İstatistiksel fizik. İstatistiksel fizik
Termodinamik ve istatistiksel fizik
Yönergeler ve kontrol görevleri uzaktan eğitim öğrencileri için
Shelkunova Z.V., Saneev E.L.
Uzaktan eğitim mühendisliği ve teknolojik uzmanlık öğrencileri için metodolojik talimatlar ve kontrol görevleri. "İstatistiksel Fizik", "Termodinamik" programlarının bölümlerini, tipik problem çözme örneklerini ve kontrol görevleri için seçenekleri içerirler.
Anahtar Kelimeler: İçsel enerji, sıcaklık, iş; izoprosesler, entropi: dağılım fonksiyonları: Maxwell, Boltzmann, Bose - Einstein; Fermi - Dirac; Fermi enerjisi, ısı kapasitesi, Einstein ve Debye karakteristik sıcaklığı.
Editör T.Yu.Artyunina
Baskı için hazırlanmıştır d Format 6080 1/16
R.l. ; uh.-ed.l. 3.0; Dolaşım ____ kopya. Sipariş numarası
___________________________________________________
RIO ESGTU, Ulan-Ude, Klyuchevskaya, 40a
ESGTU, Ulan-Ude'nin rota baskısında basılmıştır,
Klyuchevskaya, 42.
Federal Eğitim Ajansı
Doğu Sibirya Devleti
Teknoloji Üniversitesi
FİZİK №4
(Termodinamik ve istatistiksel fizik)
Metodik talimatlar ve kontrol görevleri
uzaktan eğitim öğrencileri için
Derleyen: Shelkunova Z.V.
Saneev E.L.
ESGTÜ yayınevi
Ulan-Üde, 2009
İstatistiksel fizik ve termodinamik
konu 1
Fizikte dinamik ve istatistiksel yasalar. Termodinamik ve istatistiksel yöntemler. Moleküler-kinetik teorinin unsurları. makroskopik durum. Fiziksel nicelikler ve fiziksel sistemlerin durumları. Ortalama değerler olarak makroskopik parametreler. Termal denge. İdeal gaz modeli. İdeal bir gazın hal denklemi. Sıcaklık kavramı.
Tema 2
transfer fenomeni. Difüzyon. Termal iletkenlik. difüzyon katsayısı. Termal iletkenlik katsayısı. termal yayılım. Gazlarda, sıvılarda ve katılarda difüzyon. viskozite. Gazların ve sıvıların viskozite katsayısı.
Tema 3
Termodinamiğin unsurları. Termodinamiğin birinci yasası. İçsel enerji. Yoğun ve kapsamlı parametreler.
Tema 4
Tersinir ve tersinmez süreçler. Entropi. Termodinamiğin ikinci yasası. Termodinamik potansiyeller ve denge koşulları. kimyasal potansiyel. Kimyasal denge koşulları. Karnot döngüsü.
Tema 5
dağıtım fonksiyonları. mikroskobik parametreler. Olasılık ve dalgalanmalar. Maxwell dağılımı. Orta kinetik enerji parçacıklar. Boltzmann dağılımı. Çok atomlu gazların ısı kapasitesi. Klasik ısı kapasitesi teorisinin sınırlandırılması.
Tema 6
Gibbs dağılımı. Termostattaki sistemin modeli. Kanonik Gibbs dağılımı. Termodinamik potansiyeller ve sıcaklığın istatistiksel anlamı. Serbest enerjinin rolü.
Tema 7
Değişken sayıda parçacık içeren bir sistem için Gibbs dağılımı. Entropi ve olasılık. Bir mikro-durumun istatistiksel ağırlığı aracılığıyla bir denge sisteminin entropisinin belirlenmesi.
Tema 8
Bose ve Fermi dağıtım fonksiyonları. Planck'ın ağırlıksız termal radyasyon formülü. Doğada düzen ve düzensizlik. Kaosun nicel bir ölçüsü olarak entropi. Artan entropi ilkesi. Düzenden düzensizliğe geçiş, termal denge durumu ile ilgilidir.
Tema 9
Kristallerin titreşim spektrumunu incelemek için deneysel yöntemler. Fonon kavramı. Akustik ve optik fononlar için dağılım yasaları. Düşük ve yüksek sıcaklıklarda kristallerin ısı kapasitesi. Elektronik ısı kapasitesi ve termal iletkenlik.
Tema 10
Elektronlar kristallerde. Güçlü ve zayıf kuplajın yaklaştırılması. Serbest elektron modeli. Fermi seviyesi. Kristallerin bant teorisinin elemanları. Bloch işlevi. Elektronların enerji spektrumunun bant yapısı.
Tema 11
Fermi yüzeyi. Banttaki elektronik durum sayısının sayısı ve yoğunluğu. Bölge dolguları: metaller, dielektrikler ve yarı iletkenler. Yarı iletkenlerin elektriksel iletkenliği. Delik iletkenliği kavramı. İçsel ve dışsal yarı iletkenler. kavramı Pn kavşağı. Transistör.
Tema 12
Metallerin elektriksel iletkenliği. Metallerde akım taşıyıcıları. Klasik elektron teorisinin yetersizliği. Bir metalde elektronik Fermi gazı. Kuasipartiküller olarak akım taşıyıcıları. Süperiletkenlik olgusu. Elektronların Cooper eşleşmesi. tünel teması. Josephson etkisi ve uygulamaları. Yakalama ve niceleme manyetik akı. Yüksek sıcaklık iletkenliği kavramı.
İSTATİSTİK FİZİK. TERMODİNAMİK
Temel formüller
1. Homojen bir gazın madde miktarı (mol olarak):
nerede N-gaz moleküllerinin sayısı; N A- Avogadro'nun numarası; m-gaz kütlesi; gazın molar kütlesidir.
Sistem birkaç gaz karışımı ise, sistemdeki madde miktarı
![]() ,
,
![]() ,
,
nerede i , N i , m i , i - sırasıyla madde miktarı, molekül sayısı, kütle, molar kütle i karışımın inci bileşeni.
2. Clapeyron-Mendeleev denklemi (ideal gaz hal denklemi):
![]()
nerede m- gaz kütlesi; - molar kütle; R- Evrensel gaz sabiti; = m/ - madde miktarı; T Kelvin cinsinden termodinamik sıcaklıktır.
3. İzoprosesler için Clapeyron-Mendeleev denkleminin özel durumları olan deneysel gaz yasaları:
boyle-mariotte yasası
(izotermal süreç - T= sabit; m=sabit):
veya iki gaz durumu için:
nerede p 1 ve V 1 - ilk durumda gazın basıncı ve hacmi; p 2 ve V 2
Gay-Lussac yasası (izobarik süreç - p=sabit, m=sabit):
veya iki durum için:
nerede V 1 ve T 1 - başlangıç durumundaki gazın hacmi ve sıcaklığı; V 2 ve T 2 - son durumda aynı değerler;
Charles yasası (izokorik süreç - V=sabit, m=sabit):
veya iki durum için:
nerede R 1 ve T 1 - ilk durumda gazın basıncı ve sıcaklığı; R 2 ve T 2 - son durumda aynı değerler;
kombine gaz yasası (m=sabit):
nerede R 1 , V 1 , T 1 - ilk durumda gazın basıncı, hacmi ve sıcaklığı; R 2 , V 2 , T 2 son durumda aynı değerlerdir.
4. Bir gaz karışımının basıncını belirleyen Dalton yasası:
p = p 1 + p 2 + ... +p n
nerede p i - kısmi basınçlar karışım bileşeni; n- karışımın bileşenlerinin sayısı.
5. Bir gaz karışımının molar kütlesi:
![]()
nerede m i- ağırlık i karışımın -inci bileşeni; i = m i / i- madde miktarı i karışımın -inci bileşeni; n- karışımın bileşenlerinin sayısı.
6. Kütle kesri i i gaz karışımının -inci bileşeni (birim veya yüzde kesri olarak):
nerede m karışımın kütlesidir.
7. Molekül konsantrasyonu (birim hacimdeki molekül sayısı):
![]()
nerede N-sistemde bulunan molekül sayısı; maddenin yoğunluğudur. Formül sadece gazlar için değil, aynı zamanda maddenin herhangi bir kümelenme durumu için de geçerlidir.
8. Temel denklem Kinetik teori gazlar:
 ,
,
nerede<>molekülün öteleme hareketinin ortalama kinetik enerjisidir.
9. Bir molekülün öteleme hareketinin ortalama kinetik enerjisi:
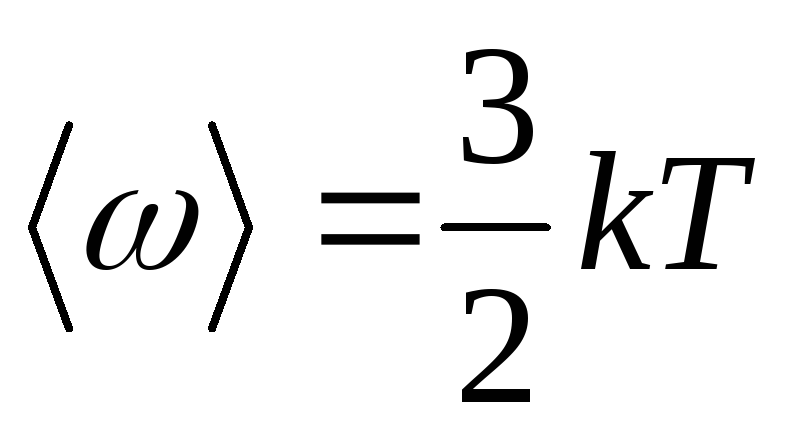 ,
,
nerede k Boltzmann sabitidir.
10. Bir molekülün ortalama toplam kinetik enerjisi:
nerede i molekülün serbestlik derecesi sayısıdır.
11. Gaz basıncının molekül konsantrasyonuna ve sıcaklığa bağımlılığı:
p = nkT.
12. Moleküllerin hızları:
Kök kare ortalama  ;
;
aritmetik ortalama 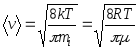 ;
;
büyük ihtimalle 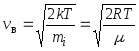 ,
,
nerede m i bir molekülün kütlesidir.
13. Bir molekülün bağıl hızı:
u = v/v içinde ,
nerede v bu molekülün hızıdır.
14. Sabit hacimde gazın özgül ısı kapasiteleri (s v) ve sabit basınç (İle birlikte R):
15. Belirli arasındaki ilişki ( İle birlikte) ve molar ( İTİBAREN) ısı kapasiteleri:
; C=c .
16. Robert Mayer Denklemi:
C p -C v = R.
17. İdeal bir gazın iç enerjisi:
![]()
18. Termodinamiğin birinci yasası:
nerede Q- sisteme iletilen ısı (gaz); dU- sistemin iç enerjisindeki değişiklik; ANCAK sistemin dış kuvvetlere karşı yaptığı iştir.
19. Gaz genleşme çalışması:
Genel olarak ;
izobarik süreçte ![]() ;
;
izotermal süreç ![]() ;
;
adyabatik bir süreçte ![]() ,
,
veya  ,
,
adyabatik üs nerede.
20. Adyabatik bir süreçte ideal bir gazın parametrelerini ilişkilendiren Poisson denklemleri:
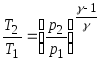 ;
;
21. Termal verimlilik Çevrim.
elektronlar, vb.), bu parçacıkların özellikleri ve aralarındaki etkileşim yoluyla.Diğer fizik dalları da makroskopik cisimleri inceliyor - termodinamik , Mekanik sürekli ortam, sürekli ortamın elektrodinamiği. Bununla birlikte, belirli problemleri bu disiplinlerin yöntemleriyle çözerken, karşılık gelen denklemler her zaman belirli bir gövdeyi karakterize eden bilinmeyen parametreleri veya işlevleri içerir. Bu nedenle, hidrodinamik problemlerini çözmek için, bir sıvı veya gazın durum denklemini, yani yoğunluğun sıcaklığa ve basınca bağımlılığını, bir sıvının ısı kapasitesini, viskozite katsayısını vb. bilmek gerekir. Tüm bu bağımlılıklar ve parametreler elbette deneysel olarak belirlenebilir; bu nedenle söz konusu yöntemlere fenomenolojik denir. İstatistiksel fizik, moleküller arasındaki etkileşim kuvvetleri biliniyorsa, en azından prensipte ve çoğu durumda fiilen tüm bu miktarları hesaplamaya izin verir. O., istatistiksel fizik cisimlerin "mikroskobik" yapısı hakkında - hangi parçacıklardan oluştukları, bu parçacıkların nasıl etkileşime girdiği hakkında bilgileri kullanır, bu nedenle buna mikroskobik teori denir.
Zamanın bir noktasında vücudun tüm parçacıklarının koordinatları ve hızları verilirse ve etkileşimlerinin yasası biliniyorsa, o zaman mekanik denklemlerini çözerek, sonraki herhangi bir noktada bu koordinatları ve hızları bulmak mümkün olacaktır. zamanla ve böylece incelenen vücudun durumunu tamamen belirler. (Basit olması için sunum klasik mekaniğin dilinde yapılır. Kuantum mekaniği durum aynı: ilkini bilmek dalga fonksiyonu sistemleri ve parçacıkların etkileşim yasası, çözerek mümkündür Schrödinger denklemi , zamanın gelecekteki tüm anlarında sistemin durumunu belirleyen dalga fonksiyonunu bulun.) Bununla birlikte, aslında, mikroskobik bir teori inşa etmenin böyle bir yolu imkansızdır, çünkü makroskobik cisimlerdeki parçacıkların sayısı çok fazladır. Örneğin, 1'de cm3 0 °C sıcaklıkta ve 1 basınçta gaz ATM yaklaşık 2.7×10 19 molekül içerir. Bu kadar çok sayıda denklemi çözmek imkansızdır ve tüm moleküllerin başlangıç koordinatları ve hızları hala bilinmemektedir.
Ancak, Büyük sayı makroskobik cisimlerdeki parçacıklar, bu tür cisimlerin davranışında yeni - istatistiksel - düzenliliklerin ortaya çıkmasına neden olur. Geniş bir aralıktaki bu davranış, belirli başlangıç koşullarına - ilk koordinatların ve parçacık hızlarının kesin değerlerine - bağlı değildir. Bu bağımsızlığın en önemli tezahürü, kendi haline bırakılan, yani dış etkilerden izole edilen bir sistemin, sonunda, özellikleri yalnızca tarafından belirlenen bir denge durumuna (termodinamik veya istatistiksel denge) geldiği deneyimlerden bilinen gerçektir. çok Genel özellikleri başlangıç durumu, parçacıkların sayısı, toplam enerjileri vb. (santimetre. termodinamik denge ). Aşağıda, esas olarak şunlara odaklanacağız: istatistiksel fizik denge durumları.
İstatistiksel düzenlilikleri tanımlayan bir teori formüle etmeden önce, teorinin gerekliliklerini makul bir şekilde sınırlamak gerekir. Yani teorinin görevi, makroskopik cisimler için çeşitli fiziksel niceliklerin tam değerlerini değil, bu niceliklerin zaman içindeki ortalama değerlerini hesaplamak olmalıdır. Örneğin, bir gazda izole edilmiş, yeterince büyük bir makroskopik hacimde bulunan molekülleri düşünün. Bu tür moleküllerin sayısı, hareketlerinden dolayı zamanla değişecektir ve moleküllerin tüm koordinatları her zaman biliniyorsa tam olarak bulunabilir. Ancak bu gerekli değildir. Hacimdeki molekül sayısındaki değişiklik, bazı ortalama değerlere göre rastgele dalgalanmaların - dalgalanmaların - doğasında olacaktır. Hacimdeki çok sayıda parçacıkla, bu dalgalanmalar ortalama parçacık sayısına kıyasla küçük olacaktır, böylece makroskopik durumu karakterize etmek için bu ortalama değeri tam olarak bilmek yeterlidir.
İstatistiksel kalıpların doğasını netleştirmek için başka bir basit örnek düşünün. İki çeşitten çok sayıda tahıl, her biri eşit derecede bir kaba konulsun ve kabın içindekiler iyice karıştırılsın. Daha sonra, günlük deneyimlere dayanarak, hala çok sayıda tahıl içeren bir kaptan alınan bir numunede, tahılların sırasına bakılmaksızın her çeşitten yaklaşık olarak eşit sayıda tahıl bulunacağından emin olunabilir. tekneye döküldü. Bu örnek, istatistiksel teorinin uygulanabilirliğini sağlayan iki önemli durumu açıkça göstermektedir. İlk olarak, hem tüm “sistemde” - tahıllı bir kapta hem de deney için seçilen “alt sistemde” - bir numunede çok sayıda tahıl ihtiyacı. (Numune sadece iki taneden oluşuyorsa, genellikle her ikisi de aynı kalitede olacaktır.) İkinci olarak, karıştırma sırasında tanelerin hareketinin karmaşıklığının, bunların hacminde düzgün dağılımlarını sağlayarak önemli bir rol oynadığı açıktır. gemi.
dağıtım işlevi. oluşan bir sistem düşünün. basitlik için parçacıkların hiçbir iç serbestlik derecesine sahip olmadığını varsayarsak. Böyle bir sistem görev tarafından tanımlanır 6 değişkenler - 3 koordinatlar ben ve 3 dürtüler pi, parçacıklar [bu değişkenlerin kümesi ( R, q)]. Belirli bir değerin zaman aralığı üzerinden ortalama değerini hesaplayalım. (p, q), bu koordinatların ve momentumun bir fonksiyonudur. Bunu yapmak için (0, t) aralığını böleriz. s eşit küçük parçalar D ta (a = 1,2,....... s). Daha sonra tanım gereği
![]() ,
,
Neresi bir ve p bir- zaman zaman koordinat ve dürtü değerleri ta. sınırda s® ¥ toplam integrale girer:
![]() (1 A)
(1 A)
6 uzayını düşünürsek, doğal bir şekilde dağılım fonksiyonu kavramı ortaya çıkar. sistemin parçacıklarının koordinatlarının ve momentumlarının değerlerinin çizildiği eksenlerde ölçümler; faz uzayı denir. zamanın her değeri için t hepsinin belirli değerlerine karşılık gelir q ve R, yani sistemin durumunu temsil eden faz uzayında bir nokta şu an zaman t. Tüm faz alanını, sistemin belirli bir durumunun karakteristik değerlerine kıyasla boyutu küçük olan elemanlara bölelim. q ve R, ama yine de o kadar büyük ki, her birinde sistemin durumunu zaman içinde farklı noktalarda gösteren birçok nokta var. t. O zaman hacim elemanındaki bu tür noktaların sayısı, bu hacmin değeri ile yaklaşık olarak orantılı olacaktır. dpdq. Orantılılık katsayısını şu şekilde ifade edersek sw(p, q), o zaman bu, bir noktada ortalanmış öğenin sayısıdır ( p, q) şu şekilde yazılacaktır:
da = sv(p, q)dpdq, (2)
Seçili faz alanı öğesinin hacmi. Ortalama değer (1), bu hacim elemanlarının küçüklüğü dikkate alınarak yeniden yazılabilir, yani.
(koordinatlar üzerinden entegrasyon, sistemin tüm hacmi üzerinde, momentum üzerinden - -¥'den ¥'ye kadar gerçekleştirilir). w( p, q, t) parçacık momentum koordinatlarına göre dağılım fonksiyonu olarak adlandırılır. Seçilen noktaların toplam sayısı s, işlev w normalizasyon koşulunu karşılar:
![]() (4)
(4)
(3) ve (4) den görülebilir ki w dpdq sistemin elemanda olma olasılığı olarak kabul edilebilir. dpdq faz boşluğu. Bu şekilde tanıtılan dağıtım işlevine başka bir yorum yapılabilir. Bunu yapmak için, aynı anda çok sayıda özdeş sistemi ele alacağız ve faz uzayındaki her noktanın böyle bir sistemin durumunu temsil ettiğini varsayacağız. O zaman (1)-(1a)'daki zaman ortalaması, bu sistemlerin toplamı üzerinden veya dedikleri gibi, üzerinden ortalama alma olarak anlaşılabilir. istatistik topluluğu . Şimdiye kadar yürütülen argümanlar, doğası gereği tamamen biçimseldi, çünkü (2)'ye göre dağılım fonksiyonunu bulmak, tüm R ve q her zaman, yani hareket denklemlerinin karşılık gelen başlangıç koşullarıyla çözümleri. Temel hüküm istatistiksel fizik bununla birlikte, termodinamik denge durumundaki bir sistem için bu işlevi genel değerlendirmelerden belirleme olasılığı hakkında bir ifadedir. Her şeyden önce, hareket sırasında sistem sayısının korunumuna dayalı olarak, dağıtım fonksiyonunun sistemin hareketinin bir integrali olduğu, yani eğer sabit kalırsa gösterilebilir. R ve q hareket denklemlerine göre değişir (bkz. Liouville teoremi ). Sürüş sırasında kapalı sistem enerjisi değişmez, bu nedenle, sistemin zaman içindeki farklı noktalarındaki durumunu gösteren faz uzayındaki tüm noktalar, enerjinin başlangıç değerine karşılık gelen bir "hiperyüzey" üzerinde yer almalıdır. E. Bu yüzeyin denklemi şu şekildedir;
Yukarıdaki formüller, alt sistemdeki parçacık sayısının verildiği duruma atıfta bulunur. Bir alt sistem olarak, tüm sistemin belirli bir hacim elemanını seçersek, yüzeyi aracılığıyla parçacıkların alt sistemi terk edip ona geri dönebileceği, o zaman alt sistemi enerjili bir durumda bulma olasılığı E n ve parçacık sayısı n Gibbs büyük kanonik dağılım formülü ile verilir:
![]() , (9)
, (9)
Ek parametre m'nin olduğu kimyasal potansiyel alt sistemdeki ortalama parçacık sayısını belirleyen ve değer normalizasyon koşulundan belirlenir [bkz. formül (11)].
Termodinamiğin istatistiksel yorumu. en önemli sonuç istatistiksel fizik- termodinamik niceliklerin istatistiksel anlamlarının oluşturulması. Bu, termodinamik yasalarını temel kavramlardan türetmeyi mümkün kılar. istatistiksel fizik ve belirli sistemler için termodinamik miktarları hesaplar. Öncelikle termodinamik içsel enerji sistemin ortalama enerjisi ile tanımlanır. Termodinamiğin birinci yasası daha sonra vücudu oluşturan parçacıkların hareketi sırasında enerjinin korunumu yasasının bir ifadesi olarak açık bir yorum alır.
Ayrıca, sistemin Hamilton fonksiyonunun bazı parametrelere (l) bağlı olmasına izin verin (sistemi içeren kabın duvarının koordinatları, dış alan, vb.). Sonra türev olacak genelleştirilmiş kuvvet
bu parametreye karşılık gelir ve ortalamadan sonraki değer verir mekanik iş Bu parametre değiştirildiğinde sistem üzerinde gerçekleştirilir. ifadeyi ayırt edersek ![]() sistemin ortalama enerjisi için, formül (6) ve normalizasyon koşulu dikkate alınarak, l ve değişkenleri dikkate alınarak T ve değeri düşünüldüğünde
aynı zamanda bu değişkenlerin bir fonksiyonu ise, o zaman kimliği elde ederiz:
sistemin ortalama enerjisi için, formül (6) ve normalizasyon koşulu dikkate alınarak, l ve değişkenleri dikkate alınarak T ve değeri düşünüldüğünde
aynı zamanda bu değişkenlerin bir fonksiyonu ise, o zaman kimliği elde ederiz:
![]() .
.
Yukarıdakilere göre, üyeyi içeren d l eşittir ortalama iş dA vücut üzerinde yapılır. Daha sonra son terim vücudun aldığı ısıdır. Bu ifadenin bağıntı ile karşılaştırılması dE = dA + TdS termodinamiğin birinci ve ikinci yasalarının birleşik kaydıdır (bkz. Termodinamiğin ikinci yasası ) için tersine çevrilebilir süreçler , bunu buluyoruz T(6)'da gerçekten cismin mutlak sıcaklığına eşittir ve türev zıt işaretle alınır. entropi . Demek oluyor var bedava enerji istatistiksel anlamının açıklığa kavuşturulduğu gövde.
Formül (8)'den çıkan entropinin istatistiksel yorumu özellikle önemlidir. Resmi olarak, g, enerji ile tüm durumlar için bu formüle toplanır. E n, ancak aslında Gibbs dağılımındaki enerji dalgalanmalarının küçüklüğü nedeniyle, ortalama enerjiye yakın bir enerjiye sahip olanlardan sadece nispeten az sayıda önemlidir. Bu temel durumların sayısını belirlemek doğaldır, bu nedenle (8)'deki toplamı aralıkla sınırlayarak, yerine E n ortalama enerjiye ve üssü toplam işaretinin altından çıkarmak. Sonra toplamı verecek ve formu alacak.
![]()
Öte yandan, termodinamiğe göre, =-TS belirli bir makroskopik durumda entropi ile mikroskobik durumların sayısı arasında bir bağlantı veren, başka bir deyişle, istatistiksel ağırlık makroskopik durum, yani olasılığı ile:
bir sıcaklıkta tamamen sıfır herhangi bir sistem belirli bir temel durumda, yani = 1, S= 0. Bu ifade şunu ifade eder: termodinamiğin üçüncü yasası . Burada, entropinin açık bir tanımı için kuantum formülünün (8) kullanılması gereklidir; tamamen klasik istatistikte, entropi yalnızca keyfi bir terime kadar tanımlanır.
Bir durumun olasılığının bir ölçüsü olarak entropinin anlamı, keyfi - mutlaka denge değil - durumlarla ilgili olarak da korunur. Bir denge durumunda, entropi, belirli dış koşullar altında mümkün olan en yüksek değere sahiptir. Bu, denge durumunun maksimum istatistiksel ağırlığa sahip durum, en olası durum olduğu anlamına gelir. Bir sistemin denge dışı durumdan denge durumuna geçiş süreci, daha az olası durumlardan daha olası olanlara geçiş sürecidir; bu, kapalı bir sistemin entropisinin yalnızca artabileceğine göre entropi artış yasasının istatistiksel anlamını aydınlatır.
Serbest enerji ile ilgili formül (8) Bölme fonksiyonu ile termodinamik miktarları metotlarla hesaplamanın temelidir. istatistiksel fizikÖzellikle, maddenin elektriksel ve manyetik özelliklerinin istatistiksel bir teorisini oluşturmak için kullanılır. Örneğin, bir cismin manyetik alandaki manyetik momentini hesaplamak için, bölme fonksiyonunu ve serbest enerjiyi hesaplamak gerekir. manyetik moment m gövde daha sonra formülle verilir:
Neresi H- dış gerilim manyetik alan. (8)'e benzer şekilde, büyük kanonik dağılımdaki (9) normalleştirme koşulu şunları belirler: termodinamik potansiyel formüle göre:
![]() . (11)
. (11)
Bu potansiyel, aşağıdaki ilişki ile serbest enerji ile ilgilidir:
![]() .
.
Uygulamalar istatistiksel fizik belirli sistemlerin belirli özelliklerinin incelenmesine, esasen, sistemin belirli özelliklerini dikkate alarak, bölme fonksiyonunun yaklaşık bir hesaplamasına indirgenir.
Çoğu durumda, bu görev, ısı kapasitesinin eşit olduğunu belirten serbestlik derecelerinde eş bölme yasası uygulanarak basitleştirilir. Özgeçmiş(en sabit hacim v) etkileşim sistemleri maddi noktalar- harmonik salınım yapan parçacıklar eşittir
c v = k(l/2 + n),
Neresi ben - toplam sayısıöteleme ve dönme serbestlik dereceleri, n- titreşim serbestlik derecesi sayısı. Kanunun ispatı, Hamilton fonksiyonunun H böyle bir sistem şöyle görünür: H =(pi) + (metrekare), kinetik enerji nerede İle homojen bir ikinci dereceden fonksiyondur ben + n dürtüler pi ve potansiyel enerji - ikinci dereceden fonksiyon n titreşim koordinatları metrekare. İstatistiksel integralde Z(8a) integralin hızlı yakınsaması nedeniyle titreşim koordinatları üzerinden entegrasyon - ¥'den ¥'ye uzatılabilir. Değişkenleri değiştirdikten sonra şunu buluruz. Z olarak sıcaklığa bağlıdır TL/2+n yani serbest enerji =-kT(ben/ 2 +n)(ln T+ sabit). Bu, ısı kapasitesi için yukarıdaki ifadeyi ifade eder, çünkü . Gerçek sistemlerde eş-bölüşüm yasasından sapmalar, öncelikle kuantum düzeltmeleri ile ilişkilidir, çünkü kuantumda istatistiksel fizik bu kanun adaletsizdir. Salınımların uyumsuzluğu ile ilgili düzeltmeler de vardır.
Ideal gaz. En basit çalışma nesnesi istatistiksel fizik ideal bir gazdır, yani molekülleri arasındaki etkileşim ihmal edilebilecek kadar nadir bulunan bir gazdır. Böyle bir gazın termodinamik fonksiyonları tam olarak hesaplanabilir. Bir gazın enerjisi, basitçe, tek tek moleküllerin enerjilerinin toplamıdır. Ancak bu, molekülleri tamamen bağımsız olarak düşünmek için hala yetersizdir. Gerçekten de, kuantum mekaniğinde, parçacıklar arasında etkileşim kuvvetleri olmasa bile, benzer kuantum mekaniksel durumlardaysa özdeş (özdeş) parçacıkların birbirleri üzerinde belirli bir etkisi vardır. Bu sözde. değişim etkileşimi . Durum başına ortalama olarak, gazın yeterince yüksek bir sıcaklığında gerçekleşen birden fazla parçacık varsa, ihmal edilebilir; böyle bir gaza dejenere olmayan denir. Aslında, atomlardan ve moleküllerden oluşan sıradan gazlar, tüm sıcaklıklarda (hâlâ gaz halinde oldukları) dejenere değildir. Dejenere olmayan bir ideal gaz için, dağıtım fonksiyonu, tek tek moleküller için dağıtım fonksiyonlarının ürününe ayrışır. aralıklarda yatmak dp x, dpy, dpz, ve koordinatlar aralıklarda dx, ölmek, dz:
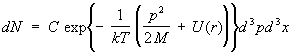 , (12) Bir dış alandaki tek atomlu bir gaz molekülünün enerjisi potansiyel enerji
(r) eşittir p 2 /2M +(r). (6) koordinatları üzerinden entegrasyon r(x, y, z) ve dürtüler R(px, p, pz) biri hariç tüm moleküllerin molekül sayısını bulabilirsiniz. dN, kimin dürtüleri
, (12) Bir dış alandaki tek atomlu bir gaz molekülünün enerjisi potansiyel enerji
(r) eşittir p 2 /2M +(r). (6) koordinatları üzerinden entegrasyon r(x, y, z) ve dürtüler R(px, p, pz) biri hariç tüm moleküllerin molekül sayısını bulabilirsiniz. dN, kimin dürtüleri
Neresi 3 p = dp x dp y dp z, d3x = dxdydz. Bu formüle Maxwell-Boltzmann dağılımı denir (bkz. Boltzmann istatistikleri ). (12) momentum üzerinden integral alırsak, dış alanda, özellikle yerçekimi alanında, parçacıkların koordinatlar üzerinden dağılımı için bir formül elde ederiz - barometrik formül . Uzayda her noktadaki hız dağılımı, Maxwell dağılımı .
İdeal bir gazın bölme işlevi, aynı zamanda, tek tek moleküllere karşılık gelen özdeş terimlerin ürününe de ayrılır. Tek atomlu bir gaz için, (8)'deki toplam, koordinatlar ve momentum üzerinden entegrasyona indirgenir, yani toplam, ![]() 3
bir parçacığın faz uzayındaki [hacimli] hücre sayısına göre. Bedava enerji
gaz atomları eşittir:
3
bir parçacığın faz uzayındaki [hacimli] hücre sayısına göre. Bedava enerji
gaz atomları eşittir:
 ,
,
Neresi g- atomun temel durumunun istatistiksel ağırlığı, yani alt durumuna karşılık gelen durum sayısı enerji seviyesi, . Nihayetinde bu, entropi ile kuantum durumlarının sayısı kavramı arasında daha önce belirtilen bağlantıdan kaynaklanmaktadır.
İki atomlu ve çok atomlu gazlar durumunda, moleküllerin titreşimleri ve dönüşü de termodinamik fonksiyonlara katkıda bulunur. Bu katkı, titreşimlerin kuantizasyonunun ve molekülün rotasyonunun etkilerinin önemli olup olmadığına bağlıdır. Titreşimsel enerji seviyeleri arasındaki mesafe, w'nin karakteristik salınım frekansı olduğu ve birinci dönme enerjisi seviyeleri arasındaki mesafenin olduğu düzendedir. ![]() , nerede
- dönen bir cismin atalet momenti, bu durumda bir molekül. Sıcaklık yeterince yüksekse, klasik istatistikler geçerlidir.
, nerede
- dönen bir cismin atalet momenti, bu durumda bir molekül. Sıcaklık yeterince yüksekse, klasik istatistikler geçerlidir.
kT>> D E.
Bu durumda, eşbölme yasasına göre, dönüş, ısı kapasitesine 1/2'ye eşit sabit bir katkı sağlar. k her bir dönme serbestlik derecesi için; özellikle, iki atomlu moleküller için bu katkı şuna eşittir: k. Dalgalanmalar, ısı kapasitesine eşit katkıda bulunur. k her bir titreşim serbestlik derecesi için (böylece iki atomlu bir molekülün titreşimsel ısı kapasitesi k). Titreşim serbestlik derecesinin katkısı, dönme ile karşılaştırıldığında, titreşimler sırasında bir moleküldeki atomların sadece kinetik değil, aynı zamanda potansiyel enerjiye sahip olması nedeniyle iki kat daha fazladır. Ters sınırlayıcı durumda, moleküller, enerjisi sıcaklığa bağlı olmayan yer titreşimi durumundadır, bu nedenle titreşimler ısı kapasitesine hiç katkıda bulunmaz. Aynı koşul altında moleküllerin dönüşü için de geçerlidir. ![]() . Sıcaklık yükseldikçe, uyarılmış titreşim ve dönme hallerinde olan moleküller ortaya çıkar ve bu serbestlik dereceleri ısı kapasitesine katkıda bulunmaya başlar - sanki kademeli olarak "açılır", sıcaklıkta daha fazla artışla klasik sınırlarına yönelirler. Böylece, kuantum etkilerinin dahil edilmesi, gazların ısı kapasitesinin sıcaklığa deneysel olarak gözlemlenen bağımlılığını açıklamayı mümkün kıldı. Çoğu molekül için "dönme kuantumunu" karakterize eden miktarın değerleri, birkaç derece veya onlarca derecedir (H 2 için 85 K, 2 için 2.4 K, H için 15 K). Aynı zamanda, "titreşimsel kuantum" için karakteristik değerler binlerce derece mertebesindedir (H2 için 6100 K, O2 için 2700 K, H için 4100 K). Bu nedenle, dönme serbestlik dereceleri, titreşimli olanlardan çok daha düşük sıcaklıklarda açılır. Şek. Şekil 1, iki atomlu bir molekül için (a) dönme ve (b) titreşim ısı kapasitelerinin sıcaklığa bağımlılığını göstermektedir (dönme ısısı kapasitesi, farklı atomlardan oluşan bir molekül için oluşturulmuştur).
. Sıcaklık yükseldikçe, uyarılmış titreşim ve dönme hallerinde olan moleküller ortaya çıkar ve bu serbestlik dereceleri ısı kapasitesine katkıda bulunmaya başlar - sanki kademeli olarak "açılır", sıcaklıkta daha fazla artışla klasik sınırlarına yönelirler. Böylece, kuantum etkilerinin dahil edilmesi, gazların ısı kapasitesinin sıcaklığa deneysel olarak gözlemlenen bağımlılığını açıklamayı mümkün kıldı. Çoğu molekül için "dönme kuantumunu" karakterize eden miktarın değerleri, birkaç derece veya onlarca derecedir (H 2 için 85 K, 2 için 2.4 K, H için 15 K). Aynı zamanda, "titreşimsel kuantum" için karakteristik değerler binlerce derece mertebesindedir (H2 için 6100 K, O2 için 2700 K, H için 4100 K). Bu nedenle, dönme serbestlik dereceleri, titreşimli olanlardan çok daha düşük sıcaklıklarda açılır. Şek. Şekil 1, iki atomlu bir molekül için (a) dönme ve (b) titreşim ısı kapasitelerinin sıcaklığa bağımlılığını göstermektedir (dönme ısısı kapasitesi, farklı atomlardan oluşan bir molekül için oluşturulmuştur).
Kusurlu gaz.Önemli başarı istatistiksel fizik- parçacıkları arasındaki etkileşimle ilişkili gazın termodinamik miktarlarında düzeltmelerin hesaplanması. Bu bakış açısından, ideal bir gazın hal denklemi, gerçek bir gazın basıncının tanecik sayısının yoğunluğunun kuvvetleri cinsinden genişlemesindeki ilk terimdir, çünkü herhangi bir gaz yeterince bir ideal gaz gibi davranır. düşük yoğunluklu. Yoğunluk arttıkça, durum denklemindeki etkileşimle ilgili düzeltmeler bir rol oynamaya başlar. Parçacık sayısının daha yüksek yoğunluk derecelerine sahip terimlerin basınç ifadesinde ortaya çıkmasına neden olurlar, böylece basınç sözde ile temsil edilir. formun viral serisi:
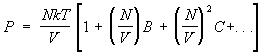 . (15)
. (15)
oranlar AT, İTİBAREN vb. sıcaklığa bağlıdır ve oluşur. ikinci, üçüncü vb. viral katsayılar. yöntemler istatistiksel fizik gaz molekülleri arasındaki etkileşim yasası biliniyorsa, bu katsayıları hesaplamayı mümkün kılar. Aynı zamanda, katsayılar AT, İTİBAREN,... iki, üç ve daha fazla moleküller. Örneğin, gaz tek atomluysa ve atomlarının etkileşiminin potansiyel enerjisi (r), o zaman ikinci virial katsayı
büyüklük sırasına göre AT eşittir, nerede r0- bir atomun karakteristik boyutu veya daha doğrusu atomlar arası kuvvetlerin etki yarıçapı. Bu, (15) serisinin aslında boyutsuz parametrenin güçlerinde bir açılım olduğu anlamına gelir. Sayı 3 / V, yeterince nadir bir gaz için küçük. Gaz atomları arasındaki etkileşim, yakın mesafelerde itme ve uzak mesafelerde çekim karakterine sahiptir. Bu yol açar AT> 0'da yüksek sıcaklıklar ve AT < 0 при низких. Поэтому давление реального газа при высоких температурах daha fazla baskı aynı yoğunlukta ve düşük - daha az ideal gaz. Yani, örneğin, helyum için T= 15.3 K faktörü AT = - 3×10 -23 cm3, ve ne zaman T= 510 bin AT= 1.8 × 10 -23 cm3. argon için AT = - 7.1×10 -23 cm3 de T = 180 bin ve AT= 4,2×10 -23 cm3 de T= 6000 K. Monatomik gazlar için, gazların davranışını oldukça geniş bir yoğunluk aralığında tanımlamayı mümkün kılan beşinci katsayı da dahil olmak üzere virial katsayıların değerleri hesaplanır (ayrıca bkz. gazlar ).
Plazma. özel bir durum ideal olmayan gaz plazma - kısmen veya tamamen iyonize gaz, bu nedenle içinde serbest elektronlar ve iyonlar bulunur. Yeterince düşük yoğunlukta, plazmanın özellikleri ideal gazın özelliklerine yakındır. İdeallikten sapmaları hesaplarken, elektronların ve iyonların Coulomb yasasına göre elektrostatik olarak etkileşmesi esastır. Coulomb kuvvetleri mesafe ile yavaş yavaş azalır ve bu, termodinamik fonksiyonlardaki ilk düzeltmeyi hesaplamak için, aynı anda iki değil, çok sayıda parçacığın etkileşimini hesaba katmak gerektiği gerçeğine yol açar, çift etkileşimini tanımlayan ikinci virial katsayıdaki (16) integral uzun mesafelerle birbirinden ayrıldığından r parçacıklar arasında. Gerçekte, Coulomb kuvvetlerinin etkisi altında, plazmadaki iyonların ve elektronların dağılımı, her parçacığın alanı taranacak şekilde değişir, yani Debye yarıçapı olarak adlandırılan belirli bir mesafede hızla azalır. Elektronlardan ve tek yüklü iyonlardan oluşan en basit plazma durumu için Debye yarıçapı rd eşit.
İSTATİSTİK FİZİK- görevi makroskopik özelliklerini ifade etmek olan bir fizik dalı. cisimler, yani çok sayıda özdeş parçacıktan (moleküller, atomlar, elektronlar vb.) oluşan sistemler, bu parçacıkların özellikleri ve aralarındaki etkileşim yoluyla.
Böylece, S. t. cisimlerin "mikroskobik" yapısı hakkında bilgi kullanılır; bu nedenle, S. f. mikroskobiktir. teori. Bu, diğer fizik dallarından farkı, aynı zamanda makroskopik olarak da çalışmasıdır. cisimler: , sürekli ortamların mekaniği ve elektrodinamiği. Bu disiplinlerin yöntemleriyle belirli problemleri çözerken, karşılık gelen denklemler her zaman belirli bir gövdeyi karakterize eden bilinmeyen parametreleri veya işlevleri içerir. Tüm bu bağımlılıklar ve parametreler deneysel olarak belirlenebilir, bu nedenle söz konusu yöntemler denir. fenomenolojik. S.f. en azından prensipte, ancak birçok yönden izin verir. durumlarda ve aslında bu miktarları hesaplayın.
Zamanın bir noktasında, vücudun tüm parçacıklarının koordinatları ve hızları verilirse ve etkileşimlerinin yasası biliniyorsa, o zaman mekanik denklemlerinden, zamanın herhangi bir sonraki noktasında koordinatları ve hızları bulmak mümkün olacaktır ve böylece vücudun durumunu tamamen belirler. Aynı durum şu durumda da meydana gelir: sistemin ilk dalga fonksiyonunu bilerek, Schrödinger denklemini çözerek, zamanın tüm gelecek anlarında sistemin durumunu belirleyen dalga fonksiyonunu bulmak mümkündür.
Gerçekte, mikroskobik bir yapı oluşturmanın böyle bir yolu makroskopik parçacıkların sayısı, çünkü teori imkansızdır. bedenleri çok büyük ve erken. Moleküllerin koordinatları ve hızları bilinmiyor. Bununla birlikte, tam olarak makroskobik boyuttaki çok sayıda parçacıktır. cisimler, bu tür cisimlerin davranışlarında yeni (istatistiksel) düzenliliklerin ortaya çıkmasına neden olur. Bu düzenlilikler, teorinin problemlerinin karşılık gelen bir kısıtlamasından sonra ortaya çıkar. makroskobik karakterize vücut parametreleri zamanla bazılarına göre rastgele küçük dalgalanmalar (dalgalanmalar) yaşar. değerler. Teorinin görevi bunları hesaplamaktır, bkz. değerler, belirli bir zamanda parametrelerin kesin değerleri değil. istatistiksel varlığı örüntüler aslında davranış olarak ifade edilir, bkz. geniş bir aralıktaki değerler, belirli bir başlangıca bağlı değildir. koşullar (ilk koordinatların ve parçacık hızlarının kesin değerlerinden). Bu düzenliliğin en önemli tezahürü, deneyimlerden bilinen bir gerçektir ki, bir sistem dıştan izole edilmiştir. etkiler, zamanla, özellikleri yalnızca başlangıcın bu genel özellikleri tarafından belirlenen belirli bir denge durumuna (termodinamik denge) gelir. parçacıkların sayısı, toplam enerjileri vb. gibi durumlar (bkz. termodinamik denge). Sistemin denge durumuna geçiş sürecine denir. gevşeme, ve bu sürecin karakteristik zamanı gevşeme zamanıdır.
dağıtım işlevi. oluşan bir sistem düşünün. N basitlik için, parçacıkların ext'ye sahip olmadığını varsayarak. özgürlük derecesi. Böyle bir sistem görev tarafından tanımlanır 6N değişkenler: 3N koordinatlar x ben ve 3N dürtüler ben parçacıklar, bu değişkenlerin kümesi olarak kısaltılacaktır ( p, x).
Gibbs dağılımları. (1)'e göre dağıtım fonksiyonunu bulmak, tüm X ve R her zaman, yani, karşılık gelen başlangıç ile hareket denklemlerinin çözümleri. koşullar. Ana S.'nin konumu f. termodinamik durumdaki bir sistem için bu durumu belirlemek için genel değerlendirmelerin olasılığı hakkında bir ifadedir. denge. Her şeyden önce, hareket sırasında parçacık sayısının korunumuna dayalı olarak, dağıtım fonksiyonunun sistem hareketinin integrali olduğu gösterilebilir (bkz. Liouville teoremi).
Kapalı bir sistem hareket ettiğinde, enerjisi değişmez, bu nedenle, sistemin zaman içindeki farklı noktalarındaki durumunu gösteren faz uzayındaki tüm noktalar, başlangıca karşılık gelen belirli bir hiper yüzeyde bulunmalıdır. enerji değeri E. Bu yüzeyin denklemi şu şekildedir: H(x, p) = E, nerede H(x,p) - Hamilton fonksiyonu sistemler. Bir sistemin hareketi birçok parçacıklar son derece kafa karıştırıcıdır, bu nedenle zamanla durumu açıklayan noktalar direğin yüzeyine dağıtılacaktır. eşit enerji (ayrıca bkz. ergodik hipotez) Böyle bir düzgün dağılım, dağıtım fonksiyonu ile tanımlanır.
yalnızca sıfır olmayan bir delta işlevi nerede H = E, A normalizasyon koşulundan (3) belirlenen bir sabittir. Dağıtım fonksiyonu (4) karşılık gelen mikrokanonik Gibbs dağılımı, ortalamayı hesaplamanızı sağlar. tüm fiziksel değerler f-le (2)'ye göre miktarlar, hareket denklemlerini çözmeden.
(4) ifadesi türetilirken, bağlı olduğu tek korunan miktarın w, sistemin enerjisidir. Elbette momentum ve açısal momentum da korunur, ancak söz konusu cismin parçacıkların momentum ve momentum verebileceği sabit bir kutu içine alındığı varsayılarak bu miktarlar elimine edilebilir.
Aslında, S. f. genellikle kapalı sistemleri değil, makroskopik olarak düşünün. küçük makroskopik cisimler. parçalar veya alt sistemler, to-l. kapalı sistem. Bir alt sistem için dağıtım işlevi (4)'ten farklıdır, ancak sistemin geri kalanının sözde belirli biçimine bağlı değildir. termostat. Alt sistemin dağıtım fonksiyonunu belirlemek için, termostat partiküllerinin momentumları ve koordinatları üzerinden flu-lu (4) entegre edilmesi gerekmektedir. Böyle bir entegrasyon, alt sistem enerjisinin termostat enerjisine göre küçüklüğü dikkate alınarak yapılabilir. Sonuç olarak, alt sistemin dağıtım fonksiyonu için ifade elde edilir.
büyüklük T bu f-le'de geçici olarak mantıklı. Normalizasyon katsayısı. normalizasyon koşulundan (3) belirlenir:
Yarım tamsayılı spinli parçacıklar için, dalga fonksiyonu herhangi bir parçacık çiftinin permütasyonu üzerine işaret değiştirmelidir, bu nedenle, bir kuantum hali birden fazla parçacık olamaz ( Pauli prensibi) Bir durumda tamsayı spinli parçacıkların sayısı herhangi biri olabilir, ancak bu durumda gerekli olan, parçacıklar burada yeniden düzenlendiğinde dalga fonksiyonunun değişmezliği de istatistiksel olarak bir değişikliğe yol açar. gaz özellikleri. Yarım tamsayılı spinli parçacıklar açıklanmıştır Fermi-Dirac istatistikleri, onlara fermiyon denir. Fermiyonlar, örneğin elektronları, protonları, nötronları, döteryum atomlarını, 3 He atomunu içerir. Tamsayı spinli (bozonlar) parçacıklar tanımlanır Bose - Einstein istatistikleri. Bunlara örneğin H, 4 He atomları, ışık kuantumları - fotonlar dahildir.
Bkz. Momentumun aralıkta olduğu birim hacimdeki gaz parçacıklarının sayısı dp, öyle, yani vb faz uzayının bir hücresindeki parçacıkların sayısıdır. O zaman Gibbs dağılımından şu sonuç çıkar: ideal gazlar fermiyonlar (üst işaret) ve bozonlar (alt işaret)
Bu f-le'de - momentumlu bir parçacığın enerjisi R,- kimya. parçacık sayısının sabitlik koşulundan belirlenen potansiyel N sistemde: ![]()
kuazipartiküller. Yakın abs. sıfır sıcaklık istatistiklere katkı toplam, enerjide temel duruma yakın olan zayıf uyarılmış kuantum durumları tarafından sağlanır. Ana enerjinin hesaplanması. durum tamamen kuantum mekaniğidir. görev, konu birçok parçacığın kuantum teorisi. Bu koşullar altında termal hareket, zayıf etkileşimli sistemdeki görünüm olarak tanımlanabilir. yarı parçacıklar enerji ve momentuma sahip (temel uyarılar) (kristallerde - yarı-momentum) R. Bağımlılığı bilerek, termodinamiğin sıcaklığa bağlı kısmını hesaplamak mümkündür. Kuasipartiküllerin istatistiklerine bağlı olarak ideal bir Fermi veya Bose gazı için f-lams ile f-yonlar. Özellikle Bose kuasipartiküllerinin küçük olması önemlidir. R makroskobik olarak tanımlanan, uzun dalga salınımlarının niceliği olarak kabul edilebilir. ur-niami. Bu nedenle, kristallerde (ve Bose sıvılarında) fononlar (ses kuantumları), mıknatıslarda - magnonlar (manyetik momentin salınımlarının kuantumları) vardır.
İki boyutlu ve tek boyutlu sistemlerde özel kuasipartikül türleri bulunur. Düz bir kristal halinde Filmde rolleri dislokasyonlar, He filmlerinde girdap filamentleri ve polimer filamentlerde solitonlar ve alan duvarları tarafından oynanır. Üç boyutlu cisimlerde bu cisimler yüksek enerjiye sahiptir ve termodinamiğe katkıda bulunmazlar. fonksiyonlar.
kristal hücre. Kafesteki atomlar, denge konumları etrafında küçük salınımlar yaparlar. Bu, termal hareketlerinin bir dizi quasipartikül (fonon) olarak kabul edilebileceği anlamına gelir (sadece düşük değil) temp-pax (bkz. Kristal kafesin titreşimleri Fotonların yanı sıra fononların da dağılımı f-loy (16) c = 0 ile verilir. ses dalgaları, elastikiyet teorisinin denklemleri ile açıklanmıştır. Onlara bağımlılık doğrusaldır, bu nedenle kristalin ısı kapasitesi. kafes orantılıdır 3. Yüksek sıcaklıklarda, ısı kapasitesinin sıcaklığa bağlı olmaması ve eşit olması için, enerjinin serbestlik derecelerine göre eşbölünmesi kanunu kullanılabilir. 3Nk, nerede N kristaldeki atom sayısıdır. keyfi bağımlılık R bir kristalde nötronların esnek olmayan saçılması üzerine deneylerden belirlenebilir veya atomların kafeslerdeki etkileşimini belirleyen "kuvvet sabitleri" değerleri ayarlanarak teorik olarak hesaplanabilir. S. f.'den önce yeni sorunlar ortaya çıktı. sözde açılması ile bağlantılı olarak. yarı periyodik molekülleri uzayda periyodik olmayan, ancak belirli bir sırayla bulunan kristaller (bkz. yarı kristal).
metaller. Metallerde termodinamiğe katkı f-tion ayrıca iletim elektronları verir. Bir metaldeki elektronun durumu, bir yarı-momentum ile karakterize edilir ve elektronlar Fermi-Dirac istatistiklerine uyduğundan, yarı-momenta üzerindeki dağılımları f-loi (16) ile verilir. Bu nedenle, elektron gazının ve dolayısıyla tüm metalin yeterince düşük sıcaklıklardaki ısı kapasitesi, aşağıdakilerle orantılıdır: T. Serbest parçacıkların Fermi gazından farkı, Fermi yüzeyinin artık bir küre değil, yarı-momentumlar uzayında karmaşık bir yüzey olmasıdır. Fermi yüzeyinin şekli ve enerjinin bu yüzeye yakın yarı-momentuma bağımlılığı deneysel olarak belirlenebilir, Ch. arr. araştırma mıknatısı metallerin özelliklerini, ayrıca sözde kullanarak teorik olarak hesaplayın. psödopotansiyel modeli. Süperiletkenlerde, bir elektronun uyarılmış durumları Fermi yüzeyinden bir boşlukla ayrılır, bu da üstelliğe yol açar. elektronik ısı kapasitesinin sıcaklığa bağımlılığı. Ferromanyet içinde. ve antiferromıknatıs. Maddelerin termodinamiğe katkısı. f-tion ayrıca manyetik dalgalanmaları da verir. anlar (dönüş dalgaları).
Dielektrik ve yarı iletkenlerde T= 0 serbest elektron yoktur. Sonlu sıcaklıklarda, içlerinde bir yük belirir. quasiparticles: negatif olan elektronlar. pozitif ile şarj ve "delikler". şarj. Bir elektron ve bir delik, bağlı bir durum oluşturabilir - adı verilen bir kuasipartikül eksiton.dr. eksiton tipi, dielektrik atomun bir kristalin içine hareket eden uyarılmış halidir. kafes.
yöntemler kuantum teorisi istatistiksel fizik alanları. Kuantum kuantum fiziğinin problemlerini çözmede, öncelikle metallerde ve mıknatıslarda kuantum sıvılarının ve elektronların özelliklerinin incelenmesinde, kuantum fiziğinde tanıtılan kuantum alan teorisi yöntemleri büyük önem taşımaktadır. Nispeten yakın zamanda. Ana Bu yöntemlerde rol oynar. Green'in işlevi makroskobik Kuantum alan teorisindeki Green fonksiyonuna benzer sistemler. e enerjisine ve momentuma bağlıdır. R, quasipartiküllerin dağılım yasası e(p) denkleminden belirlenir ![]() , çünkü kuasipartikülün enerjisi Green fonksiyonunun kutbudur. Green'in fonksiyonlarını, parçacıklar arasındaki etkileşim enerjisinin bir dizi gücü biçiminde hesaplamak için düzenli bir yöntem vardır. Bu dizinin her bir üyesi, Green'in etkileşmeyen parçacıkların fonksiyonlarından elde edilen enerjiler ve momentumlar üzerinde çoklu integraller içerir ve aşağıdakine benzer diyagramlar şeklinde grafiksel olarak gösterilebilir. Feynman diyagramları kuantumda. Bu diyagramların her birinin belirli bir fiziksel ilgi fenomeninden sorumlu terimleri sonsuz bir dizide ayırmayı ve özetlemeyi mümkün kılan anlam. Green'in sıcaklık fonksiyonlarını hesaplamak için termodinamiği bulmayı mümkün kılan bir diyagram tekniği de vardır. quasiparticles girişi olmadan doğrudan miktarlar. Bu teknikte, Green'in fonksiyonları (enerji yerine) belirli ayrık frekanslara w n bağlıdır ve enerjiler üzerindeki integraller, bu frekansların üzerindeki toplam ile değiştirilir.
, çünkü kuasipartikülün enerjisi Green fonksiyonunun kutbudur. Green'in fonksiyonlarını, parçacıklar arasındaki etkileşim enerjisinin bir dizi gücü biçiminde hesaplamak için düzenli bir yöntem vardır. Bu dizinin her bir üyesi, Green'in etkileşmeyen parçacıkların fonksiyonlarından elde edilen enerjiler ve momentumlar üzerinde çoklu integraller içerir ve aşağıdakine benzer diyagramlar şeklinde grafiksel olarak gösterilebilir. Feynman diyagramları kuantumda. Bu diyagramların her birinin belirli bir fiziksel ilgi fenomeninden sorumlu terimleri sonsuz bir dizide ayırmayı ve özetlemeyi mümkün kılan anlam. Green'in sıcaklık fonksiyonlarını hesaplamak için termodinamiği bulmayı mümkün kılan bir diyagram tekniği de vardır. quasiparticles girişi olmadan doğrudan miktarlar. Bu teknikte, Green'in fonksiyonları (enerji yerine) belirli ayrık frekanslara w n bağlıdır ve enerjiler üzerindeki integraller, bu frekansların üzerindeki toplam ile değiştirilir.
Faz geçişleri. Dahili olarak sürekli bir değişiklik ile. parametrelerin (örneğin, basınç veya sıcaklık), sistemin özellikleri, parametrelerin belirli değerleri için aniden değişebilir, yani bir faz geçişi meydana gelir. Faz geçişleri, geçişin gizli ısısının serbest bırakılması ve hacimde ani bir değişiklik (örneğin erime) ve 2. tür geçişlerin eşlik ettiği 1. tür geçişlere ayrılır. gizli ısı ve hacimde sıçrama yoktur, ancak ısı kapasitesinde bir sıçrama vardır (örneğin, bir süper iletken duruma geçiş). 2. türün geçişi sırasında vücudun simetrisi değişir. Bu değişiklik sayısal sipariş parametresi, fazlardan birinde sıfırdan farklıdır ve geçiş noktasında kaybolur. istatistiksel Faz geçişleri teorisi, S. ph'ın önemli ama yine de tam bir alanından uzaktır. maks. teorik zorluk çalışmalar yakın maddenin özelliklerini temsil eder kritik nokta, faz geçişi 1. tür ve doğrudan. ikinci dereceden faz geçişi hattının yakınlığı. (Bu hattan belirli bir uzaklıkta, ikinci türden bir geçiş şu şekilde tanımlanır: Landau teorisi.) Burada dalgalanmalar anormal bir şekilde artar ve S. f'nin yaklaşık yöntemleri. uygulanamaz. Bu nedenle, önemli bir rol oynar tam olarak çözülebilir modeller geçişlerin olduğu (bkz. 2D Kafes Modelleri). Yaratık. dalgalanmaların inşasında ilerleme. faz geçişleri teorisi yöntemle elde edilir epsilon açılımları. İçinde, geçiş, boyutların sayısı ile hayali bir uzayda araştırılır ve sonuçlar, yani üç boyutlu gerçek uzaya tahmin edilir. İki boyutlu sistemlerde, belirli bir sıcaklıkta dislokasyonlar veya girdap filamentleri göründüğünde özel faz geçişleri mümkündür. Geçiş noktasındaki sipariş parametresi aniden kaybolur ve ısı kapasitesi süreklidir.
Düzensiz sistemler. S.f.'de tuhaf bir yer. işgal etmek bardak- atomları abs'de bile rastgele düzenlenmiş katılar. sıfır sıcaklık Kesin olarak konuşursak, böyle bir durum dengesizdir, ancak aşırı uzun bir gevşeme süresine sahiptir, bu nedenle dengesizlik aslında kendini göstermez. Camların düşük sıcaklıklardaki ısı kapasitesi doğrusal olarak aşağıdakilere bağlıdır: T. Bu, şu ifadeden çıkar: Z(8) şeklindedir. bağımlı olduğunda T davranış tarafından belirlenir g(E) küçük için E. Ama için düzensiz sistemler anlam E = 0 tahsis edilmedi, bu yüzden g(0)elbette, Z = ANCAK + e(0)T ve c ~ T. İlginç bir özellik cam, gözlemlenen ısı kapasitesi değerlerinin ölçüm süresine bağımlılığıdır. Bu, enerji seviyelerinin küçük olması gerçeğiyle açıklanmaktadır. Eçok zaman gerektiren yüksek potansiyelli bir bariyer aracılığıyla atomların kuantum tünellemesi ile ilişkilidir. ilginç özellikler spin gözlük- bir magn değerine sahip rastgele düzenlenmiş atom sistemleri. anlar.
Dengesiz süreçlerin istatistiksel fiziği. Gittikçe daha fazla önem kazanıyor fiziksel kinetik- S. f.'nin, dengede olmayan durumlardaki sistemlerdeki süreçleri inceledikleri bölümü. Burada sorunun iki formülasyonu mümkündür: sistem belirli bir denge dışı durumda düşünülebilir ve bir denge durumuna geçişi izlenebilir; Dengesizlik durumu dışarıdan sağlanan bir sistemi düşünmek mümkündür. koşullar, örn. sıcaklık gradyanının ayarlandığı gövde elektriksel olarak akar. akım, vb. veya AC'deki bir gövde. harici alan.
Dengeden sapma küçükse, sistemin dengesiz özellikleri sözde ile tanımlanır. kinetik katsayılar. Bu tür katsayılara örnekler. katsayılardır. metallerin viskozitesi, ısıl iletkenliği ve elektriksel iletkenliği vb. Bu miktarlar kinetik simetri ilkesini karşılar. zaman işaretindeki değişime göre mekanik denklemlerinin simetrisini ifade eden katsayılar (bkz. Onsager teoremi).
Daha Genel kavram dır-dir genelleştirilmiş duyarlılık değişikliği açıklayan bkz. belirli bir fiziksel sürünün değerleri. miktarları X küçük bir "genelleştirilmiş kuvvet" eylemi altında f, sistemin Hamiltonyeninde yer alan formda, kuantum mekaniği nerede. karşılık gelen operatör X. Eğer bir f zamana bağlı olarak değişiklik şu şekilde yazılabilir: ![]() . Karmaşık değer, genelleştirilmiş duyarlılıktır; sistemin dışsal olana göre davranışını tanımlar. darbe. Öte yandan, rahatlamayı da belirler. özellikler: noktasında, değer yasaya göre denge değerine gevşer, burada karmaşık değişken w'nin alt yarı düzleminde kendisine en yakın fonksiyonun gerçek eksenden tekilliğine olan uzaklıktır. S. f.'nin görevleri arasında. Dengesizlik süreçleri, dalgalanmaların zamana bağımlılığının incelenmesini de içerir. Bu bağımlılık bir zaman korelasyonu ile tanımlanır. değerdeki dalgalanmaların ortalamasının alındığı fonksiyon X farklı alındı zaman içindeki noktalar t:
. Karmaşık değer, genelleştirilmiş duyarlılıktır; sistemin dışsal olana göre davranışını tanımlar. darbe. Öte yandan, rahatlamayı da belirler. özellikler: noktasında, değer yasaya göre denge değerine gevşer, burada karmaşık değişken w'nin alt yarı düzleminde kendisine en yakın fonksiyonun gerçek eksenden tekilliğine olan uzaklıktır. S. f.'nin görevleri arasında. Dengesizlik süreçleri, dalgalanmaların zamana bağımlılığının incelenmesini de içerir. Bu bağımlılık bir zaman korelasyonu ile tanımlanır. değerdeki dalgalanmaların ortalamasının alındığı fonksiyon X farklı alındı zaman içindeki noktalar t: ![]() argümanının çift fonksiyonudur. Klasik S. f. ile büyüklük gevşeme yasası arasında bir bağlantı vardır. Gevşeme belirli bir lineer diferansiyel ile tanımlanırsa denge değerinden sapma denklemi, daha sonra aynı denklemi sağlar t > 0.
argümanının çift fonksiyonudur. Klasik S. f. ile büyüklük gevşeme yasası arasında bir bağlantı vardır. Gevşeme belirli bir lineer diferansiyel ile tanımlanırsa denge değerinden sapma denklemi, daha sonra aynı denklemi sağlar t > 0.
ve kümeler arasındaki ilişki dalgalanma-dağılım teoremi.Teorem, Fourier dönüşümünün bağıntılı olduğunu belirtir. fonksiyonlar 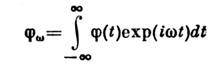
aşağıdaki gibi ifade edilir:
Özel bir durum (17) Nyquist formülü.Kinetik hesabının yanı sıra, kuvvetle denge dışı durumların açıklaması. katsayı kullanılarak üretilen Boltzmann'ın kinetik denklemi. Bu denklem bir tam diferansiyeldir. tek parçacıklı bir dağılım fonksiyonu için ur-tion (kuantum durumunda - tek parçacıklı bir yoğunluk matrisi veya bir istatistiksel operatör için). İki tür üye içerir. Bazıları, parçacıklar harici olarak hareket ettiğinde dağılımın f-tionundaki değişikliği tanımlar. alanlar, diğerleri - parçacıkların çarpışmalarında. Dengesiz bir sistemin entropisinde bir artışa, yani gevşemeye yol açan çarpışmalardır. Kapalı, yani başka miktarlarda kinetik içermeyen. ur-tion, içeri girmek imkansız Genel görünüm. Bunu türetirken, bu özel problemde mevcut olan küçük parametreleri kullanmak gereklidir. En önemli örnek kinetiktir. moleküller arasındaki çarpışmalar nedeniyle bir gazda dengenin kurulmasını tanımlayan bir denklem. Moleküller arasındaki mesafelere kıyasla büyük olduğunda, yeterince nadir gazlar için geçerlidir. Bu denklemin özel şekli eff'e bağlıdır. moleküllerin enine kesitlerinin birbiri üzerine saçılması. Eğer bu kısım biliniyorsa, istenen fonksiyon ortogonal polinomlar cinsinden genişletilerek denklem çözülebilir. Bu şekilde kinetik hesaplamak mümkündür. katsayı Moleküller arasındaki bilinen etkileşim yasalarına dayanan gaz. Kinetik Denklem, moleküller arasındaki yalnızca ikili çarpışmaları hesaba katar ve bu katsayıların genişlemesinde yalnızca ilk kaybolmayan terimi tanımlar. gaz yoğunluğuna göre. Ayrıca, bir sonraki genişleme terimini hesaplamayı mümkün kılan üçlü çarpışmaları da hesaba katan daha doğru bir denklem bulmayı başardık.
Kinetiğin türetilmesi özel bir problemdir. plazma için ur-tion. Coulomb kuvvetlerinin mesafe ile yavaş azalması nedeniyle, çift çarpışmalar düşünüldüğünde bile, bu kuvvetlerin diğer parçacıklar tarafından taranması esastır. Katıların ve kuantum sıvıların denge dışı durumları, düşük sıcaklıklarda, karşılık gelen yarı-parçacıkların gazının denge dışı durumları olarak düşünülebilir. Bu nedenle, kinetik bu tür sistemlerdeki süreçler kinetik olarak tanımlanır. aralarındaki çarpışmaları ve karşılıklı dönüşüm süreçlerini hesaba katan yarı parçacıklar için denklemler. Fiziksel olarak uygulama ile yeni olanaklar açıldı. kuantum alan teorisi yöntemlerinin kinetiği. Kinetik katsayı Bir sistemin tanımı, diyagramlar kullanılarak genel bir hesaplama yöntemi olan Green fonksiyonu cinsinden ifade edilebilir. Bu, bazı durumlarda kinetik elde edilmesini sağlar. katsayı kinetik açıkça kullanılmadan. Uygulanabilirlik koşullarının karşılanmadığı durumlarda bile sistemin denge dışı özelliklerini araştırır ve keşfeder.
İstatistiksel fiziğin gelişiminde kilometre taşları. S.f. tamamen konsepte dayalı atomik yapıÖnemli olmak. Bu nedenle, başlangıç S. f.'nin gelişim dönemi atomistik gelişimi ile örtüşmektedir. temsiller. S. f.'nin gelişimi Teorinin bir bölümü olarak. fizik serde başladı. 19. yüzyıl 1859'da J. Maxwell, gaz moleküllerinin hız dağılım fonksiyonunu belirledi. 1860-70'de R. Clausius (R. Clausing) ortalama serbest yol kavramını tanıttı ve onu gazın viskozitesi ve termal iletkenliği ile ilişkilendirdi. Aynı zamanda, L. Boltzmann, Maxwell dağılımını gazın harici olduğu duruma genelleştirdi. alan, enerjinin serbestlik derecelerine göre eşit dağılımına ilişkin teoremi kanıtladı, kinetik çıkardı. ur-tion, istatistik verdi. entropinin yorumlanması ve onun artış yasasının kinetik sonucu olduğunu gösterdi. ur-tion. Klasik S. f. 1902 yılında J. W. Gibbs (J. W. Gibbs) tarafından tamamlanmıştır. Dalgalanma teorisi 1905-06'da M. Smoluchowski ve A. Einstein'ın eserlerinde geliştirildi. 1900'de M. Planck, hem kuantum mekaniğinin hem de kuantum fiziğinin gelişimini başlatan bir kara cismin radyasyon spektrumundaki enerji dağılımı yasasını çıkardı. 1924'te Sh. Bose, ışık kuantasının momentum dağılımını buldu ve bunu Planck dağılımıyla ilişkilendirdi. Einstein, Bose dağılımını belirli sayıda parçacık içeren gazlara genelledi. 1925'te E. Fermi (E. Fermi), Pauli ilkesine uyan parçacıkların dağılımının bir işlevini aldı ve P. A. M. Dirac (R. A. M. Dirac) bu dağılım ile mat ile Bose-Einstein dağılımı arasındaki bağlantıyı kurdu. kuantum mekaniği aygıtı. S. t.'nin daha da geliştirilmesi. 20. yüzyılda ana uygulamasının işareti altına girdi. belirli problemlerin incelenmesi için ilkeler.
Aydınlatılmış.: Landau L.D., L ve f sh ve c E.M., İstatistiksel fizik, bölüm 1, 3. baskı, M., 1976; Mayer J., Goeppert-Mayer M., İstatistik mekanik, çev. İngilizce'den, 2. baskı, M., 1980; Abrikosov A.A., Gorkoye L.P., Dzyaloshinsky I.E., İstatistiksel fizikte kuantum alan teorisi yöntemleri, M., 1962; X u an ng K., İstatistiksel mekanik, çev. İngilizce'den, M., 1966; Kittel Ch., Kuantum teorisi katılar, başına. İngilizce'den, M., 1967; Silin V.P., Gazların kinetik teorisine giriş, M., 1971; Basit sıvıların fiziği. Sat., başına. İngilizce'den, M., 1971; Anselm A. I., İstatistiksel fizik ve termodinamiğin temelleri, M., 1973; L ve f sh ve c E.M., Pitaevsky L.P., İstatistiksel fizik, bölüm 2, M., 1978; ve xzh e, Fiziksel kinetik, M., 1979; Balescu R., Denge ve denge dışı istatistiksel mekanik, çev. İngilizce'den, cilt 1-2, M., 1978; Bogolyubov N. N., İstatistiksel fizik üzerine seçilmiş çalışmalar, M., 1979; G ve b b s J. V., Termodinamik. İstatistiksel mekanik, çev. English, M., 1982'den; Leontovich MA, Termodinamiğe giriş. İstatistiksel Fizik, M., 1983; Boltzmann L., Seçilmiş Eserler, çev. Almancadan, Fransızcadan, M., 1984. L.P. Pitayevski.
Yöntemler Eğitim Bu site hakkında Kütüphane Matematik. forumlarKütüphane > Fizik Kitapları > İstatistiksel Fizik
istatistiksel fizik
- Aizenshitz R. Tersinmez süreçlerin istatistiksel teorisi. M.: Ed. Yabancı yak., 1963 (djvu)
- Anselm A.I. İstatistiksel fizik ve termodinamiğin temelleri. Moskova: Nauka, 1973 (djvu)
- Akhiezer A.I., Peletminsky S.V. İstatistiksel fizik yöntemleri. Moskova: Nauka, 1977 (djvu)
- Bazarov I.P. İstatistiksel fizik ve termodinamiğin metodolojik problemleri. M.: Moskova Devlet Üniversitesi Yayınevi, 1979 (djvu)
- Bogolyubov N.N. İstatistiksel fizik üzerine seçilmiş eserler. M.: Moskova Devlet Üniversitesi Yayınevi, 1979 (djvu)
- Bogolyubov N.N. (Jr.), Sadovnikov B.I. İstatistiksel mekaniğin bazı soruları. M.: Daha yüksek. okul, 1975 (djvu)
- Bonch-Bruevich V.L., Tyablikov S.V. İstatistiksel mekanikte Green'in fonksiyon yöntemi. Moskova: Fizmatlit, 1961 (djvu, 2.61Mb)
- Vasiliev A.M. İstatistiksel fiziğe giriş. M.: Daha yüksek. okul, 1980 (djvu)
- Vlasov A.A. Yerel olmayan istatistiksel mekanik. Moskova: Nauka, 1978 (djvu)
- Gibbs JW İstatistik mekaniğin temel ilkeleri (termodinamiğin rasyonel gerekçelendirilmesine özel bir uygulama ile açıklanmıştır). M.-L.: OGIZ, 1946 (djvu)
- Gurov K.P. Kinetik teorinin temelleri. Yöntem N.N. Bogolyubov. Moskova: Nauka, 1966 (djvu)
- Zaslavsky G.M. Doğrusal olmayan sistemlerde istatistiksel tersinmezlik. Moskova: Nauka, 1970 (djvu)
- Zakharov A.Yu. İstatistiksel fiziğin kafes modelleri. Veliky Novgorod: NovGU, 2006 (pdf)
- Zakharov A.Yu. Klasik istatistiksel fizikte fonksiyonel yöntemler. Veliky Novgorod: NovGU, 2006 (pdf)
- Ios G. Teorik fizik dersi. Bölüm 2. Termodinamik. İstatistiksel fizik. Kuantum teorisi. Nükleer Fizik. M.: Aydınlanma, 1964 (djvu)
- Ishihara A. İstatistiksel Fizik. M.: Mir, 1973 (djvu)
- Kadanov L., Beim G. Kuantum istatistiksel mekaniği. Denge ve denge dışı süreçler teorisinde Green fonksiyonlarının yöntemleri. M.: Mir, 1964 (djvu)
- Katz M. Fizikte olasılık ve ilgili konular. M.: Mir, 1965 (djvu)
- Katz M. Fizik ve matematiğin çeşitli olasılıksal problemleri. Moskova: Nauka, 1967 (djvu)
- Kittel Ch. Temel istatistiksel fizik. M.: IL, 1960 (djvu)
- Kittel Ch. İstatistiksel termodinamik. M: Bilim, 1977 (djvu)
- Kozlov V.V. Gibbs ve Poincare'e göre termal denge. Moskova-Izhevsk: Bilgisayar Araştırmaları Enstitüsü, 2002 (djvu)
- Kompaneets A.Ş. Fiziksel istatistik yasaları. şok dalgaları. Süper yoğun madde. M.: Nauka, 1976 (djvu)
- Kompaneets A.Ş. Teorik fizik dersi. Cilt 2. İstatistiksel yasalar. M.: Aydınlanma, 1975 (djvu)
- Kotkin G.L. İstatistiksel Fizik Dersleri, NSU (pdf)
- Krylov N.S. İstatistiksel fiziğin doğrulanması üzerinde çalışır. M.-L.: SSCB Bilimler Akademisi'nden 1950 (djvu)
- Kubo R. İstatistiksel mekanik. M.: Mir, 1967 (djvu)
- Landsberg P. (ed.) Termodinamik ve istatistiksel fizikteki problemler. M.: Mir, 1974 (djvu)
- Levich V.G. İstatistiksel Fiziğe Giriş (2. baskı) M.: GITTL, 1954 (djvu)
- Libov R. Kinetik denklemler teorisine giriş. M.: Mir, 1974 (djvu)
- Mayer J., Geppert-Mayer M. İstatistiksel mekanik. M.: Mir, 1980 (djvu)
- Minlos R.A. (ed.) Matematik. Yabancı bilimde yeni-11. Gibbs istatistiksel fizikte devletler. Makalelerin özeti. M.: Mir, 1978 (djvu)
- Nozdrev V.F., Senkevich A.A. İstatistiksel fizik dersi. M.: Daha yüksek. okul, 1965 (djvu)
- Prigogine I. Dengesizlik İstatistiksel Mekaniği. M.: Mir, 1964 (djvu)
- Radushkevich L.V. İstatistiksel fizik dersi (2. baskı) M.: Prosveshchenie, 1966 (djvu)
- Reif F. Berkeley Fizik Kursu. Cilt 5. İstatistiksel fizik. M.: Nauka, 1972 (djvu)
- Rumer Yu.B., Ryvkin M.Ş. Termodinamik, istatistiksel fizik ve kinetik. M.: Nauka, 1972 (djvu)
- Rumer Yu.B., Ryvkin M.Ş. Termodinamik İstatistiksel Fizik ve Kinetik (2. baskı). Moskova: Nauka, 1977 (djvu)
- Ruel D. İstatistiksel mekanik. M.: Mir, 1971 (djvu)
- Savukov V.V. İstatistiksel fiziğin aksiyomatik ilkelerinin iyileştirilmesi. SPb.: Balt. durum teknoloji univ. "Voenmekh", 2006
istatistiksel fizik Makroskopik cisimlerin, yani çok sayıda özdeş parçacıktan (moleküller, atomlar, elektronlar vb.) oluşan sistemlerin özelliklerini, bu parçacıkların özellikleri ve aralarındaki etkileşim yoluyla ifade etmek olan bir fizik dalı . Fiziğin diğer dalları da makroskopik cisimleri inceliyor - Termodinamik, sürekli ortam mekaniği, sürekli ortamların elektrodinamiği. Bununla birlikte, belirli problemleri bu disiplinlerin yöntemleriyle çözerken, karşılık gelen denklemler her zaman belirli bir gövdeyi karakterize eden bilinmeyen parametreleri veya işlevleri içerir. Bu nedenle, hidrodinamik problemlerini çözmek için, bir sıvı veya gazın durum denklemini, yani yoğunluğun sıcaklığa ve basınca bağımlılığını, bir sıvının ısı kapasitesini, viskozite katsayısını vb. bilmek gerekir. Tüm bu bağımlılıklar ve parametreler elbette deneysel olarak belirlenebilir; bu nedenle söz konusu yöntemlere fenomenolojik denir. İstatistiksel fizik, moleküller arasındaki etkileşim kuvvetleri biliniyorsa, en azından prensipte ve çoğu durumda fiilen tüm bu miktarları hesaplamaya izin verir. T.o., S.f. cisimlerin "mikroskobik" yapısı hakkında - hangi parçacıklardan oluştukları, bu parçacıkların nasıl etkileşime girdiği hakkında bilgileri kullanır, bu nedenle buna mikroskobik teori denir. Zamanın bir noktasında vücudun tüm parçacıklarının koordinatları ve hızları verilirse ve etkileşimlerinin yasası biliniyorsa, o zaman mekanik denklemlerini çözerek, sonraki herhangi bir noktada bu koordinatları ve hızları bulmak mümkün olacaktır. zamanla ve böylece incelenen vücudun durumunu tamamen belirler. (Basit olması açısından sunum klasik mekaniğin dilinde yapılmıştır. Ancak kuantum mekaniğinde (bkz. Kuantum mekaniği) durum aynıdır: sistemin ilk dalga fonksiyonunu (Bkz. Dalga fonksiyonu) ve sistemin etkileşim yasasını bilmek. parçacıklar, Schrödinger denklemini çözerek, zamanın gelecekteki tüm anlarında sistemin durumunu belirleyen dalga fonksiyonunu bulmak mümkündür.) Bununla birlikte, aslında, böyle bir mikroskobik teori inşa etmek imkansızdır, çünkü makroskobik cisimlerdeki parçacıkların sayısı çok fazladır. Örneğin, 1'de cm3 0 °C sıcaklıkta ve 1 basınçta gaz ATM yaklaşık 2.7․10 19 molekül içerir. Bu kadar çok sayıda denklemi çözmek imkansızdır ve tüm moleküllerin başlangıç koordinatları ve hızları hala bilinmemektedir. Bununla birlikte, bu tür cisimlerin davranışında yeni - istatistiksel - düzenliliklerin ortaya çıkmasına yol açan tam olarak makroskopik cisimlerdeki çok sayıda parçacıktır. Geniş bir aralıktaki bu davranış, belirli başlangıç koşullarına - ilk koordinatların ve parçacık hızlarının kesin değerlerine - bağlı değildir. Bu bağımsızlığın en önemli tezahürü, kendi haline bırakılan, yani dış etkilerden izole edilen bir sistemin, sonunda, özellikleri yalnızca tarafından belirlenen bir denge durumuna (termodinamik veya istatistiksel denge) geldiği deneyimlerden bilinen gerçektir. parçacıkların sayısı, toplam enerjileri vb. gibi genel özellikler başlangıç durumu. (bkz. Termodinamik denge). Gelecekte, esas olarak S. t hakkında konuşacağız. denge durumları. İstatistiksel düzenlilikleri tanımlayan bir teori formüle etmeden önce, teorinin gerekliliklerini makul bir şekilde sınırlamak gerekir. Yani teorinin görevi, makroskopik cisimler için çeşitli fiziksel niceliklerin tam değerlerini değil, bu niceliklerin zaman içindeki ortalama değerlerini hesaplamak olmalıdır. Örneğin, bir gazda izole edilmiş, yeterince büyük bir makroskopik hacimde bulunan molekülleri düşünün. Bu tür moleküllerin sayısı, hareketlerinden dolayı zamanla değişecektir ve moleküllerin tüm koordinatları her zaman biliniyorsa tam olarak bulunabilir. Ancak bu gerekli değildir. Hacimdeki molekül sayısındaki değişiklik, bazı ortalama değerlere göre rastgele dalgalanmaların - dalgalanmaların - doğasında olacaktır. Hacimdeki çok sayıda parçacıkla, bu dalgalanmalar ortalama parçacık sayısına kıyasla küçük olacaktır, böylece makroskopik durumu karakterize etmek için bu ortalama değeri tam olarak bilmek yeterlidir. İstatistiksel kalıpların doğasını netleştirmek için başka bir basit örnek düşünün. İki çeşitten çok sayıda tahıl, her biri eşit derecede bir kaba konulsun ve kabın içindekiler iyice karıştırılsın. Daha sonra, günlük deneyimlere dayanarak, hala çok sayıda tahıl içeren bir kaptan alınan bir numunede, tahılların sırasına bakılmaksızın her çeşitten yaklaşık olarak eşit sayıda tahıl bulunacağından emin olunabilir. tekneye döküldü. Bu örnek, istatistiksel teorinin uygulanabilirliğini sağlayan iki önemli durumu açıkça göstermektedir. İlk olarak, hem tüm “sistemde” - tahıllı bir kapta hem de deney için seçilen “alt sistemde” - bir numunede çok sayıda tahıl ihtiyacı. (Numune sadece iki taneden oluşuyorsa, genellikle her ikisi de aynı kalitede olacaktır.) İkinci olarak, karıştırma sırasında tanelerin hareketinin karmaşıklığının, bunların hacminde düzgün dağılımlarını sağlayarak önemli bir rol oynadığı açıktır. gemi. dağıtım işlevi. oluşan bir sistem düşünün. N basitlik için parçacıkların hiçbir iç serbestlik derecesine sahip olmadığını varsayarsak. Böyle bir sistem görev tarafından tanımlanır 6N değişkenler - 3N koordinatlar ben ve 3N dürtüler pi, parçacıklar [bu değişkenlerin kümesi ( R, q)]. Belirli bir değerin zaman aralığı üzerinden ortalama değerini hesaplayalım. F(p, q), bu koordinatların ve momentumun bir fonksiyonudur. Bunu yapmak için (0, τ) aralığını böleriz. s eşit küçük parçalar Δ ta (a = 1,2,....... s). Daha sonra tanım gereği nerede bir ve p bir- zaman zaman koordinat ve dürtü değerleri ta. sınırda s→ ∞ toplam bir integrale gider: 6 uzayını düşünürsek, doğal bir şekilde dağılım fonksiyonu kavramı ortaya çıkar. N sistemin parçacıklarının koordinatlarının ve momentumlarının değerlerinin çizildiği eksenlerde ölçümler; faz uzayı denir. zamanın her değeri için t hepsinin belirli değerlerine karşılık gelir q ve R, yani belirli bir zamanda sistemin durumunu gösteren faz uzayında bir nokta t. Tüm faz alanını, sistemin belirli bir durumunun karakteristik değerlerine kıyasla boyutu küçük olan elemanlara bölelim. q ve R, ama yine de o kadar büyük ki, her birinde sistemin durumunu zaman içinde farklı noktalarda gösteren birçok nokta var. t. O zaman hacim elemanındaki bu tür noktaların sayısı, bu hacmin değeri ile yaklaşık olarak orantılı olacaktır. dpdq. Orantılılık katsayısını şu şekilde ifade edersek sω(p, q), o zaman bu, bir noktada ortalanmış öğenin sayısıdır ( p, q) şu şekilde yazılacaktır: da = sω(p, q)dpdq, (2) dpdq = dp 1 dq 1 dp 2 dq 2 ... dp 3N dq 3N Seçili faz alanı öğesinin hacmi. Ortalama değer (1), bu hacim elemanlarının küçüklüğü dikkate alınarak yeniden yazılabilir. (koordinatlar üzerinden entegrasyon, sistemin tüm hacmi üzerinde, momentum üzerinden - -∞'den ∞'ye kadar gerçekleştirilir). fonksiyon ω( p, q, t) parçacık momentum koordinatlarına göre dağılım fonksiyonu olarak adlandırılır. Seçilen noktaların toplam sayısı s, işlev w normalizasyon koşulunu karşılar: (3) ve (4) den görülebilir ki ω dpdq sistemin elemanda olma olasılığı olarak kabul edilebilir. dpdq faz boşluğu. Bu şekilde tanıtılan dağıtım işlevine başka bir yorum yapılabilir. Bunu yapmak için, aynı anda çok sayıda özdeş sistemi ele alacağız ve faz uzayındaki her noktanın böyle bir sistemin durumunu temsil ettiğini varsayacağız. O zaman (1)-(1a)'daki zaman ortalaması, bu sistemlerin toplamı üzerinden veya dedikleri gibi, istatistiksel topluluk üzerinden ortalama alma olarak anlaşılabilir (Bkz. İstatistiksel Topluluk). Şimdiye kadar yürütülen argümanlar, doğası gereği tamamen biçimseldi, çünkü (2)'ye göre dağılım fonksiyonunu bulmak, tüm R ve q her zaman, yani hareket denklemlerinin karşılık gelen başlangıç koşullarıyla çözümleri. S. f.'nin ana konumu. bununla birlikte, termodinamik denge durumundaki bir sistem için bu işlevi genel değerlendirmelerden belirleme olasılığı hakkında bir ifadedir. Her şeyden önce, hareket sırasında sistem sayısının korunumuna dayalı olarak, dağıtım fonksiyonunun sistemin hareketinin bir integrali olduğu, yani eğer sabit kalırsa gösterilebilir. R ve q hareket denklemlerine göre değişir (bkz. Liouville teoremi). Kapalı bir sistem hareket ettiğinde, enerjisi değişmez, bu nedenle, sistemin zaman içindeki farklı noktalarındaki durumunu gösteren faz uzayındaki tüm noktalar, enerjinin başlangıç değerine karşılık gelen bazı “hiperyüzey” üzerinde yer almalıdır. E. Bu yüzeyin denklemi şu şekildedir; H(p, q) = E, nerede H(p, q) koordinatlar ve momentum cinsinden ifade edilen sistemin enerjisidir, yani Hamilton fonksiyonu. Ayrıca, birçok parçacıktan oluşan bir sistemin hareketi son derece karmaşıktır. Bu nedenle zamanla durumu anlatan noktalar yüzey üzerine dağılacaktır. sabit enerji eşit olarak, tıpkı yukarıda bahsedilen örnekte kapta karıştırma sırasında tanelerin eşit olarak dağılması gibi (ayrıca bkz. Ergodik hipotez). İzoenerjetik yüzey üzerinde böyle bir düzgün dağılım, formun bir dağılım fonksiyonu ile tanımlanır: ω( p, q) = birδ[ H(p, q) -E], (5) nerede δ[ H(p, q) -E]
- Delta işlevi, yalnızca sıfırdan farklı olduğunda H = E, yani bu yüzeyde, ANCAK normalizasyon koşulundan (4) belirlenen bir sabittir. Mikrokanonik olarak adlandırılan dağıtım işlevi (5), hareket denklemlerini çözmeden tüm fiziksel niceliklerin ortalama değerlerini formül (3) ile hesaplamanıza olanak tanır. (5) ifadesi türetilirken, ω'nin bağlı olduğu sistemin hareketi sırasında değişmeyen tek niceliğin sistemin enerjisi olduğu varsayılmıştır. Elbette momentum ve açısal momentum da korunur, ancak söz konusu cismin parçacıkların momentum ve momentum verebileceği sabit bir kutu içine alındığı varsayılarak bu miktarlar elimine edilebilir. Aslında, genellikle kapalı sistemler olarak değil, herhangi bir kapalı sistemin makroskopik olarak küçük parçaları veya alt sistemleri olan makroskopik gövdeler olarak kabul edilir. Alt sistem için dağıtım işlevi (5)'ten farklı olacaktır, ancak sistemin geri kalanının - sözde - özel doğasına bağlı olmayacaktır. termostat. Bu nedenle, alt sistemin dağıtım fonksiyonu, örneğin termostatın basitçe aşağıdakilerden oluştuğu varsayılarak belirlenebilir. N koordinatları ve momentumları ile gösterilecek olan ideal bir gazın parçacıkları Q ve R, notasyonun aksine q ve R bir alt sistem için mikrokanonik dağılım şöyledir: Burada H(p, q) alt sistemin Hamilton fonksiyonudur, M bir gaz parçacığının kütlesidir ve toplama, termostatın tüm parçacıklarının darbelerinin tüm bileşenleri üzerinde gerçekleştirilir. Alt sistem için dağıtım fonksiyonunu bulmak için, bu ifadeyi termostat parçacıklarının koordinatları ve momentumları üzerine entegre etmemiz gerekir. Termostattaki partikül sayısının alt sistemdekinden çok daha fazla olduğunu hesaba katarsak ve N→∞, oranı varsayarak E/N sabit ve 3 / 2'ye eşit kT, daha sonra alt sistemin dağıtım fonksiyonu için aşağıdaki ifade elde edilecektir: Değer T bu formülde sıcaklık anlamı vardır, k = 1,38․10 -16 erg/derece Boltzmann sabitidir. [Şart E/N→ 3 / 2 kT termostattaki gaz için olması gerektiği gibi ideal bir gaz için formül (13)'e karşılık gelir; aşağıya bakın.] Normalleştirme faktörü e F/kT normalizasyon koşulundan (4) belirlenir: Dağılım (6), kanonik Gibbs dağılımı veya basitçe kanonik dağılım (bkz. Gibbs dağılımı) olarak adlandırılır ve miktar Z- istatistiksel integral. Mikrokanonik dağılımın aksine Gibbs dağılımında sistemin enerjisi verilmez. Sistemin durumları, enerjinin ortalama değerine karşılık gelen enerji yüzeyinin etrafında ince fakat sonlu bir tabakada yoğunlaşmıştır, bu da termostat ile enerji alışverişinin mümkün olduğu anlamına gelir. Aksi takdirde, belirli bir makroskopik gövdeye uygulandığında, her iki dağılım da esasen aynı sonuçlara yol açar. Tek fark, mikrokanonik dağılım kullanılırken tüm ortalama değerlerin vücudun enerjisi cinsinden, kanonik dağılım kullanıldığında ise sıcaklık cinsinden ifade edilmesidir. Gövde, Hamilton fonksiyonlarına sahip, birbiriyle etkileşmeyen iki parça 1 ve 2'den oluşuyorsa H1 ve H2, sonra tüm vücut için H = H1 + H2 ve (6)'ya göre, cismin dağılım fonksiyonu, parçaların her biri için dağılım fonksiyonlarının çarpımına bölünür, böylece bu parçalar istatistiksel olarak bağımsız hale gelir. Bu gereklilik, Liouville teoremi ile birlikte, mikrokanonik dağılıma başvurmadan Gibbs dağılımının türetilmesi için temel olarak kullanılabilir. Formül (6), klasik mekanik tarafından açıklanan sistemler için geçerlidir. Kuantum mekaniğinde, sonlu hacimli bir sistemin enerji spektrumu ayrıktır. Bir alt sistemin enerjili durumda olma olasılığı E n(6)'ya benzer bir formülle verilir: normalleşme koşulu nerede Değer Z sistemin bölüm işlevi olarak adlandırılır; (8) ifadesindeki toplam, sistemin tüm durumları için alınır. Klasik mekanik tarafından yeterli doğrulukla tanımlanan bir sistem için (8) formülünde durumların toplamından sistemin koordinatları ve momentumları üzerinden entegrasyona geçmek mümkündür.Aynı zamanda her kuantum durumu için bir “hücre” vardır. (veya "hücre") hacminin faz uzayında - Çubuk sabittir. Başka bir deyişle, toplam nüzerinden entegrasyonu azaltır Tamamen klasik normalleştirme koşulundan (6a) bir faktör farklıdır, bu da ek bir terime yol açar. F. Yukarıdaki formüller, alt sistemdeki parçacık sayısının verildiği duruma atıfta bulunur. Bir alt sistem olarak, tüm sistemin belirli bir hacim elemanını seçersek, yüzeyi aracılığıyla parçacıkların alt sistemi terk edip ona geri dönebileceği, o zaman alt sistemi enerjili bir durumda bulma olasılığı E n ve parçacık sayısı N n Gibbs büyük kanonik dağılım formülü ile verilir: burada ek parametre μ - Alt sistemdeki ortalama partikül sayısını belirleyen kimyasal potansiyel ve Ω değeri normalizasyon koşulundan belirlenir [bkz. formül (11)]. Termodinamiğin istatistiksel yorumu. S. f.'nin en önemli sonucu. - termodinamik niceliklerin istatistiksel anlamlarının oluşturulması. Bu, termodinamik yasalarını S. f'nin temel fikirlerinden çıkarmayı mümkün kılar. ve belirli sistemler için termodinamik miktarları hesaplar. Öncelikle termodinamik iç enerji, sistemin ortalama enerjisi ile tanımlanır. Termodinamiğin birinci yasası daha sonra cismi oluşturan parçacıkların hareketi sırasında enerjinin korunumu yasasının bir ifadesi olarak açık bir yorum alır. Ayrıca, sistemin Hamilton fonksiyonunun bazı parametrelere (λ) bağlı olmasına izin verin (sistemi içeren kabın duvarının koordinatları, dış alan, vb.). Daha sonra bu parametreye karşılık gelen Genelleştirilmiş kuvvetin türevi) ve sistemin E̅ değeri, formül (6) ve normalizasyon koşulu dikkate alınarak, λ ve değişkenleri dikkate alınarak T ve değeri düşünüldüğünde F aynı zamanda bu değişkenlerin bir fonksiyonu ise, o zaman kimliği elde ederiz: Yukarıdakilere göre, üyeyi içeren dλ, ortalama işe eşittir dA vücut üzerinde yapılır. Daha sonra son terim vücudun aldığı ısıdır. Bu ifadenin bağıntı ile karşılaştırılması dE = dA + TdS Tersinir süreçler için termodinamiğin birinci ve ikinci yasalarının (bkz. Termodinamiğin ikinci yasası) birleşik kaydı olan (bkz. Tersinir süreç), T(6)'da gerçekten cismin mutlak sıcaklığına ve türevi Entropi'ye eşittir) S. Demek oluyor F istatistiksel anlamının açıklığa kavuşturulduğu vücudun Serbest Enerjisidir. Formül (8)'den çıkan entropinin istatistiksel yorumu özellikle önemlidir. Resmi olarak, g, enerji ile tüm durumlar için bu formüle toplanır. E n, ancak aslında Gibbs dağılımındaki enerji dalgalanmalarının küçüklüğü nedeniyle, ortalama enerjiye yakın bir enerjiye sahip olanlardan sadece nispeten az sayıda önemlidir. Bu temel durumların sayısı Δ̅n̅ bu nedenle doğal olarak (8)'deki toplamın Δ̅n̅ aralığıyla sınırlandırılmasıyla belirlenebilir. E n orta enerji için E̅ ve üssü toplam işaretinin altından çıkarmak. Sonra toplam Δ̅n̅ verecek ve formu alacaktır. Öte yandan, termodinamiğe göre, F = E̅ - TS, belirli bir makroskopik durumda entropinin mikroskobik durum sayısı Δ̅n̅ ile, başka bir deyişle, makroskopik durumun istatistiksel ağırlığı (bkz. İstatistiksel ağırlık) ile, yani. olasılığı ile: Mutlak sıfır sıcaklığında, herhangi bir sistem belirli bir temel durumdadır, böylece Δ̅n̅ = 1, S= 0. Bu ifade termodinamiğin üçüncü yasasını ifade eder. Burada, entropinin açık bir tanımı için kuantum formülünün (8) kullanılması gereklidir; tamamen klasik istatistikte, entropi yalnızca keyfi bir terime kadar tanımlanır. Bir durumun olasılığının bir ölçüsü olarak entropinin anlamı, keyfi - mutlaka denge değil - durumlarla ilgili olarak da korunur. Bir denge durumunda, entropi, belirli dış koşullar altında mümkün olan en yüksek değere sahiptir. Bu, denge durumunun maksimum istatistiksel ağırlığa sahip durum, en olası durum olduğu anlamına gelir. Bir sistemin denge dışı durumdan denge durumuna geçiş süreci, daha az olası durumlardan daha olası olanlara geçiş sürecidir; bu, kapalı bir sistemin entropisinin yalnızca artabileceğine göre entropi artış yasasının istatistiksel anlamını aydınlatır. Serbest enerji ile ilgili formül (8) F bölme fonksiyonu ile, termodinamik miktarları S. f yöntemleriyle hesaplamanın temelidir. Özellikle, maddenin elektriksel ve manyetik özelliklerinin istatistiksel bir teorisini oluşturmak için kullanılır. Örneğin, bir cismin manyetik alandaki manyetik momentini hesaplamak için, bölme fonksiyonunu ve serbest enerjiyi hesaplamak gerekir. manyetik moment m gövde daha sonra formülle verilir: m = nerede H- dış manyetik alanın yoğunluğu. (8)'e benzer şekilde, büyük kanonik dağılımdaki (9) normalleştirme koşulu, aşağıdaki formüle göre termodinamik potansiyeli Ω belirler: Bu potansiyel, aşağıdaki ilişki ile serbest enerji ile ilgilidir: Uygulamalar S. f. belirli sistemlerin belirli özelliklerinin incelenmesine, esasen, sistemin belirli özelliklerini dikkate alarak, bölme fonksiyonunun yaklaşık bir hesaplamasına indirgenir. Çoğu durumda, bu görev, ısı kapasitesinin eşit olduğunu belirten serbestlik derecelerinde eş bölme yasası uygulanarak basitleştirilir. Özgeçmiş(sabit bir hacimde v) etkileşimli malzeme noktaları sisteminin - harmonik salınımlar gerçekleştiren parçacıklar, eşittir c v = k(l/2 + n),
nerede ben- toplam öteleme ve dönme serbestlik derecesi sayısı, n- titreşim serbestlik derecesi sayısı. Kanunun ispatı, Hamilton fonksiyonunun H böyle bir sistem şöyle görünür: H = K(pi)+ U(metrekare), kinetik enerji nerede İle homojen bir ikinci dereceden fonksiyondur ben + n dürtüler pi ve potansiyel enerji sen- ikinci dereceden fonksiyon n titreşim koordinatları metrekare. İstatistiksel integralde Z(8a) integralin hızlı yakınsaması nedeniyle titreşim koordinatları üzerinden entegrasyon - ∞'den ∞'ye uzatılabilir. Değişkenlerin değişimini yaptıktan sonra Z sıcaklığa şu şekilde bağlıdır: TL/2+n yani serbest enerji F=-kT(ben/ 2
+n)(ln T+ sabit). Bundan, ısı kapasitesi için yukarıdaki ifade gelir, çünkü Ideal gaz. S.'nin araştırmasının en basit amacı f. ideal bir gazdır, yani molekülleri arasındaki etkileşim ihmal edilebilecek kadar nadir bulunan bir gazdır. Böyle bir gazın termodinamik fonksiyonları tam olarak hesaplanabilir. Bir gazın enerjisi, basitçe, tek tek moleküllerin enerjilerinin toplamıdır. Ancak bu, molekülleri tamamen bağımsız olarak düşünmek için hala yetersizdir. Gerçekten de, kuantum mekaniğinde, parçacıklar arasında etkileşim kuvvetleri olmasa bile, benzer kuantum mekaniksel durumlardaysa özdeş (özdeş) parçacıkların birbirleri üzerinde belirli bir etkisi vardır. Bu sözde. değişim etkileşimi. Durum başına ortalama olarak, gazın yeterince yüksek bir sıcaklığında gerçekleşen birden fazla parçacık varsa, ihmal edilebilir; böyle bir gaza dejenere olmayan denir. Aslında, atomlardan ve moleküllerden oluşan sıradan gazlar, tüm sıcaklıklarda (hâlâ gaz halinde oldukları) dejenere değildir. Dejenere olmayan bir ideal gaz için, dağıtım fonksiyonu, tek tek moleküller için dağıtım fonksiyonlarının ürününe ayrışır. aralıklarda yatmak dp x, dpy, dpz, ve koordinatlar aralıklarda dx, ölmek, dz: , (12) Potansiyel enerjili bir dış alandaki tek atomlu bir gaz molekülünün enerjisi sen(r) eşittir p 2 /2M + U(r). (6) koordinatları üzerinden entegrasyon r(x, y, z) ve dürtüler R(px, p, pz) biri hariç tüm moleküllerin molekül sayısını bulabilirsiniz. dN, kimin dürtüleri nerede 3 p = dp x dp y dp z, d3x = dxdydz. Bu formüle Maxwell-Boltzmann dağılımı denir (bkz. Boltzmann istatistikleri). (12) momentum üzerinden entegre edersek, parçacıkların harici bir alanda, özellikle yerçekimi alanında - Barometrik formülde koordinatlar üzerinden dağılımı için bir formül elde ederiz. Uzaydaki her noktadaki hızların dağılımı, Maxwell dağılımı m ile çakışmaktadır. İdeal bir gazın bölme işlevi, aynı zamanda, tek tek moleküllere karşılık gelen özdeş terimlerin ürününe de ayrılır. Tek atomlu bir gaz için, (8)'deki toplam, koordinatlar ve momentum üzerinden entegrasyona indirgenir, yani toplam, nerede g- atomun temel durumunun istatistiksel ağırlığı, yani daha düşük enerji seviyesine karşılık gelen durum sayısı, V- gaz hacmi (burada e- temel doğal logaritmalar). yüksek sıcaklıklarda g =(2J+1)(2L+1), nerede J- Spin a, a'nın değeri L- atomun yörünge momenti (bkz. Yörünge momenti) (birim olarak) ħ
). için ifadeden bedava enerji ideal bir gazın durum denkleminin, yani basıncının bağımlılığının ( R) parçacık numarası yoğunluğuna ( N/V) ve sıcaklık, şu şekildedir: PV = NkT. Monatomik bir gazın iç enerjisi ve sabit hacimdeki ısı kapasitesi eşit olur: E = 3 / 2 (NKT), c v = 3 / 2 nk, (13) Ve onun kimyasal potansiyel: Dejenere olmayan (yani, klasik mekaniğe yeterli doğrulukla uyan) bir gaz için bile, serbest enerji ve kimyasal potansiyel ifadelerinin Planck sabitini içermesi karakteristiktir. ħ
. Nihayetinde bu, entropi ile kuantum durumlarının sayısı kavramı arasında daha önce belirtilen bağlantıdan kaynaklanmaktadır. İki atomlu ve çok atomlu gazlar durumunda, moleküllerin titreşimleri ve dönüşü de termodinamik fonksiyonlara katkıda bulunur. Bu katkı, titreşimlerin kuantizasyonunun ve molekülün rotasyonunun etkilerinin önemli olup olmadığına bağlıdır. Titreşimsel enerji seviyeleri arasındaki mesafe, I - dönen bir cismin, bu durumda bir molekülün eylemsizlik momenti düzeyindedir. Sıcaklık yeterince yüksekse, klasik istatistikler geçerlidir. kT>>
Δ E. Bu durumda, eşbölme yasasına göre, dönüş, ısı kapasitesine 1/2'ye eşit sabit bir katkı sağlar. k her bir dönme serbestlik derecesi için; özellikle, iki atomlu moleküller için bu katkı şuna eşittir: k. Dalgalanmalar, ısı kapasitesine eşit katkıda bulunur. k her bir titreşim serbestlik derecesi için (böylece iki atomlu bir molekülün titreşimsel ısı kapasitesi k). Titreşim serbestlik derecesinin katkısı, dönme ile karşılaştırıldığında, titreşimler sırasında bir moleküldeki atomların sadece kinetik değil, aynı zamanda potansiyel enerjiye sahip olması nedeniyle iki kat daha fazladır. ters sınırda Kusurlu gaz. S. t.'nin önemli bir başarısı. - parçacıkları arasındaki etkileşimle ilişkili gazın termodinamik miktarlarında düzeltmelerin hesaplanması. Bu bakış açısından, ideal bir gazın hal denklemi, gerçek bir gazın basıncının tanecik sayısının yoğunluğunun kuvvetleri cinsinden genişlemesindeki ilk terimdir, çünkü herhangi bir gaz yeterince bir ideal gaz gibi davranır. düşük yoğunluklu. Yoğunluk arttıkça, durum denklemindeki etkileşimle ilgili düzeltmeler bir rol oynamaya başlar. Parçacık sayısının daha yüksek yoğunluk derecelerine sahip terimlerin basınç ifadesinde ortaya çıkmasına neden olurlar, böylece basınç sözde ile temsil edilir. formun viral serisi: oranlar AT, İTİBAREN vb. sıcaklığa bağlıdır ve oluşur. ikinci, üçüncü vb. viral katsayılar. S.'nin yöntemleri f. gaz molekülleri arasındaki etkileşim yasası biliniyorsa, bu katsayıları hesaplamayı mümkün kılar. Aynı zamanda, katsayılar AT, İTİBAREN,... iki, üç veya daha fazla molekülün eşzamanlı etkileşimini tanımlar. Örneğin, gaz tek atomluysa ve atomlarının etkileşiminin potansiyel enerjisi sen(r), o zaman ikinci virial katsayı büyüklük sırasına göre AT eşittir r 0 - bir atomun karakteristik boyutu veya daha kesin olarak atomlar arası kuvvetlerin etki yarıçapı. Bu, (15) serisinin aslında boyutsuz parametrenin güçlerinde bir açılım olduğu anlamına gelir. Sayı 3 / V, yeterince nadir bir gaz için küçük. Gaz atomları arasındaki etkileşim, yakın mesafelerde itme ve uzak mesafelerde çekim karakterine sahiptir. Bu yol açar AT> 0 yüksek sıcaklıklarda ve AT T = 15.3 K katsayısı AT = -
3․10 -23 cm3, ve ne zaman T= 510 bin AT = 1,8 ․10 -23 cm3. argon için AT = -
7,1․10 -23 cm3 de T = 180 bin ve AT = 4,2․10 -23 cm3 de T= 6000 K. Monatomik gazlar için, beşinci de dahil olmak üzere virial katsayıların değerleri hesaplanır, bu da gazların davranışını oldukça geniş bir yoğunluk aralığında tanımlamayı mümkün kılar (ayrıca bkz. Gazlar). Plazma.İdeal olmayan bir gazın özel bir durumu, Plazmadır - kısmen veya tamamen iyonize bir gazdır, bu nedenle içinde serbest elektronlar ve iyonlar bulunur. Yeterince düşük yoğunlukta, plazmanın özellikleri ideal gazın özelliklerine yakındır. İdeallikten sapmaları hesaplarken, elektronların ve iyonların Coulomb yasasına göre elektrostatik olarak etkileşmesi esastır. Coulomb kuvvetleri mesafe ile yavaş yavaş azalır ve bu, termodinamik fonksiyonlardaki ilk düzeltmeyi hesaplamak için, aynı anda iki değil, çok sayıda parçacığın etkileşimini hesaba katmak gerektiği gerçeğine yol açar, çift etkileşimini tanımlayan ikinci virial katsayıdaki (16) integral uzun mesafelerle birbirinden ayrıldığından r parçacıklar arasında. Gerçekte, Coulomb kuvvetlerinin etkisi altında, plazmadaki iyonların ve elektronların dağılımı, her parçacığın alanı taranacak şekilde değişir, yani Debye yarıçapı olarak adlandırılan belirli bir mesafede hızla azalır. Elektronlardan ve tek yüklü iyonlardan oluşan en basit plazma durumu için Debye yarıçapı rd eşittir: nerede N elektron sayısı e elektronun yüküdür. Debye yarıçapı içindeki tüm parçacıklar aynı anda etkileşimde yer alır. Bu, ilk basınç düzeltmesinin değil ile orantılı olmasına neden olur ( N/V) 2
sıradan bir gazda olduğu gibi, ancak daha düşük yoğunluk derecesi - ( N/V) 3/2
. Nicel hesaplama, kalan parçacıkların Boltzmann dağılımına göre seçilen elektron veya iyon alanında dağıldığı gerçeğine dayanmaktadır. Sonuç olarak, ilk değişiklik dikkate alınarak devlet denklemi şu şekildedir: (elektron sayısı iyon sayısına eşit olduğundan, toplam parçacık sayısı eşittir 2N). Aynı türden düzeltmeler, içinde çözünmüş maddelerin serbest iyonlarının bulunduğu elektrolitlerin termodinamik fonksiyonlarında da ortaya çıkar. Sıvılar. Bir gazın aksine, bir sıvının hal denklemindeki etkileşim terimleri küçük değildir. Bu nedenle, bir sıvının özellikleri, molekülleri arasındaki etkileşimin özel doğasına kuvvetle bağlıdır. Akışkanlar teorisinde, teoriyi basitleştirmek için kullanılabilecek küçük bir parametre genellikle yoktur. Bir sıvının termodinamik miktarları için herhangi bir analitik formül elde etmek mümkün değildir. Bu zorluğun üstesinden gelmenin bir yolu, nispeten az sayıda parçacıktan oluşan bir sistemi incelemektir - birkaç bin civarında. Bu durumda, bir bilgisayar kullanarak, parçacıkların hareket denklemlerini doğrudan çözebilir ve bu şekilde sistemi karakterize eden tüm niceliklerin ortalama değerlerini ek varsayımlar olmadan belirleyebilir. Bu durumda, böyle bir sisteme bir denge durumuna yaklaşma sürecini incelemek de mümkündür. Bu tür az sayıda parçacıktan oluşan bir sistem için istatistiksel integrali, istatistiksel integral için ana formüldeki integralleri bilgisayarda hesaplayarak (genellikle Monte Carlo yöntemini kullanarak) bulmak da mümkündür. Bununla birlikte, sistemdeki az sayıda parçacık nedeniyle gerçek sıvılara uygulandığında her iki yöntemle elde edilen sonuçlar düşük doğruluktadır. Bir sıvı teorisi oluşturmanın başka bir yolu, moleküler dağılım fonksiyonlarının kullanımına dayanmaktadır. dağıtım fonksiyonunu entegre edersek w Sistemin tüm parçacıkların momentumu açısından ve biri hariç tüm parçacıkların koordinatları açısından tek parçacıklı bir uzaysal dağılım fonksiyonu elde edilir. f1(r). entegre edersek w tüm parçacıkların momentumlarına göre ve iki parçacık hariç tüm parçacıkların koordinatlarına göre iki parçacıklı bir dağılım fonksiyonu elde edilecektir. f2(r1, r2), üçü hariç tüm parçacıkların üç parçacıklı dağılım fonksiyonudur. f3(r 1 , r 2 , r 3 ,) vb. İki parçacıklı dağılım işlevi, doğrudan gözlemlenebilir bir fiziksel niceliktir - örneğin, elastik saçılmayı ifade eder. röntgen ve sıvıdaki nötronlar. Tüm sistemin dağılım fonksiyonunun Gibbs dağılımı (6) tarafından verildiğini varsayarsak, iki-parçacık fonksiyonunu üç-parçacık fonksiyonu ve parçacıklar arasındaki etkileşim potansiyeli cinsinden ifade eden bir integral ilişki elde edilebilir. Akışkanlar teorisinde, bu kesin ilişki, üç-parçacık fonksiyonunu iki-parçacık fonksiyonu cinsinden ifade eden bazı yaklaşık değerlerle tamamlanır (homojen bir sıvıda tek parçacıklı bir fonksiyon bir sabite indirgenir). Sonuç, sayısal olarak çözülen iki parçacıklı fonksiyon için bir denklemdir. Ek ilişkiler, makul fiziksel değerlendirmeler temelinde bulunur ve enterpolasyon niteliğindedir, böylece onlara dayanan teoriler, bir sıvının özelliklerinin yalnızca nitel bir tanımını iddia edebilir. Bununla birlikte, böyle bir nitel tanımlama bile önemlidir, çünkü S.f.'nin yasalarının genelliğini ortaya koyar. (Ayrıca bkz. Akışkan). Dejenere gazlar. Gaz sıcaklığı sabit bir yoğunlukta düşürülürse, özdeş parçacıklardan oluşan bir sistemin dalga fonksiyonlarının simetri özellikleriyle ilişkili kuantum-mekanik etkiler ortaya çıkmaya başlar. Gaz "dejenere olur" (bkz. Dejenere gaz). Yarı tamsayılı spinli parçacıklar için, herhangi bir parçacık çifti değiştirildiğinde dalga fonksiyonunun işaretini değiştirmesi gerekir. Bu, özellikle, birden fazla parçacığın bir kuantum durumunda olamayacağı gerçeğine yol açar (Pauli ilkesi). Bir durumda tamsayı dönüşü olan parçacıkların sayısı herhangi biri olabilir, ancak bu durumda parçacıklar yeniden düzenlendiğinde gerekli olan dalga fonksiyonunun değişmezliği burada gazın istatistiksel özelliklerinde bir değişikliğe yol açar. Yarı tamsayı spinli parçacıklar, Fermi-Dirac istatistikleriyle tanımlanır; onlara Fermiyon denir. Fermiyonlar, örneğin elektronları, protonları, nötronları, döteryum atomlarını, hafif helyum izotopu 3 He'nin atomlarını içerir. Tamsayı spinli parçacıklar - Bozonlar - Bose-Einstein istatistikleri ile tanımlanır. Bunlara hidrojen atomları, 4 He atomu, ışık kuantası - Fotonlar dahildir. Momentumun aralıkta olduğu birim hacim başına ortalama gaz partikülü sayısı olsun. 3 p, var Bu formülde, ε = p 2 /2M momentumlu bir parçacığın enerjisidir R, μ - partikül sayısının sabitlik koşulundan belirlenen kimyasal potansiyel ( N) sistemde: Formül (19), aşağıdakiler için Boltzmann dağıtım formülüne (12) dönüşür: Fermiyonlar söz konusu olduğunda, olması gerektiği gibi, np≤ 1. Bu, fermiyon gazının (Fermi gazı) parçacıklarının ve T= 0 sıfırdan farklı bir momentuma sahiptir, çünkü sadece bir parçacık sıfır momentumlu durumda olabilir. Daha doğrusu, T= 0 Fermi gazı için np= 1 bir Fermi yüzeyinin içinde (Bkz. Fermi yüzeyi) - momentum uzayında yarıçaplı küreler Bir Bose gazında T= 0 tüm parçacıklar sıfır momentumlu bir durumda. Durumda yeterince düşük sıcaklıklarda R= 0, tüm parçacıkların son kesridir; bu parçacıklar sözde oluşturur. Bose-Einstein yoğunlaşması. Kalan parçacıklar şu durumlarda bulunur: R≠ 0 ve sayıları formül (19) ile μ = 0 ile belirlenir. Sıcaklıkta Bose-Einstein istatistiklerini uygulamanın özel bir durumu dengedir. Elektromanyetik radyasyon fotonlardan oluşan bir gaz olarak kabul edilebilir. Bir fotonun enerjisi, momentumu ile bağıntı yoluyla ilişkilidir. Kristal hücre. S.'nin başvurusu f. kristal kafesin termodinamik fonksiyonlarının hesaplanması, kafes içindeki atomların denge konumları etrafında küçük titreşimler yapmasına dayanır. Bu, kafesi birleştirilmiş harmonik osilatörlerin bir koleksiyonu olarak düşünmemizi sağlar. Böyle bir sistemde, dalgalar kendi dağılım yasalarıyla, yani frekansın ω dalga vektörüne bağımlılığıyla karakterize edilerek yayılabilir (bkz. dalga vektörü) k. Kuantum mekaniğinde, bu dalgalar sözde bir dizi olarak kabul edilebilir. temel uyarılar veya quasiparticles (Bkz. Quasiparticles) - Enerjili fononlar ħω
ve yarı-momentum ћk. Momentum benzeri ile momentum arasındaki temel fark, fonon enerjisinin, a - kafes sabiti büyüklük sırasına eşit bir periyotla yarı-momentumun periyodik bir fonksiyonu olmasıdır. Fononların quasimomenta üzerindeki dağılım fonksiyonu, μ = 0 olan Bose-Einstein dağılım formülü (19) ile verilir. Bu durumda, ε=ħω.
Böylece, bağımlılık bilgisi ω( k) kafesin ısı kapasitesinin hesaplanmasını sağlar. Bu bağımlılık, bir kristalde nötronların esnek olmayan saçılması üzerine yapılan deneylerden belirlenebilir (bkz. Nötronografi) veya bir kafes içindeki atomların etkileşimini belirleyen "kuvvet sabitlerinin" değerlerini ayarlayarak teorik olarak hesaplanabilir. Düşük sıcaklıklarda, sıradan ses dalgalarının kuantalarına karşılık gelen yalnızca düşük frekanslı fononlar önemlidir; k doğrusal. Bu, kristal kafesin ısı kapasitesinin orantılı olduğu gerçeğine yol açar. T3. Yüksek sıcaklıklarda, enerjinin serbestlik derecelerine eşit dağılımı yasası kullanılabilir, böylece ısı kapasitesi sıcaklığa bağlı olmaz ve şuna eşittir: 3Nk, nerede N kristaldeki atom sayısıdır. metaller. Metallerde iletim elektronları da termodinamik fonksiyonlara katkıda bulunur. Bir metaldeki elektronun durumu, bir yarı-momentum ile karakterize edilir ve elektronlar Fermi - Dirac istatistiklerine uyar, quasimomenta üzerindeki dağılımları formül (19) ile verilir. Bu nedenle, elektron gazının ve dolayısıyla tüm metalin yeterince düşük sıcaklıklardaki ısı kapasitesi, aşağıdakilerle orantılıdır: T. Serbest parçacıkların Fermi gazından farkı, etrafında "aktif" elektronların yoğunlaştığı Fermi yüzeyinin artık bir küre değil, yarı-momentum uzayda karmaşık bir yüzey olmasıdır. Fermi yüzeyinin şekli ve enerjinin bu yüzeye yakın yarı-momentuma bağımlılığı, esas olarak metallerin manyetik özellikleri incelenerek deneysel olarak belirlenebilir ve ayrıca sözde kullanılarak teorik olarak hesaplanabilir. yarı potansiyel modeli. Süperiletkenlerde (bkz. Süperiletkenlik), bir elektronun uyarılmış durumları Fermi yüzeyinden sonlu genişlikte bir boşlukla ayrılır, bu da elektron ısı kapasitesinin üstel sıcaklık bağımlılığına yol açar. Ferromanyetik ve antiferromanyetik maddelerde, manyetik momentlerdeki dalgalanmalar da termodinamik fonksiyonlara katkıda bulunur - Spin dalgaları. Dielektrik ve yarı iletkenlerde T= 0 serbest elektron yoktur. Sonlu sıcaklıklarda, içlerinde yüklü kuasipartiküller görünür - elektronlar negatif yük ve (eşit sayılarda) ile "delikler" pozitif yük, Bir elektron ve bir delik, bağlı bir durum oluşturabilir - eksiton adı verilen bir kuasipartikül. Dr. Bir eksiton tipi, bir kristal kafes içinde hareket eden bir dielektrik atomun uyarılmış halidir. S. f.'de kuantum alan teorisi yöntemleri. Kuantum kuantum fiziğinin problemlerini çözmede, öncelikle metallerde ve mıknatıslarda kuantum sıvılarının ve elektronların özelliklerinin incelenmesinde, kuantum fiziğinde tanıtılan kuantum alan teorisi yöntemleri büyük önem taşımaktadır. Nispeten yakın zamanda. Bu yöntemlerdeki ana rol, Green'in kuantum alan teorisindeki işlevine benzeyen makroskopik bir sistemin Green işlevi G tarafından oynanır. ε enerjisine ve momentuma bağlıdır. R, yarıparçacık dağılım yasası ε( R) denklemden belirlenir: yani, bir yarı parçacığın enerjisi, Green fonksiyonunun kutbu tarafından belirlenir. Green'in fonksiyonlarını, parçacıklar arasındaki etkileşim enerjisinin güçlerinde bir dizi olarak hesaplamak için düzenli bir yöntem vardır. Bu dizinin her terimi, Green'in etkileşmeyen parçacıkların fonksiyonlarının enerjileri ve momentumları üzerinde çoklu integraller içerir ve kuantum elektrodinamiğindeki Feynman diyagramlarına (bkz. Feynman diyagramları) benzer diyagramlar şeklinde grafiksel olarak temsil edilebilir. Bu diyagramların her birinin belirli bir fiziksel anlam Bu, ilgilenilen fenomenden sorumlu terimleri sonsuz bir dizide ayırmayı ve özetlemeyi mümkün kılar. Green fonksiyonlarının sıcaklığını hesaplamak için bir diyagram tekniği de vardır, bu da termodinamik nicelikleri kuasipartiküller eklemeden doğrudan hesaplamayı mümkün kılar. Kuasipartiküllerin çok-parçacık dağılım fonksiyonlarını kullanan sıvılar ile ilgili bölümde bahsedilen yöntemler, birçok yönden kuantum alan teorisi yöntemlerine yakındır. Bu işlevlerin kullanımı her zaman yaklaşık bir "ayrıştırmaya" dayanır - bir işlevin yüksek mertebe alt işlevleri aracılığıyla. Faz geçişleri. Dış parametrelerde (örneğin, basınç veya sıcaklık) sürekli bir değişiklik ile, sistemin özellikleri, parametrelerin bazı değerleri için aniden değişebilir, yani bir faz geçişi meydana gelir. Faz geçişleri, geçişin gizli ısısının serbest bırakılması ve hacimde bir sıçrama (bunlar örneğin Erimeyi içerir) ve gizli ısının olmadığı ikinci tür geçişlerin eşlik ettiği birinci türden geçişlere ayrılır. ve hacimde bir sıçrama (örneğin, bir süper iletken duruma geçiş). Faz geçişlerinin istatistiksel teorisi, S. f. için en büyük zorluk teorik araştırma ikinci dereceden faz geçişi çizgisine yakın ve birinci dereceden faz geçişinin kritik noktasına yakın maddenin özelliklerini temsil eder. Matematiksel bir bakış açısından, sistemin termodinamik fonksiyonları burada tekilliklere sahiptir. Bu noktaların yakınında tuhaf Kritik Olaylar meydana gelir. Aynı zamanda, burada dalgalanmalar anormal bir şekilde artar ve S. f'nin yaklaşık yöntemleri. uygulanamaz hale geldi. Bu nedenle, geçişlerin olduğu az sayıda tam olarak çözülebilir model tarafından önemli bir rol oynar (örneğin, Ising modeli olarak adlandırılır). dalgalanmalar. S.f.'nin kalbinde. gerçeği yatıyor fiziksel özellikler, makroskopik gövdeleri karakterize eden, yüksek doğrulukla ortalama değerlerine eşittir. Bu eşitlik hala yaklaşıktır, aslında, tüm miktarlar ortalama değerlerden - dalgalanmalardan küçük rastgele sapmalar yaşar. Dalgalanmaların varlığı büyük bir temel öneme sahiptir, çünkü termodinamik düzenliliklerin istatistiksel doğasını doğrudan kanıtlar. Ayrıca, dalgalanmalar gürültüye müdahale etme rolünü oynar. fiziksel ölçümler ve doğruluklarını sınırlamaktadır. Bazı değerlerdeki dalgalanmalar X onun ortalaması civarında x ortalama kare dalgalanmaları ile karakterize edilir Vakaların büyük çoğunluğunda, değer X S derecesinde dalgalanmalar yaşar, bununla orantılıdır e S/k. Bu formüle yol açar Örneğin, vücut hacmindeki ve sıcaklığındaki dalgalanmaların ortalama kareleri: Bu formüllerden göreli hacim dalgalanmalarının ve sıcaklık dalgalanmalarının N - vücuttaki partikül sayısı ile ters orantılı olduğu görülebilir. Bu, makroskopik gövdeler için dalgalanmaların küçük olmasını sağlar. Farklı miktarlardaki dalgalanmalar arasındaki ilişki x ben, x k x i ve x fonksiyonu ile karakterize edilir k istatistiksel olarak bağımsızdır, o zaman Altında x ben ve x k uzayda farklı noktalarda aynı niceliğin, örneğin yoğunluğun değerlerini de anlayabiliriz. O zaman bu fonksiyon uzaysal bir korelasyon fonksiyonu anlamına gelir. Noktalar arasındaki mesafe arttıkça, korelasyon fonksiyonu sıfır olma eğilimindedir (genellikle üstel olarak), çünkü uzayda uzak noktalarda dalgalanmalar bağımsız olarak meydana gelir. Bu fonksiyonun önemli ölçüde azaldığı mesafeye korelasyon yarıçapı denir. Dalgalanmaların zaman davranışı ve dalgalanma gürültüsünün spektral dağılımı, zaman korelasyon fonksiyonu ile tanımlanır φ( t), farklı zamanlarda alınan miktarın dalgalanmalarının ortalamasının alındığı t: Dalgalanma teorisinde önemli bir rol sözde tarafından oynanır. Bir sistemdeki dalgalanmaları, belirli dış etkilerin etkisi altında özelliklerindeki bir değişiklikle birleştiren dalgalanma-dağılım teoremi. Bu türden en basit bağıntı, harmonik osilatör a'nın potansiyel enerji ile dalgalanmaları dikkate alınarak elde edilebilir. ve dalgalanma X gerçekten kuvvetin etkisi altındaki bozulma ile ilgilidir. f. Genel durumda, dalgalanma-dağılım teoremi şu durumlarda uygulanabilir: X"genelleştirilmiş bir güç" var f, sistemin enerji operatörüne (Hamiltonian; bkz. Kuantum mekaniği) x terimi olarak dahil edilir. Gücü açma f ortalama değerde bir değişikliğe yol açacaktır x tarafından δ x, ve eğer f zamana bağlı e-i wt , bu değişiklik şu şekilde yazılabilir: α(ω) karmaşık miktarına sistemin genelleştirilmiş duyarlılığı denir. Teorem, korelasyon fonksiyonunun Fourier dönüşümünün S.f. Denge dışı süreçler. Dengesiz durumdaki sistemlerdeki süreçleri inceleyen fiziksel fiziğin dalı olan fiziksel kinetik, giderek daha fazla önem kazanıyor. Burada iki olası soru var. İlk olarak, sistem denge dışı bir durumda düşünülebilir ve denge durumuna geçişi takip edilebilir. İkinci olarak, dengesiz durumu korunan bir sistemi düşünebiliriz. dış koşullar, örneğin, bir sıcaklık gradyanının verildiği bir cisim akar elektrik vb. veya değişken bir dış alanda bulunan bir gövde. Dengeden sapma küçükse, sistemin dengesiz özellikleri sözde ile tanımlanır. kinetik katsayılar. Bu katsayılara örnek olarak viskozite katsayıları verilebilir (Bkz.![]()
![]()
![]()

![]()
![]()
![]() p ve q, integrali permütasyon sayısına bölmek gerekir. N parçacıklar, yani N! Bölme fonksiyonu için son klasik limit:
p ve q, integrali permütasyon sayısına bölmek gerekir. N parçacıklar, yani N! Bölme fonksiyonu için son klasik limit:![]()
![]()
![]()
![]()
![]()

![]() 3
hücre sayısına göre [bir N gaz atomu hacmi ile şuna eşittir:
3
hücre sayısına göre [bir N gaz atomu hacmi ile şuna eşittir:
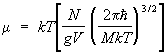

![]()
![]()
![]() n p, faz uzayının bir hücresindeki parçacıkların sayısıdır ( g = 2J+ 1, nerede J parçacık dönüşüdür). Daha sonra Gibbs dağılımından fermiyonların (üst işaret) ve bozonların (alt işaret) ideal gazları için şu sonucu çıkar:
n p, faz uzayının bir hücresindeki parçacıkların sayısıdır ( g = 2J+ 1, nerede J parçacık dönüşüdür). Daha sonra Gibbs dağılımından fermiyonların (üst işaret) ve bozonların (alt işaret) ideal gazları için şu sonucu çıkar:![]()
![]()
![]() Termal hızla hareket eden parçacıkların de Broglie dalgaları, aralarındaki ortalama mesafe kadar olur. Bu nedenle, dejenerasyon, gazdaki partikül sayısının yoğunluğu ne kadar düşükse, o kadar düşük sıcaklıklarda (ve partikülün kütlesi o kadar büyük) etkiler. M).
Termal hızla hareket eden parçacıkların de Broglie dalgaları, aralarındaki ortalama mesafe kadar olur. Bu nedenle, dejenerasyon, gazdaki partikül sayısının yoğunluğu ne kadar düşükse, o kadar düşük sıcaklıklarda (ve partikülün kütlesi o kadar büyük) etkiler. M).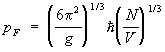 n p = 0. Sonlu fakat düşük sıcaklıklarda np kürenin içinde 1'den kürenin dışında sıfıra kademeli olarak değişir ve geçiş bölgesinin genişliği sıralıdır MkT/p F. Değer np Enerjinin bir fonksiyonu olarak bir Fermi gazı için ε şematik olarak Şek. 2 (e 0 = p F 2 /2M). Gaz sıcaklığı değiştiğinde, parçacıkların durumu sadece bu geçiş tabakasında değişir ve Fermi gazının düşük sıcaklıklardaki ısı kapasitesi ile orantılıdır. T ve şuna eşittir:
n p = 0. Sonlu fakat düşük sıcaklıklarda np kürenin içinde 1'den kürenin dışında sıfıra kademeli olarak değişir ve geçiş bölgesinin genişliği sıralıdır MkT/p F. Değer np Enerjinin bir fonksiyonu olarak bir Fermi gazı için ε şematik olarak Şek. 2 (e 0 = p F 2 /2M). Gaz sıcaklığı değiştiğinde, parçacıkların durumu sadece bu geçiş tabakasında değişir ve Fermi gazının düşük sıcaklıklardaki ısı kapasitesi ile orantılıdır. T ve şuna eşittir:![]()
![]() Faz geçişi (aşağıya bakınız). Sıfır momentumlu parçacıkların kesri kaybolur, Bose-Einstein yoğuşması kaybolur. Isı kapasitesinin sıcaklığa bağımlılık eğrisi şu noktada bulunur: Tc kırmak. Parçacıkların momentum dağılımı T > T s formül (19) ile verilir ve μ T > T s) Şekil 3'te gösterilmiştir.
Faz geçişi (aşağıya bakınız). Sıfır momentumlu parçacıkların kesri kaybolur, Bose-Einstein yoğuşması kaybolur. Isı kapasitesinin sıcaklığa bağımlılık eğrisi şu noktada bulunur: Tc kırmak. Parçacıkların momentum dağılımı T > T s formül (19) ile verilir ve μ T > T s) Şekil 3'te gösterilmiştir.![]() c ışığın boşluktaki hızıdır. foton sayısı değil verilen değer, ve kendisi termodinamik denge koşulundan belirlenir; bu nedenle, momentum dağılımları formül (19) ile μ = 0 (ayrıca, ε) ile verilir. = rs). Emisyon spektrumundaki enerji dağılımı, foton sayısı ε enerjisi ile çarpılarak elde edilir, böylece frekans aralığındaki enerji yoğunluğu dω eşittir n p alınır ε=ħω
. O. denge (siyah) radyasyon spektrumu için Planck formülü elde edilir (Planck'ın radyasyon yasasına bakınız).
c ışığın boşluktaki hızıdır. foton sayısı değil verilen değer, ve kendisi termodinamik denge koşulundan belirlenir; bu nedenle, momentum dağılımları formül (19) ile μ = 0 (ayrıca, ε) ile verilir. = rs). Emisyon spektrumundaki enerji dağılımı, foton sayısı ε enerjisi ile çarpılarak elde edilir, böylece frekans aralığındaki enerji yoğunluğu dω eşittir n p alınır ε=ħω
. O. denge (siyah) radyasyon spektrumu için Planck formülü elde edilir (Planck'ın radyasyon yasasına bakınız).![]()

![]()
![]()
![]() m - osilatör kütlesi, ω 0
kendi frekansıdır. Formül (22) kullanılarak yapılan hesaplama şunları verir: f, ortalama değer x miktara göre kaydırıldı
m - osilatör kütlesi, ω 0
kendi frekansıdır. Formül (22) kullanılarak yapılan hesaplama şunları verir: f, ortalama değer x miktara göre kaydırıldı![]()
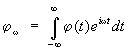
![]()






