Fizika statistikore. Fizika statistikore është
Termodinamika dhe fizika statistikore
Udhëzimet dhe detyrat e kontrollit për studentët e mësimit në distancë
Shelkunova Z.V., Saneev E.L.
Udhëzime metodologjike dhe detyra kontrolli për studentët e specialiteteve inxhinierike dhe teknologjike të mësimit në distancë. Ato përmbajnë seksione të programeve "Fizika statistikore", "Termodinamika", shembuj të zgjidhjes së problemeve tipike dhe opsione për detyrat e kontrollit.
Fjalë kyçe: Energjia e brendshme, ngrohtësi, punë; izoproceset, entropia: funksionet e shpërndarjes: Maxwell, Boltzmann, Bose - Einstein; Fermi - Dirac; Energjia Fermi, kapaciteti i nxehtësisë, temperatura karakteristike e Ajnshtajnit dhe Debye.
Redaktori T.Yu.Artyunina
Përgatitur për shtypje d.Formati 6080 1/16
R.l. ; uch.-ed.l. 3.0; Qarkullimi ____ kopje. Urdhri nr.
___________________________________________________
RIO ESGTU, Ulan-Ude, Klyuchevskaya, 40a
Shtypur në rotaprint të ESGTU, Ulan-Ude,
Klyuchevskaya, 42.
Agjencia Federale për Arsimin
Shteti i Siberisë Lindore
Universiteti i Teknologjisë
FIZIKA №4
(Termodinamika dhe fizika statistikore)
Udhëzime metodike dhe detyra kontrolli
për studentët e mësimit në distancë
Përpiluar nga: Shelkunova Z.V.
Saneev E.L.
Shtëpia botuese e ESGTU
Ulan-Ude, 2009
Fizika statistikore dhe termodinamika
Tema 1
Ligjet dinamike dhe statistikore në fizikë. Metodat termodinamike dhe statistikore. Elementet e teorisë molekulare-kinetike. gjendje makroskopike. Madhësitë fizike dhe gjendjet e sistemeve fizike. Parametrat makroskopik si vlera mesatare. Bilanci termik. Modeli ideal i gazit. Ekuacioni i gjendjes për një gaz ideal. Koncepti i temperaturës.
Tema 2
fenomenet e transferimit. Difuzioni. Përçueshmëri termike. koeficienti i difuzionit. Koeficienti i përçueshmërisë termike. difuziviteti termik. Difuzioni në gaze, lëngje dhe trupa të ngurtë. Viskoziteti. Koeficienti i viskozitetit të gazeve dhe lëngjeve.
Tema 3
Elementet e termodinamikës. Ligji i parë i termodinamikës. Energjia e brendshme. Parametrat intensivë dhe të gjerë.
Tema 4
Procese të kthyeshme dhe të pakthyeshme. Entropia. Ligji i dytë i termodinamikës. Potencialet termodinamike dhe kushtet e ekuilibrit. potencial kimik. Kushtet e ekuilibrit kimik. Cikli Carnot.
Tema 5
funksionet e shpërndarjes. parametrat mikroskopikë. Probabiliteti dhe luhatjet. Shpërndarja Maxwell. E mesme energjia kinetike grimcat. Shpërndarja Boltzmann. Kapaciteti termik i gazeve poliatomike. Kufizimi i teorisë klasike të kapacitetit të nxehtësisë.
Tema 6
Shpërndarja e Gibbs. Modeli i sistemit në termostat. Shpërndarja kanonike e Gibbs. Kuptimi statistikor i potencialeve termodinamike dhe i temperaturës. Roli i energjisë së lirë.
Tema 7
Shpërndarja Gibbs për një sistem me një numër të ndryshueshëm grimcash. Entropia dhe probabiliteti. Përcaktimi i entropisë së një sistemi ekuilibri përmes peshës statistikore të një mikrogjendjeje.
Tema 8
Funksionet e shpërndarjes Bose dhe Fermi. Formula e Planck për rrezatimin termik pa peshë. Rendi dhe çrregullimi në natyrë. Entropia si masë sasiore e kaosit. Parimi i rritjes së entropisë. Kalimi nga rendi në çrregullim ka të bëjë me gjendjen e ekuilibrit termik.
Tema 9
Metodat eksperimentale për studimin e spektrit vibrues të kristaleve. Koncepti i fononeve. Ligjet e dispersionit për fononet akustike dhe optike. Kapaciteti termik i kristaleve në temperatura të ulëta dhe të larta. Kapaciteti elektronik i nxehtësisë dhe përçueshmëria termike.
Tema 10
Elektronet në kristale. Përafrimi i bashkimit të fortë dhe të dobët. Modeli i elektroneve të lira. Niveli i Fermit. Elementet e teorisë së brezit të kristaleve. Funksioni i Bloch. Struktura e brezit të spektrit energjetik të elektroneve.
Tema 11
Sipërfaqja e Fermit. Numri dhe dendësia e numrit të gjendjeve elektronike në brez. Mbushjet e zonave: metale, dielektrikë dhe gjysmëpërçues. Përçueshmëria elektrike e gjysmëpërçuesve. Koncepti i përçueshmërisë së vrimës. Gjysmëpërçuesit e brendshëm dhe të jashtëm. Koncepti i p-n kryqëzim. Transistor.
Tema 12
Përçueshmëria elektrike e metaleve. Transportuesit e rrymës në metale. Pamjaftueshmëria e teorisë klasike të elektroneve. Gazi elektronik Fermi në një metal. Bartësit aktual si kuazigrimca. Fenomeni i superpërcjellshmërisë. Çiftimi i elektroneve me bakër. kontakti i tunelit. Efekti Josephson dhe aplikimet e tij. Kapja dhe kuantizimi fluksi magnetik. Koncepti i përçueshmërisë në temperaturë të lartë.
FIZIKA STATISTIKE. TERMODINAMIKA
Formulat bazë
1. Sasia e substancës së një gazi homogjen (në mol):
ku N-numri i molekulave të gazit; N A- Numri i Avogadro-s; m-masa e gazit; është masa molare e gazit.
Nëse sistemi është një përzierje e disa gazeve, atëherë sasia e substancës në sistem
![]() ,
,
![]() ,
,
ku i , N i , m i , i - përkatësisht sasia e substancës, numri i molekulave, masa, masë molare i përbërësi i përzierjes.
2. Ekuacioni Clapeyron-Mendeleev (ekuacioni i gjendjes së gazit ideal):
![]()
ku m- masa e gazit; - masa molare; R- konstante universale e gazit; = m/ - sasia e substancës; Tështë temperatura termodinamike në Kelvin.
3. Ligjet eksperimentale të gazit, të cilat janë raste të veçanta të ekuacionit Clapeyron-Mendeleev për izoproceset:
ligji boyle-mariotte
(procesi izotermik - T= konst; m=konst):
ose për dy gjendje gazi:
ku fq 1 dhe V 1 - presioni dhe vëllimi i gazit në gjendjen fillestare; fq 2 dhe V 2
Ligji i Gay-Lussac (procesi izobarik - p=konst, m=konst):
ose për dy shtete:
ku V 1 dhe T 1 - vëllimi dhe temperatura e gazit në gjendjen fillestare; V 2 dhe T 2 - të njëjtat vlera në gjendjen përfundimtare;
Ligji i Charles (procesi izokor - V=konst, m=konst):
ose për dy shtete:
ku R 1 dhe T 1 - presioni dhe temperatura e gazit në gjendjen fillestare; R 2 dhe T 2 - të njëjtat vlera në gjendjen përfundimtare;
të kombinuara ligji i gazit (m=konst):
ku R 1 , V 1 , T 1 - presioni, vëllimi dhe temperatura e gazit në gjendjen fillestare; R 2 , V 2 , T 2 janë të njëjtat vlera në gjendjen përfundimtare.
4. Ligji i Daltonit, i cili përcakton presionin e një përzierje gazesh:
p = p 1 + fq 2 + ... +fq n
ku fq i - presione të pjesshme përbërësi i përzierjes; n- numri i përbërësve të përzierjes.
5. Masa molare e një përzierje gazesh:
![]()
ku m i- peshë i-përbërësi i tretë i përzierjes; i = m i / i- sasia e substancës i-përbërësi i tretë i përzierjes; n- numri i përbërësve të përzierjes.
6. Pjesa masive i i-përbërësi i tretë i përzierjes së gazit (në fraksione të njësisë ose përqindjes):
ku mështë masa e përzierjes.
7. Përqendrimi i molekulave (numri i molekulave për njësi vëllimi):
![]()
ku N-numri i molekulave që përmban sistemi; është dendësia e substancës. Formula është e vlefshme jo vetëm për gazet, por edhe për çdo gjendje grumbullimi të materies.
8. Ekuacioni bazë teoria kinetike gazrat:
 ,
,
ku<>është energjia mesatare kinetike e lëvizjes përkthimore të molekulës.
9. Energjia mesatare kinetike e lëvizjes përkthimore të një molekule:
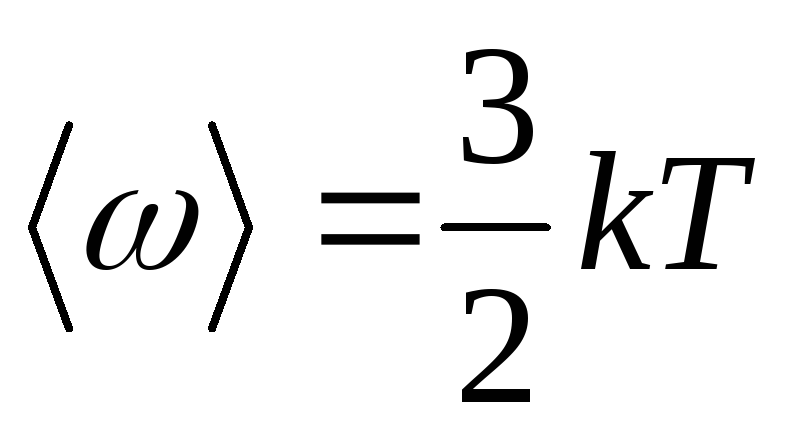 ,
,
ku kështë konstanta e Boltzmann-it.
10. Energjia mesatare totale kinetike e një molekule:
ku iështë numri i shkallëve të lirisë së molekulës.
11. Varësia e presionit të gazit nga përqendrimi i molekulave dhe temperatura:
p = nkT.
12. Shpejtësia e molekulave:
rrënja mesatare katrore  ;
;
mesatare aritmetike 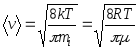 ;
;
me shumë gjasa 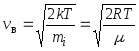 ,
,
ku m iështë masa e një molekule.
13. Shpejtësia relative e një molekule:
u = v/v në ,
ku vështë shpejtësia e kësaj molekule.
14. Kapacitetet termike specifike të gazit në vëllim konstant (s v) dhe në presion konstant (Me R):
15. Marrëdhënia ndërmjet specifike ( Me) dhe molare ( NGA) kapacitetet e nxehtësisë:
; C=c .
16. Ekuacioni i Robert Mayer:
C fq -C v = R.
17. Energjia e brendshme e një gazi ideal:
![]()
18. Ligji i parë i termodinamikës:
ku P- nxehtësia që i komunikohet sistemit (gazit); dU- ndryshimi i energjisë së brendshme të sistemit; PORështë puna e bërë nga sistemi kundër forcave të jashtme.
19. Puna e zgjerimit të gazit:
në përgjithësi ;
në procesin izobarik ![]() ;
;
procesi izotermik ![]() ;
;
në një proces adiabatik ![]() ,
,
ose  ,
,
ku është eksponenti adiabatik.
20. Ekuacionet e Poisson-it që lidhen me parametrat e një gazi ideal në një proces adiabatik:
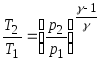 ;
;
21. Efikasiteti termik ciklit.
elektronet etj.), nëpërmjet vetive të këtyre grimcave dhe ndërveprimit ndërmjet tyre.Degë të tjera të fizikës po studiojnë gjithashtu trupat makroskopikë - termodinamika , Mekanikë media e vazhdueshme, elektrodinamika e mediave të vazhdueshme. Sidoqoftë, kur zgjidhen probleme specifike me metodat e këtyre disiplinave, ekuacionet përkatëse përfshijnë gjithmonë parametra ose funksione të panjohura që karakterizojnë një trup të caktuar. Pra, për të zgjidhur problemet e hidrodinamikës, është e nevojshme të dihet ekuacioni i gjendjes së një lëngu ose gazi, d.m.th., varësia e densitetit nga temperatura dhe presioni, kapaciteti i nxehtësisë së një lëngu, koeficienti i viskozitetit të tij, etj. Të gjitha këto varësi dhe parametra, natyrisht, mund të përcaktohen eksperimentalisht, prandaj, metodat në fjalë quhen fenomenologjike. Fizika statistikore lejon, të paktën në parim, dhe në shumë raste në fakt, të llogariten të gjitha këto sasi, nëse dihen forcat e ndërveprimit midis molekulave. Se., fizika statistikore përdor informacione për strukturën "mikroskopike" të trupave - se nga cilat grimca përbëhen, si ndërveprojnë këto grimca, prandaj quhet teoria mikroskopike.
Nëse në një moment në kohë jepen koordinatat dhe shpejtësitë e të gjitha grimcave të trupit dhe dihet ligji i bashkëveprimit të tyre, atëherë, duke zgjidhur ekuacionet e mekanikës, do të ishte e mundur të gjenden këto koordinata dhe shpejtësi në çdo pikë pasuese. në kohë dhe në këtë mënyrë të përcaktojë plotësisht gjendjen e trupit në studim. (Për thjeshtësi, prezantimi bëhet në gjuhën e mekanikës klasike. Por edhe në Mekanika kuantike situata është e njëjtë: njohja e inicialit funksioni i valës sistemeve dhe ligjit të bashkëveprimit të grimcave, është e mundur, duke zgjidhur ekuacioni i Shrodingerit , gjeni funksionin valor që përcakton gjendjen e sistemit në të gjitha momentet e ardhshme të kohës.) Megjithatë, në fakt, një mënyrë e tillë e ndërtimit të një teorie mikroskopike është e pamundur, pasi numri i grimcave në trupat makroskopikë është shumë i madh. Për shembull, në 1 cm 3 gaz në një temperaturë prej 0 °C dhe një presion prej 1 atm përmban afërsisht 2,7×10 19 molekula. Është e pamundur të zgjidhet një numër i tillë ekuacionesh, dhe koordinatat dhe shpejtësitë fillestare të të gjitha molekulave janë ende të panjohura.
Megjithatë, ajo numër i madh grimcat në trupat makroskopikë çojnë në shfaqjen e rregullsive të reja - statistikore - në sjelljen e trupave të tillë. Kjo sjellje në një gamë të gjerë nuk varet nga kushtet specifike fillestare - nga vlerat e sakta të koordinatave fillestare dhe shpejtësive të grimcave. Manifestimi më i rëndësishëm i kësaj pavarësie është fakti i njohur nga përvoja se një sistem, i lënë në vetvete, d.m.th., i izoluar nga ndikimet e jashtme, përfundimisht vjen në një gjendje ekuilibri (ekuilibër termodinamik ose statistikor), vetitë e të cilit përcaktohen vetëm nga të tilla karakteristikat e përgjithshme gjendja fillestare, si numri i grimcave, energjia totale e tyre etj. (cm. Ekuilibri termodinamik ). Në vijim do të fokusohemi kryesisht në fizika statistikore gjendjet e ekuilibrit.
Para se të formulohet një teori që përshkruan rregullsitë statistikore, duhet të kufizohen në mënyrë të arsyeshme vetë kërkesat për teorinë. Domethënë, detyra e teorisë duhet të jetë të llogaritë jo vlerat e sakta të sasive të ndryshme fizike për trupat makroskopikë, por vlerat mesatare të këtyre sasive me kalimin e kohës. Konsideroni, për shembull, molekulat e vendosura në një vëllim mjaft të madh makroskopik të izoluar në një gaz. Numri i molekulave të tilla do të ndryshojë me kalimin e kohës për shkak të lëvizjes së tyre, dhe mund të gjendet saktësisht nëse të gjitha koordinatat e molekulave në çdo kohë ishin të njohura. Kjo, megjithatë, nuk është e nevojshme. Ndryshimi në numrin e molekulave në vëllim do të jetë në natyrën e luhatjeve të rastësishme - luhatjeve - në lidhje me një vlerë mesatare. Me një numër të madh grimcash në vëllim, këto luhatje do të jenë të vogla në krahasim me numrin mesatar të grimcave, kështu që për të karakterizuar gjendjen makroskopike, mjafton të dihet vetëm kjo vlerë mesatare.
Për të sqaruar natyrën e modeleve statistikore, merrni parasysh një shembull tjetër të thjeshtë. Lëreni një numër të madh kokrrash të dy varieteteve të vendosen në një enë, secila shkallë në mënyrë të barabartë, dhe përmbajtja e enës përzihet plotësisht. Pastaj, në bazë të përvojës së përditshme, mund të sigurohet se në një kampion të marrë nga një enë që përmban një numër ende të madh kokrrash, do të gjendet një numër afërsisht i barabartë kokrrash të çdo varieteti, pavarësisht nga radha në të cilën janë kokrrat. u derdhën në enë. Ky shembull tregon qartë dy rrethana të rëndësishme që sigurojnë zbatueshmërinë e teorisë statistikore. Së pari, nevoja për një numër të madh kokrrash si në të gjithë "sistemin" - një enë me grurë, dhe në "nënsistemin" e zgjedhur për eksperimentin - një mostër. (Nëse kampioni përbëhet nga vetëm dy kokrra, atëherë shpesh të dyja do të jenë të së njëjtës shkallë.) Së dyti, është e qartë se kompleksiteti i lëvizjes së kokrrave gjatë përzierjes luan një rol të rëndësishëm, duke siguruar shpërndarjen e tyre uniforme në vëllimin e enës.
funksioni i shpërndarjes. Konsideroni një sistem të përbërë nga grimcat, duke supozuar për thjeshtësi se grimcat nuk kanë shkallë të brendshme lirie. Një sistem i tillë përshkruhet nga detyra 6 variablat - 3 koordinatat q i dhe 3 impulset pi, grimcat [bashkësia e këtyre variablave do të shkurtohet si ( R, q)]. Le të llogarisim vlerën mesatare në intervalin kohor të një vlere të caktuar (p, q), që është funksion i këtyre koordinatave dhe momenteve. Për ta bërë këtë, ne e ndajmë intervalin (0, t) në s segmente të vogla të barabarta D ta (a = 1,2,....... s). Pastaj sipas përkufizimit
![]() ,
,
Ku q a dhe p a- vlerat e koordinatave dhe impulseve nganjëherë ta. Në kufi s® ¥ shuma shkon në integral:
![]() (1a)
(1a)
Koncepti i funksionit të shpërndarjes në mënyrë të natyrshme lind nëse marrim parasysh hapësirën 6 matje, në boshtet e të cilave vizatohen vlerat e koordinatave dhe momenteve të grimcave të sistemit; quhet hapësira fazore. Për çdo vlerë të kohës t korrespondojnë me vlera të caktuara të të gjithave q dhe R, pra një pikë në hapësirën fazore që përfaqëson gjendjen e sistemit në ky moment koha t. Le ta ndajmë të gjithë hapësirën e fazës në elementë, madhësia e të cilave është e vogël në krahasim me vlerat karakteristike të një gjendjeje të caktuar të sistemit q dhe R, por ende aq i madh sa në secilën prej tyre ka shumë pika që përshkruajnë gjendjen e sistemit në momente të ndryshme kohore t. Atëherë numri i pikave të tilla në elementin e vëllimit do të jetë afërsisht proporcional me vlerën e këtij vëllimi dpdq. Nëse shënojmë koeficientin e proporcionalitetit përmes sw(p, q), atëherë ky është numri për elementin e përqendruar në një pikë ( p, q) do të shkruhet si:
da = sw(p, q)dpdq, (2)
Vëllimi i elementit të zgjedhur të hapësirës së fazës. Vlera mesatare (1), duke marrë parasysh vogëlsinë e këtyre elementeve të vëllimit, mund të rishkruhet si , d.m.th.
(integrimi mbi koordinata kryhet në të gjithë vëllimin e sistemit, mbi momentin - nga -¥ në ¥). w( p, q, t) quhet funksioni i shpërndarjes në lidhje me koordinatat e momentit të grimcave. Meqenëse numri i përgjithshëm i pikëve të zgjedhura është s, funksion w plotëson kushtin e normalizimit:
![]() (4)
(4)
Mund të shihet nga (3) dhe (4) se w dpdq mund të konsiderohet si probabiliteti që sistemi të jetë në element dpdq hapësirë fazore. Funksionit të shpërndarjes i prezantuar në këtë mënyrë mund t'i jepet një interpretim tjetër. Për ta bërë këtë, ne do të konsiderojmë njëkohësisht një numër të madh sistemesh identike dhe do të supozojmë se çdo pikë në hapësirën e fazës përfaqëson gjendjen e një sistemi të tillë. Atëherë koha mesatare në (1)-(1a) mund të kuptohet si mesatare mbi tërësinë e këtyre sistemeve, ose, siç thonë ata, mbi ansambël statistikor . Argumentet e deritanishme kanë qenë thjesht formale, që nga ajo kohë gjetja e funksionit të shpërndarjes, sipas (2), kërkon njohuri të të gjithëve R dhe q në çdo kohë, d.m.th., zgjidhjet e ekuacioneve të lëvizjes me kushtet fillestare përkatëse. Dispozita bazë fizika statistikoreështë, megjithatë, një deklaratë në lidhje me mundësinë e përcaktimit të këtij funksioni nga konsideratat e përgjithshme për një sistem në një gjendje ekuilibri termodinamik. Para së gjithash, mund të tregohet, bazuar në ruajtjen e numrit të sistemeve gjatë lëvizjes, se funksioni i shpërndarjes është një integral i lëvizjes së sistemit, d.m.th., mbetet konstant nëse R dhe q ndryshojnë sipas ekuacioneve të lëvizjes (shih Teorema e Liouville ). Gjatë vozitjes sistem i mbyllur energjia e tij nuk ndryshon, prandaj të gjitha pikat në hapësirën fazore, që përshkruajnë gjendjen e sistemit në momente të ndryshme kohore, duhet të shtrihen në një "hipersipërfaqe" që korrespondon me vlerën fillestare të energjisë. E. Ekuacioni i kësaj sipërfaqeje ka formën;
Formulat e mësipërme i referohen rastit kur jepet numri i grimcave në nënsistem. Nëse zgjedhim si nënsistem një element vëllimor të caktuar të të gjithë sistemit, përmes sipërfaqes së të cilit grimcat mund të largohen nga nënsistemi dhe të kthehen në të, atëherë probabiliteti për të gjetur nënsistemin në një gjendje me energji E n dhe numri i grimcave nështë dhënë nga formula e madhe kanonike e shpërndarjes Gibbs:
![]() , (9)
, (9)
Në të cilin është parametri shtesë m potencial kimik , i cili përcakton numrin mesatar të grimcave në nënsistem, dhe vlera përcaktohet nga kushti i normalizimit [shih formula (11)].
Interpretimi statistikor i termodinamikës. Rezultati më i rëndësishëm fizika statistikore- vendosja e kuptimit statistikor të madhësive termodinamike. Kjo bën të mundur nxjerrjen e ligjeve të termodinamikës nga konceptet bazë fizika statistikore dhe llogaritni sasitë termodinamike për sisteme specifike. Para së gjithash, termodinamik energjia e brendshme identifikohet me energjinë mesatare të sistemit. Ligji i parë i termodinamikës pastaj merr një interpretim të qartë si shprehje e ligjit të ruajtjes së energjisë gjatë lëvizjes së grimcave që përbëjnë trupin.
Më tej, le të varet funksioni Hamilton i sistemit nga disa parametra l (koordinatat e murit të anijes që përmban sistemin, fusha e jashtme, etj.). Atëherë derivati do të jetë forcë e përgjithësuar
që korrespondon me këtë parametër, dhe vlera pas mesatares jep punë mekanike kryhet në sistem kur ky parametër ndryshohet. Nëse e dallojmë shprehjen ![]() për energjinë mesatare të sistemit, duke marrë parasysh formulën (6) dhe gjendjen e normalizimit, duke marrë parasysh variablat l dhe T dhe duke pasur parasysh se vlera
është gjithashtu një funksion i këtyre variablave, atëherë marrim identitetin:
për energjinë mesatare të sistemit, duke marrë parasysh formulën (6) dhe gjendjen e normalizimit, duke marrë parasysh variablat l dhe T dhe duke pasur parasysh se vlera
është gjithashtu një funksion i këtyre variablave, atëherë marrim identitetin:
![]() .
.
Sipas sa më sipër, anëtari që përmban d l është e barabartë me punë mesatare dA kryhet në trup. Pastaj termi i fundit është nxehtësia e marrë nga trupi. Krahasimi i kësaj shprehjeje me relacionin dE = dA + TdS, i cili është një rekord i kombinuar i ligjeve të parë dhe të dytë të termodinamikës (shih Fig. Ligji i dytë i termodinamikës ) për proceset e kthyeshme , ne e gjejmë atë T në (6) është vërtet e barabartë me temperaturë absolute trup, dhe derivati - merret me shenjën e kundërt entropia . Do të thotë se ka energji e lirë organ, nga i cili sqarohet kuptimi statistikor i tij.
Me rëndësi të veçantë është interpretimi statistikor i entropisë, i cili rrjedh nga formula (8). Formalisht, g përmblidhet në këtë formulë mbi të gjitha gjendjet me energji E n, por në fakt, për shkak të vogëlsisë së luhatjeve të energjisë në shpërndarjen Gibbs, vetëm një numër relativisht i vogël i tyre me një energji afër energjisë mesatare është i rëndësishëm. Është e natyrshme të përcaktohet numri i këtyre gjendjeve thelbësore, prandaj, duke kufizuar mbledhjen në (8) në intervalin, duke zëvendësuar E n te energjia mesatare dhe nxjerrja e eksponentit nga nën shenjën e shumës. Pastaj shuma do të japë dhe do të marrë formularin.
![]()
Nga ana tjetër, sipas termodinamikës, =-TS, e cila jep një lidhje midis entropisë dhe numrit të gjendjeve mikroskopike në një gjendje të caktuar makroskopike, me fjalë të tjera, me peshë statistikore gjendja makroskopike, d.m.th me probabilitetin e saj:
Në temperaturën e zeros absolute, çdo sistem është në një gjendje të caktuar bazë, pra = 1, S= 0. Ky pohim shpreh ligji i tretë i termodinamikës . Është thelbësore këtu që për një përkufizim të qartë të entropisë është e nevojshme të përdoret formula kuantike (8); në statistikat thjesht klasike, entropia përcaktohet vetëm deri në një term arbitrar.
Kuptimi i entropisë si masë e probabilitetit të një gjendjeje ruhet gjithashtu në lidhje me gjendjet arbitrare - jo domosdoshmërisht ekuilibër. Në një gjendje ekuilibri, entropia ka vlerën maksimale të mundshme në kushte të jashtme të dhëna. Kjo do të thotë se gjendja e ekuilibrit është gjendja me peshën maksimale statistikore, gjendja më e mundshme. Procesi i kalimit të një sistemi nga një gjendje jo ekuilibër në një gjendje ekuilibri është një proces i kalimit nga gjendjet më pak të mundshme në ato më të mundshme; kjo sqaron kuptimin statistikor të ligjit të rritjes së entropisë, sipas të cilit entropia e një sistemi të mbyllur mund të rritet vetëm.
Formula (8) që lidh energjinë e lirë me një funksion ndarjeje, është baza për llogaritjen e madhësive termodinamike me metoda fizika statistikore Përdoret, në veçanti, për të ndërtuar një teori statistikore të vetive elektrike dhe magnetike të materies. Për shembull, për të llogaritur momentin magnetik të një trupi në një fushë magnetike, duhet të llogaritet funksioni i ndarjes dhe energjia e lirë. Moment magnetik m trupi më pas jepet me formulën:
Ku H- tensioni i jashtëm fushë magnetike. Ngjashëm me (8), kushti i normalizimit në shpërndarjen e madhe kanonike (9) përcakton potenciali termodinamik sipas formulës:
![]() . (11)
. (11)
Ky potencial lidhet me energjinë e lirë nga relacioni:
![]() .
.
Aplikacionet fizika statistikore për studimin e veçorive të caktuara të sistemeve specifike reduktohen në thelb në një llogaritje të përafërt të funksionit të ndarjes, duke marrë parasysh vetitë specifike të sistemit.
Në shumë raste, kjo detyrë thjeshtohet duke zbatuar ligjin e barazisë në shkallë lirie, i cili thotë se kapaciteti i nxehtësisë cv(në vëllim konstant v) sistemet e ndërveprimit pikat materiale- grimcat që bëjnë lëkundje harmonike është e barabartë me
c v = k(l/2 + n),
Ku l - numri total shkallët përkthimore dhe rrotulluese të lirisë, n- numri i shkallëve vibruese të lirisë. Prova e ligjit bazohet në faktin se funksioni i Hamiltonit H një sistem i tillë duket si ky: H =(pi) + (q m), ku energjia kinetike teështë një funksion kuadratik homogjen i l + n impulset pi dhe energjinë potenciale - funksioni kuadratik i n koordinatat vibruese q m. Në integralin statistikor Z(8a) integrimi mbi koordinatat vibruese për shkak të konvergjencës së shpejtë të integralit mund të zgjerohet nga - ¥ në ¥. Pasi kemi bërë ndryshimin e variablave, gjejmë se Z varet nga temperatura si Tl/2+n, pra energjia e lirë =-kT(l/ 2 +n) (ln T+ konst). Kjo nënkupton shprehjen e mësipërme për kapacitetin e nxehtësisë, pasi . Devijimet nga ligji i barazisë në sistemet reale shoqërohen kryesisht me korrigjime kuantike, pasi në kuantike fizika statistikore ky ligj është i padrejtë. Ka edhe korrigjime që lidhen me joharmonicitetin e lëkundjeve.
Gaz ideal. Objekti më i thjeshtë i studimit fizika statistikoreështë një gaz ideal, domethënë një gaz aq i rrallë saqë ndërveprimi ndërmjet molekulave të tij mund të neglizhohet. Funksionet termodinamike të një gazi të tillë mund të llogariten plotësisht. Energjia e një gazi është thjesht shuma e energjive të molekulave individuale. Megjithatë, kjo ende nuk mjafton për t'i konsideruar molekulat si plotësisht të pavarura. Në të vërtetë, në mekanikën kuantike, edhe nëse nuk ka forca ndërveprimi midis grimcave, ekziston një ndikim i caktuar i grimcave identike (identike) mbi njëra-tjetrën nëse ato janë në gjendje të ngjashme mekanike kuantike. Ky është i ashtuquajturi. ndërveprim shkëmbimi . Mund të neglizhohet nëse, mesatarisht, ka shumë më pak se një grimcë për gjendje, e cila, në çdo rast, ndodh në një temperaturë mjaft të lartë të gazit; një gaz i tillë quhet jo i degjeneruar. Në fakt, gazrat e zakonshëm, të përbërë nga atome dhe molekula, nuk janë të degjeneruar në të gjitha temperaturat (në të cilat ato janë ende të gazta). Për një gaz ideal jo të degjeneruar, funksioni i shpërndarjes zbërthehet në produktin e funksioneve të shpërndarjes për molekulat individuale. shtrihen në intervale dp x, dpy, dpz, dhe koordinatat janë në intervale dx, dy, dz:
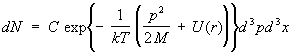 , (12) Energjia e një molekule gazi monatomike në një fushë të jashtme me energji potenciale
(r) është e barabartë me p 2 /2M +(r). Integrimi i (6) mbi koordinatat r(x, y, z) dhe impulset R(p x, py, pz) nga të gjitha molekulat përveç njërës, mund të gjeni numrin e molekulave dN, impulset e të cilit
, (12) Energjia e një molekule gazi monatomike në një fushë të jashtme me energji potenciale
(r) është e barabartë me p 2 /2M +(r). Integrimi i (6) mbi koordinatat r(x, y, z) dhe impulset R(p x, py, pz) nga të gjitha molekulat përveç njërës, mund të gjeni numrin e molekulave dN, impulset e të cilit
Ku d 3 f = dp x dp y dp z, d3x = dxdydz. Kjo formulë quhet shpërndarja Maxwell-Boltzmann (shih Fig. Statistikat e Boltzmann ). Nëse integrojmë (12) mbi momentin, atëherë marrim një formulë për shpërndarjen e grimcave mbi koordinatat në një fushë të jashtme, në veçanti, në një fushë gravitacionale - formula barometrike . Shpërndarja në terma të shpejtësive në çdo pikë të hapësirës përkon me Shpërndarja Maxwell .
Funksioni i ndarjes së një gazi ideal gjithashtu zbërthehet në produktin e termave identikë që korrespondojnë me molekulat individuale. Për një gaz monoatomik, shuma në (8) zvogëlohet në integrim mbi koordinatat dhe momentin, d.m.th., shuma zëvendësohet nga një mbi integrale ![]() 3
në përputhje me numrin e qelizave [me vëllim] në hapësirën fazore të një grimce. Energji e lirë
atomet e gazit janë të barabarta me:
3
në përputhje me numrin e qelizave [me vëllim] në hapësirën fazore të një grimce. Energji e lirë
atomet e gazit janë të barabarta me:
 ,
,
Ku g- pesha statistikore e gjendjes bazë të atomit, d.m.th. numri i gjendjeve që korrespondojnë me më të ulëtën e tij niveli i energjisë, . Në fund të fundit, kjo është për shkak të lidhjes së vërejtur më parë midis entropisë dhe konceptit të numrit të gjendjeve kuantike.
Në rastin e gazeve diatomike dhe poliatomike, dridhjet dhe rrotullimi i molekulave gjithashtu kontribuojnë në funksionet termodinamike. Ky kontribut varet nga fakti nëse efektet e kuantizimit të dridhjeve dhe rrotullimit të molekulës janë të rëndësishme. Distanca ndërmjet niveleve të energjisë vibruese është e rendit , ku w është frekuenca karakteristike e lëkundjeve dhe distanca ndërmjet niveleve të para të energjisë rrotulluese është e rendit ![]() , ku
- momenti i inercisë së një trupi rrotullues, në këtë rast të një molekule. Statistikat klasike janë të vlefshme nëse temperatura është mjaft e lartë në mënyrë që
, ku
- momenti i inercisë së një trupi rrotullues, në këtë rast të një molekule. Statistikat klasike janë të vlefshme nëse temperatura është mjaft e lartë në mënyrë që
kT>> D E.
Në këtë rast, në përputhje me ligjin e barazisë, rrotullimi jep një kontribut të vazhdueshëm në kapacitetin e nxehtësisë, të barabartë me 1/2 k për çdo shkallë rrotulluese të lirisë; në veçanti, për molekulat diatomike ky kontribut është i barabartë me k. Luhatjet japin një kontribut në kapacitetin e nxehtësisë të barabartë me k për çdo shkallë lirie vibruese (në mënyrë që kapaciteti i nxehtësisë vibruese të një molekule diatomike është k). Kontributi i shkallës vibruese të lirisë, krahasuar me atë rrotulluese, është dy herë më i madh për faktin se, gjatë dridhjeve, atomet në një molekulë kanë energji jo vetëm kinetike, por edhe potenciale. Në rastin e kundërt kufizues, molekulat janë në gjendjen e tyre vibruese tokësore, energjia e të cilave nuk varet nga temperatura, kështu që dridhjet nuk kontribuojnë fare në kapacitetin e nxehtësisë. E njëjta gjë vlen edhe për rrotullimin e molekulave sipas kushtit ![]() . Me rritjen e temperaturës, shfaqen molekula që janë në gjendje të ngacmuara vibruese dhe rrotulluese, dhe këto shkallë lirie fillojnë të kontribuojnë në kapacitetin e nxehtësisë - sikur ato gradualisht "ndizen", duke u prirur në kufirin e tyre klasik me një rritje të mëtejshme të temperaturës. Kështu, përfshirja e efekteve kuantike bëri të mundur shpjegimin e varësisë së vëzhguar eksperimentalisht të kapacitetit të nxehtësisë së gazeve nga temperatura. Vlerat e sasisë që karakterizon "kuantumin rrotullues" për shumicën e molekulave janë të rendit të disa gradëve ose dhjetëra gradë (85 K për H2, 2.4 K për 2, 15 K për H). Në të njëjtën kohë, vlerat karakteristike për "kuantumin vibrues" janë të rendit të mijëra gradëve (6100 K për H2, 2700 K për O2, 4100 K për H). Prandaj, shkallët rrotulluese të lirisë ndizen në temperatura shumë më të ulëta se ato vibruese. Në fig. Figura 1 tregon varësinë nga temperatura e (a) kapaciteteve të nxehtësisë rrotulluese dhe (b) vibruese për një molekulë diatomike (kapaciteti i nxehtësisë rrotulluese është ndërtuar për një molekulë të atomeve të ndryshme).
. Me rritjen e temperaturës, shfaqen molekula që janë në gjendje të ngacmuara vibruese dhe rrotulluese, dhe këto shkallë lirie fillojnë të kontribuojnë në kapacitetin e nxehtësisë - sikur ato gradualisht "ndizen", duke u prirur në kufirin e tyre klasik me një rritje të mëtejshme të temperaturës. Kështu, përfshirja e efekteve kuantike bëri të mundur shpjegimin e varësisë së vëzhguar eksperimentalisht të kapacitetit të nxehtësisë së gazeve nga temperatura. Vlerat e sasisë që karakterizon "kuantumin rrotullues" për shumicën e molekulave janë të rendit të disa gradëve ose dhjetëra gradë (85 K për H2, 2.4 K për 2, 15 K për H). Në të njëjtën kohë, vlerat karakteristike për "kuantumin vibrues" janë të rendit të mijëra gradëve (6100 K për H2, 2700 K për O2, 4100 K për H). Prandaj, shkallët rrotulluese të lirisë ndizen në temperatura shumë më të ulëta se ato vibruese. Në fig. Figura 1 tregon varësinë nga temperatura e (a) kapaciteteve të nxehtësisë rrotulluese dhe (b) vibruese për një molekulë diatomike (kapaciteti i nxehtësisë rrotulluese është ndërtuar për një molekulë të atomeve të ndryshme).
Gaz i papërsosur. Arritje e rëndësishme fizika statistikore- llogaritja e korrigjimeve të sasive termodinamike të gazit që lidhen me bashkëveprimin midis grimcave të tij. Nga ky këndvështrim, ekuacioni i gjendjes së një gazi ideal është termi i parë në zgjerimin e presionit të një gazi real për sa i përket densitetit të numrit të grimcave, pasi çdo gaz sillet si një gaz ideal në një nivel të mjaftueshëm. densitet të ulët. Ndërsa densiteti rritet, korrigjimet e ndërveprimit në ekuacionin e gjendjes fillojnë të luajnë një rol. Ato çojnë në paraqitjen në shprehjen për presion të termave me shkallë më të lartë të densitetit të numrit të grimcave, kështu që presioni përfaqësohet me të ashtuquajturat. seritë virale të formës:
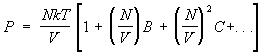 . (15)
. (15)
Shanset AT, NGA etj. varen nga temperatura dhe formohen. e dyta, e treta etj. koeficientët virialë. Metodat fizika statistikore bëjnë të mundur llogaritjen e këtyre koeficientëve nëse dihet ligji i bashkëveprimit ndërmjet molekulave të gazit. Në të njëjtën kohë, koeficientët AT, NGA,... përshkruaj bashkëveprimin e njëkohshëm të dy, tre dhe më shumë molekulat. Për shembull, nëse gazi është monoatomik dhe energjia potenciale e bashkëveprimit të atomeve të tij (r), atëherë koeficienti i dytë virial është
Sipas rendit të madhësisë AT e barabartë , ku r0- madhësia karakteristike e një atomi, ose, më saktë, rrezja e veprimit të forcave ndëratomike. Kjo do të thotë se seria (15) është në fakt një zgjerim i fuqive të parametrit pa dimension Nr 3 /V, i vogël për një gaz mjaft të rrallë. Ndërveprimi ndërmjet atomeve të gazit ka karakterin e zmbrapsjes në distanca të afërta dhe të tërheqjes në ato të largëta. Kjo çon në AT> 0 në temperaturat e larta dhe AT < 0 при низких. Поэтому давление реального газа при высоких температурах më shumë presion gaz ideal me të njëjtën densitet, dhe në të ulët - më pak. Kështu, për shembull, për heliumin në T= 15,3 K faktor AT = - 3×10 -23 cm 3, dhe kur T= 510 K AT= 1,8 × 10 -23 cm 3. Për argonin AT = - 7.1×10 -23 cm 3 në T = 180 K dhe AT= 4,2×10 -23 cm 3 në T= 6000 K. Për gazet monatomike, llogariten vlerat e koeficientëve virialë, përfshirë të pestin, gjë që bën të mundur përshkrimin e sjelljes së gazeve në një gamë mjaft të gjerë densitetesh (shih gjithashtu gazrat ).
Plazma. Një rast i veçantë gazi joideal është plazma - gaz pjesërisht ose plotësisht i jonizuar, në të cilin ka elektrone dhe jone të lirë. Në një densitet mjaft të ulët, vetitë e plazmës janë afër atyre të një gazi ideal. Kur llogariten devijimet nga idealiteti, është thelbësore që elektronet dhe jonet të ndërveprojnë elektrostatikisht sipas ligjit të Kulombit. Forcat e Kulombit zvogëlohen ngadalë me distancën, dhe kjo çon në faktin se edhe për të llogaritur korrigjimin e parë të funksioneve termodinamike, është e nevojshme të merret parasysh ndërveprimi i jo dy, por një numri i madh grimcash menjëherë. meqenëse integrali në koeficientin e dytë virial (16), i cili përshkruan ndërveprimin e çiftit, divergjent nga distanca të gjata r midis grimcave. Në realitet, nën ndikimin e forcave të Kulombit, shpërndarja e joneve dhe elektroneve në plazmë ndryshon në atë mënyrë që fusha e secilës grimcë të kontrollohet, d.m.th., zvogëlohet me shpejtësi në një distancë të caktuar, e quajtur rrezja Debye. Për rastin më të thjeshtë të një plazme të përbërë nga elektrone dhe jone të vetëm të ngarkuar, rrezja Debye rD të barabartë.
FIZIKA STATISTIKE- një degë e fizikës, detyra e së cilës është të shprehë vetitë e makroskopisë. trupa, d.m.th., sisteme që përbëhen nga një numër shumë i madh grimcash identike (molekula, atome, elektrone etj.), nëpërmjet vetive të këtyre grimcave dhe ndërveprimit ndërmjet tyre.
Kështu, në S. t. përdoret informacioni për strukturën "mikroskopike" të trupave; prandaj, S. f. është mikroskopike. teori. Ky është ndryshimi i tij nga degët e tjera të fizikës, duke studiuar gjithashtu makroskopik. trupat: , mekanika dhe elektrodinamika e kontinumeve. Kur zgjidhen probleme specifike me metodat e këtyre disiplinave, ekuacionet përkatëse përfshijnë gjithmonë parametra ose funksione të panjohura që karakterizojnë një trup të caktuar. Të gjitha këto varësi dhe parametra mund të përcaktohen në mënyrë eksperimentale, ndaj quhen metodat në fjalë. fenomenologjike. S. f. lejon, të paktën në parim, por në shumë mënyra. rastet dhe realisht llogaritin këto sasi.
Nëse në një moment në kohë jepen koordinatat dhe shpejtësitë e të gjitha grimcave të trupit dhe dihet ligji i bashkëveprimit të tyre, atëherë nga ekuacionet e mekanikës do të ishte e mundur të gjenden koordinatat dhe shpejtësitë në çdo moment të mëpasshëm të kohës dhe duke përcaktuar plotësisht gjendjen e trupit. E njëjta situatë ndodh në: duke ditur funksionin valor fillestar të sistemit, është e mundur, duke zgjidhur ekuacionin e Schrödinger-it, të gjendet funksioni valor që përcakton gjendjen e sistemit në të gjitha momentet e ardhshme kohore.
Në realitet, një mënyrë e tillë e ndërtimit të një mikroskopike teoria është e pamundur, sepse numri i grimcave në makroskopike. trupat janë shumë të mëdhenj dhe të hershëm. koordinatat dhe shpejtësitë e molekulave janë të panjohura. Megjithatë, është pikërisht numri i madh i grimcave në makroskop organet çon në shfaqjen e rregullsive të reja (statistikore) në sjelljen e organeve të tilla. Këto rregullsi zbulohen pas një kufizimi përkatës të problemeve të teorisë. duke karakterizuar makroskopike parametrat e trupit përjetojnë me kalimin e kohës luhatje (luhatje) të vogla të rastësishme në raport me disa kf. vlerat. Detyra e teorisë është t'i llogaritë këto kf. vlerat, jo vlerat e sakta të parametrave në një kohë të caktuar. Prania e statistikave modelet shprehet në faktin se sjellja kf. vlerat në një gamë të gjerë nuk varen nga fillimi specifik. kushtet (nga vlerat e sakta të koordinatave fillestare dhe shpejtësive të grimcave). Manifestimi më i rëndësishëm i kësaj rregullsie është fakti i njohur nga përvoja se një sistem i izoluar nga jashtë ndikimet, me kalimin e kohës vjen në një gjendje të caktuar ekuilibri (ekuilibri termodinamik), vetitë e të cilit përcaktohen vetëm nga karakteristika të tilla të përgjithshme të fillimit. gjendje, si numri i grimcave, energjia totale e tyre, etj. (shih ekuilibri termodinamik). Procesi i kalimit të sistemit në një gjendje ekuilibri quhet. relaksim, dhe koha karakteristike e këtij procesi është koha e relaksimit.
funksioni i shpërndarjes. Konsideroni një sistem të përbërë nga N grimcat, për thjeshtësi, duke supozuar se grimcat nuk kanë ext. shkallët e lirisë. Një sistem i tillë përshkruhet nga detyra 6N variablat: 3N koordinatat x i dhe 3N impulset p i grimca, grupi i këtyre variablave do të shkurtohet si ( p, x).
Shpërndarjet Gibbs. Argumentet e kryera deri më tani ishin të një natyre formale, pasi gjetja e funksionit të shpërndarjes, sipas (1), kërkon njohuri për të gjitha X dhe R në çdo kohë, d.m.th., zgjidhjet e ekuacioneve të lëvizjes me inicialen përkatëse. kushtet. Kryesor Pozicioni i S. f. është një deklaratë në lidhje me mundësinë e konsideratave të përgjithshme për të përcaktuar këtë f-tion për një sistem në një gjendje termodinamike. ekuilibër. Para së gjithash, bazuar në ruajtjen e numrit të grimcave gjatë lëvizjes, mund të tregohet se funksioni i shpërndarjes është integrali i lëvizjes së sistemit (shih Fig. Teorema e Liouville).
Kur një sistem i mbyllur lëviz, energjia e tij nuk ndryshon, prandaj, të gjitha pikat në hapësirën fazore, që përshkruajnë gjendjen e sistemit në pika të ndryshme të kohës, duhet të shtrihen në një hipersipërfaqe të caktuar që korrespondon me fillimin. vlera e energjisë E. Ekuacioni për këtë sipërfaqe ka formën H(x, p) = E, ku H(x,p) - Funksioni Hamilton sistemeve. Lëvizja e një sistemi nga shumë grimcat janë jashtëzakonisht konfuze, kështu që me kalimin e kohës, pikat që përshkruajnë gjendjen do të shpërndahen në sipërfaqen e postës. energji në mënyrë të barabartë (shih gjithashtu Hipoteza Ergodike Një shpërndarje e tillë uniforme përshkruhet nga funksioni i shpërndarjes
ku është një funksion delta që është jozero vetëm kur H = E, Aështë një konstante e përcaktuar nga kushti i normalizimit (3). Funksioni i shpërndarjes (4) që korrespondon me shpërndarje mikrokanonike Gibbs, ju lejon të llogaritni mesataren. vlerat e të gjitha fizike sasitë sipas f-le (2), pa zgjidhur ekuacionet e lëvizjes.
Gjatë nxjerrjes së shprehjes (4), u supozua se e vetmja sasi e ruajtur nga e cila varet w,është energjia e sistemit. Natyrisht, momenti dhe momenti këndor ruhen gjithashtu, por këto sasi mund të eliminohen duke supozuar se trupi në fjalë është i mbyllur në një kuti fikse, të cilës grimcat mund t'i japin vrull dhe vrull.
Në fakt, në S. f. zakonisht konsiderohen jo sisteme të mbyllura, por makroskopike. trupa që janë të vegjël makroskopikë. pjesë, ose nënsisteme, për-l. sistem i mbyllur. Funksioni i shpërndarjes për një nënsistem është i ndryshëm nga (4), por nuk varet nga forma specifike e pjesës tjetër të sistemit, e ashtuquajtura. termostat. Për të përcaktuar funksionin e shpërndarjes së nënsistemit, është e nevojshme të integrohet f-lu (4) mbi momentin dhe koordinatat e grimcave të termostatit. Një integrim i tillë mund të kryhet duke marrë parasysh vogëlsinë e energjisë së nënsistemit në krahasim me energjinë e termostatit. Si rezultat, për funksionin e shpërndarjes së nënsistemit, fitohet shprehja
magnitudë T në këtë f-le ka kuptim temp-ry. Koeficienti i normalizimit. përcaktohet nga gjendja e normalizimit (3):
Për grimcat me një rrotullim gjysmë të plotë, funksioni i valës duhet të ndryshojë shenjën pas ndërrimit të çdo çifti grimcash, prandaj, në një gjendje kuantike nuk mund të ketë më shumë se një grimcë ( Parimi Pauli Numri i grimcave me spin numër të plotë në një gjendje mund të jetë çdo, por e kërkuara në këtë rast, pandryshueshmëria e funksionit të valës kur grimcat riorganizohen këtu gjithashtu çon në një ndryshim në statistikë. vetitë e gazit. Përshkruhen grimcat me rrotullim gjysmë të plotë Statistikat e Fermi-Dirac, quhen fermione. Fermionet përfshijnë, për shembull, elektronet, protonet, neutronet, atomet e deuteriumit, 3 atome He. Përshkruhen grimcat me spin me numër të plotë (bozonet). Statistikat Bose - Ajnshtajni. Këto përfshijnë, për shembull, atomet H, 4 He, kuantet e dritës - fotone.
Le të kf. numri i grimcave të gazit për njësi vëllimi me momentin që shtrihet në interval dp, është , kështu etjështë numri i grimcave në një qelizë të hapësirës fazore. Pastaj nga shpërndarja Gibbs rrjedh se për gazet ideale fermionet (shenja e sipërme) dhe bozonet (shenja e poshtme)
Në këtë f-le - energjia e një grimce me momentum R,- kim. potenciali i përcaktuar nga kushti i qëndrueshmërisë së numrit të grimcave N në sistem: ![]()
Kuazigrimca. Pranë abs. temperaturë zero. kontribut në statistikat shuma kontribuohet nga gjendjet kuantike të ngacmuara dobët, afër gjendjes bazë në energji. Llogaritja e energjisë së kryesore. gjendja është thjesht mekanike kuantike. detyrë, lëndë teoria kuantike e shumë grimcave. Lëvizja termike në kushte të tilla mund të përshkruhet si shfaqja në sistemin e bashkëveprimit të dobët kuazigrimcave(ngacmimet elementare) që kanë energji dhe vrull (në kristale - kuazi-moment) R. Duke ditur varësinë, është e mundur të llogaritet pjesa e varur nga temperatura e termodinamikës. f-tionet nga f-lames për një gaz ideal Fermi ose Bose në varësi të statistikave të kuazigrimcave. Është veçanërisht e rëndësishme që kuazigrimcat Bose me të vogla R mund të konsiderohen si kuante të lëkundjeve me valë të gjata, të përshkruara në mënyrë makroskopike. ur-niami. Pra, në kristale (dhe lëngje Bose) ka fonone (kuanta të tingullit), në magnet - magnone (kuantet e lëkundjeve të momentit magnetik).
Lloje të veçanta kuazigrimcash ekzistojnë në sistemet dydimensionale dhe njëdimensionale. Në një kristal të sheshtë Në film roli i tyre luhet nga dislokimet, në filmat He nga fijet e vorbullës dhe në fijet polimere nga solitonet dhe muret e domenit. Në trupat tredimensionale, këto objekte kanë energji të lartë dhe nuk kontribuojnë në termodinamikë. funksione.
Qelizë kristalore. Atomet në rrjetë bëjnë lëkundje të vogla rreth pozicioneve të tyre të ekuilibrit. Kjo do të thotë që lëvizja e tyre termike mund të konsiderohet si një grup kuazigrimcash (fononesh) fare (dhe jo vetëm të ulët) temp-pax (shih Fig. Dridhjet e rrjetës kristalore Shpërndarja e fononeve, si dhe e fotoneve, jepet nga f-loy (16) c = 0. Në temperatura të ulëta, vetëm fononet me gjatësi vale të gjatë janë të rëndësishme, të cilat janë kuante. valët e zërit, përshkruar nga ekuacionet e teorisë së elasticitetit. Varësia për ta është lineare, kështu që kapaciteti i nxehtësisë së kristalit. rrjeta është proporcionale me T 3. Në temperatura të larta, mund të përdoret ligji i barazisë së energjisë mbi shkallët e lirisë, në mënyrë që kapaciteti i nxehtësisë të mos varet nga temperatura dhe të jetë i barabartë me 3 Nk, ku Nështë numri i atomeve në kristal. Varësia në arbitrare R mund të përcaktohet nga eksperimentet mbi shpërndarjen joelastike të neutroneve në një kristal ose të llogaritet teorikisht duke vendosur vlerat e "konstantave të forcës" që përcaktojnë ndërveprimin e atomeve në rrjeta. Probleme të reja lindën përpara S. f. në lidhje me hapjen e të ashtuquajturit. thuajse periodike kristalet, molekulat e të cilave ndodhen në hapësirë në mënyrë jo periodike, por në një rend të caktuar (shih. Kuazikristal).
Metalet. Në metale, kontributi në termodinamikë f-tion japin edhe elektrone përcjellëse. Gjendja e një elektroni në një metal karakterizohet nga një kuazi-moment, dhe meqenëse elektronet i binden statistikave Fermi-Dirac, shpërndarja e tyre mbi kuazi-momentet jepet nga f-loi (16). Prandaj, kapaciteti i nxehtësisë i gazit elektronik dhe, rrjedhimisht, i të gjithë metalit në temperatura mjaft të ulëta është proporcional me T. Dallimi nga gazi Fermi i grimcave të lira është se sipërfaqja e Fermit nuk është më një sferë, por është një sipërfaqe komplekse në hapësirën e kuazi-momenteve. Forma e sipërfaqes së Fermit, si dhe varësia e energjisë nga kuazi-momenti pranë kësaj sipërfaqeje, mund të përcaktohen eksperimentalisht, Ch. arr. magnet hulumtues. vetitë e metaleve, si dhe të llogaritet teorikisht duke përdorur të ashtuquajturat. model pseudopotencial. Në superpërçuesit, gjendjet e ngacmuara të një elektroni ndahen nga sipërfaqja e Fermit nga një hendek, i cili çon në eksponencial. varësia e kapacitetit elektronik të nxehtësisë nga temperatura. Në feromagnet. dhe antiferromagnet. Kontributi i substancave në termodinamikë. f-tion japin edhe luhatje të magnetikes. momente (valë rrotulluese).
Në dielektrikë dhe gjysmëpërçues T= 0 nuk ka elektrone të lira. Në temperatura të fundme, në to shfaqet një ngarkesë. kuazigrimca: elektrone me negative. ngarkesë dhe "vrima" me pozitive. ngarkuar. Një elektron dhe një vrimë mund të formojnë një gjendje të lidhur - një kuazigrimcë e quajtur eksiton.dr. Lloji i eksitonit është një gjendje e ngacmuar e atomit dielektrik, duke lëvizur në një kristalor. grilë.
Metodat teoria kuantike fusha në fizikën statistikore. Në zgjidhjen e problemeve të fizikës kuantike, kryesisht në studimin e vetive të lëngjeve dhe elektroneve kuantike në metale dhe magnet, metodat e teorisë së fushës kuantike të prezantuara në fizikën kuantike kanë një rëndësi të madhe. relativisht kohët e fundit. Kryesor luan një rol në këto metoda. Funksioni i Green makroskopike sisteme të ngjashme me funksionin e Green-it në teorinë kuantike të fushës. Varet nga energjia e dhe momenti R, ligji i dispersionit të kuazigrimcave e(p) përcaktohet nga ekuacioni ![]() , meqenëse energjia e kuazigrimcave është poli i funksionit të Gjelbër. Ekziston një metodë e rregullt për llogaritjen e funksioneve të Green-it në formën e një sërë fuqish të energjisë së ndërveprimit midis grimcave. Çdo anëtar i kësaj serie përmban integrale të shumta mbi energjitë dhe momentet nga funksionet e Green-it të grimcave jo bashkëvepruese dhe mund të paraqitet grafikisht në formën e diagrameve të ngjashme me Diagramet e Feynman në kuantike. Secila prej këtyre diagrameve ka një specifikë fizike kuptimi, i cili bën të mundur ndarjen në një seri të pafundme të termave përgjegjës për fenomenin e interesit dhe përmbledhjen e tyre. Ekziston edhe një teknikë diagrami për llogaritjen e funksioneve të temperaturës së Green-it, të cilat bëjnë të mundur gjetjen e termodinamikës. sasi direkt, pa futjen e kuazigrimcave. Në këtë teknikë, funksionet e Green-it varen (në vend të energjisë) nga disa frekuenca diskrete w n dhe integralet mbi energjitë zëvendësohen nga shuma mbi këto frekuenca.
, meqenëse energjia e kuazigrimcave është poli i funksionit të Gjelbër. Ekziston një metodë e rregullt për llogaritjen e funksioneve të Green-it në formën e një sërë fuqish të energjisë së ndërveprimit midis grimcave. Çdo anëtar i kësaj serie përmban integrale të shumta mbi energjitë dhe momentet nga funksionet e Green-it të grimcave jo bashkëvepruese dhe mund të paraqitet grafikisht në formën e diagrameve të ngjashme me Diagramet e Feynman në kuantike. Secila prej këtyre diagrameve ka një specifikë fizike kuptimi, i cili bën të mundur ndarjen në një seri të pafundme të termave përgjegjës për fenomenin e interesit dhe përmbledhjen e tyre. Ekziston edhe një teknikë diagrami për llogaritjen e funksioneve të temperaturës së Green-it, të cilat bëjnë të mundur gjetjen e termodinamikës. sasi direkt, pa futjen e kuazigrimcave. Në këtë teknikë, funksionet e Green-it varen (në vend të energjisë) nga disa frekuenca diskrete w n dhe integralet mbi energjitë zëvendësohen nga shuma mbi këto frekuenca.
Tranzicionet fazore. Me një ndryshim të vazhdueshëm në ext. parametrat (p.sh. presioni ose temperatura), vetitë e sistemit mund të ndryshojnë papritur për vlera të caktuara të parametrave, d.m.th., ndodh një tranzicion fazor. Tranzicionet fazore ndahen në tranzicione të llojit të 1-të, të shoqëruara nga lëshimi i nxehtësisë latente të tranzicionit dhe një ndryshim i papritur i vëllimit (për shembull, shkrirja), dhe tranzicione të llojit të dytë, në të cilin nxehtësi latente dhe nuk ka kërcime në vëllim, por ka një kërcim në kapacitetin e nxehtësisë (për shembull, një kalim në një gjendje superpërcjellëse). Gjatë kalimit të llojit të dytë, simetria e trupit ndryshon. Ky ndryshim është sasior parametri i rendit, e cila është e ndryshme nga zero në njërën nga fazat dhe zhduket në pikën e tranzicionit. Statistikore Teoria e tranzicioneve fazore përbën një zonë të rëndësishme, por ende larg nga kompletimi i S. ph. maksimumi vështirësi për teorike studimet paraqesin vetitë e materies afër pikë kritike, tranzicioni fazor Lloji i parë dhe drejtpërdrejt. afërsia e vijës së tranzicionit fazor të rendit të dytë. (Në një distancë të caktuar nga kjo linjë, një tranzicion i llojit të dytë përshkruhet nga Teoria e Landau.) Këtu luhatjet rriten në mënyrë anormale dhe metodat e përafërta të S. f. nuk aplikohet. Prandaj, një rol të rëndësishëm luhet modele saktësisht të zgjidhshme, në të cilën ka tranzicione (shih Modelet e grilave 2D).Krijesa. progresi në ndërtimin e luhatjeve. teoria e kalimeve fazore arrihet me metodën zgjerimet epsilon. Në të, tranzicioni hetohet në një hapësirë imagjinare me numrin e dimensioneve, dhe rezultatet ekstrapolohen në hapësirën reale të tre dimensioneve. Në sistemet dy-dimensionale, tranzicionet e veçanta të fazës janë të mundshme, kur zhvendosjet ose fijet e vorbullës shfaqen në një temperaturë të caktuar. Parametri i rendit në pikën e tranzicionit zhduket papritur dhe kapaciteti i nxehtësisë është i vazhdueshëm.
Sisteme të çrregulluara. Një vend i veçantë në S. f. zënë xhami- trupat e ngurtë, atomet e të cilave janë renditur rastësisht edhe në abs. temperaturë zero. Në mënyrë të rreptë, një gjendje e tillë është jo ekuilibër, por me një kohë relaksimi jashtëzakonisht të gjatë, në mënyrë që joekuilibri të mos shfaqet në fakt. Kapaciteti termik i gotave në temperatura të ulëta varet në mënyrë lineare T. Kjo rrjedh nga shprehja për Z në formën (8). Kur varet nga T përcaktuar nga sjellja g(E) për të vogla E. Por për sisteme të çrregullta kuptimi E = 0 nuk ndahet, pra g(0) sigurisht, Z = POR + e(0)T dhe c ~ T. Një veçori interesante xhami është varësia e vlerave të vëzhguara të kapacitetit të nxehtësisë nga koha e matjes. Kjo shpjegohet me faktin se nivelet e energjisë me të vogla E e lidhur me tunelizimin kuantik të atomeve përmes një pengese të lartë potenciale, e cila kërkon shumë kohë. Karakteristikat interesante syzet me rrotullim- sistemet e atomeve të renditura rastësisht që kanë një magn. momente.
Fizika statistikore e proceseve joekuilibri. Ajo po merr gjithnjë e më shumë rëndësi kinetika fizike- seksioni i S. f., në të cilin studiojnë proceset në sisteme që janë në gjendje jo ekuilibër. Dy formulime të pyetjes janë të mundshme këtu: mund ta konsiderojmë sistemin në një gjendje të caktuar jo-ekuilibri dhe të ndjekim kalimin e tij në një gjendje ekuilibri; është e mundur të merret në konsideratë një sistem, një gjendje jo-ekuilibri i të cilit ruhet nga jashtë. kushtet, p.sh. trupi, në të cilin është vendosur gradienti i temperaturës, rrjedh elektrikisht. rrymë, etj., ose një trup në AC. ext. fushë.
Nëse devijimi nga ekuilibri është i vogël, vetitë joekuilibërore të sistemit përshkruhen nga të ashtuquajturat. koeficientët kinetikë. Shembuj të koeficientëve të tillë. janë koeficientë. viskoziteti, përçueshmëria termike dhe përçueshmëria elektrike e metaleve, etj. Këto madhësi plotësojnë parimin e simetrisë së kinetikës. koeficientët që shprehin simetrinë e ekuacioneve të mekanikës në lidhje me ndryshimin e shenjës së kohës (shih. Teorema e Onsager-it).
Më shumë koncept i përgjithshëmështë ndjeshmëri e përgjithësuar duke përshkruar ndryshimin kf. vlerat e një tufe të caktuar fizike. sasive X nën veprimin e një "force të përgjithësuar" të vogël f, e cila përfshihet në Hamiltonianin e sistemit në formën , ku është mekanika kuantike. operatori që korrespondon me X. Nese nje f varet nga koha si , ndryshimi mund të shkruhet si ![]() . Vlera komplekse është ndjeshmëria e përgjithësuar; ajo përshkruan sjelljen e sistemit në lidhje me të jashtmen. ndikimi. Nga ana tjetër, përcakton edhe relaksimin. vetitë: në , vlera relaksohet në vlerën e saj ekuilibër sipas ligjit, ku është distanca nga boshti real deri tek singulariteti i funksionit më të afërt me të në gjysmërrafshin e poshtëm të ndryshores komplekse w. Ndër detyrat e S. f. Proceset jo-ekuilibër përfshijnë gjithashtu studimin e varësisë së luhatjeve nga koha. Kjo varësi përshkruhet nga një korrelacion kohor. funksion, në të cilin mesatarizohen luhatjet e vlerës X të marra në të ndryshme pika në kohë t:
. Vlera komplekse është ndjeshmëria e përgjithësuar; ajo përshkruan sjelljen e sistemit në lidhje me të jashtmen. ndikimi. Nga ana tjetër, përcakton edhe relaksimin. vetitë: në , vlera relaksohet në vlerën e saj ekuilibër sipas ligjit, ku është distanca nga boshti real deri tek singulariteti i funksionit më të afërt me të në gjysmërrafshin e poshtëm të ndryshores komplekse w. Ndër detyrat e S. f. Proceset jo-ekuilibër përfshijnë gjithashtu studimin e varësisë së luhatjeve nga koha. Kjo varësi përshkruhet nga një korrelacion kohor. funksion, në të cilin mesatarizohen luhatjet e vlerës X të marra në të ndryshme pika në kohë t: ![]() është një funksion çift i argumentit të tij. Në klasiken S. f. ekziston një lidhje midis dhe ligjit të relaksimit të madhësisë. Nëse relaksimi përshkruhet me një diferencial të caktuar linear ekuacioni për devijimin nga vlera e ekuilibrit, atëherë ai plotëson të njëjtin ekuacion në t > 0.
është një funksion çift i argumentit të tij. Në klasiken S. f. ekziston një lidhje midis dhe ligjit të relaksimit të madhësisë. Nëse relaksimi përshkruhet me një diferencial të caktuar linear ekuacioni për devijimin nga vlera e ekuilibrit, atëherë ai plotëson të njëjtin ekuacion në t > 0.
Marrëdhënia midis dhe grupeve teorema luhatje-shpërndarje.Teorema thotë se transformimi i Furierit është i ndërlidhur. funksione 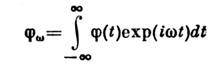
shprehet si më poshtë:
Një rast i veçantë (17) është Formula Nyquist.Përshkrimi i gjendjeve fort joekuilibri, si dhe llogaritja e kinetikës. Koeficient prodhuar duke përdorur Ekuacioni kinetik i Boltzmann-it. Ky ekuacion është një integro-diferencial. ur-tion për një funksion të shpërndarjes me një grimcë (në rastin kuantik - për një matricë densiteti me një grimcë, ose një operator statistikor). Ai përmban anëtarë të dy llojeve. Disa përshkruajnë ndryshimin në f-tion të shpërndarjes kur grimcat lëvizin në ekst. fusha, të tjera - në përplasjet e grimcave. Janë përplasjet që çojnë në një rritje të entropisë së një sistemi joekuilibri, d.m.th., në relaksim. E mbyllur, d.m.th., që nuk përmban sasi të tjera kinetike. ur-tion, e pamundur për të hyrë pamje e përgjithshme. Gjatë nxjerrjes së tij, është e nevojshme të përdoren parametrat e vegjël të disponueshëm në këtë problem të veçantë. Shembulli më i rëndësishëm është kinetika një ekuacion që përshkruan vendosjen e ekuilibrit në një gaz për shkak të përplasjeve midis molekulave. Është i vlefshëm për gazra mjaft të rrallë, kur është i madh në krahasim me distancat midis molekulave. Forma specifike e këtij ekuacioni varet nga eff. duke shpërndarë seksione tërthore të molekulave mbi njëra-tjetrën. Nëse dihet ky seksion, ekuacioni mund të zgjidhet duke zgjeruar funksionin e kërkuar në terma të polinomeve ortogonale. Në këtë mënyrë është e mundur të llogaritet kinetika Koeficient gaz, bazuar në ligjet e njohura të bashkëveprimit ndërmjet molekulave. Kinetike Ekuacioni merr parasysh vetëm përplasjet në çift midis molekulave dhe përshkruan vetëm termin e parë që nuk zhduket në zgjerimin e këtyre koeficientëve. nga dendësia e gazit. Gjithashtu arritëm të gjejmë një ekuacion më të saktë, i cili gjithashtu merr parasysh përplasjet e trefishta, të cilat bënë të mundur llogaritjen e afatit të ardhshëm të zgjerimit.
Një problem i veçantë është derivimi i kinetikës ur-tion për plazmën. Për shkak të uljes së ngadaltë të forcave të Kulombit me distancën, edhe kur merren parasysh përplasjet në çift, është thelbësore që këto forca të kontrollohen nga grimca të tjera. Gjendjet jo ekuilibër të trupave të ngurtë dhe lëngjeve kuantike mund të konsiderohen në temperatura të ulëta si gjendje jo ekuilibër të gazit të kuazi-grimcave përkatëse. Prandaj, kinetike proceset në sisteme të tilla përshkruhen kinetike. ekuacione për kuazi grimcat që marrin parasysh përplasjet midis tyre dhe proceset e transformimit të tyre të ndërsjellë. Mundësi të reja u hapën me aplikimin fizik. kinetika e metodave të teorisë kuantike të fushës. Kinetike Koeficient i një sistemi mund të shprehet me funksionin e tij Green's, për të cilin ekziston një metodë e përgjithshme llogaritjeje duke përdorur diagrame. Kjo lejon në disa raste për të marrë kinetike. Koeficient pa përdorimin e qartë të kinetikës. ur-tion dhe eksplorojnë vetitë jo-ekuilibruese të sistemit edhe në rastet kur nuk plotësohen kushtet e zbatueshmërisë së tij.
Pikat kryesore në zhvillimin e fizikës statistikore. S. f. bazuar tërësisht në konceptin e struktura atomikeçështje. Prandaj, fillimi periudha e zhvillimit të S. f. përkon me zhvillimin e atomistikës. përfaqësime. Zhvillimi i S. f. si pjesë e teorisë. fizika filloi në ser. Shekulli i 19 Në 1859, J. Maxwell përcaktoi funksionin e shpërndarjes së shpejtësisë së molekulave të gazit. Në 1860-70 R. Clausius (R. Clausing) prezantoi konceptin e rrugës mesatare të lirë dhe e lidhi atë me viskozitetin dhe përçueshmërinë termike të gazit. Rreth të njëjtën kohë, L. Boltzmann përgjithësoi shpërndarjen Maxwell në rastin kur gazi është në ekst. fushë, vërtetoi teoremën mbi barazinë e energjisë mbi shkallët e lirisë, nxori kinetiken. ur-tion, dha statistikore. interpretimi i entropisë dhe tregoi se ligji i rritjes së saj është pasojë e kinetikës. ur-tion. Ndërtimi i S. f. klasike. u përfundua deri në vitin 1902 në veprën e J. W. Gibbs (J. W. Gibbs). Teoria e luhatjeve u zhvillua në 1905-06 në veprat e M. Smoluchowski dhe A. Einstein. Në vitin 1900, M. Planck nxori ligjin e shpërndarjes së energjisë në spektrin e rrezatimit të një trupi të zi, duke filluar zhvillimin e mekanikës kuantike dhe fizikës kuantike. Në vitin 1924, Sh. Bose gjeti shpërndarjen e momentit të kuanteve të dritës dhe e lidhi atë me shpërndarjen Planck. Ajnshtajni përgjithësoi shpërndarjen Bose në gaze me një numër të caktuar grimcash. E. Fermi (E. Fermi) në vitin 1925 mori një funksion të shpërndarjes së grimcave që i binden parimit Pauli, dhe P. A. M. Dirac (R. A. M. Dirac) vendosi lidhjen midis kësaj shpërndarjeje dhe shpërndarjes Bose-Einstein me mat. aparate të mekanikës kuantike. Zhvillimi i mëtejshëm i S. t. në shekullin e 20-të shkoi nën shenjën e aplikimit të saj kryesore. parimet për studimin e problemeve specifike.
Lit.: Landau L. D., L dhe f sh dhe c E. M., Statistical Physics, pjesa 1, botimi i 3-të, M., 1976; M ayer J., Goeppert-Mayer M., Statistical mechanics, trans. nga anglishtja, botimi i dytë, M., 1980; Abrikosov A. A., Gorkoye L. P., Dzyaloshinsky I. E., Metodat e teorisë kuantike të fushës në fizikën statistikore, M., 1962; X u a ng K., Mekanika statistikore, përkth. nga anglishtja, M., 1966; Kittel Ch., Teoria kuantike të ngurta, per. nga anglishtja, M., 1967; Silin V.P., Hyrje në teorinë kinetike të gazeve, M., 1971; Fizika e lëngjeve të thjeshta. Sht., per. nga anglishtja, M., 1971; Anselm A. I., Bazat e fizikës statistikore dhe termodinamikës, M., 1973; L dhe f sh dhe c E. M., Pitaevsky L. P., Fizika statistikore, pjesa 2, M., 1978; dhe xzh e, Kinetika fizike, M., 1979; Balescu R., Mekanika statistikore e ekuilibrit dhe jo ekuilibrit, përkth. nga anglishtja, vëll.1-2, M., 1978; Bogolyubov N. N., Vepra të zgjedhura mbi fizikën statistikore, M., 1979; G dhe b b s J. V., Termodinamika. Mekanika statistikore, përkth. nga anglishtja, M., 1982; Leontovitch MA, Hyrje në termodinamikë. Fizika Statistikore, M., 1983; Boltzmann L., Vepra të zgjedhura, përkth. nga gjermanishtja, frëngjishtja, M., 1984. L. P. Pitaevsky.
Metodat Edukimi Rreth kësaj faqeje Biblioteka Math. forumeBiblioteka > Librat e fizikës > Fizika statistikore
fizika statistikore
- Aizenshitz R. Teoria statistikore e proceseve të pakthyeshme. M.: Ed. I huaj lit., 1963 (djvu)
- Anselm A.I. Bazat e fizikës statistikore dhe termodinamikës. Moskë: Nauka, 1973 (djvu)
- Akhiezer A.I., Peletminsky S.V. Metodat e fizikës statistikore. Moskë: Nauka, 1977 (djvu)
- Bazarov I.P. Probleme metodologjike të fizikës statistikore dhe termodinamikës. M.: Shtëpia Botuese e Universitetit Shtetëror të Moskës, 1979 (djvu)
- Bogolyubov N.N. Punime të zgjedhura për fizikën statistikore. M.: Shtëpia Botuese e Universitetit Shtetëror të Moskës, 1979 (djvu)
- Bogolyubov N.N. (Jr.), Sadovnikov B.I. Disa pyetje të mekanikës statistikore. M.: Më e lartë. shkolla, 1975 (djvu)
- Bonch-Bruevich V.L., Tyablikov S.V. Metoda e funksionit të Green-it në mekanikën statistikore. Moskë: Fizmatlit, 1961 (djvu, 2.61 Mb)
- Vasiliev A.M. Hyrje në fizikën statistikore. M.: Më e lartë. shkolla, 1980 (djvu)
- Vlasov A.A. Mekanika statistikore jolokale. Moskë: Nauka, 1978 (djvu)
- Gibbs JW Parimet themelore të mekanikës statistikore (shpjeguar me një aplikim të veçantë për justifikimin racional të termodinamikës). M.-L.: OGIZ, 1946 (djvu)
- Gurov K.P. Bazat e teorisë kinetike. Metoda N.N. Bogolyubov. Moskë: Nauka, 1966 (djvu)
- Zaslavsky G.M. Parikthyeshmëria statistikore në sistemet jolineare. Moskë: Nauka, 1970 (djvu)
- Zakharov A.Yu. Modelet e rrjetave të fizikës statistikore. Veliky Novgorod: NovGU, 2006 (pdf)
- Zakharov A.Yu. Metodat funksionale në fizikën statistikore klasike. Veliky Novgorod: NovGU, 2006 (pdf)
- Ios G. Kursi i fizikës teorike. Pjesa 2. Termodinamika. Fizika statistikore. Teoria kuantike. Fizika bërthamore. M.: Iluminizmi, 1964 (djvu)
- Ishihara A. Fizika Statistikore. M.: Mir, 1973 (djvu)
- Kadanov L., Beim G. Mekanika statistikore kuantike. Metodat e funksioneve të Green-it në teorinë e proceseve të ekuilibrit dhe joekuilibrit. M.: Mir, 1964 (djvu)
- Katz M. Probabiliteti dhe çështjet e lidhura me të në fizikë. M.: Mir, 1965 (djvu)
- Katz M. Disa probleme probabilistike të fizikës dhe matematikës. Moskë: Nauka, 1967 (djvu)
- Kittel Ch. Fizika statistikore elementare. M.: IL, 1960 (djvu)
- Kittel Ch. Termodinamika statistikore. M: Science, 1977 (djvu)
- Kozlov V.V. Ekuilibri termik sipas Gibbs dhe Poincare. Moskë-Izhevsk: Instituti për Kërkime Kompjuterike, 2002 (djvu)
- Kompaneets A.S. Ligjet e statistikave fizike. valët e goditjes. Substancë super e dendur. M.: Nauka, 1976 (djvu)
- Kompaneets A.S. Kursi i fizikës teorike. Vëllimi 2. Ligjet statistikore. M.: Iluminizmi, 1975 (djvu)
- Kotkin G.L. Leksione për Fizikën Statistikore, NSU (pdf)
- Krylov N.S. Punon për vërtetimin e fizikës statistikore. M.-L.: Nga Akademia e Shkencave e BRSS, 1950 (djvu)
- Kubo R. Mekanika statistikore. M.: Mir, 1967 (djvu)
- Landsberg P. (red.) Probleme në termodinamikë dhe fizikë statistikore. M.: Mir, 1974 (djvu)
- Levich V.G. Hyrje në fizikën statistikore (botim i dytë) M.: GITTL, 1954 (djvu)
- Libov R. Hyrje në teorinë e ekuacioneve kinetike. M.: Mir, 1974 (djvu)
- Mayer J., Geppert-Mayer M. Mekanika statistikore. M.: Mir, 1980 (djvu)
- Minlos R.A. (red.) Matematikë. E re në shkencën e huaj-11. Gibbs deklaron në fizikën statistikore. Përmbledhje e artikujve. M.: Mir, 1978 (djvu)
- Nozdrev V.F., Senkevich A.A. Kursi i fizikës statistikore. M.: Më e lartë. shkolla, 1965 (djvu)
- Prigogine I. Mekanika Statistikore Joekuilibërore. M.: Mir, 1964 (djvu)
- Radushkevich L.V. Kursi i fizikës statistikore (red. 2.) M.: Prosveshchenie, 1966 (djvu)
- Kursi i fizikës Reif F. Berkeley. Vëllimi 5. Fizika statistikore. M.: Nauka, 1972 (djvu)
- Rumer Yu.B., Ryvkin M.Sh. Termodinamika, fizika statistikore dhe kinetika. M.: Nauka, 1972 (djvu)
- Rumer Yu.B., Ryvkin M.Sh. Termodinamika Statistikore Fizika dhe Kinetika (Botimi 2). Moskë: Nauka, 1977 (djvu)
- Ruel D. Mekanika statistikore. M.: Mir, 1971 (djvu)
- Savukov V.V. Përsosja e parimeve aksiomatike të fizikës statistikore. SPb.: Balt. shteti teknologjisë. univ. "Voenmekh", 2006
fizika statistikore një degë e fizikës, detyra e së cilës është të shprehë vetitë e trupave makroskopikë, domethënë të sistemeve që përbëhen nga një numër shumë i madh grimcash identike (molekula, atome, elektrone, etj.), nëpërmjet vetive të këtyre grimcave dhe ndërveprimit ndërmjet tyre. . Trupat makroskopikë po studiojnë edhe degë të tjera të fizikës - Termodinamika, mekanika e vazhdimësisë, elektrodinamika e kontinuumeve. Sidoqoftë, kur zgjidhen probleme specifike me metodat e këtyre disiplinave, ekuacionet përkatëse përfshijnë gjithmonë parametra ose funksione të panjohura që karakterizojnë një trup të caktuar. Pra, për të zgjidhur problemet e hidrodinamikës, është e nevojshme të dihet ekuacioni i gjendjes së një lëngu ose gazi, d.m.th., varësia e densitetit nga temperatura dhe presioni, kapaciteti i nxehtësisë së një lëngu, koeficienti i viskozitetit të tij, etj. Të gjitha këto varësi dhe parametra, natyrisht, mund të përcaktohen eksperimentalisht, prandaj, metodat në fjalë quhen fenomenologjike. Fizika statistikore lejon, të paktën në parim, dhe në shumë raste në fakt, të llogariten të gjitha këto sasi, nëse dihen forcat e ndërveprimit midis molekulave. T. o., S. f. përdor informacione për strukturën "mikroskopike" të trupave - se nga cilat grimca përbëhen, si ndërveprojnë këto grimca, prandaj quhet teoria mikroskopike. Nëse në një moment në kohë jepen koordinatat dhe shpejtësitë e të gjitha grimcave të trupit dhe dihet ligji i bashkëveprimit të tyre, atëherë, duke zgjidhur ekuacionet e mekanikës, do të ishte e mundur të gjenden këto koordinata dhe shpejtësi në çdo pikë pasuese. në kohë dhe në këtë mënyrë të përcaktojë plotësisht gjendjen e trupit në studim. (Për thjeshtësi, prezantimi bëhet në gjuhën e mekanikës klasike. Por në mekanikën kuantike (Shih mekanikën kuantike) situata është e njëjtë: njohja e funksionit valor fillestar (shih funksionin e valës) të sistemit dhe ligjit të bashkëveprimit të grimcave, është e mundur, duke zgjidhur ekuacionin e Shrodingerit, të gjejmë funksionin valor, i cili përcakton gjendjen e sistemit në të gjitha momentet e ardhshme të kohës.) Megjithatë, në fakt, një mënyrë e tillë për të ndërtuar një teori mikroskopike është e pamundur, pasi numri i grimcave në trupat makroskopikë është shumë i madh. Për shembull, në 1 cm 3 gaz në një temperaturë prej 0 °C dhe një presion prej 1 atm përmban afërsisht 2.7․10 19 molekula. Është e pamundur të zgjidhet një numër i tillë ekuacionesh, dhe koordinatat dhe shpejtësitë fillestare të të gjitha molekulave janë ende të panjohura. Megjithatë, është pikërisht numri i madh i grimcave në trupat makroskopikë që çon në shfaqjen e rregullsive të reja - statistikore - në sjelljen e trupave të tillë. Kjo sjellje në një gamë të gjerë nuk varet nga kushtet specifike fillestare - nga vlerat e sakta të koordinatave fillestare dhe shpejtësive të grimcave. Shfaqja më e rëndësishme e kësaj pavarësie është fakti i njohur nga përvoja se një sistem i lënë në vetvete, d.m.th., i izoluar nga ndikimet e jashtme, përfundimisht vjen në një gjendje ekuilibri (ekuilibër termodinamik ose statistikor), vetitë e të cilit përcaktohen vetëm nga karakteristika të tilla të përgjithshme gjendja fillestare, si numri i grimcave, energjia totale e tyre, etj. (shih ekuilibrin termodinamik). Në të ardhmen do të flasim kryesisht për S. t. gjendjet e ekuilibrit. Para se të formulohet një teori që përshkruan rregullsitë statistikore, duhet të kufizohen në mënyrë të arsyeshme vetë kërkesat për teorinë. Domethënë, detyra e teorisë duhet të jetë të llogaritë jo vlerat e sakta të sasive të ndryshme fizike për trupat makroskopikë, por vlerat mesatare të këtyre sasive me kalimin e kohës. Konsideroni, për shembull, molekulat e vendosura në një vëllim mjaft të madh makroskopik të izoluar në një gaz. Numri i molekulave të tilla do të ndryshojë me kalimin e kohës për shkak të lëvizjes së tyre, dhe mund të gjendet saktësisht nëse të gjitha koordinatat e molekulave në çdo kohë ishin të njohura. Kjo, megjithatë, nuk është e nevojshme. Ndryshimi në numrin e molekulave në vëllim do të jetë në natyrën e luhatjeve të rastësishme - luhatjeve - në lidhje me një vlerë mesatare. Me një numër të madh grimcash në vëllim, këto luhatje do të jenë të vogla në krahasim me numrin mesatar të grimcave, kështu që për të karakterizuar gjendjen makroskopike, mjafton të dihet vetëm kjo vlerë mesatare. Për të sqaruar natyrën e modeleve statistikore, merrni parasysh një shembull tjetër të thjeshtë. Lëreni një numër të madh kokrrash të dy varieteteve të vendosen në një enë, secila shkallë në mënyrë të barabartë, dhe përmbajtja e enës përzihet plotësisht. Pastaj, në bazë të përvojës së përditshme, mund të sigurohet se në një kampion të marrë nga një enë që përmban një numër ende të madh kokrrash, do të gjendet një numër afërsisht i barabartë kokrrash të çdo varieteti, pavarësisht nga radha në të cilën janë kokrrat. u derdhën në enë. Ky shembull tregon qartë dy rrethana të rëndësishme që sigurojnë zbatueshmërinë e teorisë statistikore. Së pari, nevoja për një numër të madh kokrrash si në të gjithë "sistemin" - një enë me grurë, dhe në "nënsistemin" e zgjedhur për eksperimentin - një mostër. (Nëse kampioni përbëhet nga vetëm dy kokrra, atëherë shpesh të dyja do të jenë të së njëjtës shkallë.) Së dyti, është e qartë se kompleksiteti i lëvizjes së kokrrave gjatë përzierjes luan një rol të rëndësishëm, duke siguruar shpërndarjen e tyre uniforme në vëllimin e enës. funksioni i shpërndarjes. Konsideroni një sistem të përbërë nga N grimcat, duke supozuar për thjeshtësi se grimcat nuk kanë shkallë të brendshme lirie. Një sistem i tillë përshkruhet nga detyra 6N variablat - 3N koordinatat q i dhe 3N impulset pi, grimcat [bashkësia e këtyre variablave do të shkurtohet si ( R, q)]. Le të llogarisim vlerën mesatare në intervalin kohor të një vlere të caktuar F(p, q), që është funksion i këtyre koordinatave dhe momenteve. Për ta bërë këtë, ne e ndajmë intervalin (0, τ) në s segmente të vogla të barabartë Δ ta (a = 1,2,....... s). Pastaj sipas përkufizimit ku q a dhe p a- vlerat e koordinatave dhe impulseve nganjëherë ta. Në kufi s→ ∞ shuma shkon në një integral: Koncepti i funksionit të shpërndarjes në mënyrë të natyrshme lind nëse marrim parasysh hapësirën 6 N matje, në boshtet e të cilave vizatohen vlerat e koordinatave dhe momenteve të grimcave të sistemit; quhet hapësira fazore. Për çdo vlerë të kohës t korrespondojnë me vlera të caktuara të të gjithave q dhe R, pra një pikë në hapësirën e fazës, që përshkruan gjendjen e sistemit në një kohë të caktuar t. Le ta ndajmë të gjithë hapësirën e fazës në elementë, madhësia e të cilave është e vogël në krahasim me vlerat karakteristike të një gjendjeje të caktuar të sistemit q dhe R, por ende aq i madh sa në secilën prej tyre ka shumë pika që përshkruajnë gjendjen e sistemit në momente të ndryshme kohore t. Atëherë numri i pikave të tilla në elementin e vëllimit do të jetë afërsisht proporcional me vlerën e këtij vëllimi dpdq. Nëse shënojmë koeficientin e proporcionalitetit përmes sω(p, q), atëherë ky është numri për elementin e përqendruar në një pikë ( p, q) do të shkruhet si: da = sω(p, q)dpdq, (2) dpdq = dp 1 dq 1 dp 2 dq 2 ... dp 3N dq 3N Vëllimi i elementit të zgjedhur të hapësirës së fazës. Vlera mesatare (1), duke marrë parasysh vogëlsinë e këtyre elementeve të vëllimit, mund të rishkruhet si (integrimi mbi koordinata kryhet në të gjithë vëllimin e sistemit, mbi momentet - nga -∞ në ∞). Funksioni ω( p, q, t) quhet funksioni i shpërndarjes në lidhje me koordinatat e momentit të grimcave. Meqenëse numri i përgjithshëm i pikëve të zgjedhura është s, funksion w plotëson kushtin e normalizimit: Mund të shihet nga (3) dhe (4) se ω dpdq mund të konsiderohet si probabiliteti që sistemi të jetë në element dpdq hapësirë fazore. Funksionit të shpërndarjes i prezantuar në këtë mënyrë mund t'i jepet një interpretim tjetër. Për ta bërë këtë, ne do të konsiderojmë njëkohësisht një numër të madh sistemesh identike dhe do të supozojmë se çdo pikë në hapësirën e fazës përfaqëson gjendjen e një sistemi të tillë. Atëherë koha e mesatares në (1)-(1a) mund të kuptohet si mesatare mbi tërësinë e këtyre sistemeve, ose, siç thonë ata, mbi ansamblin statistikor (Shih Ansamblin Statistikor). Argumentet e deritanishme kanë qenë thjesht formale, që nga ajo kohë gjetja e funksionit të shpërndarjes, sipas (2), kërkon njohuri të të gjithëve R dhe q në çdo kohë, d.m.th., zgjidhjet e ekuacioneve të lëvizjes me kushtet fillestare përkatëse. Pozicioni kryesor i S. f. është, megjithatë, një deklaratë në lidhje me mundësinë e përcaktimit të këtij funksioni nga konsideratat e përgjithshme për një sistem në një gjendje ekuilibri termodinamik. Para së gjithash, mund të tregohet, bazuar në ruajtjen e numrit të sistemeve gjatë lëvizjes, se funksioni i shpërndarjes është një integral i lëvizjes së sistemit, d.m.th., mbetet konstant nëse R dhe q ndryshimi në përputhje me ekuacionet e lëvizjes (shih teoremën e Liouville). Kur një sistem i mbyllur lëviz, energjia e tij nuk ndryshon, prandaj, të gjitha pikat në hapësirën fazore, që përshkruajnë gjendjen e sistemit në momente të ndryshme të kohës, duhet të shtrihen në një "hipersipërfaqe" që korrespondon me vlerën fillestare të energjisë. E. Ekuacioni i kësaj sipërfaqeje ka formën; H(p, q) =E, ku H(p, q) është energjia e sistemit, e shprehur në terma të koordinatave dhe momentit, pra funksioni i tij Hamilton. Për më tepër, lëvizja e një sistemi të shumë grimcave është jashtëzakonisht e ndërlikuar. Prandaj, me kalimin e kohës, pikat që përshkruajnë gjendjen do të shpërndahen në sipërfaqe energji konstante në mënyrë të barabartë, ashtu si kokrrat shpërndahen në mënyrë të barabartë gjatë trazimit në enë në shembullin e përmendur më sipër (shih edhe hipotezën Ergodike). Një shpërndarje e tillë uniforme mbi sipërfaqen izoenergjetike përshkruhet nga një funksion shpërndarjeje të formës: ω( p, q) = Aδ[ H(p, q) - E], (5) ku δ[ H(p, q) - E]
- Funksioni Delta, jo zero vetëm kur H = E dmth në këtë sipërfaqe, PORështë një konstante e përcaktuar nga kushti i normalizimit (4). Funksioni i shpërndarjes (5), i quajtur mikrokanonik, ju lejon të llogaritni vlerat mesatare të të gjitha sasive fizike me formulën (3), pa zgjidhur ekuacionet e lëvizjes. Gjatë nxjerrjes së shprehjes (5), supozohej se e vetmja sasi që mbetet e pandryshuar gjatë lëvizjes së sistemit, nga e cila varet ω, është energjia e sistemit. Sigurisht, momenti dhe momenti këndor ruhen gjithashtu, por këto sasi mund të eliminohen duke supozuar se trupi në fjalë është i mbyllur në një kuti fikse, së cilës grimcat mund t'i japin vrull dhe vrull. Në fakt, zakonisht nuk konsiderohen sisteme të mbyllura, por trupa makroskopikë, të cilët janë pjesë të vogla makroskopike, ose nënsisteme të çdo sistemi të mbyllur. Funksioni i shpërndarjes për nënsistemin do të jetë i ndryshëm nga (5), por nuk do të varet nga natyra specifike e pjesës tjetër të sistemit - i ashtuquajturi. termostat. Prandaj, funksioni i shpërndarjes së nënsistemit mund të përcaktohet duke supozuar, për shembull, se termostati përbëhet thjesht nga N grimcat e një gazi ideal, koordinatat dhe momenti i të cilit do të shënohen me P dhe R, në ndryshim nga shënimi q dhe R për një nënsistem, atëherë shpërndarja mikrokanonike është: Këtu H(p, q) është funksioni Hamilton i nënsistemit, Mështë masa e një grimce gazi, dhe përmbledhja kryhet mbi të gjithë përbërësit e impulseve të të gjitha grimcave të termostatit. Për të gjetur funksionin e shpërndarjes për nënsistemin, duhet ta integrojmë këtë shprehje mbi koordinatat dhe momentet e grimcave të termostatit. Nëse atëherë marrim parasysh se numri i grimcave në termostat është shumë më i madh se në nënsistem, dhe përpiqemi N→∞, duke supozuar se raporti E/N konstante dhe e barabartë me 3/2 kT, atëherë për funksionin e shpërndarjes së nënsistemit do të fitohet shprehja e mëposhtme: Vlera T në këtë formulë ka kuptimin e temperaturës, k = 1,38․10 -16 erg/degështë konstanta e Boltzmann-it. [Gjendja E/N→ 3 / 2 kT pasi gazi në termostat korrespondon, siç duhet, me formulën (13) për një gaz ideal; shih më poshtë.] Faktori i normalizimit e F/kT përcaktohet nga kushti i normalizimit (4): Shpërndarja (6) quhet shpërndarja kanonike e Gibbs, ose thjesht shpërndarja kanonike (shih shpërndarjen e Gibbs), dhe sasia Z- integrali statistikor. Ndryshe nga shpërndarja mikrokanonike, energjia e sistemit në shpërndarjen Gibbs nuk është dhënë. Gjendjet e sistemit janë të përqendruara në një shtresë të hollë por të fundme rreth sipërfaqes së energjisë që korrespondon me vlerën mesatare të energjisë, që do të thotë se është e mundur shkëmbimi i energjisë me termostatin. Përndryshe, kur aplikohet në një trup të caktuar makroskopik, të dyja shpërndarjet çojnë në thelb në të njëjtat rezultate. Dallimi i vetëm është se kur përdorni shpërndarjen mikrokanonike, të gjitha vlerat mesatare shprehen në terma të energjisë së trupit, dhe kur përdorni shpërndarjen kanonike, në terma të temperaturës. Nëse trupi përbëhet nga dy pjesë që nuk ndërveprojnë 1 dhe 2 me funksione Hamiltoniane H1 dhe H2, pastaj për të gjithë trupin H = H1 + H2 dhe, sipas (6), funksioni i shpërndarjes së trupit ndahet në produktin e funksioneve të shpërndarjes për secilën nga pjesët, në mënyrë që këto pjesë të rezultojnë statistikisht të pavarura. Kjo kërkesë, së bashku me teoremën e Liouville, mund të përdoret si bazë për nxjerrjen e shpërndarjes Gibbs pa përdorur shpërndarjen mikrokanonike. Formula (6) është e vlefshme për sistemet që përshkruhen nga mekanika klasike. Në mekanikën kuantike, spektri i energjisë i një sistemi me vëllim të kufizuar është diskret. Probabiliteti që një nënsistem të jetë në gjendje me energji E n jepet nga një formulë e ngjashme me (6): ku kushti i normalizimit Vlera Z quhet funksioni i ndarjes së sistemit; shuma në shprehjen (8) merret mbi të gjitha gjendjet e sistemit. Për një sistem të përshkruar me saktësi të mjaftueshme nga mekanika klasike, në formulën (8) është e mundur të kalohet nga përmbledhja mbi gjendjet në integrimin mbi koordinatat dhe momentet e sistemit. Në të njëjtën kohë, për çdo gjendje kuantike ekziston një "qelizë" (ose "qeliza") në hapësirën fazore të vëllimit ħ - Shiriti është konstant. Me fjalë të tjera, përmbledhja ka përfunduar n redukton në integrimin mbi Ai ndryshon nga një faktor nga gjendja thjesht klasike e normalizimit (6a), e cila çon në një term shtesë në F. Formulat e mësipërme i referohen rastit kur jepet numri i grimcave në nënsistem. Nëse zgjedhim si nënsistem një element vëllimor të caktuar të të gjithë sistemit, përmes sipërfaqes së të cilit grimcat mund të largohen nga nënsistemi dhe të kthehen në të, atëherë probabiliteti për të gjetur nënsistemin në një gjendje me energji E n dhe numri i grimcave N nështë dhënë nga formula e madhe kanonike e shpërndarjes Gibbs: në të cilin parametri shtesë μ - Potenciali kimik, i cili përcakton numrin mesatar të grimcave në nënsistem, dhe vlera e Ω përcaktohet nga kushti i normalizimit [shih. formula (11)]. Interpretimi statistikor i termodinamikës. Rezultati më i rëndësishëm i S. f. - vendosja e kuptimit statistikor të madhësive termodinamike. Kjo bën të mundur nxjerrjen e ligjeve të termodinamikës nga idetë themelore të S. f. dhe llogaritni sasitë termodinamike për sisteme specifike. Para së gjithash, energjia e brendshme termodinamike identifikohet me energjinë mesatare të sistemit. Ligji i parë i termodinamikës merr një interpretim të qartë si shprehje e ligjit të ruajtjes së energjisë gjatë lëvizjes së grimcave që përbëjnë trupin. Më tej, le të varet funksioni Hamilton i sistemit nga disa parametra λ (koordinatat e murit të anijes që përmban sistemin, fusha e jashtme, etj.). Pastaj derivati i forcës së përgjithësuar) që korrespondon me këtë parametër, dhe vlera E̅ e sistemit, duke marrë parasysh formulën (6) dhe gjendjen e normalizimit, duke marrë parasysh variablat λ dhe T dhe duke pasur parasysh se vlera Fështë gjithashtu një funksion i këtyre variablave, atëherë marrim identitetin: Sipas sa më sipër, anëtari që përmban dλ, është e barabartë me punën mesatare dA kryhet në trup. Pastaj termi i fundit është nxehtësia e marrë nga trupi. Krahasimi i kësaj shprehjeje me relacionin dE = dA + TdS, i cili është një rekord i kombinuar i ligjit të parë dhe të dytë të termodinamikës (shih ligjin e dytë të termodinamikës) për proceset e kthyeshme (shih procesi i kthyeshëm), ne gjejmë se T në (6) është me të vërtetë e barabartë me temperaturën absolute të trupit dhe derivatin e Entropisë) S. Do të thotë se Fështë Energjia e Lirë e trupit, nga e cila sqarohet kuptimi statistikor i tij. Me rëndësi të veçantë është interpretimi statistikor i entropisë, i cili rrjedh nga formula (8). Formalisht, g përmblidhet në këtë formulë mbi të gjitha gjendjet me energji E n, por në fakt, për shkak të vogëlsisë së luhatjeve të energjisë në shpërndarjen Gibbs, vetëm një numër relativisht i vogël i tyre me një energji afër energjisë mesatare është i rëndësishëm. Prandaj, numri i këtyre gjendjeve thelbësore Δ̅n̅ mund të përcaktohet natyrshëm duke kufizuar përmbledhjen në (8) në intervalin Δ̅n̅, duke zëvendësuar E n për energji mesatare E̅ dhe nxjerrja e eksponentit nga nën shenjën e shumës. Atëherë shuma do të japë Δ̅n̅ dhe do të marrë formën. Nga ana tjetër, sipas termodinamikës, F = E̅ - TS, i cili jep marrëdhënien e entropisë me numrin e gjendjeve mikroskopike Δ̅n̅ në një gjendje të caktuar makroskopike, me fjalë të tjera, me peshën statistikore (Shih peshën statistikore) të gjendjes makroskopike, d.m.th. me probabilitetin e saj: Në temperaturën e zeros absolute, çdo sistem është në një gjendje të caktuar bazë, kështu që Δ̅n̅ = 1, S= 0. Ky pohim shpreh ligjin e tretë të termodinamikës. Është thelbësore këtu që për një përkufizim të qartë të entropisë është e nevojshme të përdoret formula kuantike (8); në statistikat thjesht klasike, entropia përcaktohet vetëm deri në një term arbitrar. Kuptimi i entropisë si masë e probabilitetit të një gjendjeje ruhet gjithashtu në lidhje me gjendjet arbitrare - jo domosdoshmërisht ekuilibër. Në një gjendje ekuilibri, entropia ka vlerën maksimale të mundshme në kushte të jashtme të dhëna. Kjo do të thotë se gjendja e ekuilibrit është gjendja me peshën maksimale statistikore, gjendja më e mundshme. Procesi i kalimit të një sistemi nga një gjendje jo ekuilibër në një gjendje ekuilibri është një proces i kalimit nga gjendjet më pak të mundshme në ato më të mundshme; kjo sqaron kuptimin statistikor të ligjit të rritjes së entropisë, sipas të cilit entropia e një sistemi të mbyllur mund të rritet vetëm. Formula (8) që lidh energjinë e lirë F me funksion ndarës, është baza për llogaritjen e madhësive termodinamike me metodat e S. f. Përdoret, në veçanti, për të ndërtuar një teori statistikore të vetive elektrike dhe magnetike të materies. Për shembull, për të llogaritur momentin magnetik të një trupi në një fushë magnetike, duhet të llogaritet funksioni i ndarjes dhe energjia e lirë. Moment magnetik m trupi më pas jepet me formulën: m = ku H- intensiteti i fushës magnetike të jashtme. Ngjashëm me (8), gjendja e normalizimit në shpërndarjen e madhe kanonike (9) përcakton potencialin termodinamik Ω sipas formulës: Ky potencial lidhet me energjinë e lirë nga relacioni: Aplikacionet S. f. për studimin e veçorive të caktuara të sistemeve specifike reduktohen në thelb në një llogaritje të përafërt të funksionit të ndarjes, duke marrë parasysh vetitë specifike të sistemit. Në shumë raste, kjo detyrë thjeshtohet duke zbatuar ligjin e barazisë në shkallë lirie, i cili thotë se kapaciteti i nxehtësisë cv(në një vëllim konstant v) i një sistemi pikash materiale ndërvepruese - grimca që kryejnë lëkundje harmonike, është e barabartë me c v = k(l/2 + n),
ku l- numri i përgjithshëm i shkallëve përkthimore dhe rrotulluese të lirisë, n- numri i shkallëve vibruese të lirisë. Prova e ligjit bazohet në faktin se funksioni i Hamiltonit H një sistem i tillë duket si ky: H = K(pi)+ U(q m), ku energjia kinetike teështë një funksion kuadratik homogjen i l + n impulset pi dhe energjinë potenciale U- funksioni kuadratik i n koordinatat vibruese q m. Në integralin statistikor Z(8a) integrimi mbi koordinatat vibruese për shkak të konvergjencës së shpejtë të integralit mund të zgjerohet nga - ∞ në ∞. Pas kryerjes së ndryshimit të variablave Z varet nga temperatura si Tl/2+n, pra energjia e lirë F=-kT(l/ 2
+n) (ln T+ konst). Nga kjo rrjedh shprehja e mësipërme për kapacitetin e nxehtësisë, pasi Gaz ideal. Objekti më i thjeshtë i kërkimit të S. f. është një gaz ideal, domethënë një gaz aq i rrallë saqë ndërveprimi ndërmjet molekulave të tij mund të neglizhohet. Funksionet termodinamike të një gazi të tillë mund të llogariten plotësisht. Energjia e një gazi është thjesht shuma e energjive të molekulave individuale. Megjithatë, kjo ende nuk mjafton për t'i konsideruar molekulat si plotësisht të pavarura. Në të vërtetë, në mekanikën kuantike, edhe nëse nuk ka forca ndërveprimi midis grimcave, ekziston një ndikim i caktuar i grimcave identike (identike) mbi njëra-tjetrën nëse ato janë në gjendje të ngjashme mekanike kuantike. Ky është i ashtuquajturi. ndërveprim shkëmbimi. Mund të neglizhohet nëse, mesatarisht, ka shumë më pak se një grimcë për gjendje, e cila, në çdo rast, ndodh në një temperaturë mjaft të lartë të gazit; një gaz i tillë quhet jo i degjeneruar. Në fakt, gazrat e zakonshëm, të përbërë nga atome dhe molekula, nuk janë të degjeneruar në të gjitha temperaturat (në të cilat ato janë ende të gazta). Për një gaz ideal jo të degjeneruar, funksioni i shpërndarjes zbërthehet në produktin e funksioneve të shpërndarjes për molekulat individuale. shtrihen në intervale dp x, dpy, dpz, dhe koordinatat janë në intervale dx, dy, dz: , (12) Energjia e një molekule gazi monatomike në një fushë të jashtme me energji potenciale U(r) është e barabartë me p 2 /2M + U(r). Integrimi i (6) mbi koordinatat r(x, y, z) dhe impulset R(p x, py, pz) nga të gjitha molekulat përveç njërës, mund të gjeni numrin e molekulave dN, impulset e të cilit ku d 3 f = dp x dp y dp z, d3x = dxdydz. Kjo formulë quhet shpërndarja Maxwell-Boltzmann (shih statistikat Boltzmann). Nëse integrojmë (12) mbi momentin, atëherë marrim një formulë për shpërndarjen e grimcave mbi koordinatat në një fushë të jashtme, veçanërisht në një fushë gravitacionale - Formula barometrike. Shpërndarja e shpejtësive në çdo pikë të hapësirës përkon me shpërndarjen Maxwell m. Funksioni i ndarjes së një gazi ideal gjithashtu zbërthehet në produktin e termave identikë që korrespondojnë me molekulat individuale. Për një gaz monoatomik, shuma në (8) zvogëlohet në integrim mbi koordinatat dhe momentin, d.m.th., shuma zëvendësohet nga një mbi integrale ku g- pesha statistikore e gjendjes bazë të atomit, d.m.th. numri i gjendjeve që korrespondojnë me nivelin e tij më të ulët të energjisë, V- vëllimi i gazit (këtu e- bazë logaritmet natyrore). Në temperatura të larta g =(2J+1)(2L+1), ku J- vlera e Spin a, a L- momenti i orbitalit (Shih Momenti orbital) i atomit (në njësi ħ
). Nga shprehja për energji e lirë rrjedh se ekuacioni i gjendjes së një gazi ideal, d.m.th., varësia e presionit të tij ( R) në densitetin e numrit të grimcave ( N/V) dhe temperatura, ka formën: PV = NkT. Energjia e brendshme e një gazi monatomik dhe kapaciteti i tij i nxehtësisë në vëllim konstant rezulton të jetë i barabartë: E = 3 / 2 (NkT), c v = 3 / 2 Nk, (13) Dhe e tij potencial kimik: Është karakteristikë që edhe për një gaz jo të degjeneruar (d.m.th., që i bindet mekanikës klasike me saktësi të mjaftueshme), shprehjet për energjinë e lirë dhe potencialin kimik përmbajnë konstantën e Plankut. ħ
. Në fund të fundit, kjo është për shkak të lidhjes së vërejtur më parë midis entropisë dhe konceptit të numrit të gjendjeve kuantike. Në rastin e gazeve diatomike dhe poliatomike, dridhjet dhe rrotullimi i molekulave gjithashtu kontribuojnë në funksionet termodinamike. Ky kontribut varet nga fakti nëse efektet e kuantizimit të dridhjeve dhe rrotullimit të molekulës janë të rëndësishme. Distanca midis niveleve të energjisë vibruese është e rendit të I - momenti i inercisë së një trupi rrotullues, në këtë rast një molekule. Statistikat klasike janë të vlefshme nëse temperatura është mjaft e lartë në mënyrë që kT>>
Δ E. Në këtë rast, në përputhje me ligjin e barazisë, rrotullimi jep një kontribut të vazhdueshëm në kapacitetin e nxehtësisë, të barabartë me 1/2 k për çdo shkallë rrotulluese të lirisë; në veçanti, për molekulat diatomike ky kontribut është i barabartë me k. Luhatjet japin një kontribut në kapacitetin e nxehtësisë të barabartë me k për çdo shkallë lirie vibruese (në mënyrë që kapaciteti i nxehtësisë vibruese të një molekule diatomike është k). Kontributi i shkallës vibruese të lirisë, krahasuar me atë rrotulluese, është dy herë më i madh për faktin se, gjatë dridhjeve, atomet në një molekulë kanë energji jo vetëm kinetike, por edhe potenciale. Në kufirin e kundërt Gaz i papërsosur. Një arritje e rëndësishme e S. t. - llogaritja e korrigjimeve të sasive termodinamike të gazit që lidhen me bashkëveprimin midis grimcave të tij. Nga ky këndvështrim, ekuacioni i gjendjes së një gazi ideal është termi i parë në zgjerimin e presionit të një gazi real për sa i përket densitetit të numrit të grimcave, pasi çdo gaz sillet si një gaz ideal në një nivel të mjaftueshëm. densitet të ulët. Ndërsa densiteti rritet, korrigjimet e ndërveprimit në ekuacionin e gjendjes fillojnë të luajnë një rol. Ato çojnë në paraqitjen në shprehjen për presion të termave me shkallë më të lartë të densitetit të numrit të grimcave, kështu që presioni përfaqësohet me të ashtuquajturat. seritë virale të formës: Shanset AT, NGA etj. varen nga temperatura dhe formohen. e dyta, e treta etj. koeficientët virialë. Metodat e S. f. bëjnë të mundur llogaritjen e këtyre koeficientëve nëse dihet ligji i bashkëveprimit ndërmjet molekulave të gazit. Në të njëjtën kohë, koeficientët AT, NGA,... përshkruajnë bashkëveprimin e njëkohshëm të dy, tre ose më shumë molekulave. Për shembull, nëse gazi është monoatomik dhe energjia potenciale e bashkëveprimit të atomeve të tij U(r), atëherë koeficienti i dytë virial është Sipas rendit të madhësisë ATështë e barabartë me r 0 - madhësia karakteristike e një atomi, ose, më saktë, rrezja e veprimit të forcave ndëratomike. Kjo do të thotë se seria (15) është në fakt një zgjerim i fuqive të parametrit pa dimension Nr 3 /V, i vogël për një gaz mjaft të rrallë. Ndërveprimi ndërmjet atomeve të gazit ka karakterin e zmbrapsjes në distanca të afërta dhe të tërheqjes në ato të largëta. Kjo çon në AT> 0 në temperatura të larta dhe AT T = 15,3 K koeficient AT = -
3․10 -23 cm 3, dhe kur T= 510 K AT = 1,8 ․10 -23 cm 3. Për argonin AT = -
7,1․10 -23 cm 3 në T = 180 K dhe AT = 4,2․10 -23 cm 3 në T= 6000 K. Për gazet monatomike, llogariten vlerat e koeficientëve virialë, përfshirë të pestin, gjë që bën të mundur përshkrimin e sjelljes së gazeve në një gamë mjaft të gjerë densiteti (shih gjithashtu Gazet). Plazma. Një rast i veçantë i një gazi jo ideal është plazma - një gaz i jonizuar pjesërisht ose plotësisht, në të cilin ka elektrone dhe jone të lirë. Në një densitet mjaft të ulët, vetitë e plazmës janë afër atyre të një gazi ideal. Kur llogariten devijimet nga idealiteti, është thelbësore që elektronet dhe jonet të ndërveprojnë elektrostatikisht sipas ligjit të Kulombit. Forcat e Kulombit zvogëlohen ngadalë me distancën, dhe kjo çon në faktin se edhe për të llogaritur korrigjimin e parë të funksioneve termodinamike, është e nevojshme të merret parasysh ndërveprimi i jo dy, por një numri i madh grimcash menjëherë. meqenëse integrali në koeficientin e dytë virial (16), i cili përshkruan ndërveprimin e çiftit, divergjent nga distanca të gjata r midis grimcave. Në realitet, nën ndikimin e forcave të Kulombit, shpërndarja e joneve dhe elektroneve në plazmë ndryshon në atë mënyrë që fusha e secilës grimcë të kontrollohet, d.m.th., zvogëlohet me shpejtësi në një distancë të caktuar, e quajtur rrezja Debye. Për rastin më të thjeshtë të një plazme të përbërë nga elektrone dhe jone të vetëm të ngarkuar, rrezja Debye rD barazohet me: ku N numri i elektroneve eështë ngarkesa e një elektroni. Të gjitha grimcat brenda rrezes së Debye marrin pjesë në bashkëveprim njëkohësisht. Kjo rezulton që korrigjimi i parë i presionit të jetë proporcional me jo ( N/V) 2
si në një gaz të zakonshëm, por një shkallë më e ulët densiteti - ( N/V) 3/2
. Llogaritja sasiore bazohet në faktin se grimcat e mbetura shpërndahen në fushën e elektronit ose jonit të zgjedhur sipas shpërndarjes Boltzmann. Si rezultat, ekuacioni i gjendjes, duke marrë parasysh ndryshimin e parë, ka formën: (meqenëse numri i elektroneve është i barabartë me numrin e joneve, numri i përgjithshëm i grimcave është i barabartë me 2N). Korrigjime të të njëjtit lloj lindin edhe në funksionet termodinamike të elektroliteve në të cilat ka jone të lira të substancave të tretura. Lëngjet. Ndryshe nga një gaz, termat e ndërveprimit në ekuacionin e gjendjes për një lëng nuk janë të vogla. Prandaj, vetitë e një lëngu varen fuqimisht nga natyra specifike e ndërveprimit midis molekulave të tij. Në teorinë e lëngjeve, në përgjithësi nuk ka asnjë parametër të vogël që mund të përdoret për të thjeshtuar teorinë. Nuk është e mundur të merret ndonjë formula analitike për sasitë termodinamike të një lëngu. Një mënyrë për të kapërcyer këtë vështirësi është studimi i një sistemi të përbërë nga një numër relativisht i vogël grimcash - në rendin e disa mijërave. Në këtë rast, duke përdorur një kompjuter, mund të zgjidhen drejtpërdrejt ekuacionet e lëvizjes së grimcave dhe në këtë mënyrë të përcaktohen vlerat mesatare të të gjitha sasive që karakterizojnë sistemin pa supozime shtesë. Në këtë rast, është gjithashtu e mundur të studiohet procesi i afrimit të një sistemi të tillë në një gjendje ekuilibri. Është gjithashtu e mundur të gjendet integrali statistikor për një sistem të tillë të një numri të vogël grimcash duke llogaritur integralet në formulën kryesore për integralin statistikor në një kompjuter (zakonisht duke përdorur metodën Monte Carlo). Rezultatet e marra nga të dyja metodat janë, megjithatë, me saktësi të ulët kur aplikohen në lëngje reale për shkak të numrit të vogël të grimcave në sistem. Një mënyrë tjetër për të ndërtuar një teori të lëngut bazohet në përdorimin e funksioneve të shpërndarjes molekulare. Nëse integrojmë funksionin e shpërndarjes w të sistemit për sa i përket momentit të të gjitha grimcave dhe për sa i përket koordinatave të të gjitha grimcave, përveç njërës, fitohet funksioni i shpërndarjes hapësinore me një grimcë. f1(r). Nëse integrohemi w sipas momentit të të gjitha grimcave dhe sipas koordinatave të të gjitha grimcave, përveç dy, do të fitohet një funksion i shpërndarjes me dy grimca. f2(r1, r2), nga të gjitha grimcat përveç tre, është funksioni i shpërndarjes me tre grimca f 3(r 1 , r 2 , r 3 ,) etj. Funksioni i shpërndarjes me dy grimca është një sasi fizike e vëzhgueshme drejtpërdrejt - shpreh, për shembull, shpërndarjen elastike rrezet x dhe neutronet në lëng. Duke supozuar se funksioni i shpërndarjes i të gjithë sistemit është dhënë nga shpërndarja Gibbs (6), mund të merret një relacion integral që shpreh funksionin me dy grimca në terma të funksionit me tre grimca dhe potencialin e ndërveprimit midis grimcave. Në teorinë e lëngjeve, kjo lidhje e saktë plotësohet nga disa të përafërta që shprehin funksionin me tre grimca në funksion të funksionit me dy grimca (një funksion me një grimcë në një lëng homogjen reduktohet në një konstante). Rezultati është një ekuacion për funksionin me dy grimca, i cili zgjidhet numerikisht. Marrëdhëniet shtesë gjenden në bazë të konsideratave fizike të besueshme dhe janë të një natyre interpolimi, kështu që teoritë e bazuara në to mund të pretendojnë vetëm një përshkrim cilësor të vetive të një lëngu. Sidoqoftë, edhe një përshkrim i tillë cilësor është i rëndësishëm, pasi zbulon përgjithësinë e ligjeve të S. f. (shih gjithashtu Fluid). Gazrat e degjeneruara. Nëse temperatura e gazit ulet me një densitet konstant, fillojnë të shfaqen efektet kuanto-mekanike të lidhura me vetitë simetrike të funksioneve valore të një sistemi grimcash identike. Gazi "degjeneron" (shih Gazi i degjeneruar). Për grimcat me rrotullim gjysmë të plotë, funksioni i valës duhet të ndryshojë shenjën kur ndërrohet ndonjë palë grimcash. Kjo, në veçanti, çon në faktin se më shumë se një grimcë nuk mund të jenë në një gjendje kuantike (parimi Pauli). Numri i grimcave me rrotullim të plotë në një gjendje mund të jetë çdo, por pandryshueshmëria e funksionit të valës që kërkohet në këtë rast kur grimcat janë riorganizuar çon këtu në një ndryshim në vetitë statistikore të gazit. Grimcat me rrotullim gjysmë të plotë përshkruhen nga statistikat Fermi-Dirac; quhen Fermione. Fermionet përfshijnë, për shembull, elektronet, protonet, neutronet, atomet e deuteriumit, atomet e izotopit të lehtë të heliumit 3 He. Grimcat me spin me numër të plotë - Bozon - përshkruhen nga statistikat Bose-Einstein. Këto përfshijnë atomet e hidrogjenit, 4 atome He, kuantet e dritës - Fotonet. Lëreni numrin mesatar të grimcave të gazit për njësi vëllimi me moment të shtrirë në interval d 3 f, ka Në këtë formulë, ε = p 2 /2Mështë energjia e një grimce me momentum R, μ - potenciali kimik i përcaktuar nga kushti i qëndrueshmërisë së numrit të grimcave ( N) në sistem: Formula (19) shndërrohet në formulën e shpërndarjes Boltzmann (12) për Në rastin e fermioneve, siç duhet të jetë, np≤ 1. Kjo çon në faktin se grimcat e gazit fermion (gazi Fermi) dhe në T= 0 kanë momente jozero, pasi vetëm një grimcë mund të jetë në gjendje me momentum zero. Më saktësisht, në T= 0 për gazin Fermi np= 1 brenda një sipërfaqeje Fermi (Shih sipërfaqen e Fermit) - sferat në hapësirën e momentit me rreze Në një gaz Bose në T= 0 të gjitha grimcat janë në një gjendje me momentum zero. Në temperatura mjaft të ulëta në shtetin me R= 0 është fraksioni përfundimtar i të gjitha grimcave; këto grimca formojnë të ashtuquajturat. Kondensata Bose-Einstein. Grimcat e mbetura janë në gjendje me R≠ 0, dhe numri i tyre përcaktohet me formulën (19) me μ = 0. Në temperaturë Një rast i veçantë i aplikimit të statistikave Bose-Einstein është ekuilibri rrezatimi elektromagnetik, i cili mund të konsiderohet si një gaz i përbërë nga fotone. Energjia e një fotoni lidhet me momentin e tij nga relacioni Qelizë kristalore. Aplikimi i S. f. për llogaritjen e funksioneve termodinamike të rrjetës kristalore bazohet në faktin se atomet në rrjetë bëjnë dridhje të vogla rreth pozicioneve të tyre të ekuilibrit. Kjo na lejon të konsiderojmë rrjetën si një koleksion oshilatorësh harmonikë të çiftuar. Në një sistem të tillë, valët mund të përhapen, të karakterizuara nga ligji i tyre i shpërndarjes, d.m.th., varësia e frekuencës ω nga vektori i valës (Shih vektorin e valës) k. Në mekanikën kuantike, këto valë mund të konsiderohen si një grup i të ashtuquajturave. ngacmimet elementare, ose kuazigrimcat (Shih Kuazigrimcat) - Fonone me energji ħω
dhe pothuajse vrull ћk. Dallimi kryesor midis një kuazi-momenti dhe një momenti është se energjia e fononit është një funksion periodik i kuazi-momentit me një periudhë të barabartë në rendin e madhësisë me a, konstanta e rrjetës. Funksioni i shpërndarjes së fononeve mbi kuazimomenta jepet nga formula e shpërndarjes Bose-Einstein (19) me μ = 0. Në këtë rast, ε=ħω.
Kështu, njohja e varësisë ω( k) lejon llogaritjen e kapacitetit të nxehtësisë së rrjetës. Kjo varësi mund të përcaktohet nga eksperimentet mbi shpërndarjen joelastike të neutroneve në një kristal (shih Neutronografinë) ose të llogaritet teorikisht duke vendosur vlerat e "konstantave të forcës" që përcaktojnë ndërveprimin e atomeve në një grilë. Në temperatura të ulëta, vetëm fononet me frekuencë të ulët janë domethënëse, që korrespondojnë me kuantet e valëve të zakonshme të zërit, për të cilat lidhja ω me k lineare. Kjo çon në faktin se kapaciteti i nxehtësisë i rrjetës kristalore është proporcional me T3. Në temperatura të larta, mund të përdoret ligji i shpërndarjes së barabartë të energjisë mbi shkallët e lirisë, në mënyrë që kapaciteti i nxehtësisë të mos varet nga temperatura dhe të jetë i barabartë me 3 Nk, ku Nështë numri i atomeve në kristal. Metalet. Në metale, elektronet përçuese gjithashtu kontribuojnë në funksionet termodinamike. Gjendja e një elektroni në një metal karakterizohet nga një kuazi-moment, dhe, meqë elektronet i binden statistikave Fermi - Dirac, shpërndarja e tyre mbi kuazimomenta jepet me formulën (19). Prandaj, kapaciteti i nxehtësisë i gazit elektronik dhe, rrjedhimisht, i të gjithë metalit në temperatura mjaft të ulëta është proporcional me T. Dallimi nga gazi Fermi i grimcave të lira është se sipërfaqja Fermi, rreth së cilës janë përqendruar elektronet "aktive", nuk është më një sferë, por është një sipërfaqe komplekse në hapësirën kuazi-momentale. Forma e sipërfaqes së Fermit, si dhe varësia e energjisë nga kuazi-momenti pranë kësaj sipërfaqeje, mund të përcaktohet në mënyrë eksperimentale, kryesisht duke studiuar vetitë magnetike të metaleve, dhe gjithashtu mund të llogaritet teorikisht duke përdorur të ashtuquajturat. modeli kuazipotencial. Në superpërçuesit (shih Superpërçueshmëria), gjendjet e ngacmuara të një elektroni ndahen nga sipërfaqja e Fermit nga një hendek me gjerësi të fundme, që çon në një varësi eksponenciale të kapacitetit të nxehtësisë së elektronit nga temperatura. Në substancat ferromagnetike dhe antiferromagnetike, luhatjet në momentet magnetike kontribuojnë gjithashtu në funksionet termodinamike - Valët spin. Në dielektrikë dhe gjysmëpërçues T= 0 nuk ka elektrone të lira. Në temperatura të fundme, në to shfaqen kuazigrimca të ngarkuara - elektrone me ngarkesë negative dhe (në numër të barabartë) "vrima" me ngarkesë pozitive, Një elektron dhe një vrimë mund të formojnë një gjendje të lidhur - një kuazigrimcë e quajtur eksiton. Dr. Një lloj eksitoni është një gjendje e ngacmuar e një atomi dielektrik që lëviz në një rrjetë kristali. Metodat e teorisë kuantike të fushës në S. f. Në zgjidhjen e problemeve të fizikës kuantike, kryesisht në studimin e vetive të lëngjeve kuantike dhe të elektroneve në metale dhe magnet, metodat e teorisë së fushës kuantike të paraqitura në fizikën kuantike kanë një rëndësi të madhe. relativisht kohët e fundit. Rolin kryesor në këto metoda e luan funksioni G Green i një sistemi makroskopik, i cili është i ngjashëm me funksionin e Green-it në teorinë kuantike të fushës. Varet nga energjia ε dhe momenti R, ligji i dispersionit të kuazi grimcave ε( R) përcaktohet nga ekuacioni: d.m.th., energjia e një quasigrimce përcaktohet nga poli i funksionit të Gjelbër. Ekziston një metodë e rregullt për llogaritjen e funksioneve të Green-it si një seri në fuqitë e energjisë së ndërveprimit midis grimcave. Çdo term i kësaj serie përmban integrale të shumta mbi energjitë dhe momentet e funksioneve të Green-it të grimcave jo bashkëvepruese dhe mund të paraqitet grafikisht në formën e diagrameve të ngjashme me diagramet e Feynman-it (Shih diagramet e Feynman-it) në elektrodinamikën kuantike. Secila prej këtyre diagrameve ka një specifikë kuptimi fizik, e cila bën të mundur ndarjen në një seri të pafundme të termave përgjegjës për fenomenin e interesit dhe përmbledhjen e tyre. Ekziston edhe një teknikë diagrami për llogaritjen e temperaturës Funksionet e Green-it, e cila bën të mundur llogaritjen e sasive termodinamike drejtpërdrejt, pa futur kuazigrimca. Metodat e përmendura në seksionin për lëngjet, të cilat përdorin funksionet e shpërndarjes me shumë grimca të kuazigrimcave, janë në shumë aspekte të afërta me metodat e teorisë kuantike të fushës. Përdorimi i këtyre funksioneve bazohet gjithmonë në një "shkëputje" të përafërt - shprehja e një funksioni mbi rendit të lartë përmes funksioneve të ulët. Tranzicionet fazore. Me një ndryshim të vazhdueshëm në parametrat e jashtëm (për shembull, presioni ose temperatura), vetitë e sistemit mund të ndryshojnë papritur për disa vlera të parametrave, d.m.th., ndodh një tranzicion fazor. Tranzicionet fazore ndahen në tranzicione të llojit të parë, të shoqëruara nga lëshimi i nxehtësisë latente të tranzicionit dhe një kërcim në vëllim (këto përfshijnë, për shembull, shkrirjen), dhe tranzicione të llojit të dytë, në të cilat nuk ka nxehtësi latente. dhe një kërcim në vëllim (për shembull, një kalim në një gjendje superpërcjellëse). Teoria statistikore e tranzicioneve fazore përbën një zonë të rëndësishme, por ende larg nga kompletimi i S. f. Vështirësia më e madhe për hulumtim teorik përfaqësojnë vetitë e materies pranë vijës së një tranzicioni fazor të rendit të dytë dhe afër pikës kritike të një tranzicioni fazor të rendit të parë. Nga pikëpamja matematikore, funksionet termodinamike të sistemit këtu kanë singularitete. Pranë këtyre pikave ndodhin fenomene të veçanta Kritike. Në të njëjtën kohë, këtu luhatjet rriten në mënyrë anormale dhe metodat e përafërta të S. f. rezultojnë të pazbatueshme. Prandaj, një rol të rëndësishëm luhet nga një numër i vogël modelesh saktësisht të zgjidhshme në të cilat ka tranzicione (për shembull, i ashtuquajturi model Ising). luhatjet. Në zemër të S. f. qëndron fakti se sasive fizike, që karakterizojnë trupat makroskopikë, janë të barabartë me vlerat mesatare të tyre me saktësi të lartë. Kjo barazi është ende e përafërt, në fakt, të gjitha sasitë përjetojnë devijime të vogla të rastësishme nga vlerat mesatare - luhatje. Ekzistenca e luhatjeve është e një rëndësie të madhe themelore, sepse vërteton drejtpërdrejt natyrën statistikore të rregullsive termodinamike. Përveç kësaj, luhatjet luajnë rolin e ndërhyrjes së zhurmës matjet fizike dhe duke kufizuar saktësinë e tyre. Luhatje me disa vlera X rreth mesatares së saj x̅ karakterizohen nga luhatje mesatare katrore Në shumicën dërrmuese të rasteve, vlera X përjeton luhatje të rendit S është proporcional me e S/k. Kjo çon në formulën Për shembull, katrorët mesatarë të luhatjeve në vëllimin e trupit dhe temperaturën janë: Nga këto formula mund të shihet se luhatjet relative të vëllimit dhe luhatjet e temperaturës janë në përpjesëtim të zhdrejtë me N - numrin e grimcave në trup. Kjo siguron vogëlsinë e luhatjeve për trupat makroskopikë. Marrëdhënia midis luhatjeve të sasive të ndryshme x i, x k karakterizohet nga funksioni x i dhe x k atëherë janë statistikisht të pavarura Nën x i dhe x k mund të kuptohen edhe vlerat e së njëjtës sasi, për shembull dendësia, në pika të ndryshme të hapësirës. Atëherë ky funksion ka kuptimin e funksionit të korrelacionit hapësinor. Ndërsa distanca midis pikave rritet, funksioni i korrelacionit tenton në zero (zakonisht në mënyrë eksponenciale), sepse luhatjet në pika të largëta të hapësirës ndodhin në mënyrë të pavarur. Distanca në të cilën ky funksion zvogëlohet ndjeshëm quhet rrezja e korrelacionit. Sjellja kohore e luhatjeve dhe shpërndarja spektrale e zhurmës së luhatjeve përshkruhen nga funksioni i korrelacionit kohor φ( t), në të cilin mesatarizohen luhatjet e sasisë së marrë në kohë të ndryshme t: Një rol të rëndësishëm në teorinë e luhatjeve luajnë të ashtuquajturat Teorema luhatje-shpërndarje, e cila lidh luhatjet në një sistem me një ndryshim në vetitë e tij nën ndikimin e ndikimeve të caktuara të jashtme. Lidhja më e thjeshtë e këtij lloji mund të merret duke marrë parasysh luhatjet e oshilatorit harmonik a me energjinë potenciale dhe luhatje X lidhet realisht me turbimin nën ndikimin e forcës f. Në rastin e përgjithshëm, teorema luhatje-shpërndarje është e zbatueshme nëse për X ekziston një "forcë e përgjithësuar" f, i cili përfshihet në operatorin energjetik të sistemit (Hamiltonian; shih Mekanikë kuantike) si term x. Ndezja e energjisë f do të çojë në një ndryshim në vlerën mesatare x̅ nga δ x̅, dhe nëse f varet nga koha e-i wt, ky ndryshim mund të shkruhet si: madhësia komplekse α(ω) quhet ndjeshmëri e përgjithësuar e sistemit. Teorema thotë se transformimi Furier i funksionit të korrelacionit S. f. proceset jo ekuilibër. Kinetika fizike, dega e fizikës fizike që studion proceset në sisteme në gjendje jo ekuilibër, po merr një rëndësi gjithnjë e më të madhe. Këtu ka dy pyetje të mundshme. Së pari, mund ta konsiderojmë sistemin në një gjendje jo-ekuilibri dhe të ndjekim kalimin e tij në gjendjen e ekuilibrit. Së dyti, ne mund të konsiderojmë një sistem, gjendja jo ekuilibër e të cilit ruhet kushtet e jashtme, për shembull, rrjedh një trup në të cilin është dhënë një gradient i temperaturës elektricitet etj., ose një trup i vendosur në një fushë të jashtme të ndryshueshme. Nëse devijimi nga ekuilibri është i vogël, vetitë joekuilibërore të sistemit përshkruhen nga të ashtuquajturat. koeficientët kinetikë. Shembuj të koeficientëve të tillë janë koeficientët e viskozitetit (Shih![]()
![]()
![]()

![]()
![]()
![]() p dhe q, është e nevojshme të pjesëtohet integrali me numrin e permutacioneve nga N grimcat, d.m.th N! Kufiri klasik përfundimtar për funksionin e ndarjes është:
p dhe q, është e nevojshme të pjesëtohet integrali me numrin e permutacioneve nga N grimcat, d.m.th N! Kufiri klasik përfundimtar për funksionin e ndarjes është:![]()
![]()
![]()
![]()
![]()

![]() 3
në përputhje me numrin e qelizave [me një vëllim të atomeve të gazit N është i barabartë me:
3
në përputhje me numrin e qelizave [me një vëllim të atomeve të gazit N është i barabartë me:
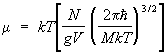

![]()
![]()
![]() n p është numri i grimcave në një qelizë të hapësirës fazore ( g = 2J+ 1, ku Jështë rrotullimi i grimcave). Pastaj nga shpërndarja Gibbs rrjedh se për gazet ideale të fermioneve (shenja e sipërme) dhe bozoneve (shenja e poshtme):
n p është numri i grimcave në një qelizë të hapësirës fazore ( g = 2J+ 1, ku Jështë rrotullimi i grimcave). Pastaj nga shpërndarja Gibbs rrjedh se për gazet ideale të fermioneve (shenja e sipërme) dhe bozoneve (shenja e poshtme):![]()
![]()
![]() Valët de Broglie të grimcave që lëvizin me shpejtësi termike bëhen të rendit të distancës mesatare ndërmjet tyre. Kështu, degjenerimi ndikon në temperatura sa më e ulët, aq më e ulët është dendësia e numrit të grimcave në gaz (dhe sa më e madhe të jetë masa e grimcave M).
Valët de Broglie të grimcave që lëvizin me shpejtësi termike bëhen të rendit të distancës mesatare ndërmjet tyre. Kështu, degjenerimi ndikon në temperatura sa më e ulët, aq më e ulët është dendësia e numrit të grimcave në gaz (dhe sa më e madhe të jetë masa e grimcave M).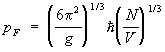 n p = 0. Në temperatura të fundme por të ulëta np ndryshon nga 1 brenda sferës në zero jashtë sferës gradualisht, dhe gjerësia e rajonit të tranzicionit është e rendit MkT/p F. Vlera np për një gaz Fermi në funksion të energjisë ε është paraqitur skematikisht në fig. 2 (ε 0 = p F 2 /2M). Kur ndryshon temperatura e gazit, gjendja e grimcave ndryshon vetëm në këtë shtresë kalimtare, dhe kapaciteti i nxehtësisë së gazit Fermi në temperatura të ulëta është në proporcion me T dhe është e barabartë me:
n p = 0. Në temperatura të fundme por të ulëta np ndryshon nga 1 brenda sferës në zero jashtë sferës gradualisht, dhe gjerësia e rajonit të tranzicionit është e rendit MkT/p F. Vlera np për një gaz Fermi në funksion të energjisë ε është paraqitur skematikisht në fig. 2 (ε 0 = p F 2 /2M). Kur ndryshon temperatura e gazit, gjendja e grimcave ndryshon vetëm në këtë shtresë kalimtare, dhe kapaciteti i nxehtësisë së gazit Fermi në temperatura të ulëta është në proporcion me T dhe është e barabartë me:![]()
![]() Tranzicioni i fazës (shih më poshtë). Pjesa e grimcave me vrull zero zhduket. Kondensimi Bose-Einstein zhduket. Kurba e varësisë së kapacitetit të nxehtësisë nga temperatura ka në pikë T c thyej. Shpërndarja e momentit të grimcave në T > T s jepet me formulën (19) dhe μ T > T s) janë paraqitur në figurën 3.
Tranzicioni i fazës (shih më poshtë). Pjesa e grimcave me vrull zero zhduket. Kondensimi Bose-Einstein zhduket. Kurba e varësisë së kapacitetit të nxehtësisë nga temperatura ka në pikë T c thyej. Shpërndarja e momentit të grimcave në T > T s jepet me formulën (19) dhe μ T > T s) janë paraqitur në figurën 3.![]() c është shpejtësia e dritës në vakum. Numri i fotoneve nuk është vlerën e dhënë, dhe vetë përcaktohet nga gjendja e ekuilibrit termodinamik; prandaj, shpërndarja e momentit të tyre jepet me formulën (19) me μ = 0 (për më tepër, ε = rs). Shpërndarja e energjisë në spektrin e emetimit fitohet duke shumëzuar numrin e fotoneve me energjinë ε, në mënyrë që dendësia e energjisë në diapazonin e frekuencës dω është e barabartë me n p merret në ε=ħω
. Se. fitohet formula e Plankut për spektrin e rrezatimit të ekuilibrit (i zi) (shih ligjin e rrezatimit të Plankut).
c është shpejtësia e dritës në vakum. Numri i fotoneve nuk është vlerën e dhënë, dhe vetë përcaktohet nga gjendja e ekuilibrit termodinamik; prandaj, shpërndarja e momentit të tyre jepet me formulën (19) me μ = 0 (për më tepër, ε = rs). Shpërndarja e energjisë në spektrin e emetimit fitohet duke shumëzuar numrin e fotoneve me energjinë ε, në mënyrë që dendësia e energjisë në diapazonin e frekuencës dω është e barabartë me n p merret në ε=ħω
. Se. fitohet formula e Plankut për spektrin e rrezatimit të ekuilibrit (i zi) (shih ligjin e rrezatimit të Plankut).![]()

![]()
![]()
![]() m - masë oshilator, ω 0
është frekuenca e vet. Llogaritja duke përdorur formulën (22) jep: f, vlerën mesatare x̅ zhvendosur nga shuma
m - masë oshilator, ω 0
është frekuenca e vet. Llogaritja duke përdorur formulën (22) jep: f, vlerën mesatare x̅ zhvendosur nga shuma![]()
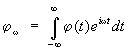
![]()






