Përkufizimi i logaritmit

Logaritmi i numrit b në bazën a është eksponenti në të cilin duhet të ngrini a për të marrë b.

Numri e në matematikë, është zakon të shënohet kufiri në të cilin priret shprehja

Numri eështë numër irracional - një numër i pakrahasueshëm me një, ai nuk mund të shprehet saktësisht as në tërësi as si thyesë racionale numri.

Letër e- shkronja e parë fjalë latine exonere- për të lëvduar, prandaj emri në matematikë eksponenciale- funksioni eksponencial.

Numri e përdoret gjerësisht në matematikë dhe në të gjitha shkencat, në një mënyrë ose në një tjetër duke përdorur llogaritjet matematikore për nevojat e tyre.

Logaritmet. Vetitë e logaritmeve

Përkufizimi: Logaritmi bazë i një numri pozitiv b është eksponenti c në të cilin duhet të rritet numri a për të marrë numrin b.

Identiteti bazë logaritmik:

7) Formula për kalimin në një bazë të re:

lna = log e a, e ≈ 2,718…

Detyra dhe teste me temën “Logaritmet. Vetitë e logaritmeve »

  • Logaritmet - Tema të rëndësishme për përsëritjen e provimit në matematikë

Për të përfunduar me sukses detyrat në këtë temë, duhet të dini përkufizimin e logaritmit, vetitë e logaritmeve, identitetin bazë logaritmik, përkufizimet e logaritmeve dhjetore dhe natyrore. Llojet kryesore të detyrave në këtë temë janë detyrat për llogaritjen dhe konvertimin e shprehjeve logaritmike. Le të shqyrtojmë zgjidhjen e tyre në shembujt e mëposhtëm.

Zgjidhja: Duke përdorur vetitë e logaritmeve, marrim

Zgjidhja: duke përdorur vetitë e shkallës, marrim

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Vetitë e logaritmeve, formulimet dhe vërtetimet.

Logaritmet kanë një sërë veçorish karakteristike. Në këtë artikull, ne do të analizojmë ato kryesore vetitë e logaritmeve. Këtu japim formulimet e tyre, shkruajmë vetitë e logaritmeve në formën e formulave, tregojmë shembuj të zbatimit të tyre dhe gjithashtu japim prova të vetive të logaritmeve.

Navigimi i faqes.

Vetitë themelore të logaritmeve, formula

Për lehtësinë e kujtimit dhe përdorimit, ne paraqesim vetitë themelore të logaritmeve si një listë formulash. Në pjesën tjetër, ne japim formulimet e tyre, provat, shembujt e përdorimit dhe shpjegimet e nevojshme.

  • Vetia e regjistrit të njësisë: log a 1=0 për çdo a>0, a≠1.
  • Logaritmi i një numri të barabartë me bazën: log a a=1 për a>0 , a≠1 .
  • Vetia e logaritmit të shkallës bazë: log a a p =p , ku a>0 , a≠1 dhe p është çdo numër real.
  • Logaritmi i prodhimit të dy numrave pozitivë: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
    dhe vetia e logaritmit të prodhimit të n numrave pozitivë: log a (x 1 x 2 ... x n) \u003d log a x 1 + log a x 2 + ... + log a x n, a>0, a≠1 , x 1 >0, x 2 >0, …, xn >0 .
  • Vetia private e logaritmit: , ku a>0, a≠1, x>0, y>0.
  • Logaritmi i fuqisë së një numri: log a b p =p log a |b| , ku a>0, a≠1, b dhe p janë numra të tillë që shkalla e b p ka kuptim dhe b p >0.
  • Pasoja: , ku a>0 , a≠1 , n është një numër natyror më i madh se një, b>0 .
  • Përfundimi 1: , a>0, a≠1, b>0, b≠1.
  • Pasoja 2: , a>0 , a≠1 , b>0 , p dhe q janë numra realë, q≠0 , në veçanti, për b=a kemi .

    • Deklarata dhe prova të pronave

    Kalojmë në formulimin dhe vërtetimin e vetive të regjistruara të logaritmeve. Të gjitha vetitë e logaritmeve vërtetohen në bazë të përcaktimit të logaritmit dhe identitetit bazë logaritmik që rrjedh prej tij, si dhe vetive të shkallës.

    Le të fillojmë me vetitë e logaritmit të unitetit. Formulimi i tij është si më poshtë: logaritmi i unitetit është i barabartë me zero, d.m.th. log a 1=0 për çdo a>0, a≠1. Vërtetimi është i drejtpërdrejtë: meqenëse a 0 =1 për çdo a që plotëson kushtet e mësipërme a>0 dhe a≠1, atëherë logi i vërtetuar i barazisë a 1=0 rrjedh menjëherë nga përkufizimi i logaritmit.

    Le të japim shembuj të zbatimit të vetive të shqyrtuara: log 3 1=0 , lg1=0 dhe .

    Le të kalojmë në pronën tjetër: logaritmi i një numri të barabartë me bazën është i barabartë me një, kjo eshte, log a a=1 për a>0, a≠1. Në të vërtetë, meqenëse a 1 =a për çdo a , atëherë sipas përkufizimit të logaritmit log a a=1 .

    Shembuj të përdorimit të kësaj vetie të logaritmeve janë log 5 5=1 , log 5.6 5.6 dhe lne=1 .

    Logaritmi i fuqisë së një numri të barabartë me bazën e logaritmit është i barabartë me eksponentin. Kjo veti e logaritmit korrespondon me një formulë të formës log a a p =p, ku a>0 , a≠1 dhe p është çdo numër real. Kjo veti rrjedh drejtpërdrejt nga përkufizimi i logaritmit. Vini re se ju lejon të specifikoni menjëherë vlerën e logaritmit, nëse është e mundur të përfaqësoni numrin nën shenjën e logaritmit si një shkallë bazë, ne do të flasim më shumë për këtë në artikullin për llogaritjen e logaritmit.

    Për shembull, log 2 2 7 =7 , log10 -4 =-4 dhe .

    Logaritmi i prodhimit të dy numrave pozitivë x dhe y është i barabartë me prodhimin e logaritmeve të këtyre numrave: log a (x y)=log a x+log a y, a>0 , a≠1 . Le të vërtetojmë vetinë e logaritmit të produktit. Për shkak të vetive të shkallës a log a x + log a y =a log a x a log a y , dhe meqenëse sipas identitetit logaritmik kryesor një log a x =x dhe një log a y =y , atëherë një log a x a log a y =x y . Kështu, a log a x+log a y =x y , nga ku barazia e kërkuar pasohet nga përkufizimi i logaritmit.

    Le të tregojmë shembuj të përdorimit të vetive të logaritmit të produktit: log 5 (2 3)=log 5 2+log 5 3 dhe .

    Vetia e logaritmit të produktit mund të përgjithësohet në prodhimin e një numri të fundëm n të numrave pozitivë x 1 , x 2 , …, x n si log a (x 1 x 2 ... x n)= log a x 1 +log a x 2 +...+log a x n. Kjo barazi mund të vërtetohet lehtësisht me metodën e induksionit matematik.

    Për shembull, logaritmi natyror i një produkti mund të zëvendësohet nga shuma e tre logaritmeve natyrore të numrave 4 , e , dhe .

    Logaritmi i herësit të dy numrave pozitivë x dhe y është e barabartë me diferencën ndërmjet logaritmeve të këtyre numrave. Vetia e logaritmit koeficient korrespondon me një formulë të formës , ku a>0, a≠1, x dhe y janë disa numra pozitivë. Vlefshmëria e kësaj formule vërtetohet si formula për logaritmin e produktit: pasi , pastaj me përcaktimin e logaritmit .

    Këtu është një shembull i përdorimit të kësaj vetie të logaritmit: .

    Le të kalojmë në veti e logaritmit të shkallës. Logaritmi i një shkalle është i barabartë me prodhimin e eksponentit dhe logaritmit të modulit të bazës së kësaj shkalle. Ne e shkruajmë këtë veti të logaritmit të shkallës në formën e një formule: log a b p =p log a |b|, ku a>0, a≠1, b dhe p janë numra të tillë që shkalla e b p ka kuptim dhe b p >0.

    Së pari e vërtetojmë këtë veti për b pozitive. Identiteti bazë logaritmik na lejon të paraqesim numrin b si një log a b , pastaj b p =(a log a b) p , dhe shprehja që rezulton, për shkak të vetive të fuqisë, është e barabartë me një p log a b . Pra, arrijmë te barazia b p =a p log a b , nga e cila, me përkufizimin e logaritmit, arrijmë në përfundimin se log a b p =p log a b .

    Mbetet të vërtetohet kjo veti për b negative. Këtu vërejmë se shprehja log a b p për negativin b ka kuptim vetëm për eksponentët çift p (pasi vlera e shkallës b p duhet të jetë më e madhe se zero, përndryshe logaritmi nuk do të ketë kuptim), dhe në këtë rast b p =|b| fq . Atëherë b p =|b| p =(a log a |b|) p =a p log a |b| , prej nga log a b p =p log a |b| .

    Për shembull, dhe ln(-3) 4 =4 ln|-3|=4 ln3 .

    Kjo rrjedh nga prona e mëparshme veti e logaritmit nga rrënja: logaritmi i rrënjës së shkallës së n-të është i barabartë me prodhimin e thyesës 1/n dhe logaritmit të shprehjes rrënjësore, pra ku a>0, a≠1, n është një numër natyror më i madh se një, b>0.

    Vërtetimi bazohet në një barazi (shih përkufizimin e eksponentit me një eksponent thyesor), i cili është i vlefshëm për çdo b pozitiv, dhe vetinë e logaritmit të shkallës: .

    Këtu është një shembull i përdorimit të kësaj prone: .

    Tani le të provojmë formula e konvertimit në bazën e re të logaritmit lloj . Për ta bërë këtë, mjafton të vërtetohet vlefshmëria e logit të barazisë c b=log a b log c a . Identiteti bazë logaritmik na lejon të paraqesim numrin b si log a b , pastaj log c b=log c a log a b . Mbetet të përdoret vetia e logaritmit të shkallës: log c a log a b = log a b log c a . Kështu, vërtetohet barazia log c b=log a b log c a, që do të thotë se vërtetohet edhe formula e kalimit në një bazë të re të logaritmit. .

    Le të tregojmë disa shembuj të zbatimit të kësaj vetie të logaritmeve: dhe .

    Formula për kalimin në një bazë të re ju lejon të kaloni në punën me logaritme që kanë një bazë "të përshtatshme". Për shembull, mund të përdoret për të kaluar në logaritme natyrore ose dhjetore në mënyrë që të mund të llogarisni vlerën e logaritmit nga një tabelë logaritmesh. Formula për kalimin në një bazë të re të logaritmit gjithashtu lejon në disa raste gjetjen e vlerës së një logaritmi të caktuar, kur dihen vlerat e disa logaritmeve me baza të tjera.

    Përdoret shpesh rast i veçantë formulat për kalimin në një bazë të re të logaritmit për c=b të formës . Kjo tregon se log a b dhe log b a janë numra reciprokisht të anasjelltë. Për shembull, .

    Shpesh përdoret edhe formula, e cila është e përshtatshme për gjetjen e vlerave të logaritmit. Për të konfirmuar fjalët tona, ne do të tregojmë se si llogaritet vlera e logaritmit të formularit duke përdorur atë. Ne kemi . Për të vërtetuar formulën, mjafton të përdoret formula e kalimit në bazën e re të logaritmit a: .

    Mbetet për të vërtetuar vetitë e krahasimit të logaritmeve.

    Le të përdorim metodën e kundërt. Supozoni se për një 1 >1 , a 2 >1 dhe a 1 2 dhe për 0 1 log a 1 b≤log a 2 b është e vërtetë. Nga vetitë e logaritmeve, këto pabarazi mund të rishkruhen si dhe përkatësisht, dhe prej tyre rrjedh se përkatësisht log b a 1 ≤log b a 2 dhe log b a 1 ≥log b a 2. Pastaj, sipas vetive të fuqive me baza të njëjta, duhet të plotësohen barazitë b log b a 1 ≥b log b a 2 dhe b log b a 1 ≥b log b a 2, pra a 1 ≥a 2 . Kështu, kemi arritur në një kontradiktë me kushtin a 1 2 . Kjo plotëson provën.

    Vetitë themelore të logaritmeve

    • Materialet për mësimin
    • Shkarkoni të gjitha formulat

      • Logaritmet, si çdo numër, mund të shtohen, zbriten dhe konvertohen në çdo mënyrë të mundshme. Por meqenëse logaritmet nuk janë numra krejt të zakonshëm, këtu ka rregulla, të cilat thirren vetitë themelore.

      Këto rregulla duhet të dihen - asnjë problem serioz logaritmik nuk mund të zgjidhet pa to. Për më tepër, ka shumë pak prej tyre - gjithçka mund të mësohet brenda një dite. Pra, le të fillojmë.

      Mbledhja dhe zbritja e logaritmeve

      Konsideroni dy logaritme me të njëjtën bazë: log a x dhe log a y . Pastaj ato mund të shtohen dhe zbriten, dhe:

      Pra, shuma e logaritmeve është e barabartë me logaritmin e produktit, dhe ndryshimi është logaritmi i herësit. Ju lutemi vini re: pika kryesore këtu është - baza të njëjta. Nëse bazat janë të ndryshme, këto rregulla nuk funksionojnë!

      Këto formula do të ndihmojnë në llogaritjen e shprehjes logaritmike edhe kur pjesët e saj individuale nuk merren parasysh (shihni mësimin "Çfarë është logaritmi"). Hidhini një sy shembujve - dhe shikoni:

      Një detyrë. Gjeni vlerën e shprehjes: log 6 4 + log 6 9.

      Meqenëse bazat e logaritmeve janë të njëjta, ne përdorim formulën e shumës:
      log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

      Një detyrë. Gjeni vlerën e shprehjes: log 2 48 − log 2 3.

      Bazat janë të njëjta, ne përdorim formulën e ndryshimit:
      log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

      Një detyrë. Gjeni vlerën e shprehjes: log 3 135 − log 3 5.

      Përsëri, bazat janë të njëjta, kështu që kemi:
      log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

      Siç mund ta shihni, shprehjet origjinale përbëhen nga logaritme "të këqija", të cilat nuk konsiderohen veçmas. Por pas transformimeve dalin numra mjaft normalë. Bazuar në këtë fakt, shumë letrat e testimit. Po, ai kontroll - shprehje të ngjashme me gjithë seriozitetin (nganjëherë - praktikisht pa ndryshime) ofrohen në provim.

      Heqja e eksponentit nga logaritmi

      Tani le ta komplikojmë pak detyrën. Po sikur të ketë një shkallë në bazën ose argumentin e logaritmit? Atëherë eksponenti i kësaj shkalle mund të hiqet nga shenja e logaritmit sipas rregullave të mëposhtme:

    • log a x n = n log a x;

      • Është e lehtë të shihet se rregulli i fundit ndjek dy të parat e tyre. Por është më mirë ta mbani mend gjithsesi - në disa raste do të zvogëlojë ndjeshëm sasinë e llogaritjeve.

      Natyrisht, të gjitha këto rregulla kanë kuptim nëse respektohet logaritmi ODZ: a > 0, a ≠ 1, x > 0. Dhe një gjë tjetër: mësoni të zbatoni të gjitha formulat jo vetëm nga e majta në të djathtë, por edhe anasjelltas, d.m.th. mund të futni numrat para shenjës së logaritmit në vetë logaritmin. Kjo është ajo që kërkohet më shpesh.

      Një detyrë. Gjeni vlerën e shprehjes: log 7 49 6 .

      Le të heqim qafe shkallën në argument sipas formulës së parë:
      log 7 49 6 = 6 log 7 49 = 6 2 = 12

      Një detyrë. Gjeni vlerën e shprehjes:

      [Titulli i figurës]

      Vini re se emëruesi është një logaritëm baza dhe argumenti i të cilit janë fuqi të sakta: 16 = 2 4 ; 49 = 72. Ne kemi:

      [Titulli i figurës]

      Mendoj se shembulli i fundit ka nevojë për sqarim. Ku kanë shkuar logaritmet? Deri në momentin e fundit, ne punojmë vetëm me emëruesin. Ata paraqitën bazën dhe argumentin e logaritmit që qëndron atje në formën e shkallëve dhe nxorën treguesit - morën një fraksion "trekatësh".

      Tani le të shohim fraksionin kryesor. Numëruesi dhe emëruesi kanë të njëjtin numër: log 2 7. Meqenëse log 2 7 ≠ 0, ne mund ta zvogëlojmë thyesën - 2/4 do të mbetet në emërues. Sipas rregullave të aritmetikës, katër mund të transferohen në numërues, gjë që u bë. Rezultati është përgjigja: 2.

      Kalimi në një themel të ri

      Duke folur për rregullat e mbledhjes dhe zbritjes së logaritmeve, theksova veçanërisht se ato punojnë vetëm me të njëjtat baza. Po sikur bazat të jenë të ndryshme? Po sikur të mos jenë fuqi të sakta të të njëjtit numër?

      Formulat për kalimin në një bazë të re vijnë në shpëtim. Ne i formulojmë ato në formën e një teoreme:

      Le të jepet logaritmi log a x. Atëherë për çdo numër c të tillë që c > 0 dhe c ≠ 1, barazia është e vërtetë:

      [Titulli i figurës]

      Në veçanti, nëse vendosim c = x, marrim:

      [Titulli i figurës]

      Nga formula e dytë rezulton se është e mundur të ndërrohet baza dhe argumenti i logaritmit, por në këtë rast e gjithë shprehja është "përmbysur", d.m.th. logaritmi është në emërues.

      Këto formula rrallë gjenden në shprehjet e zakonshme numerike. Është e mundur të vlerësohet se sa të përshtatshëm janë vetëm kur vendosni ekuacionet logaritmike dhe pabarazitë.

      Megjithatë, ka detyra që nuk mund të zgjidhen fare, përveçse duke kaluar në një themel të ri. Le të shqyrtojmë disa nga këto:

      Një detyrë. Gjeni vlerën e shprehjes: log 5 16 log 2 25.

      Vini re se argumentet e të dy logaritmave janë eksponentë të saktë. Le të nxjerrim treguesit: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

      Tani le të kthejmë logaritmin e dytë:

      [Titulli i figurës]

      Meqenëse produkti nuk ndryshon nga ndërrimi i faktorëve, ne shumëzuam me qetësi katër dhe dy, dhe më pas kuptuam logaritmet.

      Një detyrë. Gjeni vlerën e shprehjes: log 9 100 lg 3.

      Baza dhe argumenti i logaritmit të parë janë fuqi të sakta. Le ta shkruajmë dhe të heqim qafe treguesit:

      [Titulli i figurës]

      Tani le të heqim qafe logaritmin dhjetor duke kaluar në një bazë të re:

      [Titulli i figurës]

      Identiteti bazë logaritmik

      Shpesh në procesin e zgjidhjes kërkohet të paraqitet një numër si logaritëm në një bazë të caktuar. Në këtë rast, formulat do të na ndihmojnë:

    1. n = log a a n

    2. Në rastin e parë, numri n bëhet eksponent në argument. Numri n mund të jetë absolutisht çdo gjë, sepse është vetëm vlera e logaritmit.

      Formula e dytë është në fakt një përkufizim i parafrazuar. Quhet identiteti bazë logaritmik.

      Në të vërtetë, çfarë do të ndodhë nëse numri b ngrihet në një fuqi të tillë që numri b në këtë fuqi të japë numrin a? Është e drejtë: ky është i njëjti numër a . Lexojeni përsëri këtë paragraf me kujdes - shumë njerëz "varen" në të.

      Ashtu si formulat e reja të konvertimit të bazës, identiteti logaritmik bazë është ndonjëherë e vetmja zgjidhje e mundshme.

      [Titulli i figurës]

      Vini re se log 25 64 = log 5 8 - thjesht merrni katrorin e bazës dhe argumentin e logaritmit. Duke pasur parasysh rregullat për shumëzimin e fuqive me të njëjtën bazë, marrim:

      [Titulli i figurës]

      Nëse dikush nuk është në dijeni, kjo ishte një detyrë e vërtetë nga Provimi i Unifikuar i Shtetit 🙂

      Njësia logaritmike dhe zero logaritmike

      Si përfundim, do të jap dy identitete që është e vështirë të quhen veti - përkundrazi, këto janë pasoja nga përkufizimi i logaritmit. Gjenden vazhdimisht në probleme dhe çuditërisht krijojnë probleme edhe për nxënësit “të avancuar”.

      1. log a a = 1 është njësia logaritmike. Mbani mend një herë e përgjithmonë: logaritmi për çdo bazë a nga vetë ajo bazë është i barabartë me një.
      2. log a 1 = 0 është zero logaritmike. Baza a mund të jetë çdo gjë, por nëse argumenti është një - logaritmi është zero! Sepse një 0 = 1 është një pasojë e drejtpërdrejtë e përkufizimit.

      Këto janë të gjitha pronat. Sigurohuni që të praktikoni zbatimin e tyre! Shkarkoni fletën e mashtrimit në fillim të mësimit, printojeni - dhe zgjidhni problemet.

      Logaritmi. Vetitë e logaritmit (mbledhja dhe zbritja).

      Vetitë e logaritmit ndiqen nga përkufizimi i tij. Dhe kështu logaritmi i numrit b nga arsyeja a përkufizohet si eksponent në të cilin duhet të ngrihet një numër a për të marrë numrin b(logaritmi ekziston vetëm për numrat pozitivë).

      Nga ky formulim del se llogaritja x=log a b, është e barabartë me zgjidhjen e ekuacionit sëpatë=b. Për shembull, regjistri 2 8 = 3 sepse 8 = 2 3 . Formulimi i logaritmit bën të mundur justifikimin se nëse b=a c, pastaj logaritmi i numrit b nga arsyeja a barazohet Me. Është gjithashtu e qartë se tema e logaritmit është e lidhur ngushtë me temën e fuqisë së një numri.

      Me logaritme, si me çdo numër, mund të kryeni veprimet e mbledhjes, zbritjes dhe transformohen në çdo mënyrë të mundshme. Por duke pasur parasysh faktin se logaritmet nuk janë numra krejt të zakonshëm, këtu zbatohen rregullat e tyre të veçanta, të cilat quhen vetitë themelore.

      Mbledhja dhe zbritja e logaritmeve.

      Merrni dy logaritme me të njëjtën bazë: log x dhe log a y. Pastaj hiqni, është e mundur të kryhen operacione të mbledhjes dhe zbritjes:

      Siç e shohim, shuma e logaritmeve barazohet me logaritmin e produktit, dhe ndryshim logaritme- logaritmi i herësit. Dhe kjo është e vërtetë nëse numrat a, X dhe në pozitive dhe a ≠ 1.

      Është e rëndësishme të theksohet se aspekti kryesor në këto formula janë të njëjtat baza. Nëse bazat ndryshojnë nga njëra-tjetra, këto rregulla nuk zbatohen!

      Rregullat për mbledhjen dhe zbritjen e logaritmeve me të njëjtat baza lexohen jo vetëm nga e majta në të djathtë, por edhe anasjelltas. Si rezultat, kemi teoremat për logaritmin e produktit dhe logaritmin e herësit.

      Logaritmi i produktit dy numra pozitivë është e barabartë me shumën logaritmet e tyre ; duke parafrazuar këtë teoremë, marrim sa vijon, nëse numrat a, x dhe në pozitive dhe a ≠ 1, pastaj:

      Logaritmi i herësit i dy numrave pozitivë është i barabartë me diferencën ndërmjet logaritmeve të dividendit dhe pjesëtuesit. Me fjalë të tjera, nëse numrat a, X dhe në pozitive dhe a ≠ 1, pastaj:

      Zbatojmë teoremat e mësipërme për të zgjidhur shembuj:

      Nëse numrat x dhe në atëherë janë negative formula e logaritmit të produktit bëhet e pakuptimtë. Pra, është e ndaluar të shkruhet:

      meqenëse shprehjet log 2 (-8) dhe log 2 (-4) nuk janë fare të përcaktuara (funksioni logaritmik në= regjistri 2 X të përcaktuara vetëm për vlerat pozitive të argumentit X).

      Teorema e produktitështë i zbatueshëm jo vetëm për dy, por edhe për një numër të pakufizuar faktorësh. Kjo do të thotë se për çdo natyrore k dhe çdo numër pozitiv x 1 , x 2 , . . . ,x n ka një identitet:

      Nga teorema të logaritmit të herësit mund të merret edhe një veti e logaritmit. Dihet mirë se log a 1 = 0, pra,

      Pra, ekziston një barazi:

      Logaritmet e dy numrave reciprokë në të njëjtën bazë do të ndryshojnë nga njëri-tjetri vetëm në shenjë. Kështu që:

      Logaritmi. Vetitë e logaritmeve

      Logaritmi. Vetitë e logaritmeve

      Merrni parasysh barazinë. Na tregoni vlerat dhe ne duam të gjejmë vlerën e .

      Kjo do të thotë, ne jemi duke kërkuar për një eksponent tek i cili duhet të drejtoheni për të marrë .

      Le variabla mund të marrë çdo vlerë reale, atëherë kufizimet e mëposhtme u vendosen variablave: o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/ >

      Nëse i dimë vlerat e dhe , dhe përballemi me detyrën për të gjetur të panjohurën, atëherë për këtë qëllim prezantohet një operacion matematikor, i cili quhet logaritmi.

      Për të gjetur vlerën që marrim logaritmi i një numri në themeli :

      Logaritmi i një numri në bazë është eksponenti në të cilin duhet të ngrini për të marrë .

      Kjo eshte identiteti bazë logaritmik:

      o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>

      është në thelb një shënim matematikor përkufizimet e logaritmit.

      Logaritmi i operacionit matematikor është inversi i fuqisë, pra vetitë e logaritmeve janë të lidhura ngushtë me vetitë e gradës.

      Ne rendisim kryesore vetitë e logaritmeve:

      (o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>, 0,

      d>0″/>, 1″ titull =”d1″/>

      4.

      5.

      Grupi i mëposhtëm i vetive ju lejon të përfaqësoni eksponentin e shprehjes nën shenjën e logaritmit, ose qëndrimin në bazën e logaritmit si një koeficient përpara shenjës së logaritmit:

      6.

      7.

      8.

      9.

      Grupi tjetër i formulave ju lejon të kaloni nga një logaritëm me një bazë të caktuar në një logaritëm me një bazë arbitrare, dhe quhet formulat e kalimit në një bazë të re:

      10.

      12. (përfundim nga prona 11)

      Tre vetitë e mëposhtme nuk janë të njohura mirë, por ato përdoren shpesh kur zgjidhen ekuacionet logaritmike ose kur thjeshtohen shprehjet që përmbajnë logaritme:

      13.

      14.

      15.

      Raste të veçanta:

      — logaritmi dhjetor

      — logaritmi natyror

      Kur thjeshtohen shprehjet që përmbajnë logaritme, zbatohet një qasje e përgjithshme:

      1. Prezantimi dhjetore në formën e zakonshme.

      2. numra të përzier të paraqitura si thyesa të papërshtatshme.

      3. Numrat në bazën e logaritmit dhe nën shenjën e logaritmit zbërthehen në faktorë të thjeshtë.

      4. Ne përpiqemi t'i sjellim të gjitha logaritmet në të njëjtën bazë.

      5. Zbatoni vetitë e logaritmeve.

      Le të shohim shembuj të thjeshtimit të shprehjeve që përmbajnë logaritme.

      Shembulli 1

      Llogaritni:

      Le të thjeshtojmë të gjithë eksponentët: detyra jonë është t'i sjellim në logaritme, baza e të cilave është e njëjtë me bazën e eksponentit.

      ==(nga vetia 7)=(nga vetia 6) =

      Zëvendësoni treguesit që kemi marrë në shprehjen origjinale. Ne marrim:

      Përgjigje: 5.25

      Shembulli 2 Llogaritni:

      Ne i sjellim të gjitha logaritmet në bazën 6 (në këtë rast, logaritmet nga emëruesi i thyesës do të "migrojnë" te numëruesi):

      Le t'i zbërthejmë numrat nën shenjën e logaritmit në faktorë të thjeshtë:

      Aplikoni vetitë 4 dhe 6:

      Ne prezantojmë zëvendësimin

      Ne marrim:

      Përgjigje: 1

      Logaritmi . Identiteti bazë logaritmik.

      Vetitë e logaritmeve. Logaritmi dhjetor. logaritmi natyror.

      logaritmi numër pozitiv N në bazë (b > 0, b 1) quhet eksponenti x tek i cili duhet të ngrihet b për të marrë N .

      Kjo hyrje është e barabartë me sa vijon: b x = N .

      SHEMBUJ: log 3 81 = 4 meqenëse 3 4 = 81 ;

      log 1/3 27 = – 3 sepse (1/3) - 3 = 3 3 = 27 .

      Përkufizimi i mësipërm i logaritmit mund të shkruhet si një identitet:

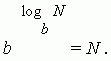
      Vetitë themelore të logaritmeve.

      2) log 1 = 0 sepse b 0 = 1 .

      3) Logaritmi i produktit është i barabartë me shumën e logaritmeve të faktorëve:

      4) Logaritmi i herësit është i barabartë me diferencën midis logaritmeve të dividendit dhe pjesëtuesit:

      5) Logaritmi i shkallës është i barabartë me produktin e eksponentit dhe logaritmin e bazës së tij:

      Pasoja e kësaj prone është si më poshtë: rrënjë log është e barabartë me logaritmin e numrit të rrënjës pjesëtuar me fuqinë e rrënjës:

      6) Nëse baza e logaritmit është një shkallë, atëherë vlera reciproku i eksponentit mund të hiqet nga shenja e regjistrit të rimës:

      Dy vetitë e fundit mund të kombinohen në një:

      7) Formula për modulin e tranzicionit (d.m.th. kalimi nga një bazë e logaritmit në një bazë tjetër):

      Në një rast të veçantë, kur N = a ne kemi:

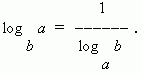
      Logaritmi dhjetor thirrur logaritmi bazë 10. Shënohet lg, d.m.th. regjistri 10 N= log N. Logaritmet e numrave 10, 100, 1000, . p janë 1, 2, 3, ..., përkatësisht, d.m.th. kanë kaq shumë pozitive

      njësitë, sa zero janë në numrin logaritëm pas një. Logaritmet e numrave 0.1, 0.01, 0.001, . p janë –1, –2, –3, …, përkatësisht, d.m.th. të ketë aq negative sa ka zero në numrin logaritmik përpara atij (duke përfshirë zero numra të plotë). Logaritmet e numrave të mbetur kanë një pjesë thyesore të quajtur mantisa. Pjesa e plotë e logaritmit quhet karakteristike. Për aplikime praktike, logaritmet dhjetore janë më të përshtatshmet.

      logaritmi natyror thirrur logaritmi bazë e. Ajo shënohet me ln, d.m.th. log e N=n N. Numri eështë irracionale, vlera e përafërt e saj është 2.718281828. Është kufiri drejt të cilit numri (1 + 1 / n) n me rritje të pakufizuar n(cm. kufiri i parë i mrekullueshëm në faqen Kufijtë e sekuencës së numrave).
      Sado e çuditshme mund të duket, logaritmet natyrore doli të ishin shumë të përshtatshme kur kryenin operacione të ndryshme që lidhen me analizën e funksioneve. Llogaritja e logaritmeve bazë e shumë më shpejt se çdo bazë tjetër.

    • Si të merrni një certifikatë të regjistrimit shtetëror të pronësisë së një apartamenti? Në përputhje me Kushtetutën e Federatës Ruse, shtetit i është besuar funksioni i garantuesit të së drejtës së pronës private. Shteti ka kompetencat e tij në këtë fushë […] Dënimi për mosdorëzimin e raporteve SZV-M dhe RSV-1 në NjIF Në fund të çdo periudhe raportimi dhe shlyerjeje, i siguruari duhet të paraqesë llogaritjen e nevojshme në fondin pensional në Formulari RSV-1. Nëse për ndonjë arsye […]
    • Kur dhe si të merrni pjesën e financuar të pensionit në Sberbank? Sberbank është një bankë partnere e fondit shtetëror të pensioneve. Në bazë të kësaj, qytetarët që kanë lëshuar pension të financuar mund të transferojnë financimin e […]
    • Si të merrni subvencione për faturat e shërbimeve (qira)? Subvencionet për faturat e shërbimeve u ofrohen kategorive të caktuara të qytetarëve në përputhje me legjislacionin e strehimit të Federatës Ruse. Për të mësuar më shumë rreth procedurës […]
    • Informacion falas nga TIN ose OGRN nga regjistri tatimor në të gjithë Rusinë - në internet Në Portalin e Unifikuar të Shërbimeve Tatimore, informacione për regjistrimin shtetëror të personave juridikë, sipërmarrësve individualë, […]
    • Cesspool: kodet dhe rregulloret sanitare dhe ndërtimore Për rregullimin e kanalizimeve në një vilë verore ose parcelë qyteti, është e nevojshme të ndiqni jo vetëm standardet e ndërtimit, por edhe standardet legjislative. Cesspool: normat dhe rregullat për rregullimin e tij […]

    Ne lidhje me

    mund të vendoset detyra për të gjetur cilindo nga tre numrat nga dy të tjerët, të dhënë. Jepet a dhe pastaj N gjendet me fuqizim. Nëse jepen N dhe atëherë a gjendet duke nxjerrë rrënjën e fuqisë x (ose fuqisë). Tani merrni parasysh rastin kur, duke pasur parasysh a dhe N, kërkohet të gjendet x.

    Le të jetë numri N pozitiv: numri a është pozitiv dhe jo i barabartë me një: .

    Përkufizimi. Logaritmi i numrit N në bazën a është eksponenti në të cilin duhet të ngrini a për të marrë numrin N; logaritmi shënohet me

    Kështu, në barazinë (26.1), eksponenti gjendet si logaritëm i N ndaj bazës a. Regjistrimet

    kanë të njëjtin kuptim. Barazia (26.1) nganjëherë quhet identiteti bazë i teorisë së logaritmeve; në fakt, ai shpreh përkufizimin e konceptit të logaritmit. Nga këtë përkufizim baza e logaritmit a është gjithmonë pozitive dhe e ndryshme nga uniteti; numri i logaritmit N është pozitiv. Numrat negativë dhe zeroja nuk kanë logaritme. Mund të vërtetohet se çdo numër me një bazë të caktuar ka një logaritëm të mirëpërcaktuar. Prandaj barazia përfshin. Vini re se kushti është thelbësor këtu, përndryshe përfundimi nuk do të justifikohej, pasi barazia është e vërtetë për çdo vlerë të x dhe y.

    Shembulli 1. Gjeni

    Zgjidhje. Për të marrë numrin, duhet të ngrini bazën 2 në fuqi Prandaj.

    Ju mund të regjistroni kur zgjidhni shembuj të tillë në formën e mëposhtme:

    Shembulli 2. Gjeni .

    Zgjidhje. Ne kemi

    Në shembujt 1 dhe 2, ne gjetëm lehtësisht logaritmin e dëshiruar duke paraqitur numrin e logarithmueshëm si një shkallë të bazës me një eksponent racional. Në rastin e përgjithshëm, për shembull, për etj., kjo nuk mund të bëhet, pasi logaritmi ka një vlerë irracionale. Le t'i kushtojmë vëmendje një pyetjeje në lidhje me këtë deklaratë. Në § 12 ne dhamë konceptin e mundësisë së përcaktimit të çdo fuqie reale të një numri të dhënë pozitiv. Kjo ishte e nevojshme për futjen e logaritmeve, të cilat, në përgjithësi, mund të jenë numra irracionalë.

    Shqyrtoni disa veti të logaritmeve.

    Vetia 1. Nëse numri dhe baza janë të barabarta, atëherë logaritmi është i barabartë me një dhe, anasjelltas, nëse logaritmi është i barabartë me një, atëherë numri dhe baza janë të barabarta.

    Dëshmi. Le Nga përkufizimi i logaritmit, kemi dhe nga

    Anasjelltas, le Pastaj sipas përkufizimit

    Vetia 2. Logaritmi i njësisë për çdo bazë është i barabartë me zero.

    Dëshmi. Sipas përkufizimit të logaritmit (fuqia zero e çdo baze pozitive është e barabartë me një, shih (10.1)). Nga këtu

    Q.E.D.

    Deklarata e kundërt është gjithashtu e vërtetë: nëse , atëherë N = 1. Në të vërtetë, ne kemi .

    Përpara se të shprehim vetinë e mëposhtme të logaritmeve, le të pranojmë të themi se dy numra a dhe b qëndrojnë në të njëjtën anë të një numri të tretë c, nëse të dy janë më të mëdhenj se c ose më të vegjël se c. Nëse njëri prej këtyre numrave është më i madh se c dhe tjetri më i vogël se c, atëherë themi se ata shtrihen në anët e kundërta të c.

    Vetia 3. Nëse numri dhe baza qëndrojnë në të njëjtën anë të unitetit, atëherë logaritmi është pozitiv; nëse numri dhe baza qëndrojnë në anët e kundërta të unitetit, atëherë logaritmi është negativ.

    Vërtetimi i vetive 3 bazohet në faktin se shkalla e a është më e madhe se një nëse baza është më e madhe se një dhe eksponenti është pozitiv, ose baza është më e vogël se një dhe eksponenti është negativ. Shkalla është më e vogël se një nëse baza është më e madhe se një dhe eksponenti është negativ, ose baza është më e vogël se një dhe eksponenti është pozitiv.

    Janë katër raste që duhen marrë parasysh:

    Ne kufizohemi në analizën e të parës prej tyre, pjesa tjetër lexuesi do t'i shqyrtojë vetë.

    Le të jetë atëherë eksponenti në barazi as negativ dhe as i barabartë me zero, pra, ai është pozitiv, d.m.th., që kërkohej të vërtetohej.

    Shembulli 3. Gjeni se cilët nga logaritmat e mëposhtëm janë pozitivë dhe cilët negativë:

    Zgjidhja, a) meqenëse numri 15 dhe baza 12 janë të vendosura në të njëjtën anë të njësisë;

    b) , pasi 1000 dhe 2 ndodhen në të njëjtën anë të njësisë; në të njëjtën kohë, nuk është thelbësore që baza të jetë më e madhe se numri logaritmik;

    c), pasi 3.1 dhe 0.8 shtrihen në anët e kundërta të unitetit;

    G) ; pse?

    e) ; pse?

    Vetitë e mëposhtme 4-6 quhen shpesh rregulla të logaritmit: ato lejojnë, duke ditur logaritmet e disa numrave, të gjejmë logaritmet e prodhimit të tyre, herësin, shkallën e secilit prej tyre.

    Vetia 4 (rregulli për logaritmin e produktit). Logaritmi i prodhimit të disa numrave pozitivë në një bazë të caktuar është i barabartë me shumën e logaritmeve të këtyre numrave në të njëjtën bazë.

    Dëshmi. Le të jepen numra pozitivë.

    Për logaritmin e produktit të tyre, shkruajmë barazinë (26.1) duke përcaktuar logaritmin:

    Nga këtu gjejmë

    Duke krahasuar eksponentët e shprehjes së parë dhe të fundit, marrim barazinë e kërkuar:

    Vini re se kushti është thelbësor; logaritmi i prodhimit të dy numrave negativ ka kuptim, por në këtë rast marrim

    Në përgjithësi, nëse prodhimi i disa faktorëve është pozitiv, atëherë logaritmi i tij është i barabartë me shumën e logaritmeve të moduleve të këtyre faktorëve.

    Vetia 5 (rregulli i logaritmit të herësit). Logaritmi i një herësi numrash pozitivë është i barabartë me diferencën midis logaritmeve të dividendit dhe pjesëtuesit, të marra në të njëjtën bazë. Dëshmi. Gjeni vazhdimisht

    Q.E.D.

    Vetia 6 (rregulli i logaritmit të shkallës). Logaritmi i fuqisë së çdo numri pozitiv është i barabartë me logaritmin e atij numri shumëfish i eksponentit.

    Dëshmi. Ne shkruajmë përsëri identitetin kryesor (26.1) për numrin:

    Q.E.D.

    Pasoja. Logaritmi i rrënjës së një numri pozitiv është i barabartë me logaritmin e numrit të rrënjës të pjesëtuar me eksponentin e rrënjës:

    Ne mund të vërtetojmë vlefshmërinë e kësaj përfundimi duke paraqitur mënyrën dhe përdorimin e vetisë 6.

    Shembulli 4. Logaritmi për bazën a:

    a) (supozohet se të gjitha vlerat b, c, d, e janë pozitive);

    b) (supozohet se ).

    Zgjidhja, a) Është e përshtatshme të kalohet në këtë shprehje te fuqitë thyesore:

    Bazuar në barazitë (26.5)-(26.7) tani mund të shkruajmë:

    Vëmë re se në logaritmet e numrave kryhen veprime më të thjeshta se sa në vetë numrat: gjatë shumëzimit të numrave shtohen logaritmet e tyre, kur ndahen zbriten etj.

    Kjo është arsyeja pse logaritmet janë përdorur në praktikën llogaritëse (shih seksionin 29).

    Veprimi i kundërt ndaj logaritmit quhet fuqizim, përkatësisht: fuqizim është veprimi me të cilin vetë ky numër gjendet me logaritmin e dhënë të një numri. Në thelb, fuqizimi nuk është ndonjë veprim i veçantë: vjen deri te ngritja e bazës në një fuqi (të barabartë me logaritmin e numrit). Termi "potenciim" mund të konsiderohet sinonim me termin "përforcim".

    Gjatë fuqizimit, është e nevojshme të përdoren rregullat që janë të kundërta me rregullat e logaritmit: zëvendësoni shumën e logaritmeve me logaritmin e produktit, diferencën e logaritmeve me logaritmin e herësit, etj. Në veçanti, nëse ka çdo faktor përballë shenjës së logaritmit, atëherë gjatë fuqizimit duhet të bartet në shkallët e treguesit nën shenjën e logaritmit.

    Shembulli 5. Gjeni N nëse dihet se

    Zgjidhje. Në lidhje me rregullin e fuqizimit që sapo u tha, faktorët 2/3 dhe 1/3, të cilët janë përballë shenjave të logaritmeve në anën e djathtë të kësaj barazie, do të transferohen te eksponentët nën shenjat e këtyre logaritmeve; marrim

    Tani ndryshimin e logaritmeve e zëvendësojmë me logaritmin e herësit:

    për të marrë thyesën e fundit në këtë zinxhir barazish, ne e çliruam thyesën e mëparshme nga irracionaliteti në emërues (seksioni 25).

    Vetia 7. Nëse baza është më e madhe se një, atëherë më shumë ka një logaritëm më të madh (dhe një më i vogël ka një më të vogël), nëse baza është më e vogël se një, atëherë një numër më i madh ka një logaritëm më të vogël (dhe një më i vogël ka një më të madh).

    Kjo veti formulohet gjithashtu si rregull për logaritmin e pabarazive, të dyja pjesët e së cilës janë pozitive:

    Kur merret logaritmi i pabarazive me bazë më të madhe se një, ruhet shenja e pabarazisë, dhe kur merret logaritmi me bazë më të vogël se një, shenja e pabarazisë kthehet mbrapsht (shih edhe pikën 80).

    Vërtetimi bazohet në vetitë 5 dhe 3. Shqyrtoni rastin kur Nëse , atëherë dhe, duke marrë logaritmin, marrim

    (a dhe N/M shtrihen në të njëjtën anë të unitetit). Nga këtu

    Në rastin a vijon, lexuesi do ta kuptojë vetë.

    Çfarë është një logaritëm?

    Kujdes!
    Ka shtesë
    materiali në Seksionin Special 555.
    Për ata që fort "jo shumë..."
    Dhe për ata që "shumë...")

    Çfarë është një logaritëm? Si të zgjidhni logaritmet? Këto pyetje ngatërrojnë shumë maturantë. Tradicionalisht, tema e logaritmeve konsiderohet komplekse, e pakuptueshme dhe e frikshme. Sidomos - ekuacionet me logaritme.

    Kjo nuk është absolutisht e vërtetë. Absolutisht! Nuk besoj? Mirë. Tani, për rreth 10-20 minuta ju:

    1. Kuptoni çfarë është një logaritëm.

    2. Mësoni të zgjidhni një klasë të tërë ekuacionesh eksponenciale. Edhe nëse nuk keni dëgjuar për to.

    3. Mësoni të llogaritni logaritme të thjeshta.

    Për më tepër, për këtë do t'ju duhet vetëm të dini tabelën e shumëzimit dhe se si një numër ngrihet në një fuqi ...

    Ndjej se dyshoni ... Epo, mbani kohë! Shkoni!

    Së pari, zgjidhni ekuacionin e mëposhtëm në mendjen tuaj:

    Nëse ju pëlqen kjo faqe...

    Nga rruga, unë kam disa faqe më interesante për ju.)

    Ju mund të praktikoni zgjidhjen e shembujve dhe të zbuloni nivelin tuaj. Testimi me verifikim të menjëhershëm. Mësimi - me interes!)

    mund të njiheni me funksionet dhe derivatet.

    (nga greqishtja λόγος - "fjalë", "lidhje" dhe ἀριθμός - "numër") numra b nga arsyeja a(log α b) quhet një numër i tillë c, dhe b= një c, domethënë log α b=c dhe b=ac janë ekuivalente. Logaritmi ka kuptim nëse a > 0, a ≠ 1, b > 0.

    Me fjale te tjera logaritmi numrat b nga arsyeja a formuluar si një eksponent tek i cili duhet të ngrihet një numër a për të marrë numrin b(logaritmi ekziston vetëm për numrat pozitivë).

    Nga ky formulim del se llogaritja x= log α b, është ekuivalente me zgjidhjen e ekuacionit a x =b.

    Për shembull:

    log 2 8 = 3 sepse 8=2 3 .

    Vëmë re se formulimi i treguar i logaritmit bën të mundur përcaktimin e menjëhershëm vlera e logaritmit kur numri nën shenjën e logaritmit është një fuqi e caktuar e bazës. Në të vërtetë, formulimi i logaritmit bën të mundur justifikimin se nëse b=a c, pastaj logaritmi i numrit b nga arsyeja a barazohet Me. Është gjithashtu e qartë se tema e logaritmit është e lidhur ngushtë me temën shkalla e numrit.

    Referohet llogaritja e logaritmit logaritmi. Logaritmi është operacioni matematik i marrjes së një logaritmi. Kur merret një logaritëm, produktet e faktorëve shndërrohen në shuma termash.

    Potencimiështë operacioni matematik i anasjelltë me logaritmin. Gjatë fuqizimit, baza e dhënë ngrihet në fuqinë e shprehjes mbi të cilën kryhet fuqizimi. Në këtë rast, shumat e termave shndërrohen në produkt faktorësh.

    Shumë shpesh përdoren logaritmet reale me baza 2 (binare), e Euler-it e ≈ 2,718 (logaritmi natyror) dhe 10 (dhjetor).

    Në këtë fazë, ia vlen të merret në konsideratë mostrat e logaritmeve regjistri 7 2 , ln √ 5, lg0.0001.

    Dhe hyrjet lg (-3), log -3 3.2, log -1 -4.3 nuk kanë kuptim, pasi në të parën prej tyre vendoset një numër negativ nën shenjën e logaritmit, në të dytin - një numër negativ në bazën, dhe në të tretën - dhe një numër negativ nën shenjën e logaritmit dhe njësisë në bazë.

    Kushtet për përcaktimin e logaritmit.

    Vlen të merren parasysh veçmas kushtet a > 0, a ≠ 1, b > 0. përkufizimi i një logaritmi. Le të shqyrtojmë pse janë marrë këto kufizime. Kjo do të na ndihmojë me një barazi të formës x = log α b, i quajtur identiteti bazë logaritmik, i cili rrjedh drejtpërdrejt nga përkufizimi i logaritmit të dhënë më sipër.

    Merre kushtin a≠1. Meqenëse një është e barabartë me një për çdo fuqi, atëherë barazia x=log α b mund të ekzistojë vetëm kur b=1, por regjistri 1 1 do të jetë çdo numër real. Për të eliminuar këtë paqartësi, marrim a≠1.

    Le të vërtetojmë domosdoshmërinë e kushtit a>0. Në a=0 sipas formulimit të logaritmit, mund të ekzistojë vetëm kur b=0. Dhe pastaj në përputhje me rrethanat regjistri 0 0 mund të jetë çdo numër real jo zero, pasi zero për çdo fuqi jozero është zero. Për të eliminuar këtë paqartësi, kushti a≠0. Dhe kur a<0 do të duhej të refuzonim analizën e vlerave racionale dhe irracionale të logaritmit, pasi eksponenti me një eksponent racional dhe irracional përcaktohet vetëm për baza jo negative. Është për këtë arsye që gjendja a>0.

    Dhe kushti i fundit b>0 rrjedh nga pabarazia a>0, pasi x=log α b, dhe vlera e gradës me bazë pozitive a gjithmonë pozitive.

    Karakteristikat e logaritmeve.

    Logaritmet karakterizohet nga dallues veçoritë, gjë që çoi në përdorimin e tyre të gjerë për të lehtësuar shumë llogaritjet e mundimshme. Në kalimin "në botën e logaritmeve", shumëzimi shndërrohet në një mbledhje shumë më të lehtë, ndarja në zbritje dhe ngritja në fuqi dhe marrja e rrënjës shndërrohen në shumëzim dhe pjesëtim me një eksponent, përkatësisht.

    Formulimi i logaritmeve dhe një tabelë e vlerave të tyre (për funksionet trigonometrike) u botua për herë të parë në 1614 nga matematikani skocez John Napier. Tabelat logaritmike, të zmadhuara dhe të detajuara nga shkencëtarë të tjerë, u përdorën gjerësisht në llogaritjet shkencore dhe inxhinierike dhe mbetën të rëndësishme derisa kalkulatorët dhe kompjuterët elektronikë filluan të përdoren.

    rrjedh nga përkufizimi i tij. Dhe kështu logaritmi i numrit b nga arsyeja a përkufizohet si eksponent në të cilin duhet të ngrihet një numër a për të marrë numrin b(logaritmi ekziston vetëm për numrat pozitivë).

    Nga ky formulim del se llogaritja x=log a b, është e barabartë me zgjidhjen e ekuacionit sëpatë=b. Për shembull, regjistri 2 8 = 3 sepse 8 = 2 3 . Formulimi i logaritmit bën të mundur justifikimin se nëse b=a c, pastaj logaritmi i numrit b nga arsyeja a barazohet Me. Është gjithashtu e qartë se tema e logaritmit është e lidhur ngushtë me temën e fuqisë së një numri.

    Me logaritme, si me çdo numër, mund të kryeni veprimet e mbledhjes, zbritjes dhe transformohen në çdo mënyrë të mundshme. Por duke pasur parasysh faktin se logaritmet nuk janë numra krejt të zakonshëm, këtu zbatohen rregullat e tyre të veçanta, të cilat quhen vetitë themelore.

    Mbledhja dhe zbritja e logaritmeve.

    Merrni dy logaritme me të njëjtën bazë: log x dhe log a y. Pastaj hiqni, është e mundur të kryhen operacione të mbledhjes dhe zbritjes:

    log a x+ log a y= log a (x y);

    log a x - log a y = log a (x:y).

    log a(x 1 . x 2 . x 3 ... x k) = log x 1 + log x 2 + log x 3 + ... + log a x k.

    Nga teorema të logaritmit të herësit mund të merret edhe një veti e logaritmit. Dihet mirë se log a 1 = 0, pra,

    log a 1 /b= log a 1 - log a b= -log a b.

    Pra, ekziston një barazi:

    log a 1 / b = - log a b.

    Logaritmet e dy numrave reciprokë në të njëjtën bazë do të ndryshojnë nga njëri-tjetri vetëm në shenjë. Kështu që:

    Regjistri 3 9= - log 3 1 / 9 ; log 5 1 / 125 = -log 5 125.