Shënime leksioni mbi këtë temë

MEKANIKA TEORIKE

Për studentët e specialitetit:

260501.65 Teknologjia e shërbimit të ushqimit,

Forma e arsimit me kohë të plotë

Shënimet e leksionit bazohen në:

1. Butorin L.V., Busygina E.B. Mekanika teorike. Udhëzues edukativ dhe praktik. - M., MGU TU, 2004

2. Targ S.M. Kurs i shkurtër mekanika teorike. - M.: shkollë e diplomuar, 2001 - Me.

3. Yablonsky A.A., Nikiforova V.N. Kursi i mekanikës teorike. M. "Lan", 2000

Prezantimi

Moderne prodhimit industrial, duke përfshirë ushqimin, janë industri shumë të mekanizuara. Zgjidhja e detyrave gjithnjë e më komplekse u caktohet pajisjeve teknologjike, e cila nga ana tjetër çon në ndërlikimin e pajisjeve. Formimi i një inxhinieri modern është i paimagjinueshëm pa njohuri të disiplinave themelore. Një nga këto disiplina është mekanika teorike .

Mekanika teorike është një degë e mekanikës që përcakton ligjet bazë të lëvizjes mekanike dhe bashkëveprimit mekanik të trupave materiale. Lëvizja mekanike quhet ndryshimi me kalimin e kohës i pozicionit relativ në hapësirë ​​të trupave materialë, mekanike ndërveprim- një ndërveprim i tillë, si rezultat i të cilit ndryshon lëvizja mekanike ose ndryshon pozicioni relativ i pjesëve të trupit.

Mekanika teorike zakonisht ndahet në: statika, kinematika dhe dinamika .

Në statikë studiohen kushtet ekuilibri trupat materiale dhe metodat e transformimit identik të sistemit të forcave. Ekuilibri Një gjendje në të cilën një trup qëndron i palëvizshëm ose lëviz në mënyrë të njëtrajtshme në një vijë të drejtë nën veprimin e forcave.

Në kinematikë merren parasysh karakteristikat e përgjithshme gjeometrike të lëvizjes së trupave. Forcat që veprojnë në trup nuk merren parasysh. Është dhënë ligji i lëvizjes. Ligji i lëvizjes së trupitështë varësia e pozicionit të trupit në hapësirë ​​nga koha.

Në dinamikë studiohen ligjet e përgjithshme të lëvizjes së trupave nën veprimin e forcave.

1. C tatika trup i fortë

1.1 Konceptet bazë të statikës

Trup absolutisht i ngurtë (trup i ngurtë, trup)- një trup material, distanca midis çdo pike në të cilën nuk ndryshon. Si pasojë, madhësia dhe forma e trupit nuk ndryshojnë.

Pika materialeështë një trup, dimensionet e të cilit, sipas kushteve të problemit, mund të neglizhohen.

trup i lirshëm- një trup, në lëvizjen e të cilit nuk vendosen kufizime.

Trup jo i lirë (i lidhur).– një trup, lëvizja e të cilit është e kufizuar.

Lidhjet- trupa që pengojnë lëvizjen e objektit në shqyrtim (një trup ose një sistem trupash).

sistemi mekanik- një grup trupash ose pikash materiale të ndërlidhura.

Një trup i ngurtë mund të konsiderohet si një sistem mekanik, pozicionet dhe distancat midis pikave të të cilit nuk ndryshojnë.

Forcë- një sasi vektoriale që karakterizon veprimin mekanik të një trupi material mbi një tjetër.

Forca si vektor karakterizohet nga pika e aplikimit, drejtimi i veprimit dhe vlera absolute (Fig. 1.1). Njësia matëse për modulin e forcës është Njutoni.

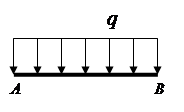Fig.1.1. Fig.1.2.

linja e forcësështë vija e drejtë përgjatë së cilës është drejtuar vektori i forcës.

Fuqia e përqendruarështë forca e aplikuar në një pikë.

Forcat e shpërndara (ngarkesa e shpërndarë)- forcat që veprojnë në të gjitha pikat e vëllimit, sipërfaqes ose gjatësisë së trupit (Fig. 1.2).

Ngarkesa e shpërndarë përcaktohet nga forca që vepron për njësi vëllimi (sipërfaqja, gjatësia).Dimensioni i ngarkesës së shpërndarë është N / m 3 (N / m 2, N / m).

Forca e jashtmeështë një forcë që vepron nga një trup që nuk i përket sistemit mekanik të konsideruar.

force e brendshme- forca që vepron pika materiale sistemi mekanik nga ana e një pike tjetër materiale që i përket sistemit në shqyrtim.

Sistemi i forcës- një grup forcash që veprojnë në një sistem mekanik.

Sistemi i sheshtë i forcave- një sistem forcash, linjat e veprimit të të cilëve shtrihen në të njëjtin rrafsh.

Sistemi hapësinor i forcave- një sistem forcash, linjat e veprimit të të cilëve nuk shtrihen në të njëjtin rrafsh.

Sistemi i forcave konvergjente- një sistem forcash linjat e veprimit të të cilave kryqëzohen në një pikë (Fig. 1.3).

Sistemi arbitrar i forcave- një sistem forcash linjat e veprimit të të cilëve nuk kryqëzohen në një pikë. (Fig. 1.4)

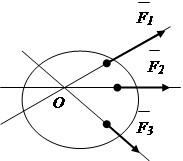Fig.1.3 Fig.1.4

Sistemet ekuivalente të forcave- sisteme të tilla forcash, zëvendësimi i të cilave njëri me tjetrin nuk ndryshon gjendjen mekanike të trupit. Shënimi i pranuar:

Sistemi i balancuar i forcave- një sistem forcash që, kur zbatohet në një trup të ngurtë të lirë, nuk e ndryshon gjendjen e tij mekanike (nuk e çekuilibron atë).

forcë rezultante- një forcë, veprimi i së cilës në një trup është i barabartë me veprimin e një sistemi forcash.

Momenti i fuqisë- një vlerë që karakterizon aftësinë rrotulluese të forcës.

Çifti i fuqisë- një sistem me dy forca paralele, të barabarta në vlerë absolute, të drejtuara në mënyrë të kundërt. Emërtimi i pranuar është () Nën veprimin e një çifti forcash, trupi do të kryejë lëvizje rrotulluese.

Projeksioni i forcës në bosht- një segment i mbyllur midis pingulave të tërhequr nga fillimi dhe fundi i vektorit të forcës në këtë aks (Fig. 1.5).

Projeksioni është pozitiv nëse drejtimi i segmentit përkon me drejtimin pozitiv të boshtit.

Projeksioni i forcës në një aeroplan- një vektor në një rrafsh të mbyllur midis pingulave të tërhequr nga fillimi dhe fundi i vektorit të forcës në këtë plan (Fig. 1.6).

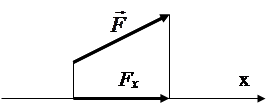
Fig.1.5 Fig.1.6

1.2. Aksiomat e statikës

Parimet teorike të statikës bazohen në një sërë aksiomash. Një aksiomë është një ligj i formuluar si rezultat i përgjithësimit të rezultateve të vëzhgimeve.

1. Aksioma e ekuilibrit.

Dy forcat që veprojnë në një trup të ngurtë balancohen vetëm nëse janë të barabarta në vlerë absolute dhe veprojnë përgjatë një vije të drejtë në drejtime të kundërta (Fig. 1.7).

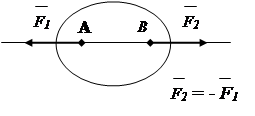
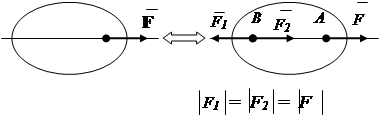
Fig.1.7 Fig.1.8

2. Aksioma e shtimit (përjashtimit) të një sistemi të ekuilibruar forcash.

Veprimi i një sistemi forcash në një trup të ngurtë nuk do të ndryshojë nëse i shtohet ose përjashtohet një sistem i balancuar forcash (Fig. 1.8).

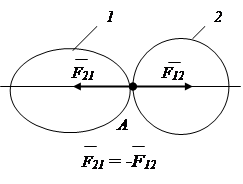
3. Aksioma për paralelogramin e forcave.

Një sistem me dy forca të aplikuara në një pikë të një trupi të ngurtë ka një forcë rezultante të aplikuar në të njëjtën pikë. Vektori rezultant është diagonalja e paralelogramit të ndërtuar mbi këto forca (Fig. 1.9).

Oriz. 1.9 Fig.1.10

4. Aksioma e kundërveprimit.

Kur një trup i ngurtë vepron mbi një tjetër, lind një forcë reagimi, e barabartë në vlerë absolute, e kundërt me forcën vepruese (Fig. 1.10).

Shënim. Forca veprimi i së cilës është dhënë quhet forcë aktive, quhet forca e reaksionit reagimi .

5. Aksioma e lidhjeve.

Çdo trup jo i lirë mund të konsiderohet i lirë, nëse është i çliruar mendërisht nga lidhjet, duke e zëvendësuar veprimin e tij me reaksionet përkatëse.

1.3 Lidhjet dhe reagimet e tyre

Trupat që pengojnë lëvizjen e objektit në shqyrtim do të quhen kufizime. Forca me të cilën lidhja vepron në objektin në fjalë quhet reagimi i lidhjes. Gjatë përcaktimit të reaksioneve të mundshme të bashkimit, duhet të vazhdohet nga fakti se reaksioni është një forcë që pengon lëvizjen e trupit në fjalë. Reagimi drejtohet në drejtim të kundërt me atë ku lidhja nuk e lejon trupin të lëvizë.

Le të shohim disa lidhje të zakonshme.

Sipërfaqe e lëmuar kufizon lëvizjen përgjatë normales në sipërfaqen mbështetëse. Reaksioni drejtohet pingul me sipërfaqen (Fig. 1.11).

Mbështetje e lëvizshme e artikuluar kufizon lëvizjen e trupit përgjatë normales në rrafshin referues. Reaksioni drejtohet përgjatë normales në sipërfaqen mbështetëse (Fig. 1.12)

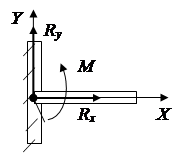
Mbështetje fikse e artikuluar kundërvepron çdo lëvizje në një rrafsh pingul me boshtin e rrotullimit. Në llogaritje, reaksioni Fr, si rregull, paraqitet si dy komponentë përgjatë boshteve X dhe Y (Fig. 1.13).

Shufra e artikuluar pa peshë kundërvepron lëvizjen e trupit përgjatë vijës së shufrës. Reaksioni do të drejtohet përgjatë vijës së shufrës (Fig. 1.14).

Përfundimi i verbër kundërvepron çdo lëvizje dhe rrotullim në rrafsh (Fig. 1.15). Veprimi i tij mund të zëvendësohet nga një forcë e paraqitur në formën e dy komponentëve dhe një çifti forcash me një moment.

Fig.1.11 1.12 Fig.1.13 Fig.1.14 Fig.1.15

1.4 Moment rreth një pike

Nën veprimin e një force, një trup i ngurtë, së bashku me lëvizjen përkthimore, mund të rrotullohet rreth një qendre të caktuar. Aftësia rrotulluese e një force karakterizohet nga një moment force. Efekti rrotullues i forcës varet nga moduli i forcës, distanca nga qendra në vijën e veprimit të forcës dhe drejtimi i rrotullimit në rrafshin e rrotullimit.

Vlera absolute e momentit është e barabartë me produktin e modulit të forcës dhe distancës më të shkurtër h nga qendra e rrotullimit në vijën e veprimit të forcës. Largësia h thirrur shpatulla e forcës (Fig. 1.16).

M 0 () = F× h , (1.1)

Momenti konsiderohet pozitiv nëse forca tenton të rrotullojë krahun h në drejtim të kundërt dhe negativ kur rrotullohet në drejtim të akrepave të orës.

Vetitë e momentit të forcës rreth një pike:

1. Momenti i forcës nuk do të ndryshojë kur pika e aplikimit të forcës lëvizet përgjatë vijës së veprimit të forcës.

2. Momenti i forcës është i barabartë me zero nëse vija e veprimit e forcës kalon nëpër pikën e zbatimit të forcës.

3. Momenti i forcës rezultante rreth një pike është e barabartë me shumën momentet e termave të forcave rreth kësaj pike.

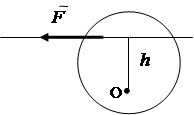Fig.1.16. Fig.1.17.

1.5. Momenti i forcës rreth boshtit

Momenti i forcës rreth një boshti është momenti i projeksionit të kësaj force në një rrafsh pingul me boshtin, në lidhje me pikën e kryqëzimit të boshtit me rrafshin.

Momenti konsiderohet pozitiv nëse, nga skaji pozitiv i boshtit, rrotullimi që kërkon të bëjë forca shihet se ndodh në drejtim të kundërt, dhe negativ nëse është në drejtim të akrepave të orës.

. (1.3)

Për të gjetur momentin e forcës rreth boshtit, ju duhet (Figura 1.17);

1. Vizatoni një rrafsh pingul me boshtin z.

2. Projektoni forcën në këtë rrafsh dhe llogarisni vlerën e projeksionit .

3. Mbajeni shpatullën h nga pika e prerjes së boshtit me rrafshin në vijën e veprimit të projeksionit të forcës dhe llogaritni gjatësinë e saj.

4. Gjeni produktin e kësaj shpatulle dhe projeksionin e forcës me shenjën përkatëse /

Vetitë e momentit të forcës rreth një boshti

Momenti i forcës rreth boshtit është zero nëse:

1. , d.m.th. forca është paralele me boshtin.

2. h =0 , d.m.th. vija e veprimit e forcës e pret boshtin.

1.6. Momenti i një çifti forcash

Një palë forcash ushtron një efekt rrotullues në trup. Momenti i një çifti forcash është i barabartë me produktin e një force me distancën më të shkurtër ndërmjet vijave të veprimit të forcave të çiftit, që quhet shpatulla e çiftit (Fig. 1.18)

, (1.4)

ku: - forcat që përbëjnë dyshen;

h- supin e çiftit

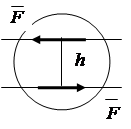Fig.1.18.

Momenti i çiftit konsiderohet pozitiv nëse forcat tentojnë të rrotullojnë krahun në drejtim të kundërt të akrepave të orës.

Forcimi i vetive të çiftit

1. Shuma e projeksioneve të forcave të një çifti në çdo bosht është zero.

2. Pa ndryshuar momentin e çiftit, mund të ndryshoni në të njëjtën kohë vlerën e forcave dhe shpatullën e çiftit, përkatësisht.

3. Një çift mund të transferohet në rrafshin e veprimit të tij, ndërsa efekti i çiftit në trup nuk do të ndryshojë.

1.7. Transformimi identik i sistemeve të forcave

Transformimi mund të bëhet në mënyrë grafike ose analitike.

1.7.1. Transformimi i një sistemi konvergjent të forcave

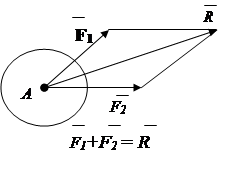
Rezultante R i dy forcave konvergjente gjendet në bazë të aksiomës së paralelogramit të forcave. (fig.1.9). Shuma gjeometrike e çdo numri forcash konvergjente mund të përcaktohet duke shtuar në mënyrë të njëpasnjëshme dy forca (Fig. 1.19) - metoda e shumëkëndëshit vektor.

konkluzioni : sistemi i forcave konvergjente ( n ) reduktohet në një forcë rezultante .

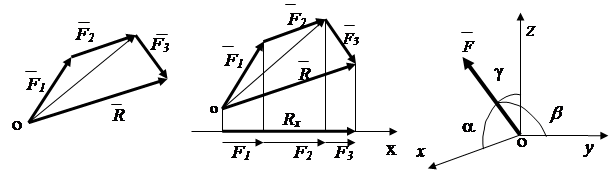
Fig.1.19 Fig.1.20. Fig.1.21.

Në mënyrë analitike, forca rezultante mund të përcaktohet përmes projeksioneve të saj në boshtet koordinative

, (1.5)

Sipas teoremës: projeksioni i rezultantes në bosht është i barabartë me shumën e projeksioneve të termave të forcave në këtë bosht (Fig. 1.20). Rx = F 1 x + F 2 x + F 3 x, ose në përgjithësi

R x = å F kx (1.6)

Duke marrë parasysh (1.6), rezultanti përcaktohet nga shprehja

Drejtimi i vektorit rezultues përcaktohet nga kosinuset e këndeve ndërmjet vektorit dhe boshteve x , y, z(fig.1.20)

1.7.2. Transformimi i një sistemi arbitrar forcash .

Është e pamundur të zbatohet rregulli paralelogram i forcave drejtpërdrejt në një sistem arbitrar forcash, pasi linjat e veprimit të forcave nuk kryqëzohen në një pikë. Më parë, sistemi i forcave sillet në një qendër në bazë të teoremës mbi transferimin paralel të forcës.

Teorema: një forcë e aplikuar në një trup të ngurtë, pa ndryshuar veprimin e tij, mund të transferohet paralelisht në një pikë tjetër të trupit, duke shtuar një palë forcash me një moment të barabartë me momentin e forcës së transferuar në lidhje me pikën në të cilën ndodhet. transferuar (Fig. 1.22).

Si rezultat i këtij transformimi, fitohet një sistem forcash konvergjente dhe shuma e momenteve të çifteve të forcave. Veprimi i sistemit konvergjent të forcave zëvendësohet nga veprimi i forcës totale, veprimi i momenteve - me momentin total. Vektori total * quhet vektori kryesor sistemet e forcës, momenti total * - nxjerr në pah sistemet e forcës.

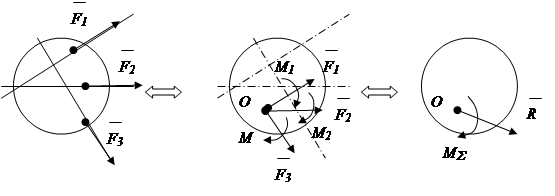
Fig.1.22

konkluzioni: një sistem arbitrar forcash si rezultat i një transformimi identik reduktohet në vektorin kryesor * dhe pika kryesore * sistemet e forcës.

Në mënyrë analitike vektori kryesor dhe momenti kryesor i sistemit të forcave mund të përcaktohet përmes projeksioneve të tyre në boshtet koordinative

1.8 Kushtet për ekuilibrin e sistemeve të forcave

1.8.1. Ekuilibri i një sistemi forcash konvergjente

Sipas përkufizimit (shih pikën 1.1), veprimi i një sistemi forcash konvergjente është i barabartë me veprimin e një force rezultante. Për ekuilibrin e trupit, është e nevojshme dhe e mjaftueshme që rezultanti të jetë i barabartë me zero = 0.

Nga formula (1.7) rrjedh se për ekuilibrin e një sistemi hapësinor të forcave konvergjente është e nevojshme dhe e mjaftueshme që shuma e projeksioneve të të gjitha forcave mbi akset X,Y,Z ishte e barabartë me zero

å F kx = 0

å Fky= 0 (1,10) F k z = 0

Për ekuilibrin e një sistemi të sheshtë konvergjent të forcave, është e nevojshme dhe e mjaftueshme që shuma e projeksioneve të të gjitha forcave në boshtet X, Y të jetë e barabartë me zero.

å F kx = 0

å Fky = 0 (1.11)

1.8.2. Ekuilibri i një sistemi arbitrar forcash.

Veprimi i një sistemi arbitrar forcash është i barabartë me veprimin e vektorit kryesor dhe momentit kryesor. Për ekuilibër është e nevojshme dhe e mjaftueshme që kushti

Për ekuilibrin e një sistemi arbitrar forcash, është e nevojshme dhe e mjaftueshme që shuma e projeksioneve të të gjitha forcave në boshtet X, Y, Z dhe shuma e momenteve të të gjitha forcave në lidhje me akset X,Y,Z ishin të barabarta me zero.

å F kx = 0

å Fky = 0

å Fkz = 0 (1.13)

å M x(k) = 0

å M y(k) = 0

å M z(k) = 0

Për ekuilibrin e një sistemi të sheshtë arbitrar forcash, është e nevojshme dhe e mjaftueshme që shuma e projeksioneve të vektorit kryesor në boshtet X, Y dhe shuma algjebrike e momenteve të forcave në lidhje me qendrën O të jetë e barabartë me zero.

åF ky = 0 (1.14)

EM o (k) = 0

1.9. Pyetje për vetëkontroll në rubrikën

1. Jepni një përkufizim të një trupi absolutisht të ngurtë, një pikë materiale, një forcë, një linjë veprimi të një force, një sistem forcash (të sheshta, hapësinore, konverguese) të një sistemi arbitrar forcash.

2. Si quhet projeksioni i forcës në bosht, në rrafsh?

3. Si quhet momenti i forcës, si përcaktohet momenti i forcës në raport me një pikë?

4. A ndryshon momenti i forcës në lidhje me një pikë të caktuar kur forca bartet përgjatë vijës së veprimit të saj?

5. Në cilin rast momenti i forcës në lidhje me një pikë të caktuar është i barabartë me zero?

6. Cili sistem forcash quhet çift forcash, cili është momenti i një çifti forcash?

7. Çfarë quhet lidhje? Cili është parimi i çlirimit nga obligacionet? Listoni llojet kryesore të lidhjeve, tregoni reagimet e tyre.

8. Cilat janë kushtet dhe ekuacionet për ekuilibrin e një sistemi sistemesh konvergjente dhe arbitrare të forcave të vendosura në hapësirë ​​dhe në një rrafsh?

9. Formuloni procedurën për zgjidhjen e problemave të statikës.

2. Kinematika

Kinematika- një seksion i mekanikës teorike, i cili merr në konsideratë vetitë e përgjithshme gjeometrike të lëvizjes mekanike, si një proces që ndodh në hapësirë ​​dhe kohë. Objektet në lëvizje trajtohen si pika gjeometrike ose trupat gjeometrikë. Prandaj, studimi ndahet në kinematikë të pikës dhe kinematikë të trupit të ngurtë

2.1 Konceptet bazë të kinematikës

Ligji i lëvizjes së një pike (trupi)- varësia e pozicionit të një pike (trupi) në hapësirë ​​nga koha.

Trajektorja e pikës- vendndodhja e pozicioneve të një pike në hapësirë ​​gjatë lëvizjes së saj.

Shpejtësia e pikës (trupit).- një karakteristikë e ndryshimit në kohë të pozicionit të një pike (trupi) në hapësirë.

Nxitimi i pikës (trupit).- karakteristikë e ndryshimit të kohës në shpejtësinë e një pike (trupi)

2.2. Kinematika e pikave

2.2.1 Metodat për përcaktimin e lëvizjes së pikës

Të vendosësh lëvizjen e një pike do të thotë të vendosësh një ndryshim në pozicionin e saj në lidhje me sistemin e zgjedhur të referencës. Ekzistojnë tre sisteme kryesore të referencës: vektor, koordinativ, natyror. Prandaj, ekzistojnë tre mënyra për të specifikuar lëvizjen e një pike.

Në një sistem vektorial, pozicioni i një pike në lidhje me origjinën jepet nga vektori i rrezes (Fig. 2.1). Ligji i lëvizjes

Pozicioni i një pike në sistemin koordinativ OXYZ jepet me tre Koordinatat X,Y,Z(fig.2.2). Ligji i lëvizjes x = x ( t ), y = y ( t ), z = z ( t ).

Pozicioni i një pike në sistemin natyror të referencës jepet nga distanca S nga origjina deri në këtë pikë përgjatë trajektores (Fig. 2.3). Ligji i lëvizjes s = s ( t ).

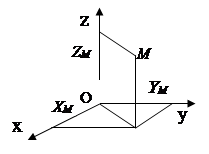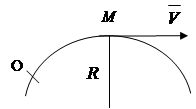
Fig.2.1 Oriz. 2.2 Fig.2.3

Lëvizja e një pike në mënyrën e natyrshme të specifikimit të lëvizjes përcaktohet nëse dihen sa vijon:

1. Trajektorja e lëvizjes.

2. Fillimi dhe drejtimi i numërimit të koordinatës së harkut.

3. Ekuacioni i lëvizjes.

Me metodën natyrale të specifikimit të lëvizjes, ndryshe nga metodat e tjera, përdoren boshtet e koordinatave të lëvizshme, duke lëvizur së bashku me pikën përgjatë trajektores. Akset e tilla janë (Fig. 2.4).

Tangjenta () - e drejtuar në drejtim të rritjes së koordinatave të harkut në mënyrë tangjenciale me trajektoren.

Normale kryesore ( P) drejtohet kah konkaviteti i kurbës.

Binormale ( në) drejtohet pingul me boshtet t, n.

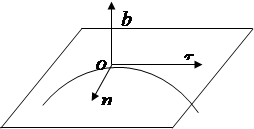Oriz. 2.4

2.2.2 Përcaktimi i karakteristikave kinematike të një pike

Trajektorja e pikës

Në sistemin e referencës vektoriale, trajektorja përshkruhet nga shprehja

Në sistemin e referencës së koordinatave, trajektorja përcaktohet sipas ligjit të lëvizjes së pikës dhe përshkruhet nga shprehjet z = f ( x , y ) - në hapësirë, ose y = f(x) - në rrafsh.

Në një sistem referimi natyror, trajektorja është e paracaktuar.

Shpejtësia e pikës

Sipas përkufizimit (shih paragrafin 2.1), shpejtësia karakterizon ndryshimin në kohë të pozicionit të një pike (trupi) në hapësirë.

Përcaktimi i shpejtësisë së një pike në një sistem koordinativ vektorial

Kur specifikoni lëvizjen e një pike në një sistem koordinativ vektorial, raporti i lëvizjes me një interval kohor quhet vlera mesatare e shpejtësisë në këtë interval kohor.

Duke marrë intervalin kohor si një vlerë pafundësisht të vogël, merret vlera e shpejtësisë në ky moment koha (vlera e shpejtësisë së menjëhershme)

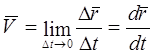(2.1)

Vektori i shpejtësisë mesatare drejtohet përgjatë vektorit në drejtim të lëvizjes së pikës, vektori i shpejtësisë së menjëhershme drejtohet tangjencialisht në trajektoren në drejtim të lëvizjes së pikës (Fig. 2.5).

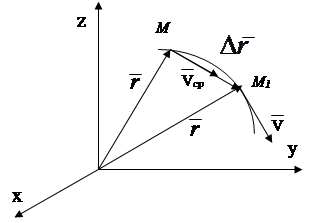Fig.2.5

konkluzioni: shpejtësia e një pike është një sasi vektoriale e barabartë me derivatin e ligjit të lëvizjes në lidhje me kohën.

Ne vërejmë dhe përdorim në arsyetimin e mëtejshëm vetinë e mëposhtme të derivatit : derivati ​​kohor i një sasie përcakton shkallën e ndryshimit të asaj sasie.

Përcaktimi i shpejtësisë së një pike në një sistem referimi koordinativ

Bazuar në vetinë e derivatit, përcaktojmë shpejtësinë e ndryshimit të koordinatave të pikës

Moduli i shpejtësisë së plotë të një pike me sistem koordinativ drejtkëndor do të jetë i barabartë me

(2.3)

Drejtimi i vektorit të shpejtësisë përcaktohet nga kosinuset e këndeve të drejtimit

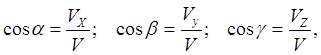
ku janë këndet ndërmjet vektorit të shpejtësisë dhe boshteve të koordinatave.

Përcaktimi i shpejtësisë së një pike në një sistem referimi natyror

Shpejtësia e një pike në një sistem referimi natyror përcaktohet si derivat i ligjit të lëvizjes së një pike

V = (2.4)

Sipas përfundimeve të mëparshme, vektori i shpejtësisë drejtohet në mënyrë tangjenciale në trajektoren në drejtim të lëvizjes së pikës dhe në boshtet n.b. përcaktuar nga vetëm një projeksion.

nxitimi i pikës

Sipas përkufizimit, nxitimi karakterizon ndryshimin e shpejtësisë, d.m.th. shkalla e ndryshimit të shpejtësisë.

Përshpejtimet e një pike në një kornizë vektoriale referimi

Bazuar në vetinë e derivatit

Vektori i shpejtësisë mund të ndryshojë në madhësi dhe drejtim. Për të përcaktuar rritjen e një vektori, ne përputhim fillimet e vektorëve (Fig.2.6). Vektori i nxitimit drejtohet përgjatë vijës së rritjes së vektorit të shpejtësisë, d.m.th., drejt lakimit të trajektores.

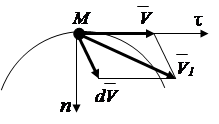
Fig.2.6

Nxitimi i një pike në një sistem referimi koordinativ

Nxitimi i ndryshimit në koordinatat e një pike është i barabartë me derivatin kohor të shpejtësive të ndryshimit të këtyre koordinatave

një x =; një y =; a z = .

Nxitimi total në një sistem koordinativ drejtkëndor do të përcaktohet nga shprehja

a = , (2.6)

Kosinuset e drejtimit të vektorit të nxitimit

.

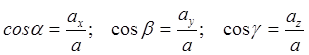Përshpejtimi i një pike në sistemin e referencës natyrore

Rritja e vektorit të shpejtësisë (Fig. 2.7) mund të zbërthehet në komponentë paralelë me boshtet sistemi natyror koordinatat

, (2.7)

Pjesëtimi i anës së majtë dhe të djathtë të barazisë (2.7) me dt, marrim

, (2.8)

ku: - nxitimi tangjencial, (2.9)

Nxitimi normal, (shih nxjerrjen, pika 43)

ku R është rrezja e lakimit të trajektores në afërsi të pikës

Oriz. 2.7

2.3. Kinematika e trupit të ngurtë

Në ndryshim nga kinematika e një pike, dy detyra kryesore zgjidhen në kinematikën e trupave të ngurtë:

Vendosja e lëvizjes dhe përcaktimi i karakteristikave kinematike të trupit në tërësi;

Përcaktimi i karakteristikave kinematike të pikave të trupit.

Metodat për vendosjen dhe përcaktimin e karakteristikave kinematike varen nga llojet e lëvizjes së trupave.

Në këtë manual, merren parasysh tre lloje lëvizjesh: përkthimore, rrotulluese rreth një boshti fiks dhe lëvizja paralele në plan të një trupi të ngurtë.

2.3.1. Lëvizja përkthimore e një trupi të ngurtë

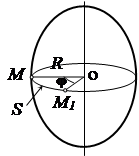
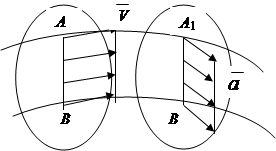
Translational është një lëvizje në të cilën një vijë e drejtë e tërhequr nëpër dy pika të trupit mbetet paralele me pozicionin e saj origjinal (Fig. 2.8).

Teorema vërtetoi: në lëvizjen përkthimore, të gjitha pikat e trupit lëvizin përgjatë të njëjtave trajektore dhe në çdo moment të kohës kanë të njëjtën shpejtësi dhe nxitim në vlerë dhe drejtim absolut (Fig. 2.8).

konkluzioni: Lëvizja përkthimore e një trupi të ngurtë përcaktohet nga lëvizja e ndonjë prej pikave të tij, dhe për këtë arsye, detyra dhe studimi i lëvizjes së tij reduktohet në kinematikën e një pike.

Oriz. 2.8 Fig. 2.9

2.3.2 Lëvizja rrotulluese e një trupi të ngurtë rreth një boshti fiks.

Rrotulluese rreth një boshti fiks është lëvizja e një trupi të ngurtë, në të cilin dy pika që i përkasin trupit mbeten të palëvizshme gjatë gjithë kohës së lëvizjes.

Pozicioni i trupit përcaktohet nga këndi i rrotullimit j (Fig. 2.9). Njësia matëse për një kënd është radianet. (radian - këndi qendror një rreth, gjatësia e harkut të të cilit është e barabartë me rrezen, kënd i plotë rrethi përmban 2p radiane.)

Ligji i lëvizjes rrotulluese të një trupi rreth një boshti fiks j = j(t). Shpejtësia këndore dhe nxitimi këndor i trupit do të përcaktohen me metodën e diferencimit

Shpejtësia këndore, rad/s; (2.10)

Nxitimi këndor, rad/s 2 (2.11)

Në lëvizje rrotulluese trupat rreth një boshti fiks, pikat e tij që nuk shtrihen në boshtin e rrotullimit lëvizin në rrathë me qendër në boshtin e rrotullimit.

Nëse e presim trupin me një rrafsh pingul me boshtin, zgjidhni një pikë në boshtin e rrotullimit NGA dhe pikë arbitrare M, pastaj pikë M do të përshkruajë rreth pikës NGA rrethi me rreze R(Fig. 2.9). Gjatë dt ka një rrotullim elementar nëpër këndin , ndërsa pika M do të lëvizë përgjatë trajektores për një distancë.Le të përcaktojmë modulin e shpejtësisë lineare:

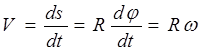(2.12)

nxitimi i pikës M sepse një trajektore e njohur përcaktohet nga përbërësit e saj, shih (2.8)

,

Duke zëvendësuar shprehjen (2.12) në formula, marrim:

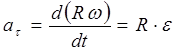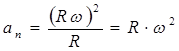, ., (2.13)

ku: - nxitimi tangjencial,

Nxitimi normal.

2.3.3. Lëvizja plan-paralele e një trupi të ngurtë

Plan-paralel është lëvizja e një trupi të ngurtë, në të cilin të gjitha pikat e tij lëvizin në rrafshe paralelisht me një rrafsh të palëvizshëm (Fig. 2.10). Për të studiuar lëvizjen e një trupi, mjafton të studiohet lëvizja e një seksioni S ky trup nga një rrafsh paralel me rrafshin fiks. Lëvizja e seksionit S në rrafshin e tij mund të konsiderohet si kompleks, i përbërë nga dy lëvizje elementare: a) përkthimore dhe rrotulluese; b) rrotulluese në lidhje me qendrën e lëvizshme (të çastit).

Në variantin e parë lëvizja e seksionit mund të jepet nga ekuacionet e lëvizjes së njërës prej pikave të saj (polit) dhe rrotullimit të seksionit rreth polit (Fig. 2.11). Çdo pikë e seksionit mund të merret si shtyllë.

Oriz. 2.10 Fig. 2.11

Ekuacionet e lëvizjes do të shkruhen si:

X A = X A ( t )

Y POR = Y POR ( t ) (2.14)

j POR = j POR ( t )

Karakteristikat kinematike të polit përcaktohen nga ekuacionet e lëvizjes së tij.

Shpejtësia e çdo pike të një figure të rrafshët që lëviz në rrafshin e vet është shuma e shpejtësisë së polit (e zgjedhur në mënyrë arbitrare në seksionin e pikës POR) dhe shpejtësia e rrotullimit rreth polit (rrotullimi i pikës AT rreth pikës POR).

Nxitimi i një pike të një figure të sheshtë lëvizëse është shuma e nxitimit të polit në raport me kornizën fikse të referencës dhe nxitimit për shkak të lëvizjes rrotulluese rreth polit.

(2.15)

(2.16)

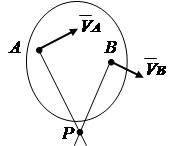
Në variantin e dytë lëvizja e seksionit konsiderohet si rrotulluese rreth një qendre të lëvizshme (të menjëhershme). P(Fig. 1.12). Në këtë rast, shpejtësia e çdo pike B të seksionit do të përcaktohet nga formula për lëvizjen rrotulluese

(2.17)

Shpejtësia këndore rreth qendrës së menjëhershme R mund të përcaktohet nëse dihet shpejtësia e ndonjë pike të seksionit, për shembull, pika A.

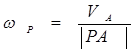(2.18)

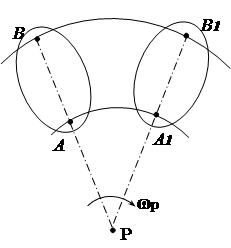
Fig.2.12

Pozicioni i qendrës së menjëhershme të rrotullimit mund të përcaktohet në bazë të vetive të mëposhtme:

Vektori i shpejtësisë së pikës është pingul me rreze;

Moduli i shpejtësisë së një pike është proporcional me distancën nga pika në qendrën e rrotullimit ( V = w ∙ R) ;

Shpejtësia në qendër të rrotullimit është zero.

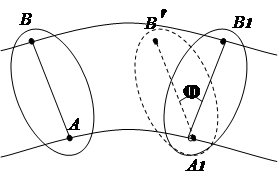
Le të shqyrtojmë disa raste të përcaktimit të pozicionit të qendrës së çastit.

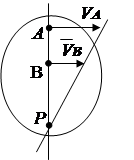
1. Dihen drejtimet e shpejtësive të dy pikave të një figure të sheshtë (Fig. 2.13). Le të vizatojmë vija rrezesh. Qendra e menjëhershme e rrotullimit R të vendosura në kryqëzimin e pingulave të tërhequr me vektorët e shpejtësisë.

2. Shpejtësitë e pikave A dhe B janë të njohura, dhe vektorët dhe janë paralel me njëri-tjetrin, dhe drejtëza. AB pingul (Fig. 2. 14). Në këtë rast, qendra e menjëhershme e rrotullimit shtrihet në vijë AB. Për ta gjetur, vizatojmë një vijë proporcionaliteti të shpejtësive bazuar në varësinë V = w R .

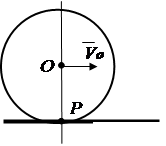
3. Trupi rrotullohet pa rrëshqitur në sipërfaqen e fiksuar të një trupi tjetër (Fig. 2.15). Pika e kontaktit të trupave për momentin ka shpejtësi zero, ndërsa shpejtësitë e pikave të tjera të trupit nuk janë të barabarta me zero. pikë prekjeje R do të jetë qendra e menjëhershme e rrotullimit.

Oriz. 2.13 Oriz. 2.14 Oriz. 2.15

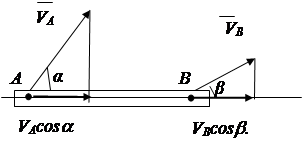
Përveç opsioneve të shqyrtuara, shpejtësia e një pike seksioni mund të përcaktohet në bazë të teoremës mbi projeksionet e shpejtësive të dy pikave të një trupi të ngurtë.

Teorema: projeksionet e shpejtësive të dy pikave të një trupi të ngurtë në një vijë të drejtë të tërhequr nëpër këto pika janë të barabarta dhe të drejtuara njësoj .

Vërtetim: Distanca AB nuk mund të ndryshojë, prandaj

V Dhe cosa nuk mund të jetë pak a shumë V Në cosb (Fig. 2.16).

Oriz. 2.16

konkluzioni: V POR cosa= V AT cosb. (2.19)

2.4. Lëvizja komplekse e pikës

Në paragrafët e mëparshëm, u mor në konsideratë lëvizja e një pike në lidhje me një kornizë fikse referimi, e ashtuquajtura lëvizje absolute. Në praktikë, ka probleme në të cilat dihet lëvizja e një pike në lidhje me një sistem koordinativ, i cili lëviz në lidhje me një sistem fiks. Në këtë rast, kërkohet të përcaktohen karakteristikat kinematike të pikës në lidhje me sistemin fiks.

Është zakon të quhet: lëvizja e një pike në lidhje me një sistem lëvizës - i afërm, lëvizja e një pike së bashku me sistemin lëvizës - portative, lëvizja e një pike në lidhje me një sistem fiks - absolute. Prandaj, shpejtësitë dhe nxitimet quhen:

farefisnore - figurative; -absolut.

Sipas teoremës së mbledhjes së shpejtësisë, shpejtësia absolute e një pike është e barabartë me shumën vektoriale të shpejtësive relative dhe translative (Fig.).

, (2.20)

Vlera absolute e shpejtësisë përcaktohet nga ligji i kosinusit

, (2.21)

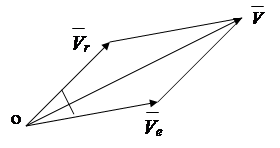
Fig.2.17

Nxitimi sipas rregullit të paralelogramit përcaktohet nga vetëm në lëvizje përkthimore

, (2.22)

Me lëvizjen e lëvizshme jo-përkthyese, shfaqet një komponent i tretë i nxitimit, i quajtur rrotullues ose Coriolis.

, (2.23)

ku

Nxitimi i Coriolis është numerikisht i barabartë me

,

ku a është këndi ndërmjet vektorëve dhe

Është i përshtatshëm për të përcaktuar drejtimin e vektorit të nxitimit Coriolis sipas N.E. Zhukovsky: projektoni vektorin në një plan pingul me boshtin e rrotullimit përkthimor, rrotulloni projeksionin me 90 gradë në drejtim të rrotullimit përkthimor. Drejtimi që rezulton do të korrespondojë me drejtimin e nxitimit të Coriolis.

2.5 Pyetje për vetëkontroll në seksion

1. Cilat janë detyrat kryesore të kinematikës? Emërtoni karakteristikat kinematike.

2. Emërtoni metodat për përcaktimin e lëvizjes së një pike dhe përcaktimin e karakteristikave kinematike.

3. Jepni një përkufizim të lëvizjes përkthimore, rrotulluese rreth një boshti fiks, lëvizjes plan-paralele të një trupi.

4. Si përcaktohet lëvizja e një trupi të ngurtë gjatë përkthimit, rrotullimit rreth një boshti fiks dhe lëvizjes plan-paralele të trupit dhe si përcaktohet shpejtësia dhe nxitimi i një pike gjatë këtyre lëvizjeve të trupit?

3. Dinamika

3.1 Probleme të dinamikës

Dy lloje problemesh zgjidhen në dinamikë. E para është për të përcaktuar forcat aktive duke pasur parasysh ligjin e lëvizjes së një objekti material (pikës ose sistemit). Detyra e dytë është e kundërta e së parës: ligji i lëvizjes së një objekti material përcaktohet me forca të njohura që veprojnë mbi të.

3.2. Konceptet themelore të dinamikës

inercia- vetia e trupave materialë për të mbajtur një gjendje pushimi ose lëvizje drejtvizore uniforme derisa forcat e jashtme ta ndryshojnë këtë gjendje.

Pesha- një masë sasiore e inercisë së trupit. Njësia e masës është kilogrami (kg).

Pika materiale- një trup me masë, përmasat e të cilit neglizhohen gjatë zgjidhjes së këtij problemi.

Qendra e masës së një sistemi mekanik- një pikë gjeometrike, koordinatat e së cilës përcaktohen me formula.

ku m k , x k , y k , z k- masa dhe koordinatat e k - ajo pikë e sistemit mekanik,

mështë masa e sistemit.

Në një fushë uniforme të gravitetit, pozicioni i qendrës së masës përkon me pozicionin e qendrës së gravitetit.

Momenti i inercisë së një trupi material rreth boshtitështë një masë sasiore e inercisë gjatë lëvizjes rrotulluese.

Momenti i inercisë së një pike materiale rreth boshtit është i barabartë me produktin e masës së pikës dhe katrorit të distancës së pikës nga boshti.

J Z = m × r 2 (3.2)

Momenti i inercisë së sistemit (trupit) rreth boshtit është i barabartë me shumën aritmetike të momenteve të inercisë të të gjitha pikave.

J Z = å m k × rk 2 (3.3)

Forca e inercisë së një pike materiale- një sasi vektoriale e barabartë në vlerë absolute me produktin e masës së një pike dhe modulit të nxitimit dhe e drejtuar në kundërshtim me vektorin e nxitimit

(3.4)

Forca e inercisë së një trupi material- një sasi vektoriale e barabartë në vlerë absolute me produktin e masës trupore dhe modulin e nxitimit të qendrës së masës së trupit dhe e drejtuar në kundërshtim me vektorin e nxitimit të qendrës së masës

, (3.5)

ku është nxitimi i qendrës së masës së trupit.

Impulsi i forcës elementare- sasi vektoriale e barabartë me produktin e vektorit të forcës me një interval kohor infinitimal dt

, (3.6)

Forca totale e impulsit për D tështë e barabartë me integralin e impulseve elementare

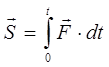(3.7)

punë elementare forcë- vlera skalare dA, e barabartë me produktin skalar të vektorit të forcës dhe zhvendosjes infiniteminale d .

Produkti skalar i vektorëve është i barabartë me produktin e moduleve të tyre dhe kosinusin e këndit ndërmjet drejtimeve të vektorëve.

dA = F × ds × cos a , (3.8)

ku a është këndi ndërmjet drejtimeve të vektorëve të zhvendosjes dhe forcës.

Puna e forcës në zhvendosjen përfundimtare të pikës së zbatimit të saj është e barabartë me integralin e punës elementare, të marrë mbi zhvendosjen.

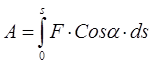(3.9)

Njësia e punës është Xhaul (1 J=1 N×m).

Sasia e lëvizjes së një pike materiale- një sasi vektoriale e barabartë me prodhimin e masës m dhe shpejtësisë së saj.

Momenti i një sistemi mekanik është i barabartë me shumën vektoriale të momentit të pikave të tij.

(3.11)

ose duke marrë parasysh formulat (3.1).

ku: m është masa e sistemit mekanik,

Vektori i shpejtësisë së qendrës së masës së sistemit.

Energjia kinetike e një pike materiale- vlera skalare T, e barabartë me gjysmën e produktit të masës së një pike dhe katrorit të shpejtësisë së saj.

T = (3.13)

Energjia kinetike e një sistemi mekanik është e barabartë me shumën energjitë kinetike të gjitha pikat e saj.

3.3. Aksiomat e dinamikës

Aksioma e parë është ligji i inercisë .

Nëse në një pikë të lirë materiale nuk vepron asnjë forcë ose nuk vepron një sistem i balancuar forcash, atëherë pika do të jetë në qetësi ose lëvizje drejtvizore uniforme.

Aksioma e dytë është ligji i proporcionalitetit të nxitimit .

Nxitimi i dhënë një pike materiale nga forca që vepron mbi të është proporcionale me këtë forcë dhe përkon në drejtim me drejtimin e forcës.

Shprehja (3.15) quhet ligji bazë i dinamikës .

Aksioma e tretë është ligji i kundërveprimit .

Forcat me të cilat dy pika materiale veprojnë mbi njëra-tjetrën janë të barabarta në vlerë absolute dhe të drejtuara përgjatë vijës së drejtë që lidh këto pika në drejtime të kundërta.

Aksioma e katërt është ligji i pavarësisë së veprimit të forcave .

Kur një sistem forcash vepron në një pikë materiale, nxitimi total i kësaj pike është i barabartë me shumën gjeometrike të nxitimeve nga veprimi i secilës forcë.

3.4. Ekuacionet diferenciale të dinamikës

Ekuacionet diferenciale të lëvizjes së një pike lidhin nxitimin e një pike me forcat që veprojnë në të. Në fakt, ekuacionet diferenciale janë një regjistrim i ligjit bazë të dinamikës në një formë të qartë diferenciale.

Për lëvizjen absolute të një pike (lëvizja në një kornizë inerciale referimi), ekuacioni diferencial ka formën

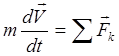, (3.18)

Ekuacioni vektorial (3.17) mund të shkruhet në projeksione në boshtet e një sistemi koordinativ inercial drejtkëndor

,

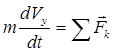, (3.19)

,

Me një trajektore të njohur të pikës, ekuacioni (3.18) mund të shkruhet në projeksione në boshtet e sistemit të koordinatave natyrore

, (3.20)

Duke marrë parasysh (2.8), ekuacionet marrin formën

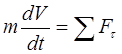(3.21)

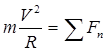
3.5 Teorema të përgjithshme të dinamikës

Teoremat e përgjithshme të dinamikës vendosin marrëdhëniet midis masave të lëvizjes mekanike dhe bashkëveprimit mekanik. Përfundimet e teoremave janë rezultat i një transformimi identik të ligjit bazë të dinamikës.

Teorema mbi ndryshimin e momentit : ndryshimi në momentin e një pike materiale (sistemi mekanik) gjatë një periudhe të kufizuar kohore është i barabartë me shumën e impulseve forcat e jashtme për të njëjtën periudhë kohore

- për një pikë materiale; (3.22)

- për sistemin mekanik. (3.23)

Teorema e ndryshimit të energjisë kinetike : ndryshimi i energjisë kinetike të një pike (sistemi mekanik) gjatë lëvizjes së saj është i barabartë me shumën e punës së të gjitha forcave të jashtme që veprojnë në këtë lëvizje.

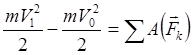- për një pikë materiale (3.24)

- për një sistem mekanik (3.25)

Energjia kinetike e një sistemi mekanik përcaktohet në përputhje me (3.14), ndërsa varësitë e mëposhtme janë nxjerrë për trupat e ngurtë

Me lëvizjen përkthimore të trupit, (3.26)

Gjatë lëvizjes rrotulluese të trupit, (3.27)

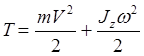- me një lëvizje plan-paralele të trupit. (3.28)

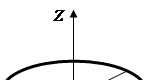
Momentet e inercisë së disa trupave homogjenë

Oriz. 3.1 Fig.3.2. R Figura 3.3.

Momenti i inercisë së cilindrit në lidhje me boshtin (Fig. 3.1.)

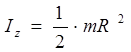
Momenti i inercisë së shufrës rreth boshtit z (Fig. 3.2)

Momenti i inercisë së një pllake drejtkëndore rreth boshteve x dhe y (Fig. 3.3)

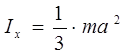
Momenti i inercisë së topit përcaktohet nga formula:

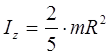
Në rastin e përgjithshëm, puna e forcave përcaktohet në përputhje me (3.8), (3.9) Në një numër rastesh të veprimit të forcave, puna mund të përcaktohet nga varësi të veçanta.

Puna e gravitetit

ku: - gravitetit,

Ndryshimi i pozicionit të trupit vertikalisht.

Puna e forcës gjatë lëvizjes rrotulluese të trupit

, (3.30)

ku: - momenti i forcës,

Shpejtësia këndore e trupit.

Mbani në mend se puna, si një sasi skalare, mund të jetë pozitive ose negative. Puna do të jetë pozitive nëse drejtimi i forcës përkon me drejtimin e lëvizjes.

Parimi 3.6 d'Alembert

Metodat e mësipërme për studimin e lëvizjes së trupave bazohen në ligjet e Njutonit. Janë zhvilluar metoda të bazuara në parime të tjera. Një prej tyre është Parimi i d'Alembert.Parimi është formuluar: nëse në çdo moment të kohës forcat e inercisë u shtohen forcave që veprojnë në pikë, atëherë sistemi i forcave që rezulton do të balancohet

, (3.31)

ose për sistemin mekanik

Parimi d'Alembert na lejon të aplikojmë më shumë për zgjidhjen e problemeve të dinamikës metoda të thjeshta statike, kështu që përdoret gjerësisht në praktikën inxhinierike.

3.7. Pyetje për vetëkontroll në rubrikën

1. Formuloni detyrat kryesore të dinamikës.

2. Jepni përkufizime të masës, momentit të inercisë, impulsit të forcës, punës së forcës, momentit, energjisë kinetike.

3. Formuloni ligjet bazë të dinamikës.

4. Çfarë barazimi quhet ekuacioni diferencial folësit? Cili është algoritmi për zgjidhjen e problemeve të dinamikës duke përdorur ekuacione diferenciale?

5. Formuloni teorema të përgjithshme të dinamikës.

6. Formuloni parimin d'Alembert. Si përcaktohen forcat e inercisë?

7. Formuloni parimin e lëvizjeve të mundshme. Në çfarë kushtesh zbatohet parimi i zhvendosjeve të mundshme?

Në këtë kapitull shqyrtohen problemet për përcaktimin e punës së bërë nga një forcë konstante dhe fuqia e zhvilluar gjatë lëvizjes përkthimore dhe rrotulluese të trupave (E. M. Nikitin, § 81-87).

§ 44. Puna dhe fuqia në lëvizjen përkthimore

Puna e një force konstante P në një seksion të drejtë të shtegut s, të përshkuar nga pika e aplikimit të forcës, përcaktohet nga formula
(1) A = Ps cos α,
ku α është këndi ndërmjet drejtimit të forcës dhe drejtimit të lëvizjes.

Në α = 90°
cos α = cos 90° = 0 dhe A = 0,
d.m.th., puna e një force që vepron pingul me drejtimin e lëvizjes është zero.

Nëse drejtimi i forcës përkon me drejtimin e lëvizjes, atëherë α = 0, prandaj cos α = cos 0 = 1 dhe formula (1) thjeshtohet:
(1") A = Ps.

Jo një forcë, por disa, zakonisht vepron në një pikë ose në një trup, prandaj, gjatë zgjidhjes së problemeve, këshillohet të përdoret teorema mbi funksionimin e sistemit rezultant të forcave (E. M. Nikitin, § 83):
(2) A R = ∑ A i ,
d.m.th., puna e rezultantes së çdo sistemi forcash në një rrugë të caktuar është e barabartë me shumën algjebrike të punës së të gjitha forcave të këtij sistemi në të njëjtën rrugë.

Në një rast të veçantë, kur sistemi i forcave është i balancuar (trupi lëviz në mënyrë të njëtrajtshme dhe në vijë të drejtë), rezultanta e sistemit të forcave është e barabartë me zero dhe, për rrjedhojë, A R = 0. Prandaj, me një lëvizje uniforme dhe drejtvizore të një pike ose trupi, ekuacioni (2) merr formën
(2") ∑ Ai = 0,
d.m.th., shuma algjebrike e punës së një sistemi të balancuar forcash në një rrugë të caktuar është e barabartë me zero.

Në të njëjtën kohë, forcat, puna e të cilave është pozitive quhen forca lëvizëse, dhe forcat, puna e të cilave është negative quhen forca të rezistencës. Për shembull, kur një trup lëviz poshtë - graviteti - forca lëvizëse dhe puna e tij është pozitive, dhe kur trupi lëviz lart, graviteti i tij është një forcë rezistente dhe puna e gravitetit është negative.

Gjatë zgjidhjes së problemeve në rastet kur forca P është e panjohur, puna e së cilës duhet të përcaktohet, mund të rekomandohen dy metoda (metoda).

1. Duke përdorur forcat e specifikuara në gjendjen e problemit, përcaktoni forcën P dhe më pas, duke përdorur formulën (1) ose (1"), llogaritni punën e saj.

2. Pa përcaktuar drejtpërdrejt forcën P, përcaktoni A p - punën e forcës së kërkuar duke përdorur formulat (2) dhe (2"), duke shprehur teoremën mbi punën e rezultantes.

Fuqia e zhvilluar gjatë punës së një force konstante përcaktohet nga formula
(3) N = A/t ose N = (Ps cos α)/t.

Nëse, gjatë përcaktimit të punës së forcës P, shpejtësia e pikës v \u003d s / t mbetet konstante, atëherë
(3") N = Pv cos α.

Nëse shpejtësia e pikës ndryshon, atëherë s / t \u003d v cf - Shpejtësia mesatare dhe më pas formula (2") heq fuqinë mesatare
N av = Pv av cos α.

Koeficient veprim i dobishëm(k.p.d.) kur bën punë mund të përkufizohet si raport i punës
(4) η = Një fushë /A,
ku Një kat - punë e dobishme; A është e gjithë puna e bërë, ose si raport i kapaciteteve përkatëse:
(4") η = N kati /N.

Njësia e punës SI është 1 xhaul (J) = 1 N * 1 m.

Njësia e fuqisë SI është 1 vat (W) = 1 J / 1 sek.

Një njësi e njohur e fuqisë jashtë sistemit është kuajfuqi (hp):
1000 W = 1,36 litra. Me. ose 1 l. Me. = 736 W.

Për të kaluar midis watts dhe kuaj-fuqi, përdorni formulat
N (kW) = 1,36 N (hp)
N (hp) \u003d 0,736 N (kW).

Leksioni 2. Puna. Fuqia. Teorema mbi ndryshimin e energjisë kinetike të një pike.

Ky leksion mbulon pyetjet e mëposhtme:

Punë me forcë.

Fuqia.

Shembuj të llogaritjes së punës.

Energji potenciale

Energjia kinetike

Teorema mbi ndryshimin e energjisë kinetike të një pike.

Teorema e momentit.

Studimi i këtyre çështjeve është i nevojshëm për dinamikën e qendrës së masës së një sistemi mekanik, dinamikën e lëvizjes rrotulluese të një trupi të ngurtë, momentin kinetik të një sistemi mekanik, për zgjidhjen e problemeve në disiplinat "Teoria e makinave dhe mekanizmat" dhe "Pjese makinerish".

Punë me forcë. Fuqia.

Për të karakterizuar veprimin e ushtruar nga një forcë mbi një trup me një farë zhvendosjeje, prezantohet koncepti i punës së një force.

Fig.16

Në këtë rast, vepra karakterizon veprimin e forcës, e cila përcakton ndryshimin modul shpejtësia e pikës lëvizëse.

Le të prezantojmë fillimisht konceptin e punës elementare të një force në një zhvendosje infiniteminale ds. Puna elementare e një force (Fig. 16) është një sasi skalare:

ku është projeksioni i forcës mbi tangjenten me trajektoren e drejtuar në drejtim të zhvendosjes së pikës dhe është zhvendosja pafundësisht e vogël e pikës e drejtuar përgjatë kësaj tangjente.

Ky përkufizim korrespondon me konceptin e punës, si karakteristikë e veprimit të një force që çon në ndryshimin e modulit të shpejtësisë së një pike. Në të vërtetë, nëse e zbërthejmë forcën në komponentë dhe , atëherë vetëm komponenti do të ndryshojë modulin e shpejtësisë së pikës, duke i dhënë një nxitim tangjencial pikës. Komponenti ose ndryshon drejtimin e vektorit të shpejtësisë v(i jep një nxitim normal pikës), ose, nëse lëvizja nuk është e lirë, ndryshon presionin në lidhje. Komponenti nuk do të ndikojë në modulin e shpejtësisë, d.m.th., siç thonë ata, forca "nuk do të prodhojë punë".

Duke vërejtur këtë, marrim:

. (1)

Në këtë mënyrë, punë elementare forca është e barabartë me projeksionin e forcës në drejtimin e lëvizjes së pikës, shumëzuar me zhvendosjen elementare, ose puna elementare e forcës është e barabartë me produktin e modulit të forcës nga zhvendosja elementare dhe kosinusi i këndi ndërmjet drejtimit të forcës dhe drejtimit të zhvendosjes.

Nëse këndi është akut, atëherë puna është pozitive. Në veçanti, për punë elementare .

Nëse këndi është i mpirë, atëherë puna është negative. Në veçanti, për punë elementare .

Nëse këndi , d.m.th. nëse forca drejtohet pingul me zhvendosjen, atëherë puna elementare e forcës është zero.

Le të gjejmë një shprehje analitike për punën elementare. Për ta bërë këtë, ne e zbërthejmë forcën në komponentë , , në drejtimet e boshteve të koordinatave (Fig. 17; vetë forca nuk tregohet në vizatim).

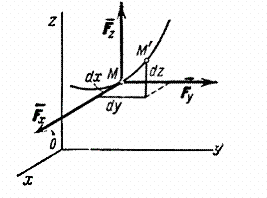
Fig.17

Një zhvendosje elementare është e përbërë nga zhvendosjet , , përgjatë boshteve koordinative, ku x, y, z - koordinatat e pikave M. Atëherë puna e forcës në zhvendosje mund të llogaritet si shuma e punës së përbërësve të saj , , mbi zhvendosjet , , .

Por vetëm komponenti punon në zhvendosjen, dhe puna e tij është e barabartë me . Puna në zhvendosje dhe llogaritet në mënyrë të ngjashme. Më në fund gjejmë:

Formula jep një shprehje analitike për punën elementare të një force.

Puna e kryer nga një forcë në çdo zhvendosje të fundme M 0 M 1 llogaritet si shuma integrale e punimeve elementare përkatëse dhe do të jetë e barabartë me:

ose

.

Rrjedhimisht, puna e forcës në çdo zhvendosje M 0 M 1 është e barabartë me integralin e punës elementare të marrë përgjatë kësaj zhvendosjeje. Kufijtë e integralit korrespondojnë me vlerat e variablave të integrimit në pika M 0 dhe M 1 .

Fig.18

Nëse vlera është konstante (= konst), atëherë tregon zhvendosjen M 0 M 1 përmes marrim: .

Një rast i tillë mund të ndodhë kur forca vepruese është konstante në modul dhe drejtim ( F= konst), dhe pika në të cilën zbatohet forca lëviz në një vijë të drejtë (Fig. 18). Në këtë rast dhe puna e forcës .

Njësia SI për punë është xhaul (1 j = 1 hm).

Fuqia.

Fuqiaështë sasia që përcakton punën e bërë nga forca për njësi të kohës. Nëse puna bëhet në mënyrë të barabartë, atëherë fuqia

ku t - koha gjatë së cilës është kryer puna A. Në përgjithësi

.

Prandaj, fuqia është e barabartë me produktin e komponentit tangjencial të forcës dhe shpejtësisë së lëvizjes.

Njësia e fuqisë në sistem SIështë vat (1 E martë= 1 j/sek). Në inxhinieri, 1 kuaj fuqi shpesh merret si njësi fuqie, e barabartë me 75 kgm/sek ose 736 e martë.

Puna e bërë nga një makinë mund të matet nga produkti i fuqisë së saj dhe koha që ajo ka punuar. Nga kjo lindi njësia e matjes së punës, kilovat-orë, e përdorur zakonisht në teknologji (1 kWh = 3,6j 367100 kgm).

Nga ekuacioni mund të shihet se për një motor me një fuqi të caktuar W, forca tërheqëse do të jetë sa më e madhe, aq më e ulët është shpejtësia e lëvizjes V. Prandaj, për shembull, në një përpjetë ose në një pjesë të keqe të rrugës, makina përfshin marshe më të ulëta, të cilat lejojnë, me fuqi të plotë, të lëvizë me një shpejtësi më të ulët dhe të zhvillojë më shumë tërheqje.

Shembuj të llogaritjes së punës.

Shembujt e konsideruar më poshtë japin rezultate që mund të përdoren drejtpërdrejt në zgjidhjen e problemeve.

1) Puna e gravitetit. Lëreni pikën M, mbi të cilat vepron forca e rëndesës , lëviz nga pozicioni M ­ 0 (x­ 0 , në 0 , z 0 ) në pozicion M 1 (X 1 , y 1 , z 1 ). Ne zgjedhim boshtet e koordinatave në mënyrë që boshti Oz drejtohej vertikalisht lart (Fig. 19).

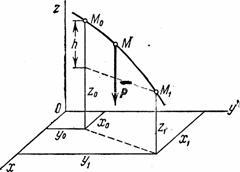
Fig.19

Pastaj R x=0, R y=0, P z=- R. Zëvendësimi i këtyre vlerave dhe duke marrë parasysh variablin e integrimit z:

Nëse pika M 0 lart M 1 , ku h- vlera e lëvizjes vertikale të pikës;

Nëse pika M 0 poshtë pikës M 1 pastaj .

Më në fund marrim: .

Rrjedhimisht, puna e gravitetit është e barabartë me produktin e modulit të forcës, të marrë me një shenjë plus ose minus, dhe zhvendosjen vertikale të pikës së zbatimit të saj. Puna është pozitive nëse pika e fillimit është më e lartë se pika e fundit, dhe negative nëse pika e fillimit është më e ulët se pika e fundit. Nga rezultati i marrë rezulton se puna e gravitetit nuk varet nga lloji i trajektores përgjatë së cilës lëviz pika e zbatimit të saj.

Forcat me këtë veti quhen forca potenciale.

2) Puna e forcës elastike. Merrni parasysh ngarkesën M, shtrirë në një rrafsh horizontal dhe ngjitur në skajin e lirë të disa susta (Fig. 20a). Shënoni në aeroplan me një pikë O pozicioni i zënë nga fundi i sustës kur nuk është i sforcuar (është gjatësia e sustës së patheksuar), dhe ne e marrim këtë pikë si origjinë. Nëse tani e largojmë ngarkesën nga pozicioni i ekuilibrit O, duke e shtrirë sustën në një vlerë , atëherë mbi ngarkesën do të veprohet nga forca elastike e sustës F, drejtuar në pikën O.

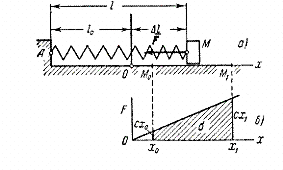
Fig.20

Sipas ligjit të Hukut, madhësia e kësaj force është proporcionale me zgjatjen e sustës. Që në rastin tonë, atëherë modulo.

Koeficient Me thirrur koeficienti i ngurtësisë burimet. Në inxhinieri, zakonisht matet Me në h/cm, duke supozuar koeficientin Me numerikisht e barabartë me forcën që duhet të aplikohet në sustë për ta shtrirë atë me 1 cm.

Gjeni punën e bërë nga forca elastike kur lëvizni ngarkesën nga pozicioni në pozicion . Meqenëse në këtë rast , , atëherë marrim:

(I njëjti rezultat mund të merret nga grafiku i varësisë F nga X (fig.20, b) duke llogaritur sipërfaqen e trapezit të hijezuar në vizatim dhe duke marrë parasysh shenjën e punës.) Në formulën që rezulton, përfaqëson zgjatjen fillestare të sustës, dhe zgjatja fundore e pranverës. Rrjedhimisht,

,

ato. puna e forcës elastike është e barabartë me gjysmën e prodhimit të koeficientit të ngurtësisë dhe diferencës ndërmjet katrorëve të zgjatimeve (ose ngjeshjeve) fillestare dhe përfundimtare të sustës.

Puna do të jetë pozitive kur , d.m.th. kur fundi i pranverës kalon në pozicionin e ekuilibrit, dhe negativ kur , d.m.th. fundi i sustës largohet nga pozicioni i ekuilibrit. Mund të vërtetohet se formula mbetet e vlefshme edhe në rastin kur zhvendosja e pikës M nuk është lineare.

Kështu, rezulton se puna e forcës F varet vetëm nga vlerat dhe dhe nuk varet nga lloji i trajektores së pikës M. Prandaj, forca elastike është gjithashtu potenciale.

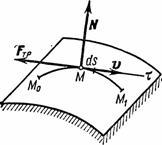
Fig.21

3) Puna e forcës së fërkimit. Konsideroni një pikë që lëviz përgjatë një sipërfaqeje të ashpër (Fig. 21) ose një kurbë. Forca e fërkimit që vepron në pikë është e barabartë në vlerë absolute fN, ku fështë koeficienti i fërkimit dhe është reagimi normal i sipërfaqes. Forca e fërkimit drejtohet në kundërshtim me zhvendosjen e pikës. Rrjedhimisht, F tr = - fN dhe sipas formulës

.

Nëse forca e fërkimit është konstante, atëherë , ku s-gjatësia e harkut të kurbës M 0 M 1 përgjatë së cilës lëviz pika.

Në këtë mënyrë, Puna e bërë nga forca e fërkimit rrëshqitës është gjithmonë negative. Sasia e kësaj pune varet nga gjatësia e harkut M 0 M 1 . Prandaj, forca e fërkimit është forca jo potencial.

4) Puna e një force të aplikuar në një trup që rrotullohet rreth një boshti të caktuar.

Në këtë rast (Fig. 22), pika e aplikimit të forcës lëviz përgjatë një rrethi me rreze r. Punë elementare, nga (1), , ku.

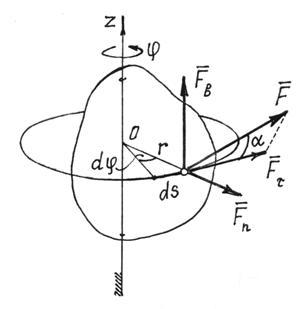
Fig.22

Kjo është arsyeja pse .

Kjo nuk është e vështirë të përcaktohet duke e zbërthyer forcën në tre komponentë (Fig. 22). (Momentet e forcave dhe janë të barabarta me zero). Do të thotë,

(2)

Në veçanti, nëse momenti i forcës rreth boshtit , puna e forcës kur trupi rrotullohet nëpër një kënd është e barabartë me

. (3)

Shenja e punës përcaktohet nga shenjat e momentit të forcës dhe këndit të rrotullimit. Nëse janë të njëjta, puna është pozitive.

Formula (3) nënkupton edhe rregullin për përcaktimin e punës së një çifti forcash. Nëse një çift me një moment m ndodhet në një rrafsh pingul me boshtin e rrotullimit të trupit, atëherë puna e tij kur trupi rrotullohet përmes një këndi

Nëse një palë forcash vepron në një rrafsh jo pingul me boshtin e rrotullimit, atëherë ai duhet të zëvendësohet me dy çifte. Vendoseni njërën në rrafshin pingul me boshtin, tjetrin në rrafshin paralel me boshtin. Momentet e tyre përcaktohen nga zgjerimi i vektorit të momentit në drejtimet përkatëse: . Natyrisht, vetëm çifti i parë me momentin do të bëjë punën, ku është këndi midis vektorit dhe boshtit të rrotullimit z,

. (5)

Energji potenciale

Pjesa e hapësirës në të cilën një forcë që vepron në një pikë materiale të vendosur aty, në varësi të vendndodhjes së pikës, quhet fushë force.

Për më tepër, kjo forcë përcaktohet duke përdorur funksionin e forcës u = u(x, y, z). Nëse nuk varet nga koha, atëherë një fushë e tillë quhet e palëvizshme. Nëse është e njëjtë në të gjitha pikat, atëherë fusha është homogjene.

Nëse projeksionet e forcës në boshtet karteziane janë derivate të pjesshme të funksionit të forcës në lidhje me koordinatat përkatëse

atëherë një fushë e tillë quhet potencial.

Llogaritni punën e forcës fushë potenciale kur lëviz një pikë nga një pozicion M 1 në pozicion M 2. (Fig. 23).

Fig.23

punë elementare,

Ky është diferenciali total i funksionit të forcës.

Duke punuar në udhëtimin përfundimtar

(7)

ku u 2 dhe u 1 - vlerat e funksionit të forcës në pika M 2 dhe M 1 .

Rrjedhimisht, puna e forcës potenciale të fushës nuk varet nga trajektorja e pikës, por përcaktohet vetëm nga vlerat e funksionit të forcës në pozicionet fillestare dhe përfundimtare të pikës.

Natyrisht, nëse pika kthehet në pozicionin e saj fillestar, puna e forcës do të jetë zero. Puna do të jetë e barabartë me zero dhe kur lëviz në një pikë tjetër M 3 nëse vlera e funksionit të forcës atje është e njëjtë si në pozicionin fillestar.

Është e lehtë të merret me mend se pikat me të njëjtat vlera të funksionit të forcës do të formojnë një sipërfaqe të tërë. Dhe se fusha e forcës është një hapësirë ​​e shtresuar e përbërë nga sipërfaqe të tilla (Fig. 23). Këto sipërfaqe quhen sipërfaqet e nivelit ose sipërfaqet ekuipotenciale. Ekuacionet e tyre janë: u(x, y, z)= C (C- konstante, e barabartë me vlerën u pika në këtë sipërfaqe). Dhe funksioni i forcës quhet, përkatësisht, potencial fusha.

Natyrisht, sipërfaqet ekuipotenciale nuk kryqëzohen. Përndryshe, do të kishte pika fushore me një potencial të pacaktuar.

Meqenëse, kur lëviz një pikë përgjatë një sipërfaqe ekuipotenciale, puna e forcës është zero, atëherë vektori i forcës është pingul me sipërfaqen.

Ndër këto sipërfaqe zgjedhim një dhe e quajmë sipërfaqja zero (vëmë u= u 0 ).

Puna që do të bëjë forca kur pika lëviz nga një vend i caktuar M në sipërfaqen zero quhet energjia potenciale e pikës në këtë vend specifik M:

. (8)

vini re, se energji potenciale në të njëjtën pikë të fushës varet nga zgjedhja e sipërfaqes nule.

Nga (8) funksioni i forcës . Prandaj, projeksionet e forcës në akset karteziane, sipas (6), pasi ,

dhe vektori i forcës .

Konsideroni disa fusha të mundshme.

1) Fusha e gravitetit.

Pranë sipërfaqes së Tokës, forca e gravitetit në të gjitha pikat është e njëjtë, e barabartë me peshën e trupit. Kjo do të thotë se kjo fushë e forcës është uniforme. Meqenëse kur një pikë lëviz në një plan horizontal, puna e forcës është zero, sipërfaqet ekuipotenciale do të jenë plane horizontale (Fig. 24), dhe ekuacionet e tyre: u = z = C.

Fig.24

Nëse rrafshi është caktuar si sipërfaqe zero xOy, pastaj energjia potenciale e një pike në pozicion M do të jetë e barabartë me punën e gravitetit:

2) Fusha e forcës elastike.

Kur një trup elastik, siç është një susta, deformohet, shfaqet një forcë. Domethënë, pranë këtij trupi lind një fushë force, forcat e së cilës janë proporcionale me deformimin e trupit dhe të drejtuara drejt gjendjes së padeformuar. Në pranverë - deri në pikën M 0 , ku ndodhet fundi i sustës së padeformuar (Fig. 25).

Fig.25

Nëse e lëvizni fundin e sustës në mënyrë që gjatësia e saj të mos ndryshojë, atëherë puna e forcës elastike do të jetë zero. Kjo do të thotë që sipërfaqet ekuipotenciale janë sipërfaqe sferike të përqendruara në pikën O.

Cakto sipërfaqen zero sferës që kalon nëpër pikë M 0 , deri në fund të pranverës së padeformuar. Pastaj energjia potenciale e sustës në pozicion M: .

Me një zgjedhje të tillë të sipërfaqes zero, energjia potenciale do të jetë gjithmonë pozitive (P>0), si në gjendje të shtrirë ashtu edhe në gjendje të ngjeshur.

Teorema mbi ndryshimin e energjisë kinetike të një pike.

Konsideroni një pikë me masë t, duke lëvizur nën veprimin e forcave të aplikuara në të nga një pozicion M 0 , ku ka shpejtësi , në pozicion M 1, ku është shpejtësia e tij.

Për të marrë varësinë e dëshiruar, i drejtohemi ekuacionit që shpreh ligjin bazë të dinamikës. Projektimi i të dy pjesëve të kësaj barazie në tangjenten me trajektoren e pikës M, drejtuar në drejtim të lëvizjes, marrim:

Vlera e nxitimit tangjencial në të majtë mund të përfaqësohet si

.

Si rezultat do të kemi:

.

Duke shumëzuar të dyja anët e këtij ekuacioni me ds, do të prezantojmë t nën shenjën e diferencialit. Pastaj, duke vënë re se ku - puna elementare e forcës F k marrim shprehjen e teoremës për ndryshimin e energjisë kinetike në formë diferenciale.

Puna e gravitetit. gravitetit R masë e pikës materiale t pranë sipërfaqes së Tokës mund të konsiderohet një konstante, e barabartë me mg

drejtuar vertikalisht poshtë.

Puna POR forcë R në lëvizje nga pika M 0 drejt e në temë M

ku h = z 0 - z x - lartësia e uljes së pikës.

Puna e gravitetit është e barabartë me produktin e kësaj force dhe lartësinë e uljes (puna është pozitive) ose lartësia e ngritjes (puna është negative). Puna e gravitetit nuk varet nga forma e trajektores midis pikave M 0 dhe M|, dhe nëse këto pika përkojnë, atëherë puna e gravitetit është e barabartë me zero (rasti i një shtegu të mbyllur). Është gjithashtu e barabartë me zero nëse pikat M 0 dhe M shtrihen në të njëjtin rrafsh horizontal.

Puna e forcës lineare të elasticitetit. Forca elastike lineare (ose forca lineare e rivendosjes) është forca që vepron sipas ligjit të Hukut (Fig. 63):

F = - Mer,

ku r- largësia nga pika e ekuilibrit statik, ku forca është zero, deri në pikën e konsideruar M; Me- konstante koeficient - koeficient ngurtësi.

A=--().

Sipas kësaj formule llogaritet puna e forcës elastike lineare. Nëse pika M 0 përkon me një pikë ekuilibër statik O, kështu atëherë r 0 \u003d 0 dhe për punën e forcës në zhvendosjen nga pika O drejt e në temë M ne kemi

Vlera r- distanca më e shkurtër ndërmjet pikës së konsideruar dhe pikës së ekuilibrit statik. E shënojmë me λ dhe e quajmë deformim. Pastaj

Puna e forcës elastike lineare në zhvendosjen nga gjendja e ekuilibrit statik është gjithmonë negative dhe e barabartë me gjysmën e produktit të koeficientit të ngurtësisë dhe katrorit të deformimit. Puna e forcës elastike lineare nuk varet nga forma e zhvendosjes dhe puna në çdo zhvendosje të mbyllur është zero. Është gjithashtu e barabartë me zero nëse pikat Mo dhe M shtrihen në të njëjtën sferë të kufizuar nga pika e ekuilibrit statik.

Puna e një force të ndryshueshme në lëvizjen kurvilineare.

Puna e forcës në një seksion të lakuar

Shqyrtoni rastin e përgjithshëm të gjetjes së punës së një force të ndryshueshme, pika e aplikimit të së cilës lëviz përgjatë një trajektoreje lakor. Lëreni pikën M të aplikimit të forcës së ndryshueshme F të lëvizë përgjatë një lakore të vazhdueshme arbitrare. Shënoni me vektorin e zhvendosjes pafundësisht të vogël të pikës M. Ky vektor drejtohet tangjencialisht në kurbë në të njëjtin drejtim si vektori i shpejtësisë.

Puna elementare e një force të ndryshueshme F në një zhvendosje pafundësisht të vogël

ds quhet prodhim skalar i vektorëve F dhe ds:

ku a- këndi ndërmjet vektorëve F dhe ds

Kjo do të thotë, puna elementare e forcës është e barabartë me produktin e moduleve të vektorëve të forcës dhe një zhvendosje pafundësisht të vogël, të shumëzuar me kosinusin e këndit midis këtyre vektorëve.

Ne e zbërthejmë vektorin e forcës F në dy komponentë: - drejtuar përgjatë tangjentes me trajektoren - dhe - drejtuar përgjatë normales. linja e forcës

është pingul me tangjenten me rrugën përgjatë së cilës lëviz pika dhe puna e saj është zero. Pastaj:

dA= Ftds.

Për të llogaritur punën e forcës së ndryshueshme F në seksionin përfundimtar të lakores nga a në b, duhet llogaritur integrali i punës elementare:

Energjia e mundshme dhe kinetike.

Energji potenciale P matpika serike në shqyrtimpika ime fushë force M thirrje pune, të kryera nga forcatla duke vepruar në një pikë materiale kur e lëviz atë nga një pikëMderi në pikën e fillimitM 0 , d.m.th.

P = Amm 0

P = =-U=- U

Konstanta С 0 është e njëjtë për të gjitha pikat e fushës, varësisht se cila pikë e fushës zgjidhet si fillestare. Është e qartë se energjia potenciale mund të futet vetëm për një fushë force potenciale në të cilën puna nuk varet nga forma e lëvizjes midis pikave. M dhe M 0 . Një fushë force jopotenciale nuk ka energji potenciale dhe nuk ka asnjë funksion force për të.

dA = dU= -dP; POR = U - U 0 = P 0 - P

Nga formulat e mësipërme rezulton se P përcaktohet deri në një konstante arbitrare, e cila varet nga zgjedhja e pikës së fillimit, por kjo konstante arbitrare nuk ndikon në forcat e llogaritura përmes energjisë potenciale dhe punës së këtyre forcave. Duke pasur parasysh këtë:

P= - U+ konst ose P =- U.

Energjia potenciale në çdo pikë të fushës, deri në një konstante arbitrare, mund të përcaktohet si vlera e funksionit të forcës në të njëjtën pikë, e marrë me një shenjë minus.

Energjia kinetike sistemi quhet një vlerë skalare T, e barabartë me shumën e energjive kinetike të të gjitha pikave të sistemit:

Energjia kinetike është një karakteristikë e lëvizjeve përkthimore dhe rrotulluese të sistemit. Energjia kinetike është një sasi skalare dhe, për më tepër, në thelb pozitive. Prandaj, nuk varet nga drejtimet e lëvizjes së pjesëve të sistemit dhe nuk karakterizon ndryshimet në këto drejtime.

Le të vërejmë edhe rrethanë e mëposhtme të rëndësishme. Forcat e brendshme veprojnë në pjesë të sistemit në drejtime reciproke të kundërta. Ndryshimet në energjinë kinetike ndikohen nga veprimi i forcave të jashtme dhe të brendshme.

Lëvizja uniforme e një pike.

Lëvizja me variabël të barabartë të një pike- lëvizje, me Krom kasat. nxitimi ω t pikë (në rastin e lëvizjes drejtvizore, nxitimi total ω ) vazhdimisht. Ligji i lëvizjes uniforme të një pike dhe ligji i ndryshimit të shpejtësisë së saj υ gjatë kësaj lëvizjeje jepen nga barazitë:

ku s është distanca e pikës së matur përgjatë harkut të trajektores nga pika e referencës e zgjedhur në trajektore, t- koha, s 0 - vlera e s në fillim. momenti i kohës t = = 0. - beg. shpejtësi pikë. Kur shenjat υ dhe ω lëvizje identike, uniforme. përshpejtohet, dhe kur ndryshon - ngadalësohet.

Kur vepron. lëvizje uniforme e një trupi të ngurtë, të gjitha sa më sipër zbatohen për secilën pikë të trupit; me rrotullim uniform rreth një boshti fiks këndi. nxitimi e i trupit është konstant, dhe ligji i rrotullimit dhe ligji i ndryshimit të këndit. shpejtësitë ω të trupit jepen nga barazitë

ku φ është këndi i rrotullimit të trupit, φ 0 është vlera e φ në fillim. momenti i kohës t= 0, ω 0 - lyp. ang. shpejtësia e trupit. Kur shenjat e ω dhe ε përputhen, rrotullimi përshpejtohet dhe kur nuk përputhen, është i ngadalshëm.

Puna e një force konstante në lëvizjen drejtvizore.

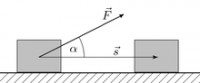
Le të përcaktojmë punën për rastin kur forca vepruese është konstante në madhësi dhe drejtim, dhe pika e zbatimit të saj lëviz përgjatë një trajektoreje drejtvizore. Konsideroni një pikë materiale C, në të cilën zbatohet një forcë konstante në vlerë dhe drejtim (Fig. 134, a).

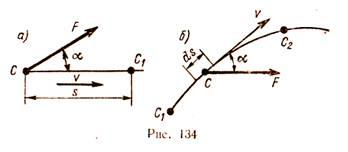
Për një periudhë të caktuar kohore t, pika C ka lëvizur në pozicionin C1 përgjatë një trajektoreje drejtvizore në një distancë s.

Puna W e një force konstante gjatë lëvizjes drejtvizore të pikës së zbatimit të saj është e barabartë me produktin e modulit të forcës F shumëfish i distancës s dhe kosinusit të këndit ndërmjet drejtimit të forcës dhe drejtimit të lëvizjes, d.m.th.

Këndi α ndërmjet drejtimit të forcës dhe drejtimit të lëvizjes mund të ndryshojë nga 0 në 180°. Për α< 90° работа положительна, при α >90° është negative, në α = 90° puna është zero.

Nëse forca bën një kënd të mprehtë me drejtimin e lëvizjes, quhet forca lëvizëse, puna e forcës është gjithmonë pozitive. Nëse këndi ndërmjet drejtimeve të forcës dhe lëvizjes është i mpirë, forca i reziston lëvizjes, kryen punë negative dhe quhet forcë e rezistencës. Shembuj të forcave të rezistencës janë forcat e prerjes, fërkimit, rezistencës së ajrit dhe të tjera, të cilat drejtohen gjithmonë në drejtim të kundërt me lëvizjen.

Kur α = 0°, d.m.th., kur drejtimi i forcës përkon me drejtimin e shpejtësisë, atëherë W = F s, pasi cos 0° = 1. Produkti F cos α është projeksioni i forcës në drejtimin e lëvizja e pikës materiale. Prandaj, puna e një force mund të përkufizohet si produkt i zhvendosjes s dhe projeksionit të forcës dhe drejtimit të lëvizjes së pikës.

33. Forcat e inercisë së një trupi të ngurtë

Në mekanikën klasike, paraqitjet e forcave dhe vetitë e tyre bazohen në ligjet e Njutonit dhe janë të lidhura pazgjidhshmërisht me konceptin e kornizës inerciale të referencës.

Në të vërtetë, sasia fizike e quajtur forcë është futur në konsideratë nga ligji i dytë i Njutonit, ndërsa vetë ligji është formuluar vetëm për sistemet inerciale referencë. Prandaj, koncepti i forcës fillimisht rezulton të jetë i përcaktuar vetëm për korniza të tilla referimi.

Ekuacioni i ligjit të dytë të Njutonit, i cili lidh nxitimin dhe masën e një pike materiale me forcën që vepron mbi të, shkruhet si

Nga ekuacioni rrjedh drejtpërdrejt se vetëm forcat janë shkaku i nxitimit të trupave dhe anasjelltas: veprimi i forcave të pakompensuara mbi një trup domosdoshmërisht shkakton nxitimin e tij.

Ligji i tretë i Njutonit plotëson dhe zhvillon atë që u tha për forcat në ligjin e dytë.

forca është një masë e veprimit mekanik në një trup të caktuar material të trupave të tjerë

në përputhje me ligjin e tretë të Njutonit, forcat mund të ekzistojnë vetëm në çifte, dhe natyra e forcave në çdo çift të tillë është e njëjtë.

çdo forcë që vepron mbi një trup ka burimin e origjinës në formën e një trupi tjetër. Me fjalë të tjera, forcat janë domosdoshmërisht rezultati ndërveprimet tel.

Asnjë forcë tjetër në mekanikë nuk merret në konsideratë ose përdoret. Mundësia e ekzistencës së forcave që kanë lindur në mënyrë të pavarur, pa trupa ndërveprues, nuk lejohet nga mekanika.

Edhe pse emrat e forcave të inercisë Euler dhe d'Alembert përmbajnë fjalën forcë, këto madhësi fizike nuk janë forca në kuptimin e pranuar në mekanikë.

34. Koncepti i lëvizjes plan-paralele të një trupi të ngurtë

Lëvizja e një trupi të ngurtë quhet plan-paralel nëse të gjitha pikat e trupit lëvizin në rrafshe paralelisht me një rrafsh të palëvizshëm (rrafshin kryesor). Lëreni një trup V të bëjë një lëvizje plani, π - rrafshi kryesor. Nga përkufizimi i lëvizjes plan-paralele dhe vetitë e një trupi absolutisht të ngurtë, rezulton se çdo segment i drejtëzës AB, pingul me rrafshin π, do të bëjë lëvizje progresive. Kjo do të thotë, trajektoret, shpejtësitë dhe nxitimet e të gjitha pikave të segmentit AB do të jenë të njëjta. Kështu, lëvizja e secilës pikë të seksionit s paralel me rrafshin π përcakton lëvizjen e të gjitha pikave të trupit V që shtrihen në segmentin pingul me seksionin në këtë pikë. Shembuj të lëvizjes plan-paralele janë: rrotullimi i rrotës përgjatë një segmenti të drejtë, pasi të gjitha pikat e saj lëvizin në rrafshe paralel me rrafshin pingul me boshtin e rrotës; një rast i veçantë i një lëvizjeje të tillë është rrotullimi i një trupi të ngurtë rreth një boshti fiks, në fakt, të gjitha pikat e një trupi rrotullues lëvizin në plane paralele me një plan fiks pingul me boshtin e rrotullimit.

35. Forcat e inercise ne levizjen drejtvizore dhe te lakuar te nje pike materiale

Forca me të cilën një pikë i reziston ndryshimit të lëvizjes quhet forca e inercisë së një pike materiale. Forca e inercisë drejtohet e kundërta me nxitimin e pikës dhe është e barabartë me masën shumëfishuar nxitimin.

Në vijë të drejtë drejtimi i nxitimit përkon me trajektoren. Forca e inercisë drejtohet në drejtim të kundërt me nxitimin, dhe vlera e saj numerike përcaktohet nga formula:

Me lëvizjen e përshpejtuar, drejtimet e nxitimit dhe shpejtësisë përkojnë dhe forca e inercisë drejtohet në drejtim të kundërt me lëvizjen. Në lëvizjen e ngadaltë, kur nxitimi drejtohet në drejtim të kundërt me shpejtësinë, forca e inercisë vepron në drejtim të lëvizjes.

Nëlakuar dhe të pabarabartëlëvizjes nxitimi mund të zbërthehet në normal një dhe tangjente në komponentët. Në mënyrë të ngjashme, forca e inercisë së një pike gjithashtu përbëhet nga dy përbërës: normale dhe tangjenciale.

Normale komponenti i forcës inerciale është i barabartë me produktin e masës së pikës dhe nxitimit normal dhe është i drejtuar kundër këtij nxitimi:

Tangjente komponenti i forcës inerciale është i barabartë me produktin e masës së pikës dhe nxitimit tangjencial dhe është i drejtuar në kundërshtim me këtë nxitim:

Është e qartë se fuqi të plotë pikë inercie Mështë e barabartë me shumën gjeometrike të përbërësve normalë dhe tangjentë, d.m.th.

Duke marrë parasysh që përbërësit tangjencial dhe normal janë reciprokisht pingul, forca totale e inercisë është:

36. Teorema mbi mbledhjen e shpejtësive dhe nxitimeve të një pike në lëvizje komplekse

Teorema e shtimit të shpejtësisë:

Në mekanikë, shpejtësia absolute e një pike është e barabartë me shumën vektoriale të shpejtësive të saj relative dhe përkthimore:

Shpejtësia e trupit në lidhje me kornizën fikse të referencës është e barabartë me shumën vektoriale të shpejtësisë së këtij trupi në raport me kornizën lëvizëse të referencës dhe shpejtësinë (në raport me kornizën fikse) të pikës së kornizës lëvizëse ku trupi ndodhet.

në një lëvizje komplekse, shpejtësia absolute e një pike është e barabartë me shumën gjeometrike të shpejtësisë përkthimore dhe relative. Madhësia e shpejtësisë absolute përcaktohet ku α është këndi ndërmjet vektorëv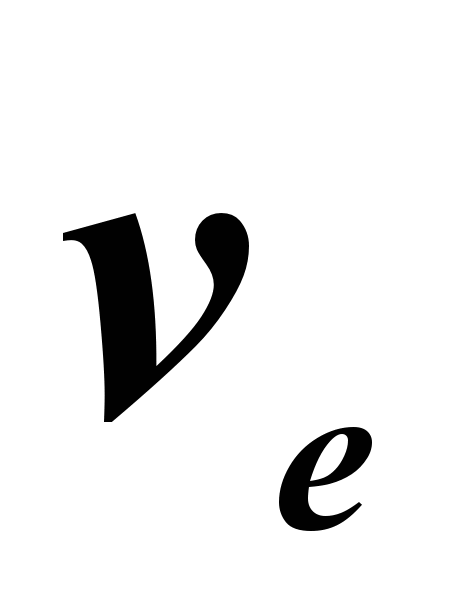e dhe .

Teorema e mbledhjes së nxitimit ( TEOREMA E CORIOLIS)

acor = aper + afrom + acor

Formula shpreh teoremën e mëposhtme të Koriolisit mbi mbledhjen e të përshpejtuarve

renium: 1 për lëvizje komplekse, nxitimi i një pike është i barabartë me gjeometrik

shuma e tre nxitimeve: relativ, translator dhe rrotullues, ose

Coriolis.

acor = 2 (ω × votë)

37. Parimi d'Alembert

Parimi i d'Alembert për një pikë materiale: në çdo moment të lëvizjes së një pike materiale, forcat aktive, reaksionet e lidhjeve dhe forca e inercisë formojnë një sistem të ekuilibruar forcash.

Parimi i D'Alembert- në mekanikë: një nga parimet bazë të dinamikës, sipas të cilit, nëse forcat e inercisë u shtohen forcave të dhëna që veprojnë në pikat e sistemit mekanik dhe reaksioneve të lidhjeve të imponuara, atëherë një sistem i balancuar forcash do të të merret.

Sipas këtij parimi, për çdo pikë të i-të të sistemit, barazia

ku është forca aktive që vepron në këtë pikë, është reaksioni i lidhjes që imponohet në pikë, është forca e inercisë, numerikisht e barabartë me produktin e masës së pikës dhe nxitimit të saj dhe e drejtuar kundër këtij nxitimi ().

Në fakt, bëhet fjalë për transferimin e termit ma nga e djathta në të majtë në ligjin e dytë të Njutonit () të kryer veçmas për secilën nga pikat materiale të konsideruara dhe për censurimin e këtij termi nga forca e inercisë d'Alembert.

Parimi d'Alembert bën të mundur aplikimin e metodave më të thjeshta të statikës për zgjidhjen e problemeve të dinamikës, prandaj përdoret gjerësisht në praktikën inxhinierike, të ashtuquajturat. metoda kinetostatike. Është veçanërisht i përshtatshëm për ta përdorur atë për të përcaktuar reagimet e kufizimeve në rastet kur ligji i lëvizjes së vazhdueshme njihet ose gjendet nga zgjidhja e ekuacioneve përkatëse.

Një nga konceptet më të rëndësishme në mekanikë fuqi punëtore .

Punë me forcë

Të gjitha trupat fizikë në botën përreth nesh janë vënë në lëvizje me forcë. Nëse një trup që lëviz në drejtim të njëjtë ose të kundërt ndikohet nga një forcë ose disa forca nga një ose më shumë trupa, atëherë ata thonë se puna është bërë .

Domethënë, puna mekanike kryhet nga forca që vepron në trup. Pra, forca tërheqëse e një lokomotivë elektrike vë në lëvizje të gjithë trenin, duke bërë kështu punë mekanike. Biçikleta shtyhet nga forca muskulore e këmbëve të çiklistit. Prandaj kjo forcë bën edhe punë mekanike.

në fizikë puna e forcës thirrur sasi fizike, e barabartë me produktin e modulit të forcës, modulit të zhvendosjes së pikës së aplikimit të forcës dhe kosinusit të këndit ndërmjet vektorëve të forcës dhe zhvendosjes.

A = F s cos (F, s) ,

ku F moduli i forcës,

s- moduli i lëvizjes .

Puna kryhet gjithmonë nëse këndi midis erërave të forcës dhe zhvendosjes nuk është i barabartë me zero. Nëse forca vepron në drejtim të kundërt me drejtimin e lëvizjes, sasia e punës është negative.

Puna nuk kryhet nëse nuk veprojnë forca në trup, ose nëse këndi midis forcës së aplikuar dhe drejtimit të lëvizjes është 90 o (cos 90 o \u003d 0).

Nëse kali e tërheq karrocën, atëherë forca muskulore e kalit, ose forca tërheqëse e drejtuar në drejtim të karrocës, bën punën. Dhe forca e gravitetit, me të cilën shoferi shtyp karrocën, nuk funksionon, pasi është e drejtuar poshtë, pingul me drejtimin e lëvizjes.

Puna e një force është një sasi skalare.

Njësia e punës SI - xhaul. 1 xhaul është puna e bërë nga një forcë prej 1 njuton në një distancë prej 1 m nëse drejtimi i forcës dhe zhvendosja janë të njëjta.

Nëse në një trup ose pikë materiale veprojnë disa forca, atëherë ata flasin për punën e bërë nga forca e tyre rezultante.

Nëse forca e aplikuar nuk është konstante, atëherë puna e saj llogaritet si një integral:

Fuqia

Forca që e vë trupin në lëvizje kryen punë mekanike. Por se si bëhet kjo punë, shpejt ose ngadalë, ndonjëherë është shumë e rëndësishme të dihet në praktikë. Për të njëjtën punë mund të bëhet në kohë të ndryshme. Puna që bën një motor elektrik i madh mund të bëhet nga një motor i vogël. Por atij do t'i duhet shumë më shumë kohë për ta bërë këtë.

Në mekanikë, ekziston një sasi që karakterizon shpejtësinë e punës. Kjo vlerë quhet pushtet.

Fuqia është raporti i punës së bërë në një periudhë të caktuar kohore me vlerën e kësaj periudhe.

N= A /∆ t

Sipas përkufizimit A = F s cos α , a s/∆ t = v , Rrjedhimisht

N= F v cos α = F v ,

ku F - forcë, v shpejtësia, α është këndi ndërmjet drejtimit të forcës dhe drejtimit të shpejtësisë.

Kjo eshte fuqi - është prodhim skalar i vektorit të forcës dhe vektorit të shpejtësisë së trupit.

AT sistemit ndërkombëtar Fuqia SI matet në vat (W).

Fuqia prej 1 vat është puna e 1 xhaul (J) e bërë në 1 sekondë (s).

Fuqia mund të rritet duke rritur forcën që kryen punën, ose shpejtësinë me të cilën kryhet kjo punë.