16. Teorema e Sternit.

Nëse dihet momenti i inercisë së një trupi rreth një boshti që kalon nga qendra e masës së tij, atëherë momenti i inercisë rreth çdo boshti tjetër paralel përcaktohet nga teorema e Shtajnerit. : momenti i inercisë së trupit J në lidhje me një bosht arbitrar është i barabartë me momentin e tij të inercisë Jc në lidhje me një bosht paralel që kalon nga qendra e masës NGA trupi, i shtuar në produktin e masës t trup për distancë katrore a ndërmjet boshteve:

17. Ekuacioni i dinamikës lëvizje rrotulluese trup i fortë.

Iε = M. Ky është ekuacioni bazë i dinamikës së lëvizjes rrotulluese të një trupi të ngurtë. Nxitimi këndor ε dhe çift rrotullimi M në këtë ekuacion janë madhësi algjebrike. Zakonisht, drejtimi pozitiv i rrotullimit është në drejtim të kundërt të akrepave të orës.

Është gjithashtu e mundur një formë vektoriale e ekuacionit bazë të dinamikës së lëvizjes rrotulluese, në të cilën sasitë përcaktohen si vektorë të drejtuar përgjatë boshtit të rrotullimit. Gjatë studimit të lëvizjes përkthimore të trupave, prezantohet koncepti i momentit të trupit. Në mënyrë të ngjashme, kur studiojmë lëvizjen rrotulluese, prezantohet koncepti i momentit këndor. Momenti këndor i një trupi rrotullues është një sasi fizike e barabartë me produktin e momentit të inercisë së trupit I dhe shpejtësisë këndore ω të rrotullimit të tij. Momenti këndor shënohet me shkronjën L: Momenti këndor i të gjithë trupit përcaktohet si shuma vektoriale e Li. L = Iω. Ky ekuacion, i marrë këtu për rastin kur I = konst, vlen edhe në rastin e përgjithshëm kur momenti i inercisë së trupit ndryshon gjatë lëvizjes.

18. Energjia kinetike e një trupi rrotullues.

Konsideroni një trup absolutisht të ngurtë (shih § 1) që rrotullohet rreth një boshti fiks z që kalon nëpër të (Fig. 24). Le ta ndajmë mendërisht këtë trup në vëllime të vogla me masa elementare t 1 , t 2 ,..., t n , në një distancë r 1 , r 2 ,..., rn nga boshti.

Kur një trup i ngurtë rrotullohet rreth një boshti fiks, vëllimet e tij elementare individuale me masa m i të përshkruajë rrathë me rreze të ndryshme r i, dhe kanë shpejtësi të ndryshme lineare v i . Por meqenëse po shqyrtojmë një trup absolutisht të ngurtë, shpejtësia këndore e rrotullimit të këtyre vëllimeve është e njëjtë: (17.1) Ne gjejmë energjinë kinetike të një trupi rrotullues si shumën e energjive kinetike të vëllimeve të tij elementare:

ose Duke përdorur shprehjen (17.1), marrim

ku Jz- momenti i inercisë së trupit rreth boshtit z. Në këtë mënyrë, energjia kinetike trup rrotullues (17.2)

Nga një krahasim i formulës (17.2) me shprehjen (12.1) për energjinë kinetike të një trupi që lëviz përpara (T=mv 2 /2), Nga kjo rrjedh se momenti i inercisë është masë e inercisë së trupit gjatë lëvizjes rrotulluese. Formula (17.2) është e vlefshme për një trup që rrotullohet rreth një boshti fiks. Në rastin e një lëvizjeje në rrafsh të një trupi, për shembull, një cilindër që rrotullohet poshtë një plani të pjerrët pa rrëshqitje, energjia e lëvizjes është shuma e energjisë së lëvizjes përkthimore dhe energjisë së rrotullimit: ku m- masa e trupit rrotullues; vc- shpejtësia e qendrës së masës së trupit; Jc- momenti i inercisë së trupit rreth boshtit që kalon nëpër qendrën e tij të masës; wështë shpejtësia këndore e trupit. Puna e forcës së jashtme në rrotullimin e trupit F=Fi+Fr+Fk. Puna e forcës së një trupi rrotullues A=M* ∆φ

19. Fusha gravitacionale.

Ndërveprimi gravitacional ndërmjet trupave kryhet me ndihmën e fushës gravitacionale, ose fushës gravitacionale. Kjo fushë krijohet nga trupat dhe është një formë e ekzistencës së materies. Vetia kryesore e fushës gravitacionale është ajo për çdo trup me masë t, e sjellë në këtë fushë, forca gravitacionale vepron, d.m.th. (24.1)

Vektori g nuk varet nga m dhe quhet forca e fushës gravitacionale. Intensiteti i fushës gravitacionale përcaktohet nga forca që vepron nga ana e fushës në pikën materiale të një njësie masë, dhe përkon në drejtim me forcën vepruese. Ka tension karakteristikë e fuqisë fushat e gravitetit. Fusha gravitacionale quhet homogjene nëse intensiteti i saj është i njëjtë në të gjitha pikat, dhe qendrore nëse në të gjitha pikat e fushës vektorët e intensitetit janë të drejtuar përgjatë vijave të drejta që kryqëzohen në një pikë. (A) i palëvizshëm në lidhje me çdo kornizë inerciale të referencës (Fig. 38). Për një paraqitje grafike të fushës së forcës përdoren linjat e forcës (linjat e tensionit). Linjat e fushës janë zgjedhur në mënyrë që vektori i forcës së fushës të drejtohet në mënyrë tangjenciale në vijën e fushës.

Vlera është karakteristikë e energjisë Fusha gravitacionale quhet potencial. Potenciali i fushës gravitacionale j- një sasi skalare e përcaktuar nga energjia potenciale e një trupi me masë njësi në një pikë të caktuar të fushës ose nga puna e lëvizjes së një njësie masë nga një pikë e caktuar e fushës në pafundësi. Kështu, potenciali i fushës gravitacionale të krijuar nga një trup me masë M, barazohet me (25.4) ku R- largësia nga ky trup deri në pikën në fjalë. Nga formula (25.4) rrjedh se vendndodhja e pikave me të njëjtin potencial formon një sipërfaqe sferike ( R= konst). Sipërfaqet e tilla për të cilat potenciali është konstant quhen ekuipotenciale. Merrni parasysh marrëdhënien midis potencialit ( j) fusha gravitacionale dhe intensiteti i saj (g). Nga shprehjet (25.1) dhe (25.4) del se puna elementare d A, kryhet nga forcat fushore me zhvendosje të vogël të një trupi me masë t,është e barabartë me

20. Presioni në lëngje dhe gazra. Ligjet e Paskalit dhe Arkimedit.

Njësia e presionit - paskal(Pa): 1 Pa është e barabartë me presionin e krijuar nga një forcë prej 1 N, e shpërndarë në mënyrë uniforme mbi një sipërfaqe normale me të me një sipërfaqe prej 1m 2 (1 Pa \u003d 1 N / m 2).

Presioni në ekuilibrin e lëngjeve (gazeve) i bindet ligjit të Paskalit: presioni në çdo vend të një lëngu në qetësi është i njëjtë në të gjitha drejtimet dhe presioni transmetohet në mënyrë të barabartë në të gjithë vëllimin e zënë nga lëngu në qetësi. Le të shqyrtojmë se si pesha e një lëngu ndikon në shpërndarjen e presionit brenda një lëngu të papërshtatshëm në qetësi. Kur një lëng është në ekuilibër, presioni horizontal është gjithmonë i njëjtë, përndryshe nuk do të kishte ekuilibër. Prandaj, sipërfaqja e lirë e një lëngu në qetësi është gjithmonë horizontale larg mureve të anijes. Nëse një lëng është i pakompresueshëm, atëherë dendësia e tij është e pavarur nga presioni. Pastaj për seksionin kryq S kolona e lëngshme, lartësia e saj h dhe dendësia r pesha P=rgSh, dhe presioni në bazën e poshtme

(28.1) pra presioni ndryshon në mënyrë lineare me lartësinë. Presioni rgh quhet presion hidrostatik. Sipas formulës (28.1), forca e presionit në shtresat e poshtme të lëngut do të jetë më e madhe se në ato të sipërme, prandaj, një forcë e përcaktuar nga ligji i Arkimedit vepron në një trup të zhytur në një lëng (gaz): një e drejtuar forca vepron në një trup të zhytur në një lëng (gaz). forcë lëvizëse lart e barabartë me peshën e lëngut (gazit) të zhvendosur nga trupi: F POR = PgV, ku R - dendësia e lëngjeve, V- vëllimi i një trupi të zhytur në një lëng.

21. Linja dhe tubi i rrymës. Teorema e vazhdimësisë së avionit.

Lëvizja e lëngjeve quhet rrjedhje, dhe grumbullimi i grimcave të një lëngu në lëvizje quhet rrjedhje. Grafikisht, lëvizja e lëngjeve përshkruhet duke përdorur vija rrjedhëse, të cilat vizatohen në mënyrë që tangjentet ndaj tyre të përkojnë në drejtim me vektorin e shpejtësisë së lëngut në pikat përkatëse në hapësirë ​​(Fig. 45). Linjat rrjedhëse vizatohen në atë mënyrë që dendësia e tyre, e cila karakterizohet nga raporti i numrit të vijave me sipërfaqen e zonës pingul me to, nëpër të cilën ato kalojnë, të jetë më e madhe aty ku shpejtësia e rrjedhjes së lëngut është më e madhe, dhe më pak ku lëngu rrjedh më ngadalë. Kështu, sipas modelit të vijave rrjedhëse, mund të gjykohet drejtimi dhe moduli i shpejtësisë në pika të ndryshme në hapësirë, d.m.th., mund të përcaktohet gjendja e lëvizjes së lëngut. Pjesa e lëngut e kufizuar nga linja rrjedhëse quhet tubi i rrjedhës. Rrjedha e një lëngu quhet e qëndrueshme (ose e palëvizshme) nëse forma dhe vendndodhja e linjave rrjedhëse, si dhe vlerat e shpejtësive në secilën prej pikave të tij, nuk ndryshojnë me kalimin e kohës.

Konsideroni çdo tub të rrymës. Ne zgjedhim dy nga seksionet e tij S 1 dhe S 2 , pingul me drejtimin e shpejtësisë (Fig. 46). Për kohën D t përmes seksionit S vëllimi i lëngut që kalon Sv D t; prandaj, për 1 sekondë S 1 do të kalojë vëllimin e lëngut S 1 v 1 , ku v 1 - shpejtësia e rrjedhjes së lëngut në seksion kryq S 1 . Përmes seksionit S 2 për 1 s do të kalojë vëllimin e lëngut S 2 v 2 , ku v 2 - shpejtësia e rrjedhjes së lëngut në seksion kryq S 2 . Këtu supozohet se shpejtësia e lëngut në seksion kryq është konstante. Nëse lëngu është i pakompresueshëm (r=const), atëherë përmes prerjes tërthore S 2 do të kalojë të njëjtin vëllim lëngu si nëpër seksion S 1 , dmth. (29.1) Rrjedhimisht, produkti i shpejtësisë së rrjedhës së një lëngu të pangjeshur dhe seksionit kryq të tubit aktual është një vlerë konstante për këtë tub aktual. Lidhja (29.1) quhet ekuacioni i vazhdimësisë për një lëng të pakompresueshëm.

ekuacioni i Bernulit

Sipas ekuacionit të vazhdimësisë për një lëng të pakompresueshëm , vëllimi i zënë nga lëngu mbetet konstant, d.m.th. pjesëtimi i shprehjes (30.5) me D V, arri ku R - dendësia e lëngshme. Por meqenëse seksionet u zgjodhën në mënyrë arbitrare, ne mund të shkruajmë (30.6)

Shprehja (30.6) është nxjerrë nga fizikani zviceran D. Bernoulli dhe quhet ekuacioni i Bernulit. Siç mund të shihet nga derivimi i tij, ekuacioni i Bernulit është një shprehje e ligjit të ruajtjes së energjisë siç zbatohet për një rrjedhë të qëndrueshme të një lëngu ideal. Gjithashtu funksionon mirë për lëngjet reale, fërkimi i brendshëm i të cilave nuk është shumë i lartë. Vlera R në formulën (30.6) quhet presioni statik (presioni i lëngut në sipërfaqen e trupit që qarkullon prej tij), vlera rv 2 / 2 - presion dinamik. Siç u përmend më lart, vlera rghështë presioni hidrostatik.

Për një tub të rrymës horizontale ( h 1 =h 2 ) shprehja (30.6) bëhet (30.7)

ku p+rv 2 / 2 quhet presion total. Nga ekuacioni i Bernoulli (30.7) për një tub horizontal të rrymës dhe ekuacioni i vazhdimësisë (29.1) rrjedh se kur një lëng rrjedh nëpër një tub horizontal me seksione të ndryshme, shpejtësia e lëngut është më e madhe në vendet e ngushtimit dhe presioni statik është më e madhe në vende më të gjera, pra aty ku shpejtësia është më e ngadaltë. Kjo mund të demonstrohet duke vendosur një seri matësish presioni përgjatë tubit (Fig. 48).

23. Formula Torricelli.

Le të shqyrtojmë një enë cilindrike me një lëng, në murin anësor të së cilës ka një vrimë të vogël në një thellësi nën nivelin e lëngut (Fig. 51). Konsideroni dy seksione (në nivel h 1 sipërfaqe e lirë e lëngut në enë dhe në nivel h 2 dalja e saj nga vrima) dhe shkruani ekuacionin e Bernulit:

Që nga presioni R 1 dhe R 2 në lëng në nivelet e seksionit të parë dhe të dytë janë të barabarta me ato atmosferike, d.m.th. R 1 =p 2 , atëherë ekuacioni do të duket si

Nga ekuacioni i vazhdimësisë (29.1) rezulton se v 2 /v 1 =S 1 /S 2 , ku S 1 dhe S 2 - zonat e prerjes tërthore të enës dhe hapja. Nese nje S 1 >>S 2 , pastaj anëtar v/2 mund të neglizhohet dhe

Kjo shprehje quhet formula Torricelli. Formula për shkallën e rrjedhjes së lëngut nga një vrimë në një enë të hapur

24. Viskoziteti, ligji i Njutonit. Regjimet e rrjedhës.

Viskoziteti (fërkimi i brendshëm) është vetia e lëngjeve reale për t'i rezistuar lëvizjes së një pjese të lëngut në raport me një tjetër. Kur disa shtresa të një lëngu real lëvizin në krahasim me të tjerat, lindin forca të brendshme të fërkimit, të drejtuara në mënyrë tangjenciale në sipërfaqen e shtresave. Veprimi i këtyre forcave manifestohet në faktin se nga ana e shtresës që lëviz më shpejt, shtresa që lëviz më ngadalë ndikohet nga një forcë përshpejtuese. Nga ana e shtresës që lëviz më ngadalë, shtresa që lëviz më shpejt ndikohet nga një forcë vonuese.

Forca e brendshme e fërkimit F është sa më e madhe, aq më e madhe është sipërfaqja e konsideruar e sipërfaqes së shtresës S(Fig. 52), dhe varet nga sa shpejt ndryshon shpejtësia e rrjedhës së lëngut gjatë kalimit nga shtresa në shtresë. Drejtimi në të cilin llogaritet distanca midis shtresave, pingul normat e rrjedhjes së shtresave. Vlera tregon se sa shpejt ndryshon shpejtësia kur lëvizni nga shtresa në shtresë në drejtim X, pingul me drejtimin e lëvizjes së shtresave dhe quhet gradient i shpejtësisë. Kështu, moduli i forcës së fërkimit të brendshëm (31.1), ku koeficienti i proporcionalitetit m, e cila varet nga natyra e lëngut, quhet viskozitet dinamik (ose thjesht viskozitet). Njësia e viskozitetit është sekonda paskal (Pa×s). Sa më i madh të jetë viskoziteti, aq më shumë lëngu ndryshon nga ai ideal, aq më të mëdha shfaqen forcat e fërkimit të brendshëm në të. Ekzistojnë dy mënyra të rrjedhjes së lëngut. Rrjedha quhet laminare (shtresore) nëse secila shtresë e hollë e përzgjedhur rrëshqet përgjatë rrjedhës në krahasim me ato fqinje pa u përzier me to, dhe turbulente (vorbull) nëse formimi intensiv i vorbullës dhe përzierja e lëngshme (gazit) ndodh përgjatë rrjedhës. Rrjedha laminare e një lëngu vërehet me shpejtësi të ulëta të lëvizjes së tij. Shtresa e jashtme e lëngut ngjitur me sipërfaqen e tubit në të cilin rrjedh, për shkak të forcave të kohezionit molekular, ngjitet në të dhe mbetet e palëvizshme. Profili i shpejtësisë mesatare për rrjedhën e turbullt në tuba (Fig. 53) ndryshon nga profili parabolik për rrjedhjen laminare nga një rritje më e shpejtë e shpejtësisë pranë mureve të tubit dhe më pak lakim në pjesën qendrore të rrjedhës. Natyra e rrjedhjes varet nga një sasi pa dimensione e quajtur Numri Reynolds: ku n = h/p-viskoziteti kinematik; R- dendësia e lëngshme;<v>-shpejtësia mesatare e lëngut mbi seksionin e tubit; d- dimensioni karakteristik linear, siç është diametri i tubit. Në vlera të ulëta të numrit Reynolds, vërehet një rrjedhje laminare, kalimi nga rrjedha laminare në atë të turbullt ndodh në rajon dhe në (për tubat e lëmuar) rrjedha është e turbullt.

26. Formula Poiseuille. Metodat për përcaktimin e viskozitetit.

Metoda e Stokes. Kjo metodë e përcaktimit të viskozitetit bazohet në matjen e shpejtësisë së trupave të vegjël sferikë që lëvizin ngadalë në një lëng. Tre forca veprojnë në një top që bie vertikalisht në një lëng: graviteti P= 4 / 3 pr 3 rg(r- dendësia e topit), forca e Arkimedit P= 4 / 3 pr 3 r "g (r" - dendësia e lëngshme) dhe forca e rezistencës e vendosur në mënyrë empirike nga J. Stokes: F= 6phrv, ku rështë rrezja e topit, v- shpejtësinë e tij. Kur topi lëviz në mënyrë uniforme, ku

Duke matur shpejtësinë e lëvizjes uniforme të topit, mund të përcaktohet viskoziteti i një lëngu (gazi). Metoda Poiseuille. Kjo metodë bazohet në rrjedhën laminare të lëngut në një kapilar të hollë. Konsideroni një kapilar me një rreze R dhe gjatësia l. Në një lëng, ne zgjedhim mendërisht një shtresë cilindrike me një rreze r dhe trashësia d r(Fig. 54). Forca e fërkimit të brendshëm (shih (31.1)), që vepron në sipërfaqen anësore të kësaj shtrese, ku d S- sipërfaqe anësore shtresa cilindrike; shenja minus do të thotë që me rritjen e rrezes, shpejtësia zvogëlohet. Pas integrimit, duke supozuar se ngjitja e lëngut ndodh pranë mureve, d.m.th., shpejtësia në një distancë R nga boshti është i barabartë me zero, marrim Gjatë kohës t një lëng do të rrjedhë nga tubi, vëllimi i të cilit vjen nga viskoziteti

27. Ekuacioni i lëkundjeve harmonike të lira për lavjerrësit.

Lëkundjet quhen të lira (ose natyrore) nëse kryhen për shkak të energjisë së dhënë fillimisht me mungesën e mëvonshme të ndikimeve të jashtme në sistemin oscilues (sistemi që lëkundet). Lloji më i thjeshtë i lëkundjeve janë lëkundjet harmonike - lëkundjet në të cilat vlera e lëkundjeve ndryshon me kalimin e kohës sipas ligjit të sinusit (kosinusi ). Lavjerrësi pranverorështë një ngarkesë në masë t, i pezulluar në një burim krejtësisht elastik dhe duke kryer lëkundje harmonike nën veprimin e një force elastike F= -kx, ku k- ngurtësi e pranverës. Ekuacioni i lëvizjes së lavjerrësit

Nga shprehjet rezulton se lavjerrësi i sustës kryen lëkundje harmonike sipas ligjit x=A cos (w 0 t+ j) me frekuencë ciklike (142.2) dhe periodë (142.3) Formula (142.3) vlen për lëkundjet elastike brenda kufijve në të cilët plotësohet ligji i Hukut, d.m.th kur masa e sustës është e vogël në krahasim me masën e trupit. Energjia potenciale e lavjerrësit të sustës është lavjerrës fizik- Ky është një trup i ngurtë që, nën veprimin e gravitetit, lëkundet rreth një boshti të palëvizshëm horizontal që kalon nëpër një pikë O, që nuk përkon me qendrën e masës NGA trupi (Fig. 201). Nëse lavjerrësi devijohet nga pozicioni i tij ekuilibër me një kënd a, atëherë, në përputhje me ekuacionin e dinamikës së lëvizjes rrotulluese të një trupi të ngurtë (18.3), momenti M forca rivendosëse mund të shkruhet si (142.4) ku J- momenti i inercisë së lavjerrësit rreth boshtit që kalon nëpër pikën e pezullimit Oh l- distanca midis tij dhe qendrës së masës së lavjerrësit, F t \u003d -mg sina» -mga. - rikthimi i forcës (shenja minus është për faktin se drejtimet F t dhe a gjithmonë përballë; mëkat a» a i përgjigjet lëkundjeve të vogla të lavjerrësit, d.m.th. devijime të vogla të lavjerrësit nga pozicioni i ekuilibrit). Për lëkundje të vogla, lavjerrësi fizik kryen lëkundje harmonike me një frekuencë ciklike w 0 dhe një period

Ku L=J/(ml) - gjatësia e reduktuar e lavjerrësit fizik.

Lavjerrësi matematikor- kjo është idealizuar një sistem i përbërë nga një pikë materiale me një masë t, i varur në një fije pa peshë të pazgjatur dhe që lëkundet nën ndikimin e gravitetit. Një përafrim i mirë i një lavjerrës matematik është një top i vogël dhe i rëndë i varur nga një fije e hollë dhe e gjatë. Momenti i inercisë së lavjerrësit matematik

(142.8) ku lështë gjatësia e lavjerrësit. Meqenëse lavjerrësi matematik mund të paraqitet si rast i veçantë lavjerrës fizik, duke supozuar se e gjithë masa e tij është e përqendruar në një pikë - qendra e masës, atëherë, duke zëvendësuar shprehjen (142.8) në formulën (1417), marrim një shprehje për periudhën e lëkundjeve të vogla të një lavjerrës matematikor (142.9) Krahasimi i formulave (142.7 ) dhe (142.9), shohim, çka nëse gjatësia e dhënë L lavjerrësi fizik është i barabartë me gjatësinë l një lavjerrës matematikor, atëherë periudhat e lëkundjes së këtyre lavjerrësve janë të njëjta. Prandaj, gjatësia e reduktuar e një lavjerrësi fizik është gjatësia e një lavjerrësi të tillë matematikor, periudha e lëkundjes së të cilit përkon me periudhën e lëkundjes së një lavjerrësi të caktuar fizik.

28. Kinematika e lëkundjeve të lira harmonike.

Lëkundje mekanike harmonike është një lëvizje drejtvizore jo uniforme në të cilën koordinatat e një trupi lëkundës (pikës materiale) ndryshojnë sipas ligjit të kosinusit ose sinusit në varësi të kohës. Sipas këtij përkufizimi, ligji i ndryshimit të koordinatave në varësi të kohës ka formën: , ku wt është vlera nën shenjën e kosinusit ose sinusit; w- koeficienti, kuptimi fizik të cilën do ta zbulojmë më poshtë; A është amplituda e lëkundjeve harmonike mekanike. Ekuacionet (4.1) janë ekuacionet kryesore kinematike të dridhjeve mekanike harmonike.

për një pikë materiale që kryen lëkundje mekanike harmonike, vlera e w mund të interpretohet si numri i lëkundjeve për një cikël të caktuar kohor, i barabartë me 2l. Prandaj, vlera e w u quajt frekuencë ciklike (ose rrethore). Nëse pika M e fillon lëvizjen jo nga pika 1 por nga pika 2, atëherë ekuacioni (4.1) do të marrë formën: Vlera e f0 quhet fazë fillestare.

29. Dridhjet e amortizuara.

Le të shqyrtojmë lëkundjet e lira të amortizuara - lëkundjet, amplituda e të cilave zvogëlohet me kalimin e kohës për shkak të humbjeve të energjisë nga një sistem real oscilues. Ekuacioni diferencial lëkundjet e lira të amortizuara sistemi linear jepet në formë

(146.1), ku s- një vlerë e luhatshme që përshkruan një ose një tjetër procesi fizik, d=konst - koeficienti i zbutjes, w 0 - frekuenca ciklike e lirë i pamposhtur lëkundjet e të njëjtit sistem oscilues, pra në d = 0 (në mungesë të humbjeve të energjisë) quhet frekuenca natyrore e sistemit oscilues.

- amplituda e lëkundjeve të amortizuara, a POR 0 - amplituda fillestare. Nese nje A(t) dhe POR(t+ T) - amplituda e dy lëkundjeve të njëpasnjëshme që korrespondojnë me kohët që ndryshojnë nga një periudhë, atëherë raporti quhet zvogëlimi i amortizimit, dhe logaritmin e tij (146.7)- zvogëlimi logaritmik i amortizimit; N e - numri i lëkundjeve të bëra gjatë kohës kur amplituda zvogëlohet me e herë. Zvogëlimi logaritmik i amortizimit është një vlerë konstante për një sistem të caktuar oscilues. Për të karakterizuar një sistem oscilues, përdoret koncepti faktor cilësor P, e cila për vlera të vogla të zvogëlimit logaritmik është e barabartë me (146.8). Nga formula (146.8) rezulton se faktori i cilësisë është proporcional me numrin e lëkundjeve N e , kryhet nga sistemi gjatë kohës së relaksimit.

30. Dridhje të detyruara, rezonancë.

Lëkundjet që lindin nën veprimin e një force të jashtme që ndryshon periodikisht ose një EMF të jashtme që ndryshon periodikisht quhen përkatësisht lëkundje mekanike të detyruara dhe elektromagnetike të detyruara. Merrni parasysh varësinë amplituda A dridhjet e detyruara nga frekuenca w. Lëkundjet mekanike dhe elektromagnetike do të konsiderohen njëkohësisht, duke quajtur vlerën ose zhvendosjen e lëkundjes (X) një trup lëkundës nga një pozicion ekuilibri, ose nga një ngarkesë (P) kondensator.

Nga formula (147.8) del se amplituda POR zhvendosja (ngarkesa) ka një maksimum. Për të përcaktuar frekuencën rezonante w prerë, - frekuenca në të cilën amplituda POR zhvendosja (ngarkesa) arrin një maksimum - ju duhet të gjeni maksimumin e funksionit (147.8), ose, çfarë është e njëjta, minimumin e shprehjes radikale. Diferencimi i shprehjes radikale në lidhje me w dhe duke e barazuar atë me zero, marrim kushtin që përcakton w prerje: Kjo barazi vlen për w=0, ± , për të cilën vetëm një vlerë pozitive ka kuptim fizik. Rrjedhimisht, frekuenca rezonante (148.1) Fenomeni i një rritjeje të mprehtë të amplitudës së lëkundjeve të detyruara kur frekuenca e forcës lëvizëse (frekuenca e tensionit të alternuar lëvizës) i afrohet një frekuence të barabartë ose afër frekuencës natyrore të oscilatorit. sistemi quhet rezonancë (mekanike ose elektrike, përkatësisht). Kur vlera w prerja pothuajse përkon me frekuencën natyrore w 0 sistemi oscilues. Duke zëvendësuar (148.1) në formulën (147.8), marrim (148.2)

Në fig. 210 tregon varësinë e amplitudës së lëkundjeve të detyruara nga frekuenca për vlera të ndryshme d. Nga (148.1) dhe (148.2) rrjedh se sa më pak d, aq më i lartë dhe djathtas qëndron maksimumi i kësaj kurbë. Nese nje w® 0, pastaj të gjitha kthesat (shih gjithashtu (147.8)) arrijnë të njëjtën vlerë kufi jozero , që quhet devijimi statik. Në rastin e dridhjeve mekanike , në rastin e elektromagnetikës U m / (L). Nese nje w®¥, atëherë kurbat në mënyrë asimptotike priren në zero. Grupi i reduktuar i kthesave quhet kthesa rezonancë.

Ligji i ruajtjes së energjisë thotë se energjia e trupit nuk zhduket kurrë dhe nuk rishfaqet, ajo mund të kthehet vetëm nga një formë në tjetrën. Ky ligj është universal. Ka formulimin e vet në degë të ndryshme të fizikës. Mekanika klasike shqyrton ligjin e ruajtjes së energjisë mekanike.

Energjia totale mekanike e një sistemi të mbyllur trupat fizikë, ndërmjet të cilave veprojnë forcat konservatore, është një vlerë konstante. Kështu është formuluar ligji i ruajtjes së energjisë në mekanikën e Njutonit.

E mbyllur, ose e izoluar, konsiderohet të jetë sistemi fizik, i cili nuk ndikohet nga forcat e jashtme. Ai nuk shkëmben energji me hapësirën përreth dhe energjia e vet, të cilën e posedon, mbetet e pandryshuar, pra ruhet. Në një sistem të tillë, vetëm forcat e brendshme, dhe trupat ndërveprojnë me njëri-tjetrin. Ai mund të shndërrojë vetëm energjinë potenciale në energji kinetike dhe anasjelltas.

Shembulli më i thjeshtë i një sistemi të mbyllur është një pushkë snajper dhe një plumb.

Llojet e forcave mekanike

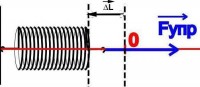
Forcat që veprojnë brenda një sistemi mekanik zakonisht ndahen në konservatore dhe jo konservatore.

konservatore konsiderohen forcat, puna e të cilave nuk varet nga trajektorja e trupit në të cilin zbatohen, por përcaktohet vetëm nga pozicioni fillestar dhe përfundimtar i këtij trupi. Quhen edhe forcat konservatore potencial. Puna e forcave të tilla në një lak të mbyllur është zero. Shembuj të forcave konservatore − forca e gravitetit, forca elastike.

Të gjitha forcat e tjera quhen jo konservatore. Kjo perfshin forca e fërkimit dhe forca e tërheqjes. Ata quhen gjithashtu shpërhapëse forcat. Këto forca kryejnë punë negative gjatë çdo lëvizjeje në një sistem mekanik të mbyllur dhe nën veprimin e tyre energjia totale mekanike e sistemit zvogëlohet (shpërndahet). Ai kalon në lloje të tjera, jo mekanike të energjisë, për shembull, në nxehtësi. Prandaj, ligji i ruajtjes së energjisë në një sistem mekanik të mbyllur mund të përmbushet vetëm nëse nuk ka forca jo konservatore në të.

Energjia totale e një sistemi mekanik përbëhet nga energjia kinetike dhe potenciale dhe është shuma e tyre. Këto lloj energjish mund të shndërrohen në njëra-tjetrën.

Energji potenciale

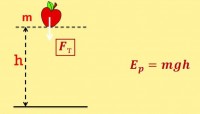
Energji potenciale quhet energjia e bashkëveprimit të trupave fizikë ose pjesëve të tyre me njëri-tjetrin. Ajo përcaktohet nga rregullimi i tyre i ndërsjellë, domethënë distanca midis tyre dhe është e barabartë me punën që duhet bërë për të lëvizur trupin nga pika e referencës në një pikë tjetër në fushën e forcave konservatore.

Energjia potenciale ka çdo trup fizik të palëvizshëm, të ngritur në një farë lartësie, pasi ndikohet nga graviteti, i cili është një forcë konservatore. Një energji e tillë zotërohet nga uji në buzë të një ujëvare, një sajë në majë të një mali.

Nga erdhi kjo energji? Ndërsa trupi fizik po ngrihej në një lartësi, punohej dhe harxhohej energji. Është kjo energji që ruhej në trupin e ngritur. Dhe tani kjo energji është gati për të bërë punë.

Vlera e energjisë potenciale të trupit përcaktohet nga lartësia në të cilën ndodhet trupi në lidhje me një nivel fillestar. Ne mund të marrim çdo pikë që zgjedhim si pikënisje.

Nëse marrim parasysh pozicionin e trupit në raport me Tokën, atëherë energji potenciale trupi në sipërfaqen e Tokës është zero. Dhe në krye h llogaritet me formulën:

E p = mɡ h ,

ku m - masa trupore

ɡ - nxitimi i gravitetit

h – lartësia e qendrës së masës së trupit në raport me Tokën

ɡ \u003d 9,8 m/s 2

Kur një trup bie nga një lartësi h1 deri në lartësi h2 graviteti funksionon. Kjo punë është e barabartë me ndryshimin e energjisë potenciale dhe ka një vlerë negative, pasi madhësia e energjisë potenciale zvogëlohet me rënien e trupit.

A = - ( E p2 - E p1) = - ∆ E f ,

ku E p1 është energjia potenciale e trupit në lartësi h1 ,

E p2 - energjia potenciale e një trupi në lartësi h2 .

Nëse trupi ngrihet në një lartësi të caktuar, atëherë punohet kundër forcave të gravitetit. Në këtë rast, ajo ka një vlerë pozitive. Dhe vlera e energjisë potenciale të trupit rritet.

Një trup i deformuar elastik (i ngjeshur ose pranverë e shtrirë). Vlera e saj varet nga ngurtësia e sustës dhe nga sa kohë është ngjeshur ose shtrirë, dhe përcaktohet nga formula:

E p \u003d k (∆x) 2 / 2 ,

ku k - koeficienti i ngurtësisë,

∆x - zgjatje ose tkurrje e trupit.

Energjia potenciale e pranverës mund të bëjë punë.

Energjia kinetike

Përkthyer nga greqishtja "kinema" do të thotë "lëvizje". Energjia që merr një trup fizik si rezultat i lëvizjes së tij quhet kinetike. Vlera e saj varet nga shpejtësia e lëvizjes.

Një top futbolli që rrotullohet nëpër fushë, një sajë që rrotullohet nga një mal dhe vazhdon të lëvizë, një shigjetë e gjuajtur nga një hark - të gjithë kanë energji kinetike.

Nëse një trup është në qetësi, energjia e tij kinetike është zero. Sapo një forcë ose disa forca të veprojnë në trup, ai do të fillojë të lëvizë. Dhe meqenëse trupi është duke lëvizur, forca që vepron mbi të funksionon. Puna e forcës, nën ndikimin e së cilës trupi nga prehja do të hyjë në lëvizje dhe do të ndryshojë shpejtësinë e tij nga zero në ν , quhet energjia kinetike masë trupore m .

Nëse, në momentin fillestar të kohës, trupi ishte tashmë në lëvizje dhe shpejtësia e tij kishte vlerën v 1 , dhe në fund ishte e barabartë me v 2 , atëherë puna e bërë nga forca ose forcat që veprojnë në trup do të jetë e barabartë me rritjen e energjisë kinetike të trupit.

∆ E k = E k 2 - E k 1

Nëse drejtimi i forcës përkon me drejtimin e lëvizjes, atëherë bëhet punë pozitive dhe energjia kinetike e trupit rritet. Dhe nëse forca drejtohet në drejtim të kundërt me drejtimin e lëvizjes, atëherë bëhet punë negative dhe trupi lëshon energji kinetike.

Ligji i ruajtjes së energjisë mekanike

Ek 1 + E p1= E k 2 + E p2

Çdo trup fizik i vendosur në një lartësi ka energji potenciale. Por kur bie, fillon ta humbasë këtë energji. Ku shkon ajo? Rezulton se nuk zhduket askund, por shndërrohet në energjinë kinetike të të njëjtit trup.

Supozoni , në një lartësi, një ngarkesë fiksohet pa lëvizje. Energjia e tij potenciale në këtë pikë është e barabartë me vlerën maksimale. Nëse e lëmë të shkojë, do të fillojë të bjerë me një shpejtësi të caktuar. Prandaj, do të fillojë të fitojë energji kinetike. Por në të njëjtën kohë, energjia e saj potenciale do të fillojë të ulet. Në pikën e goditjes, energjia kinetike e trupit do të arrijë maksimumin, dhe energjia potenciale do të ulet në zero.

Energjia potenciale e një topi të hedhur nga një lartësi zvogëlohet, ndërsa energjia kinetike rritet. Slitë në pushim në majë të një mali kanë energji potenciale. Energjia e tyre kinetike në këtë moment është zero. Por kur ato fillojnë të rrokullisen, energjia kinetike do të rritet, dhe energjia potenciale do të ulet me të njëjtën sasi. Dhe shuma e vlerave të tyre do të mbetet e pandryshuar. Energjia potenciale e një molle të varur në një pemë shndërrohet në energjinë e saj kinetike kur ajo bie.

Këta shembuj konfirmojnë qartë ligjin e ruajtjes së energjisë, i cili thotë se energjia totale e një sistemi mekanik është një vlerë konstante . Vlera e energjisë totale të sistemit nuk ndryshon, dhe energjia potenciale shndërrohet në energji kinetike dhe anasjelltas.

Me çfarë sasie zvogëlohet energjia potenciale, energjia kinetike do të rritet me të njëjtën sasi. Shuma e tyre nuk do të ndryshojë.

Për një sistem të mbyllur trupash fizikë, barazia
E k1 + E p1 = E k2 + E p2,
ku E k1, E p1 - energjitë kinetike dhe potenciale të sistemit përpara çdo ndërveprimi, E k2, E p2 - energjitë përkatëse pas saj.

Procesi i shndërrimit të energjisë kinetike në energji potenciale dhe anasjelltas mund të shihet duke parë një lavjerrës që lëkundet.

Klikoni mbi foto

Duke qenë në pozicionin ekstrem të djathtë, lavjerrësi duket se ngrin. Në këtë moment, lartësia e tij mbi pikën e referencës është maksimale. Prandaj, energjia potenciale është gjithashtu maksimale. Dhe kinetika është zero, pasi nuk lëviz. Por në momentin tjetër lavjerrësi fillon të lëvizë poshtë. Shpejtësia e saj rritet, dhe për këtë arsye energjia e saj kinetike rritet. Por me uljen e lartësisë, zvogëlohet edhe energjia potenciale. Në pikën e poshtme, ajo do të bëhet e barabartë me zero, dhe energjia kinetike do të arrijë vlerën e saj maksimale. Lavjerrësi do të kalojë këtë pikë dhe do të fillojë të ngrihet lart majtas. Energjia e saj potenciale do të fillojë të rritet, dhe energjia e saj kinetike do të ulet. etj.

Për të demonstruar transformimin e energjisë, shpiku Isak Njutoni sistemi mekanik, e cila quhet djepi i Njutonit ose Topat e Njutonit .

Klikoni mbi foto

Nëse topi i parë devijohet dhe më pas lëshohet, energjia dhe momenti i tij do të transferohen tek i fundit përmes tre topave të ndërmjetëm, të cilët do të mbeten të palëvizshëm. Dhe topi i fundit do të devijojë me të njëjtën shpejtësi dhe do të ngrihet në të njëjtën lartësi si i pari. Pastaj topi i fundit do të transferojë energjinë dhe vrullin e tij përmes topave të ndërmjetëm tek i pari, e kështu me radhë.

Një top i lënë mënjanë ka energjinë maksimale potenciale. Energjia e tij kinetike në këtë moment është zero. Duke filluar të lëvizë, humbet energjinë potenciale dhe fiton energji kinetike, e cila arrin maksimumin e saj në momentin e përplasjes me topin e dytë, dhe energjia potenciale bëhet e barabartë me zero. Më tej, energjia kinetike transferohet në topat e dytë, pastaj të tretë, të katërt dhe të pestë. Ky i fundit, pasi ka marrë energji kinetike, fillon të lëvizë dhe ngrihet në të njëjtën lartësi në të cilën ishte topi i parë në fillim të lëvizjes. Energjia e saj kinetike në këtë moment është e barabartë me zero, dhe energjia potenciale është e barabartë me vlerën maksimale. Pastaj fillon të bjerë dhe në të njëjtën mënyrë transferon energjinë te topat në rend të kundërt.

Kjo vazhdon për një kohë mjaft të gjatë dhe mund të vazhdojë pafundësisht nëse nuk do të kishte forca jo konservatore. Por në realitet, forcat shpërndarëse veprojnë në sistem, nën ndikimin e të cilave topat humbasin energjinë e tyre. Shpejtësia dhe amplituda e tyre gradualisht ulen. Dhe përfundimisht ata ndalojnë. Kjo konfirmon se ligji i ruajtjes së energjisë plotësohet vetëm në mungesë të forcave jo konservatore.

Energjia totale mekanike karakterizon lëvizjen dhe bashkëveprimin e trupave, prandaj varet nga shpejtësia dhe pozicioni relativ i trupave.

Energjia totale mekanike e një sistemi mekanik të mbyllur është e barabartë me shumën e energjive kinetike dhe potenciale të trupave të këtij sistemi:

Ligji i ruajtjes së energjisë

Ligji i ruajtjes së energjisë është një ligj themelor i natyrës.

Në mekanikën e Njutonit, ligji i ruajtjes së energjisë formulohet si më poshtë:

Energjia totale mekanike e një sistemi të izoluar (të mbyllur) trupash mbetet konstante.

Me fjale te tjera:

Energjia nuk lind nga asgjëja dhe nuk zhduket askund, ajo mund të kalojë vetëm nga një formë në tjetrën.

Shembuj klasikë të këtij pohimi janë: një lavjerrës susta dhe një lavjerrës në një fije (me amortizimin e papërfillshëm). Në rastin e një lavjerrës sustë, në procesin e lëkundjes, energjia potenciale e një sustë të deformuar (që ka një maksimum në pozicionet ekstreme të ngarkesës) shndërrohet në energjinë kinetike të ngarkesës (duke arritur maksimumin në momentin që ngarkesa kalon pozicionin e ekuilibrit) dhe anasjelltas. Në rastin e një lavjerrës në një fije, energjia potenciale e ngarkesës shndërrohet në energji kinetike dhe anasjelltas.

2 Pajisjet

2.1 Dinamometri.

2.2 Stenda laboratorike.

2.3 Ngarkesa me peshë 100 g - 2 copë.

2.4 Vizitor matës.

2.5 copë indet e buta ose të ndjerë.

3 Baza teorike

Skema e konfigurimit eksperimental është paraqitur në Figurën 1.

Dinamometri është i fiksuar vertikalisht në këmbën e trekëmbëshit. Një copë leckë e butë ose ndjesi vendoset në një trekëmbësh. Kur varni ngarkesat nga dinamometri, tensioni i sustës së dinamometrit përcaktohet nga pozicioni i treguesit. Në këtë rast, zgjatja maksimale (ose zhvendosja statike) e sustës X 0 ndodh kur forca elastike e një sustë me ngurtësi k balancon forcën e rëndesës së ngarkesës me masën t:

kx 0 = mg, (1)

ku g = 9,81 - nxitimi i rënies së lirë.

Rrjedhimisht,

Zhvendosja statike karakterizon pozicionin e ri të ekuilibrit O" të skajit të poshtëm të sustës (Fig. 2).

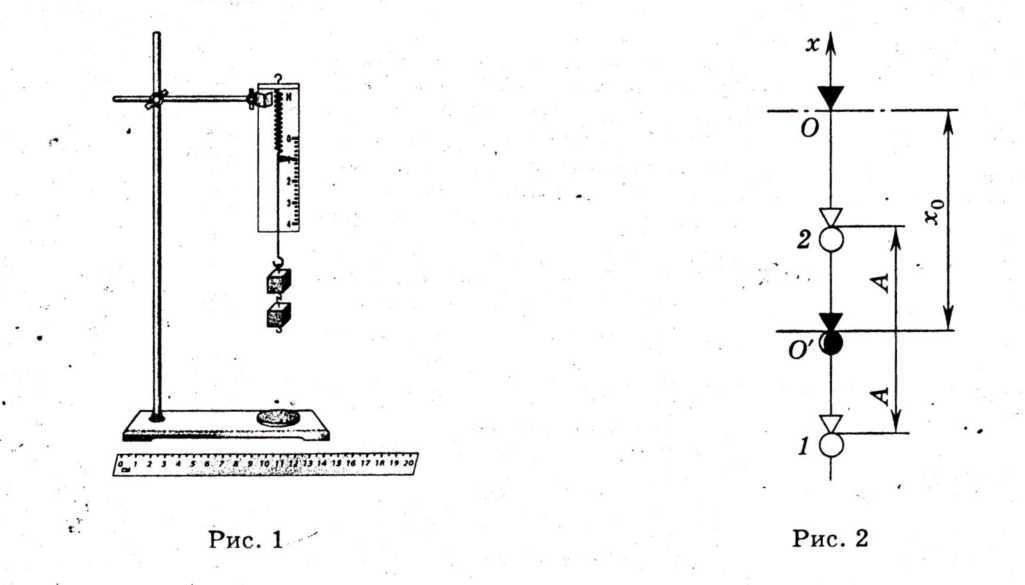
Nëse ngarkesa tërhiqet në një distancë POR nga pika O” dhe lirimi në pikën 1, atëherë ndodhin lëkundje periodike të ngarkesës. Në pika 1 dhe 2, të quajtura pika kthese, ngarkesa ndalon, duke ndryshuar drejtimin e lëvizjes. Prandaj, në këto pika, shpejtësia e ngarkesës v = 0.

Shpejtesi maksimale v m sëpatë ngarkesa do të ketë në pikën e mesit O". Në ngarkesën lëkundëse veprojnë dy forca: forca konstante e gravitetit. mg dhe forcë elastike e ndryshueshme kx. Energjia potenciale e një trupi në një fushë gravitacionale në një pikë arbitrare me koordinatë X është e barabartë me mgx. Energjia potenciale e trupit të deformuar, përkatësisht, është e barabartë me .

Në këtë rast, pika X = 0, që korrespondon me pozicionin e treguesit për një sustë të pashtrirë.

Energjia totale mekanike e ngarkesës në një pikë arbitrare është shuma e potencialit të saj dhe energjisë kinetike. Duke neglizhuar forcat e fërkimit, ne përdorim ligjin e ruajtjes së energjisë totale mekanike.

Le të barazojmë energjinë totale mekanike të ngarkesës në pikën 2 me koordinatën - (X 0 -POR) dhe në pikën O" me koordinatë -X 0 :

Duke zgjeruar kllapat dhe duke kryer transformime të thjeshta, ne sjellim formulën (3) në formë

Pastaj moduli i shpejtësisë maksimale të ngarkesave

Ngurtësia e një suste mund të gjendet duke matur zhvendosjen statike X 0 . Siç vijon nga formula (1),

3.5. Ligjet e ruajtjes dhe ndryshimit të energjisë

3.5.1. Ligji i Ndryshimit energjia totale mekanike

Një ndryshim në energjinë totale mekanike të një sistemi trupash ndodh kur puna kryhet nga forcat që veprojnë si midis trupave të sistemit ashtu edhe nga trupat e jashtëm.

Ndryshimi i energjisë mekanike ∆E të një sistemi trupash përcaktohet nga me ligjin e ndryshimit të energjisë totale mekanike:

∆E \u003d E 2 - E 1 \u003d A ext + A tr (rezistoj),

ku E 1 është energjia totale mekanike e gjendjes fillestare të sistemit; E 2 - energjia totale mekanike e gjendjes përfundimtare të sistemit; A e jashtme - puna e bërë në trupat e sistemit nga forcat e jashtme; A tr (rezistoj) - puna e bërë nga forcat e fërkimit (rezistenca) që veprojnë brenda sistemit.

Shembulli 30. Në një lartësi të caktuar, një trup në prehje ka një energji potenciale të barabartë me 56 J. Në kohën kur ai bie në Tokë, trupi ka një energji kinetike të barabartë me 44 J. Përcaktoni punën e forcave të rezistencës së ajrit.

Zgjidhje. Figura tregon dy pozicione të trupit: në një lartësi të caktuar (e para) dhe në momentin e rënies në Tokë (e dyta). Niveli zero i energjisë potenciale zgjidhet në sipërfaqen e Tokës.

Energjia totale mekanike e një trupi në lidhje me sipërfaqen e Tokës përcaktohet nga shuma e energjisë potenciale dhe kinetike:

• në njëfarë lartësie

E 1 \u003d W p 1 + W k 1;

• në momentin që bie në tokë

E 2 \u003d W p 2 + W k 2,

ku W p 1 = 56 J është energjia potenciale e trupit në një lartësi të caktuar; W k 1 = 0 - energjia kinetike e një trupi që qëndron në një lartësi të caktuar; W p 2 = 0 J - energjia potenciale e trupit në momentin e rënies në Tokë; W k 2 \u003d 44 J - energjia kinetike e trupit në kohën kur bie në Tokë.

Ne gjejmë punën e forcave të rezistencës së ajrit nga ligji i ndryshimit të energjisë totale mekanike të trupit:

ku E 1 = W p 1 është energjia totale mekanike e trupit në një lartësi të caktuar; E 2 \u003d W k ​​2 - energjia totale mekanike e trupit deri në kohën kur bie në Tokë; A ext \u003d 0 - puna e forcave të jashtme (forcat e jashtme mungojnë); Një rezistencë - puna e forcave të rezistencës ajrore.

Puna e dëshiruar e forcave të rezistencës ajrore përcaktohet kështu nga shprehja

Një rezistencë = W k 2 − W p 1 .

Le të bëjmë llogaritjen:

Një rezistencë \u003d 44 - 56 \u003d -12 J.

Puna e forcave të rezistencës ajrore është një vlerë negative.

Shembulli 31. Dy susta me faktor ngurtësie 1,0 kN/m dhe 2,0 kN/m lidhen paralelisht. Çfarë pune duhet bërë për të shtrirë sistemin e sustave me 20 cm?

Zgjidhje. Figura tregon dy susta me shpejtësi të ndryshme susta të lidhura paralelisht.

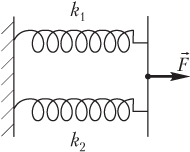
Forca e jashtme F → , që shtrin burimet, varet nga madhësia e deformimit të sustës së përbërë, prandaj, llogaritja e punës së forcës së specifikuar duke përdorur formulën për llogaritjen e punës së një force konstante është e paligjshme.

Për të llogaritur punën, ne përdorim ligjin e ndryshimit në energjinë totale mekanike të sistemit:

E 2 − E 1 = Një ext + Një rezistencë,

ku E 1 është energjia totale mekanike e sustës së përbërë në gjendje të padeformuar; E 2 - energjia totale mekanike e sustës së deformuar; Një e jashtme - punë e forcës së jashtme (vlera e dëshiruar); Një rezistencë = 0 - puna e forcave të rezistencës.

Energjia totale mekanike e një suste të përbërë është energjia potenciale e deformimit të saj:

• për pranverë të padeformuar

E 1 \u003d W p 1 \u003d 0,

• për pranverë të zgjatur

E 2 \u003d W p 2 \u003d k total (Δ l) 2 2,

ku k total - ngurtësia totale e sustës së përbërë; ∆l - madhësia e shtrirjes së sustës.

Ngurtësia totale e dy sustave të lidhura paralelisht është shuma

k total \u003d k 1 + k 2,

ku k 1 - koeficienti i ngurtësisë së sustës së parë; k 2 - koeficienti i ngurtësisë së pranverës së dytë.

Ne gjejmë punën e forcës së jashtme nga ligji i ndryshimit të energjisë totale mekanike të trupit:

Një ext \u003d E 2 - E 1,

duke zëvendësuar në këtë shprehje formulat që përcaktojnë E 1 dhe E 2, si dhe shprehjen për koeficientin e ngurtësisë totale të sustës së përbërë:

Një ext \u003d k total (Δ l) 2 2 − 0 \u003d (k 1 + k 2) (Δ l) 2 2.

Le të bëjmë llogaritjen:

Një ext \u003d (1,0 + 2,0) ⋅ 10 3 ⋅ (20 ⋅ 10 − 2) 2 2 \u003d 60 J.

Shembulli 32. Një plumb me masë 10.0 g që fluturon me shpejtësi 800 m/s godet një mur. Moduli i forcës së rezistencës ndaj lëvizjes së një plumbi në mur është konstant dhe arrin në 8.00 kN. Përcaktoni se sa larg do të depërtojë plumbi në mur.

Zgjidhje. Figura tregon dy pozicione të plumbit: kur i afrohet murit (i pari) dhe në momentin që plumbi ndalon (ngulitet) në mur (i dyti).

Energjia totale mekanike e një plumbi është energjia kinetike e lëvizjes së tij:

• kur një plumb godet një mur

E 1 \u003d W k ​​1 \u003d m v 1 2 2;

• në momentin që plumbi ndalet (ngulitet) në mur

E 2 \u003d W k ​​2 \u003d m v 2 2 2,

ku W k 1 - energjia kinetike e plumbit kur i afrohet murit; W k 2 - energjia kinetike e plumbit në momentin që ndalon (ngec) në mur; m është masa e plumbit; v 1 - moduli i shpejtësisë së plumbit kur i afroheni murit; v 2 \u003d 0 - vlera e shpejtësisë së plumbit në momentin e ndalimit (ngecjes) në mur.

Distanca në të cilën plumbi do të shkojë thellë në mur, e gjejmë nga ligji i ndryshimit të energjisë totale mekanike të plumbit:

E 2 − E 1 = Një ext + Një rezistencë,

ku E 1 \u003d m v 1 2 2 - energjia totale mekanike e plumbit kur i afrohet murit; E 2 \u003d 0 - energjia totale mekanike e plumbit deri në kohën kur ndalon (ngec) në mur; A ext \u003d 0 - puna e forcave të jashtme (forcat e jashtme mungojnë); Një rezistencë - puna e forcave të rezistencës.

Puna e forcave të rezistencës përcaktohet nga produkti:

A rezistojë = F rezistojë l cos α ,

ku F rezistojnë - moduli i forcës së rezistencës ndaj lëvizjes së plumbit; l - distanca që plumbi do të shkojë thellë në mur; α = 180° - këndi ndërmjet drejtimeve të forcës së tërheqjes dhe drejtimit të plumbit.

Kështu, ligji i ndryshimit në energjinë totale mekanike të një plumbi në një formë të qartë është si më poshtë:

− m v 1 2 2 = F rezistoj l cos 180 ° .

Distanca e dëshiruar përcaktohet nga raporti

l = − m v 1 2 2 F rezistoj cos 180 ° = m v 1 2 2 F rezistoj

l = 10,0 ⋅ 10 − 3 ⋅ 800 2 2 ⋅ 8,00 ⋅ 10 3 = 0,40 m = 400 mm.

Faqe 1

Energjia totale mekanike e trupit nuk ndryshon. Energjia ndryshon vetëm nga një formë në tjetrën.

Energjia e përgjithshme mekanike e një trupi, e cila nuk ndikohet nga forcat e fërkimit dhe rezistencës, mbetet e pandryshuar gjatë lëvizjes së tij.

Energjia totale mekanike e një trupi është shuma e energjive të tij kinetike dhe potenciale. Konsideroni plot energji trupi që bie lirshëm në kohë të ndryshme.

A ndryshon energjia totale mekanike e trupit kur ai bie.

Ajo që quhet energjia e përgjithshme mekanike e trupit.

Kështu, energjia totale mekanike e një trupi që kryen lëkundje harmonike është proporcionale me katrorin e amplitudës së lëkundjes. Prandaj, amplituda A e lëkundjeve gjithashtu nuk varet nga koha.

Siç shihet nga (44.13), energjia totale mekanike e trupit gjatë lëkundjeve të amortizuara zvogëlohet me kalimin e kohës sipas një ligji eksponencial.

Shuma e energjive kinetike dhe potenciale formon energjinë totale mekanike të trupit.

Një ndikim absolutisht elastik është një ndikim i tillë në të cilin ruhet energjia totale mekanike e trupave. Së pari, energjia kinetike konvertohet pjesërisht ose plotësisht në energjinë potenciale të deformimit elastik. Pastaj trupat kthehen në formën e tyre origjinale, duke zmbrapsur njëri-tjetrin. Si rezultat, energjia potenciale e deformimit elastik kthehet përsëri në energji kinetike dhe trupat fluturojnë larg me shpejtësi të përcaktuara nga dy kushte - ruajtja e energjisë totale dhe impuls total tel.

Një ndikim absolutisht elastik është një ndikim i tillë në të cilin ruhet energjia totale mekanike e trupave. Së pari, energjia kinetike konvertohet pjesërisht ose plotësisht në energjinë potenciale të deformimit elastik. Pastaj trupat kthehen në formën e tyre origjinale, duke zmbrapsur njëri-tjetrin. Si rezultat, energjia potenciale e deformimit elastik kthehet përsëri në energji kinetike dhe trupat fluturojnë larg me shpejtësi të përcaktuara nga dy kushte - ruajtja e energjisë totale dhe momenti i përgjithshëm i trupave.

Një ndikim absolutisht elastik është një ndikim i tillë në të cilin ruhet energjia totale mekanike e trupave. Së pari, energjia kinetike konvertohet pjesërisht ose plotësisht në energjinë potenciale të deformimit elastik. Pastaj trupat kthehen në formën e tyre origjinale, duke zmbrapsur njëri-tjetrin. Si rezultat, energjia potenciale e deformimit elastik kthehet përsëri në energji kinetike dhe trupat fluturojnë larg me shpejtësi të përcaktuara nga dy kushte - ruajtja e energjisë totale dhe momenti i përgjithshëm i trupave.

Kjo punë shpenzohet për shpërndarjen e energjisë ose ndryshimin e energjisë totale mekanike të trupit.

Sipas ligjit të ndryshimit të energjisë (shih § 28), puna e forcës së rezistencës (forca e jashtme) është e barabartë me rritjen e energjisë totale mekanike të trupit.

Ky rezultat është i parashikueshëm, pasi forca elastike nën të cilën lëviz trupi është konservatore, prandaj, ligji i ruajtjes së energjisë përmbushet - energjia totale mekanike e trupit ruhet.

Energjia mekanike karakterizon aftësinë e një trupi për të kryer punë mekanike. Energjia e përgjithshme mekanike e një trupi është shuma e energjisë kinetike dhe potenciale.