Fizică statistică. Fizica statistică este
Termodinamică și fizică statistică
Orientări și sarcini de control pentru studenții din învățământul la distanță
Shelkunova Z.V., Saneev E.L.
Instructiuni metodologice si sarcini de control pentru studentii de la inginerie si specialitati tehnologice la distanta. Acestea conțin secțiuni din programele „Fizică statistică”, „Termodinamică”, exemple de rezolvare a problemelor tipice și opțiuni pentru sarcini de control.
Cuvinte cheie: Energie interna, căldură, muncă; izoprocese, entropie: funcții de distribuție: Maxwell, Boltzmann, Bose - Einstein; Fermi - Dirac; Energia Fermi, capacitatea termică, temperatura caracteristică Einstein și Debye.
Editor T.Yu.Artyunina
Pregătit pentru tipărire d. Format 6080 1/16
R.l. ; uch.-ed.l. 3,0; Tiraj ____ exemplare. Comandă nu.
___________________________________________________
RIO ESGTU, Ulan-Ude, Klyuchevskaya, 40a
Tipărit pe rotaprint al ESGTU, Ulan-Ude,
Klyuchevskaya, 42.
Agenția Federală pentru Educație
Statul Siberiei de Est
Universitatea de Tehnologie
FIZICA №4
(Termodinamica si fizica statistica)
Instrucțiuni metodice și sarcini de control
pentru studenții din învățământul la distanță
Alcătuit de: Shelkunova Z.V.
Saneev E.L.
Editura ESGTU
Ulan-Ude, 2009
Fizică statistică și termodinamică
Subiectul 1
Legile dinamice și statistice în fizică. Metode termodinamice și statistice. Elemente de teorie molecular-cinetică. stare macroscopică. Mărimi și stări fizice ale sistemelor fizice. Parametrii macroscopici ca valori medii. Echilibrul termic. Model gaz ideal. Ecuația de stare pentru un gaz ideal. Conceptul de temperatură.
Tema 2
fenomene de transfer. Difuzie. Conductivitate termică. coeficientul de difuzie. Coeficient de conductivitate termică. difuzivitate termică. Difuzia în gaze, lichide și solide. Viscozitate. Coeficientul de vâscozitate al gazelor și lichidelor.
Tema 3
Elemente de termodinamică. Prima lege a termodinamicii. Energie interna. Parametri intensivi și extensivi.
Tema 4
Procese reversibile și ireversibile. Entropie. A doua lege a termodinamicii. Potențiale termodinamice și condiții de echilibru. potential chimic. Condiții de echilibru chimic. Ciclul Carnot.
Tema 5
functii de distributie. parametrii microscopici. Probabilitate și fluctuații. Distribuția Maxwell. Mediu energie kinetică particule. Distribuția Boltzmann. Capacitatea termică a gazelor poliatomice. Limitarea teoriei clasice a capacității termice.
Tema 6
distribuția Gibbs. Modelul sistemului din termostat. Distribuție canonică Gibbs. Semnificația statistică a potențialelor termodinamice și a temperaturii. Rolul energiei libere.
Tema 7
Distribuția Gibbs pentru un sistem cu un număr variabil de particule. Entropie și probabilitate. Determinarea entropiei unui sistem de echilibru prin ponderea statistică a unei microstări.
Tema 8
Funcții de distribuție Bose și Fermi. Formula lui Planck pentru radiații termice fără greutate. Ordine și dezordine în natură. Entropia ca măsură cantitativă a haosului. Principiul creșterii entropiei. Trecerea de la ordine la dezordine se referă la starea de echilibru termic.
Tema 9
Metode experimentale pentru studierea spectrului vibrațional al cristalelor. Conceptul de fononi. Legile de dispersie pentru fononi acustici și optici. Capacitatea termică a cristalelor la temperaturi scăzute și ridicate. Capacitate de căldură electronică și conductivitate termică.
Tema 10
Electroni în cristale. Aproximarea cuplajului puternic și slab. Modelul electronilor liberi. Nivelul Fermi. Elemente ale teoriei benzilor a cristalelor. Funcția Bloch. Structura de bandă a spectrului energetic al electronilor.
Subiectul 11
Suprafata Fermi. Numărul și densitatea numărului de stări electronice din bandă. Umpluturi de zonă: metale, dielectrici și semiconductori. Conductibilitatea electrică a semiconductorilor. Conceptul de conductivitate a găurii. Semiconductori intrinseci și extrinseci. Conceptul de joncțiune p-n. tranzistor.
Subiectul 12
Conductibilitatea electrică a metalelor. Purtători de curent în metale. Insuficiența teoriei electronilor clasice. Gaz Fermi electronic într-un metal. Purtători de curent ca cvasiparticule. Fenomenul de supraconductivitate. Perechea de electroni Cooper. contact tunel. Efectul Josephson și aplicațiile sale. Captură și cuantizare flux magnetic. Conceptul de conductivitate la temperatură înaltă.
FIZICA STATISTICĂ. TERMODINAMICĂ
Formule de bază
1. Cantitatea de substanță a unui gaz omogen (în moli):
Unde N-numarul de molecule de gaz; N A- numărul lui Avogadro; m-masa gazului; este masa molară a gazului.
Dacă sistemul este un amestec de mai multe gaze, atunci cantitatea de substanță din sistem
![]() ,
,
![]() ,
,
Unde i , N i , m i , i - respectiv cantitatea de substanță, numărul de molecule, masa, Masă molară i a-lea component al amestecului.
2. Ecuația Clapeyron-Mendeleev (ecuația de stare a gazului ideal):
![]()
Unde m- masa gazului; - Masă molară; R- constanta universala a gazului; = m/ - cantitate de substanță; T este temperatura termodinamică în Kelvin.
3. Legile experimentale ale gazelor, care sunt cazuri speciale ale ecuației Clapeyron-Mendeleev pentru izoprocese:
legea boyle-mariotte
(proces izoterm - T= const; m=const):
sau pentru două stări de gaz:
Unde p 1 și V 1 - presiunea si volumul gazului in stare initiala; p 2 și V 2
Legea lui Gay-Lussac (proces izobar - p=const, m=const):
sau pentru două stări:
Unde V 1 și T 1 - volumul si temperatura gazului in starea initiala; V 2 și T 2 - aceleași valori în starea finală;
legea lui Charles (procesul izocor - V=const, m=const):
sau pentru două stări:
Unde R 1 și T 1 - presiunea si temperatura gazului in starea initiala; R 2 și T 2 - aceleași valori în starea finală;
combinate legea gazelor (m=const):
Unde R 1 , V 1 , T 1 - presiunea, volumul si temperatura gazului in stare initiala; R 2 , V 2 , T 2 sunt aceleași valori în starea finală.
4. Legea lui Dalton, care determină presiunea unui amestec de gaze:
p = p 1 + p 2 + ... +p n
Unde p i - presiuni parțiale componenta amestecului; n- numărul de componente ale amestecului.
5. Masa molară a unui amestec de gaze:
![]()
Unde m i- greutate i-a-a componentă a amestecului; i = m i / i- cantitate de substanță i-a-a componentă a amestecului; n- numărul de componente ale amestecului.
6. Fracția de masă i i-a-a componentă a amestecului de gaze (în fracțiuni de unitate sau procent):
Unde m este masa amestecului.
7. Concentrația moleculelor (număr de molecule pe unitatea de volum):
![]()
Unde N-numarul de molecule continute in sistem; este densitatea substanței. Formula este valabilă nu numai pentru gaze, ci și pentru orice stare de agregare a materiei.
8. Ecuația de bază teoria cinetică gaze:
 ,
,
Unde<>este energia cinetică medie a mișcării de translație a moleculei.
9. Energia cinetică medie a mișcării de translație a unei molecule:
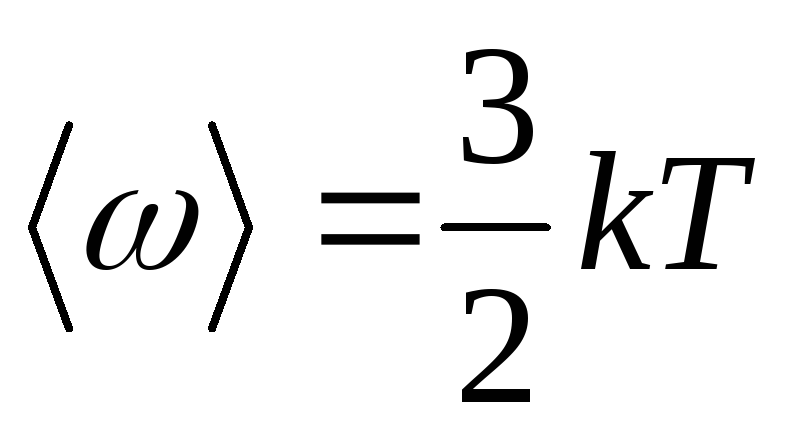 ,
,
Unde k este constanta Boltzmann.
10. Energia cinetică totală medie a unei molecule:
Unde i este numărul de grade de libertate ale moleculei.
11. Dependența presiunii gazului de concentrația de molecule și temperatură:
p = nkT.
12. Vitezele moleculelor:
rădăcină medie pătrată  ;
;
medie aritmetică 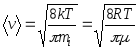 ;
;
cel mai probabil 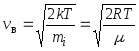 ,
,
Unde m i este masa unei molecule.
13. Viteza relativă a unei molecule:
u = v/v în ,
Unde v este viteza acestei molecule.
14. Capacități termice specifice ale gazului la volum constant (s v) și la presiune constantă (Cu R):
15. Relația dintre anumite ( Cu) și molar ( DIN) capacitati termice:
; C=c .
16. Ecuația lui Robert Mayer:
C p -C v = R.
17. Energia internă a unui gaz ideal:
![]()
18. Prima lege a termodinamicii:
Unde Q- caldura comunicata sistemului (gaz); dU- modificarea energiei interne a sistemului; DAR este munca efectuată de sistem împotriva forțelor externe.
19. Lucrări de expansiune a gazului:
în general ;
în proces izobaric ![]() ;
;
proces izotermic ![]() ;
;
într-un proces adiabatic ![]() ,
,
sau  ,
,
unde este exponentul adiabatic.
20. Ecuațiile lui Poisson care raportează parametrii unui gaz ideal într-un proces adiabatic:
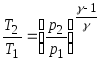 ;
;
21. Eficienta termica ciclu.
electroni etc.), prin proprietățile acestor particule și interacțiunea dintre ele.Alte ramuri ale fizicii studiază, de asemenea, corpurile macroscopice - termodinamica , Mecanica medii continue, electrodinamica mediilor continue. Cu toate acestea, atunci când se rezolvă probleme specifice prin metodele acestor discipline, ecuațiile corespunzătoare includ întotdeauna parametri sau funcții necunoscute care caracterizează un corp dat. Deci, pentru a rezolva problemele de hidrodinamică, este necesar să se cunoască ecuația de stare a unui lichid sau gaz, adică dependența densității de temperatură și presiune, capacitatea termică a unui lichid, coeficientul său de vâscozitate etc. Toate aceste dependențe și parametri pot fi, desigur, determinați experimental; prin urmare, metodele în cauză sunt numite fenomenologice. Fizica statistică permite, cel puțin în principiu, și în multe cazuri efectiv, să se calculeze toate aceste mărimi, dacă se cunosc forțele de interacțiune dintre molecule. Acea., fizica statistica folosește informații despre structura „microscopică” a corpurilor - despre ce particule constau, cum interacționează aceste particule, de aceea se numește teoria microscopică.
Dacă la un moment dat sunt date coordonatele și vitezele tuturor particulelor corpului și se cunoaște legea interacțiunii lor, atunci, prin rezolvarea ecuațiilor mecanicii, ar fi posibil să se găsească aceste coordonate și viteze în orice punct ulterior. în timp şi prin aceasta determină complet starea organismului studiat. (Pentru simplitate, prezentarea este realizată în limbajul mecanicii clasice. Dar chiar și în mecanica cuantică situația este aceeași: cunoașterea inițialei funcția de undă sisteme și legea interacțiunii particulelor, este posibil, prin rezolvare Ecuația Schrödinger , găsiți funcția de undă care determină starea sistemului în toate momentele viitoare de timp.) De fapt, totuși, un astfel de mod de a construi o teorie microscopică este imposibil, deoarece numărul de particule din corpurile macroscopice este foarte mare. De exemplu, în 1 cm 3 gaz la o temperatură de 0 °C și o presiune de 1 ATM conţine aproximativ 2,7×10 19 molecule. Este imposibil să rezolvi un astfel de număr de ecuații, iar coordonatele și vitezele inițiale ale tuturor moleculelor sunt încă necunoscute.
Cu toate acestea, acesta număr mare particulele din corpurile macroscopice duce la apariția unor noi - statistici - regularități în comportamentul unor astfel de corpuri. Acest comportament într-o gamă largă nu depinde de condițiile inițiale specifice - de valorile exacte ale coordonatelor inițiale și ale vitezelor particulelor. Cea mai importantă manifestare a acestei independențe este faptul cunoscut din experiență că un sistem lăsat singur, adică izolat de influențele externe, ajunge în cele din urmă la o stare de echilibru (echilibru termodinamic sau statistic), ale cărei proprietăți sunt determinate doar de astfel de caracteristici generale starea inițială, ca numărul de particule, energia lor totală etc. (cm. Echilibru termodinamic ). În cele ce urmează, ne vom concentra în principal asupra fizica statistica stări de echilibru.
Înainte de a formula o teorie care descrie regularitățile statistice, ar trebui să limitezi în mod rezonabil însăși cerințele pentru teorie. Și anume, sarcina teoriei ar trebui să fie să calculeze nu valorile exacte ale diferitelor cantități fizice pentru corpurile macroscopice, ci valorile medii ale acestor cantități în timp. Luați în considerare, de exemplu, moleculele situate într-un volum macroscopic suficient de mare izolat într-un gaz. Numărul de astfel de molecule se va schimba în timp datorită mișcării lor și ar putea fi găsit exact dacă toate coordonatele moleculelor ar fi cunoscute în orice moment. Acest lucru, însă, nu este necesar. Modificarea numărului de molecule din volum va fi de natura fluctuațiilor aleatorii - fluctuații - în raport cu o anumită valoare medie. Cu un număr mare de particule în volum, aceste fluctuații vor fi mici în comparație cu numărul mediu de particule, astfel încât pentru a caracteriza starea macroscopică, este suficient să cunoaștem exact această valoare medie.
Pentru a clarifica natura tiparelor statistice, luați în considerare un alt exemplu simplu. Să se pună într-un vas un număr mare de boabe de două soiuri, fiecare grad în mod egal, iar conținutul vasului să fie bine amestecat. Apoi, pe baza experienței cotidiene, se poate fi sigur că într-o probă prelevată dintr-un vas care conține încă un număr mare de boabe, se va găsi un număr aproximativ egal de boabe din fiecare soi, indiferent de ordinea în care boabele. au fost turnate în vas. Acest exemplu arată clar două împrejurări importante care asigură aplicabilitatea teoriei statistice. În primul rând, necesitatea unui număr mare de boabe atât în întregul „sistem” - un vas cu cereale, cât și în „subsistemul” ales pentru experiment - o probă. (Dacă proba constă din doar două boabe, atunci deseori ambele vor fi de aceeași calitate.) În al doilea rând, este clar că complexitatea mișcării boabelor în timpul amestecării joacă un rol semnificativ, asigurând distribuția lor uniformă în volumul de vasul.
funcția de distribuție. Luați în considerare un sistem format din particule, presupunând pentru simplitate că particulele nu au grade interne de libertate. Un astfel de sistem este descris de sarcină 6 variabile - 3 coordonate q iși 3 impulsuri pi, particule [setul acestor variabile va fi prescurtat ca ( R, q)]. Să calculăm valoarea medie pe intervalul de timp a unei anumite valori (p, q), care este o funcție a acestor coordonate și momente. Pentru a face acest lucru, împărțim intervalul (0, t) în s segmente mici egale D ta (A = 1,2,....... s). Apoi, prin definiție
![]() ,
,
Unde q ași p a- valori ale coordonatelor și impulsurilor uneori ta. In limita s® ¥ suma intră în integrală:
![]() (1a)
(1a)
Conceptul de funcție de distribuție în mod natural apare dacă luăm în considerare spațiul 6 măsurători, pe axele cărora sunt trasate valorile coordonatelor și momentelor particulelor sistemului; se numește spațiu fazelor. Pentru fiecare valoare a timpului t corespund anumitor valori ale tuturor qși R, adică un punct din spațiul fazelor reprezentând starea sistemului în acest moment timp t. Să împărțim întregul spațiu de fază în elemente, a căror dimensiune este mică în comparație cu valorile caracteristice unei anumite stări a sistemului qși R, dar încă atât de mare încât în fiecare dintre ele există multe puncte care descriu starea sistemului în momente diferite în timp t. Atunci numărul de astfel de puncte din elementul de volum va fi aproximativ proporțional cu valoarea acestui volum dpdq. Dacă notăm coeficientul de proporționalitate prin sw(p, q), atunci acesta este numărul pentru elementul centrat la un moment dat ( p, q) se va scrie ca:
da = sw(p, q)dpdq, (2)
Volumul elementului de spațiu de fază selectat. Valoarea medie (1), ținând cont de micimea acestor elemente de volum, poate fi rescrisă ca , i.e.
(integrarea peste coordonate se realizează pe întregul volum al sistemului, pe momente - de la -¥ la ¥). w( p, q, t) se numește funcție de distribuție în raport cu coordonatele momentului particulelor. Deoarece numărul total de puncte selectate este s, funcție w satisface condiția de normalizare:
![]() (4)
(4)
Se poate observa din (3) și (4) că w dpdq poate fi considerată probabilitatea ca sistemul să fie în element dpdq spațiu fazelor. Funcția de distribuție astfel introdusă poate primi o altă interpretare. Pentru a face acest lucru, vom lua în considerare simultan un număr mare de sisteme identice și vom presupune că fiecare punct din spațiul fazelor reprezintă starea unui astfel de sistem. Atunci media temporală din (1)-(1a) poate fi înțeleasă ca o medie asupra totalității acestor sisteme sau, după cum se spune, peste ansamblu statistic . Argumentele purtate până acum au fost de natură pur formală, de atunci găsirea funcției de distribuție, conform (2), necesită cunoașterea tuturor Rși qîn orice moment, adică soluții ale ecuațiilor de mișcare cu condițiile inițiale corespunzătoare. Dispoziție de bază fizica statistica este, totuși, o afirmație despre posibilitatea de a determina această funcție din considerații generale pentru un sistem în stare de echilibru termodinamic. În primul rând, se poate demonstra, pe baza conservării numărului de sisteme în timpul mișcării, că funcția de distribuție este o integrală a mișcării sistemului, adică rămâne constantă dacă Rși q se modifică în funcție de ecuațiile mișcării (vezi Teorema Liouville ). Când conduceți sistem închis energia sa nu se schimbă, prin urmare toate punctele din spațiul fazelor, care ilustrează starea sistemului în diferite momente în timp, trebuie să se afle pe o „hipersuprafață” corespunzătoare valorii inițiale a energiei. E. Ecuația acestei suprafețe are forma;
Formulele de mai sus se referă la cazul în care este dat numărul de particule din subsistem. Dacă alegem ca subsistem un anumit element de volum al întregului sistem, prin suprafața căruia particulele pot părăsi subsistemul și se pot întoarce la el, atunci probabilitatea de a găsi subsistemul într-o stare cu energie. E nși numărul de particule n este dat de formula mare de distribuție canonică a lui Gibbs:
![]() , (9)
, (9)
În care parametrul suplimentar m este potential chimic , care determină numărul mediu de particule din subsistem, iar valoarea este determinată din condiția de normalizare [vezi formula (11)].
Interpretarea statistică a termodinamicii. Cel mai important rezultat fizica statistica- stabilirea semnificaţiei statistice a mărimilor termodinamice. Acest lucru face posibilă derivarea legilor termodinamicii din conceptele de bază fizica statisticași calculați mărimile termodinamice pentru sisteme specifice. În primul rând, termodinamică energie interna se identifică cu energia medie a sistemului. Prima lege a termodinamicii apoi primește o interpretare evidentă ca expresie a legii conservării energiei în timpul mișcării particulelor care alcătuiesc corpul.
Mai mult, funcția Hamilton a sistemului depinde de un parametru l (coordonatele peretelui vasului care conține sistemul, câmpul extern etc.). Atunci derivata va fi forta generalizata
corespunzătoare acestui parametru, iar valoarea după mediere dă munca mecanica efectuate pe sistem atunci când acest parametru este modificat. Dacă deosebim expresia ![]() pentru energia medie a sistemului, luând în considerare formula (6) și condiția de normalizare, având în vedere variabilele l și T si avand in vedere ca valoarea
este, de asemenea, o funcție a acestor variabile, atunci obținem identitatea:
pentru energia medie a sistemului, luând în considerare formula (6) și condiția de normalizare, având în vedere variabilele l și T si avand in vedere ca valoarea
este, de asemenea, o funcție a acestor variabile, atunci obținem identitatea:
![]() .
.
Conform celor de mai sus, membrul care contine d l este egal cu job mediu dA efectuate asupra corpului. Apoi ultimul termen este căldura primită de corp. Comparând această expresie cu relația dE = dA + TdS, care este o înregistrare combinată a primei și a doua legi ale termodinamicii (vezi Fig. A doua lege a termodinamicii ) pentru procese reversibile , aflăm că Tîn (6) este într-adevăr egal cu temperatura absolută corp, iar derivatul - luat cu semnul opus entropie . Înseamnă că există energie gratis corp, din care se clarifică semnificația lui statistică.
De o importanță deosebită este interpretarea statistică a entropiei, care decurge din formula (8). Formal, g se însumează la această formulă peste toate stările cu energie E n, dar de fapt, din cauza micșorării fluctuațiilor de energie în distribuția Gibbs, doar un număr relativ mic dintre ele cu o energie apropiată de energia medie este semnificativ. Este firesc să se determine numărul acestor stări esențiale, prin urmare, prin limitarea însumării din (8) la intervalul , înlocuind E n la energia medie și scoaterea exponentului de sub semnul sumei. Apoi suma va da și va lua forma.
![]()
Pe de altă parte, conform termodinamicii, =-TS, care oferă o legătură între entropie și numărul de stări microscopice într-o stare macroscopică dată, cu alte cuvinte, cu ponderea statistica stare macroscopică, adică cu probabilitatea sa:
La temperatura de zero absolut, orice sistem se află într-o anumită stare fundamentală, deci = 1, S= 0. Această afirmaţie exprimă a treia lege a termodinamicii . Este esențial aici ca pentru o definiție neechivocă a entropiei este necesar să se utilizeze formula cuantică (8); în statistica pur clasică, entropia este definită doar până la un termen arbitrar.
Sensul entropiei ca măsură a probabilității unei stări este păstrat și în raport cu stările arbitrare - nu neapărat de echilibru. Într-o stare de echilibru, entropia are valoarea maximă posibilă în condiții externe date. Aceasta înseamnă că starea de echilibru este starea cu ponderea statistică maximă, starea cea mai probabilă. Procesul de trecere a unui sistem de la o stare de neechilibru la o stare de echilibru este un proces de trecere de la stările mai puțin probabile la cele mai probabile; acest lucru elucidează semnificația statistică a legii de creștere a entropiei, conform căreia entropia unui sistem închis nu poate decât să crească.
Formula (8) care raportează energia liberă cu o funcție de partiție, este baza pentru calcularea mărimilor termodinamice prin metode fizica statistica Este folosit, în special, pentru a construi o teorie statistică a proprietăților electrice și magnetice ale materiei. De exemplu, pentru a calcula momentul magnetic al unui corp într-un câmp magnetic, ar trebui să se calculeze funcția de partiție și energia liberă. Moment magnetic m corpul este apoi dat de formula:
Unde H- tensiune exterioară camp magnetic. Similar cu (8), condiția de normalizare în marea distribuție canonică (9) determină potenţialul termodinamic dupa formula:
![]() . (11)
. (11)
Acest potențial este legat de energia liberă prin relația:
![]() .
.
Aplicații fizica statistica la studiul anumitor proprietăți ale unor sisteme specifice se reduc în esență la un calcul aproximativ al funcției de partiție, ținând cont de proprietățile specifice ale sistemului.
În multe cazuri, această sarcină este simplificată prin aplicarea legii echipartiției în grade de libertate, care prevede că capacitatea termică CV(la volum constant v) sisteme de interacţiune puncte materiale- particulele care fac oscilații armonice este egală cu
c v = k(l/2 + n),
Unde l - numărul total grade de libertate de translație și rotație, n- numărul de grade de libertate vibraționale. Dovada legii se bazează pe faptul că funcția Hamilton H un astfel de sistem arată astfel: H =(pi) + (q m), unde energia cinetică La este o funcție pătratică omogenă a l + n impulsuri piși energia potențială - funcţia pătratică a n coordonate vibraționale q m. În integrala statistică Z(8a) integrarea peste coordonatele vibraționale datorită convergenței rapide a integralei poate fi extinsă de la -¥ la ¥. După ce am făcut schimbarea variabilelor, constatăm că Z depinde de temperatura ca Tl/2+n, deci energia liberă =-kT(l/ 2 +n)(ln T+ const). Aceasta implică expresia de mai sus pentru capacitatea termică, deoarece . Abaterile de la legea echipartiției în sistemele reale sunt asociate în primul rând cu corecțiile cuantice, deoarece în cuantică fizica statistica aceasta lege este nedreapta. Există și corecții legate de nearmonicitatea oscilațiilor.
Gaz ideal. Cel mai simplu obiect de studiu fizica statistica este un gaz ideal, adică un gaz atât de rarefiat încât interacțiunea dintre moleculele sale poate fi neglijată. Funcțiile termodinamice ale unui astfel de gaz pot fi calculate complet. Energia unui gaz este pur și simplu suma energiilor moleculelor individuale. Acest lucru, cu toate acestea, este încă insuficient pentru a considera moleculele ca fiind complet independente. Într-adevăr, în mecanica cuantică, chiar dacă nu există forțe de interacțiune între particule, există o anumită influență a particulelor identice (identice) unele asupra celeilalte dacă acestea se află în stări similare de mecanică cuantică. Acesta este așa-numitul. interacțiune de schimb . Poate fi neglijat dacă, în medie, există mult mai puțin de o particulă pe stare, care în orice caz are loc la o temperatură suficient de ridicată a gazului; un astfel de gaz se numește nedegenerat. De fapt, gazele obișnuite, formate din atomi și molecule, sunt nedegenerate la toate temperaturile (la care sunt încă gazoase). Pentru un gaz ideal nedegenerat, funcția de distribuție se descompune în produsul funcțiilor de distribuție pentru molecule individuale. se află în intervale dp x, dpy, dpz, iar coordonatele sunt în intervale dx, dy, dz:
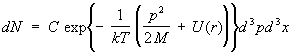 , (12) Energia unei molecule de gaz monoatomic într-un câmp extern cu energie potențială
(r) este egal cu p2/2M+(r). Integrarea (6) peste coordonate r(x, y, z) și impulsuri R(p x, py, pz) dintre toate moleculele cu excepția uneia, puteți găsi numărul de molecule dN, ale căror impulsuri
, (12) Energia unei molecule de gaz monoatomic într-un câmp extern cu energie potențială
(r) este egal cu p2/2M+(r). Integrarea (6) peste coordonate r(x, y, z) și impulsuri R(p x, py, pz) dintre toate moleculele cu excepția uneia, puteți găsi numărul de molecule dN, ale căror impulsuri
Unde d 3 p = dp x dp y dp z, d3x = dxdydz. Această formulă se numește distribuție Maxwell-Boltzmann (vezi Fig. Statistica Boltzmann ). Dacă integrăm (12) pe momente, atunci obținem o formulă pentru distribuția particulelor peste coordonate într-un câmp extern, în special, într-un câmp gravitațional - formula barometrică . Distribuția vitezei în fiecare punct din spațiu coincide cu Distribuția Maxwell .
Funcția de partiție a unui gaz ideal se descompune și în produsul termenilor identici corespunzători moleculelor individuale. Pentru un gaz monoatomic, însumarea din (8) se reduce la integrare peste coordonate și momente, adică suma este înlocuită cu o integrală peste ![]() 3
în conformitate cu numărul de celule [cu volum] din spațiul de fază al unei particule. Energie gratis
atomi de gaz este egal cu:
3
în conformitate cu numărul de celule [cu volum] din spațiul de fază al unei particule. Energie gratis
atomi de gaz este egal cu:
 ,
,
Unde g- ponderea statistică a stării fundamentale a atomului, adică numărul de stări corespunzător celui mai mic al acestuia nivel de energie, . În cele din urmă, acest lucru se datorează conexiunii menționate anterior dintre entropie și conceptul de număr de stări cuantice.
În cazul gazelor diatomice și poliatomice, la funcțiile termodinamice contribuie și vibrațiile și rotația moleculelor. Această contribuție depinde dacă efectele cuantizării vibrațiilor și rotației moleculei sunt semnificative. Distanța dintre nivelurile de energie vibrațională este de ordinul , unde w este frecvența caracteristică de oscilație, iar distanța dintre primele niveluri de energie de rotație este de ordinul ![]() , Unde
- momentul de inerție al unui corp în rotație, în acest caz o moleculă. Statisticile clasice sunt valabile dacă temperatura este suficient de ridicată astfel încât
, Unde
- momentul de inerție al unui corp în rotație, în acest caz o moleculă. Statisticile clasice sunt valabile dacă temperatura este suficient de ridicată astfel încât
kT>> D E.
În acest caz, în conformitate cu legea echipartiției, rotația aduce o contribuție constantă la capacitatea termică, egală cu 1/2 k pentru fiecare grad de libertate de rotație; în special, pentru moleculele diatomice această contribuție este egală cu k. Fluctuațiile contribuie la capacitatea termică egală cu k pentru fiecare grad de libertate vibrațional (astfel încât capacitatea de căldură vibrațională a unei molecule diatomice este k). Contribuția gradului de libertate vibrațional, față de cel rotațional, este de două ori mai mare datorită faptului că, în timpul vibrațiilor, atomii dintr-o moleculă au nu numai energie cinetică, ci și potențială. În cazul limitator opus, moleculele sunt în starea lor de vibrație fundamentală, a căror energie nu depinde de temperatură, astfel încât vibrațiile nu contribuie deloc la capacitatea termică. Același lucru este valabil și pentru rotația moleculelor în condiții ![]() . Pe măsură ce temperatura crește, apar molecule care se află în stări vibraționale și rotaționale excitate, iar aceste grade de libertate încep să contribuie la capacitatea de căldură - ca și cum treptat „se pornesc”, tinzând spre limita lor clasică cu o creștere suplimentară a temperaturii. Astfel, includerea efectelor cuantice a făcut posibilă explicarea dependenței observate experimental a capacității termice a gazelor de temperatură. Valorile mărimii care caracterizează „cuantumul rotațional” pentru majoritatea moleculelor sunt de ordinul mai multor grade sau zeci de grade (85 K pentru H 2, 2,4 K pentru 2, 15 K pentru H). În același timp, valorile caracteristice pentru „cuantumul vibrațional” sunt de ordinul miilor de grade (6100 K pentru H 2 , 2700 K pentru O 2 , 4100 K pentru H). Prin urmare, gradele de libertate de rotație sunt activate la temperaturi mult mai scăzute decât cele vibraționale. Pe fig. Figura 1 arată dependența de temperatură a capacităților de căldură (a) rotaționale și (b) vibraționale pentru o moleculă diatomică (capacitatea termică rotațională este construită pentru o moleculă de atomi diferiți).
. Pe măsură ce temperatura crește, apar molecule care se află în stări vibraționale și rotaționale excitate, iar aceste grade de libertate încep să contribuie la capacitatea de căldură - ca și cum treptat „se pornesc”, tinzând spre limita lor clasică cu o creștere suplimentară a temperaturii. Astfel, includerea efectelor cuantice a făcut posibilă explicarea dependenței observate experimental a capacității termice a gazelor de temperatură. Valorile mărimii care caracterizează „cuantumul rotațional” pentru majoritatea moleculelor sunt de ordinul mai multor grade sau zeci de grade (85 K pentru H 2, 2,4 K pentru 2, 15 K pentru H). În același timp, valorile caracteristice pentru „cuantumul vibrațional” sunt de ordinul miilor de grade (6100 K pentru H 2 , 2700 K pentru O 2 , 4100 K pentru H). Prin urmare, gradele de libertate de rotație sunt activate la temperaturi mult mai scăzute decât cele vibraționale. Pe fig. Figura 1 arată dependența de temperatură a capacităților de căldură (a) rotaționale și (b) vibraționale pentru o moleculă diatomică (capacitatea termică rotațională este construită pentru o moleculă de atomi diferiți).
Gaz imperfect. Realizare importantă fizica statistica- calculul corecțiilor la cantitățile termodinamice ale gazului asociate cu interacțiunea dintre particulele acestuia. Din acest punct de vedere, ecuația de stare a unui gaz ideal este primul termen în expansiunea presiunii unui gaz real în puteri ale densității numărului de particule, deoarece orice gaz se comportă ca un gaz ideal la o temperatură suficientă. densitate scazuta. Pe măsură ce densitatea crește, corecțiile legate de interacțiune la ecuația de stare încep să joace un rol. Acestea duc la apariția în expresia pentru presiune a termenilor cu grade mai mari de densitate a numărului de particule, astfel încât presiunea este reprezentată de așa-numita. seria virală de forma:
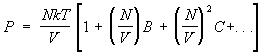 . (15)
. (15)
Cote LA, DIN etc. depind de temperatură și se formează. al doilea, al treilea etc. coeficienți viriali. Metode fizica statistica fac posibilă calcularea acestor coeficienți dacă se cunoaște legea interacțiunii dintre moleculele de gaz. În același timp, coeficienții LA, DIN,... descrie interacțiunea simultană a doi, trei și Mai mult molecule. De exemplu, dacă gazul este monoatomic și energia potențială de interacțiune a atomilor săi (r), atunci al doilea coeficient virial este
În ordinea mărimii LA este egal, unde r0- dimensiunea caracteristică a unui atom sau, mai precis, raza de acțiune a forțelor interatomice. Aceasta înseamnă că seria (15) este de fapt o extindere a puterilor parametrului adimensional Nr 3 /V, mic pentru un gaz suficient de rarefiat. Interacțiunea dintre atomii de gaz are caracter de repulsie la distanțe apropiate și de atracție la distanțe îndepărtate. Asta duce la LA> 0 la temperaturi mariși LA < 0 при низких. Поэтому давление реального газа при высоких температурах mai multa presiune gaz ideal de aceeași densitate și la scăzut - mai puțin. Deci, de exemplu, pentru heliu la T= factor 15,3 K LA = - 3×10 -23 cm 3, și atunci când T= 510 K LA= 1,8 × 10 -23 cm 3. Pentru argon LA = - 7,1×10 -23 cm 3 la T = 180 K și LA= 4,2×10 -23 cm 3 la T= 6000 K. Pentru gazele monoatomice, se calculează valorile coeficienților viriali, inclusiv al cincilea, ceea ce face posibilă descrierea comportamentului gazelor într-o gamă destul de largă de densități (vezi și gazele ).
Plasma. Un caz special gazul neideal este plasmă - gaz parțial sau total ionizat, în care deci există electroni și ioni liberi. La o densitate suficient de mică, proprietățile plasmei sunt apropiate de cele ale unui gaz ideal. Când se calculează abaterile de la idealitate, este esențial ca electronii și ionii să interacționeze electrostatic conform legii Coulomb. Forțele Coulomb scad încet odată cu distanța, ceea ce duce la faptul că, pentru a calcula prima corecție a funcțiilor termodinamice, este necesar să se ia în considerare interacțiunea nu a două, ci a unui număr mare de particule simultan, întrucât integrala din al doilea coeficient virial (16), care descrie interacțiunea perechilor, diverge pe distanțe mari rîntre particule. În realitate, sub influența forțelor Coulomb, distribuția ionilor și electronilor în plasmă se modifică în așa fel încât câmpul fiecărei particule este ecranat, adică scade rapid la o anumită distanță, numită raza Debye. Pentru cel mai simplu caz al unei plasme constând din electroni și ioni încărcați individual, raza Debye rD egal.
FIZICA STATISTICĂ- o ramură a fizicii, a cărei sarcină este de a exprima proprietățile macroscopice. corpuri, adică sisteme formate dintr-un număr foarte mare de particule identice (molecule, atomi, electroni etc.), prin proprietățile acestor particule și interacțiunea dintre ele.
Astfel, în S. t. se folosesc informații despre structura „microscopică” a corpurilor; prin urmare, S. f. este microscopică. teorie. Aceasta este diferența sa față de alte ramuri ale fizicii, studiind și macroscopică. corpuri: , mecanica și electrodinamica continuumurilor. La rezolvarea unor probleme specifice prin metodele acestor discipline, ecuațiile corespunzătoare includ întotdeauna parametri sau funcții necunoscute care caracterizează un corp dat. Toate aceste dependențe și parametri pot fi determinați experimental, deci se numesc metodele în cauză. fenomenologice. S. f. permite, cel puțin în principiu, dar în multe feluri. cazuri și calculează efectiv aceste cantități.
Dacă la un moment dat coordonatele și vitezele tuturor particulelor corpului sunt date și legea interacțiunii lor este cunoscută, atunci din ecuațiile mecanicii ar fi posibil să se găsească coordonatele și vitezele în orice moment ulterior în timp și determină astfel complet starea corpului. Aceeași situație are loc și în : cunoscând funcția de undă inițială a sistemului, este posibil, prin rezolvarea ecuației Schrödinger, să se găsească funcția de undă care determină starea sistemului în toate momentele viitoare de timp.
În realitate, un astfel de mod de a construi un microscopic teoria este imposibilă, deoarece numărul de particule în macroscopic. corpurile sunt foarte mari și timpurii. coordonatele și vitezele moleculelor sunt necunoscute. Cu toate acestea, este tocmai numărul mare de particule din macroscopic corpuri duce la apariția de noi regularități (statistice) în comportamentul unor astfel de corpuri. Aceste regularități sunt relevate după o restrângere corespunzătoare a problemelor teoriei. caracterizarea macroscopicului parametrii corpului experimentează în timp mici fluctuații aleatorii (fluctuații) în raport cu unele cf. valorile. Sarcina teoriei este de a calcula aceste cf. valorile, nu valorile exacte ale parametrilor la un moment dat. Prezența statisticilor tipare se exprimă în faptul că comportamentul cf. valorile pe o gamă largă nu depind de începutul specific. condiții (din valorile exacte ale coordonatelor inițiale și ale vitezelor particulelor). Cea mai importantă manifestare a acestei regularități este faptul cunoscut din experiență că un sistem izolat de exterior influențează, în timp ajunge la o anumită stare de echilibru (echilibru termodinamic), ale cărei proprietăți sunt determinate doar de astfel de caracteristici generale ale începutului. stări, cum ar fi numărul de particule, energia lor totală etc. (vezi echilibru termodinamic). Procesul de tranziție a sistemului la o stare de echilibru se numește. relaxare, iar timpul caracteristic acestui proces este timpul de relaxare.
funcția de distribuție. Luați în considerare un sistem format din N particule, pentru simplitate, presupunând că particulele nu au ext. grade de libertate. Un astfel de sistem este descris de sarcină 6N variabile: 3N coordonate x iși 3N impulsuri p i particule, setul acestor variabile va fi prescurtat ca ( p, x).
Distribuții Gibbs. Argumentele efectuate până acum au fost de natură formală, întrucât găsirea funcției de distribuție, conform (1), necesită cunoașterea tuturor Xși Rîn orice moment, adică soluții ale ecuațiilor de mișcare cu inițiala corespunzătoare. conditii. Principal pozitia lui S. f. este o afirmație despre posibilitatea unor considerații generale de a determina această f-ție pentru un sistem în stare termodinamică. echilibru. În primul rând, pe baza conservării numărului de particule în timpul mișcării, se poate demonstra că funcția de distribuție este integrala mișcării sistemului (vezi Fig. Teorema Liouville).
Când un sistem închis se mișcă, energia sa nu se modifică, prin urmare, toate punctele din spațiul fazelor, care descriu starea sistemului în diferite momente în timp, trebuie să se afle pe o anumită suprafață corespunzătoare începutului. valoare energetică E. Ecuația pentru această suprafață are forma H(x, p) = E, Unde H(x,p) - Funcția Hamilton sisteme. Mișcarea unui sistem din multe particulele este extrem de confuz, așa că în timp, punctele care descriu starea vor fi distribuite pe suprafața stâlpului. energie în mod uniform (vezi de asemenea Ipoteza ergodica).O astfel de distribuție uniformă este descrisă de funcția de distribuție
unde este o funcție delta care este diferită de zero numai când H = E, A este o constantă determinată din condiția de normalizare (3). Funcția de distribuție (4) corespunzătoare distribuția Gibbs microcanonică, vă permite să calculați valoarea medie. valorile tuturor fizice mărimi conform f-le (2), fără a rezolva ecuațiile mișcării.
La derivarea expresiei (4), s-a presupus că singura cantitate conservată de care depinde w, este energia sistemului. Desigur, impulsul și momentul unghiular sunt de asemenea conservate, dar aceste cantități pot fi eliminate presupunând că corpul în cauză este închis într-o cutie fixă, căreia particulele îi pot da impuls și impuls.
De fapt, în S. f. de obicei nu iau în considerare sistemele închise, ci macroscopice. corpuri care sunt macroscopice mici. părți, sau subsisteme, to-l. sistem închis. Funcția de distribuție pentru un subsistem este diferită de (4), dar nu depinde de forma specifică a restului sistemului, așa-numitul. termostat. Pentru a determina funcția de distribuție a subsistemului, este necesar să se integreze f-lu (4) peste momentul și coordonatele particulelor termostatului. O astfel de integrare poate fi realizată ținând cont de micimea energiei subsistemului în comparație cu energia termostatului. Ca urmare, pentru funcția de distribuție a subsistemului se obține expresia
magnitudinea Tîn acest f-le are sens temp-ry. Coeficient de normalizare. se determină din condiția de normalizare (3):
Pentru particulele cu spin pe jumătate întreg, funcția de undă trebuie să-și schimbe semnul la permutarea oricărei perechi de particule, prin urmare, într-o singură pereche de particule. stare cuantică nu poate exista mai mult de o particulă ( principiul Pauli Numărul de particule cu spin întreg într-o stare poate fi oricare, dar necesar în acest caz, invarianța funcției de undă atunci când particulele sunt rearanjate aici duce, de asemenea, la o schimbare în statistică. proprietățile gazului. Sunt descrise particule cu spin semiîntreg Statistica Fermi-Dirac, se numesc fermioni. Fermionii includ, de exemplu, electroni, protoni, neutroni, atomi de deuteriu, 3 atomi de He. Sunt descrise particule cu spin întreg (bosoni). Statistici Bose - Einstein. Acestea includ, de exemplu, atomi de H, 4 He, cuante de lumină - fotoni.
Să cf. numărul de particule de gaz pe unitate de volum cu momentele aflate în interval dp, este , deci etc este numărul de particule dintr-o celulă a spațiului de fază. Apoi, din distribuția Gibbs rezultă că pentru gaze ideale fermioni (semnul superior) și bosonii (semnul inferior)
În acest f-le - energia unei particule cu impuls R,- chimic. potențial determinat din condiția de constanță a numărului de particule N in sistem: ![]()
Cvasiparticule. Aproape de abdomene. temperatura zero. contribuția la statistică suma este contribuită de stările cuantice slab excitate apropiate ca energie de starea fundamentală. Calculul energiei principalului. starea este pur mecanică cuantică. sarcină, subiect teoria cuantică a multor particule. Mișcarea termică în astfel de condiții poate fi descrisă ca apariția în sistemul de interacțiune slabă cvasiparticule(excitații elementare) care au energie și impuls (în cristale - cvasi-impuls) R. Cunoscând dependența, este posibil să se calculeze partea dependentă de temperatură a termodinamicii. f-tions prin f-lames pentru un gaz Fermi sau Bose ideal, în funcție de statisticile cvasiparticulelor. Este deosebit de important ca Bose cvasiparticule cu mici R pot fi considerate cuante de oscilații de unde lungi, descrise macroscopic. ur-niami. Deci, în cristale (și lichidele Bose) există fononi (cuante de sunet), în magneți - magnoni (cuante de oscilații ale momentului magnetic).
Tipuri speciale de cvasiparticule există în sisteme bidimensionale și unidimensionale. Într-un cristalin plat În film rolul lor este jucat de dislocații, în filmele de He prin filamente de vortex, iar în filamentele polimerice de solitoni și pereții domeniului. În corpurile tridimensionale, aceste obiecte au energie mare și nu contribuie la termodinamică. funcții.
Celulă de cristal. Atomii din rețea fac mici oscilații în jurul pozițiilor lor de echilibru. Aceasta înseamnă că mișcarea lor termică poate fi considerată ca un set de cvasiparticule (fononi) la toate (și nu doar scăzute) temp-pax (vezi Fig. Vibrații ale rețelei cristaline Distribuția fononilor, precum și a fotonilor, este dată de f-loy (16) c = 0. La temperaturi scăzute sunt semnificativi doar fononii cu lungimi de undă lungi, care sunt cuantice. unde sonore, descris de ecuațiile teoriei elasticității. Dependența pentru ele este liniară, deci capacitatea de căldură a cristalului. zăbrele este proporțională cu T 3. La temperaturi ridicate, se poate folosi legea echipartiției energiei în grade de libertate, astfel încât capacitatea termică să nu depindă de temperatură și să fie egală cu 3Nk, Unde N este numărul de atomi din cristal. Dependența la arbitrar R poate fi determinată din experimente privind împrăștierea inelastică a neutronilor într-un cristal sau calculată teoretic prin stabilirea valorilor „constantelor de forță” care determină interacțiunea atomilor din rețele. Noi probleme au apărut înaintea S. f. în legătură cu deschiderea aşa-zisului. cvasiperiodică cristale, ale căror molecule sunt situate în spațiu neperiodic, dar într-o anumită ordine (vezi. Quasicristal).
Metalele. În metale, contribuția la termodinamică f-tion da, de asemenea, electroni de conducere. Starea unui electron într-un metal este caracterizată de un cvasi-moment și, deoarece electronii se supun statisticilor Fermi-Dirac, distribuția lor pe cvasi-moment este dată de f-loi (16). Prin urmare, capacitatea termică a gazului de electroni și, în consecință, a întregului metal la temperaturi suficient de scăzute este proporțională cu T. Diferența față de gazul Fermi al particulelor libere este că suprafața Fermi nu mai este o sferă, ci este o suprafață complexă în spațiul cvasi-impulsurilor. Forma suprafeței Fermi, precum și dependența energiei de cvasi-impulsul din apropierea acestei suprafețe, pot fi determinate experimental, Ch. arr. magnet de cercetare. proprietățile metalelor, precum și calculați teoretic folosind așa-numitele. model pseudopotenţial. În supraconductori, stările excitate ale unui electron sunt separate de suprafața Fermi printr-un interval, ceea ce duce la exponențial. dependența capacității electronice de căldură de temperatură. În feromagnet. și antiferomagnet. contribuția substanțelor la termodinamică. f-tion oferă, de asemenea, fluctuații ale magneticului. momente (spin waves).
În dielectrici și semiconductori T= 0 nu există electroni liberi. La temperaturi finite, apare o sarcină în ele. cvasiparticule: electroni cu negativ. încărcătură și „găuri” cu pozitiv. încărca. Un electron și o gaură pot forma o stare legată - o cvasiparticulă numită exciton.dr. tipul de exciton este o stare excitată a atomului dielectric, deplasându-se într-un cristalin. zăbrele.
Metode teoria cuantica domenii ale fizicii statistice. În rezolvarea problemelor de fizică cuantică cuantică, în primul rând în studiul proprietăților lichidelor cuantice și ale electronilor din metale și magneți, metodele de teorie cuantică a câmpurilor introduse în fizica cuantică sunt de mare importanță. relativ recent. Principal joacă un rol în aceste metode. Funcția lui Green macroscopic sisteme similare cu funcția lui Green în teoria câmpului cuantic. Depinde de energia e și de impuls R, legea de dispersie a cvasiparticulelor e(p) este determinată din ecuație ![]() , deoarece energia cvasiparticulei este polul funcției lui Green. Există o metodă obișnuită pentru calcularea funcțiilor lui Green sub forma unei serii de puteri de interacțiune a energiei între particule. Fiecare membru al acestei serii conține mai multe integrale asupra energiilor și momentelor din funcțiile lui Green ale particulelor care nu interacționează și poate fi reprezentat grafic sub formă de diagrame similare cu Diagramele Feynmanîn cuantică. Fiecare dintre aceste diagrame are un specific fizic sens, care face posibilă separarea într-o serie infinită a termenilor responsabili de fenomenul de interes și rezumarea lor. Există, de asemenea, o tehnică de diagramă pentru calcularea funcțiilor de temperatură ale lui Green, care fac posibilă găsirea termodinamicii. cantități direct, fără introducerea de cvasiparticule. În această tehnică, funcțiile lui Green depind (în loc de energie) de anumite frecvențe discrete w n și integralele asupra energiilor sunt înlocuite cu suma peste aceste frecvențe.
, deoarece energia cvasiparticulei este polul funcției lui Green. Există o metodă obișnuită pentru calcularea funcțiilor lui Green sub forma unei serii de puteri de interacțiune a energiei între particule. Fiecare membru al acestei serii conține mai multe integrale asupra energiilor și momentelor din funcțiile lui Green ale particulelor care nu interacționează și poate fi reprezentat grafic sub formă de diagrame similare cu Diagramele Feynmanîn cuantică. Fiecare dintre aceste diagrame are un specific fizic sens, care face posibilă separarea într-o serie infinită a termenilor responsabili de fenomenul de interes și rezumarea lor. Există, de asemenea, o tehnică de diagramă pentru calcularea funcțiilor de temperatură ale lui Green, care fac posibilă găsirea termodinamicii. cantități direct, fără introducerea de cvasiparticule. În această tehnică, funcțiile lui Green depind (în loc de energie) de anumite frecvențe discrete w n și integralele asupra energiilor sunt înlocuite cu suma peste aceste frecvențe.
Tranziții de fază. Cu o schimbare continuă în ext. parametrii (de exemplu, presiunea sau temperatura), proprietățile sistemului se pot schimba brusc pentru anumite valori ale parametrilor, adică are loc o tranziție de fază. Tranzițiile de fază sunt împărțite în tranziții de primul fel, însoțite de eliberarea de căldură latentă a tranziției și o schimbare bruscă a volumului (de exemplu, topire) și tranziții de al 2-lea fel, în care căldură latentăși nu există salturi de volum, dar există un salt în capacitatea de căldură (de exemplu, o tranziție la o stare supraconductoare). În timpul tranziției celui de al 2-lea fel, simetria corpului se modifică. Această modificare este cuantificată parametrul de comandă, care este diferit de zero într-una dintre faze și dispare în punctul de tranziție. Statistic Teoria tranzițiilor de fază constituie o zonă importantă, dar încă departe de a fi completă, a S. ph. max. dificultate pentru teoretic studiile reprezintă proprietățile materiei din apropiere punct critic, faza de tranzitie Primul fel și direct. apropierea liniei tranziției de fază de ordinul doi. (La o anumită distanță de această linie, o tranziție de al doilea fel este descrisă de teoria Landau.) Aici fluctuaţiile cresc anormal, iar metodele aproximative ale lui S. f. Nu se aplică. Prin urmare, se joacă un rol important modele exact rezolvabile, în care există tranziții (vezi Modele 2D Lattice).Creatură. progrese în construirea fluctuaţiilor. teoria tranzițiilor de fază se realizează prin metoda expansiuni epsilon. În ea, tranziția este investigată într-un spațiu imaginar cu numărul de dimensiuni, iar rezultatele sunt extrapolate la, adică, spațiul real de trei dimensiuni. În sistemele bidimensionale, sunt posibile tranziții de fază deosebite, atunci când dislocațiile sau filamentele vortex apar la o anumită temperatură. Parametrul de comandă în punctul de tranziție dispare brusc, iar capacitatea termică este continuă.
Sisteme dezordonate. Un loc deosebit în S. f. ocupa sticlă- solide, ale căror atomi sunt aranjați aleatoriu chiar și la abs. temperatura zero. Strict vorbind, o astfel de stare este de neechilibru, dar cu un timp de relaxare extrem de lung, astfel încât dezechilibrul nu se manifestă efectiv. Capacitatea termică a paharelor la temperaturi scăzute depinde liniar de T. Aceasta rezultă din expresia pentru Z sub forma (8). Când depinde de T determinat de comportament GE) pentru mici E. Dar pentru sisteme dezordonate sens E = 0 nu este alocat, deci g(0)desigur, Z = DAR + e(0)Tși c ~ T. O caracteristică interesantă sticla este dependența valorilor observate ale capacității termice de timpul de măsurare. Acest lucru se explică prin faptul că nivelul de energie cu mic E asociat cu tunelarea cuantică a atomilor printr-o barieră cu potențial ridicat, ceea ce necesită mult timp. Proprietăți interesante spin ochelari- sisteme de atomi dispuși aleatoriu având un magn. momente.
Fizica statistică a proceselor de neechilibru. Câștigă din ce în ce mai multă importanță cinetica fizica- secţiunea din S. f., în care se studiază procese în sisteme care se află în stări de neechilibru. Două formulări ale întrebării sunt posibile aici: se poate considera sistemul într-o anumită stare de neechilibru și se poate urmări tranziția acestuia la o stare de echilibru; este posibil să se considere un sistem a cărui stare de neechilibru este menținută în exterior. conditii, de ex. corpul, în care este setat gradientul de temperatură, curge electric. curent etc., sau un corp în AC. ext. camp.
Dacă abaterea de la echilibru este mică, proprietățile de neechilibru ale sistemului sunt descrise de așa-numitul. coeficienții cinetici. Exemple de astfel de coeficienți. sunt coeficienți. vâscozitatea, conductibilitatea termică și conductibilitatea electrică a metalelor etc. Aceste mărimi satisfac principiul simetriei cineticii. coeficienți care exprimă simetria ecuațiilor mecanicii în raport cu schimbarea semnului timpului (vezi. Teorema lui Onsager).
Mai mult concept general este susceptibilitate generalizată descriind schimbarea cf. valorile unui anumit roi de fizică. cantități X sub acțiunea unei mici „forțe generalizate” f, care este inclus în Hamiltonianul sistemului sub forma , unde este mecanica cuantică. operator corespunzător X. În cazul în care un f depinde de timp ca , modificarea poate fi scrisă ca ![]() . Valoarea complexă este susceptibilitatea generalizată; ea descrie comportamentul sistemului în raport cu exteriorul. impact. Pe de altă parte, determină și relaxarea. proprietăți: la , valoarea se relaxează la valoarea ei de echilibru conform legii, unde este distanța de la axa reală la singularitatea funcției cea mai apropiată de aceasta în semiplanul inferior al variabilei complexe w. Printre sarcinile lui S. f. Procesele de neechilibru includ, de asemenea, studiul dependenței fluctuațiilor de timp. Această dependență este descrisă de o corelație în timp. funcţie, în care se face media fluctuaţiilor valorii X luate în diferite puncte în timp t:
. Valoarea complexă este susceptibilitatea generalizată; ea descrie comportamentul sistemului în raport cu exteriorul. impact. Pe de altă parte, determină și relaxarea. proprietăți: la , valoarea se relaxează la valoarea ei de echilibru conform legii, unde este distanța de la axa reală la singularitatea funcției cea mai apropiată de aceasta în semiplanul inferior al variabilei complexe w. Printre sarcinile lui S. f. Procesele de neechilibru includ, de asemenea, studiul dependenței fluctuațiilor de timp. Această dependență este descrisă de o corelație în timp. funcţie, în care se face media fluctuaţiilor valorii X luate în diferite puncte în timp t: ![]() este o funcție uniformă a argumentului său. În S. f. clasică. există o legătură între și legea relaxării mărimii. Dacă relaxarea este descrisă de o anumită diferenţială liniară ecuația pentru abaterea de la valoarea de echilibru, apoi satisface aceeași ecuație la t > 0.
este o funcție uniformă a argumentului său. În S. f. clasică. există o legătură între și legea relaxării mărimii. Dacă relaxarea este descrisă de o anumită diferenţială liniară ecuația pentru abaterea de la valoarea de echilibru, apoi satisface aceeași ecuație la t > 0.
Relația dintre și seturi teorema fluctuaţiei- disipare.Teorema afirmă că transformata Fourier este corelată. funcții 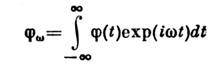
se exprimă după cum urmează:
Un caz special (17) este formula Nyquist.Descrierea stărilor puternic de neechilibru, precum și calculul cineticii. coeficient produs folosind Ecuația cinetică a lui Boltzmann. Această ecuație este o integro-diferențială. ur-țiune pentru o funcție de distribuție cu o particulă (în cazul cuantic - pentru o matrice de densitate a unei particule sau un operator statistic). Conține membri de două tipuri. Unii descriu modificarea f-ției distribuției atunci când particulele se mișcă în ext. câmpuri, altele - în ciocniri de particule. Ciocnirile sunt cele care duc la o creștere a entropiei unui sistem de neechilibru, adică la relaxare. Închis, adică nu conține alte cantități de cinetică. ur-tion, imposibil de intrat vedere generala. Atunci când o derivăm, este necesar să folosiți parametrii mici disponibili în această problemă specială. Cel mai important exemplu este cinetica o ecuație care descrie stabilirea echilibrului într-un gaz din cauza ciocnirilor dintre molecule. Este valabil pentru gazele suficient de rarefiate, când este mare în comparație cu distanțele dintre molecule. Forma specifică a acestei ecuații depinde de eff. împrăștierea secțiunilor transversale ale moleculelor unele pe altele. Dacă această secțiune este cunoscută, ecuația poate fi rezolvată prin extinderea funcției necesare în termeni de polinoame ortogonale. În acest fel este posibil să se calculeze cinetica coeficient gaz, bazat pe legile cunoscute ale interacțiunii dintre molecule. Cinetică Ecuația ia în considerare doar coliziunile perechi între molecule și descrie doar primul termen care nu dispare în extinderea acestor coeficienți. prin densitatea gazului. De asemenea, am reușit să găsim o ecuație mai precisă, care să ia în considerare și triple coliziuni, ceea ce a făcut posibilă calcularea următorului termen de expansiune.
O problemă specială este derivarea cineticii ur-ţie pentru plasmă. Din cauza scăderii lente a forțelor Coulomb cu distanța, chiar și atunci când se iau în considerare coliziunile de perechi, este esențial ca aceste forțe să fie ecranate de alte particule. Stările de neechilibru ale solidelor și ale lichidelor cuantice pot fi considerate la temperaturi scăzute ca stări de neechilibru ale gazului cvasiparticulelor corespunzătoare. Prin urmare, cinetica procesele din astfel de sisteme sunt descrise cinetice. ecuații pentru cvasiparticule care iau în considerare ciocnirile dintre ele și procesele de transformare reciprocă a acestora. S-au deschis noi posibilități prin aplicarea în fizic. cinetica metodelor de teorie cuantică a câmpurilor. Cinetică coeficient a unui sistem poate fi exprimat în termenii funcției lui Green, pentru care există o metodă generală de calcul folosind diagrame. Acest lucru permite în unele cazuri obținerea cinetică. coeficient fără utilizarea explicită a cineticii. ur-ţiune şi explorează proprietăţile de neechilibru ale sistemului chiar şi în cazurile în care nu sunt îndeplinite condiţiile de aplicabilitate a acestuia.
Repere în dezvoltarea fizicii statistice. S. f. în întregime bazată pe conceptul de structura atomica materie. Prin urmare, începutul perioada de dezvoltare a lui S. f. coincide cu dezvoltarea atomismului. reprezentări. Dezvoltarea S. f. ca o secţiune a teoriei. fizica a început în ser. secolul al 19-lea În 1859, J. Maxwell a determinat funcția de distribuție a vitezei a moleculelor de gaz. În 1860-70 R. Clausius (R. Clausing) a introdus conceptul de cale liberă medie și l-a legat de vâscozitatea și conductibilitatea termică a gazului. Aproximativ în același timp, L. Boltzmann a generalizat distribuția Maxwell în cazul în care gazul este în ext. câmp, a demonstrat teorema privind echipartiția energiei în grade de libertate, a dedus cinetica. ur-tion, a dat statistice. interpretarea entropiei și a arătat că legea creșterii acesteia este o consecință a cineticii. ur-tion. Construcția S. f. clasică. a fost finalizată până în 1902 în lucrarea lui J. W. Gibbs (J. W. Gibbs). Teoria fluctuației a fost dezvoltată în 1905-06 în lucrările lui M. Smoluchowski și A. Einstein. În 1900, M. Planck a derivat legea distribuției energiei în spectrul de radiații al unui corp negru, inițiind dezvoltarea atât a mecanicii cuantice, cât și a fizicii cuantice. În 1924, Sh. Bose a găsit distribuția de impuls a cuantelor de lumină și a conectat-o cu distribuția Planck. Einstein a generalizat distribuția Bose la gaze cu un număr dat de particule. E. Fermi (E. Fermi) în 1925 a primit o funcție de distribuție a particulelor care respectă principiul Pauli, iar P. A. M. Dirac (R. A. M. Dirac) a stabilit legătura dintre această distribuție și distribuția Bose-Einstein cu mat. aparat de mecanică cuantică. Dezvoltarea ulterioară a lui S. t. în secolul al XX-lea a trecut sub semnul aplicării principalelor sale. principii pentru studiul problemelor specifice.
Lit.: Landau L. D., L and f sh and c E. M., Statistical physics, part 1, 3rd ed., M., 1976; M ayer J., Goeppert-Mayer M., Mecanica statistică, trad. din engleză, ed. a II-a, M., 1980; Abrikosov A. A., Gorkoye L. P., Dzyaloshinsky I. E., Methods of quantum field theory in statistical physics, M., 1962; X u a ng K., Mecanica statistică, trad. din engleză, M., 1966; Kittel Ch., Teoria cuantică solide, per. din engleză, M., 1967; Silin V.P., Introducere în teoria cinetică a gazelor, M., 1971; Fizica lichidelor simple. sat., per. din engleză, M., 1971; Anselm A. I., Fundamentele fizicii statistice și termodinamicii, M., 1973; L și f sh și c E. M., Pitaevsky L. P., Statistical physics, part 2, M., 1978; şi xzh e, Physical kinetics, M., 1979; Balescu R., Mecanica statistică de echilibru și neechilibru, trad. din engleză, vol. 1-2, M., 1978; Bogolyubov N. N., Lucrări alese despre fizica statistică, M., 1979; G și b b s J. V., Termodinamică. Mecanica statistica, trad. din engleză, M., 1982; Leontovitch MA, Introducere în termodinamică. Fizica Statistică, M., 1983; Boltzmann L., Opere alese, trad. din germană, franceză, M., 1984. L. P. Pitaevski.
Metode Educație Despre acest site Biblioteca Matematică. forumuriBibliotecă > Cărți de fizică > Fizică statistică
fizica statistica
- Aizenshitz R. Teoria statistică a proceselor ireversibile. M.: Ed. Străin lit., 1963 (djvu)
- Anselm A.I. Fundamentele fizicii statistice și termodinamicii. Moscova: Nauka, 1973 (djvu)
- Akhiezer A.I., Peletminsky S.V. Metode ale fizicii statistice. Moscova: Nauka, 1977 (djvu)
- Bazarov I.P. Probleme metodologice de fizică statistică și termodinamică. M.: Editura Universității de Stat din Moscova, 1979 (djvu)
- Bogolyubov N.N. Lucrări alese de fizică statistică. M.: Editura Universității de Stat din Moscova, 1979 (djvu)
- Bogolyubov N.N. (Jr.), Sadovnikov B.I. Câteva întrebări de mecanică statistică. M.: Mai sus. scoala, 1975 (djvu)
- Bonch-Bruevich V.L., Tyablikov S.V. Metoda funcției lui Green în mecanică statistică. Moscova: Fizmatlit, 1961 (djvu, 2,61 Mb)
- Vasiliev A.M. Introducere în fizica statistică. M.: Mai sus. scoala, 1980 (djvu)
- Vlasov A.A. Mecanica statistică nelocală. Moscova: Nauka, 1978 (djvu)
- Gibbs JW Principii de bază ale mecanicii statistice (expuse cu o aplicație specială la justificarea rațională a termodinamicii). M.-L.: OGIZ, 1946 (djvu)
- Gurov K.P. Fundamentele teoriei cinetice. Metoda N.N. Bogolyubov. Moscova: Nauka, 1966 (djvu)
- Zaslavsky G.M. Ireversibilitatea statistică în sisteme neliniare. Moscova: Nauka, 1970 (djvu)
- Zaharov A.Yu. Modele latice ale fizicii statistice. Veliky Novgorod: NovGU, 2006 (pdf)
- Zaharov A.Yu. Metode funcționale în fizica statistică clasică. Veliky Novgorod: NovGU, 2006 (pdf)
- Ios G. Curs de fizică teoretică. Partea 2. Termodinamică. Fizică statistică. Teoria cuantica. Fizica nucleara. M.: Iluminismul, 1964 (djvu)
- Ishihara A. Fizica Statistică. M.: Mir, 1973 (djvu)
- Kadanov L., Beim G. Mecanica statistică cuantică. Metode ale funcțiilor lui Green în teoria proceselor de echilibru și de neechilibru. M.: Mir, 1964 (djvu)
- Katz M. Probabilitatea și problemele conexe în fizică. M.: Mir, 1965 (djvu)
- Katz M. Mai multe probleme probabilistice de fizică și matematică. Moscova: Nauka, 1967 (djvu)
- Kittel Ch. Fizică statistică elementară. M.: IL, 1960 (djvu)
- Kittel Ch. Termodinamică statistică. M: Science, 1977 (djvu)
- Kozlov V.V. Echilibru termic după Gibbs și Poincare. Moscova-Izhevsk: Institutul de Cercetare în Calculatoare, 2002 (djvu)
- Kompaneets A.S. Legile statisticii fizice. unde de soc. Substanță super densă. M.: Nauka, 1976 (djvu)
- Kompaneets A.S. Curs de fizică teoretică. Volumul 2. Legi statistice. M.: Iluminismul, 1975 (djvu)
- Kotkin G.L. Prelegeri de fizică statistică, NSU (pdf)
- Krylov N.S. Lucrări de fundamentare a fizicii statistice. M.-L.: De la Academia de Științe a URSS, 1950 (djvu)
- Kubo R. Mecanica statistică. M.: Mir, 1967 (djvu)
- Landsberg P. (ed.) Probleme în termodinamică și fizică statistică. M.: Mir, 1974 (djvu)
- Levich V.G. Introducere în fizica statistică (ed. a II-a) M.: GITTL, 1954 (djvu)
- Libov R. Introducere în teoria ecuaţiilor cinetice. M.: Mir, 1974 (djvu)
- Mayer J., Geppert-Mayer M. Mecanica statistică. M.: Mir, 1980 (djvu)
- Minlos R.A. (ed.) Matematică. Nou în știința străină-11. Gibbs afirmă în fizica statistică. Rezumat de articole. M.: Mir, 1978 (djvu)
- Nozdrev V.F., Senkevich A.A. Curs de fizică statistică. M.: Mai sus. scoala, 1965 (djvu)
- Prigogine I. Mecanica Statistică de Neechilibru. M.: Mir, 1964 (djvu)
- Radushkevici L.V. Curs de fizică statistică (ed. a II-a) M.: Prosveshchenie, 1966 (djvu)
- Curs de fizică Reif F. Berkeley. Volumul 5. Fizică statistică. M.: Nauka, 1972 (djvu)
- Rumer Yu.B., Ryvkin M.Sh. Termodinamică, fizică statistică și cinetică. M.: Nauka, 1972 (djvu)
- Rumer Yu.B., Ryvkin M.Sh. Termodinamică Fizică statistică și cinetică (ed. a II-a). Moscova: Nauka, 1977 (djvu)
- Ruel D. Mecanica statistică. M.: Mir, 1971 (djvu)
- Savukov V.V. Perfecţionarea principiilor axiomatice ale fizicii statistice. SPb.: Balt. stat tehnologie. univ. „Voenmekh”, 2006
fizica statistica o ramură a fizicii a cărei sarcină este de a exprima proprietățile corpurilor macroscopice, adică sisteme formate dintr-un număr foarte mare de particule identice (molecule, atomi, electroni etc.), prin proprietățile acestor particule și interacțiunea dintre ele. . Alte ramuri ale fizicii studiază și corpurile macroscopice - Termodinamica, mecanica continuumurilor, electrodinamica continuumurilor. Cu toate acestea, atunci când se rezolvă probleme specifice prin metodele acestor discipline, ecuațiile corespunzătoare includ întotdeauna parametri sau funcții necunoscute care caracterizează un corp dat. Deci, pentru a rezolva problemele de hidrodinamică, este necesar să se cunoască ecuația de stare a unui lichid sau gaz, adică dependența densității de temperatură și presiune, capacitatea termică a unui lichid, coeficientul său de vâscozitate etc. Toate aceste dependențe și parametri pot fi, desigur, determinați experimental; prin urmare, metodele în cauză sunt numite fenomenologice. Fizica statistică permite, cel puțin în principiu, și în multe cazuri efectiv, să se calculeze toate aceste mărimi, dacă se cunosc forțele de interacțiune dintre molecule. T. o., S. f. folosește informații despre structura „microscopică” a corpurilor - despre ce particule constau, cum interacționează aceste particule, de aceea se numește teoria microscopică. Dacă la un moment dat sunt date coordonatele și vitezele tuturor particulelor corpului și se cunoaște legea interacțiunii lor, atunci, prin rezolvarea ecuațiilor mecanicii, ar fi posibil să se găsească aceste coordonate și viteze în orice punct ulterior. în timp şi prin aceasta determină complet starea organismului studiat. (Pentru simplitate, prezentarea este realizată în limbajul mecanicii clasice. Dar în mecanica cuantică (Vezi Mecanica cuantică) situația este aceeași: cunoașterea funcției inițiale de undă (Vezi funcția de undă) a sistemului și a legii de interacțiune a particule, este posibil, prin rezolvarea ecuației Schrödinger, să se găsească funcția de undă , care determină starea sistemului în toate momentele viitoare de timp.) De fapt, totuși, un astfel de mod de a construi o teorie microscopică este imposibil, deoarece numărul de particule din corpurile macroscopice este foarte mare. De exemplu, în 1 cm 3 gaz la o temperatură de 0 °C și o presiune de 1 ATM conţine aproximativ 2,7․1019 molecule. Este imposibil să rezolvi un astfel de număr de ecuații, iar coordonatele și vitezele inițiale ale tuturor moleculelor sunt încă necunoscute. Cu toate acestea, tocmai numărul mare de particule din corpurile macroscopice este cel care duce la apariția unor noi regularități - statistice - în comportamentul unor astfel de corpuri. Acest comportament într-o gamă largă nu depinde de condițiile inițiale specifice - de valorile exacte ale coordonatelor inițiale și ale vitezelor particulelor. Cea mai importantă manifestare a acestei independențe este faptul cunoscut din experiență că un sistem lăsat singur, adică izolat de influențele externe, ajunge în cele din urmă la o stare de echilibru (echilibru termodinamic sau statistic), ale cărei proprietăți sunt determinate doar de astfel de caracteristici generale starea inițială, cum ar fi numărul de particule, energia lor totală etc. (vezi Echilibru termodinamic). În viitor, vom vorbi în principal despre S. t. stări de echilibru. Înainte de a formula o teorie care descrie regularitățile statistice, ar trebui să limitezi în mod rezonabil însăși cerințele pentru teorie. Și anume, sarcina teoriei ar trebui să fie să calculeze nu valorile exacte ale diferitelor cantități fizice pentru corpurile macroscopice, ci valorile medii ale acestor cantități în timp. Luați în considerare, de exemplu, moleculele situate într-un volum macroscopic suficient de mare izolat într-un gaz. Numărul de astfel de molecule se va schimba în timp datorită mișcării lor și ar putea fi găsit exact dacă toate coordonatele moleculelor ar fi cunoscute în orice moment. Acest lucru, însă, nu este necesar. Modificarea numărului de molecule din volum va fi de natura fluctuațiilor aleatorii - fluctuații - în raport cu o anumită valoare medie. Cu un număr mare de particule în volum, aceste fluctuații vor fi mici în comparație cu numărul mediu de particule, astfel încât pentru a caracteriza starea macroscopică, este suficient să cunoaștem exact această valoare medie. Pentru a clarifica natura tiparelor statistice, luați în considerare un alt exemplu simplu. Să se pună într-un vas un număr mare de boabe de două soiuri, fiecare grad în mod egal, iar conținutul vasului să fie bine amestecat. Apoi, pe baza experienței cotidiene, se poate fi sigur că într-o probă prelevată dintr-un vas care conține încă un număr mare de boabe, se va găsi un număr aproximativ egal de boabe din fiecare soi, indiferent de ordinea în care boabele. au fost turnate în vas. Acest exemplu arată clar două împrejurări importante care asigură aplicabilitatea teoriei statistice. În primul rând, necesitatea unui număr mare de boabe atât în întregul „sistem” - un vas cu cereale, cât și în „subsistemul” ales pentru experiment - o probă. (Dacă proba constă din doar două boabe, atunci deseori ambele vor fi de aceeași calitate.) În al doilea rând, este clar că complexitatea mișcării boabelor în timpul amestecării joacă un rol semnificativ, asigurând distribuția lor uniformă în volumul de vasul. funcția de distribuție. Luați în considerare un sistem format din N particule, presupunând pentru simplitate că particulele nu au grade interne de libertate. Un astfel de sistem este descris de sarcină 6N variabile - 3N coordonate q iși 3N impulsuri pi, particule [setul acestor variabile va fi prescurtat ca ( R, q)]. Să calculăm valoarea medie pe intervalul de timp a unei anumite valori F(p, q), care este o funcție a acestor coordonate și momente. Pentru a face acest lucru, împărțim intervalul (0, τ) în s segmente mici egale Δ ta (A = 1,2,....... s). Apoi, prin definiție Unde q ași p a- valori ale coordonatelor și impulsurilor uneori ta. In limita s→ ∞ suma intră într-o integrală: Conceptul de funcție de distribuție în mod natural apare dacă luăm în considerare spațiul 6 N măsurători, pe axele cărora sunt trasate valorile coordonatelor și momentelor particulelor sistemului; se numește spațiu fazelor. Pentru fiecare valoare a timpului t corespund anumitor valori ale tuturor qși R, adică un punct din spațiul fazelor, ilustrând starea sistemului la un moment dat t. Să împărțim întregul spațiu de fază în elemente, a căror dimensiune este mică în comparație cu valorile caracteristice unei anumite stări a sistemului qși R, dar încă atât de mare încât în fiecare dintre ele există multe puncte care descriu starea sistemului în momente diferite în timp t. Atunci numărul de astfel de puncte din elementul de volum va fi aproximativ proporțional cu valoarea acestui volum dpdq. Dacă notăm coeficientul de proporționalitate prin sω(p, q), atunci acesta este numărul pentru elementul centrat la un moment dat ( p, q) se va scrie ca: da = sω(p, q)dpdq, (2) dpdq = dp 1 dq 1 dp 2 dq 2 ... dp 3N dq 3N Volumul elementului de spațiu de fază selectat. Valoarea medie (1), ținând cont de micimea acestor elemente de volum, poate fi rescrisă ca (integrarea peste coordonate se realizează pe întregul volum al sistemului, pe momente - de la -∞ la ∞). Funcția ω( p, q, t) se numește funcție de distribuție în raport cu coordonatele momentului particulelor. Deoarece numărul total de puncte selectate este s, funcție w satisface condiția de normalizare: Din (3) și (4) se poate observa că ω dpdq poate fi considerată probabilitatea ca sistemul să fie în element dpdq spațiu fazelor. Funcția de distribuție astfel introdusă poate primi o altă interpretare. Pentru a face acest lucru, vom lua în considerare simultan un număr mare de sisteme identice și vom presupune că fiecare punct din spațiul fazelor reprezintă starea unui astfel de sistem. Atunci media temporală din (1)-(1a) poate fi înțeleasă ca o medie asupra totalității acestor sisteme sau, după cum se spune, asupra ansamblului statistic (vezi Ansamblul statistic). Argumentele purtate până acum au fost de natură pur formală, de atunci găsirea funcției de distribuție, conform (2), necesită cunoașterea tuturor Rși qîn orice moment, adică soluții ale ecuațiilor de mișcare cu condițiile inițiale corespunzătoare. Poziția principală a lui S. f. este, totuși, o afirmație despre posibilitatea de a determina această funcție din considerații generale pentru un sistem în stare de echilibru termodinamic. În primul rând, se poate demonstra, pe baza conservării numărului de sisteme în timpul mișcării, că funcția de distribuție este o integrală a mișcării sistemului, adică rămâne constantă dacă Rși q schimbare în conformitate cu ecuațiile de mișcare (vezi teorema Liouville). Când un sistem închis se mișcă, energia sa nu se modifică, prin urmare, toate punctele din spațiul fazelor, care ilustrează starea sistemului în diferite momente în timp, trebuie să se afle pe o „hipersuprafață” corespunzătoare valorii inițiale a energiei. E. Ecuația acestei suprafețe are forma; H(p, q) = E, Unde H(p, q) este energia sistemului, exprimată în coordonate și momente, adică funcția Hamilton. În plus, mișcarea unui sistem de multe particule este extrem de complicată. Prin urmare, în timp, punctele care descriu starea vor fi distribuite pe suprafață energie constantă uniform, așa cum boabele sunt distribuite uniform în timpul amestecării în vas în exemplul menționat mai sus (vezi și ipoteza ergodică). O astfel de distribuție uniformă pe suprafața izoenergetică este descrisă de o funcție de distribuție de forma: ω( p, q) = Aδ[ H(p, q) - E], (5) unde δ[ H(p, q) - E]
- Funcția Delta, diferită de zero numai când H = E, adică pe această suprafață, DAR este o constantă determinată din condiția de normalizare (4). Funcția de distribuție (5), numită microcanonic, vă permite să calculați valorile medii ale tuturor mărimilor fizice prin formula (3), fără a rezolva ecuațiile mișcării. La derivarea expresiei (5), s-a presupus că singura mărime care rămâne neschimbată în timpul mișcării sistemului, de care depinde ω, este energia sistemului. Desigur, impulsul și momentul unghiular sunt de asemenea conservate, dar aceste cantități pot fi eliminate presupunând că corpul în cauză este închis într-o cutie fixă, căreia particulele îi pot da impuls și impuls. De fapt, de obicei nu sunt considerate sisteme închise, ci corpuri macroscopice, care sunt părți macroscopice mici, sau subsisteme, ale oricărui sistem închis. Funcția de distribuție pentru subsistem va fi diferită de (5), dar nu va depinde de natura specifică a restului sistemului - așa-numitul. termostat. Prin urmare, funcția de distribuție a subsistemului poate fi determinată presupunând, de exemplu, că termostatul constă pur și simplu din N particulele unui gaz ideal, ale căror coordonate și momente vor fi notate cu Qși R, spre deosebire de notație qși R pentru un subsistem, atunci distribuția microcanonică este: Aici H(p, q) este funcția Hamilton a subsistemului, M este masa unei particule de gaz, iar însumarea se realizează asupra tuturor componentelor impulsurilor tuturor particulelor termostatului. Pentru a găsi funcția de distribuție pentru subsistem, trebuie să integrăm această expresie peste coordonatele și momentele particulelor termostatului. Dacă ținem cont de faptul că numărul de particule din termostat este mult mai mare decât în subsistem și ne străduim N→∞, presupunând că raportul E/N constantă și egală cu 3/2 kT, apoi pentru funcția de distribuție a subsistemului se va obține următoarea expresie: Valoare Tîn această formulă are sensul de temperatură, k = 1,38․10 -16 erg/deg este constanta Boltzmann. [Condiție E/N→ 3 / 2 kT pentru gazul din termostat corespunde, așa cum ar trebui să fie, formulei (13) pentru un gaz ideal; vezi mai jos.] Factorul de normalizare e F/kT se determină din condiția de normalizare (4): Distribuția (6) se numește distribuție canonică Gibbs, sau pur și simplu distribuție canonică (vezi distribuția Gibbs) și cantitatea Z- integrală statistică. Spre deosebire de distribuția microcanonică, energia sistemului în distribuția Gibbs nu este dată. Stările sistemului sunt concentrate într-un strat subțire dar finit în jurul suprafeței de energie corespunzătoare valorii medii a energiei, ceea ce înseamnă că este posibil să se schimbe energie cu termostatul. În caz contrar, atunci când sunt aplicate unui anumit corp macroscopic, ambele distribuții conduc în esență la aceleași rezultate. Singura diferență este că, atunci când se utilizează distribuția microcanonică, toate valorile medii sunt exprimate în termeni de energie a corpului, iar atunci când se utilizează distribuția canonică, în termeni de temperatură. Dacă corpul este format din două părți 1 și 2 care nu interacționează cu funcții hamiltoniene H1și H2, apoi pentru tot corpul H = H1 + H2și, conform (6), funcția de distribuție a corpului este împărțită în produsul funcțiilor de distribuție pentru fiecare dintre părți, astfel încât aceste părți se dovedesc a fi independente statistic. Această cerință, împreună cu teorema lui Liouville, poate fi folosită ca bază pentru derivarea distribuției Gibbs fără a recurge la distribuția microcanonică. Formula (6) este valabilă pentru sistemele descrise de mecanica clasică. În mecanica cuantică, spectrul de energie al unui sistem de volum finit este discret. Probabilitatea ca un subsistem să fie într-o stare cu energie E n este dat de o formulă similară cu (6): unde starea de normalizare Valoare Z se numește funcția de partiție a sistemului; suma din expresia (8) este preluată asupra tuturor stărilor sistemului. Pentru un sistem descris cu suficientă precizie de mecanica clasică, în formula (8) este posibilă trecerea de la însumarea stărilor la integrarea în coordonatele și momentele sistemului.Totodată, pentru fiecare stare cuantică există o „celulă” (sau „celulă”) în spațiul de fază al volumului ħ - Bara este constantă. Cu alte cuvinte, însumarea s-a terminat n reduce la integrare peste Se deosebește printr-un factor de condiția de normalizare pur clasică (6a), care duce la un termen suplimentar în F. Formulele de mai sus se referă la cazul în care este dat numărul de particule din subsistem. Dacă alegem ca subsistem un anumit element de volum al întregului sistem, prin suprafața căruia particulele pot părăsi subsistemul și se pot întoarce la el, atunci probabilitatea de a găsi subsistemul într-o stare cu energie. E nși numărul de particule N n este dat de formula mare de distribuție canonică a lui Gibbs: în care parametrul suplimentar μ - Potențialul chimic, care determină numărul mediu de particule din subsistem, și valoarea lui Ω este determinată din condiția de normalizare [vezi. formula (11)]. Interpretarea statistică a termodinamicii. Cel mai important rezultat al lui S. f. - stabilirea semnificaţiei statistice a mărimilor termodinamice. Aceasta face posibilă deducerea legilor termodinamicii din ideile de bază ale lui S. f. și calculați mărimile termodinamice pentru sisteme specifice. În primul rând, energia termodinamică internă se identifică cu energia medie a sistemului. Prima lege a termodinamicii primește apoi o interpretare evidentă ca expresie a legii conservării energiei în timpul mișcării particulelor care alcătuiesc corpul. Mai mult, funcția Hamilton a sistemului depinde de un parametru λ (coordonatele peretelui vasului care conține sistemul, câmpul extern etc.). Apoi derivata Forței Generalizate) corespunzătoare acestui parametru și valoarea E̅ a sistemului, ținând cont de formula (6) și de condiția de normalizare, având în vedere variabilele λ și T si avand in vedere ca valoarea F este, de asemenea, o funcție a acestor variabile, atunci obținem identitatea: Conform celor de mai sus, membrul care contine dλ, este egal cu munca medie dA efectuate asupra corpului. Apoi ultimul termen este căldura primită de corp. Comparând această expresie cu relația dE = dA + TdS, care este o înregistrare combinată a primei și a doua legi ale termodinamicii (a se vedea a doua lege a termodinamicii) pentru procesele reversibile (a se vedea Procesul reversibil), aflăm că Tîn (6) este într-adevăr egală cu temperatura absolută a corpului și derivata Entropia) S. Înseamnă că F este Energia Liberă a corpului, din care se clarifică semnificația sa statistică. De o importanță deosebită este interpretarea statistică a entropiei, care decurge din formula (8). Formal, g se însumează la această formulă peste toate stările cu energie E n, dar de fapt, din cauza micșorării fluctuațiilor de energie în distribuția Gibbs, doar un număr relativ mic dintre ele cu o energie apropiată de energia medie este semnificativ. Numărul acestor stări esențiale Δ̅n̅ poate fi deci determinat natural prin limitarea însumării din (8) la intervalul Δ̅n̅, înlocuind E n pentru energie medie E̅și scoțând exponentul de sub semnul sumei. Apoi suma va da Δ̅n̅ și va lua forma. Pe de altă parte, conform termodinamicii, F = E̅ - TS, care dă legătura entropiei cu numărul de stări microscopice Δ̅n̅ într-o stare macroscopică dată, cu alte cuvinte, cu ponderea statistică (Vezi ponderea statistică) a stării macroscopice, adică cu probabilitatea ei: La temperatura de zero absolut, orice sistem se află într-o anumită stare fundamentală, astfel încât Δ̅n̅ = 1, S= 0. Această afirmație exprimă a treia lege a termodinamicii. Este esențial aici ca pentru o definiție neechivocă a entropiei este necesar să se utilizeze formula cuantică (8); în statistica pur clasică, entropia este definită doar până la un termen arbitrar. Sensul entropiei ca măsură a probabilității unei stări este păstrat și în raport cu stările arbitrare - nu neapărat de echilibru. Într-o stare de echilibru, entropia are valoarea maximă posibilă în condiții externe date. Aceasta înseamnă că starea de echilibru este starea cu ponderea statistică maximă, starea cea mai probabilă. Procesul de trecere a unui sistem de la o stare de neechilibru la o stare de echilibru este un proces de trecere de la stările mai puțin probabile la cele mai probabile; acest lucru elucidează semnificația statistică a legii de creștere a entropiei, conform căreia entropia unui sistem închis nu poate decât să crească. Formula (8) care raportează energia liberă F cu o funcție de partiție, stă la baza calculării mărimilor termodinamice prin metodele lui S. f. Este folosit, în special, pentru a construi o teorie statistică a proprietăților electrice și magnetice ale materiei. De exemplu, pentru a calcula momentul magnetic al unui corp într-un câmp magnetic, ar trebui să se calculeze funcția de partiție și energia liberă. Moment magnetic m corpul este apoi dat de formula: m = Unde H- intensitatea câmpului magnetic extern. Similar cu (8), condiția de normalizare în marea distribuție canonică (9) determină potențialul termodinamic Ω conform formulei: Acest potențial este legat de energia liberă prin relația: Aplicatii S. f. la studiul anumitor proprietăți ale unor sisteme specifice se reduc în esență la un calcul aproximativ al funcției de partiție, ținând cont de proprietățile specifice ale sistemului. În multe cazuri, această sarcină este simplificată prin aplicarea legii echipartiției în grade de libertate, care prevede că capacitatea termică CV(la un volum constant v) a unui sistem de puncte materiale care interacționează - particule care efectuează oscilații armonice, este egal cu c v = k(l/2 + n),
Unde l- numărul total de grade de libertate de translație și rotație, n- numărul de grade de libertate vibraționale. Dovada legii se bazează pe faptul că funcția Hamilton H un astfel de sistem arată astfel: H = K(pi)+ U(q m), unde energia cinetică La este o funcție pătratică omogenă a l + n impulsuri piși energia potențială U- funcţia pătratică a n coordonate vibraționale q m. În integrala statistică Z(8a) integrarea peste coordonatele vibraționale datorită convergenței rapide a integralei poate fi extinsă de la - ∞ la ∞. După efectuarea modificării variabilelor Z depinde de temperatură ca Tl/2+n, deci energia liberă F=-kT(l/ 2
+n)(ln T+ const). De aici rezultă expresia de mai sus pentru capacitatea termică, deoarece Gaz ideal. Cel mai simplu obiect al cercetării lui S. f. este un gaz ideal, adică un gaz atât de rarefiat încât interacțiunea dintre moleculele sale poate fi neglijată. Funcțiile termodinamice ale unui astfel de gaz pot fi calculate complet. Energia unui gaz este pur și simplu suma energiilor moleculelor individuale. Acest lucru, cu toate acestea, este încă insuficient pentru a considera moleculele ca fiind complet independente. Într-adevăr, în mecanica cuantică, chiar dacă nu există forțe de interacțiune între particule, există o anumită influență a particulelor identice (identice) unele asupra celeilalte dacă acestea se află în stări similare de mecanică cuantică. Acesta este așa-numitul. interacțiune de schimb. Poate fi neglijat dacă, în medie, există mult mai puțin de o particulă pe stare, care în orice caz are loc la o temperatură suficient de ridicată a gazului; un astfel de gaz se numește nedegenerat. De fapt, gazele obișnuite, formate din atomi și molecule, sunt nedegenerate la toate temperaturile (la care sunt încă gazoase). Pentru un gaz ideal nedegenerat, funcția de distribuție se descompune în produsul funcțiilor de distribuție pentru molecule individuale. se află în intervale dp x, dpy, dpz, iar coordonatele sunt în intervale dx, dy, dz: , (12) Energia unei molecule de gaz monoatomic într-un câmp extern cu energie potențială U(r) este egal cu p 2 /2M + U(r). Integrarea (6) peste coordonate r(x, y, z) și impulsuri R(p x, py, pz) dintre toate moleculele cu excepția uneia, puteți găsi numărul de molecule dN, ale căror impulsuri Unde d 3 p = dp x dp y dp z, d3x = dxdydz. Această formulă se numește distribuția Maxwell-Boltzmann (vezi statistica Boltzmann). Dacă integrăm (12) pe momente, atunci obținem o formulă pentru distribuția particulelor peste coordonate într-un câmp extern, în special într-un câmp gravitațional - Formula barometrică. Distribuția vitezelor în fiecare punct din spațiu coincide cu distribuția Maxwell m. Funcția de partiție a unui gaz ideal se descompune și în produsul termenilor identici corespunzători moleculelor individuale. Pentru un gaz monoatomic, însumarea din (8) se reduce la integrare peste coordonate și momente, adică suma este înlocuită cu o integrală peste Unde g- greutatea statistică a stării fundamentale a atomului, adică numărul de stări corespunzător nivelului său de energie inferior, V- volumul de gaz (aici e- baza logaritmi naturali). La temperaturi ridicate g =(2J+1)(2L+1), Unde J- valoarea Spin a, a L- momentul orbitalului (vezi Momentul orbital) atomului (în unități ħ
). Din expresia pentru energie gratis rezultă că ecuația de stare a unui gaz ideal, adică dependența presiunii acestuia ( R) privind densitatea numărului de particule ( N/V) și temperatura, are forma: PV = NkT. Energia internă a unui gaz monoatomic și capacitatea sa de căldură la volum constant se dovedesc a fi egale: E = 3 / 2 (NkT), c v = 3 / 2 Nk, (13) Si a lui potential chimic: Este caracteristic că chiar și pentru un gaz nedegenerat (adică, care se supune mecanicii clasice cu suficientă precizie), expresiile pentru energia liberă și potențialul chimic conțin constanta lui Planck. ħ
. În cele din urmă, acest lucru se datorează conexiunii menționate anterior dintre entropie și conceptul de număr de stări cuantice. În cazul gazelor diatomice și poliatomice, la funcțiile termodinamice contribuie și vibrațiile și rotația moleculelor. Această contribuție depinde dacă efectele cuantizării vibrațiilor și rotației moleculei sunt semnificative. Distanța dintre nivelurile de energie vibrațională este de ordinul lui I - momentul de inerție al unui corp în rotație, în acest caz o moleculă. Statisticile clasice sunt valabile dacă temperatura este suficient de ridicată astfel încât kT>>
Δ E. În acest caz, în conformitate cu legea echipartiției, rotația aduce o contribuție constantă la capacitatea termică, egală cu 1/2 k pentru fiecare grad de libertate de rotație; în special, pentru moleculele diatomice această contribuție este egală cu k. Fluctuațiile contribuie la capacitatea termică egală cu k pentru fiecare grad de libertate vibrațional (astfel încât capacitatea de căldură vibrațională a unei molecule diatomice este k). Contribuția gradului de libertate vibrațional, față de cel rotațional, este de două ori mai mare datorită faptului că, în timpul vibrațiilor, atomii dintr-o moleculă au nu numai energie cinetică, ci și potențială. În limita opusă Gaz imperfect. O realizare importantă a lui S. t. - calculul corecțiilor la cantitățile termodinamice ale gazului asociate cu interacțiunea dintre particulele acestuia. Din acest punct de vedere, ecuația de stare a unui gaz ideal este primul termen în expansiunea presiunii unui gaz real în puteri ale densității numărului de particule, deoarece orice gaz se comportă ca un gaz ideal la o temperatură suficientă. densitate scazuta. Pe măsură ce densitatea crește, corecțiile legate de interacțiune la ecuația de stare încep să joace un rol. Acestea duc la apariția în expresia pentru presiune a termenilor cu grade mai mari de densitate a numărului de particule, astfel încât presiunea este reprezentată de așa-numita. seria virală de forma: Cote LA, DIN etc. depind de temperatură și se formează. al doilea, al treilea etc. coeficienți viriali. metodele lui S. f. fac posibilă calcularea acestor coeficienți dacă se cunoaște legea interacțiunii dintre moleculele de gaz. În același timp, coeficienții LA, DIN,... descrie interacțiunea simultană a două, trei sau mai multe molecule. De exemplu, dacă gazul este monoatomic și energia potențială de interacțiune a atomilor săi U(r), atunci al doilea coeficient virial este În ordinea mărimii LA este egal cu r 0 - dimensiunea caracteristică a unui atom sau, mai precis, raza de acțiune a forțelor interatomice. Aceasta înseamnă că seria (15) este de fapt o extindere a puterilor parametrului adimensional Nr 3 /V, mic pentru un gaz suficient de rarefiat. Interacțiunea dintre atomii de gaz are caracter de repulsie la distanțe apropiate și de atracție la distanțe îndepărtate. Asta duce la LA> 0 la temperaturi ridicate și LA T = 15,3 K coeficient LA = -
3․10 -23 cm 3, și atunci când T= 510 K LA = 1,8 ․10 -23 cm 3. Pentru argon LA = -
7,1․10 -23 cm 3 la T = 180 K și LA = 4,2․10 -23 cm 3 la T= 6000 K. Pentru gazele monoatomice, se calculează valorile coeficienților viriali, inclusiv al cincilea, ceea ce face posibilă descrierea comportamentului gazelor într-o gamă destul de largă de densități (vezi și Gaze). Plasma. Un caz special al unui gaz neideal este Plasma - un gaz parțial sau complet ionizat, în care, prin urmare, există electroni și ioni liberi. La o densitate suficient de mică, proprietățile plasmei sunt apropiate de cele ale unui gaz ideal. Când se calculează abaterile de la idealitate, este esențial ca electronii și ionii să interacționeze electrostatic conform legii Coulomb. Forțele Coulomb scad încet odată cu distanța, ceea ce duce la faptul că, pentru a calcula prima corecție a funcțiilor termodinamice, este necesar să se ia în considerare interacțiunea nu a două, ci a unui număr mare de particule simultan, întrucât integrala din al doilea coeficient virial (16), care descrie interacțiunea perechilor, diverge pe distanțe mari rîntre particule. În realitate, sub influența forțelor Coulomb, distribuția ionilor și electronilor în plasmă se modifică în așa fel încât câmpul fiecărei particule este ecranat, adică scade rapid la o anumită distanță, numită raza Debye. Pentru cel mai simplu caz al unei plasme constând din electroni și ioni încărcați individual, raza Debye rD este egal cu: Unde N numărul de electroni e este sarcina unui electron. Toate particulele din raza Debye participă simultan la interacțiune. Astfel, prima corecție a presiunii este proporțională cu nu ( N/V) 2
ca într-un gaz obișnuit, dar un grad mai scăzut de densitate - ( N/V) 3/2
. Calculul cantitativ se bazează pe faptul că particulele rămase sunt distribuite în câmpul electronului sau ionului selectat conform distribuției Boltzmann. Ca urmare, ecuația de stat, ținând cont de prima modificare, are forma: (deoarece numărul de electroni este egal cu numărul de ioni, numărul total de particule este egal cu 2N). Corecții de același fel apar și în funcțiile termodinamice ale electroliților în care există ioni liberi ai substanțelor dizolvate. Lichide. Spre deosebire de un gaz, termenii de interacțiune din ecuația de stare pentru un lichid nu sunt mici. Prin urmare, proprietățile unui lichid depind puternic de natura specifică a interacțiunii dintre moleculele sale. În teoria fluidelor, în general, nu există un parametru mic care ar putea fi utilizat pentru a simplifica teoria. Nu este posibil să se obțină formule analitice pentru cantitățile termodinamice ale unui lichid. O modalitate de a depăși această dificultate este studierea unui sistem format dintr-un număr relativ mic de particule - de ordinul a câteva mii. În acest caz, folosind un computer, se pot rezolva direct ecuațiile de mișcare a particulelor și, în acest fel, se pot determina valorile medii ale tuturor cantităților care caracterizează sistemul fără ipoteze suplimentare. În acest caz, este, de asemenea, posibil să se studieze procesul de apropiere a unui astfel de sistem la o stare de echilibru. De asemenea, este posibil să se găsească integrala statistică pentru un astfel de sistem a unui număr mic de particule prin calcularea integralelor din formula principală pentru integrala statistică pe un computer (de obicei folosind metoda Monte Carlo). Rezultatele obținute prin ambele metode sunt, totuși, de o precizie scăzută atunci când sunt aplicate lichidelor reale, din cauza numărului mic de particule din sistem. O altă modalitate de a construi o teorie a lichidului se bazează pe utilizarea funcțiilor de distribuție moleculară. Dacă integrăm funcţia de distribuţie w a sistemului în termeni de moment al tuturor particulelor și în termeni de coordonatele tuturor particulelor, cu excepția uneia, se obține o funcție de distribuție spațială a unei particule f1(r). Dacă ne integrăm wîn funcție de momentul tuturor particulelor și în funcție de coordonatele tuturor particulelor, cu excepția a două, se va obține o funcție de distribuție a două particule f2(r1, r2), a tuturor particulelor, cu excepția a trei, este funcția de distribuție a trei particule f 3(r 1 , r 2 , r 3 ,) etc. Funcția de distribuție a două particule este o mărime fizică direct observabilă - exprimă, de exemplu, împrăștierea elastică raze Xși neutroni în lichid. Presupunând că funcția de distribuție a întregului sistem este dată de distribuția Gibbs (6), se poate obține o relație integrală care exprimă funcția cu două particule în termenii funcției cu trei particule și potențialul de interacțiune dintre particule. În teoria fluidelor, această relație exactă este completată de unele aproximative care exprimă funcția cu trei particule în termenii funcției cu două particule (o funcție cu o particulă într-un lichid omogen este redusă la o constantă). Rezultatul este o ecuație pentru funcția cu două particule, care se rezolvă numeric. Relațiile suplimentare se găsesc pe baza unor considerații fizice plauzibile și sunt de natură de interpolare, astfel încât teoriile bazate pe acestea nu pot pretinde decât o descriere calitativă a proprietăților unui lichid. Cu toate acestea, chiar și o astfel de descriere calitativă este importantă, deoarece ea relevă generalitatea legilor lui S. f. (vezi și Fluid). Gaze degenerate. Dacă temperatura gazului este scăzută la o densitate constantă, încep să apară efecte mecanice cuantice asociate proprietăților de simetrie ale funcțiilor de undă ale unui sistem de particule identice. Gazul „degenerează” (vezi Gaz degenerat). Pentru particulele cu spin semiîntreg, funcția de undă trebuie să-și schimbe semnul atunci când orice pereche de particule este schimbată. Acest lucru, în special, duce la faptul că mai mult de o particulă nu poate fi într-o stare cuantică (principiul Pauli). Numărul de particule cu spin întreg într-o stare poate fi oricare, dar invarianța funcției de undă necesară în acest caz atunci când particulele sunt rearanjate duce aici la o schimbare a proprietăților statistice ale gazului. Particulele cu spin semiîntreg sunt descrise de statisticile Fermi-Dirac; se numesc Fermions. Fermionii includ, de exemplu, electroni, protoni, neutroni, atomi de deuteriu, atomi ai izotopului ușor de heliu 3 He. Particulele cu spin întreg - bosonii - sunt descrise de statisticile Bose-Einstein. Acestea includ atomi de hidrogen, 4 atomi de He, cuante de lumină - Fotoni. Fie numărul mediu de particule de gaz pe unitate de volum cu momentele situate în interval d 3 p, există În această formulă, ε = p2/2M este energia unei particule cu impuls R, μ - potențial chimic determinat din condiția de constanță a numărului de particule ( N) în sistem: Formula (19) se transformă în formula de distribuție Boltzmann (12) pentru În cazul fermionilor, așa cum ar trebui să fie, np≤ 1. Aceasta duce la faptul că particulele de gaz fermion (gazul Fermi) și la T= 0 au un moment diferit de zero, deoarece o singură particulă poate fi în starea cu impuls zero. Mai precis, la T= 0 pentru gazul Fermi np= 1 în interiorul unei suprafețe Fermi (vezi suprafața Fermi) - sfere în spațiul de impuls cu rază Într-un gaz Bose la T= 0 toate particulele sunt într-o stare cu impuls zero. La temperaturi suficient de scăzute în stat cu R= 0 este fracția finală a tuturor particulelor; aceste particule formează așa-numitele. Condens Bose-Einstein. Particulele rămase sunt în stări cu R≠ 0, iar numărul lor este determinat de formula (19) cu μ = 0. La temperatură Un caz special de aplicare a statisticii Bose-Einstein este echilibrul radiatie electromagnetica, care poate fi considerat ca un gaz format din fotoni. Energia unui foton este legată de impulsul său prin relație Celulă de cristal. cererea lui S. f. la calculul funcțiilor termodinamice ale rețelei cristaline se bazează pe faptul că atomii din rețea fac mici vibrații în jurul pozițiilor lor de echilibru. Acest lucru ne permite să considerăm rețeaua ca o colecție de oscilatoare armonice cuplate. Într-un astfel de sistem, undele se pot propaga, caracterizate de propria lor lege de dispersie, adică dependența frecvenței ω de vectorul de undă (vezi vectorul de undă) k. În mecanica cuantică, aceste unde pot fi considerate ca un set de așa-numite. excitații elementare sau cvasiparticule (vezi cvasiparticule) - Fononi cu energie ħω
și cvasi-impuls ћk. Principala diferență dintre un cvasi-impuls și un moment este că energia fononului este o funcție periodică a cvasi-momentului cu o perioadă egală în ordinea mărimii cu a - constanta rețelei. Funcția de distribuție a fononilor peste quasimoment este dată de formula de distribuție Bose-Einstein (19) cu μ = 0. În acest caz, ε=ħω.
Astfel, cunoașterea dependenței ω( k) permite să se calculeze capacitatea termică a rețelei. Această dependență poate fi determinată din experimente privind împrăștierea inelastică a neutronilor într-un cristal (vezi Neutronografie) sau calculată teoretic prin stabilirea valorilor „constantelor de forță” care determină interacțiunea atomilor într-o rețea. La temperaturi scăzute, doar fononii de joasă frecvență sunt semnificativi, corespunzătoare cuantelor de unde sonore obișnuite, pentru care relația ω cu k liniar. Acest lucru duce la faptul că capacitatea termică a rețelei cristaline este proporțională cu T3. La temperaturi ridicate, se poate folosi legea distribuției egale a energiei pe grade de libertate, astfel încât capacitatea termică să nu depindă de temperatură și să fie egală cu 3Nk, Unde N este numărul de atomi din cristal. Metalele. În metale, electronii de conducere contribuie și ei la funcțiile termodinamice. Starea unui electron într-un metal este caracterizată de un cvasi-impuls și, din moment ce electronii se supun statisticii Fermi - Dirac, distribuția lor pe quasimomenturi este dată de formula (19). Prin urmare, capacitatea termică a gazului de electroni și, în consecință, a întregului metal la temperaturi suficient de scăzute este proporțională cu T. Diferența față de gazul Fermi al particulelor libere este că suprafața Fermi, în jurul căreia sunt concentrați electronii „activi”, nu mai este o sferă, ci este o suprafață complexă în spațiul cvasi-impuls. Forma suprafeței Fermi, precum și dependența energiei de cvasi-momentul din apropierea acestei suprafețe, pot fi determinate experimental, în principal prin studierea proprietăților magnetice ale metalelor, și pot fi calculate și teoretic folosind așa-numitele. model cvasipotențial. În supraconductori (vezi Supraconductivitate), stările excitate ale unui electron sunt separate de suprafața Fermi printr-un interval de lățime finită, ceea ce duce la o dependență exponențială de temperatură a capacității de căldură a electronului. În substanțele feromagnetice și antiferomagnetice, fluctuațiile momentelor magnetice contribuie și ele la funcțiile termodinamice - undele de spin. În dielectrici și semiconductori T= 0 nu există electroni liberi. La temperaturi finite, în ele apar cvasiparticule încărcate - electroni cu sarcina negativași (în număr egal) „găuri” cu sarcină pozitivă, Un electron și o gaură pot forma o stare legată - o cvasiparticulă numită exciton. Dr. Un tip de exciton este o stare excitată a unui atom dielectric care se mișcă într-o rețea cristalină. Metode ale teoriei cuantice a câmpurilor în S. f.În rezolvarea problemelor de fizică cuantică cuantică, în primul rând în studierea proprietăților lichidelor cuantice și a electronilor din metale și magneți, metodele de teorie cuantică a câmpurilor introduse în fizica cuantică sunt de mare importanță. relativ recent. Rolul principal în aceste metode este jucat de funcția lui Green G a unui sistem macroscopic, care este similară cu funcția lui Green în teoria câmpului cuantic. Depinde de energia ε și de impuls R, legea dispersiei cvasiparticulelor ε( R) se determină din ecuația: adică, energia unei cvasiparticule este determinată de polul funcției lui Green. Există o metodă obișnuită pentru calcularea funcțiilor lui Green ca o serie de puteri de interacțiune a energiei dintre particule. Fiecare termen al acestei serii conține mai multe integrale asupra energiilor și momentelor funcțiilor lui Green ale particulelor care nu interacționează și poate fi reprezentat grafic sub formă de diagrame similare diagramelor Feynman (vezi diagramele Feynman) în electrodinamica cuantică. Fiecare dintre aceste diagrame are un specific sens fizic, care face posibilă separarea într-o serie infinită a termenilor responsabili de fenomenul de interes și rezumarea acestora. Există și o tehnică de diagramă pentru calcularea funcțiilor lui Green de temperatură, care face posibilă calcularea cantităților termodinamice în mod direct, fără a introduce cvasiparticule. Metodele menționate în secțiunea despre lichide, care utilizează funcții de distribuție a mai multor particule ale cvasiparticulelor, sunt în multe privințe apropiate de metodele teoriei câmpurilor cuantice. Utilizarea acestor funcții se bazează întotdeauna pe o „decuplare” aproximativă - expresia unei funcții peste ordin înalt prin funcţiile de jos. Tranziții de fază. Cu o schimbare continuă a parametrilor externi (de exemplu, presiunea sau temperatura), proprietățile sistemului se pot schimba brusc pentru unele valori ale parametrilor, adică are loc o tranziție de fază. Tranzițiile de fază sunt împărțite în tranziții de primul fel, însoțite de eliberarea de căldură latentă a tranziției și un salt în volum (acestea includ, de exemplu, Topirea) și tranziții de al doilea fel, în care nu există căldură latentă. și un salt în volum (de exemplu, o tranziție la o stare supraconductoare). Teoria statistică a tranzițiilor de fază constituie o zonă importantă, dar încă departe de a fi completă a S. f. Cea mai mare dificultate pentru cercetare teoretică reprezintă proprietățile materiei în apropierea liniei unei tranziții de fază de ordinul doi și în apropierea punctului critic al unei tranziții de fază de ordinul întâi. Din punct de vedere matematic, funcțiile termodinamice ale sistemului au aici singularități. În apropierea acestor puncte apar fenomene critice deosebite. În același timp, fluctuațiile cresc anormal aici, iar metodele aproximative ale lui S. f. se dovedesc a fi inaplicabile. Prin urmare, un rol important îl joacă un număr mic de modele exact rezolvabile în care există tranziții (de exemplu, așa-numitul model Ising). fluctuatii.În inima S. f. stă faptul că mărimi fizice, care caracterizează corpurile macroscopice, sunt egale cu valorile lor medii cu mare precizie. Această egalitate este încă aproximativă, de fapt, toate cantitățile experimentează mici abateri aleatorii de la valorile medii - fluctuații. Existenţa fluctuaţiilor are o mare importanţă fundamentală, deoarece demonstrează direct natura statistică a regularităţilor termodinamice. În plus, fluctuațiile joacă rolul de a interfera cu zgomotul măsurători fiziceși limitând acuratețea acestora. Fluctuații de o oarecare valoare Xîn jurul mediei sale X sunt caracterizate prin fluctuații pătratice medii În marea majoritate a cazurilor, valoarea X experimentează fluctuații de ordin S este proporțională cu e S/k. Aceasta duce la formula De exemplu, pătratele medii ale fluctuațiilor volumului și temperaturii corpului sunt: Din aceste formule se poate observa că fluctuațiile relative ale volumului și ale temperaturii sunt invers proporționale cu N - numărul de particule din corp. Acest lucru asigură micimea fluctuațiilor pentru corpurile macroscopice. Relația dintre fluctuațiile diferitelor cantități x i, x k caracterizată prin funcția x i și x k sunt statistic independente, atunci Sub x iși x k se pot înțelege și valorile aceleiași cantități, de exemplu densitatea, în diferite puncte din spațiu. Atunci această funcție are semnificația unei funcții de corelare spațială. Pe măsură ce distanța dintre puncte crește, funcția de corelare tinde spre zero (de obicei exponențial), deoarece fluctuațiile în puncte îndepărtate din spațiu apar independent. Distanța la care această funcție scade semnificativ se numește raza de corelație. Comportamentul în timp al fluctuațiilor și distribuția spectrală a zgomotului de fluctuație sunt descrise de funcția de corelație în timp φ( t), în care se face media fluctuațiilor cantității luate în momente diferite t: Un rol important în teoria fluctuațiilor îl joacă așa-numitele teorema fluctuației- disipare, care leagă fluctuațiile dintr-un sistem cu o modificare a proprietăților acestuia sub influența anumitor influențe externe. Cea mai simplă relație de acest fel poate fi obținută luând în considerare fluctuațiile oscilatorului armonic a cu energia potențială și fluctuație X este într-adevăr legată de perturbarea sub influența forței f. În cazul general, teorema fluctuației- disipare este aplicabilă dacă pt X există o „forță generalizată” f, care este inclus în operatorul energetic al sistemului (Hamiltonian; vezi Mecanica cuantică) ca termen x. Pornirea alimentării f va duce la o modificare a valorii medii X prin δ X, si daca f depinde de timp e-i wt , această modificare poate fi scrisă ca: mărimea complexă α(ω) se numește susceptibilitate generalizată a sistemului. Teorema afirmă că transformata Fourier a funcției de corelație S. f. procese de neechilibru. Cinetica fizică, ramura fizicii fizice care studiază procesele din sistemele în stări de neechilibru, capătă o importanță din ce în ce mai mare. Există două întrebări posibile aici. În primul rând, se poate considera sistemul într-o stare de neechilibru și se poate urmări tranziția lui la starea de echilibru. În al doilea rând, putem considera un sistem a cărui stare de neechilibru este menținută conditii externe, de exemplu, curge un corp în care este dat un gradient de temperatură electricitate etc., sau un corp situat într-un câmp extern variabil. Dacă abaterea de la echilibru este mică, proprietățile de neechilibru ale sistemului sunt descrise de așa-numitul. coeficienții cinetici. Exemple de astfel de coeficienți sunt coeficienții de vâscozitate (vezi![]()
![]()
![]()

![]()
![]()
![]() p și q, este necesar să se împartă integrala la numărul de permutări din N particule, adică pe N! Limita clasică finală pentru funcția de partiție este:
p și q, este necesar să se împartă integrala la numărul de permutări din N particule, adică pe N! Limita clasică finală pentru funcția de partiție este:![]()
![]()
![]()
![]()
![]()

![]() 3
în funcție de numărul de celule [cu un volum de N atomi de gaz este egal cu:
3
în funcție de numărul de celule [cu un volum de N atomi de gaz este egal cu:
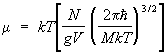

![]()
![]()
![]() n p este numărul de particule dintr-o celulă a spațiului de fază ( g = 2J+ 1, unde J este spinul particulei). Apoi, din distribuția Gibbs rezultă că pentru gazele ideale ale fermionilor (semnul superior) și bosonilor (semnul inferior):
n p este numărul de particule dintr-o celulă a spațiului de fază ( g = 2J+ 1, unde J este spinul particulei). Apoi, din distribuția Gibbs rezultă că pentru gazele ideale ale fermionilor (semnul superior) și bosonilor (semnul inferior):![]()
![]()
![]() Undele de Broglie ale particulelor care se deplasează cu viteza termică devin de ordinul distanței medii dintre ele. Astfel, degenerarea afectează la temperaturi cu cât este mai mică, cu atât densitatea numărului de particule din gaz este mai mică (și masa particulei este mai mare). M).
Undele de Broglie ale particulelor care se deplasează cu viteza termică devin de ordinul distanței medii dintre ele. Astfel, degenerarea afectează la temperaturi cu cât este mai mică, cu atât densitatea numărului de particule din gaz este mai mică (și masa particulei este mai mare). M).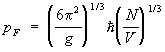 n p = 0. La temperaturi finite dar scăzute np variază de la 1 în interiorul sferei la zero în afara sferei treptat, iar lățimea regiunii de tranziție este de ordin MkT/p F. Valoare np pentru un gaz Fermi în funcție de energia ε este prezentat schematic în fig. 2 (ε 0 = pF2/2M). Când temperatura gazului se schimbă, starea particulelor se schimbă numai în acest strat de tranziție, iar capacitatea termică a gazului Fermi la temperaturi scăzute este proporțională cu T si este egal cu:
n p = 0. La temperaturi finite dar scăzute np variază de la 1 în interiorul sferei la zero în afara sferei treptat, iar lățimea regiunii de tranziție este de ordin MkT/p F. Valoare np pentru un gaz Fermi în funcție de energia ε este prezentat schematic în fig. 2 (ε 0 = pF2/2M). Când temperatura gazului se schimbă, starea particulelor se schimbă numai în acest strat de tranziție, iar capacitatea termică a gazului Fermi la temperaturi scăzute este proporțională cu T si este egal cu:![]()
![]() Tranziție de fază (vezi mai jos). Fracția de particule cu impuls zero dispare Condensarea Bose-Einstein dispare. Curba de dependență a capacității termice de temperatură are în punct T c pauză. Distribuția de impuls a particulelor la T > T s este dat de formula (19) și μ Т > T s) sunt prezentate în Figura 3.
Tranziție de fază (vezi mai jos). Fracția de particule cu impuls zero dispare Condensarea Bose-Einstein dispare. Curba de dependență a capacității termice de temperatură are în punct T c pauză. Distribuția de impuls a particulelor la T > T s este dat de formula (19) și μ Т > T s) sunt prezentate în Figura 3.![]() c este viteza luminii în vid. Numărul de fotoni nu este valoare dată, și ea însăși este determinată din condiția echilibrului termodinamic; prin urmare, distribuția lor de impuls este dată de formula (19) cu μ = 0 (în plus, ε = rs). Distribuția energiei în spectrul de emisie se obține prin înmulțirea numărului de fotoni cu energia ε, astfel încât densitatea energiei în domeniul de frecvență dω este egal cu n p este luat la ε=ħω
. Acea. se obține formula Planck pentru spectrul radiației de echilibru (negru) (vezi legea radiației lui Planck).
c este viteza luminii în vid. Numărul de fotoni nu este valoare dată, și ea însăși este determinată din condiția echilibrului termodinamic; prin urmare, distribuția lor de impuls este dată de formula (19) cu μ = 0 (în plus, ε = rs). Distribuția energiei în spectrul de emisie se obține prin înmulțirea numărului de fotoni cu energia ε, astfel încât densitatea energiei în domeniul de frecvență dω este egal cu n p este luat la ε=ħω
. Acea. se obține formula Planck pentru spectrul radiației de echilibru (negru) (vezi legea radiației lui Planck).![]()

![]()
![]()
![]() m - masa oscilatorului, ω 0
este propria frecvență. Calculul folosind formula (22) dă: f, valoarea medie X deplasat cu suma
m - masa oscilatorului, ω 0
este propria frecvență. Calculul folosind formula (22) dă: f, valoarea medie X deplasat cu suma![]()
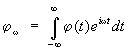
![]()






