16. Teorema lui Stern.

Dacă se cunoaște momentul de inerție al unui corp în jurul unei axe care trece prin centrul său de masă, atunci momentul de inerție în jurul oricărei alte axe paralele este determinat de teorema Steiner. : momentul de inerție al corpului J relativ la o axă arbitrară este egală cu momentul ei de inerție Jc faţă de o axă paralelă care trece prin centrul de masă DIN corp, adăugat la produsul masei t corp pe distanță pătrată A intre axe:

17. Ecuația dinamicii mișcare de rotație corp solid.

Iε = M. Aceasta este ecuația de bază a dinamicii mișcării de rotație a unui corp rigid. Accelerația unghiulară ε și cuplul M în această ecuație sunt mărimi algebrice. De obicei, sensul pozitiv de rotație este în sens invers acelor de ceasornic.

Este posibilă și o formă vectorială a ecuației de bază a dinamicii mișcării de rotație, în care mărimile sunt definite ca vectori direcționați de-a lungul axei de rotație. Când se studiază mișcarea de translație a corpurilor, se introduce conceptul de impuls al corpului. În mod similar, atunci când se studiază mișcarea de rotație, este introdus conceptul de moment unghiular. Momentul unghiular al unui corp în rotație se numește mărime fizică egală cu produsul dintre momentul de inerție al corpului I și viteza unghiulară ω de rotație a acestuia. Momentul unghiular este notat cu litera L: Momentul unghiular al întregului corp este definit ca suma vectorială a lui Li. L = Iω. Această ecuație, obținută aici pentru cazul când I = const, este valabilă și în cazul general când momentul de inerție al corpului se modifică în timpul mișcării.

18. Energia cinetică a unui corp în rotație.

Considerăm un corp absolut rigid (vezi § 1) care se rotește în jurul unei axe fixe z care trece prin el (Fig. 24). Să împărțim mental acest corp în volume mici cu mase elementare t 1 , t 2 ,..., t n , de la distanță r 1 , r 2 ,..., rn din axa.

Când un corp rigid se rotește în jurul unei axe fixe, volumele sale elementare individuale cu mase m i descrie cercuri de diferite raze r i, și au viteze liniare diferite v i . Dar, întrucât luăm în considerare un corp absolut rigid, viteza unghiulară de rotație a acestor volume este aceeași: (17.1) Găsim energia cinetică a unui corp în rotație ca fiind suma energiilor cinetice ale volumelor sale elementare:

sau Folosind expresia (17.1), obținem

Unde Jz- momentul de inerție al corpului față de axa z. În acest fel, energie kinetică corp rotativ (17.2)

Dintr-o comparație a formulei (17.2) cu expresia (12.1) pentru energia cinetică a unui corp care se deplasează înainte (T=mv 2 /2), Rezultă că momentul de inerție este măsura inerției corpuluiîn timpul mișcării de rotație. Formula (17.2) este valabilă pentru un corp care se rotește în jurul unei axe fixe. În cazul unei mișcări plane a unui corp, de exemplu, un cilindru care se rostogolește pe un plan înclinat fără alunecare, energia mișcării este suma energiei mișcării de translație și a energiei de rotație: Unde m- masa corpului de rulare; vc- viteza centrului de masă al corpului; Jc- momentul de inerție al corpului față de axa care trece prin centrul său de masă; w este viteza unghiulară a corpului. Lucrul forței externe asupra rotației corpului F=Fi+Fr+Fk. Lucrul forței unui corp în rotație A=M* ∆φ

19. Câmp gravitațional.

Interacțiunea gravitațională dintre corpuri se realizează cu ajutorul câmpului gravitațional, sau câmpului gravitațional. Acest câmp este generat de corpuri și este o formă de existență a materiei. Principala proprietate a câmpului gravitațional este aceea pentru orice corp de masă t, adusă în acest câmp, forța gravitațională acționează, adică (24.1)

Vectorul g nu depinde de m și se numește puterea câmpului gravitațional. Intensitatea câmpului gravitațional este determinată de forța care acționează din partea câmpului asupra punctului material al unei unități de masă și coincide în direcție cu forța care acționează. Există tensiune caracteristica de putere câmpuri gravitaționale. Câmpul gravitațional se numește omogen dacă intensitatea lui este aceeași în toate punctele și central dacă în toate punctele câmpului vectorii de intensitate sunt direcționați de-a lungul liniilor drepte care se intersectează într-un punct. (A) nemișcatîn raport cu orice cadru inerțial de referință (Fig. 38). Pentru o reprezentare grafică a câmpului de forță se folosesc linii de forță (linii de tensiune). Liniile de câmp sunt alese astfel încât vectorul intensității câmpului să fie direcționat tangențial la linia câmpului.

Valoarea este caracteristică energetică câmpul gravitațional se numește potențial. Potențialul câmpului gravitațional j- o mărime scalară determinată de energia potențială a unui corp de unitate de masă într-un punct dat al câmpului sau de munca de mutare a unei unități de masă dintr-un punct dat al câmpului la infinit. Astfel, potențialul câmpului gravitațional creat de un corp de masă M, este egal cu (25.4) unde R- distanţa de la acest corp până la punctul în cauză. Din formula (25.4) rezultă că locul punctelor cu același potențial formează o suprafață sferică ( R= const). Asemenea suprafețe pentru care potențialul este constant se numesc echipotențial. Luați în considerare relația dintre potențial ( j) câmpul gravitațional și intensitatea acestuia (g). Din expresiile (25.1) și (25.4) rezultă că lucrarea elementară d A, efectuate de forţele câmpului cu o mică deplasare a unui corp cu o masă t, este egal cu

20. Presiunea în lichide și gaze. Legile lui Pascal și Arhimede.

unitate de presiune - pascal(Pa): 1 Pa este egal cu presiunea creată de o forță de 1 N, distribuită uniform pe o suprafață normală cu o suprafață de 1m 2 (1 Pa \u003d 1 N / m 2).

Presiunea la echilibrul lichidelor (gazelor) respectă legea lui Pascal: presiunea în orice loc a unui fluid în repaus este aceeași în toate direcțiile, iar presiunea este transmisă în mod egal în volumul ocupat de fluidul în repaus. Să luăm în considerare modul în care greutatea unui fluid afectează distribuția presiunii în interiorul unui fluid incompresibil în repaus. Când un lichid este în echilibru, presiunea orizontală este întotdeauna aceeași, altfel nu ar exista echilibru. Prin urmare, suprafața liberă a unui fluid în repaus este întotdeauna orizontală departe de pereții vasului. Dacă un fluid este incompresibil, atunci densitatea lui este independentă de presiune. Apoi pentru secțiunea transversală S coloana de lichid, înălțimea acesteia h si densitate r greutatea P=rgSh,și presiunea pe baza inferioară

(28.1) adică presiunea se modifică liniar cu înălțimea. Presiune rgh numită presiune hidrostatică. Conform formulei (28.1), forța de presiune asupra straturilor inferioare ale lichidului va fi mai mare decât a celor superioare, prin urmare, asupra unui corp scufundat într-un lichid (gaz) acționează o forță determinată de legea lui Arhimede: o forță direcționată. forța acționează asupra unui corp scufundat într-un lichid (gaz).forță de plutire în sus egală cu greutatea lichidului (gazului) deplasat de corp: F DAR =PgV, Unde R - densitatea fluidului, V- volumul unui corp scufundat într-un lichid.

21. Linie și tub de curent. Teorema continuității jetului.

Mișcarea fluidelor se numește flux, iar colecția de particule dintr-un fluid în mișcare se numește flux. Grafic, mișcarea fluidelor este descrisă folosind linii de curgere, care sunt desenate astfel încât tangentele la acestea să coincidă în direcția cu vectorul viteză a fluidului în punctele corespunzătoare din spațiu (Fig. 45). Liniile de curgere sunt desenate în așa fel încât densitatea lor, care este caracterizată prin raportul dintre numărul de linii și aria zonei perpendiculare pe ele, prin care trec, este mai mare acolo unde viteza de curgere a fluidului este mai mare și mai puțin acolo unde fluidul curge mai lent. Astfel, conform modelului liniilor de curgere, se poate judeca direcția și modulul vitezei în diferite puncte din spațiu, adică se poate determina starea mișcării fluidului. Partea de fluid delimitată de linii de curgere se numește streamtube. Curgerea unui fluid se numește constant (sau staționar) dacă forma și locația liniilor de curgere, precum și valorile vitezelor în fiecare dintre punctele sale, nu se modifică în timp.

Luați în considerare orice tub de curent. Alegem două dintre secțiunile sale S 1 și S 2 , perpendicular pe direcția vitezei (Fig. 46). Pentru timpul D t prin sectiune S volumul trecerilor de lichid Sv D t; prin urmare, timp de 1 s S 1 va trece volumul de lichid S 1 v 1 , Unde v 1 - viteza de curgere a fluidului la secțiunea transversală S 1 . Prin sectiune S 2 timp de 1 s va trece volumul de lichid S 2 v 2 , Unde v 2 - viteza de curgere a fluidului la secțiunea transversală S 2 . Se presupune aici că viteza fluidului în secțiune transversală este constantă. Dacă fluidul este incompresibil (r=const), atunci prin secțiune transversală S 2 va trece același volum de lichid ca prin secțiune S 1 , adică (29.1) În consecință, produsul dintre viteza de curgere a unui fluid incompresibil și secțiunea transversală a tubului de curent este o valoare constantă pentru acest tub de curent. Relația (29.1) se numește ecuația de continuitate pentru un fluid incompresibil.

ecuația lui Bernoulli

Conform ecuației de continuitate pentru un fluid incompresibil , volumul ocupat de lichid rămâne constant, adică împărțind expresia (30.5) la D V, ajunge unde R - densitatea lichidului. Dar din moment ce secțiunile au fost alese arbitrar, putem scrie (30.6)

Expresia (30.6) a fost derivată de fizicianul elvețian D. Bernoulli și se numește ecuația lui Bernoulli. După cum se poate vedea din derivarea sa, ecuația lui Bernoulli este o expresie a legii conservării energiei aplicată unui flux constant al unui fluid ideal. Funcționează bine și pentru fluide reale, a căror frecare internă nu este foarte mare. Valoare Rîn formula (30.6) se numește presiune statică (presiunea fluidului pe suprafața corpului înconjurată de acesta), valoarea rv 2 / 2 - presiune dinamică. După cum am menționat deja mai sus, valoarea rgh este presiunea hidrostatică.

Pentru un tub de curent orizontal ( h 1 =h 2 ) expresia (30.6) devine (30.7)

Unde p+rv 2 / 2 se numește presiune totală. Din ecuația Bernoulli (30.7) pentru un tub orizontal de curent și ecuația de continuitate (29.1) rezultă că atunci când un lichid curge printr-o conductă orizontală având secțiuni diferite, viteza fluidului este mai mare în locurile de îngustare, iar presiunea statică. este mai mare în locuri mai largi, adică unde viteza este mai mică. Acest lucru poate fi demonstrat prin plasarea unei serii de manometre de-a lungul conductei (Fig. 48).

23. Formula Torricelli.

Să considerăm un vas cilindric cu un lichid, în peretele lateral al căruia există o mică gaură la o anumită adâncime sub nivelul lichidului (Fig. 51). Luați în considerare două secțiuni (la nivel h 1 suprafata libera a lichidului in vas si la nivel h 2 ieșirea sa din gaură) și scrieți ecuația lui Bernoulli:

Din moment ce presiunea R 1 și R 2 în lichid la nivelurile primei și celei de-a doua secțiuni sunt egale cu cele atmosferice, i.e. R 1 =p 2 , atunci ecuația va arăta ca

Din ecuaţia de continuitate (29.1) rezultă că v 2 /v 1 =S 1 /S 2 , Unde S 1 și S 2 - zonele de secțiune transversală ale vasului și deschidere. În cazul în care un S 1 >>S 2 , apoi membru v/2 poate fi neglijat şi

Această expresie se numește formula Torricelli. Formula pentru viteza de scurgere a fluidului dintr-o gaură dintr-un vas deschis

24. Vâscozitatea, legea lui Newton. Regimuri de curgere.

Vâscozitatea (frecarea internă) este proprietatea lichidelor reale de a rezista mișcării unei părți a lichidului față de alta. Când unele straturi ale unui fluid real se mișcă în raport cu altele, apar forțe de frecare interioare, direcționate tangențial la suprafața straturilor. Acțiunea acestor forțe se manifestă prin faptul că din partea stratului care se mișcă mai repede, stratul care se mișcă mai lent este afectat de o forță acceleratoare. Din partea stratului care se mișcă mai lent, stratul care se mișcă mai repede este afectat de o forță de întârziere.

Forța de frecare internă F este cu atât mai mare, cu atât aria considerată a suprafeței stratului este mai mare S(Fig. 52) și depinde de cât de repede se modifică debitul fluidului în timpul tranziției de la strat la strat. Direcția în care se numără distanța dintre straturi, perpendicular debitele stratului. Valoarea arată cât de repede se schimbă viteza atunci când treceți de la un strat la altul în direcția X, perpendicular pe direcția de mișcare a straturilor și se numește gradient de viteză. Astfel, modulul forței de frecare internă (31.1), unde coeficientul de proporționalitate m, care depinde de natura lichidului, se numește vâscozitate dinamică (sau pur și simplu vâscozitate). Unitatea de unitate de vâscozitate este pascal secundă (Pa×s). Cu cât vâscozitatea este mai mare, cu atât lichidul diferă mai mult de cel ideal, cu atât în ​​el apar forțele de frecare internă mai mari. Există două moduri de curgere a fluidului. Curgerea se numește laminar (stratificat) dacă fiecare strat subțire selectat alunecă de-a lungul fluxului în raport cu cele învecinate fără a se amesteca cu acestea, și turbulent (vortex) dacă de-a lungul curgerii au loc formarea intensivă de vortex și amestecarea lichidului (gaz). Curgerea laminară a unui lichid este observată la viteze mici ale mișcării sale. Stratul exterior de lichid adiacent suprafeței conductei în care curge, datorită forțelor de coeziune moleculară, aderă la acesta și rămâne imobil. Profilul de viteză medie pentru curgerea turbulentă în conducte (Fig. 53) diferă de profilul parabolic pentru curgerea laminară printr-o creștere mai rapidă a vitezei în apropierea pereților conductei și o curbură mai mică în partea centrală a fluxului. Natura fluxului depinde de o mărime adimensională numită numărul Reynolds: Unde n = h/p-vâscozitatea cinematică; R- densitatea lichidului;<v>-viteza medie a fluidului peste sectiunea conductei; d- dimensiune liniară caracteristică, cum ar fi diametrul conductei. La valori scăzute ale numărului Reynolds, se observă un flux laminar, trecerea de la fluxul laminar la cel turbulent are loc în regiune și la (pentru conducte netede) curgerea este turbulentă.

26. Formula Poiseuille. Metode de determinare a vâscozității.

Metoda Stokes. Această metodă de determinare a vâscozității se bazează pe măsurarea vitezei unor corpuri sferice mici care se mișcă încet într-un lichid. Trei forțe acționează asupra unei mingi care cade vertical într-un lichid: gravitația P= 4 / 3 relatii cu publicul 3 rg(r- densitatea mingii), forța lui Arhimede P= 4 / 3 relatii cu publicul 3 r "g (r" - densitatea lichidului) și forța de rezistență stabilită empiric de J. Stokes: F= 6phrv, Unde r este raza mingii, v- viteza lui. Când mingea se mișcă uniform, unde

Măsurând viteza de mișcare uniformă a mingii, se poate determina vâscozitatea unui lichid (gaz). Metoda Poiseuille. Această metodă se bazează pe fluxul laminar de lichid într-un capilar subțire. Luați în considerare un capilar cu o rază R si lungime l. Într-un lichid, selectăm mental un strat cilindric cu o rază rși grosimea d r(Fig. 54). Forța de frecare internă (vezi (31.1)), care acționează pe suprafața laterală a acestui strat, unde D S- suprafata laterala strat cilindric; semnul minus înseamnă că pe măsură ce raza crește, viteza scade. După integrare, presupunând că lipirea fluidului are loc în apropierea pereților, adică viteza la distanță R de la axa este egal cu zero, obținem În timpul t din conductă va curge un lichid, al cărui volum este de unde vascozitatea

27. Ecuația oscilațiilor armonice libere pentru pendule.

Oscilațiile se numesc libere (sau naturale) dacă sunt efectuate datorită energiei inițial impartite cu absența ulterioară a influențelor externe asupra sistemului oscilator (sistemul care oscilează). Cel mai simplu tip de oscilații sunt oscilațiile armonice - oscilațiile în care valoarea oscilației se modifică în timp conform legii sinusului (cosinusul ). Pendul de primăvară este o sarcină de masă t, suspendat pe un arc perfect elastic si care efectueaza oscilatii armonice sub actiunea unei forte elastice F= -kx, Unde k- rigiditatea arcului. Ecuația de mișcare a pendulului

Din expresii rezultă că pendulul cu arc efectuează oscilații armonice conform legii x=A cos (w 0 t+ j) cu frecvență ciclică (142.2) și perioadă (142.3) Formula (142.3) este valabilă pentru oscilațiile elastice în limitele în care este îndeplinită legea lui Hooke, adică atunci când masa arcului este mică în comparație cu masa corpului. Energia potențială a pendulului cu arc este pendul fizic- acesta este un corp rigid care, sub acțiunea gravitației, oscilează în jurul unei axe orizontale fixe care trece printr-un punct O, care nu coincide cu centrul de masă DIN corp (Fig. 201). Dacă pendulul este deviat de la poziția sa de echilibru cu un anumit unghi A, apoi, în conformitate cu ecuația dinamicii mișcării de rotație a unui corp rigid (18.3), momentul M forța de restabilire poate fi scrisă ca (142.4) unde J- momentul de inerție al pendulului în jurul axei care trece prin punctul de suspensie Oh, eu distanța dintre acesta și centrul de masă al pendulului, F t \u003d -mg sina» -mga. - forța de restabilire (semnul minus se datorează faptului că direcțiile F tși A mereu opus; păcat A» A corespunde micilor oscilații ale pendulului, adică. mici abateri ale pendulului de la poziţia de echilibru). Pentru oscilații mici, pendulul fizic efectuează oscilații armonice cu o frecvență ciclică w 0 și o perioadă

Unde L=J/(ml) - lungime redusă a pendulului fizic.

Pendul matematic- aceasta este idealizat un sistem format dintr-un punct material cu o masă t, suspendat pe un fir inextensibil fără greutate și oscilând sub influența gravitației. O bună aproximare a unui pendul matematic este o minge mică și grea suspendată de un fir subțire și lung. Momentul de inerție al unui pendul matematic

(142.8) unde l este lungimea pendulului. Întrucât pendulul matematic poate fi reprezentat ca caz special pendul fizic, presupunând că toată masa sa este concentrată într-un punct - centrul de masă, apoi, substituind expresia (142.8) în formula (1417), obținem o expresie pentru perioada de mici oscilații a unui pendul matematic (142.9) Comparând formulele (142.7). ) și (142.9), vedem ce se întâmplă dacă lungimea dată L pendulul fizic este egal cu lungimea l un pendul matematic, atunci perioadele de oscilație ale acestor pendul sunt aceleași. Prin urmare, lungimea redusă a unui pendul fizic este lungimea unui astfel de pendul matematic, a cărui perioadă de oscilație coincide cu perioada de oscilație a unui pendul fizic dat.

28. Cinematica oscilațiilor armonice libere.

Oscilația armonică mecanică este o mișcare rectilinie neuniformă în care coordonatele unui corp oscilant (punct material) se modifică conform legii cosinusului sau sinusului în funcție de timp. Conform acestei definiții, legea modificării coordonatelor în funcție de timp are forma: , unde wt este valoarea sub semnul cosinus sau sinus; coeficientul w, sens fizic pe care le vom dezvălui mai jos; A este amplitudinea oscilațiilor armonice mecanice. Ecuațiile (4.1) sunt principalele ecuații cinematice ale vibrațiilor armonice mecanice.

pentru un punct material care efectuează oscilații mecanice armonice, valoarea lui w poate fi interpretată ca numărul de oscilații pentru un anumit ciclu de timp, egal cu 2l. Prin urmare, valoarea lui w a fost numită frecvență ciclică (sau circulară). Dacă punctul M își începe mișcarea nu din punctul 1 ci din punctul 2, atunci ecuația (4.1) va lua forma: Valoarea lui f0 se numește faza inițială.

29. Vibrații amortizate.

Să considerăm oscilații amortizate libere - oscilații ale căror amplitudini scad în timp din cauza pierderilor de energie de către un sistem oscilator real. Ecuație diferențială oscilații amortizate libere sistem liniar este dat sub formă

(146.1), unde s- o valoare fluctuantă care descrie una sau alta proces fizic, d=const - coeficient de atenuare, w 0 - frecvența ciclică a liberului neamortizat oscilații ale aceluiași sistem oscilator, adică la d = 0 (în absența pierderilor de energie) se numește frecvența naturală a sistemului oscilator.

- amplitudinea oscilațiilor amortizate, A DAR 0 - amplitudinea initiala. În cazul în care un La)și DAR(t+ T) - amplitudini a două oscilații succesive corespunzătoare unor timpi care diferă cu o perioadă, atunci se numește raportul scădere de amortizare,și logaritmul acestuia (146.7)- scaderea amortizarii logaritmice; N e - numărul de oscilaţii efectuate în timpul în care amplitudinea scade de e ori. Decrementul de amortizare logaritmică este o valoare constantă pentru un sistem oscilator dat. Pentru a caracteriza un sistem oscilator se folosește conceptul factor de calitate Q, care pentru valori mici ale decrementului logaritmic este egal cu (146,8). Din formula (146.8) rezultă că factorul de calitate este proporțional cu numărul de oscilații N e , efectuate de sistem în timpul de relaxare.

30. Vibrații forțate, rezonanță.

Oscilațiile care apar sub acțiunea unei forțe externe care se schimbă periodic sau a unei feme exterioare care se schimbă periodic se numesc oscilații mecanice forțate și, respectiv, electromagnetice forțate. Luați în considerare dependența amplitudinea A vibratii fortate de la frecvența w. Oscilațiile mecanice și electromagnetice vor fi luate în considerare simultan, denumind valoarea oscilante sau deplasarea (X) un corp oscilant dintr-o poziție de echilibru sau printr-o sarcină (Q) condensator.

Din formula (147.8) rezultă că amplitudinea DAR deplasarea (sarcina) are un maxim. Pentru a determina frecvența de rezonanță w cut, - frecvența la care amplitudinea DAR deplasarea (sarcina) atinge un maxim - trebuie să găsiți maximul funcției (147,8) sau, ceea ce este același, minimul expresiei radicalului. Diferenţierea expresiei radicale în raport cu wși echivalând cu zero, obținem condiția care determină w a tăia: Această egalitate este valabilă pentru w=0, ± , pentru care doar o valoare pozitivă are semnificație fizică. În consecință, frecvența de rezonanță (148.1) Fenomenul de creștere bruscă a amplitudinii oscilațiilor forțate când frecvența forței de antrenare (frecvența tensiunii alternative de antrenare) se apropie de o frecvență egală sau apropiată de frecvența proprie a oscilației. sistem se numește rezonanță (mecanic sau respectiv electric). Când valoare w tăierea aproape coincide cu frecvența naturală w 0 sistem oscilant. Înlocuind (148.1) în formula (147.8), obținem (148.2)

Pe fig. 210 prezintă dependenţele amplitudinii oscilaţiilor forţate de frecvenţă pentru diferite valori d. Din (148.1) și (148.2) rezultă că cu cât mai puțin d, cu cât se află mai sus și la dreapta maximul acestei curbe. În cazul în care un w® 0, atunci toate curbele (vezi și (147.8)) ating aceeași valoare limită diferită de zero , care se numește abaterea statică. În cazul vibraţiilor mecanice , în cazul electromagnetic U m / (L). În cazul în care un w®¥, atunci curbele tind asimptotic spre zero. Setul redus de curbe se numește curbe de rezonanță.

Legea conservării energiei spune că energia corpului nu dispare niciodată și nu reapare, ea se poate transforma doar de la o formă la alta. Această lege este universală. Are propria sa formulare în diferite ramuri ale fizicii. Mecanica clasică are în vedere legea conservării energiei mecanice.

Energia mecanică totală a unui sistem închis corpuri fizice, între care acţionează forţele conservatoare, este o valoare constantă. Așa se formulează legea conservării energiei în mecanica newtoniană.

Închis, sau izolat, este considerat a fi sistem fizic, care nu este afectat de forțele externe. Nu face schimb de energie cu spațiul înconjurător, iar propria sa energie, pe care o posedă, rămâne neschimbată, adică se păstrează. Doar într-un astfel de sistem forțe interne, iar corpurile interacționează între ele. Poate converti doar energia potențială în energie cinetică și invers.

Cel mai simplu exemplu de sistem închis este o pușcă cu lunetă și un glonț.

Tipuri de forțe mecanice

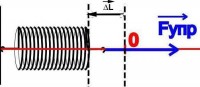
Forțele care acționează în interiorul unui sistem mecanic sunt de obicei împărțite în conservative și neconservative.

conservator se consideră forţe a căror activitate nu depinde de traiectoria corpului căruia i se aplică, ci este determinată doar de poziţia iniţială şi finală a acestui corp. Se mai numesc si fortele conservatoare potenţial. Lucrul acestor forțe într-o buclă închisă este zero. Exemple de forțe conservative − forță gravitațională, forță elastică.

Toate celelalte forțe sunt numite neconservator. Acestea includ forța de frecare și forța de tracțiune. Se mai numesc si ei disipativ forte. Aceste forțe efectuează un lucru negativ în timpul oricăror mișcări într-un sistem mecanic închis, iar sub acțiunea lor energia mecanică totală a sistemului scade (se disipă). Trece în alte tipuri de energie, nemecanice, de exemplu, în căldură. Prin urmare, legea conservării energiei într-un sistem mecanic închis poate fi îndeplinită numai dacă nu există forțe neconservative în el.

Energia totală a unui sistem mecanic este formată din energia cinetică și potențială și este suma lor. Aceste tipuri de energii se pot transforma unele în altele.

Energie potențială

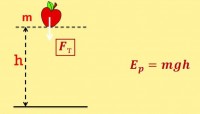
Energie potențială se numește energia de interacțiune a corpurilor fizice sau a părților lor între ele. Este determinată de aranjarea lor reciprocă, adică de distanța dintre ele, și este egală cu munca care trebuie făcută pentru a muta corpul de la punctul de referință în alt punct din câmpul forțelor conservatoare.

Energia potențială are orice corp fizic nemișcat, ridicat la o anumită înălțime, deoarece este afectat de gravitație, care este o forță conservatoare. O astfel de energie este deținută de apa de la marginea unei cascade, de o sanie în vârful unui munte.

De unde a venit această energie? În timp ce corpul fizic era ridicat la o înălțime, se lucra și se consuma energie. Această energie este stocată în corpul ridicat. Și acum această energie este gata să lucreze.

Valoarea energiei potențiale a corpului este determinată de înălțimea la care se află corpul față de un anumit nivel inițial. Putem lua orice punct pe care îl alegem ca punct de plecare.

Dacă luăm în considerare poziția corpului față de Pământ, atunci energie potențială corpul de pe suprafața Pământului este zero. Și deasupra h se calculeaza cu formula:

E p = mɡ h ,

Unde m - masa corpului

ɡ - accelerarea gravitației

h – înălțimea centrului de masă al corpului față de Pământ

ɡ \u003d 9,8 m/s 2

Când un corp cade de la înălțime h1 pana la inaltime h2 gravitația funcționează. Această muncă este egală cu modificarea energiei potențiale și are o valoare negativă, deoarece magnitudinea energiei potențiale scade pe măsură ce corpul cade.

A = - ( E p2 - E p1) = - ∆ E p ,

Unde E p1 este energia potențială a corpului la înălțime h1 ,

E p2 - energia potenţială a unui corp la înălţime h2 .

Dacă corpul este ridicat la o anumită înălțime, atunci se lucrează împotriva forțelor gravitaționale. În acest caz, are o valoare pozitivă. Și valoarea energiei potențiale a corpului crește.

Un corp deformat elastic (comprimat sau primăvară întinsă). Valoarea sa depinde de rigiditatea arcului și de cât timp a fost comprimat sau întins și este determinată de formula:

E p \u003d k (∆x) 2 / 2 ,

Unde k - coeficientul de rigiditate,

∆x - alungirea sau contractia corpului.

Energia potențială a izvorului poate funcționa.

Energie kinetică

Tradus din greacă „kinema” înseamnă „mișcare”. Energia pe care o primește un corp fizic ca urmare a mișcării sale se numește cinetică. Valoarea acestuia depinde de viteza de mișcare.

O minge de fotbal care se rostogolește pe teren, o sanie care se rostogolește pe un munte și continuă să se miște, o săgeată trasă dintr-un arc - toate au energie cinetică.

Dacă un corp este în repaus, energia lui cinetică este zero. De îndată ce o forță sau mai multe forțe acționează asupra corpului, acesta va începe să se miște. Și din moment ce corpul se mișcă, forța care acționează asupra lui funcționează. Lucrul forței, sub influența căreia corpul din repaus va intra în mișcare și își va schimba viteza de la zero la ν , se numește energie kinetică masa corpului m .

Dacă, în momentul inițial de timp, corpul era deja în mișcare, iar viteza lui avea valoarea v 1 , iar la final a fost egal cu v 2 , atunci munca efectuată de forța sau forțele care acționează asupra corpului va fi egală cu creșterea energiei cinetice a corpului.

∆ E k = E k 2 - E k 1

Dacă direcția forței coincide cu direcția mișcării, atunci se efectuează o muncă pozitivă, iar energia cinetică a corpului crește. Și dacă forța este îndreptată în direcția opusă direcției de mișcare, atunci se face un lucru negativ, iar corpul emite energie cinetică.

Legea conservării energiei mecanice

Ek 1 + E p1= E k 2 + E p2

Orice corp fizic situat la o anumită înălțime are energie potențială. Dar când cade, începe să piardă această energie. Unde merge ea? Se dovedește că nu dispare nicăieri, ci se transformă în energia cinetică a aceluiași corp.

Presupune , la o anumită înălțime, o sarcină este fixă ​​nemișcată. Energia sa potențială în acest punct este egală cu valoarea maximă. Dacă îi dăm drumul, va începe să cadă cu o anumită viteză. Prin urmare, va începe să dobândească energie cinetică. Dar, în același timp, energia sa potențială va începe să scadă. În punctul de impact, energia cinetică a corpului va atinge un maxim, iar energia potențială va scădea la zero.

Energia potențială a unei mingi aruncate de la înălțime scade, în timp ce energia cinetică crește. Săniile în repaus în vârful unui munte au energie potențială. Energia lor cinetică în acest moment este zero. Dar când încep să se rostogolească în jos, energia cinetică va crește, iar energia potențială va scădea cu aceeași cantitate. Și suma valorilor lor va rămâne neschimbată. Energia potențială a unui măr agățat de un copac este transformată în energia sa cinetică atunci când acesta cade.

Aceste exemple confirmă în mod clar legea conservării energiei, care spune că energia totală a unui sistem mecanic este o valoare constantă . Valoarea energiei totale a sistemului nu se modifică, iar energia potențială este convertită în energie cinetică și invers.

Cu ce ​​cantitate scade energia potențială, energia cinetică va crește cu aceeași cantitate. Suma lor nu se va schimba.

Pentru un sistem închis de corpuri fizice, egalitatea
E k1 + E p1 = E k2 + E p2,
Unde E k1, Ep1 - energiile cinetice și potențiale ale sistemului înainte de orice interacțiune, E k2, E p2 - energiile corespunzătoare după el.

Procesul de conversie a energiei cinetice în energie potențială și invers poate fi văzut urmărind un pendul oscilant.

Click pe imagine

Fiind în poziția de extremă dreaptă, pendulul pare să înghețe. În acest moment, înălțimea sa deasupra punctului de referință este maximă. Prin urmare, energia potențială este și ea maximă. Și cinetica este zero, deoarece nu se mișcă. Dar în clipa următoare pendulul începe să se miște în jos. Viteza lui crește și, prin urmare, energia cinetică crește. Dar pe măsură ce înălțimea scade, la fel și energia potențială. În punctul de jos, acesta va deveni egal cu zero, iar energia cinetică va atinge valoarea maximă. Pendulul va trece de acest punct și va începe să se ridice spre stânga. Energia sa potențială va începe să crească, iar energia cinetică va scădea. etc.

Pentru a demonstra transformarea energiei, Isaac Newton a inventat sistem mecanic, Care e numit leagănul lui Newton sau mingile lui Newton .

Click pe imagine

Dacă prima bilă este deviată și apoi eliberată, energia și impulsul acesteia vor fi transferate ultimei prin trei bile intermediare, care vor rămâne nemișcate. Și ultima minge se va devia cu aceeași viteză și se va ridica la aceeași înălțime ca prima. Apoi, ultima bilă își va transfera energia și impulsul prin bilele intermediare către prima și așa mai departe.

O minge lăsată deoparte are energia potențială maximă. Energia sa cinetică în acest moment este zero. După ce a început să se miște, pierde energie potențială și dobândește energie cinetică, care atinge maximul în momentul ciocnirii cu a doua bilă, iar energia potențială devine egală cu zero. În plus, energia cinetică este transferată la a doua, apoi la a treia, a patra și a cincea bile. Acesta din urmă, după ce a primit energie cinetică, începe să se miște și se ridică la aceeași înălțime la care se afla prima minge la începutul mișcării. Energia sa cinetică în acest moment este egală cu zero, iar energia potențială este egală cu valoarea maximă. Apoi începe să cadă și în același mod transferă energie bilelor în ordine inversă.

Acest lucru continuă destul de mult timp și ar putea continua la nesfârșit dacă nu ar exista forțe neconservatoare. Dar, în realitate, în sistem acționează forțe disipative, sub influența cărora bilele își pierd energia. Viteza și amplitudinea lor scad treptat. Și până la urmă se opresc. Acest lucru confirmă faptul că legea conservării energiei este îndeplinită numai în absența forțelor neconservative.

Energia mecanică totală caracterizează mișcarea și interacțiunea corpurilor, prin urmare, depinde de viteze și de poziția relativă a corpurilor.

Energia mecanică totală a unui sistem mecanic închis este egală cu suma energiilor cinetice și potențiale ale corpurilor acestui sistem:

Legea conservării energiei

Legea conservării energiei este o lege fundamentală a naturii.

În mecanica newtoniană, legea conservării energiei este formulată după cum urmează:

Energia mecanică totală a unui sistem izolat (închis) de corpuri rămâne constantă.

Cu alte cuvinte:

Energia nu ia naștere din nimic și nu dispare nicăieri, ea poate trece doar de la o formă la alta.

Exemple clasice ale acestei afirmații sunt: ​​un pendul cu arc și un pendul pe filet (cu amortizare neglijabilă). În cazul pendulului cu arc, în procesul de oscilație, energia potențială a unui arc deformat (având un maxim în pozițiile extreme ale sarcinii) este convertită în energia cinetică a sarcinii (atingând un maxim în momentul sarcina trece de poziția de echilibru) și invers. În cazul unui pendul pe un fir, energia potențială a sarcinii este convertită în energie cinetică și invers.

2 Echipamente

2.1 Dinamometru.

2.2 Stand de laborator.

2.3 Sarcina cu greutatea de 100 g - 2 buc.

2.4 Riglă de măsurare.

2,5 bucată țesut moale sau simțit.

3 Context teoretic

Schema configurației experimentale este prezentată în Figura 1.

Dinamometrul este fixat vertical la piciorul trepiedului. O bucată de pânză moale sau pâslă este așezată pe un trepied. La suspendarea sarcinilor de pe dinamometru, tensiunea arcului dinamometrului este determinată de poziția indicatorului. În acest caz, alungirea maximă (sau deplasarea statică) a arcului X 0 apare atunci când forța elastică a unui arc cu rigiditate k echilibrează forța de gravitație a sarcinii cu masa t:

kx 0 =mg, (1)

Unde g = 9,81 - accelerație în cădere liberă.

Prin urmare,

Deplasarea statică caracterizează noua poziție de echilibru O" a capătului inferior al arcului (Fig. 2).

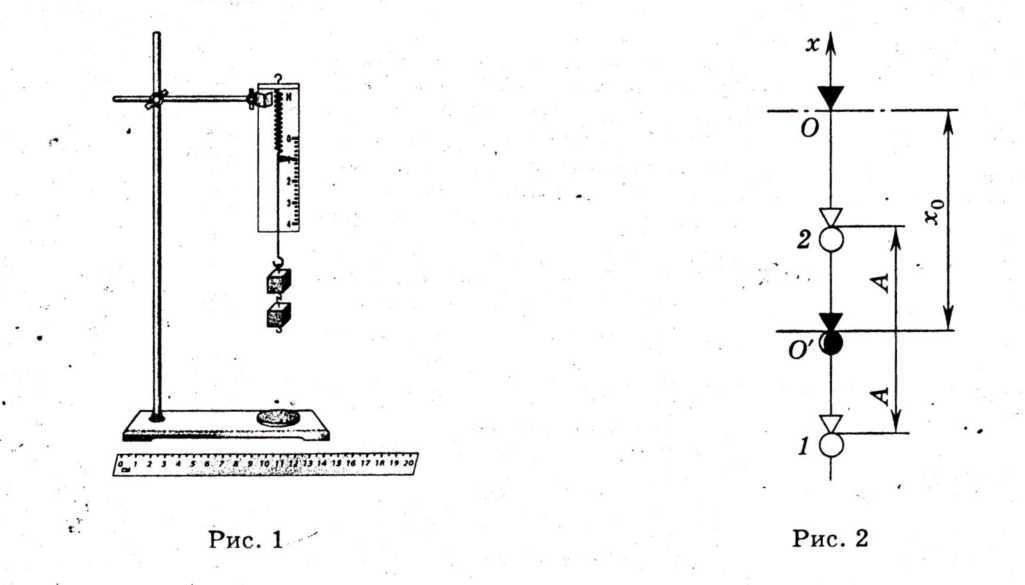
Dacă sarcina este trasă în jos o distanţă DAR din punctul O" și eliberați în punctul 1, apoi apar oscilații periodice ale sarcinii. În puncte 1 iar 2, numite puncte de cotitură, sarcina se oprește, inversând direcția de mișcare. Prin urmare, în aceste puncte, viteza încărcăturii v = 0.

viteza maxima v m topor sarcina va avea la mijlocul O". Două forţe acţionează asupra sarcinii oscilante: forţa constantă a gravitaţiei mg și forță elastică variabilă kx. Energia potențială a unui corp într-un câmp gravitațional într-un punct arbitrar cu coordonate X este egal cu mgx. Energia potențială a corpului deformat, respectiv, este egală cu .

În acest caz, ideea X = 0, corespunzătoare poziției indicatorului pentru un arc neîntins.

Energia mecanică totală a sarcinii într-un punct arbitrar este suma energiei sale potențiale și cinetice. Neglijând forțele de frecare, folosim legea conservării energiei mecanice totale.

Să echivalăm energia mecanică totală a sarcinii din punctul 2 cu coordonatele -(X 0 -DAR) iar în punctul O" cu coordonata -X 0 :

Extinzând parantezele și efectuând transformări simple, aducem formula (3) în formular

Apoi modulul vitezei maxime a sarcinilor

Rigiditatea unui arc poate fi găsită prin măsurarea deplasării statice X 0 . După cum rezultă din formula (1),

3.5. Legile conservării și schimbării energiei

3.5.1. Legea Schimbării energie mecanică totală

O modificare a energiei mecanice totale a unui sistem de corpuri are loc atunci când munca este efectuată de forțe care acționează atât între corpurile sistemului, cât și din corpurile externe.

Modificarea energiei mecanice ∆E a unui sistem de corpuri este determinată de prin legea modificării energiei mecanice totale:

∆E \u003d E 2 - E 1 \u003d A ext + A tr (rezist),

unde E 1 este energia mecanică totală a stării inițiale a sistemului; E 2 - energia mecanică totală a stării finale a sistemului; A extern - munca efectuată asupra corpurilor sistemului de către forțele externe; A tr (rezist) - lucrul efectuat de forțele de frecare (rezistență) care acționează în interiorul sistemului.

Exemplul 30. La o anumită înălțime, un corp în repaus are o energie potențială egală cu 56 J. În momentul în care cade pe Pământ, corpul are o energie cinetică egală cu 44 J. Determinați lucrul forțelor de rezistență ale aerului.

Soluţie. Figura prezintă două poziții ale corpului: la o anumită înălțime (prima) și în momentul căderii pe Pământ (a doua). Nivelul zero al energiei potențiale este ales pe suprafața Pământului.

Energia mecanică totală a unui corp în raport cu suprafața Pământului este determinată de suma energiei potențiale și cinetice:

• la o oarecare înălțime

E 1 \u003d W p 1 + W k 1;

• până când lovește pământul

E 2 \u003d W p 2 + W k 2,

unde W p 1 = 56 J este energia potențială a corpului la o anumită înălțime; W k 1 = 0 - energia cinetică a unui corp care se odihnește la o anumită înălțime; W p 2 = 0 J - energia potențială a corpului în momentul căderii pe Pământ; W k 2 \u003d 44 J - energia cinetică a corpului în momentul în care acesta cade pe Pământ.

Găsim munca forțelor de rezistență a aerului din legea modificării energiei mecanice totale a corpului:

unde E 1 = W p 1 este energia mecanică totală a corpului la o anumită înălțime; E 2 \u003d W k ​​​​2 - energia mecanică totală a corpului în momentul în care acesta cade pe Pământ; A ext \u003d 0 - munca forțelor externe (forțele externe sunt absente); O rezistență - munca forțelor de rezistență a aerului.

Lucrul dorit al forțelor de rezistență a aerului este astfel determinat de expresie

A rezist = W k 2 − W p 1 .

Hai sa facem calculul:

O rezistență \u003d 44 - 56 \u003d -12 J.

Munca forțelor de rezistență a aerului este o valoare negativă.

Exemplul 31. Două arcuri cu factori de rigiditate de 1,0 kN/m și 2,0 kN/m sunt conectate în paralel. Ce lucru trebuie făcut pentru a întinde sistemul cu arc cu 20 cm?

Soluţie. Figura prezintă două arcuri cu viteze diferite de arc conectate în paralel.

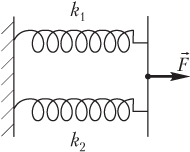
Forța externă F → , întinderea arcurilor, depinde de mărimea deformației arcului compozit, prin urmare, calculul muncii forței specificate folosind formula de calcul a muncii unei forțe constante este ilegal.

Pentru a calcula lucrul, folosim legea modificării energiei mecanice totale a sistemului:

E 2 − E 1 = A ext + A rezist,

unde E 1 este energia mecanică totală a arcului compozit în stare neformată; E 2 - energia mecanică totală a arcului deformat; A extern - lucrare a forței externe (valoarea dorită); A rezist = 0 - lucrul forțelor de rezistență.

Energia mecanică totală a unui arc compozit este energia potențială a deformarii acestuia:

• pentru primavara neformata

E 1 \u003d W p 1 \u003d 0,

• pentru primavara prelungita

E 2 \u003d W p 2 \u003d k total (Δ l) 2 2,

unde k total - rigiditatea totală a arcului compozit; ∆l - mărimea întinderii arcului.

Rigiditatea totală a două arcuri conectate în paralel este suma

k total \u003d k 1 + k 2,

unde k 1 - coeficientul de rigiditate al primului arc; k 2 - coeficientul de rigiditate al celui de-al doilea arc.

Găsim munca forței externe din legea schimbării în energia mecanică totală a corpului:

A ext \u003d E 2 - E 1,

înlocuind în această expresie formulele care determină E 1 și E 2, precum și expresia pentru coeficientul de rigiditate totală al arcului compozit:

A ext \u003d k total (Δ l) 2 2 − 0 \u003d (k 1 + k 2) (Δ l) 2 2.

Hai sa facem calculul:

O extensie \u003d (1,0 + 2,0) ⋅ 10 3 ⋅ (20 ⋅ 10 − 2) 2 2 \u003d 60 J.

Exemplul 32. Un glonț cu o masă de 10,0 g care zboară cu o viteză de 800 m/s lovește un perete. Modulul forței de rezistență la mișcarea unui glonț în perete este constant și se ridică la 8,00 kN. Stabiliți cât de departe va pătrunde glonțul în perete.

Soluţie. Figura prezintă două poziții ale glonțului: când se apropie de perete (primul) și în momentul în care glonțul se oprește (se blochează) în perete (al doilea).

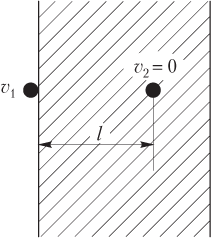
Energia mecanică totală a unui glonț este energia cinetică a mișcării sale:

• când un glonț lovește un perete

E 1 \u003d W k ​​​​1 \u003d m v 1 2 2;

• până când glonțul se oprește (se blochează) în perete

E 2 \u003d W k ​​​​2 \u003d m v 2 2 2,

unde W k 1 - energia cinetică a glonțului la apropierea de perete; W k 2 - energia cinetică a glonțului în momentul în care acesta se oprește (se blochează) în perete; m este masa glonțului; v 1 - modul de viteză a glonțului la apropierea de perete; v 2 \u003d 0 - valoarea vitezei glonțului în momentul opririi (blocarea) în perete.

Distanța la care glonțul va intra adânc în perete, găsim din legea schimbării energiei mecanice totale a glonțului:

E 2 − E 1 = A ext + A rezist,

unde E 1 \u003d m v 1 2 2 - energia mecanică totală a glonțului la apropierea de perete; E 2 \u003d 0 - energia mecanică totală a glonțului în momentul în care se oprește (se blochează) în perete; A ext \u003d 0 - munca forțelor externe (forțele externe sunt absente); O rezistență - opera forțelor de rezistență.

Munca forțelor de rezistență este determinată de produsul:

A rezist = F rezist l cos α ,

unde F resist - modulul forței de rezistență la mișcarea glonțului; l - distanța la care glonțul va intra adânc în perete; α = 180° - unghiul dintre direcțiile forței de tracțiune și direcția glonțului.

Astfel, legea modificării energiei mecanice totale a unui glonț într-o formă explicită este următoarea:

− m v 1 2 2 = F rezist l cos 180 ° .

Distanța dorită este determinată de raport

l = − m v 1 2 2 F rezist cos 180 ° = m v 1 2 2 F reziste

l = 10,0 ⋅ 10 − 3 ⋅ 800 2 2 ⋅ 8,00 ⋅ 10 3 = 0,40 m = 400 mm.

Pagina 1

Energia mecanică totală a corpului nu se modifică. Energia se schimbă doar de la o formă la alta.

Energia mecanică totală a unui corp, care nu este afectată de forțele de frecare și rezistență, rămâne neschimbată în timpul mișcării sale.

Energia mecanică totală a unui corp este suma energiilor sale cinetice și potențiale. Considera energie deplină corp în cădere liberă în momente diferite.

Se schimbă energia mecanică totală a corpului când acesta cade?

Ceea ce se numește energia mecanică totală a corpului.

Astfel, energia mecanică totală a unui corp care efectuează oscilații armonice este proporțională cu pătratul amplitudinii oscilației. Prin urmare, amplitudinea A a oscilațiilor, de asemenea, nu depinde de timp.

După cum se poate observa din (44.13), energia mecanică totală a corpului în timpul oscilațiilor amortizate scade cu timpul conform unei legi exponențiale.

Suma energiilor cinetice și potențiale formează energia mecanică totală a corpului.

Un impact absolut elastic este un astfel de impact la care energia mecanică totală a corpurilor este conservată. În primul rând, energia cinetică este convertită parțial sau complet în energia potențială de deformare elastică. Apoi corpurile revin la forma lor originală, respingându-se reciproc. Ca urmare, energia potențială a deformarii elastice se transformă din nou în energie cinetică și corpurile se despart cu viteze determinate de două condiții - conservarea energiei totale și impuls total tel.

Un impact absolut elastic este un astfel de impact la care energia mecanică totală a corpurilor este conservată. În primul rând, energia cinetică este convertită parțial sau complet în energia potențială de deformare elastică. Apoi corpurile revin la forma lor originală, respingându-se reciproc. Ca urmare, energia potențială a deformării elastice se transformă din nou în energie cinetică și corpurile se despart cu viteze determinate de două condiții - conservarea energiei totale și a impulsului total al corpurilor.

Un impact absolut elastic este un astfel de impact la care energia mecanică totală a corpurilor este conservată. În primul rând, energia cinetică este convertită parțial sau complet în energia potențială de deformare elastică. Apoi corpurile revin la forma lor originală, respingându-se reciproc. Ca urmare, energia potențială a deformării elastice se transformă din nou în energie cinetică și corpurile se despart cu viteze determinate de două condiții - conservarea energiei totale și a impulsului total al corpurilor.

Această muncă este cheltuită pentru disiparea energiei sau modificarea energiei mecanice totale a corpului.

Conform legii schimbării energiei (vezi § 28), munca forței de rezistență (forța externă) este egală cu creșterea energiei mecanice totale a corpului.

Acest rezultat este previzibil, deoarece forța elastică sub care se mișcă corpul este conservatoare, prin urmare, legea de conservare a energiei este îndeplinită - energia mecanică totală a corpului este conservată.

Energia mecanică caracterizează capacitatea unui corp de a efectua lucrări mecanice. Energia mecanică totală a unui corp este suma energiei cinetice și potențiale.