Note de curs pe subiect

MECANICA TEORETICĂ

Pentru studenții specialității:

260501.65 Tehnologia serviciilor alimentare,

Forma de învățământ cu normă întreagă

Notele cursului se bazează pe:

1. Butorin L.V., Busygina E.B. Mecanica teoretică. Ghid educațional și practic. - M., MGU TU, 2004

2. Targ S.M. Curs scurt mecanică teoretică. – M.: facultate, 2001 - Cu.

3. Yablonsky A.A., Nikiforova V.N. Curs de mecanică teoretică. M. „Lan”, 2000

Introducere

Modern productie industriala, inclusiv alimentația, sunt industrii puternic mecanizate. Rezolvarea sarcinilor din ce în ce mai complexe este atribuită echipamentelor tehnologice, ceea ce duce, la rândul său, la complicarea echipamentelor. Formarea unui inginer modern este de neconceput fără cunoașterea disciplinelor fundamentale. Una dintre aceste discipline este mecanică teoretică .

Mecanica teoretică este o ramură a mecanicii care stabilește legile de bază ale mișcării mecanice și ale interacțiunii mecanice a corpurilor materiale. Mișcare mecanică se numește schimbarea în timp a poziției relative în spațiu a corpurilor materiale, mecanic interacţiune- o astfel de interacțiune, în urma căreia se modifică mișcarea mecanică sau se modifică poziția relativă a părților corpului.

Mecanica teoretică este de obicei împărțită în: statica, cinematica si dinamica .

În statică se studiază condițiile echilibru corpuri materiale şi metode de transformare identică a sistemului de forţe. Echilibru O stare în care un corp rămâne staționar sau se mișcă uniform în linie dreaptă sub acțiunea forțelor.

În cinematică se iau în considerare caracteristicile geometrice generale ale mișcării corpurilor. Forțele care acționează asupra corpului nu sunt luate în considerare. Legea mișcării este dată. Legea mișcării corpului este dependența de timp a poziției corpului în spațiu.

În dinamică se studiază legile generale ale mișcării corpurilor sub acțiunea forțelor.

1. C tatika corp solid

1.1 Concepte de bază ale staticii

corp absolut rigid (corp rigid, corp)- un corp material, distanța dintre orice puncte în care nu se modifică. În consecință, dimensiunea și forma corpului nu se schimbă.

Punct material este un corp ale cărui dimensiuni, în funcție de condițiile problemei, pot fi neglijate.

corp liber- un corp, asupra căruia nu se impun restricții.

Corp neliber (legat).– un corp a cărui mișcare este restricționată.

Conexiuni- corpuri care impiedica miscarea obiectului luat in considerare (un corp sau un sistem de corpuri).

sistem mecanic- un set de corpuri interconectate sau puncte materiale.

Un corp rigid poate fi considerat ca un sistem mecanic ale cărui poziții și distanțe între puncte nu se modifică.

Putere- o mărime vectorială care caracterizează acţiunea mecanică a unui corp material asupra altuia.

Forța ca vector este caracterizată de punctul de aplicare, direcția de acțiune și valoarea absolută (Fig. 1.1). Unitatea de măsură pentru modulul de forță este Newton.

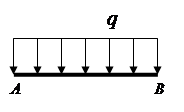Fig.1.1. Fig.1.2.

linie de forţă este linia dreaptă de-a lungul căreia este îndreptat vectorul forță.

Putere concentrată este forța aplicată într-un punct.

Forțe distribuite (sarcină distribuită)- forte care actioneaza in toate punctele volumului, suprafetei sau lungimii corpului (Fig. 1.2).

Sarcina distribuită este stabilită de forța care acționează pe unitatea de volum (suprafață, lungime).Dimensiunea sarcinii distribuite este N / m 3 (N / m 2, N / m).

Forta externa este o forță care acționează dintr-un corp care nu aparține sistemului mecanic considerat.

Forta interioara- acționează forța asupra punct material sistem mecanic din partea unui alt punct material aparţinând sistemului în cauză.

Sistemul de forță- un set de forte care actioneaza asupra unui sistem mecanic.

Sistem plat de forțe- un sistem de forțe ale căror linii de acțiune se află în același plan.

Sistemul spațial de forțe- un sistem de forțe ale căror linii de acțiune nu se află în același plan.

Sistemul de forțe convergente- un sistem de forţe ale căror linii de acţiune se intersectează într-un punct (fig. 1.3).

Sistem arbitrar de forțe- un sistem de forțe ale căror linii de acțiune nu se intersectează într-un punct (fig. 1.4).

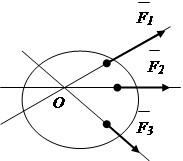Fig.1.3 Fig.1.4

Sisteme de forțe echivalente- astfel de sisteme de forțe, a căror înlocuire unul cu altul nu schimbă starea mecanică a corpului. Notare acceptată:

Sistem echilibrat de forțe- un sistem de forțe care, atunci când este aplicat unui corp solid liber, nu își schimbă starea mecanică (nu îl dezechilibrează).

forță rezultantă- o forță a cărei acțiune asupra unui corp este echivalentă cu acțiunea unui sistem de forțe.

Moment de putere- o valoare care caracterizează capacitatea de rotație a forței.

Cuplu de putere- un sistem de două forțe paralele, egale în valoare absolută, direcționate opus. Denumirea acceptată este (). Sub acțiunea unei perechi de forțe, corpul va efectua mișcare de rotație.

Proiecția forței pe axă- un segment închis între perpendiculare trasate de la începutul și sfârșitul vectorului forță pe această axă (Fig. 1.5).

Proiecția este pozitivă dacă direcția segmentului coincide cu direcția pozitivă a axei.

Proiecția forței pe un plan- un vector pe un plan închis între perpendiculare trasate de la începutul și sfârșitul vectorului forță până în acest plan (Fig. 1.6).

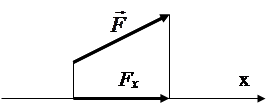
Fig.1.5 Fig.1.6

1.2. Axiomele staticii

Principiile teoretice ale staticii se bazează pe o serie de axiome. O axiomă este o lege formulată ca urmare a generalizării rezultatelor observațiilor.

1. Axioma echilibrului.

Două forțe care acționează asupra unui corp rigid sunt echilibrate numai dacă sunt egale în valoare absolută și acționează de-a lungul unei linii drepte în direcții opuse (Fig. 1.7).

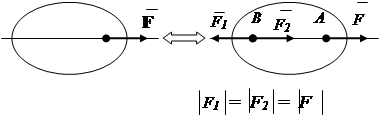
Fig.1.7 Fig.1.8

2. Axioma adunării (excluderii) a unui sistem echilibrat de forțe.

Acțiunea unui sistem de forțe asupra unui corp rigid nu se va modifica dacă la acesta se adaugă sau se exclude un sistem echilibrat de forțe (Fig. 1.8).

3. Axioma despre paralelogramul de forțe.

Un sistem de două forțe aplicate într-un punct al unui corp rigid are o forță rezultantă aplicată în același punct. Vectorul rezultant este diagonala paralelogramului construit pe aceste forțe (Fig. 1.9).

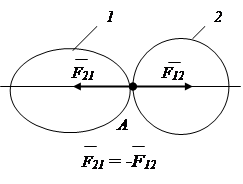
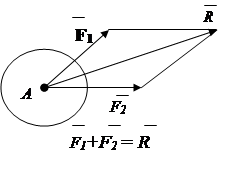
Orez. 1.9 Fig.1.10

4. Axioma contracarării.

Când un corp solid acţionează asupra altuia, apare o forţă de reacţie, egală în valoare absolută, opusă forţei care acţionează (fig. 1.10).

Notă. Forța a cărei acțiune este dată se numește forță activă, forța de reacție se numește reacţie .

5. Axioma conexiunilor.

Orice corp neliber poate fi considerat ca fiind liber, dacă este eliberat mental de legături, înlocuindu-și acțiunea cu reacțiile corespunzătoare.

1.3 Legături și reacțiile lor

Corpurile care împiedică mișcarea obiectului luat în considerare vor fi numite constrângeri. Se numește forța cu care acționează legătura asupra obiectului în cauză reacție de legătură. Atunci când se determină posibile reacții de cuplare, ar trebui să se pornească de la faptul că reacția este o forță care împiedică mișcarea corpului în cauză. Reacția este îndreptată în direcția opusă acolo unde conexiunea nu permite corpului să se miște.

Să ne uităm la câteva conexiuni comune.

Suprafață netedă restricționează mișcarea de-a lungul normalului la suprafața de sprijin. Reacția este îndreptată perpendicular pe suprafață (Fig. 1.11).

Suport mobil articulat limitează mișcarea corpului de-a lungul normalului la planul de referință. Reacția este direcționată de-a lungul normalei la suprafața de sprijin (Fig. 1.12)

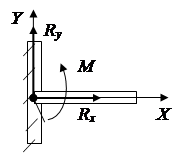
Suport fix articulat contracarează orice mișcare într-un plan perpendicular pe axa de rotație. În calcule, reacția Fr, de regulă, este prezentată ca două componente de-a lungul axelor X și Y (Fig. 1.13).

Lansetă articulată fără greutate contracarează mișcarea corpului de-a lungul liniei tijei. Reacția va fi direcționată de-a lungul liniei tijei (Fig. 1.14).

Terminare oarbă contracarează orice mișcare și rotație în plan (Fig. 1.15). Actiunea sa poate fi inlocuita cu o forta prezentata sub forma a doua componente si o pereche de forte cu un moment.

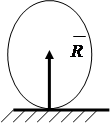Fig.1.11 1.12 Fig.1.13 Fig.1.14 Fig.1.15

1.4 Moment despre un punct

Sub acțiunea unei forțe, un corp rigid, împreună cu mișcarea de translație, se poate roti în jurul unui anumit centru. Capacitatea de rotație a unei forțe este caracterizată de un moment de forță. Efectul de rotație al forței depinde de modulul forței, de distanța de la centru până la linia de acțiune a forței și de direcția de rotație în planul de rotație.

Valoarea absolută a momentului este egală cu produsul dintre modulul de forță și distanța cea mai scurtă h de la centrul de rotație la linia de acțiune a forței. Distanţă h numit umărul forţei (Fig. 1.16).

M0 () = F× h , (1.1)

Momentul este considerat pozitiv dacă forța tinde să rotească brațul hîn sens invers acelor de ceasornic și negativ când se rotește în sensul acelor de ceasornic.

Proprietățile momentului de forță despre un punct:

1. Momentul forței nu se va schimba atunci când punctul de aplicare al forței este deplasat de-a lungul liniei de acțiune a forței.

2. Momentul forței este egal cu zero dacă linia de acțiune a forței trece prin punctul de aplicare al forței.

3. Momentul forței rezultante în jurul unui punct este egală cu suma momente ale termenilor de forţe despre acest punct.

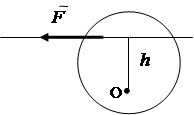Fig.1.16. Fig.1.17.

1.5. Moment de forță în jurul axei

Momentul de forță în jurul unei axe este momentul de proiecție a acestei forțe pe un plan perpendicular pe axa, raportat la punctul de intersecție al axei cu planul.

Momentul este considerat pozitiv dacă, de la capătul pozitiv al axei, rotația pe care forța încearcă să o facă este văzută ca având loc în sens invers acelor de ceasornic și negativă dacă este în sensul acelor de ceasornic.

. (1.3)

Pentru a găsi momentul forței în jurul axei, aveți nevoie (Figura 1.17);

1. Desenați un plan perpendicular pe axa z.

2. Proiectați forța pe acest plan și calculați valoarea de proiecție.

3. Ține-ți de umăr h de la punctul de intersecție a axei cu planul până la linia de acțiune a proiecției forței și calculați lungimea acesteia.

4. Aflați produsul acestui umăr și proiecția forței cu semnul corespunzător /

Proprietățile momentului de forță față de o axă

Momentul de forță în jurul axei este zero dacă:

1. , adică forța este paralelă cu axa.

2. h =0 , adică linia de acţiune a forţei intersectează axa.

1.6. Momentul unei perechi de forțe

O pereche de forțe exercită un efect de rotație asupra corpului. Momentul unei perechi de forțe este egal cu produsul unei forțe cu cea mai scurtă distanță dintre liniile de acțiune ale forțelor perechii, care se numește umărul perechii (Fig. 1.18)

, (1.4)

unde: - forţele care alcătuiesc perechea;

h- umărul cuplului

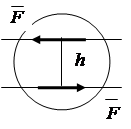Fig.1.18.

Momentul cuplului este considerat pozitiv dacă forțele tind să rotească brațul în sens invers acelor de ceasornic.

Proprietățile cuplului de forță

1. Suma proiecțiilor forțelor unei perechi pe orice axă este zero.

2. Fără a modifica momentul perechii, puteți modifica simultan valoarea forțelor și, respectiv, umărul perechii.

3. O pereche poate fi transferată în planul acțiunii sale, în timp ce efectul perechii asupra corpului nu se va schimba.

1.7. Transformarea identică a sistemelor de forțe

Transformarea se poate face grafic sau analitic.

1.7.1. Transformarea unui sistem convergent de forțe

Rezultat R a două forțe convergente se găsește pe baza axiomei paralelogramului de forțe. (fig.1.9). Suma geometrică a oricărui număr de forțe convergente poate fi determinată prin adăugarea succesivă a două forțe (Fig. 1.19) - metoda poligonului vectorial.

Concluzie : sistem de forțe convergente ( n ) se reduce la o forță rezultantă .

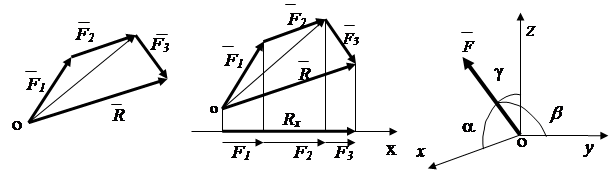
Fig.1.19 Fig.1.20. Fig.1.21.

Analitic, forța rezultantă poate fi determinată prin proiecțiile sale pe axele de coordonate

, (1.5)

Conform teoremei: proiecția rezultantei pe axă este egală cu suma proiecțiilor termenilor forțelor pe această axă (Fig. 1.20). Rx = F 1 X + F 2 X + F 3 X, sau în general

R X = å F kx (1.6)

Ținând cont de (1.6), rezultanta este determinată de expresie

Direcția vectorului rezultant este determinată de cosinusurile unghiurilor dintre vector și axe X , y, z(fig.1.20)

1.7.2. Transformarea unui sistem arbitrar de forțe .

Este imposibil să se aplice regula forțelor paralelogramului direct unui sistem arbitrar de forțe, deoarece liniile de acțiune ale forțelor nu se intersectează într-un punct. Anterior, sistemul de forțe este adus la un centru pe baza teoremei privind transferul paralel de forță.

Teorema: o forță aplicată unui corp rigid poate, fără a-și modifica acțiunea, să fie transferată în paralel cu un alt punct al corpului, adăugând în același timp o pereche de forțe cu un moment egal cu momentul forței transferate față de punctul în care se află transferat (Fig. 1.22).

În urma acestei transformări se obține un sistem de forțe convergent și suma momentelor perechilor de forțe. Acțiunea sistemului de forțe convergente este înlocuită cu acțiunea forței totale, acțiunea momentelor - cu momentul total. Se numește vectorul total * vector principal sisteme de forță, moment total * - a scoate in evidenta sisteme de forță.

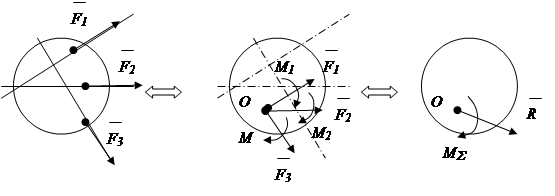
Fig.1.22

Concluzie: un sistem arbitrar de forţe ca urmare a unei transformări identice se reduce la vectorul principal * și punctul principal * sisteme de forță.

Analitic vector principal iar momentul principal al sistemului de forţe poate fi determinat prin proiecţiile acestora pe axele de coordonate

1.8 Condiții pentru echilibrul sistemelor de forțe

1.8.1. Echilibrul unui sistem de forțe convergente

Prin definiție (vezi clauza 1.1), acțiunea unui sistem de forțe convergente este echivalentă cu acțiunea unei forțe rezultante. Pentru echilibrul corpului, este necesar și suficient ca rezultatul să fie egal cu zero = 0.

Din formula (1.7) rezultă că pentru echilibrul unui sistem spațial de forțe convergente este necesar și suficient ca suma proiecțiilor tuturor forțelor asupra axele X,Y,Z a fost egal cu zero

å F kx = 0

å Fky= 0 (1,10) Fk z = 0

Pentru echilibrul unui sistem de forțe convergent plat, este necesar și suficient ca suma proiecțiilor tuturor forțelor pe axele X, Y să fie egală cu zero.

å F kx = 0

å Fky = 0 (1.11)

1.8.2. Echilibrul unui sistem arbitrar de forțe.

Acțiunea unui sistem arbitrar de forțe este echivalentă cu acțiunea vectorului principal și a momentului principal. Pentru echilibru, este necesar și suficient ca condiția

Pentru echilibrul unui sistem arbitrar de forțe, este necesar și suficient ca suma proiecțiilor tuturor forțelor pe axele X, Y, Z și suma momentelor tuturor forțelor raportate la axele X,Y,Z au fost egale cu zero.

å F kx = 0

å Fky = 0

å Fkz = 0 (1.13)

å M x(k) = 0

å M y(k) = 0

å M z(k) = 0

Pentru echilibrul unui sistem arbitrar de forțe plat, este necesar și suficient ca suma proiecțiilor vectorului principal pe axele X, Y și suma algebrică a momentelor de forțe în jurul centrului O să fie egală cu zero. .

åF ky = 0 (1,14)

EM o (k) = 0

1.9. Întrebări pentru autocontrol în secțiune

1. Dați o definiție a unui corp absolut rigid, a unui punct material, a unei forțe, a unei linii de acțiune a unei forțe, a unui sistem de forțe (plat, spațial, convergent) al unui sistem arbitrar de forțe.

2. Ce se numește proiecția forței pe axă, pe plan?

3. Ce se numește momentul forței, cum se determină momentul forței relativ la un punct?

4. Se modifică momentul forței în raport cu un punct dat când forța este transferată de-a lungul liniei de acțiune a acesteia?

5. În ce caz momentul de forță relativ la un punct dat este egal cu zero?

6. Ce sistem de forțe se numește pereche de forțe, care este momentul unei perechi de forțe?

7. Ce se numește conexiune? Care este principiul eliberării de legături? Enumerați principalele tipuri de conexiuni, arătați reacțiile lor.

8. Care sunt condițiile și ecuațiile pentru echilibrul unui sistem de sisteme de forțe convergente și arbitrare situate în spațiu și în plan?

9. Formulaţi procedura de rezolvare a problemelor de statică.

2. Cinematica

Cinematică- o ramură a mecanicii teoretice, care consideră proprietățile geometrice generale ale mișcării mecanice, ca un proces care se produce în spațiu și timp. Obiectele în mișcare sunt tratate ca puncte geometrice sau corpuri geometrice. În consecință, studiul este împărțit în cinematică punctuală și cinematică a corpului rigid

2.1 Concepte de bază ale cinematicii

Legea mișcării unui punct (corp)- dependenţa de timp a poziţiei unui punct (corp) în spaţiu.

Traiectoria punctului- locul pozițiilor unui punct din spațiu în timpul mișcării acestuia.

Viteza punctului (corpului).- o caracteristică a schimbării în timp a poziţiei unui punct (corp) în spaţiu.

Accelerație punct (corp).- caracteristica schimbării timpului în viteza unui punct (corp)

2.2. Cinematica punctuală

2.2.1 Metode de specificare a mișcării punctului

A seta mișcarea unui punct înseamnă a seta o modificare a poziției acestuia față de sistemul de referință ales. Există trei sisteme principale de referință: vector, coordonat, natural. În consecință, există trei moduri de a specifica mișcarea unui punct.

Într-un sistem vectorial, poziția unui punct în raport cu originea este dată de vectorul rază (Fig. 2.1). Legea mișcării

Poziția unui punct în sistemul de coordonate OXYZ este dată de trei Coordonatele X,Y,Z(fig.2.2). Legea mișcării X = X ( t ), y = y ( t ), z = z ( t ).

Poziția unui punct în sistemul natural de referință este dată de distanță S de la origine până în acest punct de-a lungul traiectoriei (Fig. 2.3). Legea mișcării s = s ( t ).

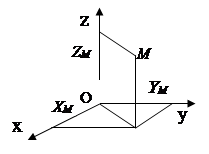Fig.2.1 Orez. 2.2 Fig.2.3

Mișcarea unui punct în modul natural de precizare a mișcării este determinată dacă se cunosc următoarele:

1. Traiectoria mișcării.

2. Începutul și direcția de numărare a coordonatei arcului.

3. Ecuația mișcării.

Cu metoda naturală de specificare a mișcării, spre deosebire de alte metode, sunt utilizate axe de coordonate mobile, deplasându-se împreună cu punctul de-a lungul traiectoriei. Astfel de axe sunt (Fig. 2.4).

Tangenta () - direcționată în direcția de creștere a coordonatelor arcului tangențial la traiectorie.

principal normal ( P) este îndreptată spre concavitatea curbei.

binormal ( în) este îndreptată perpendicular pe axele t, n.

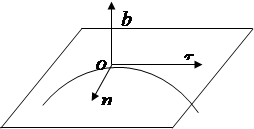Orez. 2.4

2.2.2 Determinarea caracteristicilor cinematice ale unui punct

Traiectoria punctului

În sistemul de referință vectorială, traiectoria este descrisă prin expresie

În sistemul de referință de coordonate, traiectoria este determinată conform legii mișcării punctului și este descrisă de expresiile z = f ( X , y ) - în spațiu, sau y = f(x) - în plan.

Într-un sistem de referință natural, traiectoria este predeterminată.

Viteza punctului

Conform definiției (vezi paragraful 2.1), viteza caracterizează schimbarea în timp a poziției unui punct (corp) în spațiu.

Determinarea vitezei unui punct dintr-un sistem de coordonate vectoriale

Când se specifică mișcarea unui punct într-un sistem de coordonate vectoriale, raportul dintre mișcare și un interval de timp se numește valoarea medie a vitezei în acest interval de timp.

Luând intervalul de timp ca valoare infinitezimală, se obține valoarea vitezei în acest moment timp (valoarea vitezei instantanee)

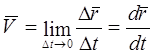(2.1)

Vectorul viteză medie este direcționat de-a lungul vectorului în direcția mișcării punctului, vectorul viteză instantanee este direcționat tangențial la traiectoria în direcția mișcării punctului (Fig. 2.5).

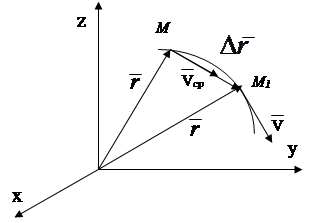Fig.2.5

Concluzie: viteza unui punct este o mărime vectorială egală cu derivata legii mișcării în raport cu timpul.

Notăm și folosim în continuarea raționamentului următoarea proprietate a derivatei : derivata în timp a unei mărimi determină rata de modificare a acelei mărimi.

Determinarea vitezei unui punct într-un sistem de referință de coordonate

Pe baza proprietății derivatei, determinăm viteza de modificare a coordonatelor punctului

Modulul vitezei maxime a unui punct cu un sistem de coordonate dreptunghiular va fi egal cu

(2.3)

Direcția vectorului viteză este determinată de cosinusurile unghiurilor de direcție

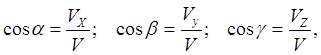
unde sunt unghiurile dintre vectorul viteză și axele de coordonate.

Determinarea vitezei unui punct dintr-un sistem de referință natural

Viteza unui punct într-un sistem de referință natural este definită ca derivata legii mișcării unui punct

V = (2.4)

Conform concluziilor anterioare, vectorul viteză este direcționat tangențial la traiectorie în direcția mișcării punctului și în axe. n.b. determinat de o singură proiecţie.

accelerație punctuală

Prin definiție, accelerația caracterizează schimbarea vitezei, adică. rata de schimbare a vitezei.

Accelerațiile unui punct într-un cadru de referință vectorial

Pe baza proprietății derivatului

Vectorul viteză se poate schimba în mărime și direcție. Pentru a determina incrementul unui vector, potrivim începuturile vectorilor (Fig.2.6). Vectorul accelerație este îndreptat de-a lungul liniei de creștere a vectorului viteză, adică spre curbura traiectoriei.

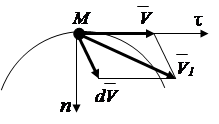
Fig.2.6

Accelerația unui punct într-un sistem de referință de coordonate

Accelerația modificării coordonatelor unui punct este egală cu derivata în timp a ratelor de modificare a acestor coordonate

un x =; Ay =; a z = .

Accelerația totală într-un sistem de coordonate dreptunghiular va fi determinată de expresie

A = , (2.6)

Cosinusurile de direcție ale vectorului accelerație

.

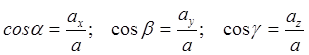Accelerația unui punct în sistemul de referință natural

Creșterea vectorului viteză (Fig. 2.7) poate fi descompusă în componente paralele cu axele sistem natural coordonate

, (2.7)

Împărțirea părților stângă și dreaptă ale egalității (2.7) la dt, primim

, (2.8)

unde: - accelerația tangențială, (2.9)

Accelerație normală, (vezi derivația, articolul 43)

unde R este raza de curbură a traiectoriei în vecinătatea punctului

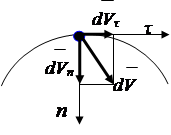Orez. 2.7

2.3. Cinematica corpului rigid

Spre deosebire de cinematica unui punct, în cinematica corpurilor rigide sunt rezolvate două sarcini principale:

Stabilirea mișcării și determinarea caracteristicilor cinematice ale corpului în ansamblu;

Determinarea caracteristicilor cinematice ale punctelor corpului.

Metodele de stabilire și de determinare a caracteristicilor cinematice depind de tipurile de mișcare a corpurilor.

În acest manual, sunt luate în considerare trei tipuri de mișcare: de translație, de rotație în jurul unei axe fixe și mișcare plan-paralelă a unui corp rigid

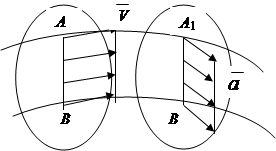
2.3.1. Mișcarea de translație a unui corp rigid

Translația este o mișcare în care o linie dreaptă trasată prin două puncte ale corpului rămâne paralelă cu poziția inițială (Fig. 2.8).

Teorema demonstrată: în mișcarea de translație, toate punctele corpului se mișcă pe aceleași traiectorii și în fiecare moment de timp au aceeași viteză și accelerație în valoare și direcție absolută (Fig. 2.8).

Concluzie: Mișcarea de translație a unui corp rigid este determinată de mișcarea oricăruia dintre punctele sale și, prin urmare, sarcina și studiul mișcării sale sunt reduse la cinematica unui punct.

Orez. 2.8 Fig. 2.9

2.3.2 Mișcarea de rotație a unui corp rigid în jurul unei axe fixe.

Rotația în jurul unei axe fixe este mișcarea unui corp rigid, în care două puncte aparținând corpului rămân staționare pe toată durata mișcării.

Poziția corpului este determinată de unghiul de rotație j (fig. 2.9). Unitatea de măsură pentru un unghi este radianii. (radian - colțul central un cerc a cărui lungime a arcului este egală cu raza, unghi complet cercul conține 2p radiani.)

Legea mișcării de rotație a unui corp în jurul unei axe fixe j = j(t). Viteza unghiulară și accelerația unghiulară a corpului vor fi determinate prin metoda diferențierii

Viteza unghiulara, rad/s; (2,10)

Accelerație unghiulară, rad/s 2 (2,11)

La mișcare de rotație corpurile în jurul unei axe fixe, punctele sale care nu se află pe axa de rotație se deplasează în cercuri centrate pe axa de rotație.

Dacă tăiem corpul cu un plan perpendicular pe axă, alegeți un punct pe axa de rotație DINși punct arbitrar M, apoi punct M va descrie în jurul punctului DIN cerc cu raza R(Fig. 2.9). Pe parcursul dt există o rotație elementară prin unghiul , în timp ce punctul M se va deplasa de-a lungul traiectoriei pe o distanță. Să determinăm modulul de viteză liniară:

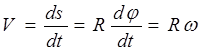(2.12)

accelerație punctuală M pentru că o traiectorie cunoscută este determinată de componentele sale, vezi (2.8)

,

Înlocuind expresia (2.12) în formule, obținem:

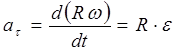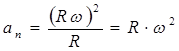, ., (2.13)

unde: - accelerația tangențială,

Accelerație normală.

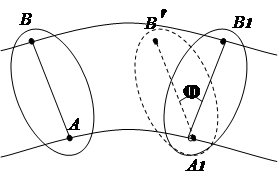
2.3.3. Mișcarea plan-paralelă a unui corp rigid

Plan-paralel este mișcarea unui corp rigid, în care toate punctele sale se mișcă în planuri paralele cu un plan fix (Fig. 2.10). Pentru a studia mișcarea unui corp, este suficient să studiem mișcarea unei secțiuni S acest corp printr-un plan paralel cu planul fix. mișcarea secțiunii Sîn planul său poate fi considerat ca unul complex, format din două mişcări elementare: a) de translaţie şi de rotaţie; b) rotaţional faţă de centrul mobil (instantaneu).

În prima variantă mișcarea secțiunii poate fi dată de ecuațiile de mișcare a unuia dintre punctele sale (polul) și rotația secțiunii în jurul stâlpului (fig. 2.11). Orice punct al secțiunii poate fi luat drept stâlp.

Orez. 2.10 Fig. 2.11

Ecuațiile mișcării se vor scrie astfel:

X A = X A ( t )

Y DAR = Y DAR ( t ) (2.14)

j DAR = j DAR ( t )

Caracteristicile cinematice ale polului sunt determinate din ecuațiile mișcării acestuia.

Viteza oricărui punct al unei figuri plane care se mișcă în propriul plan este suma vitezei polului (aleasă în mod arbitrar în secțiunea punctului DAR) și viteza de rotație în jurul polului (rotația punctului LAîn jurul punctului DAR).

Accelerația unui punct al unei figuri plate în mișcare este suma accelerației polului în raport cu cadrul fix de referință și a accelerației datorate mișcării de rotație în jurul polului.

(2.15)

(2.16)

În a doua variantă mișcarea secțiunii este considerată ca rotațională în jurul centrului mobil (instantaneu). P(Fig. 1.12). În acest caz, viteza oricărui punct B al secțiunii va fi determinată de formula pentru mișcarea de rotație

(2.17)

Viteza unghiulară în jurul centrului instantaneu R poate fi determinat dacă viteza oricărui punct al secțiunii este cunoscută, de exemplu, punctul A.

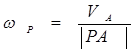(2.18)

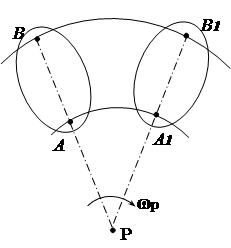
Fig.2.12

Poziția centrului instantaneu de rotație poate fi determinată pe baza următoarelor proprietăți:

Vectorul viteză al punctului este perpendicular pe rază;

Modulul de viteză al unui punct este proporțional cu distanța de la punct la centrul de rotație ( V = w ∙ R) ;

Viteza în centrul de rotație este zero.

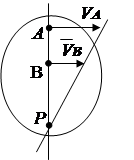
Să luăm în considerare câteva cazuri de determinare a poziției centrului instantaneu.

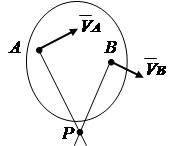
1. Se cunosc direcțiile vitezelor a două puncte ale unei figuri plane (Fig. 2.13). Să desenăm linii de raze. Centru de rotație instantaneu R situat la intersecția perpendicularelor trasate pe vectorii viteză.

2. Sunt cunoscute vitezele punctelor A și B, iar vectorii și sunt paraleli între ei, iar linia AB perpendicular (Fig. 2. 14). În acest caz, centrul de rotație instantaneu se află pe linie AB. Pentru a-l găsi, trasăm o linie de proporționalitate a vitezelor pe baza dependenței V = w R .

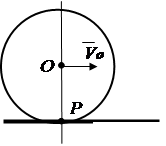
3. Caroseria se rostogolește fără alunecare pe suprafața fixă ​​a altui corp (Fig. 2.15). Punctul de contact al corpurilor în acest moment are viteză zero, în timp ce vitezele altor puncte ale corpului nu sunt egale cu zero. punct de atingere R va fi centrul de rotație instantaneu.

Orez. 2.13 Orez. 2.14 Orez. 2.15

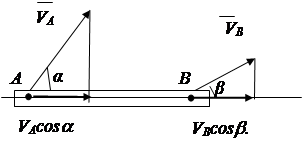
Pe lângă opțiunile luate în considerare, viteza unui punct de secțiune poate fi determinată pe baza teoremei privind proiecțiile vitezelor a două puncte ale unui corp rigid.

Teorema: proiecțiile vitezelor a două puncte ale unui corp rigid pe o linie dreaptă trasată prin aceste puncte sunt egale și egal direcționate .

Dovada: distanta AB nu se poate schimba, prin urmare

VȘi cosa nu poate fi mai mult sau mai puțin VÎn cosb (Fig. 2.16).

Orez. 2.16

Concluzie: V DAR cosa= V LA cosb. (2,19)

2.4. Mișcare complexă a punctului

În paragrafele precedente s-a luat în considerare mișcarea unui punct față de un cadru fix de referință, așa-numita mișcare absolută. În practică, există probleme în care este cunoscută mișcarea unui punct în raport cu un sistem de coordonate, care se mișcă în raport cu un sistem fix. În acest caz, este necesară determinarea caracteristicilor cinematice ale punctului în raport cu sistemul fix.

Se obișnuiește să se numească: mișcarea unui punct în raport cu un sistem în mișcare - relativ, mișcarea unui punct împreună cu sistemul de mișcare - portabil, mișcarea unui punct în raport cu un sistem fix - absolut. În consecință, vitezele și accelerațiile se numesc:

relativ; - figurat; -absolut.

Conform teoremei adiției vitezei, viteza absolută a unui punct este egală cu suma vectorială a vitezelor relative și de translație (Fig.).

, (2.20)

Valoarea absolută a vitezei este determinată de legea cosinusurilor

, (2.21)

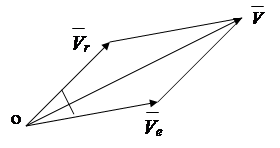
Fig.2.17

Accelerația conform regulii paralelogramului este determinată de numai în mişcare de translaţie

, (2.22)

Cu mișcarea portabilă netranslațională, apare o a treia componentă a accelerației, numită rotativă sau Coriolis.

, (2.23)

Unde

Accelerația Coriolis este numeric egală cu

,

unde a este unghiul dintre vectori și

Este convenabil să se determine direcția vectorului de accelerație Coriolis conform N.E. Jukovski: proiectați vectorul pe un plan perpendicular pe axa de rotație de translație, rotiți proiecția cu 90 de grade în direcția de rotație de translație. Direcția rezultată va corespunde cu direcția accelerației Coriolis.

2.5 Întrebări pentru autocontrol în secțiune

1. Care sunt principalele sarcini ale cinematicii? Numiți caracteristicile cinematice.

2. Numiți metodele de precizare a mișcării unui punct și de determinare a caracteristicilor cinematice.

3. Dați o definiție a mișcării de translație, rotație în jurul unei axe fixe, plan-paralel a unui corp.

4. Cum este specificată mișcarea unui corp rigid în timpul translației, rotației în jurul unei axe fixe și mișcării plan-paralele a corpului și cum se determină viteza și accelerația unui punct în timpul acestor mișcări ale corpului?

3. Dinamica

3.1 Probleme de dinamică

Două tipuri de probleme sunt rezolvate în dinamică. Primul este de a defini forte active dată fiind legea mișcării unui obiect material (punct sau sistem). A doua sarcină este inversul primei: legea de mișcare a unui obiect material este determinată cu forțe cunoscute care acționează asupra acestuia.

3.2. Concepte de bază ale dinamicii

inerţie- proprietatea corpurilor materiale de a menține o stare de repaus sau o mișcare rectilinie uniformă până când forțele externe schimbă această stare.

Greutate- o măsură cantitativă a inerției corpului. Unitatea de masă este kilogramul (kg).

Punct material- un corp cu o masă ale cărui dimensiuni sunt neglijate la rezolvarea acestei probleme.

Centrul de masă al unui sistem mecanic- un punct geometric ale cărui coordonate sunt determinate de formule.

Unde m k , x k , y k , z k- masa și coordonatele lui k - acel punct al sistemului mecanic,

m este masa sistemului.

Într-un câmp uniform de greutate, poziția centrului de masă coincide cu poziția centrului de greutate.

Momentul de inerție al unui corp material în jurul axei este o măsură cantitativă a inerției în timpul mișcării de rotație.

Momentul de inerție al unui punct material în jurul axei este egal cu produsul dintre masa punctului și pătratul distanței punctului față de axă.

J Z = m × r 2 (3.2)

Momentul de inerție al sistemului (corpului) în jurul axei este egal cu suma aritmetică a momentelor de inerție ale tuturor punctelor.

J Z = å m k × rk 2 (3.3)

Forța de inerție a unui punct material- o mărime vectorială egală în valoare absolută cu produsul dintre masa unui punct și modulul de accelerație și direcționată opus vectorului accelerație

(3.4)

Forța de inerție a unui corp material- o mărime vectorială egală în valoare absolută cu produsul dintre masa corporală și modulul de accelerație al centrului de masă al corpului și îndreptată opus vectorului de accelerație al centrului de masă

, (3.5)

unde este accelerația centrului de masă al corpului.

Impulsul de forță elementară- mărime vectorială egală cu produsul vectorului forță cu un interval de timp infinitezimal dt

, (3.6)

Forța totală de impuls pentru D t este egală cu integrala impulsurilor elementare

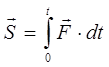(3.7)

munca elementara putere- cantitatea scalară dA, egal cu produsul scalar al vectorului forță și deplasarea infinitezimală d .

Produsul scalar al vectorilor este egal cu produsul modulelor lor și cosinusul unghiului dintre direcțiile vectorilor.

dA = F × ds × cos A , (3.8)

unde a este unghiul dintre direcțiile vectorilor de deplasare și forță.

Lucrul forței asupra deplasării finale a punctului de aplicare a acesteia este egal cu integrala muncii elementare, preluată deplasarea.

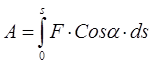(3.9)

Unitatea de lucru este Joule (1 J=1 N×m).

Cantitatea de mișcare a unui punct material- o mărime vectorială egală cu produsul dintre masa m și viteza acesteia.

Momentul unui sistem mecanic este egal cu suma vectorială a impulsului punctelor sale.

(3.11)

sau luând în considerare formulele (3.1).

unde: m este masa sistemului mecanic,

Vectorul viteză al centrului de masă al sistemului.

Energia cinetică a unui punct material- valoarea scalară T, egală cu jumătate din produsul dintre masa punctului și pătratul vitezei acestuia.

T = (3.13)

Energia cinetică a unui sistem mecanic este egală cu suma energiile cinetice toate punctele sale.

3.3. Axiomele dinamicii

Prima axiomă este legea inerției .

Dacă nu acționează nicio forță asupra unui punct material liber sau un sistem echilibrat de forțe acționează, atunci punctul va fi în repaus sau mișcare rectilinie uniformă.

A doua axiomă este legea proporționalității accelerației .

Accelerația dată unui punct material de forța care acționează asupra acestuia este proporțională cu această forță și coincide în direcția cu direcția forței.

Se numește expresia (3.15). legea fundamentală a dinamicii .

A treia axiomă este legea contraacțiunii .

Forțele cu care două puncte materiale acționează unul asupra celuilalt sunt egale în valoare absolută și sunt direcționate de-a lungul liniei drepte care leagă aceste puncte în direcții opuse

A patra axiomă este legea independenței acțiunii forțelor .

Când un sistem de forțe acționează asupra unui punct material, accelerația totală a acestui punct este egală cu suma geometrică a accelerațiilor din acțiunea fiecărei forțe.

3.4. Ecuații diferențiale ale dinamicii

Ecuațiile diferențiale ale mișcării unui punct relaționează accelerația unui punct de forțele care acționează asupra acestuia. De fapt, ecuațiile diferențiale sunt o înregistrare a legii de bază a dinamicii într-o formă diferențială explicită.

Pentru mișcarea absolută a unui punct (mișcarea într-un cadru de referință inerțial), ecuația diferențială are forma

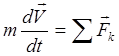, (3.18)

Ecuația vectorială (3.17) poate fi scrisă în proiecții pe axele unui sistem de coordonate inerțiale dreptunghiulare

,

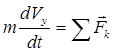, (3.19)

,

Cu o traiectorie cunoscută a punctului, ecuația (3.18) poate fi scrisă în proiecții pe axele sistemului natural de coordonate

, (3.20)

Ținând cont de (2.8), ecuațiile iau forma

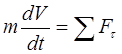(3.21)

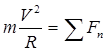
3.5 Teoreme generale ale dinamicii

Teoremele generale de dinamică stabilesc relația dintre măsurile mișcării mecanice și interacțiunea mecanică. Concluziile teoremelor sunt rezultatul unei transformări identice a legii de bază a dinamicii.

Teorema privind modificarea impulsului : modificarea impulsului unui punct material (sistem mecanic) într-o perioadă finită de timp este egală cu suma impulsurilor forțe externe pentru aceeași perioadă de timp

- pentru un punct material; (3,22)

- pentru sistemul mecanic. (3,23)

Teorema schimbării energiei cinetice : modificarea energiei cinetice a unui punct (sistem mecanic) în timpul mișcării acestuia este egală cu suma muncii tuturor forțelor externe care acționează asupra acestei mișcări

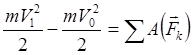- pentru un punct material (3.24)

- pentru un sistem mecanic (3.25)

Energia cinetică a unui sistem mecanic este determinată în conformitate cu (3.14), în timp ce următoarele dependențe sunt derivate pentru solide

Cu mișcarea de translație a corpului, (3.26)

În timpul mișcării de rotație a corpului, (3.27)

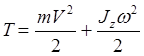- cu o miscare plan-paralela a corpului. (3,28)

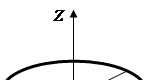
Momentele de inerție ale unor corpuri omogene

Orez. 3.1 Fig.3.2. R Figura 3.3.

Momentul de inerție al cilindrului față de axă (Fig. 3.1.)

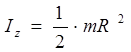
Momentul de inerție al tijei în jurul axei z (Fig. 3.2)

Momentul de inerție al unei plăci dreptunghiulare în jurul axelor x și y (Fig. 3.3)

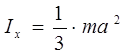
Momentul de inerție al mingii este determinat de formula:

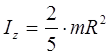
În cazul general, munca forțelor este determinată în conformitate cu (3.8), (3.9).În un număr de cazuri de acțiune a forțelor, munca poate fi determinată de dependențe particulare.

Lucrarea gravitației

Unde: - gravitatie,

Schimbarea poziției corpului pe verticală.

Munca forței în timpul mișcării de rotație a corpului

, (3.30)

unde: - momentul de forta,

Viteza unghiulară a corpului.

Rețineți că munca, ca mărime scalară, poate fi pozitivă sau negativă. Lucrul va fi pozitiv dacă direcția forței coincide cu direcția mișcării.

3.6 principiul d'Alembert

Metodele de mai sus pentru studierea mișcării corpurilor se bazează pe legile lui Newton. Au fost dezvoltate metode bazate pe alte principii. Unul dintre ei este principiul lui d'Alembert.Principiul este formulat: dacă în orice moment se adaugă forțele de inerție la forțele care acționează asupra punctului, atunci sistemul de forțe rezultat va fi echilibrat

, (3.31)

sau pentru sistem mecanic

Principiul d'Alembert face posibil să se aplice mai mult la rezolvarea problemelor de dinamică metode simple statică, deci este utilizat pe scară largă în practica inginerească.

3.7. Întrebări pentru autocontrol în secțiune

1. Formulați principalele sarcini ale dinamicii.

2. Dați definiții de masă, moment de inerție, impuls de forță, lucru de forță, impuls, energie cinetică.

3. Formulați legile de bază ale dinamicii.

4. Ce ecuație se numește ecuație diferențială difuzoare? Care este algoritmul pentru rezolvarea problemelor de dinamică folosind ecuații diferențiale?

5. Formulați teoreme generale de dinamică.

6. Formulaţi principiul d'Alembert. Cum se determină forțele de inerție?

7. Formulați principiul mișcărilor posibile. În ce condiții se aplică principiul posibilelor deplasări?

În acest capitol sunt luate în considerare probleme pentru determinarea muncii efectuate de o forță constantă și a puterii dezvoltate în timpul mișcării de translație și rotație a corpurilor (E. M. Nikitin, § 81-87).

§ 44. Munca și puterea în mișcare de translație

Lucrul unei forțe constante P pe o secțiune dreaptă a traseului s, parcurs de punctul de aplicare al forței, este determinat de formula
(1) A = Ps cos α,
unde α este unghiul dintre direcția forței și direcția mișcării.

La α = 90°
cos α = cos 90° = 0 și A = 0,
adică, munca unei forțe care acționează perpendicular pe direcția de mișcare este zero.

Dacă direcția forței coincide cu direcția de mișcare, atunci α = 0, prin urmare cos α = cos 0 = 1 și formula (1) este simplificată:
(1") A = Ps.

Nu o singură forță, ci mai multe, acționează de obicei asupra unui punct sau asupra unui corp, prin urmare, atunci când rezolvați probleme, este recomandabil să folosiți teorema privind funcționarea sistemului rezultant de forțe (E. M. Nikitin, § 83):
(2) A R = ∑ A i ,
adică, munca rezultantei oricărui sistem de forțe pe o anumită cale este egală cu suma algebrică a muncii tuturor forțelor acestui sistem pe aceeași cale.

Într-un caz particular, când sistemul de forțe este echilibrat (corpul se mișcă uniform și în linie dreaptă), rezultanta sistemului de forțe este egală cu zero și, prin urmare, A R =0. Prin urmare, cu o mișcare uniformă și rectilinie a unui punct sau corp, ecuația (2) ia forma
(2") ∑ Ai = 0,
adică suma algebrică a muncii unui sistem echilibrat de forțe pe o anumită cale este egală cu zero.

În acest caz, forțele al căror lucru este pozitiv se numesc forțe motrice, iar forțele al căror lucru este negativ se numesc forțe de rezistență. De exemplu, când corpul se mișcă în jos - gravitație - forta motrice iar munca sa este pozitivă, iar atunci când corpul se mișcă în sus, gravitația sa este o forță de rezistență, iar munca gravitației este negativă.

La rezolvarea problemelor în cazurile în care forța P este necunoscută, a căror lucru trebuie determinat, se pot recomanda două metode (metode).

1. Folosind forțele specificate în starea problemei, determinați forța P și apoi utilizați formula (1) sau (1") pentru a calcula lucrul acesteia.

2. Fără a determina direct forța P, se determină A p - lucrul forței necesare folosind formulele (2) și (2"), exprimând teorema asupra lucrului rezultantei.

Puterea dezvoltată în timpul lucrului unei forțe constante este determinată de formula
(3) N = A/t sau N = (Ps cos α)/t.

Dacă, la determinarea muncii forței P, viteza punctului v \u003d s / t rămâne constantă, atunci
(3") N = Pv cos α.

Dacă viteza punctului se modifică, atunci s / t \u003d v cf - viteza medie iar apoi formula (2") scade puterea medie
N av = Pv av cos α.

Coeficient acțiune utilă(k.p.d.) când se lucrează poate fi definit ca raportul dintre muncă
(4) η = Un câmp /A,
unde A etaj - lucru util; A este toată munca efectuată sau ca raport al capacităților respective:
(4") η = N etaj /N.

Unitatea de lucru SI este 1 joule (J) = 1 N * 1 m.

Unitatea SI de putere este 1 watt (W) = 1 J / 1 sec.

O unitate populară de putere în afara sistemului este cai putere (CP):
1000 W = 1,36 litri. Cu. sau 1 l. Cu. = 736 W.

Pentru a comuta între wați și cai putere, utilizați formulele
N (kW) = 1,36 N (CP)
N (CP) \u003d 0,736 N (kW).

Curs 2. Lucrare. Putere. Teorema privind modificarea energiei cinetice a unui punct.

Această prelegere acoperă următoarele întrebări:

Munca de forță.

Putere.

Exemple de calcul de lucru.

Energie potențială

Energie kinetică

Teorema privind modificarea energiei cinetice a unui punct.

Teorema momentului.

Studiul acestor probleme este necesar pentru dinamica centrului de masă al unui sistem mecanic, dinamica mișcării de rotație a unui corp rigid, momentul cinetic al unui sistem mecanic, pentru rezolvarea problemelor la disciplinele „Teoria mașinilor și mecanisme” și „Piese de mașini”.

Munca de forță. Putere.

Pentru a caracteriza acțiunea exercitată de o forță asupra unui corp cu o anumită deplasare, se introduce conceptul de lucru al unei forțe.

Fig.16

În acest caz, munca caracterizează acțiunea forței, care determină schimbarea modul viteza punctului de mișcare.

Să introducem mai întâi conceptul de lucru elementar al unei forțe pe o deplasare infinitezimală ds. Lucrul elementar al unei forțe (Fig. 16) este o mărime scalară:

unde este proiecția forței pe tangente la traiectorie îndreptată în direcția deplasării punctului și este deplasarea infinit mică a punctului direcționat de-a lungul acestei tangente.

Această definiție corespunde conceptului de lucru, ca caracteristică a acțiunii unei forțe care duce la modificarea modulului vitezei unui punct. Într-adevăr, dacă descompunem forța în componente și , atunci numai componenta va modifica modulul vitezei punctului, conferind o accelerație tangențială punctului. Componenta sau schimbă direcția vectorului viteză. v(oferă o accelerație normală până la punct), sau, dacă mișcarea nu este liberă, modifică presiunea asupra conexiunii. Componenta nu va afecta modulul de viteză, adică, după cum se spune, forța „nu va produce lucru”.

Observând că, obținem:

. (1)

În acest fel, munca elementara forța este egală cu proiecția forței pe direcția de mișcare a punctului, înmulțită cu deplasarea elementară, sau lucrul elementar al forței este egal cu produsul dintre modulul de forță prin deplasarea elementară și cosinusul forței. unghiul dintre direcția forței și direcția deplasării.

Dacă unghiul este ascuțit, atunci lucrul este pozitiv. În special, pentru munca elementară .

Dacă unghiul este obtuz, atunci lucrul este negativ. În special, pentru munca elementară .

Dacă unghiul , adică dacă forța este direcționată perpendicular pe deplasare, atunci lucrul elementar al forței este zero.

Să găsim o expresie analitică pentru lucrarea elementară. Pentru a face acest lucru, descompunem forța în componente , , în direcțiile axelor de coordonate (Fig. 17; forța în sine nu este prezentată în desen).

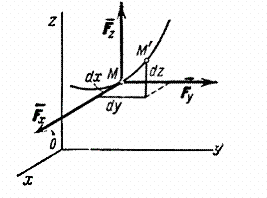
Fig.17

O deplasare elementară este compusă din deplasări , , de-a lungul axelor de coordonate, unde X, y, z - coordonatele punctului M. Atunci lucrul forței asupra deplasării poate fi calculat ca sumă a muncii componentelor sale , , pe deplasări , , .

Dar numai componenta funcționează asupra deplasării, iar munca sa este egală cu . Se lucrează pe deplasări și se calculează în mod similar. In sfarsit gasim:

Formula oferă o expresie analitică pentru munca elementară a unei forțe.

Lucrul efectuat de o forță în orice deplasare finită M 0 M 1 se calculează ca suma integrală a lucrărilor elementare corespunzătoare și va fi egal cu:

sau

.

Prin urmare, munca de forta pe orice deplasare M 0 M 1 este egală cu integrala muncii elementare luate de-a lungul acestei deplasări. Limitele integralei corespund valorilor variabilelor de integrare la puncte M 0 și M 1 .

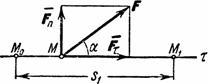
Fig.18

Dacă valoarea este constantă (= const), atunci indicând deplasarea M 0 M 1 prin obținem: .

Un astfel de caz poate avea loc atunci când forța care acționează este constantă în modul și direcție ( F= const), iar punctul în care se aplică forța se deplasează în linie dreaptă (Fig. 18). În acest caz și munca forței .

Unitatea SI pentru lucru este joule (1 j = 1 hm).

Putere.

Putere este mărimea care determină munca efectuată de forță pe unitatea de timp. Dacă munca este făcută uniform, atunci puterea

Unde t - timpul în care lucrarea a fost efectuată A. În general

.

Prin urmare, puterea este egală cu produsul dintre componentele tangenţiale a forţei şi viteza de mişcare.

Unitatea de putere din sistem SI este watt (1 Mar= 1 j/sec).În inginerie, 1 cai putere este adesea luat ca unitate de putere, egală cu 75 kgm/sec sau 736 mar.

Munca efectuată de o mașină poate fi măsurată prin produsul puterii sale și timpul în care a funcționat. Din aceasta a apărut unitatea de măsură a muncii, kilowatt-oră, folosită în mod obișnuit în tehnologie (1 kWh = 3,6j 367100 kgm).

Din ecuație se poate observa că pentru un motor cu o putere dată W, forța de tracțiune va fi cu atât mai mare, cu atât viteza de mișcare este mai mică V. Prin urmare, de exemplu, pe o pantă sau pe o porțiune proastă de drum, mașina include trepte inferioare, care permit, la putere maximă, să se deplaseze cu o viteză mai mică și să dezvolte mai multă tracțiune.

Exemple de calcul de lucru.

Exemplele considerate mai jos oferă rezultate care pot fi utilizate direct în rezolvarea problemelor.

1) Lucrarea gravitației. Lasă punctul M, asupra căruia acționează forța gravitației , se mișcă din poziție M ­ 0 (X­ 0 , la 0 , z 0 ) în poziție M 1 (X 1 , y 1 , z 1 ). Alegem axele de coordonate astfel încât axa Oz a fost îndreptată vertical în sus (Fig. 19).

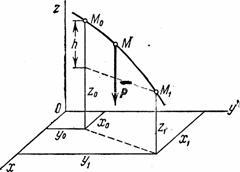
Fig.19

Apoi R x=0, R y=0, P z=- R. Înlocuind aceste valori și luând în considerare variabila de integrare z:

Dacă punct M 0 mai sus M 1 , Unde h- valoarea mișcării verticale a punctului;

Dacă punctul M 0 sub punct M 1 apoi .

În sfârșit obținem: .

În consecință, lucrul gravitației este egal cu produsul dintre modulul de forță, luat cu semnul plus sau minus, și deplasarea verticală a punctului de aplicare a acestuia. Lucrul este pozitiv dacă punctul de început este mai mare decât punctul final și negativ dacă punctul de început este mai mic decât punctul final. Din rezultatul obținut rezultă că munca gravitațională nu depinde de tipul traiectoriei de-a lungul căreia se mișcă punctul de aplicare a acesteia.

Forțele cu această proprietate se numesc forțe potențiale.

2) Lucrul forței elastice. Luați în considerare încărcătura M, culcat pe un plan orizontal și atașat de capătul liber al unui arc (Fig. 20a). Marcați în avion cu un punct O pozitia ocupata de capatul arcului cand acesta nu este solicitat ( este lungimea arcului netensionat) si luam ca origine acest punct. Dacă acum tragem sarcina departe de poziţia de echilibru O, extinzând arcul la o valoare , atunci sarcina va fi acționată de forța elastică a arcului F, îndreptată la obiect O.

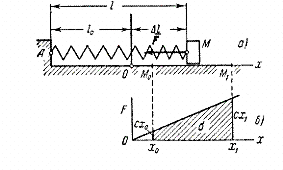
Fig.20

Conform legii lui Hooke, mărimea acestei forțe este proporțională cu alungirea arcului. Deoarece în cazul nostru , atunci modulo .

Coeficient Cu numit factor de rigiditate izvoare. În inginerie, de obicei se măsoară Cuîn h/cm, presupunând coeficient Cu egal numeric cu forța care trebuie aplicată arcului pentru a-l întinde cu 1 cm.

Găsiți munca efectuată de forța elastică la mutarea sarcinii dintr-o poziție în alta . Întrucât în ​​acest caz , , atunci obținem:

(Același rezultat poate fi obținut din graficul dependenței F din X (fig.20, b) calculând aria trapezului umbrită în desen și ținând cont de semnul de lucru.) În formula rezultată, reprezintă alungirea inițială a arcului și prelungirea de capăt a arcului. Prin urmare,

,

acestea. lucrul forței elastice este egal cu jumătate din produsul coeficientului de rigiditate și diferența dintre pătratele alungirilor (sau compresiunilor) inițiale și finale ale arcului.

Lucrul va fi pozitiv când , adică când capătul arcului se deplasează în poziția de echilibru, și negativ când , adică. capătul arcului se îndepărtează de poziția de echilibru. Se poate dovedi că formula rămâne valabilă chiar și în cazul în care deplasarea punctului M nu este liniară.

Astfel, se dovedește că munca forței F depinde numai de valori și și nu depinde de tipul traiectoriei punctului M. Prin urmare, forța elastică este de asemenea potențială.

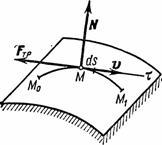
Fig.21

3) Lucrul forței de frecare. Luați în considerare un punct care se deplasează de-a lungul unei suprafețe aspre (Fig. 21) sau o curbă. Forța de frecare care acționează asupra punctului este egală în valoare absolută fN, Unde f este coeficientul de frecare și este reacția normală a suprafeței. Forța de frecare este îndreptată opus deplasării punctului. Prin urmare, F tr = - fN iar conform formulei

.

Dacă forța de frecare este constantă, atunci , Unde s-lungimea arcului de curbă M 0 M 1 de-a lungul căruia se mișcă punctul.

În acest fel, Munca efectuată de forța de frecare de alunecare este întotdeauna negativă. Cantitatea acestui lucru depinde de lungimea arcului M 0 M 1 . Prin urmare, forța de frecare este forța nepotenţial.

4) Lucrul unei forțe aplicate unui corp care se rotește în jurul unei axe fixe.

În acest caz (Fig. 22), punctul de aplicare a forței se deplasează de-a lungul unui cerc de rază r. Lucrări elementare, de (1), , Unde .

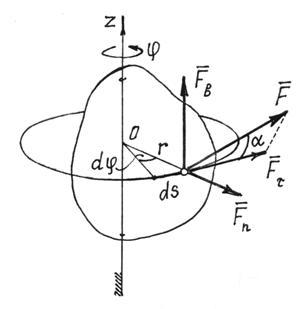
Fig.22

De aceea .

Acest lucru nu este greu de stabilit prin descompunerea forței în trei componente (Fig. 22). (Momentele forțelor și sunt egale cu zero). Mijloace,

(2)

În special, dacă momentul forței în jurul axei , lucrul forței când corpul se rotește printr-un unghi este egal cu

. (3)

Semnul muncii este determinat de semnele momentului de forță și unghiul de rotație. Dacă sunt la fel, munca este pozitivă.

Formula (3) implică și regula pentru determinarea muncii unei perechi de forțe. Dacă un cuplu cu un moment m este situat într-un plan perpendicular pe axa de rotație a corpului, apoi funcționează atunci când corpul se rotește printr-un unghi

Dacă o pereche de forțe acționează într-un plan care nu este perpendicular pe axa de rotație, atunci ea trebuie înlocuită cu două perechi. Unul este plasat în planul perpendicular pe axă, celălalt - în planul paralel cu axa. Momentele lor sunt determinate de expansiunea vectorului moment în direcţiile corespunzătoare: . Desigur, doar prima pereche cu momentul va face treaba, unde este unghiul dintre vector și axa de rotație z,

. (5)

Energie potențială

Partea de spațiu în care o forță care acționează asupra unui punct material plasat acolo, în funcție de locația punctului, se numește câmp de forță.

Mai mult, această forță este determinată folosind funcția de forță u = u(x, y, z). Dacă nu depinde de timp, atunci un astfel de câmp se numește staționar. Dacă este același în toate punctele, atunci câmpul este omogen.

Dacă proiecțiile forței pe axele carteziene sunt derivate parțiale ale funcției de forță față de coordonatele corespunzătoare

atunci un astfel de câmp se numește potențial.

Calculați munca forței câmp potențial la mutarea unui punct dintr-o poziţie M 1 la poziție M 2. (Fig. 23).

Fig.23

munca elementara,

Aceasta este diferența totală a funcției de forță.

Se lucrează la călătoria finală

(7)

Unde u 2 și u 1 – valorile funcției de rezistență la puncte M 2 și M 1 .

Prin urmare, munca forței câmpului potențial nu depinde de traiectoria punctului, ci este determinată numai de valorile funcției de forță în pozițiile inițiale și finale ale punctului.

Desigur, dacă punctul revine la poziția inițială, lucrul forței va fi zero. Lucrarea va fi egală cu zero și la trecerea în alt punct M 3 dacă valoarea funcției de forță este aceeași ca în poziția inițială.

Este ușor de ghicit că punctele cu aceleași valori ale funcției de forță vor forma o suprafață întreagă. Și că câmpul de forță este un spațiu stratificat format din astfel de suprafețe (Fig. 23). Aceste suprafețe se numesc suprafete plane sau suprafete echipotentiale. Ecuațiile lor sunt: u(X, y, z)= C (C- constant, egal cu valoarea u puncte de pe această suprafață). Și funcția de forță se numește, respectiv, potenţial câmpuri.

Desigur, suprafețele echipotențiale nu se intersectează. Altfel, ar exista puncte de câmp cu un potențial nedefinit.

Deoarece, când se deplasează un punct de-a lungul unei suprafețe echipotențiale, munca forței este zero, atunci vectorul forță este perpendicular pe suprafață.

Dintre aceste suprafețe, alegem una și o numim suprafața zero (punem u= u 0 ).

Munca pe care o va face forța atunci când punctul se deplasează dintr-un anumit loc M la suprafața zero se numește energia potențială a punctului din acest loc specific M:

. (8)

observa asta energie potențialăîn același punct al câmpului depinde de alegerea suprafeței zero.

Prin (8) funcția de forță . Prin urmare, proiecțiile forțelor pe axele carteziene, conform (6), deoarece ,

și vector de forță .

Luați în considerare mai multe câmpuri potențiale.

1) Câmp gravitațional.

Aproape de suprafața Pământului, forța gravitațională în toate punctele este aceeași, egală cu greutatea corpului. Aceasta înseamnă că acest câmp de forță este uniform. Deoarece atunci când un punct se mișcă într-un plan orizontal, lucrul forței este zero, suprafețele echipotențiale vor fi plane orizontale (Fig. 24), iar ecuațiile lor: u = z = C.

Fig.24

Dacă planul este atribuit ca suprafață zero xOy, apoi energia potențială a unui punct în poziție M va fi egală cu munca gravitațională:

2) Câmpul de forță elastică.

Când un corp elastic, cum ar fi un arc, este deformat, apare o forță. Adică, în apropierea acestui corp ia naștere un câmp de forțe, ale cărui forțe sunt proporționale cu deformarea corpului și îndreptate către starea nedeformată. La primăvară - până la obiect M 0 , unde se află capătul arcului nedeformat (Fig. 25).

Fig.25

Dacă mutați capătul arcului astfel încât lungimea acestuia să nu se schimbe, atunci munca forței elastice va fi zero. Aceasta înseamnă că suprafețele echipotențiale sunt suprafețe sferice centrate în punctul O.

Atribuiți suprafața zero sferei care trece prin punct M 0 , până la capătul arcului neformat. Apoi energia potențială a arcului în poziție M: .

Cu o astfel de alegere a suprafeței zero, energia potențială va fi întotdeauna pozitivă (P>0), atât în ​​stare întinsă, cât și în cea comprimată.

Teorema privind modificarea energiei cinetice a unui punct.

Luați în considerare un punct cu masă t, deplasându-se sub acţiunea forţelor aplicate acestuia dintr-o poziţie M 0 , unde are viteza , în poziție M 1 , unde viteza sa este .

Pentru a obține dependența dorită, apelăm la ecuația care exprimă legea de bază a dinamicii. Proiectarea ambelor părți ale acestei egalități pe tangenta la traiectoria punctului M,îndreptată în direcția mișcării, obținem:

Valoarea accelerației tangențiale din stânga poate fi reprezentată ca

.

Ca urmare, vom avea:

.

Înmulțind ambele părți ale acestei ecuații cu ds, vom introduce t sub semnul diferenţialului. Apoi, observând că unde - munca elementară de forță F k obţinem expresia teoremei asupra modificării energiei cinetice în formă diferenţială.

Lucrarea gravitației. gravitatie R masa punctuală materială t lângă suprafața Pământului poate fi considerată o constantă, egală cu mg

îndreptată vertical în jos.

Muncă DAR putere Rîn mişcare de la punct M 0 până la punctul M

Unde h = z 0 - z x - înălțimea coborârii punctului.

Munca gravitației este egală cu produsul acestei forțe și înălțimea de coborâre (munca este pozitivă) sau înălțimea de ridicare (munca este negativă). Munca gravitației nu depinde de forma traiectoriei dintre puncte M 0 și M|, iar dacă aceste puncte coincid, atunci munca gravitației este egală cu zero (cazul unui drum închis). Este, de asemenea, egal cu zero dacă punctele M 0 și M se află în același plan orizontal.

Lucrul forței liniare de elasticitate. Forța elastică liniară (sau forța de restabilire liniară) este forța care acționează conform legii lui Hooke (Fig. 63):

F = - Cur,

Unde r- distanta de la punctul de echilibru static, unde forta este nula, pana la punctul considerat M; Cu- constant coeficient - coeficient rigiditate.

A=--().

Conform acestei formule, se calculează lucrul forței elastice liniare. Dacă punct M 0 coincide cu un punct echilibru static O, deci r 0 \u003d 0 și pentru munca forței asupra deplasării din punct O până la punctul M avem

Valoare r- cea mai scurta distanta intre punctul considerat si punctul de echilibru static. O notăm cu λ și o numim deformare. Apoi

Lucrul forței elastice liniare asupra deplasării din starea de echilibru static este întotdeauna negativ și egal cu jumătate din produsul coeficientului de rigiditate și pătratul deformației. Lucrul forței elastice liniare nu depinde de forma deplasării, iar lucrul pe orice deplasare închisă este zero. Este, de asemenea, egal cu zero dacă punctele luși M se află pe aceeași sferă circumscrisă din punctul de echilibru static.

Lucrul unei forțe variabile în mișcare curbilinie.

Lucrul unei forțe asupra unei secțiuni curbe

Luați în considerare cazul general al găsirii muncii unei forțe variabile, al cărei punct de aplicare se mișcă de-a lungul unei traiectorii curbilinii. Fie punctul M de aplicare a forței variabile F se mișcă de-a lungul unei curbe continue arbitrare. Se notează cu vectorul de deplasare infinit mică a punctului M. Acest vector este direcționat tangențial la curbă în aceeași direcție cu vectorul viteză.

Lucrul elementar al unei forțe variabile F pe o deplasare infinitezimală

ds se numește produsul scalar al vectorilor F și ds:

Unde A- unghiul dintre vectorii F si ds

Adică, munca elementară a forței este egală cu produsul dintre modulele vectorilor forță și o deplasare infinitezimală, înmulțit cu cosinusul unghiului dintre acești vectori.

Descompunem vectorul forță F în două componente: - direcționat de-a lungul tangentei la traiectorie - și - direcționat de-a lungul normalului. linie de forţă

este perpendiculară pe tangenta la calea de-a lungul căreia se mișcă punctul, iar lucrul său este zero. Apoi:

dA= Ftds.

Pentru a calcula lucrul forței variabile F pe secțiunea finală a curbei din A la b, ar trebui să se calculeze integrala muncii elementare:

Energia potențială și cinetică.

Energie potențială P matpunct de serie luat în considerarepunctul meu Câmp de forță M sunați la muncă, efectuate de forţela acţionând asupra unui punct material când îl mişcă dintr-un punctMpână la punctul de plecareM 0 , adică

P = Umm 0

P = =-U=- U

Constanta С 0 este aceeași pentru toate punctele câmpului, în funcție de care punct al câmpului este ales ca inițial. Este evident că energia potențială poate fi introdusă doar pentru un câmp de forță potențial în care munca nu depinde de forma de mișcare între puncte. Mși M 0 . Un câmp de forță nepotențial nu are energie potențială și nu există nicio funcție de forță pentru el.

dA = dU= -dP; DAR = U - U 0 = P 0 - P

Din formulele de mai sus rezultă că P este determinată până la o constantă arbitrară, care depinde de alegerea punctului de plecare, dar această constantă arbitrară nu afectează forțele calculate prin energia potențială și munca acestor forțe. Având în vedere acest lucru:

P= - U+ const sau P =- U.

Energia potențială în orice punct al câmpului, până la o constantă arbitrară, poate fi definită ca valoarea funcției de forță în același punct, luată cu semnul minus.

Energie kinetică sistemul se numește valoare scalară T, egală cu suma energiilor cinetice ale tuturor punctelor sistemului:

Energia cinetică este o caracteristică atât a mișcărilor de translație, cât și a mișcărilor de rotație ale sistemului. Energia cinetică este o mărime scalară și, în plus, în esență pozitivă. Prin urmare, nu depinde de direcțiile de mișcare ale părților sistemului și nu caracterizează schimbările în aceste direcții.

Să notăm, de asemenea, următoarea circumstanță importantă. Forțele interne acționează asupra părților sistemului în direcții reciproc opuse. Modificările energiei cinetice sunt influențate de acțiunea atât a forțelor externe, cât și a forțelor interne.

Mișcarea uniformă a unui punct.

Mișcarea uniformă a unui punct- mișcare, cu Krom kasat. accelerația ω t punctul (în cazul mișcării rectilinie, accelerația totală ω )în mod constant. Legea mișcării uniforme a unui punct și legea schimbării vitezei acestuia υ în timpul acestei mișcări sunt date de egalitățile:

unde s este distanța punctului măsurat de-a lungul arcului de traiectorie de la punctul de referință ales pe traiectorie, t- timpul, s 0 - valoarea lui s la început. moment de timp t = = 0. - beg. viteza punctului. Când semnele υ și ω mișcare identică, uniformă. este accelerat, iar când este diferit - încetinit.

Când acţionează. mișcarea uniformă a unui corp rigid, toate cele de mai sus se aplică fiecărui punct al corpului; cu rotire uniformă în jurul unei axe fixe de unghi. accelerația e a corpului este constantă, iar legea rotației și legea schimbării unghiului. vitezele ω ale corpului sunt date de egalităţi

unde φ este unghiul de rotație al corpului, φ 0 este valoarea lui φ la început. moment de timp t= 0, ω 0 - beg. ang. viteza corpului. Când semnele lui ω și ε se potrivesc, rotația este accelerată, iar când nu se potrivesc, este lentă.

Lucrul unei forțe constante în mișcare rectilinie.

Să definim lucrul pentru cazul în care forța care acționează este constantă ca mărime și direcție, iar punctul de aplicare a acesteia se mișcă de-a lungul unei traiectorii rectilinie. Considerăm un punct material C, căruia i se aplică o constantă de forță în valoare și direcție (Fig. 134, a).

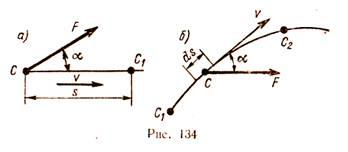
Pentru o anumită perioadă de timp t, punctul C s-a mutat în poziția C1 de-a lungul unei traiectorii rectilinie la o distanță s.

Lucrul W al unei forțe constante în timpul mișcării rectilinie a punctului de aplicare a acesteia este egal cu produsul dintre modulul de forță F înmulțit cu distanța s și cosinusul unghiului dintre direcția forței și direcția mișcării, adică.

Unghiul α dintre direcția forței și direcția mișcării poate varia de la 0 la 180°. Pentru α< 90° работа положительна, при α >90° este negativ, la α = 90° lucrul este zero.

Dacă forța formează un unghi ascuțit cu direcția mișcării, se numește forță motrice, munca forței este întotdeauna pozitivă. Dacă unghiul dintre direcțiile forței și mișcarea este obtuz, forța rezistă mișcării, efectuează un lucru negativ și se numește forță de rezistență. Exemple de forțe de rezistență sunt forțele de tăiere, frecare, rezistență la aer și altele, care sunt întotdeauna îndreptate în direcția opusă mișcării.

Când α = 0°, adică când direcția forței coincide cu direcția vitezei, atunci W = F s, deoarece cos 0° = 1. Produsul F cos α este proiecția forței pe direcție de mișcare a punctului material. Prin urmare, munca unei forțe poate fi definită ca produsul deplasării s și proiecția forței și direcția de mișcare a punctului.

33. Forțele de inerție ale unui corp rigid

În mecanica clasică, reprezentările forțelor și proprietățile lor se bazează pe legile lui Newton și sunt indisolubil legate de conceptul de cadru inerțial de referință.

Într-adevăr, mărimea fizică numită forță este introdusă în considerare de a doua lege a lui Newton, în timp ce legea însăși este formulată doar pentru sisteme inerțiale referinţă. În consecință, conceptul de forță se dovedește inițial a fi definit doar pentru astfel de cadre de referință.

Ecuația celei de-a doua legi a lui Newton, care leagă accelerația și masa unui punct material cu forța care acționează asupra acestuia, se scrie ca

Din ecuație rezultă direct că numai forțele sunt cauza accelerației corpurilor și invers: acțiunea forțelor necompensate asupra unui corp determină în mod necesar accelerația acestuia.

A treia lege a lui Newton completează și dezvoltă ceea ce s-a spus despre forțe în a doua lege.

forța este o măsură a acțiunii mecanice asupra unui corp material dat a altor corpuri

în conformitate cu a treia lege a lui Newton, forțele pot exista doar în perechi, iar natura forțelor din fiecare astfel de pereche este aceeași.

orice forţă care acţionează asupra unui corp are o sursă de origine sub forma altui corp. Cu alte cuvinte, forțele sunt în mod necesar rezultatul interacțiuni tel.

Nu sunt luate în considerare sau utilizate alte forțe în mecanică. Posibilitatea existenței unor forțe care au apărut independent, fără corpuri care interacționează, nu este permisă de mecanică.

Deși numele forțelor de inerție Euler și d'Alembert conțin cuvântul putere, aceste marimi fizice nu sunt forte in sensul acceptat in mecanica.

34. Conceptul de mișcare plan-paralelă a unui corp rigid

Mișcarea unui corp rigid se numește plan-paralel dacă toate punctele corpului se mișcă în planuri paralele cu un plan fix (planul principal). Lasă un corp V să facă o mișcare plană, π - planul principal. Din definiția mișcării plan-paralel și proprietățile unui corp absolut rigid, rezultă că orice segment de dreaptă AB, perpendicular pe planul π, va face mișcare înainte. Adică, traiectoriile, vitezele și accelerațiile tuturor punctelor segmentului AB vor fi aceleași. Astfel, mișcarea fiecărui punct al secțiunii s paralel cu planul π determină mișcarea tuturor punctelor corpului V situate pe segmentul perpendicular pe secțiune în acest punct. Exemple de mișcare plan-paralelă sunt: ​​rularea roții de-a lungul unui segment drept, deoarece toate punctele sale se mișcă în planuri paralele cu planul perpendicular pe axa roții; un caz special al unei astfel de mișcări este rotirea unui corp rigid în jurul unei axe fixe, de fapt, toate punctele unui corp în rotație se mișcă în planuri paralele cu un plan fix perpendicular pe axa de rotație.

35. Forțele de inerție în mișcarea rectilinie și curbilinie a unui punct material

Forța cu care un punct rezistă la schimbarea mișcării se numește forța de inerție a unui punct material. Forța de inerție este îndreptată opus accelerației punctului și este egală cu masa înmulțită cu accelerația.

În linie dreaptă direcția de accelerație coincide cu traiectoria. Forța de inerție este îndreptată în direcția opusă accelerației, iar valoarea sa numerică este determinată de formula:

La mișcarea accelerată, direcțiile de accelerație și viteza coincid, iar forța de inerție este îndreptată în direcția opusă mișcării. În mișcare lentă, când accelerația este îndreptată în direcția opusă vitezei, forța de inerție acționează în direcția mișcării.

Lacurbilinii și neuniformicirculaţie accelerația poate fi descompusă în normal un si tangenta la componente. În mod similar, forța de inerție a unui punct constă și din două componente: normală și tangențială.

Normal componenta forței de inerție este egală cu produsul dintre masa punctului și accelerația normală și este îndreptată opus acestei accelerații:

Tangentă componenta forței de inerție este egală cu produsul dintre masa punctului și accelerația tangențială și este îndreptată opus acestei accelerații:

Este evident că Putere deplină punct de inerție M este egală cu suma geometrică a componentelor normale și tangente, adică

Având în vedere că componentele tangenţiale şi normale sunt reciproc perpendiculare, forţa de inerţie totală este:

36. Teoreme privind adunarea vitezelor și accelerațiilor unui punct în mișcare complexă

Teorema adiției vitezei:

În mecanică, viteza absolută a unui punct este egală cu suma vectorială a vitezelor sale relative și de translație:

Viteza corpului în raport cu cadrul fix de referință este egală cu suma vectorială a vitezei acestui corp în raport cu cadrul de referință în mișcare și viteza (față de cadrul fix) a punctului cadrului în mișcare unde corpul este localizat.

într-o mișcare complexă, viteza absolută a unui punct este egală cu suma geometrică a vitezelor de translație și relative. Mărimea vitezei absolute este determinată unde α este unghiul dintre vectori și .

Teorema de adunare a accelerației ( TEOREMA LUI CORIOLIS)

acor = aper + din + acor

Formula exprimă următoarea teoremă a lui Coriolis privind adăugarea de accelerate

reniu: 1 pentru mișcarea complexă, accelerația unui punct este egală cu cea geometrică

suma a trei accelerații: relativă, translațională și rotativă sau

Coriolis.

acor = 2(ω × vot)

37. principiul d'Alembert

Principiul lui d'Alembert pentru un punct material: în fiecare moment al mișcării unui punct material, forțele active, reacțiile legăturilor și forța de inerție formează un sistem echilibrat de forțe.

Principiul D'Alembert- în mecanică: unul dintre principiile de bază ale dinamicii, conform căruia, dacă forțele de inerție se adaugă forțelor date care acționează asupra punctelor sistemului mecanic și reacțiilor legăturilor impuse, atunci un sistem echilibrat de forțe va să fie obținut.

Conform acestui principiu, pentru fiecare i-lea punct al sistemului, egalitatea

unde este forța activă care acționează asupra acestui punct, este reacția conexiunii impusă punctului, este forța de inerție, numeric egală cu produsul dintre masa punctului și accelerația acestuia și îndreptată opus acestei accelerații ().

De fapt, vorbim despre transferul termenului ma de la dreapta la stânga în cea de-a doua lege a lui Newton () efectuat separat pentru fiecare dintre punctele materiale considerate și cenzura acestui termen de către forța de inerție d'Alembert.

Principiul d'Alembert face posibilă aplicarea unor metode mai simple de statică pentru rezolvarea problemelor de dinamică, prin urmare este utilizat pe scară largă în practica inginerească, așa-numita. metoda kinetostatica. Este deosebit de convenabil să îl folosiți pentru a determina reacțiile constrângerilor în cazurile în care legea mișcării în curs este cunoscută sau găsită din soluția ecuațiilor corespunzătoare.

Unul dintre cele mai importante concepte din mecanică forta de munca .

Munca de forță

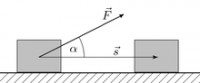
Toate corpuri fiziceîn lumea din jurul nostru sunt puse în mișcare cu forța. Dacă un corp în mișcare în aceeași direcție sau opusă este afectat de o forță sau mai multe forțe de la unul sau mai multe corpuri, atunci ei spun că munca este gata .

Adică lucrul mecanic este realizat de forța care acționează asupra corpului. Deci, forța de tracțiune a unei locomotive electrice pune în mișcare întregul tren, făcând astfel munca mecanica. Bicicleta este propulsată de forța musculară a picioarelor biciclistului. Prin urmare, această forță face și lucru mecanic.

În fizică munca de forta numit cantitate fizica, egal cu produsul dintre modulul de forță, modulul de deplasare al punctului de aplicare al forței și cosinusul unghiului dintre vectorii de forță și deplasare.

A = F s cos (F, s) ,

Unde F modulul de forță,

s- modul de mișcare .

Se lucrează întotdeauna dacă unghiul dintre vânturile de forță și deplasare nu este egal cu zero. Dacă forța acționează în direcția opusă direcției de mișcare, cantitatea de lucru este negativă.

Nu se lucrează dacă nu acționează nicio forță asupra corpului sau dacă unghiul dintre forța aplicată și direcția de mișcare este de 90 o (cos 90 o \u003d 0).

Dacă calul trage căruța, atunci forța musculară a calului sau forța de tracțiune îndreptată în direcția căruței face treaba. Iar forța gravitației, cu care șoferul apasă pe cărucior, nu funcționează, deoarece este îndreptată în jos, perpendicular pe direcția de mișcare.

Lucrul unei forțe este o mărime scalară.

Unitatea de lucru SI - Joule. 1 joule este munca efectuată de o forță de 1 newton la o distanță de 1 m dacă direcția forței și deplasarea sunt aceleași.

Dacă mai multe forțe acționează asupra unui corp sau punct material, atunci ele vorbesc despre munca făcută de forța lor rezultantă.

Dacă forța aplicată nu este constantă, atunci munca sa este calculată ca integrală:

Putere

Forța care pune corpul în mișcare face lucru mecanic. Dar cum se face această muncă, rapid sau încet, este uneori foarte important de știut în practică. Pentru aceeași muncă se poate face și în timp diferit. Munca pe care o face un motor electric mare poate fi realizată de un motor mic. Dar îi va lua mult mai mult să facă asta.

În mecanică, există o cantitate care caracterizează viteza de lucru. Această valoare este numită putere.

Puterea este raportul dintre munca depusă într-o anumită perioadă de timp și valoarea acestei perioade.

N= A /∆ t

Prin definitie A = F s cos α , A s/∆ t = v , Prin urmare

N= F v cos α = F v ,

Unde F - putere, v viteză, α este unghiul dintre direcția forței și direcția vitezei.

Acesta este putere - este produsul scalar dintre vectorul forță și vectorul viteză al corpului.

LA sistem international Puterea SI este măsurată în wați (W).

Puterea de 1 watt este munca de 1 joule (J) realizată în 1 secundă (s).

Puterea poate fi crescută prin creșterea forței care efectuează munca sau a ratei cu care se efectuează această muncă.