>>Fizica Clasa 10 >>Fizica: Energie potențială

Ce știm despre energia potențială a gravitației? Imaginează-ți suprafața pământului. Putem fi oriunde unde există gravitație, atunci energia potențială va apărea din câmpul gravitațional al masei care ne-a fost dată. Știm că dacă există un corp de masă m situat la înălțimea h într-un câmp gravitațional cu accelerație cădere liberă g sau 9,8 m/s^2. Atunci energia potențială de gravitație a acestui corp în acest punct este egală cu produsul dintre masă, accelerația căderii libere și înălțimea.

Această definiție poate fi considerată ca mărimea forței gravitaționale. Și care este energia potențială? Dacă un obiect are energie potențială și nimic nu-i oprește mișcarea, atunci va zbura în jos cu accelerație și cea mai mare parte a energiei potențiale și, de fapt, toată, se va transforma în energie cinetică. Deci, cu alte cuvinte, energia potențială este energia care este „stocată” într-un obiect sau energia pe care o are un obiect în conformitate cu locația sa. Apoi, pentru ca un corp sau obiect să aibă această energie, trebuie să vină de undeva, așa cum este cazul energiei potențiale a gravitației. Ne putem gândi la energia potențială a gravitației ca fiind munca necesară pentru a muta un obiect într-o poziție specificată.

Studiem mișcarea unui corp sub influența gravitației. Să presupunem că o bucată de stâncă cu masa m cade de la o înălțime h1 față de poalele muntelui și se oprește pe o margine la o înălțime h2. În astfel de condiții, munca se face prin gravitație: A=FS. Deoarece forța gravitației este egală cu F=gm, iar deplasarea este egală cu S=h1 - h2, atunci lucrul va fi egal cu A=mg(h1 - h2) sau A=mgh1 - mgh2. Valoarea mgh caracterizează starea corpului în câmpul gravitațional și se numește energie potențială.

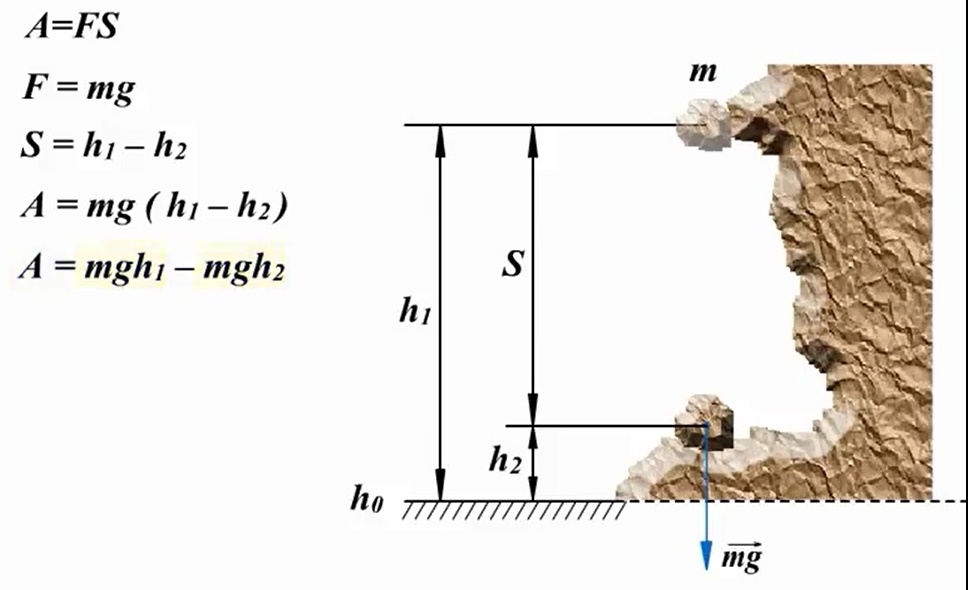
Având în vedere acest lucru, formula pentru lucrul gravitației poate fi reprezentată după cum urmează:

După cum puteți vedea, munca gravitației este o schimbare a energiei potențiale a corpului cu semnul opus. În exemplul nostru, gravitația a făcut o muncă pozitivă, iar modificarea energiei potențiale este negativă, adică. energia potenţială a scăzut.

Corpurile deformate elastic pot avea și energie potențială. Dacă deschideți o ușă cu arc, atunci forța elastică care a apărut împreună cu aceasta este capabilă să funcționeze, închizând ușa în continuare. Cu toate acestea, acest caz este special, deoarece munca va fi efectuată de o forță modulo variabilă.

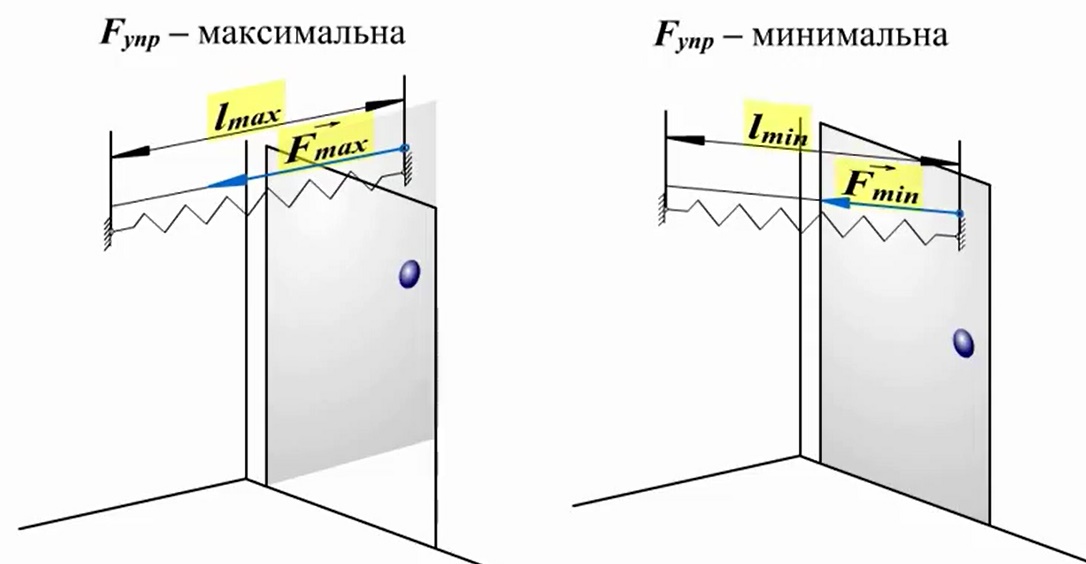
Dar, deoarece în această situație munca este efectuată datorită rezervei de energie, se poate argumenta că munca forței elastice este egală cu diferența de energii potențiale:

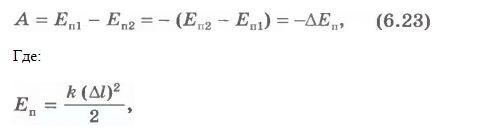
În această formulă, k este rigiditatea; Δl este cantitatea de deformare. Rezumând tot ceea ce s-a menționat mai sus, ajungem la concluzia că în toate cazurile munca forței determină o modificare a energiei corpului, de aici rezultă că munca este o măsură a schimbării energiei. Formulele de lucru pentru gravitație și forță elastică arată astfel:

Legea conservării energiei

Evident, atunci când interacționează, corpurile pot schimba energii, de exemplu, un pas de biliard în mișcare, când se ciocnește cu o minge nemișcată similară, îi transferă energia cinetică. Dacă în același timp prima minge se oprește, atunci îi va da celei de-a doua toată energia sa cinetică.

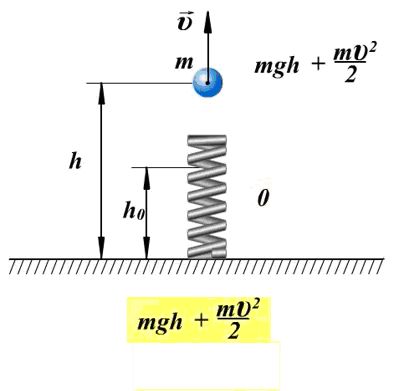
Luați în considerare un exemplu cu energie potențială. Pe un arc comprimat se află o minge de masă m, arcul este conectat printr-un fir. Mingea are energie potențială în raport cu suprafața mesei. Energia potențială a unui arc comprimat -

. Complet energie mecanică al acestui sistem de corpuri este egal cu:

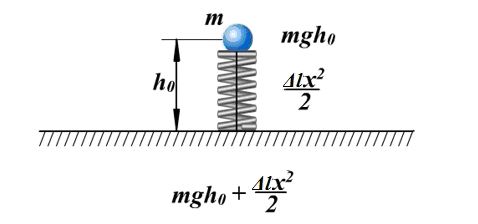
Dacă firul este ars, mingea va începe să se miște în sus, iar la un moment dat va avea o viteză ύ la o înălțime h, în același timp, energia arcului este 0 și energie totală sistemul va fi egal cu:

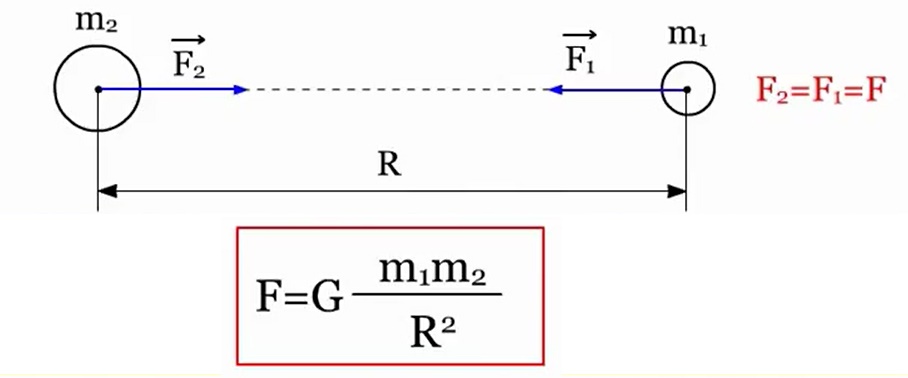
Isaac Newton este creditat cu descoperirea legii gravitatie. Iată formula sa: oricare două corpuri sunt atrase unul de celălalt cu o forță direct proporțională cu produsul maselor lor și invers proporțională cu pătratul distanței dintre ele:

Coeficientul de proporționalitate din această lege este una dintre constantele fizice fundamentale - constanta gravitațională.

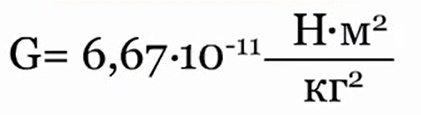
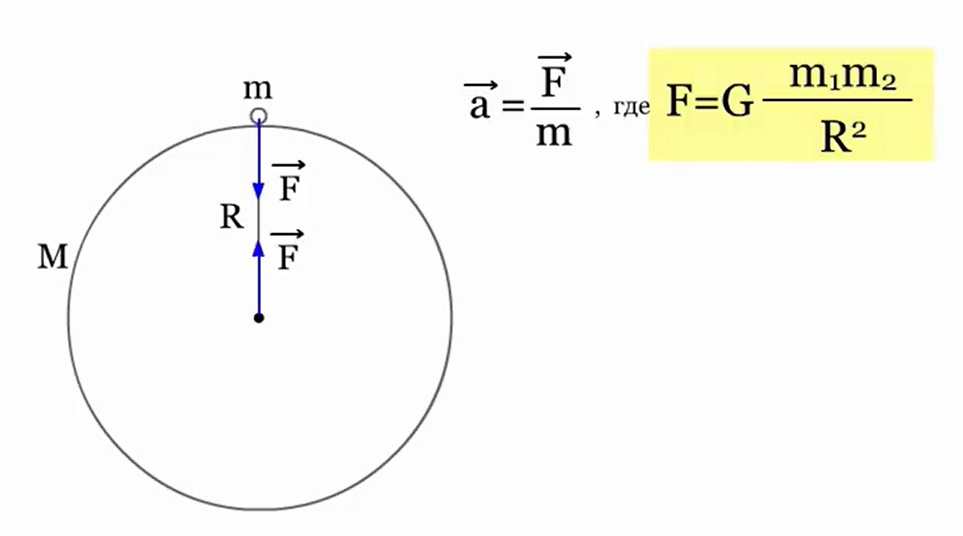
Legea este formulată pentru corpuri punctuale, i.e. pentru puncte materiale, cu toate acestea, este valabil și pentru sfere mari omogene, de exemplu, planete. În acest caz, se presupune că masa unor astfel de corpuri este concentrată în centru și distanța R este luată între centre. Există gravitația caz special manifestare a legii gravitației. Un corp cu masa m este atras de Pământul cu masa M, distanța dintre centrele lor este egală cu raza Pământului R. În conformitate cu a doua lege a lui Newton, corpul primește accelerație, unde F este forța de atracție gravitațională.

Prin urmare, accelerația corpului a și este accelerația de cădere liberă g, care este egală pentru toate corpurile și egală lângă suprafața Pământului.

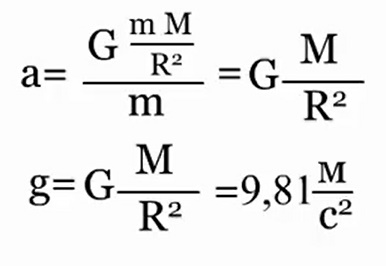
Forța care informează corpul despre această accelerație este forța gravitației: F=mg. Din formulă este evident că forța gravitației este direct proporțională cu masa corpului.

O sarcină

Un cascador care cântărea 80 kg a sărit de la o înălțime de 12 m pe o plasă de siguranță întinsă. Drept urmare, ea a cedat cu 1,5 m. Găsiți forța medie cu care cascadorul apasă pe net? Soluție: folosind legea conservării energiei, puteți face o înregistrare.

Sub energie potențialăWp corpurile care interacționează sau părți ale unui corp înțeleg SPV, care caracterizează capacitatea lor de a lucra prin schimbare poziție relativă corpuri sau părți ale aceluiași corp. Energia potențială caracterizează în mod egal toate corpurile care interacționează sau părțile lor. În același timp, între ei putere care sunt chemati conservator , munca acestor forțe nu depinde de traiectoria corpurilor, ci este determinată de pozițiile inițiale și finale ale acestora.

În prezența numai forțelor conservative, energia potențială de interacțiune a unui sistem format din N corpurile (m.t.) pot fi reprezentate ca energii potențiale ale interacțiunii lor în perechi între ele și cu corpuri externe (cu numere de la (N + 1) la (N + L)):

unde este energia potențială a interacțiunii i-acela si la- acel tel. Coeficientul (1/2) în primul termen se datorează faptului că energia potențială de interacțiune a corpurilor iși la apare aici de două ori (de exemplu, și ) și termenii cu i=k. Pentru sistem închis al doilea termen, care descrie interacțiunea corpurilor sistemului cu corpurile externe, nu va fi în formula (1.70).

Interacțiuni potențiale descris de obicei prin introducerea unui câmp de forță, și anume, se crede că un corp interacționează la locația sa cu Câmp de forță creat de alte organisme. Această abordare este convenabilă de utilizat în cazul în care mișcarea unui corp (de exemplu, primul) are un efect redus asupra mișcării altui corp (al doilea). Apoi putem presupune că primul corp se află în câmpul potențial creat de al doilea corp și atribuim energia potențială a interacțiunii lor primului corp. Deci, de exemplu, se vorbește despre energia potențială a unui corp în câmpul gravitațional al Pământului, despre energia potențială a unei sarcini într-un câmp electric etc. În acest caz, mișcarea corpului (sarcina) are un efect redus asupra câmpului de forță în care se mișcă. Să ne amintim ce se spune de obicei: corpul cade pe Pământ, iar nu Pământul cade pe corp. Acest lucru marchează faptul că mișcarea corpului practic nu schimbă poziția Pământului.

Exemple de forțe conservatoare în mecanică sunt forțele gravitației și elasticității și forțele neconservative - forțele de frecare, rezistență, tracțiune, forță reacții chimice care apar atunci când un proiectil se sparge, când este tras etc.

Denumirea de forțe „conservative” se datorează faptului că energia mecanică totală W M se păstrează sistemul de corpuri care interacționează între ele numai prin forțe conservatoare.

Să derivăm formule pentru energiile potențiale ale interacțiunii corpurilor între care acționează forțele gravitaționale și elastice.

1. Energia potențială a unui corp în câmpul gravitațional al Pământului. Între masele corporale (m.t.). m iar Pământul (bilă uniformă cu raza R З) de masă M З este afectat de forța gravitațională:

,

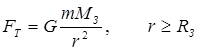Unde G este constanta gravitațională și r- distanţa de la centrul Pământului la corp (Fig. 1.24.a).

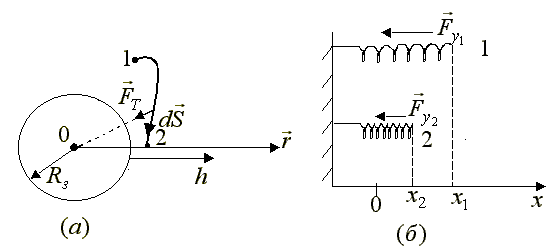
Să calculăm munca DAR 12 forțe gravitaționale în timpul tranziției corpului de la punctul 1 la punctul 2, situate respectiv la distanțe r 1 și r2 din centrul pământului:

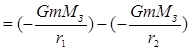(1.71)

Din formula (1.71) rezultă că munca forței gravitaționale este determinată de scăderea unor cantități care depind doar de pozițiile inițiale și finale ale corpului și ale Pământului. Deci forțele gravitaționale sunt forțe conservative , iar aceste cantități în sine reprezintă energiile potențiale ale interacțiunii gravitaționale a corpului și a Pământului:

(1.72)

Energie potențială Wp determinat până la valoare constantă, nivelul său de referință zero Wp este ales arbitrar pentru comoditatea rezolvării unor probleme specifice. Aceasta alegere se poate face in felul urmator: considera ca la

(1.73)

După cum sa menționat mai sus, formula (1.72) poate fi considerată și energia potențială a unui corp în câmpul gravitațional creat de Pământ. În acest caz, nivelul zero Wp convenabil de ales pe suprafața Pământului ( h=0, Wp=0)

unde g 0 = GM Z /R Z 2\u003d 9,81 m / s 2 - accelerație de cădere liberă la nivelul oceanului

(h = 0, r = R3); h este înălțimea corpului deasupra suprafeței Pământului.

2.Energia potențială a unui corp deformat elastic . Luați în considerare lucrul forței elastice în timpul comprimării arcului din starea 1 în starea 2 (Fig. 1.24b) cu coordonate x 1și x 2 respectiv

Din (1.75) rezultă că forța elastică este o forță conservativă, iar valoarea este energia potențială reciprocă totală a tuturor părților unui corp deformat elastic (vezi formula (1.70)).

Generalizând formulele (1.71) și (1.75), putem formula : munca forțelor conservatoare care acționează între corpuri sau părți ale unui corp este egală cu scăderea energiei potențiale reciproce..

Pentru un corp a cărui mișcare are un efect redus asupra mișcării altui corp care creează un câmp de forță, teorema energiei potenţiale poate fi formulat astfel: munca forțelor conservatoare care acționează asupra corpului este egală cu scăderea energiei potențiale a corpului în câmpul acestor forțe

1.4.5. Formula relației de energie potențială Wpși forță conservatoare

Între forța conservatoare care acționează între corpuri și energia potențială a interacțiunii lor Wp. Există anumite formule pentru relație, să le stabilim. Pentru a face acest lucru, scriem expresia pentru munca elementară a unei forțe conservatoare de-a lungul unei direcții arbitrare ( ) și înlocuiți-l în teorema energiei potențiale (1.76). Apoi

Alegând o direcție care coincide cu direcțiile axelor de coordonate, este posibil să se estimeze proiecțiile forței pe aceste axe și, prin urmare, să se scrie formula pentru relația dintre vectorul forță și energia potențială

Până acum, am luat în considerare sistemele de particule care nu interacționează. Acum ne întoarcem la considerarea unui sistem de două particule care interacționează între ele.

Să notăm forța cu care a doua particulă acționează asupra primei cu simbolul și forța cu care prima particulă acționează asupra celei de-a doua cu simbolul . Conform celei de-a treia legi a lui Newton

Introducem un vector unde și sunt vectorii de rază ai particulelor (Fig. 23.1). Distanța dintre particule este egală cu modulul acestui vector. Să presupunem că forțele au o valoare care depinde doar de distanța dintre particule și sunt direcționate de-a lungul liniei drepte care leagă particulele.

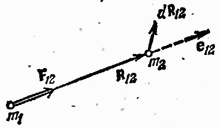
După cum știm, acest lucru este valabil pentru forțele gravitaționale și interacțiunile Coulomb (vezi formulele (11.2) și (13.1)).

Conform ipotezelor făcute, forțele pot fi reprezentate ca

unde - vector vector (Fig. 23.2), - o anumită funcție este pozitivă în cazul atracției reciproce a particulelor și negativă în cazul respingerii lor unele de altele.

Presupunând că sistemul este închis ( forțe externe nu), scriem ecuațiile de mișcare ale ambelor particule:

Înmulțiți prima ecuație cu a doua - cu și adăugați-le. Rezultatul este raportul

Partea stângă a acestei relații este creșterea energiei cinetice a sistemului în timp (vezi (19.3)), partea dreaptă este munca forțelor interne în același timp.

Luând în considerare expresiile (23.1), partea dreaptă a formulei (23.2) poate fi transformată după cum urmează:

Din fig. 23.2 se poate observa că produsul scalar este egal cu - incrementul distanței dintre particule.

În acest fel,

Expresia poate fi considerată ca o creștere a unei funcții din.Notând această funcție prin ajungem la egalitate

Prin urmare,

Ținând cont de tot ceea ce s-a spus, expresia (23.2) poate fi reprezentată ca

de unde rezultă că cantitatea pentru sistemul închis considerat este conservată. Funcția reprezintă energia potențială a interacțiunii. Depinde de distanța dintre particule.

Lăsați particulele să se miște din poziții în care distanța dintre ele a fost egală la noi poziții în care distanța dintre ele a devenit egală În conformitate cu (23.6) forțe interne. lucrați asupra particulelor

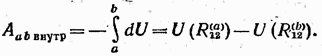
Din (23.8) rezultă că munca forțelor (23.1) nu depinde de căile pe care s-au deplasat particulele și este determinată doar de distanțele inițiale și finale dintre particule (configurațiile inițiale și finale ale sistemului). Astfel, forțele de interacțiune de forma (23-1) sunt conservatoare.

Dacă ambele particule se mișcă, energia totală a sistemului este

Să presupunem că particula 1 este fixă ​​la un moment dat, pe care îl vom lua drept origine, a coordonatelor . Ca urmare, această particulă își va pierde capacitatea de a se mișca, astfel încât energie kinetică va consta dintr-un singur termen Energia potențială în acest caz va fi doar o funcție. Prin urmare, expresia (23.9) va lua forma

(23.10)

Dacă luăm în considerare un sistem format dintr-o singură particulă 2, atunci funcția va juca rolul energiei potențiale a particulei 2 în câmpul de forțe creat de particula 1

Deși, în esență, această funcție este energia potențială a interacțiunii particulelor 1 și 2. În general, energia potențială din câmpul extern de forțe este în esență energia interacțiunii dintre corpurile sistemului și corpurile care creează. un câmp de forță extern sistemului.

Să ne întoarcem din nou la sistemul de două particule libere ("nefixate") care interacționează. Dacă, pe lângă forța internă, prima particulă este afectată de o forță externă F, iar a doua particulă este afectată de forța , atunci vor apărea termenii din partea dreaptă a relației (23.2), care în total vor da munca forțelor externe.În consecință, formula (23.7) va lua forma

În cazul în care energia cinetică totală a particulelor rămâne constantă (de exemplu, egală cu zero), relația (23.11) arată astfel:

Integrarea acestei relații de la configurația a la configurația obținem asta

(cf. formula (22.13))

Să extindem rezultatele obținute la un sistem de trei particule care interacționează. În acest caz, munca efectuată de forțele interne este

Ținând cont că vom da expresiei (23.14) forma

Presupunem că forțele interne pot fi reprezentate ca (cf. (23.1)). Apoi

Fiecare dintre produse este egal cu creșterea distanței dintre particulele corespunzătoare

Energia potențială a interacțiunii sistemului.

Este compus din energiile de interacțiune ale particulelor luate în perechi.

Echivalând suma lucrărilor, ajungem la relația (23.11), în care expresia (23.17) trebuie înțeleasă ca.

Rezultatul obținut poate fi generalizat cu ușurință la un sistem cu orice număr de particule. Pentru un sistem de N care interacționează. particule, energia potențială de interacțiune este compusă din energiile de interacțiune ale particulelor luate în perechi:

Această sumă poate fi scrisă astfel:

(23.19)

(rețineți că în expresia (23.18) pentru fiecare termen, primul indice are o valoare mai mică decât al doilea). Datorită faptului că energia de interacțiune poate fi reprezentată și sub formă

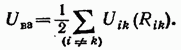
În sumele (23.19) și (23.20), indicii variază de la 1 la N, în concordanță cu condiția sau și în cazul respingerii particulelor între ele (vezi textul care urmează formulei (23.1)).

Conform (23,5)

Integrarea dă

(23.23)

La fel ca energia potențială dintr-un câmp de forță extern, energia potențială de interacțiune este determinată până la o constantă aditivă arbitrară. De obicei, se crede că atunci când energia potențială dispare (la o astfel de distanță, forța (23.22) dispare - interacțiunea dintre particule dispare). Apoi constanta aditivă din (23.23) devine egală cu zero și expresia energiei potențiale de interacțiune devine

În conformitate cu (23.13) pentru a îndepărta particulele unele de altele de la distanță până la infinit distanta lunga, fără a le modifica vitezele, este necesar să se lucreze

Înlocuirea valorilor corespunzătoare ale funcției (23.24) conduce la expresia

În cazul atracției între particule, respectiv, pentru a îndepărta particulele unele de altele, este necesar să se facă o muncă pozitivă.

În cazul respingerii particulelor unele de altele, lucrul (23.25) se dovedește a fi negativ. Această muncă trebuie făcută pentru a preveni creșterea vitezei particulelor respingătoare.