Topların çarpışmasında momentumun korunumu yasasının doğrulanması
Fizikte, çarpışmalar, yalnızca kelimenin tam anlamıyla değil - cisimlerin teması olarak değil, kelimenin geniş anlamıyla cisimler (parçacıklar) arasındaki etkileşim süreçleri olarak anlaşılır. çarpışan cisimler uzun mesafeücretsizdir. Birbirlerinden geçerek, bedenler birbirleriyle etkileşime girer, sonuç olarak çeşitli işlemler meydana gelebilir - bedenler bir bedende birleşebilir ( kesinlikle esnek olmayan etki), yeni bedenler ortaya çıkabilir ve sonunda Elastik çarpışma, bedenlerin bir miktar yaklaşımdan sonra iç durumlarını değiştirmeden tekrar ayrıldığı. Vücutların iç durumundaki bir değişikliğin eşlik ettiği çarpışmalara denir. esnek olmayan. Çarpışmaya dahil olan cisimler (parçacıklar) (çarpışmadan önce ve sonra) momentum ve enerjilerle karakterize edilir. Çarpışma süreci, etkileşimin bir sonucu olarak bu miktarlarda bir değişikliğe indirgenir. Enerjinin ve momentumun korunumu yasaları, farklı enerji türleri arasında ilişkiler kurmayı oldukça kolaylaştırır. fiziksel özellikler bedenlerin çarpışması üzerine. Burada özellikle değerli olan, korunum yasalarının çoğu zaman şu durumlarda bile kullanılabilmesidir. aktif kuvvetler Bilinmeyen. Örneğin, temel parçacık fiziğinde durum budur.
Normal koşullar altında meydana gelen makroskopik cisimlerin çarpışmaları, sadece cisimlerin bir miktar ısınmasıyla, yani kinetik enerjilerinin bir kısmının ısıya dönüştürülmesiyle birlikte oldukları için hemen hemen her zaman bir dereceye kadar esnek değildir. Yine de fizikte elastik çarpışma kavramı önemli bir rol oynar. Bu tür çarpışmaların çoğu zaman atomik fenomenler alanındaki fiziksel bir deneyde ele alınması gerekir ve sıradan çarpışmalar bile çoğu zaman yeterli bir doğruluk derecesi ile esnek olarak kabul edilebilir.
Bir çarpışmada cisimlerin (parçacıkların) momentumunun korunumu, çarpışmaya katılan cisimler kümesinin ya yalıtılmış sistem, yani dış kuvvetler veya kapalı olan, sisteme dahil olan cisimler üzerinde etki etmez: dış kuvvetler sıfır değildir ve toplam dış kuvvetler sıfıra eşittir. Çarpışmalarda enerjinin korunumu yasasının uygulanmasıyla ilgili durum biraz daha karmaşıktır. Enerjinin korunumuna başvurmak bazen çeşitli iç enerji biçimlerinin dikkate alınmasını gerektirir.
Çarpışma süreçlerinde momentum ve enerjinin korunumu yasalarının etkisinin çok çeşitli deneysel verilerle doğrulandığı söylenebilir.
esnek olmayan çarpışmalar
Kinetik enerjisi "K" olan "m" kütleli bir parçacık, "M" kütleli durağan bir parçacıkla çarpışıyor. Kesinlikle esnek olmayan bir çarpışma ("yapışma") sonucunda parçacıklar sisteminin iç enerjisinin 'Q' artışını bulun.
LSO'daki iki cismin kesinlikle esnek olmayan etkisini düşünün. Gelen parçacık çarpışmadan önce 'vec v' hızıyla 'Ox' ekseninin pozitif yönünde hareket eder, kinetik enerji parçacıklar `K = (mv^2)/2`. Kesinlikle esnek olmayan bir çarpmanın (birbirine yapışmasının) bir sonucu olarak, parçacıklar aynı "vec u" hızıyla hareket eder. Momentumun korunumu yasasına göre `mv = (m + M) u`. Enerjinin korunumu yasasına göre
`(mv^2)/2 = ((m + M)u^2)/2 + Q`.
Yukarıdaki ilişkilerden, buluruz`Q = M/(m + M) K`.
Sınırlayıcı durumlarda unutmayın
`Q=K`,
`m< < M`,
`Q = M/mK< < K`,
`m > > M`.
Gördüğümüz gibi, hafif bir parçacığın büyük bir parçacıkla (örneğin, bir atomla bir elektron) esnek olmayan bir çarpışması sırasında, kinetik enerjisinin neredeyse tam bir geçişi vardır. içsel enerji büyük parçacık.
Kütleler `(m = M)` eşit ise`Q=K/2`.
Örneğin, biri sabit, diğeri ona doğru hareket eden iki özdeş arabanın çarpışmasında, kinetik enerjinin yarısının yok olmasına neden olur.
Elastik Çarpışmalar
Pürüzsüz bir 'M' kütleli top, düz bir yatay yüzey üzerinde yer alır. 'vec v' hızında hareket eden 'm' kütleli düzgün bir top ona çarpıyor. Topların elastik bir merkezi etkisi vardır. Çarpışmadan sonra topların `vec(v_1)` ve `vec(v_2)` hızlarını bulun. Çarpışmadan sonra gelen top hangi koşulda aynı yönde hareket eder?
Çarpışma anında 'Öküz' ekseni topların merkezlerinin çizgisi boyunca yönlendirilecek olan LSO'daki sorunu ele alalım. Çarpışma sırasında bilyelere etki eden dış kuvvetler yerçekimi kuvvetleri ve kuvvetlerdir. normal reaksiyon destekler. Toplamları sıfırdır. Sonuç olarak, top sisteminin momentumu etkileşim sırasında değişmez. Momentumun korunumu yasasına göre `m vec v = m vec(v_1) + M vec(v_2)`.
`Ox` eksenindeki projeksiyonlara geçerek `mv = mv_(1x) + Mv_2` elde ederiz, burada çarpışmadan sonra gelen topun 'vec(v_1)' hızının yönünün dikkate alınmadığı dikkate alınır.bilinen. Enerjinin korunumu yasasına göre
`(mv^2)/2 = (mv_(1x)^2)/2 + (Mv_2^2)/2`.
Elde edilen ilişkileri formda yeniden yazıyoruz
`m(v - v_(1x)) = Mv_2`,
`m(v^2 - v_(1x)^2) = Mv_2^2`.
İkinci eşitliği birinci `(v != v_(1x))` ile bölerek lineer sisteme ulaşıyoruz.`v_2 = v + v_(1x)`, `m(v - v_(1x)) = Mv_2`, kimin çözümü forma sahip
`v_(1x) = (m - M)/(m + M) v`, `v_2 = (2m)/(m + M) v`.
Gelen top çarpışmadan sonra 'm > M' için aynı '(v_(1x) > 0)' yönünde hareket edecektir, yani gelen topun kütlesi duran topun kütlesinden büyükse.
İki düz elastik yuvarlak pul, düz bir yatay yüzey üzerinde 'vec(v_1)' ve 'vec(v_2)' hızlarıyla ilerler. Mükemmel elastik bir merkez dışı çarpışmadan sonra disklerin `vec(v_1^")` ve `vec(v_2^")` hızlarını bulun. "m_1" ve "m_2" pullarının kütleleri.
ISO'daki sorunu ele alalım, yatay düzlemde yer alan koordinat eksenleri 'Ox' ve 'Oy', 'Ox' ekseni ise çarpma anında rondelaların merkez çizgisi boyunca yönlendirilir.
Çarpma süresi boyunca, disk sistemine yalnızca dikey dış kuvvetler etki eder: bunlar yerçekimi kuvvetleri ve normal tepki kuvvetleridir. Toplamları sıfırdır. Daha sonra, etkileşim sürecinde yıkayıcı sisteminin momentumu korunur.
`vec(p_1) + vec(p_2) = vec(p_1^") + vec(p_2^")`,
burada `vec(p_1) = m_1 vec(v_1)`, `vec(p_2) = m_2 vec(v_2)`, `vec(p_1^") = m_1 vec(v_1^")`, `vec(p_2^" ) = m_2 vec(v_2^")` - çarpmadan önce ve sonra disk momentumu.
Pullar ideal olarak pürüzsüz olduğundan, çarpışma sırasında iç kuvvetler - elastik etkileşim kuvvetleri - sadece "Öküz" ekseni boyunca yönlendirilir. Bu kuvvetler disk momentumunun "y" bileşenlerini değiştirmez. Sonra `p_(1y) = p_(1y)^"`, `p_(2y) = p_(2y)^"` dan çarpışmadan sonra disk hızlarının `y` bileşenlerini buluruz
`vec(v_(1y)^") = v_(1y)`, `v_(2y)^" = v_(2y)`,
yani, 'Oy' ekseni üzerindeki izdüşümde, çarpışma sonucunda disklerin hızları değişmedi.
Esnek çarpışmadan sonra disklerin hızlarının 'x' bileşenlerini bulalım. Böyle bir çarpışmada kinetik enerji korunur
`(m_1 (v_(1x)^2 + v_(1y)^2))/2 + (m_2 (v_(2x)^2 + v_(2y)^2))/2 = (m_1 ((v_(1x) )^")^2 + (v_(1y)^")^2))/2 + (m_2 ((v_(2x)^")^2 + (v_(2y)^")^2))/2 `.
Eş-darbeden önce ve sonra disklerin hızlarının 'y' bileşenlerinin eşitliği dikkate alındığında, son eşitlik şu şekli alır:
`(m_1 v_(1x)^2)/2 + (m_2 v_(2x)^2)/2 = (m_1 (v_(1x)^")^2)/2 + (m_2 (v_(2x)^" )^2)/2`.
Momentumun korunumu yasasına dönelim ve disklerin momentum darbelerinin "Ox" ekseni üzerindeki izdüşümlerine geçelim.
`m_1 v_(1x) + m_2 v_(2x) = m_1 v_(1x)^" + m_2 v_(2x)^"`.
Böylece, orijinal problem, kesinlikle esnek bir merkezi etki problemine indirgenir: Bu, disklerin hızları merkezler çizgisi boyunca yönlendirilirse, enerji ve momentumun korunumu yasalarının alacağı biçimdir. Ortaya çıkan doğrusal olmayan denklem sistemi doğrusal bir sisteme indirgenebilir. Bunu yapmak için, her iki denklemde de (önceki problemde olduğu gibi), eşittir işaretinin bir tarafında, birinci yıkayıcı ile ilgili terimleri ve diğer tarafında ikinci ile ilgili terimleri birleştirir ve `(v_(1x)'i ayırır. ) != v_(1x )^")` elde edilen ilişkiler. Bu, doğrusal bir denkleme yol açar.
`v_(1x) + v_(1x)^" = v_(2x) + v_(2x)^"`.
Son iki denklemin sistemini çözerek buluruz
`v_(1x)^" = ((m_1 - m_2) v_(1x) + 2m_2 v_(2x))/(m_1 + m_2)`,
`v_(2x)^" = (2m_1 v_(1x) + (m_2 - m_1) v_(2x))/(m_1 + m_2)`.
`v_(1x)^"`, `v_(1y)^"` ve `v_(2x)^"`, `v_(2y)^"` için elde edilen bağıntılar, disklerin izdüşüm ve hız problemini çözer. çarpışma
`v_1^" = sqrt((v_(1x)^")^2 + (v_(1y)^")^2)`, `v_2^" = sqrt((v_(2x)^")^2 + ( v_(2y)^")^2)`,
ve ayrıca "vec(v_1^")" ve "vec(v_2^"" hız vektörlerinin "Ox" ekseninin pozitif yönü ile oluşturduğu "alpha_1" ve "alpha_2" açıları hakkında:
`bbb"tg" alpha_1 = (v_(1y)^")/(v_(1x)^")`, `bbb"tg" alpha_2 = (v_(2y)^")/(v_(2x)^") `.
yerleşik Genel görünüm elastik merkezi ve merkezi olmayan çarpışma problemlerini çözmek, dikkate alınan modelin cisimlerin (parçacıkların) etkileşiminin doğasına karşılık geldiği bir dizi problemin analizine yol açar.
İki düzgün topun elastik ve esnek olmayan etkisi 1. Giriş Hareket eden cisimlerin çarpışmaları, Evrenin tüm seviyelerinde doğaldır - mikroskobikten kozmik seviyeye, bu nedenle çarpma olayları çok çeşitlidir. Dinamikte, çarpışmaların mekanik sistemlerin hareketi üzerindeki etkisi incelenir. Bu problem, H. Huygens, I. Newton, J. d'Alembert, S. Punchon, G. Darboux, E. J. Routh, A.M. Lyapunova, N.E. Zhukovski, S.P. Timoşenko ve diğerleri. Grevlerin özgüllüğü, yoğunlukları ve geçicilikleridir. Bu özellik hem kazık çakmakta, cevher madenciliği yapmakta veya top oynamakta olduğu gibi faydalı hem de trafik kazalarında olduğu gibi tehlikeli olabilir. Bu nedenle, çarpma sorunu sadece teorisyenler için değil, aynı zamanda tasarımcılar, sürücüler, sporcular vb. için de önemlidir. 2. Darbe teorisindeki yaklaşımlar Fiziksel bir bakış açısından, çarpma kuvvetleri, temas alanı yakınında meydana gelen ve bu cisimlerde dalgalar halinde yayılan deformasyonlara bir tepkidir. Matematiksel modeller bu süreci az ya da çok yansıtır. Klasik çarpma teorisinde, deformasyonlar dikkate alınmaz ve sorun, çarpma kuvvetlerinin bütünleyici özelliklerini - dürtülerini belirlemeye indirgenir. Bu teori, mekanik yasalarına ve bazı ek hipotezlere dayanmaktadır. Örneğin, kütleleri olan iki topun doğrudan çarpmasının en basit problemini düşünün. m 1 ve m2 .
|
 | |||||||
|
 P 2 P 1
θ
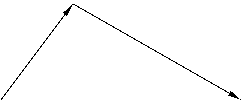
P Enerjinin korunumu yasası şu şekilde yazılabilir: P 2 /m 1 \u003d P 2 1 /m 1 + P 2 2 /m 2Çünkü P = mv ve mv 2 \u003d P 2 / m herhangi biri için. Vektör P2 açı yapar θ
vektör ile P, duran top bir açıyla sekecek θ
ilk topun ilk hızına, ardından vektörlerin üçgeninden: P 2 1 = P 2 2 + P 2 - 2 P P 2 cos θ Enerjinin sabitliğini hesaba katarak, hariç tutuyoruz P1 ve biz alırız P 2 \u003d 2 m 2 P cos θ / (m 1 + m 2) \u003d β P cos θ β \u003d 2 m 2 / (m 1 + m 2) Buradan da anlaşılacağı gibi, aralarındaki genel ilişki R2 ve R açıya bağlıdır θ
ve kütle oranı m1/m2 .İki durum ayırt edilmelidir: m1 > m2 ve m 1< m 2
. İlk durumda β < 1
Ağır top hafif olana çarpıyor. Vektörün sonu R2çapı olan bir daireyi tanımlar βР. Çarpmanın ardından her iki top da ilk topun ilk hareketi yönünde uçar. açı değeri θ
0'dan değişir π/2. İlk topun sapma açısı 0'dan bazılarına kadar değişebilir. φ maks.. bir değer φ
iki değeri eşleştir θ.
P 2 P 1
θ
P Enerjinin korunumu yasası şu şekilde yazılabilir: P 2 /m 1 \u003d P 2 1 /m 1 + P 2 2 /m 2Çünkü P = mv ve mv 2 \u003d P 2 / m herhangi biri için. Vektör P2 açı yapar θ
vektör ile P, duran top bir açıyla sekecek θ
ilk topun ilk hızına, ardından vektörlerin üçgeninden: P 2 1 = P 2 2 + P 2 - 2 P P 2 cos θ Enerjinin sabitliğini hesaba katarak, hariç tutuyoruz P1 ve biz alırız P 2 \u003d 2 m 2 P cos θ / (m 1 + m 2) \u003d β P cos θ β \u003d 2 m 2 / (m 1 + m 2) Buradan da anlaşılacağı gibi, aralarındaki genel ilişki R2 ve R açıya bağlıdır θ
ve kütle oranı m1/m2 .İki durum ayırt edilmelidir: m1 > m2 ve m 1< m 2
. İlk durumda β < 1
Ağır top hafif olana çarpıyor. Vektörün sonu R2çapı olan bir daireyi tanımlar βР. Çarpmanın ardından her iki top da ilk topun ilk hareketi yönünde uçar. açı değeri θ
0'dan değişir π/2. İlk topun sapma açısı 0'dan bazılarına kadar değişebilir. φ maks.. bir değer φ
iki değeri eşleştir θ.
 β < 1
Р 2
Р 1
А В Р φ βР
A B βP
R2
β < 1
Р 2
Р 1
А В Р φ βР
A B βP
R2
4. Cisimlerin esnek olmayan çarpışması
Kesinlikle esnek olmayan bir darbe böyle bir darbedir, bundan sonra çarpışan her iki cismin hızları aynıdır. Bunu mümkün kılmak için, çarpışan cisimler, deformasyonlarından kaynaklanan kuvvetlerin deformasyonun büyüklüğüne değil, deformasyonun değişim hızına bağlı olduğu özelliklere sahip olmalıdır. Bu özellikler, örneğin yumuşak kil, hamuru gibi doğaldır. Esnek olmayan bir çarpışmada aşağıdakiler meydana gelir. Çarpmanın ilk anında, deformasyon oranı yüksektir (bilyeler sıkıştırılır), bu nedenle, her iki bilyeye zıt yönlerde yönlendirilen ivmeler veren önemli kuvvetler ortaya çıkar. Darbe geliştikçe bilyelerin deformasyon oranları azalır ve bilyelerin hızları eşitlenene kadar deformasyonların kendileri artar. Bu anda topların deformasyonları değişmeyi bırakacak, kuvvetler ortadan kalkacak ve her iki top da aynı hızda hareket edecektir. Kesinlikle esnek olmayan bir etkide, momentumun ve toplam enerjinin korunumu yasaları karşılanır. Çarpma öncesi cisimlerin mekanik enerjisi daha fazladır. mekanik enerjiçarpmadan sonra, kısmen (veya tamamen) bedenlerin iç enerjisine geçtiği ve bedenlerin deformasyonu üzerinde çalışmaya harcandığı için. Etkileşimden sonra cisimlerin hızını belirlemek için kapalı bir sistem oluşturan iki topun (maddi noktalar) etkisini düşünün. top yığınları m 1 ve m2,çarpmadan önceki hız V 1 ben ve V 2 ben. Korunum yasasına göre, topların çarpmadan önceki toplam momentumu, çarpmadan sonraki ile aynı olmalıdır: m 1 V 1i + m 2 V 2i \u003d (m 1 + m 2) U Burada U, çarpmadan sonraki hızdır, her iki top için de aynıdır. Denklemden şunu çıkar: U \u003d (m 1 V 1i + m 2 V 2i) / (m 1 + m 2)İncelenen topların esnek olmayan etkisi için enerji korunumu yasası aşağıdaki forma sahiptir: m 1 V 1 ben 2 / 2 + m 2 V 2i 2 / 2 = (m 1 + m 2) U 2 + W burada W, sistemin iç enerjisindeki değişimdir. Çarpmadan önce cisimlerin kinetik enerjisi aşağıdaki değere sahiptir: W 1 \u003d m 1 V 1 ben 2 / 2 + m 2 V 2i 2 / 2 Ve çarpmadan sonraki kinetik enerji: W 2 \u003d (m 1 + m 2) U 2 / 2 \u003d (m 1 V 1i + m 2 V 2i) 2 / 2 (m 1 + m 2) Mekanik enerjinin kaybı veya enerjinin termal forma dönüştürülmüş kısmı: W \u003d W 1 - W 2 \u003d m 1 m 2 (V 1i - V 2i) 2 / 2 (m 1 + m 2) Değer V 1i – V 2içarpmadan önceki cismin göreli hızını temsil eder. Bu nedenle, ısıya dönüştürülen enerji, çarpışan cisimlerin kütlelerinin oranına bağlıdır. m 1 m 2 /(m 1 + m 2) ve çarpmadan önceki göreceli hızları. Kayıp enerji, bazılarının kinetik enerjisi olarak kabul edilebilir. etkin kütle: m 0 \u003d m 1 m 2 / (m 1 + m 2) bağıl hız V ile hareket " ben \u003d V 1i - V 2i. Belirli hız hesaplamaları için, darbelerin seçilen yönlere oranını tasarlamanız gerekir. Çarpmadan önce topların hızları, merkezlerinden geçen düz bir çizgi boyunca yönlendirilirse, çarpmaya merkezi denir. Böyle bir darbeden sonra topların hızı aynı düz çizgi boyunca yönlendirilecektir. Bu nedenle, momentum korunum denklemi skaler bir denklem olarak kabul edilebilir. Ancak bu durumda hızlar, bir yöne yönlendirildiklerinde işarette çakışıyor ve zıt yönlere yönlendirildiklerinde zıt işarette olarak kabul edilmelidir. Bazı özel durumları ele alalım. 1. Toplar aynı yönde hareket eder. Hız varsa etki mümkündür V 1 ben ve V 2i farklı. Örneğin, V2i > V1i, yani ikinci top birinciyi yakalar. Çarpmanın ardından toplar, birinci topun hızından daha büyük, ikinci topun hızından daha düşük bir hızla aynı yönde hareket edecektir. Topların kütleleri aynı ise U = (V 1i + V 2i) / 2 2. Toplar birbirine doğru hareket eder. Çarpmanın ardından toplar, büyük bir momentuma sahip topun hareket ettiği yönde birlikte hareket edecektir. Her iki topun momentumu eşit büyüklükte ise, çarpmadan sonra her iki top da duracaktır. 3. Merkez dışı bir darbe durumunda (Şekil 3.6.2a), hızlar V 1i ve V 2i bileşenlere ayrılabilir 1X ve 2X bilyelerin merkezlerini (X ekseni) ve bileşenleri birleştiren çizgi yönünde 1Y ve V2Y dikey yönde (y ekseni). Bileşenler için V 1X , V 2X ve V1Y ,V2Y Merkezi bir çarpma durumunda olduğu gibi momentumun korunumu yasasını yazın ve ortaya çıkan hızın bileşenini belirleyin. Esnek olmayan bir etkiyi daha ayrıntılı olarak ele alalım. Esnek olmayan bir darbede, gelen topun kinetik enerjisinin bir kısmı, ısının serbest bırakılmasıyla kaybolur. Kesinlikle esnek olmayan bir çarpmanın sınırlayıcı durumunda, gelen cisim duran cisimle birlikte yapışır, göreli hareketlerinin kinetik enerjisi yok olur ve tek bir cisim olarak hareket etmeye devam ederler. Çoğu pratik durumda, bir çarpışmadan sonra vücutta deformasyon salınımları uyarıldığında, zamanla azalan kısmen elastik bir darbe ile uğraşıyoruz. Bu tür salınımların uyarılması, bir yay ile birbirine bağlanmış iki özdeş top kullanılarak modellenebilir. Mükemmel elastik bir topun bir yaylı osilatörle çarpıştığını varsayalım. Topların kütleleri aynı ve eşittir m. Çarpma anında yay henüz hareket etmediğinden, uçan top durur ve osilatörün sol topu, uçan topun hızında harekete geçer. v. Bu durumda, osilatörün kütle merkezi bir hızla hareket eder. v/2. Zamanla, osilatörün salınımları sönecek ve hızla ilerlemeye devam edecektir. v/2 ve tüm sistemin toplam enerjisi, gelen topun enerjisinin sadece yarısı olacaktır. Diğer yarısı osilatörde ısı olarak salınacaktır. Sıradan esnek olmayan cisimlerin etkisi, ideal olarak elastik ve tamamen esnek olmayan darbeler arasındaki bir ara duruma karşılık gelir. Bu, çarpma süresinin ilk yarısında belirli bir değere sıkıştırıldığında, çarpmadan sonra orijinal boyutlarını almayacak olan esnek olmayan bir yay aracılığıyla iki topun çarpmasına benzer bir darbeye benzer; veya sıkıştırma sırasındaki itme kuvveti, yay genişlediğinde çarpma süresinin ikinci yarısından daha büyük olacaktır. Yayın potansiyel sıkıştırma enerjisinin bir kısmı ısıya dönüşecek ve hareketin kinetik enerjisine dönüşmeyecektir. Bu nedenle, mekanik enerjinin korunumu yasası bu durumda uygulanamaz. Çarpmadan sonra hızların eşitliği koşulu da, tamamen esnek olmayan bir çarpmada olduğu gibi geçerli olmayacaktır, çünkü çarpmadan sonra her iki cisim de farklı hızlarda hareket eder. Esnek olmayan bir darbe, çarpma sırasında ısıya dönüştürülen deformasyon enerjisinin o kısmı ile karakterize edilebilir. Ancak Newton bile, belirli bir malzemeden yapılmış topların esnek olmayan bir çarpması sırasında, çarpmadan önceki ve sonraki göreceli hızların sabit bir oranda olduğunu buldu ve böyle bir çarpma ile karakterize edilir. çarpmadan sonra bağıl hız kurtarma faktörü: e \u003d | V 2 - V 1 | / |V 2i – V 1i | nerede V 2i – V 1içarpmadan önceki nispi hızdır ve V2 - V1- çarpmadan sonra. Deneyimler, belirli bir doğruluk derecesi ile kişinin değeri hesaplayabileceğini göstermektedir. e sabittir ve yalnızca çarpışan topların malzemesine bağlıdır. Mükemmel elastik bir darbe ile, bağıl hız büyüklük olarak aynı kalır, ancak işaretini değiştirir: V 1i - V 2i \u003d - (V 1 - V 2) Geri kazanım katsayısı her zaman birden azdır, çünkü elastik bir etki ile bire eşittir, tamamen esnek olmayan bir etki ile sıfıra eşittir, çünkü bu durumda V 2 - V1 \u003d 0 Katsayının bilinmesi e, çarpma ve enerji kaybından sonra topların hızını hesaplayabiliriz. Kullanılmış Kitaplar: 1. D.V. Sivukhin, " Genel kurs fizik. Mekanik", Bilim, 1979 2. O.D. Shebalin, " Fiziksel temeller mekanik ve akustik", Yüksek okul, 1981 3. S.P. Strelkov, "Mechanics", Nauka, 1975 4. K. Schwartz, T. Goldfarb, "Fiziksel dünyada kalıpları arayın", İngilizce'den çevrildi, Moskova , Mir, 1977 5. Fizikte laboratuvar çalışmaları, LL Goldin, Moskova, Nauka, 1983 tarafından düzenlendi 6. AI Ivanov, "Regularities of effect in mekanik sistemler", Doğa, 1999, Sayı 10Bakanina L. Çarpışmalarda momentumun korunumu yasası // Kvant. - 1977. - No. 3. - S. 46-51.
Yayın kurulu ve "Kvant" dergisinin editörleri ile özel anlaşma ile
Momentumun (momentum) korunumu yasası, kapalı sistemler için, yani etkileşen tüm cisimleri içerenler için karşılanır, böylece sistemin herhangi bir gövdesine hiçbir dış kuvvet etki etmez. Ancak, çoğu çözerken fiziksel görevler momentumun kapalı olmayan sistemler için de sabit kalabileceği ortaya çıktı. Doğru, bu durumda momentum sadece yaklaşık olarak korunur. Burada neler olduğunu anlamaya çalışalım.
Açık bir sistemin momentumundaki değişim, dış kuvvetlerin toplam momentumuna eşittir. Δ zaman aralığı boyunca sisteme etki eden dış kuvvetin ortalama değeri ile gösteriniz. t. O zamanlar
Bu kuvvetin mutlak değeri çok büyük değilse ve kuvvetin etki ettiği süre küçükse, çarpım da küçük olacaktır. Bu durumda, sistemin momentumunun hangi doğrulukla değişmeden kabul edilebileceğini tahmin etmek gerekli hale gelir.
Ayrıca momentumun bir vektör olduğunu unutmamalıyız ve bu nedenle bu vektörün herhangi bir yönde izdüşümünün korunumu hakkında konuşabiliriz. Gerçekten de, sistem kapalı değilse, ancak dış kuvvetler, belirli bir yöndeki tüm kuvvetlerin izdüşümlerinin toplamı sıfıra eşit olacak şekilde ise, sistemin momentumunun bu yöne izdüşümü sabit kalır. Değil kapalı sistem bu yönde kapalı olana benzer.
Kısa süreli etkileşimler, örneğin patlamalar, atışlar, çarpışmalar sırasında ortaya çıkar. Bu tür bir sorunu tartışacağız. Her bir özel durumda, momentumun korunumu yasasının sağlanıp sağlanmadığını ve neye bağlı olduğunu bulmaya çalışacağız.
Görev 1. Sürtünme olmadan kayan bir toptan eğik düzlem ve yolu çoktan geçti ben, yatay yönde bir atış yapılır (Şekil 1). Ateş ettikten sonra silah merminin hangi hızında duracak? mermi ağırlığı m silahın kütlesinden çok daha az M, düzlem eğim açısı α.
Atıştan önce silah (mermi ile birlikte), yolu geçti ben, eğik düzlem boyunca yönlendirilmiş momentuma sahiptir. Bu momentumun modülü, enerjinin korunumu yasasından bulunabilir:
![]()
Atıştan hemen sonra silah durdu ve mermi yatay yönde uçtu. Böylece, silah ve mermi arasındaki etkileşimin kısa süresine rağmen, bu sistemin momentumu korunmaz. Neden? Niye?
Atış sırasında, tabancanın eğik düzlem üzerindeki basınç kuvveti keskin bir şekilde artar, bu da düzlemin yanından gelen reaksiyon kuvvetinin de arttığı anlamına gelir, böylece bu kuvvetin darbesi yeterince büyük olur. Daha sonra silahın ve merminin toplam momentumunu değiştirir.

Bununla birlikte, eğik düzlem boyunca yönde, reaksiyon kuvvetinin izdüşümü sıfıra eşittir ve yerçekimi impulsunun kısa bir atış süresi için izdüşümü Δ t küçüktür ve ateşlendiğinde artmaz. Bu nedenle, bir dereceye kadar doğrulukla, eğik düzlem boyunca yönde, tabanca mermi sisteminin momentumunun projeksiyonunun korunduğu varsayılabilir. Bu nedenle projeksiyon toplam dürtü atıştan önceki silah ve mermi, atıştan sonraki merminin izdüşümüne eşittir (silah hareketsizdir):
Dolayısıyla atıştan hemen sonra mermi hızı modülü
Bu problemi çözerken eğik düzlem boyunca top-mermi sisteminin kapalı bir sistem gibi davrandığını varsaydık. Bununla birlikte, etkileşimde bulunan organlar sistemi karmaşık olduğundan ve böyle bir değerlendirme için gerekli veriler bulunmadığından, bunun doğru olma derecesini tahmin edemeyiz.
Şimdi iki sorunu daha fazla analiz edelim. basit etkileşim nerede böyle bir tahmin yapılabilir.
Görev 2. Tahta bir kütle topunun içine M= 1 kg hızla düşüyor V 0 = 1 m / s, aşağıdan silahla ateş edin ve delin. Bundan hemen sonra topun hızı ne olacak? Mermi hızı υ 0 = 300 m/s, topu terk ettikten sonra υ = 100 m/s, mermi kütlesi m= 10 gr.
Etkileşim süresi, nerede d- bilye çapı, bir υ cf - ortalama sürat topun içindeki mermiler. Topun çapı, ρ ağacının yoğunluğunun, \u003d 10 3 kg / m3'teki ρ su yoğunluğuna yaklaşık olarak eşit olduğu bilinerek tahmin edilebilir:
![]()
![]()
![]()
yani Δ t≈ 5 10–4 sn. Bu süre boyunca sistemin yerçekiminin momentumu (ve dolayısıyla top ve merminin toplam momentumundaki değişim)
p = (M+m)· gΔ t≈ 5 10 -3 N sn.
Etkileşimden önce sistemin hareket miktarı
p 0 = mυ 0 – MV 0 = 2 N s.
sonra ilişki
![]()
ve sonuç olarak, %0,2 doğrulukla, sistemin momentumunun etkileşim sırasında değişmediğini varsayabiliriz.
Dikey olarak yukarı eksene momentum izdüşümü için korunum yasasını yazalım:
mυ 0 – MV 0 = mυ+ Mv y.
Dolayısıyla etkileşimden sonra topun hızının izdüşümü
![]()
yani top 1 m/s hızla yukarı doğru hareket etmeye başlayacaktır.
Görev 3. Bir top dikey olarak υ 0 = 1 m/s hızla yukarı doğru fırlatılıyor. Yükselişin en üst noktasına ulaştığında, aynı top 2υ 0 başlangıç hızıyla atılır. Çarpışma tamamen esnek olarak kabul edilebilirse, çarpışmadan sonra topların hızını belirleyin.
Önceki probleme benzer şekilde, her şeyden önce, çarpışma sırasında iki top sisteminin kapalı kabul edilebileceği doğruluk derecesini tahmin ediyoruz. Bunu yapmak için çarpma öncesi sistemin momentumunu, çarpma sırasındaki yerçekiminin momentumunu bulup birbirleriyle karşılaştırıyoruz.
Topların yükseklikte çarpışmasına izin verin h Zaman boyunca t ikinci topun hareketinin başlamasından sonra (Şekil 2). Sonra ilk top için
![]()
maksimum kaldırma yüksekliği nerede. ikinci top için
![]()
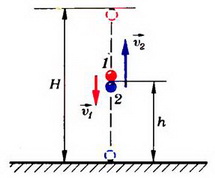
Bu nedenle, çarpışmadan hemen önceki her iki topun hızları eşittir.
ilk top aşağı, ikincisi yukarı hareket ederken.
Böylece, etkileşimden önce sistemin hareket miktarı
p 0 = m u 2 - mυ 1 \u003d 1.5 mυ 0 .
Şimdi bu süre boyunca etkileşim süresini ve yerçekimi momentumunu tahmin etmeye çalışalım. Bunu yapmak için, çarpışma sürecinin nasıl gerçekleştiğini hayal etmeliyiz. Önce iki özdeş çubuğun uçlarından çarpışmasını ele alalım. Darbenin sonunda, çubuk boyunca yayılan elastik deformasyon meydana gelir, yani çubukta bir ses dalgası ortaya çıkar. Çubuğun karşı ucuna ulaşan dalga yansır ve geri gelir. Çarpışma sürecinin burada bittiğini ve çubukların etkileşim süresinin geçiş süresine eşit olduğunu söyleyebiliriz. ses dalgasıçubuk boyunca ve arkada. Aslında, etkileşimin resmi çok daha karmaşıktır ve sonuçta ortaya çıkan elastik dalganın düzlem olmadığı toplarda, hatta daha da karmaşıktır. Bununla birlikte, burada tahmin etmek için, bir büyüklük sırasına kadar, çarpma süresinin, topun içindeki ses dalgasının yayılma süresine eşit olduğunu da varsayıyoruz: . içindeki ses hızı katılar saniyede birkaç kilometre mertebesinde. Topun çapı yaklaşık bir santimetre ise, o zaman Δ t~ 10–5 s ve yerçekimi momentumunun mutlak değeri, etkileşimden önceki topların momentumundan birçok kez daha azdır:
![]()
Dolayısıyla bu durumda da çarpışan bilyeler sisteminin kapalı olduğunu düşünebiliriz. (Tabii ki, topların daha fazla hareketi esas olarak yerçekimi kuvvetine bağlıdır.) Topların etkisi kesinlikle esnek olduğundan, mekanik enerjinin korunumu yasalarını ve dikey olarak yukarı doğru yönlendirilmiş bir eksende momentum izdüşümü kullanacağız. :
![]()
Burada υ 1 ve υ 2 için karşılık gelen değerleri değiştirerek:
![]()
Elastik bir darbede, eşit kütleli toplar hız değiştirir.
Bununla birlikte, çarpışmalarda dış kuvvetlerin etkisini her zaman ihmal edip sistemin kapalı olduğunu düşünmemek gerekir. Örneğin, aşağıdaki sorunu düşünün.
Görev 4. Bir torba un, bir yükseklikten başlangıç hızı olmadan kayar. H Ufka α = 60° açıyla eğimli düz bir tahta üzerinde. İnişten sonra çanta yatay, pürüzlü bir zemine düşer. Torbanın zemindeki sürtünme katsayısı μ = 0.7. Çanta nerede duracak?
Tahtadan indikten sonra, çanta tahta boyunca yönlendirilmiş bir hıza sahiptir (Şekil 3). Tahta pürüzsüz olduğundan ve enerji kaybı olmadığından, mutlak değeri mekanik enerjinin korunumu yasasından bulunabilir:

Yatay yönde, modülü olan torbaya bir kayma sürtünme kuvveti etki eder. Darbe sırasında bu kuvvetin momentumu eşittir
yani, desteğin tepki kuvvetinin hangi yasaya göre değiştiğine (ve dolayısıyla çantanın zemindeki basınç kuvvetine) veya çarpma süresine bağlı değildir. Torbanın momentumunun yatay izdüşümündeki değişimi bulalım. ekseni yönlendirelim X yatay olarak sağa, sonra Newton'un ikinci yasasına göre,
Bu nedenle, torbanın zemin boyunca hareket etmeye başlayacağı hızın izdüşümü,
Eksi işareti ne anlama geliyor? Resmen, eksi işareti, çarpmadan sonra torbanın sola hareket etmesi gerektiğini veya başka bir deyişle, sürtünme kuvvetinin momentumunun, torbanın momentumunun ilk yatay izdüşümünden daha büyük olduğunu gösterir. Bu, çarpışma sürecinde bir anda torba hızının eksen üzerindeki izdüşümü anlamına gelir. X sıfıra döndü. Bu noktadan sonra kararımız yanlış olur. Gerçekten de, sürtünme kuvvetinin modülü μ'ye eşittir. N cp sadece kayarken, hareketsizken sürtünme kuvveti 0 ile μ arasında herhangi bir değer alabilir N cp, vücuda hangi kuvvetlerin (sürtünme kuvveti hariç) etki ettiğine bağlı olarak. Bizim durumumuzda, başka hiçbir kuvvetin yatay yönde izdüşümü yoktur, bu nedenle torba hızının yatay izdüşümü ortadan kalktığı anda, sürtünme kuvveti de ortadan kalkar. Böylece çanta yerde hiç hareket etmeyecektir.
Son olarak, cisimlerin çarpışmasıyla ilgili oldukça iyi bilinen bir sorunu daha tartışalım. Bu problem çözülürken, genellikle kaba yaklaşımlar kullanılır, bunun bir yaklaşım olduğu hiçbir şekilde şart koşulmaz, hiçbir koşulda kullanılamaz.
Görev 5. Düz bir yatay yüzey üzerinde duran bir kütle kama üzerinde M yüksekten h düşen kütle topu m ve yatay yönde seker (Şekil 4). Çarpmadan sonra kama hızının yatay izdüşümünü bulun. Sürtünmeyi göz ardı edin ve darbenin tamamen esnek olduğunu varsayın.
Önceki tüm problemlerden farklı olarak, burada iki değil, üç cismin çarpışmasını dikkate almak gerekir - bir top, bir kama ve bir yatay düzlem. Genel durumda, darbe mekanizması hakkında herhangi bir ek varsayım yapılmadan bu sorun çözülemez. Bu problemin en yaygın çözümünde, (herhangi bir çekince olmaksızın) bilyenin kama ve kamanın yatay düzlem ile çarpışmalarının aynı anda meydana gelmesi ve çarpışmadan sonraki kamanın sadece yatay bir hız izdüşümüne sahip olması zımnendir. Daha sonra mekanik enerji ve momentumun korunumu yasalarının denklemleri yazılır:
nerede Vx ve υ x- sırasıyla, kama ve topun hızlarının sağa yönlendirilmiş yatay eksen üzerindeki izdüşümü. Buradan
![]()

Bununla birlikte, böyle bir çözümde, topun momentumunun dikey izdüşümünün nereye gittiği hiç açık değildir. Sonuçta, çarpışma kesinlikle esnekse, sistemin momentumunun dikey izdüşümü kaybolmaz, sadece işaret değiştirir! Çarpmanın ardından top yatay bir yönde seker, düzlem genellikle hareketsizdir. Bu, çarpmadan sonra kamanın sıçraması gerektiği anlamına gelir. Ve bu hareketle ilişkili enerji yukarıdaki çözümde hesaba katılmaz.
Çarpmanın fiziksel resmi, ilk başta topun sadece kama ile çarpıştığı ve daha sonra bu çarpışma sonucunda bir miktar hız kazanan kamanın yatay düzlem ile etkileştiği varsayımıyla daha tutarlıdır. İlk darbeden sonra, kama hızının dikey izdüşümü
Çarpma sırasında ağırlık merkezinden geçer Ö kama (Şekil 5).

Ayrıca, çarpışmadan sonra topun yatay olarak zıplayabilmesi için, kama açısının α, topun ve kamanın kütlelerine bağlı olarak iyi tanımlanmış bir değere sahip olması gerektiğini not ediyoruz.
Sonuç olarak, bağımsız çözüm için çeşitli görevler sunuyoruz.
Egzersizler
1. Kütle topunun merkezine m 1 = 300 gr masanın kenarında yatay olarak uçan bir kütle mermisi çarpıyor m 2 = 10 g ve delip geçiyor. Top uzakta yere düşüyor s 1 = 6 m masadan ve mermi uzakta s 2 = 15 m Masa yüksekliği H= 1 m Merminin ilk hızını belirleyin.
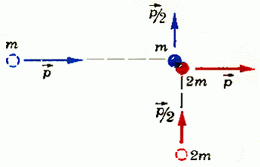
2. Kütleli iki parçacık m ve 2 m, momentuma sahip ve karşılıklı olarak dik yönlerde hareket ediyor. Çarpışmadan sonra parçacıklar momentum değiştirir (Şekil 6). Darbe sırasında açığa çıkan ısı miktarını belirleyin.
3. Bir torba un, bir yükseklikten başlangıç hızı olmadan kayar. H\u003d 2 m, ufka α \u003d 45 ° açıyla eğimli bir tahta boyunca. İnişten sonra çanta yatay bir yüzeye düşer. Torbanın tahtaya ve yatay yüzeye sürtünme katsayısı μ = 0,5'tir. Tahtanın sonundan ne kadar uzakta çanta duracak?
Yanıtlar
1. ![]()
3.![]()
Enerjinin korunumu yasası, herhangi bir nedenle vücut üzerindeki iyileştirici etkilerin bilinmediği durumlarda mekanik sorunları çözmeyi mümkün kılar. Böyle bir duruma ilginç bir örnek, iki cismin çarpışmasıdır. Bu örnek özellikle ilginçtir, çünkü analizinde yalnızca enerjinin korunumu yasasıyla yapmak imkansızdır. Momentumun (momentumun) korunumu yasasını da dahil etmek gerekir.
Günlük yaşamda ve teknolojide, çoğu zaman cisimlerin çarpışması ile uğraşılmaz, atom fiziği ve atomik parçacıklarçarpışmalar çok yaygındır.
Basit olması için, ilk önce kütleleri ikincisi durağan olan ve birincisi hızla ikinciye doğru hareket eden iki topun çarpışmasını ele alacağız.Hareketin her iki topun merkezlerini birleştiren çizgi boyunca gerçekleştiğini varsayalım (Şek. 205), böylece toplar çarpıştığında, merkezi veya önden çarpma olarak adlandırılan aşağıdaki gerçekleşir. Çarpışmadan sonra her iki topun hızları nedir?
Çarpışmadan önce, ikinci topun kinetik enerjisi sıfır ve birincidir. Her iki topun enerjilerinin toplamı:
![]()
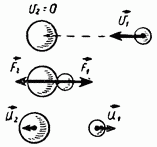
Çarpışmadan sonra birinci top bir hızla hareket etmeye başlayacak Hızı sıfıra eşit olan ikinci top da bir miktar hız alacaktır.
![]()
Enerjinin korunumu yasasına göre, bu toplam, çarpışmadan önceki topların enerjisine eşit olmalıdır:
![]()
![]()
Bu tek denklemden, elbette, iki bilinmeyen hız bulamayız: İkinci korunum yasasının kurtarmaya geldiği yer burasıdır - momentumun korunumu yasası. Topların çarpışmasından önce birinci topun momentumu eşit, ikincinin momentumu sıfırdı. İki topun toplam momentumu şuna eşitti:
![]()
Çarpışmadan sonra, her iki topun momentumu değişti ve eşit oldu ve toplam momentum
![]()
Momentumun korunumu yasasına göre, bir çarpışma sırasında toplam momentum değişemez. Bu nedenle şunu yazmalıyız:
![]()
Hareket düz bir çizgide olduğu için, vektör denklemi cebirsel yazılabilir (hızların çarpmadan önceki ilk topun hızı boyunca yönlendirilen koordinat ekseni üzerindeki izdüşümleri için):
Şimdi iki denklemimiz var:
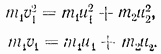
Böyle bir denklem sistemi, çarpışmadan sonra topların ve topların bilinmeyen hızları için de çözülebilir. Bunu yapmak için aşağıdaki gibi yeniden yazıyoruz:

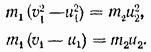
İlk denklemi ikinciye bölerek şunu elde ederiz:
Şimdi bu denklemi ikinci denklemle birlikte çözelim
(kendin yap), çarpmadan sonraki ilk topun bir hızla hareket edeceğini görüyoruz.
![]()
ve ikincisi - hızla
![]()
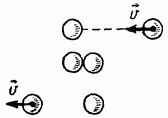
Her iki top da aynı kütleye sahipse, bu, birinci topun ikinciyle çarpışarak hızını kendisine aktardığı ve kendisinin durduğu anlamına gelir (Şekil 206).
Böylece, enerjinin ve momentumun korunumu yasalarını kullanarak, cisimlerin çarpışmadan önceki hızlarını bilerek, çarpışmadan sonraki hızlarını belirlemek mümkündür.
Ve topların merkezlerinin mümkün olduğunca yakın olduğu anda, çarpışma sırasındaki durum nasıldı?
Bu sırada belli bir hızla birlikte hareket ettikleri açıktır. Aynı vücut kütleleriyle toplam kütleleri 2 tondur. Momentumun korunumu yasasına göre, her iki topun ortak hareketi sırasında, momentumları çarpışmadan önceki toplam momentuma eşit olmalıdır:
Bu nedenle şu şekildedir:
Böylece, her iki topun eklem hareketi sırasındaki hızı yarıya eşittir.
bunlardan birinin çarpışmadan önceki hızı. Bu an için her iki topun kinetik enerjisini bulalım:
![]()
çarpışmadan önce toplam enerji iki top da eşitti
Sonuç olarak, topların çarpışması anında kinetik enerji yarıya indi. Kinetik enerjinin yarısı nereye gitti? Burada enerjinin korunumu yasasının ihlali var mı?
Enerji, elbette, topların eklem hareketi sırasında aynı kaldı. Gerçek şu ki, çarpışma sırasında her iki top da deforme oldu ve bu nedenle elastik etkileşimin potansiyel enerjisine sahipti. Tam olarak bunun boyutu potansiyel enerji ve topların kinetik enerjisi azaldı.







