Soru 1. Elektromanyetik alan. EMF vektörleri. Alanların grafik gösterimi Elektromanyetik alan- elektrik yüklü cisimlerle ve ayrıca kendi dipolü ve çok kutuplu elektrik ve manyetik momentleri olan cisimlerle etkileşime giren temel bir fiziksel alan. Belirli koşullar altında birbirini üretebilen elektrik ve manyetik alanların bir kombinasyonudur, ancak aslında bunlar elektro tensör aracılığıyla biçimlendirilmiş tek bir varlıktır. manyetik alan.

Elektromanyetik alan vektörleri:

Elektrik alanı. Elektromanyetik alanın ana vektör özelliklerinden biri, tansiyon Elektrik alanı. Elektrik alan kuvveti altında, elektrik alanının alana eklenen pozitif birim nokta yük üzerinde etki ettiği kuvvet kastedilmektedir.

(1)

Fizikte bu belirtilir: q yükü, bu alanı oluşturan elektrik yüklerinin dağılımındaki değişimin ihmal edilebilmesi için yeterince küçük olmalıdır.

Bu süreci klasik teori içinde basitleştirilmiş bir şekilde ele alalım:

Madde atomlardan oluşur. Bir atom, pozitif bir çekirdek ve negatif elektronlardan oluşur. Atomların birleşimi bir molekül oluşturur. Polar ve polar olmayan moleküllere sahip maddeler vardır. Polar olmayan atomlar veya moleküller durumunda, negatif yüklere etki eden tüm kuvvetlerin bileşkesinin uygulama noktası, pozitif yüklere etki eden tüm kuvvetlerin bileşkesinin uygulama noktası ile çakışır. Bu, molekülün ağırlık merkezinin protonların ağırlık merkeziyle çakışması durumunda mümkündür. Polar moleküllerde bu merkezler çakışmaz ve bir polar molekül, temel bir dipole, yani. uzayda bir mesafe ile ayrılmış iki zıt yükten oluşan bir sistem ben. Dipoller, bir dipol momenti ile karakterize edilir:

Madde polarizasyonunun etkisi, toplam dipol momenti ile karakterize edilir: dikkate alınan hacim dV'de:

(4) - tek tek atomlara veya moleküllere karşılık gelen dipol momenti. formül (4) geometrik toplama V hacminde gerçekleştirilir.

Elektrik alan kuvveti ile birlikte bir vektör miktarı daha kullanılır: - elektrik indüksiyon vektörü veya elektrik yer değiştirme vektörü: (8); ;

Dolayısıyla, elektrik yüklerinin aynı düzeni ve büyüklüğü için vektör alanının ortamın özelliklerine bağlı olmadığı sonucu çıkar.

Bildiğiniz gibi, bir manyetik alanda hareket eden pozitif bir nokta elektrik yüküne etki eden kuvvet Lorentz kuvveti tarafından belirlenir: (1),

nerede (2) ; (3) ; .

Manyetik kuvvet, yükün hareket hızı ile orantılıdır ve yükün hareket yönüne dik olarak yönlendirilir.

Fiziksel anlam: değere manyetik indüksiyon vektörü denir ve manyetik alanın kendisine dik bir yönde birim hızda hareket eden pozitif bir nokta yüküne etki ettiği kuvvete eşittir.

Alanlar, kuvvet çizgileri kullanılarak tasvir edilmiştir. "Güç" ile, her noktasında teğetlerin tasvir edilen alanın yönünü tasvir ettiği çizgiler kastedilmektedir. Alanın genliğindeki değişiklik, kuvvet çizgilerine dik yüzeyin birim alanı başına kuvvet çizgilerinin sayısı ile gösterilir. Bir vektör alanı olsun ANCAK, uzaydaki her noktada Kartezyen sistemde ifade edilebilir:

ben- alan çizgisi alanlar ANCAK, - birim vektörler. Alan çizgisinin diferansiyel denklemini elde ederiz: dr, izdüşümü cinsinden yazılabilir: (1),

Alan çizgisini tanımlayan fonksiyonun bilindiğini varsayıyoruz:

İtibaren vektör analizi karşılık gelen projeksiyonların oranları eşitse, iki vektörün paralel olduğu bilinmektedir:

Bu alan çizgisinin diferansiyel denklemidir.

Soru 2. Maxwell'in integral ve diferansiyel formlardaki ilk denklemi.

Maxwell'in ilk denklemi, toplam akım yasasının (Ampère yasası) bir genellemesidir. Maxwell öncesi formülasyonda, bu denklem şu şekilde formüle edilebilir: yoğunluk vektörünün sirkülasyonu H kapalı bir devre boyunca manyetik alan Г, bu devreye giren akıma eşittir:

Maxwell'den önce akım / sadece iletim akımını anladı. Genel durumda, G devresi içindeki / içindeki akımın dağılımı düzgün olmayabilir. nerede

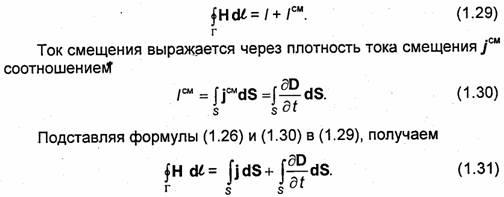
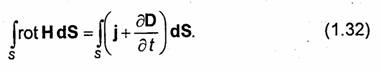
Soru 3. İntegral ve diferansiyel formlarda Maxwell'in ikinci denklemi.

Maxwell'in ikinci denklemi

Faraday'ın indüksiyon yasasının genelleştirilmesi, aşağıdaki gibi formüle edilir: eğer kapalı bir devreye Г bir değişken nüfuz ediyorsa manyetik akıФ, sonra devrede bu akışın değişim hızına eşit bir EMF e belirir:

Formül (1.34)'ün sağ tarafındaki eksi işareti, devrede ortaya çıkan emk'nin her zaman olduğu gibi, bu devreye giren akışta bir değişikliği önleme eğiliminde olduğu anlamına gelir. Bu hüküm "Lenz kuralı" olarak bilinir.

İlişki (1.37) sonlu boyutların bir konturu için formüle edilmiştir ve Maxwell'in ikinci denklemi integral formda. Maxwell ayrıca bu denklemi diferansiyel biçimde formüle etti.

Soru 4. İntegral ve diferansiyel formlarda Maxwell'in üçüncü denklemi.

Üçüncü Maxwell denklemi, Gauss yasasının değişken süreçler için genelleştirilmiş halidir. Gauss yasası, elektrik yer değiştirme vektörünün keyfi bir kapalı S yüzeyinden akışını, bu yüzeyin içinde yoğunlaşan Q yükü ile ilişkilendirir:

nerede dS = n Ö dS ; n 0 - S yüzeyinin dış normalinin birim vektörü.

(1.41)'i (1.40) yerine koyarsak, şunu elde ederiz:

Denklem (1.43) genellikle denir Maxwell'in üçüncü denklemi integral formda. Diferansiyel forma gitmek için

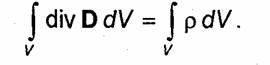
Bu eşitlik keyfi bir hacim için geçerli olmalıdır V, bu ancak mümkünse

Soru 5. İntegral ve diferansiyel formlarda Maxwell'in dördüncü denklemi.

Maxwell'in integral biçimindeki dördüncü denklemi, aşağıdaki gibi formüle edilebilen bir manyetik alan için Gauss yasasıyla örtüşür. vektör akışı AT herhangi bir kapalı yüzey boyunca S sıfıra eşittir, yani.

Bu, vektör çizgisi olmadığı anlamına gelir. AT sadece kapalı S yüzeyine giren (veya tersine sadece S yüzeyinden çıkan): her zaman ona nüfuz ederler (Şekil 1.9).

Denklem (1.46) denir Maxwell'in dördüncü denklemi integral formda.Üçüncü Maxwell denkleminde olduğu gibi, Ostrogradsky-Gauss teoremi kullanılarak denklemin (1.46) diferansiyel formuna geçilebilir. Sonuç olarak, alıyoruz

divB = 0 (1.47)

Denklem (1.47) Maxwell'in dördüncü denklemidir. Doğada aynı işarete sahip tek bir manyetik yükün olmadığını gösterir. Ayrıca bu denklemden, vektörün çizgilerinin AT(manyetik alanın alan çizgileri) süreklidir.

Maxwell'in denklem sistemi dört temel denklem içerir

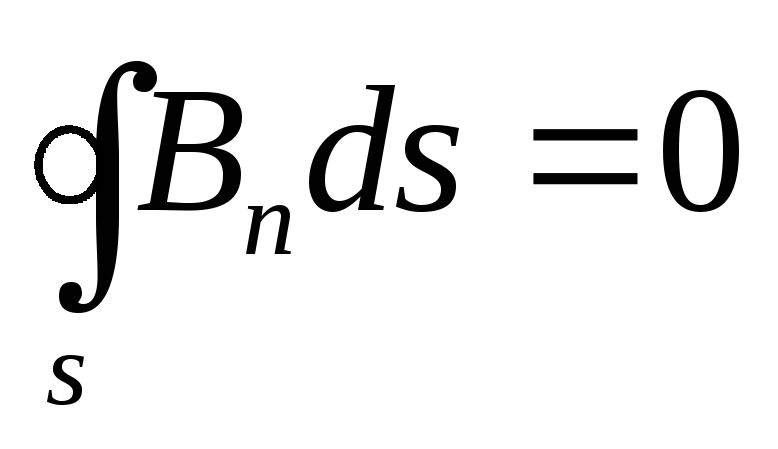, (3.2)

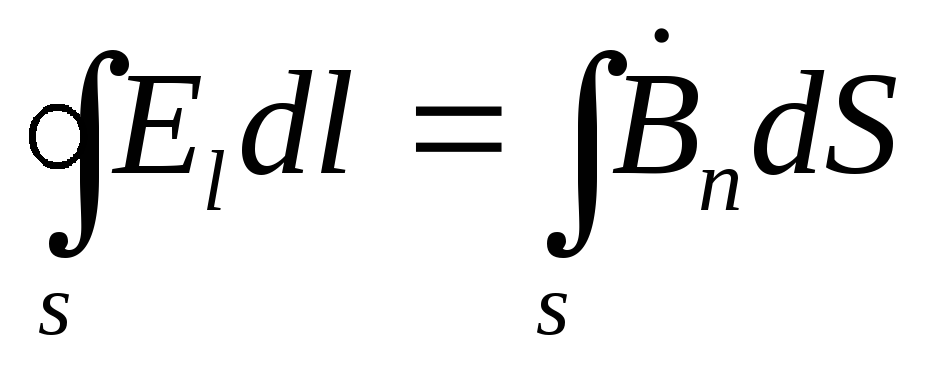, (3.3)

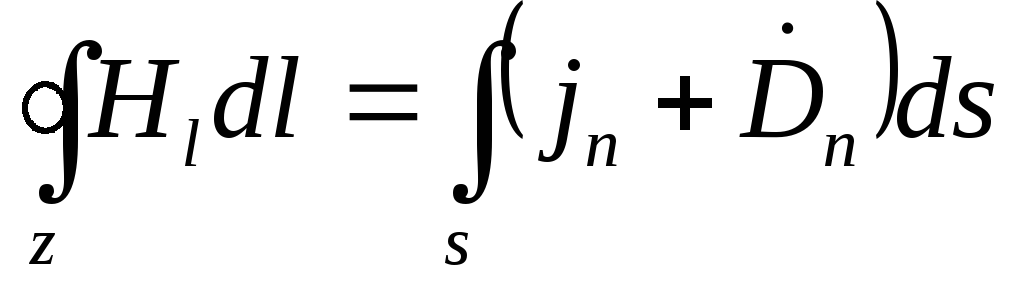. (3.4)

Bu sistem üç ile tamamlanmaktadır. malzeme denklemleri, bağlama fiziksel özellikler Maxwell denklemlerine dahil edilmiştir:

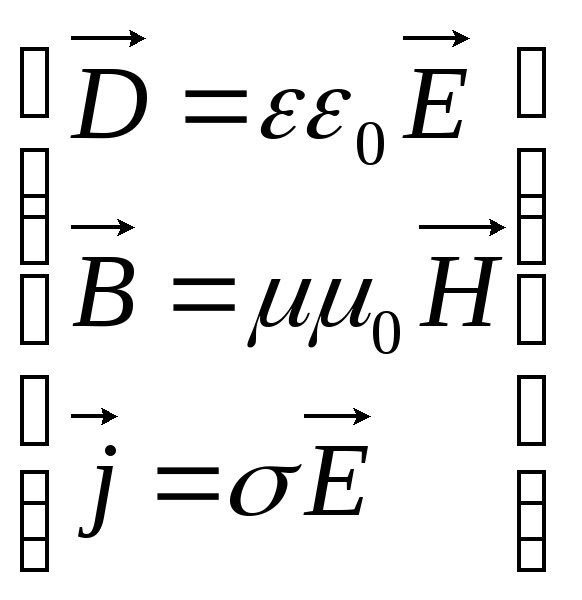(3.5)

Hatırlayalım fiziksel anlam bu matematiksel ifadeler.

İlk denklem (3.1) şunu belirtir: elektrostatik alan sadece elektrik yükleri tarafından oluşturulabilir.Bu denklemde 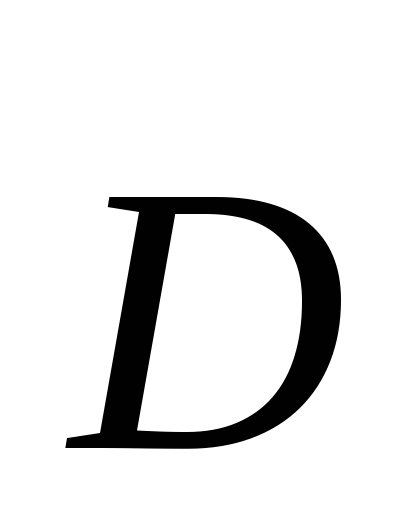elektrik yer değiştirme vektörüdür, ρ elektrik yükünün hacim yoğunluğudur.

Elektrik yer değiştirme vektörünün herhangi bir kapalı yüzeyden akışı, bu yüzeyin içindeki yüke eşittir.

Deneyin gösterdiği gibi, manyetik indüksiyon vektörünün kapalı bir yüzeyden akışı her zaman sıfıra (3.2) eşittir.

(3.2) ve (3.1) denklemlerinin karşılaştırılması, doğada manyetik yüklerin olmadığı sonucuna varmamızı sağlar.

Denklemler (3.3) ve (3.4) büyük ilgi ve öneme sahiptir. Burada elektrik gücü vektörlerinin dolaşımını ele alıyoruz ( ) ve manyetik ( ) kapalı bir kontur boyunca alanlar.

Denklem (3.3), alternatif manyetik alanın ( 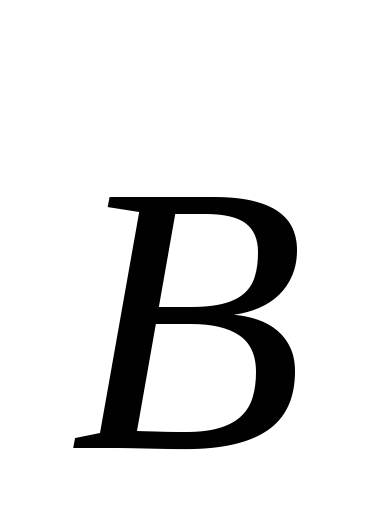) girdap elektrik alanının kaynağıdır ( ).Bu, Faraday'ın elektromanyetik indüksiyon fenomeninin matematiksel bir kaydından başka bir şey değildir.

Denklem (3.4), manyetik alan ile alternatif elektrik alanı arasında bir bağlantı kurar. Bu denkleme göre, manyetik alan sadece iletim akımı tarafından oluşturulamaz ( 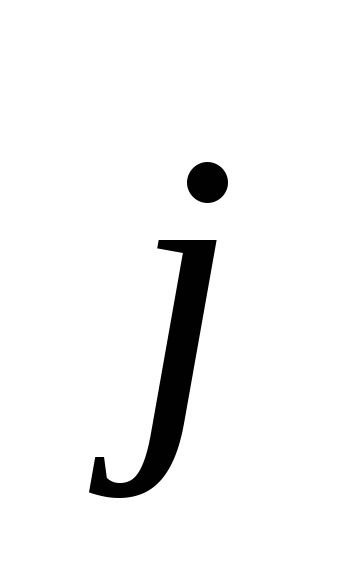), aynı zamanda alternatif bir elektrik alanı ile .

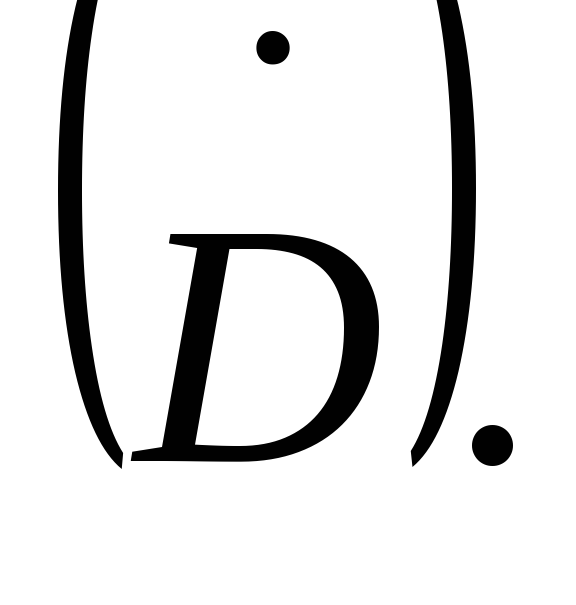Bu denklemlerde:

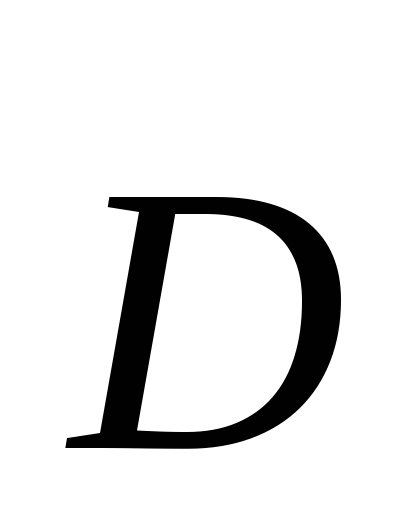elektrik yer değiştirme vektörüdür,

H- manyetik alan kuvveti,

E- elektrik alan şiddeti,

j iletim akımı yoğunluğu,

μ - ortamın manyetik geçirgenliği,

ε ortamın dielektrik sabitidir.

1. Elektromanyetik dalgalar. Elektromanyetik dalgaların özellikleri

Geçen dönem, klasik Maxwell elektrodinamiğinin denklemler sisteminin değerlendirilmesini tamamlayarak, son iki denklemin ortak çözümünün (vektörlerin dolaşımı üzerine) olduğunu bulduk. ve ) bir diferansiyel dalga denklemine yol açar.

Böylece "Y" dalgasının dalga denklemini elde ettik:

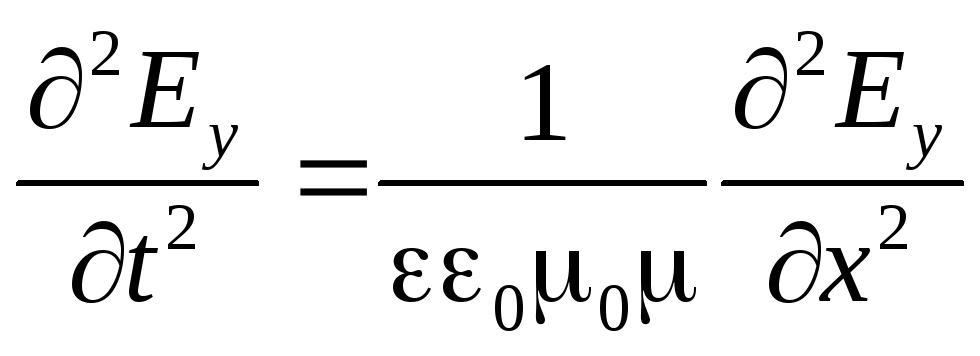. (3.6)

Elektrik bileşeni y - dalga, X ekseninin pozitif yönünde faz hızıyla yayılır

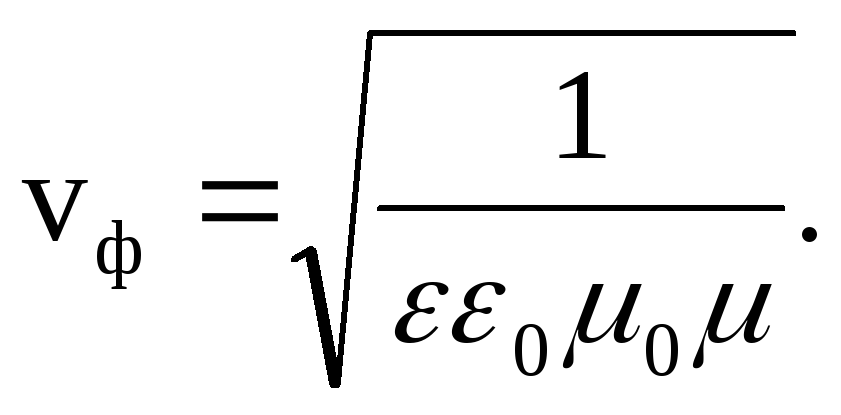(3.7)

Benzer bir denklem, manyetik alan y - dalgalarının uzay ve zamandaki değişimini tanımlar:

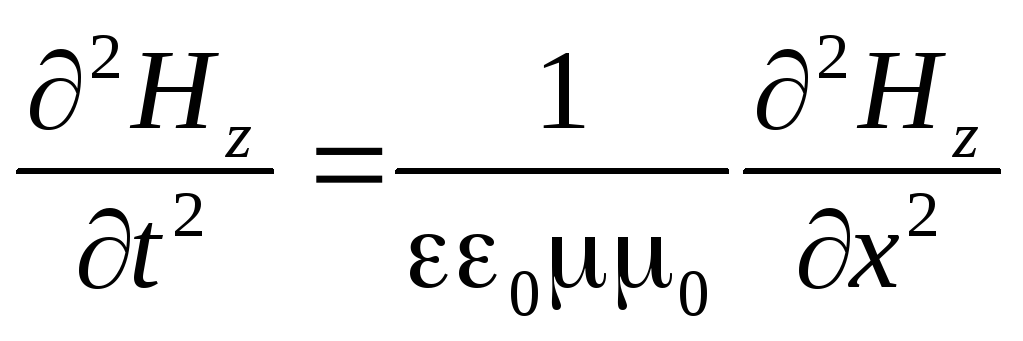. (3.8)

Elde edilen sonuçları analiz ederek, elektromanyetik dalgaların doğasında bulunan bir takım özellikleri formüle etmek mümkündür.

1. Düzlem "y" - dalga, doğrusal olarak polarize edilmiş bir enine dalgadır. Elektrik gücü vektörleri ( 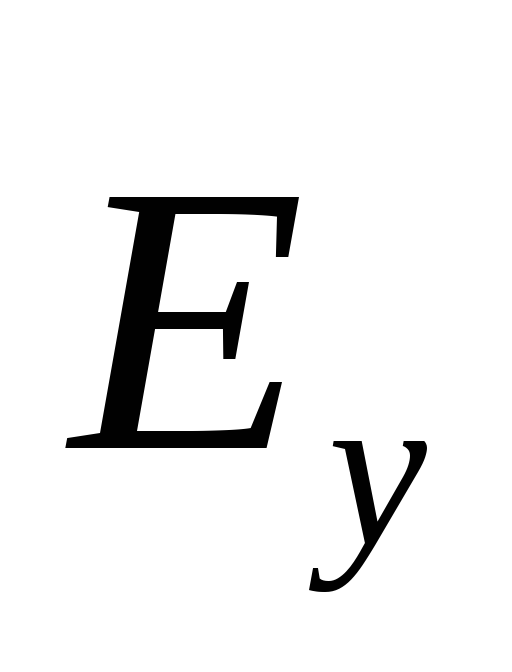), manyetik ( 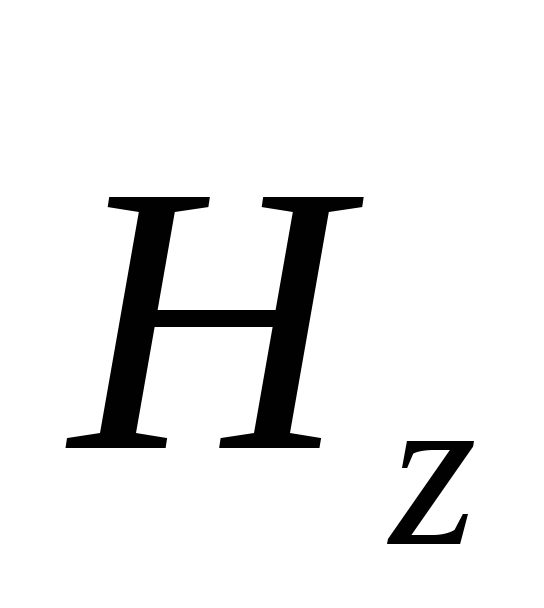) dalganın alan ve faz hızı ( 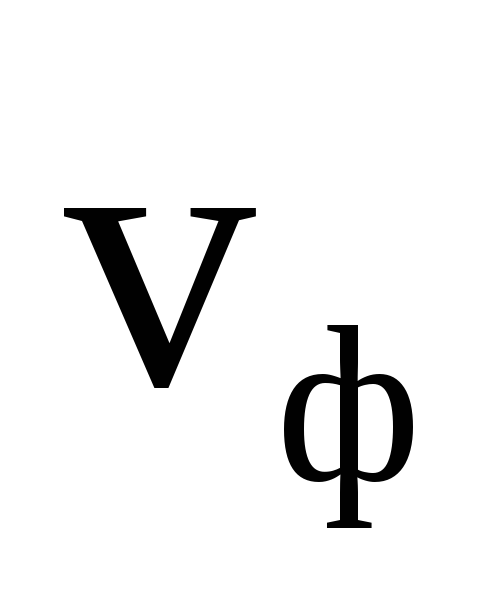) karşılıklı olarak diktir ve “sağ elini kullanan” bir sistem oluşturur (Şekil 3.1).

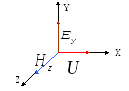
2. Dalga bileşeninin uzayındaki her noktada H z elektrik alan kuvvetiyle orantılıdır E y:

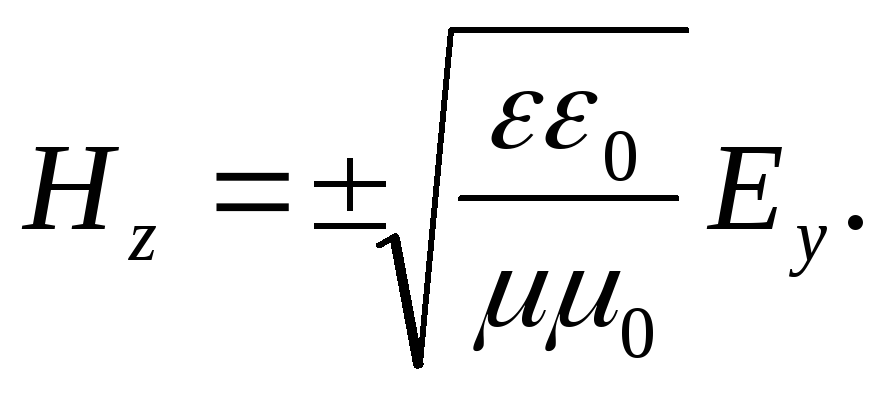
Burada, "+" işareti, X ekseninin pozitif yönünde yayılan bir dalgaya karşılık gelir. "-" - işareti, negatif yönde.

3. Bir elektromanyetik dalga, X ekseni boyunca bir faz hızıyla hareket eder.

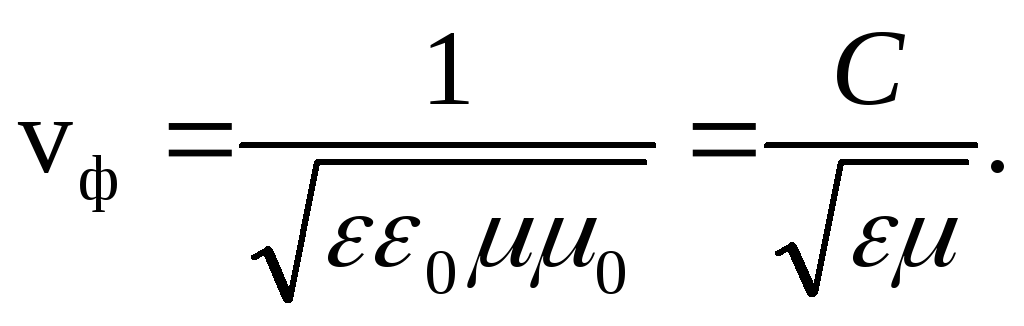
Burada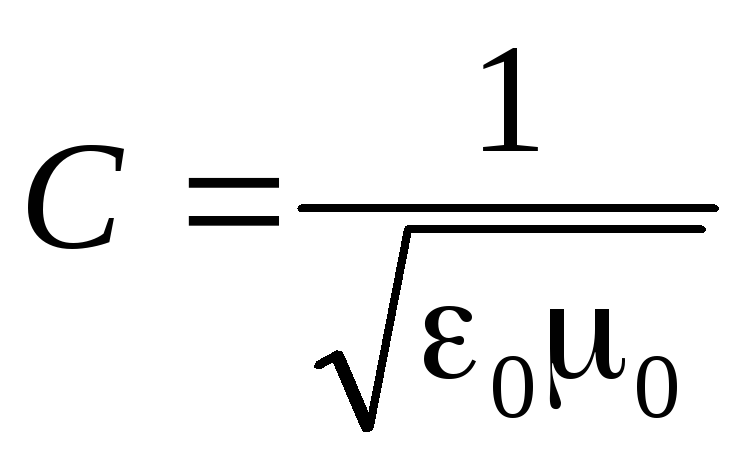

.

Bir elektromanyetik dalga vakumda yayıldığında (ε = 1, μ = 1), faz hızı

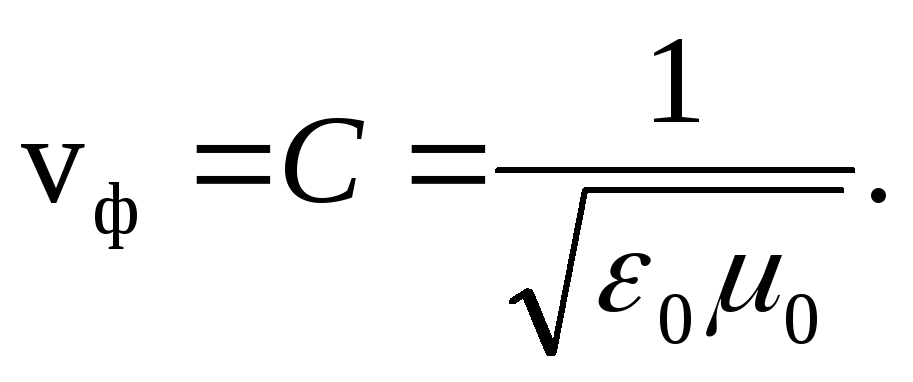
Burada elektrik sabiti ε 0 = 8.85 10 -12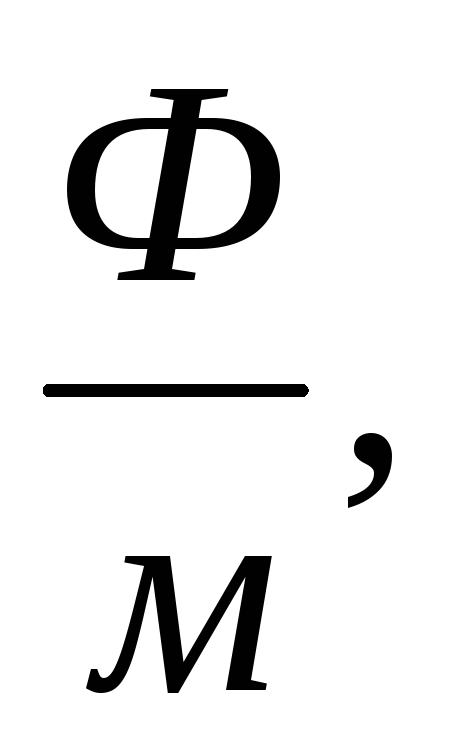

manyetik sabit μ 0 = 4π 10 -7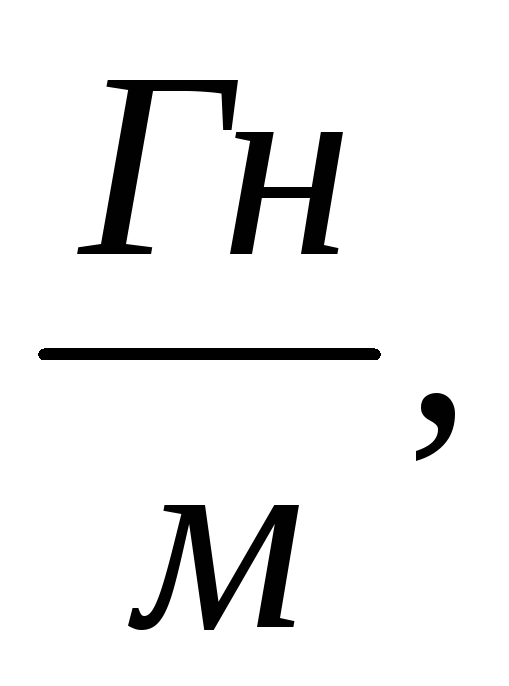

.

.

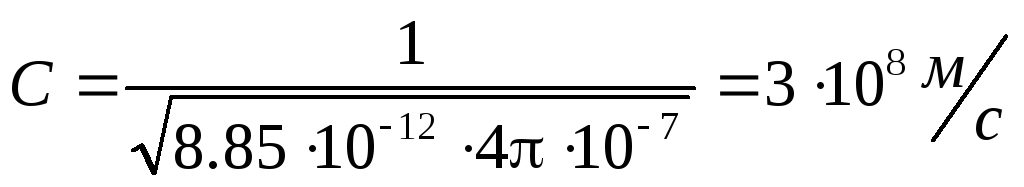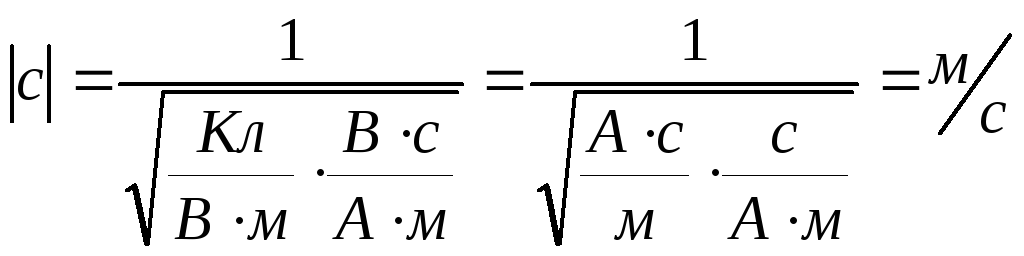Bir elektromanyetik dalganın boşluktaki hızı ile ışık hızının çakışması, ışığın elektromanyetik doğasının ilk kanıtıydı.

Vakumda, dalgadaki manyetik ve elektrik alanların gücü arasındaki ilişki basitleştirilir.

.

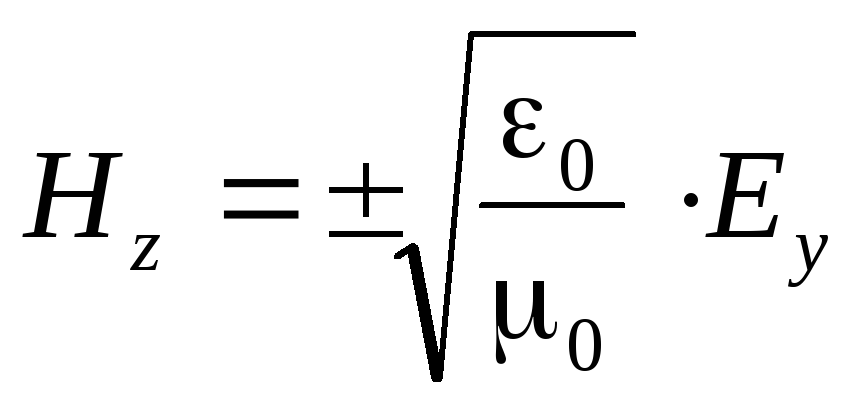Bir elektromanyetik dalga bir dielektrik ortamda yayıldığında (μ = 1)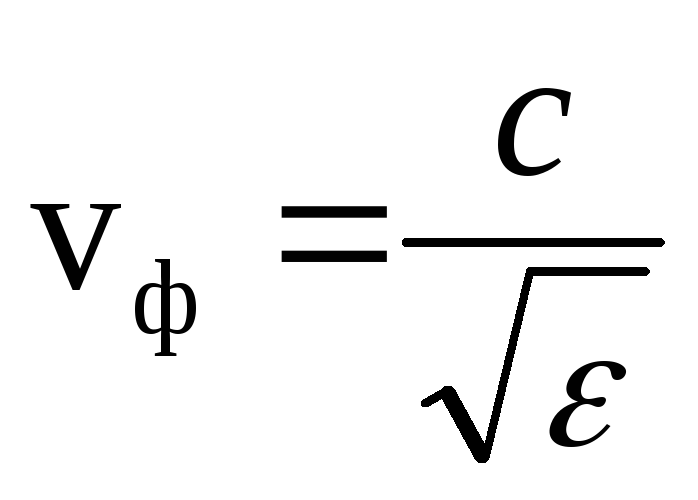

ve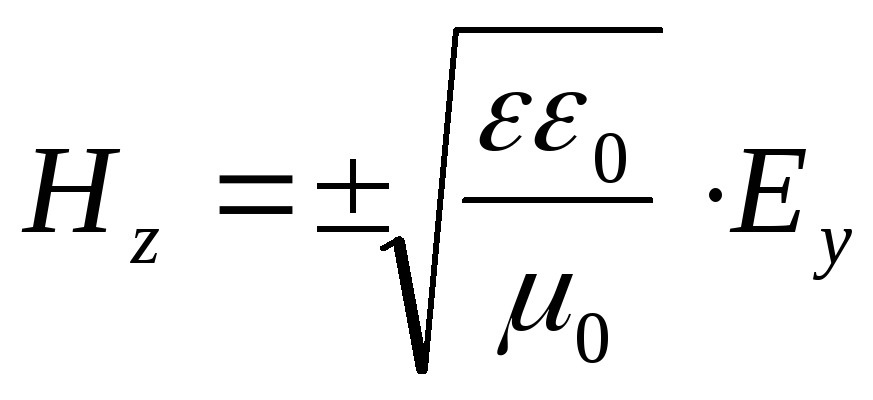

.

Maxwell tarafından yer değiştirme akımı kavramının tanıtılması, onu yarattığı elektromanyetik alanın birleşik makroskopik teorisinin tamamlanmasına götürdü, bu da birleşik bir bakış açısıyla sadece elektriksel ve manyetik olayları açıklamayı değil, aynı zamanda tahmin etmeyi de mümkün kıldı. daha sonra varlığı doğrulanan yenileri.

Maxwell'in teorisi yukarıda tartışılan dört denkleme dayanmaktadır:

1. Elektrik alanı (bkz. § 137) hem potansiyel ( e q) ve girdap ( E B), yani toplam alanın gücü E=E S+ E b. Vektörün dolaşımından beri e q sıfıra eşittir (bkz. (137.3)) ve vektörün dolaşımı E B ifadesi (137.2) ile belirlenir, ardından toplam alan kuvveti vektörünün dolaşımı

Bu denklem, elektrik alan kaynaklarının sadece elektrik yükleri değil, aynı zamanda zamanla değişen manyetik alanlar olabileceğini göstermektedir.

2. Genelleştirilmiş vektör sirkülasyon teoremi H(bkz. (138.4)):

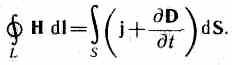
Bu denklem, manyetik alanların ya hareketli yükler (elektrik akımları) ya da alternatif elektrik alanları tarafından uyarılabileceğini gösterir.

3. Alan için Gauss teoremi D(bkz. (89.3)):

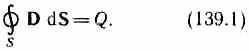
Yük, kütle yoğunluğu  olan kapalı bir yüzey içinde sürekli olarak dağıtılırsa, formül (139.1) şu şekilde yazılacaktır:

4. B alanı için Gauss teoremi (bkz. (120.3)):

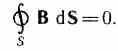
Ve 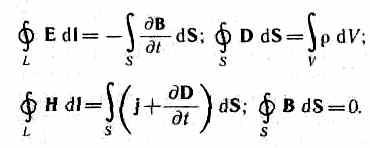Yani, integral formda Maxwell denklemlerinin tam sistemi:

Maxwell denklemlerine dahil edilen miktarlar bağımsız değildir ve aralarında aşağıdaki ilişki vardır (izotropik ferroelektrik olmayan ve ferromanyetik olmayan ortam):

D= 0 E,

B= 0 H,

j=E,

burada  0 ve  0 sırasıyla elektrik ve manyetik sabitlerdir,  ve  - sırasıyla dielektrik ve manyetik geçirgenlik,  - maddenin spesifik iletkenliği.

Maxwell denklemlerinden, bir elektrik alanının kaynaklarının ya elektrik yükleri ya da zamanla değişen manyetik alanlar olabileceği ve manyetik alanların ya hareket eden elektrik yükleri (elektrik akımları) ya da alternatif elektrik alanları tarafından uyarılabileceği sonucu çıkar. Maxwell denklemleri elektrik ve manyetik alanlara göre simetrik değildir. Bunun nedeni, doğada elektrik yüklerinin olması, ancak manyetik yüklerin olmamasıdır.

D 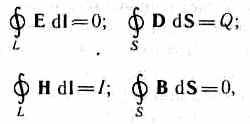sabit alanlar için (E= const ve AT= sabit) Maxwell denklemleri formu al

yani, bu durumda elektrik alan kaynakları yalnızca elektrik yükleridir, manyetik alan kaynakları yalnızca iletim akımlarıdır. Bu durumda, elektrik ve manyetik alanlar birbirinden bağımsızdır, bu da ayrı ayrı çalışmayı mümkün kılar. kalıcı elektrik ve manyetik alanlar.

Vektör analizinden bilinen Stokes ve Gauss teoremlerini kullanarak, m 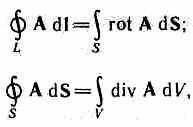biri hayal edebilir diferansiyel formda Maxwell denklemlerinin tam sistemi(alanı uzaydaki her noktada karakterize ederek):

Yükler ve akımlar uzayda sürekli olarak dağıtılırsa, Maxwell denklemlerinin her iki formu da integraldir.

ve 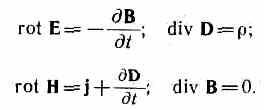diferansiyel - eşdeğer. Ancak, var olduğunda kırılma yüzeyleri- ortamın veya alanların özelliklerinin aniden değiştiği yüzeyler, daha sonra denklemlerin integral formu daha geneldir.

Maxwell'in diferansiyel formdaki denklemleri, uzay ve zamandaki tüm niceliklerin sürekli değiştiğini varsayar. Maxwell denklemlerinin her iki formunun da matematiksel denkliğini elde etmek için diferansiyel form tamamlanır. sınır şartları, iki ortam arasındaki arayüzde elektromanyetik alan tarafından karşılanması gereken. Maxwell denklemlerinin integral formu bu koşulları içerir. Bunlar daha önce değerlendirilmiştir (bkz. § 90, 134):

D 1 n = D 2 n , E 1  = E 2  , B 1 n = B 2 n , H 1  = H 2 

(ilk ve son denklemler, arayüzde ne serbest yüklerin ne de iletim akımlarının olmadığı durumlara karşılık gelir).

Maxwell denklemleri, elektrik ve manyetik alanlar için en genel denklemlerdir. dinlenme ortamları. Elektromanyetizma teorisinde Newton'un mekanikteki yasalarıyla aynı rolü oynarlar. Maxwell denklemlerinden, alternatif bir manyetik alanın her zaman onun ürettiği elektrik alanıyla ilişkili olduğunu ve alternatif bir elektrik alanının her zaman onun ürettiği manyetik alanla ilişkili olduğunu, yani elektrik ve manyetik alanların ayrılmaz bir şekilde birbirine bağlı olduğunu izler - tek oluştururlar elektromanyetik alan.

Maxwell'in teorisi, elektriksel ve manyetik fenomenlerin temel yasalarının bir genellemesi olarak, sadece zaten bilinen deneysel gerçekleri açıklamakla kalmadı, aynı zamanda bunun önemli bir sonucuydu, aynı zamanda yeni fenomenleri de öngördü. Bu teorinin önemli sonuçlarından biri, Maxwell'in varlığını tahmin etmesine izin veren manyetik bir yer değiştirme akımı alanının varlığıydı (bkz. § 138). elektromanyetik dalgalar- uzayda sınırlı bir hızla yayılan alternatif bir elektromanyetik alan. Daha sonra, bir serbest elektromanyetik alanın (yükler ve akımlarla ilgili olmayan) boşlukta yayılma hızının, ışık hızı c = 3 10 8 m/s'ye eşit olduğu kanıtlandı. Bu sonuç ve elektromanyetik dalgaların özelliklerinin teorik olarak incelenmesi, Maxwell'in ışığın da elektromanyetik dalgalar olduğuna göre elektromanyetik ışık teorisini yaratmasına yol açtı. Elektromanyetik dalgalar, uyarılma ve yayılma yasalarının tamamen Maxwell denklemleriyle tanımlandığını kanıtlayan Alman fizikçi G. Hertz (1857-1894) tarafından deneysel olarak elde edildi. Böylece Maxwell'in teorisi deneysel olarak doğrulandı.

İle elektromanyetik alan Elektromanyetik dalgaların boşlukta tüm referans çerçevelerinde aynı hızla yayıldığı gerçeğinden dolayı sadece Einstein'ın görelilik ilkesi uygulanabilir. İle birlikte Galileo'nun görelilik ilkesiyle bağdaşmaz.

Göre Einstein'ın görelilik ilkesi tüm eylemsiz referans çerçevelerinde mekanik, optik ve elektromanyetik olaylar aynı şekilde ilerler, yani aynı denklemlerle tanımlanırlar. Maxwell denklemleri Lorentz dönüşümleri altında değişmezdir: geçerken formları değişmez

birinden atalet sistemi değerlere rağmen bir diğerine referans E, V,D, N belirli kurallara göre dönüştürülürler.

Görelilik ilkesinden, elektrik ve manyetik alanların ayrı bir değerlendirmesinin göreceli bir anlamı olduğu sonucu çıkar. Dolayısıyla, elektrik alanı bir sabit yükler sistemi tarafından yaratılıyorsa, o zaman bu yükler, bir eylemsiz referans çerçevesine göre sabitlendiğinde, diğerine göre hareket eder ve bu nedenle, sadece bir elektrik değil, aynı zamanda bir manyetik alan da üretecektir. . Benzer şekilde, bir eylemsiz referans çerçevesine göre sabit bir akım iletkeni, uzayda her noktada sabit bir manyetik alan uyandırır, diğer eylemsiz çerçevelere göre hareket eder ve onun tarafından oluşturulan alternatif manyetik alan bir girdap elektrik alanı uyarır. Böylece, Maxwell'in teorisi, deneysel onayı ve Einstein'ın görelilik ilkesi, elektromanyetik alan fikrine dayanan birleşik bir elektrik, manyetik ve optik fenomen teorisine yol açar.

Elektromanyetik alanla ilgili olarak ortam sınıflandırmaları

Ortamın elektromanyetik alana göre özellikleri parametreler tarafından belirlenir.

Orta iletkenlik

Bu parametreler alanın büyüklüğüne bağlıysa, o zaman doğrusal ortam ve en az 1 parametre alan değerine bağlıysa, ortam doğrusal olmayan.

Doğrusal ortam 4 gruba ayrılır

1. Homojen, burada bu parametreler koordinatlara bağlı değildir.

2. Homojen olmayan, burada bu parametreler koordinatlara bağlıdır.

3. İzotropik, özellikleri her yönde aynıdır.

4. Anizotropik, özellikler her yönde farklıdır.

Maxwell denklemleri diferansiyel, integral ve karmaşık formlarda

1 Maxwell denklemi diferansiyel formda: Elektrik şarjı elektriksel indüksiyon kaynağıdır.

2 Maxwell denklemi. Manyetik yük yok

3 Maxwell denklemi. Manyetik indüksiyondaki değişiklik bir girdap elektrik alanı oluşturur

4 Maxwell denklemi. Elektrik ve elektrik indüksiyonundaki bir değişiklik bir girdap manyetik alanı oluşturur

Aynı sırayla, integral gösterimi

Kapalı bir yüzeyden elektrik indüksiyon akışı s hacimdeki ücretsiz ücret miktarıyla orantılı v yüzeyi çevreleyen s.

Kapalı bir yüzeyden geçen manyetik indüksiyon akısı sıfırdır (manyetik yükler yoktur).

Açık bir yüzeyden geçen manyetik indüksiyon akısındaki değişim s, zıt işaret ile alındığında, kapalı bir döngüde elektrik alanının dolaşımı ile orantılıdır. ben s.

Serbest yüklerin toplam elektrik akımı ve açık bir yüzey boyunca elektrik indüksiyon akışındaki değişim s, kapalı bir devrede manyetik alanın dolaşımı ile orantılıdır. ben, yüzeyin sınırı olan s.

Karmaşık genlikler için Maxwell denklemleri

3. Anlık güç değerlerinin denge denklemi

1.1'de belirtildiği gibi, elektromanyetik alan maddenin biçimlerinden biridir. Diğer tüm madde formları gibi, enerjiye sahiptir. Bu enerji uzayda yayılabilir ve diğer enerji biçimlerine dönüştürülebilir.

Belirli bir hacme göre anlık güç değerleri için denge denklemini formüle edelim. V, S yüzeyi ile sınırlandırılmıştır (Şekil 1.23). Hacim ver V, homojen bir izotropik ortamla dolu, üçüncü taraf kaynaklar var. Genel fiziksel kavramlardan, üçüncü taraf kaynaklar tarafından salınan gücün Joule kayıplarına ve içerideki elektromanyetik alanın enerjisini değiştirmeye harcanabileceği açıktır. V, ve ayrıca S yüzeyinden çevreleyen alana kaçarak kısmen dağılabilir. Bu durumda eşitlik

nerede R st, üçüncü taraf kaynakların gücüdür; R P - hacim içindeki Joule kayıplarının gücü V; R Σ S yüzeyinden geçen güç; W- bir hacimde yoğunlaşan elektromanyetik alanın enerjisi V, a dW/dt- Hacimdeki enerjiyi değiştirmek için harcanan güç v.

AT bu bölüm durum denklemleri (1.53) kullanılacaktır. Bu denklemler ortamın polarizasyonu ve manyetizasyonu sırasındaki enerji kayıplarının hesaba katılmasına izin vermez. Bu nedenle, terim R P içinde eşitlik (1.120), aslında V hacmindeki Joule kayıplarının gücünü belirler. , İletim akımından kaynaklanır.

Denklem (1.120), enerji ilişkileri hakkında yalnızca niteliksel bir fikir verir. Nicel ilişkiler elde etmek için Maxwell denklemlerini kullanmanız gerekir. Dış akımları (1.111) hesaba katarak ilk Maxwell denklemini düşünün. Bu denklemin tüm üyeleri, A/m 2 boyutuna sahip vektör miktarlarıdır.

(1.120)'ye benzer bir denklem elde etmek için, birinci Maxwell denklemini (1.111) terimlerini watt cinsinden ölçülen skaler nicelikler olacak şekilde değiştirmeniz gerekir. Bunu yapmak için, belirtilen eşitliğin tüm terimlerini vektörle skaler olarak çarpmak yeterlidir. E ve ardından elde edilen ifadeyi birim üzerine entegre edin v. Bir vektörle skaler çarpımdan sonra E alırız

Vektör analizinden bilinen div formülünü kullanma = = H rot E - E rot H, ilişkinin (1.121) sol tarafını dönüştürüyoruz ve rot E'yi ikinci Maxwell denkleminden (1.39) değeriyle değiştiriyoruz:

Bu ifadeyi (1.121) yerine koyarsak, şunu elde ederiz:

(1.122)'nin sağ tarafındaki son terimde, vektörlerin skaler çarpımındaki faktörlerin sırası değiştirilir. dB/dt ve H. Buna izin verilir çünkü H dB/dt = dAT/dtH. Bu değişiklik temel değildir ve anlık güç değerleri için burada ele alınan denge denkleminin türetilmesinde herhangi bir avantaj sağlamaz. Ancak, böyle bir gösterimle, denklem (1.122) tüm terimlerinde ikinci faktör (vektörler) j Aziz, j, BDIDt ve H), daha önce ilk Maxwell denklemine dahil edilmiş bir vektördür. Bu durum gelecekte (bakınız 1.8.4) monokromatik bir alan (karmaşık gücün denge denklemi) durumunda denge denkleminin türetilmesini bir şekilde basitleştirmeyi mümkün kılacaktır. Hacim üzerinden terim terim denklemi (1.122) entegre etme V, alırız

elemanın yönü nerede dS(1.122)'den (1.123)'e geçerken, Ostrogradsky-Gauss teoremi, hacim integralini div['den çevirmek için kullanılır. E, H] vektör ürününün yüzey integraline [ E, H]. Notasyonu tanıtıyoruz

ve son terimdeki integrali (1.123'ün sağ tarafında) dönüştürün:

(1.124) ve (1.125)'i (1.123) yerine koyarak ve entegrasyon ve farklılaşma sırasını değiştirerek elde ederiz.

(1.126) denkleminde yer alan ifadelerin fiziksel anlamlarını bulalım.

(1.126)'nın sağ tarafındaki ilk terimi ele alalım. Hacmi hayal edelim V uzunlukları sonsuz küçük silindirlerin toplamı olarak dl, hangi uçları ( dS ) akımın yönüne dik (vektör j). O zamanlar EjdV=EjdV=(Edl)(jdS) = dUdl = dP n , nerede dl=jdS kabul edilen sonsuz küçük silindirden akan akımdır; dU = Edl- uzunluk boyunca potansiyelde değişiklik dl, a dP n, hacimdeki Joule kayıplarının gücüdür d V . Bu nedenle, söz konusu terim, hacimdeki Joule kayıplarının Р p gücüdür. v. oranı kullanma j = σЕ, için R P diğer temsiller elde edilebilir:

Formüller (1.127), iletken bir hacim için geçerli genelleştirilmiş bir Joule-Lenz yasası olarak kabul edilebilir. V keyfi şekil.

(1.126)'nın sol tarafındaki integral, sağ taraftaki ilk terimden yalnızca, j dahil j c t Bu nedenle, üçüncü taraf kaynakların gücünü belirlemelidir. Elektromanyetik alana dış akımların verdiği pozitif gücü ele alacağız. Elektrik akımı, yüklü parçacıkların düzenli bir hareketidir. Akımın pozitif yönü hareket yönüdür. pozitif masraflar. Akım, kendisini oluşturan yüklü parçacıklar yavaşladığında elektromanyetik alana enerji verir. Bunun için elektrik alan şiddeti vektörünün E mevcut yönün tersine yönlendirilmiş bir bileşeni vardı, yani. vektörlerin nokta çarpımına E ve j st negatifti ( Ej Aziz<0). При этом левая часть равенства (1.126) будет поло­жительной величиной. Таким образом, мгновенное значение мощ­ности, отдаваемой сторонними токами электромагнитному полю в объеме V, ifade ile tanımlanır

(1.126) denkleminin sağ tarafındaki son terimin fiziksel anlamını anlamak için özel bir durumu ele alıyoruz. Diyelim ki hacim V S yüzeyi ile çakışan mükemmel iletken bir kabuk ile çevrilidir. Daha sonra vektörün teğet bileşeni E yüzeyinde S sıfıra eşit olacaktır. Yüzey elemanı dS dış normal ile aynı doğrultuda n 0 . Sonuç olarak, denklem (1.126)'daki yüzey integrali, vektör ürününün normal bileşeni [ E, H], Vektörlerinin teğet bileşenleri tarafından belirlenir. Ayrıca, birim içindeki ortamın V iletkenliği yok σ = 0). Bu durumda, söz konusu bölgede Joule kaybı olmayacak ve denklemin (1.126) sağ tarafındaki ilk integral de sıfıra eşit olacaktır. Sonuç olarak, alıyoruz

Açıkçası, söz konusu durumda, dış kaynakların gücü yalnızca elektromanyetik alanın enerjisini değiştirmek için harcanabilir. Böylece eşitliğin sağ tarafı (1.129), hacimde depolanan elektromanyetik alanın enerjisinin değişim hızıdır. V,şunlar. terime karşılık gelir dW/dt(1.126) denkleminde. (1.129)'un sağ tarafındaki integralin V hacminde yoğunlaşan elektromanyetik alanın enerjisine eşit olduğunu varsaymak doğaldır:

Kesin konuşmak gerekirse, bu integral aşağıdakilerden farklı olabilir: W bazı işlevlere g = g(x, y, z) zamandan bağımsız. işlevin doğru olduğunu doğrulamak kolaydır. d sıfıra eşittir. (1.130) olarak yeniden yazalım. W \u003d B E + W M, nerede

Elektrik ve manyetik alanların sabit olduğunu varsayın (zamana bağlı değil). Bu durumda, fizik dersinden bilindiği gibi (ayrıca Bölüm 3 ve 4'e bakınız), (1.131) ve (1.132) ifadeleri hacimdeki sırasıyla elektrik ve manyetik alanların enerjisini belirler. v. Ancak bu, g = 0 olduğu anlamına gelir ve bu ifadeler, hacimdeki elektrik ve manyetik alanların enerjisinin anlık değerlerini belirler. V zamana herhangi bir bağımlılık için, formül (1.130) ile belirlenen toplamları, gerçekten de hacimdeki elektromanyetik alanın enerjisinin anlık değerine eşittir. v.

(1.126) denklemindeki yüzey integralinin fiziksel özünü netleştirmek için kalır. hacimde olduğunu varsayıyoruz V kayıp yoktur ve ayrıca elektromanyetik enerji miktarı sabit kalır (W= const). Bu durumda denklem (1.126) şeklini alır.

Aynı zamanda, bu özel durumda, üçüncü taraf kaynakların tüm gücünün çevreleyen alana gitmesi gerektiği fiziksel temsillerden açıktır. (R Aziz = Р). Bu nedenle, denklemin (1.133) sağ tarafı, S yüzeyinden geçen enerji akışına eşittir (zaman içinde S'den geçen enerji miktarının oranının limiti). Δt de Δt→0),şunlar.

vektörü olduğunu varsaymak doğaldır. P enerji akı yoğunluğunu temsil eder (alandan geçen enerji akısının oranının sınırı ∆S enerji yayılım yönüne dik olarak yerleştirilmiş, ∆S de ∆S→0). Biçimsel olarak, matematiksel olarak, bu varsayım açık değildir, çünkü vektörün değiştirilmesi Püzerinde P 1 = P + çürüme a, nerede a- keyfi vektör, değeri değiştirmez R Σ . Ancak bu doğrudur ve özellikle elektromanyetik alanın göreli kuramından doğrudan çıkar.

Böylece eşitlik (1.126), (1.120)'ye benzer ve elektromanyetik alanın gücünün anlık değerlerinin dengesi için denklemi temsil eder. 1884 yılında Poynting tarafından elde edilmiştir ve İşaret teoremi. Buna göre vektör P Poynting vektörü denir. İsimler de sıklıkla kullanılır "Umov-Poynting teoremi" ve "Umov-İşaretleme vektörü" enerji akısı kavramının ve yoğunluğunu karakterize eden bir vektörün tanıtılmasıyla enerjinin korunumu yasasının genel bir biçimde formüle edilmesinin ilk kez N.A. 1874 yılında Umov.

Enerjinin hacme girebileceğini unutmayın. V sadece dış kaynaklardan değil. Örneğin, S yüzeyinden geçen enerji akışı çevreleyen alandan hacme yönlendirilebilir. v. Aynı zamanda, güç PΣ hacimden çıkan enerji akışı pozitif kabul edildiğinden negatif olacaktır Vçevreleyen alana (eleman yönü dS S yüzeyinin dış normalinin yönü ile çakışır).

Üçüncü taraf kaynaklar sadece enerji vermekle kalmaz, aynı zamanda elektromanyetik alandan da alır. Bu durumda, üçüncü taraf kaynakların gücü negatif olacaktır. Gerçekten de, elektromanyetik alan, akımı oluşturan yüklü parçacıkların hareketini hızlandırırsa, iletim akımına enerji verir. Bunun için elektrik alan şiddeti vektörü E akış çizgileri boyunca yönlendirilmiş bir bileşene sahip olmalıdır, yani böylece E vektörlerinin skaler çarpımı ve j st sıfırdan büyüktü.

Elektromanyetik alanın enerjisini belirleyen formülleri daha ayrıntılı olarak ele alalım. integraller

sırasıyla elektrik ve manyetik alanların hacimsel enerji yoğunluklarının anlık değerleri ve bunların toplamı olarak yorumlanabilir.

Elektromanyetik alanın toplam enerjisinin hacim yoğunluğu olarak.

Elektrik ve manyetik alan vektörleri tarafından sağlanan süperpozisyon ilkesinin enerji için geçerli olmadığını vurguluyoruz. Gerçekten de, alan enerjilerinin E 1, H 1 ve E 2, H 2, bölgede ayrı olarak mevcut V, sırasıyla eşit 1 ve W2. Daha sonra toplam alanın enerjisi E \u003d E 1 + E 2, H \u003d H 1 + H 2 ifade ile belirlenir

Alanların karşılıklı enerjisi. karşılıklı enerji K 12 hem olumlu hem de olumsuz olabilir. vektörler ise E1 ve E2, birlikte H1 ve H2 karşılıklı olarak dik, o zaman W 12 = 0.

Değişken süreçlerde elektromanyetik enerjinin dağılımı sürekli değişir. Herhangi bir noktadaki bu değişiklik, uygun bir şekilde şu şekilde temsil edilen (1.122) denklemi temelinde belirlenebilir.

nerede p st \u003d- Ej st ve pn = Ej- sırasıyla üçüncü taraf kaynakların güç yoğunluklarının ve Joule kayıplarının gücünün anlık değerleri. (1.122) bağıntısından (1.136) denklemine geçilirken (1.125) ve (1.135) formülleri dikkate alınır. Denklem (1.136) Poynting teoreminin diferansiyel formu.

4 DALGA DENKLEMLERİ

Genel dava

Elektrodinamiğin doğrudan problemlerini çözerken, vektörleri bulmak gerekir. E ve H bilinen (belirtilen) üçüncü taraf kaynaklara göre. Dış kaynakların sonsuz homojen bir izotropik ortamda bulunduğunu varsayalım. Dönüşümleri basitleştirmek için, σ = 0 olduğunu varsayacağız. Bu özel durum için Maxwell denklemlerini yazarsak, şunu elde ederiz:

vektörlerin tanımı E ve H(2.25) denklem sisteminden doğrudan elde edilmesi zordur. Bu nedenle, vektörü ortadan kaldırarak dönüştürülmesi tavsiye edilir. E veya bir vektör H, yani vektörlerden sadece birini içeren böyle bir diferansiyel denklem elde edin. E veya H. Bunu yapmak için, rotoru sistemin ikinci denkleminin (2.25) her iki kısmından alıyoruz ve zaman ve uzaysal koordinatlarda farklılaşma sırasını değiştiriyoruz. Vektör analizinden bilinen eşitliği dikkate alarak

nerede Δ 2 ≡Δ-Laplace operatörü ve söz konusu sistemin üçüncü eşitliği, denkleme ulaşırız

Benzer şekilde, vektör için denklem türetilir H:

(2.27) ve (2.28) vektör denklemlerinin her biri, vektör denkleminin eksenlere yansıtılmasıyla elde edilen üç skaler denkleme eşdeğerdir. X, Y ve Kartezyen koordinat sisteminin Z'si. Bu skaler denklemler şu şekildedir:

nerede w ve f(x, y, z, f)-sırasıyla aranan ve verilen (bilinen) fonksiyonlar. Bilindiği gibi, (2.29) biçimindeki denklemler dalga süreçlerini tanımlar ve parametre v bu sürecin hızına eşittir. Bu tür denklemler denir homojen olmayan d'Alembert denklemleri veya homojen olmayan dalga denklemleri.(2.27) ve (2.28) denklemleri (2.29)'dan sadece içerdikleri fonksiyonların vektör fonksiyonları olması bakımından farklıdır. Bu tür denklem denir homojen olmayan vektör d'Alembert denklemleri veya homojen olmayan vektör dalga denklemleri. Sağ kenarları sıfıra eşit olan benzer denklemlere denir. homojen vektör d'Alembert denklemleri (homojen vektör dalga denklemleri). Daha sonra parametrenin bir analogu olan (2.27) ve (2.28) denklemlerine giren parametrenin v(2.29)'de kayıpsız bir ortam söz konusu olduğunda, elektromanyetik alanın yayılma hızı da bulunur ve dikkate alınan ortamdaki ışığın hızına eşittir. Işık, belirli bir frekans aralığındaki elektromanyetik dalgalar olduğu için bu sonuç beklenmedik değildir.

Vektörler için benzer denklemler zorlanmadan yazılabilir E ve H ve σ≠0 olduğu durumda (bkz., örneğin, ).

tek renkli alan

Tek renkli bir alan durumunda, harici elektrik kaynaklarını dikkate alarak karmaşık biçimdeki Maxwell denklemlerinin tam sistemi şu şekildedir:

Uzayın düşünülen kısmını dolduran ortamın homojen ve izotropik olduğunu varsayalım. Sistemin ikinci denkleminin (2.30) her iki kısmından da kıvrımı alalım ve vektörü hariç tutalım. H, ilk denklemi kullanarak Formül (2.26) ve homojen bir izotropik ortam için geçerli eşitliği dikkate alarak denkleme ulaşırız.

nerede vektör için H benzer şekilde elde ederiz

Aynı denklemlerin karmaşık genlikleri ilişkilendirdiği açıktır.

Söz konusu alanda herhangi bir dış kaynak yoksa, denklemler (2.31) ve (2.32) basitleştirilmiştir:

(2.30)-(2.34) denklemlerinde kayıpsız ortam durumuna geçmek için . Her biri

(2.33) ve (2.34) vektör denklemlerinden, karşılık gelen vektörün Kartezyen bileşenleri için aynı tipteki üç skaler denkleme eşdeğerdir: ∆ 2w+ k 2w= 0, nerede w- bileşenlerden herhangi biri