Statistička fizika. Statistička fizika jeste
Termodinamika i statistička fizika
Smjernice i kontrolni zadaci za studente učenja na daljinu
Shelkunova Z.V., Saneev E.L.
Metodološka uputstva i kontrolni zadaci za studente inženjerskih i tehnoloških specijalnosti na daljinu. Sadrže odjeljke programa "Statistička fizika", "Termodinamika", primjere rješavanja tipičnih problema i opcije kontrolnih zadataka.
Ključne riječi: Unutrašnja energija, toplina, rad; izoprocesi, entropija: funkcije distribucije: Maxwell, Boltzmann, Bose - Einstein; Fermi - Dirac; Fermijeva energija, toplotni kapacitet, Einstein i Debye karakteristična temperatura.
Urednik T.Yu.Artyunina
Pripremljeno za štampu d. Format 6080 1/16
R.l. ; uch.-ed.l. 3.0; Tiraž ____ primjeraka. Narudžba br.
___________________________________________________
RIO ESGTU, Ulan-Ude, Klyuchevskaya, 40a
Štampano na rotaprintu ESGTU, Ulan-Ude,
Ključevskaja, 42.
Federalna agencija za obrazovanje
Istočnosibirska država
Tehnološki univerzitet
FIZIKA №4
(Termodinamika i statistička fizika)
Metodička uputstva i kontrolni zadaci
za studente učenja na daljinu
Sastavio: Shelkunova Z.V.
Saneev E.L.
Izdavačka kuća ESGTU
Ulan-Ude, 2009
Statistička fizika i termodinamika
Tema 1
Dinamički i statistički zakoni u fizici. Termodinamičke i statističke metode. Elementi molekularno-kinetičke teorije. makroskopsko stanje. Fizičke veličine i stanja fizičkih sistema. Makroskopski parametri kao srednje vrijednosti. Toplotna ravnoteža. Idealan plinski model. Jednačina stanja za idealni gas. Koncept temperature.
Tema 2
transfer fenomena. Difuzija. Toplotna provodljivost. koeficijent difuzije. Koeficijent toplotne provodljivosti. termička difuzivnost. Difuzija u gasovima, tečnostima i čvrstim materijama. Viskoznost. Koeficijent viskoznosti gasova i tečnosti.
Tema 3
Elementi termodinamike. Prvi zakon termodinamike. Unutrašnja energija. Intenzivni i ekstenzivni parametri.
Tema 4
Reverzibilni i ireverzibilni procesi. Entropija. Drugi zakon termodinamike. Termodinamički potencijali i uslovi ravnoteže. hemijski potencijal. Uslovi hemijske ravnoteže. Carnot ciklus.
Tema 5
funkcije distribucije. mikroskopski parametri. Vjerovatnoća i fluktuacije. Maxwellova distribucija. Srednje kinetička energijačestice. Boltzmannova distribucija. Toplotni kapacitet poliatomskih gasova. Ograničenje klasične teorije toplotnog kapaciteta.
Tema 6
Gibbsova distribucija. Model sistema u termostatu. Kanonska Gibbsova distribucija. Statističko značenje termodinamičkih potencijala i temperature. Uloga slobodne energije.
Tema 7
Gibbsova distribucija za sistem s promjenjivim brojem čestica. Entropija i vjerovatnoća. Određivanje entropije ravnotežnog sistema kroz statističku težinu mikrostanja.
Tema 8
Bose i Fermijeve distribucijske funkcije. Plankova formula za bestežinsko toplotno zračenje. Red i nered u prirodi. Entropija kao kvantitativna mjera haosa. Princip povećanja entropije. Prijelaz iz reda u nered odnosi se na stanje termičke ravnoteže.
Tema 9
Eksperimentalne metode za proučavanje vibracionog spektra kristala. Koncept fonona. Zakoni disperzije za akustičke i optičke fonone. Toplotni kapacitet kristala na niskim i visokim temperaturama. Elektronski toplotni kapacitet i toplotna provodljivost.
Tema 10
Elektroni u kristalima. Aproksimacija jake i slabe sprege. Model slobodnih elektrona. Fermi nivo. Elementi pojasne teorije kristala. Blochova funkcija. Pojasna struktura energetskog spektra elektrona.
Tema 11
Fermijeva površina. Broj i gustina broja elektronskih stanja u opsegu. Ispune zona: metali, dielektrici i poluprovodnici. Električna provodljivost poluprovodnika. Koncept provodljivosti rupa. Unutrašnji i ekstrinzični poluprovodnici. Koncept od p-n spoj. Tranzistor.
Tema 12
Električna provodljivost metala. Nosači struje u metalima. Nedostatak klasične teorije elektrona. Elektronski Fermi plin u metalu. Nosioci struje kao kvazičestice. Fenomen supravodljivosti. Kuperovo uparivanje elektrona. tunelski kontakt. Josephsonov efekat i njegove primjene. Hvatanje i kvantizacija magnetni fluks. Koncept visokotemperaturne provodljivosti.
STATISTIČKA FIZIKA. TERMODINAMIKA
Osnovne formule
1. Količina supstance homogenog gasa (u molovima):
gdje N-broj molekula gasa; N A- Avogadrov broj; m-masa gasa; molarna masa gasa.
Ako je sistem mješavina nekoliko plinova, onda je količina tvari u sistemu
![]() ,
,
![]() ,
,
gdje i , N i , m i , i - odnosno količina supstance, broj molekula, masa, molarna masa i th komponenta smjese.
2. Clapeyron-Mendeleev jednadžba (idealna plinska jednačina stanja):
![]()
gdje m- masa gasa; - molarna masa; R- univerzalna plinska konstanta; = m/ - količina supstance; T je termodinamička temperatura u Kelvinima.
3. Eksperimentalni plinski zakoni, koji su posebni slučajevi Clapeyron-Mendelejevske jednadžbe za izoprocese:
boyle-mariotte zakon
(izotermni proces - T= const; m=const):
ili za dva gasna stanja:
gdje str 1 i V 1 - pritisak i zapremina gasa u početnom stanju; str 2 i V 2
Gay-Lussacov zakon (izobarni proces - p=konst., m=konst):
ili za dvije države:
gdje V 1 i T 1 - zapreminu i temperaturu gasa u početnom stanju; V 2 i T 2 - iste vrijednosti u konačnom stanju;
Charlesov zakon (izohorni proces - V=konst, m=konst):
ili za dvije države:
gdje R 1 i T 1 - pritisak i temperatura gasa u početnom stanju; R 2 i T 2 - iste vrijednosti u konačnom stanju;
kombinovano zakon o gasu (m=konst):
gdje R 1 , V 1 , T 1 - pritisak, zapremina i temperatura gasa u početnom stanju; R 2 , V 2 , T 2 su iste vrijednosti u konačnom stanju.
4. Daltonov zakon, koji određuje pritisak mješavine plinova:
p = p 1 + str 2 + ... +str n
gdje str i - parcijalni pritisci komponenta mješavine; n- broj komponenti smeše.
5. Molarna masa mješavine plinova:
![]()
gdje m i- težina i-ta komponenta smeše; i = m i / i- količina supstance i-ta komponenta smeše; n- broj komponenti smeše.
6. Maseni udio i i-ta komponenta mješavine plinova (u udjelima jedinice ili postotku):
gdje m je masa smjese.
7. Koncentracija molekula (broj molekula po jedinici zapremine):
![]()
gdje N-broj molekula sadržanih u sistemu; je gustina supstance. Formula vrijedi ne samo za plinove, već i za bilo koje agregatno stanje materije.
8. Osnovna jednadžba kinetička teorija gasovi:
 ,
,
gdje<>je prosječna kinetička energija translacijskog kretanja molekula.
9. Prosječna kinetička energija translacijskog kretanja molekula:
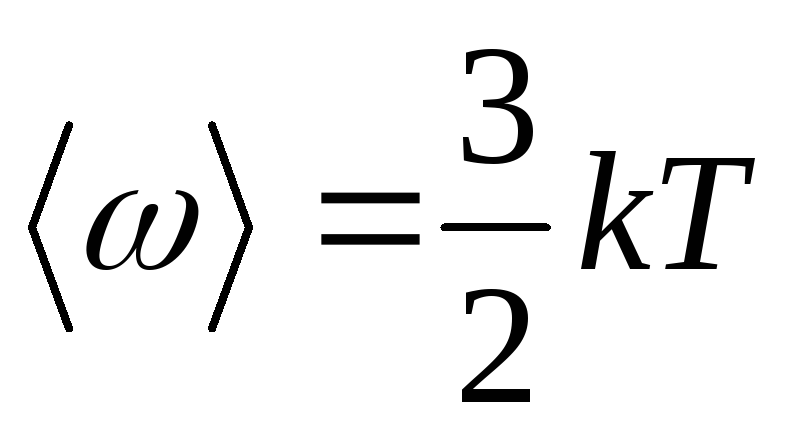 ,
,
gdje k je Boltzmannova konstanta.
10. Prosječna ukupna kinetička energija molekula:
gdje i je broj stupnjeva slobode molekula.
11. Ovisnost tlaka plina od koncentracije molekula i temperature:
p = nkT.
12. Brzine molekula:
srednji kvadratni korijen  ;
;
aritmetička sredina 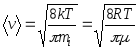 ;
;
najvjerovatnije 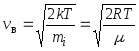 ,
,
gdje m i je masa jednog molekula.
13. Relativna brzina molekula:
u = v/v in ,
gdje v je brzina ovog molekula.
14. Specifični toplotni kapaciteti gasa pri konstantnoj zapremini (s v) i at konstantan pritisak (With R):
15. Odnos između specifičnih ( With) i kutnjak ( OD) toplotni kapaciteti:
; C=c .
16. Jednačina Roberta Mayera:
C str -C v = R.
17. Unutrašnja energija idealnog gasa:
![]()
18. Prvi zakon termodinamike:
gdje Q- toplota koja se prenosi na sistem (gas); dU- promjena unutrašnje energije sistema; ALI je rad koji sistem obavlja protiv vanjskih sila.
19. Radovi na proširenju plina:
Uglavnom ;
u izobarnom procesu ![]() ;
;
izotermni proces ![]() ;
;
u adijabatskom procesu ![]() ,
,
ili  ,
,
gdje je adijabatski eksponent.
20. Poissonove jednadžbe koje se odnose na parametre idealnog plina u adijabatskom procesu:
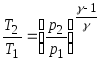 ;
;
21. Toplotna efikasnost ciklus.
elektrona, itd.), kroz svojstva ovih čestica i interakciju između njih.Ostale grane fizike takođe proučavaju makroskopska tela - termodinamika , Mehanika kontinuirani mediji, elektrodinamika kontinuiranih medija. Međutim, kada se specifični problemi rješavaju metodama ovih disciplina, odgovarajuće jednadžbe uvijek uključuju nepoznate parametre ili funkcije koje karakteriziraju dato tijelo. Dakle, za rješavanje problema hidrodinamike potrebno je poznavati jednačinu stanja tekućine ili plina, odnosno ovisnost gustoće o temperaturi i tlaku, toplinski kapacitet tekućine, njen koeficijent viskoznosti itd. Sve ove zavisnosti i parametri se, naravno, mogu eksperimentalno odrediti, pa se dotične metode nazivaju fenomenološkim. Statistička fizika dozvoljava, barem u principu, au mnogim slučajevima i stvarno, izračunavanje svih ovih veličina, ako su poznate sile interakcije između molekula. to., statistička fizika koristi informacije o "mikroskopskoj" strukturi tijela - o tome od kojih se čestica sastoje, kako te čestice međusobno djeluju, pa se naziva mikroskopska teorija.
Ako su u nekom trenutku date koordinate i brzine svih čestica tijela i poznat je zakon njihove interakcije, tada bi rješavanjem jednadžbi mehanike bilo moguće pronaći te koordinate i brzine u bilo kojoj narednoj tački na vrijeme i time u potpunosti odrediti stanje tijela koje se proučava. (Radi jednostavnosti, prezentacija je izvedena na jeziku klasične mehanike. Ali čak i u kvantna mehanika situacija je ista: poznavanje početnog valna funkcija sistema i zakona interakcije čestica, moguće je rješavanjem Schrödingerova jednadžba , pronaći talasnu funkciju koja određuje stanje sistema u svim budućim trenucima vremena.) U stvari, međutim, takav način konstruisanja mikroskopske teorije je nemoguć, jer broj čestica u makroskopskim tijelima je vrlo velik. Na primjer, u 1 cm 3 gas na temperaturi od 0 °C i pritisku od 1 atm sadrži približno 2,7×10 19 molekula. Nemoguće je riješiti toliki broj jednačina, a početne koordinate i brzine svih molekula su još uvijek nepoznate.
Međutim, to veliki brojčestica u makroskopskim tijelima dovodi do pojave novih – statističkih – pravilnosti u ponašanju takvih tijela. Ovo ponašanje u širokom rasponu ne ovisi o specifičnim početnim uvjetima - o točnim vrijednostima početnih koordinata i brzina čestica. Najvažnija manifestacija ove nezavisnosti je iz iskustva poznata činjenica da sistem, prepušten sam sebi, tj. izolovan od spoljašnjih uticaja, na kraju dolazi u neko ravnotežno stanje (termodinamičko, ili statističko, ravnotežno), čija su svojstva određena samo od strane takvih opšte karakteristike početno stanje, kao broj čestica, njihova ukupna energija itd. (cm. Termodinamička ravnoteža ). U nastavku ćemo se fokusirati uglavnom na statistička fizika ravnotežna stanja.
Prije formulisanja teorije koja opisuje statističke pravilnosti, treba razumno ograničiti same zahtjeve za teoriju. Naime, zadatak teorije trebao bi biti da izračuna ne točne vrijednosti različitih fizičkih veličina za makroskopska tijela, već prosječne vrijednosti tih veličina tokom vremena. Razmotrimo, na primjer, molekule smještene u dovoljno velikom makroskopskom volumenu izoliranom u plinu. Broj takvih molekula će se vremenom mijenjati zbog njihovog kretanja, a mogao bi se točno naći kada bi se znale sve koordinate molekula u svakom trenutku. To, međutim, nije neophodno. Promjena broja molekula u volumenu će biti u prirodi nasumičnih fluktuacija - fluktuacija - u odnosu na neku prosječnu vrijednost. Sa velikim brojem čestica u zapremini, ove fluktuacije će biti male u odnosu na prosječan broj čestica, tako da je za karakterizaciju makroskopskog stanja dovoljno znati samo ovu prosječnu vrijednost.
Da biste razjasnili prirodu statističkih obrazaca, razmotrite još jedan jednostavan primjer. Neka se u posudu stavi veliki broj zrna dve sorte, svake sorte podjednako, a sadržaj posude dobro promeša. Tada se, na osnovu svakodnevnog iskustva, može uveriti da će se u uzorku uzetom iz posude, koja još uvek sadrži veliki broj zrna, naći približno jednak broj zrna svake sorte, bez obzira na redosled. zrna su sipana u posudu. Ovaj primjer jasno pokazuje dvije važne okolnosti koje osiguravaju primjenjivost statističke teorije. Prvo, potreba za velikim brojem zrna kako u cijelom "sistemu" - posudi sa zrnom, tako iu "podsistemu" odabranom za eksperiment - uzorku. (Ako se uzorak sastoji od samo dva zrna, onda će često oba biti istog kvaliteta.) Drugo, jasno je da složenost kretanja zrna tokom miješanja igra značajnu ulogu, osiguravajući njihovu ravnomjernu distribuciju u zapremini posude.
funkcija distribucije. Zamislite sistem koji se sastoji od čestice, uz pretpostavku radi jednostavnosti da čestice nemaju unutrašnje stepene slobode. Takav sistem je opisan zadatkom 6 varijable - 3 koordinate q i i 3 impulsi pi, čestice [skup ovih varijabli će biti skraćen kao ( R, q)]. Izračunajmo prosječnu vrijednost u vremenskom intervalu određene vrijednosti (p, q), što je funkcija ovih koordinata i impulsa. Da bismo to učinili, podijelimo interval (0, t) na s jednaki mali segmenti D ta (a = 1,2,....... s). Onda po definiciji
![]() ,
,
Gdje q a i p a- vrijednosti koordinata i impulsa povremeno ta. U limitu s® ¥ zbir ide u integral:
![]() (1a)
(1a)
Koncept funkcije distribucije na prirodan način nastaje ako uzmemo u obzir prostor 6 mjerenja, na čijim osama su ucrtane vrijednosti koordinata i impulsa čestica sistema; naziva se fazni prostor. Za svaku vrijednost vremena t odgovaraju određenim vrijednostima svih q i R, tj. neka tačka u faznom prostoru koja predstavlja stanje sistema u ovog trenutka vrijeme t. Podijelimo cijeli fazni prostor na elemente čija je veličina mala u odnosu na vrijednosti karakteristične za dato stanje sistema q i R, ali i dalje toliko veliki da u svakoj od njih postoji mnogo tačaka koje prikazuju stanje sistema u različitim vremenskim trenucima t. Tada će broj takvih tačaka u elementu volumena biti približno proporcionalan vrijednosti ovog volumena dpdq. Ako označimo koeficijent proporcionalnosti kroz sw(p, q), onda je ovo broj za element sa centrom u nekoj tački ( p, q) biće napisan kao:
da = sw(p, q)dpdq, (2)
Volumen odabranog elementa faznog prostora. Prosječna vrijednost (1), uzimajući u obzir malenost ovih elemenata zapremine, može se prepisati kao , tj.
(integracija preko koordinata se vrši po celoj zapremini sistema, po momentima - od -¥ do ¥). w( p, q, t) naziva se funkcija raspodjele u odnosu na koordinate impulsa čestice. Budući da je ukupan broj odabranih bodova s, funkcija w zadovoljava uslov normalizacije:
![]() (4)
(4)
Iz (3) i (4) se može vidjeti da je w dpdq može se smatrati vjerovatnoćom da se sistem nalazi u elementu dpdq fazni prostor. Ovako uvedena funkcija distribucije može dobiti još jednu interpretaciju. Da bismo to uradili, istovremeno ćemo razmotriti veliki broj identičnih sistema i pretpostaviti da svaka tačka u faznom prostoru predstavlja stanje jednog takvog sistema. Tada se vremensko usrednjavanje u (1)-(1a) može shvatiti kao usrednjavanje po ukupnosti ovih sistema, ili, kako kažu, preko statistički ansambl . Argumenti koji su do sada sprovedeni bili su čisto formalne prirode, od tada pronalaženje funkcije raspodjele, prema (2), zahtijeva poznavanje svega R i q u svakom trenutku, tj. rješenja jednačina kretanja sa odgovarajućim početnim uslovima. Osnovna odredba statistička fizika je, međutim, tvrdnja o mogućnosti određivanja ove funkcije iz općih razmatranja za sistem u stanju termodinamičke ravnoteže. Pre svega, može se pokazati, na osnovu očuvanja broja sistema tokom kretanja, da je funkcija distribucije integral kretanja sistema, tj. ostaje konstantna ako R i q mijenjati prema jednadžbi kretanja (vidi Liouvilleova teorema ). Tokom vožnje zatvoreni sistem njegova energija se ne mijenja, stoga sve tačke u faznom prostoru, koje oslikavaju stanje sistema u različitim vremenskim točkama, moraju ležati na nekoj "hiperpovršini" koja odgovara početnoj vrijednosti energije E. Jednačina ove površine ima oblik;
Gore navedene formule odnose se na slučaj kada je dat broj čestica u podsistemu. Ako kao podsistem odaberemo određeni volumenski element čitavog sistema, kroz čiju površinu čestice mogu napustiti podsistem i vratiti se u njega, tada je vjerovatnoća da se podsistem nađe u stanju sa energijom E n i broj čestica n je dan Gibbsovom formulom velike kanonske distribucije:
![]() , (9)
, (9)
U kojoj je dodatni parametar m hemijski potencijal , koji određuje prosječan broj čestica u podsistemu, a vrijednost se određuje iz uslova normalizacije [vidi formula (11)].
Statistička interpretacija termodinamike. Najvažniji rezultat statistička fizika- utvrđivanje statističkog značenja termodinamičkih veličina. Ovo omogućava izvođenje zakona termodinamike iz osnovnih pojmova statistička fizika i izračunati termodinamičke veličine za specifične sisteme. Prije svega, termodinamički unutrašnja energija identifikuje se sa prosečnom energijom sistema. Prvi zakon termodinamike tada dobija očiglednu interpretaciju kao izraz zakona održanja energije tokom kretanja čestica koje čine telo.
Dalje, neka Hamiltonova funkcija sistema zavisi od nekog parametra l (koordinate zida posude u kojoj se nalazi sistem, spoljašnje polje, itd.). Tada će derivat biti generalizovana sila
koji odgovara ovom parametru, a vrijednost nakon usrednjavanja daje mehanički rad izvršeno na sistemu kada se ovaj parametar promijeni. Ako razlikujemo izraz ![]() za prosječnu energiju sistema, uzimajući u obzir formulu (6) i uvjet normalizacije, s obzirom na varijable l i T a s obzirom da je vrijednost
je također funkcija ovih varijabli, tada dobijamo identitet:
za prosječnu energiju sistema, uzimajući u obzir formulu (6) i uvjet normalizacije, s obzirom na varijable l i T a s obzirom da je vrijednost
je također funkcija ovih varijabli, tada dobijamo identitet:
![]() .
.
Prema gore navedenom, član koji sadrži d l je jednako prosečan posao dA izvodi na tijelu. Tada je posljednji pojam toplina koju primi tijelo. Upoređujući ovaj izraz sa relacijom dE = dA + TdS, koji je kombinovani zapis prvog i drugog zakona termodinamike (vidi sl. Drugi zakon termodinamike ) za reverzibilni procesi , nalazimo to T u (6) je zaista jednako apsolutna temperatura tijelo, a derivat - uzet sa suprotnim predznakom entropija . To znači da tu je slobodna energija tijelo, iz kojeg se pojašnjava njegovo statističko značenje.
Od posebne je važnosti statistička interpretacija entropije, koja slijedi iz formule (8). Formalno, g se sabira u ovu formulu preko svih stanja sa energijom E n, ali u stvari, zbog male fluktuacije energije u Gibsovoj distribuciji, značajan je samo relativno mali broj njih sa energijom bliskom prosječnoj. Prirodno je odrediti broj ovih bitnih stanja, stoga, ograničavanjem sumiranja u (8) na interval , zamjenom E n na srednju energiju i uzimanje eksponenta ispod predznaka zbira. Tada će zbroj dati i poprimiti oblik.
![]()
S druge strane, prema termodinamici, =-TS, što daje vezu između entropije i broja mikroskopskih stanja u datom makroskopskom stanju, drugim riječima, sa statistička težina makroskopsko stanje, tj. sa svojom vjerovatnoćom:
Na temperaturi apsolutne nule, bilo koji sistem je u određenom osnovnom stanju, pa je = 1, S= 0. Ova izjava izražava treći zakon termodinamike . Ovdje je bitno da je za jednoznačnu definiciju entropije potrebno koristiti kvantnu formulu (8); u čisto klasičnoj statistici, entropija je definisana samo do proizvoljnog pojma.
Značenje entropije kao mere verovatnoće stanja je takođe očuvano u odnosu na proizvoljna - ne nužno ravnotežna - stanja. U stanju ravnoteže, entropija ima najveću moguću vrijednost pod datim vanjskim uvjetima. To znači da je stanje ravnoteže stanje sa maksimalnom statističkom težinom, najvjerovatnije stanje. Proces prelaska sistema iz neravnotežnog stanja u ravnotežno stanje je proces prelaska iz manje verovatnih stanja u verovatnija; ovo razjašnjava statističko značenje zakona povećanja entropije, prema kojem entropija zatvorenog sistema može samo rasti.
Formula (8) koja povezuje slobodnu energiju sa particionom funkcijom, je osnova za izračunavanje termodinamičkih veličina po metodama statistička fizika Koristi se, posebno, za izgradnju statističke teorije o električnim i magnetskim svojstvima materije. Na primjer, da bi se izračunao magnetni moment tijela u magnetskom polju, treba izračunati particijsku funkciju i slobodnu energiju. Magnetski trenutak m tijelo se tada daje formulom:
Gdje H- spoljna napetost magnetsko polje. Slično (8), uslov normalizacije u velikoj kanonskoj distribuciji (9) određuje termodinamički potencijal prema formuli:
![]() . (11)
. (11)
Ovaj potencijal je povezan sa slobodnom energijom relacijom:
![]() .
.
Prijave statistička fizika na proučavanje određenih svojstava specifičnih sistema u suštini se svode na približno izračunavanje particione funkcije, uzimajući u obzir specifična svojstva sistema.
U mnogim slučajevima, ovaj zadatak se pojednostavljuje primjenom zakona ekviparticije u stupnjevima slobode, koji kaže da je toplinski kapacitet životopis(kod konstantan volumen v) sistemi interakcije materijalne tačke- čestice koje prave harmonijske oscilacije je jednako
c v = k(l/2 + n),
Gdje l - ukupan broj translacioni i rotacioni stepeni slobode, n- broj vibracionih stepeni slobode. Dokaz zakona se zasniva na činjenici da je Hamiltonova funkcija H takav sistem izgleda ovako: H =(pi) + (q m), gdje je kinetička energija To je homogena kvadratna funkcija od l + n impulsi pi i potencijalnu energiju - kvadratna funkcija od n vibracijske koordinate q m. U statističkom integralu Z(8a) integracija preko vibracionih koordinata zbog brze konvergencije integrala može se proširiti od - ¥ do ¥. Nakon promjene varijabli, nalazimo to Z zavisi od temperature kao Tl/2+n, dakle slobodna energija =-kT(l/ 2 +n)(ln T+ const). To implicira gornji izraz za toplinski kapacitet, budući da . Odstupanja od zakona ekviparticije u realnim sistemima povezana su prvenstveno sa kvantnim korekcijama, jer u kvantnom statistička fizika ovaj zakon je nepravedan. Postoje i korekcije vezane za neharmoničnost oscilacija.
Idealan gas. Najjednostavniji predmet proučavanja statistička fizika je idealan plin, odnosno plin toliko razrijeđen da se interakcija između njegovih molekula može zanemariti. Termodinamičke funkcije takvog plina mogu se u potpunosti izračunati. Energija gasa je jednostavno zbir energija pojedinačnih molekula. To je, međutim, još uvijek nedovoljno da se molekuli smatraju potpuno nezavisnim. Zaista, u kvantnoj mehanici, čak i ako nema interakcijskih sila između čestica, postoji određeni utjecaj identičnih (identičnih) čestica jedna na drugu ako su u sličnim kvantnomehaničkim stanjima. Ovo je tzv. interakcija razmene . Može se zanemariti ako, u prosjeku, postoji mnogo manje od jedne čestice po stanju, što se, u svakom slučaju, odvija pri dovoljno visokoj temperaturi plina; takav gas se naziva nedegenerisanim. U stvari, obični plinovi, koji se sastoje od atoma i molekula, nisu degenerirani na svim temperaturama (na kojima su još uvijek plinoviti). Za nedegenerirani idealni plin, funkcija distribucije se razlaže u proizvod funkcija raspodjele za pojedinačne molekule. leže u intervalima dp x, dpy, dpz, a koordinate su u intervalima dx, dy, dz:
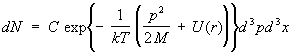 , (12) Energija jednoatomske molekule plina u vanjskom polju s potencijalna energija
(r) je jednako p 2 /2M +(r). Integriranje (6) preko koordinata r(x, y, z) i impulse R(p x, py, pz) od svih molekula osim jednog, možete pronaći broj molekula dN, čiji impulsi
, (12) Energija jednoatomske molekule plina u vanjskom polju s potencijalna energija
(r) je jednako p 2 /2M +(r). Integriranje (6) preko koordinata r(x, y, z) i impulse R(p x, py, pz) od svih molekula osim jednog, možete pronaći broj molekula dN, čiji impulsi
Gdje d 3 str = dp x dp y dp z, d3x = dxdydz. Ova formula se naziva Maxwell-Boltzmannova distribucija (vidi sl. Boltzmannova statistika ). Ako integriramo (12) preko impulsa, onda ćemo dobiti formulu za raspodjelu čestica po koordinatama u vanjskom polju, posebno u gravitacijskom polju - barometrijska formula . Raspodjela brzine u svakoj tački u prostoru poklapa se sa Maxwellova distribucija .
Razdjelna funkcija idealnog plina također se razlaže na proizvod identičnih pojmova koji odgovaraju pojedinačnim molekulima. Za jednoatomni gas, sumiranje u (8) se svodi na integraciju preko koordinata i impulsa, tj. zbir se zamjenjuje integralom po ![]() 3
u skladu sa brojem ćelija [sa zapreminom] u faznom prostoru jedne čestice. Besplatna energija
atoma gasa je jednako:
3
u skladu sa brojem ćelija [sa zapreminom] u faznom prostoru jedne čestice. Besplatna energija
atoma gasa je jednako:
 ,
,
Gdje g- statistička težina osnovnog stanja atoma, odnosno broj stanja koja odgovaraju njegovom nižem nivo energije, . Konačno, to je zbog prethodno uočene veze između entropije i koncepta broja kvantnih stanja.
U slučaju dvoatomskih i poliatomskih plinova, vibracije i rotacija molekula također doprinose termodinamičkim funkcijama. Ovaj doprinos zavisi od toga da li su efekti kvantizacije vibracija i rotacije molekula značajni. Udaljenost između nivoa energije vibracije je reda , gdje je w karakteristična frekvencija oscilacije, a udaljenost između prvih nivoa energije rotacije je od ![]() , gdje
- moment inercije rotirajućeg tijela, u ovom slučaju molekula. Klasična statistika je važeća ako je temperatura dovoljno visoka za to
, gdje
- moment inercije rotirajućeg tijela, u ovom slučaju molekula. Klasična statistika je važeća ako je temperatura dovoljno visoka za to
kT>> D E.
U ovom slučaju, u skladu sa zakonom ekviparticije, rotacija daje konstantan doprinos toplotnom kapacitetu, jednak 1/2 k za svaki stepen slobode rotacije; posebno, za dvoatomske molekule ovaj doprinos je jednak k. Fluktuacije daju doprinos toplotnom kapacitetu jednak k za svaki vibracioni stepen slobode (tako da je vibracioni toplotni kapacitet dvoatomske molekule k). Doprinos vibracionog stepena slobode, u poređenju sa rotacionim, dvostruko je veći zbog činjenice da prilikom vibracija atomi u molekulu imaju ne samo kinetičku, već i potencijalnu energiju. U suprotnom graničnom slučaju, molekuli su u svom osnovnom vibracionom stanju, čija energija ne zavisi od temperature, tako da vibracije uopšte ne doprinose toplotnom kapacitetu. Isto važi i za rotaciju molekula pod uslovom ![]() . Kako temperatura raste, pojavljuju se molekuli koji su u pobuđenim vibracijskim i rotacijskim stanjima, a ovi stupnjevi slobode počinju doprinositi toplinskom kapacitetu - kao da se postupno "uključuju", težeći svojoj klasičnoj granici s daljnjim povećanjem temperature. Stoga je uključivanje kvantnih efekata omogućilo da se objasni eksperimentalno uočena zavisnost toplotnog kapaciteta gasova o temperaturi. Vrijednosti veličine koja karakterizira "rotacijski kvant" za većinu molekula su reda nekoliko stupnjeva ili desetina stupnjeva (85 K za H 2, 2,4 K za 2, 15 K za H). Istovremeno, karakteristične vrijednosti za "vibracioni kvant" su reda hiljada stepeni (6100 K za H2, 2700 K za O2, 4100 K za H). Stoga se rotacijski stupnjevi slobode uključuju na mnogo nižim temperaturama od vibracijskih. Na sl. Na slici 1 prikazana je temperaturna zavisnost (a) rotacionog i (b) vibracionog toplotnog kapaciteta za dvoatomski molekul (rotacioni toplotni kapacitet je konstruisan za molekul različitih atoma).
. Kako temperatura raste, pojavljuju se molekuli koji su u pobuđenim vibracijskim i rotacijskim stanjima, a ovi stupnjevi slobode počinju doprinositi toplinskom kapacitetu - kao da se postupno "uključuju", težeći svojoj klasičnoj granici s daljnjim povećanjem temperature. Stoga je uključivanje kvantnih efekata omogućilo da se objasni eksperimentalno uočena zavisnost toplotnog kapaciteta gasova o temperaturi. Vrijednosti veličine koja karakterizira "rotacijski kvant" za većinu molekula su reda nekoliko stupnjeva ili desetina stupnjeva (85 K za H 2, 2,4 K za 2, 15 K za H). Istovremeno, karakteristične vrijednosti za "vibracioni kvant" su reda hiljada stepeni (6100 K za H2, 2700 K za O2, 4100 K za H). Stoga se rotacijski stupnjevi slobode uključuju na mnogo nižim temperaturama od vibracijskih. Na sl. Na slici 1 prikazana je temperaturna zavisnost (a) rotacionog i (b) vibracionog toplotnog kapaciteta za dvoatomski molekul (rotacioni toplotni kapacitet je konstruisan za molekul različitih atoma).
Nesavršen gas. Važno dostignuće statistička fizika- proračun korekcija termodinamičkih količina gasa povezanih sa interakcijom između njegovih čestica. Sa ove tačke gledišta, jednadžba stanja idealnog gasa je prvi član u širenju pritiska realnog gasa u smislu gustine broja čestica, budući da se svaki gas ponaša kao idealan gas pri dovoljnoj niske gustine. Kako se gustoća povećava, korekcije jednačine stanja povezane s interakcijom počinju igrati ulogu. One dovode do pojave u izrazu za pritisak pojmova sa većim stepenom gustine broja čestica, tako da se pritisak predstavlja tzv. viralne serije oblika:
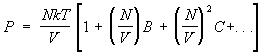 . (15)
. (15)
Odds AT, OD itd. zavise od temperature i formiraju se. drugi, treći itd. virijski koeficijenti. Metode statistička fizika omogućavaju izračunavanje ovih koeficijenata ako je poznat zakon interakcije između molekula gasa. Istovremeno, koeficijenti AT, OD,... opisuju istovremenu interakciju dva, tri i više molekule. Na primjer, ako je plin jednoatomski i potencijalna energija interakcije njegovih atoma (r), tada je drugi virijski koeficijent
Po redu veličine AT jednako , gdje r0- karakteristična veličina atoma, ili, preciznije, radijus djelovanja međuatomskih sila. To znači da je serija (15) zapravo ekspanzija snaga bezdimenzionalnog parametra Nr 3 /V, mali za dovoljno razrijeđen plin. Interakcija između atoma plina ima karakter odbijanja na bliskim udaljenostima i privlačenja na udaljenim. Ovo vodi do AT> 0 at visoke temperature i AT < 0 при низких. Поэтому давление реального газа при высоких температурах veći pritisak idealan gas iste gustine, a pri niskoj - manje. Tako, na primjer, za helijum na T= 15,3 K faktor AT = - 3×10 -23 cm 3, i kada T= 510 K AT= 1,8 × 10 -23 cm 3. Za argon AT = - 7,1×10 -23 cm 3 at T = 180 K i AT= 4,2×10 -23 cm 3 at T= 6000 K. Za jednoatomske plinove izračunavaju se vrijednosti virijalnih koeficijenata, uključujući i peti, što omogućava da se opiše ponašanje plinova u prilično širokom rasponu gustina (vidi također gasovi ).
Plazma. Poseban slučaj neidealan gas je plazma - djelomično ili potpuno jonizirani plin, u kojem se stoga nalaze slobodni elektroni i joni. Pri dovoljno niskoj gustini, svojstva plazme su bliska onima idealnog gasa. Prilikom izračunavanja odstupanja od idealnosti, bitno je da elektroni i ioni međusobno djeluju elektrostatički prema Kulonovom zakonu. Coulombove sile polako opadaju s rastojanjem, a to dovodi do činjenice da je čak i za izračunavanje prve korekcije termodinamičkih funkcija potrebno uzeti u obzir interakciju ne dvije, već velikog broja čestica odjednom, budući da se integral u drugom virjalnom koeficijentu (16), koji opisuje interakciju para, divergira za velike udaljenosti r između čestica. U stvarnosti, pod utjecajem Coulomb sila, distribucija jona i elektrona u plazmi se mijenja na način da se polje svake čestice ekranizira, odnosno brzo opada na određenoj udaljenosti, koja se naziva Debajev radijus. Za najjednostavniji slučaj plazme koja se sastoji od elektrona i jednostruko nabijenih jona, Debyeov radijus rD jednaka.
STATISTIČKA FIZIKA- grana fizike, čiji je zadatak da izrazi svojstva makroskopskog. tijela, odnosno sisteme koji se sastoje od vrlo velikog broja identičnih čestica (molekula, atoma, elektrona itd.), kroz svojstva ovih čestica i interakciju između njih.
Dakle, u S. t. koristi se informacija o "mikroskopskoj" strukturi tijela, stoga S. f. je mikroskopski. teorija. To je njegova razlika u odnosu na druge grane fizike, koje također proučavaju makroskopiju. tijela: , mehanika i elektrodinamika kontinuuma. Prilikom rješavanja konkretnih problema metodama ovih disciplina, odgovarajuće jednadžbe uvijek uključuju nepoznate parametre ili funkcije koje karakteriziraju dato tijelo. Sve ove zavisnosti i parametri mogu se odrediti eksperimentalno, pa se nazivaju dotične metode. fenomenološki. S. f. dozvoljava, barem u principu, ali na mnogo načina. slučajevima i stvarno izračunati ove količine.
Ako su u nekom trenutku date koordinate i brzine svih čestica tijela i poznat je zakon njihove interakcije, tada bi iz jednadžbi mehanike bilo moguće pronaći koordinate i brzine u bilo kojem sljedećem trenutku i čime se u potpunosti utvrđuje stanje organizma. Ista situacija se dešava u: poznavajući početnu talasnu funkciju sistema, moguće je, rešavanjem Schrödingerove jednačine, pronaći talasnu funkciju koja određuje stanje sistema u svim budućim trenucima vremena.
U stvarnosti, takav način konstruisanja mikroskopskog teorija je nemoguća, jer je broj čestica u makroskopskom. tijela je veoma velika i rano. koordinate i brzine molekula su nepoznate. Međutim, to je upravo veliki broj čestica u makroskopu tijela dovodi do pojave novih (statističkih) pravilnosti u ponašanju takvih tijela. Ove pravilnosti se otkrivaju nakon odgovarajućeg ograničavanja problema teorije. karakterizira makroskopsko tjelesni parametri tokom vremena doživljavaju nasumične male fluktuacije (fluktuacije) u odnosu na neke up. vrijednosti. Zadatak teorije je da izračuna ove upor. vrijednosti, a ne tačne vrijednosti parametara u datom trenutku. Prisustvo statističkih obrazaca izražava se u činjenici da ponašanje usp. vrijednosti u širokom rasponu ne zavise od konkretnog početka. uslove (od tačnih vrednosti početnih koordinata i brzina čestica). Najvažnija manifestacija ove pravilnosti je činjenica poznata iz iskustva da je sistem izolovan od spoljašnjeg uticaja, vremenom dolazi do određenog ravnotežnog stanja (termodinamička ravnoteža), čija svojstva su određena samo takvim opštim karakteristikama početka. stanja, kao što je broj čestica, njihova ukupna energija, itd. (vidi termodinamička ravnoteža). Proces prelaska sistema u ravnotežno stanje naziva se. opuštanje, a karakteristično vrijeme ovog procesa je vrijeme relaksacije.
funkcija distribucije. Zamislite sistem koji se sastoji od Nčestice, radi jednostavnosti, pod pretpostavkom da čestice nemaju ekst. stepena slobode. Takav sistem je opisan zadatkom 6N varijable: 3N koordinate x i i 3N impulsi p ičestice, skup ovih varijabli će biti skraćen kao ( p, x).
Gibbsove distribucije. Argumenti koji su do sada izvedeni bili su formalne prirode, budući da pronalaženje funkcije distribucije, prema (1), zahtijeva poznavanje svih X i R u svakom trenutku, tj. rješenja jednadžbi kretanja sa odgovarajućim početnim. uslovima. Main Položaj S. f. je izjava o mogućnosti općih razmatranja za određivanje ove f-cije za sistem u termodinamičkom stanju. balans. Pre svega, na osnovu očuvanja broja čestica tokom kretanja, može se pokazati da je funkcija raspodele integral kretanja sistema (vidi Sl. Liouvilleova teorema).
Kada se zatvoreni sistem kreće, njegova energija se ne mijenja, stoga sve tačke u faznom prostoru, koje oslikavaju stanje sistema u različitim vremenskim točkama, moraju ležati na određenoj hiperpovršini koja odgovara početku. energetska vrijednost E. Jednačina za ovu površinu ima oblik H(x, p) = E, gdje H(x,p) - Hamiltonova funkcija sistemima. Kretanje sistema od mnogih čestice je izuzetno zbunjujuće, tako da će se tokom vremena tačke koje opisuju stanje rasporediti po površini stuba. energiju ravnomjerno (vidi također Ergodična hipoteza Takva uniformna raspodjela je opisana funkcijom raspodjele
gdje je delta funkcija koja nije nula samo kada H = E, A je konstanta određena iz uslova normalizacije (3). Funkcija distribucije (4) koja odgovara mikrokanonska Gibbsova distribucija, omogućava vam da izračunate prosj. vrijednosti svih fizičkih veličine prema f-le (2), bez rješavanja jednačina kretanja.
Prilikom izvođenja izraza (4) pretpostavljeno je da je jedina očuvana veličina od koje zavisi w, je energija sistema. Naravno, količina gibanja i ugaoni moment su također očuvani, ali se te veličine mogu eliminirati pod pretpostavkom da je dotično tijelo zatvoreno u fiksnu kutiju, kojoj čestice mogu dati zamah i zamah.
Zapravo, u S. f. obično ne smatraju zatvorenim sistemima, već makroskopskim. tijela koja su mala makroskopska. dijelovi, ili podsistemi, do-l. zatvoreni sistem. Funkcija distribucije za podsistem se razlikuje od (4), ali ne zavisi od specifičnog oblika ostatka sistema, tzv. termostat. Da bi se odredila funkcija distribucije podsistema, potrebno je integrirati f-lu (4) preko impulsa i koordinata čestica termostata. Takva integracija se može izvesti uzimajući u obzir malenost energije podsistema u odnosu na energiju termostata. Kao rezultat, za funkciju distribucije podsistema dobija se izraz
magnitude T u ovom f-le ima smisla privremeno. Koeficijent normalizacije. određuje se iz uslova normalizacije (3):
Za čestice sa polucijelim spinom, valna funkcija mora promijeniti predznak nakon permutacije bilo kojeg para čestica, dakle u jednom kvantno stanje ne može postojati više od jedne čestice ( Paulijev princip Broj čestica sa celobrojnim spinom u jednom stanju može biti bilo koji, ali zahtevana u ovom slučaju, invarijantnost talasne funkcije kada se čestice ovde preuređuju takođe dovodi do promene u statistici. svojstva gasa. Opisane su čestice sa polucijelim spinom Fermi-Dirac statistika, nazivaju se fermioni. Fermioni uključuju, na primjer, elektrone, protone, neutrone, atome deuterija, 3 He atoma. Opisane su čestice sa cjelobrojnim spinom (bozoni). Bose - Einstein statistika. To uključuje, na primjer, atome H, 4 He, kvante svjetlosti - fotone.
Neka cf. broj gasnih čestica po jedinici zapremine sa momentima koji se nalaze u intervalu dp, je , tako itd je broj čestica u jednoj ćeliji faznog prostora. Tada iz Gibbsove distribucije slijedi da za idealnih gasova fermioni (gornji znak) i bozoni (donji znak)
U ovom f-le - energija čestice sa impulsom R,- chem. potencijal određen iz uslova konstantnosti broja čestica N u sistemu: ![]()
Kvazičestice. Blizu trbušnjaka. nulta temp. doprinos statistici zbroju doprinose slabo pobuđena kvantna stanja bliska po energiji osnovnom stanju. Proračun energije glavnog. stanje je čisto kvantno mehaničko. zadatak, predmet kvantna teorija mnogih čestica. Toplotno kretanje u takvim uslovima može se opisati kao pojava u sistemu slabo interakcije kvazičestice(elementarne pobude) koje imaju energiju i impuls (u kristalima - kvazi impuls) R. Poznavajući zavisnost, moguće je izračunati temperaturno ovisan dio termodinamike. f-cije po f-lameovima za idealan Fermi ili Bose gas u zavisnosti od statistike kvazičestica. Posebno je važno da Bose kvazičestice sa malim R se mogu posmatrati kao kvanti dugotalasnih oscilacija, opisanih makroskopski. ur-niami. Dakle, u kristalima (i Bose tekućinama) postoje fononi (kvantovi zvuka), u magnetima - magnoni (kvantovi oscilacija magnetskog momenta).
Posebni tipovi kvazičestica postoje u dvodimenzionalnim i jednodimenzionalnim sistemima. U ravnom kristalu Na filmu njihovu ulogu imaju dislokacije, u He filmovima vrtložni filamenti, a u polimernim filamentima solitoni i domenski zidovi. U trodimenzionalnim tijelima ovi objekti imaju veliku energiju i ne doprinose termodinamici. funkcije.
Kristalna ćelija. Atomi u rešetki prave male oscilacije oko svojih ravnotežnih položaja. To znači da se njihovo toplotno kretanje može smatrati skupom kvazičestica (fonona) na svim (a ne samo niskim) temp-paxima (vidi Sl. Vibracije kristalne rešetke Distribucija fonona, kao i fotona, data je sa f-loy (16) c = 0. Na niskim temperaturama značajni su samo dugotalasni fononi, koji su kvanti zvučni talasi, opisana jednadžbama teorije elastičnosti. Ovisnost za njih je linearna, dakle toplotni kapacitet kristala. rešetka je proporcionalna T 3. Pri visokim temperaturama može se koristiti zakon ekvipodjele energije preko stupnjeva slobode, tako da toplinski kapacitet ne ovisi o temperaturi i jednak je 3Nk, gdje N je broj atoma u kristalu. Zavisnost na proizvoljno R može se odrediti iz eksperimenata neelastičnog raspršenja neutrona u kristalu ili izračunati teoretski postavljanjem vrijednosti "konstanti sile" koje određuju interakciju atoma u rešetkama. Novi problemi su se pojavili prije S. f. u vezi sa otvaranjem tzv. kvaziperiodični kristali, čiji se molekuli nalaze u prostoru neperiodično, već određenim redoslijedom (vidi. Kvazikristal).
Metali. U metalima, doprinos termodinamici f-cije takođe daju elektrone provodljivosti. Stanje elektrona u metalu karakterizira kvazi-impuls, a budući da se elektroni povinuju Fermi-Diracovoj statistici, njihova raspodjela po kvazi-momentima je data pomoću f-loi (16). Stoga je toplinski kapacitet elektronskog plina, a time i cijelog metala na dovoljno niskim temperaturama, proporcionalan T. Razlika od Fermijevog plina slobodnih čestica je u tome što Fermijeva površina više nije sfera, već je neka složena površina u prostoru kvazi impulsa. Oblik Fermijeve površine, kao i ovisnost energije o kvazi-momentu u blizini ove površine, može se odrediti eksperimentalno, Ch. arr. istraživački magnet. svojstva metala, kao i izračunati teoretski koristeći tzv. pseudopotencijalni model. U supravodnicima, pobuđena stanja elektrona su odvojena od Fermijeve površine prazninom, što dovodi do eksponencijalnog. zavisnost elektronskog toplotnog kapaciteta o temperaturi. U feromagnetu. i antiferomagnet. doprinose tvari termodinamici. f-cije također daju fluktuacije magnetskog. momenti (spin talasi).
U dielektricima i poluprovodnicima T= 0 nema slobodnih elektrona. Na konačnim temperaturama u njima se pojavljuje naboj. kvazičestice: elektroni sa negativnim. naboj i "rupe" sa pozitivnim. naplatiti. Elektron i rupa mogu formirati vezano stanje - kvazičesticu tzv eksciton.dr. Ekscitonski tip je pobuđeno stanje dielektričnog atoma, koji se kreće u kristalno. rešetka.
Metode kvantna teorija oblasti statističke fizike. U rješavanju problema kvantne kvantne fizike, prvenstveno u proučavanju svojstava kvantnih tekućina i elektrona u metalima i magnetima, od velike su važnosti metode kvantne teorije polja uvedene u kvantnu fiziku. relativno nedavno. Main igra ulogu u ovim metodama. Greenova funkcija makroskopski sistemi slični Grinovoj funkciji u kvantnoj teoriji polja. Zavisi od energije e i impulsa R, zakon disperzije kvazičestica e(p) je određen iz jednačine ![]() , budući da je energija kvazičestice pol Greenove funkcije. Postoji redovna metoda za izračunavanje Greenovih funkcija u obliku niza snaga interakcije energije između čestica. Svaki član ove serije sadrži višestruke integrale nad energijama i momentima iz Greenovih funkcija čestica koje nisu u interakciji i može se grafički predstaviti u obliku dijagrama sličnih Feynmanovi dijagrami u kvantnom. Svaki od ovih dijagrama ima svoje specifičnosti fizički značenja, što omogućava da se u beskonačan niz odvoje pojmovi odgovorni za pojavu od interesa i sažmu ih. Postoji i dijagramska tehnika za izračunavanje Greenovih temperaturnih funkcija, koje omogućavaju pronalaženje termodinamike. količine direktno, bez unošenja kvazičestica. U ovoj tehnici, Greenove funkcije zavise (umjesto energije) o određenim diskretnim frekvencijama w n i integrali nad energijama se zamjenjuju zbrojem ovih frekvencija.
, budući da je energija kvazičestice pol Greenove funkcije. Postoji redovna metoda za izračunavanje Greenovih funkcija u obliku niza snaga interakcije energije između čestica. Svaki član ove serije sadrži višestruke integrale nad energijama i momentima iz Greenovih funkcija čestica koje nisu u interakciji i može se grafički predstaviti u obliku dijagrama sličnih Feynmanovi dijagrami u kvantnom. Svaki od ovih dijagrama ima svoje specifičnosti fizički značenja, što omogućava da se u beskonačan niz odvoje pojmovi odgovorni za pojavu od interesa i sažmu ih. Postoji i dijagramska tehnika za izračunavanje Greenovih temperaturnih funkcija, koje omogućavaju pronalaženje termodinamike. količine direktno, bez unošenja kvazičestica. U ovoj tehnici, Greenove funkcije zavise (umjesto energije) o određenim diskretnim frekvencijama w n i integrali nad energijama se zamjenjuju zbrojem ovih frekvencija.
Fazni prijelazi. Uz kontinuiranu promjenu ekst. parametara (npr. pritisak ili temperatura), svojstva sistema se mogu naglo promeniti za određene vrednosti parametara, tj. dolazi do faznog prelaza. Fazni prijelazi se dijele na prijelaze 1. vrste, praćene oslobađanjem latentne topline prijelaza i naglom promjenom volumena (na primjer, topljenje), i prijelaze 2. vrste, u kojima latentna toplota i nema skokova u zapremini, ali postoji skok toplotnog kapaciteta (na primjer, prijelaz u supravodljivo stanje). Tokom tranzicije 2. vrste, mijenja se simetrija tijela. Ova promjena je kvantificirana parametar naloga, koji je različit od nule u jednoj od faza i nestaje u prelaznoj tački. Statistički Teorija faznih prijelaza predstavlja važno, ali još uvijek daleko od cjelovitog područja S. ph. max. teškoća za teoretsku studije predstavljaju svojstva materije u blizini kritična tačka, fazni prelaz 1. vrste i direktno. blizina linije faznog prelaza drugog reda. (Na određenoj udaljenosti od ove linije, prijelaz druge vrste je opisan sa Landau teorija.) Ovdje se fluktuacije anomalno povećavaju, a približne metode S. f. nije primjenjivo. Stoga se igra važna uloga tačno rješivi modeli, u kojem postoje prijelazi (vidi 2D rešetkasti modeli).Stvorenje. napredak u izgradnji fluktuacija. teorija faznih prelaza postiže se metodom epsilon ekspanzije. U njemu se tranzicija istražuje u imaginarnom prostoru s brojem dimenzija , a rezultati se ekstrapoliraju na, odnosno realni prostor od tri dimenzije. U dvodimenzionalnim sistemima mogući su neobični fazni prijelazi, kada se na određenoj temperaturi pojave dislokacije ili vrtložni filamenti. Parametar reda na prelaznoj tački naglo nestaje, a toplotni kapacitet je kontinuiran.
Neuređeni sistemi. Neobično mjesto u S. f. okupirati staklo- čvrste materije, čiji su atomi raspoređeni nasumično čak i na abs. nulta temp. Strogo govoreći, takvo stanje je neravnotežno, ali sa izuzetno dugim vremenom relaksacije, tako da se neravnoteža zapravo i ne manifestuje. Toplotni kapacitet stakla na niskim temperaturama linearno zavisi od T. Ovo slijedi iz izraza za Z u obliku (8). Kada zavisi od T određeno ponašanjem g(E) za male E. Ali za poremećeni sistemi značenje E = 0 nije dodijeljeno, dakle g(0)naravno, Z = ALI + e(0)T i c ~ T. Zanimljiva karakteristika staklo je zavisnost posmatranih vrednosti toplotnog kapaciteta o vremenu merenja. Ovo se objašnjava činjenicom da su nivoi energije sa malim E povezano s kvantnim tuneliranjem atoma kroz visoku potencijalnu barijeru, što zahtijeva mnogo vremena. Interesantne nekretnine spin čaše- sistemi nasumično raspoređenih atoma koji imaju magn. momente.
Statistička fizika neravnotežnih procesa. Sve više dobija na značaju fizička kinetika- odjeljak S. f., u kojem proučavaju procese u sistemima koji su u neravnotežnim stanjima. Ovdje su moguće dvije formulacije pitanja: može se posmatrati sistem u određenom neravnotežnom stanju i pratiti njegov prelazak u ravnotežno stanje; moguće je razmotriti sistem čije se neravnotežno stanje održava spolja. uslovi, npr. tijelo, u kojem je postavljen temperaturni gradijent, teče električnim putem. struja, itd., ili tijelo u naizmjeničnom stanju. lok. polje.
Ako je odstupanje od ravnoteže malo, neravnotežna svojstva sistema opisuju se tzv. kinetički koeficijenti. Primjeri takvih koeficijenata. su koeficijenti. viskoznost, toplotna provodljivost i električna provodljivost metala itd. Ove veličine zadovoljavaju princip simetrije kinetike. koeficijenti koji izražavaju simetriju jednadžbi mehanike u odnosu na promjenu predznaka vremena (vidi. Onsagerova teorema).
Više opšti koncept je generalizovana osetljivost opisivanje promjene usp. vrijednosti određenog roja fizičkih. količine X pod dejstvom male "generalizovane sile" f, koji je uključen u Hamiltonijan sistema u obliku , gdje je kvantno mehanički. operator koji odgovara X. Ako a f ovisi o vremenu kao , promjena se može napisati kao ![]() . Kompleksna vrijednost je generalizirana osjetljivost, ona opisuje ponašanje sistema u odnosu na eksterno. uticaj. S druge strane, on također određuje opuštanje. svojstva: na , vrijednost opušta na svoju ravnotežnu vrijednost prema zakonu, gdje je udaljenost od realne ose do singularnosti funkcije koja joj je najbliža u donjoj poluravni kompleksne varijable w. Među zadacima S. f. Neravnotežni procesi takođe uključuju proučavanje zavisnosti fluktuacija o vremenu. Ova zavisnost je opisana vremenskom korelacijom. funkcija, u kojoj su fluktuacije vrijednosti u prosjeku X uzeti u različitim tačke u vremenu t:
. Kompleksna vrijednost je generalizirana osjetljivost, ona opisuje ponašanje sistema u odnosu na eksterno. uticaj. S druge strane, on također određuje opuštanje. svojstva: na , vrijednost opušta na svoju ravnotežnu vrijednost prema zakonu, gdje je udaljenost od realne ose do singularnosti funkcije koja joj je najbliža u donjoj poluravni kompleksne varijable w. Među zadacima S. f. Neravnotežni procesi takođe uključuju proučavanje zavisnosti fluktuacija o vremenu. Ova zavisnost je opisana vremenskom korelacijom. funkcija, u kojoj su fluktuacije vrijednosti u prosjeku X uzeti u različitim tačke u vremenu t: ![]() je parna funkcija njegovog argumenta. U klasičnom S. f. postoji veza između i zakona veličine. Ako je relaksacija opisana određenim linearnim diferencijalom jednadžba za odstupanje od ravnotežne vrijednosti, onda ona zadovoljava istu jednačinu na t > 0.
je parna funkcija njegovog argumenta. U klasičnom S. f. postoji veza između i zakona veličine. Ako je relaksacija opisana određenim linearnim diferencijalom jednadžba za odstupanje od ravnotežne vrijednosti, onda ona zadovoljava istu jednačinu na t > 0.
Odnos između i skupova teorema fluktuacije i disipacije.Teorema kaže da je Fourierova transformacija korelirana. funkcije 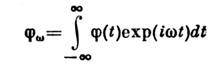
izražava se na sljedeći način:
Poseban slučaj (17) je Nyquist formula.Opis jako neravnotežnih stanja, kao i proračun kinetičkih. koeficijent proizvedeno upotrebom Boltzmannova kinetička jednačina. Ova jednadžba je integro-diferencijalna. ur-cija za funkciju raspodjele jedne čestice (u kvantnom slučaju - za matricu gustine jedne čestice ili statistički operator). Sadrži članove dvije vrste. Neki opisuju promjenu f-cije distribucije kada se čestice kreću u ekst. polja, drugi - u sudarima čestica. Upravo sudari dovode do povećanja entropije neravnotežnog sistema, odnosno do relaksacije. Zatvorena, tj. koja ne sadrži druge kinetičke količine. ur-cija, nemoguće je ući opšti pogled. Prilikom njegovog izvođenja potrebno je koristiti male parametre dostupne u ovom konkretnom problemu. Najvažniji primjer je kinetički jednadžba koja opisuje uspostavljanje ravnoteže u plinu uslijed sudara između molekula. Vrijedi za dovoljno razrijeđene plinove, kada je velika u odnosu na udaljenosti između molekula. Specifičan oblik ove jednačine zavisi od eff. raspršivanje presjeka molekula jedan na drugom. Ako je ovaj dio poznat, jednadžba se može riješiti proširenjem tražene funkcije u terminima ortogonalnih polinoma. Na ovaj način je moguće izračunati kinetiku koeficijent gas, zasnovan na poznatim zakonima interakcije između molekula. Kinetic Jednačina uzima u obzir samo sudare u paru između molekula i opisuje samo prvi član koji ne iščezava u ekspanziji ovih koeficijenata. po gustini gasa. Također smo uspjeli pronaći tačniju jednačinu koja također uzima u obzir trostruke sudare, što je omogućilo izračunavanje sljedećeg člana ekspanzije.
Poseban problem je izvođenje kinetike ur-cija za plazmu. Zbog sporog opadanja Coulombovih sila s rastojanjem, čak i kada se razmatraju sudari parova, bitno je da te sile budu zaštićene drugim česticama. Neravnotežna stanja čvrstih tijela i kvantnih tekućina na niskim temperaturama mogu se smatrati neravnotežnim stanjima plina odgovarajućih kvazičestica. Dakle, kinetički procesi u takvim sistemima se opisuju kinetički. jednadžbe za kvazičestice koje uzimaju u obzir kolizije između njih i procese njihove međusobne transformacije. Nove mogućnosti su otvorene primjenom u fizičkom. kinetika metoda kvantne teorije polja. Kinetic koeficijent sistema se može izraziti u terminima njegove Greenove funkcije, za koju postoji opći način izračunavanja pomoću dijagrama. Ovo u nekim slučajevima omogućava postizanje kinetike. koeficijent bez eksplicitne upotrebe kinetike. ur-ciju i istražiti neravnotežna svojstva sistema čak iu slučajevima kada nisu ispunjeni uslovi njegove primenljivosti.
Prekretnice u razvoju statističke fizike. S. f. u potpunosti zasnovan na konceptu atomska struktura stvar. Dakle, početak period razvoja S. f. poklapa se sa razvojem atomističke. reprezentacije. Razvoj S. f. kao deo teorije. fizika je počela u ser. 19. vijek Godine 1859, J. Maxwell je odredio funkciju raspodjele brzina molekula plina. 1860-70 R. Clausius (R. Clausing) uveo je koncept srednjeg slobodnog puta i povezao ga sa viskozitetom i toplotnom provodljivošću gasa. Otprilike u isto vrijeme, L. Boltzmann je generalizirao Maxwellovu raspodjelu na slučaj kada je plin u ekst. polju, dokazao teoremu o jednakoj podjeli energije na stepene slobode, izveo kinetičku. ur-cija, dao statističku. tumačenje entropije i pokazao da je zakon njenog povećanja posljedica kinetičke. ur-tion. Konstrukcija klasične S. f. dovršen je do 1902. u djelu J. W. Gibbsa (J. W. Gibbs). Teorija fluktuacije razvijena je 1905-06 u radovima M. Smoluchowskog i A. Einsteina. M. Planck je 1900. godine izveo zakon raspodjele energije u spektru zračenja crnog tijela, čime je započeo razvoj i kvantne mehanike i kvantne fizike. Godine 1924. Sh. Bose je pronašao raspodjelu impulsa svjetlosnih kvanta i povezao je sa Planckovom raspodjelom. Ajnštajn je generalizovao Boseovu raspodelu na gasove sa datim brojem čestica. E. Fermi (E. Fermi) je 1925. godine dobio funkciju raspodjele čestica po Paulijevom principu, a P. A. M. Dirac (R. A. M. Dirac) je uspostavio vezu između ove raspodjele i Bose-Einsteinove raspodjele sa mat. aparat kvantne mehanike. Dalji razvoj S. t. u 20. veku išao pod znakom primjene svog glavnog. principe za proučavanje specifičnih problema.
Lit.: Landau L. D., L i f sh i c E. M., Statistička fizika, dio 1, 3. izd., M., 1976; M ayer J., Goeppert-Mayer M., Statistička mehanika, trans. s engleskog, 2. izd., M., 1980; Abrikosov A. A., Gorkoye L. P., Dzyaloshinsky I. E., Metode kvantne teorije polja u statističkoj fizici, M., 1962; X u a ng K., Statistička mehanika, trans. sa engleskog, M., 1966; Kittel Ch., Kvantna teorija čvrste materije, per. sa engleskog, M., 1967; Silin V.P., Uvod u kinetičku teoriju gasova, M., 1971; Fizika jednostavnih tečnosti. Sub., per. sa engleskog, M., 1971; Anselm A.I., Osnove statističke fizike i termodinamike, M., 1973; L i f š i c E. M., Pitaevsky L. P., Statistička fizika, 2. dio, M., 1978; i xzh e, Fizička kinetika, M., 1979; Balescu R., Ekvilibrijumska i neravnotežna statistička mehanika, trans. sa engleskog, tom 1-2, M., 1978; Bogolyubov N. N., Izabrani radovi iz statističke fizike, M., 1979; G i b b s J. V., Termodinamika. Statistička mehanika, trans. sa engleskog, M., 1982; Leontovitch MA, Uvod u termodinamiku. Statistička fizika, M., 1983; Boltzmann L., Izabrana djela, trans. sa njemačkog, francuskog, M., 1984. L. P. Pitaevsky.
Metode Obrazovanje O ovoj stranici Library Math. forumimaBiblioteka > Knjige iz fizike > Statistička fizika
statistička fizika
- Aizenshitz R. Statistička teorija ireverzibilnih procesa. M.: Ed. Strani lit., 1963 (djvu)
- Anselm A.I. Osnove statističke fizike i termodinamike. Moskva: Nauka, 1973 (djvu)
- Akhiezer A.I., Peletminsky S.V. Metode statističke fizike. Moskva: Nauka, 1977 (djvu)
- Bazarov I.P. Metodološki problemi statističke fizike i termodinamike. M.: Izdavačka kuća Moskovskog državnog univerziteta, 1979 (djvu)
- Bogolyubov N.N. Odabrani radovi iz statističke fizike. M.: Izdavačka kuća Moskovskog državnog univerziteta, 1979 (djvu)
- Bogolyubov N.N. (mlađi), Sadovnikov B.I. Neka pitanja statističke mehanike. M.: Više. škola, 1975 (djvu)
- Bonch-Bruevich V.L., Tyablikov S.V. Metoda Greenove funkcije u statističkoj mehanici. Moskva: Fizmatlit, 1961 (djvu, 2,61Mb)
- Vasiliev A.M. Uvod u statističku fiziku. M.: Više. škola, 1980 (djvu)
- Vlasov A.A. Nelokalna statistička mehanika. Moskva: Nauka, 1978 (djvu)
- Gibbs JW Osnovni principi statističke mehanike (izloženi sa posebnom primjenom na racionalno utemeljenje termodinamike). M.-L.: OGIZ, 1946 (djvu)
- Gurov K.P. Osnove kinetičke teorije. Metoda N.N. Bogolyubov. Moskva: Nauka, 1966 (djvu)
- Zaslavsky G.M. Statistička ireverzibilnost u nelinearnim sistemima. Moskva: Nauka, 1970 (djvu)
- Zakharov A.Yu. Rešetkasti modeli statističke fizike. Veliki Novgorod: NovGU, 2006 (pdf)
- Zakharov A.Yu. Funkcionalne metode u klasičnoj statističkoj fizici. Veliki Novgorod: NovGU, 2006 (pdf)
- Ios G. Kurs teorijske fizike. Dio 2. Termodinamika. Statistička fizika. Kvantna teorija. Nuklearna fizika. M.: Prosvjeta, 1964 (djvu)
- Ishihara A. Statistical Physics. M.: Mir, 1973 (djvu)
- Kadanov L., Beim G. Kvantna statistička mehanika. Metode Greenovih funkcija u teoriji ravnotežnih i neravnotežnih procesa. M.: Mir, 1964 (djvu)
- Katz M. Vjerovatnoća i srodna pitanja u fizici. M.: Mir, 1965 (djvu)
- Katz M. Nekoliko probabilističkih problema fizike i matematike. Moskva: Nauka, 1967 (djvu)
- Kittel Ch. Elementarna statistička fizika. M.: IL, 1960 (djvu)
- Kittel Ch. Statistička termodinamika. M: Nauka, 1977 (djvu)
- Kozlov V.V. Termička ravnoteža prema Gibbsu i Poincareu. Moskva-Iževsk: Institut za kompjuterska istraživanja, 2002 (djvu)
- Kompaneets A.S. Zakoni fizičke statistike. udarni talasi. Super gusta supstanca. M.: Nauka, 1976 (djvu)
- Kompaneets A.S. Kurs teorijske fizike. Tom 2. Statistički zakoni. M.: Prosvjeta, 1975 (djvu)
- Kotkin G.L. Predavanja iz statističke fizike, NSU (pdf)
- Krylov N.S. Radovi na potkrepljivanju statističke fizike. M.-L.: Iz Akademije nauka SSSR-a, 1950. (djvu)
- Kubo R. Statistička mehanika. M.: Mir, 1967 (djvu)
- Landsberg P. (ur.) Problemi u termodinamici i statističkoj fizici. M.: Mir, 1974 (djvu)
- Levich V.G. Uvod u statističku fiziku (2. izdanje) M.: GITTL, 1954 (djvu)
- Libov R. Uvod u teoriju kinetičkih jednačina. M.: Mir, 1974 (djvu)
- Mayer J., Geppert-Mayer M. Statistička mehanika. M.: Mir, 1980 (djvu)
- Minlos R.A. (ur.) Matematika. Novo u stranoj nauci-11. Gibbsova stanja u statističkoj fizici. Sažetak članaka. M.: Mir, 1978 (djvu)
- Nozdrev V.F., Senkevič A.A. Kurs statističke fizike. M.: Više. škola, 1965 (djvu)
- Prigogine I. Neravnotežna statistička mehanika. M.: Mir, 1964 (djvu)
- Radushkevich L.V. Kurs statističke fizike (2. izdanje) M.: Prosveshchenie, 1966 (djvu)
- Reif F. Berkeley Physics Course. Tom 5. Statistička fizika. M.: Nauka, 1972 (djvu)
- Rumer Yu.B., Ryvkin M.Sh. Termodinamika, statistička fizika i kinetika. M.: Nauka, 1972 (djvu)
- Rumer Yu.B., Ryvkin M.Sh. Thermodynamics Statistical Physics and Kinetics (2. ed.). Moskva: Nauka, 1977 (djvu)
- Ruel D. Statistička mehanika. M.: Mir, 1971 (djvu)
- Savukov V.V. Rafiniranje aksiomatskih principa statističke fizike. SPb.: Balt. stanje tech. univ. "Voenmekh", 2006
statistička fizika grana fizike čiji je zadatak da izrazi svojstva makroskopskih tijela, odnosno sistema koji se sastoje od vrlo velikog broja identičnih čestica (molekula, atoma, elektrona itd.), kroz svojstva ovih čestica i interakciju između njih . Ostale grane fizike takođe proučavaju makroskopska tela - termodinamiku, mehaniku kontinuuma, elektrodinamiku kontinuuma. Međutim, kada se specifični problemi rješavaju metodama ovih disciplina, odgovarajuće jednadžbe uvijek uključuju nepoznate parametre ili funkcije koje karakteriziraju dato tijelo. Dakle, za rješavanje problema hidrodinamike potrebno je poznavati jednačinu stanja tekućine ili plina, odnosno ovisnost gustoće o temperaturi i tlaku, toplinski kapacitet tekućine, njen koeficijent viskoznosti itd. Sve ove zavisnosti i parametri se, naravno, mogu eksperimentalno odrediti, pa se dotične metode nazivaju fenomenološkim. Statistička fizika dozvoljava, barem u principu, au mnogim slučajevima i stvarno, izračunavanje svih ovih veličina, ako su poznate sile interakcije između molekula. T. o., S. f. koristi informacije o "mikroskopskoj" strukturi tijela - o tome od kojih se čestica sastoje, kako te čestice međusobno djeluju, pa se naziva mikroskopska teorija. Ako su u nekom trenutku date koordinate i brzine svih čestica tijela i poznat je zakon njihove interakcije, tada bi rješavanjem jednadžbi mehanike bilo moguće pronaći te koordinate i brzine u bilo kojoj narednoj tački na vrijeme i time u potpunosti odrediti stanje tijela koje se proučava. (Radi jednostavnosti, prezentacija je izvedena na jeziku klasične mehanike. Ali u kvantnoj mehanici (Vidi Kvantna mehanika) situacija je ista: poznavanje početne valne funkcije (Vidi Talasna funkcija) sistema i zakona interakcije čestica, moguće je, rješavanjem Schrödingerove jednadžbe, pronaći talasnu funkciju , koja određuje stanje sistema u svim budućim trenucima vremena.) U stvari, međutim, takav način konstruisanja mikroskopske teorije je nemoguć, jer broj čestica u makroskopskim tijelima je vrlo velik. Na primjer, u 1 cm 3 gas na temperaturi od 0 °C i pritisku od 1 atm sadrži približno 2,7․10 19 molekula. Nemoguće je riješiti toliki broj jednačina, a početne koordinate i brzine svih molekula su još uvijek nepoznate. Međutim, upravo veliki broj čestica u makroskopskim tijelima dovodi do pojave novih – statističkih – pravilnosti u ponašanju takvih tijela. Ovo ponašanje u širokom rasponu ne ovisi o specifičnim početnim uvjetima - o točnim vrijednostima početnih koordinata i brzina čestica. Najvažnija manifestacija ove nezavisnosti je iz iskustva poznata činjenica da sistem, prepušten sam sebi, tj. izolovan od spoljašnjih uticaja, na kraju dolazi u neko ravnotežno stanje (termodinamičko, ili statističko, ravnotežno), čija su svojstva određena samo po takvim opštim karakteristikama početnog stanja, kao što je broj čestica, njihova ukupna energija itd. (vidi Termodinamička ravnoteža). U budućnosti ćemo uglavnom govoriti o S. t. ravnotežna stanja. Prije formulisanja teorije koja opisuje statističke pravilnosti, treba razumno ograničiti same zahtjeve za teoriju. Naime, zadatak teorije trebao bi biti da izračuna ne točne vrijednosti različitih fizičkih veličina za makroskopska tijela, već prosječne vrijednosti tih veličina tokom vremena. Razmotrimo, na primjer, molekule smještene u dovoljno velikom makroskopskom volumenu izoliranom u plinu. Broj takvih molekula će se vremenom mijenjati zbog njihovog kretanja, a mogao bi se točno naći kada bi se znale sve koordinate molekula u svakom trenutku. To, međutim, nije neophodno. Promjena broja molekula u volumenu će biti u prirodi nasumičnih fluktuacija - fluktuacija - u odnosu na neku prosječnu vrijednost. Sa velikim brojem čestica u zapremini, ove fluktuacije će biti male u odnosu na prosječan broj čestica, tako da je za karakterizaciju makroskopskog stanja dovoljno znati samo ovu prosječnu vrijednost. Da biste razjasnili prirodu statističkih obrazaca, razmotrite još jedan jednostavan primjer. Neka se u posudu stavi veliki broj zrna dve sorte, svake sorte podjednako, a sadržaj posude dobro promeša. Tada se, na osnovu svakodnevnog iskustva, može uveriti da će se u uzorku uzetom iz posude, koja još uvek sadrži veliki broj zrna, naći približno jednak broj zrna svake sorte, bez obzira na redosled. zrna su sipana u posudu. Ovaj primjer jasno pokazuje dvije važne okolnosti koje osiguravaju primjenjivost statističke teorije. Prvo, potreba za velikim brojem zrna kako u cijelom "sistemu" - posudi sa zrnom, tako iu "podsistemu" odabranom za eksperiment - uzorku. (Ako se uzorak sastoji od samo dva zrna, onda će često oba biti istog kvaliteta.) Drugo, jasno je da složenost kretanja zrna tokom miješanja igra značajnu ulogu, osiguravajući njihovu ravnomjernu distribuciju u zapremini posude. funkcija distribucije. Zamislite sistem koji se sastoji od Nčestice, uz pretpostavku radi jednostavnosti da čestice nemaju unutrašnje stepene slobode. Takav sistem je opisan zadatkom 6N varijable - 3N koordinate q i i 3N impulsi pi, čestice [skup ovih varijabli će biti skraćen kao ( R, q)]. Izračunajmo prosječnu vrijednost u vremenskom intervalu određene vrijednosti F(p, q), što je funkcija ovih koordinata i impulsa. Da bismo to učinili, podijelimo interval (0, τ) na s jednaki mali segmenti Δ ta (a = 1,2,....... s). Onda po definiciji gdje q a i p a- vrijednosti koordinata i impulsa povremeno ta. U limitu s→ ∞ zbir ide u integral: Koncept funkcije distribucije na prirodan način nastaje ako uzmemo u obzir prostor 6 N mjerenja, na čijim osama su ucrtane vrijednosti koordinata i impulsa čestica sistema; naziva se fazni prostor. Za svaku vrijednost vremena t odgovaraju određenim vrijednostima svih q i R, tj. neka tačka u faznom prostoru, koja prikazuje stanje sistema u datom trenutku t. Podijelimo cijeli fazni prostor na elemente čija je veličina mala u odnosu na vrijednosti karakteristične za dato stanje sistema q i R, ali i dalje toliko veliki da u svakoj od njih postoji mnogo tačaka koje prikazuju stanje sistema u različitim vremenskim trenucima t. Tada će broj takvih tačaka u elementu volumena biti približno proporcionalan vrijednosti ovog volumena dpdq. Ako označimo koeficijent proporcionalnosti kroz sω(p, q), onda je ovo broj za element sa centrom u nekoj tački ( p, q) biće napisan kao: da = sω(p, q)dpdq, (2) dpdq = dp 1 dq 1 dp 2 dq 2 ... dp 3N dq 3N Volumen odabranog elementa faznog prostora. Prosječna vrijednost (1), uzimajući u obzir malenost ovih elemenata zapremine, može se prepisati kao (integracija preko koordinata se vrši po čitavom volumenu sistema, po impulsima - od -∞ do ∞). Funkcija ω( p, q, t) naziva se funkcija raspodjele u odnosu na koordinate impulsa čestice. Budući da je ukupan broj odabranih bodova s, funkcija w zadovoljava uslov normalizacije: Iz (3) i (4) se može vidjeti da je ω dpdq može se smatrati vjerovatnoćom da se sistem nalazi u elementu dpdq fazni prostor. Ovako uvedena funkcija distribucije može dobiti još jednu interpretaciju. Da bismo to uradili, istovremeno ćemo razmotriti veliki broj identičnih sistema i pretpostaviti da svaka tačka u faznom prostoru predstavlja stanje jednog takvog sistema. Tada se vremensko usrednjavanje u (1)-(1a) može shvatiti kao usrednjavanje po ukupnosti ovih sistema, ili, kako se kaže, po statističkom ansamblu (vidi Statistički ansambl). Argumenti koji su do sada sprovedeni bili su čisto formalne prirode, od tada pronalaženje funkcije raspodjele, prema (2), zahtijeva poznavanje svega R i q u svakom trenutku, tj. rješenja jednačina kretanja sa odgovarajućim početnim uslovima. Glavni stav S. f. je, međutim, tvrdnja o mogućnosti određivanja ove funkcije iz općih razmatranja za sistem u stanju termodinamičke ravnoteže. Pre svega, može se pokazati, na osnovu očuvanja broja sistema tokom kretanja, da je funkcija distribucije integral kretanja sistema, tj. ostaje konstantna ako R i q promijeniti u skladu sa jednadžbama kretanja (vidi Liouville teorem). Kada se zatvoreni sistem kreće, njegova energija se ne menja, stoga sve tačke u faznom prostoru, koje prikazuju stanje sistema u različitim vremenskim tačkama, moraju ležati na nekoj „hiperpovršini“ koja odgovara početnoj vrednosti energije. E. Jednačina ove površine ima oblik; H(p, q) = E, gdje H(p, q) je energija sistema, izražena u koordinatama i momentima, odnosno njegova Hamiltonova funkcija. Nadalje, kretanje sistema mnogih čestica je izuzetno zamršeno. Stoga će se tokom vremena tačke koje opisuju stanje rasporediti po površini konstantna energija ravnomerno, kao što su zrna ravnomerno raspoređena tokom mešanja u posudi u gore pomenutom primeru (videti i Ergodičku hipotezu). Takva uniformna raspodjela po izoenergetskoj površini opisuje se funkcijom raspodjele oblika: ω( p, q) = Aδ[ H(p, q) - E], (5) gdje je δ[ H(p, q) - E]
- Delta funkcija, različita od nule samo kada H = E, tj. na ovoj površini, ALI je konstanta određena iz uslova normalizacije (4). Funkcija distribucije (5), nazvana mikrokanonska, omogućava vam da izračunate prosječne vrijednosti svih fizičkih veličina po formuli (3), bez rješavanja jednadžbi kretanja. Prilikom izvođenja izraza (5) pretpostavljeno je da je jedina veličina koja ostaje nepromijenjena tokom kretanja sistema, od koje zavisi ω, energija sistema. Naravno, zamah i ugaoni moment su takođe očuvani, ali se ove veličine mogu eliminisati pretpostavkom da je dotično telo zatvoreno u fiksnu kutiju, kojoj čestice mogu da daju zamah i zamah. U stvari, obično se ne razmatraju zatvoreni sistemi, već makroskopska tijela, koja su makroskopski mali dijelovi, ili podsistemi, bilo kojeg zatvorenog sistema. Funkcija distribucije za podsistem će se razlikovati od (5), ali neće zavisiti od specifičnosti ostatka sistema - tzv. termostat. Stoga se funkcija distribucije podsistema može odrediti pretpostavkom, na primjer, da se termostat sastoji jednostavno od Nčestice idealnog gasa, čije koordinate i momenti će biti označeni sa Q i R, za razliku od notacije q i R za podsistem, onda je mikrokanonska distribucija: Evo H(p, q) je Hamiltonova funkcija podsistema, M je masa čestice gasa, a zbrajanje se vrši po svim komponentama impulsa svih čestica termostata. Da bismo pronašli funkciju distribucije za podsistem, moramo integrirati ovaj izraz preko koordinata i momenta čestica termostata. Ako tada uzmemo u obzir da je broj čestica u termostatu mnogo veći nego u podsistemu, te težimo N→∞, uz pretpostavku da je omjer E/N konstantan i jednak 3/2 kT, tada će se za funkciju distribucije podsistema dobiti sljedeći izraz: Vrijednost T u ovoj formuli ima značenje temperature, k = 1,38․10 -16 erg/deg je Boltzmannova konstanta. [Stanje E/N→ 3 / 2 kT za gas u termostatu odgovara, kako bi trebalo da bude, formuli (13) za idealan gas; vidi ispod.] Faktor normalizacije e F/kT određuje se iz uslova normalizacije (4): Distribucija (6) se naziva kanonska Gibbsova distribucija, ili jednostavno kanonska distribucija (vidi Gibbsova distribucija), a količina Z- statistički integral. Za razliku od mikrokanonske distribucije, energija sistema u Gibsovoj distribuciji nije data. Stanja sistema su koncentrisana u tankom, ali konačnom sloju oko energetske površine koja odgovara prosečnoj energetskoj vrednosti, što znači da je moguća razmena energije sa termostatom. Inače, kada se primjenjuju na određeno makroskopsko tijelo, obje distribucije u suštini dovode do istih rezultata. Jedina razlika je u tome što se pri korištenju mikrokanonske distribucije sve prosječne vrijednosti izražavaju u smislu energije tijela, a kada se koristi kanonska distribucija, u smislu temperature. Ako se tijelo sastoji od dva dijela 1 i 2 koji nisu u interakciji s Hamiltonovim funkcijama H1 i H2, zatim za cijelo tijelo H = H1 + H2 a prema (6) funkcija distribucije tijela je podijeljena na umnožak funkcija raspodjele za svaki od dijelova, tako da ovi dijelovi ispadaju statistički nezavisni. Ovaj zahtjev, zajedno sa Liouvilleovom teoremom, može se koristiti kao osnova za izvođenje Gibbsove raspodjele bez pribjegavanja mikrokanonskoj raspodjeli. Formula (6) vrijedi za sisteme koji su opisani klasičnom mehanikom. U kvantnoj mehanici, energetski spektar sistema konačnog volumena je diskretan. Verovatnoća da podsistem bude u stanju sa energijom E n je data formulom sličnom (6): gde je uslov normalizacije Vrijednost Z naziva se particiona funkcija sistema; zbir u izrazu (8) uzima se za sva stanja sistema. Za sistem koji je sa dovoljno preciznošću opisan klasičnom mehanikom, u formuli (8) moguće je preći sa sumiranja po stanjima na integraciju po koordinatama i momentima sistema.Istovremeno, za svako kvantno stanje postoji „ćelija“ (ili “ćelija”) u faznom prostoru zapremine ħ - Traka je konstantna. Drugim riječima, sumiranje je završeno n svodi na integraciju preko Razlikuje se za faktor od čisto klasičnog normalizacijskog uvjeta (6a), što dovodi do dodatnog člana u F. Gore navedene formule odnose se na slučaj kada je dat broj čestica u podsistemu. Ako kao podsistem odaberemo određeni volumenski element čitavog sistema, kroz čiju površinu čestice mogu napustiti podsistem i vratiti se u njega, tada je vjerovatnoća da se podsistem nađe u stanju sa energijom E n i broj čestica N n je dan Gibbsovom formulom velike kanonske distribucije: u kojoj je dodatni parametar μ - Hemijski potencijal, koji određuje prosječan broj čestica u podsistemu, a vrijednost Ω određena je iz uslova normalizacije [vidi. formula (11)]. Statistička interpretacija termodinamike. Najvažniji rezultat S. f. - utvrđivanje statističkog značenja termodinamičkih veličina. Ovo omogućava izvođenje zakona termodinamike iz osnovnih ideja S. f. i izračunati termodinamičke veličine za specifične sisteme. Prije svega, termodinamička unutrašnja energija se poistovjećuje sa prosječnom energijom sistema. Prvi zakon termodinamike tada dobija očiglednu interpretaciju kao izraz zakona održanja energije tokom kretanja čestica koje čine telo. Dalje, neka Hamiltonova funkcija sistema zavisi od nekog parametra λ (koordinate zida posude u kojoj se nalazi sistem, spoljašnje polje, itd.). Zatim derivacija generalizovane sile) koja odgovara ovom parametru, i vrednost E̅ sistema, uzimajući u obzir formulu (6) i uslov normalizacije, s obzirom na varijable λ i T a s obzirom da je vrijednost F je također funkcija ovih varijabli, tada dobijamo identitet: Prema gore navedenom, član koji sadrži dλ, jednako je prosječnom radu dA izvodi na tijelu. Tada je posljednji pojam toplina koju primi tijelo. Upoređujući ovaj izraz sa relacijom dE = dA + TdS, koji je kombinovani zapis prvog i drugog zakona termodinamike (vidi Drugi zakon termodinamike) za reverzibilne procese (vidi Reverzibilni proces), nalazimo da T u (6) je zaista jednak apsolutnoj temperaturi tijela, i derivaciji Entropije) S. To znači da F je Slobodna energija tijela, iz koje se razjašnjava njeno statističko značenje. Od posebne je važnosti statistička interpretacija entropije, koja slijedi iz formule (8). Formalno, g se sabira u ovu formulu preko svih stanja sa energijom E n, ali u stvari, zbog male fluktuacije energije u Gibsovoj distribuciji, značajan je samo relativno mali broj njih sa energijom bliskom prosječnoj. Broj ovih bitnih stanja Δ̅n̅ se stoga može prirodno odrediti ograničavanjem sumiranja u (8) na interval Δ̅n̅, zamjenom E n za srednju energiju E̅ i uzimanje eksponenta ispod znaka zbira. Tada će zbir dati Δ̅n̅ i poprimiti oblik. S druge strane, prema termodinamici, F = E̅ - TS, koji daje odnos entropije sa brojem mikroskopskih stanja Δ̅n̅ u datom makroskopskom stanju, drugim riječima, sa statističkom težinom (vidi Statistička težina) makroskopskog stanja, odnosno sa njegovom vjerovatnoćom: Na temperaturi apsolutne nule, bilo koji sistem je u određenom osnovnom stanju, tako da je Δ̅n̅ = 1, S= 0. Ova izjava izražava treći zakon termodinamike. Ovdje je bitno da je za jednoznačnu definiciju entropije potrebno koristiti kvantnu formulu (8); u čisto klasičnoj statistici, entropija je definisana samo do proizvoljnog pojma. Značenje entropije kao mere verovatnoće stanja je takođe očuvano u odnosu na proizvoljna - ne nužno ravnotežna - stanja. U stanju ravnoteže, entropija ima najveću moguću vrijednost pod datim vanjskim uvjetima. To znači da je stanje ravnoteže stanje sa maksimalnom statističkom težinom, najvjerovatnije stanje. Proces prelaska sistema iz neravnotežnog stanja u ravnotežno stanje je proces prelaska iz manje verovatnih stanja u verovatnija; ovo razjašnjava statističko značenje zakona povećanja entropije, prema kojem entropija zatvorenog sistema može samo rasti. Formula (8) koja povezuje slobodnu energiju F sa particionom funkcijom, je osnova za izračunavanje termodinamičkih veličina po metodama S. f. Koristi se, posebno, za izgradnju statističke teorije o električnim i magnetskim svojstvima materije. Na primjer, da bi se izračunao magnetni moment tijela u magnetskom polju, treba izračunati particijsku funkciju i slobodnu energiju. Magnetski trenutak m tijelo se tada daje formulom: m = gdje H- intenzitet vanjskog magnetnog polja. Slično (8), uslov normalizacije u velikoj kanonskoj distribuciji (9) određuje termodinamički potencijal Ω prema formuli: Ovaj potencijal je povezan sa slobodnom energijom relacijom: Prijave S. f. na proučavanje određenih svojstava specifičnih sistema u suštini se svode na približno izračunavanje particione funkcije, uzimajući u obzir specifična svojstva sistema. U mnogim slučajevima, ovaj zadatak se pojednostavljuje primjenom zakona ekviparticije u stupnjevima slobode, koji kaže da je toplinski kapacitet životopis(pri konstantnoj zapremini v) sistema interakcijskih materijalnih tačaka - čestica koje vrše harmonijske oscilacije, jednaka je c v = k(l/2 + n),
gdje l- ukupan broj translacionih i rotacionih stepeni slobode, n- broj vibracionih stepeni slobode. Dokaz zakona se zasniva na činjenici da je Hamiltonova funkcija H takav sistem izgleda ovako: H = K(pi)+ U(q m), gdje je kinetička energija To je homogena kvadratna funkcija od l + n impulsi pi i potencijalnu energiju U- kvadratna funkcija od n vibracijske koordinate q m. U statističkom integralu Z(8a) integracija preko vibracijskih koordinata zbog brze konvergencije integrala može se proširiti od - ∞ do ∞. Nakon izvršene promjene varijabli Z ovisi o temperaturi as Tl/2+n, dakle slobodna energija F=-kT(l/ 2
+n)(ln T+ const). Iz ovoga slijedi gornji izraz za toplinski kapacitet, jer Idealan gas. Najjednostavniji predmet S.-ovog istraživanja f. je idealan plin, odnosno plin toliko razrijeđen da se interakcija između njegovih molekula može zanemariti. Termodinamičke funkcije takvog plina mogu se u potpunosti izračunati. Energija gasa je jednostavno zbir energija pojedinačnih molekula. To je, međutim, još uvijek nedovoljno da se molekuli smatraju potpuno nezavisnim. Zaista, u kvantnoj mehanici, čak i ako nema interakcijskih sila između čestica, postoji određeni utjecaj identičnih (identičnih) čestica jedna na drugu ako su u sličnim kvantnomehaničkim stanjima. Ovo je tzv. interakcija razmene. Može se zanemariti ako, u prosjeku, postoji mnogo manje od jedne čestice po stanju, što se, u svakom slučaju, odvija pri dovoljno visokoj temperaturi plina; takav gas se naziva nedegenerisanim. U stvari, obični plinovi, koji se sastoje od atoma i molekula, nisu degenerirani na svim temperaturama (na kojima su još uvijek plinoviti). Za nedegenerirani idealni plin, funkcija distribucije se razlaže u proizvod funkcija raspodjele za pojedinačne molekule. leže u intervalima dp x, dpy, dpz, a koordinate su u intervalima dx, dy, dz: , (12) Energija jednoatomske molekule plina u vanjskom polju s potencijalnom energijom U(r) je jednako p 2 /2M + U(r). Integriranje (6) preko koordinata r(x, y, z) i impulse R(p x, py, pz) od svih molekula osim jednog, možete pronaći broj molekula dN, čiji impulsi gdje d 3 str = dp x dp y dp z, d3x = dxdydz. Ova formula se zove Maxwell-Boltzmannova distribucija (vidi Boltzmannova statistika). Ako integrišemo (12) preko impulsa, onda dobijamo formulu za raspodelu čestica po koordinatama u spoljašnjem polju, posebno u gravitacionom polju - Barometrijska formula. Raspodjela brzina u svakoj tački u prostoru poklapa se sa Maxwellovom raspodjelom m. Razdjelna funkcija idealnog plina također se razlaže na proizvod identičnih pojmova koji odgovaraju pojedinačnim molekulima. Za jednoatomni gas, sumiranje u (8) se svodi na integraciju preko koordinata i impulsa, tj. zbir se zamjenjuje integralom po gdje g- statističku težinu osnovnog stanja atoma, odnosno broj stanja koja odgovaraju njegovom nižem energetskom nivou, V- zapremina gasa (ovde e- baza prirodni logaritmi). Na visokim temperaturama g =(2J+1)(2L+1), gdje J- vrijednost Spin a, a L- moment orbitale (vidi Orbitalni moment) atoma (u jedinicama ħ
). Iz izraza za slobodna energija iz toga proizlazi da je jednadžba stanja idealnog gasa, tj. zavisnost njegovog pritiska ( R) na gustinu broja čestica ( N/V) i temperature, ima oblik: PV = NkT. Unutrašnja energija jednoatomnog gasa i njegov toplotni kapacitet pri konstantnoj zapremini su jednaki: E = 3 / 2 (NkT), c v = 3 / 2 Nk, (13) I njegov hemijski potencijal: Karakteristično je da čak i za nedegenerisan (tj. povinuje se klasičnoj mehanici sa dovoljnom tačnošću) gas, izrazi za slobodnu energiju i hemijski potencijal sadrže Planckovu konstantu ħ
. Konačno, to je zbog prethodno uočene veze između entropije i koncepta broja kvantnih stanja. U slučaju dvoatomskih i poliatomskih plinova, vibracije i rotacija molekula također doprinose termodinamičkim funkcijama. Ovaj doprinos zavisi od toga da li su efekti kvantizacije vibracija i rotacije molekula značajni. Udaljenost između nivoa energije vibracije je reda I - moment inercije rotirajućeg tijela, u ovom slučaju molekula. Klasična statistika je važeća ako je temperatura dovoljno visoka za to kT>>
Δ E. U ovom slučaju, u skladu sa zakonom ekviparticije, rotacija daje konstantan doprinos toplotnom kapacitetu, jednak 1/2 k za svaki stepen slobode rotacije; posebno, za dvoatomske molekule ovaj doprinos je jednak k. Fluktuacije daju doprinos toplotnom kapacitetu jednak k za svaki vibracioni stepen slobode (tako da je vibracioni toplotni kapacitet dvoatomske molekule k). Doprinos vibracionog stepena slobode, u poređenju sa rotacionim, dvostruko je veći zbog činjenice da prilikom vibracija atomi u molekulu imaju ne samo kinetičku, već i potencijalnu energiju. U suprotnoj granici Nesavršen gas. Važno dostignuće S. t. - proračun korekcija termodinamičkih količina gasa povezanih sa interakcijom između njegovih čestica. Sa ove tačke gledišta, jednadžba stanja idealnog gasa je prvi član u širenju pritiska realnog gasa u smislu gustine broja čestica, budući da se svaki gas ponaša kao idealan gas pri dovoljnoj niske gustine. Kako se gustoća povećava, korekcije jednačine stanja povezane s interakcijom počinju igrati ulogu. One dovode do pojave u izrazu za pritisak pojmova sa većim stepenom gustine broja čestica, tako da se pritisak predstavlja tzv. viralne serije oblika: Odds AT, OD itd. zavise od temperature i formiraju se. drugi, treći itd. virijski koeficijenti. S. metode f. omogućavaju izračunavanje ovih koeficijenata ako je poznat zakon interakcije između molekula gasa. Istovremeno, koeficijenti AT, OD,... opisuju istovremenu interakciju dva, tri ili više molekula. Na primjer, ako je plin jednoatomski i potencijalna energija interakcije njegovih atoma U(r), tada je drugi virijski koeficijent Po redu veličine AT jednak je r 0 - karakterističnoj veličini atoma, ili, preciznije, radijusu djelovanja međuatomskih sila. To znači da je serija (15) zapravo ekspanzija snaga bezdimenzionalnog parametra Nr 3 /V, mali za dovoljno razrijeđen plin. Interakcija između atoma plina ima karakter odbijanja na bliskim udaljenostima i privlačenja na udaljenim. Ovo vodi do AT> 0 na visokim temperaturama i AT T = 15,3 K koeficijent AT = -
3․10 -23 cm 3, i kada T= 510 K AT = 1,8 ․10 -23 cm 3. Za argon AT = -
7,1․10 -23 cm 3 at T = 180 K i AT = 4,2․10 -23 cm 3 at T= 6000 K. Za jednoatomne gasove izračunavaju se vrednosti virijalnih koeficijenata, uključujući i peti, što omogućava da se opiše ponašanje gasova u prilično širokom opsegu gustina (vidi i Gasovi). Plazma. Poseban slučaj neidealnog plina je plazma - djelomično ili potpuno ionizirani plin, u kojem se stoga nalaze slobodni elektroni i ioni. Pri dovoljno niskoj gustini, svojstva plazme su bliska onima idealnog gasa. Prilikom izračunavanja odstupanja od idealnosti, bitno je da elektroni i ioni međusobno djeluju elektrostatički prema Kulonovom zakonu. Coulombove sile polako opadaju s rastojanjem, a to dovodi do činjenice da je čak i za izračunavanje prve korekcije termodinamičkih funkcija potrebno uzeti u obzir interakciju ne dvije, već velikog broja čestica odjednom, budući da se integral u drugom virjalnom koeficijentu (16), koji opisuje interakciju para, divergira za velike udaljenosti r između čestica. U stvarnosti, pod utjecajem Coulomb sila, distribucija jona i elektrona u plazmi se mijenja na način da se polje svake čestice ekranizira, odnosno brzo opada na određenoj udaljenosti, koja se naziva Debajev radijus. Za najjednostavniji slučaj plazme koja se sastoji od elektrona i jednostruko nabijenih jona, Debyeov radijus rD jednako: gdje N broj elektrona e je naboj elektrona. Sve čestice unutar Debyeovog radijusa učestvuju u interakciji istovremeno. Ovo rezultira da je prva korekcija pritiska proporcionalna ne ( N/V) 2
kao u običnom gasu, ali nižeg stepena gustine - ( N/V) 3/2
. Kvantitativni proračun se zasniva na činjenici da su preostale čestice raspoređene u polju odabranog elektrona ili jona prema Boltzmannovoj raspodjeli. Kao rezultat toga, jednadžba stanja, uzimajući u obzir prvi amandman, ima oblik: (pošto je broj elektrona jednak broju jona, ukupan broj čestica je jednak 2N). Ispravke iste vrste nastaju i u termodinamičkim funkcijama elektrolita u kojima se nalaze slobodni joni otopljenih tvari. Tečnosti. Za razliku od gasa, članovi interakcije u jednačini stanja za tečnost nisu mali. Stoga svojstva tekućine jako zavise od specifične prirode interakcije između njenih molekula. U teoriji fluida generalno ne postoji mali parametar koji bi se mogao koristiti za pojednostavljenje teorije. Nije moguće dobiti nikakve analitičke formule za termodinamičke količine tečnosti. Jedan od načina za prevazilaženje ove teškoće je proučavanje sistema koji se sastoji od relativno malog broja čestica - reda veličine nekoliko hiljada. U ovom slučaju se pomoću računara mogu direktno riješiti jednačine kretanja čestica i na taj način odrediti prosječne vrijednosti svih veličina koje karakterišu sistem bez dodatnih pretpostavki. U ovom slučaju moguće je proučavati i proces približavanja takvog sistema ravnotežnom stanju. Takođe je moguće pronaći statistički integral za takav sistem od malog broja čestica izračunavanjem integrala u glavnoj formuli za statistički integral na računaru (obično koristeći Monte Carlo metod). Rezultati dobijeni obema metodama su, međutim, niske tačnosti kada se primenjuju na stvarne tečnosti zbog malog broja čestica u sistemu. Drugi način za izgradnju teorije tekućine temelji se na korištenju funkcija molekularne distribucije. Ako integriramo funkciju distribucije w sistema u smislu impulsa svih čestica i u smislu koordinata svih čestica, osim jedne, dobija se jednočestična funkcija prostorne distribucije f1(r). Ako se integrišemo w prema impulsima svih čestica i prema koordinatama svih čestica, osim dvije, dobit će se funkcija raspodjele s dvije čestice f2(r1, r2), od svih čestica osim tri, je funkcija raspodjele od tri čestice f 3(r 1 , r 2 , r 3 ,) itd. Funkcija raspodjele s dvije čestice je fizička veličina koja se može direktno promatrati - izražava, na primjer, elastično raspršenje x-zrake i neutrona u tečnosti. Uz pretpostavku da je funkcija distribucije cijelog sistema data Gibbsovom raspodjelom (6), može se dobiti integralna relacija koja izražava funkciju dvije čestice u terminima funkcije tri čestice i interakcijskog potencijala između čestica. U teoriji tekućina, ova tačna relacija je dopunjena nekim približnim koji izražavaju funkciju tri čestice u terminima funkcije dvije čestice (funkcija od jedne čestice u homogenoj tekućini svodi se na konstantu). Rezultat je jednačina za funkciju dvije čestice, koja se rješava numerički. Dodatne relacije se nalaze na osnovu vjerodostojnih fizičkih razmatranja i interpolacijske su prirode, tako da teorije zasnovane na njima mogu tražiti samo kvalitativni opis svojstava tekućine. Ipak, čak je i takav kvalitativni opis važan, jer otkriva općenitost zakona S. f. (vidi i Fluid). Degenerisani gasovi. Ako se temperatura gasa snizi pri konstantnoj gustini, počinju da se pojavljuju kvantno-mehanički efekti povezani sa svojstvima simetrije talasnih funkcija sistema identičnih čestica. Gas "degeneriše" (vidi Degenerisani gas). Za čestice sa polucijelim spinom, valna funkcija mora promijeniti predznak kada se bilo koji par čestica zamijeni. Ovo, posebno, dovodi do činjenice da više od jedne čestice ne može biti u jednom kvantnom stanju (Paulijev princip). Broj čestica sa cjelobrojnim spinom u jednom stanju može biti bilo koji, ali invarijantnost valne funkcije potrebna u ovom slučaju kada su čestice preuređene dovodi ovdje do promjene statističkih svojstava plina. Čestice sa polucijelim spinom opisane su Fermi-Diracovom statistikom; zovu se fermioni. Fermioni uključuju, na primjer, elektrone, protone, neutrone, atome deuterija, atome lakog izotopa helijuma 3 He. Čestice sa cjelobrojnim spinom - bozoni - opisane su Bose-Einstein statistikom. To uključuje atome vodika, 4 atoma He, svjetlosne kvante - fotone. Neka prosječan broj čestica plina po jedinici volumena sa impulsima leži u intervalu d 3 str, tu je U ovoj formuli, ε = p 2 /2M je energija čestice sa impulsom R, μ - hemijski potencijal određen iz uslova konstantnosti broja čestica ( N) u sistemu: Formula (19) se pretvara u Boltzmannovu formulu raspodjele (12) za U slučaju fermiona, kako bi trebalo da bude, np≤ 1. To dovodi do činjenice da čestice fermionskog gasa (Fermi gas) i na T= 0 imaju impuls različit od nule, pošto samo jedna čestica može biti u stanju sa nultim impulsom. Tačnije, kod T= 0 za Fermi gas np= 1 unutar Fermijeve površine (vidi Fermijevu površinu) - sfere u prostoru impulsa sa radijusom U Bose gas u T= 0 sve čestice su u stanju sa nultim impulsom. Na dovoljno niskim temperaturama u stanju s R= 0 je konačni udio svih čestica; ove čestice formiraju tzv. Bose-Einstein kondenzat. Preostale čestice su u stanjima sa R≠ 0, a njihov broj je određen formulom (19) sa μ = 0. Na temperaturi Poseban slučaj primjene Bose-Einstein statistike je ravnoteža elektromagnetno zračenje, koji se može smatrati gasom koji se sastoji od fotona. Energija fotona povezana je sa njegovim momentom relacijom Kristalna ćelija. Prijava S. f. Izračunavanje termodinamičkih funkcija kristalne rešetke zasniva se na činjenici da atomi u rešetki prave male vibracije oko svojih ravnotežnih položaja. Ovo nam omogućava da posmatramo rešetku kao skup spregnutih harmonijskih oscilatora. U takvom sistemu, talasi se mogu širiti, što karakteriše sopstveni zakon disperzije, tj. zavisnost frekvencije ω od talasnog vektora (vidi talasni vektor) k. U kvantnoj mehanici ovi valovi se mogu smatrati skupom tzv. elementarne pobude, ili kvazičestice (vidi kvazičestice) - fononi sa energijom ħω
i kvazi impuls ćk. Glavna razlika između kvazi impulsa i impulsa je u tome što je energija fonona periodična funkcija kvazi impulsa s periodom jednakim po redu veličine a, konstanti rešetke. Funkcija raspodjele fonona preko kvazimomenta data je Bose-Einstein formulom raspodjele (19) sa μ = 0. U ovom slučaju, ε=ħω.
Dakle, poznavanje zavisnosti ω( k) omogućava izračunavanje toplotnog kapaciteta rešetke. Ova ovisnost se može odrediti iz eksperimenata neelastičnog raspršenja neutrona u kristalu (vidi Neutronografija) ili izračunati teoretski postavljanjem vrijednosti "konstanti sile" koje određuju interakciju atoma u rešetki. Na niskim temperaturama značajni su samo fononi niske frekvencije, koji odgovaraju kvantima običnih zvučnih talasa, za koje je relacija ω sa k linearno. To dovodi do činjenice da je toplinski kapacitet kristalne rešetke proporcionalan T3. Pri visokim temperaturama može se koristiti zakon jednake raspodjele energije po stupnjevima slobode, tako da toplinski kapacitet ne ovisi o temperaturi i jednak je 3Nk, gdje N je broj atoma u kristalu. Metali. U metalima, elektroni provodljivosti također doprinose termodinamičkim funkcijama. Stanje elektrona u metalu karakteriše kvazi-impuls, i, pošto elektroni se pokoravaju Fermi - Dirac statistici, njihova raspodjela po kvazimomentima je data formulom (19). Stoga je toplinski kapacitet elektronskog plina, a time i cijelog metala na dovoljno niskim temperaturama, proporcionalan T. Razlika od Fermijevog plina slobodnih čestica je u tome što Fermijeva površina, oko koje su koncentrisani "aktivni" elektroni, više nije sfera, već je neka složena površina u prostoru kvazi momenta. Oblik Fermijeve površine, kao i ovisnost energije o kvazi momentu u blizini ove površine, može se odrediti eksperimentalno, uglavnom proučavanjem magnetskih svojstava metala, a može se i teorijski izračunati pomoću tzv. kvazipotencijalni model. U superprovodnicima (vidi Superprovodljivost), pobuđena stanja elektrona su odvojena od Fermijeve površine prazninom konačne širine, što dovodi do eksponencijalne zavisnosti toplotnog kapaciteta elektrona o temperaturi. U feromagnetnim i antiferomagnetskim supstancama fluktuacije magnetnih momenata također doprinose termodinamičkim funkcijama - Spin valovima. U dielektricima i poluprovodnicima T= 0 nema slobodnih elektrona. Na konačnim temperaturama u njima se pojavljuju nabijene kvazičestice - elektroni s negativni naboj i (u jednakom broju) "rupe" sa pozitivan naboj, Elektron i rupa mogu formirati vezano stanje - kvazičesticu koja se zove eksiton. dr. Ekscitonski tip je pobuđeno stanje dielektričnog atoma koji se kreće u kristalnoj rešetki. Metode kvantne teorije polja u S. f. U rješavanju problema kvantne kvantne fizike, prvenstveno u proučavanju svojstava kvantnih tekućina i elektrona u metalima i magnetima, od velike su važnosti metode kvantne teorije polja uvedene u kvantnu fiziku. relativno nedavno. Glavnu ulogu u ovim metodama igra Grinova funkcija G makroskopskog sistema, koja je slična Grinovoj funkciji u kvantnoj teoriji polja. Zavisi od energije ε i impulsa R, zakon disperzije kvazičestica ε( R) se određuje iz jednačine: tj. energija kvazičestice određena je polom Greenove funkcije. Postoji redovna metoda za izračunavanje Greenovih funkcija kao niza snaga interakcije energije između čestica. Svaki član ove serije sadrži višestruke integrale nad energijama i momentima Greenovih funkcija čestica koje nisu u interakciji i može se grafički predstaviti u obliku dijagrama sličnih Feynmanovim dijagramima (vidi Feynmanove dijagrame) u kvantnoj elektrodinamici. Svaki od ovih dijagrama ima svoje specifičnosti fizičko značenje, što omogućava da se termini odgovorni za fenomen od interesa razdvoje u beskonačan niz i sumiraju se. Postoji i dijagramska tehnika za izračunavanje Greenovih funkcija temperature, koja omogućava direktno izračunavanje termodinamičkih veličina, bez uvođenja kvazičestica. Metode spomenute u odjeljku o tekućinama, koje koriste funkcije raspodjele više čestica kvazičestica, po mnogo čemu su bliske metodama kvantne teorije polja. Upotreba ovih funkcija uvijek se temelji na približnom "razdvajanju" - izrazu funkcije preko high order kroz funkcije nižeg. Fazni prijelazi. Uz kontinuiranu promjenu vanjskih parametara (na primjer, pritisak ili temperatura), svojstva sistema mogu se naglo promijeniti za neke vrijednosti parametara, tj. dolazi do faznog prijelaza. Fazni prijelazi se dijele na prijelaze prve vrste, praćene oslobađanjem latentne topline prijelaza i skokom volumena (to uključuje, na primjer, topljenje), i prijelaze druge vrste, u kojima nema latentne topline i skok volumena (na primjer, prijelaz u supravodljivo stanje). Statistička teorija faznih prijelaza predstavlja važno, ali još uvijek daleko od cjelovitog područja S. f. Najveća poteškoća za teorijsko istraživanje predstavljaju svojstva materije blizu linije faznog prelaza drugog reda i blizu kritične tačke faznog prelaza prvog reda. Sa matematičke tačke gledišta, termodinamičke funkcije sistema ovde imaju singularnosti. Blizu ovih tačaka javljaju se neobični kritični fenomeni. Istovremeno, fluktuacije se ovdje anomalno povećavaju, a aproksimativne metode S. f. ispostavilo se da je neprimjenjivo. Stoga važnu ulogu igra mali broj tačno rješivih modela u kojima postoje prijelazi (na primjer, tzv. Izingov model). fluktuacije. U srcu S. f. leži činjenica da fizičke veličine, koji karakteriziraju makroskopska tijela, jednaki su njihovim prosječnim vrijednostima sa velikom preciznošću. Ova jednakost je još uvijek približna, u stvari, sve veličine doživljavaju mala nasumična odstupanja od prosječnih vrijednosti - fluktuacije. Postojanje fluktuacija je od velike fundamentalne važnosti, jer direktno dokazuje statističku prirodu termodinamičkih pravilnosti. Osim toga, fluktuacije igraju ulogu ometanja buke fizička mjerenja i ograničavanje njihove tačnosti. Fluktuacije neke vrijednosti X oko svog proseka x̅ karakteriziraju srednje kvadratne fluktuacije U velikoj većini slučajeva, vrijednost X doživljava fluktuacije reda S je proporcionalno e S/k. Ovo vodi do formule Na primjer, srednji kvadrati fluktuacija tjelesne zapremine i temperature su: Iz ovih formula se može vidjeti da su relativne fluktuacije volumena i fluktuacije temperature obrnuto proporcionalne N – broju čestica u tijelu. Ovo osigurava male fluktuacije za makroskopska tijela. Odnos između fluktuacija različitih veličina x i, x k karakterizirana funkcijama x i i x k su dakle statistički nezavisni Ispod x i i x k također se mogu razumjeti vrijednosti iste količine, na primjer gustine, u različitim tačkama u prostoru. Tada ova funkcija ima značenje funkcije prostorne korelacije. Kako se rastojanje između tačaka povećava, korelaciona funkcija teži nuli (obično eksponencijalno), jer fluktuacije na udaljenim tačkama u prostoru se javljaju nezavisno. Udaljenost na kojoj se ova funkcija značajno smanjuje naziva se korelacijski radijus. Vremensko ponašanje fluktuacija i spektralna distribucija buke fluktuacije opisani su funkcijom vremenske korelacije φ( t), u kojem su fluktuacije količine uzete u različito vrijeme prosječne t: Važnu ulogu u teoriji fluktuacija imaju tzv teorema fluktuacije-disipacije, koja povezuje fluktuacije u sistemu sa promjenom njegovih svojstava pod utjecajem određenih vanjskih utjecaja. Najjednostavniji odnos ove vrste može se dobiti razmatranjem fluktuacija harmonijskog oscilatora a sa potencijalnom energijom i fluktuacija X je zaista vezan za perturbaciju pod uticajem sile f. U opštem slučaju, teorema fluktuacije-disipacije je primjenjiva ako je za X postoji "generalizovana sila" f, koji je uključen u energetski operator sistema (Hamiltonian; vidi Kvantna mehanika) kao pojam x. Uključivanje napajanja fće dovesti do promjene prosječne vrijednosti x̅ od δ x̅, i ako f zavisi od vremena e-i wt , ova promjena se može napisati kao: kompleksna veličina α(ω) naziva se generalizovana osetljivost sistema. Teorema kaže da je Fourierova transformacija korelacijske funkcije S. f. neravnotežni procesi. Fizička kinetika, grana fizičke fizike koja proučava procese u sistemima u neravnotežnim stanjima, dobija sve veći značaj. Ovdje postoje dva moguća pitanja. Prvo, može se posmatrati sistem u nekom neravnotežnom stanju i pratiti njegov prelazak u ravnotežno stanje. Drugo, možemo razmotriti sistem čije se neravnotežno stanje održava spoljni uslovi, na primjer, tijelo u kojem je zadan temperaturni gradijent teče struja itd., ili tijelo koje se nalazi u promjenljivom vanjskom polju. Ako je odstupanje od ravnoteže malo, neravnotežna svojstva sistema opisuju se tzv. kinetički koeficijenti. Primjeri takvih koeficijenata su koeficijenti viskoznosti (vidi![]()
![]()
![]()

![]()
![]()
![]() p i q, potrebno je podijeliti integral sa brojem permutacija od Nčestice, tj. na N! Konačna klasična granica za particionu funkciju je:
p i q, potrebno je podijeliti integral sa brojem permutacija od Nčestice, tj. na N! Konačna klasična granica za particionu funkciju je:![]()
![]()
![]()
![]()
![]()

![]() 3
u skladu sa brojem ćelija [sa zapreminom atoma N gasa jednaka je:
3
u skladu sa brojem ćelija [sa zapreminom atoma N gasa jednaka je:
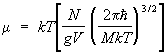

![]()
![]()
![]() n p je broj čestica u jednoj ćeliji faznog prostora ( g = 2J+ 1, gdje J je spin čestice). Tada iz Gibbsove raspodjele slijedi da za idealne plinove fermiona (gornji predznak) i bozona (donji predznak):
n p je broj čestica u jednoj ćeliji faznog prostora ( g = 2J+ 1, gdje J je spin čestice). Tada iz Gibbsove raspodjele slijedi da za idealne plinove fermiona (gornji predznak) i bozona (donji predznak):![]()
![]()
![]() De Broglieovi talasi čestica koje se kreću toplotnom brzinom postaju reda veličine prosečne udaljenosti između njih. Dakle, degeneracija utiče na temperaturama što je niža, manja gustina broja čestica u gasu (i što je veća masa čestice). M).
De Broglieovi talasi čestica koje se kreću toplotnom brzinom postaju reda veličine prosečne udaljenosti između njih. Dakle, degeneracija utiče na temperaturama što je niža, manja gustina broja čestica u gasu (i što je veća masa čestice). M).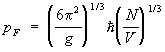 n p = 0. Na konačnim ali niskim temperaturama np varira od 1 unutar sfere do nule izvan sfere postepeno, a širina prelaznog područja je reda MkT/p F. Vrijednost np za Fermi gas kao funkcija energije ε je shematski prikazana na sl. 2 (ε 0 = p F 2 /2M). Kada se temperatura gasa promeni, stanje čestica se menja samo u ovom prelaznom sloju, a toplotni kapacitet Fermijevog gasa na niskim temperaturama je proporcionalan T i jednak je:
n p = 0. Na konačnim ali niskim temperaturama np varira od 1 unutar sfere do nule izvan sfere postepeno, a širina prelaznog područja je reda MkT/p F. Vrijednost np za Fermi gas kao funkcija energije ε je shematski prikazana na sl. 2 (ε 0 = p F 2 /2M). Kada se temperatura gasa promeni, stanje čestica se menja samo u ovom prelaznom sloju, a toplotni kapacitet Fermijevog gasa na niskim temperaturama je proporcionalan T i jednak je:![]()
![]() Fazni prijelaz (vidi dolje). Frakcija čestica sa nultim momentom nestaje Bose-Einstein kondenzacija nestaje. Kriva zavisnosti toplotnog kapaciteta od temperature ima u tački T c break. Raspodjela momenta čestica pri T > T s je dato formulom (19) i μ T > T s) prikazani su na slici 3.
Fazni prijelaz (vidi dolje). Frakcija čestica sa nultim momentom nestaje Bose-Einstein kondenzacija nestaje. Kriva zavisnosti toplotnog kapaciteta od temperature ima u tački T c break. Raspodjela momenta čestica pri T > T s je dato formulom (19) i μ T > T s) prikazani su na slici 3.![]() c je brzina svjetlosti u vakuumu. Broj fotona nije datu vrijednost, a sam je određen iz uslova termodinamičke ravnoteže, pa je njihova raspodjela impulsa data formulom (19) sa μ = 0 (štaviše, ε = rs). Distribucija energije u spektru emisije dobija se množenjem broja fotona sa energijom ε, tako da se gustina energije u frekvencijskom opsegu dω je jednako n p se uzima na ε=ħω
. To. dobija se Plankova formula za spektar ravnotežnog (crnog) zračenja (vidi Plankov zakon zračenja).
c je brzina svjetlosti u vakuumu. Broj fotona nije datu vrijednost, a sam je određen iz uslova termodinamičke ravnoteže, pa je njihova raspodjela impulsa data formulom (19) sa μ = 0 (štaviše, ε = rs). Distribucija energije u spektru emisije dobija se množenjem broja fotona sa energijom ε, tako da se gustina energije u frekvencijskom opsegu dω je jednako n p se uzima na ε=ħω
. To. dobija se Plankova formula za spektar ravnotežnog (crnog) zračenja (vidi Plankov zakon zračenja).![]()

![]()
![]()
![]() m - masa oscilatora, ω 0
je vlastita frekvencija. Proračun po formuli (22) daje: f, srednju vrijednost x̅ pomaknut za iznos
m - masa oscilatora, ω 0
je vlastita frekvencija. Proračun po formuli (22) daje: f, srednju vrijednost x̅ pomaknut za iznos![]()
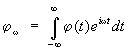
![]()






