Bilješke s predavanja na ovu temu

TEORIJSKA MEHANIKA

Za studente specijalnosti:

260501.65 Tehnologija usluživanja hrane,

Redovni oblik obrazovanja

Bilješke sa predavanja su zasnovane na:

1. Butorin L.V., Busygina E.B. Teorijska mehanika. Edukativni i praktični vodič. - M., MGU TU, 2004

2. Targ S.M. Kratki kurs teorijske mehanike. – M.: postdiplomske škole, 2001 - Sa.

3. Yablonsky A.A., Nikiforova V.N. Kurs teorijske mehanike. M. "Lan", 2000

Uvod

Moderna industrijska proizvodnja, uključujući i prehrambenu, visoko su mehanizirane industrije. Rješavanje sve složenijih zadataka pripisuje se tehnološkoj opremi, što opet dovodi do kompliciranja opreme. Formiranje modernog inženjera nezamislivo je bez poznavanja fundamentalnih disciplina. Jedna od ovih disciplina je teorijska mehanika .

Teorijska mehanika je grana mehanike koja postavlja osnovne zakone mehaničkog kretanja i mehaničke interakcije materijalnih tijela. Mehanički pokret naziva se promjena relativnog položaja materijalnih tijela tokom vremena u prostoru, mehanički interakcija- takva interakcija, uslijed koje se mijenja mehaničko kretanje ili se mijenja relativni položaj dijelova tijela.

Teorijska mehanika se obično dijeli na: statiku, kinematiku i dinamiku .

U statici se proučavaju uslovi ravnoteža materijalna tela i metode identične transformacije sistema sila. Equilibrium Stanje u kojem tijelo ostaje nepomično ili se ravnomjerno kreće pravolinijski pod djelovanjem sila.

U kinematici se razmatraju opšte geometrijske karakteristike kretanja tela. Sile koje djeluju na tijelo se ne uzimaju u obzir. Dat je zakon kretanja. Zakon o kretanju tijela je zavisnost položaja tijela u prostoru od vremena.

U dinamici se proučavaju opći zakoni kretanja tijela pod djelovanjem sila.

1. C tatika čvrsto telo

1.1 Osnovni koncepti statike

Apsolutno kruto tijelo (kruto tijelo, tijelo)- materijalno tijelo, rastojanje između bilo koje tačke u kojem se ne mijenja. Posljedično, veličina i oblik tijela se ne mijenjaju.

Materijalna tačka je tijelo čije se dimenzije, prema uslovima problema, mogu zanemariti.

opušteno tijelo- tijelo čije kretanje se ne ograničava.

Neslobodno (vezano) tijelo– tijelo čije je kretanje ograničeno.

Veze- tela koja sprečavaju kretanje predmetnog objekta (tela ili sistema tela).

mehanički sistem- skup međusobno povezanih tijela ili materijalnih tačaka.

Kruto tijelo se može posmatrati kao mehanički sistem čiji se položaji i udaljenosti između tačaka ne mijenjaju.

Snaga- vektorska veličina koja karakterizira mehaničko djelovanje jednog materijalnog tijela na drugo.

Silu kao vektor karakterišu tačka primene, smer delovanja i apsolutna vrednost (slika 1.1). Jedinica mjere za modul sile je Njutn.

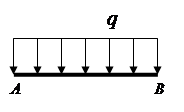Sl.1.1. Sl.1.2.

linija sile je prava linija duž koje je usmjeren vektor sile.

Koncentrisana snaga je sila primijenjena u jednoj tački.

Raspodijeljene sile (distribuirano opterećenje)- sile koje deluju na sve tačke zapremine, površine ili dužine tela (slika 1.2).

Raspodijeljeno opterećenje je postavljeno silom koja djeluje po jedinici volumena (površina, dužina) Dimenzija raspoređenog opterećenja je N / m 3 (N / m 2, N / m).

Spoljna sila je sila koja djeluje iz tijela koje ne pripada razmatranom mehaničkom sistemu.

unutrašnja snaga- sila koja deluje na materijalna tačka mehanički sistem sa strane druge materijalne tačke koja pripada sistemu koji se razmatra.

Sistem sile- skup sila koje djeluju na mehanički sistem.

Ravni sistem sila- sistem sila čije linije djelovanja leže u istoj ravni.

Prostorni sistem snaga- sistem sila čije linije delovanja ne leže u istoj ravni.

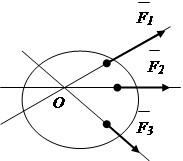
Sistem konvergentnih sila- sistem sila čije se linije djelovanja seku u jednoj tački (slika 1.3).

Proizvoljni sistem sila- sistem sila čije se linije delovanja ne seku u jednoj tački (slika 1.4)

Sl.1.3 Sl.1.4

Ekvivalentni sistemi sila- takvi sistemi sila čija zamjena jedne za druge ne mijenja mehaničko stanje tijela. Prihvaćena notacija:

Uravnotežen sistem snaga- sistem sila koji, kada se primijeni na slobodno čvrsto tijelo, ne mijenja njegovo mehaničko stanje (ne izbalansira ga).

rezultujuća sila- sila čije je djelovanje na tijelo ekvivalentno djelovanju sistema sila.

Trenutak snage- vrijednost koja karakterizira sposobnost rotacije sile.

Moćni par- sistem od dvije paralelne, jednake po apsolutnoj vrijednosti, suprotno usmjerene sile. Prihvaćena oznaka je () Pod dejstvom para sila, telo će izvršiti rotaciono kretanje.

Projekcija sile na osu- segment zatvoren između okomica povučenih od početka i kraja vektora sile na ovu os (slika 1.5).

Projekcija je pozitivna ako se smjer segmenta poklapa s pozitivnim smjerom ose.

Projekcija sile na ravan- vektor na ravni zatvorenoj između okomica povučenih od početka i kraja vektora sile na ovu ravan (slika 1.6).

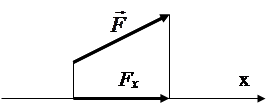
Sl.1.5 Sl.1.6

1.2. Aksiomi statike

Teorijski principi statike zasnovani su na brojnim aksiomima. Aksiom je zakon formulisan kao rezultat generalizacije rezultata posmatranja.

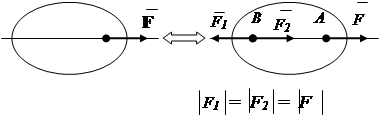
1. Aksiom ravnoteže.

Dvije sile koje djeluju na kruto tijelo su uravnotežene samo ako su jednake po apsolutnoj vrijednosti i djeluju duž jedne prave u suprotnim smjerovima (slika 1.7).

Sl.1.7 Sl.1.8

2. Aksiom sabiranja (isključivanja) uravnoteženog sistema sila.

Djelovanje sistema sila na kruto tijelo neće se promijeniti ako mu se doda ili izuzme uravnoteženi sistem sila (slika 1.8).

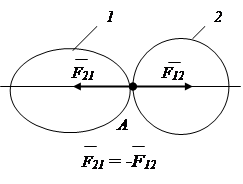
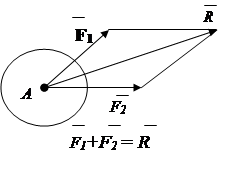
3. Aksiom o paralelogramu sila.

Sistem od dvije sile primijenjene u jednoj tački krutog tijela ima rezultantnu silu primijenjenu na istoj tački. Rezultantni vektor je dijagonala paralelograma izgrađenog na ovim silama (slika 1.9).

Rice. 1.9 Sl.1.10

4. Aksiom protivdejstva.

Kada jedno čvrsto tijelo djeluje na drugo, javlja se sila reakcije, jednaka po apsolutnoj vrijednosti, suprotna sili koja djeluje (slika 1.10).

Bilješka. Zove se sila čija je akcija data aktivna snaga, sila reakcije se zove reakcija .

5. Aksiom veza.

Svako neslobodno tijelo može se smatrati slobodnim ako je mentalno oslobođeno veza, zamjenjujući njihovo djelovanje odgovarajućim reakcijama.

1.3 Obveznice i njihove reakcije

Tijela koja sprječavaju kretanje predmeta koji se razmatra nazvat ćemo ograničenja. Zove se sila kojom veza djeluje na predmetni predmet reakcija veze. Pri određivanju mogućih reakcija sprega treba polaziti od činjenice da je reakcija sila koja sprečava kretanje dotičnog tijela. Reakcija je usmjerena u suprotnom smjeru od mjesta gdje veza ne dozvoljava tijelu da se kreće.

Pogledajmo neke uobičajene veze.

Glatka površina ograničava kretanje duž normale na površinu potpore. Reakcija je usmjerena okomito na površinu (slika 1.11).

Zglobni pokretni oslonac ograničava kretanje tijela duž normale na referentnu ravan. Reakcija je usmjerena duž normale na površinu oslonca (slika 1.12)

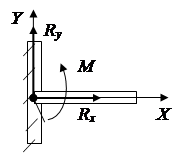
Zglobni fiksni oslonac suprotstavlja se svakom kretanju u ravni okomitoj na os rotacije. U proračunima se reakcija Fr, po pravilu, predstavlja kao dvije komponente duž X i Y osi (slika 1.13).

Zglobni bestežinski štap sprečava kretanje tijela duž linije štapa. Reakcija će biti usmjerena duž linije štapa (slika 1.14).

Slijepi prekid suprotstavlja se svakom kretanju i rotaciji u ravni (slika 1.15). Njegovo djelovanje može se zamijeniti silom predstavljenom u obliku dvije komponente i parom sila s momentom.

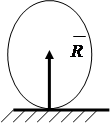Sl.1.11 1.12 Sl.1.13 Sl.1.14 Sl.1.15

1.4 Trenutak o bodu

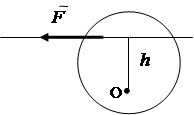
Pod djelovanjem sile, kruto tijelo, uz translatorno kretanje, može rotirati oko određenog centra. Rotacionu sposobnost sile karakteriše moment sile. Rotacijski učinak sile ovisi o modulu sile, udaljenosti od centra do linije djelovanja sile i smjeru rotacije u ravni rotacije.

Apsolutna vrijednost momenta jednaka je proizvodu modula sile i najkraće udaljenosti h od centra rotacije do linije djelovanja sile. Razdaljina h pozvao rame snage (slika 1.16).

M 0 () = F× h , (1.1)

Moment se smatra pozitivnim ako sila teži rotaciji ruke h suprotno od kazaljke na satu i negativan kada se okreće u smjeru kazaljke na satu.

Svojstva momenta sile oko tačke:

1. Moment sile se neće promijeniti kada se tačka primjene sile pomjeri duž linije djelovanja sile.

2. Moment sile je jednak nuli ako linija djelovanja sile prolazi kroz tačku primjene sile.

3. Moment rezultantne sile oko tačke jednak je zbiru momente sila oko ove tačke.

Sl.1.16. Sl.1.17.

1.5. Moment sile oko ose

Moment sile oko ose je moment projekcije ove sile na ravan okomitu na osu, u odnosu na tačku preseka ose sa ravninom.

Moment se smatra pozitivnim ako se, s pozitivnog kraja ose, rotacija koju sila nastoji napraviti smatra da se događa suprotno od kazaljke na satu, a negativna ako je u smjeru kazaljke na satu.

. (1.3)

Da biste pronašli moment sile oko ose, trebate (slika 1.17);

1. Nacrtajte ravan okomitu na z-osu.

2. Projicirajte silu na ovu ravan i izračunajte vrijednost projekcije.

3. Držite se za rame h od tačke preseka ose sa ravninom do linije dejstva projekcije sile i izračunati njenu dužinu.

4. Pronađite proizvod ovog ramena i projekcije sile sa odgovarajućim znakom /

Svojstva momenta sile oko ose

Moment sile oko ose je nula ako:

1. , tj. sila je paralelna sa osom.

2. h =0 , tj. linija djelovanja sile siječe osu.

1.6. Moment para sila

Par sila vrši rotirajući efekat na tijelo. Moment para sila jednak je umnošku jedne sile na najkraću udaljenost između linija djelovanja sila para, koja se naziva rame para (slika 1.18)

, (1.4)

gdje su: - sile koje čine par;

h- rame para

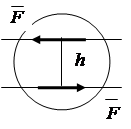Fig.1.18.

Trenutak para se smatra pozitivnim ako sile teže da rotiraju ruku u smjeru suprotnom od kazaljke na satu.

Force par svojstva

1. Zbir projekcija sila para na bilo koju osu je nula.

2. Bez mijenjanja momenta para, možete istovremeno promijeniti vrijednost sila i ramena para, respektivno.

3. Par se može prenijeti u ravni njegovog djelovanja, dok se djelovanje para na tijelo neće promijeniti.

1.7. Identična transformacija sistema sila

Transformacija se može izvršiti grafički ili analitički.

1.7.1. Transformacija konvergentnog sistema sila

Rezultat R dvije konvergirajuće sile nalazi se na osnovu aksioma paralelograma sila. (sl.1.9). Geometrijski zbir bilo kog broja sila koje se konvergiraju može se odrediti sukcesivnim sabiranjem dvije sile (slika 1.19) - metoda vektorskog poligona.

Zaključak : sistem konvergentnih sila ( n ) se svodi na jednu rezultantnu silu .

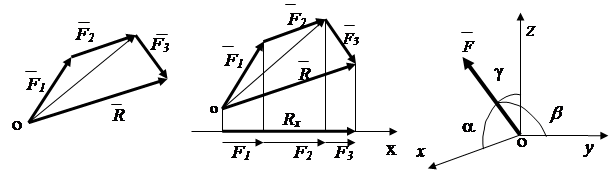
Sl.1.19 Sl.1.20. Sl.1.21.

Analitički, rezultantna sila se može odrediti kroz njene projekcije na koordinatne ose

, (1.5)

Prema teoremi: projekcija rezultante na osu jednaka je zbiru projekcija članova sila na ovu osu (slika 1.20). R x = F 1 x + F 2 x + F 3 x, ili općenito

R x = å F kx (1.6)

Uzimajući u obzir (1.6), rezultanta je određena izrazom

Smjer rezultujućeg vektora određen je kosinusima uglova između vektora i osi x , y, z(sl.1.20)

1.7.2. Transformacija proizvoljnog sistema sila .

Nemoguće je primijeniti pravilo paralelograma sila direktno na proizvoljan sistem sila, jer se linije djelovanja sila ne seku u jednoj tački. Prethodno je sistem sila doveden u jedan centar na osnovu teoreme o paralelnom prenosu sile.

Teorema: sila primijenjena na kruto tijelo može se, bez promjene njenog djelovanja, prenijeti paralelno na drugu tačku tijela, pri čemu se dodaje par sila sa momentom jednakim momentu prenesene sile u odnosu na tačku u kojoj se nalazi prenesena (slika 1.22).

Kao rezultat ove transformacije, dobija se konvergentni sistem sila i zbir momenata parova sila. Djelovanje konvergentnog sistema sila zamjenjuje se djelovanjem ukupne sile, djelovanje momenata - ukupnim momentom. Ukupni vektor * se zove glavni vektor sistemi sila, ukupni moment * - highlight sistemi sila.

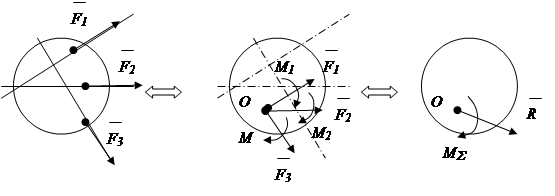
Sl.1.22

zaključak: proizvoljan sistem sila kao rezultat identične transformacije svodi se na glavni vektor * i glavna poenta * sistemi sila.

Analitički glavni vektor a glavni moment sistema sila se može odrediti kroz njihove projekcije na koordinatne ose

1.8. Uslovi za ravnotežu sistema sila

1.8.1. Ravnoteža sistema konvergentnih sila

Po definiciji (vidi klauzulu 1.1), djelovanje sistema konvergirajućih sila je ekvivalentno djelovanju jedne rezultantne sile. Za ravnotežu tijela potrebno je i dovoljno da rezultanta bude nula = 0.

Iz formule (1.7) proizlazi da je za ravnotežu prostornog sistema konvergentnih sila potrebno i dovoljno da zbir projekcija svih sila na ose X,Y,Z je bilo jednako nuli

å F kx = 0

å Fky= 0 (1.10) Fk z = 0

Za ravnotežu ravnog konvergentnog sistema sila, potrebno je i dovoljno da zbir projekcija svih sila na ose X, Y bude jednak nuli

å F kx = 0

å Fky = 0 (1.11)

1.8.2. Ravnoteža proizvoljnog sistema sila.

Djelovanje proizvoljnog sistema sila je ekvivalentno djelovanju glavnog vektora i glavnog momenta. Za ravnotežu je neophodno i dovoljno da uslov

Za ravnotežu proizvoljnog sistema sila potrebno je i dovoljno da zbir projekcija svih sila na ose X, Y, Z i zbir momenata svih sila u odnosu na ose X,Y,Z bile jednake nuli.

å F kx = 0

å Fky = 0

å Fkz = 0 (1.13)

å M x(k) = 0

å M y(k) = 0

å M z(k) = 0

Za ravnotežu ravnog proizvoljnog sistema sila, potrebno je i dovoljno da zbir projekcija glavnog vektora na ose X, Y i algebarski zbir momenata sila u odnosu na centar O budu jednaki nula.

åF ky = 0 (1.14)

EM o ( k) = 0

1.9. Pitanja za samokontrolu u odjeljku

1. Dajte definiciju apsolutno krutog tijela, materijalne tačke, sile, linije djelovanja sile, sistema sila (ravnog, prostornog, konvergentnog) proizvoljnog sistema sila.

2. Šta se zove projekcija sile na osu, na ravan?

3. Šta se zove moment sile, kako se određuje moment sile u odnosu na tačku?

4. Da li se moment sile mijenja u odnosu na datu tačku kada se sila prenosi duž linije njenog djelovanja?

5. U kom slučaju je moment sile u odnosu na datu tačku jednak nuli?

6. Koji sistem sila se naziva par sila, koliki je moment para sila?

7. Šta se zove veza? Koji je princip oslobađanja od veza? Navedite glavne vrste veza, pokažite njihove reakcije.

8. Koji su uslovi i jednačine za ravnotežu sistema konvergirajućih i proizvoljnih sistema sila koje se nalaze u prostoru i u ravni?

9. Formulirati postupak rješavanja problema statike.

2. Kinematika

Kinematika- dio teorijske mehanike, koji razmatra opšta geometrijska svojstva mehaničkog kretanja, kao procesa koji se odvija u prostoru i vremenu. Pokretni objekti se tretiraju kao geometrijske tačke ili geometrijska tijela. U skladu s tim, studija je podijeljena na kinematiku tačke i kinematiku krutog tijela

2.1 Osnovni pojmovi kinematike

Zakon gibanja tačke (tijela)- zavisnost položaja tačke (tijela) u prostoru od vremena.

Putanja tačke- lokus položaja tačke u prostoru tokom njenog kretanja.

Brzina tačke (tela).- karakteristika promjene u vremenu položaja tačke (tijela) u prostoru.

Ubrzanje u tački (tijelo).- karakteristika vremenske promjene brzine tačke (tijela)

2.2. Kinematika tačke

2.2.1 Metode za određivanje kretanja tačke

Podešavanje kretanja tačke znači podesiti promenu njenog položaja u odnosu na izabrani referentni sistem. Postoje tri glavna referentna sistema: vektorski, koordinatni, prirodni. Prema tome, postoje tri načina da se odredi kretanje tačke.

U vektorskom sistemu, položaj tačke u odnosu na početak je dat vektorom radijusa (slika 2.1). Zakon kretanja

Položaj tačke u OXYZ koordinatnom sistemu je dat sa tri X,Y,Z koordinate(sl.2.2). Zakon kretanja x = x ( t ), y = y ( t ), z = z ( t ).

Položaj tačke u prirodnom referentnom sistemu je dat rastojanjem S od početka do ove tačke duž putanje (slika 2.3). Zakon kretanja s = s ( t ).

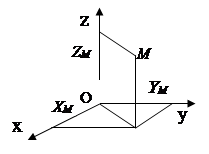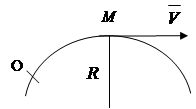
Sl.2.1 Rice. 2.2 Sl.2.3

Kretanje tačke na prirodan način specificiranja kretanja određuje se ako je poznato sljedeće:

1. Putanja kretanja.

2. Početak i smjer odbrojavanja lučne koordinate.

3. Jednačina kretanja.

Kod prirodne metode specificiranja kretanja, za razliku od drugih metoda, koriste se pomične koordinatne ose, koje se kreću zajedno sa tačkom duž putanje. Takve ose su (slika 2.4).

Tangenta () - usmjerena u smjeru povećanja koordinata luka tangencijalno na putanju.

Glavni normalan ( P) je usmjerena prema udubljenosti krive.

binormalni ( in) je usmjeren okomito na ose t, n.

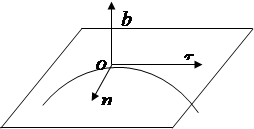Rice. 2.4

2.2.2 Određivanje kinematičkih karakteristika tačke

Putanja tačke

U vektorskom referentnom sistemu, putanja je opisana izrazom

U koordinatnom referentnom sistemu putanja je određena prema zakonu kretanja tačke i opisana je izrazima z = f ( x , y ) - u prostoru, ili y = f(x) - u ravni.

U prirodnom referentnom sistemu, putanja je unaprijed određena.

Tačkasta brzina

Prema definiciji (vidi paragraf 2.1), brzina karakteriše vremensku promenu položaja tačke (tijela) u prostoru.

Određivanje brzine tačke u vektorskom koordinatnom sistemu

Kada se specificira kretanje tačke u vektorskom koordinatnom sistemu, odnos kretanja i vremenskog intervala naziva se prosečna vrednost brzine u ovom vremenskom intervalu.

Uzimajući vremenski interval kao beskonačno malu vrijednost, vrijednost brzine se dobija u ovog trenutka vrijeme (trenutna vrijednost brzine)

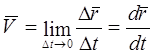(2.1)

Vektor prosječne brzine usmjeren je duž vektora u smjeru kretanja tačke, vektor trenutne brzine je usmjeren tangencijalno na putanju u smjeru kretanja točke (slika 2.5).

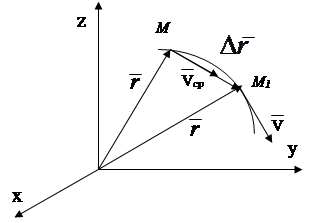Sl.2.5

zaključak: brzina tačke je vektorska veličina jednaka izvodu zakona kretanja u odnosu na vrijeme.

Napominjemo i koristimo u daljem rasuđivanju sljedeće svojstvo izvoda : vremenski izvod veličine određuje brzinu promjene te količine.

Određivanje brzine tačke u koordinatnom referentnom sistemu

Na osnovu svojstva derivacije određujemo brzinu promjene koordinata tačke

Modul pune brzine tačke sa pravougaonim koordinatnim sistemom biće jednak

(2.3)

Smjer vektora brzine određen je kosinusima uglova upravljanja

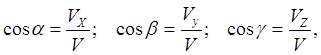
gdje su uglovi između vektora brzine i koordinatnih osa.

Određivanje brzine tačke u prirodnom referentnom sistemu

Brzina tačke u prirodnom referentnom sistemu se definiše kao derivat zakona kretanja tačke

V = (2.4)

Prema prethodnim zaključcima, vektor brzine je usmjeren tangencijalno na putanju u smjeru kretanja točke i u osi n.b. određena samo jednom projekcijom.

tačka ubrzanje

Po definiciji, ubrzanje karakterizira promjenu brzine, tj. brzina promjene brzine.

Ubrzanja tačke u vektorskom referentnom okviru

Na osnovu svojstva derivata

Vektor brzine se može mijenjati po veličini i smjeru. Da bismo odredili prirast vektora, uparujemo početke vektora (Sl.2.6). Vektor ubrzanja je usmjeren duž linije prirasta vektora brzine, odnosno prema krivini putanje.

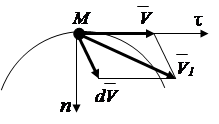
Sl.2.6

Ubrzanje tačke u koordinatnom referentnom sistemu

Ubrzanje promjene koordinata tačke jednako je vremenskom izvodu brzina promjene ovih koordinata

sjekira =; a y =; a z = .

Ukupno ubrzanje u pravougaonom koordinatnom sistemu biće određeno izrazom

a = , (2.6)

Kosinus smjera vektora ubrzanja

.

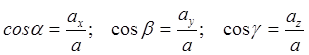Ubrzanje tačke u prirodnom referentnom sistemu

Povećanje vektora brzine (slika 2.7) može se razložiti na komponente paralelne osi prirodni sistem koordinate

, (2.7)

Dijeljenje lijeve i desne strane jednakosti (2.7) sa dt, dobijamo

, (2.8)

gdje je: - tangencijalno ubrzanje, (2.9)

Normalno ubrzanje, (vidi izvod, tačka 43)

gdje je R polumjer zakrivljenosti putanje u blizini tačke

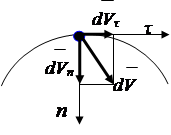Rice. 2.7

2.3. Kinematika krutog tijela

Za razliku od kinematike tačke, u kinematici krutih tijela rješavaju se dva glavna zadatka:

Određivanje kretanja i određivanje kinematičkih karakteristika tijela u cjelini;

Određivanje kinematičkih karakteristika tjelesnih tačaka.

Metode za postavljanje i određivanje kinematičkih karakteristika zavise od vrste kretanja tijela.

U ovom priručniku razmatraju se tri tipa kretanja: translacijsko, rotacijsko oko fiksne ose i ravno-paralelno kretanje krutog tijela.

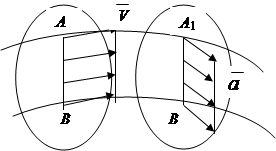
2.3.1. Translacijsko kretanje krutog tijela

Translacijsko je kretanje u kojem prava linija povučena kroz dvije tačke tijela ostaje paralelna svom prvobitnom položaju (slika 2.8).

Dokazana teorema: u translatornom kretanju, sve tačke tela kreću se duž istih putanja i u svakom trenutku imaju istu brzinu i ubrzanje u apsolutnoj vrednosti i pravcu (slika 2.8).

zaključak: Translacijsko kretanje krutog tijela određeno je kretanjem bilo koje njegove tačke, pa se stoga zadatak i proučavanje njegovog kretanja svodi na kinematiku tačke.

Rice. 2.8 Sl. 2.9

2.3.2 Rotacijsko kretanje krutog tijela oko fiksne ose.

Rotacija oko fiksne ose je kretanje krutog tela, pri čemu dve tačke koje pripadaju telu ostaju nepokretne tokom čitavog vremena kretanja.

Položaj tijela je određen uglom rotacije j (slika 2.9). Mjerna jedinica za ugao je radijani. (radijan - centralni ugao krug čija je dužina luka jednaka poluprečniku, puni ugao krug sadrži 2p radijana.)

Zakon rotacionog kretanja tijela oko fiksne ose j = j(t). Ugaona brzina i kutno ubrzanje tijela odredit će se metodom diferencijacije

Ugaona brzina, rad/s; (2.10)

Kutno ubrzanje, rad/s 2 (2.11)

At rotaciono kretanje tijela oko fiksne ose, njegove tačke koje ne leže na osi rotacije kreću se u krugovima sa središtem na osi rotacije.

Ako tijelo presečemo ravninom koja je okomita na osu, odaberite tačku na osi rotacije OD i proizvoljna tačka M, onda pokažite Mće opisati oko tačke OD krug radijusa R(Sl. 2.9). Tokom dt postoji elementarna rotacija kroz ugao , dok je tačka Mće se kretati duž putanje za jednu udaljenost. Odredimo modul linearne brzine:

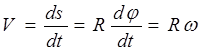(2.12)

tačka ubrzanje M jer je poznata putanja određena njenim komponentama, vidi (2.8)

,

Zamjenom izraza (2.12) u formule dobijamo:

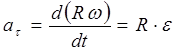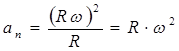, ., (2.13)

gdje je: - tangencijalno ubrzanje,

Normalno ubrzanje.

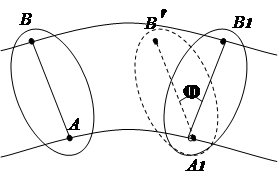
2.3.3. Ravnoparalelno kretanje krutog tijela

Ravnoparalelno je kretanje krutog tijela, u kojem se sve njegove tačke kreću u ravnima paralelnim s jednom fiksnom ravninom (slika 2.10). Za proučavanje kretanja tijela dovoljno je proučiti kretanje jednog dijela S ovo tijelo ravninom koja je paralelna fiksnoj ravni. Pokret sekcije S u svojoj ravni može se smatrati kompleksnim, koji se sastoji od dva elementarna kretanja: a) translacionog i rotacionog; b) rotacijski u odnosu na mobilni (trenutni) centar.

U prvoj varijanti kretanje presjeka može se dati jednačinama kretanja jedne od njegovih tačaka (pola) i rotacije presjeka oko pola (slika 2.11). Bilo koja tačka preseka može se uzeti kao stub.

Rice. 2.10 Sl. 2.11

Jednačine kretanja će biti zapisane kao:

X A = X A ( t )

Y ALI = Y ALI ( t ) (2.14)

j ALI = j ALI ( t )

Kinematske karakteristike pola određuju se iz jednačina njegovog kretanja.

Brzina bilo koje tačke ravne figure koja se kreće u svojoj ravni je zbir brzine pola (proizvoljno odabranog u presjeku tačke ALI) i brzinu rotacije oko pola (rotacija tačke AT oko tačke ALI).

Ubrzanje tačke ravne figure koja se kreće je zbir ubrzanja pola u odnosu na fiksni referentni okvir i ubrzanja zbog rotacionog kretanja oko pola.

(2.15)

(2.16)

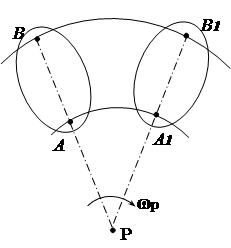
U drugoj varijanti kretanje sekcije se smatra rotacijskim oko pokretnog (trenutnog) centra P(Sl. 1.12). U ovom slučaju, brzina bilo koje tačke B presjeka bit će određena formulom za rotacijsko kretanje

(2.17)

Ugaona brzina oko trenutnog centra R može se odrediti ako je poznata brzina bilo koje tačke odsjeka, na primjer, tačke A.

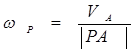(2.18)

Sl.2.12

Položaj trenutnog centra rotacije može se odrediti na osnovu sljedećih svojstava:

Vektor brzine tačke je okomit na radijus;

Modul brzine tačke je proporcionalan udaljenosti od tačke do centra rotacije ( V = w ∙ R) ;

Brzina u centru rotacije je nula.

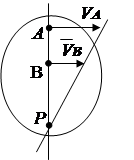
Razmotrimo neke slučajeve određivanja položaja trenutnog centra.

1. Smjerovi brzina dviju tačaka ravne figure su poznati (slika 2.13). Nacrtajmo linije radijusa. Trenutni centar rotacije R koji se nalazi na presjeku okomica povučenih na vektore brzina.

2. Brzine tačaka A i B su poznate, a vektori i su međusobno paralelni, a prava AB okomito (sl. 2. 14). U ovom slučaju, trenutni centar rotacije leži na liniji AB. Da bismo ga pronašli, povlačimo liniju proporcionalnosti brzina na osnovu zavisnosti V = w R .

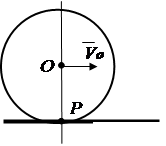
3. Tijelo se kotrlja bez klizanja po fiksnoj površini drugog tijela (slika 2.15). Tačka dodira tijela u ovom trenutku ima brzinu nula, dok brzine ostalih tačaka tijela nisu jednake nuli. dodirna tačka Rće biti trenutno središte rotacije.

Rice. 2.13 Rice. 2.14 Rice. 2.15

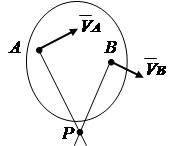
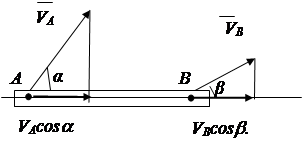
Pored razmatranih opcija, brzina tačke preseka može se odrediti na osnovu teoreme o projekcijama brzina dve tačke krutog tela.

Teorema: projekcije brzina dviju tačaka krutog tijela na pravu liniju povučenu kroz ove tačke su jednake i jednako usmjerene .

Dokaz: udaljenost AB ne može se promeniti, dakle

V A cosa ne može biti više ili manje V U cosb (sl. 2.16).

Rice. 2.16

zaključak: V ALI cosa= V AT cosb. (2.19)

2.4. Složeno kretanje tačke

U prethodnim paragrafima razmatrano je kretanje tačke u odnosu na fiksni referentni okvir, takozvano apsolutno kretanje. U praksi postoje problemi u kojima je poznato kretanje tačke u odnosu na koordinatni sistem, koja se kreće u odnosu na fiksni sistem. U tom slučaju je potrebno odrediti kinematičke karakteristike tačke u odnosu na fiksni sistem.

Uobičajeno je da se zove: kretanje tačke u odnosu na sistem koji se kreće - relativno, kretanje tačke zajedno sa pokretnim sistemom - prenosiv, kretanje tačke u odnosu na fiksni sistem - apsolutno. Prema tome, brzine i ubrzanja se nazivaju:

- figurativni; -apsolutno.

Prema teoremi sabiranja brzina, apsolutna brzina tačke je jednaka vektorska suma relativne i prenosive brzine (sl.).

, (2.20)

Apsolutna vrijednost brzine određena je zakonom kosinusa

, (2.21)

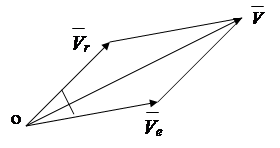
Sl.2.17

Ubrzanje prema pravilu paralelograma određuje se pomoću samo u translatornom kretanju

, (2.22)

Kod netranslacionog prijenosnog kretanja pojavljuje se treća komponenta ubrzanja, nazvana rotacijski ili Coriolis.

, (2.23)

gdje

Coriolisovo ubrzanje je numerički jednako

,

gdje je a ugao između vektora i

Pogodno je odrediti smjer Coriolisovog vektora ubrzanja prema N.E. Žukovski: projektirati vektor na ravan okomitu na osu translacijske rotacije, rotirati projekciju za 90 stepeni u smjeru translacijske rotacije. Rezultirajući smjer će odgovarati smjeru Coriolisovog ubrzanja.

2.5 Pitanja za samokontrolu u odjeljku

1. Koji su glavni zadaci kinematike? Navedite kinematičke karakteristike.

2. Imenujte metode za određivanje kretanja tačke i određivanje kinematičkih karakteristika.

3. Dajte definiciju translacijskog, rotacijskog oko fiksne ose, ravno-paralelnog kretanja tijela.

4. Kako se određuje kretanje krutog tijela pri translacijskom, rotacijskom oko fiksne ose i ravnoparalelnom kretanju tijela i kako se određuje brzina i ubrzanje tačke pri tim kretanjima tijela?

3. Dinamika

3.1 Problemi dinamike

U dinamici se rješavaju dvije vrste problema. Prvi je definisati aktivne snage dat zakon kretanja materijalnog objekta (tačke ili sistema). Drugi zadatak je suprotan prvom: zakon kretanja materijalnog objekta određuje se poznatim silama koje na njega djeluju.

3.2. Osnovni pojmovi dinamike

inercija- svojstvo materijalnih tijela da održavaju stanje mirovanja ili ravnomjernog pravolinijskog kretanja sve dok vanjske sile ne promijene ovo stanje.

Težina- kvantitativna mjera inercije tijela. Jedinica mase je kilogram (kg).

Materijalna tačka- tijelo s masom, čije se dimenzije zanemaruju pri rješavanju ovog problema.

Centar mase mehaničkog sistema- geometrijska tačka čije su koordinate određene formulama.

gdje m k , x k , y k , zk- masa i koordinate k - ta tačka mehaničkog sistema,

m je masa sistema.

U jednoličnom polju gravitacije, položaj centra mase se poklapa sa položajem težišta.

Moment inercije materijalnog tijela oko ose je kvantitativna mjera inercije tokom rotacionog kretanja.

Moment inercije materijalne tačke oko ose jednak je proizvodu mase tačke i kvadrata udaljenosti tačke od ose.

J Z = m × r 2 (3.2)

Moment inercije sistema (tijela) oko ose jednak je aritmetičkom zbiru momenata inercije svih tačaka.

J Z = å m k × rk 2 (3.3)

Sila inercije materijalne tačke- vektorska veličina jednaka apsolutnoj vrijednosti proizvodu mase tačke i modula ubrzanja i usmjerena suprotno vektoru ubrzanja

(3.4)

Sila inercije materijalnog tijela- vektorska veličina jednaka apsolutnoj vrijednosti umnošku mase tijela i modula ubrzanja centra mase tijela i usmjerena suprotno vektoru ubrzanja centra mase

, (3.5)

gdje je ubrzanje centra mase tijela.

Impuls elementarne sile- vektorska količina jednaka proizvodu vektora sile na beskonačno mali vremenski interval dt

, (3.6)

Ukupna impulsna sila za D t jednak je integralu elementarnih impulsa

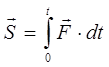(3.7)

elementarni rad snagu- skalarna vrijednost dA, jednako skalarnom proizvodu vektora sile i beskonačno malog pomaka d .

Skalarni proizvod vektora jednak je umnošku njihovih modula i kosinusa ugla između pravaca vektora.

dA = F × ds × cos a , (3.8)

gdje je a ugao između smjerova vektora pomaka i sile.

Rad sile na konačnom pomaku tačke njene primene jednak je integralu elementarnog rada, preuzetog nad pomakom.

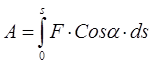(3.9)

Jedinica rada je džul (1 J=1 N×m).

Količina kretanja materijalne tačke- vektorska veličina jednaka proizvodu mase m i njene brzine.

Zamah mehaničkog sistema jednak je vektorskom zbiru impulsa njegovih tačaka.

(3.11)

ili uzimajući u obzir formule (3.1).

gdje je: m masa mehaničkog sistema,

Vektor brzine centra mase sistema.

Kinetička energija materijalne tačke- skalarna vrijednost T, jednaka polovini proizvoda mase tačke i kvadrata njene brzine.

T = (3.13)

Kinetička energija mehaničkog sistema jednaka je zbiru kinetičke energije sve njegove tačke.

3.3. Aksiomi dinamike

Prvi aksiom je zakon inercije .

Ako na slobodnu materijalnu tačku ne djeluju sile ili ako djeluje uravnotežen sistem sila, tada će tačka biti u mirovanju ili ravnomjerno pravolinijsko kretati.

Drugi aksiom je zakon proporcionalnosti ubrzanja .

Ubrzanje koje materijalnoj tački daje sila koja djeluje na nju je proporcionalna ovoj sili i podudara se u smjeru sa smjerom sile.

Izraz (3.15) se poziva osnovni zakon dinamike .

Treći aksiom je zakon protivdejstva .

Sile kojima dvije materijalne tačke djeluju jedna na drugu su jednake po apsolutnoj vrijednosti i usmjerene duž prave linije koja povezuje ove tačke u suprotnim smjerovima

Četvrti aksiom je zakon nezavisnosti djelovanja sila .

Kada sistem sila djeluje na materijalnu tačku, ukupno ubrzanje ove tačke jednako je geometrijskom zbiru ubrzanja od djelovanja svake sile

3.4. Diferencijalne jednadžbe dinamike

Diferencijalne jednadžbe kretanja tačke povezuju ubrzanje tačke sa silama koje na nju djeluju. U stvari, diferencijalne jednadžbe su zapis osnovnog zakona dinamike u eksplicitnom diferencijalnom obliku.

Za apsolutno kretanje tačke (gibanje u inercijalnom referentnom okviru), diferencijalna jednadžba ima oblik

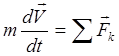, (3.18)

Vektorska jednadžba (3.17) može se napisati u projekcijama na osi pravokutnog inercijalnog koordinatnog sistema

,

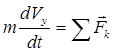, (3.19)

,

Uz poznatu putanju tačke, jednačina (3.18) se može napisati u projekcijama na osi prirodnog koordinatnog sistema

, (3.20)

Uzimajući u obzir (2.8), jednačine dobijaju oblik

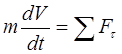(3.21)

3.5 Opće teoreme dinamike

Opće teoreme dinamike uspostavljaju odnos između mjera mehaničkog kretanja i mehaničke interakcije. Zaključci teorema su rezultat identične transformacije osnovnog zakona dinamike.

Teorema o promjeni impulsa : promjena impulsa materijalne tačke (mehaničkog sistema) u konačnom vremenskom periodu jednaka je zbiru impulsa spoljne sile za isti vremenski period

- za materijalnu tačku; (3.22)

- za mehanički sistem. (3.23)

Teorema promjene kinetičke energije : promjena kinetičke energije tačke (mehaničkog sistema) tokom njenog kretanja jednaka je zbiru rada svih vanjskih sila koje djeluju na ovo kretanje

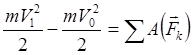- za materijalnu tačku (3.24)

- za mehanički sistem (3.25)

Kinetička energija mehaničkog sistema određena je u skladu sa (3.14), dok su za čvrsta tela izvedene sledeće zavisnosti

Sa translatornim kretanjem tijela, (3.26)

Tokom rotacionog kretanja tijela, (3.27)

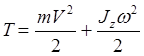- sa ravnoparalelnim kretanjem tijela. (3.28)

Momenti inercije nekih homogenih tijela

Rice. 3.1 Sl.3.2. R Slika 3.3.

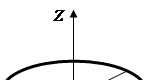
Moment inercije cilindra u odnosu na osu (slika 3.1.)

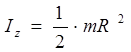
Moment inercije štapa oko z-ose (slika 3.2)

Moment inercije pravokutne ploče oko osa x i y (slika 3.3)

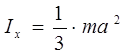
Moment inercije lopte određen je formulom:

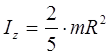
U opštem slučaju rad sila se određuje u skladu sa (3.8), (3.9), a u nizu slučajeva delovanja sila rad se može odrediti posebnim zavisnostima.

Rad gravitacije

gdje: - gravitacije,

Promjena položaja tijela okomito.

Rad sile pri rotacijskom kretanju tijela

, (3.30)

gdje: - moment sile,

Ugaona brzina tijela.

Imajte na umu da rad, kao skalarna veličina, može biti pozitivan ili negativan. Rad će biti pozitivan ako se smjer sile poklapa sa smjerom kretanja.

3.6 d'Alambertov princip

Gore navedene metode za proučavanje kretanja tijela zasnivaju se na Newtonovim zakonima. Razvijene su metode zasnovane na drugim principima. Jedan od njih je d'Alambertov princip.Princip je formuliran: ako se u bilo kojem trenutku sile inercije dodaju silama koje djeluju na tačku, tada će rezultirajući sistem sila biti uravnotežen

, (3.31)

ili za mehanički sistem

D'Alembertov princip omogućava da se više primjenjuje na rješavanje problema dinamike jednostavne metode statike, pa se široko koristi u inženjerskoj praksi.

3.7. Pitanja za samokontrolu u odjeljku

1. Formulirajte glavne zadatke dinamike.

2. Dajte definicije mase, momenta inercije, impulsa sile, rada sile, momenta kretanja, kinetičke energije.

3. Formulirati osnovne zakone dinamike.

4. Kako se zove jednačina diferencijalna jednadžba zvučnici? Koji je algoritam za rješavanje problema dinamike korištenjem diferencijalnih jednadžbi?

5. Formulirati opće teoreme dinamike.

6. Formulirajte d'Alembertov princip. Kako se određuju sile inercije?

7. Formulirajte princip mogućih pokreta. Pod kojim uslovima se primenjuje princip mogućih pomeranja?

U ovom poglavlju razmatraju se problemi za određivanje rada konstantne sile i razvijene snage tokom translacionog i rotacionog kretanja tela (E. M. Nikitin, § 81-87).

§ 44. Rad i snaga u translatornom kretanju

Rad konstantne sile P na ravnom odsjeku puta s, koji prelazi tačka primjene sile, određuje se formulom
(1) A = Ps cos α,
gdje je α ugao između smjera sile i smjera kretanja.

Na α = 90°
cos α = cos 90° = 0 i A = 0,
tj. rad sile koja djeluje okomito na smjer kretanja jednak je nuli.

Ako se smjer sile poklapa sa smjerom kretanja, tada je α = 0, dakle cos α = cos 0 = 1 i formula (1) je pojednostavljena:
(1") A = Ps.

Ne jedna sila, već nekoliko, obično deluje na tačku ili na telo, pa je pri rešavanju zadataka preporučljivo koristiti teoremu o delovanju rezultantnog sistema sila (E. M. Nikitin, § 83):
(2) A R = ∑ A i ,
tj. rad rezultante bilo kojeg sistema sila na određenom putu jednak je algebarskom zbiru rada svih sila ovog sistema na istoj putanji.

U konkretnom slučaju, kada je sistem sila uravnotežen (telo se kreće ravnomerno i pravolinijski), rezultanta sistema sila je jednaka nuli i, prema tome, A R =0. Stoga, kod ravnomjernog i pravolinijskog kretanja tačke ili tijela, jednačina (2) poprima oblik
(2") ∑ Ai = 0,
tj. algebarski zbir rada uravnoteženog sistema sila na određenom putu jednak je nuli.

U ovom slučaju, sile čiji je rad pozitivan nazivaju se pokretačke sile, a sile čiji je rad negativan nazivaju se sile otpora. Na primjer, kada se tijelo kreće prema dolje - gravitacija - pokretačka snaga i njegov rad je pozitivan, a kada se tijelo kreće prema gore, njegova gravitacija je sila otpora, a rad gravitacije je negativan.

Prilikom rješavanja zadataka u slučajevima kada je sila P nepoznata, čiji rad treba odrediti, mogu se preporučiti dvije metode (metode).

1. Koristeći sile navedene u uslovu zadatka, odredite silu P, a zatim pomoću formule (1) ili (1") izračunajte njen rad.

2. Bez direktnog određivanja sile P, odrediti A p - rad tražene sile koristeći formule (2) i (2"), izražavajući teoremu o radu rezultante.

Snaga razvijena tokom rada konstantne sile određena je formulom
(3) N = A/t ili N = (Ps cos α)/t.

Ako, prilikom određivanja rada sile P, brzina točke v = s / t ostane konstantna, tada
(3") N = Pv cos α.

Ako se brzina točke promijeni, tada s / t \u003d v cf - prosječna brzina a onda formula (2") ispušta prosječnu snagu
N av = Pv av cos α.

Koeficijent korisna akcija(k.p.d.) pri obavljanju posla može se definisati kao omjer rada
(4) η = A polje /A,
gdje A sprat - koristan rad; A je sav obavljen posao, ili kao omjer odgovarajućih kapaciteta:
(4") η = N sprat /N.

SI jedinica rada je 1 džul (J) = 1 N * 1 m.

SI jedinica snage je 1 vat (W) = 1 J / 1 sek.

Popularna vansistemska jedinica snage je konjska snaga (KS):
1000 W = 1,36 litara. With. ili 1 l. With. = 736 W.

Za prebacivanje između vati i konjskih snaga, koristite formule
N (kW) = 1,36 N (hp)
N (KS) \u003d 0,736 N (kW).

Predavanje 2. Rad. Snaga. Teorema o promjeni kinetičke energije tačke.

Ovo predavanje pokriva sljedeća pitanja:

Prisilni rad.

Snaga.

Primjeri obračuna rada.

Potencijalna energija

Kinetička energija

Teorema o promjeni kinetičke energije tačke.

Teorema trenutka.

Proučavanje ovih pitanja neophodno je za dinamiku centra mase mehaničkog sistema, dinamiku rotacionog kretanja krutog tela, kinetički moment mehaničkog sistema, za rešavanje zadataka u disciplinama „Teorija mašina i mehanizmi" i "Mašinski dijelovi".

Prisilni rad. Snaga.

Da bi se okarakteriziralo djelovanje sile na tijelo s nekim pomakom, uvodi se pojam rada sile.

Fig.16

U ovom slučaju rad karakterizira djelovanje sile, koja određuje promjenu modul brzina pokretne tačke.

Hajde da prvo uvedemo koncept elementarnog rada sile na beskonačno mali pomak ds. Elementarni rad sile (slika 16) je skalarna veličina:

gdje je projekcija sile na tangentu na putanju usmjerenu u smjeru pomaka tačke, i beskonačno mali pomak točke usmjeren duž ove tangente.

Ova definicija odgovara pojmu rada, kao karakteristike djelovanja sile koja dovodi do promjene modula brzine tačke. Zaista, ako razložimo silu na komponente i , tada će samo komponenta promijeniti modul brzine tačke, dajući tangencijalno ubrzanje tački. Komponenta ili mijenja smjer vektora brzine v(daje normalno ubrzanje do točke), ili, ako kretanje nije slobodno, mijenja pritisak na spoj. Komponenta neće utjecati na modul brzine, odnosno, kako kažu, sila "neće proizvesti rad".

Primetivši to, dobijamo:

. (1)

Na ovaj način, elementarni rad sila je jednaka projekciji sile na smjer kretanja tačke, pomnoženoj sa elementarnim pomakom, ili je elementarni rad sile jednak umnošku modula sile elementarnim pomakom i kosinusom od ugao između smjera sile i smjera pomaka.

Ako je ugao oštar, onda je rad pozitivan. Posebno za elementarni rad .

Ako je ugao tup, tada je rad negativan. Posebno za elementarni rad .

Ako je ugao, tj. ako je sila usmjerena okomito na pomak, tada je elementarni rad sile nula.

Nađimo analitički izraz za elementarni rad. Da bismo to učinili, razlažemo silu na komponente , , u smjerovima koordinatnih osa (slika 17; sama sila nije prikazana na crtežu).

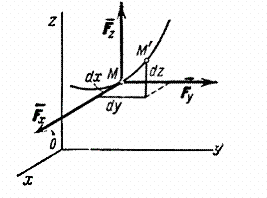
Fig.17

Elementarni pomak se sastoji od pomaka , , duž koordinatnih osa, gdje je x, y, z - koordinate tačke M. Tada se rad sile na pomaku može izračunati kao zbir rada njenih komponenti , , na pomacima , , .

Ali samo komponenta radi na pomaku, a njen rad je jednak . Rad na pomacima i izračunava se slično. Konačno nalazimo:

Formula daje analitički izraz za elementarni rad sile.

Rad koji vrši sila u bilo kojem konačnom pomaku M 0 M 1 se izračunava kao integralni zbir odgovarajućih elementarnih radova i biće jednak:

ili

.

shodno tome, rad sile na bilo koji pomak M 0 M 1 jednak je integralu elementarnog rada obavljenog duž ovog pomaka. Granice integrala odgovaraju vrijednostima varijabli integracije u tačkama M 0 i M 1 .

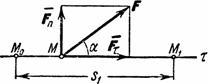
Fig.18

Ako je vrijednost konstantna (= const), onda označava pomak M 0 M 1 kroz dobijamo: .

Takav slučaj se može dogoditi kada je sila koja djeluje konstantna po modulu i smjeru ( F= const), a tačka na koju se primenjuje sila kreće se pravolinijski (slika 18). U ovom slučaju i rad snaga .

SI jedinica za rad je joule (1 j = 1 hm).

Snaga.

Snaga je veličina koja određuje rad sile u jedinici vremena. Ako se posao obavlja ravnomjerno, onda snaga

gdje t - vrijeme tokom kojeg je posao obavljen A. Uglavnom

.

Dakle, snaga je jednaka proizvodu tangencijalne komponente sile i brzine kretanja.

Jedinica snage u sistemu SI je watt (1 uto= 1 j/sec). U inženjerstvu se 1 konjska snaga često uzima kao jedinica snage, jednaka 75 kgm/sec ili 736 uto.

Rad koji obavlja mašina može se mjeriti umnoškom njene snage i vremena rada. Iz toga je nastala mjerna jedinica rada, kilovat-sat, koja se obično koristi u tehnici (1 kWh = 3,6j 367100 kgm).

Iz jednačine se vidi da za motor date snage W, vučna sila će biti veća, što je niža brzina kretanja V. Stoga, na primjer, na usponu ili na lošem dijelu puta, automobil uključuje niže stupnjeve prijenosa, koji omogućavaju, pri punoj snazi, da se kreću manjom brzinom i razvijaju veću vuču.

Primjeri obračuna rada.

Primjeri razmatrani u nastavku daju rezultate koji se mogu direktno koristiti u rješavanju problema.

1) Rad gravitacije. Pusti poentu M, na koje deluje sila gravitacije , pomera sa pozicije M ­ 0 (x­ 0 , at 0 , z 0 ) u poziciju M 1 (X 1 , y 1 , z 1 ). Koordinatne osi biramo tako da os Oz bila usmjerena okomito prema gore (sl. 19).

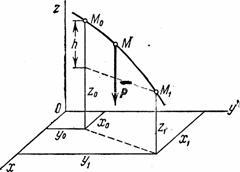
Fig.19

Onda R x=0, R y=0, P z=- R. Zamjena ovih vrijednosti i razmatranje integracijske varijable z:

Ako tačka M 0 iznad M 1 , gdje h- vrijednost vertikalnog kretanja tačke;

Ako je poenta M 0 ispod tačke M 1 onda .

Konačno dobijamo: .

Prema tome, rad gravitacije jednak je proizvodu modula sile, uzetog sa predznakom plus ili minus, i vertikalnog pomaka tačke njene primjene. Rad je pozitivan ako je početna tačka viša od krajnje tačke, a negativan ako je početna tačka niža od krajnje tačke. Iz dobivenog rezultata slijedi da rad gravitacije ne ovisi o vrsti putanje duž koje se kreće tačka njene primjene.

Sile sa ovim svojstvom nazivaju se potencijalne sile.

2) Rad elastične sile. Uzmite u obzir teret M, koji leži na horizontalnoj ravni i pričvršćen za slobodni kraj neke opruge (slika 20a). Označite na avionu tačkom O položaj koji zauzima kraj opruge kada nije napregnut ( je dužina nenapregnute opruge), a ovu tačku uzimamo kao ishodište. Ako sada povučemo teret iz ravnotežnog položaja O, produžujući oprugu do vrijednosti , tada će na opterećenje djelovati elastična sila opruge F, usmjeren na stvar O.

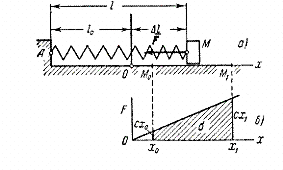
Fig.20

Prema Hookeovom zakonu, veličina ove sile je proporcionalna izduženju opruge. Pošto je u našem slučaju , onda po modulu .

Koeficijent With pozvao koeficijent krutosti opruge. U inženjerstvu se obično mjeri With in h/cm, uz pretpostavku koeficijenta With brojčano jednaka sili koja se mora primijeniti na oprugu da se istegne za 1 cm.

Pronađite rad elastične sile pri pomicanju tereta iz položaja u položaj . Pošto u ovom slučaju , , tada dobijamo:

(Isti rezultat se može dobiti iz grafa zavisnosti F od X (sl.20, b) izračunavanje površine trapeza osenčenog na crtežu i uzimanje u obzir predznaka rada.) U dobijenoj formuli, predstavlja početno izduženje opruge, a krajnji nastavak opruge. shodno tome,

,

one. rad elastične sile jednak je polovini umnoška koeficijenta krutosti i razlike između kvadrata početnog i krajnjeg izduženja (ili kompresije) opruge.

Rad će biti pozitivan kada , tj. kada se kraj opruge pomeri u ravnotežni položaj, a negativan kada , tj. kraj opruge se udaljava od ravnotežnog položaja. Može se dokazati da formula ostaje važeća i u slučaju kada je pomak tačke M nije linearan.

Tako se ispostavlja da je rad sile F zavisi samo od vrednosti i ne zavisi od tipa putanje tačke M. Stoga je i sila elastičnosti potencijalna.

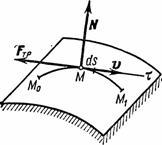
Fig.21

3) Rad sile trenja. Zamislite tačku koja se kreće duž neke grube površine (slika 21) ili krivulje. Sila trenja koja djeluje na tačku jednaka je po apsolutnoj vrijednosti fN, gdje f je koeficijent trenja i normalna reakcija površine. Sila trenja je usmjerena suprotno od pomaka točke. shodno tome, F tr = - fN i po formuli

.

Ako je sila trenja konstantna, onda , gdje s-dužina luka krive M 0 M 1 duž koje se tačka kreće.

Na ovaj način, Rad koji vrši sila trenja klizanja je uvijek negativan. Količina ovog posla zavisi od dužine luka M 0 M 1 . Dakle, sila trenja je sila nepotencijalni.

4) Rad sile primijenjene na tijelo koje rotira oko fiksne ose.

U ovom slučaju (slika 22), tačka primjene sile se kreće duž kruga polumjera r. Elementarni rad, od (1), , gdje .

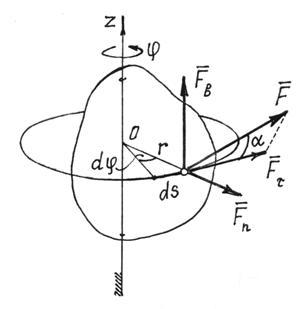
Fig.22

Zbog toga .

Ovo nije teško utvrditi razlaganjem sile na tri komponente (slika 22). (Momenti sila i jednaki su nuli). znači,

(2)

Posebno, ako je moment sile oko ose , rad sile kada se tijelo rotira pod uglom jednak je

. (3)

Predznak rada je određen predznacima momenta sile i ugla rotacije. Ako su isti, rad je pozitivan.

Formula (3) podrazumijeva i pravilo za određivanje rada para sila. Ako par sa trenutak m nalazi se u ravni okomitoj na os rotacije tijela, tada njen rad kada se tijelo rotira kroz ugao

Ako par sila djeluje u ravni koja nije okomita na os rotacije, tada se mora zamijeniti s dva para. Jedan je postavljen u ravnini okomitoj na osu, a drugi - u ravnini paralelnoj sa osom. Njihovi momenti su određeni širenjem vektora momenta u odgovarajućim smjerovima: . Naravno, samo će prvi par sa momentom obaviti posao, gdje je ugao između vektora i ose rotacije z,

. (5)

Potencijalna energija

Dio prostora u kojem sila djeluje na materijalnu tačku koja je tamo smještena, ovisno o lokaciji točke, naziva se polje sile.

Štaviše, ova sila se određuje pomoću funkcije sile u = u(x, y, z). Ako ne zavisi od vremena, onda se takvo polje naziva stacionarnim. Ako je ista u svim tačkama, onda je polje homogeno.

Ako su projekcije sile na kartezijanske ose parcijalne derivacije funkcije sile u odnosu na odgovarajuće koordinate

onda se takvo polje naziva potencijalnim.

Izračunajte rad sile potencijalno polje kada pomerate tačku sa pozicije M 1 na poziciju M 2. (Sl. 23).

Fig.23

elementarni rad,

Ovo je ukupni diferencijal funkcije sile.

Rad na završnom putovanju

(7)

gdje u 2 i u 1 – vrijednosti funkcije snage u tačkama M 2 i M 1 .

shodno tome, rad sile potencijalnog polja ne ovisi o putanji točke, već je određen samo vrijednostima funkcije sile u početnoj i krajnjoj poziciji točke.

Naravno, ako se tačka vrati u početni položaj, rad sile će biti nula. Rad će biti jednak nuli i pri prelasku u drugu tačku M 3 ako je vrijednost funkcije sile tamo ista kao u početnoj poziciji.

Lako je pretpostaviti da će tačke s istim vrijednostima funkcije sile formirati cijelu površinu. I da je polje sile slojevit prostor koji se sastoji od takvih površina (slika 23). Ove površine se nazivaju ravnim površinama ili ekvipotencijalne površine. Njihove jednačine su: u(x, y, z)= C (C- konstantno, jednako vrijednosti u tačke na ovoj površini). A funkcija sile se zove, respektivno, potencijal polja.

Naravno, ekvipotencijalne površine se ne seku. Inače bi postojale tačke polja sa neograničenim potencijalom.

Budući da je pri pomicanju točke duž ekvipotencijalne površine rad sile jednak nuli, tada je vektor sile okomit na površinu.

Među ovim površinama biramo jednu i nazivamo je nultom površinom (stavljamo u= u 0 ).

Rad koji će sila obaviti kada se tačka pomjeri sa određenog mjesta M na nultu površinu naziva se potencijalna energija tačke na ovom određenom mjestu M:

. (8)

primeti, to potencijalna energija u istoj tački polja zavisi od izbora nulte površine.

Po (8) funkcija sile . Prema tome, projekcije sile na kartezijanske ose, prema (6), budući da ,

i vektor sile .

Razmotrite nekoliko potencijalnih polja.

1) Gravitaciono polje.

U blizini površine Zemlje, sila gravitacije u svim tačkama je ista, jednaka težini tijela. To znači da je ovo polje sile uniformno. Budući da kada se tačka kreće u horizontalnoj ravni, rad sile je nula, ekvipotencijalne površine će biti horizontalne ravni (slika 24), a njihove jednačine: u = z = C.

Fig.24

Ako je ravnina dodijeljena kao nulta površina xOy, zatim potencijalna energija tačke u položaju M biće jednak radu gravitacije:

2) Polje elastične sile.

Kada se elastično tijelo, kao što je opruga, deformiše, pojavljuje se sila. Odnosno, u blizini ovog tijela nastaje polje sile čije su sile proporcionalne deformaciji tijela i usmjerene prema nedeformiranom stanju. Na izvoru - do tačke M 0 , gdje se nalazi kraj nedeformisane opruge (slika 25).

Fig.25

Ako pomaknete kraj opruge tako da se njena dužina ne promijeni, tada će rad elastične sile biti nula. To znači da su ekvipotencijalne površine sferne površine sa centrom u tački O.

Dodijelite nultu površinu sferi koja prolazi kroz tačku M 0 , kroz kraj nedeformisane opruge. Zatim potencijalna energija opruge u položaju M: .

S takvim izborom nulte površine, potencijalna energija će uvijek biti pozitivna (P>0), kako u rastegnutom tako iu komprimiranom stanju.

Teorema o promjeni kinetičke energije tačke.

Razmotrite tačku sa masom t, krećući se pod dejstvom sila koje se na njega primenjuju iz pozicije M 0 , gdje ima brzinu , u poziciju M 1 , gdje je njegova brzina .

Da bismo dobili željenu zavisnost, okrećemo se jednadžbi koja izražava osnovni zakon dinamike. Projektovanje oba dela ove jednakosti na tangentu putanje tačke M, usmjereno u smjeru kretanja, dobijamo:

Vrijednost tangencijalnog ubrzanja na lijevoj strani može se predstaviti kao

.

Kao rezultat, imaćemo:

.

Pomnožite obje strane ove jednadžbe sa ds, mi ćemo predstaviti t pod znakom diferencijala. Zatim, primetivši da gde - elementarnog rada sile F k dobijamo izraz teoreme o promeni kinetičke energije u diferencijalnom obliku.

Rad gravitacije. gravitacije R masa materijalne tačke t blizu Zemljine površine može se smatrati konstantom, jednakom mg

usmjerena okomito prema dolje.

Posao ALI snagu R u pokretu od tačke M 0 do tačke M

gdje h = z 0 - z x - visina spuštanja tačke.

Rad gravitacije jednak je proizvodu ove sile i visine spuštanja (rad je pozitivan) ili visine uzdizanja (rad je negativan). Rad gravitacije ne zavisi od oblika putanje između tačaka M 0 i M|, a ako se ove tačke poklapaju, onda je rad gravitacije jednak nuli (slučaj zatvorene putanje). Također je jednako nuli ako su tačke M 0 i M leže u istoj horizontalnoj ravni.

Rad linearne sile elastičnosti. Linearna elastična sila (ili linearna sila vraćanja) je sila koja djeluje prema Hookeovom zakonu (slika 63):

F = - Withr,

gdje r- udaljenost od tačke statičke ravnoteže, u kojoj je sila nula, do razmatrane tačke M; With- konstantno koeficijent - koeficijent rigidnost.

A=--().

Prema ovoj formuli izračunava se rad linearne elastične sile. Ako tačka M 0 poklapa se sa tačkom statička ravnoteža O, pa onda r 0 \u003d 0 i za rad sile na pomaku iz tačke O do tačke M imamo

Vrijednost r- najkraća udaljenost između razmatrane tačke i tačke statičke ravnoteže. Označavamo ga sa λ i nazivamo deformacijom. Onda

Rad linearne elastične sile na pomaku iz stanja statičke ravnoteže uvijek je negativan i jednak je polovini umnoška koeficijenta krutosti i kvadrata deformacije. Rad linearne elastične sile ne ovisi o obliku pomaka i rad na bilo kojem zatvorenom pomaku je nula. Također je jednako nuli ako su tačke Mo i M leže na istoj sferi opisanoj od tačke statičke ravnoteže.

Rad promjenljive sile pri krivolinijskom kretanju.

Rad sile na zakrivljenom presjeku

Razmotrimo opći slučaj pronalaženja rada promjenjive sile čija se tačka primjene kreće duž krivolinijske putanje. Neka se tačka M primjene promjenljive sile F kreće duž proizvoljne kontinuirane krivulje. Označimo vektorom beskonačno malog pomaka tačke M. Ovaj vektor je usmjeren tangencijalno na krivu u istom smjeru kao i vektor brzine.

Elementarni rad promjenljive sile F na beskonačno malom pomaku

ds naziva se skalarni proizvod vektora F i ds:

gdje a- ugao između vektora F i ds

To jest, elementarni rad sile jednak je proizvodu modula vektora sile i beskonačno malog pomaka, pomnoženog kosinusom ugla između ovih vektora.

Vektor sile F rastavljamo na dvije komponente: - usmjerena duž tangente na putanju - i - usmjerena duž normale. linija sile

je okomita na tangentu na putanju duž koje se tačka kreće, a njen rad je nula. onda:

dA= Ftds.

Da bi se izračunao rad promjenljive sile F na konačnom dijelu krive iz a do b, treba izračunati integral elementarnog rada:

Potencijalna i kinetička energija.

Potencijalna energija P matserijska tačka u razmatranjumoja poenta polje sile M poziv posao, izvršile snagela deluje na materijalnu tačku kada je pomera iz tačkeMdo početne tačkeM 0 , tj.

P = Umm 0

P = =-U=- U

Konstanta C 0 je ista za sve tačke polja, zavisno od toga koja je tačka polja izabrana kao početna. Očigledno, potencijalna energija se može uvesti samo za polje potencijalne sile u kojem rad ne zavisi od oblika kretanja između tačaka M i M 0 . Nepotencijalno polje sila nema potencijalnu energiju i za njega ne postoji funkcija sile.

dA = dU= -dP; ALI = U - U 0 = P 0 - P

Iz gornjih formula proizilazi da P je određena do proizvoljne konstante, koja zavisi od izbora početne tačke, ali ova proizvoljna konstanta ne utiče na sile izračunate kroz potencijalnu energiju i rad tih sila. S obzirom na ovo:

P= - U+ const ili P =- U.

Potencijalna energija u bilo kojoj tački polja, do proizvoljne konstante, može se definirati kao vrijednost funkcije sile u istoj tački, uzeta sa predznakom minus.

Kinetička energija sistem se naziva skalarna vrijednost T, jednaka zbroju kinetičkih energija svih tačaka sistema:

Kinetička energija je karakteristika translacionog i rotacionog kretanja sistema. Kinetička energija je skalarna veličina i, osim toga, suštinski pozitivna. Dakle, ne zavisi od pravca kretanja delova sistema i ne karakteriše promene u tim smerovima.

Napomenimo i sljedeću bitnu okolnost. Unutrašnje sile djeluju na dijelove sistema u međusobno suprotnim smjerovima. Promjene kinetičke energije su pod utjecajem djelovanja vanjskih i unutrašnjih sila.

Ujednačeno kretanje tačke.

Ujednačeno kretanje tačke- pokret, sa Krom kasatom. ubrzanje ω t tačke (u slučaju pravolinijskog kretanja, ukupno ubrzanje ω )stalno. Zakon ravnomjernog kretanja tačke i zakon promjene njene brzine υ tokom ovog kretanja date su jednakostima:

gdje je s udaljenost točke mjerene duž luka putanje od referentne točke odabrane na putanji, t- vrijeme, s 0 - vrijednost s na početku. trenutak vremena t = = 0. - poč. tačka brzina. Kada znakovi υ i ω identično, ujednačeno kretanje. je ubrzan, a kada je drugačiji - usporen.

Kada glumi. ravnomjerno kretanje krutog tijela, sve navedeno vrijedi za svaku tačku tijela; sa ravnomernom rotacijom oko fiksne ose ugla. ubrzanje e tijela je konstantno, a zakon rotacije i zakon promjene ugla. brzine ω tijela date su jednakostima

gdje je φ ugao rotacije tijela, φ 0 je vrijednost φ na početku. trenutak vremena t= 0, ω 0 - poč. ang. telesna brzina. Kada se znaci ω i ε poklapaju, rotacija je ubrzana, a kada se ne poklapaju, spora.

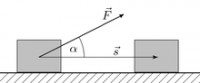
Rad stalne sile u pravolinijskom kretanju.

Definirajmo rad za slučaj kada je sila koja djeluje konstantna po veličini i smjeru, a tačka njene primjene kreće se po pravocrtnoj putanji. Posmatrajmo materijalnu tačku C, na koju se primjenjuje konstanta sile u vrijednosti i smjeru (slika 134, a).

Za određeni vremenski period t, tačka C se pomjerila u poziciju C1 duž pravolinijske putanje na udaljenosti s.

Rad W konstantne sile pri pravolinijskom kretanju tačke njene primjene jednak je proizvodu modula sile F puta udaljenosti s i kosinusa ugla između smjera sile i smjera kretanja, tj.

Ugao α između smjera sile i smjera kretanja može varirati od 0 do 180°. Za α< 90° работа положительна, при α >90° je negativan, pri α = 90° rad je nula.

Ako sila čini oštar ugao sa smjerom kretanja, naziva se pokretačka sila, rad sile je uvijek pozitivan. Ako je kut između smjera sile i kretanja tup, sila se opire kretanju, vrši negativan rad i naziva se sila otpora. Primjeri sila otpora su sile rezanja, trenja, otpora zraka i druge, koje su uvijek usmjerene u smjeru suprotnom kretanju.

Kada je α = 0°, tj. kada se smjer sile poklapa sa smjerom brzine, tada je W = F s, budući da je cos 0° = 1. Proizvod F cos α je projekcija sile na smjer kretanje materijalne tačke. Stoga se rad sile može definirati kao proizvod pomaka s i projekcije sile i smjera kretanja tačke.

33. Sile inercije krutog tijela

U klasičnoj mehanici, prikazi sila i njihovih svojstava zasnovani su na Newtonovim zakonima i neraskidivo su povezani sa konceptom inercijalnog referentnog okvira.

Zaista, fizička veličina koja se zove sila je uvedena u razmatranje drugim Newtonovim zakonom, dok je sam zakon formuliran samo za inercijski sistemi referenca. Prema tome, ispostavilo se da je koncept sile u početku definisan samo za takve referentne okvire.

Jednadžba drugog Newtonovog zakona, koja povezuje ubrzanje i masu materijalne tačke sa silom koja na nju djeluje, zapisuje se kao

Iz jednačine direktno proizilazi da su samo sile uzrok ubrzanja tijela, i obrnuto: djelovanje nekompenziranih sila na tijelo nužno uzrokuje njegovo ubrzanje.

Njutnov treći zakon dopunjuje i razvija ono što je rečeno o silama u drugom zakonu.

sila je mjera mehaničkog djelovanja na dato materijalno tijelo drugih tijela

u skladu sa trećim Newtonovim zakonom, sile mogu postojati samo u parovima, a priroda sila u svakom takvom paru je ista.

svaka sila koja djeluje na tijelo ima izvor u obliku drugog tijela. Drugim riječima, sile su nužno rezultat interakcije tel.

Nikakve druge sile u mehanici se ne uzimaju u obzir niti koriste. Mogućnost postojanja sila koje su nastale samostalno, bez međusobnog djelovanja tijela, mehanika ne dopušta.

Iako nazivi Eulerove i d'Alembertove sile inercije sadrže tu riječ snagu, ove fizičke veličine nisu sile u smislu prihvaćenom u mehanici.

34. Koncept ravnoparalelnog kretanja krutog tijela

Kretanje krutog tijela naziva se ravnoparalelno ako se sve tačke tijela kreću u ravnima paralelnim nekoj fiksnoj ravni (glavnoj ravni). Neka se neko tijelo V kreće u ravninu, π - glavna ravan. Iz definicije ravnoparalelnog kretanja i svojstava apsolutno krutog tijela slijedi da će svaki segment AB okomit na ravan π činiti kretanje napred. Odnosno, putanje, brzine i ubrzanja svih tačaka segmenta AB će biti iste. Dakle, kretanje svake tačke preseka s paralelno sa ravninom π određuje kretanje svih tačaka tela V koje leže na segmentu okomitom na presek u ovoj tački. Primeri ravnoparalelnog kretanja su: točak koji se kotrlja duž pravog segmenta, jer se sve njegove tačke kreću u ravnima paralelnim ravnini koja je okomita na osu točka; poseban slučaj takvog kretanja je rotacija krutog tijela oko fiksne ose, zapravo, sve točke rotacionog tijela kreću se u ravninama paralelnim nekoj fiksnoj ravni okomitoj na os rotacije.

35. Sile inercije u pravolinijskom i krivolinijskom kretanju materijalne tačke

Sila kojom se tačka opire promjeni kretanja naziva se sila inercije materijalne tačke. Sila inercije usmjerena je suprotno od ubrzanja tačke i jednaka je masi pomnoženoj s ubrzanjem.

U pravoj liniji smjer ubrzanja poklapa se s putanjom. Sila inercije usmjerena je u smjeru suprotnom od ubrzanja, a njena numerička vrijednost određena je formulom:

Kod ubrzanog kretanja pravci ubrzanja i brzine se poklapaju, a sila inercije je usmjerena u smjeru suprotnom kretanju. Kod usporenog kretanja, kada je ubrzanje usmjereno u smjeru suprotnom brzini, sila inercije djeluje u smjeru kretanja.

Atkrivolinijski i neujednačenipokret ubrzanje se može razložiti na normalno an i tangenta at komponente. Slično tome, sila inercije tačke se takođe sastoji od dve komponente: normalne i tangencijalne.

Normalno komponenta inercijalne sile jednaka je umnošku mase tačke i normalnog ubrzanja i usmjerena je suprotno od ovog ubrzanja:

Tangenta komponenta inercijalne sile jednaka je umnošku mase tačke i tangencijalnog ubrzanja i usmjerena je suprotno od ovog ubrzanja:

Očigledno je da puna snaga tačka inercije M jednak je geometrijskom zbiru normalne i tangentne komponente, tj.

S obzirom da su tangencijalna i normalna komponenta međusobno okomite, ukupna sila inercije je:

36. Teoreme o sabiranju brzina i ubrzanja tačke u kompleksnom kretanju

Teorema o dodavanju brzine:

U mehanici je apsolutna brzina tačke jednaka vektorskom zbroju njene relativne i translacione brzine:

Brzina tijela u odnosu na fiksni referentni okvir jednaka je vektorskom zbroju brzine ovog tijela u odnosu na pokretni referentni okvir i brzine (u odnosu na fiksni okvir) tačke pokretnog okvira u kojoj je tijelo se nalazi.

u složenom kretanju, apsolutna brzina tačke jednaka je geometrijskom zbiru translacione i relativne brzine. Veličina apsolutne brzine je određena gdje α je ugao između vektora 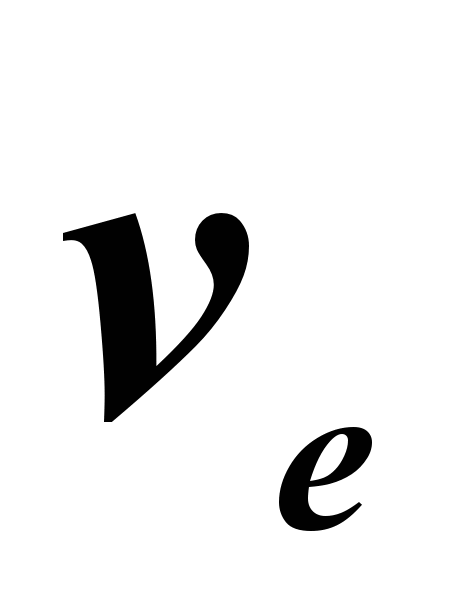i .

Teorema zbrajanja ubrzanja ( TEOREMA KORIOLISA)

acor = aper + from + acor

Formula izražava sljedeći Coriolisov teorem o dodavanju ubrzanog

renijum: 1 za složeno kretanje, ubrzanje tačke je jednako geometrijskom

zbir tri ubrzanja: relativnog, translacionog i rotacionog, ili

Coriolis.

ako = 2(ω × vot)

37. d'Alambertov princip

d'Alambertov princip za materijalnu tačku: u svakom trenutku kretanja materijalne tačke, aktivne sile, reakcije veza i sila inercije čine uravnoteženi sistem sila.

d'Alambertov princip- u mehanici: jedan od osnovnih principa dinamike, prema kojem, ako se datim silama koje djeluju na tačke mehaničkog sistema i reakcijama superponiranih veza dodaju sile inercije, tada će biti uravnotežen sistem sila dobiti.

Po ovom principu, za svaku i-tu tačku sistema, jednakost

gdje je aktivna sila koja djeluje na ovu tačku, je reakcija veze nametnute točki, je sila inercije, brojčano jednaka proizvodu mase točke i njenog ubrzanja i usmjerena suprotno od ovog ubrzanja ().

Zapravo, govorimo o prijenosu pojma ma s desna na lijevo u drugom Newtonovom zakonu () koji se vrši zasebno za svaku od razmatranih materijalnih tačaka i osudi ovog pojma d'Alembertovom silom inercije.

D'Alembertov princip omogućava primjenu jednostavnijih metoda statike na rješavanje problema dinamike, pa se u inženjerskoj praksi široko koristi tzv. kinetostatska metoda. Posebno je pogodno koristiti ga za određivanje reakcija ograničenja u slučajevima kada je zakon tekućeg kretanja poznat ili pronađen iz rješenja odgovarajućih jednačina.

Jedan od najvažnijih koncepata u mehanici radna snaga .

Prisilni rad

Sve fizička tijela u svetu oko nas se pokreće silom. Ako na tijelo koje se kreće u istom ili suprotnom smjeru djeluje sila ili više sila jednog ili više tijela, onda kažu da posao je obavljen .

Odnosno, mehanički rad obavlja sila koja djeluje na tijelo. Dakle, vučna sila električne lokomotive pokreće cijeli voz, čime se mehanički rad. Bicikl se pokreće mišićnom snagom nogu bicikliste. Dakle, ova sila vrši i mehanički rad.

U fizici rad sile pozvao fizička količina, jednak proizvodu modula sile, modula pomaka tačke primjene sile i kosinusa ugla između vektora sile i pomaka.

A = F s cos (F, s) ,

gdje F modul sile,

s- modul pokreta .

Rad se uvijek obavlja ako ugao između vjetrova sile i pomaka nije jednak nuli. Ako sila djeluje u smjeru suprotnom od smjera kretanja, količina rada je negativna.

Rad se ne obavlja ako na tijelo ne djeluju sile, ili ako je kut između primijenjene sile i smjera kretanja 90 o (cos 90 o = 0).

Ako konj vuče kola, tada mišićna sila konja, ili vučna sila usmjerena u smjeru kolica, obavlja posao. A sila gravitacije, kojom vozač pritiska kolica, ne radi, jer je usmjerena prema dolje, okomito na smjer kretanja.

Rad sile je skalarna veličina.

SI jedinica rada - džul. 1 džul je rad koji izvrši sila od 1 njutna na udaljenosti od 1 m ako su smjer sile i pomaka isti.

Ako na tijelo ili materijalnu tačku djeluje više sila, onda govore o radu koji je izvršila njihova rezultantna sila.

Ako primijenjena sila nije konstantna, tada se njen rad izračunava kao integral:

Snaga

Sila koja pokreće tijelo vrši mehanički rad. Ali kako se ovaj posao obavlja, brzo ili sporo, ponekad je veoma važno znati u praksi. Za isti posao se može obaviti u drugačije vrijeme. Posao koji obavlja veliki električni motor može obaviti mali motor. Ali za to će mu trebati mnogo više vremena.

U mehanici postoji veličina koja karakteriše brzinu rada. Ova vrijednost se zove moć.

Snaga je odnos rada obavljenog u određenom vremenskom periodu i vrijednosti tog perioda.

N= A /∆ t

Po definiciji A = F s cos α , a s/∆ t = v , Shodno tome

N= F v cos α = F v ,

gdje F - snaga, v brzina, α je ugao između smjera sile i smjera brzine.

To je snaga - je skalarni proizvod vektora sile i vektora brzine tijela.

AT međunarodni sistem SI snaga se mjeri u vatima (W).

Snaga 1 vata je rad od 1 džula (J) obavljen u 1 sekundi (s).

Snaga se može povećati povećanjem sile koja obavlja rad, ili brzine kojom se taj rad obavlja.