16. Stern-ova teorema.

Ako je poznat moment inercije tijela oko ose koja prolazi kroz njegovo središte mase, tada je moment inercije oko bilo koje druge paralelne ose određen Steinerovom teoremom : moment inercije tela J u odnosu na proizvoljnu osu jednako je njenom momentu inercije Jc u odnosu na paralelnu osu koja prolazi kroz centar mase OD tijelo, dodano proizvodu mase t tijela po kvadratnoj udaljenosti a između osovina:

17. Jednačina dinamike rotaciono kretanječvrsto telo.

Iε = M. Ovo je osnovna jednadžba dinamike rotacionog kretanja krutog tijela. Kutno ubrzanje ε i moment M u ovoj jednačini su algebarske veličine. Obično je pozitivan smjer rotacije u smjeru suprotnom od kazaljke na satu.

Moguća je i vektorska forma osnovne jednadžbe dinamike rotacijskog kretanja, u kojoj su veličine definirane kao vektori usmjereni duž ose rotacije. Prilikom proučavanja translacionog kretanja tijela uvodi se pojam impulsa tijela. Slično, kada se proučava rotacijsko kretanje, uvodi se koncept ugaonog momenta. Ugaoni moment rotirajućeg tijela je fizička veličina jednaka proizvodu momenta inercije tijela I i ugaone brzine ω njegove rotacije. Ugaoni moment je označen slovom L: Ugaoni moment cijelog tijela definiran je kao vektorski zbir Li. L = Iω. Ova jednačina, dobijena ovde za slučaj kada je I = const, važi i u opštem slučaju kada se moment inercije tela menja tokom kretanja.

18. Kinetička energija rotirajućeg tijela.

Zamislite apsolutno kruto tijelo (vidi § 1) koje rotira oko fiksne ose z koja prolazi kroz njega (slika 24). Podelimo mentalno ovo telo na male zapremine sa elementarnim masama t 1 , t 2 ,..., t n , na daljinu r 1 , r 2 ,..., r n od ose.

Kada se kruto tijelo rotira oko fiksne ose, njegovi pojedinačni elementarni volumeni s masama m i opisuju krugove različitih poluprečnika r i, i imaju različite linearne brzine v i . Ali pošto razmatramo apsolutno kruto tijelo, ugaona brzina rotacije ovih volumena je ista: (17.1) Nalazimo kinetičku energiju rotirajućeg tijela kao zbir kinetičkih energija njegovih elementarnih volumena:

ili Koristeći izraz (17.1), dobijamo

gdje Jz- moment inercije tijela oko z-ose. Na ovaj način, kinetička energija rotirajuće tijelo (17.2)

Iz poređenja formule (17.2) sa izrazom (12.1) za kinetičku energiju tijela koje se kreće naprijed (T=mv 2 /2), Iz toga slijedi da je moment inercije mjera inercije tijela tokom rotacionog kretanja. Formula (17.2) vrijedi za tijelo koje rotira oko fiksne ose. U slučaju ravnog gibanja tijela, na primjer, cilindra koji se kotrlja niz nagnutu ravan bez klizanja, energija gibanja je zbir energije translacijskog kretanja i energije rotacije: gdje m- masa kotrljajućeg tijela; vc- brzina centra mase tijela; Jc- moment inercije tijela oko ose koja prolazi kroz njegovo središte mase; w je ugaona brzina tijela. Rad vanjske sile na rotaciju tijela F=Fi+Fr+Fk. Rad sile rotirajućeg tijela A=M* ∆φ

19. Gravitaciono polje.

Gravitaciona interakcija između tijela odvija se uz pomoć gravitacionog polja, odnosno gravitacionog polja. Ovo polje stvaraju tijela i predstavlja oblik postojanja materije. Glavno svojstvo gravitacionog polja je ono za bilo koje tijelo mase t, dovedena u ovo polje, deluje gravitaciona sila, tj. (24.1)

Vektor g ne zavisi od m i naziva se jačinom gravitacionog polja. Intenzitet gravitacionog polja određen je silom koja djeluje sa strane polja na materijalnu tačku jedinične mase, a poklapa se u smjeru sa silom koja djeluje. Postoji napetost karakteristika snage gravitacionih polja. Gravitaciono polje se naziva homogenim ako je njegov intenzitet isti u svim tačkama, a centralnim ako su u svim tačkama polja vektori intenziteta usmereni duž pravih linija koje se seku u jednoj tački (A) nepomično u odnosu na bilo koji inercijski referentni okvir (slika 38). Za grafički prikaz polja sila koriste se linije sile (linije napetosti). Linije polja su odabrane tako da je vektor jačine polja usmjeren tangencijalno na liniju polja.

Vrijednost je energetska karakteristika gravitaciono polje naziva se potencijal. Potencijal gravitacionog polja j- skalarna veličina određena potencijalnom energijom tijela jedinične mase u datoj tački polja ili radom pomjeranja jedinične mase iz date tačke polja u beskonačnost. Dakle, potencijal gravitacionog polja stvorenog od tijela mase M, jednako (25.4) gdje je R- udaljenost od ovog tijela do tačke o kojoj je riječ. Iz formule (25.4) slijedi da lokus tačaka sa istim potencijalom formira sfernu površinu ( R= const). Takve površine za koje je potencijal konstantan nazivaju se ekvipotencijalne. Razmotrite odnos između potencijala ( j) gravitaciono polje i njegov intenzitet (g). Iz izraza (25.1) i (25.4) proizilazi da je elementarni rad d A, koje vrše sile polja sa malim pomakom tijela s masom t, je jednako

20. Pritisak u tečnostima i gasovima. Pascalovi i Arhimedovi zakoni.

Jedinica pritiska - pascal(Pa): 1 Pa je jednak pritisku koji stvara sila od 1 N, ravnomjerno raspoređena po površini koja je normalna na nju s površinom od ​​1m 2 (1 Pa = 1 N / m 2).

Pritisak u ravnoteži tečnosti (gasova) podleže Pascalovom zakonu: pritisak na bilo kom mestu fluida koji miruje je isti u svim pravcima, a pritisak se podjednako prenosi kroz zapreminu koju zauzima fluid u mirovanju. Razmotrimo kako težina fluida utiče na raspodjelu pritiska unutar nestišljivog fluida u mirovanju. Kada je tečnost u ravnoteži, horizontalni pritisak je uvek isti, inače ne bi bilo ravnoteže. Zbog toga je slobodna površina fluida u mirovanju uvijek horizontalna udaljena od zidova posude. Ako je fluid nestišljiv, tada je njegova gustina nezavisna od pritiska. Zatim za poprečni presjek S stub tečnosti, njegova visina h i gustina r težina P=rgSh, i pritisak na donju bazu

(28.1) tj. pritisak se linearno mijenja sa visinom. Pritisak rgh naziva hidrostatički pritisak. Prema formuli (28.1), sila pritiska na donje slojeve tečnosti biće veća nego na gornje, stoga na telo uronjeno u tečnost (gas) deluje sila određena Arhimedovim zakonom: usmerena sila deluje na telo uronjeno u tečnost (gas). sila uzgona prema gore jednaka težini tečnosti (gasa) koju je telo istisnulo: F ALI =PgV, gdje R - gustina tečnosti, V- zapremine tela uronjenog u tečnost.

21. Vod i cijev struje. Teorema kontinuiteta mlaza.

Kretanje fluida naziva se strujanje, a sakupljanje čestica fluida koji se kreće naziva se strujanje. Grafički je kretanje fluida prikazano pomoću strujnih linija, koje su nacrtane tako da se tangente na njih poklapaju u pravcu sa vektorom brzine fluida u odgovarajućim tačkama u prostoru (slika 45). Linije strujanja su nacrtane na način da je njihova gustina, koju karakteriše odnos broja linija i površine okomitog na njih, kroz koju prolaze, veća tamo gde je brzina strujanja fluida veća, a manje tamo gde tečnost sporije teče. Dakle, prema obrascu strujnih linija može se suditi o smjeru i modulu brzine u različitim tačkama u prostoru, odnosno može se odrediti stanje kretanja fluida. Dio tekućine omeđen strujnim linijama naziva se strujna cijev. Protok tekućine naziva se stacionarnim (ili stacionarnim) ako se oblik i položaj strujnih linija, kao i vrijednosti brzina u svakoj od njegovih točaka, ne mijenjaju s vremenom.

Uzmite u obzir bilo koju strujnu cijev. Biramo dva njegova odjeljka S 1 i S 2 , okomito na pravac brzine (Sl. 46). Za vrijeme D t kroz sekciju S zapremina tečnosti prolazi Sv D t dakle, kroz 1 s S 1 će proći zapreminu tečnosti S 1 v 1 , gdje v 1 - brzina protoka fluida na poprečnom presjeku S 1 . Kroz sekciju S 2 za 1 s će proći zapreminu tečnosti S 2 v 2 , gdje v 2 - brzina protoka fluida na poprečnom presjeku S 2 . Ovdje se pretpostavlja da je brzina fluida u poprečnom presjeku konstantna. Ako je fluid nestišljiv (r=const), onda kroz poprečni presjek S 2 će proći istu zapreminu tečnosti kao kroz sekciju S 1 , tj. (29.1) Prema tome, proizvod brzine protoka nestišljivog fluida i poprečnog presjeka strujne cijevi je konstantna vrijednost za ovu strujnu cijev. Relacija (29.1) se naziva jednačina kontinuiteta za nestišljiv fluid.

Bernoullijeva jednadžba

Prema jednačini kontinuiteta za nestišljiv fluid , zapremina koju zauzima tečnost ostaje konstantna, tj. Deljenje izraza (30.5) sa D V, dobiti gde R - gustina tečnosti. Ali pošto su sekcije odabrane proizvoljno, možemo pisati (30.6)

Izraz (30.6) je izveo švajcarski fizičar D. Bernuli i naziva se Bernulijeva jednačina. Kao što se može vidjeti iz njegovog izvođenja, Bernoullijeva jednačina je izraz zakona održanja energije primijenjenog na stabilan tok idealnog fluida. Takođe dobro funkcioniše za prave tečnosti, čije unutrašnje trenje nije jako veliko. Vrijednost R u formuli (30.6) naziva se statički pritisak (pritisak tečnosti na površini tela koje oblijeće oko njega), vrednost rv 2 / 2 - dinamički pritisak. Kao što je već spomenuto, vrijednost rgh je hidrostatički pritisak.

Za horizontalnu strujnu cijev ( h 1 =h 2 ) izraz (30.6) postaje (30.7)

gdje p+rv 2 / 2 se naziva ukupni pritisak. Iz Bernoullijeve jednadžbe (30.7) za horizontalnu strujnu cijev i jednačine kontinuiteta (29.1) slijedi da kada tečnost teče kroz horizontalnu cijev različitih presjeka, brzina fluida je veća u tačkama suženja, a statički pritisak je veća na širim tačkama, odnosno tamo gde je brzina sporija. To se može pokazati postavljanjem niza mjerača tlaka duž cijevi (Sl. 48).

23. Torricelli formula.

Razmotrimo cilindričnu posudu sa tečnošću, u čijoj se bočnoj stijenci nalazi mala rupa na nekoj dubini ispod nivoa tečnosti (Sl. 51). Razmotrite dva dijela (na nivou h 1 slobodna površina tečnosti u posudi i na nivou h 2 njegov izlaz iz rupe) i napišite Bernoullijevu jednačinu:

Od pritiska R 1 i R 2 u tečnosti na nivoima prve i druge sekcije jednaki su atmosferskim, tj. R 1 =p 2 , tada će jednačina izgledati ovako

Iz jednačine kontinuiteta (29.1) slijedi da v 2 /v 1 =S 1 /S 2 , gdje S 1 i S 2 - površine poprečnog presjeka posude i otvora. Ako a S 1 >>S 2 , ondačlan v/2 može se zanemariti i

Ovaj izraz se naziva Torričelijeva formula. Formula za brzinu istjecanja tekućine iz rupe u otvorenoj posudi

24. Viskozitet, Newtonov zakon. Režimi protoka.

Viskoznost (unutrašnje trenje) je svojstvo stvarnih tečnosti da se odupru kretanju jednog dela tečnosti u odnosu na drugi. Kada se neki slojevi stvarnog fluida pomiču u odnosu na druge, nastaju sile unutrašnjeg trenja, usmjerene tangencijalno na površinu slojeva. Djelovanje ovih sila očituje se u činjenici da sa strane sloja koji se kreće brže, na sloj koji se kreće sporije djeluje sila ubrzanja. Sa strane sloja koji se kreće sporije, na sloj koji se kreće brže utiče sila usporavanja.

Sila unutrašnjeg trenja F je veća, što je veća razmatrana površina površine sloja S(Sl. 52), a zavisi od toga koliko se brzo menja brzina protoka fluida tokom prelaska iz sloja u sloj. Smjer u kojem se broji razmak između slojeva, okomito protoka sloja. Vrijednost pokazuje koliko se brzo mijenja brzina kada se krećete od sloja do sloja u smjeru X, okomito na smjer kretanja slojeva, a naziva se gradijent brzine. Dakle, modul sile unutrašnjeg trenja (31.1), gdje je koeficijent proporcionalnosti m, koji zavisi od prirode tečnosti, naziva se dinamička viskoznost (ili jednostavno viskoznost). Jedinica za viskozitet je paskal sekunda (Pa×s). Što je viskoznost veća, što se tekućina više razlikuje od idealne, to se u njoj pojavljuju veće sile unutrašnjeg trenja. Postoje dva načina protoka tečnosti. Strujanje se naziva laminarnim (slojevitim) ako svaki odabrani tanki sloj klizi duž toka u odnosu na susjedne bez miješanja s njima, a turbulentnim (vorteksnim) ako se uz tok odvija intenzivno formiranje vrtloga i miješanje tekućine (plina). Laminarni tok tečnosti se posmatra pri malim brzinama njenog kretanja. Vanjski sloj tekućine uz površinu cijevi u koju teče, zbog sila molekularne kohezije, lijepi se za nju i ostaje nepokretan. Prosječni profil brzine za turbulentno strujanje u cijevima (slika 53) razlikuje se od paraboličnog profila za laminarni tok po bržem porastu brzine u blizini stijenki cijevi i manjoj zakrivljenosti u središnjem dijelu toka. Priroda protoka ovisi o bezdimenzionalnoj količini tzv Reynoldsov broj: gdje n = h/p-kinematička viskoznost; R- gustina tečnosti;<v>-prosječna brzina fluida preko dijela cijevi; d- karakteristične linearne dimenzije, kao što je promjer cijevi. Pri niskim vrijednostima Reynoldsovog broja uočava se laminarni tok, u području se javlja prijelaz iz laminarnog u turbulentno strujanje, a kod (za glatke cijevi) strujanje je turbulentno.

26. Poiseuilleova formula. Metode za određivanje viskoznosti.

Stokes metoda. Ova metoda određivanja viskoznosti zasniva se na mjerenju brzine malih sfernih tijela koja se polako kreću u tekućini. Na loptu koja pada okomito u tečnosti djeluju tri sile: gravitacija P= 4 / 3 pr 3 rg(r- gustina lopte), Arhimedova sila P= 4 / 3 pr 3 r "g (r" - gustina tečnosti) i sila otpora koju je empirijski utvrdio J. Stokes: F= 6phrv, gdje r je poluprečnik lopte, v- njegovu brzinu. Kada se lopta kreće ravnomerno, gde

Mjerenjem brzine ravnomjernog kretanja lopte može se odrediti viskozitet tečnosti (gasa). Poiseuilleova metoda. Ova metoda se zasniva na laminarnom protoku tečnosti u tankoj kapilari. Razmotrimo kapilaru s radijusom R i dužina l. Mentalno izdvojimo cilindrični sloj u tekućini polumjera r i debljina d r(Sl. 54). Sila unutrašnjeg trenja (vidi (31.1)), koja djeluje na bočnu površinu ovog sloja, gdje d S- bočna površina cilindrični sloj; znak minus znači da kako se radijus povećava, brzina se smanjuje. Nakon integracije, pod pretpostavkom da se tečnost zalijepi u blizini zidova, tj. brzina na udaljenosti R od ose je jednaka nuli, dobijamo Tokom vremena t iz cijevi će istjecati tekućina čija je zapremina otuda i viskozitet

27. Jednačina slobodnih harmonijskih oscilacija za klatna.

Oscilacije se nazivaju slobodnim (ili pravilnim) ako se izvode zbog prvobitno prenesene energije uz naknadno odsustvo vanjskih utjecaja na oscilatorni sistem (sistem koji osciluje). Najjednostavniji tip oscilacija su harmonijske oscilacije - oscilacije kod kojih se oscilirajuća vrijednost mijenja s vremenom prema zakonu sinusa (kosinus ). Opružno klatno je opterećenje mase t, visi na savršeno elastičnoj oprugi i izvodi harmonijske oscilacije pod djelovanjem elastične sile F= –kx, gdje k- krutost opruge. Jednačina kretanja klatna

Iz izraza proizilazi da opružno klatno vrši harmonijske oscilacije po zakonu x=A cos (w 0 t+ j) sa cikličnom frekvencijom (142.2) i periodom (142.3) Formula (142.3) vrijedi za elastične oscilacije u granicama u kojima je ispunjen Hookeov zakon, odnosno kada je masa opruge mala u odnosu na masu tijela. Potencijalna energija opružnog klatna je fizičko klatno- ovo je kruto tijelo koje pod djelovanjem gravitacije oscilira oko fiksne horizontalne ose koja prolazi kroz tačku O, ne poklapa se sa centrom mase OD telo (sl. 201). Ako se klatno od ravnotežnog položaja odbije za neki ugao a, tada, u skladu sa jednačinom dinamike rotacionog kretanja krutog tijela (18.3), moment M sila vraćanja može se zapisati kao (142.4) gdje J- moment inercije klatna oko ose koja prolazi kroz tačku vešanja Oh ja- udaljenost između njega i centra mase klatna, F t \u003d -mg sina» -mga. - obnavljajuća sila (znak minus je zbog činjenice da su pravci F t i a uvijek suprotno; grijeh a» a odgovara malim oscilacijama klatna, tj. mala odstupanja klatna od ravnotežnog položaja). Za male oscilacije, fizičko klatno vrši harmonijske oscilacije sa cikličkom frekvencijom w 0 i periodom

Gdje L=J/(ml) - smanjena dužina fizičkog klatna.

Matematičko klatno- ovo je idealizovan sistem koji se sastoji od materijalne tačke sa masom t, visi na nerasteznoj bestežinskoj niti i osciluje pod uticajem gravitacije. Dobra aproksimacija matematičkog klatna je mala, teška lopta okačena na tanku, dugačku nit. Moment inercije matematičkog klatna

(142.8) gdje l je dužina klatna. Pošto se matematičko klatno može predstaviti kao poseban slučaj fizičko klatno, pod pretpostavkom da je sva njegova masa koncentrisana u jednoj tački - centru mase, onda, zamjenom izraza (142.8) u formulu (1417), dobijamo izraz za period malih oscilacija matematičkog klatna (142.9) Poređenje formula (142.7) ) i (142.9), vidimo, šta ako je data dužina L fizičko klatno je jednako dužini l matematičko klatno, onda su periodi oscilovanja ovih klatna isti. Dakle, smanjena dužina fizičkog klatna je dužina takvog matematičkog klatna, čiji se period oscilovanja poklapa sa periodom oscilovanja datog fizičkog klatna.

28. Kinematika slobodnih harmonijskih oscilacija.

Mehanička harmonijska oscilacija je pravolinijsko neujednačeno kretanje u kojem se koordinate oscilirajućeg tijela (materijalne tačke) mijenjaju prema kosinusnom ili sinusnom zakonu ovisno o vremenu. Prema ovoj definiciji, zakon promjene koordinata u zavisnosti od vremena ima oblik: , gdje je wt vrijednost ispod predznaka kosinusa ili sinusa; w- koeficijent, fizičko značenje koje ćemo otkriti u nastavku; A je amplituda mehaničkih harmonijskih oscilacija. Jednačine (4.1) su glavne kinematičke jednačine mehaničkih harmonijskih vibracija.

za materijalnu tačku koja vrši harmonijske mehaničke oscilacije, vrijednost w može se tumačiti kao broj oscilacija za određeni vremenski ciklus, jednak 2l. Stoga je vrijednost w nazvana cikličkom (ili kružnom) frekvencijom. Ako tačka M krene svoje kretanje ne od tačke 1, već od tačke 2, tada će jednačina (4.1) dobiti oblik: Vrijednost f0 naziva se početna faza.

29. Prigušene vibracije.

Razmotrimo slobodne prigušene oscilacije - oscilacije čije amplitude opadaju tokom vremena zbog gubitaka energije realnog oscilatornog sistema. Diferencijalna jednadžba slobodne prigušene oscilacije linearni sistem je dat u formi

(146.1), gdje s- fluktuirajuća veličina koja opisuje jedno ili drugo fizički proces, d=const - koeficijent slabljenja, w 0 - ciklična frekvencija slobodnog neprigušeni oscilacije istog oscilatornog sistema, tj. na d = 0 (u odsustvu gubitaka energije) naziva se prirodna frekvencija oscilatornog sistema.

- amplituda prigušenih oscilacija, a ALI 0 - početna amplituda. Ako a A(t) i ALI(t+ T) - amplitude dvije uzastopne oscilacije koje odgovaraju vremenima koja se razlikuju za period, tada se omjer naziva dekrement prigušenja, i njegov logaritam (146.7)- dekrement logaritamskog prigušenja; N e - broj oscilacija napravljenih za vrijeme kada se amplituda smanji za e puta. Logaritamski dekrement prigušenja je konstantna vrijednost za dati oscilatorni sistem. Za karakterizaciju oscilatornog sistema koristi se koncept faktor kvaliteta Q,što je za male vrijednosti logaritamskog dekrementa jednako (146,8). Iz formule (146.8) proizlazi da je faktor kvaliteta proporcionalan broju oscilacija N e , koje sistem izvodi tokom vremena opuštanja.

30. Prisilne vibracije, rezonancija.

Oscilacije koje nastaju pod dejstvom spoljašnje periodično promenljive sile ili spoljašnje periodično promenljive emf nazivaju se prinudne mehaničke, odnosno prisilne elektromagnetne oscilacije. Uzmite u obzir zavisnost amplituda A prisilne vibracije od frekvencija w. Mehaničke i elektromagnetne oscilacije će se razmatrati istovremeno, nazivajući oscilirajuću vrijednost ili pomak (X) oscilirajućeg tijela iz ravnotežnog položaja ili naelektrisanja (Q) kondenzator.

Iz formule (147.8) proizilazi da je amplituda ALI pomak (naboj) ima maksimum. Za određivanje rezonantne frekvencije w rez, - frekvencija na kojoj je amplituda ALI pomak (naboj) dostiže maksimum - potrebno je pronaći maksimum funkcije (147,8), ili, što je isto, minimum radikalnog izraza. Razlikovanje radikalnog izraza u odnosu na w i izjednačavajući ga sa nulom, dobijamo uslov koji određuje w rezati: Ova jednakost važi za w=0, ± , za koje samo pozitivna vrijednost ima fizičko značenje. Posljedično, rezonantna frekvencija (148.1) Fenomen naglog povećanja amplitude prisilnih oscilacija kada se frekvencija pokretačke sile (frekvencija pogonskog naizmjeničnog napona) približi frekvenciji jednakoj ili bliskoj prirodnoj frekvenciji oscilatornog sistem se zove rezonancija (mehanička, odnosno električna). Kada vrijednost w rez se skoro poklapa sa prirodnom frekvencijom w 0 oscilirajući sistem. Zamjenom (148.1) u formulu (147.8) dobijamo (148.2)

Na sl. 210 prikazane su ovisnosti amplitude prisilnih oscilacija o frekvenciji za različite vrijednosti d. Iz (148.1) i (148.2) slijedi da je manje d, što je više i desno nalazi maksimum ove krive. Ako a w® 0, tada sve krive (vidi također (147.8)) dostižu istu graničnu vrijednost različitu od nule , što se naziva statička devijacija. U slučaju mehaničkih vibracija , u slučaju elektromagnetnih U m / (L). Ako a w®¥, tada krive asimptotski teže nuli. Redukovani skup krivulja naziva se rezonantne krive.

Zakon održanja energije kaže da energija tijela nikada ne nestaje i ne pojavljuje se ponovo, može samo prelaziti iz jednog oblika u drugi. Ovaj zakon je univerzalan. Ima svoju formulaciju u raznim granama fizike. Klasična mehanika razmatra zakon održanja mehaničke energije.

Ukupna mehanička energija zatvorenog sistema fizička tijela, između kojih djeluju konzervativne sile, je konstantna vrijednost. Ovako je formulisan zakon održanja energije u Njutnovoj mehanici.

Zatvorenim ili izolovanim se smatra fizički sistem, na koju ne utiču spoljne sile. Ne razmjenjuje energiju sa okolnim prostorom, a vlastita energija koju posjeduje ostaje nepromijenjena, odnosno očuvana. Samo u takvom sistemu unutrašnje sile, a tijela međusobno djeluju. Može samo pretvoriti potencijalnu energiju u kinetičku i obrnuto.

Najjednostavniji primjer zatvorenog sistema je snajperska puška i metak.

Vrste mehaničkih sila

Sile koje djeluju unutar mehaničkog sistema obično se dijele na konzervativne i nekonzervativne.

konzervativan smatraju se sile čiji rad ne zavisi od putanje tela na koje se primenjuju, već je određen samo početnim i konačnim položajem ovog tela. Konzervativne snage se takođe nazivaju potencijal. Rad takvih sila u zatvorenoj petlji je nula. Primjeri konzervativnih sila − sila gravitacije, sila elastičnosti.

Sve ostale sile se zovu nekonzervativan. To uključuje sila trenja i sila otpora. Takođe se zovu disipativno snage. Ove sile vrše negativan rad pri bilo kojem kretanju u zatvorenom mehaničkom sistemu, a pod njihovim djelovanjem ukupna mehanička energija sistema opada (raspada). Prelazi u druge, nemehaničke vrste energije, na primjer, u toplinu. Dakle, zakon održanja energije u zatvorenom mehaničkom sistemu može biti ispunjen samo ako u njemu nema nekonzervativnih sila.

Ukupna energija mehaničkog sistema sastoji se od kinetičke i potencijalne energije i njihov je zbir. Ove vrste energija mogu se transformisati jedna u drugu.

Potencijalna energija

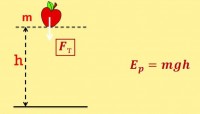
Potencijalna energija naziva se energija interakcije fizičkih tijela ili njihovih dijelova međusobno. Ona je određena njihovim međusobnim rasporedom, odnosno rastojanjem između njih, i jednaka je radu koji je potrebno obaviti da se tijelo premjesti iz referentne točke u drugu tačku u polju konzervativnih sila.

Potencijalnu energiju ima svako nepomično fizičko tijelo, podignuto na određenu visinu, budući da na njega djeluje gravitacija, koja je konzervativna sila. Takvu energiju posjeduje voda na rubu vodopada, sanke na vrhu planine.

Odakle ova energija? Dok se fizičko tijelo dizalo na visinu, radilo se i energija se trošila. To je ta energija koja je pohranjena u podignutom tijelu. I sada je ova energija spremna za rad.

Vrijednost potencijalne energije tijela određena je visinom na kojoj se tijelo nalazi u odnosu na neki početni nivo. Za početnu tačku možemo uzeti bilo koju tačku koju odaberemo.

Ako uzmemo u obzir položaj tijela u odnosu na Zemlju, onda potencijalna energija tijelo na površini Zemlje je nula. I na vrhu h izračunava se po formuli:

E p = mɡ h ,

gdje m - tjelesna masa

ɡ - ubrzanje gravitacije

h – visina centra mase tijela u odnosu na Zemlju

ɡ \u003d 9,8 m / s 2

Kada telo padne sa visine h1 do visine h2 gravitacija radi. Ovaj rad jednak je promjeni potencijalne energije i ima negativnu vrijednost, jer se veličina potencijalne energije smanjuje kako tijelo pada.

A = - ( E p2 - E p1) = - ∆ E str ,

gdje E p1 je potencijalna energija tijela na visini h1 ,

E p2 - potencijalna energija tijela na visini h2 .

Ako se tijelo podigne na određenu visinu, tada se radi protiv sila gravitacije. U ovom slučaju ima pozitivnu vrijednost. I povećava se vrijednost potencijalne energije tijela.

Elastično deformirano tijelo (komprimirano ili rastegnuta opruga). Njegova vrijednost ovisi o krutosti opruge i o tome koliko dugo je bila stisnuta ili rastegnuta, a određuje se po formuli:

E p \u003d k (∆x) 2 / 2 ,

gdje k - koeficijent krutosti,

∆x - produženje ili kontrakcija tijela.

Potencijalna energija opruge može obaviti rad.

Kinetička energija

U prijevodu s grčkog "kinema" znači "kretanje". Energija koju fizičko tijelo primi kao rezultat svog kretanja naziva se kinetički. Njegova vrijednost ovisi o brzini kretanja.

Fudbalska lopta koja se kotrlja po terenu, sanke koje se kotrljaju niz planinu i nastavljaju da se kreću, strijela ispaljena iz luka - svi imaju kinetičku energiju.

Ako tijelo miruje, njegova kinetička energija je nula. Čim sila ili više sila djeluje na tijelo, ono će se početi kretati. A pošto se tijelo kreće, sila koja djeluje na njega radi. Rad sile pod čijim će se djelovanjem tijelo iz mirovanja pokrenuti i promijeniti brzinu od nule do ν , zove se kinetička energija tjelesne mase m .

Ako je tijelo u početnom trenutku već bilo u pokretu i njegova brzina je imala vrijednost v 1 , a na kraju je bilo jednako v 2 , tada će rad sile ili sila koje djeluju na tijelo biti jednak priraštaju kinetičke energije tijela.

∆ E k = E k 2 - E k 1

Ako se smjer sile poklapa sa smjerom kretanja, tada se vrši pozitivan rad, a kinetička energija tijela se povećava. A ako je sila usmjerena u smjeru suprotnom od smjera kretanja, tada se vrši negativan rad i tijelo odaje kinetičku energiju.

Zakon održanja mehaničke energije

Ek 1 + E p1= E k 2 + E p2

Svako fizičko tijelo koje se nalazi na nekoj visini ima potencijalnu energiju. Ali kada padne, počinje da gubi ovu energiju. Gde ona ide? Ispostavilo se da ne nestaje nigdje, već se pretvara u kinetičku energiju istog tijela.

Pretpostavimo , na nekoj visini, teret je nepomično fiksiran. Njegova potencijalna energija u ovoj tački jednaka je maksimalnoj vrijednosti. Ako ga pustimo, počeće da pada određenom brzinom. Stoga će početi dobivati ​​kinetičku energiju. Ali u isto vrijeme, njegova potencijalna energija će se početi smanjivati. U tački udara, kinetička energija tijela će dostići maksimum, a potencijalna energija će se smanjiti na nulu.

Potencijalna energija lopte bačene s visine se smanjuje, dok kinetička energija raste. Sanke koje miruju na vrhu planine imaju potencijalnu energiju. Njihova kinetička energija u ovom trenutku je nula. Ali kada počnu da se kotrljaju, kinetička energija će se povećati, a potencijalna će se smanjiti za isti iznos. A zbir njihovih vrijednosti će ostati nepromijenjen. Potencijalna energija jabuke koja visi na drvetu pretvara se u njenu kinetičku energiju kada padne.

Ovi primjeri jasno potvrđuju zakon održanja energije koji to govori ukupna energija mehaničkog sistema je konstantna vrijednost . Vrijednost ukupne energije sistema se ne mijenja, a potencijalna energija se pretvara u kinetičku energiju i obrnuto.

Za koliko se smanjuje potencijalna energija, za isti će se povećati i kinetička energija. Njihov iznos se neće mijenjati.

Za zatvoreni sistem fizičkih tijela, jednakost
E k1 + E p1 = E k2 + E p2,
gdje E k1 , E p1 - kinetičke i potencijalne energije sistema prije bilo kakve interakcije, E k2 , E p2 - odgovarajuće energije nakon njega.

Proces pretvaranja kinetičke energije u potencijalnu i obrnuto može se vidjeti promatranjem klatna.

Kliknite na sliku

Nalazeći se u krajnje desnoj poziciji, čini se da se klatno zamrzava. U ovom trenutku, njegova visina iznad referentne tačke je maksimalna. Stoga je i potencijalna energija maksimalna. A kinetika je nula, jer se ne kreće. Ali sljedećeg trenutka klatno počinje da se kreće prema dolje. Njegova brzina se povećava, a samim tim i kinetička energija. Ali kako se visina smanjuje, smanjuje se i potencijalna energija. U donjoj tački, ona će postati jednaka nuli, a kinetička energija će dostići svoju maksimalnu vrijednost. Klatno će proći ovu tačku i početi da se diže ulijevo. Njegova potencijalna energija će početi rasti, a kinetička će se smanjivati. itd.

Kako bi demonstrirao transformaciju energije, izumio je Isaac Newton mehanički sistem, koji se zove Newtonova kolevka ili Njutnova muda .

Kliknite na sliku

Ako se prva lopta odbije, a zatim pusti, njena energija i zamah će se prenijeti na posljednju kroz tri međuloptice, koje će ostati nepomične. I posljednja lopta će se skrenuti istom brzinom i podići na istu visinu kao prva. Tada će posljednja lopta prenijeti svoju energiju i zamah kroz međuloptice na prvu, i tako dalje.

Lopta položena u stranu ima maksimalnu potencijalnu energiju. Njegova kinetička energija u ovom trenutku je nula. Kada se krene, gubi potencijalnu energiju i dobija kinetičku energiju, koja dostiže svoj maksimum u trenutku sudara sa drugom loptom, a potencijalna energija postaje jednaka nuli. Nadalje, kinetička energija se prenosi na drugu, zatim na treću, četvrtu i petu kuglu. Potonji, nakon što je primio kinetičku energiju, počinje se kretati i diže se na istu visinu na kojoj je bila prva lopta na početku kretanja. Njegova kinetička energija u ovom trenutku je jednaka nuli, a potencijalna energija jednaka maksimalnoj vrijednosti. Tada počinje da pada i na isti način prenosi energiju na kuglice obrnutim redoslijedom.

To traje dosta dugo i moglo bi se nastaviti u nedogled da nema nekonzervativnih snaga. Ali u stvarnosti u sistemu djeluju disipativne sile, pod čijim utjecajem kuglice gube energiju. Njihova brzina i amplituda postepeno se smanjuju. I na kraju prestaju. Ovo potvrđuje da je zakon održanja energije zadovoljen samo u odsustvu nekonzervativnih sila.

Ukupna mehanička energija karakterizira kretanje i međudjelovanje tijela, stoga ovisi o brzinama i relativnom položaju tijela.

Ukupna mehanička energija zatvorenog mehaničkog sistema jednaka je zbiru kinetičke i potencijalne energije tijela ovog sistema:

Zakon o očuvanju energije

Zakon održanja energije je osnovni zakon prirode.

U Njutnovoj mehanici, zakon održanja energije je formulisan na sledeći način:

Ukupna mehanička energija izolovanog (zatvorenog) sistema tela ostaje konstantna.

Drugim riječima:

Energija ne nastaje ni iz čega i nigde ne nestaje, može samo prelaziti iz jednog oblika u drugi.

Klasični primjeri ove tvrdnje su: opružno klatno i klatno na niti (sa zanemarljivim prigušenjem). U slučaju opružnog klatna, u procesu oscilovanja, potencijalna energija deformisane opruge (koja ima maksimum u ekstremnim položajima tereta) se pretvara u kinetičku energiju tereta (dostiže maksimum u trenutku kada opterećenje prelazi ravnotežni položaj) i obrnuto. U slučaju klatna na niti, potencijalna energija tereta se pretvara u kinetičku energiju i obrnuto.

2 Oprema

2.1 Dinamometar.

2.2 Laboratorijski stalak.

2.3 Teret težine 100 g - 2 kom.

2.4 Mjerni lenjir.

2.5 Piece mekana maramica ili osjetio.

3 Teorijska osnova

Šema eksperimentalne postavke prikazana je na slici 1.

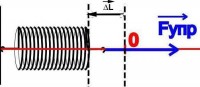
Dinamometar je fiksiran okomito u podnožju stativa. Na stativ se stavlja komad meke tkanine ili filca. Prilikom vješanja tereta sa dinamometra, napetost opruge dinamometra određuje se položajem kazaljke. U ovom slučaju, maksimalno izduženje (ili statički pomak) opruge X 0 nastaje kada elastična sila opruge sa krutošću k balansira silu gravitacije tereta sa masom t:

kx 0 =mg, (1)

gdje g = 9,81 - ubrzanje slobodnog pada.

shodno tome,

Statički pomak karakteriše novi ravnotežni položaj O" donjeg kraja opruge (slika 2).

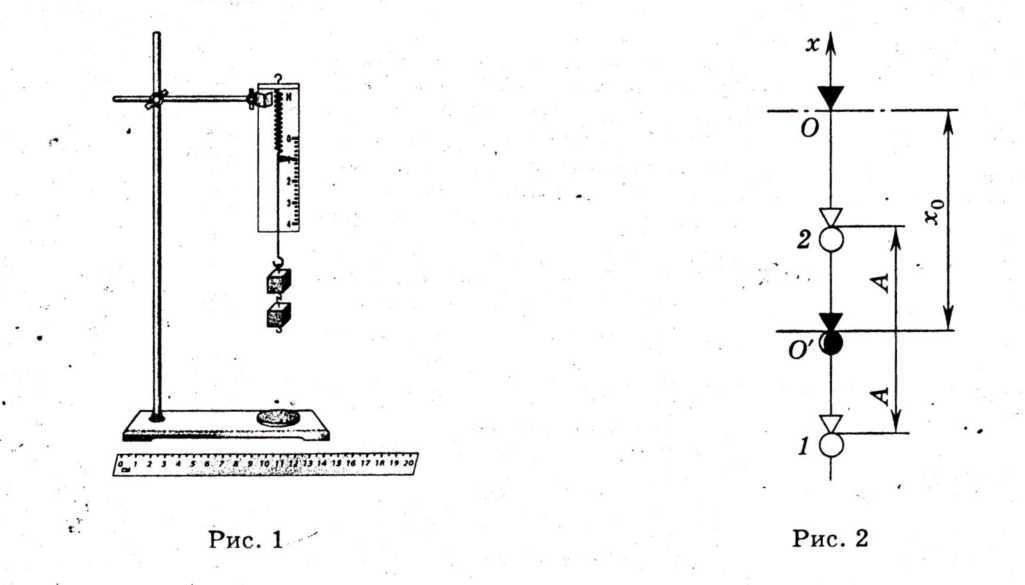
Ako se teret povuče na dole ALI iz tačke O" i otpuštanje u tački 1, tada dolazi do periodičnih oscilacija tereta. U tačkama 1 i 2, zvane okretne tačke, opterećenje se zaustavlja, mijenjajući smjer kretanja. Dakle, u ovim tačkama, brzina opterećenja v = 0.

Max brzina v m sjekira opterećenje će imati u sredini O". Dvije sile djeluju na oscilirajuće opterećenje: konstantna sila gravitacije mg i promjenljiva elastična sila kx. Potencijalna energija tijela u gravitacionom polju u proizvoljnoj tački sa koordinatom X je jednako mgx. Potencijalna energija deformiranog tijela, respektivno, jednaka je .

U ovom slučaju, poenta X = 0, što odgovara položaju pokazivača za neispruženu oprugu.

Ukupna mehanička energija tereta u proizvoljnoj tački je zbir njegove potencijalne i kinetičke energije. Zanemarujući sile trenja, koristimo zakon održanja ukupne mehaničke energije.

Izjednačimo ukupnu mehaničku energiju tereta u tački 2 sa koordinatom -(X 0 -ALI) i u tački O" sa koordinatom -X 0 :

Proširujući zagrade i izvodeći jednostavne transformacije, dovodimo formulu (3) u formu

Zatim modul maksimalne brzine opterećenja

Krutost opruge može se utvrditi mjerenjem statičkog pomaka X 0 . Kao što slijedi iz formule (1),

3.5. Zakoni održanja i promjene energije

3.5.1. Zakon promjene ukupna mehanička energija

Promjena ukupne mehaničke energije sistema tijela nastaje kada rad obavljaju sile koje djeluju i između tijela sistema i od vanjskih tijela.

Promjenu mehaničke energije ∆E sistema tijela određuje po zakonu promjene ukupne mehaničke energije:

∆E \u003d E 2 - E 1 \u003d A ext + A tr (otpor),

gdje je E 1 ukupna mehanička energija početnog stanja sistema; E 2 - ukupna mehanička energija konačnog stanja sistema; Eksterni - rad koji na telima sistema vrše spoljne sile; A tr (otpor) - rad koji obavljaju sile trenja (otpora) koje djeluju unutar sistema.

Primjer 30. Na određenoj visini tijelo u mirovanju ima potencijalnu energiju od 56 J. U trenutku pada na Zemlju, tijelo ima kinetičku energiju od 44 J. Odrediti rad sila otpora zraka.

Rješenje. Na slici su prikazana dva položaja tijela: na određenoj visini (prvi) i u trenutku pada na Zemlju (drugi). Na površini Zemlje bira se nulti nivo potencijalne energije.

Ukupna mehanička energija tijela u odnosu na površinu Zemlje određena je zbrojem potencijalne i kinetičke energije:

• na nekoj visini

E 1 \u003d W p 1 + W k 1;

• do trenutka kada udari o tlo

E 2 \u003d W p 2 + W k 2,

gdje je W p 1 = 56 J potencijalna energija tijela na određenoj visini; W k 1 = 0 - kinetička energija tijela koje miruje na određenoj visini; W p 2 = 0 J - potencijalna energija tijela u trenutku pada na Zemlju; W k 2 \u003d 44 J - kinetička energija tijela do trenutka kada padne na Zemlju.

Rad sila otpora vazduha nalazimo iz zakona promene ukupne mehaničke energije tela:

gdje je E 1 = W p 1 ukupna mehanička energija tijela na određenoj visini; E 2 \u003d W k ​​2 - ukupna mehanička energija tijela u trenutku pada na Zemlju; A ext \u003d 0 - rad vanjskih sila (spoljne sile su odsutne); Otpor - rad sila otpora zraka.

Željeni rad sila otpora vazduha je stoga određen izrazom

A otpor = W k 2 − W p 1 .

Uradimo računicu:

Otpor \u003d 44 - 56 \u003d -12 J.

Rad sila otpora zraka je negativna vrijednost.

Primjer 31. Dvije opruge sa faktorima krutosti 1,0 kN/m i 2,0 kN/m spojene su paralelno. Koji posao treba obaviti da se opružni sistem rastegne za 20 cm?

Rješenje. Na slici su prikazane dvije opruge s različitim brzinama opruga spojene paralelno.

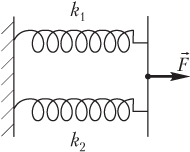
Vanjska sila F → , koja rasteže opruge, ovisi o veličini deformacije kompozitne opruge, stoga je proračun rada navedene sile korištenjem formule za izračunavanje rada konstantne sile nezakonit.

Za izračunavanje rada koristimo zakon promjene ukupne mehaničke energije sistema:

E 2 − E 1 = A ekst + A otpor,

gdje je E 1 ukupna mehanička energija kompozitne opruge u nedeformisanom stanju; E 2 - ukupna mehanička energija deformisane opruge; Eksterni - rad vanjske sile (željena vrijednost); A otpor = 0 - rad otpornih sila.

Ukupna mehanička energija kompozitne opruge je potencijalna energija njene deformacije:

• za nedeformisanu oprugu

E 1 = W p 1 = 0,

• za produženu oprugu

E 2 \u003d W p 2 \u003d k ukupno (Δ l) 2 2,

gdje je k ukupno - ukupna krutost kompozitne opruge; ∆l - veličina istezanja opruge.

Ukupna krutost dvije paralelno spojene opruge je zbir

k ukupno \u003d k 1 + k 2,

gdje je k 1 - koeficijent krutosti prve opruge; k 2 - koeficijent krutosti druge opruge.

Rad vanjske sile nalazimo iz zakona promjene ukupne mehaničke energije tijela:

Ekst = E 2 - E 1,

zamjenjujući u ovaj izraz formule koje određuju E 1 i E 2, kao i izraz za ukupni koeficijent krutosti kompozitne opruge:

Ekst = k ukupno (Δ l) 2 2 − 0 = (k 1 + k 2) (Δ l) 2 2.

Uradimo računicu:

A ekst = (1,0 + 2,0) ⋅ 10 3 ⋅ (20 ⋅ 10 − 2) 2 2 = 60 J.

Primjer 32. Metak mase 10,0 g koji leti brzinom od 800 m/s udari u zid. Modul sile otpora kretanju metka u zidu je konstantan i iznosi 8,00 kN. Odredite koliko će metak probiti zid.

Rješenje. Na slici su prikazana dva položaja metka: kada se približi zidu (prvi) i u trenutku kada se metak zaustavi (zaglavi) u zidu (drugi).

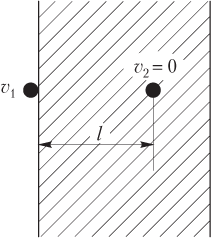
Ukupna mehanička energija metka je kinetička energija njegovog kretanja:

• kada metak udari u zid

E 1 = W k 1 = m v 1 2 2;

• do trenutka kada se metak zaustavi (zaglavi) u zidu

E 2 \u003d W k ​​2 \u003d m v 2 2 2,

gdje je W k 1 - kinetička energija metka pri približavanju zidu; W k 2 - kinetička energija metka do trenutka kada se zaustavi (zaglavi) u zidu; m je masa metka; v 1 - modul brzine metka pri približavanju zidu; v 2 \u003d 0 - vrijednost brzine metka u trenutku zaustavljanja (zaglavljivanja) u zidu.

Udaljenost na kojoj će metak ući duboko u zid, nalazimo iz zakona promjene ukupne mehaničke energije metka:

E 2 − E 1 = A ekst + A otpor,

gdje je E 1 \u003d m v 1 2 2 - ukupna mehanička energija metka pri približavanju zidu; E 2 \u003d 0 - ukupna mehanička energija metka do trenutka kada se zaustavi (zaglavi) u zidu; A ext \u003d 0 - rad vanjskih sila (spoljne sile su odsutne); Otpor - rad snaga otpora.

Rad sila otpora određen je proizvodom:

A otpor = F otpor l cos α ,

gdje je F otpor - modul sile otpora kretanju metka; l - udaljenost na kojoj će metak ući duboko u zid; α = 180° - ugao između smjera sile otpora i smjera metka.

Dakle, zakon promjene ukupne mehaničke energije metka u eksplicitnom obliku je sljedeći:

− m v 1 2 2 = F otpor l cos 180 ° .

Željena udaljenost je određena omjerom

l = − m v 1 2 2 F otpor cos 180 ° = m v 1 2 2 F otpor

l = 10,0 ⋅ 10 − 3 ⋅ 800 2 2 ⋅ 8,00 ⋅ 10 3 = 0,40 m = 400 mm.

Stranica 1

Ukupna mehanička energija tijela se ne mijenja. Energija se samo mijenja iz jednog oblika u drugi.

Ukupna mehanička energija tijela, na koju ne djeluju sile trenja i otpora, ostaje nepromijenjena tokom njegovog kretanja.

Ukupna mehanička energija tijela je zbir njegove kinetičke i potencijalne energije. Razmislite puna energija slobodno padajuće tijelo u različito vrijeme.

Da li se ukupna mehanička energija tijela mijenja kada padne.

Ono što se zove ukupna mehanička energija tijela.

Dakle, ukupna mehanička energija tijela koje vrši harmonijske oscilacije proporcionalna je kvadratu amplitude oscilacije. Dakle, amplituda A oscilacija takođe ne zavisi od vremena.

Kao što se može vidjeti iz (44.13), ukupna mehanička energija tijela tokom prigušenih oscilacija opada s vremenom prema eksponencijalnom zakonu.

Zbir kinetičke i potencijalne energije čini ukupnu mehaničku energiju tijela.

Apsolutno elastičan udar je takav udar pri kojem se održava ukupna mehanička energija tijela. Prvo, kinetička energija se djelomično ili potpuno pretvara u potencijalnu energiju elastične deformacije. Tada se tijela vraćaju u prvobitni oblik odbijajući se jedno od drugog. Kao rezultat toga, potencijalna energija elastične deformacije ponovo se pretvara u kinetičku energiju i tijela se razlijeću brzinama koje određuju dva uslova - očuvanje ukupne energije i totalni impuls tel.

Apsolutno elastičan udar je takav udar pri kojem se održava ukupna mehanička energija tijela. Prvo, kinetička energija se djelomično ili potpuno pretvara u potencijalnu energiju elastične deformacije. Tada se tijela vraćaju u prvobitni oblik odbijajući se jedno od drugog. Kao rezultat toga, potencijalna energija elastične deformacije ponovo se pretvara u kinetičku energiju i tijela se razlijeću brzinama koje određuju dva uvjeta - očuvanje ukupne energije i ukupni impuls tijela.

Apsolutno elastičan udar je takav udar pri kojem se održava ukupna mehanička energija tijela. Prvo, kinetička energija se djelomično ili potpuno pretvara u potencijalnu energiju elastične deformacije. Tada se tijela vraćaju u prvobitni oblik odbijajući se jedno od drugog. Kao rezultat toga, potencijalna energija elastične deformacije ponovo se pretvara u kinetičku energiju i tijela se razlijeću brzinama koje određuju dva uvjeta - očuvanje ukupne energije i ukupni impuls tijela.

Ovaj rad se troši na rasipanje energije ili promjenu ukupne mehaničke energije tijela.

Prema zakonu promene energije (vidi § 28), rad sile otpora (spoljne sile) jednak je priraštaju ukupne mehaničke energije tela.

Ovaj rezultat je predvidljiv, budući da je elastična sila pod kojom se tijelo kreće konzervativna, dakle, zakon održanja energije je zadovoljen – ukupna mehanička energija tijela je očuvana.

Mehanička energija karakterizira sposobnost tijela da izvrši mehanički rad. Ukupna mehanička energija tijela je zbir kinetičke i potencijalne energije.