Întrebarea 1. Câmp electromagnetic. vectori EMF. Reprezentarea grafică a câmpurilor Câmp electromagnetic- un câmp fizic fundamental care interacționează cu corpuri încărcate electric, precum și cu corpuri care au propriile momente electrice și magnetice dipol și multipol. Este o combinație de câmpuri electrice și magnetice care, în anumite condiții, se pot genera reciproc, dar de fapt sunt o singură entitate formalizată prin electrotensorul. camp magnetic.

Vectori de câmp electromagnetic:

Câmp electric. Una dintre principalele caracteristici vectoriale ale câmpului electromagnetic este tensiune câmp electric. Prin intensitatea câmpului electric se înțelege forța cu care câmpul electric acționează asupra unei sarcini punctuale unitare pozitive introdusă în câmp.

(1)

În fizică se specifică acest lucru: sarcina q trebuie să fie suficient de mică pentru ca modificarea distribuției sarcinilor electrice care formează acest câmp să poată fi neglijată.

Să luăm în considerare acest proces într-un mod simplificat în cadrul teoriei clasice:

Materia este formată din atomi. Un atom este format dintr-un nucleu pozitiv și electroni negativi. Combinația de atomi formează o moleculă. Există substanțe cu molecule polare și nepolare. În cazul atomilor sau moleculelor nepolare, punctul de aplicare al rezultantei tuturor forțelor care acționează asupra sarcinilor negative coincide cu punctul de aplicare al rezultantei tuturor forțelor care acționează asupra sarcinilor pozitive. Acest lucru este posibil dacă centrul de greutate al moleculei coincide cu centrul de greutate al protonilor. În moleculele polare, acești centri nu coincid, iar o moleculă polară poate fi asemănată cu un dipol elementar, adică. un sistem format din două sarcini opuse separate în spațiu de o distanță l. Dipolii sunt caracterizați de un moment dipol:

Efectul polarizării substanței este caracterizat de momentul dipol total: în volumul considerat dV:

(4) - moment dipol corespunzător atomilor sau moleculelor individuali. Formulă (4) însumarea geometrică se efectuează în volumul V.

Alături de intensitatea câmpului electric, se mai folosește o mărime vectorială: - vector de inducție electrică, sau vector de deplasare electrică: (8); ;

De aici rezultă că pentru aceeași aranjare și mărime a sarcinilor electrice, câmpul vectorial nu depinde de proprietățile mediului.

După cum știți, forța care acționează asupra unei sarcini electrice punctiforme pozitive care se mișcă într-un câmp magnetic este determinată de forța Lorentz: (1),

Unde (2) ; (3) ; .

Forța magnetică este proporțională cu viteza de mișcare a sarcinii și este direcționată perpendicular pe direcția de mișcare a sarcinii.

Semnificație fizică: valoarea se numește vectorul inducției magnetice și este egală cu forța cu care acționează câmpul magnetic asupra unei sarcini punctiforme pozitive care se deplasează cu viteză unitară într-o direcție perpendiculară pe aceasta.

Câmpurile sunt reprezentate folosind linii de forță. Prin „putere” se înțelege linii, în fiecare punct al cărora tangentele descriu direcția câmpului reprezentat. Modificarea amplitudinii câmpului este indicată de numărul de linii de forță pe unitatea de suprafață a suprafeței perpendiculare pe liniile de forță. Să existe un câmp vectorial DAR, care în fiecare punct al spațiului poate fi exprimat în sistemul cartezian:

l- linia de forță câmpuri DAR, - vectori unitari. Obținem ecuația diferențială a dreptei câmpului: dr poate fi scris în termenii proiecției sale: (1),

Presupunem că funcția care descrie linia câmpului este cunoscută:

Din analiza vectoriala se știe că doi vectori sunt paraleli dacă rapoartele proiecțiilor corespunzătoare sunt egale:

Aceasta este ecuația diferențială a liniei câmpului.

Întrebarea 2. Prima ecuație a lui Maxwell în forme integrale și diferențiale.

Prima ecuație a lui Maxwell este o generalizare a legii curentului total (legea lui Ampère). În formularea pre-Maxwelliană, această ecuație ar putea fi formulată astfel: circulația vectorului de intensitate H câmpul magnetic de-a lungul unui circuit închis Г este egal cu curentul / care pătrunde în acest circuit:

Înainte de Maxwell, curentul / înțelegea doar curentul de conducție. În cazul general, distribuția curentului / în interiorul circuitului G poate fi neuniformă. în care

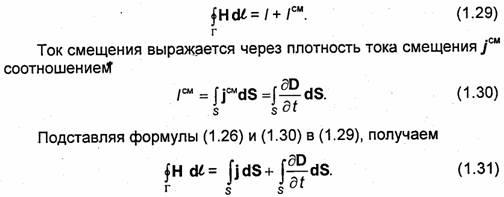
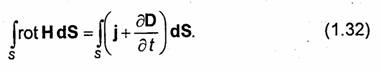
Întrebarea 3. A doua ecuație a lui Maxwell în forme integrale și diferențiale.

A doua ecuație a lui Maxwell este

generalizarea legii lui Faraday a inducției, care se formulează astfel: dacă un circuit închis Г este pătruns cu o variabilă flux magneticФ, atunci apare un EMF e în circuit, egal cu rata de modificare a acestui flux:

Semnul minus din partea dreaptă a formulei (1.34) înseamnă că EMF care apare în circuit pare să tinde întotdeauna să prevină o modificare a fluxului care pătrunde în acest circuit. Această prevedere este cunoscută sub numele de „regula lui Lenz”.

Relația (1.37) este formulată pentru un contur de dimensiuni finite și se numește A doua ecuație a lui Maxwell în formă integrală. Maxwell a formulat, de asemenea, această ecuație în formă diferențială.

Întrebarea 4. A treia ecuație a lui Maxwell în forme integrale și diferențiale.

A treia ecuație Maxwell este o generalizare a legii Gauss pentru cazul proceselor variabile. Legea Gauss leagă fluxul vectorului electric deplasare printr-o suprafață închisă arbitrară S cu sarcina Q concentrată în interiorul acestei suprafețe:

Unde dS = n o dS ; n 0 - vector unitar al normalei exterioare la suprafața S.

Înlocuind (1.41) în (1.40), obținem

Ecuația (1.43) este de obicei numită A treia ecuație a lui Maxwell în formă integrală. Pentru a merge la forma diferențială

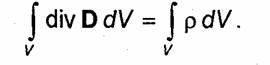
Această egalitate trebuie să fie valabilă pentru un volum arbitrar V, ceea ce este posibil numai dacă

Întrebarea 5. A patra ecuație a lui Maxwell în forme integrale și diferențiale.

A patra ecuație a lui Maxwell în formă integrală coincide cu legea Gauss pentru un câmp magnetic, care poate fi formulată după cum urmează. Fluxul vectorial LA prin orice suprafață închisă S este egal cu zero, adică.

Aceasta înseamnă că nu există linii vectoriale LA, care nu intră decât în ​​suprafața închisă S (sau, dimpotrivă, nu ies decât pe suprafața S): o pătrund întotdeauna (Fig. 1.9).

Ecuația (1.46) se numește A patra ecuație a lui Maxwell în formă integrală. Se poate trece la forma diferențială a ecuației (1.46) folosind teorema Ostrogradsky-Gauss în același mod în care s-a procedat în cazul celei de-a treia ecuații Maxwell. Drept urmare, obținem

divB = 0 (1.47)

Ecuația (1.47) este a patra ecuație a lui Maxwell. Arată că în natură nu există sarcini magnetice solitare de același semn. De asemenea, din această ecuație rezultă că liniile vectorului LA(liniile de câmp ale câmpului magnetic) sunt continue.

Sistemul de ecuații al lui Maxwell include patru ecuații de bază

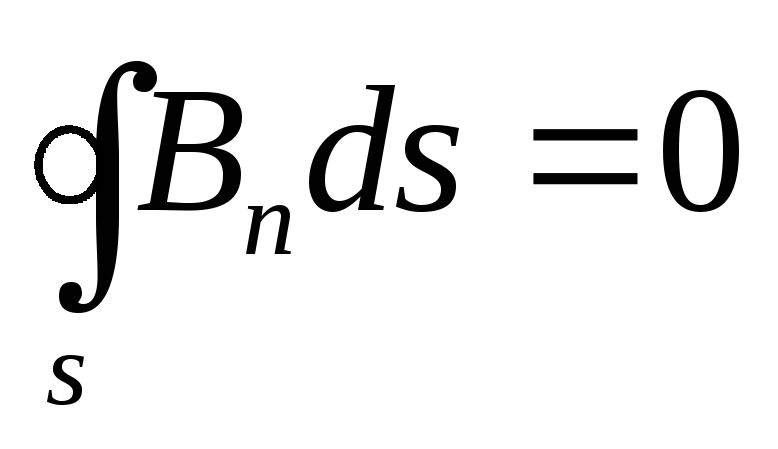, (3.2)

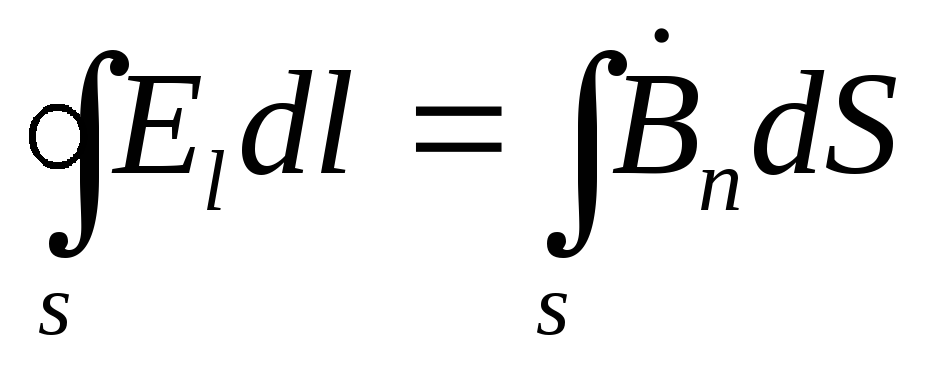, (3.3)

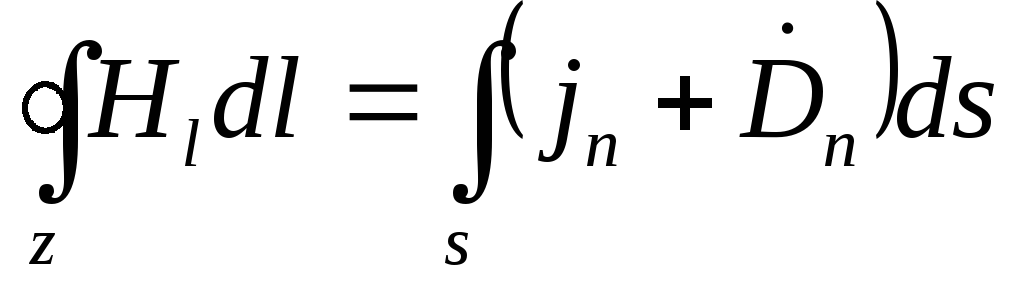. (3.4)

Acest sistem este completat de trei ecuații materiale, legarea mărimi fizice incluse în ecuațiile Maxwell:

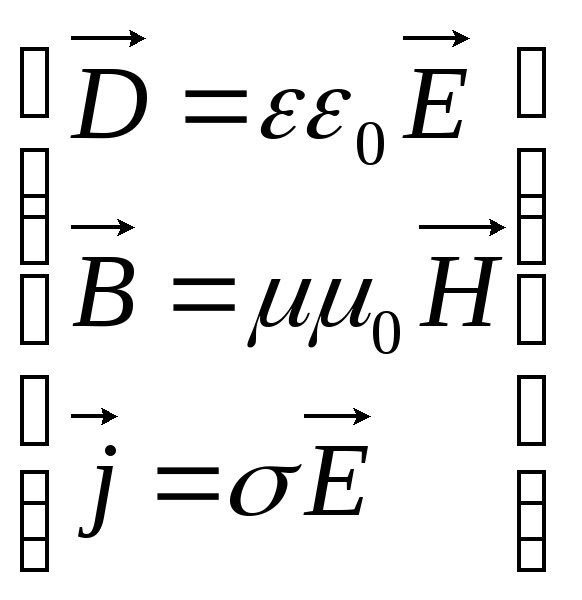(3.5)

Să ne amintim sens fizic aceste fraze matematice.

Prima ecuație (3.1) afirmă că electrostatic câmpul poate fi creat numai de sarcini electrice.În această ecuaţie 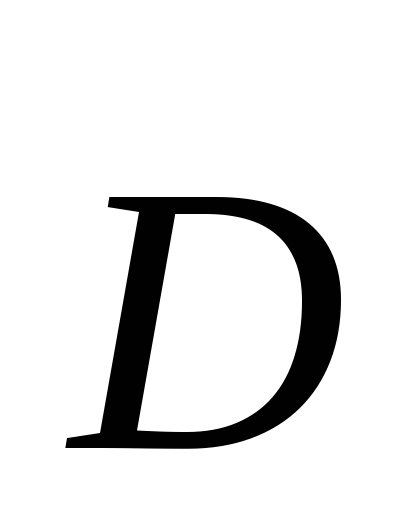este vectorul deplasării electrice, ρ este densitatea de volum a sarcinii electrice.

Fluxul vectorului de deplasare electrică prin orice suprafață închisă este egal cu sarcina închisă în interiorul acestei suprafețe.

După cum arată experimentul, fluxul vectorului de inducție magnetică printr-o suprafață închisă este întotdeauna egal cu zero (3.2)

Compararea ecuațiilor (3.2) și (3.1) ne permite să concluzionăm că nu există sarcini magnetice în natură.

Ecuațiile (3.3) și (3.4) sunt de mare interes și importanță. Aici luăm în considerare circulația vectorilor forței electrice ( ) și magnetice ( ) câmpuri de-a lungul unui contur închis.

Ecuația (3.3) arată că câmpul magnetic alternativ ( 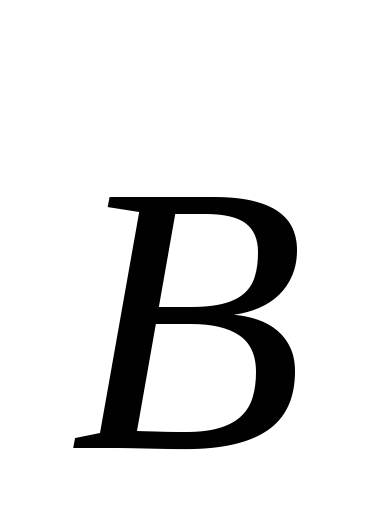) este sursa câmpului electric vortex ( ).Aceasta nu este altceva decât o înregistrare matematică a fenomenului inducției electromagnetice a lui Faraday.

Ecuația (3.4) stabilește o legătură între câmpul magnetic și câmpul electric alternativ. Conform acestei ecuații, câmpul magnetic poate fi creat nu numai de curentul de conducție ( 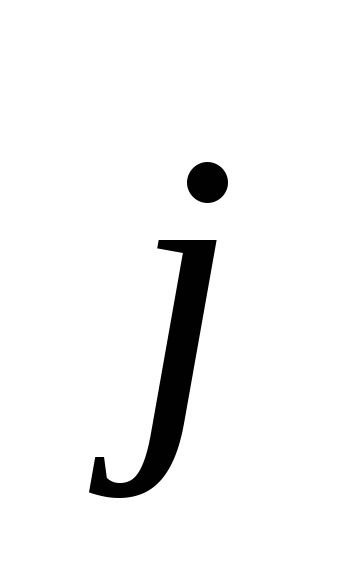), dar și printr-un câmp electric alternativ .

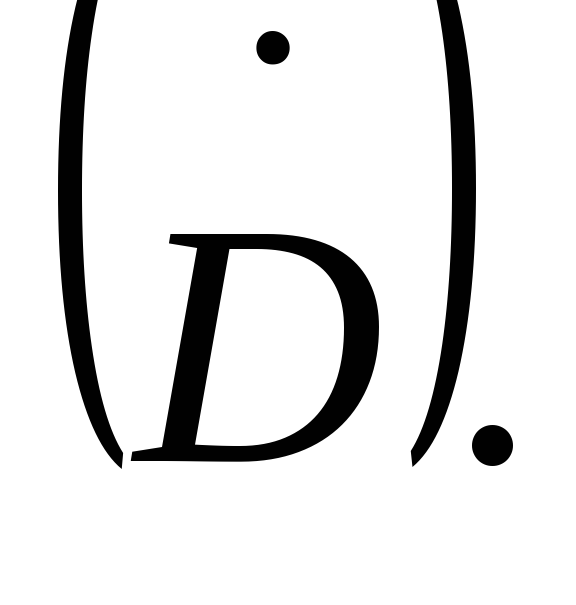În aceste ecuații:

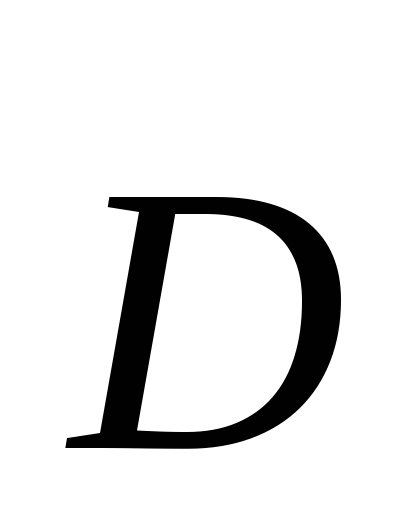este vectorul deplasării electrice,

H- intensitatea câmpului magnetic,

E- intensitatea câmpului electric,

j este densitatea curentului de conducere,

μ - permeabilitatea magnetică a mediului,

ε este constanta dielectrică a mediului.

1. Undele electromagnetice. Proprietățile undelor electromagnetice

Semestrul trecut, completând considerația sistemului de ecuații al electrodinamicii Maxwell clasice, am constatat că soluția comună a ultimelor două ecuații (asupra circulației vectorilor și ) conduce la o ecuație de undă diferențială.

Deci am obținut ecuația de undă a undei „Y”:

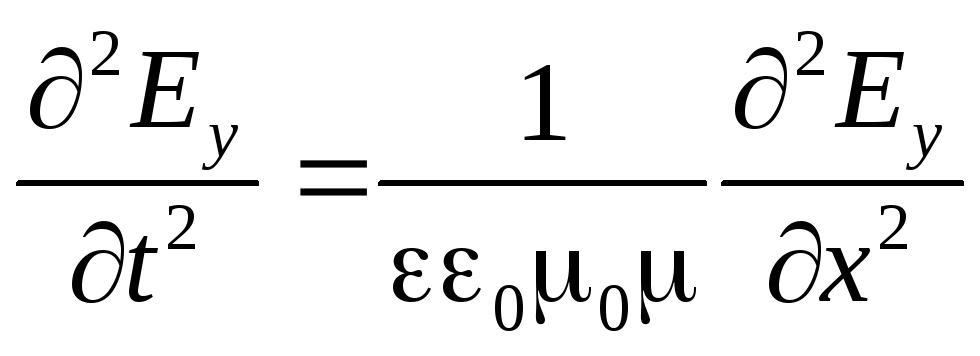. (3.6)

Componenta electrică y - unda se propagă în direcția pozitivă a axei X cu viteza de fază

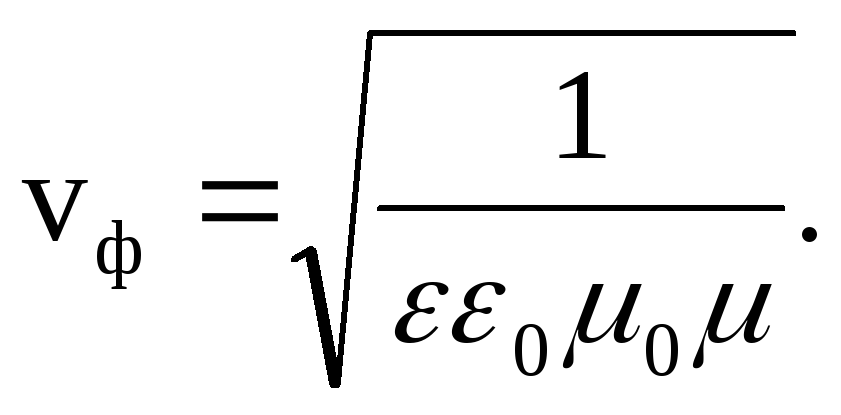(3.7)

O ecuație similară descrie schimbarea în spațiu și timp a câmpului magnetic undele y:

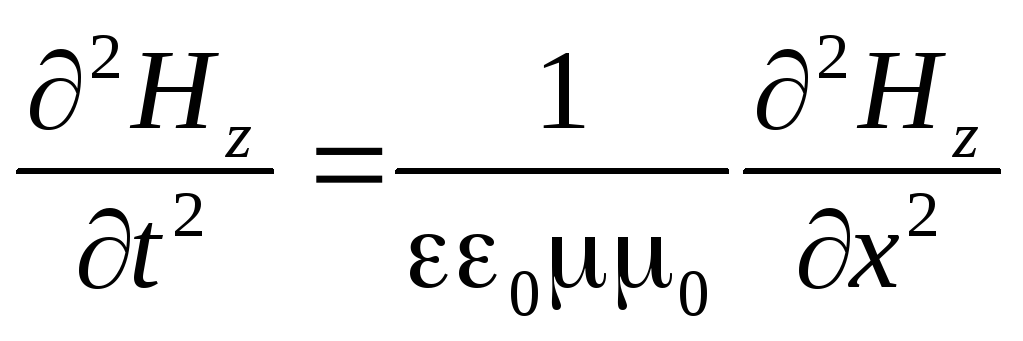. (3.8)

Analizând rezultatele obținute, se pot formula o serie de proprietăți inerente undelor electromagnetice.

1. Planul „y” – unda este o undă transversală polarizată liniar. Vectori de putere electrică ( 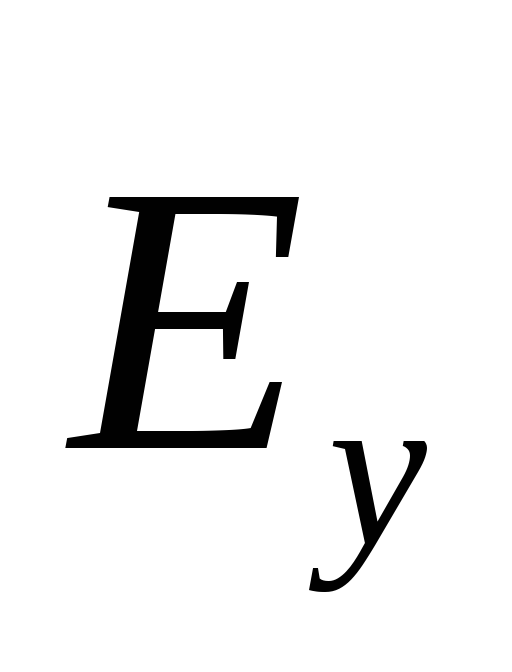), magnetic ( 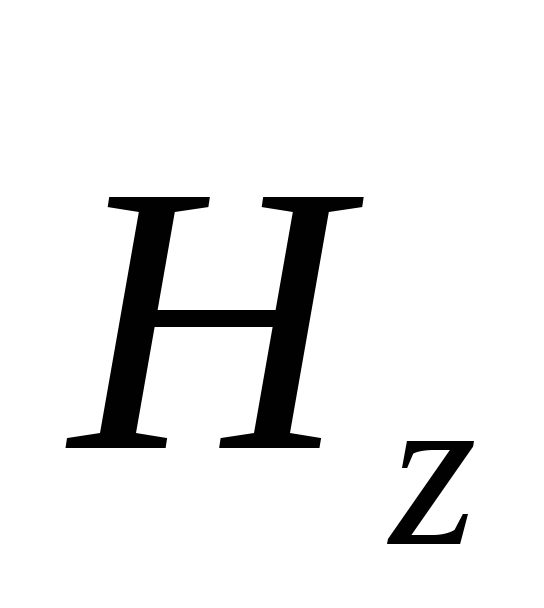) câmpul și viteza de fază a undei ( 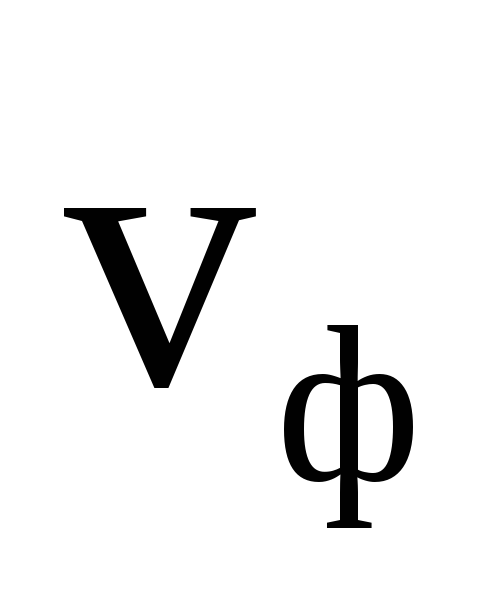) sunt reciproc perpendiculare și formează un sistem „dreapci” (Fig. 3.1).

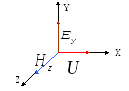
2. În fiecare punct din spațiul componentei undei H z este proporțional cu intensitatea câmpului electric E y:

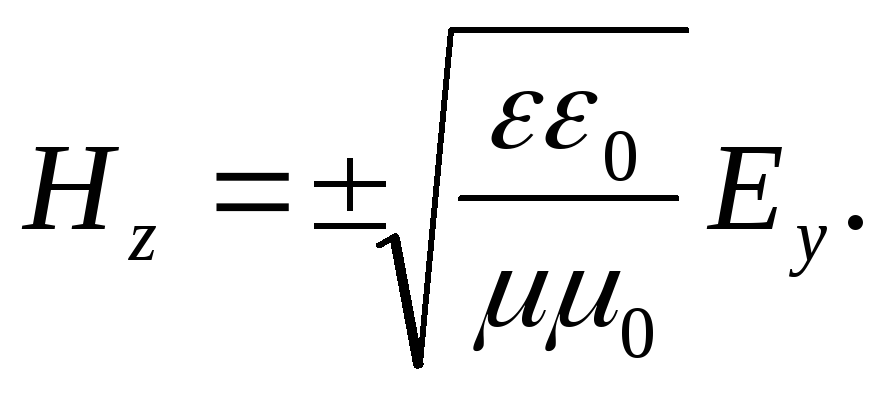
Aici, semnul „+” corespunde unei unde care se propagă în direcția pozitivă a axei X. Semnul „-” - în direcția negativă.

3. O undă electromagnetică se deplasează de-a lungul axei X cu o viteză de fază

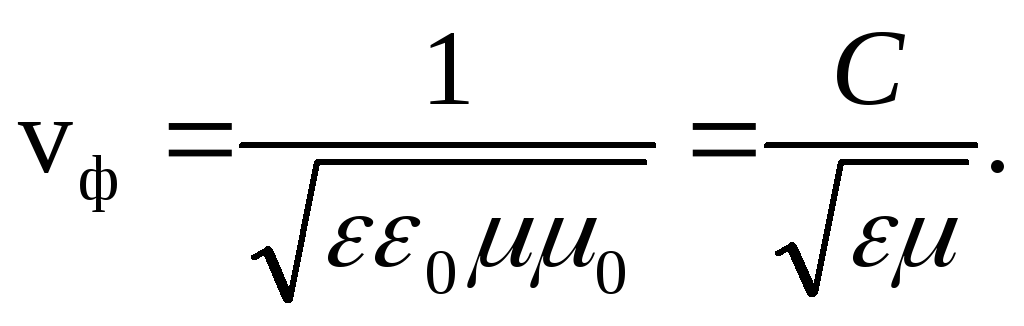
Aici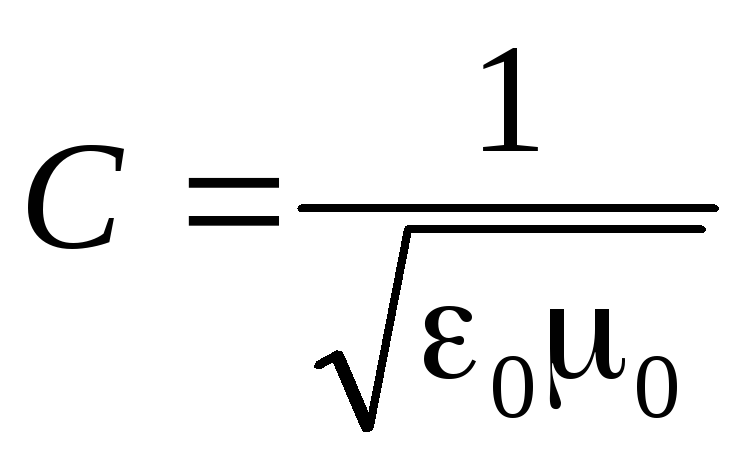

.

Când o undă electromagnetică se propagă în vid (ε = 1, μ = 1), viteza de fază

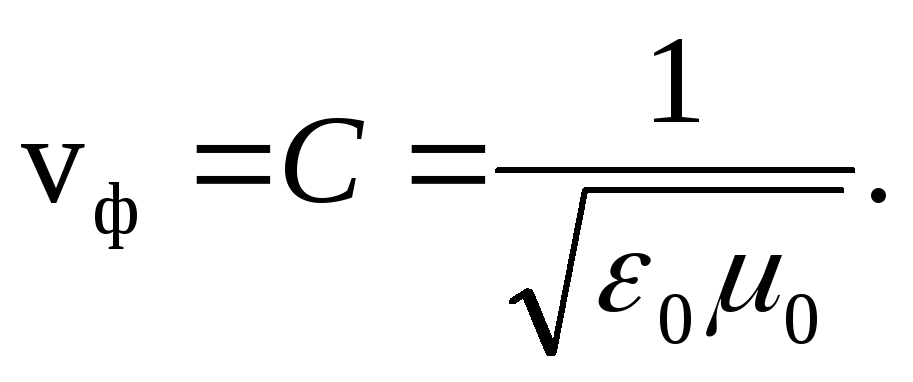
Aici constanta electrică ε 0 = 8,85 10 -12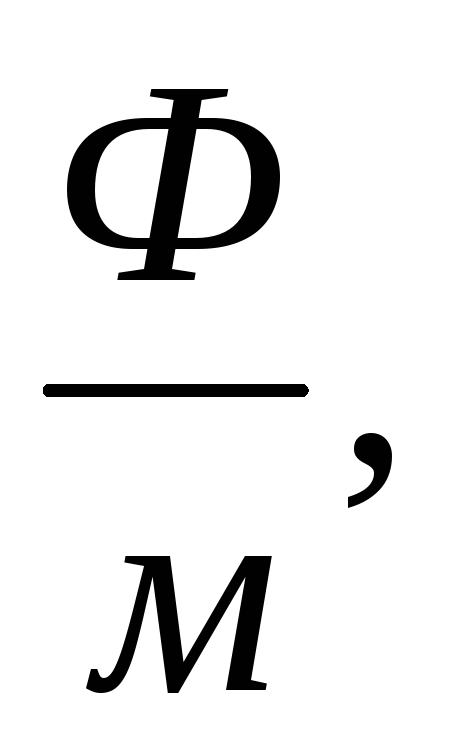

constantă magnetică μ 0 = 4π 10 -7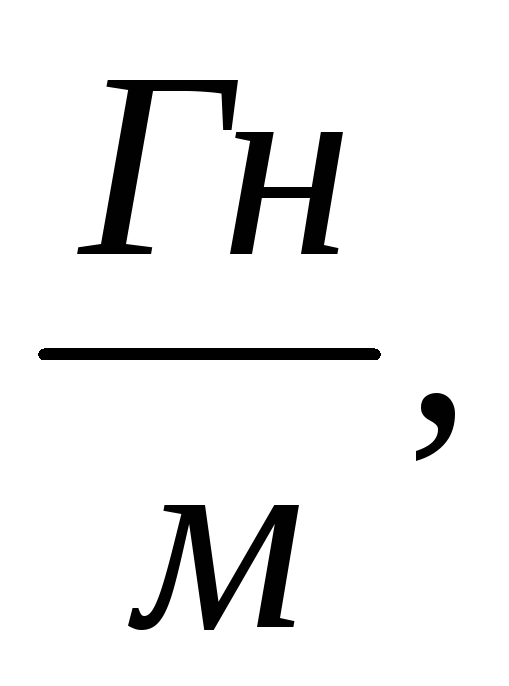

.

.

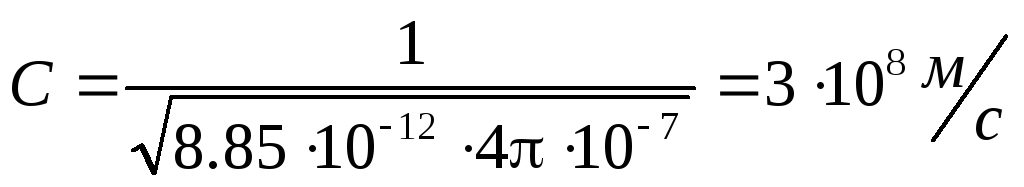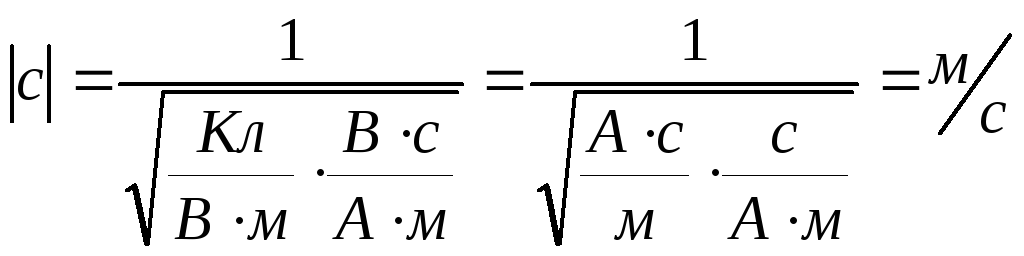Coincidența vitezei unei unde electromagnetice în vid cu viteza luminii a fost prima dovadă a naturii electromagnetice a luminii.

În vid, relația dintre puterea câmpurilor magnetice și electrice din undă este simplificată.

.

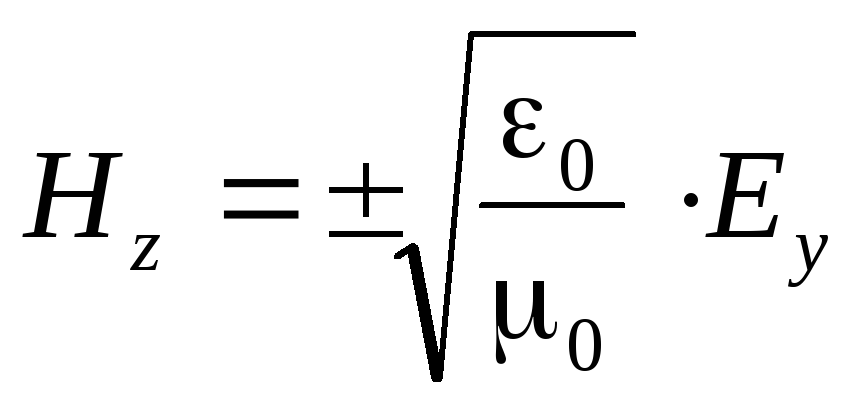Când o undă electromagnetică se propagă într-un mediu dielectric (μ = 1)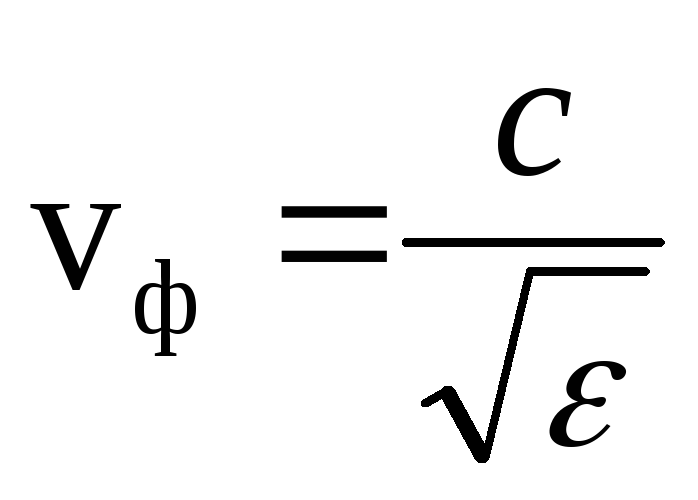

și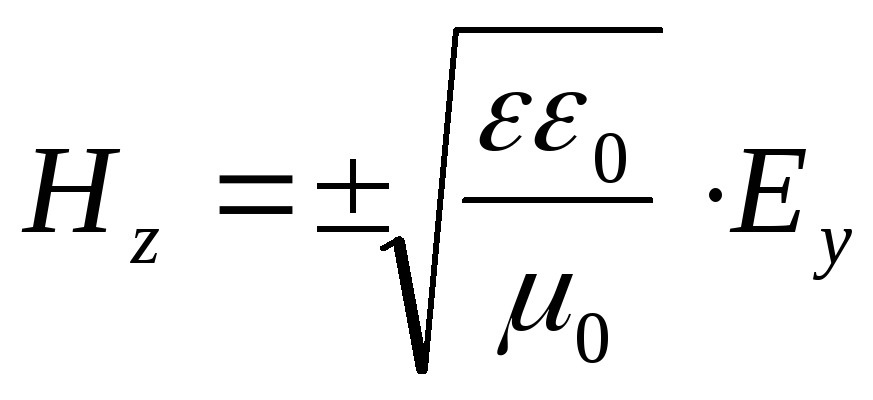

.

Introducerea conceptului de curent de deplasare de către Maxwell l-a condus la finalizarea teoriei macroscopice unificate a câmpului electromagnetic pe care a creat-o, ceea ce a făcut posibilă dintr-un punct de vedere unitar nu numai explicarea fenomenelor electrice și magnetice, ci și predicția. altele noi, a căror existență a fost ulterior confirmată.

Teoria lui Maxwell se bazează pe cele patru ecuații discutate mai sus:

1. Câmpul electric (vezi § 137) poate fi atât potențial ( e q) și vortex ( E B), deci puterea câmpului total E=E Q+ E b. Din moment ce circulaţia vectorului e q este egal cu zero (vezi (137.3)), iar circulația vectorului E B se determină prin expresia (137.2), apoi circulația vectorului intensității câmpului total

Această ecuație arată că sursele câmpului electric pot fi nu numai sarcini electrice, ci și câmpuri magnetice care variază în timp.

2. Teorema generalizată a circulației vectoriale H(vezi (138.4)):

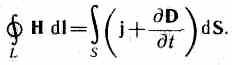
Această ecuație arată că câmpurile magnetice pot fi excitate fie prin sarcini în mișcare (curenți electrici), fie prin câmpuri electrice alternative.

3. Teorema lui Gauss pentru câmp D(vezi (89.3)):

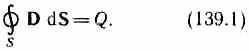
Dacă sarcina este distribuită continuu în interiorul unei suprafețe închise cu o densitate în vrac , atunci formula (139.1) se va scrie ca

4. Teorema lui Gauss pentru câmpul B (vezi (120.3)):

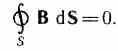
Și 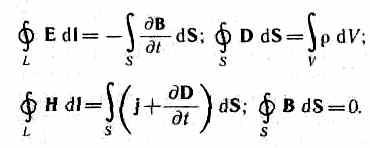Asa de, sistem complet de ecuații Maxwell în formă integrală:

Mărimile incluse în ecuațiile Maxwell nu sunt independente și există următoarea relație între ele (medii izotrope neferoelectrice și neferomagnetice):

D= 0 E,

B= 0 H,

j=E,

unde  0 și  0 sunt, respectiv, constante electrice și magnetice,  și  - respectiv permeabilitate dielectrică şi magnetică,  - conductivitate specifică substanţei.

Din ecuațiile lui Maxwell rezultă că sursele unui câmp electric pot fi fie sarcini electrice, fie câmpuri magnetice variabile în timp, iar câmpurile magnetice pot fi excitate fie prin sarcini electrice în mișcare (curenți electrici), fie prin câmpuri electrice alternative. Ecuațiile lui Maxwell nu sunt simetrice în raport cu câmpurile electrice și magnetice. Acest lucru se datorează faptului că în natură există sarcini electrice, dar nu există sarcini magnetice.

D 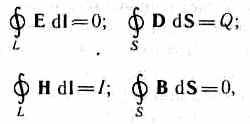pentru câmpuri staționare (E= const şi LA= const) Ecuațiile lui Maxwell ia forma

adică, sursele câmpului electric în acest caz sunt doar sarcini electrice, sursele câmpului magnetic sunt doar curenți de conducție. În acest caz, câmpurile electrice și magnetice sunt independente unul de celălalt, ceea ce face posibilă studierea separată permanent câmpuri electrice și magnetice.

Folosind teoremele Stokes și Gauss cunoscute din analiza vectorială, m 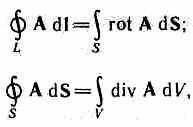se poate imagina sistemul complet de ecuații lui Maxwell în formă diferențială(caracterizarea câmpului în fiecare punct din spațiu):

Dacă sarcinile și curenții sunt distribuiți în spațiu continuu, atunci ambele forme ale ecuațiilor lui Maxwell sunt integrale

și 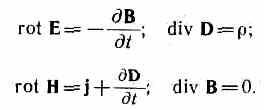diferenţial - echivalent. Totuși, când există suprafete de fractura- suprafete pe care proprietatile mediului sau campurilor se modifica brusc, atunci forma integrala a ecuatiilor este mai generala.

Ecuațiile lui Maxwell sub formă diferențială presupun că toate mărimile din spațiu și timp se modifică continuu. Pentru a obține echivalența matematică a ambelor forme ale ecuațiilor lui Maxwell, forma diferențială este completată Condiții de frontieră, care trebuie să fie satisfăcut de câmpul electromagnetic de la interfaţa dintre două medii. Forma integrală a ecuațiilor lui Maxwell conține aceste condiții. Ele au mai fost luate în considerare (vezi § 90, 134):

D 1 n = D 2 n , E 1  = E 2  , B 1 n = B 2 n , H 1  = H 2 

(prima și ultima ecuație corespund cazurilor în care nu există nici sarcini libere, nici curenți de conducție la interfață).

Ecuațiile lui Maxwell sunt cele mai generale ecuații pentru câmpurile electrice și magnetice în medii de odihnă. Ei joacă același rol în teoria electromagnetismului ca legile lui Newton în mecanică. Din ecuațiile lui Maxwell rezultă că un câmp magnetic alternativ este întotdeauna asociat cu câmpul electric generat de acesta, iar un câmp electric alternativ este întotdeauna asociat cu câmpul magnetic generat de acesta, adică câmpurile electrice și magnetice sunt indisolubil legate între ele - formează un singur câmp electromagnetic.

Teoria lui Maxwell, fiind o generalizare a legilor de bază ale fenomenelor electrice și magnetice, a putut explica nu numai fapte experimentale deja cunoscute, care este și consecința sa importantă, ci și a prezis fenomene noi. Una dintre concluziile importante ale acestei teorii a fost existența unui câmp magnetic de curenți de deplasare (vezi § 138), care i-a permis lui Maxwell să prezică existența. undele electromagnetice- un câmp electromagnetic alternant care se propagă în spațiu cu o viteză finită. Ulterior s-a dovedit că viteza de propagare a unui câmp electromagnetic liber (care nu are legătură cu sarcinile și curenții) în vid este egală cu viteza luminii c = 3 10 8 m/s. Această concluzie și studiul teoretic al proprietăților undelor electromagnetice l-au determinat pe Maxwell să creeze teoria electromagnetică a luminii, conform căreia lumina este și unde electromagnetice. Undele electromagnetice au fost obținute experimental de către fizicianul german G. Hertz (1857-1894), care a demonstrat că legile excitației și propagării lor sunt complet descrise de ecuațiile lui Maxwell. Astfel, teoria lui Maxwell a fost confirmată experimental.

La câmp electromagnetic este aplicabil doar principiul relativității lui Einstein, deoarece undele electromagnetice se propagă în vid în toate cadrele de referință cu aceeași viteză. Cu incompatibil cu principiul relativității lui Galileo.

Conform Principiul relativității al lui Einstein fenomenele mecanice, optice și electromagnetice din toate cadrele de referință inerțiale decurg în același mod, adică sunt descrise prin aceleași ecuații. Ecuațiile lui Maxwell sunt invariante sub transformările Lorentz: forma lor nu se schimbă la trecere

de la unul sistem inerțial referire la altul, deși valorile E, V,D, N sunt convertite după anumite reguli.

Din principiul relativității rezultă că o luare în considerare separată a câmpurilor electrice și magnetice are un sens relativ. Deci, dacă câmpul electric este creat de un sistem de sarcini fixe, atunci aceste sarcini, fiind fixe față de un cadru de referință inerțial, se deplasează față de altul și, prin urmare, vor genera nu numai un câmp electric, ci și un câmp magnetic. . În mod similar, un conductor de curent fix în raport cu un cadru de referință inerțial, excitând un câmp magnetic constant în fiecare punct din spațiu, se mișcă în raport cu alte cadre inerțiale, iar câmpul magnetic alternant creat de acesta excită un câmp electric vortex. Astfel, teoria lui Maxwell, confirmarea sa experimentală, precum și principiul relativității lui Einstein conduc la o teorie unificată a fenomenelor electrice, magnetice și optice bazată pe ideea unui câmp electromagnetic.

Clasificări ale mediilor în raport cu câmpul electromagnetic

Proprietățile mediului în raport cu câmpul electromagnetic sunt determinate de parametri

Conductivitate medie

Dacă acești parametri depind de mărimea câmpului, atunci liniar mediu, iar dacă cel puțin 1 parametru depinde de valoarea câmpului, atunci mediul este neliniară.

Mediile liniare sunt împărțite în 4 grupuri

1. Omogen, unde acești parametri nu depind de coordonate.

2. Neomogen, unde acești parametri depind de coordonate.

3. Izotrop, proprietățile sunt aceleași în toate direcțiile.

4. Anizotrope, proprietățile sunt diferite în toate direcțiile.

Ecuațiile lui Maxwell în forme diferențiale, integrale și complexe

1 Ecuație Maxwell sub formă diferențială: Incarcare electrica este o sursă de inducție electrică.

2 Ecuația lui Maxwell. Nu există sarcini magnetice

3 Ecuația lui Maxwell. Schimbarea inducției magnetice generează un câmp electric vortex

4 Ecuația lui Maxwell. Electricitate iar o schimbare a inducției electrice generează un câmp magnetic vortex

În aceeași ordine, notația integrală

Flux de inducție electrică printr-o suprafață închisă s proporțional cu cantitatea de încărcare gratuită din volum v care inconjoara suprafata s.

Fluxul inducției magnetice printr-o suprafață închisă este zero (sarcinile magnetice nu există).

Modificarea fluxului de inducție magnetică care trece printr-o suprafață deschisă s, luată cu semnul opus, este proporțională cu circulația câmpului electric într-o buclă închisă l s.

Curentul electric total al sarcinilor libere și modificarea fluxului de inducție electrică printr-o suprafață deschisă s, sunt proporționale cu circulația câmpului magnetic într-un circuit închis l, care este limita suprafeței s.

Ecuațiile lui Maxwell pentru amplitudini complexe

3. Ecuația de echilibrare a valorilor puterii instantanee

După cum sa menționat în 1.1, câmpul electromagnetic este una dintre formele materiei. Ca orice altă formă de materie, are energie. Această energie se poate răspândi prin spațiu și poate fi convertită în alte forme de energie.

Să formulăm ecuația de echilibru pentru valorile instantanee ale puterii în raport cu un anumit volum V, delimitată de suprafaţa S (Fig. 1.23). Lasati in volum V, umplute cu un mediu izotrop omogen, există surse terțe. Din conceptele fizice generale, este evident că puterea eliberată de surse terțe poate fi cheltuită pentru pierderi în Joule și pentru modificarea energiei câmpului electromagnetic din interior. V,și poate fi, de asemenea, parțial împrăștiat, scăpând în spațiul înconjurător prin suprafața S. În acest caz, egalitatea

Unde R st este puterea surselor terțe; R P - pierderile de putere ale Joule în interiorul volumului V; R Σ este puterea care trece prin suprafața S; W- energia unui câmp electromagnetic concentrat într-un volum V, A dW/dt- puterea cheltuită pentru a schimba energia în volum v.

LA aceasta sectiune se vor folosi ecuaţiile de stare (1.53). Aceste ecuații nu permit luarea în considerare a pierderilor de energie în timpul polarizării și magnetizării mediului. Prin urmare, termenul R P în egalitatea (1.120) determină de fapt puterea pierderilor Joule în volumul V , cauzate de curentul de conducere.

Ecuația (1.120) oferă doar o idee calitativă a relațiilor energetice. Pentru a obține relații cantitative, trebuie să utilizați ecuațiile lui Maxwell. Se consideră prima ecuație Maxwell, ținând cont de curenții externi (1.111). Toți membrii acestei ecuații sunt mărimi vectoriale având dimensiunea A/m 2 .

Pentru a obține o ecuație similară cu (1.120), trebuie să modificați prima ecuație a lui Maxwell (1.111) astfel încât termenii săi să devină mărimi scalare măsurate în wați. Pentru a face acest lucru, este suficient să înmulțiți scalar toți termenii egalității indicate cu vectorul E, și apoi integrați expresia rezultată peste volum v. După înmulțirea scalară cu un vector E primim

Folosind formula div cunoscută din analiza vectorială = = H rot E - E rot H, transformăm partea stângă a relației (1.121) și înlocuim rot E cu valoarea sa din a doua ecuație Maxwell (1.39):

Înlocuind această expresie în (1.121), obținem

În ultimul termen din partea dreaptă a lui (1.122), ordinea factorilor în produsul scalar al vectorilor este schimbată dB/dtși H. Acest lucru este permis deoarece H dB/dt = dLA/dtH. Această modificare nu este fundamentală și nu oferă niciun avantaj în derivarea ecuației de echilibru luate în considerare aici pentru valorile puterii instantanee. Cu toate acestea, cu o astfel de notație, în toți termenii ecuației (1.122) al doilea factor (vectori j Sf, j, BDIDtși H) este un vector care a fost inclus anterior în prima ecuație Maxwell. Această împrejurare va face posibilă în viitor (vezi 1.8.4) să se simplifice oarecum derivarea ecuației de echilibru în cazul unui câmp monocromatic (ecuația de echilibru a puterii complexe). Integrarea ecuației termen cu termen (1.122) peste volum V, primim

unde este direcția elementului dS coincide cu direcția normalei exterioare la suprafața S. Trecând de la (1.122) la (1.123), teorema Ostrogradsky-Gauss este folosită pentru a transla integrala de volum din div[ E, H] în integrala de suprafață a produsului vectorial [ E, H]. Introducem notația

și transformă integrandul în ultimul termen din partea dreaptă a (1.123):

Înlocuind (1.124) și (1.125) în (1.123) și schimbând ordinea integrării și diferențierii, obținem

Să aflăm semnificația fizică a expresiilor incluse în ecuația (1.126).

Luați în considerare primul termen din partea dreaptă a (1.126). Să ne imaginăm volumul V ca o sumă de cilindri infinitezimali de lungime dl, ale căror capete ( dS ) perpendicular pe direcția curentului (vector j). Apoi EjdV=EjdV=(Edl)(jdS) = dUdl = dP n , Unde dl=jdS este curentul care curge prin cilindrul infinitezimal considerat; dU = Edl- modificarea potenţialului pe lungime dl, A dP n este puterea pierderilor Joule în volum d V . Prin urmare, termenul luat în considerare este puterea pierderilor Joule Р p în volum v. Folosind raportul j = σЕ, pentru R P se pot obtine alte reprezentari:

Formulele (1.127) pot fi considerate drept o lege Joule-Lenz generalizată valabilă pentru un volum conductor V formă arbitrară.

Integrala din partea stângă a (1.126) diferă de primul termen din partea dreaptă doar prin aceea din integrand în loc de j inclus j c t. Prin urmare, trebuie să determine puterea surselor terțe. Vom lua în considerare puterea pozitivă eliberată de curenții externi câmpului electromagnetic. Curentul electric este o mișcare ordonată a particulelor încărcate. Direcția pozitivă a curentului este direcția de mișcare sarcini pozitive. Curentul eliberează energie câmpului electromagnetic atunci când particulele încărcate care îl formează încetinesc. Pentru aceasta, este necesar ca vectorul intensității câmpului electric E avea o componentă orientată opus direcției curentului, adică. la produsul punctual al vectorilor Eși j st a fost negativ ( E j Sf<0). При этом левая часть равенства (1.126) будет поло­жительной величиной. Таким образом, мгновенное значение мощ­ности, отдаваемой сторонними токами электромагнитному полю в объеме V, este definit de expresia

Pentru a înțelege semnificația fizică a ultimului termen din partea dreaptă a ecuației (1.126), luăm în considerare un caz special. Să presupunem că volumul Vînconjurat de un înveliș perfect conducător care coincide cu suprafața S. Apoi componenta tangentă a vectorului E pe suprafata S va fi egal cu zero. Element de suprafață dS coincide în direcția cu normala exterioară n 0 . În consecință, integrala de suprafață din ecuația (1.126) va fi egală cu zero, deoarece componenta normală a produsului vectorial [ E, H] este determinată de componentele tangente ale Vectorilor săi. În plus, să presupunem că mediul în interiorul volumului V nu are conductivitate σ = 0). În acest caz, nu vor exista pierderi Joule în regiunea luată în considerare, iar prima integrală din partea dreaptă a ecuației (1.126) va fi, de asemenea, egală cu zero. Drept urmare, obținem

Evident, în cazul în cauză, puterea surselor externe poate fi cheltuită doar pentru modificarea energiei câmpului electromagnetic. Astfel, partea dreaptă a egalității (1.129) este rata de modificare a energiei câmpului electromagnetic stocat în volum. V, acestea. corespunde termenului dW/dtîn ecuația (1.126). Este firesc să presupunem că integrala din partea dreaptă a lui (1.129) este egală cu energia câmpului electromagnetic concentrat în volumul V:

Strict vorbind, această integrală poate diferi W la o anumită funcție g = g(x, y, z) independent de timp. Este ușor de verificat dacă funcția d este egal cu zero. Să rescriem (1.130) ca W \u003d W E + W M, Unde

Să presupunem că câmpurile electrice și magnetice sunt constante (nu depind de timp). În acest caz, după cum se știe din cursul fizicii (vezi și capitolele 3 și 4), expresiile (1.131) și (1.132) determină energia câmpului electric și respectiv magnetic în volum. v. Dar aceasta înseamnă că g = 0 și aceste expresii determină valorile instantanee ale energiei câmpurilor electrice și magnetice în volum V pentru orice dependență de timp, suma lor, determinată de formula (1.130), este într-adevăr egală cu valoarea instantanee a energiei câmpului electromagnetic în volum v.

Rămâne să clarificăm esența fizică a integralei de suprafață din ecuația (1.126). Presupunem că în volum V nu există pierderi și, în plus, cantitatea de energie electromagnetică rămâne constantă (W= const). În acest caz, ecuația (1.126) ia forma

În același timp, din reprezentările fizice este evident că, în acest caz particular, toată puterea surselor terțe ar trebui să meargă în spațiul înconjurător. (R Sf = Р Σ). Prin urmare, partea dreaptă a ecuației (1.133) este egală cu fluxul de energie prin suprafața S (limita raportului dintre cantitatea de energie care trece prin S în timp Δt la Δt→0), acestea.

Este firesc să presupunem că vectorul P reprezintă densitatea fluxului de energie (limita raportului fluxului de energie prin zonă ∆S, situat perpendicular pe direcția de propagare a energiei, spre ∆S la ∆S→0). Din punct de vedere formal, matematic, această presupunere nu este evidentă, deoarece înlocuirea vectorului P pe P 1 = P + putregai A, Unde A- vector arbitrar, nu modifică valoarea R Σ . Cu toate acestea, este adevărat și, în special, decurge direct din teoria relativistă a câmpului electromagnetic.

Astfel, egalitatea (1.126) este similară cu (1.120) și reprezintă ecuația pentru bilanţul valorilor instantanee ale puterii câmpului electromagnetic. A fost obținut de Poynting în 1884 și se numește Teorema punctării.În consecință, vectorul P se numește vectorul Poynting. Numele sunt, de asemenea, adesea folosite „Teorema Umov-Poynting”și "Vector de indicare Umov" pentru a sublinia faptul că formularea legii conservării energiei într-o formă generală cu introducerea conceptului de flux energetic și de vector care caracterizează densitatea acestuia a fost dată mai întâi de N.A. Umov în 1874.

Rețineți că energia poate intra în volum V nu numai din surse exterioare. De exemplu, fluxul de energie prin suprafața S poate fi direcționat din spațiul înconjurător în volum v.În același timp, puterea PΣ va fi negativ, deoarece fluxul de energie care iese din volum este considerat pozitiv Vîn spațiul înconjurător (direcția elementului dS coincide cu direcția normalei exterioare la suprafața S).

Sursele terțe pot nu numai să ofere energie, ci și să o primească din câmpul electromagnetic. În acest caz, puterea surselor terțe va fi negativă. Într-adevăr, câmpul electromagnetic emite energie curentului de conducere dacă accelerează mișcarea particulelor încărcate care formează curentul. Pentru aceasta, vectorul intensității câmpului electric E trebuie să aibă o componentă orientată de-a lungul liniilor de curgere, adică astfel încât produsul scalar al vectorilor E şi j st a fost mai mare decât zero.

Să luăm în considerare mai detaliat formulele care determină energia câmpului electromagnetic. Integrale în

pot fi interpretate ca valorile instantanee ale densităților volumetrice de energie ale câmpurilor electrice și respectiv magnetice și suma acestora

Ca densitate de volum a energiei totale a câmpului electromagnetic.

Subliniem că principiul suprapunerii, care este satisfăcut de vectorii puterilor câmpurilor electrice și magnetice, nu se aplică energiei. Într-adevăr, lăsați energiile câmpului E1, H1 şi E2, H2, existenta separat in zona V, egal, respectiv W 1și W2. Apoi energia câmpului total E \u003d E 1 + E 2, H \u003d H 1 + H 2 este determinată de expresie

Energia reciprocă a câmpurilor. Energie reciprocă W 12 poate fi atât pozitiv, cât și negativ. Dacă vectorii E 1și E 2, precum și H1și H 2 reciproc perpendiculare, deci W 12 = 0.

În cazul proceselor variabile, distribuția energiei electromagnetice se modifică continuu. Această modificare în orice punct dat poate fi determinată pe baza ecuației (1.122), care este reprezentată în mod convenabil ca

unde p st \u003d- E j st și p n = E j- valorile instantanee ale densităților de putere ale surselor terțe și, respectiv, ale pierderilor de putere în Joule. La trecerea de la relația (1.122) la ecuația (1.136), se iau în considerare formulele (1.125) și (1.135). Ecuația (1.136) este forma diferențială a teoremei lui Poynting.

4 ECUATII DE UNDE

Caz general

Când se rezolvă probleme directe de electrodinamică, se cere găsirea vectorilor Eși H conform surselor terțe cunoscute (specificate). Să presupunem că sursele externe sunt situate într-un mediu izotrop omogen infinit. Pentru a simplifica transformările, vom presupune că σ= 0. Scriind ecuațiile Maxwell pentru acest caz particular, obținem

Definiţia vectors Eși H direct din sistemul de ecuații (2.25) este dificil. Prin urmare, este recomandabil să-l transformi prin eliminarea fie a vectorului E, sau un vector H, adică obțineți din aceasta o astfel de ecuație diferențială, care să includă doar unul dintre vectori E sau H. Pentru a face acest lucru, luăm rotorul din ambele părți ale celei de-a doua ecuații a sistemului (2.25) și schimbăm ordinea diferențierii în timp și în coordonate spațiale. Luând în considerare egalitatea cunoscută din analiza vectorială

unde Δ 2 ≡Δ-operator Laplace și a treia egalitate a sistemului luat în considerare, ajungem la ecuație

În mod similar, ecuația pentru vector este derivată H:

Fiecare dintre ecuațiile vectoriale (2.27) și (2.28) este echivalentă cu trei ecuații scalare obținute prin proiectarea ecuației vectoriale pe axe X Yși Z al sistemului de coordonate carteziene. Aceste ecuații scalare sunt de forma

Unde wși f(x, y, z, f)-funcții căutate și, respectiv, date (cunoscute). După cum se știe, ecuațiile de forma (2.29) descriu procesele undei și parametrul v egală cu viteza acestui proces. Astfel de ecuații se numesc ecuații d'Alembert neomogene sau ecuații de undă neomogene. Ecuațiile (2.27) și (2.28) diferă de (2.29) doar prin faptul că funcțiile pe care le conțin sunt funcții vectoriale. Acest tip de ecuație se numește ecuații d'Alembert vectoriale neomogene sau ecuații de undă vectorială neomogene. Se numesc ecuații analoge ale căror părți din dreapta sunt egale cu zero ecuații vector omogene d'Alembert (ecuații de undă vectorială omogene). Mai târziu se va arăta că parametrul intră în ecuațiile (2.27) și (2.28), care este un analog al parametrului vîn (2.29), în cazul unui mediu fără pierderi, este și viteza de propagare a câmpului electromagnetic și este egală cu viteza luminii în mediul considerat. Acest rezultat nu este neașteptat, deoarece lumina sunt unde electromagnetice dintr-un anumit interval de frecvență.

Ecuații similare pentru vectori pot fi scrise fără dificultate Eși H iar în cazul când σ≠0 (vezi, de exemplu, ).

câmp monocromatic

În cazul unui câmp monocromatic, sistemul complet de ecuații lui Maxwell în formă complexă, ținând cont de sursele electrice externe, are forma

Să presupunem că mediul care umple partea considerată a spațiului este omogen și izotrop. Să luăm bucla din ambele părți ale celei de-a doua ecuații a sistemului (2.30) și să excludem vectorul H, folosind prima ecuație. Ținând cont de formula (2.26) și de egalitatea valabilă pentru un mediu izotrop omogen, ajungem la ecuație

unde Pentru vector H obținem în mod similar

Este evident că aceleași ecuații relaționează amplitudinile complexe

Dacă nu există surse externe în zona luată în considerare, ecuațiile (2.31) și (2.32) sunt simplificate:

Pentru a trece la cazul unui mediu fără pierderi în ecuațiile (2.30)-(2.34) trebuie să punem . Fiecare

din ecuațiile vectoriale (2.33) și (2.34) este echivalentă cu trei ecuații scalare de același tip pentru componentele carteziene ale vectorului corespunzător: ∆ 2w+ k 2w= 0, unde w- oricare dintre componente