§ 15. POTENȚIAL. ENERGIA SISTEMULUI DE ÎNCĂRCĂRI ELECTRICE. LUCRĂRI LA MUTAREA ÎNCĂRCĂRII ÎN CÂMP

Formule de bază

 Potenţial câmp electric este o cantitate egală cu raportul dintre energia potențială a unei sarcini pozitive punctiforme plasate în punct dat câmpuri, la această taxă;

=P/ Q,

sau potențialul câmpului electric este o mărime egală cu raportul dintre munca forțelor câmpului pentru a muta o sarcină pozitivă punctuală dintr-un punct dat al câmpului la infinit la această sarcină:

=A/ Q.

Potențialul câmpului electric la infinit este considerat condiționat egal cu zero.

Rețineți că atunci când o sarcină se mișcă într-un câmp electric, funcționează A v.s forțele externe este egală în valoare absolută cu munca A s.p. intensitatea câmpului și este opus acesteia în semn:

A v.s = – A s.p. .

 Potențialul câmpului electric creat de o sarcină punctiformă Q pe distanta r din sarcina

 Potențialul câmpului electric creat de metal, purtând o taxă Q sferă cu rază R, la o distanță de centrul sferei:

în interiorul sferei ( r<R)

;

pe suprafața unei sfere ( r=R)


;

fara scop (r> R)

.

În toate formulele date pentru potențialul unei sfere încărcate,  este permisivitatea unui dielectric infinit omogen care înconjoară sfera.

 Potenţialul câmpului electric creat de sistem P sarcinile punctuale, într-un punct dat, în conformitate cu principiul suprapunerii câmpurilor electrice, este egală cu suma algebrică a potențialelor  1 , 2 , ... , n, creat de taxe punctuale individuale Q 1 ,Q 2 , ...,Q n :


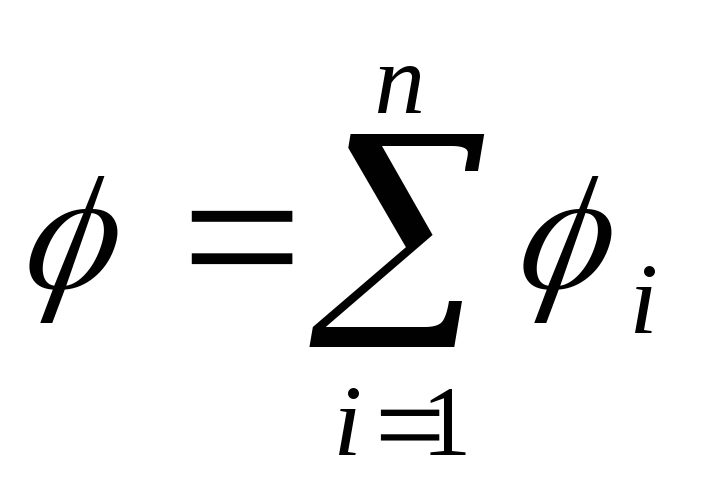
 Energie W interacțiunile unui sistem de sarcini punctiforme Q 1 ,Q 2 , ...,Q n este determinată de munca pe care o poate face acest sistem de sarcini atunci când sunt îndepărtate unul față de celălalt la infinit și este exprimat prin formula


,

unde  i- potenţialul câmpului creat de toţi P- 1 taxe (excluzând prima) în punctul în care se află taxa Q i .

 Potențialul este legat de puterea câmpului electric prin relație

E= -grad.

În cazul unui câmp electric cu simetrie sferică, această relație este exprimată prin formula


,

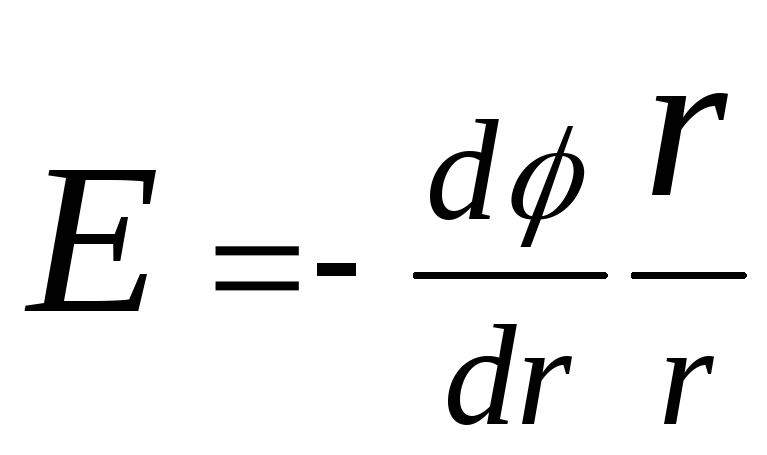sau sub formă scalară


,

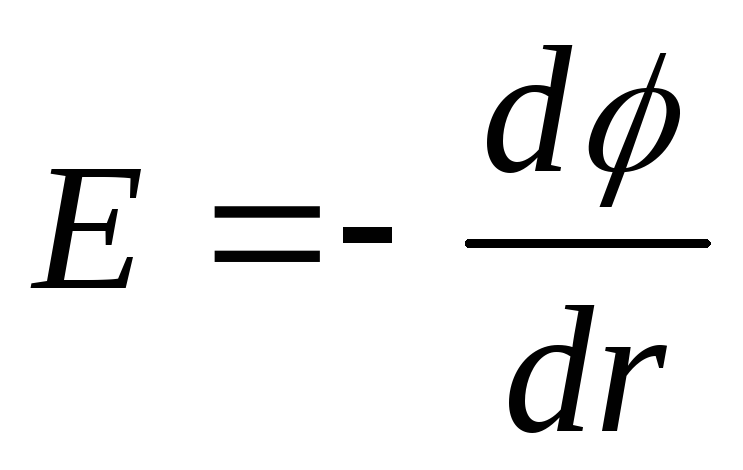iar în caz câmp omogen, adică un câmp a cărui intensitate în fiecare punct este aceeași atât ca valoare absolută, cât și ca direcție,

E=( 1 – 2 ,)/d,

unde  1 și 2 - potenţialele punctelor a două suprafeţe echipotenţiale; d - distanța dintre aceste suprafețe de-a lungul circuitului electric linia de câmp.

 Lucrul efectuat de un câmp electric la deplasarea unei sarcini punctiforme Q dintr-un punct al câmpului cu un potenţial  1 , într-un altul cu un potențial  2 ,

A=Q( 1 - 2 ), sau

,

Unde E l - proiecția vectorului de tensiune E la direcția de mișcare; dl - circulaţie.

În cazul unui câmp omogen, ultima formulă ia forma

A= QElcos,

Unde l- deplasarea; - unghiul dintre directiile vectorului Eși deplasare l.

Exemple de rezolvare a problemelor

Exemplul 1 sarcini pozitive Q 1 \u003d 3 μC și Q 2 \u003d 20 nC sunt în vid la distanță r 1 =l.5 m distanta. Definiți un loc de muncă A, ceea ce trebuie făcut pentru a apropia încărcăturile la distanță r 2 = 1 m.

Soluţie. Să presupunem că prima încărcare Q 1 rămâne staționar și celălalt Q 2 sub acţiunea forţelor externe se deplasează în câmpul creat de sarcină Q 1 apropiindu-se de el de la distanţă r 1 =t,5 m până la r 2 = 1 m .

Muncă DAR" forță externă pentru deplasarea încărcăturii Q dintr-un punct al câmpului cu potenţial  1 în altul, al cărui potenţial 2 , egal în valoare absolută și opus în semn să lucreze DAR forțe de câmp pentru mișcarea sarcinii între aceleași puncte:

A "= -A.

Muncă DAR forțe de câmp la deplasarea sarcinii A=Q( 1 - 2 ). Atunci lucrează DAR" forțele externe pot fi scrise ca

A" = –Q( 1 - 2 )=Q( 2 - 1 ). (1)

Potențialele punctelor de început și de sfârșit ale traseului sunt exprimate prin formule


;

.

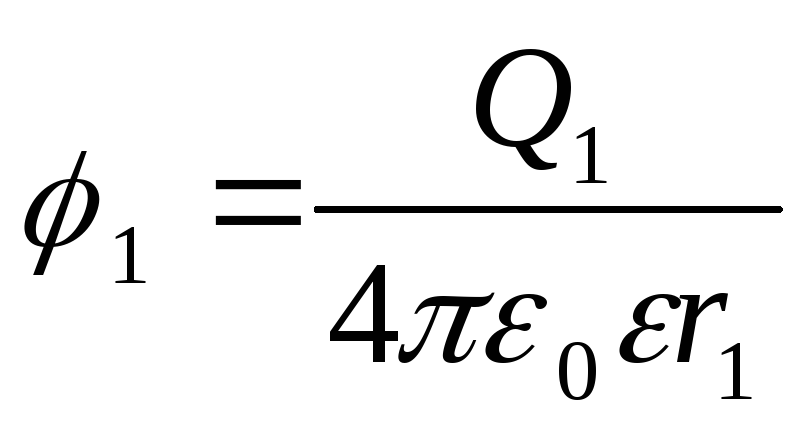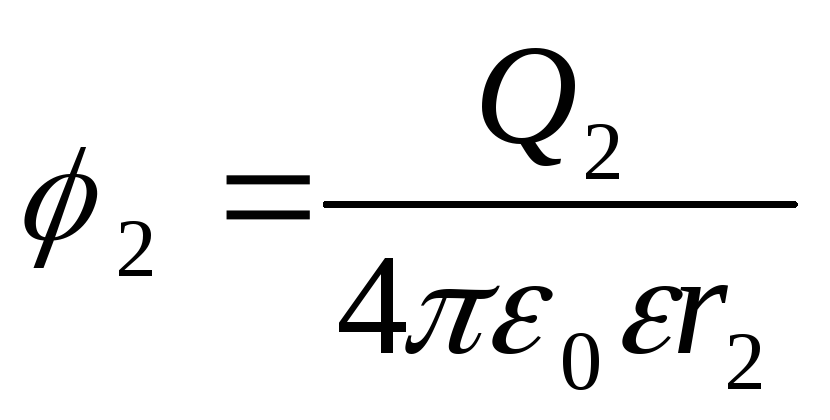Înlocuind expresiile  1 și 2 în formula (1) și ținând cont că pentru acest caz taxa transferată Q=Q 2 , primim


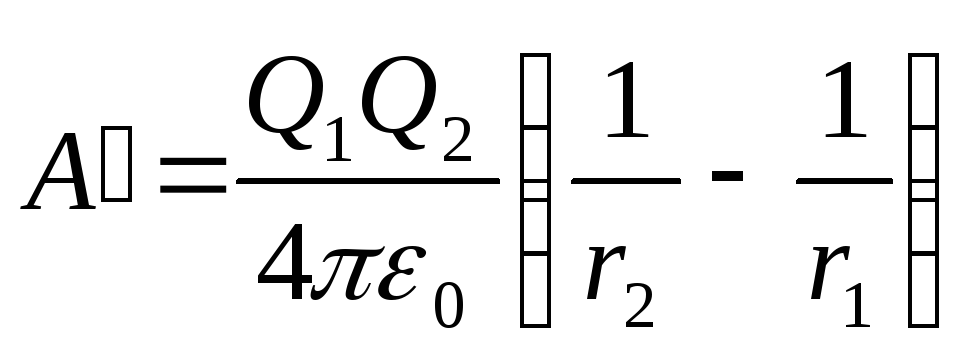. (2)

Având în vedere că 1/(4 0 )=910 9 m/F, apoi după înlocuirea valorilor cantităților în formula (2) și calculul, găsim

A„=180 uJ.

Exemplul 2 Gaseste o slujba DAR câmpuri de transfer de taxe Q=10 nC de la punct 1 exact 2 (Fig. 15.1), situat între două încărcate opus, cu o densitate de suprafață  \u003d 0,4 μC / m 2 planuri paralele infinite, distanță l intre ele este de 3 cm.

R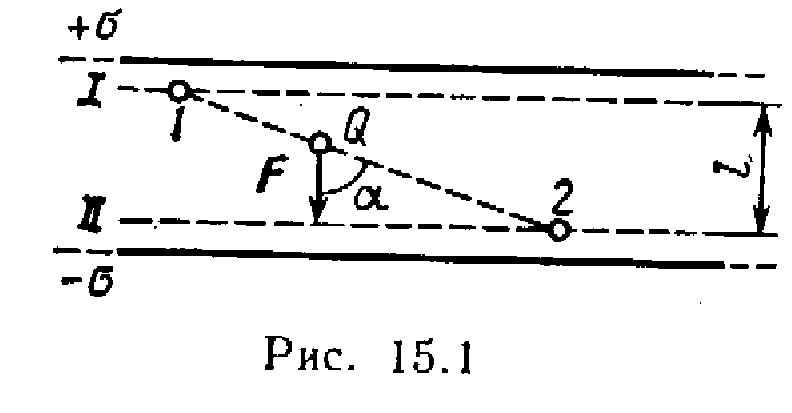

soluţie. Există două moduri de a rezolva problema.

1-a cale. Lucrarea câmpului forțează să miște sarcina Q din punct 1 domenii cu potenţial 1 exact 2 domenii cu potenţial 2 găsi prin formulă

A=Q( 1 - 2 ). (1)

Pentru a determina potențialele în puncte 1 și 2 Să desenăm suprafețele echipotențiale I și II prin aceste puncte. Aceste suprafețe vor fi plane, deoarece câmpul dintre două plane paralele infinit încărcate uniform este uniform. Pentru un astfel de domeniu, relația

1 - 2 =El, (2)

Unde E - intensitatea câmpului; l - distanța dintre suprafețele echipotențiale.

Intensitatea câmpului între planuri paralele infinite încărcate opus E=/ 0 . Înlocuind această expresie Eîn formula (2) și apoi expresia 1 - 2 în formula (1), obținem

A= Q(/ 0 ) l.

a 2-a cale. Deoarece câmpul este uniform, forța care acționează asupra sarcinii Q, este constantă pe măsură ce se mișcă. Prin urmare, munca de mutare a încărcăturii din punct 1 exact 2 poate fi calculat folosind formula

A=F r cos, (3)

Unde F - forță care acționează asupra unei sarcini r- modul de transfer de incarcare Q dintr-un punct 1 exact 2;  este unghiul dintre direcțiile deplasării și forței . Dar F= QE= Q(/ 0 ). Înlocuind această expresie Fîn egalitate (3), precum și observând că  r cos= l, primim

A=Q(/ 0 )l. (4)

Astfel, ambele soluții duc la același rezultat.

Înlocuind în expresia (4) valoarea mărimilor Q, , 0 și l, găsi

A\u003d 13,6 μJ.

Exemplul 3 Pe un fir subțire îndoit de-a lungul unui arc de cerc cu o rază R, sarcină uniform distribuită cu densitate liniară=10 nC/m. Definiți tensiunea Eși potențialul  al câmpului electric creat de un astfel de p

sarcină distribuită într-un punct O, care coincide cu centrul de curbură al arcului. Lungime l firul este 1/3 din circumferinta si este egal cu 15 cm.

Soluţie. Alegem axele de coordonate astfel încât originea coordonatelor să coincidă cu centrul de curbură al arcului, iar axa la era situat simetric fata de capetele arcului (Fig. 15.2). Selectați un element de lungime d pe fir l. Încărcat Q=d l, situat în zona selectată, poate fi considerat ca punct.

Să determinăm puterea câmpului electric în punct O. Pentru a face acest lucru, găsim mai întâi tensiunea d E câmp creat de taxa d Q:


,

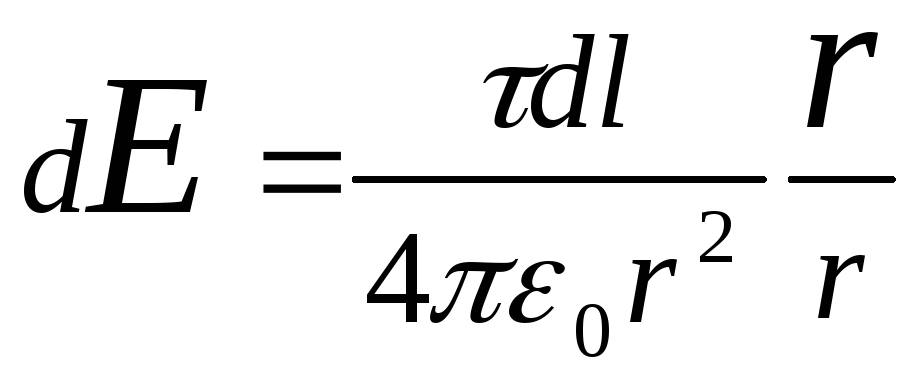Unde r-raza-vector îndreptat departe de elementul d l până la punctul în care se calculează tensiunea. Exprimăm vectorul d E prin proiecție dE X cși dE y pe axa de coordonate:


,

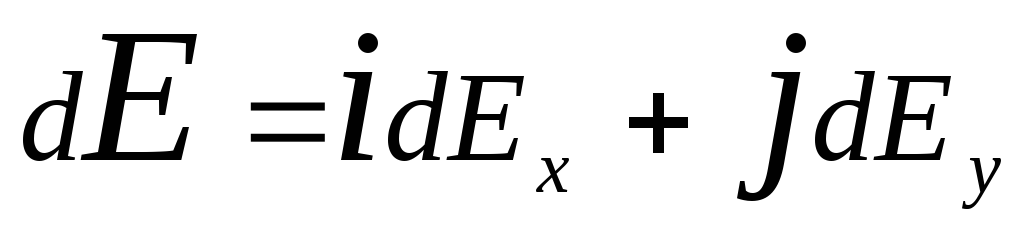Unde iși j- vectori de direcție unitară (orte).

tensiune E găsiți prin integrare:


.

Integrarea se realizează de-a lungul arcului de lungime l. Datorită simetriei, integrala este egal cu zero. Apoi


, (1)

Unde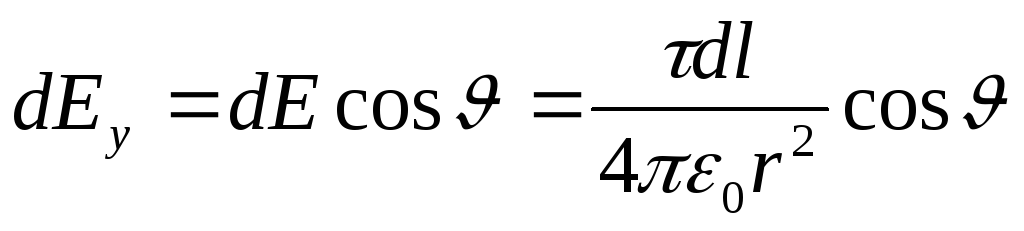

. pentru că r=R= const și d l=R d. apoi


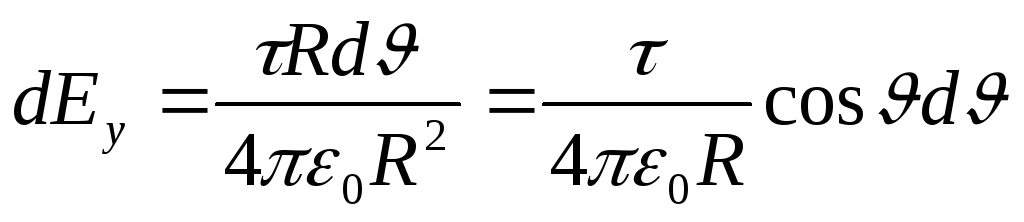
Înlocuiți expresia găsită dE yîn (1) și, ținând cont de locația simetrică a arcului în raport cu axa OU, luăm limitele de integrare de la 0 la /3, și dublăm rezultatul;


.

Înlocuind aceste limite și exprimând R prin lungimea arcului (3 l= 2 r), primim


.

Această formulă arată că vectorul E coincide cu direcția pozitivă a axei OUÎnlocuind valoarea și lîn ultima formulă și făcând calculele, găsim

E\u003d 2,18 kV / m.

Să determinăm potențialul câmpului electric în punct O. Să găsim mai întâi potențialul d creat de sarcina punctiformă d Q la punct O:


Să înlocuim r pe Rși efectuează integrarea:


.Pentru că l=2 R/3, apoi

=/(6 0 ).

Făcând calcule conform acestei formule, obținem

Exemplu4 . Câmpul electric este creat de un cilindru lung cu o rază R= 1 cm , încărcat uniform cu densitatea liniară=20 nC/m. Determinați diferența de potențial a două puncte din acest câmp situate la distanțe A 1 =0,5 cm și A 2 \u003d 2 cm de suprafața cilindrului, în partea mijlocie.

Soluţie. Pentru a determina diferența de potențial, folosim relația dintre intensitatea câmpului și modificarea potențialului E= -grad. Pentru un câmp cu simetrie axială, care este câmpul unui cilindru, această relație poate fi scrisă ca

E= -( d/d r) , sau d= - E d r.

Integrând ultima expresie, găsim diferența de potențial a două puncte separate prin r 1 și r 2 din axa cilindrului;


. (1)

Deoarece cilindrul este lung și punctele sunt luate în apropierea părții sale din mijloc, puterea câmpului poate fi exprimată folosind formula

. Înlocuind această expresie Eîn egalitate (1), obținem


(2)

Din moment ce cantitatile r 2 și r 1 introduceți formula ca raport, apoi pot fi exprimate în oricare, dar numai în aceleași unități:

r 1 =R+a 1 = 1,5 cm; r 2 =R+A 2 = 3 cm .

Înlocuind valorile mărimii , 0 ,r 1 și r 2 în formula (2) și calculând, găsim

1 - 2 =250 V.

Exemplul 5 Câmpul electric este creat de o tijă subțire care poartă o sarcină =0,1 μC/m distribuită uniform pe lungimea sa. Determinați potențialul  al câmpului într-un punct îndepărtat de capetele tijei la distanță, egal cu lungimea tijă.

Soluţie. Sarcina de pe tijă nu poate fi considerată o sarcină punctuală, prin urmare, aplicați direct formula pentru a calcula potențialul


, (1)

valabil doar pentru taxe punctuale, este imposibil. Dar dacă împărțim tija în segmente elementare d l, apoi taxad l situate pe fiecare dintre ele pot fi considerate ca punct și atunci formula (1) va fi valabilă. Aplicând această formulă, obținem


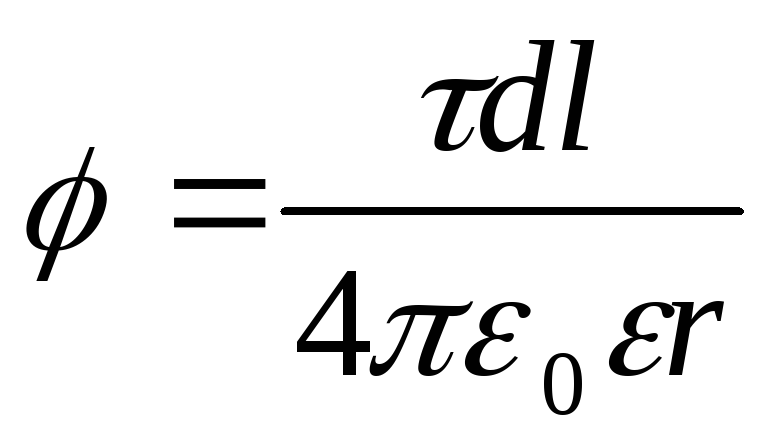, (2)

Unde r - distanța dintre punctul în care este determinat potențialul până la elementul tijei.

Din fig. 15.3 că d l=(r d/cos). Înlocuind această expresie d lîn formula (2), găsim

.

Integrarea expresiei rezultate în limitele lui  1 da 2 , obținem potențialul creat de întreaga sarcină distribuită pe tijă: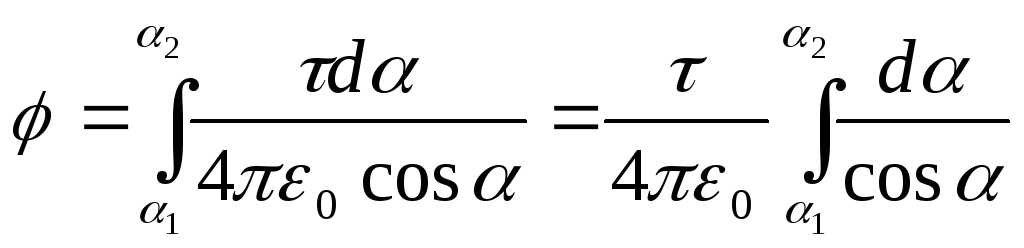

.

LA 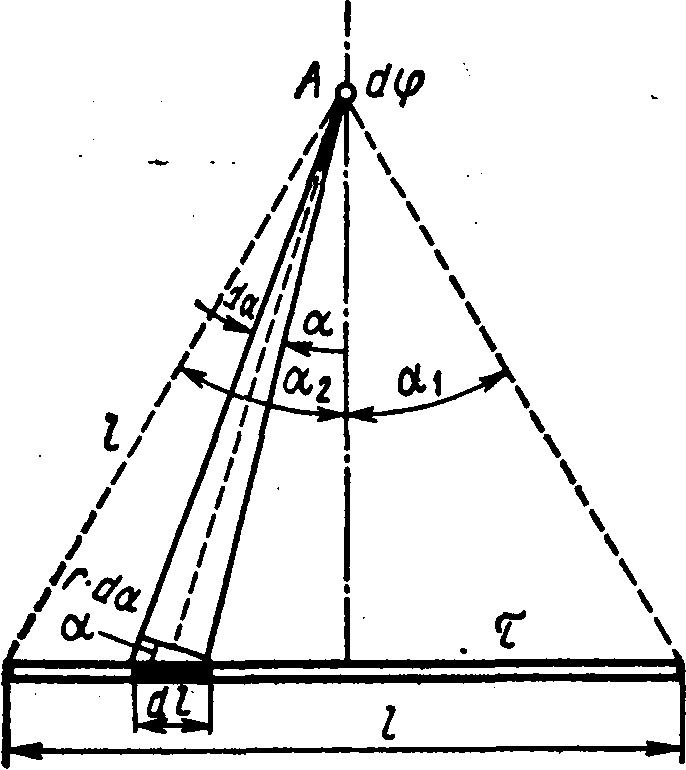forța de simetrie a punctului DAR raportat la capetele tijei avem  2 = 1 prin urmare

.

Prin urmare,


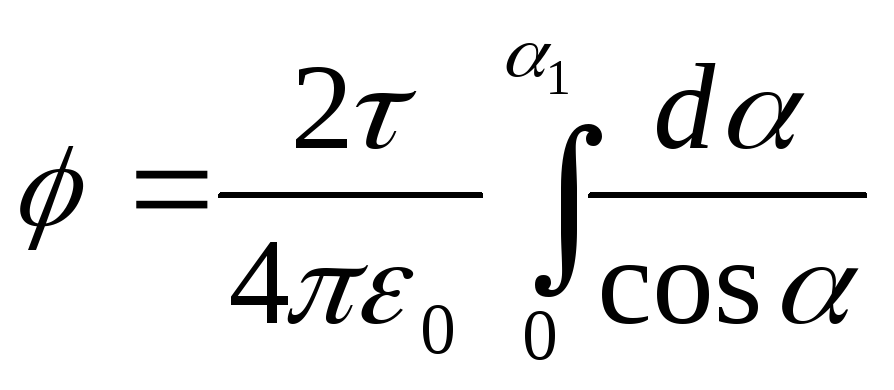.Pentru că

(vezi tabelul 2), atunci

.

Înlocuind limitele integrării, obținem

După ce am făcut calcule conform acestei formule, găsim

Exemplul 6 Un electron cu viteza v=1,8310 6 m/s a zburat într-un câmp electric uniform în direcția opusă vectorului intensității câmpului. Ce diferență de potențial U trebuie să treacă un electron pentru a avea energie E i\u003d 13,6 eV *? (Având o astfel de energie, un electron îl poate ioniza atunci când se ciocnește cu un atom de hidrogen. Energia de 13,6 eV se numește energia de ionizare a hidrogenului.)

Soluţie. Electronul trebuie să treacă de o astfel de diferență de potențial tu, astfel încât energia dobândită W combinat cu energia cinetică T, pe care electronul o avea înainte de a intra în câmp, se ridica la o energie egală cu energia de ionizare E i , adică W+ T= E i . Exprimând în această formulă W= UEși T=(m v 2 /2), obținem UE+(m v 2 /2)=E i. De aici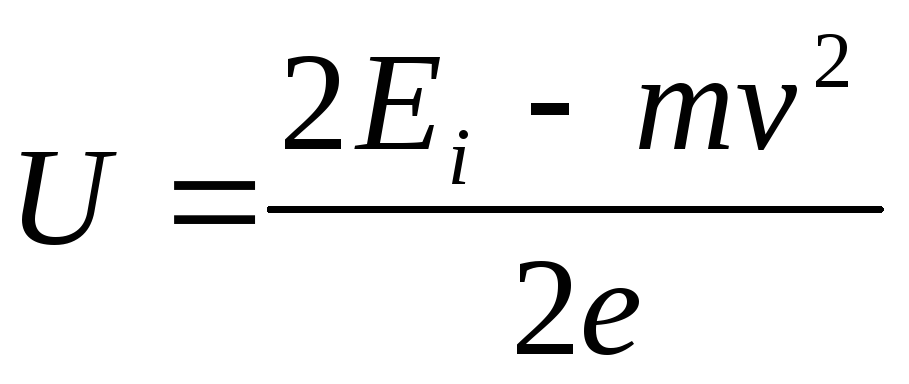

.

___________________

* Electron-volt (eV) - energia pe care o dobândește o particulă, având o sarcină egală cu sarcina unui electron, trecând printr-o diferență de potențial de 1 V. Această unitate de energie non-sistemică este în prezent aprobată pentru utilizare în fizică.

Să facem calcule în unități SI:

U=4,15 LA.

Exemplul 7 Determinați viteza inițială υ 0 apropierea protonilor situati la o suficient distanta lunga unul de altul dacă distanța minimă r min , prin care se pot apropia, este de 10 -11 cm.

Soluție: Există forțe de respingere între cei doi protoni, drept urmare mișcarea protonilor va fi lentă. Prin urmare, problema poate fi rezolvată ca sistem inerțial coordonate (asociate cu centrul de masă a doi protoni) și în neinerțial (asociate cu unul dintre protonii care se mișcă rapid). În al doilea caz, legile lui Newton nu sunt valabile. Aplicarea principiului d'Alembert este dificilă datorită faptului că acceleraţia sistemului va fi variabilă. Prin urmare, este convenabil să luăm în considerare problema într-un cadru de referință inerțial.

Să plasăm originea coordonatelor în centrul de masă a doi protoni. Deoarece avem de-a face cu particule identice, centrul de masă va fi în punctul care traversează segmentul care leagă particulele. Față de centrul de masă, particulele vor avea în orice moment aceleași viteze modulo. Când particulele se află la o distanță suficient de mare unele de altele, viteza υ 1 fiecare particulă este egală cu jumătate υ 0 , adică υ 1 =υ 0 /2.

Pentru a rezolva problema, aplicăm legea conservării energiei, conform căreia energia mecanică totală E sistem izolat este constant, adică

E=T+ P ,

Unde T- suma energiilor cinetice ale ambilor protoni fata de centrul de masa; P este energia potențială a sistemului de sarcini.

Exprimăm energia potențială în momentele inițiale P 1 și P 2 finale ale mișcării.

La momentul inițial, după starea problemei, protonii se aflau la mare distanță, deci energia potențială poate fi neglijată (P 1 =0). Prin urmare, pentru momentul inițial energie totală va fi egală cu energia cinetică T 1 protoni, adică

E=T l . (1)

În momentul final, când protonii se apropie cât mai aproape posibil, viteza și energia cinetică sunt egale cu zero, iar energia totală va fi egală cu energia potențială P 2, adică.

E= P 2 . (2)

Echivalând părțile corecte ale egalităților (1) și (2), obținem

T 1 \u003d P 2. (3)

Energia cinetică este egală cu suma energiilor cinetice ale protonilor:


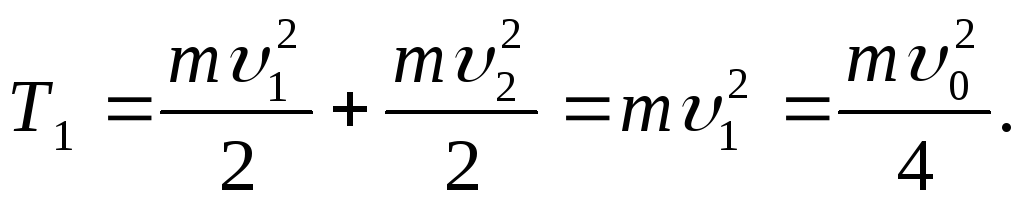(4)

Energia potențială a unui sistem de două sarcini Q 1 și Q 2 în vid este determinat de formula

, Unde r- distanta dintre incarcari. Folosind această formulă, obținem


(5)

Luând în considerare egalitățile (4) și (5), formula (3) ia forma


Unde

După efectuarea calculelor după formula obținută, găsim υ 0 =2,35 mm/s

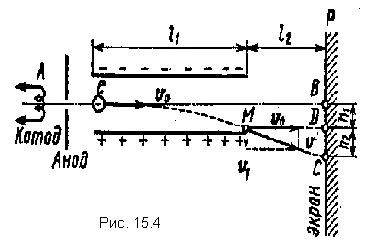Exemplul 8 Un electron fără viteză inițială a depășit diferența de potențial U 0 =10 kV și a zburat în spațiul dintre plăcile unui condensator plat încărcat la o diferență de potențial U l \u003d 100 V, de-a lungul liniei AB, paralel cu plăcile (Fig. 15.4). Distanţă dîntre plăci este de 2 cm.Lungime l 1 plăci condensatoare în direcția zborului electronilor este egală cu 20 cm. Determinați distanța Soare pe ecran R, departe de condensator l 2 \u003d 1 m.

Soluție.Mișcarea unui electron în interiorul condensatorului constă din două mișcări: 1) prin inerție de-a lungul liniei AB cu o viteză constantă υ 0 , dobandit sub actiunea unei diferente de potential U 0 , pe care electronul a trecut la condensator; 2) mișcare accelerată uniform în direcția verticală către o placă încărcată pozitiv sub acțiunea unei forțe constante de câmp a condensatorului. După părăsirea condensatorului, electronul se va mișca uniform cu o viteză υ, pe care o avea la punct M la momentul iesirii din condensator.

Din fig. 15.4 arată că distanța dorită | | BC|=h 1 +h 2 , de unde h 1 - distanța pe care electronul se va deplasa în direcția verticală în timp ce se deplasează în condensator; h 2 - distanța dintre punctul D de pe ecran, în care ar cădea electronul, mișcându-se la ieșirea din condensator în direcția vitezei inițiale υ 0 și punctul C, unde electronul lovește efectiv.

Exprimați separat h 1 și h 2 . Folosind formula pentru lungimea traseului mișcării uniform accelerate, găsim


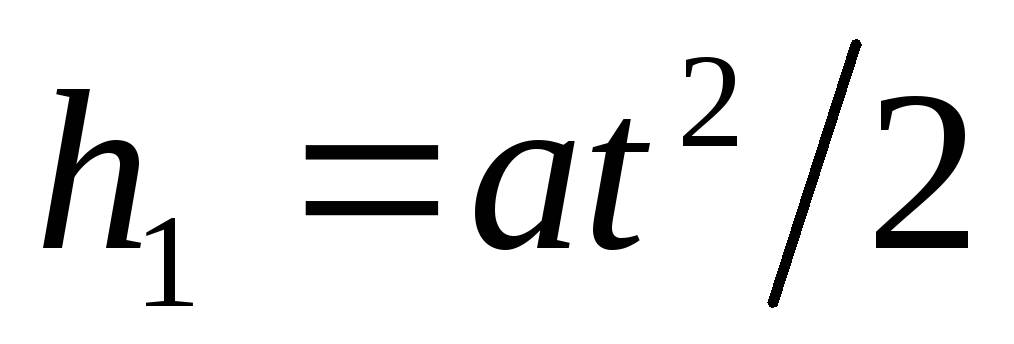. (1)

Unde A- acceleratia primita de electron sub actiunea campului condensatorului; t- timpul de zbor al unui electron în interiorul unui condensator.

Conform celei de-a doua legi a lui Newton a=F/m, Unde F- forta cu care actioneaza campul asupra electronului; t- masa acestuia. La randul lui, F=eE=eU 1 /d, Unde e- sarcina electronilor; U 1 - diferența de potențial dintre plăcile condensatorului; d- distanta dintre ele. Găsim timpul de zbor al unui electron în interiorul condensatorului din formula pentru calea mișcării uniforme

, Unde


Unde l 1 este lungimea condensatorului în direcția de zbor a electronilor. Găsim expresia vitezei din condiția de egalitate a muncii efectuate de câmp la mișcarea electronului și a energiei cinetice dobândite de acesta:

. De aici


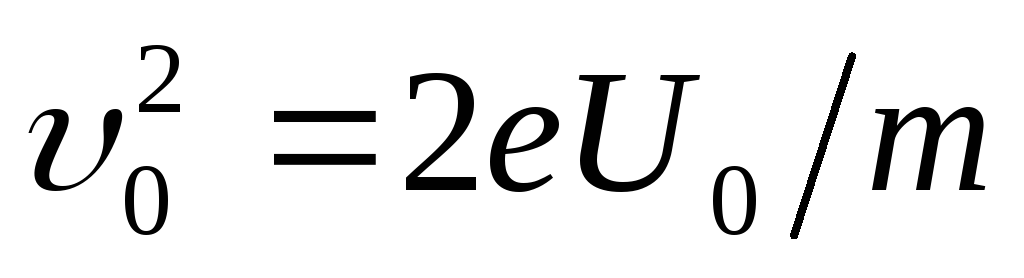(2)

Înlocuind în formula (1) succesiv valorile A,F, tși υ 0 2 din expresiile corespunzătoare, obținem

Lungimea tăiată h 2 găsiți din asemănarea triunghiurilor MDCși vector:


(3)

Unde υ 1 - viteza electronului în direcția verticală într-un punct M;l 2 - distanța de la condensator la ecran.

Viteză υ 1 găsim prin formula υ 1 =la, care, ținând cont de expresiile pentru a, Fși t va lua forma


Înlocuind expresia υ 1 în formula (3), obținem

, sau prin înlocuire υ 0 2 prin formula (3), găsim


În sfârșit pentru distanța necesară | î.Hr| vom avea

|î.Hr|=

­

Înlocuirea valorilor cantităților U 1 ,U 0 ,d,l 1 și l 2 în ultima expresie și efectuând calcule, obținem | î.Hr|=5,5 cm.

Sarcini

Energia potențială și potențialul de câmp al sarcinilor punctuale

15.1. taxă punctuală Q\u003d 10 nC, fiind într-un anumit punct al câmpului, are o energie potențială P \u003d 10 μJ. Găsiți potențialul φ al acestui punct de câmp.

5.2. Când mutați încărcarea Q=20 nC între două puncte ale câmpului, munca a fost făcută de forțe externe A=4µJ. Definiți un loc de muncă A 1 forțele câmpului și diferența Δφ a potențialelor acestor puncte ale câmpului.

15.3. Câmpul electric este creat de o sarcină punctiformă pozitivă Q 1 \u003d 6 nC. sarcină pozitivă Q 2 este transferat din punct DAR acest câmp până la un punct LA(Fig. 15.5). Care este modificarea energiei potențiale ΔP pe unitatea de sarcină transferată, dacă r 1 =20 cm și r 2 \u003d 50 cm?

15.4. Câmp electric creat de o sarcină punctiformă Q l \u003d 50 nC. Fără a folosi conceptul de potențial, calculați munca DARîn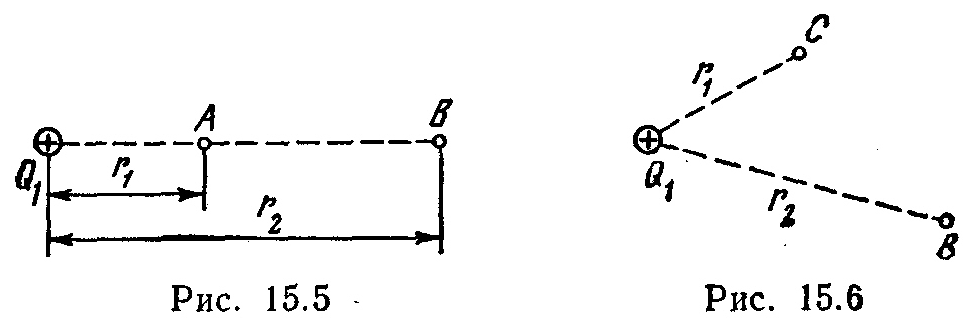

forțe externe pentru a deplasa o sarcină punctiformă Q 2 = -2 nC din punct DIN exact LA

(Fig. 15.6), dacă r 1 =10 cm, r 2 \u003d 20 cm.Determină, de asemenea, modificarea ΔP a energiei potențiale a sistemului de sarcini.

15.5. Câmpul este creat de o încărcare punctiformă Q=1 nC. Determinați potențialul φ al câmpului într-un punct îndepărtat de sarcină la distanță r= 20 cm.

15.6. Determinați potențialul φ al câmpului electric într-un punct îndepărtat de sarcini Q 1 = -0,2 uC și Q 2 =0,5 μC, respectiv, on r 1 =15 mass media r 2 \u003d 25 cm.Determină, de asemenea, distanțele minime și maxime dintre sarcini pentru care este posibilă o soluție.

15.7. Taxe Q 1 \u003d 1 μC și Q 2 = -1 μC sunt la distanță d\u003d 10 cm. Determinați tensiunea Eși potențialul φ al câmpului într-un punct îndepărtat la distanță r= 10 cm de prima sarcină și întins pe o linie care trece prin prima sarcină perpendicular pe direcția de la Q 1 la Q 2 .

15.8. Calculați energia potențială P a unui sistem de două sarcini punctiforme Q 1 =100 nC și Q 2 =10 nC la distanta d= 10 cm distanță.

15.9. Aflați energia potențială P a unui sistem de trei sarcini punctiforme Q 1 \u003d 10 nC, Q 2 =20 nCl și Q 3 \u003d -30 nC, situat la vârfurile unui triunghi echilateral cu lungimea laturii A= 10 cm.

15.10. Ce este energie potențialăП sisteme de patru sarcini punctiforme identice Q\u003d 10 nC, situat la vârfurile unui pătrat cu lungimea laturii A\u003d 10 cm? .

15.11. Determinați energia potențială P a unui sistem de patru sarcini punctiforme situate la vârfurile unui pătrat cu lungimea laturii A\u003d 10 cm. Taxele sunt aceleași ca modul Q=10 nC, dar două dintre ele sunt negative. Luați în considerare două cazuri posibile de aranjare a taxelor.



15.12 . Câmpul este creat de două taxe punctiforme + 2Qși -Q, de la distanță d= 12 cm distanță. Determinați locul punctelor din planul pentru care potențialul este zero (scrieți ecuația pentru dreapta potențialului zero).

5.13. Sistemul este format din trei încărcări - două de aceeași dimensiune Q 1 = |Q 2 |=1 μC și opus în semn și sarcină Q=20 nC, situat în punctul 1 din mijloc între celelalte două sarcini ale sistemului (Fig. 15.7). Determinați modificarea energiei potențiale ΔP a sistemului în timpul transferului de sarcină Q de la punctul 1 la punctul 2. Aceste puncte sunt îndepărtate din sarcina negativă Q 1 pe distanta a= 0,2 m.

Potenţialul câmpului sarcinilor distribuite liniar

15.14. De-a lungul unui inel subțire cu o rază R= 10 cm sarcină uniform distribuită cu o densitate liniară τ= 10 nC/m. Determinați potențialul φ într-un punct situat pe axa inelului, la distanță a= 5 cm de centru.

15.15. Pe un segment de conductor drept subțire, o sarcină este distribuită uniform cu o densitate liniară τ=10 nC/m. Calculați potențialul φ creat de această sarcină într-un punct situat pe axa conductorului și îndepărtat de cel mai apropiat capăt al segmentului cu o distanță egală cu lungimea acestui segment.

Câmpul electrostatic este potențial, forțele Coulomb sunt forțe conservative, iar munca forțelor conservatoare poate fi reprezentată ca o scădere a energiei potențiale, adică.

unde C este constanta de integrare, care este de obicei aleasă astfel încât atunci când sarcina q este îndepărtată la infinit - W р = 0, i.e. C=0.

Vom investiga ESP folosind taxe de testare q pr 1 , q pr 2 , q pr 3 –

Potențialul unui câmp electrostatic este energia caracteristică a câmpului, numeric egală cu raportul dintre energia potențială a testului incarcare electrica, plasat într-un punct dat al câmpului, la mărimea sarcinii.

Apoi, folosind relațiile (7.1) și (7.7), obținem:

Cunoscând distribuția sarcinilor, putem găsi potențialul de câmp al oricărui sistem.

Potențialele de câmp sunt adăugate algebric, prin urmare, calculul potențialelor este de obicei mai simplu decât calculul puterilor EF.

În SI, unitatea de potențial este [ j ] \u003d 1J / C \u003d 1V

O unitate de lucru de 1 eV (electron volt) este egală cu munca efectuată de forțele câmpului asupra sarcinii egal cu taxa electron, când trece printr-o diferență de potențial de 1 V.

1 eV = 1,6´10 -19 C ´ 1V=1,6´10 -19 J

Model video: 1) Mișcarea sarcinilor într-un câmp electric; 2) Spectrometru de masă.

Un corp situat într-un câmp potențial de forțe (un câmp electrostatic) are energie potențială datorită căreia munca este efectuată de forțele câmpului. Lucrarea forțelor conservatoare se realizează din cauza pierderii de energie potențială. Prin urmare, munca forțelor câmpului electrostatic poate fi reprezentată ca diferența de energii potențiale deținute de taxă punctuală Q 0 la punctele de început și de sfârșit ale câmpului de încărcare Q: , de unde rezultă că energia potenţială a sarcinii q0în câmpul de taxare Q este egal cu . Este definit în mod ambiguu și până la o constantă arbitrară DIN. Dacă presupunem că atunci când sarcina este îndepărtată la infinit ( r®¥) energia potențială dispare ( U=0), apoi DIN=0 și energia potențială a sarcinii Q 0 , situat în domeniul de sarcină Q la o distanta r ​​de acesta, este egal cu . Pentru taxe similare Q 0 Q> 0 și energia potențială a interacțiunii lor (repulsie) este pozitivă, pentru sarcini opuse Q 0 Q<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Potenţial jîn orice punct al câmpului electrostatic există o mărime fizică determinată de energia potențială a unei unități de sarcină pozitivă plasată în acest punct. Din care rezultă că potenţialul câmpului creat de o sarcină punctiformă Q, este egal cu . Munca efectuată de forțele câmpului electrostatic la deplasarea sarcinii Q 0 din punct 1 exact 2 , poate fi reprezentat ca , adică egal cu produsul sarcinii transferate și diferența de potențial la punctele inițiale și finale. Diferenta potentiala două puncte 1 și 2 într-un câmp electrostatic este determinată de munca efectuată de forțele câmpului la deplasarea unei unități de sarcină pozitivă dintr-un punct 1 exact 2 . Munca forțelor de câmp la deplasarea încărcăturii Q 0 din punct 1 exact 2 poate fi scris și sub formă . Expresia pentru diferența de potențial: , unde integrarea poate fi realizată de-a lungul oricărei linii care leagă punctele de început și de sfârșit, deoarece munca forțelor câmpului electrostatic nu depinde de traiectoria mișcării.

Dacă mutați încărcarea Q 0 dintr-un punct arbitrar din afara câmpului, adică până la infinit, unde, prin condiție, potențialul este zero, atunci lucrul forțelor câmpului electrostatic A ¥ =Q 0 j Unde

Potenţial- o mărime fizică determinată de munca de mutare a unei unități de sarcină pozitivă atunci când aceasta este îndepărtată dintr-un punct dat al câmpului la infinit. Această muncă este numeric egală cu munca efectuată forțe externe(împotriva forțelor câmpului electrostatic) prin mutarea unei unități de sarcină pozitivă de la infinit la un punct dat din câmp. Unitate potențială - volt(B): 1 V este potențialul unui astfel de punct din câmp la care o sarcină de 1 C are o energie potențială de 1 J (1 V = 1 J/C).

În cazul unui câmp electrostatic, energia potențială servește ca măsură a interacțiunii sarcinilor. Să existe un sistem de sarcini punctuale în spațiu Q i(i = 1, 2, ... ,n). Energia de interacțiune a tuturor n taxele este determinată de raport

Unde rij- distanța dintre sarcinile corespunzătoare și însumarea se realizează astfel încât interacțiunea dintre fiecare pereche de sarcini să fie luată în considerare o singură dată.

De aici rezultă că potențialul câmpului sistemului de sarcini este egal cu algebric suma potențialelor de câmp ale tuturor acestor sarcini:


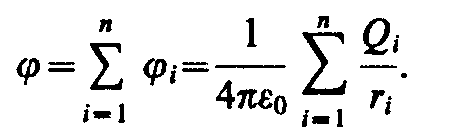
Având în vedere câmpul electric creat de un sistem de sarcini, ar trebui să folosiți principiul suprapunerii pentru a determina potențialul câmpului:

Potențialul câmpului electric al unui sistem de sarcini într-un punct dat din spațiu este egal cu suma algebrică a potențialelor câmpurilor electrice create într-un punct dat din spațiu de fiecare sarcină a sistemului separat:



6. Suprafețele echipotențiale și proprietățile acestora. Relația dintre diferența de potențial și intensitatea câmpului electrostatic.
O suprafață imaginară, ale cărei toate punctele au același potențial, se numește suprafață echipotențială. Ecuația acestei suprafețe

Dacă câmpul este creat de o sarcină punctiformă, atunci potențialul său Astfel, suprafețele echipotențiale în acest caz sunt sfere concentrice. Pe de altă parte, liniile de tensiune în cazul unei sarcini punctuale sunt drepte radiale. Prin urmare, liniile de tensiune în cazul unei sarcini punctiforme perpendicular suprafete echipotentiale.


Toate punctele suprafeței echipotențiale au același potențial, astfel încât munca de deplasare a sarcinii de-a lungul acestei suprafețe este zero, adică forțele electrostatice care acționează asupra sarcinii, mereuîndreptate de-a lungul normalelor către suprafeţele echipotenţiale. Prin urmare, vectorul E este întotdeauna normală cu suprafețele echipotențiale,şi deci liniile vectorului E ortogonale pe aceste suprafeţe.

Există un număr infinit de suprafețe echipotențiale în jurul fiecărei sarcini și fiecărui sistem de sarcini. Cu toate acestea, acestea sunt de obicei efectuate astfel încât diferențele de potențial dintre oricare două suprafețe echipotențiale adiacente să fie aceleași. Apoi, densitatea suprafețelor echipotențiale caracterizează clar intensitatea câmpului în diferite puncte. Acolo unde aceste suprafețe sunt mai dense, intensitatea câmpului este mai mare.

Deci, cunoscând locația liniilor de intensitate a câmpului electrostatic, este posibil să se construiască suprafețe echipotențiale și, invers, din locația cunoscută a suprafețelor echipotențiale, este posibil să se determine modulul și direcția intensității câmpului în fiecare punct al camp.

Să găsim relația dintre puterea câmpului electrostatic, care este a acestuia caracteristica de putere, si potential - energie caracteristică câmpului.

Lucrari de mutare singur sarcină pozitivă punctuală de la un punct al câmpului la altul de-a lungul axei X cu condiţia ca punctele să fie infinit apropiate unele de altele şi X 2 -X 1 = d X, este egal cu ex d X. Aceeași lucrare este j 1 -j 2 =dj. Echivalând ambele expresii, putem scrie

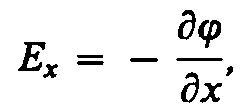
unde simbolul derivatei parțiale subliniază că diferențierea se face numai în raport cu X. Repetând raționament similar pentru axe lași z, putem găsi vectorul E:


Unde i, j, k- vectori unitari ai axelor de coordonate x, y, z.

Din definiția unui gradient rezultă că

adică tensiune E câmpul este egal cu gradientul potențial cu semnul minus. Semnul minus este determinat de faptul că vectorul intensitate E câmpuri îndreptate către direcție în jos potenţial.

Pentru o reprezentare grafică a distribuției potențiale a câmpului electrostatic, ca și în cazul câmpului gravitațional, utilizați suprafete echipotentiale- suprafeţe, în toate punctele cărora potenţialul j are acelasi sens.