§ 15. POTENCIALI. ENERGJIA E SISTEMIT TË NDRYSHIMEVE ELEKTRIKE. PUNA PËR LËVIZJEN E TARKESËS NË FUSHË

Formulat bazë

 Potenciali fushe elektrikeështë një sasi e barabartë me raportin e energjisë potenciale të një pikë ngarkese pozitive të vendosur në pikë e dhënë fusha, për këtë tarifë;

=P/ P,

ose potenciali i fushës elektrike është një sasi e barabartë me raportin e punës së forcave të fushës për të lëvizur një pikë ngarkesë pozitive nga një pikë e caktuar e fushës në pafundësi në këtë ngarkesë:

=A/ P.

Potenciali i fushës elektrike në pafundësi merret kushtimisht i barabartë me zero.

Vini re se kur një ngarkesë lëviz në një fushë elektrike, puna A v.s forcat e jashtme janë të barabarta në vlerë absolute me veprën A s.p. forca e fushës dhe është e kundërt me të në shenjë:

A v.s = – A s.p. .

 Potenciali i fushës elektrike i krijuar nga një ngarkesë pikë P në distancë r nga akuza

 Potenciali i fushës elektrike të krijuar nga metali, duke mbajtur një pagesë P sferë me rreze R, në një distancë nga qendra e sferës:

brenda sferës ( r<R)

;

në sipërfaqen e një sfere ( r=R)

;

jashtë fushës (r> R)

.

Në të gjitha formulat e dhëna për potencialin e një sfere të ngarkuar,  është lejueshmëria e një dielektrike homogjene të pafundme që rrethon sferën.

 Potenciali i fushës elektrike të krijuar nga sistemi P ngarkesat pikësore, në një pikë të caktuar, në përputhje me parimin e mbivendosjes së fushave elektrike, është e barabartë me shumën algjebrike të potencialeve  1 , 2 , ... , n, krijuar nga tarifat individuale të pikëve P 1 ,P 2 , ...,P n :

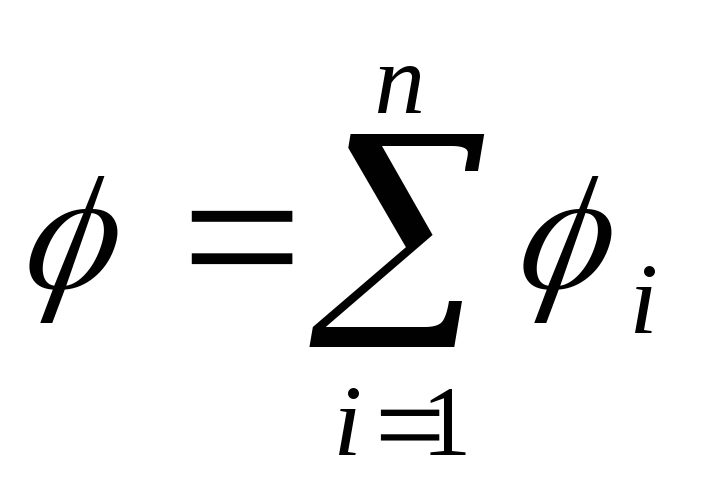
 Energjia W ndërveprimet e një sistemi ngarkesash pikash P 1 ,P 2 , ...,P n përcaktohet nga puna që mund të bëjë ky sistem ngarkesash kur ato hiqen në raport me njëri-tjetrin deri në pafundësi dhe shprehet me formulën

,

ku  i- potenciali i fushës i krijuar nga të gjithë P- 1 tarifë (me përjashtim të 1-tës) në pikën ku ndodhet tarifa P i .

 Potenciali lidhet me fuqinë e fushës elektrike nga relacioni

E= -grad.

Në rastin e një fushe elektrike me simetri sferike, kjo marrëdhënie shprehet me formulën

,

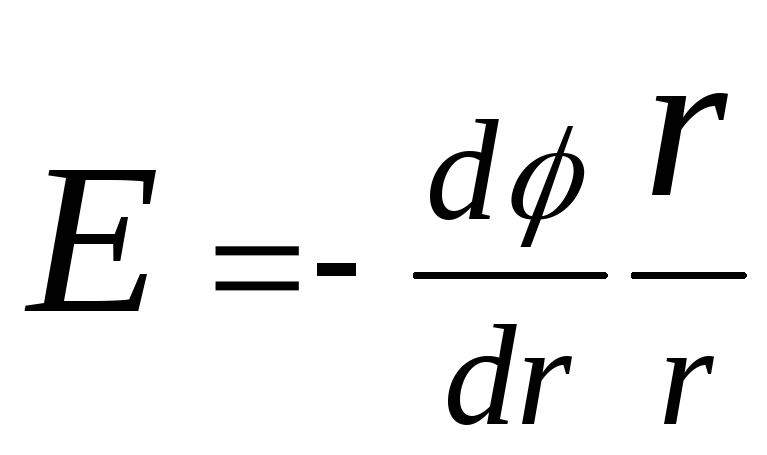ose në formë skalare

,

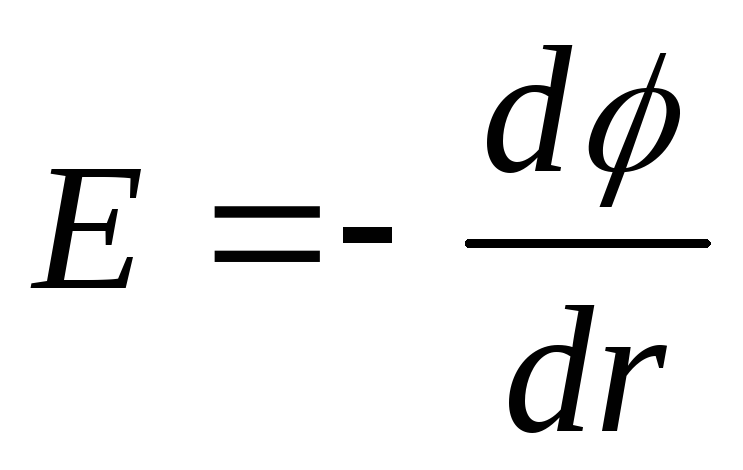dhe në rast fushë homogjene, d.m.th., një fushë, intensiteti i së cilës në çdo pikë është i njëjtë si në vlerë absolute ashtu edhe në drejtim,

E=( 1 – 2 ,)/d,

ku  1 dhe 2 - potencialet e pikave të dy sipërfaqeve ekuipotenciale; d - distanca ndërmjet këtyre sipërfaqeve përgjatë elektricitetit linjë fushore.

 Puna e kryer nga një fushë elektrike kur lëviz një ngarkesë pikësore P nga një pikë e fushës me një potencial  1 , në një tjetër me një potencial  2 ,

A=P( 1 - 2 ), ose

,

ku E l - projeksioni i vektorit të tensionit E në drejtimin e lëvizjes; dl - lëvizjes.

Në rastin e një fushe homogjene, formula e fundit merr formën

A= QElcos ,

ku l- zhvendosja; - këndi ndërmjet drejtimeve të vektorit E dhe zhvendosja l.

Shembuj të zgjidhjes së problemeve

Shembulli 1 ngarkesa pozitive P 1 \u003d 3 μC dhe P 2 \u003d 20 nC janë në vakum në distancë r 1 =l.5 m larg njëra-tjetrës. Përcaktoni një punë A, që duhet bërë për të afruar akuzat në distancë r 2 =1 m.

Zgjidhje. Le të supozojmë se ngarkesa e parë P 1 mbetet i palëvizshëm dhe tjetri P 2 nën veprimin e forcave të jashtme lëviz në fushën e krijuar nga ngarkesa P 1 duke iu afruar nga larg r 1 =t,5 m deri në r 2 =1 m .

Puna POR" forcë e jashtme për të lëvizur ngarkesën P nga një pikë e fushës me potencial  1 në një tjetër, potenciali i të cilit 2 , i barabartë në vlerë absolute dhe i kundërt në shenjë me punën POR forcat fushore për lëvizjen e ngarkesës ndërmjet të njëjtave pika:

A "= -A.

Puna POR forcat në terren në zhvendosjen e ngarkesës A=P( 1 - 2 ). Pastaj punoni POR" forcat e jashtme mund të shkruhen si

A" = –P( 1 - 2 )=P( 2 - 1 ). (1)

Potencialet e pikave të fillimit dhe të fundit të shtegut shprehen me formula

;

.

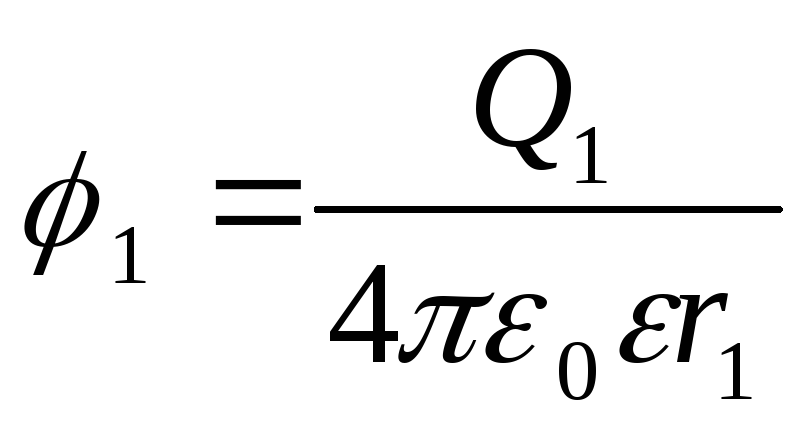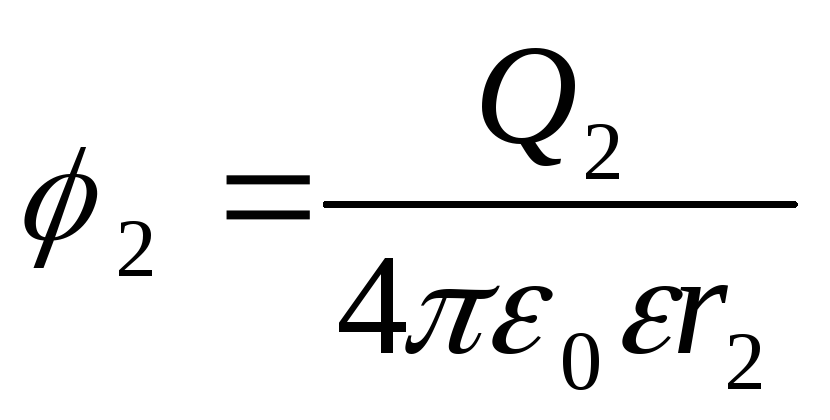Zëvendësimi i shprehjeve  1 dhe 2 në formulën (1) dhe duke marrë parasysh se për këtë rast ngarkesa e transferuar P=P 2 , marrim

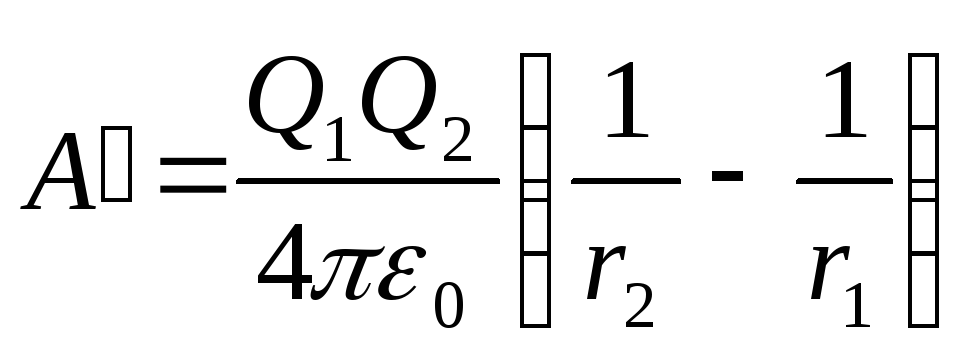. (2)

Duke marrë parasysh se 1/(4 0 )=910 9 m/F, më pas pasi zëvendësojmë vlerat e sasive në formulën (2) dhe kemi llogaritur, gjejmë

A"=180 µJ.

Shembulli 2 Gjej një punë POR fushat e transferimit të tarifave P=10 nC nga pika 1 pikërisht 2 (Fig. 15.1), i vendosur midis dy atyre të ngarkuar në mënyrë të kundërt me një densitet sipërfaqësor  \u003d 0,4 μC / m 2 plane paralele të pafundme, largësi l ndërmjet tyre është 3 cm.

R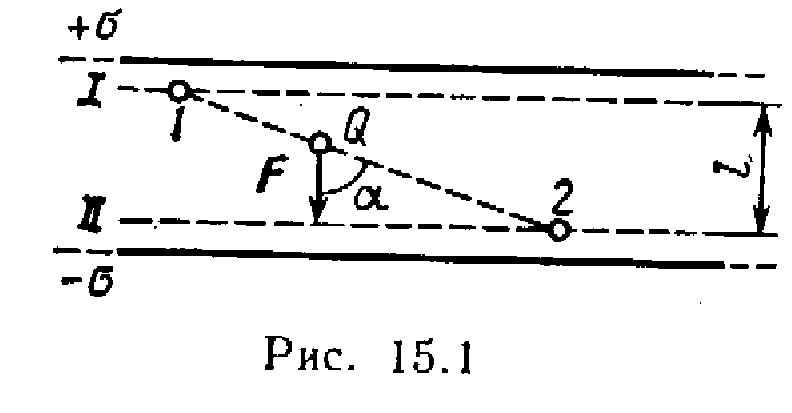

zgjidhje. Ka dy mënyra për të zgjidhur problemin.

Mënyra e parë. Puna e fushës detyron të lëvizë ngarkesën Q nga pika 1 fusha me potencial 1 pikërisht 2 fusha me potencial 2 gjeni sipas formulës

A=P( 1 - 2 ). (1)

Për të përcaktuar potencialet në pika 1 dhe 2 Le të vizatojmë sipërfaqet ekuipotenciale I dhe II përmes këtyre pikave. Këto sipërfaqe do të jenë rrafshe, pasi fusha midis dy rrafsheve paralele të pafundme të ngarkuara në mënyrë uniforme është uniforme. Për një fushë të tillë, relacioni

 1 - 2 =El, (2)

ku E - forca e fushës; l - distanca ndërmjet sipërfaqeve ekuipotenciale.

Forca e fushës ndërmjet planeve paralele të pafundme me ngarkesë të kundërt E=/ 0 . Duke zëvendësuar këtë shprehje E në formulën (2) dhe më pas shprehjen 1 - 2 në formulën (1), marrim

A= P( /  0 ) l.

Mënyra e 2-të. Meqenëse fusha është uniforme, forca që vepron në ngarkesë P, është konstante ndërsa lëviz. Prandaj, puna e lëvizjes së ngarkesës nga pika 1 pikërisht 2 mund të llogaritet duke përdorur formulën

A=F  r cos, (3)

ku F - forcë që vepron mbi një ngarkesë r- Moduli i transferimit të ngarkesës P nga një pikë 1 pikërisht 2;  është këndi ndërmjet drejtimeve të zhvendosjes dhe forcës . Por F= QE= P( /  0 ). Duke zëvendësuar këtë shprehje F në barazi (3), si dhe duke vërejtur se  r cos= l, marrim

A=P(/ 0 )l. (4)

Kështu, të dyja zgjidhjet çojnë në të njëjtin rezultat.

Zëvendësimi në shprehjen (4) i vlerës së sasive P, , 0 dhe l, Gjej

A\u003d 13,6 μJ.

Shembulli 3 Në një fije të hollë të përkulur përgjatë një harku të një rrethi me një rreze R, ngarkesë e shpërndarë në mënyrë uniforme me dendësi lineare=10 nC/m. Përcaktoni tensionin E dhe potenciali  i fushës elektrike të krijuar nga një p

tarifa e shpërndarë në një pikë O, që përkon me qendrën e lakimit të harkut. Gjatësia l filli është 1/3 e perimetrit dhe është i barabartë me 15 cm.

Zgjidhje. Ne zgjedhim boshtet e koordinatave në mënyrë që origjina e koordinatave të përkojë me qendrën e lakimit të harkut dhe boshtin në ishte vendosur në mënyrë simetrike në lidhje me skajet e harkut (Fig. 15.2). Zgjidhni një element me gjatësi d në fije l. I ngarkuar P=d l, i vendosur në zonën e zgjedhur, mund të konsiderohet si një pikë.

Le të përcaktojmë forcën e fushës elektrike në pikë O. Për ta bërë këtë, së pari gjejmë tensionin d E fusha e krijuar nga ngarkesa d P:

,

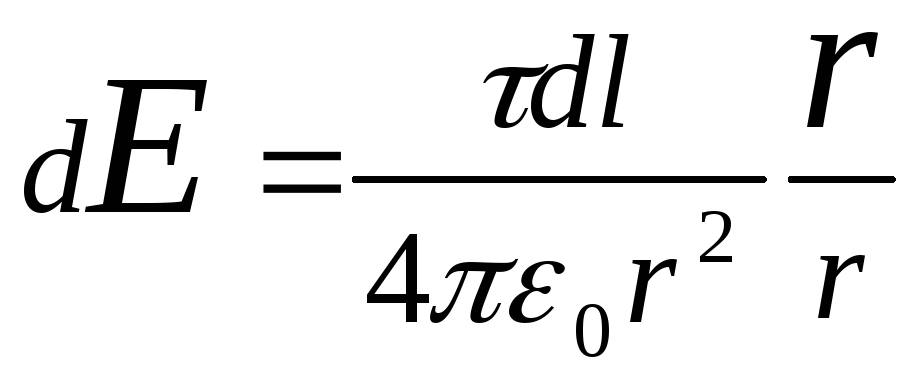ku r-rrezja-vektor i drejtuar larg elementit d l deri në pikën në të cilën llogaritet tensioni. Shprehim vektorin d E përmes projeksionit dE x c dhe dE y në boshtin koordinativ:

,

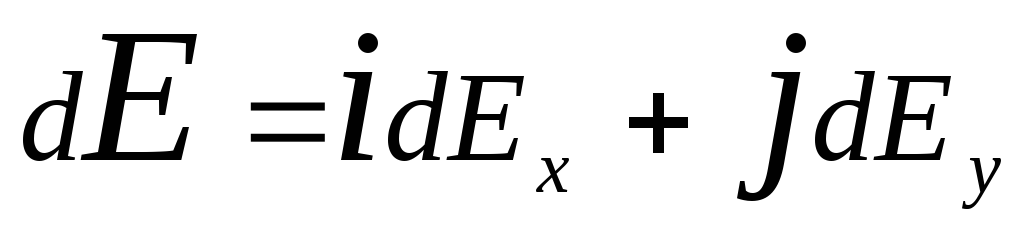ku i dhe j- vektorët e drejtimit njësi (ortat).

tensioni E gjeni me integrim:

.

Integrimi kryhet përgjatë harkut të gjatësisë l. Për shkak të simetrisë, integrali barazohet me zero. Pastaj

, (1)

ku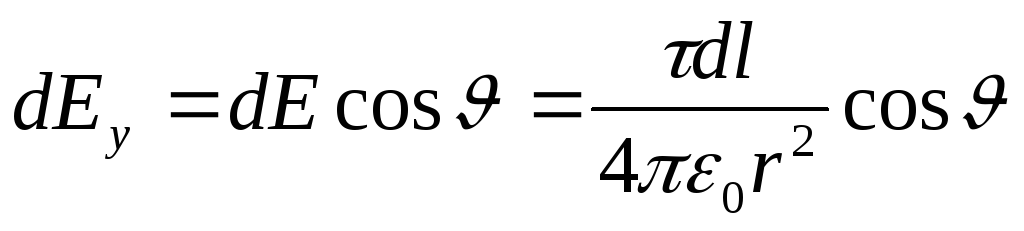

. Sepse r=R= konst dhe d l=R d. pastaj

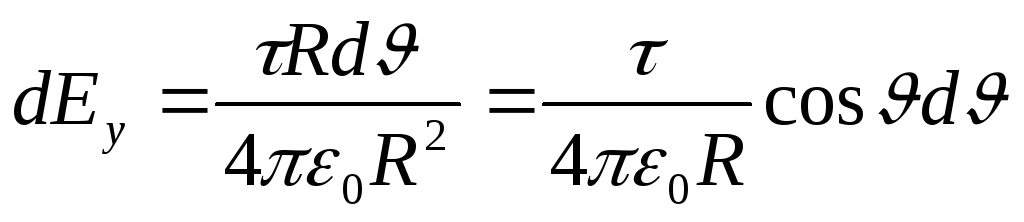
Zëvendësoni shprehjen e gjetur dE y në (1) dhe, duke marrë parasysh vendndodhjen simetrike të harkut në lidhje me boshtin OU, marrim kufijtë e integrimit nga 0 në /3 dhe dyfishojmë rezultatin;

.

Zëvendësimi i këtyre kufijve dhe shprehja R përmes gjatësisë së harkut (3 l= 2 r), marrim

.

Kjo formulë tregon se vektori E përkon me drejtimin pozitiv të boshtit OU Zëvendësimi i vlerës dhe l në formulën e fundit dhe duke bërë llogaritjet, gjejmë

E\u003d 2,18 kV / m.

Le të përcaktojmë potencialin e fushës elektrike në pikë O. Le të gjejmë fillimisht potencialin d të krijuar nga ngarkesa pikësore d P në pikën O:

Le të zëvendësojmë r në R dhe kryeni integrimin:

.Sepse l=2  R/3, pastaj

=/(6 0 ).

Pasi kemi bërë llogaritjet sipas kësaj formule, marrim

Shembull4 . Fusha elektrike krijohet nga një cilindër i gjatë me rreze R= 1cm , ngarkuar në mënyrë të njëtrajtshme me dendësi lineare=20 nC/m. Përcaktoni ndryshimin potencial të dy pikave të kësaj fushe të vendosura në largësi a 1 =0,5 cm dhe a 2 \u003d 2 cm nga sipërfaqja e cilindrit, në pjesën e mesme të tij.

Zgjidhje. Për të përcaktuar diferencën potenciale, ne përdorim marrëdhënien midis fuqisë së fushës dhe ndryshimit të potencialit E= -grad. Për një fushë me simetri boshtore, e cila është fusha e një cilindri, kjo lidhje mund të shkruhet si

E= -( d/d r) , ose d= - E d r.

Duke integruar shprehjen e fundit, gjejmë ndryshimin potencial të dy pikave të ndara me r 1 dhe r 2 nga boshti i cilindrit;

. (1)

Meqenëse cilindri është i gjatë dhe pikat janë marrë afër pjesës së mesme të tij, forca e fushës mund të shprehet duke përdorur formulën

. Duke zëvendësuar këtë shprehje E në barazi (1), marrim

(2)

Që nga sasitë r 2 dhe r 1 futni formulën si raport, atëherë ato mund të shprehen në çdo, por vetëm të njëjtat njësi:

r 1 =R+a 1 = 1,5 cm; r 2 =R+a 2 = 3 cm .

Zëvendësimi i vlerave të madhësisë , 0 ,r 1 dhe r 2 në formulën (2) dhe duke llogaritur, gjejmë

 1 - 2 = 250 V.

Shembulli 5 Fusha elektrike krijohet nga një shufër e hollë që mban ngarkesë =0,1 μC/m të shpërndarë në mënyrë uniforme përgjatë gjatësisë së saj. Përcaktoni potencialin  të fushës në një pikë të largët nga skajet e shufrës në një distancë, e barabartë me gjatësinë kallam.

Zgjidhje. Ngarkesa në shufër nuk mund të konsiderohet si një ngarkesë pikë, prandaj zbatoni drejtpërdrejt formulën për të llogaritur potencialin

, (1)

e vlefshme vetëm për tarifat me pikë, është e pamundur. Por nëse e ndajmë shufrën në segmente elementare d l, pastaj ngarkesad l që ndodhet në secilën prej tyre mund të konsiderohet si një pikë dhe atëherë formula (1) do të jetë e vlefshme. Duke aplikuar këtë formulë, marrim

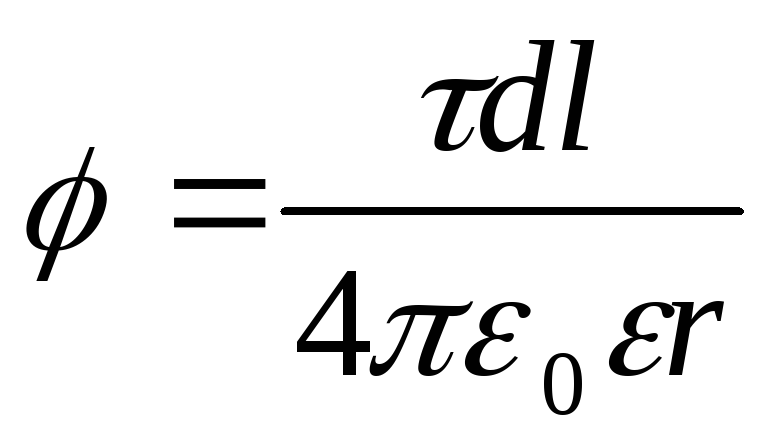, (2)

ku r - distanca e pikës në të cilën përcaktohet potenciali me elementin e shufrës.

Nga fig. 15.3 që d l=(r d/cos). Zëvendësimi i kësaj shprehjeje d l në formulën (2), gjejmë

.

Integrimi i shprehjes që rezulton brenda kufijve të  1 po 2 , marrim potencialin e krijuar nga e gjithë ngarkesa e shpërndarë në shufër: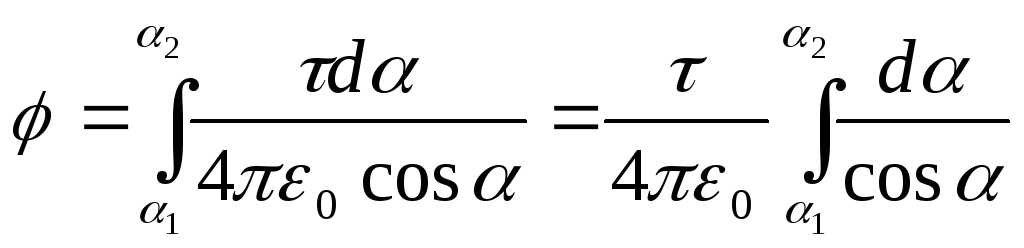

.

AT 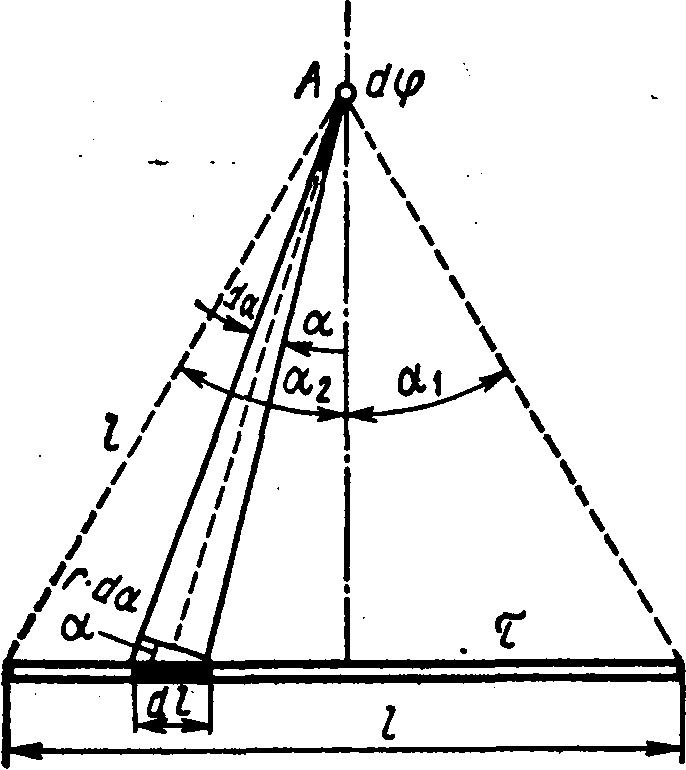forca e simetrisë së pikës POR në raport me skajet e shufrës kemi  2 = 1 dhe për këtë arsye

.

Rrjedhimisht,

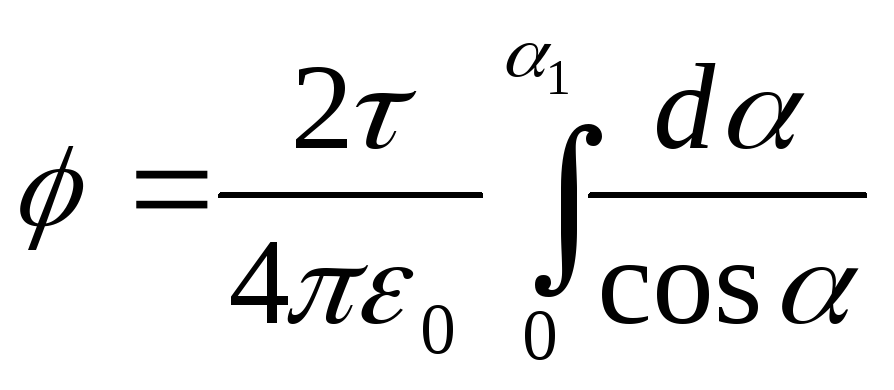.Sepse

(shih tabelën 2), më pas

.

Duke zëvendësuar kufijtë e integrimit, ne marrim

Pasi kemi bërë llogaritjet sipas kësaj formule, gjejmë

Shembulli 6 Një elektron me shpejtësi v=1,8310 6 m/s fluturoi në një fushë elektrike uniforme në drejtim të kundërt me vektorin e forcës së fushës. Çfarë ndryshimi potencial U një elektron duhet të kalojë që të ketë energji E i\u003d 13,6 eV *? (Duke pasur një energji të tillë, një elektron mund ta jonizojë atë kur përplaset me një atom hidrogjeni. Energjia prej 13.6 eV quhet energji jonizuese e hidrogjenit.)

Zgjidhje. Elektroni duhet të kalojë një ndryshim të tillë potencial ju, në mënyrë që energjia e fituar W e kombinuar me energjinë kinetike T, që elektroni kishte përpara se të hynte në fushë, arriti në një energji të barabartë me energjinë e jonizimit E i , dmth. W+ T= E i . Duke u shprehur në këtë formulë W= BE dhe T=(m v 2 /2), marrim BE+(m v 2 /2)=E i. Nga këtu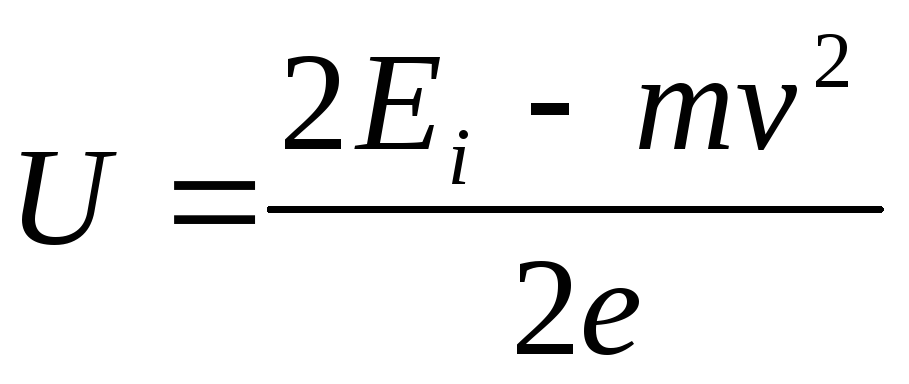

.

___________________

* Elektron-volt (eV) - energjia që merr një grimcë, që ka një ngarkesë të barabartë me ngarkesën e një elektroni, duke kaluar përmes një ndryshimi potencial prej 1 V. Kjo njësi energjie josistematike aktualisht është miratuar për përdorim në fizikë.

Le të bëjmë llogaritjet në njësitë SI:

U=4.15 AT.

Shembulli 7 Përcaktoni shpejtësinë fillestare υ 0 afrimi i protoneve të vendosura në një mjaftueshëm distancë e madhe nga njëri-tjetri nëse distanca minimale r min , me të cilën mund të afrohen, është 10 -11 cm.

Zgjidhja: Midis dy protoneve ka forca refuzuese, si rezultat i të cilave lëvizja e protoneve do të jetë e ngadaltë. Prandaj, problemi mund të zgjidhet si sistemi inercial koordinatat (të lidhura me qendrën e masës së dy protoneve), dhe në joinerciale (të lidhura me një nga protonet që lëvizin shpejt). Në rastin e dytë, ligjet e Njutonit nuk vlejnë. Zbatimi i parimit d'Alembert është i vështirë për faktin se nxitimi i sistemit do të jetë i ndryshueshëm. Prandaj, është e përshtatshme të shqyrtohet problemi në një kornizë inerciale referimi.

Le të vendosim origjinën e koordinatave në qendër të masës së dy protoneve. Meqenëse kemi të bëjmë me grimca identike, qendra e masës do të jetë në pikën që përgjysmon segmentin që lidh grimcat. Në lidhje me qendrën e masës, grimcat do të kenë në çdo kohë të njëjtat modul shpejtësie. Kur grimcat janë në një distancë mjaft të madhe nga njëra-tjetra, shpejtësia υ 1 çdo grimcë është e barabartë me gjysmën υ 0 , dmth. υ 1 =υ 0 /2.

Për të zgjidhur problemin zbatojmë ligjin e ruajtjes së energjisë, sipas të cilit energjia totale mekanike E sistemi i izoluar është konstant, d.m.th.

E=T+ P ,

ku T- shuma e energjive kinetike të të dy protoneve në raport me qendrën e masës; P është energjia potenciale e sistemit të ngarkesave.

Ne e shprehim energjinë potenciale në momentet fillestare P 1 dhe P 2 të fundit të lëvizjes.

Në momentin fillestar, sipas gjendjes së problemit, protonet ishin në një distancë të madhe, kështu që energjia potenciale mund të neglizhohet (P 1 =0). Prandaj, për momentin fillestar energji totale do të jetë e barabartë me energjinë kinetike T 1 protonet, d.m.th.

E=T l . (1)

Në momentin përfundimtar, kur protonet afrohen sa më afër, shpejtësia dhe energjia kinetike janë të barabarta me zero, dhe energjia totale do të jetë e barabartë me energjinë potenciale P 2, d.m.th.

E= P 2 . (2)

Duke barazuar pjesët e duhura të barazive (1) dhe (2), marrim

T 1 \u003d P 2. (3)

Energjia kinetike është e barabartë me shumën e energjive kinetike të protoneve:

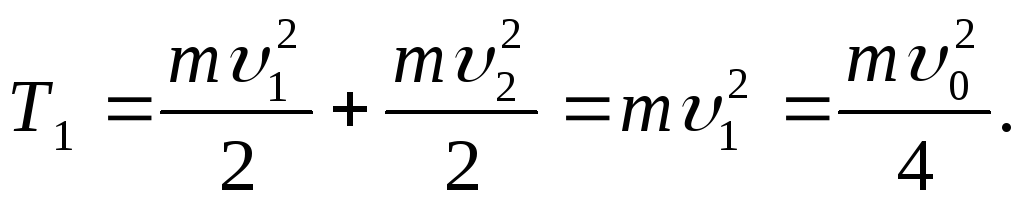(4)

Energjia potenciale e një sistemi me dy ngarkesa P 1 dhe P 2 në vakum përcaktohet nga formula

, ku r- distanca midis tarifave. Duke përdorur këtë formulë, marrim

(5)

Duke marrë parasysh barazitë (4) dhe (5), formula (3) merr formën

ku

Pas kryerjes së llogaritjeve sipas formulës së përftuar, gjejmë υ 0 =2,35 mm/s

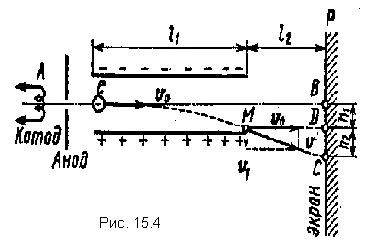Shembulli 8 Një elektron pa një shpejtësi fillestare ka kaluar diferencën e potencialit U 0 =10 kV dhe fluturoi në hapësirën midis pllakave të një kondensatori të sheshtë të ngarkuar me një ndryshim potencial U l \u003d 100 V, përgjatë vijës AB, paralel me pllakat (Fig. 15.4). Largësia d ndërmjet pllakave është 2 cm.Gjatësia l 1 pllakë kondensator në drejtim të fluturimit të elektroneve është e barabartë me 20 cm. Përcaktoni distancën dielli në ekran R, larg kondensatorit l 2 \u003d 1 m.

Zgjidhje Lëvizja e një elektroni brenda kondensatorit përbëhet nga dy lëvizje: 1) me inerci përgjatë vijës AB me një shpejtësi konstante υ 0 , të fituara nën veprimin e një ndryshimi potencial U 0 , të cilin elektroni ia kaloi kondensatorit; 2) lëvizje e përshpejtuar në mënyrë uniforme në drejtim vertikal në një pllakë të ngarkuar pozitivisht nën veprimin e një force konstante të fushës së kondensatorit. Pasi të largohet nga kondensatori, elektroni do të lëvizë në mënyrë të njëtrajtshme me një shpejtësi υ, që kishte në atë pikë M në momentin e daljes nga kondensatori.

Nga fig. 15.4 tregon se distanca e dëshiruar | | BC|=h 1 +h 2 , prej nga h 1 - distanca që elektroni do të lëvizë në drejtim vertikal gjatë lëvizjes në kondensator; h 2 - distanca midis pikës D në ekran, në të cilën elektroni do të binte, duke lëvizur në dalje nga kondensatori në drejtim të shpejtësisë fillestare υ 0, dhe pika C, ku elektroni godet në të vërtetë.

Shprehni veçmas h 1 dhe h 2 . Duke përdorur formulën për gjatësinë e shtegut të lëvizjes së përshpejtuar uniformisht, gjejmë

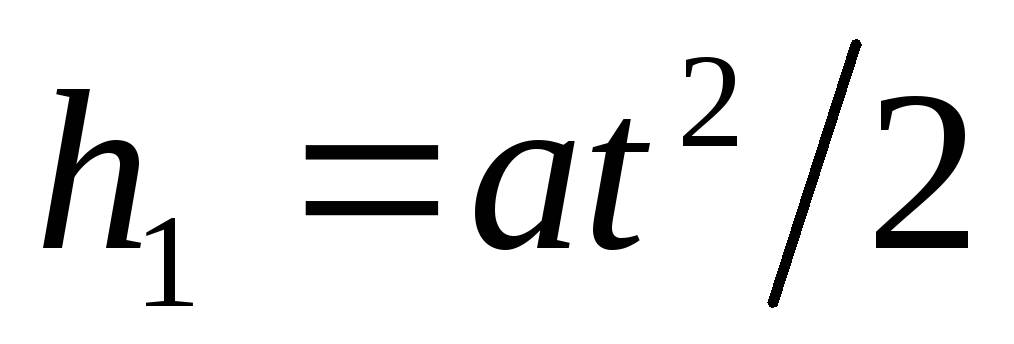. (1)

ku a- nxitimi i marrë nga elektroni nën veprimin e fushës së kondensatorit; t- koha e fluturimit të një elektroni brenda një kondensatori.

Sipas ligjit të dytë të Njutonit a=F/m, ku F- forca me të cilën fusha vepron në elektron; t- masën e saj. Nga ana e tij, F=eE=eU 1 /d, ku e- ngarkesa elektronike; U 1 - ndryshimi i potencialit midis pllakave të kondensatorit; d- distanca midis tyre. Kohën e fluturimit të një elektroni brenda kondensatorit e gjejmë nga formula për rrugën e lëvizjes uniforme

, ku

ku l 1 është gjatësia e kondensatorit në drejtim të fluturimit të elektroneve. Shprehjen për shpejtësinë e gjejmë nga kushti i barazisë së punës së fushës gjatë lëvizjes së elektronit dhe energjisë kinetike të fituar prej tij:

. Nga këtu

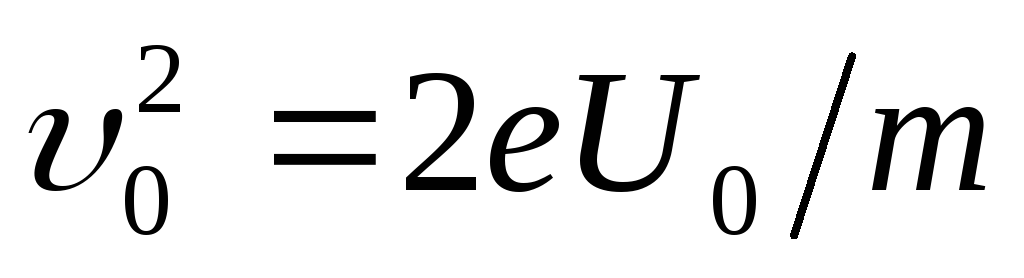(2)

Zëvendësimi në formulën (1) në mënyrë të njëpasnjëshme të vlerave a,F, t dhe υ 0 2 nga shprehjet përkatëse, marrim

Gjatësia e prerjes h 2 gjeni nga ngjashmëria e trekëndëshave MDC dhe vektor:

(3)

ku υ 1 - shpejtësia e elektronit në drejtimin vertikal në një pikë M;l 2 - distanca nga kondensatori në ekran.

Shpejtësia υ 1 e gjejmë sipas formulës υ 1 = në, e cila duke marrë parasysh shprehjet për a, F dhe t do të marrë formën

Zëvendësimi i shprehjes υ 1 në formulën (3), marrim

, ose duke e zëvendësuar υ 0 2 sipas formulës (3), gjejmë

Më në fund për distancën e kërkuar | para Krishtit| do të ketë

|para Krishtit|=

­

Zëvendësimi i vlerave të sasive U 1 ,U 0 ,d,l 1 dhe l 2 në shprehjen e fundit dhe duke kryer llogaritjet, marrim | para Krishtit|=5,5 cm.

Detyrat

Energjia potenciale dhe potenciali fushor i ngarkesave pika

15.1. tarifë pikë P\u003d 10 nC, duke qenë në një pikë të caktuar në fushë, ka një energji potenciale P \u003d 10 μJ. Gjeni potencialin φ të kësaj pike fushore.

5.2. Kur lëviz ngarkesa Q=20 nC midis dy pikave të fushës, puna bëhej nga forcat e jashtme A=4µJ. Përcaktoni një punë A 1 forcat e fushës dhe diferenca Δφ e potencialeve të këtyre pikave të fushës.

15.3. Fusha elektrike krijohet nga një pikë ngarkesë pozitive P 1 \u003d 6 nC. ngarkesë pozitive P 2 transferohet nga pika POR këtë fushë deri në një pikë AT(Fig. 15.5). Sa është ndryshimi i energjisë potenciale ΔP për njësi të ngarkesës së transferuar nëse r 1 =20 cm dhe r 2 \u003d 50 cm?

15.4. Fusha elektrike e krijuar nga një ngarkesë pikë P l \u003d 50 nC. Pa përdorur konceptin e potencialit, llogaritni punën POR në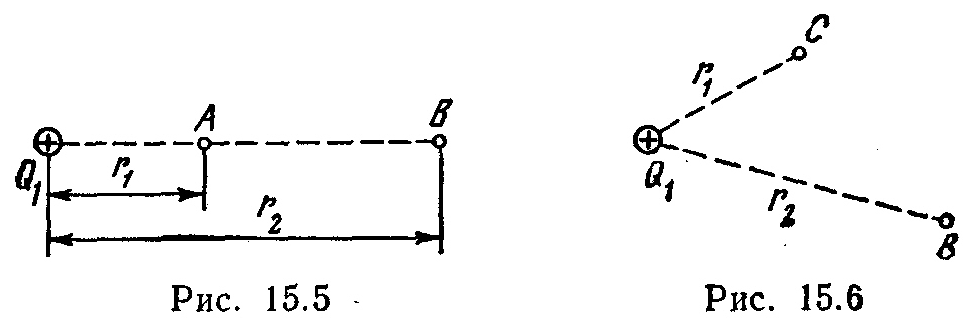

forcat e jashtme për të lëvizur një ngarkesë pikë P 2 = -2 nC nga pika NGA pikërisht AT

(Fig. 15.6), nëse r 1 =10 cm, r 2 \u003d 20 cm Përcaktoni gjithashtu ndryshimin ΔP të energjisë potenciale të sistemit të ngarkesave.

15.5. Fusha krijohet nga një ngarkesë pikë P=1 nC. Përcaktoni potencialin φ të fushës në një pikë të largët nga ngarkesa në një distancë r= 20 cm.

15.6. Përcaktoni potencialin φ të fushës elektrike në një pikë të largët nga ngarkesat P 1 = -0,2 µC dhe P 2 =0,5 μC, përkatësisht, në r 1 =15 masmedia r 2 \u003d 25 cm Përcaktoni gjithashtu distancat minimale dhe maksimale midis ngarkesave për të cilat është e mundur një zgjidhje.

15.7. Akuzat P 1 \u003d 1 μC dhe P 2 = -1 μC janë në distancë d\u003d 10 cm Përcaktoni tensionin E dhe potenciali φ i fushës në një pikë të largët në një distancë r= 10 cm nga ngarkesa e parë dhe shtrirë në një vijë që kalon përmes ngarkesës së parë pingul me drejtimin nga P 1 deri në P 2 .

15.8. Llogaritni energjinë potenciale P të një sistemi me ngarkesa me dy pika P 1 =100 nC dhe P 2 =10 nC në distancë d= 10 cm larg njëri-tjetrit.

15.9. Gjeni energjinë potenciale P të një sistemi me ngarkesa me tre pika P 1 \u003d 10 nC, P 2 =20 nCl dhe P 3 \u003d -30 nC, e vendosur në kulmet e një trekëndëshi barabrinjës me gjatësi anësore a= 10 cm.

15.10. Cfare eshte energji potenciale P sisteme me katër ngarkesa pikash identike P\u003d 10 nC, e vendosur në kulmet e një katrori me gjatësi anësore a\u003d 10 cm? .

15.11. Përcaktoni energjinë potenciale P të një sistemi me ngarkesa me katër pika të vendosura në kulmet e një katrori me gjatësi anësore a\u003d 10 cm Ngarkesat janë të njëjta në modul P=10 nC, por dy prej tyre janë negative. Konsideroni dy raste të mundshme të rregullimit të tarifave.

15.12 . Fusha krijohet nga ngarkesa me dy pika + 2P dhe -Py, në një distancë d= 12 cm larg. Përcaktoni vendndodhjen e pikave në rrafshin për të cilin potenciali është zero (shkruani ekuacionin për vijën e potencialit zero).

5.13. Sistemi përbëhet nga tre ngarkesa - dy të së njëjtës madhësi P 1 = |P 2 |=1 μC dhe e kundërta në shenjë dhe ngarkesë Q=20 nC, e vendosur në pikën 1 në mes midis dy ngarkesave të tjera të sistemit (Fig. 15.7). Përcaktoni ndryshimin në energjinë potenciale ΔP të sistemit gjatë transferimit të ngarkesës P nga pika 1 në pikën 2. Këto pika hiqen nga ngarkesa negative P 1 për distancë a= 0,2 m.

Potenciali i fushës së ngarkesave të shpërndara në mënyrë lineare

15.14. Përgjatë një unaze të hollë me një rreze R= 10 cm ngarkesë e shpërndarë në mënyrë uniforme me dendësi lineare τ= 10 nC/m. Përcaktoni potencialin φ në një pikë të shtrirë në boshtin e unazës, në një distancë a= 5 cm nga qendra.

15.15. Në një segment të një përcjellësi të hollë të drejtë, një ngarkesë shpërndahet në mënyrë të njëtrajtshme me një densitet linear τ=10 nC/m. Llogaritni potencialin φ të krijuar nga kjo ngarkesë në një pikë të vendosur në boshtin e përcjellësit dhe të largët nga skaji më i afërt i segmentit me një distancë të barabartë me gjatësinë e këtij segmenti.

Fusha elektrostatike është potenciale, forcat e Kulonit janë forca konservatore dhe puna e forcave konservatore mund të përfaqësohet si një rënie e energjisë potenciale, d.m.th.

ku C është konstanta e integrimit, e cila zakonisht zgjidhet në mënyrë që kur ngarkesa q të hiqet në pafundësi - W р = 0, d.m.th. C=0.

Ne do të hetojmë ESP duke përdorur tarifat e provës q pr 1 , q pr 2 , q pr 3 -

Potenciali i një fushe elektrostatike është karakteristikë energjetike e fushës, numerikisht e barabartë me raportin e energjisë potenciale të provës ngarkesë elektrike, vendosur në një pikë të caktuar të fushës, në madhësinë e ngarkesës.

Pastaj, duke përdorur relacionet (7.1) dhe (7.7), marrim:

Duke ditur shpërndarjen e tarifave, ne mund të gjejmë potencialin në terren të çdo sistemi.

Potencialet e fushës shtohen në mënyrë algjebrike Prandaj, llogaritja e potencialeve është zakonisht më e thjeshtë se llogaritja e fuqive EF.

Në SI, njësia e potencialit është [ j ] \u003d 1J / C \u003d 1V

Një njësi pune prej 1 eV (elektron volt) është e barabartë me punën e bërë nga forcat e fushës në ngarkesë e barabartë me ngarkesën elektron, kur kalon një diferencë potenciale prej 1 V.

1 eV = 1.6´10 -19 C ´ 1V=1.6´10 -19 J

Modeli video: 1) Lëvizja e ngarkesave në një fushë elektrike; 2) Spektometri i masës.

Një trup i vendosur në një fushë potenciale forcash (një fushë elektrostatike) ka energji potenciale për shkak të së cilës puna kryhet nga forcat e fushës. Puna e forcave konservatore kryhet për shkak të humbjes së energjisë potenciale. Prandaj, puna e forcave të fushës elektrostatike mund të përfaqësohet si ndryshim në energjitë potenciale të zotëruara nga tarifë pikë P 0 në pikat e fillimit dhe të fundit të fushës së karikimit P: , prej nga rrjedh se energjia potenciale e ngarkesës q0 në fushën e ngarkimit Pështë e barabartë me . Përcaktohet në mënyrë të paqartë dhe deri në një konstante arbitrare NGA. Nëse supozojmë se kur ngarkesa hiqet në pafundësi ( r®¥) energjia potenciale zhduket ( U=0), pastaj NGA=0 dhe energjia potenciale e ngarkesës P 0 , ndodhet në fushën e ngarkimit P në një distancë r prej saj, është e barabartë me . Për tarifa të ngjashme P 0 P> 0 dhe energjia potenciale e bashkëveprimit të tyre (zmbrapsjes) është pozitive, për ngarkesa të kundërta P 0 P<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Potenciali j në çdo pikë të fushës elektrostatike ekziston një sasi fizike e përcaktuar nga energjia potenciale e një njësie ngarkese pozitive të vendosur në këtë pikë. Nga ku del se potenciali i fushës i krijuar nga një ngarkesë pikë P, është e barabartë me . Puna e bërë nga forcat e fushës elektrostatike gjatë lëvizjes së ngarkesës P 0 nga pika 1 pikërisht 2 , mund të përfaqësohet si , d.m.th. i barabartë me produktin e ngarkesës së transferuar dhe diferencën potenciale në pikat fillestare dhe përfundimtare. Diferencë potenciale dy pika 1 dhe 2 në një fushë elektrostatike përcaktohet nga puna e bërë nga forcat e fushës kur lëviz një ngarkesë pozitive njësi nga një pikë 1 pikërisht 2 . Puna e forcave të fushës gjatë lëvizjes së ngarkesës P 0 nga pika 1 pikërisht 2 mund të shkruhet edhe në formë . Shprehja për diferencën potenciale: , ku integrimi mund të kryhet përgjatë çdo linje që lidh pikën e fillimit dhe të fundit, pasi puna e forcave të fushës elektrostatike nuk varet nga trajektorja e lëvizjes.

Nëse e lëvizni ngarkesën P 0 nga një pikë arbitrare jashtë fushës, pra deri në pafundësi, ku, sipas kushtit, potenciali është zero, atëherë puna e forcave të fushës elektrostatike A ¥ =Q 0 j ku

Potenciali- një sasi fizike e përcaktuar nga puna e lëvizjes së një ngarkese pozitive njësi kur ajo hiqet nga një pikë e caktuar e fushës në pafundësi. Kjo punë është numerikisht e barabartë me punën e bërë forcat e jashtme(kundër forcave të fushës elektrostatike) duke lëvizur një ngarkesë pozitive njësi nga pafundësia në një pikë të caktuar të fushës. Njësia e mundshme - volt(B): 1 V është potenciali i një pike të tillë në fushë në të cilën një ngarkesë prej 1 C ka një energji potenciale prej 1 J (1 V = 1 J/C).

Në rastin e një fushe elektrostatike, energjia potenciale shërben si masë e ndërveprimit të ngarkesave. Le të ketë një sistem ngarkesash pikash në hapësirë Q i(i = 1, 2, ... ,n). Energjia e ndërveprimit të të gjithëve n tarifat përcaktohet nga raporti

ku rij- distanca ndërmjet ngarkesave përkatëse dhe përmbledhja kryhet në atë mënyrë që ndërveprimi ndërmjet çdo çifti ngarkesash të merret parasysh një herë.

Nga kjo rezulton se potenciali i fushës së sistemit të ngarkesave është i barabartë me algjebrike shuma e potencialeve të fushës së të gjitha këtyre ngarkesave:

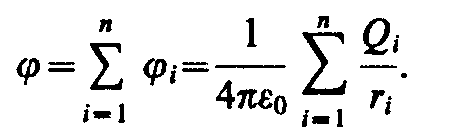
Duke marrë parasysh fushën elektrike të krijuar nga një sistem ngarkesash, duhet të përdoret parimi i mbivendosjes për të përcaktuar potencialin e fushës:

Potenciali i fushës elektrike të një sistemi ngarkesash në një pikë të caktuar në hapësirë ​​është i barabartë me shumën algjebrike të potencialeve të fushave elektrike të krijuara në një pikë të caktuar të hapësirës nga secila ngarkesë e sistemit veç e veç:

6. Sipërfaqet ekuipotenciale dhe vetitë e tyre. Marrëdhënia midis ndryshimit të potencialit dhe fuqisë së fushës elektrostatike.
Një sipërfaqe imagjinare, të gjitha pikat e së cilës kanë të njëjtin potencial, quhet sipërfaqe ekuipotenciale. Ekuacioni i kësaj sipërfaqeje

Nëse fusha krijohet nga një ngarkesë pikë, atëherë potenciali i saj Kështu, sipërfaqet ekuipotenciale në këtë rast janë sfera koncentrike. Nga ana tjetër, linjat e tensionit në rastin e një ngarkese pika janë vija të drejta radiale. Prandaj, linjat e tensionit në rastin e një ngarkese pikë pingul sipërfaqet ekuipotenciale.

Të gjitha pikat e sipërfaqes ekuipotenciale kanë të njëjtin potencial, kështu që puna e lëvizjes së ngarkesës përgjatë kësaj sipërfaqeje është zero, d.m.th., forcat elektrostatike që veprojnë në ngarkesë, gjithmonë drejtuar përgjatë normaleve në sipërfaqet ekuipotenciale. Prandaj, vektori E është gjithmonë normale me sipërfaqet ekuipotenciale, dhe rrjedhimisht vijat e vektorit E ortogonale me këto sipërfaqe.

Ka një numër të pafund sipërfaqesh ekuipotenciale rreth çdo ngarkese dhe çdo sistemi ngarkesash. Sidoqoftë, ato zakonisht kryhen në mënyrë që ndryshimet e mundshme midis çdo dy sipërfaqesh ekuipotenciale ngjitur të jenë të njëjta. Pastaj dendësia e sipërfaqeve ekuipotenciale karakterizon qartë forcën e fushës në pika të ndryshme. Aty ku këto sipërfaqe janë më të dendura, forca e fushës është më e madhe.

Pra, duke ditur vendndodhjen e linjave të fuqisë së fushës elektrostatike, është e mundur të ndërtohen sipërfaqe ekuipotenciale dhe, anasjelltas, nga vendndodhja e njohur e sipërfaqeve ekuipotenciale, është e mundur të përcaktohet moduli dhe drejtimi i forcës së fushës në secilën pikë të fushë.

Le të gjejmë marrëdhënien midis fuqisë së fushës elektrostatike, e cila është e saj funksioni i fuqisë, dhe potencial - karakteristikë energjetike e fushës.

Puna e zhvendosjes beqare pika e ngarkesës pozitive nga një pikë e fushës në tjetrën përgjatë boshtit X me kusht që pikat të jenë pafundësisht afër njëra-tjetrës dhe x 2 -x 1 = d x,është e barabartë me E x d x. E njëjta punë është j 1 -j 2 =dj. Duke barazuar të dyja shprehjet, mund të shkruajmë

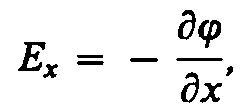
ku simboli i derivatit të pjesshëm thekson se diferencimi bëhet vetëm në lidhje me X. Përsëritja e arsyetimit të ngjashëm për sëpatat në dhe z, ne mund të gjejmë vektorin E:

ku i, j, k- vektorët njësi të boshteve koordinative x, y, z.

Nga përkufizimi i një gradienti rezulton se

dmth tensioni E fusha është e barabartë me gradientin potencial me shenjën minus. Shenja minus përcaktohet nga fakti se vektori i intensitetit E fushat e drejtuara në drejtim në rënie potencial.

Për një paraqitje grafike të shpërndarjes së potencialit të fushës elektrostatike, si në rastin e fushës gravitacionale, përdorni sipërfaqet ekuipotenciale- sipërfaqet, në të gjitha pikat e të cilave ka potencial j ka të njëjtin kuptim.