Verifikimi i ligjit të ruajtjes së momentit në përplasjen e topave
Në fizikë, përplasjet kuptohen si procese të bashkëveprimit midis trupave (grimcave) në kuptimin e gjerë të fjalës, dhe jo vetëm në kuptimin e drejtpërdrejtë - si kontakt i trupave. trupat që përplasen në distancë e madhe janë të lira. Duke kaluar pranë njëri-tjetrit, trupat ndërveprojnë me njëri-tjetrin, si rezultat, mund të ndodhin procese të ndryshme - trupat mund të kombinohen në një trup ( ndikim absolutisht joelastik), mund të lindin trupa të rinj dhe, më në fund, mund të ketë përplasje elastike, në të cilën trupat, pas një afrimi, ndryshojnë përsëri pa ndryshuar gjendjen e tyre të brendshme. Përplasjet e shoqëruara me ndryshim të gjendjes së brendshme të trupave quhen joelastike. Trupat (grimcat) e përfshirë në përplasje karakterizohen (para dhe pas përplasjes) nga momentet dhe energjitë. Procesi i përplasjes reduktohet në një ndryshim në këto sasi si rezultat i ndërveprimit. Ligjet e ruajtjes së energjisë dhe momentit e bëjnë mjaft të lehtë vendosjen e marrëdhënieve midis të ndryshmeve sasive fizike pas përplasjes së trupave. Veçanërisht e vlefshme këtu është rrethana që shpesh ligjet e ruajtjes mund të përdoren edhe në rastet kur forcat aktive i panjohur. Ky është rasti, për shembull, në fizikën e grimcave elementare.
Përplasjet e trupave makroskopikë që ndodhin në kushte normale janë pothuajse gjithmonë joelastike në një shkallë ose në një tjetër, qoftë edhe vetëm sepse shoqërohen nga njëfarë nxehjeje të trupave, d.m.th., shndërrimi i një pjese të energjisë së tyre kinetike në nxehtësi. Sidoqoftë, në fizikë koncepti i përplasjeve elastike luan një rol të rëndësishëm. Përplasje të tilla shpesh duhet të trajtohen në një eksperiment fizik në fushën e fenomeneve atomike, madje edhe përplasjet e zakonshme shpesh mund të konsiderohen elastike me një shkallë të mjaftueshme saktësie.
Ruajtja e momentit të trupave (grimcave) në një përplasje është për faktin se grupi i trupave që marrin pjesë në përplasje është ose sistem i izoluar, d.m.th., forcat e jashtme, ose ato të mbyllura, nuk veprojnë në trupat e përfshirë në sistem: forcat e jashtme janë jo zero, dhe shuma forcat e jashtme barazohet me zero. Situata me zbatimin e ligjit të ruajtjes së energjisë në përplasje është disi më e ndërlikuar. Apeli për ruajtjen e energjisë ndonjëherë kërkon marrjen parasysh të formave të ndryshme të energjisë së brendshme.
Mund të thuhet se veprimi i ligjeve të ruajtjes së momentit dhe energjisë në proceset e përplasjes vërtetohet nga një gamë e gjerë të dhënash eksperimentale.
Përplasjet joelastike
Një grimcë me masë `m` me energji kinetike `K` përplaset me një grimcë të palëvizshme me masë `M`. Gjeni shtimin `Q` të energjisë së brendshme të sistemit të grimcave si rezultat i një përplasjeje absolutisht joelastike ("ngjitje").
Konsideroni një ndikim absolutisht joelastik të dy trupave në LSO. Grimca e rënë lëviz përpara përplasjes në drejtim pozitiv të boshtit "Ox" me shpejtësinë "vec v", energjia kinetike grimcat `K = (mv^2)/2`. Si rezultat i një ndikimi absolutisht joelastik (duke ngjitur së bashku), grimcat lëvizin me të njëjtën shpejtësi `vec u`. Sipas ligjit të ruajtjes së momentit `mv = (m + M) u`. Sipas ligjit të ruajtjes së energjisë
`(mv^2)/2 = ((m + M)u^2)/2 + Q`.
Nga marrëdhëniet e mësipërme, ne gjejmë`Q = M/(m + M) K`.
Vini re se në rastet kufizuese
`Q=K`,
`m< < M`,
`Q = M/m K< < K`,
`m > > M`.
Siç mund ta shohim, gjatë një përplasjeje joelastike të një grimce të lehtë me një masë (për shembull, një elektron me një atom), ka një tranzicion pothuajse të plotë të energjisë së saj kinetike në energjia e brendshme grimcë masive.
Nëse masat janë të barabarta `(m = M)``Q=K/2`.
Nga kjo rrjedh, për shembull, se në përplasjen e dy makinave identike, njëra prej të cilave është e palëvizshme dhe tjetra lëviz në drejtimin drejt saj, gjysma e energjisë kinetike shkon në shkatërrim.
Përplasjet elastike
Një top i lëmuar me masë "M" shtrihet në një sipërfaqe të lëmuar horizontale. Ai goditet nga një top i lëmuar me masë `m` që lëviz me një shpejtësi prej `vec v`. Ka një ndikim qendror elastik të topave. Gjeni shpejtësitë `vec(v_1)` dhe `vec(v_2)` të topave pas përplasjes. Në çfarë kushtesh do të lëvizë topi i incidentit në të njëjtin drejtim pas përplasjes?
Le të shqyrtojmë problemin në LSO, boshti `Ox` i të cilit do të drejtohet përgjatë vijës së qendrave të topave në momentin e përplasjes. Forcat e jashtme që veprojnë në topa gjatë përplasjes janë forcat e gravitetit dhe forcat reagim normal mbështet. Shuma e tyre është zero. Rrjedhimisht, momenti i sistemit të topave nuk ndryshon gjatë ndërveprimit. Sipas ligjit të ruajtjes së momentit `m vec v = m vec(v_1) + M vec(v_2)`.
Duke kaluar te projeksionet në boshtin `Ox`, marrim `mv = mv_(1x) + Mv_2`, këtu merret parasysh se drejtimi i shpejtësisë `vec(v_1)` i topit të përplasjes pas përplasjes nuk ështëi njohur. Sipas ligjit të ruajtjes së energjisë
`(mv^2)/2 = (mv_(1x)^2)/2 + (Mv_2^2)/2`.
Marrëdhëniet e marra i rishkruajmë në formë
`m(v - v_(1x)) = Mv_2`,
`m(v^2 - v_(1x)^2) = Mv_2^2`.
Duke pjesëtuar barazinë e dytë me të parën `(v != v_(1x))`, arrijmë në sistemin linear`v_2 = v + v_(1x)`, `m(v - v_(1x)) = Mv_2`, zgjidhja e të cilit ka formën
`v_(1x) = (m - M)/(m + M) v`, `v_2 = (2m)/(m + M) v`.
Topi në hyrje do të lëvizë pas përplasjes në të njëjtin drejtim `(v_(1x) > 0)` për `m > M`, d.m.th. nëse masa e topit në hyrje është më e madhe se masa e topit të prerë.
Dy rondele të rrumbullakëta elastike të lëmuara lëvizin përpara në një sipërfaqe të lëmuar horizontale me shpejtësi `vec(v_1)` dhe `vec(v_2)`. Gjeni shpejtësitë `vec(v_1^")` dhe `vec(v_2^")` të topave pas një përplasjeje të përkryer elastike jashtë qendrës. Masat e rondele `m_1` dhe `m_2`.
Le të shqyrtojmë problemin në ISO, boshtet e koordinatave `Ox` dhe `Oy` që shtrihen në rrafshin horizontal, ndërsa boshti `Ox` drejtohet përgjatë vijës qendrore të rondele në momentin e goditjes.
Gjatë kohës së goditjes, vetëm forcat e jashtme vertikale veprojnë në sistemin e topit: këto janë forcat e gravitetit dhe forcat e reagimit normal. Shuma e tyre është zero. Pastaj ruhet momenti i sistemit të rondele në procesin e ndërveprimit
`vec(p_1) + vec(p_2) = vec(p_1^") + vec(p_2^")`,
këtu `vec(p_1) = m_1 vec(v_1)`, `vec(p_2) = m_2 vec(v_2)`, `vec(p_1^") = m_1 vec(v_1^")`, `vec(p_2^" ) = m_2 vec(v_2^")` - vrulli i shpimit para dhe pas goditjes.
Meqenëse rondelet janë idealisht të lëmuara, gjatë përplasjes, forcat e brendshme - forcat e ndërveprimit elastik - drejtohen vetëm përgjatë boshtit "Ox". Këto forca nuk i ndryshojnë komponentët `y` të momentit të topit. Pastaj nga `p_(1y) = p_(1y)^"`, `p_(2y) = p_(2y)^"` gjejmë `y`-përbërësit e shpejtësive të topit pas përplasjes
`vec(v_(1y)^") = v_(1y)`, `v_(2y)^" = v_(2y)`,
d.m.th., në projeksionin në boshtin 'Oy', shpejtësitë e topave nuk ndryshuan si rezultat i përplasjes.
Le të gjejmë komponentët `x` të shpejtësive të topave pas përplasjes elastike. Në një përplasje të tillë, energjia kinetike ruhet
`(m_1 (v_(1x)^2 + v_(1y)^2))/2 + (m_2 (v_(2x)^2 + v_(2y)^2))/2 = (m_1 ((v_(1x )^")^2 + (v_(1y)^")^2))/2 + (m_2 ((v_(2x)^")^2 + (v_(2y)^")^2))/2 `.
Duke marrë parasysh barazinë e komponentëve `y` të shpejtësive të topave para dhe pas goditjes së përbashkët, barazia e fundit merr formën
`(m_1 v_(1x)^2)/2 + (m_2 v_(2x)^2)/2 = (m_1 (v_(1x)^")^2)/2 + (m_2 (v_(2x)^" )^2)/2`.
Le t'i drejtohemi ligjit të ruajtjes së momentit dhe të kalojmë në projeksionet e impulseve të momentit të topave në boshtin "Ox"
`m_1 v_(1x) + m_2 v_(2x) = m_1 v_(1x)^" + m_2 v_(2x)^"`.
Kështu, problemi fillestar reduktohet në problemin e një ndikimi qendror absolutisht elastik: kjo është forma që do të merrnin ligjet e ruajtjes së energjisë dhe momentit nëse shpejtësitë e topave do të drejtoheshin përgjatë vijës së qendrave. Sistemi jolinear i ekuacioneve që rezulton mund të reduktohet në një sistem linear. Për ta bërë këtë, vijon (si në problemin e mëparshëm) në të dy ekuacionet, në njërën anë të shenjës së barabartë, kombinoni termat që lidhen me rondele e parë, dhe nga ana tjetër me të dytën, dhe ndani `(v_(1x ) != v_(1x )^")` marrë relacione. Kjo çon në një ekuacion linear
`v_(1x) + v_(1x)^" = v_(2x) + v_(2x)^"`.
Duke zgjidhur sistemin e dy ekuacioneve të fundit, gjejmë
`v_(1x)^" = ((m_1 - m_2) v_(1x) + 2m_2 v_(2x))/(m_1 + m_2)`,
`v_(2x)^" = (2m_1 v_(1x) + (m_2 - m_1) v_(2x))/(m_1 + m_2)`.
Marrëdhëniet e fituara për `v_(1x)^"`, `v_(1y)^"` dhe `v_(2x)^"`, `v_(2y)^"` zgjidh problemin e projeksioneve dhe shpejtësive të topave pas përplasjen
`v_1^" = sqrt((v_(1x)^")^2 + (v_(1y)^")^2)`, `v_2^" = sqrt((v_(2x)^")^2 + ( v_(2y)^")^2)`,
dhe gjithashtu për këndet "alfa_1" dhe "alfa_2" që vektorët e shpejtësisë "vec(v_1^")" dhe "vec(v_2^"" formojnë me drejtimin pozitiv të boshtit "Ox":
`bbb"tg" alfa_1 = (v_(1y)^")/(v_(1x)^")`, `bbb"tg" alfa_2 = (v_(2y)^")/(v_(2x)^") `.
I ndertuar pamje e përgjithshme zgjidhja e problemeve të përplasjeve elastike qendrore dhe joqendrore i hap rrugën analizës së një numri problemesh për të cilat modeli i konsideruar korrespondon me natyrën e bashkëveprimit të trupave (grimcave).
Ndikim elastik dhe joelastik i dy topave uniforme 1. Hyrje Përplasjet e trupave në lëvizje janë të natyrshme në të gjitha nivelet e Universit - nga mikroskopik në kozmik, prandaj fenomenet e ndikimit janë shumë të ndryshme. Në dinamikë studiohet ndikimi i përplasjeve në lëvizjen e sistemeve mekanike. Ky problem tërhoqi vëmendjen e shumë shkencëtarëve të famshëm, duke përfshirë H. Huygens, I. Newton, J. d'Alembert, S. Punchon, G. Darboux, E. J. Routh, A.M. Lyapunova, N.E. Zhukovsky, S.P. Timoshenko dhe shumë të tjerë. Specifikimi i goditjeve është intensiteti dhe kalueshmëria e tyre. Kjo veçori mund të jetë edhe e dobishme, si në drejtimin e shtyllave, nxjerrjen e mineralit ose lojën e topit, dhe e rrezikshme, si në aksidente trafiku. Prandaj, problemi i ndikimit është i rëndësishëm jo vetëm për teoricienët, por edhe për projektuesit, automobilistët, atletët, etj. 2. Qasje në teorinë e ndikimit Nga pikëpamja fizike, forcat e goditjes janë një përgjigje ndaj deformimeve që ndodhin pranë zonës së kontaktit dhe përhapen në valë në këto trupa. Modele matematikore pasqyrojnë këtë proces në një shkallë më të madhe ose më të vogël. Në teorinë klasike të ndikimit, deformimet nuk merren parasysh dhe problemi reduktohet në përcaktimin e karakteristikave integrale të forcave të goditjes - impulseve të tyre. Kjo teori bazohet në ligjet e mekanikës dhe disa hipoteza shtesë. Konsideroni, për shembull, problemin më të thjeshtë të një ndikimi të drejtpërdrejtë të dy topave me masa m 1 dhe m2 .
|
 | |||||||
|
 |
|||
P 2 P 1
θ
P Ligji i ruajtjes së energjisë mund të shkruhet si: P 2 /m 1 \u003d P 2 1 /m 1 + P 2 2 /m 2 Sepse P = mv dhe mv 2 \u003d P 2 / m për çdo trup. Vektor P2 bën një kënd θ
me vektor P, topi në pushim do të kërcejë në një kënd θ
në shpejtësinë fillestare të topit të parë, pastaj nga trekëndëshi i vektorëve vijon: P 2 1 = P 2 2 + P 2 - 2 P P 2 cos θ Duke marrë parasysh qëndrueshmërinë e energjisë, ne e përjashtojmë P1 dhe marrim P 2 \u003d 2 m 2 P cos θ / (m 1 + m 2) \u003d β P cos θ β \u003d 2 m 2 / (m 1 + m 2) Nga kjo mund të shihet se marrëdhënia e përgjithshme ndërmjet R 2 dhe R varet nga këndi θ
dhe raporti i masës m 1 / m 2 . Duhet të dallohen dy raste: m1 > m2 dhe m 1< m 2
. Në rastin e parë β < 1
Topi i rëndë godet atë të lehtë. Fundi i vektorit R 2 përshkruan një rreth me diametër βР. Të dy topat pas goditjes fluturojnë në drejtim të lëvizjes fillestare të topit të parë. Vlera e këndit θ
ndryshon nga 0 në π/2. Këndi i devijimit të topit të parë mund të ndryshojë nga 0 në disa φ max.. Një vlerë φ
përputhen me dy vlera θ.
β < 1
Р 2
Р 1
А В Р φ βР
A B βP
R 2
4. Përplasja joelastike e trupave
Një goditje absolutisht joelastike është një goditje e tillë, pas së cilës shpejtësitë e të dy trupave që përplasen janë të njëjta. Për ta bërë të mundur këtë, trupat që përplasen duhet të kenë veti të tilla që forcat që rrjedhin nga deformimi i tyre të mos varen nga madhësia e deformimit, por nga shpejtësia e ndryshimit të deformimit. Karakteristikat e tilla janë të natyrshme, për shembull, në argjilën e butë, plastelinë. Në një përplasje joelastike, ndodh si më poshtë. Në momentin fillestar të goditjes, shkalla e deformimit është e lartë (topat janë të ngjeshur), prandaj lindin forca të rëndësishme që u japin të dy topave përshpejtime, të drejtuara në drejtime të kundërta. Me zhvillimin e ndikimit, shkalla e deformimit të topave zvogëlohet dhe vetë deformimet rriten derisa shpejtësia e topave të jetë e barabartë. Në këtë moment, deformimet e topave do të ndalojnë së ndryshuari, forcat do të zhduken dhe të dy topat do të lëvizin me të njëjtën shpejtësi. Në një ndikim absolutisht joelastik, ligjet e ruajtjes së momentit dhe energjisë totale plotësohen. Energjia mekanike e trupave para goditjes është më e madhe energji mekanike pas goditjes, pasi pjesërisht (ose plotësisht) kalon në energjinë e brendshme të trupave dhe harxhohet në punën për deformimin e trupave. Për të përcaktuar shpejtësinë e trupave pas bashkëveprimit, merrni parasysh ndikimin e dy topave (pikave materiale) që formojnë një sistem të mbyllur. Masat e topave m 1 dhe m2, shpejtësia para goditjes V 1 i dhe V 2 i. Sipas ligjit të ruajtjes, momenti total i topave përpara goditjes duhet të jetë i njëjtë me atë pas goditjes: m 1 V 1i + m 2 V 2i \u003d (m 1 + m 2) U ku U është shpejtësia pas goditjes, e njëjtë për të dy topat. Nga ekuacioni rezulton se: U \u003d (m 1 V 1i + m 2 V 2i) / (m 1 + m 2) Ligji i ruajtjes së energjisë për ndikimin joelastik të topave në shqyrtim ka formën e mëposhtme: m 1 V 1 i 2 / 2 + m 2 V 2i 2 / 2 = (m 1 + m 2) U 2 + W ku W është ndryshimi i energjisë së brendshme të sistemit. Energjia kinetike e trupave para goditjes ka vlerën e mëposhtme: W 1 \u003d m 1 V 1 i 2 / 2 + m 2 V 2i 2 / 2 Dhe energjia kinetike pas goditjes: W 2 \u003d (m 1 + m 2) U 2 / 2 \u003d (m 1 V 1i + m 2 V 2i) 2 / 2 (m 1 + m 2) Humbja e energjisë mekanike, ose pjesa e energjisë që është shndërruar në formë termike, është: W \u003d W 1 - W 2 \u003d m 1 m 2 (V 1i - V 2i) 2 / 2 (m 1 + m 2) Vlera V 1i – V 2i paraqet shpejtësinë relative të trupave para goditjes. Prandaj, energjia e shndërruar në nxehtësi varet nga raporti i masave të trupave që përplasen m 1 m 2 / (m 1 + m 2) dhe shpejtësinë e tyre relative përpara goditjes. Energjia e humbjes mund të konsiderohet si energjia kinetike e disave masa efektive: m 0 \u003d m 1 m 2 / (m 1 + m 2) duke lëvizur me shpejtësi relative V " i \u003d V 1i - V 2i. Për llogaritjet specifike të shpejtësisë, duhet të hartoni raportin e impulseve me drejtimet e zgjedhura. Nëse, përpara goditjes, shpejtësitë e topave drejtohen përgjatë një linje të drejtë që kalon nëpër qendrat e tyre, goditja quhet qendrore. Shpejtësia e topave pas një ndikimi të tillë do të drejtohet përgjatë së njëjtës vijë të drejtë. Prandaj, ekuacioni i ruajtjes së momentit mund të konsiderohet si skalar. Por shpejtësitë në këtë rast duhet të konsiderohen të përkojnë në shenjë kur drejtohen në një drejtim dhe të kundërta në shenjë kur drejtohen në drejtime të kundërta. Le të shqyrtojmë disa raste të veçanta. 1. Topat lëvizin në të njëjtin drejtim. Ndikimi është i mundur nëse shpejtësia V 1 i dhe V 2i të ndryshme. Për shembull, V2i > V1i, d.m.th. topi i dytë arrin të parin. Pas goditjes, topat do të lëvizin në të njëjtin drejtim me një shpejtësi më të madhe se shpejtësia e topit të parë dhe më e vogël se shpejtësia e topit të dytë. Nëse masat e topave janë të njëjta, atëherë U = (V 1i + V 2i) / 2 2. Topat lëvizin drejt njëri-tjetrit. Pas goditjes, topat do të lëvizin së bashku në drejtimin në të cilin lëvizi topi me një vrull të madh. Nëse momenti i të dy topave është i barabartë në madhësi, atëherë të dy topat do të ndalen pas goditjes. 3. Në rastin e një goditjeje jashtë qendrës (Fig. 3.6.2a), shpejtësitë V 1i dhe V 2i mund të zbërthehet në përbërës V 1X dhe V 2X në drejtim të vijës që lidh qendrat e topave (boshti X) dhe përbërësit V 1Y dhe V2Y në drejtim pingul (boshti y). Për komponentët V 1X, V 2X dhe V 1Y ,V 2Y shkruani ligjin e ruajtjes së momentit në të njëjtën formë si në rastin e një goditjeje qendrore dhe përcaktoni përbërësin e shpejtësisë që rezulton. Le të shqyrtojmë më në detaje një ndikim joelastik. Në një goditje joelastike, një pjesë e energjisë kinetike të topit të përplasjes humbet me lëshimin e nxehtësisë. Në rastin kufizues të një ndikimi absolutisht joelastik, trupi i rënë ngjitet së bashku me trupin në qetësi, energjia kinetike e lëvizjes së tyre relative zhduket dhe ata vazhdojnë të lëvizin si një trup i vetëm. Në shumicën e rasteve praktike, kemi të bëjmë me një ndikim pjesërisht elastik, kur në trup ngacmohen lëkundjet e deformimit pas një përplasjeje, të cilat prishen me kalimin e kohës. Ngacmimi i lëkundjeve të tilla mund të modelohet duke përdorur dy topa identikë të lidhur me një pranverë. Supozoni se një top krejtësisht elastik përplaset me një oshilator sustë. Masat e topave janë të njëjta dhe të barabarta m. Meqenëse në momentin e goditjes susta nuk është ende duke vepruar, topi fluturues ndalon dhe topi i majtë i oshilatorit vihet në lëvizje me shpejtësinë e topit fluturues. v. Në këtë rast, qendra e masës së oshilatorit lëviz me një shpejtësi v/2. Me kalimin e kohës, lëkundjet e oshilatorit do të shuhen dhe ai do të vazhdojë të ecë përpara me një shpejtësi v/2, dhe energjia totale e të gjithë sistemit do të jetë vetëm gjysma e energjisë së topit të përplasjes. Gjysma tjetër do të lëshohet si nxehtësi në oshilator. Ndikimi i trupave joelastikë të zakonshëm korrespondon me një rast të ndërmjetëm midis ndikimeve ideale elastike dhe plotësisht joelastike. Është analoge me një goditje të ngjashme me një goditje të dy topave përmes një suste joelastike, e cila, duke u ngjeshur në një vlerë të caktuar gjatë gjysmës së parë të kohës së goditjes, nuk do të marrë dimensionet e saj origjinale pas goditjes; ose forca repulsive gjatë shtypjes do të jetë më e madhe se gjatë gjysmës së dytë të kohës së goditjes kur susta zgjerohet. Një pjesë e energjisë potenciale të ngjeshjes së sustës do të shndërrohet në nxehtësi dhe nuk do të shndërrohet në energji kinetike të lëvizjes. Prandaj, ligji i ruajtjes së energjisë mekanike nuk mund të zbatohet në këtë rast. Kushti i barazisë së shpejtësive pas goditjes gjithashtu nuk do të qëndrojë, siç ishte me një ndikim krejtësisht joelastik, pasi pas goditjes të dy trupat lëvizin me shpejtësi të ndryshme. Një goditje joelastike mund të karakterizohet nga ajo pjesë e energjisë së deformimit që shndërrohet në nxehtësi gjatë goditjes. Por edhe Njutoni zbuloi se gjatë një goditjeje joelastike të topave të bërë nga një material i caktuar, shpejtësitë relative para dhe pas goditjes janë në një raport konstant, dhe një ndikim i tillë karakterizohet nga faktori i rikuperimit të shpejtësisë relative pas goditjes: e \u003d | V 2 - V 1 | / |V 2i – V 1i | ku V 2i – V 1iështë shpejtësia relative përpara goditjes, dhe V 2 - V 1- pas ndikimit. Përvoja tregon se, me një shkallë të caktuar saktësie, mund të llogaritet vlera e konstante dhe e varur vetëm nga materiali i topave që përplasen. Me një ndikim krejtësisht elastik, shpejtësia relative mbetet e njëjtë në madhësi, por ndryshon shenjën e saj: V 1i - V 2i \u003d - (V 1 - V 2) Koeficienti i rikuperimit është gjithmonë më i vogël se uniteti, sepse me një ndikim elastik është i barabartë me një, me një ndikim plotësisht joelastik është i barabartë me zero, pasi në këtë rast V 2 - V 1 \u003d 0 Njohja e koeficientit e, mund të llogarisim shpejtësinë e topave pas goditjes dhe humbjes së energjisë. Libra të përdorur: 1. D.V. Sivukhin, " Kursi i përgjithshëm fizikës. Mekanika", Shkenca, 1979 2. O.D. Shebalin, " Bazat fizike mekanika dhe akustika", Shkolla e lartë, 1981 3. S.P. Strelkov, "Mekanikë", Nauka, 1975 4. K. Schwartz, T. Goldfarb, "Kërkimi i modeleve në botën fizike", përkthyer nga anglishtja, Moskë , Mir, 1977 5. Studime laboratorike në fizikë, redaktuar nga LL Goldin, Moskë, Nauka, 1983 6. AI Ivanov, "Regularities of ndikim në sistemet mekanike“, Natyra, 1999, nr 10Bakanina L. Ligji i ruajtjes së momentit në përplasje // Kvant. - 1977. - Nr 3. - S. 46-51.
Me marrëveshje të veçantë me redaksinë dhe redaktorët e revistës "Kvant"
Ligji i ruajtjes së momentit (momentumit) është i kënaqur për sistemet e mbyllura, domethënë ato që përfshijnë të gjithë trupat ndërveprues, në mënyrë që asnjë forcë e jashtme të mos veprojë në asnjë nga trupat e sistemit. Megjithatë, kur zgjidhen shumë detyrat fizike rezulton se momenti mund të mbetet konstant edhe për sistemet jo të mbyllura. Vërtetë, në këtë rast momenti ruhet vetëm përafërsisht. Le të përpiqemi të kuptojmë se çfarë po ndodh këtu.
Ndryshimi në momentin e një sistemi të hapur është i barabartë me momentin total të forcave të jashtme. Shënoni me vlerën mesatare të forcës së jashtme që rezulton që vepron në sistem gjatë intervalit kohor Δ t. Pastaj
Nëse vlera absolute e kësaj force nuk është shumë e madhe dhe koha gjatë së cilës vepron forca është e vogël, atëherë edhe produkti do të jetë i vogël. Në këtë rast, bëhet e nevojshme të vlerësohet me çfarë saktësie momenti i sistemit mund të konsiderohet i pandryshuar.
Për më tepër, nuk duhet të harrojmë se momenti është një vektor, dhe, për rrjedhojë, mund të flasim për ruajtjen e projeksionit të këtij vektori në çdo drejtim. Në të vërtetë, nëse sistemi nuk është i mbyllur, por forcat e jashtme janë të tilla që shuma e projeksioneve të të gjitha forcave në një drejtim të caktuar është e barabartë me zero, atëherë projeksioni i momentit të sistemit në këtë drejtim mbetet konstant. Jo sistem i mbyllur në këtë drejtim është i ngjashëm me një të mbyllur.
Ndërveprimet afatshkurtra lindin, për shembull, gjatë shpërthimeve, të shtëna, përplasje. Ne do të diskutojmë këtë lloj problemi. Ne do të përpiqemi të zbulojmë në çdo rast specifik nëse ligji i ruajtjes së momentit është i kënaqur apo jo dhe nga çfarë varet.
Detyra 1. Nga një top që rrëshqet pa fërkim përgjatë plan i pjerrët dhe tashmë e ka kaluar rrugën l, lëshohet një e shtënë në drejtim horizontal (Fig. 1). Me çfarë shpejtësie të predhës do të ndalet arma pas shkrepjes? Pesha e predhës m shumë më pak se masa e armës M, këndi i pjerrësisë së rrafshët α.
Para goditjes, arma (së bashku me predhën), kaloi rrugën l, ka vrull të drejtuar përgjatë rrafshit të pjerrët. Moduli i këtij momenti mund të gjendet nga ligji i ruajtjes së energjisë:
Menjëherë pas goditjes, arma ndaloi dhe predha fluturoi në drejtim horizontal. Kështu, pavarësisht nga kohëzgjatja e shkurtër e ndërveprimit midis armës dhe predhës, momenti i këtij sistemi nuk ruhet. Pse?
Gjatë gjuajtjes, forca e presionit të armës në rrafshin e pjerrët rritet ndjeshëm, që do të thotë se forca e reagimit nga ana e avionit gjithashtu rritet, kështu që impulsi i kësaj force rezulton mjaft i madh. Më pas ndryshon vrullin total të armës dhe predhës.
Sidoqoftë, në drejtimin përgjatë planit të pjerrët, projeksioni i forcës së reagimit është i barabartë me zero, dhe projeksioni i impulsit të gravitetit për një kohë të shkurtër goditjeje Δ t i vogël dhe nuk rritet kur shkrehet. Prandaj, mund të supozohet, me një shkallë saktësie, se në drejtimin përgjatë rrafshit të pjerrët, ruhet projeksioni i momentit të sistemit të armës-predhës. Prandaj projeksioni impuls total arma dhe predha para goditjes është e barabartë me projeksionin e predhës pas goditjes (arma është në qetësi):
Prandaj moduli i shpejtësisë së predhës menjëherë pas goditjes
Gjatë zgjidhjes së këtij problemi, supozuam se në drejtimin përgjatë rrafshit të pjerrët, sistemi i predhës me armë sillet si një sistem i mbyllur. Megjithatë, ne nuk mund të vlerësojmë shkallën e saktësisë me të cilën kjo është e vërtetë, pasi sistemi i trupave ndërveprues është kompleks dhe nuk ka të dhëna të nevojshme për një vlerësim të tillë.
Le të analizojmë tani dy probleme me më shumë ndërveprim i thjeshtë ku mund të bëhet një vlerësim i tillë.
Detyra 2. Në një top druri në masë M= 1 kg që bie me shpejtësi V 0 = 1 m / s, qëlloni nga poshtë me një armë dhe shpojeni atë. Çfarë shpejtësie do të ketë topi menjëherë pas kësaj? Shpejtësia e plumbit υ 0 = 300 m/s, pas largimit nga topi υ = 100 m/s, masa e plumbit m= 10 g.
Koha e ndërveprimit, ku d- diametri i topit, a υ cf - Shpejtësia mesatare plumba brenda topit. Diametri i topit mund të vlerësohet duke ditur se dendësia e pemës ρ është afërsisht e barabartë me densitetin e ujit ρ në \u003d 10 3 kg / m 3:
Pra Δ t≈ 5 10–4 s. Momenti i gravitetit të sistemit gjatë kësaj kohe (dhe rrjedhimisht ndryshimi në momentin total të topit dhe plumbit)
fq = (M+m)· gΔ t≈ 5 10 -3 N s.
Sasia e lëvizjes së sistemit para ndërveprimit
fq 0 = mυ 0 – MV 0 = 2 N s.
Pastaj relacioni
dhe, rrjedhimisht, me një saktësi prej 0.2%, mund të supozojmë se momenti i sistemit nuk ndryshon gjatë ndërveprimit.
Le të shkruajmë ligjin e ruajtjes për projeksionin e momentit në boshtin vertikalisht lart:
mυ 0 – MV 0 = mυ+ MV y.
Prandaj projeksioni i shpejtësisë së topit pas ndërveprimit
domethënë, topi do të fillojë të lëvizë lart me një shpejtësi prej 1 m / s.
Detyra 3. Një top hidhet vertikalisht lart me një shpejtësi υ 0 = 1 m/s. Kur të arrijë në pikën më të lartë të ngjitjes, i njëjti top hidhet me shpejtësi fillestare 2υ 0 . Përcaktoni shpejtësinë e topave pas përplasjes, nëse përplasja mund të konsiderohet krejtësisht elastike.
Ngjashëm me problemin e mëparshëm, para së gjithash vlerësojmë shkallën e saktësisë me të cilën sistemi i dy topave gjatë përplasjes mund të konsiderohet i mbyllur. Për ta bërë këtë, ne gjejmë momentin e sistemit përpara goditjes, momentin e gravitetit gjatë goditjes dhe i krahasojmë ato me njëri-tjetrin.
Lërini topat të përplasen në lartësi h Përmes kohës t pas fillimit të lëvizjes së topit të dytë (Fig. 2). Pastaj për topin e parë
ku është lartësia maksimale e ngritjes. Për topin e dytë
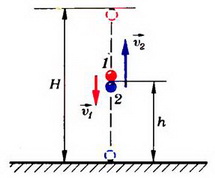
Prandaj, dhe shpejtësitë e të dy topave menjëherë para përplasjes janë të barabarta
me topin e parë që lëviz poshtë, dhe i dyti - lart.
Pra, sasia e lëvizjes së sistemit para ndërveprimit
fq 0 = mυ 2 - mυ 1 \u003d 1.5 mυ 0 .
Tani le të përpiqemi të vlerësojmë kohën e ndërveprimit dhe momentin e gravitetit gjatë kësaj kohe. Për ta bërë këtë, ne duhet të imagjinojmë se si ndodh procesi i përplasjes. Le të shqyrtojmë fillimisht përplasjen e dy shufrave identike nga skajet. Pas goditjes në fund, ndodh deformimi elastik, i cili përhapet përgjatë shufrës, domethënë një valë zanore lind në shufër. Pasi ka arritur në skajin e kundërt të shufrës, vala reflektohet dhe kthehet. Mund të themi se procesi i përplasjes përfundon këtu, dhe koha e bashkëveprimit të shufrave është e barabartë me kohën e kalimit valë zanore përgjatë shufrës dhe mbrapa. Në fakt, fotografia e ndërveprimit është shumë më e ndërlikuar, dhe në rastin e topave, ku vala elastike që rezulton nuk është e rrafshët, aq më tepër. Megjithatë, për të vlerësuar këtu, supozojmë gjithashtu se, deri në një renditje të madhësisë, koha e ndikimit është e barabartë me kohën e përhapjes së valës së zërit brenda topit: . Shpejtësia e zërit në të ngurta në rendin e disa kilometrave në sekondë. Nëse diametri i topit është rreth një centimetër, atëherë Δ t~ 10–5 s, dhe vlera absolute e momentit të gravitetit është shumë herë më e vogël se momenti i topave përpara ndërveprimit:
Kështu, edhe në këtë rast, sistemi i përplasjes së topave mund të konsiderohet i mbyllur. (Sigurisht, lëvizja e mëtejshme e topave në thelb varet nga forca e gravitetit.) Meqenëse ndikimi i topave është absolutisht elastik, ne do të përdorim ligjet e ruajtjes së energjisë mekanike dhe projeksionin e momentit në një bosht të drejtuar vertikalisht lart. :
Duke zëvendësuar këtu vlerat përkatëse për υ 1 dhe υ 2:
Në një goditje elastike, topa me masa të barabarta shkëmbejnë shpejtësi.
Sidoqoftë, nuk duhet menduar se në përplasje gjithmonë mund të neglizhohet veprimi i forcave të jashtme dhe të konsiderohet sistemi i mbyllur. Për shembull, merrni parasysh problemin e mëposhtëm.
Detyra 4. Një qese me miell rrëshqet pa shpejtësi fillestare nga një lartësi H në një dërrasë të lëmuar të prirur në një kënd α = 60° ndaj horizontit. Pas zbritjes, çanta bie në një dysheme të ashpër horizontale. Koeficienti i fërkimit të çantës në dysheme μ = 0.7. Ku do të ndalojë çanta?
Pas zbritjes nga tabela, çanta ka një shpejtësi të drejtuar përgjatë tabelës (Fig. 3). Vlera e saj absolute mund të gjendet nga ligji i ruajtjes së energjisë mekanike, pasi pllaka është e lëmuar dhe nuk ka humbje energjie:
Në drejtimin horizontal, një forcë rrëshqitëse e fërkimit vepron në qese, moduli i së cilës është . Momenti i kësaj force gjatë goditjes është i barabartë me
domethënë, nuk varet nga ligji që ndryshon forca e reagimit të mbështetësit (dhe si rrjedhojë forca e presionit të qeskës në dysheme), as nga koha e goditjes. Le të gjejmë ndryshimin në projeksionin horizontal të momentit të çantës. Le të drejtojmë boshtin X horizontalisht në të djathtë, atëherë, sipas ligjit të dytë të Njutonit,
Prandaj projeksioni i shpejtësisë me të cilën çanta do të fillojë të lëvizë përgjatë dyshemesë,
Çfarë do të thotë shenja minus? Formalisht, shenja minus tregon se pas goditjes qesja duhet të lëvizë majtas, ose, me fjalë të tjera, se momenti i forcës së fërkimit doli të jetë më i madh se projeksioni fillestar horizontal i momentit të qeses. Kjo do të thotë që në një moment në procesin e përplasjes, projeksioni i shpejtësisë së qeses në bosht X u kthye në zero. Nga ky moment, vendimi ynë bëhet i pasaktë. Në të vërtetë, moduli i forcës së fërkimit është i barabartë me μ N cp vetëm kur rrëshqet, ndërsa në qetësi forca e fërkimit mund të marrë çdo vlerë nga 0 në μ N cp në varësi të forcave (përveç forcës së fërkimit) që veprojnë në trup. Në rastin tonë, asnjë forcë tjetër nuk ka projeksione në drejtimin horizontal, prandaj, në momentin kur projeksioni horizontal i shpejtësisë së qeses zhduket, edhe forca e fërkimit zhduket. Kështu, çanta nuk do të lëvizë fare në dysheme.
Së fundi, le të diskutojmë një problem tjetër mjaft të njohur mbi përplasjen e trupave. Gjatë zgjidhjes së këtij problemi, zakonisht përdoren përafrime mjaft të përafërta, pa përcaktuar në asnjë mënyrë që kjo është një përafrim, në asnjë rrethanë nuk mund të përdoret.
Detyra 5. Në një pykë masive që qëndron në një sipërfaqe të lëmuar horizontale M nga lart h rënie e topit të masës m dhe kërcen në drejtimin horizontal (Fig. 4). Gjeni projeksionin horizontal të shpejtësisë së pykës pas goditjes. Injoroni fërkimin dhe supozoni se ndikimi është krejtësisht elastik.
Ndryshe nga të gjitha problemet e mëparshme, këtu është e nevojshme të merret parasysh përplasja e jo dy, por tre trupave - një top, një pykë dhe një plan horizontal. Në rastin e përgjithshëm, pa bërë ndonjë supozim shtesë për mekanizmin e ndikimit, ky problem nuk mund të zgjidhet. Në zgjidhjen më të zakonshme të këtij problemi, është në mënyrë implicite (pa asnjë rezervë) që përplasjet e topit me pykën dhe pykën me planin horizontal ndodhin njëkohësisht, dhe pyka pas përplasjes ka vetëm një projeksion të shpejtësisë horizontale. Pastaj shkruhen ekuacionet e ligjeve të ruajtjes së energjisë mekanike dhe momentit:
ku Vx dhe υ x- përkatësisht projeksioni i shpejtësive të pykës dhe topit në boshtin horizontal të drejtuar djathtas. Nga këtu
Megjithatë, në një zgjidhje të tillë nuk është aspak e qartë se ku ka shkuar projeksioni vertikal i momentit të topit. Në fund të fundit, nëse përplasja është absolutisht elastike, projeksioni vertikal i momentit të sistemit nuk zhduket, por vetëm ndryshon shenjën! Topi pas goditjes kërcen në një drejtim horizontal, avioni është përgjithësisht i palëvizshëm. Kjo do të thotë që pyka duhet të kërcejë pas goditjes. Dhe energjia e lidhur me këtë lëvizje nuk merret parasysh në zgjidhjen e mësipërme.
Pamja fizike e goditjes përputhet më shumë me supozimin se në fillim topi përplaset vetëm me pykën dhe më pas pyka, e cila ka marrë njëfarë shpejtësie si rezultat i kësaj përplasjeje, ndërvepron me rrafshin horizontal. Pas goditjes së parë, projeksioni vertikal i shpejtësisë së pykës
Kalon nëpër qendrën e gravitetit gjatë goditjes O pykë (Fig. 5).
Përveç kësaj, vërejmë se në mënyrë që topi të kërcejë horizontalisht pas përplasjes, këndi i pykës α duhet të ketë një vlerë të përcaktuar mirë, në varësi të masave të topit dhe pykës.
Si përfundim, ne ofrojmë disa detyra për zgjidhje të pavarur.
Ushtrime
1. Në qendër të topit të masës m 1 = 300 g i shtrirë në skajin e tavolinës goditet nga një plumb në masë që fluturon horizontalisht m 2 = 10 g dhe e shpon atë. Topi bie në dysheme në distancë s 1 = 6 m nga tabela, dhe plumbi është në një distancë s 2 = 15 m Lartësia e tavolinës H= 1 m Përcaktoni shpejtësinë fillestare të plumbit.
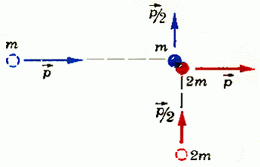
2. Dy grimca me masë m dhe 2 m, duke pasur moment dhe , lëvizin në drejtime pingule reciproke. Pas përplasjes, grimcat shkëmbejnë momentin (Fig. 6). Përcaktoni sasinë e nxehtësisë së lëshuar gjatë goditjes.
3. Një qese me miell rrëshqet pa shpejtësi fillestare nga një lartësi H\u003d 2 m përgjatë një dërrase të prirur në një kënd α \u003d 45 ° në horizont. Pas zbritjes, çanta bie në një sipërfaqe horizontale. Koeficienti i fërkimit të çantës ndaj tabelës dhe sipërfaqes horizontale është μ = 0,5. Sa larg nga fundi i tabelës do të ndalojë çanta?
Përgjigjet
1. 
3.
Ligji i ruajtjes së energjisë bën të mundur zgjidhjen e problemeve mekanike në ato raste kur, për ndonjë arsye, efektet shëruese në trup janë të panjohura. Një shembull interesant i një rasti të tillë është përplasja e dy trupave. Ky shembull është veçanërisht interesant sepse në analizën e tij është e pamundur të bëhet vetëm me ligjin e ruajtjes së energjisë. Është gjithashtu e nevojshme të përfshihet ligji i ruajtjes së momentit (momentum).
Në jetën e përditshme dhe në teknologji, nuk duhet të merret shpesh me përplasje trupash, por në fizikën e atomit dhe grimcat atomike përplasjet janë shumë të zakonshme.
Për thjeshtësi, fillimisht do të shqyrtojmë përplasjen e dy topave me masat e të cilave i dyti është në qetësi dhe i pari lëviz drejt të dytit me shpejtësi. Supozojmë se lëvizja ndodh përgjatë vijës që lidh qendrat e të dy topave (Fig. 205), kështu që kur topat përplasen, ndodh e mëposhtme e quajtur goditje qendrore ose ballore. Sa janë shpejtësitë e të dy topave pas përplasjes?
Para përplasjes, energjia kinetike e topit të dytë është zero, dhe e para. Shuma e energjive të të dy topave është:
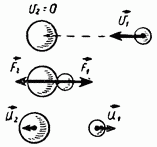
Pas përplasjes, topi i parë do të fillojë të lëvizë me një farë shpejtësie Topi i dytë, shpejtësia e të cilit ishte e barabartë me zero, do të marrë gjithashtu një shpejtësi. Prandaj, pas përplasjes, shuma e energjive kinetike të dy topave do të bëhet e barabartë me
Sipas ligjit të ruajtjes së energjisë, kjo shumë duhet të jetë e barabartë me energjinë e topave para përplasjes:
Nga ky ekuacion, natyrisht, nuk mund të gjejmë dy shpejtësi të panjohura: Këtu vjen në ndihmë ligji i dytë i ruajtjes - ligji i ruajtjes së momentit. Para përplasjes së topave, vrulli i topit të parë ishte i barabartë dhe vrulli i të dytit ishte zero. Momenti i përgjithshëm i dy topave ishte i barabartë me:
Pas përplasjes, momenti i të dy topave ndryshoi dhe u bë i barabartë dhe vrulli total u bë
Sipas ligjit të ruajtjes së momentit, momenti i përgjithshëm nuk mund të ndryshojë gjatë një përplasjeje. Prandaj, duhet të shkruajmë:
Meqenëse lëvizja është përgjatë një linje të drejtë, në vend të ekuacioni vektorial mund të shkruhet algjebrike (për projeksionet e shpejtësive në boshtin koordinativ të drejtuar përgjatë shpejtësisë së topit të parë përpara goditjes):
Tani kemi dy ekuacione:
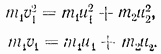
Një sistem i tillë ekuacionesh mund të zgjidhet edhe për shpejtësitë e panjohura të tyre dhe topave pas një përplasjeje. Për ta bërë këtë, ne e rishkruajmë atë si më poshtë:
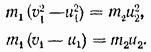
Duke pjesëtuar ekuacionin e parë me të dytin, marrim:
Tani duke zgjidhur këtë ekuacion së bashku me ekuacionin e dytë
(bëjeni vetë), zbulojmë se topi i parë pas goditjes do të lëvizë me një shpejtësi
dhe e dyta - me shpejtësi
Nëse të dy topat kanë të njëjtat masa, atëherë kjo do të thotë që topi i parë, duke u përplasur me të dytin, transferoi shpejtësinë e tij tek ai dhe vetë ndaloi (Fig. 206).
Kështu, duke përdorur ligjet e ruajtjes së energjisë dhe momentit, është e mundur, duke ditur shpejtësitë e trupave para përplasjes, të përcaktohen shpejtësitë e tyre pas përplasjes.
Dhe si ishte situata gjatë vetë përplasjes, në momentin kur qendrat e topave ishin sa më afër?
Është e qartë se në këtë kohë ata lëviznin së bashku me një shpejtësi të caktuar. Me të njëjtat masa trupash, masa e tyre totale është 2 tonë. Sipas ligjit të ruajtjes së momentit, gjatë lëvizjes së përbashkët të të dy topave, momenti i tyre duhet të jetë i barabartë me momentin total përpara përplasjes:
Prandaj rrjedh se
Kështu, shpejtësia e të dy topave gjatë lëvizjes së tyre të përbashkët është e barabartë me gjysmën
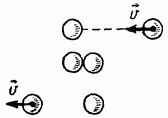
shpejtësia e njërit prej tyre para përplasjes. Le të gjejmë energjinë kinetike të të dy topave për këtë moment:
Para përplasjes energji totale të dy topat ishin të barabartë
Për rrjedhojë, pikërisht në momentin e përplasjes së topave, energjia kinetike u përgjysmua. Ku shkoi gjysma e energjisë kinetike? A ka shkelje të ligjit të ruajtjes së energjisë këtu?
Energjia, natyrisht, mbeti e njëjtë gjatë lëvizjes së përbashkët të topave. Fakti është se gjatë përplasjes të dy topat u deformuan dhe për këtë arsye kishin energjinë potenciale të ndërveprimit elastik. Pikërisht përmasat e kësaj energji potenciale dhe energjia kinetike e topave është zvogëluar.
