Pitanje 1. Elektromagnetno polje. EMF vektori. Grafički prikaz polja Elektromagnetno polje- osnovno fizičko polje u interakciji sa električno nabijenim telima, kao i sa tijelima koja imaju svoje dipolne i multipolne električne i magnetne momente. To je kombinacija električnog i magnetskog polja koja mogu, pod određenim uslovima, generisati jedno drugo, ali su u stvari jedan entitet formalizovan kroz elektrotenzor magnetsko polje.

Vektori elektromagnetnog polja:

Električno polje. Jedna od glavnih vektorskih karakteristika elektromagnetnog polja je tenzija električno polje. Pod jačinom električnog polja podrazumijeva se sila kojom električno polje djeluje na pozitivni jedinični tačkasti naboj uveden u polje.

(1)

U fizici je ovo specificirano: naboj q mora biti dovoljno mali da se može zanemariti promjena u distribuciji električnih naboja koji formiraju ovo polje.

Razmotrimo ovaj proces na pojednostavljen način u okviru klasične teorije:

Materija se sastoji od atoma. Atom se sastoji od pozitivnog jezgra i negativnih elektrona. Kombinacija atoma formira molekulu. Postoje supstance sa polarnim i nepolarnim molekulima. U slučaju nepolarnih atoma ili molekula, tačka primjene rezultante svih sila koje djeluju na negativne naboje poklapa se s točkom primjene rezultante svih sila koje djeluju na pozitivne naboje. To je moguće ako se težište molekula poklapa sa težištem protona. Kod polarnih molekula ovi centri se ne poklapaju, a polarni molekul se može uporediti sa elementarnim dipolom, tj. sistem koji se sastoji od dva suprotna naelektrisanja razdvojena u prostoru razdaljinom l. Dipole karakterizira dipolni moment:

Učinak polarizacije tvari karakterizira ukupni dipolni moment: u razmatranom volumenu dV:

(4) - dipolni moment koji odgovara pojedinačnim atomima ili molekulama. Formula (4) geometrijsko zbrajanje se vrši u volumenu V.

Uz jačinu električnog polja koristi se još jedna vektorska veličina: - vektor električne indukcije, ili vektor električnog pomaka: (8); ;

Otuda slijedi da za isti raspored i veličinu električnih naboja vektorsko polje ne ovisi o svojstvima medija.

Kao što znate, sila koja djeluje na pozitivni električni naboj koji se kreće u magnetskom polju određena je Lorentzovom silom: (1),

gdje (2) ; (3) ; .

Magnetna sila je proporcionalna brzini kretanja naboja i usmjerena je okomito na smjer kretanja naboja.

Fizičko značenje: vrijednost se naziva vektor magnetske indukcije i jednaka je sili kojom magnetsko polje djeluje na pozitivni tačkasti naboj koji se kreće jediničnom brzinom u smjeru okomitom na njega.

Polja su prikazana pomoću linija sile. Pod "snagom" podrazumijevaju linije, u čijoj tački tangente opisuju smjer prikazanog polja. Promjena amplitude polja je označena brojem linija sile po jedinici površine površine okomito na linije sile. Neka postoji vektorsko polje ALI, koji se u svakoj tački prostora može izraziti u kartezijanskom sistemu:

l- linija polja polja ALI, - jedinični vektori. Dobijamo diferencijalnu jednadžbu linije polja: dr se može napisati u terminima njene projekcije: (1),

Pretpostavljamo da je funkcija koja opisuje liniju polja poznata:

Od vektorska analiza poznato je da su dva vektora paralelna ako su omjeri odgovarajućih projekcija jednaki:

Ovo je diferencijalna jednadžba linije polja.

Pitanje 2. Maxwellova prva jednačina u integralnom i diferencijalnom obliku.

Maxwellova prva jednačina je generalizacija zakona ukupne struje (Amperov zakon). U pre-Maxwellovoj formulaciji, ova se jednadžba može formulirati na sljedeći način: cirkulacija vektora intenziteta H magnetno polje duž zatvorenog kola G jednako je struji / koja prodire kroz ovo kolo:

Prije Maxwella, struja / je razumjela samo struju provodljivosti. U opštem slučaju, raspodela struje / unutar kola G može biti neujednačena. Gde

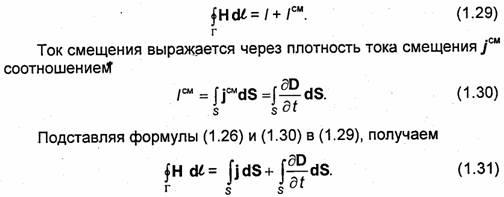
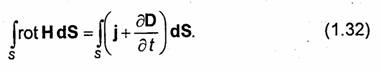
Pitanje 3. Maxwellova druga jednačina u integralnom i diferencijalnom obliku.

Maxwellova druga jednačina je

generalizacija Faradejevog zakona indukcije, koja je formulisana na sledeći način: ako je zatvoreni krug G prožet promenljivom magnetni fluks F, tada se u krugu pojavljuje EMF e, jednak brzini promjene ovog protoka:

Znak minus na desnoj strani formule (1.34) znači da se čini da EMF koji nastaje u krugu uvijek teži da spriječi promjenu protoka koji prodire u ovo kolo. Ova odredba je poznata kao "Lenzovo pravilo".

Relacija (1.37) je formulisana za konturu konačnih dimenzija i naziva se Maxwellova druga jednadžba u integralnom obliku. Maxwell je također formulirao ovu jednačinu u diferencijalnom obliku.

Pitanje 4. Maxwellova treća jednačina u integralnom i diferencijalnom obliku.

Treća Maxwellova jednačina je generalizacija Gaussovog zakona za slučaj promjenjivih procesa. Gaussov zakon povezuje tok vektora električnog pomaka kroz proizvoljnu zatvorenu površinu S sa nabojem Q koncentriranim unutar ove površine:

gdje dS = n o dS ; n 0 - jedinični vektor vanjske normale na površinu S.

Zamjenom (1.41) u (1.40) dobijamo

Jednačina (1.43) se obično naziva Maxwellova treća jednačina u integralnom obliku. Da pređemo na diferencijalni oblik

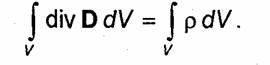
Ova jednakost mora vrijediti za proizvoljan volumen V, što je moguće samo ako

Pitanje 5. Maxwellova četvrta jednačina u integralnom i diferencijalnom obliku.

Maxwellova četvrta jednačina u integralnom obliku poklapa se sa Gaussovim zakonom za magnetno polje, koji se može formulirati na sljedeći način. Vektorski tok AT kroz bilo koju zatvorenu površinu S je jednako nuli, tj.

To znači da nema vektorskih linija AT, koji samo ulaze u zatvorenu površinu S (ili, obrnuto, samo izlaze iz površine S): uvijek prodiru u nju (slika 1.9).

Jednačina (1.46) se zove Maxwellova četvrta jednačina u integralnom obliku. Može se prijeći na diferencijalni oblik jednadžbe (1.46) koristeći Ostrogradsky-Gaussovu teoremu na isti način kao što je to učinjeno u slučaju treće Maxwellove jednadžbe. Kao rezultat, dobijamo

divB = 0 (1.47)

Jednačina (1.47) je Maxwellova četvrta jednačina. To pokazuje da u prirodi ne postoje usamljeni magnetni naboji istog znaka. Iz ove jednačine također slijedi da su linije vektora AT(linije polja magnetnog polja) su kontinuirane.

Maxwellov sistem jednačina uključuje četiri osnovne jednačine

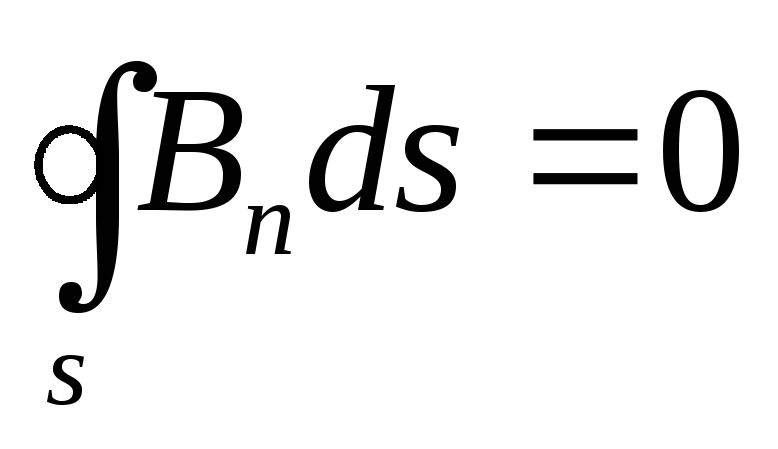, (3.2)

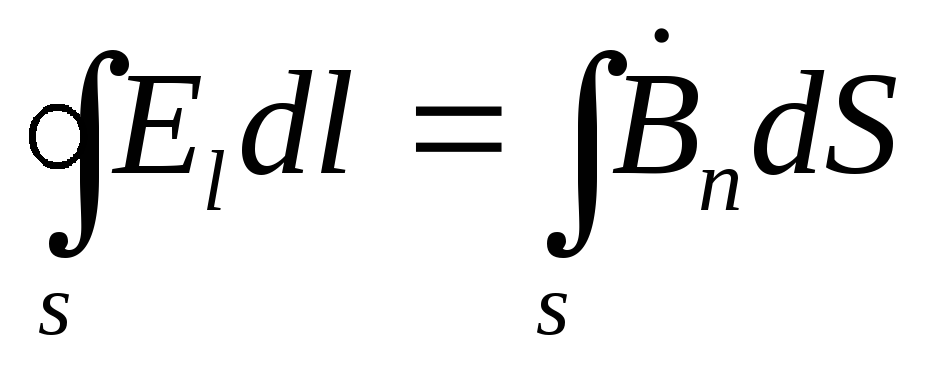, (3.3)

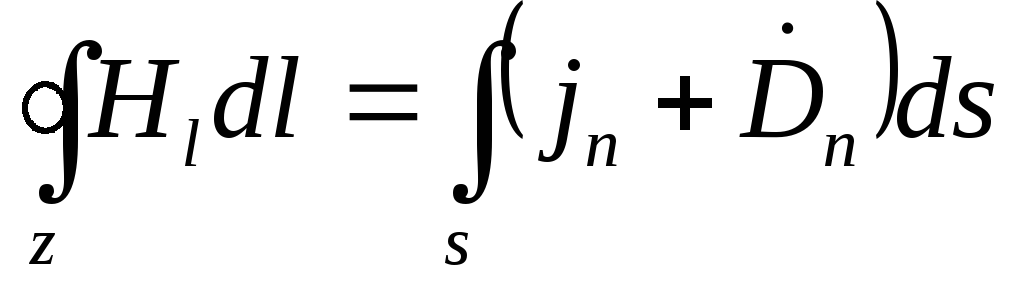. (3.4)

Ovaj sistem je dopunjen sa tri materijalne jednačine, povezivanje fizičke veličine uključeno u Maxwellove jednačine:

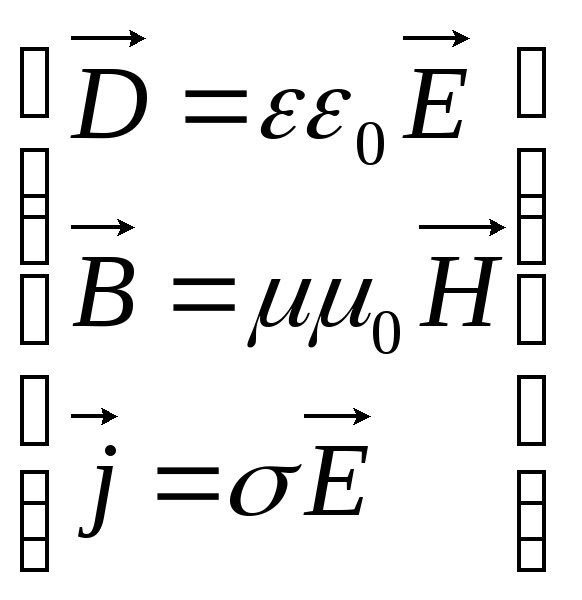(3.5)

Podsjetimo se fizičko značenje ove matematičke fraze.

Prva jednačina (3.1) to kaže elektrostatički polje se može stvoriti samo električnim nabojem.U ovoj jednačini 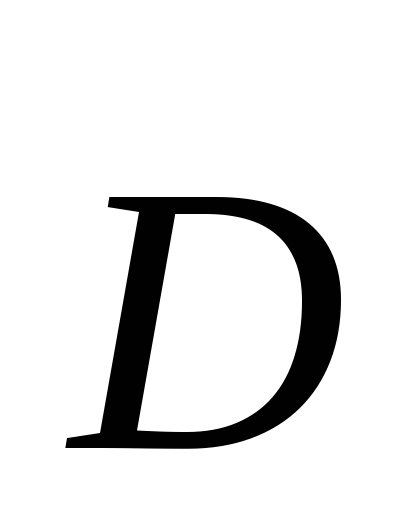je vektor električnog pomaka, ρ je zapreminska gustina električnog naboja.

Protok vektora električnog pomaka kroz bilo koju zatvorenu površinu jednak je naboju zatvorenom unutar ove površine.

Kao što eksperiment pokazuje, tok vektora magnetske indukcije kroz zatvorenu površinu uvijek je jednak nuli (3.2)

Poređenje jednačina (3.2) i (3.1) omogućava nam da zaključimo da u prirodi nema magnetnih naboja.

Jednačine (3.3) i (3.4) su od velikog interesa i značaja. Ovdje razmatramo kruženje vektora električne snage ( ) i magnetni ( ) polja duž zatvorene konture.

Jednačina (3.3) kaže da naizmjenično magnetsko polje ( 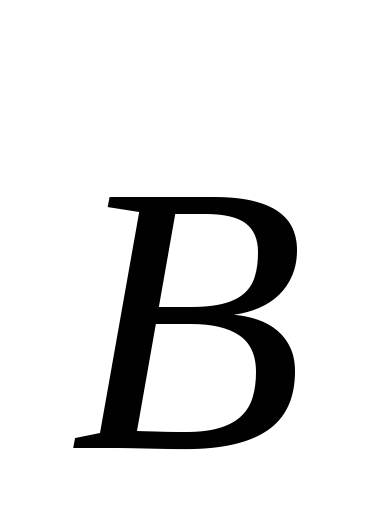) je izvor vrtložnog električnog polja ( ).Ovo nije ništa drugo do matematički zapis fenomena Faradejeve elektromagnetne indukcije.

Jednačina (3.4) uspostavlja vezu između magnetnog polja i naizmjeničnog električnog polja. Prema ovoj jednačini, magnetsko polje može biti stvoreno ne samo strujom provodljivosti ( 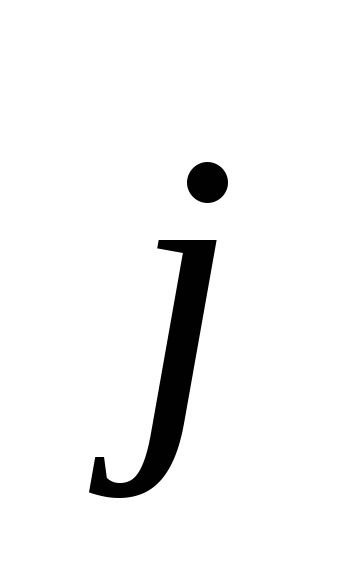), ali i naizmjeničnim električnim poljem .

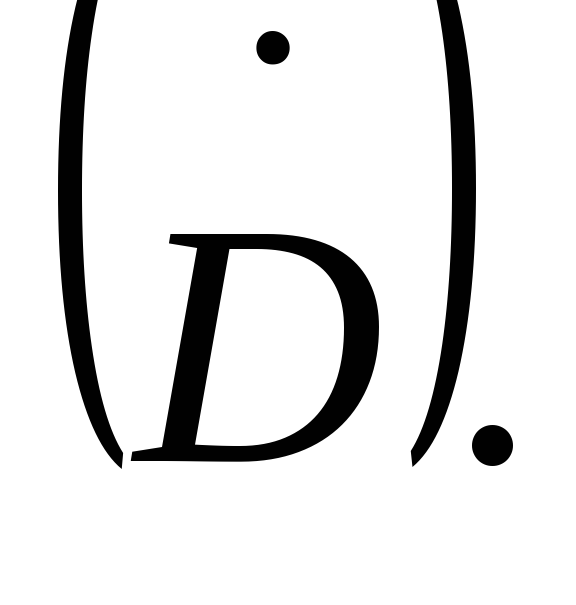U ovim jednačinama:

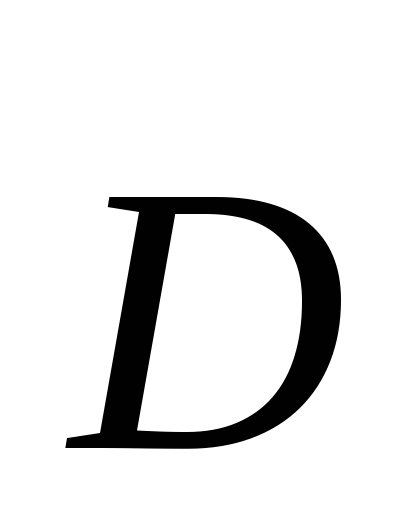je vektor električnog pomaka,

H- jačina magnetnog polja,

E- jačina električnog polja,

j je gustina struje provodljivosti,

μ - magnetna permeabilnost medija,

ε je dielektrična konstanta medija.

1. Elektromagnetski talasi. Osobine elektromagnetnih talasa

Prošlog semestra, završavajući razmatranje sistema jednačina klasične Maksvelove elektrodinamike, ustanovili smo da je zajedničko rešenje poslednje dve jednačine (o kruženju vektora i ) dovodi do diferencijalne valne jednačine.

Tako smo dobili talasnu jednačinu "Y" talasa:

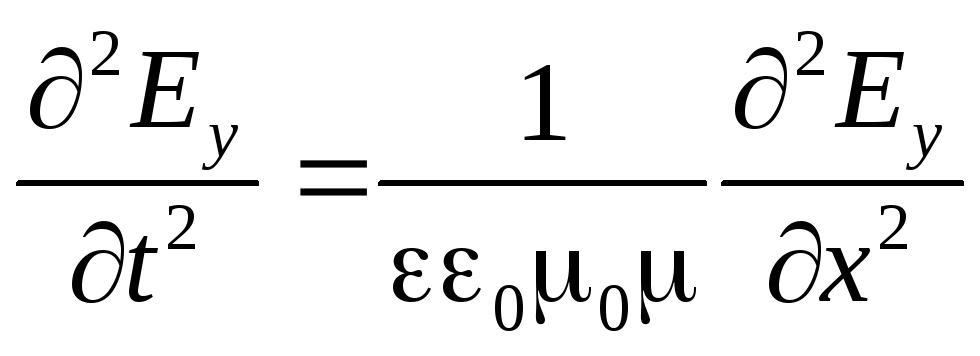. (3.6)

Električna komponenta y - val se širi u pozitivnom smjeru ose X faznom brzinom

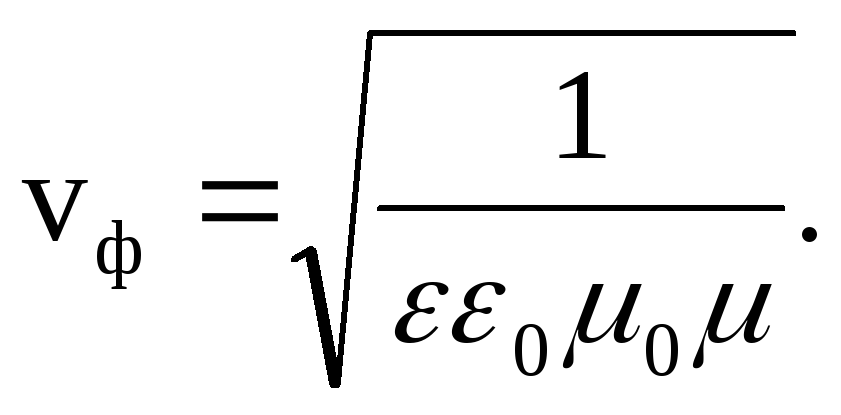(3.7)

Slična jednadžba opisuje promjenu u prostoru i vremenu magnetskog polja y - valova:

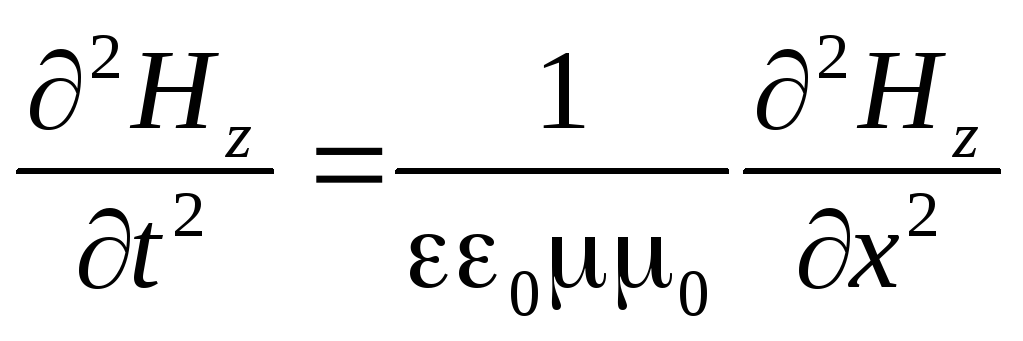. (3.8)

Analizirajući dobijene rezultate, moguće je formulisati niz svojstava svojstvenih elektromagnetnim talasima.

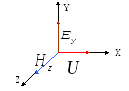
1. Ravan "y" - talas je linearno polarizovan poprečni talas. Vektori električne snage ( 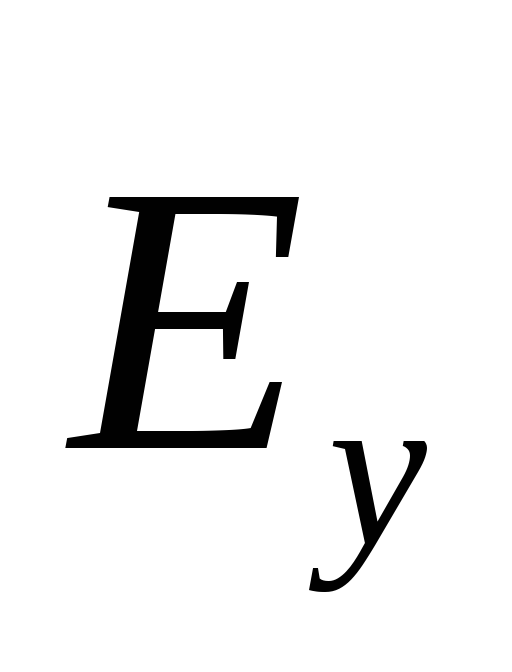), magnetni ( 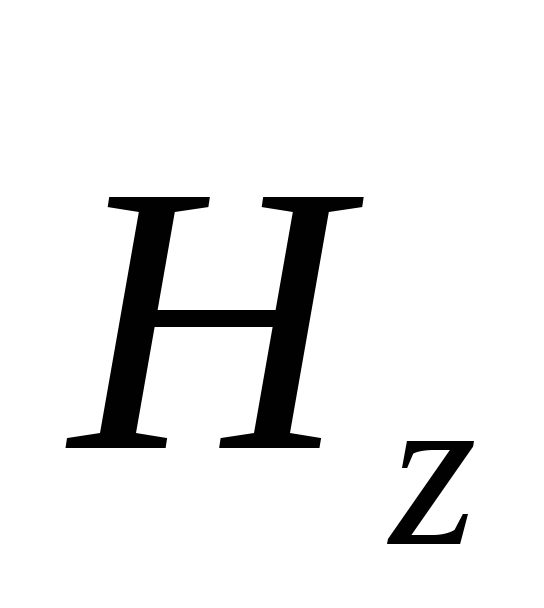) polje i fazna brzina talasa ( 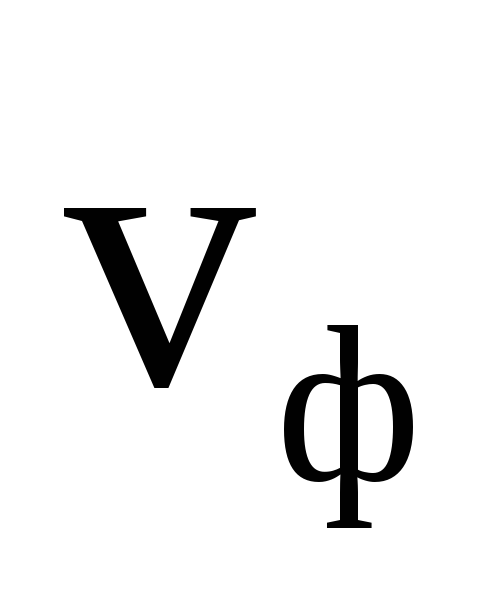) su međusobno okomite i čine „desnoruki“ sistem (slika 3.1).

2. U svakoj tački u prostoru valne komponente H z je proporcionalna jačini električnog polja E y:

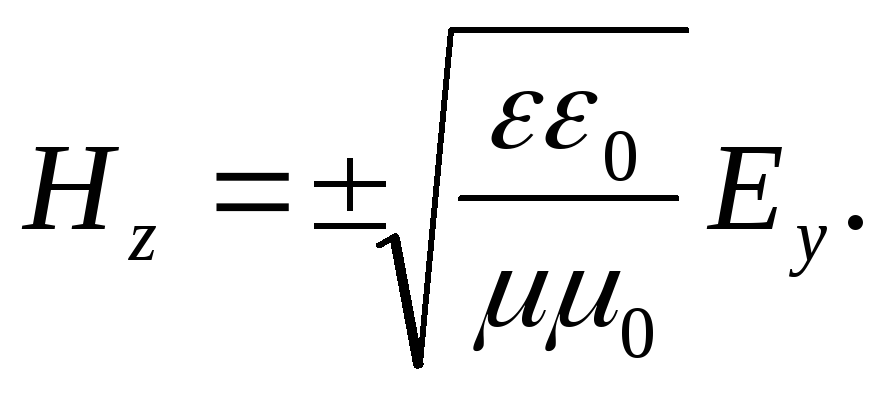
Ovdje znak "+" odgovara valu koji se širi u pozitivnom smjeru ose X. Znak "-" - u negativnom smjeru.

3. Elektromagnetski talas se kreće duž X ose faznom brzinom

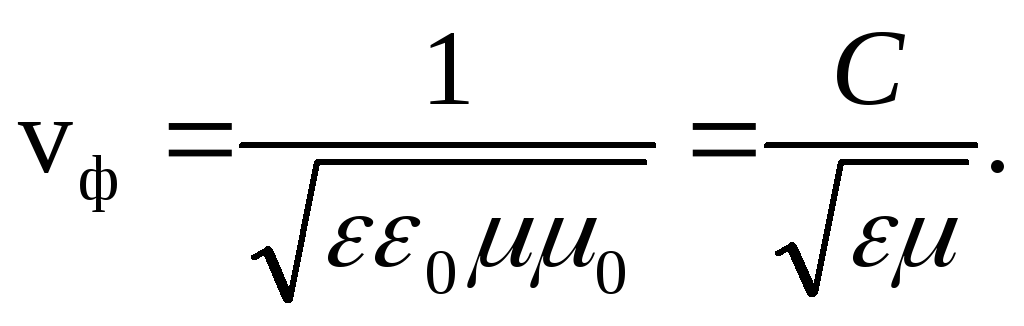
Evo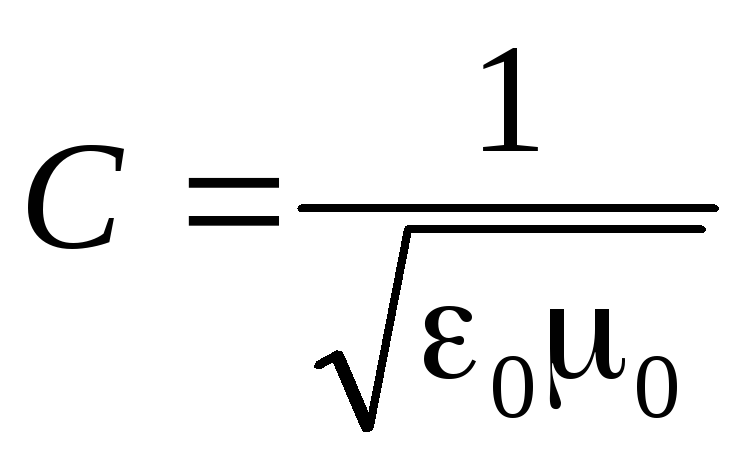

.

Kada se elektromagnetski talas širi u vakuumu (ε = 1, μ = 1), fazna brzina

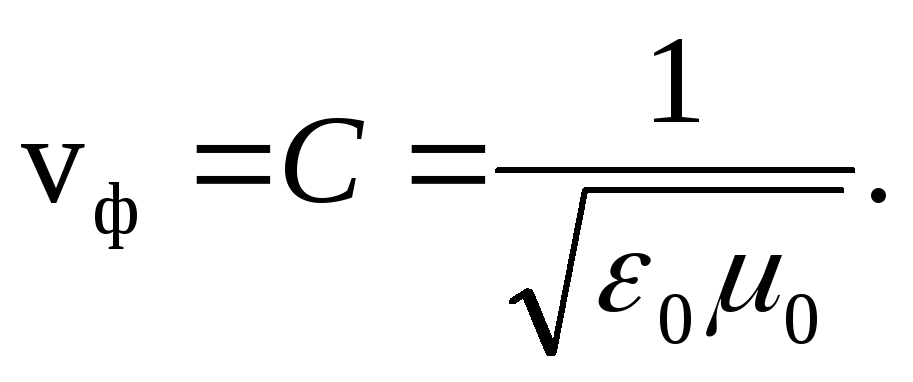
Ovdje je električna konstanta ε 0 = 8,85 10 -12

magnetna konstanta μ 0 = 4π 10 -7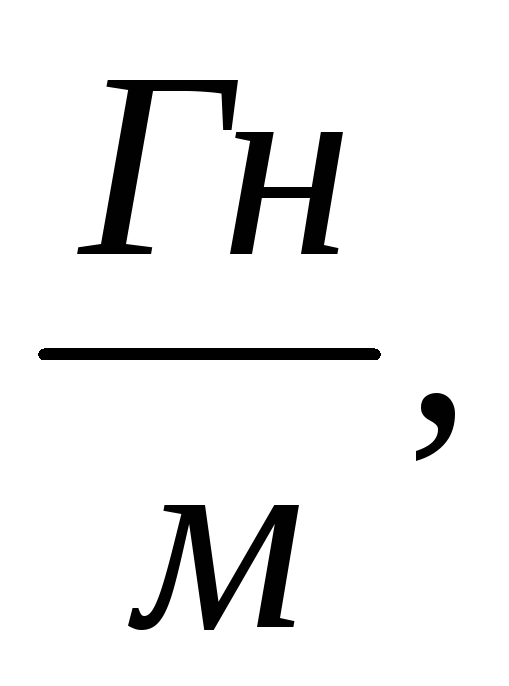

.

.

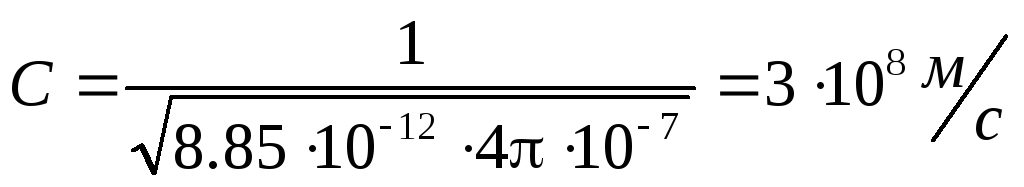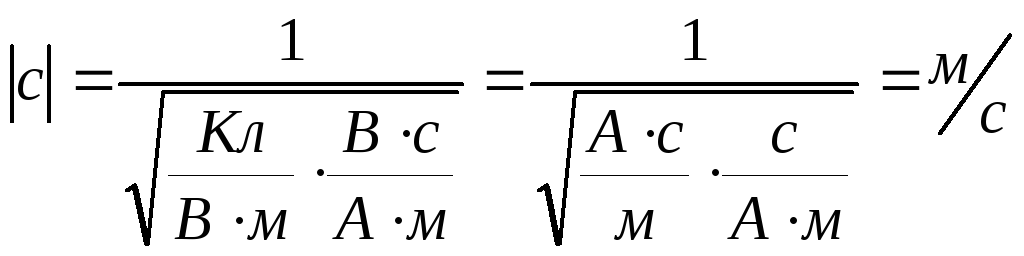Podudarnost brzine elektromagnetnog talasa u vakuumu sa brzinom svetlosti bio je prvi dokaz elektromagnetne prirode svetlosti.

U vakuumu, odnos između jačine magnetnog i električnog polja u talasu je pojednostavljen.

.

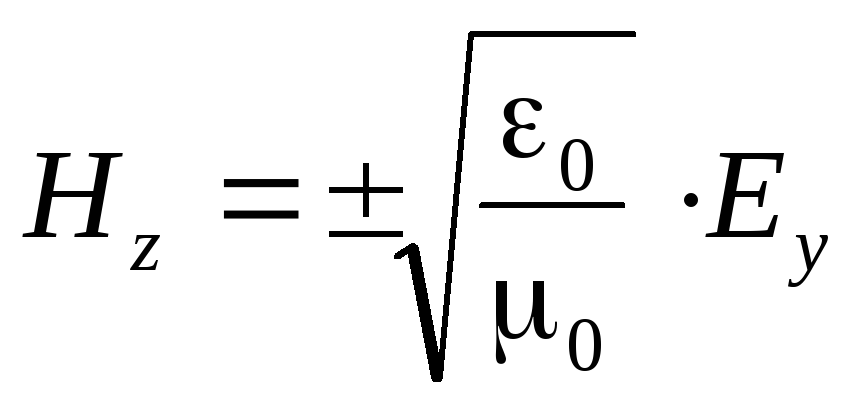Kada se elektromagnetski talas širi u dielektričnom mediju (μ = 1)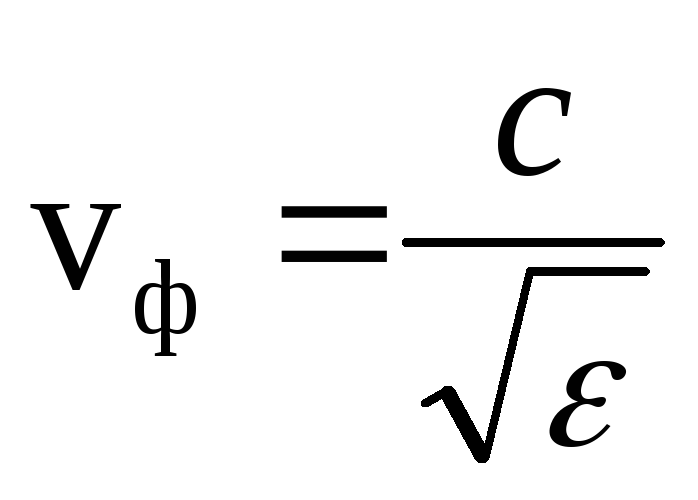

i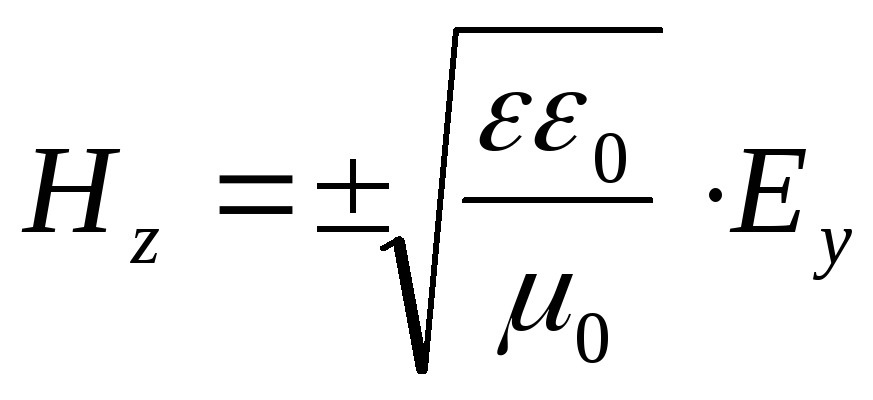

.

Uvođenje koncepta struje pomaka od strane Maxwella dovelo ga je do završetka jedinstvene makroskopske teorije elektromagnetnog polja koje je stvorio, što je omogućilo sa jedinstvene tačke gledišta ne samo da objasni električne i magnetske pojave, već i da predvidi nove, čije je postojanje naknadno potvrđeno.

Maxwellova teorija zasniva se na četiri gore navedene jednačine:

1. Električno polje (vidi § 137) može biti i potencijalno ( e q) i vrtlog ( E B), dakle jačina ukupnog polja E=E Q+ E b. Od cirkulacije vektora e q je jednak nuli (vidi (137.3)), a cirkulacija vektora E B je određen izrazom (137.2), zatim cirkulacija vektora ukupne jačine polja

Ova jednadžba pokazuje da izvori električnog polja mogu biti ne samo električni naboji, već i magnetska polja koja se mijenjaju u vremenu.

2. Generalizirana teorema vektorske cirkulacije H(vidi (138.4)):

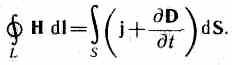
Ova jednadžba pokazuje da se magnetna polja mogu pobuđivati ​​bilo pokretnim nabojima (električnim strujama) ili naizmjeničnim električnim poljima.

3. Gaussova teorema za polje D(vidi (89.3)):

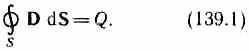
Ako se naboj kontinuirano distribuira unutar zatvorene površine sa zapreminskom gustinom , tada će formula (139.1) biti zapisana kao

4. Gaussova teorema za polje B (vidi (120.3)):

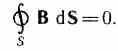
I 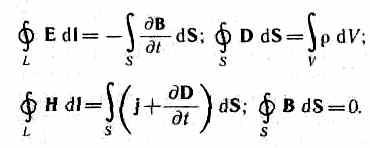dakle, kompletan sistem Maksvelovih jednačina u integralnom obliku:

Veličine uključene u Maxwellove jednadžbe nisu nezavisne i između njih postoji sljedeći odnos (izotropni neferoelektrični i neferomagnetni mediji):

D= 0 E,

B= 0 H,

j=E,

gdje su  0 i  0 električna i magnetska konstanta,  i  - dielektrična i magnetna permeabilnost,  - specifična provodljivost supstance.

Iz Maxwellovih jednadžbi proizlazi da izvori električnog polja mogu biti ili električni naboji ili magnetska polja koja se mijenjaju u vremenu, a magnetska polja mogu biti pobuđena bilo pokretnim električnim nabojima (električnim strujama) ili naizmjeničnim električnim poljima. Maxwellove jednadžbe nisu simetrične u odnosu na električna i magnetska polja. To je zbog činjenice da u prirodi postoje električni naboji, ali nema magnetnih naboja.

D 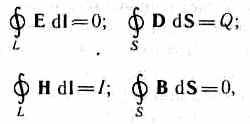za stacionarna polja (E= const and AT= const) Maxwellove jednadžbe uzmi formu

tj. izvori električnog polja u ovom slučaju su samo električni naboji, izvori magnetskog polja su samo provodne struje. U ovom slučaju, električno i magnetsko polje su neovisni jedno o drugom, što omogućava odvojeno proučavanje trajno električna i magnetna polja.

Koristeći Stokesove i Gaussove teoreme poznate iz vektorske analize, m 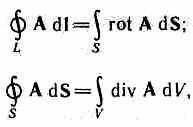može se zamisliti kompletan sistem Maksvelovih jednačina u diferencijalnom obliku(karakteriziranje polja u svakoj tački u prostoru):

Ako su naboji i struje kontinuirano raspoređeni u prostoru, tada su oba oblika Maxwellovih jednadžbi integralna

i 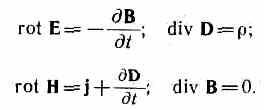diferencijal - ekvivalent. Međutim, kada postoje površine loma- površine na kojima se svojstva sredine ili polja naglo mijenjaju, tada je integralni oblik jednadžbi opštiji.

Maxwellove jednadžbe u diferencijalnom obliku pretpostavljaju da se sve veličine u prostoru i vremenu kontinuirano mijenjaju. Da bi se postigla matematička ekvivalencija oba oblika Maxwellovih jednadžbi, diferencijalni oblik je dopunjen granični uslovi, koje mora zadovoljiti elektromagnetno polje na granici između dva medija. Integralni oblik Maksvelovih jednačina sadrži ove uslove. Oni su već razmatrani (vidi § 90, 134):

D 1 n = D 2 n , E 1  = E 2  , B 1 n = B 2 n , H 1  = H 2 

(prva i posljednja jednadžba odgovaraju slučajevima u kojima nema ni slobodnih naboja ni provodnih struja na sučelju).

Maxwellove jednadžbe su najopćenitije jednadžbe za električna i magnetna polja u okruženja za odmor. Oni igraju istu ulogu u teoriji elektromagnetizma kao i Newtonovi zakoni u mehanici. Iz Maxwellovih jednadžbi proizilazi da je naizmjenično magnetsko polje uvijek povezano s električnim poljem koje on stvara, a naizmjenično električno polje uvijek je povezano s magnetskim poljem koje on stvara, odnosno, električno i magnetsko polje su neraskidivo povezane sa svakim drugo - čine singl elektromagnetno polje.

Maxwellova teorija, kao generalizacija osnovnih zakona električnih i magnetskih pojava, mogla je objasniti ne samo već poznate eksperimentalne činjenice, što je također važna posljedica toga, već je i predvidjela nove pojave. Jedan od važnih zaključaka ove teorije bilo je postojanje magnetnog polja struja pomaka (vidi § 138), što je omogućilo Maxwellu da predvidi postojanje elektromagnetnih talasa- naizmjenično elektromagnetno polje koje se širi u prostoru konačnom brzinom. Kasnije je dokazano da je brzina prostiranja slobodnog elektromagnetnog polja (nevezanog za naelektrisanja i struje) u vakuumu jednaka brzini svjetlosti c = 3 10 8 m/s. Ovaj zaključak i teorijsko proučavanje svojstava elektromagnetnih talasa doveli su Maxwella do stvaranja elektromagnetne teorije svjetlosti, prema kojoj je svjetlost također elektromagnetni valovi. Elektromagnetne valove eksperimentalno je dobio njemački fizičar G. Hertz (1857-1894), koji je dokazao da su zakoni njihovog pobuđivanja i širenja potpuno opisani Maxwellovim jednačinama. Tako je Maxwellova teorija eksperimentalno potvrđena.

To elektromagnetno polje primjenjiv je samo Einsteinov princip relativnosti, budući da se elektromagnetski valovi šire u vakuumu u svim referentnim okvirima istom brzinom With nespojivo sa Galilejevim principom relativnosti.

Prema Ajnštajnov princip relativnosti mehaničke, optičke i elektromagnetne pojave u svim inercijalnim referentnim okvirima odvijaju se na isti način, odnosno opisuju se istim jednačinama. Maxwellove jednadžbe su invarijantne u odnosu na Lorentzove transformacije: njihov oblik se ne mijenja prilikom prolaska

od jednog inercijski sistem upućivanje na drugo, iako vrijednosti E, V,D, N oni se pretvaraju prema određenim pravilima.

Iz principa relativnosti slijedi da odvojeno razmatranje električnog i magnetskog polja ima relativno značenje. Dakle, ako je električno polje stvoreno sistemom fiksnih naboja, onda se ti naboji, koji su fiksirani u odnosu na jedan inercijski referentni okvir, pomiču u odnosu na drugi i stoga će generirati ne samo električno, već i magnetsko polje. . Slično, provodnik fiksne struje u odnosu na jedan inercijski referentni okvir, pobuđujući konstantno magnetsko polje u svakoj tački prostora, kreće se u odnosu na druge inercijalne okvire, a naizmjenično magnetsko polje koje stvara pobuđuje vrtložno električno polje. Dakle, Maxwellova teorija, njena eksperimentalna potvrda, kao i Einsteinov princip relativnosti dovode do jedinstvene teorije električnih, magnetskih i optičkih pojava zasnovanih na ideji elektromagnetnog polja.

Klasifikacije medija u odnosu na elektromagnetno polje

Svojstva medija u odnosu na elektromagnetno polje određuju se parametrima

Srednja provodljivost

Ako ovi parametri zavise od veličine polja, onda linearno okruženje, a ako barem 1 parametar ovisi o vrijednosti polja, onda je okruženje nelinearne.

Linearni mediji su podijeljeni u 4 grupe

1. Homogeni, gdje ovi parametri ne zavise od koordinata.

2. Nehomogena, gdje ovi parametri zavise od koordinata.

3. Izotropna, svojstva su ista u svim smjerovima.

4. Anizotropna, svojstva su različita u svim smjerovima.

Maxwellove jednadžbe u diferencijalnom, integralnom i kompleksnom obliku

1 Maxwellova jednadžba u diferencijalnom obliku: Električno punjenje je izvor električne indukcije.

2 Maxwellova jednadžba. Nema magnetnih naboja

3 Maxwellova jednadžba. Promjena magnetne indukcije stvara vrtložno električno polje

4 Maxwellova jednadžba. Struja i promjena električne indukcije stvaraju vrtložno magnetsko polje

Istim redom, integralna notacija

Električni indukcijski tok kroz zatvorenu površinu s proporcionalno iznosu besplatne naknade u volumenu v koja okružuje površinu s.

Tok magnetske indukcije kroz zatvorenu površinu je nula (magnetna naelektrisanja ne postoje).

Promjena toka magnetske indukcije koja prolazi kroz otvorenu površinu s, uzet sa suprotnim predznakom, proporcionalan je kruženju električnog polja u zatvorenoj petlji l s.

Ukupna električna struja slobodnih naboja i promjena toka električne indukcije kroz otvorenu površinu s, proporcionalni su kruženju magnetnog polja u zatvorenom kolu l, što je granica površine s.

Maxwellove jednadžbe za kompleksne amplitude

3. Jednačina ravnoteže trenutnih vrijednosti snage

Kao što je navedeno u 1.1, elektromagnetno polje je jedan od oblika materije. Kao i svaki drugi oblik materije, ima energiju. Ova energija se može širiti kroz prostor i pretvoriti u druge oblike energije.

Formulirajmo jednadžbu ravnoteže za trenutne vrijednosti snage u odnosu na određeni volumen V, ograničena površinom S (slika 1.23). Pustite u volumen V, ispunjeni homogenim izotropnim medijem, postoje izvori trećih strana. Iz općih fizičkih koncepata, očito je da se snaga koju oslobađaju izvori trećih strana može potrošiti na džulove gubitke i na promjenu energije elektromagnetnog polja unutar V, a mogu se i djelomično raspršiti, bježeći u okolni prostor kroz površinu S. U ovom slučaju, jednakost

gdje R st je snaga izvora trećih strana; R P - snaga Joule gubitaka unutar zapremine V; R Σ je snaga koja prolazi kroz površinu S; W- energija elektromagnetnog polja koncentrisanog u zapremini V, a dW/dt- snaga utrošena na promjenu volumena energije v.

AT ovaj odeljak koristit će se jednačine stanja (1.53). Ove jednačine ne dozvoljavaju uzimanje u obzir gubitaka energije tokom polarizacije i magnetizacije medija. Dakle, termin R P in Jednakost (1.120) zapravo određuje snagu Jouleovih gubitaka u volumenu V , uzrokovano strujom provodljivosti.

Jednačina (1.120) daje samo kvalitativnu ideju o energetskim odnosima. Da biste dobili kvantitativne odnose, morate koristiti Maxwellove jednadžbe. Razmotrimo prvu Maxwellovu jednačinu, uzimajući u obzir vanjske struje (1.111). Svi članovi ove jednačine su vektorske veličine koje imaju dimenziju A/m 2 .

Da biste dobili jednačinu sličnu (1.120), trebate modificirati Maxwellovu prvu jednačinu (1.111) tako da njeni članovi postanu skalarne veličine mjerene u vatima. Da biste to učinili, dovoljno je skalarno pomnožiti sve članove navedene jednakosti vektorom E, a zatim integrirajte rezultirajući izraz preko volumena v. Nakon skalarnog množenja vektorom E dobijamo

Korištenje div formule poznate iz vektorske analize = = H rot E - E rot H, transformiramo lijevu stranu relacije (1.121) i zamjenjujemo rot E njegovom vrijednošću iz druge Maxwellove jednačine (1.39):

Zamjenom ovog izraza u (1.121) dobijamo

U posljednjem članu na desnoj strani (1.122), redoslijed faktora u skalarnom proizvodu vektora se mijenja dB/dt i H. Ovo je dozvoljeno jer H dB/dt = dAT/dtH. Ova promjena nije fundamentalna i ne daje nikakve prednosti u izvođenju jednadžbe ravnoteže koja se ovdje razmatra za trenutne vrijednosti snage. Međutim, uz takvu notaciju, u svim terminima jednačine (1.122) drugi faktor (vektori j st, j, BDIDt i H) je vektor koji je prethodno bio uključen u prvu Maxwellovu jednačinu. Ova okolnost će omogućiti da se u budućnosti (vidi 1.8.4) donekle pojednostavi izvođenje jednadžbe ravnoteže u slučaju monohromatskog polja (jednačina ravnoteže kompleksne snage). Integriranje jednačine po članu (1.122) preko volumena V, dobijamo

gdje je smjer elementa dS poklapa se sa smjerom vanjske normale na površinu S. U prelasku od (1.122) do (1.123), Ostrogradsky-Gaussova teorema se koristi za prevođenje integrala volumena iz div[ E, H] u površinski integral vektorskog proizvoda [ E, H]. Uvodimo notaciju

i transformirajte integrand u posljednjem članu na desnoj strani (1.123):

Zamjenom (1.124) i (1.125) u (1.123) i promjenom redoslijeda integracije i diferencijacije dobijamo

Hajde da saznamo fizičko značenje izraza uključenih u jednačinu (1.126).

Razmotrimo prvi član na desnoj strani (1.126). Zamislimo volumen V kao zbir beskonačno malih cilindara dužine dl,čiji krajevi ( dS ) okomito na smjer struje (vektor j). Onda EjdV=EjdV=(Edl)(jdS) = dUdl = dP n , gdje dl=jdS je struja koja teče kroz razmatrani infinitezimalni cilindar; dU = Edl- promjena potencijala duž dužine dl, a dP n je snaga džula gubitaka u zapremini d V . Prema tome, termin koji se razmatra je snaga džulovih gubitaka R p u zapremini v. Koristeći omjer j = σE, for R P mogu se dobiti i druge reprezentacije:

Formule (1.127) se mogu smatrati generalizovanim Joule-Lenzovim zakonom koji vrijedi za provodni volumen V proizvoljan oblik.

Integral na lijevoj strani (1.126) razlikuje se od prvog člana na desnoj strani samo po tome što je u integrandu umjesto u j uključeno j c t. Stoga mora odrediti snagu izvora trećih strana. Razmotrićemo pozitivnu snagu koju daju vanjske struje elektromagnetnom polju. Električna struja je uređeno kretanje nabijenih čestica. Pozitivan smjer struje je smjer kretanja pozitivnih naboja. Struja odaje energiju elektromagnetnom polju kada se nabijene čestice koje je formiraju usporavaju. Za to je potrebno da vektor jakosti električnog polja E imao komponentu orijentisanu suprotno od smera struje, tj. tačkasti proizvod vektora E i j st je bio negativan ( Ej st<0). При этом левая часть равенства (1.126) будет поло­жительной величиной. Таким образом, мгновенное значение мощ­ности, отдаваемой сторонними токами электромагнитному полю в объеме V, je definisan izrazom

Da bismo razumjeli fizičko značenje posljednjeg člana na desnoj strani jednačine (1.126), razmatramo poseban slučaj. Pretpostavimo da je volumen V okružen savršeno vodljivom ljuskom koja se poklapa s površinom S. Tada je tangentna komponenta vektora E na površini S će biti jednaka nuli. Površinski element dS poklapa se u smjeru sa vanjskom normalom n 0 . Prema tome, površinski integral u jednačini (1.126) će biti jednak nuli, budući da je normalna komponenta vektorskog proizvoda [ E, H] je određen tangentnim komponentama njegovih vektora. Uz to, pretpostavimo da je okruženje unutar volumena V nema provodljivost σ = 0). U ovom slučaju neće biti džule gubitaka u području koje se razmatra, a prvi integral na desnoj strani jednačine (1.126) će također biti jednak nuli. Kao rezultat, dobijamo

Očigledno, u slučaju koji se razmatra, snaga vanjskih izvora može se potrošiti samo na promjenu energije elektromagnetnog polja. Dakle, desna strana jednakosti (1.129) je brzina promjene energije elektromagnetnog polja pohranjenog u volumenu V, one. odgovara terminu dW/dt u jednačini (1.126). Prirodno je pretpostaviti da je integral na desnoj strani (1.129) jednak energiji elektromagnetnog polja koncentrisanog u zapremini V:

Strogo govoreći, ovaj integral se može razlikovati od W na neku funkciju g = g(x, y, z) nezavisno od vremena. Lako je provjeriti da li je funkcija d jednako nuli. Prepišimo (1.130) kao W \u003d W E + W M, gdje

Pretpostavimo da su električno i magnetsko polje konstantno (ne zavise od vremena). U ovom slučaju, kao što je poznato iz kursa fizike (vidi i poglavlja 3 i 4), izrazi (1.131) i (1.132) određuju energiju električnog i magnetskog polja u zapremini v. Ali to znači da je g = 0 i ovi izrazi određuju trenutne vrijednosti energije električnog i magnetskog polja u volumenu V za bilo koju ovisnost o vremenu, njihov zbir, određen formulom (1.130), zaista je jednak trenutnoj vrijednosti energije elektromagnetnog polja u zapremini v.

Ostaje da se razjasni fizička suština površinskog integrala u jednačini (1.126). Pretpostavljamo da u volumenu V nema gubitaka i, osim toga, količina elektromagnetne energije ostaje konstantna (W= const). U ovom slučaju, jednačina (1.126) ima oblik

Istovremeno, iz fizičkih predstava je očito da bi u ovom konkretnom slučaju sva snaga izvora trećih strana trebala otići u okolni prostor (R st = R Σ). Dakle, desna strana jednačine (1.133) jednaka je protoku energije kroz površinu S (granica odnosa količine energije koja prolazi kroz S u vremenu Δt at Δt→0), one.

Prirodno je pretpostaviti da je vektor P predstavlja gustinu energetskog toka (granicu omjera energetskog toka kroz područje ∆S, koji se nalazi okomito na pravac prostiranja energije, do ∆S at ∆S→0). Formalno, matematički, ova pretpostavka nije očigledna, budući da je zamjena vektora P na P 1 = P + rot a, gdje a- proizvoljan vektor, ne mijenja vrijednost R Σ . Međutim, to je tačno i, posebno, direktno sledi iz relativističke teorije elektromagnetnog polja.

Dakle, jednakost (1.126) je slična (1.120) i predstavlja jednadžbu za ravnotežu trenutnih vrijednosti snage elektromagnetnog polja. Dobio ga je Poynting 1884. i zove se Pointingova teorema. Shodno tome, vektor P naziva se Poyntingov vektor. Imena se takođe često koriste "Umov-Poyntingova teorema" i "Vektor koji pokazuje Umov" da bi se naglasila činjenica da je formulaciju zakona održanja energije u opštem obliku sa uvođenjem koncepta energetskog fluksa i vektora koji karakteriše njegovu gustinu prvi dao N.A. Umov 1874. godine.

Imajte na umu da energija može ući u volumen V ne samo iz vanjskih izvora. Na primjer, protok energije kroz površinu S može se usmjeriti iz okolnog prostora u volumen v. Istovremeno, moć PΣće biti negativan, jer se protok energije koji napušta volumen smatra pozitivnim V u okolni prostor (smjer elementa dS poklapa se sa smjerom vanjske normale na površinu S).

Izvori trećih strana ne mogu samo davati energiju, već je i primati iz elektromagnetnog polja. U ovom slučaju, snaga izvora trećih strana bit će negativna. Zaista, elektromagnetno polje daje energiju struji provodljivosti ako ubrza kretanje nabijenih čestica koje formiraju struju. Za ovo, vektor jačine električnog polja E mora imati komponentu orijentisanu duž strujnih linija, tj. tako da je skalarni proizvod vektora E i j st je bio veći od nule.

Razmotrimo detaljnije formule koje određuju energiju elektromagnetnog polja. Integrali u

može se tumačiti kao trenutne vrijednosti zapreminskih gustoća energije električnog i magnetskog polja, odnosno njihov zbir

Kao zapreminska gustina ukupne energije elektromagnetnog polja.

Naglašavamo da se princip superpozicije, koji zadovoljavaju vektori jačine električnog i magnetskog polja, ne odnosi na energiju. Zaista, neka energija polja E 1, H 1 i E 2, H 2, koji postoji odvojeno na području V, jednake respektivno W 1 i W2. Zatim energija ukupnog polja E \u003d E 1 + E 2, H \u003d H 1 + H 2 je određen izrazom

Međusobna energija polja. Međusobna energija W 12 može biti i pozitivno i negativno. Ako vektori E 1 i E 2, kao i H1 i H 2 onda međusobno okomite W 12 = 0.

U slučaju promjenjivih procesa, distribucija elektromagnetne energije se kontinuirano mijenja. Ova promjena u bilo kojoj datoj tački može se odrediti na osnovu jednačine (1.122), koja je prikladno predstavljena kao

gdje je p st \u003d- Ej st i p n = Ej- trenutne vrijednosti gustoće snage izvora treće strane i snage Jouleovih gubitaka, respektivno. Prilikom prelaska sa relacije (1.122) na jednačinu (1.136) uzimaju se u obzir formule (1.125) i (1.135). Jednačina (1.136) je diferencijalni oblik Poyntingove teoreme.

4 TALASNE JEDNAČINE

Opšti slučaj

Prilikom rješavanja direktnih zadataka elektrodinamike potrebno je pronaći vektore E i H prema poznatim (specificiranim) izvorima trećih strana. Pretpostavimo da se vanjski izvori nalaze u beskonačnom homogenom izotropnom mediju. Da bismo pojednostavili transformacije, pretpostavljamo da je σ= 0. Pišući Maxwellove jednadžbe za ovaj konkretni slučaj, dobijamo

Definicija vektora E i H direktno iz sistema jednačina (2.25) je teško. Stoga je preporučljivo transformirati ga eliminacijom bilo kojeg vektora E, ili vektor H, tj. dobiti iz nje takvu diferencijalnu jednačinu, koja bi uključivala samo jedan od vektora E ili H. Da bismo to uradili, uzimamo rotor iz oba dela druge jednačine sistema (2.25) i menjamo red diferencijacije u vremenu iu prostornim koordinatama. Uzimajući u obzir jednakost poznatu iz vektorske analize

gdje je Δ 2 ≡Δ-Laplaceov operator, i treća jednakost sistema koji se razmatra, dolazimo do jednačine

Slično je izvedena jednačina za vektor H:

Svaka od vektorskih jednadžbi (2.27) i (2.28) je ekvivalentna trima skalarnim jednadžbama koje se dobiju projektiranjem vektorske jednadžbe na ose X, Y i Z kartezijanskog koordinatnog sistema. Ove skalarne jednačine su u obliku

gdje w i f(x, y, z, f)-tražene i zadane (poznate) funkcije, respektivno. Kao što je poznato, jednačine oblika (2.29) opisuju talasne procese i parametar v jednaka brzini ovog procesa. Takve jednačine se nazivaju nehomogene d'Alembertove jednadžbe ili nehomogene talasne jednačine. Jednačine (2.27) i (2.28) se razlikuju od (2.29) samo po tome što su funkcije koje sadrže vektorske funkcije. Ova vrsta jednadžbe se zove nehomogene vektorske d'Alembertove jednadžbe ili nehomogene vektorske valne jednačine. Analogne jednačine čije su desne strane jednake nuli nazivaju se homogene vektorske d'Alembertove jednadžbe (homogene vektorske valne jednačine). Kasnije će se pokazati da parametar koji ulazi u jednačine (2.27) i (2.28), koji je analog parametra v u (2.29), u slučaju sredine bez gubitaka, je i brzina širenja elektromagnetnog polja i jednaka je brzini svjetlosti u razmatranom mediju. Ovaj rezultat nije neočekivan, budući da su svjetlost elektromagnetski valovi određenog frekvencijskog opsega.

Slične jednačine za vektore mogu se napisati bez poteškoća E i H iu slučaju kada je σ≠0 (vidi, na primjer, ).

monohromatsko polje

U slučaju monohromatskog polja, kompletan sistem Maksvelovih jednačina u kompleksnom obliku, uzimajući u obzir spoljne električne izvore, ima oblik

Pretpostavimo da je medij koji ispunjava razmatrani dio prostora homogen i izotropan. Uzmimo zavojnicu iz oba dijela druge jednadžbe sistema (2.30) i isključimo vektor H, koristeći prvu jednačinu. Uzimajući u obzir formulu (2.26) i jednakost koja važi za homogenu izotropnu sredinu, dolazi se do jednačine

gdje Za vektor H dobijamo slično

Očigledno je da iste jednačine povezuju kompleksne amplitude

Ako nema eksternih izvora u području koje se razmatra, jednačine (2.31) i (2.32) se pojednostavljuju:

Da bismo prešli na slučaj sredine bez gubitaka u jednačinama (2.30)-(2.34) moramo staviti . Svaki

iz vektorskih jednadžbi (2.33) i (2.34) je ekvivalentan trima skalarnim jednačinama istog tipa za kartezijanske komponente odgovarajućeg vektora: ∆ 2w+ k 2w= 0, gdje w- bilo koju od komponenti