§ 15. POTENCIJAL. ENERGIJA SISTEMA ELEKTRIČNIH NAPUNJENJA. RAD NA PREMJEŠTANJU NABAVKA NA TERENU

Osnovne formule

 Potencijal električno polje je količina jednaka omjeru potencijalne energije tačke pozitivnog naboja smještenog u dati poen polja, na ovu naknadu;

=P/ Q,

ili potencijal električnog polja je veličina jednaka omjeru rada sila polja da pomjeri tačkasti pozitivni naboj iz date tačke polja u beskonačnost do ovog naboja:

=A/ Q.

Potencijal električnog polja u beskonačnosti uslovno se uzima jednak nuli.

Imajte na umu da kada se naboj kreće u električnom polju, rad A v.s vanjske sile je po apsolutnoj vrijednosti jednaka radu A s.p. jačina polja i suprotan joj je znakom:

A v.s = – A s.p. .

 Potencijal električnog polja stvoren tačkastim nabojem Q na daljinu r od optužbe

 Potencijal električnog polja koje stvara metal, noseći naboj Q sfera sa radijusom R, na udaljenosti od centra sfere:

unutar sfere ( r<R)

;

na površini kugle ( r=R)

;

van delokruga (r> R)

.

U svim formulama datim za potencijal nabijene sfere,  je permitivnost homogenog beskonačnog dielektrika koji okružuje sferu.

 Potencijal električnog polja stvorenog od strane sistema P tačkasti naboj, u datoj tački, u skladu sa principom superpozicije električnih polja, jednak je algebarskom zbiru potencijala  1 , 2 , ... , n, kreiran pojedinačnim bodovima Q 1 ,Q 2 , ...,Q n :

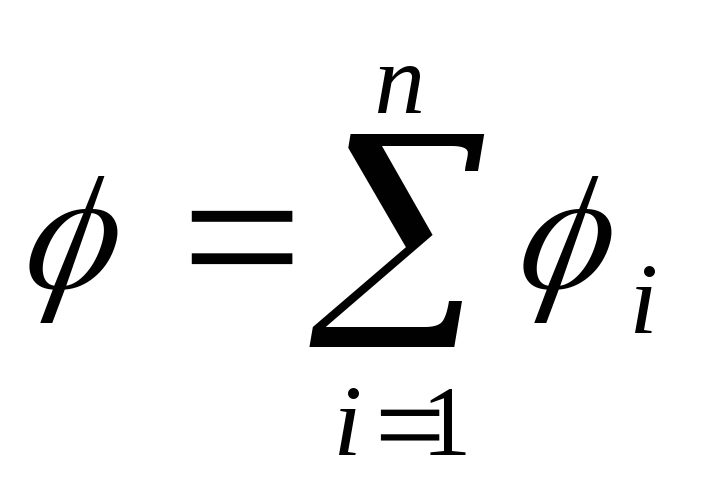
 Energija W interakcije sistema tačkastih naelektrisanja Q 1 ,Q 2 , ...,Q n određen je poslom koji ovaj sistem naboja može obaviti kada se uklone jedno u odnosu na drugo do beskonačnosti, a izražava se formulom

,

gdje je  i- potencijal polja koji stvaraju svi P- 1 punjenje (isključujući 1.) na mjestu gdje se punjenje nalazi Q i .

 Potencijal je povezan sa jačinom električnog polja relacijom

E= -grad.

U slučaju električnog polja sa sfernom simetrijom, ovaj odnos se izražava formulom

,

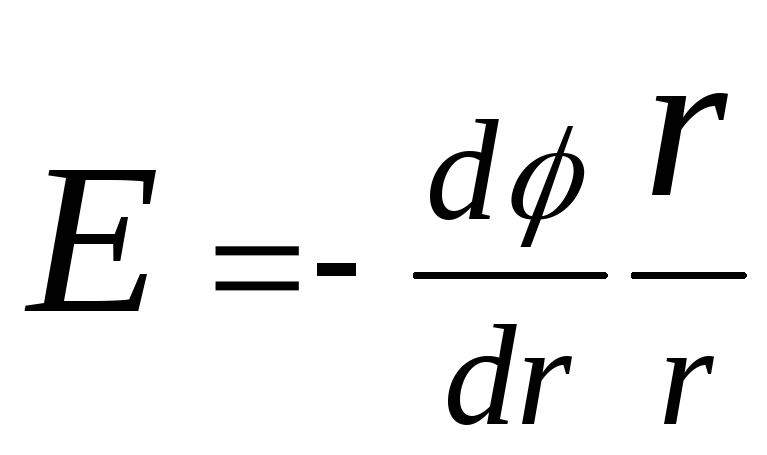ili u skalarnom obliku

,

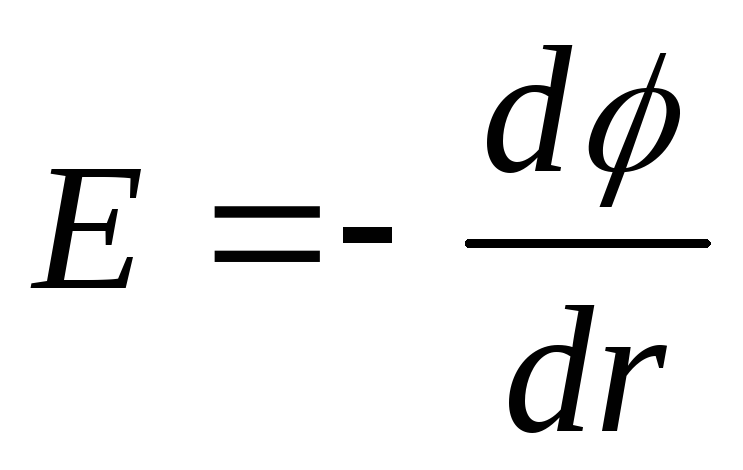i u slučaju uniformno polje, tj. polje čiji je intenzitet u svakoj tački isti i po apsolutnoj vrijednosti i po pravcu,

E=( 1 – 2 ,)/d,

gdje je  1 i 2 - potencijali tačaka dvije ekvipotencijalne površine; d - udaljenost između ovih površina duž električne linija polja.

 Rad električnog polja pri pomicanju tačkastog naboja Q iz jedne tačke polja sa potencijalom  1 , u drugu s potencijalom  2 ,

A=Q( 1 - 2 ), ili

,

gdje E l - projekcija vektora napetosti E u pravcu kretanja; dl - pokret.

U slučaju homogenog polja, posljednja formula poprima oblik

A= QElcos ,

gdje l- pomak  - ugao između vektorskih pravaca E i raseljavanje l.

Primjeri rješavanja problema

Primjer 1 pozitivnih naboja Q 1 \u003d 3 μC i Q 2 \u003d 20 nC su u vakuumu na udaljenosti r 1 =l.5 m međusobno. Definišite posao A, što se mora učiniti kako bi se naboji približili na daljinu r 2 =1 m.

Rješenje. Pretpostavimo da je prvo punjenje Q 1 ostaje nepomičan a drugi Q 2 pod dejstvom spoljnih sila kreće se u polju koje stvara naelektrisanje Q 1 prilazeći mu iz daljine r 1 =t,5 m do r 2 =1 m .

Posao ALI" spoljna sila koja pokreće naboj Q iz jedne tačke polja sa potencijalom  1 u drugu, čiji potencijal 2 , jednak po apsolutnoj vrijednosti i suprotan po predznaku radu ALI sile polja za kretanje naboja između istih tačaka:

A "= -A.

Posao ALI sile polja pri pomeranju naboja A=Q( 1 - 2 ). Onda radi ALI" spoljne sile se mogu zapisati kao

A" = –Q( 1 - 2 )=Q( 2 - 1 ). (1)

Potencijali početne i krajnje tačke putanje izraženi su formulama

;

.

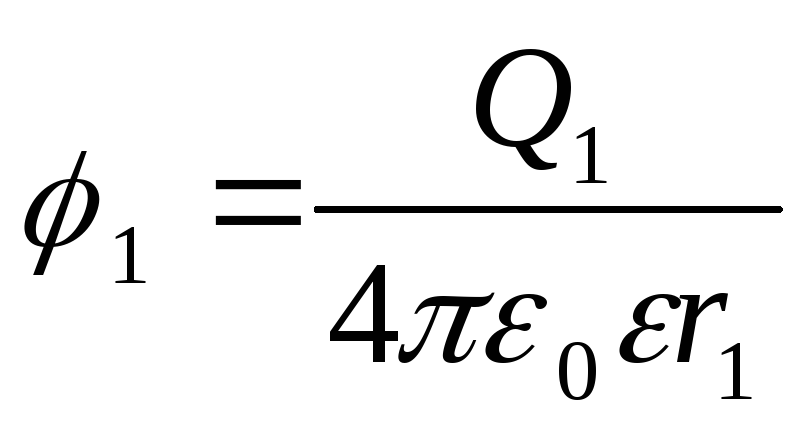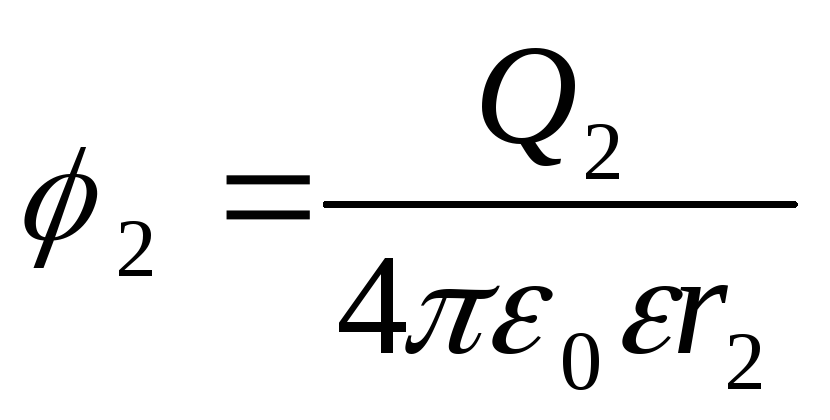Zamjenjivanje izraza  1 i 2 u formulu (1) i uzimajući u obzir da je za ovaj slučaj preneseni naboj Q=Q 2 , dobijamo

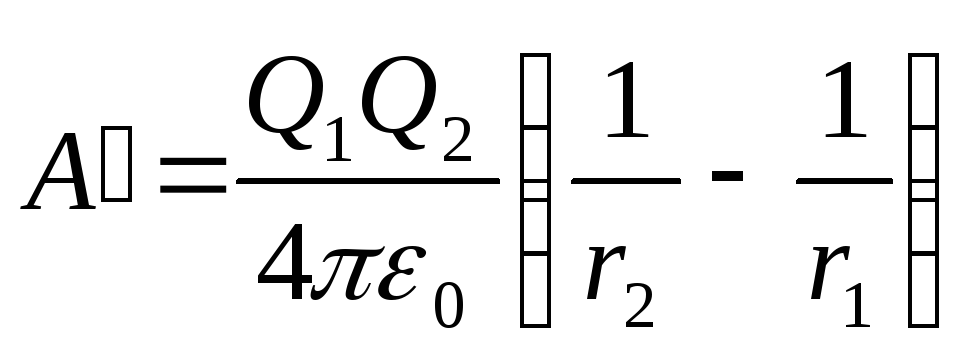. (2)

S obzirom da je 1/(4 0 )=910 9 m/F, tada nakon zamjene vrijednosti veličina u formulu (2) i izračunavanja, nalazimo

A"=180 µJ.

Primjer 2 Nađi posao ALI polja za prijenos naplate Q=10 nC od tačke 1 upravo 2 (Sl. 15.1), koji se nalazi između dva suprotno nabijena s površinskom gustinom  \u003d 0,4 μC / m 2 beskonačne paralelne ravni, udaljenost l između njih je 3 cm.

R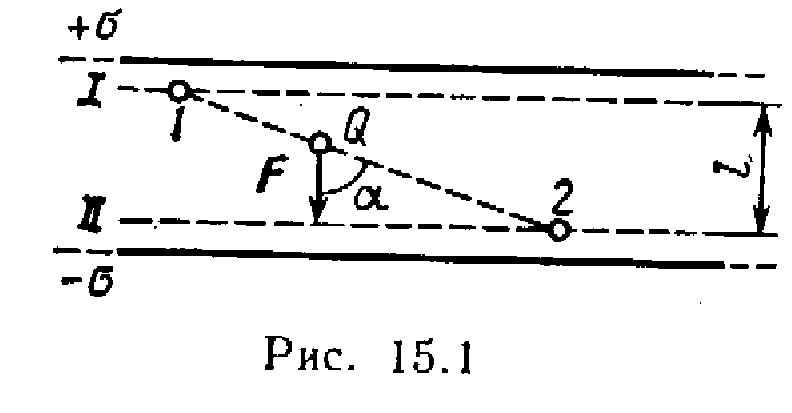

rješenje. Postoje dva načina za rješavanje problema.

1. način. Rad polja prisiljava na pomjeranje naboja Q iz tačke 1 polja sa potencijalom 1 upravo 2 polja sa potencijalom 2 pronađite po formuli

A=Q( 1 - 2 ). (1)

Odrediti potencijale u tačkama 1 i 2 Kroz ove tačke povucimo ekvipotencijalne površine I i II. Ove površine će biti ravni, jer je polje između dvije jednolično nabijene beskonačne paralelne ravni uniformno. Za takvo polje, relacija

 1 - 2 =El, (2)

gdje E - jačina polja; l - udaljenost između ekvipotencijalnih površina.

Jačina polja između paralelnih beskonačnih suprotno naelektrisanih ravni E=/ 0 . Zamjena ovog izraza E u formulu (2), a zatim u izraz 1 - 2 u formulu (1), dobijamo

A= Q( /  0 ) l.

2nd way. Pošto je polje uniformno, sila koja deluje na naelektrisanje Q, je konstantan dok se kreće. Dakle, rad pomjeranja naboja iz tačke 1 upravo 2 može se izračunati pomoću formule

A=F  r cos, (3)

gdje F - sila koja deluje na naelektrisanje r- modul za prijenos punjenja Q iz tačke 1 upravo 2;  je ugao između smjerova pomaka i sile . Ali F= QE= Q( /  0 ). Zamjena ovog izraza F u jednakost (3), kao i uočavanje da je  r cos= l, dobijamo

A=Q(/ 0 )l. (4)

Dakle, oba rješenja dovode do istog rezultata.

Zamjena u izraz (4) vrijednosti veličina Q, , 0 i l, nađi

A\u003d 13,6 μJ.

Primjer 3 Na tankoj niti savijenoj duž luka kruga polumjera R, ravnomerno raspoređeno naelektrisanje sa linearnom gustinom=10 nC/m. Definišite napetost E i potencijal  električnog polja stvorenog takvim p

distribuirani naboj u jednoj tački O, koji se poklapa sa centrom zakrivljenosti luka. Dužina l konac je 1/3 obima i jednak je 15 cm.

Rješenje. Koordinatne osi biramo tako da se ishodište koordinata poklapa sa centrom zakrivljenosti luka, a os at bio simetrično lociran u odnosu na krajeve luka (slika 15.2). Odaberite element dužine d na navoju l. Naplaćeno Q=d l, koji se nalazi u odabranom području, može se smatrati točkom.

Odredimo jačinu električnog polja u tački O. Da bismo to učinili, prvo pronađemo napetost d E polje stvoreno naplatom d Q:

,

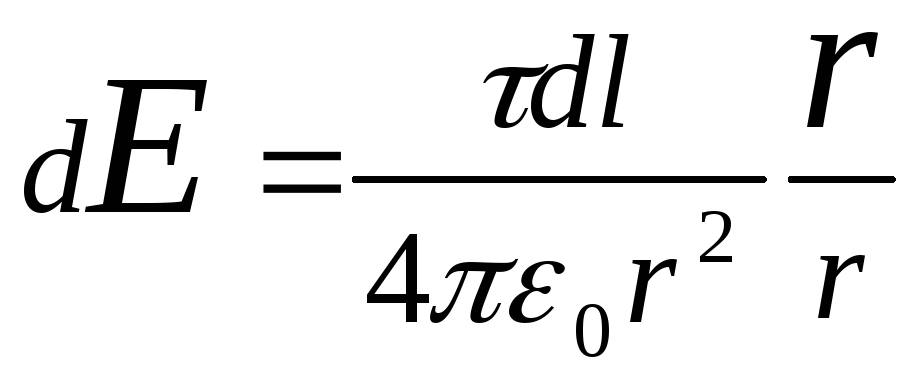gdje r-vektor radijusa usmjeren od elementa d l do tačke u kojoj se izračunava napetost. Izražavamo vektor d E kroz projekciju dE x c i dE y na koordinatnoj osi:

,

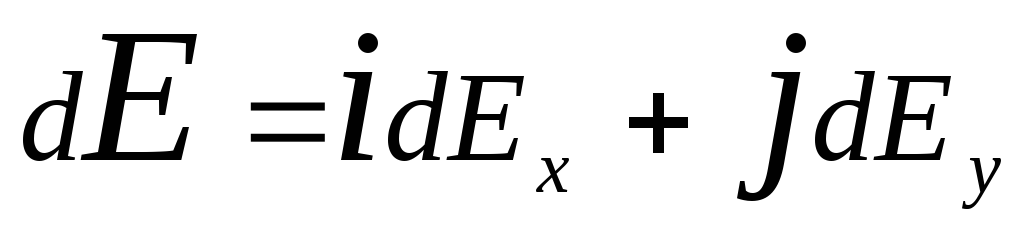gdje i i j- jedinični vektori smjera (orths).

tenzija E pronađi integracijom:

.

Integracija se vrši duž luka dužine l. Zbog simetrije, integral jednako nuli. Onda

, (1)

gdje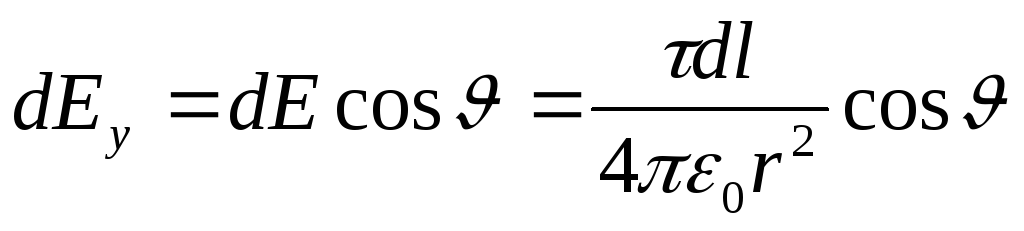

. Jer r=R= const i d l=R d. onda

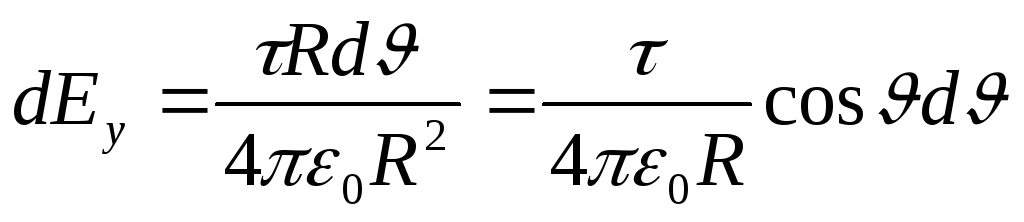
Zamijenite pronađeni izraz dE y u (1) i, uzimajući u obzir simetričnu lokaciju luka u odnosu na osu OU, uzimamo granice integracije od 0 do /3, i udvostručujemo rezultat;

.

Zamjena ovih granica i izražavanje R kroz dužinu luka (3 l= 2 r), dobijamo

.

Ova formula pokazuje da je vektor E poklapa se s pozitivnim smjerom ose OU Zamjena vrijednosti and l u posljednju formulu i radeći proračune, nalazimo

E\u003d 2,18 kV / m.

Odredimo potencijal električnog polja u tački O. Nađimo prvo potencijal d stvoren tačkastim nabojem d Q u tački O:

Zamenimo r na R i izvršite integraciju:

.Zato l=2  R/3, onda

=/(6 0 ).

Nakon što smo izvršili proračune prema ovoj formuli, dobijamo

Primjer4 . Električno polje stvara dugi cilindar poluprečnika R= 1cm , jednoliko naelektrisan sa linearnom gustinom=20 nC/m. Odredite razliku potencijala dvije tačke ovog polja koje se nalaze na udaljenostima a 1 =0,5 cm i a 2 \u003d 2 cm od površine cilindra, u njegovom srednjem dijelu.

Rješenje. Da bismo odredili potencijalnu razliku, koristimo odnos između jačine polja i promjene potencijala E= -grad. Za polje sa aksijalnom simetrijom, koje je polje cilindra, ova relacija se može zapisati kao

E= -( d/d r) , ili d= - E d r.

Integracijom posljednjeg izraza nalazimo potencijalnu razliku dvije tačke razdvojene sa r 1 i r 2 od ose cilindra;

. (1)

Pošto je cilindar dugačak i tačke su uzete blizu njegovog srednjeg dela, jačina polja se može izraziti pomoću formule

. Zamjena ovog izraza E u jednakost (1), dobijamo

(2)

Pošto količine r 2 i r 1 unesite formulu kao omjer, tada se mogu izraziti u bilo kojoj, ali samo u istim jedinicama:

r 1 =R+a 1 = 1,5 cm; r 2 =R+a 2 =3cm .

Zamjena vrijednosti veličine , 0 ,r 1 i r 2 u formulu (2) i računajući, nalazimo

 1 - 2 =250 V.

Primjer 5 Električno polje stvara tanka šipka koja nosi naboj =0,1 μC/m ravnomjerno raspoređen duž svoje dužine. Odredite potencijal  polja u tački udaljenoj od krajeva štapa na udaljenosti, jednaka dužini rod.

Rješenje. Naboj na štapu se ne može smatrati tačkastim nabojem, stoga direktno primijenite formulu za izračunavanje potencijala

, (1)

važi samo za bodovne naknade, to je nemoguće. Ali ako podijelimo štap na elementarne segmente d l, zatim punjenjed l koja se nalazi na svakoj od njih može se smatrati tačkom i tada će formula (1) biti važeća. Primjenom ove formule dobijamo

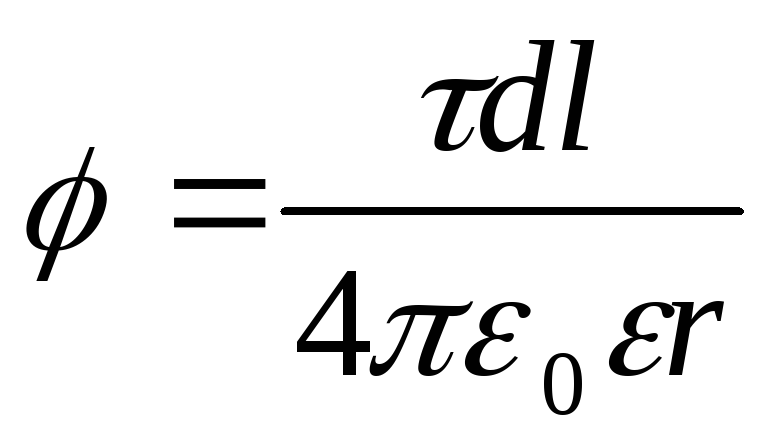, (2)

gdje r - udaljenost tačke u kojoj je potencijal određen do elementa štapa.

Od sl. 15.3 da d l=(r d/cos). Zamjena ovog izraza d l u formulu (2), nalazimo

.

Integriranje rezultirajućeg izraza u granicama  1 da 2 , dobijamo potencijal koji stvara cijeli naboj raspoređen na štapu: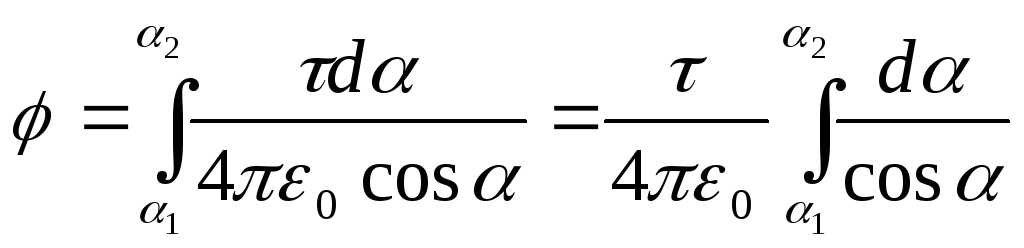

.

AT 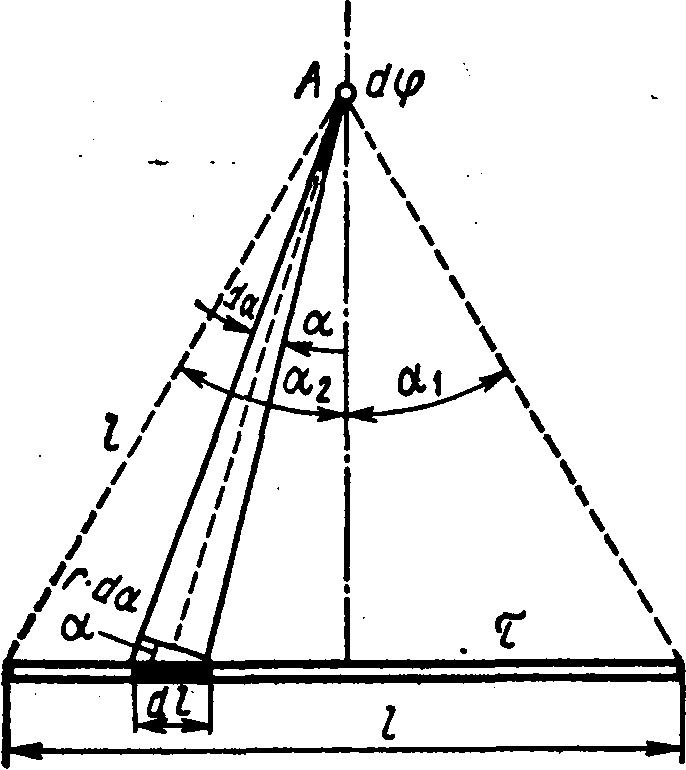sila simetrije tačke ALI u odnosu na krajeve štapa imamo  2 = 1 i zbog toga

.

shodno tome,

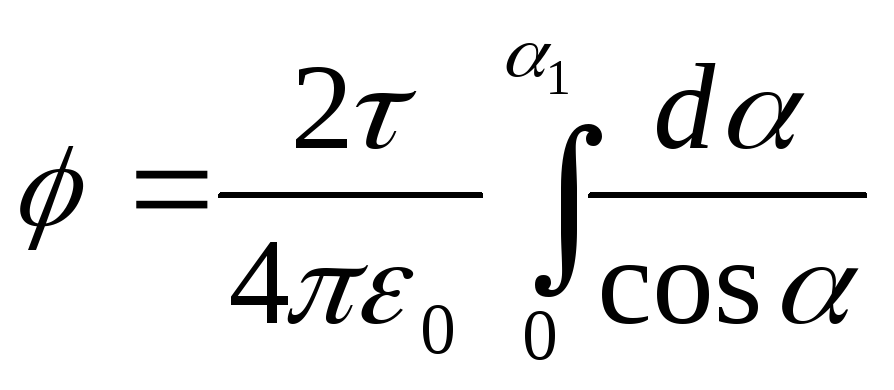.Zato

(vidi tabelu 2), zatim

.

Zamjenom granica integracije dobijamo

Nakon što smo izvršili proračune prema ovoj formuli, nalazimo

Primjer 6 Elektron brzine v=1,8310 6 m/s uletio je u jednolično električno polje u smjeru suprotnom od vektora jačine polja. Kakva potencijalna razlika U elektron mora proći da bi imao energiju E i\u003d 13,6 eV *? (Imajući takvu energiju, elektron ga može jonizirati kada se sudari s atomom vodonika. Energija od 13,6 eV naziva se energija ionizacije vodonika.)

Rješenje. Elektron mora proći takvu potencijalnu razliku u, tako da stečena energija W u kombinaciji sa kinetičkom energijom T, koju je elektron imao prije ulaska u polje, iznosila je energiju jednaku energiji jonizacije E i , tj. W+ T= E i . Izražavanje u ovoj formuli W= EU i T=(m v 2 /2), dobijamo EU+(m v 2 /2)=E i. Odavde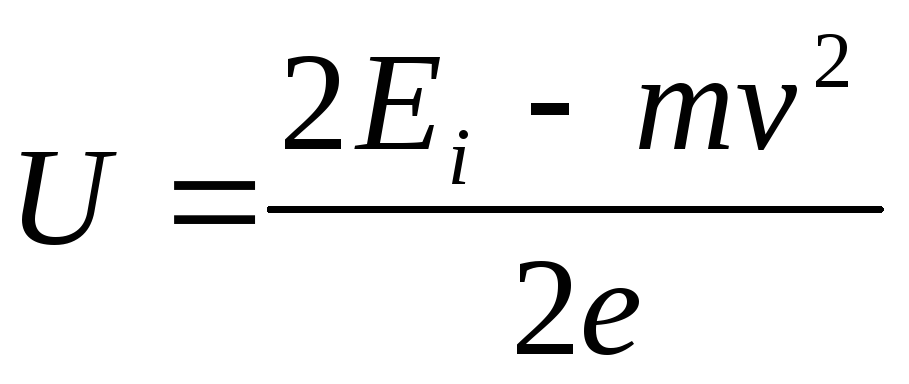

.

___________________

* Elektron-volt (eV) - energija koju dobija čestica koja ima naelektrisanje jednako naelektrisanju elektrona koji je prošao kroz potencijalnu razliku od 1 V. Ova nesistemska jedinica energije trenutno je odobrena za upotrebu u fizici.

Izračunajmo u SI jedinicama:

U=4,15 AT.

Primjer 7 Odredite početnu brzinu υ 0 pristup protona lociranih na dovoljno velika udaljenost jedan od drugog ako je minimalna udaljenost r min, do kojeg se mogu približiti, iznosi 10 -11 cm.

Rješenje: Između dva protona postoje odbojne sile, zbog čega će kretanje protona biti sporo. Dakle, problem se može riješiti kao inercijski sistem koordinatama (povezano sa centrom mase dva protona), iu neinercijalnim (povezano sa jednim od protona koji se brzo kreću). U drugom slučaju, Newtonovi zakoni ne vrijede. Primjena d'Alembertovog principa je teška zbog činjenice da će ubrzanje sistema biti promjenjivo. Stoga je zgodno razmotriti problem u inercijskom referentnom okviru.

Postavimo početak koordinata u centar mase dva protona. Pošto imamo posla sa identičnim česticama, centar mase će biti u tački koja deli segment koji povezuje čestice. U odnosu na centar mase, čestice će u svakom trenutku imati iste brzine po modulu. Kada su čestice na dovoljno velikoj udaljenosti jedna od druge, brzina υ 1 svaka čestica jednaka je polovini υ 0 , tj. υ 1 =υ 0 /2.

Za rješavanje problema primjenjujemo zakon održanja energije, prema kojem ukupna mehanička energija E izolovani sistem je konstantan, tj.

E=T+ P ,

gdje T- zbir kinetičkih energija oba protona u odnosu na centar mase; P je potencijalna energija sistema naelektrisanja.

Potencijalnu energiju izražavamo u početnom P 1 i konačnom P 2 momentu kretanja.

U početnom trenutku, prema uslovu zadatka, protoni su bili na velikoj udaljenosti, pa se potencijalna energija može zanemariti (P ​​1 =0). Dakle, za početni trenutak ukupna energija biće jednaka kinetičkoj energiji T 1 protona, tj.

E=T l . (1)

U konačnom trenutku, kada se protoni približavaju što bliže, brzina i kinetička energija su jednake nuli, a ukupna energija će biti jednaka potencijalnoj energiji P 2, tj.

E= P 2 . (2)

Izjednačavanjem pravih dijelova jednakosti (1) i (2) dobijamo

T 1 \u003d P 2. (3)

Kinetička energija jednaka je zbiru kinetičkih energija protona:

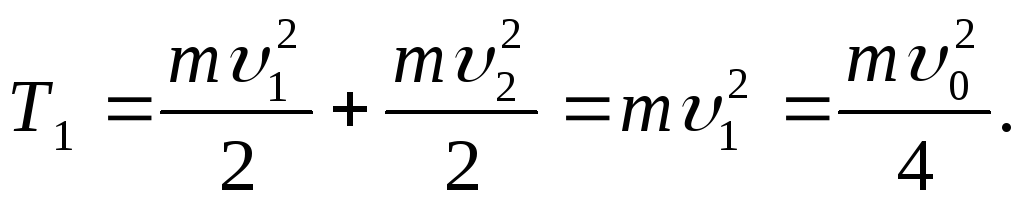(4)

Potencijalna energija sistema od dva naelektrisanja Q 1 i Q 2 u vakuumu određuje se formulom

, gdje r- udaljenost između punjenja. Koristeći ovu formulu, dobijamo

(5)

Uzimajući u obzir jednakosti (4) i (5), formula (3) dobija oblik

gdje

Nakon izvođenja proračuna prema dobijenoj formuli, nalazimo υ 0 =2,35 mm/s

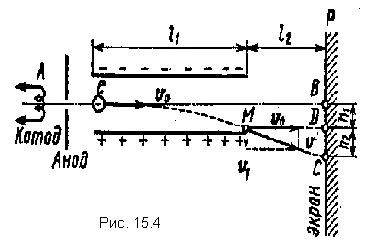Primjer 8 Elektron bez početne brzine prošao je potencijalnu razliku U 0 =10 kV i odleteo u prostor između ploča ravnog kondenzatora napunjenog do razlike potencijala U l \u003d 100 V, duž linije AB, paralelno sa pločama (sl. 15.4). Razdaljina d između ploča je 2 cm dužine l 1 ploča kondenzatora u smjeru leta elektrona jednaka je 20cm. Odredite udaljenost Ned na ekranu R, dalje od kondenzatora l 2 \u003d 1 m.

Rješenje Kretanje elektrona unutar kondenzatora sastoji se od dva kretanja: 1) po inerciji duž linije AB konstantnom brzinom υ 0 , stečena pod dejstvom potencijalne razlike U 0 , koju je elektron prešao na kondenzator; 2) jednoliko ubrzano kretanje u vertikalnom pravcu do pozitivno naelektrisane ploče pod dejstvom konstantne sile polja kondenzatora. Nakon što napusti kondenzator, elektron će se kretati ravnomjerno brzinom υ, koju je imao u tom trenutku M u trenutku izlaska iz kondenzatora.

Od sl. 15.4 pokazuje da je željena udaljenost | | BC|=h 1 +h 2 , odakle h 1 - udaljenost na kojoj će se elektron kretati u vertikalnom smjeru dok se kreće u kondenzatoru; h 2 - udaljenost između tačke D na ekranu, u koju bi elektron pao, krećući se na izlazu iz kondenzatora u smjeru početne brzine υ 0 i tačku C, gdje elektron zapravo udara.

Ekspres posebno h 1 i h 2 . Koristeći formulu za dužinu putanje jednoliko ubrzanog kretanja, nalazimo

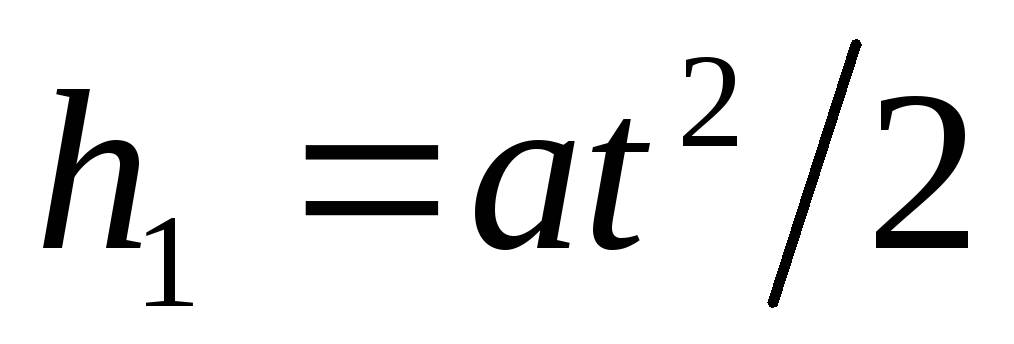. (1)

gdje a- ubrzanje koje prima elektron pod dejstvom polja kondenzatora; t- vrijeme leta elektrona unutar kondenzatora.

Prema drugom Newtonovom zakonu a=F/m, gdje F- sila kojom polje deluje na elektron; t- svoju masu. sa svoje strane, F=eE=eU 1 /d, gdje e- naelektrisanje elektrona; U 1 - razlika potencijala između ploča kondenzatora; d- udaljenost između njih. Vrijeme leta elektrona unutar kondenzatora nalazimo iz formule za putanju ravnomjernog kretanja

, gdje

gdje l 1 je dužina kondenzatora u smjeru leta elektrona. Izraz za brzinu nalazimo iz uvjeta jednakosti rada polja pri kretanju elektrona i kinetičke energije koju on dobija:

. Odavde

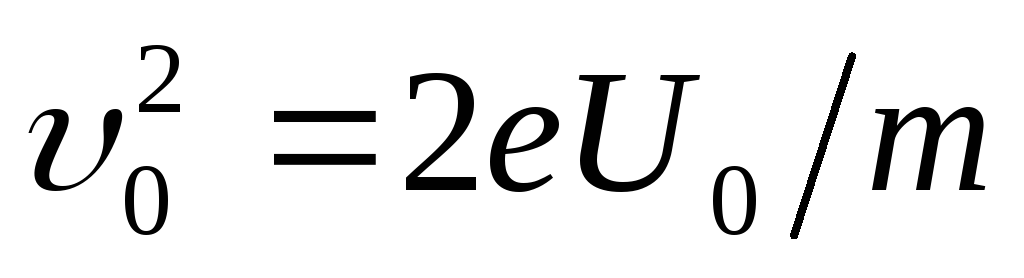(2)

Zamjenjujući u formulu (1) sukcesivno vrijednosti a,F, t i υ 0 2 iz odgovarajućih izraza dobijamo

Dužina rezanja h 2 naći iz sličnosti trouglova MDC i vektor:

(3)

gdje υ 1 - brzina elektrona u vertikalnom smjeru u tački M;l 2 - udaljenost od kondenzatora do ekrana.

Brzina υ 1 nalazimo po formuli υ 1 =na,što, uzimajući u obzir izraze za a, F i tće poprimiti formu

Zamjena izraza υ 1 u formulu (3), dobijamo

, ili zamenom υ 0 2 po formuli (3), nalazimo

Konačno za potrebnu udaljenost | BC| će imati

|BC|=

­

Zamjena vrijednosti količina U 1 ,U 0 ,d,l 1 i l 2 u posljednji izraz i izvođenjem proračuna dobijamo | BC|=5,5 cm.

Zadaci

Potencijalna energija i potencijal polja tačkastih naelektrisanja

15.1. tačka naboj Q\u003d 10 nC, u određenoj tački polja, ima potencijalnu energiju P = 10 μJ. Pronađite potencijal φ ove tačke polja.

5.2. Pri pomicanju punjenja Q=20 nC između dvije tačke polja, rad su obavljale vanjske sile A=4µJ. Definišite posao A 1 sile polja i razlika Δφ potencijala ovih tačaka polja.

15.3. Električno polje je stvoreno tačkastim pozitivnim nabojem Q 1 \u003d 6 nC. pozitivan naboj Q 2 se prenosi iz tačke ALI ovo polje do neke tačke AT(Sl. 15.5). Kolika je promjena potencijalne energije ΔP po jedinici prenesenog naboja, ako r 1 =20 cm i r 2 \u003d 50 cm?

15.4. Električno polje stvoreno tačkastim nabojem Q l \u003d 50 nC. Bez korištenja koncepta potencijala, izračunajte rad ALI in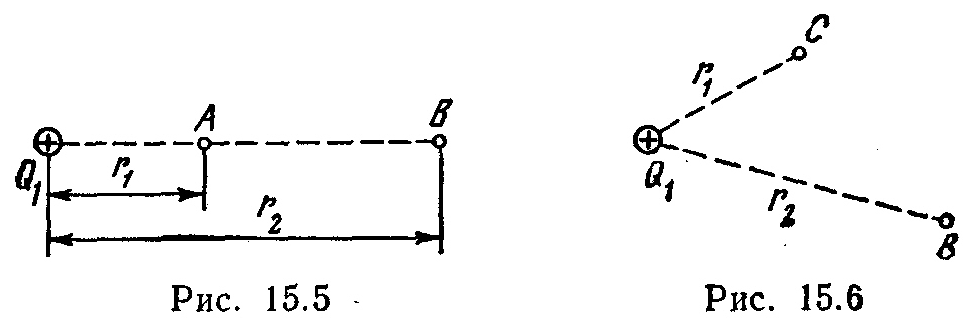

spoljne sile za pomeranje tačkastog naboja Q 2 = -2 nC od tačke OD upravo AT

(Sl. 15.6), ako r 1 =10 cm, r 2 = 20 cm Odredite i promjenu ΔP potencijalne energije sistema naboja.

15.5. Polje je stvoreno tačkastim nabojem Q=1 nC. Odrediti potencijal φ polja u tački udaljenoj od naboja na udaljenosti r=20 cm.

15.6. Odredite potencijal φ električnog polja u tački udaljenoj od naboja Q 1 = -0,2 µC i Q 2 =0,5 μC, respektivno, uključeno r 1 =15 masovni medij r 2 \u003d 25 cm. Također odredite minimalne i maksimalne udaljenosti između naboja za koje je moguće rješenje.

15.7. Naplate Q 1 \u003d 1 μC i Q 2 = -1 μC su na udaljenosti d\u003d 10 cm. Odredite napetost E i potencijal φ polja u tački udaljenoj na daljinu r= 10 cm od prvog naboja i leži na pravoj koja prolazi kroz prvo naelektrisanje okomito na pravac od Q 1 to Q 2 .

15.8. Izračunajte potencijalnu energiju P sistema od dva tačkasta naelektrisanja Q 1 =100 nC i Q 2 =10 nC na daljinu d=10 cm međusobno.

15.9. Odredite potencijalnu energiju P sistema naelektrisanja u tri tačke Q 1 \u003d 10 nC, Q 2 =20 nCl i Q 3 \u003d -30 nC, koji se nalazi na vrhovima jednakostraničnog trokuta sa dužinom stranice a=10 cm.

15.10. Šta je potencijalna energija P sistemi od četiri identična tačkasta naboja Q\u003d 10 nC, koji se nalazi na vrhovima kvadrata sa dužinom stranice a\u003d 10 cm? .

15.11. Odrediti potencijalnu energiju P sistema od četiri tačkasta naelektrisanja koja se nalaze na vrhovima kvadrata sa dužinom stranice a\u003d 10 cm Naboji su isti u modulu Q=10 nC, ali su dva negativna. Razmotrimo dva moguća slučaja uređenja naknada.

15.12 . Polje se stvara pomoću dva tačkastog naboja + 2Q i -Q, na daljinu d=12 cm jedan od drugog. Odrediti geometrijsko mjesto tačaka na ravni za koju je potencijal jednak nuli (napisati jednačinu za liniju nultog potencijala).

5.13. Sistem se sastoji od tri punjenja - dva iste veličine Q 1 = |Q 2 |=1 μC i suprotnog predznaka i naboja Q=20 nC, koji se nalazi u tački 1 u sredini između druga dva naelektrisanja sistema (slika 15.7). Odrediti promjenu potencijalne energije ΔP sistema tokom prijenosa naboja Q od tačke 1 do tačke 2. Ove tačke se uklanjaju iz negativnog naboja Q 1 po udaljenosti a= 0,2 m.

Potencijal polja linearno raspoređenih naelektrisanja

15.14. Duž tankog prstena poluprečnika R= 10 cm ravnomjerno raspoređenog naboja s linearnom gustinom τ= 10 nC/m. Odrediti potencijal φ u tački koja leži na osi prstena, na udaljenosti a= 5 cm od centra.

15.15. Na segmentu tankog pravog provodnika naelektrisanje je ravnomerno raspoređeno sa linearnom gustinom τ=10 nC/m. Izračunajte potencijal φ stvoren ovim nabojem u tački koja se nalazi na osi provodnika i udaljena je od najbližeg kraja segmenta za udaljenost jednaku dužini ovog segmenta.

Elektrostatičko polje je potencijalno, Kulonove sile su konzervativne sile, a rad konzervativnih sila se može predstaviti kao smanjenje potencijalne energije, tj.

gdje je C konstanta integracije, koja se obično bira tako da kada se naboj q ukloni do beskonačnosti - W r = 0, tj. C=0.

Istražit ćemo ESP koristeći test punjenja q pr 1 , q pr 2 , q pr 3 –

Potencijal elektrostatičkog polja je energetska karakteristika polja, numerički jednaka omjeru potencijalne energije testa električni naboj, postavljen u datu tačku polja, na veličinu naboja.

Zatim, koristeći relacije (7.1) i (7.7), dobijamo:

Poznavajući distribuciju naelektrisanja, možemo pronaći potencijal polja svakog sistema.

Potencijali polja se zbrajaju algebarski, stoga je proračun potencijala obično jednostavniji od proračuna EF snaga.

U SI, jedinica potencijala je [ j ] = 1J / C = 1V

Jedinica rada od 1 eV (elektron volt) jednaka je radu sila polja na naboju jednak naboju elektron, kada prođe potencijalnu razliku od 1 V.

1 eV = 1,6´10 -19 C ´ 1V=1,6´10 -19 J

Video model: 1) Kretanje naelektrisanja u električnom polju; 2) Maseni spektrometar.

Tijelo koje se nalazi u potencijalnom polju sila (elektrostatičko polje) ima potencijalnu energiju zbog koje se vrši rad silama polja. Rad konzervativnih sila obavlja se zbog gubitka potencijalne energije. Stoga se rad sila elektrostatičkog polja može predstaviti kao razlika potencijalnih energija koju posjeduje tačka naboj Q 0 na početnoj i krajnjoj tački polja punjenja Q: , odakle slijedi da je potencijalna energija naboja q0 u polju punjenja Q je jednako . Definira se dvosmisleno, do proizvoljne konstante OD. Ako pretpostavimo da kada se naboj ukloni do beskonačnosti ( r®¥) potencijalna energija nestaje ( U=0), onda OD=0 i potencijalnu energiju naboja Q 0 , nalazi u polju zaduženja Q na udaljenosti r od njega, jednako je . Za slične troškove Q 0 Q> 0 i potencijalna energija njihove interakcije (odbijanja) je pozitivna, za suprotna naelektrisanja Q 0 Q<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Potencijal j u bilo kojoj tački elektrostatičkog polja postoji fizička veličina određena potencijalnom energijom jediničnog pozitivnog naboja smještenog u ovoj tački. Iz čega slijedi da je potencijal polja stvoren tačkastim nabojem Q, je jednako . Rad koji vrše sile elektrostatičkog polja pri pomicanju naboja Q 0 od tačke 1 upravo 2 , može se predstaviti kao , tj. jednako proizvodu prenesenog naboja i potencijalne razlike u početnoj i krajnjoj tački. Razlika potencijala dva poena 1 i 2 u elektrostatičkom polju određen je radom sila polja pri pomicanju jediničnog pozitivnog naboja iz tačke 1 upravo 2 . Rad sila polja pri kretanju punjenja Q 0 od tačke 1 upravo 2 takođe može biti napisan u formi . Izraz za razliku potencijala: , gdje se integracija može izvršiti duž bilo koje linije koja povezuje početnu i krajnju tačku, budući da rad sila elektrostatičkog polja ne ovisi o putanji kretanja.

Ako pomjerite punjenje Q 0 od proizvoljne tačke izvan polja, tj. do beskonačnosti, gdje je, po uslovu, potencijal jednak nuli, tada rad sila elektrostatičkog polja A ¥ =Q 0 j gdje

Potencijal- fizička veličina određena radom pomicanja jediničnog pozitivnog naboja kada se ukloni iz date tačke polja u beskonačnost. Ovaj rad je numerički jednak obavljenom radu spoljne sile(protiv sila elektrostatičkog polja) pomicanjem jediničnog pozitivnog naboja iz beskonačnosti do date tačke u polju. Potencijalna jedinica - volt(B): 1 V je potencijal takve tačke u polju u kojoj naboj od 1 C ima potencijalnu energiju od 1 J (1 V = 1 J/C).

U slučaju elektrostatičkog polja, potencijalna energija služi kao mjera interakcije naelektrisanja. Neka postoji sistem tačkastih naelektrisanja u prostoru Q i(i = 1, 2, ... ,n). Energija interakcije svih n naknada je određena omjerom

gdje rij- udaljenost između odgovarajućih naboja, a zbrajanje se vrši na način da se interakcija između svakog para naboja uzima u obzir jednom.

Iz ovoga sledi da je potencijal polja sistema naelektrisanja jednak algebarski zbir potencijala polja svih ovih naelektrisanja:

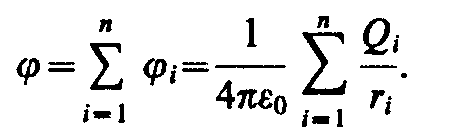
S obzirom na električno polje koje stvara sistem naelektrisanja, treba koristiti princip superpozicije za određivanje potencijala polja:

Potencijal električnog polja sistema naelektrisanja u datoj tački prostora jednak je algebarskom zbiru potencijala električnih polja stvorenih u datoj tački u prostoru svakim naelektrisanjem sistema posebno:

6. Ekvipotencijalne površine i njihova svojstva. Odnos između razlike potencijala i jačine elektrostatičkog polja.
Zamišljena površina, čije sve tačke imaju isti potencijal, naziva se ekvipotencijalna površina. Jednačina ove površine

Ako je polje stvoreno tačkastim nabojem, onda njegov potencijal Dakle, ekvipotencijalne površine u ovom slučaju su koncentrične sfere. S druge strane, linije napetosti u slučaju tačkastog naboja su radijalne prave. Dakle, linije napetosti u slučaju tačkastog naboja okomito ekvipotencijalne površine.

Sve tačke ekvipotencijalne površine imaju isti potencijal, pa je rad pomeranja naelektrisanja duž ove površine jednak nuli, tj. elektrostatičke sile koje deluju na naelektrisanje, uvijek usmjerena duž normala na ekvipotencijalne površine. Dakle, vektor E je uvijek normalna na ekvipotencijalne površine, a samim tim i linije vektora E ortogonalno na ove površine.

Postoji beskonačan broj ekvipotencijalnih površina oko svakog naboja i svakog sistema naelektrisanja. Međutim, obično se izvode tako da su potencijalne razlike između bilo koje dvije susjedne ekvipotencijalne površine iste. Tada gustina ekvipotencijalnih površina jasno karakteriše jačinu polja u različitim tačkama. Tamo gdje su ove površine gušće, jačina polja je veća.

Dakle, znajući lokaciju linija jačine elektrostatičkog polja, moguće je konstruisati ekvipotencijalne površine i, obrnuto, iz poznate lokacije ekvipotencijalnih površina, moguće je odrediti modul i smjer jakosti polja u svakoj tački polja. polje.

Nađimo odnos između jačine elektrostatičkog polja, koja je njegova funkcija snage, i potencijal - energetska karakteristika polja.

Radovi na selidbi single tačka pozitivnog naboja od jedne tačke polja do druge duž ose X pod uslovom da su tačke beskonačno blizu jedna drugoj i x 2 -x 1 = d x, je jednako E x d x. Isti posao je j 1 -j 2 =dj. Izjednačavajući oba izraza možemo napisati

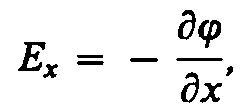
gdje simbol djelomične derivacije naglašava da se diferencijacija vrši samo u odnosu na X. Ponavljanje sličnog razmišljanja za osi at i z, možemo pronaći vektor E:

gdje i, j, k- jedinični vektori koordinatnih osa x, y, z.

Iz definicije gradijenta slijedi da

odnosno napetost E polje je jednako gradijentu potencijala sa predznakom minus. Znak minus je određen činjenicom da je vektor intenziteta E polja usmjerena na smjer prema dolje potencijal.

Za grafički prikaz raspodjele potencijala elektrostatičkog polja, kao u slučaju gravitacionog polja, koristite ekvipotencijalne površine- površine, u svim tačkama čiji je potencijal j ima isto značenje.