statica geometrica
Echilibrul a două forțe: două forțe formează un sistem echilibrat dacă sunt egale ca mărime, opuse ca direcție și au o linie comună de acțiune.
Echilibrul a trei forțe: trei forțe situate în același plan formează un sistem echilibrat dacă liniile lor de acțiune se intersectează într-un punct și pe aceste forțe, ca și pe laturi, puteți construi un triunghi de forțe închis.
Un echilibru al unui sistem arbitrar de forţe are loc dacă vector principal sistemul și momentul său principal față de un pol arbitrar O sunt egale cu zero.
Acest ecuații vectoriale echilibrul corespunde la șase ecuații de echilibru analitic. În cazul în care sunt impuse restricții asupra locației forțelor, numărul ecuațiilor de echilibru analitic scade. În tabel. Tabelul 1 prezintă ecuațiile de echilibru analitic (și variantele acestora) pentru diferite cazuri de aranjare a forțelor.
Echilibrul unui corp rigid se realizează dacă i se aplică un sistem echilibrat de forțe.
Echilibrul unui sistem variabil (deformabil) sub acțiunea forțelor poate fi considerat ca echilibrul unui corp absolut rigid, a cărui formă este identică cu forma sistemului variabil după deformare (axioma solidificării).
Echilibrul unui sistem de corpuri (seturi de corpuri legate între ele și de pământ prin legături). Numărul total de ecuații de echilibru pentru un sistem de corpuri este egal cu numărul de ecuații pentru fiecare dintre corpuri separat, înmulțit cu numărul de corpuri din sistem. LA numărul total ecuațiile pot include ecuații ale sistemului ca întreg, care au diferența că nu includ forțe interne.
Conceptul de probleme (sisteme) determinabile static și nedeterminate static. Dacă numărul de ecuații de echilibru independente pentru un sistem dat de corpuri este egal cu numărul de necunoscute din problemă, sistemul este determinat static. Dacă numărul de ecuații de echilibru pentru un sistem dat este mai mic decât numărul de necunoscute din problemă, sistemul este static nedeterminat, adică problema nu poate fi rezolvată prin metode statice. Dacă numărul m de ecuații de statică este mai mare decât numărul n de necunoscute din problemă, sistemul este schimbător și poate fi în echilibru numai sub o astfel de sarcină încât m-n ecuații echilibrele se transformă în identități. La rezolvarea unei astfel de probleme, în primul rând, este necesar să se verifice dacă, pentru un dat sarcina m-n ecuații în identități. Dacă numărul de necunoscute din problemă este egal cu numărul de ecuații rămase, sistemul este în echilibru.
Când se compilează ecuații de echilibru, ar trebui să ne străduim, prin intermediul unei alegeri raționale a axelor (și a punctelor de moment pentru o problemă plană), să împărțim sistemul de ecuații în ecuații separate, cu câte o necunoscută fiecare. În acest scop, puteți utiliza opțiunile pentru condițiile de echilibru prezentate în tabel. unu.
Tabelul 1. Variante ale ecuațiilor de echilibru analitic
Caracteristicile dispozitiei fortelor |
Numărul de ecuații |
Variante ale ecuațiilor de echilibru |
1. Forțele sunt situate în același plan |
||
|
Sistem de forțe situate pe o linie dreaptă |
||
|
Sistem de forțe convergente (O - punct de fugă) |
||
|
Sistem forte paralele |
||
|
Sistem cu abur |
||
|
Sistemul de forțe plan arbitrar |
||
2. Forțele sunt situate în spațiu (sunt indicate doar cele mai comune variante de ecuații) |
||
|
Sistem de forțe convergente (O - punct de fugă) |
unde l, m, n sunt axe arbitrare care îndeplinesc condiția: prin punctul O este imposibil să se tragă o dreaptă care să intersecteze toate cele trei axe |
|
|
Sistem de forțe paralele |
||
STATICĂ
Capitolul I CONCEPTE DE BAZĂ ȘI AXIOME DE STATICĂ
Putere. Sistemul de forță. Echilibrul unui corp perfect rigid
LA mecanică teoretică se studiază mişcarea corpurilor materiale unele faţă de altele. Aceasta presupune, în primul rând, să construim modele de obiecte și să definim conceptele cu care se ocupă mecanica. În mecanica teoretică, este considerat cel mai simplu model al spațiului tridimensional euclidian „obișnuit”. Se postulează că în acest spațiu există cel puțin un sistem de coordonate în care legile lui Newton sunt valabile ( sistem inerțial ). Numeroase experimente și măsurători arată că, cu un grad ridicat de precizie, un sistem de referință cu originea în centru sistem solar iar axele direcționate către stele „infinit depărtate fixe”, este un sistem inerțial. Dacă există cel puțin un sistem inerțial, atunci există un număr infinit de ele. Un sistem inerțial este un sistem în care se aplică legile lui Newton. Cadrele de referință inerțiale sunt numite condiționat nemişcat .
În statică, fără a introduce erori în calcule, putem presupune că sistemele de coordonate conectate rigid cu Pământul sunt nemișcate. Condițiile de echilibru relativ în alte cadre de referință non-inerțiale, în special în cadrele care se mișcă în raport cu Pământul, vor fi luate în considerare în dinamică.
Atât pentru statică, cât și pentru dinamică, unul dintre conceptele principale este conceptul de forță. Ideea principală este dată de senzațiile noastre musculare.
În mecanică, forța este înțeleasă ca o măsură a interacțiunii mecanice a corpurilor materiale, în urma căreia corpurile care interacționează își pot da accelerații între ele sau se pot deforma (își schimbă forma).
Din această definiție decurg imediat două moduri de măsurare a forțelor:
primul, dinamic metoda bazata pe masurarea acceleratiei unui corp in sistem inerțial referinţă;
al doilea, static metoda bazata pe masurarea deformarii corpurilor elastice.
În mecanică, natura fizică a forțelor nu este studiată. Forțele pot apărea din contactul direct al corpurilor (de exemplu, forța de tracțiune a unei locomotive electrice transmisă mașinilor, forța de frecare între suprafețele corpurilor care vin în contact). Forțele apar și la distanță (de exemplu, forțele de atracție corpuri cerești, forțele de interacțiune ale particulelor încărcate electric sau magnetizate etc.).
Forța este o mărime vectorială - este caracterizată printr-o valoare numerică sau modul, un punct de aplicare și o direcție. Punctul de aplicare al forței și direcția acesteia determină linia de acțiune a forței. Pe fig. 1.1 arată puterea F, aplicat la obiect DAR, lungimea segmentului ABîn scara corespunzătoare este egală cu modulul de forță, punctul LA numit sfârșitul puterii; la sfârșitul puterii; o săgeată este plasată la capătul forței, indicând direcția forței. Drept LM numit linie de forţă. Să fim de acord să desemnăm forța cu o literă aldine, de exemplu, F, și modulul său cu aceeași literă de font obișnuită, adică F.
Pentru a măsura modulul de forță, acesta este comparat cu o forță aleasă ca unitate. LA sistem international unități de măsură mărimi fizice(SI) unitatea de forță este un newton (1 H), iar în sistemul tehnic de unități (sistemul ICGSS) - un kilogram de forță (1 kg sau 1 kgf - nu trebuie confundat cu unitatea de masă SI-1 kg). Aceste unități sunt legate prin relații
1 kg ≈ 9,81 H; 1 H ≈ 0,102 kg.
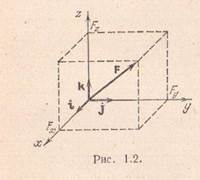 Având în vedere acțiunea forțelor asupra corpurilor materiale, vom face abstracție nu numai de natura fizică a forțelor, ci și de multe proprietăți ale corpurilor în sine. Astfel, solidele reale își schimbă de obicei puțin forma sub acțiunea forțelor aplicate lor. Prin urmare, pentru a rezolva multe probleme din mecanică, este permis să neglijăm complet deformațiile mici (adică micile modificări ale formei) și să folosiți modelul corp absolut rigid. Un corp absolut rigid este un corp în care distanțele dintre oricare două puncte ale acestuia rămân neschimbate, indiferent de acțiunea anumitor forțe.
. Pentru concizie, vom folosi adesea expresia „corp rigid” sau chiar pur și simplu „corp”, ținând cont de conceptul abia introdus de corp absolut rigid.
Având în vedere acțiunea forțelor asupra corpurilor materiale, vom face abstracție nu numai de natura fizică a forțelor, ci și de multe proprietăți ale corpurilor în sine. Astfel, solidele reale își schimbă de obicei puțin forma sub acțiunea forțelor aplicate lor. Prin urmare, pentru a rezolva multe probleme din mecanică, este permis să neglijăm complet deformațiile mici (adică micile modificări ale formei) și să folosiți modelul corp absolut rigid. Un corp absolut rigid este un corp în care distanțele dintre oricare două puncte ale acestuia rămân neschimbate, indiferent de acțiunea anumitor forțe.
. Pentru concizie, vom folosi adesea expresia „corp rigid” sau chiar pur și simplu „corp”, ținând cont de conceptul abia introdus de corp absolut rigid.
O combinație de forțe multiple F1,…, fn) se numește sistem de forțe. Dacă, fără a încălca starea corpului, un singur sistem de forțe (F1,…, fn) poate fi înlocuit cu un alt sistem (P1,…, pk) și invers, astfel de sisteme sunt numite echivalente. Simbolic, acest lucru este indicat după cum urmează:
(F1,…, fn) = (P1,…, pk).
Conceptul introdus de echivalență a sistemelor de forțe nu stabilește condițiile în care două sisteme vor fi echivalente. Înseamnă doar că sisteme echivalente de forțe provoacă aceeași stare a corpului (aceleași accelerații sau, dacă corpul nu este absolut rigid, aceleași deformații).
Când sistemul de forţe(F1,…, fn) este echivalent cu o forță R, adică
(F1,…, fn) = R,
aceasta din urmă se numește rezultanta sistemului dat de forțe. Aceasta înseamnă că o forță rezultantă poate înlocui acțiunea tuturor acestor forțe. Nu orice sistem de forțe are o rezultantă.
După cum sa menționat deja, în sistemul de coordonate inerțiale, legea inerției este îndeplinită. Aceasta înseamnă, în special, că corpul, care este inițial în repaus, rămâne în această stare dacă nu acționează alte forțe asupra lui.
Dacă un corp absolut rigid rămâne în repaus sub acţiunea unui sistem de forţe asupra lui(F1,…, fn), atunci acesta din urmă se numește un sistem echilibrat de forțe sau un sistem de forțe echivalent cu zero:
(F1,…, fn) = 0.
Se spune adesea în acest caz că corpul este în echilibru.
1.2. Axiomele staticii și consecințele lor
În axiomele staticii sunt formulate acele legi simple și generale, care sunt supuse forțelor care acționează asupra aceluiași corp, sau forțelor aplicate corpurilor care interacționează. Aceste legi au fost stabilite prin numeroase observații directe, precum și prin verificarea consecințelor (deseori îndepărtate și deloc evidente) care decurg logic din aceste axiome.
După cum rezultă din a doua lege a lui Newton, un corp sub influența unei forțe dobândește accelerație și, prin urmare, nu poate fi în repaus. Aceasta înseamnă că o singură forță nu poate constitui un sistem echilibrat de forțe. Prima axiomă stabilește condițiile în care cel mai simplu sistem de forțe va fi echilibrat.
Axioma 1. Două forțe aplicate unui corp absolut rigid vor fi echilibrate (echivalent cu zero) dacă și numai dacă sunt egale în valoare absolută, acționează într-o linie dreaptă și sunt direcționate în direcții opuse.
Aceasta înseamnă că, dacă un corp absolut rigid este în repaus sub acțiunea a două forțe, atunci aceste forțe sunt egale în valoare absolută, acționează într-o linie dreaptă și sunt direcționate în direcții opuse. În schimb, dacă căldura absolut solidă este acționată într-o linie dreaptă în direcții opuse de două forțe egale iar corpul era în repaus în momentul inițial, atunci 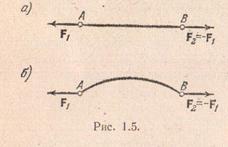 se va păstra starea de odihnă a corpului.
se va păstra starea de odihnă a corpului.
Pe fig. 1.4 prezintă forțe echilibrate care satisfac relațiile: (F1, F2) = 0, (P1, P2) = 0.
La rezolvarea unor probleme de statică, trebuie luate în considerare forțele aplicate la capetele tijelor rigide, a căror greutate poate fi neglijată, și se știe că tijele sunt în echilibru. Din axioma formulată rezultă direct că forțele asupra unei astfel de tije sunt direcționate de-a lungul unei linii drepte care trece prin capetele tijei, opuse ca direcție și egale între ele în valoare absolută. Această concluzie este valabilă și dacă axa tijei este curbilinie.
Prima axiomă stabilește condițiile necesare și suficiente pentru echilibrarea doar a două forțe, dar, desigur, un sistem echilibrat de forțe poate consta și din Mai mult forte.
Următoarele două axiome stabilesc cele mai simple acțiuni cu forțe în care starea corpului nu se schimbă.
Axioma 2. Fără a încălca starea unui corp absolut rigid, forțele îi pot fi aplicate sau respinse dacă și numai dacă ele constituie un sistem echilibrat, în special dacă acest sistem este format din două forțe egale în valoare absolută, care acționează de-a lungul unei linii drepte. și îndreptate în direcții opuse.
Corolarul rezultă din această axiomă: fără a încălca starea corpului, punctul de aplicare a forței poate fi transferat de-a lungul liniei de acțiune a acestuia.
Acest corolar arată că forța aplicată unui corp perfect rigid este un vector de alunecare.
Atât axiomele, cât și corolarul dovedit nu poate fi aplicat corpurilor deformabile, în special, transferul punctului de aplicare a forței de-a lungul liniei de acțiune a acestuia modifică starea de efort-deformare a corpului.
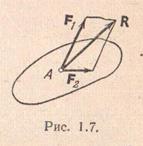 Axioma 3. Fără a schimba starea corpului, două forțe aplicate unuia dintre punctele sale pot fi înlocuite cu o forță rezultantă aplicată în același punct și egală cu suma lor geometrică.(axioma paralelogramului de forţe).
Axioma 3. Fără a schimba starea corpului, două forțe aplicate unuia dintre punctele sale pot fi înlocuite cu o forță rezultantă aplicată în același punct și egală cu suma lor geometrică.(axioma paralelogramului de forţe).
Această axiomă stabilește două circumstanțe:
prima - două forțe F1și F2, aplicate la un punct, au o rezultanta, i.e. echivalent cu o singură forță
(F1, F2) = R;
al doilea - axioma determină complet modulul, punctul de aplicare și direcția forței rezultante
R = F1 + F2.
Cu alte cuvinte, rezultatul R poate fi construită ca o diagonală a unui paralelogram cu laturile care coincid cu F1și F2.
Rețineți că a treia axiomă este aplicabilă oricăror corpuri, nu neapărat absolut rigide.
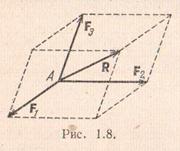 A doua și a treia axiomă ale staticii fac posibilă trecerea de la un sistem de forțe la un alt sistem echivalent cu acesta. În special, ele permit extinderea oricărei forțe R pentru doi, trei etc. componente, adică merge la un alt sistem de forțe, pentru care forța R este rezultatul. Prin stabilirea, de exemplu, a două direcții care se află cu Rîntr-un plan, puteți construi un paralelogram, în care diagonala reprezintă forța R. Apoi forțele îndreptate de-a lungul laturilor paralelogramului vor forma un sistem pentru care R va fi rezultatul. O construcție similară poate fi realizată în spațiu. Pentru aceasta, este suficient din punctul de vedere al aplicării forței R trageți trei drepte care nu se află în același plan și construiți pe ele un paralelipiped cu o diagonală reprezentând forța R, și cu marginile îndreptate de-a lungul acestor linii.
A doua și a treia axiomă ale staticii fac posibilă trecerea de la un sistem de forțe la un alt sistem echivalent cu acesta. În special, ele permit extinderea oricărei forțe R pentru doi, trei etc. componente, adică merge la un alt sistem de forțe, pentru care forța R este rezultatul. Prin stabilirea, de exemplu, a două direcții care se află cu Rîntr-un plan, puteți construi un paralelogram, în care diagonala reprezintă forța R. Apoi forțele îndreptate de-a lungul laturilor paralelogramului vor forma un sistem pentru care R va fi rezultatul. O construcție similară poate fi realizată în spațiu. Pentru aceasta, este suficient din punctul de vedere al aplicării forței R trageți trei drepte care nu se află în același plan și construiți pe ele un paralelipiped cu o diagonală reprezentând forța R, și cu marginile îndreptate de-a lungul acestor linii.
Axioma 4 (a treia lege a lui Newton). Forțele de interacțiune a două corpuri sunt egale în valoare absolută și sunt direcționate de-a lungul unei linii drepte în direcții opuse.
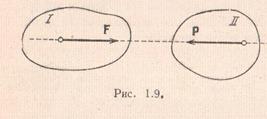 Rețineți că forțele de interacțiune dintre două corpuri nu constituie un sistem de forțe echilibrate, deoarece sunt aplicate unor corpuri diferite.
Rețineți că forțele de interacțiune dintre două corpuri nu constituie un sistem de forțe echilibrate, deoarece sunt aplicate unor corpuri diferite.
 Dacă este notat cu F forța cu care Soarele atrage Pământul, apoi Pământul atrage Soarele cu același modul, dar forță direcționată opus - F.
Dacă este notat cu F forța cu care Soarele atrage Pământul, apoi Pământul atrage Soarele cu același modul, dar forță direcționată opus - F.
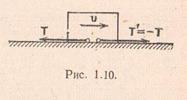
Când un corp se mișcă de-a lungul unui plan, i se va aplica o forță de frecare T, îndreptată în direcția opusă mișcării. Aceasta este forța cu care planul fix acționează asupra corpului. Pe baza axiomei 4, corpul acționează pe plan cu aceeași forță, dar direcția sa va fi opusă forței. T.
Axioma 5. Echilibrul unui corp deformabil nu este perturbat dacă punctele sale sunt legate rigid și se presupune că corpul este absolut rigid.
Această axiomă (numită uneori principiul de întărire ) sunt folosite când vorbim despre echilibrul corpurilor care nu pot fi considerate solide. Atașat de astfel de corpuri forțe externe trebuie să satisfacă condițiile de echilibru ale unui corp rigid, dar pentru corpurile nerigide aceste condiții sunt doar necesare, dar nu suficiente. Să explicăm această situație cu un exemplu simplu. Pentru echilibrul unei tije fără greutate absolut rigide, este necesar și suficient ca forțele aplicate la capetele tijei Fși F" a acționat de-a lungul unei linii drepte care leagă capetele sale, au fost egale în valoare absolută și direcționate în direcții diferite. Aceleași condiții sunt necesare pentru echilibrul unui segment al unui fir fără greutate, dar pentru un fir sunt insuficiente - este necesar să se facă suplimentar impun ca forțele care acționează asupra firului să fie de tracțiune, în timp ce pentru o tijă pot fi compresive.
În concluzie, luăm în considerare cazul echivalenței cu zero a trei forțe neparalele aplicate unui corp rigid.
Teorema despre trei forțe neparalele. Dacă sub acțiunea a trei forțe corpul este în echilibru și liniile de acțiune a două forțe se intersectează, atunci toate forțele se află în același plan și liniile lor de acțiune se intersectează într-un punct.
Fie ca un sistem de trei forțe să acționeze asupra corpului F1, F2și F3,și liniile de acțiune ale forțelor F1și F2 se intersectează într-un punct DAR. Conform corolarului axiomei 2, forțele F1și F2 poate fi mutat la punct DAR, iar conform axiomei 3 ele pot fi înlocuite cu o singură forță R, și
R=F1+F2.
În acest fel,
sistemul de forţe considerat se reduce la două forţe Rși F3. Conform condițiilor teoremei, corpul este în echilibru, prin urmare, conform axiomei 1, forțele Rși F3 trebuie să aibă o linie comună de acțiune, dar apoi liniile de acțiune ale tuturor celor trei forțe trebuie să se intersecteze într-un punct.
Exemple de rezolvare a problemelor
Secvența de rezolvare a problemelor:
- Selectați un corp (punct) al cărui echilibru ar trebui luat în considerare.
- Eliberați corpul (balamaua) din legături și descrieți forțele active care acționează asupra acestuia și reacțiile legăturilor aruncate. În plus, reacțiile tijelor ar trebui îndreptate departe de balama, deoarece se obișnuiește să se presupună că tijele sunt întinse.
- Alegeți axele de coordonate și întocmește ecuațiile de echilibru folosind condițiile de echilibru pentru sistemul de forțe convergente pe planul ∑Xi = 0; ∑Yi = 0. La alegerea axelor de coordonate, trebuie avut în vedere că ecuațiile rezultate vor fi mai ușor de rezolvat dacă una dintre axe este îndreptată perpendicular pe una dintre forțele necunoscute.
- Determinați reacțiile tijelor din soluția sistemului de ecuații indicat.
- Verificați corectitudinea rezultatelor obținute prin rezolvarea ecuațiilor de echilibru pentru coordonatele x și y nou alese.
Exemplu 1. Sarcina este suspendată de tije și frânghii și este în echilibru (Fig. 1.13). Înfățișați sistemul de forțe care acționează asupra balamalei DAR.
Soluţie
1. Reacțiile tijelor sunt direcționate de-a lungul tijelor, reacțiile legăturilor flexibile sunt direcționate de-a lungul firelor în direcția tensiunii (Fig. 1.13, a).
2. Pentru a determina directia exacta a fortelor din tije indepartam mental succesiv tijele 1 si 2. Analizam posibilele deplasari ale punctului DAR.
Nu considerăm un bloc fix cu forțe care acționează asupra lui.
3. Scoateți tija 1, punctul DAR se ridică și se îndepărtează de perete, prin urmare, reacția tijei 1 este îndreptată spre perete.
4. Scoateți tija 2, punctul DAR se ridică și se apropie de perete, prin urmare, reacția tijei 2 este îndreptată în jos de perete.
5. Funia trage spre dreapta.
6. Suntem eliberați de legături (Fig. 1.13, b).
Exemplul 2 Mingea este suspendată pe un fir și se sprijină pe un perete (Fig. 1.14a). Determinați reacțiile unui fir și a unui suport neted (perete).
Soluţie
1. Reacția firului - de-a lungul firului până la punct LAîn sus (Fig. 1.14, b).
2. Reacția unui suport neted (perete) - de-a lungul normalului de la suprafața suportului.
Exemplul 3 Imaginează-ți asta pe o bară situată orizontal AB, neglijând propria sa masă, acționează sarcina verticală F, aplicat la un punct DIN cherestea (Fig. 1.14-1, A). Capătul din stânga al grinzii DAR prins de suport printr-o balama, iar dreapta LA se sprijină pe un plan neted înclinat.
Să descriem schematic bara ca un segment AB, ca în fig. 1.14-1, b,și aplicați-l la punctul DIN forță verticală F. La punctul LA din lateral plan înclinat reacția sa este aplicată pe bară RB, direcționat perpendicular pe plan; linii de acțiune Fși R B se intersectează într-un punct O. Pe lângă aceste forțe, asupra grinzii acționează o altă forță - reacția suportului articulat-fix. Și deoarece bara este în echilibru, linia de acțiune a celei de-a treia forțe va trece și ea prin punct O, adică reacția R suportul articulat, dar fix este îndreptat de-a lungul segmentului AO.
Metoda de raționament folosită aici se numește principiul eliberării corpului de legături și înlocuirea legăturilor cu reacțiile lor.
Exemplul 4 Determinați forța în tijă CDși presiunea de sarcină DAR pe planul de referinţă EF(Fig. 1.14-2, a). Greutatea tijei CD, bloc LA, frânghia şi frecarea frânghiei pe bloc de neglijat.
Soluţie
Tensiunea cablului în toate punctele sale este aceeași și este egală cu forța gravitațională a sarcinii LA,întrucât blocul fix modifică doar direcția forței care acționează asupra frânghiei.
Luați în considerare echilibrul sistemului: tija CDși blocați La ML. Să aruncăm conexiunile și să le înlocuim acțiunea cu reacțiile corespunzătoare (Fig. 1.14-2, 6). Pentru sistemul de forțe rezultat, se poate întocmi o singură ecuație de echilibru:
Pe fig. 1.14-2, în arată forțele care acționează asupra sarcinii DAR cu o bucată de frânghie adiacentă EL. R EF - susține reacția planului.
Din moment ce marfa DAR este în echilibru, atunci
![]()
R ef \u003d Pa - Pv \u003d 600 - 400 \u003d 200 N.
Forța de presiune a sarcinii A pe planul de sprijin RA este prezentată în Fig. 1.14-2, d. Evident, R A = R EF = 200 H (forța de acțiune este egală cu forța de reacție).
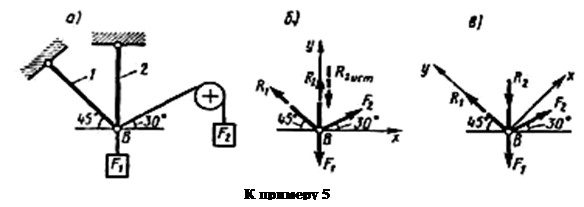
Exemplul 5 Determinați reacțiile tijelor care țin sarcinile F 1 = 70 kN și F 2 = 100 kN (Fig. a). Ignorați greutatea tijelor.
 |
Soluţie
1. Luați în considerare echilibrul balamalei B (Fig. a).
2. Eliberăm balamaua B de legături și înfățișăm forțele active care acționează asupra acesteia și reacțiile legăturilor (Fig. b).
3. Alegem un sistem de coordonate, aliniind axa y în direcția C cu reacția R 2 (Fig. b) și compunem ecuațiile de echilibru pentru sistemul de forțe care acționează asupra balamalei B:
3. Determinăm reacțiile tijelor R 1 și R 2 prin rezolvarea ecuațiilor.
Înlocuind valoarea găsită a lui R 1 în ecuația (2), obținem
Semnul minus în fața valorii R 2 indică faptul că direcția aleasă inițial a reacției este incorectă - reacția R 2 ar trebui direcționată în direcția opusă, adică. la balama B (în Fig. b, adevărata direcție a reacției R2 este prezentată printr-un vector întrerupt).
5. Verificăm corectitudinea rezultatelor obținute prin alegerea unei noi locații a axelor de coordonate x și y (Fig. a). În ceea ce privește aceste axe, compunem ecuațiile de echilibru:
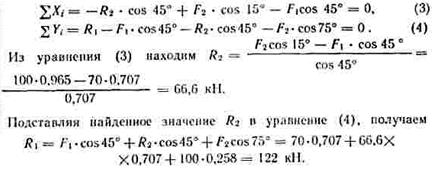
Valorile reacțiilor R 1 și R 2 obținute prin rezolvarea ecuațiilor (1) și (2) coincid ca mărime și direcție cu valorile găsite din ecuațiile (3) și (4), prin urmare, problema este rezolvată. corect.
Controlați întrebările și sarcinile
1. Care dintre sistemele de forțe date (Fig. 1.15) este echilibrat?
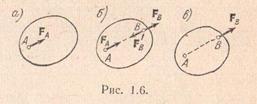
3. Corpurile 1 și 2 (Fig. 1.17) sunt în echilibru. Este posibil să se elimine sistemele de operare ale forțelor dacă corpurile sunt absolut rigide? Ce se va schimba dacă corpurile sunt reale, deformabile?
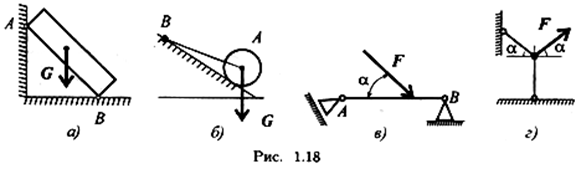
4. Specificați directie posibila reacţii în suporturi (Fig. 1.18).
Pentru a aplica teorema Huygens-Steiner, trebuie să cunoașteți momentul de inerție eu Cu corp în raport cu axa SS care trece prin centrul său de greutate (centrul de inerție). Acest moment depinde de direcția axei CC. Cu toate acestea, nu este nevoie să se calculeze eu Cu conform formulei sau măsurați-o din nou pentru fiecare axă.
Se pare că pentru orice corp solid există trei axe reciproc perpendiculare care trec prin centrul său de inerție (axele principale ale corpului), astfel încât momentul de inerție în jurul oricărei axe a CC este exprimat prin momentele de inerție ale corpului I 1 , I 2 și I 3 raportat la aceste axe principale. Astfel, sarcina de a determina momentul de inerție al unui corp față de o axă arbitrară se reduce la determinarea axelor principale și a momentelor de inerție corespunzătoare I 1 , I 2 și I 3.
Cum să găsiți axele principale de inerție ale unui corp rigid dat? Axele principale sunt ușor de determinat pentru corpuri simetrice omogene (bilă, cub, cilindru, paralelipiped dreptunghiular etc.) Axele principale de inerție ale unor astfel de corpuri coincid întotdeauna cu axele de simetrie ale corpului. De exemplu, axele principale ale unui paralelipiped dreptunghiular omogen trec prin centrul său geometric perpendicular pe fețe (poza 4)
Pentru o minge omogenă, oricare trei axe reciproc perpendiculare care trec prin centrul ei sunt principale.Se poate demonstra că un cub omogen are aceeași proprietate.Pentru corpuri axele principale de formă complexă și momentele de inerție pot fi găsite prin metode experimentale și teoretice mai complexe.
Figura 4 Axele principale de inerție ale unui paralelipiped dreptunghiular
4.6 Energia cinetică a unui corp în rotație
Energia cinetică arbitrară i-al-lea punct material cu masa m i; este egal cu
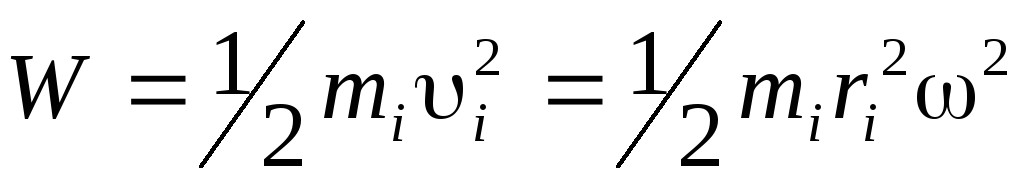 ,
(16)
,
(16)
Unde υ i= ωr i- viteza punct material, ω - viteza unghiulară, r i- distanta de la punct la axa de rotatie. Însumând energiile cinetice ale tuturor punctelor materiale, obținem energia cinetică a unui corp solid:
Formula (2 8) este valabilă atunci când corpul se rotește în jurul unei axe fixe. Dacă corpul se mișcă ca întreg și încă se rotește, atunci este energie kinetică poate fi reprezentat ca suma energiilor cinetice ale mișcărilor de translație și rotație.
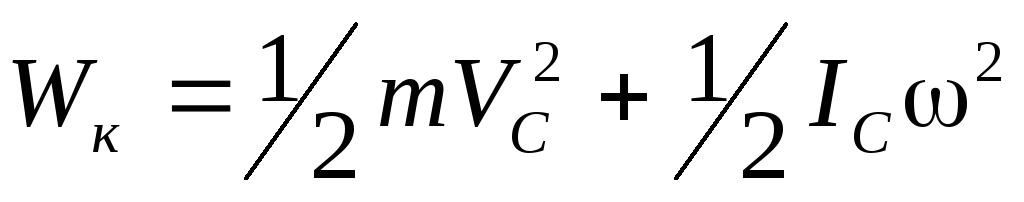 (18)
(18)
Unde V C este viteza centrului de masă (centrul de inerție) al corpului rigid; eu C este momentul de inerție în jurul axei care trece prin centrul de masă paralel cu vectorul viteză unghiulară.
4.8 Vibrații ale unui corp pe un arc. Ecuație de fluctuație mică
Oscilațiile libere sunt efectuate sub acțiunea forțelor interne ale sistemului după ce sistemul a fost scos din echilibru. Un exemplu de vibrații libere sunt vibrațiile unei sarcini pe un arc.
Pentru ca oscilațiile libere să apară conform legii armonice, este necesar ca forța care tinde să readucă corpul în poziția de echilibru să fie proporțională cu deplasarea x a corpului din poziția de echilibru.
Această condiție este îndeplinită de forța elastică a arcului F x =-kx. Coeficientul k se numește rigiditatea arcului. Toate celelalte forțe care satisfac această condiție sunt numite cvasi-elastice.
Dacă un corp atașat unui arc elastic este scos din echilibru, atunci o forță elastică din arc va începe să acționeze asupra corpului, care, conform legii lui Hooke, este proporțională cu abaterea corpului de la poziția de echilibru. Trebuie amintit că legea lui Hooke este valabilă doar pentru mici abateri de la poziția de echilibru (cantitativ, aceasta este exprimată prin inegalitatea x<< l, Unde l este lungimea arcului neîntins, x este prelungirea arcului).
Ecuația mișcării sub acțiunea unei forțe elastice are forma:
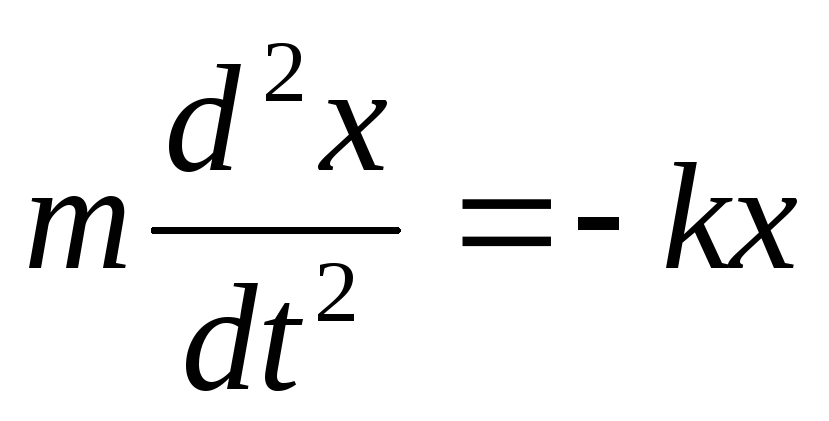 (19)
(19)
Poate fi rescris într-o altă formă introducând notația ω 2 = k/ m. Apoi
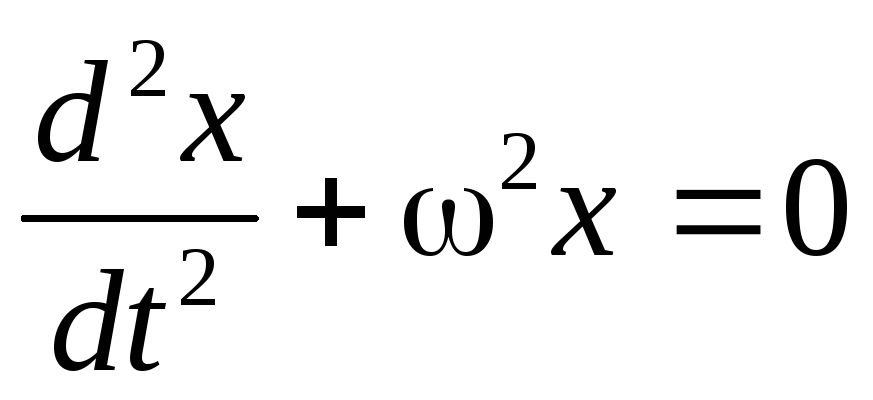 (20)
(20)
Sistemul care oscilează descris de această ecuație se numește oscilator armonic. Valoarea lui ω se numește frecvența naturală de oscilație circulară. Pentru sarcina cu arc
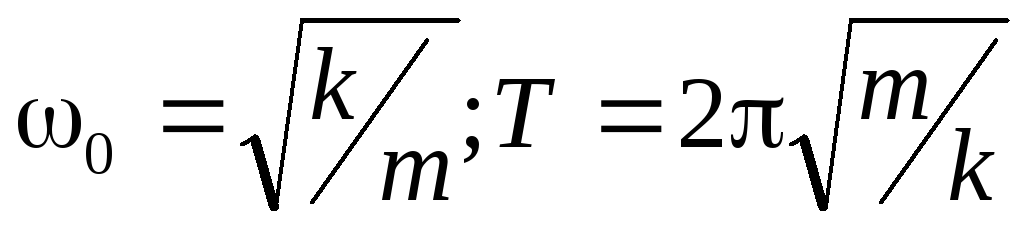 ; (21)
; (21)
Oscilațiile armonice apar conform legii
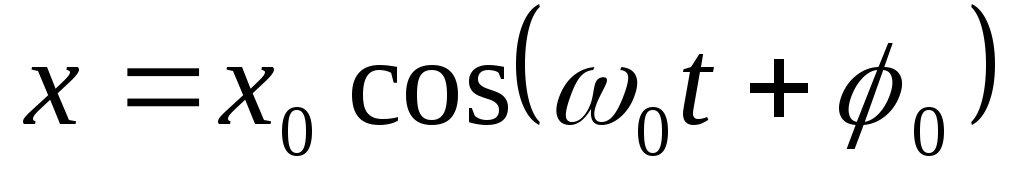 , (22)
, (22)
unde x 0 și φ 0 sunt amplitudinea și faza inițială a oscilațiilor. Aceste cantități depind de condițiile inițiale.
Cu oscilații armonice, energia cinetică și potențială se modifică periodic, dar energia mecanică totală E a unui sistem închis în care nu există forțe de rezistență rămâne neschimbată.
Pentru sarcina cu arc
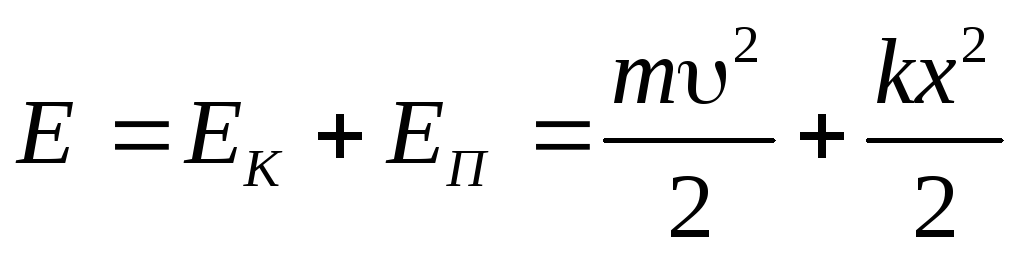 ;
;
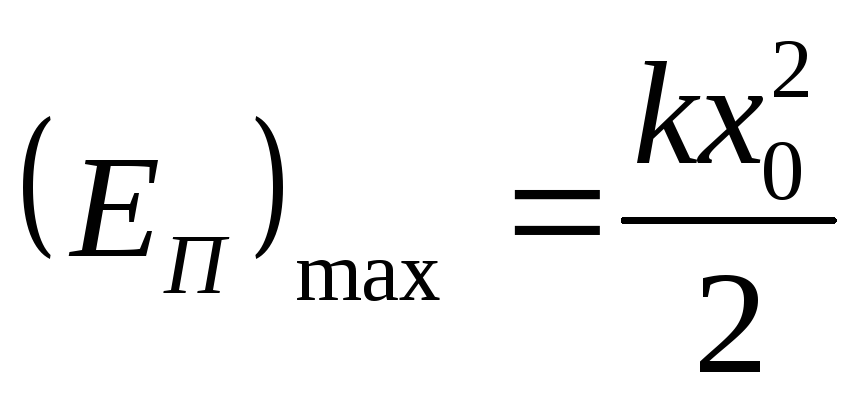 ;(23)
;(23)
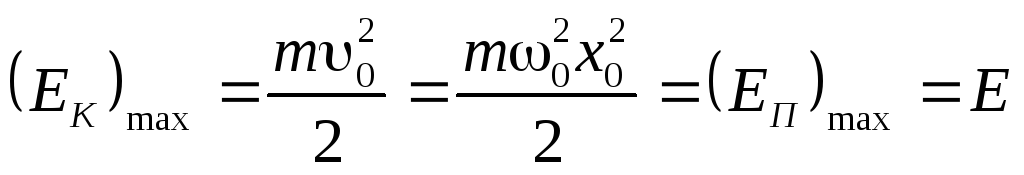 (24)
(24)
Cu oscilații armonice, are loc o transformare periodică a energiei cinetice în energie potențială și invers.
În prezența forțelor de frecare (rezistență), energia totală a sistemului scade în timp, iar oscilațiile devin amortizate.
Dacă forța de rezistență este proporțională cu viteza (frecarea vâscoasă) F tr \u003d - bυ, amplitudinea oscilației A scade conform legii
A = x0 e- δt , unde δ=b/2 m (25)
Constanta δ se numește factor de amortizare. Intervalul de timp τ = 1/δ în care amplitudinea scade în e≈2,7 ori se numește timp de dezintegrare.






