Proiecția forței pe axă este determinată de segmentul axei tăiat

perpendiculare coborâte pe axă de la începutul și sfârșitul vectorului (Fig. 3.1).

Mărimea proiecției forței pe axă este egal cu produsul dintre modulul forței și cosinusul unghiului dintre vectorul forță și direcție pozitivă topoare. Astfel, proiecția are semnul: pozitiv în aceeași direcție vectori de forţă şi axe şi negativ când este îndreptată spre axa negativă(Fig. 3.2).

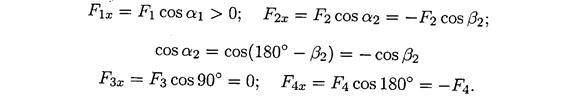
Proiecția forței pe două axe reciproc perpendiculare(Fig. 3.3).

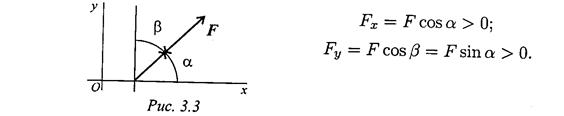
Sfârșitul lucrării -

Acest subiect aparține:

Mecanica teoretică

Mecanica teoretica... PRELARE... Subiect Concepte de baza si axiome ale staticii...

Dacă aveți nevoie de material suplimentar pe această temă, sau nu ați găsit ceea ce căutați, vă recomandăm să utilizați căutarea în baza noastră de date de lucrări:

Ce vom face cu materialul primit:

Dacă acest material s-a dovedit a fi util pentru dvs., îl puteți salva pe pagina dvs. de pe rețelele sociale:

Toate subiectele din această secțiune:

Probleme de mecanică teoretică
Mecanica teoretică este știința mișcării mecanice a solidelor materiale și a interacțiunii lor. Mișcarea mecanică este înțeleasă ca mișcarea unui corp în spațiu și timp

A treia axiomă
Fără a încălca starea mecanică a corpului, puteți adăuga sau elimina un sistem echilibrat de forțe (principiul renunțării unui sistem de forțe echivalent cu zero) (Fig. 1.3). P,=P2 P,=P.

Consecință din axiomele a doua și a treia
Forța care acționează asupra unui corp rigid poate fi deplasată de-a lungul liniei sale de acțiune (Fig. 1.6).

Legături și reacții ale obligațiunilor
Toate legile și teoremele staticii sunt valabile gratuit corp solid. Toate corpurile sunt împărțite în libere și legate. Corpuri libere- corpuri, a căror mișcare nu este limitată.

Tijă rigidă
În diagrame, tijele sunt reprezentate cu o linie groasă și continuă (Fig. 1.9). rod mozhe

balama fixă
Punctul de atașare nu poate fi mutat. Tija se poate roti liber în jurul axei balamalei. Reacția unui astfel de suport trece prin axa balamalei, dar

Sistem plan de forțe convergente
Sistemul de forțe, ale cărui linii de acțiune se intersectează într-un punct, se numește convergent (Fig. 2.1).

Rezultatul forțelor convergente
Rezultanta a două forțe care se intersectează poate fi determinată utilizând un paralelogram sau un triunghi de forțe (a patra axiomă) (Vis. 2.2).

Condiție de echilibru pentru un sistem plat de forțe convergente
Când sistemul de forțe este în echilibru, rezultanta trebuie să fie egală cu zero, prin urmare, într-o construcție geometrică, sfârșitul ultimului vector trebuie să coincidă cu începutul primului. În cazul în care un

Rezolvarea problemelor de echilibru într-un mod geometric
Este convenabil să folosiți metoda geometrică dacă există trei forțe în sistem. La rezolvarea problemelor de echilibru, corpul este considerat a fi absolut solid (solidificat). Ordinea rezolvarii problemelor:

Soluţie
1. Forțele care apar în tijele de fixare sunt egale ca mărime cu forțele cu care tijele susțin sarcina (axioma a 5-a a staticii) (Fig. 2.5a). Noi definim directii posibile reacții de legătură

Forțe într-un mod analitic
Valoarea rezultantei este egală cu suma vectorială (geometrică) a vectorilor sistemului de forțe. Determinăm rezultatul geometric. Alegem un sistem de coordonate, stabilim proiecțiile tuturor sarcinilor

Forțe convergente în formă analitică
Pe baza faptului că rezultanta este egală cu zero, obținem: Condiție

Pereche de forțe, moment pentru câteva forțe
O pereche de forțe este un sistem de două forțe care au modul egal, paralele și direcționate în direcții diferite. Luați în considerare un sistem de forțe (P; B") care formează o pereche.

Moment de forță în jurul unui punct.
O forță care nu trece prin punctul de atașare al corpului face ca corpul să se rotească în raport cu acest punct, astfel încât efectul unei astfel de forțe asupra corpului este estimat ca un moment. Moment de forță rel.

Teorema lui Poinsot privind transferul paralel de forțe
O forță poate fi transferată paralel cu linia sa de acțiune prin adăugarea unei perechi de forțe cu un moment egal cu produsul dintre modulul forței și distanța pe care a fost transferată forța.

forțe localizate
Liniile de acțiune ale unui sistem arbitrar de forțe nu se intersectează la un moment dat, prin urmare, pentru a evalua starea corpului, un astfel de sistem ar trebui simplificat. Pentru a face acest lucru, toate forțele sistemului sunt transferate la unul în mod arbitrar

Influența punctului de referință
Punctul de referință este ales în mod arbitrar. Când schimbați poziția punctului de reducere, valoarea vectorului principal nu se va modifica. Valoarea momentului principal în care punctul de reducere este mutat se va modifica,

Sistem de forță plată
1. În echilibru vector principal sistemul este zero. Definiția analitică a vectorului principal duce la concluzia:

Tipuri de sarcini
În funcție de metoda de aplicare, încărcăturile sunt împărțite în concentrate și distribuite. Dacă în realitate transferul sarcinii are loc pe o zonă neglijabilă (la un punct), sarcina se numește concentrată

Moment de forță în jurul axei
Momentul forței în jurul axei este egal cu momentul proiecției forței pe un plan perpendicular pe axă, raportat la punctul de intersecție a axei cu planul (Fig. 7.1 a). MO

Vector în spațiu
În spațiu, vectorul forță este proiectat pe trei axe de coordonate reciproc perpendiculare. Proiecțiile vectoriale formează margini cuboid, vectorul forță coincide cu diagonala (Fig. 7.2

Sistemul de forțe convergent spațial
Un sistem de forțe convergent spațial este un sistem de forțe care nu se află în același plan, ale căror linii de acțiune se intersectează într-un punct. Sistemul spațial rezultat si

Aducerea unui sistem spațial arbitrar de forțe în centrul O
Este dat un sistem spațial de forțe (Fig. 7.5a). Să-l aducem în centrul O. Forțele trebuie deplasate în paralel și se formează un sistem de perechi de forțe. Momentul fiecăreia dintre aceste perechi este

Centrul de greutate al corpurilor plate omogene
(figuri plate) Foarte des este necesar să se determine centrul de greutate al diferitelor corpuri plate și figuri geometrice plate formă complexă. Pentru corpurile plate, putem scrie: V =

Determinarea coordonatelor centrului de greutate al figurilor plate
Notă. Centrul de greutate al unei figuri simetrice se află pe axa de simetrie. Centrul de greutate al tijei este la mijlocul înălțimii. Pozițiile centrelor de greutate ale formelor geometrice simple pot

Cinematica punctuală
Aveți o idee despre spațiu, timp, traiectorie, cale, viteză și accelerație. Știți cum să setați mișcarea unui punct (natural și coordonat). Cunoașteți notația

Distanta parcursa
Calea este măsurată de-a lungul căii în direcția de mers. Denumire - S, unități de măsură - metri. Ecuația mișcării punctuale: definirea ecuației

Viteza de calatorie
Cantitatea vectorială care caracterizează în acest moment viteza și direcția mișcării de-a lungul traiectoriei se numesc viteză. Viteza este un vector direcționat de-a lungul k

accelerație punctuală
Mărimea vectorială care caracterizează viteza de schimbare a mărimii și direcției se numește accelerația unui punct. Viteza punctului la deplasarea din punctul M1

Mișcare uniformă
Mișcarea uniformă este mișcarea cu viteză constantă: v = const. Pentru mișcare uniformă rectilinie (Fig. 10.1 a)

Mișcare egal-variabilă
Mișcarea egal-variabilă este mișcarea cu accelerație tangențială constantă: at = const. Pentru mișcare uniformă rectilinie

mișcare de translație
Translația este o astfel de mișcare a unui corp rigid în care orice linie dreaptă de pe corp în timpul mișcării rămâne paralelă cu poziția sa inițială (Fig. 11.1, 11.2). La

mișcare de rotație
În timpul mișcării de rotație, toate punctele corpului descriu cercuri în jurul unei axe fixe comune. Axa fixă ​​în jurul căreia se rotesc toate punctele corpului se numește axă de rotație.

Cazuri particulare de mișcare de rotație
Rotație uniformă (viteza unghiulară este constantă): ω = const Ecuația (legea) rotației uniforme în acest caz are forma:

Vitezele și accelerațiile punctelor unui corp în rotație
Corpul se rotește în jurul punctului O. Să determinăm parametrii de mișcare ai punctului Alocat la o distanță RA față de axa de rotație (Fig. 11.6, 11.7). cale

Soluţie
1. Secțiunea 1 - mișcare neuniformă accelerată, ω \u003d φ '; ε = ω’ 2. Secțiunea 2 - viteza este constantă - mișcarea este uniformă, . ω = const 3.

Definiții de bază
O mișcare complexă este o mișcare care poate fi descompusă în mai multe mișcări simple. Mișcările simple sunt de translație și rotație. Pentru a lua în considerare mișcarea complexă a punctelor

Mișcarea plan-paralelă a unui corp rigid
Plan-paralel sau plat este o astfel de mișcare a unui corp rigid în care toate punctele corpului se mișcă paralel cu unele fixe din cadrul de referință luat în considerare

translațional și rotațional
Mișcarea plan-paralelă este descompusă în două mișcări: de translație împreună cu un anumit pol și de rotație față de acest pol. Descompunerea este folosită pentru a determina

Centru de viteze
Viteza oricărui punct al corpului poate fi determinată folosind centrul de viteze instantaneu. În acest caz, o mișcare complexă este reprezentată ca un lanț de rotații în jurul diferiților centri. O sarcină

Axiomele dinamicii
Legile dinamicii sintetizează rezultatele a numeroase experimente și observații. Legile dinamicii, care sunt de obicei considerate axiome, au fost formulate de Newton, dar prima și a patra lege au fost, de asemenea,

Conceptul de frecare. Tipuri de frecare
Frecarea este rezistența care apare atunci când un corp dur se deplasează pe suprafața altuia. Când corpurile alunecă, apare frecarea de alunecare; la rulare, apare frecarea de rulare. Natura rezistenței

frecare de rulare
Rezistența la rulare este legată de deformarea reciprocă a solului și a roții și este mult mai mică decât frecarea de alunecare. De obicei, solul este considerat mai moale decât roata, apoi solul este în principal deformat și

Puncte gratuite și negratuite
Un punct material, a cărui mișcare în spațiu nu este limitată de nicio constrângere, se numește liber. Problemele sunt rezolvate folosind legea de bază a dinamicii. Material atunci

forta de inertie
Inerția este abilitatea de a-și menține starea neschimbată; aceasta este o proprietate internă a tuturor corpurilor materiale. Forța de inerție - forța care apare la accelerarea sau frânarea corpurilor

Soluţie
Forțe active: forta motrice, forța de frecare, forța gravitațională. Reacția în suportul R. Aplicăm forța de inerție în sens invers față de accelerație. Conform principiului d'Alembert, sistemul de forţe care acţionează pe platformă

Lucrul forței rezultante
Sub acţiunea unui sistem de forţe, un punct de masă m se deplasează din poziţia M1 în poziţia M 2 (fig. 15.7). În cazul mișcării sub acțiunea unui sistem de forțe,

Putere
Pentru a caracteriza performanța și viteza de lucru, este introdus conceptul de putere. Puterea este munca efectuată pe unitatea de timp:

Putere de rotație
Orez. 16.2 Corpul se deplasează de-a lungul unui arc de rază de la punctul M1 la punctul M2 M1M2 = φr Lucrul de forță

Eficienţă
Fiecare mașină și mecanism, lucrând, cheltuiește o parte din energie pentru a depăși rezistențele dăunătoare. Astfel, mașina (mecanismul), pe lângă munca utilă, efectuează și un suplimentar

Teorema privind modificarea impulsului
Momentul unui punct material este o mărime vectorială egală cu produsul dintre masa punctului și viteza lui mv. Vectorul impuls coincide cu

Teorema schimbării energiei cinetice
Energia este capacitatea unui corp de a efectua lucrări mecanice. Există două forme energie mecanică: energie potențială, sau energia de poziție și energia cinetică,

Fundamentele dinamicii sistemului de puncte materiale
Agregat puncte materiale, interconectate prin forțe de interacțiune, se numește sistem mecanic. Orice corp material în mecanică este considerat mecanic

Ecuația de bază a dinamicii unui corp în rotație
Lăsați un corp rigid să se rotească în jurul axei Oz sub acțiunea forțelor externe cu o viteză unghiulară

Voltaj
Metoda secțiunii vă permite să determinați valoarea factorului forță internă în secțiune, dar nu face posibilă stabilirea legii distribuției forțe interne dupa sectiune. Pentru a evalua puterea lui n

Factori de forță interni, tensiuni. Complot
Aveți o idee despre forțele longitudinale, despre tensiunile normale în secțiuni transversale. Cunoașteți regulile de construire a diagramelor de forțe longitudinale și tensiuni normale, legea distribuției

Forțe longitudinale
Luați în considerare o grindă încărcată cu forțe externe de-a lungul axei. Grinda se fixează în perete (fixarea „încastrării”) (Fig. 20.2a). Împărțim fasciculul în secțiuni de încărcare. Zona de încărcare cu

Caracteristicile geometrice ale secțiunilor plate
Ai o idee despre simțul fizicși procedura de determinare a momentelor de inerție axială, centrifugă și polară, despre principalele axe centrale și principalele momente centrale de inerție.

Momentul static al ariei secțiunii
Luați în considerare o secțiune arbitrară (Fig. 25.1). Dacă împărțim secțiunea în zone infinit de mici dA și înmulțim fiecare zonă cu distanța față de axa de coordonate și integrăm rezultatul obținut

moment de inerție centrifugal
Momentul de inerție centrifugal al unei secțiuni este suma produselor ariilor elementare luate de aria totală prin ambele coordonate:

Momentele axiale de inerție
Momentul axial de inerție al unei secțiuni față de o curte situată în același plan este suma produselor ariilor elementare pe pătrat a distanței lor luate pe întreaga suprafață

Momentul polar de inerție al secțiunii
Momentul polar de inerție al unei secțiuni în raport cu un anumit punct (pol) este suma produselor ariilor elementare luate pe întreaga suprafață și pătratul distanței lor până la acest punct:

Momentele de inerție ale celor mai simple secțiuni
Momente axiale inerția dreptunghiului (Fig. 25.2) Imaginează-ți direct

Momentul polar de inerție al unui cerc
Pentru un cerc se calculează mai întâi momentul polar de inerție, apoi cele axiale. Imaginează-ți un cerc ca un set de inele infinit de subțiri (Fig. 25.3).

Deformatii de torsiune
Torsiunea unei grinzi rotunde are loc atunci când este încărcată de perechi de forțe cu momente în planuri perpendiculare pe axa longitudinală. În acest caz, generatorul fasciculului este îndoit și rotit printr-un unghi γ,

Ipoteze în torsiune
1. Este îndeplinită ipoteza secțiunilor plane: secțiunea transversală a grinzii, care este plană și perpendiculară pe axa longitudinală, rămâne plată și perpendiculară pe axa longitudinală după deformare.

Factori de forță interni în torsiune
Torsiunea se numește încărcare, în care în secțiunea transversală a fasciculului apare un singur factor de forță intern - cuplul. Încărcăturile externe sunt, de asemenea, două pro

Diagrame de cuplu
Cuplurile pot varia de-a lungul axei fasciculului. După ce am determinat valorile momentelor de-a lungul secțiunilor, construim o diagramă de cupluri de-a lungul axei barei.

Tensiuni de torsiune
Desenăm o grilă de linii longitudinale și transversale pe suprafața grinzii și luăm în considerare modelul format pe suprafață după Fig. 27.1a deformare (Fig. 27.1a). Pop

Tensiuni maxime de torsiune
Din formula de determinare a tensiunilor și diagrama de distribuție a tensiunilor tăietoare în timpul torsiune se poate observa că tensiunile maxime apar la suprafață. Determinați tensiunea maximă

Tipuri de calcule de rezistență
Există două tipuri de calcul al rezistenței 1. Calcul de proiectare - se determină diametrul grinzii (arborele) în secțiunea periculoasă:

Calculul rigidității
La calcularea rigidității, se determină deformația și se compară cu cea admisibilă. Se consideră deformarea unei bare rotunde sub acțiunea unei perechi exterioare de forțe cu un moment t (Fig. 27.4).

Definiții de bază
O îndoire este un tip de încărcare în care în secțiunea transversală a grinzii apare un factor de forță intern - un moment încovoietor. Se lucrează la bar

Factori de forță interni în încovoiere
Exemplul 1. Să considerăm o grindă, asupra căreia acţionează o pereche de forţe cu un moment t şi o forţă externă F (Fig. 29.3a). Pentru a determina factorii de forță interni, folosim metoda cu

Momente de încovoiere
Forța transversală în secțiune este considerată pozitivă dacă tinde să rotească

Dependențe diferențiale pentru îndoirea directă transversală
Construcția diagramelor forțelor tăietoare și a momentelor încovoietoare este mult simplificată atunci când se utilizează relații diferențiale între momentul încovoietor, forța tăietoare și intensitatea uniformă.

Metoda secțiunii Expresia rezultată poate fi generalizată
Forța transversală în secțiunea luată în considerare este egală cu suma algebrică a tuturor forțelor care acționează asupra grinzii până la secțiunea luată în considerare: Q = ΣFi Deoarece vorbim despre

Voltaj
Luați în considerare îndoirea unei grinzi ciupit pe dreapta și încărcat cu o forță concentrată F (Fig. 33.1).

Stare de stres la un punct
Starea de efort într-un punct este caracterizată de solicitări normale și de forfecare care apar pe toate zonele (secțiunile) care trec prin punct dat. De obicei este suficient să definiți

Conceptul de stare complexă deformată
Setul de deformații care apar în direcții diferite și în planuri diferite care trec printr-un punct determină starea deformată în acel punct. Deformări complexe

Calculul unei bare rotunde pentru îndoire cu torsiune
În cazul calculării unei grinzi rotunde sub acțiunea de încovoiere și torsiune (Fig. 34.3), este necesar să se țină cont de tensiunile normale și de forfecare, deoarece valorile maxime ale tensiunii apar în ambele cazuri.

Conceptul de echilibru stabil și instabil
Lansetele relativ scurte și masive se bazează pe compresie, deoarece. ele eșuează ca urmare a distrugerii sau a deformărilor reziduale. Tije lungi cu secțiune transversală mică sub acțiune

Calculul durabilității
Calculul stabilității constă în determinarea forței de compresiune admisă și, în comparație cu aceasta, a forței care acționează:

Calcul prin formula lui Euler
Problema determinării forței critice a fost rezolvată matematic de L. Euler în 1744. Pentru o tijă articulată pe ambele părți (Fig. 36.2), formula Euler are forma

Tensiuni critice.
Tensiunea critică este tensiunea de compresiune corespunzătoare forței critice. Tensiunea de la forța de compresiune este determinată de formula

Limitele de aplicabilitate ale formulei Euler
Formula Euler este valabilă numai în limitele deformațiilor elastice. Astfel, efortul critic trebuie să fie mai mic decât limita elastică a materialului. Prev

teorema lui Varignon. Dacă sistemul plan de forțe luat în considerare este redus la o rezultantă, atunci momentul acestei rezultante față de orice punct este egal cu suma algebrică a momentelor tuturor forțelor sistemului dat față de același punct. Să presupunem că sistemul de forțe este redus la rezultanta R care trece prin punctul O. Să luăm acum un alt punct O 1 ca centru de reducere. Momentul principal (5.5) despre acest punct este egală cu suma momentele tuturor forţelor în formă generală: M O1 =ƩM o1 (F k). În cazul nostru, avem M O1 =M Ol (R), deoarece momentul principal pentru centrul de reducere O este egal cu zero (M O =0). Comparând relaţiile, se obţine M O1 (R)=ƩM Ol (F k); h.t.d.

18.Mod analitic de stabilire a forței Alegem sistemul de coordonate Oxyz. Un vector se poate construi cunoscând modulul şi unghiurile dintre vector şi axele corespunzătoare.Atribuirea acestor mărimi determină forţa. Punctul de aplicare a forței trebuie specificat suplimentar prin coordonatele x, y, z. În plus, forța poate fi setată prin proiecții pe axă. Apoi

Aceste formule permit, cunoscând proiecțiile forței pe axele de coordonate, să se găsească modulul și unghiurile acesteia cu axele, i.e. determina puterea. Cunoscând proiecțiile, puteți construi un vector geometric.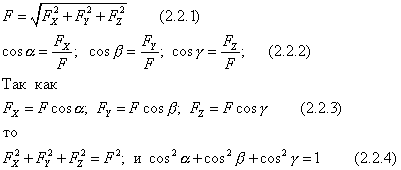

Pentru un plan se vor scrie formulele (2.2.1) și (2.2.2) Construcția în plan se realizează conform axiomei a IV-a a staticii.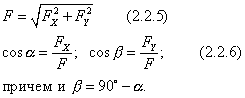

19. Dispozitive suport ale sistemelor de fascicule

Se folosesc următoarele tipuri de suporturi: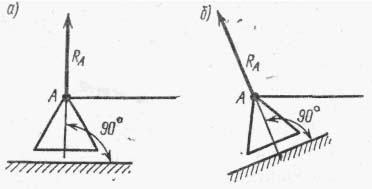

Balamale - suport mobil

Aici valoarea numerică a reacției suport RA rămâne necunoscută. Trebuie remarcat faptul că suprafața de sprijin a suportului articulat poate să nu fie paralelă cu axa grinzii (Fig.b). Reacția RA în acest caz nu va fi perpendiculară pe axa grinzii, deoarece este perpendiculară pe suprafața de sprijin.

Balamale - suport fix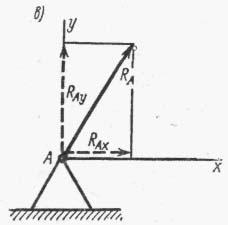

Acest suport permite rotirea în jurul axei balamalei, dar nu permite nicio mișcare liniară. În acest caz, se cunoaște doar punctul de aplicare al reacției suport - centrul balamalei; direcția și valoarea reacției suport sunt necunoscute. De obicei, în loc să se determine sensul și direcția reacției (totale) RA, se găsesc componentele acesteia RAx și RAy.

Atașare rigidă (prindere) Un astfel de suport nu permite nici mișcarea liniară, nici rotația.În acest caz, nu se cunosc doar valoarea și direcția reacției, ci și punctul de aplicare a acesteia. Prin urmare, terminația rigidă este înlocuită cu o forță de reacție RA și un cuplu de forțe cu un moment MA.

Pentru determinarea reacției suport trebuie găsite trei necunoscute: componentele RAx și RAy ale reacției suport de-a lungul axelor de coordonate și momentul reactiv MA.

20. Proiecția forței pe axă și pe plan

O valoare scalară egală cu lungimea segmentului luat cu semnul corespunzător, închisă între proiecțiile începutului și sfârșitului forței, se numește proiecția forței pe axă.

Proiecția are semnul plus dacă mișcarea de la început până la sfârșit are loc în direcția pozitivă a axei, iar semnul minus dacă este în sens negativ.

Astfel, proiecțiile unei forțe date pe orice axe paralele și egal direcționate sunt egale între ele.

Proiecția forței pe axa Ox se notează cu To, proiecția forței pe axă este egală cu produsul dintre modulul forței și cosinusul unghiului dintre direcția forței și direcția pozitivă a axa.

Dacă o forță este perpendiculară pe o axă, atunci proiecția ei pe acea axă este zero.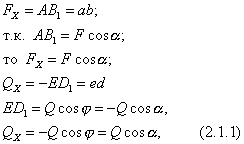

Proiecția forței pe planul Oxy este vectorul cuprins între proiecțiile începutului și sfârșitului forței F pe acest plan (Fig. 13).

Proiecția unei forțe pe un plan este o mărime vectorială și se caracterizează atât prin modul cât și prin direcția în planul Oxy. Modulul de proiecție a forței pe planul Oxy este exprimat ca Apoi proiecțiile pe axele Ox și Oy:

21. descompunerea forţelor. A descompune o forță dată în mai multe componente înseamnă a găsi un astfel de sistem de mai multe forțe pentru care forța dată este rezultatul. Această problemă este nedefinită și are o soluție unică numai atunci când sunt specificate condiții suplimentare. Să luăm în considerare două cazuri speciale:

a) expansiunea forței în două direcții date. Problema se reduce la construirea unui astfel de paralelogram, în care forța extinsă este o diagonală, iar laturile sunt paralele cu direcțiile date.

b) expansiunea forţei în trei direcţii date. Dacă direcțiile date nu se află în același plan, atunci problema „este definită și se reduce la construirea unui astfel de paralelipiped, în care diagonala înfățișează forța R dată, iar muchiile sunt paralele cu direcțiile date. În cele mai simple cazuri. , metoda descompunerii poate fi folosită pentru determinarea forțelor de presiune asupra legăturilor Pentru a face acest lucru, forța dată care acționează asupra corpului (structurii) trebuie descompusă în direcțiile reacției de legătură, întrucât, conform legii de acțiune și reacție, forța de presiune asupra legăturii și reacția de legătură sunt direcționate de-a lungul aceleiași linii drepte.

O valoare scalară egală cu lungimea segmentului luat cu semnul corespunzător, închisă între proiecțiile începutului și sfârșitului forței, se numește proiecția forței pe axă.

Proiecția are semnul plus dacă mișcarea de la început până la sfârșit are loc în direcția pozitivă a axei, iar semnul minus dacă este în sens negativ.

Astfel, proiecțiile unei forțe date pe orice axe paralele și egal direcționate sunt egale între ele.

Proiecția forței pe axa Ox se notează ca (Fig. 12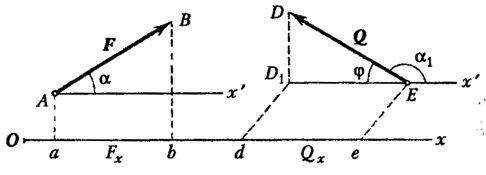

).

Urmând Figura 12 și definiția, obținem

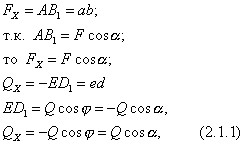
Adică, proiecția forței pe axă este egală cu produsul dintre modulul de forță și cosinusul unghiului dintre direcția forței și direcția pozitivă a axei.

Dacă o forță este perpendiculară pe o axă, atunci proiecția ei pe acea axă este zero.

Proiecția forței pe planul Oxy este vectorul cuprins între proiecțiile începutului și sfârșitului forței F pe acest plan (Fig. 13).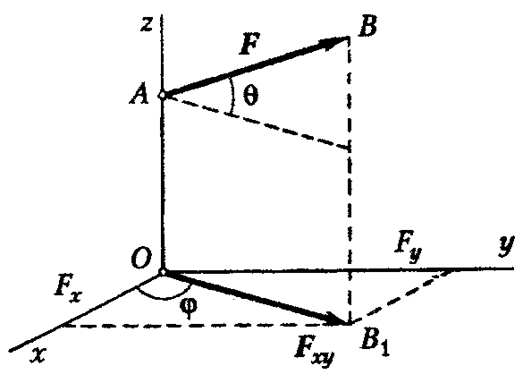

).

Proiecția unei forțe pe un plan este o mărime vectorială și se caracterizează atât prin modul cât și prin direcția în planul Oxy. Modulul de proiecție a forței pe planul Oxy este exprimat ca

Apoi proiecțiile pe axele Ox și Oy:

Alegem sistemul de coordonate Oxyz. Un vector poate fi construit cunoscând modulul și unghiurile dintre vector și axele corespunzătoare (Fig. 14). ).

Atribuirea acestor mărimi determină forța. Punctul de aplicare a forței trebuie specificat suplimentar prin coordonatele x, y, z. În plus, forța poate fi specificată prin proiecții pe axe. Apoi

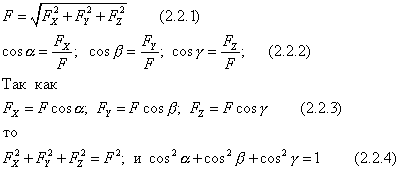
Aceste formule permit, cunoscând proiecțiile forței pe axele de coordonate, să se găsească modulul și unghiurile acesteia cu axele, i.e. determina puterea. Cunoscând proiecțiile, puteți construi un vector geometric.

Pentru un plan se scriu formulele (2.2.1) și (2.2.2).

Construcția în plan se realizează conform celei de-a 4-a axiome a staticii.

Să luăm acum în considerare metoda analitică de adunare a forțelor. Relația dintre vectori și proiecțiile lor este dată de următoarea teoremă:

Proiecția vectorului sumă pe o anumită axă este egală cu suma algebrică a proiecțiilor termenilor vectorilor pe aceeași axă (Fig. 15). ).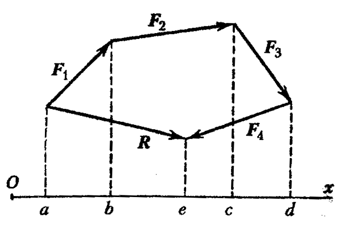

Aceste relații fac posibilă adăugarea analitică a forțelor. Se poate observa identitatea formulelor (2.2.1)-(2.2.4) și (2.2.9)-(2.2.11).

Rezolvarea problemelor de statică este adesea asociată cu operația de adunare din algebra vectorială. Să ne amintim vechile trucuri și să introducem câteva definiții.

Se numește o mărime egală cu suma geometrică a forțelor oricărui sistem vector principal sisteme.

Suma geometrică a forțelor nu trebuie confundată cu rezultanta. Pentru multe sisteme de forțe, nu există o rezultantă, iar vectorul principal poate fi calculat pentru oricare.

Luați în considerare adăugarea a două forțe pe un plan. Suma geometrică a forțelor se găsește conform regulii paralelogramului prin construirea unui triunghi de forțe (Fig. 16).

).

Modulul R al rezultantei este definit ca latura triunghiului:

unghiurile se găsesc prin teorema sinusului, dat fiind că , primim

În continuare mod geometric adunarea forțelor, să ne amintim adăugarea a trei forțe care nu se află în acest plan.

Suma geometrică a trei forțe, care nu se află în același plan, este reprezentată de diagonala unui paralelipiped construit pe aceste forțe (Fig. 17). ).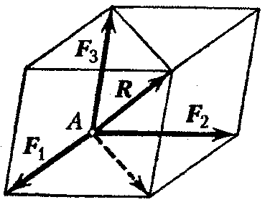

Aici este necesar să subliniem analogia completă a figurilor 14 și 17, unde , și, respectiv, joacă rolul. În consecință, putem folosi formule (2.2.1-2.2.4).

Având în vedere un sistem plat de forțe convergente, este necesar să se ia în considerare poziția unui astfel de sistem de forțe.

Suma geometrică (vectorul principal) a oricărui sistem de forțe este determinată de construcția unui poligon de forțe sau de adăugarea succesivă a forțelor sistemului. Lasă sistemul forțe convergente (Fig. 18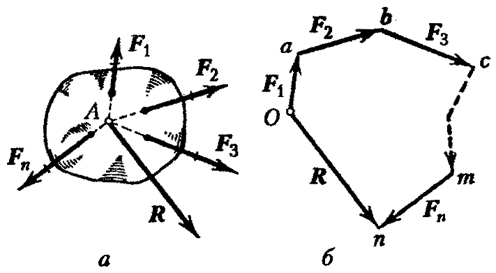

).

Pentru a construi un poligon de forță, selectați un punct arbitrar O și mutați începutul la el, apoi mutați începutul la sfârșitul vectorului și așa mai departe. după transferul vectorului, capătul vectorului va fi la un punct N. Legăm punctele O și N cu un vector. Acest vector de închidere va fi vectorul principal al sistemului.

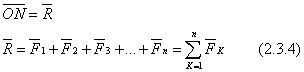
Odată cu adunarea succesivă a forțelor (Fig. 18, a), toate acestea sunt transferate de-a lungul liniilor de acțiune către punctul de intersecție A. În mod constant, conform regulii paralelogramului, se adună forțele, se obține vectorul:

care este rezultanta, egală cu vectorul principal al tuturor forțelor și aplicată în punctul de intersecție a acestora.

Liniile de acțiune a trei forțe neparalele echilibrate reciproc aflate în același plan se intersectează într-un punct.

Fie ca putere să fie dată. Deoarece ele se află în același plan și nu sunt paralele, liniile lor de acțiune se vor intersecta într-un punct O. Aplicăm forțe în acest punct și le înlocuim cu rezultanta.Atunci sunt două forțe și se aplică în punctul O (Fig. 19). ).

Dacă corpul este în echilibru, atunci, conform primei teoreme a staticii, și trebuie să fie depus de-a lungul unei linii drepte, i.e. . Prin urmare, trece prin punctul A. Acesta este ceea ce s-a cerut să fie demonstrat.

Teorema este o demonstrație necesară, dar insuficientă, a stării de echilibru pentru un corp rigid liber sub acțiunea a trei forțe.

După cum a fost definit, forțele convergente sunt forțe ale căror linii de acțiune se intersectează într-un punct. Ținând cont de teorema celor trei forțe și de axioma paralelogramului de forțe, constatăm că sistemul de forțe convergente are o rezultantă egală cu suma geometrică (vectorul principal) a acestor forțe și aplicată în punctul de intersecție a acestora. Construcția sau definirea rezultatului a fost efectuată în paragraful 2 al acestui capitol (vezi formulele 2.3.3, 2.3.4).

După ce am determinat rezultanta, putem trece la determinarea condițiilor de echilibru pentru un corp rigid liber sub acțiunea unui sistem de forțe convergente.

Dacă un sistem echilibrat de forțe acționează asupra unui corp, atunci corpul este în repaus sau se mișcă prin inerție.

Pentru echilibrul unui sistem de forțe convergente aplicate unui corp solid, este necesar și suficient ca rezultanta acestor forțe să fie egală cu zero. Condițiile pe care trebuie să le îndeplinească aceste forțe pot fi exprimate în formă geometrică sau analitică.

1) Condiția de echilibru geometric.

Deoarece rezultanta forțelor convergente este definită ca vectorul de închidere al poligonului de forță, ea poate să dispară atunci când poligonul se închide. Adică, pentru echilibrul sistemului de forțe convergente, este necesar și suficient ca poligonul de forțe construit din aceste forțe să fie închis.

2) Condiții de echilibru analitic. Analitic, rezultatul este definit ca

Deoarece suma numerelor pozitive este sub rădăcină, atunci R va fi egal cu zero dacă și numai dacă în același timp.

Adică egalitățile

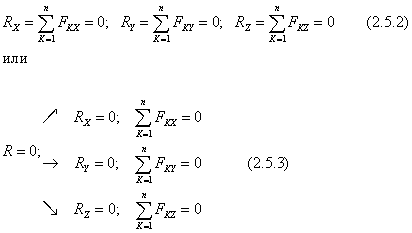
Acestea sunt condițiile pentru echilibrul unui corp rigid liber sub acțiunea unui sistem de forțe convergente.

Pentru echilibrul unui sistem spațial de forțe convergente, este necesar și suficient ca sumele proiecțiilor acestor forțe pe axele de coordonate să fie egale cu zero.

Pentru un sistem plat de forțe convergente, ecuațiile (2.5.3) se reduc la următoarele:

Împreună cu mișcare progresivă un corp rigid se poate roti în jurul unui centru (punct).

Rotația este caracterizată de un moment de forță.

Lăsați forța să fie aplicată în punctul A. Are tendința de a roti corpul în jurul centrului fix O (Fig. 20).

). Perpendiculara h coborâtă din punctul O pe linia de acțiune a forței se numește umărul forței față de centrul O.

Deoarece punctul de aplicare al forței poate fi deplasat de-a lungul liniei de acțiune a forței, rotația corpului va depinde de:

1) modulul de forță și umărul h.

2) pozițiile planului OAB,

Lăsați întregul sistem de forțe să se afle într-un singur plan, apoi direcția poate fi caracterizată printr-un semn. Oferim următoarea definiție a momentului de forță:

Momentul de forță în jurul centrului O se numește valoare egală cu produsul dintre modulul de forță și lungimea brațului, luat cu semnul corespunzător.

Momentul de forță este notat astfel:

Alegem semnul plus dacă forța încearcă să rotească corpul în sens invers acelor de ceasornic, în caz contrar luăm semnul minus.

Unități de măsură: (newton pe metru), (kilogram pe metru).

Proprietățile momentului de forță:

1) momentul forței nu se va schimba atunci când punctul de aplicare a forței este transferat de-a lungul liniei sale de acțiune;

2) momentul forței este egal cu zero dacă și numai dacă forța este egală cu zero, sau linia sa de acțiune trece prin centrul O. (h = 0).

3) momentul forței este numeric egal cu dublul aria triunghiului OAB.

Momentul sistemului plat rezultant de forțe convergente față de orice centru este egal cu suma algebrică a momentelor termenilor forțelor față de același centru.

Luați în considerare sistemul de forțe convergând în punctul A (Fig. 21 ).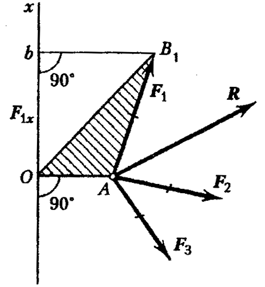

Pentru o schemă de grinzi dată, este necesar să se găsească reacțiile de sprijin dacă l=14 m, a=3,8 m, b=5 m, M=11 kN m, F=10 kN.

Soluţie. Deoarece nu există încărcare orizontală, suportul A are doar o reacție verticală RA. Compunem ecuațiile de echilibru sub forma momentelor tuturor forțelor raportate la punctele A și B.

unde găsim

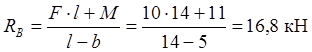
Pentru a verifica, compunem o ecuație de echilibru pentru axa verticală:

întrebări de testare

punctul de forță al balamalei fasciculului

> Cum este proiecția forței pe axă?

Proiecția forței pe axă este o mărime algebrică egală cu produsul dintre modulul de forță și cosinusul unghiului dintre direcția pozitivă a axei și vectorul forță (adică acesta este segmentul reprezentat de forța pe axele corespunzătoare).

Px=Pcos?=Pcos90o=0;

Rx=Rcos? = -R cos(180o-?).

Proiecția forței pe axă este pozitivă, fig. 2 a) dacă 0 ? ?< ?/2.

> În ce caz proiecția forței pe axă este egală cu zero?

Proiecția forței pe axă poate fi nulă, fig. 2 b) dacă? = ?/2.)

> În ce caz proiecția forței pe axă este egală cu modulul forței?

Proiecția forței pe axă este egală cu modulul forței, dacă? =0?.

> În ce caz proiecția forței pe axă este negativă?

Proiecția forței pe axă poate fi negativă, fig. 2 c) dacă?/2< ? ? ?.

> Câte ecuații de echilibru sunt întocmite pentru un sistem de forțe convergent plat?

Forțele se numesc convergente dacă liniile lor de acțiune se intersectează într-un punct. Distingeți un sistem plat de forțe convergente, când liniile de acțiune ale tuturor acestor forțe se află în același plan.

Echilibrul unui sistem de forțe convergente.

Din legile mecanicii rezultă că un corp solid, asupra căruia se acționează echilibrat reciproc forțe externe, poate nu numai să fie în repaus, ci să facă și o mișcare, pe care o vom numi mișcare „prin inerție”. O astfel de mișcare va fi, de exemplu, mișcarea uniformă de translație și rectilinie a corpului.

De aici obținem două concluzii importante:

1) Condițiile pentru echilibrul staticii sunt îndeplinite de forțele care acționează atât asupra unui corp în repaus, cât și asupra unui corp care se deplasează „prin inerție”.

2) Echilibrul de forțe aplicat unui corp solid liber este o condiție necesară dar nu suficientă pentru echilibrul (repausul) corpului însuși; in acest caz, corpul va fi in repaus doar daca a fost in repaus si pana in momentul in care i-au fost aplicate forte echilibrate.

Pentru echilibrul unui sistem de forțe convergente aplicate unui corp solid, este necesar și suficient ca rezultanta acestor forțe să fie egală cu zero. Condițiile pe care forțele în sine trebuie să le îndeplinească în acest caz pot fi exprimate în formă geometrică sau analitică.

1. Condiția de echilibru geometric. Deoarece rezultanta forțelor convergente este definită ca latura de închidere a poligonului de forță construit din aceste forțe, ea poate dispărea dacă și numai dacă sfârșitul ultimei forțe din poligon coincide cu începutul primei, adică atunci când poligonul se închide. .

În consecință, pentru echilibrul sistemului, forțe convergente, este necesar și suficient ca poligonul de forță construit din aceste forțe să fie închis.

2. Condiții de echilibru analitic. Analitic, rezultanta unui sistem de forțe convergente este determinată de formula

Deoarece suma termenilor pozitivi este sub rădăcină, R va dispărea numai atunci când ambii

adică atunci când forțele care acționează asupra corpului vor satisface egalitățile:

Egalitățile exprimă condițiile de echilibru într-o formă analitică: pentru echilibrul unui sistem spațial de forțe convergente, este necesar și suficient ca sumele proiecțiilor acestor forțe pe fiecare dintre cele trei axe de coordonate să fie egale cu zero.

Dacă toate forțele convergente care acționează asupra corpului se află în același plan, atunci ele formează un sistem plat de forțe convergente. În cazul unui sistem plat de forțe convergente, obținem evident doar două condiții de echilibru

Egalitățile exprimă și condițiile (sau ecuațiile) necesare pentru echilibrul unui corp rigid liber sub acțiunea forțelor convergente.

> În ce direcție este îndreptată reacția unei tije cu capete articulate?

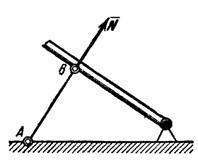
În unele construcții, legătura este tija AB, fixată la capete cu balamale (Fig. 3). Să presupunem că greutatea tijei în comparație cu sarcina pe care o percepe poate fi neglijată. Apoi, asupra tijei vor acționa doar două forțe aplicate la balamalele A și B. Dar dacă tija AB este în echilibru, atunci forțele aplicate în punctele A și B trebuie direcționate de-a lungul unei linii drepte, adică de-a lungul axei tijei. . În consecință, o tijă încărcată la capete, a cărei greutate poate fi neglijată în comparație cu aceste sarcini, funcționează doar în tensiune sau compresie. Dacă o astfel de tijă este o legătură, atunci reacția tijei va fi direcționată de-a lungul axei tijei.

> Cum este momentul de forță în legătură cu un punct?

Momentul forței relativ la un punct este determinat de produsul dintre modulul de forță și lungimea perpendicularei căzute de la punct la linia de acțiune a forței (Fig. 4, a). Când un corp este fixat în punctul O, forța tinde să-l rotească în jurul acestui punct. Punctul O, relativ la care este luat momentul, se numește centrul momentului, iar lungimea perpendicularei a se numește umărul forței față de centrul momentului.

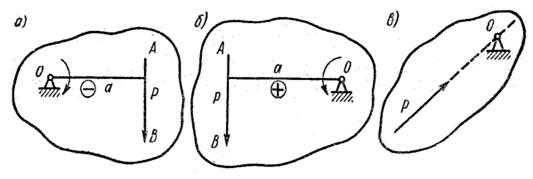
Momentele forțelor se măsoară în newtonometre (N m) sau kilograme metri (kgf m) sau în unitățile multiple și submultiple corespunzătoare, precum și momentele de perechi.