Varësia e diferencës potenciale nga distanca. Dallimi i mundshëm, energjia e ngarkimit në një fushë elektrike. Potenciali
Në paragrafin e mëparshëm, ne diskutuam karakteristikat kryesore fushe elektrike- tensioni i tij. Siç del nga vetë përkufizimi, kjo është një karakteristikë e fuqisë, dhe për rrjedhojë një vektor. Në disa raste, karakteristikat skalare janë më të përshtatshme, për të cilat, rezulton, gjithashtu mund të futen fushë elektrostatike– ndryshimi dhe potenciali potencial. Në këtë rast, ne do të mbështetemi në një veti të rëndësishme themelore të forcave që veprojnë në një ngarkesë në një fushë elektrostatike - konservatorizmi i tyre.
Kujtojmë se forcat quhen konservatore, puna e të cilave nuk varet nga forma e trajektores së trupit. Puna e forcave të tilla përcaktohet vetëm nga koordinatat e pikave fillestare dhe përfundimtare të zhvendosjes. Bazuar në njohuritë tona për vetitë e karakteristikave të saj të fuqisë së fushës elektrostatike të krijuar nga një sistem arbitrar ngarkesash, do të ishte e mundur të kryhej një provë e detajuar e barazisë së punës kur një ngarkesë lëviz midis dy pikave të saj. Por ne do ta shkurtojmë disi këtë procedurë, duke kujtuar teoremën "mbi konservativitetin e forcave qendrore", të cilën e vërtetuam në seksionin mbi mekanikën.
Një ngarkesë pikë e palëvizshme është burimi i "fushës së forcave qendrore" - kjo rrjedh drejtpërdrejt nga formulimi i ligjit bazë të elektrostatikës - ligji i Kulombit. Nga parimi i mbivendosjes së fushave elektrike rrjedh se puna e bërë kur një ngarkesë provë lëviz në fushën e çdo sistemi duke pushuar tarifat është shuma algjebrike e punës në fushën e secilës prej ngarkesave veç e veç. Kjo do të thotë se fusha e forcave të tilla (“forcat Coulomb” *)) është gjithashtu një fushë e forcave konservatore. Kjo është ajo që duhej vërtetuar.
Kështu, puna e forcave të fushës elektrostatike **) në lëvizjen e një ngarkese pikë (provuese) ndërmjet dy pikave e karakterizon këtë fushë. Por kjo varet edhe nga madhësia e ngarkesës së provës q 0 . Këtë e dëshmon përvoja, por edhe kjo është e kuptueshme, bazuar në njohuritë tona për forcat “Kulomb”. Sepse janë proporcionale me ngarkesën q 0 në çdo pikë të trajektores 1®2 (bazuar në ligjin e Kulombit), dhe puna është proporcionale me forcën. Për të karakterizuar fushën dhe vetëm fushën, mund ta ndani punën me vlerën e tarifës së provës. Ajo që ndodh është "ndryshimi i mundshëm". Këtu është një përkufizim i këtij koncepti të rëndësishëm:
(ODA .) Diferencë potenciale ndërmjet pikave të fushës elektrostatike 1 dhe 2 quhet qëndrim puna fushat duke lëvizur ngarkesën e provës nga pika 1pikërisht 2në vlerën e kësaj tarife :
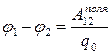 . (3.1)
. (3.1)
Në sistemin SI, njësia e diferencës së potencialit quhet 1 volt (1 V = 1 J/C). Nëse mësojmë se si të përcaktojmë disi ndryshimin e mundshëm j 1 –j 2 për fushën e një sistemi ngarkesash në qetësi (teorikisht ose eksperimentalisht), kjo do të na lejojë të gjejmë punën e fushës duke lëvizur ndonjë përcaktoj ngarkuar q në këtë fushë:
![]() . (3.2)
. (3.2)
Pra, ndryshimi potencial është karakteristikë e energjisë fushë elektrike, pasi lidhet drejtpërdrejt me konceptin e punës.
Në mekanikë, ne prezantuam konceptin e "energjisë potenciale" për forcat konservatore (tani themi: "fushat e forcave konservatore"). Në të njëjtën kohë, ne u udhëhoqëm nga parimi i mëposhtëm: “puna e forcave të terrenit është e barabartë me humbjen energji potenciale". Ne e zyrtarizojmë këtë parim në një shënim analitik:
Këtu U 1 dhe U 2 janë energjia potenciale në gjendjet "fillestare" ("1") dhe "përfundimtare" ("2") të sistemit, përkatësisht. Në rastin në diskutim, fushat e sistemit të tarifave fikse janë energjia tarifë pikë q në pozicionin "1" (me koordinata ( x 1 ,y 1 ,z 1 )) dhe pozicioni "2" (me koordinata ( x 2 ,y 2 ,z 2 )) fushë elektrostatike. Ato. energjia potenciale e ngarkesës në këtë fushë është një funksion skalar i koordinatave të pikave të fushës U = U( x,y,z) (ose ). Duke krahasuar (3.2) dhe (3.3), shohim se është e përshtatshme të supozohet se ndryshimi i mundshëm është ndryshimi në vlerat e një funksioni tjetër skalar të koordinatave të pikave të fushës. j(x, y, z). Ajo lidhet me funksionin U( x,y,z) (energjia potenciale) nga një lidhje e thjeshtë: U( x,y,z) = q× j(x, y, z). Ose sepse
thuhet se është "numerikisht e barabartë me energjinë potenciale të një ngarkese pozitive njësi" në një pikë të caktuar të fushës. Dhe kjo vlerë quhet j"potenciali" i një pike të caktuar të fushës elektrostatike.
Gjëja më e rëndësishme është se si të gjendet ky funksion për fushën e një sistemi të caktuar tarifash? Cila është procedura?
Para së gjithash, duhet të biem dakord për kushtet e normalizimit *): duhet të zgjedhim një pikë R 0, në të cilën potenciali i ngarkimit të testimit do të supozohet të jetë i barabartë me zero. Më shpesh, një pikë e tillë zgjidhet "pafundësisht" në distancë, ku fusha mungon **). Për ta bërë këtë, ju duhet të gjeni punën "specifike" të fushës - d.m.th. punë në lidhje me sasinë e ngarkesës testuese të transferuar (ose, siç thuhet shpesh, "duke lëvizur një ngarkesë njësi pozitive") nga një pikë e caktuar në terren R(x,y,z) deri në pikën e normalizimit R 0 . Në formë analitike, kjo përkufizim potenciali mund të shkruhet si më poshtë:
(Def. ) j P(x,y,z) = . (3.5)
A është e mundur të shprehim vlerat e prezantuara rishtazi nga ne - ndryshimi i mundshëm dhe potenciali përmes karakteristikës së fuqisë, të cilën tashmë kemi mësuar se si ta llogarisim me vendndodhjen e dhënë ngarkesa në hapësirë? Po, sigurisht që mundeni. Le të shkruajmë një zinxhir barazish që janë kuptuar mirë për ne:
 .
.
Le të shkruajmë përsëri ekuacionin e fundit
 . (3.6)
. (3.6)
Ai jep një "recetë" për kërkimin e një ndryshimi potencial duke përdorur një funksion të njohur tensioni. Në mënyrë të ngjashme për potencialin:
Dhe së fundi për potencialin e një pike arbitrare të fushës R me koordinata ( x,y,z):
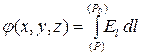 . (3.7)
. (3.7)
· Potenciali i fushës së një ngarkese pikë
Bazuar në procedurën e llogaritjes së potencialit, marrim një shprehje për rastin e fushës së ngarkesës me pikë. Kjo është shumë e rëndësishme për llogaritjet e mëtejshme të potencialit në terren të një sistemi ngarkesash të vendosura në mënyrë arbitrare në hapësirë.
2. Zgjedhja e trajektores. Le një pikë arbitrare R(x,y,z) është në distancë r nga tarifa burimore. Meqenëse rezultati nuk varet nga forma e trajektores, për llogaritjen e integralit lakor të formës (3.7) zgjedhim vijën e drejtë më të thjeshtë të drejtuar radialisht nga një pikë e caktuar e fushës përgjatë vijës së fushës dhe "duke shkuar në pafundësi".
3. Llogaritja. Në përputhje me përcaktimin e potencialit, ne llogarisim punën "specifike" të fushës të krijuar nga një ngarkesë pikë q mbi transferimin e ngarkesës së provës përgjatë trajektores së zgjedhur. Zinxhiri i mëposhtëm i barazive, shpresojmë se duket mjaft “transparent”. Megjithatë, ne do të japim një koment minimal për të. Para së gjithash, vërejmë se, për shkak të zgjedhjes sonë të një trajektoreje në formën e një rrezeje të drejtuar në mënyrë radiale nga ngarkesa, mund të shënojmë E l dhe dl(kurbë arbitrare " L") ndryshoni në Er dhe dr(boshti polar" r"). Për më tepër, meqenëse vektori drejtohet në mënyrë radiale, për çdo zhvendosje të vogël përgjatë trajektores, projeksioni i vektorit të stresit është thjesht i barabartë me modulin e këtij vektori E(r). Si rezultat, ne gjithashtu mund të bëjmë një hap të rëndësishëm në llogaritjen tonë - të bëjmë kalimin nga integrali lakor në atë të zakonshëm të caktuar:
 .*)
.*)
Tani, pasi zëvendësojmë shprehjen për modulin e forcës së fushës së një ngarkese pika (3.5), na mbetet vetëm një "rutinë" matematikore:
Le ta shkruajmë përsëri rezultatin, duke e plotësuar atë me praninë e mundshme të një mediumi dielektrik homogjen të gaztë ose të lëngshëm me lejueshmëri e, e cila mbush të gjithë hapësirën që rrethon ngarkesën pikë:
 . (3.8)
. (3.8)
Potenciali i fushës së një ngarkese pika, siç e shohim, zvogëlohet me distancën sipas ligjit 1/ r.
· Sipërfaqet ekuipotenciale
Kur diskutohet karakteristikat e fuqisë fushë elektrostatike, ne ishim të bindur për frytshmërinë e konceptit linjat e forcës(linjat e tensionit). Për karakteristikën energjetike të fushës - potencial - është gjithashtu e dobishme të futet një karakteristikë ilustruese shtesë - një sistem "sipërfaqesh ekuipotenciale". Nga vetë emri është e qartë ("equi" do të thotë "e barabartë") se këto janë sipërfaqe me potencial konstant, të cilat karakterizojnë aftësinë e forcave të fushës për të bërë punë kur lëvizin një ngarkesë. Përgjatë sipërfaqeve të tilla, natyrisht, nuk punohet fare. Është maksimale në drejtimet përgjatë të cilave dendësia (densiteti) i sipërfaqeve ekuipotenciale është maksimale. Në këto vende, forca e fushës është gjithashtu maksimale. Është e lehtë të kuptosh se cili është orientimi i ndërsjellë i linjave të forcës dhe sipërfaqeve ekuipotenciale në kryqëzimet e tyre: ato janë pingul reciprokisht. Në fund të fundit, për çdo zhvendosje të vogël përgjatë sipërfaqes ekuipotenciale punë elementareështë e barabartë me zero, dhe kjo është e mundur vetëm nëse komponenti tangjent i vektorit të stresit është i barabartë me zero, d.m.th. drejtohet rreptësisht përgjatë normales në sipërfaqe. Më poshtë japim një zinxhir që korrespondojnë me këto fjalë, shpresojmë, barazi mjaft të dukshme:

Së bashku me Fig. 3. ... ata vërtetojnë, në fakt, deklaratën tashmë të formuluar: linjat e forcës kryqëzohen (ose "duke ardhur në...") sipërfaqet ekuipotenciale në kënde të drejta !
Le të japim një pamje të sipërfaqeve ekuipotenciale (dhe linjave të forcës gjithashtu) për disa nga rastet më të thjeshta të një fushe elektrostatike që tashmë janë të njohura për ne: a) fusha e një tarife pikë; b) fusha e dy ngarkesave me pikë të kundërta identike në vlerë absolute; në) fusha ndërmjet dy rrafsheve të ngarkuara në mënyrë të kundërt - paralele të mëdha (në krahasim me distancën ndërmjet tyre) - shih fig. 3.1.
Le të kthehemi tani te një ngarkesë sferike (pikore). Më sipër tregohet se forca e fushës elektrike e krijuar nga një ngarkesë e shpërndarë në mënyrë uniforme mbi sferën P, nuk varet nga rrezja e sferës. Imagjinoni që në një distancë
r nga qendra e sferës është një ngarkesë provë q. Forca e fushës në pikën ku ndodhet ngarkesa, 
Figura tregon një grafik të varësisë së fuqisë së bashkëveprimit elektrostatik midis ngarkesave pika nga distanca midis tyre. Për të gjetur punën e fushës elektrike gjatë lëvizjes së ngarkesës provë q nga një largësi r deri në një distancë R, ndajeni këtë interval me pikë r 1 , r 2 ,..., rP në seksione të barabarta. Forca mesatare që vepron mbi një ngarkesë q brenda segmentit [ rr 1 ] është e barabartë me ![]()
Puna e kësaj force në këtë fushë:
![]()
Shprehje të ngjashme për punë do të merren për të gjitha seksionet e tjera. Pra, puna e plotë është:
Termat identikë me shenja të kundërta shkatërrohen dhe më në fund marrim:
është puna e fushës në akuzë ![]()
- diferencë potenciale ![]()
Tani, për të gjetur potencialin e pikës së fushës në lidhje me pafundësinë, ne drejtojmë R deri në pafundësi dhe më në fund marrim:
Pra, potenciali i fushës së një ngarkese pika është në përpjesëtim të zhdrejtë me distancën nga ngarkesa.
24. Energjia potenciale e një ngarkese në fushën e një sistemi ngarkesash. Parimi i mbivendosjes për potencialet. Parimi i mbivendosjes për potencialet
Çdo fushë elektrostatike arbitrarisht komplekse mund të përfaqësohet si një mbivendosje e fushave të ngarkesave pika. Çdo fushë e tillë në pikën e zgjedhur ka një potencial të caktuar. Meqenëse potenciali është një sasi skalare, potenciali rezultues i fushës së të gjitha ngarkesave pika është shuma algjebrike e potencialeve 1, 2, 3, ... të fushave të ngarkesave individuale: = 1 + 2 + 3 + .. Kjo lidhje është pasojë e drejtpërdrejtë e parimit të mbivendosjes së fushave elektrike.
Energjia potenciale e një ngarkese në një fushë elektrike. Vazhdojmë krahasimin e bashkëveprimit gravitacional të trupave dhe bashkëveprimit elektrostatik të ngarkesave. masë trupore m në fushën gravitacionale të Tokës ka energji potenciale. Puna e gravitetit është e barabartë me ndryshimin e energjisë potenciale, marrë me shenjën e kundërt:
A=-(W p2 - W p1) = mgh.
(Këtu dhe më poshtë do të shënojmë energjinë me shkronjë W.) Ashtu si një trup në masë m në fushën e gravitetit ka një energji potenciale proporcionale me masën e trupit, një ngarkesë elektrike në një fushë elektrostatike ka një energji potenciale W p , proporcionale me ngarkesën q. Puna e forcave të fushës elektrostatike PORështë e barabartë me ndryshimin e energjisë potenciale të ngarkesës në fushën elektrike, marrë me shenjën e kundërt:
A=-(W p2 - W p1) . (40.1)
25. Diferenca e mundshme. Sipërfaqet ekuipotenciale
Sipërfaqe ekuipotenciale- një sipërfaqe, secila pikë e së cilës ka të njëjtin potencial.
Si vijon nga lidhja midis punës dhe potencialeve:
kur ngarkesa transferohet përgjatë sipërfaqeve ekuipotenciale, fusha elektrike nuk funksionon, pasi .
Puna me një forcë jozero është zero vetëm nëse vektori i forcës është pingul me vektorin e zhvendosjes. Nga kjo rezulton se linjat e tensionit janë pingul me sipërfaqet ekuipotenciale. Shembuj të sipërfaqeve ekuipotenciale janë sferat për fushën e ngarkesës pikësore dhe rrafshet paralele për fushat homogjene (Fig. 3).

Diferenca e mundshme (tensioni) ndërmjet dy pikave është i barabartë me raportin e punës në terren kur lëvizni ngarkesën nga pika e fillimit në pikën përfundimtare në modulin e kësaj ngarkese: U\u003d φ 1 - φ 2 \u003d -Δφ \u003d A / q, A \u003d - (W p2 - W p1) \u003d -q (φ 2 - φ 1) \u003d -qΔφ
Diferenca e potencialit matet në volt (V = J / C) Marrëdhënia midis fuqisë së fushës elektrostatike dhe diferencës së potencialit: E x = Δφ / Δ x Fuqia e fushës elektrostatike drejtohet në drejtim të zvogëlimit të potencialit. Matur në volt të ndarë me metra (V/m)
§ 15. POTENCIALI. ENERGJIA E SISTEMIT TË NDRYSHIMEVE ELEKTRIKE. PUNA PËR LËVIZJEN E TARKESËS NË FUSHË
Formulat bazë
Potenciali i një fushe elektrike është një vlerë e barabartë me raportin e energjisë potenciale të një pikë ngarkese pozitive të vendosur në pikë e dhënë fusha, për këtë tarifë;
=P/ P,
ose potenciali i fushës elektrike është një sasi e barabartë me raportin e punës së forcave të fushës për të lëvizur një pikë ngarkesë pozitive nga një pikë e caktuar e fushës në pafundësi në këtë ngarkesë:
=A/ P.
Potenciali i fushës elektrike në pafundësi merret kushtimisht i barabartë me zero.
Vini re se kur një ngarkesë lëviz në një fushë elektrike, puna A v.s forcat e jashtme janë të barabarta në vlerë absolute me veprën A s.p. forca e fushës dhe është e kundërt me të në shenjë:
A v.s = – A s.p. .
Potenciali i fushës elektrike i krijuar nga një ngarkesë pikë P në distancë r nga akuza
Potenciali i fushës elektrike të krijuar nga metali, duke mbajtur një pagesë P sferë me rreze R, në një distancë nga qendra e sferës:
brenda sferës ( r<R)
 ;
;
në sipërfaqen e një sfere ( r=R)
 ;
;
jashtë fushës (r>
R)
 .
.
Në të gjitha formulat e dhëna për potencialin e një sfere të ngarkuar, është lejueshmëria e një dielektrike homogjene të pafundme që rrethon sferën.
Potenciali i fushës elektrike të krijuar nga sistemi P ngarkesat pikësore, në një pikë të caktuar, në përputhje me parimin e mbivendosjes së fushave elektrike, është e barabartë me shumën algjebrike të potencialeve 1 , 2 , ... , n, krijuar nga tarifat individuale të pikëve P 1 ,P 2 , ...,P n :
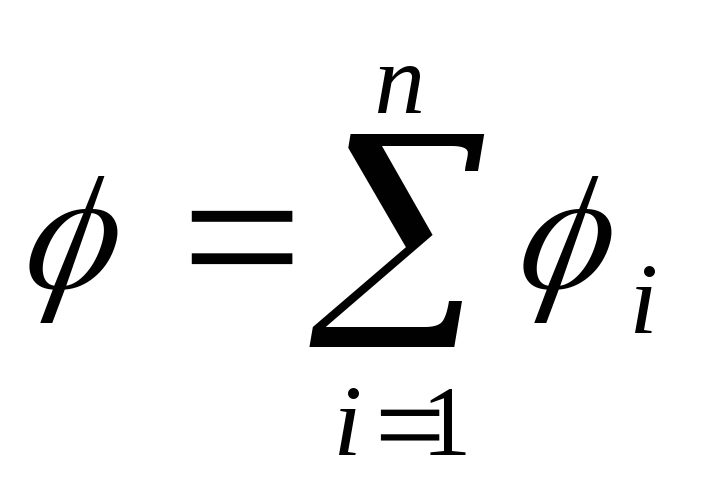
Energjia W ndërveprimet e një sistemi ngarkesash pikash P 1 ,P 2 , ...,P n përcaktohet nga puna që mund të bëjë ky sistem ngarkesash kur ato hiqen në raport me njëri-tjetrin deri në pafundësi dhe shprehet me formulën
 ,
,
ku i- potenciali i fushës i krijuar nga të gjithë P- 1 tarifë (me përjashtim të 1-tës) në pikën ku ndodhet tarifa P i .
Potenciali lidhet me fuqinë e fushës elektrike nga relacioni
E= -grad.
Në rastin e një fushe elektrike me simetri sferike, kjo marrëdhënie shprehet me formulën
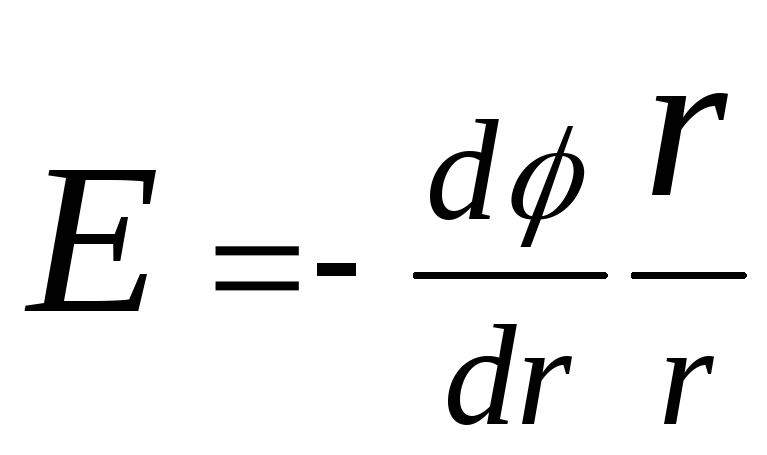 ,
,
ose në formë skalare
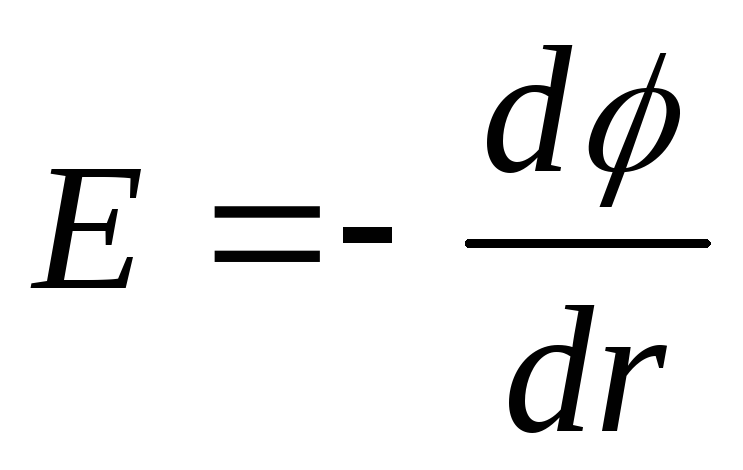 ,
,
dhe në rast fushë uniforme, d.m.th., një fushë, intensiteti i së cilës në çdo pikë është i njëjtë si në vlerë absolute ashtu edhe në drejtim,
E=( 1 – 2 ,)/d,
ku 1 dhe 2 - potencialet e pikave të dy sipërfaqeve ekuipotenciale; d - distanca ndërmjet këtyre sipërfaqeve përgjatë vijës së fushës elektrike.
Puna e kryer nga një fushë elektrike kur lëviz një ngarkesë pikësore P nga një pikë e fushës me një potencial 1 , në një tjetër me një potencial 2 ,
A=P( 1
- 2
), ose  ,
,
ku E l - projeksioni i vektorit të tensionit E në drejtimin e lëvizjes; dl - lëvizjes.
Në rastin e një fushe homogjene, formula e fundit merr formën
A= QElcos ,
ku l- zhvendosja; - këndi ndërmjet drejtimeve të vektorit E dhe zhvendosja l.
Shembuj të zgjidhjes së problemeve
Shembulli 1 ngarkesa pozitive P 1 \u003d 3 μC dhe P 2 \u003d 20 nC janë në vakum në distancë r 1 =l.5 m larg njëra-tjetrës. Përcaktoni një punë A, që duhet bërë për të afruar akuzat në distancë r 2 =1 m.
Zgjidhje. Le të supozojmë se ngarkesa e parë P 1 mbetet i palëvizshëm dhe tjetri P 2 nën veprimin e forcave të jashtme lëviz në fushën e krijuar nga ngarkesa P 1 duke iu afruar nga larg r 1 =t,5 m deri në r 2 =1 m .
Puna POR" forcë e jashtme për të lëvizur ngarkesën P nga një pikë e fushës me potencial 1 në një tjetër, potenciali i të cilit 2 , i barabartë në vlerë absolute dhe i kundërt në shenjë me punën POR forcat fushore për lëvizjen e ngarkesës ndërmjet të njëjtave pika:
A "= -A.
Puna POR forcat në terren në zhvendosjen e ngarkesës A=P( 1 - 2 ). Pastaj punoni POR" forcat e jashtme mund të shkruhen si
A" = –P( 1 - 2 )=P( 2 - 1 ). (1)
Potencialet e pikave të fillimit dhe të fundit të shtegut shprehen me formula
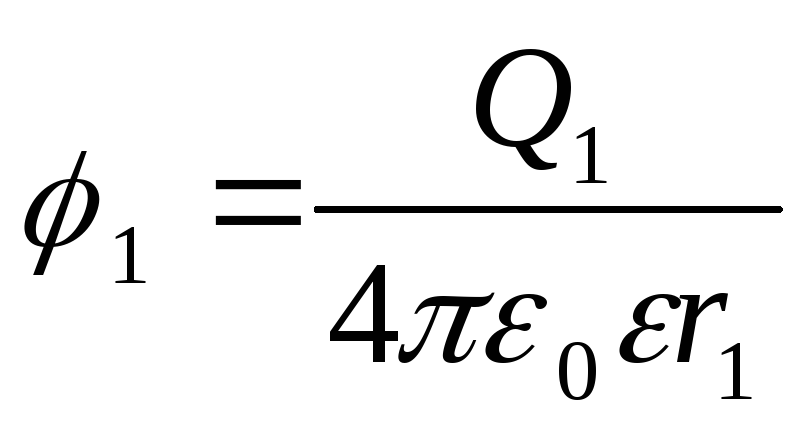 ;
;
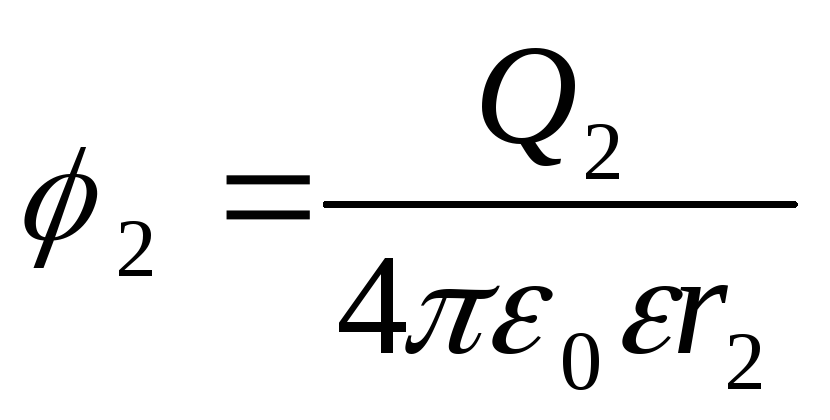 .
.
Zëvendësimi i shprehjeve 1 dhe 2 në formulën (1) dhe duke marrë parasysh se për këtë rast ngarkesa e transferuar P=P 2 , marrim
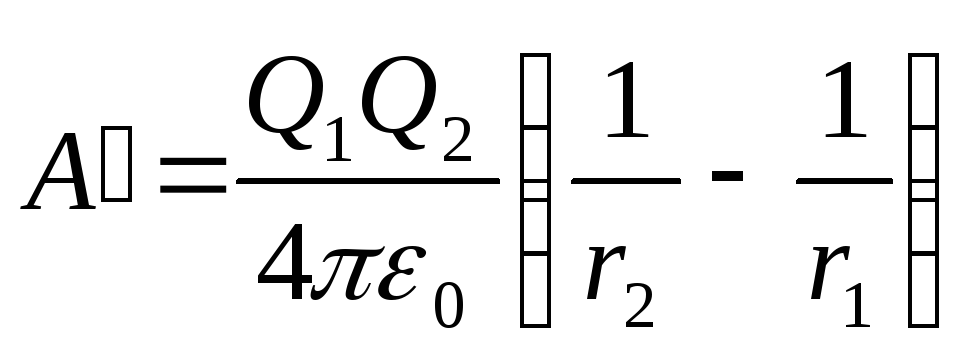 . (2)
. (2)
Duke marrë parasysh se 1/(4 0 )=910 9 m/F, më pas pasi zëvendësojmë vlerat e sasive në formulën (2) dhe kemi llogaritur, gjejmë
A"=180 µJ.
Shembulli 2 Gjej një punë POR fushat e transferimit të tarifave P=10 nC nga pika 1 pikërisht 2 (Fig. 15.1), i vendosur midis dy atyre të ngarkuar në mënyrë të kundërt me një densitet sipërfaqësor \u003d 0,4 μC / m 2 plane paralele të pafundme, largësi l ndërmjet tyre është 3 cm.
R 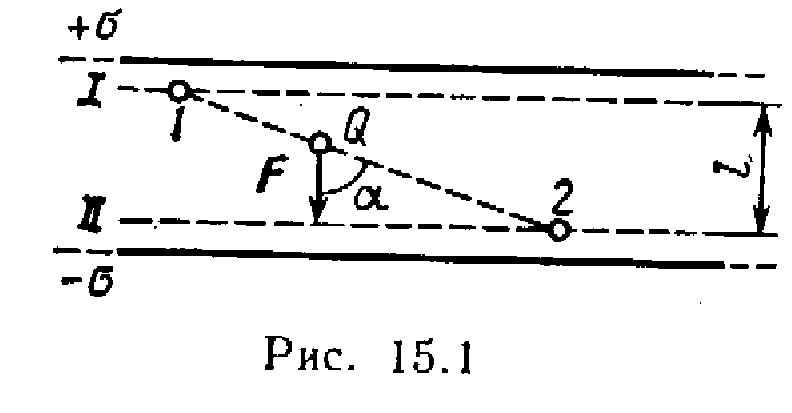 zgjidhje. Ka dy mënyra për të zgjidhur problemin.
zgjidhje. Ka dy mënyra për të zgjidhur problemin.
Mënyra e parë. Puna e fushës detyron të lëvizë ngarkesën Q nga pika 1 fusha me potencial 1 pikërisht 2 fusha me potencial 2 gjeni sipas formulës
A=P( 1 - 2 ). (1)
Për të përcaktuar potencialet në pika 1 dhe 2 Le të vizatojmë sipërfaqet ekuipotenciale I dhe II përmes këtyre pikave. Këto sipërfaqe do të jenë rrafshe, pasi fusha midis dy rrafsheve paralele të pafundme të ngarkuara në mënyrë uniforme është uniforme. Për një fushë të tillë, relacioni
1 - 2 =El, (2)
ku E - forca e fushës; l - distanca ndërmjet sipërfaqeve ekuipotenciale.
Forca e fushës ndërmjet planeve paralele të pafundme me ngarkesë të kundërt E=/ 0 . Duke zëvendësuar këtë shprehje E në formulën (2) dhe më pas shprehjen 1 - 2 në formulën (1), marrim
A= P( / 0 ) l.
Mënyra e 2-të. Meqenëse fusha është uniforme, forca që vepron në ngarkesë P, është konstante ndërsa lëviz. Prandaj, puna e lëvizjes së ngarkesës nga pika 1 pikërisht 2 mund të llogaritet duke përdorur formulën
A=F r cos, (3)
ku F - forcë që vepron mbi një ngarkesë r- Moduli i transferimit të ngarkesës P nga një pikë 1 pikërisht 2; është këndi ndërmjet drejtimeve të zhvendosjes dhe forcës . Por F= QE= P( / 0 ). Duke zëvendësuar këtë shprehje F në barazi (3), si dhe duke vërejtur se r cos= l, marrim
A=P(/ 0 )l. (4)
Kështu, të dyja zgjidhjet çojnë në të njëjtin rezultat.
Zëvendësimi në shprehjen (4) i vlerës së sasive P, , 0 dhe l, Gjej
A\u003d 13,6 μJ.
Shembulli 3 Në një fije të hollë të përkulur përgjatë një harku të një rrethi me një rreze R,
ngarkesë e shpërndarë në mënyrë uniforme me dendësi lineare=10 nC/m. Përcaktoni tensionin E dhe potenciali i fushës elektrike të krijuar nga një p  ngarkesa e shpërndarë në një pikë O, që përkon me qendrën e lakimit të harkut. Gjatësia l filli është 1/3 e perimetrit dhe është i barabartë me 15 cm.
ngarkesa e shpërndarë në një pikë O, që përkon me qendrën e lakimit të harkut. Gjatësia l filli është 1/3 e perimetrit dhe është i barabartë me 15 cm.
Zgjidhje. Ne zgjedhim boshtet e koordinatave në mënyrë që origjina e koordinatave të përkojë me qendrën e lakimit të harkut dhe boshtin në ishte vendosur në mënyrë simetrike në lidhje me skajet e harkut (Fig. 15.2). Zgjidhni një element me gjatësi d në fije l. I ngarkuar P=d l, i vendosur në zonën e zgjedhur, mund të konsiderohet si një pikë.
Le të përcaktojmë forcën e fushës elektrike në pikë O. Për ta bërë këtë, së pari gjejmë tensionin d E fusha e krijuar nga ngarkesa d P:
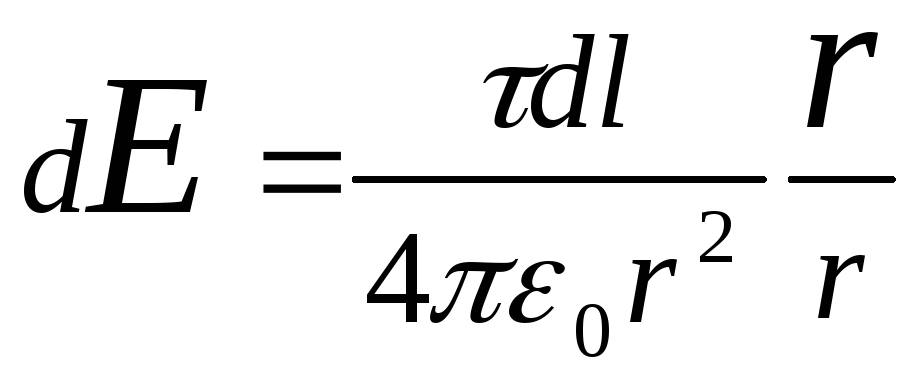 ,
,
ku r-rrezja-vektor i drejtuar larg elementit d l deri në pikën në të cilën llogaritet tensioni. Shprehim vektorin d E përmes projeksionit dE x c dhe dE y në boshtin koordinativ:
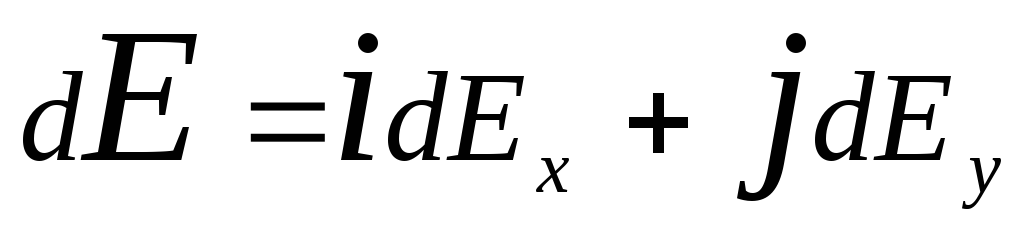 ,
,
ku i dhe j- vektorët e drejtimit njësi (ortat).
tensioni E gjeni me integrim:
 .
.
Integrimi kryhet përgjatë harkut të gjatësisë l. Për shkak të simetrisë, integrali  barazohet me zero. Pastaj
barazohet me zero. Pastaj
 , (1)
, (1)
ku 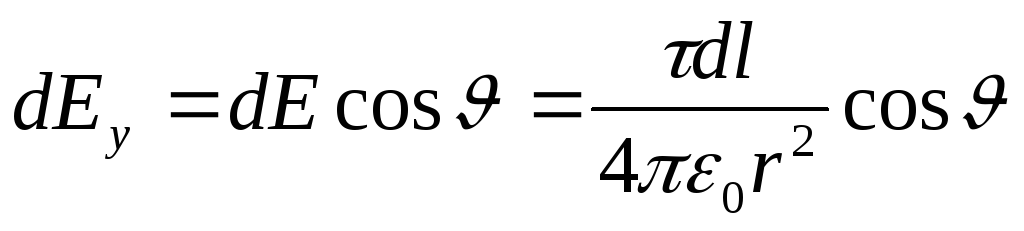 . Sepse r=R= konst dhe d l=R d. pastaj
. Sepse r=R= konst dhe d l=R d. pastaj
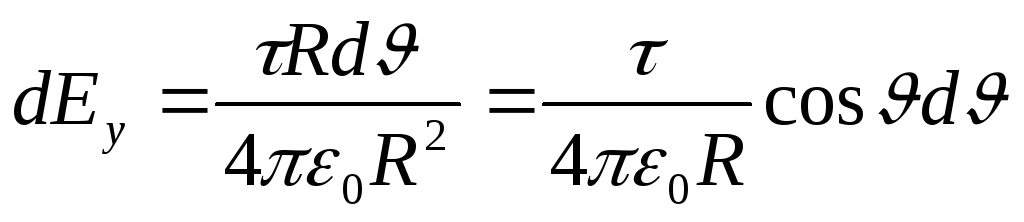
Zëvendësoni shprehjen e gjetur dE y në (1) dhe, duke marrë parasysh vendndodhjen simetrike të harkut në lidhje me boshtin OU, marrim kufijtë e integrimit nga 0 në /3 dhe dyfishojmë rezultatin;
 .
.
Zëvendësimi i këtyre kufijve dhe shprehja R përmes gjatësisë së harkut (3 l= 2 r), marrim
 .
.
Kjo formulë tregon se vektori E përkon me drejtimin pozitiv të boshtit OU Zëvendësimi i vlerës dhe l në formulën e fundit dhe duke bërë llogaritjet, gjejmë
E\u003d 2,18 kV / m.
Le të përcaktojmë potencialin e fushës elektrike në pikë O. Le të gjejmë fillimisht potencialin d të krijuar nga ngarkesa pikësore d P në pikën O:

Le të zëvendësojmë r në R dhe kryeni integrimin:
 .Sepse l=2
R/3,
pastaj
.Sepse l=2
R/3,
pastaj
=/(6 0 ).
Pasi kemi bërë llogaritjet sipas kësaj formule, marrim
Shembull4 . Fusha elektrike krijohet nga një cilindër i gjatë me rreze R= 1cm , ngarkuar në mënyrë të njëtrajtshme me dendësi lineare=20 nC/m. Përcaktoni ndryshimin potencial të dy pikave të kësaj fushe të vendosura në largësi a 1 =0,5 cm dhe a 2 \u003d 2 cm nga sipërfaqja e cilindrit, në pjesën e mesme të tij.
Zgjidhje. Për të përcaktuar diferencën potenciale, ne përdorim marrëdhënien midis fuqisë së fushës dhe ndryshimit të potencialit E= -grad. Për një fushë me simetri boshtore, e cila është fusha e një cilindri, kjo lidhje mund të shkruhet si
E= -( d/d r) , ose d= - E d r.
Duke integruar shprehjen e fundit, gjejmë ndryshimin potencial të dy pikave të ndara me r 1 dhe r 2 nga boshti i cilindrit;
![]() . (1)
. (1)
Meqenëse cilindri është i gjatë dhe pikat janë marrë afër pjesës së mesme të tij, forca e fushës mund të shprehet duke përdorur formulën  . Duke zëvendësuar këtë shprehje E në barazi (1), marrim
. Duke zëvendësuar këtë shprehje E në barazi (1), marrim
 (2)
(2)
Që nga sasitë r 2 dhe r 1 futni formulën si raport, atëherë ato mund të shprehen në çdo, por vetëm të njëjtat njësi:
r 1 =R+a 1 = 1,5 cm; r 2 =R+a 2 = 3 cm .
Zëvendësimi i vlerave të madhësisë , 0 ,r 1 dhe r 2 në formulën (2) dhe duke llogaritur, gjejmë
1 - 2 = 250 V.
Shembulli 5 Fusha elektrike krijohet nga një shufër e hollë që mban ngarkesë =0,1 μC/m të shpërndarë në mënyrë uniforme përgjatë gjatësisë së saj. Përcaktoni potencialin të fushës në një pikë të largët nga skajet e shufrës në një distancë, e barabartë me gjatësinë kallam.
Zgjidhje. Ngarkesa në shufër nuk mund të konsiderohet si një ngarkesë pikë, prandaj zbatoni drejtpërdrejt formulën për të llogaritur potencialin
 , (1)
, (1)
e vlefshme vetëm për tarifat me pikë, është e pamundur. Por nëse e ndajmë shufrën në segmente elementare d l, pastaj ngarkesad l që ndodhet në secilën prej tyre mund të konsiderohet si një pikë dhe atëherë formula (1) do të jetë e vlefshme. Duke aplikuar këtë formulë, marrim
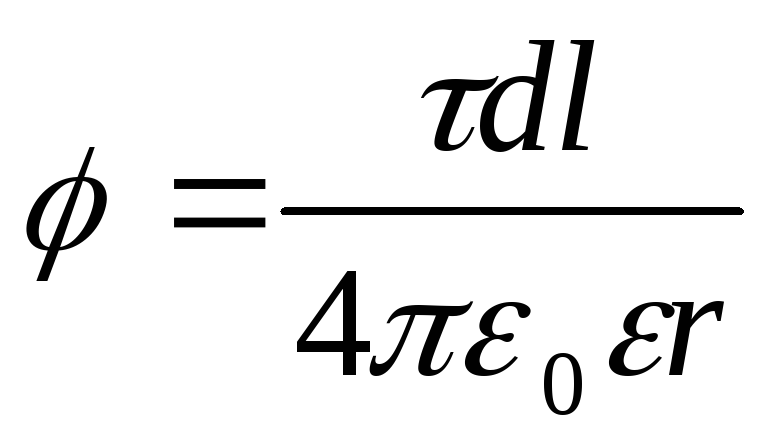 , (2)
, (2)
ku r - distanca e pikës në të cilën përcaktohet potenciali me elementin e shufrës.
Nga fig. 15.3 që d l=(r d/cos). Zëvendësimi i kësaj shprehjeje d l në formulën (2), gjejmë  .
.
Integrimi i shprehjes që rezulton brenda kufijve të 1
po 2
, marrim potencialin e krijuar nga e gjithë ngarkesa e shpërndarë në shufër: 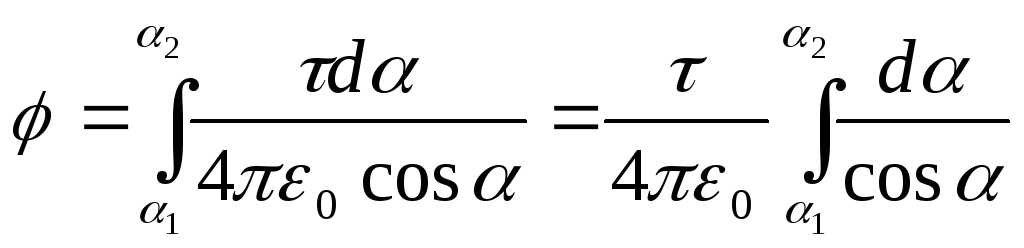 .
.
AT 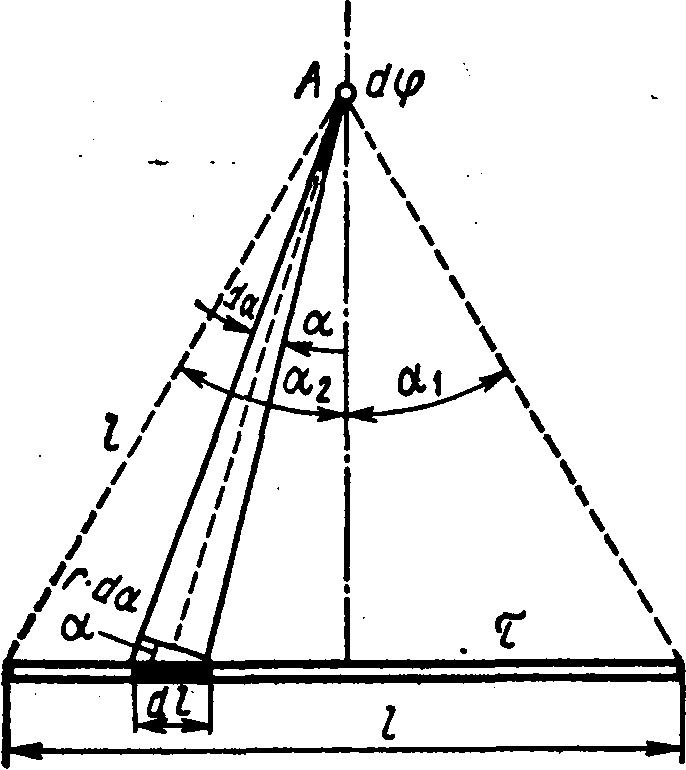 forca e simetrisë së pikës POR në raport me skajet e shufrës kemi 2
= 1
dhe për këtë arsye
forca e simetrisë së pikës POR në raport me skajet e shufrës kemi 2
= 1
dhe për këtë arsye  .
.
Rrjedhimisht,
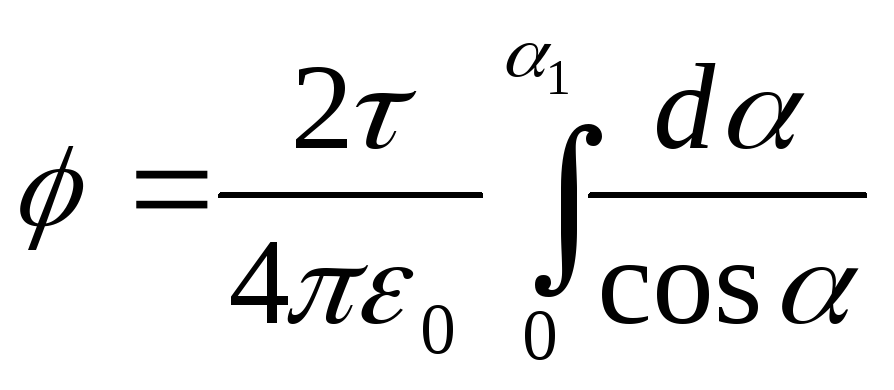 .Sepse
.Sepse 
(shih tabelën 2), më pas  .
.
Duke zëvendësuar kufijtë e integrimit, ne marrim
Pasi kemi bërë llogaritjet sipas kësaj formule, gjejmë
Shembulli 6 Një elektron me shpejtësi v=1,8310 6 m/s fluturoi në një fushë elektrike uniforme në drejtim të kundërt me vektorin e forcës së fushës. Çfarë ndryshimi potencial U një elektron duhet të kalojë që të ketë energji E i\u003d 13,6 eV *? (Duke pasur një energji të tillë, një elektron mund ta jonizojë atë kur përplaset me një atom hidrogjeni. Energjia prej 13.6 eV quhet energji jonizuese e hidrogjenit.)
Zgjidhje. Elektroni duhet të kalojë një ndryshim të tillë potencial ju, në mënyrë që energjia e fituar W e kombinuar me energjinë kinetike T, që elektroni kishte përpara se të hynte në fushë, arriti në një energji të barabartë me energjinë e jonizimit E i ,
dmth. W+
T=
E i .
Duke u shprehur në këtë formulë W=
BE dhe T=(m v 2
/2), marrim BE+(m v 2
/2)=E i. Nga këtu 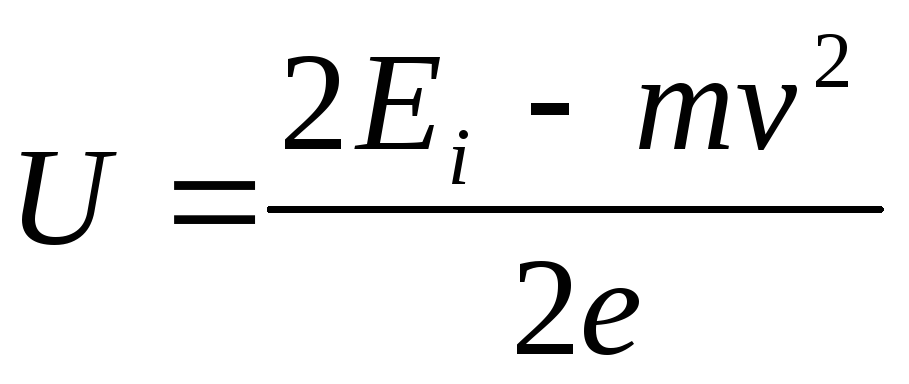 .
.
___________________
* Elektron-volt (eV) - energjia e fituar nga një grimcë që ka një ngarkesë të barabartë me ngarkesën e një elektroni që ka kaluar përmes një ndryshimi potencial prej 1 V. Kjo njësi energjie josistematike është miratuar aktualisht për përdorim në fizikë.
Le të bëjmë llogaritjet në njësitë SI:
U=4.15 AT.
Shembulli 7 Përcaktoni shpejtësinë fillestare υ 0 afrimi i protoneve të vendosura në një mjaftueshëm distancë e madhe nga njëri-tjetri nëse distanca minimale r min , me të cilën mund të afrohen, është 10 -11 cm.
Zgjidhja: Midis dy protoneve ka forca refuzuese, si rezultat i të cilave lëvizja e protoneve do të jetë e ngadaltë. Prandaj, problemi mund të zgjidhet si sistemi inercial koordinatat (të lidhura me qendrën e masës së dy protoneve), dhe në joinerciale (të lidhura me një nga protonet që lëvizin shpejt). Në rastin e dytë, ligjet e Njutonit nuk vlejnë. Zbatimi i parimit d'Alembert është i vështirë për faktin se nxitimi i sistemit do të jetë i ndryshueshëm. Prandaj, është e përshtatshme të shqyrtohet problemi në një kornizë inerciale referimi.
Le të vendosim origjinën e koordinatave në qendër të masës së dy protoneve. Meqenëse kemi të bëjmë me grimca identike, qendra e masës do të jetë në pikën që përgjysmon segmentin që lidh grimcat. Në lidhje me qendrën e masës, grimcat do të kenë në çdo kohë të njëjtat modul shpejtësie. Kur grimcat janë në një distancë mjaft të madhe nga njëra-tjetra, shpejtësia υ 1 çdo grimcë është e barabartë me gjysmën υ 0 , dmth. υ 1 =υ 0 /2.
Për të zgjidhur problemin zbatojmë ligjin e ruajtjes së energjisë, sipas të cilit energjia totale mekanike E sistemi i izoluar është konstant, d.m.th.
E=T+ P ,
ku T- shuma e energjive kinetike të të dy protoneve në raport me qendrën e masës; P është energjia potenciale e sistemit të ngarkesave.
Ne e shprehim energjinë potenciale në momentet fillestare P 1 dhe P 2 të fundit të lëvizjes.
Në momentin fillestar, sipas gjendjes së problemit, protonet ishin në një distancë të madhe, kështu që energjia potenciale mund të neglizhohet (P 1 =0). Prandaj, për momentin fillestar energji totale do të jetë e barabartë me energjinë kinetike T 1 protonet, d.m.th.
E=T l . (1)
Në momentin përfundimtar, kur protonet afrohen sa më afër, shpejtësia dhe energjia kinetike janë të barabarta me zero, dhe energjia totale do të jetë e barabartë me energjinë potenciale P 2, d.m.th.
E= P 2 . (2)
Duke barazuar pjesët e duhura të barazive (1) dhe (2), marrim
T 1 \u003d P 2. (3)
Energjia kinetike është e barabartë me shumën e energjive kinetike të protoneve:
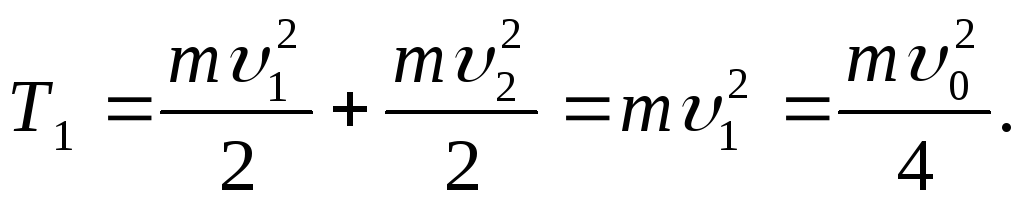 (4)
(4)
Energjia potenciale e një sistemi me dy ngarkesa P 1 dhe P 2 në vakum përcaktohet nga formula  , ku r- distanca midis tarifave. Duke përdorur këtë formulë, marrim
, ku r- distanca midis tarifave. Duke përdorur këtë formulë, marrim
 (5)
(5)
Duke marrë parasysh barazitë (4) dhe (5), formula (3) merr formën
 ku
ku 
Pas kryerjes së llogaritjeve sipas formulës së përftuar, gjejmë υ 0 =2,35 mm/s
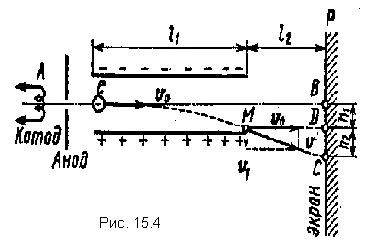 Shembulli 8 Një elektron pa një shpejtësi fillestare ka kaluar diferencën e potencialit U 0 =10
kV dhe fluturoi në hapësirën midis pllakave të një kondensatori të sheshtë të ngarkuar me një ndryshim potencial U l \u003d 100 V, përgjatë vijës AB, paralel me pllakat (Fig. 15.4). Largësia d ndërmjet pllakave është 2 cm.Gjatësia l 1 pllakë kondensator në drejtim të fluturimit të elektroneve është e barabartë me 20 cm. Përcaktoni distancën dielli në ekran R, larg kondensatorit l 2 \u003d 1 m.
Shembulli 8 Një elektron pa një shpejtësi fillestare ka kaluar diferencën e potencialit U 0 =10
kV dhe fluturoi në hapësirën midis pllakave të një kondensatori të sheshtë të ngarkuar me një ndryshim potencial U l \u003d 100 V, përgjatë vijës AB, paralel me pllakat (Fig. 15.4). Largësia d ndërmjet pllakave është 2 cm.Gjatësia l 1 pllakë kondensator në drejtim të fluturimit të elektroneve është e barabartë me 20 cm. Përcaktoni distancën dielli në ekran R, larg kondensatorit l 2 \u003d 1 m.
Zgjidhje Lëvizja e një elektroni brenda kondensatorit përbëhet nga dy lëvizje: 1) me inerci përgjatë vijës AB me një shpejtësi konstante υ 0 , të fituara nën veprimin e një ndryshimi potencial U 0 , të cilin elektroni ia kaloi kondensatorit; 2) lëvizje e përshpejtuar në mënyrë uniforme në drejtim vertikal në një pllakë të ngarkuar pozitivisht nën veprimin e një force konstante të fushës së kondensatorit. Pasi të largohet nga kondensatori, elektroni do të lëvizë në mënyrë të njëtrajtshme me një shpejtësi υ, që kishte në atë pikë M në momentin e daljes nga kondensatori.
Nga fig. 15.4 tregon se distanca e dëshiruar | | BC|=h 1 +h 2 , prej nga h 1 - distanca që elektroni do të lëvizë në drejtim vertikal gjatë lëvizjes në kondensator; h 2 - distanca midis pikës D në ekran, në të cilën elektroni do të binte, duke lëvizur në dalje nga kondensatori në drejtim të shpejtësisë fillestare υ 0, dhe pika C, ku elektroni godet në të vërtetë.
Shprehni veçmas h 1 dhe h 2 . Duke përdorur formulën për gjatësinë e shtegut të lëvizjes së përshpejtuar uniformisht, gjejmë
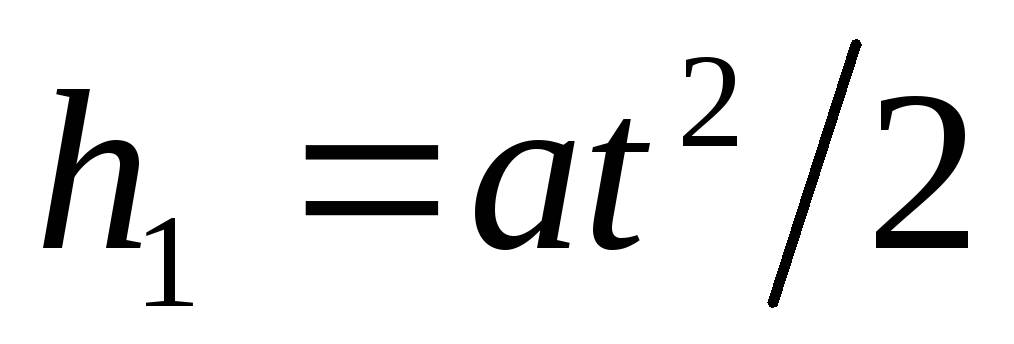 .
(1)
.
(1)
ku a- nxitimi i marrë nga elektroni nën veprimin e fushës së kondensatorit; t- koha e fluturimit të një elektroni brenda një kondensatori.
Sipas ligjit të dytë të Njutonit a=F/m, ku F- forca me të cilën fusha vepron në elektron; t- masën e saj. Nga ana e tij, F=eE=eU 1 /d, ku e- ngarkesa elektronike; U 1 - ndryshimi i potencialit midis pllakave të kondensatorit; d- distanca midis tyre. Kohën e fluturimit të një elektroni brenda kondensatorit e gjejmë nga formula për rrugën e lëvizjes uniforme  ,
ku
,
ku

ku l 1
është gjatësia e kondensatorit në drejtim të fluturimit të elektroneve. Shprehjen për shpejtësinë e gjejmë nga kushti i barazisë së punës së fushës gjatë lëvizjes së elektronit dhe energjisë kinetike të fituar prej tij:  .
Nga këtu
.
Nga këtu
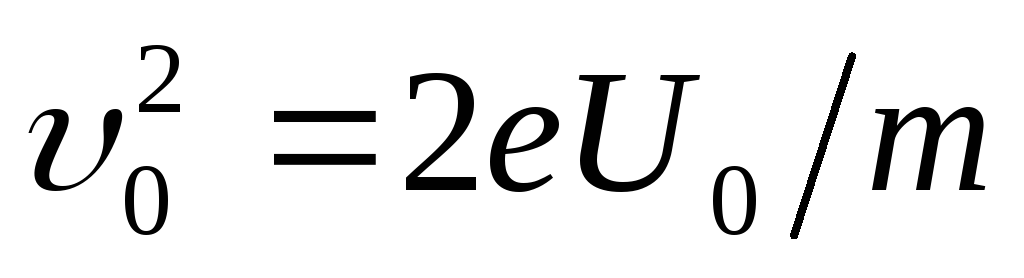 (2)
(2)
Zëvendësimi në formulën (1) në mënyrë të njëpasnjëshme të vlerave a,F, t dhe υ
0 2
nga shprehjet përkatëse, marrim 
Gjatësia e prerjes h 2 gjeni nga ngjashmëria e trekëndëshave MDC dhe vektor:
 (3)
(3)
ku υ 1 - shpejtësia e elektronit në drejtimin vertikal në një pikë M;l 2 - distanca nga kondensatori në ekran.
Shpejtësia υ 1 e gjejmë sipas formulës υ 1 = në, e cila duke marrë parasysh shprehjet për a, F dhe t do të marrë formën

Zëvendësimi i shprehjes υ
1 në formulën (3), marrim  ,
ose duke e zëvendësuar υ
0 2 sipas formulës (3), gjejmë
,
ose duke e zëvendësuar υ
0 2 sipas formulës (3), gjejmë

Më në fund për distancën e kërkuar | para Krishtit| do të ketë
|para Krishtit|=
Zëvendësimi i vlerave të sasive U 1 ,U 0 ,d,l 1 dhe l 2 në shprehjen e fundit dhe duke kryer llogaritjet, marrim | para Krishtit|=5,5 cm.
Detyrat
Energjia potenciale dhe potenciali fushor i ngarkesave pika
15.1. tarifë pikë P\u003d 10 nC, duke qenë në një pikë të caktuar në fushë, ka një energji potenciale P \u003d 10 μJ. Gjeni potencialin φ të kësaj pike fushore.
5.2. Kur lëviz ngarkesa Q=20 nC midis dy pikave të fushës, puna bëhej nga forcat e jashtme A=4µJ. Përcaktoni një punë A 1 forcat e fushës dhe diferenca Δφ e potencialeve të këtyre pikave të fushës.
15.3. Fusha elektrike krijohet nga një pikë ngarkesë pozitive P 1 \u003d 6 nC. ngarkesë pozitive P 2 transferohet nga pika POR këtë fushë deri në një pikë AT(Fig. 15.5). Sa është ndryshimi i energjisë potenciale ΔP për njësi të ngarkesës së transferuar, nëse r 1 =20 cm dhe r 2 \u003d 50 cm?
15.4.
Fusha elektrike e krijuar nga një ngarkesë pikë P l \u003d 50 nC. Pa përdorur konceptin e potencialit, llogaritni punën POR në 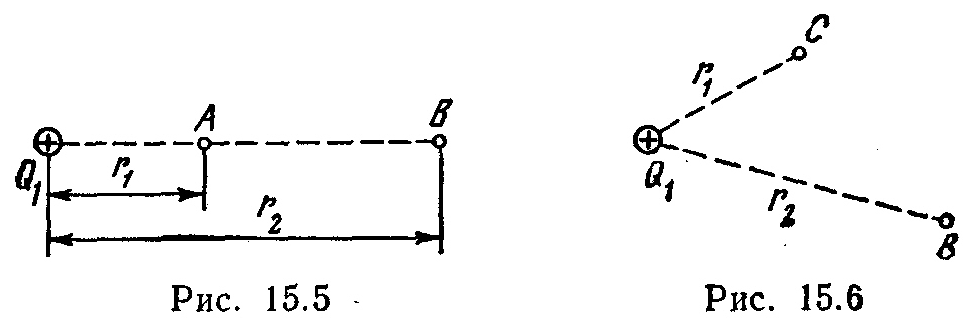 forcat e jashtme për të lëvizur një ngarkesë pikë P 2 = -2 nC nga pika NGA pikërisht AT
forcat e jashtme për të lëvizur një ngarkesë pikë P 2 = -2 nC nga pika NGA pikërisht AT
(Fig. 15.6), nëse r 1 =10 cm, r 2 \u003d 20 cm Përcaktoni gjithashtu ndryshimin ΔP të energjisë potenciale të sistemit të ngarkesave.
15.5. Fusha krijohet nga një ngarkesë pikë P=1 nC. Përcaktoni potencialin φ të fushës në një pikë të largët nga ngarkesa në një distancë r= 20 cm.
15.6. Përcaktoni potencialin φ të fushës elektrike në një pikë të largët nga ngarkesat P 1 = -0,2 µC dhe P 2 =0,5 μC, përkatësisht, në r 1 =15 masmedia r 2 \u003d 25 cm Përcaktoni gjithashtu distancat minimale dhe maksimale midis ngarkesave për të cilat është e mundur një zgjidhje.
15.7. Akuzat P 1 \u003d 1 μC dhe P 2 = -1 μC janë në distancë d\u003d 10 cm Përcaktoni tensionin E dhe potenciali φ i fushës në një pikë të largët në një distancë r= 10 cm nga ngarkesa e parë dhe shtrirë në një vijë që kalon përmes ngarkesës së parë pingul me drejtimin nga P 1 deri në P 2 .
15.8. Llogaritni energjinë potenciale P të një sistemi me ngarkesa me dy pika P 1 =100 nC dhe P 2 =10 nC në distancë d= 10 cm larg njëri-tjetrit.
15.9. Gjeni energjinë potenciale P të një sistemi me ngarkesa me tre pika P 1 \u003d 10 nC, P 2 =20 nCl dhe P 3 \u003d -30 nC, e vendosur në kulmet e një trekëndëshi barabrinjës me gjatësi anësore a= 10 cm.
15.10. Sa është energjia potenciale P e një sistemi me katër ngarkesa pika identike P\u003d 10 nC, e vendosur në kulmet e një katrori me gjatësi anësore a\u003d 10 cm? .
15.11. Përcaktoni energjinë potenciale P të një sistemi me ngarkesa me katër pika të vendosura në kulmet e një katrori me gjatësi anësore a\u003d 10 cm Ngarkesat janë të njëjta në modul P=10 nC, por dy prej tyre janë negative. Konsideroni dy raste të mundshme të rregullimit të tarifave.
 15.12
. Fusha krijohet nga ngarkesa me dy pika +
2P dhe -Py, në një distancë d= 12 cm larg. Përcaktoni vendndodhjen e pikave në rrafshin për të cilin potenciali është zero (shkruani ekuacionin për vijën e potencialit zero).
15.12
. Fusha krijohet nga ngarkesa me dy pika +
2P dhe -Py, në një distancë d= 12 cm larg. Përcaktoni vendndodhjen e pikave në rrafshin për të cilin potenciali është zero (shkruani ekuacionin për vijën e potencialit zero).
5.13. Sistemi përbëhet nga tre ngarkesa - dy të së njëjtës madhësi P 1 = |P 2 |=1 μC dhe e kundërta në shenjë dhe ngarkesë Q=20 nC, e vendosur në pikën 1 në mes midis dy ngarkesave të tjera të sistemit (Fig. 15.7). Përcaktoni ndryshimin në energjinë potenciale ΔP të sistemit gjatë transferimit të ngarkesës P nga pika 1 në pikën 2. Këto pika hiqen nga ngarkesa negative P 1 për distancë a= 0,2 m.
Potenciali i fushës së ngarkesave të shpërndara në mënyrë lineare
15.14. Përgjatë një unaze të hollë me një rreze R= 10 cm ngarkesë e shpërndarë në mënyrë uniforme me dendësi lineare τ= 10 nC/m. Përcaktoni potencialin φ në një pikë të shtrirë në boshtin e unazës, në një distancë a= 5 cm nga qendra.
15.15. Në një segment të një përcjellësi të hollë të drejtë, një ngarkesë shpërndahet në mënyrë të njëtrajtshme me një dendësi lineare τ=10 nC/m. Llogaritni potencialin φ të krijuar nga kjo ngarkesë në një pikë të vendosur në boshtin e përcjellësit dhe të largët nga skaji më i afërt i segmentit me një distancë të barabartë me gjatësinë e këtij segmenti.
Leksioni 6. Potenciali i fushës elektrike. Testi nr. 2
Potenciali është një nga konceptet më komplekse të elektrostatikës. Nxënësit mësojnë përkufizimin e potencialit të një fushe elektrostatike, zgjidhin probleme të shumta, por nuk kanë ndjenjën e potencialit, kanë vështirësi në lidhjen e teorisë me realitetin. Prandaj, roli i eksperimentit edukativ në formimin e konceptit të potencialit është shumë i lartë. Ne kemi nevojë për eksperimente të tilla që, nga njëra anë, do të ilustrojnë ide teorike abstrakte për potencialin dhe, nga ana tjetër, do të tregojnë vlefshmërinë e plotë të eksperimentit për prezantimin e konceptit të potencialit. Është më tepër e dëmshme sesa e dobishme të përpiqemi për saktësi të veçantë të rezultateve sasiore në këto eksperimente.
6.1. Potenciali i fushës elektrostatike
Le ta rregullojmë trupin përcjellës në një mbështetëse izoluese dhe ta ngarkojmë atë. Ne varim një top përçues të lehtë në një fije të gjatë të izoluar dhe i japim një ngarkesë provë, që është i njëjti emër si ngarkesa e trupit. Topi do të kërcejë nga trupi dhe do të dalë jashtë pozicionit 1 do të lëvizë në pozicion 2. Meqenëse lartësia e topit në fushën gravitacionale është rritur me h, energjia potenciale e ndërveprimit të saj me Tokën është rritur me mgh. Kjo do të thotë se fusha elektrike e trupit të ngarkuar ka bërë disa punë në ngarkesën e provës.
Le të përsërisim eksperimentin, por në momentin fillestar, jo thjesht të lëshojmë topin e provës, por ta shtyjmë atë në një drejtim arbitrar, duke i dhënë asaj njëfarë energjie kinetike. Në të njëjtën kohë, ne gjejmë se lëvizja nga pozicioni 1 përgjatë një trajektoreje komplekse, topi përfundimisht do të ndalet në pozicion 2 . Informuar me topin në momentin fillestar energjia kinetike, padyshim, është shpenzuar për tejkalimin e forcave të fërkimit gjatë lëvizjes së topit, dhe fusha elektrike bëri të njëjtën punë me topin si në rastin e parë. Në të vërtetë, nëse heqim trupin e ngarkuar, atëherë e njëjta shtytje e topit të provës çon në faktin se nga pozicioni 2 ai kthehet në pozicion 1 .
Kështu, eksperimenti sugjeron që puna e fushës elektrike në ngarkesë nuk varet nga trajektorja e ngarkesës, por përcaktohet vetëm nga pozicionet e pikave fillestare dhe përfundimtare të saj. Me fjalë të tjera, në një trajektore të mbyllur, puna e fushës elektrostatike është gjithmonë zero. Fushat me këtë veti quhen potencial.
6.2. Potenciali i fushës qendrore
Përvoja tregon se në një fushë elektrostatike të krijuar nga një top përcjellës i ngarkuar, forca që vepron në ngarkesën e provës drejtohet gjithmonë nga qendra e topit të ngarkuar, ajo zvogëlohet në mënyrë monotonike me rritjen e distancës dhe ka të njëjtat vlera në distanca të barabarta. prej saj. Një fushë e tillë quhet qendrore. Duke përdorur figurën, është e lehtë të verifikohet se fusha qendrore është potenciale.

6.3. Energjia e mundshme e ngarkimit në një fushë elektrostatike
Fusha gravitacionale, si ajo elektrostatike, është potenciale. Për më tepër, shënimi matematik i ligjit të gravitetit universal përkon me shënimin e ligjit të Kulombit. Prandaj, kur studiojmë një fushë elektrostatike, ka kuptim të mbështetemi në analogjinë midis fushave gravitacionale dhe elektrostatike.
Në një zonë të vogël afër sipërfaqes së Tokës, fusha gravitacionale mund të konsiderohet uniforme (Fig. a).
Një trup me masë m në këtë fushë i nënshtrohet një force që është konstante në madhësi dhe drejtim f= t g. Nëse një trup i lënë në vetvete bie nga pozicioni 1 në pozicion 2 , atëherë forca gravitacionale funksionon A = fs = mgs = mg (h 1 – h 2).
Mund të themi të njëjtën gjë ndryshe. Kur trupi ishte në pozicion 1
, sistemi Tokë-trup kishte energji potenciale (d.m.th., aftësinë për të bërë punë) W 1 = mgh një. Kur trupi është në pozicion 2
, sistemi në shqyrtim filloi të kishte energji potenciale W 2 = mgh 2. Puna e bërë në këtë rast është e barabartë me diferencën midis energjive potenciale të sistemit në gjendjen përfundimtare dhe fillestare, të marra me shenjën e kundërt: POR
= – (W 2 – W 1). 
Tani le t'i drejtohemi fushës elektrike, e cila, kujtojmë, si ajo gravitacionale, është potenciale. Imagjinoni që nuk ka gravitacion, dhe në vend të sipërfaqes së Tokës ka një pllakë përcjellëse të sheshtë, të ngarkuar (për definicion) negativisht (Fig. b). Shkruani boshtin e koordinatave Y dhe vendosni një ngarkesë pozitive mbi pjatë q. Është e qartë se, meqenëse ngarkesa në vetvete nuk ekziston, ka një trup të një mase të caktuar mbi pllakën, që mban një ngarkesë elektrike. Por, meqenëse e konsiderojmë fushën gravitacionale të munguar, atëherë nuk do të marrim parasysh masën e trupit të ngarkuar.
Pra, për një ngarkesë pozitive q nga ana e planit të ngarkuar negativisht, forca e tërheqjes f = q E , ku E është forca e fushës elektrike. Meqenëse fusha elektrike është uniforme, e njëjta forcë vepron mbi ngarkesën në të gjitha pikat e saj. Nëse ngarkesa lëviz nga pozicioni 1 në pozicion 2 , atëherë forca elektrostatike punon mbi të POR = fs = qEs = qE(y 1 – y 2).
Të njëjtën gjë mund ta shprehim me fjalë të tjera. Shtatzëna 1 Një ngarkesë në një fushë elektrostatike ka një energji potenciale W 1 = qEy 1, dhe në pozicion 2 - energji potenciale W 2 = qEy 2. Kur ngarkesa kalon nga pozicioni 1 në pozicion 2 fusha elektrike e rrafshit të ngarkuar ka bërë punë në të POR = –(W 2 – W 1).
Kujtoni se energjia potenciale përcaktohet vetëm deri në një term: nëse vlera zero e energjisë potenciale zgjidhet diku tjetër në bosht Y, atëherë në thelb asgjë nuk do të ndryshojë.
6.4. Potenciali i një fushe elektrostatike homogjene
Nëse energjia potenciale e një ngarkese në një fushë elektrostatike pjesëtohet me vlerën e kësaj ngarkese, atëherë marrim karakteristikën e energjisë së vetë fushës, e cila u quajt potencial:
Potenciali në sistemin SI shprehet në volt: 1 V = 1 J / 1 C.
Nëse në një fushë elektrike uniforme boshti Y dërgoni paralelisht me vektorin e tensionit E , atëherë potenciali i një pike arbitrare të fushës do të jetë proporcional me koordinatën e pikës: për më tepër, koeficienti i proporcionalitetit është forca e fushës elektrike.
6.5. Diferencë potenciale
Energjia dhe potenciali potencial përcaktohen vetëm deri në një konstante arbitrare, në varësi të zgjedhjes së vlerave të tyre zero. Sidoqoftë, puna e fushës ka një kuptim shumë të caktuar, pasi përcaktohet nga ndryshimi në energjitë e mundshme në dy pika të fushës:
POR = –(W 2 – W 1) = –( 2 q – 1 q) = q( 1 – 2).
Puna e lëvizjes së një ngarkese elektrike ndërmjet dy pikave të fushës është e barabartë me produktin e ngarkesës dhe diferencën potenciale të pikave të fillimit dhe të mbarimit. Diferenca potenciale quhet gjithashtu tensioni.
Tensioni midis dy pikave është i barabartë me raportin e punës në terren kur lëvizni ngarkesën nga pika fillestare në atë përfundimtare në këtë ngarkesë:
![]()
Tensioni, si potenciali, shprehet në volt.
6.6. Diferenca dhe tensioni i mundshëm
Në një fushë elektrike uniforme, forca drejtohet në drejtim të zvogëlimit të potencialit dhe, sipas formulës = Po, diferenca potenciale është U = 1 – 2 = E(në 1 – y 2). Duke treguar ndryshimin në koordinatat e pikave në 1 – y 2 = d, marrim U = Ed.
Në një eksperiment, në vend që të matet drejtpërdrejt forca, është më e lehtë të përcaktohet diferenca potenciale dhe më pas të llogaritet moduli i forcës duke përdorur formulën
ku dështë distanca ndërmjet dy pikave të fushës që janë të vendosura ngushtë në drejtim të vektorit E . Në të njëjtën kohë, jo një njuton për varëse përdoret si njësi tensioni, por një volt për metër:
![]()
6.7. Potenciali i një fushe elektrostatike arbitrare
Përvoja tregon se raporti i punës për të lëvizur një ngarkesë nga pafundësia në një pikë të caktuar të fushës me vlerën e kësaj ngarkese mbetet i pandryshuar: = POR/q. Kjo marrëdhënie quhet potenciali i një pike të caktuar të fushës elektrostatike, duke marrë potencialin në pafundësi të barabartë me zero.
6.8. Parimi i mbivendosjes për potencialet
Çdo fushë elektrostatike arbitrarisht komplekse mund të përfaqësohet si një mbivendosje e fushave të ngarkesave pika. Çdo fushë e tillë në pikën e zgjedhur ka një potencial të caktuar. Meqenëse potenciali është një sasi skalare, potenciali rezultues i fushës së të gjitha ngarkesave pika është shuma algjebrike e potencialeve 1, 2, 3, ... të fushave të ngarkesave individuale: = 1 + 2 + 3 + .. Kjo lidhje është pasojë e drejtpërdrejtë e parimit të mbivendosjes së fushave elektrike.
6.9. Potenciali i fushës së një ngarkese pikë
Le të kthehemi tani te një ngarkesë sferike (pikore). Më sipër tregohet se forca e fushës elektrike e krijuar nga një ngarkesë e shpërndarë në mënyrë uniforme mbi sferën P, nuk varet nga rrezja e sferës. Imagjinoni që në një distancë r nga qendra e sferës është një ngarkesë provë q. Forca e fushës në pikën ku ndodhet ngarkesa, 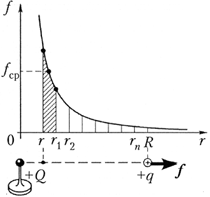
Figura tregon një grafik të varësisë së fuqisë së bashkëveprimit elektrostatik midis ngarkesave pika nga distanca midis tyre. Për të gjetur punën e fushës elektrike gjatë lëvizjes së ngarkesës provë q nga një largësi r deri në një distancë R, ndajeni këtë interval me pikë r 1 , r 2 ,...,
r fq në seksione të barabarta. Forca mesatare që vepron mbi një ngarkesë q brenda segmentit [ rr 1 ] është e barabartë me ![]()
Puna e kësaj force në këtë fushë:
![]()
Shprehje të ngjashme për punë do të merren për të gjitha seksionet e tjera. Pra, puna e plotë është:
Termat identikë me shenja të kundërta shkatërrohen dhe më në fund marrim:
është puna e fushës në akuzë ![]()
- diferencë potenciale ![]()
Tani, për të gjetur potencialin e pikës së fushës në lidhje me pafundësinë, ne drejtojmë R deri në pafundësi dhe më në fund marrim:
Pra, potenciali i fushës së një ngarkese pika është në përpjesëtim të zhdrejtë me distancën nga ngarkesa.
6.10. Sipërfaqet ekuipotenciale
Quhet një sipërfaqe në të cilën potenciali i fushës elektrike ka të njëjtën vlerë në çdo pikë ekuipotencial. Nuk është e vështirë të demonstrosh sipërfaqet ekuipotenciale të fushës së një topi të ngarkuar me një ngarkesë provë të pezulluar në një fije, siç tregohet në figurë.
Në figurën e dytë, fusha elektrostatike e dy ngarkesave të kundërta është paraqitur me vija të forcës (të ngurtë) dhe ekuipotenciale (të ndërprera).
Hulumtimi 6.1. Diferencë potenciale
Ushtrimi. Zhvilloni një eksperiment të thjeshtë që prezanton konceptin e ndryshimit të potencialit, ose tensionit.
Opsioni i ekzekutimit. Vendosni dy disqe metalikë në mbështetëse izoluese paralel me njëri-tjetrin në një distancë prej rreth 10 cm. Ngarkoni disqet me ngarkesa të barabarta në madhësi dhe të kundërta në shenjë. Ngarkoni topin e një dinamometri elektrostatik me një ngarkesë, për shembull, q= 5 nC (shih studimin 3.6) dhe futeni në zonën midis disqeve. Në këtë rast, gjilpëra e dinamometrit do të tregojë një vlerë të caktuar të forcës që vepron në top. Duke ditur parametrat e dinamometrit, llogaritni vlerën e modulit të forcës (shih studimin 3.6). Për shembull, në një nga eksperimentet tona, gjilpëra e dinamometrit tregoi vlerën X\u003d 2 cm, pra, sipas formulës, moduli i forcës f = Kx= 17 10 -5 N.
Duke lëvizur dinamometrin, tregoni se në të gjitha pikat e fushës midis disqeve të ngarkuar, e njëjta forcë vepron në ngarkesën e provës. Duke lëvizur dinamometrin në mënyrë që ngarkesa e provës të kalojë rrugën s\u003d 5 cm në drejtim të forcës që vepron mbi të, pyesni studentët: çfarë pune bën fusha elektrike në ngarkesë? Arritni të kuptoni se puna e fushës në modulin e ngarkimit është e barabartë me
POR = fs= 8,5 10 -6 J, (6,3)
për më tepër, është pozitive nëse ngarkesa lëviz në drejtim të fuqisë së fushës dhe negative nëse në drejtim të kundërt. Llogaritni ndryshimin potencial midis pozicioneve fillestare dhe përfundimtare të topit të dinamometrit: U = POR/q\u003d 1,7 10 3 V.
Nga njëra anë, forca e fushës elektrike midis pllakave:
![]()
Nga ana tjetër, sipas formulës (6.1), për d=s:
![]()
Kështu, përvoja tregon se forca e fushës elektrike mund të përcaktohet në dy mënyra, të cilat, natyrisht, çojnë në të njëjtat rezultate.
Studimi 6.2. Kalibrimi i tensionit të elektrometrit
Ushtrimi. Hartoni një eksperiment për të treguar se një elektrometër tregues demonstrues mund të masë tensionin.
Opsioni i ekzekutimit. Konfigurimi eksperimental është paraqitur në mënyrë skematike në figurë. Duke përdorur një dinamometër elektrostatik, përcaktoni forcën e një fushe elektrike uniforme dhe përdorni formulën U = Ed llogaritni diferencën e potencialit midis pllakave përçuese. Duke përsëritur këto hapa, kalibroni elektrometrin për tension në mënyrë që të merrni një voltmetër elektrostatik.
Hulumtimi 6.3. Potenciali i fushës së një ngarkese sferike
Ushtrimi. Përcaktoni në mënyrë eksperimentale punën që duhet bërë kundër fushës elektrostatike në mënyrë që ngarkesa e provës të zhvendoset nga pafundësia në një pikë të fushës së krijuar nga sfera e ngarkuar.
Opsioni i ekzekutimit. Ngjitni një top stiropor të mbështjellë me letër alumini në shtyllën izoluese. Ngarkoni atë nga një burim piezoelektrik ose një burim tjetër (shih pikën 1.10) dhe ngarkoni një top provë në shufrën e një dinamometri elektrostatik me të njëjtën ngarkesë. Ngarkesa e provës është pafundësisht larg asaj të hetuar, nëse dinamometri elektrostatik nuk regjistron forcat e bashkëveprimit elektrostatik midis ngarkesave. Në eksperiment, është e përshtatshme të lini dinamometrin elektrostatik të palëvizshëm dhe të lëvizni ngarkesën në studim.
Gradualisht afrojeni topin e ngarkuar në bazën izoluese me topin e dinamometrit elektrostatik. Në rreshtin e parë të tabelës shkruani vlerat e distancës r midis ngarkesave, në rreshtin e dytë - vlerat përkatëse të forcës së ndërveprimit elektrostatik. Është i përshtatshëm për të shprehur distancën në centimetra, dhe forcën në njësitë konvencionale, në të cilat shkalla e dinamometrit është kalibruar. Bazuar në të dhënat e marra, ndërtoni një grafik të varësisë së forcës nga distanca. Ju keni ndërtuar tashmë një grafik të ngjashëm në Studimin 3.5.
Tani gjeni varësinë e punës nga lëvizja e ngarkesës nga pafundësia në një pikë të caktuar në fushë. Kushtojini vëmendje faktit që në eksperiment forca e bashkëveprimit të ngarkesave bëhet pothuajse e barabartë me zero në një distancë relativisht të vogël të një ngarkese nga tjetra.
Ndani të gjithë gamën e ndryshimeve në distancën midis ngarkesave në seksione të barabarta, për shembull, 1 cm secila. Është më i përshtatshëm të filloni përpunimin e të dhënave eksperimentale nga fundi i grafikut. Në zonën nga 16 në 12 cm, vlera mesatare e forcës f cf është 0.13 arb. njësi, pra punë elementare POR në këtë zonë është e barabartë me 0,52 arb. njësive Në zonën nga 12 deri në 10 cm, duke argumentuar në mënyrë të ngjashme, marrim një punë elementare prej 0,56 njësi konvencionale. njësive Më tej, është e përshtatshme për të marrë seksione të gjata 1 cm. Në secilën prej tyre, gjeni vlerën mesatare të forcës dhe shumëzojeni atë me gjatësinë e seksionit. Vlerat e marra të punës në terren A në të gjitha fushat, futeni në rreshtin e katërt të tabelës.
Për të gjetur punën POR bërë nga fusha elektrike kur lëvizni ngarkesën nga pafundësia në një distancë të caktuar, mblidhni punën elementare përkatëse dhe shkruani vlerat që rezultojnë në rreshtin e pestë të tabelës. Në rreshtin e fundit shkruani vlerat e 1/ r, reciproke e distancës ndërmjet ngarkesave.
Vizatoni punën e fushës elektrike në reciproke të distancës dhe sigurohuni që të keni një vijë të drejtë (figura në të djathtë).
Kështu, përvoja tregon se puna e një fushe elektrike kur një ngarkesë lëviz nga pafundësia në një pikë të caktuar të fushës është në përpjesëtim të zhdrejtë me distancën nga kjo pikë në ngarkesën që krijon fushën.
Studimi 6.4. Burimi i tensionit të lartë
Informacion. Për eksperimentin e fizikës shkollore, industria aktualisht po prodhon burime të shkëlqyera të tensionit të lartë. Ata kanë dy terminale dalëse ose dy elektroda të tensionit të lartë, diferenca e potencialit ndërmjet të cilave rregullohet vazhdimisht nga 0 në 25 kV. Treguesi ose matësi dixhital i tensionit i integruar në pajisje ju lejon të përcaktoni ndryshimin e mundshëm midis poleve të burimit. Pajisjet e tilla rrisin nivelin e eksperimentit arsimor në elektrostatikë.
Ushtrimi. Hartoni një eksperiment edukativ demonstrues që tregon se potenciali i një topi të ngarkuar, i përcaktuar eksperimentalisht në përputhje me formulën (6.2) për një ngarkesë pikë, është i barabartë me potencialin që i jepet këtij topi nga një burim energjie me tension të lartë.
Opsioni i ekzekutimit. Rimontoni konfigurimin eksperimental, të përbërë nga një dinamometër elektrostatik me një top provë dhe një top përçues në një mbështetëse izoluese (shih studimet 3.4 dhe 6.3). Matni parametrat e të gjithë elementëve të instalimit.
Për saktësi, theksojmë se në një nga eksperimentet kemi përdorur një dinamometër elektrostatik, parametrat e të cilit tregohen në studimin 3.4: a= 5 10 -3 m, b= 55 10 -3 m, Me= 100 10 -3 m, t= 0,94 10 -3 kg, dhe topat ishin të njëjtë dhe kishin një rreze R= 7.5 10 -3 m Për këtë dinamometër faktori i kalibrimit K, i cili konverton njësitë arbitrare të forcës në njuton, jepet me formula ![]() (Shih studimin 3.6).
(Shih studimin 3.6).
Orari i punës për lëvizjen e një ngarkese provë nga pafundësia në një pikë të caktuar të fushës është paraqitur në figurën në f. 31. Për të kaluar nga njësitë konvencionale të punës në joule në këtë grafik, është e nevojshme, në përputhje me formulën A = f e mërkurë r përktheni vlerat e distancës në centimetra në metra, forconi vlerat në arb. njësive (cm) konvertohet në arb. njësive (m) dhe shumëzojeni me K. Në këtë mënyrë: A(J) = 10 -4 KA(arb. njësitë). 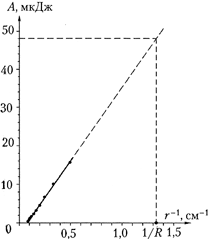
Grafiku përkatës i punës kundrejt distancës reciproke është paraqitur më poshtë. Duke e ekstrapoluar atë në R\u003d 7.5 mm, ne zbulojmë se puna për të lëvizur ngarkesën e provës nga pafundësia në sipërfaqen e topit të ngarkuar POR\u003d 57 10 -4 K \u003d 4.8 10 -5 J. Meqenëse ngarkesat e topave ishin të njëjta dhe arritën në q\u003d 6.6 10 -9 C (shih studimin 3.6), pastaj potenciali i dëshiruar \u003d POR/q= 7300 V.

Ndizni burimin e tensionit të lartë dhe vendosni tensionin e daljes në të me rregullatorin, për shembull, U= 15 kV. Prekni topat përçues një nga një me njërën nga elektrodat dhe fikni burimin. Në këtë rast, secili nga topat fiton një potencial prej = 7.5 kV në lidhje me Tokën. Përsëriteni eksperimentin për përcaktimin e ngarkesave të topave me metodën e Kulombit (hulumtimi 3.6) dhe do të merrni një vlerë afër 7 nC.
Kështu, në eksperiment, ngarkesat e topave përcaktohen në dy mënyra të pavarura. Metoda e parë bazohet në përdorimin e drejtpërdrejtë të përcaktimit të potencialit, e dyta bazohet në komunikimin e një potenciali të caktuar me topat duke përdorur një burim të tensionit të lartë dhe matjen pasuese të ngarkesës së tyre duke përdorur ligjin e Kulombit. Në të njëjtën kohë, u morën rezultate të njëjta.
Sigurisht, asnjë nga nxënësit e shkollës nuk dyshon se instrumentet moderne matin saktë vlerat e sasive fizike. Por tani janë të bindur se pikërisht ato sasi që studiojnë në dukuritë më të thjeshta maten drejt. Është krijuar një lidhje e fortë midis bazave të fizikës dhe teknologjisë moderne, dhe hendeku midis njohurive shkollore dhe jetës reale është eliminuar.
Pyetje dhe detyra për vetëkontroll
1. Si të vërtetohet eksperimentalisht se fusha elektrostatike është potenciale?
2. Cili është thelbi i analogjisë ndërmjet fushave gravitacionale dhe elektrostatike?
3. Cila është marrëdhënia ndërmjet intensitetit dhe ndryshimit të potencialit të fushës elektrostatike?
4. Sugjeroni një eksperiment që vërteton drejtpërdrejt vlefshmërinë e parimit të mbivendosjes për potencialet.
5. Llogaritni potencialin e fushës së një ngarkese pika duke përdorur llogaritjen integrale. Krahasoni derivimin tuaj të formulës me derivimin elementar të dhënë në leksion.
6. Zbuloni pse, në një eksperiment për të përcaktuar ndryshimin potencial midis dy disqeve përçuese (hulumtimi 6.1), është e pamundur të lëvizni matësin e tensionit në mënyrë që topi i tij i testimit të kalojë të gjithë distancën nga një disk në tjetrin.
7. Pasi të keni kalibruar elektrometrin për tension (hulumtimi 6.2), krahasoni rezultatin me vlerat e ndjeshmërisë së tensionit të pajisjes që jepen në të dhënat e pasaportës së elektrometrit.
9. Zhvilloni në detaje një metodologji për formimin në mendjet e studentëve të një bindjeje të arsyeshme se koncepti i potencialit të fushës elektrike i paraqitur në studimin e elektrostatikës korrespondon saktësisht me atë të përdorur. shkenca moderne dhe teknologjisë.
Letërsia
Butikov E.I., Kondratiev A.S. Fizikë: Proc. shtesa: Në 3 libra. Libër. 2. Elektrodinamika. Optika. – M.: Fizmatlit, 2004.
Voskanyan A.G.., Marlensky A.D., Shibaev A.F. Demonstrimi i ligjit të Kulombit bazuar në matjet sasiore: Në Sat. "Eksperiment mësimor në elektrodinamikë", vëll. 7. - M .: Shkolla-Shtypi, 1996.
Kasyanov V.A. Fizikë-10. - M.: Bustard, 2003.
Myakishev G.Ya., Sinyakov A.Z.., Slobodskov B.A.. Fizikë: Elektrodinamikë. 10–11 qeliza: Proc. për ang. studimi i fizikës. - M.: Bustard, 2002.
Pajisje edukative për klasat e fizikës së përgjithshme institucionet arsimore: Ed. G.G. Nikiforova. - M.: Bustard, 2005.
Tema 3. POTENCIALI DHE PUNA E FUSHËS ELEKTROSTATIKE. MARRËDHËNIET E FORCËS ME POTENCIALIN
3.4. Dipol në një fushë elektrike
3.5. Marrëdhënia midis fuqisë dhe potencialit të një fushe elektrostatike
3.6. Linjat e terrenit dhe sipërfaqet ekuipotenciale
3.7. Llogaritja e diferencëspotencialet sipas fuqisë së fushës së fushave elektrostatike më të thjeshta
3.1. Puna e forcave të fushës elektrostatike
Forca që vepron në një ngarkesë pikësore të vendosur në fushën e një ngarkese tjetër pika të palëvizshme është qendrore. Drejtimi i forcës që vepron në çdo pikë të hapësirës mbi një ngarkesë kalon nëpër qendrën e ngarkesës që krijon fushën dhe vlera e forcës varet vetëm nga distanca me këtë ngarkesë. deri në pikën e vëzhgimit. (Për shembull, fusha e gravitetit është fusha e forcave qendrore).
deri në pikën e vëzhgimit. (Për shembull, fusha e gravitetit është fusha e forcave qendrore). E
Oriz. 3.1
Nëse një trup vendoset në kushte të tilla që në çdo pikë të hapësirës i nënshtrohet ndikimit të trupave të tjerë me një forcë që ndryshon natyrshëm nga pika në pikë, atëherë ky trup quhet në fushën e forcave. Fusha qendrore e forcave është potencialisht. Le të sigurohemi që fusha elektrike të jetë potenciale. Llogaritni punën e bërë nga forcat e fushës së një ngarkese me pikë fikse q mbi një ngarkesë pikë që lëviz në këtë fushë  (Fig. 3.1). Punoni në rrugën elementare
(Fig. 3.1). Punoni në rrugën elementare 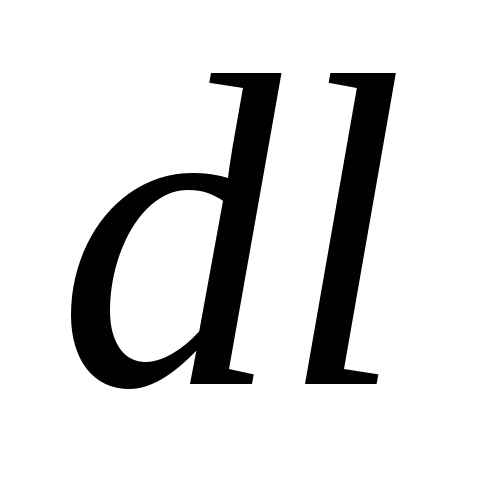 është e barabartë me:
është e barabartë me: 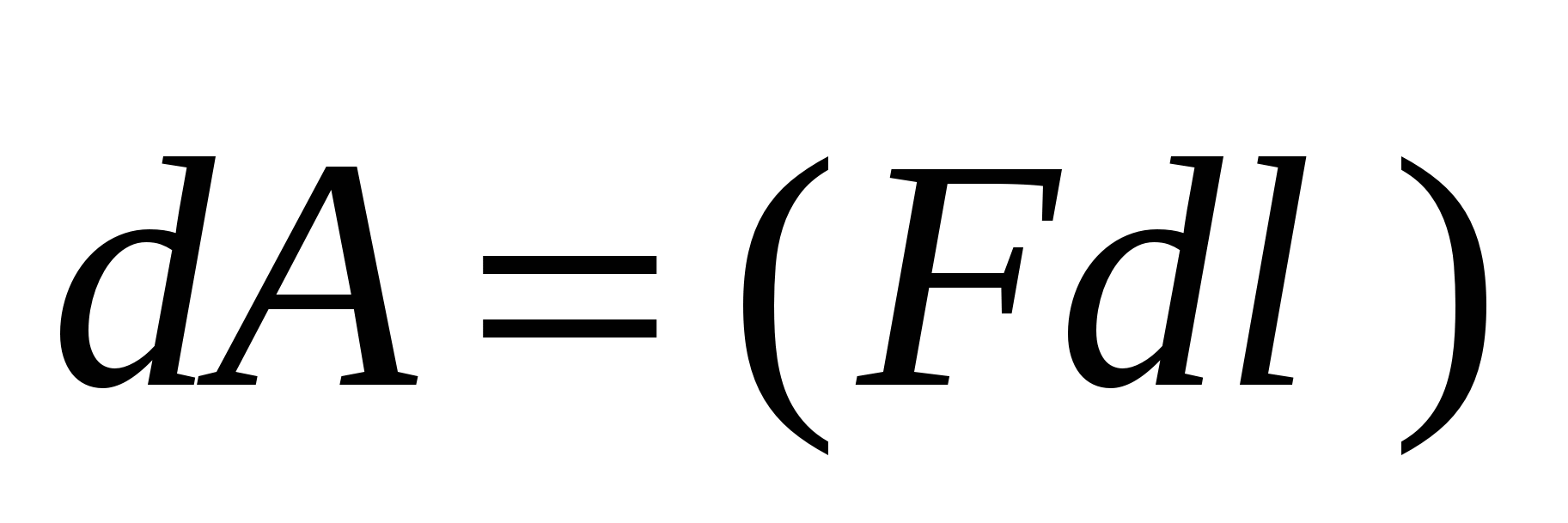 ose
ose
Sepse  . Nga këtu në rrugën 1–2
. Nga këtu në rrugën 1–2
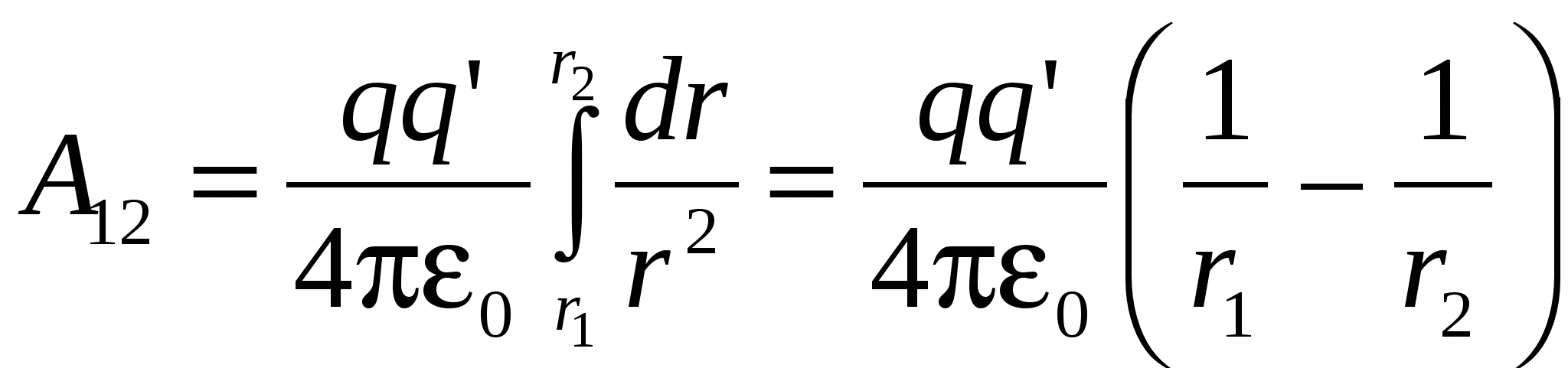 (1)
(1)
Mund të shihet se puna nuk varet nga rruga përgjatë së cilës ngarkesa lëvizte në fushën elektrike q"
, por varet vetëm nga pozicionet fillestare dhe përfundimtare të kësaj ngarkese (në r 1 dhe r 2). Prandaj, forcat që veprojnë në ngarkesë q"
në fushën e një ngarkese të palëvizshme q, janë konservatore, dhe fusha e këtyre forcave potencial. Ky përfundim mund të shtrihet lehtësisht në fushën e çdo sistemi ngarkesash fikse, pasi forca  duke vepruar në një ngarkesë pikë q" në një fushë të tillë, mund të përfaqësohet nga parimi i mbivendosjes në formë
duke vepruar në një ngarkesë pikë q" në një fushë të tillë, mund të përfaqësohet nga parimi i mbivendosjes në formë  , ku
, ku  - detyrimi i duhur i- ngarkesa e sistemit të krijimit të fushës. Puna në këtë rast është e barabartë me shumën algjebrike të punës së kryer nga forcat individuale:
- detyrimi i duhur i- ngarkesa e sistemit të krijimit të fushës. Puna në këtë rast është e barabartë me shumën algjebrike të punës së kryer nga forcat individuale:  . Secili prej termave në anën e djathtë të kësaj shprehjeje është i pavarur nga shtegu. Prandaj nuk varet nga rruga dhe puna POR.
. Secili prej termave në anën e djathtë të kësaj shprehjeje është i pavarur nga shtegu. Prandaj nuk varet nga rruga dhe puna POR.
Nga mekanika dihet se forcat potenciale në një rrugë të mbyllur është zero. Puna e bërë nga forcat e terrenit në ngarkim q"
kur kalon një lak të mbyllur, mund të përfaqësohet si  , ku
, ku  –projeksion vektorial
–projeksion vektorial 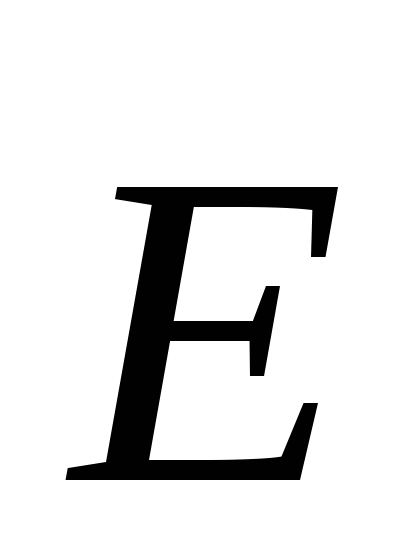 në drejtimin e zhvendosjes elementare, atëherë, pra:
në drejtimin e zhvendosjes elementare, atëherë, pra:
 (2)
(2)
Kjo marrëdhënie duhet të qëndrojë për çdo lak të mbyllur. Duhet të kihet parasysh se (21) vlen vetëm për një fushë elektrostatike. Fusha e ngarkesave lëvizëse (domethënë fusha që ndryshon me kalimin e kohës) nuk është potenciale. Për rrjedhojë, kushti (21) nuk është i plotësuar për të.
Shprehja e formës  quhet qarkullimi i vektorit
quhet qarkullimi i vektorit  përgjatë këtij konture. Në këtë mënyrë, karakteristikë e një fushe elektrostatike është se qarkullimi i vektorit të intensitetit përgjatë çdo qarku të mbyllur është zero.
përgjatë këtij konture. Në këtë mënyrë, karakteristikë e një fushe elektrostatike është se qarkullimi i vektorit të intensitetit përgjatë çdo qarku të mbyllur është zero.
3.2. Teorema e qarkullimit të vektorit të fushës elektrostatike
Kështu, pohojmë se qarkullimi i vektorit 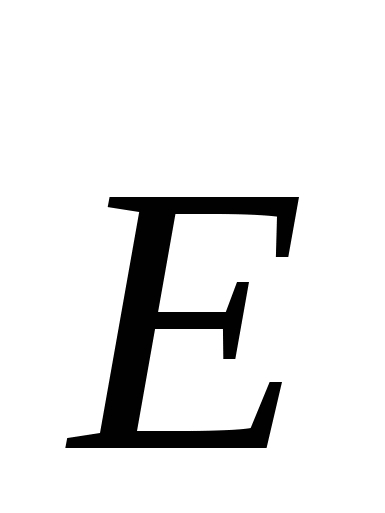 në çdo fushë elektrostatike është zero, d.m.th. . Ky pohim quhet teorema e qarkullimit të vektorit.
në çdo fushë elektrostatike është zero, d.m.th. . Ky pohim quhet teorema e qarkullimit të vektorit.
Lëreni një ngarkesë të lëvizë përgjatë një rruge të mbyllur 1a2b1 në një fushë të caktuar me forcë. Për të vërtetuar teoremën, ne ndajmë një shteg të mbyllur arbitrar në dy pjesë 1a2 dhe 2b1 (shih figurën). Le të gjejmë një punë për të lëvizur tarifën q nga pika 1 në pikën 2. Meqenëse puna në një fushë të caktuar nuk varet nga forma e shtegut, puna për të lëvizur ngarkesën përgjatë shtegut 1a2 është e barabartë me punën për të lëvizur ngarkesën përgjatë shtegut 1b2 ose 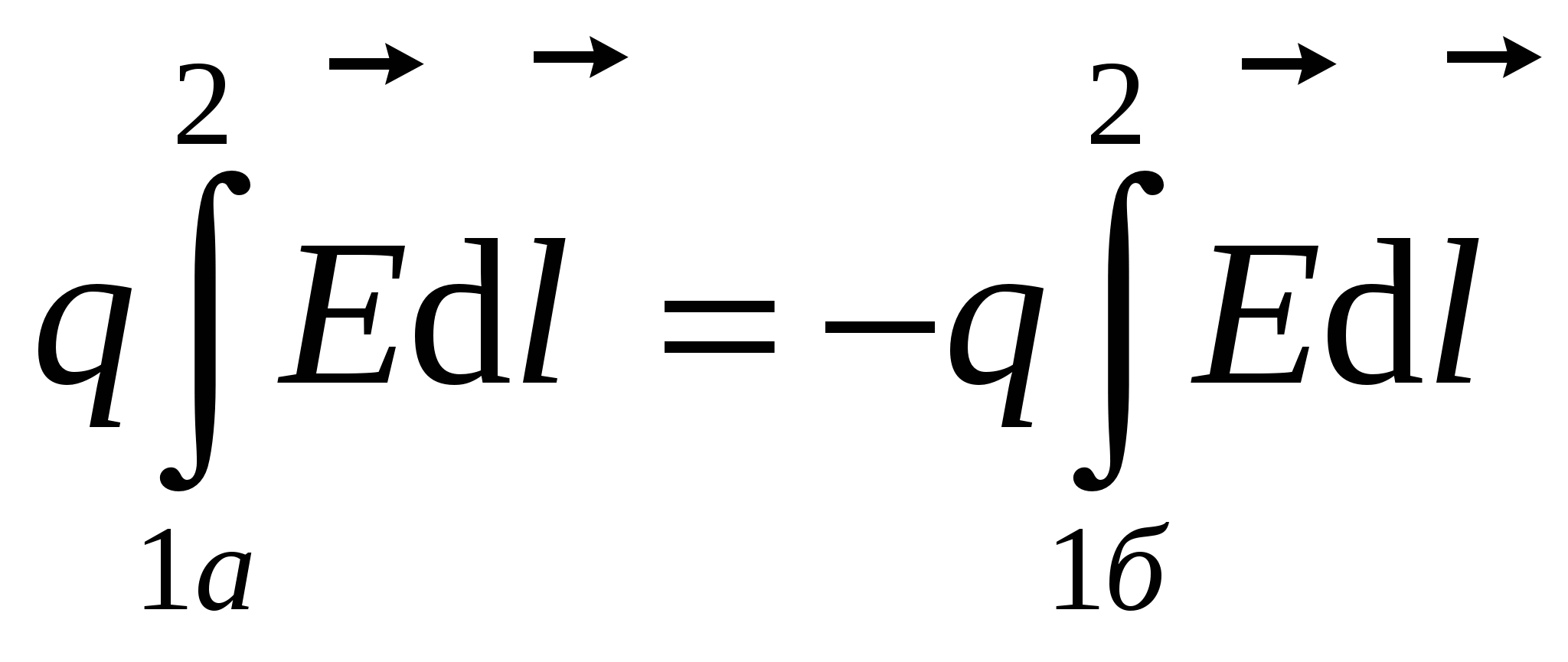

Figura 3.2
Nga sa më sipër rezulton se

(Integralet e modulit janë të barabartë, por shenjat janë të kundërta). Pastaj punoni në një rrugë të mbyllur:
 (3)
(3)
ose 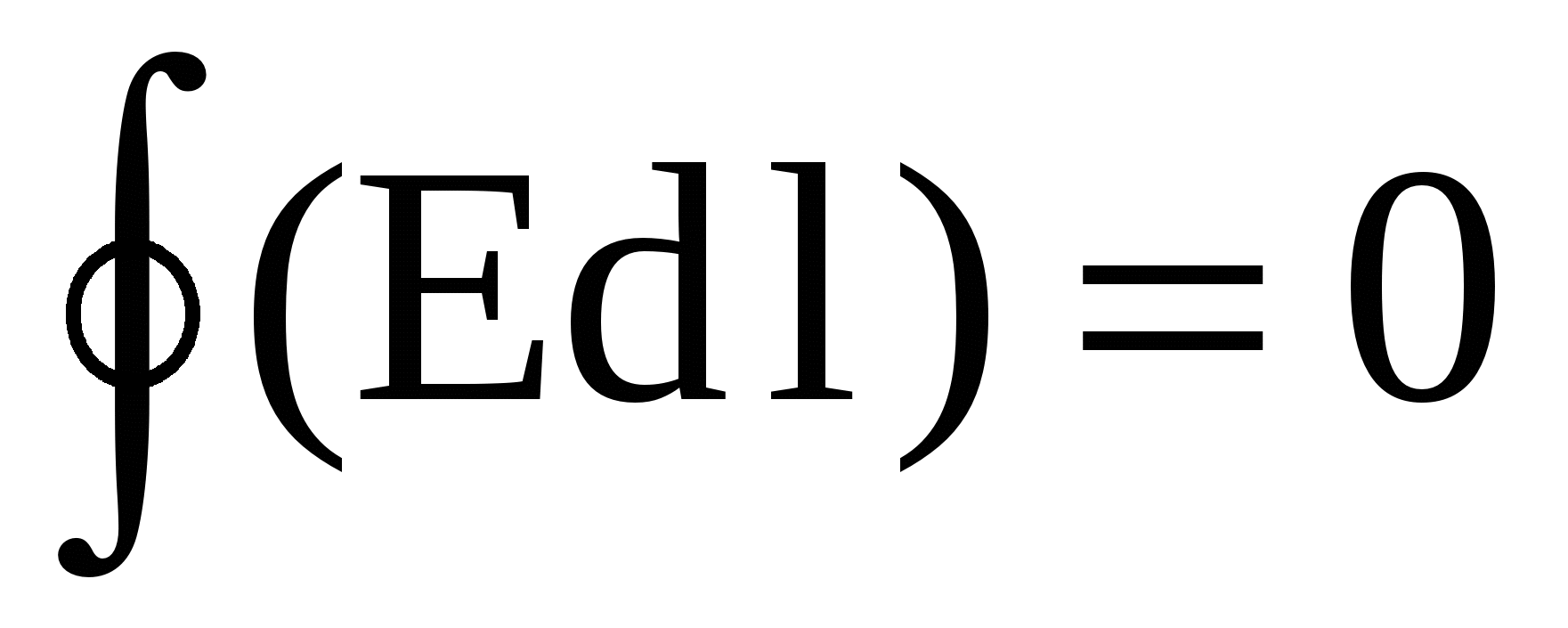 (4)
(4)
Një fushë me këto veti quhet potencial . Çdo fushë elektrostatike është potenciale.
Teorema e qarkullimit na lejon të nxjerrim një sërë përfundimesh të rëndësishme, praktikisht pa iu drejtuar llogaritjeve. Le të shqyrtojmë dy shembuj të thjeshtë që konfirmojnë këtë përfundim. 
Ne përdorim teoremën e Stokes, e cila thotë se qarkullimi i vektorit  përgjatë një konture arbitrare Lështë e barabartë me rrjedhën e rotorit të këtij vektori nëpër çdo sipërfaqe të shtrirë nga kjo kontur, d.m.th.
përgjatë një konture arbitrare Lështë e barabartë me rrjedhën e rotorit të këtij vektori nëpër çdo sipërfaqe të shtrirë nga kjo kontur, d.m.th.  . Në rastin e një fushe elektrostatike, kemi
. Në rastin e një fushe elektrostatike, kemi 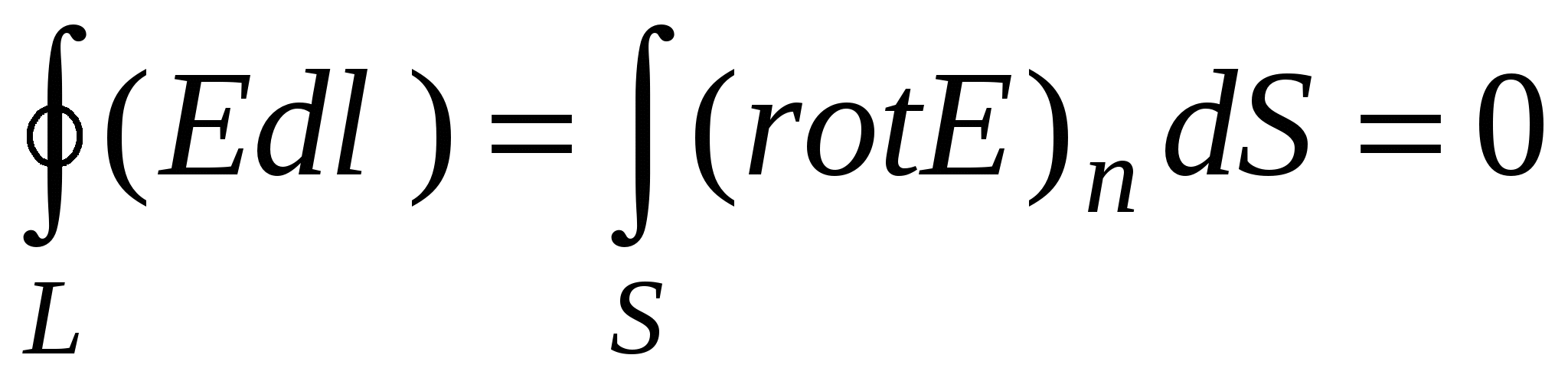 , pra, për shkak të arbitraritetit të formës së sipërfaqes, marrim
, pra, për shkak të arbitraritetit të formës së sipërfaqes, marrim 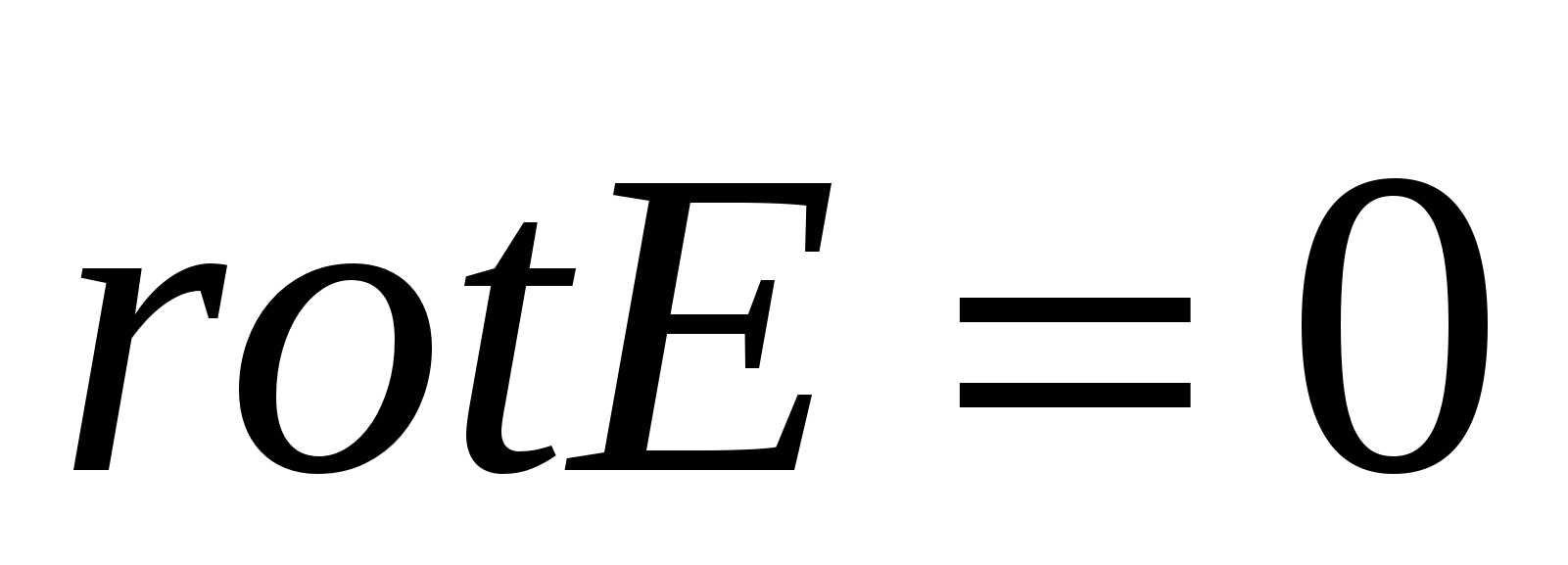 . Prandaj, nga natyra potenciale e fushës elektrostatike, rrjedh se fusha elektrostatike nuk është vorbull nëse .
(5)
. Prandaj, nga natyra potenciale e fushës elektrostatike, rrjedh se fusha elektrostatike nuk është vorbull nëse .
(5)
3.3. Energjia potenciale dhe potenciali i fushës elektrostatike
Një trup i vendosur në fushën e forcave potenciale ka energji potenciale, për shkak të së cilës puna kryhet nga forcat e fushës. Prandaj, puna mund të përfaqësohet si ndryshim në vlerat e energjive të mundshme që zotëron ngarkesa q" në pikat 1 dhe 2 të fushës së karikimit q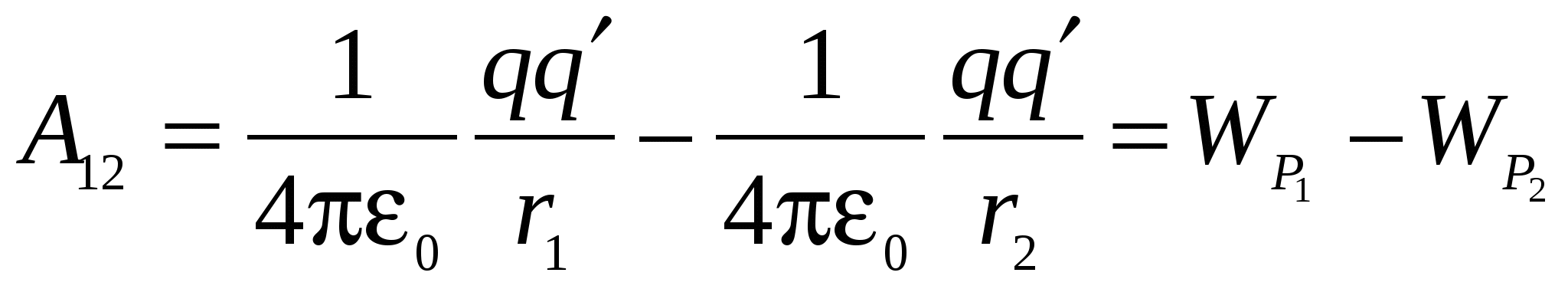
Mund të tregohet gjithashtu se, pasi 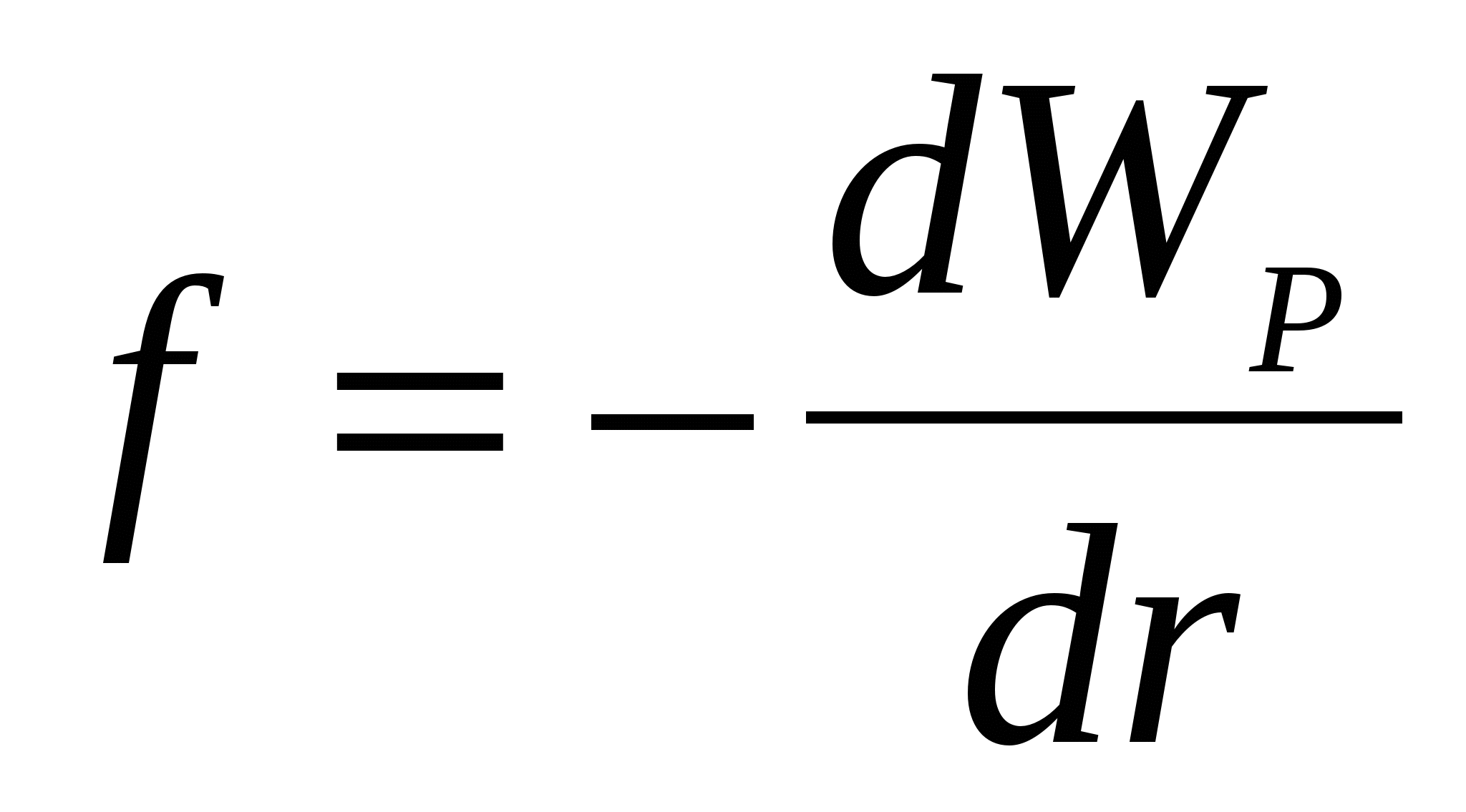 ,
, 
![]() .
.
Prandaj, për energjinë potenciale të ngarkesës në fushën e ngarkesës q marrim:
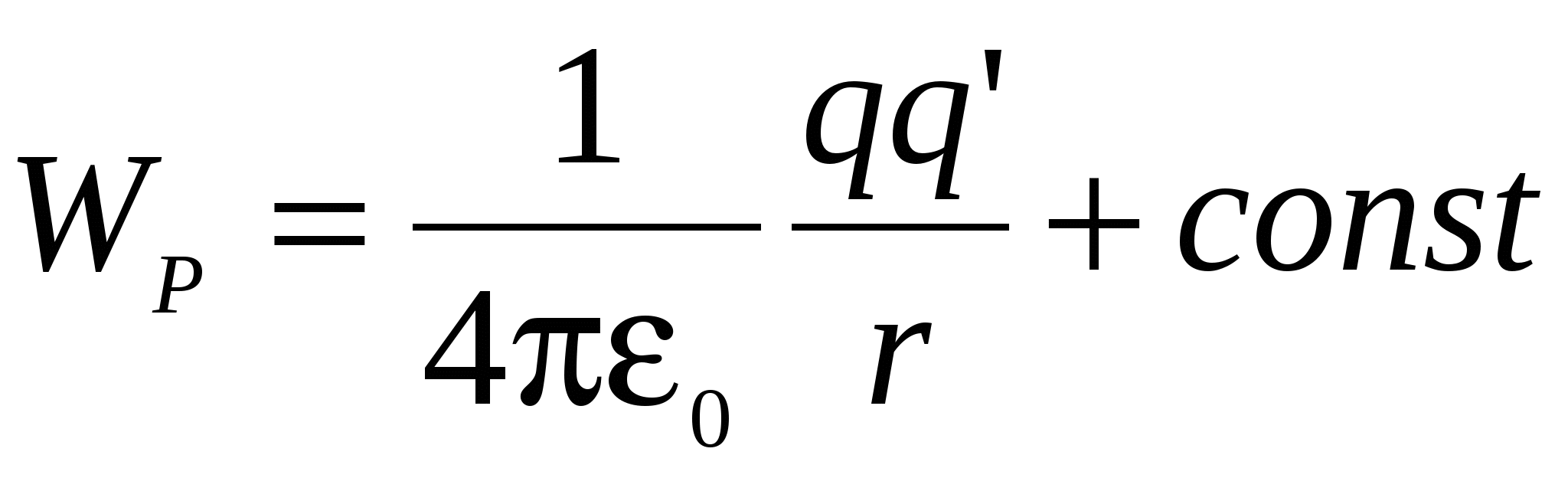 (6)
(6)
Kuptimi konst në (6) zakonisht zgjidhet në atë mënyrë që kur të hiqet ngarkesa q"
në pafundësi (  ) energjia potenciale zhduket. Në këtë kusht, rezulton se
) energjia potenciale zhduket. Në këtë kusht, rezulton se
 (7)
(7)
supozojmë q"
tarifë testimi. Atëherë energjia potenciale që zotëron ngarkesa e provës varet jo vetëm nga vlera e saj 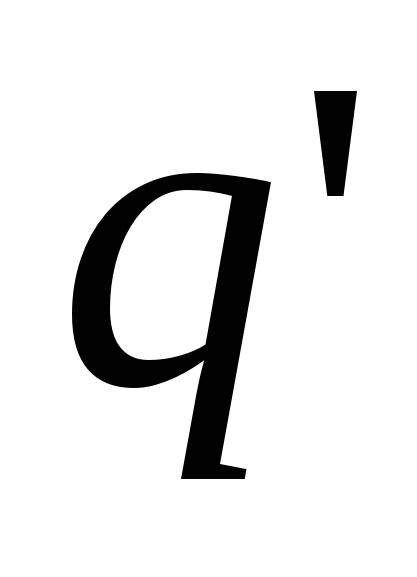 , por edhe mbi vlerën q dhe r, duke përcaktuar fushën. Prandaj, kjo energji mund të përdoret për të përshkruar fushën, ashtu siç është përdorur forca që vepron në një ngarkesë provë për këtë qëllim.
, por edhe mbi vlerën q dhe r, duke përcaktuar fushën. Prandaj, kjo energji mund të përdoret për të përshkruar fushën, ashtu siç është përdorur forca që vepron në një ngarkesë provë për këtë qëllim.
Tarifa të ndryshme testimi  ,
, 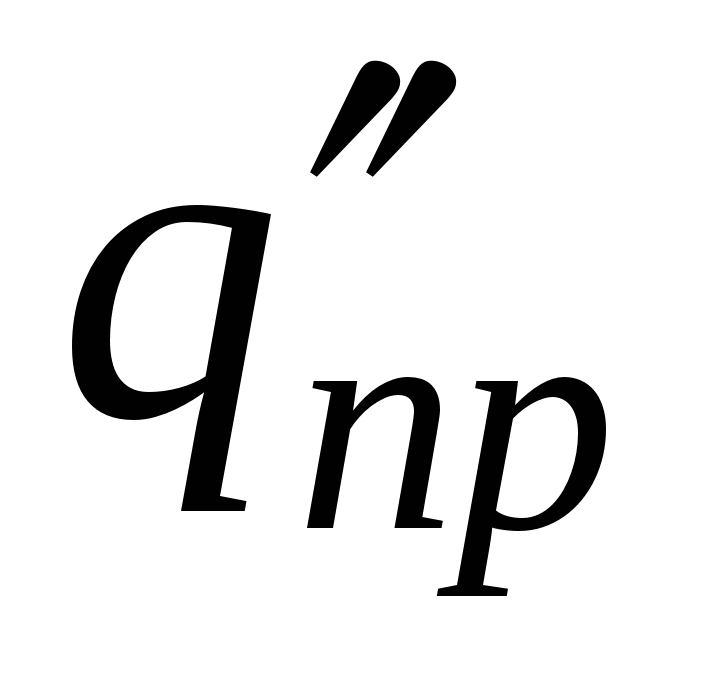 do të ketë energji të ndryshme në të njëjtën pikë të fushës
do të ketë energji të ndryshme në të njëjtën pikë të fushës  ,
, 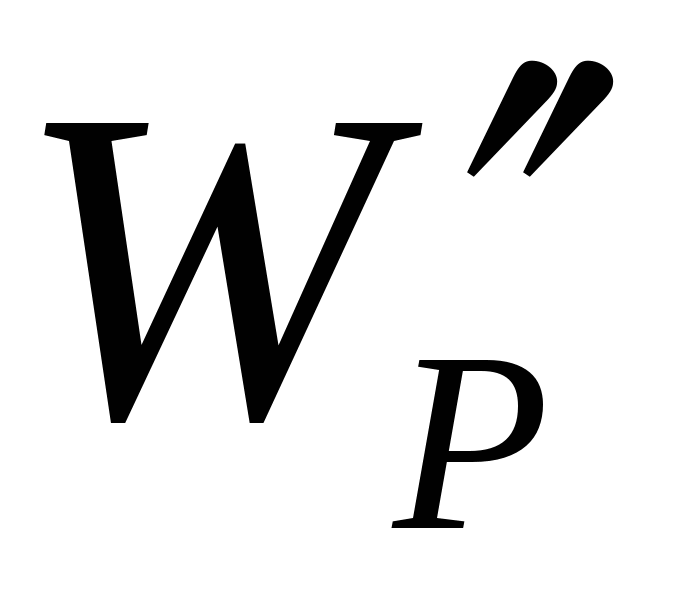 etj. Megjithatë, qëndrimi
etj. Megjithatë, qëndrimi 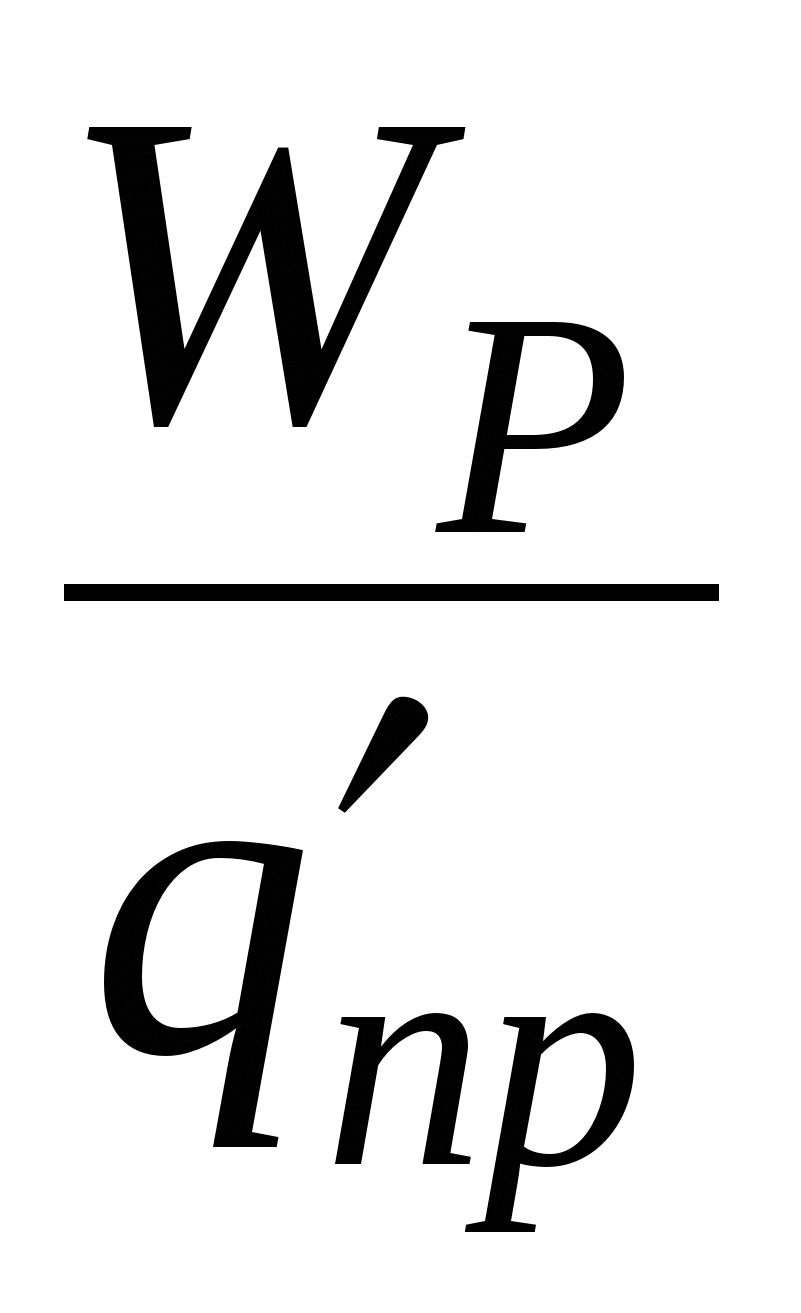 do të jetë e njëjtë për të gjitha tarifat. Vlera
do të jetë e njëjtë për të gjitha tarifat. Vlera
 (8)
(8)
thirrur potencial fushë në një pikë të caktuar dhe përdoret së bashku me forcën e fushës për të përshkruar fushat elektrike.
Siç vijon nga (8) Potenciali numerikisht është i barabartë me energjinë potenciale që ka një njësi ngarkesë pozitive në një pikë të caktuar të fushës.
Kështu, për fushën e mundshme të një ngarkese pikë, marrim shprehja e mëposhtme:
 (9)
(9)
Nëse fusha krijohet nga një sistem ngarkesash pikash q 1
, q 2
, …, q n, të vendosura përkatësisht në distanca r 1
, r 2
,…, r n deri në pikën e fushës ku ndodhet ngarkesa  , më pas puna e bërë nga forcat e kësaj fushe në ngarkim
, më pas puna e bërë nga forcat e kësaj fushe në ngarkim  , do të jetë e barabartë me shumën algjebrike të punës së forcave për secilën nga ngarkesat veç e veç:
, do të jetë e barabartë me shumën algjebrike të punës së forcave për secilën nga ngarkesat veç e veç:
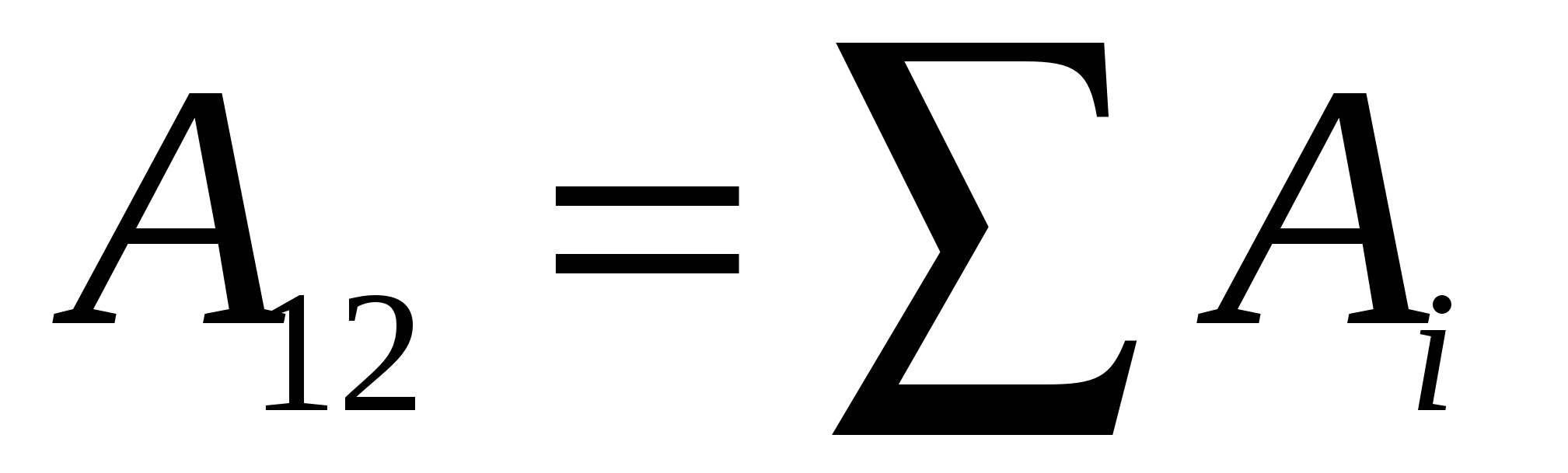 .
.
Por secila prej veprave  është e barabartë me:
është e barabartë me:
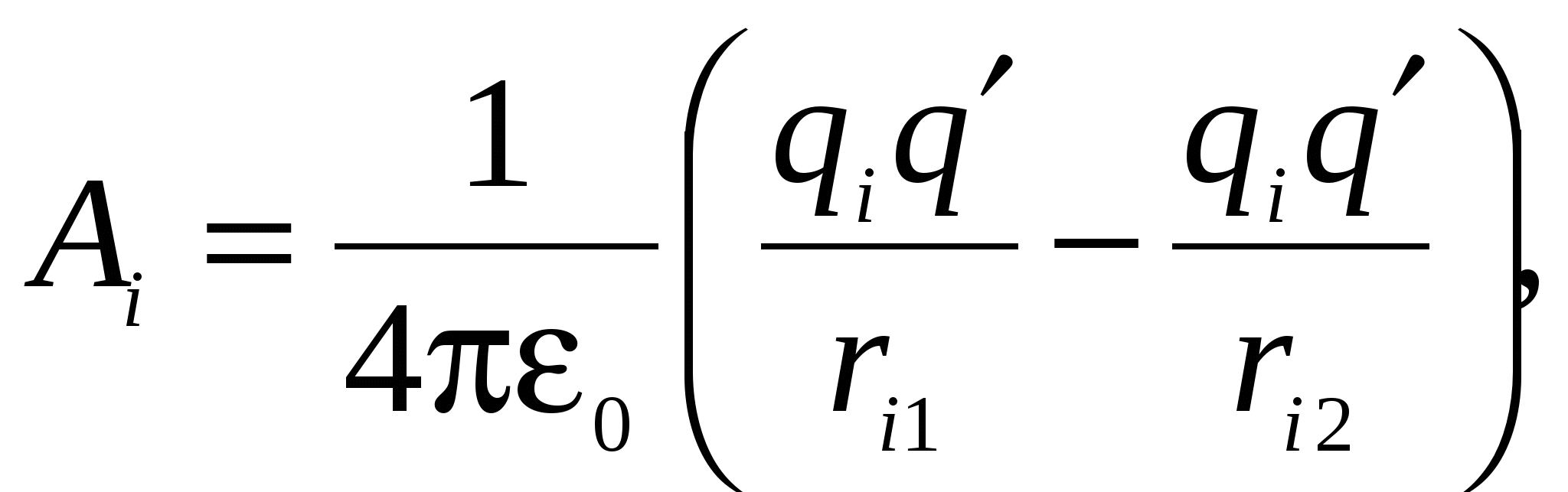
Ku  distanca e karikimit
distanca e karikimit 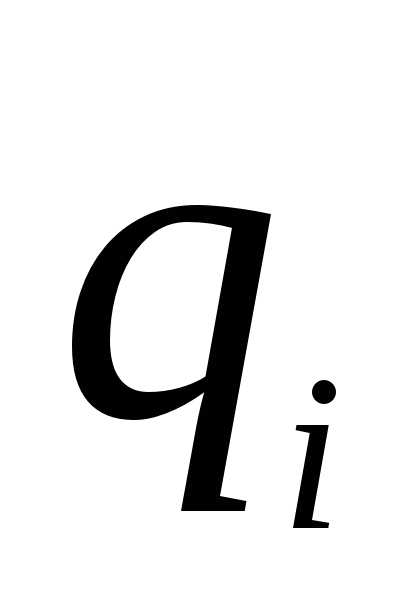 në pozicionin fillestar të ngarkesës,
në pozicionin fillestar të ngarkesës,  distanca nga ngarkesa në pozicionin përfundimtar të ngarkesës.
distanca nga ngarkesa në pozicionin përfundimtar të ngarkesës.
Rrjedhimisht:
 .
.
Krahasimi i kësaj shprehjeje me relacionin 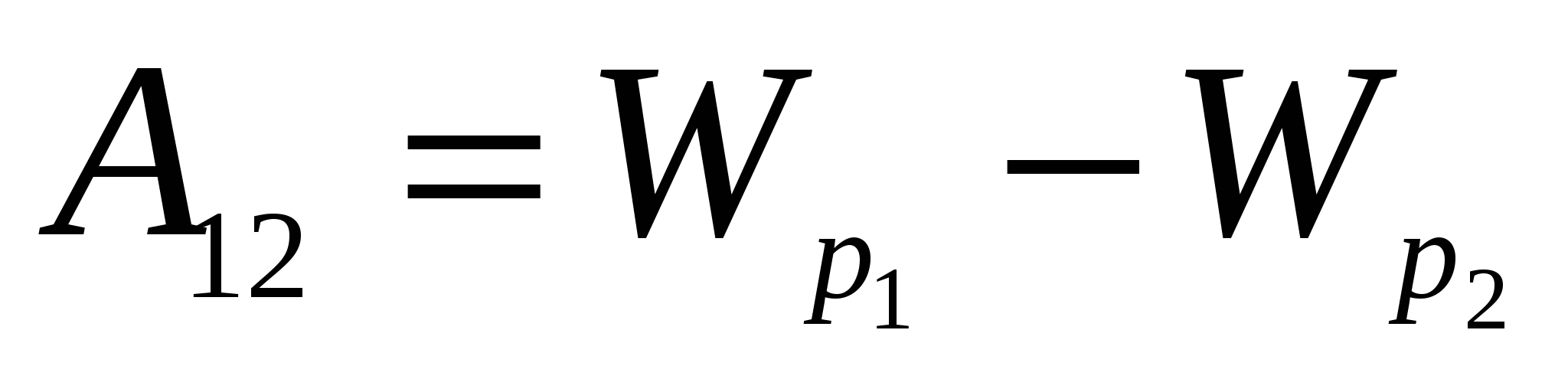 , marrim shprehjen për energjinë potenciale të ngarkesës në fushën e sistemit të ngarkesave:
, marrim shprehjen për energjinë potenciale të ngarkesës në fushën e sistemit të ngarkesave:
 , (10)
, (10)
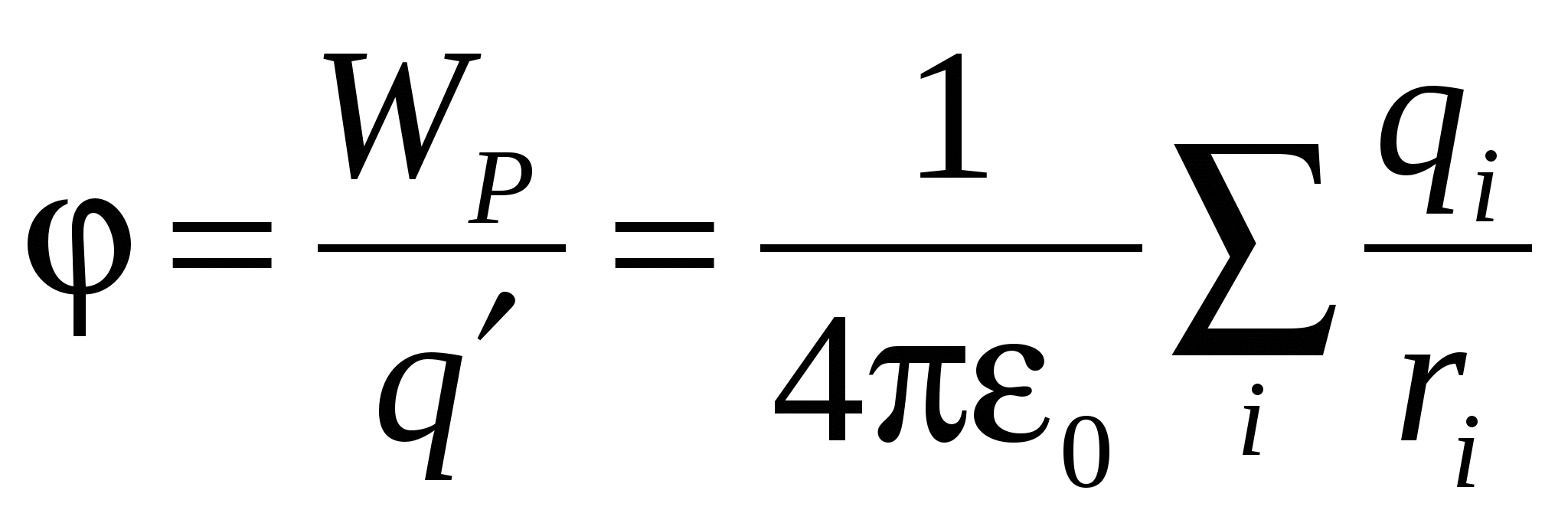 . (11).
. (11).
Për rrjedhojë, potenciali i fushës së krijuar nga sistemi i ngarkesave është i barabartë me shumën algjebrike të potencialeve të krijuara nga secila prej ngarkesave veç e veç.
Nga marrëdhënia 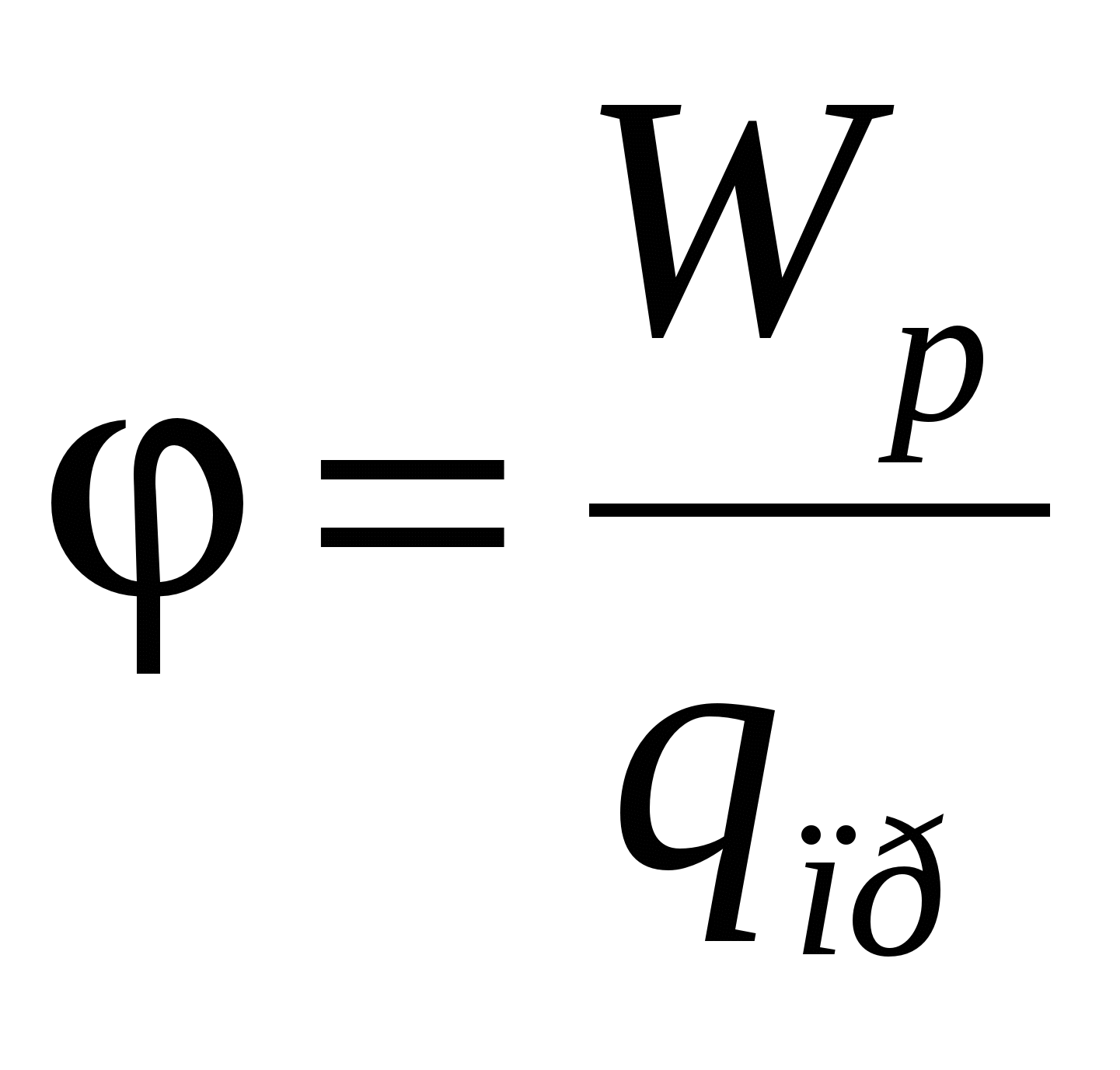 rrjedh se ngarkesa
rrjedh se ngarkesa  , i vendosur në pikën e fushës me potencial
, i vendosur në pikën e fushës me potencial  , ka energji potenciale
, ka energji potenciale  . Prandaj, puna e forcave të fushës në ngarkesë mund të shprehet në termat e ndryshimit potencial:
. Prandaj, puna e forcave të fushës në ngarkesë mund të shprehet në termat e ndryshimit potencial:
Pra, puna e bërë në akuzë forcat fushore, është e barabartë me produktin e ngarkesës dhe diferencën potenciale në pikat fillestare dhe përfundimtare. Nëse ngarkesa nga një pikë me potencial hiqet deri në pafundësi (ku potenciali është i barabartë me zero sipas kushtit), puna e forcave të fushës do të jetë e barabartë me
 ose
ose 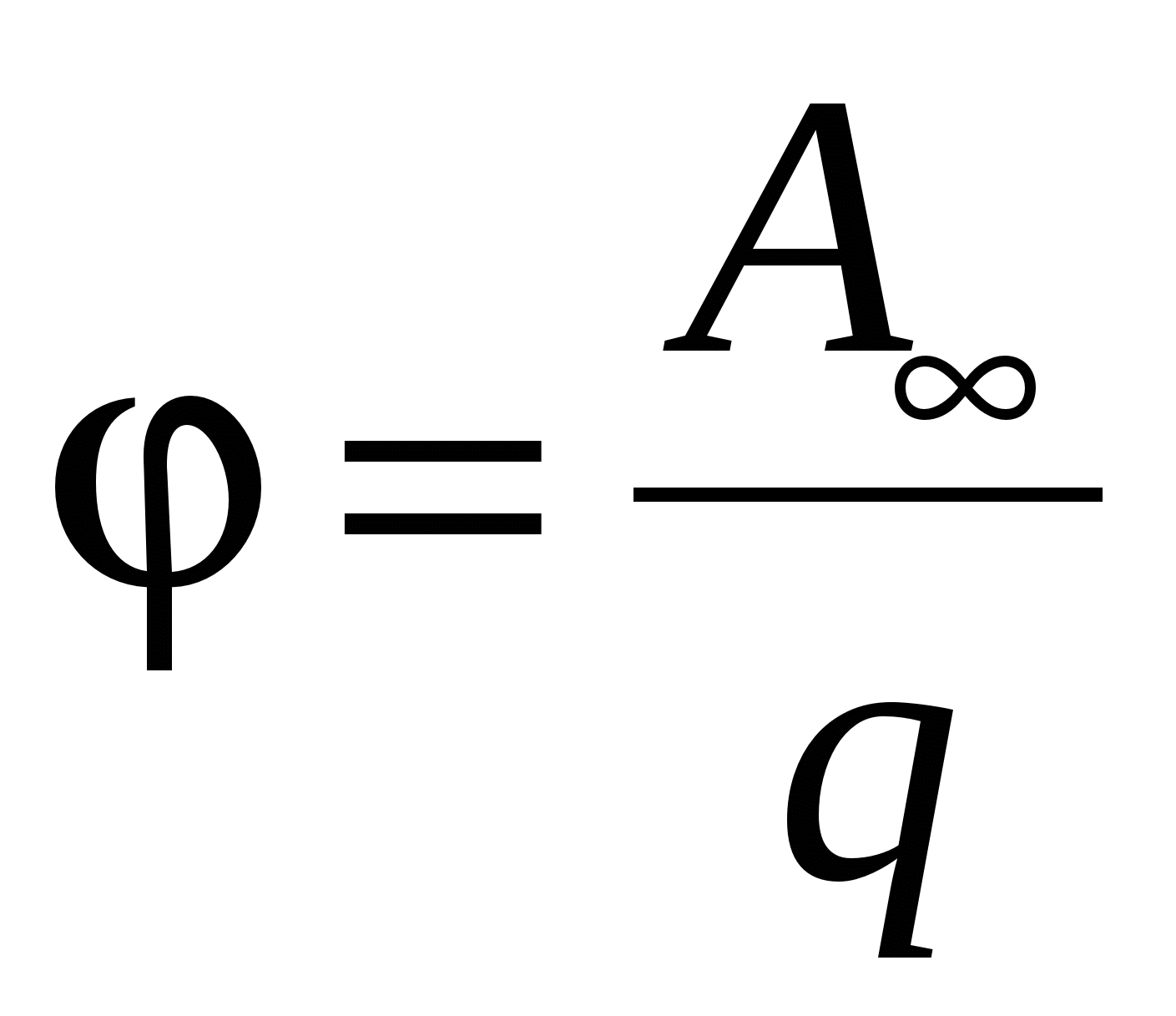 ,
,
T. e, potencial numerikisht është e barabartë me punë, e cila kryhet nga forcat e fushës në një ngarkesë pozitive njësi kur ajo largohet nga një pikë e caktuar e fushës në pafundësi, ose puna që duhet bërë kundër forcave të fushës elektrike për të zhvendosur një ngarkesë pozitive njësi nga pafundësi në një pikë të caktuar të fushës.
Njësia potenciale duhet marrë si potencial në një pikë të tillë të fushës, në mënyrë që të zhvendoset ngarkesa në të cilën nga pafundësia është e nevojshme të kryhet punë e barabartë me
1 xhaul (sistemi i njësive "Ci")

Nga këtu 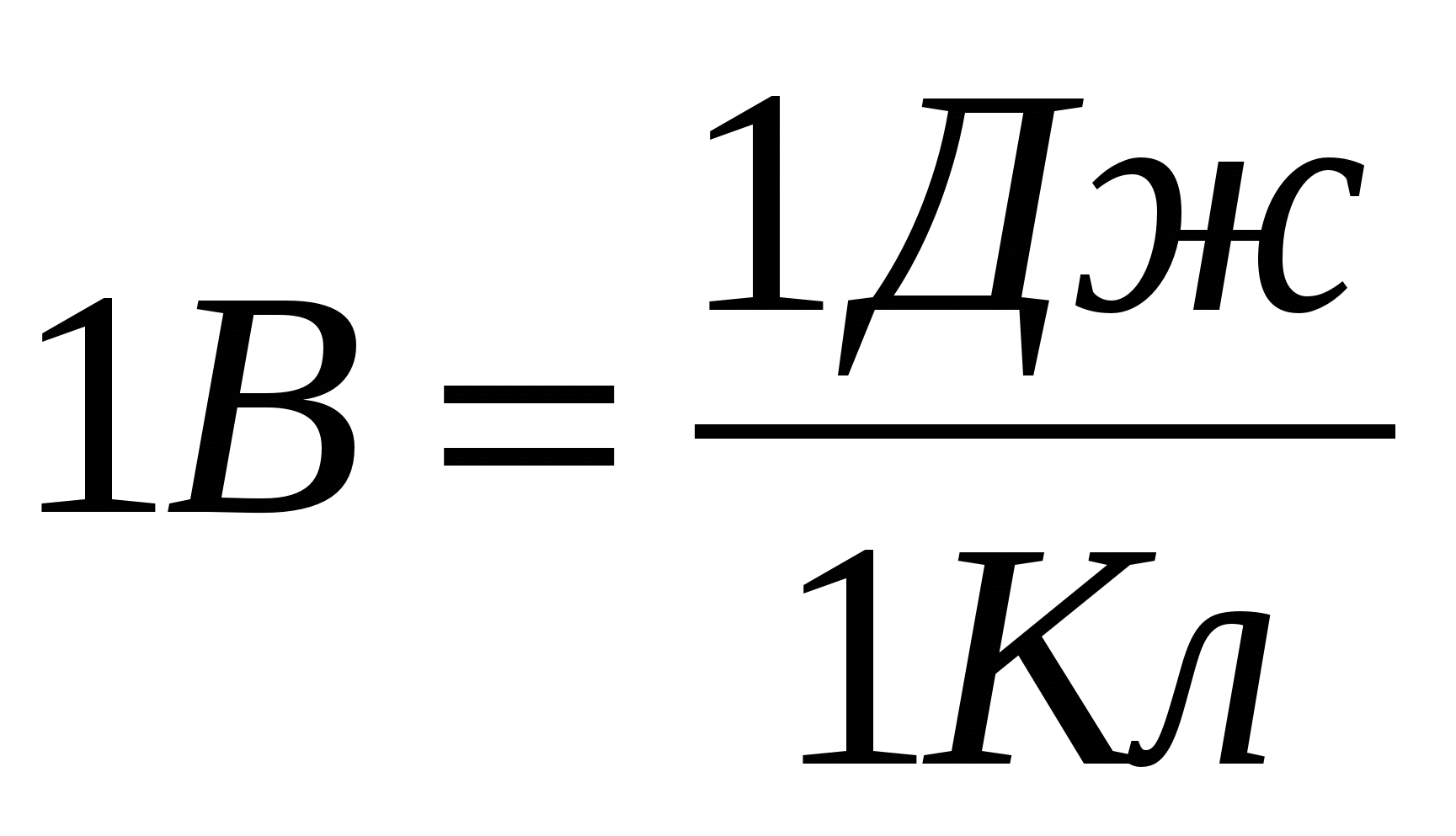 .
.
3.4. Dipol në një fushë elektrostatike
E 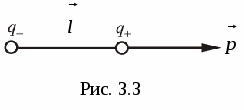 dipol elektrik
quhet kombinimi i dy tarifa të barabarta shenjë e kundërt, e vendosur në një distancë nga njëra-tjetra l, e cila është e vogël në krahasim me distancën e tyre me pikat në të cilat përcaktohet fusha dipole.
dipol elektrik
quhet kombinimi i dy tarifa të barabarta shenjë e kundërt, e vendosur në një distancë nga njëra-tjetra l, e cila është e vogël në krahasim me distancën e tyre me pikat në të cilat përcaktohet fusha dipole.
Produkti i ngarkesës dhe distanca ndërmjet ngarkesave p=ql
thirrur moment dipol
. Për një përcaktim të plotë të dipolit, është gjithashtu e nevojshme të specifikohet orientimi i boshtit të dipolit në hapësirë. Prandaj, momenti dipol duhet të konsiderohet si një vektor  . Këtij vektori i caktohet një drejtim nga ngarkesa negative në pozitive(fig.3.3). Nëse futni rreze - vektor
. Këtij vektori i caktohet një drejtim nga ngarkesa negative në pozitive(fig.3.3). Nëse futni rreze - vektor 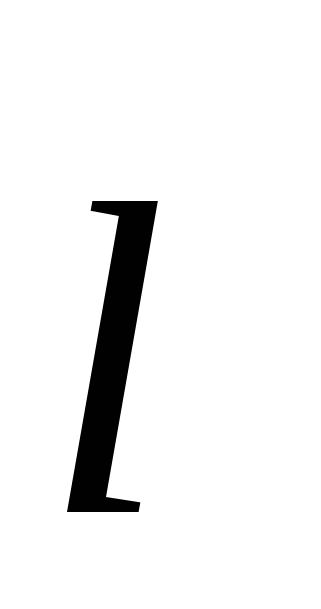 shpenzuar nga - q te + q, atëherë momenti dipol mund të përfaqësohet si:
shpenzuar nga - q te + q, atëherë momenti dipol mund të përfaqësohet si:
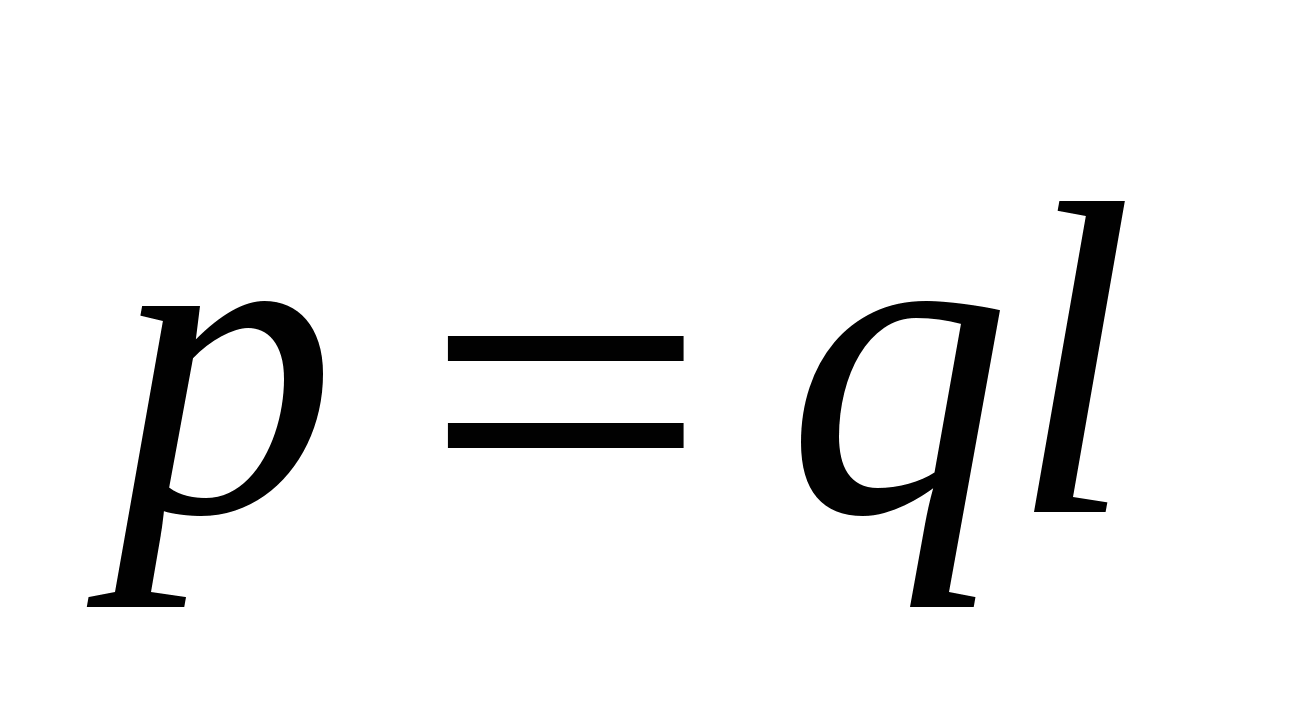 .
(13)
.
(13)
Nëse një dipol vendoset në një fushë elektrike uniforme, ngarkesat që formojnë dipolin janë q dhe + q
veprohet nga forca me përmasa të barabarta, por me drejtim të kundërt  dhe
dhe  (Fig. 14). Këto forca formojnë një palë forcash, krahu i të cilave është i barabartë me
(Fig. 14). Këto forca formojnë një palë forcash, krahu i të cilave është i barabartë me 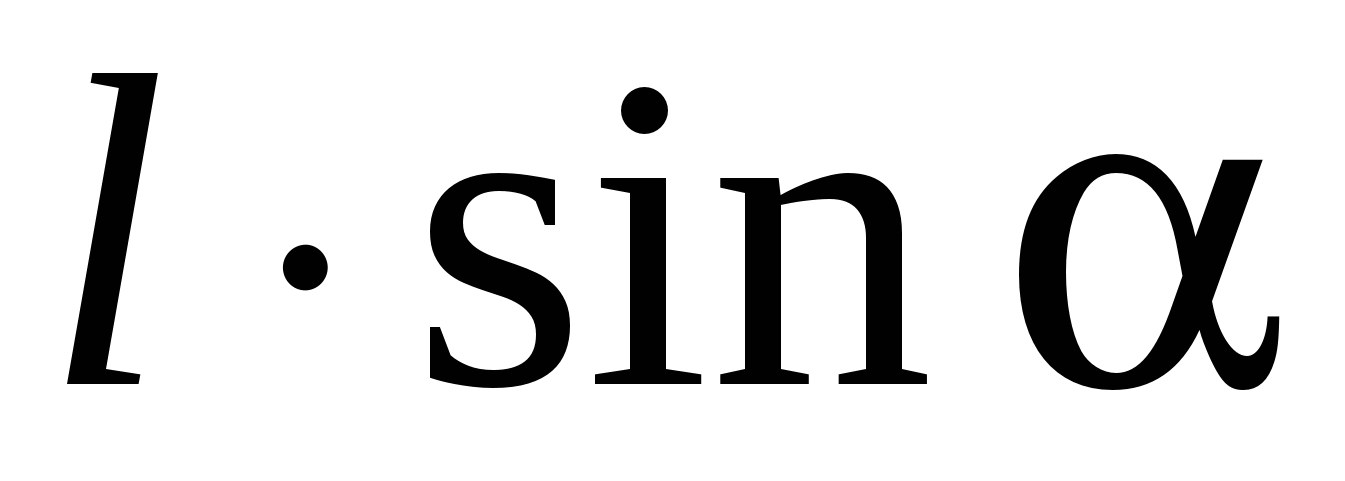 , d.m.th., varet nga orientimi i dipolit në lidhje me fushën. Moduli i secilës prej forcave është qE. Duke e shumëzuar me shpatullën, marrim vlerën e momentit të një çifti forcash që veprojnë në dipol:
, d.m.th., varet nga orientimi i dipolit në lidhje me fushën. Moduli i secilës prej forcave është qE. Duke e shumëzuar me shpatullën, marrim vlerën e momentit të një çifti forcash që veprojnë në dipol:
Ku R– moment elektrik dipol.
AT  forma vektoriale:
forma vektoriale:
 .
(15)
.
(15)
Moment  tenton të rrotullojë dipolin në mënyrë që momenti i tij
tenton të rrotullojë dipolin në mënyrë që momenti i tij  vendosur në drejtim të fushës.
vendosur në drejtim të fushës.
Për të rritur këndin ndërmjet vektorëve dhe në dα Puna duhet të bëhet kundër forcave që veprojnë në dipol:
Kjo punë shkon për të rritur energjinë potenciale W, e cila ka një dipol në një fushë elektrike, d.m.th.
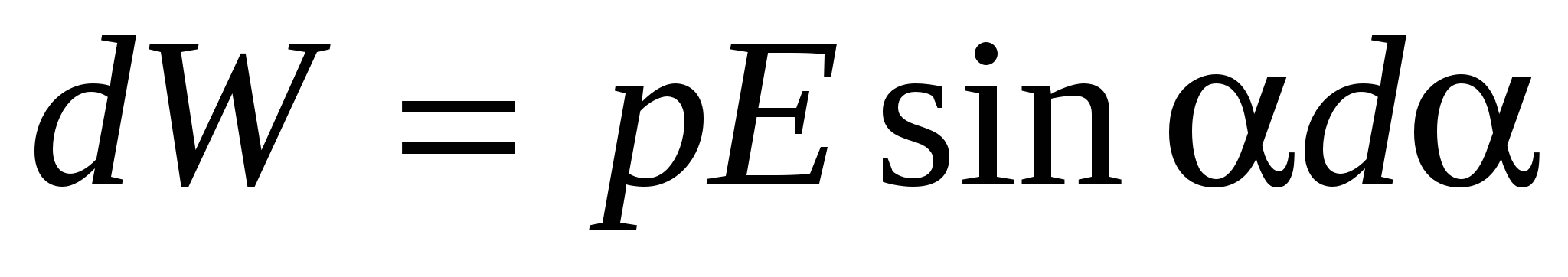 (16)
(16)
Integrimi (16) jep shprehjen për energjinë potenciale të një dipoli në një fushë elektrike:
Duke supozuar konst=0 , marrim
AT  duke zgjedhur konst=0
, supozojmë se energjia e dipolit do të jetë zero kur dipoli vendoset pingul me drejtimin e fushës. Vlera më e vogël e energjisë e barabartë me ( -pe), fitohet kur dipoli është i orientuar në drejtim të fushës, më i madhi, i barabartë me pE, kur drejtohet në drejtim të kundërt me vektorin
.
duke zgjedhur konst=0
, supozojmë se energjia e dipolit do të jetë zero kur dipoli vendoset pingul me drejtimin e fushës. Vlera më e vogël e energjisë e barabartë me ( -pe), fitohet kur dipoli është i orientuar në drejtim të fushës, më i madhi, i barabartë me pE, kur drejtohet në drejtim të kundërt me vektorin
.
Në një fushë johomogjene, forcat që veprojnë në ngarkesat e dipolit nuk janë të njëjta. Për dipolet e vogla të forcës f 1 dhe
f 2 mund të konsiderohet afërsisht kolinear. Le të supozojmë se fusha ndryshon më shpejt në drejtim X, që përkon me drejtimin
në vendin ku ndodhet dipoli (Fig. 3.5). ngarkesë pozitive dipoli zhvendoset në lidhje me negativin në drejtim X nga shuma 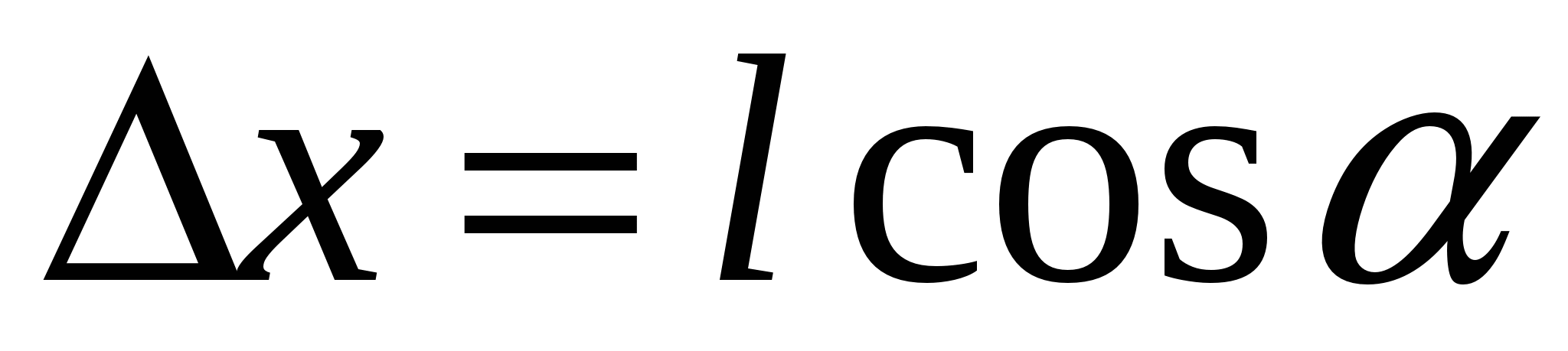 . Prandaj, forca e fushës në pikat ku vendosen ngarkesat ndryshon me Δ E. Që nga shuma e forcave
. Prandaj, forca e fushës në pikat ku vendosen ngarkesat ndryshon me Δ E. Që nga shuma e forcave  dhe
dhe 
 ose ,
(19)
ose ,
(19)
 , pastaj
, pastaj
 , (20)
, (20)
Ku  është gradienti i vektorit të forcës së fushës elektrike. Kështu, në një fushë elektrike johomogjene, përveç momentit rrotullues, ekziston edhe një forcë f, nën veprimin e së cilës dipoli ose do të tërhiqet në rajonin e një fushe më të fortë (α 0) ose do të shtyhet jashtë saj (α> 90 0).
është gradienti i vektorit të forcës së fushës elektrike. Kështu, në një fushë elektrike johomogjene, përveç momentit rrotullues, ekziston edhe një forcë f, nën veprimin e së cilës dipoli ose do të tërhiqet në rajonin e një fushe më të fortë (α 0) ose do të shtyhet jashtë saj (α> 90 0).
Shprehja për forcën mund të merret nga (18), duke marrë parasysh se f= – .
.
3.5. Marrëdhënia midis fuqisë dhe potencialit të fushës elektrostatike
Forca e fushës elektrike - madhësia, numerikisht e barabartë me forcën duke vepruar sipas akuzës. Potenciali është një vlerë numerikisht e barabartë me energjinë potenciale të ngarkesës. Kështu, duhet të ketë një marrëdhënie midis këtyre sasive, e ngjashme me marrëdhënien midis energjisë potenciale dhe forcës (d.m.th.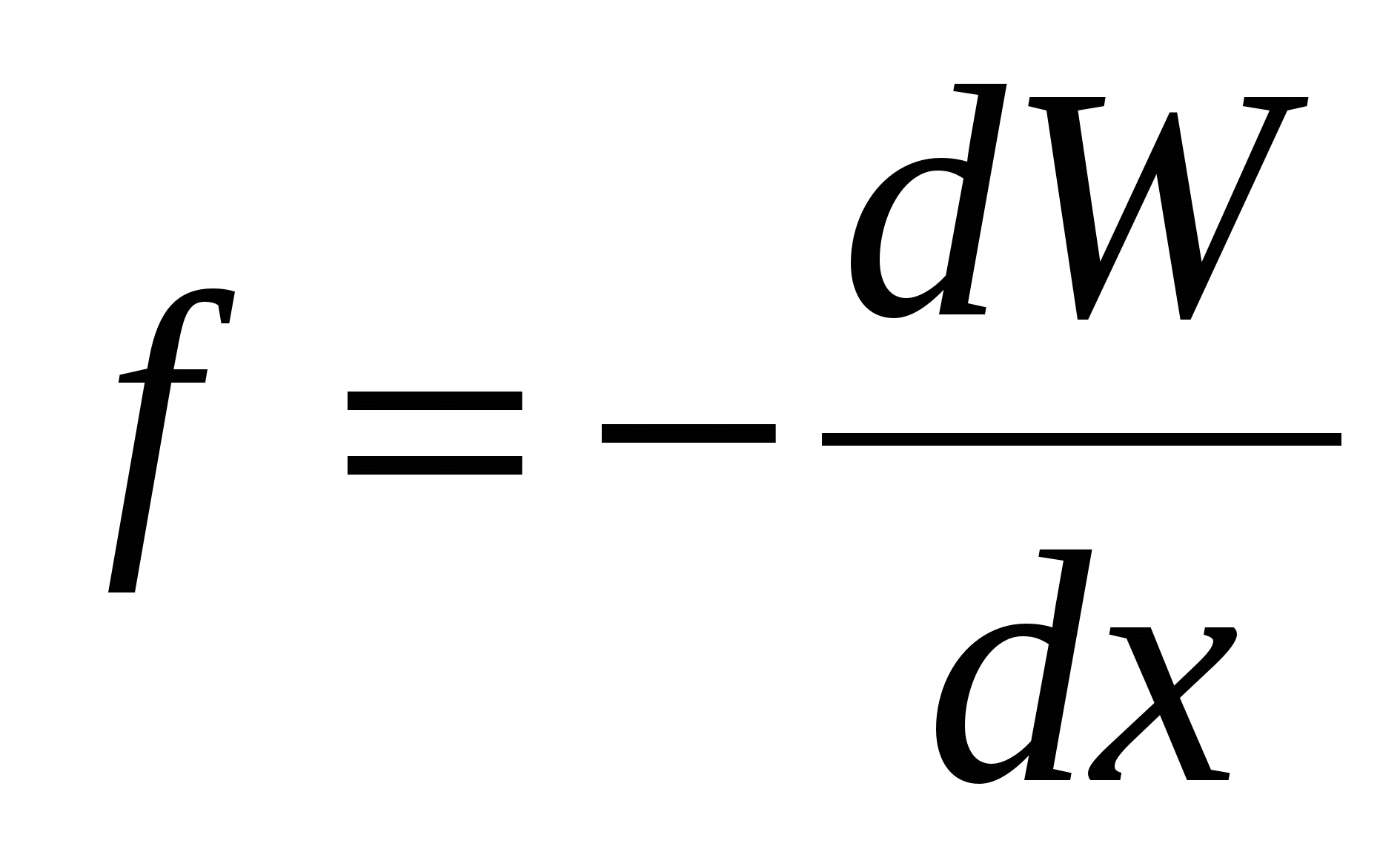 ). Puna e forcave të fushës mbi ngarkesën në segmentin e rrugës mund të paraqitet si
). Puna e forcave të fushës mbi ngarkesën në segmentin e rrugës mund të paraqitet si  , dhe zvogëlimi i energjisë potenciale të ngarkesës, që do të lindë në këtë rast: . Prej barazisë
, dhe zvogëlimi i energjisë potenciale të ngarkesës, që do të lindë në këtë rast: . Prej barazisë  ne gjejme:
ne gjejme: 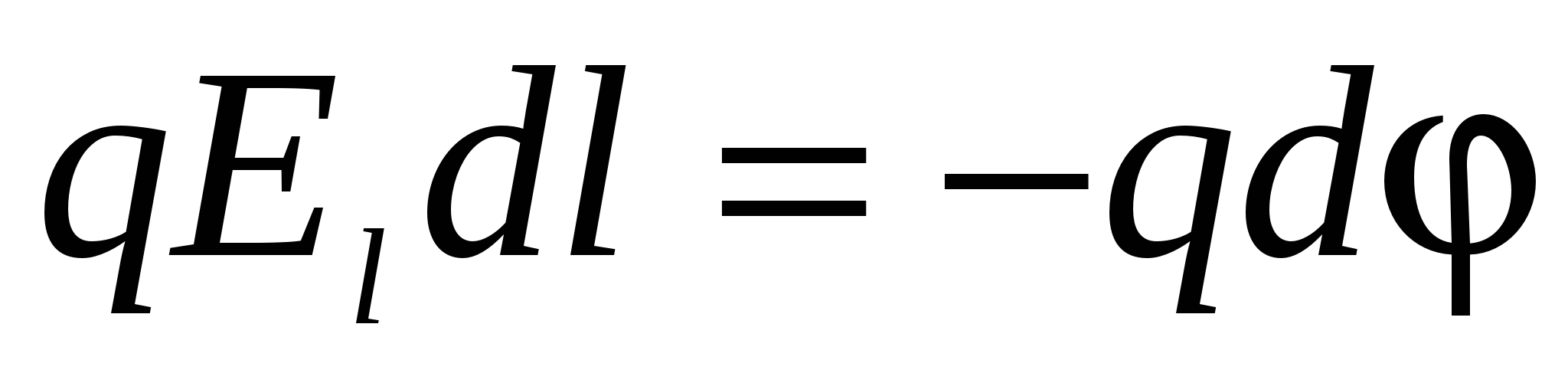 ose
ose 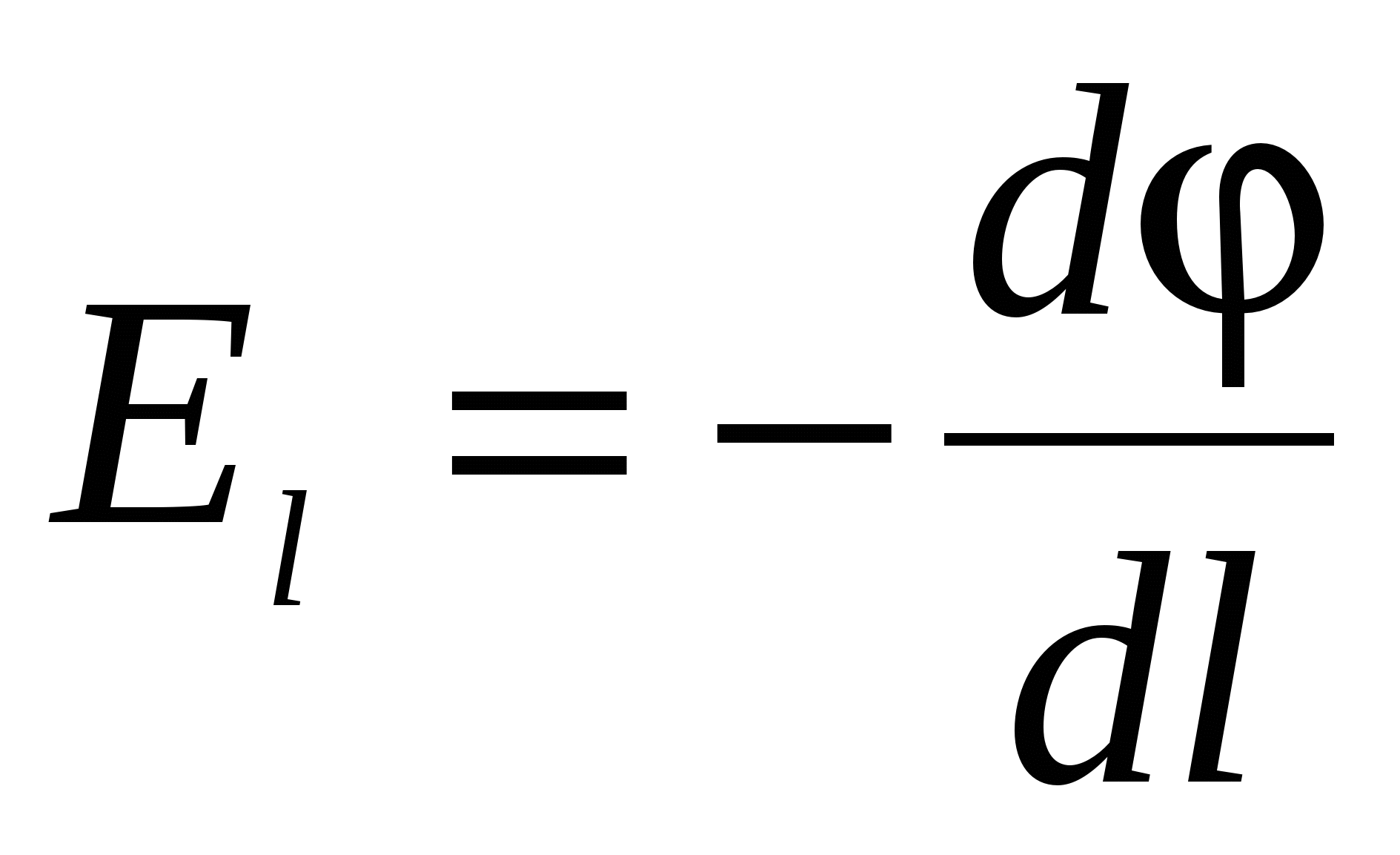 , (21)
, (21)
Ku përmes  drejtim i zgjedhur në mënyrë arbitrare.
drejtim i zgjedhur në mënyrë arbitrare.
 ,
, 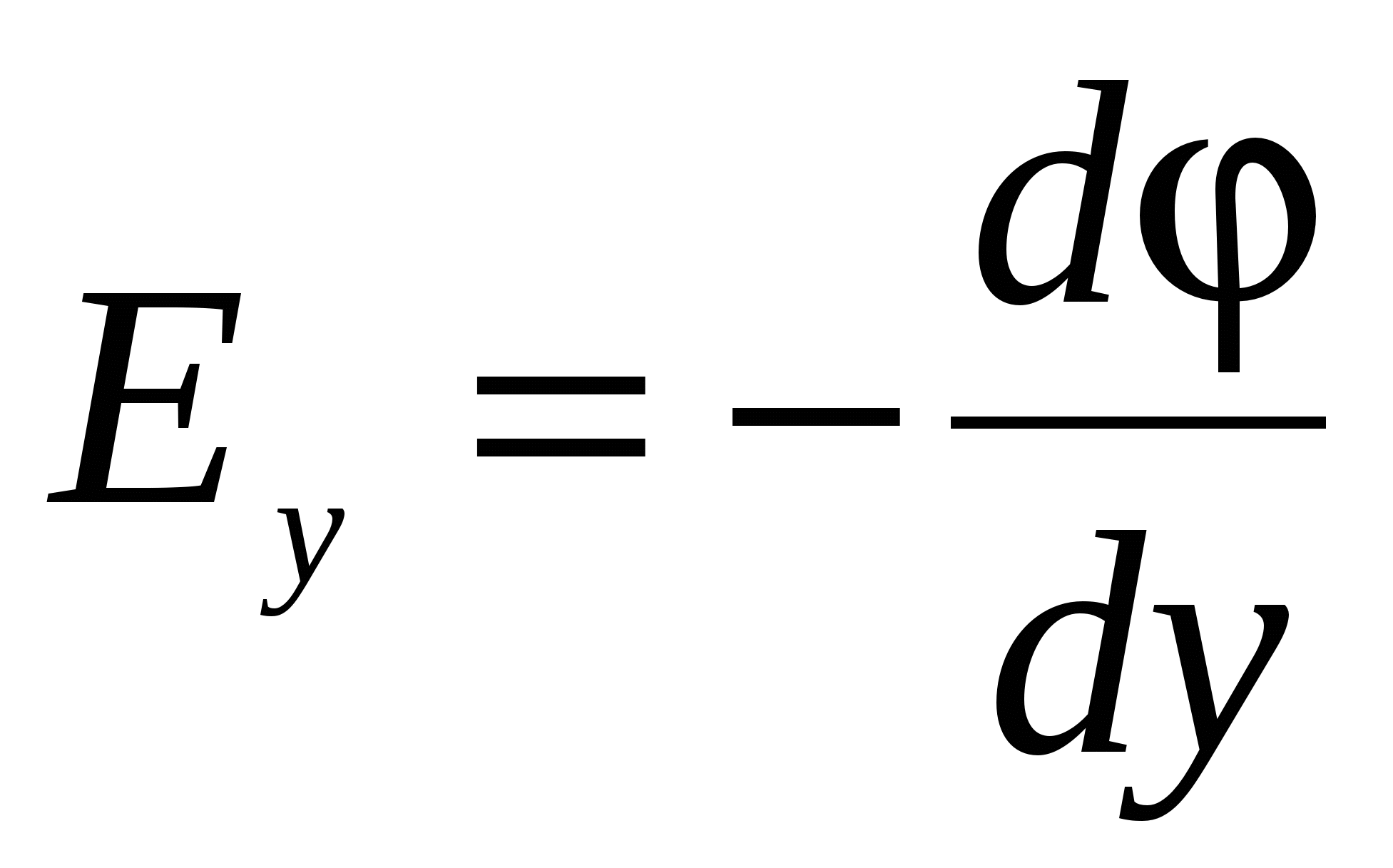 ,
,  , (22)
, (22)
Ku  ortet e boshteve të koordinatave, d.m.th., vektorët njësi. Vektor me komponentë
ortet e boshteve të koordinatave, d.m.th., vektorët njësi. Vektor me komponentë 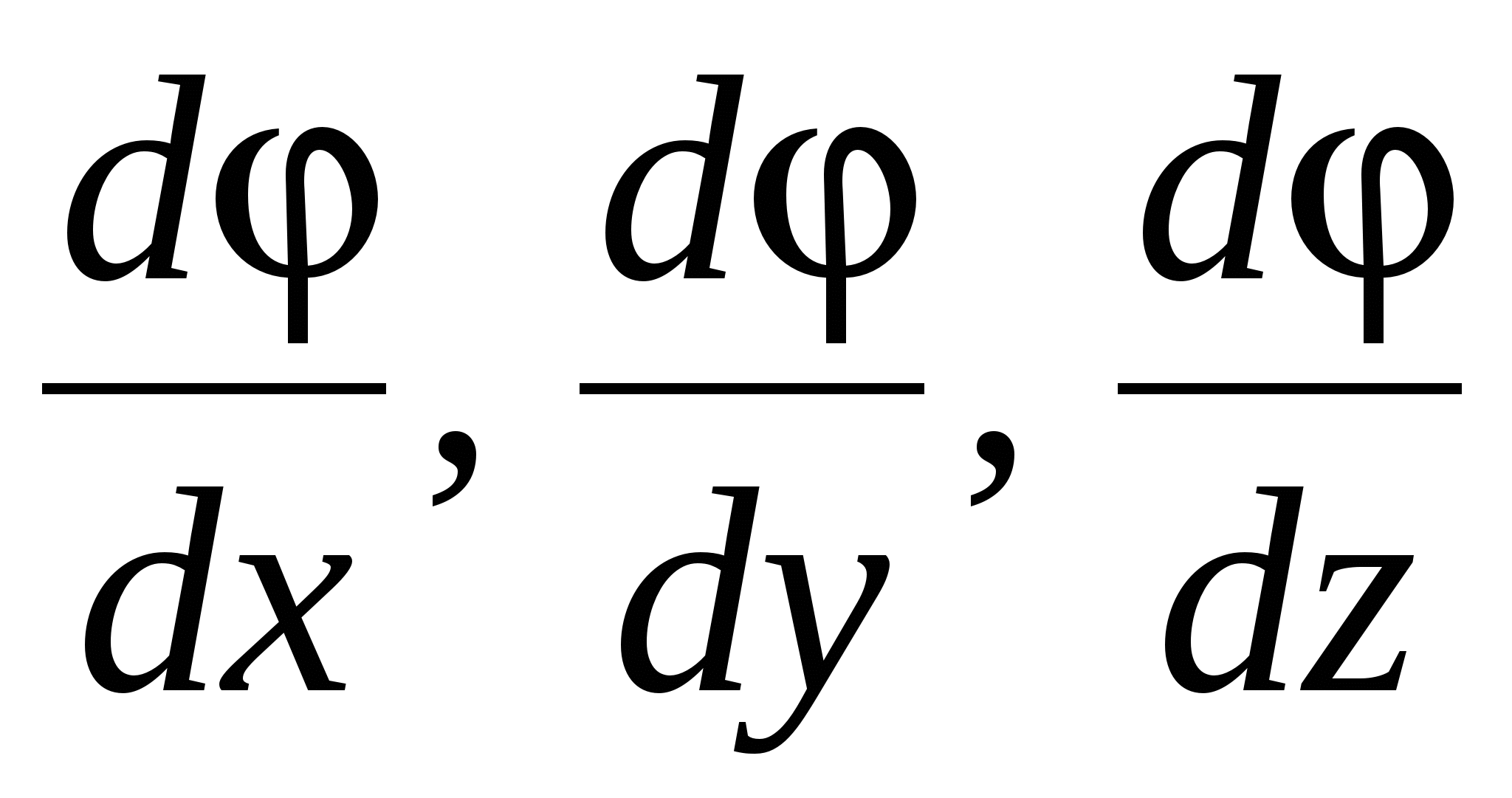 , ku
, ku  funksioni skalar i koordinatave
funksioni skalar i koordinatave  thirrur gradient funksionon dhe shënohet me simbolin
thirrur gradient funksionon dhe shënohet me simbolin  (ose
(ose 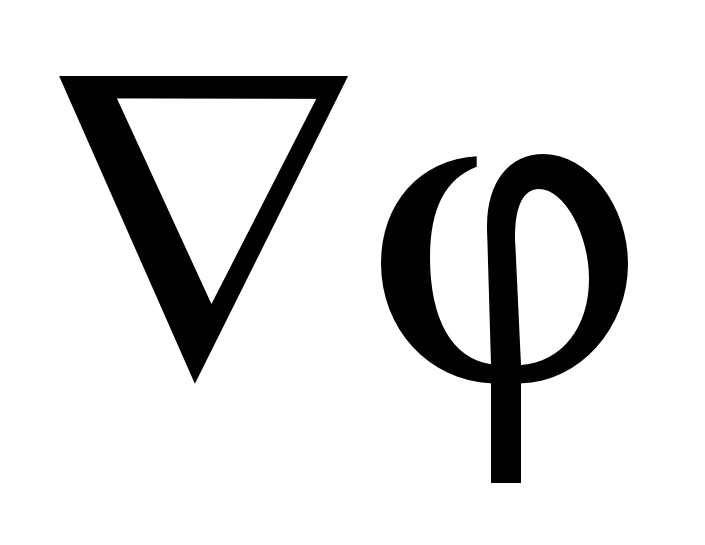 , ku
, ku  është operatori nabla). Pra, gradienti i mundshëm është:
është operatori nabla). Pra, gradienti i mundshëm është:
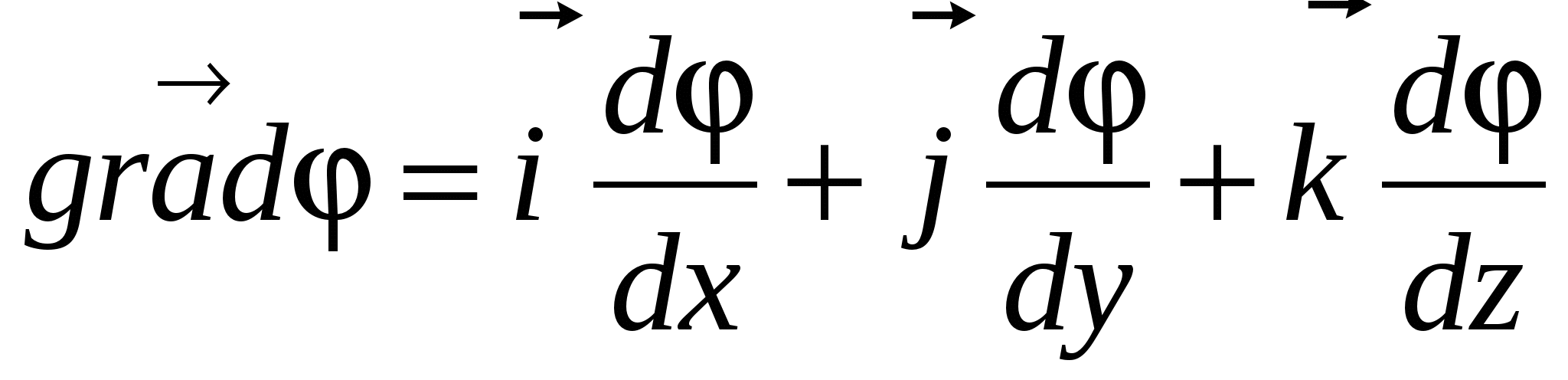 (24)
(24)
Dhe nga (23) dhe (24) rrjedh se
 (25)
(25)
Meqenëse gradienti është një vektor që tregon drejtimin e ndryshimit më të shpejtë të një sasie, vlera e së cilës ndryshon nga një pikë në hapësirë në tjetrën, atëherë gradienti i potencialit 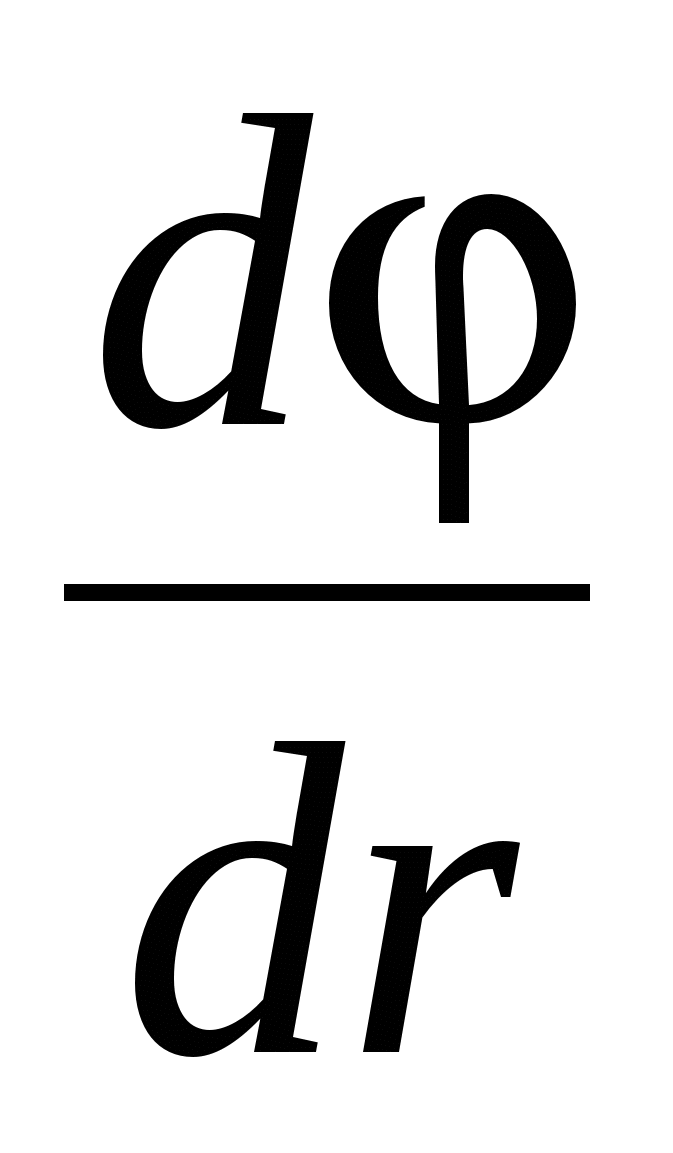 (ku r-radius-vektor) është një vektor i drejtuar në drejtim të rritjes më të shpejtë të potencialit, numerikisht i barabartë me shpejtësinë e ndryshimit të tij për njësi gjatësi në këtë drejtim.
(ku r-radius-vektor) është një vektor i drejtuar në drejtim të rritjes më të shpejtë të potencialit, numerikisht i barabartë me shpejtësinë e ndryshimit të tij për njësi gjatësi në këtë drejtim.
Sepse 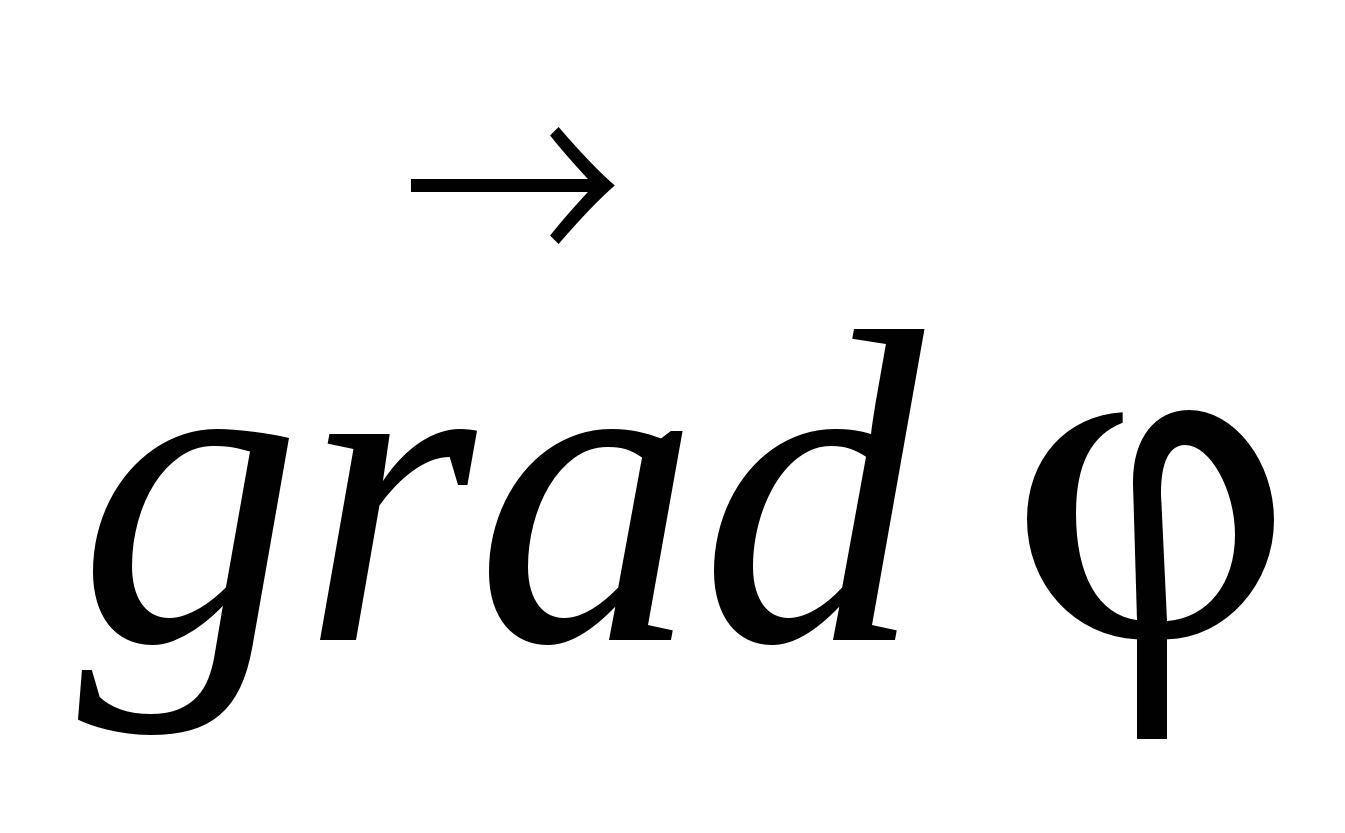 është një sasi vektoriale, atëherë moduli i saj shprehet si:
është një sasi vektoriale, atëherë moduli i saj shprehet si:
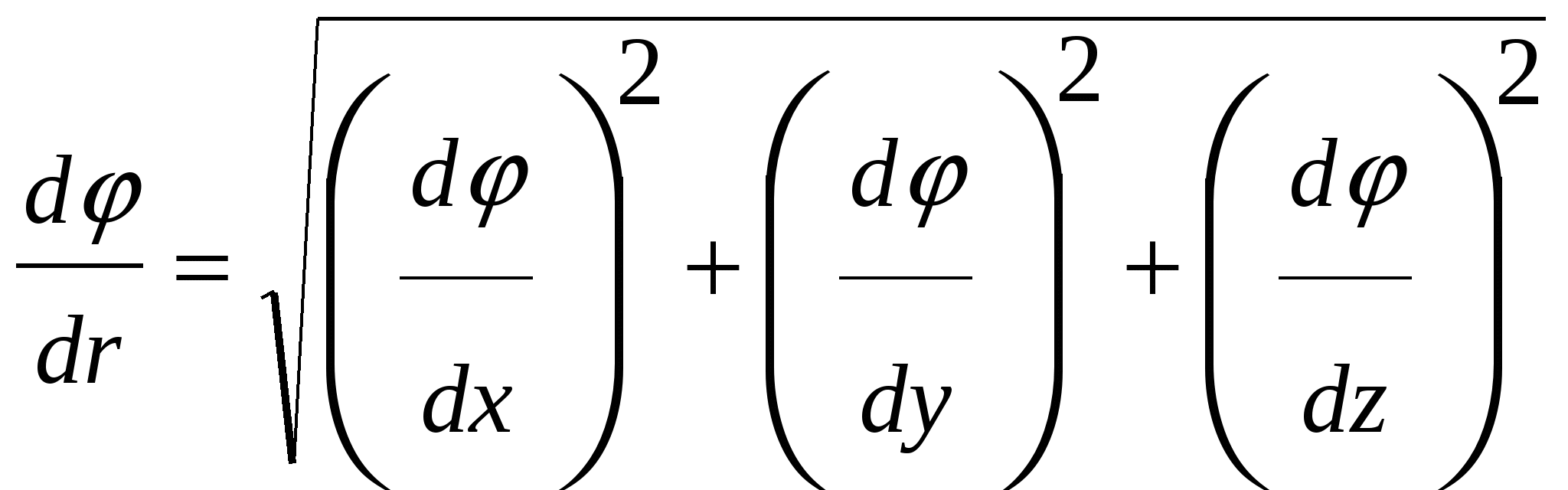 , (26)
, (26)
Ashtu si moduli i një vektori 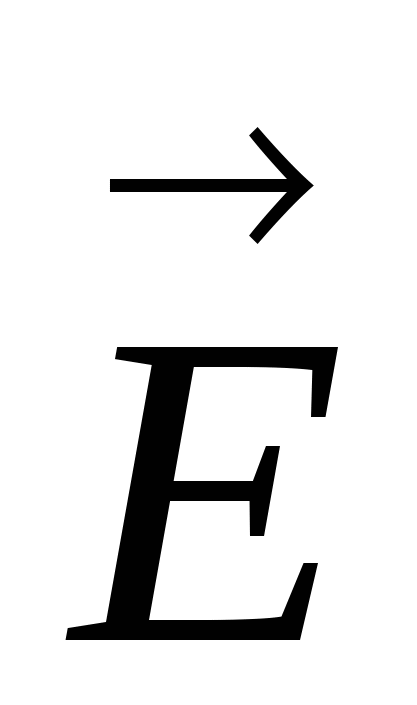 :
:
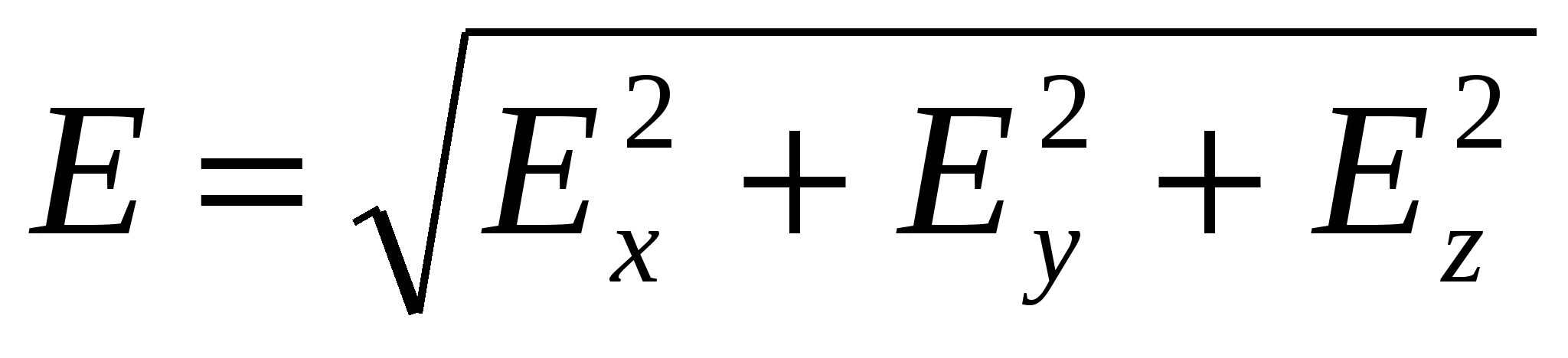 (27)
(27)
Shenja “–” (25) tregon që tensioni drejtohet në drejtim të uljes së potencialit. Formula (25) ju lejon të gjeni forcën e fushës në çdo pikë nga vlerat e njohura ose të zgjidhni problemin e anasjelltë, d.m.th., nga vlerat e dhëna në secilën pikë, të gjeni ndryshimin e mundshëm midis dy pikave arbitrare të fushës.
3.6. Sipërfaqet ekuipotenciale
Potenciali i një fushe elektrostatike është një funksion që ndryshon nga pika në pikë. Sidoqoftë, në çdo rast real, është e mundur të veçohen një grup pikash, potencialet e të cilave janë të njëjta.G  vendndodhja gjeometrike e pikave me potencial konstant quhet një sipërfaqe me potencial të barabartë ose një sipërfaqe ekuipotenciale.
vendndodhja gjeometrike e pikave me potencial konstant quhet një sipërfaqe me potencial të barabartë ose një sipërfaqe ekuipotenciale.
Merrni një plan të pafund të ngarkuar në mënyrë uniforme (Fig. 3.6). Fusha e krijuar nga një rrafsh i tillë është homogjen, dhe linjat e tensionit janë normale me rrafshin. Nga kjo rrjedh se puna e lëvizjes së një ngarkese nga një pikë e caktuar AT 1 në çdo pikë tjetër AT 2 , i vendosur në të njëjtën distancë nga sipërfaqja e ngarkuar si pika AT 1 barazohet me zero. Në të vërtetë, kur lëviz një ngarkesë q në vijë të drejtë AT 1 AT 2 forca që vepron në ngarkesë nga ana e fushës do të jetë gjithmonë pingul me zhvendosjen, dhe, për rrjedhojë, puna e saj është zero. Por kjo vepër mund të përfaqësohet, nga ana tjetër, në formën:
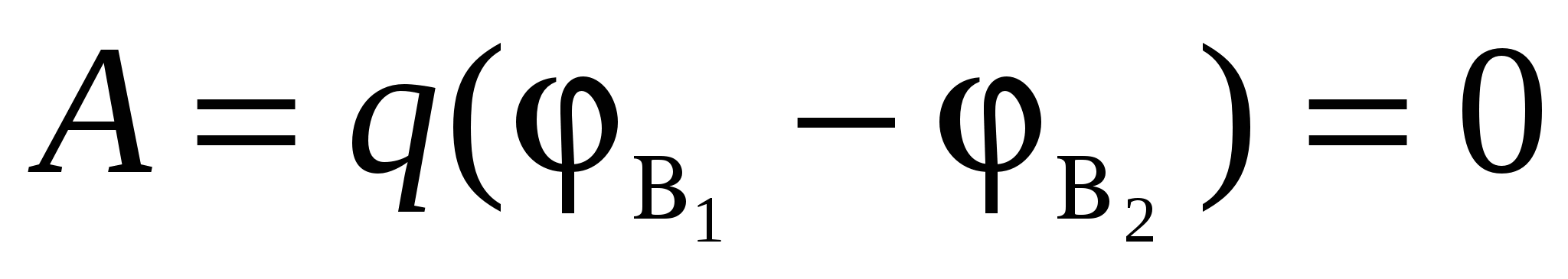 , (28)
, (28)
G  de
de  dhe
dhe  janë përkatësisht potencialet e pikave AT 1
dhe AT 2
. Prandaj, sepse A = 0, atëherë =, d.m.th., potencialet e pikave të barabarta nga rrafshi i ngarkuar janë të njëjta. Kështu, sipërfaqet me potencial të barabartë (sipërfaqet ekuipotenciale) janë rrafshe paralele me rrafshin e ngarkuar. Nëse rrafshi është i ngarkuar pozitivisht, atëherë vlera e potencialit zvogëlohet me distancën nga rrafshi i ngarkuar. Është e qartë se sipërfaqet me potencial të barabartë janë të vendosura në mënyrë simetrike në të dy anët e planit të ngarkuar.
janë përkatësisht potencialet e pikave AT 1
dhe AT 2
. Prandaj, sepse A = 0, atëherë =, d.m.th., potencialet e pikave të barabarta nga rrafshi i ngarkuar janë të njëjta. Kështu, sipërfaqet me potencial të barabartë (sipërfaqet ekuipotenciale) janë rrafshe paralele me rrafshin e ngarkuar. Nëse rrafshi është i ngarkuar pozitivisht, atëherë vlera e potencialit zvogëlohet me distancën nga rrafshi i ngarkuar. Është e qartë se sipërfaqet me potencial të barabartë janë të vendosura në mënyrë simetrike në të dy anët e planit të ngarkuar.
Sipërfaqet ekuipotenciale të fushës së ngarkesës pikësore janë sfera me rreze r
, qendra e të cilit është në qendër të një ngarkese pikë, d.m.th.  (Fig. 3.7). Në fig. 3.6 dhe fig. 3.7 vektori i intensitetit është pingul me sipërfaqet ekuipotenciale.
(Fig. 3.7). Në fig. 3.6 dhe fig. 3.7 vektori i intensitetit është pingul me sipërfaqet ekuipotenciale.
Le të tregojmë se vektori i intensitetit është pingul me sipërfaqen ekuipotenciale. Konsideroni punën e lëvizjes së një ngarkese mbi një sipërfaqe me potencial të barabartë në një pjesë të vogël të shtegut ∆ S
(Fig. 3.7). Në të njëjtën kohë, punoni forcë elektrike  në këtë rrugë do të jetë:
në këtë rrugë do të jetë:
Ku α është këndi ndërmjet drejtimit të forcës f
dhe zhvendosja ∆ S. Nga ana tjetër, kjo punë mund të shprehet si produkt i vlerës së ngarkesës lëvizëse dhe diferencës së mundshme në pozicionet fillestare dhe përfundimtare të ngarkesës, d.m.th. 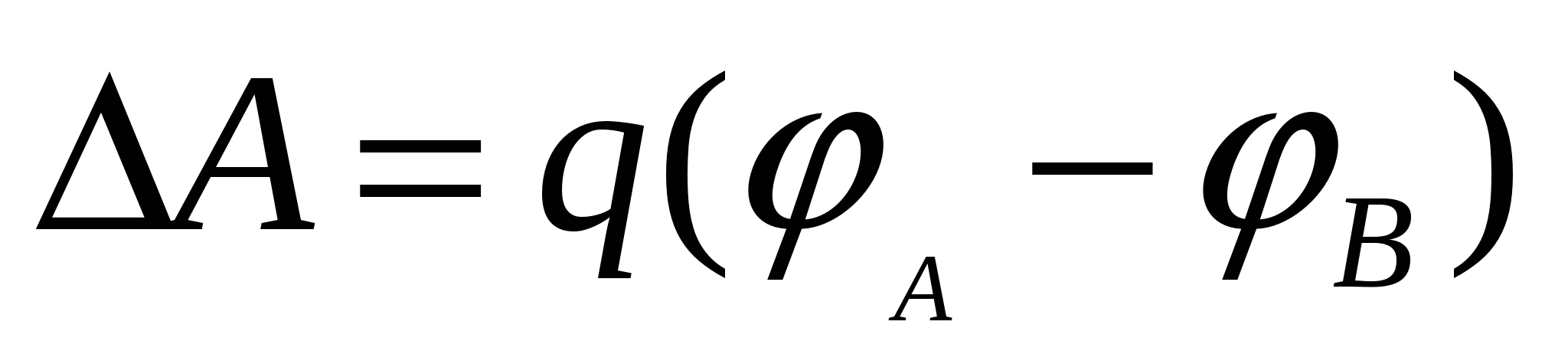 .
.
Meqenëse lëvizja shkon përgjatë sipërfaqes ekuipotenciale, diferenca potenciale 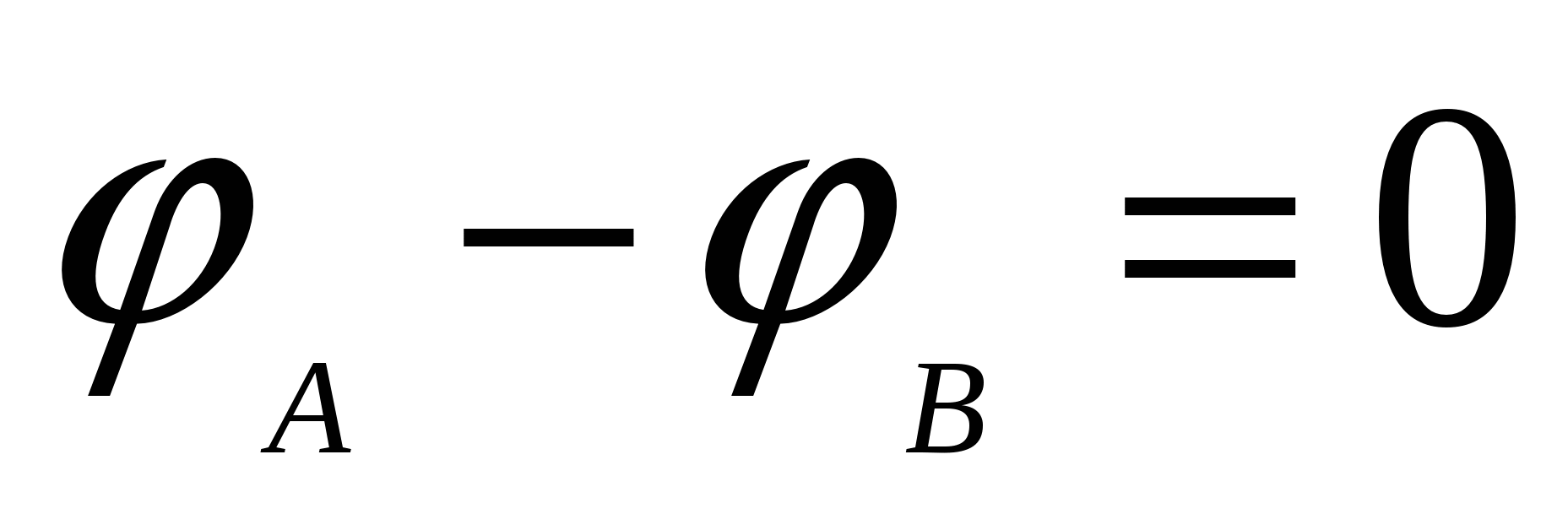 dhe
dhe  , ose cosα = 0, pra α = 90 0 d.m.th. këndi ndërmjet drejtimit të forcës dhe zhvendosjes ∆ Sështë e barabartë me 90 0 . Por, d.m.th. drejtimet dhe
përputhen, pra këndi ndërmjet
dhe ∆ S, α=90 0 d.m.th. drejtimi i vektorit të fushës elektrostatike është gjithmonë pingul me sipërfaqen ekuipotenciale.
, ose cosα = 0, pra α = 90 0 d.m.th. këndi ndërmjet drejtimit të forcës dhe zhvendosjes ∆ Sështë e barabartë me 90 0 . Por, d.m.th. drejtimet dhe
përputhen, pra këndi ndërmjet
dhe ∆ S, α=90 0 d.m.th. drejtimi i vektorit të fushës elektrostatike është gjithmonë pingul me sipërfaqen ekuipotenciale.
Ju mund të vizatoni sa më shumë sipërfaqe ekuipotenciale rreth një trupi të ngarkuar sa të doni. Nga dendësia e sipërfaqeve ekuipotenciale, mund të gjykohet vlera , megjithatë, me kusht që diferenca potenciale ndërmjet dy sipërfaqeve të baraspotenciale ngjitur të jetë e barabartë me një vlerë konstante.
Formula shpreh marrëdhënien midis potencialit dhe forcës dhe lejon përdorimin e vlerave të njohura të φ për të gjetur forcën e fushës në çdo pikë. Gjithashtu është e mundur të zgjidhet problemi invers, d.m.th. sipas vlerave të njohura në çdo pikë të fushës gjeni ndryshimin potencial ndërmjet dy pikave arbitrare të fushës. Për ta bërë këtë, ne përdorim faktin se puna e bërë nga terreni forcon ngarkesën q kur zhvendoset nga pika 1 në pikën 2 mund të llogaritet si:
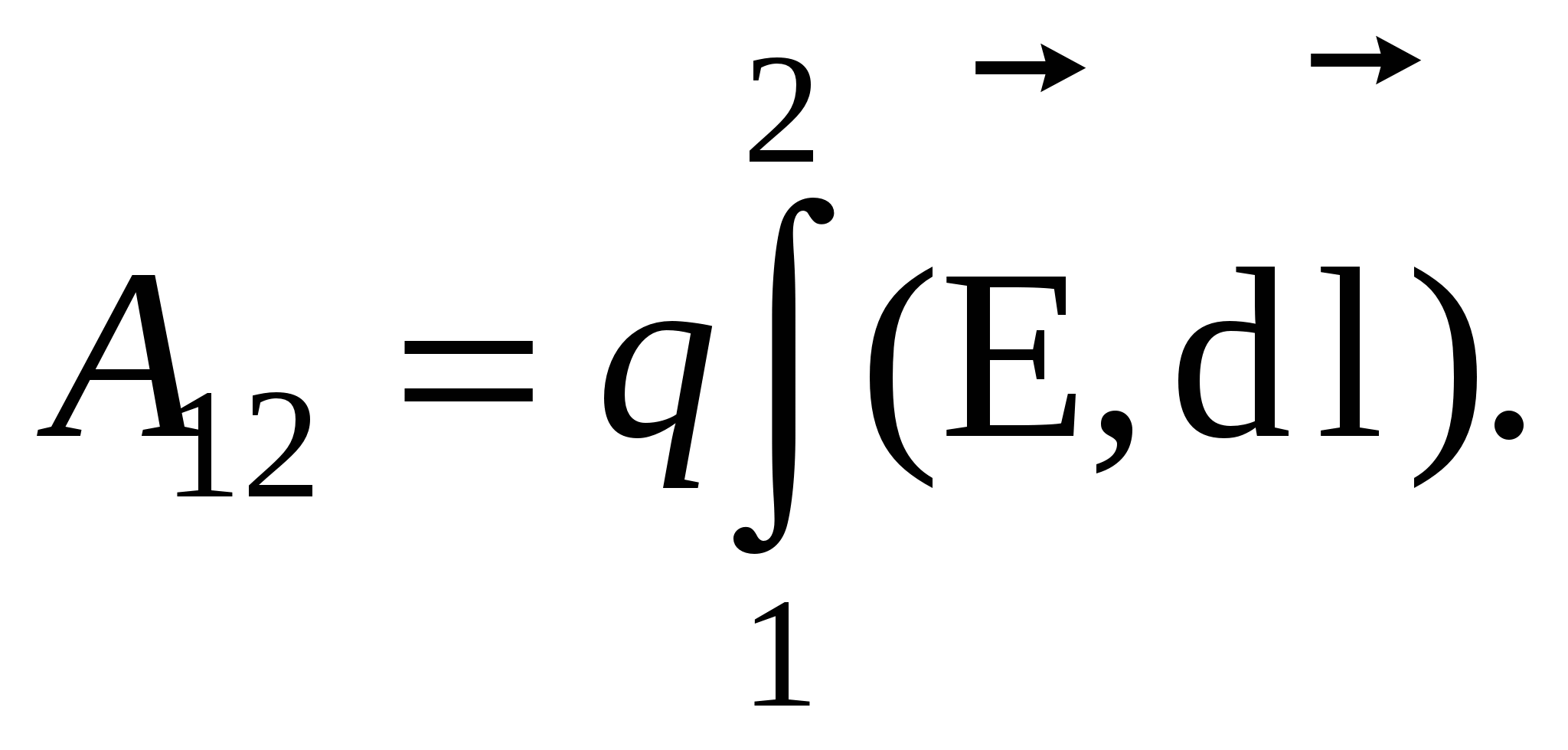
Nga ana tjetër, puna mund të përfaqësohet si:
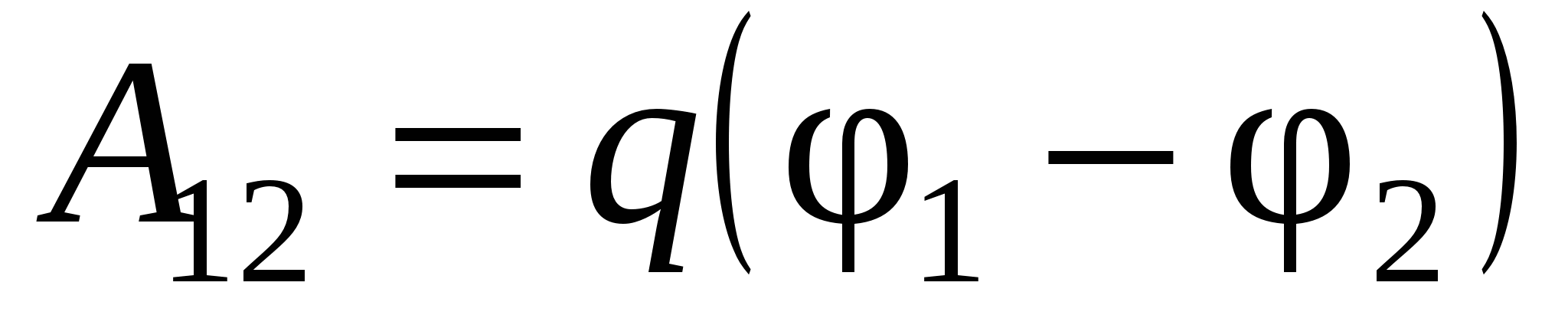 , pastaj
, pastaj 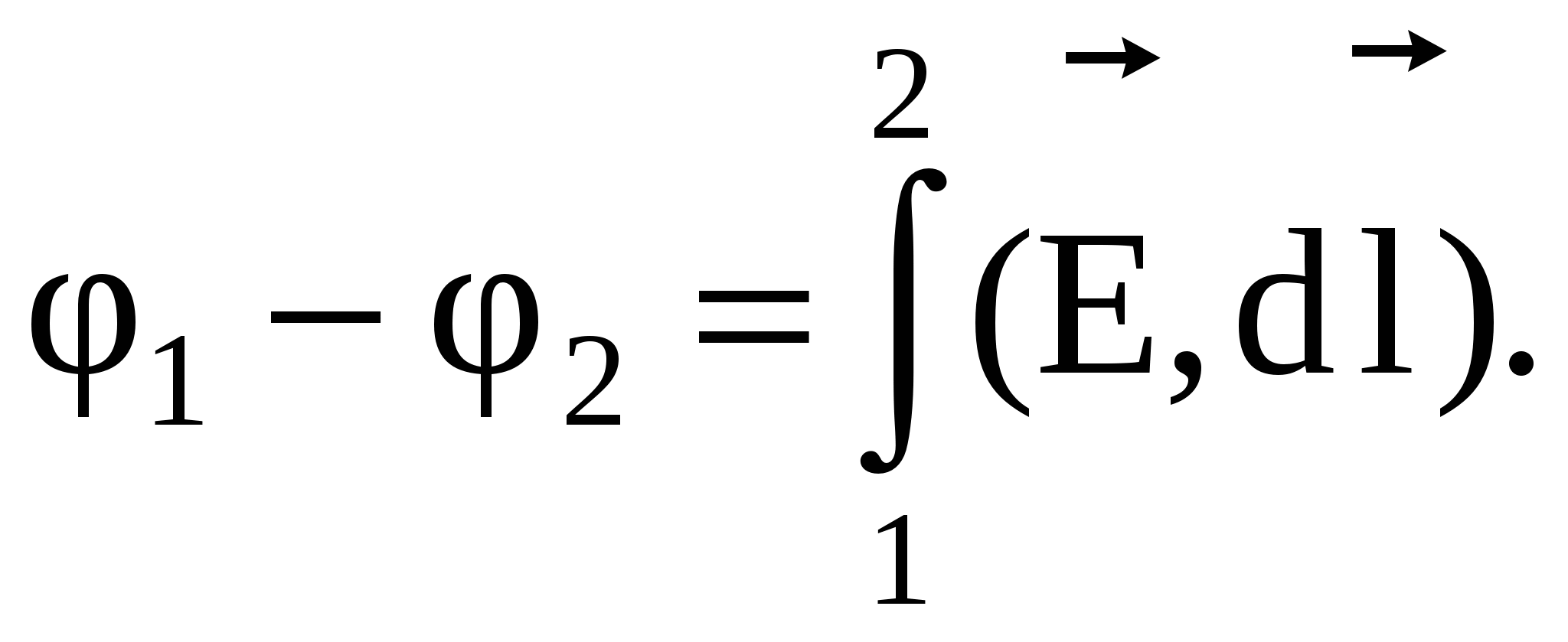
Integrali mund të merret përgjatë çdo linje që lidh pikën 1 dhe pikën 2, pasi puna e forcave fushore nuk varet nga rruga.
Kur kalon një lak të mbyllur 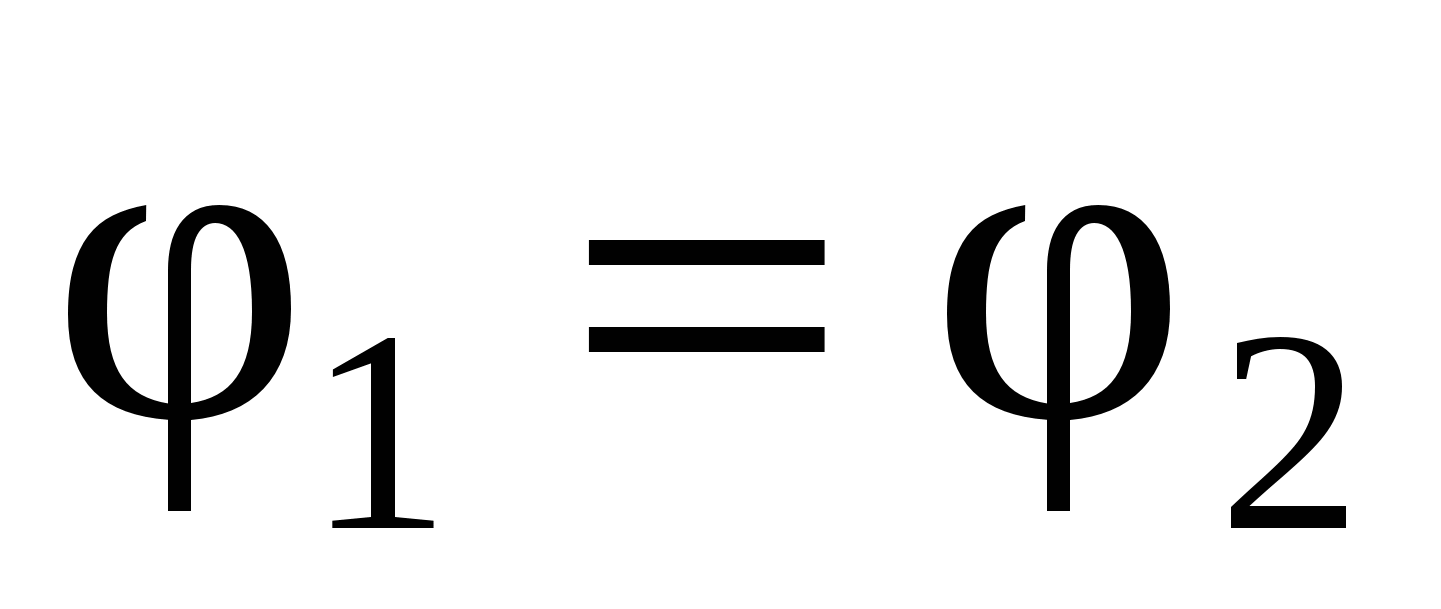 marrim:
marrim:

ato. erdhi në teoremën e njohur mbi qarkullimin e vektorit të intensitetit: qarkullimi i vektorit të forcës së fushës elektrostatike përgjatë çdo laku të mbyllur është i barabartë me zero.
Një fushë me këtë veti quhet potencial.
Nga zhdukja e qarkullimit të vektorit rezulton se linjat e fushës elektrostatike nuk mund të mbyllen.:ato fillojnë me ngarkesa pozitive(origjinën )dhe me radhë ngarkesa negative mbaroj(kullon )ose shkoni në pafundësi.
Le të përgjithësojmë teoremën e Gausit dhe teoremën mbi qarkullimin e vektorit të forcës së fushës elektrostatike në vakum. Që nga , a 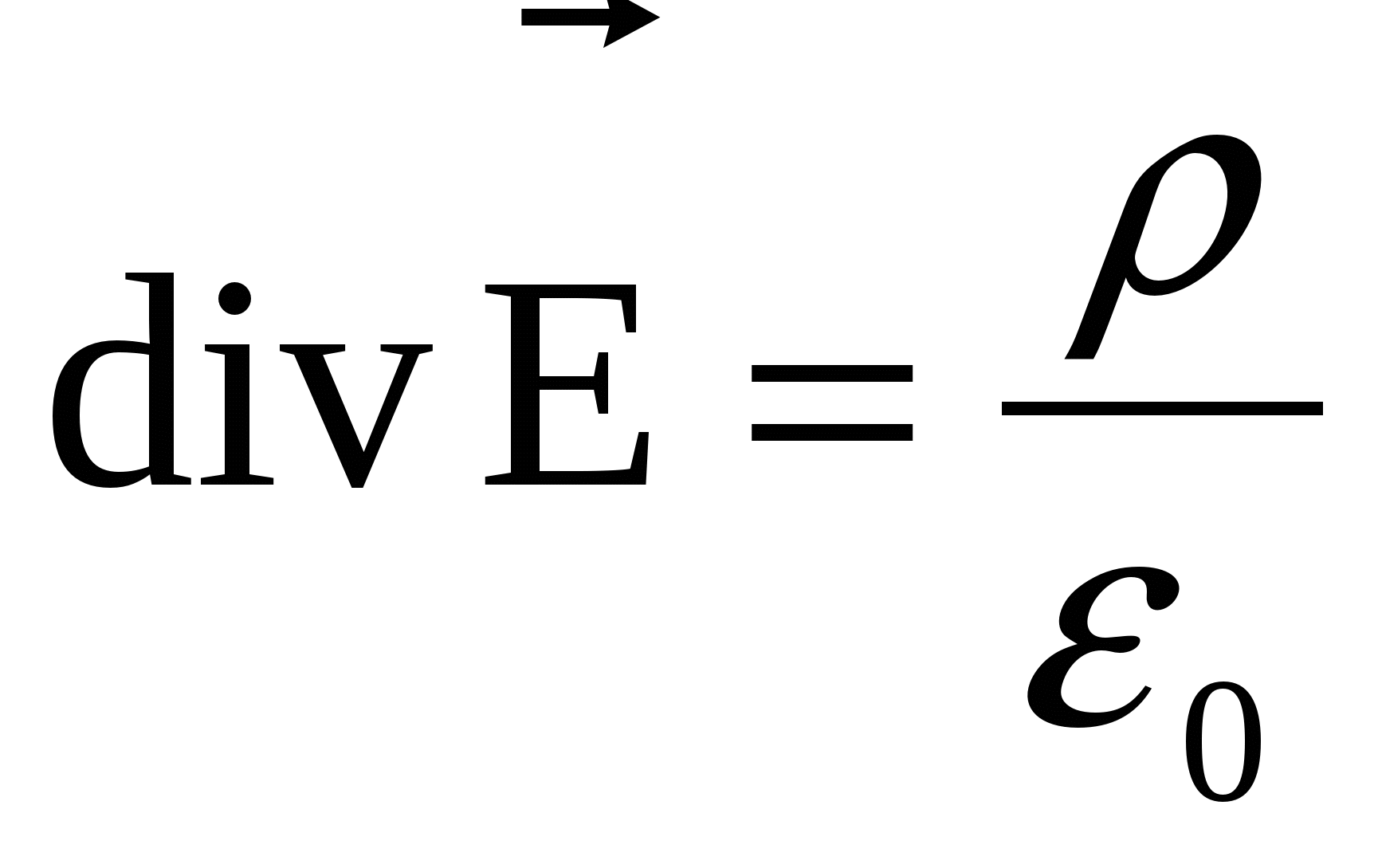 , pastaj
, pastaj 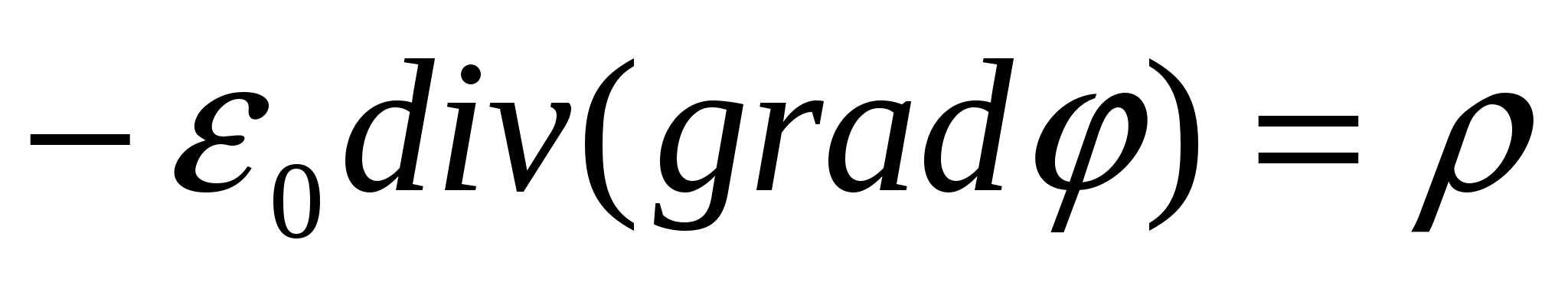 . Sepse
. Sepse  (
( është operatori Laplace), atëherë për potencialin φ marrim shprehjen
është operatori Laplace), atëherë për potencialin φ marrim shprehjen  ose
ose  , e cila quhet Ekuacioni Poisson.
, e cila quhet Ekuacioni Poisson.
Ky ekuacion lejon, sipas shpërndarjes së njohur të ngarkesës 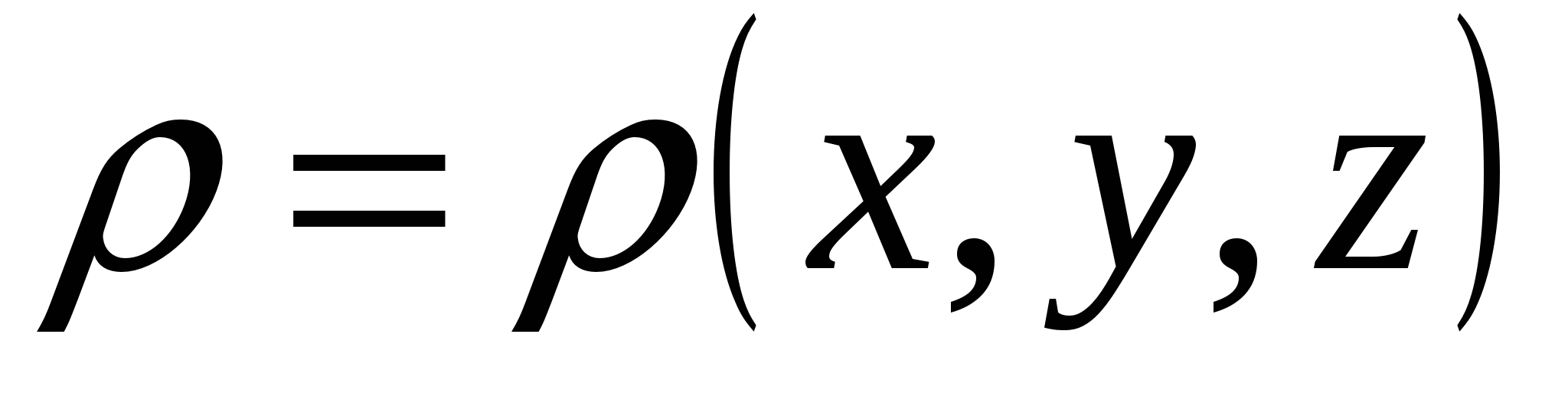 dhe kushti i dhënë kufitar për potencialin φ për të përcaktuar vlerat
dhe kushti i dhënë kufitar për potencialin φ për të përcaktuar vlerat 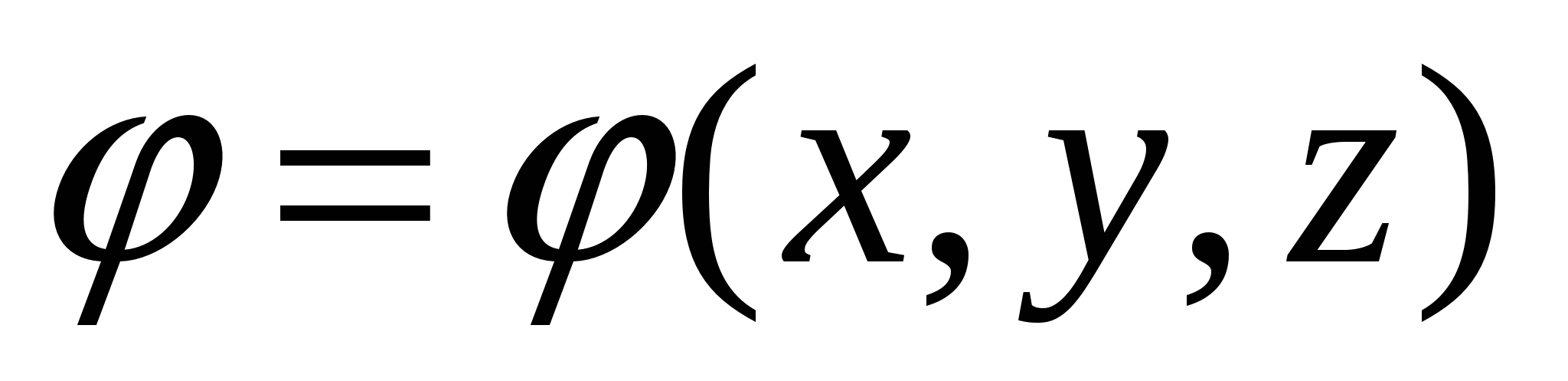 në të gjitha pikat e fushës, dhe më pas duke përdorur formulën për të gjetur tensionin
në të gjitha pikat e fushës, dhe më pas duke përdorur formulën për të gjetur tensionin 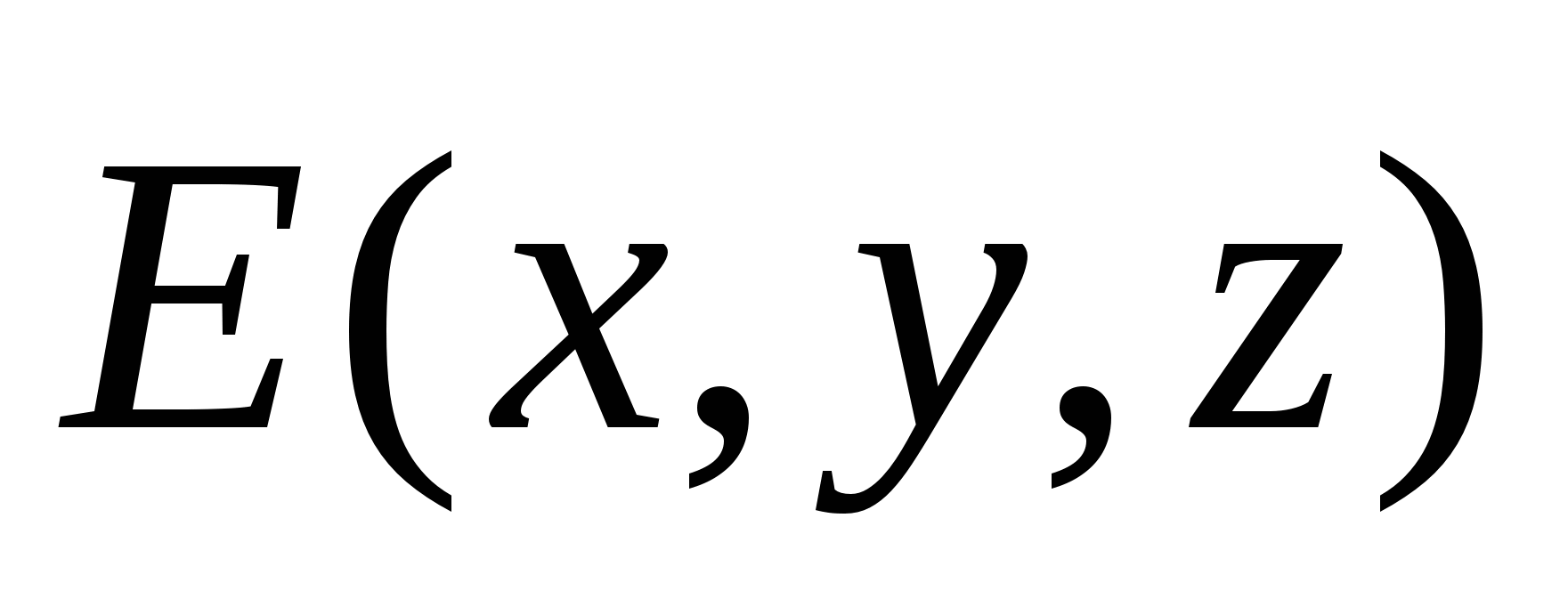 fusha, d.m.th. zgjidh problemin e drejtpërdrejtë të elektrostatikës.
fusha, d.m.th. zgjidh problemin e drejtpërdrejtë të elektrostatikës.
3.7. Llogaritja e diferencës së potencialit nga forca e fushës së fushave elektrostatike më të thjeshta
Marrëdhënia e vendosur midis forcës dhe potencialit lejon, nga forca e njohur e fushës, të gjendet diferenca potenciale midis dy pikave arbitrare të kësaj fushe.
Le të shqyrtojmë disa shembuj të llogaritjes së diferencës së mundshme midis pikave të fushës të krijuara nga disa trupa të ngarkuar.
1. Fusha e një rrafshi të pafund të ngarkuar në mënyrë uniforme
Fusha e një rrafshi të pafund të ngarkuar në mënyrë uniforme, e gjetur duke përdorur teoremën Ostrogradsky-Gauss, përcaktohet nga formula  , ku σ është dendësia e ngarkesës sipërfaqësore. Diferenca e mundshme midis pikave të shtrira në distancë x 1
dhe
x 2
nga avioni, është e barabartë me
, ku σ është dendësia e ngarkesës sipërfaqësore. Diferenca e mundshme midis pikave të shtrira në distancë x 1
dhe
x 2
nga avioni, është e barabartë me ![]() .
.
- d E \u003d 0, midis pllakave potenciali zvogëlohet sipas një ligji logaritmik, dhe pllaka e dytë (jashtë cilindrave) ekranizon fushën elektrike dhe φ dhe E janë të barabarta me zero.

Figura 3.10
Në fig. 3.10 tregon varësinë e tensionit E dhe kapaciteti
 nga r.
nga r.4. Fusha e një sipërfaqeje sferike të ngarkuar në mënyrë uniforme
Duke marrë parasysh shembuj të aplikimit të teoremës Ostrogradsky-Gauss, zbuluam se forca e fushës së sferës përcaktohet nga formula:
 (Fig. 3.11). Dhe që nga ajo kohë
(Fig. 3.11). Dhe që nga ajo kohë  , pastaj
, pastaj
Figura 3.11
. Nëse pranohet r 1 = r , a r 2 =∞, atëherë potenciali jashtë sipërfaqes sferike përcaktohet nga shprehja), përcaktohet nga formula
Duke zgjedhur nivelin e potencialit zero në pikë r 2 =∞ Potenciali i çdo pike brenda topit të ngarkuar mund të gjendet si më poshtë: . Pas integrimit, ne marrim
. Pas integrimit, ne marrim  .
. 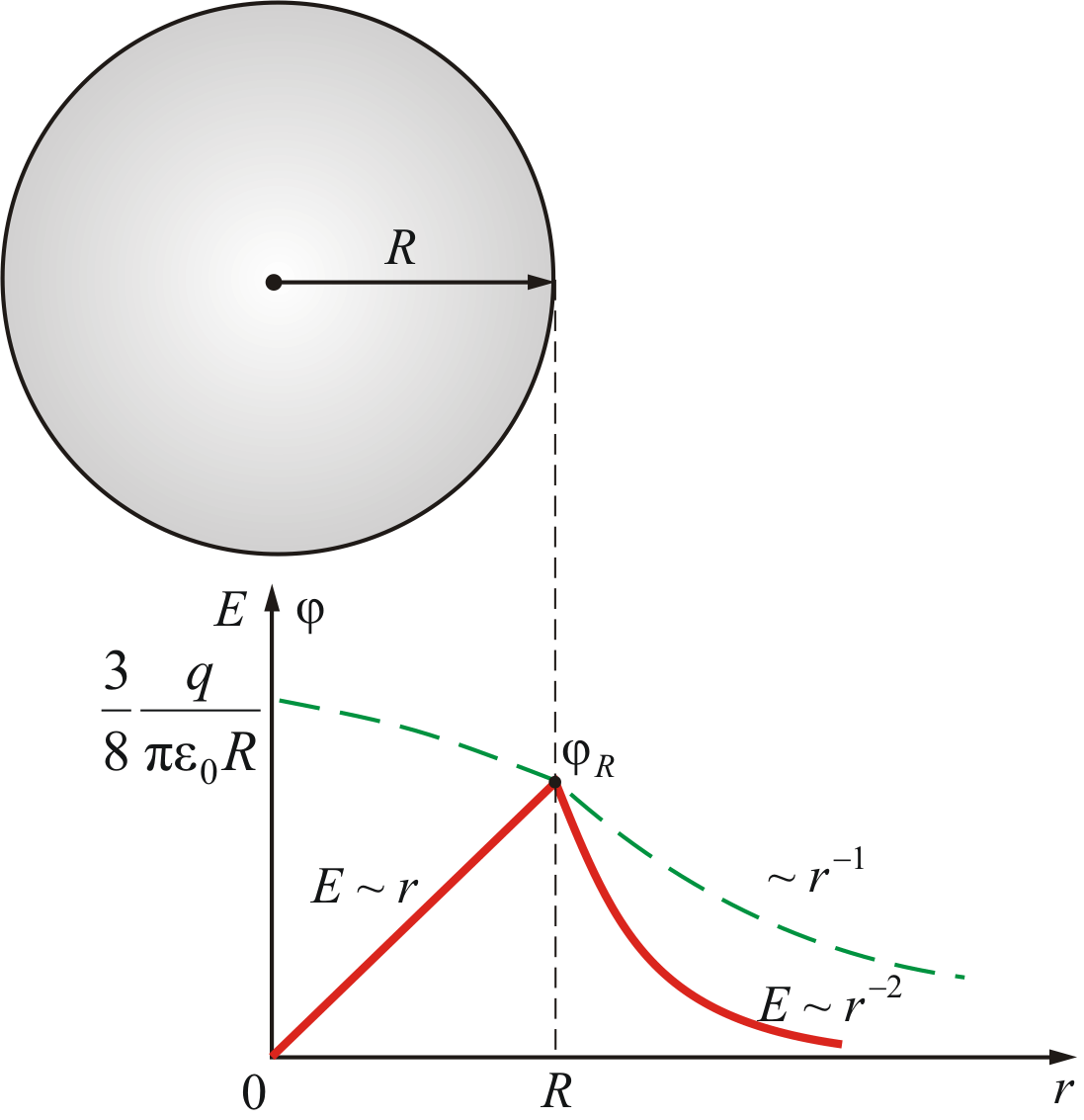
Figura 3.12
Duke marrë parasysh atë
 , pastaj
, pastaj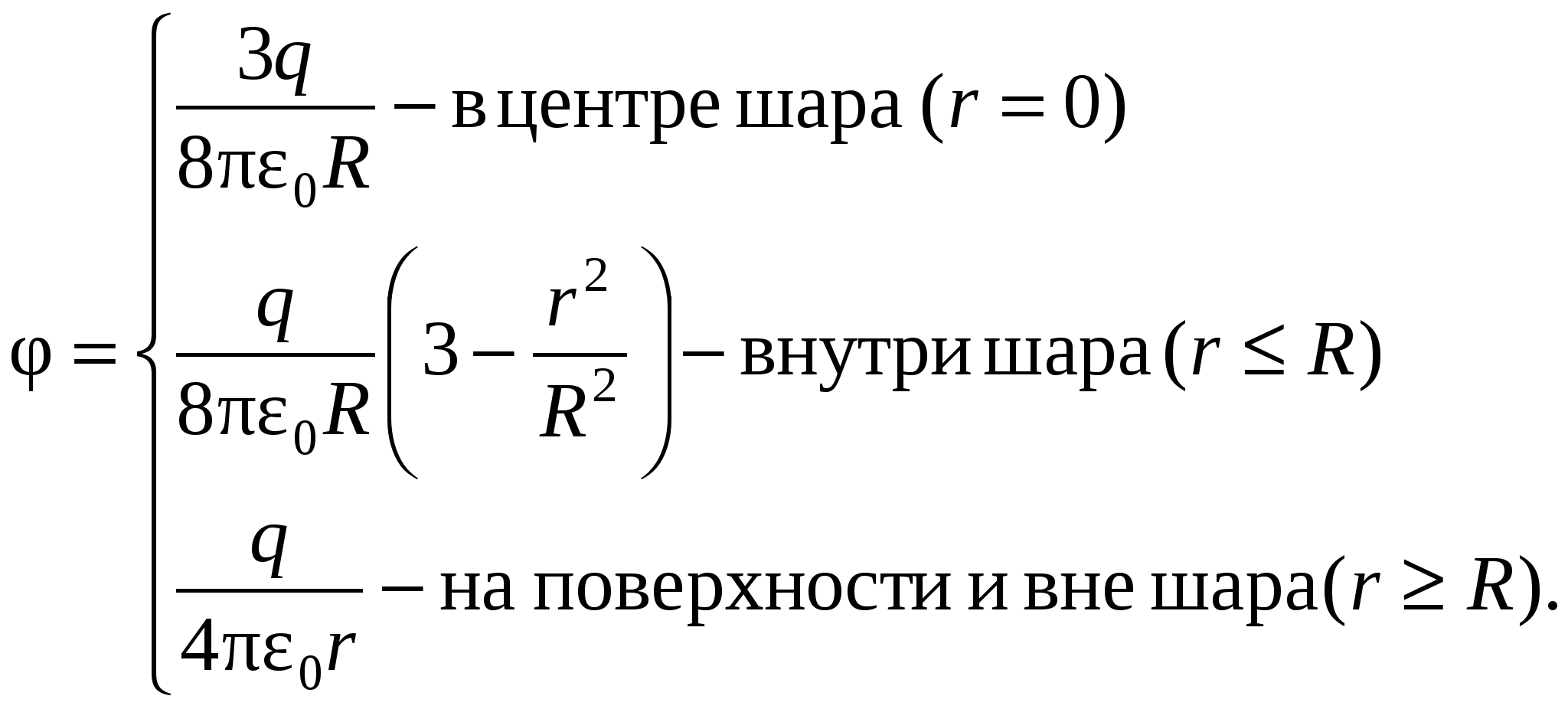 ( 38
)
( 38
)
Nga relacionet e marra mund të bëjmë sa vijon konkluzionet .
Duke përdorur teoremën e Gausit, është relativisht e lehtë për të llogaritur E dhe φ nga sipërfaqe të ndryshme të ngarkuara.
Fuqia e fushës në vakum ndryshon papritur kur kalon nëpër një sipërfaqe të ngarkuar.
Potenciali në terren - gjithmonë funksion të vazhdueshëm koordinatat.
pyetjet e testit
Si të tregohet se një fushë elektrostatike është potenciale?
Çfarë është potenciali?
Si quhet qarkullimi i vektorit të tensionit?
Cila është marrëdhënia midis tensionit dhe potencialit? Si të vizatoni një pamje të linjave të fushës nga fotografia e sipërfaqeve ekuipotenciale?
Cila është puna e bërë për të lëvizur një ngarkesë në një sipërfaqe ekuipotenciale?
Jepni shembuj të llogaritjes së diferencës së potencialit të fushave elektrostatike më të thjeshta.
Si sillet një dipol në një fushë të jashtme elektrostatike?






