Energji potenciale ngarkesë në një fushë elektrike. Puna e bërë nga forcat fushe elektrike kur lëviz një ngarkesë pikë pozitive q nga pozicioni 1 në pozicionin 2, përfaqësojnë si një ndryshim në energjinë potenciale të kësaj ngarkese:

ku W n1 dhe W n2 - energjitë e mundshme të ngarkesës q në pozicionet 1 dhe 2. Për të vogla lëvizja e ngarkesës q në fushën e krijuar nga një ngarkesë pikë pozitive P, ndryshimi i energjisë potenciale është

.

Me lëvizjen përfundimtare të ngarkesës q nga pozicioni 1 në pozicionin 2, i vendosur në distanca r 1 dhe r 2 pa pagesë P,

Nëse fusha është krijuar nga sistemi tarifat me pikë P 1 ,P 2 ,¼ , P n , atëherë ndryshimi në energjinë potenciale të ngarkesës q në këtë fushë:

.

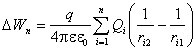Formulat e mësipërme ju lejojnë të gjeni vetëm ndryshim energjia potenciale e një ngarkese pikë q sesa vetë energjia potenciale. Për të përcaktuar energjinë potenciale, është e nevojshme të bini dakord se në cilën pikë të fushës ta konsideroni atë të barabartë me zero. Për energjinë potenciale të një ngarkese pikë q, i vendosur në një fushë elektrike të krijuar nga një ngarkesë tjetër pikë P, marrim

,

ku Cështë një konstante arbitrare. Le të jetë energjia potenciale zero për pafundësi distancë e madhe nga ngarkesa P(në r® ¥ ), pastaj konstante C= 0 dhe shprehja e mëparshme bëhet

Në këtë rast, energjia potenciale përcaktohet si puna e bërë për të lëvizur një ngarkesë nga një pikë e caktuar në një pikë në pafundësi. Në rastin e një fushe elektrike të krijuar nga një sistem ngarkesash pikash, energjia potenciale e ngarkesës q:

.

Energjia potenciale e një sistemi ngarkesash pikash. Kur fushë elektrostatike energjia potenciale shërben si masë e ndërveprimit të ngarkesave. Le të ketë një sistem ngarkesash pikash në hapësirë Q i(i = 1, 2, ... , n). Energjisë ndërveprimin e të gjithëve n tarifat përcaktohet nga raporti

,

ku rij- distanca ndërmjet ngarkesave përkatëse dhe përmbledhja kryhet në atë mënyrë që ndërveprimi ndërmjet çdo çifti ngarkesash të merret parasysh një herë.

Potenciali i fushës elektrostatike. Fusha e forcës konservatore mund të përshkruhet jo vetëm funksioni vektor, por një përshkrim ekuivalent i kësaj fushe mund të merret duke përcaktuar një vlerë skalare të përshtatshme në secilën nga pikat e saj. Për një fushë elektrostatike, kjo sasi është potenciali i fushës elektrostatike, i përcaktuar si raporti i energjisë potenciale të ngarkesës së provës q për madhësinë e kësaj ngarkese, j = W P / q, prej nga rrjedh se potenciali numerikisht është i barabartë me energjinë potenciale që zotëron një njësi ngarkesë pozitive në një pikë të caktuar të fushës. Njësia e potencialit është Volt (1 V).

Potenciali i fushës së një ngarkese pikë P në një mjedis izotropik homogjen me lejueshmëria e :

Parimi i mbivendosjes. Potenciali është një funksion skalar, parimi i mbivendosjes është i vlefshëm për të. Pra, për potencialin e fushës së një sistemi ngarkesash pikash P 1, P 2 ¼ ,Pn ne kemi

,

ku ri- largësia nga pika e fushës, e cila ka potencial j, para ngarkimit Q i. Nëse ngarkesa shpërndahet rastësisht në hapësirë, atëherë

,

ku r- largësia nga vëllimi elementar d x, d y, d z drejt e në temë ( x, y, z), ku përcaktohet potenciali; Vështë vëllimi i hapësirës në të cilën shpërndahet ngarkesa.

Potenciali dhe puna e forcave të fushës elektrike. Bazuar në përcaktimin e potencialit, mund të tregohet se puna e fushës elektrike forcon kur lëviz një ngarkesë pikë q nga një pikë e fushës në tjetrën është e barabartë me produktin e madhësisë së kësaj ngarkese dhe ndryshimin potencial në pikat fillestare dhe përfundimtare të rrugës, A=q (j 1 - j 2 ) .
Nëse, për analogji me energjinë potenciale, supozojmë se në pika pafundësisht të largëta nga ngarkesat elektrike - burimet e fushës, potenciali është zero, atëherë puna e forcave të fushës elektrike kur lëviz ngarkesën q nga pika 1 deri në pafundësi mund të paraqitet si A ¥ = qj 1 .
Kështu, potenciali â në një pikë të caktuar të fushës elektrostatike është sasi fizike, numerikisht e barabartë me punën kryhet nga forcat e fushës elektrike kur lëviz një ngarkesë e vetme pikë pozitive nga një pikë e caktuar e fushës në një pafundësisht të largët: j = A ¥ / q.
Në disa raste, potenciali i fushës elektrike përcaktohet më qartë si sasi fizike numerikisht e barabartë me punën e forcave të jashtme kundër forcave të fushës elektrike kur lëviz një ngarkesë me pikë pozitive nga pafundësia në pikë e dhënë . Përkufizimi i fundit mund të shkruhet lehtësisht si më poshtë:

AT shkenca moderne dhe teknologjia, veçanërisht kur përshkruhen dukuritë që ndodhin në mikrokozmos, shpesh përdoret një njësi pune dhe energjie, e quajtur elektron volt(eV). Kjo është puna e bërë në lëvizjen e ngarkesës. e barabartë me ngarkesën elektron, ndërmjet dy pikave me diferencë potenciale 1 V: 1 eV = 1,60 × 10 - 1 9 Cl × 1 V = 1,60 × 10 - 1 9 J.

Pyetje

1) Jepni përkufizimin e potencialit të një pike të caktuar të fushës dhe ndryshimin potencial të dy pikave të fushës.

2) Jepni grafikët e fuqisë së fushës dhe potencialit kundrejt distancës për një sipërfaqe sferike të ngarkuar në mënyrë uniforme. Jepni shpjegimin dhe arsyetimin e tyre.

Fillojmë duke diskutuar energjinë potenciale që ka një ngarkesë në një fushë elektrostatike. Para së gjithash, është e nevojshme të kujtojmë kushtet në të cilat përgjithësisht është e mundur të prezantohet koncepti i energjisë potenciale.

4.1 Forcat konservatore

Një forcë quhet konservatore (ose potenciale) nëse puna e kësaj force nuk varet nga forma e trajektores dhe përcaktohet vetëm nga pozicionet fillestare dhe përfundimtare të trupit.

Le të, për shembull, trupi nën veprimin e një force konservatore ~ ​​lëvizur nga fillestari

pika 1 deri te pika e fundit 2 (Fig. 16). Atëherë puna e bërë nga forca varet vetëm nga pozicioni

vetë pikat 1 dhe 2, por jo nga trajektorja e trupit. Për shembull, për trajektoret 1 ! a! 2 dhe 1! b! 2 vlera e A do të jetë e njëjtë.

Oriz. 16. Mbi konceptin e forcës konservatore

Vini re se puna e bërë nga një forcë konservatore përgjatë çdo rruge të mbyllur është zero. Në të vërtetë, le të lëmë pikën 1 përgjatë trajektores 1! a! 2 dhe kthehuni përgjatë trajektores 2! b! 1. Në trajektoren e parë, forca do të bëjë punën A, dhe në trajektoren e dytë, puna do të jetë e barabartë me A. Si rezultat, puna totale do të jetë zero.

Pra, koncepti i energjisë potenciale mund të prezantohet vetëm në rastin e një force konservatore. Energjia potenciale W është një shprehje matematikore që varet nga koordinatat e trupit, e tillë që puna e forcës është e barabartë me ndryshimin në këtë shprehje me një shenjë minus:

Ose, e cila është e njëjtë:

A = (W2 W1) = W1 W2:

Siç mund ta shihni, puna e një force konservatore është ndryshimi midis vlerave të energjisë potenciale të llogaritura për pozicionet fillestare dhe përfundimtare të trupit, përkatësisht.

Shembujt e forcave konservatore janë të njohur për ju. Për shembull, graviteti është konservator. Forca e pranverës është gjithashtu konservatore. Kjo është arsyeja pse ne mund të flasim për energjinë potenciale të një trupi të ngritur mbi tokë, ose për energjinë potenciale të një burimi të deformuar.

Por forca e fërkimit nuk është konservatore: puna e forcës së fërkimit varet nga forma e trajektores dhe nuk është e barabartë me zero në një shteg të mbyllur. Prandaj, nuk ka ¾energji potenciale të trupit në fushën e forcës së fërkimit¿.

4.2 Potenciali i fushës elektrostatike

Rezulton se forca me të cilën fusha elektrostatike vepron në një trup të ngarkuar është gjithashtu konservatore. Puna e kësaj force, e kryer gjatë lëvizjes së ngarkesës, quhet puna e fushës elektrostatike. Pra, kemi faktin më të rëndësishëm:

Puna e fushës elektrostatike nuk varet nga forma e trajektores përgjatë së cilës lëviz ngarkesa, dhe përcaktohet vetëm nga pozicionet fillestare dhe përfundimtare të ngarkesës. Puna e fushës përgjatë një rruge të mbyllur është zero.

Ky fakt quhet edhe potenciali i fushës elektrostatike. Ashtu si fusha e gravitetit, fusha elektrostatike është potenciale. Puna e një fushe elektrostatike është e njëjtë për të gjitha shtigjet përgjatë të cilave një ngarkesë mund të lëvizë nga një pikë fikse në hapësirë ​​në tjetrën.

Një provë rigoroze matematikore e potencialit të një fushe elektrostatike është jashtë fushëveprimit kurrikula shkollore. Megjithatë, ¾në nivelin fizik të ashpërsisë¿ ne mund të verifikojmë vlefshmërinë e këtij fakti me ndihmën e arsyetimit të thjeshtë të mëposhtëm.

Është e lehtë të shihet se nëse fusha elektrostatike nuk do të ishte potenciale, atëherë do të ishte e mundur të ndërtohej një makinë me lëvizje të përhershme! Në të vërtetë, atëherë do të kishte një trajektore të mbyllur, kur ngarkesa lëviz përgjatë së cilës fusha do të bënte punë pozitive (dhe nuk do të ndodhnin ndryshime në trupat përreth). Ne e kthejmë ngarkesën tonë përgjatë kësaj trajektore, ne tërheqim një sasi të pakufizuar energjie nga askund dhe të gjitha problemet energjetike të njerëzimit zgjidhen :-) Por kjo, mjerisht, nuk respektohet, bie në kundërshtim me ligjin e ruajtjes së energjisë.

Meqenëse fusha elektrostatike është potenciale, mund të flasim për energjinë potenciale të ngarkesës në këtë fushë. Le të fillojmë me një rast të thjeshtë dhe të rëndësishëm.

4.3 Energjia e mundshme e ngarkesës në një fushë uniforme

Energjia potenciale e një trupi të ngritur mbi tokë është e barabartë me mgh. Rasti i një ngarkese në një fushë uniforme rezulton të jetë shumë i ngjashëm me këtë situatë mekanike.

Konsideroni një fushë elektrostatike uniforme E, vijat e intensitetit të së cilës drejtohen përgjatë boshtit X (Fig. 17). Lëreni ngarkesën pozitive q të lëvizë përgjatë vijës së forcës nga pika 1 (me koordinatë x1) në pikën 2 (me koordinatë x2).

0x1

Oriz. 17. Lëvizja e një ngarkese në një fushë uniforme

Fusha vepron mbi ngarkesën me një forcë ~ , e cila drejtohet përgjatë vijave të tensionit. Puna

Kjo forcë, siç shihet lehtë, do të jetë e barabartë me:

A = F (x2 x1) = qE (x2 x1):

Çfarë do të ndryshojë nëse pikat 1 dhe 2 nuk shtrihen në të njëjtën linjë tensioni? Nuk rezulton asgjë! Formula për punën në terren do të mbetet e njëjtë. Këtë do ta verifikojmë me ndihmën e Fig. tetëmbëdhjetë .

0x1

Oriz. 18. Lëvizja e një ngarkese në një fushë uniforme

Duke kaluar nga pika 1 në pikën 2, le të zgjedhim rrugën 1! 3! 2, ku pika 3 shtrihet në të njëjtën vijë fushe me pikën 1. Atëherë puna A32 në seksionin 32 është zero sepse ne lëvizim pingul me forcën. Si rezultat, marrim:

A = A13 + A32 = A13 = qE(x2 x1):

Shohim që puna e fushës varet vetëm nga abshisa e pozicioneve fillestare dhe përfundimtare të ngarkesës. Ne shkruajmë formulën që rezulton si më poshtë:

A = qEx2 qEx1 = ((qEx2 ) (qEx1 )) = (W2 W1 ) = W:

Këtu W1 = qEx1, W2 = qEx2. Puna e fushës, në përputhje me formulën (8), rezulton të jetë e barabartë me ndryshimin me një shenjë minus të vlerës

Kjo vlerë është energjia potenciale e ngarkesës në një fushë uniforme elektrostatike. X shënon abshisën e pikës në të cilën kërkohet energjia potenciale. Niveli zero i energjisë potenciale në këtë rast korrespondon me origjinën x = 0 dhe është paraqitur në figura me një vijë me pika pingul me vijat e tensionit4.

Kujtojmë se, për momentin, konsiderohet q > 0. Nga formula (9) rrjedh se kur një ngarkesë lëviz përgjatë një linje fushe, energjia potenciale zvogëlohet me rritjen e x. Kjo është e natyrshme: në fund të fundit, fusha bën punë pozitive, duke përshpejtuar ngarkesën dhe energjia kinetike ngarkesa rritet për shkak të zvogëlimit të energjisë së saj potenciale.

Është e lehtë të tregohet se formula (9) mbetet e vlefshme për q< 0. В этом случае потенциальная энергия возрастает с ростом x. Это тоже понятно: ведь сила, с которой поле действует на заряд, теперь будет направлена влево, так что движение заряда вправо будет осуществляться против действия поля. Заряд тормозится полем, кинетическая энергия заряда уменьшается, а потенциальная энергия увеличивается.

Pra, një përfundim i rëndësishëm: në formulën për energjinë potenciale, q tregon vlerën algjebrike të ngarkesës (duke marrë parasysh shenjën), dhe jo modulin e saj.

4 Në fakt, niveli zero i energjisë potenciale mund të zgjidhet kudo. Me fjalë të tjera, energjia potenciale përcaktohet vetëm deri në një konstante shtesë arbitrare C, d.m.th. W = qEx+C. Nuk ka asgjë të keqe me një pasiguri të tillë: vetë energjia potenciale ka kuptim fizik, dhe ndryshimi në energjitë e mundshme është i barabartë me punën e fushës. Në këtë ndryshim, konstanta C anulohet.

4.4 Energjia potenciale e bashkëveprimit të ngarkesave pika

Le të jenë dy ngarkesa me pikë q1 dhe q2 në vakum në një distancë r nga njëra-tjetra. Mund të tregohet se energjia potenciale e bashkëveprimit të tyre jepet nga formula:

		kq1 q2

Ne e pranojmë formulën (10) pa prova. Dy veçori të kësaj formule duhet të diskutohen.

Së pari, ku është niveli zero i energjisë potenciale? Në fund të fundit, energjia potenciale, siç mund të shihet nga formula (10), nuk mund të kthehet në zero. Por në fakt, niveli zero ekziston dhe është në pafundësi. Me fjalë të tjera, kur ngarkesat janë të vendosura pafundësisht larg njëra-tjetrës, energjia potenciale e ndërveprimit të tyre supozohet të jetë zero (gjë që është logjike në këtë rast, ngarkesat tashmë ¾nuk ndërveprojnë¿).

Së dyti, q1 dhe q2 janë përsëri sasi algjebrike të ngarkesave, d.m.th., ngarkesave, duke marrë parasysh shenjën e tyre.

Për shembull, energjia potenciale e bashkëveprimit të dy ngarkesave të ngjashme do të jetë pozitive. Pse? Nëse i lëmë të shkojnë, ata do të fillojnë të përshpejtohen dhe të largohen nga njëri-tjetri. Energjia e tyre kinetike rritet, kështu që energjia e tyre potenciale zvogëlohet. Por në pafundësi, energjia potenciale zhduket, dhe meqenëse zvogëlohet në zero, atëherë është pozitive.

Por energjia potenciale e bashkëveprimit të ngarkesave të kundërta rezulton të jetë negative. Në të vërtetë, le t'i heqim ato në një distancë shumë të madhe nga njëra-tjetra në mënyrë që energjia potenciale të jetë zero dhe t'i lëmë të shkojnë. Ngarkesat do të fillojnë të përshpejtohen, afrohen dhe energjia potenciale zvogëlohet përsëri. Por nëse ishte zero, atëherë ku duhet të ulet? Vetëm drejt vlerave negative.

Formula (10) gjithashtu ndihmon për të llogaritur energjinë potenciale të një sistemi ngarkesash nëse numri i ngarkesave është më shumë se dy. Për ta bërë këtë, ju duhet të përmblidhni energjitë e çdo çifti ngarkesash. Ne nuk do të lëshojmë formulë e përgjithshme; Le të ilustrojmë më mirë atë që është thënë me një shembull të thjeshtë, të paraqitur në figurën 19.

Oriz. 19. Ndërveprimi i tre ngarkesave

Nëse ngarkesat q1, q2, q3 janë në kulmet e një trekëndëshi me brinjë a, b, c, atëherë energjia potenciale e bashkëveprimit të tyre është e barabartë me:

		kq1 q2		kq2 q3		kq1 q3

4.5 Potenciali

Nga formula W = qEx shohim se energjia potenciale e një ngarkese q në një fushë uniforme është drejtpërdrejt proporcionale me këtë ngarkesë.

E shohim të njëjtën gjë nga formula W = kq1 q2 =r: energjia potenciale e një ngarkese q1 e vendosur në fushën e një ngarkese pika q2 është drejtpërdrejt proporcionale me ngarkesën q1 .

Nese nje trup elektrik vepron në trupat e ngarkuar elektrikisht, atëherë është në gjendje të bëjë punën e lëvizjes së trupave të ngarkuar. Fusha elektrostatike e krijuar nga një ngarkesë pikë është qendrore, domethënë, forca që vepron në një ngarkesë pikë në një fushë të tillë drejtohet përgjatë vijës së drejtë që lidh ngarkesën burimore dhe ngarkesën e provës. Më parë treguam se çdo forcë qendrore është potenciale, domethënë, puna e kësaj force nuk varet nga forma e trajektores, por përcaktohet vetëm nga pozicioni fillestar dhe përfundimtar i trupit.

Le të kujtojmë shkurtimisht provën e këtij pohimi më të rëndësishëm. Lëreni një ngarkesë testuese me pikë q të lëvizë në fushën qendrore të krijuar nga një ngarkesë fikse Q (Fig. 174). Forca që vepron në ngarkesën e provës përcaktohet nga ligji i Kulombit

Ku është vektori i tërhequr nga ngarkesa burimore Q në pikën A, ku ndodhet ngarkesa testuese. Kur një ngarkesë lëviz përgjatë harqeve të rrathëve të përqendruar në ngarkesën Q (për shembull, përgjatë harqeve AB, CD), punoni forcë elektrikeështë e barabartë me zero, kështu që vektorët e forcës dhe zhvendosjes janë reciprokisht pingul. Kur lëvizni në drejtimin radial (për shembull, përgjatë segmenteve BC, DE), puna varet vetëm nga distanca fillestare dhe përfundimtare me ngarkesën e burimit. Pra, puna e fushës elektrostatike kur lëviz përgjatë segmenteve DE dhe D1E1 është padyshim e barabartë. Prova më e bukur e kësaj deklarate lidhet me simetrinë e fushës - le ta rrotullojmë sistemin tonë rreth boshtit që kalon përmes burimit, në mënyrë që segmenti D1E1 të përkojë me segmentin DE - shpërndarja e fushës nuk do të ndryshojë, pse duhet puna e terrenit ndryshim?

Meqenëse parimi i mbivendosjes është i vlefshëm për forcën e një fushe elektrostatike, çdo fushë elektrostatike është potenciale. Në të vërtetë, le të jetë një ngarkesë pikë q në një fushë elektrike të krijuar nga një sistem ngarkesash me pikë fikse Q1, Q2, … ,QN . Kur lëvizni ngarkesën në një vektor të vogël zhvendosjeje, sipas përkufizimit, fusha elektrike do të bëjë punën, ku

Forca rezultuese që vepron mbi ngarkesën lëvizëse q, e barabartë me shumën e forcave që veprojnë nga secila prej ngarkesave me pikë fikse Qk. Puna e kësaj force mund të llogaritet me formulë

Për të llogaritur punën në seksionin përfundimtar të trajektores, është e nevojshme të ndahet trajektorja në seksione të vogla (Fig. 175), pastaj të përdoret formula (1) për të llogaritur punën në çdo seksion të vogël dhe më pas t'i përmbledhë ato.

. (2) Në fakt, kjo shumë është dyfish, pasi çdo forcë rezultante është shuma e forcave, sipas formulës (1). Vini re se në formulën (2) forca që rezulton ndryshon, pasi llogaritet në pika të ndryshme trajektoret.

Siç treguam më herët, puna e fushës elektrike të një ngarkese pika nuk varet nga forma e trajektores, domethënë, çdo term nga formula (1) nuk varet nga forma e trajektores, prandaj, e gjithë shuma nuk varet nga forma e trajektores. Kështu, çdo fushë elektrostatike është potenciale.

Prandaj, për një ngarkesë pikë në një fushë elektrostatike, mund të prezantohet energjia potenciale e bashkëveprimit U(x, y, z). Ky funksion ka kuptimin fizik të mëposhtëm: puna e fushës elektrike kur lëviz një ngarkesë pikë nga një pikë me koordinata (x1,y1,z1) në tjetrën, me koordinata (x2,y2,z2) është e barabartë me ndryshimin e potencialit. energji, marrë me shenjën e kundërt:

. (3) Ndryshimi i hyrjes këtë përkufizim mjaft logjikisht: nëse fusha elektrike ka bërë punë pozitive (A > 0), atëherë energjia e saj zvogëlohet (ΔU< 0). Для вычисления работы силы взаимодействия между двумя точечными заряженными телами достаточно подсчитать эту работу при движении вдоль радиального отрезка при изменении расстояния от r1 до r2 (Рис. 176). Если построить зависимость силы взаимодействия между зарядами от расстояния r между телами, тогда площадь под графиком этой зависимости в указанных пределах и будет равна искомой работе (Рис. 177). Зависимость силы электростатического взаимодействия от расстояния аналогична силе гравитационного взаимодействия, с одним существенным отличием: гравитационная сила всегда есть сила притяжения, а электрическая может быть как силой притяжения, так и силой отталкивания. В частности два ngarkesë pozitive zmbraps. Prandaj, shprehja për punën e fushës elektrike do të jetë e ngjashme me formulën për punën e forcës gravitacionale, por do të ketë shenjën e kundërt.

Kjo punë është e barabartë me uljen e energjisë potenciale të bashkëveprimit, domethënë, nga kjo shprehje, mund të përcaktoni shprehjen për energjinë potenciale të bashkëveprimit elektrostatik të dy ngarkesave pika. (4) Me këtë përkufizim, energjia potenciale e bashkëveprimit të dy ngarkesave të së njëjtës shenjë është pozitive dhe tenton në zero në një distancë të pafundme ndërmjet trupave. Forca e bashkëveprimit të ngarkesave të shenjave të kundërta drejtohet në drejtim të kundërt, kështu që puna e kësaj force me një rritje të distancës midis ngarkesave do të jetë negative. Sidoqoftë, nuk kemi nevojë të bëjmë ndonjë rezervë shtesë, pasi formula (4) automatikisht merr parasysh shenjat e ngarkesave - nëse ngarkesat janë të kundërta, atëherë produkti i tyre (përkatësisht, energjia) është negativ. Shenja e energjisë potenciale të bashkëveprimit të ngarkesave ka një kuptim shumë të qartë. Ngarkesat e së njëjtës shenjë zmbrapsen, prandaj, kur ato "ikin" në një distancë pafundësisht të madhe, fusha elektrike do të bëjë punë pozitive - prandaj, fillimisht sistemi i këtyre ngarkesave ka aftësinë për të punuar, prandaj energjia e tij është pozitive, kur ngarkesat largohen nga njëra-tjetra, energjia e tyre zvogëlohet në zero. Ngarkesat e shenjave të kundërta tërhiqen, për t'i larguar ato në një distancë të pafundme, forcat e jashtme duhet të bëjnë punë pozitive. Në këtë rast, energjia e një palë ngarkesash duhet të rritet, prandaj, fillimisht është negative, dhe kur ngarkesat hiqen nga njëra-tjetra, rritet në zero. Në përgjithësi, situata e zakonshme është që tërheqja korrespondon me energjinë negative, dhe zmbrapsja - pozitive. Vëmë re vetëm se një provë e tillë është e vlefshme vetëm kur zgjedhim nivelin zero të energjisë potenciale në pafundësi. Formula (4) përcakton energjinë potenciale të bashkëveprimit të dy trupave të ngarkuar me pikë. Vlerat e ngarkesave të trupave Q dhe q hyjnë, siç pritej, në mënyrë simetrike në këtë formulë. Ndarja e tarifave në një tarifë burimore dhe një tarifë testimi është e kushtëzuar, ato mund të shkëmbehen plotësisht. Prandaj, preferohet të shkruhet kjo formulë në një formë simetrike: energjia e ndërveprimit të dy ngarkesave pika q1 dhe q2 është , ose të dyja ngarkesat lëvizin, në fund, pavarësisht nga trajektoret e lëvizjes së të dy ngarkesave. Më tej, është e pamundur të thuhet se cilës ngarkesë të veçantë "i përket" kjo energji, në të ardhmen do të tregojmë se energjia e bashkëveprimit të ngarkesave është pjesë e energjisë së vetë fushës elektrostatike, domethënë është "e lyer" në të gjithë hapësirën ku ekziston fusha e krijuar nga këto ngarkesa. Nëse sistemi përbëhet nga më shumë se dy ngarkesa, atëherë për të llogaritur energjinë e ndërveprimit të këtyre ngarkesave, është e nevojshme të përmblidhen energjitë e ndërveprimit të të gjitha palëve të ngarkesave.

këtu Uik është energjia e ndërveprimit të ngarkesave qi dhe qk të vendosura në një distancë rik nga njëra-tjetra (Fig. 178).

40 Pyetje:

Fusha elektrostatike - el. fushë ngarkese e palëvizshme.

Feli, duke vepruar në ngarkim, e lëviz atë, duke bërë punë. Në një fushë elektrike uniforme Fel = qE - konstante

Puna e fushës (forca elektronike) nuk varet nga forma e trajektores dhe nga një trajektore e mbyllur = zero.

ENERGJIA POTENCIALE E NJË TRUPI TË NGARKUAR NË NJË FUSHË ELEKTROSTATIKE HOMOGJENE

Energjia elektrostatike është energjia potenciale e një sistemi trupash të ngarkuar (sepse ata ndërveprojnë dhe janë në gjendje të bëjnë punë).

Meqenëse puna e fushës nuk varet nga forma e trajektores, atëherë në të njëjtën kohë

duke krahasuar formulat e punës, marrim energjinë potenciale të ngarkesës në një fushë elektrostatike uniforme

Nëse fusha bën punë pozitive (së bashku linjat e forcës), pastaj energjia potenciale

i një trupi të ngarkuar zvogëlohet (por sipas ligjit të ruajtjes së energjisë, energjia kinetike rritet) dhe anasjelltas.

POTENCIALI I FUSHËS ELEKTROSTATIKE

Karakteristikë energjetike el. fusha.

Është e barabartë me raportin e energjisë potenciale të ngarkesës në fushë me këtë ngarkesë.

Një vlerë skalare që përcakton energjinë potenciale të tarifës në çdo pikë të emailit. fusha.

Vlera e mundshme konsiderohet në lidhje me nivelin zero të zgjedhur.

DIFERENCA POTENCIALE (ose ndryshe TENSION)

Ky është ndryshimi i mundshëm në pikën fillestare dhe fundore të trajektores së ngarkesës.

Tensioni ndërmjet dy pikave (U) është i barabartë me diferencën potenciale të këtyre pikave dhe është i barabartë me punën e fushës në lëvizjen e një ngarkese njësi.

MARRËDHËNIET MIDIS FORCËS SË FUSHËS DHE DIFERENCAVE POTENCIALE

§ 12.3 Puna e forcave të fushës elektrostatike. Potenciali. Sipërfaqet ekuipotenciale

Një ngarkesë q pr e vendosur në një pikë arbitrare të një fushe elektrostatike me forcë E i nënshtrohet një force F = q pr E. Nëse ngarkesa nuk është fikse, atëherë forca do ta bëjë atë të lëvizë dhe, për rrjedhojë, do të punohet. . Puna elementare e bërë nga forca F kur lëviz një ngarkesë elektrike pikë q pr nga pika a e fushës elektrike në pikën b në një segment të shtegut dℓ, sipas përkufizimit, është e barabartë me

(α është këndi ndërmjet F dhe drejtimit të lëvizjes) (Fig. 12.13).

Nëse bëhet puna forcat e jashtme, pastaj dA< 0 , если силами поля, то dA >0. Duke integruar shprehjen e fundit, marrim se puna kundër fushës forcon kur lëviz q pr nga pika a në pikën b

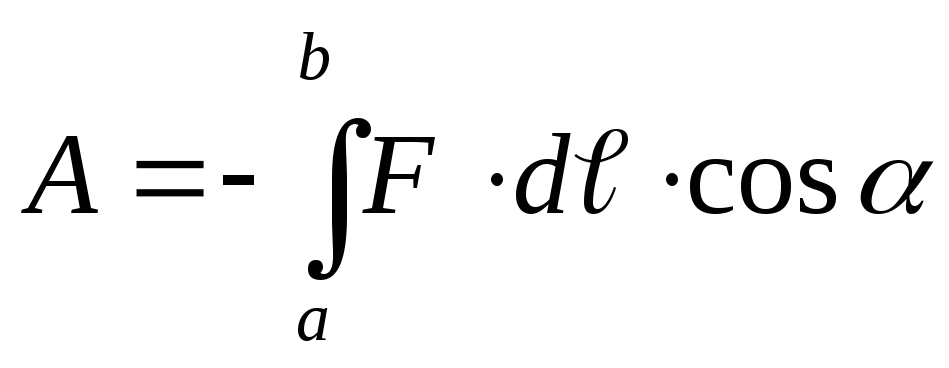(12.20)

Figura -12.13

(

- Forca e Kulonit që vepron në ngarkesën e provës q pr në çdo pikë të fushës me forcë E).

Pastaj punoni

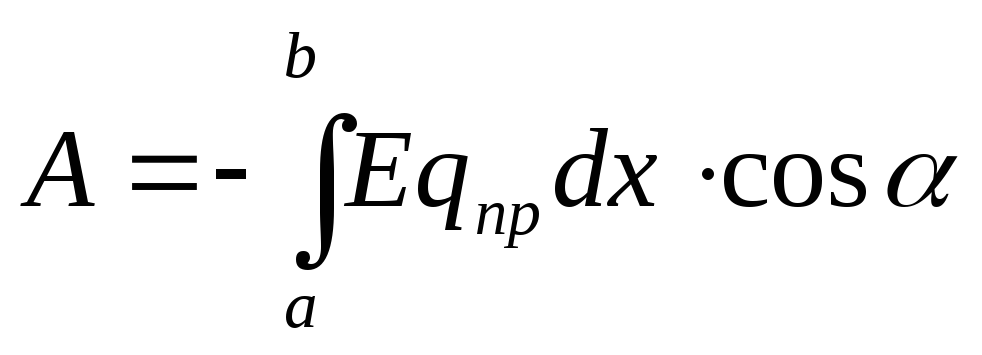(12.21)

Lëvizja është pingul me vektorin , pra cosα =1, puna e transferimit të ngarkesës test q pr nga a te bështë e barabartë me

(12.22)

Puna e forcave të fushës elektrike gjatë lëvizjes së ngarkesës nuk varet nga forma e shtegut, por varet vetëm nga pozicioni relativ pikat e fillimit dhe të fundit të trajektores.

Prandaj, fusha elektrostatike e një ngarkese pika ështëpotencial , dhe forcat elektrostatike janëkonservatore .

Kjo është një pronë e fushave të mundshme. Nga ai rrjedh se puna e bërë në një fushë elektrike përgjatë një qarku të mbyllur është e barabartë me zero:

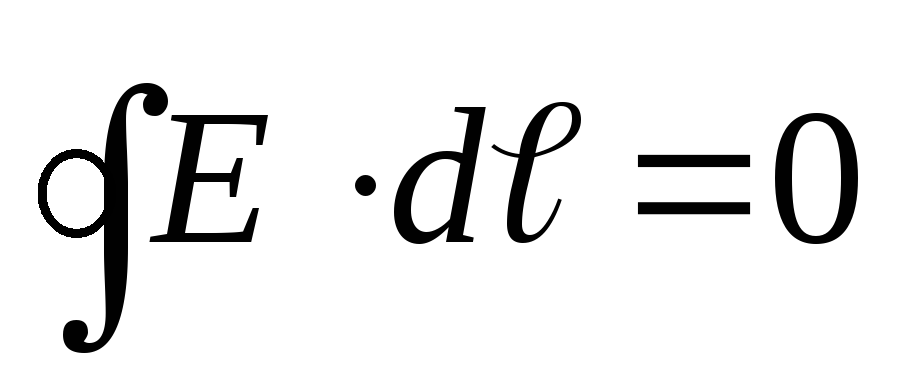(12.23)

Integrale

thirrur qarkullimi i vektorit të tensionit . Nga zhdukja e qarkullimit të vektorit E, rezulton se linjat e forcës së fushës elektrostatike nuk mund të mbyllen, ato fillojnë me ngarkesë pozitive dhe përfundojnë me ngarkesa negative.

Siç e dini, puna e forcave konservatore kryhet për shkak të humbjes së energjisë potenciale. Prandaj, puna e forcave të fushës elektrostatike mund të përfaqësohet si ndryshim në energjitë potenciale që ka një ngarkesë pikë q pr në pikat fillestare dhe përfundimtare të fushës së ngarkesës q:

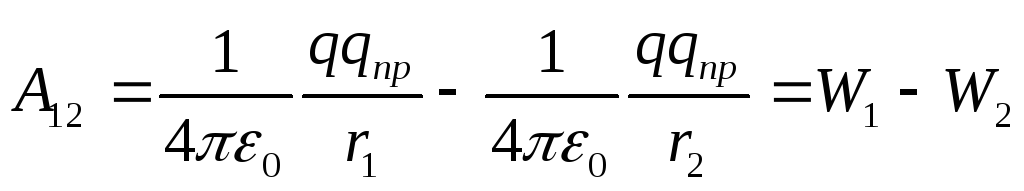(12.24)

prej nga rrjedh se energjia potenciale e ngarkesës q pr në fushën e ngarkesës q është e barabartë me

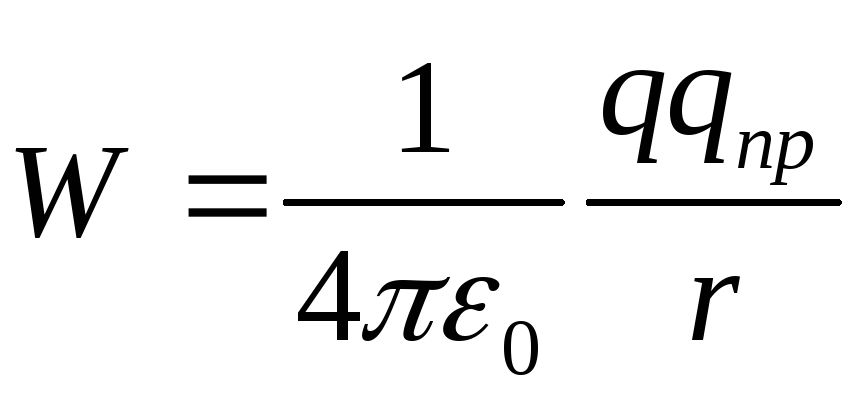(12.25)

Për ngarkesat e ngjashme q pr q >0 dhe energjia potenciale e bashkëveprimit të tyre (zmbrapsja) është pozitive, për ngarkesat e ndryshme q pr q< 0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Nëse fusha krijohet nga një sistem prej n ngarkesash pikash q 1, q 2, .... q n , atëherë energjia potenciale U e ngarkesës q pr e vendosur në këtë fushë është e barabartë me shumën e energjive të saj potenciale U i krijuar nga secila prej ngarkesave veç e veç:

(12.26)

Qëndrimi 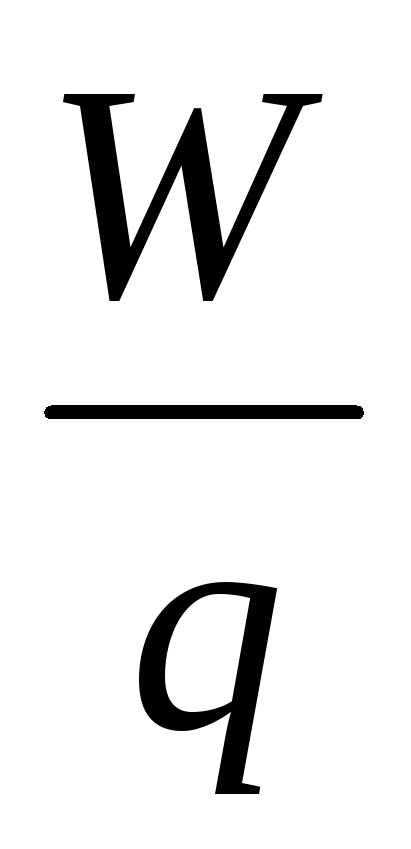nuk varen nga ngarkesa q dhe është karakteristikë energjetike e fushës elektrostatike.

Një sasi fizike skalare, e matur nga raporti i energjisë potenciale të një ngarkese provë në një fushë elektrostatike me vlerën e kësaj ngarkese, quhetpotenciali i fushës elektrostatike.

(12.27)

Potenciali i fushës i krijuar nga një ngarkesë pikë q është e barabartë me

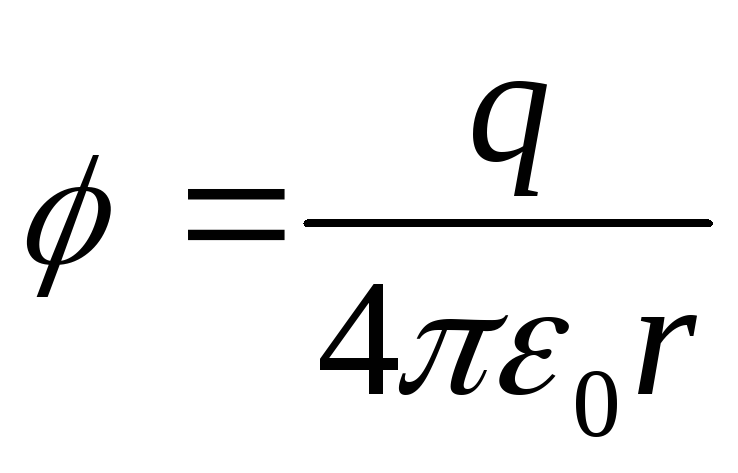(12.28)

Njësia e mundshme - volt.

Puna e bërë nga forcat e fushës elektrostatike kur lëviz ngarkesa q pr nga pika 1 në pikën 2 mund të përfaqësohet si

ato. është e barabartë me produktin e ngarkesës së transferuar dhe diferencën potenciale në pikat e fillimit dhe të përfundimit.

Diferenca potenciale e dy pikave të fushës elektrostatike φ 1 -φ 2 është e barabartë me tensionin. Pastaj

Raporti i punës së bërë nga një fushë elektrostatike kur lëviz një ngarkesë provë nga një pikë e fushës në tjetrën, me vlerën e kësaj ngarkese quhettensionit ndërmjet këtyre pikave.

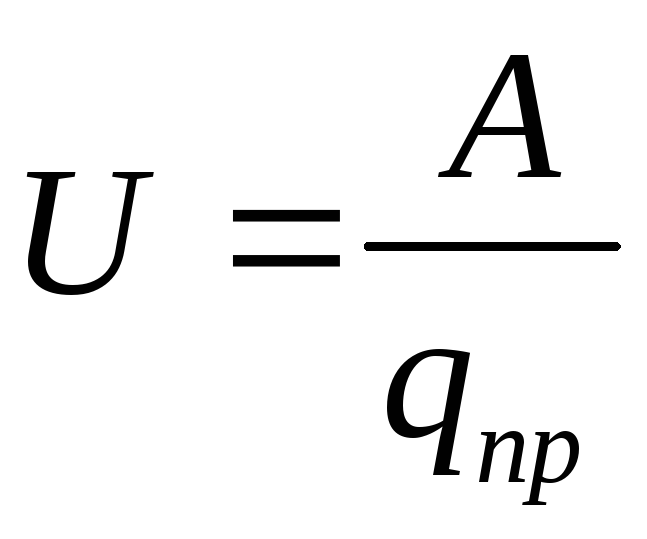(12.30)

Grafikisht, fusha elektrike mund të përshkruhet jo vetëm me ndihmën e linjave të tensionit, por edhe me ndihmën e sipërfaqeve ekuipotenciale.

Ekuipotencial sipërfaqeve është një grup pikash që kanë të njëjtin potencial. Figura tregon se vijat e tensionit (rrezet radiale) janë pingul me vijat ekuipotenciale.

E ka një numër të pafund sipërfaqesh potenciale rreth çdo ngarkese dhe çdo sistemi ngarkesash (Fig. 12.14). Megjithatë, ato kryhen në mënyrë që ndryshimet e mundshme midis çdo dy sipërfaqesh ekuipotenciale ngjitur të jenë të njëjta. Pastaj dendësia e sipërfaqeve ekuipotenciale karakterizon qartë forcën e fushës në pika të ndryshme. Aty ku këto sipërfaqe janë më të dendura, forca e fushës është më e madhe. Duke ditur vendndodhjen e linjave (sipërfaqeve) ekuipotenciale, është e mundur të ndërtohen linja tensioni, ose nga një vendndodhje e njohur e linjave të tensionit, mund të ndërtohen sipërfaqe ekuipotenciale.

§ 12.4Marrëdhënia midis tensionit dhe potencialit

Një fushë elektrostatike ka dy karakteristika: fuqinë (forcën) dhe energjinë (potencialin). Tensioni dhe potenciali janë karakteristika të ndryshme të së njëjtës pikë fushore, prandaj duhet të ketë një lidhje midis tyre.

Puna e lëvizjes së një ngarkese pozitive me pikë të vetme nga një pikë në tjetrën përgjatë boshtit x, me kusht që pikat të jenë pafundësisht afër njëra-tjetrës dhe x 1 - x 2 \u003d dx, është e barabartë me qE x dx. E njëjta punë është e barabartë me q(φ 1 - φ 2)= -dφq. Duke barazuar të dyja shprehjet, mund të shkruajmë

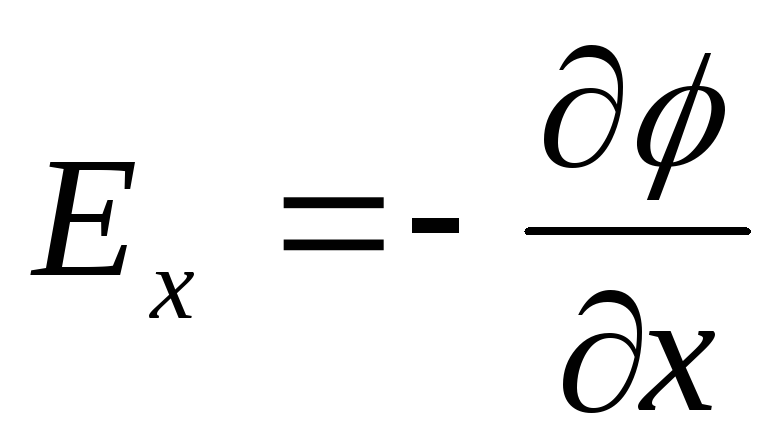
Duke përsëritur arsyetime të ngjashme për boshtet y dhe z, mund të gjejmë vektorin :

ku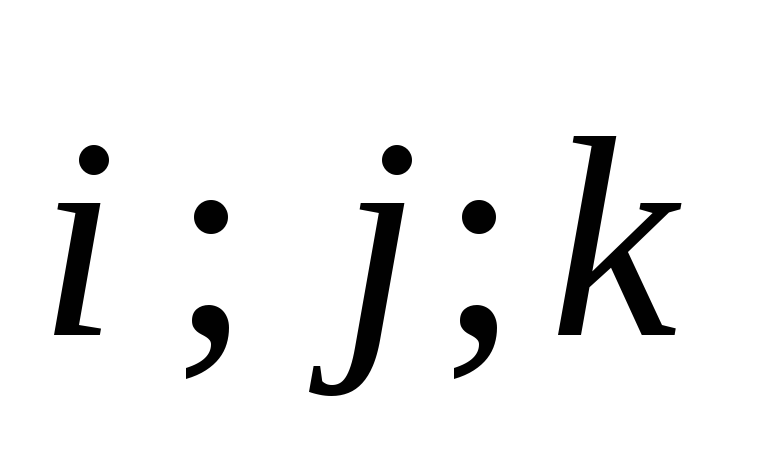

- vektorët njësi të boshteve të koordinatave x, y, z.

Nga përkufizimi i një gradienti rezulton 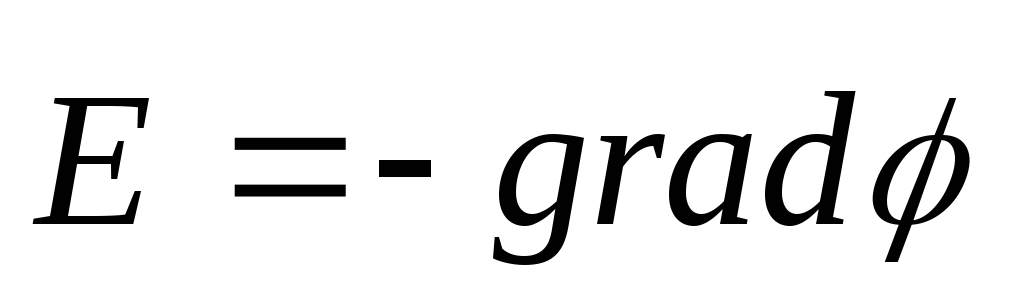se

ose

(12.31)

ato. forca e fushës E është e barabartë me gradientin potencial me shenjën minus. Shenja minus përcaktohet nga fakti se vektori i tensionit E fusha drejtohet në drejtim të zvogëlimit të potencialit.

Marrëdhënia e vendosur midis forcës dhe potencialit lejon, me forcën e njohur të fushës, të gjejë diferencën potenciale midis dy pikave arbitrare të kësaj fushe.

Fusha e një sfere të ngarkuar në mënyrë uniforme rrezeR

Forca e fushës jashtë sferës përcaktohet nga formula

(r>R)

Diferenca potenciale ndërmjet pikave r 1 dhe r 2 (r 1 >R; r 2 >R) përcaktohet duke përdorur relacionin

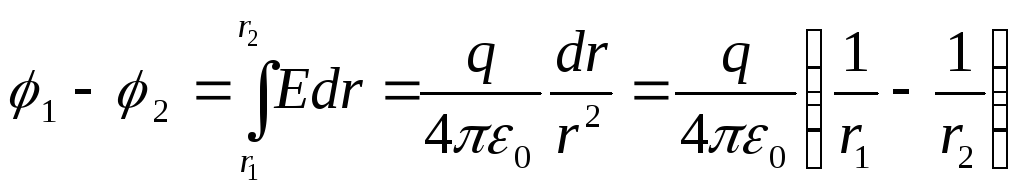
Ne marrim potencialin e sferës nëse r 1 = R, r 2 → ∞:

Fusha e një cilindri pafundësisht të gjatë të ngarkuar në mënyrë uniforme

Forca e fushës jashtë cilindrit (r > R) përcaktohet nga formula

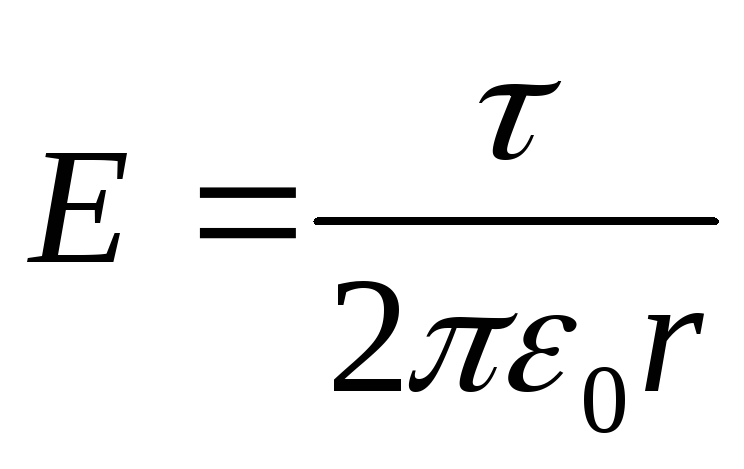
(τ është dendësia lineare).

Diferenca potenciale midis dy pikave që ndodhen në një distancë r 1 dhe r 2 (r 1 >R; r 2 >R) nga boshti i cilindrit është i barabartë me

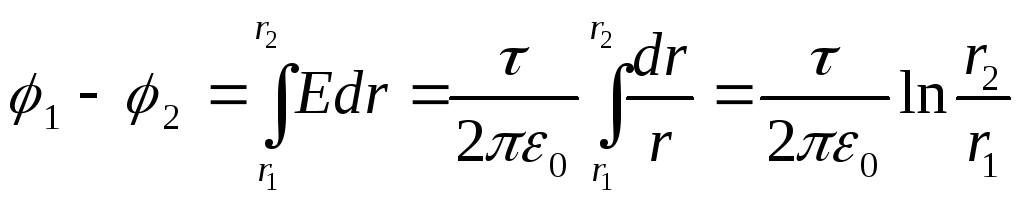(12.32)

Fusha e një rrafshi të pafund të ngarkuar në mënyrë uniforme

Forca e fushës së këtij rrafshi përcaktohet nga formula

(σ - dendësia e sipërfaqes).

Diferenca potenciale midis pikave që shtrihen në një distancë x 1 dhe x 2 nga rrafshi është e barabartë me

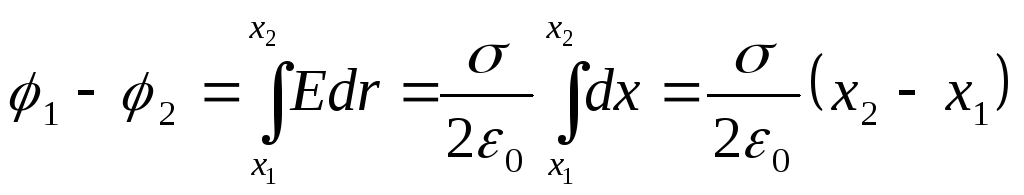(12.33)

Fusha e dy planeve paralele të pafundme me ngarkesë të kundërt

Forca e fushës së këtyre planeve përcaktohet nga formula

Dallimi potencial midis avionëve është

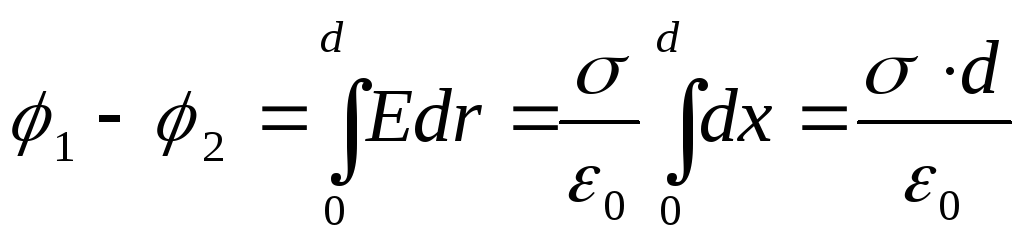(12.34)

(d është distanca ndërmjet avionëve).

Shembuj të zgjidhjes së problemeve

Shembulli 12.1 . Ngarkesat me tre pika Q 1 \u003d 2nC, Q 2 \u003d 3nC dhe Q 3 \u003d -4nC janë të vendosura në kulmet e një trekëndëshi barabrinjës me gjatësi anësore a= 10 cm. Përcaktoni energjinë potenciale të këtij sistemi.

E dhënë : Q 1 \u003d 2nCl \u003d 2∙10 -9 C; Q 2 \u003d 3nCl \u003d 3 ∙ 10 -9 C; dhe Q 3 \u003d -4nCl \u003d 4∙10 -9 C; a=10cm=0.1m.

Gjej : U.

R Zgjidhja: Energjia potenciale e një sistemi ngarkesash është e barabartë me shumën algjebrike të energjive të bashkëveprimit të secilit prej çifteve ndërvepruese të ngarkesave, d.m.th.

U=U 12 +U 13 +U 23

ku, respektivisht, energjitë e mundshme të njërës prej ngarkesave të vendosura në fushën e një ngarkese tjetër në distancë a prej tij, të barabartë

;

;

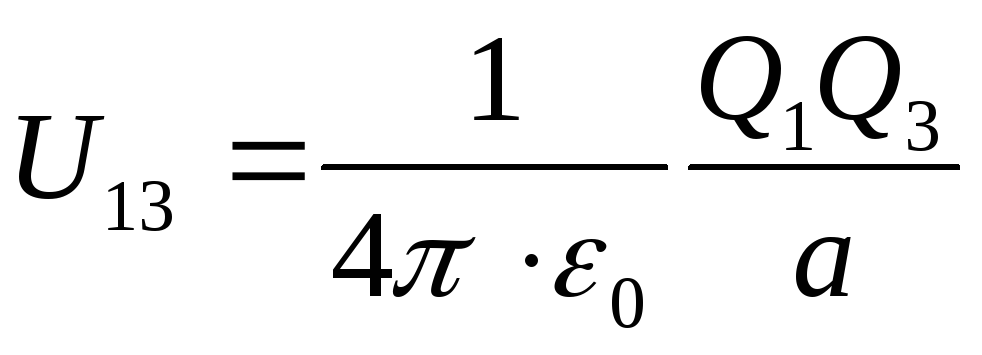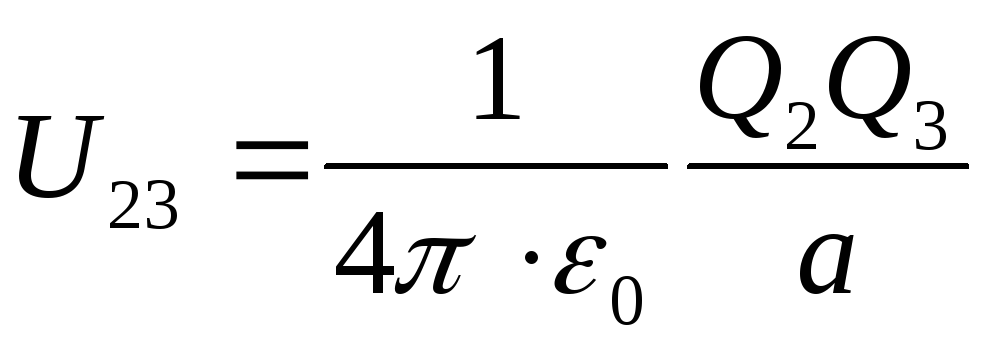(2)

Ne zëvendësojmë formulat (2) në shprehjen (1), gjejmë energjinë e dëshiruar potenciale të sistemit të ngarkesave

Përgjigje: U \u003d -0,126 μJ.

Shembulli 12.2 . Përcaktoni potencialin në qendër të unazës me rreze të brendshme R 1 =30cm dhe R 2 =60cm të jashtme, nëse ngarkesa q=5nC është e shpërndarë në mënyrë të barabartë mbi të.

E dhënë: R 1 \u003d 30 cm \u003d 0,3 m; R 2 \u003d 60 cm \u003d 0,6 m; q=5nCl=5∙10 -9 C

Gjej : φ .

Zgjidhja: Unazën e ndajmë në unaza koncentrike pafundësisht të holla me një rreze të brendshme r dhe një rreze të jashtme (r+dr).

Sipërfaqja e unazës së hollë të konsideruar (shih figurën) dS=2πrdr.

P 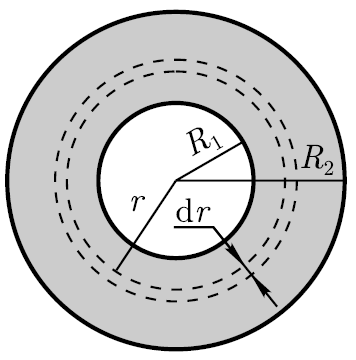potenciali në qendër të unazës, i krijuar nga një unazë pafundësisht e hollë,

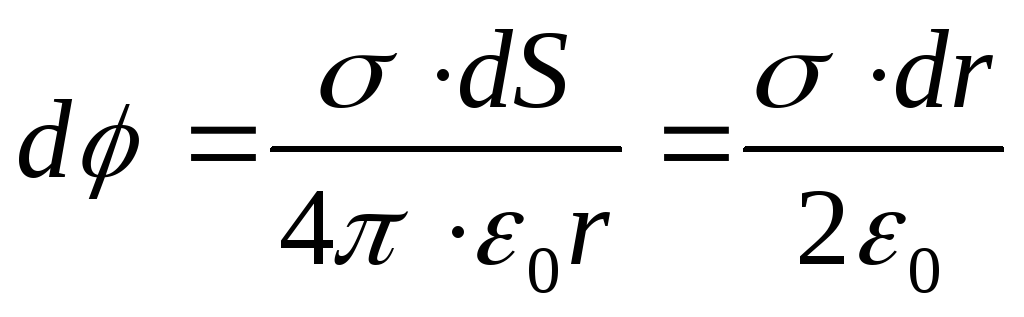
ku është dendësia e ngarkesës sipërfaqësore.

Për të përcaktuar potencialin në qendër të unazës, duhet të shtoni aritmetikisht dφ nga të gjitha unazat pafundësisht të hollë. Pastaj

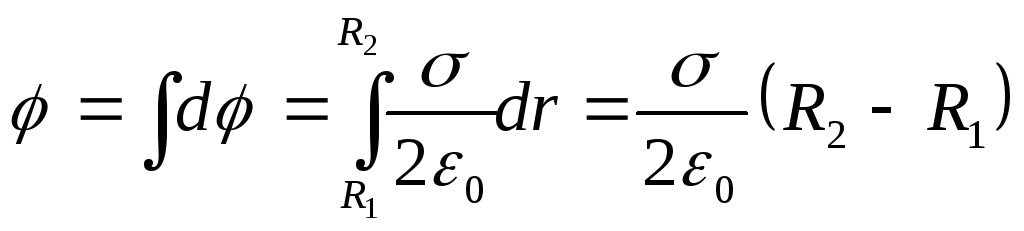
Duke marrë parasysh që ngarkesa e unazës Q=σS, ku S= π(R 2 2 -R 1 2) është sipërfaqja e unazës, marrim potencialin e dëshiruar në qendër të unazës.

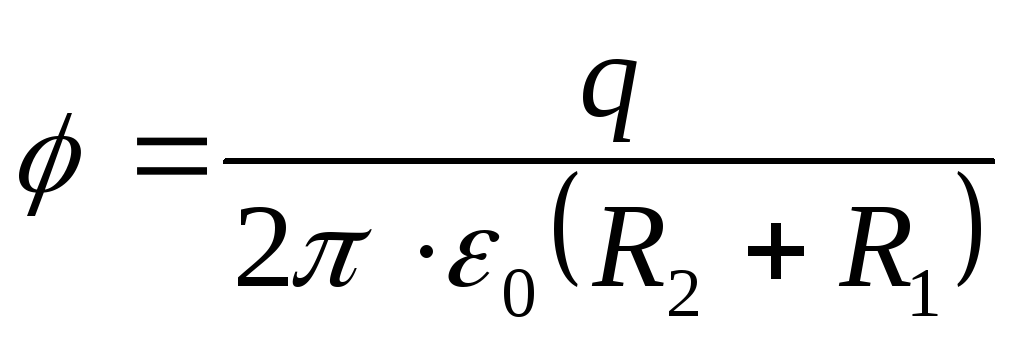
Përgjigju : φ=25V

Shembulli 12.3. dy pika akuza me të njëjtin emër (q 1 =2nC dheq 2 \u003d 5nC) janë në vakum në distancër 1 = 20 cm. Përcaktoni punën A që duhet bërë për t'i afruar ato me distancënr 2 = 5 cm.

E dhënë: q 1 =2nCl=2∙10 -9 C; q 2 =5nCl=5∙10 -9 C ; r 1 = 20cm=0,2m;r 2 =5cm=0,05m.

Gjej : POR.

Zgjidhja: Puna e bërë nga forcat e fushës elektrostatike kur lëviz ngarkesa Q nga një pikë në fushë me një potencial φ 1 në një pikë me një potencial φ 2.

A 12 \u003d q (φ 1 - φ 2)

Kur ngarkesa të ngjashme i afrohen njëra-tjetrës, puna kryhet nga forca të jashtme, kështu që puna e këtyre forcave është e barabartë në vlerë absolute, por në shenjë e kundërt me punën e forcave të Kulonit:

A \u003d -q (φ 1 - φ 2) \u003d q (φ 2 - φ 1). (një)

Potencialet e pikave 1 dhe 2 të fushës elektrostatike

;

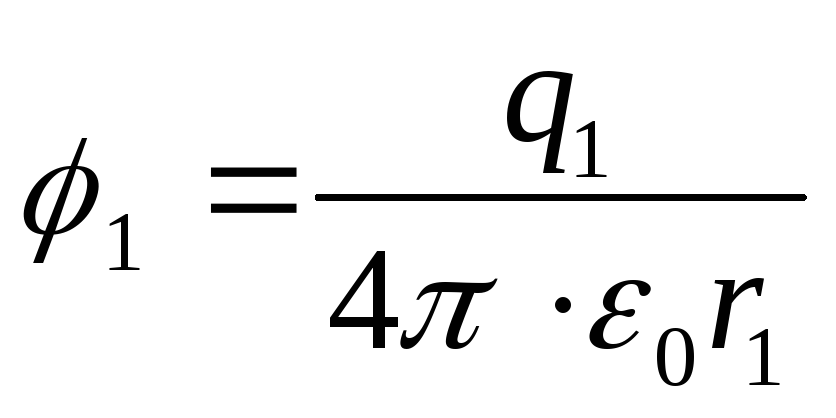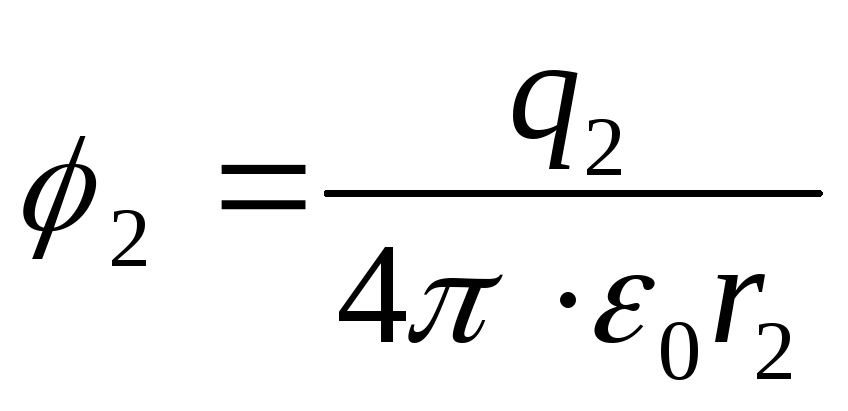(2)

Duke zëvendësuar formulat (2) në shprehjen (1), gjejmë punën e dëshiruar që duhet bërë për të afruar ngarkesat,

Përgjigje: A=1,35 μJ.

Shembulli 12.4. Një fushë elektrostatike krijohet nga një filament i pafund i ngarkuar pozitivisht. Një proton që lëviz nën veprimin e një fushe elektrostatike përgjatë vijës së tensionit nga filamenti nga një distancër 1 = 2 cm derir 2 =10cm, ndryshoi shpejtësinë ngaυ 1 =1Mm/s deri nëυ 2 = 5 mm/s. Përcaktoni densitetin linear τ të ngarkesës së fillit.

E dhënë: q=1,6∙10 -19 C; m=1,67∙10 -27 kg; r 1 \u003d 2 cm \u003d 2 ∙ 10 -2 m; r 2 \u003d 10 cm \u003d 0,1 m; r 2 \u003d 5 cm \u003d 0,05 m; υ 1 \u003d 1 Mm / s \u003d 1 ∙ 10 6 m / s; deri në υ 2 \u003d 5 Mm / s \u003d 5 ∙ 10 6 m / s.

Gjej : τ .

Zgjidhja: Puna e bërë nga forcat e fushës elektrostatike kur lëviz një proton nga një pikë e fushës me një potencial φ 1 në një pikë me një potencial φ 2 shkon për të rritur energjinë kinetike të protonit

q(φ 1 - φ 2) \u003d ΔT (1)

Në rastin e një filamenti, fusha elektrostatike është simetrike në aksi, pra

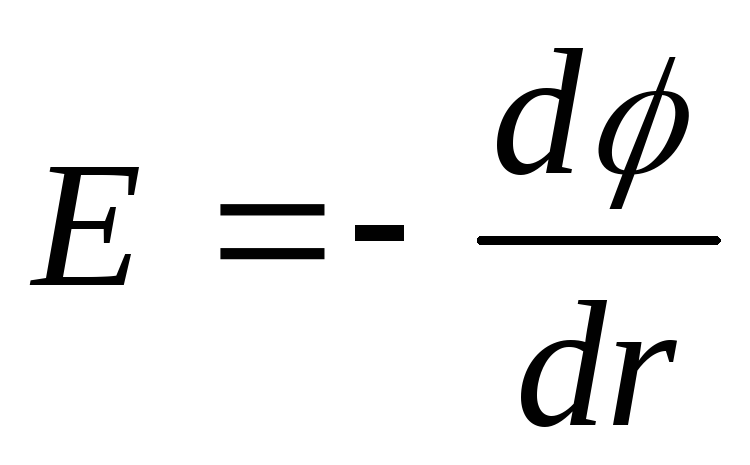ose dφ=-Edr,

atëherë diferenca potenciale midis dy pikave të vendosura në një distancë r 1 dhe r 2 nga filli,

(ne kemi marrë parasysh se forca e fushës e krijuar nga një fije e pafundme e ngarkuar në mënyrë uniforme,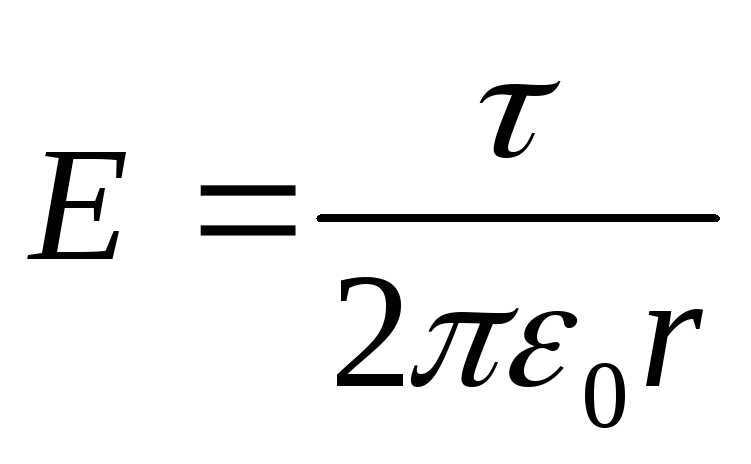

).

Zëvendësimi i shprehjes (2) në formulën (1) dhe duke marrë parasysh atë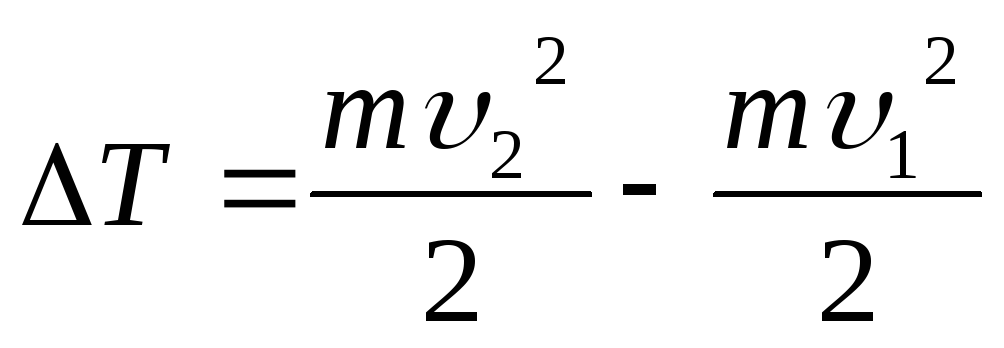

, marrim

Ku është dendësia e dëshiruar lineare e ngarkesës së fillit

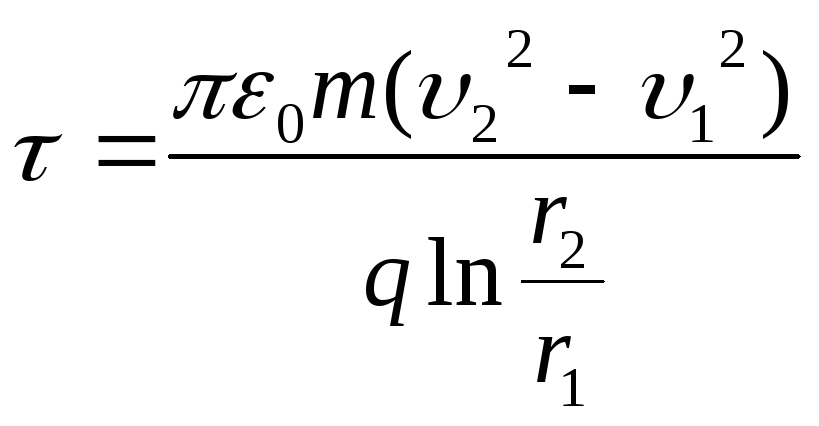
Përgjigju : τ = 4,33 µC/m.

Shembulli 12.5. Një fushë elektrostatike krijohet në një vakum nga një top me një rrezeR=8cm, i ngarkuar në mënyrë të njëtrajtshme me dendësi të madhe ρ=10nC/m 3 . Përcaktoni ndryshimin potencial midis dy pikave të kësaj fushe që shtrihen në distancë nga qendra e topit: 1)r 1 = 10 cm dher 2 = 15 cm; 2)r 3 = 2 cm dher 4 = 5 cm..

E dhënë: R=8cm=8∙10 -2 m; ρ=10nC/m 3 =10∙10 -9 nC/m 3; r 1 \u003d 10 cm \u003d 10 ∙ 10 -2 m;

r 2 \u003d 15 cm \u003d 15 ∙ 10 -2 m; r 3 \u003d 2cm \u003d 2 ∙ 10 -2 m; r 4 \u003d 5 cm \u003d 5 ∙ 10 -2 m.

Gjej : 1) φ 1 - φ 2 ; 2) φ 3 - φ 4 .

Zgjidhja: 1) Diferenca e mundshme midis dy pikave që shtrihen në një distancë r 1 dhe r 2 nga qendra e topit.

(1)

ku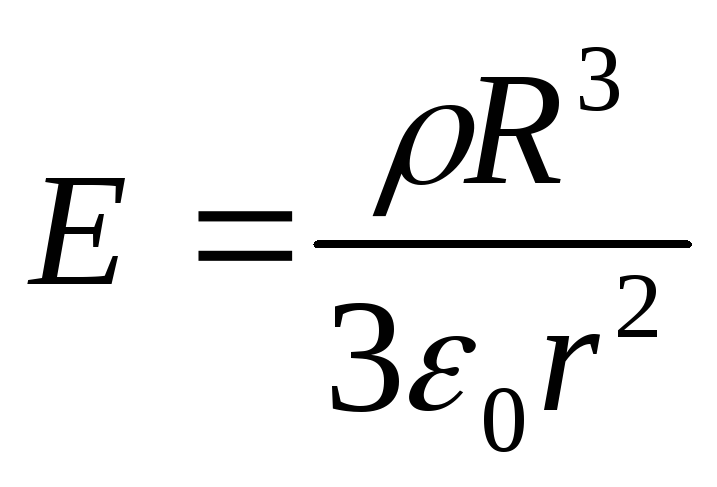

është forca e fushës e krijuar nga një top i ngarkuar në mënyrë uniforme me një densitet të madh ρ në çdo pikë jashtë topit në një distancë r nga qendra e tij.

Duke e zëvendësuar këtë shprehje në formulën (1) dhe duke e integruar, marrim diferencën e dëshiruar të potencialit

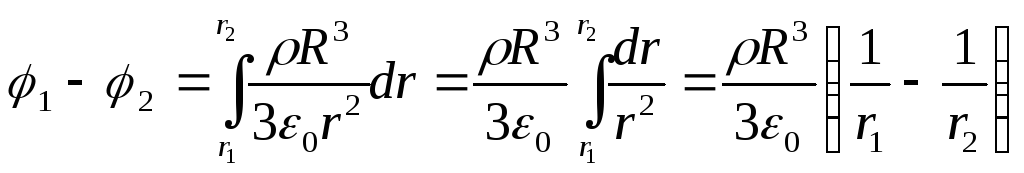
2) Diferenca e mundshme midis dy pikave të vendosura në një distancë r 3 dhe r 4 nga qendra e topit,

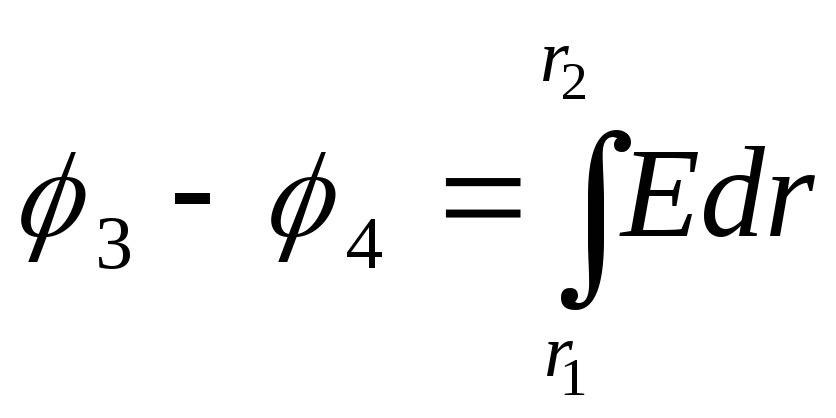(2)

ku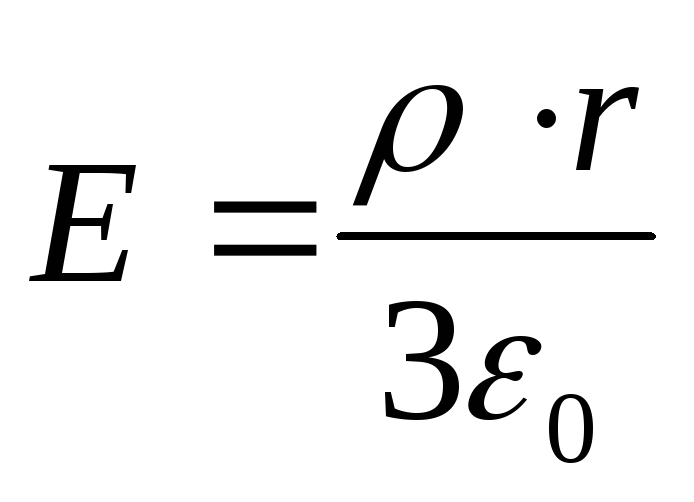

është forca e fushës e gjeneruar nga një top i ngarkuar në mënyrë uniforme me një densitet vëllimi ρ në çdo pikë që ndodhet brenda topit në një distancë r nga qendra e tij.

Duke e zëvendësuar këtë shprehje në formulën (2) dhe duke e integruar, marrim diferencën e dëshiruar të potencialit

Përgjigju : 1) φ 1 - φ 2 \u003d 0,643 V; 2) φ 3 - φ 4 \u003d 0,395 V

Le të llogarisim energjinë potenciale të ngarkesave elektrike për rastet e veçanta më të thjeshta, por shumë të rëndësishme.
Energjia potenciale e një ngarkese në një fushë homogjene Lëreni ngarkesën q të lëvizë në një fushë elektrike uniforme me forcë E nga pika 1 në pikën 2. Pozicioni i pikës 1 përcaktohet nga vektori i rrezes dhe i pikës 2 nga vektori i rrezes r2 . Forca që vepron në ngarkesën F = qE është konstante. Puna e forcës F nuk varet nga forma e pikave lidhëse të trajektores 1 dhe 2. Kjo rrjedh nga vërtetimi i përgjithshëm i potencialit të fushës elektrostatike. Është gjithashtu e mundur të kryhet një vërtetim duke llogaritur drejtpërdrejt punën e bërë kur një ngarkesë lëviz përgjatë shtigjeve të ndryshme në të njëjtën mënyrë siç është bërë në Mekanikë për forcat gravitacionale. Tani nuk do ta bëjmë.
Mënyra më e lehtë për të llogaritur punën është nëse ngarkesa lëviz përgjatë vijës së drejtë që lidh pikën 1 dhe pikën 2 (Fig. 1.78). Vektori i zhvendosjes Dg = r2 - rv Puna është e barabartë me produktin skalar të forcës dhe zhvendosjes:
A = F Ar^qE (r2-r1) = qE r2-qE gg (1.18.1)
Nga ana tjetër, sipas (1.17.1), A \u003d ~ (W 2 ~ Duke krahasuar shprehjet (1.18.1) dhe (1.17.1), marrim një shprehje për energjinë potenciale të një ngarkese në një fushë uniforme :
Wp ~ -qE g. (1.18.2)
Një fushë uniforme krijohet, veçanërisht, në hapësirën midis pllakave paralele, bartja e ngarkesave shenja të kundërta (Fig. 1.79). Është e natyrshme të zgjedhësh sistemin e koordinatave në mënyrë që boshti X të drejtohet pingul me pllakat. Atëherë projeksionet En dhe E, janë të barabarta me zero dhe shprehen
në z
më i ulët (1.18.2) merr formën:
Wp = -q(Exx + Eyy + Ezz) = ~qExx. (1.18.3)

Formula (1.18.3) është e ngjashme me formulën Wp = mgh për energjinë potenciale të një trupi mbi sipërfaqen e Tokës. Roli i masës luhet nga ngarkesa, nxitimi renie e lireështë forca e fushës, dhe në vend të lartësisë h është koordinata x. Por shenja e energjisë është e ndryshme: minus në vend të plusit. Çështja këtu është kjo. Masa është gjithmonë pozitive, dhe forca e gravitetit është e drejtuar domosdoshmërisht vertikalisht poshtë. Duke marrë parasysh këto rrethana, u shkrua formula Wp = mgh. Ai përmban modulin e nxitimit të rënies së lirë, dhe lartësia h matet nga sipërfaqja e Tokës. Formula (1.18.3) është më e përgjithshme. Ngarkesa q mund të jetë pozitive ose negative; forca e fushës mund të drejtohet kudo, dhe projeksioni i saj mund të jetë pozitiv ose negativ, në varësi të zgjedhjes së sistemit të koordinatave.
Në veçanti, nëse forca e fushës E drejtohet vertikalisht poshtë, dhe boshti X është lart, atëherë
Wp = qE\x\ (1.18.4)
në përputhje të saktë me shprehjen Wp = mgh.
Nëse fusha elektrike bën punë pozitive, atëherë energjia e një trupi të ngarkuar në fushë zvogëlohet: AW 0. Një lëvizje e tillë e një grimce të ngarkuar është e ngjashme me lëvizjen e një guri të hedhur lart. Në këtë rast, energjia potenciale e grimcave rritet, ndërsa energjia kinetike zvogëlohet: grimca ngadalësohet.
Energji potenciale zero
Energjia potenciale në elektrodinamikë përcaktohet, si në mekanikë, deri në një konstante arbitrare. Në vend të shprehjes (1.18.2) mund të shkruajmë:
W=-qE-r + C, (1.18.5)
ku C është një konstante arbitrare. Në këtë rast, ndryshimi i energjisë potenciale mbetet i njëjtë, dhe puna përcakton saktësisht ndryshimin në energjinë potenciale, dhe jo vetë energjinë. Duke shkruar formulën (1.18.2), ne në fakt e barazuam konstanten C me zero. Kjo korrespondon me një zgjedhje të caktuar të nivelit zero të energjisë potenciale. Për shembull, për rastin e paraqitur në figurën 1.79, energjia potenciale supozohet të jetë zero në sipërfaqen e pllakës B. Por, si me veprimin e forcave gravitacionale, niveli zero i energjisë potenciale zgjidhet në mënyrë arbitrare. Mund të supozojmë se W - O në një distancë nga pllaka B. Pastaj
wp=-qExx-qExx y
Nuk është vetë energjia potenciale ajo që ka kuptim fizik, por ndryshimi në vlerat e saj, i përcaktuar nga puna e fushës kur ngarkesa lëviz nga pozicioni fillestar në atë përfundimtar.
Energjia e ndërveprimit të ngarkesave pika
Në kursin e mekanikës, u mor një shprehje për energjinë e ndërveprimit të trupave pika:
tі u "W \u003d -G---.
R g
Nëse në vend të masave pikash marrim dy ngarkesa q1 dhe q2 të shenjave të kundërta (ngarkesat tërhiqen), atëherë mund të marrim një shprehje të ngjashme për energjinë potenciale të bashkëveprimit të tyre:
w (1.18.6)
R y"
Për ngarkesat e së njëjtës shenjë (ngarkesat zmbrapsen), shenja e energjisë potenciale do të jetë e kundërt:
w (1.18.7)
R y"
Formulat (1.18.6) dhe (1.18.7) mund të kombinohen në një nëse në vend të moduleve të ngarkesës marrim vlerat e tyre algjebrike:
W. (1.18.8)
R r v "
Shenja e energjisë potenciale automatikisht do të dalë e saktë.
Nëse ngarkesat ql dhe q2 kanë të njëjtat shenja, atëherë energjia potenciale e bashkëveprimit të tyre është pozitive (Fig. 1.80, a). Sa më e madhe, aq më e vogël është distanca midis ngarkesave, pasi puna që mund të bëjnë forcat e Kulonit kur ngarkesat zmbrapsen nga njëra-tjetra do të jetë më e madhe. Nëse ngarkesat kanë shenja të kundërta, atëherë energjia është negative dhe vlera maksimale e saj, e barabartë me zero, arrihet në r -> oo (Fig. 1.80, b). Sa më i madh r, aq më shumë punë do të bëhet nga forcat tërheqëse kur ngarkesat i afrohen njëra-tjetrës.

Oriz. 1.80
Kur shkruani energjinë potenciale në formën (1.18.8), tashmë është bërë një zgjedhje e caktuar e nivelit zero të energjisë potenciale. Besohet se energjia potenciale e ngarkesave pafundësisht të largëta është e barabartë me zero: Wp -» 0 kur r -» oo. Kjo zgjedhje e nivelit zero është e përshtatshme, por nuk kërkohet. Në vend të shprehjes (1.18.8), mund të shkruhet po aq mirë
(1.18.9)
rg y"
ku C është një konstante arbitrare. Kjo tregon se vlera pozitive ose negative e energjisë potenciale të një speciale sensi fizik nuk ka. Shenja e energjisë potenciale do të përcaktohet duke fiksuar një konstante arbitrare C. Duke ndryshuar vlerën e C, ne mund të ndryshojmë shenjën e Wp për një distancë të caktuar r ndërmjet ngarkesave.
Energjia potenciale e një sistemi ngarkesash pikash
Energjia potenciale e një sistemi ngarkesash pikësore qv q2, ..., qN është e barabartë me shumën e energjive potenciale të të gjitha çifteve të ngarkesave ndërvepruese. Për tre akuza
w kbSi+hbS*+hwz l
R G1.2 G1.3 G2.3
Provoni vetë duke përdorur trukun e mëposhtëm. Fillimisht, ngarkesat q2 dhe qz janë në një distancë të pafundme nga ngarkesa qv Më pas ngarkesa q2 lëviz në një pikë që ndodhet në një distancë gl 2 nga ngarkesa e parë. Pas kësaj, ngarkesa qz lëviz në një pikë në një distancë r1 3 nga ngarkesa e parë dhe r2 3 nga e dyta. Është e nevojshme të llogaritet puna e forcave të Kulonit të kryera gjatë këtyre zhvendosjeve dhe të barazohet me ndryshimin e energjisë potenciale, marrë me shenjën e kundërt.
Në përgjithësi, N akuza
N N
wp=llk7rh> (1.18.11)
i=lfc=l (i*k)
ku r; k - distanca midis ngarkesave të bojës së numrave. Koeficienti - 1
2 fitohet për faktin se gjatë përmbledhjes, energjia potenciale merret parasysh dy herë në formën identike
ri, k rk, i
Formulat për energjinë potenciale ngarkesë elektrike në një fushë homogjene (1.18.2) dhe për ngarkesat me dy pika (1.18.8) këshillohet të mbani mend. Ata do të takohen mjaft shpesh.
? 1. A është e mundur të krijohet një elektrostatik
le, vijat e tensionit të të cilave janë paralele- ^^^^^^^
lelny, dhe moduli i intensitetit të moshës është
em në drejtim pingul me
nijam (Fig. 1.81)? Oriz. 1.81
Vizatoni një grafik të varësisë së energjisë potenciale të grimcave të ngarkuara në mënyrë të kundërt nga distanca, me kusht që konstanta arbitrare C në formulën (1.18.9) të jetë pozitive.
Si do të duket formula (1.18.8) nëse ngarkesat janë në një mjedis me një konstante dielektrike є?