2. Fusha elektrike. Fushe elektrike tarifë pikë. Linjat e energjisë.

Sipas koncepteve moderne, ngarkesat elektrike nuk veprojnë drejtpërdrejt mbi njëra-tjetrën. Çdo trup i ngarkuar krijon në hapësirën përreth fushe elektrike . Kjo fushë ka një efekt force mbi trupat e tjerë të ngarkuar. Prona kryesore fushe elektrike- veprim mbi ngarkesat elektrike me një forcë të caktuar. Kështu, bashkëveprimi i trupave të ngarkuar nuk kryhet nga veprimi i tyre i drejtpërdrejtë mbi njëri-tjetrin, por përmes fushave elektrike që rrethojnë trupat e ngarkuar.

Fusha elektrike që rrethon një trup të ngarkuar mund të hetohet duke përdorur të ashtuquajturat tarifë provë - një tarifë e vogël pikë, e cila nuk prodhon një rishpërndarje të dukshme të akuzave të hetuara.

Për të përcaktuar sasinë e fushës elektrike, paraqitet pushtet karakteristike forca e fushës elektrike .

Forca e fushës elektrike quhet një sasi fizike e barabartë me raportin e forcës me të cilën fusha vepron në një ngarkesë testuese pozitive të vendosur në një pikë të caktuar të hapësirës me madhësinë e kësaj ngarkese:

Forca e fushës elektrike është një sasi fizike vektoriale. Drejtimi i vektorit në çdo pikë të hapësirës përkon me drejtimin e forcës që vepron në ngarkesën pozitive të provës.

Fusha elektrike e ngarkesave të palëvizshme dhe të pandryshueshme me kohën quhet elektrostatike . Në shumë raste, për shkurtim, kjo fushë shënohet me termin e përgjithshëm - fushë elektrike

Nëse një fushë elektrike e krijuar nga disa trupa të ngarkuar hetohet duke përdorur një ngarkesë provë, atëherë forca që rezulton rezulton të jetë e barabartë me shumën gjeometrike të forcave që veprojnë në ngarkesën e provës nga secili trup i ngarkuar veçmas. Rrjedhimisht, forca e fushës elektrike e krijuar nga sistemi i ngarkesave në një pikë të caktuar në hapësirë ​​është e barabartë me shumën vektoriale të fuqive të fushave elektrike të krijuara në të njëjtën pikë nga ngarkesat veç e veç:

Kjo fushë quhet Kulombi . Në fushën Kulomb, drejtimi i vektorit varet nga shenja e ngarkesës P: nëse P> 0, atëherë vektori drejtohet përgjatë rrezes nga ngarkesa, nëse P < 0, то вектор направлен к заряду.

Për një paraqitje vizuale të fushës elektrike, përdorni linjat e forcës . Këto vija janë tërhequr në mënyrë që drejtimi i vektorit në secilën pikë të përputhet me drejtimin e tangjentes në linjë fushore(Fig. 1.2.1). Kur përshkruani një fushë elektrike duke përdorur linjat e forcës, dendësia e tyre duhet të jetë proporcionale me modulin e vektorit të forcës së fushës.

Vijat e forcës të fushave të Kulonit të ngarkesave pika pozitive dhe negative janë paraqitur në fig. 1.2.2. Meqenëse fusha elektrostatike e krijuar nga çdo sistem ngarkesash mund të përfaqësohet si një mbivendosje e fushave të Kulonit të ngarkesave pika, të paraqitura në Fig. 1.2.2 Fushat mund të konsiderohen si njësi strukturore elementare ("tulla") të çdo fushe elektrostatike.

Fusha e Kulonit e një ngarkese pikë Pështë i përshtatshëm për të shkruar në formë vektoriale. Për ta bërë këtë, duhet të vizatoni një vektor rreze nga ngarkesa P në pikën e vëzhgimit. Pastaj në P> 0 vektori është paralel, dhe kur P < 0 вектор антипараллелен Следовательно, можно записать:

ku rështë moduli i vektorit të rrezes .

Si shembull i zbatimit të parimit të mbivendosjes së fushave në fig. 1.2.3. shfaqet një foto e vijave të fushës dipol elektrik - sistemet e dy ngarkesave identike të modulit të shenjave të ndryshme q dhe - q ndodhet në një distancë l.

Një karakteristikë e rëndësishme e një dipoli elektrik është i ashtuquajturi moment dipol

ku është një vektor i drejtuar nga një ngarkesë negative në një pozitive, moduli i dipolit mund të shërbejë si një model elektrik i shumë molekulave.

Për shembull, një molekulë uji neutrale (H 2 O) ka një moment dipoli elektrik, pasi qendrat e dy atomeve të hidrogjenit nuk janë të vendosura në të njëjtën vijë të drejtë me qendrën e atomit të oksigjenit, por në një kënd prej 105 ° (Fig. 1.2.4). Momenti dipol i një molekule uji fq= 6,2 10 -30 C m.

3. Teorema elektrostatike e Gausit. Vërtetimi i teoremës së Gausit për një rast të veçantë (një ngarkesë pikë është e vendosur brenda një sfere me rreze R). Përgjithësimi i teoremës së Gausit nëN tarifat me pikë. Përgjithësimi i teoremës së Gausit në rastin e një ngarkese të shpërndarë vazhdimisht. Teorema e Gausit në formë diferenciale.

Le të gjejmë rrjedhën e vektoritE përmes një sipërfaqe sferikeS, në qendër të së cilës është një ngarkesë pikëq.

Në këtë rast, që nga drejtimet E dhe n përkojnë në të gjitha pikat e sipërfaqes sferike.

Duke marrë parasysh forcën e fushës së një ngarkese pikë dhe fakti që marrim sipërfaqen e sferës

Një sasi algjebrike në varësi të shenjës së ngarkesës. Për shembull, kur q<0 линии E e drejtuar kah ngarkesa dhe e kundërt me drejtimin e normales së jashtme n. Prandaj, në këtë rast, fluksi është negativ.<0 .

Lëreni sipërfaqen e mbyllur rreth ngarkesës q ka një formë arbitrare. Është e qartë se sipërfaqja është e prerë nga i njëjti numër vijash E, që është sipërfaqja S. Prandaj, rrjedha e vektorit E përmes një sipërfaqe arbitrare përcaktohet edhe nga formula që rezulton .

Nëse ngarkesa është jashtë sipërfaqes së mbyllur, atëherë, padyshim, sa më shumë rreshta të hyjnë në zonën e mbyllur, i njëjti numër do të largohet prej saj. Si rezultat, rrjedha vektoriale E do të jetë e barabartë me zero.

Nëse fusha elektrike krijohet nga një sistem ngarkesash pikësore atëherë sipas parimit të mbivendosjes,

Dëshmia e një rasti të veçantë:

Teorema e Gausit pretendon:

Rrjedha e vektorit të forcës elektrostatike të fushës përmes një sipërfaqe të mbyllur arbitrare është e barabartë me shumën algjebrike të ngarkesave të vendosura brenda kësaj sipërfaqeje, pjesëtuar me konstanten elektrike ε 0 .

ku Rështë rrezja e sferës. Rrjedha Φ nëpër një sipërfaqe sferike do të jetë e barabartë me produktin E në zonën e sferës 4π R 2. Rrjedhimisht,

Tani le ta rrethojmë ngarkesën pikësore me një sipërfaqe të mbyllur arbitrare S dhe konsideroni një sferë ndihmëse me rreze R 0 (Fig. 1.3.3).

Konsideroni një kon me të vogla kënd i fortë ΔΩ në krye. Ky kon veçon një zonë të vogël Δ në sferë S 0, dhe në sipërfaqe S– platforma Δ S. Rrjedhat elementare ΔΦ 0 dhe ΔΦ nëpër këto zona janë të njëjta. Vërtet,

Këtu Δ S" = Δ S cos α është zona e përcaktuar nga një kon me një kënd të fortë ΔΩ në sipërfaqen e një sfere me rreze n.

Që nga një prandaj rrjedh se rrjedha totale e fushës elektrike të një ngarkese pika përmes një sipërfaqe arbitrare që mbyll ngarkesën është e barabartë me rrjedhën Φ 0 nëpër sipërfaqen e sferës ndihmëse:

Në mënyrë të ngjashme mund të tregohet se nëse një sipërfaqe e mbyllur S nuk mbulon një tarifë pikë q, atëherë rrjedha Φ = 0. Një rast i tillë është paraqitur në Fig. 1.3.2. Të gjitha linjat e forcës së fushës elektrike të një ngarkese pika depërtojnë në një sipërfaqe të mbyllur S përmes. Sipërfaqja e brendshme S nuk ka akuza, prandaj, në këtë rajon, linjat e forcës nuk prishen dhe nuk lindin.

Përgjithësimi i teoremës së Gausit në rastin e një shpërndarje arbitrare të ngarkesave rrjedh nga parimi i mbivendosjes. Fusha e çdo shpërndarjeje ngarkese mund të përfaqësohet si një shumë vektoriale e fushave elektrike të ngarkesave pika. Rrjedha Φ e një sistemi ngarkesash nëpër një sipërfaqe të mbyllur arbitrare S do të përbëhet nga flukse Φ i fushat elektrike të ngarkesave individuale. Nëse ngarkesa q i ishte brenda sipërfaqes S, atëherë jep një kontribut në rrjedhë, nëse kjo ngarkesë është jashtë sipërfaqes, atëherë kontributi i fushës së saj elektrike në rrjedhë do të jetë i barabartë me zero.

Kështu, vërtetohet teorema e Gausit.

Për çdo numër tarifash

Hapi i fundit është i thjeshtë. Ai konsiston në zbatimin e parimit të mbivendosjes.

Nëse, për çdo ngarkesë pikë, fusha e prodhuar prej saj (kur nuk ka ngarkesa të tjera) krijon një fluks nëpër sipërfaqe që plotëson teoremën e Gausit (d.m.th., për çdo ngarkesë brenda sipërfaqes dhe 0 për secilën jashtë sipërfaqes) , pastaj fluksi nga fusha totale

është e barabartë me shumën e flukseve të krijuara nga çdo ngarkesë në mungesë të të tjerave, është thjesht e barabartë me

ku shuma është vetëm mbi ngarkesat brenda sipërfaqes (secila prej atyre jashtë kontribuon me 0).

Teorema është vërtetuar.

ANIMI ELEKTRIKE

Formulat bazë

 Forca e fushës elektrike

E=F/P,

ku Fështë forca që vepron në një pikë ngarkesë pozitive P vendosur në pikën e dhënë të fushës.

 Forca që vepron mbi një ngarkesë pikë P, vendosur në një fushë elektrike,

F=PE.

E fushe elektrike:

a) përmes një sipërfaqe arbitrare S, vendosur në një fushë johomogjene,

ose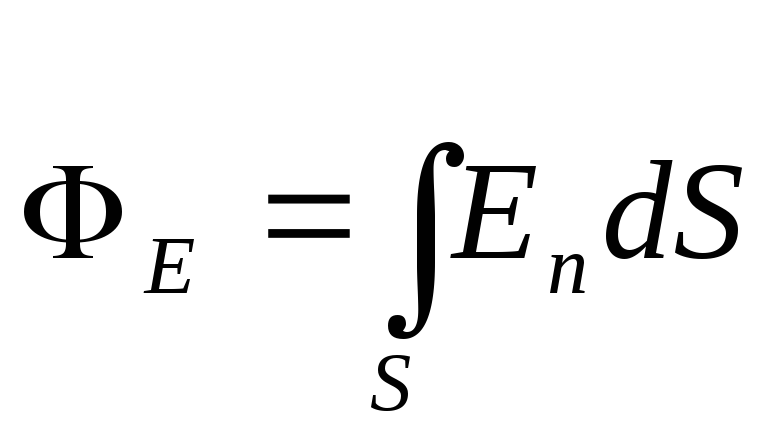

,

ku  është këndi ndërmjet vektorit të intensitetit E dhe normale n në një element sipërfaqësor; d S- zona e elementit të sipërfaqes; E n- projeksioni i vektorit të tensionit në normale;

b) përmes një sipërfaqeje të sheshtë të vendosur në një fushë elektrike uniforme,

F E =ES cos.

 Rrjedha vektoriale e tensionit E përmes një sipërfaqe të mbyllur

,

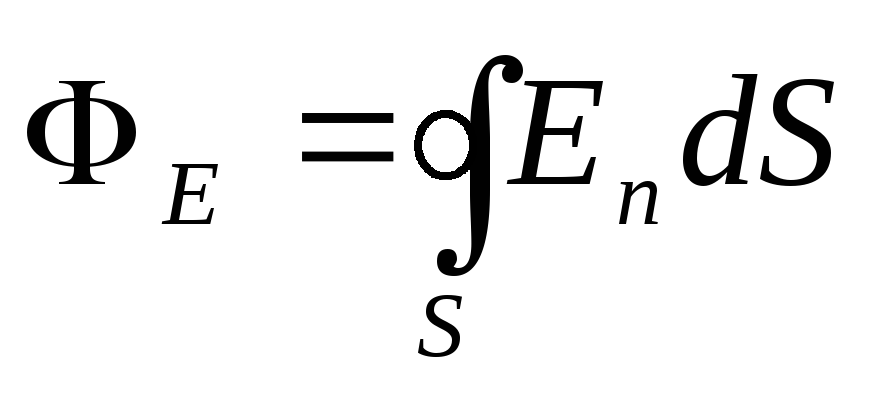ku integrimi kryhet në të gjithë sipërfaqen.

 Teorema Ostrogradsky-Gauss. Rrjedha Vektoriale e Tensionit E përmes çdo ngarkese rrethuese të sipërfaqes së mbyllur P l , P 2 , . . ., P n ,

,

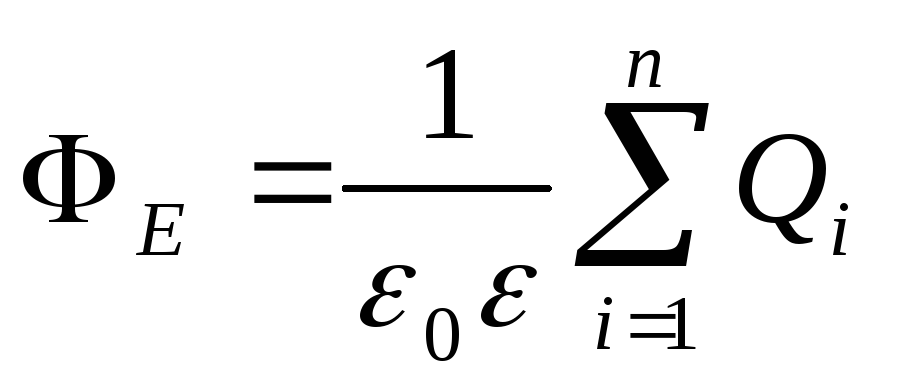ku 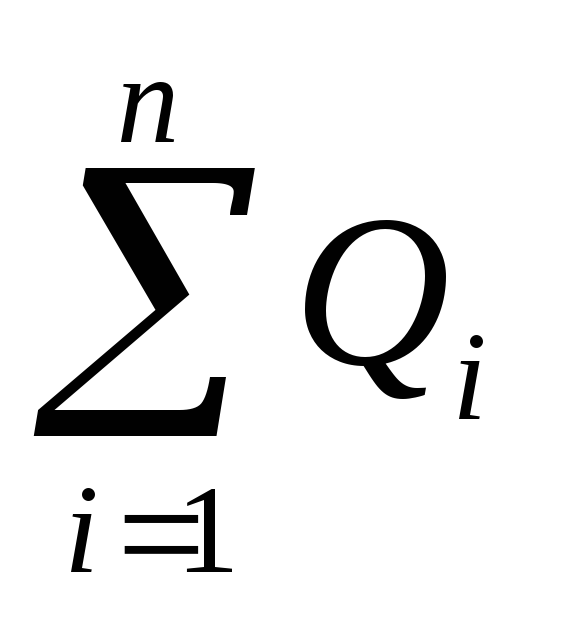- shuma algjebrike e ngarkesave të mbyllura brenda një sipërfaqe të mbyllur; P - numri i tarifave.

 Intensiteti i fushës elektrike të krijuar nga një ngarkesë pikë P në distancë r nga akuza

.

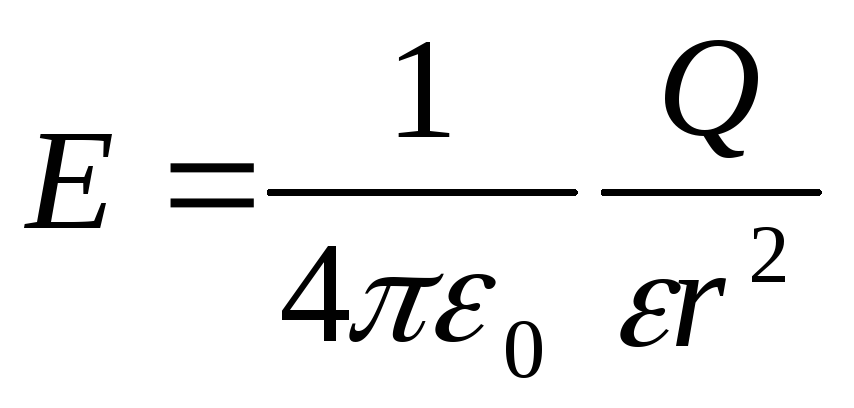Forca e fushës elektrike e krijuar nga një sferë metalike me rreze R, duke mbajtur një pagesë P, në distancë r nga qendra e sferës:

a) brenda sferës (r<.R)

b) në sipërfaqen e një sfere (r=R)

;

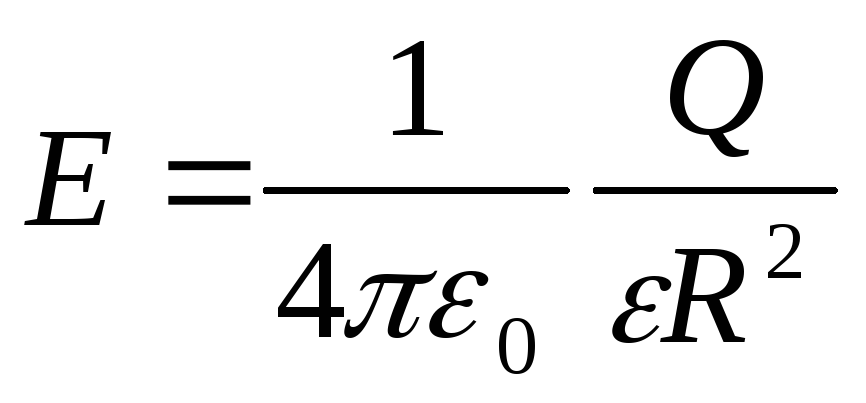c) jashtë sferës (r>R)

.

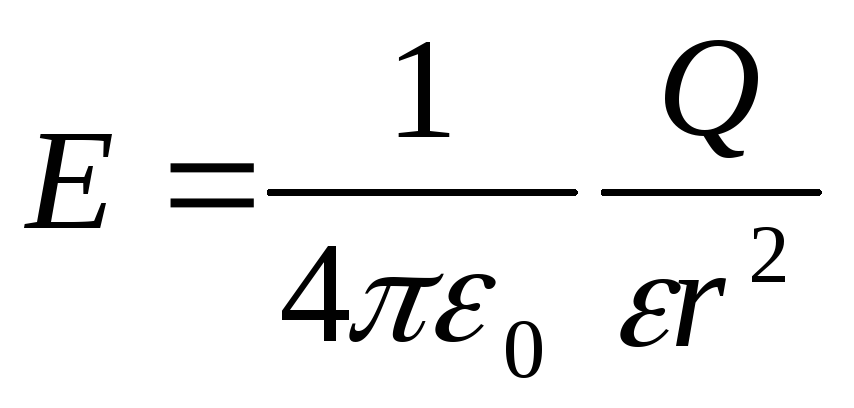 Parimi i mbivendosjes (superpozicionit) të fushave elektrike, sipas të cilit intensiteti E e fushës që rezulton e krijuar nga dy (ose më shumë) ngarkesa pika është e barabartë me shumën vektoriale (gjeometrike) të fuqive të fushave të shtuara:

E=E 1 +E 2 +...+E n .

Në rastin e dy fushave elektrike me forca E 1 dhe E 2 moduli i vektorit të forcës

ku  është këndi ndërmjet vektorëve E 1 dhe E 2 .

 Intensiteti i fushës së krijuar nga një fije (ose cilindër) pafundësisht e gjatë e ngarkuar në mënyrë uniforme në një distancë r nga boshti i saj

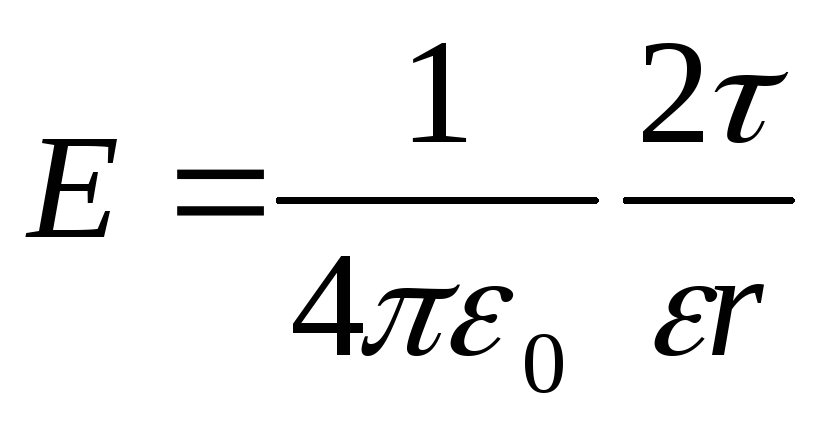, ku  është dendësia lineare e ngarkesës.

Dendësia lineare e ngarkesës është një vlerë e barabartë me raportin e ngarkesës së shpërndarë përgjatë fillit me gjatësinë e fillit (cilindri):

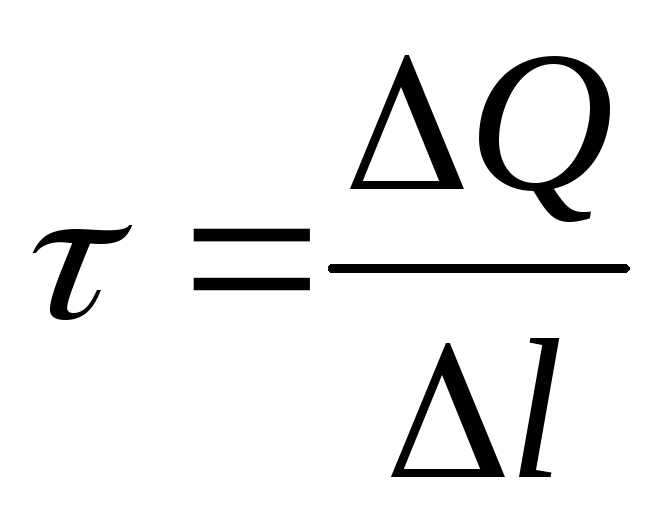
 Intensiteti i fushës së krijuar nga një aeroplan i pafund i ngarkuar në mënyrë uniforme,

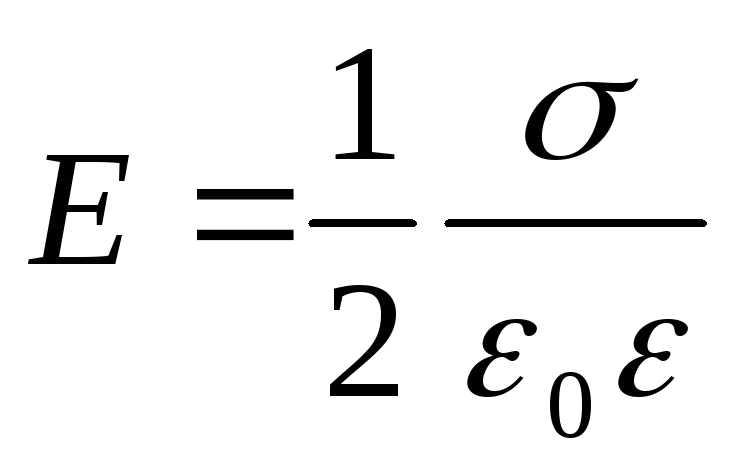
ku  është dendësia e ngarkesës sipërfaqësore.

Dendësia e ngarkesës sipërfaqësore është një vlerë e barabartë me raportin e ngarkesës së shpërndarë në sipërfaqe me zonën e kësaj sipërfaqeje:

.

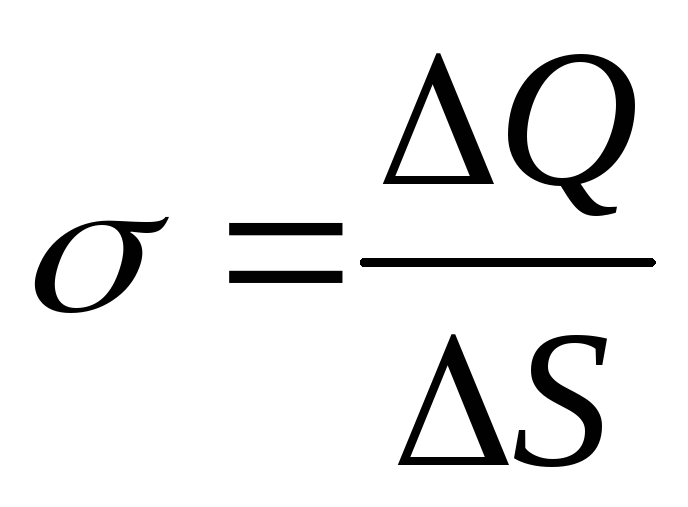 Intensiteti i fushës së krijuar nga dy plane paralele të pafundme të ngarkuara në mënyrë të njëtrajtshme dhe të kundërta, me të njëjtin modul të densitetit të ngarkesës sipërfaqësore (fusha e një kondensatori të sheshtë)

.

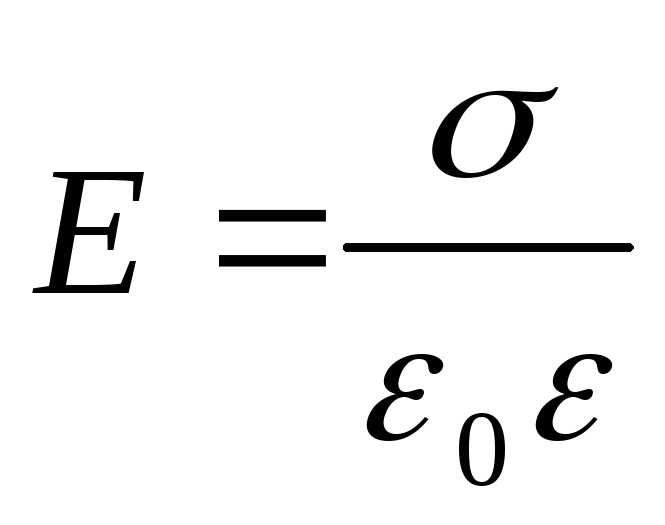Formula e mësipërme është e vlefshme për llogaritjen e forcës së fushës midis pllakave të një kondensatori të sheshtë (në pjesën e mesme të tij) vetëm nëse distanca midis pllakave është shumë më e vogël se dimensionet lineare të pllakave të kondensatorit.

 Zhvendosja elektrike D lidhur me tensionin E raporti i fushës elektrike

D= 0 E.

Kjo lidhje vlen vetëm për dielektrikët izotropikë.

 Rrjedha e vektorit të zhvendosjes elektrike shprehet në mënyrë të ngjashme me rrjedhën e vektorit të forcës së fushës elektrike:

a) në rastin e një fushe uniforme, rrjedha nëpër një sipërfaqe të sheshtë

;

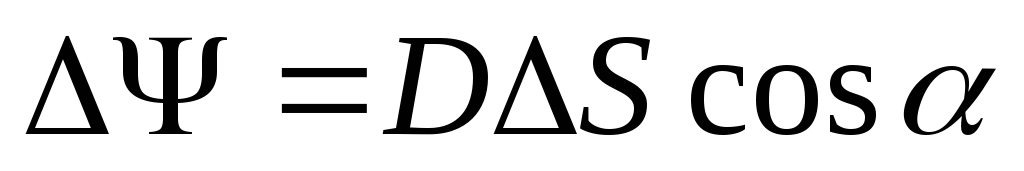b) në rastin e një fushe johomogjene dhe një sipërfaqe arbitrare

,

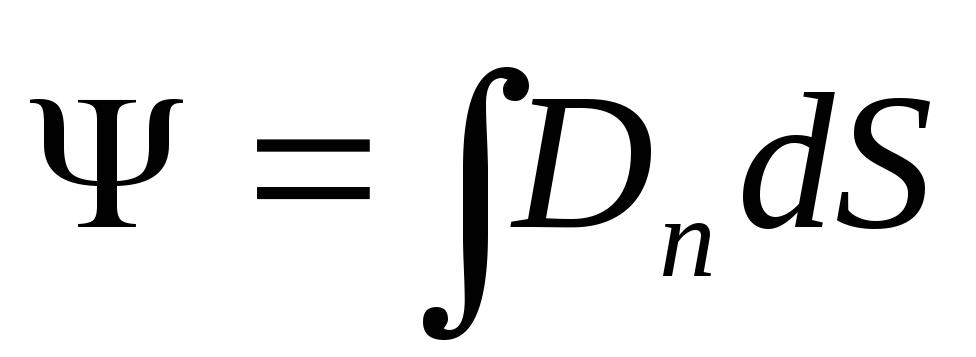ku D n - projeksion vektorial D në drejtimin e elementit normal në sipërfaqe, sipërfaqja e të cilit është e barabartë me d S.

 Teorema Ostrogradsky-Gauss. Fluksi i vektorit të zhvendosjes elektrike përmes çdo ngarkese të sipërfaqes së mbyllur P 1 ,P 2 , ...,P n ,

,

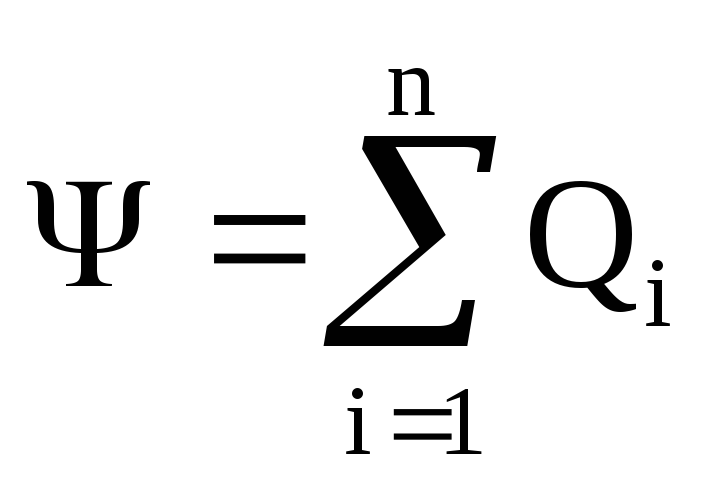ku P- numri i ngarkesave (me shenjën e vet) të mbyllur brenda një sipërfaqe të mbyllur.

 Qarkullimi i vektorit të forcës së fushës elektrike është një vlerë numerikisht e barabartë me punën e lëvizjes së një ngarkese pozitive me pikë të vetme përgjatë një laku të mbyllur. Qarkullimi shprehet me integralin me qark të mbyllur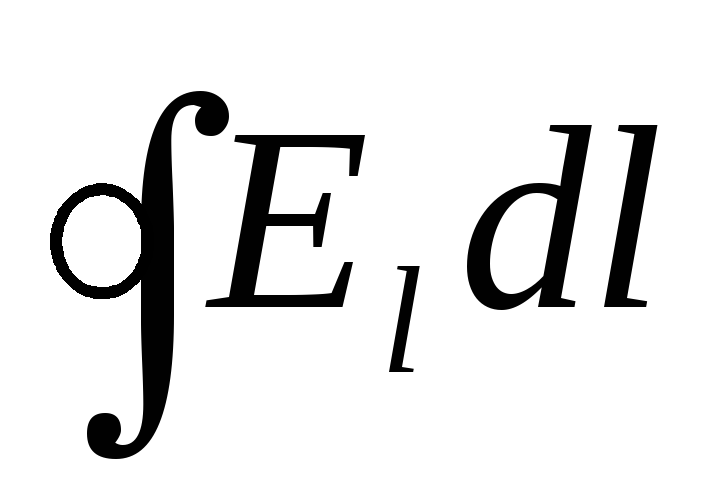

, ku E l - projeksioni i vektorit të intensitetit E në një pikë të caktuar të konturit në drejtimin e tangjentes me konturin në të njëjtën pikë.

Në rastin e një fushe elektrostatike, qarkullimi i vektorit të intensitetit është zero:

.

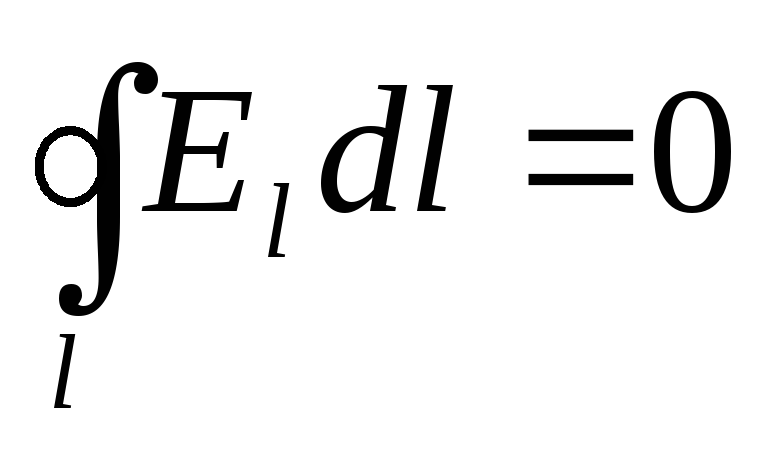Shembuj të zgjidhjes së problemeve

P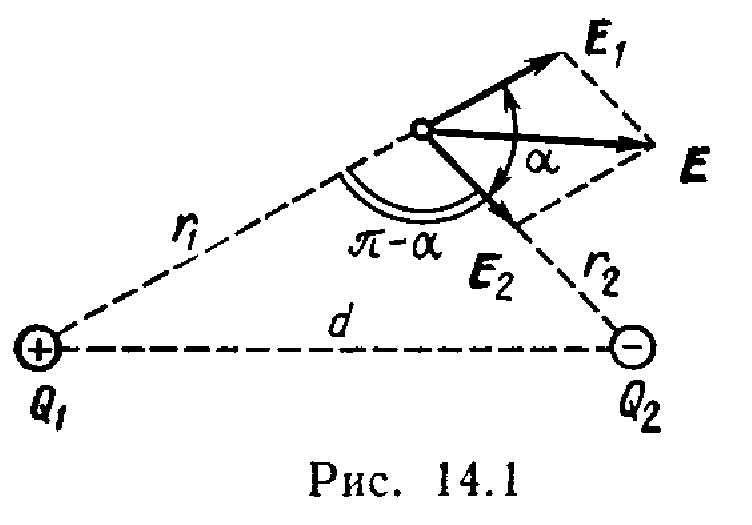

shembulli 1. Fusha elektrike krijohet nga dy ngarkesa pika: P 1 =30nC dhe P 2 = –10 nC. Largësia d ndërmjet ngarkesave është 20 cm Përcaktoni forcën e fushës elektrike në një pikë të vendosur në distancë r 1 =15cm nga e para dhe në distancë r 2 =10 cm nga ngarkesat e dyta.

Zgjidhje. Sipas parimit të mbivendosjes së fushave elektrike, çdo ngarkesë krijon një fushë, pavarësisht nga prania e ngarkesave të tjera në hapësirë. Prandaj tensioni E fusha elektrike në pikën e dëshiruar mund të gjendet si shuma vektoriale e forcave E 1 dhe E 2 fushat e krijuara nga secila tarifë veç e veç: E=E 1 +E 2 .

Fuqitë e fushës elektrike të krijuar në vakum nga ngarkesat e para dhe të dyta janë, përkatësisht, të barabarta me

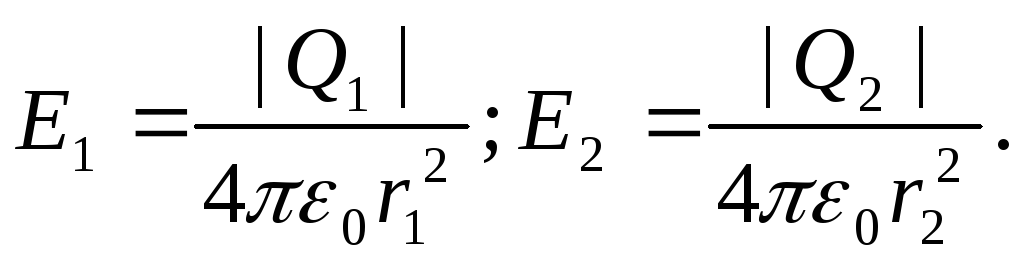(1)

Vektor E 1 (Fig. 14.1) drejtohet përgjatë vijës fushore nga ngarkesa P 1 , që nga akuza P 1 >0;vektor E 2 drejtuar edhe përgjatë vijës së forcës, por drejt ngarkesës P 2 , sepse P 2 <0.

Moduli vektorial E gjeni sipas ligjit të kosinusit:

ku këndi  mund të gjendet nga një trekëndësh me brinjë r 1 , r 2 dhe d:

.

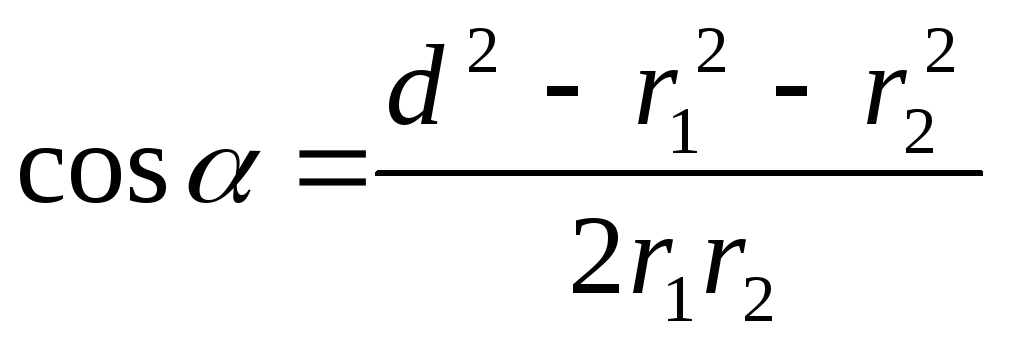Në këtë rast, për të shmangur hyrjet e rënda, ne llogarisim vlerën e cos veçmas.Duke përdorur këtë formulë, gjejmë

Zëvendësimi i shprehjeve E 1 dhe E 2 dhe me formula (1) në barazi (2) dhe duke hequr faktorin e përbashkët 1/(4 0 ) për shenjën rrënjë, marrim

.

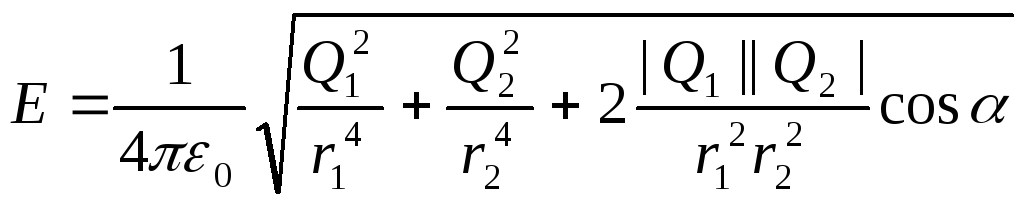Zëvendësimi i vlerave të  ,  0 , P 1 , P 2 , r 1 -,r 2 dhe  në formulën e fundit dhe duke kryer llogaritjet, gjejmë

Shembulli 2 Fusha elektrike krijohet nga dy plane paralele të ngarkuara të pafundme me densitet të ngarkesës sipërfaqësore  1 \u003d 0,4 μC / m 2 dhe 2 \u003d 0,1 μC / m 2. Përcaktoni forcën e fushës elektrike të krijuar nga këto plane të ngarkuara.

R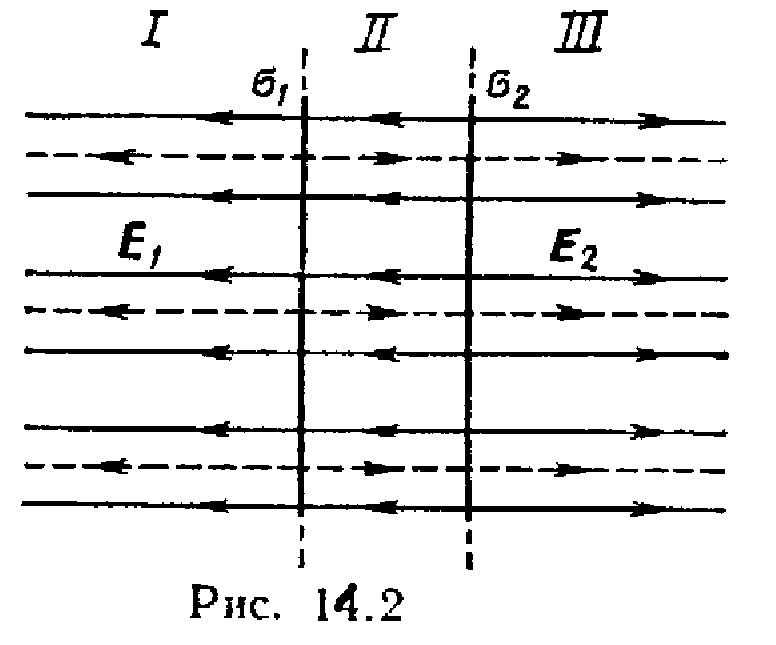

zgjidhje. Sipas parimit të mbivendosjes, fushat e krijuara nga secili rrafsh i ngarkuar individualisht mbivendosen mbi njëra-tjetrën, ku secili plan i ngarkuar krijon një fushë elektrike pavarësisht nga prania e një rrafshi tjetër të ngarkuar (Fig. 14.2).

Fuqitë e fushave elektrike homogjene të krijuara nga rrafshi i parë dhe i dytë janë përkatësisht të barabarta me:

;

.

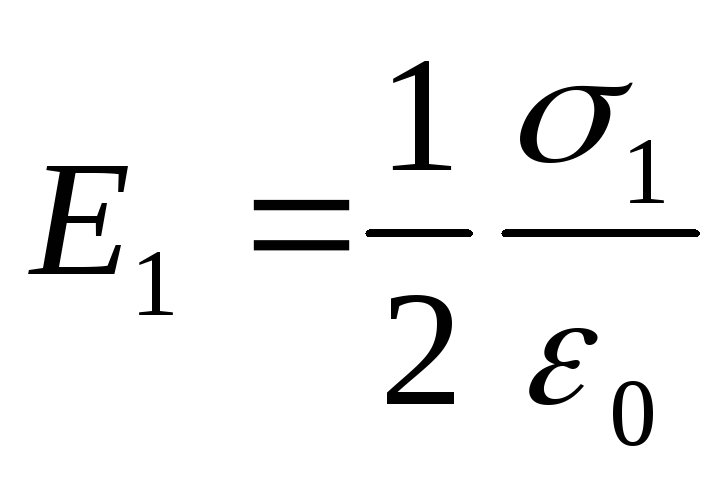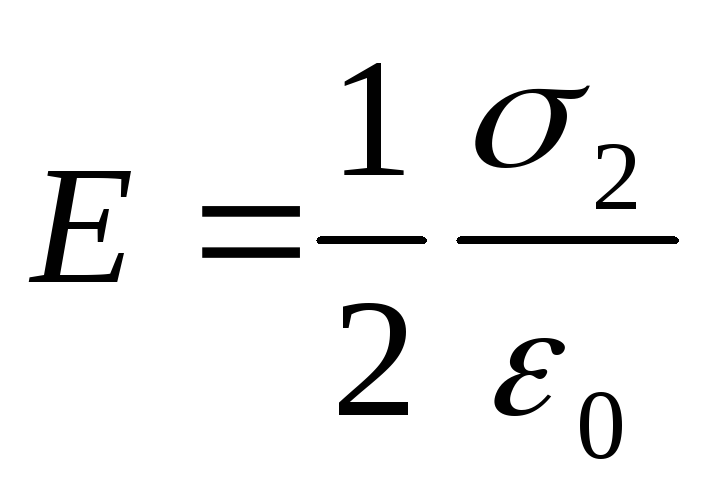Planet e ndajnë të gjithë hapësirën në tre rajone: I, II dhe III. Siç shihet nga figura, në rajonin e parë dhe të tretë, linjat elektrike të forcës së të dy fushave janë të drejtuara në të njëjtin drejtim dhe, rrjedhimisht, forcat e fushave totale. E (Unë) dhe E(III) në rajonin e parë dhe të tretë janë të barabartë me njëri-tjetrin dhe të barabartë me shumën e fuqive të fushës të krijuar nga rrafshi i parë dhe i dytë: E (Unë) =E(III) = E 1 +E 2 , ose

E (Unë) =E (III) =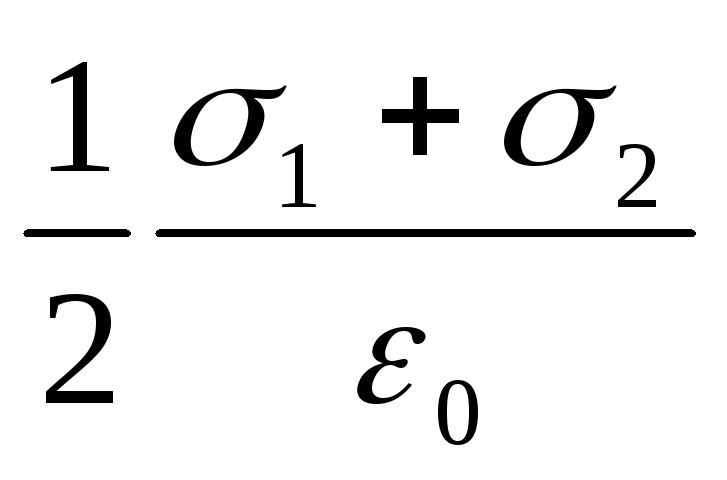

.

Në rajonin e dytë (midis aeroplanëve), linjat elektrike të forcës së fushave drejtohen në drejtime të kundërta dhe, për rrjedhojë, forca e fushës. E (II)është e barabartë me ndryshimin në forcat e fushës të krijuar nga rrafshi i parë dhe i dytë: E (II) =|E 1 -E 2 | , ose

.

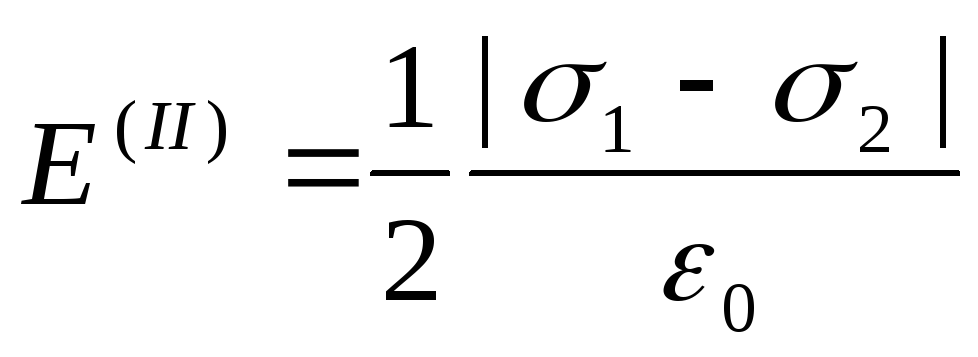Duke zëvendësuar të dhënat dhe duke bërë llogaritjet, marrim

E (Unë) =E (III) =28,3 kV/m=17 kV/m.

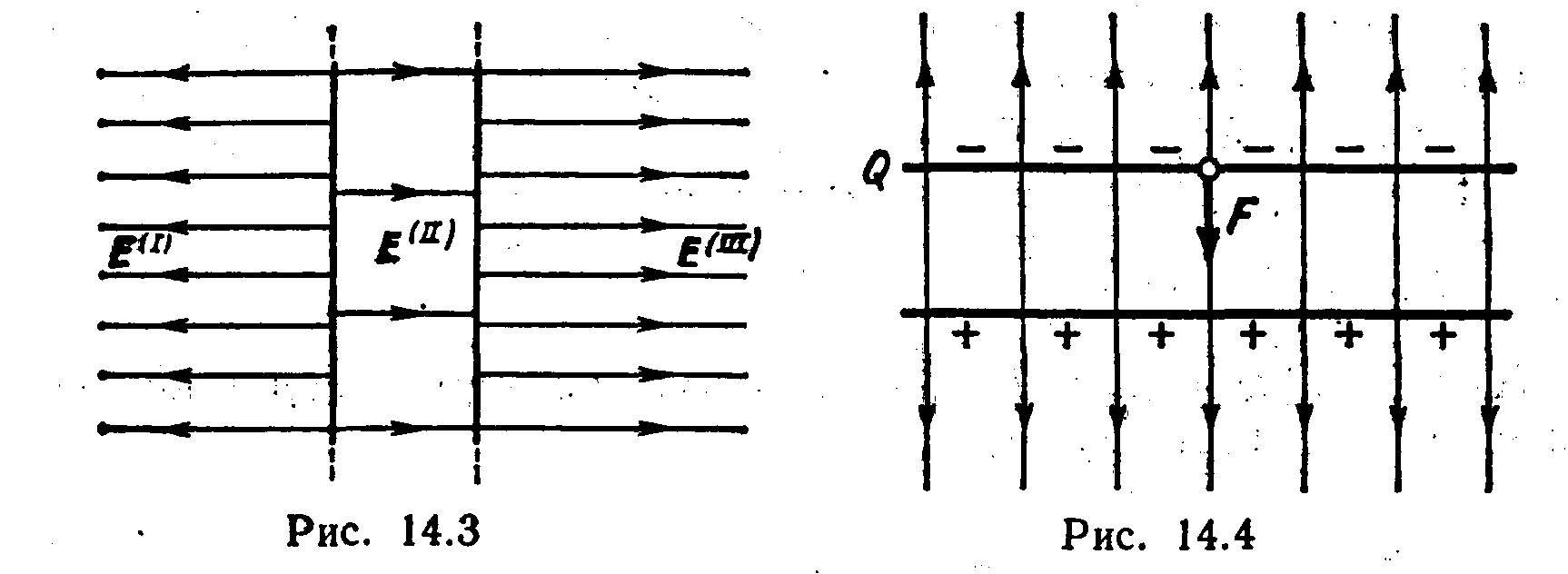
Fotografia e shpërndarjes së linjave të forcës së fushës totale është paraqitur në fig. 14.3.

Shembulli 3. Në pllakat e një kondensatori ajri të sheshtë ka një ngarkesë P=10nC. Sheshi Sçdo pllakë e kondensatorit është e barabartë me 100 cm 2 Përcaktoni forcën F, me të cilat tërhiqen pllakat. Fusha midis pllakave supozohet të jetë uniforme.

Zgjidhje. Ngarkimi P njëra pllakë është në fushën e krijuar nga ngarkesa e pllakës tjetër të kondensatorit. Prandaj, një forcë vepron në ngarkesën e parë (Fig. 14.4)

F=E 1 P,(1)

ku E 1 - forca e fushës e krijuar nga ngarkesa e një pllake. Por

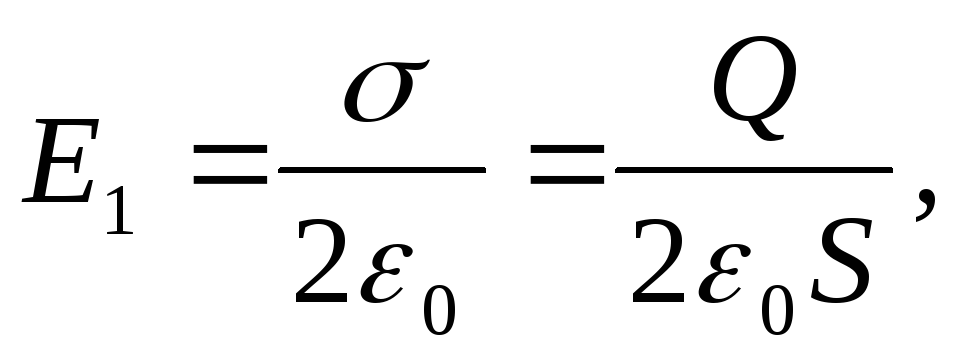ku  është dendësia e ngarkesës sipërfaqësore të pllakës.

Formula (1) duke marrë parasysh shprehjen për E 1 do të marrë formën

F=P 2 /(2 0 S).

Zëvendësimi i vlerave të sasive P, 0 dhe S në këtë formulë dhe duke bërë llogaritjet, marrim

F\u003d 565 μN.

Shembulli 4 Fusha elektrike krijohet nga një rrafsh i pafund i ngarkuar me një densitet sipërfaqësor  = 400 nC/m 2 , dhe një fije e drejtë e pafundme e ngarkuar me dendësi lineare =100 nC/m. Në distancë r\u003d 10 cm nga filli ka një ngarkesë pikë P=10 nC. Përcaktoni forcën që vepron në ngarkesë, drejtimin e saj, nëse ngarkesa dhe filli shtrihen në të njëjtin rrafsh paralel me rrafshin e ngarkuar.

Zgjidhje. Forca që vepron në një ngarkesë të vendosur në një fushë

F=EQ, (1)

ku E -P.

Le të përcaktojmë tensionin E fushë e krijuar, sipas gjendjes së problemit, nga një rrafsh i ngarkuar i pafund dhe një fije e pafundme e ngarkuar. Fusha e krijuar nga një aeroplan i ngarkuar pafund është uniform dhe intensiteti i saj në çdo pikë

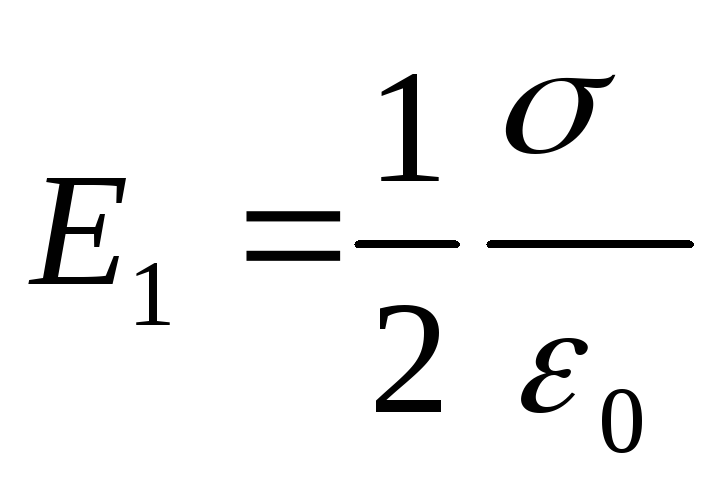. (2)

Fusha e krijuar nga një linjë e pafundme e ngarkuar është jo uniforme. Intensiteti i tij varet nga distanca dhe përcaktohet nga formula

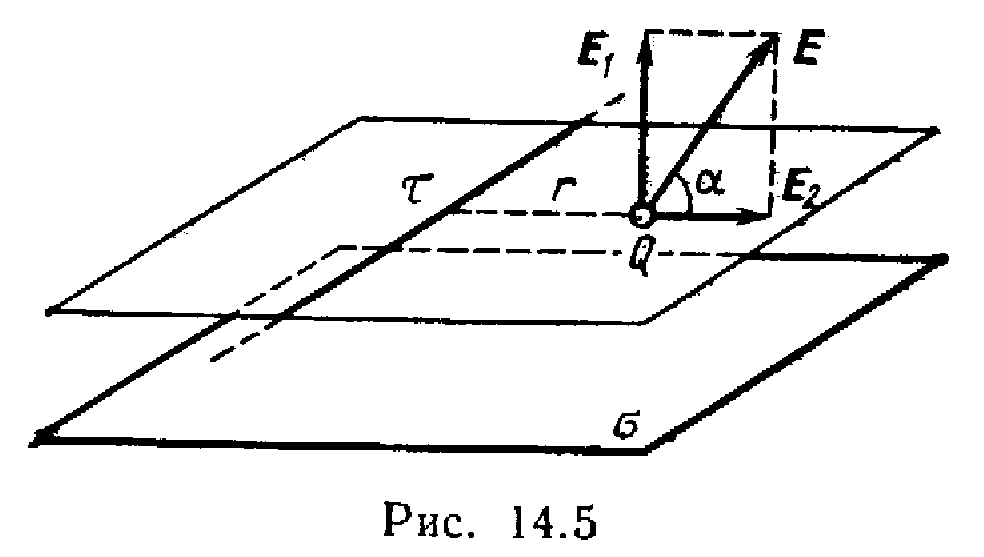
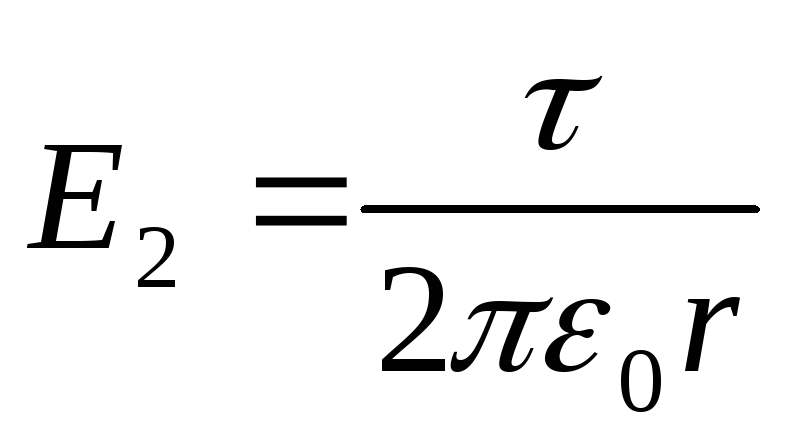. (3)

Sipas parimit të mbivendosjes së fushave elektrike, forca e fushës në pikën ku është ngarkesa P, është e barabartë me shumën vektoriale të intensiteteve E 1 dhe E 2 (Fig. 14.5): E=E 1 +E 2 .Sepse vektorët E 1 dhe E 2 reciprokisht pingul, atëherë

.

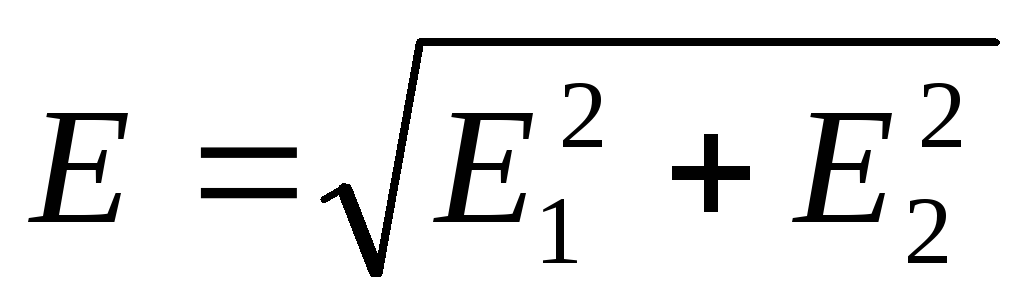Zëvendësimi i shprehjeve E 1 dhe E 2 formulat (2) dhe (3) në këtë barazi, marrim

,

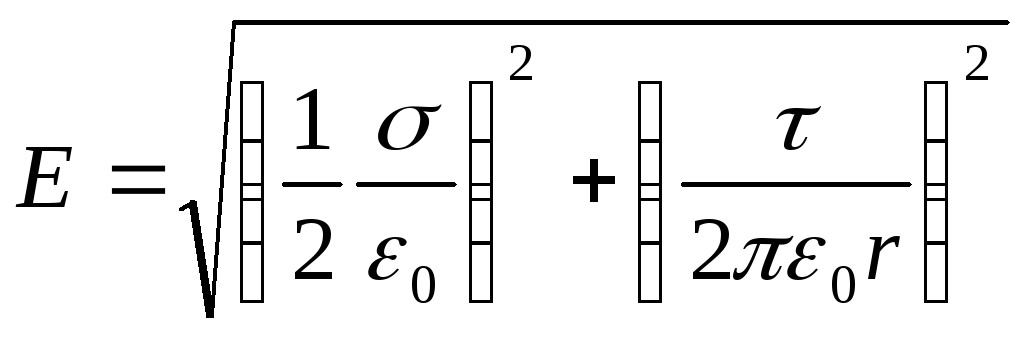ose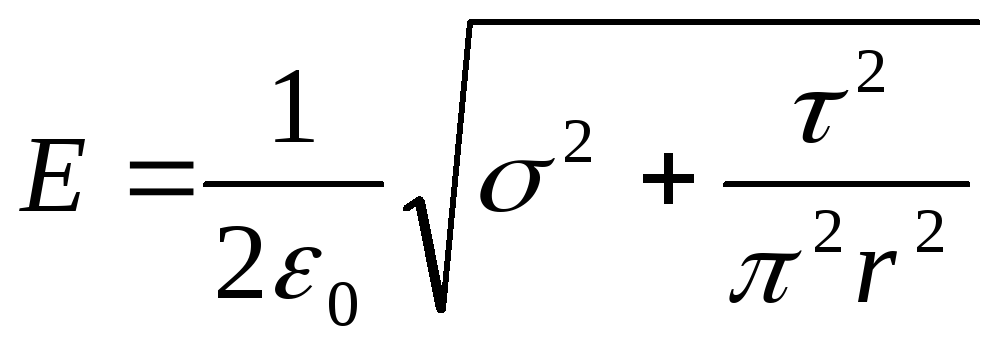

.

Tani le të gjejmë forcën F, duke vepruar sipas akuzës, duke zëvendësuar shprehjen E në formulën (1):

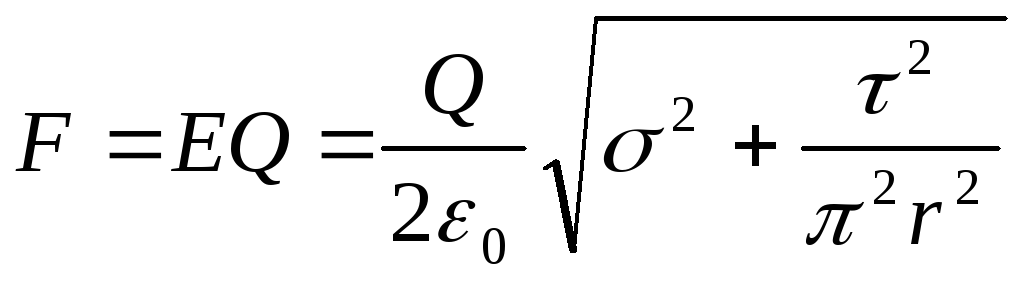. (4)

Zëvendësimi i vlerave të sasive P, 0 ,,,dhe r në formulën (4) dhe duke bërë llogaritjet, gjejmë

F\u003d 289 μN.

Drejtimi i forcës F, duke vepruar në një ngarkesë pozitive P, përkon me drejtimin e vektorit të intensitetit E fusha. Drejtimi i njëjti vektor E jepet nga këndi  ndaj planit të ngarkuar. Nga fig. 14.5 rrjedh se

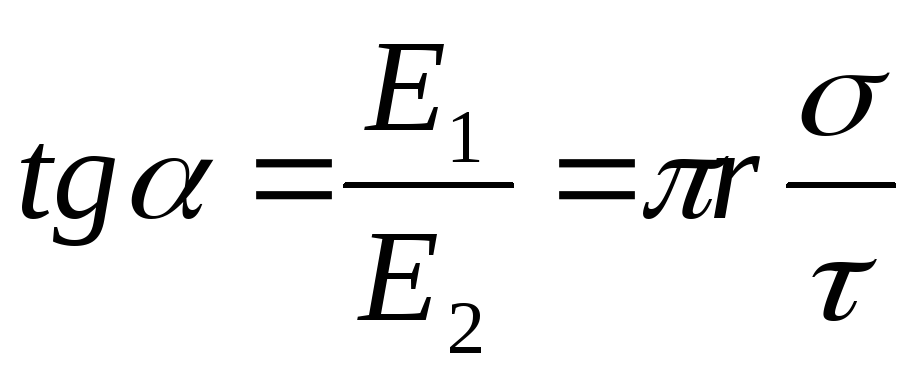, ku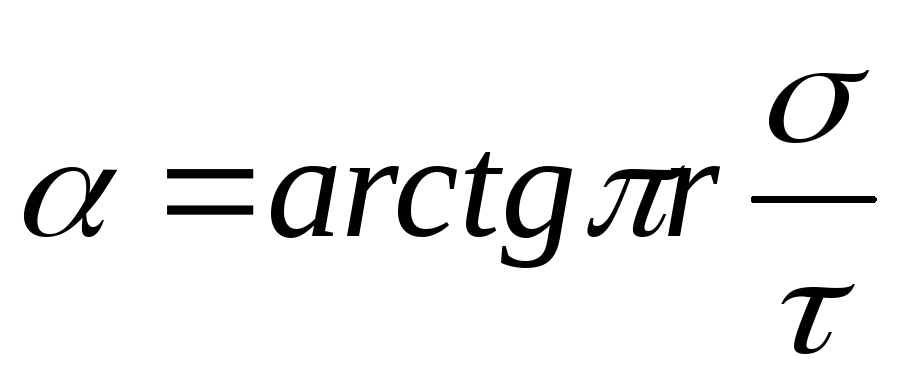

.

Zëvendësimi i vlerave të , r,dhenë këtë shprehje dhe duke llogaritur, marrim

Shembulli 5 tarifë pikë P\u003d 25nC është në zero e krijuar nga një cilindër i drejtë i pafund me një rreze R= 1 cm, i ngarkuar në mënyrë uniforme me një densitet sipërfaqësor  = 2 μC / m 2. Përcaktoni forcën që vepron në një ngarkesë të vendosur në një distancë nga boshti i cilindrit r= 10 cm.

Zgjidhje. Forca që vepron mbi një ngarkesë P, i vendosur në fushë,

F=QE,(1)

ku E - forca e fushës në pikën ku ndodhet ngarkesa P.

Siç dihet, forca e fushës së një cilindri pafundësisht të gjatë të ngarkuar në mënyrë uniforme

E=/(2 0 r), (2)

ku  është dendësia lineare e ngarkesës.

Dendësinë lineare  e shprehim me dendësinë e sipërfaqes . Për ta bërë këtë, zgjidhni një element cilindri me gjatësi l dhe shpreh akuzën për të P 1 dy mënyra:

P 1 =  S= 2  Rl dhe Q 1 = l.

Duke barazuar pjesët e duhura të këtyre barazive, marrim  l=2 Rl . Pas shkurtimit të l gjeni=2 R . Me këtë në mendje, formula (2) merr formën E=R /( 0 r). Duke zëvendësuar këtë shprehje E në formulën (1), gjejmë forcën e dëshiruar:

F=Q R/( 0 r).(3)

Sepse R dhe r përfshihen në formulë si raport, atëherë ato mund të shprehen në çdo, por vetëm të njëjtat njësi.

Pas kryerjes së llogaritjeve duke përdorur formulën (3), gjejmë

F\u003d 2510 -9 210 -6 10 -2 / (8,8510 -12 1010 -2)H==56510 -6 H=565μH.

Drejtimi i forcës F përkon me drejtimin e vektorit të tensionit E, dhe kjo e fundit, për shkak të simetrisë (cilindri është pafundësisht i gjatë) drejtohet pingul me cilindrin.

Shembulli 6 Fusha elektrike krijohet nga një fije e hollë pafundësisht e gjatë, e ngarkuar në mënyrë uniforme me densitet linear =30 nC/m. Në distancë a\u003d 20 cm nga filli ka një zonë të rrumbullakët të sheshtë me një rreze r\u003d 1 cm Përcaktoni rrjedhën e vektorit të tensionit nëpër këtë zonë nëse rrafshi i tij bën një kënd  \u003d 30 ° me vijën e tensionit që kalon në mes të zonës.

Zgjidhje. Fusha e krijuar pafundësisht në mënyrë uniforme nga një filament i ngarkuar është johomogjene. Fluksi vektorial i intensitetit në këtë rast shprehet me integralin

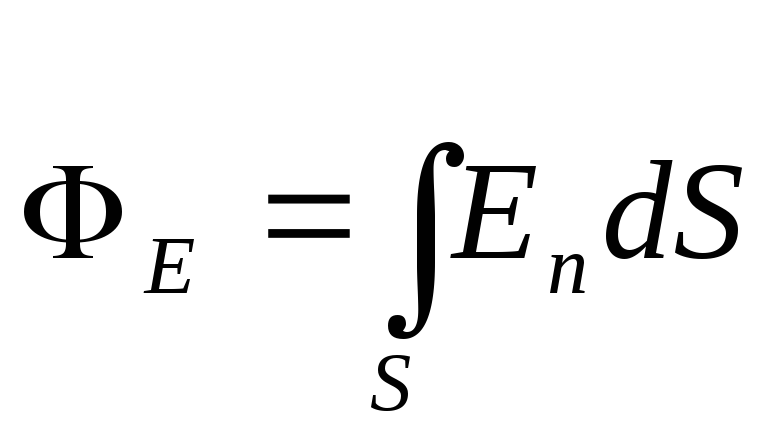, (1)

ku E n - projeksion vektorial E në normale n në sipërfaqen e vendit dS. Integrimi kryhet në të gjithë sipërfaqen e faqes, e cila është e shpuar nga linjat e tensionit.

P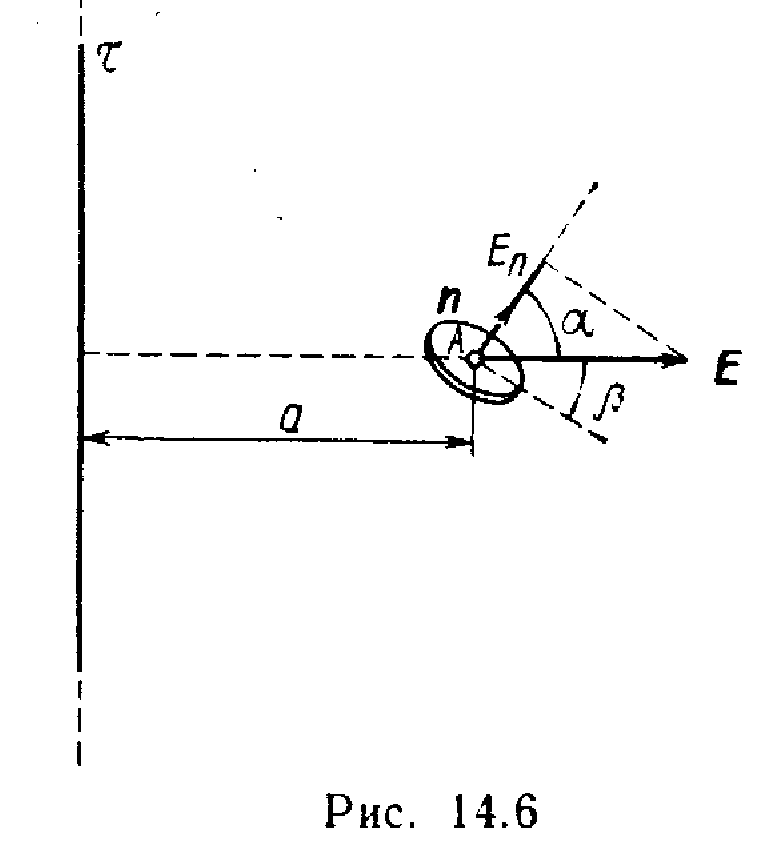

projeksioni E P Vektori i tensionit është i barabartë, siç mund të shihet nga Fig. 14.6,

E P =E ko,

ku  është këndi ndërmjet drejtimit të vektorit dhe normales n. Me këtë në mendje, formula (1) merr formën

.

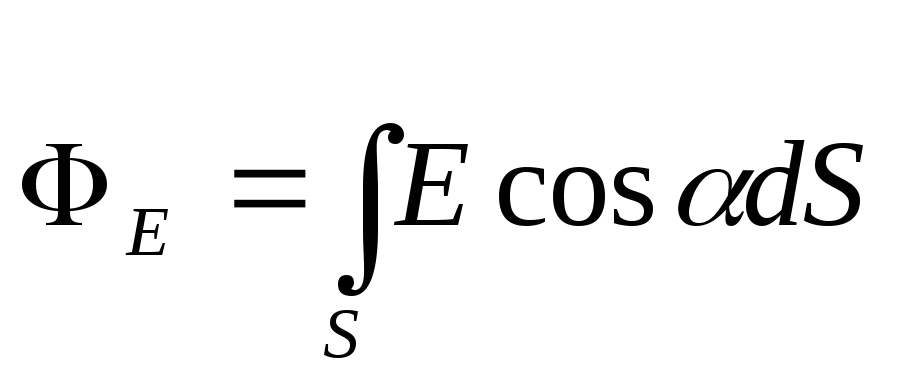Meqenëse dimensionet e sipërfaqes janë të vogla në krahasim me distancën nga filli (r<E shume pak. ndryshon në vlerë absolute dhe drejtim brenda faqes, gjë që ju lejon të zëvendësoni vlerat nën shenjën integrale E dhe cos vlerat mesatare të tyre<E> dhe dhe hiqni ato nga shenja integrale:

Duke integruar dhe zëvendësuar<E> dhe vlerat e tyre të përafërta E A dhe cos  A , llogaritur për pikën e mesit të faqes, marrim

F E =E A cos  A S= r 2 E A cos A . (2)

tensioni E A llogaritur me formulë E A=/(2 0 a). Nga

oriz. 14.6 vijon cos  A=cos(/2 -  )= mëkat.

Duke pasur parasysh shprehjen E A dhe cos  A barazia (2.) merr formën

.

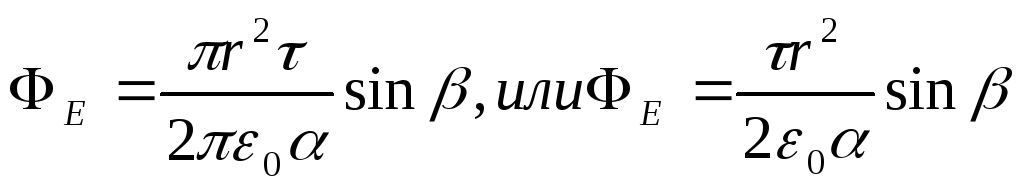Duke zëvendësuar të dhënat në formulën e fundit dhe duke kryer llogaritjet, gjejmë

F E=424 mV.m.

Shembull7 . Dy sfera përçuese koncentrike me rreze R 1 =6cm dhe R 2 = 10cm bart respektivisht ngarkesa P 1 \u003d lnKl dhe P 2 =–0,5 nC. Gjeni tensionin E fushat në pika të ndara nga qendra e sferave në largësi r 1 = 5 cm, r 2 = 9 cm r 3 = 15 cm. Ndërtimi i grafikut E(r).

R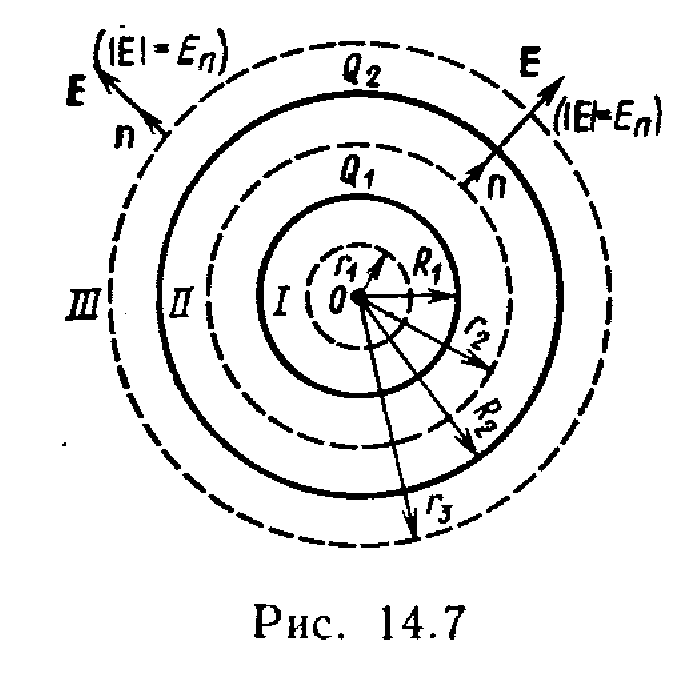

zgjidhje. Vini re se pikat në të cilat dëshironi të gjeni forcën e fushës elektrike shtrihen në tre zona (Fig. 14.7): zona I ( r<R 1 ), rajoni II ( R 1 <r 2 <R 2 ), rajoni III ( r 3 >R 2 ).

1. Për të përcaktuar tensionin E 1 vizatoni një sipërfaqe sferike në zonën I S 1 rreze r 1 dhe përdorni teoremën Ostrogradsky-Gauss. Meqenëse brenda rajonit I nuk ka ngarkesa, atëherë, sipas teoremës së treguar, marrim barazinë

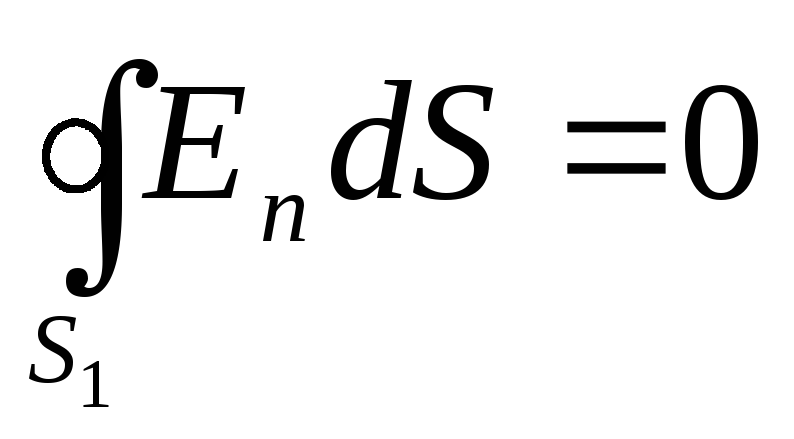, (1)

ku E nështë përbërësi normal i forcës së fushës elektrike.

Për arsye simetrie, komponenti normal E n duhet të jetë e barabartë me vetë tensionin dhe konstante për të gjitha pikat e sferës, d.m.th. En=E 1 = konst.Prandaj mund të nxirret nga shenja integrale. Barazia (1) merr formën

.

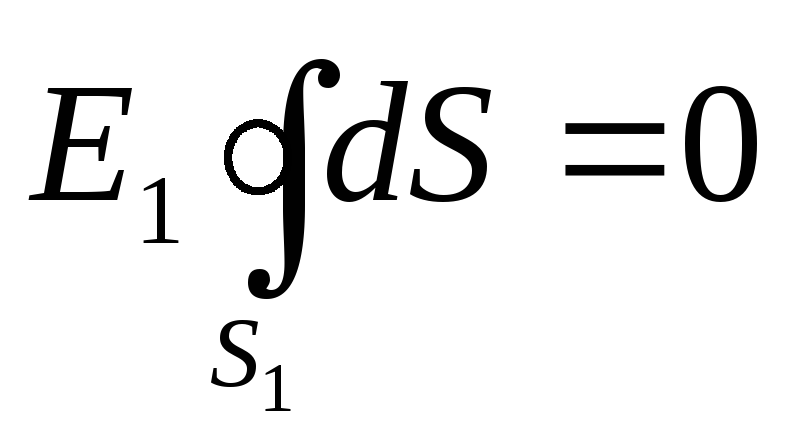Meqenëse sipërfaqja e një sfere nuk është zero, atëherë

E 1 =0,

d.m.th., forca e fushës në të gjitha pikat që plotësojnë kushtin r 1 <.R 1 , do të jetë e barabartë me zero.

2. Në rajonin II, vizatojmë një sipërfaqe sferike me rreze r 2 .Meqenëse brenda kësaj sipërfaqeje ka një ngarkesë P 1 , atëherë për të, sipas teoremës Ostrogradsky-Gauss, mund të shkruajmë barazinë

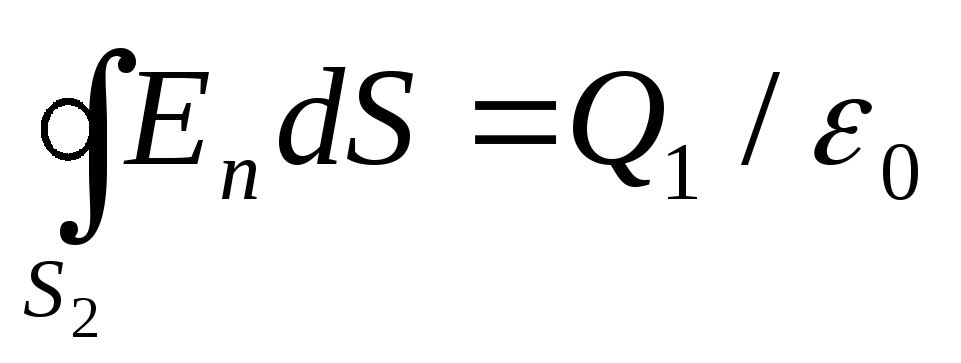. (2)

Sepse E n =E 2 = konst, atëherë nënkuptojnë kushtet e simetrisë

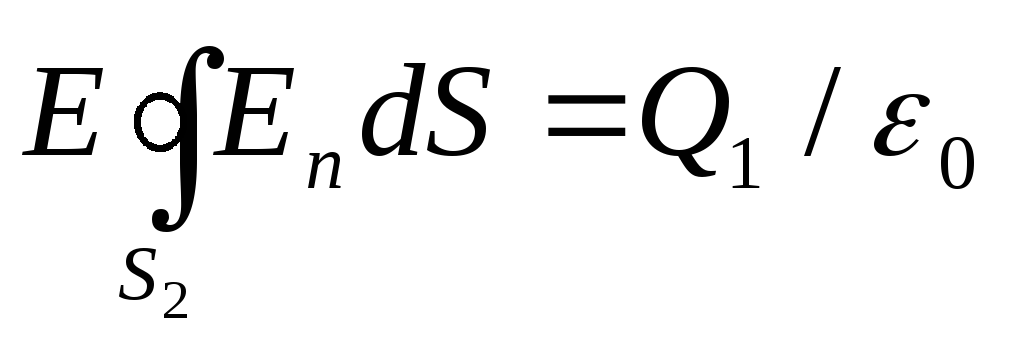, ose ES 2 =P 1 / 0 ,

E 2 =P 1 /( 0 S 2 ).

Duke zëvendësuar këtu shprehjen për zonën e sferës, marrim

E 2 =P/(4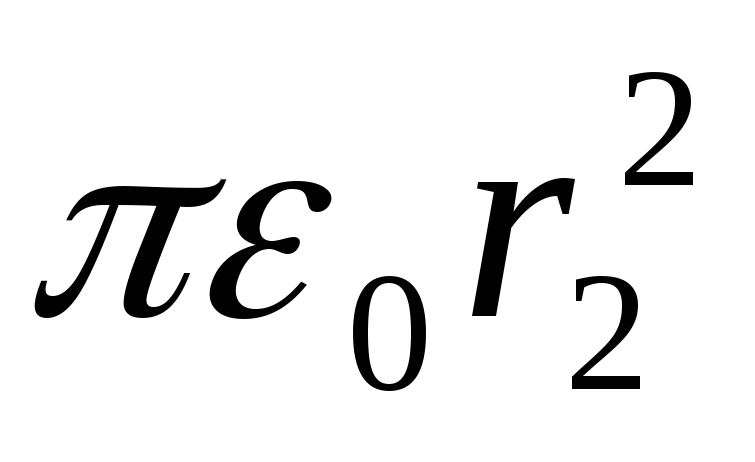

). (3)

3. Në rajonin III vizatojmë një sipërfaqe sferike me rreze r 3 . Kjo sipërfaqe mbulon ngarkesën totale P 1 +P 2 . Prandaj, për të, ekuacioni i shkruar në bazë të teoremës Ostrogradsky-Gauss do të ketë formën

.

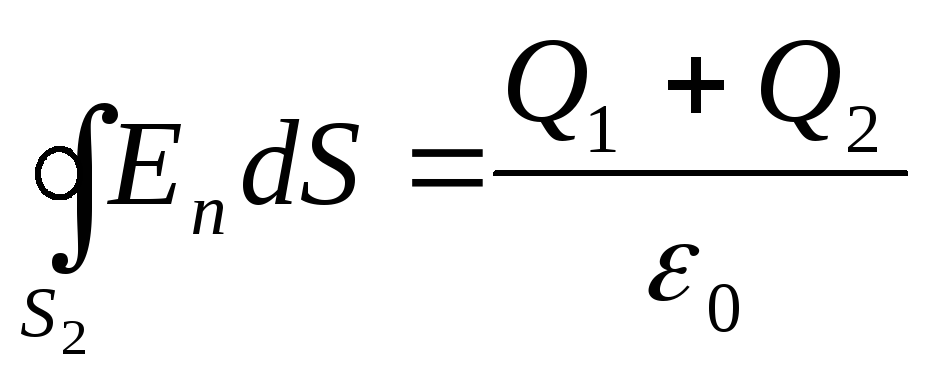Pra, duke përdorur dispozitat e zbatuara në dy rastet e para, konstatojmë

Le të sigurohemi që pjesët e duhura të barazive (3) dhe (4) të japin njësinë e forcës së fushës elektrike;

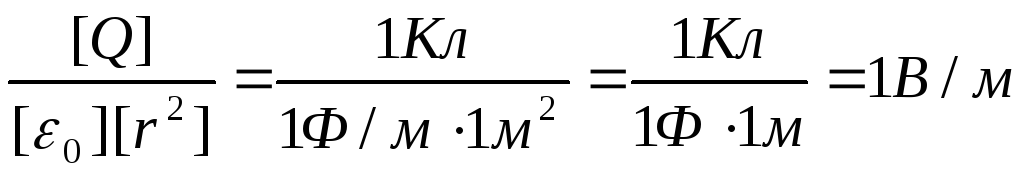
Ne i shprehim të gjitha sasitë në njësi SI ( P 1 \u003d 10 -9 C, P 2 = –0,510 -9 C, r 1 =0.09m, r 2 = 15 m , l/(4 0 )=910 9 m/F) dhe kryeni llogaritjet:

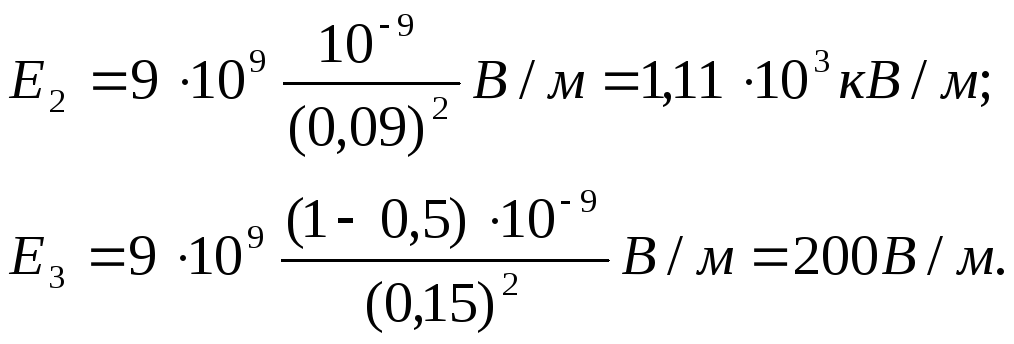
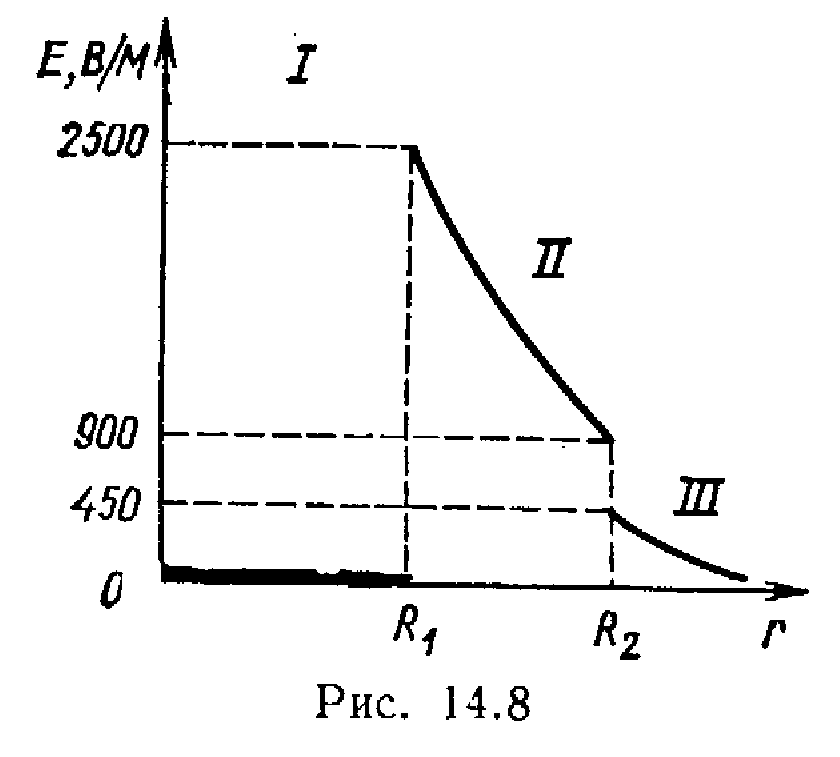
4. Le të ndërtojmë një grafik E(r).AT zona I ( r 1 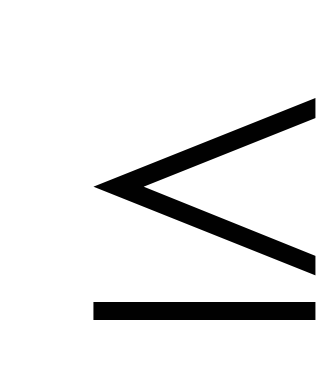1 ) tensioni E=0. Në zonën II (R 1 r<.R 2 ) tensioni E 2 (r) ndryshon sipas ligjit l/r 2 .Pika r=R 1 tensioni E 2 (R 1 )=Q 1 /(4 0 R 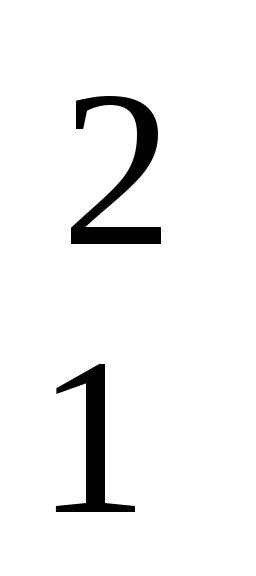)=2500 V/m.Në pikën r=R 1 (r tenton të R 1 majtas) E 2 (R 2 )=Q 1 /(4 0 R 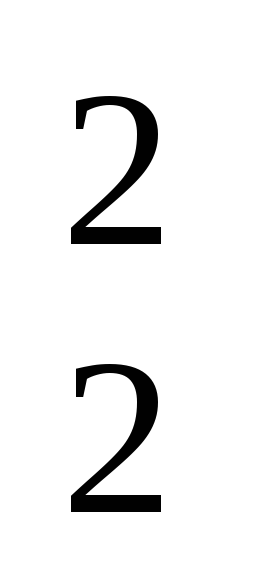)=900V/m. Në zonën III ( r>R 2 )E 3 (r) ndryshon sipas ligjit 1/ r 2 , dhe në pikën r=R 2 (r tenton të R 2 djathtas) E 3 (R 2 ) =(P 1 –|P 2 |)/(4 0 R 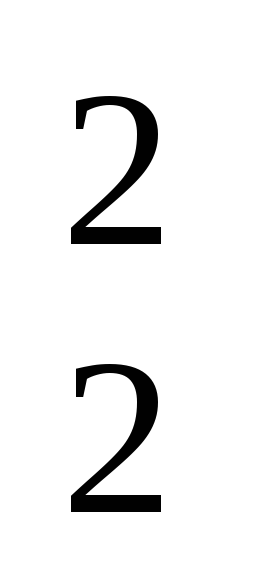)=450 V/m. Pra funksioni E(r) në pika r=R 1 dhe r=R 2 pëson një pushim. grafiku i varësisë E(r) treguar në fig. 14.8.

Detyrat

Forca e fushës së ngarkesave pika

14.1. Përcaktoni tensionin E fushë elektrike e krijuar nga një ngarkesë pikë P=10 nC në distancë r\u003d 10 cm nga ajo. Dielektrik - vaj.

14.2. Largësia d ndërmjet dy tarifave pikë P 1 =+8 nC dhe P 2 \u003d -5,3 nC është e barabartë me 40 cm. Llogaritni intensitetin E fushë në një pikë në mes të rrugës ndërmjet akuzave. Sa është intensiteti nëse ngarkesa e dytë është pozitive?

14.3. P 1 =10nC dhe P 2 = –20 nC, e vendosur në një distancë d= 20 cm largësi. Përcaktoni tensionin E fushë në një pikë të largët nga ngarkimi i parë nga r 1 =30cm dhe nga e dyta në r 2 = 50 cm.

14.4. Largësia d ndërmjet dy pikave ngarkesave pozitive P 1 =9P dhe P 2 \u003d Q është 8 cm. Në cilën distancë r nga ngarkesa e parë është pika në të cilën intensiteti E fusha e ngarkimit është zero? Ku do të ishte kjo pikë nëse ngarkesa e dytë do të ishte negative?

14.5. Tarifa me dy pikë P 1 =2P dhe P 2 = –P janë në distancë d nga njeri tjetri. Gjeni pozicionin e një pike në një vijë të drejtë që kalon nëpër këto ngarkesa, intensitetin E fusha në të cilat është e barabartë me zero,

14.6. Fusha elektrike e krijuar nga ngarkesat me dy pika P 1 =40nC dhe P 2 = –10 nC, e vendosur në një distancë d= 10 cm larg njëri-tjetrit. Përcaktoni tensionin E fushë në një pikë të largët nga ngarkimi i parë nga r 1 \u003d 12 cm dhe nga e dyta në r 2 =6 cm.

Fuqia e fushës së ngarkesës shpërndahet mbi unazë dhe sferë

14.7. Një unazë e hollë me një rreze R\u003d 8 cm mbart një ngarkesë të shpërndarë në mënyrë uniforme me një densitet linear  \u003d 10 nC/m. Cili është tensioni E fushë elektrike në një pikë të barabartë nga të gjitha pikat e unazës në një distancë r\u003d 10 cm?

14.8. Hemisfera mbart një ngarkesë të shpërndarë në mënyrë uniforme me një densitet sipërfaqësor=1,nC/m 2 . Gjeni tensionin E fushë elektrike në qendrën gjeometrike të hemisferës.

14.9. Në një sferë metalike me rreze R\u003d 10 cm është një tarifë P\u003d lnKl. Përcaktoni tensionin E fushë elektrike në pikat e mëposhtme: 1) në distancë r 1 =8 cm nga qendra e sferës; 2) në sipërfaqen e saj; 3) në distancë r 2 =15 cm nga qendra e sferës. Grafiku i varësisë nga vizatimi E nga r.

14.10. Dy sfera koncentrike të ngarkuara metalike me rreze R 1 =6cm dhe R 2 \u003d 10 cm bartje, respektivisht P 1 =1 nC dhe P 2 = – 0,5 nC. Gjeni tensionin E fushat me pika. të ndara nga qendra e sferave në largësi r 1 = 5 cm, r 2 = 9 cm, r 3 \u003d 15 cm Varësia e parcelës E(r).

Fuqia e fushës së linjës së ngarkuar

14.11. Një tel i drejtë shumë i gjatë i hollë mbart një ngarkesë të shpërndarë në mënyrë të barabartë përgjatë gjithë gjatësisë së tij. Llogaritni densitetin linear  të ngarkesës nëse intensiteti E fusha në distancë a\u003d 0,5 m nga teli në mes të tij është 200 V / m.

14.12. Largësia d ndërmjet dy telave të gjatë të hollë paralel me njëri-tjetrin është 16 cm Telat janë të ngarkuar në mënyrë të njëtrajtshme me ngarkesa të kundërta me dendësi lineare ||=^150. µC/m. Cili është tensioni E fushat në një pikë të largët r\u003d 10 cm nga teli i parë dhe i dytë?

14.13. Diametri i drejtë i shufrës metalike d= 5 cm dhe i gjatë l\u003d 4 m mbart një ngarkesë të shpërndarë në mënyrë uniforme në sipërfaqen e saj P= 500 nC. Përcaktoni tensionin E fushë në një pikë përballë mesit të shufrës në një distancë a=1 cm nga sipërfaqja e tij.

14.14. Një tub metalik pafundësisht i gjatë me mure të hollë me rreze R\u003d 2 cm mbart një ngarkesë të shpërndarë në mënyrë të barabartë në sipërfaqe ( \u003d 1 nC / m 2). Përcaktoni tensionin E fushat në pika të ndara nga boshti i tubit në distanca r 1 =lcm, r 2 \u003d 3 cm Varësia e parcelës E(r).

14.15. Dy tuba koaksial me mure të hollë të gjatë me rreze R 1 =2cm dhe R 2 \u003d 4 cm bartin ngarkesa të shpërndara në mënyrë uniforme përgjatë gjatësisë me dendësi lineare  1 \u003d ln C / m dhe  2 = -0,5 nC/m. Hapësira midis tubave është e mbushur me ebonit. Përcaktoni tensionin E fushat në pikat e vendosura në distanca r 1 \u003d 1 cm, r 2 = 3 cm, r 3 \u003d 5 cm nga boshti i tubave; Grafiku i varësisë nga vizatimi E nga r.