Materiali teorik

Lidhje Një trup që pengon një trup tjetër të lëvizë nën veprimin e një force.

Reagimi i komunikimit- forca që lind brenda vetë lidhjes. Reagimi është gjithmonë i kundërt me drejtimin në të cilin lidhja pengon lëvizjen e trupit. Të gjithë trupat mund të jenë të lirë dhe jo të lirë. Trupi i lirë nuk ka asnjë lidhje. Çdo trup jo i lirë mund të përfaqësohet si i lirë nëse lidhjet që veprojnë në të zëvendësohen me reaksione.

Llojet e lidhjeve:

a) Sipërfaqe ose plan i lëmuar, domethënë një sipërfaqe pa fërkime. Reagimi i kësaj lidhjeje është gjithmonë i drejtuar pingul me pikën e kontaktit. R - reaksioni i lidhjes

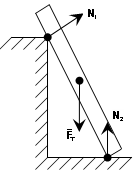b) mbështetje e qetë Reaksionet e kësaj lidhjeje janë të drejtuara pingul me pikën e kontaktit. (Reaksioni është një forcë brenda një strukture). Vlera e saj varet nga materiali, madhësia dhe forca e jashtme.

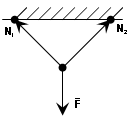në) Lidhje fleksibël- një lidhje që funksionon vetëm në tension, e cila kryhet nga një kabllo, litar, zinxhir. Reagimi i një lidhjeje fleksibël drejtohet përgjatë vetë lidhjes deri në pikën e lidhjes, domethënë në kundërshtim me drejtimin e forcës.

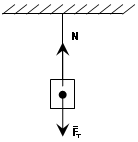
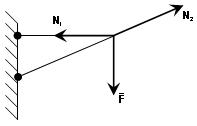G) Shufra të ngurtë. Ajo kryhet nga trarë të ndryshëm, I-trarë, kanale. Lidhja funksionon si në tension ashtu edhe në ngjeshje. Nëse shufra është në tension, atëherë reagimi drejtohet përgjatë shufrës në vendin e fiksimit, nëse është në ngjeshje, atëherë reagimi drejtohet përtej shufrës.

e) mbështetje e artikuluar. Mbështetësit janë të lëvizshëm dhe të fiksuar. Mbështetja fikse ka dy reaksione të vendosura pingul me njëri-tjetrin. Mbështetja e lëvizshme ka një reagim, pingul me sipërfaqen.

Mbështetje e lëvizshme Mbështetje fikse

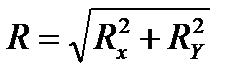
Detyrat për të përfunduar punën

1. Vizatoni vizatimet e versionit tuaj.

2. Përshkruani vizatimin.

3. Përcaktoni llojin e lidhjes dhe zëvendësoni ato me reaksione.

Opsioni 18

1.

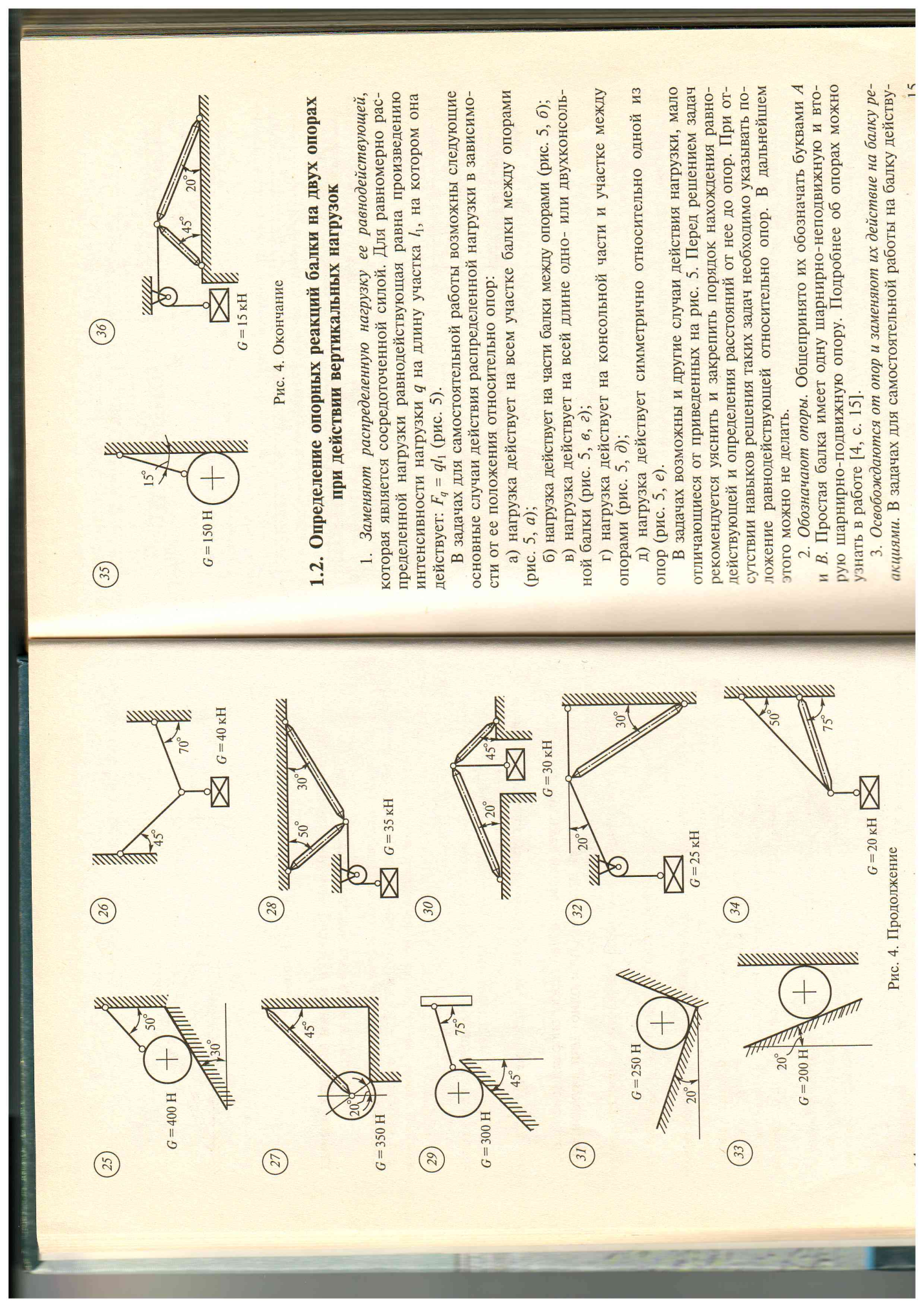2.

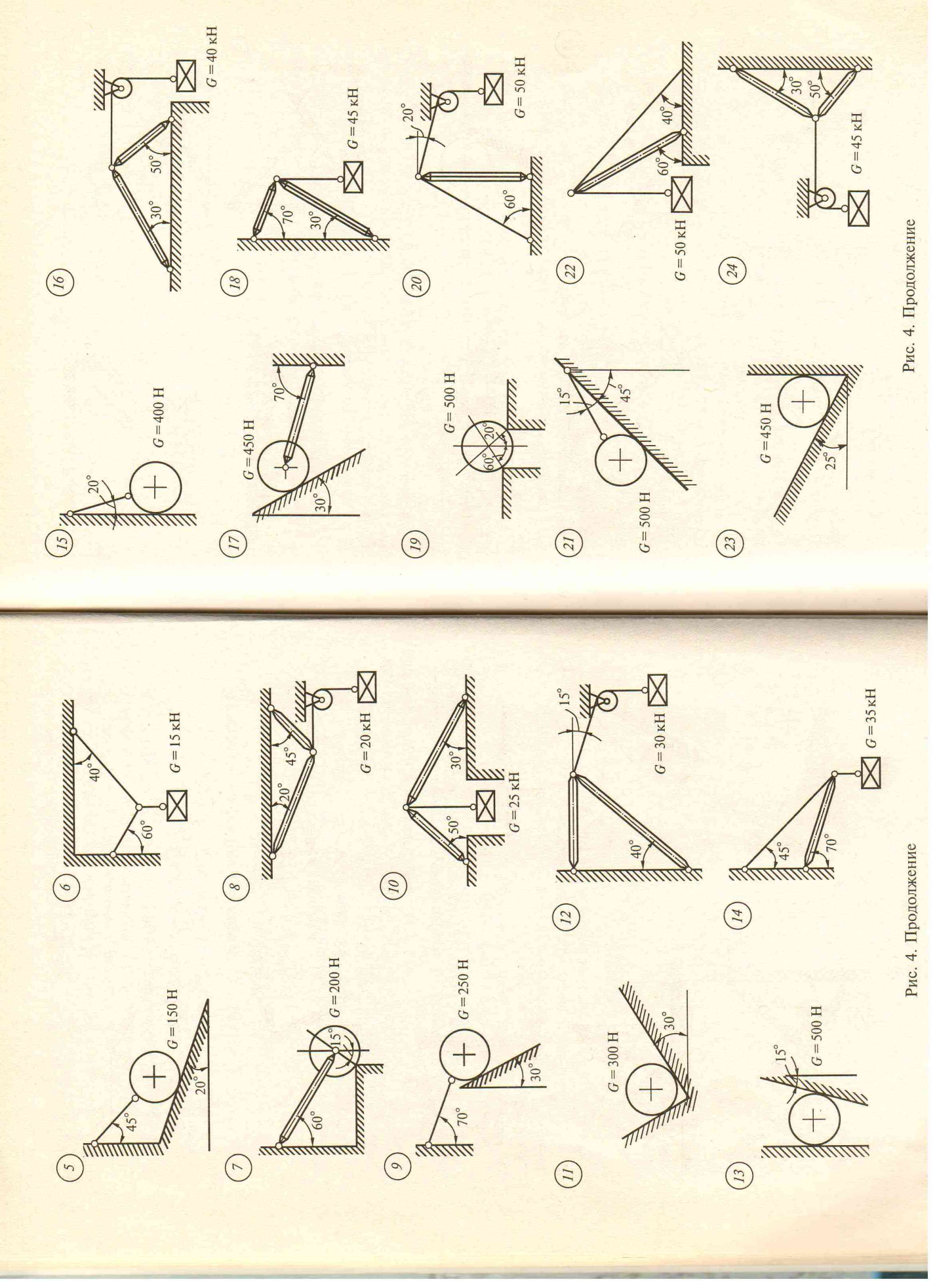3.

Pyetjet e testit:

1. Cili është ndryshimi midis boshtit dhe projeksionit?

2. Sa ekuacione ekuilibri keni bërë gjatë zgjidhjes së problemës?

3. Metodologjia e zgjidhjes së problemave të SHPSF-së.

4. Përcaktoni një sistem të sheshtë forcash konvergjente.

5. Cili është projeksioni i forcës në planin koordinativ?

Literatura:

1. Verein L.I. Mekanika Teknike - M: Akademia, 2006.

2. Movnin M.S. Bazat e mekanikës teknike - Shën Petersburg: Politeknik, 2003.

3. Molchanova E.V., Shurygina G.N. Statika dhe forca e materialeve - Tomsk, 2008.

Puna praktike №2

Tema e mësimit: Përcaktimi i reaksioneve të bashkimit të një sistemi të sheshtë forcash konvergjente.

Lloji i mësimit: konsolidimi i njohurive të marra.

Qëllimi i mësimit: Mësoni të përcaktoni reaksionet e lidhjes së një sistemi të sheshtë forcash konvergjente

Sigurimi i mjeteve:

1. udhëzim metodologjik për kryerjen e punës;

2. detyrë individuale;

3. fletore për punë praktike;

7. kalkulator.

Teknologjia e punës:

1. Studioni me kujdes udhëzime, materiali teorik i propozuar.

2. Në përputhje me opsionin, kryeni detyrën sipas metodologjisë së paraqitur më poshtë.

3. Nxirrni përfundime për punën e bërë.

4. Përgjigjuni pyetjeve të sigurisë.

Materiali teorik

Kushtet dhe ekuacionet e ekuilibrit të një sistemi të sheshtë të forcave të vendosura në mënyrë arbitrare.

Kur sistemi i forcave reduktohet në një pikë, fitohen R hl dhe M hl.

Nëse sistemi i forcave është në ekuilibër, atëherë R ch \u003d 0, M ch \u003d 0.

Le të shkruajmë tre lloje të ekuacioneve të ekuilibrit për këtë sistem.

Pamja e parë

Pamja e dytë

Metoda gjeometrike konsiston në ndërtimin e një poligoni të forcës, ajo analitike në përcaktimin e shumës së projeksioneve të të gjitha forcat aktive në dy boshte reciprokisht pingul.

Me një metodë grafike për përcaktimin e rezultantit, vektorët e forcës mund të vizatohen në çdo rend, rezultati (madhësia dhe drejtimi i rezultantit) nuk do të ndryshojë.

Vektori rezultues është i drejtuar drejt vektorët e forcave-terms.

Rendi i ndërtimit të shumëkëndëshit të forcës

1. Zgjidhni shtyllën e ndërtimit.

2. Fillimin e vektorit të parë F 2 e vendosim në pol (vektorët e forcës mund të vizatohen sipas çdo radhe) duke e lëvizur paralelisht me vetveten, duke ruajtur vlerën e tij.

3. Vendosni fillimin e F 1 të dytë në fund të vektorit të parë. Vizatojmë njëri pas tjetrit në të njëjtin rend vektorët e forcave të mbetura F 4 , F 3 .

4. Vektori rezultant mbyll vijën e thyer që rezulton ; lidh fillimin e vektorit të parë me fundin e të fundit dhe drejtohet drejt tij.

Kur ndryshoni rendin e vizatimit të vektorëve në një shumëkëndësh, the pamje shifrat. Rendi i vizatimit nuk ndikon në rezultatin.

Kushti i ekuilibrit gjeometrik për PSSS: shumëkëndëshi i forcës duhet të jetë i mbyllur.

Përcaktimi i rezultantit në mënyrë analitike

Moduli (vlera) e rezultantit përcaktohet nga projeksionet e njohura:

Drejtimi i vektorit rezultant mund të përcaktohet nga madhësitë dhe shenjat e kosinuseve të këndeve të formuara nga rezultanta me boshtet koordinative (Fig. 3.5).

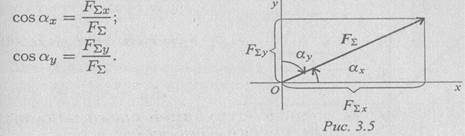
Projeksioni i forcës në bosht

Projeksioni i forcës në bosht përcaktohet nga segmenti i boshtit të prerë nga pingulët e rënë mbi bosht nga fillimi dhe fundi i vektorit

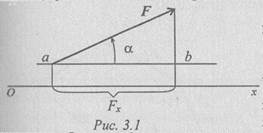
Madhësia e projeksionit të forcës në boshtështë e barabartë me prodhimin e modulit të forcës dhe kosinusit të këndit ndërmjet vektorit të forcës dhe drejtim pozitiv sëpata. Kështu, projeksioni ka shenjën: pozitive në të njëjtin drejtim vektorët dhe boshtet e forcës dhe negativ kur drejtohet drejt boshtit negativ(Fig. 3.2).

Kushti analitik i ekuilibrit për PSSS: shuma e projeksioneve të të gjitha forcave në dy boshte reciprokisht pingul duhet të jetë e barabartë me zero.

ΣFx=0

ΣF y =0

Në problema, boshtet e koordinatave zgjidhen në mënyrë që zgjidhja të jetë më e thjeshta. Është e dëshirueshme që të paktën një forcë e panjohur të përkojë me boshtin koordinativ.

Tema 1.3. Sistemi planar i forcave të vendosura në mënyrë arbitrare

Momenti i forcës rreth një pike

Një forcë që nuk kalon nëpër pikën e lidhjes së trupit bën që trupi të rrotullohet në lidhje me pikën, kështu që efekti i një force të tillë në trup vlerësohet si një moment.

Momenti i fuqisë në raport me pikën numerikisht është i barabartë me prodhimin e modulit të forcës dhe të krahut.

Shpatull - distanca më e shkurtër nga pika në vijën e veprimit të forcës ( pingul e ulur nga pika në vijën e veprimit të forcës) (Fig. 4.4).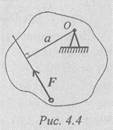

Përcaktimi i momentit M o ( F) osem o ( F);m 0 (F) = Fa.

njësi matëse m o (F)= N m

Momenti konsiderohet pozitiv nëse forca përpiqet ta kthejë trupin në drejtim të akrepave të orës.

Momenti i forcës rreth një pike është zero nëse vija e veprimit e forcës kalon nëpër pikë, pasi në këtë rast distanca nga pika në forcë është zero.

Sistemi planar i forcave të vendosura në mënyrë arbitrare

Vektori kryesorështë e barabartë me shumën gjeometrike të vektorëve të një sistemi të planit arbitrar të forcave. Ne projektojmë të gjitha forcat e sistemit në boshtet koordinative dhe, duke shtuar projeksionet përkatëse në akset, marrim projeksionet e vektorit kryesor.

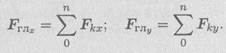
Nga madhësia e projeksioneve të vektorit kryesor në boshtet e koordinatave, gjejmë modulin e vektorit kryesor:

Pika kryesore sistemi i forcave është i barabartë me shumën algjebrike momente forcat e sistemit në lidhje me pikën e reduktimit.

Kështu, PSPRS reduktohet në një forcë(vektori kryesor i sistemit të forcave) dhe një moment(momenti kryesor i sistemit të forcave).

Tre forma të gjendjes së ekuilibrit të PSPRS

Për raste të ndryshme përdoren tre grupe ekuacionesh të ekuilibrit.

Për një rast të veçantë, nëse sistemi është i balancuar forcat paralele, ka vetëm dy ekuacione ekuilibri:

Sistemet e trarëve. Përcaktimi i reaksioneve mbështetëse dhe momenteve të shtrëngimit

Llojet e ngarkesave

Sipas metodës së aplikimit, ngarkesat ndahen në të përqendruara dhe të shpërndara. Nëse në realitet transferimi i ngarkesës ndodh në një zonë të papërfillshme (në një pikë), ngarkesa quhet të përqendruara.

Shpesh ngarkesa shpërndahet në një zonë ose linjë të konsiderueshme (presioni i ujit në digë, presioni i borës në çati, etj.), atëherë ngarkesa merret parasysh të shpërndara.

Në problemet e statikës për trupat absolutisht të ngurtë, ngarkesa e shpërndarë mund të zëvendësohet nga rezultante forca e përqendruar (Fig. 6.1).

q

l/2P

q- intensiteti i ngarkesës, N/m;

l- linja e veprimit të ngarkesës së shpërndarë, m;

Q = ql- ngarkesa e shpërndarë rezultante.

Llojet e mbështetësve të sistemeve të trarëve(shih reagimet dhe lidhjet e tyre) Tra - një pjesë strukturore në formën e një trau të drejtë, të fiksuar në mbështetëse dhe të përkulur nga forcat e aplikuara në të.

Lartësia e seksionit të rrezes është e parëndësishme në krahasim me gjatësinë. Përfundim i ngurtë (prishje)(Fig. 6.2)

Mbështetja nuk lejon lëvizjen dhe rrotullimin. Përfundimi zëvendësohet nga dy forca përbërëse Rax dhe R A y dhe një çift me një moment Z. A.

Për të përcaktuar këto të panjohura, është e përshtatshme të përdoret një sistem ekuacionesh në formë

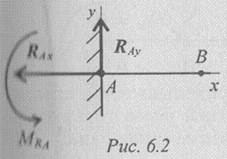
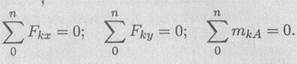
Çdo ekuacion ka një sasi e panjohur dhe zgjidhet pa zëvendësime. Për të kontrolluar korrektësinë e vendimeve, përdoret një shtrirje shtesë e momenteve në lidhje me çdo pikë në rreze, për shembull, B.

Për një skemë të caktuar të rrezeve kërkohet gjetja e reaksioneve mbështetëse nëse l=14 m, a=3,8 m, b=5 m, M=11 kN m, F=10 kN.

Zgjidhje. Meqenëse nuk ka ngarkesë horizontale, mbështetja A ka vetëm një reagim vertikal RA. Ne përpilojmë ekuacionet e ekuilibrit në formën e momenteve të të gjitha forcave në lidhje me pikat A dhe B.

ku gjejmë

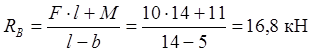
Për të kontrolluar, ne hartojmë një ekuacion ekuilibri për boshtin vertikal:

pyetjet e testit

pika e forcës së menteshës së traut

> Si është projeksioni i forcës në bosht?

Projeksioni i forcës në bosht është një sasi algjebrike e barabartë me produktin e modulit të forcës dhe kosinusit të këndit ndërmjet drejtimit pozitiv të boshtit dhe vektorit të forcës (d.m.th., ky është segmenti i paraqitur nga forca në boshtet përkatëse).

Px=Pcos?=Pcos90o=0;

Rx=Rcos? = -R cos(180o-?).

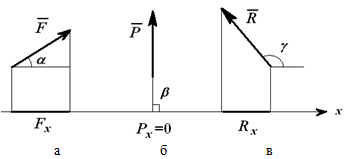
Projeksioni i forcës në bosht është pozitiv, fig. 2 a) nëse 0 ? ?< ?/2.

> Në cilin rast projeksioni i forcës në bosht është i barabartë me zero?

Projeksioni i forcës në bosht mund të jetë zero, fig. 2 b) nëse? = ?/2.)

> Në cilin rast projeksioni i forcës në bosht është i barabartë me modulin e forcës?

Projeksioni i forcës në bosht është i barabartë me modulin e forcës, nëse? =0?.

> Në cilin rast projeksioni i forcës në bosht është negativ?

Projeksioni i forcës në bosht mund të jetë negativ, fig. 2 c) nëse?/2< ? ? ?.

> Sa ekuacione të ekuilibrit janë hartuar për një sistem konvergjent të sheshtë forcash?

Forcat quhen konvergjente nëse linjat e tyre të veprimit kryqëzohen në një pikë. Dalloni një sistem të sheshtë forcash konvergjente, kur linjat e veprimit të të gjitha këtyre forcave shtrihen në të njëjtin rrafsh.

Ekuilibri i një sistemi forcash konvergjente.

Nga ligjet e mekanikës del se të ngurta, mbi të cilat veprojnë forcat e jashtme të balancuara reciproke, jo vetëm që mund të pushojnë, por edhe të bëjnë një lëvizje, të cilën do ta quajmë lëvizje "me inerci". Një lëvizje e tillë do të jetë, për shembull, lëvizja uniforme përkthimore dhe drejtvizore e trupit.

Nga kjo nxjerrim dy përfundime të rëndësishme:

1) Kushtet për ekuilibrin e statikës plotësohen nga forcat që veprojnë si në një trup në qetësi ashtu edhe në një trup që lëviz "nga inercia".

2) Ekuilibri i forcave të aplikuara në një trup të ngurtë të lirë është një kusht i domosdoshëm, por jo i mjaftueshëm për ekuilibrin (pushimin) e vetë trupit; në këtë rast, trupi do të jetë në qetësi vetëm nëse ka qenë në qetësi dhe deri në momentin kur ndaj tij janë aplikuar forca të balancuara.

Për ekuilibrin e një sistemi forcash konvergjente të aplikuara në një trup të ngurtë, është e nevojshme dhe e mjaftueshme që rezultanta e këtyre forcave të jetë e barabartë me zero. Kushtet që duhet të plotësojnë vetë forcat në këtë rast mund të shprehen në formë gjeometrike ose analitike.

1. Gjendja e ekuilibrit gjeometrik. Meqenëse rezultanta e forcave konvergjente përkufizohet si ana mbyllëse e poligonit të forcës së ndërtuar nga këto forca, ajo mund të zhduket nëse dhe vetëm nëse fundi i forcës së fundit në poligon përkon me fillimin e së parës, d.m.th. kur poligoni mbyllet. .

Për rrjedhojë, për ekuilibrin e sistemit, forcat konvergjente, është e nevojshme dhe e mjaftueshme që poligoni i forcës i ndërtuar nga këto forca të jetë i mbyllur.

2. Kushtet analitike të ekuilibrit. Në mënyrë analitike, rezultanta e një sistemi forcash konvergjente përcaktohet nga formula

Meqenëse shuma e termave pozitivë është nën rrënjë, R do të zhduket vetëm kur të dyja

dmth kur forcat që veprojnë në trup do të plotësojnë barazitë:

Barazitë shprehin kushtet e ekuilibrit në një formë analitike: për ekuilibrin e një sistemi hapësinor të forcave konvergjente, është e nevojshme dhe e mjaftueshme që shumat e projeksioneve të këtyre forcave në secilin nga tre boshtet koordinative të jenë të barabarta me zero.

Nëse të gjitha forcat konvergjente që veprojnë në trup shtrihen në të njëjtin rrafsh, atëherë ato formojnë një sistem të sheshtë forcash konvergjente. Në rastin e një sistemi të sheshtë forcash konvergjente, padyshim fitojmë vetëm dy kushte ekuilibri

Barazitë shprehin gjithashtu kushtet (ose ekuacionet) e nevojshme për ekuilibrin e një trupi të ngurtë të lirë nën veprimin e forcave konvergjente.

> Në cilin drejtim drejtohet reaksioni i shufrës me skaje të varura?

Lëreni në disa konstruksione, lidhja është shufra AB, e fiksuar në skajet me mentesha (Fig. 3). Le të supozojmë se pesha e shufrës në krahasim me ngarkesën që ajo percepton mund të neglizhohet. Atëherë në shufër do të veprojnë vetëm dy forca të aplikuara në menteshat A dhe B. Por nëse shufra AB është në ekuilibër, atëherë forcat e aplikuara në pikat A dhe B duhet të drejtohen përgjatë një linje të drejtë, d.m.th. përgjatë boshtit të shufrës. . Rrjedhimisht, një shufër e ngarkuar në skajet, pesha e së cilës mund të neglizhohet në krahasim me këto ngarkesa, funksionon vetëm në tension ose në shtypje. Nëse një shufër e tillë është një lidhje, atëherë reagimi i shufrës do të drejtohet përgjatë boshtit të shufrës.

> Si është momenti i forcës rreth një pike?

Momenti i forcës në lidhje me një pikë përcaktohet nga produkti i modulit të forcës dhe gjatësisë së pingulit të rënë nga pika në vijën e veprimit të forcës (Fig. 4, a). Kur një trup është i fiksuar në pikën O, forca tenton ta rrotullojë atë rreth kësaj pike. Pika O, në lidhje me të cilën merret momenti, quhet qendra e momentit, dhe gjatësia e pingulës a quhet shpatulla e forcës në lidhje me qendrën e momentit.

Momentet e forcave maten në njutonometra (N m) ose kilogram metra (kgf m) ose në njësitë përkatëse të shumëfishta dhe nën shumëfishe, si dhe momentet e çifteve.

Projeksioni i forcës në bosht përcaktohet nga segmenti i boshtit të prerë

pingulet ranë mbi bosht nga fillimi dhe fundi i vektorit (Fig. 3.1).

Madhësia e projeksionit të forcës në boshtështë e barabartë me prodhimin e modulit të forcës dhe kosinusit të këndit ndërmjet vektorit të forcës dhe drejtim pozitiv sëpata. Kështu, projeksioni ka shenjën: pozitive në të njëjtin drejtim vektorët dhe boshtet e forcës dhe negativ kur drejtohet drejt boshtit negativ(Fig. 3.2).

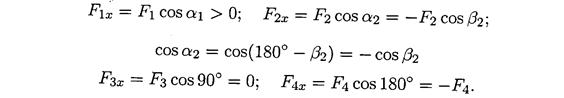
Projeksioni i forcës në dy boshte reciprokisht pingul(Fig. 3.3).

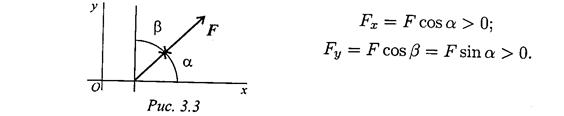
Fundi i punës -

Kjo temë i përket:

Mekanika teorike

Mekanika teorike... LEKTURA... Tema Konceptet themelore dhe aksiomat e statikes...

Nëse keni nevojë për materiale shtesë për këtë temë, ose nuk keni gjetur atë që po kërkoni, ju rekomandojmë të përdorni kërkimin në bazën e të dhënave tona të veprave:

Çfarë do të bëjmë me materialin e marrë:

Nëse ky material doli të jetë i dobishëm për ju, mund ta ruani në faqen tuaj në rrjetet sociale:

Të gjitha temat në këtë seksion:

Probleme të mekanikës teorike
Mekanika teorike është shkenca e lëvizjes mekanike të lëndëve të ngurta materiale dhe ndërveprimit të tyre. Lëvizja mekanike kuptohet si lëvizja e një trupi në hapësirë ​​dhe kohë përgjatë

Aksioma e tretë
Pa cenuar gjendjen mekanike të trupit, mund të shtoni ose hiqni një sistem të balancuar forcash (parimi i hedhjes së një sistemi forcash të barazvlefshëm me zero) (Fig. 1.3). P,=P2 P,=P.

Pasojë nga aksioma e dytë dhe e tretë
Forca që vepron në një trup të ngurtë mund të lëvizet përgjatë vijës së veprimit të tij (Fig. 1.6).

Lidhjet dhe reaksionet e obligacioneve
Të gjitha ligjet dhe teoremat e statikës janë të vlefshme për një trup të ngurtë të lirë. Të gjithë trupat ndahen në të lirë dhe të lidhur. Trupa të lirshëm- trupat, lëvizja e të cilëve nuk është e kufizuar.

Shufra e ngurtë
Në diagrame, shufrat përshkruhen me një vijë të trashë të fortë (Fig. 1.9). shufra mozhe

mentesha e fiksuar
Pika e lidhjes nuk mund të zhvendoset. Shufra mund të rrotullohet lirshëm rreth boshtit të menteshës. Reagimi i një mbështetjeje të tillë kalon përmes boshtit të menteshës, por

Sistemi planar i forcave konvergjente
Sistemi i forcave, vijat e veprimit të të cilit kryqëzohen në një pikë, quhet konvergjent (Fig. 2.1).

Rezultat i forcave konvergjente
Rezultantja e dy forcave të kryqëzuara mund të përcaktohet duke përdorur një paralelogram ose një trekëndësh forcash (aksioma e 4-të) (Vis. 2.2).

Kushti i ekuilibrit për një sistem të sheshtë forcash konvergjente
Kur sistemi i forcave është në ekuilibër, rezultanta duhet të jetë e barabartë me zero, prandaj, në një ndërtim gjeometrik, fundi i vektorit të fundit duhet të përkojë me fillimin e të parit. Nese nje

Zgjidhja e problemeve të ekuilibrit në mënyrë gjeometrike
Është i përshtatshëm për të përdorur metodën gjeometrike nëse ka tre forca në sistem. Gjatë zgjidhjes së problemeve të ekuilibrit, trupi konsiderohet të jetë absolutisht i ngurtë (i ngurtësuar). Rendi i zgjidhjes së problemeve:

Zgjidhje
1. Forcat që lindin në shufrat e fiksimit janë të barabarta në madhësi me forcat me të cilat shufrat mbështesin ngarkesën (aksioma e 5-të e statikës) (Fig. 2.5a). Ne përcaktojmë drejtimet e mundshme reaksionet e lidhjes

Forcat në mënyrë analitike
Vlera e rezultantes është e barabartë me shumën vektoriale (gjeometrike) të vektorëve të sistemit të forcave. Rezultantin e përcaktojmë gjeometrikisht. Ne zgjedhim një sistem koordinativ, përcaktojmë parashikimet e të gjitha detyrave

Forcat konvergjente në formë analitike
Duke u bazuar në faktin se rezultanta është e barabartë me zero, marrim: Kushti

Dy forca, momenti nja dy forcash
Një palë forcash është një sistem i dy forcave që janë të barabarta në modul, paralel dhe të drejtuar në drejtime të ndryshme. Konsideroni një sistem forcash (P; B") që formojnë një çift.

Momenti i forcës rreth një pike.
Një forcë që nuk kalon nëpër pikën e lidhjes së trupit bën që trupi të rrotullohet në lidhje me pikën, kështu që efekti i një force të tillë në trup vlerësohet si një moment. Momenti i forcës rel.

Teorema e Poinsot-it mbi transferimin paralel të forcave
Një forcë mund të bartet paralelisht me vijën e saj të veprimit duke shtuar një palë forcash me një moment të barabartë me produktin e modulit të forcës dhe distancën mbi të cilën është bartur forca.

forcat e vendosura
Linjat e veprimit të një sistemi arbitrar forcash nuk kryqëzohen në një pikë, prandaj, për të vlerësuar gjendjen e trupit, një sistem i tillë duhet të thjeshtohet. Për ta bërë këtë, të gjitha forcat e sistemit transferohen në një në mënyrë arbitrare

Ndikimi i pikës së referencës
Pika e referencës zgjidhet në mënyrë arbitrare. Kur ndryshoni pozicionin e pikës së reduktimit, vlera e vektorit kryesor nuk do të ndryshojë. Vlera e momentit kryesor kur zhvendoset pika e reduktimit do të ndryshojë,

Sistemi i forcës së sheshtë
1. Në ekuilibër vektori kryesor sistemi është zero. Përkufizimi analitik i vektorit kryesor çon në përfundimin:

Llojet e ngarkesave
Sipas metodës së aplikimit, ngarkesat ndahen në të përqendruara dhe të shpërndara. Nëse në realitet transferimi i ngarkesës ndodh në një zonë të papërfillshme (në një pikë), ngarkesa quhet e përqendruar

Momenti i forcës rreth boshtit
Momenti i forcës rreth boshtit është i barabartë me momentin e projeksionit të forcës në një rrafsh pingul me boshtin, në lidhje me pikën e kryqëzimit të boshtit me rrafshin (Fig. 7.1 a). MO

Vektor në hapësirë
Në hapësirë, vektori i forcës projektohet në tre akse koordinative reciprokisht pingul. Projeksionet vektoriale formojnë skaje kuboid, vektori i forcës përkon me diagonalen (Fig. 7.2

Sistemi konvergjent hapësinor i forcave
Një sistem konvergjent hapësinor i forcave është një sistem forcash që nuk shtrihen në të njëjtin rrafsh, linjat e veprimit të të cilave kryqëzohen në një pikë. Sistemi hapësinor rezultant si

Sjellja e një sistemi hapësinor arbitrar të forcave në qendrën O
Jepet një sistem hapësinor forcash (Fig. 7.5a). Le ta sjellim në qendër O. Forcat duhet të lëvizin paralelisht dhe formohet një sistem çiftesh forcash. Momenti i secilës prej këtyre çifteve është

Qendra e gravitetit të trupave homogjenë të sheshtë
(figura të sheshta) Shumë shpesh është e nevojshme të përcaktohet qendra e gravitetit të trupave të ndryshëm të sheshtë dhe figurave të sheshta gjeometrike formë komplekse. Për trupat e sheshtë, mund të shkruajmë: V =

Përcaktimi i koordinatave të qendrës së gravitetit të figurave të sheshta
Shënim. Qendra e gravitetit të një figure simetrike është në boshtin e simetrisë. Qendra e gravitetit të shufrës është në mes të lartësisë. Pozicionet e qendrave të gravitetit të formave të thjeshta gjeometrike mund

Kinematika e pikave
Të ketë një ide për hapësirën, kohën, trajektoren, shtegun, shpejtësinë dhe nxitimin.Të dijë të vendosë lëvizjen e një pike (natyrore dhe koordinative). Njihni shënimin

Distanca e përshkuar
Shtegu matet përgjatë shtegut në drejtim të udhëtimit. Emërtimi - S, njësitë matëse - metra. Ekuacioni i lëvizjes së pikës: Përcaktimi i ekuacionit

Shpejtësia e udhëtimit
Sasia vektoriale që karakterizon në ky moment shpejtësia dhe drejtimi i lëvizjes përgjatë trajektores quhet shpejtësi. Shpejtësia është një vektor i drejtuar përgjatë k

nxitimi i pikës
Madhësia vektoriale që karakterizon shpejtësinë e ndryshimit të shpejtësisë në madhësi dhe drejtim quhet nxitimi i një pike. Shpejtësia e pikës kur lëviz nga pika M1

Lëvizje uniforme
Lëvizja e njëtrajtshme është lëvizja me shpejtësi konstante: v = konst. Për lëvizje të njëtrajtshme drejtvizore (Fig. 10.1 a)

Lëvizje me variabël të barabartë
Lëvizja me variabël të barabartë është lëvizje me nxitim tangjencial konstant: at = konst. Për lëvizje të njëtrajtshme drejtvizore

lëvizje përkthimore
Translational është një lëvizje e tillë e një trupi të ngurtë në të cilën çdo vijë e drejtë në trup gjatë lëvizjes mbetet paralele me pozicionin e tij fillestar (Fig. 11.1, 11.2). Në

lëvizje rrotulluese
Gjatë lëvizjes rrotulluese, të gjitha pikat e trupit përshkruajnë rrathë rreth një boshti të përbashkët fiks. Boshti fiks rreth të cilit rrotullohen të gjitha pikat e trupit quhet bosht i rrotullimit.

Raste të veçanta të lëvizjes rrotulluese
Rrotullimi uniform (shpejtësia këndore është konstante): ω = konst Ekuacioni (ligji) i rrotullimit uniform në këtë rast ka formën:

Shpejtësitë dhe nxitimet e pikave të një trupi rrotullues
Trupi rrotullohet rreth pikës O. Le të përcaktojmë parametrat e lëvizjes së pikës së vendosur në një distancë RA nga boshti i rrotullimit (Fig. 11.6, 11.7). Rrugë

Zgjidhje
1. Seksioni 1 - lëvizje e përshpejtuar e pabarabartë, ω \u003d φ '; ε = ω’ 2. Seksioni 2 - shpejtësia është konstante - lëvizja është uniforme, . ω = konst 3.

Përkufizimet bazë
Një lëvizje komplekse është një lëvizje që mund të zbërthehet në disa të thjeshta. Lëvizjet e thjeshta janë përkthimore dhe rrotulluese. Për të marrë parasysh lëvizjen komplekse të pikave

Lëvizja plan-paralele e një trupi të ngurtë
Rrafsh paralele, ose e sheshtë, është një lëvizje e tillë e një trupi të ngurtë në të cilin të gjitha pikat e trupit lëvizin paralelisht me një fikse në kornizën e referencës në shqyrtim.

përkthimore dhe rrotulluese
Lëvizja plan-paralele zbërthehet në dy lëvizje: përkthimore së bashku me një pol të caktuar dhe rrotulluese në lidhje me këtë pol. Zbërthimi përdoret për të përcaktuar

Qendra e shpejtësive
Shpejtësia e çdo pike të trupit mund të përcaktohet duke përdorur qendrën e menjëhershme të shpejtësive. Në këtë rast, një lëvizje komplekse përfaqësohet si një zinxhir rrotullimesh rreth qendrave të ndryshme. Një detyrë

Aksiomat e dinamikës
Ligjet e dinamikës përmbledhin rezultatet e eksperimenteve dhe vëzhgimeve të shumta. Ligjet e dinamikës, të cilat zakonisht konsiderohen si aksioma, u formuluan nga Njutoni, por ligjet e parë dhe të katërt u formuluan gjithashtu.

Koncepti i fërkimit. Llojet e fërkimit
Fërkimi është rezistenca që ndodh kur një trup i ashpër lëviz mbi sipërfaqen e një tjetri. Kur trupat rrëshqasin, lind fërkimi rrëshqitës; kur rrotullohen, ndodh fërkimi i rrotullimit. Natyra e rezistencës

fërkimi rrotullues
Rezistenca e rrotullimit lidhet me deformimin e ndërsjellë të tokës dhe rrotës dhe është shumë më pak se fërkimi i rrëshqitjes. Zakonisht toka konsiderohet më e butë se rrota, atëherë toka kryesisht deformohet dhe

Pika falas dhe jo të lira
Një pikë materiale, lëvizja e së cilës në hapësirë ​​nuk kufizohet nga asnjë kufizim, quhet e lirë. Problemet zgjidhen duke përdorur ligjin bazë të dinamikës. Materiali pastaj

forca e inercisë
Inercia është aftësia për të mbajtur të pandryshuar gjendjen e dikujt; kjo është një veti e brendshme e të gjithë trupave materialë. Forca inerciale - forca që shfaqet gjatë përshpejtimit ose frenimit të trupave

Zgjidhje
Forcat aktive: forca lëvizëse, forca e fërkimit, forca e gravitetit. Reaksioni në mbështetësin R. Forcën e inercisë e zbatojmë në drejtim të kundërt nga nxitimi. Sipas parimit d'Alembert, sistemi i forcave që veprojnë në platformë

Puna e forcës rezultante
Nën veprimin e një sistemi forcash, një pikë me masë m lëviz nga pozicioni M1 në pozicionin M 2 (Fig. 15.7). Në rastin e lëvizjes nën veprimin e një sistemi forcash,

Fuqia
Për të karakterizuar performancën dhe shpejtësinë e punës, prezantohet koncepti i fuqisë. Fuqia është puna e bërë për njësi të kohës:

Fuqi rrotulluese
Oriz. 16.2 Trupi lëviz përgjatë një harku me rreze nga pika M1 në pikën M2 M1M2 = φr Puna e forcës

Efikasiteti
Çdo makinë dhe mekanizëm, duke kryer punë, shpenzon një pjesë të energjisë për të kapërcyer rezistencat e dëmshme. Kështu, makina (mekanizmi), përveç punës së dobishme, kryen edhe një shtesë

Teorema mbi ndryshimin e momentit
Momenti i një pike materiale është një sasi vektoriale e barabartë me produktin e masës së pikës dhe shpejtësisë së saj mv. Vektori i momentit përkon me

Teorema e ndryshimit të energjisë kinetike
Energjia është aftësia e një trupi për të kryer punë mekanike. Ka dy forma energji mekanike: energji potenciale, ose energjia e pozicionit dhe energjia kinetike,

Bazat e dinamikës së sistemit të pikave materiale
Agregat pikat materiale, i ndërlidhur nga forcat e ndërveprimit, quhet sistem mekanik. Çdo trup material në mekanikë konsiderohet si mekanik

Ekuacioni themelor i dinamikës së një trupi rrotullues
Lëreni një trup të ngurtë të rrotullohet rreth boshtit Oz nën veprimin e forcave të jashtme me një shpejtësi këndore

Tensioni
Metoda e seksionit ju lejon të përcaktoni vlerën e faktorit të forcës së brendshme në seksion, por nuk bën të mundur vendosjen e ligjit të shpërndarjes forcat e brendshme sipas seksionit. Për të vlerësuar forcën e n

Faktorët e forcës së brendshme, sforcimet. Komploti
Keni një ide për forcat gjatësore, për sforcimet normale në prerje tërthore. Të njohë rregullat për ndërtimin e diagrameve të forcave gjatësore dhe sforcimeve normale, ligjin e shpërndarjes

Forcat gjatësore
Konsideroni një rreze të ngarkuar me forca të jashtme përgjatë boshtit. Trari është i fiksuar në mur (fiksimi i "ngulitjes") (Fig. 20.2a). Ne e ndajmë rrezen në seksione ngarkimi. Zona e ngarkimit me

Karakteristikat gjeometrike të seksioneve të sheshta
Keni një ide për sensi fizik dhe procedurën për përcaktimin e momenteve boshtore, centrifugale dhe polare të inercisë, rreth boshteve qendrore kryesore dhe momenteve qendrore kryesore të inercisë.

Momenti statik i zonës seksionale
Konsideroni një seksion arbitrar (Fig. 25.1). Nëse e ndajmë seksionin në zona pafundësisht të vogla dA dhe e shumëzojmë secilën zonë me distancën nga boshti koordinativ dhe integrojmë atë të marrë

momenti centrifugal i inercisë
Momenti centrifugal i inercisë së një seksioni është shuma e produkteve të zonave elementare të marra nga sipërfaqja totale nga të dy koordinatat:

Momentet aksiale të inercisë
Momenti boshtor i inercisë së seksionit në lidhje me disa oborr që shtrihen në të njëjtin rrafsh është shuma e produkteve të zonave elementare për katror të distancës së tyre të marrë në të gjithë sipërfaqen

Momenti polar i inercisë së seksionit
Momenti polar i inercisë së një seksioni në lidhje me një pikë (pol) të caktuar është shuma e produkteve të zonave elementare të marra në të gjithë zonën dhe katrori i distancës së tyre deri në këtë pikë:

Momentet e inercisë së seksioneve më të thjeshta
Momentet aksiale inercia drejtkëndëshe (Fig. 25.2) Imagjinoni drejtpërdrejt

Momenti polar i inercisë së një rrethi
Për një rreth, fillimisht llogaritet momenti polar i inercisë, pastaj ai boshtor. Imagjinoni një rreth si një grup unazash pafundësisht të holla (Fig. 25.3).

Deformimet përdredhëse
Përdredhja e një trau të rrumbullakët ndodh kur ai ngarkohet nga çifte forcash me momente në plane pingul me boshtin gjatësor. Në këtë rast, gjeneratori i rrezes është i përkulur dhe i kthyer përmes një këndi γ,

Hipotezat në përdredhje
1. Përmbushet hipoteza e prerjeve të sheshta: prerja tërthore e traut, e cila është e sheshtë dhe pingul me boshtin gjatësor, pas deformimit mbetet e sheshtë dhe pingul me boshtin gjatësor.

Faktorët e forcës së brendshme në përdredhje
Përdredhja quhet ngarkim, në të cilin vetëm një faktor i brendshëm i forcës lind në seksionin kryq të rrezes - çift rrotullimi. Ngarkesat e jashtme janë gjithashtu dy pro

Komplotet e rrotullimit
Çiftet rrotulluese mund të ndryshojnë përgjatë boshtit të rrezes. Pas përcaktimit të vlerave të momenteve përgjatë seksioneve, ne ndërtojmë një parcelë çift rrotullues përgjatë boshtit të shiritit.

Sforcimet përdredhëse
Ne vizatojmë një rrjet vijash gjatësore dhe tërthore në sipërfaqen e rrezes dhe marrim parasysh modelin e formuar në sipërfaqe pas Fig. 27.1a deformim (Fig. 27.1a). Pop

Sforcimet maksimale përdredhëse
Nga formula për përcaktimin e sforcimeve dhe diagrami i shpërndarjes së sforcimeve prerëse gjatë përdredhjes shihet se sforcimet maksimale ndodhin në sipërfaqe. Përcaktoni tensionin maksimal

Llojet e llogaritjeve të forcës
Ekzistojnë dy lloje të llogaritjes së forcës 1. Llogaritja e projektimit - përcaktohet diametri i rrezes (boshtit) në seksionin e rrezikshëm:

Llogaritja e ngurtësisë
Gjatë llogaritjes së ngurtësisë, deformimi përcaktohet dhe krahasohet me atë të lejuar. Konsideroni deformimin e një shufreje të rrumbullakët nën veprimin e një çifti të jashtëm forcash me një moment t (Fig. 27.4).

Përkufizimet bazë
Një kthesë është një lloj ngarkese në të cilën një faktor i brendshëm i forcës lind në seksionin kryq të rrezes - një moment lakimi. Bar duke punuar në

Faktorët e forcës së brendshme në përkulje
Shembulli 1. Konsideroni një rreze mbi të cilën vepron një çift forcash me një moment t dhe forcë e jashtme F (Fig. 29.3a). Për të përcaktuar faktorët e forcës së brendshme, ne përdorim metodën me

Momentet e përkuljes
Forca tërthore në seksion konsiderohet pozitive nëse tenton të kthejë

Varësi diferenciale për përkuljen e drejtpërdrejtë tërthore
Ndërtimi i diagrameve të forcave prerëse dhe momenteve të përkuljes thjeshtohet shumë kur përdoren marrëdhëniet diferenciale midis momentit të përkuljes, forcës prerëse dhe intensitetit uniform.

Metoda e seksionit Shprehja që rezulton mund të përgjithësohet
Forca tërthore në seksionin në shqyrtim është e barabartë me shumën algjebrike të të gjitha forcave që veprojnë në tra deri në seksionin në shqyrtim: Q = ΣFi Meqenëse po flasim për

Tensioni
Konsideroni lakimin e një trau të mbërthyer në të djathtë dhe të ngarkuar me një forcë të përqendruar F (Fig. 33.1).

Gjendja e stresit në një pikë
Gjendja e stresit në një pikë karakterizohet nga sforcimet normale dhe prerëse që lindin në të gjitha zonat (seksionet) që kalojnë nëpër pikë e dhënë. Zakonisht është e mjaftueshme për të përcaktuar

Koncepti i një gjendje komplekse të deformuar
Tërësia e sforcimeve që ndodhin në drejtime të ndryshme dhe në rrafshe të ndryshme që kalojnë nëpër një pikë përcaktojnë gjendjen e deformuar në atë pikë. Deformime komplekse

Llogaritja e një shufre të rrumbullakët për përkulje me përdredhje
Në rastin e llogaritjes së një shufre të rrumbullakët nën veprimin e përkuljes dhe përdredhjes (Fig. 34.3), është e nevojshme të merren parasysh streset normale dhe prerëse, pasi vlerat maksimale të stresit ndodhin në të dyja rastet.

Koncepti i ekuilibrit të qëndrueshëm dhe të paqëndrueshëm
Shufrat relativisht të shkurtra dhe masive mbështeten në ngjeshje, sepse. ato dështojnë si pasojë e shkatërrimit ose deformimeve të mbetura. Shufra të gjata me prerje të vogël nën veprim

Llogaritja e qëndrueshmërisë
Llogaritja e qëndrueshmërisë konsiston në përcaktimin e forcës së lejueshme të shtypjes dhe, në krahasim me të, forcës vepruese:

Llogaritja me formulën e Euler-it
Problemi i përcaktimit të forcës kritike u zgjidh matematikisht nga L. Euler në 1744. Për një shufër të varur në të dy anët (Fig. 36.2), formula e Euler-it ka formën

Stresi kritik.
Stresi kritik është sforcimi i shtypjes që korrespondon me forcën kritike. Stresi nga forca shtypëse përcaktohet nga formula

Kufijtë e zbatueshmërisë së formulës së Euler-it
Formula e Euler-it vlen vetëm brenda kufijve të deformimeve elastike. Kështu, stresi kritik duhet të jetë më i vogël se kufiri elastik i materialit. Prev

Një vlerë skalare e barabartë me gjatësinë e segmentit të marrë me shenjën përkatëse, e mbyllur midis projeksioneve të fillimit dhe fundit të forcës, quhet projeksion i forcës në bosht.

Projeksioni ka një shenjë plus nëse lëvizja nga fillimi në fund ndodh në drejtimin pozitiv të boshtit dhe një shenjë minus nëse është në drejtim negativ.

Kështu, projeksionet e një force të caktuar në çdo bosht paralel dhe të drejtuar po aq janë të barabarta me njëra-tjetrën.

Projeksioni i forcës në boshtin Ox shënohet si (Fig. 12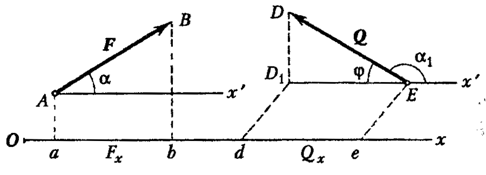

).

Duke ndjekur figurën 12 dhe përkufizimin, marrim

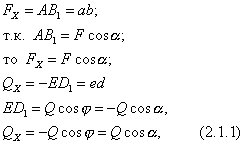
Kjo do të thotë, projeksioni i forcës në bosht është i barabartë me produktin e modulit të forcës dhe kosinusit të këndit midis drejtimit të forcës dhe drejtimit pozitiv të boshtit.

Nëse një forcë është pingul me një bosht, atëherë projeksioni i saj në atë bosht është zero.

Projeksioni i forcës në rrafshin Oxy është vektori i mbyllur midis projeksioneve të fillimit dhe fundit të forcës F në këtë plan (Fig. 13

).

Projeksioni i një force mbi një plan është një sasi vektoriale dhe karakterizohet si nga moduli ashtu edhe nga drejtimi në rrafshin Oxy. Moduli i projeksionit të forcës në rrafshin Oxy shprehet si

Pastaj projeksionet në akset Ox dhe Oy:

Ne zgjedhim sistemin e koordinatave Oxyz. Një vektor mund të ndërtohet duke ditur modulin dhe këndet ndërmjet vektorit dhe boshteve përkatëse (Fig. 14 ).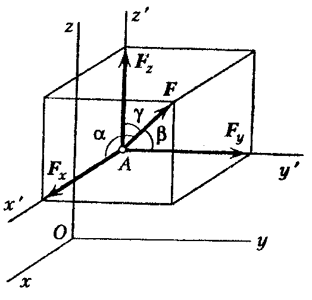

Caktimi i këtyre madhësive përcakton forcën. Pika e aplikimit të forcës duhet të specifikohet shtesë nga koordinatat x, y, z. Për më tepër, forca mund të specifikohet nga projeksionet në akset. Pastaj

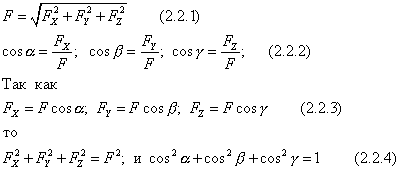
Këto formula lejojnë, duke ditur projeksionet e forcës në boshtet koordinative, të gjejmë modulin dhe këndet e saj me boshtet, d.m.th. përcaktoni forcën. Duke ditur projeksionet, mund të ndërtoni një vektor gjeometrikisht.

Për një plan shkruhen formulat (2.2.1) dhe (2.2.2).

Ndërtimi në rrafsh kryhet sipas aksiomës së 4-të të statikës.

Le të shqyrtojmë tani metodën analitike të shtimit të forcave. Marrëdhënia midis vektorëve dhe projeksioneve të tyre jepet nga teorema e mëposhtme:

Projeksioni i vektorit të shumës në një bosht është i barabartë me shumën algjebrike të projeksioneve të termave të vektorëve në të njëjtin bosht (Fig. 15 ).

Këto marrëdhënie bëjnë të mundur shtimin e forcave në mënyrë analitike. Mund të vërehet identiteti i formulave (2.2.1)-(2.2.4) dhe (2.2.9)-(2.2.11).

Zgjidhja e problemeve në statikë shpesh shoqërohet me operacionin e mbledhjes nga algjebra vektoriale. Le të kujtojmë truket e vjetra dhe të prezantojmë disa përkufizime.

Quhet një sasi e barabartë me shumën gjeometrike të forcave të çdo sistemi vektori kryesor sistemeve.

Shuma gjeometrike e forcave nuk duhet të ngatërrohet me rezultatin. Për shumë sisteme forcash, nuk ka asnjë rezultat, dhe vektori kryesor mund të llogaritet për cilindo.

Konsideroni shtimin e dy forcave në një aeroplan. Shuma gjeometrike e forcave gjendet sipas rregullit të paralelogramit duke ndërtuar një trekëndësh të forcës (Fig. 16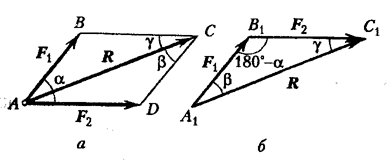

).

Moduli R i rezultantit përcaktohet si brinja e trekëndëshit:

këndet gjenden nga teorema e sinusit, duke pasur parasysh se , marrim

Në vazhdim të metodës gjeometrike të mbledhjes së forcave, kujtojmë mbledhjen e tre forcave që nuk shtrihen në këtë rrafsh.

Shuma gjeometrike e tre forcave, jo të shtrira në të njëjtin rrafsh, përshkruhet nga diagonalja e një paralelipipedi të ndërtuar mbi këto forca (Fig. 17 ).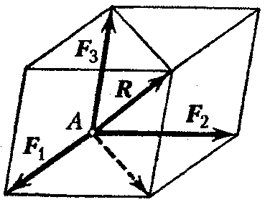

Këtu është e nevojshme të theksohet analogjia e plotë e figurave 14 dhe 17, ku , dhe , respektivisht, luajnë rolin. Prandaj, ne mund të përdorim formula (2.2.1-2.2.4).

Duke marrë parasysh një sistem të sheshtë të forcave konvergjente, është e nevojshme të merret parasysh pozicioni i një sistemi të tillë forcash.

Shuma gjeometrike (vektori kryesor) i çdo sistemi forcash përcaktohet nga ndërtimi i një poligoni forcash ose nga mbledhja e njëpasnjëshme e forcave të sistemit. Lëreni sistemin forcat konvergjente (Fig. 18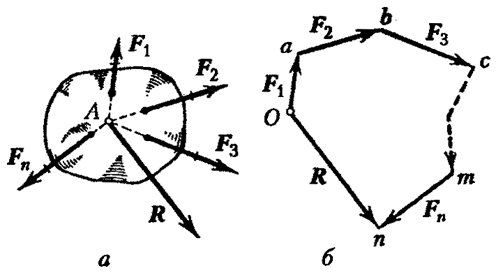

).

Për të ndërtuar një poligon të forcës, zgjidhni një pikë arbitrare O dhe zhvendoseni fillimin në të, pastaj zhvendoseni fillimin në fund të vektorit, e kështu me radhë. pas bartjes së vektorit, fundi i vektorit do të jetë në një pikë N. Pikat O dhe N i lidhim me një vektor. Ky vektor mbyllës do të jetë vektori kryesor i sistemit.

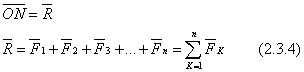
Me shtimin e njëpasnjëshëm të forcave (Fig. 18, a), ato transferohen të gjitha përgjatë vijave të veprimit në pikën e kryqëzimit A. Në mënyrë konsistente, sipas rregullit të paralelogramit, forcat shtohen, fitohet vektori:

e cila është rezultante, e barabartë me vektorin kryesor të të gjitha forcave dhe e aplikuar në pikën e kryqëzimit të tyre.

Linjat e veprimit të tre forcave joparalele të balancuara reciproke që shtrihen në të njëjtin rrafsh kryqëzohen në një pikë.

Të jepet forca. Meqenëse ato shtrihen në të njëjtin rrafsh dhe nuk janë paralele, vijat e tyre të veprimit do të kryqëzohen në një pikë O. Ne zbatojmë forcat në këtë pikë dhe i zëvendësojmë ato me rezultanten. Pastaj janë dy forca dhe zbatohen në pikën O (Fig. 19 ).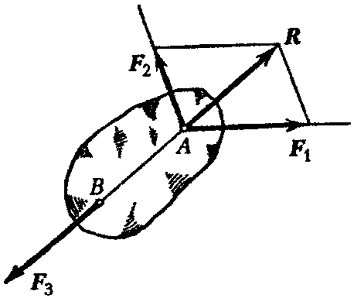

Nëse trupi është në ekuilibër, atëherë, sipas teoremës së parë të statikës, dhe duhet të depozitohet përgjatë një vije të drejtë, d.m.th. . Prandaj kalon në pikën A. Kjo është ajo që kërkohej të vërtetohej.

Teorema është një provë e nevojshme, por e pamjaftueshme e kushtit të ekuilibrit për një trup të ngurtë të lirë nën veprimin e tre forcave.

Siç u përcaktua, forcat konvergjente janë forca linjat e veprimit të të cilave kryqëzohen në një pikë. Duke marrë parasysh teoremën mbi tre forcat dhe aksiomën e paralelogramit të forcave, gjejmë se sistemi i forcave konvergjente ka një rezultante të barabartë me shumën gjeometrike (vektorin kryesor) të këtyre forcave dhe të aplikuar në pikën e kryqëzimit të tyre. Ndërtimi ose përkufizimi i rezultantit u krye në paragrafin 2 të këtij kapitulli (shih formulat 2.3.3, 2.3.4).

Pasi të kemi përcaktuar rezultatin, mund të vazhdojmë me përcaktimin e kushteve të ekuilibrit për një trup të ngurtë të lirë nën veprimin e një sistemi forcash konvergjente.

Nëse një sistem i balancuar i forcave vepron mbi një trup, atëherë trupi është në qetësi ose lëviz me inerci.

Për ekuilibrin e një sistemi forcash konvergjente të aplikuara në një trup të ngurtë, është e nevojshme dhe e mjaftueshme që rezultanta e këtyre forcave të jetë e barabartë me zero. Kushtet që këto forca duhet të plotësojnë mund të shprehen në formë gjeometrike ose analitike.

1) Gjendja e ekuilibrit gjeometrik.

Meqenëse rezultanti i forcave konvergjente përcaktohet si vektor mbyllës i poligonit të forcës, ai mund të zhduket kur poligoni mbyllet. Domethënë, për ekuilibrin e sistemit të forcave konvergjente, është e nevojshme dhe e mjaftueshme që poligoni i forcës i ndërtuar nga këto forca të jetë i mbyllur.

2) Kushtet analitike të ekuilibrit. Në mënyrë analitike, rezultanti përcaktohet si

Meqenëse shuma e numrave pozitivë është nën rrënjë, atëherë R do të jetë e barabartë me zero nëse dhe vetëm nëse në të njëjtën kohë.

Domethënë barazitë

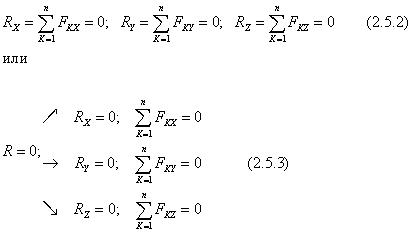
Këto janë kushtet për ekuilibrin e një trupi të ngurtë të lirë nën veprimin e një sistemi forcash konvergjente.

Për ekuilibrin e një sistemi hapësinor të forcave konvergjente, është e nevojshme dhe e mjaftueshme që shumat e projeksioneve të këtyre forcave në boshtet koordinative të jenë të barabarta me zero.

Për një sistem të sheshtë forcash konvergjente, ekuacionet (2.5.3) reduktohen në sa vijon:

Së bashku me lëvizje progresive një trup i ngurtë mund të rrotullohet rreth një qendre (pike).

Rrotullimi karakterizohet nga një moment force.

Le të zbatohet forca në pikën A. Ajo tenton të rrotullojë trupin rreth qendrës fikse O (Fig. 20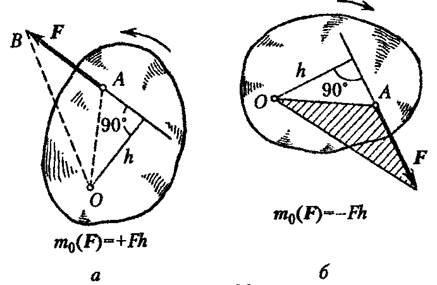

). h pingul i ulur nga pika O në vijën e veprimit të forcës quhet shpatulla e forcës në raport me qendrën O.

Meqenëse pika e aplikimit të forcës mund të zhvendoset përgjatë vijës së veprimit të forcës, rrotullimi i trupit do të varet nga:

1) moduli i forcës dhe shpatulla h.

2) pozicionet e aeroplanit OAB,

Lëreni të gjithë sistemin e forcave të shtrihet në një plan, atëherë drejtimi mund të karakterizohet nga një shenjë. Ne japim përkufizimin e mëposhtëm të momentit të forcës:

Momenti i forcës rreth qendrës O quhet një vlerë e barabartë me produktin e modulit të forcës dhe gjatësisë së krahut, marrë me shenjën përkatëse.

Momenti i forcës shënohet si:

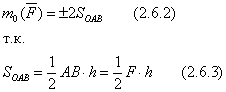
Ne zgjedhim shenjën plus nëse forca përpiqet të rrotullojë trupin në drejtim të kundërt të akrepave të orës, përndryshe marrim shenjën minus.

Njësitë matëse: (njuton për metër), (kilogram për metër).

Vetitë e momentit të forcës:

1) momenti i forcës nuk do të ndryshojë kur pika e aplikimit të forcës transferohet përgjatë vijës së saj të veprimit;

2) momenti i forcës është i barabartë me zero nëse dhe vetëm nëse forca është e barabartë me zero, ose vija e tij e veprimit kalon nëpër qendrën O. (h = 0).

3) momenti i forcës është numerikisht i barabartë me dyfishin e sipërfaqes së trekëndëshit OAB.

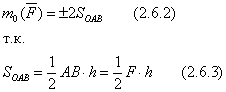
Momenti i sistemit të sheshtë rezultant të forcave konvergjente në lidhje me çdo qendër është i barabartë me shumën algjebrike të momenteve të termave të forcave në lidhje me të njëjtën qendër.

Konsideroni sistemin e forcave duke konverguar në pikën A (Fig. 21 ).