Dependența diferenței de potențial de distanță. Diferența de potențial, energia de încărcare într-un câmp electric. Potenţial

În paragraful anterior, am discutat despre caracteristica principală câmp electric- tensiunea lui. După cum rezultă din definiția în sine, aceasta este o caracteristică de putere și, prin urmare, un vector. În unele cazuri, caracteristicile scalare sunt mai convenabile, care, se pare, pot fi introduse și pentru câmp electrostatic– diferența de potențial și potențial. În acest caz, ne vom baza pe o proprietate fundamentală importantă a forțelor care acționează asupra unei sarcini într-un câmp electrostatic - conservatorismul lor.

Amintiți-vă că forțele sunt numite conservatoare, a căror activitate nu depinde de forma traiectoriei corpului. Munca unor astfel de forțe este determinată numai de coordonatele punctelor inițiale și finale de deplasare. Pe baza cunoștințelor noastre despre proprietățile caracteristicilor sale de putere ale câmpului electrostatic creat de un sistem arbitrar de sarcini, ar fi posibil să se efectueze o demonstrație detaliată a egalității muncii atunci când o sarcină se mișcă între oricare dintre două puncte ale sale. Dar vom scurta oarecum această procedură, amintind teorema „cu privire la conservativitatea forțelor centrale”, pe care am demonstrat-o în secțiunea despre mecanică.

O sarcină punctiformă staționară este sursa „câmpului de forțe centrale” - aceasta decurge direct din formularea legii de bază a electrostaticii - legea lui Coulomb. Din principiul suprapunerii câmpurilor electrice rezultă că munca efectuată atunci când o sarcină de test se mișcă în câmpul oricărui sistem odihnindu-se taxe este suma algebrică a muncii în câmpul fiecărei sarcini separat. Aceasta înseamnă că câmpul unor astfel de forțe („Forțe Coulomb” *)) este, de asemenea, un câmp de forțe conservatoare. Acesta este ceea ce trebuia dovedit.

Astfel, lucrul forțelor câmpului electrostatic **) asupra deplasării unei sarcini punctuale (de probă) între două puncte caracterizează acest câmp. Dar depinde și de mărimea sarcinii de testare q 0 . Acest lucru este dovedit de experiență, dar acest lucru este și de înțeles, pe baza cunoștințelor noastre despre forțele „Coulomb”. Pentru că sunt proporționale cu taxa q 0 în fiecare punct al traiectoriei 1®2 (pe baza legii lui Coulomb), iar munca este proporțională cu forța. Pentru a caracteriza câmpul și numai câmpul, puteți împărți munca la valoarea taxei de testare. Ceea ce se întâmplă este „diferența de potențial”. Iată o definiție a acestui concept important:

(AOD .) Diferenta potentiala între punctele de câmp electrostatic 1 și 2 se numește atitudine muncă câmpuri prin deplasarea încărcăturii de testare din punct 1exact 2la valoarea acestei taxe :

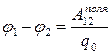. (3.1)

În sistemul SI, unitatea diferenței de potențial se numește 1 volt (1 V = 1 J/C). Dacă învățăm cum să determinăm diferența de potențial j 1 –j 2 pentru câmpul unui sistem de sarcini în repaus (teoretic sau experimental), aceasta ne va permite să găsim munca câmpului prin deplasarea oricărui repera cu precizieîncărca qîn acest domeniu:

. (3.2)

Deci diferența de potențial este caracteristică energetică câmp electric, deoarece este direct legat de conceptul de muncă.

În mecanică, am introdus conceptul de „energie potențială” pentru forțele conservatoare (acum spunem: „câmpuri de forțe conservatoare”). În același timp, ne-am ghidat după următorul principiu: „munca forțelor de câmp este egală cu pierderea energie potențială". Oficializăm acest principiu într-o notație analitică:

Aici U 1 și U 2 sunt energia potențială în stările „inițiale” („1”) și, respectiv, „finale” („2”) ale sistemului. În cazul în discuție, câmpurile sistemului de sarcini fixe sunt energia taxă punctuală qîn poziția „1” (cu coordonatele ( X 1 ,y 1 ,z 1 )) și poziția „2” (cu coordonatele ( X 2 ,y 2 ,z 2 )) câmp electrostatic. Acestea. energia potențială a sarcinii din acest câmp este o funcție scalară a coordonatelor punctelor câmpului U = U( X,y,z) (sau ). Comparând (3.2) și (3.3), vedem că este convenabil să presupunem că diferența de potențial este diferența dintre valorile unei alte funcții scalare ale coordonatelor punctelor de câmp j(x,y,z). Este legat de funcția U( X,y,z) (energie potențială) printr-o relație simplă: U( X,y,z) = q× j(x,y,z). Sau pentru că

se spune că este „egal numeric cu energia potențială a unei unități de sarcină pozitivă” într-un punct dat al câmpului. Și această valoare se numește j„potenţialul” unui punct dat al câmpului electrostatic.

Cel mai important lucru este cum să găsiți această funcție pentru domeniul unui anumit sistem de taxe? Care este procedura?

În primul rând, trebuie să cădem de acord asupra condițiilor de normalizare *): trebuie să alegem un punct R 0 , în care potențialul de încărcare de testare se va presupune a fi egal cu zero . Cel mai adesea, un astfel de punct este ales „la infinit” la distanță, unde câmpul este absent **). Pentru a face acest lucru, trebuie să găsiți munca „specifică” a domeniului - adică. lucru legat de cantitatea de sarcină de test transferată (sau, după cum se spune adesea, „prin mutarea unei unități de sarcină pozitivă”) dintr-un punct dat din câmp R(X,y,z) până la punctul de normalizare R 0 . În formă analitică, aceasta definiție potentialul poate fi scris astfel:

(Def. ) j P(X,y,z) = . (3.5)

Este posibil să exprimăm valorile nou introduse de noi - diferența de potențial și potențialul prin caracteristica puterii, pe care am învățat deja cum să le calculăm prin locație dată taxe în spațiu? Da, cu siguranță poți. Să scriem un lanț de egalități pe care le înțelegem bine:

Să scriem din nou ultima ecuație

. (3.6)

Oferă o „rețetă” pentru căutarea unei diferențe de potențial folosind o funcție cunoscută de tensiune. În mod similar pentru potențial:

Și în sfârșit pentru potențialul unui punct arbitrar al câmpului R cu coordonate ( X,y,z):

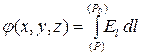. (3.7)

· Potenţialul câmpului unei sarcini punctiforme

Pe baza procedurii de calcul al potențialului, obținem o expresie pentru cazul unui câmp de sarcină punctiformă. Acest lucru este foarte important pentru calculele ulterioare ale potențialului de câmp al unui sistem de sarcini situate arbitrar în spațiu.

2. Alegerea traiectoriei. Să fie un punct arbitrar R(X,y,z) se află la distanță r din taxa sursă. Deoarece rezultatul nu depinde de forma traiectoriei, pentru calcularea integralei curbilinii a formei (3.7) alegem cea mai simplă linie dreaptă direcționată radial dintr-un punct dat al câmpului de-a lungul liniei câmpului și „mergând la infinit”.

3. Calcul. În conformitate cu definiția potențialului, calculăm munca „specifică” a câmpului creat de o sarcină punctiformă q asupra transferului sarcinii de testare de-a lungul traiectoriei alese. Următorul lanț de egalități, sperăm, pare destul de „transparent”. Cu toate acestea, vom oferi în continuare un comentariu minim. În primul rând, observăm că, datorită alegerii noastre a unei traiectorii sub forma unei raze îndreptate radial de la sarcină, putem denota E lși dl(curba arbitrara " L") schimba in Erși dr(axa polară" r"). Mai mult, deoarece vectorul este direcționat radial, pentru orice deplasare mică de-a lungul traiectoriei, proiecția vectorului de stres este pur și simplu egală cu modulul acestui vector. E(r). Ca rezultat, putem face, de asemenea, un pas important în calculul nostru - pentru a face tranziția de la integrala curbilinie la cea definită obișnuită:

.*)

Acum, după înlocuirea expresiei pentru modulul intensității câmpului unei sarcini punctiforme (3.5), rămânem doar cu o „rutină” matematică:

Să scriem din nou rezultatul, completându-l cu posibila prezență a unui mediu dielectric omogen gazos sau lichid cu o permitivitate e, care umple întregul spațiu din jurul sarcinii punctiforme:

. (3.8)

Potențialul de câmp al unei sarcini punctiforme, după cum vedem, scade cu distanța conform legii 1/ r.

· Suprafețe echipotențiale

Când discutăm caracteristicile puterii câmp electrostatic, ne-am convins de rodnicia conceptului linii de forță(linii de tensiune). Pentru caracteristica energetică a câmpului - potențial - este utilă și introducerea unei caracteristici ilustrative suplimentare - un sistem de „suprafețe echipotențiale”. Din numele însuși este clar („equi” înseamnă „egal”) că acestea sunt suprafețe cu potențial constant, care caracterizează capacitatea forțelor de câmp de a lucra atunci când mișcă o sarcină. De-a lungul unor astfel de suprafețe, evident, nu se lucrează deloc. Este maximă în direcțiile de-a lungul cărora densitatea (densitatea) suprafețelor echipotențiale este maximă. În aceste locuri, intensitatea câmpului este, de asemenea, maximă. Este ușor să ne dăm seama care este orientarea reciprocă a liniilor de forță și a suprafețelor echipotențiale la intersecțiile lor: sunt reciproc perpendiculare. La urma urmei, pentru orice deplasare mică de-a lungul suprafeței echipotențiale munca elementara este egal cu zero, iar acest lucru este posibil numai dacă componenta tangentă a vectorului de stres este egală cu zero, adică. este îndreptată strict de-a lungul normalului la suprafață. Mai jos dăm un lanț de corespunzătoare acestor cuvinte, sperăm, egalități destul de evidente:

Împreună cu Fig. 3. ... dovedesc, de fapt, afirmația deja formulată: liniile de forță se încrucișează (sau „vin la...”) suprafețe echipotențiale în unghi drept !

Să dăm o imagine a suprafețelor echipotențiale (și a liniilor de forță) pentru unele dintre cele mai simple cazuri de câmp electrostatic care ne sunt deja bine cunoscute: A) câmpul unei sarcini punctiforme; b) câmpul a două sarcini punctuale opuse identice în valoare absolută; în) câmpul dintre două plăci mari plan-paralele încărcate opus (comparativ cu distanța dintre ele) - vezi fig. 3.1.

Să ne întoarcem acum la o sarcină sferică (punctivă). Se arată mai sus că puterea câmpului electric creat de o sarcină distribuită uniform pe sferă Q, nu depinde de raza sferei. Imaginați-vă că la o oarecare distanță r din centrul sferei este o sarcină de test q. Intensitatea câmpului în punctul în care este localizată sarcina,

Figura prezintă un grafic al dependenței puterii interacțiunii electrostatice dintre sarcinile punctuale de distanța dintre ele. Pentru a găsi lucrul câmpului electric la mutarea sarcinii de testare q de la o distanta r pana la distanta R, împărțiți acest interval la puncte r 1 , r 2 ,..., rPîn secțiuni egale. Forța medie care acționează asupra unei sarcini qîn cadrul segmentului [ rr 1 ] este egal cu

Munca acestei forțe în acest domeniu:

Expresii similare pentru lucru vor fi obținute pentru toate celelalte secțiuni. Deci, treaba completă este:

Termenii identici cu semne opuse sunt distruși și în final obținem:

este lucrarea câmpului pe sarcină

- diferenta potentiala

Acum, pentru a găsi potențialul punctului de câmp față de infinit, ne direcționăm R la infinit și în final obținem:

Deci, potențialul câmpului unei sarcini punctiforme este invers proporțional cu distanța până la sarcină.

24. Energia potențială a unei sarcini în câmpul unui sistem de sarcini. Principiul suprapunerii pentru potențiale. Principiul suprapunerii pentru potențiale

Orice câmp electrostatic arbitrar complex poate fi reprezentat ca o suprapunere a câmpurilor de sarcini punctuale. Fiecare astfel de câmp în punctul selectat are un anumit potențial. Deoarece potențialul este o mărime scalară, potențialul rezultat al câmpului tuturor sarcinilor punctiforme este suma algebrică a potențialelor 1, 2, 3, ... a câmpurilor sarcinilor individuale: = 1 + 2 + 3 + .. Această relație este o consecință directă a principiului suprapunerii câmpurilor electrice.

Energia potențială a unei sarcini într-un câmp electric. Să continuăm comparația dintre interacțiunea gravitațională a corpurilor și interacțiunea electrostatică a sarcinilor. masa corpului mîn câmpul gravitațional al Pământului are energie potențială. Lucrul gravitației este egal cu modificarea energiei potențiale, luată cu semnul opus:

A=-(W p2 - W p1) = mgh.

(Aici și mai jos vom desemna energia prin literă W.) Exact ca un corp de masă mîn câmpul gravitațional are o energie potențială proporțională cu masa corpului, o sarcină electrică într-un câmp electrostatic are o energie potențială W p , proporțional cu sarcina q. Lucrarea forțelor câmpului electrostatic DAR este egală cu modificarea energiei potențiale a sarcinii în câmpul electric, luată cu semnul opus:

A=-(W p2 - W p1) . (40.1)

25. Diferența de potențial. Suprafețe echipotențiale

Suprafata echipotentiala- o suprafață, fiecare punct având același potențial.

După cum urmează din legătura dintre muncă și potențiale:

când sarcina este transferată de-a lungul suprafețelor echipotențiale, câmpul electric nu funcționează, deoarece .

Lucrul cu o forță diferită de zero este zero numai dacă vectorul forță este perpendicular pe vectorul deplasare. De aici rezultă că liniile de tensiune sunt perpendiculare pe suprafețele echipotențiale. Exemple de suprafețe echipotențiale sunt sferele pentru câmpul unei sarcini punctuale și planurile paralele pentru câmpurile omogene (Fig. 3).

Diferența de potențial (tensiune)între două puncte este egal cu raportul lucrărilor de câmp la mutarea sarcinii de la punctul de pornire la punctul final la modulul acestei sarcini: U\u003d φ 1 - φ 2 \u003d -Δφ \u003d A / q, A \u003d - (W p2 - W p1) \u003d -q (φ 2 - φ 1) \u003d -qΔφ

Diferența de potențial se măsoară în volți (V = J / C) Relația dintre puterea câmpului electrostatic și diferența de potențial: E X = Δφ / Δ X Puterea câmpului electrostatic este direcționată în direcția potențialului de scădere. Măsurată în volți împărțit la metri (V/m)

§ 15. POTENȚIAL. ENERGIA SISTEMULUI DE ÎNCĂRCĂRI ELECTRICE. LUCRĂRI LA MUTAREA ÎNCĂRCĂRII ÎN CÂMP

Formule de bază

 Potențialul unui câmp electric este o valoare egală cu raportul dintre energia potențială a unei sarcini pozitive punctiforme plasate în punct dat câmpuri, la această taxă;

=P/ Q,

sau potențialul câmpului electric este o mărime egală cu raportul dintre munca forțelor câmpului pentru a muta o sarcină pozitivă punctuală dintr-un punct dat al câmpului la infinit la această sarcină:

=A/ Q.

Potențialul câmpului electric la infinit este considerat condiționat egal cu zero.

Rețineți că atunci când o sarcină se mișcă într-un câmp electric, funcționează A v.s forțele externe este egală în valoare absolută cu munca A s.p. intensitatea câmpului și este opusă acesteia în semn:

A v.s = – A s.p. .

 Potențialul câmpului electric creat de o sarcină punctiformă Q pe distanta r din sarcina

 Potențialul câmpului electric creat de metal, purtând o taxă Q sferă cu rază R, la o distanță de centrul sferei:

în interiorul sferei ( r<R)

;

pe suprafața unei sfere ( r=R)

;

fara scop (r> R)

.

În toate formulele date pentru potențialul unei sfere încărcate,  este permisivitatea unui dielectric infinit omogen care înconjoară sfera.

 Potenţialul câmpului electric creat de sistem P sarcinile punctuale, într-un punct dat, în conformitate cu principiul suprapunerii câmpurilor electrice, este egală cu suma algebrică a potențialelor  1 , 2 , ... , n, creat de taxe punctuale individuale Q 1 ,Q 2 , ...,Q n :

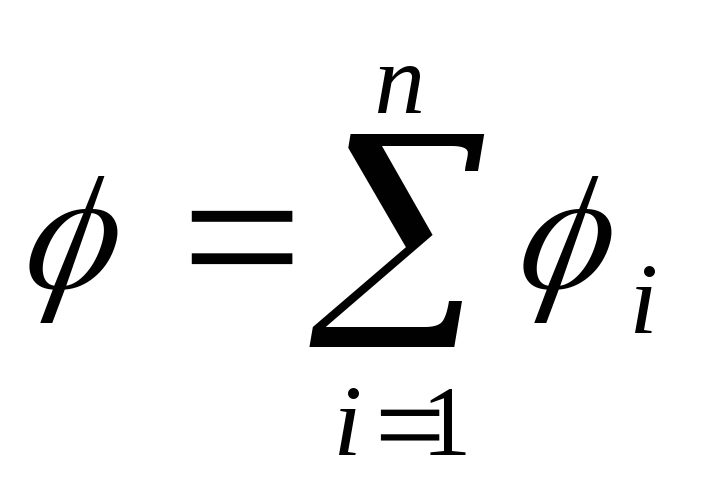
 Energie W interacțiunile unui sistem de sarcini punctiforme Q 1 ,Q 2 , ...,Q n este determinată de munca pe care o poate face acest sistem de sarcini atunci când sunt îndepărtate unul față de celălalt la infinit și este exprimat prin formula

unde  i- potenţialul câmpului creat de toţi P- 1 taxe (excluzând prima) în punctul în care se află taxa Q i .

 Potențialul este legat de puterea câmpului electric prin relație

E= -grad.

În cazul unui câmp electric cu simetrie sferică, această relație este exprimată prin formula

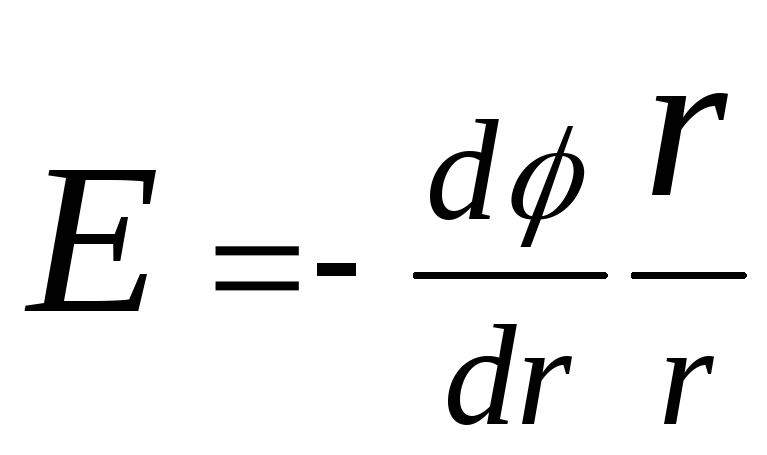sau sub formă scalară

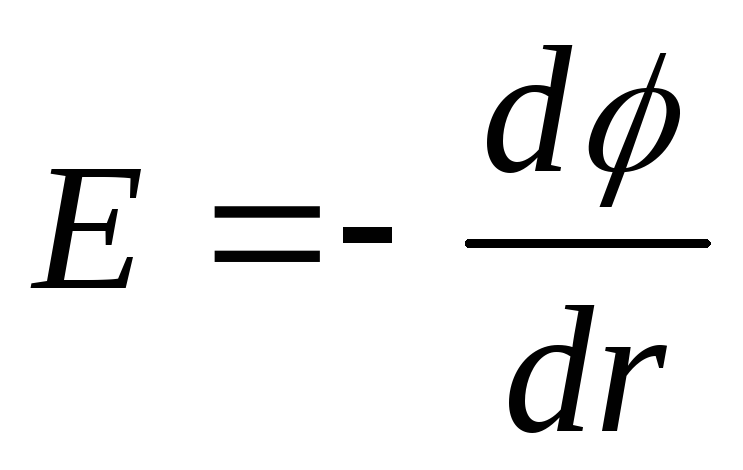iar în caz câmp uniform, adică un câmp a cărui intensitate în fiecare punct este aceeași atât ca valoare absolută, cât și ca direcție,

E=( 1 – 2 ,)/d,

unde  1 și 2 - potenţialele punctelor a două suprafeţe echipotenţiale; d - distanța dintre aceste suprafețe de-a lungul liniei câmpului electric.

 Lucrul efectuat de un câmp electric la deplasarea unei sarcini punctiforme Q dintr-un punct al câmpului cu un potenţial  1 , într-un altul cu un potențial  2 ,

A=Q( 1 - 2 ), sau

,

Unde E l - proiecția vectorului de tensiune E la direcția de mișcare; dl - circulaţie.

În cazul unui câmp omogen, ultima formulă ia forma

A= QElcos ,

Unde l- deplasarea; - unghiul dintre directiile vectorului Eși deplasare l.

Exemple de rezolvare a problemelor

Exemplul 1 sarcini pozitive Q 1 \u003d 3 μC și Q 2 \u003d 20 nC sunt în vid la distanță r 1 =l.5 m distanta. Definiți un loc de muncă A, ceea ce trebuie făcut pentru a apropia încărcăturile de la distanță r 2 = 1 m.

Soluţie. Să presupunem că prima încărcare Q 1 rămâne staționar și celălalt Q 2 sub acţiunea forţelor externe se deplasează în câmpul creat de sarcină Q 1 apropiindu-se de el de la distanţă r 1 =t,5 m până la r 2 = 1 m .

Muncă DAR" forță externă pentru deplasarea încărcăturii Q dintr-un punct al câmpului cu potenţial  1 în altul, al cărui potenţial 2 , egal în valoare absolută și opus în semn să lucreze DAR forțe de câmp pentru mișcarea sarcinii între aceleași puncte:

A"= -A.

Muncă DAR forțe de câmp la deplasarea sarcinii A=Q( 1 - 2 ). Atunci lucrează DAR" forțele externe pot fi scrise ca

A" = –Q( 1 - 2 )=Q( 2 - 1 ). (1)

Potențialele punctelor de început și de sfârșit ale traseului sunt exprimate prin formule

;

.

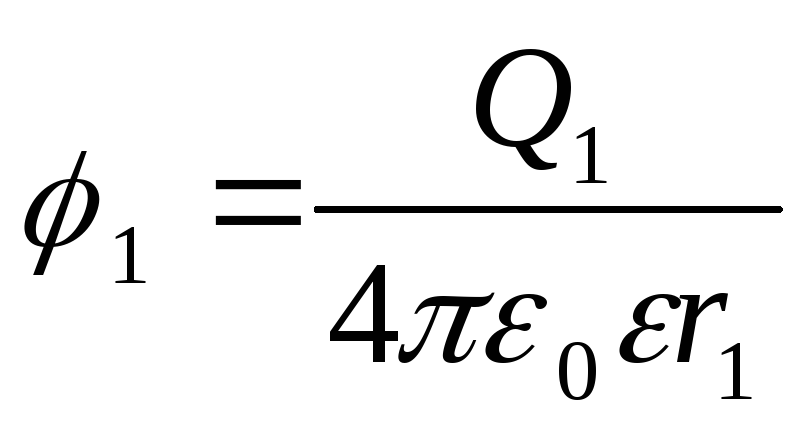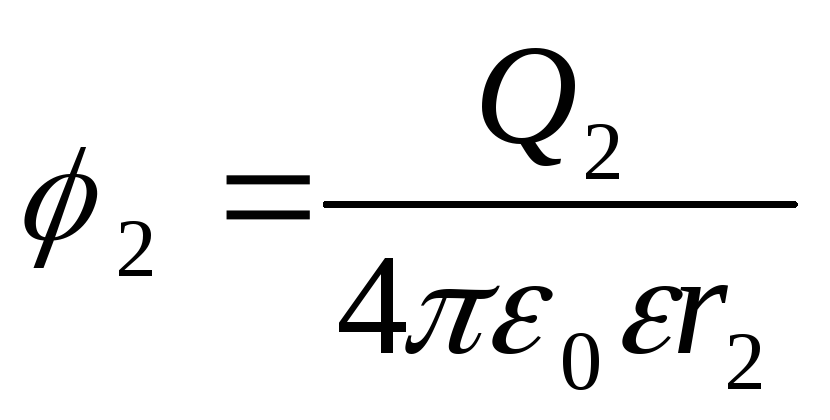Înlocuind expresiile  1 și 2 în formula (1) și ținând cont că pentru acest caz taxa transferată Q=Q 2 , primim

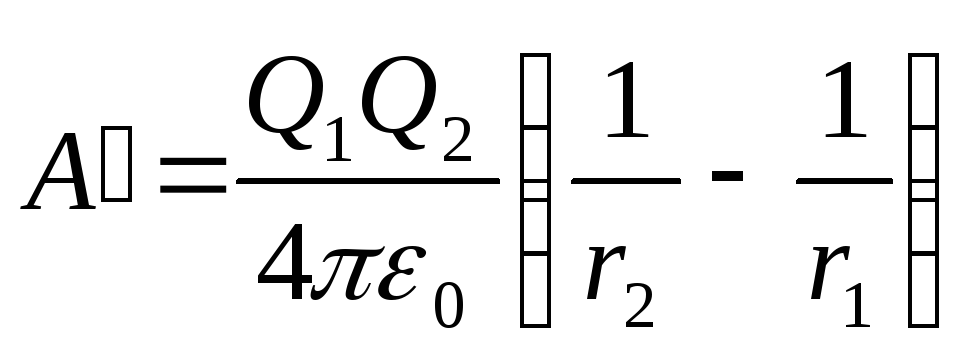. (2)

Având în vedere că 1/(4 0 )=910 9 m/F, apoi după înlocuirea valorilor cantităților în formula (2) și calculul, găsim

A„=180 pJ.

Exemplul 2 Gaseste o slujba DAR câmpuri de transfer de taxe Q=10 nC de la punct 1 exact 2 (Fig. 15.1), situat între două încărcate opus, cu o densitate de suprafață  \u003d 0,4 μC / m 2 planuri paralele infinite, distanță l intre ele este de 3 cm.

R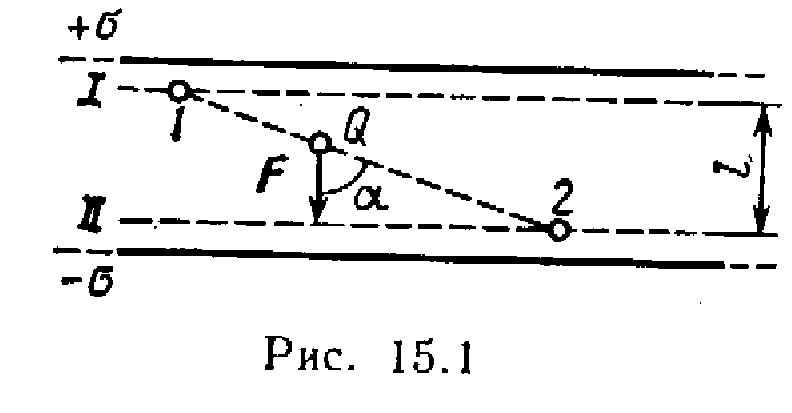

soluţie. Există două moduri de a rezolva problema.

1-a cale. Lucrarea câmpului forțează să miște sarcina Q din punct 1 domenii cu potenţial 1 exact 2 domenii cu potenţial 2 găsi prin formulă

A=Q( 1 - 2 ). (1)

Pentru a determina potențialele în puncte 1 și 2 Să desenăm suprafețele echipotențiale I și II prin aceste puncte. Aceste suprafețe vor fi plane, deoarece câmpul dintre două plane paralele infinit încărcate uniform este uniform. Pentru un astfel de domeniu, relația

 1 - 2 =El, (2)

Unde E - intensitatea câmpului; l - distanța dintre suprafețele echipotențiale.

Intensitatea câmpului între planuri paralele infinite încărcate opus E=/ 0 . Înlocuind această expresie Eîn formula (2) și apoi expresia 1 - 2 în formula (1), obținem

A= Q( /  0 ) l.

a 2-a cale. Deoarece câmpul este uniform, forța care acționează asupra sarcinii Q, este constantă pe măsură ce se mișcă. Prin urmare, munca de mutare a încărcăturii din punct 1 exact 2 poate fi calculat folosind formula

A=F  r cos, (3)

Unde F - forță care acționează asupra unei sarcini r- modul de transfer de incarcare Q dintr-un punct 1 exact 2;  este unghiul dintre direcțiile deplasării și forței . Dar F= QE= Q( /  0 ). Înlocuind această expresie Fîn egalitate (3), precum și observând că  r cos= l, primim

A=Q(/ 0 )l. (4)

Astfel, ambele soluții duc la același rezultat.

Înlocuind în expresia (4) valoarea mărimilor Q, , 0 și l, găsi

A\u003d 13,6 μJ.

Exemplul 3 Pe un fir subțire îndoit de-a lungul unui arc de cerc cu o rază R, sarcină uniform distribuită cu densitate liniară=10 nC/m. Definiți tensiunea Eși potențialul  al câmpului electric creat de un astfel de p

sarcină distribuită într-un punct O, care coincide cu centrul de curbură al arcului. Lungime l firul este 1/3 din circumferinta si este egal cu 15 cm.

Soluţie. Alegem axele de coordonate astfel încât originea coordonatelor să coincidă cu centrul de curbură al arcului, iar axa la era situat simetric fata de capetele arcului (Fig. 15.2). Selectați un element de lungime d pe fir l. Încărcat Q=d l, situat în zona selectată, poate fi considerat ca punct.

Să determinăm puterea câmpului electric în punct O. Pentru a face acest lucru, găsim mai întâi tensiunea d E câmp creat de taxa d Q:

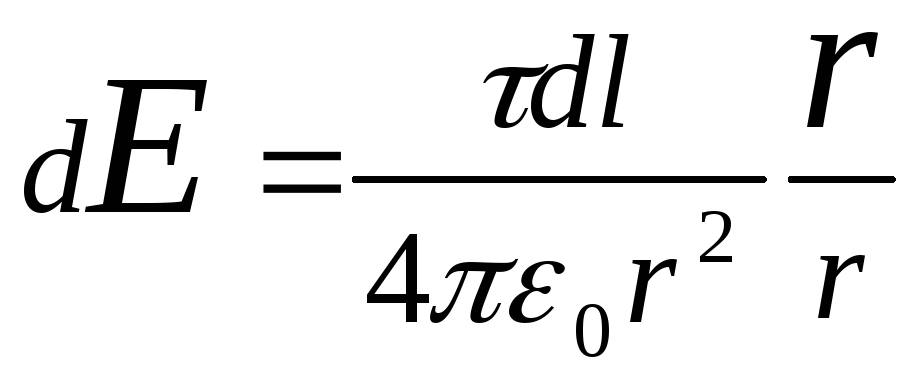Unde r-raza-vector îndreptat departe de elementul d l până la punctul în care se calculează tensiunea. Exprimăm vectorul d E prin proiecție dE X cși dE y pe axa de coordonate:

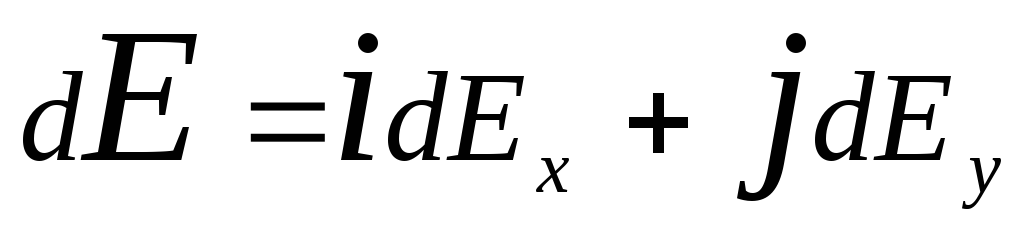Unde iși j- vectori de direcție unitară (orte).

tensiune E găsiți prin integrare:

Integrarea se realizează de-a lungul arcului de lungime l. Prin simetrie, integrala este egal cu zero. Apoi

, (1)

Unde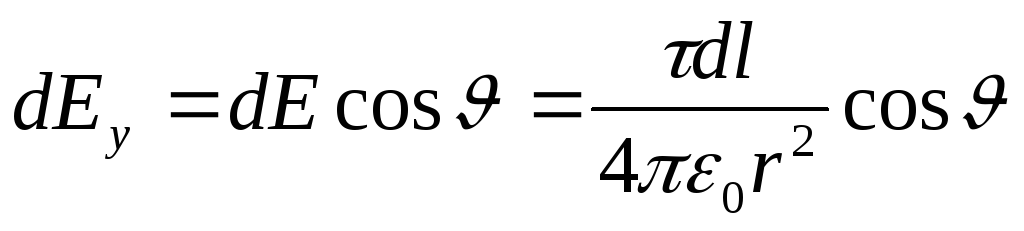

. pentru că r=R= const și d l=R d. apoi

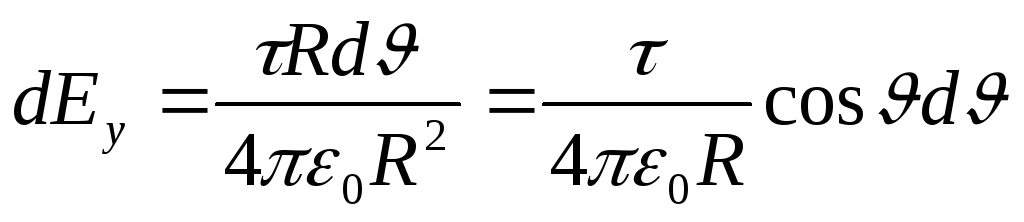
Înlocuiți expresia găsită dE yîn (1) și, ținând cont de locația simetrică a arcului în raport cu axa OU, luăm limitele de integrare de la 0 la /3, și dublăm rezultatul;

Înlocuind aceste limite și exprimând R prin lungimea arcului (3 l= 2 r), primim

Această formulă arată că vectorul E coincide cu direcția pozitivă a axei OUÎnlocuind valoarea și lîn ultima formulă și făcând calculele, găsim

E\u003d 2,18 kV / m.

Să determinăm potențialul câmpului electric în punct O. Să găsim mai întâi potențialul d creat de sarcina punctiformă d Q la punct O:

Să înlocuim r pe Rși efectuează integrarea:

.Pentru că l=2  R/3, apoi

=/(6 0 ).

Făcând calcule conform acestei formule, obținem

Exemplu4 . Câmpul electric este creat de un cilindru lung cu o rază R= 1 cm , încărcat uniform cu densitatea liniară=20 nC/m. Determinați diferența de potențial a două puncte din acest câmp situate la distanțe A 1 =0,5 cm și A 2 \u003d 2 cm de suprafața cilindrului, în partea sa din mijloc.

Soluţie. Pentru a determina diferența de potențial, folosim relația dintre intensitatea câmpului și modificarea potențialului E= -grad. Pentru un câmp cu simetrie axială, care este câmpul unui cilindru, această relație poate fi scrisă ca

E= -( d/d r) , sau d= - E d r.

Integrând ultima expresie, găsim diferența de potențial a două puncte separate prin r 1 și r 2 din axa cilindrului;

. (1)

Deoarece cilindrul este lung și punctele sunt luate în apropierea părții sale din mijloc, puterea câmpului poate fi exprimată folosind formula

. Înlocuind această expresie Eîn egalitate (1), obținem

(2)

Din moment ce cantitatile r 2 și r 1 introduceți formula ca raport, apoi pot fi exprimate în oricare, dar numai în aceleași unități:

r 1 =R+a 1 = 1,5 cm; r 2 =R+A 2 = 3 cm .

Înlocuind valorile mărimii , 0 ,r 1 și r 2 în formula (2) și calculând, găsim

 1 - 2 =250 V.

Exemplul 5 Câmpul electric este creat de o tijă subțire care poartă o sarcină =0,1 μC/m distribuită uniform pe lungimea sa. Determinați potențialul  al câmpului într-un punct îndepărtat de capetele tijei la distanță, egal cu lungimea tijă.

Soluţie. Sarcina de pe tijă nu poate fi considerată o sarcină punctuală, prin urmare, aplicați direct formula pentru a calcula potențialul

, (1)

valabil doar pentru taxe punctuale, este imposibil. Dar dacă împărțim tija în segmente elementare d l, apoi taxad l situate pe fiecare dintre ele pot fi considerate ca punct și atunci formula (1) va fi valabilă. Aplicând această formulă, obținem

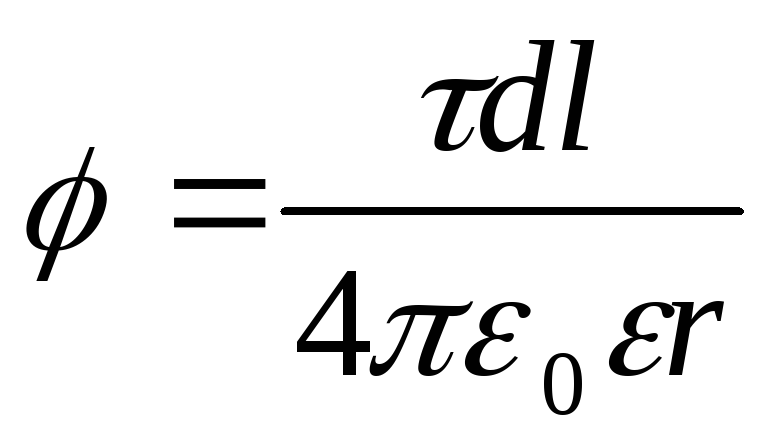, (2)

Unde r - distanța dintre punctul în care se determină potențialul până la elementul tijei.

Din fig. 15.3 că d l=(r d/cos). Înlocuind această expresie d lîn formula (2), găsim

.

Integrarea expresiei rezultate în limitele lui  1 da 2 , obținem potențialul creat de întreaga sarcină distribuită pe tijă: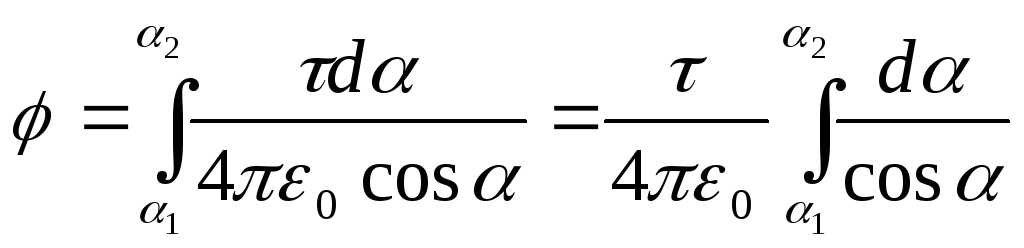

.

LA 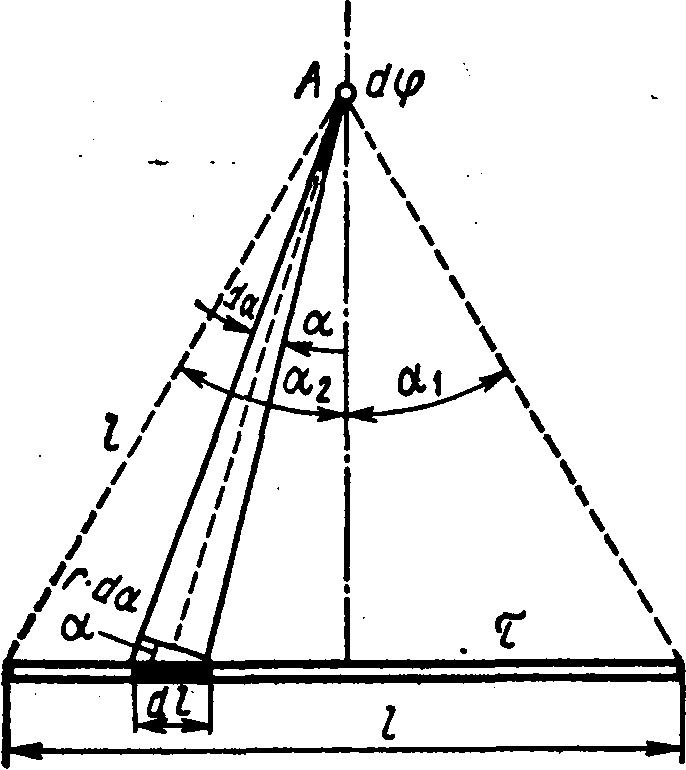forța de simetrie a punctului DAR relativ la capetele tijei avem  2 = 1 prin urmare

.

Prin urmare,

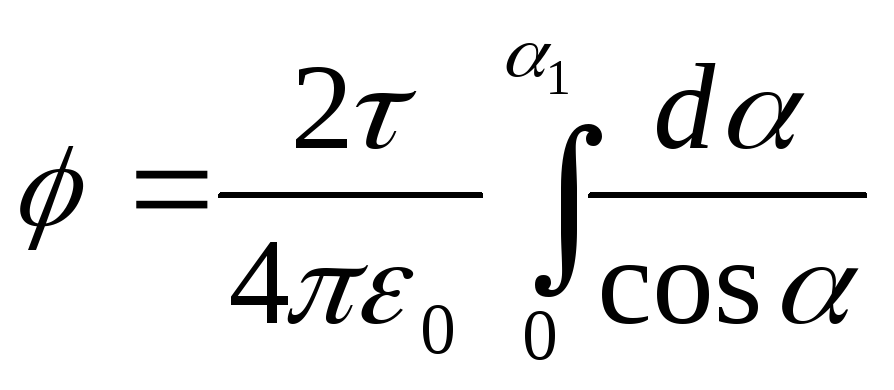.Pentru că

(vezi tabelul 2), atunci

.

Înlocuind limitele integrării, obținem

După ce am făcut calcule conform acestei formule, găsim

Exemplul 6 Un electron cu viteza v=1,8310 6 m/s a zburat într-un câmp electric uniform în direcția opusă vectorului intensității câmpului. Ce diferență de potențial U trebuie să treacă un electron pentru a avea energie E i\u003d 13,6 eV *? (Având o astfel de energie, un electron îl poate ioniza atunci când se ciocnește cu un atom de hidrogen. Energia de 13,6 eV se numește energia de ionizare a hidrogenului.)

Soluţie. Electronul trebuie să treacă de o astfel de diferență de potențial tu, astfel încât energia dobândită W combinat cu energia cinetică T, pe care electronul o avea înainte de a intra în câmp, se ridica la o energie egală cu energia de ionizare E i , adică W+ T= E i . Exprimând în această formulă W= UEși T=(m v 2 /2), obținem UE+(m v 2 /2)=E i. De aici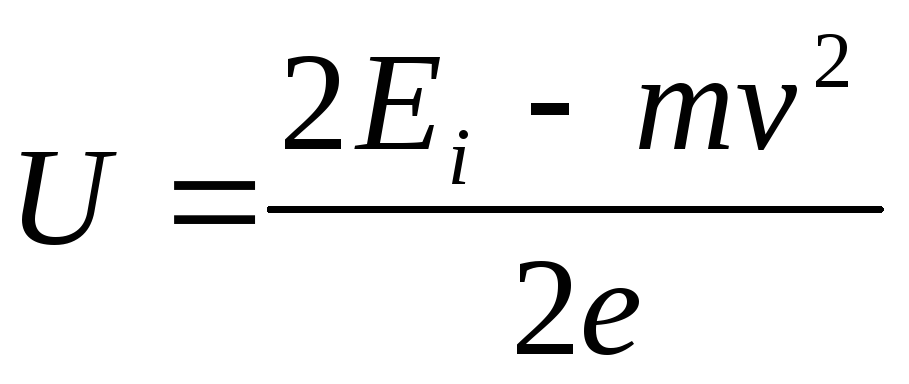

.

___________________

* Electron-volt (eV) - energia pe care o dobândește o particulă, având o sarcină egală cu sarcina unui electron, trecând printr-o diferență de potențial de 1 V. Această unitate de energie non-sistemică este în prezent aprobată pentru utilizare în fizică.

Să facem calcule în unități SI:

U=4,15 LA.

Exemplul 7 Determinați viteza inițială υ 0 apropierea protonilor situati la un suficient distanta lunga unul de altul dacă distanța minimă r min , prin care se pot apropia, este de 10 -11 cm.

Soluție: Între cei doi protoni există forțe de respingere, în urma cărora mișcarea protonilor va fi lentă. Prin urmare, problema poate fi rezolvată ca sistem inerțial coordonate (asociate cu centrul de masă a doi protoni) și în non-inerțial (asociate cu unul dintre protonii care se mișcă rapid). În al doilea caz, legile lui Newton nu sunt valabile. Aplicarea principiului d'Alembert este dificilă datorită faptului că acceleraţia sistemului va fi variabilă. Prin urmare, este convenabil să luăm în considerare problema într-un cadru de referință inerțial.

Să plasăm originea coordonatelor în centrul de masă a doi protoni. Deoarece avem de-a face cu particule identice, centrul de masă va fi în punctul care traversează segmentul care leagă particulele. Față de centrul de masă, particulele vor avea în orice moment aceleași viteze modulo. Când particulele se află la o distanță suficient de mare unele de altele, viteza υ 1 fiecare particulă este egală cu jumătate υ 0 , adică υ 1 =υ 0 /2.

Pentru a rezolva problema, aplicăm legea conservării energiei, conform căreia energia mecanică totală E sistem izolat este constant, adică

E=T+ P ,

Unde T- suma energiilor cinetice ale ambilor protoni fata de centrul de masa; P este energia potențială a sistemului de sarcini.

Exprimăm energia potențială în momentele inițiale P 1 și P 2 finale ale mișcării.

La momentul inițial, după starea problemei, protonii se aflau la mare distanță, deci energia potențială poate fi neglijată (P 1 =0). Prin urmare, pentru momentul inițial energie totală va fi egală cu energia cinetică T 1 protoni, adică

E=T l . (1)

În momentul final, când protonii se apropie cât mai aproape posibil, viteza și energia cinetică sunt egale cu zero, iar energia totală va fi egală cu energia potențială P 2, adică.

E= P 2 . (2)

Echivalând părțile corecte ale egalităților (1) și (2), obținem

T 1 \u003d P 2. (3)

Energia cinetică este egală cu suma energiilor cinetice ale protonilor:

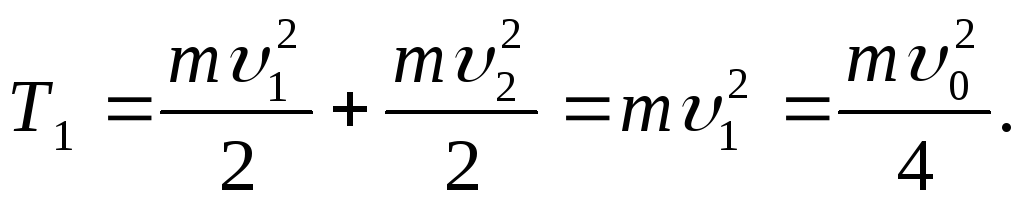(4)

Energia potențială a unui sistem de două sarcini Q 1 și Q 2 în vid este determinat de formula

, Unde r- distanta dintre incarcari. Folosind această formulă, obținem

(5)

Luând în considerare egalitățile (4) și (5), formula (3) ia forma

Unde

După efectuarea calculelor după formula obținută, găsim υ 0 =2,35 mm/s

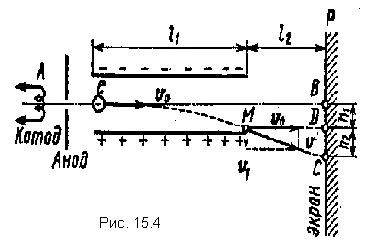Exemplul 8 Un electron fără viteză inițială a depășit diferența de potențial U 0 =10 kV și a zburat în spațiul dintre plăcile unui condensator plat încărcat la o diferență de potențial U l \u003d 100 V, de-a lungul liniei AB, paralel cu plăcile (Fig. 15.4). Distanţă dîntre plăci este de 2 cm.Lungime l 1 plăci de condensator în direcția zborului electronilor este egală cu 20 cm. Determinați distanța soare pe ecran R, departe de condensator l 2 \u003d 1 m.

Soluție.Mișcarea unui electron în interiorul condensatorului constă din două mișcări: 1) prin inerție de-a lungul liniei AB cu viteză constantă υ 0 , dobandit sub actiunea unei diferente de potential U 0 , pe care electronul a trecut la condensator; 2) mișcare accelerată uniform în direcția verticală către o placă încărcată pozitiv sub acțiunea unei forțe constante de câmp a condensatorului. După părăsirea condensatorului, electronul se va mișca uniform cu o viteză υ, pe care o avea la punct M la părăsirea condensatorului.

Din fig. 15.4 arată că distanța dorită | | BC|=h 1 +h 2 , de unde h 1 - distanța pe care electronul se va deplasa în direcția verticală în timp ce se deplasează în condensator; h 2 - distanța dintre punctul D de pe ecran, în care electronul ar cădea, deplasându-se din condensator în direcția vitezei inițiale υ 0 și punctul C, unde electronul lovește efectiv.

Exprimați separat h 1 și h 2 . Folosind formula pentru lungimea traseului mișcării uniform accelerate, găsim

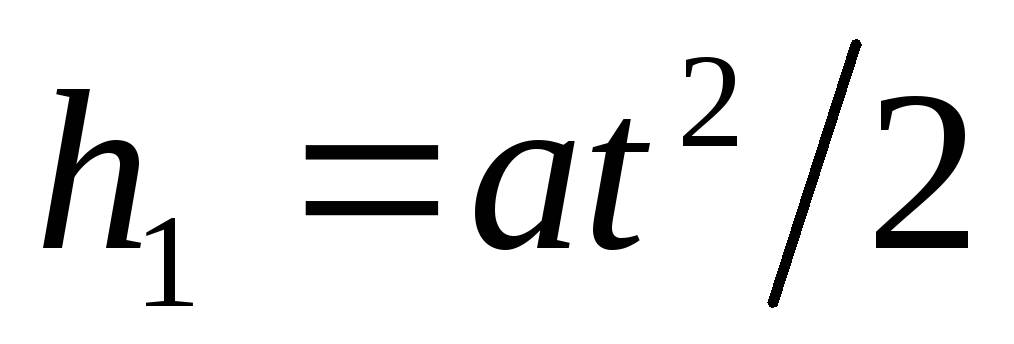. (1)

Unde A- acceleratia primita de electron sub actiunea campului condensatorului; t- timpul de zbor al unui electron în interiorul unui condensator.

Conform celei de-a doua legi a lui Newton a=F/m, Unde F- forta cu care actioneaza campul asupra electronului; t- masa lui. La randul lui, F=eE=eU 1 /d, Unde e- sarcina electronilor; U 1 - diferența de potențial dintre plăcile condensatorului; d- distanta dintre ele. Găsim timpul de zbor al unui electron în interiorul condensatorului din formula pentru calea mișcării uniforme

, Unde

Unde l 1 este lungimea condensatorului în direcția de zbor a electronilor. Găsim expresia vitezei din condiția de egalitate a muncii efectuate de câmp la mișcarea electronului și a energiei cinetice dobândite de acesta:

. De aici

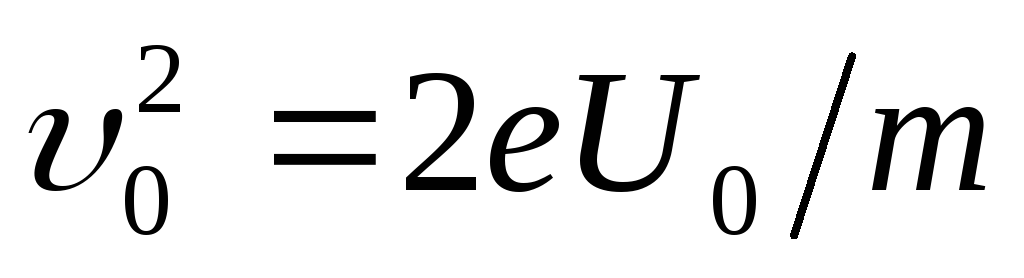(2)

Înlocuind în formula (1) succesiv valorile A,F, tși υ 0 2 din expresiile corespunzătoare, obținem

Lungimea tăiată h 2 găsiți din asemănarea triunghiurilor MDCși vector:

(3)

Unde υ 1 - viteza electronului în direcția verticală într-un punct M;l 2 - distanța de la condensator la ecran.

Viteză υ 1 găsim prin formula υ 1 =la, care, ținând cont de expresiile pentru a, Fși t va lua forma

Înlocuind expresia υ 1 în formula (3), obținem

, sau prin înlocuire υ 0 2 prin formula (3), găsim

În sfârșit pentru distanța necesară | î.Hr| vom avea

|î.Hr|=

Înlocuirea valorilor cantităților U 1 ,U 0 ,d,l 1 și l 2 în ultima expresie și efectuând calcule, obținem | î.Hr|=5,5 cm.

Sarcini

Energia potențială și potențialul de câmp al sarcinilor punctuale

15.1. taxă punctuală Q\u003d 10 nC, fiind într-un anumit punct al câmpului, are o energie potențială P \u003d 10 μJ. Găsiți potențialul φ al acestui punct de câmp.

5.2. Când mutați încărcarea Q=20 nC între două puncte ale câmpului, munca a fost făcută de forțe externe A=4µJ. Definiți un loc de muncă A 1 forțele câmpului și diferența Δφ a potențialelor acestor puncte ale câmpului.

15.3. Câmpul electric este creat de o sarcină pozitivă punctiformă Q 1 \u003d 6 nC. sarcină pozitivă Q 2 este transferat din punct DAR acest câmp până la un punct LA(Fig. 15.5). Care este modificarea energiei potențiale ΔP pe unitatea de sarcină transferată, dacă r 1 =20 cm și r 2 \u003d 50 cm?

15.4. Câmp electric creat de o sarcină punctiformă Q l \u003d 50 nC. Fără a folosi conceptul de potențial, calculați munca DARîn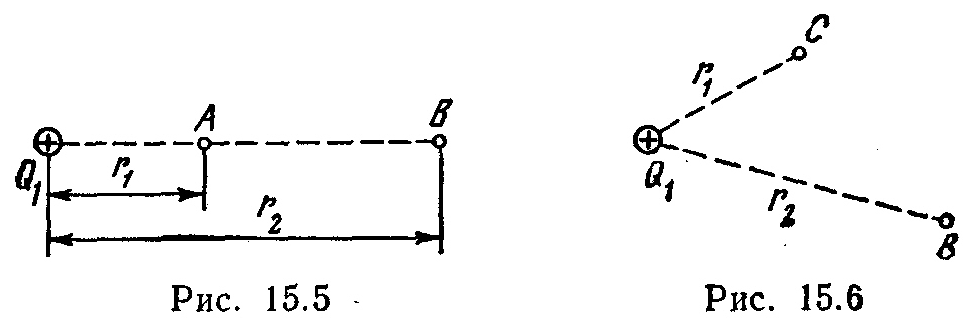

forțe externe pentru a deplasa o sarcină punctiformă Q 2 = -2 nC din punct DIN exact LA

(Fig. 15.6), dacă r 1 =10 cm, r 2 \u003d 20 cm.Determină, de asemenea, modificarea ΔP a energiei potențiale a sistemului de sarcini.

15.5. Câmpul este creat de o încărcare punctiformă Q=1 nC. Determinați potențialul φ al câmpului într-un punct îndepărtat de sarcină la distanță r\u003d 20 cm.

15.6. Determinați potențialul φ al câmpului electric într-un punct îndepărtat de sarcini Q 1 = -0,2 uC și Q 2 =0,5 μC, respectiv, on r 1 =15 mass media r 2 \u003d 25 cm.Determină, de asemenea, distanțele minime și maxime dintre sarcini pentru care este posibilă o soluție.

15.7. Taxe Q 1 \u003d 1 μC și Q 2 = -1 μC sunt la distanță d\u003d 10 cm. Determinați tensiunea Eși potențialul φ al câmpului într-un punct îndepărtat la distanță r= 10 cm de prima sarcină și întins pe o linie care trece prin prima sarcină perpendicular pe direcția de la Q 1 la Q 2 .

15.8. Calculați energia potențială P a unui sistem de două sarcini punctiforme Q 1 =100 nC și Q 2 =10 nC la distanta d= 10 cm distanță.

15.9. Aflați energia potențială P a unui sistem de trei sarcini punctiforme Q 1 \u003d 10 nC, Q 2 =20 nCl și Q 3 \u003d -30 nC, situat la vârfurile unui triunghi echilateral cu lungimea laturii A\u003d 10 cm.

15.10. Care este energia potențială P a unui sistem de patru sarcini punctiforme identice Q\u003d 10 nC, situat la vârfurile unui pătrat cu lungimea laturii A\u003d 10 cm? .

15.11. Determinați energia potențială P a unui sistem de patru sarcini punctiforme situate la vârfurile unui pătrat cu lungimea laturii A\u003d 10 cm. Taxele sunt aceleași în modul Q=10 nC, dar două dintre ele sunt negative. Luați în considerare două cazuri posibile de aranjare a taxelor.

15.12 . Câmpul este creat de două taxe punctiforme + 2Qși -Q, de la distanță d= 12 cm distanță. Determinați locul punctelor din planul pentru care potențialul este zero (scrieți ecuația pentru dreapta potențialului zero).

5.13. Sistemul este format din trei încărcări - două de aceeași dimensiune Q 1 = |Q 2 |=1 μC și opus în semn și sarcină Q=20 nC, situat în punctul 1 din mijloc între celelalte două sarcini ale sistemului (Fig. 15.7). Determinați modificarea energiei potențiale ΔP a sistemului în timpul transferului de sarcină Q de la punctul 1 la punctul 2. Aceste puncte sunt îndepărtate din sarcina negativă Q 1 pe distanta a= 0,2 m.

Potenţialul câmpului sarcinilor distribuite liniar

15.14. De-a lungul unui inel subțire cu o rază R= 10 cm sarcină uniform distribuită cu o densitate liniară τ= 10 nC/m. Determinați potențialul φ într-un punct situat pe axa inelului, la distanță a= 5 cm de centru.

15.15. Pe un segment de conductor drept subțire, o sarcină este distribuită uniform cu o densitate liniară τ=10 nC/m. Calculați potențialul φ creat de această sarcină într-un punct situat pe axa conductorului și îndepărtat de cel mai apropiat capăt al segmentului cu o distanță egală cu lungimea acestui segment.

Curs 6. Potențialul câmpului electric. Testul nr. 2

Potentialul este unul dintre cele mai complexe concepte de electrostatica. Elevii învață definiția potențialului unui câmp electrostatic, rezolvă numeroase probleme, dar nu au simțul potențialului, au dificultăți în a raporta teoria la realitate. Prin urmare, rolul experimentului educațional în formarea conceptului de potențial este foarte mare. Avem nevoie de astfel de experimente care, pe de o parte, să ilustreze idei teoretice abstracte despre potențial și, pe de altă parte, să arate validitatea deplină a experimentului pentru introducerea conceptului de potențial. Este mai degrabă dăunător decât util să ne străduim pentru o acuratețe specială a rezultatelor cantitative în aceste experimente.

6.1. Potenţialitatea câmpului electrostatic

Să fixăm corpul conductor pe un suport izolator și să-l încărcăm. Atârnăm o minge conducătoare de lumină pe un fir lung izolat și îi dăm o încărcare de test, care este același nume cu încărcarea corpului. Mingea va sari de pe corp si va iesi din pozitie 1 se va muta pe poziție 2. Deoarece înălțimea mingii în câmpul gravitațional a crescut cu h, energia potențială a interacțiunii sale cu Pământul a crescut cu mgh. Aceasta înseamnă că câmpul electric al corpului încărcat a lucrat la sarcina de testare.

Să repetăm experimentul, dar la momentul inițial, să nu lăsăm doar mingea de test, ci să o împingem într-o direcție arbitrară, dându-i o energie cinetică. În același timp, constatăm că trecerea de la poziție 1 de-a lungul unei traiectorii complexe, mingea se va opri în cele din urmă în poziție 2 . Informat la minge în momentul inițial energie kinetică, evident, a fost cheltuit pentru depășirea forțelor de frecare în timpul mișcării mingii, iar câmpul electric a făcut același lucru asupra mingii ca în primul caz. Într-adevăr, dacă scoatem corpul încărcat, atunci aceeași împingere a mingii de testare duce la faptul că din poziție 2 se întoarce pe poziție 1 .

Astfel, experimentul sugerează că munca câmpului electric asupra sarcinii nu depinde de traiectoria sarcinii, ci este determinată doar de pozițiile punctelor sale inițiale și finale. Cu alte cuvinte, pe o traiectorie închisă, munca câmpului electrostatic este întotdeauna zero. Câmpurile cu această proprietate sunt numite potenţial.

6.2. Potenţialitatea câmpului central

Experiența arată că într-un câmp electrostatic creat de o bilă conducătoare încărcată, forța care acționează asupra sarcinii de testare este întotdeauna direcționată din centrul bilei încărcate, scade monoton odată cu creșterea distanței și are aceleași valori la distanțe egale. din ea. Un astfel de câmp se numește central. Folosind figură, este ușor de verificat dacă câmpul central este potențial.

6.3. Energia potențială de încărcare într-un câmp electrostatic

Câmpul gravitațional, ca și cel electrostatic, este potențial. În plus, notația matematică a legii gravitației universale coincide cu notația legii lui Coulomb. Prin urmare, atunci când studiem un câmp electrostatic, este logic să ne bazăm pe analogia dintre câmpurile gravitaționale și electrostatice.

Într-o zonă mică din apropierea suprafeței Pământului, câmpul gravitațional poate fi considerat uniform (Fig. A).

Un corp de masă m în acest câmp este supus unei forțe care este constantă ca mărime și direcție f= t g. Dacă un corp lăsat pentru el însuși cade din poziție 1 în poziție 2 , atunci forța gravitațională funcționează A = fs = mgs = mg (h 1 – h 2).

Același lucru îl putem spune altfel. Când corpul era în poziție 1 , sistemul Pământ-corp avea energie potențială (adică capacitatea de a lucra) W 1 = mgh unu . Când corpul este în poziție 2 , sistemul luat în considerare a început să aibă energie potențială W 2 = mgh 2. Munca efectuată în acest caz este egală cu diferența dintre energiile potențiale ale sistemului în starea finală și inițială, luate cu semnul opus: DAR = – (W 2 – W 1).

Să ne întoarcem acum la câmpul electric, care, ne amintim, ca și cel gravitațional, este potențial. Imaginați-vă că nu există gravitație și în locul suprafeței Pământului există o placă conducătoare plată, încărcată (pentru claritate) negativ (Fig. b). Introduceți axa de coordonate Yși puneți o sarcină pozitivă peste placă q. Este clar că, deoarece sarcina în sine nu există, există un corp cu o anumită masă deasupra plăcii, purtând o sarcină electrică. Dar, întrucât considerăm că câmpul gravitațional este absent, atunci nu vom lua în considerare masa corpului încărcat.

Deci, pentru o sarcină pozitivă q din partea planului încărcat negativ, forța de atracție f = q E , Unde E este puterea câmpului electric. Deoarece câmpul electric este uniform, aceeași forță acționează asupra sarcinii în toate punctele ei. Dacă sarcina se mișcă din poziție 1 în poziție 2 , atunci forța electrostatică lucrează asupra ei DAR = fs = qEs = qE(y 1 – y 2).

Putem exprima același lucru cu alte cuvinte. Gravidă 1 O sarcină într-un câmp electrostatic are o energie potențială W 1 = qEy 1 și în poziție 2 - energie potențială W 2 = qEy 2. Când sarcina trece din poziție 1 în poziție 2 câmpul electric al planului încărcat a lucrat asupra lui DAR = –(W 2 – W 1).

Amintiți-vă că energia potențială este definită doar până la un termen: dacă valoarea zero a energiei potențiale este aleasă în altă parte a axei Y, atunci practic nimic nu se va schimba.

6.4. Potenţialul unui câmp electrostatic omogen

Dacă energia potențială a unei sarcini într-un câmp electrostatic este împărțită la valoarea acestei sarcini, atunci obținem energia caracteristică a câmpului însuși, care a fost numită potenţial:

Potențialul din sistemul SI este exprimat în volți: 1 V = 1 J / 1 C.

Dacă într-un câmp electric uniform axa Y trimite paralel cu vectorul de tensiune E , atunci potențialul unui punct arbitrar al câmpului va fi proporțional cu coordonata punctului: în plus, coeficientul de proporționalitate este puterea câmpului electric.

6.5. Diferenta potentiala

Energia potențială și potențialul sunt determinate numai până la o constantă arbitrară, în funcție de alegerea valorilor lor zero. Cu toate acestea, munca câmpului are o semnificație foarte clară, deoarece este determinată de diferența de energii potențiale în două puncte ale câmpului:

DAR = –(W 2 – W 1) = –( 2 q – 1 q) = q( 1 – 2).

Munca de mutare a unei sarcini electrice între două puncte ale câmpului este egală cu produsul sarcinii și diferența de potențial dintre punctele de început și de sfârșit. Se mai numește și diferența de potențial tensiune.

Tensiunea dintre două puncte este egală cu raportul muncii de câmp la mutarea sarcinii de la punctul de pornire la cel final la această sarcină:

Tensiunea, ca și potențialul, este exprimată în volți.

6.6. Diferență de potențial și tensiune

Într-un câmp electric uniform, puterea este direcționată în direcția potențialului descrescător și, conform formulei = Da, diferența de potențial este U = 1 – 2 = E(la 1 – y 2). Indicând diferența în coordonatele punctelor la 1 – y 2 = d, primim U = Ed.

Într-un experiment, în loc să se măsoare direct rezistența, este mai ușor să se determine diferența de potențial și apoi să se calculeze modulul de rezistență folosind formula

Unde d este distanța dintre două puncte de câmp care sunt strâns distanțate în direcția vectorului E . În același timp, nu un newton per pandantiv este folosit ca unitate de tensiune, ci un volt pe metru:

6.7. Potenţialul unui câmp electrostatic arbitrar

Experiența arată că raportul dintre muncă pentru a muta o sarcină de la infinit la un punct dat al câmpului și valoarea acestei sarcini rămâne neschimbat: = DAR/q. Această relație se numește potențialul unui punct dat al câmpului electrostatic, luând potențialul la infinit egal cu zero.

6.8. Principiul suprapunerii pentru potențiale

6.9. Potenţialul câmpului unei sarcini punctiforme

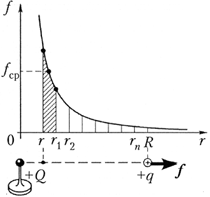
Figura prezintă un grafic al dependenței puterii interacțiunii electrostatice dintre sarcinile punctuale de distanța dintre ele. Pentru a găsi lucrul câmpului electric la mutarea sarcinii de testare q de la o distanta r pana la distanta R, împărțiți acest interval la puncte r 1 , r 2 ,..., r pîn secțiuni egale. Forța medie care acționează asupra unei sarcini qîn cadrul segmentului [ rr 1 ] este egal cu

Munca acestei forțe în acest domeniu:

Expresii similare pentru lucru vor fi obținute pentru toate celelalte secțiuni. Deci, treaba completă este:

Termenii identici cu semne opuse sunt distruși și în final obținem:

este lucrarea câmpului pe sarcină

- diferenta potentiala

Acum, pentru a găsi potențialul punctului de câmp față de infinit, ne direcționăm R la infinit și în final obținem:

Deci, potențialul câmpului unei sarcini punctiforme este invers proporțional cu distanța până la sarcină.

6.10. Suprafețe echipotențiale

Se numește o suprafață în care potențialul câmpului electric are aceeași valoare în fiecare punct echipotenţială. Nu este dificil să se demonstreze suprafețele echipotențiale ale câmpului unei mingi încărcate cu o sarcină de test suspendată pe un fir, așa cum se arată în figură.

În a doua figură, câmpul electrostatic a două sarcini opuse este reprezentat prin linii de forță (solide) și echipotențiale (întrerupte).

Cercetare 6.1. Diferenta potentiala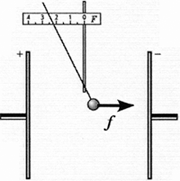

Exercițiu. Dezvoltați un experiment simplu care introduce conceptul de diferență de potențial sau tensiune.

Opțiune de execuție. Așezați două discuri metalice pe suporturi izolatoare paralele între ele la o distanță de aproximativ 10 cm. Încărcați discurile cu sarcini egale și opuse ca mărime. Încărcați bila unui dinamometru electrostatic cu o încărcare, de exemplu, q= 5 nC (vezi studiul 3.6) și introduceți-l în zona dintre discuri. În acest caz, acul dinamometrului va indica o anumită valoare a forței care acționează asupra bilei. Cunoscând parametrii dinamometrului, se calculează valoarea modulului de forță (vezi studiul 3.6). De exemplu, într-unul dintre experimentele noastre, acul dinamometrului a arătat valoarea X\u003d 2 cm, prin urmare, conform formulei, modulul de forță f = Kx= 17 10 –5 N.

Prin deplasarea dinamometrului, arătați că în toate punctele câmpului dintre discurile încărcate, aceeași forță acționează asupra sarcinii de testare. Prin deplasarea dinamometrului astfel încât sarcina de probă să parcurgă calea s\u003d 5 cm în direcția forței care acționează asupra acesteia, întrebați elevii: ce lucru efectuează câmpul electric asupra sarcinii? Realizați o înțelegere a faptului că munca câmpului pe modulo de sarcină este egală cu

DAR = fs= 8,5 10 -6 J, (6,3)

în plus, este pozitiv dacă sarcina se mișcă în direcția intensității câmpului și negativ dacă în direcția opusă. Calculați diferența de potențial dintre pozițiile inițiale și finale ale bilei dinamometrului: U = DAR/q\u003d 1,7 10 3 V.

Pe de o parte, intensitatea câmpului electric dintre plăci:

Pe de altă parte, conform formulei (6.1), pt d=s:

Astfel, experiența arată că puterea câmpului electric poate fi determinată în două moduri, care, desigur, duc la aceleași rezultate.

Studiul 6.2. Calibrarea tensiunii electrometrului

Exercițiu. Proiectați un experiment pentru a arăta că un electrometru cu indicator demonstrativ poate măsura tensiunea.

Opțiune de execuție. Configurația experimentală este prezentată schematic în figură. Folosind un dinamometru electrostatic, determinați puterea unui câmp electric uniform și utilizați formula U = Ed calculați diferența de potențial dintre plăcile conductoare. Repetând acești pași, calibrați electrometrul pentru tensiune, astfel încât să obțineți un voltmetru electrostatic.

Cercetare 6.3. Potențialul de câmp al unei sarcini sferice

Exercițiu. Determinați experimental munca care trebuie făcută împotriva câmpului electrostatic pentru a muta sarcina de testare de la infinit la un punct din câmpul creat de sfera încărcată.

Opțiune de execuție. Atașați o minge de polistiren învelită în folie de aluminiu la stâlpul izolator. Încărcați-l de la o sursă piezoelectrică sau altă sursă (vezi punctul 1.10) și încărcați o minge de testare pe tija unui dinamometru electrostatic cu aceeași sarcină. Sarcina de testare este infinit de departe de cea investigată, dacă dinamometrul electrostatic nu înregistrează forțele de interacțiune electrostatică dintre sarcini. În experiment, este convenabil să lăsați dinamometrul electrostatic staționar și să mutați sarcina studiată.

Apropiați treptat bila încărcată de pe suportul izolator de bila dinamometrul electrostatic. În primul rând al tabelului, notați valorile distanței rîntre sarcini, în a doua linie - valorile corespunzătoare ale forței de interacțiune electrostatică. Este convenabil să exprimați distanța în centimetri și forța în unități convenționale, în care scara dinamometrului este calibrată. Pe baza datelor obținute, construiți un grafic al dependenței forței de distanță. Ați construit deja un grafic similar în Studiul 3.5.

Acum găsiți dependența lucrării de mutarea sarcinii de la infinit la un punct dat din câmp. Acordați atenție faptului că în experiment forța de interacțiune a sarcinilor devine aproape egală cu zero la o distanță relativ mică a unei sarcini de alta.

Împărțiți întregul interval de modificări ale distanței dintre sarcini în secțiuni egale, de exemplu, câte 1 cm fiecare. Este mai convenabil să începeți procesarea datelor experimentale de la sfârșitul graficului. În zona de la 16 la 12 cm, valoarea medie a forței f cf este 0,13 arb. unități, deci muncă elementară DARîn această zonă este egală cu 0,52 arb. unitati În zona de la 12 la 10 cm, argumentând în mod similar, obținem o lucrare elementară de 0,56 unități convenționale. unitati În plus, este convenabil să luați secțiuni lungi de 1 cm. Pe fiecare dintre ele, găsiți valoarea medie a forței și înmulțiți-o cu lungimea secțiunii. Valori obținute de lucru pe teren Aîn toate zonele, introduceți în a patra linie a tabelului.

Pentru a afla meseria DAR realizat de câmpul electric atunci când mutați sarcina de la infinit la o distanță dată, adunați munca elementară corespunzătoare și scrieți valorile rezultate în al cincilea rând al tabelului. În ultimul rând scrieți valorile lui 1/ r, reciproca distanței dintre sarcini.

Trasează munca câmpului electric pe inversul distanței și asigură-te că obții o linie dreaptă (figura din dreapta).

Astfel, experiența arată că munca unui câmp electric atunci când o sarcină se deplasează de la infinit la un punct dat al câmpului este invers proporțională cu distanța de la acest punct la sarcina care creează câmpul.

Studiul 6.4. Sursă de tensiune înaltă

Informație. Pentru experimentul de fizică școlară, industria produce în prezent surse excelente de tensiune de înaltă tensiune. Au două terminale de ieșire sau doi electrozi de înaltă tensiune, diferența de potențial dintre care este reglabilă continuu de la 0 la 25 kV. Indicatorul sau contorul digital de tensiune încorporat în dispozitiv vă permite să determinați diferența de potențial dintre polii sursei. Astfel de dispozitive cresc nivelul de experiment educațional în electrostatică.

Exercițiu. Proiectați un experiment educațional demonstrativ care să arate că potențialul unei mingi încărcate, determinat experimental în conformitate cu formula (6.2) pentru o sarcină punctiformă, este egal cu potențialul transmis acestei mingi de o sursă de energie de înaltă tensiune.

Opțiune de execuție. Reasamblați configurația experimentală, constând dintr-un dinamometru electrostatic cu o bilă de testare și o bilă conductoare pe un suport izolator (a se vedea studiile 3.4 și 6.3). Măsurați parametrii tuturor elementelor instalației.

Pentru certitudine, subliniem că într-unul dintre experimente am folosit un dinamometru electrostatic, ai cărui parametri sunt indicați în studiul 3.4: A= 5 10 –3 m, b= 55 10 -3 m, Cu= 100 10 -3 m, t= 0,94 10 -3 kg, iar bilele erau aceleași și aveau o rază R= 7,5 10 -3 m. Pentru acest dinamometru, factorul de calibrare K, care convertește unități arbitrare de forță în newtoni, este dat de formula (Vezi studiul 3.6).

Programul de lucru pentru mutarea unei sarcini de testare de la infinit la un punct dat al câmpului este prezentat în figura de la p. 31. Pentru a trece de la unitățile convenționale de lucru la jouli din acest grafic, este necesar, în conformitate cu formula A = f mier r traduceți valorile distanței în centimetri în metri, valorile forței în arb. unitati (cm) converti în arb. unitati (m) și înmulțiți cu K. În acest fel: A(J) = 10-4 KA(unități arb.).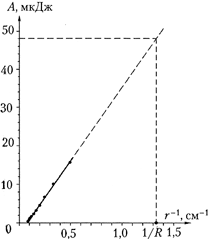

Graficul corespunzătoare de lucru în funcție de distanța reciprocă este prezentat mai jos. Extrapolând-o la R\u003d 7,5 mm, constatăm că munca pentru a muta sarcina de testare de la infinit la suprafața bilei încărcate DAR\u003d 57 10 -4 K \u003d 4,8 10 -5 J. Deoarece încărcăturile bilelor erau aceleași și se ridicau la q\u003d 6,6 10 -9 C (a se vedea studiul 3.6), apoi potențialul dorit \u003d DAR/q= 7300 V.

Porniți sursa de înaltă tensiune și setați tensiunea de ieșire pe ea cu regulatorul, de exemplu, U= 15 kV. Atingeți bilele conductoare una câte una cu unul dintre electrozi și opriți sursa. În acest caz, fiecare dintre bile dobândește un potențial de = 7,5 kV față de Pământ. Repetați experimentul pentru determinarea sarcinilor bilelor prin metoda Coulomb (cercetarea 3.6) și veți obține o valoare apropiată de 7 nC.

Astfel, în experiment, încărcăturile bilelor sunt determinate în două moduri independente. Prima metodă se bazează pe utilizarea directă a determinării potențialului, a doua se bazează pe comunicarea unui anumit potențial la bile folosind o sursă de înaltă tensiune și măsurarea ulterioară a sarcinii lor folosind legea Coulomb. În același timp, s-au obținut rezultate identice.

Desigur, niciunul dintre școlari nu se îndoiește de faptul că instrumentele moderne măsoară corect valorile mărimilor fizice. Dar acum sunt convinși că tocmai acele cantități pe care le studiază în cele mai simple fenomene sunt măsurate corect. S-a stabilit o conexiune puternică între fundamentele fizicii și tehnologia modernă, iar decalajul dintre cunoștințele școlare și viața reală a fost eliminat.

Întrebări și sarcini pentru autocontrol

1. Cum se demonstrează experimental că câmpul electrostatic este potențial?

2. Care este esența analogiei dintre câmpurile gravitaționale și electrostatice?

3. Care este relația dintre intensitatea și diferența de potențial a câmpului electrostatic?

4. Propuneți un experiment care să justifice în mod direct validitatea principiului de suprapunere pentru potențiale.

5. Calculați potențialul de câmp al unei sarcini punctiforme folosind calcul integral. Comparați derivația dvs. a formulei cu derivarea elementară dată în prelegere.

6. Aflați de ce, într-un experiment pentru determinarea diferenței de potențial dintre două discuri conductoare (cercetarea 6.1), este imposibil să mutați tensiometrul astfel încât bila sa de test să treacă toată distanța de la un disc la altul.

7. După calibrarea electrometrului pentru tensiune (cercetarea 6.2), comparați rezultatul cu valorile sensibilității dispozitivului pentru tensiune, care sunt date în datele pașaportului electrometrului.

9. Elaborați în detaliu o metodologie pentru formarea în mintea studenților a unei convingeri rezonabile că conceptul de potențial de câmp electric introdus în studiul electrostaticei corespunde exact celui utilizat stiinta modernași tehnologie.

Literatură

Butikov E.I., Kondratiev A.S. Fizica: Proc. indemnizație: În 3 cărți. Carte. 2. Electrodinamica. Optica. – M.: Fizmatlit, 2004.

Voskanyan A.G.., Marlensky A.D., Shibaev A.F. Demonstrarea legii lui Coulomb pe baza măsurătorilor cantitative: În Sat. „Experiment didactic în electrodinamică”, voi. 7. - M .: Şcoală-Presă, 1996.

Kasyanov V.A. Fizica-10. – M.: Dropia, 2003.

Myakishev G.Ya., Sinyakov A.Z.., Slobodskov B.A.. Fizica: electrodinamica. 10–11 celule: Proc. pentru ang. studiul fizicii. – M.: Dropia, 2002.

Echipamente educaționale pentru sălile de fizică generală institutii de invatamant: Ed. G.G. Nikiforova. – M.: Dropia, 2005.

Tema 3. POTENȚIALUL ȘI LUCRĂRII CÂMPULUI ELECTROstatic. RELATIA DE FORTA CU POTENTIAL

3.4. Dipol într-un câmp electric

3.5. Relația dintre puterea și potențialul unui câmp electrostatic

3.6. Linii de câmp și suprafețe echipotențiale

3.7. Calculul diferențeipotenţiale în funcţie de intensitatea câmpului celor mai simple câmpuri electrostatice

3.1. Lucrarea forțelor câmpului electrostatic

Forța care acționează asupra unei sarcini punctiforme situate în câmpul unei alte sarcini punctiforme staționare este centrală. Direcția forței care acționează în orice punct al spațiului asupra unei sarcini trece prin centrul sarcinii care creează câmpul, iar valoarea forței depinde doar de distanța până la această sarcină.

până la punctul de observație. (De exemplu, câmpul gravitațional este câmpul forțelor centrale).

E
Orez. 3.1
Dacă un corp este plasat în astfel de condiții încât în fiecare punct al spațiului este supus influenței altor corpuri cu o forță care se schimbă în mod natural de la un punct la altul, atunci se spune că acest corp se află în câmpul de forțe. Câmpul central de forțe este potențial. Să ne asigurăm că câmpul electric este potențial. Calculați munca efectuată de forțele câmpului unei sarcini de punct fix q peste o sarcină punctiformă care se deplasează în acest câmp (Fig. 3.1). Lucrați pe calea elementară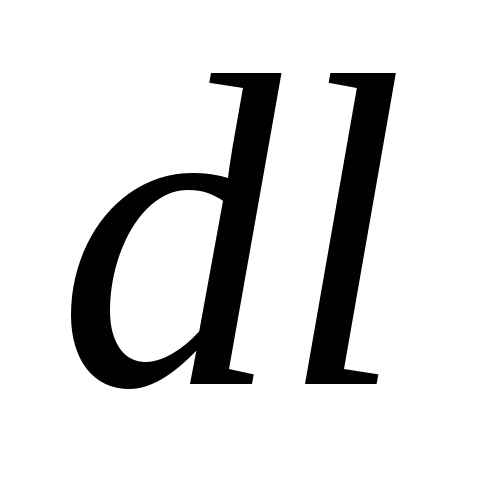

este egal cu:

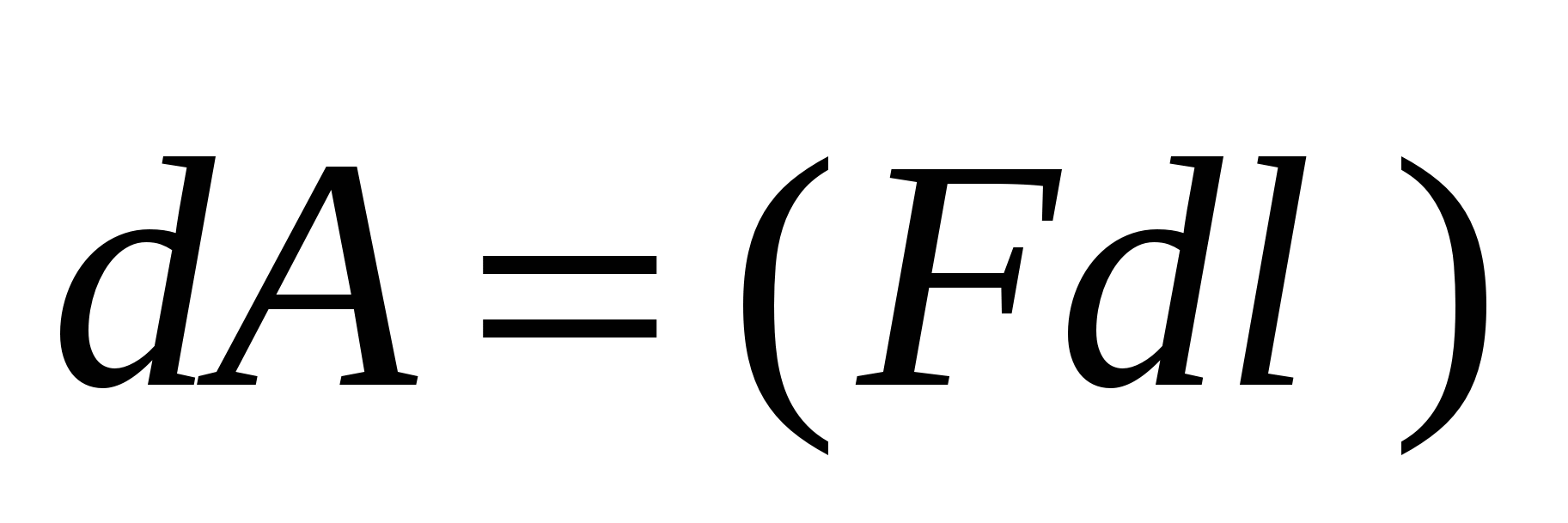sau

pentru că

. De aici pe calea 1–2

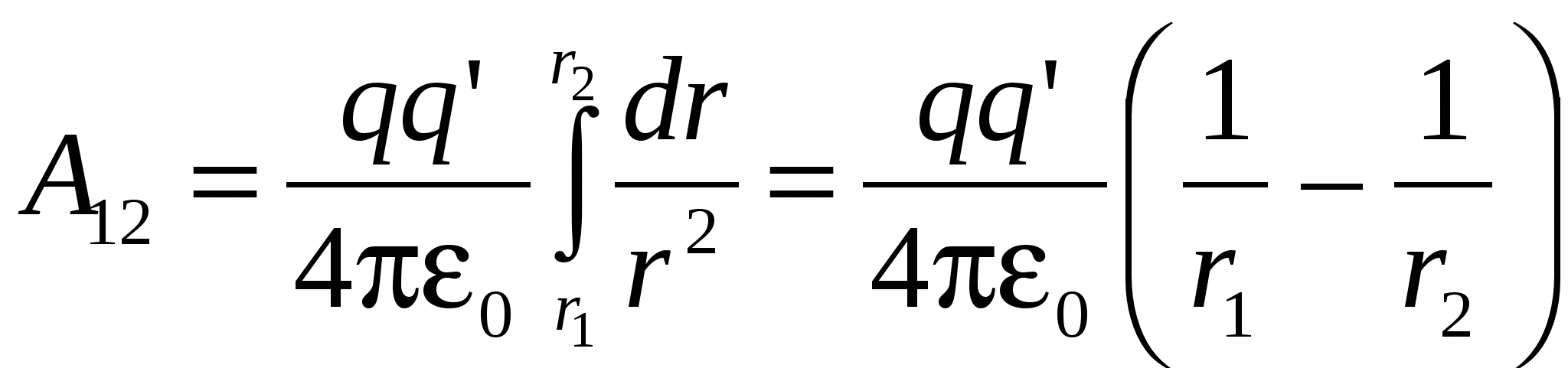(1)

Se poate observa că munca nu depinde de calea pe care s-a deplasat sarcina în câmpul electric q" , dar depinde numai de pozițiile inițiale și finale ale acestei taxe (pe r 1 și r 2). Prin urmare, forțele care acționează asupra sarcinii q" în domeniul unei sarcini staţionare q, sunt conservatoare, iar câmpul acestor forțe potenţial. Această concluzie poate fi extinsă cu ușurință în domeniul oricărui sistem de sarcini fixe, începând cu forța acţionând cu o taxă punctuală q„ într-un astfel de domeniu, poate fi reprezentat de principiul suprapunerii în formă

, Unde - forța datorată i-a încărcătură a sistemului de creare a câmpului. Lucrul în acest caz este egal cu suma algebrică a muncii efectuate de forțele individuale:

. Fiecare dintre termenii din partea dreaptă a acestei expresii este independent de cale. Prin urmare, nu depinde de cale și de muncă DAR.

Din mecanică se știe că munca forțelor potențiale pe o cale închisă este zero. Munca efectuată de forțele de câmp la încărcătură q" la parcurgerea unei bucle închise, poate fi reprezentat ca

, Unde – proiectie vectoriala la direcția deplasării elementare, deci:

(2)

Această relație trebuie să fie valabilă pentru orice buclă închisă. Trebuie reținut că (21) este valabil doar pentru un câmp electrostatic. Câmpul sarcinilor în mișcare (adică câmpul care se modifică în timp) nu este potențial. În consecință, condiția (21) nu este îndeplinită pentru aceasta.

Exprimarea formei

se numeste circulatia vectorului de-a lungul acestui contur. În acest fel, caracteristica unui câmp electrostatic este aceea că circulația vectorului de intensitate de-a lungul oricărui circuit închis este zero.

3.2. Teorema circulației vectorului câmp electrostatic

Astfel, susținem că circulația vectorului în orice câmp electrostatic este zero, adică . Această afirmație se numește teorema circulației vectoriale.

Lasă o sarcină să se miște pe o cale închisă 1a2b1 într-un câmp dat cu intensitate. Pentru a demonstra teorema, împărțim o cale închisă arbitrară în două părți 1a2 și 2b1 (vezi figura). Să găsim o slujbă pentru a muta taxa q de la punctul 1 la punctul 2. Deoarece munca într-un anumit câmp nu depinde de forma traseului, munca de deplasare a sarcinii de-a lungul căii 1a2 este egală cu munca de mutare a încărcăturii de-a lungul căii 1b2 sau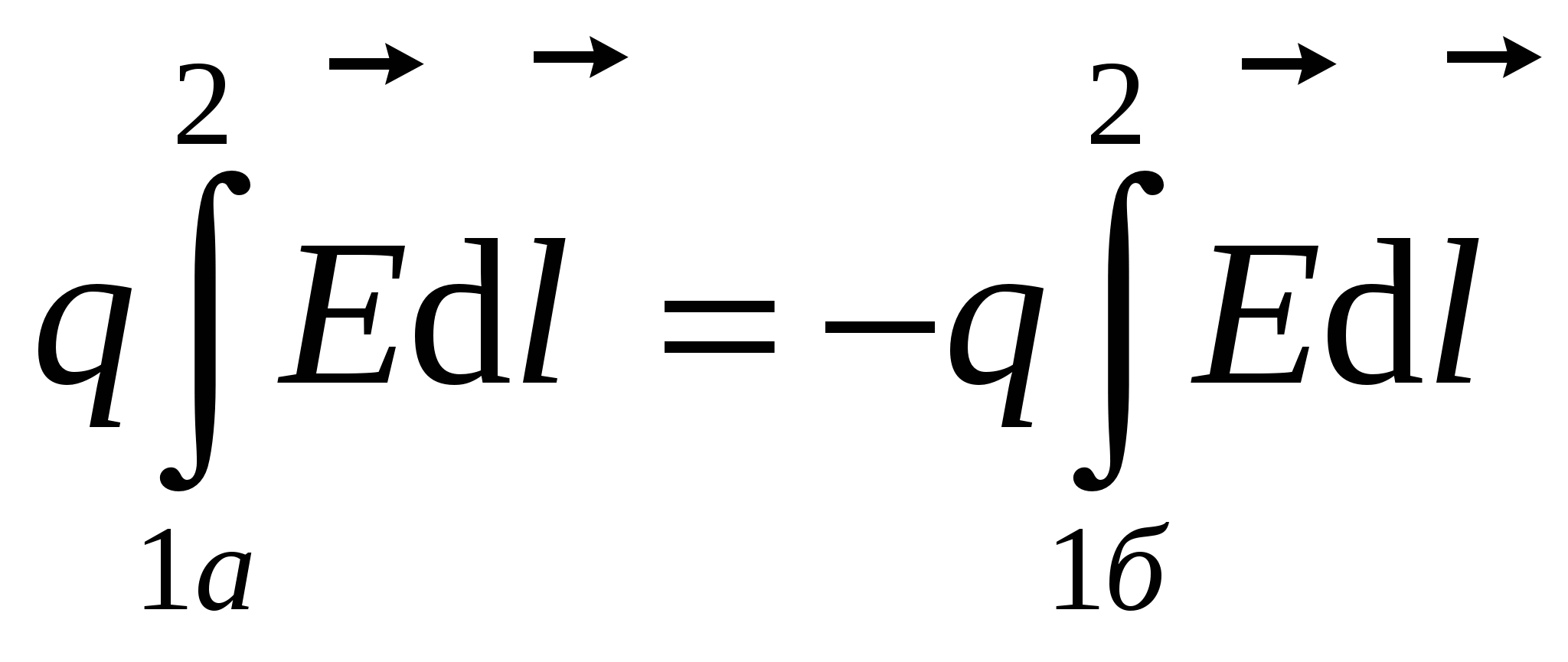

Figura 3.2

Din cele de mai sus rezultă că

(Integralele modulo sunt egale, dar semnele sunt opuse). Apoi lucrați pe o cale închisă:

(3)

sau

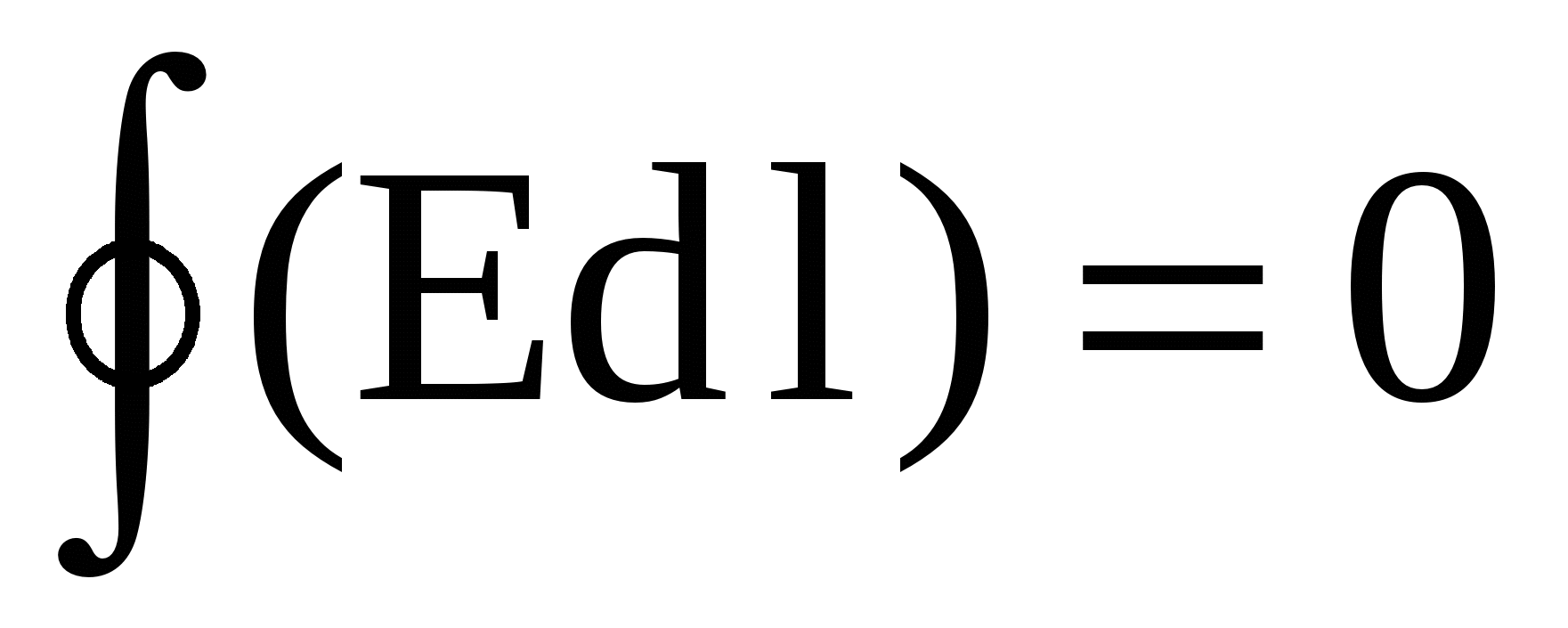(4)

Un câmp cu aceste proprietăți este numit potenţial . Orice câmp electrostatic este potențial.

Teorema circulației ne permite să tragem o serie de concluzii importante, practic fără a recurge la calcule. Să luăm în considerare două exemple simple care confirmă această concluzie.

Folosim teorema Stokes, care afirmă că circulația vectorului de-a lungul unui contur arbitrar L este egal cu curgerea rotorului acestui vector prin orice suprafață acoperită de acest contur, i.e.

. În cazul unui câmp electrostatic, avem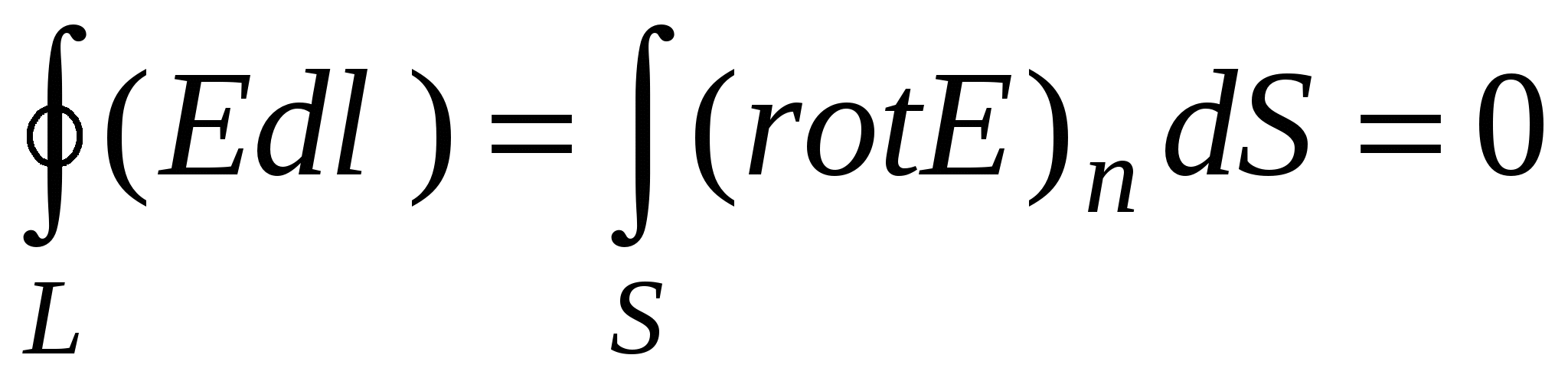

, prin urmare, datorită arbitrarului formei suprafeței, obținem

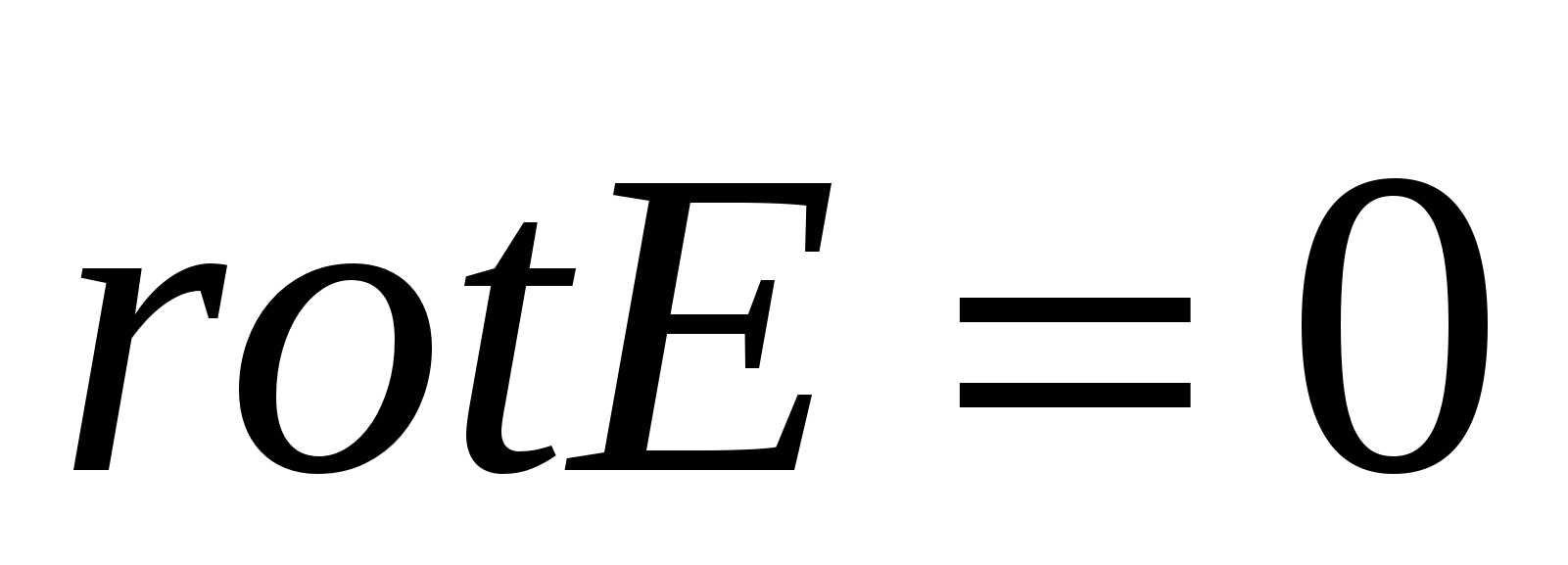. Prin urmare, din natura potențială a câmpului electrostatic rezultă că câmpul electrostatic nu este vortex dacă . (5)

3.3. Energia potențială și potențialul câmpului electrostatic

Un corp situat în câmpul de forțe potențiale are energie potențială, datorită căreia munca este efectuată de forțele câmpului. Prin urmare, munca poate fi reprezentată ca diferența dintre valorile energiilor potențiale deținute de sarcină q" la punctele 1 și 2 din câmpul de încărcare q

Se mai poate arăta că, din moment ce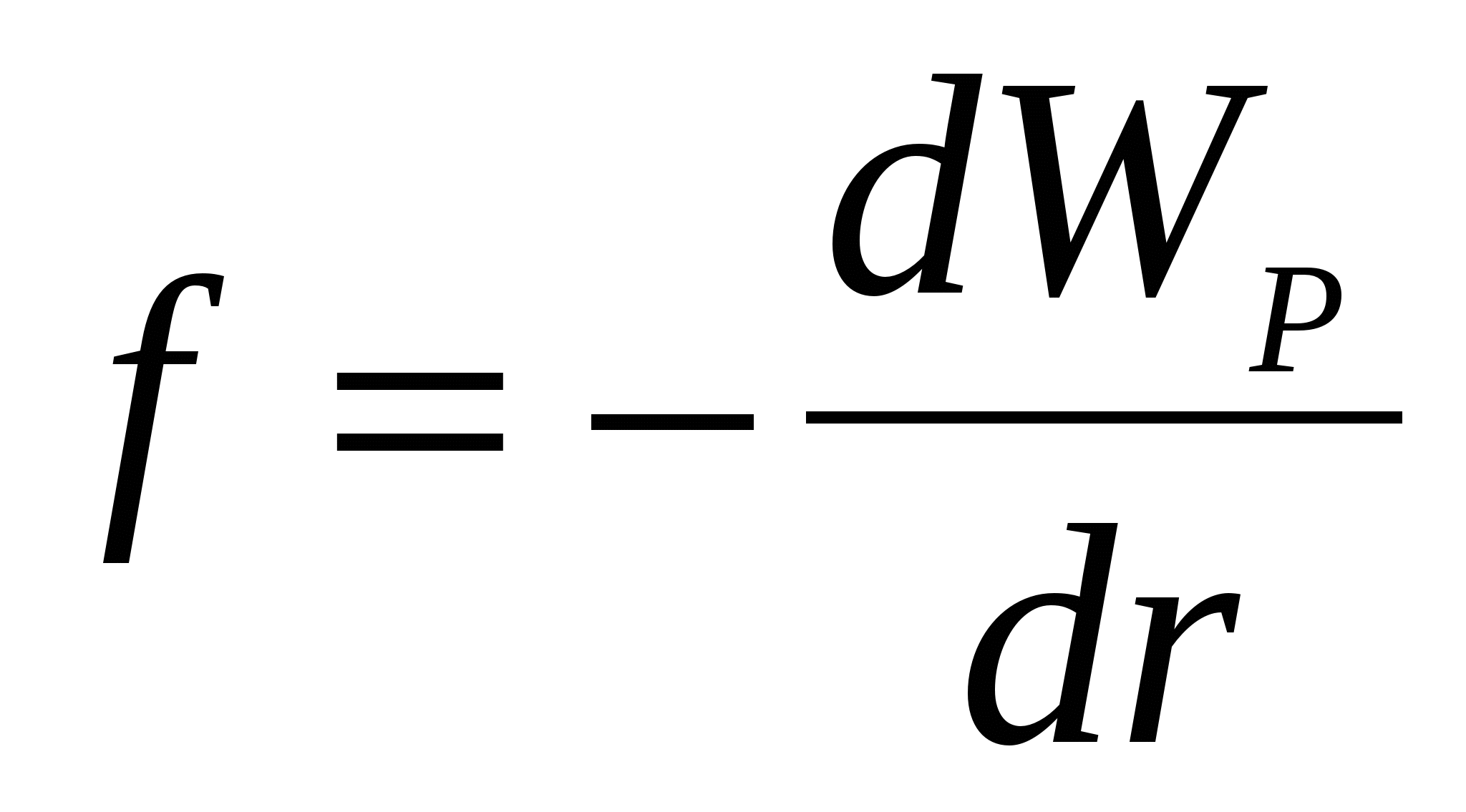

,

Prin urmare, pentru energia potențială a sarcinii în câmpul de sarcină q primim:

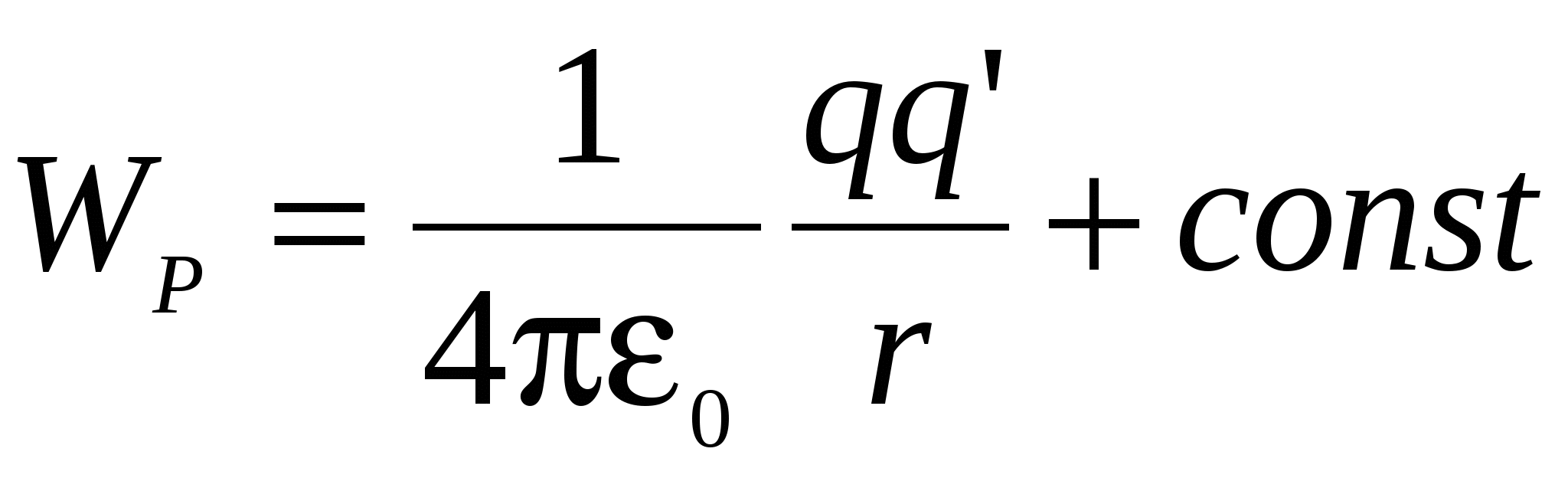(6)

Sens constîn (6) este de obicei aleasă în așa fel încât atunci când încărcarea este îndepărtată q" catre infinit (

) energia potențială dispare. În această condiție, se dovedește că

(7)

Presupunem q" acuzație de probă. Atunci energia potențială deținută de sarcina de testare depinde nu numai de valoarea acesteia 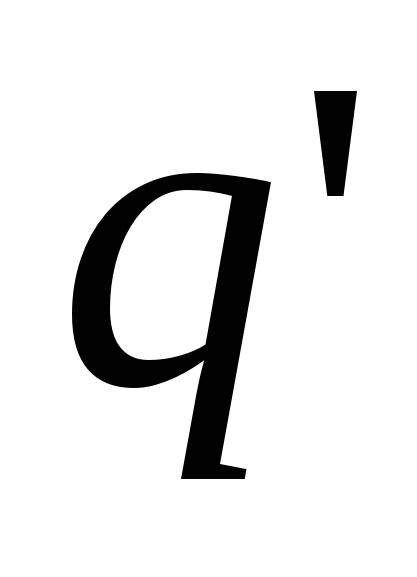, dar și asupra valorii qși r, definind domeniul. Prin urmare, această energie poate fi folosită pentru a descrie câmpul, așa cum a fost folosită în acest scop forța care acționează asupra unei sarcini de testare.

Diverse taxe de testare

,

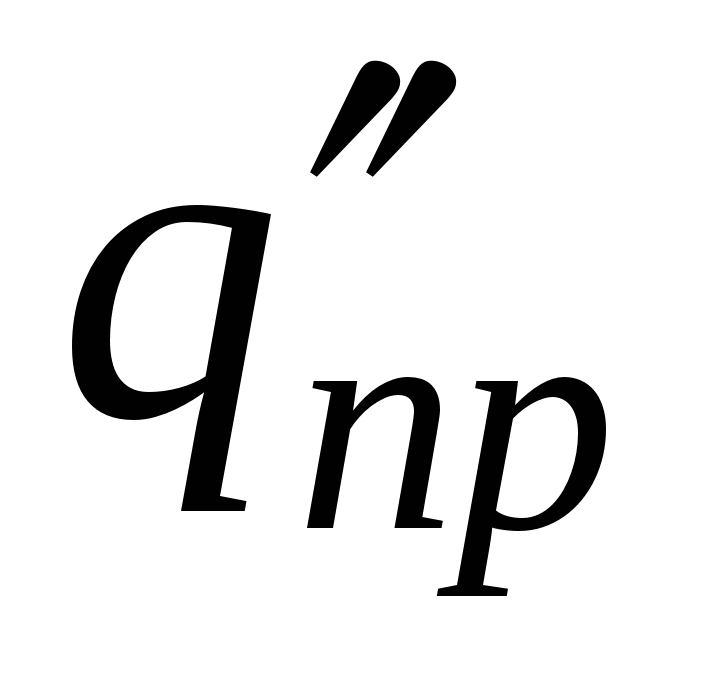va avea energii diferite în același punct al câmpului

,

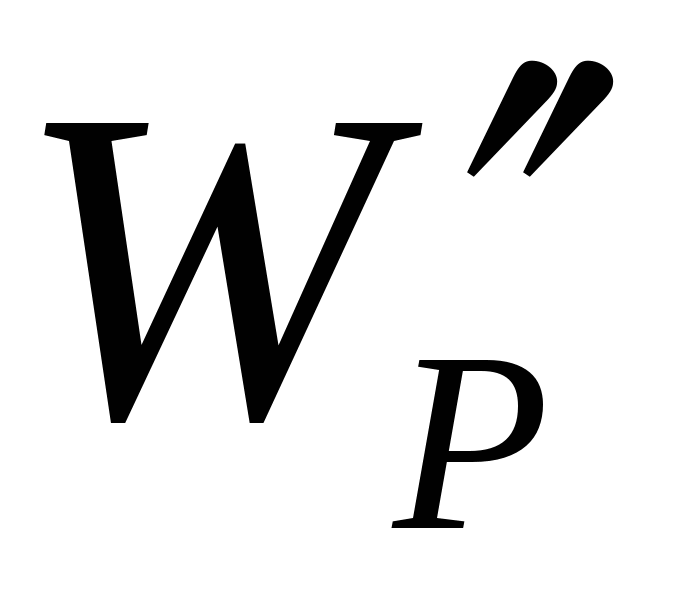etc. Cu toate acestea, atitudinea

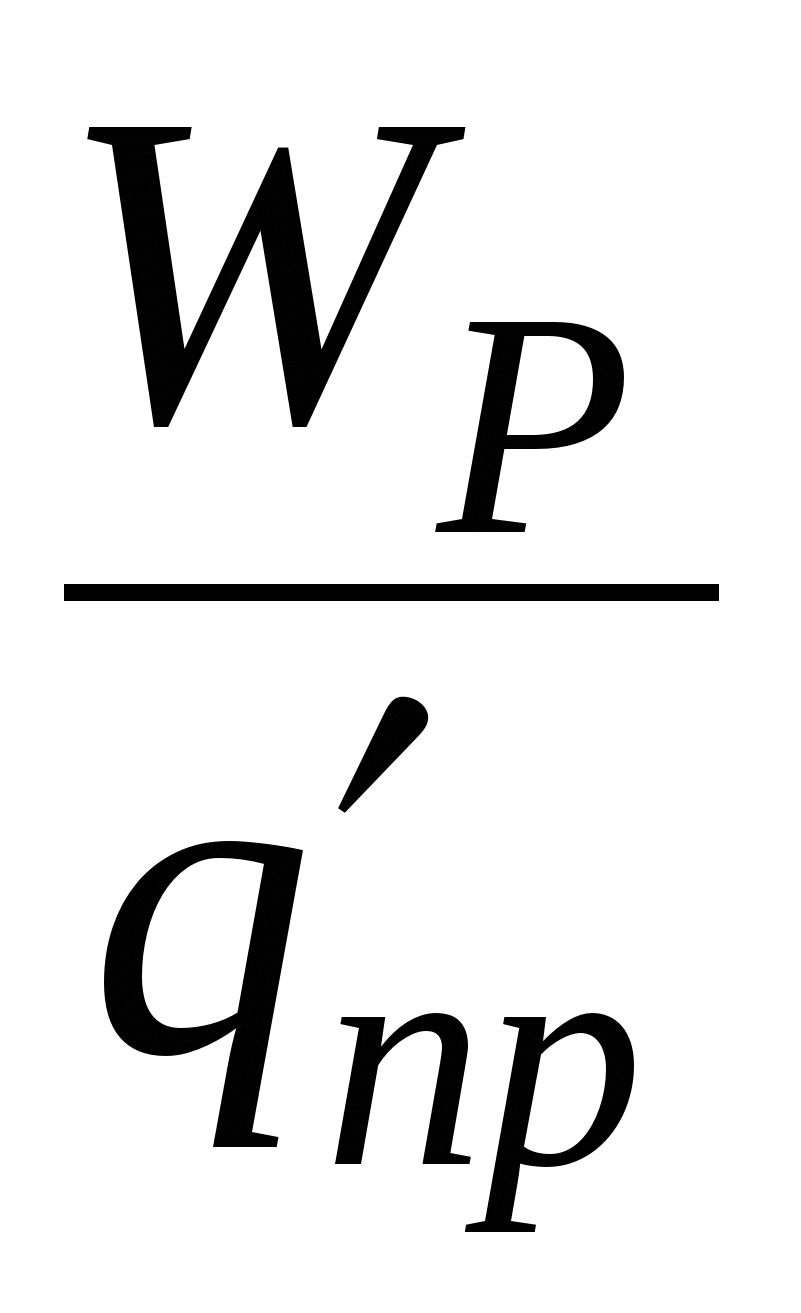va fi la fel pentru toate taxele. Valoare

(8)

numit potenţial câmp într-un punct dat și este utilizat împreună cu intensitatea câmpului pentru a descrie câmpurile electrice.

După cum urmează din (8) potențialul este numeric egal cu energia potențială pe care o unitate de sarcină pozitivă o are într-un punct dat al câmpului.

Prin urmare câmp potențial taxă punctuală pe care o primim următoarea expresie:

(9)

Dacă câmpul este creat de un sistem de taxe punctiforme q 1 , q 2 , …, q n, situate respectiv la distante r 1 , r 2 ,…, r n până la punctul câmpului unde se află încărcătura , apoi munca făcută de forțele acestui câmp asupra încărcăturii , va fi egal cu suma algebrică a muncii forțelor datorate fiecărei sarcini separat:

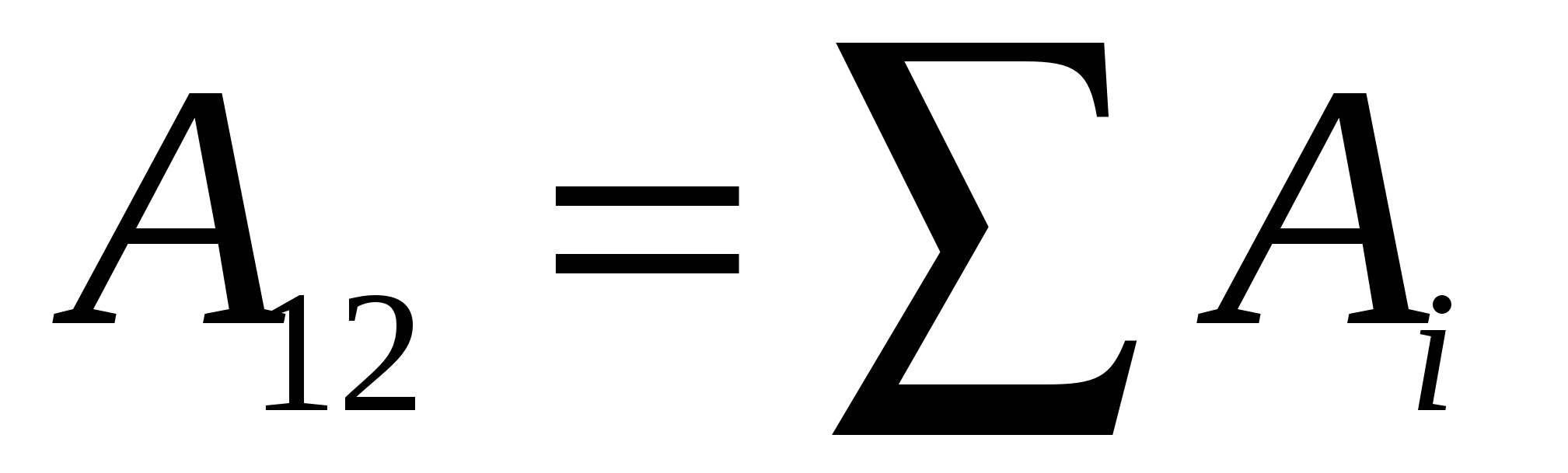Dar fiecare dintre lucrări este egal cu:

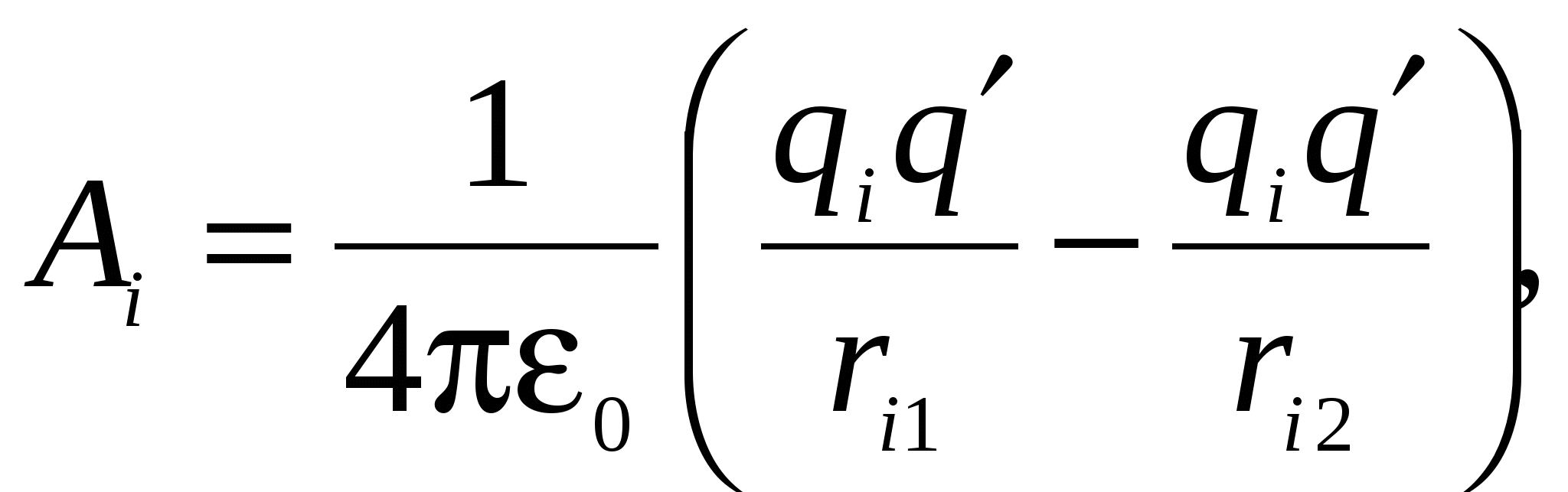
Unde

distanta de incarcare 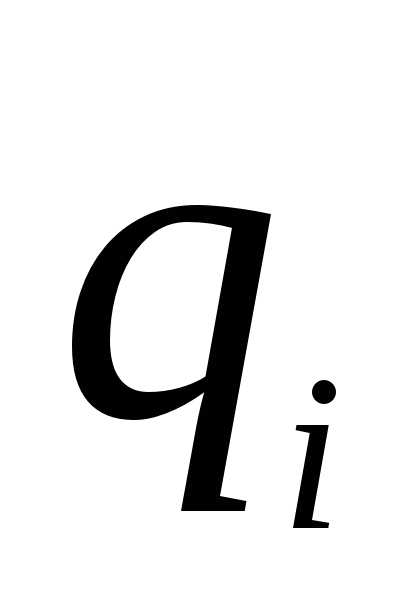la poziția inițială a încărcăturii,

distanta de la sarcina pana la pozitia finala a incarcarii.

Prin urmare:

Comparând această expresie cu relația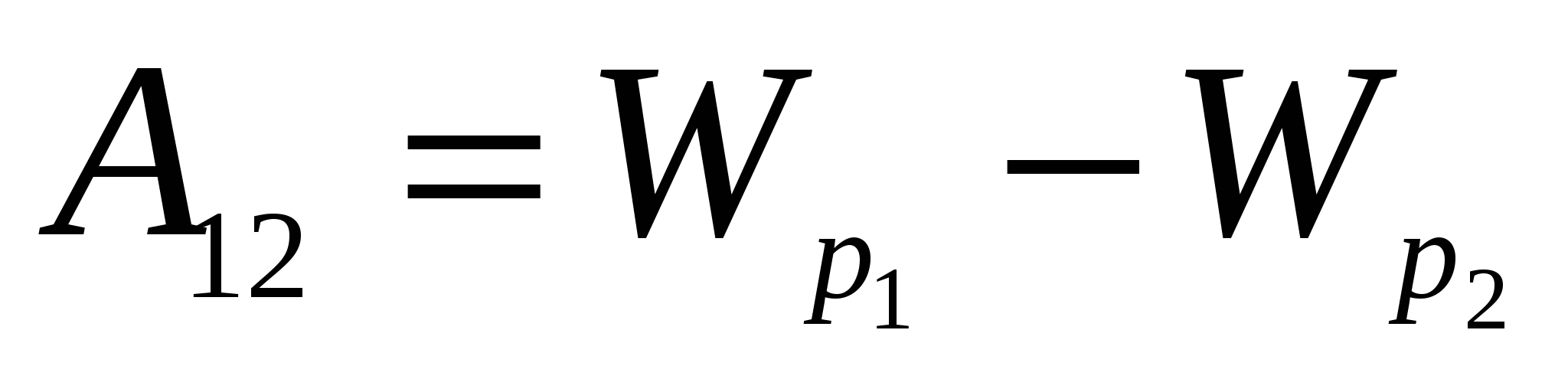

, obținem expresia pentru energia potențială a sarcinii în câmpul sistemului de sarcini:

, (10)

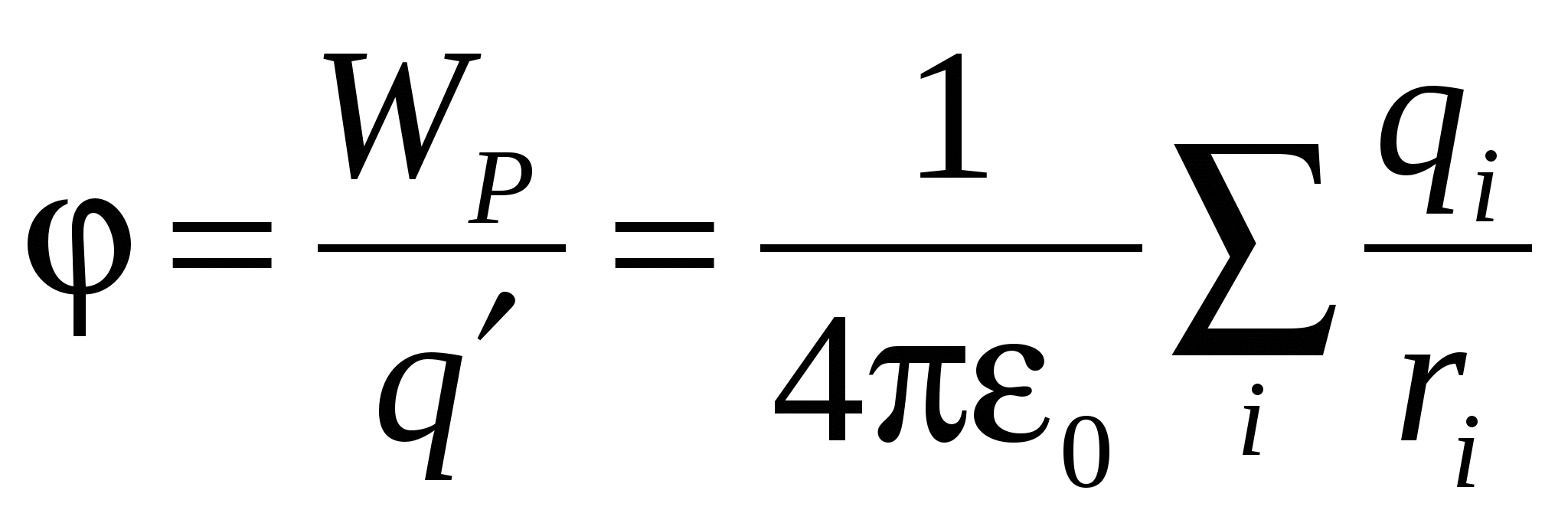. (11).

În consecință, potențialul câmpului creat de sistemul de sarcini este egal cu suma algebrică a potențialelor create de fiecare dintre sarcini separat.

Din relatie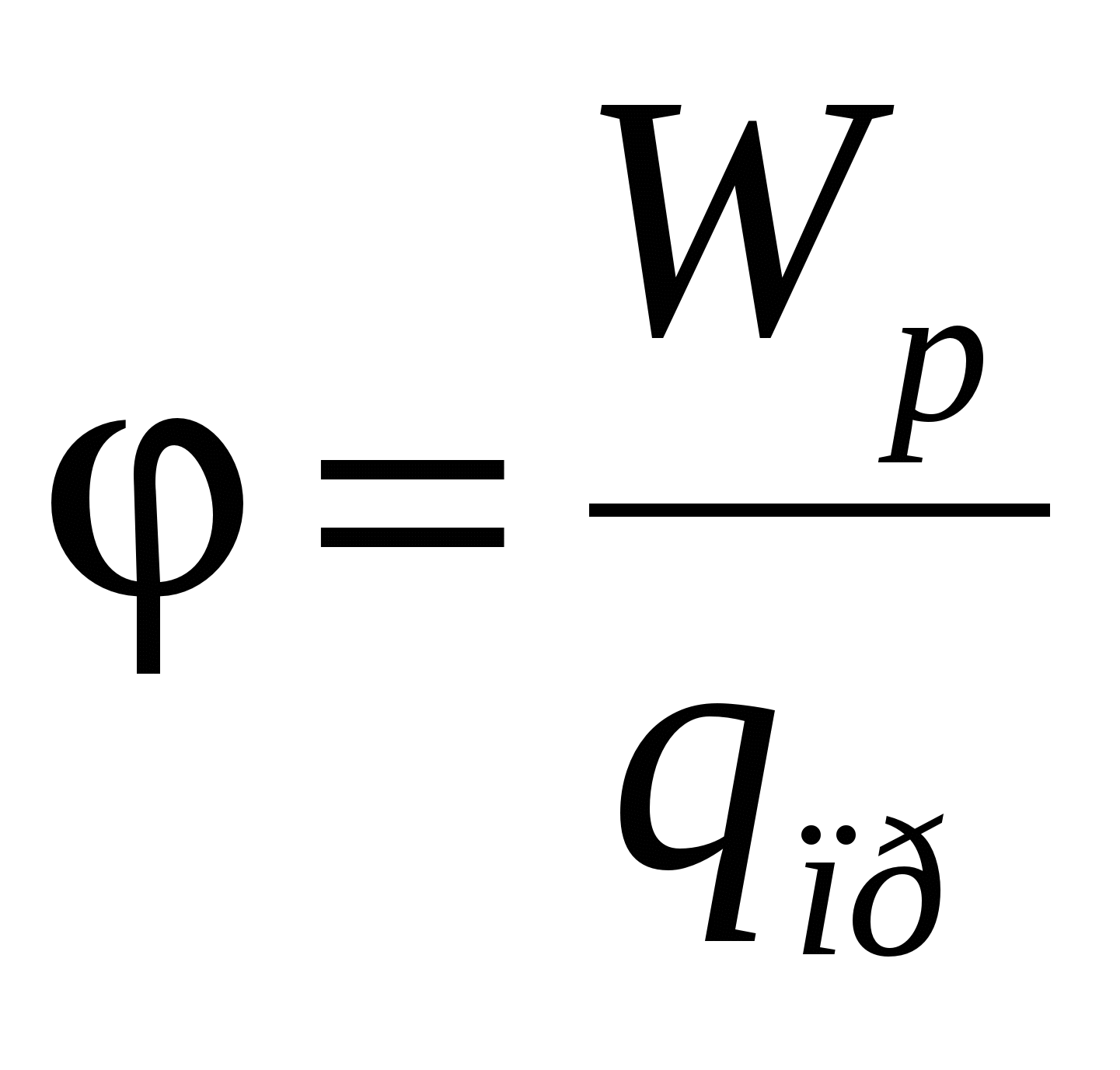

rezultă că taxa , situat în punctul câmpului cu potențial , are energie potenţială

. Prin urmare, munca forțelor câmpului asupra sarcinii poate fi exprimată în termeni de diferență de potențial:

Deci munca făcută pe taxă forţelor de câmp, este egal cu produsul dintre sarcina și diferența de potențial la punctele inițiale și finale. Dacă sarcina dintr-un punct cu un potențial este îndepărtată la infinit (unde potențialul este egal cu zero prin condiție), munca forțelor câmpului va fi egală cu

sau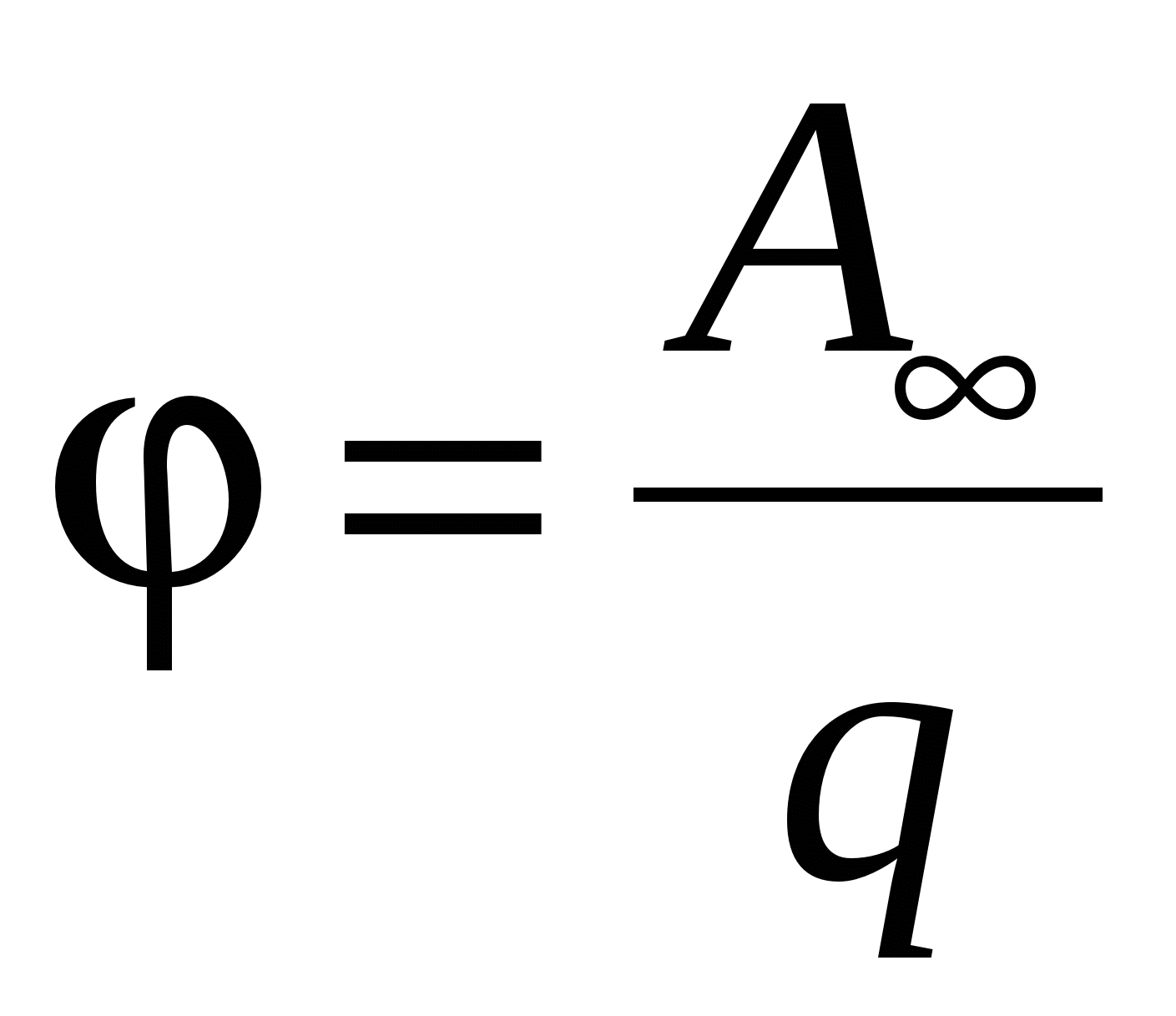

,

T. e, potenţial numeric este egal cu munca, care este efectuată de forțele câmpului asupra unei unități de sarcină pozitivă atunci când aceasta este îndepărtată dintr-un punct dat al câmpului la infinit, sau munca care trebuie făcută împotriva forțelor câmpului electric pentru a muta o unitate de sarcină pozitivă din infinit până la un punct dat al câmpului.

Unitatea de potențial trebuie luată ca potențial într-un astfel de punct al câmpului, pentru a muta sarcina la care de la infinit este necesar să se efectueze un lucru egal cu

1 Joule (sistemul de unități „Ci”)

De aici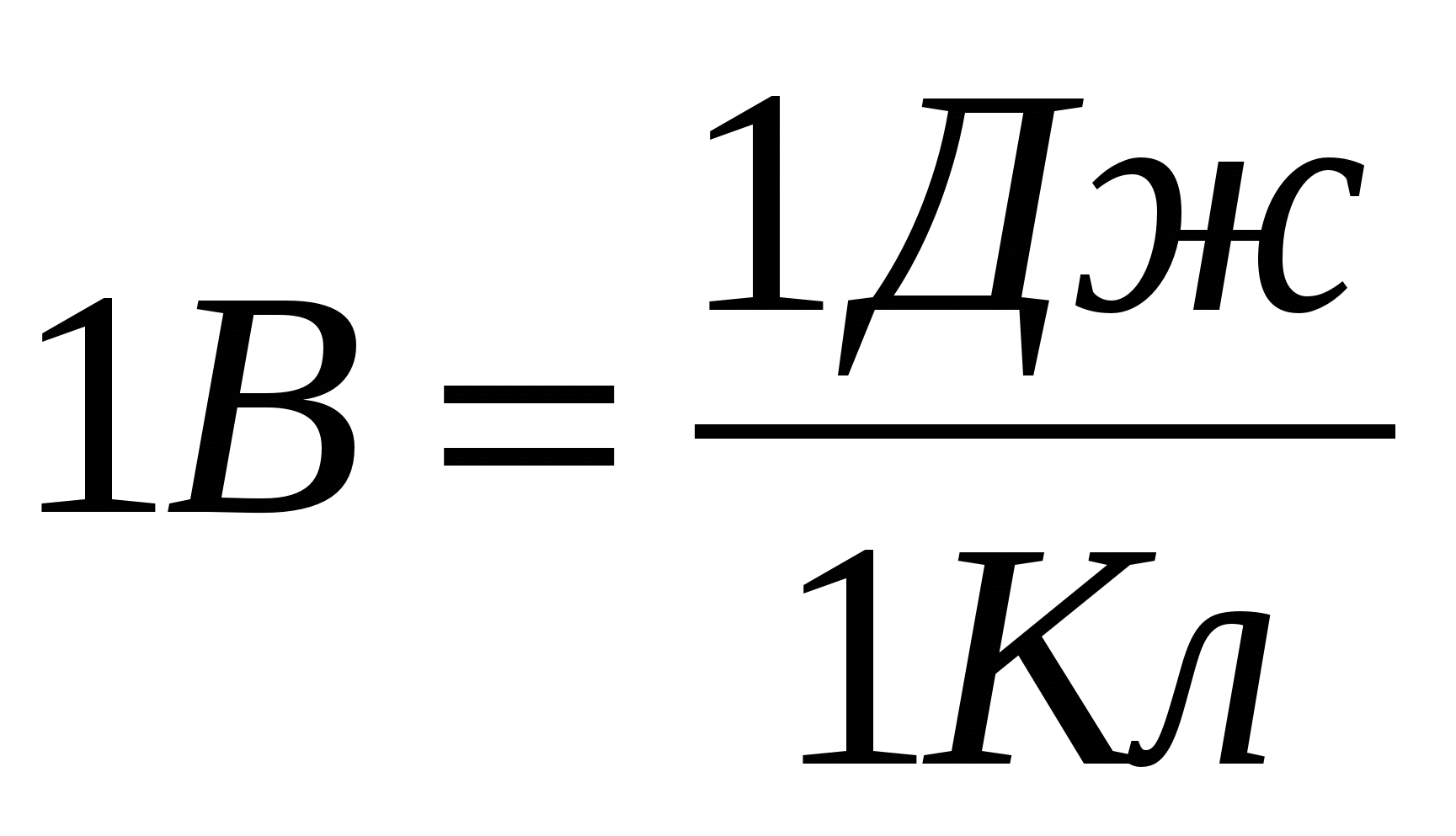

.

3.4. Dipol într-un câmp electrostatic

E 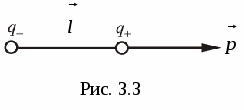dipol electric numită combinația a două taxe egale semn opus, situate la distanță unul de celălalt l, care este mic în comparație cu distanța lor până la punctele în care este determinat câmpul dipol.

Produsul sarcinii și distanța dintre sarcini p=ql numit moment dipol . Pentru o definiție completă a dipolului, este de asemenea necesar să se precizeze orientarea axei dipolului în spațiu. În consecință, momentul dipolar ar trebui considerat ca un vector . Acest vector are o direcție de la negativ la pozitiv(fig.3.3). Dacă introduceți raza - vector 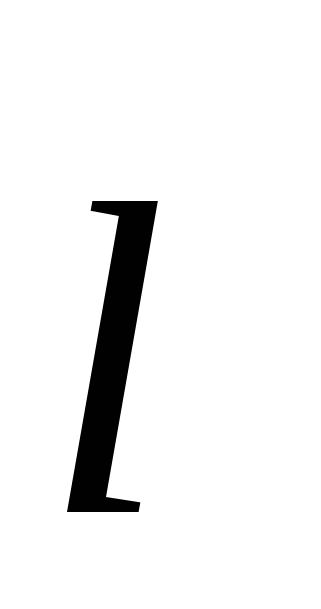cheltuit din - q la + q, atunci momentul dipolar poate fi reprezentat ca:

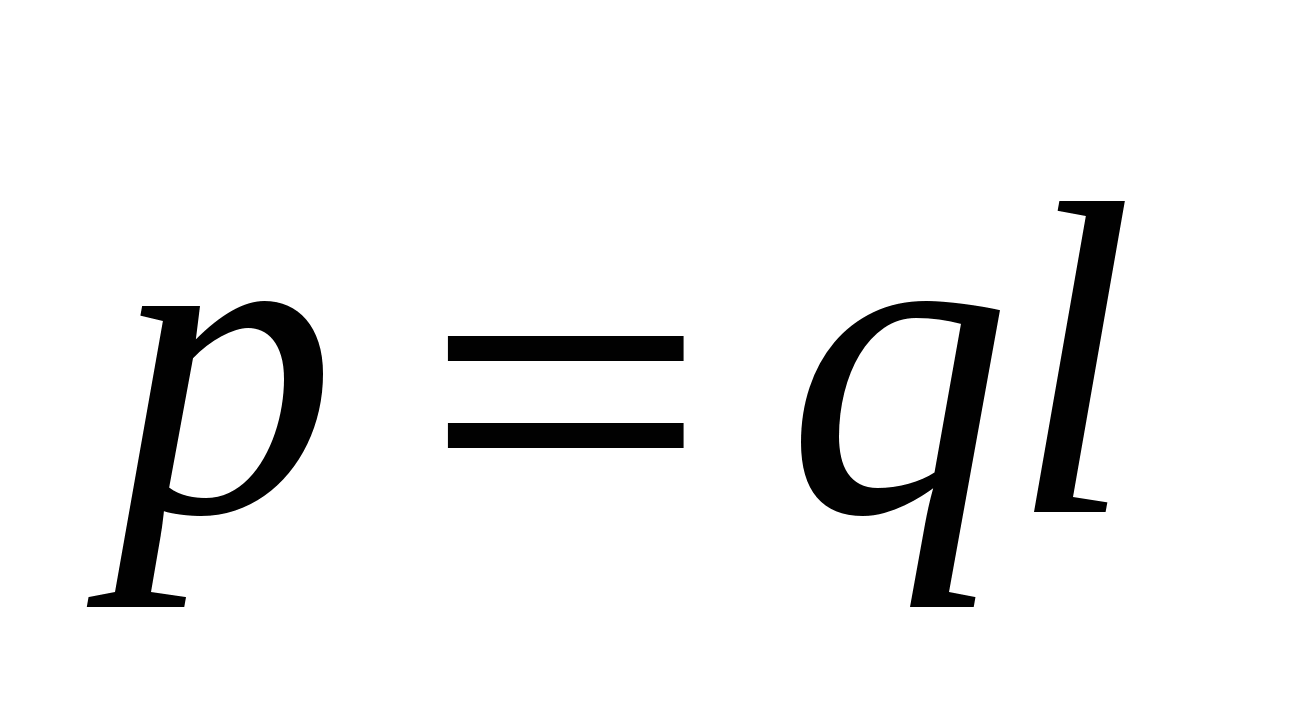. (13)

Dacă un dipol este plasat într-un câmp electric uniform, sarcinile care formează dipolul sunt qși + q acţionat asupra unor forţe de mărime egală, dar de direcţie opusă și (Fig. 14). Aceste forțe formează o pereche de forțe, al căror braț este egal cu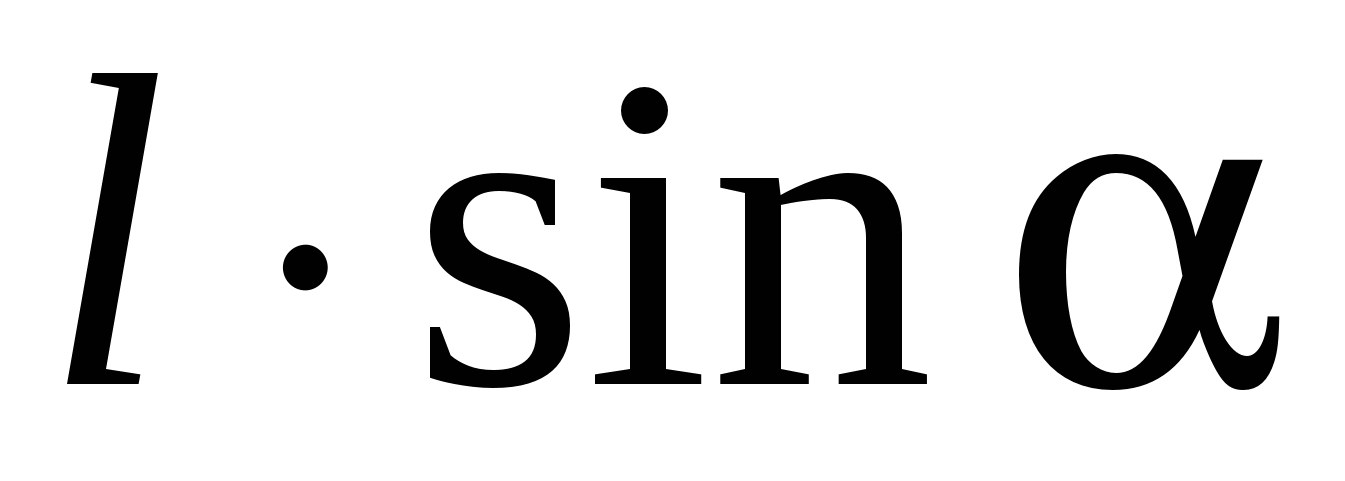

, adică depinde de orientarea dipolului față de câmp. Modulul fiecăreia dintre forțe este qE. Înmulțind cu umărul, obținem valoarea momentului unei perechi de forțe care acționează asupra dipolului:

Unde R– moment electric dipol.

LA forma vectoriala:

. (15)

Moment

tinde să rotească dipolul astfel încât momentul său aşezat în direcţia câmpului.

Pentru a crește unghiul dintre vectori și pe dα trebuie să se lucreze împotriva forțelor care acționează asupra dipolului:

Acest lucru duce la creșterea energiei potențiale W, care are un dipol într-un câmp electric, adică:

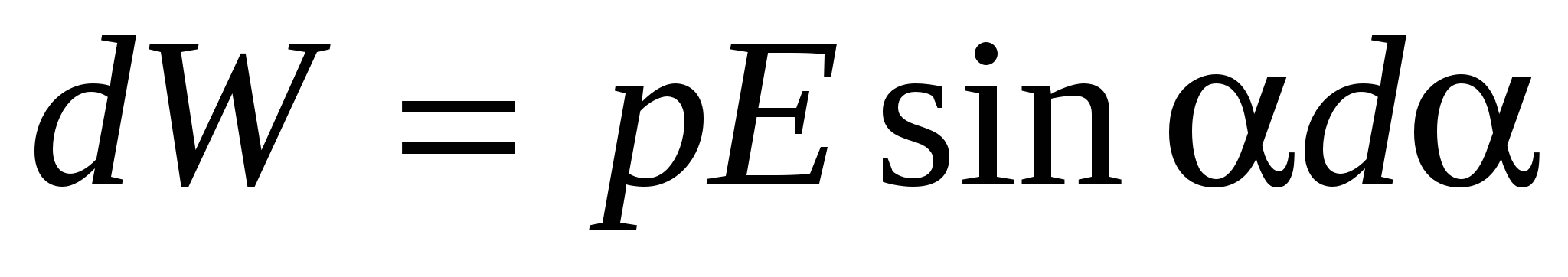(16)

Integrarea (16) dă expresia energiei potențiale a unui dipol într-un câmp electric:

Presupunând const=0 , primim

LA prin alegere const=0 , presupunem că energia dipolului va fi zero atunci când dipolul este setat perpendicular pe direcția câmpului. Cea mai mică valoare energetică egală cu ( -pe), se obţine atunci când dipolul este orientat în direcţia câmpului, cel mai mare, egal cu pE, când este îndreptată în direcția opusă vectorului .

Într-un câmp neomogen, forțele care acționează asupra sarcinilor dipolului nu sunt aceleași. Pentru dipoli mici de forță f 1 și f 2 poate fi considerat aproximativ coliniar. Să presupunem că câmpul se schimbă cel mai rapid în direcția X, care coincide cu direcția în locul unde se află dipolul (Fig. 3.5). sarcină pozitivă dipolul este deplasat față de negativ în direcția X prin suma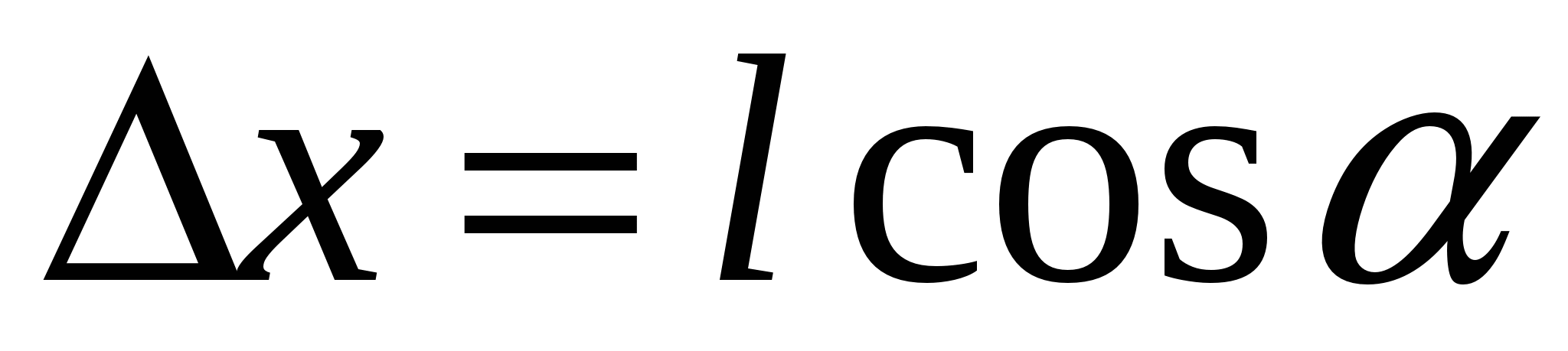

. Prin urmare, intensitatea câmpului în punctele în care sunt plasate sarcinile diferă cu Δ E. Din moment ce suma forţelor

și

sau , (19)

, apoi

, (20)

Unde

este gradientul vectorului intensității câmpului electric. Astfel, într-un câmp electric neomogen, pe lângă momentul de rotație, există o forță f, sub influența căruia dipolul fie va fi atras în regiunea unui câmp mai puternic (α 0), fie împins în afara acestuia (α> 90 0).

Expresia forței poate fi obținută din (18), ținând cont de faptul că f= –

.

3.5. Relația dintre intensitatea câmpului electrostatic și potențial

Intensitatea câmpului electric - magnitudine, numeric egal cu puterea acţionând asupra acuzaţiei. Potenţial este o valoare egală numeric cu energia potențială a sarcinii. Astfel, trebuie să existe o relație între aceste mărimi, similară relației dintre energia potențială și forță (adică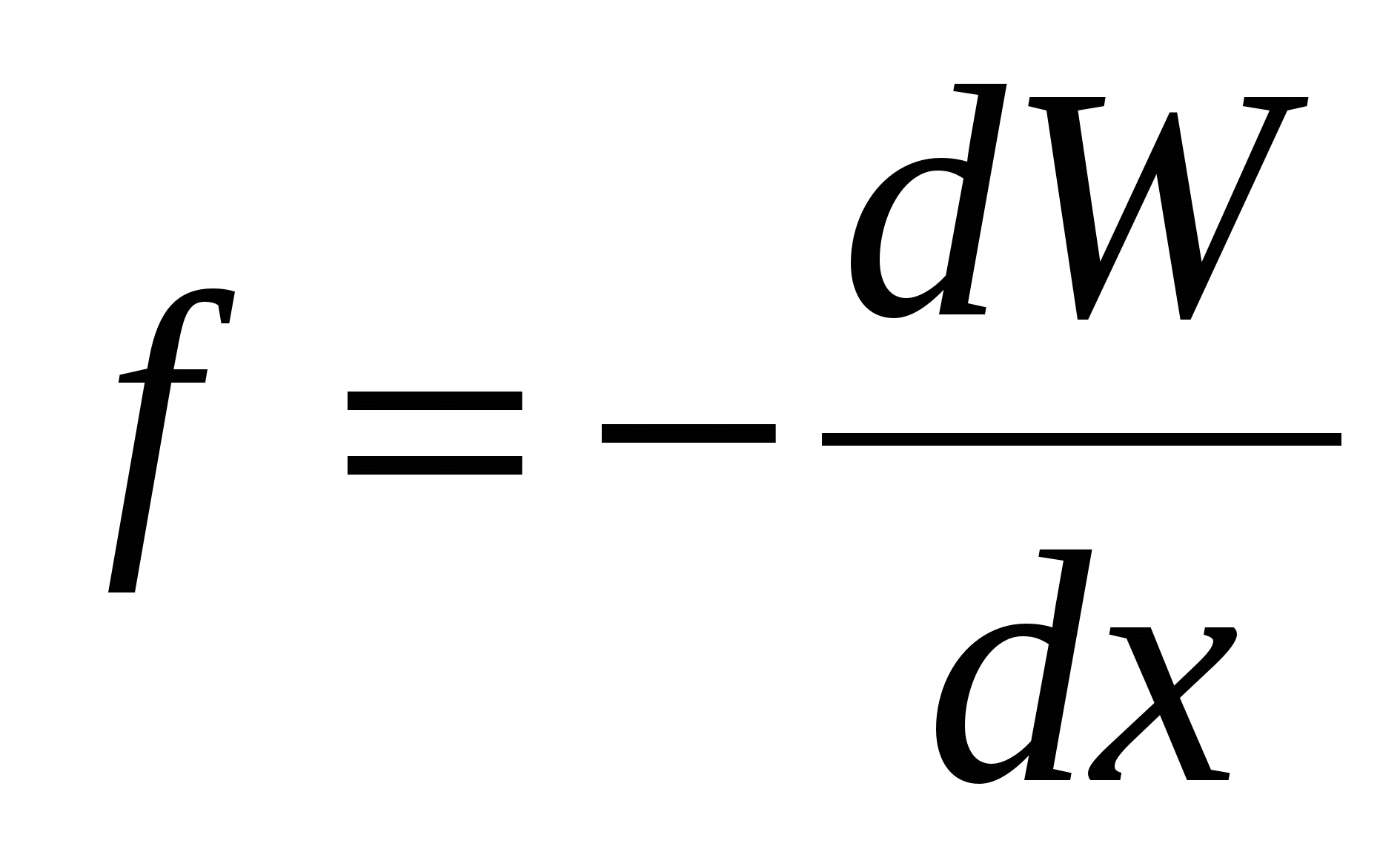

). Lucrarea forțelor câmpului asupra sarcinii pe segmentul de cale poate fi reprezentată ca

, și scăderea energiei potențiale a sarcinii, care va apărea în acest caz: . De unde de la egalitate

găsim:

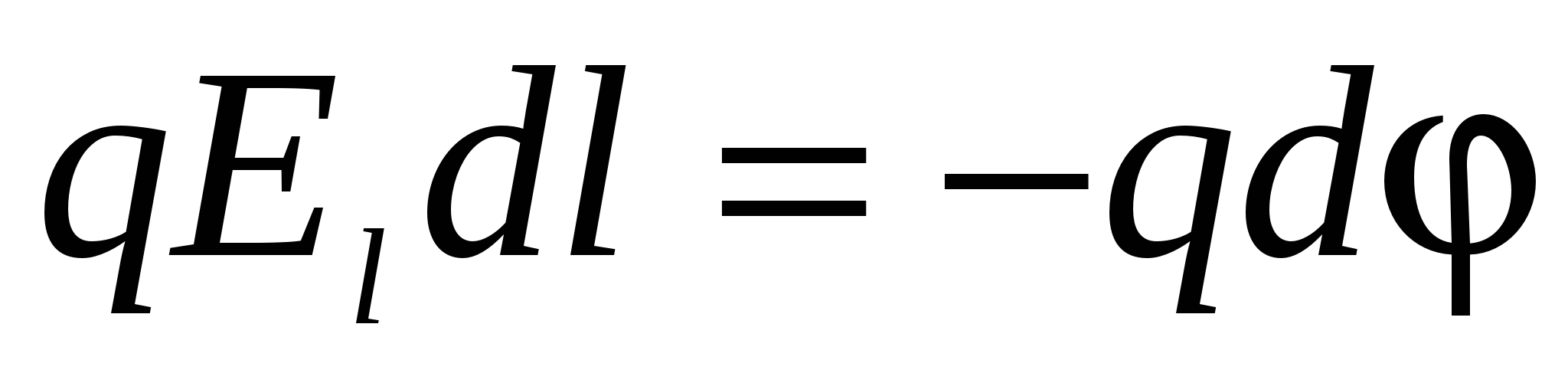sau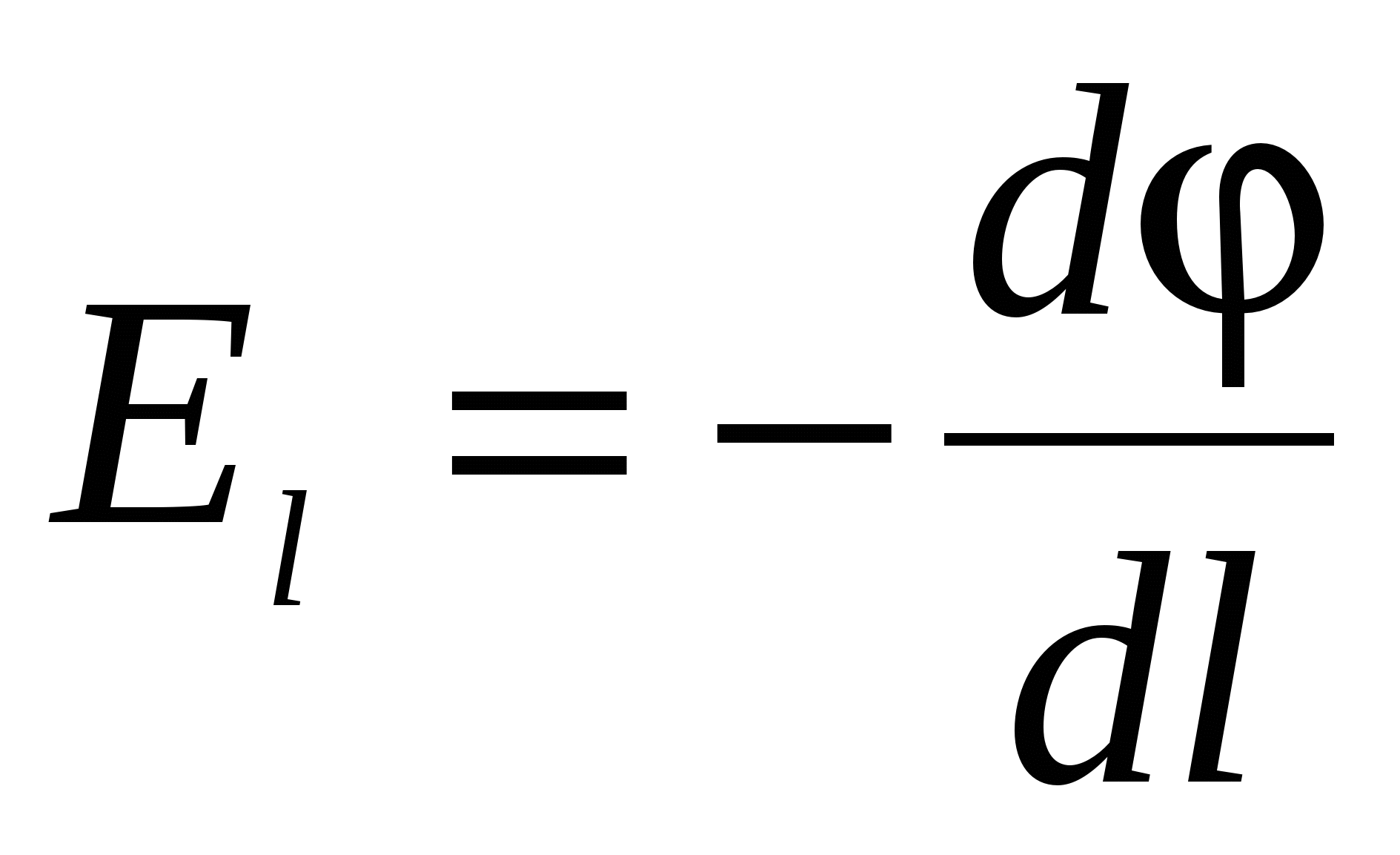

, (21)

Unde prin direcție aleasă în mod arbitrar.

,

,

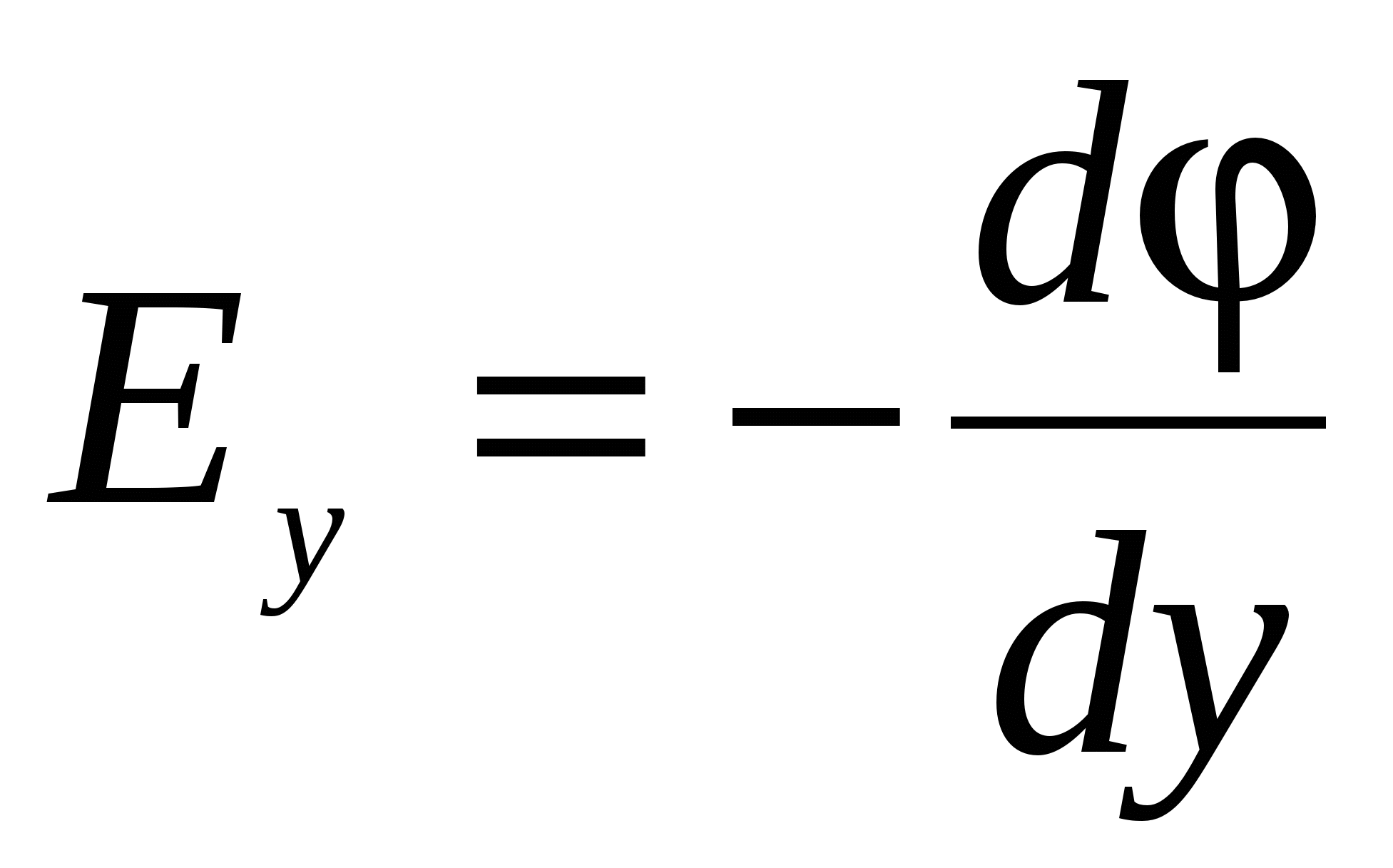, (22)

Unde

orte de axe de coordonate, adică vectori unitari. Vector cu componente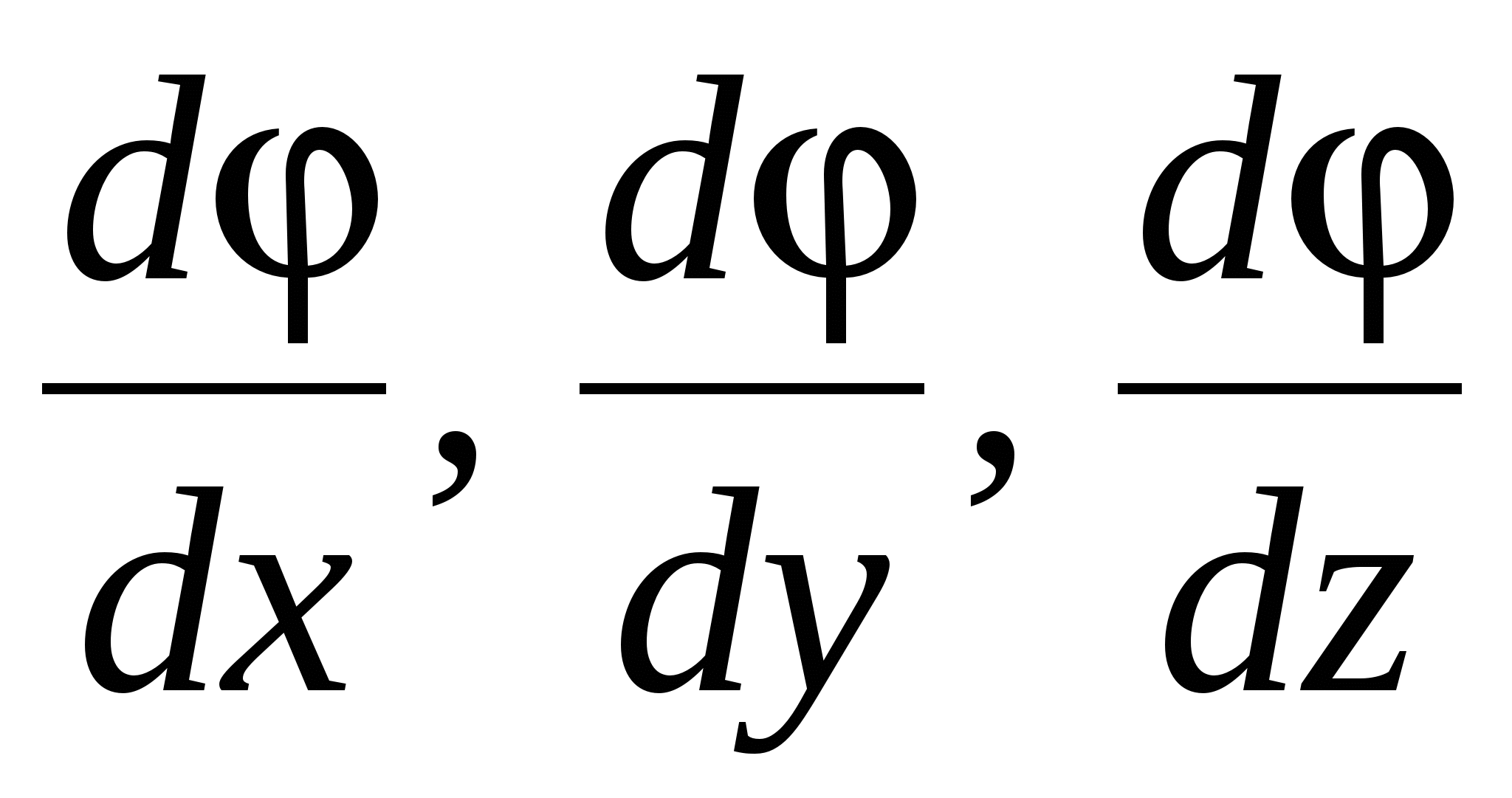

, Unde

funcția scalară a coordonatelor

numit gradient funcţionează şi este notat cu simbolul

(sau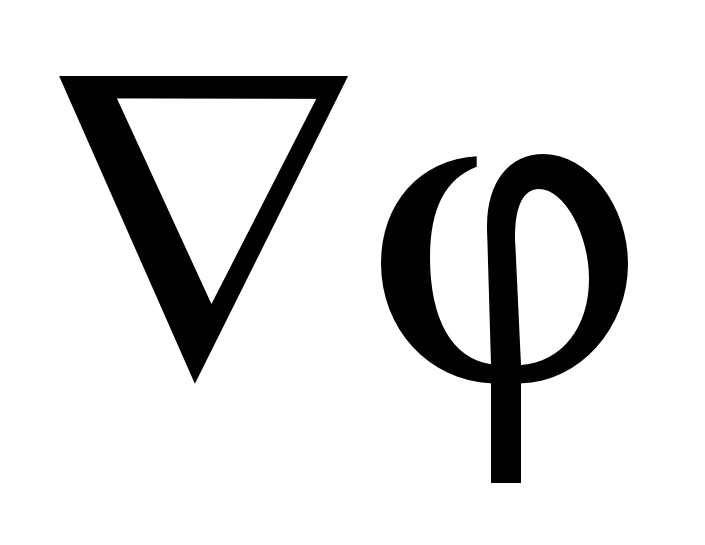

, Unde - operator nabla). Deci gradientul potențial este:

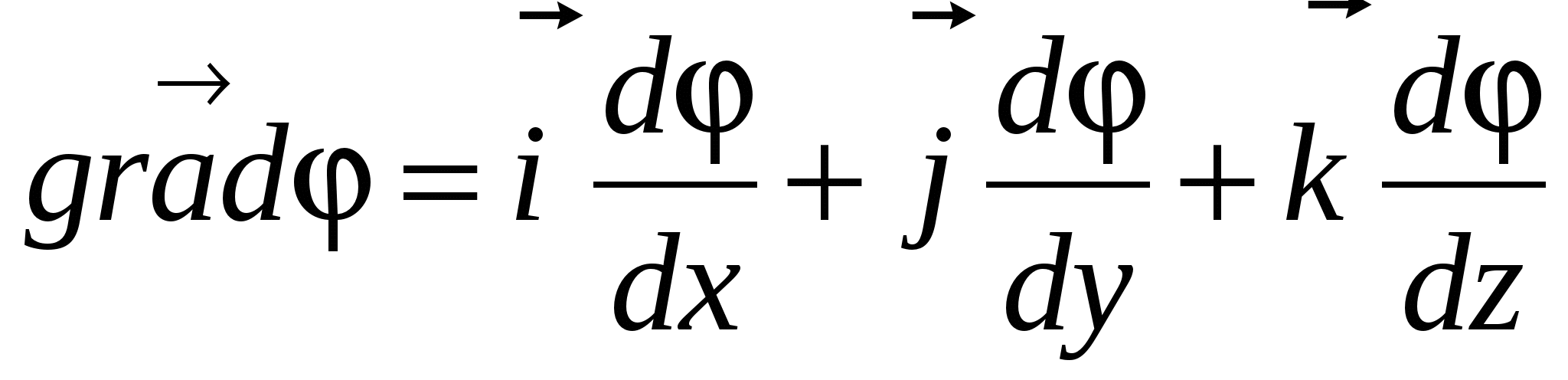(24)

Și din (23) și (24) rezultă că

(25)

Deoarece gradientul este un vector care arată direcția celei mai rapide modificări a unei cantități, a cărei valoare se schimbă de la un punct în spațiu la altul, atunci gradientul potențialului 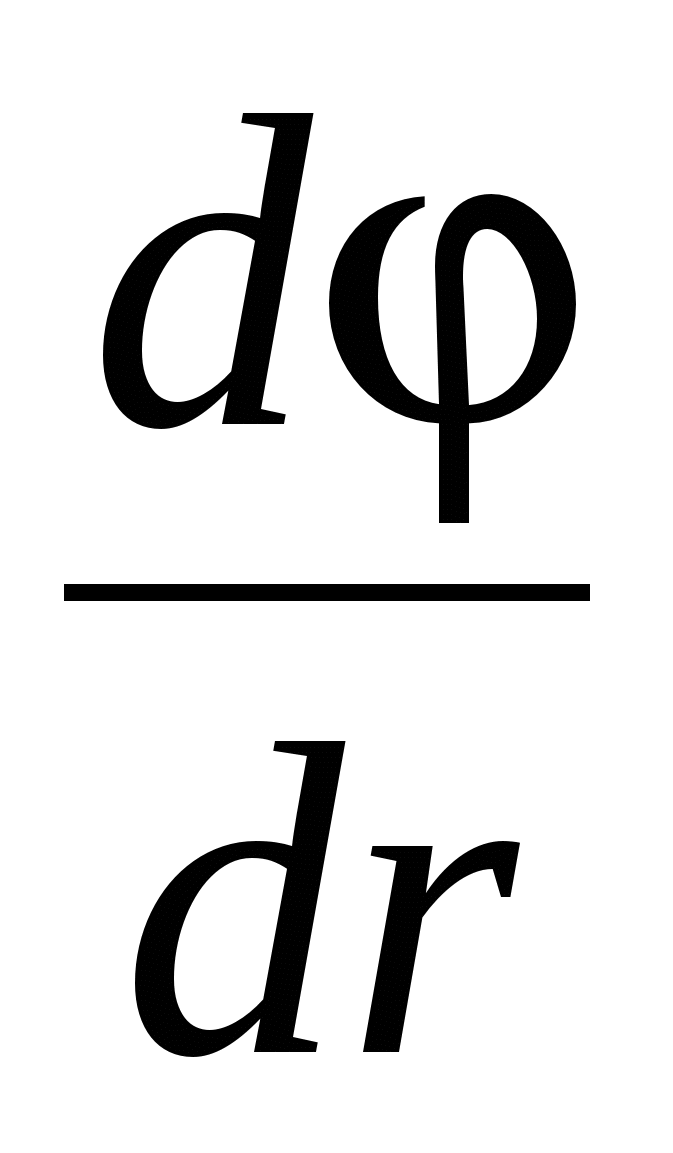(Unde r-radius-vector) este un vector îndreptat în direcția celei mai rapide creșteri a potențialului, numeric egal cu rata de modificare a acestuia pe unitatea de lungime în această direcție.

Pentru că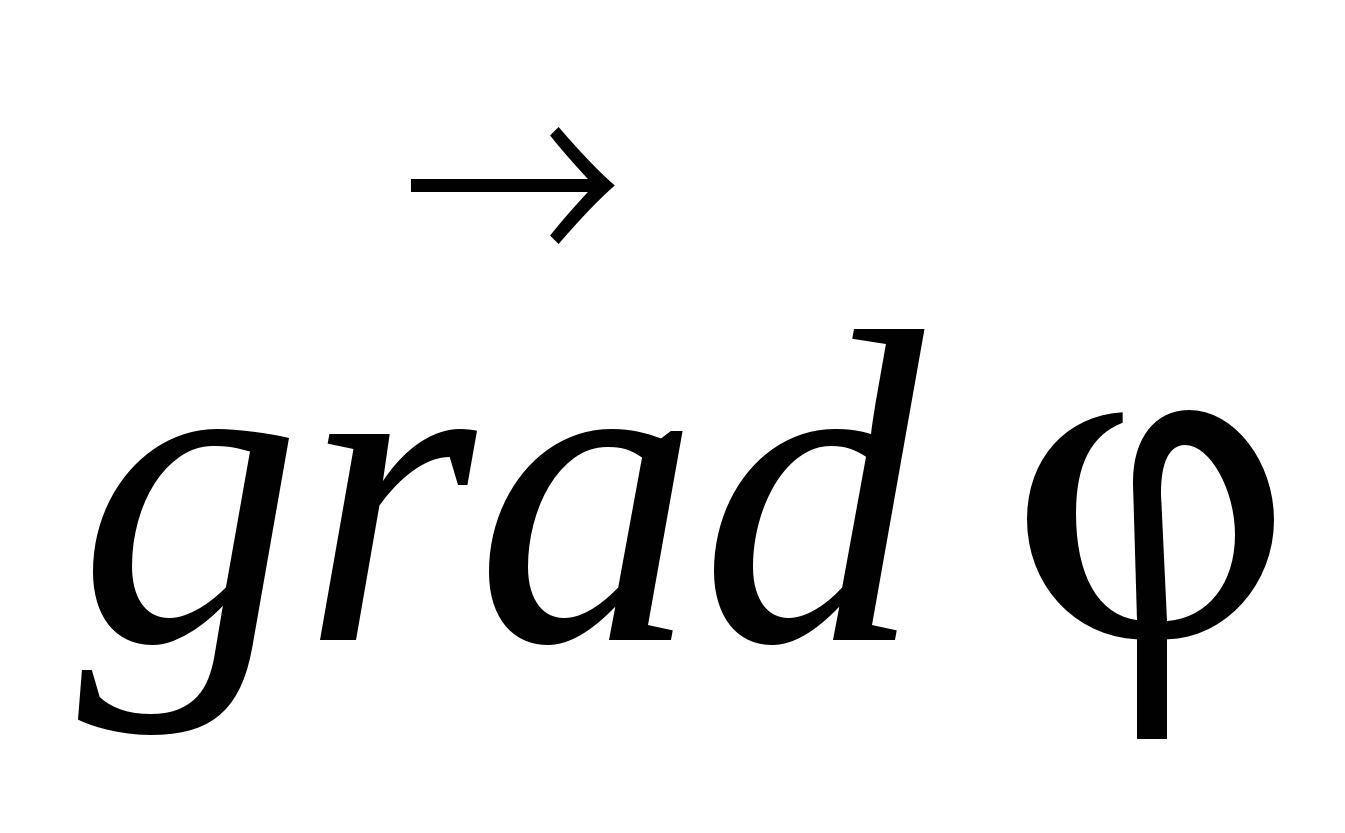

este o mărime vectorială, atunci modulul său se exprimă astfel:

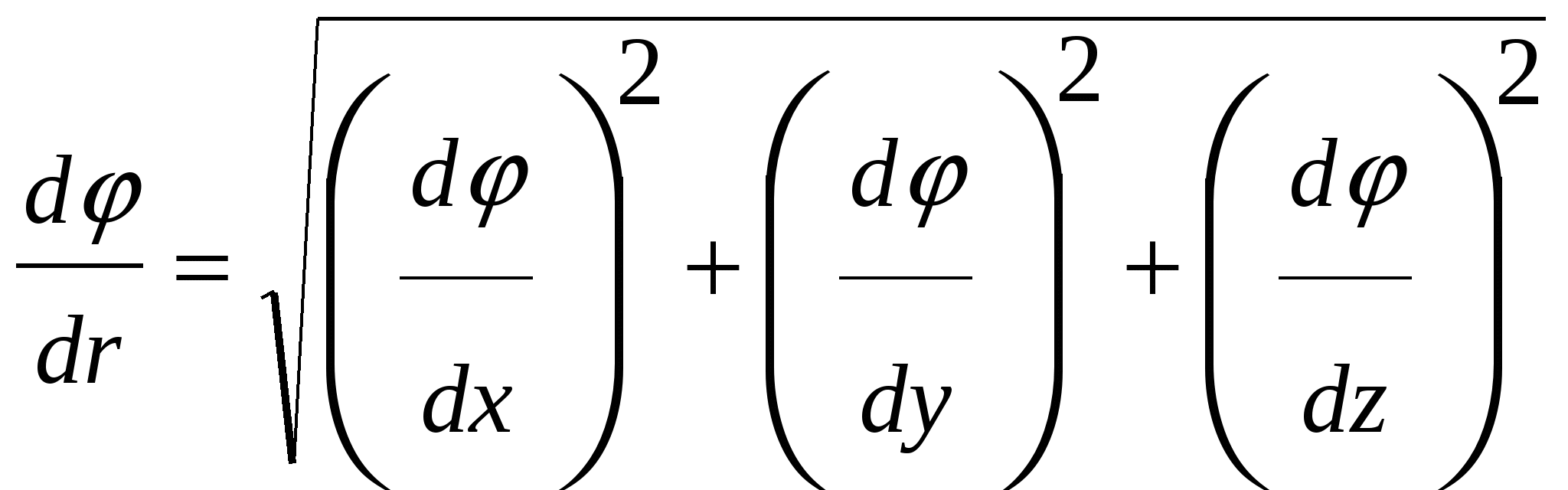, (26)

La fel ca modulul unui vector :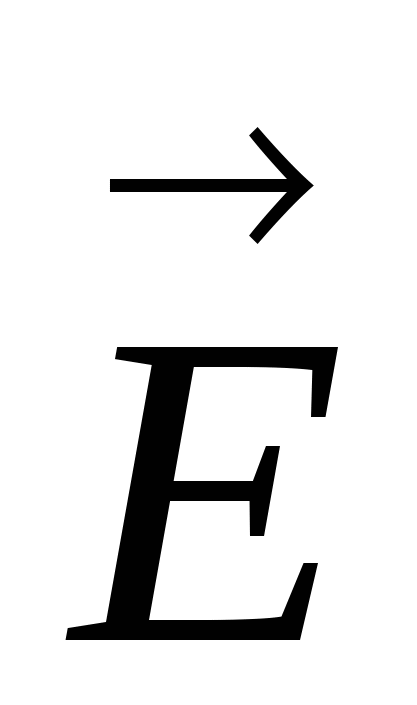

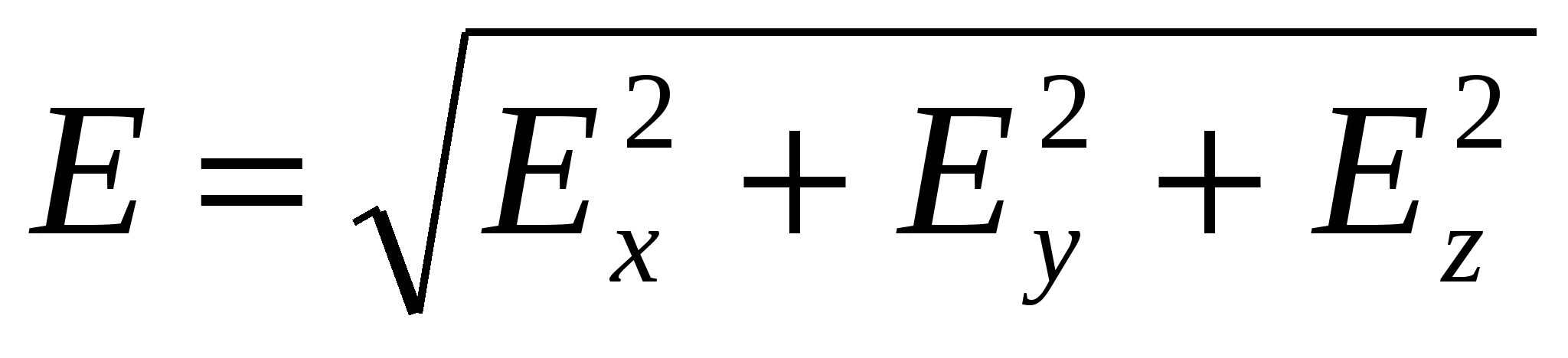(27)

Semnul „–” (25) indică faptul că tensiunea este direcționată în direcția potențialului de scădere. Formula (25) vă permite să găsiți intensitatea câmpului în fiecare punct din valori cunoscute sau să rezolvați problema inversă, adică din valorile date în fiecare punct, să găsiți diferența de potențial dintre două puncte arbitrare ale câmpului.

3.6. Suprafețe echipotențiale

Potențialul unui câmp electrostatic este o funcție care variază de la un punct la altul. Cu toate acestea, în orice caz real, este posibil să se evidențieze un set de puncte ale căror potențiale sunt aceleași.

G 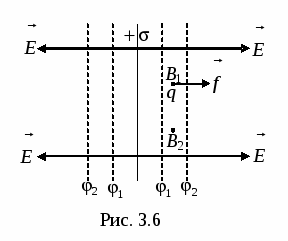locul geometric al punctelor cu potențial constant se numește suprafață cu potențial egal sau suprafață echipotențială.

Luați un plan infinit încărcat uniform (Fig. 3.6). Câmpul creat de un astfel de plan este omogen, iar liniile de tensiune sunt normale cu planul. Rezultă că munca de mutare a unei sarcini dintr-un anumit punct LA 1 la orice alt punct LA 2 , situat la aceeași distanță de suprafața încărcată cu punctul LA 1 este egal cu zero. Într-adevăr, atunci când se mută o încărcătură qîn linie dreaptă LA 1 LA 2 forța care acționează asupra sarcinii din partea câmpului va fi întotdeauna perpendiculară pe deplasare și, prin urmare, lucrul acesteia este zero. Dar această lucrare poate fi reprezentată, pe de altă parte, sub forma:

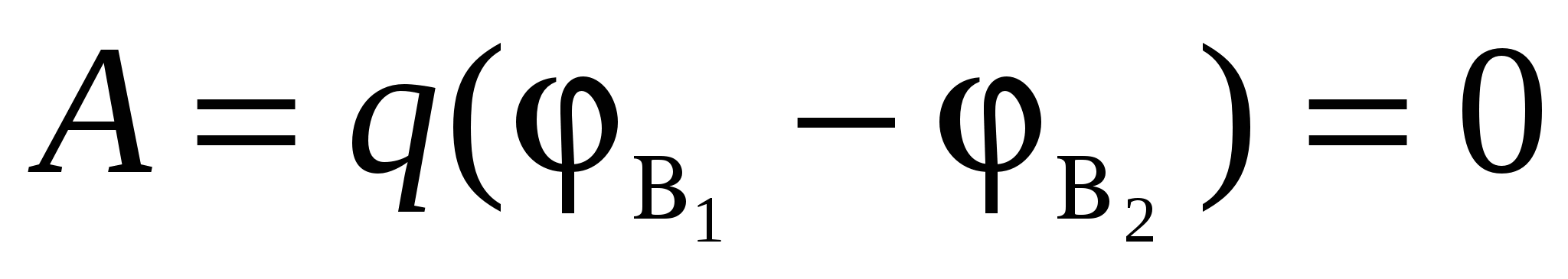, (28)

G de și

sunt, respectiv, potenţialele punctelor LA 1 și LA 2 . Prin urmare, pentru că A = 0, atunci =, adică potențialele punctelor echidistante de planul încărcat sunt aceleași. Astfel, suprafețele cu potențial egal (suprafețele echipotențiale) sunt plane paralele cu planul încărcat. Dacă planul este încărcat pozitiv, atunci valoarea potențialului scade odată cu distanța față de planul încărcat. Este evident că suprafețele cu potențial egal sunt situate simetric pe ambele părți ale planului încărcat.

Suprafețele echipotențiale ale câmpului unei sarcini punctuale sunt sfere cu o rază r , al cărui centru se află în centrul unei sarcini punctiforme, adică

(Fig. 3.7). Pe fig. 3.6 și fig. 3.7 vectorul intensitate este perpendicular pe suprafețele echipotențiale.

Să arătăm că vectorul intensitate este perpendicular pe suprafața echipotențială. Luați în considerare munca de deplasare a unei sarcini pe o suprafață de potențial egal pe o secțiune mică a drumului ∆ S (Fig. 3.7). În același timp, munca forta electrica

pe acest drum va fi:

Unde α este unghiul dintre direcția forței f și deplasarea ∆ S. Pe de altă parte, această lucrare poate fi exprimată ca produsul dintre valoarea sarcinii în mișcare și diferența de potențial în pozițiile inițiale și finale ale sarcinii, i.e.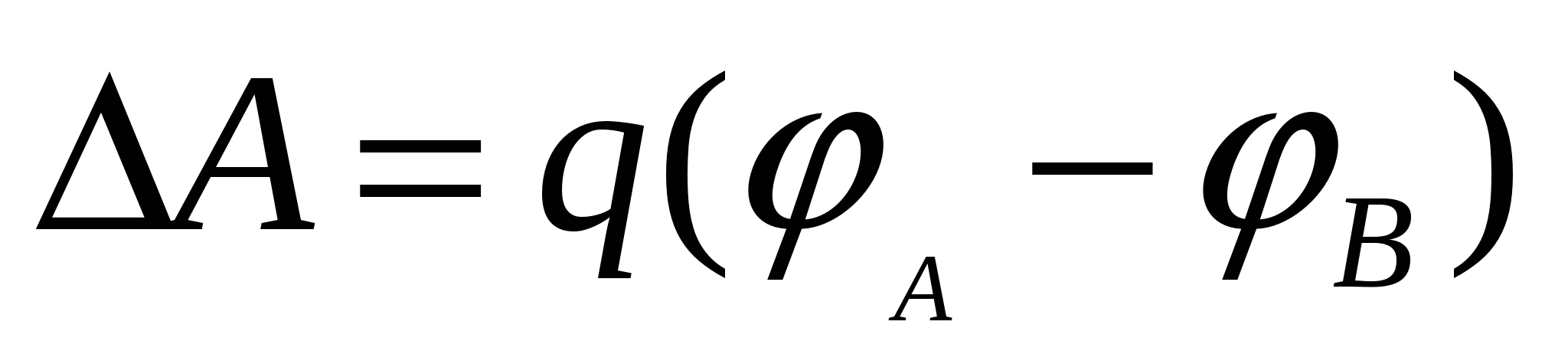

.

Deoarece mișcarea merge de-a lungul suprafeței echipotențiale, diferența de potențial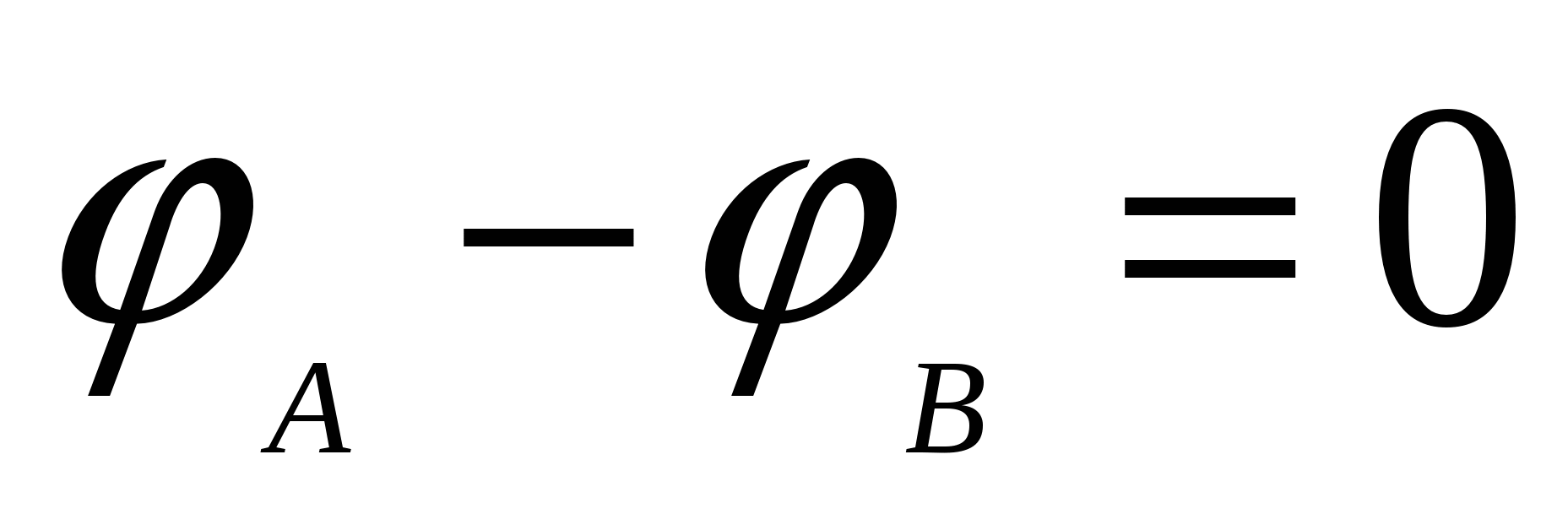

și

, sau cosα = 0, deci α = 90 0 i.e. unghiul dintre direcția forței și deplasarea ∆ S este egal cu 90 0 . Dar, i.e. direcții și potrivi, deci unghiul dintre și ∆ S, α=90 0 i.e. direcția vectorului câmp electrostatic este întotdeauna perpendiculară pe suprafața echipotențială.

Puteți desena câte suprafețe echipotențiale în jurul unui corp încărcat doriți. După densitatea suprafețelor echipotențiale, se poate judeca valoarea , cu toate acestea, cu condiția ca diferența de potențial dintre două suprafețe echipotențiale adiacente să fie egală cu o valoare constantă.

Formula exprimă relația dintre potențial și putere și permite utilizarea valorilor cunoscute ale lui φ pentru a găsi intensitatea câmpului în fiecare punct. De asemenea, este posibil să se rezolve problema inversă, adică. prin valori cunoscute în fiecare punct al câmpului găsiți diferența de potențial între două puncte arbitrare ale câmpului. Pentru a face acest lucru, folosim faptul că munca depusă de câmpul forțează pe încărcătură q la mutarea lui de la punctul 1 la punctul 2 poate fi calculată astfel:

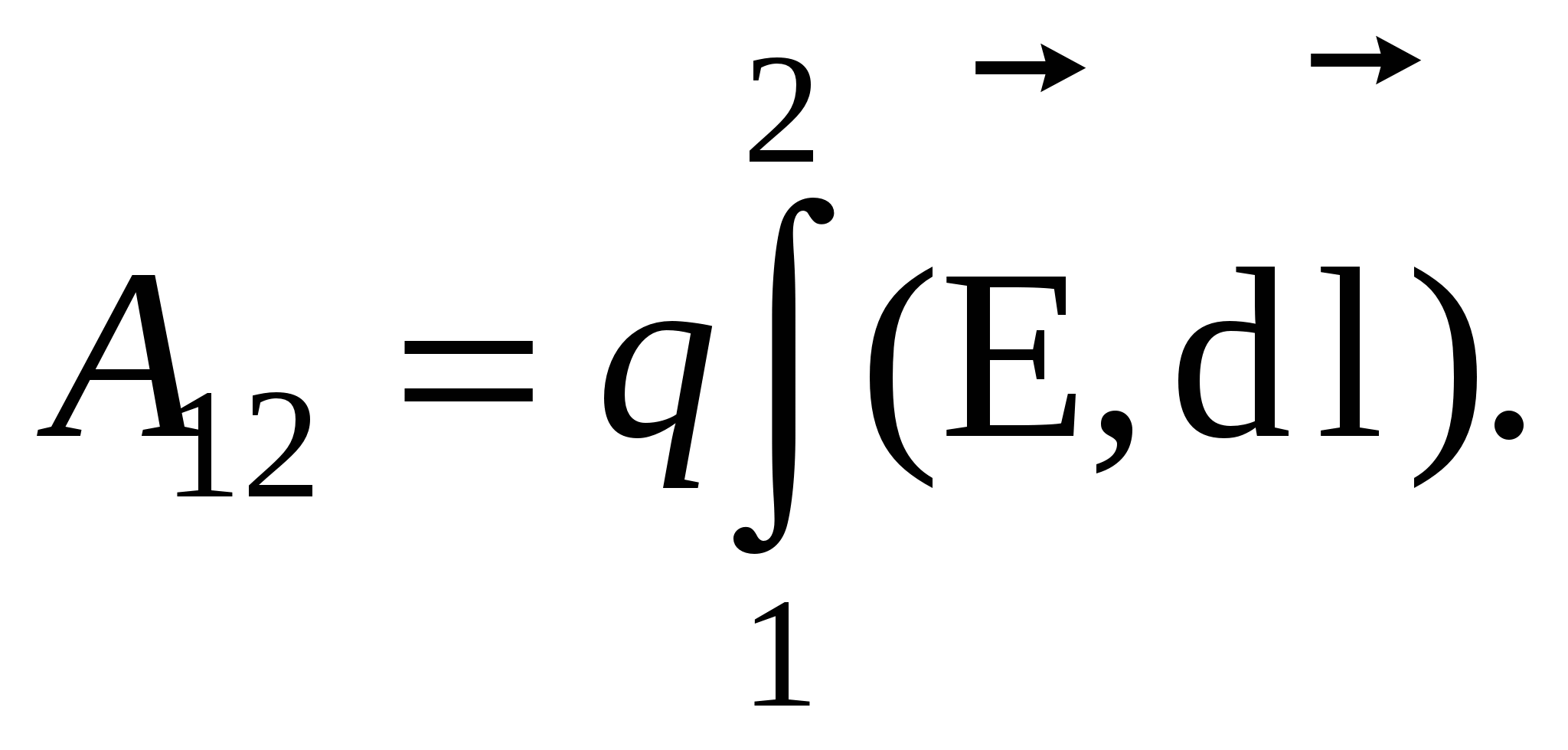
Pe de altă parte, lucrarea poate fi reprezentată astfel:

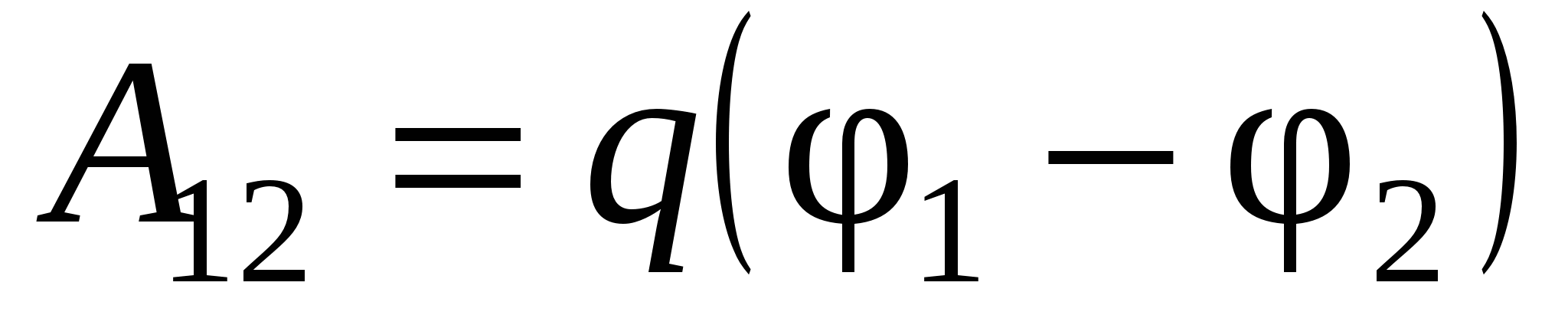, apoi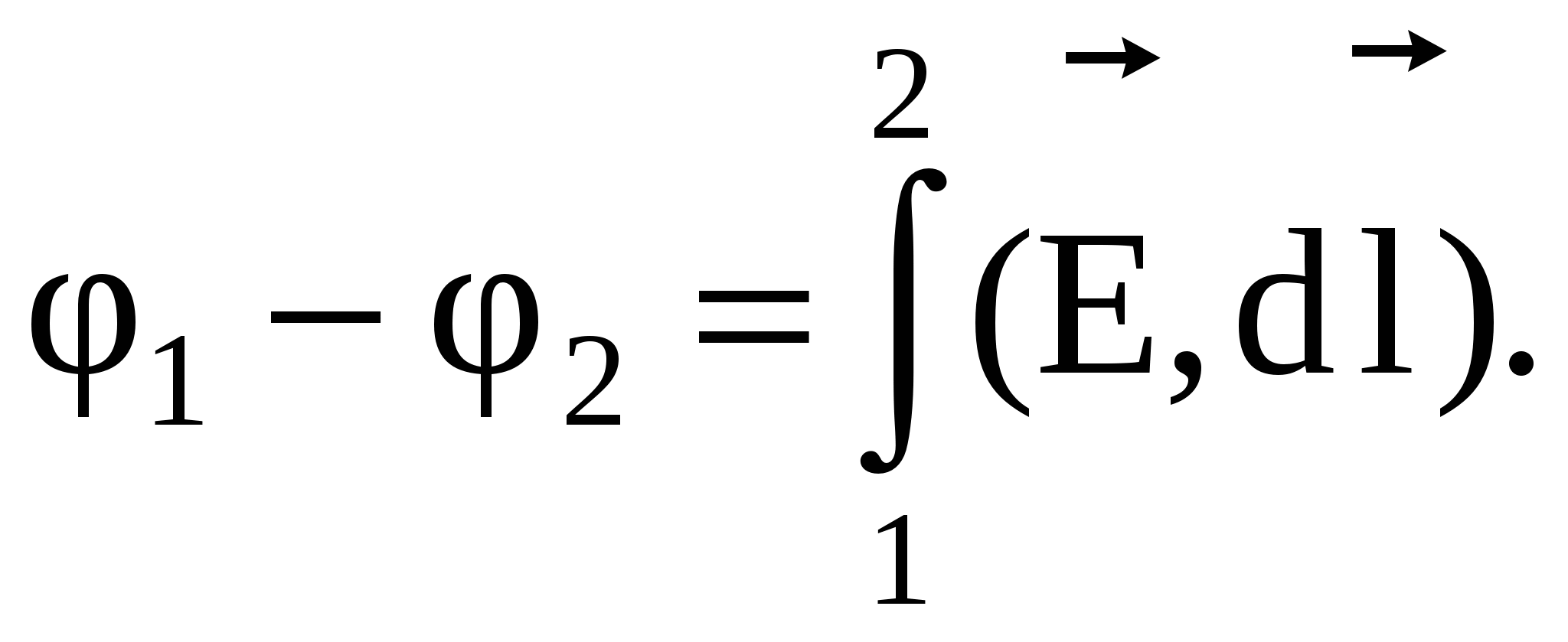

Integrala poate fi luată de-a lungul oricărei linii care leagă punctul 1 și punctul 2, deoarece munca forțelor de câmp nu depinde de cale.

La traversarea unei bucle închise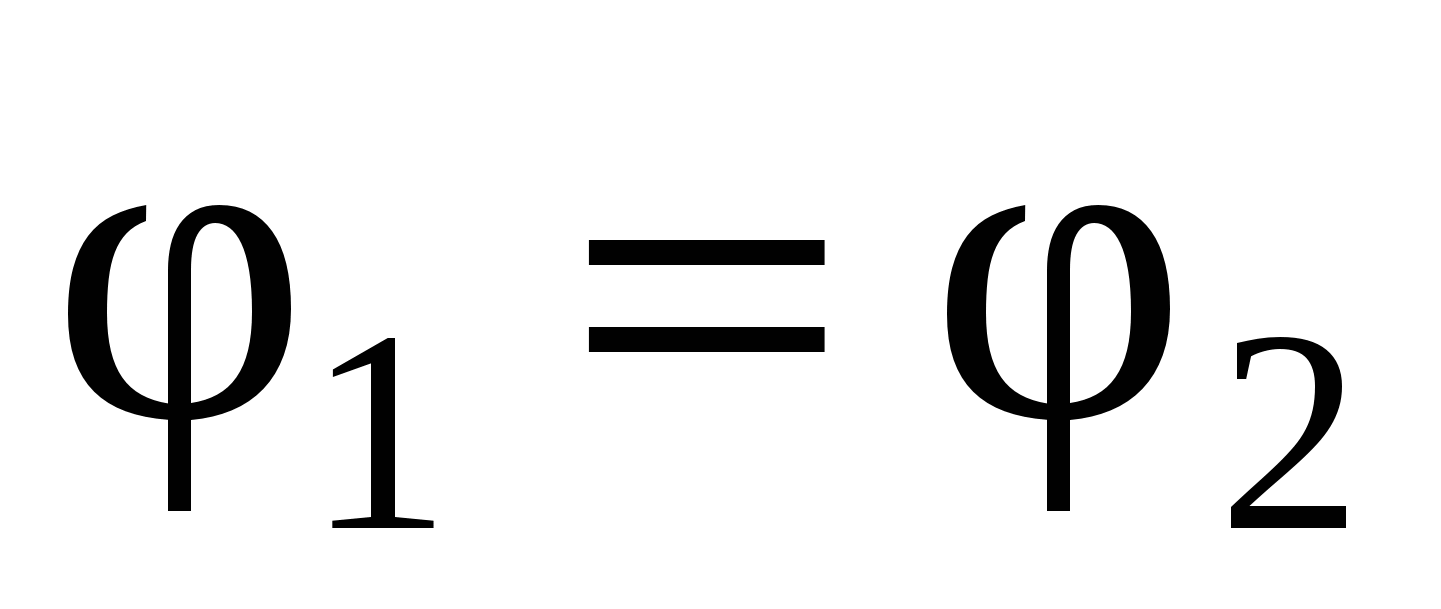

primim:

acestea. a ajuns la binecunoscuta teoremă privind circulația vectorului intensitate: circulația vectorului intensității câmpului electrostatic de-a lungul oricărei bucle închise este egală cu zero.

Un câmp cu această proprietate se numește potențial.

Din dispariția circulației vectorului rezultă că liniile câmpului electrostatic nu pot fi închise:ele încep cu sarcini pozitive(origini )și pe sarcini negative a alerga afară(drenuri )sau mergi la infinit.

Să generalizăm teorema Gauss și teorema privind circulația vectorului intensității câmpului electrostatic în vid. Din moment ce, a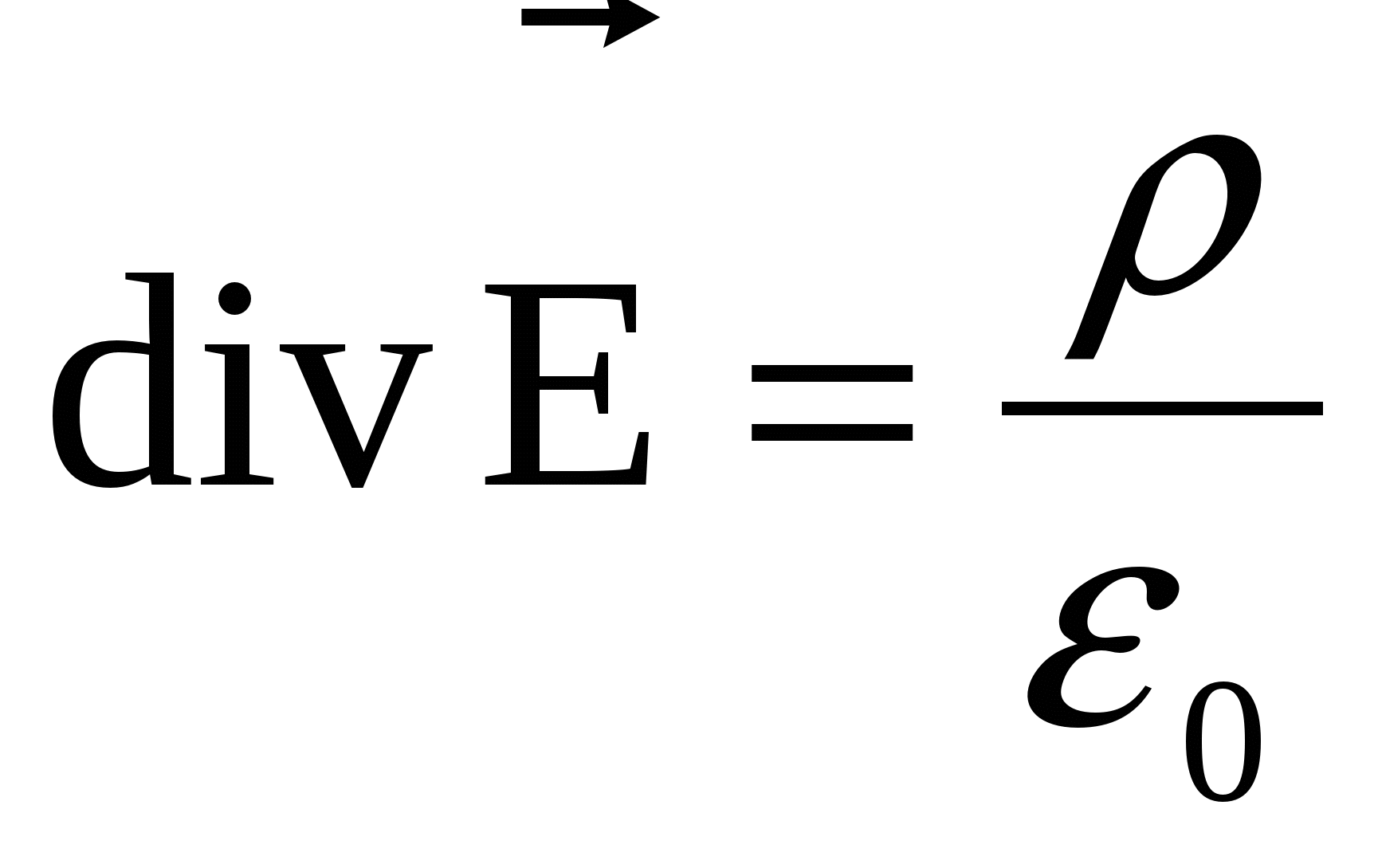

, apoi

. Pentru că

(

este operatorul Laplace), atunci pentru potențialul φ obținem expresia

sau

, Care e numit Ecuația Poisson.

Această ecuație permite, conform distribuției de sarcină cunoscute

și condiția la limită dată pentru potențialul φ pentru a determina valorile

în toate punctele câmpului și apoi folosind formula pentru a găsi tensiunea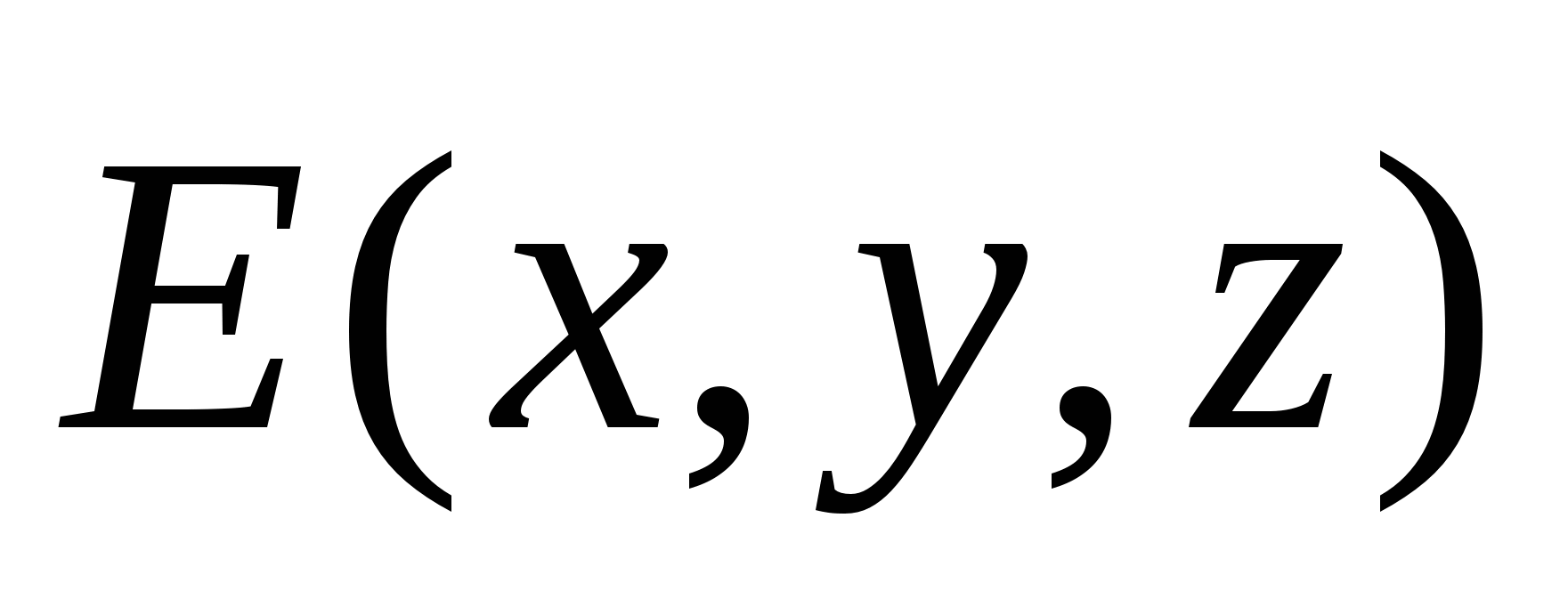

câmpuri, adică rezolva problema directa a electrostaticii.

3.7. Calculul diferenței de potențial față de intensitatea câmpului celor mai simple câmpuri electrostatice

Relația stabilită între putere și potențial permite, din puterea cunoscută a câmpului, să se găsească diferența de potențial dintre două puncte arbitrare ale acestui câmp.

Să luăm în considerare câteva exemple de calcul a diferenței de potențial dintre punctele câmpului create de unele corpuri încărcate.

1. Câmpul unui plan infinit încărcat uniform

Câmpul unui plan infinit încărcat uniform, găsit folosind teorema Ostrogradsky-Gauss, este determinat de formula

, unde σ este densitatea de sarcină la suprafață. Diferența de potențial între punctele aflate la distanțe X 1 și X 2 din avion, egal cu

.

d E = 0, între plăci potențialul scade conform legii logaritmice, iar a doua placă (în afara cilindrilor) protejează câmpul electric și φ și E sunt egale cu zero.
Figura 3.10
Pe fig. 3.10 arată dependența de tensiune E si capacitate din r.
4. Câmp al unei suprafețe sferice încărcate uniform
Luând în considerare exemple de aplicare a teoremei Ostrogradsky-Gauss, am constatat că intensitatea câmpului sferei este determinată de formula:

(Fig. 3.11). Și de când

, apoi

Figura 3.11
. Dacă acceptă r 1 = r , A r 2 =∞, atunci potențialul din afara suprafeței sferice este determinat de expresie), este determinat de formula
Prin alegerea nivelului potențialului zero la punct r 2 =∞ potențialul oricărui punct din interiorul bilei încărcate poate fi găsit după cum urmează:

. După integrare, obținem

.

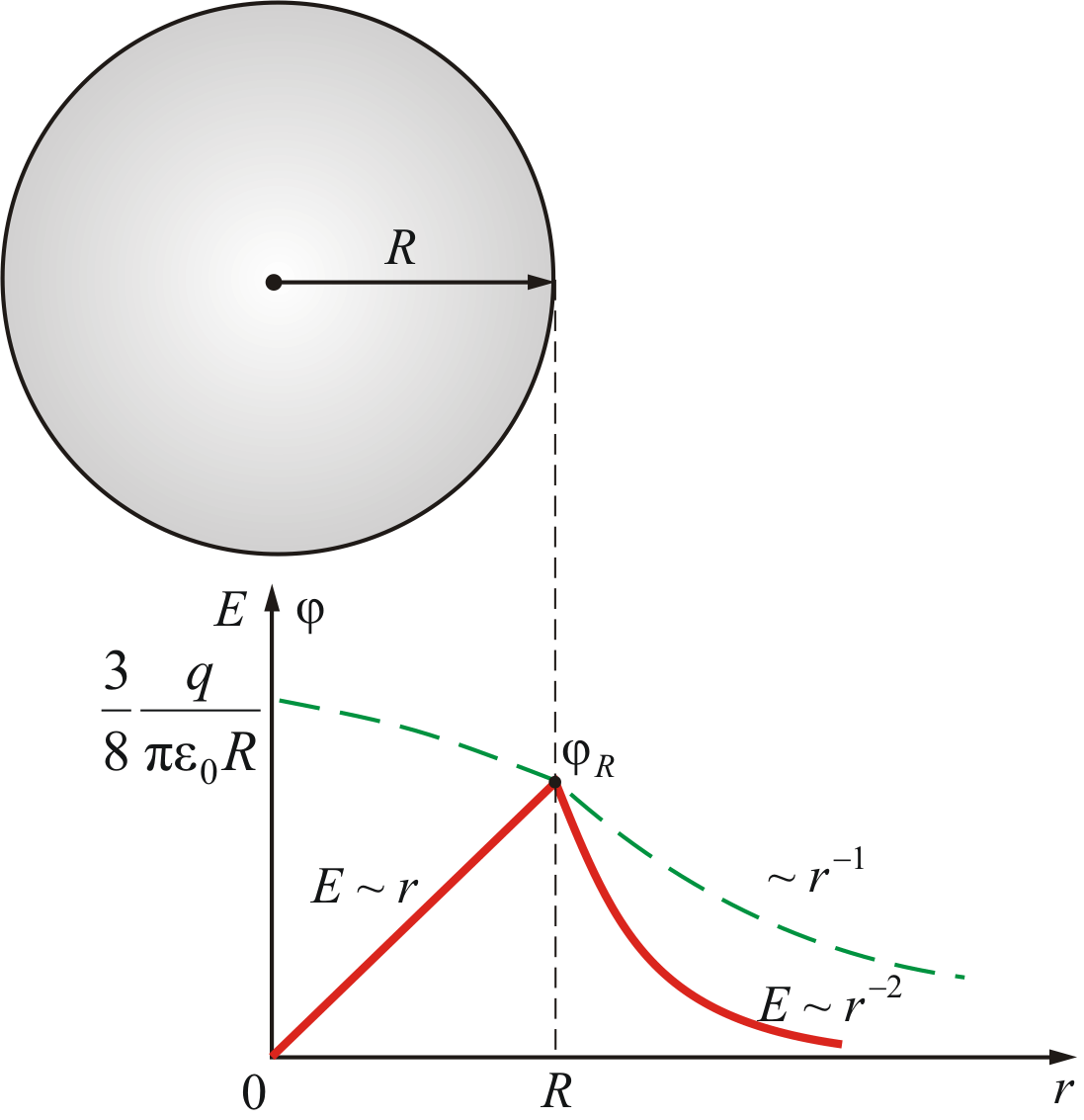
Figura 3.12
Având în vedere că

, apoi

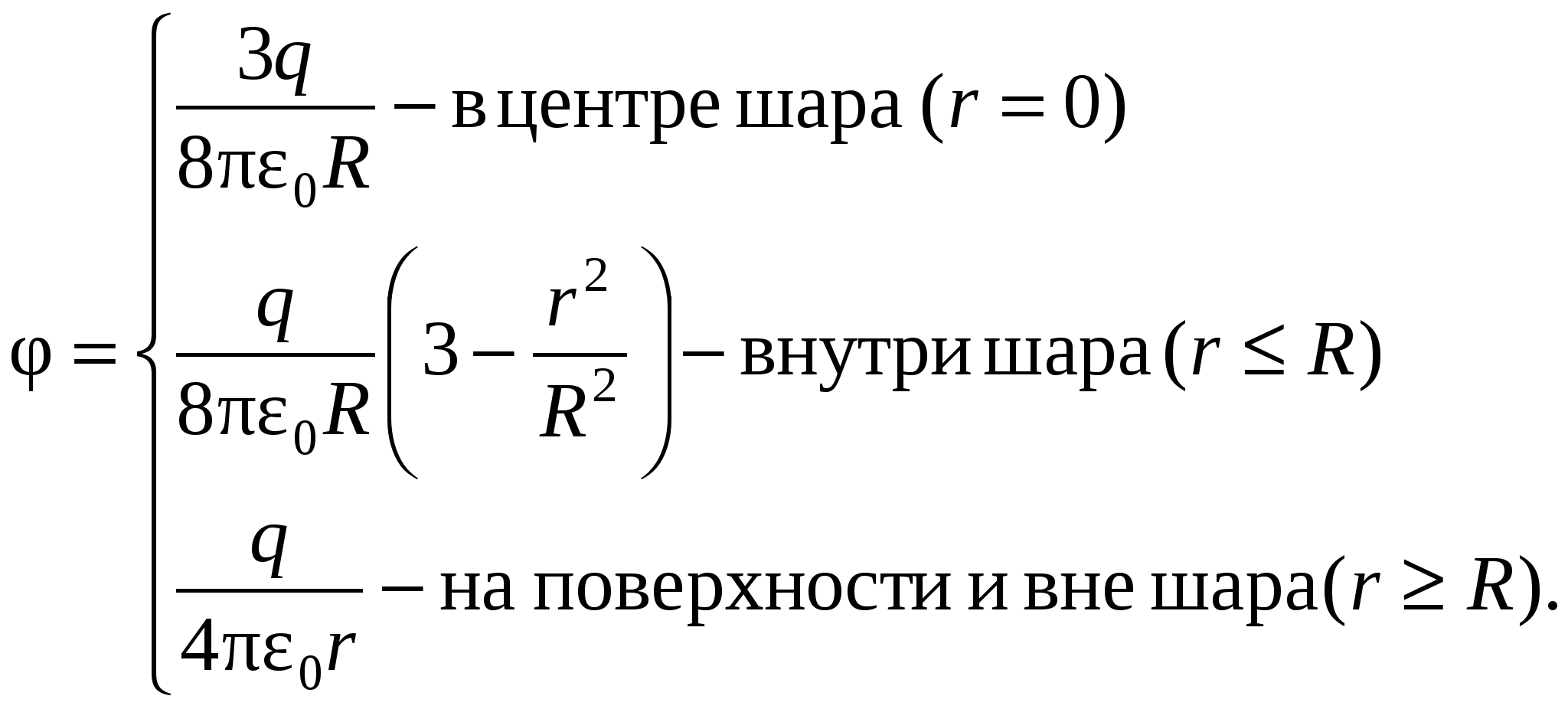( 38 )
Din relațiile obținute putem face următoarele concluzii .
- Folosind teorema Gauss, este relativ ușor să calculezi E și φ de la diferite suprafețe încărcate.
- Intensitatea câmpului în vid se modifică brusc atunci când trece printr-o suprafață încărcată.
- Potențial de câmp - întotdeauna funcție continuă coordonate.
întrebări de test
1. Cum să arăți că un câmp electrostatic este potențial?
2. Ce este potențialul?
3. Cum se numește circulația vectorului de tensiune?
4. Care este relația dintre tensiune și potențial? Cum se desenează o imagine a liniilor de câmp din imaginea suprafețelor echipotențiale?
5. Care este munca efectuată pentru a muta o sarcină pe o suprafață echipotențială?
6. Dați exemple de calcul a diferenței de potențial a celor mai simple câmpuri electrostatice.
7. Cum se comportă un dipol într-un câmp electrostatic extern?