Energie potențială sarcina intr-un camp electric. Munca făcută de forțe câmp electric când se deplasează o sarcină punctiformă pozitivă q de la poziția 1 la poziția 2, reprezintă o modificare a energiei potențiale a acestei sarcini:

Unde W n1 și W n2 - energiile potențiale ale sarcinii qîn poziţiile 1 şi 2. Pentru mici mișcarea de încărcare qîn câmpul creat de o sarcină punctiformă pozitivă Q, modificarea energiei potenţiale este

.

Odată cu mișcarea finală a încărcăturii q de la poziția 1 la poziția 2, situată la distanțe r 1 și r 2 reducere Q,

Dacă câmpul a fost creat de sistem taxe punctuale Q 1 ,Q 2 ,¼ , Q n , apoi modificarea energiei potențiale a sarcinii qîn acest domeniu:

.

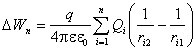Formulele de mai sus vă permit să găsiți numai Schimbare energia potenţială a unei sarcini punctiforme q mai degrabă decât energia potenţială în sine. Pentru a determina energia potențială, este necesar să cădem de acord în ce punct al câmpului să o considerăm egală cu zero. Pentru energia potențială a unei sarcini punctiforme q, situat într-un câmp electric creat de o altă sarcină punctuală Q, primim

,

Unde C este o constantă arbitrară. Fie energia potențială zero pentru infinit distanta lunga din sarcina Q(la r® ¥ ), apoi constanta C= 0 și expresia anterioară devine

În acest caz, energia potențială este definită ca munca efectuată pentru a muta o sarcină dintr-un punct dat într-un punct la infinit. În cazul unui câmp electric creat de un sistem de sarcini punctuale, energia potențială a sarcinii q:

.

Energia potențială a unui sistem de sarcini punctiforme. Când câmp electrostatic energia potențială servește ca măsură a interacțiunii sarcinilor. Să existe un sistem de sarcini punctuale în spațiu Q i(i = 1, 2, ... , n). Energie interacțiunea tuturor n taxele este determinată de raport

,

Unde rij- distanța dintre sarcinile corespunzătoare și însumarea se realizează astfel încât interacțiunea dintre fiecare pereche de sarcini să fie luată în considerare o singură dată.

Potențialul câmpului electrostatic. Câmpul de forță conservator poate fi descris nu numai funcție vectorială, dar o descriere echivalentă a acestui câmp poate fi obținută prin definirea unei valori scalare adecvate în fiecare dintre punctele sale. Pentru un câmp electrostatic, această mărime este potențial de câmp electrostatic, definit ca raportul dintre energia potențială a sarcinii de testare q la mărimea acestei sarcini, j = W P / q, de unde rezultă că potențialul este numeric egal cu energia potențială pe care o unitate de sarcină pozitivă o are într-un punct dat al câmpului. Unitatea de măsură a potențialului este Volt (1 V).

Potenţialul câmpului unei sarcini punctiforme Qîntr-un mediu izotrop omogen cu permisivitatea e :

Principiul suprapunerii. Potențialul este o funcție scalară, principiul suprapunerii este valabil pentru acesta. Deci pentru potențialul de câmp al unui sistem de sarcini punctuale Q 1, Q 2 ¼ ,Qn avem

,

Unde ri- distanta fata de punctul campului, care are potentialul j, înainte de încărcare Q i. Dacă sarcina este distribuită aleatoriu în spațiu, atunci

,

Unde r- distanta fata de volumul elementar d X, d y, d z până la punctul ( X, y, z), unde potenţialul este determinat; V este volumul spațiului în care este distribuită sarcina.

Potențialul și munca forțelor câmpului electric. Pe baza definiției potențialului, se poate demonstra că munca câmpului electric forțează la deplasarea unei sarcini punctiforme q de la un punct al câmpului la altul este egal cu produsul dintre mărimea acestei sarcini și diferența de potențial la punctele inițiale și finale ale căii, A=q (j 1 - j 2 ) .
Dacă, prin analogie cu energia potențială, presupunem că în puncte infinit îndepărtate de sarcinile electrice - sursele de câmp, potențialul este zero, atunci munca forțelor câmpului electric atunci când se deplasează sarcina q de la punctul 1 la infinit poate fi reprezentat ca A ¥ = qj 1 .
Astfel, potențialul â într-un punct dat al câmpului electrostatic este cantitate fizica, numeric egal cu munca, efectuată de forțele câmpului electric atunci când se deplasează o unitate de sarcină punctuală pozitivă dintr-un punct dat al câmpului la un infinit îndepărtat: j = A ¥ / q.
În unele cazuri, potențialul câmpului electric este definit mai clar ca mărime fizică egală numeric cu munca forțelor externe împotriva forțelor câmpului electric atunci când se deplasează o singură sarcină punctiformă pozitivă de la infinit la punct dat . Ultima definiție poate fi scrisă convenabil după cum urmează:

LA stiinta modernași tehnologie, în special atunci când descriem fenomene care au loc în microlume, este adesea folosită o unitate de muncă și energie, numită electron volt(eV). Aceasta este munca efectuată în deplasarea încărcăturii. egal cu taxa electron, între două puncte cu o diferență de potențial de 1 V: 1 eV = 1,60 × 10 - 1 9 cl × 1 V = 1,60 × 10 - 1 9 J.

Întrebări

1) Dați definiția potențialului unui punct dat al câmpului și diferența de potențial a două puncte ale câmpului.

2) Oferiți grafice ale intensității câmpului și potențialului față de distanță pentru o suprafață sferică încărcată uniform. Dați-le explicația și justificarea.

Începem prin a discuta energia potențială pe care o are o sarcină într-un câmp electrostatic. În primul rând, este necesar să reamintim condițiile în care este în general posibilă introducerea conceptului de energie potențială.

4.1 Forțele conservatoare

O forță se numește conservatoare (sau potențială) dacă munca acestei forțe nu depinde de forma traiectoriei și este determinată doar de pozițiile inițiale și finale ale corpului.

Fie, de exemplu, corpul sub acțiunea unei forțe conservatoare ~ deplasat de la inițială

de la punctul 1 până la punctul final 2 (Fig. 16). Atunci munca efectuată de forță depinde doar de poziție

punctele 1 și 2 în sine, dar nu din traiectoria corpului. De exemplu, pentru traiectorii 1 ! A! 2 si 1! b! 2 valoarea lui A va fi aceeași.

Orez. 16. Despre conceptul de forță conservatoare

Rețineți că munca efectuată de o forță conservatoare de-a lungul oricărei căi închise este zero. Într-adevăr, să lăsăm punctul 1 de-a lungul traiectoriei 1! A! 2 și întoarceți-vă pe traiectoria 2! b! 1. Pe prima traiectorie, forța va face lucrul A, iar pe a doua traiectorie, munca va fi egală cu A. Ca urmare, munca totală va fi zero.

Deci, conceptul de energie potențială poate fi introdus doar în cazul unei forțe conservatoare. Energia potențială W este o expresie matematică care depinde de coordonatele corpului, astfel încât munca forței să fie egală cu modificarea acestei expresii cu semnul minus:

Sau, care este la fel:

A = (W2 W1 ) = W1 W2 :

După cum puteți vedea, munca unei forțe conservatoare este diferența dintre valorile energiei potențiale calculate pentru pozițiile inițiale și, respectiv, finale ale corpului.

Exemple de forțe conservatoare vă sunt bine cunoscute. De exemplu, gravitația este conservatoare. Forța arcului este, de asemenea, conservatoare. De aceea se poate vorbi despre energia potențială a unui corp ridicat deasupra solului, sau despre energia potențială a unui arc deformat.

Dar forța de frecare nu este conservativă: munca forței de frecare depinde de forma traiectoriei și nu este egală cu zero pe o cale închisă. Prin urmare, nu există ¾energie potențială a corpului în câmpul forței de frecare¿.

4.2 Potenţialitatea câmpului electrostatic

Se dovedește că forța cu care acționează câmpul electrostatic asupra unui corp încărcat este, de asemenea, conservativă. Lucrul acestei forțe, efectuat la deplasarea sarcinii, se numește lucrul câmpului electrostatic. Astfel, avem cel mai important fapt:

Lucrarea câmpului electrostatic nu depinde de forma traiectoriei de-a lungul căreia se mișcă sarcina și este determinată doar de pozițiile inițiale și finale ale sarcinii. Lucrul câmpului de-a lungul unei căi închise este zero.

Acest fapt se mai numește și potențialul câmpului electrostatic. Ca și câmpul gravitațional, câmpul electrostatic este potențial. Lucrarea unui câmp electrostatic este aceeași pentru toate căile pe care o sarcină se poate deplasa dintr-un punct fix în spațiu în altul.

O demonstrație matematică riguroasă a potențialității unui câmp electrostatic este în afara scopului curiculumul scolar. Totuși, ¾la nivel fizic de rigoare¿ putem verifica validitatea acestui fapt cu ajutorul următorului raționament simplu.

Este ușor de observat că, dacă câmpul electrostatic nu ar fi potențial, atunci ar fi posibil să se construiască o mașină cu mișcare perpetuă! Într-adevăr, atunci ar exista o traiectorie închisă, când sarcina se mișcă de-a lungul căreia câmpul ar face o muncă pozitivă (și nicio modificare nu ar avea loc în corpurile înconjurătoare). Ne întoarcem sarcina pe această traiectorie, extragem o cantitate nelimitată de energie de nicăieri și toate problemele energetice ale omenirii sunt rezolvate :-) Dar asta, din păcate, nu se observă, contrazice în mod flagrant legea conservării energiei.

Deoarece câmpul electrostatic este potențial, putem vorbi despre energia potențială a sarcinii în acest câmp. Să începem cu un caz simplu și important.

4.3 Energia potențială de încărcare într-un câmp uniform

Energia potențială a unui corp ridicat deasupra solului este egală cu mgh. Cazul unei sarcini într-un câmp uniform se dovedește a fi foarte asemănător cu această situație mecanică.

Se consideră un câmp electrostatic uniform E, ale cărui linii de intensitate sunt îndreptate de-a lungul axei X (Fig. 17). Lăsați sarcina pozitivă q să se miște de-a lungul liniei de forță de la punctul 1 (cu coordonata x1) la punctul 2 (cu coordonata x2).

0x1

Orez. 17. Mișcarea unei sarcini într-un câmp uniform

Câmpul acționează asupra sarcinii cu o forță ~ , care este îndreptată de-a lungul liniilor de tensiune. Muncă

această forță, după cum este ușor de văzut, va fi egală cu:

A = F (x2 x1 ) = qE(x2 x1 ):

Ce se va schimba dacă punctele 1 și 2 nu se află pe aceeași linie de tensiune? Se dovedește că nimic! Formula pentru munca de teren va rămâne aceeași. Vom verifica acest lucru cu ajutorul Fig. optsprezece .

0x1

Orez. 18. Mișcarea unei sarcini într-un câmp uniform

Trecând de la punctul 1 la punctul 2, să alegem calea 1! 3! 2, unde punctul 3 se află pe aceeași linie de câmp cu punctul 1. Atunci lucrul A32 din secțiunea 32 este zero deoarece ne deplasăm perpendicular pe forță. Ca rezultat, obținem:

A = A13 + A32 = A13 = qE(x2 x1 ):

Vedem că munca câmpului depinde doar de abscisa pozițiilor inițiale și finale ale sarcinii. Scriem formula rezultată după cum urmează:

A = qEx2 qEx1 = ((qEx2 ) (qEx1 )) = (W2 W1 ) = W:

Aici W1 = qEx1 , W2 = qEx2 . Lucrarea câmpului, în conformitate cu formula (8), se dovedește a fi egală cu modificarea cu semnul minus al valorii

Această valoare este energia potențială a sarcinii într-un câmp electrostatic uniform. X indică abscisa punctului în care se caută energia potențială. Nivelul zero al energiei potențiale în acest caz corespunde originii x = 0 și este reprezentat în figuri printr-o linie punctată perpendiculară pe liniile de tensiune4.

Reamintim că, deocamdată, se consideră q > 0. Din formula (9) rezultă că atunci când o sarcină se mișcă de-a lungul unei linii de câmp, energia potențială scade odată cu creșterea x. Acest lucru este firesc: la urma urmei, câmpul face o activitate pozitivă, accelerând încărcarea și energie kinetică sarcina crește datorită scăderii energiei sale potențiale.

Este ușor de arătat că formula (9) rămâne valabilă pentru q< 0. В этом случае потенциальная энергия возрастает с ростом x. Это тоже понятно: ведь сила, с которой поле действует на заряд, теперь будет направлена влево, так что движение заряда вправо будет осуществляться против действия поля. Заряд тормозится полем, кинетическая энергия заряда уменьшается, а потенциальная энергия увеличивается.

Deci, o concluzie importantă: în formula pentru energia potențială, q denotă valoarea algebrică a sarcinii (ținând cont de semn), și nu modulul acesteia.

4 De fapt, nivelul zero al energiei potențiale poate fi ales oriunde. Cu alte cuvinte, energia potențială este definită numai până la o constantă aditivă arbitrară C, adică W = qEx+C. Nu este nimic greșit cu o astfel de incertitudine: energia potențială în sine are sens fizic, iar diferența de energii potențiale este egală cu munca câmpului. În această diferență, constanta C se anulează.

4.4 Energia potențială de interacțiune a sarcinilor punctiforme

Fie două sarcini punctiforme q1 și q2 să fie în vid la o distanță r una de cealaltă. Se poate demonstra că energia potențială a interacțiunii lor este dată de formula:

		kq1 q2

Acceptăm formula (10) fără dovezi. Două caracteristici ale acestei formule ar trebui discutate.

În primul rând, unde este nivelul zero al energiei potențiale? La urma urmei, energia potențială, așa cum se poate vedea din formula (10), nu poate ajunge la zero. Dar, de fapt, nivelul zero există și este la infinit. Cu alte cuvinte, atunci când sarcinile sunt situate infinit departe una de cealaltă, se presupune că energia potențială a interacțiunii lor este zero (ceea ce este logic în acest caz, încărcăturile deja ¾nu interacționează¿).

În al doilea rând, q1 și q2 sunt din nou cantități algebrice de sarcini, adică sarcini, ținând cont de semnul lor.

De exemplu, energia potențială a interacțiunii a două sarcini similare va fi pozitivă. De ce? Dacă le lăsăm să plece, vor începe să accelereze și să se îndepărteze unul de celălalt. Energia lor cinetică crește, astfel încât energia lor potențială scade. Dar la infinit, energia potențială dispare și, deoarece scade la zero, atunci este pozitivă.

Dar energia potențială de interacțiune a sarcinilor opuse se dovedește a fi negativă. Într-adevăr, să le îndepărtăm la o distanță foarte mare unul de celălalt, astfel încât energia potențială să fie zero și să eliberăm. Sarcinile vor începe să se accelereze, se apropie, iar energia potențială scade din nou. Dar dacă era zero, atunci unde ar trebui să scadă? Doar spre valori negative.

Formula (10) ajută și la calcularea energiei potențiale a unui sistem de sarcini dacă numărul de sarcini este mai mare de două. Pentru a face acest lucru, trebuie să însumați energiile fiecărei perechi de sarcini. Nu vom emite formula generala; Să ilustrăm mai bine ceea ce s-a spus cu un exemplu simplu, prezentat în Fig. 19.

Orez. 19. Interacțiunea a trei sarcini

Dacă sarcinile q1, q2, q3 sunt la vârfurile unui triunghi cu laturile a, b, c, atunci energia potențială a interacțiunii lor este egală cu:

		kq1 q2		kq2 q3		kq1 q3

4.5 Potenţial

Din formula W = qEx vedem că energia potențială a unei sarcini q într-un câmp uniform este direct proporțională cu această sarcină.

Același lucru îl vedem și din formula W = kq1 q2 =r: energia potențială a unei sarcini q1 situată în câmpul unei sarcini punctuale q2 este direct proporțională cu sarcina q1 .

În cazul în care un corp electric acționează asupra corpurilor încărcate electric, atunci este capabil să facă munca de mișcare a corpurilor încărcate. Câmpul electrostatic creat de o sarcină punctiformă este central, adică forța care acționează asupra unei sarcini punctiforme într-un astfel de câmp este îndreptată de-a lungul liniei drepte care leagă sarcina sursă și sarcina de testare. Mai devreme am arătat că orice forță centrală este potențială, adică munca acestei forțe nu depinde de forma traiectoriei, ci este determinată doar de poziția inițială și finală a corpului.

Să ne amintim pe scurt dovada acestei cele mai importante afirmații. Fie ca o sarcină de testare punctuală q să se miște în câmpul central creat de o sarcină fixă ​​Q (Fig. 174). Forța care acționează asupra sarcinii de testare este determinată de legea lui Coulomb

Unde este vectorul tras de la sarcina sursă Q până la punctul A, unde se află sarcina de testare. Când o sarcină se mișcă de-a lungul arcurilor de cerc centrate pe sarcina Q (de exemplu, de-a lungul arcurilor AB, CD), se lucrează forta electrica este egal cu zero, deci vectorii forței și deplasării sunt reciproc perpendiculari. Când se deplasează în direcția radială (de exemplu, de-a lungul segmentelor BC, DE), munca depinde numai de distanța inițială și finală până la sarcina sursă. Deci munca câmpului electrostatic atunci când se deplasează de-a lungul segmentelor DE și D1E1 sunt în mod evident egale. Cea mai frumoasă dovadă a acestei afirmații este legată de simetria câmpului - să ne rotim sistemul în jurul axei care trece prin sursă, astfel încât segmentul D1E1 să coincidă cu segmentul DE - distribuția câmpului nu se va schimba, de ce ar trebui munca câmpului se schimbă?

Deoarece principiul suprapunerii este valabil pentru intensitatea unui câmp electrostatic, orice câmp electrostatic este potențial. Într-adevăr, să fie o sarcină punctiformă q într-un câmp electric creat de un sistem de sarcini punctiforme fixe Q1, Q2, … ,QN . Când mutați sarcina la un vector de deplasare mică, prin definiție, câmpul electric va face treaba, unde

Forța rezultată care acționează asupra sarcinii în mișcare q, egală cu suma forțelor care acționează din fiecare dintre sarcinile punctuale Qk. Lucrul acestei forțe poate fi calculat prin formula

Pentru a calcula munca pe secțiunea finală a traiectoriei, este necesar să împărțiți traiectoria în secțiuni mici (Fig. 175), apoi să utilizați formula (1) pentru a calcula munca pe fiecare secțiune mică și apoi să le însumați

. (2) De fapt, această sumă este dublă, deoarece fiecare forță rezultantă este suma forțelor, conform formulei (1). Rețineți că în formula (2) forța rezultată se modifică, deoarece este calculată în puncte diferite traiectorii.

După cum am arătat mai devreme, munca câmpului electric al unei sarcini punctuale nu depinde de forma traiectoriei, adică fiecare termen din formula (1) nu depinde de forma traiectoriei, prin urmare, întreaga sumă. nu depinde de forma traiectoriei. Astfel, orice câmp electrostatic este potențial.

Prin urmare, pentru o sarcină punctiformă într-un câmp electrostatic, se poate introduce energia potențială a interacțiunii U(x, y, z). Această funcție are următoarea semnificație fizică: munca câmpului electric la mutarea unei sarcini punctiforme dintr-un punct cu coordonatele (x1,y1,z1) în altul, cu coordonatele (x2,y2,z2) este egală cu modificarea potențialului energie, luată cu semnul opus:

. (3) Schimbare de conectare această definiție destul de logic: dacă câmpul electric a făcut lucru pozitiv (A > 0), atunci energia sa scade (ΔU< 0). Для вычисления работы силы взаимодействия между двумя точечными заряженными телами достаточно подсчитать эту работу при движении вдоль радиального отрезка при изменении расстояния от r1 до r2 (Рис. 176). Если построить зависимость силы взаимодействия между зарядами от расстояния r между телами, тогда площадь под графиком этой зависимости в указанных пределах и будет равна искомой работе (Рис. 177). Зависимость силы электростатического взаимодействия от расстояния аналогична силе гравитационного взаимодействия, с одним существенным отличием: гравитационная сила всегда есть сила притяжения, а электрическая может быть как силой притяжения, так и силой отталкивания. В частности два sarcină pozitivă respinge. Prin urmare, expresia pentru lucrul câmpului electric va fi similară cu formula pentru lucrul forței gravitaționale, dar va avea semnul opus

Această muncă este egală cu scăderea energiei potențiale de interacțiune, adică Din această expresie, puteți determina expresia energiei potențiale a interacțiunii electrostatice a două sarcini punctuale. (4) Cu această definiție, energia potențială de interacțiune a două sarcini de același semn este pozitivă și tinde spre zero la o distanță infinită între corpuri. Forța de interacțiune a sarcinilor de semne opuse este îndreptată în sens opus, deci lucrul acestei forțe cu creșterea distanței dintre sarcini va fi negativ. Cu toate acestea, nu trebuie să facem rezerve suplimentare, deoarece formula (4) ia în considerare automat semnele sarcinilor - dacă sarcinile sunt opuse, atunci produsul lor (respectiv, energia) este negativ. Semnul energiei potențiale a interacțiunii sarcinilor are o semnificație foarte clară. Sarcinile de același semn se resping, prin urmare, atunci când „fug” la o distanță infinit de mare, câmpul electric va face lucru pozitiv - prin urmare, inițial sistemul acestor sarcini are capacitatea de a lucra, prin urmare energia sa este pozitivă, când sarcinile se îndepărtează una de cealaltă, energia lor scade la zero. Sarcinile de semne opuse se atrag, pentru a le îndepărta la o distanță infinită, forțele externe trebuie să facă un lucru pozitiv. În acest caz, energia unei perechi de sarcini ar trebui să crească, prin urmare, inițial este negativă, iar atunci când sarcinile sunt îndepărtate una de cealaltă, crește la zero. În general, situația obișnuită este aceea că atracția corespunde energiei negative, iar repulsia - pozitivă. Observăm doar că astfel de dovezi sunt valabile numai atunci când se alege nivelul zero al energiei potențiale la infinit. Formula (4) determină energia potențială a interacțiunii a două corpuri încărcate punctiforme. Valorile sarcinilor corpurilor Q și q intră, așa cum era de așteptat, simetric în această formulă. Împărțirea taxelor într-o taxă sursă și o taxă de test este condiționată, acestea putând fi complet interschimbate. Prin urmare, este de preferat să scriem această formulă într-o formă simetrică: energia de interacțiune a două sarcini punctuale q1 și q2 este , sau ambele sarcini se mișcă, în sfârșit, indiferent de traiectoriile de mișcare ale ambelor sarcini. În plus, este imposibil să spunem cărei sarcină particulară „aparține” această energie, în viitor vom arăta că energia interacțiunii sarcinilor face parte din energia câmpului electrostatic în sine, adică este „untată” pe întregul spațiu în care există câmpul creat de aceste sarcini. Dacă sistemul este format din mai mult de două sarcini, atunci pentru a calcula energia de interacțiune a acestor sarcini, este necesar să se însumeze energiile de interacțiune ale tuturor perechilor de sarcini.

aici Uik este energia de interacțiune a sarcinilor qi și qk situate la distanță rik una de cealaltă (Fig. 178).

40 Întrebare:

Câmp electrostatic - el. câmp de sarcină staționară.

Fel, acționând în funcție de încărcătură, o mută, lucrând. Într-un câmp electric uniform Fel = qE - constant

Lucrul câmpului (forța electronică) nu depinde de forma traiectoriei și de o traiectorie închisă = zero.

ENERGIA POTENȚIALĂ A UNUI CORPS ÎNCĂRCAT ÎN UN CÂMP ELECTROSTATIC HOMOGEN

Energia electrostatică este energia potențială a unui sistem de corpuri încărcate (deoarece interacționează și sunt capabile să lucreze).

Deoarece munca câmpului nu depinde de forma traiectoriei, atunci în același timp

comparând formulele de lucru, obținem energia potențială a sarcinii într-un câmp electrostatic uniform

Dacă câmpul face o activitate pozitivă (împreună linii de forță), apoi energia potențială

a unui corp încărcat scade (dar conform legii conservării energiei, energia cinetică crește) și invers.

POTENȚIALUL CÂMPULUI ELECTROstatic

Caracteristica energetică el. câmpuri.

Este egal cu raportul dintre energia potențială a sarcinii din câmp și această sarcină.

O valoare scalară care determină energia potențială a încărcării în orice punct al e-mailului. câmpuri.

Valoarea potențială este considerată relativ la nivelul zero selectat.

DIFERENTA DE POTENȚIAL (sau altfel TENSIUNE)

Aceasta este diferența de potențial la punctele de început și de sfârșit ale traiectoriei de încărcare.

Tensiunea dintre două puncte (U) este egală cu diferența de potențial a acestor puncte și este egală cu munca câmpului în deplasarea unei unități de sarcină.

RELAȚIA DINTRE FORȚA CÂMPULUI ȘI DIFERENȚA DE POTENȚIAL

§ 12.3 Lucrul forţelor câmpului electrostatic. Potenţial. Suprafețe echipotențiale

O sarcină q pr plasată într-un punct arbitrar al unui câmp electrostatic cu o putere E este supusă unei forțe F = q pr E. Dacă sarcina nu este fixă, atunci forța o va face să se miște și, prin urmare, se va lucra. . Lucrul elementar efectuat de forța F la deplasarea unei sarcini electrice punctiforme q pr din punctul a al câmpului electric în punctul b pe un segment al drumului dℓ, prin definiție, este egal cu

(α este unghiul dintre F și direcția de mișcare) (Fig. 12.13).

Dacă se lucrează forțe externe, apoi dA< 0 , если силами поля, то dA >0. Integrând ultima expresie, obținem că lucrează împotriva forțelor câmpului la deplasarea q pr din punct A la punctul b

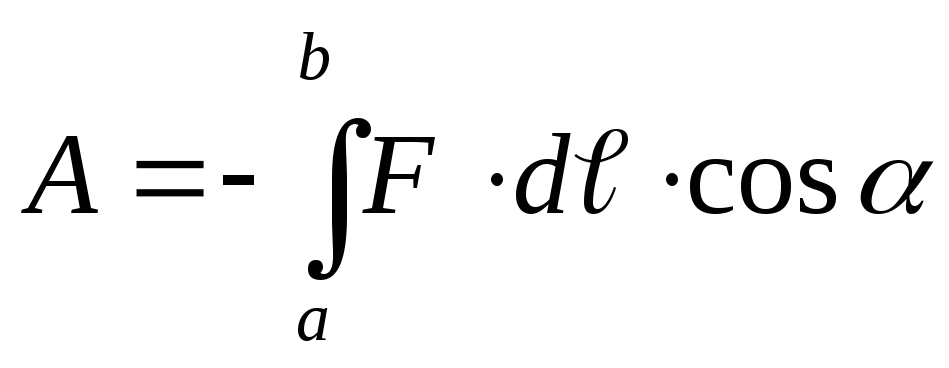(12.20)

Figura -12.13

(

- Forța Coulomb care acționează asupra sarcinii de încercare q pr în fiecare punct al câmpului cu puterea E).

Atunci lucrează

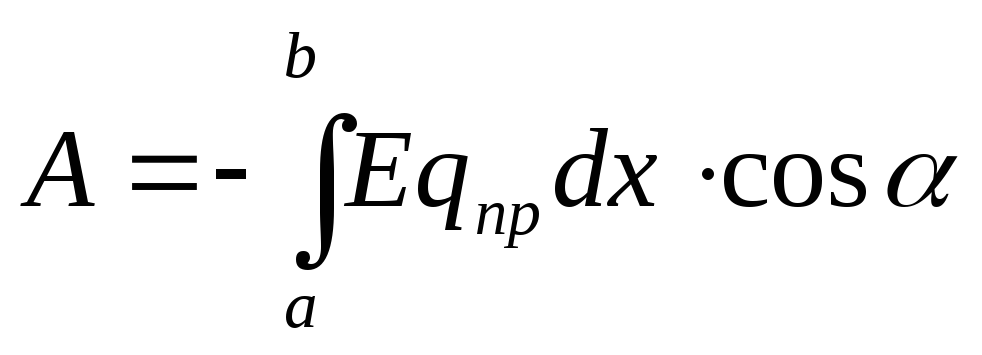(12.21)

Mișcarea este perpendiculară pe vector , deci cosα =1, lucru de transfer de sarcină de test q pr din A la b este egal cu

(12.22)

Lucrarea forțelor câmpului electric la deplasarea sarcinii nu depinde de forma căii, ci depinde doar de poziție relativă punctele de început și de sfârșit ale traiectoriei.

Prin urmare, câmpul electrostatic al unei sarcini punctuale estepotenţial , iar forțele electrostatice suntconservator .

Aceasta este o proprietate a câmpurilor potențiale. Din aceasta rezultă că munca efectuată într-un câmp electric de-a lungul unui circuit închis este egal cu zero:

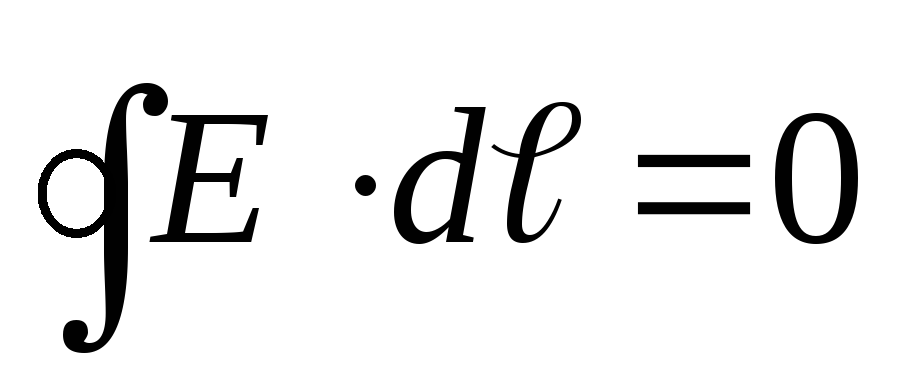(12.23)

Integral

numit circulația vectorului de tensiune . Din dispariția circulației vectorului E, rezultă că liniile intensității câmpului electrostatic nu pot fi închise, ele încep pe sarcini pozitive și se termină pe sarcini negative.

După cum știți, munca forțelor conservatoare este efectuată din cauza pierderii de energie potențială. Prin urmare, munca forțelor câmpului electrostatic poate fi reprezentată ca diferența de energii potențiale pe care o sarcină punctiformă q pr o are în punctele inițiale și finale ale câmpului de sarcină q:

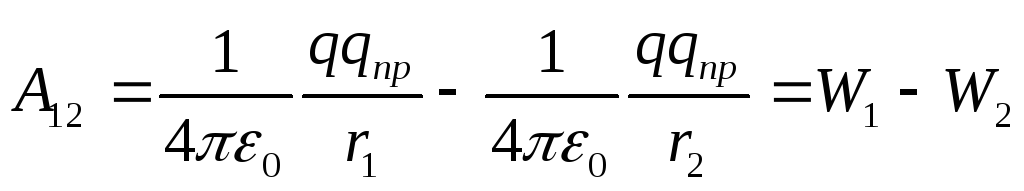(12.24)

de unde rezultă că energia potenţială a sarcinii q pr în câmpul sarcinii q este egală cu

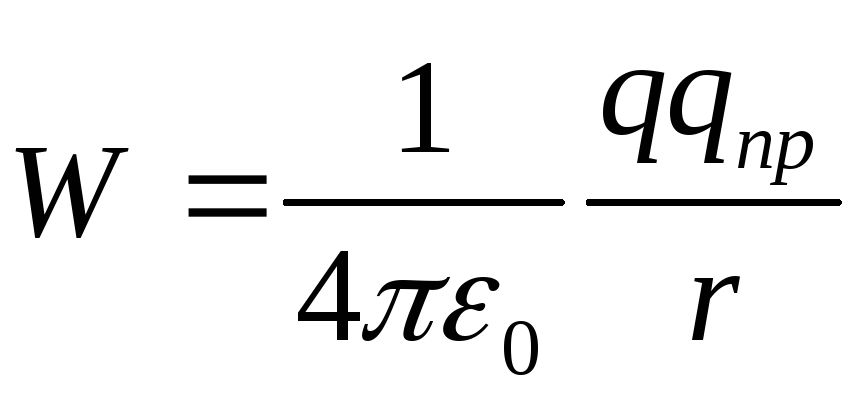(12.25)

Pentru sarcini asemănătoare q pr q >0 și energia potențială a interacțiunii lor (repulsie) este pozitivă, pentru sarcini diferite q pr q< 0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Dacă câmpul este creat de un sistem de n sarcini punctiforme q 1, q 2, .... q n , atunci energia potențială U a sarcinii q pr situată în acest câmp este egală cu suma energiilor sale potențiale U i create de fiecare dintre sarcini separat:

(12.26)

Atitudine 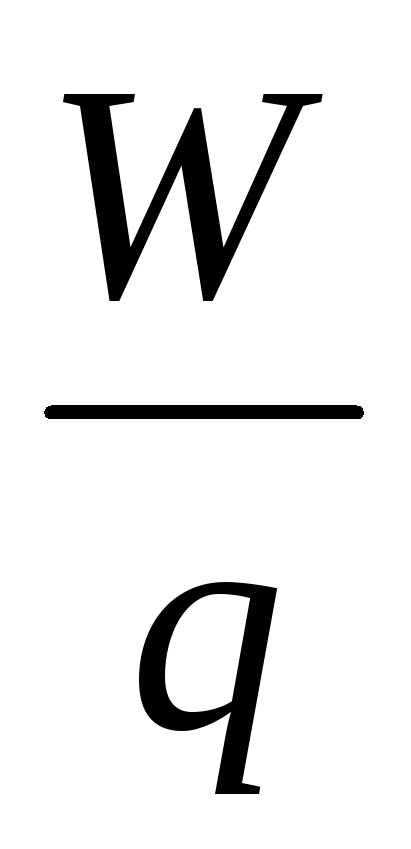nu depind de sarcina q și este energia caracteristică câmpului electrostatic.

O mărime fizică scalară, măsurată prin raportul dintre energia potențială a unei sarcini de testare într-un câmp electrostatic și valoarea acestei sarcini, se numeștepotenţialul câmpului electrostatic.

(12.27)

Potențialul câmpului creat de o sarcină punctiformă q este egal cu

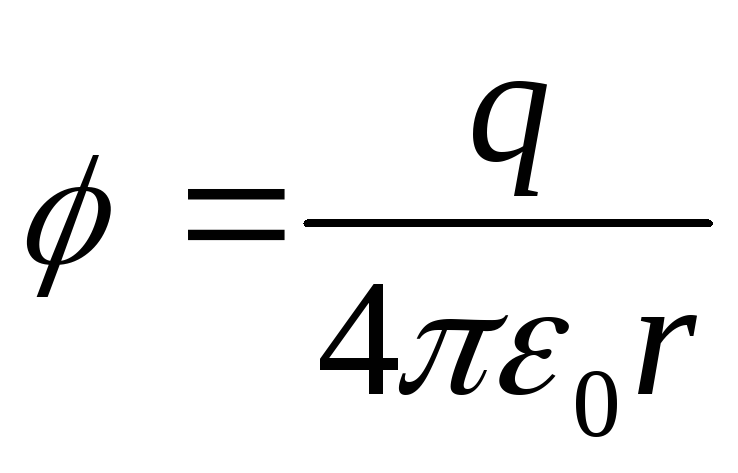(12.28)

Unitate potențială - volt.

Lucrul efectuat de forțele câmpului electrostatic la deplasarea sarcinii q pr de la punctul 1 la punctul 2 poate fi reprezentat ca

acestea. este egal cu produsul dintre sarcina transferată și diferența de potențial la punctele de început și de sfârșit.

Diferența de potențial a două puncte ale câmpului electrostatic φ 1 -φ 2 este egală cu tensiunea. Apoi

Raportul dintre munca efectuată de un câmp electrostatic la mutarea unei sarcini de testare dintr-un punct al câmpului în altul, la valoarea acestei sarcini se numeștetensiune intre aceste puncte.

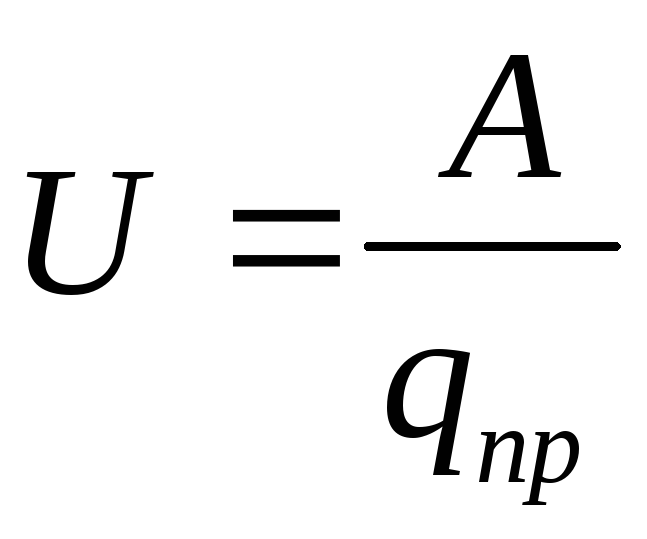(12.30)

Grafic, câmpul electric poate fi reprezentat nu numai cu ajutorul liniilor de tensiune, ci și cu ajutorul suprafețelor echipotențiale.

Echipotențial suprafete este o mulțime de puncte având același potențial. Figura arată că liniile de tensiune (razele radiale) sunt perpendiculare pe liniile echipotențiale.

E există un număr infinit de suprafețe potențiale în jurul fiecărei sarcini și a fiecărui sistem de sarcini (Fig. 12.14). Cu toate acestea, acestea sunt efectuate astfel încât diferențele de potențial dintre oricare două suprafețe echipotențiale adiacente să fie aceleași. Apoi, densitatea suprafețelor echipotențiale caracterizează clar intensitatea câmpului în diferite puncte. Acolo unde aceste suprafețe sunt mai dense, intensitatea câmpului este mai mare. Cunoscând locația liniilor echipotențiale (suprafețelor), este posibil să se construiască linii de tensiune, sau dintr-o locație cunoscută a liniilor de tensiune, se pot construi suprafețe echipotențiale.

§ 12.4Relația dintre tensiune și potențial

Un câmp electrostatic are două caracteristici: putere (putere) și energie (potențial). Tensiunea și potențialul sunt caracteristici diferite ale aceluiași punct de câmp, prin urmare, trebuie să existe o legătură între ele.

Lucrarea de mutare a unei sarcini pozitive punctuale de la un punct la altul de-a lungul axei x, cu condiția ca punctele să fie infinit aproape unele de altele și x 1 - x 2 \u003d dx, este egală cu qE x dx. Aceeași muncă este egală cu q(φ 1 - φ 2)= -dφq. Echivalând ambele expresii, putem scrie

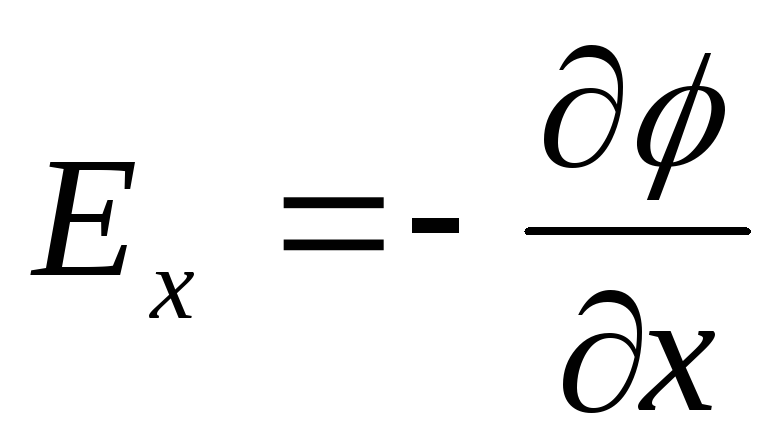
Repetând un raționament similar pentru axele y și z, putem găsi vectorul :

Unde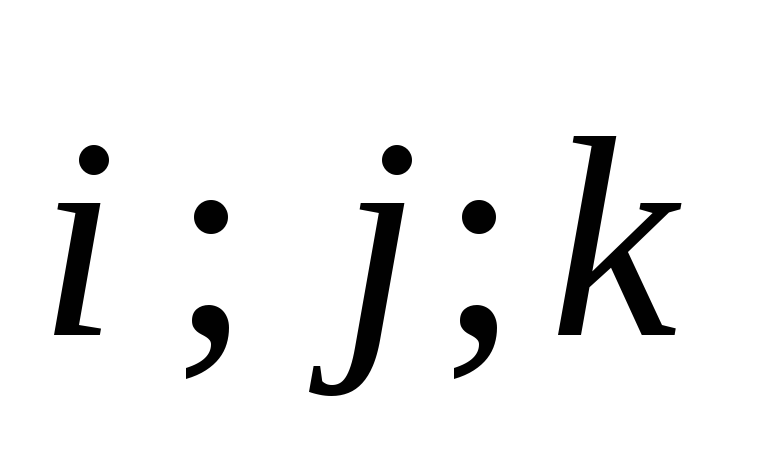

- vectori unitari ai axelor de coordonate x, y, z.

Din definiția unui gradient rezultă că

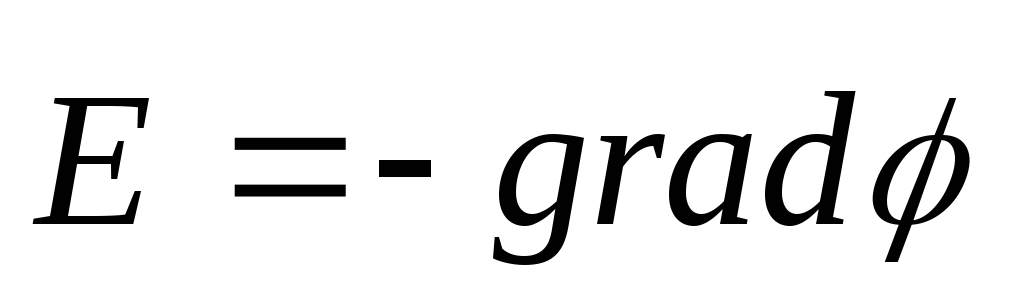sau

(12.31)

acestea. intensitatea câmpului E este egală cu gradientul de potențial cu semnul minus. Semnul minus este determinat de faptul că vector de tensiune E câmpul este îndreptat în direcția potențialului descrescător.

Relația stabilită între putere și potențial permite, prin intensitatea câmpului cunoscută, să se găsească diferența de potențial între două puncte arbitrare ale acestui câmp.

Câmpul unei sfere încărcate uniform razăR

Intensitatea câmpului în afara sferei este determinată de formulă

(r>R)

Diferența de potențial dintre punctele r 1 și r 2 (r 1 >R; r 2 >R) se determină folosind relația

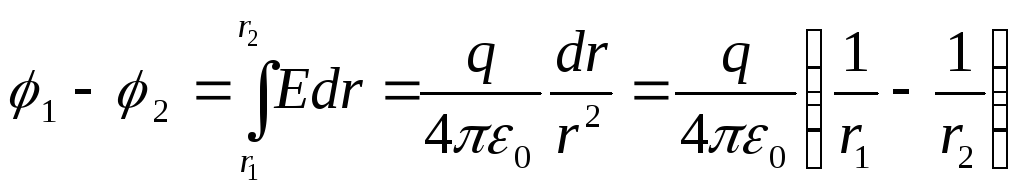
Obținem potențialul sferei dacă r 1 = R, r 2 → ∞:

Câmpul unui cilindru infinit de lung încărcat uniform

Intensitatea câmpului în afara cilindrului (r > R) este determinată de formulă

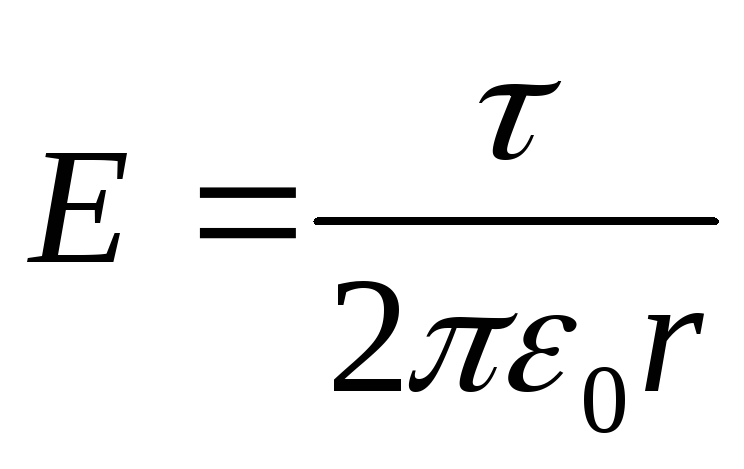
(τ este densitatea liniară).

Diferența de potențial dintre două puncte situate la distanța r 1 și r 2 (r 1 >R; r 2 >R) de axa cilindrului este egală cu

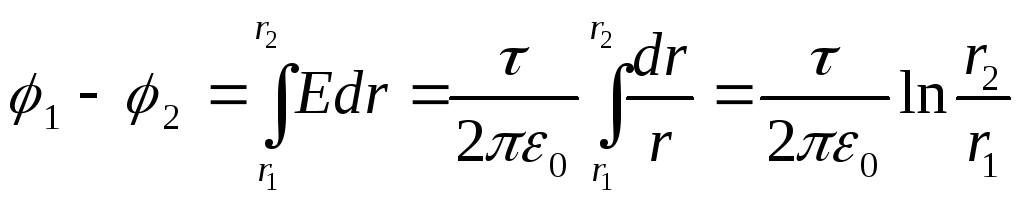(12.32)

Câmp al unui plan infinit încărcat uniform

Intensitatea câmpului acestui plan este determinată de formulă

(σ - densitatea suprafeței).

Diferența de potențial dintre punctele situate la o distanță x 1 și x 2 de plan este egală cu

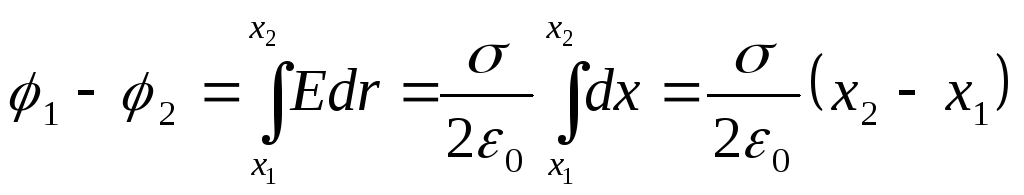(12.33)

Câmp de două plane paralele infinite încărcate opus

Intensitatea câmpului acestor planuri este determinată de formulă

Diferența de potențial dintre avioane este

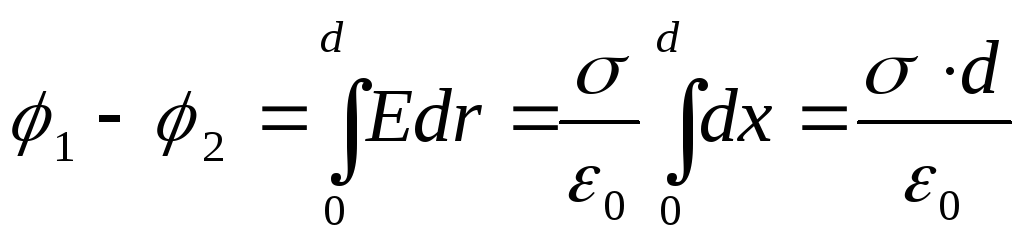(12.34)

(d este distanța dintre avioane).

Exemple de rezolvare a problemelor

Exemplul 12.1 . Trei sarcini punctuale Q 1 \u003d 2nC, Q 2 \u003d 3nC și Q 3 \u003d -4nC sunt situate la vârfurile unui triunghi echilateral cu lungimea laturii A= 10 cm. Determinați energia potențială a acestui sistem.

Dat : Q 1 \u003d 2nCl \u003d 2∙10 -9 C; Q 2 \u003d 3nCl \u003d 3 ∙ 10 -9 C; și Q 3 \u003d -4nCl \u003d 4∙10 -9 C; A= 10 cm = 0,1 m.

Găsi : U.

R Soluţie: Energia potențială a unui sistem de sarcini este egală cu suma algebrică a energiilor de interacțiune ale fiecăreia dintre perechile de sarcini care interacționează, i.e.

U=U 12 +U 13 +U 23

unde, respectiv, energiile potențiale ale uneia dintre sarcinile situate în câmpul altei sarcini la distanță A de la el, egal

;

;

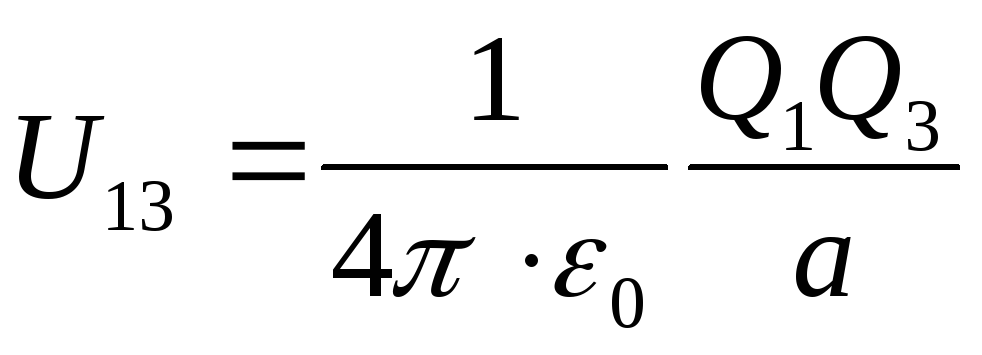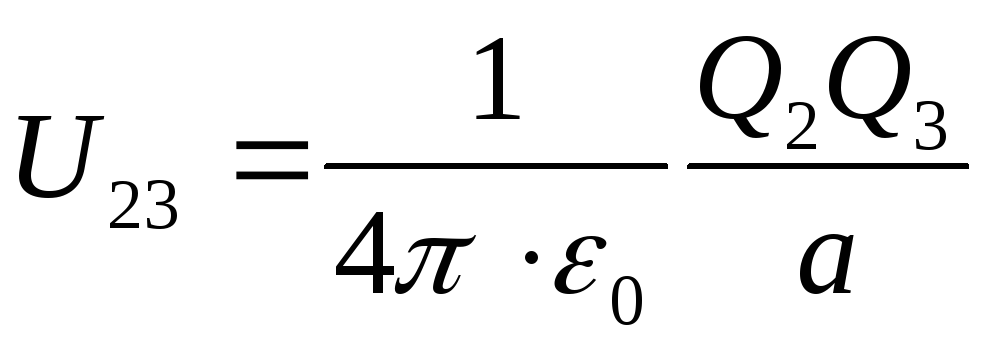(2)

Inlocuim formulele (2) in expresia (1), gasim energia potentiala dorita a sistemului de sarcini

Răspuns: U \u003d -0,126 μJ.

Exemplul 12.2 . Determinați potențialul din centrul inelului cu o rază interioară R 1 =30cm și una exterioară R 2 =60cm, dacă sarcina q=5nC este distribuită uniform pe acesta.

Dat: R 1 \u003d 30 cm \u003d 0,3 m; R 2 \u003d 60 cm \u003d 0,6 m; q=5nCl=5∙10 -9 C

Găsi : φ .

Soluţie: Împărțim inelul în inele concentrice infinit subțiri cu o rază interioară r și o rază exterioară (r+dr).

Aria inelului subțire considerat (vezi figura) dS=2πrdr.

P 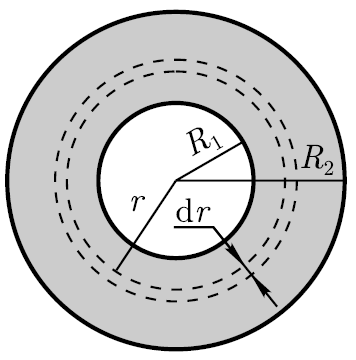potențial în centrul inelului, creat de un inel infinit de subțire,

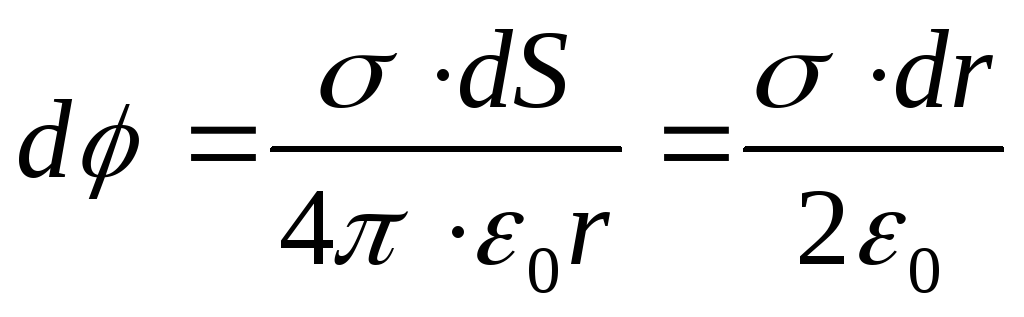
unde este densitatea sarcinii de suprafață.

Pentru a determina potențialul din centrul inelului, ar trebui să adăugați aritmetic dφ din toate inelele infinit subțiri. Apoi

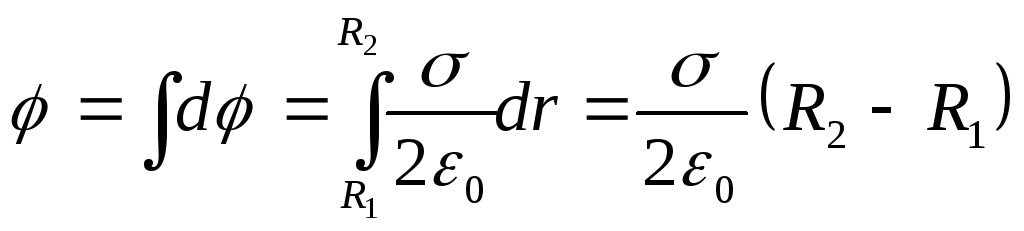
Având în vedere că sarcina inelului Q=σS, unde S= π(R 2 2 -R 1 2) este aria inelului, obținem potențialul dorit în centrul inelului

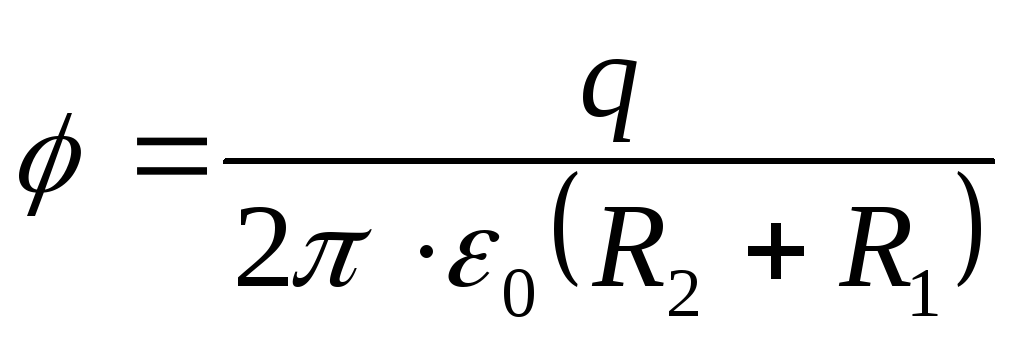
Răspuns : φ=25V

Exemplul 12.3. Două încărcături punctiforme cu același nume (q 1 =2nC șiq 2 \u003d 5nC) sunt în vid la distanțăr 1 = 20 cm. Determinați munca A care trebuie făcută pentru a le apropia de distanțăr 2 = 5 cm.

Dat: q 1 =2nCl=2∙10 -9 C; q 2 =5nCl=5∙10 -9 C ; r 1 = 20cm=0,2m;r 2 =5cm=0,05m.

Găsi : DAR.

Soluţie: Lucrul efectuat de forțele câmpului electrostatic la mutarea sarcinii Q dintr-un punct din câmp cu un potențial φ 1 într-un punct cu un potențial φ 2.

A 12 \u003d q (φ 1 - φ 2)

Când sarcini similare se apropie una de cealaltă, munca este efectuată de forțe externe, astfel încât munca acestor forțe este egală ca valoare absolută, dar semn opus muncii forțelor Coulomb:

A \u003d -q (φ 1 - φ 2) \u003d q (φ 2 - φ 1). (unu)

Potențialele punctelor 1 și 2 ale câmpului electrostatic

;

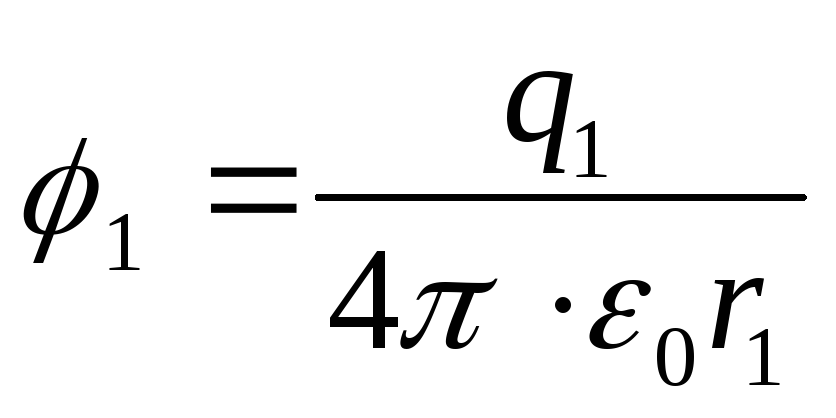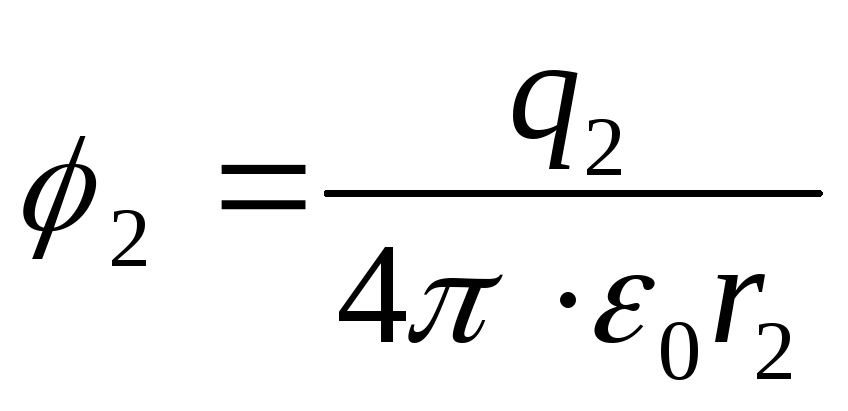(2)

Înlocuind formulele (2) în expresia (1), găsim munca dorită care trebuie făcută pentru a apropia sarcinile,

Răspuns: A=1,35 μJ.

Exemplul 12.4. Un câmp electrostatic este creat de un filament fără sfârșit încărcat pozitiv. Un proton care se deplasează sub acțiunea unui câmp electrostatic de-a lungul liniei de tensiune din filament de la distanțăr 1 = 2 cm lar 2 =10cm, și-a schimbat viteza de laυ 1 =1Mm/s până laυ 2 = 5 mm/s. Determinați densitatea liniară τ a sarcinii firului.

Dat: q=1,6∙10-19 C; m=1,67∙10 -27 kg; r 1 \u003d 2 cm \u003d 2 ∙ 10 -2 m; r 2 \u003d 10cm \u003d 0,1m; r 2 \u003d 5 cm \u003d 0,05 m; υ 1 \u003d 1 Mm / s \u003d 1 ∙ 10 6 m / s; până la υ 2 \u003d 5 Mm / s \u003d 5 ∙ 10 6 m / s.

Găsi : τ .

Soluţie: Munca efectuată de forțele câmpului electrostatic la mutarea unui proton dintr-un punct al câmpului cu potențial φ 1 într-un punct cu potențial φ 2 duce la creșterea energiei cinetice a protonului.

q(φ 1 - φ 2) \u003d ΔT (1)

În cazul unui filament, câmpul electrostatic este simetric axial, deci

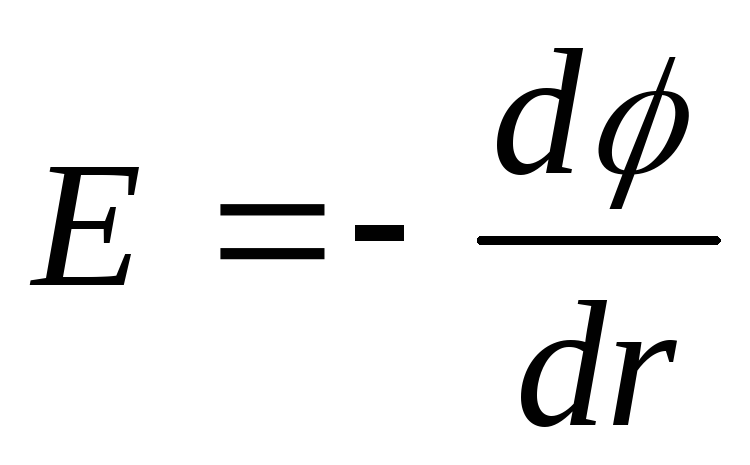sau dφ=-Edr,

apoi diferența de potențial dintre două puncte situate la distanța r 1 și r 2 de fir,

(am luat în considerare faptul că puterea câmpului creat de un fir infinit încărcat uniform,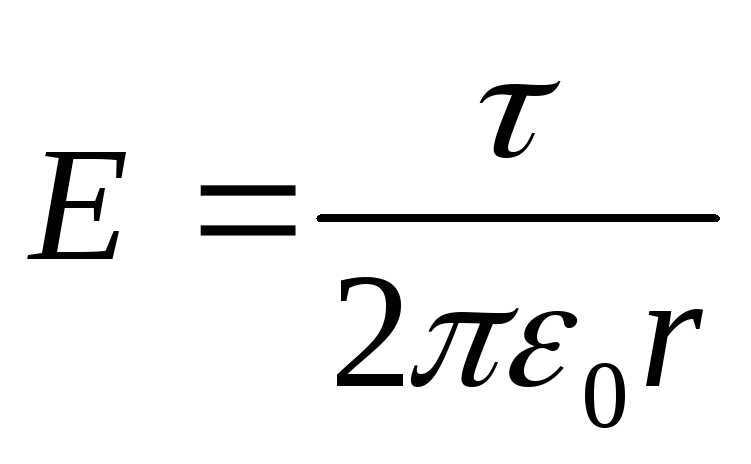

).

Inlocuind expresia (2) in formula (1) si tinand cont de faptul ca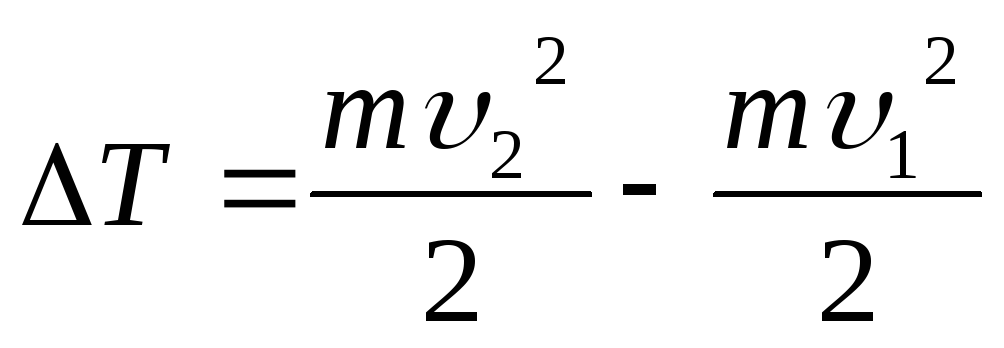

, primim

Unde este densitatea de sarcină liniară dorită a firului

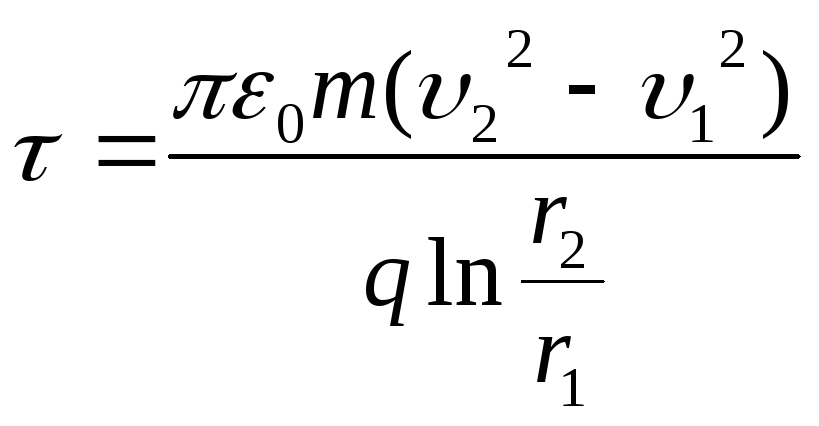
Răspuns : τ = 4,33 uC/m.

Exemplul 12.5. Un câmp electrostatic este creat în vid de o minge cu o razăR=8cm, încărcat uniform cu densitatea în vrac ρ=10nC/m 3 . Determinați diferența de potențial dintre două puncte ale acestui câmp situate la distanțe de centrul mingii: 1)r 1 = 10 cm șir 2 =15cm; 2)r 3 = 2 cm șir 4 = 5 cm..

Dat: R=8cm=8∙10 -2 m; ρ=10nC/m3 =10∙10 -9 nC/m3; r 1 \u003d 10 cm \u003d 10 ∙ 10 -2 m;

r 2 \u003d 15 cm \u003d 15 ∙ 10 -2 m; r 3 \u003d 2cm \u003d 2 ∙ 10 -2 m; r 4 \u003d 5 cm \u003d 5 ∙ 10 -2 m.

Găsi : 1) φ 1 - φ 2 ; 2) φ 3 - φ 4 .

Soluţie: 1) Diferența de potențial dintre două puncte situate la distanța r 1 și r 2 de centrul mingii.

(1)

Unde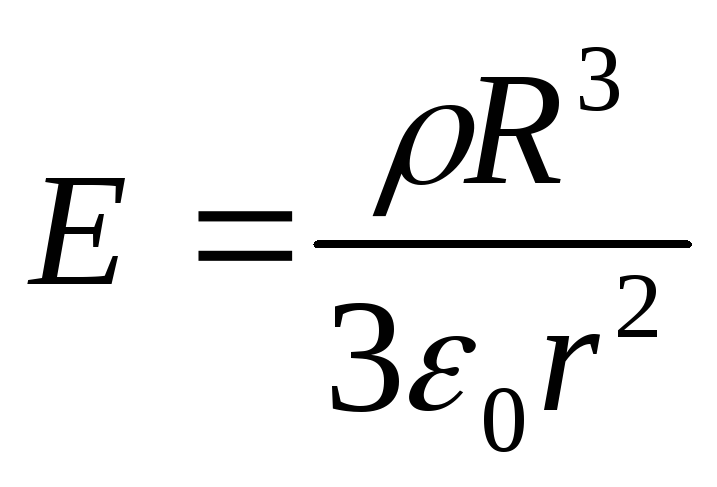

este intensitatea câmpului generată de o minge încărcată uniform cu o densitate în vrac ρ în orice punct din afara mingii la o distanță r de centrul acesteia.

Înlocuind această expresie în formula (1) și integrând, obținem diferența de potențial dorită

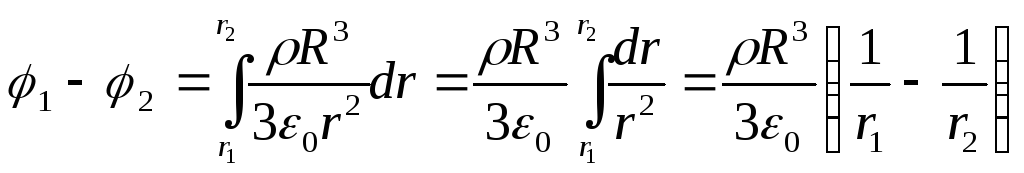
2) Diferența de potențial dintre două puncte situate la distanța r 3 și r 4 de centrul mingii,

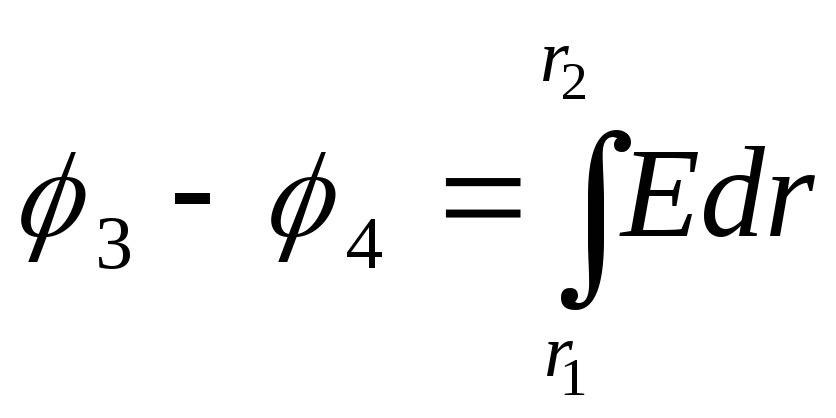(2)

Unde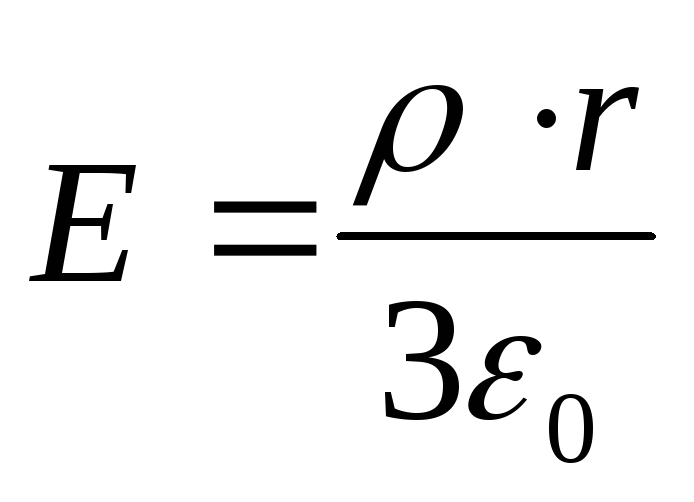

este intensitatea câmpului generată de o minge încărcată uniform cu o densitate de volum ρ în orice punct situat în interiorul mingii la o distanță r de centrul acesteia.

Înlocuind această expresie în formula (2) și integrând, obținem diferența de potențial dorită

Răspuns : 1) φ 1 - φ 2 \u003d 0,643 V; 2) φ 3 - φ 4 \u003d 0,395 V

Să calculăm energia potențială a sarcinilor electrice pentru cele mai simple, dar foarte importante cazuri speciale.
Energia potențială a unei sarcini într-un câmp omogen Fie ca sarcina q să se miște într-un câmp electric uniform cu o putere E de la punctul 1 la punctul 2. Poziția punctului 1 este determinată de vectorul rază și a punctului 2 de vectorul rază r2 . Forța care acționează asupra sarcinii F = qE este constantă. Lucrul forței F nu depinde de forma traiectoriei care leagă punctele 1 și 2. Aceasta rezultă din demonstrația generală a potențialității câmpului electrostatic. De asemenea, este posibil să se efectueze o demonstrație folosind un calcul direct al muncii efectuate atunci când o sarcină se mișcă pe căi diferite, în același mod ca în Mecanica forțelor gravitaționale. Acum nu vom face asta.
Cel mai simplu mod de a calcula munca este dacă sarcina se deplasează de-a lungul liniei drepte care leagă punctul 1 și punctul 2 (Fig. 1.78). Vector deplasare Dg = r2 - rv Lucrul este egal cu produsul scalar al forței și deplasării:
A = F Ar^qE (r2-r1) = qE r2-qE gg (1.18.1)
Pe de altă parte, conform (1.17.1), A \u003d ~ (W 2 ~ Comparând expresiile (1.18.1) și (1.17.1), obținem o expresie pentru energia potențială a unei sarcini într-un câmp uniform :
Wp ~ -qE g. (1.18.2)
Un câmp uniform este creat, în special, în spațiul dintre plăcile paralele, purtarea de taxe semne opuse (fig. 1.79). Este firesc să alegeți sistemul de coordonate astfel încât axa X să fie direcționată perpendicular pe plăci. Atunci proiecțiile En și E, sunt egale cu zero și sunt exprimate
la z
inferior (1.18.2) ia forma:
Wp = -q(Exx + Eyy + Ezz) = ~qExx. (1.18.3)

Formula (1.18.3) este similară cu formula Wp = mgh pentru energia potențială a unui corp deasupra suprafeței Pământului. Rolul masei îl joacă sarcina, accelerația cădere liberă este intensitatea câmpului, iar în loc de înălțime h este coordonata x. Dar semnul energiei este diferit: minus în loc de plus. Ideea aici este aceasta. Masa este întotdeauna pozitivă, iar forța gravitației este în mod necesar îndreptată vertical în jos. Ținând cont de aceste circumstanțe s-a scris formula Wp = mgh. Conține modulul de accelerație în cădere liberă, iar înălțimea h este măsurată de la suprafața Pământului. Formula (1.18.3) este mai generală. Sarcina q poate fi fie pozitivă, fie negativă; intensitatea câmpului poate fi direcționată oriunde, iar proiecția sa poate fi fie pozitivă, fie negativă, în funcție de alegerea sistemului de coordonate.
În special, dacă intensitatea câmpului E este îndreptată vertical în jos, iar axa X este în sus, atunci
Wp = qE\x\ (1.18.4)
în conformitate exactă cu expresia Wp = mgh.
Dacă câmpul electric efectuează lucru pozitiv, atunci energia unui corp încărcat în câmp scade: AW 0. O astfel de mișcare a unei particule încărcate este similară cu mișcarea unei pietre aruncate în sus. În acest caz, energia potențială a particulei crește, în timp ce energia cinetică scade: particula este decelerată.
Energie potențială zero
Energia potențială în electrodinamică este determinată, ca și în mecanică, până la o constantă arbitrară. În loc de expresia (1.18.2) am putea scrie:
W=-qE-r + C, (1,18,5)
unde C este o constantă arbitrară. În acest caz, modificarea energiei potențiale rămâne aceeași, iar munca determină tocmai schimbarea energiei potențiale, și nu energia în sine. Notând formula (1.18.2), am echivalat de fapt constanta C cu zero. Aceasta corespunde unei anumite alegeri a nivelului zero al energiei potențiale. De exemplu, pentru cazul prezentat în figura 1.79, se presupune că energia potențială este zero pe suprafața plăcii B. Dar, ca și în cazul acțiunii forțelor gravitaționale, nivelul zero al energiei potențiale este ales în mod arbitrar. Putem presupune că W - O la o distanţă de placa B. Atunci
wp=-qExx-qExx y
Nu energia potențială în sine are sens fizic, ci diferența de valori, determinată de munca câmpului atunci când sarcina se deplasează din poziția inițială în cea finală.
Energia de interacțiune a sarcinilor punctiforme
În cursul mecanicii, s-a obținut o expresie pentru energia de interacțiune a corpurilor punctuale:
tі u "W \u003d -G---.
R g
Dacă în loc de mase punctiforme luăm două sarcini q1 și q2 de semne opuse (sarcinile sunt atrase), atunci putem obține o expresie similară pentru energia potențială a interacțiunii lor:
w (1.18.6)
R y"
Pentru sarcinile de același semn (sarcinele se resping), semnul energiei potențiale va fi opus:
w (1.18.7)
R y"
Formulele (1.18.6) și (1.18.7) pot fi combinate într-una singură dacă în loc de modulele de încărcare le luăm valorile algebrice:
W. (1.18.8)
R r v "
Semnul de energie potențială se va dovedi automat a fi corect.
Dacă sarcinile ql și q2 au aceleași semne, atunci energia potențială a interacțiunii lor este pozitivă (fig. 1.80, a). Cu cât este mai mare, cu atât distanța dintre sarcini este mai mică, deoarece munca pe care o pot face forțele Coulomb atunci când sarcinile sunt respinse una de cealaltă va fi mai mare. Dacă sarcinile au semne opuse, atunci energia este negativă și valoarea sa maximă, egală cu zero, se realizează la r -> oo (Fig. 1.80, b). Cu cât r este mai mare, cu atât forțele de atracție vor lucra mai mult atunci când sarcinile se apropie una de cealaltă.

Orez. 1,80
Când scrieți energia potențială în forma (1.18.8), a fost deja făcută o anumită alegere a nivelului zero al energiei potențiale. Se crede că energia potențială a sarcinilor infinit îndepărtate este egală cu zero: Wp -» 0 când r -» oo. Această alegere a nivelului zero este convenabilă, dar nu este necesară. În loc de expresie (1.18.8), s-ar putea la fel de bine să scrie asta
(1.18.9)
rg y"
unde C este o constantă arbitrară. Acest lucru arată că valoarea pozitivă sau negativă a energiei potențiale a unui special simțul fizic nu are. Semnul energiei potențiale va fi determinat prin fixarea unei constante arbitrare C. Modificând valoarea lui C, putem schimba semnul lui Wp pentru o anumită distanță r între sarcini.
Energia potențială a unui sistem de sarcini punctiforme
Energia potențială a unui sistem de sarcini punctiforme qv q2, ..., qN este egală cu suma energiilor potențiale ale tuturor perechilor de sarcini care interacționează. Pentru trei taxe
w kbSi+hbS*+hwz l
R G1.2 G1.3 G2.3
Demonstrați-o singur folosind următorul truc. Inițial, sarcinile q2 și qz sunt la o distanță infinită de sarcina qv Apoi sarcina q2 se deplasează într-un punct situat la o distanță gl 2 de prima sarcină. După aceea, sarcina qz se deplasează într-un punct la o distanță r1 3 de prima sarcină și r2 3 de a doua. Este necesar să se calculeze munca forțelor Coulomb efectuate în timpul acestor deplasări și să se echivaleze cu modificarea energiei potențiale, luată cu semnul opus.
În general, N taxează
N N
wp=llk7rh> (1.18.11)
i=lfc=l (i*k)
unde r; k - distanța dintre sarcinile de cerneală numere. Coeficient - 1
2 se obține datorită faptului că la însumare, energia potențială este luată în considerare de două ori sub formă de
ri, k rk, i
Formule pentru energia potențială incarcare electricaîntr-un câmp omogen (1.18.2) și pentru încărcături de două puncte (1.18.8) este indicat să reținem. Se vor întâlni destul de des.
? 1. Este posibil să se creeze un electrostatic
le, ale căror linii de tensiune sunt paralele- ^^^^^^^
lelny, iar modulul de intensitate a vârstei este
em în direcția perpendiculară pe
niyam (Fig. 1.81)? Orez. 1,81
Desenați un grafic al dependenței energiei potențiale a particulelor încărcate opus de distanță, cu condiția ca constanta arbitrară C din formula (1.18.9) să fie pozitivă.
Cum va arăta formula (1.18.8) dacă sarcinile sunt într-un mediu cu o constantă dielectrică є?