Ovisnost razlike potencijala o udaljenosti. Razlika potencijala, energija naboja u električnom polju. Potencijal

U prethodnom pasusu govorili smo o glavnoj karakteristici električno polje- njegovu napetost. Kao što slijedi iz same definicije, ovo je karakteristika snage, a samim tim i vektor. U nekim slučajevima su prikladnije skalarne karakteristike, za koje se, ispostavilo se, također mogu uvesti elektrostatičko polje– potencijalna razlika i potencijal. U ovom slučaju ćemo se osloniti na važno fundamentalno svojstvo sila koje djeluju na naboj u elektrostatičkom polju – njihov konzervativizam.

Podsjetimo da se sile nazivaju konzervativne, čiji rad ne ovisi o obliku putanje tijela. Rad takvih sila određen je samo koordinatama početne i krajnje točke pomaka. Na osnovu našeg poznavanja svojstava njegovih karakteristika snage elektrostatičkog polja stvorenog proizvoljnim sistemom naelektrisanja, bilo bi moguće izvesti detaljan dokaz jednakosti rada kada se naelektrisanje kreće između bilo koje dve njegove tačke. Ali ćemo ovaj postupak donekle skratiti, podsjetivši na teoremu „o konzervativnosti centralnih sila“, koju smo dokazali u dijelu o mehanici.

Stacionarno tačkasto naelektrisanje je izvor "polja centralnih sila" - ovo direktno sledi iz formulacije osnovnog zakona elektrostatike - Coulombovog zakona. Iz principa superpozicije električnih polja proizilazi da rad obavljen kada se probni naboj kreće u polju bilo kojeg sistema mirovanje naboji je algebarski zbir rada u polju svakog od naboja posebno. To znači da je polje takvih sila („Kulonove sile“ *)) takođe polje konzervativnih sila. To je ono što je trebalo dokazati.

Dakle, rad sila elektrostatičkog polja **) na kretanje tačkastog (probnog) naboja između dve tačke karakteriše ovo polje. Ali to također ovisi o veličini probnog naboja q 0 . O tome svjedoči iskustvo, ali i to je razumljivo, na osnovu naših saznanja o "kulonskim" silama. Zato što su proporcionalni naboju q 0 u svakoj tački putanje 1®2 (na osnovu Coulombovog zakona), a rad je proporcionalan sili. Da biste okarakterizirali polje i samo polje, rad možete podijeliti vrijednošću probnog punjenja. Ono što se dešava je "potencijalna razlika". Evo definicije ovog važnog koncepta:

(ODA .) Razlika potencijala između tačaka elektrostatičkog polja 1 i 2 naziva se stav rad polja pomeranjem testnog naboja iz tačke 1upravo 2na vrijednost ove naknade :

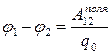. (3.1)

U SI sistemu jedinica za potencijalnu razliku naziva se 1 volt (1 V = 1 J/C). Ako naučimo kako nekako odrediti razliku potencijala j 1 –j 2 za polje sistema naelektrisanja u mirovanju (teorijski ili eksperimentalno), to će nam omogućiti da pronađemo rad polja pomeranjem bilo kojeg pinpoint naplatiti q u ovoj oblasti:

. (3.2)

Dakle, potencijalna razlika je energetska karakteristika električno polje, budući da je direktno povezano sa pojmom rada.

U mehanici smo uveli koncept "potencijalne energije" za konzervativne sile (sada kažemo: "polja konzervativnih sila"). Istovremeno, vodili smo se sljedećim principom: „Rad snaga na terenu jednak je gubitku potencijalna energija". Ovaj princip formaliziramo u analitičkoj notaciji:

Ovdje su U 1 i U 2 potencijalna energija u "početnom" ("1") i "konačnom" ("2") stanju sistema, respektivno. U slučaju koji se razmatra, polja sistema fiksnih naelektrisanja su energija tačka naboj q na poziciji "1" (sa koordinatama ( x 1 ,y 1 ,z 1 )) i pozicija "2" (sa koordinatama ( x 2 ,y 2 ,z 2 )) elektrostatičko polje. One. potencijalna energija naboja u ovom polju je skalarna funkcija koordinata tačaka polja U = U( x,y,z) (ili ). Uspoređujući (3.2) i (3.3), vidimo da je zgodno pretpostaviti da je razlika potencijala razlika u vrijednostima druge skalarne funkcije koordinata tačaka polja j(x,y,z). Vezano je za funkciju U( x,y,z) (potencijalna energija) jednostavnom relacijom: U( x,y,z) = q× j(x,y,z). Ili zato

kaže se da je "numerički jednak potencijalnoj energiji jediničnog pozitivnog naboja" u datoj tački polja. I ova vrijednost se zove j"potencijal" date tačke elektrostatičkog polja.

Najvažnije je kako pronaći ovu funkciju za polje određenog sistema naelektrisanja? Koja je procedura?

Prije svega, moramo se dogovoriti oko uslova normalizacije *): trebamo odabrati tačku R 0, u kojem će se pretpostaviti da je potencijal probnog naboja jednak nuli. Najčešće se takva tačka bira "beskonačno" udaljena, gdje polje nema **). Da biste to učinili, potrebno je pronaći "specifičan" rad na terenu - tj. rad vezan za količinu prenesenog testnog naboja (ili, kako se često kaže, "pomicanjem jediničnog pozitivnog" naboja) iz date tačke u polju R(x,y,z) do tačke normalizacije R 0 . U analitičkom obliku, ovo definicija potencijal se može napisati na sljedeći način:

(Def. ) j P(x,y,z) = . (3.5)

Da li je moguće vrijednosti koje smo novo uveli - potencijalnu razliku i potencijal izraziti kroz karakteristiku snage, koju smo već naučili izračunati pomoću datu lokaciju naelektrisanja u svemiru? Da, svakako možete. Zapišimo lanac jednakosti koje smo dobro razumjeli:

Hajde da ponovo napišemo poslednju jednačinu

. (3.6)

Daje "recept" za traženje razlike potencijala koristeći poznatu funkciju napetosti. Slično za potencijal:

I konačno za potencijal proizvoljne tačke polja R sa koordinatama ( x,y,z):

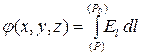. (3.7)

· Potencijal polja tačkastog naboja

Na osnovu procedure za izračunavanje potencijala dobijamo izraz za slučaj polja tačkastog naelektrisanja. Ovo je veoma važno za dalje proračune potencijala polja sistema naelektrisanja proizvoljno lociranih u prostoru.

2. Izbor putanje. Neka proizvoljna tačka R(x,y,z) je na udaljenosti r od izvornog punjenja. Kako rezultat ne ovisi o obliku putanje, za izračunavanje krivolinijskog integrala oblika (3.7) biramo najjednostavniju radijalno usmjerenu pravu liniju iz date tačke polja duž linije polja i „ide u beskonačnost“.

3. Kalkulacija. U skladu sa definicijom potencijala, izračunavamo "specifičan" rad polja stvorenog tačkastim nabojem q o prijenosu probnog naboja duž odabrane putanje. Sljedeći lanac jednakosti, nadamo se, izgleda prilično "transparentno". Međutim, mi ćemo ipak dati minimalan komentar na to. Prije svega, napominjemo da, zbog našeg izbora putanje u obliku zraka usmjerenog radijalno od naboja, možemo označiti E l i dl(proizvoljna kriva" L") promijeniti u Er i dr(polarna osa" r"). Štoviše, budući da je vektor usmjeren radijalno, za bilo koji mali pomak duž putanje, projekcija vektora naprezanja jednostavno je jednaka modulu ovog vektora E(r). Kao rezultat toga, također možemo napraviti važan korak u našem proračunu - napraviti prijelaz sa krivolinijskog integrala na uobičajeni definitivni:

.*)

Sada, nakon zamjene izraza za modul jačine polja tačkastog naboja (3.5), ostaje nam samo matematička “rutina”:

Zapišimo ponovo rezultat, dopunivši ga mogućim prisustvom plinovitog ili tekućeg homogenog dielektričnog medija s permitivnošću e, koji ispunjava cijeli prostor oko tačkastog naboja:

. (3.8)

Potencijal polja tačkastog naelektrisanja, kao što vidimo, opada sa rastojanjem prema zakonu 1/ r.

· Ekvipotencijalne površine

Kada se raspravlja karakteristike snage elektrostatičkog polja, uverili smo se u plodnost koncepta linije sile(napetostne linije). Za energetsku karakteristiku polja - potencijal - takođe je korisno uvesti dodatnu ilustrativnu karakteristiku - sistem "ekvipotencijalnih površina". Iz samog naziva jasno je („equi“ znači „jednak“) da su to površine konstantnog potencijala, koje karakterišu sposobnost sila polja da obavljaju rad prilikom kretanja naelektrisanja. Na takvim površinama se, očigledno, ne radi uopšte. Maksimalna je u pravcima duž kojih je gustina (gustina) ekvipotencijalnih površina maksimalna. Na ovim mestima je i jačina polja maksimalna. Lako je odgonetnuti kakva je međusobna orijentacija linija sile i ekvipotencijalnih površina na njihovim sjecištima: oni su međusobno okomiti. Uostalom, za bilo koji mali pomak duž ekvipotencijalne površine elementarni rad je jednak nuli, a to je moguće samo ako je tangentna komponenta vektora napona jednaka nuli, tj. usmjerena je striktno duž normale na površinu. U nastavku dajemo lanac odgovarajućih riječi, nadamo se, prilično očiglednih jednakosti:

Zajedno sa sl. 3. ... dokazuju, zapravo, već formulisanu tvrdnju: ukrštaju se linije sile (ili "dolazak u...") ekvipotencijalne površine pod pravim uglom !

Hajde da damo sliku ekvipotencijalnih površina (i linija sila) za neke od najjednostavnijih slučajeva elektrostatičkog polja koji su nam već dobro poznati: a) polje tačkastog naboja; b) polje dva identična po apsolutnoj vrijednosti suprotna tačkasta naboja; in) polje između dve suprotno naelektrisane, ravni paralelne velike (u poređenju sa rastojanjem između njih) ploče - videti sl. 3.1.

Okrenimo se sada sfernom (tačkastom) naboju. Gore je prikazano da je jačina električnog polja stvorenog naelektrisanjem jednoliko raspoređenim po sferi Q, ne zavisi od poluprečnika sfere. Zamislite to na nekoj udaljenosti r iz centra sfere je probni naboj q. Jačina polja na mjestu gdje se nalazi naboj,

Na slici je prikazan graf zavisnosti jačine elektrostatičke interakcije između tačkastih naelektrisanja od udaljenosti između njih. Pronaći rad električnog polja pri kretanju ispitnog naboja q iz daljine r do udaljenosti R, podijelite ovaj interval po točkama r 1 , r 2 ,..., rP na jednake delove. Prosječna sila koja djeluje na naboj q unutar intervala [ rr 1 ] je jednako

Rad ove snage u ovoj oblasti:

Slični izrazi za rad će se dobiti i za sve ostale dijelove. Dakle, kompletan posao je:

Identični pojmovi sa suprotnim predznacima se uništavaju i konačno dobijamo:

je rad polja na naboju

– razlika potencijala

Sada, da bismo pronašli potencijal tačke polja u odnosu na beskonačnost, usmjeravamo R do beskonačnosti i konačno dobijamo:

Dakle, potencijal polja tačkastog naelektrisanja obrnuto je proporcionalan udaljenosti do naelektrisanja.

24. Potencijalna energija naelektrisanja u polju sistema naelektrisanja. Princip superpozicije potencijala. Princip superpozicije potencijala

Bilo koje proizvoljno složeno elektrostatičko polje može se predstaviti kao superpozicija polja tačkastih naelektrisanja. Svako takvo polje u odabranoj tački ima određeni potencijal. Pošto je potencijal skalarna veličina, rezultujući potencijal polja svih tačkastih naelektrisanja je algebarski zbir potencijala 1, 2, 3, ... polja pojedinačnih naelektrisanja: = 1 + 2 + 3 + .. Ovaj odnos je direktna posledica principa superpozicije električnih polja.

Potencijalna energija naboja u električnom polju. Nastavimo sa poređenjem gravitacijske interakcije tijela i elektrostatičke interakcije naelektrisanja. tjelesne mase m u Zemljinom gravitacionom polju ima potencijalnu energiju. Rad gravitacije jednak je promjeni potencijalne energije, uzetoj sa suprotnim predznakom:

A=-(W p2 -W p1) = mgh.

(Ovdje i dolje ćemo energiju označiti slovom W.) Baš kao tijelo mase m u polju gravitacije ima potencijalnu energiju proporcionalnu masi tijela, električni naboj u elektrostatičkom polju ima potencijalnu energiju W p , proporcionalno naelektrisanju q. Rad sila elektrostatičkog polja ALI jednaka je promjeni potencijalne energije naboja u električnom polju, uzeta sa suprotnim predznakom:

A=-(W p2 -W p1) . (40.1)

25. Razlika potencijala. Ekvipotencijalne površine

Ekvipotencijalna površina- površina, čija svaka tačka ima isti potencijal.

Kako slijedi iz veze između rada i potencijala:

kada se naboj prenosi duž ekvipotencijalnih površina, električno polje ne radi, jer .

Rad sa silom različitom od nule je nula samo ako je vektor sile okomit na vektor pomaka. Iz ovoga slijedi da su linije napetosti okomite na ekvipotencijalne površine. Primjeri ekvipotencijalnih površina su sfere za polje tačkastog naboja i paralelne ravni za homogena polja (slika 3).

Razlika potencijala (napon) između dvije tačke jednak je omjeru rada na terenu pri pomicanju punjenja od početne do krajnje tačke do modula ovog naboja: U\u003d φ 1 - φ 2 \u003d -Δφ \u003d A / q, A \u003d - (W p2 - W p1) = -q (φ 2 - φ 1) = -qΔφ

Razlika potencijala se mjeri u voltima (V = J/C) Odnos između jačine elektrostatičkog polja i razlike potencijala: E x = Δφ / Δ x Jačina elektrostatičkog polja usmjerena je u smjeru opadanja potencijala. Izmjereno u voltima podijeljeno metrima (V/m)

§ 15. POTENCIJAL. ENERGIJA SISTEMA ELEKTRIČNIH NAPUNJENJA. RAD NA PREMJEŠTANJU NABAVKA NA TERENU

Osnovne formule

 Potencijal električnog polja je vrijednost jednaka omjeru potencijalne energije pozitivnog naelektrisanja u tački dati poen polja, na ovu naknadu;

=P/ Q,

ili potencijal električnog polja je veličina jednaka omjeru rada sila polja za pomicanje pozitivnog naboja iz određene tačke polja u beskonačnost do ovog naboja:

=A/ Q.

Potencijal električnog polja u beskonačnosti uslovno se uzima jednak nuli.

Imajte na umu da kada se naboj kreće u električnom polju, rad A v.s vanjske sile je po apsolutnoj vrijednosti jednaka radu A s.p. jačina polja i suprotan joj je znakom:

A v.s = – A s.p. .

 Potencijal električnog polja stvoren tačkastim nabojem Q na daljinu r od optužbe

 Potencijal električnog polja koje stvara metal, noseći naboj Q sfera sa radijusom R, na udaljenosti od centra sfere:

unutar sfere ( r<R)

;

na površini kugle ( r=R)

;

van delokruga (r> R)

.

U svim formulama datim za potencijal nabijene sfere,  je permitivnost homogenog beskonačnog dielektrika koji okružuje sferu.

 Potencijal električnog polja stvorenog od strane sistema P tačkasti naboj, u datoj tački, u skladu sa principom superpozicije električnih polja, jednak je algebarskom zbiru potencijala  1 , 2 , ... , n, kreiran pojedinačnim bodovima Q 1 ,Q 2 , ...,Q n :

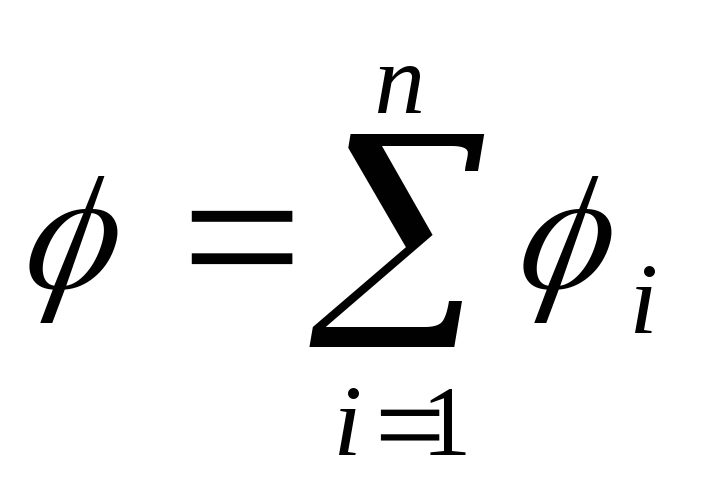
 Energija W interakcije sistema tačkastih naelektrisanja Q 1 ,Q 2 , ...,Q n određen je poslom koji ovaj sistem naboja može obaviti kada se uklone jedno u odnosu na drugo do beskonačnosti, a izražava se formulom

gdje je  i- potencijal polja koji stvaraju svi P- 1 punjenje (isključujući 1.) na mjestu gdje se punjenje nalazi Q i .

 Potencijal je povezan sa jačinom električnog polja relacijom

E= -grad.

U slučaju električnog polja sa sfernom simetrijom, ovaj odnos se izražava formulom

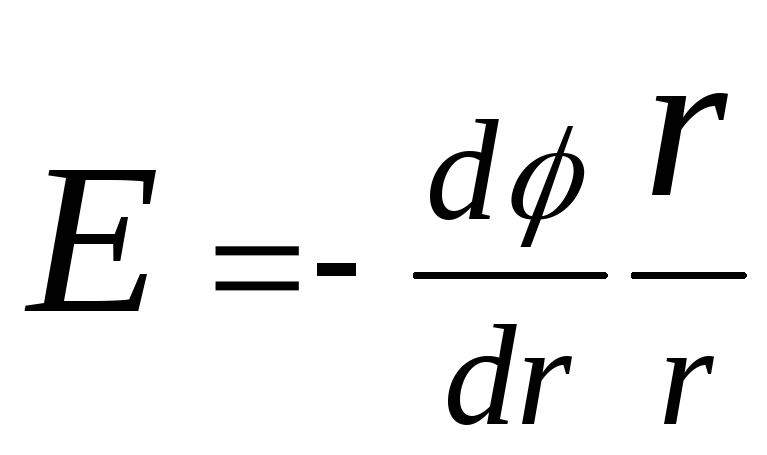ili u skalarnom obliku

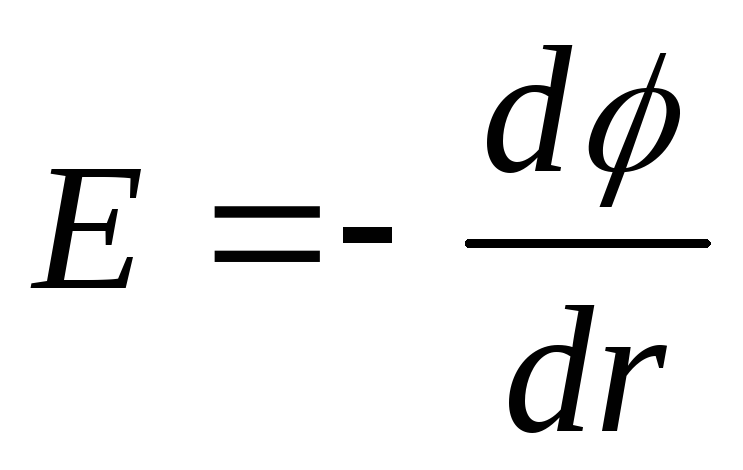i u slučaju homogeno polje, tj. polje čiji je intenzitet u svakoj tački isti i po apsolutnoj vrijednosti i po pravcu,

E=( 1 – 2 ,)/d,

gdje je  1 i 2 - potencijali tačaka dvije ekvipotencijalne površine; d - udaljenost između ovih površina duž linije električnog polja.

 Rad električnog polja pri pomicanju tačkastog naboja Q iz jedne tačke polja sa potencijalom  1 , u drugu s potencijalom  2 ,

A=Q( 1 - 2 ), ili

,

gdje E l - projekcija vektora napetosti E u pravcu kretanja; dl - pokret.

U slučaju homogenog polja, posljednja formula poprima oblik

A= QElcos ,

gdje l- pomak  - ugao između vektorskih pravaca E i raseljavanje l.

Primjeri rješavanja problema

Primjer 1 pozitivnih naboja Q 1 \u003d 3 μC i Q 2 \u003d 20 nC su u vakuumu na udaljenosti r 1 =l.5 m međusobno. Definišite posao A, što se mora učiniti kako bi se naboji približili na daljinu r 2 =1 m.

Rješenje. Pretpostavimo da je prvo punjenje Q 1 ostaje nepomičan a drugi Q 2 pod dejstvom spoljnih sila kreće se u polju koje stvara naelektrisanje Q 1 prilazeći mu iz daljine r 1 =t,5 m do r 2 =1 m .

Posao ALI" spoljna sila koja pokreće naboj Q iz jedne tačke polja sa potencijalom  1 u drugu, čiji potencijal 2 , jednak po apsolutnoj vrijednosti i suprotan po predznaku radu ALI sile polja za kretanje naboja između istih tačaka:

A "= -A.

Posao ALI sile polja pri pomeranju naboja A=Q( 1 - 2 ). Onda radi ALI" spoljne sile se mogu zapisati kao

A" = –Q( 1 - 2 )=Q( 2 - 1 ). (1)

Potencijali početne i krajnje tačke putanje izraženi su formulama

;

.

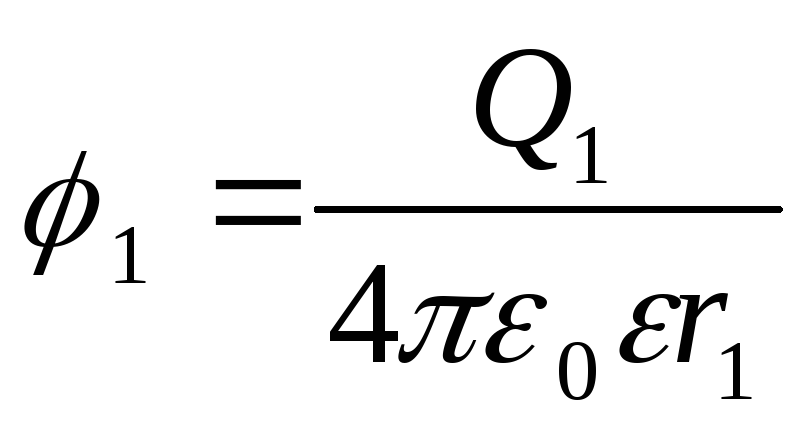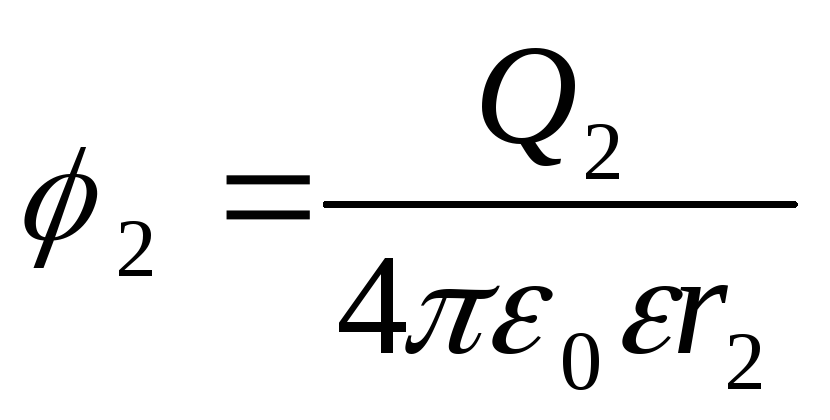Zamjenjivanje izraza  1 i 2 u formulu (1) i uzimajući u obzir da je za ovaj slučaj preneseni naboj Q=Q 2 , dobijamo

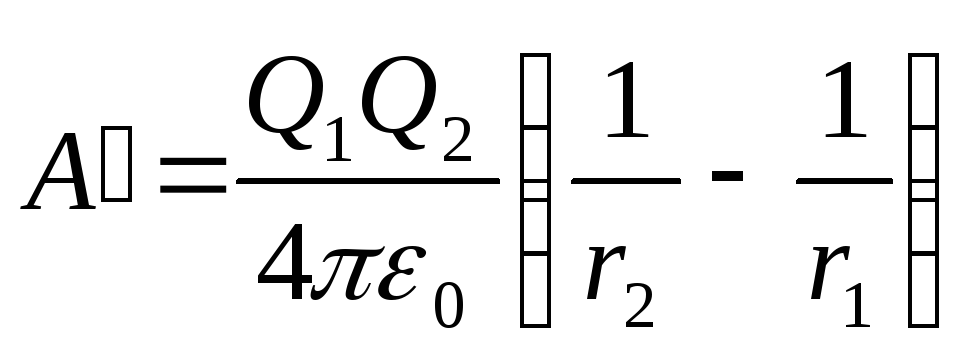. (2)

S obzirom da je 1/(4 0 )=910 9 m/F, tada nakon zamjene vrijednosti veličina u formulu (2) i izračunavanja, nalazimo

A"=180 µJ.

Primjer 2 Nađi posao ALI polja za prijenos naplate Q=10 nC od tačke 1 upravo 2 (Sl. 15.1), koji se nalazi između dva suprotno nabijena s površinskom gustinom  \u003d 0,4 μC / m 2 beskonačne paralelne ravni, udaljenost l između njih je 3 cm.

R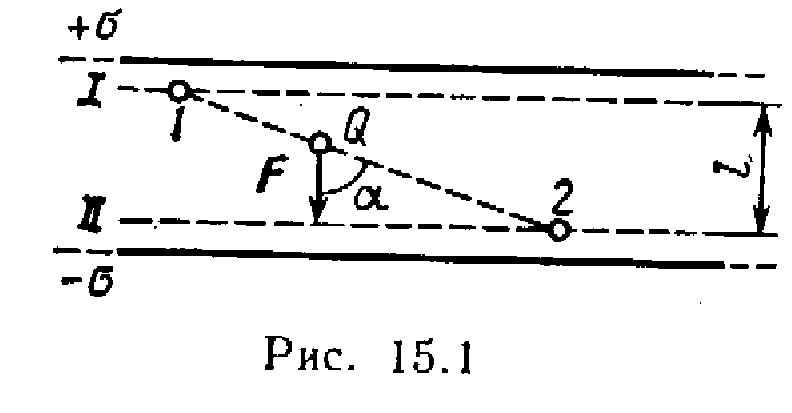

rješenje. Postoje dva načina za rješavanje problema.

1. način. Rad polja prisiljava na pomjeranje naboja Q iz tačke 1 polja sa potencijalom 1 upravo 2 polja sa potencijalom 2 pronađite po formuli

A=Q( 1 - 2 ). (1)

Odrediti potencijale u tačkama 1 i 2 Kroz ove tačke povucimo ekvipotencijalne površine I i II. Ove površine će biti ravni, jer je polje između dvije jednolično nabijene beskonačne paralelne ravni uniformno. Za takvo polje, relacija

 1 - 2 =El, (2)

gdje E - jačina polja; l - udaljenost između ekvipotencijalnih površina.

Jačina polja između paralelnih beskonačnih suprotno naelektrisanih ravni E=/ 0 . Zamjena ovog izraza E u formulu (2), a zatim u izraz 1 - 2 u formulu (1), dobijamo

A= Q( /  0 ) l.

2nd way. Pošto je polje uniformno, sila koja deluje na naelektrisanje Q, je konstantan dok se kreće. Dakle, rad pomeranja naboja iz tačke 1 upravo 2 može se izračunati pomoću formule

A=F  r cos, (3)

gdje F - sila koja deluje na naelektrisanje r- modul za prijenos punjenja Q iz tačke 1 upravo 2;  je ugao između smjerova pomaka i sile . Ali F= QE= Q( /  0 ). Zamjena ovog izraza F u jednakost (3), kao i uočavanje da je  r cos= l, dobijamo

A=Q(/ 0 )l. (4)

Dakle, oba rješenja dovode do istog rezultata.

Zamjena u izraz (4) vrijednosti veličina Q, , 0 i l, nađi

A\u003d 13,6 μJ.

Primjer 3 Na tankoj niti savijenoj duž luka kruga polumjera R, ravnomerno raspoređeno naelektrisanje sa linearnom gustinom=10 nC/m. Definišite napetost E i potencijal  električnog polja stvorenog takvim p

distribuirani naboj u jednoj tački O, koji se poklapa sa centrom zakrivljenosti luka. Dužina l konac je 1/3 obima i jednak je 15 cm.

Rješenje. Koordinatne osi biramo tako da se ishodište koordinata poklapa sa centrom zakrivljenosti luka, a os at bio simetrično lociran u odnosu na krajeve luka (slika 15.2). Odaberite element dužine d na navoju l. Naplaćeno Q=d l, koji se nalazi u odabranom području, može se smatrati točkom.

Odredimo jačinu električnog polja u tački O. Da bismo to učinili, prvo pronalazimo napetost d E polje stvoreno naplatom d Q:

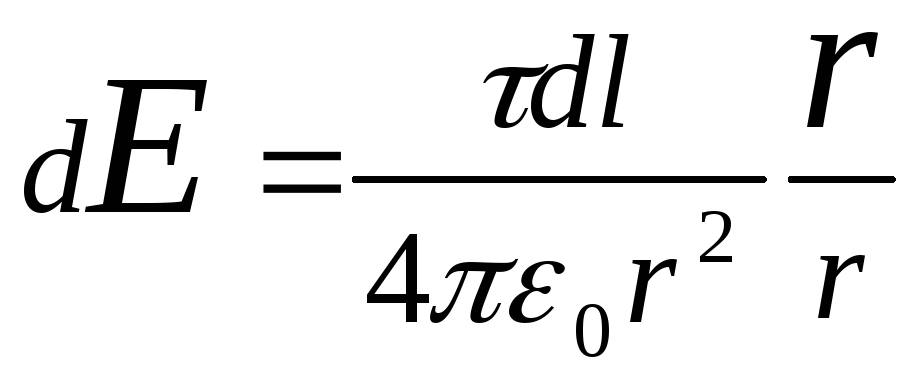gdje r-vektor radijusa usmjeren od elementa d l do tačke u kojoj se izračunava napetost. Izražavamo vektor d E kroz projekciju dE x c i dE y na koordinatnoj osi:

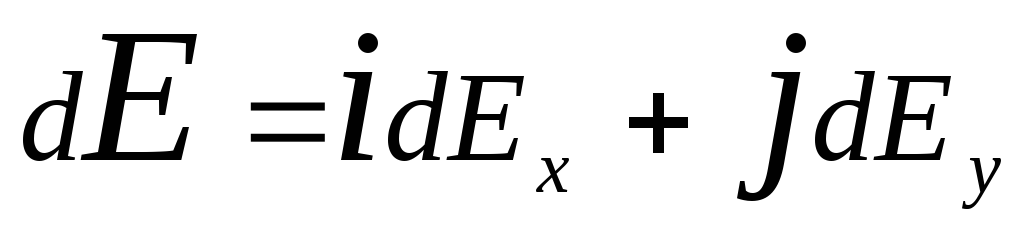gdje i i j- jedinični vektori smjera (orths).

tenzija E pronađi integracijom:

Integracija se vrši duž luka dužine l. Zbog simetrije, integral jednako nuli. Onda

, (1)

gdje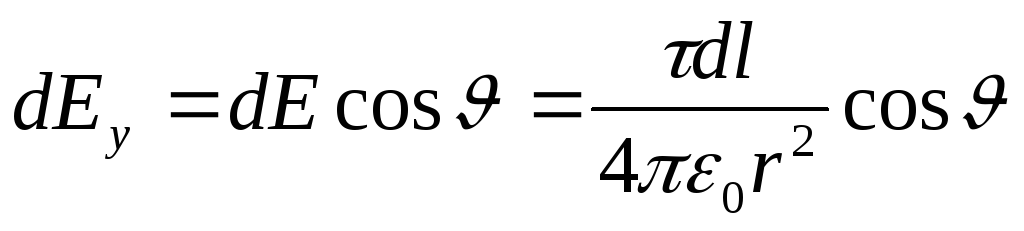

. Jer r=R= const i d l=R d. onda

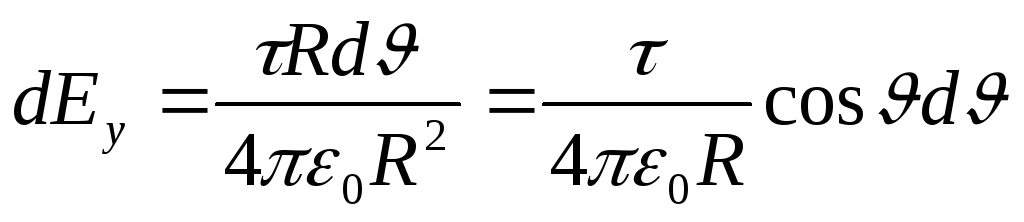
Zamijenite pronađeni izraz dE y u (1) i, uzimajući u obzir simetričnu lokaciju luka u odnosu na osu OU, uzimamo granice integracije od 0 do /3, i udvostručujemo rezultat;

Zamjena ovih granica i izražavanje R kroz dužinu luka (3 l= 2 r), dobijamo

Ova formula pokazuje da je vektor E poklapa se s pozitivnim smjerom ose OU Zamjena vrijednosti and l u posljednju formulu i radeći proračune, nalazimo

E\u003d 2,18 kV / m.

Odredimo potencijal električnog polja u tački O. Nađimo prvo potencijal d stvoren tačkastim nabojem d Q u tački O:

Zamenimo r na R i izvršite integraciju:

.Zato što l=2  R/3, onda

=/(6 0 ).

Nakon što smo izvršili proračune prema ovoj formuli, dobijamo

Primjer4 . Električno polje stvara dugi cilindar poluprečnika R= 1cm , jednoliko naelektrisan sa linearnom gustinom=20 nC/m. Odredite razliku potencijala dvije tačke ovog polja koje se nalaze na udaljenostima a 1 =0,5 cm i a 2 \u003d 2 cm od površine cilindra, u njegovom srednjem dijelu.

Rješenje. Da bismo odredili potencijalnu razliku, koristimo odnos između jačine polja i promjene potencijala E= -grad. Za polje sa aksijalnom simetrijom, koje je polje cilindra, ova relacija se može zapisati kao

E= -( d/d r) , ili d= - E d r.

Integracijom posljednjeg izraza nalazimo potencijalnu razliku dvije tačke razdvojene sa r 1 i r 2 od ose cilindra;

. (1)

Pošto je cilindar dugačak i tačke su uzete blizu njegovog srednjeg dela, jačina polja se može izraziti pomoću formule

. Zamjena ovog izraza E u jednakost (1), dobijamo

(2)

Pošto količine r 2 i r 1 unesite formulu kao omjer, tada se mogu izraziti u bilo kojoj, ali samo u istim jedinicama:

r 1 =R+a 1 = 1,5 cm; r 2 =R+a 2 =3cm .

Zamjena vrijednosti veličine , 0 ,r 1 i r 2 u formulu (2) i računajući, nalazimo

 1 - 2 =250 V.

Primjer 5 Električno polje stvara tanka šipka koja nosi naboj =0,1 μC/m ravnomjerno raspoređen duž svoje dužine. Odredite potencijal  polja u tački udaljenoj od krajeva štapa na udaljenosti, jednaka dužini rod.

Rješenje. Naboj na štapu se ne može smatrati tačkastim nabojem, stoga direktno primijenite formulu za izračunavanje potencijala

, (1)

važi samo za bodovne naknade, to je nemoguće. Ali ako podijelimo štap na elementarne segmente d l, zatim punjenjed l koja se nalazi na svakoj od njih može se smatrati tačkom i tada će formula (1) biti važeća. Primjenom ove formule dobijamo

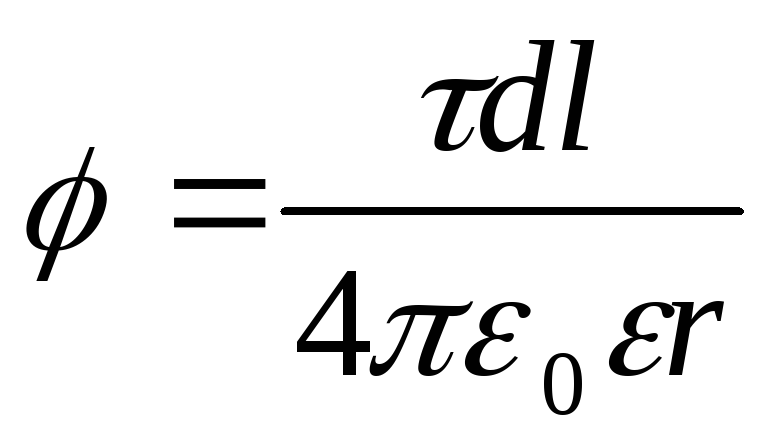, (2)

gdje r - udaljenost tačke u kojoj je potencijal određen do elementa štapa.

Od sl. 15.3 da d l=(r d/cos). Zamjena ovog izraza d l u formulu (2), nalazimo

.

Integriranje rezultirajućeg izraza u granicama  1 da 2 , dobijamo potencijal koji stvara cijeli naboj raspoređen na štapu: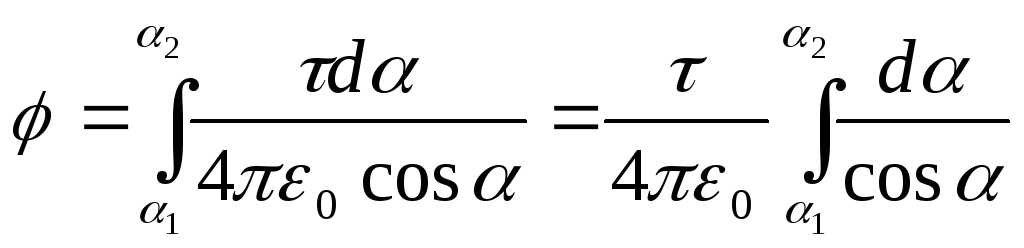

.

AT 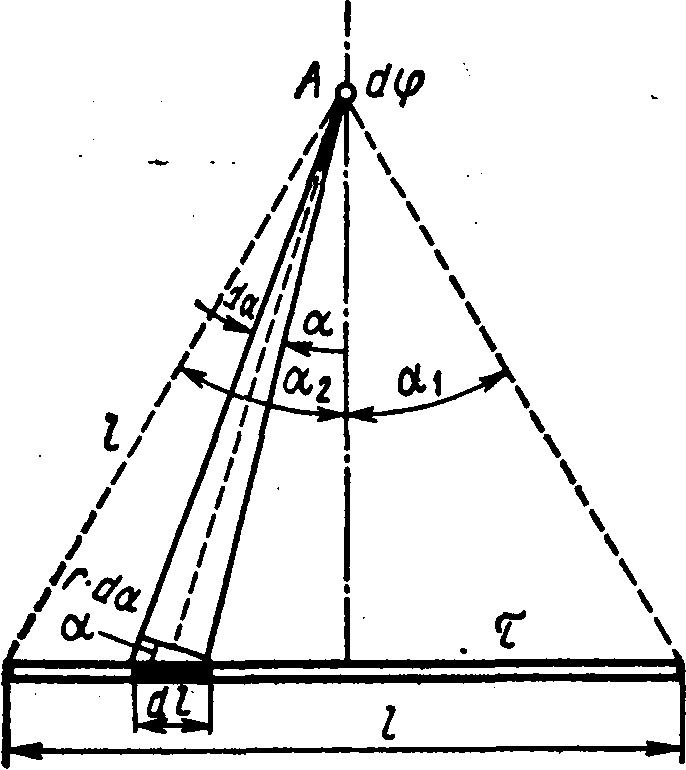sila simetrije tačke ALI u odnosu na krajeve štapa imamo  2 = 1 i zbog toga

.

shodno tome,

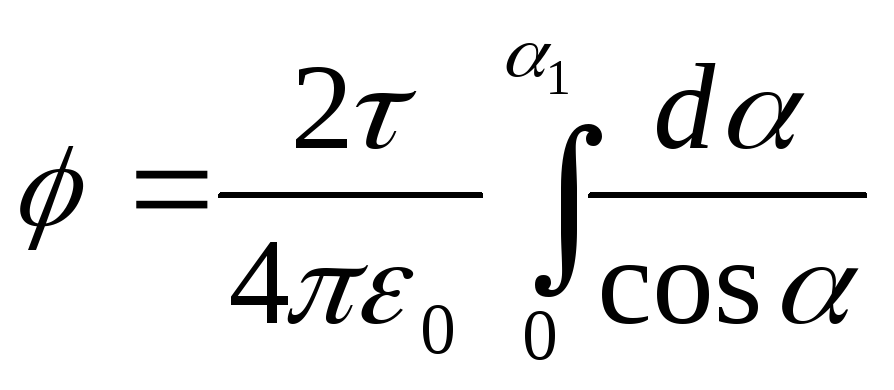.Zato što

(vidi tabelu 2), zatim

.

Zamjenom granica integracije dobijamo

Nakon što smo izvršili proračune prema ovoj formuli, nalazimo

Primjer 6 Elektron brzine v=1,8310 6 m/s uletio je u jednolično električno polje u smjeru suprotnom od vektora jačine polja. Kakva potencijalna razlika U elektron mora proći da bi imao energiju E i\u003d 13,6 eV *? (Imajući takvu energiju, elektron ga može jonizirati kada se sudari s atomom vodonika. Energija od 13,6 eV naziva se energija ionizacije vodonika.)

Rješenje. Elektron mora proći takvu potencijalnu razliku u, tako da stečena energija W u kombinaciji sa kinetičkom energijom T, koju je elektron imao prije ulaska u polje, iznosila je energiju jednaku energiji jonizacije E i , tj. W+ T= E i . Izražavanje u ovoj formuli W= EU i T=(m v 2 /2), dobijamo EU+(m v 2 /2)=E i. Odavde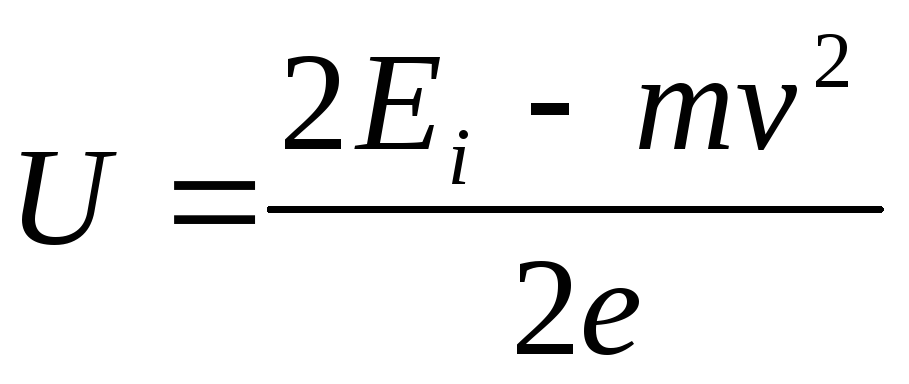

.

___________________

* Elektron-volt (eV) - energija koju čestica dobija, koja ima naelektrisanje jednako naelektrisanju elektrona, prolazeći kroz potencijalnu razliku od 1 V. Ova nesistemska jedinica energije trenutno je odobrena za upotrebu u fizici.

Izračunajmo u SI jedinicama:

U=4,15 AT.

Primjer 7 Odredite početnu brzinu υ 0 pristup protona lociranih na dovoljno velika udaljenost jedan od drugog ako je minimalna udaljenost r min, do kojeg se mogu približiti, iznosi 10 -11 cm.

Rješenje: Između dva protona postoje odbojne sile, zbog čega će kretanje protona biti sporo. Dakle, problem se može riješiti kao inercijski sistem koordinatama (povezano sa centrom mase dva protona), iu neinercijalnim (povezano sa jednim od protona koji se brzo kreću). U drugom slučaju, Newtonovi zakoni ne vrijede. Primjena d'Alembertovog principa je teška zbog činjenice da će ubrzanje sistema biti promjenjivo. Stoga je zgodno razmotriti problem u inercijskom referentnom okviru.

Postavimo početak koordinata u centar mase dva protona. Pošto imamo posla sa identičnim česticama, centar mase će biti u tački koja deli segment koji povezuje čestice. U odnosu na centar mase, čestice će u svakom trenutku imati iste brzine po modulu. Kada su čestice na dovoljno velikoj udaljenosti jedna od druge, brzina υ 1 svaka čestica jednaka je polovini υ 0 , tj. υ 1 =υ 0 /2.

Za rješavanje problema primjenjujemo zakon održanja energije, prema kojem ukupna mehanička energija E izolovani sistem je konstantan, tj.

E=T+ P ,

gdje T- zbir kinetičkih energija oba protona u odnosu na centar mase; P je potencijalna energija sistema naelektrisanja.

Potencijalnu energiju izražavamo u početnom P 1 i konačnom P 2 momentu kretanja.

U početnom trenutku, prema uslovu zadatka, protoni su bili na velikoj udaljenosti, pa se potencijalna energija može zanemariti (P 1 =0). Dakle, za početni trenutak ukupna energija biće jednaka kinetičkoj energiji T 1 protona, tj.

E=T l . (1)

U konačnom trenutku, kada se protoni približavaju što bliže, brzina i kinetička energija su jednake nuli, a ukupna energija će biti jednaka potencijalnoj energiji P 2, tj.

E= P 2 . (2)

Izjednačavanjem pravih dijelova jednakosti (1) i (2) dobijamo

T 1 \u003d P 2. (3)

Kinetička energija jednaka je zbiru kinetičkih energija protona:

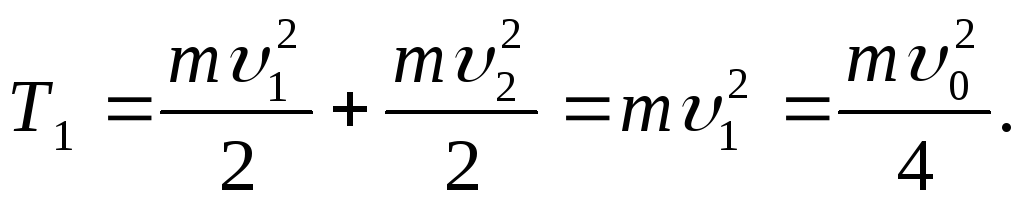(4)

Potencijalna energija sistema od dva naelektrisanja Q 1 i Q 2 u vakuumu određuje se formulom

, gdje r- udaljenost između punjenja. Koristeći ovu formulu, dobijamo

(5)

Uzimajući u obzir jednakosti (4) i (5), formula (3) dobija oblik

gdje

Nakon izvođenja proračuna prema dobijenoj formuli, nalazimo υ 0 =2,35 mm/s

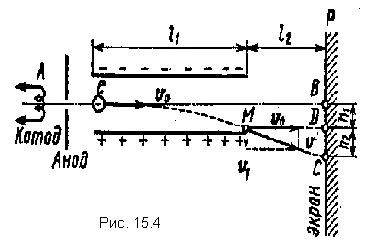Primjer 8 Elektron bez početne brzine prošao je potencijalnu razliku U 0 =10 kV i odleteo u prostor između ploča ravnog kondenzatora napunjenog do razlike potencijala U l \u003d 100 V, duž linije AB, paralelno sa pločama (sl. 15.4). Razdaljina d između ploča je 2 cm dužine l 1 ploča kondenzatora u smjeru leta elektrona jednaka je 20cm. Odredite udaljenost Ned na ekranu R, dalje od kondenzatora l 2 \u003d 1 m.

Rješenje Kretanje elektrona unutar kondenzatora sastoji se od dva kretanja: 1) po inerciji duž linije AB konstantnom brzinom υ 0 , stečena pod dejstvom potencijalne razlike U 0 , koju je elektron prešao na kondenzator; 2) jednoliko ubrzano kretanje u vertikalnom pravcu do pozitivno naelektrisane ploče pod dejstvom konstantne sile polja kondenzatora. Nakon što napusti kondenzator, elektron će se kretati ravnomjerno brzinom υ, koju je imao u tom trenutku M u trenutku izlaska iz kondenzatora.

Od sl. 15.4 pokazuje da je željena udaljenost | | BC|=h 1 +h 2 , odakle h 1 - udaljenost na kojoj će se elektron kretati u vertikalnom smjeru dok se kreće u kondenzatoru; h 2 - udaljenost između tačke D na ekranu, u koju bi elektron pao, krećući se na izlazu iz kondenzatora u smjeru početne brzine υ 0 i tačku C, gdje elektron zapravo udara.

Ekspres posebno h 1 i h 2 . Koristeći formulu za dužinu putanje jednoliko ubrzanog kretanja, nalazimo

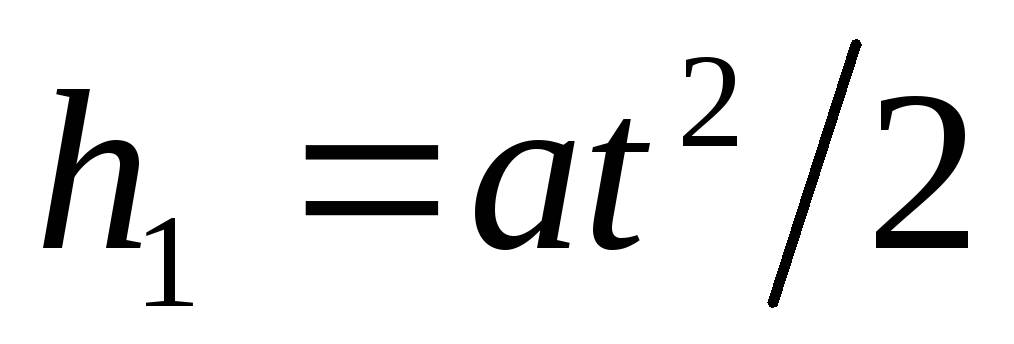. (1)

gdje a- ubrzanje koje prima elektron pod dejstvom polja kondenzatora; t- vrijeme leta elektrona unutar kondenzatora.

Prema drugom Newtonovom zakonu a=F/m, gdje F- sila kojom polje deluje na elektron; t- svoju masu. sa svoje strane, F=eE=eU 1 /d, gdje e- naelektrisanje elektrona; U 1 - razlika potencijala između ploča kondenzatora; d- udaljenost između njih. Vrijeme leta elektrona unutar kondenzatora nalazimo iz formule za putanju ravnomjernog kretanja

, gdje

gdje l 1 je dužina kondenzatora u smjeru leta elektrona. Izraz za brzinu nalazimo iz uvjeta jednakosti rada polja pri kretanju elektrona i kinetičke energije koju on dobija:

. Odavde

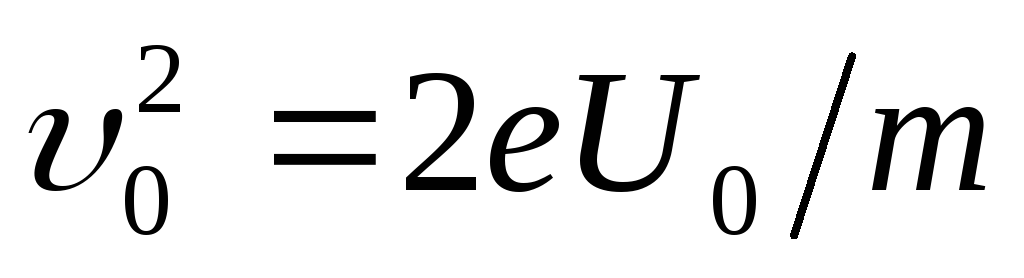(2)

Zamjenjujući u formulu (1) sukcesivno vrijednosti a,F, t i υ 0 2 iz odgovarajućih izraza dobijamo

Dužina rezanja h 2 naći iz sličnosti trouglova MDC i vektor:

(3)

gdje υ 1 - brzina elektrona u vertikalnom smjeru u tački M;l 2 - udaljenost od kondenzatora do ekrana.

Brzina υ 1 nalazimo po formuli υ 1 =na,što, uzimajući u obzir izraze za a, F i tće poprimiti formu

Zamjena izraza υ 1 u formulu (3), dobijamo

, ili zamenom υ 0 2 po formuli (3), nalazimo

Konačno za potrebnu udaljenost | BC| će imati

|BC|=

Zamjena vrijednosti količina U 1 ,U 0 ,d,l 1 i l 2 u posljednji izraz i izvođenjem proračuna dobijamo | BC|=5,5 cm.

Zadaci

Potencijalna energija i potencijal polja tačkastih naelektrisanja

15.1. tačka naboj Q\u003d 10 nC, u određenoj tački polja, ima potencijalnu energiju P = 10 μJ. Pronađite potencijal φ ove tačke polja.

5.2. Pri pomicanju punjenja Q=20 nC između dvije tačke polja, rad su obavljale vanjske sile A=4µJ. Definišite posao A 1 sile polja i razlika Δφ potencijala ovih tačaka polja.

15.3. Električno polje je stvoreno tačkastim pozitivnim nabojem Q 1 \u003d 6 nC. pozitivan naboj Q 2 se prenosi iz tačke ALI ovo polje do neke tačke AT(Sl. 15.5). Kolika je promjena potencijalne energije ΔP po jedinici prenesenog naboja, ako r 1 =20 cm i r 2 \u003d 50 cm?

15.4. Električno polje stvoreno tačkastim nabojem Q l \u003d 50 nC. Bez korištenja koncepta potencijala, izračunajte rad ALI in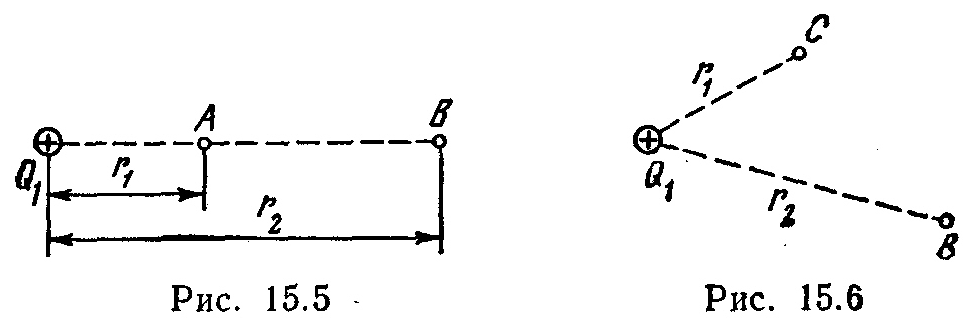

spoljne sile za pomeranje tačkastog naboja Q 2 = -2 nC od tačke OD upravo AT

(Sl. 15.6), ako r 1 =10 cm, r 2 = 20 cm Odredite i promjenu ΔP potencijalne energije sistema naboja.

15.5. Polje je stvoreno tačkastim nabojem Q=1 nC. Odrediti potencijal φ polja u tački udaljenoj od naboja na udaljenosti r=20 cm.

15.6. Odredite potencijal φ električnog polja u tački udaljenoj od naboja Q 1 = -0,2 µC i Q 2 =0,5 μC, respektivno, uključeno r 1 =15 masovni medij r 2 \u003d 25 cm. Također odredite minimalne i maksimalne udaljenosti između naboja za koje je moguće rješenje.

15.7. Naplate Q 1 \u003d 1 μC i Q 2 = -1 μC su na udaljenosti d\u003d 10 cm. Odredite napetost E i potencijal φ polja u tački udaljenoj na daljinu r= 10 cm od prvog naboja i leži na pravoj koja prolazi kroz prvo naelektrisanje okomito na pravac od Q 1 to Q 2 .

15.8. Izračunajte potencijalnu energiju P sistema od dva tačkasta naelektrisanja Q 1 =100 nC i Q 2 =10 nC na daljinu d=10 cm međusobno.

15.9. Odredite potencijalnu energiju P sistema naelektrisanja u tri tačke Q 1 \u003d 10 nC, Q 2 =20 nCl i Q 3 \u003d -30 nC, koji se nalazi na vrhovima jednakostraničnog trokuta sa dužinom stranice a=10 cm.

15.10. Kolika je potencijalna energija P sistema od četiri identična tačkasta naelektrisanja Q\u003d 10 nC, koji se nalazi na vrhovima kvadrata sa dužinom stranice a\u003d 10 cm? .

15.11. Odrediti potencijalnu energiju P sistema od četiri tačkasta naelektrisanja koja se nalaze na vrhovima kvadrata sa dužinom stranice a\u003d 10 cm Naboji su isti u modulu Q=10 nC, ali su dva negativna. Razmotrimo dva moguća slučaja uređenja naknada.

15.12 . Polje se stvara pomoću dva tačkastog naboja + 2Q i -Q, na daljinu d=12 cm jedan od drugog. Odrediti geometrijsko mjesto tačaka na ravni za koju je potencijal jednak nuli (napisati jednačinu za liniju nultog potencijala).

5.13. Sistem se sastoji od tri punjenja - dva iste veličine Q 1 = |Q 2 |=1 μC i suprotnog predznaka i naboja Q=20 nC, koji se nalazi u tački 1 u sredini između druga dva naelektrisanja sistema (slika 15.7). Odrediti promjenu potencijalne energije ΔP sistema tokom prijenosa naboja Q od tačke 1 do tačke 2. Ove tačke se uklanjaju iz negativnog naboja Q 1 po udaljenosti a= 0,2 m.

Potencijal polja linearno raspoređenih naelektrisanja

15.14. Duž tankog prstena poluprečnika R= 10 cm ravnomjerno raspoređenog naboja s linearnom gustinom τ= 10 nC/m. Odrediti potencijal φ u tački koja leži na osi prstena, na udaljenosti a= 5 cm od centra.

15.15. Na segmentu tankog pravog provodnika naelektrisanje je ravnomerno raspoređeno sa linearnom gustinom τ=10 nC/m. Izračunajte potencijal φ stvoren ovim nabojem u tački koja se nalazi na osi provodnika i udaljena je od najbližeg kraja segmenta za udaljenost jednaku dužini ovog segmenta.

Predavanje 6. Potencijal električnog polja. Test br. 2

Potencijal je jedan od najsloženijih koncepata elektrostatike. Studenti uče definiciju potencijala elektrostatičkog polja, rješavaju brojne probleme, ali nemaju osjećaj potencijala, teško povezuju teoriju sa stvarnošću. Stoga je uloga obrazovnog eksperimenta u formiranju koncepta potencijala vrlo velika. Potrebni su nam eksperimenti koji bi, s jedne strane, ilustrovali apstraktne teorijske ideje o potencijalu, a s druge strane pokazali punu valjanost eksperimenta za uvođenje pojma potencijala. Više je štetno nego korisno težiti posebnoj tačnosti kvantitativnih rezultata u ovim eksperimentima.

6.1. Potencijal elektrostatičkog polja

Pričvrstimo provodno tijelo na izolacijski nosač i napunimo ga. Okačimo svjetlovodnu kuglicu na dugu izoliranu nit i damo joj probni naboj, koji je isto ime kao i tjelesni naboj. Lopta će se odbiti od tijela i van pozicije 1 će se pomeriti na poziciju 2. Od kada se visina lopte u gravitacionom polju povećala za h, potencijalna energija njegove interakcije sa Zemljom se povećala za mgh. To znači da je električno polje naelektrisanog tela izvršilo neki rad na probnom naelektrisanju.

Ponovimo eksperiment, ali u početnom trenutku nemojmo samo pustiti test loptu, već je gurnuti u proizvoljnom smjeru, dajući joj neku kinetičku energiju. Istovremeno, nalazimo da se kreće sa pozicije 1 duž složene putanje, lopta će se na kraju zaustaviti u poziciji 2 . Obaviješten na loptu u početnom trenutku kinetička energija, očigledno je potrošeno na savladavanje sila trenja pri kretanju lopte, a električno polje je izvršilo isti rad na loptici kao u prvom slučaju. Zaista, ako uklonimo nabijeno tijelo, tada isti guranje test lopte dovodi do činjenice da iz položaja 2 vraća se na poziciju 1 .

Dakle, eksperiment sugerira da rad električnog polja na naboju ne ovisi o putanji naboja, već je određen samo položajima njegove početne i krajnje točke. Drugim riječima, na zatvorenoj putanji rad elektrostatičkog polja je uvijek nula. Polja sa ovim svojstvom se pozivaju potencijal.

6.2. Potencijal centralnog polja

Iskustvo pokazuje da je u elektrostatičkom polju stvorenom nabijenom provodljivom kuglom, sila koja djeluje na probni naboj uvijek usmjerena od centra nabijene kuglice, monotono opada s povećanjem udaljenosti i ima iste vrijednosti na jednakim udaljenostima od toga. Takvo polje se zove centralno. Koristeći sliku, lako je provjeriti da li je centralno polje potencijalno.

6.3. Potencijalna energija naboja u elektrostatičkom polju

Gravitaciono polje, kao i elektrostatičko, je potencijalno. Osim toga, matematička notacija zakona univerzalne gravitacije poklapa se sa notacijom Coulombovog zakona. Stoga, kada se proučava elektrostatičko polje, ima smisla osloniti se na analogiju između gravitacionog i elektrostatičkog polja.

Na malom području blizu Zemljine površine, gravitacijsko polje se može smatrati uniformnim (Sl. a).

Na tijelo mase m u ovom polju djeluje sila konstantne veličine i smjera f= t g. Ako tijelo prepušteno samo sebi ispadne iz položaja 1 u poziciju 2 , tada gravitaciona sila radi A = fs = mgs = mg (h 1 – h 2).

Možemo reći istu stvar drugačije. Kada je tijelo bilo u položaju 1 , sistem Zemlja-telo je imao potencijalnu energiju (tj. sposobnost da obavlja rad) W 1 = mgh jedan . Kada je telo u poziciji 2 , sistem koji se razmatra počeo je imati potencijalnu energiju W 2 = mgh 2. Rad obavljen u ovom slučaju jednak je razlici između potencijalnih energija sistema u konačnom i početnom stanju, uzetih sa suprotnim predznakom: ALI = – (W 2 – W 1).

Okrenimo se sada električnom polju, koje je, podsjetimo, kao i gravitacijsko, potencijalno. Zamislite da nema gravitacije, a umjesto Zemljine površine postoji ravna provodna ploča, nabijena (za sigurno) negativno (sl. b). Unesite koordinatnu os Y i postavite pozitivno naelektrisanje preko ploče q. Jasno je da, pošto sam naboj ne postoji, iznad ploče postoji neko tijelo određene mase koje nosi električni naboj. Ali, pošto smatramo da gravitaciono polje nema, onda nećemo uzeti u obzir masu naelektrisanog tela.

Dakle, za pozitivan naboj q sa strane negativno nabijene ravni, sila privlačenja f = q E , gdje E je jačina električnog polja. Pošto je električno polje uniformno, ista sila djeluje na naboj u svim njegovim tačkama. Ako se punjenje pomjeri sa pozicije 1 u poziciju 2 , tada na njega radi elektrostatička sila ALI = fs = qEs = qE(y 1 – y 2).

Isto možemo izraziti i drugim riječima. Trudna 1 Naelektrisanje u elektrostatičkom polju ima potencijalnu energiju W 1 = qEy 1 i na poziciji 2 - potencijalna energija W 2 = qEy 2. Kada punjenje prođe sa pozicije 1 u poziciju 2 električno polje naelektrisane ravni je izvršilo rad na njemu ALI = –(W 2 – W 1).

Podsjetimo da je potencijalna energija definirana samo do izraza: ako je nulta vrijednost potencijalne energije odabrana na drugom mjestu na osi Y, onda se u osnovi ništa neće promijeniti.

6.4. Potencijal homogenog elektrostatičkog polja

Ako se potencijalna energija naboja u elektrostatičkom polju podijeli s vrijednošću ovog naboja, onda se dobije energetska karakteristika samog polja, koja se naziva potencijal:

Potencijal u SI sistemu se izražava u volti: 1 V = 1 J / 1 C.

Ako je u jednoličnom električnom polju os Y poslati paralelno sa vektorom napetosti E , tada će potencijal proizvoljne tačke polja biti proporcionalan koordinati tačke: štaviše, koeficijent proporcionalnosti je jačina električnog polja.

6.5. Razlika potencijala

Potencijalna energija i potencijal se određuju samo do proizvoljne konstante, ovisno o izboru njihovih nultih vrijednosti. Međutim, rad polja ima sasvim određeno značenje, jer je određen razlikom potencijalnih energija u dvije tačke polja:

ALI = –(W 2 – W 1) = –( 2 q – 1 q) = q( 1 – 2).

Rad kretanja električnog naboja između dvije tačke polja jednak je proizvodu naboja i potencijalne razlike početne i krajnje tačke. Razlika potencijala se također naziva voltaža.

Napon između dvije tačke jednak je omjeru rada na polju pri pomicanju naboja od početne do krajnje tačke na ovo punjenje:

Napon je, kao i potencijal, izražen u voltima.

6.6. Razlika potencijala i napetost

U jednoličnom električnom polju, snaga je usmjerena u smjeru opadanja potencijala i, prema formuli = Yey, razlika potencijala je U = 1 – 2 = E(at 1 – y 2). Označavanje razlike u koordinatama tačaka at 1 – y 2 = d, dobijamo U = Ed.

U eksperimentu, umjesto direktnog mjerenja čvrstoće, lakše je odrediti razliku potencijala, a zatim izračunati modul čvrstoće koristeći formulu

gdje d je udaljenost između dvije tačke polja koje su blisko razmaknute u smjeru vektora E . Istovremeno, ne koristi se njutn po privjesku kao jedinica napetosti, već volt po metru:

6.7. Potencijal proizvoljnog elektrostatičkog polja

Iskustvo pokazuje da omjer rada za pomicanje naboja iz beskonačnosti u datu tačku polja i vrijednosti ovog naboja ostaje nepromijenjen: = ALI/q. Ovaj odnos se zove potencijal date tačke elektrostatičkog polja, uzimajući potencijal u beskonačnosti jednak nuli.

6.8. Princip superpozicije potencijala

6.9. Potencijal polja tačkastog naboja

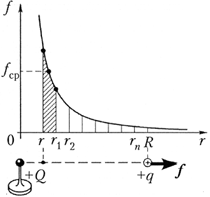
Na slici je prikazan graf zavisnosti jačine elektrostatičke interakcije između tačkastih naelektrisanja od udaljenosti između njih. Pronaći rad električnog polja pri kretanju ispitnog naboja q iz daljine r do udaljenosti R, podijelite ovaj interval po točkama r 1 , r 2 ,..., r p na jednake delove. Prosječna sila koja djeluje na naboj q unutar intervala [ rr 1 ] je jednako

Rad ove snage u ovoj oblasti:

Slični izrazi za rad će se dobiti i za sve ostale dijelove. Dakle, kompletan posao je:

Identični pojmovi sa suprotnim predznacima se uništavaju i konačno dobijamo:

je rad polja na naboju

– razlika potencijala

Sada, da bismo pronašli potencijal tačke polja u odnosu na beskonačnost, usmjeravamo R do beskonačnosti i konačno dobijamo:

Dakle, potencijal polja tačkastog naelektrisanja obrnuto je proporcionalan udaljenosti do naelektrisanja.

6.10. Ekvipotencijalne površine

Zove se površina u kojoj potencijal električnog polja ima istu vrijednost u svakoj tački ekvipotencijalni. Nije teško demonstrirati ekvipotencijalne površine polja nabijene kuglice sa ispitnim nabojem okačenim na niti, kao što je prikazano na slici.

Na drugoj slici, elektrostatičko polje dva suprotna naelektrisanja predstavljeno je silama (puna) i ekvipotencijalnim (isprekidanim) linijama.

Istraživanje 6.1. Razlika potencijala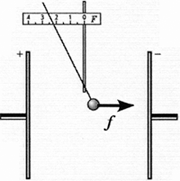

Vježbajte. Razvijte jednostavan eksperiment koji uvodi koncept razlike potencijala ili napona.

Opcija izvršenja. Postavite dva metalna diska na izolacione nosače paralelno jedan s drugim na udaljenosti od oko 10 cm Napunite diskove naelektrisanjem jednakim po veličini i suprotnog znaka. Napunite kuglicu elektrostatičkog dinamometra nabojom, na primjer, q= 5 nC (vidi studiju 3.6), i unesite ga u područje između diskova. U tom slučaju, igla dinamometra će pokazati određenu vrijednost sile koja djeluje na loptu. Poznavajući parametre dinamometra, izračunajte vrijednost modula sile (vidi studiju 3.6). Na primjer, u jednom od naših eksperimenata, igla dinamometra je pokazala vrijednost X\u003d 2 cm, dakle, prema formuli, modul sile f = Kx= 17 10 –5 N.

Pomjeranjem dinamometra pokazati da u svim tačkama polja između nabijenih diskova na probni naboj djeluje ista sila. Pomicanjem dinamometra tako da probno punjenje putuje putem s\u003d 5 cm u smjeru sile koja djeluje na njega, pitajte učenike: kakav rad električno polje vrši na naboju? Postići razumijevanje da je rad polja na modulu naelektrisanja jednak

ALI = fs= 8,5 10 -6 J, (6,3)

osim toga, pozitivan je ako se naboj kreće u smjeru jačine polja, a negativan ako se kreće u suprotnom smjeru. Izračunajte potencijalnu razliku između početnog i konačnog položaja kuglice dinamometra: U = ALI/q\u003d 1,7 10 3 V.

S jedne strane, jačina električnog polja između ploča:

S druge strane, prema formuli (6.1), for d=s:

Dakle, iskustvo pokazuje da se jačina električnog polja može odrediti na dva načina, što, naravno, dovodi do istih rezultata.

Studija 6.2. Kalibracija napona elektrometra

Vježbajte. Osmislite eksperiment da pokažete da pokazni elektrometar može mjeriti napon.

Opcija izvršenja. Eksperimentalna postavka je shematski prikazana na slici. Pomoću elektrostatičkog dinamometra odredite jačinu jednolikog električnog polja i koristite formulu U = Ed izračunati razliku potencijala između provodnih ploča. Ponavljajući ove korake, kalibrirajte elektrometar za napon tako da dobijete elektrostatički voltmetar.

Istraživanje 6.3. Potencijal polja sfernog naboja

Vježbajte. Eksperimentalno odredite rad koji se mora obaviti protiv elektrostatičkog polja da bi se probni naboj pomjerio iz beskonačnosti u neku tačku u polju koje stvara nabijena sfera.

Opcija izvršenja. Pričvrstite kuglicu od stiropora umotanu u aluminijumsku foliju na izolacioni stub. Napunite ga iz piezoelektričnog ili drugog izvora (vidi tačku 1.10) i istim nabojom napunite ispitnu kuglu na štapu elektrostatičkog dinamometra. Probni naboj je beskonačno daleko od ispitivanog, ako elektrostatički dinamometar ne bilježi sile elektrostatičke interakcije između naboja. U eksperimentu je zgodno ostaviti elektrostatički dinamometar da miruje i pomjeriti naboj koji se proučava.

Postepeno približavajte nabijenu kuglicu na izolacijskom postolju kugli elektrostatičkog dinamometra. U prvi red tabele upišite vrijednosti udaljenosti r između naboja, u drugom redu - odgovarajuće vrijednosti sile elektrostatičke interakcije. Pogodno je udaljenost izraziti u centimetrima, a silu u konvencionalnim jedinicama, u kojima je kalibrirana skala dinamometra. Na osnovu dobijenih podataka konstruisati graf zavisnosti sile od udaljenosti. Već ste napravili sličan grafikon u Studiji 3.5.

Sada pronađite zavisnost rada od pomeranja naelektrisanja od beskonačnosti do date tačke u polju. Obratite pažnju na činjenicu da u eksperimentu sila interakcije naelektrisanja postaje gotovo jednaka nuli na relativno maloj udaljenosti jednog naboja od drugog.

Cijeli raspon promjena udaljenosti između naboja podijelite na jednake dijelove, na primjer, svaki po 1 cm. Pogodnije je započeti obradu eksperimentalnih podataka s kraja grafikona. U području od 16 do 12 cm, prosječna vrijednost sile f cf je 0,13 arb. jedinice, dakle elementarni rad ALI u ovoj oblasti je jednako 0,52 arb. jedinice U području od 12 do 10 cm, argumentirajući na sličan način, dobivamo elementarni rad od 0,56 konvencionalnih jedinica. jedinice Dalje, prikladno je uzeti odsječke dužine 1 cm. Na svakom od njih pronađite prosječnu vrijednost sile i pomnožite je sa dužinom presjeka. Dobijene vrijednosti rada na terenu A u svim oblastima unesite u četvrti red tabele.

Da saznam posao ALI koje stvara električno polje pri pomicanju naboja iz beskonačnosti na zadatu udaljenost, zbrojite odgovarajući elementarni rad i upišite rezultirajuće vrijednosti u peti red tabele. U zadnji red upišite vrijednosti 1/ r, recipročna udaljenost između naboja.

Nacrtajte rad električnog polja na recipročnoj udaljenosti i vodite računa da dobijete pravu liniju (slika desno).

Dakle, iskustvo pokazuje da je rad električnog polja kada se naboj kreće od beskonačnosti do date tačke polja obrnuto proporcionalan udaljenosti od ove tačke do naboja koji stvara polje.

Studija 6.4. Izvor visokog napona

Informacije. Za školski eksperiment fizike, industrija trenutno proizvodi odlične izvore napona visokog napona. Imaju dva izlazna terminala ili dvije visokonaponske elektrode, između kojih je potencijalna razlika kontinuirano podesiva od 0 do 25 kV. Pokazivač ili digitalni mjerač napona ugrađen u uređaj omogućava vam da odredite potencijalnu razliku između polova izvora. Ovakvi uređaji povećavaju nivo edukativnog eksperimenta u elektrostatici.

Vježbajte. Osmisliti demonstrativni edukativni eksperiment koji pokazuje da je potencijal nabijene lopte, eksperimentalno određen u skladu sa formulom (6.2) za tačkasto naelektrisanje, jednak potencijalu koji ovoj loptici daje visokonaponski izvor napajanja.

Opcija izvršenja. Ponovo sastavite eksperimentalnu postavku koja se sastoji od elektrostatičkog dinamometra sa ispitnom loptom i provodljive lopte na izolacionom postolju (vidi studije 3.4 i 6.3). Izmjerite parametre svih elemenata instalacije.

Za određenost ističemo da smo u jednom od eksperimenata koristili elektrostatički dinamometar, čiji su parametri naznačeni u studiji 3.4: a= 5 10 –3 m, b= 55 10 -3 m, With= 100 10 -3 m, t= 0,94 10 -3 kg, a kuglice su bile iste i imale su poluprečnik R= 7,5 10 -3 m. Za ovaj dinamometar, faktor kalibracije K, koji pretvara proizvoljne jedinice sile u njutne, dat je formulom (Vidi studiju 3.6).

Na slici na str. 31. Za prelazak sa konvencionalnih jedinica rada na džule na ovom grafikonu, potrebno je, u skladu sa formulom A = f sri r prevedite vrijednosti udaljenosti u centimetrima u metre, vrijednosti sile u arb. jedinice (cm) pretvoriti u arb. jedinice (m) i pomnožite sa K. Na ovaj način: A(J) = 10 -4 KA(arb. jedinice).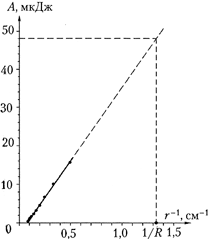

Odgovarajući grafikon rada u odnosu na recipročnu udaljenost je prikazan ispod. Ekstrapolirajući to na R\u003d 7,5 mm, nalazimo da je rad na pomicanju testnog naboja iz beskonačnosti na površinu nabijene lopte ALI\u003d 57 10 -4 K \u003d 4,8 10 -5 J. Pošto su naboji loptica bili isti i iznosili su q\u003d 6,6 10 -9 C (vidi studiju 3.6), zatim željeni potencijal \u003d ALI/q= 7300 V.

Uključite izvor visokog napona i podesite izlazni napon na njemu pomoću regulatora, na primjer, U= 15 kV. Dodirnite jednu po jednu provodljive kuglice jednom od elektroda i isključite izvor. U ovom slučaju, svaka od kuglica dobija potencijal od = 7,5 kV u odnosu na Zemlju. Ponovite eksperiment za određivanje naboja kuglica Kulonovom metodom (istraživanje 3.6) i dobićete vrijednost blizu 7 nC.

Dakle, u eksperimentu se naboji kuglica određuju na dva nezavisna načina. Prva metoda se zasniva na direktnoj upotrebi određivanja potencijala, druga se zasniva na komunikaciji određenog potencijala kuglicama pomoću izvora visokog napona i naknadnom merenju njihovog naboja primenom Kulombovog zakona. Istovremeno su dobijeni identični rezultati.

Naravno, niko od školaraca ne sumnja da savremeni instrumenti ispravno mjere vrijednosti fizičkih veličina. Ali sada su uvjereni da se upravo one veličine koje proučavaju u najjednostavnijim pojavama mjere ispravno. Uspostavljena je snažna veza između osnova fizike i moderne tehnologije, a jaz između školskog znanja i stvarnog života je eliminisan.

Pitanja i zadaci za samokontrolu

1. Kako eksperimentalno dokazati da je elektrostatičko polje potencijalno?

2. Koja je suština analogije između gravitacionog i elektrostatičkog polja?

3. Kakav je odnos između intenziteta i razlike potencijala elektrostatičkog polja?

4. Predložite eksperiment koji direktno potvrđuje valjanost principa superpozicije za potencijale.

5. Izračunajte potencijal polja tačkastog naboja koristeći integralni račun. Uporedite svoj izvod formule sa elementarnim izvođenjem datim na predavanju.

6. Otkrijte zašto je u eksperimentu za određivanje razlike potencijala između dva provodna diska (istraživanje 6.1) nemoguće pomjeriti mjerač napetosti tako da njegova ispitna kugla pređe cijelu udaljenost od jednog diska do drugog.

7. Nakon što ste kalibrirali elektrometar za napon (istraživanje 6.2), uporedite rezultat sa vrijednostima osjetljivosti uređaja na napon, koje su date u podacima pasoša elektrometra.

9. Razviti detaljno metodologiju za formiranje u svijesti studenata razumnog uvjerenja da koncept potencijala električnog polja uveden u proučavanje elektrostatike tačno odgovara onom koji se koristi moderna nauka i tehnologije.

Književnost

Butikov E.I., Kondratiev A.S. Fizika: Proc. dodatak: U 3 knjige. Book. 2. Elektrodinamika. Optika. – M.: Fizmatlit, 2004.

Voskanyan A.G.., Marlensky A.D., Shibaev A.F. Demonstracija Coulombovog zakona na osnovu kvantitativnih mjerenja: U sat. "Nastavni eksperiment iz elektrodinamike", knj. 7. - M.: Škola-Press, 1996.

Kasyanov V.A. Fizika-10. – M.: Drfa, 2003.

Myakishev G.Ya., Sinyakov A.Z.., Slobodskov B.A.. Fizika: Elektrodinamika. 10–11 ćelija: Proc. za ang. studija fizike. – M.: Drfa, 2002.

Obrazovna oprema za kabinete opšte fizike obrazovne institucije: Ed. G.G. Nikiforova. – M.: Drfa, 2005.

Tema 3. POTENCIJAL I RAD ELEKTROstatičkog POLJA. ODNOS SNAGE I POTENCIJALA

3.4. Dipol u električnom polju

3.5. Odnos snage i potencijala elektrostatičkog polja

3.6. Linije polja i ekvipotencijalne površine

3.7. Proračun razlikepotencijali prema jačini polja najjednostavnijih elektrostatičkih polja

3.1. Rad sila elektrostatičkog polja

Sila koja deluje na tačkasto naelektrisanje koje se nalazi u polju drugog stacionarnog punjenja je centralna. Smjer sile koja djeluje u bilo kojoj tački prostora na naboj prolazi kroz centar naboja koji stvara polje, a vrijednost sile ovisi samo o udaljenosti do tog naboja

do tačke posmatranja. (Na primjer, polje gravitacije je polje centralnih sila).

E
Rice. 3.1
Ako je tijelo postavljeno u takve uslove da je u svakoj tački prostora podložno utjecaju drugih tijela sa silom koja se prirodno mijenja od tačke do tačke, onda se za ovo tijelo kaže da se nalazi u polju sila. Centralno polje snaga je potencijalno. Uvjerimo se da je električno polje potencijalno. Izračunajte rad koji vrše sile polja naelektrisanja u fiksnoj tački q preko tačkastog naboja koji se kreće u ovom polju (Sl. 3.1). Radite na elementarnom putu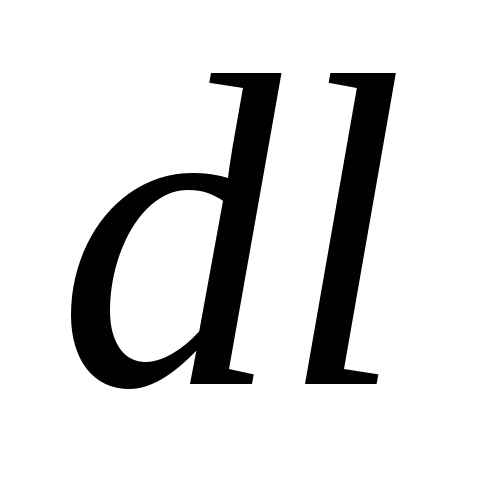

je jednako:

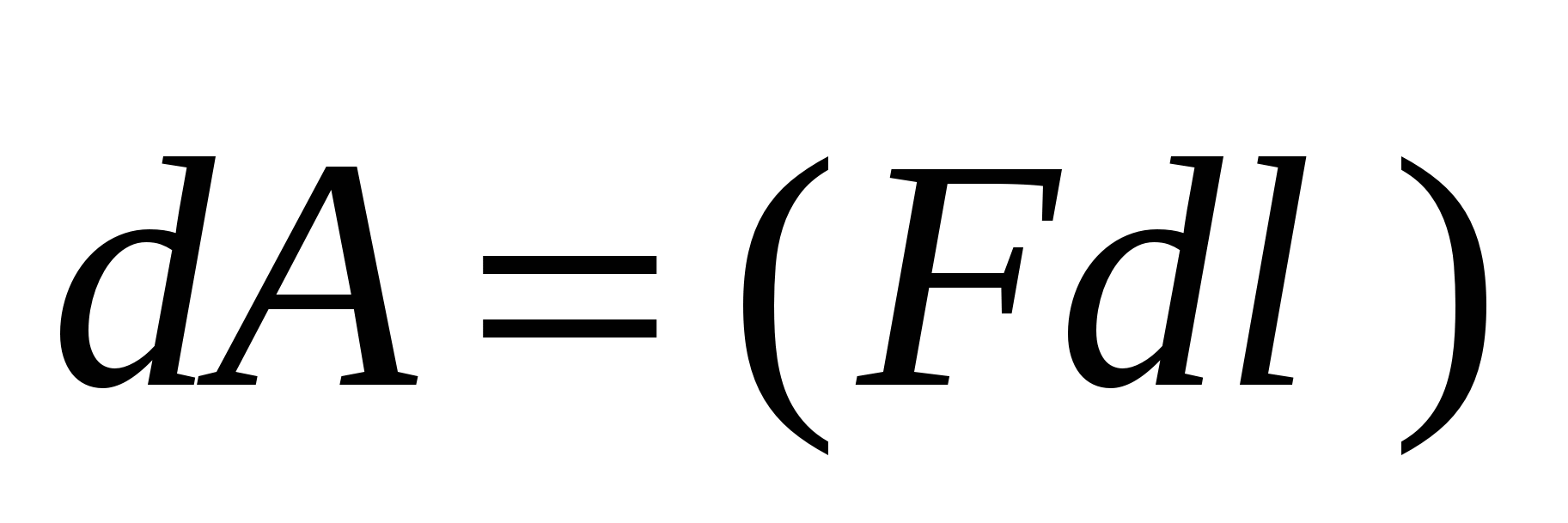ili

Jer

. Odavde na putu 1–2

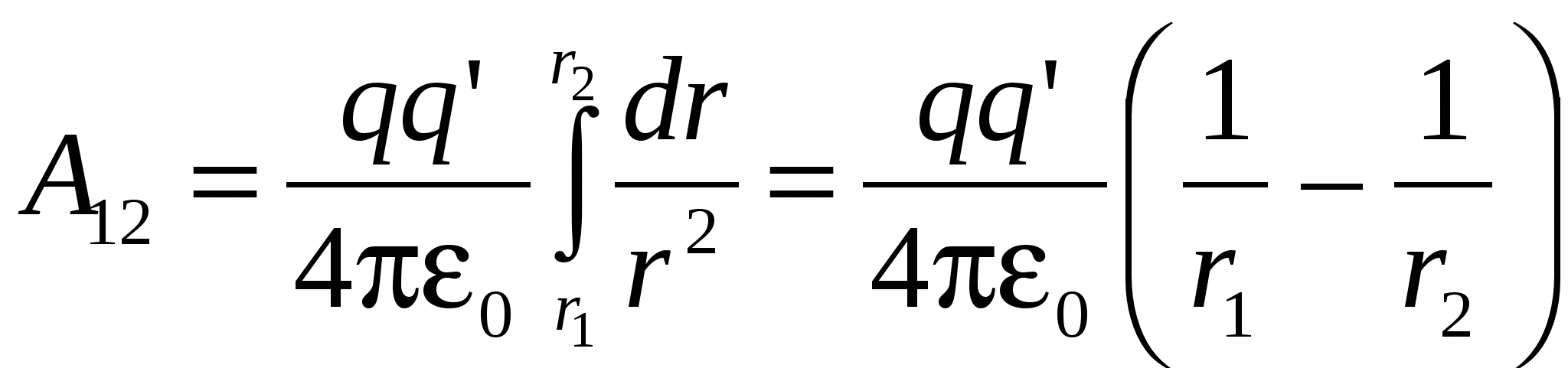(1)

Vidi se da rad ne zavisi od putanje po kojoj se naelektrisanje kretalo u električnom polju q" , ali zavisi samo od početne i krajnje pozicije ovog naboja (na r 1 i r 2). Dakle, sile koje djeluju na naboj q" u polju stacionarnog punjenja q, su konzervativne i polje ovih sila potencijal. Ovaj zaključak se lako može proširiti na polje bilo kojeg sistema fiksnih naelektrisanja, od sile djelujući na osnovu punjenja q" u takvom polju, može se predstaviti principom superpozicije u obliku

, gdje - prinudno i-to punjenje sistema za stvaranje polja. Rad u ovom slučaju jednak je algebarskom zbiru rada pojedinačnih sila:

. Svaki od pojmova na desnoj strani ovog izraza je nezavisan od putanje. Dakle, ne zavisi od puta i posla ALI.

Iz mehanike je poznato da je rad potencijalnih sila na zatvorenom putu jednak nuli. Posao obavljen od strane terenskih snaga na napadu q" kada se prelazi kroz zatvorenu petlju, može se predstaviti kao

, gdje –vektorska projekcija 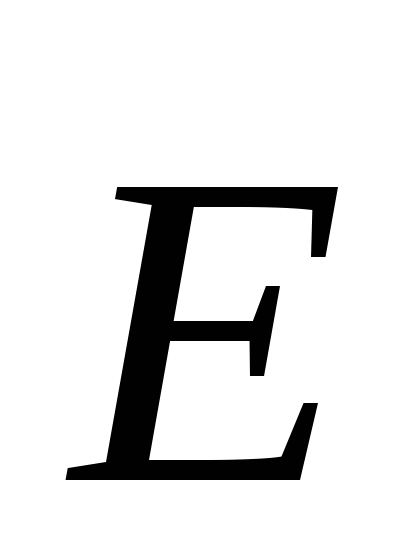u smjeru elementarnog pomaka , dakle:

(2)

Ovaj odnos mora da važi za svaku zatvorenu petlju. Treba imati na umu da (21) vrijedi samo za elektrostatičko polje. Polje pokretnih naboja (tj. polje koje se mijenja s vremenom) nije potencijalno. Shodno tome, uslov (21) za njega nije zadovoljen.

Izražavanje forme

naziva se cirkulacija vektora duž ove konture. Na ovaj način, karakteristika elektrostatičkog polja je da je cirkulacija vektora intenziteta duž bilo kojeg zatvorenog kola nula.

3.2. Teorema cirkulacije vektora elektrostatičkog polja

Dakle, tvrdimo da je cirkulacija vektora 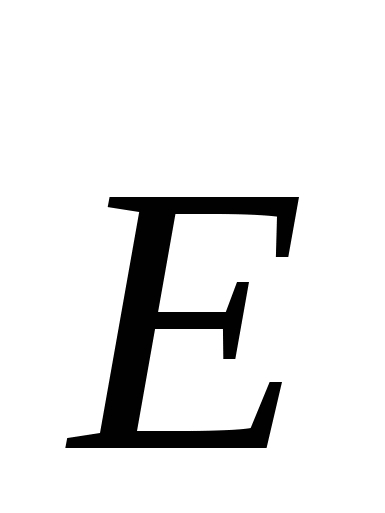u bilo kom elektrostatičkom polju je nula, tj. . Ova izjava se zove teorema vektorske cirkulacije.

Neka se naelektrisanje kreće po zatvorenoj putanji 1a2b1 u datom polju sa jačinom. Da bismo dokazali teoremu, podijelimo proizvoljan zatvoreni put na dva dijela 1a2 i 2b1 (vidi sliku). Hajde da nađemo posao da pomerimo naboj q od tačke 1 do tačke 2. Pošto rad u datom polju ne zavisi od oblika putanje, rad pomeranja naelektrisanja duž putanje 1a2 jednak je radu pomeranja naelektrisanja duž putanje 1b2 ili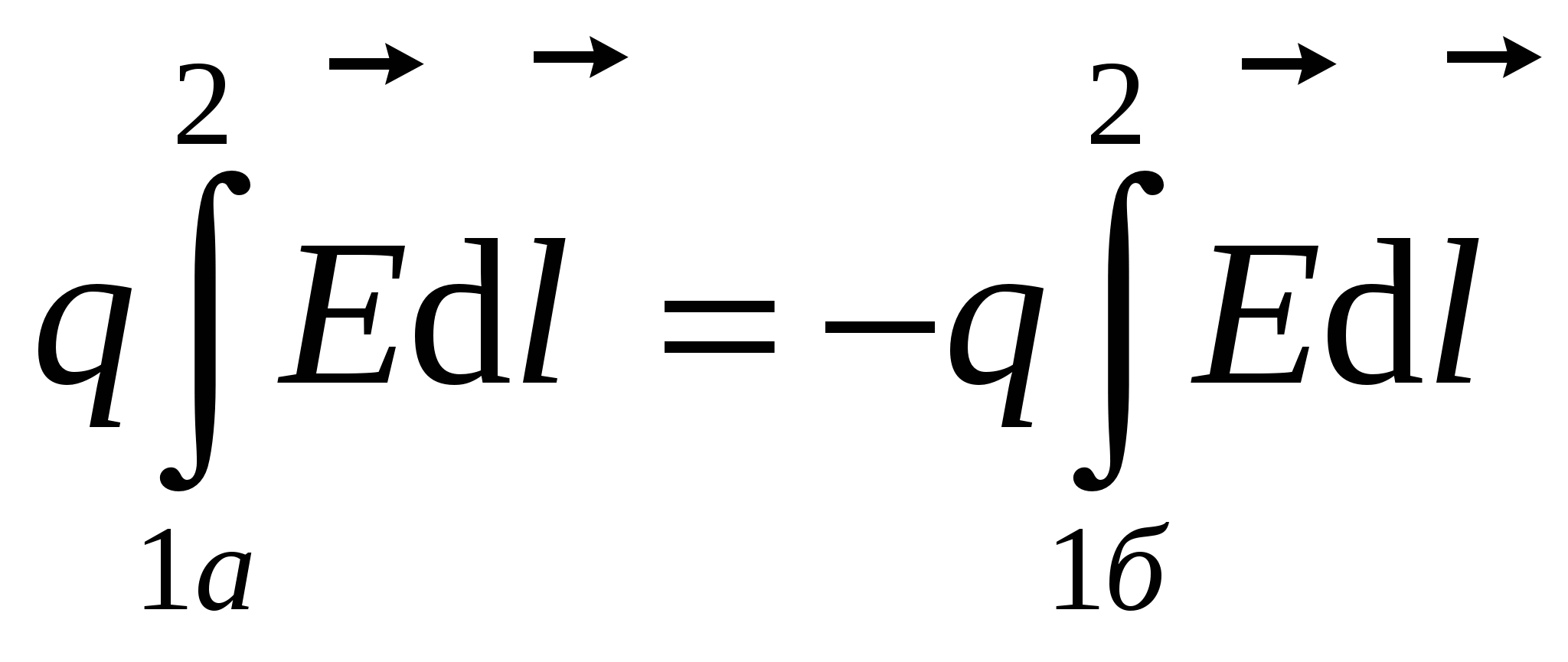

Slika 3.2

Iz navedenog proizilazi da

(Modulo integrali su jednaki, ali su predznaci suprotni). Zatim radite na zatvorenom putu:

(3)

ili

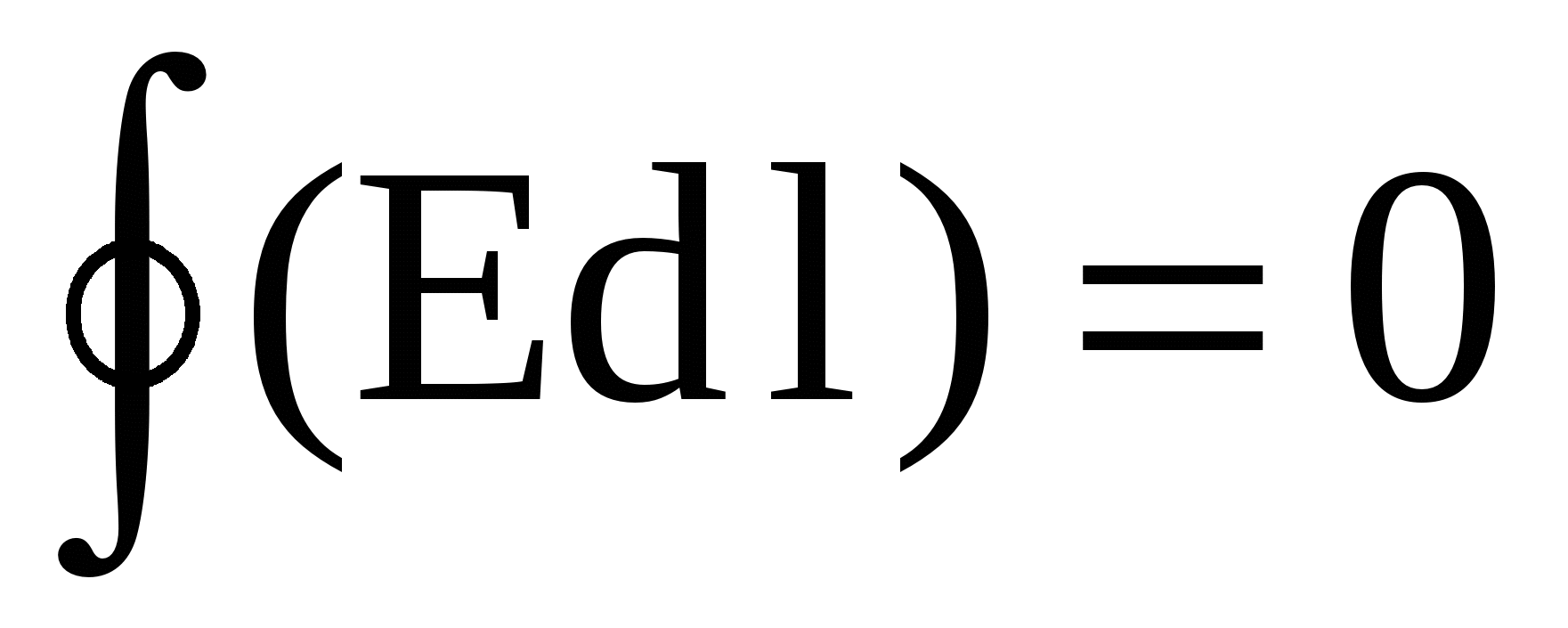(4)

Polje sa ovim svojstvima se zove potencijal . Svako elektrostatičko polje je potencijalno.

Teorema o cirkulaciji omogućava nam da izvučemo niz važnih zaključaka, praktično bez pribjegavanja proračunima. Razmotrimo dva jednostavna primjera koji potvrđuju ovaj zaključak.

Koristimo Stokesovu teoremu, koja kaže da je cirkulacija vektora duž proizvoljne konture L jednak je protoku rotora ovog vektora kroz bilo koju površinu koju obuhvata ova kontura, tj.

. U slučaju elektrostatičkog polja imamo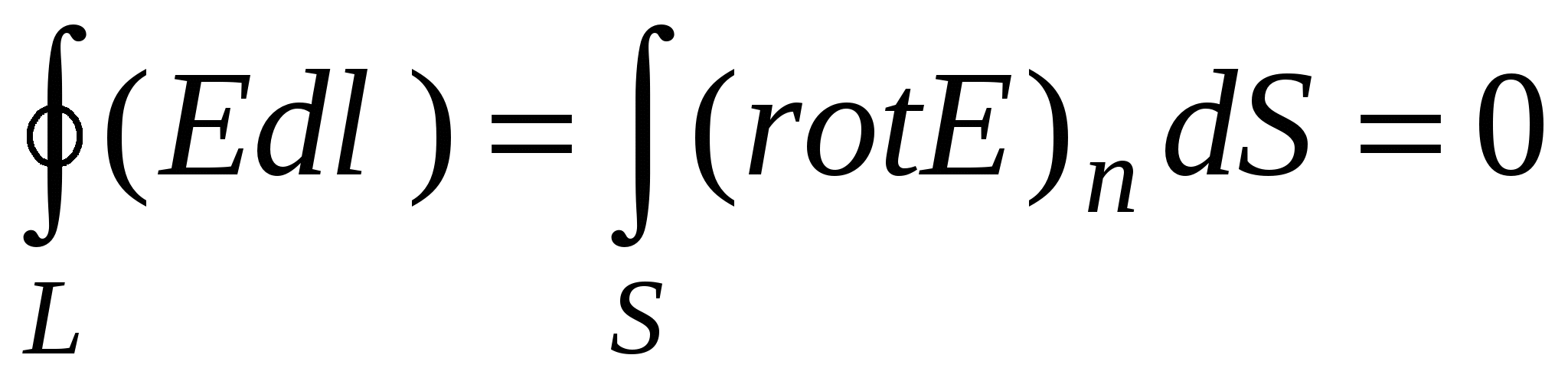

, dakle, zbog proizvoljnosti oblika površine, dobijamo

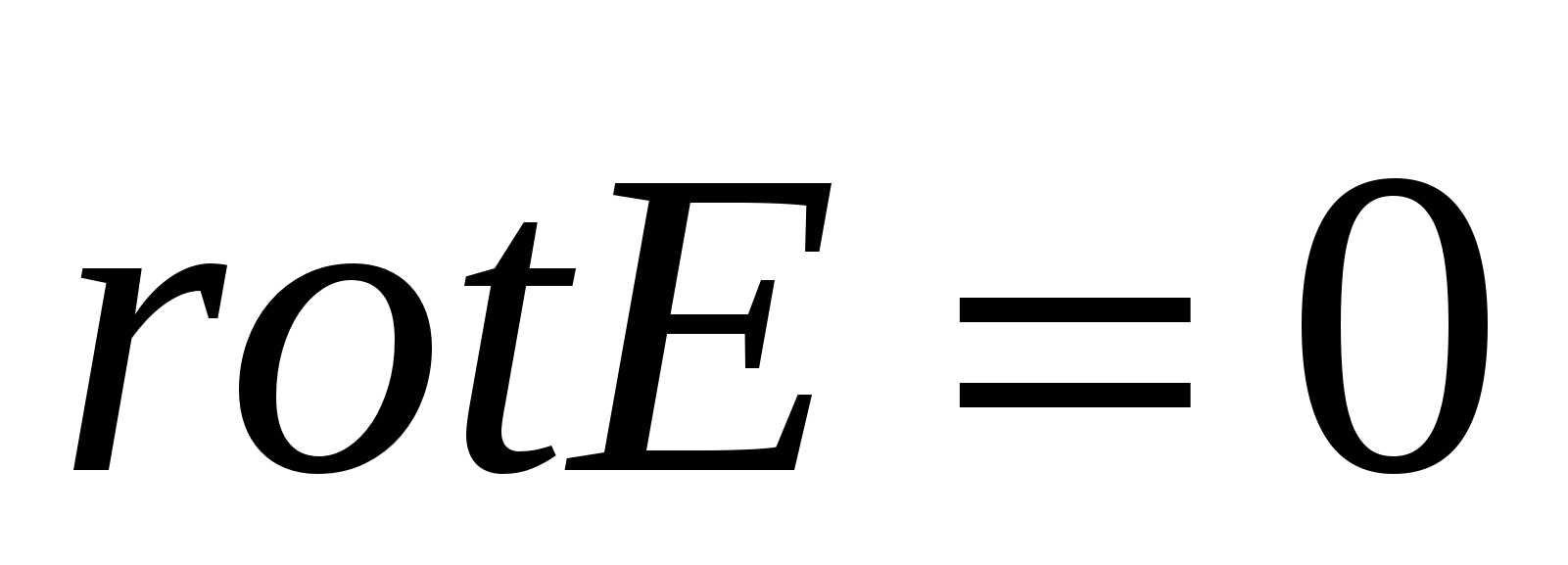. Stoga, iz potencijalne prirode elektrostatičkog polja, slijedi da elektrostatičko polje nije vrtložno ako . (5)

3.3. Potencijalna energija i potencijal elektrostatičkog polja

Tijelo koje se nalazi u polju potencijalnih sila ima potencijalnu energiju, zbog koje se rad obavlja silama polja. Stoga se rad može predstaviti kao razlika u vrijednostima potencijalnih energija koje posjeduje naboj q" u tačkama 1 i 2 polja naelektrisanja q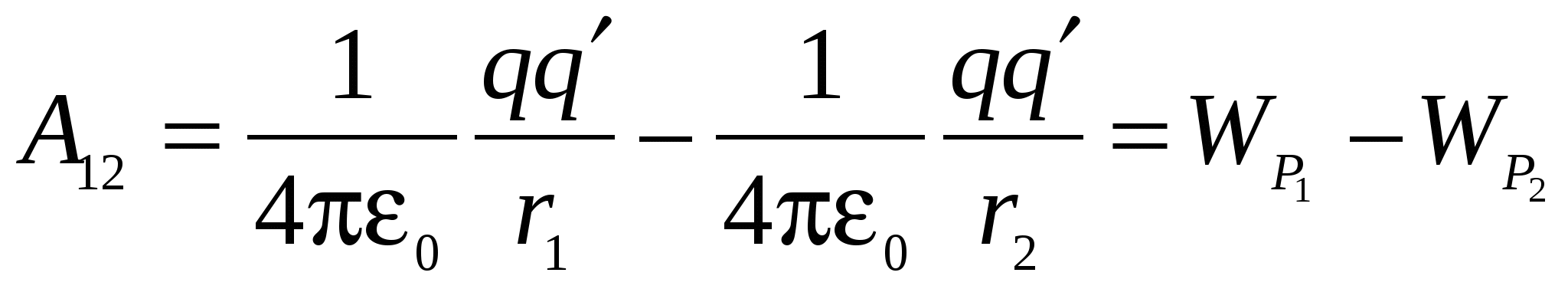

Takođe se može pokazati da, pošto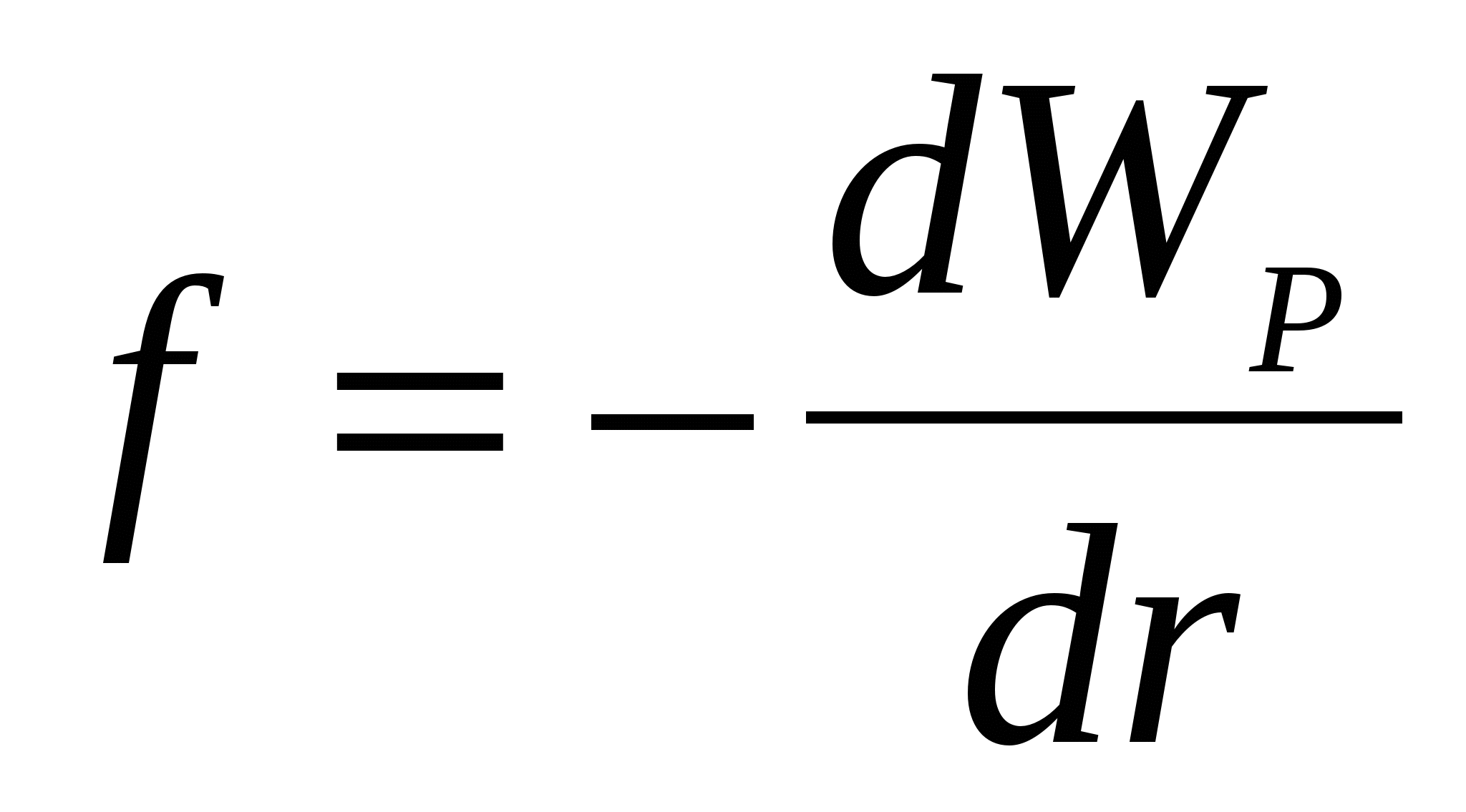

,

Dakle, za potencijalnu energiju naboja u polju naelektrisanja q dobijamo:

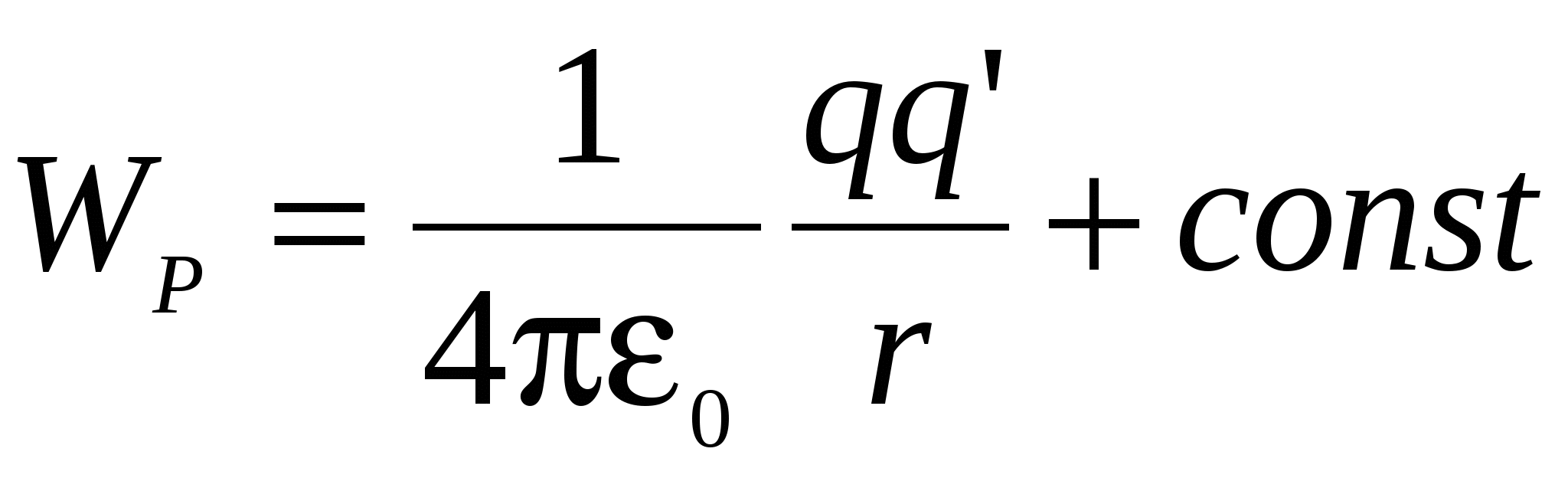(6)

Značenje konst u (6) se obično bira na takav način da kada se naboj ukloni q" do beskonačnosti (

) potencijalna energija nestaje. Pod ovim uslovom ispada da

(7)

Pretpostavljamo q" sudska optužba. Tada potencijalna energija koju posjeduje probni naboj ne ovisi samo o njegovoj vrijednosti 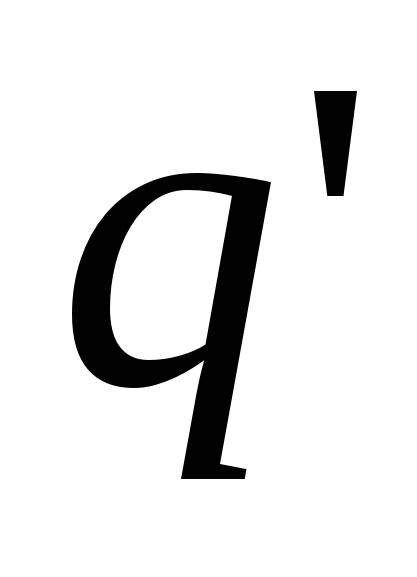, ali i na vrijednost q i r, definiranje polja. Stoga se ova energija može koristiti za opisivanje polja, kao što je za tu svrhu korištena sila koja djeluje na probni naboj.

Razne naknade za testiranje

,

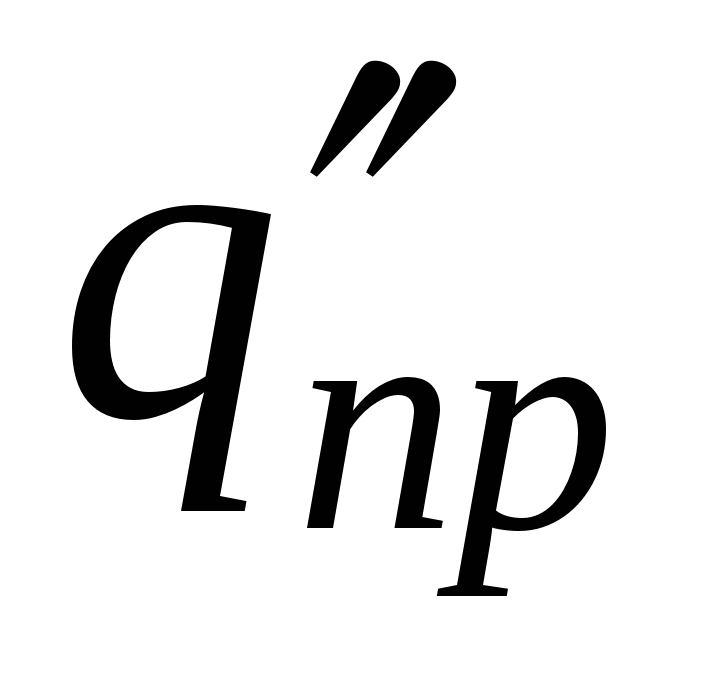imaće različite energije u istoj tački polja

,

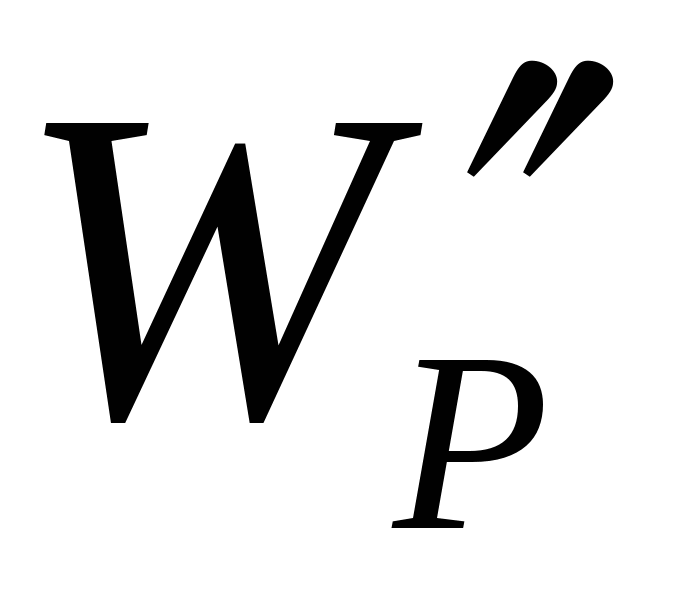itd. Međutim, stav

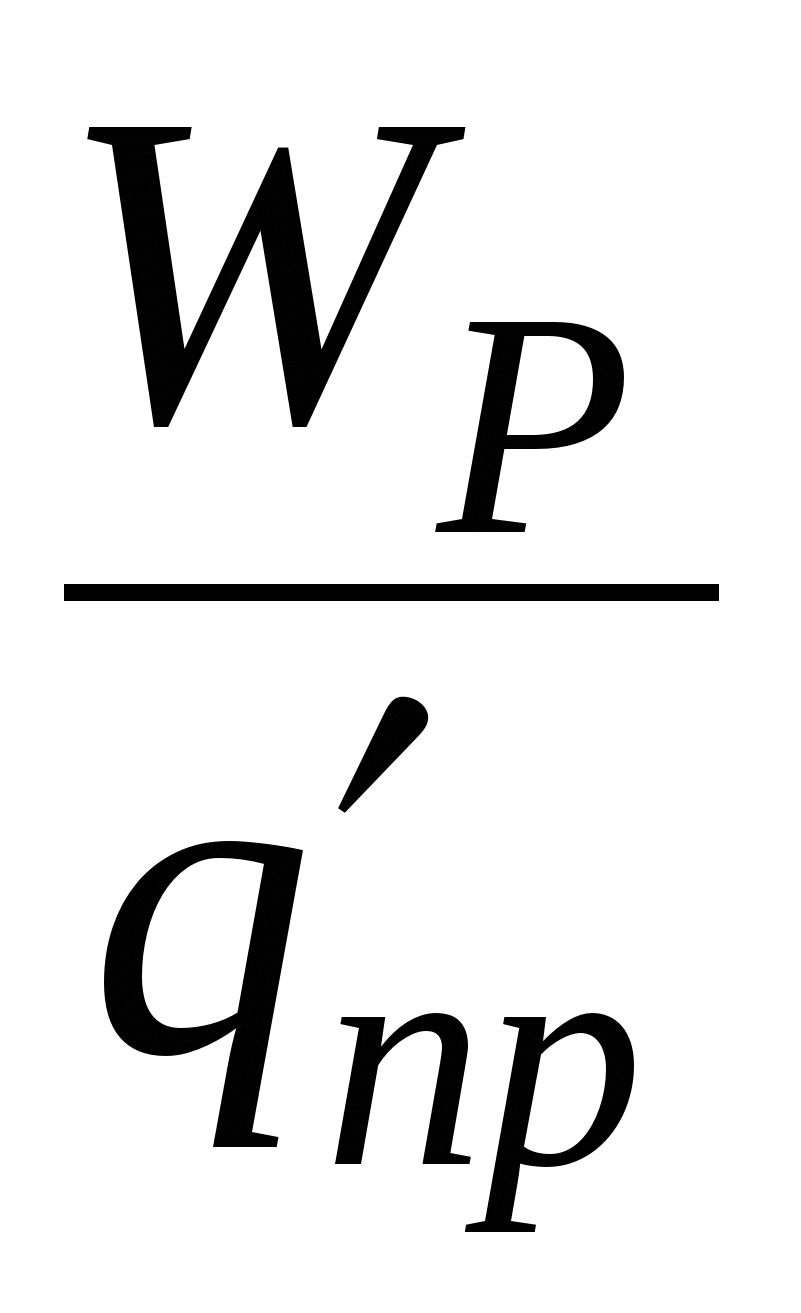bit će isti za sve naknade. Vrijednost

(8)

pozvao potencijal polje u datoj tački i koristi se zajedno sa jačinom polja za opisivanje električnih polja.

Kako slijedi iz (8) potencijal je numerički jednak potencijalnoj energiji koju jedinični pozitivni naboj ima u datoj tački polja.

Dakle za potencijalno polje tačka punjenja dobijamo sledeći izraz:

(9)

Ako je polje kreirano sistemom bodovnih naplata q 1 , q 2 , …, q n, koji se nalaze na udaljenostima respektivno r 1 , r 2 ,…, r n do tačke polja gde se nalazi naboj , zatim rad koji vrše sile ovog polja na naboju , bit će jednak algebarskom zbiru rada sila zbog svakog od naboja posebno:

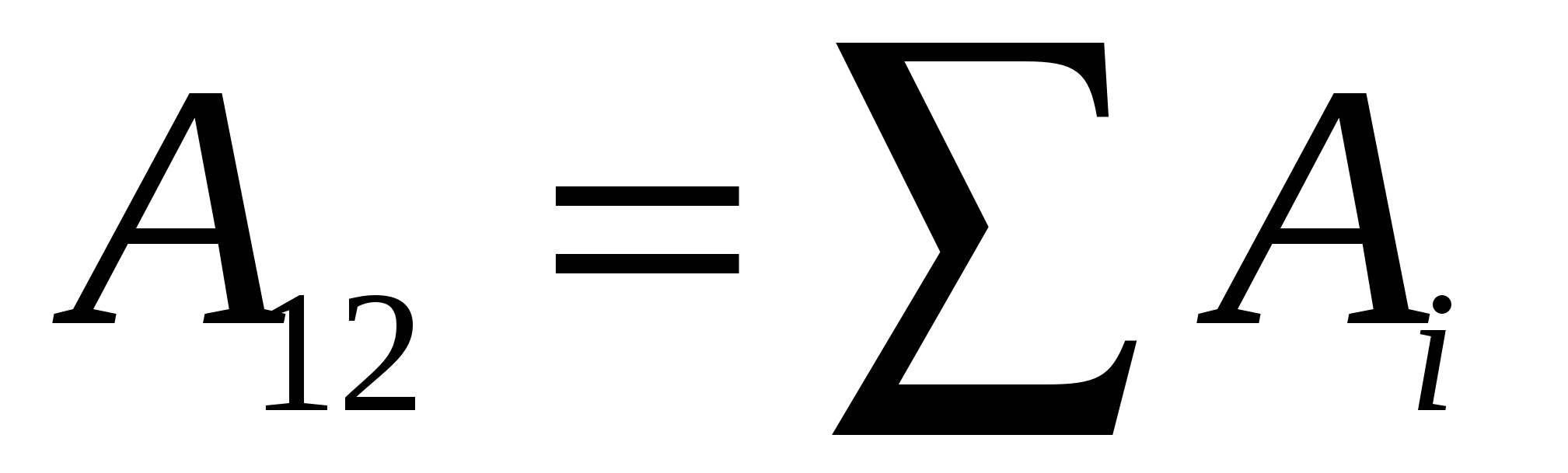Ali svaki od radova je jednako:

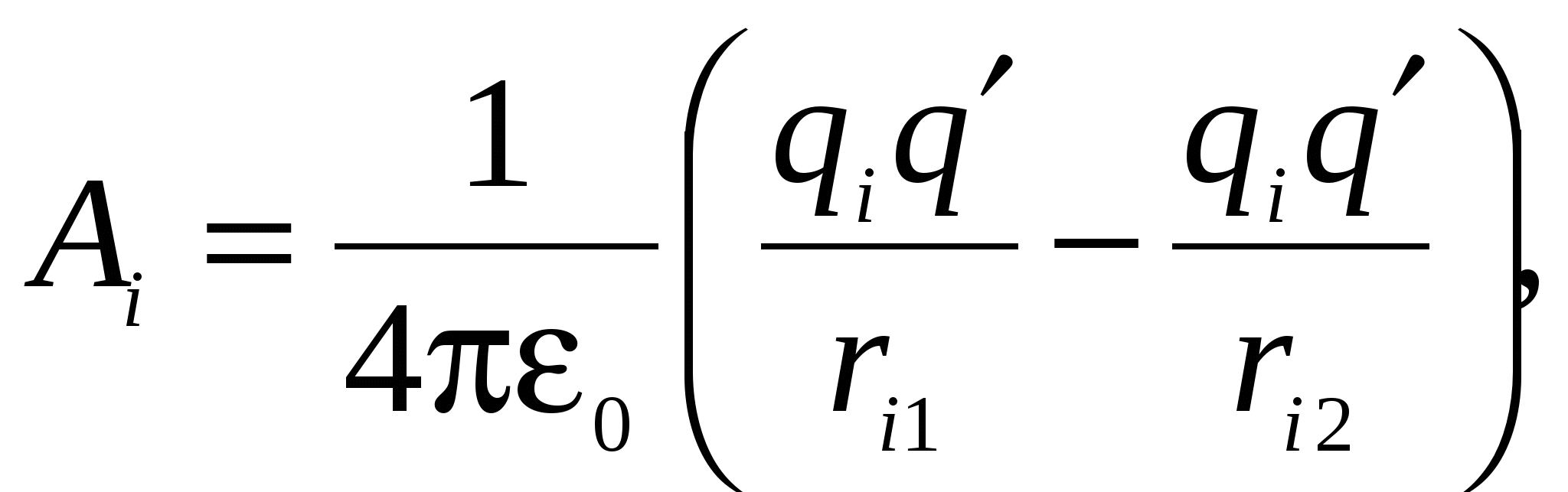
Gdje

udaljenost punjenja 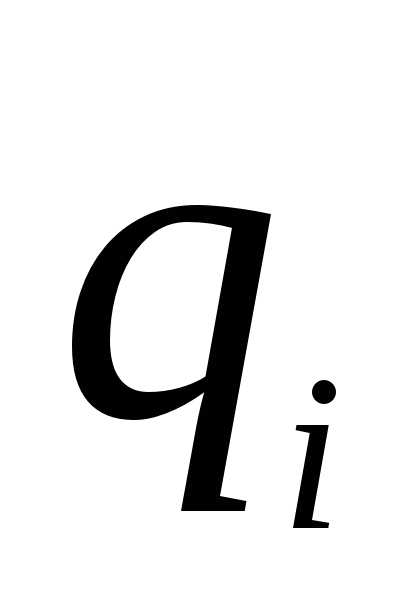u početni položaj punjenja,

udaljenost od naboja do krajnjeg položaja naboja.

posljedično:

Upoređujući ovaj izraz sa relacijom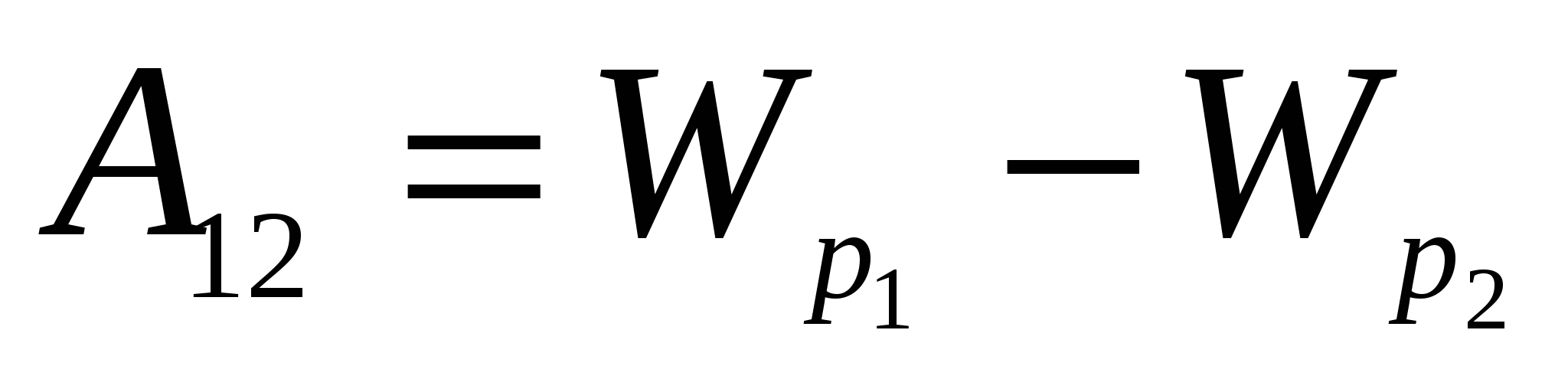

, dobijamo izraz za potencijalnu energiju naelektrisanja u polju sistema naelektrisanja:

, (10)

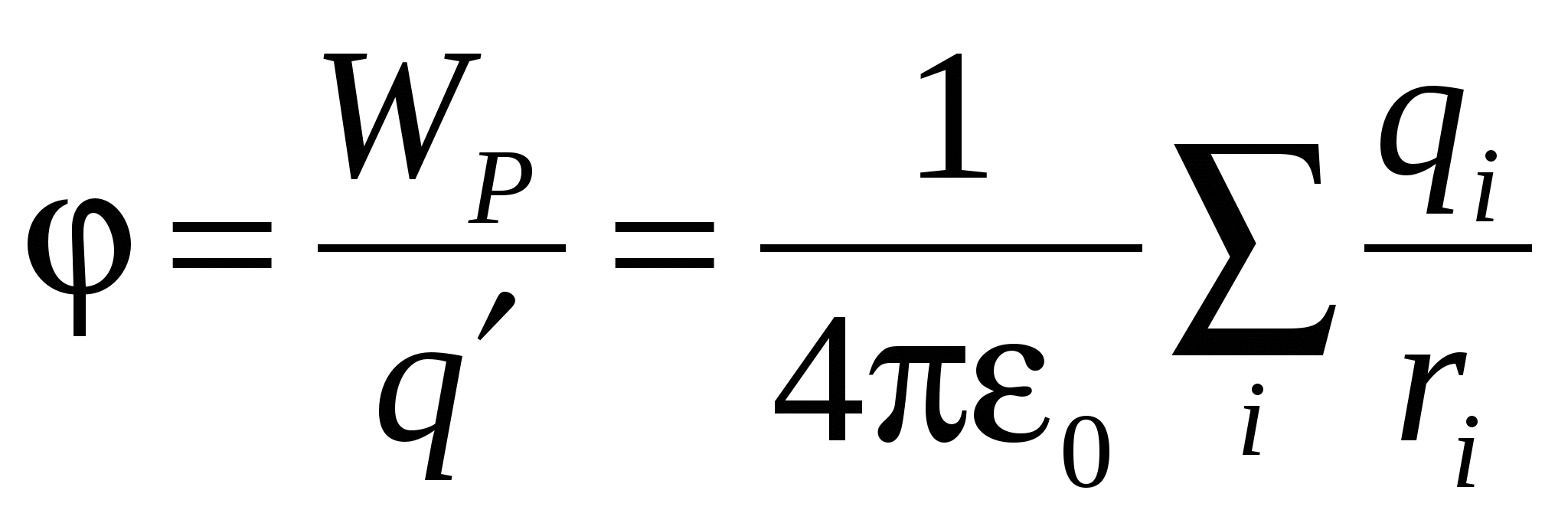. (11).

Shodno tome, potencijal polja stvorenog sistemom naelektrisanja jednak je algebarskom zbiru potencijala koje stvara svako od naelektrisanja posebno.

Iz odnosa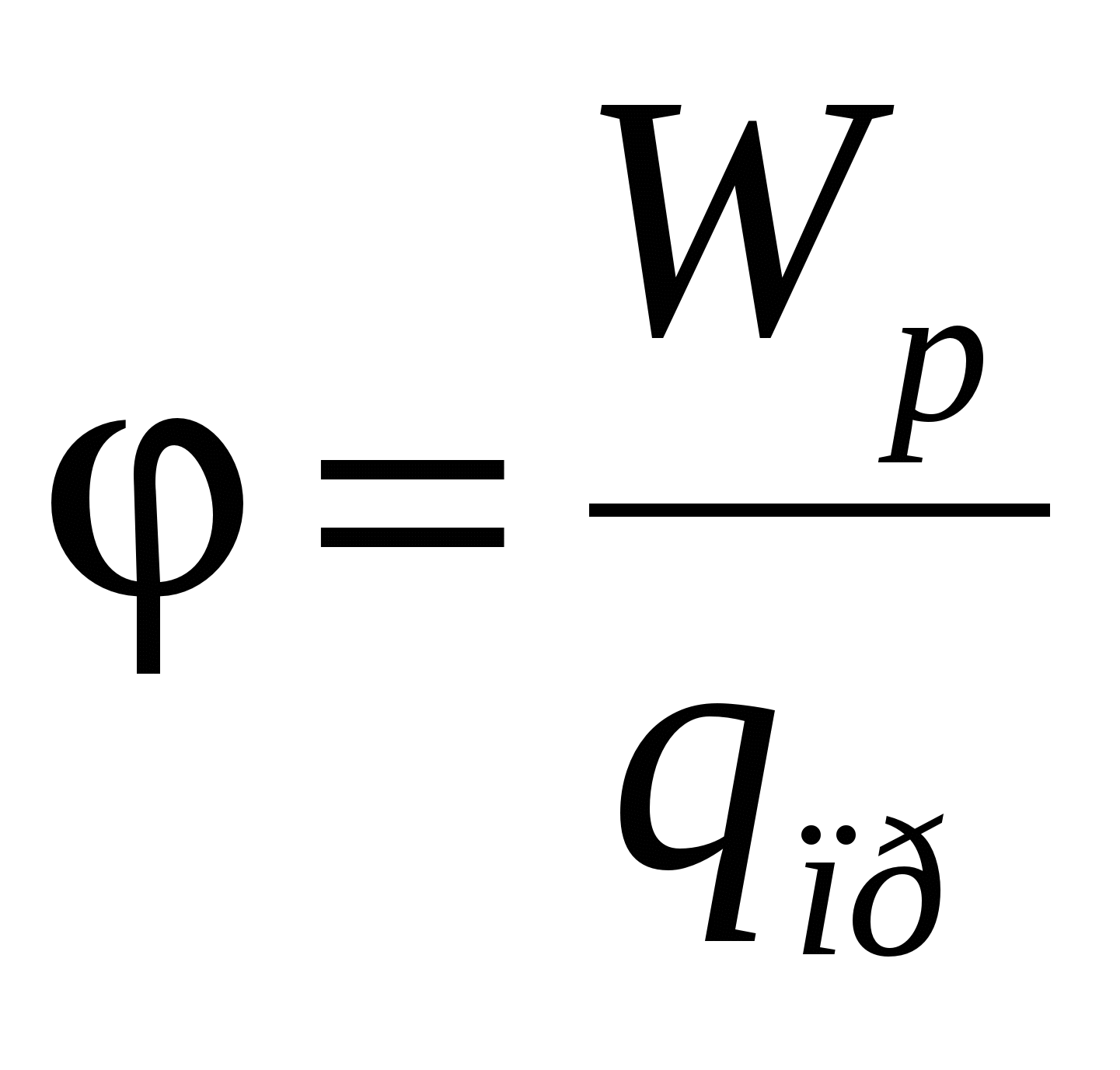

slijedi da je optužba , koji se nalazi na tački polja sa potencijalom , ima potencijalnu energiju

. Stoga se rad sila polja na naboju može izraziti kroz razliku potencijala:

Dakle, posao obavljen na naplati terenske snage, jednak je proizvodu naboja i potencijalne razlike u početnoj i krajnjoj tački. Ako se naboj iz tačke sa potencijalom ukloni u beskonačnost (gde je potencijal jednak nuli prema uslovu), rad sila polja će biti jednak

ili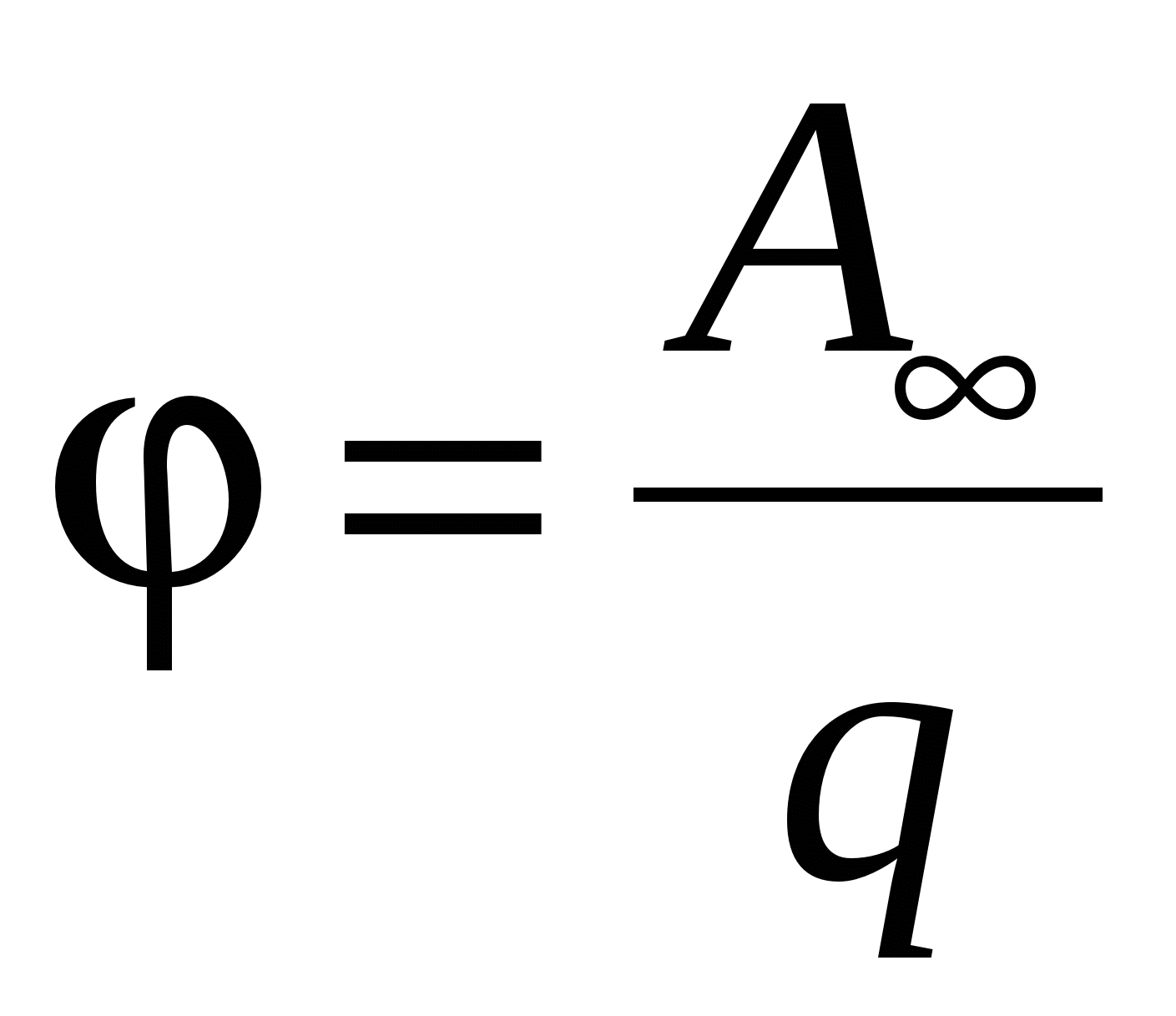

,

T. e, potencijal brojčano jednako radu, koju vrše sile polja na jediničnom pozitivnom naboju kada se udalji iz date tačke polja u beskonačnost, ili rad koji se mora izvršiti protiv sila električnog polja da bi se jedinični pozitivni naboj pomerio iz beskonačnost do date tačke polja.

Potencijalnu jedinicu treba uzeti kao potencijal u takvoj tački polja, da bi se pomaknuo naboj do kojeg je iz beskonačnosti potrebno izvršiti rad jednak

1 džul (sistem jedinica “Ci”)

Odavde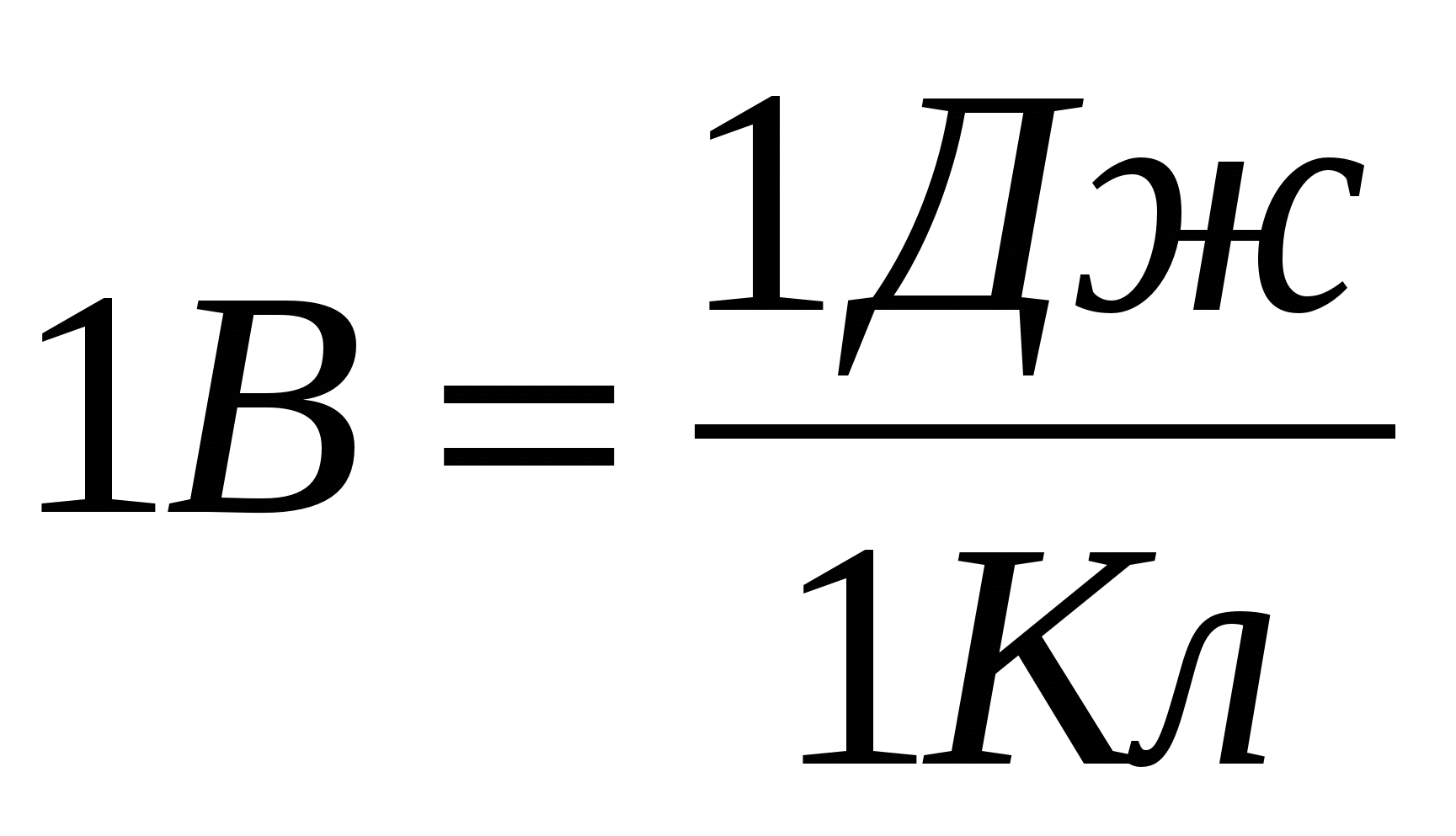

.

3.4. Dipol u elektrostatičkom polju

E 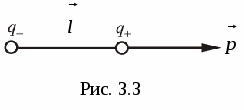električni dipol nazvana kombinacija dva jednake naplate suprotni znak, koji se nalaze na udaljenosti jedan od drugog l, što je malo u odnosu na njihovu udaljenost do tačaka u kojima je određeno dipolno polje.

Umnožak naboja i udaljenosti između naboja p=ql pozvao dipolni moment . Za potpunu definiciju dipola potrebno je navesti i orijentaciju ose dipola u prostoru. Shodno tome, dipolni moment treba posmatrati kao vektor . Ovom vektoru je dodijeljen smjer od negativnog naboja do pozitivnog(sl.3.3). Ako unesete radijus - vektor 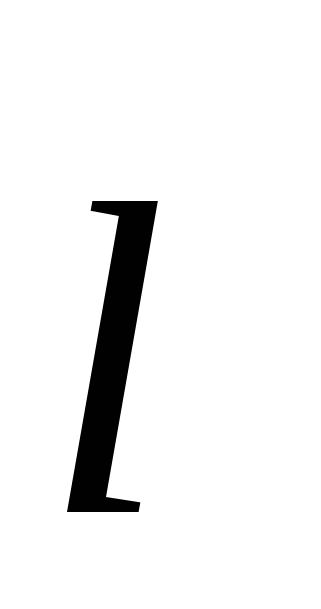potrošeno od – q do + q, tada se dipolni moment može predstaviti kao:

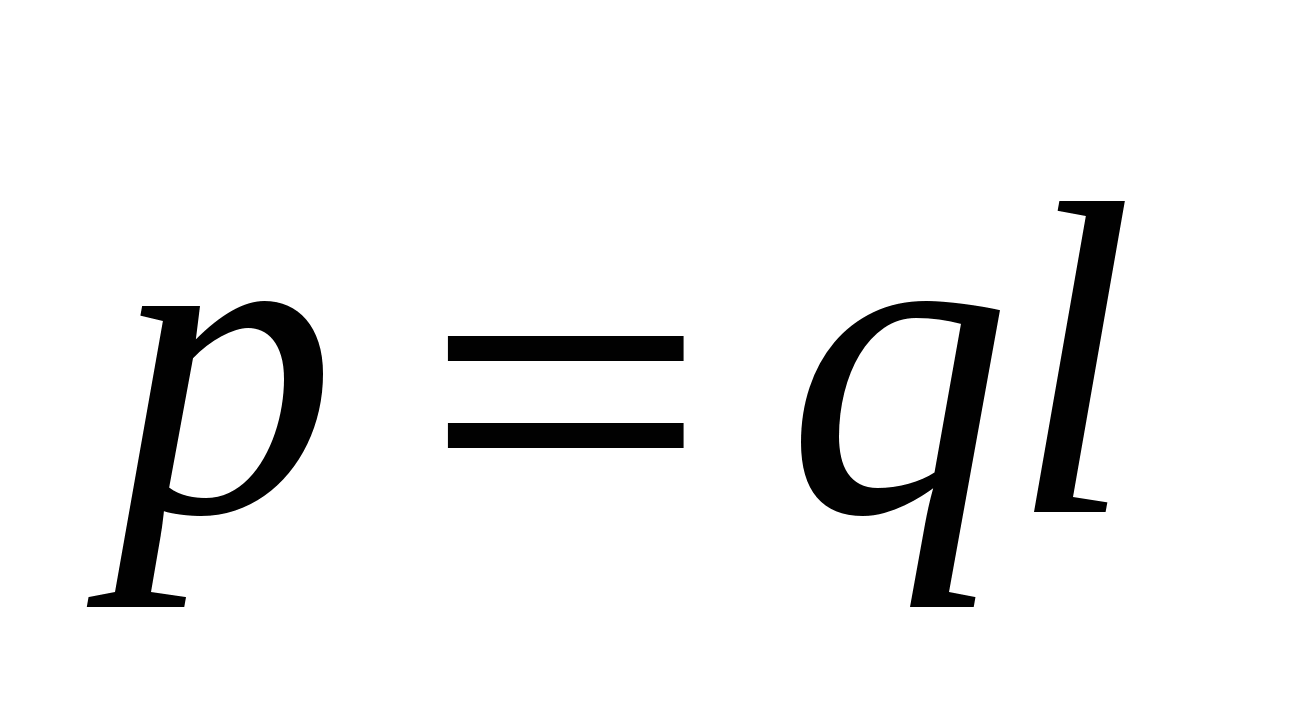. (13)

Ako se dipol postavi u jednolično električno polje, naelektrisanja koja formiraju dipol su q i + q na koje djeluju sile jednake veličine, ali suprotnog smjera i (Sl. 14). Ove sile čine par sila čiji je krak jednak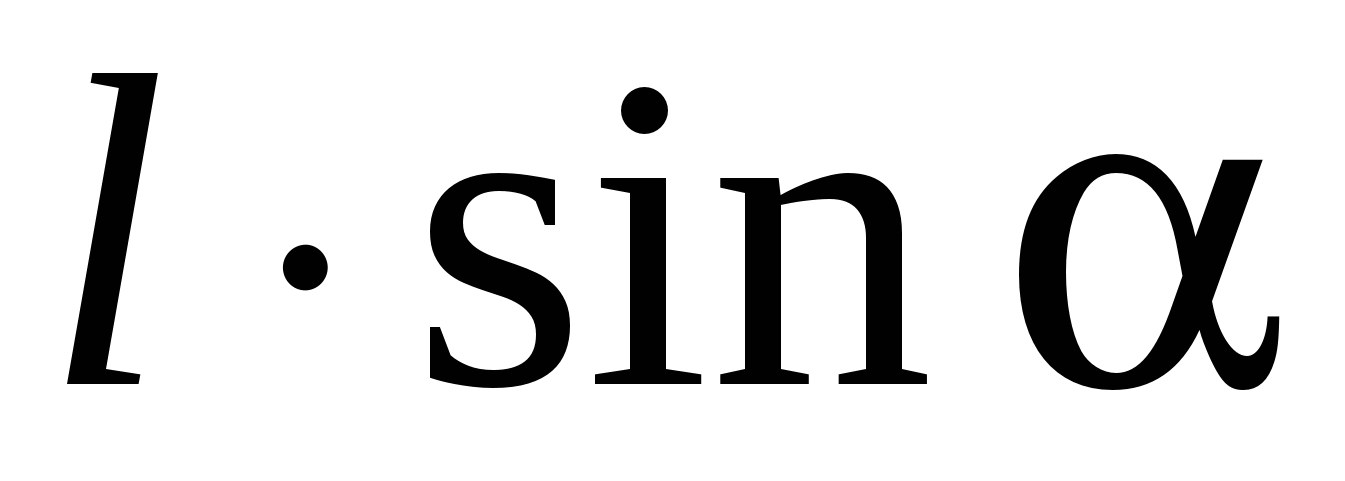

, tj. zavisi od orijentacije dipola u odnosu na polje. Modul svake od sila je qE. Pomnoživši ga sa ramenom, dobivamo vrijednost momenta para sila koje djeluju na dipol:

Gdje R– električni moment dipol.

AT vektorski oblik:

. (15)

Momenat

teži da zarotira dipol tako da njegov moment postaviti u pravcu polja.

Za povećanje ugla između vektora i na dα mora se raditi protiv sila koje djeluju na dipol:

Ovaj rad ide na povećanje potencijalne energije W, koji ima dipol u električnom polju, tj.:

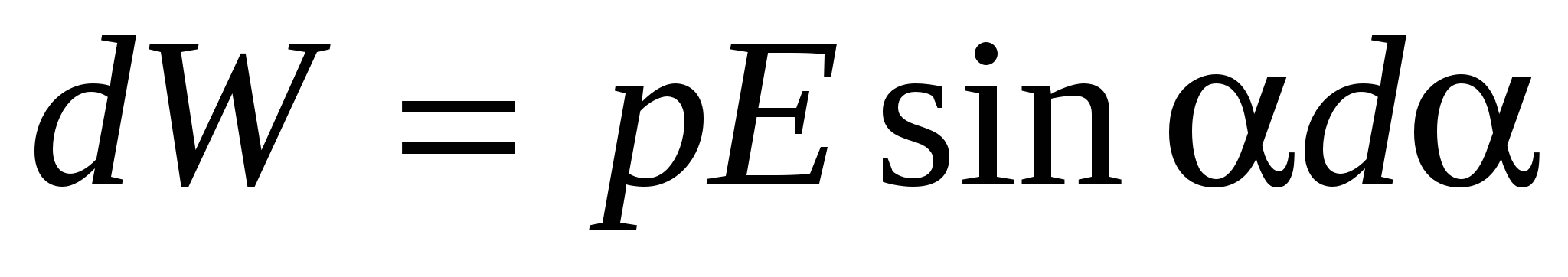(16)

Integracija (16) daje izraz za potencijalnu energiju dipola u električnom polju:

Pretpostavljam konst=0 , dobijamo

AT biranjem konst=0 , pretpostavljamo da će energija dipola biti nula kada se dipol postavi okomito na smjer polja. Najmanja energetska vrijednost jednaka ( -pe), se dobija kada je dipol orijentisan duž pravca polja, najvećeg, jednakog pE, kada je usmjerena u smjeru suprotnom od vektora .

U nehomogenom polju, sile koje djeluju na naboje dipola nisu iste. Za male dipole sile f 1 i f 2 se može smatrati približno kolinearnim. Pretpostavimo da se polje najbrže mijenja u smjeru X, koji se poklapa sa smjerom na mestu gde se nalazi dipol (slika 3.5). pozitivan naboj dipol je pomjeren u odnosu na negativ u smjeru X po iznosu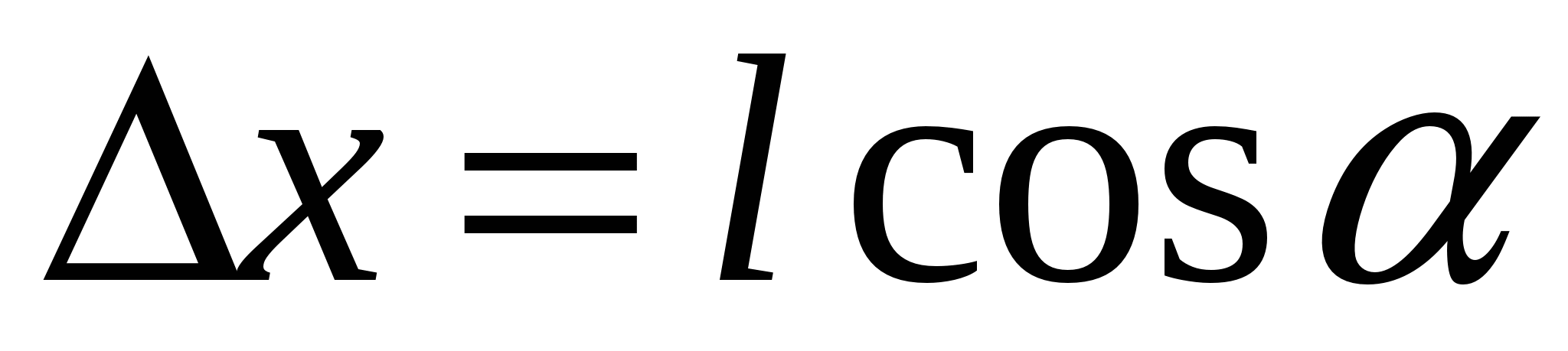

. Prema tome, jačina polja u tačkama gde su naelektrisanja se razlikuje za Δ E. Pošto je zbir sila

i

ili , (19)

, onda

, (20)

Gdje

je gradijent vektora jakosti električnog polja. Dakle, u nehomogenom električnom polju, pored rotacionog momenta, postoji i sila f, pod čijim će djelovanjem dipol biti ili uvučen u područje jačeg polja (α 0) ili istisnut iz njega (α> 90 0).

Izraz za silu se može dobiti iz (18), uzimajući u obzir to f= –

.

3.5. Odnos između jačine elektrostatičkog polja i potencijala

Jačina električnog polja - veličina, brojčano jednaka snazi postupajući po optužbi. Potencijal je vrijednost numerički jednaka potencijalnoj energiji naboja. Dakle, mora postojati odnos između ovih veličina, sličan odnosu između potencijalne energije i sile (tj.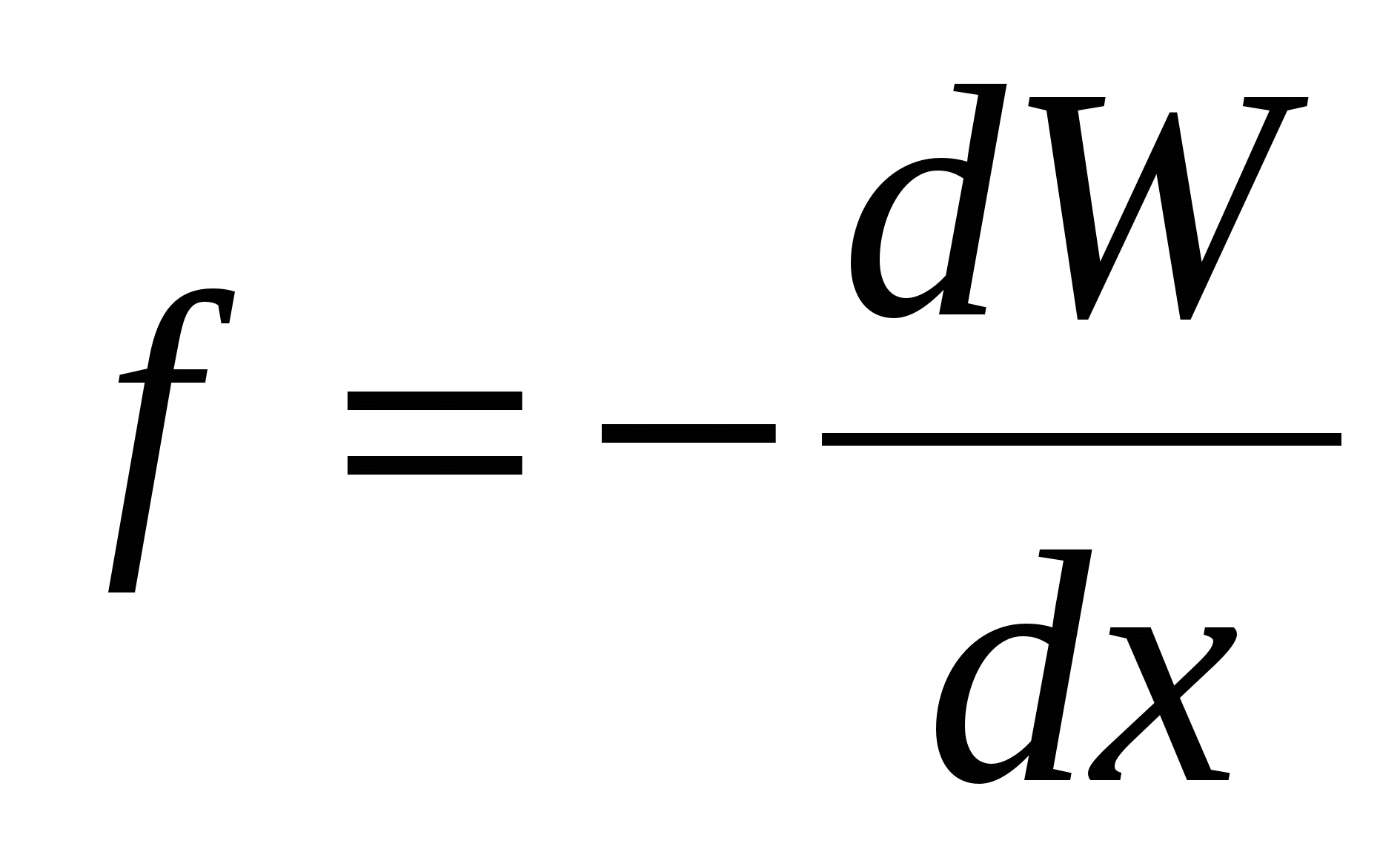

). Rad sila polja na naboju na segmentu puta se može predstaviti kao

, i smanjenje potencijalne energije naboja, koje će u ovom slučaju nastati: . Otkud jednakost

mi nalazimo:

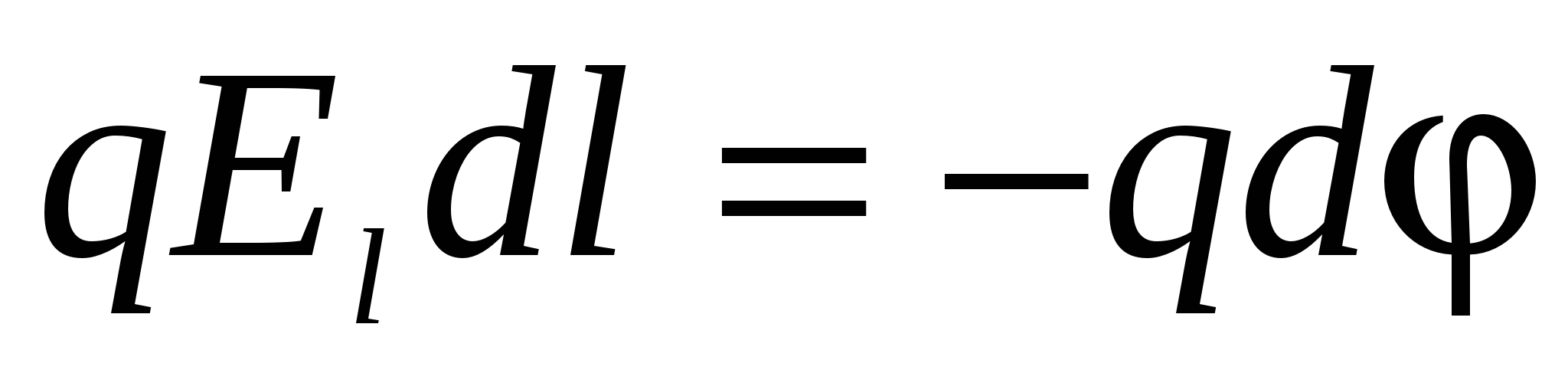ili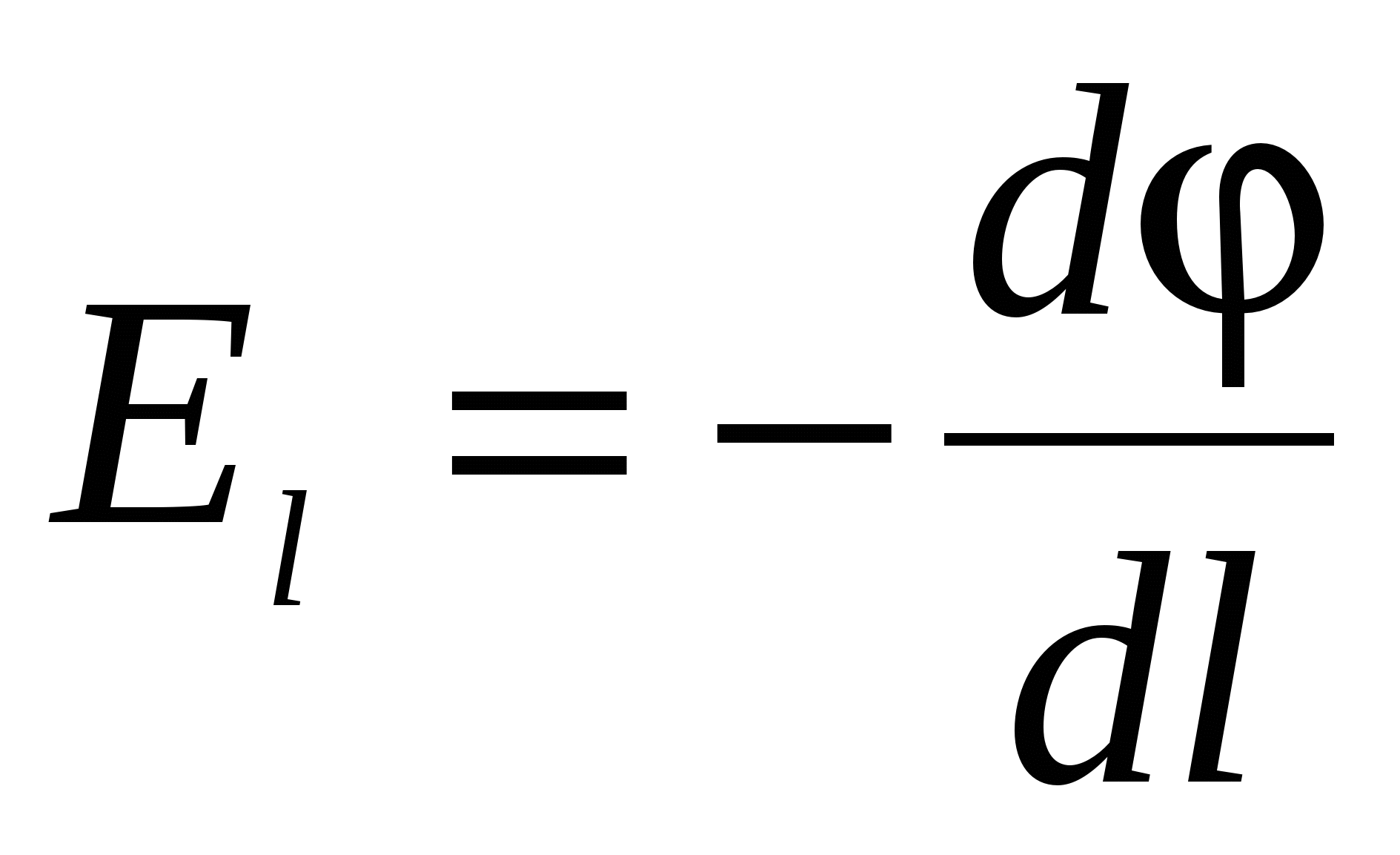

, (21)

Gdje kroz proizvoljno odabranom pravcu.

,

,

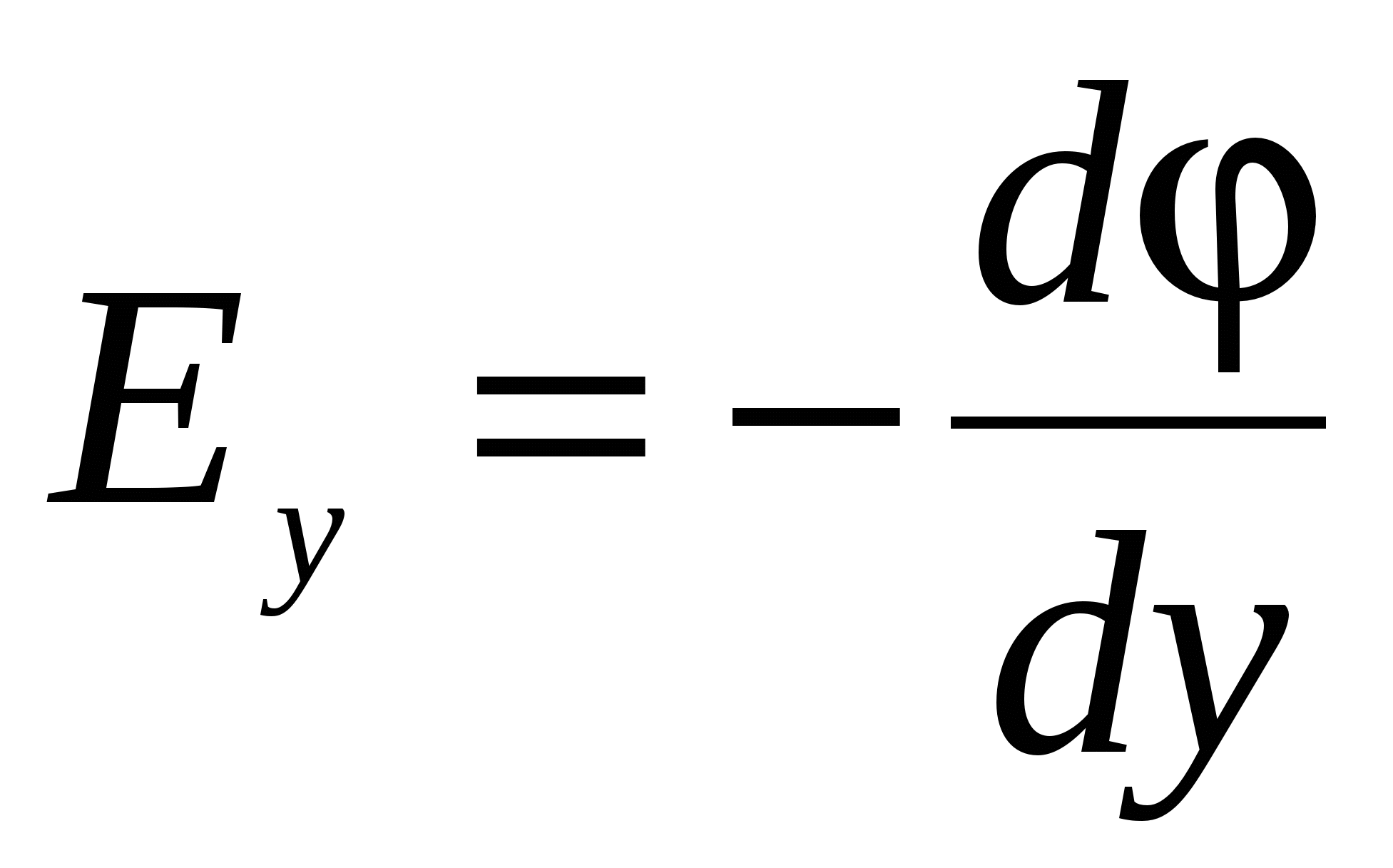, (22)

Gdje

ortove koordinatnih osa, tj. jediničnih vektora. Vektor sa komponentama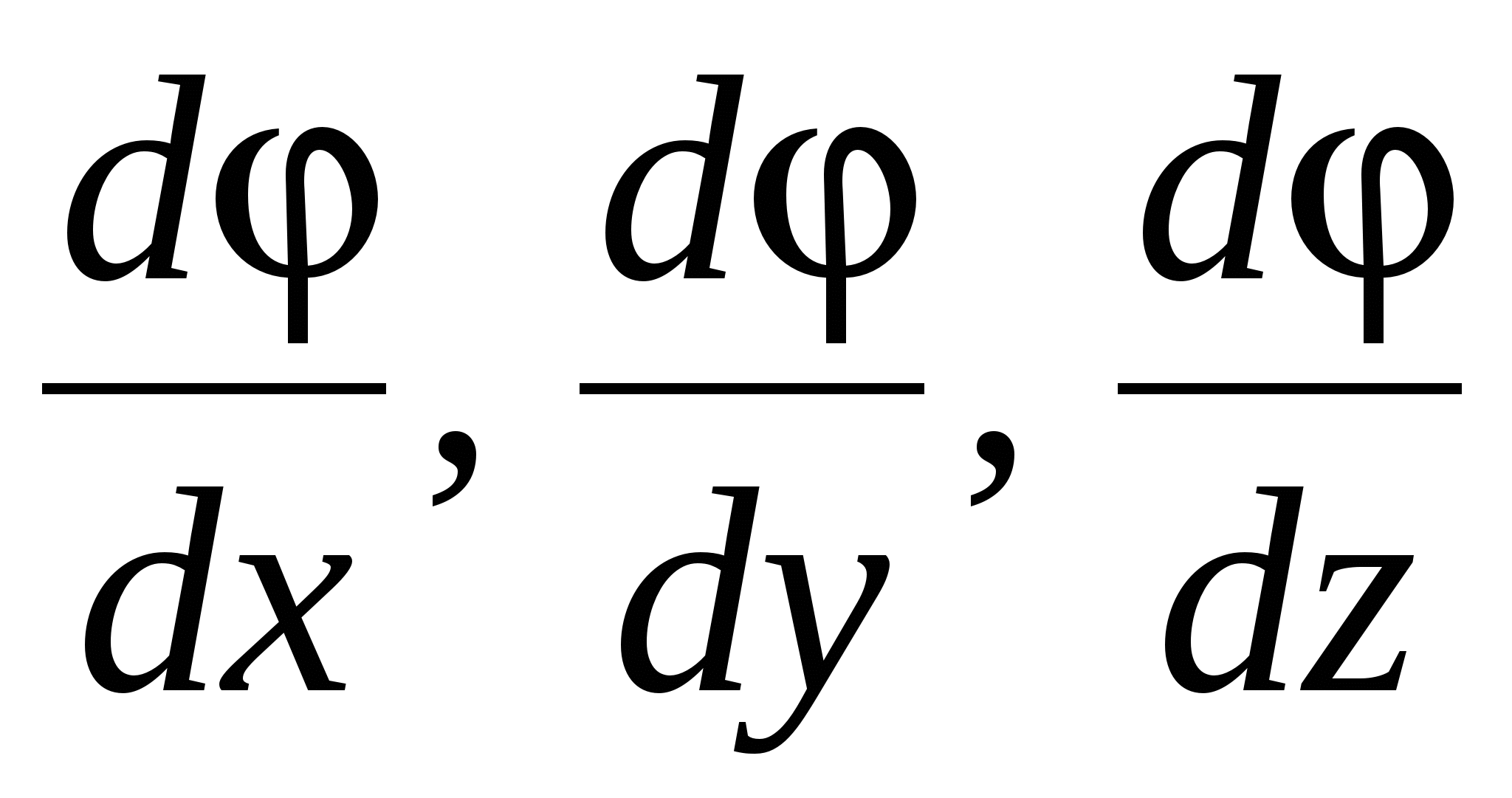

, gdje

skalarna funkcija koordinata

pozvao gradijent funkcije i označava se simbolom

(ili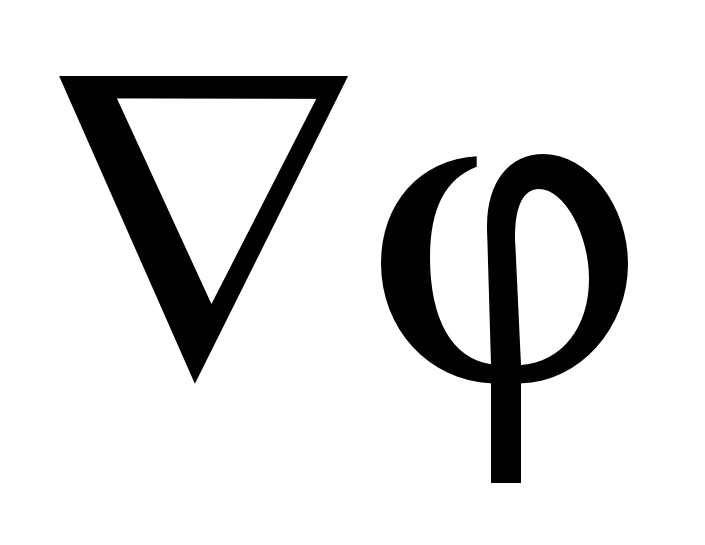

, gdje je nabla operator). Dakle, potencijalni gradijent je:

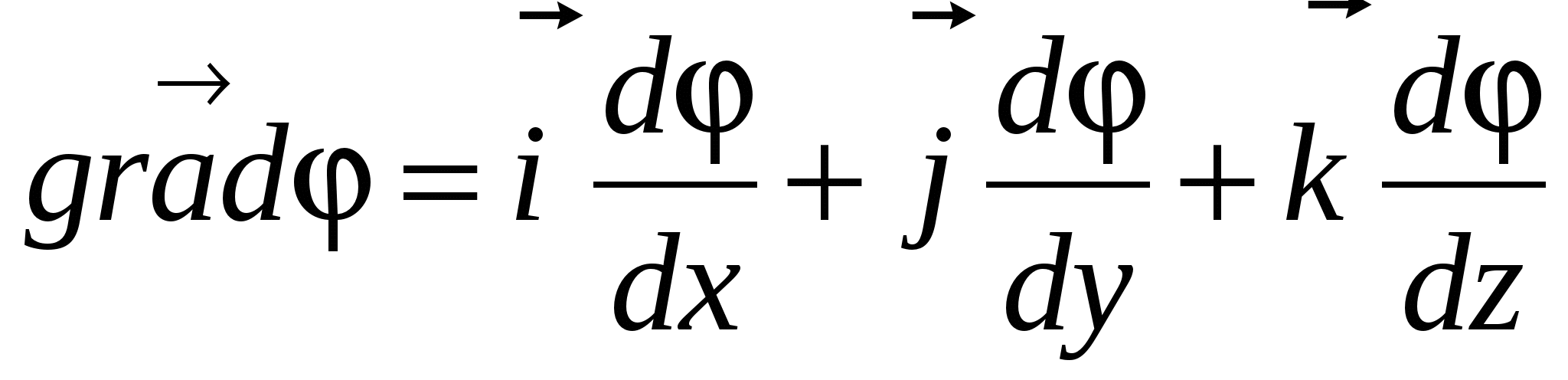(24)

A iz (23) i (24) proizilazi da

(25)

Budući da je gradijent vektor koji pokazuje smjer najbrže promjene neke veličine, čija se vrijednost mijenja od jedne tačke u prostoru do druge, onda gradijent potencijala 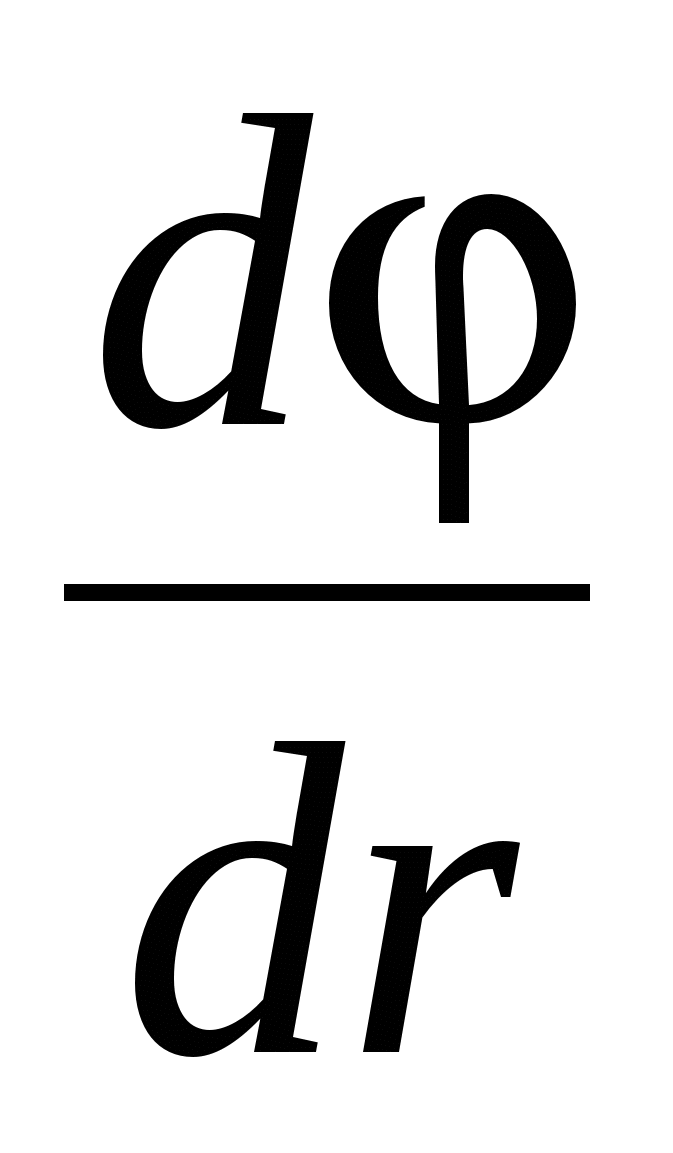(gde r-radijus-vektor) je vektor usmjeren u smjeru najbržeg povećanja potencijala, numerički jednak brzini njegove promjene po jedinici dužine u tom smjeru.

Zbog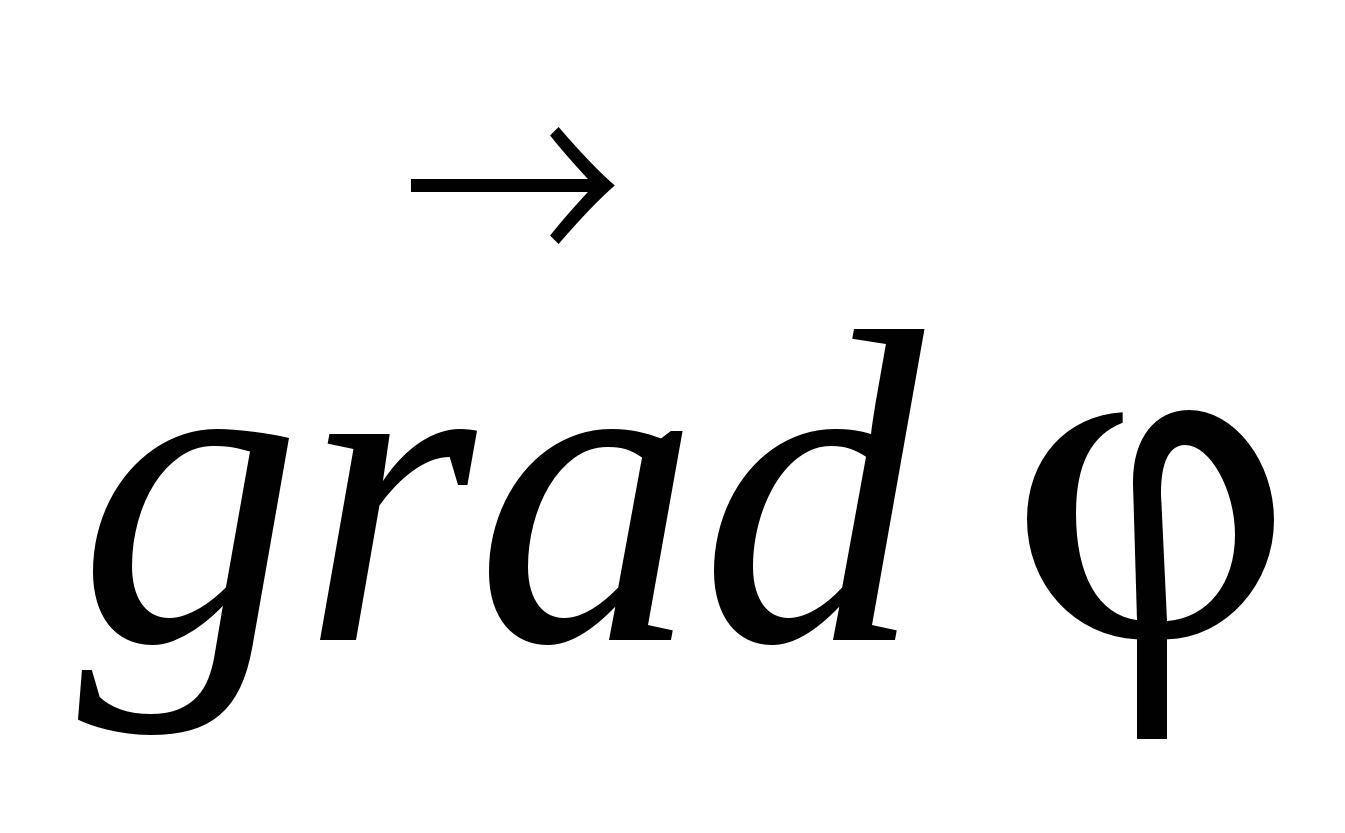

je vektorska veličina, tada se njen modul izražava kao:

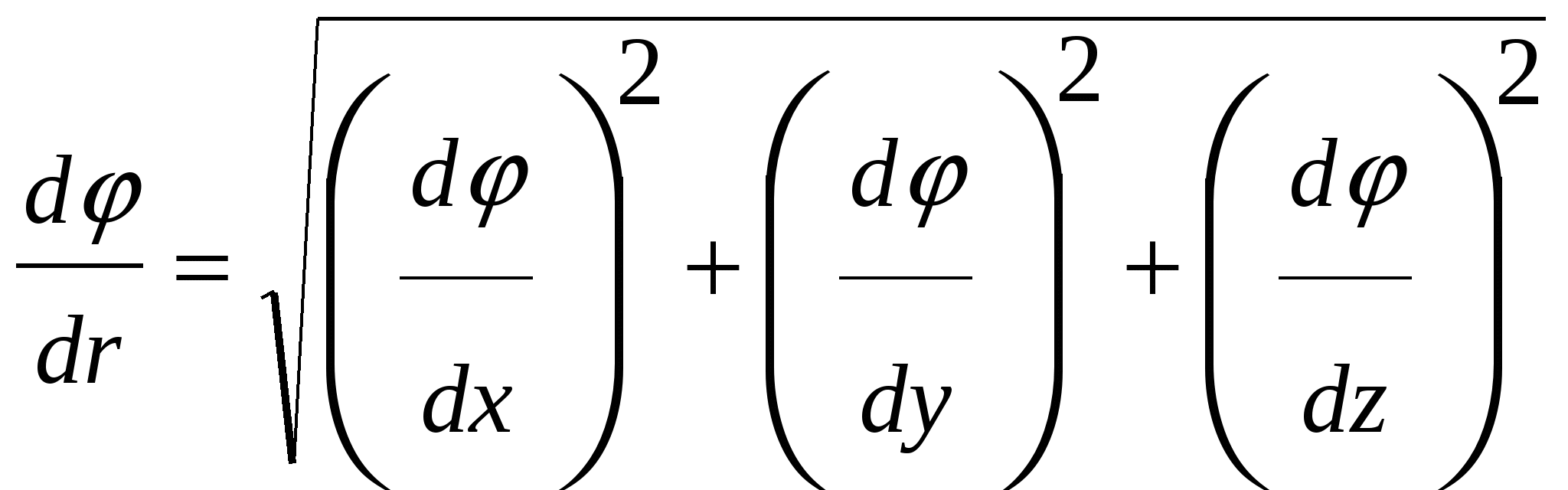, (26)

Baš kao modul vektora :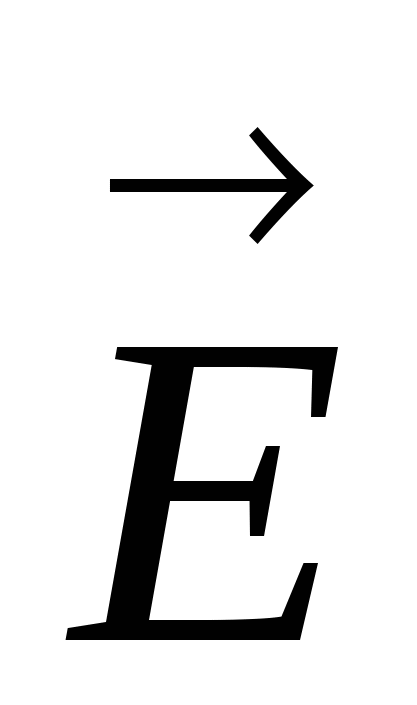

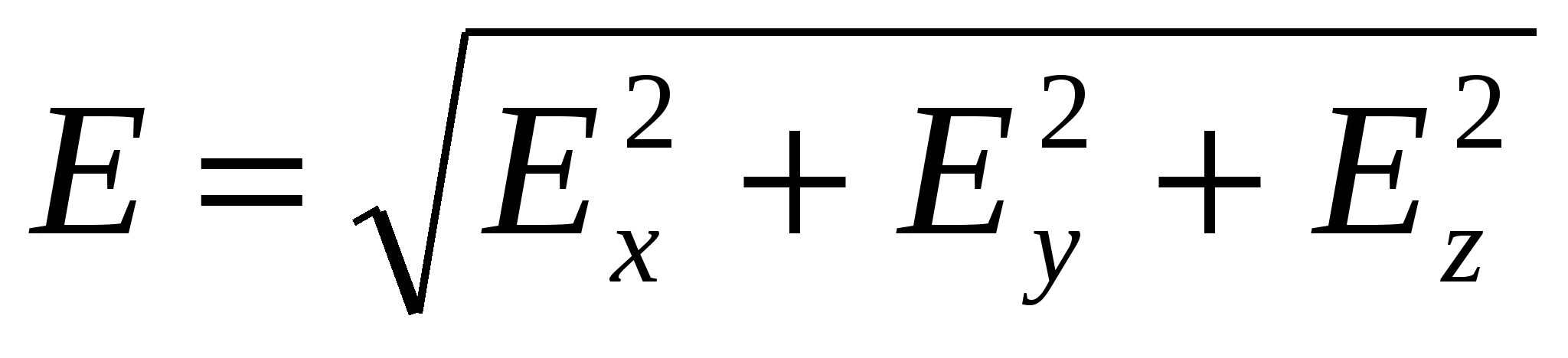(27)

Znak “–” (25) označava da je napetost usmjerena u smjeru opadanja potencijala. Formula (25) vam omogućava da pronađete jačinu polja u svakoj tački od poznatih vrijednosti ili riješite inverzni problem, odnosno da iz zadanih vrijednosti u svakoj tački pronađete razliku potencijala između dvije proizvoljne tačke polja.

3.6. Ekvipotencijalne površine

Potencijal elektrostatičkog polja je funkcija koja varira od tačke do tačke. Međutim, u svakom realnom slučaju moguće je izdvojiti skup tačaka čiji su potencijali isti.

G 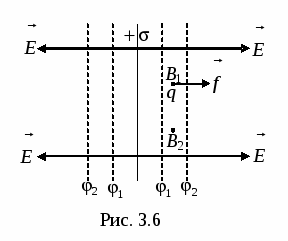geometrijsko mjesto tačaka konstantnog potencijala naziva se površina jednakog potencijala ili ekvipotencijalna površina.

Uzmite jednolično nabijenu beskonačnu ravan (slika 3.6). Polje koje stvara takva ravan je homogeno, a linije napetosti su normalne na ravan. Iz toga slijedi da je rad pomjeranja naboja iz određene tačke AT 1 na bilo koju drugu tačku AT 2 , koji se nalazi na istoj udaljenosti od nabijene površine kao i tačka AT 1 jednako nuli. Zaista, pri pomicanju nekog naboja q u pravoj liniji AT 1 AT 2 sila koja djeluje na naboj sa strane polja uvijek će biti okomita na pomak, pa je stoga njen rad jednak nuli. Ali ovaj rad se, s druge strane, može predstaviti u obliku:

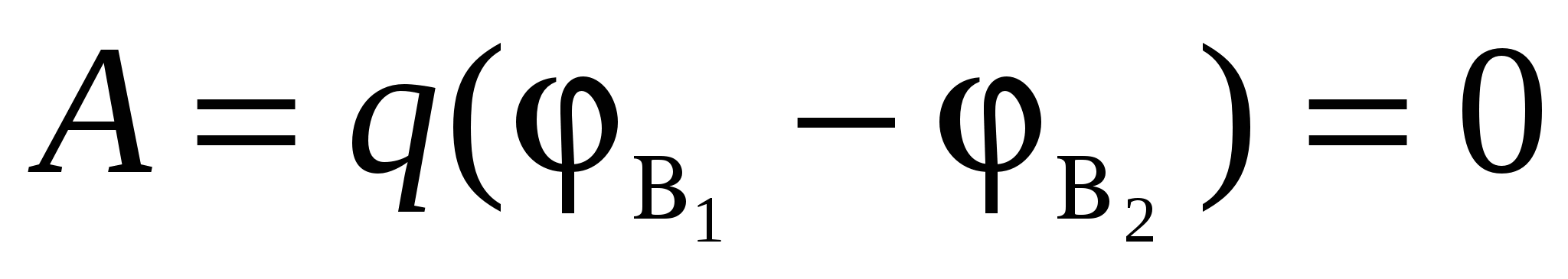, (28)

G de i

su, respektivno, potencijali tačaka AT 1 i AT 2 . Dakle, jer A = 0, zatim =, tj. potencijali tačaka jednako udaljenih od nabijene ravni su isti. Dakle, površine jednakog potencijala (ekvipotencijalne površine) su ravni paralelne naelektrisanoj ravni. Ako je ravan pozitivno nabijena, tada vrijednost potencijala opada s rastojanjem od nabijene ravni. Očigledno je da se površine jednakog potencijala nalaze simetrično na obje strane nabijene ravni.

Ekvipotencijalne površine polja tačkastog naelektrisanja su sfere poluprečnika r , čiji je centar u centru tačkastog naboja, tj.

(Sl. 3.7). Na sl. 3.6 i sl. 3.7 vektor intenziteta je okomit na ekvipotencijalne površine.

Pokažimo da je vektor intenziteta okomit na ekvipotencijalnu površinu. Razmotrimo rad kretanja naelektrisanja preko površine jednakog potencijala na malom dijelu puta ∆ S (Sl. 3.7). Istovremeno, rad električna sila

na ovom putu će biti:

Gdje je α ugao između smjera sile f i pomaka ∆ S. S druge strane, ovaj rad se može izraziti kao proizvod vrijednosti pokretnog naboja i potencijalne razlike u početnoj i krajnjoj poziciji naelektrisanja, tj.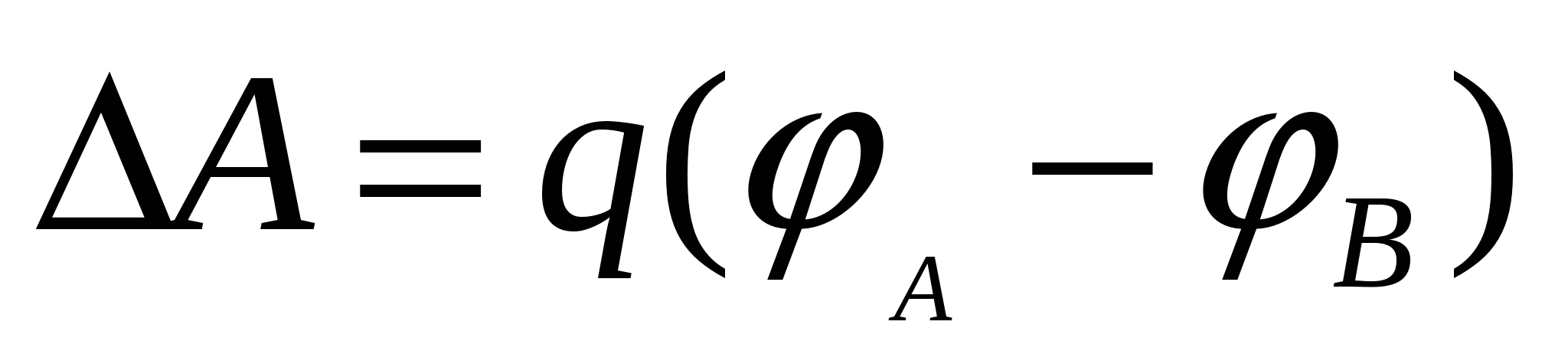

.

Budući da kretanje ide duž ekvipotencijalne površine, razlika potencijala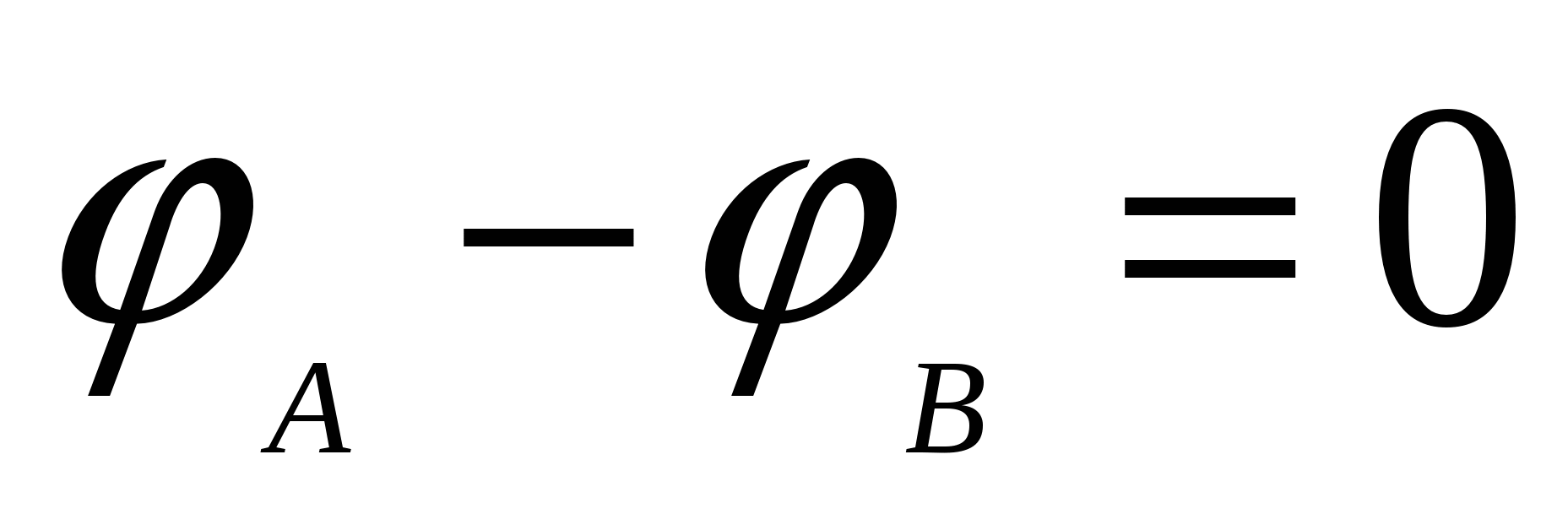

i

, ili cosα = 0, pa je α = 90 0 tj. ugao između smjera sile i pomaka ∆ S je jednako 90 0 . Ali, tj. uputstva i podudaraju, dakle ugao između i ∆ S, α=90 0 tj. smjer vektora elektrostatičkog polja uvijek je okomit na ekvipotencijalnu površinu.

Možete nacrtati koliko god želite ekvipotencijalnih površina oko nabijenog tijela. Po gustini ekvipotencijalnih površina može se suditi o vrednosti , međutim, pod uvjetom da je razlika potencijala između dvije susjedne ekvipotencijalne površine jednaka konstantnoj vrijednosti.

Formula izražava odnos između potencijala i jačine i omogućava korištenje poznatih vrijednosti φ za pronalaženje jačine polja u svakoj tački. Moguće je riješiti i inverzni problem, tj. prema poznatim vrijednostima u svakoj tački polja pronađite razliku potencijala između dvije proizvoljne tačke polja. Da bismo to učinili, koristimo se činjenicom da je rad terenskih snaga izvršen na naboju q kada se pomera od tačke 1 do tačke 2 može se izračunati kao:

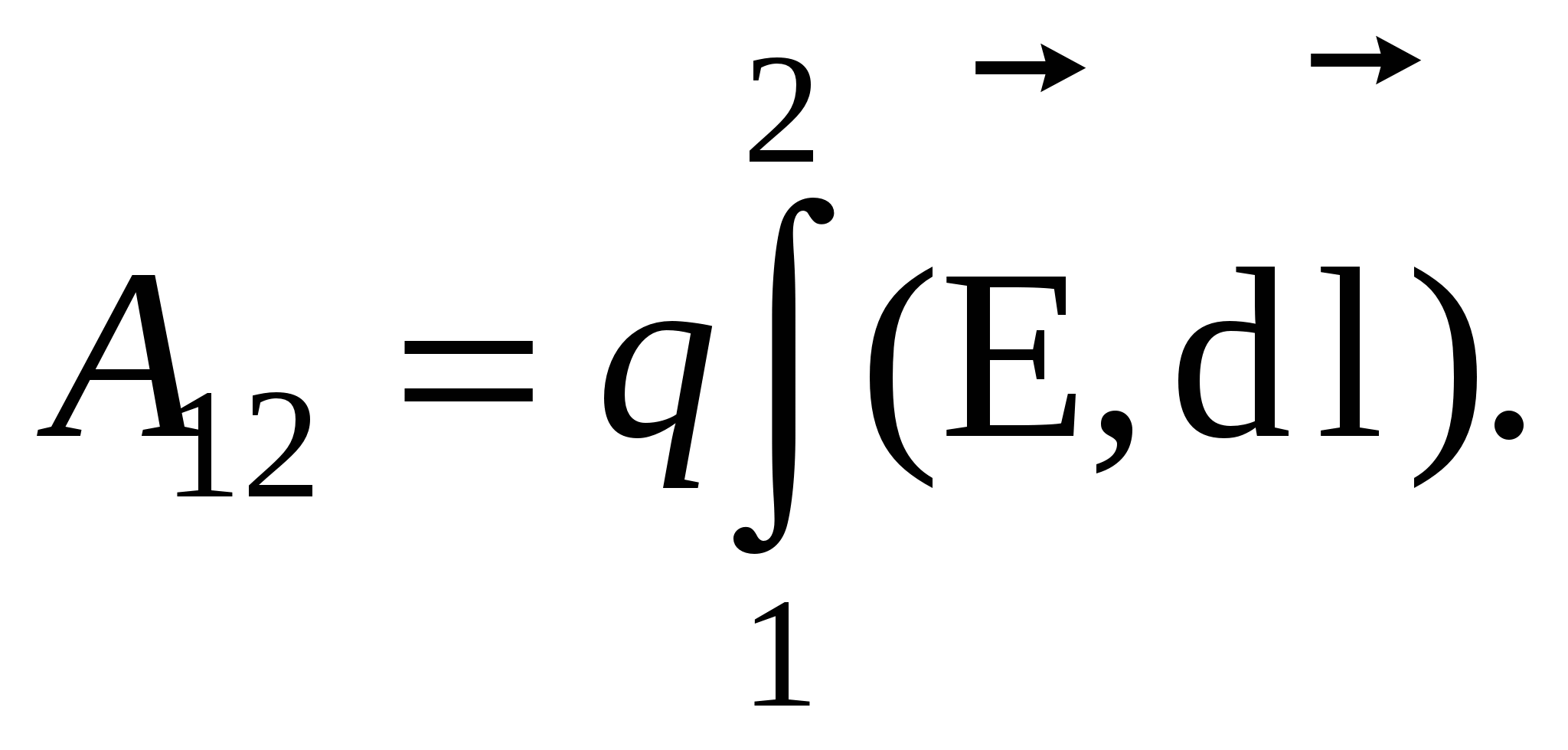
S druge strane, rad se može predstaviti kao:

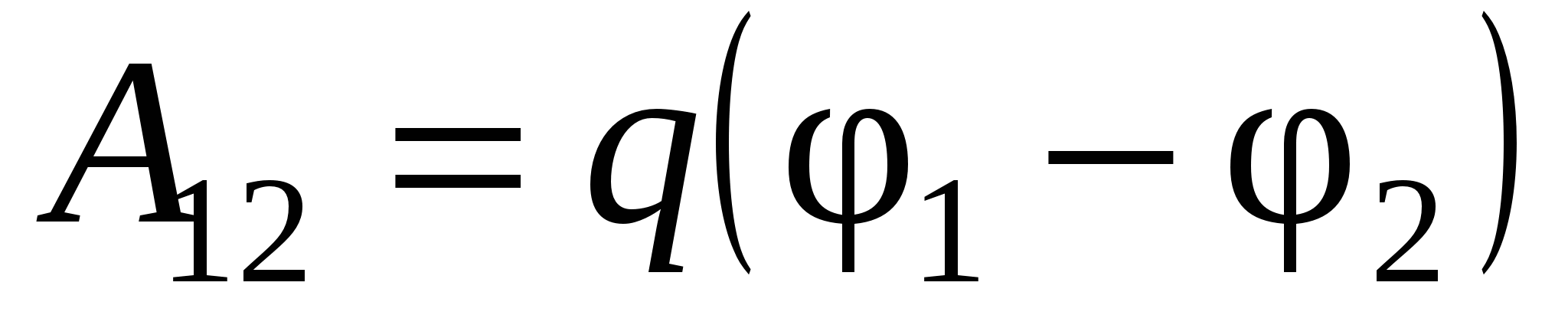, onda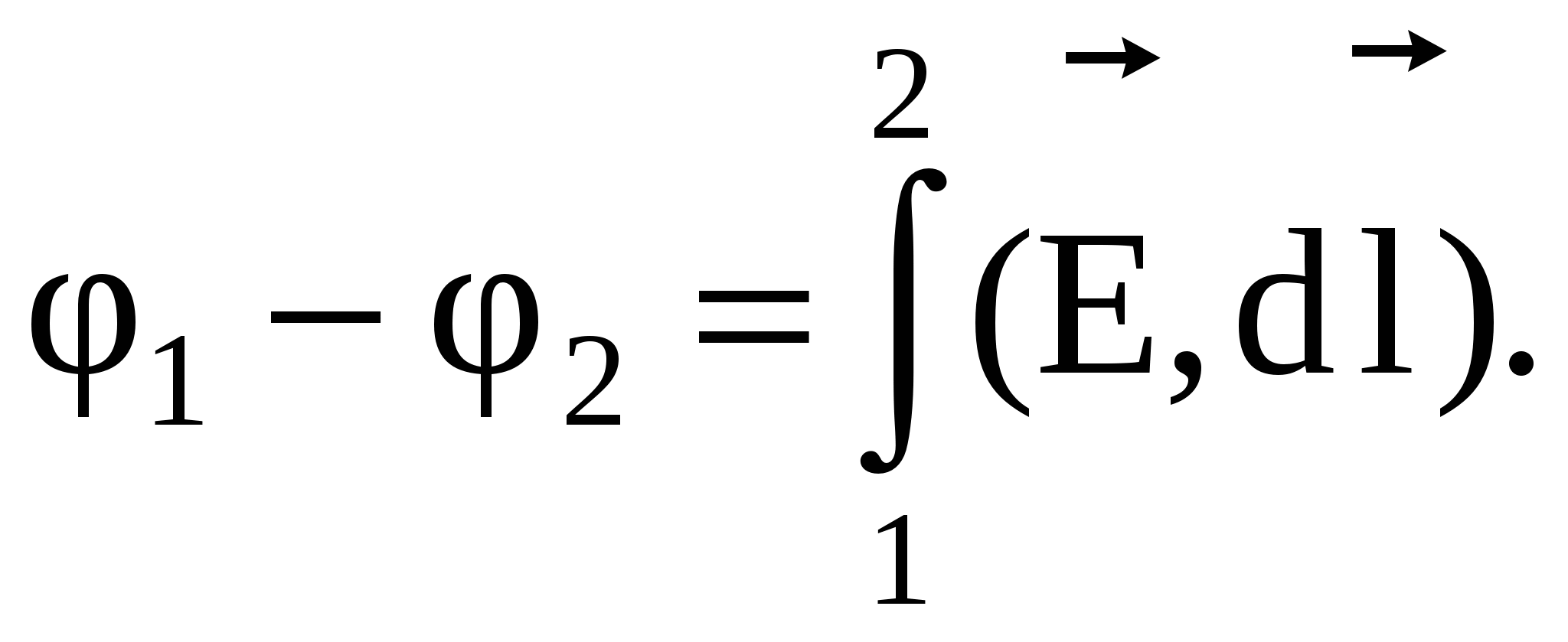

Integral se može uzeti duž bilo koje linije koja povezuje tačku 1 i tačku 2, pošto rad snaga polja ne zavisi od putanje.

Prilikom prelaska zatvorene petlje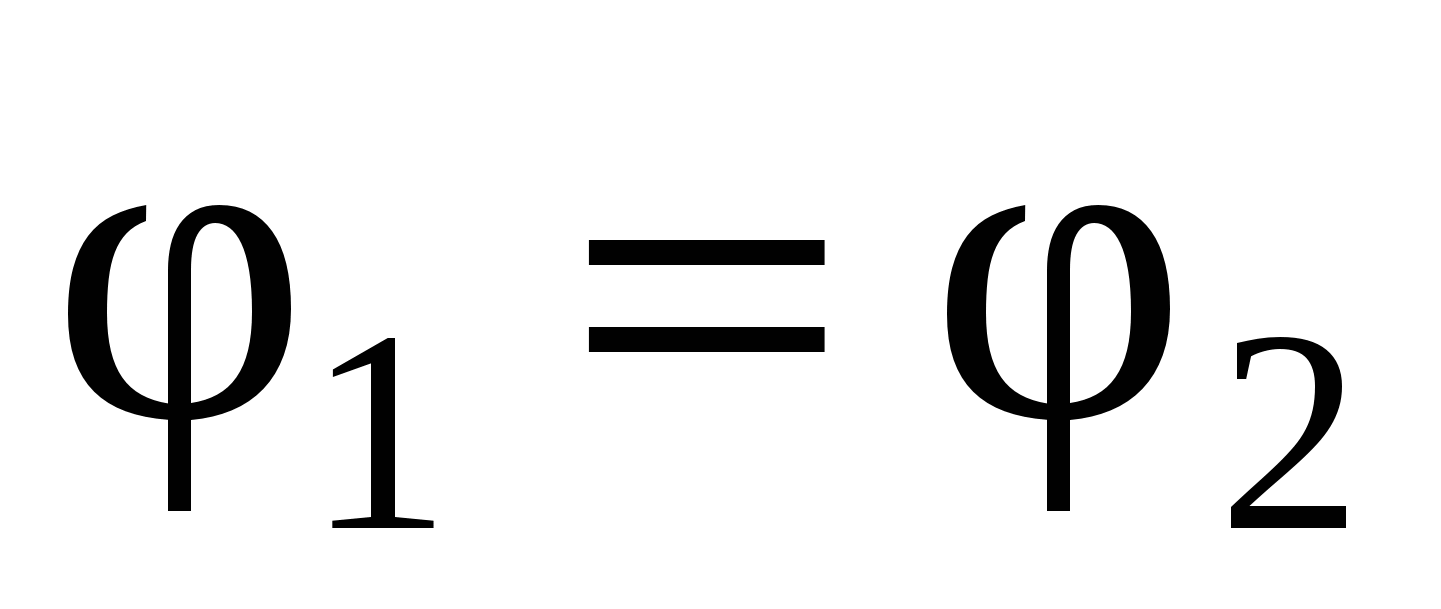

dobijamo:

one. došao do dobro poznate teoreme o cirkulaciji vektora intenziteta: cirkulacija vektora jačine elektrostatičkog polja duž bilo koje zatvorene petlje jednaka je nuli.

Polje sa ovim svojstvom naziva se potencijal.

Iz nestajanja cirkulacije vektora slijedi da se linije elektrostatičkog polja ne mogu zatvoriti:počinju sa pozitivnim nabojem(porijeklo )i dalje negativnih naboja istrčati(odvodi )ili idi u beskonačnost.

Hajde da generalizujemo Gaussovu teoremu i teoremu o kruženju vektora jačine elektrostatičkog polja u vakuumu. Od , a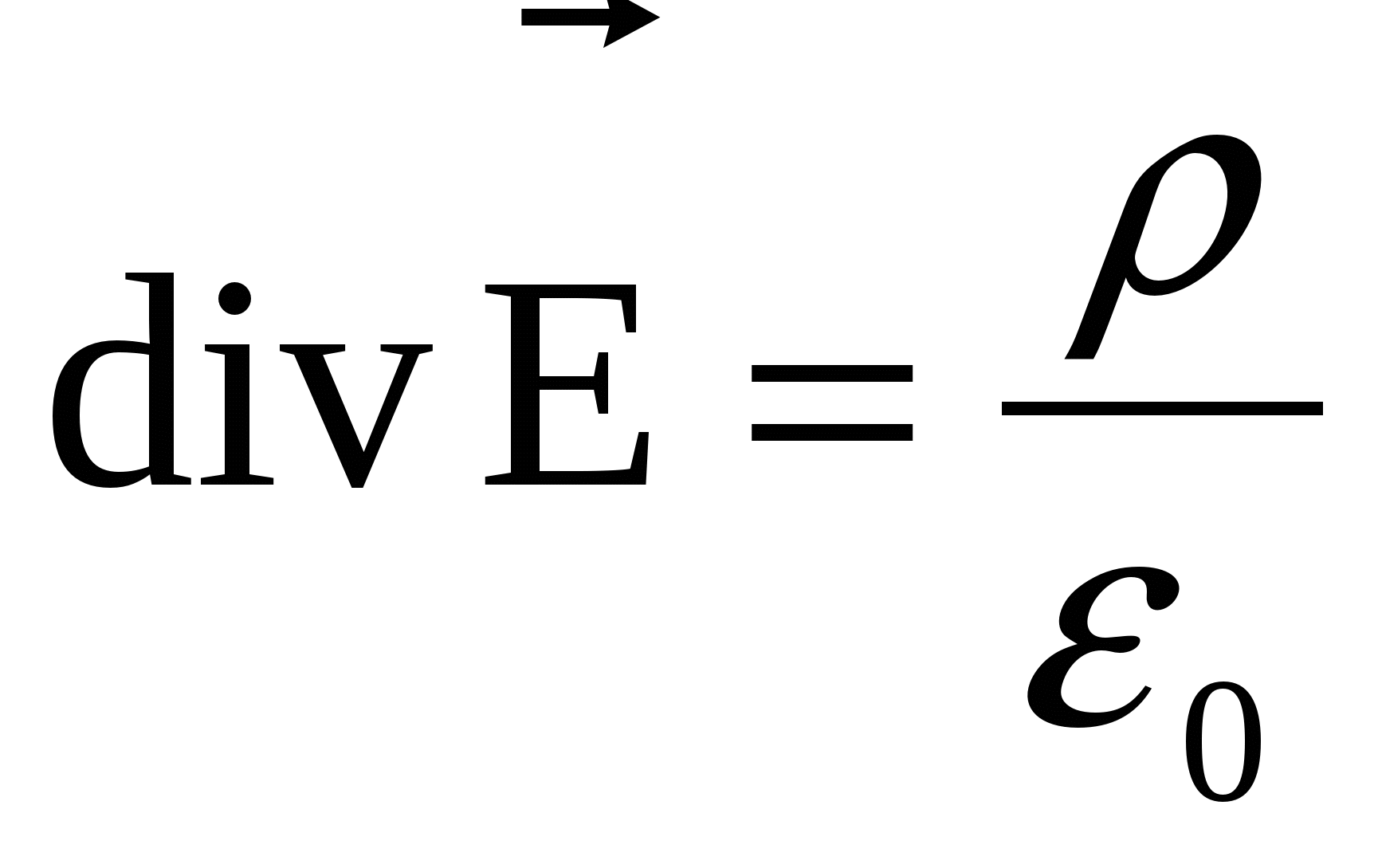

, onda

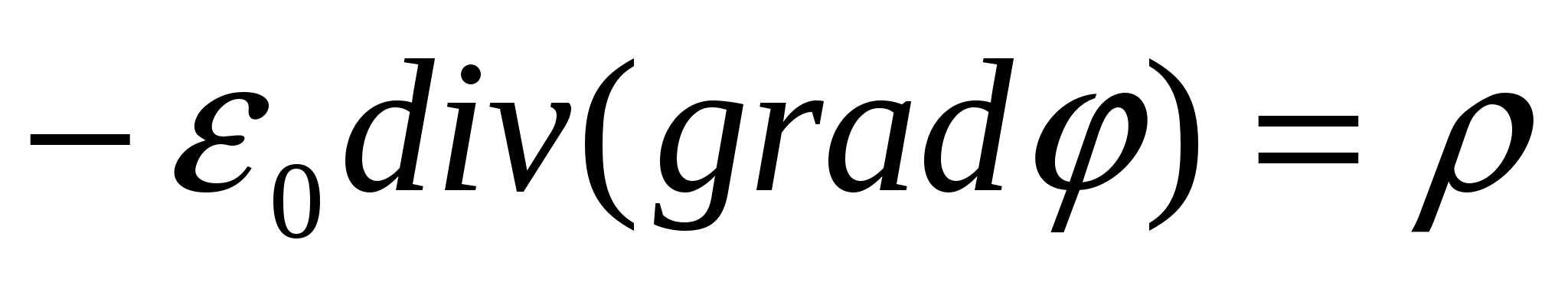. Zbog

(

je Laplaceov operator), tada za potencijal φ dobijamo izraz

ili

, koji se zove Poissonova jednadžba.

Ova jednačina dozvoljava, prema poznatoj raspodjeli naboja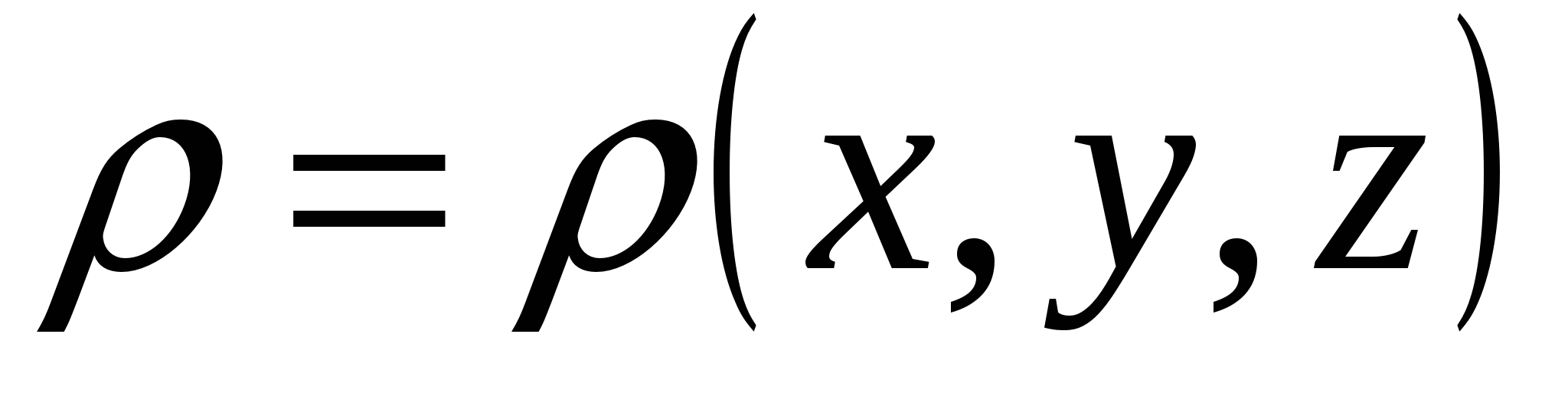

i dati granični uvjet za potencijal φ za određivanje vrijednosti

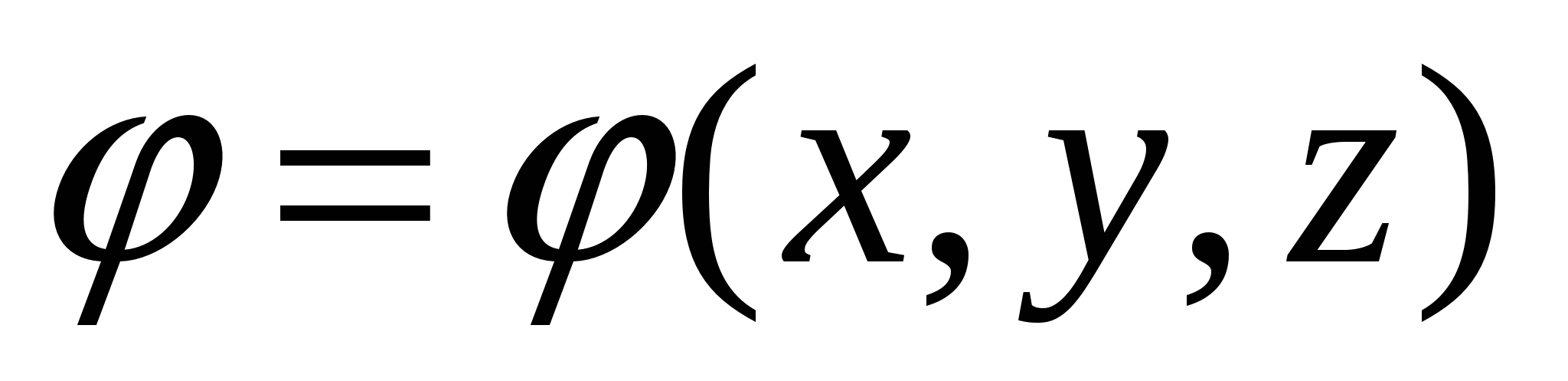na svim tačkama polja, a zatim pomoću formule pronaći napetost

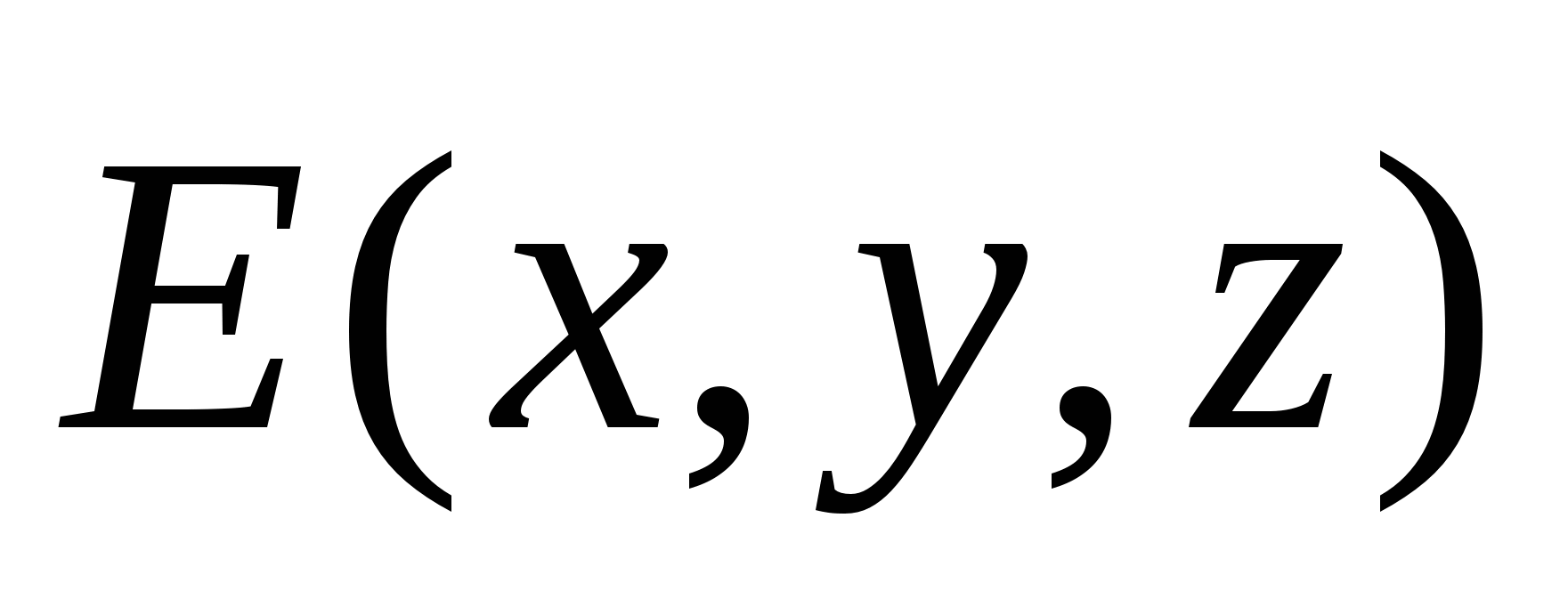polja, tj. riješiti direktni problem elektrostatike.

3.7. Proračun razlike potencijala iz jačine polja najjednostavnijih elektrostatičkih polja

Uspostavljena veza između intenziteta i potencijala omogućava da se pomoću poznate jačine polja pronađe potencijalna razlika između dvije proizvoljne tačke ovog polja.

Razmotrimo nekoliko primjera izračunavanja razlike potencijala između tačaka polja koje stvaraju neka nabijena tijela.

1. Polje jednolično nabijene beskonačne ravni

Polje jednolično nabijene beskonačne ravni, pronađeno korištenjem Ostrogradskog-Gaussove teoreme, određeno je formulom

, gdje je σ površinska gustina naboja. Razlika potencijala između tačaka koje leže na udaljenostima x 1 i x 2 iz ravni, jednako je

.

d E \u003d 0, između ploča potencijal se smanjuje prema logaritamskom zakonu, a druga ploča (izvan cilindara) zaklanja električno polje i φ i E jednake su nuli.
Slika 3.10
Na sl. 3.10 prikazuje zavisnost napetosti E i kapacitet od r.
4. Polje jednoliko nabijene sferne površine
Uzimajući u obzir primjere primjene Ostrogradsky-Gauss teoreme, otkrili smo da je jačina polja sfere određena formulom:

(Sl. 3.11). I od tada

, onda

Slika 3.11
. Ako prihvatite r 1 = r , a r 2 =∞, tada je potencijal izvan sferne površine određen izrazom), određen je formulom
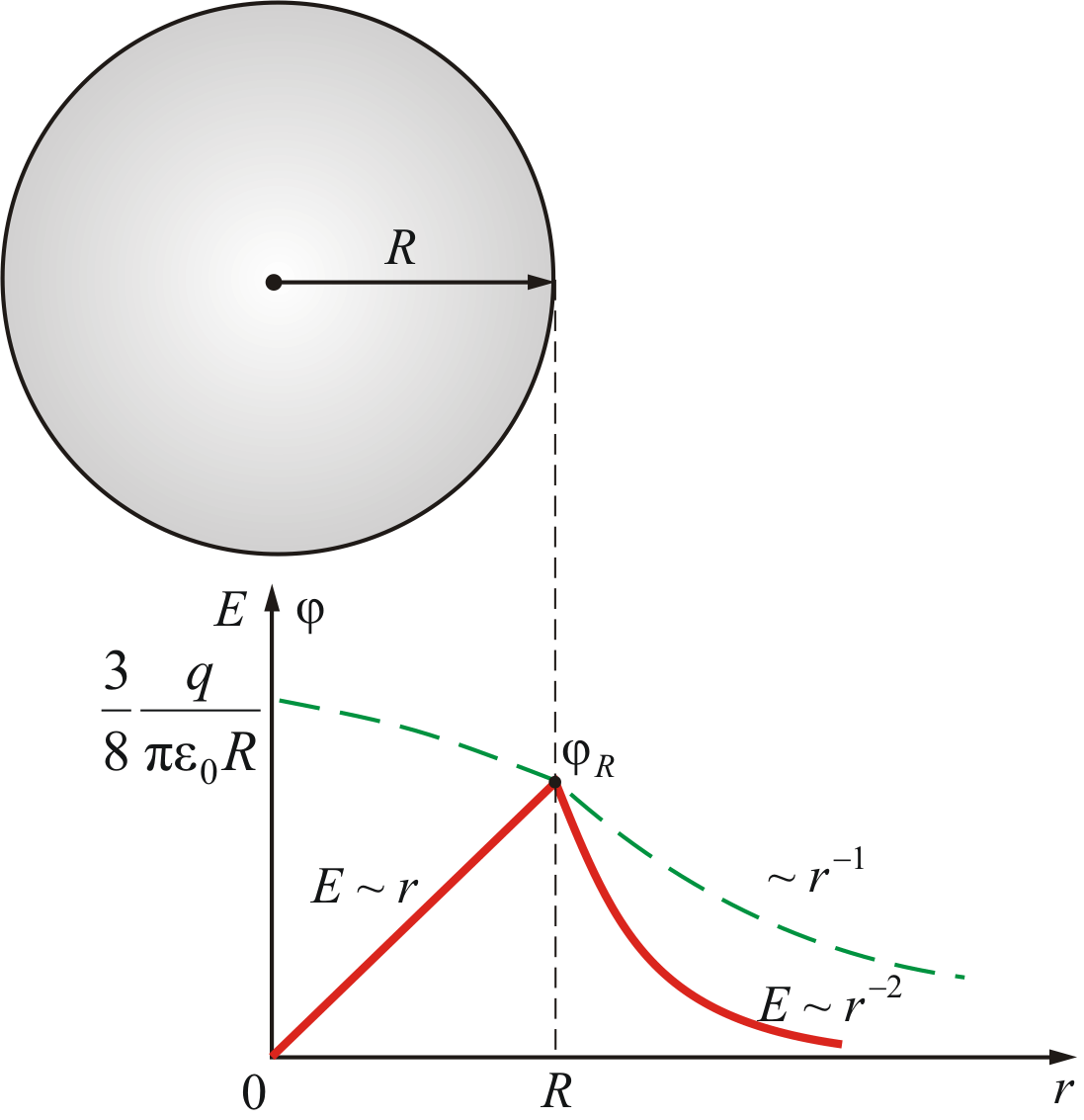
Odabirom nivoa nultog potencijala u tački r 2 =∞ potencijal bilo koje tačke unutar nabijene kuglice može se naći na sljedeći način:

. Nakon integracije dobijamo

.

Slika 3.12
S obzirom na to

, onda

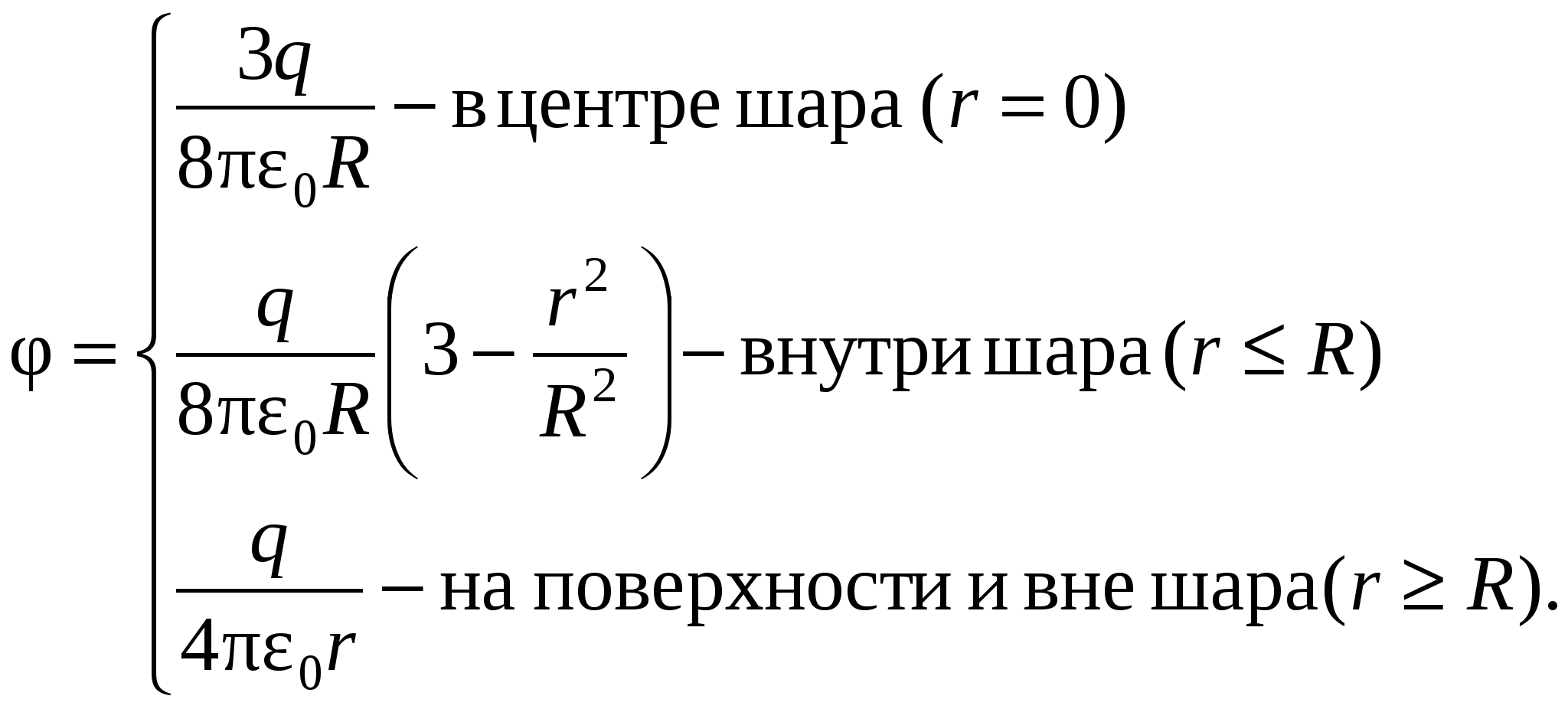( 38 )
Iz dobijenih relacija možemo zaključiti sljedeće zaključci .
- Koristeći Gaussov teorem, relativno je lako izračunati E i φ iz različitih nabijenih površina.
- Jačina polja u vakuumu se naglo mijenja kada prođe kroz nabijenu površinu.
- Potencijal polja - uvijek kontinuirana funkcija koordinate.
test pitanja
1. Kako pokazati da je elektrostatičko polje potencijalno?
2. Šta je potencijal?
3. Šta se naziva cirkulacija vektora napetosti?
4. Kakav je odnos između napetosti i potencijala? Kako nacrtati sliku linija polja sa slike ekvipotencijalnih površina?
5. Koliki je rad obavljen da se naboj pomjeri preko ekvipotencijalne površine?
6. Navedite primjere izračunavanja razlike potencijala najjednostavnijih elektrostatičkih polja.
7. Kako se dipol ponaša u vanjskom elektrostatičkom polju?