2. Električno polje. Električno polje tačka naboj. Električni vodovi.

Prema modernim konceptima, električni naboji ne djeluju direktno jedno na drugo. Svako naelektrisano telo stvara u okolnom prostoru električno polje . Ovo polje ima efekat sile na druga naelektrisana tela. Glavna nekretnina električno polje- djelovanje na električna naelektrisanja određenom silom. Dakle, interakcija nabijenih tijela se ne odvija njihovim direktnim djelovanjem jedno na drugo, već kroz električna polja koja okružuju nabijena tijela.

Električno polje koje okružuje naelektrisano tijelo može se istražiti pomoću tzv sudska optužba - mali tačkasti naboj, koji ne proizvodi primjetnu preraspodjelu istraženih naboja.

Za kvantificiranje električnog polja uvodi se moć karakteristika jačina električnog polja .

Jačina električnog polja naziva se fizička veličina jednaka omjeru sile kojom polje djeluje na pozitivan probni naboj smješten u datoj tački prostora i veličinom ovog naboja:

Jačina električnog polja je vektorska fizička veličina. Smjer vektora u svakoj tački u prostoru poklapa se sa smjerom sile koja djeluje na pozitivno naelektrisanje.

Električno polje stacionarnih i nepromjenjivih naelektrisanja s vremenom naziva se elektrostatički . U mnogim slučajevima, radi kratkoće, ovo polje se označava opštim pojmom - električno polje

Ako se električno polje koje stvara nekoliko nabijenih tijela istražuje pomoću probnog naboja, tada se rezultirajuća sila pokazuje da je jednaka geometrijskom zbroju sila koje djeluju na probno naelektrisanje iz svakog nabijenog tijela posebno. Prema tome, jačina električnog polja stvorenog sistemom naelektrisanja u datoj tački u prostoru jednaka je vektorskom zbiru jačina električnih polja stvorenih naelektrisanjem odvojeno u istoj tački:

Ovo polje se zove Coulomb . U Kulonovom polju smjer vektora ovisi o predznaku naboja Q: ako Q> 0, tada je vektor usmjeren duž radijusa od naboja, ako Q < 0, то вектор направлен к заряду.

Za vizuelni prikaz električnog polja, koristite linije sile . Ove linije su nacrtane tako da se smjer vektora u svakoj tački poklapa sa smjerom tangente na linija polja(Slika 1.2.1). Kada se električno polje prikazuje pomoću linija sile, njihova gustoća treba biti proporcionalna modulu vektora jačine polja.

Linije sile Kulonovog polja pozitivnih i negativnih tačkastih naelektrisanja prikazane su na sl. 1.2.2. Pošto se elektrostatičko polje koje stvara bilo koji sistem naelektrisanja može predstaviti kao superpozicija Kulombovih polja tačkastih naelektrisanja, prikazanih na Sl. 1.2.2 polja se mogu smatrati elementarnim strukturnim jedinicama ("ciglama") bilo kojeg elektrostatičkog polja.

Kulonovo polje tačkastog naboja Q zgodno je pisati u vektorskom obliku. Da biste to učinili, morate nacrtati radijus vektor iz naboja Q do tačke posmatranja. Zatim u Q> 0 vektor je paralelan i kada Q < 0 вектор антипараллелен Следовательно, можно записать:

gdje r je modul radijus vektora .

Kao primjer primjene principa superpozicije polja na sl. 1.2.3. prikazana je slika linija polja električni dipol - sistemi dva identična modulna naelektrisanja različitih predznaka q i - q nalazi na određenoj udaljenosti l.

Važna karakteristika električnog dipola je tzv dipolni moment

gdje je vektor usmjeren od negativnog na pozitivan naboj, dipolni modul može poslužiti kao električni model mnogih molekula.

Na primjer, neutralna molekula vode (H 2 O) ima električni dipolni moment, budući da se centri dvaju atoma vodika ne nalaze na istoj pravoj liniji sa centrom atoma kisika, već pod kutom od 105° (sl. 1.2.4). Dipolni moment molekula vode str= 6,2 10 -30 C m.

3. Elektrostatička Gaussova teorema. Dokaz Gaussove teoreme za određeni slučaj (tačkasti naboj se nalazi unutar sfere poluprečnika R). Generalizacija Gaussove teoreme naN tačkaste naknade. Generalizacija Gaussove teoreme na slučaj kontinuirano distribuiranog naboja. Gaussova teorema u diferencijalnom obliku.

Nađimo tok vektoraE kroz sfernu površinuS, u čijem je centru tačkasto naelektrisanjeq.

U ovom slučaju, pošto uputstva E i n poklapaju u svim tačkama sferne površine.

Uzimajući u obzir jačinu polja tačkastog naboja i činjenica da površinu sfere dobijemo

Algebarska veličina u zavisnosti od predznaka naboja. Na primjer, kada q<0 линии E usmjereno prema naboju i suprotno od smjera vanjske normale n. Stoga je u ovom slučaju protok negativan.<0 .

Pustite zatvorenu površinu oko punjenja q ima proizvoljan oblik. Očigledno je da površinu siječe isti broj linija E,što je površina S. Dakle, tok vektora E kroz proizvoljnu površinu je također određena rezultujućom formulom .

Ako je naboj izvan zatvorene površine, onda, očito, koliko god linija uđe u zatvoreno područje, isti broj će ga napustiti. Kao rezultat, vektorski tok Eće biti jednaka nuli.

Ako je električno polje stvoreno sistemom tačkastih naelektrisanja zatim po principu superpozicije,

Dokaz o posebnom slučaju:

Gaussova teorema tvrdi:

Vektorski fluks jačine elektrostatičkog polja kroz proizvoljnu zatvorenu površinu jednak je algebarskom zbiru naboja koji se nalaze unutar ove površine, podijeljen s električnom konstantom ε 0 .

gdje R je poluprečnik sfere. Protok Φ kroz sfernu površinu bit će jednak proizvodu E na površinu sfere 4π R 2. shodno tome,

Okružimo sada tačkasti naboj sa proizvoljnom zatvorenom površinom S i razmotrimo pomoćnu sferu poluprečnika R 0 (slika 1.3.3).

Zamislite konus sa malim solidan ugao ΔΩ na vrhu. Ovaj konus izdvaja malu površinu Δ na sferi S 0 i na površini S– platforma Δ S. Elementarni tokovi ΔΦ 0 i ΔΦ kroz ove oblasti su isti. stvarno,

Ovdje Δ S" = Δ S cos α je površina definisana konusom sa čvrstim uglom ΔΩ na površini sfere poluprečnika n.

Od a otuda slijedi da je ukupan protok električnog polja tačkastog naboja kroz proizvoljnu površinu koja obuhvata naboj jednak protoku Φ 0 kroz površinu pomoćne sfere:

Na sličan način može se pokazati da ako je zatvorena površina S ne pokriva bodovnu naknadu q, tada je protok Φ = 0. Takav slučaj je prikazan na sl. 1.3.2. Sve linije sile električnog polja tačkastog naboja prodiru kroz zatvorenu površinu S kroz. Unutrašnja površina S nema naboja, dakle, u ovoj regiji, linije sile se ne lome i ne nastaju.

Generalizacija Gaussove teoreme na slučaj proizvoljne raspodjele naboja slijedi iz principa superpozicije. Polje bilo koje distribucije naboja može se predstaviti kao vektorski zbir električnih polja tačkastih naelektrisanja. Protok Φ sistema naelektrisanja kroz proizvoljnu zatvorenu površinu Sće se sastojati od tokova Φ i električna polja pojedinačnih naelektrisanja. Ako je naplata q i bio unutar površine S, tada daje doprinos protoku, koji je jednak ako je ovaj naboj izvan površine, tada će doprinos njegovog električnog polja protoku biti jednak nuli.

Dakle, Gaussova teorema je dokazana.

Za bilo koji broj troškova

Poslednji korak je jednostavan. Sastoji se u primjeni principa superpozicije.

Ako za svaki tačkasti naboj polje koje stvara (kada nema drugih naboja) stvara protok kroz površinu koji zadovoljava Gaussov teorem (tj. za svaki naboj unutar površine i 0 za svaki izvan površine), zatim fluks iz ukupnog polja

jednak je zbiru protoka stvorenih od strane svakog naboja u odsustvu ostalih, jednostavno je jednak

gdje je zbrajanje samo preko naboja unutar površine (svako od onih izvan doprinosi 0).

Teorema je dokazana.

ELECTRICAL BIAS

Osnovne formule

 Jačina električnog polja

E=F/Q,

gdje F je sila koja djeluje na pozitivno naelektrisanje tačke Q postavljen na datoj tački polja.

 Sila koja djeluje na tačkasti naboj Q, postavljen u električno polje,

F=QE.

E električno polje:

a) kroz proizvoljnu površinu S, postavljen u nehomogeno polje,

ili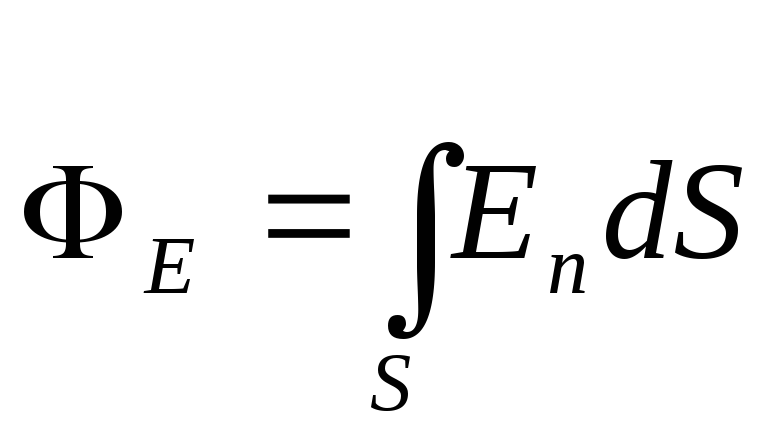

,

gdje je  ugao između vektora intenziteta E i normalno n na površinski element; d S- površina elementa površine; E n- projekcija vektora napetosti na normalu;

b) kroz ravnu površinu postavljenu u jednolično električno polje,

F E =ES cos.

 Protok vektora napetosti E kroz zatvorenu površinu

,

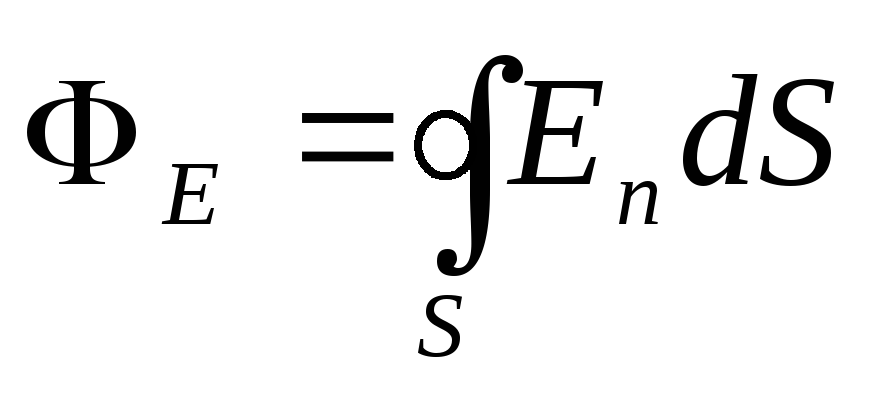gdje se integracija vrši po cijeloj površini.

 Ostrogradsky-Gaussova teorema. Protok vektora napetosti E kroz svaku zatvorenu površinu koja obuhvata naboje Q l , Q 2 , . . ., Q n ,

,

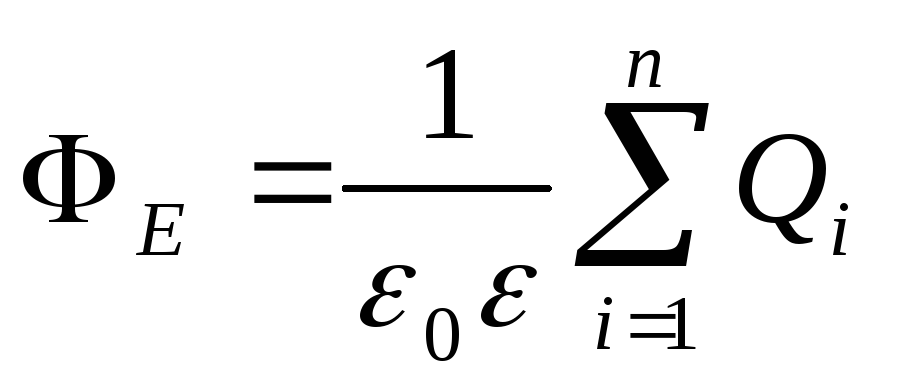gdje 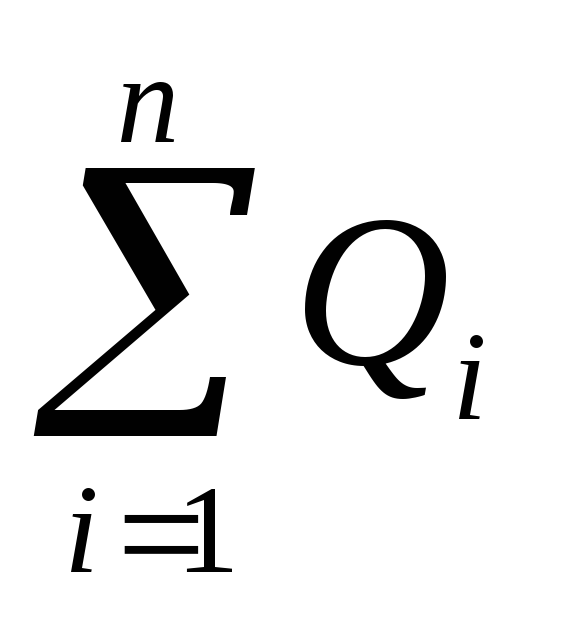- algebarski zbir naelektrisanja zatvorenih unutar zatvorene površine; P - broj punjenja.

 Intenzitet električnog polja stvorenog tačkastim nabojem Q na daljinu r od optužbe

.

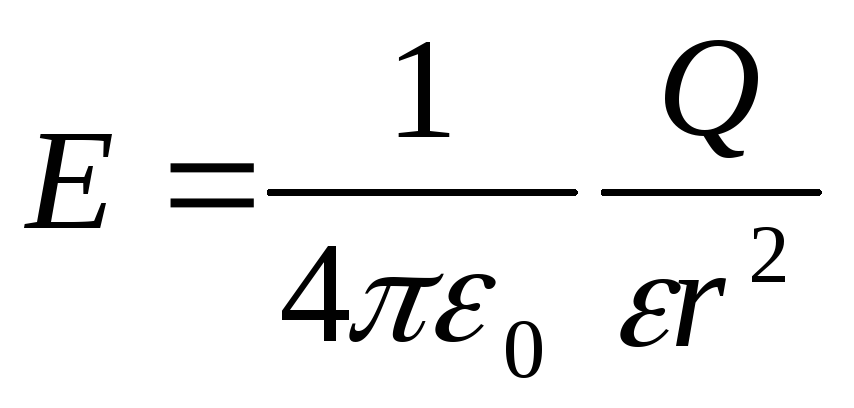Jačina električnog polja koju stvara metalna kugla poluprečnika R, noseći naboj Q,na daljinu r od centra sfere:

a) unutar sfere (r<.R)

b) na površini kugle (r=R)

;

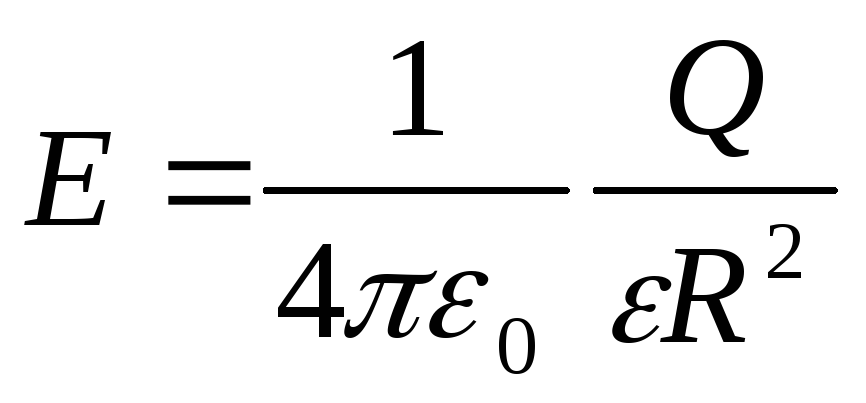c) van sfere (r>R)

.

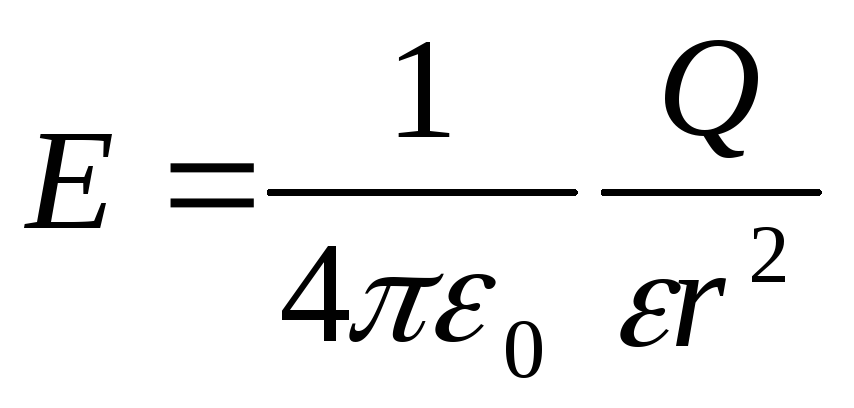 Princip superpozicije (superpozicije) električnih polja, prema kojem se intenzitet E rezultujućeg polja stvorenog sa dva (ili više) tačkastih naboja jednako je vektorskom (geometrijskom) zbroju jačina dodatih polja:

E=E 1 +E 2 +...+E n .

U slučaju dva električna polja sa jačinama E 1 i E 2 modul vektora snage

gdje je  ugao između vektora E 1 i E 2 .

 Intenzitet polja stvorenog beskonačno dugom jednolično nabijenom niti (ili cilindrom) na udaljenosti r od svoje ose

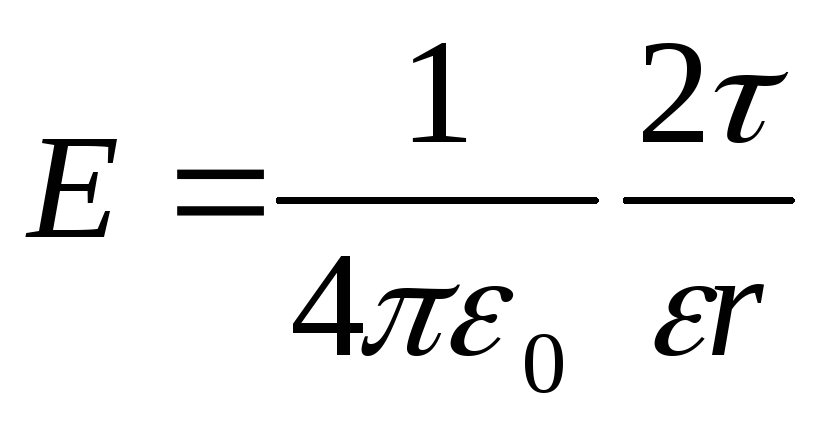, gdje je  linearna gustina naboja.

Linearna gustina naboja je vrijednost jednaka omjeru naboja raspoređenog duž konca i dužine navoja (cilindra):

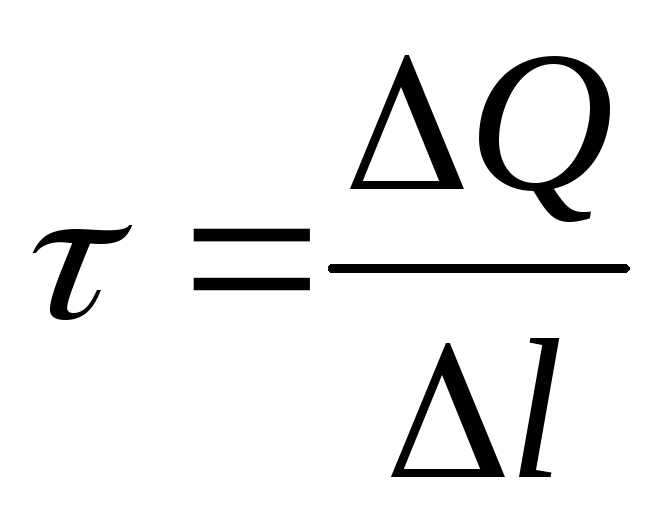
 Intenzitet polja kojeg stvara beskonačna ravnomjerno nabijena ravan,

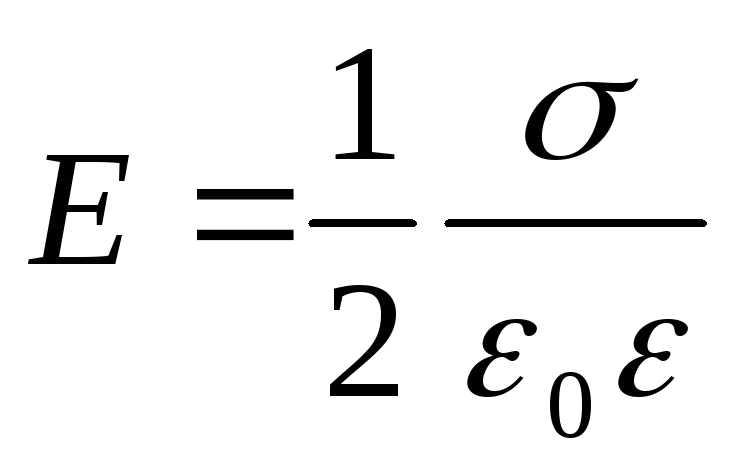
gdje je  površinska gustina naboja.

Površinska gustina naboja je vrijednost jednaka omjeru naboja raspoređenog po površini i površine ove površine:

.

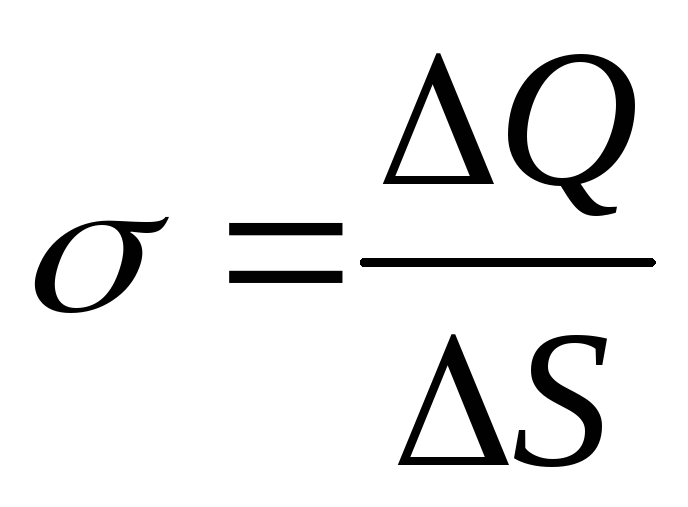 Intenzitet polja koji stvaraju dvije paralelne beskonačne ravnomjerno i suprotno nabijene ravni, sa istim modulom površinske gustine naelektrisanja (polje ravnog kondenzatora)

.

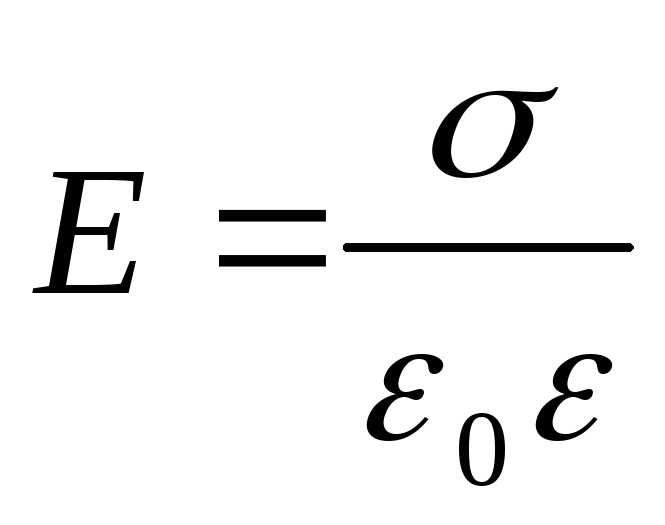Gornja formula vrijedi za izračunavanje jačine polja između ploča ravnog kondenzatora (u njegovom srednjem dijelu) samo ako je razmak između ploča mnogo manji od linearnih dimenzija ploča kondenzatora.

 Električni pomak D povezana sa tenzijom E omjer električnog polja

D= 0 E.

Ova relacija vrijedi samo za izotropne dielektrike.

 Protok vektora električnog pomaka izražava se slično protoku vektora jačine električnog polja:

a) u slučaju jednolikog polja, strujanje kroz ravnu površinu

;

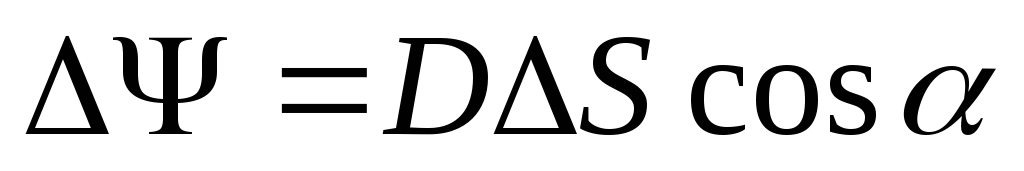b) u slučaju nehomogenog polja i proizvoljne površine

,

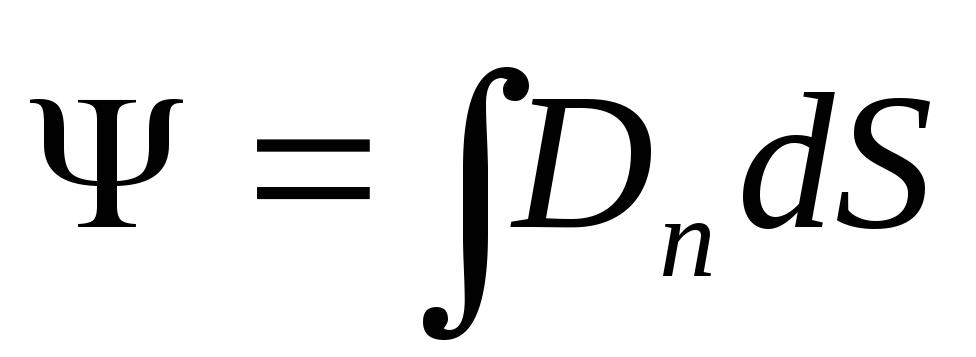gdje D n - vektorska projekcija D u smjeru normale na element površine, čija je površina jednaka d S.

 Ostrogradsky-Gaussova teorema. Protok vektora električnog pomaka kroz bilo koju zatvorenu površinu koja obuhvata naboje Q 1 ,Q 2 , ...,Q n ,

,

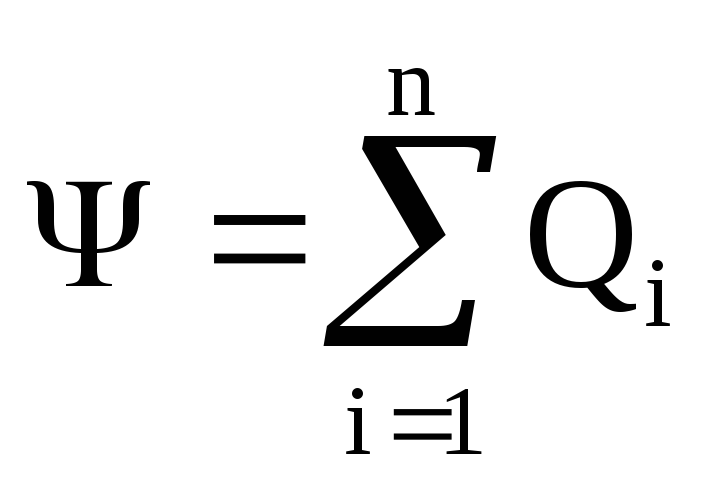gdje P- broj naboja (sa svojim predznakom) zatvorenih unutar zatvorene površine.

 Kruženje vektora jakosti električnog polja je brojčano jednaka radu pomicanja pozitivnog naboja jedne tačke duž zatvorene petlje. Cirkulacija je izražena integralom zatvorene petlje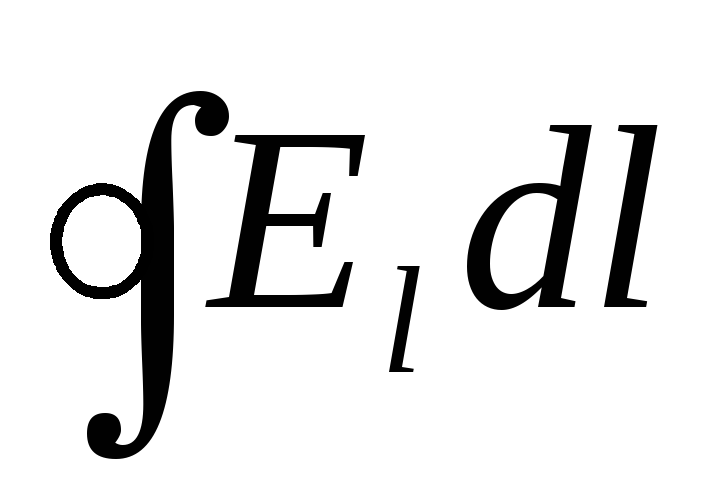

,gdje E l - projekcija vektora intenziteta E u datoj tački konture na pravac tangente na konturu u istoj tački.

U slučaju elektrostatičkog polja, cirkulacija vektora intenziteta je nula:

.

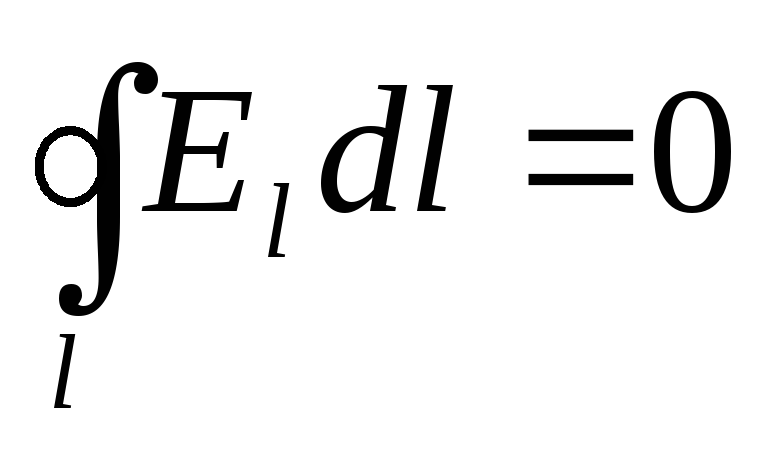Primjeri rješavanja problema

P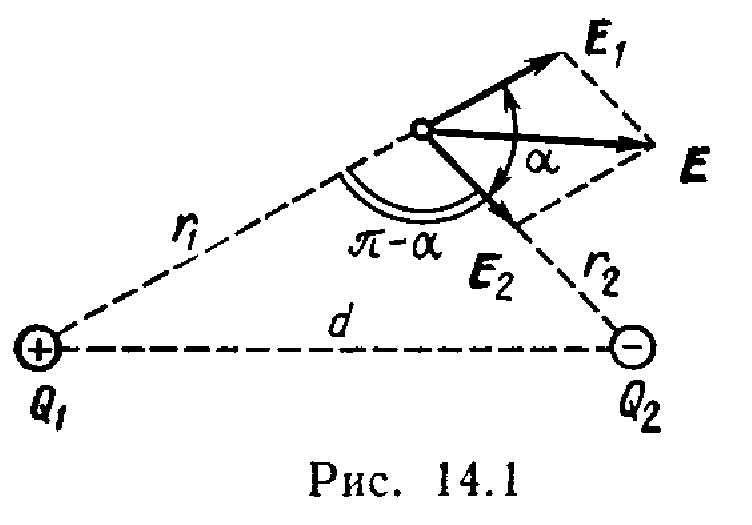

primjer 1. Električno polje stvaraju dva tačkasta naboja: Q 1 =30nC i Q 2 = –10 nC. Razdaljina d između naelektrisanja je 20 cm Odrediti jačinu električnog polja u tački koja se nalazi na udaljenosti r 1 =15cm od prve i na udaljenosti r 2 =10 cm od drugog punjenja.

Rješenje. Prema principu superpozicije električnih polja, svako naelektrisanje stvara polje, bez obzira na prisustvo drugih naelektrisanja u prostoru. Stoga napetost E električno polje u željenoj tački može se naći kao vektorski zbir snaga E 1 i E 2 polja kreirana svakim naplatom posebno: E=E 1 +E 2 .

Jačine električnog polja koje u vakuumu stvaraju prvi i drugi naboj jednake su

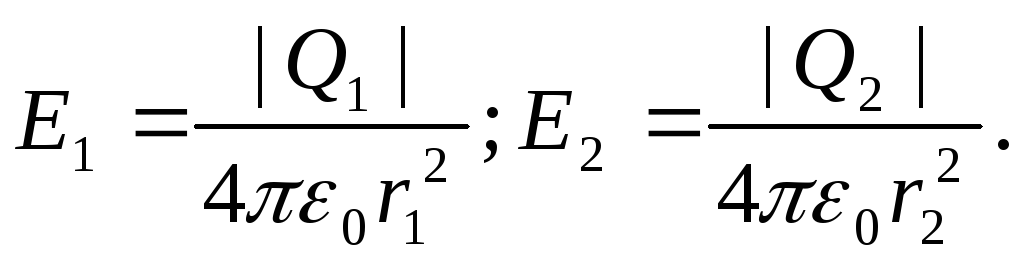(1)

Vector E 1 (Sl. 14.1) je usmjerena duž linije polja od naboja Q 1 , od optužbe Q 1 >0;vektor E 2 također usmjerena duž linije sile, ali prema naboju Q 2 ,jer Q 2 <0.

Vektorski modul E naći po zakonu kosinusa:

gdje se ugao  može naći iz trougla sa stranicama r 1 , r 2 i d:

.

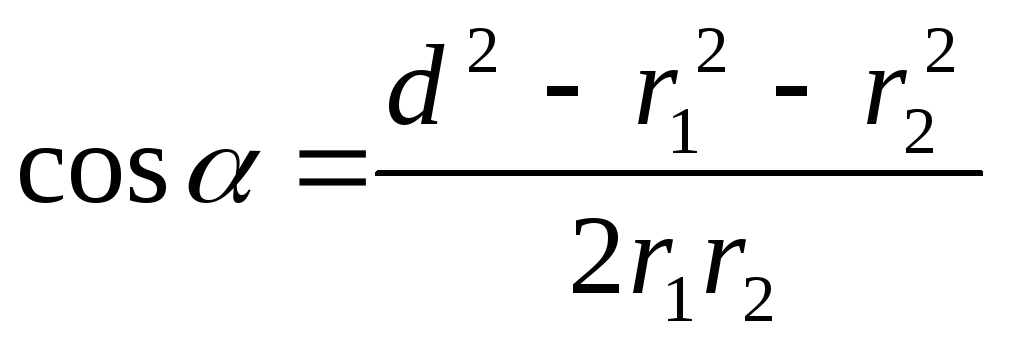U ovom slučaju, kako bismo izbjegli glomazne unose, posebno izračunavamo vrijednost cos Koristeći ovu formulu, nalazimo

Zamjena izraza E 1 i E 2 i po formulama (1) u jednakost (2) i uzimajući zajednički faktor 1/(4 0 ) za korijenski znak, dobijamo

.

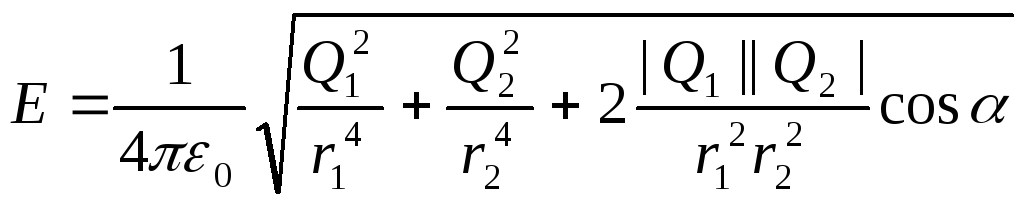Zamjena vrijednosti  ,  0 , Q 1 , Q 2 , r 1 -,r 2 i  u posljednju formulu i izvodeći proračune, nalazimo

Primjer 2 Električno polje stvaraju dvije paralelne beskonačno nabijene ravni s površinskom gustinom naboja  1 \u003d 0,4 μC / m 2 i 2 \u003d 0,1 μC / m 2. Odredite jačinu električnog polja koje stvaraju ove naelektrisane ravni.

R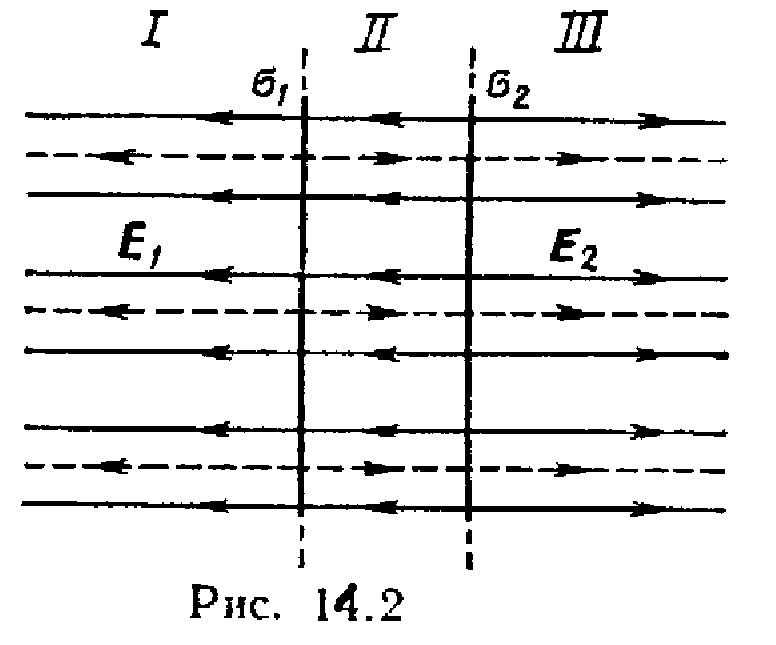

rješenje. Prema principu superpozicije, polja koja stvara svaka naelektrisana ravan pojedinačno su superponirana jedno na drugo, pri čemu svaka naelektrisana ravan stvara električno polje bez obzira na prisustvo druge naelektrisane ravni (slika 14.2).

Jačine homogenih električnih polja koje stvaraju prva i druga ravnina jednake su:

;

.

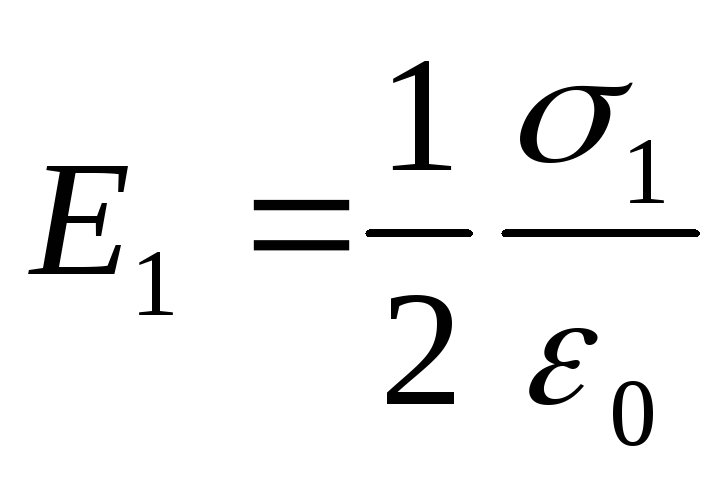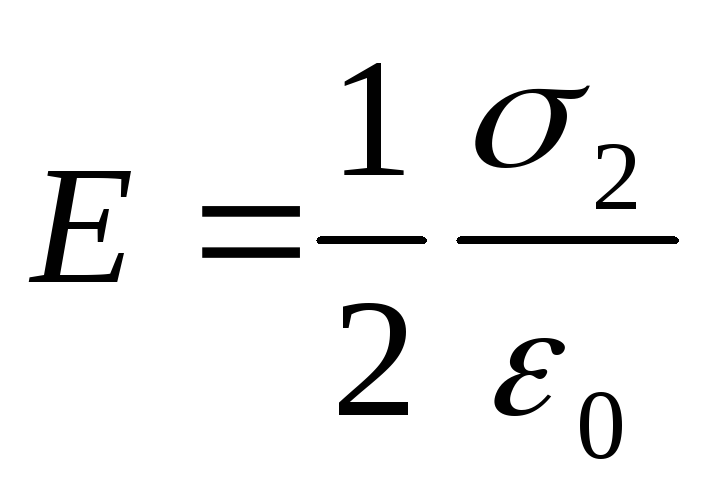Avioni dijele sav prostor na tri regije: I, II i III. Kao što se može vidjeti sa slike, u prvom i trećem području, električne linije sile oba polja su usmjerene u istom smjeru i, posljedično, jačine ukupnih polja E (ja) i E(III) u prvom i trećem području jednake su jedna drugoj i jednake zbroju jačine polja koje stvaraju prva i druga ravnina: E (ja) =E(III) = E 1 +E 2 , ili

E (ja) =E (III) =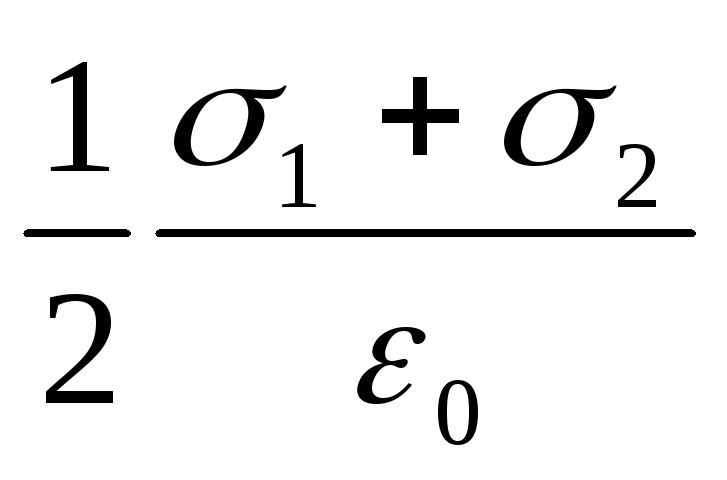

.

U drugom području (između ravnina), električne linije sile polja su usmjerene u suprotnim smjerovima i, prema tome, jačina polja E (II) jednaka je razlici u jačini polja koju stvaraju prva i druga ravnina: E (II) =|E 1 -E 2 | , ili

.

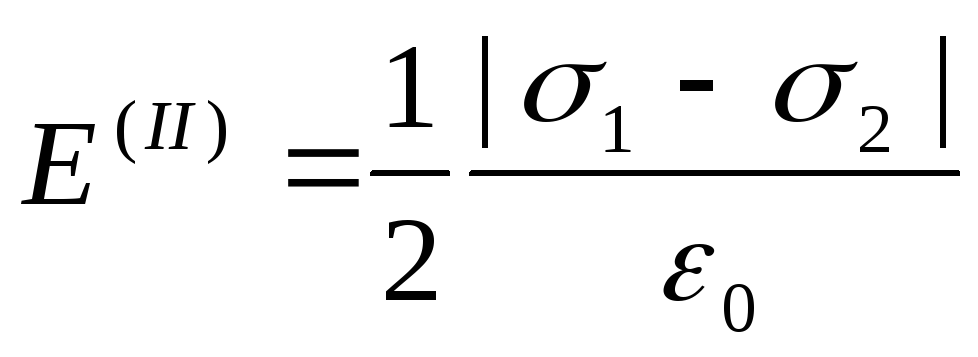Zamjenom podataka i proračunima dobijamo

E (ja) =E (III) =28,3 kV/m=17 kV/m.

Slika raspodjele linija sila ukupnog polja prikazana je na sl. 14.3.

Primjer 3. Na pločama ravnog zračnog kondenzatora postoji punjenje Q=10nC. Square S svaka ploča kondenzatora je jednaka 100 cm 2 Odredite silu F, kojim se ploče privlače. Pretpostavlja se da je polje između ploča jednolično.

Rješenje. Napunite Q jedna ploča je u polju stvorenom naelektrisanjem druge ploče kondenzatora. Dakle, na prvo naelektrisanje deluje sila (slika 14.4)

F=E 1 Q,(1)

gdje E 1 - jačina polja stvorenog naelektrisanjem jedne ploče. Ali

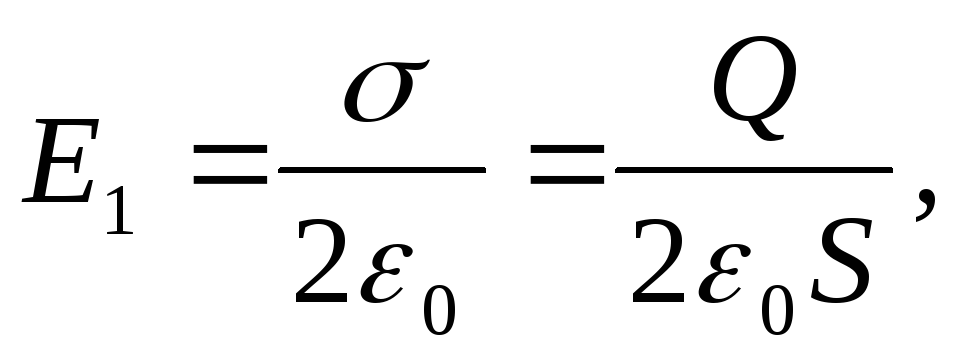gdje je  površinska gustina naboja ploče.

Formula (1) uzimajući u obzir izraz za E 1 poprimiće formu

F=Q 2 /(2 0 S).

Zamjena vrijednosti količina Q, 0 i S u ovu formulu i radeći proračune, dobijamo

F\u003d 565 μN.

Primjer 4 Električno polje stvara beskonačna ravan nabijena površinskom gustinom  = 400 nC/m 2 , i beskonačnu ravnu nit nabijenu linearnom gustinom =100 nC/m. Na daljinu r\u003d 10 cm od konca nalazi se tačkasto punjenje Q=10 nC. Odrediti silu koja djeluje na naboj, njegov smjer, ako naboj i nit leže u istoj ravni paralelno s nabijenom ravninom.

Rješenje. Sila koja deluje na naelektrisanje postavljeno u polje

F=EQ, (1)

gdje E -Q.

Hajde da definišemo napetost E polje stvoreno, prema uslovu zadatka, beskonačno nabijenom ravninom i beskonačno nabijenom niti. Polje koje stvara beskonačno nabijena ravan je uniformno, a njegov intenzitet u bilo kojoj tački

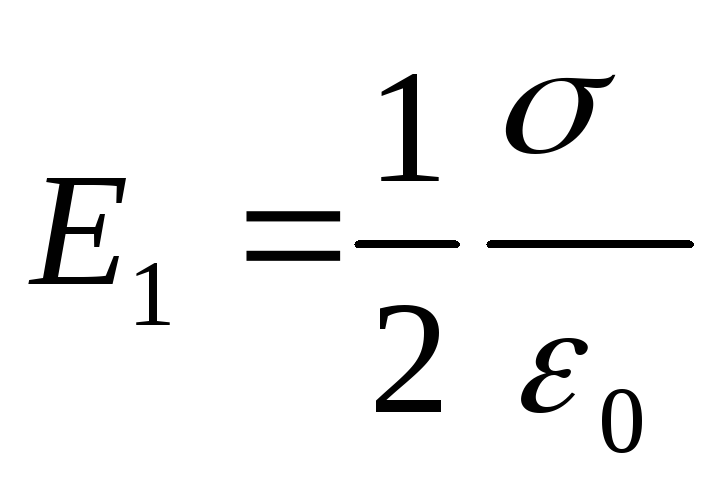. (2)

Polje koje stvara beskonačna nabijena linija je neujednačeno. Njegov intenzitet ovisi o udaljenosti i određen je formulom

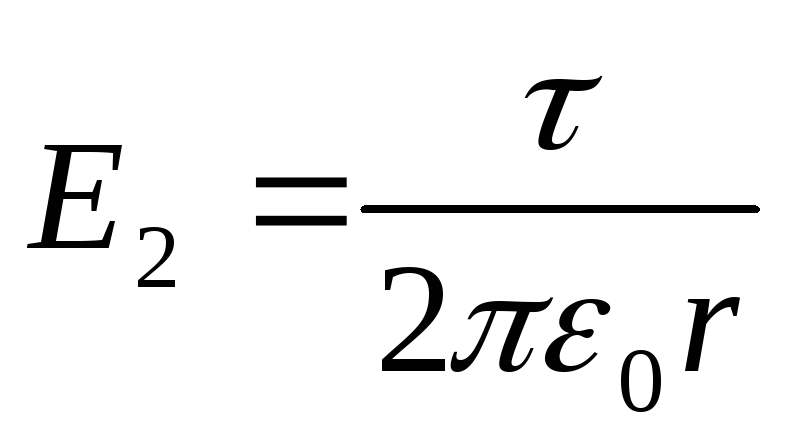. (3)

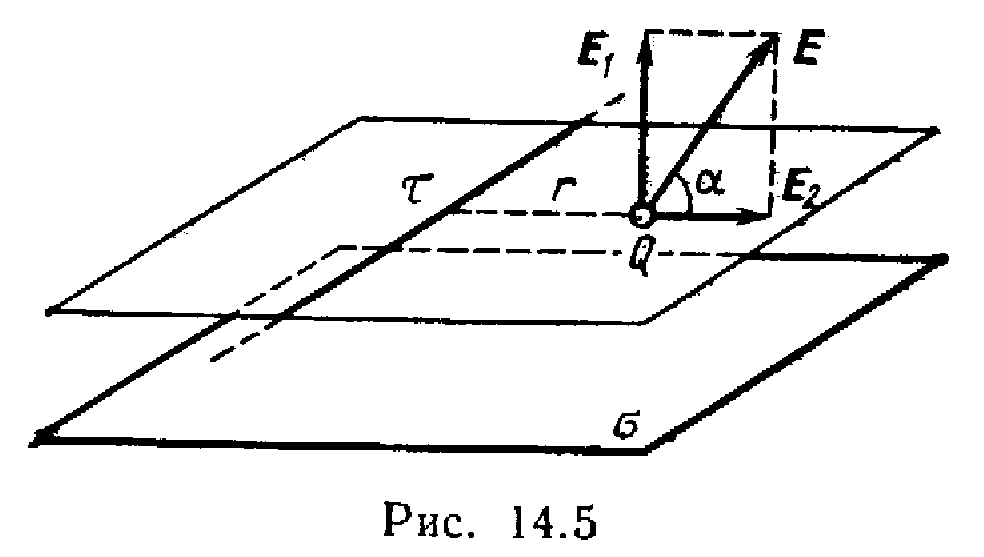
Prema principu superpozicije električnih polja, jačina polja u tački gde je naelektrisanje Q, jednak je vektorskom zbiru intenziteta E 1 i E 2 (Sl. 14.5): E=E 1 +E 2 .Zato što su vektori E 1 i E 2 onda međusobno okomite

.

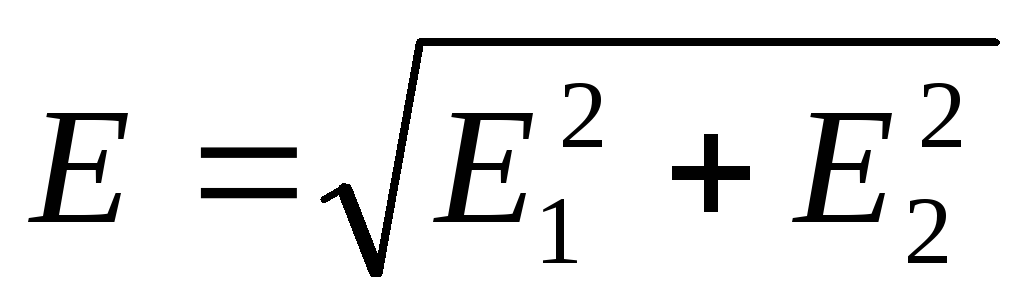Zamjena izraza E 1 i E 2 formule (2) i (3) u ovu jednakost, dobijamo

,

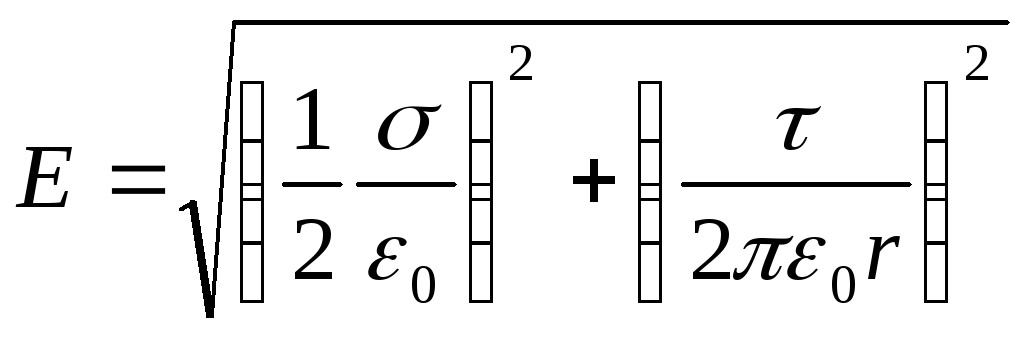ili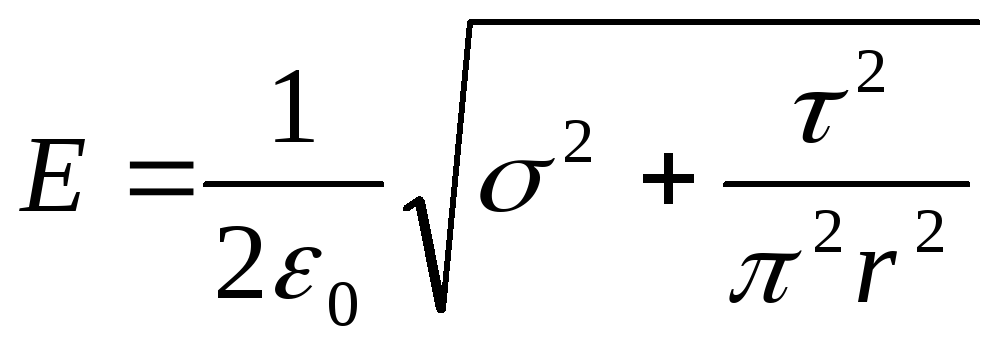

.

Hajde sada da nađemo snagu F, djelujući na naboj, zamjenjujući izraz E u formulu (1):

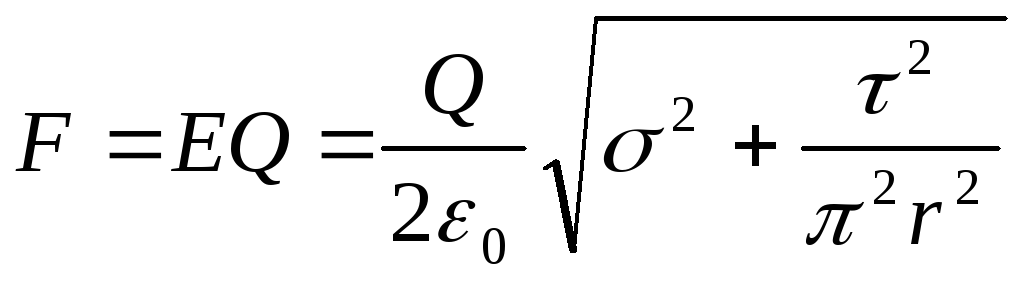. (4)

Zamjena vrijednosti količina Q, 0 ,,,i r u formulu (4) i vršeći proračune, nalazimo

F\u003d 289 μN.

Smjer sile F, djelujući na pozitivan naboj Q, poklapa se sa smjerom vektora intenziteta E polja. Smjer isti vektor E je dat uglom  u odnosu na nabijenu ravan. Od sl. 14.5 iz toga slijedi

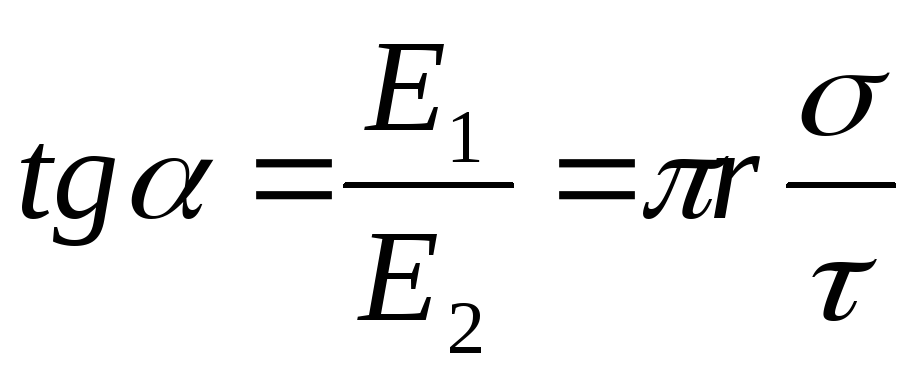, gdje

.

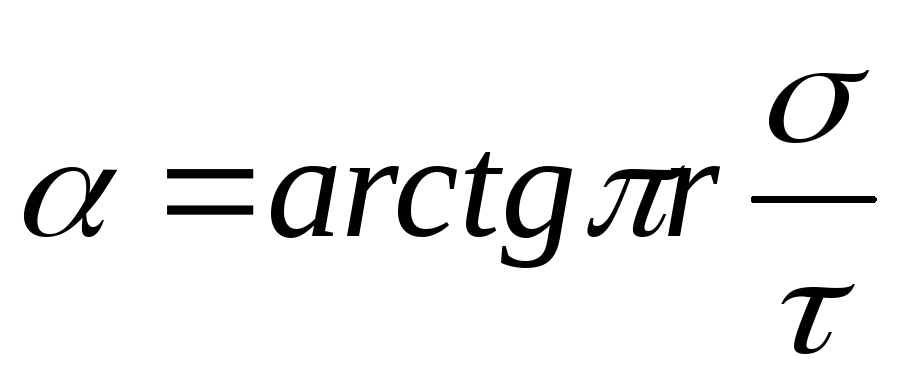Zamjena vrijednosti , r,iu ovom izrazu i računanju, dobijamo

Primjer 5 tačka naboj Q\u003d 25nC je u nuli koju stvara pravi beskonačan cilindar polumjera R= 1 cm, jednoliko naelektrisan sa površinskom gustinom  = 2 μC / m 2. Odrediti silu koja djeluje na naboj smješten na udaljenosti od ose cilindra r\u003d 10 cm.

Rješenje. Sila koja djeluje na naboj Q, nalazi se na terenu,

F=QE,(1)

gdje E - jačina polja na mestu gde se nalazi naelektrisanje Q.

Kao što je poznato, jačina polja beskonačno dugog jednoliko nabijenog cilindra

E=/(2 0 r), (2)

gdje je  linearna gustina naboja.

Linearnu gustoću  izražavamo preko površinske gustine . Da biste to učinili, odaberite element cilindra s dužinom l i izrazi naplatu na njemu Q 1 dva načina:

Q 1 =  S= 2  Rl i Q 1 = l.

Izjednačavajući prave dijelove ovih jednakosti, dobijamo  l=2 Rl . Nakon skraćivanja na l find=2 R . Imajući to na umu, formula (2) poprima oblik E=R /( 0 r). Zamjena ovog izraza E u formulu (1), nalazimo željenu silu:

F=Q R/( 0 r).(3)

Jer R i r su uključeni u formulu kao omjer, onda se mogu izraziti u bilo kojoj, ali samo u istim jedinicama.

Nakon izvođenja proračuna pomoću formule (3), nalazimo

F\u003d 2510 -9 210 -6 10 -2 / (8,8510 -12 1010 -2)H==56510 -6 H=565μH.

Smjer sile F poklapa se sa smjerom vektora napetosti E, a potonji je zbog simetrije (cilindar je beskonačno dugačak) usmjeren okomito na cilindar.

Primjer 6 Električno polje stvara tanka beskonačno duga nit, jednoliko nabijena linearne gustine =30 nC/m. Na daljinu a\u003d 20 cm od navoja nalazi se ravno okruglo područje s radijusom r\u003d 1 cm Odredite tok vektora napetosti kroz ovo područje ako njegova ravnina čini ugao  \u003d 30 ° sa linijom napetosti koja prolazi sredinom područja.

Rješenje. Polje stvoreno beskonačno ravnomjerno nabijenim filamentom je nehomogeno. Tok vektora intenziteta u ovom slučaju je izražen integralom

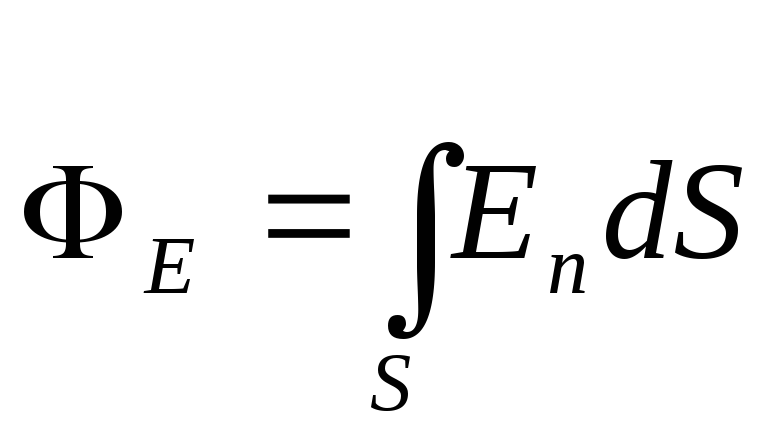, (1)

gdje E n - vektorska projekcija E do normalnog n na površinu lokacije dS. Integracija se vrši preko cijele površine lokacije koja je probijena linijama napetosti.

P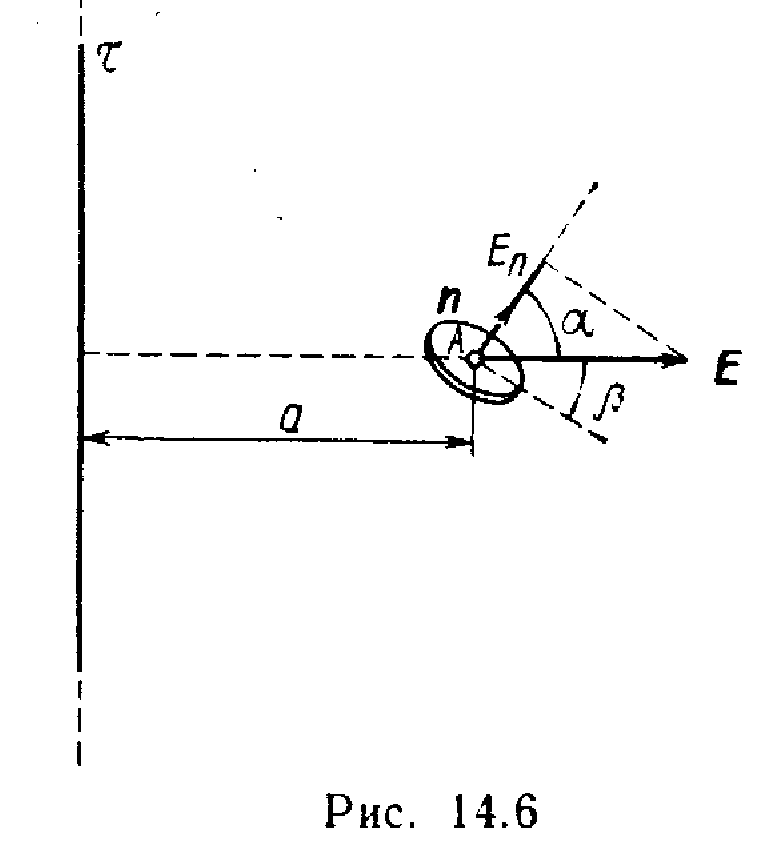

projekcija E P vektor napetosti je jednak, kao što se može videti sa Sl. 14.6,

E P =E cos,

gdje je  ugao između smjera vektora i normale n. Imajući to na umu, formula (1) poprima oblik

.

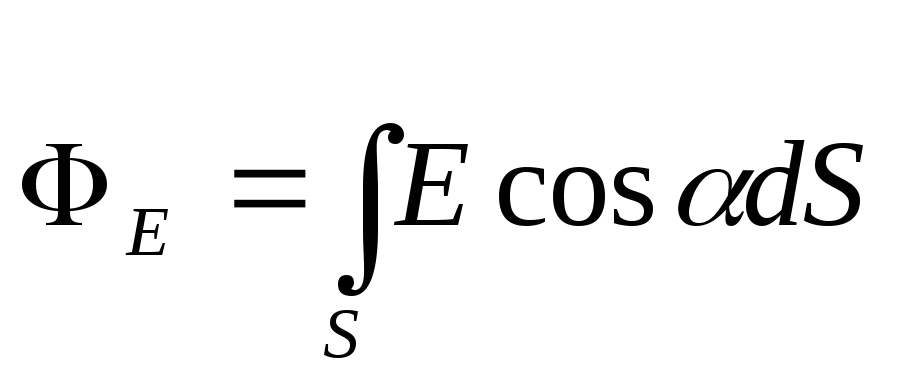Budući da su dimenzije površine male u odnosu na udaljenost do konca (r<E veoma malo. varira u apsolutnoj vrijednosti i smjeru unutar stranice, što vam omogućava zamjenu vrijednosti pod znakom integrala E i cos njihove prosječne vrijednosti<E> i i izvadi ih iz integralnog znaka:

Integracijom i zamjenom<E> i njihove približne vrijednosti E A i cos  A , izračunato za sredinu lokacije, dobijamo

F E =E A cos  A S= r 2 E A cos A . (2)

tenzija E A izračunato po formuli E A=/(2 0 a). Od

pirinač. 14.6 slijedi cos  A=cos(/2 -  )=sin.

S obzirom na izraz E A i cos  A jednakost (2.) poprima oblik

.

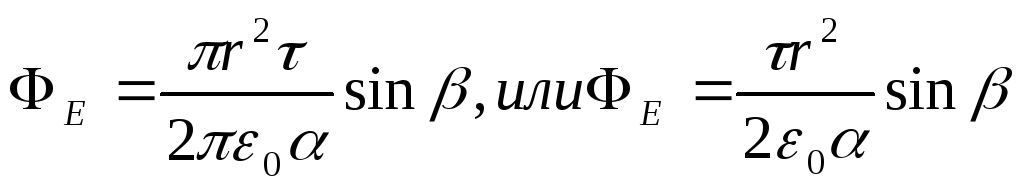Zamjenom podataka u posljednju formulu i izvođenjem proračuna nalazimo

F E=424 mV.m.

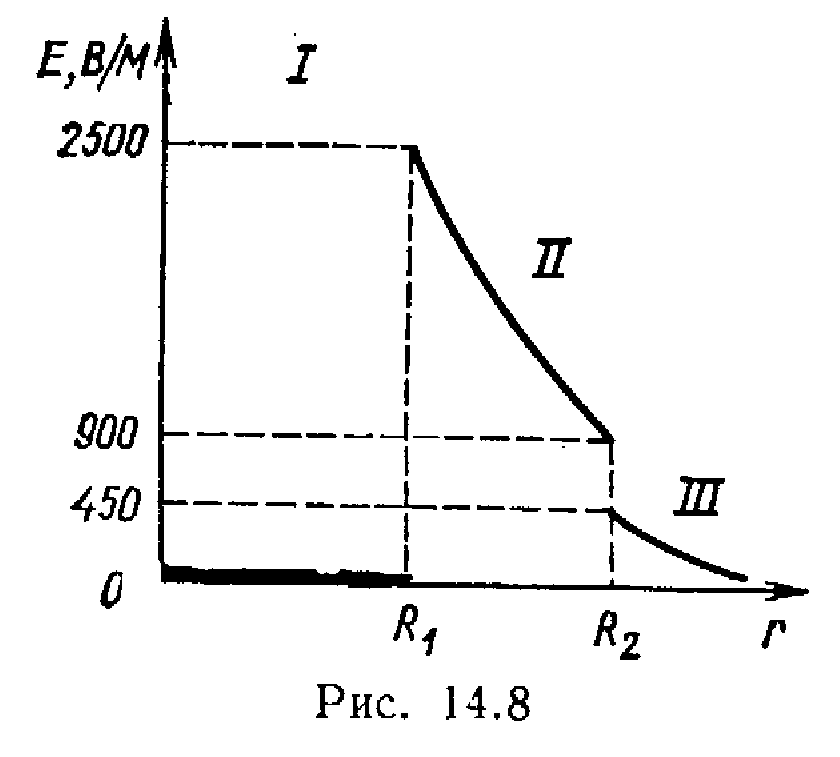
Primjer7 . Dvije koncentrične provodne sfere poluprečnika R 1 =6cm i R 2 = 10cm nose respektivno punjenja Q 1 \u003d lnKl i Q 2 =–0,5 nC. Pronađite napetost E polja u tačkama odvojenim od središta sfera na udaljenostima r 1 =5cm, r 2 =9 cm r 3 =15cm. Build Graph E(r).

R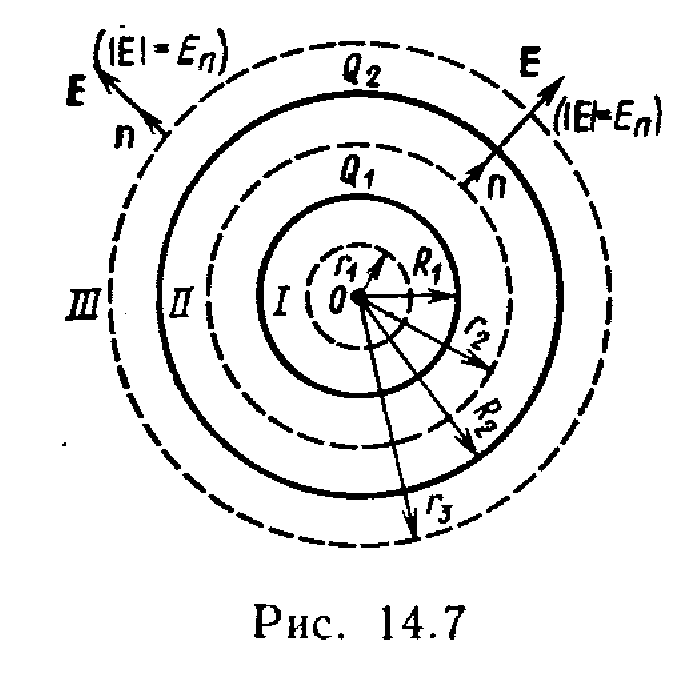

rješenje. Imajte na umu da tačke u kojima želite da pronađete jačinu električnog polja leže u tri oblasti (slika 14.7): oblast I ( r<R 1 ), regija II( R 1 <r 2 <R 2 ), regija III ( r 3 >R 2 ).

1. Odrediti napetost E 1 nacrtati sfernu površinu u području I S 1 radijus r 1 i koristite Ostrogradsky-Gaussovu teoremu. Kako unutar područja I nema naboja, onda prema navedenoj teoremi dobijamo jednakost

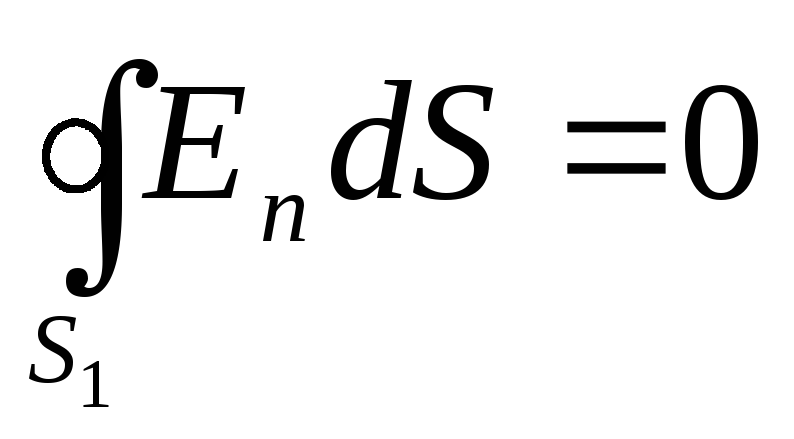, (1)

gdje E n je normalna komponenta jačine električnog polja.

Iz razloga simetrije, normalna komponenta E n mora biti jednaka samoj napetosti i konstantna za sve tačke sfere, tj. En=E 1 = konst.. Stoga se može izvaditi iz predznaka integrala. Jednakost (1) ima oblik

.

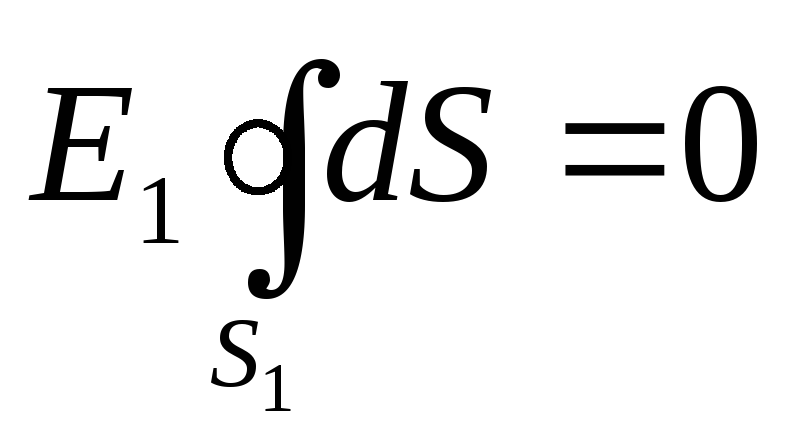Pošto površina sfere nije nula, onda

E 1 =0,

tj. jačina polja u svim tačkama koje zadovoljavaju uslov r 1 <.R 1 , će biti jednaka nuli.

2. U području II crtamo sfernu površinu polumjera r 2 .Pošto postoji naelektrisanje unutar ove površine Q 1 , onda za njega, prema Ostrogradsky-Gauss teoremi, možemo napisati jednakost

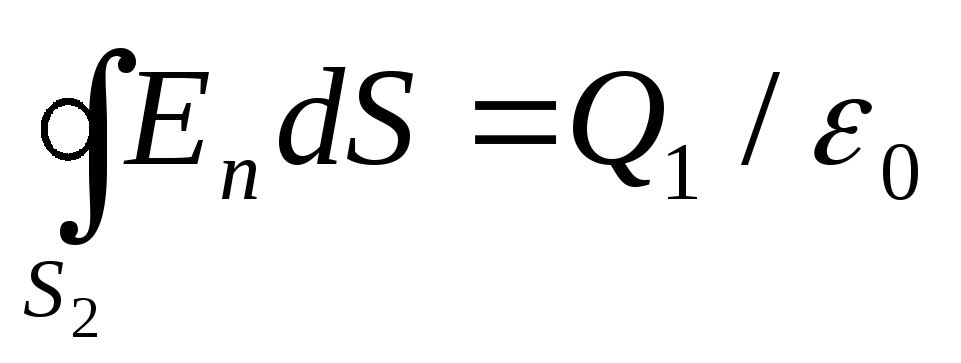. (2)

Jer E n =E 2 = const, onda uslovi simetrije impliciraju

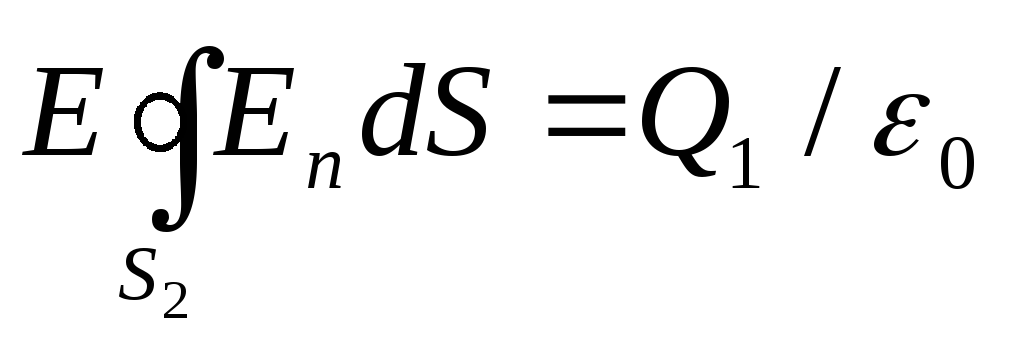, ili ES 2 =Q 1 / 0 ,

E 2 =Q 1 /( 0 S 2 ).

Zamjenjujući ovdje izraz za površinu sfere, dobijamo

E 2 =Q/(4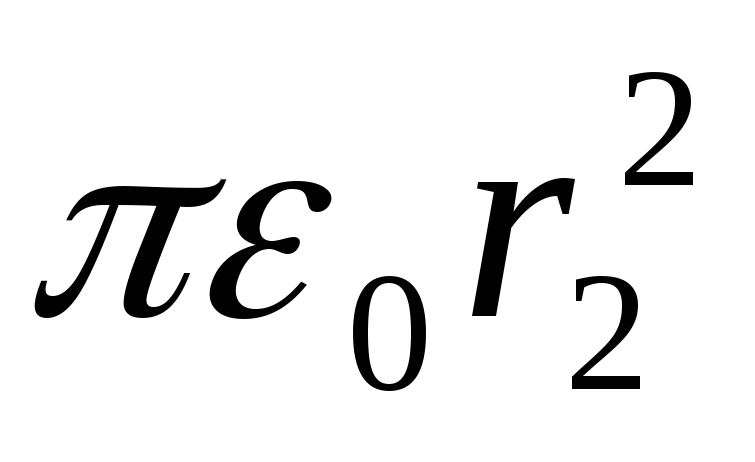

). (3)

3. U području III crtamo sfernu površinu polumjera r 3 . Ova površina pokriva ukupni naboj Q 1 +Q 2 . Stoga će za njega jednadžba napisana na osnovu Ostrogradskog-Gaussove teoreme imati oblik

.

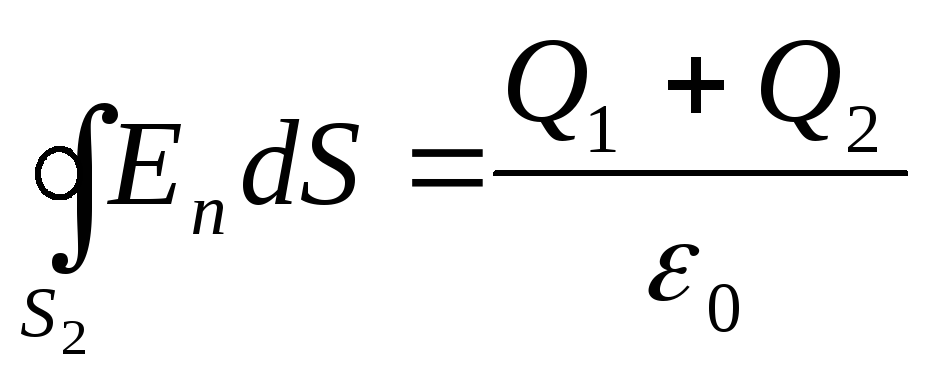Dakle, koristeći odredbe primijenjene u prva dva slučaja, nalazimo

Uvjerimo se da pravi dijelovi jednakosti (3) i (4) daju jedinicu jačine električnog polja;

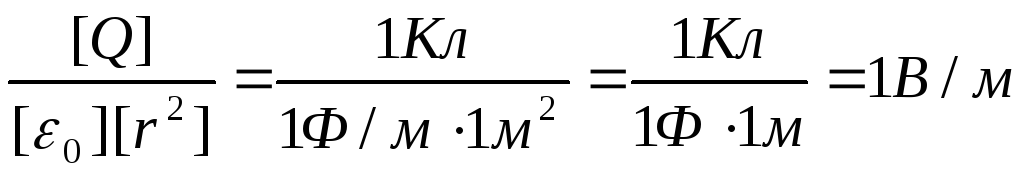
Sve količine izražavamo u SI jedinicama ( Q 1 \u003d 10 -9 C, Q 2 = –0,510 -9 C, r 1 =0,09m, r 2 =15m , l/(4 0 )=910 9 m/F) i izvršite proračune:

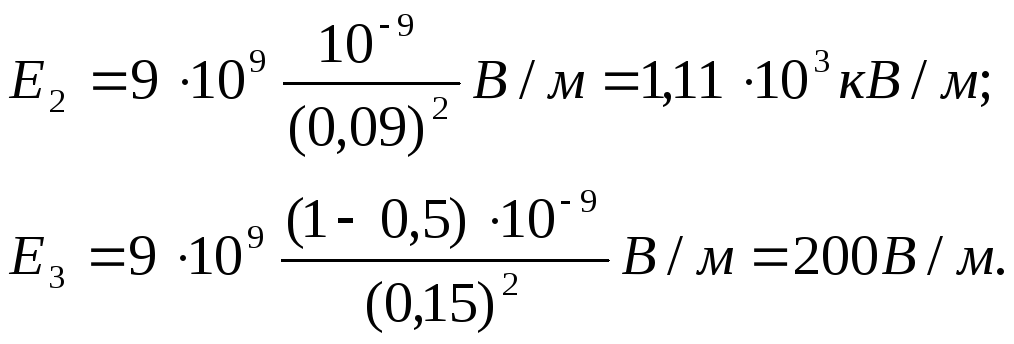
4. Napravimo graf E(r).AT područje I ( r 1 1 ) tenzija E=0. U području II (R 1 r<.R 2 ) tenzija E 2 (r) varira u skladu sa zakonom l/r 2 .Point r=R 1 tenzija E 2 (R 1 )=Q 1 /(4 0 R 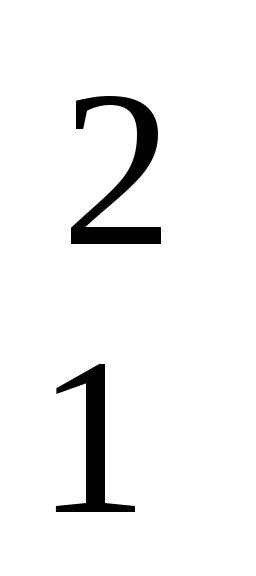)=2500 V/m U tački r=R 1 (r teži da R 1 lijevo) E 2 (R 2 )=Q 1 /(4 0 R 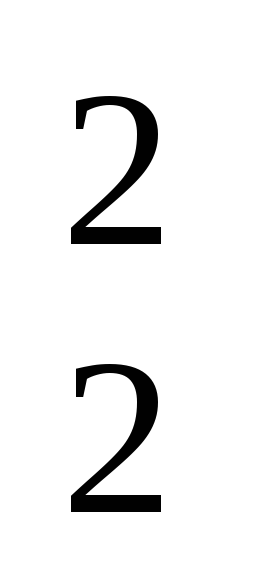)=900V/m. U oblasti III( r>R 2 )E 3 (r) varira u skladu sa zakonom 1/ r 2 , i u točki r=R 2 (r teži da R 2 desno) E 3 (R 2 ) =(Q 1 –|P 2 |)/(4 0 R 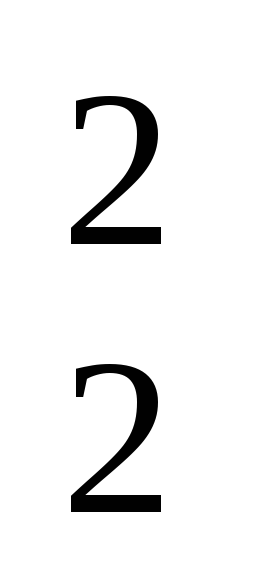)=450 V/m. Dakle, funkcija E(r) u tačkama r=R 1 i r=R 2 pretrpi pauzu. graf zavisnosti E(r) prikazano na sl. 14.8.

Zadaci

Jačina polja tačkastih naelektrisanja

14.1. Definišite napetost E električno polje koje stvara tačkasti naboj Q=10 nC na udaljenosti r\u003d 10 cm od njega. Dielektrik - ulje.

14.2. Razdaljina d između dva tačkastog naboja Q 1 =+8 nC i Q 2 \u003d -5,3 nC je jednako 40 cm. Izračunajte intenzitet E polje u tački na sredini između naelektrisanja. Koliki je intenzitet ako je drugi naboj pozitivan?

14.3. Q 1 =10nC i Q 2 = –20 nC, nalazi se na udaljenosti d=20cm jedan od drugog. Definišite napetost E polje na tački udaljenoj od prvog punjenja r 1 =30cm i od drugog do r 2 =50 cm.

14.4. Razdaljina d između dva pozitivna naboja Q 1 =9Q i Q 2 \u003d Q je 8 cm. Na kojoj udaljenosti r od prvog naboja je tačka u kojoj je intenzitet E polje punjenja je nula? Gdje bi bila ta tačka da je drugi naboj negativan?

14.5. Naboj u dva boda Q 1 =2Q i Q 2 = –Q su na udaljenosti d jedno od drugog. Pronađite položaj tačke na pravoj liniji koja prolazi kroz ove naboje, intenzitet E polja u kojima je jednako nuli,

14.6. Električno polje koje stvaraju dva tačkasta naelektrisanja Q 1 =40nC i Q 2 = –10 nC, nalazi se na udaljenosti d=10 cm međusobno. Definišite napetost E polje na tački udaljenoj od prvog punjenja r 1 \u003d 12 cm i od drugog do r 2 =6 cm.

Jačina polja naelektrisanja raspoređena po prstenu i sferi

14.7. Tanak prsten sa radijusom R\u003d 8 cm nosi naboj ravnomjerno raspoređen s linearnom gustoćom  \u003d 10 nC/m. Kakva je napetost E električno polje u tački koja je jednako udaljena od svih tačaka prstena na udaljenosti r\u003d 10 cm?

14.8. Hemisfera nosi naelektrisanje ravnomerno raspoređeno sa površinskom gustinom =1,nC/m 2 . Pronađite napetost E električno polje u geometrijskom centru hemisfere.

14.9. Na metalnoj sferi poluprečnika R\u003d 10 cm je punjenje Q\u003d lnKl. Definišite napetost E električno polje u sljedećim tačkama: 1) na udaljenosti r 1 =8 cm od centra sfere; 2) na svojoj površini; 3) na daljinu r 2 =15 cm od centra sfere. Grafikon zavisnosti E od r.

14.10. Dvije koncentrične metalne nabijene kugle polumjera R 1 =6cm i R 2 \u003d 10 cm nosi naboje, respektivno Q 1 =1 nC i Q 2 = – 0,5 nC. Pronađite napetost E tačkasta polja. udaljeni od središta sfera na udaljenostima r 1 =5 cm, r 2 =9 cm, r 3 \u003d 15 cm. Ovisnost parcele E(r).

Jačina polja napunjene linije

14.11. Vrlo duga tanka ravna žica nosi naboj ravnomjerno raspoređen po cijeloj dužini. Izračunajte linearnu gustoću naboja  ako je intenzitet E polja u daljini a\u003d 0,5 m od žice u odnosu na njenu sredinu je 200 V / m.

14.12. Razdaljina d između dvije dugačke tanke žice paralelne jedna s drugom iznosi 16 cm. Žice su jednoliko nabijene suprotnim nabojima linearne gustine ||=^150. µC/m. Kakva je napetost E polja u tački udaljenoj na r\u003d 10 cm od prve i druge žice?

14.13. Prečnik ravne metalne šipke d=5cm i dužine l\u003d 4 m nosi naboj ravnomjerno raspoređen po svojoj površini Q=500nC. Definišite napetost E polje u tački suprotno od sredine štapa na udaljenosti a=1 cm od njegove površine.

14.14. Beskonačno duga metalna cijev tankih stijenki radijusa R\u003d 2 cm nosi naboj ravnomjerno raspoređen po površini ( \u003d 1 nC / m 2). Definišite napetost E polja u tačkama odvojenim od ose cijevi na udaljenostima r 1 =lcm, r 2 \u003d 3 cm. Ovisnost parcele E(r).

14.15. Dvije duge koaksijalne cijevi tankih stijenki poluprečnika R 1 =2cm i R 2 \u003d 4 cm nose naboje ravnomjerno raspoređene duž dužine s linearnim gustoćama  1 \u003d ln C / m i  2 = -0,5 nC/m. Prostor između cijevi ispunjen je ebonitom. Definišite napetost E polja u tačkama koje se nalaze na udaljenostima r 1 =1 cm, r 2 =3cm, r 3 \u003d 5 cm od ose cijevi; Grafikon zavisnosti E od r.