U fizici se sudari shvataju kao procesi interakcije između tijela (čestica) u širem smislu riječi, a ne samo u doslovnom smislu - kao kontakt tijela. sudarajućih tijela velika udaljenost su besplatni. Prolazeći jedno pored drugog, tijela međusobno djeluju, kao rezultat toga mogu se pojaviti različiti procesi - tijela se mogu kombinirati u jedno tijelo ( apsolutno neelastičan udar), mogu nastati nova tijela i, konačno, mogu postojati elastični sudar, pri čemu se tijela nakon nekog približavanja ponovo razilaze bez promjene unutrašnjeg stanja. Zovu se sudari praćeni promjenom unutrašnjeg stanja tijela neelastično. Tijela (čestice) uključene u sudar karakteriziraju (prije i nakon sudara) momenti i energije. Proces sudara se svodi na promjenu ovih veličina kao rezultat interakcije. Zakoni održanja energije i impulsa olakšavaju uspostavljanje odnosa između različitih fizičke veličine prilikom sudara tela. Ovdje je posebno vrijedna okolnost da se zakoni o očuvanju često mogu koristiti čak iu slučajevima kada aktivne snage nepoznato. To je slučaj, na primjer, u fizici elementarnih čestica.

Sudari makroskopskih tijela do kojih dolazi u normalnim uvjetima gotovo su uvijek neelastični u ovom ili onom stupnju, makar samo zato što su praćeni nekim zagrijavanjem tijela, odnosno pretvaranjem dijela njihove kinetičke energije u toplinu. Ipak, u fizici koncept elastičnih sudara igra važnu ulogu. Takvi sudari se često moraju rješavati u fizičkom eksperimentu na polju atomskih fenomena, a čak se i obični sudari često mogu smatrati elastičnim s dovoljnim stepenom tačnosti.

Očuvanje količine kretanja tijela (čestica) u sudaru je zbog činjenice da je skup tijela koja učestvuju u sudaru ili izolovani sistem, odnosno vanjske sile, ili zatvorena, ne djeluju na tijela uključena u sistem: vanjske sile su različite od nule, a zbir spoljne sile jednako nuli. Situacija s primjenom zakona održanja energije u sudarima je nešto složenija. Apel na očuvanje energije ponekad zahtijeva uzimanje u obzir različitih oblika unutrašnje energije.

Može se reći da je djelovanje zakona održanja impulsa i energije u procesima sudara potvrđeno širokim spektrom eksperimentalnih podataka.

Neelastični sudari

Čestica mase `m` sa kinetičkom energijom `K` sudara se sa stacionarnom česticom mase `M`. Naći priraštaj `Q` unutrašnje energije sistema čestica kao rezultat apsolutno neelastičnog sudara ("lepljenja").

Uzmite u obzir apsolutno neelastičan udar dva tijela u LSO. Upadna čestica se kreće prije sudara u pozitivnom smjeru ose `Ox` brzinom `vec v`, kinetička energijačestice `K = (mv^2)/2`. Kao rezultat apsolutno neelastičnog udara (lijepljenja), čestice se kreću istom brzinom `vec u`. Prema zakonu održanja impulsa `mv = (m + M) u`. Prema zakonu održanja energije

`(mv^2)/2 = ((m + M)u^2)/2 + Q`.

Iz gornjih relacija nalazimo`Q = M/(m + M) K`.

Imajte na umu da u graničnim slučajevima

`Q=K`,

`m< < M`,

`Q = M/m K< < K`,

`m > > M`.

Kao što vidimo, prilikom neelastičnog sudara lake čestice s masivnom (na primjer, elektrona s atomom), dolazi do gotovo potpunog prijelaza njene kinetičke energije u unutrašnja energija masivne čestice.

Ako su mase jednake `(m = M)``Q=K/2`.

Iz toga slijedi, na primjer, da u sudaru dva identična automobila, od kojih jedan miruje, a drugi se kreće u pravcu prema njemu, polovina kinetičke energije odlazi na uništenje.

Elastični sudari

Glatka lopta mase `M` leži na glatkoj horizontalnoj površini. Pogođen je glatkom kuglom mase `m` koja se kreće brzinom `vec v`. Postoji elastičan centralni udar loptica. Pronađite brzine `vec(v_1)` i `vec(v_2)` loptica nakon sudara. Pod kojim uslovom će se upadna lopta kretati u istom smjeru nakon sudara?

Razmotrimo problem u LSO-u, čija će os `Ox` biti usmjerena duž linije centara loptica u trenutku sudara. Vanjske sile koje djeluju na kuglice tokom sudara su sile gravitacije i sile normalna reakcija podržava. Njihov zbir je nula. Posljedično, impuls sistema loptica se ne mijenja tokom interakcije. Prema zakonu održanja impulsa `m vec v = m vec(v_1) + M vec(v_2)`.

Prelazeći na projekcije na osi `Ox`, dobijamo `mv = mv_(1x) + Mv_2`, ovdje se uzima u obzir da smjer brzine `vec(v_1)` upadne lopte nakon sudara nijepoznato. Prema zakonu održanja energije

`(mv^2)/2 = (mv_(1x)^2)/2 + (Mv_2^2)/2`.

Dobijene relacije prepisujemo u formu

`m(v - v_(1x)) = Mv_2`,

`m(v^2 - v_(1x)^2) = Mv_2^2`.

Dijelimo drugu jednakost prvom `(v != v_(1x))`, dolazimo do linearnog sistema`v_2 = v + v_(1x)`, `m(v - v_(1x)) = Mv_2`, čije rješenje ima oblik

`v_(1x) = (m - M)/(m + M) v`, `v_2 = (2m)/(m + M) v`.

Dolazna loptica će se kretati nakon sudara u istom smjeru `(v_(1x) > 0)` za `m > M`, tj. ako je masa nadolazeće lopte veća od mase loptice u mirovanju.

Dvije glatke elastične okrugle podloške kreću se naprijed na glatkoj horizontalnoj površini sa brzinama `vec(v_1)` i `vec(v_2)`. Pronađite brzine `vec(v_1^")` i `vec(v_2^")` pakova nakon savršeno elastičnog sudara izvan centra. Mase podložaka `m_1` i `m_2`.

Razmotrimo problem u ISO, koordinatne ose `Ox` i `Oy` koje leže u horizontalnoj ravni, dok je osa `Ox` usmjerena duž središnje linije podloški u trenutku udara.

Za vrijeme udara na sistem pak djeluju samo vertikalne vanjske sile: to su sile gravitacije i sile normalne reakcije. Njihov zbir je nula. Tada se zadržava impuls sistema podložaka u procesu interakcije

`vec(p_1) + vec(p_2) = vec(p_1^") + vec(p_2^")`,

ovdje `vec(p_1) = m_1 vec(v_1)`, `vec(p_2) = m_2 vec(v_2)`, `vec(p_1^") = m_1 vec(v_1^")`, `vec(p_2^" ) = m_2 vec(v_2^")` - impuls paka prije i poslije udara.

Pošto su podloške idealno glatke, za vreme sudara unutrašnje sile - sile elastične interakcije - su usmerene samo duž ose `Ox`. Ove sile ne mijenjaju `y`-komponente impulsa paka. Tada iz `p_(1y) = p_(1y)^"`, `p_(2y) = p_(2y)^"` nalazimo `y`-komponente brzina paka nakon sudara

`vec(v_(1y)^") = v_(1y)`, `v_(2y)^" = v_(2y)`,

tj. u projekciji na osu `Oy`, brzine pakova se nisu mijenjale kao rezultat sudara.

Nađimo `x`-komponente brzina pakova nakon elastičnog sudara. U takvom sudaru kinetička energija je očuvana

`(m_1 (v_(1x)^2 + v_(1y)^2))/2 + (m_2 (v_(2x)^2 + v_(2y)^2))/2 = (m_1 ((v_(1x) )^")^2 + (v_(1y)^")^2))/2 + (m_2 ((v_(2x)^")^2 + (v_(2y)^")^2))/2 `.

Uzimajući u obzir jednakost `y`-komponenti brzina pakova prije i nakon suudara, posljednja jednakost poprima oblik

`(m_1 v_(1x)^2)/2 + (m_2 v_(2x)^2)/2 = (m_1 (v_(1x)^")^2)/2 + (m_2 (v_(2x)^" )^2)/2`.

Okrenimo se zakonu održanja impulsa i pređimo na projekcije impulsa impulsa pakova na osu `Ox`

`m_1 v_(1x) + m_2 v_(2x) = m_1 v_(1x)^" + m_2 v_(2x)^"`.

Dakle, prvobitni problem se svodi na problem apsolutno elastičnog centralnog udara: to je oblik koji bi poprimili zakoni održanja energije i momenta kada bi se brzine pakova usmjerile duž linije centara. Rezultirajući nelinearni sistem jednačina može se svesti na linearni. Da biste to učinili, slijedi (kao u prethodnom zadatku) u obje jednačine, na jednoj strani znaka jednakosti, spojite pojmove koji se odnose na prvu podlošku, a na drugoj strani za drugu i razdvojite `(v_(1x ) != v_(1x )^")` dobijene relacije. Ovo vodi do linearne jednadžbe

`v_(1x) + v_(1x)^" = v_(2x) + v_(2x)^"`.

Rješavajući sistem posljednje dvije jednačine, nalazimo

`v_(1x)^" = ((m_1 - m_2) v_(1x) + 2m_2 v_(2x))/(m_1 + m_2)`,

`v_(2x)^" = (2m_1 v_(1x) + (m_2 - m_1) v_(2x))/(m_1 + m_2)`.

Dobijene relacije za `v_(1x)^"`, `v_(1y)^"` i `v_(2x)^"`, `v_(2y)^"` rješavaju problem projekcija i brzina pakova nakon sudara

`v_1^" = sqrt((v_(1x)^")^2 + (v_(1y)^")^2)`, `v_2^" = sqrt((v_(2x)^")^2 + ( v_(2y)^")^2)`,

kao i o uglovima `alpha_1` i `alpha_2` koje formiraju vektori brzine `vec(v_1^")` i `vec(v_2^"` sa pozitivnim smjerom ose `Ox`:

`bbb"tg" alpha_1 = (v_(1y)^")/(v_(1x)^")`, `bbb"tg" alpha_2 = (v_(2y)^")/(v_(2x)^") `.

Ugrađeno opšti pogled Rješavanje problema elastičnih centralnih i necentralnih sudara otvara put analizi niza problema za koje razmatrani model odgovara prirodi interakcije tijela (čestica).

Elastični i neelastični udar dvije jednolike lopte 1. Uvod Sudari pokretnih tijela svojstveni su svim nivoima Univerzuma - od mikroskopskih do kosmičkih, stoga su fenomeni udara vrlo raznoliki. U dinamici se proučava uticaj sudara na kretanje mehaničkih sistema. Ovaj problem je privukao pažnju mnogih poznatih naučnika, uključujući H. Huygensa, I. Newtona, J. d'Alemberta, S. Punchona, G. Darbouxa, E. J. Routha, A.M. Lyapunova, N.E. Žukovski, S.P. Timošenko i mnogi drugi. Specifičnost štrajkova je njihov intenzitet i prolaznost. Ovo svojstvo može biti i korisno, kao kod zabijanja gomila, rudarenja rude ili igranja loptom, i opasno, kao u saobraćajnim nesrećama. Stoga je problem udara važan ne samo za teoretičare, već i za dizajnere, automobiliste, sportiste itd. 2. Pristupi u teoriji udara Sa fizičke tačke gledišta, udarne sile su odgovor na deformacije koje se javljaju u blizini kontaktne površine i šire se u valovima u tim tijelima. Matematički modeli odražavaju ovaj proces u većoj ili manjoj mjeri. U klasičnoj teoriji udara deformacije se ne uzimaju u obzir i problem se svodi na određivanje integralnih karakteristika udarnih sila – njihovih impulsa. Ova teorija se zasniva na zakonima mehanike i nekim dodatnim hipotezama. Razmotrimo, na primjer, najjednostavniji problem direktnog udara dvije kugle s masama m 1 i m2 .

	v 1 - v 2 -

Na slici, kuglice mase m 1 i m2 . prije sudara brzina v 1 - iv 2 - potrebno je pronaći njihove brzine nakon udara. Zakon održanja impulsa izražava se formulom: m 1 v 1i + m 2 v 2i = m 1 v 1 + m 2 v 2 gdje v 1i i v 2i; v 1 i v 2 odgovaraju brzinama prije i nakon udara. Ova jednadžba nije dovoljna da odredi dvije nepoznate v 1 iv 2 . Izgraditi jedina odluka, može se prihvatiti jedna od sljedećih hipoteza: ukupna kinetička energija je očuvana pri udaru (apsolutno elastični udar), lopte se nakon udarca ne odvajaju, tj. v 1 = v 2 (apsolutno neelastičan udar). Može se izabrati opštija Newtonova pretpostavka, prema kojoj v 2 - v 1 = e ( v 1i - v 2i ) Omjer oporavka e , kako je Newton eksperimentalno utvrdio, ovisi o materijalu kuglica i kreće se od nule do jedan. teorija talasa udar, uzdižući se do B. Saint-Venant-a, najpotpunije opisuje naponsko stanje sudarajućih tijela. Zasnovan je na prilično složenim jednačinama matematičke fizike, koje dopuštaju tačno rješenje samo u izuzetnim slučajevima. U opštem slučaju, upotreba talasne teorije je necelishodna, a posebno se ne može koristiti za rešavanje razmatranog problema udara loptica. Kompromis između ova dva ekstremna pristupa su modeli koji djelimično uzimaju u obzir deformacije. Ideju o takvim metodama predložio je d'Alembert, koji je mentalno postavio malu oprugu (deformabilni element) na tačku dodira udarca. Sa matematičke tačke gledišta, problem uticaja se svodi na rešavanje običnog diferencijalne jednadžbe, što ne predstavlja suštinske poteškoće. U gornjem primjeru, idealna opruga ne rasipa energiju, tako da će udar biti savršeno elastičan. 3. Elastični sudar tijela Prilikom elastičnog sudara tijela, tijela podliježu elastičnoj deformaciji. U tom slučaju kinetička energija tijela koja se kreće se djelimično ili potpuno pretvara u potencijalnu energiju elastične deformacije i u unutrašnju energiju tijela. Interakciona tijela su zatvoreni sistem ako na njih ne djeluju sile drugih tijela. U zatvorenim sistemima ispunjeni su zakoni održanja energije i impulsa. Poznavajući kretanje tijela prije sudara i primjenom zakona održanja, moguće je odrediti kretanje tijela nakon sudara. Ali u isto vrijeme, nećemo saznati ništa o tome kako dolazi do samog sudara. Za rješavanje niza problema o sudaru mikročestica, po pravilu, dovoljno je znati njihovo kretanje nakon interakcije. "Model" za probleme ove vrste je problem sudara loptica. Ako se kuglice kotrljaju po glatkoj horizontalnoj površini i ako se sila trenja kotrljanja može zanemariti, onda se sistem od dvije lopte može smatrati zatvorenim. Postoje dvije ograničavajuće vrste udara: apsolutno neelastičan i apsolutno elastičan. Sudar (sudar) je kratkotrajna interakcija u kojoj se tijela direktno dodiruju. Analiza pojava koje se dešavaju pri udaru elastičnih čvrstih tijela je prilično komplikovana, stoga ćemo razmotriti najjednostavniji slučaj - centralni udar dvije homogene kugle. Sudar se naziva centralnim ako su vektori brzina kuglica prije udara usmjereni duž prave linije koja prolazi kroz njihova središta. Apsolutno elastični i neelastični sudari su idealni slučajevi. U praksi se mogu realizovati samo uz određeni stepen aproksimacije. U proizvoljnom slučaju sudara loptica vrijede zakoni održanja količine gibanja i energije: Apsolutno elastičan je takav udar, nakon kojeg u interakcijskim tijelima ne ostaju deformacije i ukupna kinetička energija koju su tijela imala prije udara je jednaka na kinetičku energiju tijela nakon udara. Da bi udar bio apsolutno elastičan, tijela u interakciji moraju imati određena svojstva. Naime, sile koje nastaju prilikom udara treba da zavise od veličine deformacije, a ne od njene brzine. Nekretnine najbliže njima su dobre sortečelik, slonovača. Do sudara takvih tijela dolazi na sljedeći način. Pri udaru dolazi do deformacija sudarajućih tijela, a time i sila koje daju ubrzanja oba tijela u suprotnim smjerovima. U nekom trenutku, brzine kuglica postaju jednake, deformacije dostižu svoju maksimalnu vrijednost, sile nastavljaju djelovati, mijenjajući brzine u istim smjerovima kao i prije. Zbog toga će se kuglice "udaljavati" jedna od druge, a deformacije će se smanjivati ​​dok potpuno ne nestanu. Do ovog trenutka, elastične sile koje nastaju u tijelima obavit će isti posao koji je utrošen na deformaciju. Kao rezultat toga, sva kinetička energija koju su tijela imala prije udara ponovo će se pretvoriti u kinetičku energiju tijela nakon udara. Da biste odredili brzinu tijela nakon elastične interakcije, razmotrite udar dvije lopte (materijalne tačke) koje čine zatvoreni sistem. 3.1. Centralno elastični sudar tijela Postoje dva sferna objekta (lopte) sa masama m 1 i m 2. Pretpostavimo da se ove kuglice kreću bez rotacije duž jedne ose i doživljavaju centralni elastični udar. U ovom slučaju, zakon održanja impulsa biće zapisan kao: m 1 v 1i + m 2 v 2i = m 1 v 1 + m 2 v 2 gdje v 1i i v 2i su početne brzine svakog objekta, i v 1 i v 2 - njihove konačne brzine. Zakon održanja energije piše se kao: m 1 v 1i 2 / 2+ m 2 v 2i 2 / 2 = m 1 v 1 2 / 2 + m 2 v 2 2 / 2 Vektori brzina kuglica nakon elastičnog udara ležat će na liniji centara kuglica, jer će sile interakcije pri udaru uslijed simetrije biti usmjerene duž iste prave linije. Zakon održanja količine kretanja može se transformirati na sljedeći način: m 1 (v 1i- v 1) = m 2 (v 2 - v 2i) Transformišemo i izraz za zakon održanja energije m 1 (v 1i 2 - v 1 2) = m 2 (v 2 2 - v 2i 2) Ako razlika između početne i konačne brzine nije jednaka nulu (odnosno, sudar se stvarno dogodio), možemo podijeliti drugu od posljednje dvije jednačine prvom, što daje: v 1i + v 1 = v 2 + v 2i ili v 1i- v 2i = v 2 - v 1 Drugim riječima, u jednodimenzionalnom slučaju elastičnih sudara, relativna brzina objekata nakon sudara jednaka je relativnoj brzini kretanja prije sudara. Da bismo dobili konačne brzine objekata u smislu njihovih početnih brzina i masa, moramo izraziti v 2 iz posljednje jednadžbe i zamijeniti je u jednačinu za zakon održanja količine kretanja. Konačno dobijamo: v 1 = v 1i( m 1 - m 2) / (m 1 + m 2) + v 2i (2 m 2) / (m 1 + m 2) Na isti način nalazimo izraz za v 2 v 2 = v 1i (2 m 1) / (m 1 + m 2) + v 2i ( m 2 - m 1) / (m 2 + m 1) Zatim pretpostavimo da se objekti iste mase sudare, tj. m 1 = m 2 = m. U ovom slučaju: v 1 = v 1i( m - m) / (m + m) + v 2i (2 m) / (m + m) v 2 = v 1i (2 m) / (m + m) + v 2i ( m - m) / (m + m) Konačno, dobijamo v 1 = v 2i and v 2 = v 1i To znači da će u slučaju centralnog elastičnog sudara objekata jednakih masa oni jednostavno zamijeniti brzine. Ako je jedan od objekata mirovao prije sudara, onda će se nakon sudara zaustaviti, a drugi objekt će početi da se kreće. U ovom slučaju, brzina drugog objekta bit će jednaka brzini prvog objekta prije sudara. U opštem slučaju centralnog i apsolutno elastičnog sudara objekata različitih masa, od kojih je jedan mirovao pre sudara ( v 2i =0), možemo pisati sledeće izraze za brzine nakon udara: v 1 = v 1i( m 1 - m 2) / (m 1 + m 2) v 2 = v 1i (2 m 1) / (m 1 + m 2) Ako je masa upadne lopte m 1 više od mase lopte u mirovanju m 2, dakle v 1 i v 2 će biti pozitivna i obje lopte nakon sudara će se kretati u istom smjeru, koji se podudara sa smjerom početnog kretanja nadolazeće lopte. Ako je masa upadne lopte m 1 je manje od mase loptice u mirovanju m 2, dakle v 1 će biti negativan i v 2 - pozitivno, a kugle će se nakon sudara raspršiti u suprotnim smjerovima. Istovremeno, pošto 2 m 1 > m 1 - m 2 , tada će se mala lopta reflektirati većom brzinom. Ovo je slika udara bilo koja dva tijela, ako je početna brzina usmjerena duž linije koja spaja centre mase ovih tijela i ako su sile interakcije usmjerene duž iste linije centara. U suprotnom, uticaj će biti složena pojava. Sa udarom loptica izvan centra, obrazac udara će biti drugačiji. 3.2. Necentralni elastični sudar tijela Ovdje se pri udaru dešava i približavanje centara loptica jedno drugom zbog njihove deformacije i klizanje površine jedne lopte preko površine druge. Očigledno je da će zbog klizanja površina nastati sile trenja koje će, zajedno sa elastičnim silama interakcije, odrediti promjenu brzine kuglica nakon udara. Osim toga, sile trenja će uzrokovati da se kuglice rotiraju oko svojih centara mase. Da bismo predstavili udarni mehanizam, dekomponirajmo vektore brzina obje lopte prije udara u smjeru linije centara kuglica iu smjeru okomitom na ovu pravu. V grad V 1i F" T V 1 p F" y F y V 2i v 2 n F T V 2 c Kao rezultat "klizanja" površine kuglica, nastat će sile trenja F"T i F T, koji zajedno sa elastičnim silama interakcije F"y i Fy odrediti promjenu brzine loptica nakon udara. Osim toga, sile trenja će uzrokovati rotaciju kuglica oko centra. Samo kada sile trenja F T vrlo male u odnosu na elastične sile Fy, tj. F T<< F y , možemo zanemariti efekat sila trenja. U ovom slučaju, problem necentralnog sudara loptica je riješen prilično jednostavno. Doista, povezivanje centara mase kuglica koje se sudaraju ravnom linijom i razlaganje brzine svake kugle na normalnu komponentu usmjerenu duž linije centara i tangencijalnu komponentu okomitu na nju. Kako, prema našoj pretpostavci, ne postoje sile trenja, pri sudaru ne nastaju nikakve tangencijalne sile i, posljedično, tangencijalne brzine kuglica se neće mijenjati. Komponente normalne brzine nakon udara mogu se odrediti na osnovu zakona održanja količine kretanja i zakona održanja energije na isti način kao i u slučaju centralnog udara. Napišimo jednačine: m 1 v 1 c + m 2 v 2 c \u003d m 1 c v "1 c + m 2 v" 2 c m 1 (v 2 1 p + v 2 1 c) + m 2 (v 2 2 p + v 2 2 c) \u003d m 1 (v "2 1 p + v 2 1 c) + m 2 (v" 2 2 p + v 2 2 c ovdje su nepoznate samo dvije veličine: v" grad i v" 2 c. Opšte pravilnosti necentralnog udara loptica u ovom slučaju mogu se pronaći na sljedeći način. Pretpostavimo da prije udarca lopta 2 miruje, a 1 se kreće. Sila interakcije u trenutku udara prolazi kroz centre kuglica (bez trenja), a njen smjer ovisi o udaljenosti "nišanja" δ, jednaka udaljenosti centra loptice u mirovanju od linije leta centra druge lopte (prije udara). Ravan crteža poklapa se sa ravninom koja prolazi kroz centre kuglica i vektorom brzine lopte 1. F 2r2 δ r1 R 1 F" Do uticaja će doći ako δ < r1 + r2, gdje r1 i r2 su poluprečniki kuglica. Ugao θ zavisi od δ i r1 + r2. Komponenta impulsa lopte 1 (udaranje), normalna na F( interakcijska sila ) , ostaje nepromijenjen. Komponente količine kretanja kuglica u smjeru sile F promijeniti u skladu sa zakonima centralnog udara. Prema zakonu konstantnog impulsa: P = P 1 + P 2 gdje P- količinu kretanja lopte 1 prije udara, P1 i P2 su impulsi loptica 1 i 2 nakon udara, respektivno. P 2 P 1 θ P Zakon održanja energije može se zapisati kao: P 2 /m 1 \u003d P 2 1 /m 1 + P 2 2 /m 2 Jer P = mv i mv 2 \u003d P 2 / m za bilo koje telo. Vector P2 pravi ugao θ sa vektorom P, lopta u mirovanju će odskočiti pod uglom θ na početnu brzinu prve lopte, a zatim iz trougla vektora slijedi: P 2 1 = P 2 2 + P 2 - 2 P P 2 cos θ Uzimajući u obzir postojanost energije, isključujemo P1 i dobijamo P 2 \u003d 2 m 2 P cos θ / (m 1 + m 2) = β P cos θ β = 2 m 2 / (m 1 + m 2) Iz ovoga se može vidjeti da je opći odnos između R 2 i R zavisi od ugla θ i omjer mase m 1 /m 2 . Treba razlikovati dva slučaja: m1 > m2 i m 1< m 2 . U prvom slučaju β < 1 Teška lopta pogađa laku. Kraj vektora R 2 opisuje krug sa prečnikom βR. Obje lopte nakon udarca lete u smjeru početnog kretanja prve lopte. Vrijednost ugla θ mijenja se od 0 do π/2. Ugao otklona prve lopte može varirati od 0 do nešto φ max.. Jedna vrijednost φ podudaraju dvije vrijednosti θ. β < 1 Р 2 Р 1 A V R φ βR A B βP R 2 A B φ Ugao φ mijenja se od 0 do π/2. Sa centralnim udarom, lopta 1 se zaustavlja, a lopta 2 se kreće dalje istom brzinom (tačka B). Ugao balona θ + φ uvek jednaka π/2. Ugao θ lako povezati sa nišanskom daljinom δ i pokaži to (r 1 + r 2)sin θ = δ Znajući δ , prečnike kuglica i njihove mase, nalazimo θ i β , prema R definisati R 2 i R 1, koji zauzvrat određuju brzinu i smjer loptica nakon udara.

4. Neelastični sudar tijela

Apsolutno neelastičan udar je takav udarac, nakon kojeg su brzine oba sudarajuća tijela iste. Da bi to bilo moguće, sudarajuća tijela moraju imati takva svojstva da sile koje proizlaze iz njihove deformacije ne ovise o veličini deformacije, već o brzini promjene deformacije. Takva svojstva su svojstvena, na primjer, mekoj glini, plastelinu. U neelastičnom sudaru događa se sljedeće. U početnom trenutku udara, brzina deformacije je visoka (kuglice su komprimirane), stoga nastaju značajne sile koje daju ubrzanja objema kuglicama, usmjerena u suprotnim smjerovima. Kako se udar razvija, stope deformacije kuglica se smanjuju, a same deformacije se povećavaju sve dok se brzine kuglica ne izjednače. U ovom trenutku deformacije kuglica će prestati da se menjaju, sile će nestati, a obe lopte će se kretati istom brzinom. U apsolutno neelastičnom udaru zadovoljeni su zakoni održanja impulsa i ukupne energije. Mehanička energija tijela prije udara je veća mehanička energija nakon udara, jer djelomično (ili potpuno) prelazi u unutrašnju energiju tijela i troši se na rad na deformaciji tijela. Da biste odredili brzinu tijela nakon interakcije, razmotrite udar dvije lopte (materijalne tačke) koje čine zatvoreni sistem. Mase loptica m 1 i m2, brzina prije udara V 1 i i V 2 i. Prema zakonu održanja, ukupni impuls loptica prije udara mora biti isti kao i nakon udara: m 1 V 1i + m 2 V 2i \u003d (m 1 + m 2) U gdje je U brzina nakon udara, ista za obje lopte. Iz jednačine slijedi da: U \u003d (m 1 V 1i + m 2 V 2i) / (m 1 + m 2) Zakon očuvanja energije za neelastični udar kugli koje se razmatraju ima sljedeći oblik: m 1 V 1 i 2 / 2 + m 2 V 2i 2 / 2 = (m 1 + m 2) U 2 + W gdje je W promjena unutrašnje energije sistema. Kinetička energija tijela prije udara ima sljedeću vrijednost: W 1 \u003d m 1 V 1 i 2 / 2 + m 2 V 2i 2 / 2 I kinetička energija nakon udara: W 2 \u003d (m 1 + m 2) U 2 / 2 = (m 1 V 1i + m 2 V 2i) 2 / 2 (m 1 + m 2) Gubitak mehaničke energije, odnosno dijela energije koji je pretvoren u toplinski oblik je: W \u003d W 1 - W 2 \u003d m 1 m 2 (V 1i - V 2i) 2 / 2 (m 1 + m 2) Vrijednost V 1i – V 2i predstavlja relativnu brzinu tijela prije udara. Dakle, energija pretvorena u toplotu zavisi od odnosa masa tela koja se sudaraju m 1 m 2 /(m 1 + m 2) i njihovu relativnu brzinu prije udara. Energija gubitka može se smatrati kinetičkom energijom nekih efektivna masa: m 0 \u003d m 1 m 2 / (m 1 + m 2) kreće se relativnom brzinom V " i \u003d V 1i - V 2i. Za specifične proračune brzine, potrebno je dizajnirati omjer impulsa prema odabranim smjerovima. Ako su prije udara brzine loptica usmjerene duž prave linije koja prolazi kroz njihova središta, udar se naziva centralnim. Brzina loptica nakon takvog udara bit će usmjerena duž iste prave linije. Stoga se jednačina održanja impulsa može smatrati skalarnom. Ali brzine se u ovom slučaju moraju smatrati podudarnim u znaku kada su usmjerene u jednom smjeru i suprotnom u znaku kada su usmjerene u suprotnim smjerovima. Razmotrimo neke posebne slučajeve. 1. Kuglice se kreću u istom smjeru. Udar je moguć ako je brzina V 1 i i V 2i drugačije. Na primjer, V2i > V1i, tj. druga lopta sustiže prvu. Nakon udarca, loptice će se kretati u istom smjeru brzinom većom od brzine prve i manjom od brzine druge. Ako su mase loptica iste, onda je U = (V 1i + V 2i) / 2 2. Kuglice se kreću jedna prema drugoj. Nakon udara, loptice će se kretati zajedno u smjeru u kojem se kretala lopta sa velikim zamahom. Ako su impulsi obje lopte jednaki po veličini, tada će se obje lopte zaustaviti nakon udara. 3. U slučaju udara izvan centra (slika 3.6.2a), brzine V 1i i V 2i mogu se razložiti na komponente V 1X i V 2X u smjeru linije koja povezuje centre kuglica (X-osa) i komponenti V 1Y i V2Y u okomitom smjeru (y-osa). Za komponente V 1X , V 2X i V 1Y ,V 2Y zapišite zakon održanja količine gibanja u istom obliku kao u slučaju centralnog udara i odredite komponentu rezultirajuće brzine. Razmotrimo detaljnije neelastični udar. U neelastičnom udaru, dio kinetičke energije upadne lopte gubi se oslobađanjem topline. U graničnom slučaju apsolutno neelastičnog udara, upadno tijelo se drži zajedno s tijelom u mirovanju, kinetička energija njihovog relativnog kretanja nestaje i oni se nastavljaju kretati kao jedno tijelo. U većini praktičnih slučajeva radi se o djelomično elastičnom udaru, kada se u tijelu nakon sudara pobuđuju deformacijske oscilacije, koje s vremenom opadaju. Pobuđivanje takvih oscilacija može se modelirati korištenjem dvije identične kuglice spojene oprugom. Pretpostavimo da se savršeno elastična lopta sudari sa opružnim oscilatorom. Mase loptica su iste i jednake m. Pošto opruga još ne djeluje u trenutku udarca, leteća lopta se zaustavlja, a lijeva lopta oscilatora se pokreće brzinom leteće lopte. v. U ovom slučaju, centar mase oscilatora kreće se brzinom v/2. Vremenom će oscilacije oscilatora nestati i on će nastaviti da se kreće naprijed brzinom v/2, a ukupna energija cijelog sistema bit će samo polovina energije upadne lopte. Druga polovina će se osloboditi kao toplota u oscilatoru. Udar običnih neelastičnih tijela odgovara srednjem slučaju između savršeno elastičnih i potpuno neelastičnih udara. Analogno je udaru sličnom udaru dvije kugle kroz neelastičnu oprugu, koja, stisnuta na određenu vrijednost tokom prve polovine vremena udara, neće poprimiti svoje prvobitne dimenzije nakon udara; ili će sila odbijanja tokom kompresije biti veća nego tokom druge polovine vremena udara kada se opruga širi. Dio potencijalne energije kompresije opruge će se pretvoriti u toplinu i neće se pretvoriti u kinetičku energiju kretanja. Stoga se u ovom slučaju ne može primijeniti zakon održanja mehaničke energije. Uslov jednakosti brzina nakon udara također neće vrijediti, kao što je bio slučaj sa potpuno neelastičnim udarom, jer se nakon udara oba tijela kreću različitim brzinama. Neelastični udar se može okarakterizirati dijelom energije deformacije koja se pretvara u toplinu tokom udara. Ali čak je i Newton otkrio da su prilikom neelastičnog udara loptica napravljenih od određenog materijala relativne brzine prije i poslije udara u konstantnom omjeru, a takav udar karakterizira faktor oporavka relativne brzine nakon udara: e \u003d | V 2 - V 1 | / |V 2i – V 1i | gdje V 2i – V 1i je relativna brzina prije udara, i V 2 - V 1- nakon udara. Iskustvo pokazuje da se sa određenim stepenom tačnosti može izračunati vrednost e konstantan i zavisan samo od materijala kuglica koje se sudaraju. Sa savršeno elastičnim udarom, relativna brzina ostaje ista po veličini, ali mijenja svoj predznak: V 1i - V 2i \u003d - (V 1 - V 2) Koeficijent oporavka je uvijek manji od jedinice, jer je kod elastičnog udara jednak jedan, a kod potpuno neelastičnog udara jednak je nuli, jer u ovom slučaju V 2 - V 1 \u003d 0 Poznavanje koeficijenta e, možemo izračunati brzinu loptica nakon udara i gubitka energije. Korištene knjige: 1. D.V. Sivukhin, " Opšti kurs fizike. Mehanika", Nauka, 1979 2. O.D. Shebalin, " Fizičke osnove mehanika i akustika", Viša škola, 1981. 3. S.P. Strelkov, "Mehanika", Nauka, 1975. 4. K. Schwartz, T. Goldfarb, "Traganje za obrascima u fizičkom svijetu", prevod s engleskog, Moskva, Mir, 1977. 5. Laboratorijske studije iz fizike, pod uredništvom LL Goldina, Moskva, Nauka, 1983. 6. AI Ivanov, „Regularnosti uticaja u mehanički sistemi“, Priroda, 1999, br. 10

Bakanina L. Zakon održanja količine gibanja u sudarima // Kvant. - 1977. - br. 3. - S. 46-51.

Po posebnom dogovoru sa uredništvom i uredništvom časopisa "Kvant"

Za zatvorene sisteme, odnosno one koji obuhvataju sva tijela u interakciji, zadovoljen je zakon održanja količine gibanja (momenta), tako da ni na jedno tijelo sistema ne djeluju vanjske sile. Međutim, prilikom rješavanja mnogih fizički zadaci ispostavilo se da zamah može ostati konstantan i za nezatvorene sisteme. Istina, u ovom slučaju impuls je samo približno očuvan. Hajde da pokušamo da shvatimo šta se ovde dešava.

Promjena momenta gibanja otvorenog sistema jednaka je ukupnom impulsu vanjskih sila. Označiti sa prosječnom vrijednošću rezultirajuće vanjske sile koja djeluje na sistem tokom vremenskog intervala Δ t. Onda

Ako apsolutna vrijednost ove sile nije prevelika i vrijeme tokom kojeg sila djeluje je malo, tada će i proizvod biti mali. U tom slučaju postaje neophodno procijeniti s kojom se tačnošću impuls sistema može smatrati nepromijenjenim.

Osim toga, ne treba zaboraviti da je impuls vektor, pa se stoga može govoriti o očuvanju projekcije ovog vektora u bilo kojem smjeru. Zaista, ako sistem nije zatvoren, ali su vanjske sile takve da je zbir projekcija svih sila na određeni pravac jednak nuli, tada projekcija impulsa sistema na ovaj pravac ostaje konstantna. Ne zatvoreni sistem u ovom pravcu je sličan zatvorenom.

Kratkotrajne interakcije nastaju, na primjer, tokom eksplozija, hitaca, sudara. Razgovaraćemo o ovoj vrsti problema. Pokušat ćemo u svakom konkretnom slučaju otkriti da li je zakon održanja impulsa zadovoljen ili ne i od čega zavisi.

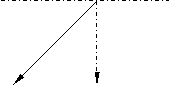
Zadatak 1. Iz topa koji klizi bez trenja kosoj ravni i već prošao put l, puca se u horizontalnom smjeru (slika 1). Pri kojoj brzini projektila će se pištolj zaustaviti nakon ispaljivanja? Težina projektila m mnogo manje od mase pištolja M, ugao nagiba ravni α.

Prije pucanja, pištolj (zajedno sa projektilom), prošao put l, ima zamah usmjeren duž nagnute ravni. Modul ovog momenta se može naći iz zakona održanja energije:

Neposredno nakon pucnja, puška je stala, a projektil je odletio u horizontalnom smjeru. Dakle, uprkos kratkom trajanju interakcije između pištolja i projektila, impuls ovog sistema nije očuvan. Zašto?

Prilikom pucanja, sila pritiska pištolja na nagnutu ravan naglo raste, što znači da se povećava i sila reakcije sa strane ravnine, tako da se impuls ove sile ispostavlja dovoljno velikim. Zatim mijenja ukupni zamah pištolja i projektila.

Međutim, u pravcu duž nagnute ravni, projekcija sile reakcije jednaka je nuli, a projekcija gravitacionog impulsa za kratko vreme udarca Δ t mali i ne povećava se pri ispaljivanju. Stoga se, s određenim stepenom tačnosti, može pretpostaviti da je u smjeru duž nagnute ravnine očuvana projekcija količine gibanja sistema top-projektil. Otuda i projekcija totalni impuls pištolj i projektil prije metka jednaki su projekciji projektila nakon metka (puška miruje):

Otuda i modul brzine projektila odmah nakon metka

Prilikom rješavanja ovog problema pretpostavili smo da se u smjeru duž nagnute ravni sistem top-projektil ponaša kao zatvoreni sistem. Međutim, ne možemo proceniti stepen tačnosti sa kojim je to tačno, jer je sistem tela u interakciji složen i ne postoje potrebni podaci za takvu procenu.

Hajde da sada analiziramo dva problema sa više jednostavna interakcija gdje se takva procjena može napraviti.

Zadatak 2. U drvenu kuglu mase M= 1 kg pada brzinom V 0 = 1 m/s, pucajte odozdo iz pištolja i probijte ga. Koju brzinu će lopta imati odmah nakon toga? Brzina metka υ 0 = 300 m/s, nakon napuštanja lopte υ = 100 m/s, masa metka m= 10 g.

Vrijeme interakcije, gdje d- prečnik lopte, a υ cf - prosječna brzina meci unutar lopte. Promjer kuglice može se procijeniti znajući da je gustina stabla ρ približno jednaka gustoći vode ρ u \u003d 10 3 kg / m 3:

Dakle Δ t≈ 5 10–4 s. Zamah gravitacije sistema za to vrijeme (a time i promjena ukupnog impulsa lopte i metka)

str = (M+m)· gΔ t≈ 5 10 -3 N s.

Količina kretanja sistema prije interakcije

str 0 = mυ 0 – MV 0 = 2 N s.

Zatim odnos

i, shodno tome, sa tačnošću od 0,2%, možemo pretpostaviti da se impuls sistema ne menja tokom interakcije.

Zapišimo zakon održanja za projekciju impulsa na vertikalno uzlaznu osu:

mυ 0 – MV 0 = mυ+ MV y.

Otuda projekcija brzine lopte nakon interakcije

to jest, lopta će se početi kretati prema gore brzinom od 1 m / s.

Zadatak 3. Lopta je bačena vertikalno naviše brzinom υ 0 = 1 m/s. Kada dostigne gornju tačku svog uspona, ista lopta se baca početnom brzinom od 2υ 0 . Odredite brzinu kuglica nakon sudara, ako se sudar može smatrati savršeno elastičnim.

Slično prethodnom problemu, prvo procjenjujemo stepen tačnosti sa kojim se sistem od dvije lopte tokom sudara može smatrati zatvorenim. Da bismo to uradili, pronalazimo zamah sistema pre udarca, zamah gravitacije tokom udara i uporedimo ih jedno sa drugim.

Pustite da se loptice sudare na visini h kroz vreme t nakon početka kretanja druge lopte (slika 2). Onda za prvu loptu

gdje je maksimalna visina dizanja. Za drugu loptu

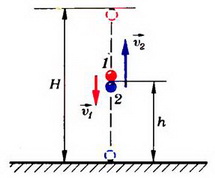
Dakle, i brzine obje lopte neposredno prije sudara su jednake

pri čemu se prva lopta kreće dolje, a druga - gore.

Dakle, količina kretanja sistema prije interakcije

str 0 = mυ 2 - mυ 1 \u003d 1.5 mυ 0 .

Pokušajmo sada procijeniti vrijeme interakcije i zamah gravitacije za to vrijeme. Da bismo to učinili, moramo zamisliti kako se odvija proces sudara. Razmotrimo prvo sudar dvaju identičnih štapova na krajevima. Pri udaru na kraju dolazi do elastične deformacije koja se širi duž štapa, odnosno u štapu nastaje zvučni val. Došavši do suprotnog kraja štapa, val se reflektira i vraća. Možemo reći da se proces sudara ovdje završava, a vrijeme interakcije štapova je jednako vremenu prolaska zvučni talas duž štapa i nazad. U stvari, slika interakcije je mnogo komplikovanija, a u slučaju kuglica, gde rezultujući elastični talas nije ravan, još više. Međutim, da bismo ovdje procijenili, također pretpostavljamo da je, do reda veličine, vrijeme udara jednako vremenu širenja zvučnog talasa unutar lopte: . Brzina zvuka unutra čvrste materije reda veličine nekoliko kilometara u sekundi. Ako je promjer kuglice oko centimetar, tada je Δ t~ 10–5 s, a apsolutna vrijednost zamaha gravitacije je mnogo puta manja od impulsa kuglica prije interakcije:

Dakle, i u ovom slučaju možemo smatrati da je sistem sudarajućih loptica zatvoren. (Naravno, daljnje kretanje kuglica bitno ovisi o sili gravitacije.) Kako je udar loptica apsolutno elastičan, koristit ćemo se zakonima održanja mehaničke energije i projekcijom količine gibanja na os usmjerenu okomito prema gore. :

Zamjenjujući ovdje odgovarajuće vrijednosti za υ 1 i υ 2:

U elastičnom udaru, loptice jednake mase razmjenjuju brzine.

Međutim, ne treba misliti da se u sudarima uvijek može zanemariti djelovanje vanjskih sila i sistem smatrati zatvorenim. Na primjer, razmotrite sljedeći problem.

Zadatak 4. Vreća brašna klizi bez početne brzine sa visine H na glatkoj dasci nagnutoj pod uglom α = 60° prema horizontu. Nakon spuštanja, torba pada na horizontalni hrapavi pod. Koeficijent trenja vreće na podu μ = 0,7. Gdje će torba stati?

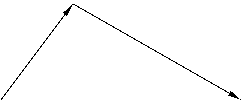
Nakon spuštanja sa daske, vreća ima brzinu usmjerenu duž daske (slika 3). Njegova apsolutna vrijednost se može naći iz zakona održanja mehaničke energije, budući da je ploča glatka i nema gubitka energije:

U horizontalnom smjeru, sila trenja klizanja djeluje na vreću, čiji je modul . Impuls ove sile pri udaru je jednak

odnosno ne zavisi od kojeg zakona se menja sila reakcije oslonca (a time i sila pritiska vreće na pod), niti od vremena udara. Nađimo promjenu horizontalne projekcije momenta torbe. Usmjerimo osu X horizontalno udesno, zatim, prema drugom Newtonovom zakonu,

Otuda projekcija brzine kojom će se vreća početi kretati po podu,

Šta znači znak minus? Formalno, znak minus označava da bi se vreća nakon udarca trebala pomaknuti ulijevo, ili, drugim riječima, da je moment sile trenja bio veći od početne horizontalne projekcije količine gibanja vreće. To znači da u nekom trenutku u procesu sudara, projekcija brzine vreće na os X okrenuo na nulu. Od ovog trenutka naša odluka postaje pogrešna. Zaista, modul sile trenja je jednak μ N cp samo prilikom klizanja, dok u mirovanju sila trenja može poprimiti bilo koju vrijednost od 0 do μ N cp u zavisnosti od toga koje sile (osim sile trenja) deluju na telo. U našem slučaju nijedna druga sila nema projekcije u horizontalnom smjeru, dakle, u trenutku kada horizontalna projekcija brzine vreće nestane, nestaje i sila trenja. Tako se torba uopće neće kretati po podu.

Na kraju, razgovarajmo o još jednom prilično poznatom problemu sudara tijela. Prilikom rješavanja ovog problema obično se koriste prilično grube aproksimacije, bez navođenja na bilo koji način da je to aproksimacija, ni pod kojim okolnostima se ne može koristiti.

Zadatak 5. Na masnom klinu koji stoji na glatkoj horizontalnoj površini M sa visokog h padajuća lopta mase m i odbija se u horizontalnom smjeru (slika 4). Pronađite horizontalnu projekciju brzine klina nakon udara. Zanemarite trenje i pretpostavite da je udar savršeno elastičan.

Za razliku od svih prethodnih problema, ovdje je potrebno razmotriti sudar ne dva, već tri tijela - lopte, klina i horizontalne ravni. U opštem slučaju, bez dodatnih pretpostavki o mehanizmu uticaja, ovaj problem se ne može rešiti. U najčešćem rješenju ovog problema implicitno je (bez ikakvih rezervi) da se sudari lopte s klinom i klina s horizontalnom ravninom događaju istovremeno, a klin nakon sudara ima samo horizontalnu projekciju brzine. Tada se pišu jednadžbe zakona održanja mehaničke energije i impulsa:

gdje Vx i υ x- odnosno projekcija brzina klina i lopte na horizontalnu osu usmjerenu udesno. Odavde

Međutim, kod takvog rješenja uopće nije jasno gdje je otišla vertikalna projekcija momenta lopte. Uostalom, ako je sudar apsolutno elastičan, vertikalna projekcija impulsa sistema ne nestaje, već samo mijenja predznak! Lopta se nakon udara odbija u horizontalnom smjeru, ravnina je općenito nepomična. To znači da klin mora odskočiti nakon udara. A energija povezana s ovim kretanjem nije uzeta u obzir u gornjem rješenju.

Fizička slika udara je konzistentnija s pretpostavkom da se u početku lopta sudari samo sa klinom, a zatim klin, koji je dobio određenu brzinu kao rezultat ovog sudara, stupa u interakciju s horizontalnom ravninom. Nakon prvog udara, vertikalna projekcija brzine klina

Prolazi kroz centar gravitacije prilikom udara O klin (sl. 5).

Osim toga, napominjemo da da bi lopta nakon sudara odskočila horizontalno, ugao klina α mora imati dobro definiranu vrijednost, ovisno o masama lopte i klina.

U zaključku nudimo nekoliko zadataka za samostalno rješavanje.

Vježbe

1. U centar kugle mase m 1 = 300 g koji leži na rubu stola pogođen je horizontalno letećim metkom mase m 2 = 10 g i probija ga. Lopta pada na pod u daljini s 1 = 6 m od stola, a metak je na udaljenosti s 2 = 15 m Visina stola H= 1 m. Odrediti početnu brzinu metka.

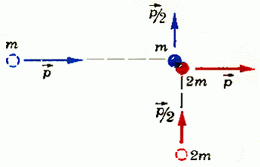
2. Dve čestice sa masama m i 2 m, imaju momente i , kreću se u međusobno okomitim smjerovima. Nakon sudara, čestice razmjenjuju zamah (slika 6). Odredite količinu toplote koja se oslobađa tokom udara.

3. Vreća brašna klizi bez početne brzine sa visine H\u003d 2 m duž daske nagnute pod uglom α = 45 ° prema horizontu. Nakon spuštanja, torba pada na vodoravnu površinu. Koeficijent trenja vreće o dasku i horizontalnu površinu je μ = 0,5. Koliko će se vreća zaustaviti od kraja ploče?

Odgovori

1.

3.

Zakon održanja energije omogućava rješavanje mehaničkih problema u onim slučajevima kada su, iz nekog razloga, nepoznati ljekoviti efekti na organizam. Zanimljiv primjer upravo takvog slučaja je sudar dva tijela. Ovaj primjer je posebno zanimljiv jer se u njegovoj analizi nemoguće baviti samo zakonom održanja energije. Također je potrebno uključiti zakon održanja količine gibanja (momenta).

U svakodnevnom životu i tehnologiji se ne mora često suočavati sa sudarima tijela, već u fizici atoma i atomske čestice sudari su veoma česti.

Radi jednostavnosti, prvo ćemo razmotriti sudar dviju kuglica s masama od kojih druga miruje, a prva se brzinom kreće prema drugoj. Pretpostavljamo da se kretanje odvija duž linije koja spaja središta obje lopte (sl. 205), tako da kada se lopte sudaraju, dolazi do sljedećeg koji se naziva centralni ili frontalni udar. Kolike su brzine obje lopte nakon sudara?

Prije sudara, kinetička energija druge lopte je nula, a prve. Zbir energija obe lopte je:

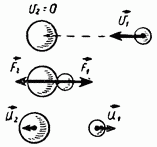
Nakon sudara, prva lopta će početi da se kreće određenom brzinom. Druga lopta, čija je brzina bila jednaka nuli, takođe će dobiti određenu brzinu. Dakle, nakon sudara, zbir kinetičkih energija dve lopte će postati jednak

Prema zakonu održanja energije, ovaj zbir mora biti jednak energiji loptica prije sudara:

Iz ove jedne jednačine, naravno, ne možemo pronaći dvije nepoznate brzine: Tu u pomoć dolazi drugi zakon održanja - zakon održanja količine kretanja. Prije sudara loptica, impuls prve lopte bio je jednak, a impuls druge nula. Ukupni impuls dvije lopte bio je jednak:

Nakon sudara, impulsi obje lopte su se promijenili i postali jednaki, a ukupni impuls je postao

Prema zakonu održanja impulsa, ukupni impuls se ne može promijeniti tokom sudara. Stoga moramo napisati:

Budući da je kretanje duž prave linije, umjesto vektorska jednadžba može se napisati algebarski (za projekcije brzina na koordinatnu osu usmjerenu duž brzine prve lopte prije udara):

Sada imamo dvije jednadžbe:

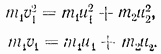
Takav sistem jednačina može se riješiti i za nepoznate brzine njih i loptica nakon sudara. Da bismo to učinili, prepisujemo ga na sljedeći način:

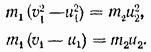
Ako prvu jednačinu podijelimo drugom, dobijamo:

Sada rješavamo ovu jednačinu zajedno sa drugom jednačinom

(uradi sam), nalazimo da će se prva lopta nakon udarca kretati brzinom

a drugi - brzinom

Ako obje lopte imaju istu masu, to znači da je prva lopta, sudarajući se sa drugom, prenijela svoju brzinu na nju, a sama se zaustavila (Sl. 206).

Dakle, koristeći zakone održanja energije i količine gibanja, moguće je, znajući brzine tijela prije sudara, odrediti njihove brzine nakon sudara.

A kakva je bila situacija prilikom samog sudara, u trenutku kada su centri lopti bili što bliže?

Očigledno je da su se u to vrijeme zajedno kretali određenom brzinom. Uz iste mase tijela, njihova ukupna masa je 2 tone. Prema zakonu održanja količine gibanja, za vrijeme zajedničkog kretanja obje lopte, njihov impuls mora biti jednak ukupnom momentu gibanja prije sudara:

Otuda to sledi

Dakle, brzina obje lopte za vrijeme njihovog zajedničkog kretanja jednaka je polovini

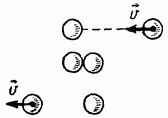
brzina jednog od njih prije sudara. Nađimo kinetičku energiju obje lopte za ovaj trenutak:

Prije sudara ukupna energija obje lopte su bile jednake

Shodno tome, u samom trenutku sudara loptica kinetička energija je prepolovljena. Gdje je otišla polovina kinetičke energije? Postoji li ovdje kršenje zakona održanja energije?

Energija je, naravno, ostala ista tokom zajedničkog kretanja loptica. Činjenica je da su se prilikom sudara obje lopte deformisale i stoga su imale potencijalnu energiju elastične interakcije. Tačna veličina ovoga potencijalna energija a kinetička energija loptica se smanjila.