Teorijski materijal

Veza Telo koje sprečava kretanje drugog tela pod dejstvom sile.

Komunikacijska reakcija- sila koja nastaje unutar same veze. Reakcija je uvijek suprotna smjeru u kojem veza ometa kretanje tijela. Sva tijela mogu biti slobodna i neslobodna. Slobodno tijelo nema veze. Svako neslobodno tijelo može se predstaviti kao slobodno ako se veze koje na njega djeluju zamijene reakcijama.

Vrste linkova:

a) Glatka površina ili ravan, odnosno površina bez trenja. Reakcija ove veze je uvijek usmjerena okomito na tačku kontakta. R - reakcija veze

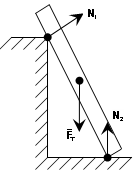b) glatka podrška Reakcije ove veze su usmjerene okomito na tačku kontakta. (Reakcija je sila unutar strukture). Njegova vrijednost ovisi o materijalu, veličini i vanjskoj sili.

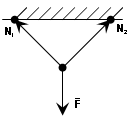u) Fleksibilna veza- veza koja radi samo u napetosti, koja se izvodi kablom, užetom, lancem. Reakcija fleksibilne veze usmjerena je duž same veze do tačke vezivanja, odnosno suprotno od smjera sile.

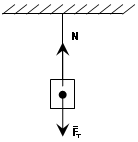
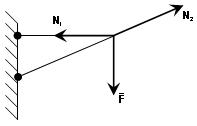G) Krute šipke. Izvodi se raznim gredama, I-gredama, kanalima. Veza radi i na napetost i na kompresiju. Ako je štap u napetosti, tada se reakcija usmjerava duž štapa do mjesta fiksiranja, ako je u kompresiji, tada je reakcija usmjerena izvan štapa.

e) artikulisana podrška. Nosači su pokretni i fiksni. Fiksni nosač ima dvije reakcije koje se nalaze okomito jedna na drugu. Pomični oslonac ima jednu reakciju, okomitu na površinu.

Pokretni nosač Fiksni nosač

Zadaci za obavljanje posla

1. Nacrtajte crteže svoje verzije.

2. Opišite crtež.

3. Odredite vrstu veze i zamijenite ih reakcijama.

Opcija 18

1.

2.

3.

Test pitanja:

1. Koja je razlika između ose i projekcije?

2. Koliko ste jednadžbi ravnoteže napravili prilikom rješavanja problema?

3. Metodologija rješavanja problema PSSS.

4. Definirajte ravan sistem konvergentnih sila.

5. Kolika je projekcija sile na koordinatnu ravan?

književnost:

1. Verein L.I. Tehnička mehanika - M: Akademija, 2006.

2. Movnin M.S. Osnove tehničke mehanike - Sankt Peterburg: Politehnika, 2003.

3. Molchanova E.V., Shurygina G.N. Statika i čvrstoća materijala - Tomsk, 2008.

Praktični rad №2

Tema lekcije: Određivanje reakcija spajanja ravnog sistema sila koje se konvergiraju.

Vrsta lekcije: učvršćivanje stečenog znanja.

Svrha lekcije: Naučite odrediti reakcije veze ravnog sistema sila koje se konvergiraju

Obezbjeđivanje sredstava:

1. metodološko uputstvo za obavljanje poslova;

2. individualni zadatak;

3. sveska za praktičan rad;

7. kalkulator.

Tehnologija rada:

1. Pažljivo proučavajte smjernice, predloženi teorijski materijal.

2. U skladu sa opcijom, izvršite zadatak prema metodologiji predstavljenoj u nastavku.

3. Izvucite zaključke o obavljenom poslu.

4. Odgovorite na sigurnosna pitanja.

Teorijski materijal

Uslovi i jednačine ravnoteže ravnog sistema proizvoljno lociranih sila.

Kada se sistem sila svede na tačku, dobijaju se R hl i M hl.

Ako je sistem sila u ravnoteži, tada je R ch = 0, M ch = 0.

Zapišimo tri vrste jednačina ravnoteže za ovaj sistem.

Prvi pogled

Drugi pogled

Geometrijska metoda se sastoji u konstruisanju poligona sila, analitička u određivanju zbira projekcija svih aktivne snage na dvije međusobno okomite ose.

Sa grafičkom metodom za određivanje rezultante, vektori sile se mogu nacrtati bilo kojim redoslijedom, rezultat (veličina i smjer rezultante) se neće promijeniti.

Rezultirajući vektor je usmjeren prema vektori sila-termina.

Redoslijed izgradnje poligona sila

1. Odaberite konstrukcijski stup.

2. Početak prvog vektora F 2 stavljamo u pol (vektori sile se mogu nacrtati bilo kojim redoslijedom) pomjerajući ga paralelno sa samim sobom, čuvajući njegovu vrijednost.

3. Postavite početak drugog F 1 na kraj prvog vektora. Crtamo jedan za drugim istim redom vektore preostalih sila F 4 , F 3 .

4. Rezultantni vektor zatvara rezultujuću izlomljenu liniju ; povezuje početak prvog vektora sa krajem posljednjeg i usmjeren je prema njemu.

Kada promijenite redoslijed crtanja vektora u poligonu, pogled figure. Redoslijed crtanja ne utječe na rezultat.

Uvjet geometrijske ravnoteže za PSSS: poligon sile mora biti zatvoren.

Određivanje rezultante na analitički način

Modul (vrijednost) rezultante je određen poznatim projekcijama:

Smjer rezultantnog vektora može se odrediti veličinama i predznacima kosinusa uglova koje formira rezultanta sa koordinatnim osa (slika 3.5).

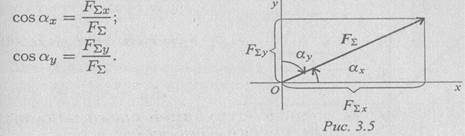
Projekcija sile na osu

Projekcija sile na os je određena segmentom ose odsječenim okomiticama spuštenim na osu s početka i kraja vektora

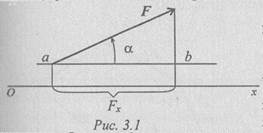
Veličina projekcije sile na osu jednak je proizvodu modula sile i kosinusa ugla između vektora sile i pozitivnog smjera sjekire. Dakle, projekcija ima predznak: pozitivno u istom pravcu vektore sile i ose i negativan kada je upućen prema negativnoj osi(Sl. 3.2).

Uslov analitičke ravnoteže za PSSS: zbir projekcija svih sila na dvije međusobno okomite ose mora biti jednak nuli.

ΣFx=0

ΣF y =0

U zadacima se koordinatne ose biraju tako da je rješenje najjednostavnije. Poželjno je da se barem jedna nepoznata sila poklapa sa koordinatnom osom.

Tema 1.3. Planarni sistem proizvoljno lociranih sila

Moment sile oko tačke

Sila koja ne prolazi kroz tačku vezivanja tela izaziva rotaciju tela u odnosu na tačku, pa se dejstvo takve sile na telo procenjuje kao moment.

Trenutak snage u odnosu na tačku je brojčano jednak proizvodu modula sile i kraka.

Rame - najkraća udaljenost od tačke do linije dejstva sile (upravno spušteno od tačke do linije dejstva sile) (slika 4.4).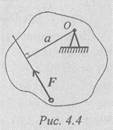

Oznaka momenta M o ( F) ilim o ( F);m 0 (F) = Fa.

jedinica mjere m o (F)= N m

Moment se smatra pozitivnim ako sila pokuša da okrene tijelo u smjeru kazaljke na satu.

Moment sile oko tačke je nula ako linija djelovanja sile prolazi kroz tačku, jer je u ovom slučaju udaljenost od tačke do sile nula.

Planarni sistem proizvoljno lociranih sila

Glavni vektor jednak je geometrijskom zbiru vektora proizvoljnog sistema sila. Projektujemo sve sile sistema na koordinatne ose i sabiranjem odgovarajućih projekcija na ose dobijamo projekcije glavnog vektora.

Po veličini projekcija glavnog vektora na koordinatne ose nalazimo modul glavnog vektora:

Glavna tačka sistem sila jednak je algebarskom zbiru momente sile sistema u odnosu na tačku redukcije.

Tako se PSPRS svodi na jednu silu(glavni vektor sistema sila) i jedan trenutak(glavni moment sistema sila).

Tri oblika uslova ravnoteže PSPRS

Za različite slučajeve koriste se tri grupe jednadžbi ravnoteže.

Za konkretan slučaj, ako je sistem uravnotežen paralelne sile, postoje samo dvije jednadžbe ravnoteže:

Sistemi greda. Određivanje reakcija potpore i momenata štipanja

Vrste opterećenja

Prema načinu primjene opterećenja se dijele na koncentrirana i raspoređena. Ako se u stvarnosti prijenos opterećenja dogodi na zanemarljivoj površini (u nekoj tački), opterećenje se naziva koncentrirano.

Često je opterećenje raspoređeno na značajno područje ili liniju (pritisak vode na branu, pritisak snijega na krov, itd.), tada se uzima u obzir opterećenje distribuirano.

U problemima statike za apsolutno kruta tijela, raspoređeno opterećenje može se zamijeniti rezultantom koncentrisana sila (slika 6.1).

q

l/2Q

q- intenzitet opterećenja, N/m;

l- linija djelovanja raspoređenog opterećenja, m;

Q = ql- rezultujuće raspoređeno opterećenje.

Vrste nosača sistema greda(vidi reakcije i njihove veze) Greda - konstrukcijski dio u obliku ravne grede, pričvršćen na nosače i savijen silama koje se na njega primjenjuju.

Visina presjeka grede je neznatna u odnosu na dužinu. Kruti završetak (štipanje)(Sl. 6.2)

Oslonac ne dozvoljava kretanje i rotaciju. Završetak je zamijenjen dvokomponentnim silama Rax i Zraka i par sa momentom g. A.

Za određivanje ovih nepoznanica zgodno je koristiti sistem jednačina u obliku

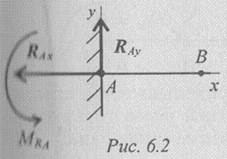
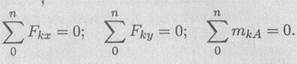
Svaka jednačina ima jednu nepoznata količina i rješava se bez zamjena. Za kontrolu ispravnosti odluka koristi se dodatno poravnanje momenata u odnosu na bilo koju tačku na gredi, na primjer, B.

Za datu shemu greda potrebno je pronaći reakcije nosača ako je l=14 m, a=3,8 m, b=5 m, M=11 kN m, F=10 kN.

Rješenje. Pošto nema horizontalnog opterećenja, oslonac A ima samo vertikalnu reakciju RA. Jednačine ravnoteže sastavljamo u obliku momenata svih sila u odnosu na tačke A i B.

gde da nađemo

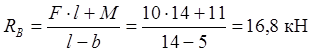
Da bismo provjerili, sastavljamo jednadžbu ravnoteže za vertikalnu osu:

test pitanja

tačka sile šarke grede

> Kako je projekcija sile na osu?

Projekcija sile na osu je algebarska veličina jednaka umnošku modula sile i kosinusa ugla između pozitivnog smjera ose i vektora sile (tj. ovo je odsječak iscrtan silom na odgovarajuće ose).

Px=Pcos?=Pcos90o=0;

Rx=Rcos? = -R cos(180o-?).

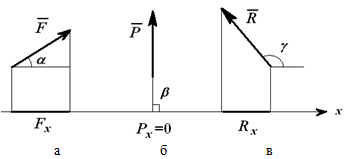
Projekcija sile na osu je pozitivna, sl. 2 a) ako je 0 ? ?< ?/2.

> U kom slučaju je projekcija sile na osu jednaka nuli?

Projekcija sile na osu može biti nula, sl. 2 b) ako? = ?/2.)

> U kom slučaju je projekcija sile na osu jednaka modulu sile?

Projekcija sile na osu jednaka je modulu sile, ako? =0?.

> U kom slučaju je projekcija sile na osu negativna?

Projekcija sile na osu može biti negativna, sl. 2 c) ako?/2< ? ? ?.

> Koliko jednačina ravnoteže je sastavljeno za ravan konvergentni sistem sila?

Sile se nazivaju konvergentne ako se njihove linije djelovanja sijeku u jednoj tački. Razlikovati ravan sistem sila koje se konvergiraju, kada linije djelovanja svih ovih sila leže u istoj ravni.

Ravnoteža sistema konvergentnih sila.

Iz zakona mehanike proizilazi da solidan, na koje djeluju međusobno uravnotežene vanjske sile, može ne samo mirovati, već i vršiti kretanje, koje ćemo nazvati kretanjem "po inerciji". Takav pokret će biti, na primjer, translatorno uniformno i pravolinijsko kretanje tijela.

Iz ovoga dolazimo do dva važna zaključka:

1) Uslove za ravnotežu statike zadovoljavaju sile koje deluju i na telo koje miruje i na telo koje se kreće „po inerciji“.

2) Ravnoteža sila primenjenih na slobodno čvrsto telo je neophodan, ali ne i dovoljan uslov za ravnotežu (odmor) samog tela; u ovom slučaju tijelo će mirovati samo ako je mirovalo i do trenutka kada su na njega primijenjene uravnotežene sile.

Za ravnotežu sistema konvergentnih sila primijenjenih na čvrsto tijelo, potrebno je i dovoljno da rezultanta ovih sila bude jednaka nuli. Uslovi koje same sile moraju da zadovolje u ovom slučaju mogu se izraziti u geometrijskom ili analitičkom obliku.

1. Uvjet geometrijske ravnoteže. Budući da je rezultanta konvergentnih sila definirana kao zatvarajuća strana poligona sila konstruiranog od ovih sila, ona može nestati ako i samo ako se kraj posljednje sile u poligonu poklopi s početkom prve, tj. kada se poligon zatvori .

Shodno tome, za ravnotežu sistema, konvergirajućih sila, neophodno je i dovoljno da poligon sila konstruisan od ovih sila bude zatvoren.

2. Uslovi analitičke ravnoteže. Analitički, rezultanta sistema konvergentnih sila određena je formulom

Budući da je zbir pozitivnih članova ispod korijena, R će nestati samo kada oba

tj. kada će sile koje djeluju na tijelo zadovoljiti jednakosti:

Jednakosti izražavaju uslove ravnoteže u analitičkom obliku: za ravnotežu prostornog sistema konvergentnih sila potrebno je i dovoljno da sumi projekcija ovih sila na svaku od tri koordinatne ose budu jednaki nuli.

Ako sve konvergirajuće sile koje djeluju na tijelo leže u istoj ravni, onda formiraju ravan sistem sila koje se konvergiraju. U slučaju ravnog sistema konvergentnih sila, očigledno dobijamo samo dva uslova ravnoteže

Jednakosti takođe izražavaju neophodne uslove (ili jednačine) za ravnotežu slobodnog krutog tela pod dejstvom sila koje se konvergiraju.

> U kom smjeru je usmjerena reakcija štapa sa zglobnim krajevima?

Neka je u nekoj konstrukciji veza šipka AB, pričvršćena na krajevima šarkama (slika 3). Pretpostavimo da se težina štapa u poređenju sa opterećenjem koje on percipira može zanemariti. Tada će na štap djelovati samo dvije sile primijenjene na šarke A i B. Ali ako je štap AB u ravnoteži, tada sile primijenjene u tačkama A i B moraju biti usmjerene duž jedne prave linije, tj. duž ose štapa . Posljedično, šipka opterećena na krajevima, čija se težina može zanemariti u usporedbi s ovim opterećenjima, radi samo na napetost ili kompresiju. Ako je takav štap veza, tada će reakcija štapa biti usmjerena duž ose štapa.

> Koliki je moment sile oko tačke?

Moment sile u odnosu na tačku određen je proizvodom modula sile i dužine okomice spuštene iz tačke na liniju djelovanja sile (slika 4, a). Kada je tijelo fiksirano u tački O, sila teži da ga rotira oko ove tačke. Tačka O, u odnosu na koju se uzima moment, naziva se centar momenta, a dužina okomice a naziva se rame sile u odnosu na centar momenta.

Momenti sila se mjere u njutonometrima (N m) ili kilogram metrima (kgf m) ili u odgovarajućim višestrukim i suvišestrukim jedinicama, kao i momenti parova.

Projekcija sile na osu je određena segmentom odsečene ose

okomite spuštene na osu s početka i kraja vektora (slika 3.1).

Veličina projekcije sile na osu jednak je proizvodu modula sile i kosinusa ugla između vektora sile i pozitivnog smjera sjekire. Dakle, projekcija ima predznak: pozitivno u istom pravcu vektore sile i ose i negativan kada je upućen prema negativnoj osi(Sl. 3.2).

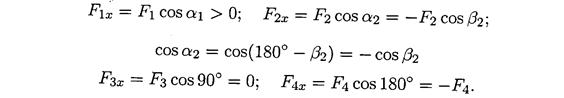
Projekcija sile na dvije međusobno okomite ose(Sl. 3.3).

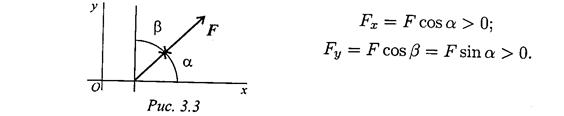
Kraj rada -

Ova tema pripada:

Teorijska mehanika

Teorijska mehanika... PREDAVANJE... Tema Osnovni pojmovi i aksiomi statike...

Ako vam je potreban dodatni materijal na ovu temu, ili niste pronašli ono što ste tražili, preporučujemo da koristite pretragu u našoj bazi radova:

Šta ćemo sa primljenim materijalom:

Ako vam se ovaj materijal pokazao korisnim, možete ga spremiti na svoju stranicu na društvenim mrežama:

Sve teme u ovoj sekciji:

Problemi teorijske mehanike
Teorijska mehanika je nauka o mehaničkom kretanju materijalnih čvrstih tela i njihovoj interakciji. Pod mehaničkim kretanjem se podrazumijeva kretanje tijela u prostoru i vremenu

Treći aksiom
Bez narušavanja mehaničkog stanja tela, možete dodati ili ukloniti uravnotežen sistem sila (princip odbacivanja sistema sila ekvivalentnih nuli) (slika 1.3). P,=P2 P,=P.

Posljedica iz druge i treće aksiome
Sila koja djeluje na kruto tijelo može se kretati duž njegove linije djelovanja (slika 1.6).

Obveznice i reakcije obveznica
Za slobodno kruto tijelo vrijede svi zakoni i teoreme statike. Sva tijela se dijele na slobodna i vezana. Loose tijela- tijela čije kretanje nije ograničeno.

Kruta šipka
Na dijagramima su šipke prikazane debelom punom linijom (slika 1.9). rod mozhe

fiksna šarka
Tačka pričvršćivanja se ne može pomjeriti. Šipka se može slobodno rotirati oko ose šarke. Reakcija takvog oslonca prolazi kroz osovinu šarke, ali

Planarni sistem konvergentnih sila
Sistem sila, čije se linije djelovanja seku u jednoj tački, naziva se konvergentnim (slika 2.1).

Rezultat konvergirajućih sila
Rezultanta dvije sile koje se sijeku može se odrediti pomoću paralelograma ili trokuta sila (4. aksiom) (Vis. 2.2).

Uslov ravnoteže za ravan sistem konvergentnih sila
Kada je sistem sila u ravnoteži, rezultanta mora biti jednaka nuli, dakle, u geometrijskoj konstrukciji, kraj posljednjeg vektora mora se podudarati s početkom prvog. Ako a

Rješavanje problema ravnoteže na geometrijski način
Pogodno je koristiti geometrijsku metodu ako u sistemu postoje tri sile. Prilikom rješavanja ravnotežnih zadataka tijelo se smatra apsolutno čvrstim (učvršćenim). Redoslijed rješavanja problema:

Rješenje
1. Sile koje nastaju u šipkama za pričvršćivanje jednake su po veličini silama kojima šipke podržavaju opterećenje (5. aksiom statike) (slika 2.5a). Mi definišemo mogućim pravcima reakcije veze

Snage na analitički način
Vrijednost rezultante jednaka je vektorskom (geometrijskom) zbiru vektora sistema sila. Rezultantu određujemo geometrijski. Biramo koordinatni sistem, određujemo projekcije svih zadataka

Konvergentne sile u analitičkom obliku
Na osnovu činjenice da je rezultanta jednaka nuli, dobijamo: Uslov

Par sila, moment par sila
Par sila je sistem od dvije sile koje su jednake po modulu, paralelne i usmjerene u različitim smjerovima. Razmotrimo sistem sila (P; B") koji formira par.

Moment sile oko tačke.
Sila koja ne prolazi kroz tačku vezivanja tela izaziva rotaciju tela u odnosu na tačku, pa se dejstvo takve sile na telo procenjuje kao moment. Moment sile rel.

Poinsotova teorema o paralelnom prijenosu sila
Sila se može prenijeti paralelno sa svojom linijom djelovanja dodavanjem para sila s momentom jednakim proizvodu modula sile i udaljenosti na koju je sila prenesena.

locirane snage
Linije djelovanja proizvoljnog sistema sila ne seku se u jednoj tački, stoga, za procjenu stanja tijela, takav sistem treba pojednostaviti. Da bi se to postiglo, sve sile sistema se proizvoljno prenose na jednu

Uticaj referentne tačke
Referentna tačka se bira proizvoljno. Kada promijenite poziciju tačke redukcije, vrijednost glavnog vektora se neće promijeniti. Promijenit će se vrijednost glavnog momenta kada se tačka redukcije pomjeri,

Ravni sistem sile
1. U ravnoteži glavni vektor sistem je nula. Analitička definicija glavnog vektora dovodi do zaključka:

Vrste opterećenja
Prema načinu primjene opterećenja se dijele na koncentrirana i raspoređena. Ako se u stvarnosti prijenos opterećenja događa na zanemarljivom području (u nekoj tački), opterećenje se naziva koncentrisanim

Moment sile oko ose
Moment sile oko ose jednak je momentu projekcije sile na ravan okomitu na osu, u odnosu na tačku preseka ose sa ravninom (slika 7.1 a). MO

Vektor u svemiru
U prostoru se vektor sile projektuje na tri međusobno okomite koordinatne ose. Vektorske projekcije formiraju rubove kuboid, vektor sile se poklapa sa dijagonalom (slika 7.2.).

Prostorni konvergentni sistem sila
Prostorni konvergentni sistem sila je sistem sila koje ne leže u istoj ravni, čije se linije delovanja seku u jednoj tački. Rezultirajući prostorni sistem si

Dovođenje proizvoljnog prostornog sistema sila u centar O
Dat je prostorni sistem sila (slika 7.5a). Dovedemo ga u centar O. Sile se moraju kretati paralelno i formira se sistem parova sila. Moment svakog od ovih parova je

Težište homogenih ravnih tijela
(ravne figure) Vrlo često je potrebno odrediti težište raznih ravnih tijela i geometrijskih ravnih figura složenog oblika. Za ravna tijela možemo napisati: V =

Određivanje koordinata težišta ravnih figura
Bilješka. Težište simetrične figure nalazi se na osi simetrije. Težište štapa je na sredini visine. Položaji centara gravitacije jednostavni geometrijski oblici svibanj

Kinematika tačke
Imati ideju o prostoru, vremenu, putanji, putanji, brzini i ubrzanju Znati kako postaviti kretanje tačke (prirodno i koordinatno). Znajte notaciju

Prijeđena udaljenost
Putanja se mjeri duž putanje u smjeru vožnje. Oznaka - S, mjerne jedinice - metri. Jednačina kretanja tačke: Definisanje jednačine

Brzina putovanja
Vektorska veličina koja karakteriše u ovog trenutka brzina i smjer kretanja duž putanje naziva se brzina. Brzina je vektor usmjeren duž k

tačka ubrzanje
Vektorska veličina koja karakterizira brzinu promjene brzine u veličini i smjeru naziva se ubrzanje tačke. Brzina tačke pri kretanju od tačke M1

Ujednačeno kretanje
Ravnomjerno kretanje je kretanje konstantnom brzinom: v = const. Za pravolinijsko ravnomjerno kretanje (slika 10.1 a)

Jednako promenljivo kretanje
Jednakopromenljivo kretanje je kretanje sa konstantnim tangencijalnim ubrzanjem: at = const. Za pravolinijsko ravnomjerno kretanje

translatorno kretanje
Translacijsko je takvo kretanje krutog tijela u kojem svaka prava linija na tijelu tokom kretanja ostaje paralelna sa svojim početnim položajem (sl. 11.1, 11.2). At

rotaciono kretanje
Tokom rotacionog kretanja, sve tačke tela opisuju kružnice oko zajedničke fiksne ose. Fiksna osa oko koje se rotiraju sve tačke tela naziva se osa rotacije.

Posebni slučajevi rotacionog kretanja
Ujednačena rotacija (ugaona brzina je konstantna): ω = const Jednačina (zakon) jednolike rotacije u ovom slučaju ima oblik:

Brzine i ubrzanja tačaka rotirajućeg tela
Telo se rotira oko tačke O. Odredimo parametre kretanja tačke koja se nalazi na udaljenosti RA od ose rotacije (sl. 11.6, 11.7). Put

Rješenje
1. Odjeljak 1 - neravnomjerno ubrzano kretanje, ω \u003d φ '; ε = ω’ 2. Sekcija 2 - brzina je konstantna - kretanje je ravnomjerno, . ω = const 3.

Osnovne definicije
Složeni pokret je pokret koji se može rastaviti na nekoliko jednostavnih. Jednostavni pokreti su translatorni i rotacijski. Razmotriti složeno kretanje tačaka

Ravnoparalelno kretanje krutog tijela
Ravnoparalelno, ili ravno, je takvo kretanje krutog tijela u kojem se sve točke tijela kreću paralelno s nekom fiksnom u referentnom okviru koji se razmatra

translatorno i rotaciono
Ravnoparalelno kretanje se razlaže na dva kretanja: translacijsko uz određeni pol i rotacijsko u odnosu na ovaj pol. Za određivanje se koristi dekompozicija

Centar brzina
Brzina bilo koje tačke tijela može se odrediti pomoću trenutnog centra brzina. U ovom slučaju, složeno kretanje je predstavljeno kao lanac rotacija oko različitih centara. Zadatak

Aksiomi dinamike
Zakoni dinamike sumiraju rezultate brojnih eksperimenata i zapažanja. Zakone dinamike, koji se obično smatraju aksiomima, formulirao je Njutn, ali su prvi i četvrti zakon takođe

Koncept trenja. Vrste trenja
Trenje je otpor koji nastaje kada se jedno grubo tijelo pomiče po površini drugog. Prilikom klizanja tijela nastaje trenje klizanja, a prilikom kotrljanja nastaje trenje kotrljanja. Priroda otpora

trenje kotrljanja
Otpor kotrljanja povezan je s međusobnom deformacijom tla i točka i mnogo je manji od trenja klizanja. Obično se tlo smatra mekšim od kotača, tada se tlo uglavnom deformira i

Besplatni i nebesplatni bodovi
Materijalna tačka, čije kretanje u prostoru nije ograničeno nikakvim ograničenjima, naziva se slobodnom. Zadaci se rješavaju korištenjem osnovnog zakona dinamike. Onda materijal

sila inercije
Inercija je sposobnost da se svoje stanje zadrži nepromenjenim; to je unutrašnje svojstvo svih materijalnih tela. Inercijska sila - sila koja se javlja prilikom ubrzanja ili kočenja tijela

Rješenje
Aktivne snage: pokretačka snaga, sila trenja, sila gravitacije. Reakcija u nosaču R. Primjenjujemo silu inercije u smjeru suprotnom od ubrzanja. Prema d'Alambertovom principu, sistem sila koje djeluju na platformu

Rad rezultujuće sile
Pod dejstvom sistema sila, tačka mase m pomera se iz položaja M1 u položaj M 2 (slika 15.7). U slučaju kretanja pod dejstvom sistema sila,

Snaga
Za karakterizaciju performansi i brzine rada uvodi se pojam snage. Snaga je rad obavljen u jedinici vremena:

Snaga rotacije
Rice. 16.2 Tijelo se kreće duž luka polumjera od tačke M1 do tačke M2 M1M2 = φr Rad sile

Efikasnost
Svaka mašina i mehanizam, radeći, troši dio energije na savladavanje štetnih otpora. Dakle, mašina (mehanizam), pored korisnog posla, obavlja i dodatni

Teorema o promjeni impulsa
Zamah materijalne tačke je vektorska veličina jednaka proizvodu mase tačke i njene brzine mv. Vektor momenta se poklapa sa

Teorema promjene kinetičke energije
Energija je sposobnost tijela da obavlja mehanički rad. Postoje dva oblika mehanička energija: potencijalna energija, ili energija položaja i kinetička energija,

Osnove dinamike sistema materijalnih tačaka
Agregat materijalne tačke, međusobno povezanih silama interakcije, naziva se mehanički sistem. Svako materijalno tijelo u mehanici se smatra mehaničkim

Osnovna jednadžba dinamike rotirajućeg tijela
Neka se kruto tijelo rotira oko ose Oz pod djelovanjem vanjskih sila ugaonom brzinom

voltaža
Metoda preseka vam omogućava da odredite vrednost unutrašnjeg faktora sile u preseku, ali ne omogućava uspostavljanje zakona raspodele unutrašnje sile po odeljku. Za procjenu snage n

Unutrašnji faktori sile, naprezanja. Plotting
Imati ideju o uzdužnim silama, o normalnim naponima u poprečnim presjecima. Poznavati pravila za konstruisanje dijagrama uzdužnih sila i normalnih napona, zakon raspodjele

Uzdužne sile
Zamislite gredu opterećenu vanjskim silama duž ose. Greda je fiksirana u zid (pričvršćivanje "ugradnje") (sl. 20.2a). Gredu dijelimo na dijelove opterećenja. Područje opterećenja sa

Geometrijske karakteristike ravnih presjeka
Imati ideju o tome fizičkog čula i postupak za određivanje aksijalnih, centrifugalnih i polarnih momenata inercije, o glavnim centralnim osi i glavnim centralnim momentima inercije.

Statički moment površine presjeka
Razmotrimo proizvoljan presek (slika 25.1). Ako podijelimo presjek na beskonačno male površine dA i pomnožimo svaku površinu s udaljenosti do koordinatne ose i integrišemo dobijenu

centrifugalni moment inercije
Centrifugalni moment inercije presjeka je zbir proizvoda elementarnih površina uzetih od ukupne površine po obje koordinate:

Aksijalni momenti inercije
Aksijalni moment inercije presjeka u odnosu na neko dvorište koje leži u istoj ravni je zbir proizvoda elementarnih površina po kvadratu njihove udaljenosti uzete preko cijele površine

Polarni moment inercije presjeka
Polarni moment inercije presjeka u odnosu na određenu tačku (pol) je zbir proizvoda elementarnih površina uzetih na cijeloj površini i kvadrata njihove udaljenosti do ove točke:

Momenti inercije najjednostavnijih sekcija
Aksijalni momenti inercija pravougaonika (slika 25.2) Zamislite direktno

Polarni moment inercije kružnice
Za krug se prvo izračunava polarni moment inercije, a zatim aksijalni. Zamislite krug kao skup beskonačno tankih prstenova (slika 25.3).

Torzione deformacije
Torzija okrugle grede nastaje kada je opterećena parovima sila s momentima u ravninama okomitim na uzdužnu os. U ovom slučaju, generatriksa snopa je savijena i okrenuta pod kutom γ,

Hipoteze u torziji
1. Ispunjena je hipoteza o ravnim presjecima: poprečni presjek grede, koji je ravan i okomit na uzdužnu os, nakon deformacije ostaje ravan i okomit na uzdužnu os.

Faktori unutrašnje sile u torziji
Torzija se naziva opterećenjem, pri čemu u poprečnom presjeku grede nastaje samo jedan unutarnji faktor sile - moment. Vanjska opterećenja su također dva profesionalna

Torque Plots
Momenti mogu varirati duž ose grede. Nakon određivanja vrijednosti momenata duž presjeka, gradimo grafikon momenta duž osi šipke.

Torziona naprezanja
Crtamo mrežu uzdužnih i poprečnih linija na površini grede i razmatramo uzorak koji se formira na površini nakon Sl. 27.1a deformacija (sl. 27.1a). Pop

Maksimalna torzijska naprezanja
Iz formule za određivanje napona i dijagrama raspodjele posmičnih naprezanja pri torziji se vidi da se na površini javljaju maksimalna naprezanja. Odredite maksimalni napon

Vrste proračuna čvrstoće
Postoje dva tipa proračuna čvrstoće 1. Projektni proračun - određuje se prečnik grede (vrata) u opasnom preseku:

Proračun krutosti
Pri proračunu krutosti određuje se deformacija i uspoređuje s dopuštenom. Razmotrimo deformaciju okrugle šipke pod dejstvom spoljnog para sila sa momentom t (slika 27.4).

Osnovne definicije
Savijanje je vrsta opterećenja u kojoj u poprečnom presjeku grede nastaje faktor unutrašnje sile - moment savijanja. Bar radi

Interni faktori sile pri savijanju
Primjer 1. Razmotrimo gredu na koju djeluje par sila sa momentom t i spoljna sila F (Sl. 29.3a). Za određivanje unutrašnjih faktora sile koristimo metodu sa

Momenti savijanja
Poprečna sila u presjeku smatra se pozitivnom ako teži okretanju

Diferencijalne zavisnosti za direktno poprečno savijanje
Konstrukcija dijagrama posmičnih sila i momenata savijanja uvelike je pojednostavljena kada se koriste diferencijalni odnosi između momenta savijanja, posmične sile i ujednačenog intenziteta.

Metoda preseka Dobijeni izraz se može generalizovati
Poprečna sila u razmatranom presjeku jednaka je algebarskom zbiru svih sila koje djeluju na gredu do presjeka koji se razmatra: Q = ΣFi Pošto je riječ o

voltaža
Razmotrimo savijanje grede stisnute s desne strane i opterećene koncentriranom silom F (slika 33.1).

Stanje stresa u jednom trenutku
Stanje naprezanja u tački karakteriziraju normalni i posmični naponi koji nastaju na svim područjima (presjecima) koji prolaze kroz dati poen. Obično je dovoljno definisati

Koncept složenog deformisanog stanja
Skup deformacija koje se javljaju u različitim smjerovima iu različitim ravnima prolazeći kroz tačku određuju deformirano stanje u toj tački. Kompleksna deformacija

Proračun okrugle šipke za savijanje sa torzijom
U slučaju proračuna okrugle šipke pod djelovanjem savijanja i torzije (slika 34.3), potrebno je uzeti u obzir normalna i posmična naprezanja, jer se u oba slučaja javljaju maksimalne vrijednosti naprezanja.

Koncept stabilne i nestabilne ravnoteže
Relativno kratke i masivne šipke oslanjaju se na kompresiju, jer. propadaju kao rezultat razaranja ili zaostalih deformacija. Dugačke šipke malog presjeka pod djelovanjem

Proračun održivosti
Proračun stabilnosti sastoji se u određivanju dopuštene tlačne sile i, u poređenju s njom, djelujuće sile:

Proračun po Ojlerovoj formuli
Problem određivanja kritične sile matematički je riješio L. Euler 1744. Za štap koji je šarkiran na obje strane (slika 36.2), Ojlerova formula ima oblik

Kritični naponi.
Kritično naprezanje je tlačno naprezanje koje odgovara kritičnoj sili. Naprezanje od tlačne sile određuje se formulom

Granice primjenjivosti Ojlerove formule
Ojlerova formula vrijedi samo u granicama elastičnih deformacija. Dakle, kritični napon mora biti manji od granice elastičnosti materijala. Prev

Skalarna vrijednost jednaka dužini segmenta uzetog s odgovarajućim predznakom, zatvorenog između projekcija početka i kraja sile, naziva se projekcija sile na os.

Projekcija ima predznak plus ako se kretanje od početka do kraja odvija u pozitivnom smjeru ose, a znak minus ako je u negativnom smjeru.

Dakle, projekcije date sile na bilo koju paralelnu i jednako usmjerenu ose su jednake jedna drugoj.

Projekcija sile na osu Ox je označena kao (slika 12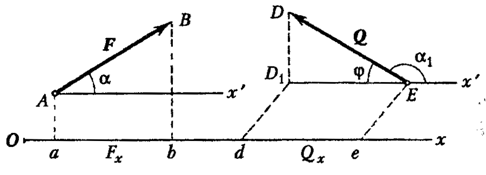

).

Prateći sliku 12 i definiciju, dobijamo

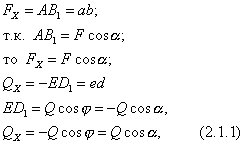
To jest, projekcija sile na os je jednaka proizvodu modula sile i kosinusa ugla između smjera sile i pozitivnog smjera ose.

Ako je sila okomita na osu, tada je njena projekcija na tu osu nula.

Projekcija sile na Oxy ravan je vektor zatvoren između projekcija početka i kraja sile F na ovu ravan (Sl. 13

).

Projekcija sile na ravan je vektorska veličina i karakteriše je i modul i pravac u ravni Oxy. Modul projekcije sile na Oxy ravan se izražava kao

Zatim projekcije na ose Ox i Oy:

Biramo koordinatni sistem Oxyz. Vektor se može konstruisati znajući modul i uglove između vektora i odgovarajućih osa (slika 14 ).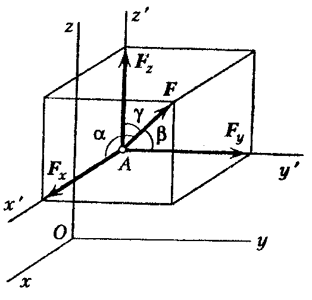

Dodjela ovih veličina određuje silu. Tačka primjene sile mora biti dodatno specificirana s koordinatama x, y, z. Osim toga, sila se može odrediti projekcijama na osi. Onda

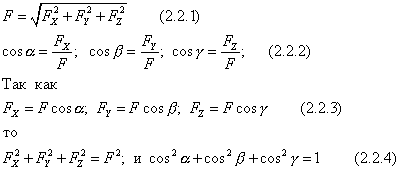
Ove formule omogućavaju, znajući projekcije sile na koordinatne ose, da se pronađe njen modul i uglovi sa osama, tj. odrediti snagu. Poznavajući projekcije, možete konstruisati vektor geometrijski.

Za ravan su napisane formule (2.2.1) i (2.2.2).

Konstrukcija u ravni je izvedena prema 4. aksiomu statike.

Razmotrimo sada analitičku metodu sabiranja sila. Odnos između vektora i njihovih projekcija je dat sljedećom teoremom:

Projekcija vektora sume na neku osu jednaka je algebarskom zbiru projekcija članova vektora na istu osu (Sl. 15 ).

Ovi odnosi omogućavaju analitički sabiranje sila. Može se uočiti identičnost formula (2.2.1)-(2.2.4) i (2.2.9)-(2.2.11).

Rješavanje problema u statici često je povezano s operacijom sabiranja iz vektorske algebre. Prisjetimo se starih trikova i uvedemo neke definicije.

Količina jednaka geometrijskom zbiru sila bilo kojeg sistema naziva se glavni vektor sistemima.

Geometrijski zbir sila ne treba brkati sa rezultantom. Za mnoge sisteme sila ne postoji rezultanta, a glavni vektor se može izračunati za bilo koji.

Razmotrimo sabiranje dvije sile na ravni. Geometrijski zbir sila nalazi se prema pravilu paralelograma konstruiranjem trokuta sila (sl. 16.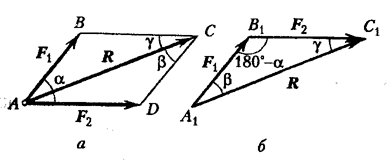

).

Modul R rezultante je definiran kao stranica trokuta:

uglovi se nalaze po sinusnoj teoremi, s obzirom na to , dobijamo

U nastavku geometrijske metode sabiranja sila, prisjećamo se sabiranja tri sile koje ne leže u ovoj ravni.

Geometrijski zbir tri sile, koje ne leže u istoj ravni, prikazan je dijagonalom paralelepipeda izgrađenog na tim silama (slika 17. ).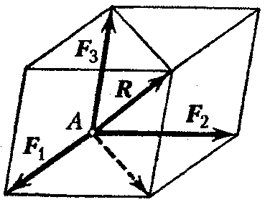

Ovdje je potrebno naglasiti potpunu analogiju slika 14 i 17, gdje ulogu igraju , odnosno . Shodno tome, možemo koristiti formule (2.2.1-2.2.4).

S obzirom na ravan sistem konvergirajućih sila, potrebno je razmotriti položaj takvog sistema sila.

Geometrijski zbir (glavni vektor) bilo kojeg sistema sila određen je konstrukcijom poligona sila ili sukcesivnim sabiranjem sila sistema. Pustite sistem konvergentne sile (slika 18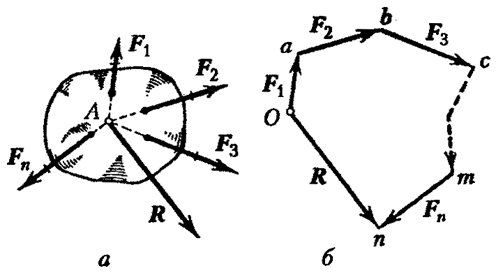

).

Da biste izgradili poligon sile, odaberite proizvoljnu tačku O i pomaknite početak do nje, zatim pomaknite početak na kraj vektora, itd. nakon prijenosa vektora, kraj vektora će biti u nekoj tački N. Vektorom povezujemo tačke O i N. Ovaj vektor zatvaranja će biti glavni vektor sistema.

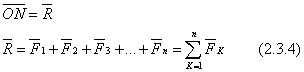
Sukcesivnim sabiranjem sila (slika 18, a) sve se prenose duž linija djelovanja do točke presjeka A. Dosljedno, prema pravilu paralelograma, sile se sabiraju, dobija se vektor:

koja je rezultanta, jednaka glavnom vektoru svih sila i primijenjena u tački njihovog presjeka.

Linije djelovanja tri neparalelne međusobno uravnotežene sile koje leže u istoj ravni seku se u jednoj tački.

Neka snaga bude data. Pošto leže u istoj ravni i nisu paralelne, njihove linije delovanja će se preseći u nekoj tački O. U ovoj tački primenjujemo sile i zamenjujemo ih rezultantom. Tada postoje dve sile koje se primenjuju u tački O (slika 19. ).

Ako je tijelo u ravnoteži, onda, prema 1. teoremi statike, mora se odložiti duž jedne prave, tj. . Dakle, prolazi kroz tačku A. To je ono što je trebalo dokazati.

Teorema je neophodan, ali nedovoljan dokaz uslova ravnoteže za slobodno kruto tijelo pod djelovanjem tri sile.

Kako je definirano, konvergentne sile su sile čije se linije djelovanja seku u jednoj tački. Uzimajući u obzir teoremu o tri sile i aksiom paralelograma sila, nalazimo da sistem konvergirajućih sila ima rezultantu jednaku geometrijskom zbiru (glavnom vektoru) ovih sila i primijenjenu u tački njihovog presjeka. Konstrukcija ili definicija rezultante izvršena je u stavu 2 ovog poglavlja (vidi formule 2.3.3, 2.3.4).

Nakon što smo odredili rezultantu, možemo pristupiti određivanju uslova ravnoteže za slobodno kruto tijelo pod djelovanjem sistema sila koje se konvergiraju.

Ako na tijelo djeluje uravnotežen sistem sila, tada tijelo miruje ili se kreće po inerciji.

Za ravnotežu sistema konvergentnih sila primijenjenih na čvrsto tijelo, potrebno je i dovoljno da rezultanta ovih sila bude jednaka nuli. Uslovi koje ove sile moraju da zadovolje mogu se izraziti u geometrijskom ili analitičkom obliku.

1) Uslov geometrijske ravnoteže.

Budući da je rezultanta konvergentnih sila definirana kao vektor zatvaranja poligona sile, može nestati kada se poligon zatvori. Odnosno, za ravnotežu sistema konvergentnih sila potrebno je i dovoljno da poligon sila konstruisan od ovih sila bude zatvoren.

2) Uslovi analitičke ravnoteže. Analitički, rezultanta je definirana kao

Budući da je zbir pozitivnih brojeva ispod korijena, tada će R biti jednak nuli ako i samo ako je u isto vrijeme.

Odnosno, jednakosti

Ovo su uslovi za ravnotežu slobodnog krutog tela pod dejstvom sistema sila koje se konvergiraju.

Za ravnotežu prostornog sistema konvergentnih sila potrebno je i dovoljno da sumi projekcija ovih sila na koordinatne ose budu jednaki nuli.

Za ravan sistem konvergentnih sila, jednadžbe (2.5.3) se svode na sljedeće:

Zajedno sa progresivno kretanje kruto tijelo može rotirati oko centra (tačke).

Rotaciju karakteriše moment sile.

Neka se sila primeni u tački A. Ona teži da rotira telo oko fiksnog centra O (Sl. 20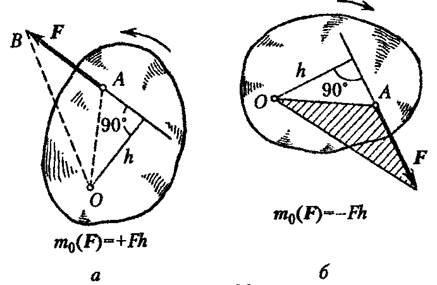

). Okomita h spuštena iz tačke O na liniju djelovanja sile naziva se rame sile u odnosu na centar O.

Pošto se tačka primene sile može pomerati duž linije delovanja sile, rotacija tela će zavisiti od:

1) modul sile i ramena h.

2) pozicije OAB ravni,

Neka cijeli sistem sila leži u jednoj ravni, tada se smjer može okarakterizirati znakom. Dajemo sljedeću definiciju momenta sile:

Momentom sile oko centra O nazivamo vrijednost jednaku proizvodu modula sile i dužine kraka, uzete s odgovarajućim predznakom.

Moment sile se označava kao:

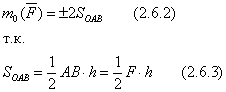
Odabiremo znak plus ako sila pokušava da rotira tijelo u smjeru suprotnom od kazaljke na satu, u suprotnom uzimamo znak minus.

Mjerne jedinice: (njutn po metru), (kilogram po metru).

Svojstva momenta sile:

1) moment sile se neće promeniti kada se tačka primene sile prenese duž njene linije dejstva;

2) moment sile je jednak nuli ako i samo ako je sila jednaka nuli, ili njena linija djelovanja prolazi kroz centar O. (h = 0).

3) moment sile je brojčano jednak dvostrukoj površini trougla OAB.

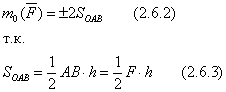
Moment rezultujućeg ravnog sistema sila koje konvergiraju u odnosu na bilo koji centar jednak je algebarskom zbiru momenata članova sila u odnosu na isti centar.

Razmotrimo sistem sila konvergirajući u tački A (slika 21 ).