It can be noted that the ratio of the temperature of the refrigerator to the temperature of the heater is equal to the ratio of the amount of heat given by the working fluid to the refrigerator to the amount of heat received from the heater. This means that for an ideal heat engine operating according to the Carnot cycle, the following relation is also satisfied: . Attitude Lorenz named reduced heat . For an elementary process, the reduced heat will be equal to . This means that during the implementation of the Carnot cycle (and it is a reversible cyclic process), the reduced heat remains unchanged and behaves as a function of the state, while, as is known, the amount of heat is a function of the process.

Using the first law of thermodynamics for reversible processes, and dividing both sides of this equation by the temperature, we get:

(3.70)

Heat cannot spontaneously transfer from a colder body to a hotter one without some other change in the system.

Entropy is a concept that was introduced in thermodynamics. With the help of this value, the measure of energy dissipation is determined. Any system experiences a confrontation that arises between heat and heat. force field. An increase in temperature leads to a decrease in the degree of order. To determine the measure of disorder, a quantity called entropy is introduced. It characterizes the degree of exchange of energy flows both in closed and in open systems Oh.

The change in entropy in isolated circuits occurs in the direction of increase along with the growth of heat. This measure of disorder reaches its maximum value in a state characterized by thermodynamic equilibrium, which is the most chaotic.

If the system is open and at the same time non-equilibrium, then the change in entropy occurs in the direction of decrease. The value of this measure in this variant is characterized by the formula. To obtain it, the summation of two quantities is carried out:
- the flow of entropy occurring due to the exchange of heat and substances with external environment;
- the magnitude of the change in the indicator of chaotic movement within the system.

The change in entropy occurs in any environment where biological, chemical and physical processes. This phenomenon is realized with a certain speed. The change in entropy can be a positive value - in this case, there is an influx of this indicator into the system from the external environment. There are cases when the value indicating the change in entropy is defined with a minus sign. Such a numerical value indicates an outflow of entropy. The system may be in In this case, the amount of entropy produced is compensated by the outflow of this indicator. An example of such a situation is the state It is non-equilibrium, but at the same time stationary. Any organism pumps entropy, which has a negative value, from its environment. The allocation of a measure of disorder from it may even exceed the amount of income.

Entropy production occurs in any complex systems. In the process of evolution, information is exchanged between them. For example, when information about the spatial arrangement of its molecules is lost. There is a process of increasing entropy. If the liquid freezes, then the uncertainty in the arrangement of the molecules decreases. In this case, the entropy decreases. Cooling a liquid causes a decrease in its internal energy. However, when the temperature reaches a certain value, despite the removal of heat from the water, the temperature of the substance remains unchanged. This means that the transition to crystallization begins. Entropy change at isothermal process of this type is accompanied by a decrease in the indicator of the measure of the randomness of the system.

A practical method that allows the heat of fusion of a substance is to carry out work, the result of which is the construction of a solidification diagram. In other words, on the basis of the data obtained as a result of the study, it is possible to draw a curve that will indicate the dependence of the temperature of a substance on time. In this case, the external conditions must remain unchanged. It is possible to determine the change in entropy by processing the data graphic image experience results. On such curves there is always a section where the line has a horizontal gap. The temperature corresponding to this segment is the solidification temperature.

A change in any substance accompanied by a transition from solid body into a liquid at a temperature of its environment equal to and vice versa, is referred to as a phase change of the first kind. This changes the density of the system, its and entropy.

The main processes in thermodynamics are:

· isochoric, flowing at constant volume;

· isobaric flowing at constant pressure;

· isothermal, occurring at a constant temperature;

· adiabatic where there is no heat exchange with the environment.

Isochoric process

In an isochoric process, the condition V= const.

From the ideal gas equation of state ( pV = RT) follows:

p/ T = R/V= const,

i.e., the gas pressure is directly proportional to its absolute temperature:

p2 / p1 = T2/T 1 .

The change in entropy in an isochoric process is determined by the formula:

s 2 -s 1 = Δ s = cv ln( p2/p 1 ) = cv ln( T2/T 1 )

isobaric process

An isobaric process is one that takes place at constant pressure. p= const.

From the equation of state for an ideal gas it follows:

V/T = R/p= const.

The change in entropy will be:

s 2 – s 1 = Δ s = cp ln( T 2 / T 1 ).

Isothermal process

In an isothermal process, the temperature of the working fluid remains constant T= const, so:

pV = RT= const

The change in entropy is:

s 2 -s 1 = Δ s = R ln( p1/p 2 ) = R ln( V2/V 1 ).

adiabatic process

An adiabatic process is a change in the state of a gas that occurs without heat exchange with the environment ( Q = 0).

Curve Equation adiabatic process(adiabatics) in p-V diagram looks like:

pV k= const.

In this expression k is called adiabatic exponent(also called Poisson's ratio).

The change in entropy is:

Δ S = S 2 – S 1 = 0, those.S 2 = S 1 .

Phase transitions

In a reversible phase transition, the temperature remains constant, and the heat phase transition at constant pressure is H fp, so the change in entropy is:

.

During melting and boiling, heat is absorbed, so the entropy in these processes increases: S tv< S and< S d. In this case, the entropy of the environment decreases by the value S f.p. , so the change in the entropy of the Universe is 0, as expected for a reversible process in isolated system.

The Second Law of Thermodynamics and the "Heat Death of the Universe"

Clausius, considering the second law of thermodynamics, came to the conclusion that the entropy of the Universe as a closed system tends to a maximum, and eventually all macroscopic processes in the Universe will end. This state of the Universe is called "thermal death" - global chaos, in which no more process is possible. On the other hand, Boltzmann expressed the opinion that the current state of the Universe is a gigantic fluctuation, which implies that most of the time the Universe is still in a state of thermodynamic equilibrium (“thermal death”).

According to Landau, the key to resolving this contradiction lies in the field of general relativity: since the Universe is a system in a variable gravitational field, the law of entropy increase is not applicable to it.

Since the second law of thermodynamics (in Clausius' formulation) is based on the assumption that the universe is a closed system, other types of criticism of this law are possible. In accordance with modern physical concepts, we can only speak about the observable part of the Universe. At this stage, humanity has no way to prove either that the Universe is a closed system, or the opposite.

Entropy measurement

In real experiments it is very difficult to measure the entropy of a system. Measurement techniques are based on the thermodynamic determination of entropy and require extremely accurate calorimetry.

For simplicity, we will explore mechanical system, the thermodynamic states of which will be determined through its volume V and pressure P. To measure the entropy of a particular state, we must first measure the heat capacity at constant volume and pressure (marked C V and C P respectively) for a successful set of states between the initial state and the desired one.

Thermal capacities are related to entropy S and with temperature T according to the formula:

where is the subscript X refers to constant volume and pressure. We can integrate to get the entropy change:

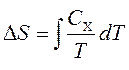
Thus, we can get the entropy value of any state ( P,V) with respect to the initial state ( P 0 ,V 0). The exact formula depends on our choice of intermediate states. For example, if the initial state has the same pressure as the final state, then

.

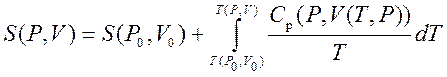In addition, if the path between the first and last states is through any first-order phase transition, latent heat associated with the transition must also be taken into account.

The entropy of the initial state must be determined independently. Ideally, the initial state is chosen as the state at an extremely high temperature, at which the system exists in the form of a gas. The entropy in this state is similar to that of a classical ideal gas, plus contributions from molecular rotations and vibrations, which can be determined spectroscopically.

Theory laboratory work

Theoretical information

In this work, it is necessary to measure the phase transition temperature - the melting point of tin, which will allow us to determine the entropy increment.

Since for reversible processes the increment of entropy d S=d Q/T, and the change in entropy during the transition of the system from the state a into a state b

,

then the change in entropy during heating and melting of tin is defined as the sum of the change in entropy during heating to the melting point and during melting of tin:

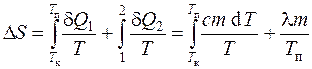or

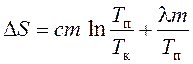, (10)

where d Q is an infinitesimal amount of heat transferred to the system at a temperature T;

d Q 1 and d Q 2 - infinitely small amounts of heat received by tin during heating and during melting;

T k is the initial (room) temperature;

T n is the melting point;

l \u003d 59 10 -3 J / kg - specific heat melting;

c = 0.23 10 -3 J/(kg K) – specific heat,

m = 0.20 kg is the mass of tin.

The macroscopic parameters of a thermodynamic system include pressure, volume, and temperature. However, there is another important physical quantity, which is used to describe states and processes in thermodynamic systems. It's called entropy.

What is entropy

This concept was first introduced in 1865 by the German physicist Rudolf Clausius. He called entropy the state function of a thermodynamic system, which determines the measure of irreversible energy dissipation.

What is entropy?

Before answering this question, let's get acquainted with the concept of "reduced heat". Any thermodynamic process that takes place in a system consists of a certain number of transitions of the system from one state to another. Reduced heat called the ratio of the amount of heat in an isothermal process to the temperature at which this heat is transferred.

Q" = Q/T .

For any open thermodynamic process there is such a function of the system, the change of which during the transition from one state to another is equal to the sum of the reduced heats. Clausius called this function " entropy and marked it with the letter S , and the ratio of the total amount of heat ∆Q to the absolute temperature T named entropy change .

Let us pay attention to the fact that the Clausius formula determines not the entropy value itself, but only its change.

What is the "irreversible dissipation of energy" in thermodynamics?

One of the formulations of the second law of thermodynamics is as follows: " A process is impossible, the only result of which is the conversion into work of the entire amount of heat received by the system". That is, part of the heat is converted into work, and some of it is dissipated. This process is irreversible. In the future, the dissipated energy can no longer do work. For example, in a real heat engine not all heat is transferred to the working body. Part of it is dissipated into the external environment, heating it.

In an ideal heat engine operating according to the Carnot cycle, the sum of all reduced heats is equal to zero. This statement is also true for any quasi-static (reversible) cycle. And it doesn't matter how many transitions from one state to another such process consists of.

If we divide an arbitrary thermodynamic process into sections of infinitesimal size, then the reduced heat in each such section will be equal to δQ/T . Full differential entropy dS = δQ/T .

Entropy is a measure of the ability of heat to dissipate irreversibly. Its change shows how much energy is randomly dissipated into the environment in the form of heat.

In a closed isolated system that does not exchange heat with the environment, the entropy does not change during reversible processes. This means that the differential dS = 0 . In real and irreversible processes, heat transfer occurs from a warm body to a cold one. In such processes, the entropy always increases ( dS ˃ 0 ). Therefore, it indicates the direction of the thermodynamic process.

The Clausius formula written as dS = δQ/T , is valid only for quasi-static processes. These are idealized processes, which are a series of equilibrium states that follow one another continuously. They were introduced into thermodynamics in order to simplify the study of real thermodynamic processes. It is considered that at any moment of time the quasi-static system is in a state of thermodynamic equilibrium. Such a process is also called quasi-equilibrium.

Of course, such processes do not exist in nature. After all, any change in the system disturbs its equilibrium state. Various transient and relaxation processes begin to occur in it, tending to return the system to a state of equilibrium. But thermodynamic processes proceeding rather slowly can be considered as quasi-static ones.

In practice, there are many thermodynamic problems, the solution of which requires the creation of complex equipment, the creation of a pressure of several hundred thousand atmospheres, the maintenance of very high temperature for a long time. And quasi-static processes make it possible to calculate the entropy for such real processes, to predict how this or that process can take place, which is very difficult to implement in practice.

Law of non-decreasing entropy

The second law of thermodynamics based on the concept of entropy is formulated as follows: “ Entropy does not decrease in an isolated system ". This law is also called the law of non-decreasing entropy.

If at some point in time the entropy of a closed system differs from the maximum, then in the future it can only increase until it reaches the maximum value. The system will come to a state of equilibrium.

Clausius believed that the universe is closed system. And if so, then its entropy tends to reach its maximum value. This means that someday all macroscopic processes in it will stop, and “thermal death” will come. But the American astronomer Edwin Powell Hubble proved that the Universe cannot be called an isolated thermodynamic system as it expands. The Soviet physicist Academician Landau believed that the law of non-decreasing entropy cannot be applied to the Universe, since it is in a variable gravitational field. modern science is not yet able to answer the question of whether our Universe is a closed system or not.

Boltzmann principle

Ludwig Boltzmann

Any closed thermodynamic system tends to a state of equilibrium. All spontaneous processes occurring in it are accompanied by an increase in entropy.

In 1877, the Austrian theoretical physicist Ludwig Boltzmann related entropy thermodynamic state with the number of microstates of the system. It is believed that the very formula for calculating the value of entropy was later developed by the German theoretical physicist Max Planck.

S = k · lnW ,

where k = 1.38 10 −23 J/K - Boltzmann's constant; W - the number of microstates of the system that implement a given macrostatic state, or the number of ways in which this state can be realized.

We see that entropy depends only on the state of the system and does not depend on how the system got to this state.

Physicists consider entropy to be a quantity that characterizes the degree of disorder in a thermodynamic system. Any thermodynamic system always strives to balance its parameters with the environment. She comes to this state spontaneously. And when the state of equilibrium is reached, the system can no longer do work. It can be assumed that it is in disarray.

Entropy characterizes the direction of the thermodynamic process of heat exchange between the system and the environment. In a closed thermodynamic system, it determines in which direction spontaneous processes proceed.

All processes occurring in nature are irreversible. Therefore, they flow in the direction of increasing entropy.

3.6. Beginnings of thermodynamics. Ideas about entropy

General information about thermodynamics

Thermodynamics is the science of the most general properties macroscopic bodies and systems in a state of thermodynamic equilibrium, and about the processes of transition from one state to another.

Classical thermodynamics studies the physical objects of the material world only in a state of thermodynamic equilibrium. This refers to a state in which, over time, a system comes under certain constant external conditions and a certain constant ambient temperature. For such equilibrium states, the concept of time is inessential. Therefore, time is not explicitly used as a parameter in thermodynamics. In its original form, this discipline was called the "mechanical theory of heat". The term "thermodynamics" was introduced into scientific literature in 1854 by W. Thomson. The equilibrium processes of classical thermodynamics also make it possible to judge the regularities of the processes that occur when an equilibrium is established, that is, it considers ways to establish thermodynamic equilibrium.

At the same time, thermodynamics considers the conditions for the existence of irreversible processes. For example, the propagation of gas molecules (the law of diffusion) eventually leads to an equilibrium state, while thermodynamics forbids the reverse transition of such a system to its original state.

The task of thermodynamics of irreversible processes was at first the study of non-equilibrium processes for states not too different from equilibrium. The emergence of the thermodynamics of irreversible processes dates back to the 1950s. the last century. It was formed on the basis of classical thermodynamics, which arose in the second half of the 19th century. The works of N. Carnot, B. Clapeyron, R. Clausius and others played an outstanding role in the development of classical thermodynamics. -Stokes are elements of future thermodynamics. Here we should name one of the pioneers of a new direction in thermodynamics - the American physicist L. Onsager ( Nobel Prize 1968), as well as the Dutch-Belgian school of I. Prigozhin, S. de Groth, P. Mazur. In 1977, Ilya Romanovich Prigozhin, a Belgian physicist and physico-chemist of Russian origin, was awarded the Nobel Prize in Chemistry “for his contribution to the theory of nonequilibrium thermodynamics, in particular to the theory of dissipative structures, and for its applications in chemistry and biology.”

Thermodynamics as a function of state

The equality of temperatures at all points of some systems or parts of one system is a condition of equilibrium.

The state of homogeneous liquids or gases is completely fixed by setting any two of the three quantities: temperature Г, volume V, pressure p. Relationship between p, V and T is called the equation of state. The French physicist B. Clapeyron in 1934 derived the equation of state for an ideal gas by combining the laws of Boyle-Mariotte and Gay-Lusac. D. I. Mendeleev combined the Clapeyron equations with the Avogadro law. According to Avogadro's law, at the same pressures R and temperature G moles of all gases occupy the same molar volume V m, so for all gases there is a molar gas constant R. Then the Clapeyron-Mendeleev equation can be written as:

pV m = R.T.

The numerical value of the molar gas constant R= 8.31 J/mol K.

First law of thermodynamics

The first law, or the first law of thermodynamics, or the law of conservation of energy for thermal systems, is convenient to consider using the example of a heat engine. The heat engine includes a heat source Q 1 , a working fluid, for example, a cylinder with a piston, under which the gas can be heated (ΔQ 1) or cooled by a refrigerator that takes heat from the working fluid ΔQ 2 . In this case, work can be done Δ A and the internal energy Δ changes U.

Thermal motion energy can be converted into mechanical motion energy, and vice versa. During these transformations, the law of conservation and transformation of energy is observed. As applied to thermodynamic processes, this is the first law of thermodynamics, established as a result of summarizing centuries-old experimental data. Experience shows that the change in internal energy ΔU is determined by the difference between the amount of heat Q 1 obtained by the system and work A:

Δ U= Q 1 – A

Q 1 = A1 + ΔU.

In differential form:

dQ= dA+ dU.

The first law of thermodynamics determines the second state function - energy, more precisely, internal energy u, which represents the energy of the chaotic movement of all molecules, atoms, ions, etc., as well as the energy of interaction of these microparticles. If the system does not exchange energy or matter with the environment (isolated system), then dU= 0, and U= const in accordance with the law of conservation of energy. It follows from this that the work BUT equal to the amount of heat Q, that is, a periodically operating engine (heat engine) cannot do more work than the energy imparted to it from the outside, which means that it is impossible to create an engine that, through some kind of energy transformation, can increase its total amount.

Circular processes (cycles). Reversible and irreversible processes

circular process(cycle) is a process in which the system goes through a series of states and returns to its original state. Such a cycle can be represented by a closed curve in the axes P, V, where P is the pressure in the system, and V is its volume. A closed curve consists of sections where the volume increases (expansion) and a section where the volume decreases (compression).

In this case, the work done per cycle is determined by the area covered by the closed curve. The cycle that flows through expansion and then compression is called direct, it is used in heat engines - periodically operating engines that do work due to heat received from outside. The cycle that goes through contraction and then expansion is called reverse and is used in refrigerating machines- periodically operating installations in which, due to the work of external forces, heat is transferred from one body to another. As a result of the circular process, the system returns to its original state:

ΔU=0, Q= A

The system can both receive heat and give it away. If the system receives Q 1 warmth, but gives Q 2 , then the thermal efficiency for the circular process

Reversible processes can occur in both forward and reverse directions.

In the ideal case, if the process occurs first in the forward and then in the opposite direction and the system returns to its original state, then in environment no change occurs. Reversible processes are an idealization of real processes in which there is always some energy loss (due to friction, thermal conductivity, etc.)

The concept of a reversible circular process was introduced into physics in 1834 by the French scientist B. Clapeyron.

The ideal cycle of a Carnot heat engine

When we talk about the reversibility of processes, it should be taken into account that this is some kind of idealization. All real processes are irreversible, and therefore the cycles they work on thermal machines, are also irreversible, and therefore nonequilibrium. However, to simplify the quantitative estimates of such cycles, it is necessary to consider them as equilibrium, that is, as if they consisted only of equilibrium processes. This is required by the well-developed apparatus of classical thermodynamics.

The famous cycle of an ideal Carnot engine is considered to be an equilibrium inverse circular process. In real conditions, any cycle cannot be ideal, since there are losses. It takes place between two heat sources constant temperatures at the heat sink T 1 and heat receiver T 2 , as well as the working body, which is taken as ideal gas(Fig. 3.1).

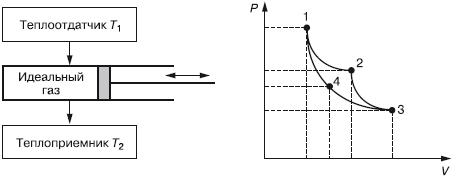
Rice. 3.1. Heat engine cycle

We believe that T 1 > T 2 and heat removal from the heat sink and heat supply to the heat sink do not affect their temperatures, T 1 and T 2 remain constant. Let us designate the gas parameters at the left extreme position of the heat engine piston: pressure - R 1 volume - V 1 , temperature T one . This is point 1 on the graph on the axes P-V. At this moment, the gas (working fluid) interacts with the heat source, the temperature of which is also T one . As the piston moves to the right, the gas pressure in the cylinder decreases and the volume increases. This will continue until the piston arrives at the position determined by point 2, where the parameters of the working fluid (gas) will take on the values ​​P 2 , V 2 , T 2 . The temperature at this point remains unchanged, since the temperature of the gas and the heat sink is the same during the transition of the piston from point 1 to point 2 (expansion). Such a process in which T does not change, is called isothermal, and curve 1–2 is called isotherm. In this process, heat is transferred from the heat source to the working fluid. Q 1 .

At point 2, the cylinder is completely isolated from the external environment (there is no heat exchange), and with further movement of the piston to the right, a decrease in pressure and an increase in volume occurs along curve 2–3, which is called adiabatic(process without heat exchange with the environment). When the piston moves to the extreme right position (point 3), the expansion process will end and the parameters will have the values ​​P 3 , V 3 , and the temperature will become equal to the temperature of the heat sink T 2. With this position of the piston, the insulation of the working fluid is reduced and it interacts with the heat sink. If we now increase the pressure on the piston, then it will move to the left at a constant temperature T 2 (compression). Hence, this compression process will be isothermal. In this process, heat Q 2 will pass from the working fluid to the heat sink. The piston, moving to the left, will come to point 4 with the parameters P 4 , V 4 and T 2 where the working fluid is again isolated from the environment. Further compression occurs along a 4–1 adiabat with an increase in temperature. At point 1, compression ends at the parameters of the working fluid P 1 , V 1 , T 1 . The piston returned to its original state. At point 1, the isolation of the working fluid from the external environment is removed and the cycle is repeated.

Efficiency of an ideal Carnot engine:

Analysis of the expression for the efficiency of the Carnot cycle allows us to draw the following conclusions:

1) The more efficient the more T 1 and less T 2 ;

2) efficiency is always less than unity;

3) Efficiency is zero at T 1 = T 2 .

The Carnot cycle gives the best use of heat, but, as mentioned above, it is idealized and is not feasible in real conditions. However, its significance is great. It allows you to determine the highest value of the efficiency of a heat engine.

The second law of thermodynamics. Entropy

The second law of thermodynamics is associated with the names of N. Carnot, W. Thomson (Kelvin), R. Clausius, L. Boltzmann, W. Nernst.

The second law of thermodynamics introduces a new state function - entropy. The term "entropy", proposed by R. Clausius, is derived from the Greek. entropia and means "transformation".

It would be appropriate to bring the concept of “entropy” in the formulation of A. Sommerfeld: “Each thermodynamic system has a state function called entropy. Entropy is calculated as follows. The system is transferred from an arbitrarily chosen initial state to the corresponding final state through a sequence of equilibrium states; all portions of heat dQ conducted to the system are calculated, each is divided by the corresponding to it absolute temperature T, and all the values ​​obtained in this way are summed up (the first part of the second law of thermodynamics). In real (non-ideal) processes, the entropy of an isolated system increases (the second part of the second law of thermodynamics)."

Accounting and conservation of the amount of energy is still not enough to judge the possibility of a particular process. Energy should be characterized not only by quantity, but also by quality. At the same time, it is essential that energy of a certain quality can spontaneously transform only into energy of a lower quality. The quantity that determines the quality of energy is entropy.

The processes in living and non-living matter as a whole proceed in such a way that the entropy in closed isolated systems increases, and the quality of energy decreases. This is the meaning of the second law of thermodynamics.

If we denote the entropy by S, then

which corresponds to the first part of the second law according to Sommerfeld.

You can substitute the expression for entropy into the equation of the first law of thermodynamics:

dU= T × dS – dU.

This formula is known in the literature as the Gibbs ratio. This fundamental equation combines the first and second laws of thermodynamics and determines, in essence, the entire equilibrium thermodynamics.

The second law establishes a certain direction of the flow of processes in nature, that is, the “arrow of time”.

The meaning of entropy is most deeply revealed in the static evaluation of entropy. In accordance with the Boltzmann principle, entropy is related to the probability of the state of the system by the known relation

S= K × LnW,

where W is the thermodynamic probability, and To is the Boltzmann constant.

The thermodynamic probability, or static weight, is understood as the number of different distributions of particles in coordinates and velocities corresponding to a given thermodynamic state. For any process that takes place in an isolated system and transfers it from state 1 to state 2, the change Δ W thermodynamic probability is positive or equal to zero:

ΔW \u003d W 2 - W 1 ≥ 0

In the case of a reversible process, ΔW = 0, that is, the thermodynamic probability, is constant. If an irreversible process occurs, then Δ W > 0 and W increases. This means that an irreversible process takes the system from a less probable state to a more probable one. The second law of thermodynamics is a statistical law, it describes the laws of the chaotic movement of a large number of particles that make up a closed system, that is, entropy characterizes the measure of randomness, randomness of particles in a system.

R. Clausius defined the second law of thermodynamics as follows:

A circular process is impossible, the only result of which is the transfer of heat from a less heated body to a hotter one (1850).

In connection with this formulation in the middle of the XIX century. the problem of the so-called heat death of the Universe was defined. Considering the Universe as a closed system, R. Clausius, relying on the second law of thermodynamics, argued that sooner or later the entropy of the Universe must reach its maximum. The transfer of heat from more heated bodies to less heated ones will lead to the fact that the temperature of all bodies of the Universe will be the same, complete thermal equilibrium will come and all processes in the Universe will stop - thermal death of the Universe will come.

The erroneous conclusion about the thermal death of the Universe is that the second law of thermodynamics cannot be applied to a system that is not a closed, but an infinitely developing system. The universe is expanding, galaxies are moving apart at ever increasing speeds. The universe is non-stationary.

The formulations of the second law of thermodynamics are based on postulates that are the result of centuries of human experience. In addition to the specified postulate of Clausius, the postulate of Thomson (Kelvin), which speaks of the impossibility of building a perpetual heat engine of the second kind (perpetuum mobile), that is, an engine that completely converts heat into work, has become most famous. According to this postulate, of all the heat received from a heat source with a high temperature - a heat sink, only a part can be converted into work. The rest must be diverted to a heat sink with a relatively low temperature, that is, for the operation of a heat engine, at least two heat sources of different temperatures are required.

This explains the reason why it is impossible to convert the heat of the atmosphere surrounding us or the heat of the seas and oceans into work in the absence of the same large-scale sources of heat with a lower temperature.

The third law of thermodynamics, or Nernst's thermal theory

Among state functions other than temperature T, internal energy U and entropy S, there are also those that contain the product T S. For example, in the study of chemical reactions, an important role is played by such state functions as free energy F= U–T S or the Gibbs potential Ф = U+ pV– TS. These state functions include the product T S. However, the value S is defined only up to an arbitrary constant S 0 , since the entropy is defined in terms of its differential dS. Therefore, without specifying S 0 , the application of the state functions becomes undefined. The question arises about the absolute value of entropy.

The thermal theory of Nernst answers this question. In Planck's formulation, it boils down to the statement: the entropy of all bodies in equilibrium tends to zero as the temperature approaches zero Kelvin:

Since the entropy is determined up to an additive constant S 0 , then it is convenient to take this constant equal to zero.

The heat theorem was formulated by Nerst at the beginning of the 20th century. (Nobel Prize in Physics in 1920). It does not follow from the first two principles, therefore, due to its generality, it can rightfully be considered as a new law of nature - the third law of thermodynamics.

Nonequilibrium thermodynamics

Non-equilibrium systems are characterized not only by thermodynamic parameters, but also by the rate of their change in time and space, which determines flows (transfer processes) and thermodynamic forces (temperature gradient, concentration gradient, etc.).

The appearance of flows in the system violates the statistical equilibrium. In any physical system, there are always processes that try to return the system to a state of equilibrium. There is a kind of confrontation between the processes of transfer, breaking the balance, and the internal processes, trying to restore it.

Processes in nonequilibrium systems have the following three properties:

1. Processes that bring the system to thermodynamic equilibrium (recovery) occur when there are no special factors that maintain a non-equilibrium state within the system itself. If the initial state is strongly non-equilibrium, and against the background of the general tendency of the system to equilibrium, subsystems of great interest are born in which the entropy locally decreases, then local subsystems arise where the order increases. In this case, the total increase for the entire system is many times greater. In an isolated system, the local decrease in entropy is, of course, temporary. In an open system, through which powerful flows flow for a long time, reducing entropy, some sort of ordered subsystems can arise. They can exist, changing and developing, for a very long time (until the flows that feed them stop).

2. The birth of local states with low entropy leads to an acceleration of the overall growth of the entropy of the entire system. Thanks to the ordered subsystems, the entire system as a whole moves faster towards more and more disordered states, towards thermodynamic equilibrium.

The presence of an ordered subsystem can speed up the exit of the entire system from a “prosperous” metastable state by millions or more times. Nothing in nature is given for free.

3. Ordered states are dissipative structures that require a large influx of energy for their formation. Such systems react to small changes in external conditions more sensitively and more diversely than the thermodynamic equilibrium state. They can easily collapse or turn into new ordered structures.

The emergence of dissipative structures has a threshold character. Nonequilibrium thermodynamics connected the threshold character with instability. The new structure is always the result of instability and arises from fluctuations.

An outstanding merit of non-equilibrium thermodynamics is the establishment of the fact that self-organization is inherent not only in "living systems". The ability to self-organize is a common property of all open systems that can exchange energy with the environment. In this case, it is nonequilibrium that serves as a source of order.

This conclusion is the main thesis for the circle of ideas of I. Prigogine's group.

The compatibility of the second law of thermodynamics with the ability of systems to self-organize is one of the greatest achievements of modern nonequilibrium thermodynamics.

Entropy and matter. Entropy change in chemical reactions

As the temperature rises, the speed increases various kinds particle motion. Hence the number of microstates of particles, and, accordingly, the thermodynamic probability W, and the entropy of matter increase. When a substance passes from solid state in the liquid, the disorder of the particles and, accordingly, the entropy (ΔS melt) increases. The disorder and, accordingly, the entropy increase especially sharply during the transition of matter from liquid state into gaseous (AS boiled). Entropy increases with the transformation of a crystalline substance into an amorphous one. The higher the hardness of a substance, the lower its entropy. The increase in atoms in a molecule and the complication of molecules leads to an increase in entropy. Entropy is measured in Cal/mol·K (entropy unit) and in J/mol·K. The entropy values ​​in the so-called standard state, that is, at 298.15 K (25 °C), are used in calculations. Then the entropy is S 0 298 . For example, the entropy of oxygen 0 3 - S 0 298 = 238.8 units e., and 0 2 - S 0 298 = 205 units e.

The absolute values ​​of the entropy of many substances are tabular and are given in reference books. For example:

H 2 0 (g) \u003d 70.8; H 2 0 (g) = 188.7; CO(g) = 197.54;

CH 4 (r) = 186.19; H 2 (g) = 130.58; HC1(g) = 186.69; HCl(p) = 56.5;

CH 3 0H (l) \u003d 126.8; Ca(k) = 41.4; Ca (OH) 2 (k) \u003d 83.4; C(diamond) = 2.38;

C (graphite) \u003d 5.74, etc.

Note: g—liquid, d—gas, j—crystals; r - solution.

The change in the entropy of the system as a result chemical reaction (Δ S) is equal to the sum of the entropies of the reaction products minus the entropies of the starting materials. For example:

CH 4 + H 2 0 (g) \u003d C0 + 3H 2 - here Δ S 0 298 = S 0 co.298 + 3 S 0 H2.298 – S 0 H4.298 – S 0 H2.298 =

197.54 \u003d 3 130.58 - 188.19 - 188.7 \u003d 214.39 J / mol K.

As a result of the reaction, the entropy increased (A S> 0), the number of moles of gaseous substances has increased.

Information entropy. Entropy in biology

Information entropy serves as a measure of the uncertainty of messages. Messages are described by a set of quantities x 1 , x 2 x n, which can be, for example, the words: p 1 , p 2 …, p n . Information entropy designate S n or H u. For a certain discrete statistical probability distribution P i use the following expression:

on condition:

Meaning S n= 0 if any probability P i= 1, and the remaining probabilities of occurrence of other quantities are equal to zero. In this case, the information is reliable, that is, there is no uncertainty in the information. The information entropy takes on its greatest value when P i are equal to each other and the uncertainty in the information is maximum.

The total entropy of several messages is equal to the sum of the entropies of individual messages (additivity property).

The American mathematician Claude Shannon, one of the founders of the mathematical theory of information, used the concept of entropy to determine the critical rate of information transfer and to create "noise-immune codes". Such an approach (the use of the probabilistic entropy function from statistical thermodynamics) turned out to be fruitful in other areas of natural science.

The concept of entropy, as shown for the first time by E. Schrödinger (1944), and then by L. Brillouin and others, is also essential for understanding many phenomena of life and even human activity.

Now it is clear that with the help of the probabilistic function of entropy it is possible to analyze all stages of the transition of the system from the state of complete chaos, which corresponds to equal probabilities and the maximum value of entropy, to the state of the maximum possible order, which corresponds to the only possible state of the elements of the system.

From the point of view of the physical and chemical processes occurring in it, a living organism can be considered as a complex open system that is in a non-equilibrium, non-stationary state. Living organisms are characterized by a balance of metabolic processes leading to a decrease in entropy. Of course, with the help of entropy it is impossible to characterize vital activity as a whole, since life is not reduced to a simple set of physical and chemical processes. It is characterized by other complex processes of self-regulation.

Questions for self-examination

1. Formulate Newton's laws of motion.

2. List the main conservation laws.

3. Name the general conditions for the validity of conservation laws.

4. Explain the essence of the symmetry principle and the connection of this principle with the laws of conservation.

5. Formulate the complementarity principle and the Heisenberg uncertainty principle.

6. What is the "collapse" of Laplacian determinism?

7. How are Einstein's postulates formulated in SRT?

8. Name and explain relativistic effects.

9. What is the essence of general relativity?

10. Why is a perpetual motion machine of the first kind impossible?

11. Explain the concept of a circular process in thermodynamics and the ideal Carnot cycle.

12. Explain the concept of entropy as a function of the state of the system.

13. Formulate the second law of thermodynamics.

14. Explain the essence of the concept of "non-equilibrium thermodynamics".

15. How is the change in entropy in chemical reactions qualitatively determined?