In 1887, Heinrich Rudolf Hertz discovered a phenomenon later called the photoelectric effect. He summed it up as follows:

If the light from a mercury lamp is directed to sodium metal, then electrons will fly out from its surface.

The modern formulation of the photoelectric effect is different:

When light quanta fall on a substance and when they are subsequently absorbed in the substance, charged particles will be partially or completely released.

In other words, when light photons are absorbed, the following is observed:

1. Emission of electrons from matter
2. Change in the electrical conductivity of a substance
3. The occurrence of photo-EMF at the interface of media with different conductivity (for example, metal-semiconductor)

Currently, there are three types of photoelectric effect:

1. Internal photoelectric effect. It consists in changing the conductivity of semiconductors. It is used in photoresistors, which are used in X-ray and ultraviolet dosimeters, and is also used in medical devices (oximeter) and in fire alarms.
2. Valve photoelectric effect. It consists in the occurrence of photo-EMF at the interface of substances with different type conductivity, as a result of carrier separation electric charge electric field. It is used in solar panels, in selenium photocells and sensors that record the level of illumination.
3. external photoelectric effect. As mentioned earlier, this is the process of electrons escaping from matter into vacuum under the action of electromagnetic radiation quanta.

Laws of the external photoelectric effect.

They were installed by Philip Lenard and Alexander Grigoryevich Stoletov at the turn of the 20th century. These scientists measured the number of ejected electrons and their speed depending on the intensity and frequency of the supply radiation.

First law (Stoletov's law):

The strength of the saturation photocurrent is directly proportional to the luminous flux, i.e. incident radiation on matter.

Theoretical formulation: When the voltage between the electrodes is equal to zero, the photocurrent is not equal to zero. This is due to the fact that after leaving the metal, the electrons have kinetic energy. In the presence of voltage between the anode and cathode, the photocurrent strength increases with increasing voltage, and at a certain voltage value, the current reaches its maximum value (saturation photocurrent). This means that all the electrons emitted every second by the cathode under the influence of electromagnetic radiation take part in the creation of the current. When the polarity is reversed, the current drops and soon becomes zero. Here the electron does work against the retarding field at the expense of the kinetic energy. With an increase in the radiation intensity (increase in the number of photons), the number of energy quanta absorbed by the metal increases, and hence the number of emitted electrons. This means that the greater the luminous flux, the greater the saturation photocurrent.

I f us ~ F, I f us = k F

k - coefficient of proportionality. The sensitivity depends on the nature of the metal. The sensitivity of a metal to the photoelectric effect increases with increasing light frequency (with decreasing wavelength).

This wording of the law is technical. It is valid for vacuum photovoltaic devices.

The number of emitted electrons is directly proportional to the density of the incident flux at its constant spectral composition.

Second law (Einstein's law):

The maximum initial kinetic energy of a photoelectron is proportional to the frequency of the incident radiant flux and does not depend on its intensity.

E kē = => ~ hυ

The third law (the law of the "red border"):

For each substance, there is a minimum frequency or maximum wavelength, beyond which the photoelectric effect is absent.

This frequency (wavelength) is called the “red border” of the photoelectric effect.

Thus, he establishes the conditions for the photoelectric effect for a given substance, depending on the work function of an electron from the substance and on the energy of the incident photons.

If the energy of a photon is less than the work function of an electron from a substance, then there is no photoelectric effect. If the photon energy exceeds the work function, then its excess after absorption of the photon goes to the initial kinetic energy of the photoelectron.

Applying it to explain the laws of the photoelectric effect.

Einstein's equation for the photoelectric effect is a special case of the law of conservation and transformation of energy. He based his theory on the laws of the still emerging quantum physics.

Einstein formulated three propositions:

1. When exposed to matter with electrons, incident photons are completely absorbed.
2. One photon interacts with only one electron.
3. One absorbed photon contributes to the release of only one photoelectron with some E kē .

The energy of a photon is spent on the work function (A out) of the electron from the substance and on its initial kinetic energy, which will be maximum if the electron leaves the surface of the substance.

E kē \u003d hυ - A out

The greater the frequency of the incident radiation, the greater the photon energy and the more (minus the work function) remains for the initial kinetic energy of photoelectrons.

The more intense the incident radiation, the more photons enter the light flux and the more electrons will be able to leave the substance and participate in the creation of the photocurrent. That is why the strength of the saturation photocurrent is promoproportional to the light flux (I f us ~ F). However, the initial kinetic energy does not depend on the intensity, because one electron absorbs the energy of only one photon.

§ 4 Energy luminosity. Stefan-Boltzmann law.

Wien's displacement law

RE(integrated energy luminosity) - energy luminosity determines the amount of energy emitted from a single surface per unit time in the entire frequency range from 0 to ∞ at a given temperature T.

Connection energy luminosity and radiance

[R e ] \u003d J / (m 2 s) \u003d W / m 2

The law of J. Stefan (Austrian scientist) and L. Boltzmann (German scientist)

where

σ \u003d 5.67 10 -8 W / (m 2 K 4) - Stef-on-Boltzmann constant.

The energy luminosity of a black body is proportional to the fourth power of thermodynamic temperature.

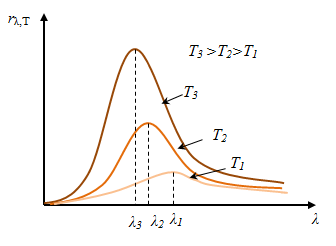Stefan-Boltzmann's law, defining dependenceREon temperature, does not give an answer regarding the spectral composition of the radiation of a completely black body. From the experimental dependence curvesrλ ,T from λ at various T it follows that the distribution of energy in the spectrum of a blackbody is uneven. All curves have a maximum, which with increasing T shifts towards shorter wavelengths. Area bounded by dependency curverλ ,T from λ, is equal to RE(this follows from geometric meaning integral) and proportional T 4 .

Wien's displacement law (1864 - 1928): Length, waves (λ max), which accounts for the maximum emissivity of an a.ch.t. at a given temperature, is inversely proportional to the temperature T.

b\u003d 2.9 10 -3 m K - Wien's constant.

The Wien shift occurs because as the temperature increases, the maximum emissivity shifts towards shorter wavelengths.

§ 5 Rayleigh-Jeans formula, Wien's formula and ultraviolet catastrophe

The Stefan-Boltzmann law allows you to determine the energy luminosityREa.h.t. by its temperature. Wien's displacement law relates body temperature to the wavelength at which the maximum emissivity falls. But neither one nor the other law solves the main problem of how great is the radiative ability per each λ in the spectrum of an A.Ch.T. at a temperature T. To do this, you need to establish a functional dependencyrλ ,T from λ and T.

Based on the concept of the continuous nature of the emission of electromagnetic waves in the law of uniform distribution of energies over degrees of freedom, two formulas were obtained for the emissivity of an a.ch.t.:

• Wine Formula

where a, b = const.

• Rayleigh-Jeans formula

k =1.38·10 -23 J/K - Boltzmann's constant.

Experimental verification showed that for a given temperature Wien's formula is correct for short waves and gives sharp discrepancies with experience in the region of long waves. The Rayleigh-Jeans formula turned out to be correct for long waves and not applicable for short ones.

The study of thermal radiation using the Rayleigh-Jeans formula showed that within the framework of classical physics it is impossible to solve the problem of the function characterizing the emissivity of an AChT. This unsuccessful attempt to explain the laws of radiation of A.Ch.T. with the help of the apparatus of classical physics, it was called the “ultraviolet catastrophe”.

If we try to calculateREusing the Rayleigh-Jeans formula, then

• “ ultraviolet catastrophe”

§6 Quantum hypothesis and Planck's formula.

In 1900, M. Planck (a German scientist) put forward a hypothesis according to which the emission and absorption of energy does not occur continuously, but in certain small portions - quanta, and the quantum energy is proportional to the oscillation frequency (Planck's formula):

h \u003d 6.625 10 -34 J s - Planck's constant or

where

Since the radiation occurs in portions, the energy of the oscillator (oscillating atom, electron) E takes only values ​​that are multiples of an integer number of elementary portions of energy, that is, only discrete values

E = n E o = nhν .

PHOTOELECTRIC EFFECT

The influence of light on the course of electrical processes was first studied by Hertz in 1887. He conducted experiments with an electric spark gap and found that when irradiated with ultraviolet radiation, the discharge occurs at a much lower voltage.

In 1889-1895. A.G. Stoletov studied the effect of light on metals using the following scheme. Two electrodes: cathode K made of the metal under study and anode A (in Stoletov's scheme - a metal mesh that transmits light) in a vacuum tube are connected to the battery so that with the help of resistance R you can change the value and sign of the voltage applied to them. When the zinc cathode was irradiated, a current flowed in the circuit, which was recorded by a milliammeter. By irradiating the cathode with light various lengths waves, Stoletov established the following basic patterns:

• The strongest effect is exerted by ultraviolet radiation;
• Under the action of light, negative charges escape from the cathode;
• The strength of the current generated by the action of light is directly proportional to its intensity.

Lenard and Thomson in 1898 measured the specific charge ( e/ m), ejected particles, and it turned out that it is equal to the specific charge of the electron, therefore, electrons are ejected from the cathode.

§ 2 External photoelectric effect. Three laws of the external photoelectric effect

The external photoelectric effect is the emission of electrons by a substance under the influence of light. Electrons escaping from a substance with an external photoelectric effect are called photoelectrons, and the current they generate is called photocurrent.

Using the Stoletov scheme, the following dependence of the photocurrent on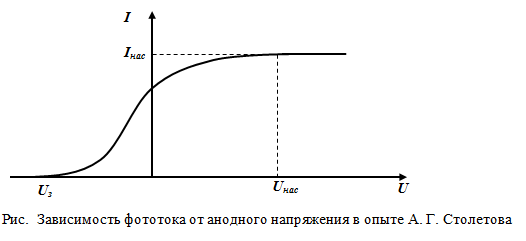

applied voltage at constant luminous flux F(that is, the I–V characteristic was obtained - current-voltage characteristic):

At some voltageUHphotocurrent reaches saturationI n - all electrons emitted by the cathode reach the anode, hence the saturation currentI n is determined by the number of electrons emitted by the cathode per unit time under the action of light. The number of released photoelectrons is proportional to the number of light quanta incident on the cathode surface. And the number of light quanta is determined by the luminous flux F falling on the cathode. Number of photonsNfalling over timet to the surface is determined by the formula:

where W- radiation energy received by the surface during the time Δt,

photon energy,

F e -luminous flux (radiation power).

1st law of external photoelectric effect (Stoletov's law):

At a fixed frequency of the incident light, the saturation photocurrent is proportional to the incident light flux:

Ius~ Ф, ν =const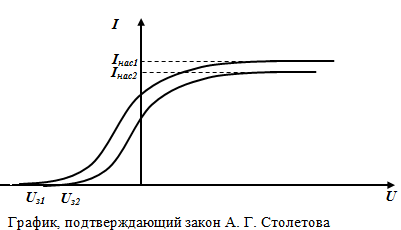

Uh - retarding voltage is the voltage at which no electron can reach the anode. Therefore, the law energy conservation in this case, we can write: the energy of the emitted electrons is equal to the retarding energy electric field

therefore, one can find the maximum velocity of the emitted photoelectronsVmax

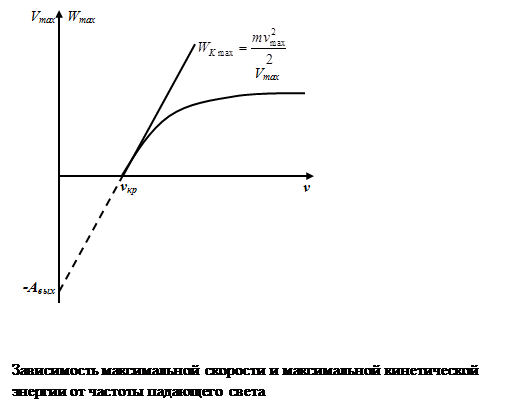
2nd law of photoelectric effect : maximum initial speedVmaxphotoelectrons does not depend on the intensity of the incident light (on F), but is determined only by its frequency ν

3rd law of photoelectric effect : for every substance there is "red border" photo effect, that is, the minimum frequency ν kp , depending on the chemical nature of the substance and the state of its surface, at which it is still possible external photoelectric effect.

The second and third laws of the photoelectric effect cannot be explained using the wave nature of light (or the classical electromagnetic theory Sveta). According to this theory, the pulling out of conduction electrons from the metal is the result of their "rocking" electromagnetic field light wave. As the light intensity increases ( F) the energy transmitted by the electron of the metal should increase, therefore, it should increaseVmax, and this contradicts the 2nd law of the photoelectric effect.

Since, according to the wave theory, the energy transmitted by the electromagnetic field is proportional to the intensity of light ( F), then any light; frequency, but a sufficiently high intensity would have to pull out electrons from the metal, that is, the red border of the photoelectric effect would not exist, which contradicts the 3rd law of the photoelectric effect. The external photoelectric effect is inertialess. BUT wave theory cannot explain his lack of inertia.

§ 3 Einstein's equation for the external photoelectric effect.

Work function

In 1905, A. Einstein explained the photoelectric effect on the basis of quantum concepts. According to Einstein, light is not only emitted by quanta in accordance with Planck's hypothesis, but propagates in space and is absorbed by matter in separate portions - quanta with energy E0 = hv. The quanta of electromagnetic radiation are called photons.

Einstein's equation (the law of conservation of energy for the external photo effect):

Incident photon energy hv is spent on pulling out an electron from the metal, that is, on the work function A out, and to the message to the emitted photoelectron kinetic energy.

The smallest energy that must be imparted to an electron in order to remove it from solid body into a vacuum is called work function.

Since the energy of Ferm to E Fdepends on temperature and E F, also changes with temperature, then, therefore, A out temperature dependent.

In addition, the work function is very sensitive to surface finish. Applying a film to the surface Sa, SG, Wa) on the WA outdecreases from 4.5 eV for pureW up to 1.5 h 2 eV for impurityW.

Einstein's equation makes it possible to explain in c e three laws of the external photo-effect,

1st law: each quantum is absorbed by only one electron. Therefore, the number of ejected photoelectrons should be proportional to the intensity ( F) Sveta

2nd law: Vmax~ ν and since A out does not depend on F, then andVmax does not depend on F

3rd law: As ν decreases,Vmax and for ν = ν 0 Vmax = 0, therefore,hν 0 = A out, therefore, i.e. there is a minimum frequency, starting from which the external photoelectric effect is possible.

The photoelectric effect is the phenomenon of pulling out the light of electrons from the metal (external)

A photoelectric effect is the emission of electrons by a substance under the action of light (or any other electromagnetic radiation). In condensed substances (solid and liquid), external and internal photoelectric effects are distinguished.

The external photoelectric effect (photoelectron emission) is the emission of electrons by a substance under the action of electromagnetic radiation. Electrons emitted from a substance by an external photoelectric effect are called photoelectrons, and electricity, formed by them during ordered movement in an external electric field, is called a photocurrent.

The internal photoelectric effect is the redistribution of electrons over energy states in solid and liquid semiconductors and dielectrics, which occurs under the action of radiation. It manifests itself in a change in the concentration of charge carriers in the medium and leads to the appearance of photoconductivity or the valve photoelectric effect.

Photoconductivity is an increase in the electrical conductivity of a substance under the influence of radiation.

The valve photoelectric effect is a kind of internal photoelectric effect - this is the occurrence of EMF (photo EMF) when illuminating the contact of two different semiconductors or a semiconductor and a metal (in the absence of an external electric field). The valve photoelectric effect opens the way for the direct conversion of solar energy into electrical energy.

The multiphoton photoelectric effect is possible if the light intensity is very high (for example, when using laser beams). In this case, an electron emitted by a metal can simultaneously receive energy not from one, but from several photons.

Stoletov's laws

First Law
Investigating the dependence of the current strength in the balloon on the voltage between the electrodes with a constant light flux to one of them, he established the first law of the photoelectric effect.

The saturation photocurrent is proportional to the light flux incident on the metal.

Because the current strength is determined by the magnitude of the charge, and the luminous flux is determined by the energy of the light beam, then we can say:

the number of electrons knocked out of a substance in 1 s is proportional to the intensity of the light falling on this substance.

Second Law

Changing the lighting conditions at the same installation, A. G. Stoletov discovered the second law of the photoelectric effect: the kinetic energy of photoelectrons does not depend on the intensity of the incident light, but depends on its frequency.

It followed from the experiment that if the frequency of light is increased, then with a constant light flux, the blocking voltage increases, and, consequently, the kinetic energy of photoelectrons also increases. Thus, the kinetic energy of photoelectrons increases linearly with the frequency of light.

third law

Replacing the material of the photocathode in the device, Stoletov established the third law of the photoelectric effect: for each substance there is a red border of the photoelectric effect, i.e. there is a minimum frequency nmin at which the photoelectric effect is still possible.

The law of conservation of energy, written by Einstein for the photoelectric effect, is the statement that the energy of a photon acquired by an electron allows it to leave the surface of the conductor, having done the work function. The rest of the energy is realized in the form of the kinetic energy of the now free electron

The energy of the incident photon is expended on the electron performing the work function A from the metal and on communicating the kinetic energy mv2max/2 to the emitted photoelectron. According to the law of conservation of energy,

(203.1)

Equation (203.1) is called the Einstein equation for the external photoelectric effect.

Compton effect

Change in the wavelength of light upon scattering by bound electrons

EXPERIMENTS OF RUTERFORD. PLANETARY MODEL OF THE ATOM

Rutherford's experiments. The mass of electrons is several thousand times less than the mass of atoms. Since the atom as a whole is neutral, therefore, the bulk of the atom falls on its positively charged part.

For pilot study distribution positive charge, and hence the mass inside the atom Ernest Rutherford proposed in 1906 to apply the probing of the atom with the help of -particles. These particles arise from the decay of radium and some other elements. Their mass is about 8000 times the mass of the electron, and the positive charge is equal in modulus to twice the charge of the electron. These are nothing but fully ionized helium atoms. The speed of -particles is very high: it is 1/15 of the speed of light.

With these particles, Rutherford bombarded the atoms of heavy elements. Electrons, due to their small mass, cannot noticeably change the trajectory of the -particle, just as a pebble of several tens of grams in a collision with a car cannot significantly change its speed.

Planetary model of the atom. Based on his experiments, Rutherford created a planetary model of the atom. In the center of the atom is located a positively charged nucleus, in which almost all the mass of the atom is concentrated. In general, the atom is neutral. Therefore, the number of intraatomic electrons, as well as the charge of the nucleus, is equal to the ordinal number of the element in the periodic system. It is clear that the electrons cannot rest inside the atom, since they would fall on the nucleus. They move around the core, just as the planets revolve around the sun. This character of the electron motion is determined by the action of the Coulomb forces of attraction from the side of the nucleus.

Planck's hypothesis, which brilliantly solved the problem of the thermal radiation of a black body, was confirmed and further developed in explaining the photoelectric effect, a phenomenon whose discovery and study played an important role in the development of quantum theory. In 1887, G. Hertz discovered that when the negative electrode is illuminated with ultraviolet rays, the discharge between the electrodes occurs at a lower voltage. This phenomenon, as shown by the experiments of V. Galvaks (1888) and A.G. Stoletov (1888–1890) is due to the knocking out of negative charges from the electrode under the action of light. Electron has not yet been discovered. Only in 1898 J.J. Thompson and F. Leonard, having measured the specific charge of the particles emitted by the body, found that these are electrons.

There are external, internal, valve and multiphoton photoelectric effects.

external photoelectric effect called the emission of electrons by a substance under the action of electromagnetic radiation. external photoelectric effect observed in solids (metals, semiconductors, dielectrics), as well as in gases on individual atoms and molecules (photoionization).

Internal photoelectric effect - is caused electromagnetic radiation transitions of electrons inside a semiconductor or dielectric from bound to free states without escaping to the outside. As a result, the concentration of current carriers inside the body increases, which leads to the appearance of photoconductivity (an increase in the electrical conductivity of a semiconductor or dielectric when it is illuminated) or to the appearance of an electromotive force (EMF).

valve photoelectric effect is a kind of internal photoelectric effect, is the occurrence of EMF (photo EMF) when illuminating the contact of two different semiconductors or a semiconductor and a metal (in the absence of an external electric field). The valve photoelectric effect opens the way for the direct conversion of solar energy into electrical energy.

Multiphoton photoelectric effect possible if the light intensity is very high (for example, when using laser beams). In this case, an electron emitted by a metal can simultaneously receive energy not from one, but from several photons.

The first fundamental studies of the photoelectric effect were carried out by the Russian scientist A.G. Stoletov. A schematic diagram for studying the photoelectric effect is shown in fig. 2.1.

	Rice. 2.1	Rice. 2.2

Two electrodes (cathode To from the material under study and the anode BUT, for which Stoletov used a metal mesh) in a vacuum tube are connected to the battery so that using a potentiometer R you can change not only the value, but also the sign of the voltage applied to them. Current generated by illuminating the cathode monochromatic light(through quartz glass), measured by a milliammeter included in the circuit.

In 1899, J. J. Thompson and F. Lenard proved that during the photoelectric effect, light knocks electrons out of matter.

Volt-ampere characteristic (VAC) of the photoelectric effect - photocurrent dependence I, formed by the electron flow, on voltage, is shown in fig. 2.2.

This dependence corresponds to two different energy illuminations of the cathode (the frequency of light is the same in both cases). As you increase U the photocurrent gradually increases, i.e. all more photoelectrons reaches the anode. The flat character of the curves shows that the electrons are emitted from the cathode at different velocities.

Maximum value saturation photocurrent is determined by such a voltage value U, at which all the electrons emitted by the cathode reach the anode:

where n is the number of electrons emitted by the cathode in 1 s.

It follows from the VAC, at U= 0 the photocurrent does not disappear. Consequently, the electrons knocked out of the cathode have some initial velocity υ, and hence a non-zero kinetic energy, so they can reach the cathode without an external field. In order for the photocurrent to become zero, it is necessary to apply retarding voltage . At , none of the electrons, even if they have the maximum speed when leaving the cathode, can overcome the retarding field and reach the anode. Consequently,

,

(2.1.1)

those. by measuring the retarding voltage , it is possible to determine the maximum values ​​of the speed and kinetic energy of the photoelectron.

When studying the current-voltage characteristics of various materials at different frequencies of the radiation incident on the cathode and different energy illumination of the cathode and generalizing the data obtained, three laws of the external photoelectric effect were established.

To view demos, click on the appropriate hyperlink:

Introduction

2. Laws of Stoletov

3. Einstein's equation

4. Internal photoelectric effect

Bibliography

Introduction

Numerous optical phenomena have been consistently explained on the basis of ideas about the wave nature of light. However, in late XIX- the beginning of the XX century. Phenomena such as the photoelectric effect, X-rays, the Compton effect, radiation of atoms and molecules were discovered and studied, thermal radiation and others, whose explanation with wave point vision was impossible. An explanation of the new experimental facts was obtained on the basis of corpuscular ideas about the nature of light. A paradoxical situation has arisen associated with the use of completely opposite physical models waves and particles to explain optical phenomena. In some phenomena, light manifested wave properties, in others - corpuscular.

Among the various phenomena in which the effect of light on matter is manifested, an important place is occupied by photoelectric effect , that is, the emission of electrons by a substance under the influence of light. The analysis of this phenomenon led to the idea of ​​light quanta and played an extremely important role in the development of modern theoretical concepts. At the same time, the photoelectric effect is used in photocells, which have received exceptionally wide application in the most diverse fields of science and technology and promise even richer prospects.

1. The history of the discovery of the photoelectric effect

The discovery of the photoelectric effect should be attributed to 1887, when Hertz discovered that illuminating the spark gap electrodes under voltage with ultraviolet light facilitates the spark between them.

The phenomenon discovered by Hertz can be observed in the following easily feasible experiment (Fig. 1).

The value of the spark gap F is selected in such a way that in a circuit consisting of a transformer T and a capacitor C, the spark jumps with difficulty (once or twice per minute). If the electrodes F, made of pure zinc, are illuminated with the light of an Hg mercury lamp, then the discharge of the capacitor is greatly facilitated: a spark begins to jump. 1. Scheme of Hertz's experiment.

The photoelectric effect was explained in 1905 by Albert Einstein (for which he received Nobel Prize) based on Max Planck's hypothesis about the quantum nature of light. Einstein's work contained an important new hypothesis- if Planck suggested that light is emitted only in quantized portions, then Einstein already believed that light exists only in the form of quantum portions. From the concept of light as particles (photons), Einstein's formula for the photoelectric effect immediately follows:

, is the kinetic energy of the emitted electron, is the work function for a given substance, is the frequency of the incident light, is Planck's constant, which turned out to be exactly the same as in Planck's formula for black body radiation.

From this formula follows the existence of the red boundary of the photoelectric effect. Thus, studies of the photoelectric effect were among the earliest quantum mechanical studies.

2. Laws of Stoletov

For the first time (1888–1890), analyzing in detail the phenomenon of the photoelectric effect, the Russian physicist A.G. Stoletov obtained fundamentally important results. Unlike previous researchers, he took a small potential difference between the electrodes. The scheme of Stoletov's experiment is shown in fig. 2.

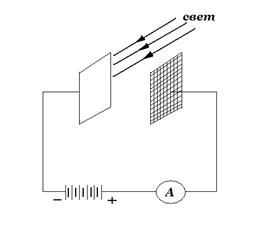
Two electrodes (one in the form of a grid, the other flat), located in a vacuum, are attached to the battery. The ammeter included in the circuit is used to measure the resulting current strength. Irradiating the cathode with light of various wavelengths, Stoletov came to the conclusion that ultraviolet rays have the most effective effect. In addition, it was found that the strength of the current generated by the action of light is directly proportional to its intensity.

In 1898, Lenard and Thomson, using the method of charge deflection in electric and magnetic fields determined the specific charge of charged particles ejected 2. Scheme of Stoletov's experiment.

light from the cathode, and received the expression

SGSE unit s/g, coinciding with the known specific charge of the electron. From this it followed that under the action of light, electrons are ejected from the material of the cathode.

By summarizing the results obtained, the following patterns photoelectric effect:

1. With a constant spectral composition of light, the strength of the saturation photocurrent is directly proportional to the light flux incident on the cathode.

2. The initial kinetic energy of the electrons ejected by the light increases linearly with the frequency of the light and does not depend on its intensity.

3. The photoelectric effect does not occur if the frequency of light is less than a certain value characteristic of each metal

called the red border.

The first pattern of the photoelectric effect, as well as the occurrence of the photoelectric effect itself, can be easily explained based on the laws of classical physics. Indeed, the light field, acting on the electrons inside the metal, excites their oscillations. The amplitude of the forced oscillations can reach such a value at which the electrons leave the metal; then the photoelectric effect is observed.

In view of the fact that, according to the classical theory, the intensity of light is directly proportional to the square electric vector, the number of ejected electrons increases with increasing light intensity.

The second and third laws of the photoelectric effect are not explained by the laws of classical physics.

Studying the dependence of the photocurrent (Fig. 3), which occurs when a metal is irradiated with a flow monochromatic light, on the potential difference between the electrodes (such a dependence is usually called the volt-ampere characteristic of the photocurrent), it was found that: 1) the photocurrent occurs not only when

, but also for ; 2) the photocurrent is different from zero to a negative value of the potential difference strictly defined for a given metal, the so-called retarding potential; 3) the magnitude of the blocking (delaying) potential does not depend on the intensity of the incident light; 4) the photocurrent increases with decreasing absolute value of the retarding potential; 5) the value of the photocurrent increases with growth and from a certain value the photocurrent (the so-called saturation current) becomes constant; 6) the value of the saturation current increases with increasing intensity of the incident light; 7) the value of the delay 3. Feature

potential depends on the frequency of the incident light; photocurrent.

8) the speed of electrons ejected under the action of light does not depend on the intensity of light, but depends only on its frequency.

3. Einstein's equation

The phenomenon of the photoelectric effect and all its laws are well explained using the quantum theory of light, which confirms quantum nature Sveta.

As already noted, Einstein (1905), developing quantum theory Planck put forward the idea that not only radiation and absorption, but also the propagation of light occurs in portions (quanta), the energy and momentum of which are:

, , is the unit vector directed along the wave vector. Applying the law of conservation of energy to the phenomenon of the photoelectric effect in metals, Einstein proposed the following formula: , (1) - the work function of the electron from the metal, - the speed of the photoelectron. According to Einstein, each quantum is absorbed by only one electron, and part of the energy of the incident photon is spent on the metal electron work function, while the remaining part imparts kinetic energy to the electron.

As follows from (1), the photoelectric effect in metals can arise only when

, otherwise the photon energy will be insufficient to eject an electron from the metal. The lowest frequency of light , under which the photoelectric effect occurs, is obviously determined from the condition , . (2)

The light frequency determined by condition (2) is called the "red border" of the photoelectric effect. The word "red" has nothing to do with the color of light in which the photoelectric effect occurs. Depending on the type of metal, the “red border” of the photoelectric effect can correspond to red, yellow, violet, ultraviolet light, etc.

With the help of Einstein's formula, other regularities of the photoelectric effect can also be explained.

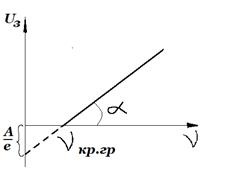
Let's assume that

, i.e. there is a retarding potential between the anode and cathode. If the kinetic energy of the electrons is sufficient, then they, having overcome the decelerating field, create a photocurrent. The photocurrent involves those electrons for which the condition is satisfied . The value of the retarding potential is determined from the condition , (3) is the maximum velocity of ejected electrons. Rice. four.

Substituting (3) into (1), we obtain

, .

Thus, the magnitude of the retarding potential does not depend on the intensity, but depends only on the frequency of the incident light.

The work function of electrons from a metal and Planck's constant can be determined by plotting the dependence

on the frequency of the incident light (Fig. 4). As you can see, the segment cut off from the potential axis gives .

In view of the fact that the light intensity is directly proportional to the number of photons, an increase in the intensity of the incident light leads to an increase in the number of ejected electrons, i.e., to an increase in the photocurrent.

Einstein's formula for the photoelectric effect in non-metals has the form

. - the work of detachment of a bound electron from an atom inside non-metals - is explained by the fact that, unlike metals, where there are free electrons, in non-metals, electrons are in a state bound to atoms. Obviously, when light falls on non-metals, part of the light energy is spent on the photoelectric effect in the atom - on the separation of the electron from the atom, and the rest is spent on the work function of the electron and imparting kinetic energy to the electron.

Conduction electrons do not spontaneously leave the metal in a noticeable amount. This is explained by the fact that the metal represents a potential well for them. It is possible to leave the metal only for those electrons whose energy is sufficient to overcome the potential barrier existing on the surface. The forces that cause this barrier have the following origin. Random removal of an electron from the outer layer positive ions lattice leads to the appearance in the place that the electron left, an excess positive charge. The Coulomb interaction with this charge causes the electron, whose speed is not very high, to return back. Thus, individual electrons leave the metal surface all the time, move away from it by several interatomic distances, and then turn back. As a result, the metal is surrounded by a thin cloud of electrons. This cloud together with the outer layer of ions forms a double electric layer (Fig. 5; circles - ions, black dots - electrons). The forces acting on an electron in such a layer are directed inside the metal. The work done against these forces when transferring an electron from the metal to the outside goes to increase the potential energy of the electron

(Fig. 5).

In this way, potential energy valence electrons inside the metal is less than outside the metal by an amount equal to the depth of the potential well

(Fig. 6). The change in energy occurs over a length of the order of several interatomic distances; therefore, the walls of the well can be considered vertical.

Potential energy of an electron

Rice. 6.

and potential

the point at which the electron is located have opposite signs. It follows from this that the potential inside the metal is greater than the potential in the immediate vicinity of its surface by .

Giving excess positive charge to the metal increases the potential both on the surface and inside the metal. The potential energy of an electron decreases accordingly (Fig. 7, a).

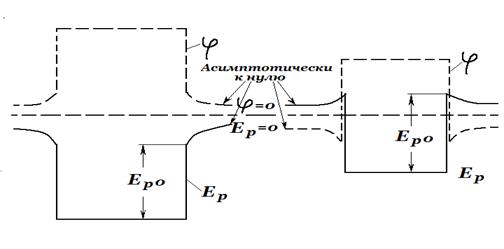
a) b)

The values ​​of the potential and potential energy at infinity are taken as the reference point. The introduction of a negative charge lowers the potential inside and outside the metal. Accordingly, the potential energy of the electron increases (Fig. 7, b).

The total energy of an electron in a metal is the sum of the potential and kinetic energies. At absolute zero the values ​​of the kinetic energy of the conduction electrons range from zero to the energy coinciding with the Fermi level

. On fig. eight energy levels The conduction bands are inscribed in the potential well (dotted lines show levels unoccupied at 0K). To move out of the metal, different electrons need to be given different energies. So, an electron located at the lowest level of the conduction band must be given energy; for an electron at the Fermi level, the energy is sufficient .

The smallest energy that must be imparted to an electron in order to remove it from a solid or liquid body into a vacuum is called exit work. The work function of an electron from a metal is determined by the expression

. (4)

We have obtained this expression under the assumption that the temperature of the metal is 0K. At other temperatures, the work function is also defined as the difference between the depth of the potential well and the Fermi level, i.e., definition (4) is extended to any temperature. The same definition applies to semiconductors.

The Fermi level depends on temperature. In addition, due to the change in the average distances between atoms due to thermal expansion, the depth of the potential well changes slightly.

. This results in the work function being slightly temperature dependent.

The work function is very sensitive to the state of the metal surface, in particular to its purity. Having chosen properly Fig. eight.

surface coating, the work function can be greatly reduced. So, for example, deposition of an oxide layer of an alkaline earth metal (Ca, Sr, Ba) on the surface of tungsten reduces the work function from 4.5 eV (for pure W) to 1.5 - 2 eV.

4. Internal photoelectric effect

Above, we talked about the release of electrons from the illuminated surface of a substance and their transition to another medium, in particular, to vacuum. This emission of electrons is called photoelectronic emission, but the phenomenon itself external photoelectric effect. Along with it is also known and widely used for practical purposes, the so-called internal photoelectric effect, at which, unlike the external one, optically excited electrons remain inside the illuminated body without violating the neutrality of the latter. In this case, the concentration of charge carriers or their mobility changes in the substance, which leads to a change electrical properties matter under the influence of light falling on it. The internal photoelectric effect is inherent only in semiconductors and dielectrics. It can be detected, in particular, by the change in the conductivity of homogeneous semiconductors when they are illuminated. Based on this phenomenon, photoconductivity a large group of light receivers has been created and is constantly being improved - photoresistors. They mainly use selenide and cadmium sulfide.

In inhomogeneous semiconductors, along with a change in conductivity, the formation of a potential difference is also observed (photo - emf). This phenomenon (photovoltaic effect) is due to the fact that, due to the homogeneity of the conductivity of semiconductors, there is a spatial separation inside the volume of the conductor of optically excited electrons carrying negative charge and microzones (holes) that appear in the immediate vicinity of atoms from which electrons have been torn off, and, like particles, carry a positive elementary charge. Electrons and holes are concentrated at different ends of the semiconductor, as a result of which electromotive force, thanks to which it is produced without the application of an external emf. electric current in a load connected in parallel with an illuminated semiconductor. In this way, a direct conversion of light energy into electrical energy is achieved. It is for this reason that photovoltaic light receivers are used not only for registering light signals, but in electrical circuits as sources of electrical energy.

The main industrial types of such receivers operate on the basis of selenium and silver sulfide. Silicon, germanium and a number of compounds - GaAs, InSb, CdTe and others are also very common. Photovoltaic cells, used to convert solar energy into electrical energy, have become particularly widespread in space research as on-board power sources. They have a relatively high rate useful action(up to 20%), very convenient in autonomous flight spaceship. In modern solar cells, depending on the semiconductor material, photo - emf. reaches 1 - 2 V, current removal from

- several tens of milliamps, and for 1 kg of mass, the output power reaches hundreds of watts.

5. Application of the phenomenon of photoelectric effect

Currently, on the basis of the external and internal photoelectric effect, countless radiation receivers are being built that convert the light signal into electrical and combined common name – photocells. They are widely used in engineering and scientific research. A variety of objective optical measurements are unthinkable in our time without the use of one or another type of photocells. Modern photometry, spectrometry and spectrophotometry in the widest range of the spectrum, spectral analysis of matter, objective measurement of very weak light fluxes, observed, for example, in the study of spectra Raman scattering light, in astrophysics, biology, etc. it is difficult to imagine without the use of photocells; registration of infrared spectra is often carried out by special photocells for the long-wavelength region of the spectrum. Photocells are unusually widely used in technology: control and management of production processes, various communication systems from image transmission and television to optical communication on lasers and space technology represent a far from complete list of the most diverse technical issues in modern industry and communications.

The history of the creation of photocells has more than 130 years. The first photoelectric cell based on the internal photoelectric effect and using the phenomenon of photoconductivity was built in 1875, the first vacuum photocell based on the external photoelectric effect was built in 1889. industrial production vacuum photocells in Russia was organized by P.V. Timofeev in 1930. It is interesting to note that photocells using the external photoelectric effect were widely developed earlier, although the internal photoelectric effect was discovered at least 50 years earlier. Only in the forties of our century, thanks to the rapid development of semiconductor physics and a detailed study of the internal photoelectric effect, the creation of new photocells based on semiconductor materials began.

The huge variety of tasks solved with the help of photocells has given rise to an extremely wide variety of types of photocells with different technical characteristics. The choice of the optimal type of photocells for solving each specific task is based on the knowledge of these characteristics. For photocells with an external photoelectric effect (vacuum photocells), knowledge of the following characteristics is required: the working region of the spectrum; relative characteristic of the spectral sensitivity (it is constructed as a dependence on the wavelength of the incident light of a dimensionless value of the ratio of the spectral sensitivity under monochromatic illumination to the sensitivity at the maximum of this characteristic); integral sensitivity (it is determined when the photocell is illuminated with a standard light source); quantum yield value (percentage ratio of the number of emitted photoelectrons to the number of photons incident on the photocathode); inertia (for vacuum photocells, it is usually determined through the time of flight of electrons from the photocathode to the anode). An important parameter is also the dark current of the photocell, which is the sum of the thermal emission of the photocathode at room temperature and the leakage current.

Depending on the material of the photocathode and the material of the photocell bulb, they can be used in the range of 0.2 - 1.1 µm. Their integrated sensitivity lies within 20 - 100 μA per 1 lm of luminous flux, and thermal emission - within

. A very important advantage of vacuum photocells is their high constancy and linearity of the connection of the light flux with the photocurrent. Therefore, for a long time they were predominantly used in objective photometry, spectrometry, spectrophotometry, and spectral analysis in the visible ultraviolet region of the spectrum. The main disadvantage of vacuum photocells for light measurements should be considered the smallness of the electrical signals generated by these light receivers. The last drawback is completely eliminated in photomultiplier tubes (PMTs), representing, as it were, the development of photocells. PMTs were first built in 1934.

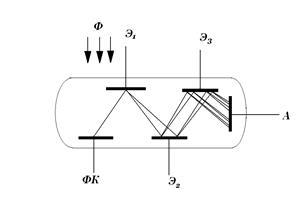
Rice. 9. Scheme of the photomultiplier device

The principle of operation of the PMT can be seen in Fig. 9. Photoelectrons emitted from the photocathode of the PC under the action of an electric field are accelerated and fall on the first intermediate electrode

. Falling on it, photoelectrons cause the emission of secondary electrons, and under certain conditions, this secondary emission can exceed the initial flux of photoelectrons by several times. The configuration of the electrodes is such that most of the photoelectrons fall on the electrode, and most of the secondary electrons fall on the next electrode, where the multiplication process is repeated, and so on. anode. The overall gain of such systems reaches , and the integral sensitivity of the PMT reaches thousands of amperes per lumen. This, of course, does not mean the possibility of obtaining large currents, but only indicates the possibility of measuring small light fluxes.

Obviously, the same technical characteristics as those of vacuum photocells, as well as the gain and its dependence on the supply voltage, completely characterize the PMT. At present, the latter are replacing vacuum photocells everywhere. The disadvantages of PMTs include the need to use a high-voltage and stabilized power supply, somewhat worse sensitivity stability, and high noise. However, by applying cooling of the photocathodes and measuring not the output current, but the number of pulses, each of which corresponds to one photoelectron, these shortcomings can be largely suppressed.

The great advantage of all light receivers using the external photoelectric effect is the fact that their photocurrent does not change when the load changes. This means that at low values ​​of the photocurrent, one can apply an almost arbitrarily large load resistance and thereby achieve a voltage drop across it that is convenient enough for recording and amplification. On the other hand, replacing the resistance with a capacitance, it is possible, by measuring the voltage across this capacitance, to obtain a value proportional to the average value of the luminous flux over a given time interval. The latter is extremely important in those cases when it is necessary to measure the luminous flux from unstable light - a situation typical for spectral analysis measurements.

Spectrometry in the infrared region of the spectrum cannot be performed using vacuum photocells and photomultipliers for the reason that modern photocathodes have a red border no higher than 1100 nm. However, materials are already known that make it possible to advance up to 3–4 μm. Therefore, in the infrared region, photocells are used that work on the basis of an internal photoelectric effect. These include uncooled photoresistors based on InSb, PbSe and PbS, which can be used down to 6 µm, and deeply cooled photoresistors based on germanium doped with gold, zinc, copper and other metals, suitable up to 40 µm.

For measurements in the longer wavelength region of the spectrum, thermal receivers are used; the latter either change their conductivity, or an emf is created on them. when heated by incident radiation.

Semiconductor photocells are not characterized by a strict linearity of the dependence of the magnitude of the electrical signal on the illumination. This disadvantage, as well as the variability of the sensitivity of the photocell, the instability of its power supply, and the drift of the amplification of the measuring circuit, are eliminated by using a two-beam system, in which not the absolute value of the intensity of the light transmitted through the absorbing substance is measured, but its ratio to the light intensity of the translucent source.

In extremely large numbers In cases where photocells are used, strict requirements are not imposed on their measuring properties. Therefore, photocells operating on the basis of the internal photoelectric effect, due to their small dimensions, low supply voltages and a number of design advantages, are widely used for automatic systems, control systems, solar energy conversion, production control, etc., except for those cases where relatively the low inertial properties of these photocells hinder their use.

Bibliography

1. Landsberg G.S. Optics. Proc. allowance. – 5th ed. correct – M.: Science. Main edition of physical and mathematical literature, 1976. - 928 p.

2. Godzhaev N.M. Optics. Proc. allowance for universities. - M .: " graduate School", 1977. - 432 p.

3. Shpolsky E.V. Atomic physics. Volume 1: Introduction to Atomic Physics. Tutorial. – 7th ed. corrected – M.: Science. Main edition of physical and mathematical literature, 1984. - 552 p.

4. Saveliev I.V. General physics course: Proc. allowance. In 3 volumes. T. 3. Quantum optics. Atomic physics. Solid state physics. Physics atomic nucleus and elementary particles. - 3rd ed. correct – M.: Nauka, Ch. ed. physical - mat. lit., 1987. - 320 p.

5. Gershenzon E.M., Malov N.N., Mansurov A.N. Optics and atomic physics: Proc. allowance for students. higher ped. textbook establishments. - M.: Publishing Center "Academy", 2000. - 408 p.