What does elementary particle mean? Elementary particles and their main characteristics. photon - a particle that carries electromagnetic interaction
ELEMENTARY PARTICLES
Introduction
E. h. in the exact meaning of this term are primary, indecomposable particles, of which, by assumption, all matter consists. In the concept of "E. h." in modern In physics, the idea of primitive entities that determine all the observable properties of the material world finds expression, an idea that originated in the early stages of the formation of natural science and has always played an important role in its development.
Stable particles are particles that cannot be decomposed due to the rate of conservation of, for example, an electron as the lightest electrically charged particle and a proton as the lightest baryon. Every particle has an antiparticle with the same values for spin and mass. The charges of antiparticles have the opposite sign. For example, the proton is positively charged, while the antiproton is negative. Some particles, all of whose charges are zero, are their own antiparticles. An example is the photon.
Leptons are particles of elementary matter that are not subject to strong interaction. As the lightest charged particle, the electron is stable. For historical reasons, the electron's antiparticle is labeled. In the production or destruction of a lepton, an antilepton is always produced or destroyed.
The concept of "E. h." was formed in close connection with the establishment of the discrete nature of the structure of matter on the microscopic. level. Discovery at the turn of the 19th-20th centuries. the smallest carriers of the properties of matter - molecules and atoms - and the establishment of the fact that molecules are built from atoms, for the first time made it possible to describe all observed substances as combinations of a finite, albeit large, number of structural components - atoms. Detection in the future constituent parts atoms - electrons and nuclei, the establishment of the complex nature of the nuclei themselves, which turned out to be built from only two particles (nucleons): protons and neutrons, significantly reduced the number of discrete elements that form the properties of matter, and gave reason to assume that the chain of constituent parts of matter ends with discrete structureless formations - E. h. 20th century the possibility of interpreting e-magn. field as a collection of special particles - photons - additionally strengthened the conviction in the correctness of this approach.
Gauge bosons - particles through the exchange of which interactions are carried out
A list of additional features can be found in the article. Unlike leptons, they carry one and are therefore subject to strong interactions. When a quark is created or destroyed, an antiquark is always created or destroyed. Quarks are never observed freely, but only bound in hadrons.
Particle exchange
The properties of quarks are described in detail in the article. Exchangeable particles mediate the interaction between elementary particles. They are predicted in the standard model, have an integer spin, and so. The physical technical expression for exchange particles is gauge bosons, since the Standard Model is an optical theory.
However, the stated assumption, generally speaking, is an extrapolation known facts and cannot be justified in any way. It is impossible to assert with certainty that particles that are elementary in the sense of the above definition exist. It is also possible that the statement "consists of ..." at some stage of the study of matter will be devoid of content. In this case, the definition of "elementary" given above will have to be abandoned. The existence of E. h. is a kind of postulate, and the verification of its validity is one of the most important tasks of physics.
The graviton is not a standard model particle, but is often mentioned in connection with other exchange particles, reflecting the hope that future models of particle physics can also properly handle the gravitational interaction. All gauge bosons, with the exception of the graviton, are confirmed by experiments; the characteristics of the graviton given in the table below should be understood as an "educated guess" and follow from the general theory of relativity.
There are a total of 8 gluons, each carrying combinations of two color charges and mediating the interaction between these two color charges. The electromagnetic interaction is mediated by only one boson. Eichbosonen himself can also bear charges and is therefore subject to interaction.
As a rule, the term "E. h." used in modern physics not in its exact meaning, but less strictly - to name a large group of the smallest observable particles of matter, subject to the condition that they are not atoms or atomic nuclei, that is, objects of a deliberately composite nature (the exception is the proton - the nucleus of a hydrogen atom). Studies have shown that this group of particles is unusually extensive. Apart from proton(R), neutron(n), electron(e) and photon(g) it includes: pi mesons(p), muons(m), tau leptons(t), neutrino three types ( v e , v m , v t), so-called. strange particles ( K-mesons and hyperons), charmed particles and lovely (beautiful) particles (D- and B-mesons and the corresponding baryons), various resonances, including mesons with hidden charm and charm ( ncu particles, upsilon particles) and, finally, open at the beginning. 80s intermediate vector bosons (W, Z)- more than 350 particles in total, mainly unstable. The number of particles included in this group as they are discovered is constantly growing, and it can be confidently asserted that it will continue to grow. Obviously, such a huge number of particles cannot act as elementary constituents of matter, and indeed, in the 70s. it was shown that most of the listed particles (all mesons and baryons) are composite systems. The particles included in this last group should be more accurately called "subnuclear" particles, since they represent specific forms of the existence of matter that is not aggregated into nuclei. The use of the name "E. h." in relation to all the mentioned particles has in the main. history, causes and is associated with the period of research (beginning of the 30s), when the unity. known representatives of this group were the proton, neutron, electron and particle el-magn. fields - photon. Then, with a certain right, these particles could lay claim to the role of E. h.
The conversion of one particle to another is mediated by exchange particles. This is a hypothetical elementary particle that has not yet been demonstrated. This is predicted based on theoretical considerations from the standard model of physics elementary particles. The Higgs boson is seen today as a necessary component, a more realistic model of particle physics that describes the real world.
Photon - a particle that carries electromagnetic interaction
With the strongest particle accelerator in the world, physicists from the European Center for Nuclear Research have discovered the so-called pentaquar particles. These five-membered quarks are a form of the constituents of matter that have so far been described only in theoretical models of particle physics.
The discovery of new microscopic particles gradually destroyed this simple picture of the structure of matter. However, the newly discovered particles in their properties were in a number of respects close to the first four known particles: either to the proton and neutron, or to the electron, or to the photon. As long as the number of such particles was not very large, the belief was maintained that they all play the fundam. role in the structure of matter, and they were included in the category of E. h. With an increase in the number of particles, this belief had to be abandoned, but traditionally. name "E. h." kept behind them.
Classification of elementary particles by spin size
Not all elementary particles are part of matter. There are five other elementary particles that transfer forces as exchange particles. If he moves around the room during a party, new listeners constantly turn to him, and others leave the male rope. Thus, the prime minister gains more weight, and similarly, the hypothetical Higgs field creates a mass of elementary particles. So a former immutable property like mass was the result of an interaction with the Higgs field - a strange idea, but not all that unusual for physicists.
In accordance with established practice, the term "E. h." will be used below as a general name for all the smallest particles of matter. In cases where we are talking about particles that claim to be primary elements matter, the term "true elementary particles".
Brief historical information
With the same picture, another conclusion from the theory can be explained: the cocktail party mechanism also works when the ear crosses the room. That's why the listeners gather and give him such a mass. Similarly, the Higgs field is expected to produce a Higgs particle. Thus, this proof is the best proof of the whole theory.
A pentaquark is made up of four quarks and an antique shop. The prediction of pentaquarks is based on the quark model. "The recent observation provides new insight into the strong interactions and bindings of quarks to particles such as protons and neutrons," says Ulrich Uwer, a physicist at the University of Heidelberg. It quickly decays into smaller particles, such as a three-quark proton. Theoretically, even states with six or more quarks are possible.
The discovery of E. h. was a natural result of the general success in studying the structure of matter, achieved by physics in con. 19th century It was prepared by detailed studies of the spectra of atoms, the study of electric. phenomena in liquids and gases, the discovery of photoelectricity, X-ray. rays, natural radioactivity, indicating the existence of a complex structure of matter.
Everything we know is made up of quarks. They are the basic components of our world, quarks are particles like protons and neutrons. A maximum of three quarks per particle, so far the equation has run. Researchers say. What is the world about the discovery of this particle?
That we can understand a little more where we come from, what happened between the Big Bang and today. This is one of the many puzzles, but a particularly addictive one. We have been searching for a long time in this area, and finally we have found something. It will not follow tomorrow's or tomorrow's statements. But this is part of the fundamental research of particle physics to understand the great whole.
Historically, the first open E. h. was an electron - the carrier of a negative elementary electric. charge in atoms. In 1897, J. J. Thomson (J. J. Thomson) convincingly showed that the so-called. cathode rays are a flow of charge. particles, to-rye were later called electrons. In 1911 E. Rutherford, skipping alpha particles from nature. radioactive source through thin foil dec. substances, came to the conclusion that he would put. the charge in atoms is concentrated in compact formations - nuclei, and in 1919 he discovered among particles knocked out of atomic nuclei, protons - particles with a unit put. charge and mass, 1840 times the mass of an electron. Another particle that is part of the nucleus, the neutron, was discovered in 1932 by J. Chadwick while studying the interaction of a-particles with beryllium. The neutron has a mass close to that of the proton, but does not have an electrical charge. charge. The discovery of the neutron completed the identification of particles, which are the structural elements of atoms and their nuclei.
What is special about this newly discovered particle? That you didn't see it. All the basic building blocks of matter that we know so far that are made up of quarks, such as the proton or neutron, are made up of two or three quarks. These are not exciting particles that we see very often. In this model, the found particle does not fit only because it consists of four quarks. This particle has been looking for a long time; that we have found it now is already a sensation.
So, when you were looking for it, was there a theory that should exist? Yes, according to quantum chromodynamics. It explains how quarks interact with each other, and in principle particles can be made up of four quarks, though not in any combination. But that was our theory. In fact, nature, however, would decide against its existence. The task of theorists is to test what this means and to predict what we do with experimental physicists. It is, of course, exciting.
The conclusion about the existence of particles e-magn. field - photon - originates from the work of M. Planck (M. Planck, 1900). To obtain a correct description of the radiation spectrum of an absolutely black body, Planck was forced to admit that the radiation energy is divided into individual. portions (quanta). Developing Planck's idea, A. Einstein suggested in 1905 that el-magn. radiation is a stream of quanta (photons) and on this basis explained the laws of the photoelectric effect. Direct experiments. proofs of the existence of the photon were given by R. Millikan in 1912-15 when studying the photoelectric effect and by A. Compton in 1922 when studying the scattering of g-quanta by electrons (see. Compton effect).
If there are particles of four quarks, then maybe five? The next step is now when the theorists tell us where this new particle should fall. This is especially important for us physicists when the second experiment looks the same regardless. This confirms that this is not possible due to the measurement accuracy of the detector.
Both were released on the same day. No, the posting time is already set, you already know what other groups are doing. In this case, it was even so that the authors partially overlapped. How big is the competition when different teams are doing research in the same area?
The idea of the existence of a neutrino, a particle that interacts only weakly with matter, belongs to W. Pauli (1930), who pointed out that such a hypothesis makes it possible to eliminate difficulties with the law of conservation of energy in the processes of beta decay of a radio act. nuclei. The existence of neutrinos was experimentally confirmed in the study of the process of inverse beta decay only in 1956 [F. Reines (F. Reines) and K. Cowan (S. Cowan)].
The staff is always professional and friendly. Of course, this is always a kind of race, but at the same time very constructive cooperation, that is, healthy competition. Our universe is extremely complex. Distant galaxies to microstructures on our own planet show that the closer we look, endless detail seemingly emerges from a corresponding abundance of trace elements. But this complexity is countered by a minimally equipped particle space. In fact, there are no more than 18 different building blocks that make up the observable world: six quarks, six leptons, and six particles of force, or bosons.
From the 30s to the early 50s the study of E. h. was closely connected with the study cosmic rays. In 1932, as part of the cosmic. rays by K. Anderson (S. Anderson) was discovered positron(e +) - a particle with an electron mass, but with a positive, electric. charge. The positron was the first to be discovered antiparticle. The existence of the positron follows directly from the relativistic theory of the electron developed by P. Dirac in 1928-31 shortly before the discovery of the positron. In 1936, Anderson and S. Neddermeyer (S. Neddermeyer) found in the study of space. rays muons (of both signs of electric charge) - particles with a mass of about 200 masses of an electron, but otherwise remarkably close to it in properties.
The building blocks of matter can be divided into quarks and leptons. The latter also include electrons and their partners. Quarks and leptons have seminumbered spins and are therefore also called fermions. All of these particles are replaced by force particles whose spin is an integer. Some particles are positive, others are negatively charged, and still others are neutral.
The fact that these fundamental building blocks can be compiled into "families" and mathematically described in terms of the "standard model of particle physics" is an achievement of recent decades. It was populated, as it did, at least to the researchers - virtually any number of particles with mass, charge, and other quantum properties.
In 1947, also in space. rays by the group of S. Powell (S. Powell) were discovered p +
- and p - mesons with a mass of 274 electron masses, which play an important role in the interaction of protons with neutrons in nuclei. The existence of such particles was proposed by H. Yukawa in 1935.
Con. 40s-beginning 50s were marked by the discovery of a large group of particles with unusual properties, called. "weird". The first particles of this group - K + - and K - mesons, L-hyperons - were discovered in space. rays, subsequent discoveries of strange particles were made on particle accelerators- installations that create intense flows of high-energy protons and electrons. Upon collision with matter, accelerated protons and electrons give rise to new E. h., to-rye are then registered with the help of complex detectors.
The order fell into chaos when physicists discovered that the world of elementary particles obeys certain symmetries. From this knowledge it is possible to obtain structures in which particles can be organized according to certain criteria - principles of organization that in some respects resemble the periodic table of the elements of chemistry. Among other things, families of particles can be classified according to which forces they obey, and against which they are certainly protected. In our universe, fortunately, there are only four of these forces, which makes it easier to order: gravity after matter, the electromagnetic force acting on electric charges, the strong force that holds atomic nuclei, for example, and the weak force, which is something less known and used, for example, in beta decay, i.e. during the decay of an atomic nucleus.
From the beginning 50s accelerators have become the main. tool for the study of E. h. In the 90s. Max. the energies of particles accelerated at accelerators amounted to hundreds of billions of electron volts (GeV), and the process of increasing energies continues. The desire to increase the energies of accelerated particles is due to the fact that this way opens up the possibility of studying the structure of matter at the shorter distances, the higher the energy of colliding particles, as well as the possibility of producing more and more heavy particles. Accelerators significantly increased the rate of obtaining new data and in a short time expanded and enriched our knowledge of the properties of the microworld.
Characteristics of elementary particles
Family: Quarks - "Creating blocks of matter." The first important family of six heads is made up of quarks. They are the essential building blocks of matter as we know them. For quarks, they are made up of atomic nuclei, and most of the visible matter is made up of these nuclei. In addition, there are only electron clouds surrounded by nuclei.
However, for mass balance, they do practically nothing. Quantum field theory can be used to estimate quark masses. Measuring them individually is not possible due to limitation. Now, however, a few more additions need to be mentioned. They don't make things difficult. Antiquarks correspond to the corresponding quark in all but one way: they carry the opposite charge. Two kinds of particles can be made up of quarks: mesons and baryons. While mesons are made up of a quark and an antiquark, baryons, as well as the already mentioned proton, are made up of three quarks.
The commissioning of proton accelerators with energies of billions of eV made it possible to discover heavy antiparticles: antiproton (1955), antineutron(1956), antisigmagi-peron (I960). In 1964, the heaviest particle from the group of hyperons, W, was discovered (with a mass of about two masses of a proton).
Since the 60s. with the help of accelerators revealed big number extremely unstable (in comparison with other unstable E. h.) particles, which received the name. resonances. The masses of most exceed the mass of a proton. [The first of them, D (1232), which decays into a p-meson and a nucleon, has been known since 1953.] It turned out that the resonances are main. part of E. h.
In 1974, massive (3-4 proton masses) and at the same time relatively stable psi-particles were discovered, with a lifetime approximately 10 3 times longer than the lifetime typical of resonances. They turned out to be closely related to the new family of charmed E. h., the first representatives of which (D mesons, L With-baryons) were discovered in 1976.
In 1977, even heavier (about 10 proton masses) upsilon particles were discovered, as well as psi particles, which are anomalously stable for particles of such large masses. They heralded the existence of another unusual family of lovely, or beautiful, particles. Its representatives - B-mesons - were discovered in 1981-83, L b-baryons - in 1992.
In 1962, it was found that in nature there is not one type of neutrino, but at least two: electronic v e and muonic v m . 1975 brought the discovery of the t-lepton, a particle almost 2 times heavier than a proton, but otherwise repeating the properties of an electron and a muon. It soon became clear that another type of neutrino was associated with it. v t.
Finally, in 1983, in the course of experiments at the proton-antiproton collider (an apparatus for carrying out colliding beams of accelerated particles), the heaviest known electron particles were discovered: charged intermediate bosons W b (m W 80 GeV) and a neutral intermediate boson Z 0 (m Z = 91 GeV).
Thus, in almost 100 years that have passed since the discovery of the electron, a huge number of various microparticles of matter have been discovered. The world of E. h. turned out to be rather complicated. Unexpected in many relations turned out to be the properties of the discovered E. h. To describe them, in addition to the characteristics borrowed from the classical. physics, such as electrical charge, mass, angular momentum, it took a lot of new specials to be introduced. characteristics, in particular to describe the strange, enchanted and lovely (beautiful) E. h. weirdness[TO. Nishijima (K. Nishijima), M. Gell-Mann (M. Gell-Mann), 1953], the charm[J. Bjorken (J. Bjorken), Sh. Glashow (Sh. Glashow), 1964], the beauty. The names of the above characteristics already reflect the unusual nature of the properties they describe.
The study of internal From its first steps, the evolution of matter and properties was accompanied by a radical revision of many established concepts and ideas. The laws that govern the behavior of matter in the small, turned out to be so different from the laws of the classical. mechanics and that required for their description completely new theoretical. constructions. Such new theories were, first of all, private (spec.) relativity theory(Einstein, 1905) and quantum mechanics(H. Bohr, L. de Broglie, W. Heisenberg, E. Schrödinger, M. Born; 1924-27). The theory of relativity and quantum mechanics marked a true revolution in the science of nature and laid the foundations for describing the phenomena of the microworld. However, it was not enough to describe the processes occurring with E. h. It took the next step - the quantization of the classical. fields (so-called. second quantization) and development quantum field theory. The most important stages on the way of its development were: the formulation quantum electrodynamics(Dirac, 1929), quantum theory beta decay [E. Fermi (E. Fermi), 1934] - the forerunners of modern. phenomenological theory of weak interactions, quantum mesodynamics (X. Yukawa, 1935). This period ended with the creation of a succession. calculate. apparatus of quantum electrodynamics [S. Tomona-ga (S. Tomonaga), P. Feynman (R. Feynman), J. Schwinger (J. Schwinger); 1944-49], based on the use of technology
This technique was later generalized to other variants of quantum field theory.
An essential stage in the subsequent development of quantum field theory was associated with the development of ideas about the so-called. calibration fields or Yanga - Mills fields(Ch. Young, P. Mills, 1954), which made it possible to establish the relationship of properties symmetry interactions with the fields. The quantum theory of gauge fields is at present the basis for describing the interactions of electromagnets. This theory has a number of serious successes, but it is still very far from completeness and cannot yet claim the role of a comprehensive theory of electromagnetism. not one restructuring of all ideas and a much deeper understanding of the relationship between the properties of microparticles and the properties of space-time before such a theory is built.
Basic properties of elementary particles. Interaction classes
All electrons are objects of exceptionally small masses and sizes. For most of them, the masses m are of the order of magnitude of the proton mass, equal to 1.6·10 -24 g (only the electron mass is noticeably smaller: 9·10 -28 g). The sizes of the proton, neutron, p- and K-mesons determined from experience are equal in order of magnitude to 10 -13 cm (see Fig. "Size" of an elementary particle). It was not possible to determine the dimensions of the electron and muon, it is only known that they are less than 10 -16 cm. Microscopic. The masses and dimensions of E. h. underlie the quantum specificity of their behavior. characteristic wavelengths, which should be attributed to E. h. in quantum theory (= /ts-Compton wavelength), which are close in order of magnitude to the typical sizes on which their interaction takes place (for example, for the p-meson /ts 1.4 10 -13 cm). This leads to the fact that quantum regularities are decisive in the behavior of E. h.
Naib. An important quantum property of all electrons is their ability to be born and destroyed (emitted and absorbed) when they interact with other particles. In this respect, they are completely analogous to photons. E. h. is specific. quanta of matter, more precisely - quanta of the corresponding fields of physical. All processes with E. h. proceed through a sequence of acts of their absorption and emission. Only on this basis can one understand, for example, the process of p + -meson production in a collision of two protons (p + pp + n + p +) or the process of an electron and a positron, when, for example, two g-quanta appear instead of disappeared particles (e + +e - g + g). But also the processes of elastic scattering of particles, for example. e - + p- >
e - + p, are also associated with the absorption of the beginning. particles and the birth of finite particles. The decay of unstable electron particles into lighter particles, accompanied by the release of energy, corresponds to the same regularity and is a process in which decay products are born at the moment of the decay itself and do not exist until that moment. In this respect, the decay of E. h. is similar to the decay of an excited atom into the main. state and photon. Examples of decays of electron particles can serve (the "tilde" sign above the particle symbol here and in what follows corresponds to the antiparticle).
Diff. Electromagnetic processes at relatively low energies [up to 10 GeV in the center-of-mass system (c.m.)] differ noticeably in the intensity of their occurrence. In accordance with this, the interactions that generate them E. h. can be phenomenologically divided into several. classes: strong interaction, electromagnetic interaction and weak interaction.All E. h. possess, in addition, gravitational interaction.
Strong interaction stands out as an interaction, a cut is responsible for the processes with E. h., proceeding with the greatest intensity in comparison with other processes. It leads to the strongest connection E. h. It is the strong interaction that determines the connection of protons and neutrons in the nuclei of atoms and provides an exception. the strength of these formations, which underlies the stability of matter under terrestrial conditions.
El-magn. interaction is characterized as an interaction, the basis of which is the connection with e-magn. field. The processes caused by it are less intense than the processes of strong interaction, and the E. h. connection generated by it is noticeably weaker. El-magn. interaction, in particular, is responsible for the processes of photon emission, for the bonding of atomic electrons with nuclei, and for the bonding of atoms in molecules.
Depending on the participation in certain types of interactions, all studied E. particles, with the exception of the photon, W- and Z-bosons, are divided into two main. groups: hadrons and leptons. Hadrons are characterized primarily by the fact that they participate in the strong interaction, along with the el-magnetic and weak interactions, while the leptons participate only in the el-magnetic and weak interactions. (The presence of a common gravitational interaction for both groups is implied.) The masses of hadrons are close in order of magnitude to the mass of a proton ( t R )
, sometimes exceeding it several times. once; min. p-meson has the mass among hadrons: t p1 /
7 m p , . The masses of leptons known before 1975-76 were small (0.1 m p) - hence their name. However, more recent data indicate the existence of heavy m-leptons with a mass of approx. two proton masses.
Hadrons are the most extensive group of known E. h. It includes all baryons and mesons, as well as the so-called. resonances (i.e., most of the mentioned 350 e. h.). As already mentioned, these particles have a complex structure and in fact cannot be considered as elementary. Leptons are represented by three charged (e, m, m) and three neutral particles ( v e , v m , v t). Photon, W +
and Z 0 -bosons together form an important group of gauge bosons that carry out the transfer of the el-weak interaction. The elementarity of particles from these last two groups has not yet been seriously questioned.
Characteristics of elementary particles
Each E. h., along with the specifics of its inherent interactions, is described by a set of discrete values determined. physical quantities or characteristics. In a number of cases these discrete values are expressed in terms of whole or fractional numbers and a certain common multiplier, a unit of measurement; these numbers are referred to as quantum numbers E. h. and set only them, omitting the units of measurement.
General characteristics of all E. h - mass ( t), lifetime (t), spin ( J) and electric. charge ( Q).
Depending on the lifetime t, E. hours are divided into stable, quasi-stable, and unstable (resonances). Stable, within the accuracy of modern. measurements are the electron (m > 2 · 10 22 years), the proton (m > 5 · 10 32 years), the photon and all types of neutrinos. Quasi-stable particles include particles that decay due to e-magnet. and weak interactions. Their lifetimes range from 900 s for a free neutron to 10 -20 s for an S 0 -hyperon. Resonance called. E. h., disintegrating due to the strong interaction. Their characteristic lifetimes are 10 -22 -10 -24 s. In table. 1 they are marked with * and instead of m a more convenient value is given: the width of the resonance Г=/т.
Spin E. h. J is an integer or half-integer multiple of the value. In these units, the spin of p- and K-mesons is equal to 0, for the proton, neutron and all leptons J= 1/2, for a photon, Wb-and Z-bosons J= 1. There are also particles with a large spin. The magnitude of the spin of an E. h. determines the behavior of an ensemble of identical (identical) particles or their statistics (Pauli, 1940). Particles of half-integer spin obey Fermi - Dirac statistics(hence the name fermions), which requires the antisymmetry of the wave function of the system with respect to the permutation of a pair of particles (or an odd number of such permutations) and, therefore, "forbids" two particles of half-integer spin to be in the same state ( Pauli principle).Particles of a whole spin obey Base - Einstein statistics(hence the name bosons), which requires a wave function with respect to permutations of particles and allows any number of particles of integer spin to be in the same state. Statistical E.'s properties of h. appear essential in those cases when at a birth or disintegration several is formed. identical particles.
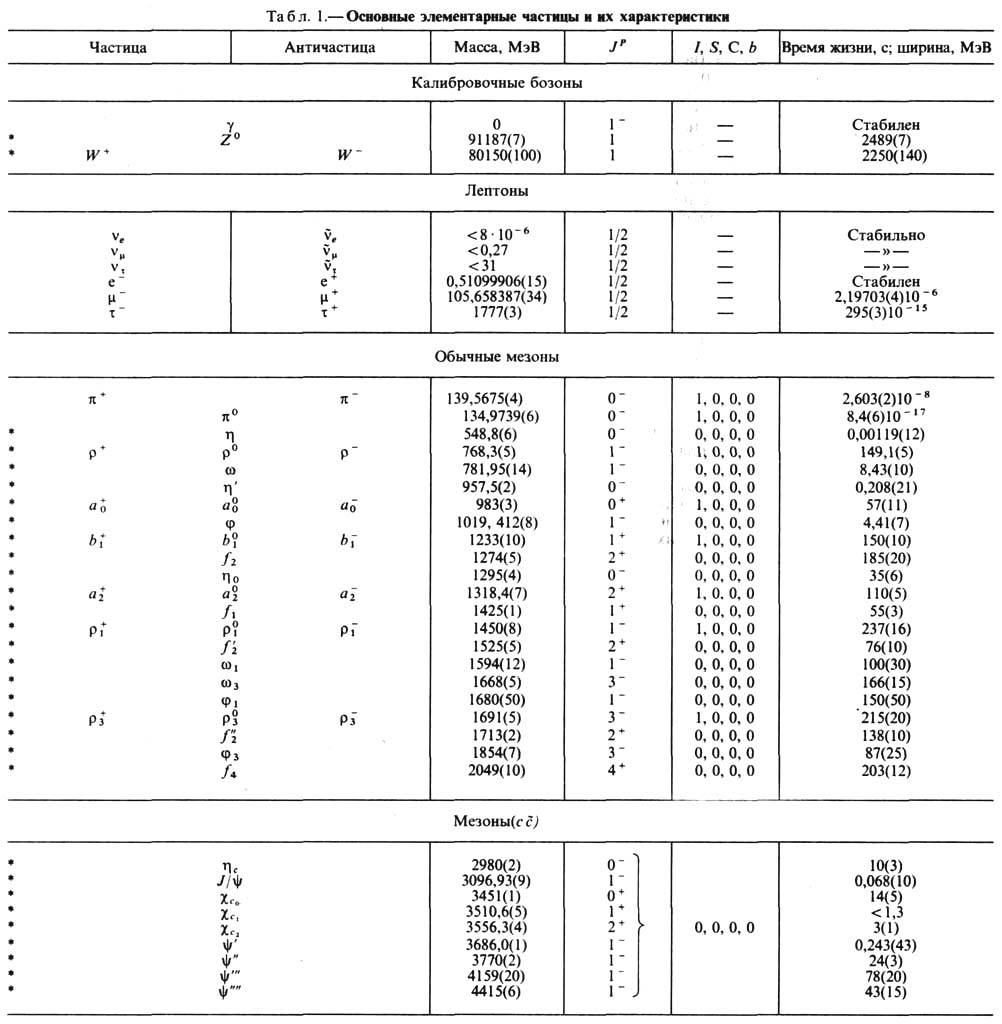
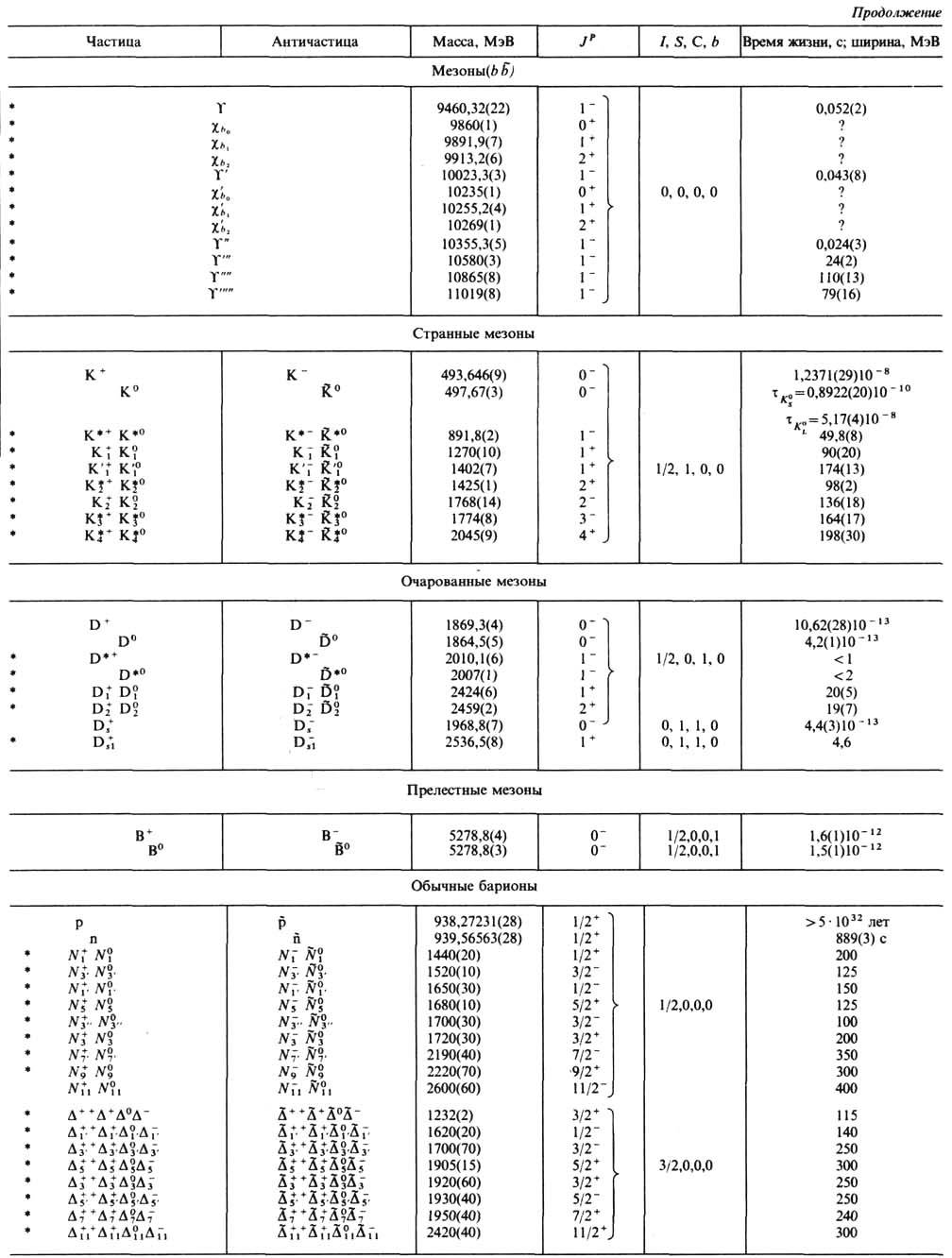
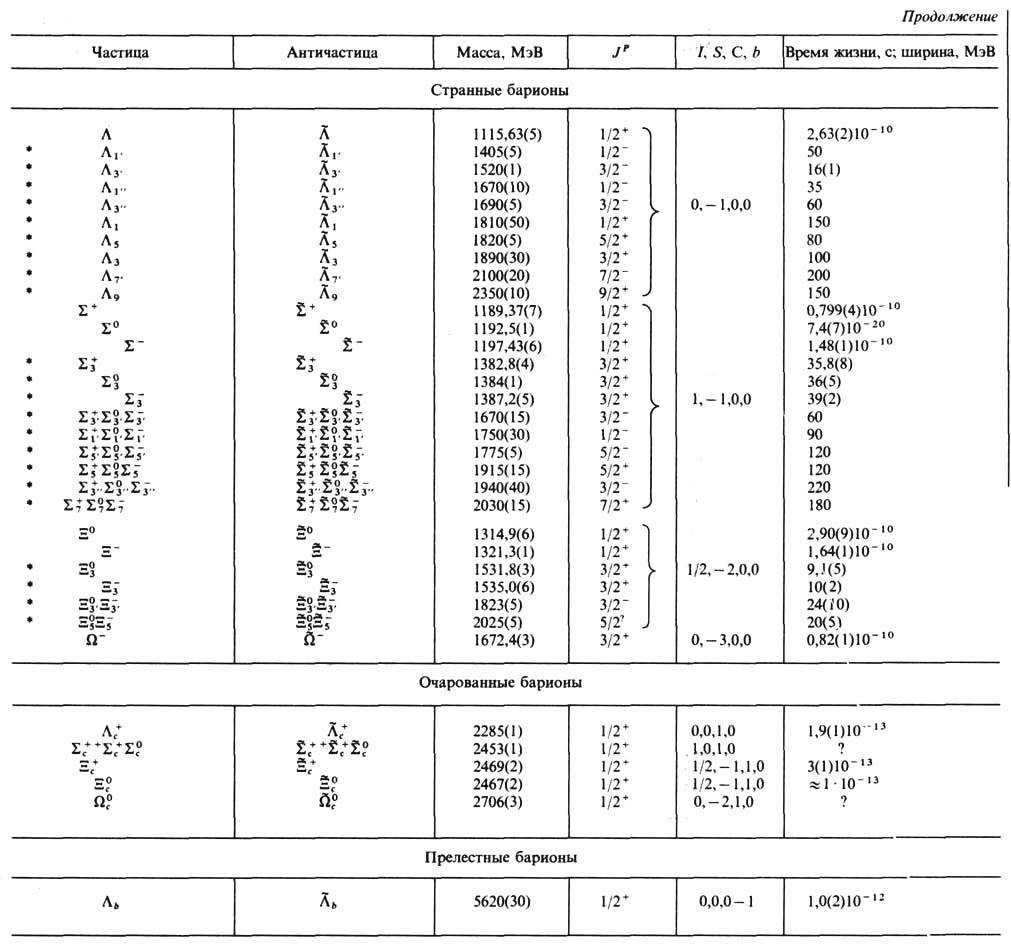
N o t e. Particles are marked with * on the left. (as a rule, resonances), for which instead of time life t is the width Г=/t. True Neutralnye particles are placed in the middle between the particles and antiparticles. Members of one isotopic multilashes are located on one line (in those cases, when the characteristics of each member of the multiwhip, - with a slight vertical offset). treasonparity sign P for antibaryons it is not indicated, equal tobut like changing signs S, C, b y of all antiparticles. For leptons and intermediate bosons, the inner parity is not an exact (conserved) quantonumber and therefore not marked. Numbers in brackets at the end of the physical quantities designate the existing error in the meaning of these quantities, relating to the last of the figures given.
Electric the charges of the studied E. h. (except) are integer multiples of e= 1.6 10 -19 C (4.8 10 -10 CGS), nas. elementary electric charge. In famous E. h. Q= 0, +
1, b2.
In addition to these quantities, E. h. are additionally characterized by a number of quantum numbers, called. "internal". Leptons are specific. lepton number (L) three types: electronic Le, equal to +1 for e - and v e, muonic L m , equal to +1 for m - and v m , and L t equal to +1 for t - and v t .
For hadrons L= 0, and this is another manifestation of their difference from leptons. In turn, that means part of the hadrons should be attributed to the so-called. baryon number B (|B| = I )
. Hadrons with B=+ 1 form a subgroup of baryons (this includes the proton, neutron, hyperons; charmed and lovely baryons; baryon resonances), and hadrons with B= 0 - a subgroup of mesons (p-mesons, K-mesons, charmed and lovely mesons, bosonic resonances). Name subgroups of hadrons come from the Greek. words baruV - heavy and mEsоV - medium, which is in the beginning. research stage E. h. reflected compare. the masses of the then known baryons and mesons. More recent data have shown that the masses of baryons and mesons are comparable. For leptons B=0. For a photon Wb- and Z-bosons B= 0 and L= 0.
The studied baryons and mesons are subdivided into the already mentioned sets: ordinary (non-strange) particles (proton, neutron, p-mesons), strange particles (hyperons, K-mesons), charmed and lovely particles. This division corresponds to the presence of special quantum numbers in hadrons: oddities S, charms C and charms (beauty) b with valid values (modulo) 0, 1, 2, 3. For ordinary particles S=C= b=0, for strange particles S 0, C= b= 0, for charmed particles С0, b= 0, and for lovely b O. Along with these quantum numbers, the quantum number is also often used hypercharge Y=B+S+C + b having, apparently, more than fundam. meaning.
Already the first studies of ordinary hadrons revealed the presence among them of families of particles close in mass and with very similar properties with respect to the strong interaction, but with decomp. electric values. charge. The proton and neutron (nucleons) were the first example of such a family. Such families were later discovered among strange, enchanted, and lovely hadrons. The commonality of the properties of particles included in such families is a reflection of the existence of the same quantum number for them - isotopic spin I, which, like the usual spin, takes integer and half-integer values. The families themselves are usually called. isotopic multiplets. Number of particles in a multiplet n associated with I ratio n = 2I+1. Particles of one isotopic. multiplet differ from each other by the value of the "projection" isotopic. back I 3 , and corresponding values Q are given by
![]()
An important characteristic of hadrons is inner parity P associated with the operation of spaces. inversions: P takes values +
1.
For all electron numbers with nonzero values of at least one of the quantum numbers Q, L, B, S, C, b there are antiparticles with the same mass values t, lifetime t, spin J and for hadrons isotopic. back I, but with opposite signs of the indicated quantum numbers, and for baryons with the opposite sign, ext. parity R. Particles that do not have antiparticles are called. true neutral particles. Truly neutral hadrons have a special - charge parity(i.e., parity with respect to the charge conjugation operation) C with the values +
one; examples of such particles are p 0 - and h-mesons (C=+1), r 0 - and f-mesons (C=-1), etc.
The quantum numbers of E. h. are divided into exact (i.e., those that are associated with physical quantities that are conserved in all processes) and inexact (for which the corresponding physical quantities are not conserved in a number of processes). Spin J is associated with a strict conservation law and therefore is an exact quantum number. Another exact quantum number is electric. charge Q. Within the accuracy of the measurements taken, the quantum numbers B and L, although there are no serious theoretical prerequisites. Moreover, the observed baryon asymmetry of the universe max. can naturally be interpreted assuming a violation of the conservation of the baryon number AT(A.D. Sakharov, 1967). Nevertheless, the observed stability of the proton is a reflection of the high degree of conservation accuracy. B and L(there is no pe + p 0 decay, for example). The decays m - e - + g, m - m - + g, etc. are also not observed. However, most of the quantum numbers of hadrons are inaccurate. Isotopic the spin, being conserved in the strong interaction, is not conserved in the e-magn. and weak interactions. Strangeness, charm and charm are preserved in strong and el-magn. interactions, but are not conserved in weak interactions. Weak interaction also changes the ext. and charge parity of the set of particles involved in the process. Combined parity is preserved with a much greater degree of accuracy CP (CP parity), however, it is also violated in certain processes due to the weak interaction. Reasons for non-conservation pl. quantum numbers of hadrons are not clear and, apparently, are connected both with the nature of these quantum numbers and with the deep structure of the el-weak interaction.
In table. 1 shows max. well-studied electron particles from the groups of leptons and hadrons and their quantum numbers. In the special group, gauge bosons are allocated. Particles and antiparticles are given separately (change P not indicated for antibaryons). True neutral particles are placed in the center of the first column. Members of one isotopic. multiplet are located in one line, sometimes with a slight shift (in those cases when the characteristics of each member of the multiplet are given).
As already noted, the group of leptons is very small, and the masses of particles in the main. small. For the masses of all types of neutrinos, there are rather strict restrictions from above, but what their true values are remains to be seen.
Main part of the E. h. is made up of hadrons. An increase in the number of known E. hours in the 60-70s. occurred solely due to the expansion of this group. Hadrons are mostly represented by resonances. Attention is drawn to the tendency for the spin to grow with the growth of the mass of resonances; it is well traced on diff. groups of mesons and baryons with given I,
S and C. It should also be noted that strange particles are somewhat more massive than ordinary particles, charmed particles are more massive than strange ones, and lovely particles are more massive than charmed ones.
Classification of elementary particles. Quark model of hadrons
If the classification of gauge bosons and leptons does not cause any special problems, then a large number of hadrons already in the beginning. 50s was the basis for the search for patterns in the distribution of masses and quantum numbers of baryons and mesons, which could form the basis of their classification. The selection of isotopic. hadron multiplets was the first step in this direction. With mother. point of view, the grouping of hadrons in isotopic. multiplets reflects the presence of a strong interaction symmetry associated with group rotation, more formally, with the unitary group SU(2) - a group of transformations in a complex two-dimensional space [see. SU symmetry ( 2
)]
. It is assumed that these transformations operate in some specific way. internal space - so-called. isotopic space other than normal. The existence of isotopic space is manifested only in the observable properties of symmetry. On math. isotopic language. multiplets are irreducible group representations symmetry SU (2).
The concept of symmetry as a factor that determines the existence of decomp. groups and families E. h. in modern. theory, is dominant in the classification of hadrons and other E. h. It is assumed that ext. quantum numbers E. h., allowing you to combine certain groups of particles, associated with special. types of symmetry that arise due to the freedom of transformations in special internal. spaces. This is where the name comes from. "internal quantum numbers".
Careful consideration shows that strange and ordinary hadrons together form broader associations of particles with similar properties than isotopic ones. multiplets. They are usually called supermulti-lashes. The number of particles included in the observed super-multiplets is 8 and 10. From the point of view of symmetry, the appearance of super-multiplets is interpreted as a manifestation of the existence of a symmetry group in the strong interaction that is wider than the group SU( 2)
, namely the unitary group SU(3) - transformation groups in three-dimensional complex space [Gell-Man, Y. Neeman, 1961]; cm. Symmetry SU(3). The corresponding symmetry is called unitary symmetry. Group SU(3) has, in particular, irreducible representations with the number of components 8 and 10, which can be associated with the observed supermultiplets: an octet and a decuplet. Examples of supermultiplets are the following groups of particles with the same values JP(i.e. with the same pairs of values J and P):
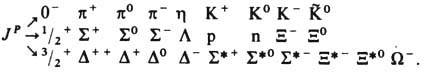
Unitary symmetry is less precise than isotopic. symmetry. Accordingly, the difference in particle masses included in octets and decuplets is quite significant. For the same reason, the partitioning of hadrons into supermultiplets is relatively easy to carry out for electron particles of not very large masses. At large masses, when there are many diff. particles with similar masses, this division is more difficult to implement.
Detection among hadrons of selected supermulti-plets of fixed dimensions, corresponding to certain cases. representations of the unitary group SU(3), was the key to the most important conclusion about the existence of special structural elements in hadrons - quarks.
The hypothesis that the observed hadrons are built from particles of an unusual nature - quarks carrying spin 1 /
2 , possessing a strong interaction, but at the same time, not belonging to the class of hadrons, was put forward by G. Zweig and independently by Gell-Mann in 1964 (see. quark models). The idea of quarks was suggested by Math. structure of representations of unitary groups. Ma-them. formalism opens up the possibility of describing all representations of the group SU(n) (and, consequently, all associated hadron multiplets) based on the multiplication of the simplest (fundam.) group representation containing n component. It is only necessary to admit the existence of special particles associated with these components, which was done by Zweig and Gell-Mann for the particular case of the group SU( 3)
. These particles were called quarks.
The specific quark composition of mesons and baryons was derived from the fact that mesons, as a rule, are included in supermultiplets with the number of particles equal to 8, and baryons - 8 and 10. This regularity is easily reproduced if we assume that mesons are composed of a quark and an antiquark, symbolically: M=(q)
, and the baryon is made up of three quarks, symbolically: B = (qqq). By virtue of the properties of the group SU(3) 9 mesons break down into supermultiplets of 1 and 8 particles, and 27 baryons into supermultiplets containing 1, 10, and twice 8 particles, which explains the observed separation of octets and decuplets.
T. o., revealed by the experiments of the 60s. the existence of supermultiplets composed of ordinary and strange hadrons led to the conclusion that all these hadrons are built from 3 quarks, usually denoted i, d, s(Table 2). The whole set of facts known at that time was in perfect agreement with this proposal.
Tab. 2.-Characteristics of quarks

* Preliminary experimental evaluation.
The subsequent discovery of psi-particles, and then upsilon particles, charmed and charmed hadrons showed that three quarks are not enough to explain their properties and it is necessary to admit the existence of two more types of quarks c and b, carrying new quantum numbers: charm and beauty. This circumstance did not shake, however, the fundamental tenets of the quark model. In particular, the center was preserved. point of her diagram of the structure of hadrons: M=(q), B = (qqq). Moreover, it was on the basis of the assumption of the quark structure of psi- and upsilon-particles that it was possible to give physical. interpretation of their largely unusual properties.
Historically, the discovery of psi- and upsilon-particles, as well as new types of charmed and lovely hadrons, was an important step in the confirmation of ideas about the quark structure of all strongly interacting particles. According to modern theoretical models (see below), one should expect the existence of one more - the sixth t-quark, which was discovered in 1995.
The above quark structure of hadrons and Mat. properties of quarks as objects associated with the fundam. group representation SU(n), lead to the following quantum numbers of quarks (Table 2). Attention is drawn to unusual (fractional) values of electric. charge Q, as well as AT, which are not found in any of the studied E. h. With index a for each type of quark qi (i= 1, 2, 3, 4, 5, 6) a special characteristic of quarks is associated - color, which the observed hadrons do not have. The index a takes on the values 1, 2, 3, i.e. each type of quark ( qi) is represented by three varieties q a i. The quantum numbers of each type of quark do not change when the color changes, so Table. 2 applies to quarks of any color. As shown later, the quantities q a (for each i) when changing a in terms of their transformations. properties should be considered as components of fundam. representations of another group SU(3), color, operating in a color three-dimensional space [see. SU color symmetry(3)].
The need to introduce color follows from the requirement of antisymmetry of the wave function of the system of quarks that form baryons. Quarks, as spin 1/2 particles, must obey Fermi-Dirac statistics. Meanwhile, there are baryons composed of three identical quarks with the same spin orientation: D ++ (), W - (), which are clearly symmetrical with respect to permutations of quarks, if the latter do not have a complement. degree of freedom. Such an addition. the degree of freedom is the color. Given the color, the required antisymmetry is easily restored. The refined functions of the structural composition of mesons and baryons look like this:
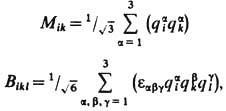
where e abg is the fully antisymmetric tensor ( Levi-chi-vita symbol)(1/
1/
- normalization factors). It is important to note that neither mesons nor baryons carry color indices (no color) and are, as is sometimes said, "white" particles.
In table. 2 shows only the "effective" quark masses. This is due to the fact that quarks in the free state, despite numerous careful searches for them, have not been observed. This, by the way, reveals another feature of quarks as particles of a completely new, unusual nature. Therefore, there are no direct data on quark masses. There are only indirect estimates of the masses of quarks, which can be extracted from their decomp. dynamic manifestations in the characteristics of hadrons (including the masses of the latter), as well as in decomp. processes occurring with hadrons (decays, etc.). For mass t-quark, a preliminary experiment is given. grade.
The whole variety of hadrons arises due to the decomp. combinations i-, d-, s-, s- and b-quarks forming bound states. Ordinary hadrons correspond to bound states constructed only from and- and d-quarks [for mesons with the possible participation of combinations ( s.), (With) and ( b)]. The presence in the bound state, along with u- and d-quarks, one s-, with- or b-quark means that the corresponding hadron is strange ( S= - 1), enchanted (C= + 1) or adorable ( b= - 1). A baryon can consist of two or three s-quark (respectively With- and b-quark), i.e., twice and thrice strange (charmed, lovely) baryons are possible. Combinations are also allowed. numbers s- and With-, b-quarks (especially in baryons), which correspond to "hybrid" forms of hadrons (strangely charming, strangely charming). Obviously, the more s-, with- or b-quarks contains a hadron, the more massive it is. If we compare the ground (unexcited) states of hadrons, this is precisely the picture that is observed (Table 1).
Since the spin of quarks is 1 /
2 , the above quark structure of hadrons has as its consequence an integer spin for mesons and a half-integer spin for baryons, in full accordance with the experiment. In this case, in the states corresponding to the orbital momentum l=0, in particular in the main. states, the values of the meson spin should be 0 or 1 (for antiparallel and parallel orientation of the quark spins), and the spin of the baryons: 1 /
2
or 3 / 2 (for spin configurations
and
). Considering that the internal the parity of the quark-antiquark system is negative, the values JP for mesons at l= 0 are equal to 0 - and 1 - , for baryons: 1 / 2 +
and 3 / 2 + . It is these values that are observed for hadrons that have the smallest mass at given values I and S, FROM, b.
As an illustration, in Table. 3 and 4 show the quark composition of mesons with JP= 0 - and baryons J P = 1 / 2 +
(the necessary summation over quark colors is assumed everywhere).
Tab. 3.- Quark composition of the studied mesons With JP=0 - ()

Tab. 4.- Quark composition of the studied baryons With JP= 1/2 + ()

Note. The symbol () means symmetrization with respect to variable particles; symbol - antisymmetrization.
T. o., quark model of nature. way explains the origin of the main. groups of hadrons and their observed quantum numbers. A more detailed dynamic consideration also allows us to draw a number of useful conclusions regarding the interrelation of masses within dec. families of hadrons.
Correctly conveying the specifics of hadrons with the smallest masses and spins, the quark model of nature. also explains in a way the total large number of hadrons and the predominance of resonances among them. The multiplicity of hadrons is a reflection of their complex structure and the possibility of existence decomp. excited states of quark systems. All excited states of quark systems are unstable with respect to fast transitions due to the strong interaction to underlying states. They form the basis. some of the resonances. A small fraction of the resonances are also quark systems with parallel spins (with the exception of W -). Quark configurations with antiparallel orientation of spins related to main. states, form quasi-stable hadrons and a stable proton.
Excitations of quark systems occur both due to a change in rotation. motion of quarks (orbital excitations), and due to changes in their spaces. location (radial excitations). In the first case, an increase in the mass of the system is accompanied by a change in the total spin J and parity P system, in the second case, the increase in mass occurs without changing JP .
When formulating the quark model, quarks were considered as hypothetical. structural elements that open up the possibility of a very convenient description of hadrons. In the years that followed, experiments were carried out which made it possible to speak of quarks as real material formations inside hadrons. The first were experiments on the scattering of electrons by nucleons at very large angles. These experiments (1968), reminiscent of the classic. Rutherford's experiments on the scattering of a-particles by atoms revealed the presence of point charges inside the nucleon. formations (see Partons). Comparison of the data of these experiments with similar data on the scattering of neutrinos by nucleons (1973-75) made it possible to draw a conclusion about cf. the size of the square of the electric the charge of these point formations. The result was close to the expected fractional values (2 / 3) 2 e 2 and (1 / 3) 2 e 2. The study of the process of hadron production during the annihilation of an electron and a positron, which presumably goes through the following stages:
indicated the presence of two groups of hadrons, the so-called. jets (see Hadron jet), genetically associated with each of the resulting quarks, and made it possible to determine the spin of the quarks. It turned out to be equal to 1/2. Total number of hadrons produced in this process also indicates that in the intermediate state each type of quark is represented by three varieties, i.e., quarks are tricolor.
T. o., the quantum numbers of quarks, given on the basis of the theoretical. considerations, received a comprehensive experiment. the confirmation. Quarks have actually acquired the status of new E. particles and are serious contenders for the role of true E. particles for strongly interacting forms of matter. The number of known types of quarks is small. Up to lengths<=10 -16
см кварки выступают как точечные бесструктурные образования. Бесструктурность
кварков, конечно, может отражать лишь достигнутый уровень исследования этих
материальных образований. Однако ряд специфич. особенностей кварков даёт известные
основания предполагать, что кварки являются частицами, замыкающими цепь структурных
составляющих сильновзаимодействующей материи.
Quarks differ from all other electromagnetic waves in that they apparently do not exist in a free state, although there is clear evidence for their existence in a bound state. This feature of quarks is most likely associated with the specifics of their interaction, generated by the exchange of special particles - gluons, leading to the fact that the forces of attraction between them do not weaken with distance. As a consequence, infinite energy is required to separate quarks from each other, which is obviously impossible (the theory of the so-called confinement or trapping of quarks; cf. Color retention). In reality, when trying to separate quarks from each other, the formation of a complement occurs. hadrons (the so-called hadronization of quarks). The impossibility of observing quarks in a free state makes them a completely new type of structural units of matter. It is not clear, for example, whether it is possible in this case to raise the question of the constituent parts of quarks and whether the sequence of structural constituents of matter is thereby interrupted. All of the above leads to the conclusion that quarks, along with leptons and gauge bosons, which also do not have observable signs of structure, form a group of E. h., which has the greatest reason to claim the role of true E. h.
Elementary particles and quantum field theory. Standard Interaction Model
To describe the properties and interactions of E. h. in modern. the theory of beings. What matters is the concept of a physical field, which is assigned to each particle. The field is specific. the form of matter distributed in space; it is described by a f-tion, given at all points in space-time and having a definite. transformer properties with respect to transformations Lorenz group(scalar, spinor, vector, etc.) and "intrinsic" groups. symmetries (isotopic scalar, isotopic spinor, etc.). El-magn. a field that has the properties of a four-dimensional vector A m ( x)(m= 1, 2, 3, 4) - historically the first example of physical. fields. The fields associated with E. h. are of a quantum nature, i.e., their energy and momentum are composed of a set of separate fields. portions - quanta, and the total energy e k and momentum p k quantum are related by the ratio of special. relativity: e 2 k =p 2 k s 2 + t 2 With four . Each such quantum is an E. h. with a mass t, with a given energy e k and momentum p k. quanta e-magn. fields are photons, quanta of other fields correspond to all other known E. h. Ma-themes. The apparatus of quantum field theory (QFT) makes it possible to describe the birth and annihilation of a particle at each space-time point.
Transform. field properties determine the main. quantum numbers of electrochemical units. Transformation properties with respect to transformations of the Lorentz group determine the spin of particles: a scalar corresponds to a spin J= 0, spinor- spin J= 1 /
2 , vector - spin J= 1 etc. Transform. properties of fields in relation to transformations "internal." spaces ("charge space", "isotopic space", "unitary space", "color space") determine the existence of such quantum numbers as L, B, I, S, FROM, b, a for quarks and gluons also colors. The introduction of "int." spaces in the apparatus of the theory is still a purely formal technique, which, however, can serve as an indication that the dimension of physical. space-time, which is reflected in the properties of E. h., is actually more than four - i.e. more than the dimension of space-time, characteristic of all macroscopic. physical processes.
The mass of E. h. is not directly related to the transformation. field properties. This is their additional characteristic, the origin of which is not fully understood.
To describe the processes that occur with E. h., QFT uses Lagrangian formalism.AT Lagrangians, constructed from the fields involved in the interaction of particles, contains all the information about the properties of particles and the dynamics of their behavior. The Lagrangian includes two Ch. terms: Lagrangian, describing the behavior of free fields, and Lagrangian of interaction, reflecting the relationship decomp. fields and the possibility of converting E. h. Knowledge of the exact form allows, in principle, using the apparatus scattering matrices (S-matrices), calculate the probabilities of transitions from the initial set of particles to a given finite set of particles, occurring under the influence of the interaction existing between them. Thus, the establishment of a structure that opens up the possibility of quantities. descriptions of processes with E. h., is one of the center. tasks of KTP.
Creatures. progress in solving this problem was achieved in the 50-70s. based on the development of the idea of vector gauge fields formulated in the already mentioned work of Yang and Mills. Starting from the well-known position that any conservation law observed experimentally is associated with the invariance of the Lagrangian describing the system with respect to transformations of a certain symmetry group ( Noether theorem), Yang and Mills demanded that this invariance be satisfied locally, i.e., take place for an arbitrary dependence of transformations on a point in space-time. It turned out that the fulfillment of this requirement, which is physically connected with the fact that the interaction cannot be instantly transmitted from point to point, is possible only with the introduction of a special Lagrangian into the structure. gauge fields of vector nature, def. transforming under transformations of the symmetry group. Moreover, the structures of the free Lagrangian turned out to be closely related in this approach: knowledge in means. measure predetermined the form
The latter circumstance is due to the fact that the requirement of local gauge invariance can be satisfied only if in all derivatives acting on free fields in , the replacement ![]() Here g- interaction constant; V a m - calibration fields; T a - generators of the symmetry group in the matrix representation corresponding to the free field; r- the size of the group.
Here g- interaction constant; V a m - calibration fields; T a - generators of the symmetry group in the matrix representation corresponding to the free field; r- the size of the group.
By virtue of what has been said in the modified Lagrangian, strictly defined terms automatically arise. structures describing the interaction of the fields originally included in with the newly introduced gauge fields. In this case, the gauge fields play the role of carriers of the interaction between the initial fields. Of course, since new gauge fields have appeared in the Lagrangian, the free Lagrangian must be supplemented by a term associated with them and subjected to the modification procedure described above. If the gauge invariance is strictly observed, the gauge fields correspond to bosons with zero mass. When symmetry is broken, the mass of bosons is nonzero.
In this approach, the task of constructing a Lagrangian that reflects the dynamics of interacting fields is essentially reduced to the correct selection of the system of fields that make up the initial free Lagrangian and fixing its shape. The latter, however, for given transformation properties with respect to the Lorentz group, is uniquely determined by the requirement of relativistic invariance and the obvious requirement that only structures that are quadratic in fields occur.
Thus, the main thing for describing the dynamics is the question of choosing a system of primary fields that form , i.e., in fact, all the same center. question of physics E. h.: "Which particles (and, accordingly, fields) should be considered the most fundamental (elementary) in the description of the observed particles of matter?".
Modern theory, as already noted, singles out as such particles structureless particles with spin 1/2: quarks and leptons. Such a choice makes it possible, relying on the principle of local gauge invariance, to construct a very successful scheme for describing the strong and elec-weak interactions of an elec- trical particle, which has received the name STANDARD MODEL.
The model proceeds primarily from the assumption that the strong interaction has an exact symmetry SUc(3), corresponding to transformations in the "color" three-dimensional space. It is assumed that the quarks are transformed in terms of fundamentals. group representation SUc(3). The fulfillment of the requirement of local gauge invariance for the quark Lagrangian leads to the appearance in the structure of the theory of eight massless gauge bosons, called gluons, interacting with quarks (and with each other) strictly defined. way (Fritzsch and Göll-Man, 1972). The scheme for describing the strong interaction developed on this basis was called. quantum chromodynamics. The correctness of her predictions has been confirmed by many. experiments, including convincing evidence of the existence of gluons. There are also serious reasons to believe that the apparatus of quantum chromodynamics contains an explanation for the phenomenon of confinement.
In constructing the theory of the weak interaction, the fact was used that the existence of pairs of leptons with the same lepton number ( L e , L v , L t), but with different electric. charge (e - , v e; m - , v m t - , v m) can be interpreted as a manifestation of the symmetry associated with the group of the so-called. weak isospin SU cl (2), and consider the pairs themselves as spinor (doublet) representations of this group. A similar interpretation is possible for pairs of quarks participating in the weak interaction. We note that, within the framework of this scheme, the weak interaction with the participation of a quark b necessarily leads to the conclusion that it has an isotopic partner quark t, constituting a pair ( t, b). Isolation by the weak interaction def. helicity(left) fermions participating in it can additionally be considered as a manifestation of the existence of symmetry U cl (1) associated with a weak hypercharge Y sl. In this case, the left and right fermions should be assigned different hypercharge values Y cl, and right fermions should be considered as isotopic scalars. In the construction adopted, the relation naturally arises Q = I 3 cl + 1 / 2 Y cl, which we have already met with hadrons.
Thus, a careful analysis of the el-weak interaction of leptons and quarks makes it possible to reveal that they have a symmetry (noticeably, however, broken) corresponding to the group SU sl (2) U cl (
1)
. If we ignore the violation of this symmetry and use the strict condition of local gauge invariance, then a theory of the weak interaction of quarks and leptons arises, in which four massless bosons appear (two charged and two neutral) and two interaction constants corresponding to the groups SU sl (2) and U sl (1). In this theory, the terms of the Lagrangian corresponding to the interaction with the charge. bosons correctly reproduce the known structure charged currents, but do not provide the short-range action observed in weak processes, which is not surprising, since the zero mass of intermediate bosons leads to long-range action. It follows only that in realistic. theories of weak interaction of the mass of intermediate bosons must be finite. This is also in accordance with the fact that the symmetry is broken SU sl (2) U sl (1).
However, a direct introduction of finite masses of intermediate bosons into the Lagrangian constructed in the manner described above is impossible, since it contradicts the requirement of local gauge invariance. It was possible to take into account the symmetry breaking in a consistent way and achieve the appearance of intermediate bosons in the theory of finite masses using the important assumption about the existence in nature of special scalar fields F ( Higgs fields), interacting with fermionic and gauge fields and having a specific self-interaction leading to the phenomenon spontaneous symmetry breaking[P. Higgs (P. Higgs), 1964]. The introduction of one doublet (according to the weak isospin group) of Higgs fields into the Lagrangian of the theory in the simplest version leads to the transition of the entire system of fields to a new, lower energy vacuum state corresponding to broken symmetry. If initially vacuum average from the field F was equal to zero<Ф>0 = 0, then in the new state<Ф>0 = Ф 0 0. Symmetry breaking and the appearance of finite F 0 in the theory leads to Higgs mechanism to the non-vanishing mass of charge. intermediate bosons W +
and to the occurrence of mixing (linear combination) of two neutral bosons that appear in the theory. As a result of mixing, there is a massless e-mag. field interacting with e-magn. current of quarks and leptons, and the field of a massive neutral boson Z 0 interacting with neutral current strictly defined structure. Mixing parameter (angle) ( Weinberg angle) of neutral bosons in this scheme is given by the ratio of the group interaction constants U sl(l) and SU sl (2) :
tgq W=g"/g. The same parameter determines the connection of the masses m W and m Z (m Z = m W / cosq W) and electrical connection. charge e s weak isospin group constant g: e = g sinq W. Detection in 1973 in the study of neutrino scattering of neutral weak currents predicted by the scheme described above, and the subsequent discovery in 1983 W- and Z-bosons with masses of 80 GeV and 91 GeV, respectively, brilliantly confirmed the whole concept of a unified description of the e-magn. and weak interactions. Experiment. determination of sin 2 q value W= 0.23 showed that the constant g and electric charge e close in size. It became clear that the "weakness" of the weak interaction at energies noticeably lower than m W and mZ, in the main due to the large mass of intermediate bosons. Indeed, the constant of the phenomenological four-fermion theory of the weak Fermi interaction G F in the above scheme is equal to G F =g 2 /8m 2 W. This means that eff. weak interaction constant at energy in sec. c. m. ~t p is equal to G F m p 2
10 -5 , and its square is close to 10 -10 , i.e. to the value given above. At energies in c.m., large or of the order m W, the only parameter characterizing the weak interaction is the quantity g 2 /
4p or e 2 /
4p, i.e. weak and e-mag. interactions become comparable in intensity and must be considered jointly.
Construction of a unified description of e-magn. and weak interactions is an important achievement in the theory of gauge fields, comparable in importance to the development by Maxwell in con. 19th century unified theory of e-magn. phenomena. Quantity. The predictions of the theory of the el-weak interaction were justified in all the measurements carried out with an accuracy of 1%. An important physical a consequence of this construction is the conclusion about the existence in nature of a particle of a new type - neutral Higgs boson. At the beginning 90s no such particle has been found. The conducted searches have shown that its mass exceeds 60 GeV. The theory does not, however, give an accurate prediction for the mass of the Higgs boson. One can only assert that the value of its mass does not exceed 1 TeV. Estimated values of the mass of this particle lie in the range of 300-400 GeV.
So, the "standard model" selects as fund-dames. particles three pairs of quarks ( and, d)(With, s) (t, b) and three pairs of leptons ( v e ,e -)(v m ,m -) ( v t, t -), usually grouped according to their masses into families (or generations) as follows:
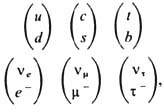
and postulates that their interactions satisfy the symmetry SU sl (3) SU sl (2) U sl(l). As a consequence, a theory is obtained in which the carriers of the interaction are gauge bosons: gluons, photon, Wb and Z. And although the "standard model" very successfully copes with the description of all known facts related to E.ch., nevertheless, most likely, it is an intermediate stage in the construction of a more perfect and comprehensive theory of E.ch. In the structure of the "standard model" there are still quite a lot of arbitrary, empirically determined parameters (values of the masses of quarks and leptons, values of interaction constants, mixing angles, etc.). The number of fermion generations in the model is also not determined. So far, the experiment confidently asserts only that the number of generations does not exceed three, if there are no heavy neutrinos with masses of several times in nature. tens of GeV.
From the point of view of the symmetry properties of interactions, it would be more natural to expect that in the comprehensive theory of E.ch. instead of a direct product of symmetry groups, one symmetry group will appear G with one interaction constant corresponding to it. Symmetry groups of the "standard model" in this case could be treated as products of the reduction of a large group when the symmetry associated with it is broken. In this way, in principle, the possibility of a Grand Unification of interactions could arise. The property of change with energy eff can serve as a formal basis for such a union. interaction constants of gauge fields gi 2/4p = a i (i=1, 2, 3), which arises when the higher orders of the theory are taken into account (the so-called running constants). In this case, the constant a 1 is associated with the group U(I); a 2 - with a group SU( 2);
a 3 - with a group SU( 3)
. The mentioned very slow (logarithmic) changes are described by the expression
linking the values of eff. constants a i (M) and a i(m) at two different energy values: M and m( M > m). The nature of these changes is different for decomp. symmetry groups (and, consequently, different interactions) and is given by the coefficients b i, which incorporate information both about the structure of the symmetry groups and about the particles participating in the interaction. Because the b 1 , b 2 and b 3 are different, it is possible that, despite the noticeable differences in the values of a i-1 (m) at the investigated energies m, at very high energies M all three values a i -1 (M) will coincide, i.e., the Great Unification of Interactions will be realized. Careful analysis, however, showed that within the framework of the standard model, using the known values of a i-1 (m), match all three values of a i -1 (M) for some large M impossible, i.e. the variant of the theory with Grand Unification is not realizable in this model. At the same time, it was found that in schemes other than the standard model, with a modified composition of the main (fund.) fields or particles, Grand unification can take place. Changes in the composition of the main particles lead to changes in the values of the coefficients " b i" and thus provide the possibility of matching a i (M) for large M.
The guiding idea when choosing a modified composition of the main. particle theory was the idea of the possible existence in the world of E. h. supersymmetry, which sets the definition. relationships between particles of integer and half-integer spin that appear in the theory. To meet the requirements of supersymmetry, for example. in the case of the standard model, each particle must be assigned a particle with a spin shifted by 1 / 2 - Moreover, in the case of exact supersymmetry, all these particles must have the same mass. Thus, quarks and leptons of spin 1/2 should be associated with their supersymmetric partners (superpartners) with spin zero, all gauge bosons with spin 1 should be associated with their superpartners with spin 1/2, and the Higgs boson with spin zero should be associated with a superpartner with spin 1/ 2. Since superpartners of quarks, leptons, and gauge bosons are obviously not observed in the studied energy region, supersymmetry, if it exists, must be noticeably broken, and the masses of superpartners must have values significantly exceeding the masses of known fermions and bosons.
A consistent expression of the supersymmetry requirement is found in the minimal supersymmetric model (MCCM), in which, in addition to the already listed changes in the composition of the standard model particles, the number of Higgs bosons increases to five (two of them are charged and three are neutral particles). Accordingly, five superpartners of Higgs bosons with spin 1 / 2 appear in the model - MCCM - the simplest generalization of the Standard Model to the case of supersymmetry. Meaning M, for which the coincidence a i (M)(Grand Unification), in the MCCM is approximately equal to 10 16 GeV.
The hypothesis of the existence of supersymmetry is associated with one of the promising possibilities for the development of the theory of gauge fields, which, moreover, resolves a number of its intrinsic values. problems associated with the stability of the parameters appearing in it. Supersymmetry, as has been noted, makes it possible to retain in the theory of electromagnetic waves the attractive possibility of a grand unification of interactions. A decisive confirmation of the fact of the existence of supersymmetry would be the discovery of superpartners of known particles. Their masses are estimated to range from hundreds of GeV to 1 TeV. Particles of such masses will be available for study at the next generation of proton colliders.
Verification of the hypothesis of the existence of supersymmetry and the search for supersymmetric particles is undoubtedly one of the most important problems in electrochemical physics, which will undoubtedly be given top priority in the near future.
Some General Problems of the Theory of Elementary Particles
The latest development of particle physics has clearly singled out from all the microcomponents of matter a group of particles that play a special role and have the greatest reason (at the beginning of the 90s) to be called truly E. h. Fundams belong to it. fermions spin 1 /
2 - leptons and quarks, which make up three generations, and gauge bosons of spin 1 (gluons, photons and intermediate bosons), which are carriers of strong and e-weak interactions. Most likely, a particle with spin 2 should be added to this group, graviton as a carrier of gravity. interaction that binds all particles. A special group is made up of particles of spin 0, the Higgs bosons, which, however, have not yet been discovered.
Many questions nevertheless remain unanswered. Thus, it remains unclear whether there is a physical a criterion fixing the number of generations of elementary fermions. It is not clear how fundamental is the difference in the properties of quarks and leptons associated with the presence of color in the former, or whether this difference is specific only to the studied energy region. Related to this question is the question of physical nature of the Grand Unification, since in its formalism quarks and leptons are considered as objects with similar properties.
It is important to understand whether the existence of various "ext." quantum numbers of quarks and leptons ( B, L, I, S, C, b etc.) to a more complex geometry of the microworld, corresponding to a larger number of dimensions than the four-dimensional macroscopic geometry that we are accustomed to. space-time. Closely related to this question is what is the max. symmetry group G, which satisfy the interactions of E. h. and in which symmetry groups are embedded, which manifest themselves in the studied energy region. The answer to this question would help to determine the limiting number of carriers of the interaction of E. h. and to clarify their properties. It is possible that max. Group G actually reflects the symmetry properties of a certain multidimensional space. This circle of ideas found a certain reflection in the theory superstrings, which are analogues of ordinary strings in spaces with more than four dimensions (usually in a space of 10 dimensions). Superstring theory interprets E. h. as manifestations of specific excitations of superstrings, corresponding to decomp. backs. It is believed that extra (over four) dimensions do not reveal themselves in observations due to the so-called. compactification, i.e., the formation of closed subspaces with characteristic dimensions of ~10 -33 cm. Ext. manifestation of the existence of these subspaces are the observed "ext." Quantum numbers of electrochemical crystals. There are as yet no data confirming the correctness of the approach to interpreting the properties of electrical superstrings associated with the concept of superstrings.
As can be seen from the foregoing, ideally, a complete theory of electron particles should not only correctly describe the interactions of a given set of particles selected as fundamental, but also contain an explanation of what factors determine the number of these particles, their quantum numbers, interaction constants, the values of their masses, etc. The reasons for the selection of the most. wide symmetry group G and, at the same time, the nature of the mechanisms that cause symmetry breaking as we move to lower energies. In this regard, the clarification of the role of the Higgs bosons in E.Ch. physics is of paramount importance. Models, to-rye offers modern. theory of E. h., are still far from satisfying all the listed criteria.
The description of EC interactions, as already noted, is connected with gauge field theories. These theories have a developed mat. apparatus, to-ry allows you to make calculations of processes with E.ch. at the same level of rigor as in quantum electrodynamics. However, in the apparatus of gauge field theories, in its modern wording, there is one being. a flaw common with quantum electrodynamics - in the process of calculations, meaningless infinitely large expressions appear in it. With the help of special method of redefining the observed quantities (masses and interaction constants) -
- it is possible to eliminate infinities from endings. calculation results. However, the renormalization procedure is a purely formal circumvention of the difficulty existing in the apparatus of the theory, which at some level of accuracy may affect the degree of agreement between the predictions of the theory and measurements.
The appearance of infinities in calculations is due to the fact that in the Lagrangians of interactions the fields of different particles are referred to one point x, i.e., it is assumed that the particles are pointlike, and the four-dimensional space-time remains flat down to the smallest distances. In fact, these assumptions, apparently, are incorrect for several. reasons:
a) truly E. h., as carriers of a finite mass, it is most natural to attribute, albeit very small, but finite dimensions, if we want to avoid the infinite density of matter;
b) the properties of space-time at small distances, most likely, are radically different from its macroscopic. properties (starting from a certain characteristic distance, which is usually called fundamental length);
c) at the smallest distances (~ 10 -33 cm) a change in the geome affects. properties of space-time due to the influence of quantum gravity. effects (fluctuations of the metric; see quantum theory of gravity).
Perhaps these reasons are closely related. So, it is the accounting of gravity. effects max. naturally leads to true E.ch. sizes. about 10 -33 cm, and funds. length may actually coincide with the so-called. Planck length l Pl \u003d 10 -33 cm, where x-gravity constant (M. Markov, 1966). Any of these reasons should lead to a modification of the theory and the elimination of infinities, although the practical implementation of this modification can be very difficult.
One of the interesting possibilities of consistently taking into account the effects of gravity is related to the extension of the ideas of supersymmetry to gravity. interaction (theory supergravity, especially extended supergravity). Joint accounting of gravity. and other types of interactions leads to a noticeable reduction in the number of divergent expressions in the theory, but whether supergravity leads to the complete elimination of divergences in calculations has not been rigorously proven.
Thus, the logical conclusion of the ideas of the Great Unification, most likely, will be the inclusion in the general scheme for considering the interactions of E. h. also gravitational. interactions, taking into account which may turn out to be fundamental at the smallest distances. It is on the basis of the simultaneous consideration of all types of interactions that Naib. likely to expect the creation of a future theory of E. h.
Lit.: Elementary particles and compensating fields. Sat. st., trans. from English, M., 1964; Kokkede Ya., Theory of quarks, trans. from English, M.. 1971; Markov M. A., On the nature of matter, M., 1976; Gle-show Sh., Quarks with color and flavor, trans. from English. UFN, 1976, v. 119, c. 4, p. 715; Bernstein, J., Spontaneous symmetry breaking, gauge theories, the Higgs mechanism, etc., in: Quantum Theory of Gauge Fields. Sat. st., trans. from English, M., 1977 (News of Fundamental Physics, v. 8); Bogolyubov H. H., Shirkov D. V., Quantum fields, 2nd ed., M., 1993; Okun L. B., Leptons and Quarks, 2nd ed., M., 1990.
- material objects that cannot be divided into component parts. In accordance with this definition, molecules, atoms and atomic nuclei that can be divided into constituent parts cannot be attributed to elementary particles - an atom is divided into a nucleus and orbital electrons, a nucleus - into nucleons. At the same time, nucleons, consisting of smaller and fundamental particles - quarks, cannot be divided into these quarks. Therefore, nucleons are classified as elementary particles. Given the fact that the nucleon and other hadrons have a complex internal structure, consisting of more fundamental particles - quarks, it is more appropriate to call hadrons not elementary particles, but simply particles.
Particles are smaller than atomic nuclei. The sizes of the nuclei are 10 -13 − 10 -12 cm. The largest particles (including nucleons) consist of quarks (two or three) and are called hadrons. Their dimensions are ≈ 10 -13 cm. There are also structureless (at the current level of knowledge) dot-like (< 10 -17 см) частицы, которые
называют фундаментальными. Это кварки, лептоны, фотон и некоторые другие.
Всего известно несколько сот частиц. Это в подавляющем большинстве адроны.
Table 1
|
Fundamental fermions |
|||||||
|---|---|---|---|---|---|---|---|
|
Interactions |
Generations | Charge Q/e |
|||||
| leptons | v e | ν μ | ν τ | ||||
| e | μ | τ | |||||
| quarks | c | t | +2/3 | ||||
| s | b | -1/3 | |||||
The fundamental particles are 6 quarks and 6 leptons (Table 1), which have spin 1/2 (these are fundamental fermions) and several particles with spin 1 (gluon, photon, W ± and Z bosons), as well as the graviton (spin 2), called fundamental bosons (Table 2). Fundamental fermions are divided into three groups (generations), each of which has 2 quarks and 2 leptons. All observable matter consists of particles of the first generation (quarks u, d, electron e -): nucleons consist of u and d quarks, nuclei consist of nucleons. Nuclei with electrons in their orbits form atoms, and so on.
table 2
| Fundamental Interactions | ||||
|---|---|---|---|---|
| Interaction | field quantum | Radius cm | Interaction constant (order of magnitude) |
Example manifestations |
| strong | gluon | 10 -13 | 1 | nucleus, hadrons |
| electromagnetic | γ quantum | 10 -2 | atom | |
| weak | W ± , Z | 10 -16 | 10 -6 | γ decay |
| gravitational | graviton | ∞ | 10 -38 | gravity |
The role of fundamental bosons is that they realize the interaction between particles, being “carriers” of interactions. In the process of various interactions, particles exchange fundamental bosons. Particles participate in four fundamental interactions - strong (1), electromagnetic (10 -2), weak (10 -6) and gravitational (10 -38). Numbers in parentheses characterize the relative strength of each interaction in the energy range below 1 GeV. Quarks (and hadrons) participate in all interactions. Leptons do not participate in the strong interaction. The carrier of the strong interaction is the gluon (8 types), the electromagnetic one is the photon, the weak one is the bosons W ± and Z, and the gravitational one is the graviton.
The vast majority of particles in the free state are unstable; breaks up. The characteristic lifetimes of particles are 10 -24 –10 -6 sec. The lifetime of a free neutron is about 900 sec. The electron, photon, electron neutrino, and possibly the proton (and their antiparticles) are stable.
The basis of the theoretical description of particles is quantum field theory. To describe electromagnetic interactions, quantum electrodynamics (QED) is used, the weak and electromagnetic interactions are jointly described by a unified theory - the electroweak model (ESM), and the strong interaction - by quantum chromodynamics (QCD). QCD and ESM, which together describe the strong, electromagnetic, and weak interactions of quarks and leptons, form a theoretical framework called the Standard Model.






