1. Periodic system of elements as a form of reflection of the periodic law . Formulations of the periodic law. The main regularities of the filling of atomic orbitals with electrons and the formation of periods. s -, p -, d - andf -elements and their location in the periodic system. The structure of the periodic system: small and large periods, main and secondary subgroups. Position of lanthanides and actinides. Modern forms of the periodic table. Periodic law as the basis for the development of inorganic chemistry. General scientific significance of the periodic law.

1 With. 41–46; 2 With. 46–55; 4 With. 30–40; 5 . With. 6–8, 21–32; 8 With. 105–106; 11 With. 75–203.

Periodic Law in modern terms: "The properties of atoms of chemical elements, as well as the composition and properties of the substances they form, are in a periodic dependence on the charges atomic nuclei».

The graphic expression of the periodic law is the table of the periodic system of elements. There is only one periodic law, and more than 500 forms of the periodic system of elements are known. Of these, the most common short period(8 cell) , semi-long period(18 cell) and long period(32 cell).

Chemical elements are arranged in the periodic table in order of increasing charge of the nuclei of their atoms. The periodic system consists of periods and groups.

Period- a number of elements arranged in order of increasing charge of the nuclei of their atoms, the electronic configuration of the external energy level of which varies from ns 1 (alkali metal) to ns 2 np 6 (noble gas). For the first period - from 1 s 1 (hydrogen) to 1 s 2 (helium). The first, second and third periods are called small(or short), the rest - big(or long). There are 7 periods in total.

The physical meaning of the period number – it is equal the number of energy levels in the atoms of chemical elements in a given period. For example, in atoms of elements of the 4th period, which are in an unexcited state, electrons are distributed on 4 energy levels (4 electron shells).

Group – vertical row elements that have similar electronic structure atoms and exhibiting therefore similar properties. As a rule, the group number indicates the number of electrons in an atom of an element that can participate in the formation of a chemical bond.

2. Periodicity of properties of atoms of chemical elements. Factors that determine the nature of the change chemical properties elements. "Configuration" and "structure" of the electron shells of the atom, their change in periods and groups. The radii of atoms and ions, the ratio of their values. Effective (covalent, ionic, metallic) and orbital radii. Changing the radii of atoms and ions by periods and groups.

Ionization energy (ionization potential) and electron affinity. Factors that determine their values: the radius of the atom, the configuration of the outer electron shell, the effective charge of the atomic nucleus. Patterns of change in ionization energy and electron affinity in periods and groups.

The concept of electronegativity. Change in the electronegativity of atoms in periods and groups. The influence of the difference in the electronegativity of atoms on the nature of the chemical bond between them. Changes in the chemical properties of elements in groups and periods depending on the structure electron shells, as well as the atomic radii.

1 With. 46–51; 2 With. 51–52, 94–98, 423; 99–103; 4 With. 40–46; 5 With. 6–9, 49–53; 7 With. 81–90; 8 With. 106–112; 11 With. 63–67.

The most important factors that determine the chemical properties of atoms of chemical elements are the configuration and structure of their electron shells. A successive increase in the charge of atomic nuclei leads to a periodic change in the electronic configuration of their outer electron shells from ns 1 to ns 2 np 6. The consequence of this is a periodic change in such characteristics of atoms as covalent, ionic and metallic radius, ionization energy, electron affinity, oxidation state, atomic volume, etc.

Strictly speaking, the size of any atom is infinite, since there is a non-zero probability of finding its electrons at an arbitrarily large distance from the nucleus. However, there is a main maximum on the curve of the radial electron density distribution for any orbital. Based on this, the concept orbital radius atom. He is equal theoretically calculated the distance from the nucleus to the main maximum on the radial distribution curve for the outer orbital.

Speaking about the size of an atom, most often they mean it effectiveradius. Its values ​​determine experimentally methods of electronography or X-ray diffraction, which make it possible to find internuclear distances in molecules, ionic and metallic crystals. Based on their values, they calculate accordingly covalent, ionic and metallic atomic radii.

The value of the effective radius of an atom depends on many factors: the structure of the substance, the nature of the chemical bond, the degree of oxidation of the element, etc. data and therefore different authors can vary greatly.

The pattern of change in the values ​​of atomic radii of chemical elements has a periodic character.

In periods as the charge of atomic nuclei increases (an increase in atomic number) the radius of the atoms decreases. For example, eight elements of the 3rd period (only s- and R-elements), the radius decreases from 190 pm (for sodium) to 99 pm (for chlorine), i.e., almost 2 times, and for ten d-elements of the 4th period, the radius decreases from 164 pm (for scandium) to 153 pm (for zinc), i.e., by only 7%.

In groups as the charge of the nuclei increases, the radius of the atoms increases, while in groups A ( s- and p-elements), such an increase occurs to a greater extent than in groups B ( d- and f-elements).

d-Elements of the 5th and 6th periods, located in the same group, have almost the same atomic radii. For example, the atomic radii of zirconium and hafnium are 160 pm and 150 pm, respectively, while those of molybdenum and tungsten are 139 pm and 141 pm, respectively. The reason for such proximity of the radii is that in the 6th period 14 f-elements, in the atoms of which the third outside is filled 4 f-energy sublevel, which strongly "shields" outer electrons from the nucleus. As a result, an increase in the charge of atomic nuclei has little effect on the magnitude of atomic radii. This effect is called lanthanide compression.

Ionization energy (E and he. ) – minimum energy required to remove 1 electron from an isolated atom BUT , which is in the ground energy state:

A 0 → A + + e – – E and he.

Distinguish the first ( E 1), second ( E 2) and subsequent ionization energies corresponding to the detachment of the first, second, and subsequent electrons. The unit of ionization energy is kJ/mol.

Ionization potential (I ) –the smallest voltage (potential difference) of the electric field at which an electron detaches from an isolated atom.

Distinguish the first ( I 1), second ( I 2) and subsequent ionization potentials corresponding to the detachment of the first, second, and subsequent electrons. The unit of the ionization potential is the electron volt, eV. One eV corresponds to 96.486 kJ/mol.

The value of the ionization energy of an atom (and its ionization potential) depends on many factors: the charge of the nucleus, the radius of the atom, the configuration of the electron shell of the atom.

Electron affinity (E cf. ) – the energy that is released or absorbed as a result of the attachment of an electron to a neutral isolated atom A 0:

A 0 + e – → A – ± E cf.

The addition of an electron to an atom is accompanied by release of energy(+e cf.), if this results in atomic particle with a stable electron shell. This is typical, for example, for halogen atoms. If, as a result of the attachment of an electron to an atom, an atomic particle with an unstable electron shell is formed, then the electron affinity of such an atom is negative, i.e. energy is absorbed(– e cf.). This is inherent, for example, in metal atoms.

Electronegativity (χ) – conditional value characterizing the ability of an atom to chemical compound attract valence electrons(common electron pairs).

The electronegativity value of an atom in the simplest case is determined based on its ionization potential and electron affinity.

There are various scales in which the values ​​of χ of the elements may differ somewhat (electronegativity according to Pauling, according to Mulliken, according to Allred-Rochov, etc.). On most scales, fluorine is the most electronegative element and francium is the least electronegative.

With increasing atomic number In a period, electronegativity increases, while in a group, as a rule, it decreases. For example, the electronegativity of oxygen is higher than that of carbon, because they are located in the same period, but oxygen is located to the right of carbon. The electronegativity of barium is lower than that of magnesium, since its values ​​decrease from top to bottom in a group.

If two atoms have the same χ values, then a covalent nonpolar chemical bond is formed between them. If the electronegativity of the atoms does not differ very much (the difference in the values ​​of the electronegativity Δχ does not exceed 1.5), then a covalent polar bond arises between the atoms. The common electron pairs that form it always shift to an atom with a higher χ, as a result of which it acquires a partial negative charge (δ–). Accordingly, the second atom acquires a partial positive charge (δ+).

The consequence of solving the Schrödinger equation for the hydrogen atom are three quantum numbers that characterize the behavior of an electron in an atom. These same quantum numbers uniquely characterize the state of the electrons of any atom of the periodic system of elements.

Principal quantum number n determines the energy of the electron and the size of the electron clouds. The energy of an electron mainly depends on the distance of the electron from the nucleus: the closer the electron is to the nucleus, the lower its energy. Therefore, we can say that the main quantum number determines the location of the electron on one or another energy level(quantum layer). The main quantum number has the values ​​of a series of integers from 1 to When the value of the main quantum number is equal to one, the electron is in the first energy level located at the minimum possible distance from the nucleus. total energy of such an electron is the smallest.

The electron at the energy level farthest from the nucleus has maximum energy. Therefore, during the transition of an electron from a more distant energy level to a closer one, portions (quanta) of energy are released. Energy levels are indicated in capital letters according to the scheme:

Orbital quantum number According to quantum mechanical calculations, electron clouds differ not only in size, but also in shape. The shape of the electron cloud is characterized by the orbital or azimuthal quantum number. The different form of electron clouds causes a change in the energy of electrons within one energy level, i.e., its splitting into energy sublevels. Each form of the electron cloud corresponds to a certain value of the mechanical momentum of the electron, determined by the orbital quantum number:

Orbital quantum number l. can have values ​​from 0 to all values. Energy sublevels are denoted by letters:

With the value of the principal quantum number equal to one, the orbital quantum number has only one value, equal to zero. This value characterizes electron clouds that have spherical symmetry (see Fig. 1.3). Electrons whose orbital quantum number is zero are called -electrons.

Only -electrons can be on the first energy level, its conditional notation When the value of the main quantum number is equal to two, the orbital quantum number has two meanings: Orbital number,

equal to one corresponds to the dumbbell-shaped form of an electron cloud (the shape of a volume eight) (Fig. 1.4. Electrons whose orbital quantum number is equal to one are called -electrons.

The second energy level can contain S- and -electrons, which form two sublevels: When the value of the main quantum number is three, the orbital quantum number has three values: An orbital quantum number equal to two corresponds to more complex shape electron clouds (Fig. 1.5). Electrons with an orbital quantum number of two are called d-electrons.

The third energy level can contain -electrons, which form three sublevels: When the value of the main quantum number is four, the orbital quantum number has four values: An orbital number equal to three corresponds to an even more complex shape of clouds. electrons,

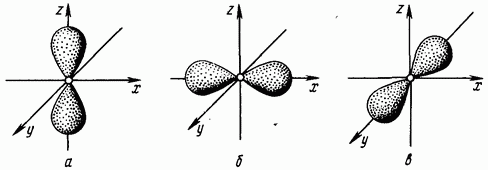
Rice. 1.4. Electronic -clouds -orbital; -orbital; in - -orbital

Rice. 1.5. Electron d-clouds - orbital; -orbital; c - orbital; - -orbital; - -orbital

whose orbital quantum number is three, are called -electrons.

The fourth energy level can contain and -electrons, which form four sublevels;

Magnetic quantum number It follows from the solution of the Schrödinger equation that the electron clouds are oriented in space. The spatial orientation of electron clouds is characterized by a magnetic quantum number.

An external magnetic or electric field changes the spatial orientation of electron clouds, therefore, when exposed to a magnetic or electric field, the energy sublevels of electrons are split. in magnetic and electric fields splitting of atomic spectral lines is observed.

The magnetic quantum number takes on any integer numerical value from to including 0. Thus, the number of possible values ​​​​of the magnetic quantum number is If the value of the orbital quantum number is zero, the magnetic quantum number has only one value, equal to zero (see Fig. 1.3). With an orbital quantum number equal to one, the magnetic quantum number has three values: Three values ​​of the magnetic number characterize three states of -electrons, which corresponds to the orientation of -clouds in space in three mutually perpendicular planes along the coordinate axes (see Fig. 1.4).

With an orbital quantum number equal to two, the magnetic quantum number has five values: . The five values ​​of the magnetic quantum number correspond to the five spatial positions of the d-electron clouds (Fig. 1.5). The orbital quantum number equal to three corresponds to seven values ​​of the magnetic number and seven spatial positions of the clouds.

Atomic orbitals (AO). Based on the concepts of quantum numbers, it is possible to refine the definition of an electron orbital in an atom. The set of positions of an electron in an atom, characterized by certain values ​​of quantum numbers, is called an atomic orbital.

2. ELECTRONIC STRUCTURE OF ATOMS. CHEMICAL BOND

Any stable state of an electron in an atom is characterized by certain values ​​of quantum numbers: n, l, ml, ms, called respectively: principal, orbital, magnetic and spin.

The state of an electron in an atom, corresponding to certain values ​​of quantum numbers n, ℓ, ml, is called an atomic orbital (a.o.). Otherwise, the atomic orbital is the space where the electron is most likely to stay.

Depending on the value of the orbital quantum number, the following designation of energy sublevels is accepted:

ℓ= 2 – d -*- ℓ= 3 – f -*-

Each type of atomic orbital has its own shape of the electron cloud. S is a spherical orbital, p is a dumbbell-shaped orbital, d is a rosette-shaped orbital, and f is an orbital of even more complex shape.

The number of orbitals of each type is determined by the number of ways to orient them in space, i.e. the number of values ​​of the magnetic quantum number - ml. The magnetic quantum number has (2ℓ + 1) values

(Table 2.1).

Graphically, an atomic orbital is depicted or -. The number (z) of atomic orbitals in an energy level is given by za.o. = n2 , where n is the principal quantum number.

According to the Pauli principle, an atom cannot have two electrons characterized by the same set of quantum numbers. It follows from this that each atomic orbital can be occupied by no more than two electrons, and their spin quantum numbers must be different, which is denoted by ↓.

Thus, the total number of electrons in the energy level is determined by the formula ze = 2n2. The number of electrons in a sublevel is determined by the formula 2(2ℓ + 1). The calculation of the number of electrons and the level structure can be presented in the form of Table. 2.2.

Knowing the structure of each sublevel and level, it is possible to compose electronic formulas of elements.

The stable (unexcited) state of a multielectron atom corresponds to such a distribution of electrons over atomic orbitals, in which the energy of the atom is minimal. Therefore, atomic orbitals are filled in the order of successive increase in their energies. The order in which atomic orbitals are filled with electrons is determined by the Klechkovsky rules, which take into account the dependence of the energy of an orbital on the values ​​of both the principal (n) and orbital (ℓ) quantum numbers. According to these rules, atomic orbitals are filled with electrons in the order of the successive increase in the sum (n + 1) (Klechkovsky's first rule), and for the same values ​​​​of this sum, in the order of the successive increase in the main number n (Klechkovsky's second rule).

The placement of electrons in atomic orbitals within one energy sublevel is determined by Hund's rule, according to which the minimum energy of an atom corresponds to such a distribution of electrons in atomic orbitals of a given sublevel, at which the absolute value of the total spin of the atom is maximum; with any other arrangement of electrons, the atom will be in an excited state, i.e. will have higher energy.

Tasks and exercises

2.1. How is the state of an electron designated: a) with n=4, ℓ=2; b) with n=5, ℓ=3.

Solution: When recording the energy state, the number indicates the number of the sublevel (n), and the letter indicates the nature of the sublevel (s, p, d, f). For n=4 and ℓ=2 we write 4d; for n=5 and ℓ=3 we write 5f.

Table 2.2

Calculation of the number of electrons

The end of the table. 2.2

2.2. How many orbitals correspond to the third energy level? How many electrons are in this level? How many sublevels does this level split into?

Solution: For the third energy level n = 3, the number of atomic orbitals is 9 (32); this number of orbitals is the sum of 1(s) + 3(p) + 5(d) = 9. According to the Pauli principle, the number of electrons in this level is 18. The third energy level is split into three sublevels: s, p, d (the number of sublevels is the same as the number of values ​​of the principal quantum number).

All chemical elements can be classified depending on the nature of the sublevels to be filled into 4 types:

s-elements - fill with electrons ns - sublevel; p-elements - fill with electrons np - sublevel; d- elements - fill with electrons (n-1) d - sublevel; f-elements - fill with electrons (n-2) f - sublevel.

To write the electronic formula of an element, you must: indicate the number of the energy level with an Arabic numeral, write the literal value of the sublevel, write the number of electrons as an exponent.

For example: 26 FeIV 1s2 2s2 2p6 3s2 3p6 4s2 3d6 .

The electronic formula is compiled taking into account the competition of sublevels, i.e. minimum energy rules. Excluding the last electronic

the formula will be written: 26 Fe1V 1s2 2s2 2p6 3s2 3p6 3d6 4s2 . The maximum valency of an element is determined by the number of valence orbitals and depends on the electronic type of the element and the period number.

The electronic structure of the elements by periods and the maximum valency are presented in Table. 2.3.

Table 2.3 Electronic structure and maximum valency of elements

2.3. Which sublevel is filled in the atom with electrons after filling the sublevel: a) 4p; b) 4s?

R Solution: a) Sublevel 4p corresponds to the sum (n + l) equal to 4+1 = 5. The same sum n+l characterizes sublevels 3d (3+2 = 5)

and 5s (5+0 = 5). However, the 3d state corresponds to a smaller value of n (n = 3) than the 4p state, so the 3d sublevel will fill up earlier than the 4p sublevel. Therefore, after filling the sublevel 4p, the sublevel 5s will be filled, which corresponds to a one greater value of n (n=5).

b) sublevel 4s corresponds to the sum n+l = 4+0 = 4. The same sum n+l characterizes sublevel 3р, but filling of this sublevel precedes filling of sublevel 4s, because the latter corresponds to a larger value of the principal quantum number. Therefore, after the sublevel 4s, the sublevel with the sum (n+l) = 5 will be filled, moreover, from all possible combinations n+ℓ corresponding to this sum (n=3, ℓ=2; n=4, ℓ=1; n= 5, ℓ=0), the combination with the lowest value of the principal quantum number will be implemented first, i.e. the 4s sublevel will be followed by the 3d sublevel.

Conclusion: Thus, the filling of sublevel d lags behind by one quantum level, the filling of sublevel f lags behind by two quantum levels.

2.4. The electronic structure of an atom is described by the formula 1s 2 2s2 2p6 3s2 3d7 4s2 . What is this element?

R Solution: This element belongs to the electronic type

d-elements 1U period, because the 3d sublevel is built up by electrons; the number of electrons 3d7 indicates that this is the seventh element in order. The total number of electrons is 27, which means the serial number is 27. This element is cobalt.

2.5. Why are phosphorus and vanadium placed in the same group of the periodic table? Why are they placed in different subgroups?

R Solution: Electronic configurations of P 1s atoms 2 2s2 2p3 3s 2 3p 3 ; V 1s2 2s2 2p6 3s2 3p6 4s 2 3d 3 . The valence electrons are underlined.

These elements have the same number of valence electrons - 5. Therefore, P and V are located in the same 5th group. At the same time, these elements are not electronic counterparts, because. build up different sublevels, so they should not be placed in the same subgroup.

chemical bond is the result of the quantum mechanical interaction of electrons.

According to the nature of the distribution of electron density between atoms, chemical bonds are divided into covalent non-polar, polar and ionic ones (the metallic bond realized in metals is not considered here). If there is no displacement of a pair of electrons, then the bond approaches a covalent non-polar one. A covalent polar bond is carried out by a common pair of electrons displaced (polarized) to the nucleus of one of the partner atoms. The ionic bond is considered as extremely polarized covalent bond. To assess the ability of an atom of a given element to attract a common electron pair to itself, the value of relative electronegativity (χ) is used (Table 5). The greater the difference in electronegativity (Δχ), the greater the polarization of the bond (the higher the ionicity of the bond). It is believed that if Δχ > 1.9, then the bond is ionic.

2.6. Calculate the difference in the relative electronegativity of atoms for H-O and E-O bonds in E(OH)2 compounds, where E are the elements Ca, Sr, Ba, and determine:

a) what N-O bond or E-O is characterized in each molecule by a greater degree of ionicity; b) what is the nature of the ionization of these molecules in an aqueous solution?

Decision: a) Calculate Δχ for the relationship between E-O and H-O:

Δχ Ca-O = 3.5 - 1.04 = 2.46 ΔχSr-O = 3.5 - 0.99 = 2.51 Δχ Ba-O = 3.5 - 0.90 = 2.60 Δχ H-O = 3.5 - 2.1 = 1.4

From the comparison of Δχ we see that E-O communication can be considered ionic, the H-O bond is polar.

b) ionization in aqueous solutions will be carried out along the most ionic bond, i.e. according to the scheme: E (OH) 2 ↔ E2 + + 2OH- (according to the type

grounds).

The strength of a chemical bond is characterized by energy (kJ/mol) and

length (nm or A) of the bond. The higher the bond energy and the shorter its length, the stronger the bond.

Chemical bond, i.e. a common electron pair can be formed in two ways: by the exchange and donor-acceptor mechanism. A chemical bond is characterized by three main properties:

1) has a certain direction in space. From this point of view, σ andπ bonds. The angle formed by the directions of two σ-bonds is called the valence angle. If a π bond combines several atoms, it is called non-localized;

2) tends to saturation, as a result of which the particles have a certain composition and structure. Possible: coordination

unsaturated, coordinatively saturated, valence-saturated and valence-unsaturated states of atoms;

3) can be polarized under the influence of various factors (depending on the electronegativity of atoms, as well as under the influence of an external electric or magnetic field, under the action of other polar molecules).

To explain the geometric structure of molecules, the concept of hybridization of atomic orbitals of the central atom is used. According to this concept, the formation of σ-bonds is preceded by a change in the shape and energy of atomic orbitals. Hybrid orbitals are formed, capable of deeper overlap and hence stronger bonds. For elements of the s and p electronic type, orbitals, including unshared electron pairs, can take part in hybridization.

2.7. Show the formation of a bond in a BF3 molecule and a BF4 - ion. Explain the structure of these particles.

Solution: 1. Compose the electronic formulas of atoms and io-

new: B 1s2 2s2 2p1 ; F 1s2 2s2 2p5 ; F- 1s2 2s2 2p6 .

2. Let us show the distribution of electrons over valence orbitals. In this case, we take into account the degree of oxidation of the boron atom in the compound (we can conditionally assume that the number of unpaired electrons in the atom corresponds to the degree of oxidation).

3. We will show the formation of all possible bonds, we will indicate the mechanism of their formation:

3 σ-bonds were formed by the exchange mechanism Based on the valence possibilities of the atom

boron and its tendency to saturation, we will show the formation of a π-bond by the donor-acceptor mechanism. But, because this bond unites more than two atoms

mov, it will be non-localized.

In the BF4 - ion, 4 σ-bonds are formed, three of them by the exchange and one by the donor-acceptor mechanism.

4. Calculate the multiplicity of the connection as a ratio total number connections toσ-bonds. In the BF3 molecule, the bond multiplicity is 1⅓; in the BF4 ion, the bond multiplicity is 1.

5. Let us define the state of the central atom in terms of saturation

bridges. In the BF3 molecule, the maximum valence is manifested due to σ and π bonds, therefore, the state of the boron atom is valence-saturated.

In the BF 4 - ion, the maximum valence is manifested due to σ-bonds, therefore, the state of the boron atom is coordinatively saturated.

6. Let's define the nature of the connection B-F in terms of polarity. Because the difference in the electronegativity value (Δχ) is 4.0-2.0 = 2.0, i.e. more than 1.9, the bond can be considered ionic.

7. Let us determine the type of hybridization of the atomic orbitals of the central atom and the geometric shape of the particles.

In the BF 3 molecule, s and 2p orbitals are involved in the formation of σ-bonds, hence the type of sp2 hybridization. The molecule is triangular

structure. In the BF4 - ion, one s and three p orbitals are involved in the formation of σ-bonds, hence the sp3 hybridization type. The ion has a tetrahedral shape.

8. Let's graphically depict the structure of particles

2.8. Show the formation of bonds in the SO3 molecule, explain the structure of the molecule.

Solution: Electronic Formulas of Elements

S 1s2 2s2 2p6 3s2 3p4 O 1s2 2s2 2p4 .

Because the oxidation state of the sulfur atom is +6, we will show the distribution of electrons over the valence orbitals of the excited sulfur atom.

The sulfur atom forms 3 σ-bonds (due to one s and two p-atomic orbitals) and 3 π-bonds (due to one p- and two d-atomic orbitals) by the exchange mechanism.

Consequently, the atom is valence-saturated, coordinatively unsaturated; bond multiplicity 6/3 = 2. S-O connection polar, common electron pairs are shifted to oxygen (Δχ = 0.5). Sp2 hybridization type. The molecule has the structure of a triangle.

3. COMPLEX COMPOUNDS

Complex compounds play an important role in the life of living organisms. Na, K, Ca, Mg ions, which perform important physiological functions in the body, are found in the blood, lymph, and tissue fluids in the form of complex compounds. Fe, Zn, Mn, Cu ions form complex compounds with proteins and are part of enzymes and vitamins. Iron is part of hemoglobin. Hemoglobin is the connection between the globin protein and the heme complex. In heme, the central ion is Fe2+.

Complex compounds are called molecular compounds, the combination of components of which leads to the formation of complex ions capable of free existence both in a crystal and in solution. In the molecules of complex compounds, internal and external spheres are distinguished. The inner sphere is enclosed in square brackets and consists of a central atom or ion, called the complexing agent, and atoms, ions, or molecules coordinated around it, called ligands.

The number of ligands coordinated around the complexing agent determines its coordination number (c.h.). The latter shows the number of σ-bonds that arise between f.p. and ligands.

Molecule c.s. electrically neutral. Inner sphere charge equal to the charge external with the opposite sign. The charge of a complex ion is equal to the algebraic sum of charges k.o. and ligands.

Classification of complex compounds

1. By the nature of the charge of the complex ion

- cationic: formed due to coordination around a positively charged c.o. neutral ligand molecules

Cl2; Cl3;

- anionic: complexing agent - positive ions, whether-

gangs are K2 anions; Na2 ;

- neutral: formed upon coordination around a neutral f.r. neutral ligands o or with simultaneous coordination around a positively charged c.o.

negatively charged and neutral ligands

2. By the nature of ligands

Hydrates or aquacomplexes Cl3 ;

Ammonia SO4 ;

- acid complexes K 2 ;

- Na hydroxocomplexes.

3. By the number of k.o.

Mononuclear Cl2 ;

Polynuclear [(NH 3 )4 Co\ / OH OH / \ Co(NH3 )4 ]Cl4 .

Rules for naming complex compounds

1) name of c.s. start with a cation;

2) in the name of a complex ion, the ligands are indicated first, then the central atom. The ending "o" is added to the names of anionic ligands, molecular ligands are called as

corresponding free molecules. Exception: NH3 - ammine; H2O - aqua; CO - carbonyl;

3) complexing agent in cationic and neutral c.s. called the Russian name of the element, in anionic - the Latin name with the addition of the ending "at";

4) oxidation state k.o. denoted by an Arabic numeral and put in

brackets after its name. K3 – potassium hexanitritocobaltate (+3); Cl3 - hexaaquachromium (+3) chloride; o is iron pentacarbonyl (0).

Behavior of complex compounds in solution

In solutions of c.s. behaves like a strong electrolyte and dissociates entirely into a complex ion and outer sphere ions:

Cl → + + Cl-

Complex ions ionize reversibly and stepwise: + ↔ + + NH3

+ ↔ Ag+ + NH3 or in total: + ↔ Ag+ + 2NH3

The ionization equilibrium constant of a complex ion is called the instability constant

It depends only on the nature of the compound and the temperature; is given in reference books (see Table 6).

4. CHEMICAL EQUILIBRIUM

Chemical equilibrium is a state that corresponds to the equality of the rates of forward and reverse reactions:

In this case, the change in the Gibbs energy is zero

Go=O; ΔΗο = T So

The state of chemical equilibrium remains unchanged at a constant external conditions. When these conditions (temperature, pressure, concentrations) change, the equilibrium is disturbed in order to be restored again, but under new conditions.

The equilibrium shift obeys the Le Chatelier principle: if one of the conditions that determine the equilibrium position is changed in an equilibrium system, then the equilibrium shifts in the direction of the process that weakens the effect of the impact. So, with an increase in the concentration of reagents, the equilibrium shifts towards the process that will cause the consumption of these reagents. The reason for this behavior of the equilibrium system is an increase in the number of collisions of particles of the indicated reagents, which causes an acceleration of the forward or reverse reaction.

In gas systems, an increase in the concentrations of reagents occurs with an increase in pressure or a decrease in the volume of the system. Therefore, with an increase in the total pressure in the system, one of the two reversible reactions that occurs with the participation of a larger number of moles of gas, i.e. the equilibrium shifts towards the formation of a smaller number of moles.

With an increase in temperature, the rate of both forward and reverse reactions increases, but the rate of endothermic increases to a greater extent.

reactions, because it has a higher temperature coefficient.

Tasks and exercises

4.1. Show the direction of equilibrium shift with decreasing H2 concentration in the equilibrium system:

CO + H2 O↔ CO2 + H2 Solution: With a decrease in CH 2, according to the principle of Le-

Chatelier, the direct reaction must prevail, because in this case, the amount of H2 will increase, and the equilibrium will be restored again.

4.2. In what direction will the equilibrium PC15 ↔ PC13 + C12 - 31 kJ mol-1 shift with increasing temperature and pressure?

Solution: As the temperature rises, the equilibrium will shift to the right, because the direct reaction proceeds with the absorption of heat, i.e. is

endothermic. As the pressure increases, the number of collisions of PC13 and C12 molecules will be greater than PC15, so the equilibrium will shift to the left.

4.3. Under what conditions in an equilibrium system

N2 g + 3H2 g ↔ 2NH3 g + 22 kJ mol-1 is it possible to maximize the yield of NH3?

Solution: To increase the NH3 output, i.e. to shift the equilibrium to the right, it is necessary:

1) increase the pressure of the gas mixture, because in this case, the rate of the direct reaction increases, because more moles;

2) increase N concentration 2 and H2 and reduce the concentration of NH3, removing it from the reaction sphere;

3) lower the temperature of the reaction mixture, because reaction about-

NH3 formation is exothermic.

The quantitative characteristic of the state of chemical equilibrium is the equilibrium constant, which reflects the law of mass action.

The equilibrium constant is related to the Gibbs energy by the relation RTlnK

= -∆G about . For process aA + bB ↔ cC + dD concentration constant

equilibrium has the form: Кс = [C] c [D] d , where [A], [B], [C], [D] – equilibrium [A]a [B]b

nye concentrations in mol/l; a, b, c, d stoichiometric coefficients.

partial pressures of gases and mixtures.

The constants Kc and Kp characterize equilibrium processes in dilute solutions of electrolytes and non-electrolytes and in gas systems at pressures close to 101.3 kPa (ideal gases).

For concentrated solutions and non-ideal gases, activity values ​​should be used:

K a = a C ca D da A a a B b

The equilibrium constant depends on the nature of the reagents and temperature, but does not depend on the concentrations of the components of the equilibrium system.

In heterogeneous systems, the concentration of the solid phase is included in the value of the equilibrium constant, since is a constant value.

If the reactions proceed in aqueous solutions with the participation of water, then the concentration of water is large and constant and will practically not affect the state of equilibrium.

We write the equilibrium constants of the processes: 4HC1g + O2 g ↔ 2H2 Og + 2C12 g

When solving problems, it is necessary to clearly define state of aggregation reacting substances, as well as to distinguish the initial concentrations of substances from equilibrium.

C equilibrium \u003d C initial - C spent

4.4. 1 mol of H2 and 1 mol of I2 were mixed in a vessel with a capacity of 1 l at 410°C. Calculate at what concentrations the chemical equilibrium is established if the equilibrium constant is 48?

Solution: H 2 + I 2 ↔ 2HI

Let us assume that X moles of H2 and I2 are consumed in the reaction. Then 2X moles of HI were formed, i.e. HI = 2 mol/l. In this case ==

We get the equation: 44X2 - 96X + 48 = 0 Solving it, we get X = 0.776. Calculate the equilibrium concentrations: HI = 2X = 2 0.776 = 1.552 mol/l

1 - X \u003d 0.222 mol / l.

4.5. In the reversible reaction CO + C12 ↔ COC12, the following equilibrium concentrations (mol/l) were established: = 0.1; = 0.4; = 4. Calculate Crav. and initial concentrations of C12 and CO.

We find the initial concentrations: Cish. = Comp. + Sizexp. . For the formation of 4 mol COC12, according to the reaction equation, 4

mol of CO and C12. Hence, the initial concentrations are: CCO = 0.1 + 4 = = 4.1 mol/l; CC1 2 \u003d 0.4 + 4 \u003d 4.4 mol / l.

4.6. Determine the volumetric composition of the mixture at the moment of equilibrium for the reaction Cgraphite + O2 g ↔ CO2 g, if at 1300 ° C Equn. = 0.289.

Solution: K p \u003d P R CO 2

Let X denote the CO2 content in volume fractions (percentage). Then the content of O2 will be (100-X). Substitute into the equation:

K \u003d 0.289 \u003d (100 X - X); X = 22.42 vol.%. The content of O2 will be

5. CHEMICAL KINETICS

Chemical kinetics studies the rate and mechanism of chemical reactions, as well as the influence of various factors on the rate. average speed chemical reaction measured by the change in the concentration of reactants per unit time:

V = ±C 2 − C 1 ,

τ2−τ1

where C2 and C1 are the concentrations of substances (mol/l) corresponding to the time τ2 and τ1 (in s or min). For heterogeneous systems, the speed is measured

change in concentration per unit surface of the solid phase (1 cm2 or 1 m2).

The rate of a chemical reaction depends on the following main factors:

- the nature and state of the reacting substances;

- the nature of the environment in which the reaction takes place;

Catalyst;

- concentration of reacting substances, and for gases and pressure;

Temperatures.

The chemical activity of substances depends on the structure of atoms or molecules, the nature of intramolecular and intermolecular bonds. Radicals have the highest activity, it is somewhat lower for ions and molecules. The state of aggregation of the reagents and the degree of dispersity are also of no small importance.

Almost always, substances react with the medium (solvent), forming solvates (hydrates). In addition, the solvent may have a catalytic effect.

Catalysts generally speed up chemical reactions by changing their path. In this case, a new reaction path corresponds to a lower activation energy. The activation energy (Ea) is the minimum energy that the particles of the reacting substances must have in order to carry out the interaction. The value of Ea is determined by the chemical nature of the substances.

The effect of concentration, pressure, and temperature on the rate of a chemical reaction is quantifiable.

Law of acting masses expresses the dependence of the rate of a chemical reaction on the concentration of the reactants: the reaction rate is directly proportional to the concentrations of the reactants raised to the power of their stoichiometric coefficients. For reaction

аА + вВ → С V = KCA a CB b ,

where CA and CB are the molar concentrations of reagents A and B;

a and b are stoichiometric coefficients for A and B;

To - the rate constant of this reaction, reflecting the influence of the nature of substances. It depends on temperature, but does not depend on the concentration of substances.

For gas systems, instead of concentrations, you can use the value

us partial pressures: V = KPA a PB b .

In heterogeneous systems, the concentrations of crystalline substances are constant values ​​and are included in the rate constant. The reason for the increase in the reaction rate with increasing concentrations of reactants can be explained by an increase in the total number of particle collisions, and hence an increase in the number of active collisions. Let us write expressions for the rates of the following reactions:

a) 2H2 g + O2 g \u003d 2H2 Og

The law of mass action is valid only for simple reactions with a small order and molecularity.

The reaction order is understood as the sum of the exponents at concentrations in the expression of the law of mass action. Reaction molecularity is determined by the minimum number of molecules involved in the act of interaction. On the basis of molecularity, reactions are divided into one-molecular (monomolecular), two-molecular (bimolecular) and three-molecular (trimolecular). Higher molecular reactions are rare, because such reactions proceed in several stages.

One-molecular reactions include reactions of decomposition and intramolecular rearrangements, for them V = K·C. Two-molecular reactions include reactions in which the interaction occurs when two molecules collide, for them V \u003d K C1 C2; for three-molecular reactions V = K·C1 ·C2 ·C3 . On the basis of the order of the reaction, there are first, second and third orders, as well as zero and fractional.

third order V = K·C3 , V = K·C1 2 ·C2 , V = K·C1 ·C2 2 .

Reactions are of zero order if the concentration of the substance does not change during the entire process and the speed is a constant value. This is possible in heterogeneous systems where crystalline substance interacts with the surface, and the concentration remains constant value. For a zero order reaction, V = K·Co . The reaction has a fractional order if the process occurs in several stages, each of which has a negligible rate.

Tasks and exercises

5.1. Determine the molecularity and order of the reaction:

С12 g + 2NOg = 2NOClg

Solution: 1 mol of C12 and 2 mol of NO enter into the reaction, therefore, the indicated reaction is trimolecular. The procedure for determining

we use the equation: V = KCCl 2 C2 NO . The response is third order.

5.2. Calculate the rate of dissolution of iron (II) hydroxide in 0.02 M H2SO4 at K = 40. Determine the molecularity and order of the reaction.

Solution: The reaction will go according to the equation:

Fe(OH)2 cr + H2 SO4 p-p = FeSO4 p-p + 2H2 Ozh

V \u003d KCH 2 SO 4, because Fe(OH)2 is in the crystalline phase. The molecularity of the reaction is 2, the order is 1. Calculate the reaction rate:

V \u003d 40 0.02 \u003d 0.8 mol / min l.

5.3. In a solution containing 1 mol of SnCl 2 and 2 mol FeCl3, the reaction proceeds according to the equation:

SnCl2 p + 2FeCl3 p ↔ SnCl4 p + 2FeCl2 p

How many times will the reaction rate decrease after the reaction

ruet 0.65 mol SnCl2?

Solution: Calculate the reaction rate in the initial

After 0.65 mol SnCl2 has reacted, the concentrations will be

have the following values: СSnCl2 = 1 - 0.65 = 0.35 mol/l; СFeCl3 = = 2 - 1.3 = 0.7 mol/l. In this case, the reaction rate will be equal to:

V1 = K 0.35 0.72 = 0.17 K.

5.4. How will the reaction rate CO2 + C12 g = COC12 g change if the volume of the gas mixture is halved?

Solution: The initial reaction rate will be:

Vo = K CCO CC1 2 . With a halving of the volume, the concentrations of all

components will double and the speed can be calculated as follows: V 1= K 2C CO2C Cl2 = 4KC COC Cl2

It is quite obvious that with a decrease in volume by 2 times, the reaction rate increases by 4 times.

The effect of temperature on the rate of a chemical reaction is also quantified. With increasing temperature, the rate of any reactions increases, which is explained by an increase in the number of active particles whose energy reaches or exceeds the activation energy Ea. The temperature dependence of the reaction rate constant is expressed as

In practice, for calculations, the van't Hoff rule is used, according to which, with an increase in temperature by 10 °, the rate or rate constant of the reaction increases by 2-4 times.

γ is the temperature coefficient.

Van't Hoff's rule gives less accurate results than the Arrhenius equation, because γ can be considered constant only in a small temperature range. For inorganic reactions γ = 2-4, for enzymatic reactions γ = 7-8.

5.5. The temperature coefficient of the decomposition rate of HI in the temperature range of 356-376o C is 2. Calculate the rate constant of this reaction at 376o C, if at 356o C it is 8.09·10-5.

The set of states of an electron in an atom with the same value n called energy level. The number of levels at which the electrons are in the ground state of the atom coincides with the number of the period in which the element is located. The numbers of these levels are indicated by numbers: 1, 2, 3, ... (less often - by letters K, L, M, ...).

Energy sublevel- a set of energy states of an electron in an atom, characterized by the same values ​​of quantum numbers n and l. Sublevels are denoted by letters: s, p, d, f... The first energy level has one sublevel, the second - two sublevels, the third - three sublevels and so on.

If the orbitals are designated in the diagram as cells (square frames), and the electrons as arrows (or ↓), then you can see that the main quantum number characterizes the energy level (EU), the combination of the main and orbital quantum numbers - the energy sublevel (EPL ), a set of principal, orbital and magnetic quantum numbers - atomic orbital, and all four quantum numbers are an electron.

Each orbital corresponds to a certain energy. The designation of the orbital includes the number of the energy level and the letter corresponding to the corresponding sublevel: 1 s, 3p, 4d etc. For each energy level, starting from the second, the existence of three equal in energy p orbitals located in three mutually perpendicular directions. At each energy level, starting from the third, there are five d-orbitals with a more complex four-leaf shape. Starting from the fourth energy level, even more complex shapes appear. f-orbitals; There are seven on each level. An atomic orbital with an electron charge distributed over it is often called an electron cloud.

Question 12.

Horizontal periodicity

Such physical properties, as the ionization energy and electron affinity, a horizontal periodicity is also manifested, associated with a periodic change in the number of electrons at the last energy sublevels:

Question 13.

Question 14.

Magnetic characteristics of an atom

The electron has its own magnetic moment, which is quantized in the direction parallel or opposite to the applied magnetic field. If two electrons occupying the same orbital have oppositely directed spins (according to the Pauli principle), then they cancel each other out. In this case, the electrons are said to be paired. Atoms with only paired electrons are pushed out of the magnetic field. Such atoms are called diamagnetic. Atoms that have one or more unpaired electrons are drawn into a magnetic field. They are called diamagnetic.

The magnetic moment of an atom, which characterizes the intensity of the interaction of an atom with magnetic field, is practically proportional to the number of unpaired electrons.

Peculiarities electronic structure atoms various elements are reflected in such energy characteristics as ionization energy and electron affinity.

Ionization energy

Energy (potential) of ionization of an atom Ei is the minimum energy required to remove an electron from an atom to infinity according to the equation

X = X + + e− . Its values ​​are known for atoms of all elements of the Periodic system. For example, the ionization energy of a hydrogen atom corresponds to the transition of an electron from 1 s- energy sublevel (−1312.1 kJ/mol) to the sublevel with zero energy and equals +1312.1 kJ/mol.

In the change of the first ionization potentials, corresponding to the removal of one electron, of atoms, the periodicity is clearly expressed with an increase in the ordinal number of the atom:

When moving from left to right along the period, the ionization energy, generally speaking, gradually increases, while increasing the serial number within the group, it decreases. The minimum first ionization potentials have alkali metals, maximum - noble gases.

For the same atom, the second, third and subsequent ionization energies always increase, since the electron has to be detached from a positively charged ion. For example, for a lithium atom, the first, second, and third ionization energies are 520.3, 7298.1, and 11814.9 kJ/mol, respectively.

The sequence of detachment of electrons is usually the reverse of the sequence of population of orbitals by electrons in accordance with the principle of minimum energy. However, the elements that are populated d-orbitals are exceptions - first of all they lose not d-, a s-electrons.

electron affinity

Affinity of an atom for an electron A e - the ability of atoms to attach an additional electron and turn into a negative ion. The measure of electron affinity is the energy released or absorbed in the process. The electron affinity is equal to the ionization energy of the negative ion X − : X − = X + e −

The halogen atoms have the highest electron affinity. For example, for a fluorine atom, the addition of an electron is accompanied by the release of 327.9 kJ/mol of energy. For a number of elements, the electron affinity is close to zero or negative, which means that there is no stable anion for this element.

Usually, the electron affinity for atoms of various elements decreases in parallel with an increase in their ionization energy. However, there are exceptions for some pairs of elements:

An explanation for this can be given based on the smaller sizes of the first atoms and the greater electron-electron repulsion in them.

Question 15.

Question 16.

Horizontal periodicity

Horizontal periodicity consists in the appearance of maximum and minimum values ​​of properties simple substances and connections within each period. It is especially noticeable for elements of group VIIIB and lanthanides (for example, lanthanides with even serial numbers are more common than those with odd ones).

In such physical properties as ionization energy and electron affinity, horizontal periodicity is also manifested, associated with a periodic change in the number of electrons at the last energy sublevels.