>>Physics Grade 10 >>Physics: Potential energy

What do we know about the potential energy of gravity? Imagine the surface of the earth. We can be anywhere where there is gravity, then the potential energy will appear from the gravitational field of the mass given to us. We know that if there is some body of mass m located at a height h in a gravitational field with acceleration free fall g, or 9.8 m/s^2. Then the potential energy of gravitation of this body at this point is equal to the product of mass, acceleration of free fall and height.

This definition can be considered as the magnitude of the gravitational force. And what is the potential energy? If an object has potential energy, and nothing stops its movement, then it will fly down with acceleration and most of the potential energy, and in fact, all of it, will turn into kinetic energy. So in other words, potential energy is the energy that is "stored" in an object, or the energy that an object has in accordance with its location. Then, in order for a body or object to have this energy, it must come from somewhere, as is the case with the potential energy of gravity. We can think of the potential energy of gravity as the work required to move an object to a specified position.

We study the motion of a body under the influence of gravity. Suppose that a piece of rock with mass m falls from a height h1 relative to the foot of the mountain and stops on a ledge at a height h2. Under such conditions, the work is done by gravity: A=FS. Since the force of gravity is equal to F=gm, and the displacement is equal to S=h1 - h2, then the work will be equal to A=mg(h1 - h2) or A=mgh1 - mgh2. The value mgh characterizes the state of the body in the gravitational field and is called potential energy.

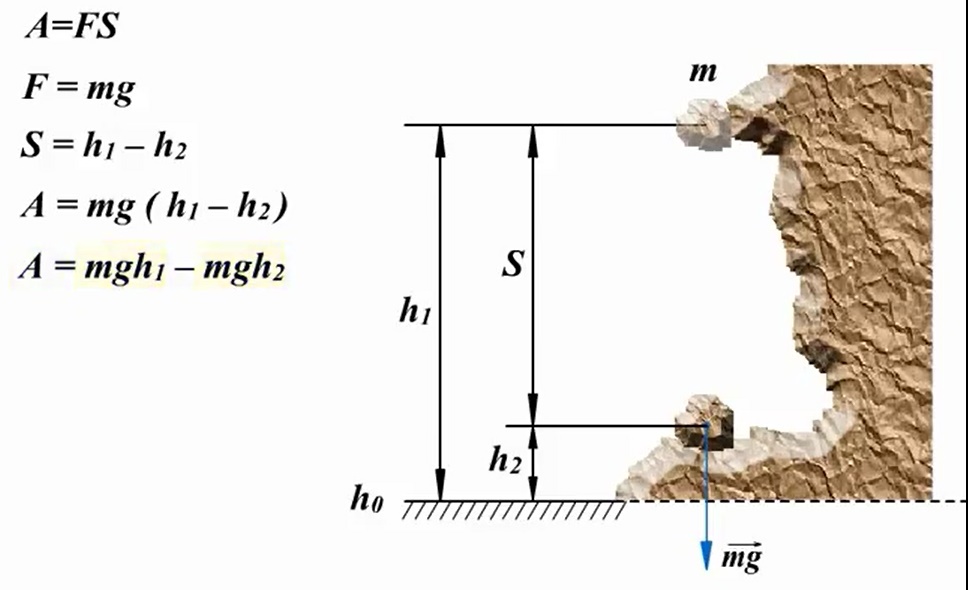
With this in mind, the formula for the work of gravity can be represented as follows:

As you can see, the work of gravity is a change in the potential energy of the body with the opposite sign. In our example, gravity has done positive work, and the change in potential energy is negative, i.e. potential energy has decreased.

Elastically deformed bodies can also possess potential energy. If you open a spring-loaded door, then the elastic force that has arisen along with this is able to do work, closing the door next. However, this case is special, since the work will be done by a variable modulo force.

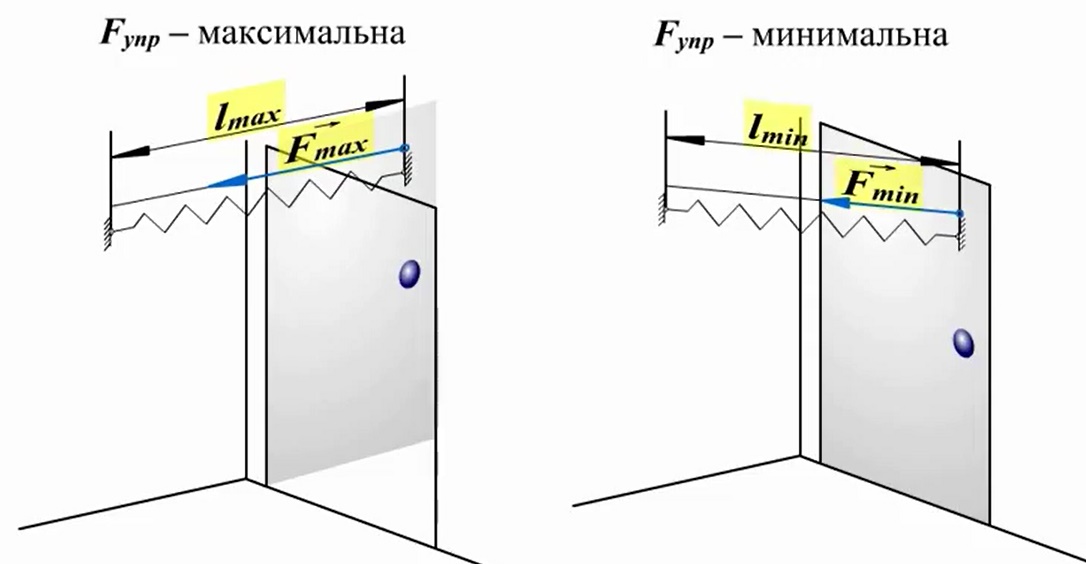
But since in this situation the work is performed due to the energy reserve, it can be argued that the work of the elastic force is equal to the difference in potential energies:

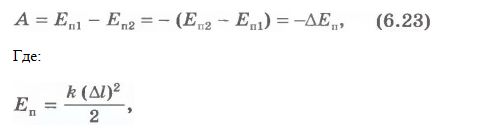
In this formula, k is the stiffness; Δl is the amount of deformation. Summing up everything mentioned above, we come to the conclusion that in all cases the work of the force causes a change in the energy of the body, from here it follows that work is a measure of the change in energy. The work formulas for gravity and elastic force look like this:

Law of energy conservation

Obviously, when interacting, bodies can exchange energies, for example, a moving billiard step, when colliding with a similar motionless ball, transfers its kinetic energy to it. If at the same time the first ball stops, then it will give the second all its kinetic energy.

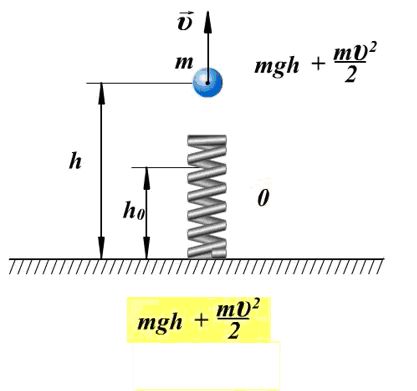
Consider an example with potential energy. A ball of mass m is located on a compressed spring, the spring is connected by a thread. The ball has potential energy with respect to the surface of the table. Potential energy of a compressed spring -

. Complete mechanical energy of this system of bodies is equal to:

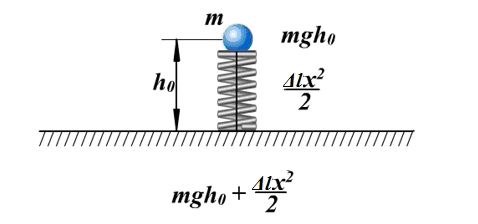
If the thread is burned, the ball will start moving upwards, and at some moment it will have a speed ύ at a height h, at the same time, the energy of the spring is 0, and total energy system will be equal to:

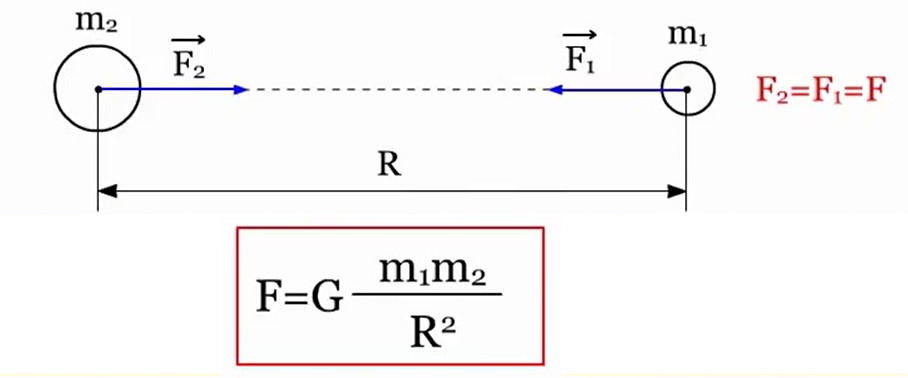
Isaac Newton is credited with discovering the law gravity. Here is his formulation: any two bodies are attracted to each other with a force directly proportional to the product of their masses and inversely proportional to the square of the distance between them:

The coefficient of proportionality in this law is one of the fundamental physical constants - the gravitational constant.

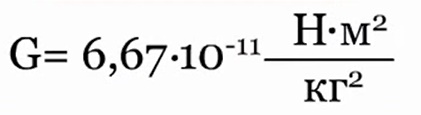
The law is formulated for point bodies, i.e. for material points, however, it is also valid for large homogeneous spheres, for example, planets. In this case, it is assumed that the mass of such bodies is concentrated in the center and the distance R is taken between the centers. There is gravity special case manifestation of the law of gravity. A body of mass m is attracted by the Earth of mass M, the distance between their centers is equal to the Earth's radius R. In accordance with Newton's second law, the body receives acceleration, where F is the force of gravitational attraction.

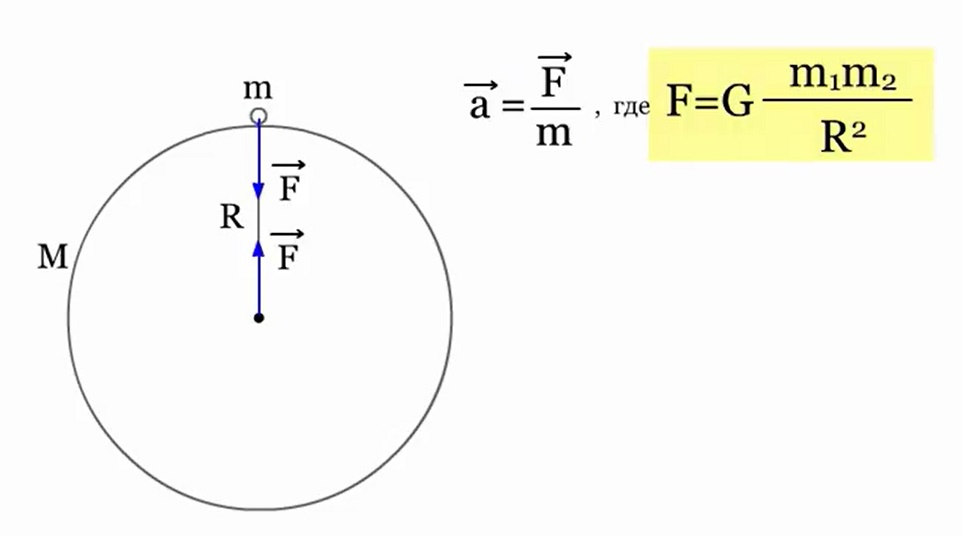
Therefore, the acceleration of the body a and is the free fall acceleration g, which is equal for all bodies and equal near the surface of the Earth.

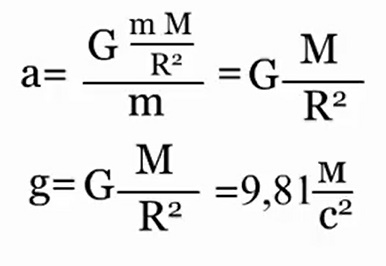
The force that informs the body of this acceleration is the force of gravity: F=mg. From the formula it is obvious that the force of gravity is directly proportional to the mass of the body.

A task

A stuntman weighing 80 kg jumped from a height of 12 m onto a stretched safety net. As a result, she caved in by 1.5 m. Find the average force with which the stuntman presses on the net? Solution: using the law of conservation of energy, you can make a record.

Under potential energyWp interacting bodies or parts of one body understand the SPV, which characterizes their ability to do work by changing relative position bodies or parts of the same body. Potential energy equally characterizes all interacting bodies or their parts. At the same time, between them strength who are called conservative , the work of these forces does not depend on the trajectory of the bodies, but is determined by their initial and final positions.

In the presence of only conservative forces, the potential energy of interaction of a system consisting of N bodies (m.t.) can be represented as potential energies of their pairwise interaction with each other and with external bodies (with numbers from (N + 1) to (N + L)):

where is the potential energy of interaction i-that and to-that tel. The coefficient (1/2) in the first term is due to the fact that the potential energy of interaction of bodies i and to occurs here twice (for example, and ) and the terms with i=k. For closed system the second term, which describes the interaction of the bodies of the system with external bodies, will not be in formula (1.70).

Potential Interactions usually described by the introduction of a force field, namely, it is believed that one body interacts at its location with force field created by other bodies. This approach is convenient to use in the case when the movement of one body (for example, the first one) has little effect on the movement of another body (the second one). Then we can assume that the first body is in the potential field created by the second body, and attribute the potential energy of their interaction to the first body. So, for example, they talk about the potential energy of a body in the Earth's gravitational field, about the potential energy of a charge in an electric field, etc. In this case, the motion of the body (charge) has little effect on the force field in which it moves. Let's remember what they usually say: the body falls to the Earth, and not the Earth falls on the body. This marks the fact that the movement of the body practically does not change the position of the Earth.

Examples of conservative forces in mechanics are the forces of gravity and elasticity, and non-conservative forces - the forces of friction, resistance, traction, force chemical reactions that occur when a projectile breaks, when fired, etc.

The name "conservative" forces is due to the fact that the total mechanical energy W M the system of bodies interacting with each other through only conservative forces is preserved.

Let us derive formulas for the potential energies of the interaction of bodies between which gravitational and elastic forces act.

1. Potential energy of a body in the Earth's gravitational field. Between body (m.t.) masses m and the Earth (uniform ball of radius R З) of mass M З is affected by the gravitational force:

,

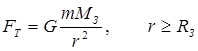where G is the gravitational constant, and r- distance from the center of the Earth to the body (Fig. 1.24.a).

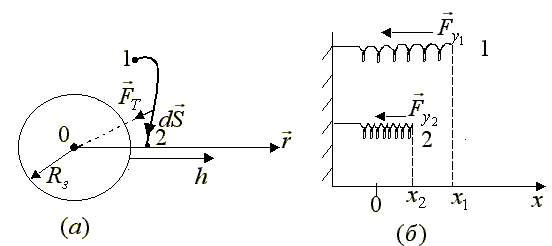
Let's calculate the work BUT 12 gravitational forces during the transition of the body from point 1 to point 2, located respectively at distances r 1 and r2 from the center of the earth:

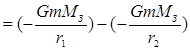(1.71)

From formula (1.71) it follows that the work of the gravitational force is determined by the decrease in quantities that depend only on the initial and final positions of the body and the Earth. So the gravitational forces are conservative forces , and these quantities themselves represent the potential energies of the gravitational interaction of the body and the Earth:

(1.72)

Potential energy Wp determined up to constant value, its zero reference level Wp is chosen arbitrarily for the convenience of solving specific problems. This choice can be made in the following way: consider that at

(1.73)

As noted above, formula (1.72) can also be considered as the potential energy of a body in the gravitational field created by the Earth. In this case, the zero level Wp convenient to choose on the surface of the Earth ( h=0, Wp=0)

where g 0 = GM Z /R Z 2\u003d 9.81m / s 2 - free fall acceleration at ocean level

(h = 0, r = R 3); h is the height of the body above the Earth's surface.

2.Potential energy of an elastically deformed body . Consider the work of the elastic force during compression of the spring from state 1 to state 2 (Fig. 1.24b) with coordinates x 1 and x 2 respectively

From (1.75) it follows that the elastic force is a conservative force, and the value is the total mutual potential energy of all parts of an elastically deformed body (see formula (1.70)).

Generalizing formulas (1.71) and (1.75), we can formulate : the work of conservative forces acting between bodies or parts of one body is equal to the decrease in their mutual potential energy.

For a body whose motion has little effect on the motion of another body that creates a force field, potential energy theorem can be formulated like this: the work of conservative forces acting on the body is equal to the decrease in the potential energy of the body in the field of these forces

1.4.5. Potential Energy Relationship Formula Wp and conservative strength

Between the conservative force acting between the bodies, and the potential energy of their interaction Wp. There are certain formulas for the relationship, let's establish them. To do this, we write the expression for the elementary work of a conservative force along an arbitrary direction ( ) and substitute it into the potential energy theorem (1.76). Then

By choosing a direction coinciding with the directions of the coordinate axes, it is possible to estimate the force projections on these axes and thereby write the formula for the relationship between the force vector and potential energy

So far, we have considered systems of noninteracting particles. Now we turn to the consideration of a system of two particles interacting with each other.

Let us denote the force with which the second particle acts on the first by the symbol and the force with which the first particle acts on the second by the symbol . According to Newton's third law

We introduce a vector where and are the radius vectors of the particles (Fig. 23.1). The distance between particles is equal to the modulus of this vector. Let us assume that the forces have a value that depends only on the distance between the particles and are directed along the straight line connecting the particles.

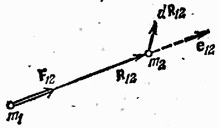
This, as we know, is true for the forces of gravitational and Coulomb interactions (see formulas (11.2) and (13.1)).

Under the assumptions made, the forces can be represented as

where - vector vector (Fig. 23.2), - some function is positive in the case of mutual attraction of particles and negative in the case of their repulsion from each other.

Assuming the system is closed ( external forces no), we write the equations of motion of both particles:

Multiply the first equation by the second - by and add them together. The result is the ratio

The left side of this relation is the increment of the kinetic energy of the system over time (see (19.3)), the right side is the work of internal forces over the same time.

Taking into account expressions (23.1), the right side of formula (23.2) can be transformed as follows:

From fig. 23.2 it can be seen that the scalar product is equal to - the increment of the distance between the particles.

In this way,

The expression can be considered as an increment of some function from. Denoting this function through we arrive at the equality

Consequently,

Taking into account all that has been said, expression (23.2) can be represented as

whence it follows that the quantity for the considered closed system is conserved. The function represents the potential energy of the interaction. It depends on the distance between the particles.

Let the particles move from positions in which the distance between them was equal to new positions in which the distance between them became equal In accordance with (23.6) internal forces. do work on the particles

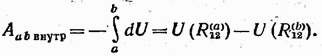
From (23.8) it follows that the work of forces (23.1) does not depend on the paths to which the particles moved, and is determined only by the initial and final distances between the particles (the initial and final configurations of the system). Thus, interaction forces of the form (23-1) are conservative.

If both particles are moving, the total energy of the system is

Suppose that particle 1 is fixed at some point, which we will take as the origin, of coordinates . As a result, this particle will lose the ability to move, so that kinetic energy will consist of only one term Potential energy in this case will be a function only Therefore, expression (23.9) will take the form

(23.10)

If we consider a system consisting of only one particle 2, then the function will play the role of the potential energy of particle 2 in the field of forces created by particle 1

Although, in essence, this function is the potential energy of the interaction of particles 1 and 2. In general, the potential energy in the external field of forces is essentially the energy of the interaction between the bodies of the system and the bodies that create a force field external to the system.

Let us turn again to the system of two interacting free ("unfixed") particles. If, in addition to the internal force, the first particle is affected by an external force F, and the second particle is affected by the force , then the terms on the right side of relation (23.2) will appear, which in total will give the work of external forces. Accordingly, formula (23.7) will take the form

In the case when the total kinetic energy of the particles remains constant (for example, equal to zero), relation (23.11) looks like this:

Integrating this relation from configuration a to configuration we get that

(cf. formula (22.13))

Let us extend the obtained results to a system of three interacting particles. In this case, the work done by the internal forces is

Taking into account that we will give the expression (23.14) the form

We assume that the internal forces can be represented as (cf. (23.1)). Then

Each of the products is equal to the increment of the distance between the corresponding particles. Therefore

Potential energy of system interaction.

It is composed of the interaction energies of particles taken in pairs.

Equating the sum of works, we arrive at relation (23.11), in which expression (23.17) should be understood as.

The result obtained can be easily generalized to a system with any number of particles. For a system of N interacting. particles, the potential energy of interaction is composed of the interaction energies of particles taken in pairs:

This amount can be written as follows:

(23.19)

(note that in expression (23.18) for each term, the first index has a value less than the second). Due to the fact that the interaction energy can also be represented in the form

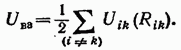
In the sums (23.19) and (23.20), the indices range from 1 to N, consistent with the condition or and in the case of repulsion of particles from each other (see the text following formula (23.1)).

According to (23.5)

Integration gives

(23.23)

Like the potential energy in an external force field, the potential energy of interaction is determined up to an arbitrary additive constant. It is usually believed that when the potential energy vanishes (at such a distance, the force (23.22) vanishes - the interaction between the particles disappears). Then the additive constant in (23.23) becomes equal to zero and the expression for the potential energy of interaction becomes

In accordance with (23.13) in order to remove particles from each other from a distance to infinitely long distance, without changing their speeds, it is required to do work

Substitution of the corresponding values ​​of the function (23.24) leads to the expression

In the case of attraction between particles, respectively, to remove particles from each other, it is required to do positive work.

In the case of repulsion of particles from each other, the work (23.25) turns out to be negative. This work has to be done to prevent the repelling particles from increasing their speed.