where the wavelength corresponds to the maximum value of the spectral density of the energy luminosity of an absolutely black body,

- constant guilt.

Planck's quantum hypothesis establishes a proportionality between the energy of a radiation quantum and the oscillation frequency

,

where

is Planck's constant.

Planck's formula for the spectral density of energy luminosity of a blackbody has the form

.

Einstein's equation for external photoelectric effect

,

where is the work function of an electron from a metal,

- maximum kinetic energy electron.

The red border of the photoelectric effect can be determined by the formulas

,

.

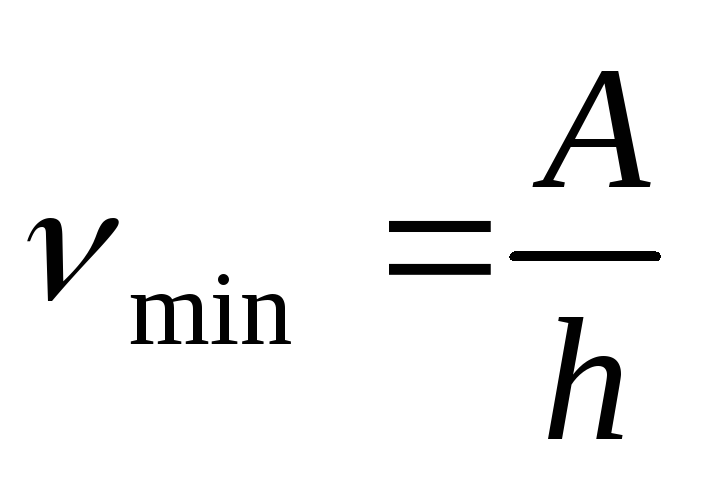The value of the blocking voltage is calculated by the formula

.

The mass of a photon is determined using the Planck and Einstein formulas

,

and its momentum is

.

The pressure of light incident normally on some surface is determined by the formula

,

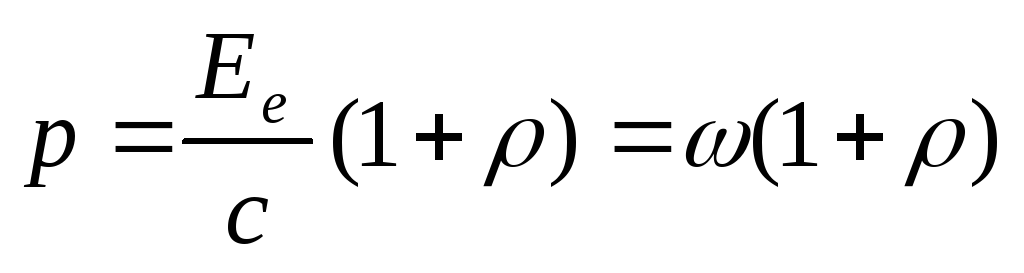where 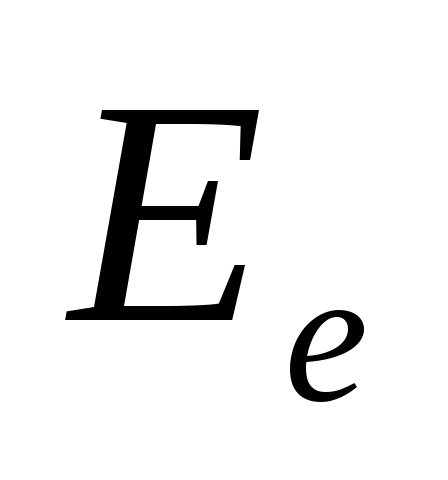is the energy of all photons incident on a unit area of ​​the surface per unit time (energy illumination of the surface), - coefficient of reflection of light from the surface, is the volume density of radiation energy.

The change in the wavelength of short-wavelength radiation during its scattering by free (or weakly bound) electrons (the Compton effect) is determined by the formula

where - scattering angle,

- Compton wavelength (for photon scattering on an electron

).

The wavelength of the short-wavelength boundary of the continuous X-ray spectrum is determined by the formula

,

where - voltage on the x-ray tube.

Examples of problem solving

Task 1. The radiation of the Sun is close in its spectral composition to the radiation of a completely black body, for which the maximum emissivity falls on the wavelength

. Find the mass lost by the Sun every second due to radiation. Estimate the time it takes for the mass of the Sun to decrease by 1%.

We use Wien's displacement law and determine the temperature of the surface of the Sun

. (2.1.1)

Then the energy luminosity of the Sun according to the Stefan-Boltzmann law and with the help of (2.1.1) will be written in the form

. (2.1.2)

Multiplying (2.1.2) by the area of ​​the radiating surface and time, we find the energy emitted by the Sun

. (2.1.3)

To determine the mass lost by the Sun due to radiation, we use the Einstein formula for the relationship between mass and energy, which, taking into account (2.1.3), will allow us to write

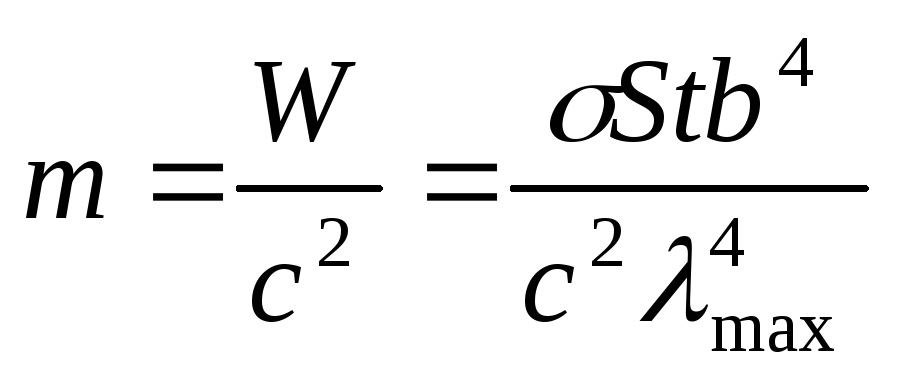. (2.1.4)

Given that the area of ​​the radiating surface (sphere)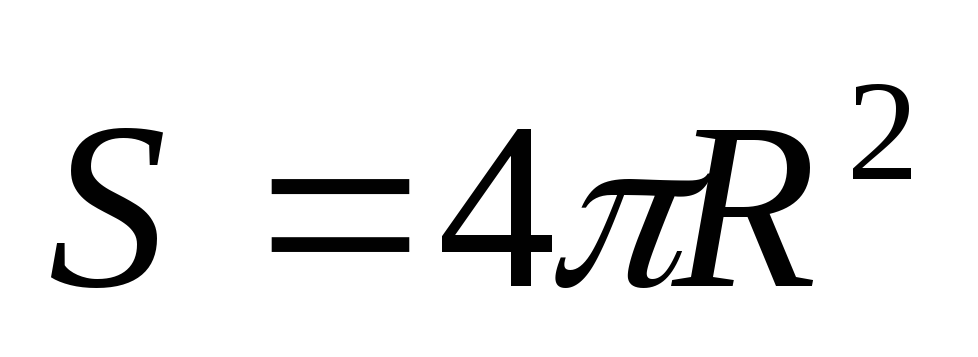

, from (2.1.4) we find

To estimate the time for a 1% decrease in the mass of the Sun, we assume that during this time the energy radiated by the Sun does not change, then

.

Task 2. Determine the steady temperature a blackened ball located at half the distance from the Earth to the Sun. Take the temperature of the Sun's surface equal to

.

Obviously, being in a state of thermal equilibrium, the ball must receive per unit time the same radiation energy from the Sun, which it itself radiates into the surrounding space. Then, denoting the power of solar radiation incident on the ball through 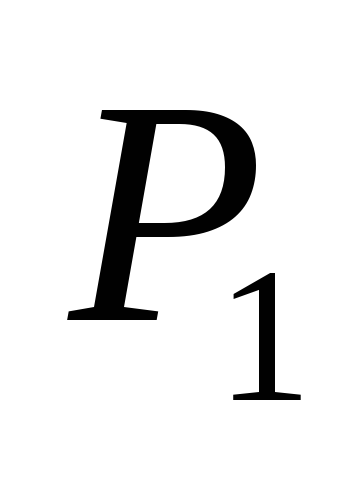, and the power radiated by the ball - through , we have

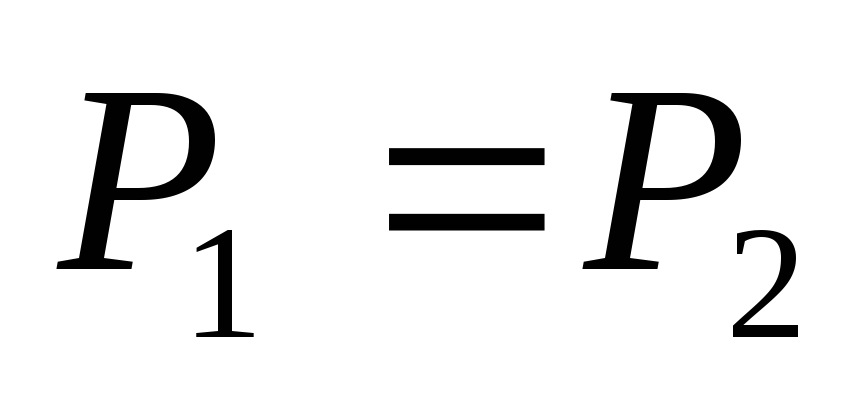. (2.1.5)

Assuming that the Sun radiates as an absolutely black body, the expression for the power of solar radiation can be written as

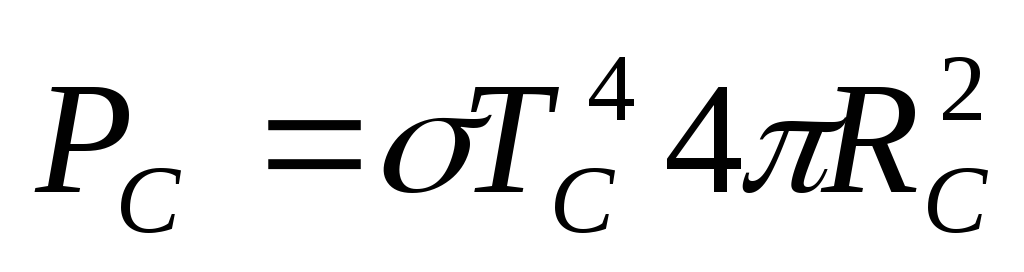, (2.1.6)

where is the temperature of the sun's surface,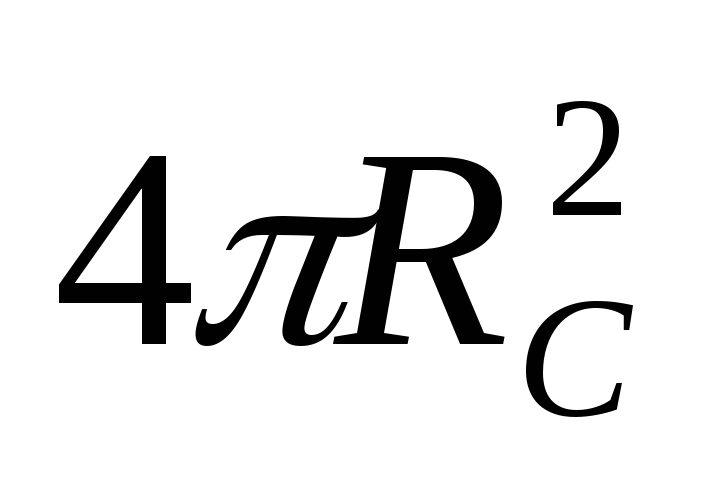

is the surface area of ​​the sun. The fraction of the power of solar radiation falling on the surface of the ball, we find from the proportion

, (2.1.7)

where

- area of ​​a circle of radius 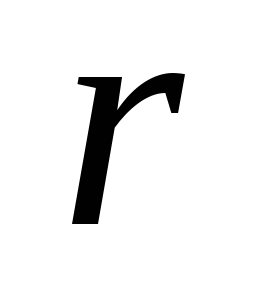, equal to the radius of the ball,

is the distance from the Earth to the Sun. From (2.1.6), (2.1.7) we find

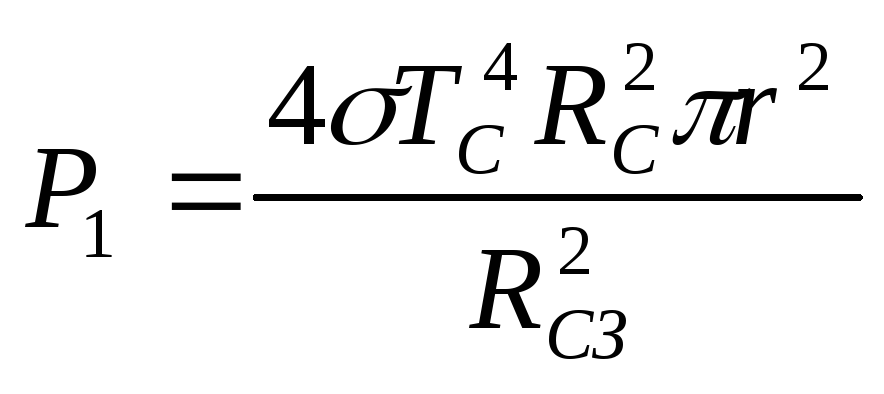. (2.1.8)

Let us now determine the radiation power of the ball, assuming that it also radiates as an absolutely black body, and the temperature of all its points is the same. Then we get

. (2.1.9)

From (2.1.5), (2.1.8), (2.1.9) it follows

.

Using tabular data, we get the answer

.

Problem 3. A copper ball removed from other bodies, under the action of light falling on it, is charged to a potential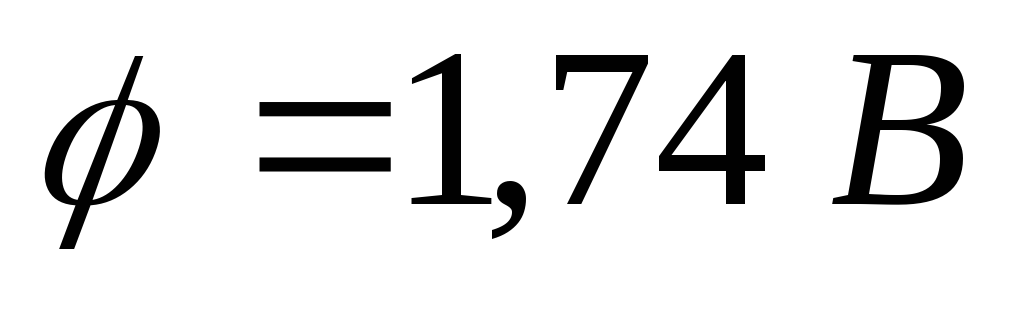

. Determine the wavelength of light.

According to the Einstein equation for the photoelectric effect, the maximum kinetic energy of photoelectrons is

. (2.1.10)

Due to the emission of electrons from the ball under the action of light, it acquires positive charge, as a result of which an electric field is created around it, which slows down the movement of the emitted electrons. The ball will be charged until the maximum kinetic energy of photoelectrons becomes equal to work decelerating electric field when moving electrons over an infinitely long distance. Since the potential of a point at infinity is zero, by the kinetic energy theorem we get

,

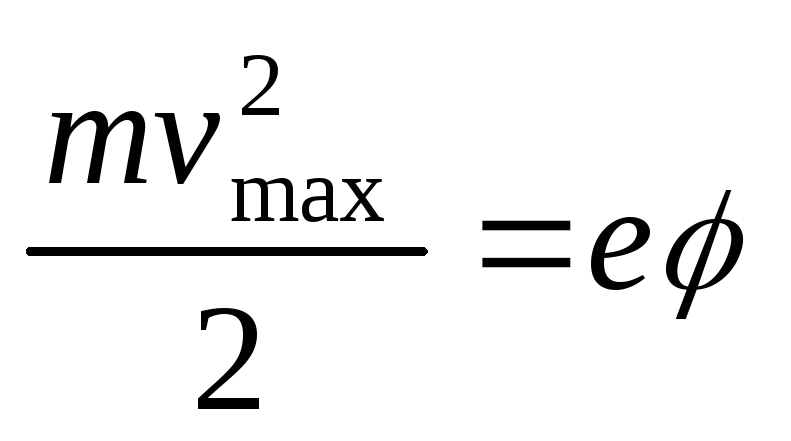which, taking into account (2.1.10), allows us to find the wavelength of light

. (2.1.11)

Substituting into (2.1.11) numerical values ​​(the work function of electrons from copper is equal to

), we find

.

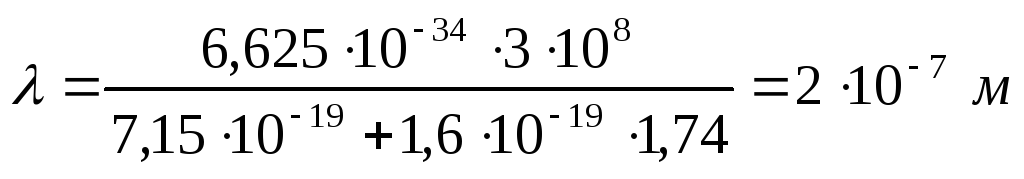Problem 4. A flat surface is illuminated by light with a wavelength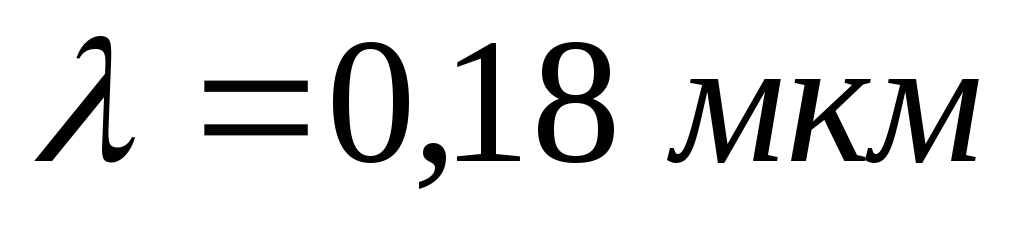

. The red border of the photoelectric effect for a given substance

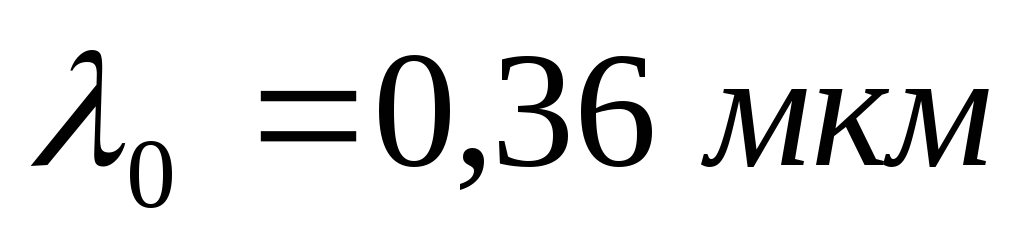. Directly at the surface, a uniform magnetic field with induction

whose lines are parallel to the surface. What is the maximum distance from the surface that photoelectrons can escape if they fly out perpendicular to the surface?

We use the Einstein equation for the photoelectric effect and determine the maximum speed of the emitted photoelectrons

. (2.1.12)

Using the formula for the red border of the photoelectric effect

,

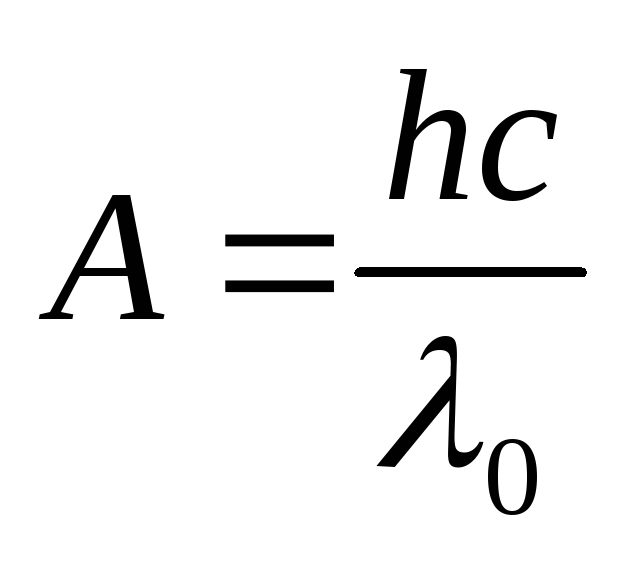expression (2.1.12) can be written as

. (2.1.13)

After leaving the surface, the electrons enter a uniform magnetic field perpendicular to the velocity vector, therefore, they move in it in a circle, and their maximum distance from the surface will be equal to the radius of this circle. The radius of a circle can be found by applying Newton's second law and using the Lorentz force formula

. (2.1.14)

Then from (2.1.13), (2.1.14) we find the maximum distance of electrons from the surface

.

Calculations give

.

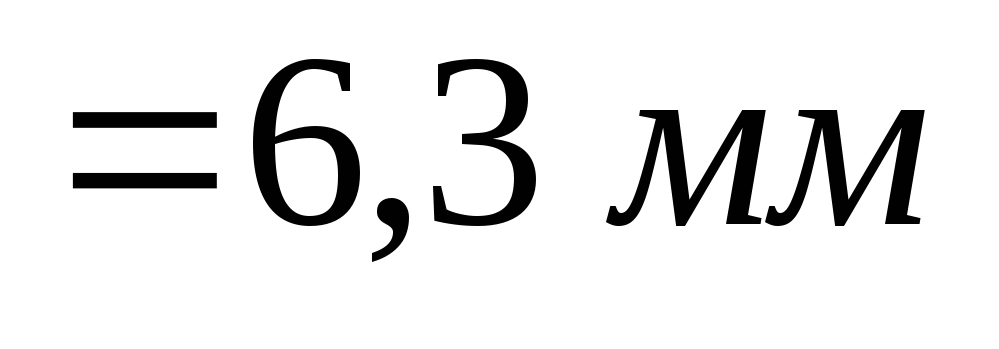Task 5. The cathode of a photocell is illuminated with monochromatic light. With a holding voltage between cathode and anode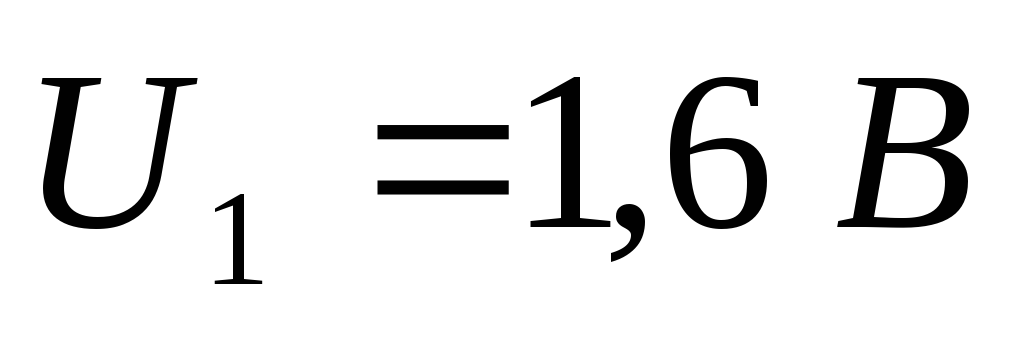

current in the circuit stops. When changing the wavelength of light in

times it was necessary to apply a delaying potential difference to the electrodes

. Determine the work function of electrons from the cathode material.

Using the Einstein equation for the photoelectric effect and the formula for the retarding voltage, we get

, (2.1.15)

, (2.1.16)

where the wavelengths are related by the condition

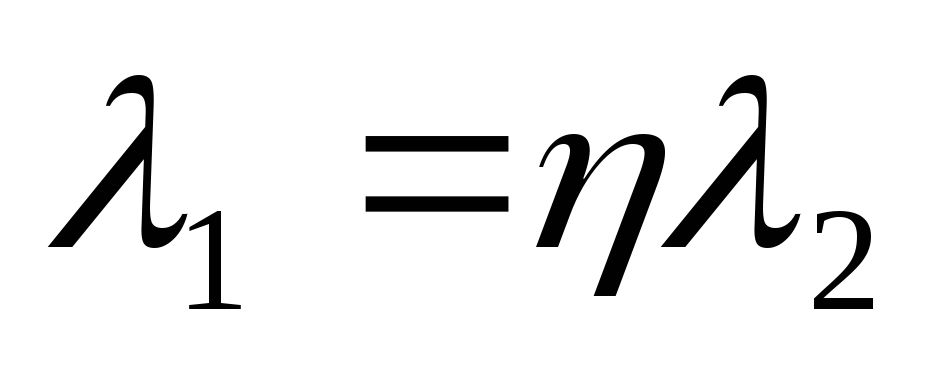. (2.1.17)

Solving the system of equations (2.1.15) - (2.1.17), we find

Task 6. Determine the speed with which an electron must move so that its momentum is equal to the momentum of a photon with a wavelength

.

Let us first compare the energy of a photon with the rest energy of an electron

Calculations show that the energy of a photon is greater than the rest energy of an electron, therefore, when solving the problem, it is necessary to use the formulas of the special theory of relativity. Equating the formulas for the momentum of a photon and a relativistic electron, we obtain

. (2.1.18)

Solving (2.1.18) with respect to the electron velocity, we obtain

.

Problem 7. A speck of density moves in space

that absorbs all the light falling on it. Knowing the radiation power of the Sun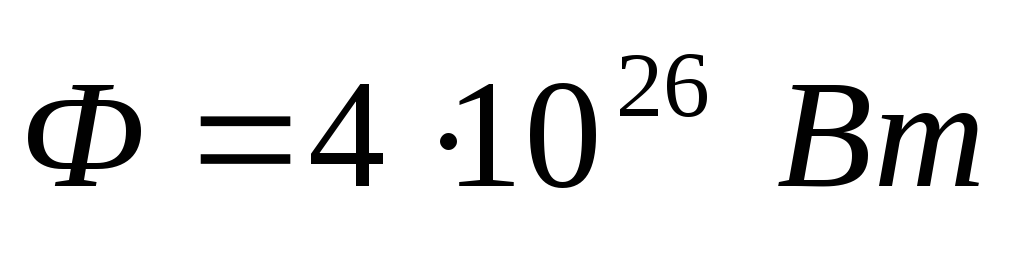

, find the radius of a dust grain at which its gravitational attraction to the Sun is compensated by the force of light pressure.

According to the condition of the problem, the force gravity must be balanced by the force of light pressure, therefore

. (2.1.19)

According to the law of gravity

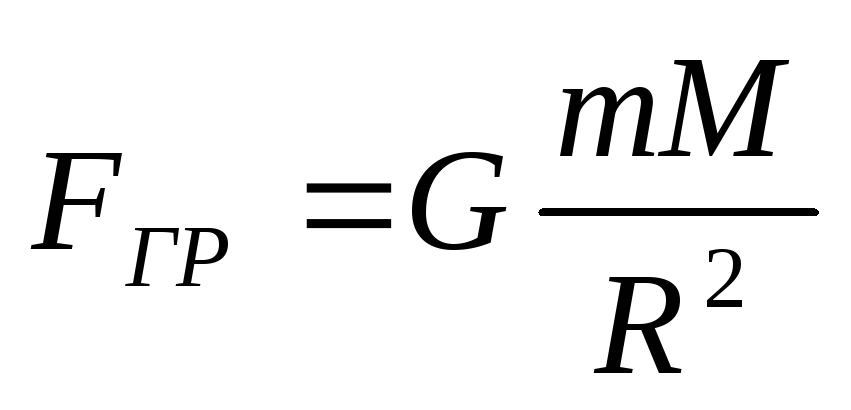, (2.1.20)

where the mass of the dust grain can be written as

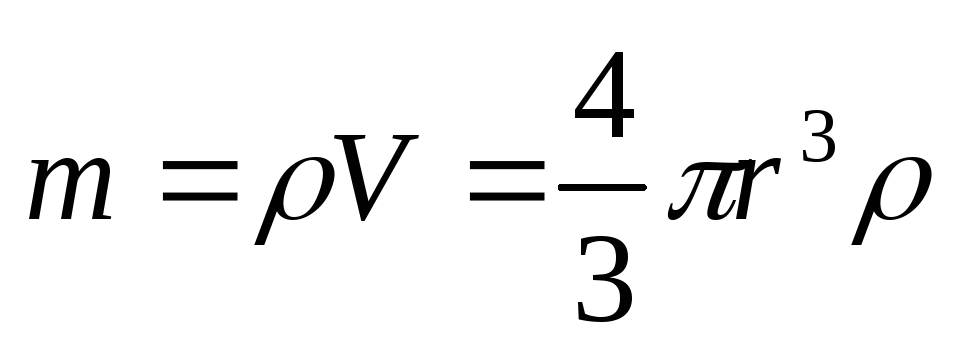; (2.1.21)

here 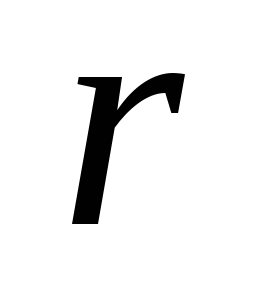is the radius of the dust particle, 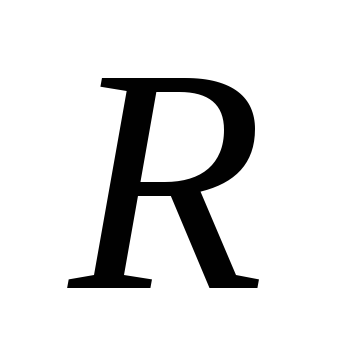is the distance from the dust grain to the Sun.

The force of light pressure is equal to

, (2.1.22)

where the projection of the surface of a dust grain onto a plane perpendicular to the sun's rays has an area

, (2.1.23)

and the pressure is related to the radiation power , penetrating the surface of a dust grain with the formula

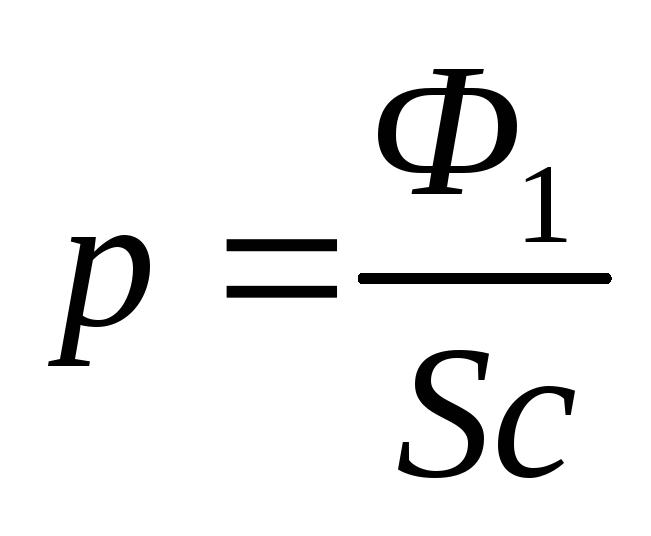. (2.1.24)

The radiation power per grain of dust can be expressed in terms of solar radiation power using the proportion

. (2.1.25)

Eliminating the unknowns from the system (2.1.19) - (2.1.25), we obtain the formula for the dust grain radius

.

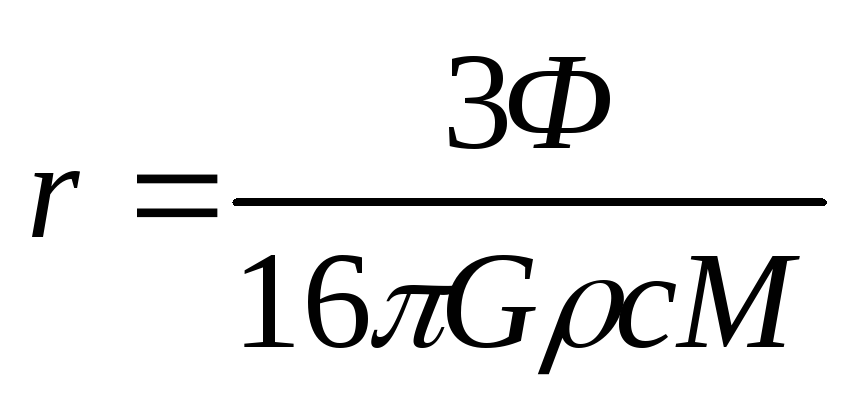Substitution of numerical values ​​gives

Problem 8. As a result of the collision of a photon and a proton flying in mutually perpendicular directions, the proton stopped, and the photon wavelength changed by

. What was the momentum of the photon? Proton speed count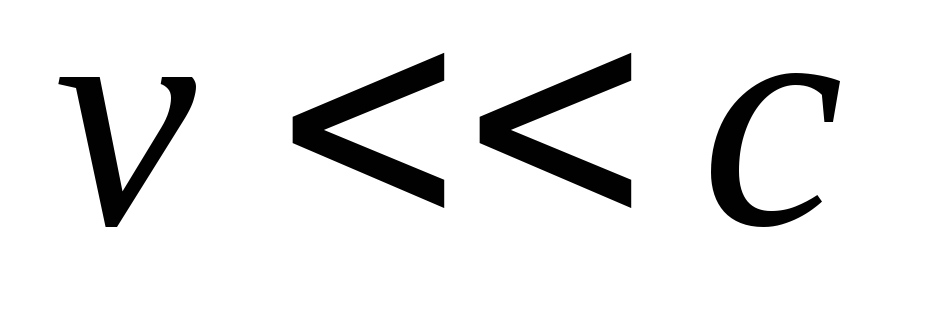

.

Let us use the laws of conservation of momentum and energy to solve the problem. Let the initial momentum of the photon axially directed

, proton momentum - along the axis

, and the photon momentum after scattering forms with axis

corner (Fig. 2.1.1). Given that the motion of a proton can be described by classical formulas, according to the law of conservation of energy, we have

. (2.1.26)

R is. 2.1.1

The law of conservation of momentum in projections on the axis

and

gives

,

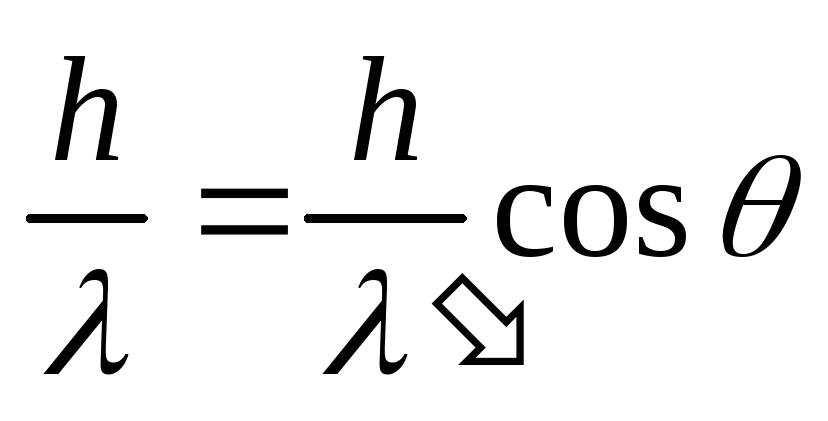. (2.1.27)

The change in the wavelength of the scattered photon satisfies the formula

. (2.1.28)

Express from (2.1.27)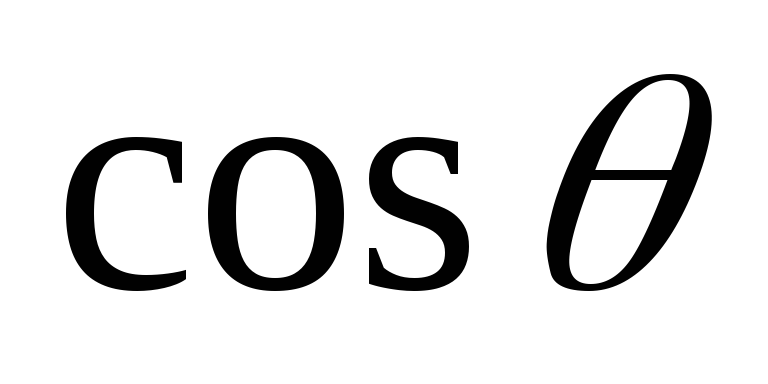

and

, we square these equations, add them up and use the basic trigonometric identity. As a result, we get

. (2.1.29)

Excluding from (2.1.26), (2.1.29)

using (2.1.28), we transform these equations to the form

, (2.1.30)

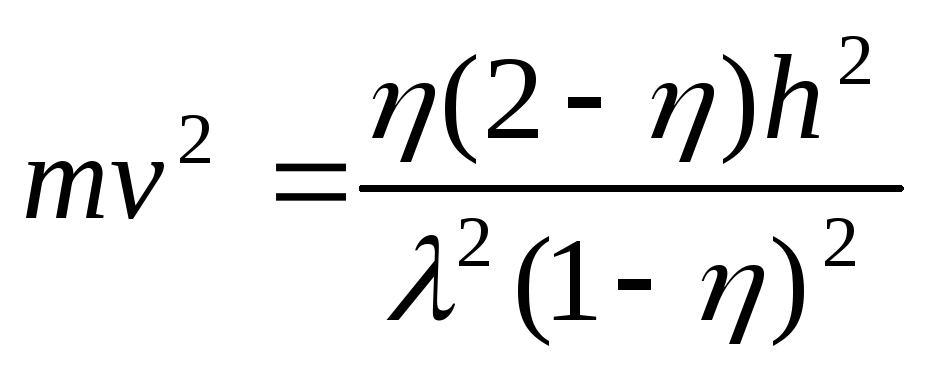. (2.1.31)

Now excluding the proton velocity from the system (2.1.30), (2.1.31), we find the photon wavelength before scattering

,

after which we determine the initial momentum of the photon

Problem 9. A narrow beam of monochromatic X-rays is incident on a scattering substance. In this case, the wavelengths of the shifted components of radiation scattered at angles

and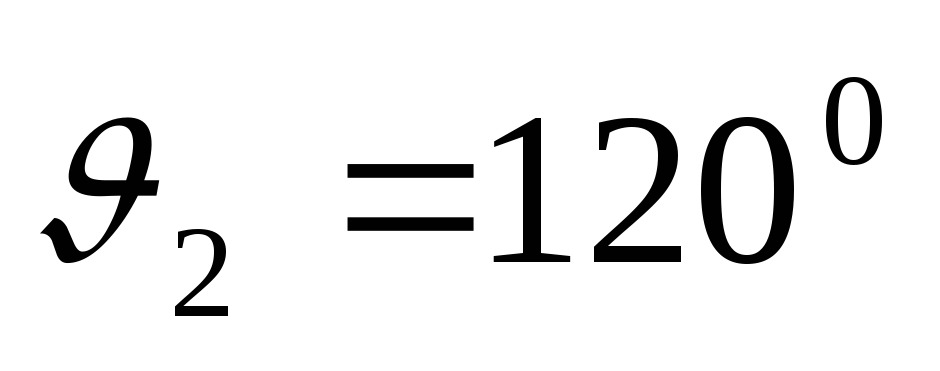

, differ from each other in

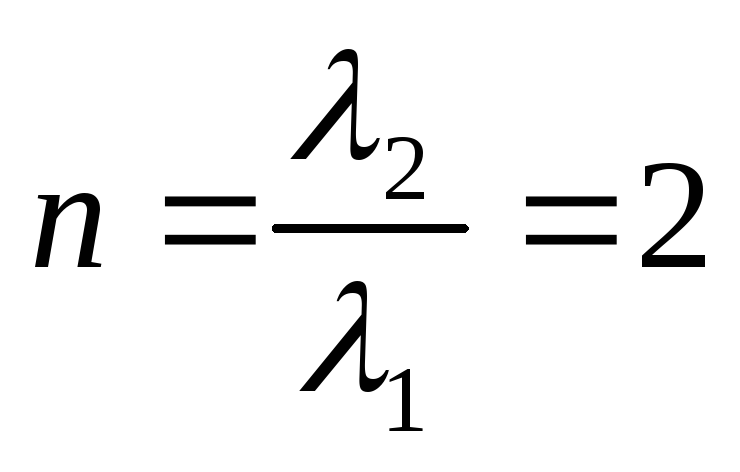times. Assuming that scattering occurs on free electrons, find the wavelength of the incident radiation.

Let us use the formulas for changing the wavelength during Compton scattering for the two scattering angles mentioned in the condition

,

. (2.1.32)

Dividing the second equation (2.1.32) by the first one, we obtain

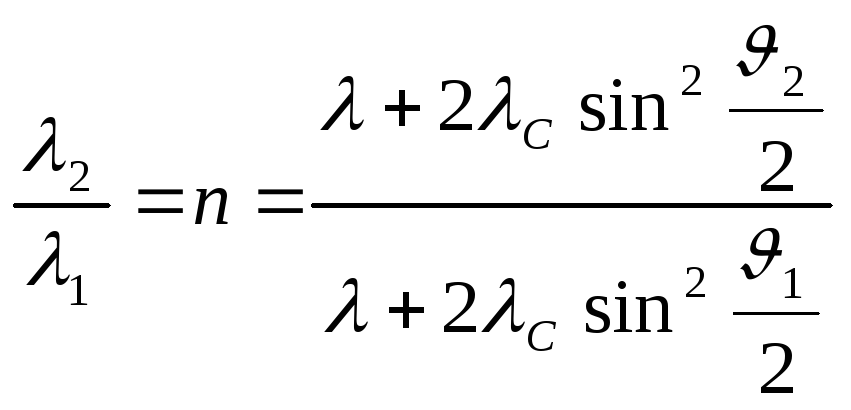. (2.1.33)

Solving (2.1.33), we find the wavelength of the radiation incident on the substance

.

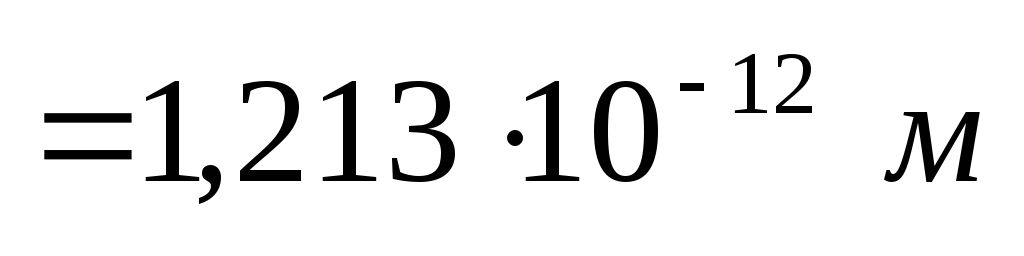Problem 10. Photon with energy, in

times greater than the rest energy of the electron, scattered back on a stationary free electron. Find the radius of curvature of the recoil electron trajectory in a magnetic field with induction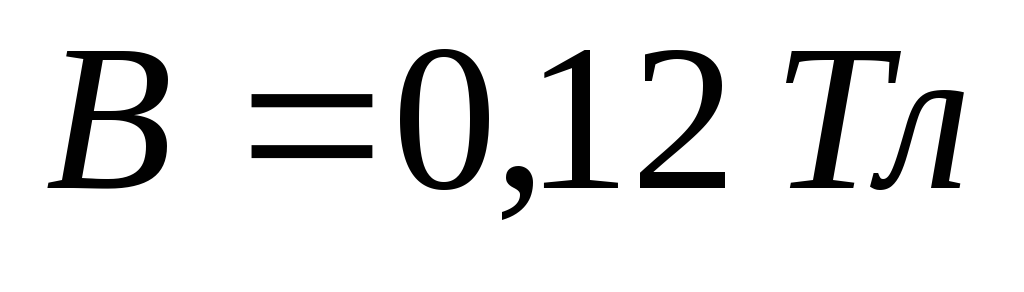

, assuming that the induction lines are perpendicular to the electron velocity vector.

Let us write the expression for the change in the wavelength of light during Compton scattering

. (2.1.34)

Let us pass in (2.1.34) from wavelengths to energies using the relation

and take into account that the scattering angle

. As a result, we get

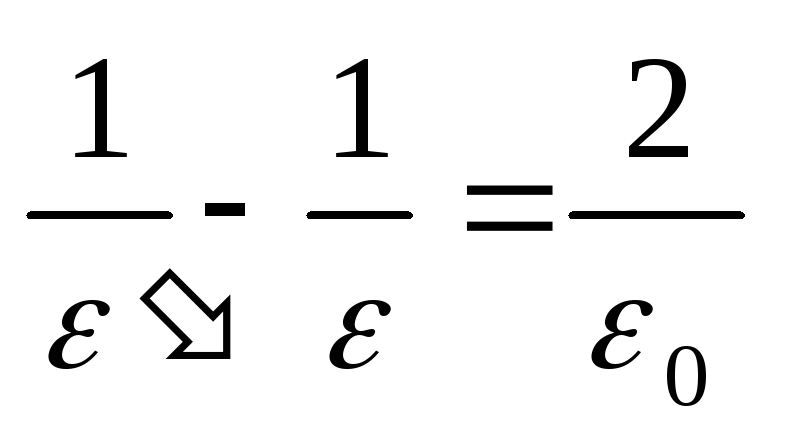, (2.1.35)

where

is the rest energy of the electron. Taking into account the fact that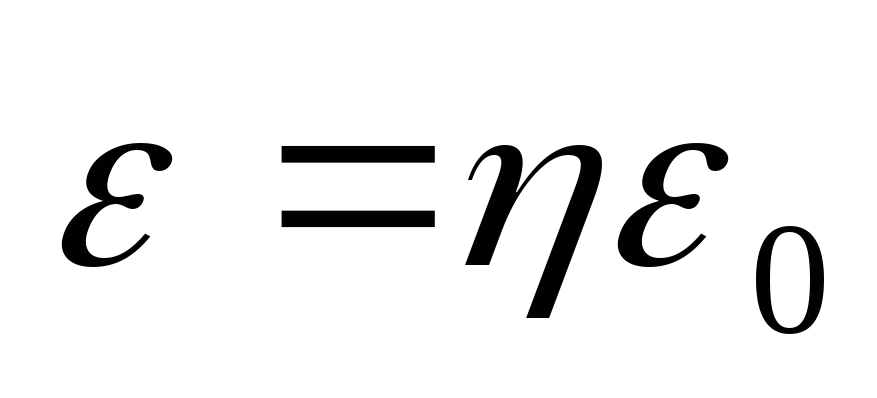

, we find from (2.1.35) the energy of the scattered photon

and the kinetic energy of the recoil electron

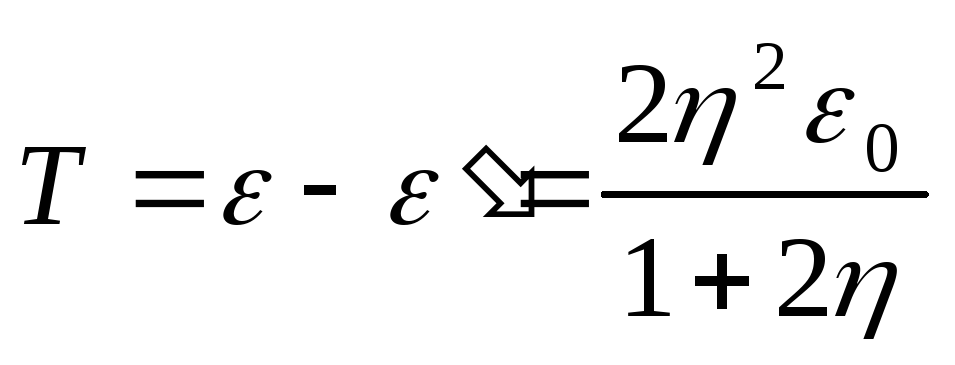. (2.1.36)

As is known, the radius of the circle along which an electron moves in a magnetic field is determined by the formula

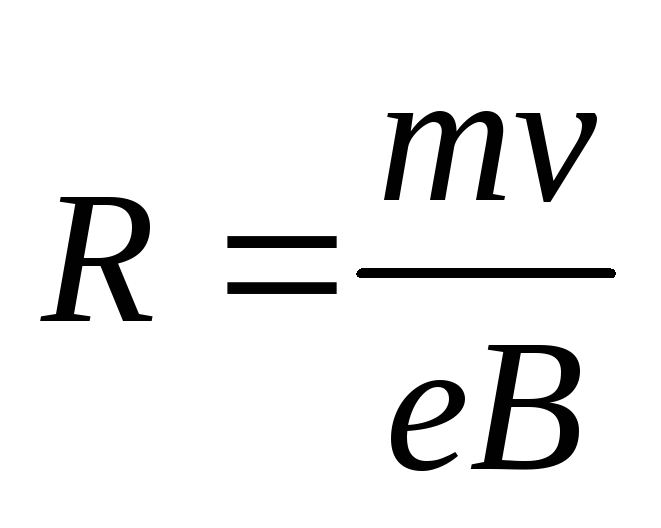, (2.1.37)

where, taking into account the relativistic nature of the electron motion

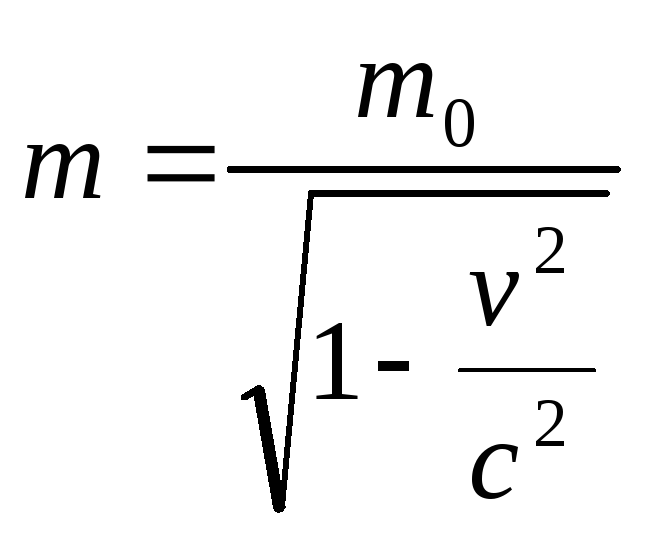. (2.1.38)

Using the relativistic formula for kinetic energy

,

from (2.1.36) after algebraic transformations one can obtain

,

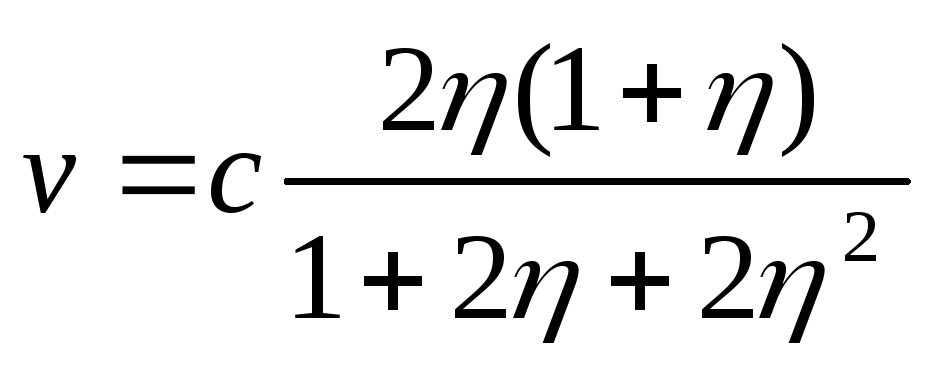which after substitution into (2.1.37), (2.1.38) allows to find the radius of curvature of the electron trajectory

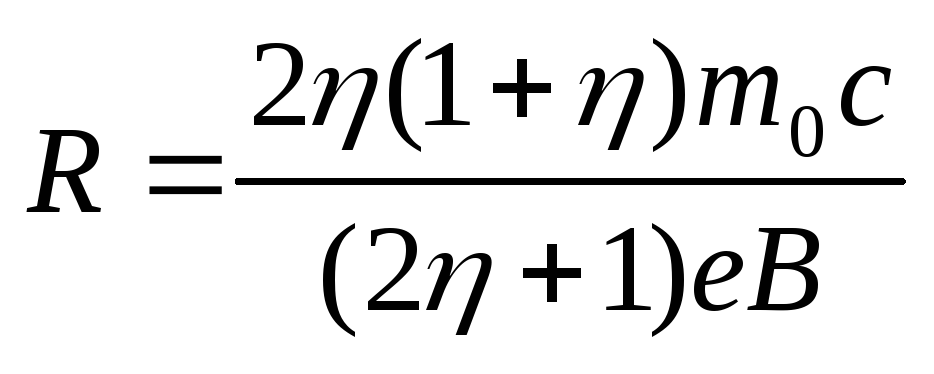. (2.1.39)

Substitution in (2.1.39) of numerical values ​​gives

.

Problem 11. With an increase in the voltage on the X-ray tube in

times the wavelength of the short-wave boundary of the continuous X-ray spectrum changed by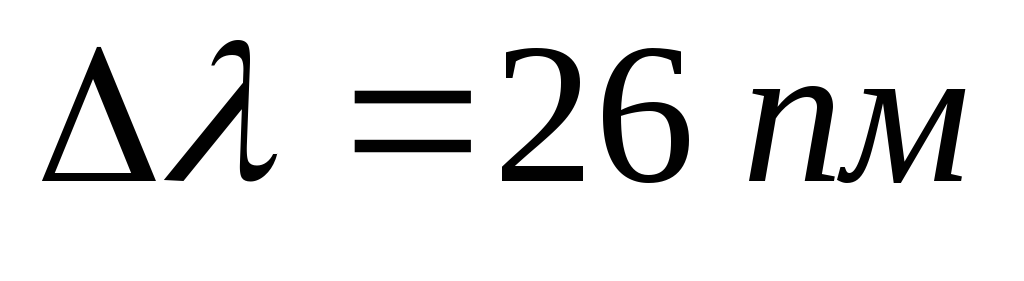

. Find the initial voltage on the tube.

We apply the formula for the wavelength of the short-wavelength boundary of the continuous X-ray spectrum for the cases before and after the change in voltage on the tube

,

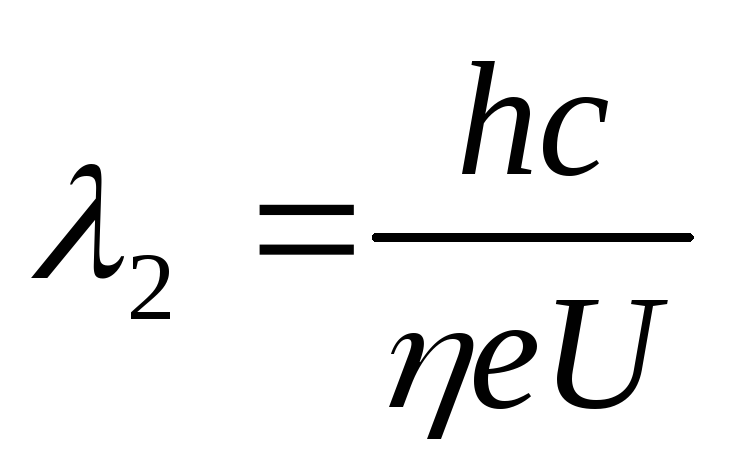. (2.1.40)

Subtracting the second from the first equation (2.1.40), we find

,

whence follows the formula for the initial stress on the tube

№1 Light falling on a metal causes the emission of electrons from the metal. If the intensity of light decreases, while its frequency remains unchanged, then ...

Solution: According to the Einstein equation for the photoelectric effect, where hυ is the photon energy; work function of electrons from metal; - the maximum kinetic energy of electrons, which depends on the energy of the photon, therefore, on the frequency of light. Since the frequency does not change, the kinetic energy remains unchanged. The intensity of light is proportional to the number of photons, and the number of ejected electrons is proportional to the number of incident photons; This means that as the light intensity decreases, the number of ejected electrons decreases.

Answer: the number of ejected electrons decreases, while their kinetic energy remains unchanged

№2 Cathode vacuum photocell illuminated by light with photon energy 10 eV. If the photocurrent stops when a delay voltage is applied to the photocell 4 AT, then the work function of electrons leaving the cathode (in eV) is equal to …

Solution: According to Einstein's equation for the photoelectric effect, , where hυ is the photon energy; work function of electrons from metal; the maximum kinetic energy of electrons, which is equal to , where is the holding voltage. Consequently,

№3 An external photoelectric effect is observed. As the wavelength of the incident light increases...

Answer: the magnitude of the retarding potential difference decreases

The figure shows the distribution of energy in the radiation spectrum of a black body depending on the wavelength for temperature. With a 2-fold increase in temperature, the wavelength (v) corresponding to the maximum radiation will be equal to ...

Answer: 250

№5 The distribution of energy in the radiation spectrum of a completely black body depending on the radiation frequency for temperatures T 1 and T 2 () is correctly shown in the figure ...

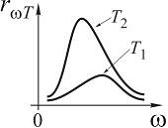
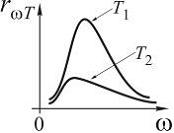
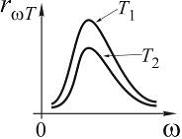
№6 The figure shows two current-voltage characteristics of a vacuum photocell. If E is the illumination of the photocell, ν is the frequency of the light incident on it, then

Solution: The current-voltage characteristics shown in the figure differ from each other by the value of the saturation current. The saturation current value is determined by the number of electrons knocked out in 1 second, which is proportional to the number of photons incident on the metal, that is, the illumination of the photocell. Therefore, the retarding voltage is the same for both curves. The value of the delay voltage is determined by the maximum speed of photoelectrons: Then the Einstein equation can be represented as . Hence, since, consequently, the kinetic energy of the electrons is the same, and hence the frequency of the light incident on the photocathode, that is

Answer:

№ 7 The figure shows the dependence curves of the spectral density of the energy luminosity of a black body on the wavelength at different temperatures. If curve 2 corresponds to the radiation spectrum of a completely black body at a temperature

1450 , then curve 1 corresponds to temperature (at ) ...

Solution. We use the Wien displacement law for blackbody radiation, where the wavelength that accounts for the maximum spectral density of the blackbody energy luminosity is its thermodynamic temperature, Wien's constant:

.

Since, according to the schedule, , then

№8 Establish a correspondence between the given characteristics of thermal equilibrium radiation and the nature of their dependence on the temperature frequency.

1. Spectral energy density in the radiation spectrum of a completely black body, according to Rayleigh-Jeans formula, with frequency increase 2. The spectral energy density in the radiation spectrum of a black body, according to Planck's formula, with increasing frequency ...

3. Energy luminosity of a completely black body with increasing temperature ...

4. Wavelength, which accounts for the maximum spectral energy density in the radiation spectrum of a completely black body, with increasing temperature ...

Answer options: (indicate the correspondence for each numbered element of the task)

1. tends to 0

2. Increases proportionately

3. Increases proportionately

4. Increases indefinitely

5. Decreases proportionally

Solution: 1. Consistent classical theory for the spectral energy density of black body radiation leads to the Rayleigh-Jeans formula. In this case, the theorem of classical physics is used on the equipartition of the energy of the system over the degrees of freedom and electromagnetic theory light, which allows you to calculate the number of degrees of freedom per unit volume of the region occupied by equilibrium monochromatic thermal radiation. Since, according to the classical theory, this number of degrees of freedom is proportional to the third power of frequency and does not depend on temperature, the spectral energy density of the equilibrium thermal radiation should increase indefinitely with increasing frequency. P. Ehrenfest figuratively called this result an ultraviolet catastrophe.

2. Planck's formula gives the distribution of energy in the radiation spectrum of a completely black body, consistent with experiment at all frequencies, that is, in the entire spectrum, and thus gives an exhaustive description of equilibrium thermal radiation. According to Planck's formula, as the frequency increases, the number of degrees of freedom per unit volume decreases, and ultraviolet catastrophe does not occur.

3. According to the Stefan-Boltzmann law, the energy luminosity of a completely black body increases proportionally with increasing temperature. From the Planck formula, integrating over all wavelengths or frequencies, one can obtain the energy luminosity of a completely black body, i.e. the Stefan-Boltzmann law, and the expression of the Stefan-Boltzmann constant through universal physical constants.

4. According to Wien's displacement law, the wavelength, which accounts for the maximum spectral energy density in the radiation spectrum of a completely black body, decreases proportionally with increasing temperature.

№9 The figure shows the radiation spectrum of a completely black body at a temperature T. The area under the curve will increase by a factor of 81 if the temperature is...

Answer: 3T

№10 A black body and a gray body have the same temperature. At the same time, the radiation intensity ...

Answer: more in a completely black body

Page 2 of 3

201. Determine the work function A of electrons from tungsten if the "red border" of the photoelectric effect for it is λ 0 = 275 nm.

202. Potassium is illuminated monochromatic light with a wavelength of 400 nm. Determine the smallest retarding voltage at which the photocurrent will stop. The work function of electrons from potassium is 2.2 eV.

203. The red border of the photoelectric effect for some metal is 500 nm. Determine: 1) the work function of electrons from this metal; 2) the maximum speed of electrons ejected from this metal by light with a wavelength of 400 nm.

204. Electrons knocked out by light during the photoelectric effect during irradiation of a photocathode visible light are completely delayed by the reverse voltage U 0 \u003d 1.2 V. Special measurements showed that the wavelength of the incident light λ \u003d 400 nm. Define the red border of the photoelectric effect.

205. The retarding voltage for a platinum plate (work function 6.3 eV) is 3.7 V. Under the same conditions for another plate, the retarding voltage is 5.3 V. Determine the work function of the electrons from this plate.

206. Determine to what potential a solitary silver ball will be charged when it is irradiated with ultraviolet light with a wavelength of λ = 208 nm. The work function of electrons from silver A = 4.7 eV.

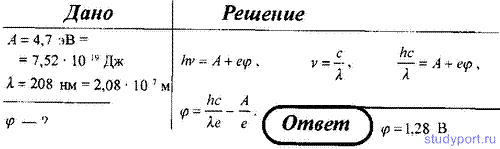
207. When a vacuum photocell is illuminated with monochromatic light with a wavelength of λ 1 \u003d 0.4 microns, it is charged to a potential difference φ 1 \u003d 2 V. Determine to what potential difference the photocell will be charged when it is illuminated with monochromatic light with a wavelength of λ 1 \u003d 0, 3 µm.

208. A flat silver electrode is illuminated by monochromatic radiation with a wavelength λ = 83 nm. Determine the maximum distance from the electrode surface that a photoelectron can move if there is a retarding electric field outside the electrode with a strength of E = 10 V/cm. The red border of the photoelectric effect for silver λ 0 = 264 nm.

209. Photons with energy ε = 5 eV pull out photoelectrons from metal with work function A = 4.7 eV. Determine the maximum momentum transferred to the surface of this metal when an electron is emitted.

210. When the cathode of a vacuum photocell is illuminated with monochromatic light with a wavelength of λ = 310 nm, the photocurrent stops at a certain retarding voltage. With an increase in wavelength by 25%, the retarding voltage is less than 0.8 V. Determine Planck's constant from these experimental data.

211. Determine the maximum speed V max of photoelectrons ejected from the surface of zinc (work function A = 4 eV), when irradiated with y-radiation with a wavelength λ = 2.47 pm.

212. Determine for a photon with a wavelength λ = 0.5 microns: 1) its energy; 2) momentum; 3) mass.

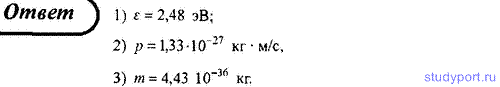
213. Determine the energy of a photon, at which its equivalent mass is equal to the rest mass of an electron. Express your answer in electron volts.

214. Determine with what speed an electron must move so that its momentum is equal to momentum photon, the wavelength of which is λ = 0.5 µm.

215. Determine the wavelength of a photon whose momentum is equal to the momentum of an electron that has passed through a potential difference U = 9.8 V.

216. Determine the temperature at which the average energy of triatomic gas molecules is equal to the energy of photons corresponding to radiation λ = 600 nm.

217. Determine with what speed an electron must move so that its kinetic energy is equal to the energy of a photon whose wavelength is λ = 0.5 microns.