Reprezentarea grafică a câmpurilor. Metodă grafică pentru reprezentarea structurii câmpurilor electrice. linii de forță

Proprietăți corpuri fizice iar obiectele sunt descrise mărimi fizice . Una dintre aceste cantitati pt câmp electric este tensiune. În conformitate cu definiția formulată anterior, descrie acțiunea forței a câmpului asupra corpurilor încărcate într-un anumit punct al câmpului electric. Dacă câmpul este neomogen, atunci intensitatea în puncte diferite câmpurile sunt diferite. Și pentru a descrie proprietățile câmpului în multe puncte, este necesar să se prezinte un număr mare de valori de intensitate. Acest lucru complică studiul domeniului și împiedică crearea în imaginația umană a ideii de domeniu în fiecare caz specific.

Puterea câmpului electric este caracteristica puterii sale.

Ajută la reprezentarea mai bună a structurii câmpului electric metoda grafica. În centrul metodei de prezentare grafică structuri de câmp electric se află fenomene reale care pot fi observate în experimente.

Fie introdusă în câmpul electric al unei bile încărcate pozitiv o particule mică dintr-o substanță, având și o sarcină pozitivă. Dacă această particulă este liberă și acțiunea câmpului gravitațional este nesemnificativă, atunci sub influența unei forțe electrice se va îndepărta de minge. Asemănător se va observa în orice punct al câmpului unei mingi încărcate (Fig. 4.20).

După ce am descris traiectoriile de mișcare ale multor particule încărcate pozitiv într-un câmp electric și indicând direcția către acestea forța de acționare, primim o poză numită spectru acest câmp.

Liniile care formează spectrul câmpului electric se numesc linii de tensiune câmp electric, sau linii de înaltă tensiune.

concept linia de câmp a fost introdus pentru prima dată în știință de M. Faraday pe baza cunoștințelor dobândite în cursul cercetării experimentale.

Experimentele cunoscute lui M. Faraday pot fi efectuate în condiții moderne.

Să luăm un conductor metalic cu benzi de hârtie atașate la el și să-l conectăm la conductorul mașinii electrofor. Dacă o punem în acțiune, atunci toate benzile de hârtie vor diverge în direcții diferite din cauza repulsiunii reciproce (Fig. 4.21). Rezultatele acestui experiment (și altele asemenea) fac posibilă construirea spectrului câmpului electric al unui singur corp încărcat. Este prezentat în fig. 4.22. Săgețile de pe liniile de forță arată direcția forței care va acționa asupra unui corp încărcat pozitiv situat într-un punct dat al câmpului.

Prin urmare, liniile de forță „părăsesc” un corp încărcat pozitiv și „intră” într-un corp încărcat negativ (Fig. 4.22). Trebuie amintit că „iese” și „intră” perpendicular pe suprafața corpului.

Liniile de intensitate a câmpului electric sunt perpendiculare pe suprafața unui corp încărcat în punctele în care încep.material de pe site

Să luăm doi conductori metalici cu benzi de hârtie și să le conectăm la conductorii mașinii electrofor. Punem în acțiune mașina de electrofor și vom vedea că benzile de hârtie vor începe să se atragă între ele (Fig. 4.23). În consecință, câmpul a două corpuri încărcate opus va avea spectrul prezentat în fig. 4.24.

Forma curbilinie a liniilor de tensiune se explică prin faptul că două forțe acționează asupra unei particule încărcate pozitiv din partea fiecărui corp. Rezultanta acestor forțe în fiecare punct al câmpului este tangentă la liniile de tensiune.

Se numesc drepte tangente la care în orice punct arată direcția forței care acționează asupra unui corp punct încărcat pozitiv linii de înaltă tensiune.

Direcţiile forţelor care vor acţiona în diferite puncte din câmpul a două corpuri încărcate sunt prezentate în fig. 4.25.

Deoarece liniile de tensiune sunt întotdeauna perpendiculare pe suprafață, spectrele câmpurilor corpurilor de diferite forme vor fi diferite (Fig. 4.26).

Pe această pagină, material pe teme:

Spectre el. câmpuri ale diferitelor corpuri încărcate
Imagine grafică a câmpului electric abstract
Imagini ale liniilor de câmp electric în experimente
A b

Cunoscând vectorul de intensitate al câmpului electrostatic în fiecare dintre punctele sale, acest câmp poate fi vizualizat cu ajutorul liniilor de forță de intensitate (linii ale vectorului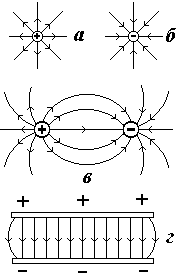 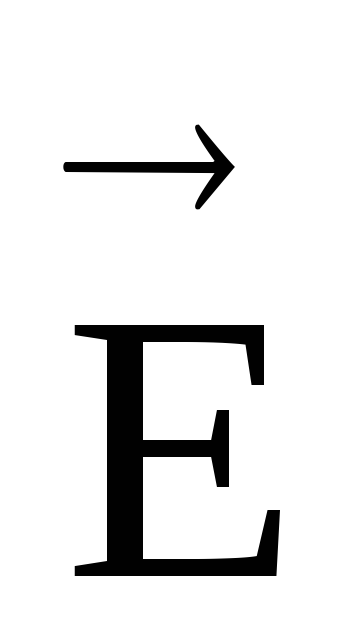). linii de forță tensiunile sunt trasate astfel încât tangenta la acestea în fiecare punct să coincidă cu direcția vectorului de tensiune (Fig. 1.4, A).
Numărul de linii care pătrund într-o singură zonă dS, perpendicular pe acestea, este trasat proporțional cu modulul vectorului (Fig. 1.4, b).
Linilor de forță li se atribuie o direcție care coincide cu direcția vectorului . Modelul rezultat al distribuției liniilor de tensiune face posibilă aprecierea configurației unui câmp electric dat în diferitele sale puncte. Liniile de câmp încep la sarcini pozitiveși se termină în sarcini negative. Pe fig. 1.5 prezintă liniile de tensiune ale sarcinilor punctiforme (Fig. 1.5, A, b); sisteme de două sarcini opuse (Fig. 1.5, în) - un exemplu de câmp electrostatic neomogen și două plane paralele încărcate opus (Fig. 1.5, G) este un exemplu de câmp electric uniform.
1.5. Distribuția taxelor
În unele cazuri, pentru a simplifica calculele matematice, este convenabil să înlocuiți distribuția adevărată a sarcinilor punctiforme discrete cu o distribuție continuă fictivă. În trecerea la o distribuție continuă a sarcinilor se folosește conceptul de densitate de sarcină - liniar , suprafață  și volumetric , i.e.

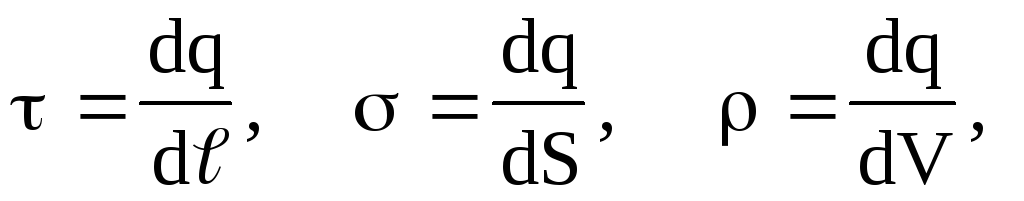(1.12)
unde dq este sarcina distribuită corespunzător pe elementul de lungime

, elementul de suprafață dS și elementul de volum dV.
Luând în considerare aceste distribuții, formula (1.11) poate fi scrisă într-o formă diferită. De exemplu, dacă sarcina este distribuită pe volum, atunci în loc de q i trebuie să utilizați dq = dV și să înlocuiți simbolul sumei cu o integrală, atunci

. (1.13)
1.6. dipol electric
Pentru a explica fenomenele asociate sarcinilor în fizică, este folosit conceptul dipol electric.
Un sistem de două sarcini punctuale opuse de mărime egală, distanța dintre care este mult mai mică decât distanța până la punctele studiate din spațiu, se numește dipol electric. Conform definiției unui dipol, +q=q= q.

O linie dreaptă care leagă sarcini opuse (poli) se numește axa dipolului; punctul 0 - centrul dipolului (Fig. 1.6). Dipolul electric este caracterizat brațul dipolului: vector , direcționată de la o sarcină negativă la una pozitivă. Caracteristica principală a unui dipol este moment dipol electric = q . (1.14)
Prin valoare absolută
p = q 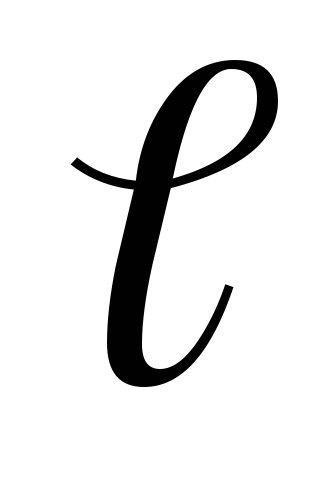. (1.15)
În SI, momentul dipolului electric este măsurat în coulombs ori pe metru (C m).
Să calculăm potențialul și puterea câmpului electric al dipolului, considerând că este un punct, dacă 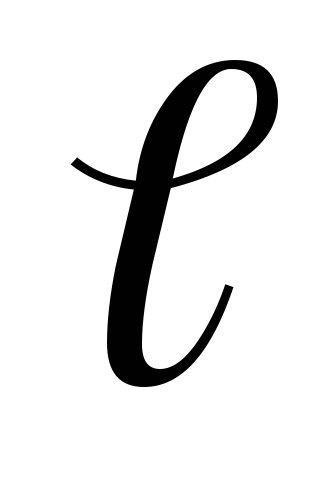 r.
Potențialul unui câmp electric creat de un sistem de sarcini punctiforme într-un punct arbitrar caracterizat printr-un vector cu rază 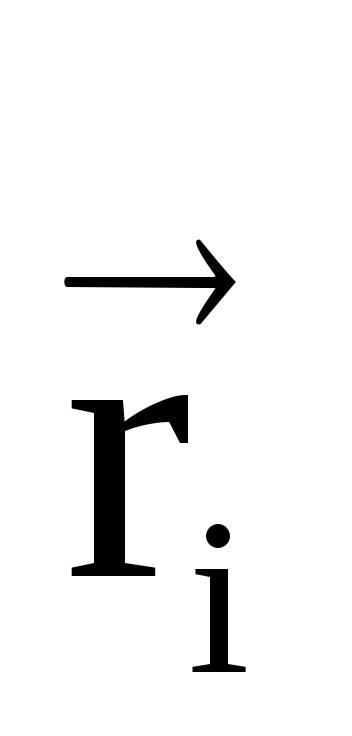, scriem sub forma: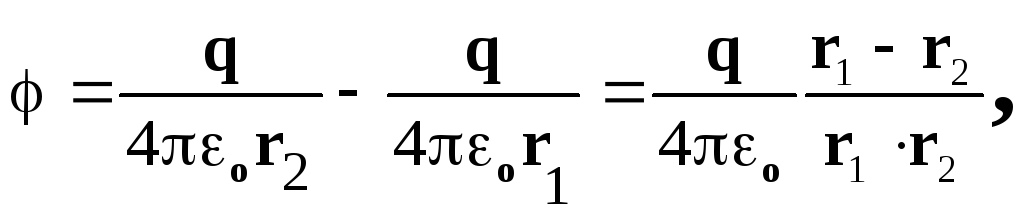

unde r 1 r 2  r 2 , r 1  r 2  r =

, deoarece 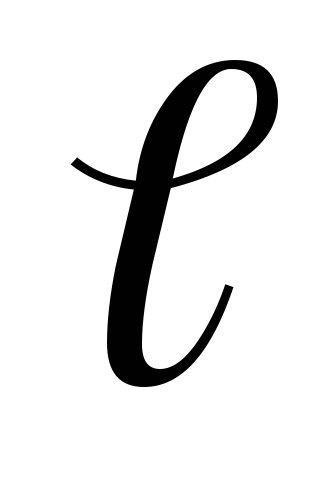r;   unghiul dintre vectorii cu rază și (Fig. 1.6) . Având în vedere acest lucru, obținem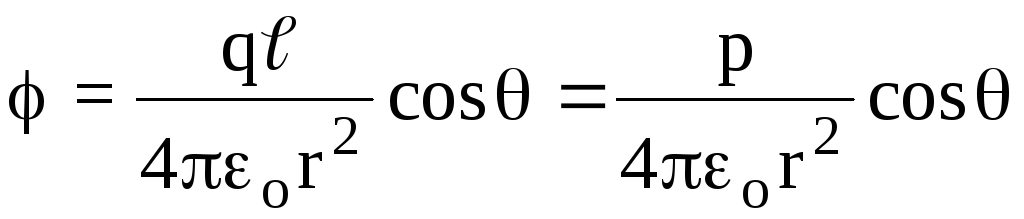

. (1.16)
Folosind formula care raportează gradientul de potențial la intensitate, găsim intensitatea creată de câmpul electric al dipolului. Să descompunăm vectorul electric câmpul dipol în două componente perpendiculare reciproce, adică

(Fig. 1. 6).
Prima dintre ele este determinată de mișcarea unui punct caracterizat de vectorul rază (pentru o valoare fixă a unghiului ), adică găsim valoarea lui E  prin diferențierea (1.81) față de r, adică.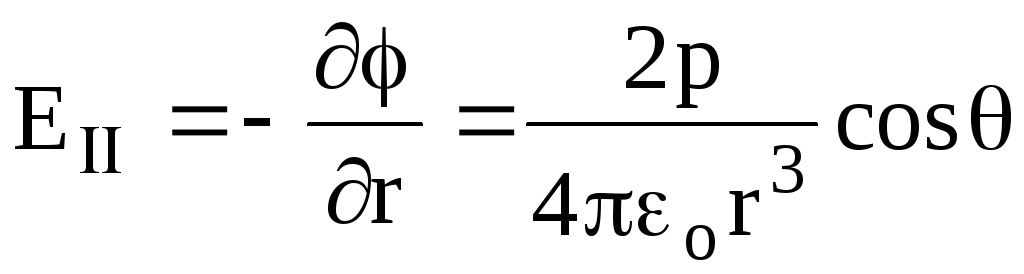

. (1.17)
A doua componentă este determinată de mișcarea punctului asociată cu o modificare a unghiului  (pentru un r fix), adică E  găsim prin diferențierea (1.16) față de :

, (1.18)
Unde

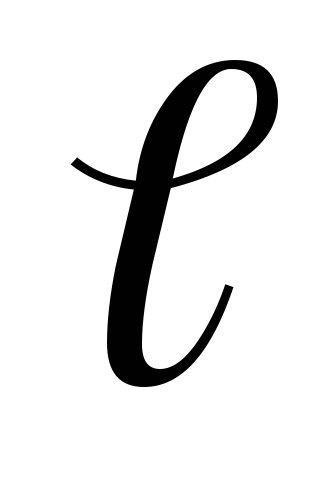,d = rd.
Tensiunea rezultată E 2 \u003d E  2 + E  2 sau după înlocuire

. (1.19)
cometariu: La  = 90 o

, (1.20)
adică intensitatea într-un punct de pe o linie dreaptă care trece prin centrul dipolului (adică O) și perpendicular pe axa dipolului.
Când  = 0 aproximativ

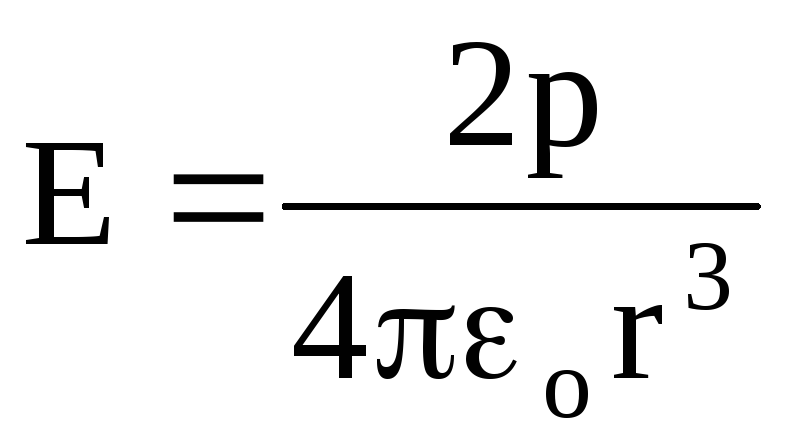, (1.21)
adică într-un punct de pe continuarea unei linii drepte care coincide cu axa dipolului.
O analiză a formulelor (1.19), (1.20), (1.21) arată că intensitatea câmpului electric al unui dipol scade cu distanța în proporție inversă cu r 3 , adică mai rapid decât pentru o sarcină punctiformă (invers proporțional cu r 2).

Pentru o mai mare claritate, câmpul electric este adesea descris folosind linii de forță și suprafețe echipotențiale.
linii de forță – acestea sunt linii continue, tangentele la care în fiecare punct prin care trec coincid cu vectorul intensității câmpului electric (Fig. 1.5). Densitatea liniilor de câmp (numărul de linii de câmp care trec printr-o unitate de suprafață) este proporțională cu puterea câmpului electric.
Suprafețe echipotențiale (echipotențiale) – suprafete cu potential egal. Acestea sunt suprafețe (linii) atunci când se deplasează de-a lungul cărora potențialul nu se modifică. În caz contrar, diferența de potențial dintre oricare două puncte ale suprafeței echipotențiale este egală cu zero. Liniile de forță sunt perpendiculare pe suprafețele echipotențiale și îndreptate în direcția celei mai puternice scăderi a potențialului. Acest fapt rezultă din ecuația (1.10) și este demonstrat în cursul analizei matematice, secțiunea „Câmpuri scalare și vectoriale”.
Luați în considerare, ca exemplu, un câmp electric generat la distanță 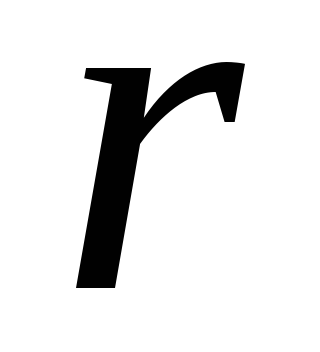dintr-o încărcare punctuală. Conform (1.11,b), vectorul intensitate coincide cu direcția vectorului dacă sarcina este pozitivă și opusă dacă sarcina este negativă. În consecință, liniile de forță diverg radial de la sarcină (Fig. 1.6, a, b). Densitatea liniilor de câmp, ca și intensitatea, este invers proporțională cu pătratul distanței (

) a încărca. Suprafețele echipotențiale ale câmpului electric al unei sarcini punctuale sunt sfere centrate în locul sarcinii.

Pe fig. 1.7 arată câmpul electric al unui sistem de două sarcini punctuale egale în valoare absolută, dar opuse ca semn. Lăsăm acest exemplu pe seama cititorilor să-l analizeze singuri. Remarcăm doar că liniile de forță încep întotdeauna pe sarcini pozitive și se termină pe cele negative. În cazul unui câmp electric cu o sarcină punctuală (Fig. 1.6, a, b), se presupune că liniile de forță se rup la sarcini foarte îndepărtate de semn opus. Se crede că universul în ansamblu este neutru. Prin urmare, dacă există o taxă pentru un semn, atunci undeva va exista cu siguranță o taxă pentru celălalt semn egală cu aceasta în valoare absolută.
1.6. Teorema lui Gauss pentru un câmp electric în vid
Sarcina principală a electrostaticei este problema de a găsi puterea și potențialul câmpului electric în fiecare punct din spațiu. În Secțiunea 1.4 am rezolvat problema câmpului unei sarcini punctuale și am luat în considerare și câmpul unui sistem de sarcini punctiforme. În această secțiune, ne vom concentra asupra unei teoreme care ne permite să calculăm câmpul electric al obiectelor încărcate mai complexe. De exemplu, un fir lung încărcat (linie dreaptă), un plan încărcat, o sferă încărcată și altele. După ce s-a calculat intensitatea câmpului electric în fiecare punct din spațiu, folosind ecuațiile (1.12) și (1.13), se poate calcula potențialul în fiecare punct sau diferența de potențial dintre oricare două puncte, de exemplu. rezolva problema de baza a electrostaticii.
Pentru o descriere matematică, introducem conceptul de flux al vectorului de intensitate sau flux al câmpului electric. Vector de flux (F). câmp electric pe o suprafață pătrată plană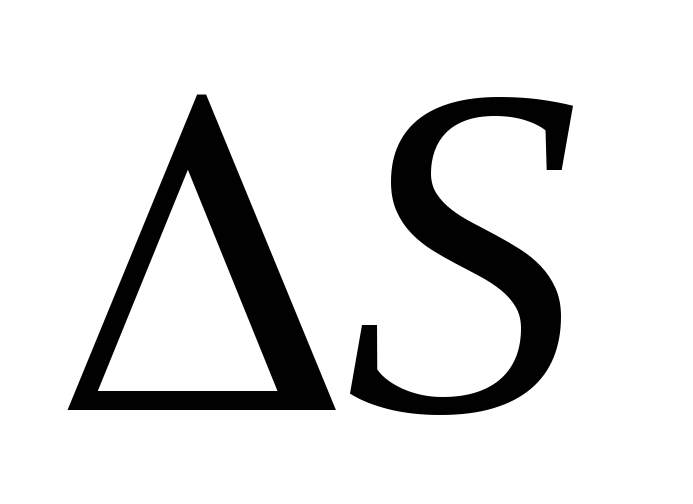

cantitatea se numeste:

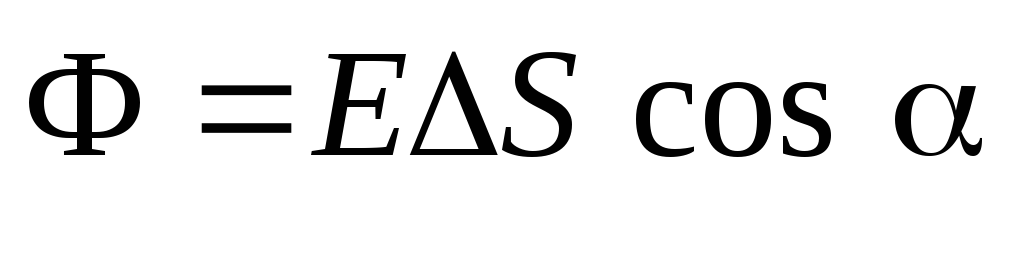, (1.16)

Unde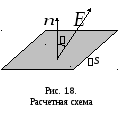 este intensitatea câmpului electric, care se presupune a fi constantă în amplasament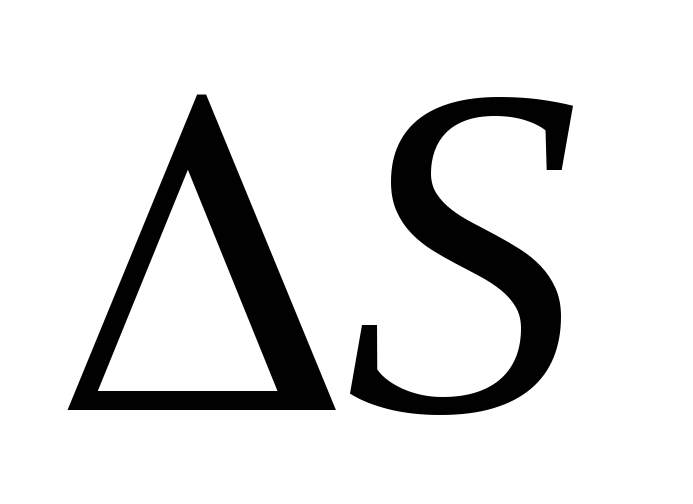

;

este unghiul dintre direcția vectorului și vectorul normal unitar 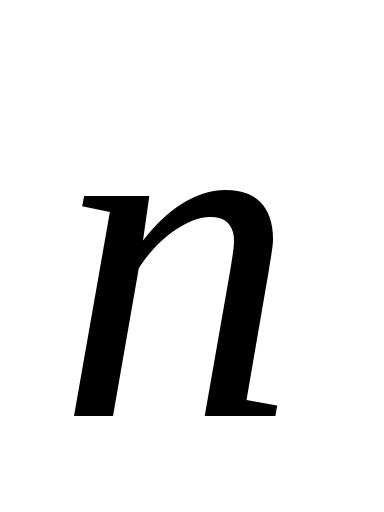la site

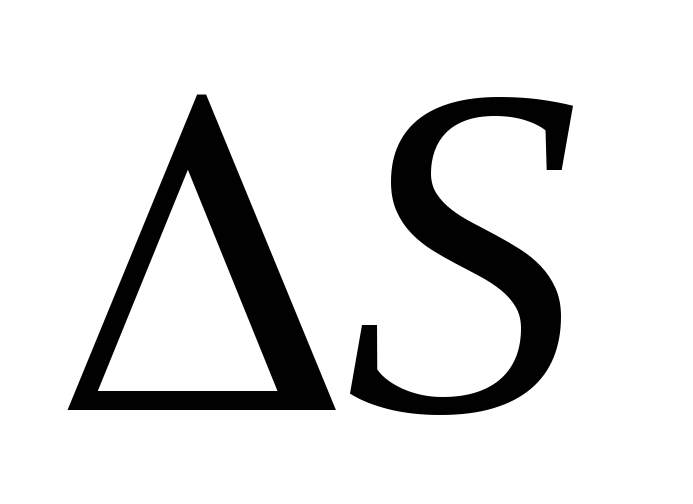(Fig. 1.8). Formula (1.16) poate fi scrisă folosind conceptul de produs scalar al vectorilor:

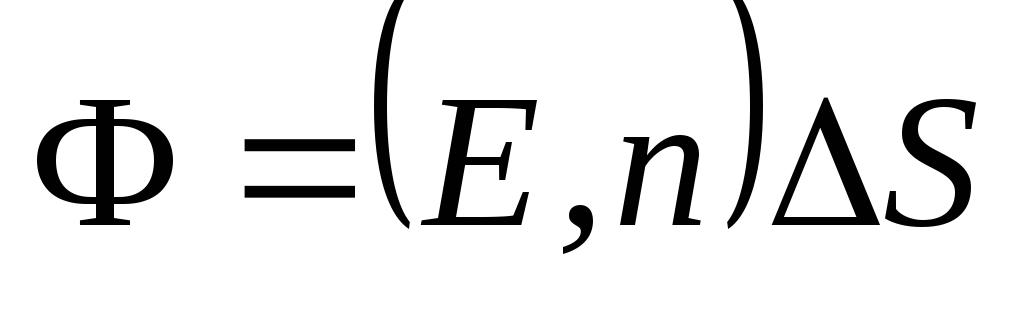. (1.15,a)
In cazul in care suprafata nu plat, pentru a calcula debitul trebuie împărțit în părți mici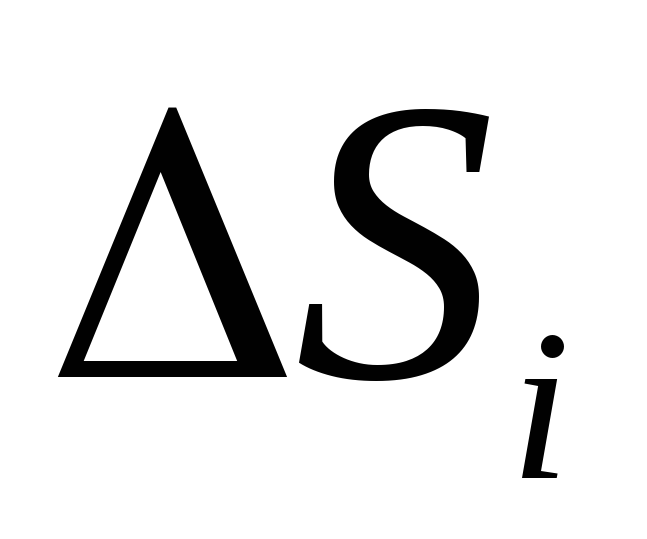

, care poate fi considerat aproximativ plat, apoi notați expresia (1.16) sau (1.16, a) pentru fiecare bucată de suprafață și adăugați-le. În limita când suprafaţa S i foarte mic (

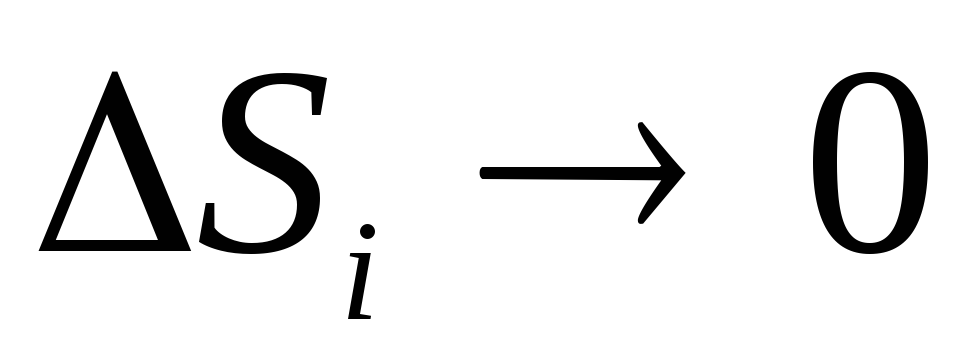), o astfel de sumă se numește integrală de suprafață și se notează

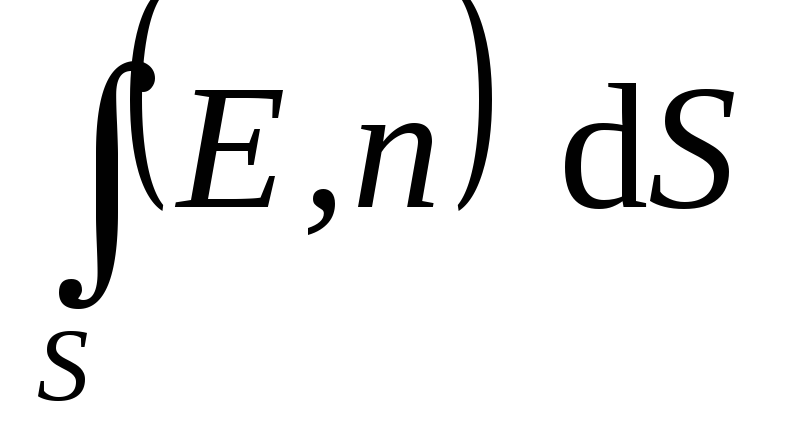. Astfel, fluxul vectorului intensității câmpului electric printr-o suprafață arbitrară este definit prin expresia:

. (1.17)
Ca exemplu, luați în considerare o sferă cu rază 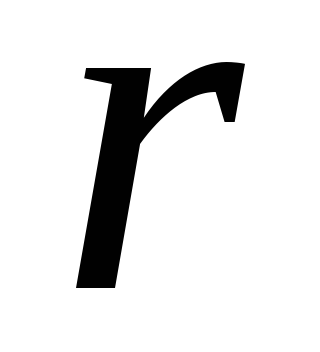, centrat pe o sarcină punctiformă pozitivă , și determinați fluxul câmpului electric prin suprafața acestei sfere. Liniile de forță (vezi, de exemplu, Fig. 1.6, a) care ies din sarcină sunt perpendiculare pe suprafața sferei, iar în fiecare punct al sferei, modulul intensității câmpului este același

.
Zona sferei

,
apoi

.
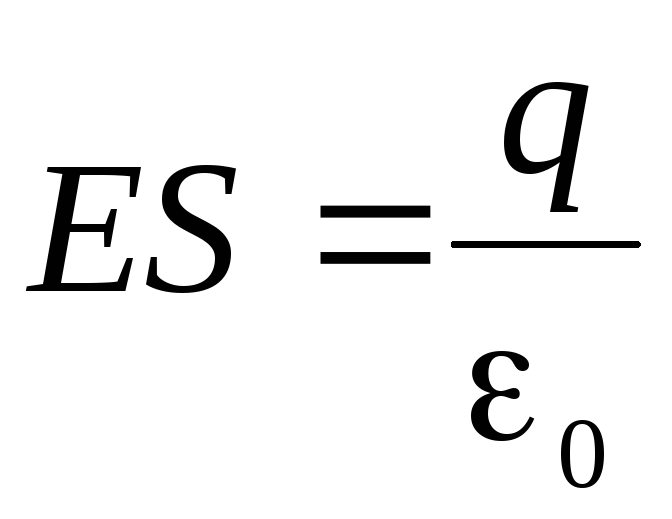Valoare

și reprezintă fluxul câmpului electric prin suprafața sferei. Astfel, primim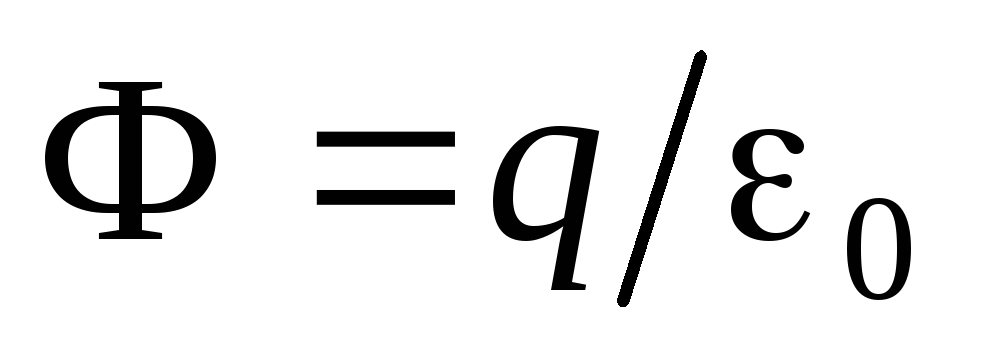

. Se poate observa că fluxul prin suprafața sferei câmpului electric nu depinde de raza sferei, ci depinde doar de sarcina în sine. . Prin urmare, dacă desenați o serie de sfere concentrice, atunci fluxul câmpului electric prin toate aceste sfere va fi același. Evident, numărul liniilor de forță care traversează aceste sfere va fi și el același. Am convenit să luăm numărul de linii de forță care ies din sarcină egal cu fluxul câmpului electric:

.
Dacă sfera este înlocuită cu orice altă suprafață închisă, atunci fluxul câmpului electric și numărul de linii de forță care o traversează nu se vor schimba. În plus, fluxul câmpului electric printr-o suprafață închisă și, prin urmare, numărul de linii de forță care pătrund în această suprafață este egal cu

nu numai pentru câmpul unei sarcini punctuale, ci și pentru câmpul creat de orice set de taxe punctiforme, în special, de un corp încărcat. Apoi valoarea ar trebui considerată ca suma algebrică a întregului set de sarcini situate în interiorul unei suprafețe închise. Aceasta este esența teoremei Gauss, care este formulată după cum urmează:
Fluxul vectorului de intensitate a câmpului electric printr-un mod arbitrarînchis suprafata este egala

, Unde

 algebric cuantumul taxelor anexateinterior această suprafață.
Matematic, teorema poate fi scrisă ca

. (1.18)
Rețineți că dacă pe o anumită suprafață S vector constantă și paralelă cu vectorul 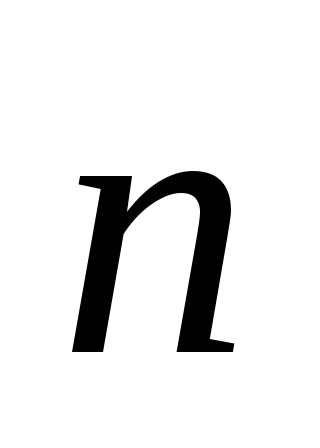, apoi curgerea printr-o astfel de suprafață. Transformând prima integrală, am profitat mai întâi de faptul că vectorii și 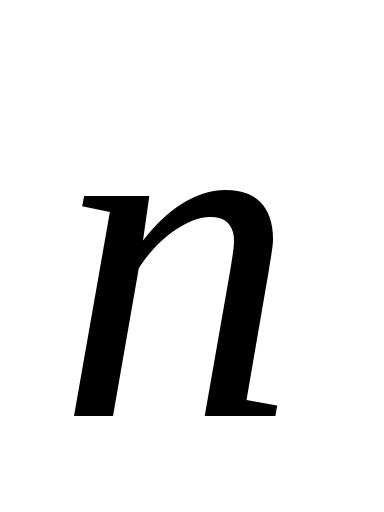paralel, ceea ce înseamnă

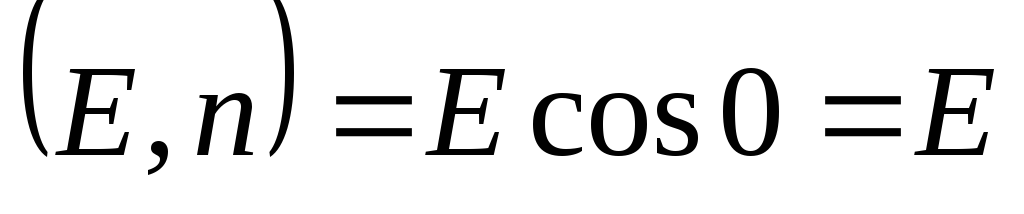. Apoi a scos valoarea pentru semnul integralei datorită faptului că este constantă în orice punct al sferei . Aplicând teorema Gauss pentru a rezolva probleme specifice, ei încearcă să aleagă o suprafață pentru care condițiile descrise mai sus sunt îndeplinite ca suprafață închisă arbitrară.
Dăm câteva exemple de aplicare a teoremei Gauss.
Exemplul 1.2. Calculați intensitatea câmpului electric al unui filament infinit încărcat uniform. Determinați diferența de potențial dintre două puncte dintr-un astfel de câmp.
Soluţie. Să presupunem pentru certitudine că firul este încărcat pozitiv. Datorită simetriei problemei, se poate susține că liniile de forță vor fi drepte divergente radial față de axa filetului (Fig. 1.9), a căror densitate scade pe măsură ce se îndepărtează de fir conform unor lege. Conform aceleiași legi, va scădea și mărimea câmpului electric 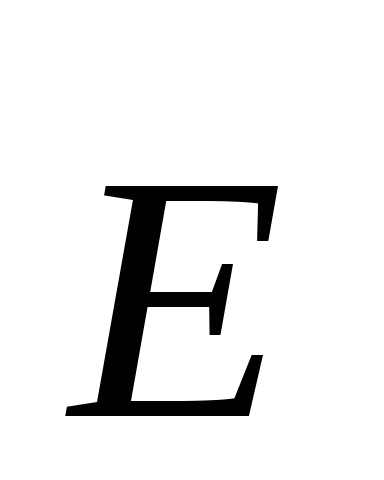. Suprafețele echipotențiale vor fi suprafețe cilindrice cu o axă care coincide cu filetul.
Fie încărcarea pe unitatea de lungime a firului . Această valoare se numește densitate de sarcină liniară și este măsurată în unități SI [C/m]. Pentru a calcula intensitatea câmpului, aplicăm teorema lui Gauss. Pentru aceasta, ca o suprafață închisă arbitrară alege un cilindru cu raza 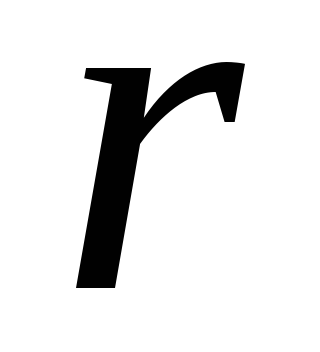si lungime , a cărui axă coincide cu filetul (Fig. 1.9). Să calculăm fluxul câmpului electric prin suprafața cilindrului. Debitul total este suma debitului prin suprafata laterala cilindru și curge prin baze
In orice caz,

, deoarece în orice punct pe bazele cilindrului

. Înseamnă că

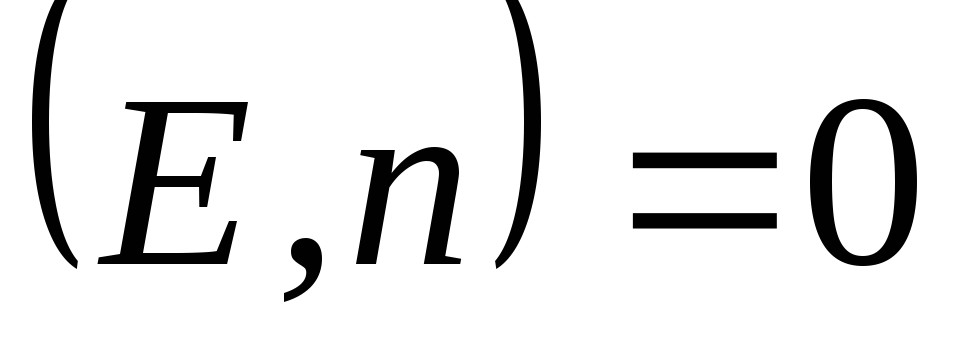in aceste puncte. Curgeți prin suprafața laterală

. După teorema lui Gauss, acest flux total este egal cu

. Astfel, am primit

.
Suma sarcinilor din interiorul cilindrului este exprimată în termeni de densitate de sarcină liniară :

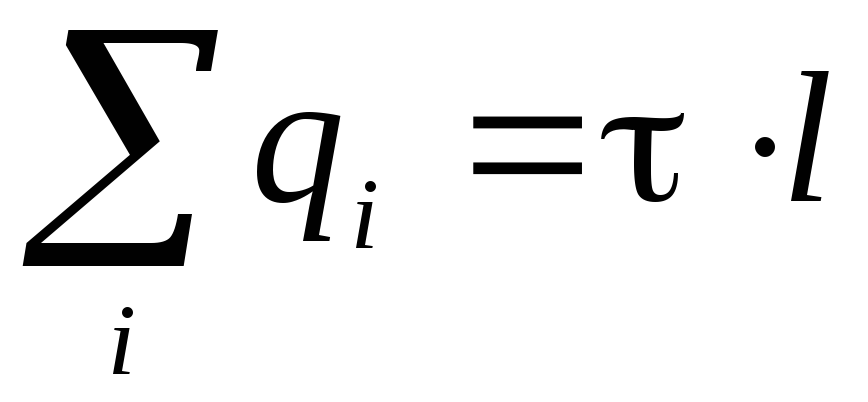. Dat fiind

, primim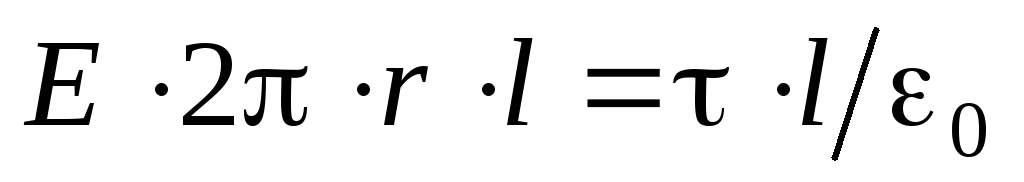

,

, (1.19)
acestea. intensitatea și densitatea liniilor de câmp electric ale unui filament infinit încărcat uniform scade invers cu distanța (

).
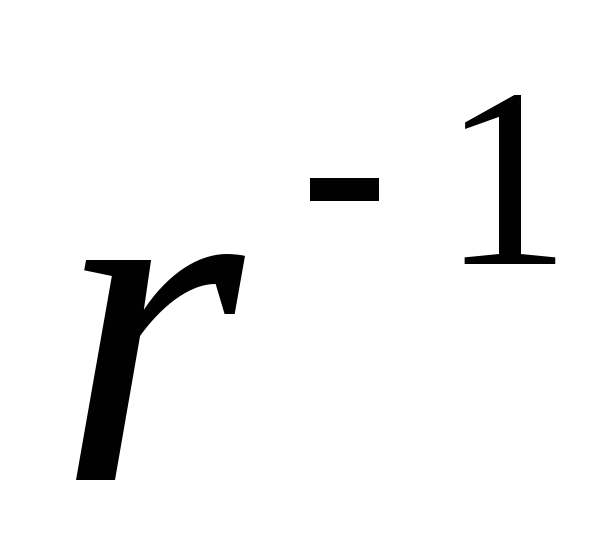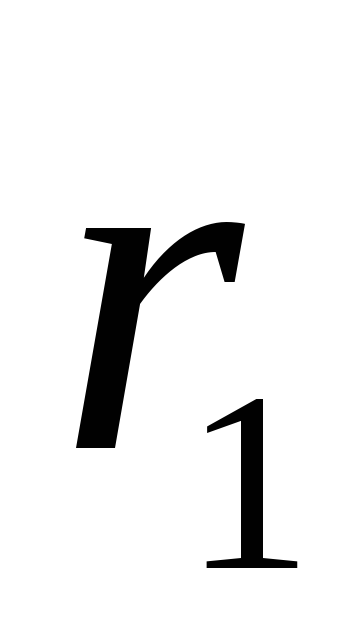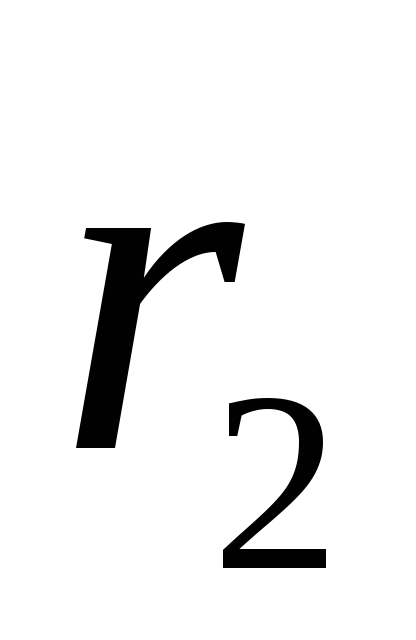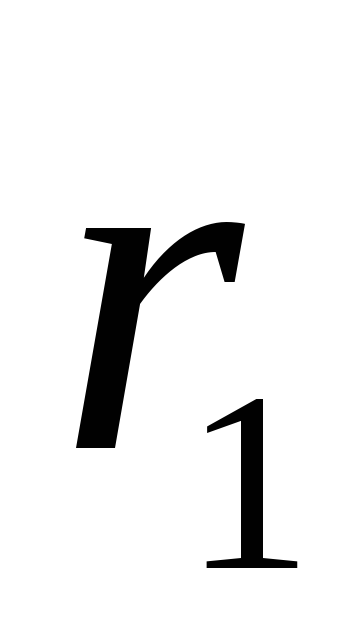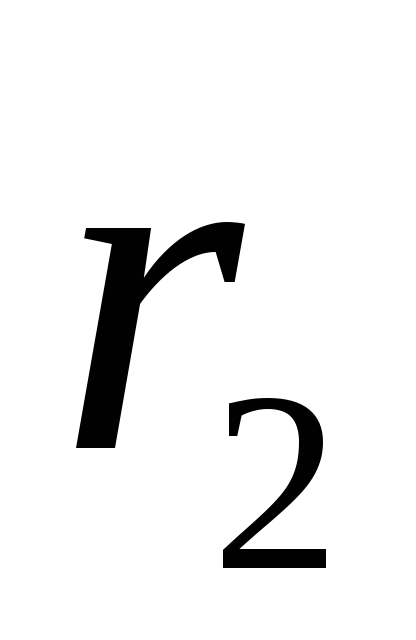Găsiți diferența de potențial dintre punctele situate la distanțe și din filet (aparținând suprafețelor cilindrice echipotențiale cu raze și ). Pentru a face acest lucru, folosim legătura dintre intensitatea câmpului electric și potențial sub forma (1.9, c):

. Ținând cont de expresia (1.19), obținem o ecuație diferențială cu variabile separabile:

.

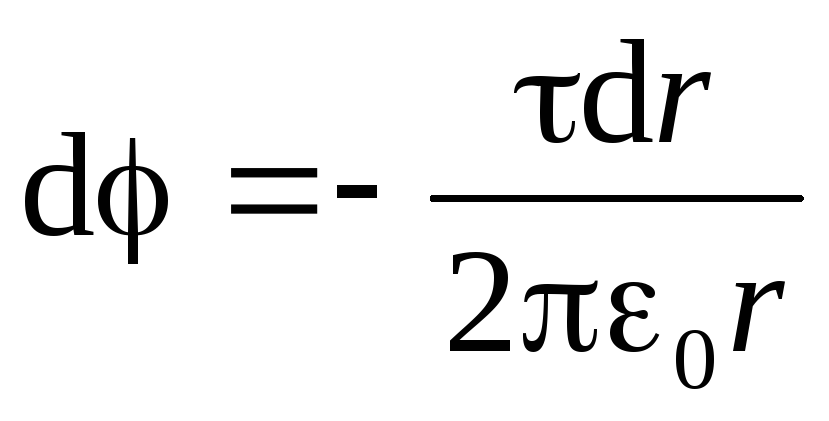
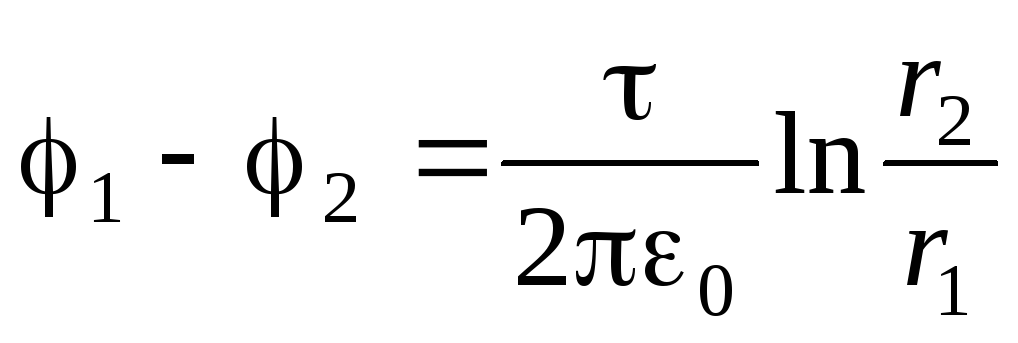Exemplul 1.3. Calculați intensitatea câmpului electric al unui plan încărcat uniform. Determinați diferența de potențial dintre două puncte dintr-un astfel de câmp.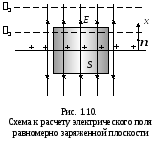
Soluţie. Câmpul electric al unui plan încărcat uniform este prezentat în fig. 1.10. Datorită simetriei, liniile de forță trebuie să fie perpendiculare pe plan. Prin urmare, putem concluziona imediat că densitatea liniei și, în consecință, intensitatea câmpului electric nu se vor schimba odată cu distanța de la plan. Suprafețele echipotențiale sunt plane paralele cu un plan încărcat dat. Fie taxa pe unitatea de suprafață a avionului . Această valoare se numește densitate de sarcină la suprafață și este măsurată în SI în unități de [C/m 2 ].
Să aplicăm teorema lui Gauss. Pentru aceasta, ca o suprafață închisă arbitrară alege un cilindru cu o lungime 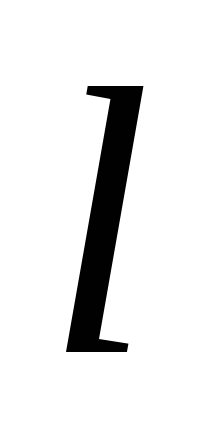, a cărui axă este perpendiculară pe plan, iar bazele sunt echidistante de acesta (fig. 1.10). Fluxul total al câmpului electric

. Debitul prin suprafața laterală este zero. Curgerea prin fiecare dintre baze este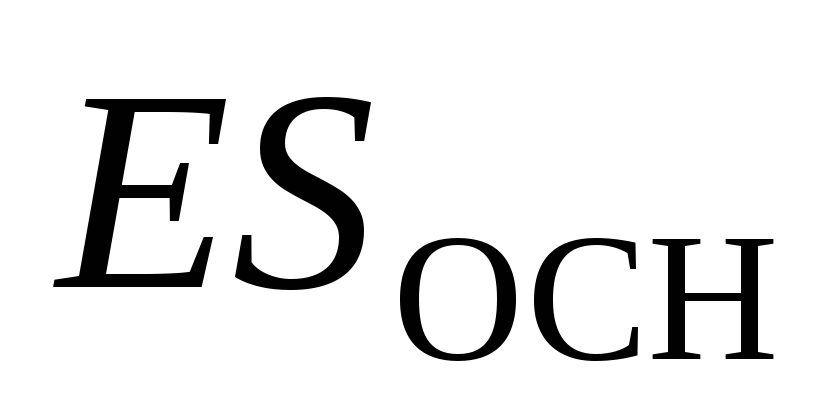

, de aceea

. Conform teoremei lui Gauss, obținem: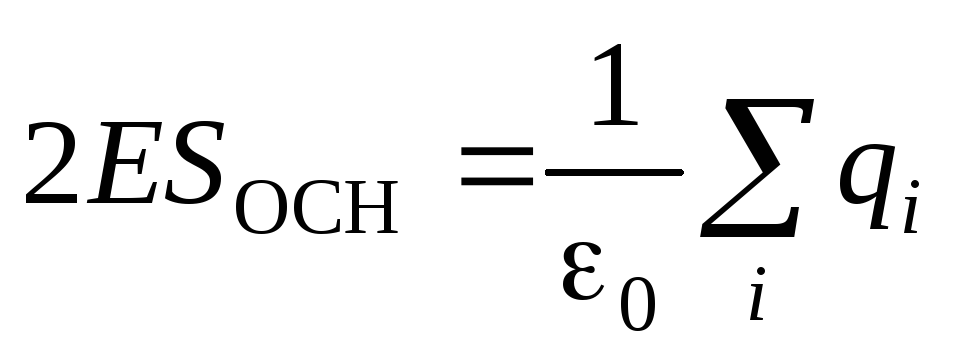

.
Suma sarcinilor din interiorul cilindrului , găsim prin densitatea de sarcină de suprafață :

. Apoi de unde:

. (1.20)
Din formula obținută se poate observa că intensitatea câmpului unui plan încărcat uniform nu depinde de distanța până la planul încărcat, adică în orice punct al spațiului (într-un semiplan) este același atât ca valoare absolută, cât și ca direcție. Un astfel de câmp se numește omogen. linii de forță câmp omogen paralel, densitatea lor nu se modifică.
Să găsim diferența de potențial dintre două puncte ale unui câmp omogen (aparținând planurilor echipotențiale și situat într-un semiplan în raport cu planul încărcat (Fig. 1.10)). Să direcționăm axa 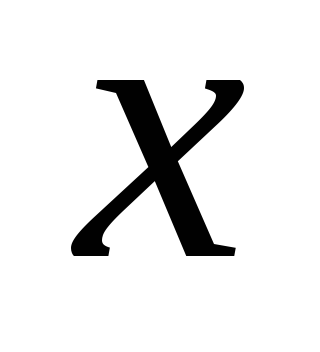vertical în sus, atunci proiecția vectorului de tensiune pe această axă este egală cu modulul vectorului de tensiune

. Folosim ecuația (1.9):

.
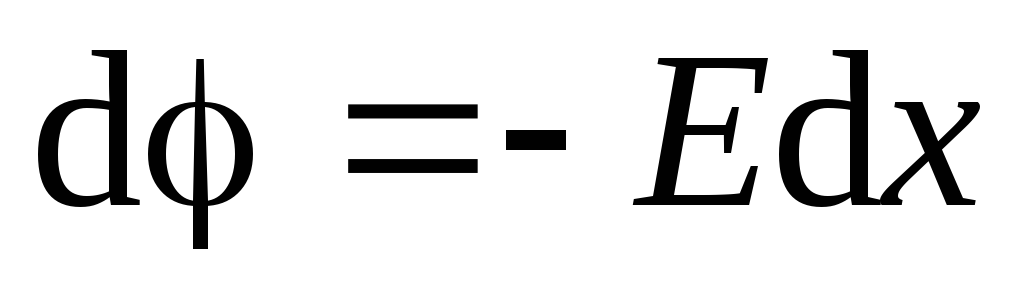
Valoare constantă (câmpul este omogen) poate fi scos de sub semnul integral: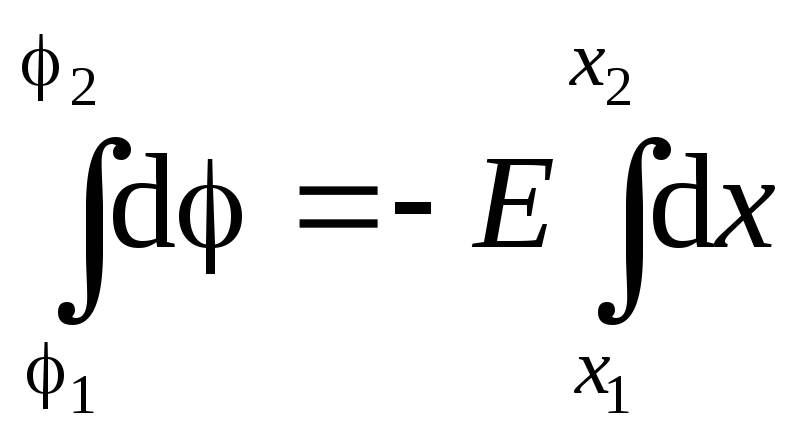

. Integrând, obținem: . Deci, potențialul unui câmp omogen depinde liniar de coordonată.
Diferența de potențial dintre două puncte ale câmpului electric este tensiunea dintre aceste puncte ( ). Să notăm distanța dintre planurile echipotențiale

. Apoi putem scrie că într-un câmp electric uniform:

. (1.21)
Subliniem încă o dată că atunci când folosim formula (1.21), trebuie să ne amintim că cantitatea - nu distanta dintre punctele 1 si 2, ci distanta dintre planurile echipotentiale carora le apartin aceste puncte.
Exemplul 1.4. Calculați intensitatea câmpului electric a două plane paralele încărcate uniform cu densitățile de sarcină de suprafață

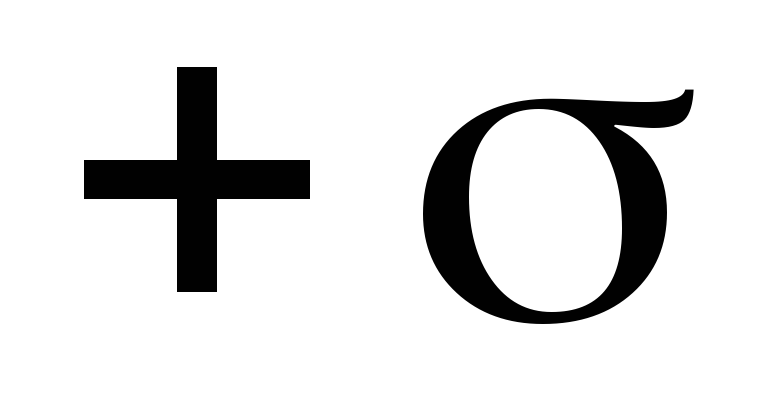și

.
Soluţie. Să folosim rezultatul exemplului 1.3 și principiul suprapunerii. Conform acestui principiu, câmpul electric rezultat în orice punct al spațiului

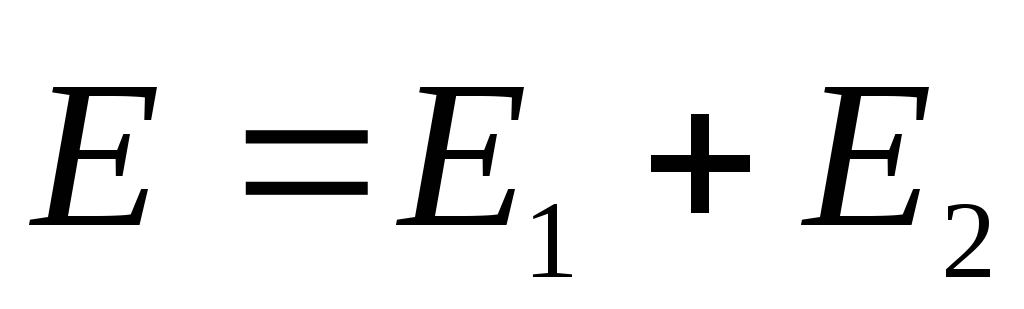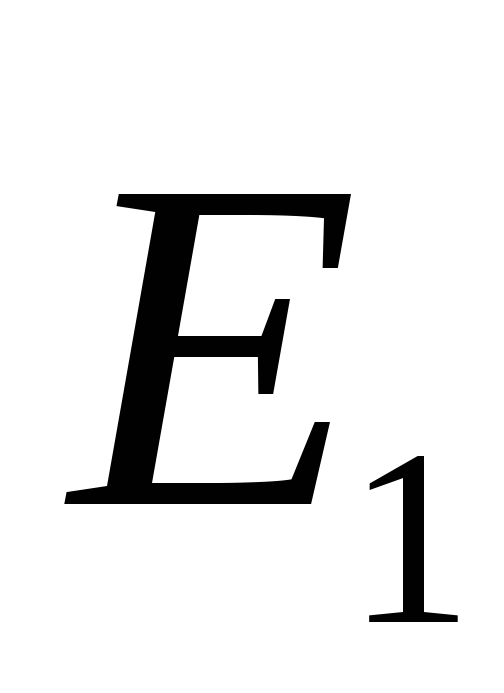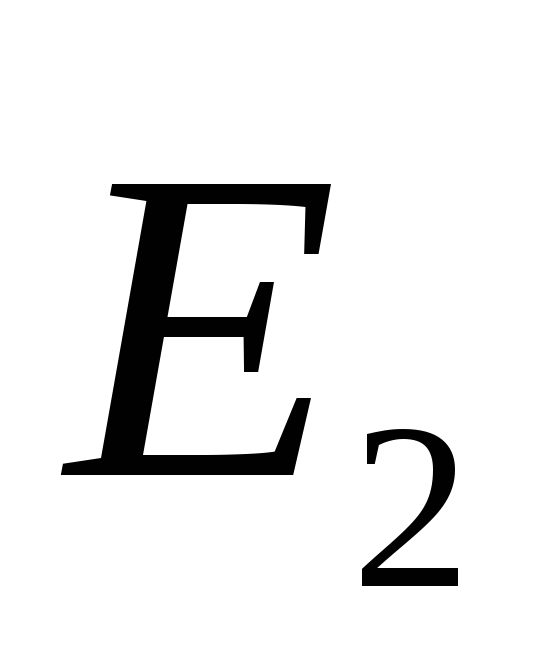, Unde și - intensitatea câmpului electric al primului și al doilea plan. În spațiul dintre planurile vectoriale 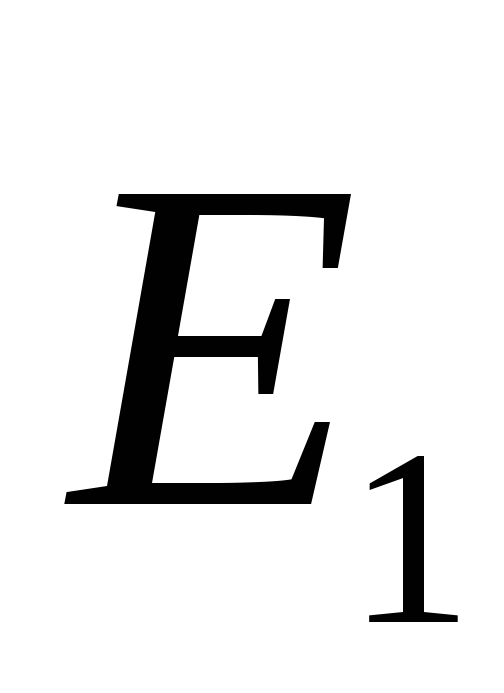și 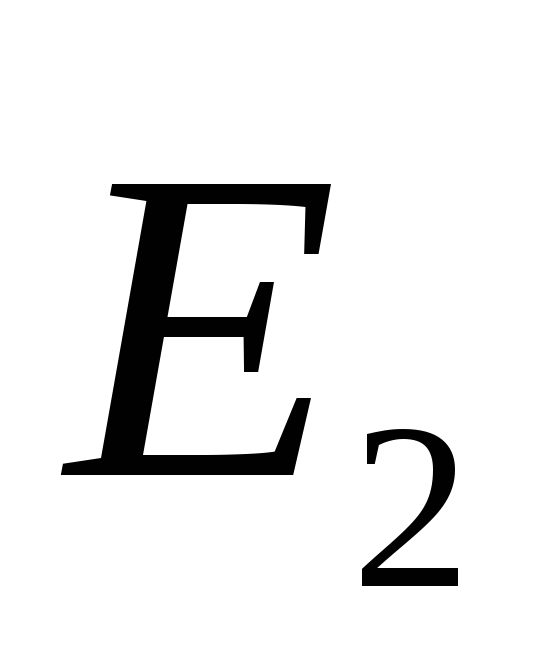direcționat într-o direcție, deci modulul intensității câmpului rezultat. În spațiul exterior al vectorulu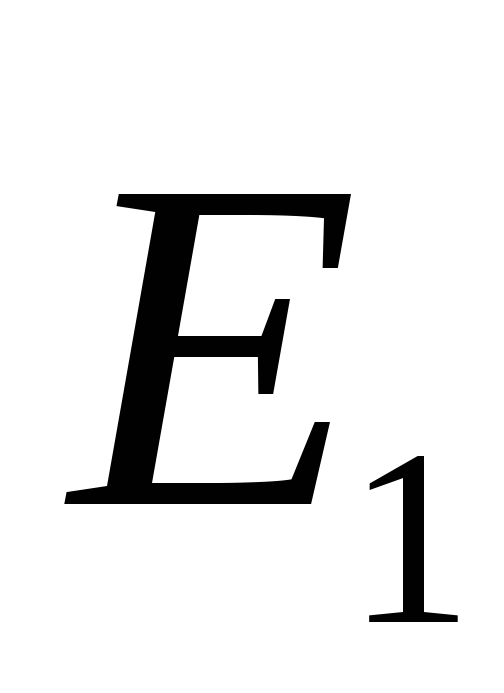i și 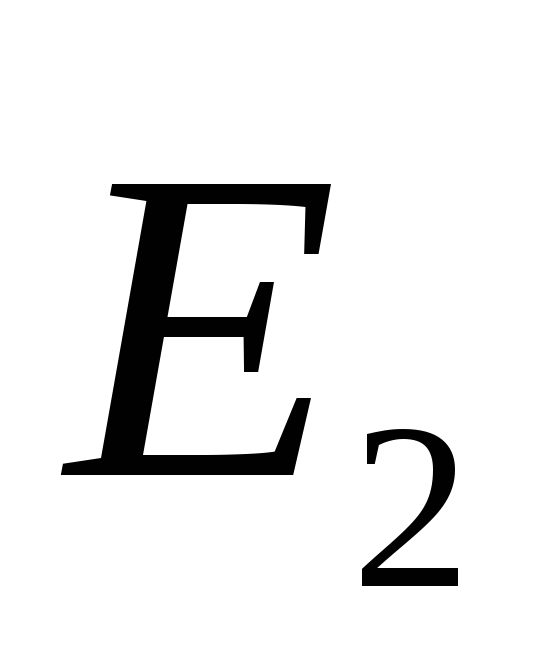îndreptate în direcţii diferite, prin urmare (Fig. 1.11). Astfel, câmpul electric există doar în spațiul dintre planuri. Este omogen, deoarece este suma a două câmpuri omogene.
Exemplul 1.5. Aflați puterea și potențialul câmpului electric al unei sfere încărcate uniform. Sarcina totală a sferei este , iar raza sferei este .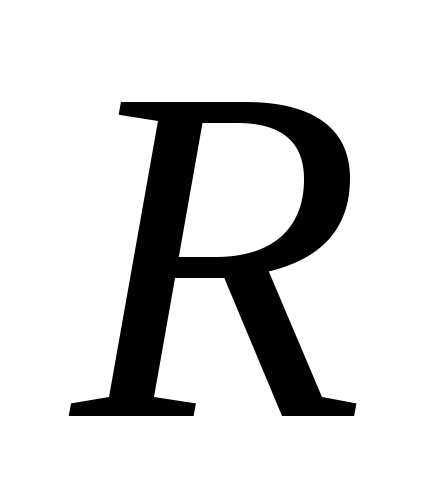
Soluţie. Datorită simetriei distribuției sarcinii, liniile de forță trebuie direcționate de-a lungul razelor sferei.
Luați în considerare o regiune în interiorul unei sfere. Ca o suprafață arbitrară alege o sferă de rază

, al cărui centru coincide cu centrul sferei încărcate. Apoi fluxul câmpului electric prin sferă S:

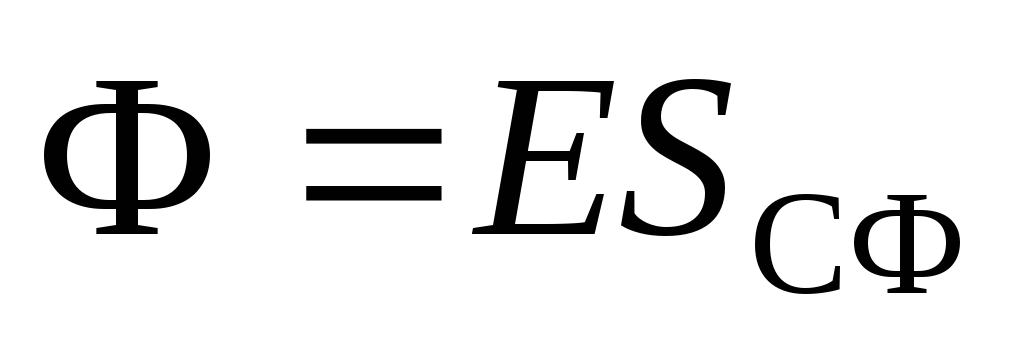. Suma sarcinilor din interiorul sferei rază 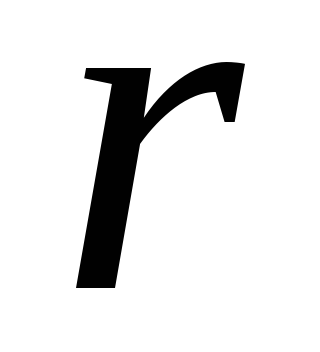este egal cu zero, deoarece toate sarcinile sunt situate pe suprafața unei sfere cu rază

. Apoi, după teorema lui Gauss: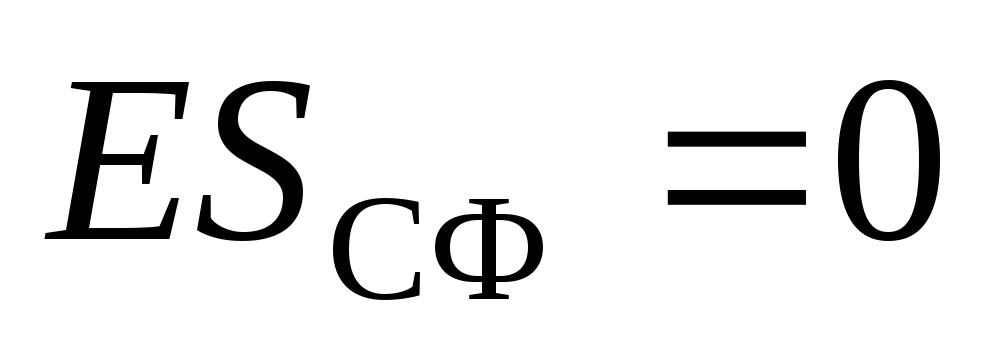

. Pentru că

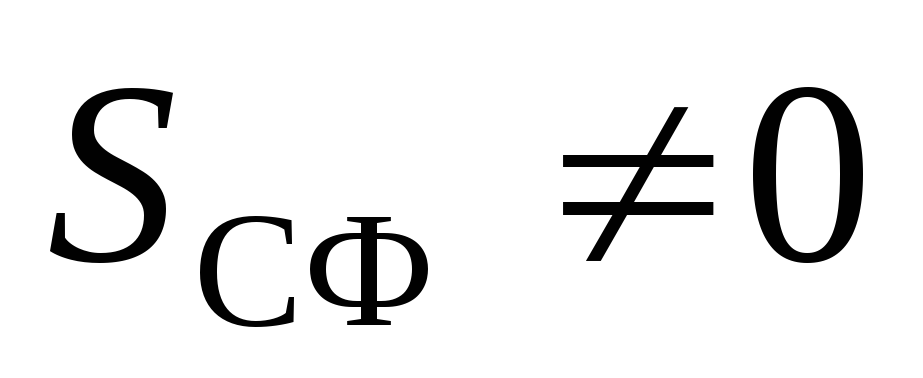, apoi

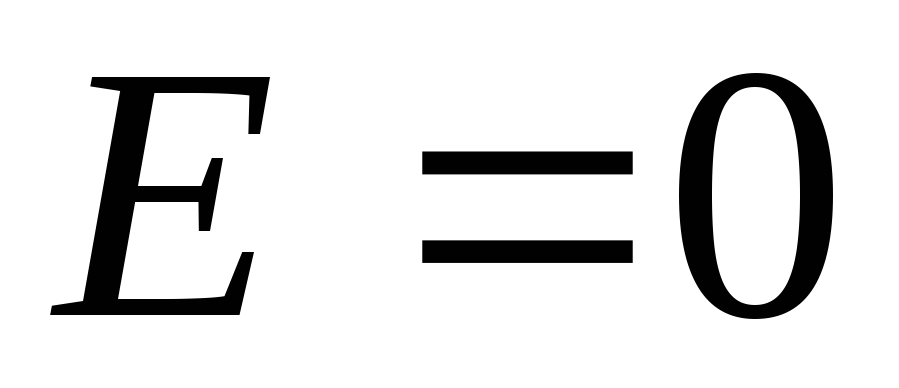. Astfel, nu există câmp în interiorul unei sfere încărcate uniform.
Luați în considerare o regiune în afara sferei. Ca o suprafață arbitrară alege o sferă de rază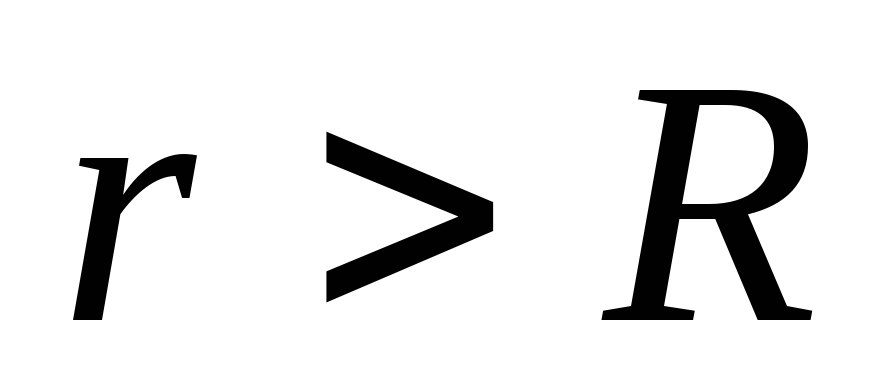

, al cărui centru coincide cu centrul sferei încărcate. Fluxul unui câmp electric printr-o sferă :

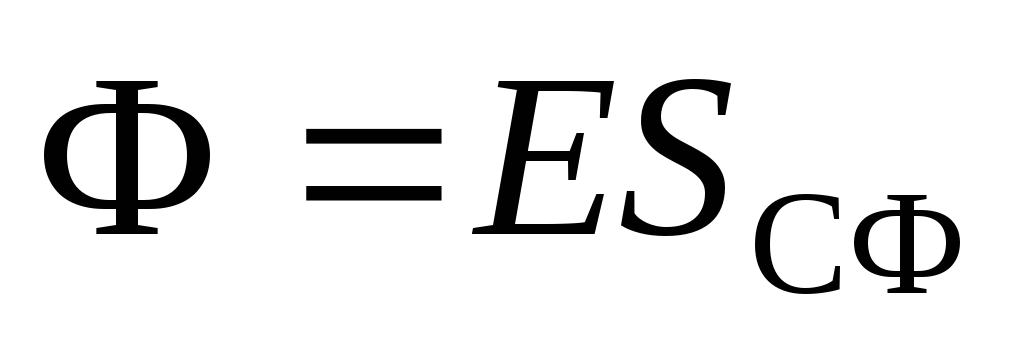. Suma sarcinilor din interiorul sferei este egală cu sarcina totală sferă încărcată de rază 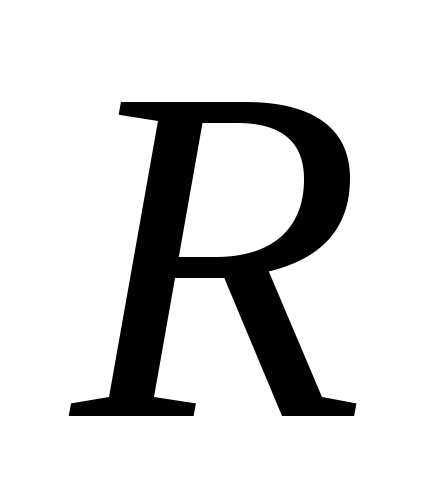. Apoi, după teorema lui Gauss:

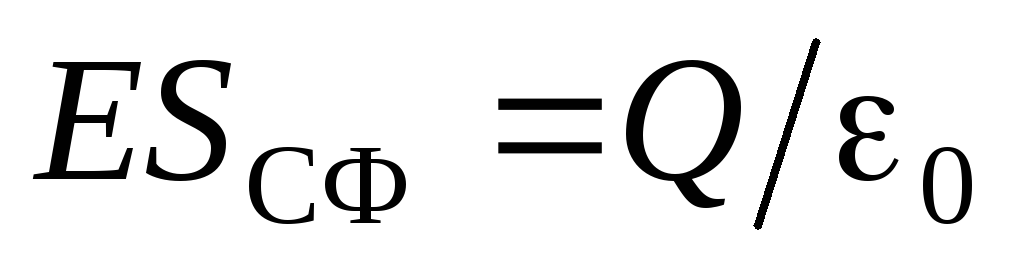. Dat fiind

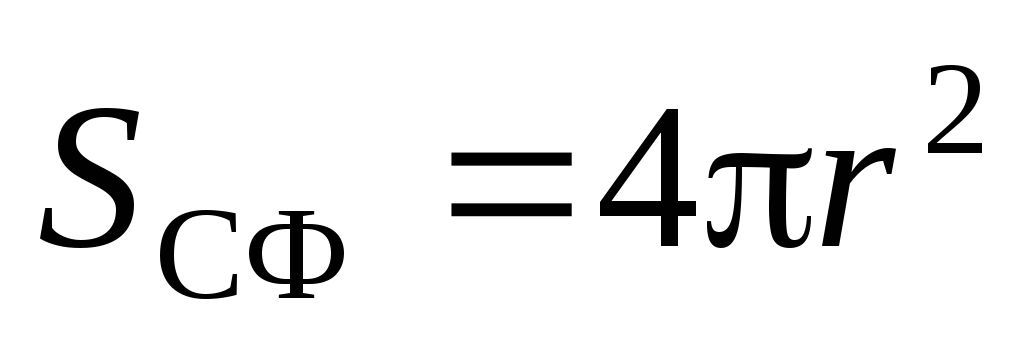, primim:

.
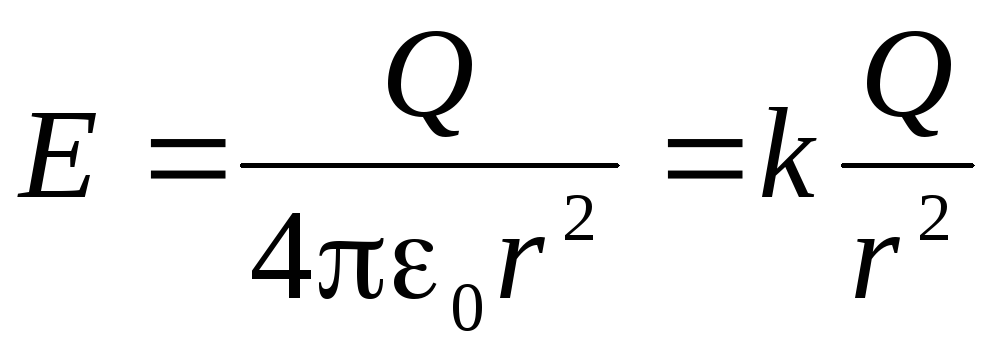Să calculăm potențialul câmpului electric. Este mai convenabil să începeți din zona exterioară

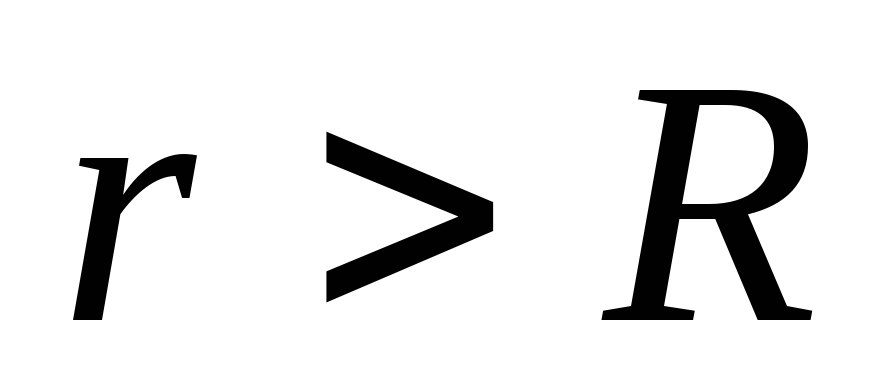, deoarece știm că la o distanță infinită de centrul sferei, se presupune că potențialul este zero. Folosind ecuația (1.11, a) obținem o ecuație diferențială cu variabile separabile:

.
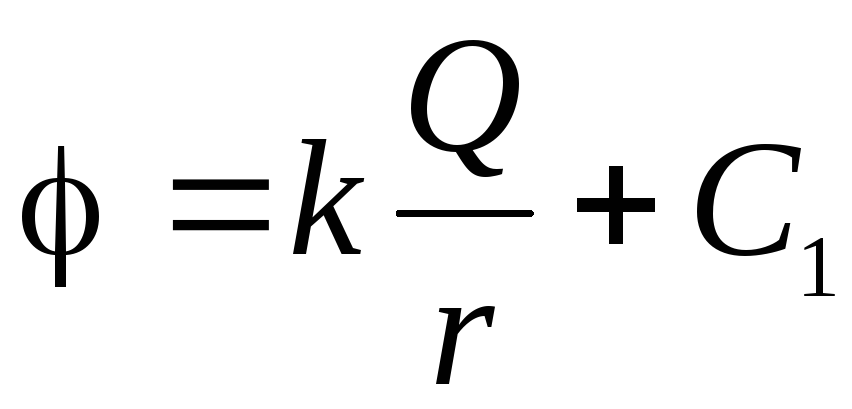Constant

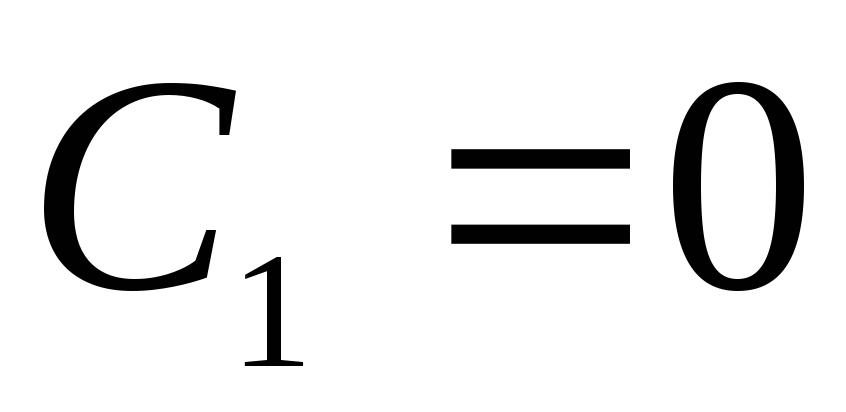, pentru că

la

. Astfel, în spațiul cosmic (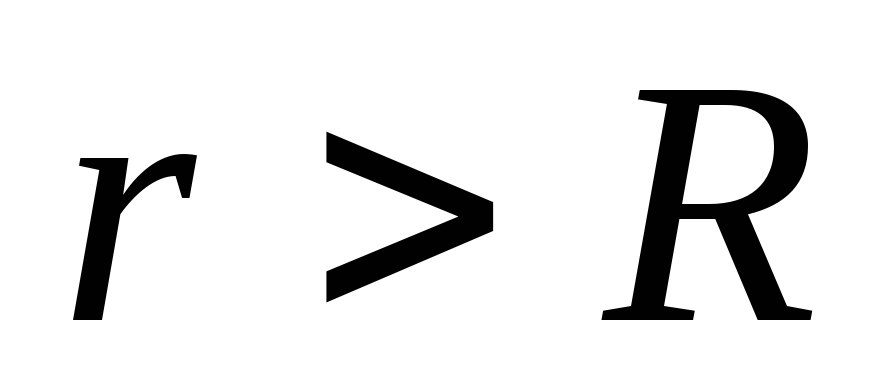

):

.
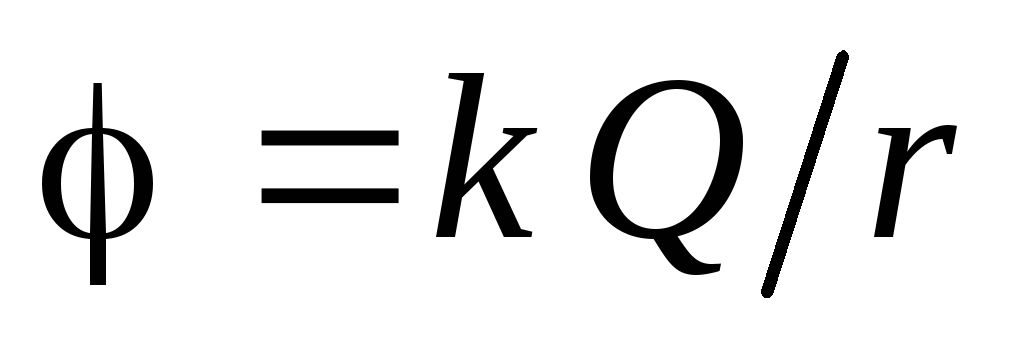Puncte de pe suprafața unei sfere încărcate (

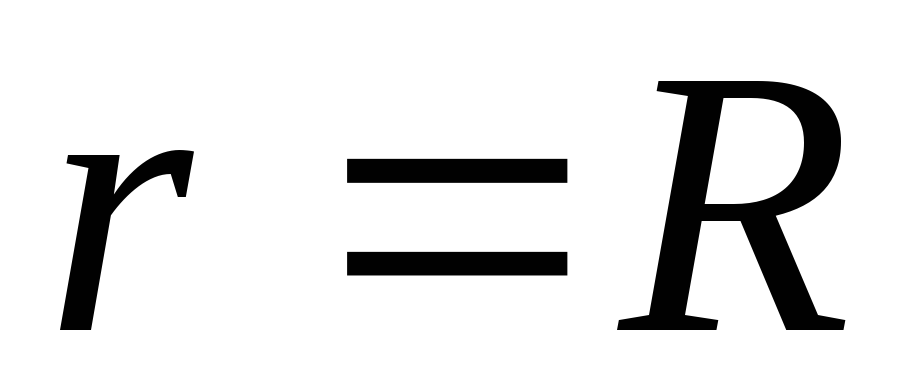) va avea potențialul

.
Luați în considerare zona

. In aceasta regiune

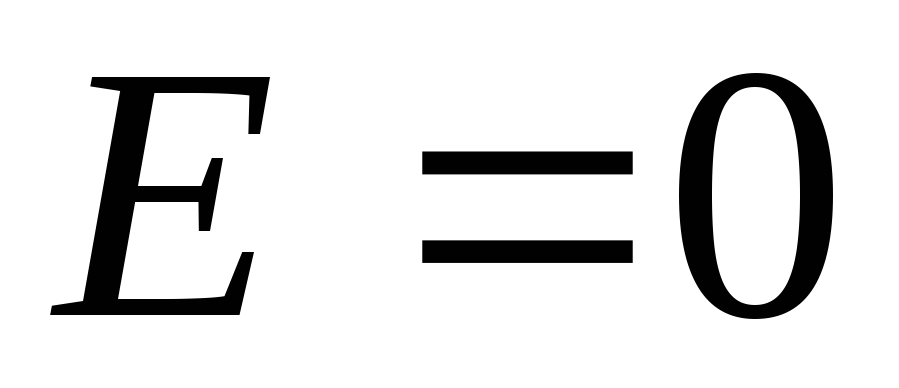, prin urmare, din ecuația (1.11, a) obținem: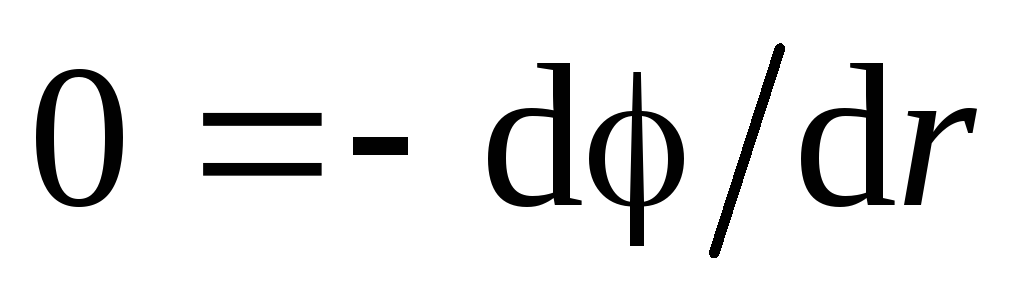

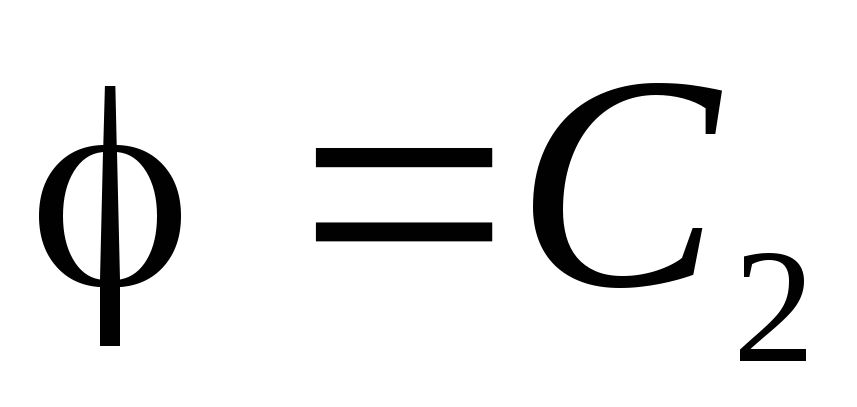. Datorita continuitatii functiei

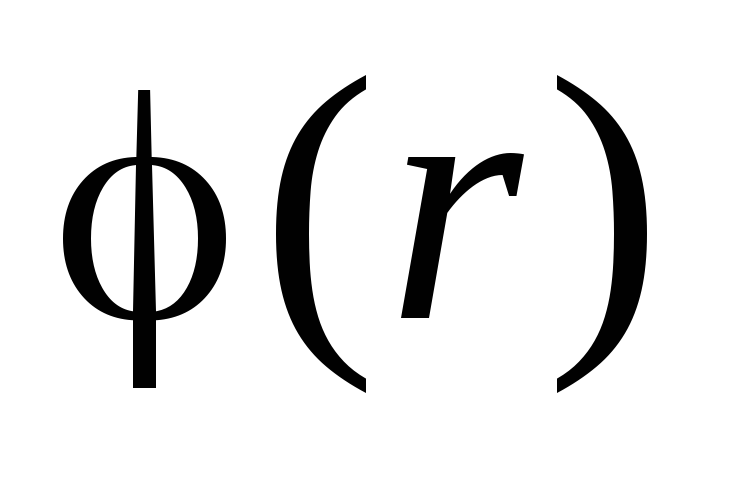constant trebuie să fie egală cu valoarea potențialului de pe suprafața sferei încărcate: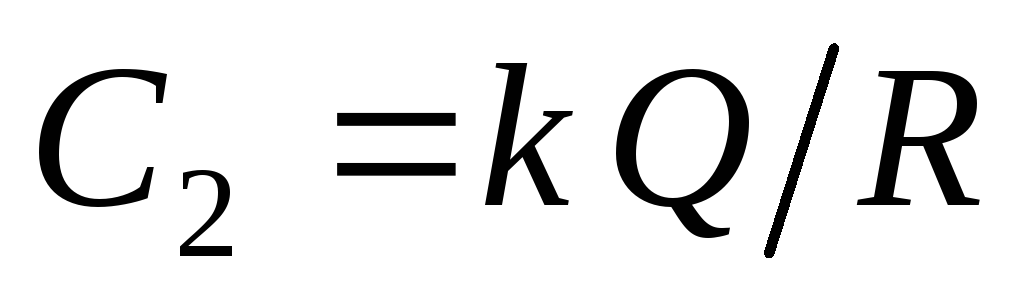

. Deci potențialul în toate punctele din interiorul sferei este:

.

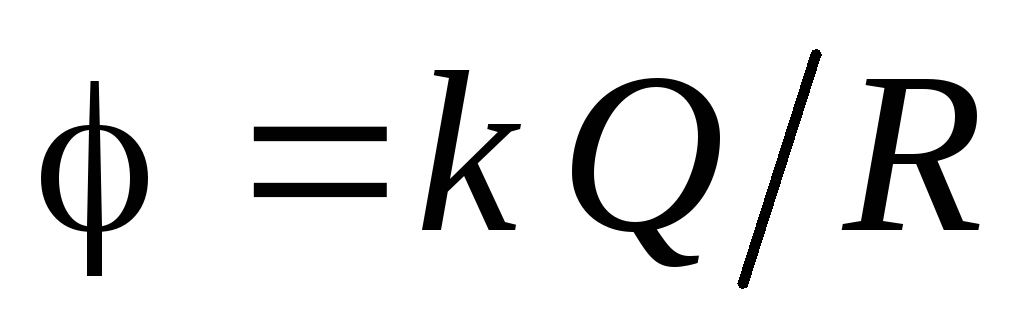Deci, am obținut că puterea și potențialul câmpului electric creat de o sferă încărcată uniform în afara sferei sunt egale cu puterea și potențialul câmpului creat de taxă punctuală aceeasi dimensiune , care este sarcina sferei plasate în centrul sferei. Nu există câmp în spațiul interior, iar potențialul este același în toate punctele. Câmpul electric (linii de câmp și suprafețe echipotențiale) al unei sfere încărcate este prezentat în fig. 1.12. Se presupune că sfera este încărcată pozitiv. În afara sferei, liniile de forță și sunt distribuite în spațiu exact în același mod ca liniile de forță ale unei sarcini punctiforme.

Pe fig. 1.13 prezintă grafice de dependență

și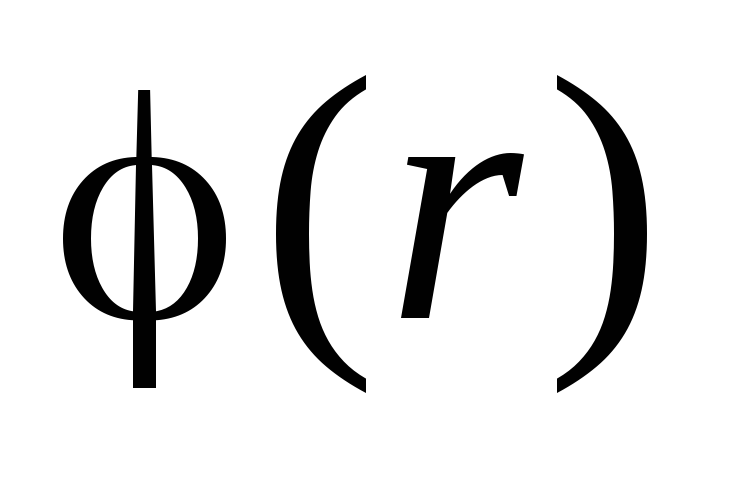

. Funcţie

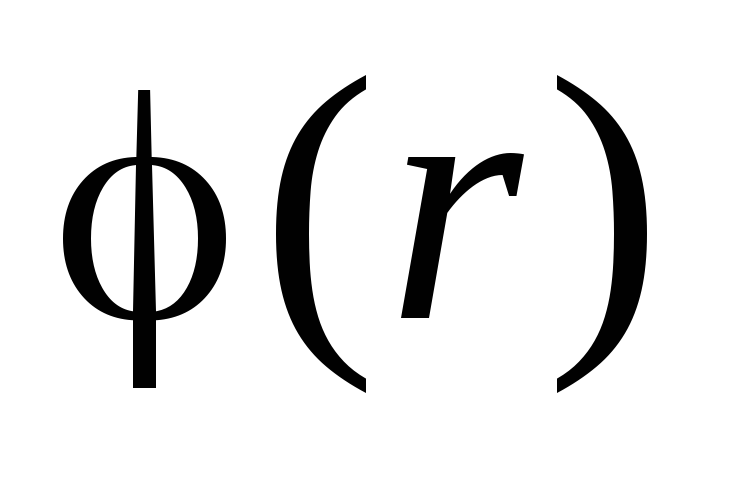este continuă, iar funcția

se modifică brusc la trecerea prin limita unei sfere încărcate. Valoarea saltului este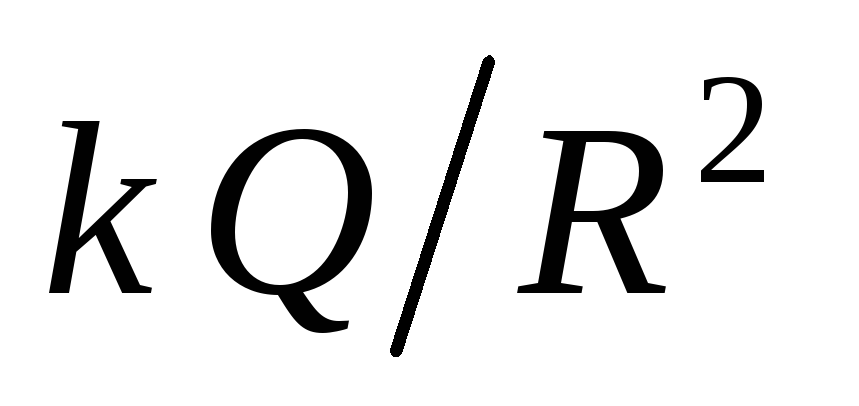

. Într-adevăr, lângă sfera încărcată (

) intensitatea câmpului în spațiul cosmic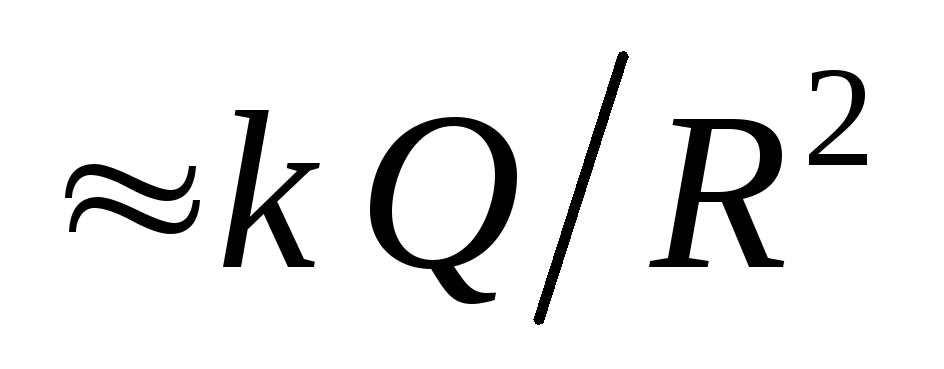

, în timp ce în interior este egal cu zero.
Mărimea saltului poate fi exprimată în termeni de densitatea sarcinii de suprafață pe sferă:

.
Rețineți că aceasta proprietate comună câmp electrostatic: pe o suprafață încărcată, proiecția intensității pe direcția normalului experimentează întotdeauna un salt

indiferent de forma suprafeței. Vă recomandăm să verificați acest principiu pentru câmpul unui plan încărcat uniform și câmpul a două plane încărcate paralele (exemplele 1.3, 1.4).
Din punct de vedere al matematicii, continuitatea potenţialului în punctele suprafeţei încărcate înseamnă că

. Din punct de vedere al fizicii, continuitatea funcției

poate fi explicată după cum urmează. Dacă potențialul de la limita unei anumite regiuni ar avea un salt (discontinuitate), atunci cu o deplasare infinit mică a unei anumite sarcini de la punctul 1, situat pe o parte a graniței, până la punctul 2, situat pe cealaltă parte, s-ar face o muncă finită

, Unde și  potenţialele punctelor 1, respectiv 2 şi valoarea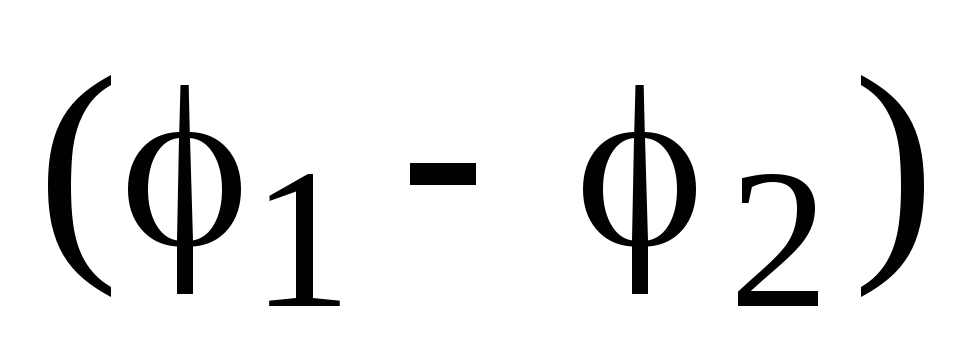

este egal cu saltul potențial la limita regiunii. Lucrarea finală efectuată pe o deplasare infinit de mică înseamnă că forțe infinit de mari ar acționa asupra interfeței, ceea ce este imposibil.
Puterea câmpului electric, în contrast cu potențialul, la limita regiunii se poate schimba foarte brusc (sărituri).
Exemplul 1.6. Două sfere concentrice de raze și (

) sunt încărcate uniform cu sarcini egale ca mărime, dar cu semne opuse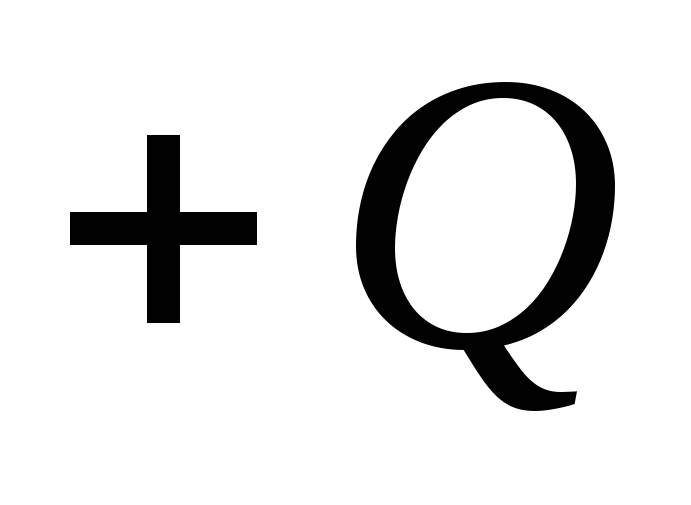

și

(condensator sferic). Determinați puterea și potențialul câmpului electric în spațiu.
Soluţie. Rezolvarea acestei probleme ar putea începe și cu aplicarea teoremei Gauss. Cu toate acestea, folosind rezultatele exemplului anterior și principiul suprapunerii (1.13, 1.14), răspunsul poate fi obținut mai rapid.
În punctele exterioare ale spațiului (

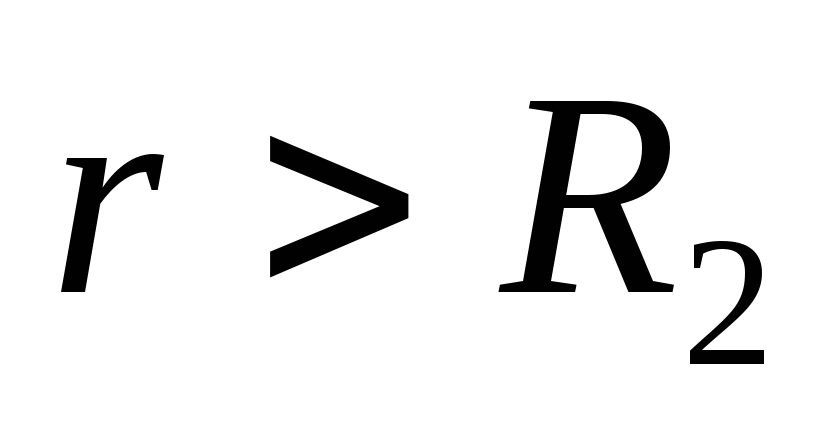) câmpul electric este creat de sarcinile ambelor sfere. Mărimea intensității câmpului primei sfere

și este îndreptată dinspre sfere de-a lungul razelor. Mărimea intensității câmpului celei de-a doua sfere este aceeași

, dar în sens invers. Prin urmare, conform principiului suprapunerii, nu va exista câmp electric în toate punctele externe din spațiu.

.
Luați în considerare punctele spațiului dintre sfere (

). Aceste puncte sunt interne sferei încărcate negativ, deci în această zonă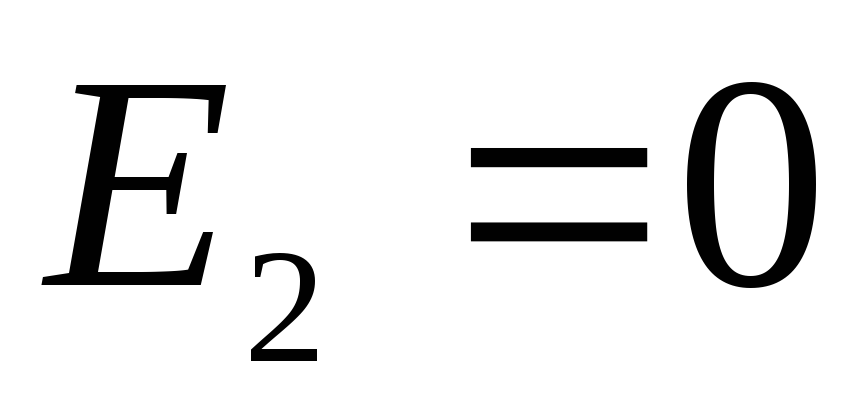

(vezi exemplul 1.5). Pentru o sferă încărcată pozitiv, aceste puncte sunt externe, deci

. Astfel, amploarea intensității câmpului în această regiune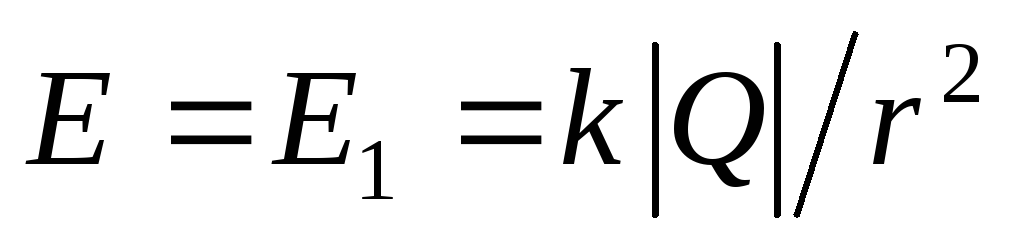

. Aici câmpul este creat doar de sarcinile sferei mai mici.
În cele din urmă, în punctele interioare ale spațiului (

)

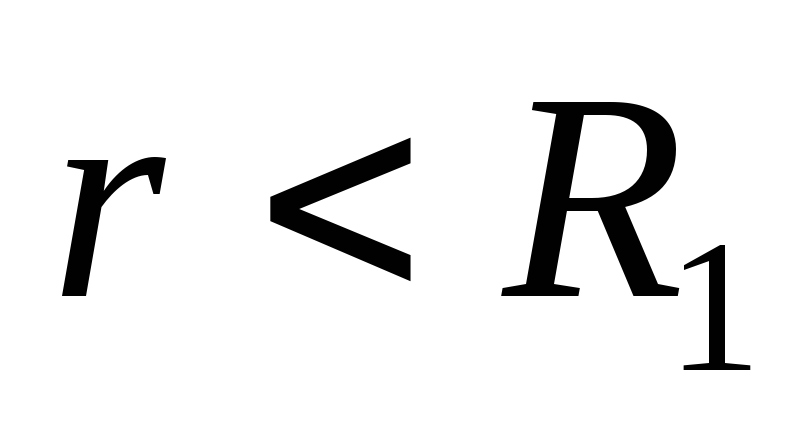și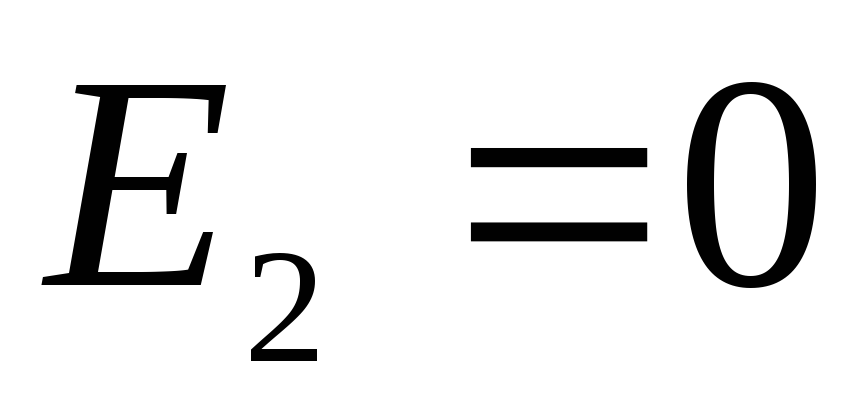

, deci nu există câmp electric în aceste puncte.
În mod similar, principiul suprapunerii poate fi aplicat potențialelor. Se obtin urmatoarele rezultate:

:

;

:

;

:

.
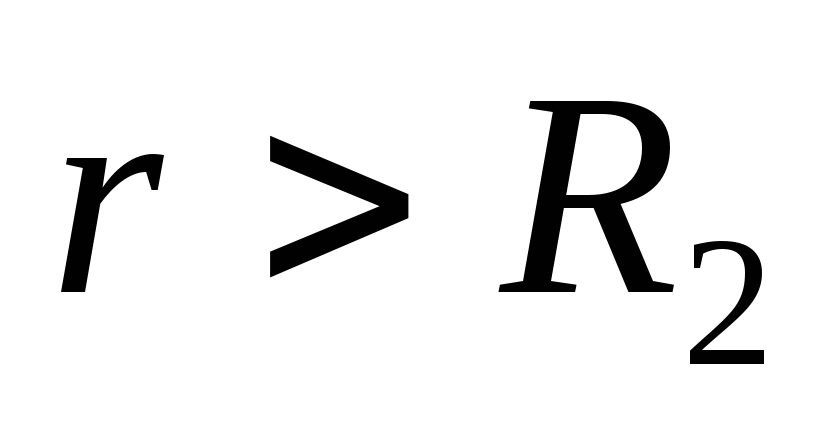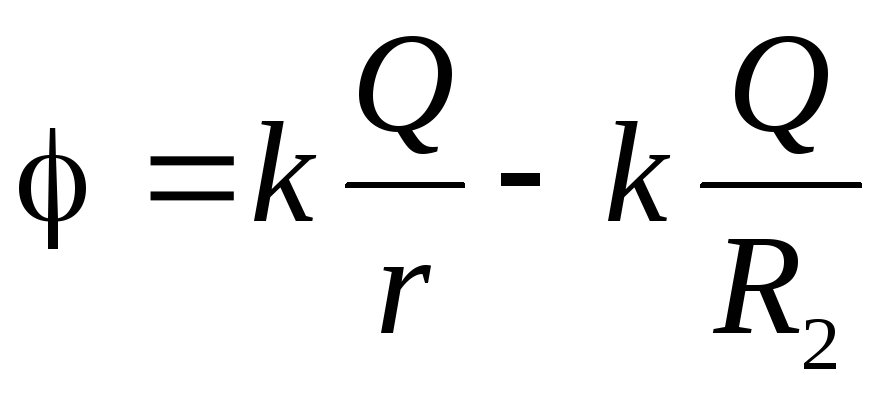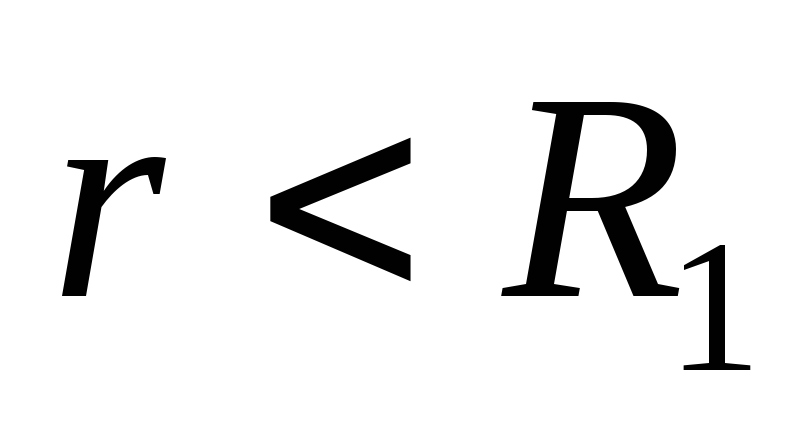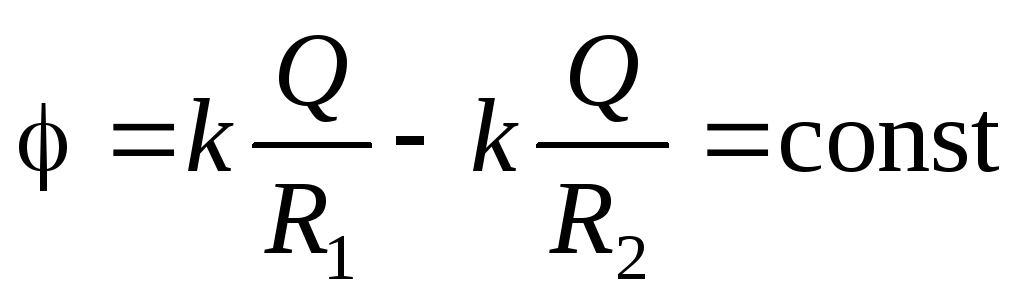Vă recomandăm să obțineți în mod independent aceste rezultate, precum și să descrieți schematic câmpul electric și să construiți grafice

și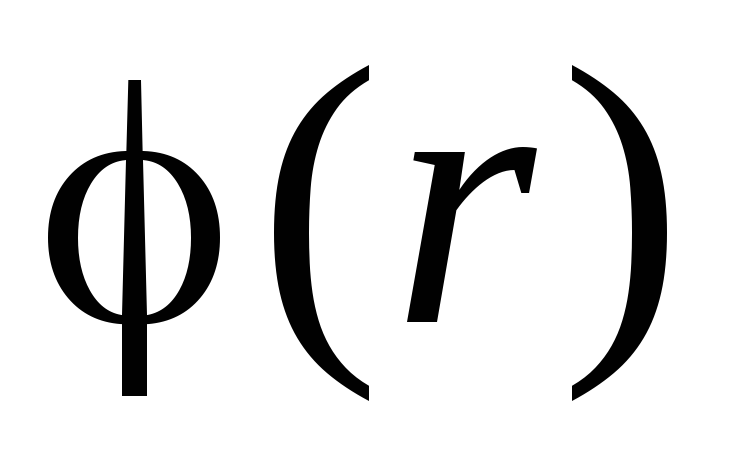

.