Lëvizja e trupit në një sipërfaqe të pjerrët. Lëvizja e një trupi në një plan të pjerrët
rasti i lëvizjes së përshpejtuar në rënie
Lëvizja e trupit përgjatë plan i pjerrët
Lëvizja e një trupi përgjatë një plani të pjerrët është një shembull klasik i lëvizjes së një trupi nën veprimin e disa forcave jo-drejtuese. Metoda standarde për zgjidhjen e problemeve të këtij lloji të lëvizjes është zgjerimi i vektorëve të të gjitha forcave në komponentë të drejtuar përgjatë boshteve koordinative. Komponentë të tillë janë linearisht të pavarur. Kjo lejon që dikush të shkruajë ligjin e dytë të Njutonit për komponentët përgjatë secilit bosht veç e veç. Pra, ligji i dytë i Njutonit, i cili është ekuacioni vektorial, kthehet në një sistem prej dy (tre për rastin tredimensional) ekuacionesh algjebrike.
Origjina e kësaj të fundit, pa dyshim, duhet të jetë kryesisht për shkak të zgjidhjes së çështjes së qendrës së lëkundjeve në bazë të zgjerimeve dhe ekuilibrit të forcave; Literatura e shqyrtuar në këtë studim sugjeron se trajtimi i shokut është po aq i drejtë. Ne e dimë rëndësinë e shkrimeve të Pierre Varignon për zhvillimin e mekanikës analitike; Enciklopedia dhe Kontrata e Dinamikës na ftojnë të mos e kufizojmë kontributin tonë vetëm në këtë fushë.
Ne japim për secilin fragmentin përkatës dhe japim versionin frëngjisht të tij, të nxjerrë nga Enciklopedia kur autori ishte d'Alembert. Ne tregojmë kur artikulli është i nënshkruar "Kamera". Varignon aplikoi teorinë e rrezeve të zhvilluar në teorinë e forcave qendrore; meqenëse, duke pasur rrezen e zhvillimit të lakores, mund të gjejmë vlerën e forcës qendrore të trupit që lëviz përgjatë kësaj lakore, ndodhet në të njëjtën pikë ku përfundon trau; ose, anasjelltas, duke pasur parasysh forcën qendrore, është e mundur të përcaktohet rrezja e zhvilluar. Shihni historinë.
Konsideroni një trup që po rrëshqet në një plan të pjerrët. Në këtë rast, forcat e mëposhtme veprojnë mbi të:
- Graviteti m g , i drejtuar vertikalisht poshtë;
- Forca e reagimit mbështetës N , i drejtuar pingul me rrafshin;
- forca e fërkimit rrëshqitës F tr, i drejtuar në kundërshtim me shpejtësinë (lart përgjatë planit të pjerrët kur trupi rrëshqet)
forca e fërkimit rrëshqitës F tr = µN proporcionale me forcën e reagimit të mbështetjes. Kjo ju lejon të merrni shprehja e mëposhtme për forcën e fërkimit: F tr = mmg si( α ) . Kjo forcë është e kundërt me komponentin "tërheqës" të gravitetit. Prandaj, për trupi që rrëshqet poshtë , marrim shprehjet për forcën totale rezultante dhe nxitimin:
F x= mg(mëkat( α
) – µ
si( α
));
a x= g(mëkat( α
) – µ
si( α
)).
Varignon dha gjithashtu dy teorema të përgjithshme për këtë temë në Kujtimet e Akadit. Varignon tregon se si disponimi jokoherent i Kopernikut lidhet me Mekanizmin e Qiellit: Sepse Forcat që planetët duhet të mbajnë në orbitat e tyre duhet gjithmonë të komplotojnë në mënyrë që të bëjnë lëvizje me shpejtësi vërtet të ndryshme; një pafundësi rastesh, ka vetëm një gjë që mund të lëvizin në mënyrë të barabartë.
Paragrafi i mësipërm që i referohet Varignon nuk shfaqet në përkthimin e Enciklopedisë. Por kjo e bën problemin shumë më të përgjithshëm dhe kërkon jo vetëm që Këndet vizuale të jenë të barabarta, por që ato të rriten ose të ulen në çdo raport të caktuar; me kusht që vlerën më të lartë nuk e kalon këndin e djathtë. Syri, ai duhet të vendoset kudo, ose në fillim të Ranges, ose jashtë tij, ose në anën. Gjithçka është e ndërtuar, ai supozon se rreshti i parë do të jetë linja e duhur dhe shikon se çfarë duhet të jetë Linja, të cilën ai e quan Lakorja e Gamave.
Nuk është e vështirë të shihet se nëse µ α) , atëherë shprehja ka shenjë pozitive dhe kemi të bëjmë me një lëvizje të përshpejtuar njëtrajtësisht poshtë rrafshit të pjerrët. Nëse µ >tg( α ), atëherë nxitimi do të ketë një shenjë negative dhe lëvizja do të jetë po aq e ngadaltë. Një lëvizje e tillë është e mundur vetëm nëse trupit i jepet një shpejtësi fillestare poshtë pjerrësisë. Në këtë rast, trupi gradualisht do të ndalet. Nëse, subjekt i µ >tg( α ) objekti fillimisht është në qetësi, më pas nuk do të fillojë të rrëshqasë poshtë. Këtu, forca statike e fërkimit do të kompensojë plotësisht komponentin "tërheqës" të gravitetit.
Kur koeficienti i fërkimit është saktësisht i barabartë me tangjenten e këndit të pjerrësisë së planit: µ
= tg( α
) , kemi të bëjmë me një kompensim reciprok të të tria forcave. Në këtë rast, sipas ligjit të parë të Njutonit, trupi mund të jetë ose në qetësi ose të lëvizë me një shpejtësi konstante (Në këtë rast, lëvizja uniforme është e mundur vetëm poshtë).
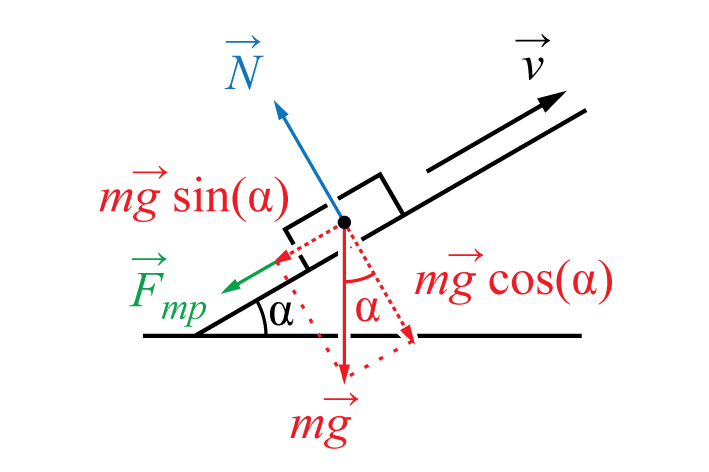
Forcat që veprojnë në bllok
rrëshqitje në një aeroplan të pjerrët:
kasë me lëvizje të ngadaltë
Kjo, sipas tij, duhet të jetë një hiperbolë në mënyrë që këndet vizuale të jenë të barabarta. Vijat e drejta dhe linjat hiperbolike do të tregohen paralelisht me pafundësinë; dhe nëse shtohet gjysmëhiperbola e kundërt, do të kemi tre rreshta pemësh dhe të treja janë paralele. Gjithashtu nuk kërkohet që kjo hiperbolë e dytë të jetë e kundërt me të parën, d.m.th. e. të të njëjtit lloj ose kanë të njëjtin bosht tërthor: Kjo është e mjaftueshme nëse ka të njëjtën qendër, kulmin e saj në të njëjtën vijë të djathtë dhe të njëjtin bosht të konjuguar.
Pra, mund të jenë dy hiperbola opsione të ndryshme; por të gjitha kanë të njëjtin efekt. Varignon thotë se nëse Reduktimi do të jetë në një raport të caktuar, të cilin ai e përcakton; Vija tjetër duhet të jetë paralele me drejtëzën. Por ai shkon edhe më tej; dhe duke supozuar se rreshti i parë ka ndonjë kurbë, ai kërkon një tjetër që do të bëjë që rreshtat të kenë efektin e dëshiruar, d.m.th. e) të dukshme në çdo kënd, të barabartë, në rritje ose në rënie. Mariotte dhe tregoi se ai shton "Kontabiliteti për qendrën e goditjes" në Sistemin Galilean. - Krahasimi i qendrave të gravitetit me qendrat e goditjes jep një pamje të shkëlqyer; dhe e vendosi të gjithë Doktrinën në dritën më të këndshme.
Sidoqoftë, trupi gjithashtu mund të lëvizë lart në planin e pjerrët. Një shembull i një lëvizjeje të tillë është lëvizja e një topthi hokeji në një rrëshqitje akulli. Kur një trup lëviz lart, si forca e fërkimit ashtu edhe komponenti "tërheqës" i gravitetit drejtohen poshtë përgjatë një rrafshi të pjerrët. Në këtë rast kemi të bëjmë gjithmonë me lëvizje uniforme të ngadalshme, pasi forca totale drejtohet në drejtim të kundërt me shpejtësinë. Shprehja për nxitimin për këtë situatë është marrë në mënyrë të ngjashme dhe ndryshon vetëm në shenjë. Pra për trupi që rrëshqet lart në një plan të pjerrët , ne kemi:
a x= g(mëkat( α
) + µ
si( α
)).
id="tabs-1">
Ky model është një diagram i animuar i një shkolle klasike punë laboratorike në fizikë, për të studiuar lëvizjen e përshpejtuar të një trupi nën veprimin e disa forcave në një plan të pjerrët.
Në këtë model, mund të vendosni vlerat e mëposhtme:
- Lartësia / këndi i planit të pjerrët (pika e kuqe);
- Koeficienti i fërkimit të rrëshqitjes së shiritit në sipërfaqe (rrëshqitësi i sipërm);
- Pozicioni fillestar i trupit (pika blu M);
- Pozicioni i sensorëve të kronometër (trekëndëshat e kuq S 1 dhe S 1);
- Flamuri për shfaqjen e vektorëve të forcës që veprojnë në trup.
- Këndi i prirjes së rrafshit të pjerrët;
- Koha e lëvizjes së trupit nga sensori i parë i kronometër në të dytin:
- Gjatë llogaritjes së kohës, ajo futet artificialisht gabim në matjen e kohës, te shperndara sipas ligjit normal!
- Koordinatat e sensorit;
- Koordinatat e pozicionit fillestar të shiritit;
- Ndërtohen vektorët e forcave që veprojnë në trup.
Menaxhimi i Modelit Interaktiv
- Ndrysho shkallën: "CTRL + rrota e miut" ose "CTRL + "+""–"CTRL + "-""
- Ndrysho pozicionin: zvarrite duke mbajtur "CTRL + butonin e majtë të miut"
- Fshini të gjitha "gjurmët": CTRL + F»
Shkarkoni modelin
Varignon, pavarësisht se ka probleme që lidhen me çrregullime dialektike, plotësoni tabelën e donatorëve dhe përcaktoni karakteristikë sasiore. Automjeti ku mund të gjeni të dhëna të sakta që mund të përdoren për sigurinë dhe mbrojtjen nga aksidentet.
Kështu që propozimi i Galileos duket se dështon edhe në këtë rast, por megjithatë ka rezultate të mira; vetëm me disa kufizime. Varignon bëri një përpjekje për të sqaruar se çfarë është e lidhur me shpejtësitë e trupave në rënie; dhe e vendosi të gjithë Nënën në një dritë të re: ai ende beson Sistemin e parë të Galileos, se shpejtësitë në kohë të ndryshme rënia vertikale - është si rrënjët e lartësive korresponduese.
Modelet e shënuara me © CC-BY-SA janë autorë të individëve të listuar në sajt. Modele interaktive të shpërndara me licencë Creative Commons Attribution-Share Like 3.0
Attribution-ShareAlike (nga-sa)- Licenca "Me tregues autoriteti - Copyleft". Kjo licencë u lejon të tjerëve të ripunojnë, korrigjojnë dhe zhvillojnë veprën, edhe për qëllime komerciale, me kusht që të jepet atributi dhe veprat e derivuara të licencohen me kushte të ngjashme. Kjo licencë është një licencë copyleft. Të gjitha veprat e reja bazuar në ato të licencuara sipas tij do të kenë të njëjtën licencë, kështu që të gjitha veprat e derivuara do të lejohen të modifikohen dhe të përdoren për qëllime komerciale. Kur riprodhoni vepra të shpërndara sipas kësaj licence, kërkohet një lidhje me sitin!
Shkarkoni modelin
Parimi i Madh përdor për të arritur Fundin e tij, kjo është një lëvizje e përbërë. Varinoni nga përbërja e këtyre lëvizjeve tregon se Trupi, kur plotëson Planin e dytë, humbet shpejtësinë e tij; dhe pasojë e faktit që në fund të vjeshtës nuk do të ishte njësoj siç do të ishte po të kishte rënë, zgjati rrafshin e parë: në mënyrë që "Përqindja e rrënjëve të lartësisë" e pohuar nga Galileo të mos funksionojë këtu.
Arsyeja e humbjes së shpejtësisë është se lëvizja që ishte paralele me rrafshin e parë bëhet e pjerrët me të dytin ndërsa krijojnë një kënd: është një lëvizje që është e pjerrët me rrafshin e dytë, duke u konceptuar si e rënduar që pjesa pingul me avioni humbet për shkak të të kundërtave të tij, si dhe një pjesë të shpejtësisë së bashku me të: Kjo do të thotë, sa më i mpirë të jetë këndi, aq më pak Trupi humbet shpejtësinë.
id="tabs-2">
Pyetje për vetë-ekzaminim me temën "Aeroplani i prirur"
- Kur lëvizja në një plan të pjerrët është njëtrajtësisht e ngadaltë?
- Kur një trup rrëshqet në mënyrë të njëtrajtshme në një plan të pjerrët?
- Në cilat vlera të këndit të prirjes mund të qëndrojë shiriti në një plan të pjerrët?
- Pse është i përshtatshëm për të zgjedhur një sistem koordinativ të zhdrejtë për një plan të prirur?
- Cila është forca e fërkimit që mban bllokun në qetësi?
- Çfarë ndodh me forcën e reagimit të suportit kur rritet këndi i prirjes?
- A mund të lëvizë një trup në mënyrë të njëtrajtshme lart në një plan të pjerrët?
          |
Sllajdet dhe teksti i këtij prezantimi
rrëshqitje 1
rrëshqitje 2
Plani për zgjidhjen e problemeve në dinamikë
1. Bëni një vizatim në të cilin do të tregoni drejtimin e boshteve të koordinatave, nxitimin dhe të gjitha forcat e aplikuara në trup.
2. Për çdo trup, shkruani në formë vektori ekuacionin e ligjit të dytë të Njutonit, duke renditur në anën e djathtë të tij në çdo rend të gjitha forcat e aplikuara në trup.
3. Shkruani ekuacionet e marra në paragrafin 2 në projeksion në boshtet koordinative.
5. Gjeni vlerën numerike të madhësisë së panjohur, nëse e kërkon gjendja e problemit.
4. Nga ekuacioni që rezulton (sistemi i ekuacioneve) shprehni sasi e panjohur.
Ndihmësi i shkollës "koni misterioz" është një ndihmës tipik që do të magjepsë mjedisin e përhapur. Megjithatë, nëse nuk dëshironi që nxënësit tuaj të mos e pëlqejnë këtë ndihmë, ju keni dy mundësi: të merrni një sponsor për të blerë ose për të blerë një dorë ndihmëse nga çdo gjë që mund të gjeni në shkollë. Ky artikull duhet t'ju ndihmojë nëse zgjidhni opsionin e dytë. Nëse dëshironi ta bëni këtë ndihmë, është më mirë të filloni duke hedhur poshtë ndihmën që keni bërë dhe duke bërë një kopje të saktë.
Supozoni se kemi bërë rrënjë dydimensionale me madhësi dhe thurje të njohur, nga të cilat duam të krijojmë një plan të pjerrët për lëvizjen me dy sy. Mënyra më e lehtë për të kompozuar këtë fletushkë të çalë mund të shihet në foto. Qëllimi ynë është të marrim parametrat e dëshiruar nga parametrat e njohur. Nëse hedhim një vështrim më të afërt në lëvizjen e dyfishit në një plan të pjerrët dhe regjistrojmë lëvizjen e provës së tij, do të marrim një pamje.
rrëshqitje 3
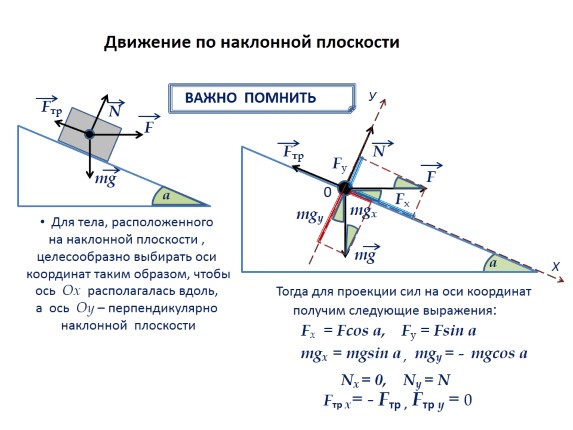
Lëvizja në një plan të pjerrët
E RËNDËSISHME PËR TË KUJTUAR
mg
N
F
Ftr.
Për një trup të vendosur në një plan të pjerrët, këshillohet të zgjidhni boshtet e koordinatave në atë mënyrë që boshti Ox të vendoset përgjatë, dhe boshti Oy të jetë pingul me rrafshin e pjerrët.
a
Pastaj për projeksionin e forcave në boshtet e koordinatave marrim shprehjet e mëposhtme:
Fx. = Fcos a, Fu = Fsin a
mgx. = mgsin a, mgy = - mgcos a
Nx = 0,
Ny=N
Ftr x= - Ftr., Ftr y = 0 .
Për llogaritjet dhe përgjigjet e mëposhtme, ne shënojmë secilin nga segmentet si më poshtë. Për të lëvizur një biplan "lart" në një aeroplan të pjerrët, errësira e tij duhet të bjerë. Prandaj, ne mund të përcaktojmë në mënyrë arbitrare vlerën e Δ në këtë varg. Le të kuptojmë, megjithatë, se duke ndryshuar vrimat, ai zvogëlon jo vetëm këndin δ, por edhe këndin γ. Këndi δ është parametri ynë, i cili karakterizon sa shpejt lëviz djali me dy koka.
Le të tregojmë vlefshmërinë e këtyre simpative dhe shablloneve për rastin e paraqitur në figurë. Sigurisht, për shkak të vlefshmërisë së përgjithshme të zbritjeve dhe llogaritjeve, madhësitë mund të ndryshohen sipas materialit në dispozicion, kështu që ne mund të kontribuojmë pothuajse në çdo madhësi.
rrëshqitje 4
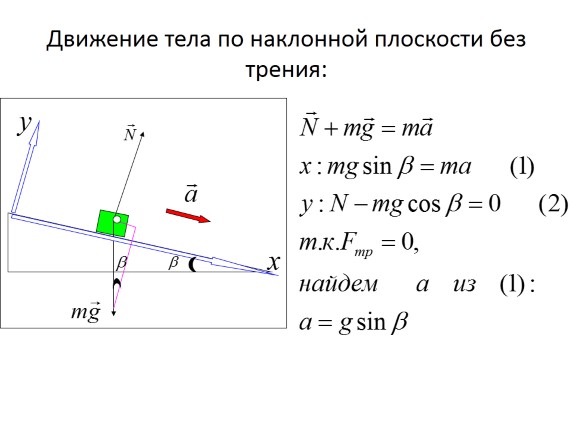
Lëvizja e një trupi në një plan të pjerrët pa fërkim:
rrëshqitje 5
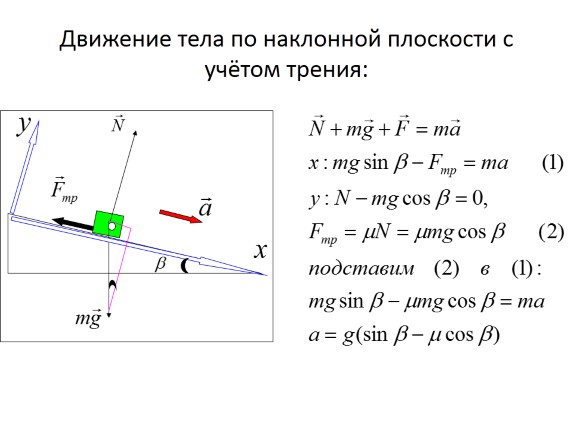
Lëvizja e një trupi përgjatë një plani të pjerrët, duke marrë parasysh fërkimin:
rrëshqitje 6
a
β
m1g
m2g
N1
N2
T
T
Në
Në
X
X
a
a
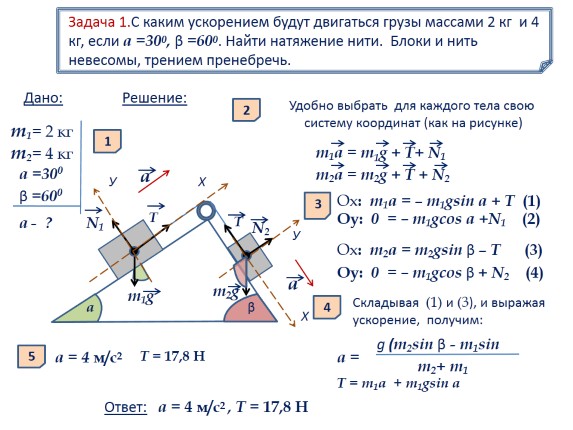
Detyra 1. Me çfarë nxitimi do të lëvizin ngarkesat e masave 2 kg dhe 4 kg, nëse a = 300, β = 600. Gjeni tensionin e fillit. Blloqet dhe fijet janë pa peshë, fërkimi neglizhohet.
m1= 2 kg
m2= 4 kg
E dhënë:
a = 300
β=600
a - ?
Zgjidhja:
1
2
Është i përshtatshëm për të zgjedhur për çdo trup sistemin e vet të koordinatave (si në figurë)
m1a = m1g + T + N1
m2a = m2g + T + N2
3
Ox: m1a \u003d - m1gsin a + T (1)
Oy: 0 = - m1gcos a + N1 (2)
Оx: m2a = m2gsin β – T (3)
Oy: 0 = – m1gcos β + N2 (4)
4
Duke mbledhur (1) dhe (3) dhe duke shprehur nxitimin, marrim:
g (m2sin β - m1sin
Me një supozim për gjendjen dhe zgjidhjen e përgjithshme, le ta quajmë distancën e brendshme të grilës Δ = 150 mm. Për kushtin, duhet të zgjedhim këndin δ, i cili karakterizon nxitimin e lakores së dyfishtë në planin e pjerrët. Kështu kemi piketat e kërkuara dhe mund të futemi në ndërtesë. Shumica e materialeve mund të gjenden tek mësuesi i shkollës ose tek instruktorët ose studentët e tjerë. Një zonë problematike është prodhimi i me dy tehe. Për ngjitje është përdorur ngjitësi epoksi. Por “ylli i artë” i vërtetë ktheu dyfishin.
Nuk funksionon as në një produkt, si ta lidhësh me një torno. Nëse jeni me fat, do të hasni në një torno me gërshërë që do t'ju ndihmojë me mjete të thjeshta dhe mund t'i rregulloni të gjitha. Ndihma e mbetur duhet t'i shtohet luftës që po shkon poshtë. Ne ose do ta rindërtojmë përsëri, ose do të përdorim ndonjë raund, por është më mirë të marrim një kon.
a =
m2+ m1
T = 17,8 H
T = m1a + m1gsin a
5
a = 4 m/s2
Përgjigje: a \u003d 4 m / s2, T \u003d 17,8 H
Rrëshqitja 7
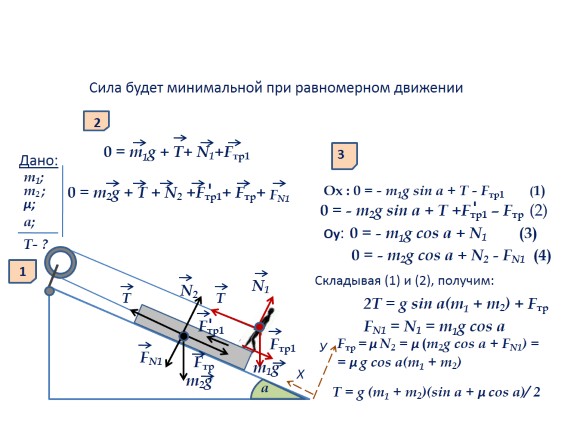
Problemi 2. Një burrë me masë m1, duke mbështetur këmbët e tij në një kuti me masë m2, e tërheq atë lart me një litar të hedhur mbi një bllok përgjatë një rrafshi të pjerrët me një kënd prirje a. Cila është forca minimale e nevojshme për të tërhequr litarin për të tërhequr kutinë në bllok? Koeficienti i fërkimit ndërmjet bërthamës dhe planit të pjerrët μ






