Paraqitja grafike e fushave. Metoda grafike për paraqitjen e strukturës së fushave elektrike. linjat e forcës

Vetitë trupat fizikë dhe objektet përshkruhen sasive fizike . Një nga këto sasi për fushe elektrikeështë tensioni. Në përputhje me përkufizimin e formuluar më parë, ai përshkruan veprimin e forcës së fushës mbi trupat e ngarkuar në një pikë të caktuar në fushën elektrike. Nëse fusha është johomogjene, atëherë intensiteti në pika të ndryshme fushat janë të ndryshme. Dhe për të përshkruar vetitë e fushës në shumë pika, është e nevojshme të paraqisni një numër të madh vlerash intensiteti. Kjo e ndërlikon studimin e fushës dhe parandalon krijimin në imagjinatën njerëzore të idesë së fushës në çdo rast specifik.

Fuqia e fushës elektrike është karakteristikë e fuqisë së saj.

Ndihmon për të përfaqësuar më mirë strukturën e fushës elektrike metodë grafike. Në zemër të metodës së paraqitjes grafike strukturat e fushës elektrike gënjeshtra dukuri reale që mund të vërehen në eksperimente.

Lëreni një grimcë të vogël të një lënde, që gjithashtu ka një ngarkesë pozitive, të futet në fushën elektrike të një topi të ngarkuar pozitivisht. Nëse kjo grimcë është e lirë dhe veprimi i fushës gravitacionale është i parëndësishëm, atëherë nën ndikimin e një force elektrike ajo do të largohet nga topi. E ngjashme do të vërehet në çdo pikë në fushën e një topi të ngarkuar (Fig. 4.20).

Duke përshkruar trajektoret e lëvizjes së shumë grimcave të ngarkuara pozitivisht në një fushë elektrike dhe duke treguar drejtimin drejt tyre forcë operative, marrim një foto të quajtur spektrit këtë fushë.

Vijat që formojnë spektrin e fushës elektrike quhen linjat e tensionit fushë elektrike, ose linjat e energjisë.

koncept linjë fushore u fut për herë të parë në shkencë nga M. Faraday mbi bazën e njohurive të marra në rrjedhën e kërkimeve eksperimentale.

Eksperimentet e njohura për M. Faraday mund të kryhen në kushte moderne.

Le të marrim një përcjellës metalik me shirita letre të ngjitura dhe ta lidhim me përçuesin e makinës elektrofore. Nëse e vëmë në veprim, atëherë të gjithë shiritat e letrës do të ndryshojnë në drejtime të ndryshme për shkak të zmbrapsjes së ndërsjellë (Fig. 4.21). Rezultatet e këtij eksperimenti (dhe të tjerëve si ai) bëjnë të mundur ndërtimin e spektrit të fushës elektrike të një trupi të vetëm të ngarkuar. Është paraqitur në fig. 4.22. Shigjetat në vijat e forcës tregojnë drejtimin e forcës që do të veprojë në një trup të ngarkuar pozitivisht të vendosur në një pikë të caktuar të fushës.

Prandaj, vijat e forcës "largohen" nga një trup i ngarkuar pozitivisht dhe "hyjnë" në një trup të ngarkuar negativisht (Fig. 4.22). Duhet mbajtur mend se ato "dalin" dhe "hyjnë" pingul me sipërfaqen e trupit.

Vijat e fuqisë së fushës elektrike janë pingul me sipërfaqen e një trupi të ngarkuar në pikat ku ato fillojnë.material nga faqja

Marrim dy përçues metalikë me shirita letre dhe i lidhim me përçuesit e makinës elektrofore. E vendosim në veprim makinën e elektroforës dhe do të shohim që shiritat e letrës do të fillojnë të tërheqin njëri-tjetrin (Fig. 4.23). Prandaj, fusha e dy trupave të ngarkuar në mënyrë të kundërt do të ketë spektrin e treguar në fig. 4.24.

Forma e lakuar e vijave të tensionit shpjegohet me faktin se dy forca veprojnë në një grimcë të ngarkuar pozitivisht nga ana e secilit trup. Rezultantja e këtyre forcave në çdo pikë të fushës është tangjente me vijat e tensionit.

Linjat tangjente në të cilat në çdo pikë tregojnë drejtimin e forcës që vepron në një trup me pikë të ngarkuar pozitivisht quhen linjat e energjisë.

Drejtimet e forcave që do të veprojnë në pika të ndryshme në fushën e dy trupave të ngarkuar janë paraqitur në fig. 4.25.

Meqenëse vijat e tensionit janë gjithmonë pingul me sipërfaqen, spektrat e fushave të trupave me forma të ndryshme do të jenë të ndryshme (Fig. 4.26).

Në këtë faqe, materiale mbi temat:

Spectra el. fushat e trupave të ndryshëm të ngarkuar
Imazhi grafik abstrakt i fushës elektrike
Imazhet e linjave të fushës elektrike në eksperimente
a b

Duke ditur vektorin e intensitetit të fushës elektrostatike në secilën prej pikave të saj, kjo fushë mund të vizualizohet me ndihmën e vijave të forcës së intensitetit (vijat e vektorit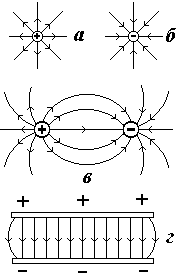 ). linjat e forcës tensionet janë tërhequr në mënyrë që tangjentja ndaj tyre në secilën pikë të përputhet me drejtimin e vektorit të tensionit (Fig. 1.4, a).
Numri i vijave që depërtojnë në një zonë të vetme dS, pingul me to, vizatohet në proporcion me modulin e vektorit (Fig. 1.4, b).
Vijave të forcës u caktohet një drejtim që përkon me drejtimin e vektorit . Modeli që rezulton i shpërndarjes së linjave të tensionit bën të mundur gjykimin e konfigurimit të një fushe elektrike të caktuar në pika të ndryshme të saj. Linjat në terren fillojnë në ngarkesa pozitive dhe përfundojnë në ngarkesa negative. Në fig. 1.5 tregon linjat e tensionit të ngarkesave pika (Fig. 1.5, a, b); sistemet e dy ngarkesave të kundërta (Fig. 1.5, në) - një shembull i një fushe elektrostatike johomogjene dhe dy plane paralele të ngarkuara në mënyrë të kundërt (Fig. 1.5, G) është një shembull i një fushe elektrike uniforme.
1.5. Shpërndarja e tarifave
Në disa raste, për të thjeshtuar llogaritjet matematikore, është i përshtatshëm për të zëvendësuar shpërndarjen e vërtetë të ngarkesave pika diskrete me një shpërndarje fiktive të vazhdueshme. Në kalimin në një shpërndarje të vazhdueshme të ngarkesave, përdoret koncepti i densitetit të ngarkesës - lineare , sipërfaqja  dhe  vëllimore, d.m.th.

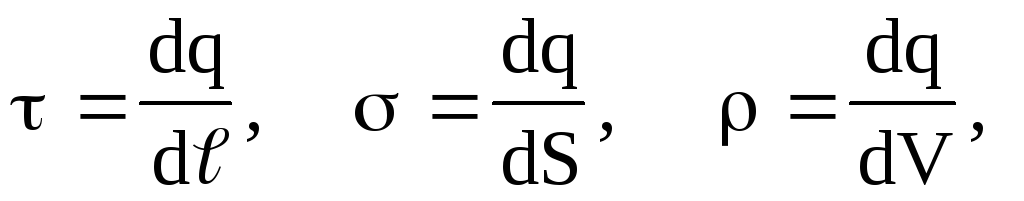(1.12)
ku dq është ngarkesa e shpërndarë në përputhje me elementin e gjatësisë

, elementi sipërfaqësor dS dhe elementi vëllimor dV.
Duke marrë parasysh këto shpërndarje, formula (1.11) mund të shkruhet në një formë tjetër. Për shembull, nëse ngarkesa shpërndahet në vëllim, atëherë në vend të q i duhet të përdorni dq = dV dhe të zëvendësoni simbolin e shumës me një integral, atëherë

. (1.13)
1.6. dipol elektrik
Për të shpjeguar dukuritë që lidhen me ngarkesat në fizikë, përdoret koncepti dipol elektrik.
Një sistem me dy ngarkesa pikash të kundërta në madhësi të barabarta, distanca midis të cilave është shumë më e vogël se distanca me pikat e studiuara në hapësirë, quhet dipol elektrik. Sipas përkufizimit të një dipoli, +q=q= q.

Një vijë e drejtë që lidh ngarkesat (polet) e kundërta quhet bosht dipol; pika 0 - qendra e dipolit (Fig. 1.6). Karakterizohet dipoli elektrik krahu dipol: vektor , drejtuar nga një ngarkesë negative në një pozitive. Karakteristika kryesore e një dipoli është momenti i dipolit elektrik = q . (1.14)
Me vlerë absolute
p = q 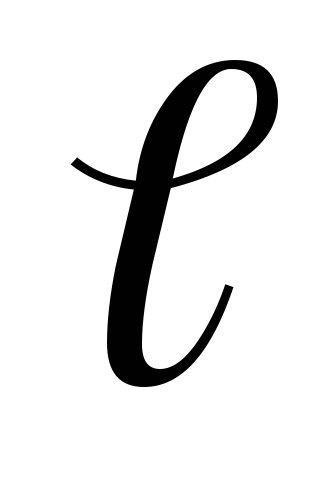. (1.15)
Në SI, momenti i dipolit elektrik matet në kulonë herë në metër (C m).
Le të llogarisim potencialin dhe forcën e fushës elektrike të dipolit, duke e konsideruar atë si një pikë, nëse 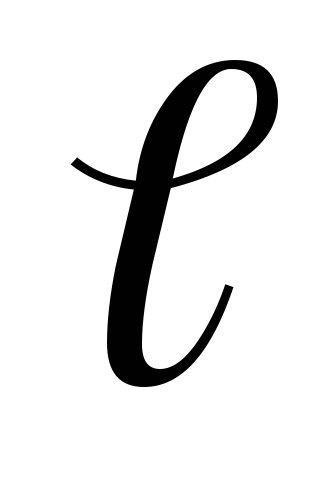 r.
Potenciali i një fushe elektrike të krijuar nga një sistem ngarkesash pikash në një pikë arbitrare të karakterizuar nga një vektor rreze , shkruajmë në formën: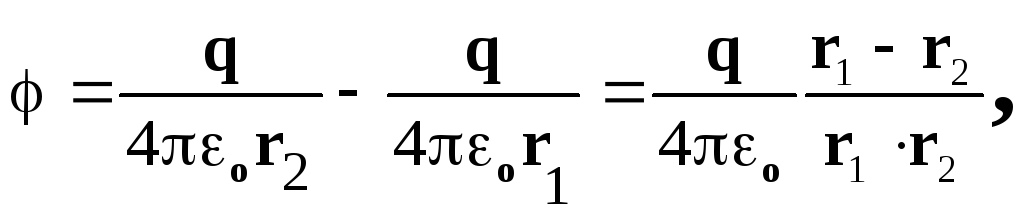

ku r 1 r 2  r 2 , r 1  r 2  r =

, sepse 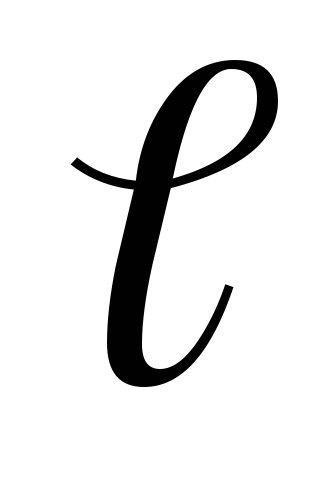r;   këndi ndërmjet vektorëve të rrezes dhe 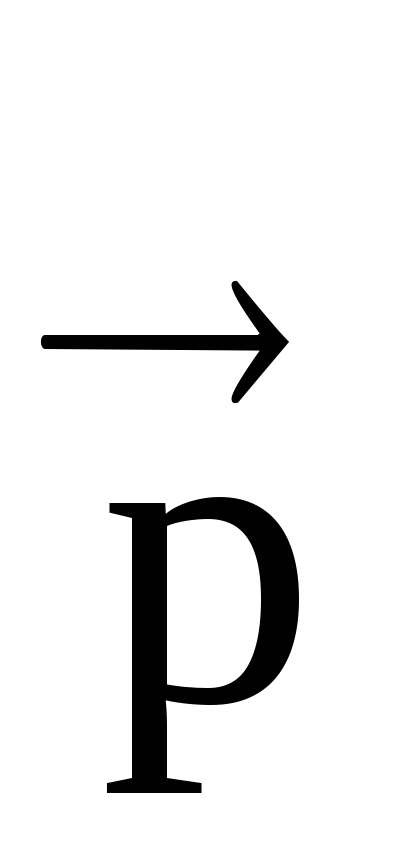(Fig. 1.6) . Me këtë në mendje, ne marrim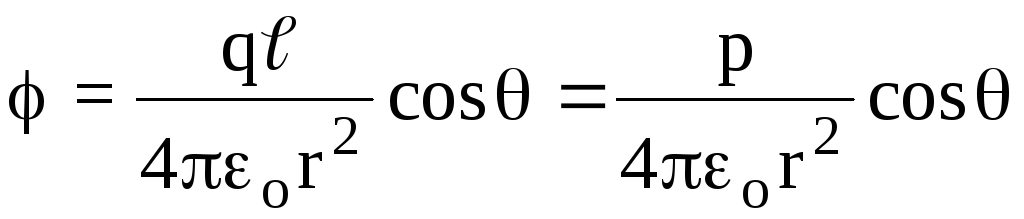

. (1.16)
Duke përdorur formulën që lidh gradientin potencial me intensitetin, gjejmë intensitetin e krijuar nga fusha elektrike e dipolit. Le të zbërthejmë vektorin elektrike fushë dipole në dy komponentë pingul reciprokisht, d.m.th.

(Fig. 1. 6).
E para prej tyre përcaktohet nga lëvizja e një pike të karakterizuar nga vektori i rrezes (për një vlerë fikse të këndit ), d.m.th., ne gjejmë vlerën e E  me diferencim (1.81) në lidhje me r, d.m.th.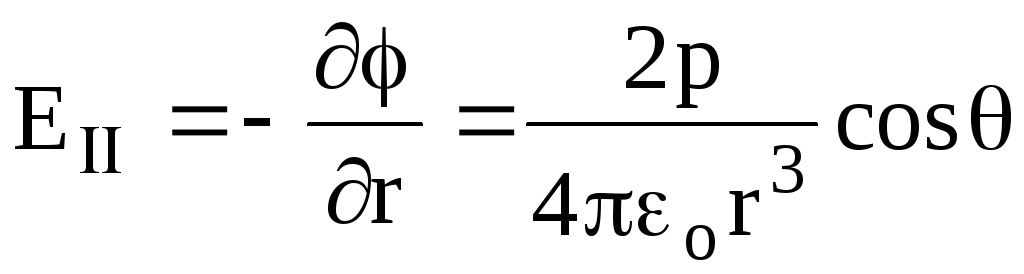

. (1.17)
Komponenti i dytë përcaktohet nga lëvizja e pikës që shoqërohet me një ndryshim në këndin  (për një r të fiksuar), d.m.th. E  gjejmë duke diferencuar (1.16) në lidhje me :

, (1.18)
ku

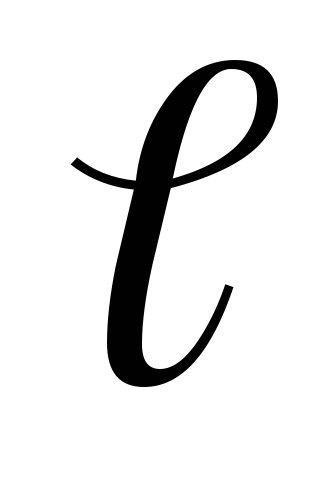, d = rd.
Tensioni që rezulton E 2 \u003d E  2 + E  2 ose pas zëvendësimit

. (1.19)
Koment: Në  = 90 o

, (1.20)
d.m.th., intensiteti në një pikë në një vijë të drejtë që kalon nga qendra e dipolit (d.m.th. O) dhe pingul me boshtin e dipolit.
Kur  = 0 rreth

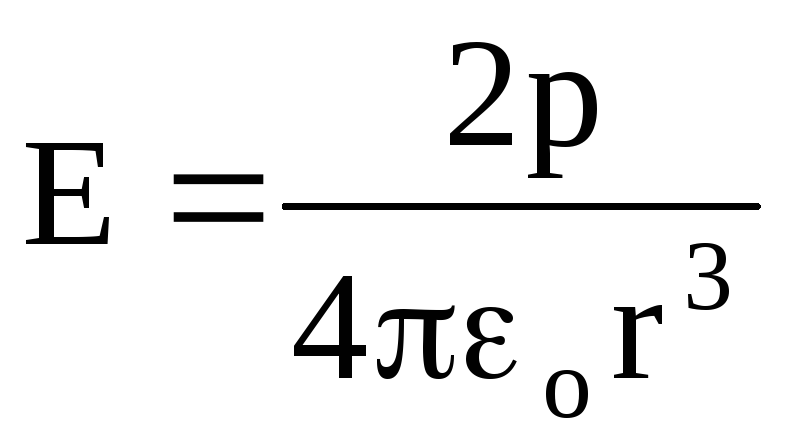, (1.21)
d.m.th., në një pikë në vazhdimin e një vije të drejtë që përkon me boshtin e dipolit.
Një analizë e formulave (1.19), (1.20), (1.21) tregon se forca e fushës elektrike të dipolit zvogëlohet me distancën në proporcion të zhdrejtë me r3, pra më shpejt se sa për një ngarkesë pikë (në përpjesëtim të zhdrejtë me r2).

Për qartësi më të madhe, fusha elektrike shpesh përshkruhet duke përdorur linjat e forcës dhe sipërfaqet ekuipotenciale.
linjat e forcës – këto janë vija të vazhdueshme, tangjentet në të cilat në secilën pikë nëpër të cilën kalojnë përputhen me vektorin e forcës së fushës elektrike (Fig. 1.5). Dendësia e vijave të fushës (numri i vijave të fushës që kalojnë nëpër një sipërfaqe njësi) është proporcionale me forcën e fushës elektrike.
Sipërfaqet ekuipotenciale (ekuipotencialet) – sipërfaqe me potencial të barabartë. Këto janë sipërfaqe (vija) kur lëvizin përgjatë të cilave potenciali nuk ndryshon. Përndryshe, diferenca potenciale ndërmjet çdo dy pikash të sipërfaqes ekuipotenciale është e barabartë me zero. Linjat e forcës janë pingul me sipërfaqet ekuipotenciale dhe të drejtuara në drejtim të uljes më të mprehtë të potencialit. Ky fakt rrjedh nga ekuacioni (1.10) dhe vërtetohet në rrjedhën e analizës matematikore, seksioni "Fushat skalare dhe vektoriale".
Konsideroni, si shembull, një fushë elektrike të krijuar në një distancë 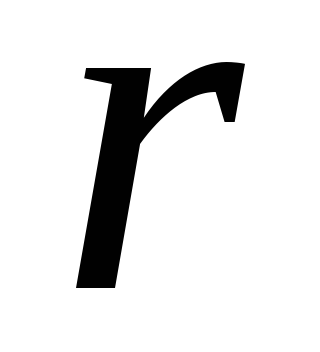nga një ngarkesë pikë. Sipas (1.11,b), vektori i intensitetit përkon me drejtimin e vektorit nëse ngarkesa është pozitive dhe e kundërta nëse ngarkesa është negative. Rrjedhimisht, linjat e forcës ndryshojnë në mënyrë radiale nga ngarkesa (Fig. 1.6, a, b). Dendësia e vijave të fushës, si intensiteti, është në përpjesëtim të zhdrejtë me katrorin e distancës (

) për të ngarkuar. Sipërfaqet ekuipotenciale të fushës elektrike të një ngarkese pika janë sfera të përqendruara në vendndodhjen e ngarkesës.

Në fig. 1.7 tregon fushën elektrike të një sistemi me dy ngarkesa të barabarta në vlerë absolute, por të kundërta në shenjë, ngarkesa pikë. Këtë shembull ua lëmë lexuesve ta analizojnë vetë. Vëmë re vetëm se linjat e forcës fillojnë gjithmonë me ngarkesa pozitive dhe përfundojnë me ato negative. Në rastin e një fushe elektrike me ngarkesë me një pikë (Fig. 1.6, a, b), supozohet se linjat e forcës shkëputen me ngarkesa shumë të largëta të shenjës së kundërt. Besohet se universi në tërësi është neutral. Prandaj, nëse ka një ngarkesë të një shenje, atëherë diku do të ketë patjetër një ngarkesë të shenjës tjetër e barabartë me të në vlerë absolute.
1.6. Teorema e Gausit për një fushë elektrike në vakum
Detyra kryesore e elektrostatikës është problemi i gjetjes së forcës dhe potencialit të fushës elektrike në çdo pikë të hapësirës. Në seksionin 1.4 ne zgjidhëm problemin e fushës së një ngarkese pikë dhe gjithashtu morëm në konsideratë fushën e një sistemi ngarkesash pikash. Në këtë seksion, ne do të përqendrohemi në një teoremë që na lejon të llogarisim fushën elektrike të objekteve më komplekse të ngarkuara. Për shembull, një fije e gjatë e ngarkuar (vijë e drejtë), një plan i ngarkuar, një sferë e ngarkuar dhe të tjera. Duke llogaritur forcën e fushës elektrike në çdo pikë të hapësirës, duke përdorur ekuacionet (1.12) dhe (1.13), mund të llogaritet potenciali në secilën pikë ose diferenca e potencialit midis çdo dy pikash, d.m.th. zgjidh problemin bazë të elektrostatikës.
Për një përshkrim matematikor, ne prezantojmë konceptin e rrjedhës së vektorit të intensitetit ose rrjedhës së fushës elektrike. Vektori i fluksit (F). fushë elektrike në një sipërfaqe të sheshtë katrore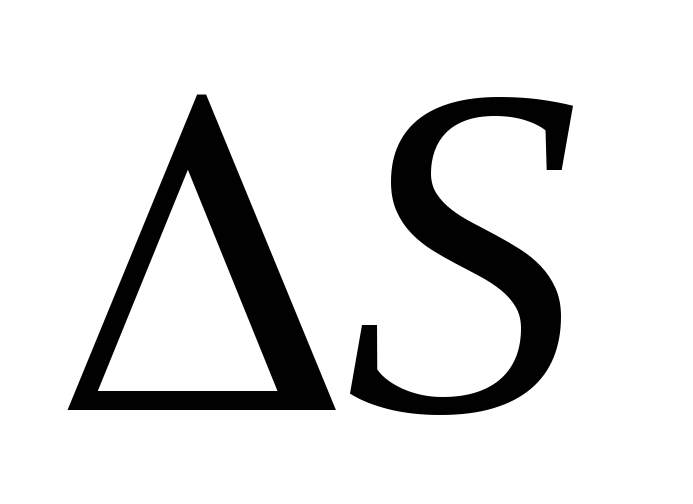

sasia quhet:

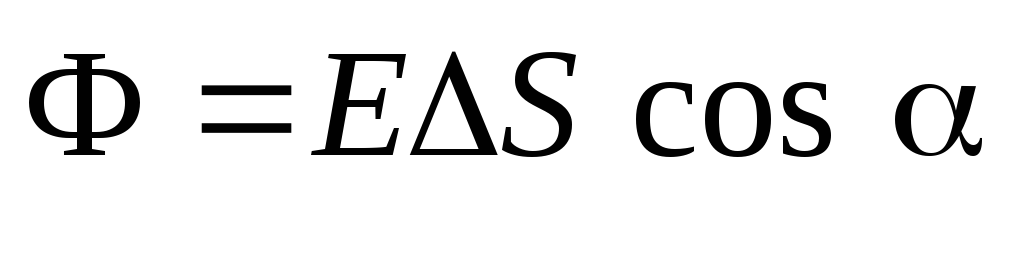, (1.16)

ku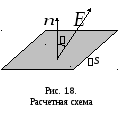 është forca e fushës elektrike, e cila supozohet të jetë konstante brenda zonës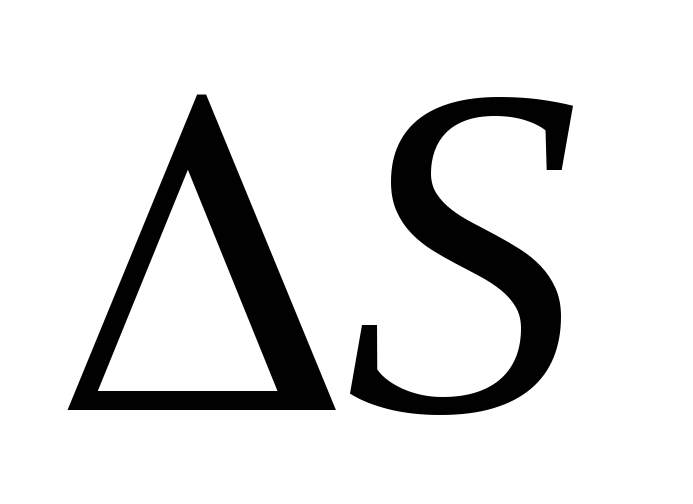

;

është këndi ndërmjet drejtimit të vektorit dhe vektor normal njësi 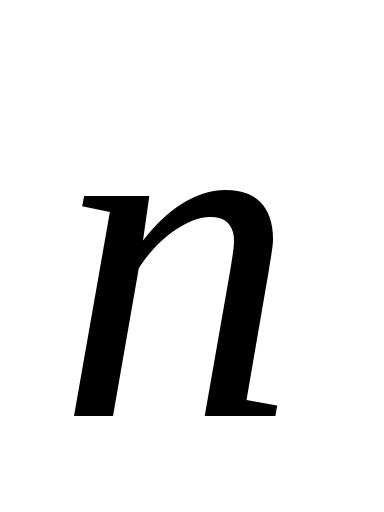te siti

(Fig. 1.8). Formula (1.16) mund të shkruhet duke përdorur konceptin e produktit skalar të vektorëve: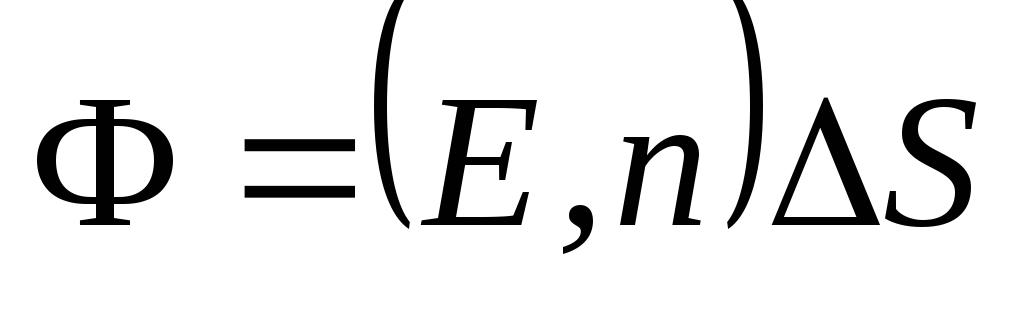

. (1.15,a)
Në rast se sipërfaqja jo e sheshtë, për të llogaritur rrjedhën duhet të ndahet në pjesë të vogla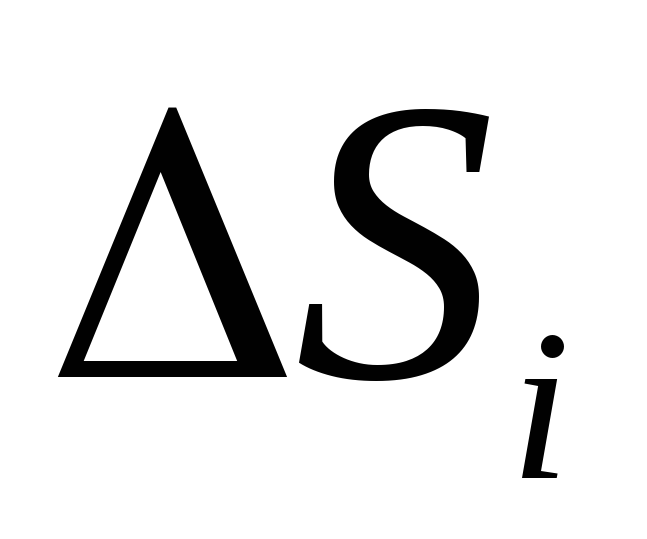

, të cilat përafërsisht mund të konsiderohen të sheshta, dhe më pas shkruani shprehjen (1.16) ose (1.16, a) për secilën pjesë të sipërfaqes dhe shtoni ato. Në kufirin kur sipërfaqja S i shumë i vogël (

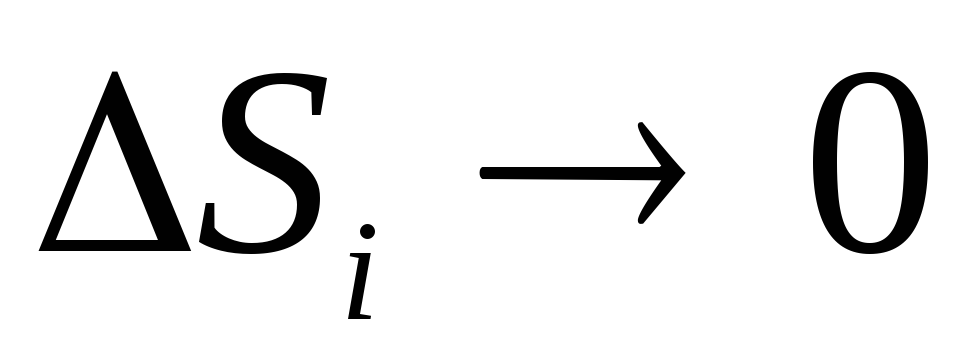), një shumë e tillë quhet integral sipërfaqësor dhe shënohet

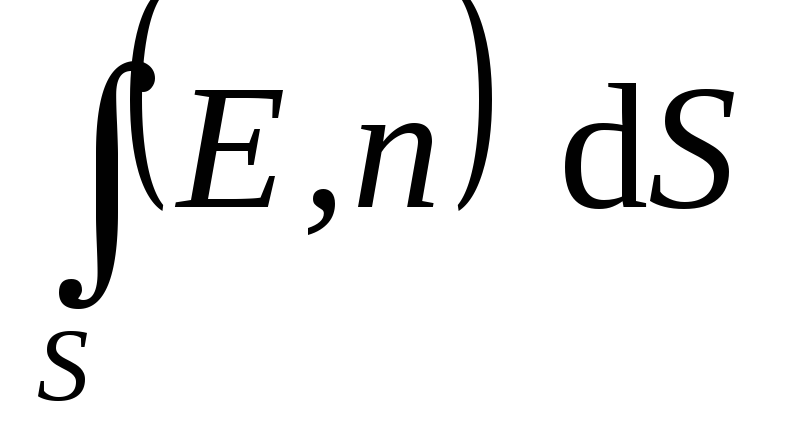. Kështu, rrjedha e vektorit të forcës së fushës elektrike nëpër një sipërfaqe arbitrare përkufizohet me shprehjen:

. (1.17)
Si shembull, merrni parasysh një sferë me rreze 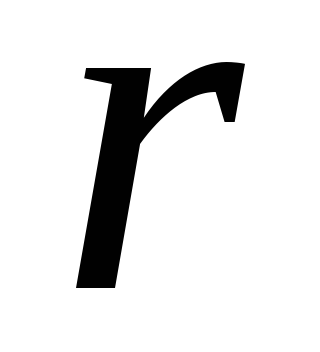, e përqendruar në një ngarkesë pikë pozitive , dhe përcaktoni fluksin e fushës elektrike nëpër sipërfaqen e kësaj sfere. Linjat e forcës (shih, për shembull, Fig. 1.6, a) që dalin nga ngarkesa janë pingul me sipërfaqen e sferës dhe në secilën pikë të sferës, moduli i forcës së fushës është i njëjtë

.
Zona e sferës

,
pastaj

.
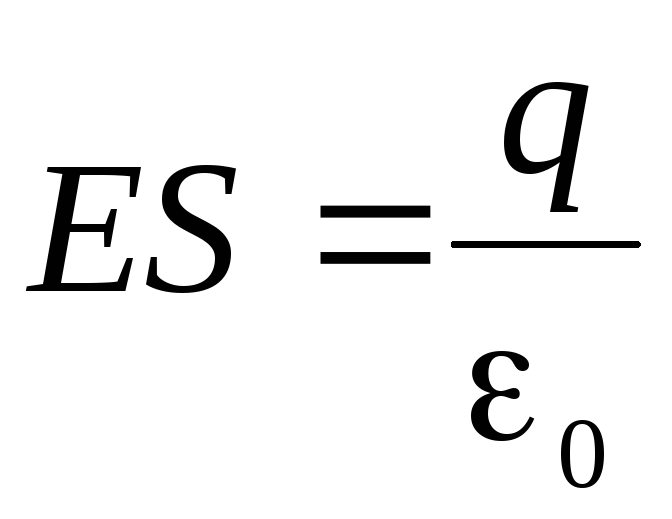Vlera

dhe paraqet rrjedhjen e fushës elektrike nëpër sipërfaqen e sferës. Kështu, ne marrim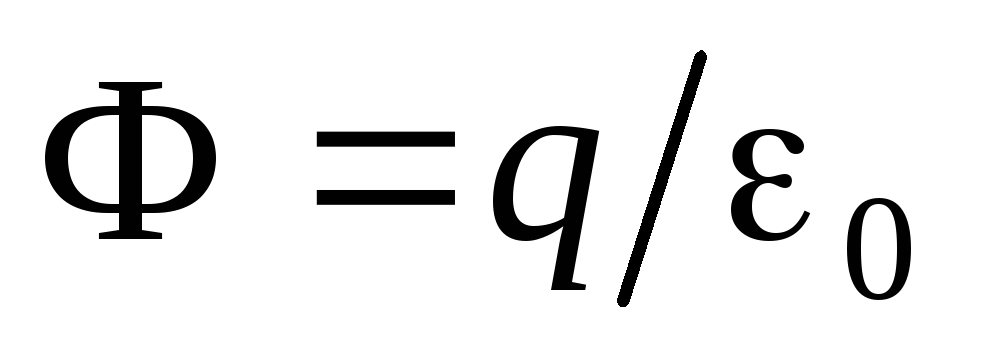

. Mund të shihet se fluksi nëpër sipërfaqen e sferës së fushës elektrike nuk varet nga rrezja e sferës, por varet vetëm nga vetë ngarkesa. . Prandaj, nëse vizatoni një seri sferash koncentrike, atëherë rrjedha e fushës elektrike nëpër të gjitha këto sfera do të jetë e njëjtë. Natyrisht, numri i linjave të forcës që kalojnë këto sfera do të jetë gjithashtu i njëjtë. Ne ramë dakord të marrim numrin e linjave të forcës që dalin nga ngarkesa e barabartë me rrjedhën e fushës elektrike:

.
Nëse sfera zëvendësohet nga ndonjë sipërfaqe tjetër e mbyllur, atëherë rrjedha e fushës elektrike dhe numri i linjave të forcës që e kalojnë atë nuk do të ndryshojnë. Për më tepër, rrjedha e fushës elektrike nëpër një sipërfaqe të mbyllur, dhe kështu numri i linjave të forcës që depërtojnë në këtë sipërfaqe, është i barabartë me

jo vetëm për fushën e një ngarkese pika, por edhe për fushën e krijuar nga çdo grup ngarkesash pikash, në veçanti, nga një trup i ngarkuar. Pastaj vlera duhet të konsiderohet si shuma algjebrike e të gjithë grupit të ngarkesave të vendosura brenda një sipërfaqe të mbyllur. Ky është thelbi i teoremës së Gausit, i cili formulohet si më poshtë:
Rrjedha e vektorit të forcës së fushës elektrike përmes një arbitrarembyllur sipërfaqja është e barabartë

, ku

 algjebrike shuma e tarifave të bashkangjiturabrenda këtë sipërfaqe.
Matematikisht, teorema mund të shkruhet si

. (1.18)
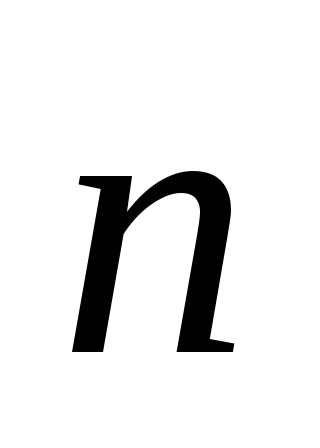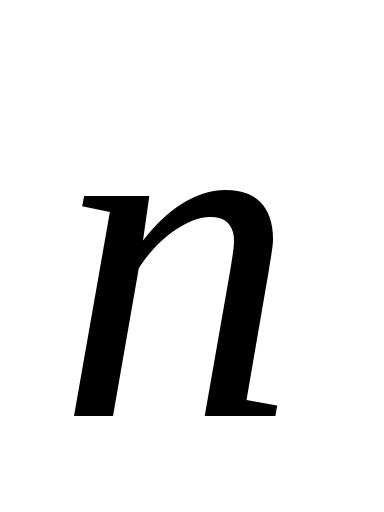Vini re se nëse në ndonjë sipërfaqe S vektoriale konstante dhe paralele me vektorin , pastaj rrjedha nëpër një sipërfaqe të tillë. Duke transformuar integralin e parë, fillimisht kemi përfituar nga fakti se vektorët dhe paralele, që do të thotë

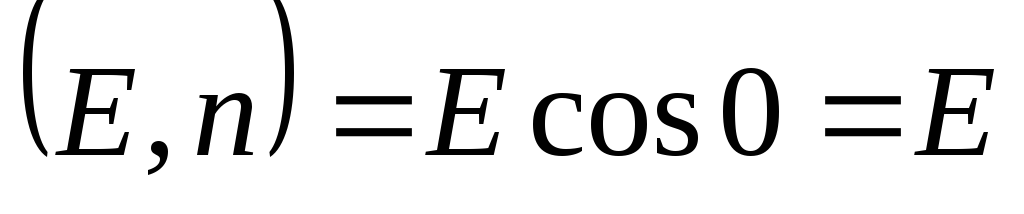. Pastaj hoqi vlerën për shenjën e integralit për faktin se ai është konstant në çdo pikë të sferës . Duke aplikuar teoremën e Gausit për të zgjidhur probleme specifike, ata përpiqen të zgjedhin një sipërfaqe për të cilën kushtet e përshkruara më sipër plotësohen si një sipërfaqe e mbyllur arbitrare.
Ne japim disa shembuj të zbatimit të teoremës së Gausit.
Shembulli 1.2. Llogaritni forcën e fushës elektrike të një filamenti të pafund të ngarkuar në mënyrë uniforme. Përcaktoni ndryshimin potencial midis dy pikave në një fushë të tillë.
Zgjidhje. Supozoni për saktësi se filli është i ngarkuar pozitivisht. Për shkak të simetrisë së problemit, mund të argumentohet se vijat e forcës do të jenë vija të drejta që ndryshojnë në mënyrë radiale nga boshti i fillit (Fig. 1.9), dendësia e të cilave zvogëlohet me distancën nga filli sipas disa ligjeve. Sipas të njëjtit ligj, do të ulet edhe madhësia e fushës elektrike 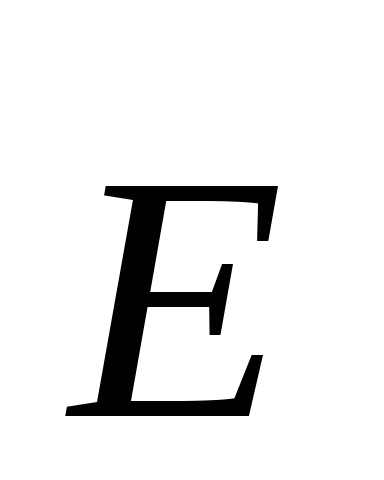. Sipërfaqet ekuipotenciale do të jenë sipërfaqe cilindrike me një bosht që përkon me fillin.
Le të jetë ngarkesa për njësi të gjatësisë së fillit . Kjo vlerë quhet dendësia lineare e ngarkesës dhe matet në njësi SI [C/m]. Për të llogaritur forcën e fushës, zbatojmë teoremën e Gausit. Për këtë, si një sipërfaqe e mbyllur arbitrare zgjidhni një cilindër me rreze 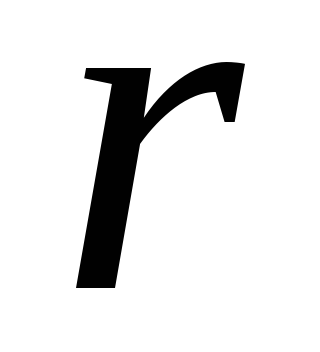dhe gjatësia , boshti i të cilit përkon me fillin (Fig. 1.9). Le të llogarisim fluksin e fushës elektrike përmes sipërfaqes së cilindrit. Rrjedha totale është shuma e rrjedhës përmes sipërfaqe anësore cilindër dhe rrjedh nëpër baza
Megjithatë,

, pasi në çdo pikë në bazat e cilindrit

. Do të thotë se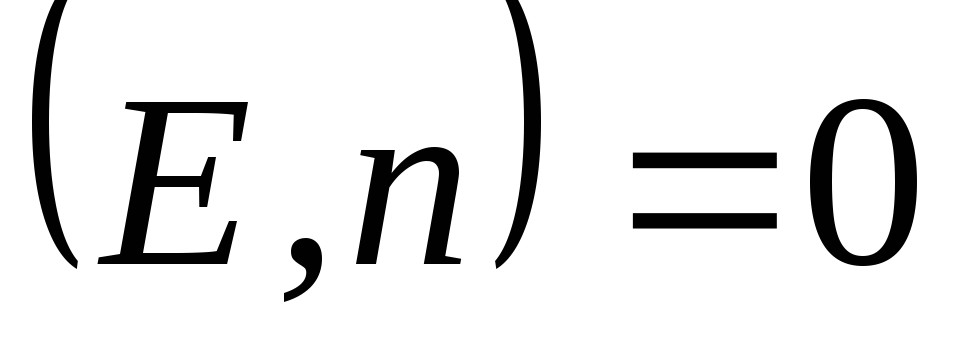

në këto pika. Rrjedhni nëpër sipërfaqen anësore

. Sipas teoremës së Gausit, kjo rrjedhë totale është e barabartë me

. Kështu, ne morëm

.
Shuma e ngarkesave brenda cilindrit shprehet në terma të densitetit linear të ngarkesës :

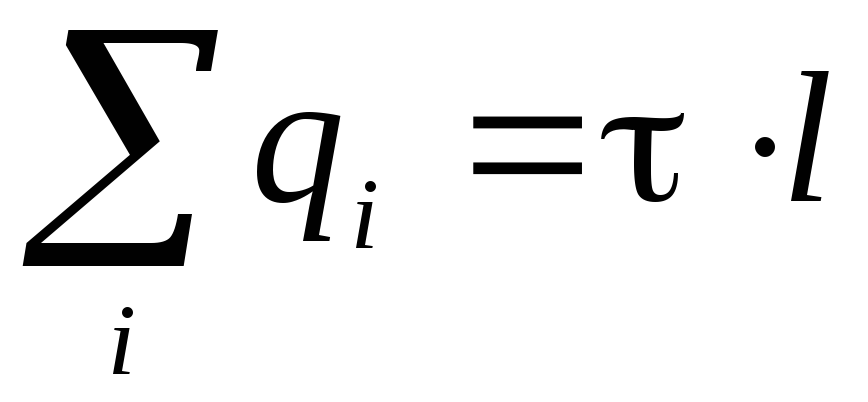. Duke pasur parasysh se

, marrim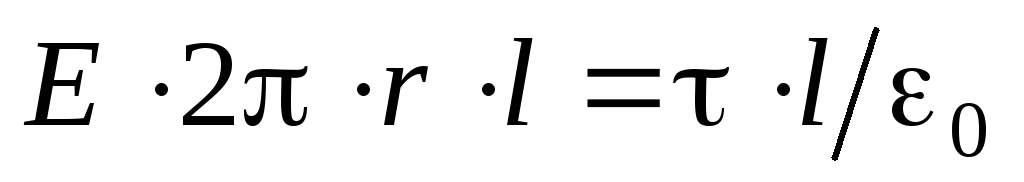

,

, (1.19)
ato. intensiteti dhe dendësia e linjave të fushës elektrike të një filamenti të pafund të ngarkuar në mënyrë uniforme zvogëlohet në mënyrë të kundërt me distancën (

).
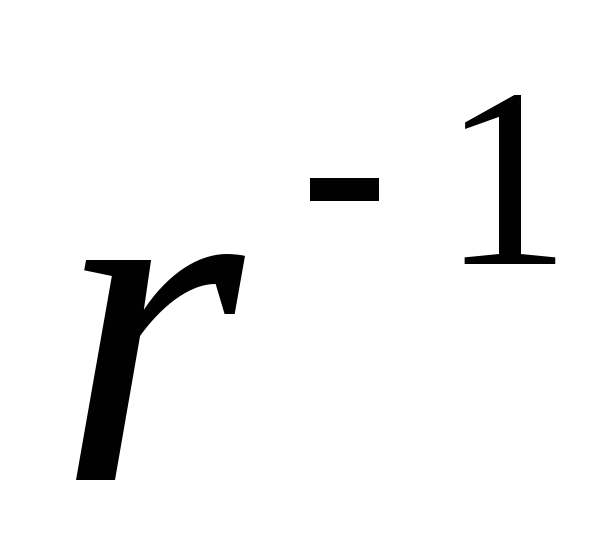Gjeni ndryshimin potencial midis pikave të vendosura në distanca 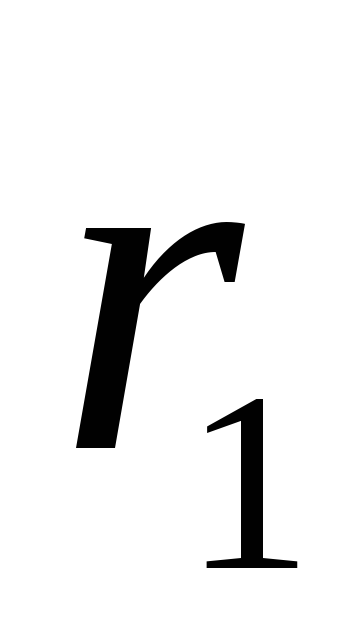dhe 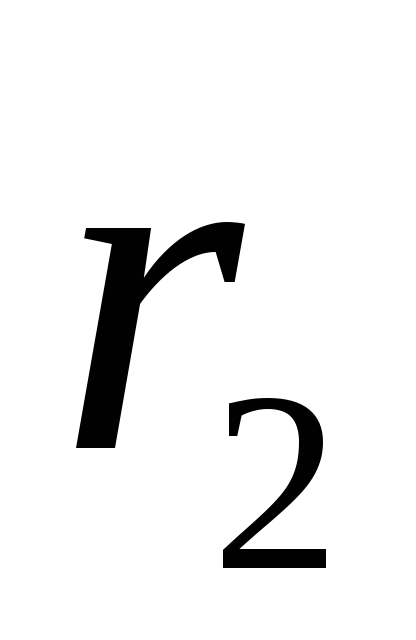nga filli (që i përkasin sipërfaqeve cilindrike ekuipotenciale me rrez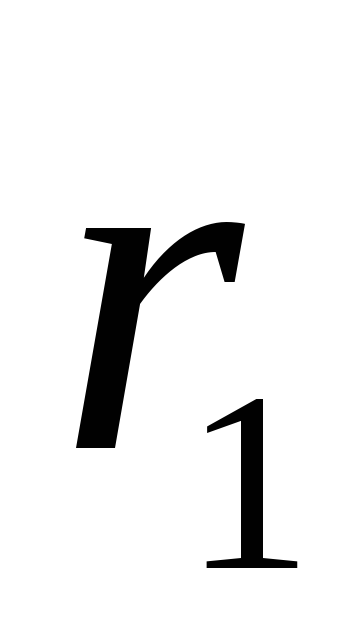e dhe 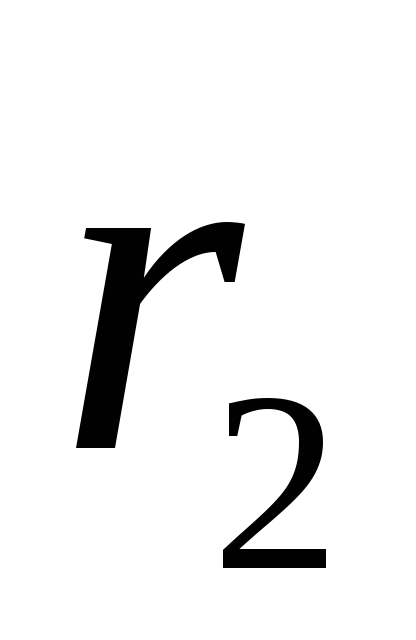). Për ta bërë këtë, ne përdorim lidhjen midis forcës së fushës elektrike dhe potencialit në formën (1.9, c):

. Duke marrë parasysh shprehjen (1.19), marrim një ekuacion diferencial me ndryshore të ndashme:

.

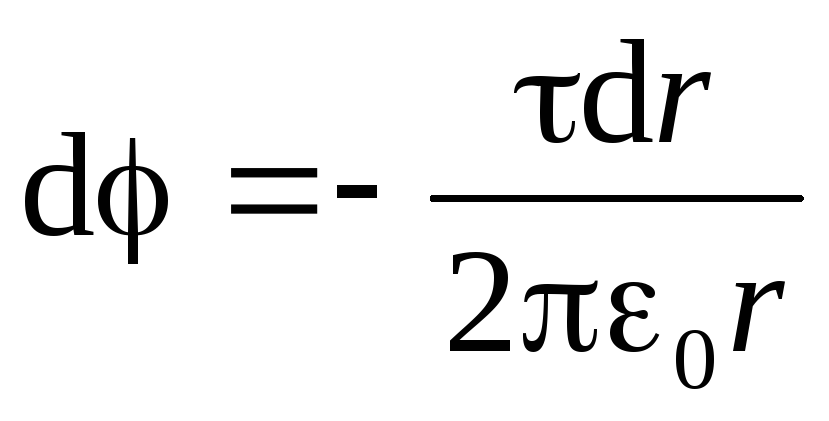
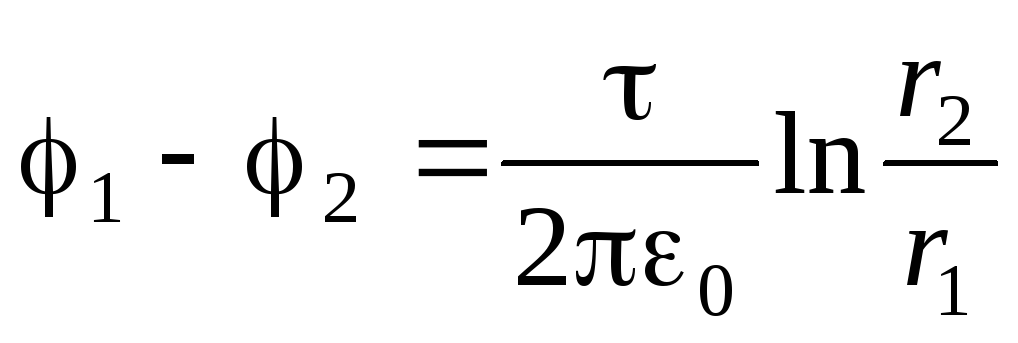Shembulli 1.3. Llogaritni forcën e fushës elektrike të një rrafshi të ngarkuar uniformisht. Përcaktoni ndryshimin potencial midis dy pikave në një fushë të tillë.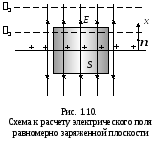
Zgjidhje. Fusha elektrike e një rrafshi të ngarkuar uniformisht është paraqitur në fig. 1.10. Për shkak të simetrisë, vijat e forcës duhet të jenë pingul me rrafshin. Prandaj, mund të konkludojmë menjëherë se dendësia e linjës dhe, rrjedhimisht, forca e fushës elektrike nuk do të ndryshojë me distancën nga rrafshi. Sipërfaqet ekuipotenciale janë rrafshe paralele me një plan të caktuar të ngarkuar. Le të jetë ngarkesa për njësi sipërfaqe të aeroplanit . Kjo vlerë quhet dendësia e ngarkesës sipërfaqësore dhe matet në SI në njësi prej [C/m 2 ].
Le të zbatojmë teoremën e Gausit. Për këtë, si një sipërfaqe e mbyllur arbitrare zgjidhni një cilindër me një gjatësi , boshti i të cilit është pingul me rrafshin, dhe bazat janë të barabarta nga ai (Fig. 1.10). Fluksi total i fushës elektrike

. Rrjedha përmes sipërfaqes anësore është zero. Rrjedha nëpër secilën prej bazave është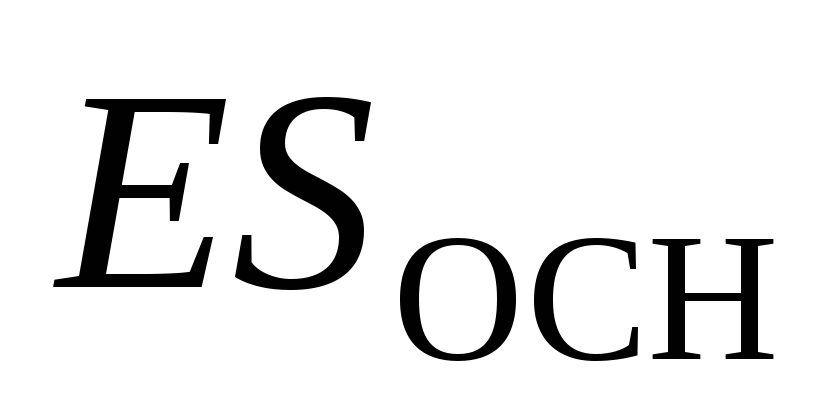

, kjo është arsyeja pse

. Sipas teoremës së Gausit, marrim: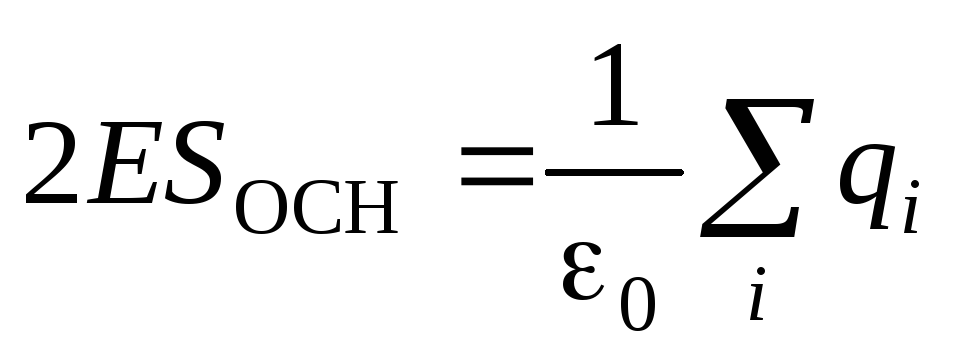

.
Shuma e ngarkesave brenda cilindrit , gjejmë përmes densitetit të ngarkesës sipërfaqësore :

. Pastaj nga ku:

. (1.20)
Nga formula e përftuar shihet se forca e fushës së një rrafshi të ngarkuar uniformisht nuk varet nga distanca në planin e ngarkuar, d.m.th. në çdo pikë të hapësirës (në një gjysmë rrafsh) është i njëjtë si në vlerë absolute ashtu edhe në drejtim. Një fushë e tillë quhet homogjene. linjat e forcës fushë uniforme paralelisht, dendësia e tyre nuk ndryshon.
Le të gjejmë ndryshimin potencial midis dy pikave të një fushe homogjene (që i përkasin planeve ekuipotenciale dhe shtrirë në një gjysmë rrafsh në raport me rrafshin e ngarkuar (Fig. 1.10)). Le të drejtojmë boshtin 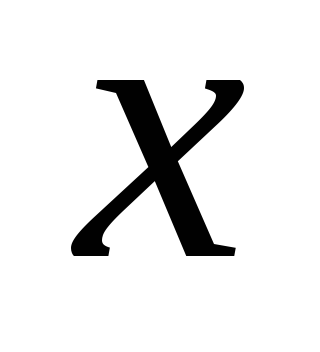vertikalisht lart, atëherë projeksioni i vektorit të tensionit në këtë bosht është i barabartë me modulin e vektorit të tensionit

. Ne përdorim ekuacionin (1.9):

.
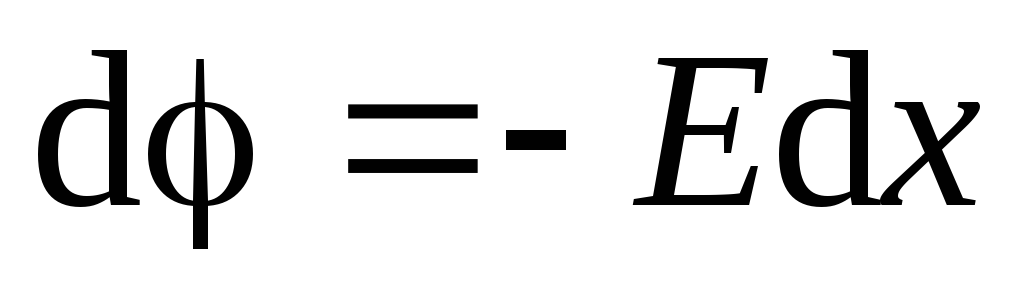
Vlera konstante (fusha është homogjene) mund të nxirret nga nën shenjën integrale: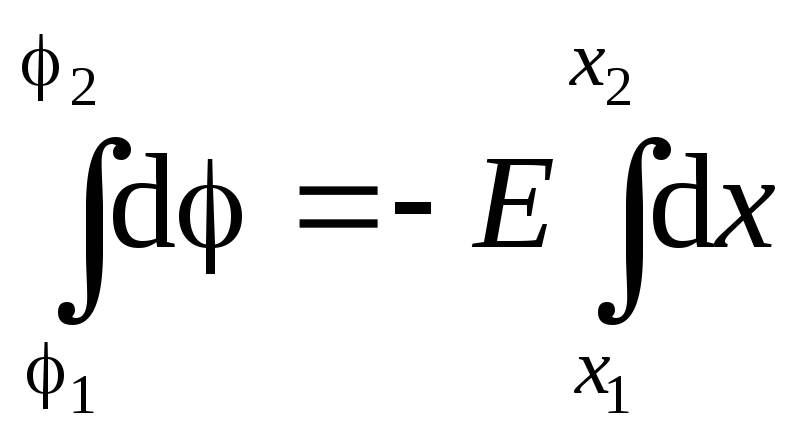

. Duke u integruar, marrim: . Pra, potenciali i një fushe homogjene varet në mënyrë lineare nga koordinata.
Dallimi potencial midis dy pikave të fushës elektrike është tensioni midis këtyre pikave ( ). Le të shënojmë distancën ndërmjet rrafsheve ekuipotenciale

. Atëherë mund të shkruajmë se në një fushë elektrike uniforme:

. (1.21)
Theksojmë edhe një herë se kur përdorim formulën (1.21), duhet të kujtojmë se sasia - jo distanca ndërmjet pikave 1 dhe 2, por distanca ndërmjet rrafsheve ekuipotenciale të cilave u përkasin këto pika.
Shembulli 1.4. Llogaritni forcën e fushës elektrike të dy rrafsheve paralele të ngarkuar në mënyrë të njëtrajtshme me densitetin e ngarkesës sipërfaqësore

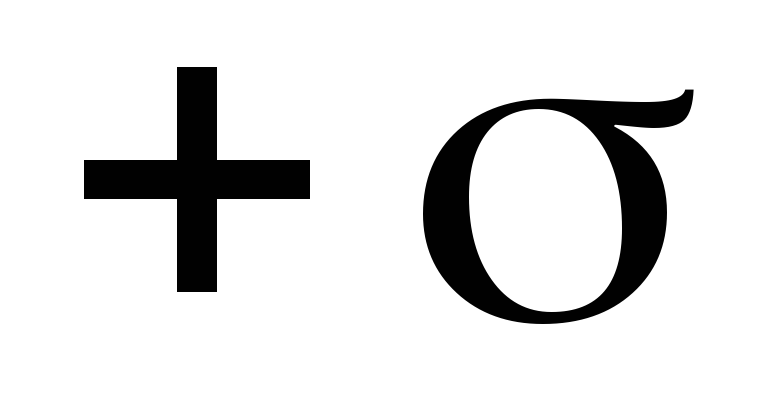dhe

.
Zgjidhje. Le të përdorim rezultatin e Shembullit 1.3 dhe parimin e mbivendosjes. Sipas këtij parimi, fusha elektrike rezulton në çdo pikë të hapësirës

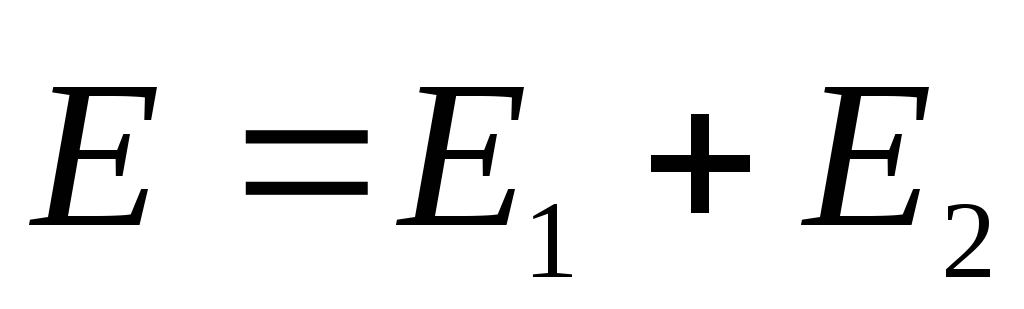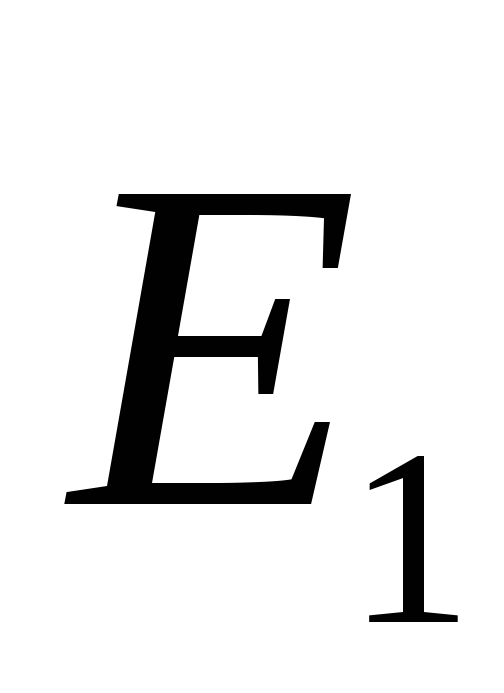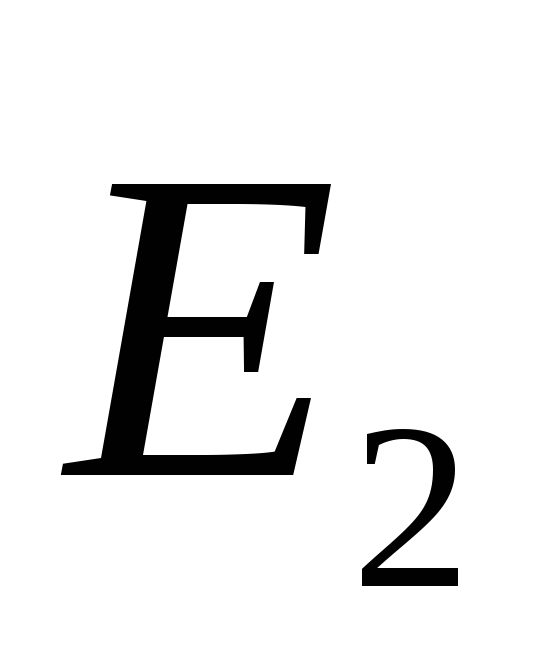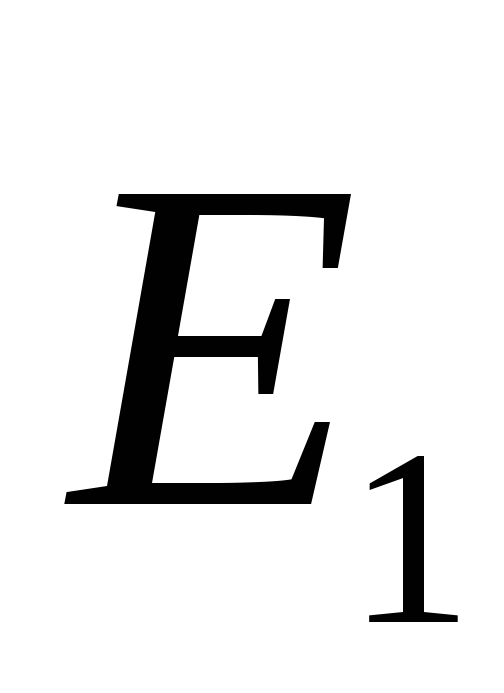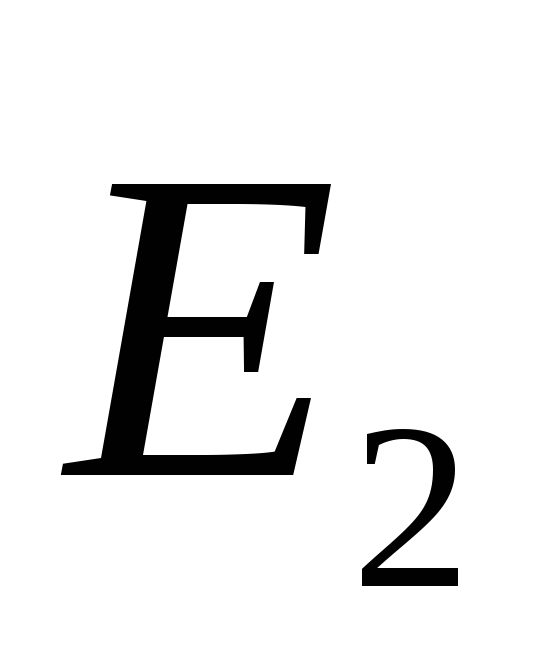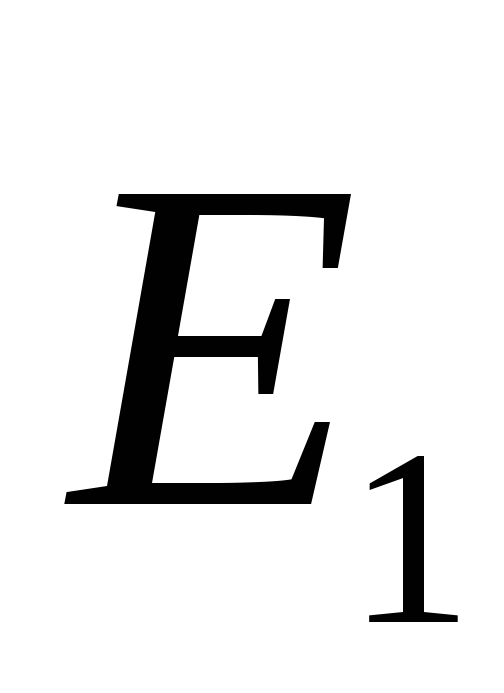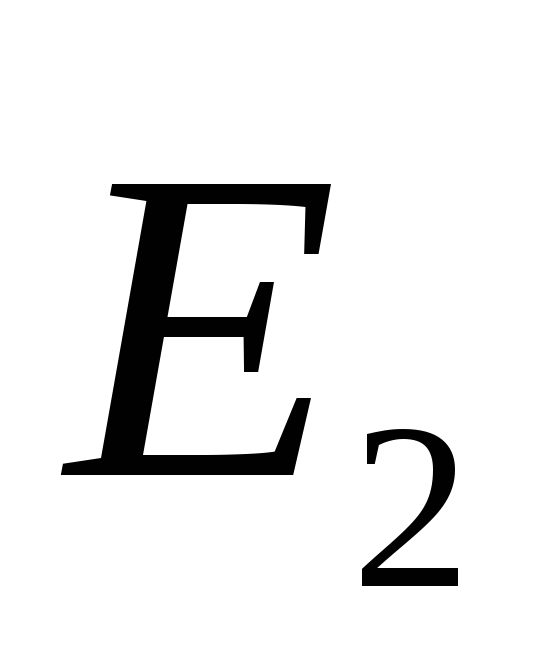, ku dhe - fuqitë e fushës elektrike të planit të parë dhe të dytë. Në hapësirën ndërmjet planeve vektoriale dhe drejtuar në një drejtim, pra moduli i forcës së fushës që rezulton. Në hapësirën e jashtme të vektorit dhe drejtuar në drejtime të ndryshme, pra (Fig. 1.11). Kështu, fusha elektrike ekziston vetëm në hapësirën ndërmjet planeve. Është homogjene, pasi është shuma e dy fushave homogjene.
Shembulli 1.5. Gjeni forcën dhe potencialin e fushës elektrike të një sfere të ngarkuar uniformisht. Ngarkesa totale e sferës është , dhe rrezja e sferës është .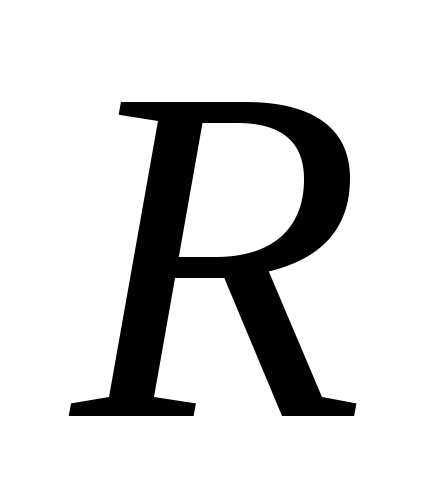
Zgjidhje. Për shkak të simetrisë së shpërndarjes së ngarkesës, linjat e forcës duhet të drejtohen përgjatë rrezeve të sferës.
Konsideroni një rajon brenda një sfere. Si një sipërfaqe arbitrare zgjidhni një sferë me rreze

, qendra e të cilit përkon me qendrën e sferës së ngarkuar. Pastaj rrjedha e fushës elektrike nëpër sferë S:

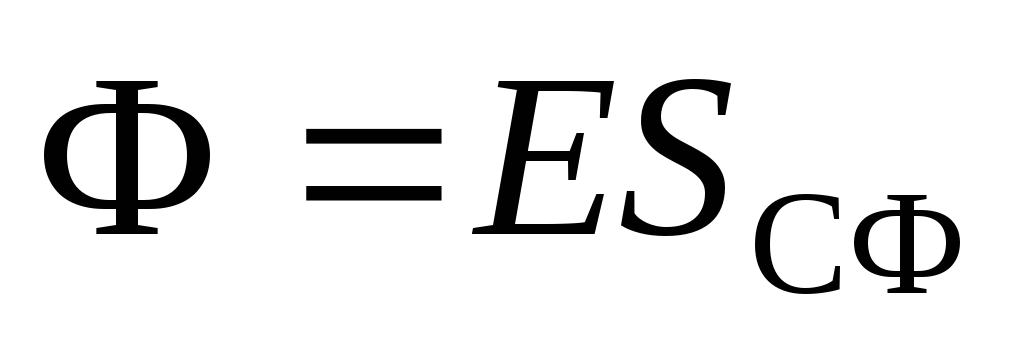. Shuma e ngarkesave brenda sferës rreze 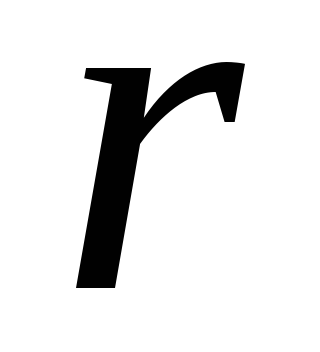është e barabartë me zero, pasi të gjitha ngarkesat janë të vendosura në sipërfaqen e një sfere me rreze

. Pastaj nga teorema e Gausit: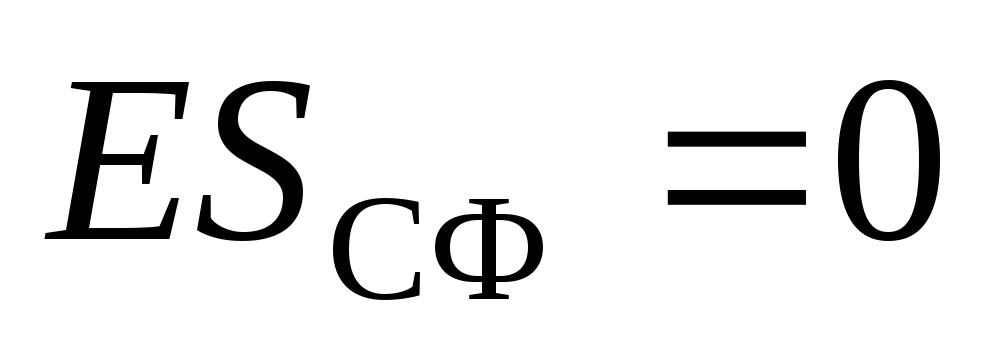

. Sepse

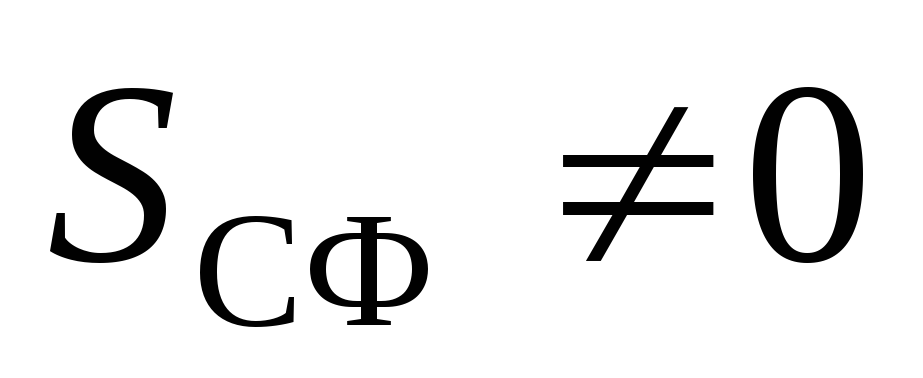, pastaj

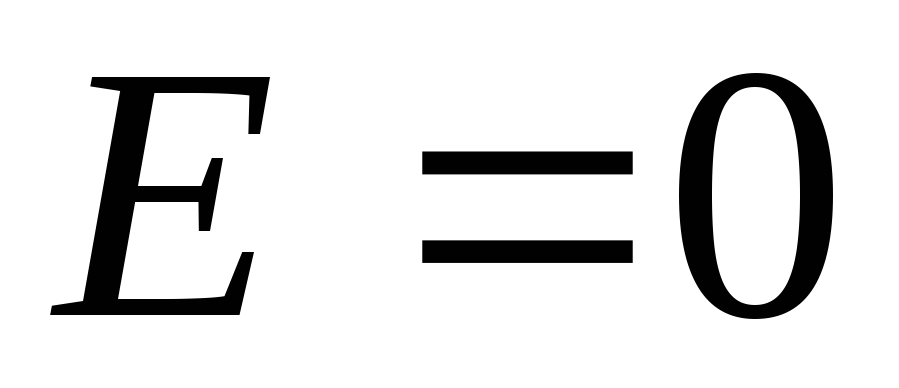. Kështu, nuk ka fushë brenda një sfere të ngarkuar në mënyrë uniforme.
Konsideroni një rajon jashtë sferës. Si një sipërfaqe arbitrare zgjidhni një sferë me rreze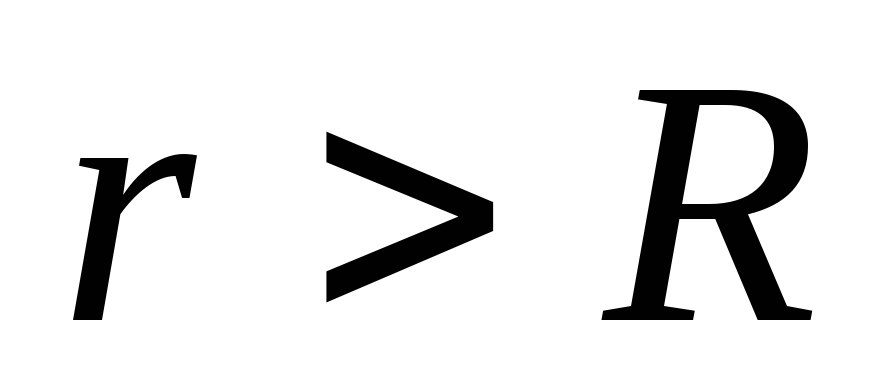

, qendra e të cilit përkon me qendrën e sferës së ngarkuar. Rrjedha e një fushe elektrike nëpër një sferë :

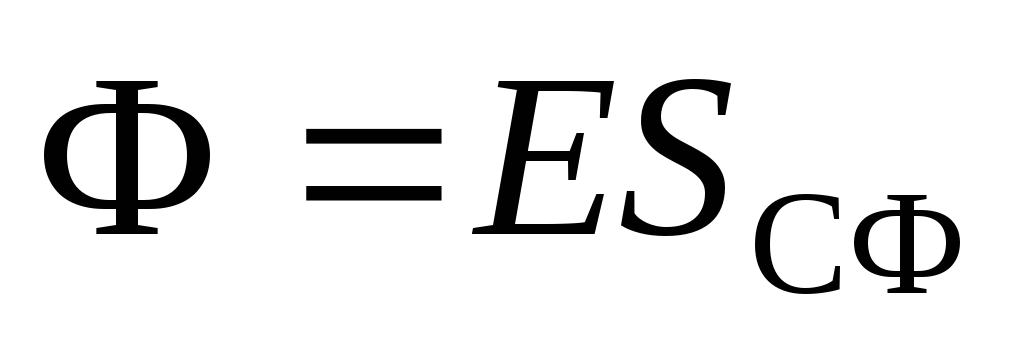. Shuma e ngarkesave brenda sferës është e barabartë me ngarkesën totale sfera e ngarkuar e rrezes 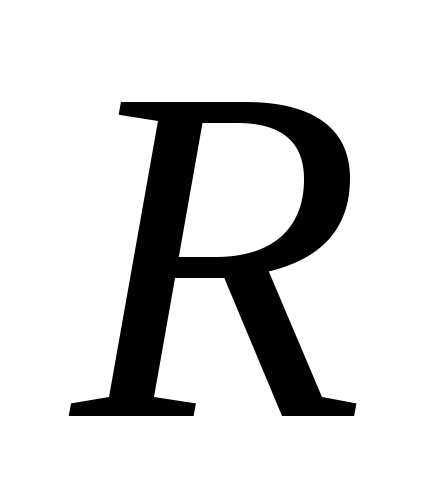. Pastaj nga teorema e Gausit:

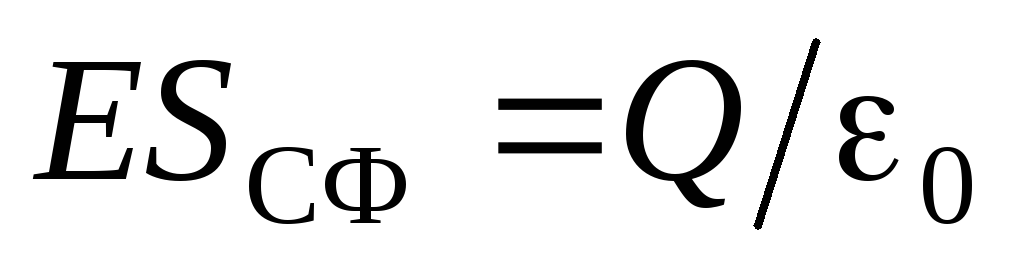. Duke pasur parasysh se

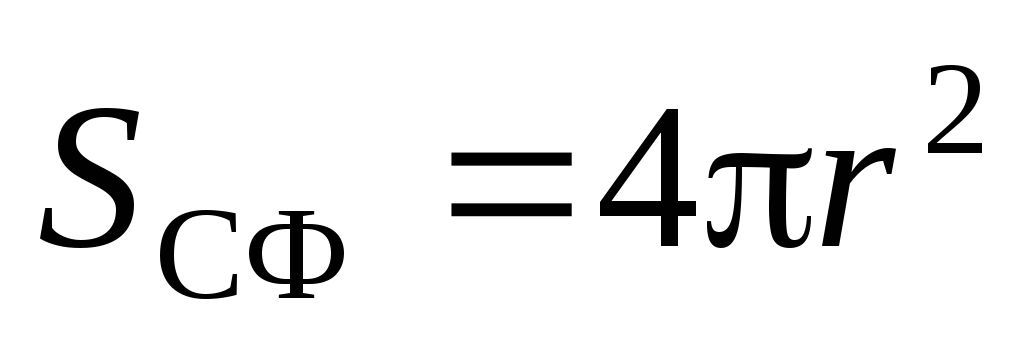, marrim:

.
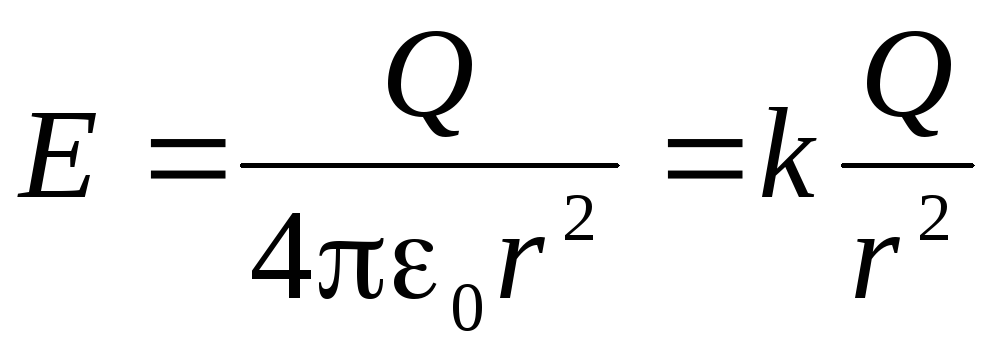Le të llogarisim potencialin e fushës elektrike. Është më i përshtatshëm për të filluar nga zona e jashtme

, pasi ne e dimë se në një distancë të pafundme nga qendra e sferës, potenciali supozohet të jetë zero. Duke përdorur ekuacionin (1.11, a) marrim një ekuacion diferencial me ndryshore të ndashme:

.
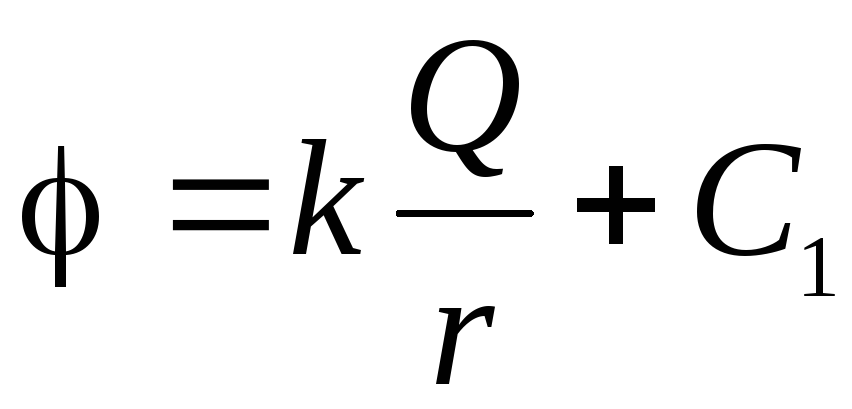Konstante

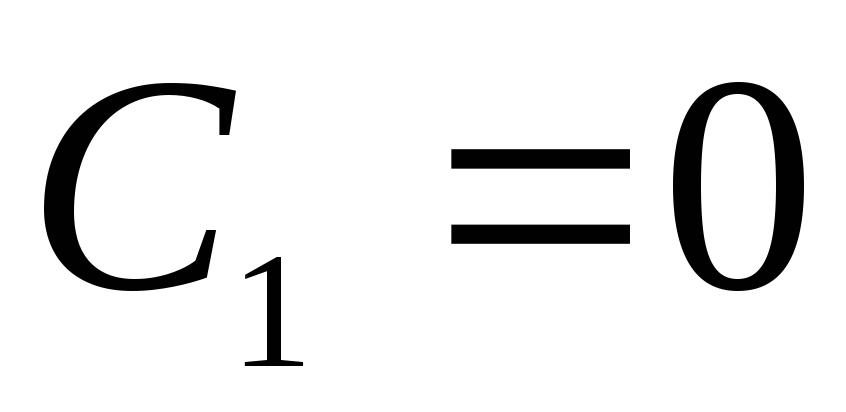, sepse

në

. Kështu, në hapësirën e jashtme (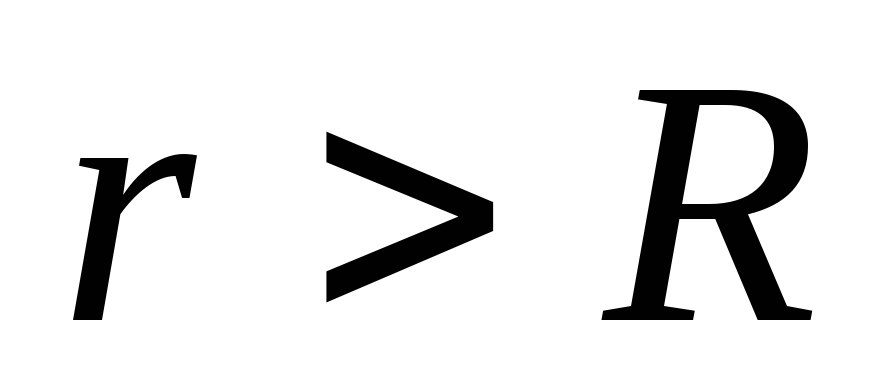

):

.
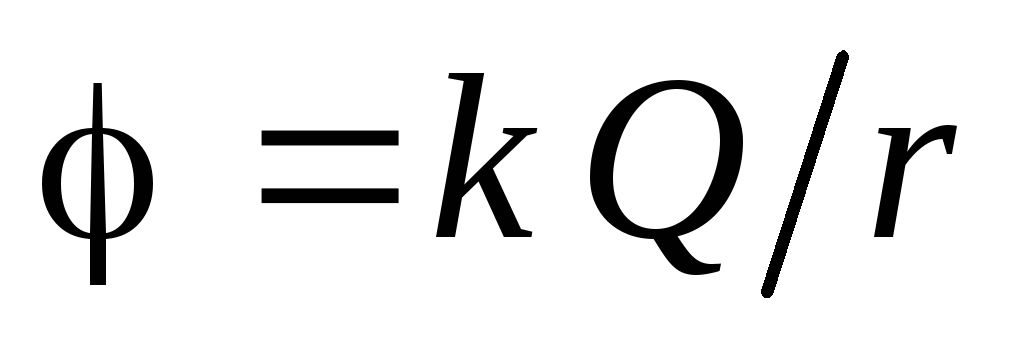Pikat në sipërfaqen e një sfere të ngarkuar (

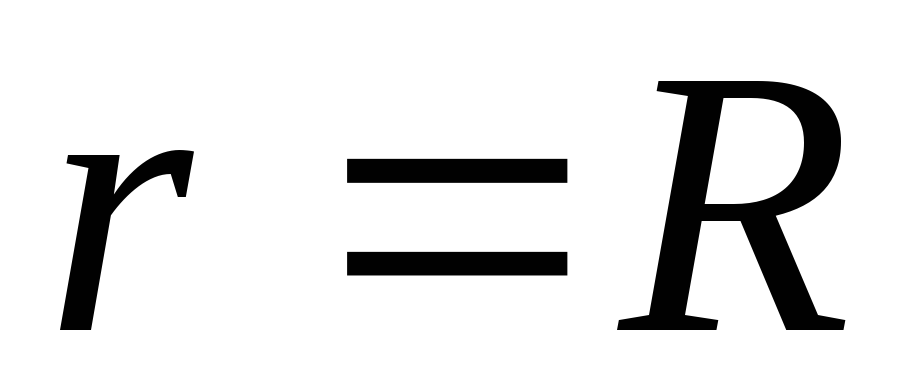) do të ketë potencial

.
Merrni parasysh zonën

. Në këtë rajon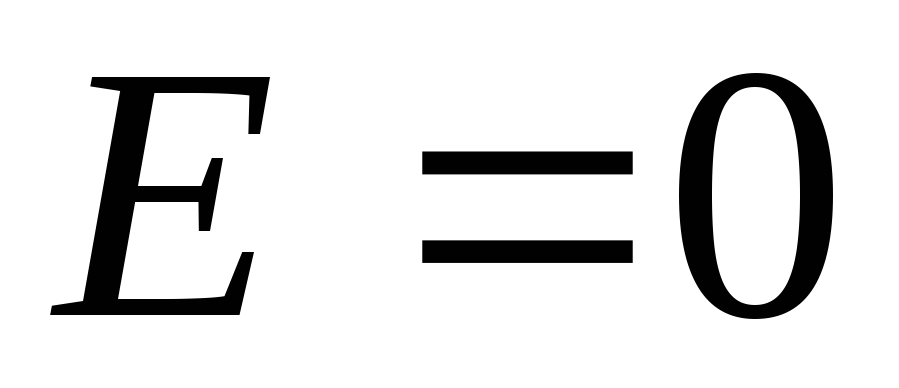

, pra, nga ekuacioni (1.11, a) marrim: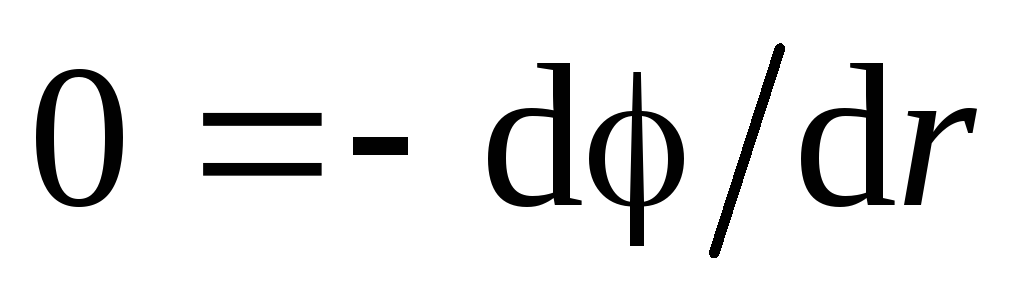

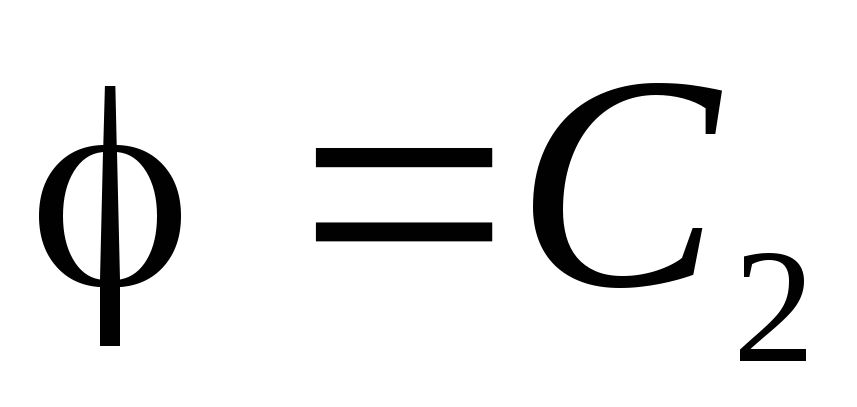. Për shkak të vazhdimësisë së funksionit

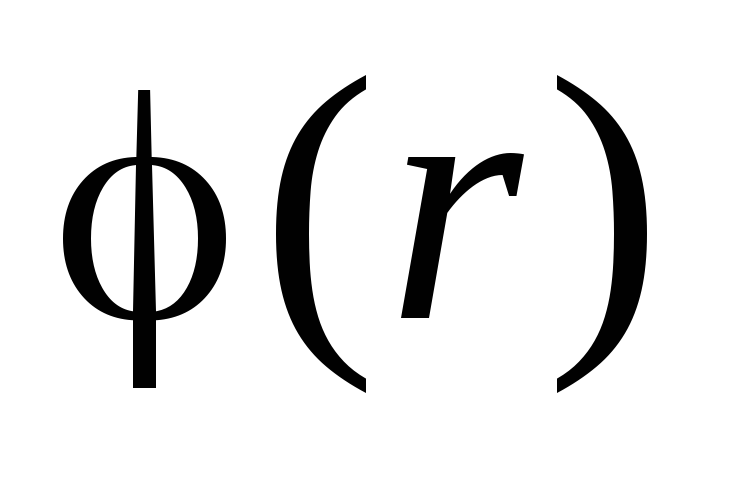konstante duhet të jetë e barabartë me vlerën e potencialit në sipërfaqen e sferës së ngarkuar: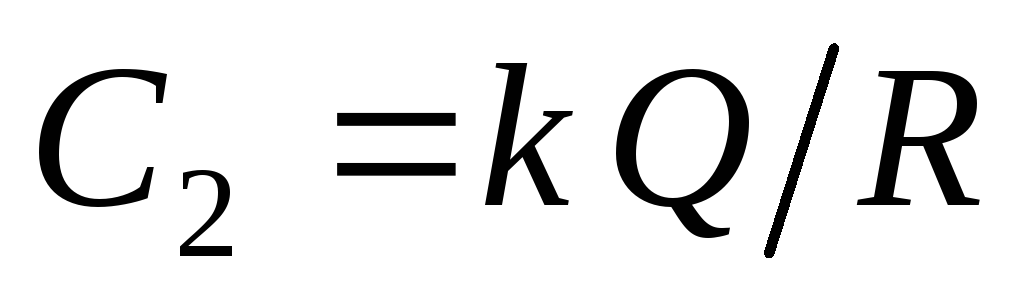

. Pra, potenciali në të gjitha pikat brenda sferës është:

.

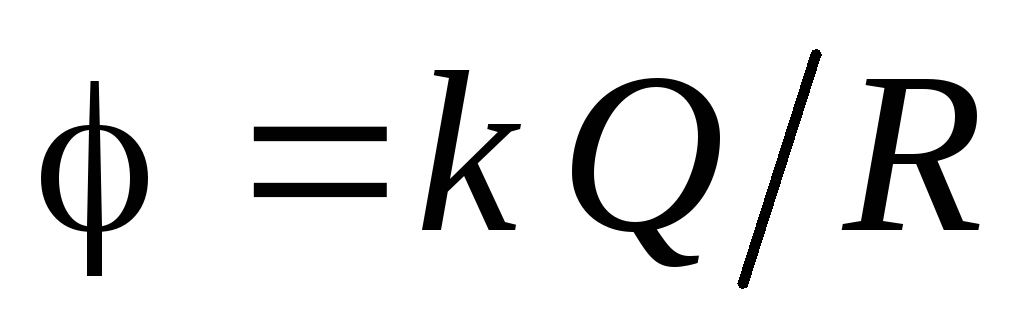Pra, kemi marrë që forca dhe potenciali i fushës elektrike të krijuar nga një sferë e ngarkuar në mënyrë uniforme jashtë sferës janë të barabarta me forcën dhe potencialin e fushës së krijuar nga tarifë pikë të njëjtën madhësi , e cila është ngarkesa e sferës e vendosur në qendër të sferës. Nuk ka fushë në hapësirën e brendshme, dhe potenciali është i njëjtë në të gjitha pikat. Fusha elektrike (vijat e fushës dhe sipërfaqet ekuipotenciale) të një sfere të ngarkuar është paraqitur në fig. 1.12. Sfera supozohet të jetë e ngarkuar pozitivisht. Jashtë sferës, linjat e forcës dhe shpërndahen në hapësirë saktësisht në të njëjtën mënyrë si linjat e forcës së një ngarkese pikë.

Në fig. 1.13 tregon grafikët e varësisë

dhe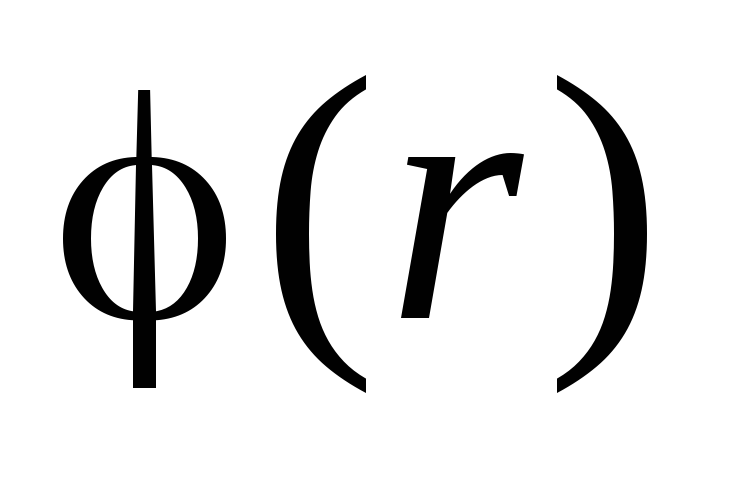

. Funksioni

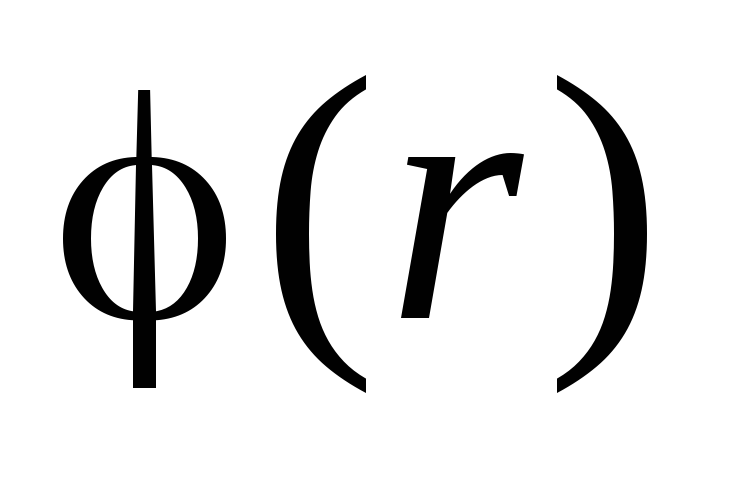është i vazhdueshëm, dhe funksioni

ndryshon befas kur kalon nëpër kufirin e një sfere të ngarkuar. Vlera e kërcimit është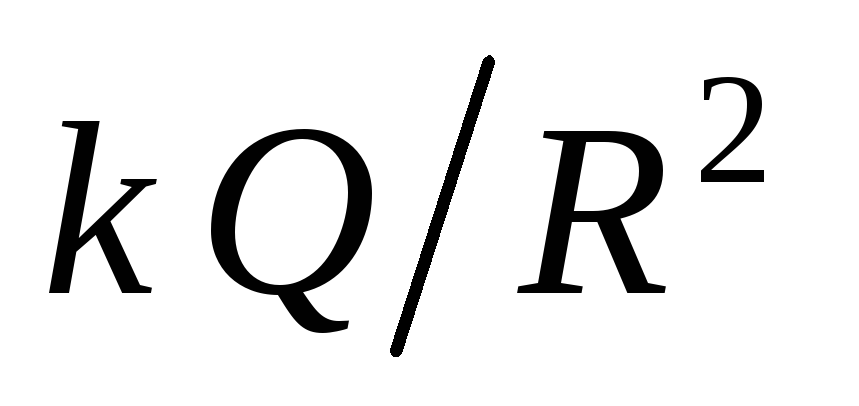

. Në të vërtetë, pranë sferës së ngarkuar (

) forca e fushës në hapësirën e jashtme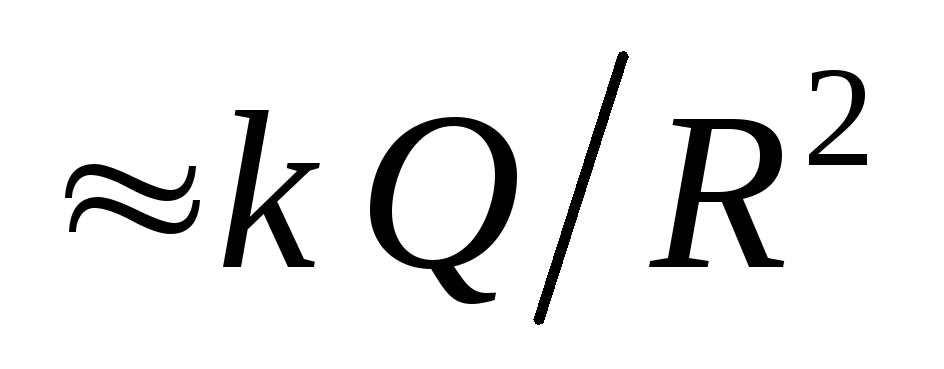

, ndërsa brenda është e barabartë me zero.
Madhësia e kërcimit mund të shprehet në termat e densitetit të ngarkesës sipërfaqësore në sferë:

.
Vini re se kjo pronë e përbashkët fushë elektrostatike: në një sipërfaqe të ngarkuar, projeksioni i intensitetit në drejtim të normales përjeton gjithmonë një kërcim

pavarësisht nga forma e sipërfaqes. Ne rekomandojmë kontrollimin e këtij parimi për fushën e një rrafshi të ngarkuar uniformisht dhe fushën e dy rrafsheve të ngarkuara paralele (shembuj 1.3, 1.4).
Nga pikëpamja e matematikës, vazhdimësia e potencialit në pikat e sipërfaqes së ngarkuar do të thotë që

. Nga pikëpamja e fizikës, vazhdimësia e funksionit

mund të shpjegohet si më poshtë. Nëse potenciali në kufirin e një rajoni të caktuar do të kishte një kërcim (diskontinuitet), atëherë me një zhvendosje pafundësisht të vogël të një ngarkese të caktuar nga pika 1, e shtrirë në njërën anë të kufirit, në pikën 2, e shtrirë në anën tjetër të saj, do të kryhej punë e fundme.

, ku dhe  potencialet e pikave 1 dhe 2, përkatësisht, dhe vlera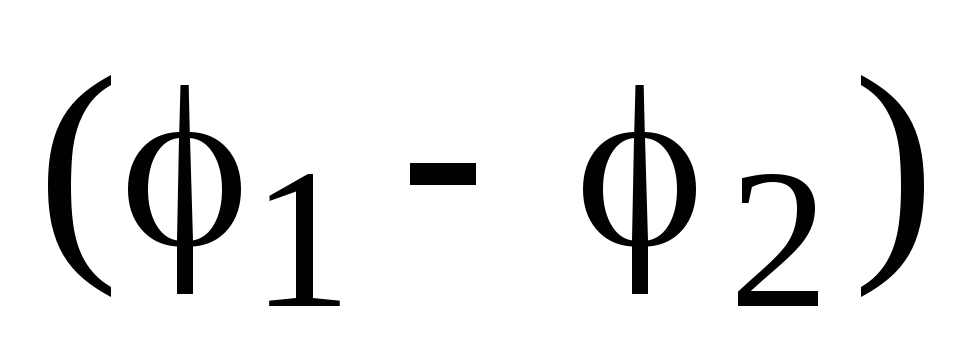

është e barabartë me kërcimin e mundshëm në kufirin e rajonit. Puna përfundimtare e bërë në një zhvendosje pafundësisht të vogël do të thotë se forca pafundësisht të mëdha do të vepronin në ndërfaqe, gjë që është e pamundur.
Forca e fushës elektrike, në kontrast me potencialin, në kufirin e rajonit mund të ndryshojë shumë ashpër (kërcimet).
Shembulli 1.6. Dy sfera koncentrike me rreze dhe (

) janë të ngarkuara në mënyrë uniforme me ngarkesa të barabarta në madhësi, por të kundërta në shenj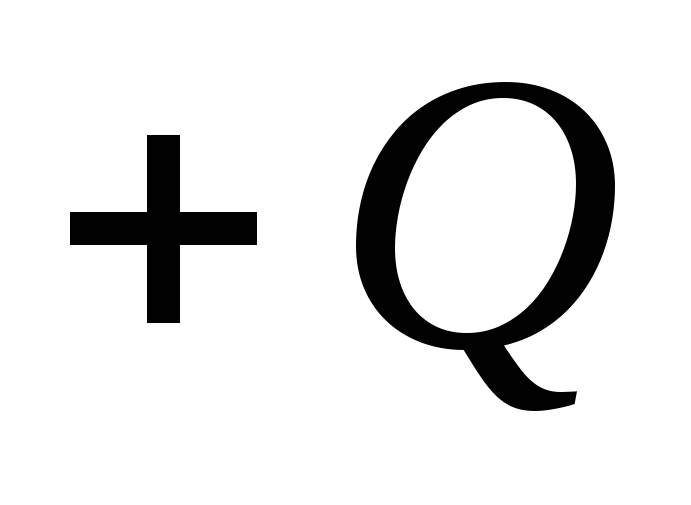ë

dhe

(kondensator sferik). Përcaktoni forcën dhe potencialin e fushës elektrike në të gjithë hapësirën.
Zgjidhje. Zgjidhja e këtij problemi mund të fillojë edhe me zbatimin e teoremës së Gausit. Sidoqoftë, duke përdorur rezultatet e shembullit të mëparshëm dhe parimin e mbivendosjes (1.13, 1.14), përgjigja mund të merret më shpejt.
Në pikat e jashtme të hapësirës (

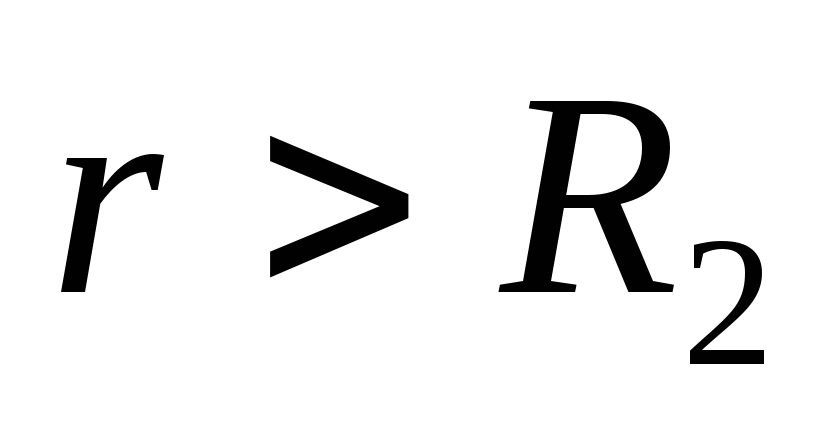) fusha elektrike krijohet nga ngarkesat e të dy sferave. Madhësia e forcës së fushës së sferës së parë

dhe drejtohet nga sferat përgjatë rrezeve. Madhësia e forcës së fushës së sferës së dytë është e njëjtë

, por në drejtim të kundërt. Prandaj, sipas parimit të mbivendosjes, nuk do të ketë fushë elektrike në të gjitha pikat e jashtme në hapësirë.

.
Konsideroni pikat e hapësirës midis sferave (

). Këto pika janë të brendshme të sferës së ngarkuar negativisht, kështu që në këtë zonë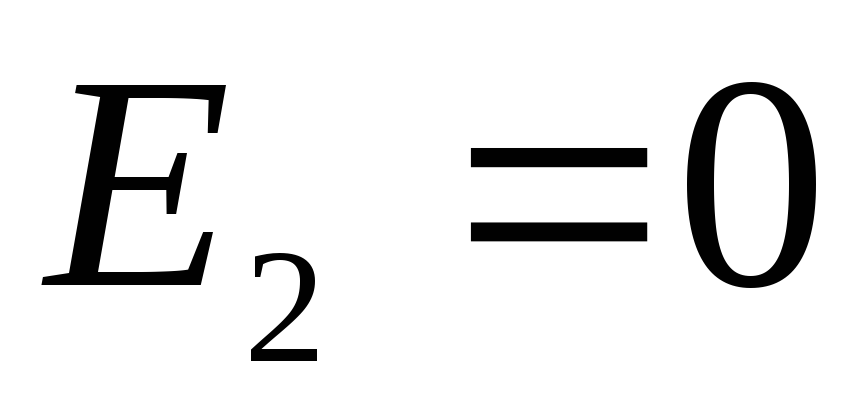

(shih shembullin 1.5). Për një sferë të ngarkuar pozitivisht, këto pika janë të jashtme, pra

. Kështu, madhësia e forcës së fushës në këtë rajon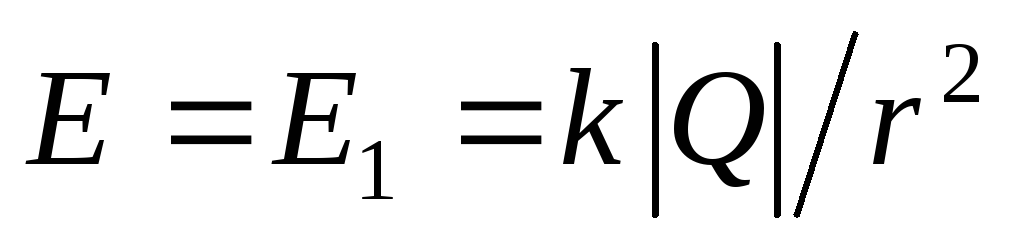

. Këtu fusha krijohet vetëm nga ngarkesat e sferës më të vogël.
Së fundi, në pikat e brendshme të hapësirës (

)

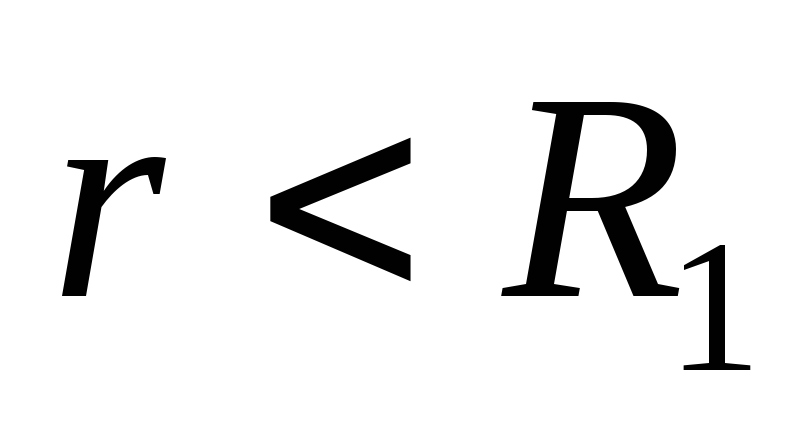dhe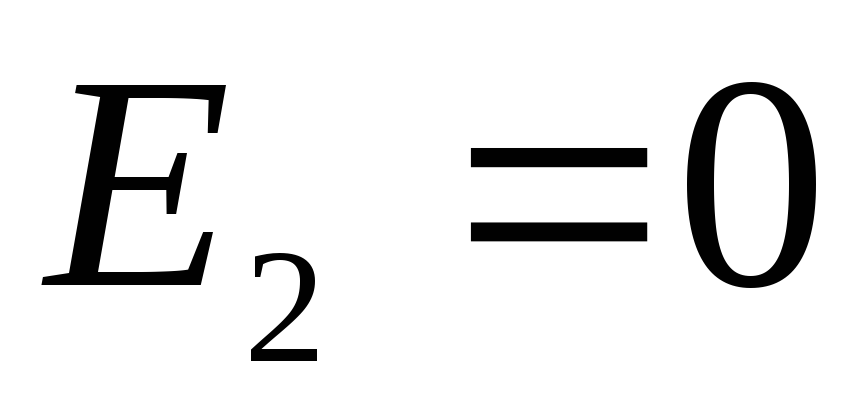

, pra nuk ka fushë elektrike në këto pika.
Në mënyrë të ngjashme, parimi i mbivendosjes mund të zbatohet për potencialet. Janë marrë rezultatet e mëposhtme:

:

;

:

;

:

.
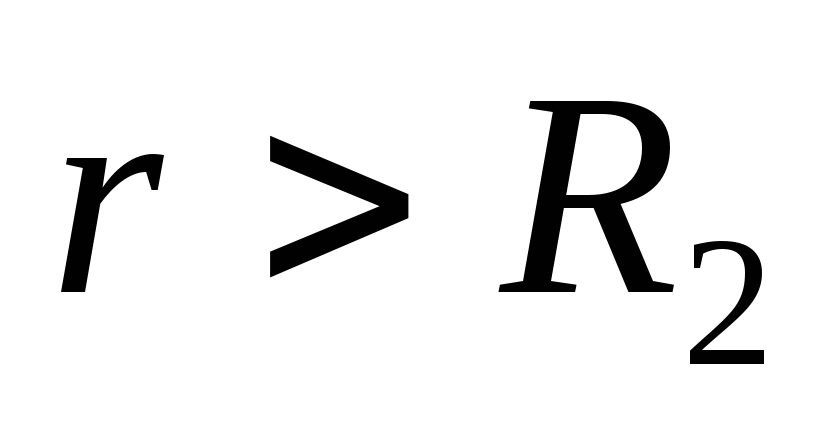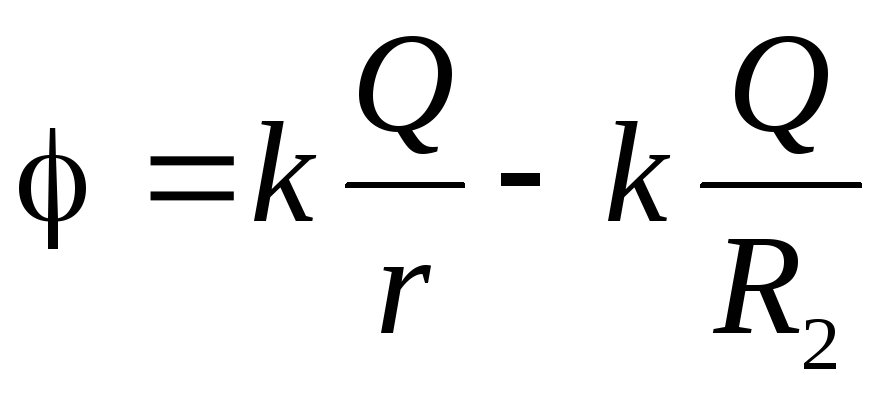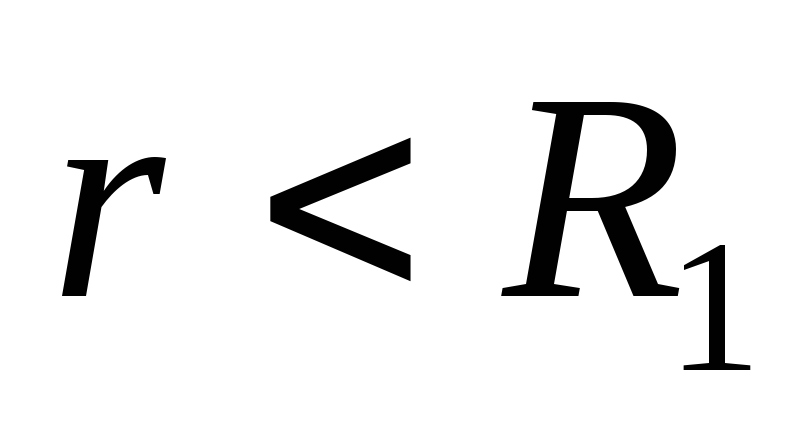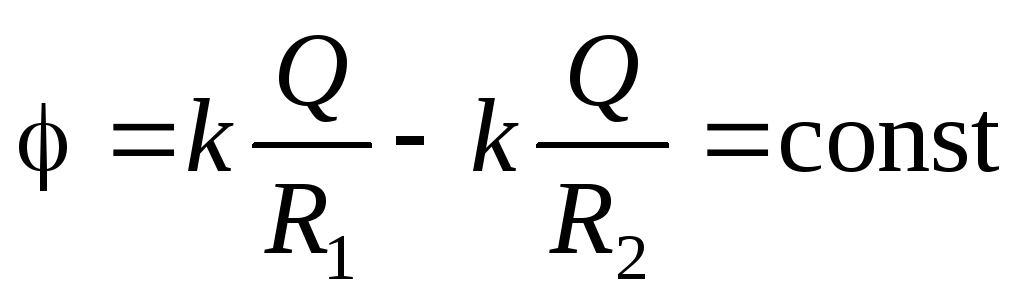Ne ju rekomandojmë që të merrni në mënyrë të pavarur këto rezultate, si dhe të përshkruani skematikisht fushën elektrike dhe të ndërtoni grafikë

dhe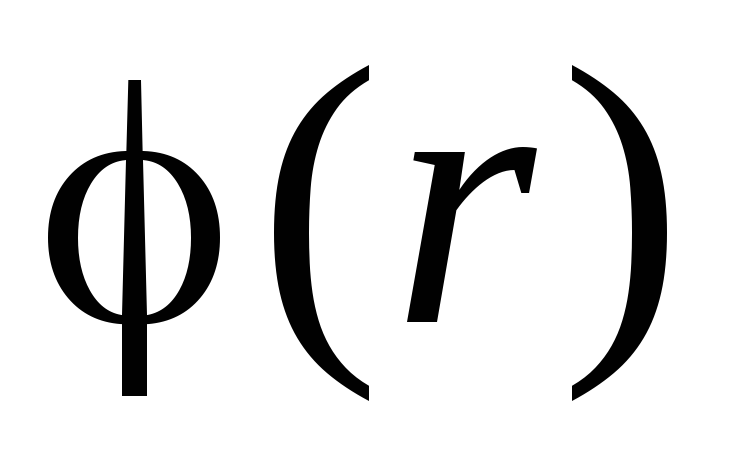

.