Bilanci i dy forcave: dy forca formojnë një sistem të balancuar nëse janë të barabarta në madhësi, të kundërta në drejtim dhe kanë një vijë të përbashkët veprimi.

Bilanci i tre forcave: tre forca që shtrihen në të njëjtin rrafsh formojnë një sistem të ekuilibruar nëse linjat e tyre të veprimit kryqëzohen në një pikë dhe mbi këto forca, si në anët, mund të ndërtoni një trekëndësh me forcë të mbyllur.

Një ekuilibër i një sistemi arbitrar forcash ndodh nëse vektori kryesor sistemi dhe momenti i tij kryesor në lidhje me një poli arbitrar O janë të barabartë me zero.

Kjo ekuacionet vektoriale ekuilibri i korrespondojnë gjashtë ekuacioneve analitike të ekuilibrit. Në rastin kur vendosen ndonjë kufizim në vendndodhjen e forcave, numri i ekuacioneve analitike të ekuilibrit zvogëlohet. Në tabelë. Tabela 1 tregon ekuacionet analitike të ekuilibrit (dhe variantet e tyre) për raste të ndryshme të renditjes së forcave.

Ekuilibri i një trupi të ngurtë kryhet nëse në të zbatohet një sistem i balancuar forcash.

Ekuilibri i një sistemi të ndryshueshëm (të deformueshëm) nën veprimin e forcave mund të konsiderohet si ekuilibri i një trupi absolutisht të ngurtë, forma e të cilit është identike me formën e sistemit të ndryshueshëm pas deformimit (aksioma e ngurtësimit).

Ekuilibri i një sistemi trupash (bashkësi trupash të lidhur me njëri-tjetrin dhe me tokën me lidhje). Numri i përgjithshëm i ekuacioneve të ekuilibrit për një sistem trupash është i barabartë me numrin e ekuacioneve për secilin prej trupave veç e veç, shumëzuar me numrin e trupave në sistem. AT numri total ekuacionet mund të përfshijnë ekuacione të sistemit në tërësi, të cilat kanë ndryshimin se nuk përfshijnë forcat e brendshme.

Koncepti i problemeve (sistemeve) statikisht të përcaktueshme dhe statikisht të papërcaktueshme. Nëse numri i ekuacioneve të pavarura të ekuilibrit për një sistem të caktuar trupash është i barabartë me numrin e të panjohurave në problem, sistemi është i përcaktuar statikisht. Nëse numri i ekuacioneve të ekuilibrit për një sistem të caktuar është më i vogël se numri i të panjohurave në problem, sistemi është statikisht i papërcaktuar, d.m.th., problemi nuk mund të zgjidhet me metoda statike. Nëse numri m i ekuacioneve të statikës është më i madh se numri n i të panjohurave në problem, sistemi është i ndryshueshëm dhe mund të jetë në ekuilibër vetëm nën një ngarkesë të tillë që ekuacionet m-n ekuilibrat kthehen në identitete. Kur zgjidhet një problem i tillë, para së gjithash, është e nevojshme të kontrollohet nëse, për një të dhënë ngarkesë m-n ekuacionet në identitete. Nëse numri i të panjohurave në problem është i barabartë me numrin e ekuacioneve të mbetura, sistemi është në ekuilibër.

Gjatë përpilimit të ekuacioneve të ekuilibrit, duhet të përpiqemi, me anë të një zgjedhjeje racionale të boshteve (dhe pikave të momentit për një problem të rrafshët), të ndajmë sistemin e ekuacioneve në ekuacione të veçanta me një të panjohur secila. Për këtë qëllim, mund të përdorni opsionet për kushtet e ekuilibrit të dhëna në tabelë. 1.

Tabela 1. Variantet e ekuacioneve analitike të ekuilibrit

STATIKA

Kapitulli I KONCEPTET THEMELORE DHE AXIOMAT E STATIKAVE

Forca. Sistemi i forcës. Ekuilibri i një trupi krejtësisht të ngurtë

AT mekanika teorike studiohet lëvizja e trupave materiale në raport me njëri-tjetrin. Kjo kërkon, para së gjithash, ndërtimin e modeleve të objekteve dhe përcaktimin e koncepteve me të cilat merret mekanika. Në mekanikën teorike, konsiderohet modeli më i thjeshtë i hapësirës "e zakonshme" tredimensionale Euklidiane. Supozohet se në këtë hapësirë ​​ekziston të paktën një sistem koordinativ në të cilin ligjet e Njutonit janë të vlefshme ( sistemi inercial ). Eksperimente dhe matje të shumta tregojnë se, me një shkallë të lartë saktësie, një sistem referimi me origjinë në qendër. sistem diellor dhe akset e drejtuara drejt yjeve "pafundësisht të largët të fiksuar", është një sistem inercial. Nëse ekziston të paktën një sistem inercial, atëherë ka një numër të pafund të tyre. Një sistem inercial është një sistem në të cilin zbatohen ligjet e Njutonit. Kornizat inerciale të referencës quhen me kusht i palëvizshëm .

Në statikë, pa futur ndonjë gabim në llogaritjet, mund të supozojmë se sistemet e koordinatave të lidhura në mënyrë të ngurtë me Tokën janë të palëvizshme. Kushtet e ekuilibrit relativ në korniza të tjera jo-inerciale të referencës, në veçanti, në sistemet që lëvizin në raport me Tokën, do të merren parasysh në dinamikë.

Si për statikën ashtu edhe për dinamikën, një nga konceptet kryesore është koncepti i forcës. Ideja kryesore për të është dhënë nga ndjesitë tona muskulore.

Në mekanikë, forca kuptohet si një masë e bashkëveprimit mekanik të trupave materialë, si rezultat i të cilit trupat ndërveprues mund t'i japin nxitime njëri-tjetrit ose të deformojnë (të ndryshojnë formën e tyre).

Dy mënyra të matjes së forcave rrjedhin menjëherë nga ky përkufizim:

e para, dinamike metodë e bazuar në matjen e nxitimit të një trupi në sistemi inercial referencë;

e dyta, statike metodë e bazuar në matjen e deformimit të trupave elastikë.

Në mekanikë, natyra fizike e forcave nuk studiohet. Forcat mund të lindin nga kontakti i drejtpërdrejtë i trupave (për shembull, forca tërheqëse e një lokomotivë elektrike që transmetohet te makina, forca e fërkimit midis sipërfaqeve të trupave kontaktues). Forcat lindin gjithashtu në një distancë (për shembull, forcat e tërheqjes trupat qiellorë, forcat e bashkëveprimit të grimcave të ngarkuara elektrike ose të magnetizuara, etj.).

Forca është një sasi vektoriale - karakterizohet nga një vlerë numerike ose modul, një pikë aplikimi dhe drejtim. Pika e aplikimit të forcës dhe drejtimi i saj përcaktojnë vijën e veprimit të forcës. Në fig. 1.1 tregon forcë F, aplikuar në pikën DHE, gjatësia e segmentit AB në shkallën përkatëse është e barabartë me modulin e forcës, pika AT quhet fundi i pushtetit; në fund të pushtetit; në fund të forcës vendoset një shigjetë, që tregon drejtimin e forcës. Drejt LM thirrur linja e forcës. Le të biem dakord të caktojmë forcën me një shkronjë të theksuar, për shembull, F, dhe moduli i tij me të njëjtën shkronjë të rregullt, d.m.th. F.

Për të matur modulin e forcës, ai krahasohet me një forcë të zgjedhur si njësi. AT sistemit ndërkombëtar njësitë matëse sasive fizike(SI) njësia e forcës është një njuton (1 H), dhe në sistemin teknik të njësive (sistemi ICGSS) - një kilogram forcë (1 kg ose 1 kgf - nuk duhet të ngatërrohet me njësinë e masës SI-1 kg). Këto njësi lidhen nga marrëdhëniet

1 kg ≈ 9,81 H; 1 H ≈ 0,102 kg.

Duke marrë parasysh veprimin e forcave mbi trupat materialë, ne do të abstragojmë jo vetëm nga natyra fizike e forcave, por edhe nga shumë veti të vetë trupave. Kështu, trupat e vërtetë zakonisht ndryshojnë pak formën e tyre nën veprimin e forcave të aplikuara ndaj tyre. Prandaj, për të zgjidhur shumë probleme në mekanikë, lejohet të neglizhohen plotësisht deformimet e vogla (d.m.th., ndryshimet e vogla në formë) dhe të përdoret modeli trup absolutisht i ngurtë. Një trup absolutisht i ngurtë është një trup në të cilin distancat midis dy pikave të tij mbeten të pandryshuara pavarësisht nga veprimi i forcave të caktuara. . Për shkurtësi, ne do të përdorim shpesh shprehjen "trup i ngurtë" ose thjesht "trup", duke pasur parasysh konceptin e sapo prezantuar të një trupi absolutisht të ngurtë.

Një kombinim i forcave të shumta F1,…, fn) quhet sistem forcash. Nëse, pa cenuar gjendjen e trupit, një sistem forcash (F1,…, fn) mund të zëvendësohet nga një sistem tjetër (P1,…, pk) dhe anasjelltas, sisteme të tilla quhen ekuivalente. Në mënyrë simbolike, kjo tregohet si më poshtë:

(F1,…, fn) = (P1,…, pk).

Koncepti i paraqitur i ekuivalencës së sistemeve të forcave nuk krijon kushte në të cilat dy sisteme do të jenë ekuivalente. Do të thotë vetëm se sistemet ekuivalente të forcave shkaktojnë të njëjtën gjendje të trupit (të njëjtat përshpejtime ose, nëse trupi nuk është absolutisht i ngurtë, të njëjtat deformime).

Kur sistemi i forcave(F1,…, fn) është e barabartë me një forcë R, d.m.th.

(F1,…, fn) = R,

kjo e fundit quhet rezultante e sistemit të caktuar të forcave. Kjo do të thotë se një forcë rezultante mund të zëvendësojë veprimin e të gjitha këtyre forcave. Jo çdo sistem forcash ka një rezultat.

Siç u përmend tashmë, në sistemin e koordinatave inerciale plotësohet ligji i inercisë. Kjo do të thotë, në veçanti, se trupi, i cili fillimisht është në qetësi, mbetet në këtë gjendje nëse mbi të nuk veprojnë forca të tjera.

Nëse një trup absolutisht i ngurtë qëndron në qetësi nën veprimin e një sistemi forcash mbi të(F1,…, fn), atëherë ky i fundit quhet një sistem i balancuar forcash ose një sistem forcash ekuivalent me zero:

(F1,…, fn) = 0.

Shpesh në këtë rast thuhet se trupi është në ekuilibër.

1.2. Aksiomat e statikës dhe pasojat e tyre

Në aksiomat e statikës, formulohen ato ligje më të thjeshta dhe të përgjithshme, të cilat u nënshtrohen forcave që veprojnë në të njëjtin trup, ose forcave të aplikuara ndaj trupave ndërveprues. Këto ligje janë vendosur nga vëzhgime të shumta të drejtpërdrejta, si dhe duke kontrolluar pasojat (shpesh të largëta dhe aspak të dukshme) që rrjedhin logjikisht nga këto aksioma.

Siç del nga ligji i dytë i Njutonit, trupi nën ndikimin e një force fiton nxitim dhe, për rrjedhojë, nuk mund të jetë në qetësi. Kjo do të thotë se një forcë nuk mund të përbëjë një sistem të balancuar forcash. Aksioma e parë përcakton kushtet në të cilat sistemi më i thjeshtë i forcave do të balancohet.

Aksioma 1. Dy forcat e aplikuara në një trup absolutisht të ngurtë do të balancohen (ekuivalente me zero) nëse dhe vetëm nëse janë të barabarta në vlerë absolute, veprojnë në një vijë të drejtë dhe drejtohen në drejtime të kundërta.

Kjo do të thotë se nëse një trup absolutisht i ngurtë është në qetësi nën veprimin e dy forcave, atëherë këto forca janë të barabarta në vlerë absolute, veprojnë në një vijë të drejtë dhe drejtohen në drejtime të kundërta. Në të kundërt, nëse nxehtësia absolutisht e ngurtë veprohet në një vijë të drejtë në drejtime të kundërta nga dy forca të barabarta dhe trupi ishte në qetësi në momentin fillestar 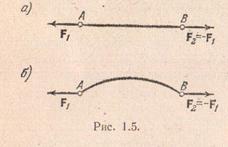gjendja e pushimit të trupit do të ruhet.

Në fig. 1.4 tregon forcat e balancuara që plotësojnë marrëdhëniet: (F1, F2) = 0, (P1, P2) = 0.

Gjatë zgjidhjes së disa problemeve të statikës, duhet të merren parasysh forcat e aplikuara në skajet e shufrave të ngurtë, pesha e të cilave mund të neglizhohet dhe dihet se shufrat janë në ekuilibër. Nga aksioma e formuluar rrjedh drejtpërdrejt se forcat në një shufër të tillë drejtohen përgjatë një vije të drejtë që kalon nëpër skajet e shufrës, të kundërta në drejtim dhe të barabarta me njëra-tjetrën në vlerë absolute. Ky përfundim është gjithashtu i vlefshëm nëse boshti i shufrës është lakor.

Aksioma e parë vendos kushtet e nevojshme dhe të mjaftueshme për balancimin e vetëm dy forcave, por, natyrisht, një sistem i balancuar forcash mund të përbëhet gjithashtu nga më shumë forcat.

Dy aksiomat e ardhshme vendosin veprimet më të thjeshta me forcat në të cilat gjendja e trupit nuk ndryshon.

Aksioma 2. Pa cenuar gjendjen e një trupi absolutisht të ngurtë, forcat mund të aplikohen ose refuzohen ndaj tij nëse dhe vetëm nëse ato përbëjnë një sistem të ekuilibruar, veçanërisht nëse ky sistem përbëhet nga dy forca të barabarta në vlerë absolute, që veprojnë përgjatë një linje të drejtë. dhe të drejtuara në drejtime të kundërta.

Përfundimi rrjedh nga kjo aksiomë: pa cenuar gjendjen e trupit, pika e aplikimit të forcës mund të bartet përgjatë vijës së veprimit të tij.

Kjo konkluzion tregon se forca e aplikuar në një trup krejtësisht të ngurtë është një vektor rrëshqitës.

Të dyja aksiomat dhe përfundimi i vërtetuar nuk mund të aplikohet për trupat e deformueshëm, në veçanti, transferimi i pikës së aplikimit të forcës përgjatë vijës së veprimit të saj ndryshon gjendjen stres-deformim të trupit.

Aksioma 3. Pa ndryshuar gjendjen e trupit, dy forca të aplikuara në njërën nga pikat e tij mund të zëvendësohen nga një forcë rezultante e aplikuar në të njëjtën pikë dhe e barabartë me shumën e tyre gjeometrike.(aksioma e paralelogramit të forcave).

Kjo aksiomë përcakton dy rrethana:

e para - dy forca F1 dhe F2, aplikuar në një pikë, kanë një rezultante, d.m.th. ekuivalente me një forcë

(F1, F2) = R;

e dyta - aksioma përcakton plotësisht modulin, pikën e aplikimit dhe drejtimin e forcës rezultante

R = F1 + F2.

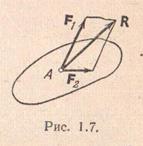
Me fjalë të tjera, rezultati R mund të ndërtohet si një diagonale e një paralelogrami me brinjë që përkojnë me F1 dhe F2.

Vini re se aksioma e tretë është e zbatueshme për çdo trup, jo domosdoshmërisht absolutisht të ngurtë.

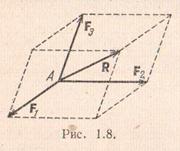Aksiomat e dyta dhe të treta të statikës bëjnë të mundur kalimin nga një sistem forcash në një sistem tjetër ekuivalent me të. Në veçanti, ato lejojnë që dikush të zgjerojë çdo forcë R për dy, tre, etj. komponentët, d.m.th. shkojnë në një sistem tjetër forcash, për të cilat forca Rështë rezultante. Duke vendosur, për shembull, dy drejtime që lidhen me R në një plan, mund të ndërtoni një paralelogram, në të cilin diagonalja përfaqëson forcën R. Atëherë forcat e drejtuara përgjatë anëve të paralelogramit do të formojnë një sistem për të cilin R do të jetë rezultati. Një ndërtim i ngjashëm mund të kryhet në hapësirë. Për këtë mjafton nga pika e aplikimit të forcës R vizatoni tre vija që nuk shtrihen në të njëjtin rrafsh dhe ndërtoni mbi to një paralelipiped me një diagonale që përfaqëson forcën R, dhe me skaje të drejtuara përgjatë këtyre vijave.

Aksioma 4 (ligji i 3-të i Njutonit). Forcat e bashkëveprimit të dy trupave janë të barabarta në vlerë absolute dhe drejtohen përgjatë një linje të drejtë në drejtime të kundërta.

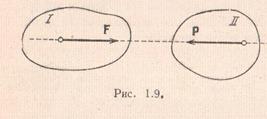Vini re se forcat e ndërveprimit midis dy trupave nuk përbëjnë një sistem forcash të balancuara, pasi ato zbatohen në trupa të ndryshëm.

Nëse shënohet me F forca me të cilën Dielli tërheq Tokën, atëherë Toka e tërheq Diellin me të njëjtin modul, por forcë të drejtuar në të kundërt - F.

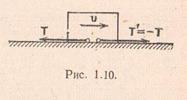
Kur një trup lëviz përgjatë një rrafshi, një forcë fërkimi do të aplikohet në të T, drejtuar në drejtim të kundërt me lëvizjen. Kjo është forca me të cilën rrafshi fiks vepron në trup. Bazuar në aksiomën 4, trupi vepron në aeroplan me të njëjtën forcë, por drejtimi i tij do të jetë i kundërt me forcën. T.

Aksioma 5. Ekuilibri i një trupi të deformueshëm nuk prishet nëse pikat e tij janë të lidhura fort dhe trupi supozohet të jetë absolutisht i ngurtë.

Kjo aksiomë (nganjëherë quhet parimi i kurimit ) përdoren kur po flasim për ekuilibrin e trupave që nuk mund të konsiderohen të ngurtë. Të bashkangjitur me trupa të tillë forcat e jashtme duhet të plotësojë kushtet e ekuilibrit të një trupi të ngurtë, por për trupat jo të ngurtë këto kushte janë vetëm të nevojshme, por jo të mjaftueshme. Le ta shpjegojmë këtë situatë me një shembull të thjeshtë. Për ekuilibrin e një shufre absolutisht të ngurtë pa peshë, është e nevojshme dhe e mjaftueshme që forcat e aplikuara në skajet e shufrës F dhe F" veproi përgjatë një linje të drejtë që lidh skajet e saj, ishin të barabarta në vlerë absolute dhe të drejtuara në drejtime të ndryshme. Të njëjtat kushte janë të nevojshme për ekuilibrin e një segmenti të një filli pa peshë, por ato janë të pamjaftueshme për një fill - është e nevojshme që gjithashtu. kërkojnë që forcat që veprojnë në fill të jenë tërheqëse, ndërsa për një shufër mund të jenë shtypëse.

Si përfundim, merrni parasysh rastin e ekuivalencës me zero të tre forcave joparalele të aplikuara në një trup të ngurtë.

Teorema rreth tre forcave jo paralele. Nëse nën veprimin e tre forcave trupi është në ekuilibër dhe vijat e veprimit të dy forcave kryqëzohen, atëherë të gjitha forcat shtrihen në të njëjtin rrafsh dhe linjat e tyre të veprimit kryqëzohen në një pikë.

Le të veprojë në trup një sistem me tre forca F1, F2 dhe F3, dhe linjat e veprimit të forcave F1 dhe F2 kryqëzohen në një pikë DHE. Sipas përfundimit të aksiomës 2, forcat F1 dhe F2 mund të zhvendoset në pikë DHE, dhe sipas aksiomës 3 ato mund të zëvendësohen me një forcë R, dhe

R=F1+F2.

Në këtë mënyrë,

sistemi i konsideruar i forcave reduktohet në dy forca R dhe F3. Sipas kushteve të teoremës, trupi është në ekuilibër, prandaj, sipas aksiomës 1, forcat R dhe F3 duhet të ketë një vijë të përbashkët veprimi, por atëherë linjat e veprimit të të tre forcave duhet të kryqëzohen në një pikë.

Shembuj të zgjidhjes së problemeve

Sekuenca e zgjidhjes së problemeve:

1. Zgjidhni një trup (pikë) ekuilibri i të cilit duhet të merret parasysh.
2. Lironi trupin (varen) nga lidhjet dhe përshkruani forcat aktive që veprojnë mbi të dhe reagimet e lidhjeve të hedhura. Për më tepër, reagimet e shufrave duhet të drejtohen larg nga mentesha, pasi është zakon të supozohet se shufrat janë shtrirë.
3. Zgjidhni boshtet e koordinatave dhe hartoni ekuacionet e ekuilibrit duke përdorur kushtet e ekuilibrit për sistemin e forcave konvergjente në rrafshin ∑Xi = 0; ∑Yi = 0. Gjatë zgjedhjes së boshteve të koordinatave duhet pasur parasysh se ekuacionet që rezultojnë do të jenë më të lehta për t'u zgjidhur nëse njëri prej boshteve është i drejtuar pingul me një nga forcat e panjohura.
4. Përcaktoni reaksionet e shufrave nga zgjidhja e sistemit të treguar të ekuacioneve.
5. Kontrolloni saktësinë e rezultateve të fituara duke zgjidhur ekuacionet e ekuilibrit për koordinatat e reja x dhe y.

Shembull 1. Ngarkesa është e varur në shufra dhe litarë dhe është në ekuilibër (Fig. 1.13). Përshkruani sistemin e forcave që veprojnë në mentesh DHE.

Vendimi

1. Reaksionet e shufrave drejtohen përgjatë shufrave, reaksionet e lidhjeve fleksibël drejtohen përgjatë fijeve në drejtim të tensionit (Fig. 1.13, a).

2. Për të përcaktuar drejtimin e saktë të forcave në shufra heqim mendërisht shufrat 1 dhe 2 radhazi. Analizojmë zhvendosjet e mundshme të pikës DHE.

Ne nuk e konsiderojmë një bllok fiks me forca që veprojnë mbi të.

3. Hiqni shufrën 1, pikë DHE ngrihet dhe largohet nga muri, prandaj, reagimi i shufrës 1 drejtohet drejt murit.

4. Hiqni shufrën 2, pikë DHE ngrihet dhe i afrohet murit, prandaj, reaksioni i shufrës 2 drejtohet poshtë nga muri.

5. Litari tërhiqet djathtas.

6. Ne çlirohemi nga lidhjet (Fig. 1.13, b).

Shembulli 2 Topi është i varur në një fije dhe mbështetet në një mur (Fig. 1.14a). Përcaktoni reagimet e një filli dhe një mbështetjeje të lëmuar (muri).

Vendimi

1. Reagimi i fillit - përgjatë fillit deri në pikën AT lart (Fig. 1.14, b).

2. Reagimi i një mbështetjeje të lëmuar (muri) - përgjatë normales nga sipërfaqja e mbështetëses.

Shembulli 3 Imagjinoni që në një shirit të vendosur horizontalisht AB, duke neglizhuar masën e vet, ngarkesa vertikale vepron F, aplikuar në një pikë NGA lëndë druri (Fig. 1.14-1, a). Fundi i majtë i rrezes DHE ngjitur në mbështetje nga një menteshë, dhe djathtas AT mbështetet në një plan të lëmuar të pjerrët.

Le të përshkruajmë shiritin në mënyrë skematike si një segment AB, si në fig. 1.14-1, b, dhe aplikoni për të në pikën NGA forca vertikale F. Në pikën AT nga ana plan i pjerrët reagimi i tij aplikohet në shirit R B, drejtuar pingul me rrafshin; linjat e veprimit F dhe R B kryqëzohen në një pikë O. Përveç këtyre forcave, një forcë tjetër vepron në rreze - reagimi i mbështetjes së fiksuar me varet. Dhe meqenëse shiriti është në ekuilibër, vija e veprimit të forcës së tretë do të kalojë gjithashtu përmes pikës O, dmth reagimi R Mbështetja e varur por e fiksuar drejtohet përgjatë segmentit AO.

Metoda e arsyetimit e përdorur këtu quhet parimi i çlirimit të trupit nga lidhjet dhe i zëvendësimit të lidhjeve me reagimet e tyre.

Shembulli 4 Përcaktoni forcën në shufër CD dhe presioni i ngarkesës DHE në rrafshin e referencës EF(Fig. 1.14-2, a). Pesha e shufrës CD, bllokoj TE, litari dhe fërkimi i litarit në bllok të neglizhohet.

Vendimi

Tensioni i litarit në të gjitha pikat e tij është i njëjtë dhe i barabartë me forcën e gravitetit të ngarkesës AT, meqë blloku fiks ndryshon vetëm drejtimin e forcës që vepron në litar.

Konsideroni ekuilibrin e sistemit: shufrën CD dhe bllokoj te ML. Le t'i heqim lidhjet dhe të zëvendësojmë veprimin e tyre me reaksionet përkatëse (Fig. 1.14-2, 6). Për sistemin e forcave që rezulton, mund të hartohet vetëm një ekuacion ekuilibri:

Në fig. 1.14-2, në tregon forcat që veprojnë në ngarkesë DHE me një copë litar ngjitur me të AI. R EF - reagimi i avionit mbështetës.

Që nga ngarkesa DHEështë në ekuilibër, atëherë

R ef \u003d Pa - Pv \u003d 600 - 400 \u003d 200 N.

Forca e presionit të ngarkesës A në rrafshin mbështetës RA është paraqitur në figurën 1.14-2, d. Natyrisht, R A = R EF = 200 H (forca e veprimit është e barabartë me forcën e reagimit).

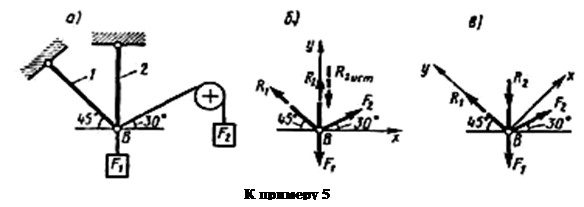
Shembulli 5 Përcaktoni reaksionet e shufrave që mbajnë ngarkesat F 1 = 70 kN dhe F 2 = 100 kN (Fig. a). Injoroni masën e shufrave.

Vendimi

1. Konsideroni ekuilibrin e menteshës B (Fig. a).

2. Lëshojmë menteshën B nga lidhjet dhe përshkruajmë forcat aktive që veprojnë mbi të dhe reaksionet e lidhjeve (Fig. b).

3. Ne zgjedhim një sistem koordinatash, duke rreshtuar boshtin y në drejtimin C me reaksionin R 2 (Fig. b) dhe hartojmë ekuacionet e ekuilibrit për sistemin e forcave që veprojnë në menteshën B:

3. Përcaktojmë reaksionet e shufrave R 1 dhe R 2 duke zgjidhur ekuacionet.

Duke zëvendësuar vlerën e gjetur të R 1 në ekuacionin (2), marrim

Shenja minus përpara vlerës R 2 tregon se drejtimi i zgjedhur fillimisht i reaksionit është i pasaktë - reagimi R 2 duhet të drejtohet në drejtim të kundërt, d.m.th. te mentesha B (në figurën b, drejtimi i vërtetë i reaksionit R 2 tregohet nga një vektor me ndërprerje).

5. Kontrollojmë korrektësinë e rezultateve të marra duke zgjedhur një vendndodhje të re të boshteve të koordinatave x dhe y (Fig. a). Në lidhje me këto boshte, ne përpilojmë ekuacionet e ekuilibrit:

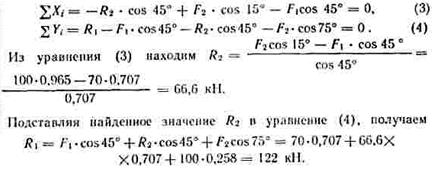
Vlerat e reaksioneve R 1 dhe R 2 të marra nga zgjidhja e ekuacioneve (1) dhe (2) përkojnë në madhësi dhe drejtim me vlerat e gjetura nga ekuacionet (3) dhe (4), prandaj, problemi është zgjidhur saktë.

Kontrolloni pyetjet dhe detyrat

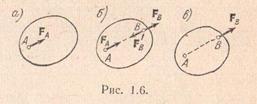
1. Cili nga sistemet e dhëna të forcave (Fig. 1.15) është i balancuar?

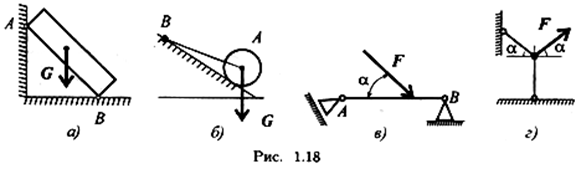
4. Specifikoni drejtimi i mundshëm reaksionet në mbështetëse (Fig. 1.18).

Për të zbatuar teoremën e Huygens-Steiner, duhet të dini momentin e inercisë I Me trup në lidhje me boshtin SS që kalon nëpër qendrën e tij të gravitetit (qendra e inercisë). Ky moment varet nga drejtimi i boshtit CC. Megjithatë, nuk ka nevojë të llogaritet I Me sipas formulës ose matet sërish për çdo bosht.

Rezulton se për ndonjë trup i fortë ka tre boshte reciprokisht pingul që kalojnë nëpër qendrën e tij të inercisë (boshtet kryesore të trupit), të tilla që momenti i inercisë rreth çdo boshti të SS shprehet përmes momenteve të inercisë së trupit I 1 , I 2 dhe I 3 në lidhje me këto akse kryesore. Kështu, detyra e përcaktimit të momentit të inercisë së një trupi në lidhje me një bosht arbitrar reduktohet në përcaktimin e akseve kryesore dhe momenteve përkatëse të inercisë I 1 , I 2 dhe I 3.

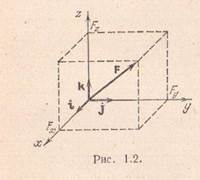
Si të gjeni boshtet kryesore të inercisë së një trupi të caktuar të ngurtë? Boshtet kryesore janë të lehta për t'u përcaktuar për trupat homogjenë simetrikë (top, kub, cilindër, paralelipiped drejtkëndor, etj.) Boshtet kryesore të inercisë së trupave të tillë përputhen gjithmonë me boshtet e simetrisë së trupit. Për shembull, boshtet kryesore të një paralelipipedi drejtkëndor homogjen kalojnë nëpër qendrën e tij gjeometrike pingul me faqet (foto 4)

Për një top homogjen, çdo tre boshte reciprokisht pingul që kalon nga qendra e tij janë kryesore. Mund të vërtetohet se një kub homogjen ka të njëjtën veti. Për trupat Boshtet kryesore të formës komplekse dhe momentet e inercisë mund të gjenden me metoda më komplekse eksperimentale dhe teorike.

Figura 4 Boshtet kryesore të inercisë së një paralelipipedi drejtkëndor

4.6 Energjia kinetike e një trupi rrotullues

Energjia kinetike arbitrare i-pika e-të materiale me masë m i; është e barabartë me

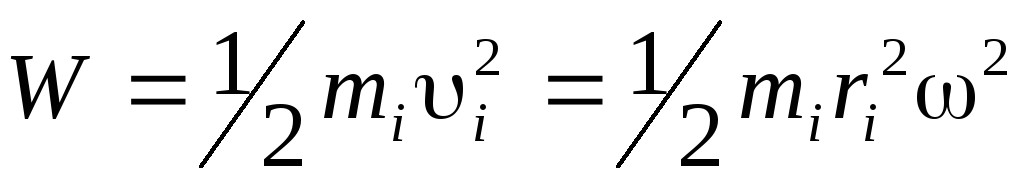, (16)

ku υ i= ωr i- shpejtësia pika materiale, ω - shpejtësi këndore, r i- distanca nga pika në boshtin e rrotullimit. Duke përmbledhur energjitë kinetike të të gjitha pikave materiale, marrim energjinë kinetike të një trupi të ngurtë:

Formula (2 8) është e vlefshme kur trupi rrotullohet rreth një boshti fiks. Nëse trupi lëviz si një i tërë dhe ende rrotullohet, atëherë është energjia kinetike mund të paraqitet si shuma e energjive kinetike të lëvizjeve përkthimore dhe rrotulluese.

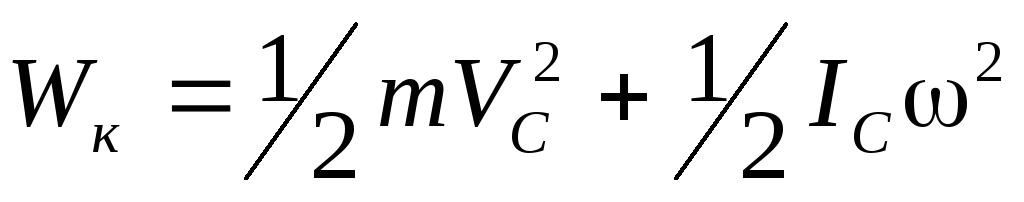(18)

ku V C është shpejtësia e qendrës së masës (qendra e inercisë) e trupit të ngurtë; I C është momenti i inercisë rreth boshtit që kalon nëpër qendrën e masës paralele me vektorin e shpejtësisë këndore.

4.8 Lëkundjet e një trupi në një sustë. Ekuacioni i luhatjeve të vogla

Lëkundjet e lira kryhen nën veprimin e forcave të brendshme të sistemit pasi sistemi të jetë nxjerrë nga ekuilibri. Një shembull i dridhjeve të lira janë dridhjet e një ngarkese në një sustë.

Në mënyrë që lëkundjet e lira të ndodhin sipas ligjit harmonik, është e nevojshme që forca që tenton ta kthejë trupin në pozicionin e ekuilibrit të jetë proporcionale me zhvendosjen x të trupit nga pozicioni i ekuilibrit.

Këtë kusht e plotëson forca elastike e sustës F x =-kx. Koeficienti k quhet ngurtësia e sustës. Të gjitha forcat e tjera që plotësojnë këtë kusht quhen kuazi-elastike.

Nëse një trup i lidhur me një sustë elastike nxirret jashtë ekuilibrit, atëherë mbi trup do të fillojë të veprojë një forcë elastike nga susta, e cila, sipas ligjit të Hukut, është proporcionale me devijimin e trupit nga pozicioni i ekuilibrit. Duhet mbajtur mend se ligji i Hooke është i vlefshëm vetëm për devijime të vogla nga pozicioni i ekuilibrit (në mënyrë sasiore, kjo shprehet me pabarazinë x<< l, ku lështë gjatësia e sustës së pashtrirë, x është zgjatja e sustës).

Ekuacioni i lëvizjes nën veprimin e një force elastike ka formën:

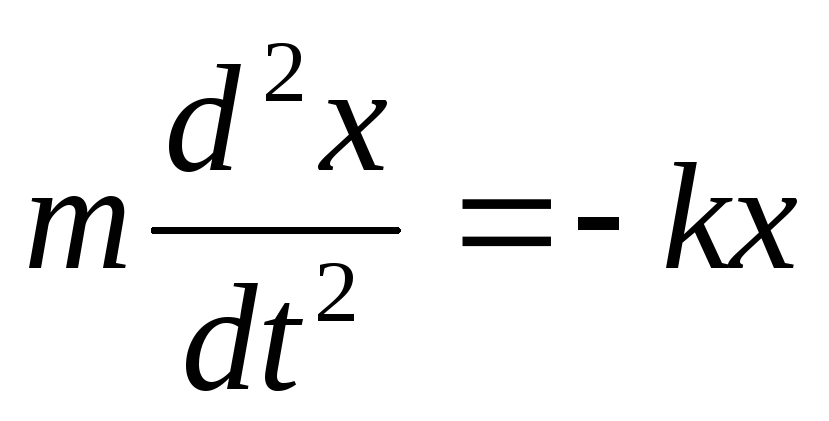(19)

Mund të rishkruhet në një formë tjetër duke futur shënimin ω 2 = k/ m. Pastaj

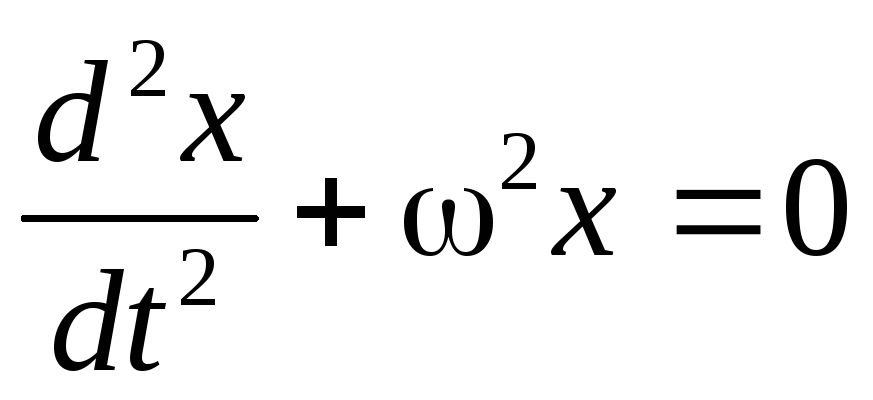(20)

Sistemi që lëkundet i përshkruar nga ky ekuacion quhet oshilator harmonik. Vlera e ω quhet frekuencë natyrore rrethore e lëkundjeve. Për ngarkesën e pranverës

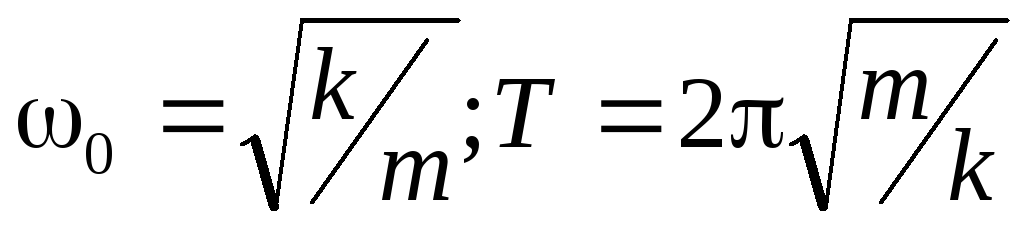; (21)

Lëkundjet harmonike ndodhin sipas ligjit

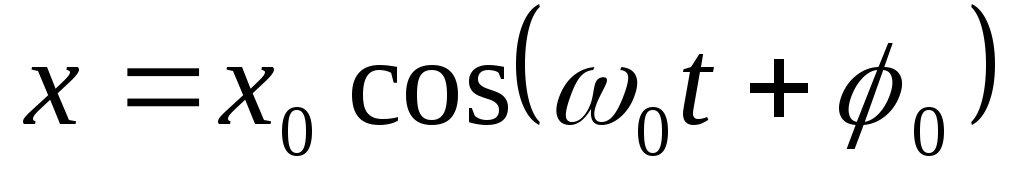, (22)

ku x 0 dhe φ 0 janë amplituda dhe faza fillestare e lëkundjeve. Këto sasi varen nga kushtet fillestare.

Me lëkundjet harmonike, energjia kinetike dhe potenciale ndryshojnë periodikisht, por energjia totale mekanike E e një sistemi të mbyllur në të cilin nuk ka forca rezistence mbetet e pandryshuar.

Për ngarkesën e pranverës

;

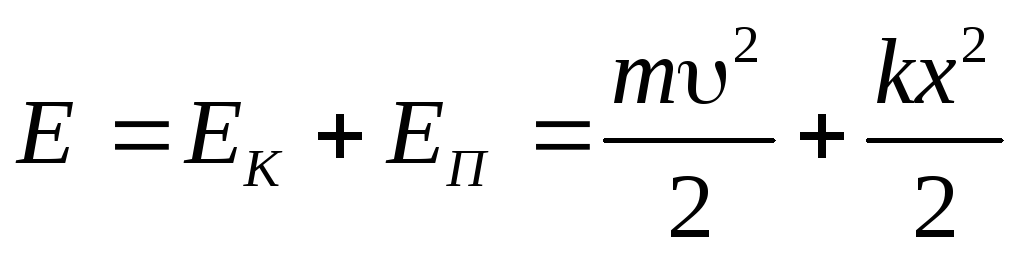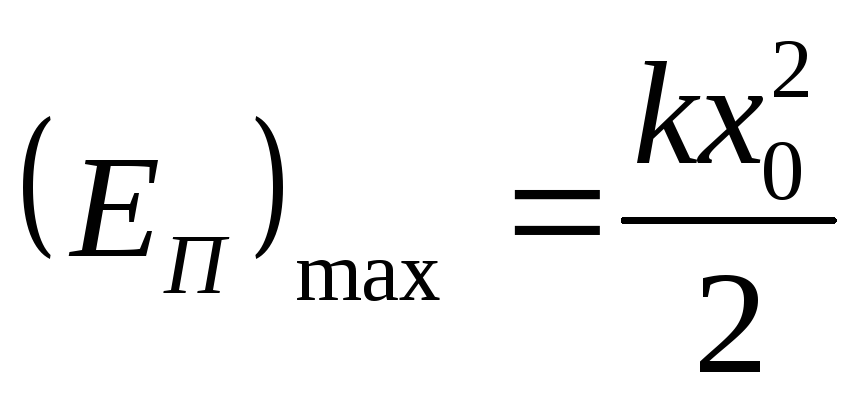;(23)

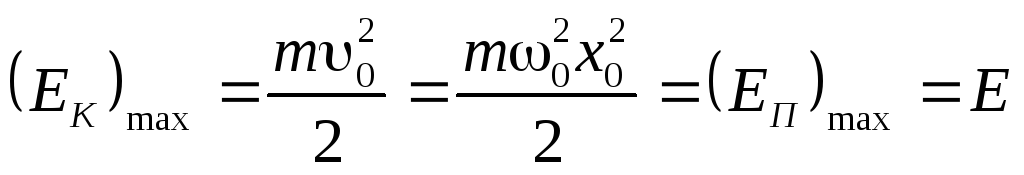(24)

Me lëkundjet harmonike, ka një transformim periodik të energjisë kinetike në energji potenciale dhe anasjelltas.

Në prani të forcave të fërkimit (rezistencës), energjia totale e sistemit zvogëlohet me kalimin e kohës, dhe lëkundjet zbehen.

Nëse forca e rezistencës është proporcionale me shpejtësinë (fërkimi viskoz) F tr \u003d - bυ, amplituda e lëkundjes A zvogëlohet sipas ligjit

A = x0 e- δt , ku δ=b/2 m (25)

Konstanta δ quhet faktor amortizimi. Intervali kohor τ = 1/δ gjatë të cilit amplituda zvogëlohet në e≈2,7 herë quhet koha e kalbjes.