The simplest of atoms, the hydrogen atom, was a kind of test object for Bohr's theory. By the time the theory was created, it had been well studied experimentally. It was known to contain a single electron. The nucleus of an atom is proton - a positively charged particle, the charge of which is equal in absolute value to the charge of the electron, and the mass is 1836 times the mass of the electron. Also in early XIX century were discovered discrete spectral lines in the visible region of radiation of the hydrogen atom (the so-called line spectrum ). Subsequently, the patterns to which the wavelengths (or frequencies) of the line spectrum obey were well studied quantitatively (I. Balmer, 1885). The set of spectral lines of the hydrogen atom in the visible part of the spectrum was called Balmer series . Later, similar series of spectral lines were found in the ultraviolet and infrared parts of the spectrum. In 1890, Johannes Rydberg derived an empirical formula for the frequencies of spectral lines:

This can lead to the formation of a compound formed by two aluminum atoms and three oxygen atoms. It will combine with two oxygen atoms to form a compound. Although the periodic table was a great success at the time, the discovery of new elements that did not fit this table led to the search for another classification system.

In addition, Mendeleev knew some rare earth elements such as lanthanum, ytterbium, erbium, terbium, praseodymium and neodymium, which did not have a place in the table. The problem was solved when it was discovered that the atomic number is a characteristic of the elements, denoting the periodicity of its properties. Today, elements are ordered from left to right and from top to bottom in ascending order of their value. atomic numbers, i.e. by the number of protons in the nucleus of their atoms.

For the Balmer series m = 2, n= 3, 4, 5, ... . For ultraviolet series (Lyman series) m = 1, n= 2, 3, 4, ... . Constant R in this formula is called Rydberg constant . Its numerical value R= 3.29 10 15 Hz. Before Bohr, the mechanism of the appearance of line spectra and the meaning of the integers included in the formulas of the spectral lines of hydrogen (and a number of other atoms) remained incomprehensible.

In the same row are placed the elements which have the same number of electron layers and whose properties change progressively, while the elements which have the same number of electrons in the last layer and which therefore have similar properties are placed in the same column. The first period, as well as the second and third, are called short periods; the fourth and fifth, with eight elements, are long, and the sixth and seventh, with 32 elements, are very long. The last two, in addition to transition metals, are rare earth elements.

Bohr's postulates determined the direction of development of a new science - the quantum physics of the atom. But they did not contain a recipe for determining the parameters of stationary states (orbits) and the corresponding energy values En.

The quantization rule leading to experimentally consistent values ​​of the energies of the stationary states of the hydrogen atom was guessed by Bohr. He suggested that the angular momentum of an electron revolving around the nucleus can only take on discrete values ​​that are multiples of Planck's constant. For circular orbits, the Bohr quantization rule is written as

Patterns in the properties of the elements of the periodic system. The classification of elements in ascending order of atomic number involves the use of two other criteria: atomic mass and similarity in properties. If these elements are ordered from smallest to highest according to their atomic mass, argine should appear in the position that potassium occupies in the modern periodic table. But argon is a noble gas and cannot be in the group of lithium and sodium, which are highly reactive metals.

If they are ordered by atomic number, argon is 18 and potassium is 19, so each is in its respective group. The reason for the similarity of the properties of elements lies precisely in the number and distribution of electrons in their atoms. Elements whose atoms have the same number of electrons in their last layer or energy level have similar Chemical properties and therefore are in the same group as the periodic table.

Here m e - electron mass, υ - its speed, rn is the radius of the stationary circular orbit. Bohr's quantization rule makes it possible to calculate the radii of the stationary orbits of an electron in a hydrogen atom and to determine the energy values. The speed of an electron rotating in a circular orbit of some radius r in the Coulomb field of the nucleus, as follows from Newton's second law, is determined by the relation

The electronic distribution of the first 10 elements is as follows. Please note that electronic levels or levels are completed as you progress beyond certain period. Helium and Neon, which are the last elements of periods 1 and 2, have their full electron layers.

All alkalis have a single electron in the last level. Its electronic configuration. All elements that are in the same group have the same configuration at the last level. All have similar properties. In general, the atoms that make up matter, whether the same or different, are combined, although in nature there are also substances formed by isolated atoms, such as the elements of a group.

where e - elementary charge, ε 0 - electrical constant. Electron velocity υ and stationary orbit radius rn are related by the Bohr quantization rule. It follows that the radii of stationary circular orbits are determined by the expression

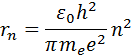
One of the characteristics of the group 18 elements is that they all have eight electrons in their outer layer, with the exception of helium, which has only two. This structure is the most stable, so that the atoms of these elements do not usually interfere with chemical reactions. Therefore, they get the nickname noble or inert gases. The way the rest of the elements try to have 8 electrons in their last layer justifies their chemical behavior.

Therefore, we can conclude that atoms tend to combine to form chemical substances with certain characteristics that are more energy unstable than the original atoms. This type of connection is called chemical bonding. A chemical bond is an attractive force that holds atoms in different atomic clusters.

The orbit closest to the nucleus corresponds to the value n= 1. The radius of the first orbit, which is called Bohr radius , is equal to

The radii of subsequent orbits increase proportionally n 2 .

Complete mechanical energy E a system of an atomic nucleus and an electron circulating in a stationary circular orbit with a radius rn, is equal to

The helium atom has a last full layer, which gives it great stability. In contrast, the hydrogen atom, which has an electron in its last and only layer, is much less stable. However, this stability increases if two hydrogen atoms are close enough to each other to connect their electron layers by sharing their electrons. Such a connection is possible because most of the outer region of the atom is empty space. The diagram shows that under these conditions a series of electrostatic forces are manifested: two nuclei have the same electric charge and repel each other, like two electrons; however, there is mutual attraction between the nuclei and electrons, and the four particles are arranged in such a way that the attractive forces exactly counteract the repulsive forces.

It should be noted that E p< 0, так как между электроном и ядром действуют силы притяжения. Подставляя в эту формулу выражения для υ 2 и rn, we get:

Integer n= 1, 2, 3, ... is called in the quantum physics of the atom principal quantum number .

When this happens, a chemical bond. Atoms that achieve their stability by sharing electrons with other atoms are bound by a covalent bond. A pair of hydrogen atoms is the most stable form of hydrogen at normal temperature.

Molecules that, like hydrogen, contain two atoms are called diatomic molecules. If they contain more than two atoms, they are called polyatomic. Two chlorine atoms are added in a similar way. An individual atom has seven electrons in its last layer. When two chlorine atoms approach each other and connect their electron layers, they have a pair of electrons. Thus, each atom can be considered surrounded by eight electrons. The two chlorine atoms remain attached as a molecule.

According to Bohr's second postulate, during the transition of an electron from one stationary orbit with energy En to another stationary orbit with energy Em < En atom emits a quantum of light, frequency ν nm which is equal to Δ Enm / h:

This formula exactly coincides with the Rydberg empirical formula for the spectral series of the hydrogen atom, if we set the constant R equal

There are many other gaseous chemical elements, which at normal temperature occur in the form of biatomic molecules, such as oxygen, nitrogen, fluorine. Representation of a covalent bond. A covalent bond is the force of attraction that two nuclei exert on the pairs of electrons between them: a pair in a single bond, two pairs in a double bond, and three pairs in a triple bond. A covalent bond can be represented in several ways; for example, a bond between two atoms in a fluoride molecule can be specified in two ways.

Substituting Numeric Values m e , e, ε 0 and h into this formula gives the result

which agrees very well with the empirical value R. Rice. 6.3.1 illustrates the formation of spectral series in the radiation of a hydrogen atom during the transition of an electron from high stationary orbits to lower ones.

On fig. 6.3.2. a diagram of the energy levels of the hydrogen atom is shown and the transitions corresponding to different spectral series are indicated.

Properties of covalent elements. Its melting and boiling points are low. Since there are no free electrons, but they are located, these elements do not conduct electricity. In covalent crystals, atoms are held together only by covalent bonds that form a three-dimensional network.

Diamond contains only carbon atoms and is therefore one of the forms in which this element is present. The carbon atom has the last four electrons in the last layer and four more are missing to have a noble gas structure and can be obtained by sharing each of these electrons with four other carbon atoms.

The excellent agreement between Bohr's theory of the hydrogen atom and experiment served as a weighty argument in favor of its validity. However, attempts to apply this theory to more complex atoms have not been successful. Bohr was unable to give a physical interpretation of the quantization rule. This was done a decade later by de Broglie based on ideas about wave properties ah particles. De Broglie proposed that each orbit in the hydrogen atom corresponds to a wave propagating in a circle around the nucleus of the atom. A stationary orbit occurs when the wave continuously repeats itself after each revolution around the nucleus. In other words, a stationary orbit corresponds to a circular standing de Broglie wave over the length of the orbit (Figure 6.3.3). This phenomenon is very similar to the stationary picture of standing waves in a string with fixed ends.

Thus, it acquires a stable electronic structure, similar to the structure of neon, with four pairs of electrons in the last layer. The substance iodine is formed by iodine molecules connected by intermolecular forces forming a crystalline or three-dimensional network. Since these attractive forces between molecules are weak, these crystals can be easily destroyed.

In the carbon structure diagram, it is observed that only the central element has the last layer. This allows each of the other four atoms to form, in turn, covalent bonds with four other atoms and thus fill their electronic layers. As each atom does this, a giant network is created.

In stationary quantum state of a hydrogen atom, according to de Broglie's idea, an integer number of wavelengths λ, i.e.,

Substituting into this relation the de Broglie wavelength λ = h / p, where p = m e υ - electron momentum, we get:

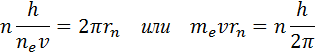
In diamond, the carbon atoms are in the form of a three-dimensional network that is extremely stable in all directions. Diamond is one of the most solids, which is known and remains in the solid state at very high temperatures. Properties of covalent atomic crystals.

All properties of these solid crystals show that very strong forces are established between the particles that form them. The theorem tells us that these forces are due to the covalent bonds between their atoms. Diamond is very hard, its melting and boiling points are very high. covalent bonds between the carbon atoms forming the network are so strong that a significant amount of energy is required to destroy the structure. Because it has no free electrons, it does not conduct electricity.

Thus, the Bohr quantization rule is related to the wave properties of electrons.

The success of Bohr's theory in explaining the spectral patterns in the study of the hydrogen atom was amazing. It became clear that atoms are quantum systems, and energy levels stationary states of atoms are discrete. Almost simultaneously with the creation of Bohr's theory, direct experimental evidence was obtained for the existence of stationary states of the atom and for energy quantization. The discreteness of the energy states of the atom was demonstrated in 1913, in the experiment of D. Frank and G. Hertz, in which the collision of electrons with mercury atoms was studied. It turned out that if the energy of electrons is less than 4.9 eV, then their collision with mercury atoms occurs according to the law of absolutely elastic impact. If the electron energy is equal to 4.9 eV, then the collision with mercury atoms acquires the character of an inelastic impact, i.e., as a result of a collision with immobile mercury atoms, the electrons completely lose their kinetic energy. This means that the mercury atoms absorb the energy of the electron and pass from the ground state to the first excited state,

When approximating two atoms, the following cases may occur. There are repulsive forces between electrons and nuclei that increase as they approach, and a bond is never formed, such as trying to approximate two helium atoms. Forces of attraction arise between the nucleus of one atom and the electrons of another, and vice versa. In this case, the energy of the system decreases by some distance; then a bond is formed between the two atoms.

In the process of bond formation, energy is always released. Therefore, in order to separate the atoms that form an element or compound, it is necessary to provide an energy equal to or greater than the energy released during the formation of a bond. Graphite is another form of carbon found in nature. In this case, the carbon atoms are arranged in six-membered rings. Each carbon atom is covalently bonded to three other atoms. Thus, the electrons leave freedom of movement, so graphite conducts electricity.

E 2 - E 1 = 4.9 eV.

According to the Bohr concept, during the reverse spontaneous transition of an atom, mercury should emit quanta with a frequency

A spectral line with such a frequency was actually detected in the ultraviolet part of the emission spectrum of mercury atoms.

It is a black substance, shiny, soft and colorless to the touch, as it is presented in slips slightly attached to each other and which slide over each other. It is used to make electrodes for their property of conducting electricity, and to make pencil shafts and printer ribbons for computers.

Metals have properties very different from other substances that enhance the existence of a particular type of bond and characteristic that makes them possible. Metallic elements usually have atoms containing 1, 2, or 3 electrons in their outer layer. These electrons are weakly bound to atomic nucleus so they can be easily recycled.

The concept of discrete states contradicts classical physics. Therefore, the question arose whether quantum theory refutes its laws.

Quantum physics has not canceled the fundamental classical laws of conservation of energy, momentum, electric discharge, etc. According to N. Bohr conformity principle , the quantum physics includes the laws of classical physics, and under certain conditions it is possible to detect a smooth transition from quantum to classical concepts. This can be seen in the example of the energy spectrum of the hydrogen atom (Fig. 6.3.2). For large quantum numbers n>> 1 discrete levels gradually approach each other, and there is a smooth transition to the region of the continuous spectrum, which follows from classical physics.

Imagine a set of atoms of a metallic element that are separated and come as close together as possible. Under these conditions, the outer electron layers of atoms overlap completely, and any electron originally emanating from a given electron layer is now not associated with any particular atom, but is shared by all the atoms in the set. These atoms are connected by a metallic bond.

A metallic crystal is formed by positively charged stationary atoms immersed in a sea of ​​electrons that delocalize and therefore do not belong to any particular atoms. Because they are very compact, the metals are quite hard, but they can be stretched to form wires, as one layer of atoms can be moved over another.

Bohr's half-hearted, semiclassical theory was an important stage in the development of quantum concepts, the introduction of which into physics required a radical restructuring of mechanics and electrodynamics. Such a restructuring was carried out in the 20s - 30s of the XX century.

Bohr's idea of ​​certain orbits along which electrons move in an atom turned out to be very conditional. In fact, the motion of an electron in an atom bears very little resemblance to the motion of planets or satellites. The physical meaning is only the probability of finding an electron in one place or another, described by the square of the modulus of the wave function |Ψ| 2. The wave function Ψ is the solution to the main equation quantum mechanics - Schrödinger equations . It turned out that the state of an electron in an atom is characterized by a whole set of quantum numbers. Principal quantum number n determines the quantization of the energy of the atom. To quantize the angular momentum, the so-called orbital quantum number l . The projection of the angular momentum onto any direction distinguished in space (for example, the direction of the vector magnetic field) also takes a discrete series of values. To quantize the projection of the angular momentum, we introduce magnetic quantum number m . quantum numbers n, l, m bound by certain quantization rules. For example, the orbital quantum number l can take integer values ​​from 0 to ( n- one). Magnetic quantum number m can take any integer values ​​in the interval ± l. Thus, each value of the principal quantum number n, which determines the energy state of the atom, corresponds to a number of combinations of quantum numbers l and m. Each such combination corresponds to a certain probability distribution |Ψ| 2 detection of an electron at various points in space ("electron cloud").

States in which the orbital quantum number l= 0 are described by spherically symmetric probability distributions. They're called s-states (1 s, 2s, ..., ns, ...). For values l> 0 the spherical symmetry of the electron cloud is broken. States since l= 1 are called p- states, with l = 2 - d-states, etc.

On fig. 6.3.4 shows the probability distribution curves ρ ( r) = 4π r 2 |Ψ| 2 detection of an electron in a hydrogen atom at various distances from the nucleus in states 1 s and 2 s.

As can be seen from fig. 6.3.4, electron in state 1 s(the ground state of the hydrogen atom) can be detected at various distances from the nucleus. FROM most likely it can be detected at a distance equal to the radius r 1 of the first Bohr orbit. Probability of finding an electron in state 2 s maximum distance r = 4r 1 from the core. In both cases, the hydrogen atom can be represented as a spherically symmetrical electron cloud, in the center of which is the nucleus.

Spectral series of the hydrogen atom.

Studies of the emission spectra of rarefied gases (i.e., the emission spectra of individual atoms) have shown that each gas has a certain ruled a spectrum consisting of individual spectral lines or groups of closely spaced lines. This is especially pronounced in the spectrum of the simplest hydrogen atom.

The Swiss scientist I. Balmer picked up an empirical formula that describes all the spectral lines of the hydrogen atom known at that time in visible region of the spectrum:

where n=3;4;5;6.

Along with the Balmer series, other series were found in the spectrum of atomic hydrogen, the wave numbers of which can be represented by similar formulas.

AT ultraviolet Lyman series areas:

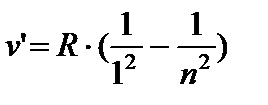n = 2;3… (8.4)

AT infrared areas:

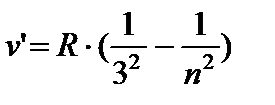- Paschen series, n =4;5…

) - Bracket's series, n = 5;6… (8.5)

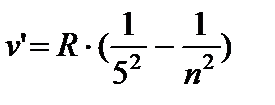- Pfund series, n = 6;7…

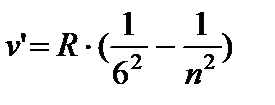- Humphrey series, n = 7;8…

Analyzing relations (8.3) - (8.5), we can say that all series of atomic hydrogen can be represented general formula called by the generalized Balmer formula:

(8.6)

where m has a constant value in each given series, m=1;2;3;4;5;6 (defines series); a n=m+1, m+2,… (defines the individual lines of this series).

The energy of the stationary state of the atom: (8.9)

The "-" sign has conditional value, pure physical meaning– the energy of an electron in the field of a positive nucleus is negative. From (8.9) it can be seen that the energy of stationary states forms a discrete series for n=1;2;3…

The postulates put forward by Bohr made it possible to calculate the spectrum of the hydrogen atom and hydrogen-like systems (systems consisting of a nucleus with a charge Ze and one electron (for example, ions Not + , Li +), and theoretically calculate the Rydberg constant.

Following Bohr, let us consider the motion of an electron in a hydrogen-like system, confining ourselves to circular stationary orbits. Potential energy interactions of an electron with a nucleus:

(9.1),

r is the radius of the orbit. Kinetic energy electron moving around the nucleus: (9.2).

Then total energy atom:


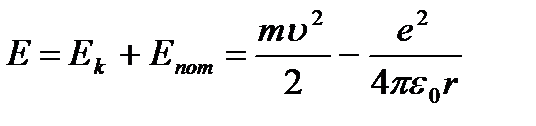(9.3).

The electron around the nucleus moves with acceleration 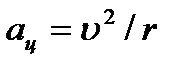under the influence of the Coulomb force: .

According to Newton's second law ( ma = F k) can be written:

(9.4);

from here 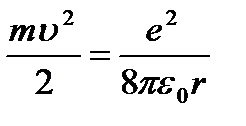(9.5).

We put (9.5) in (9.3): 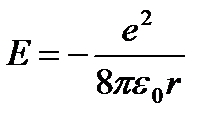(9.6).

Bohr proposed a selection rule or quantization rule (Bohr's third postulate): of all possible orbits of an electron, only those for which the angular momentum of the electron is a multiple of Planck's constant are realized:

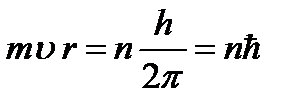(9.7),

where n=1,2,3,… is the main quantum number. Using relations (9.4) and (9.7), we determine the radius of the stationary electron orbit:

(9.8),

at (radius of the first orbit).

From (9.8) it follows 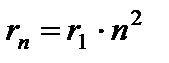. Substituting (9.8) into (9.10) we obtain an expression for stationary state energies:


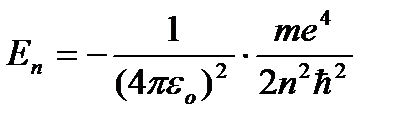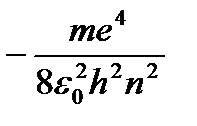= (9.9)

At - energy of the first stationary state.

In a state of energy E 1 an atom can stay indefinitely. In order to ionize the hydrogen atom, i.e. to tear off an electron from it, it needs to be given an energy of 13.55 eV.

eV; ;

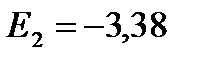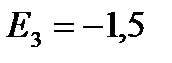eV; eV; eV, etc.

The state , ,… correspond to an excited atom. The lifetime in these states is of the order . During this time, the electron manages to make about 100 million revolutions around the nucleus.

Giving n different integer values, we obtain for the hydrogen atom, according to formula (9.9), the possible energy levels. Hydrogen atom energy with increasing P increases and the energy levels approach the boundary corresponding to the value n=¥. The hydrogen atom thus has a minimum energy (E 1 \u003d -13.55 eV) at n=1 and maximum (E ¥ =0) at P=¥ . Therefore, the value of E ¥ = 0 corresponds to the ionization of the atom (separation of an electron from it). According to Bohr's second postulate, during the transition of a hydrogen atom from the stationary state n to a steady state t a quantum is emitted with less energy:



,

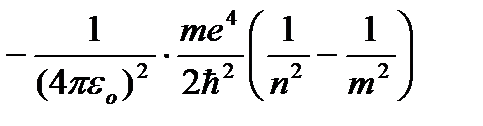whence the radiation frequency:

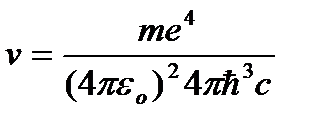
=R , (9.10)

where .

Using in the calculation R modern values universal constants, we obtain a value that coincides with the experimental value of the Rydberg constant in the empirical formulas for the hydrogen atom:

.

This coincidence proves the correctness of the formula obtained by Bohr for the energy levels of a hydrogen-like system.

Substituting, for example, into formula (9.10) m=1 and n=2, 3, 4, ..., we obtain a group of lines that form the Lyman series and correspond to the transitions of electrons from excited levels (n= 2, 3, 4, ...) on the main (t= 1). Similarly, when substituting t= 2, 3, 4, 5, 10 and their corresponding values n we get the Balmer, Paschen, Bracket, Pfund and Humphrey series (some of them are schematically presented in Fig. 9.1.). Consequently, according to Bohr's theory, which quantitatively explained the spectrum of the hydrogen atom, the spectral series correspond to radiation resulting from the transition of an atom to a given state from excited states located above this one.


Bohr's theory showed the inapplicability of classical physics to intra-atomic phenomena and the need to apply quantum laws in the microcosm. But an attempt to construct a similar theory for the helium atom failed. Bohr's theory was neither consistently classical nor consistently quantum theory. The shortcomings of Bohr's theory could be eliminated by creating a new quantum theory, in which the behavior and movement of microparticles obeys its own laws. This was done in the creation of quantum mechanics.

The state of an electron in an atom is characterized by not one, but several quantum numbers.

First their quantum numbers - principal quantum number: n= one; 2;3,… It determines the energy levels of an electron in an atom: and radii of stationary orbits . These expressions follow from the solution of the Schrödinger equation and coincide with the corresponding formulas obtained by Bohr.

Second quantum number - orbital quantum number, which at the given n can take values ​​0, 1, 2, ..., n-one . This number determines the orbital angular momentum electron relative to the nucleus. The angular momentum of an electron in an atom is quantized by the formula:

Third quantum number - magnetic quantum number, which, when given, takes the values ​​0; ±1; ±2,…, ± ; total 2+1 values. This number determines the projections of the orbital angular momentum of the electron onto some arbitrarily chosen direction Z. Only such orientations of the angular momentum vector are possible, for which the projection of the vector onto the direction of the external magnetic field (axis OZ) takes the values: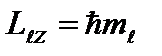

Fourth quantum number - spin(magnetic spin) quantum number m s . It can only take two values 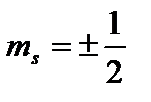and characterizes the possible values ​​of the projection onto the Z axis of the spin (intrinsic mechanical angular momentum) of the electron: 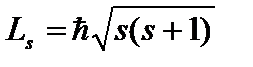, where is the spin quantum number. Spatial spin quantization means that the projection of the spin vector onto the direction of the external magnetic field is found by the formula: .

In 1924, the Swiss physicist Pauli formulated the principle that: in any atom there cannot be two electrons that are in two identical stationary states, determined by a set of four quantum numbers - the main n; orbital; magnetic m and spin m s. The Pauli principle, in addition to electrons, obeys other particles that have a half-integer spin (in units).

Let us determine the number of electrons with a certain .

Electrons with =0 are called s 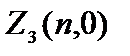= 2(2×0+1)=2.

Electrons with =1 are called R-electrons, their maximum number is 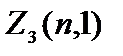=2(2×1+1)=6.

Electrons with =2 are called d-electrons, their maximum number is =2(2 2+1)=10.

Electrons with =3 are called f-electrons, their maximum number is 2(2×3+1)=14 etc.

Maximum number electrons in states determined by the value n principal quantum number

=

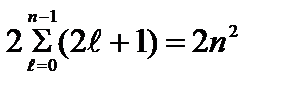
Electrons occupying a set of states with the same value of the principal quantum number n form an electron shell. There are the following electron shells (or layers): K-layer at n = 1; L- layer at n = 2; M- layer at n = 3; N- layer at n=4 etc. In each quantum shell of an atom, electrons are distributed among subshells corresponding to a certain value of the orbital quantum number; depending on the electron is in a subgroup with symbols s, p, d, f etc.

Principal quantum number Electronic shell (layer) Number of electrons in states Maximum number of electrons
s ( =0) p ( =1) d ( =2) f ( =3)
K – – –
L – –
M –
N

In a state determined by the principal quantum number n= 1, there can only be two s-electrons with two different spin orientations (see Fig. 10.1).

If a n= 2, then the circuit has the form shown in Fig. 10.2.

The sequence of filling electronic states in the atoms of chemical elements is explained by the Pauli principle.

This principle explains the periodicity of the properties of chemical elements in the periodic system created by D.I. Mendeleev.

Let us trace the construction of the periodic system (or the filling of the layers of the atom with electrons), which obey two principles: a) the filling starts from the lowest energy (the most stable state); b) the Pauli exclusion principle.

The first element in the periodic table is a hydrogen atom H, for it Z = 1. It has one electron, the quantum numbers for which are: n \u003d 1, \u003d 0, m e \u003d 0, m s \u003d +1/2 or -1/2, i.e. the electronic configuration of the hydrogen atom: 1S1.

The next element is helium Not there are two electrons, quantum numbers: n \u003d 1, \u003d 0, m e \u003d 0, m s \u003d ±1/2, i.e. the electronic configuration of the helium atom: 1S 2. Layer K with the number of electrons N = 2 is completely filled.

The third element is lithium Li. Its third electron has quantum numbers: n \u003d 2, \u003d 0, m e \u003d 0, m s \u003d +1/2 or - 1/2, i.e. the electronic configuration of the atom 1S 2 2S 1.

beryllium Ve: Z = 4 electronic configuration of the atom 1S 2 2S 2 .

The next six elements have shells filled with 2p. As a result, neon Ne with Z = 10 has the electronic configuration of the atom 1S 2 2S 2 2P 6, i.e. L- the layer is completely filled and this ends the second layer of the periodic table. He, Ne, as well as other atoms in which the s- or s- and p-subgroups are completely occupied by electrons, are similar in properties and chemically inert.

Z element symbol Element name Electronic configuration
H hydrogen 1s 1
Not helium 1s2
Li lithium 1s1 2s1
Be beryllium 1s2 2s2
B boron 1s 2 2s 2 2p 1
C carbon 1s 2 2s 2 2p 2
N nitrogen 1s 2 2s 2 2p 3
O oxygen 1s 2 2s 2 2p 4
F fluorine 1s 2 2s 2 2p 5
Ne neon 1s 2 2s 2 2p 6
Na sodium 1s 2 2s 2 2p 6 3s 1
mg magnesium 1s 2 2s 2 2p 6 3s 2
Al aluminum 1s 2 2s 2 2p 6 3s 2 3p 1
Si silicon 1s 2 2s 2 2p 6 3s 2 3p 2
R phosphorus 1s 2 2s 2 2p 6 3s 2 3p 3
S sulfur 1s 2 2s 2 2p 6 3s 2 3p 4
Cl chlorine 1s 2 2s 2 2p 6 3s 2 3p 5
Ar argon 1s 2 2s 2 2p 6 3s 2 3p 6

Violations during the filling of layers are observed in an element with Z=19 (potassium K), where the filling of the 4s shell begins with an unfilled 3d:

and so on until the 3d shell is filled.

This violation is associated with the interaction between electrons, the state of which is characterized by the main quantum numbers n=3, n=4, etc. As a result of the interaction, such a situation arises that a state with a large n, but a small one can be energetically more favorable.

A similar situation is observed in rare-earth elements, or lanthanides (atoms with numbers 58-71), in which the shells 5s, 5p, 6s are filled with an unfilled 4 f shell. They all have an outer shell 6s 2 . Another deviation applies to actinides (atoms with numbers 90-103), in which 5 f shell after filling the outer shell 7s 2 .

Topic 29. Optical quantum generators

Due to the selection rules, the atoms of many elements have energy levels from which an electron cannot directly move to a lower level. These levels are called metastable states. An electron can go to such a level when colliding with another electron or when moving from a higher high level. The duration of an electron's stay in a metastable state is on the order of 10–3 s, while in an excited state it is 10–8 s.

The radiation emitted during the spontaneous transition of an atom from an excited state to the ground state is called spontaneous emission. Spontaneous emission various atoms does not occur coherently, because each atom starts and ends radiation independently of the others (Fig. 15.1a).

The emission of energy by an atom, in which the transition from metastable state in the main is called electromagnetic radiation corresponding frequency is called forced or induced, radiation (Fig. 15.1b).

The probability of stimulated emission increases sharply when the frequency coincides electromagnetic field with the natural radiation frequency of the excited atom. Stimulated radiation has the same frequency, phase, polarization and propagation direction as the stimulating radiation. Consequently, stimulated emission strictly coherent with the stimulating radiation, that is, the emitted photon is indistinguishable from the photon incident on the atom. The emitted photons, moving in one direction and meeting other excited atoms, stimulate further induced transitions, and the number of photons grows like an avalanche.

However, along with stimulated emission, a competing process, absorption, is also possible. In a system of atoms that is in thermodynamic equilibrium, the absorption of the incident radiation will prevail over the forced one, i.e. Incident radiation will be attenuated as it passes through matter.

In order for the medium to amplify the radiation incident on it, it is necessary to create non-equilibrium state of the system, at which the number of atoms in excited states would be greater than their number in the ground state. Such states are called states. with inverse population. The process of creating a non-equilibrium state of matter (transferring the system to a state with population inversion) is called pumped. Pumping can be done by optical, electrical and other methods. Media with inverse states are called active. They can be considered as media with a negative absorption coefficient, since the incident beam of light will be amplified as it passes through these media.

For the first time, the possibility of obtaining media in which light can be amplified due to stimulated emission was pointed out in 1939 by the Russian physicist V.A. Fabrikant. He experimentally discovered the stimulated emission of mercury vapor excited by an electric discharge. The discovery of the phenomenon of amplification of electromagnetic waves and the invented method of their amplification (V.A. Fabrikant, M.M. Vudynsky, F.A. Butaeva; 1951) formed the basis of quantum electronics, the provisions of which subsequently made it possible to implement quantum amplifiers and quantum light generators.

The practically inverse state of the medium is realized in optical quantum generators, or lasers (from the first letters of the English name Light Amplification by Stimulated Emission of Radiation - light amplification by stimulated emission). Lasers generate in the visible, infrared and near ultraviolet regions (in the optical range). The idea of ​​a qualitatively new principle of amplification and generation of electromagnetic waves, applied in masers (generators and amplifiers operating in the centimeter range of radio waves) and lasers, belongs to Russian scientists N.G. Basov and A.M. Prokhorov and American physicist C. Towns, who were awarded Nobel Prize 1964

The most important of existing types lasers are solid-state, gas, semiconductor and liquid (the basis of such a division is the type of active medium). A more accurate classification also takes into account pumping methods - optical, thermal, chemical, electroionization, etc. In addition, it is necessary to take into account the generation mode - continuous or pulsed.


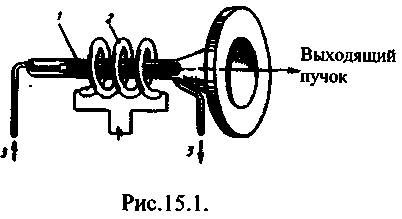The laser necessarily has three main components: 1) active environment, in which states with population inversion are created; 2) pumping system(device for creating inversions in the active medium); 3) optical resonator(a device that separates the selective direction of the photon beam into space and forms the outgoing light beam).

The first solid-state laser operating in the visible region of the spectrum (radiation wavelength 0.6943 μm) was a ruby ​​laser created in 1960 (T. Maiman, USA). Figure 16.1 shows the scheme of a ruby ​​laser. In it, the inverse population of levels is carried out according to a three-level scheme proposed in 1955 by N. G. Basov and A. M. Prokhorov. A ruby ​​crystal is aluminum oxide Al 2 Oz, in the crystal lattice of which some of the Al atoms are replaced by trivalent Cr e + ions (0.03 and 0.05% of chromium ions, respectively, of pink and red ruby). For optical pumping, a pulsed gas-discharge lamp (2) is used, spirally twisted around a ruby ​​rod (1). When a ruby ​​is intensely irradiated with the light of a powerful flash lamp, chromium atoms pass from the lower level to the levels of a wide band 3 (Fig. 16.2). Since the lifetime of chromium atoms in excited states is short (less than 10 -7 s), either spontaneous 3®1 transitions occur (they are insignificant), or the most probable nonradiative transitions to the level 2 (it is called metastable) with the transfer of excess energy to the ruby ​​crystal lattice. The 2®1 transition is forbidden by the selection rules, so the duration of the excited state 2 chromium atoms of the order of 10 -3 s, i.e. about four orders of magnitude greater than for the state 3. This leads to the "accumulation" of chromium atoms at level 2 . With sufficient pump power, their concentration at level 2 will be much higher than at level 1 , i.e., a medium arises with an inverse population of level 2.

The ruby ​​laser rod was a cylinder, the ends of which were carefully polished and covered with a layer of silver in such a way that one end completely reflected light, and the other partially reflected and partially transmitted light. When the pump lamp flashes, photons of various frequencies enter the ruby ​​rod. Chromium atoms, having absorbed part of the photons of a certain energy, go into an excited state. Due to limited spontaneous transitions, stimulated radiation can arise in the rod, which propagates strictly along its axis and is amplified by multiple reflections from the end mirrors, which play the role cavity resonator. As a result, powerful monochromatic radiation arises - a light pulse, part of which exits through a translucent mirror. The duration of such a pulse is 10–3 s. This is due to the fact that all excited chromium ions during this time pass into the unexcited state. The laser light beam is strictly directed and has a small divergence. The cavity resonator of the laser serves to create a positive feedback and to form the geometric parameters of the laser output beam.

Not all of the energy absorbed by the ruby ​​rod is converted into laser radiation. Part of it, quite significant (50%), is spent on heating the rod, so the laser design provides for cooling 3. At a rod temperature of about 1000 K, the ruby ​​laser is destroyed.

There are a large number of laser materials: glass, in which neodymium ions are introduced, calcium fluorite with samarium ions, etc. They give light radiation various lengths waves: ruby ​​laser - 0.694 microns, neodymium glass laser - 1.06 microns (infrared radiation). In lasers, gases or mixtures of gases (Ne, Ar, Ne–He, CO 2, etc.) can be used as an active medium. In gas lasers, the atoms of the active medium are often excited by a high-frequency discharge. As a rule, the emission of gas lasers is continuous. Semiconductor, chemical, gas-dynamic and other lasers have been created.

Laser radiation has the following properties:

1) temporal and spatial coherence;

2) strict monochromaticity;

3) high energy flux density;

4) very small angular divergence in the beam.

Unusual Properties laser radiation have found wide application. For example, in light-beam machines, using a laser beam, holes are made in watch stones made of ruby, diamond, in refractory alloys and hard-to-cut metals. In microelectronics, lasers are used to weld various connections for microcircuits, deposit semiconductor layers, etc.

Topic 30. Elements of quantum mechanics

The French scientist Louis de Broglie, developing ideas about the dual corpuscular-wave nature of light, put forward in 1923 a hypothesis about the universality of corpuscular-wave dualism. De Broglie argued that there is a deep analogy between the properties of light and the properties of material particles; therefore, material particles also have a dual nature, i.e. under certain conditions, their wave properties are manifested.

De Broglie postulated that a particle with momentum corresponds to the wavelength: (1.2)

This relation (de Broglie's formula) is valid for any particle with momentum R.

Soon de Broglie's hypothesis was confirmed experimentally. American physicists K. Davisson and L. Germer in 1927 studied the scattering of electrons on a nickel single crystal using the setup shown in fig. The electron beam from the electron gun 1 was directed to the nickel crystal 2, the electrons 3 scattered from the crystal were captured by a special receiver 4 connected to a sensitive galvanometer. The intensity of the reflected beam was determined from the strength of the current flowing through the galvanometer. Experiments have shown that at a given angle of incidence, electrons are reflected from the crystal surface at different angles, and maxima of the number of reflected electrons are observed in some directions, minima in others, that is, a diffraction pattern was observed. This phenomenon was observed when the de Broglie electron wavelength 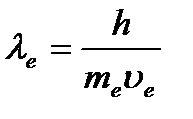is of the order of the interatomic distance in the crystal. The diffraction maxima corresponded to the Wulf-Braggs formula , and the Bragg wavelength turned out to be exactly equal to the length wave calculated by formula (1.2).

Later, PS Tartakovskii and G. Thomson investigated the passage of fast electrons through thin metal films. At the same time, on photographic plates behind these films, a diffraction pattern was obtained, the same as in diffraction x-rays on polycrystals.

In 1849, V.A. Fabrikant, L.M. Biberman and N.G. Sushkin carried out experiments on electron diffraction with a very low current in the device, that is, each electron was recorded by a photographic plate in random places. With a long exposure, the same diffraction pattern was obtained as with a short exposure with a high current strength. This means that the wave properties are inherent in each electron separately, but the diffraction of one electron does not give the entire system of points, which is obtained with diffraction from the flow. The trace of one electron will be at only one point, which is allowed by the diffraction condition. This shows the corpuscular nature of electrons, since an electron cannot spread out. In which of the places the electron will fall, it is impossible to say. We can only talk about the probability of hitting a point in space.

Thus, the electron has a dual nature, i.e. it combines the properties of both particles and waves. The wave nature of electrons is confirmed by experiments on their diffraction. The corpuscular nature of electrons is manifested in the fact that the electron acts as a whole, without breaking up into parts.

Subsequently, diffraction phenomena were also discovered for neutrons, protons, atomic and molecular beams. This finally served as a proof of the presence of wave properties of microparticles and made it possible to describe the motion of microparticles in the form of a wave process characterized by a certain wavelength calculated by the de Broglie formula (1.2).