16. Stern's theorem.

If the moment of inertia of a body about an axis passing through its center of mass is known, then the moment of inertia about any other parallel axis is determined by the Steiner theorem : moment of inertia of the body J relative to an arbitrary axis is equal to its moment of inertia Jc relative to a parallel axis passing through the center of mass FROM body, added to the product of the mass t body per square distance a between axles:

17. Equation of dynamics rotary motion solid body.

Iε = M. This is the basic equation of the dynamics of the rotational motion of a rigid body. Angular acceleration ε and torque M in this equation are algebraic quantities. Usually, the positive direction of rotation is counterclockwise.

A vector form of the basic equation of the rotational motion dynamics is also possible, in which the quantities are defined as vectors directed along the axis of rotation. When studying the translational motion of bodies, the concept of body momentum is introduced. Similarly, when studying rotational motion, the concept of angular momentum is introduced. The angular momentum of a rotating body is a physical quantity equal to the product of the moment of inertia of the body I and the angular velocity ω of its rotation. The angular momentum is denoted by the letter L: The angular momentum of the whole body is defined as the vector sum of Li. L = Iω. This equation, obtained here for the case when I = const, is also valid in the general case when the moment of inertia of the body changes during the motion.

18. Kinetic energy of a rotating body.

Consider an absolutely rigid body (see § 1) rotating about a fixed axis z passing through it (Fig. 24). Let's mentally divide this body into small volumes with elementary masses t 1 , t 2 ,..., t n , at a distance r 1 , r 2 ,..., rn from the axis.

When a rigid body rotates about a fixed axis, its individual elementary volumes with masses m i describe circles of various radii r i, and have different linear speeds v i . But since we are considering an absolutely rigid body, the angular velocity of rotation of these volumes is the same: (17.1) We find the kinetic energy of a rotating body as the sum of the kinetic energies of its elementary volumes:

or Using expression (17.1), we obtain

where Jz- moment of inertia of the body about the z-axis. In this way, kinetic energy rotating body (17.2)

From a comparison of formula (17.2) with expression (12.1) for the kinetic energy of a body moving forward (T=mv 2 /2), It follows that the moment of inertia is measure of body inertia during rotational movement. Formula (17.2) is valid for a body rotating around a fixed axis. In the case of a plane motion of a body, for example, a cylinder rolling down an inclined plane without sliding, the energy of motion is the sum of the energy of translational motion and the energy of rotation: where m- mass of the rolling body; vc- the speed of the center of mass of the body; Jc- the moment of inertia of the body about the axis passing through its center of mass; w is the angular velocity of the body. The work of the external force on the rotation of the body F=Fi+Fr+Fk. The work of the force of a rotating body A=M* ∆φ

19. Gravitational field.

Gravitational interaction between bodies is carried out with the help of the gravitational field, or gravitational field. This field is generated by bodies and is a form of existence of matter. The main property of the gravitational field is that for any body of mass t, brought into this field, the gravitational force acts, i.e. (24.1)

The vector g does not depend on m and is called the strength of the gravitational field. The intensity of the gravitational field is determined by the force acting from the side of the field on the material point of a unit mass, and coincides in direction with the acting force. There is tension power characteristic gravity fields. The gravitational field is called homogeneous if its intensity is the same at all points, and central if at all points of the field the intensity vectors are directed along straight lines that intersect at one point (A) motionless with respect to any inertial frame of reference (Fig. 38). For a graphical representation of the force field are used lines of force (lines of tension). The field lines are chosen so that the field strength vector is directed tangentially to the field line.

The value is energy characteristic gravitational field is called the potential. Gravitational field potential j- a scalar quantity determined by the potential energy of a body of unit mass at a given point in the field or by the work of moving a unit mass from a given point of the field to infinity. Thus, the potential of the gravitational field created by a body of mass M, equals (25.4) where R- the distance from this body to the point in question. From formula (25.4) it follows that the locus of points with the same potential forms a spherical surface ( R= const). Such surfaces for which the potential is constant are called equipotential. Consider the relationship between the potential ( j) gravitational field and its intensity (g). From expressions (25.1) and (25.4) it follows that the elementary work d A, performed by the field forces with a small displacement of a body with a mass t, is equal to

20. Pressure in liquids and gases. Laws of Pascal and Archimedes.

Unit of pressure - pascal(Pa): 1 Pa is equal to the pressure created by a force of 1 N, uniformly distributed over a surface normal to it with an area of ​​​​1m 2 (1 Pa \u003d 1 N / m 2).

Pressure at equilibrium of liquids (gases) obeys Pascal's law: the pressure in any place of a fluid at rest is the same in all directions, and the pressure is equally transmitted throughout the volume occupied by the fluid at rest. Let us consider how the weight of a fluid affects the distribution of pressure inside an incompressible fluid at rest. When a liquid is in equilibrium, the horizontal pressure is always the same, otherwise there would be no equilibrium. Therefore, the free surface of a fluid at rest is always horizontal away from the walls of the vessel. If a fluid is incompressible, then its density is independent of pressure. Then for the cross section S liquid column, its height h and density r the weight P=rgSh, and the pressure on the lower base

(28.1) i.e. pressure changes linearly with height. Pressure rgh called hydrostatic pressure. According to formula (28.1), the pressure force on the lower layers of the liquid will be greater than on the upper ones, therefore, a force determined by the law of Archimedes acts on a body immersed in a liquid (gas): a directed force acts on a body immersed in a liquid (gas). upward buoyant force equal to the weight of the liquid (gas) displaced by the body: F BUT =PgV, where R - fluid density, V- the volume of a body immersed in a liquid.

21. Line and tube of current. Jet continuity theorem.

The movement of fluids is called a flow, and the collection of particles of a moving fluid is called a flow. Graphically, the movement of fluids is depicted using streamlines, which are drawn so that the tangents to them coincide in direction with the fluid velocity vector at the corresponding points in space (Fig. 45). Streamlines are drawn in such a way that their density, which is characterized by the ratio of the number of lines to the area of ​​the area perpendicular to them, through which they pass, is greater where the fluid flow velocity is greater, and less where the fluid flows more slowly. Thus, according to the pattern of streamlines, one can judge the direction and modulus of velocity at different points in space, i.e., one can determine the state of fluid motion. The part of the fluid bounded by streamlines is called the streamtube. The flow of a fluid is called steady (or stationary) if the shape and location of the streamlines, as well as the values ​​of the velocities at each of its points, do not change with time.

Consider any tube of current. We choose two of its sections S 1 and S 2 , perpendicular to the direction of speed (Fig. 46). For time D t through the section S volume of liquid passes Sv D t; therefore, for 1 s through S 1 will pass the volume of liquid S 1 v 1 , where v 1 - fluid flow velocity at the cross section S 1 . Through the section S 2 for 1 s will pass the volume of liquid S 2 v 2 , where v 2 - fluid flow velocity at the cross section S 2 . It is assumed here that the fluid velocity in the cross section is constant. If the fluid is incompressible (r=const), then through the cross section S 2 will pass the same volume of liquid as through the section S 1 , i.e. (29.1) Consequently, the product of the flow velocity of an incompressible fluid and the cross section of the current tube is a constant value for this current tube. Relation (29.1) is called the continuity equation for an incompressible fluid.

Bernoulli equation

According to the continuity equation for an incompressible fluid , the volume occupied by the liquid remains constant, i.e. Dividing expression (30.5) by D V, get where R - liquid density. But since the sections were chosen arbitrarily, we can write (30.6)

Expression (30.6) was derived by the Swiss physicist D. Bernoulli and is called the Bernoulli equation. As can be seen from his derivation, Bernoulli's equation is an expression of the law of conservation of energy as applied to a steady flow of an ideal fluid. It also works well for real fluids, the internal friction of which is not very high. Value R in formula (30.6) is called static pressure (fluid pressure on the surface of the body flown around by it), the value rv 2 / 2 - dynamic pressure. As already mentioned above, the value rgh is the hydrostatic pressure.

For a horizontal current tube ( h 1 =h 2 ) expression (30.6) becomes (30.7)

where p+rv 2 / 2 is called total pressure. From the Bernoulli equation (30.7) for a horizontal tube of current and the equation of continuity (29.1) it follows that when a liquid flows through a horizontal pipe having different sections, the fluid velocity is greater in places of narrowing, and the static pressure is greater in wider places, i.e. where the speed is slower. This can be demonstrated by placing a series of pressure gauges along the pipe (Fig. 48).

23. Torricelli Formula.

Let us consider a cylindrical vessel with a liquid, in the side wall of which there is a small hole at some depth below the liquid level (Fig. 51). Consider two sections (at the level h 1 free surface of the liquid in the vessel and at the level h 2 its exit from the hole) and write the Bernoulli equation:

Since the pressure R 1 and R 2 in liquid at the levels of the first and second sections are equal to atmospheric, i.e. R 1 =p 2 , then the equation will look like

It follows from the continuity equation (29.1) that v 2 /v 1 =S 1 /S 2 , where S 1 and S 2 - cross-sectional areas of the vessel and opening. If a S 1 >>S 2 , then member v/2 can be neglected and

This expression is called the Torricelli formula. The formula for the rate of fluid outflow from a hole in an open vessel

24. Viscosity, Newton's law. Flow regimes.

Viscosity (internal friction) is the property of real liquids to resist the movement of one part of the liquid relative to another. When some layers of a real fluid move relative to others, internal friction forces arise, directed tangentially to the surface of the layers. The action of these forces is manifested in the fact that from the side of the layer moving faster, the layer moving more slowly is affected by an accelerating force. From the side of the layer moving more slowly, the layer moving faster is affected by a retarding force.

The internal friction force F is the greater, the larger the considered area of ​​the layer surface S(Fig. 52), and depends on how quickly the fluid flow rate changes during the transition from layer to layer. The direction in which the distance between the layers is counted, perpendicular layer flow rates. The value shows how quickly the speed changes when moving from layer to layer in the direction X, perpendicular to the direction of motion of the layers, and is called the velocity gradient. Thus, the modulus of the force of internal friction (31.1), where the coefficient of proportionality m, which depends on the nature of the liquid, is called dynamic viscosity (or simply viscosity). The unit of viscosity is the pascal second (Pa×s). The greater the viscosity, the more the liquid differs from the ideal one, the greater the forces of internal friction appear in it. There are two modes of fluid flow. The flow is called laminar (layered) if each selected thin layer slides along the flow relative to the neighboring ones without mixing with them, and turbulent (vortex) if intensive vortex formation and liquid (gas) mixing occur along the flow. The laminar flow of a liquid is observed at low velocities of its movement. The outer layer of liquid adjacent to the surface of the pipe in which it flows, due to the forces of molecular cohesion, sticks to it and remains immobile. The average velocity profile for turbulent flow in pipes (Fig. 53) differs from the parabolic profile for laminar flow by a faster increase in velocity near the pipe walls and less curvature in the central part of the flow. The nature of the flow depends on a dimensionless quantity called Reynolds number: where n = h/p-kinematic viscosity; R- liquid density;<v>-average fluid velocity over the pipe section; d- characteristic linear dimension, such as pipe diameter. At low values ​​of the Reynolds number, a laminar flow is observed, the transition from laminar to turbulent flow occurs in the region and at (for smooth pipes) the flow is turbulent.

26. Poiseuille formula. Methods for determining viscosity.

Stokes method. This method of determining viscosity is based on measuring the speed of small spherical bodies slowly moving in a liquid. Three forces act on a ball falling vertically in a liquid: gravity P= 4 / 3 pr 3 rg(r- ball density), Archimedes force P= 4 / 3 pr 3 r "g (r" - liquid density) and resistance force empirically established by J. Stokes: F= 6phrv, where r is the radius of the ball, v- his speed. When the ball moves uniformly, where

By measuring the speed of uniform movement of the ball, one can determine the viscosity of a liquid (gas). Poiseuille method. This method is based on the laminar flow of liquid in a thin capillary. Consider a capillary with a radius R and length l. In a liquid, we mentally select a cylindrical layer with a radius r and thickness d r(Fig. 54). The force of internal friction (see (31.1)), acting on the side surface of this layer, where d S- side surface cylindrical layer; the minus sign means that as the radius increases, the speed decreases. After integration, assuming that fluid sticking occurs near the walls, i.e., the velocity at a distance R from the axis is equal to zero, we get During the time t a liquid will flow out of the pipe, the volume of which is whence the viscosity

27. The equation of free harmonic oscillations for pendulums.

Oscillations are called free (or natural) if they are performed due to the initially imparted energy with the subsequent absence of external influences on the oscillatory system (the system that oscillates). The simplest type of oscillations are harmonic oscillations - oscillations in which the oscillating value changes with time according to the law of sine (cosine ). Spring pendulum is a load of mass t, suspended on a perfectly elastic spring and performing harmonic oscillations under the action of an elastic force F= –kx, where k- spring stiffness. The equation of motion of the pendulum

It follows from the expressions that the spring pendulum performs harmonic oscillations according to the law x=A cos (w 0 t+ j) with cyclic frequency (142.2) and period (142.3) Formula (142.3) is valid for elastic oscillations within the limits in which Hooke's law is fulfilled, i.e. when the mass of the spring is small compared to the mass of the body. The potential energy of the spring pendulum is physical pendulum- this is a rigid body that, under the action of gravity, oscillates around a fixed horizontal axis passing through a point O, not coinciding with the center of mass FROM body (Fig. 201). If the pendulum is deflected from its equilibrium position by some angle a, then, in accordance with the equation of dynamics of rotational motion of a rigid body (18.3), the moment M restoring force can be written as (142.4) where J- moment of inertia of the pendulum about the axis passing through the point of suspension Oh l- the distance between it and the center of mass of the pendulum, F t \u003d -mg sina» -mga. - restoring force (the minus sign is due to the fact that the directions F t and a always opposite; sin a» a corresponds to small oscillations of the pendulum, i.e. small deviations of the pendulum from the equilibrium position). For small oscillations, the physical pendulum performs harmonic oscillations with a cyclic frequency w 0 and a period

Where L=J/(ml) - reduced length of the physical pendulum.

Mathematical pendulum- this is idealized a system consisting of a material point with a mass t, suspended on an inextensible weightless thread, and oscillating under the influence of gravity. A good approximation of a mathematical pendulum is a small, heavy ball suspended from a thin, long thread. Moment of inertia of a mathematical pendulum

(142.8) where l is the length of the pendulum. Since the mathematical pendulum can be represented as special case physical pendulum, assuming that all its mass is concentrated at one point - the center of mass, then, substituting expression (142.8) into formula (1417), we obtain an expression for the period of small oscillations of a mathematical pendulum (142.9) Comparing formulas (142.7) and (142.9), we see, what if the given length L physical pendulum is equal to the length l a mathematical pendulum, then the periods of oscillation of these pendulums are the same. Therefore, the reduced length of a physical pendulum is the length of such a mathematical pendulum, the period of oscillation of which coincides with the period of oscillation of a given physical pendulum.

28. Kinematics of free harmonic oscillations.

Mechanical harmonic oscillation is a rectilinear non-uniform movement in which the coordinates of an oscillating body (material point) change according to the cosine or sine law depending on time. According to this definition, the law of coordinate change depending on time has the form: , where wt is the value under the cosine or sine sign; w- coefficient, physical meaning which we will reveal below; A is the amplitude of mechanical harmonic oscillations. Equations (4.1) are the main kinematic equations of mechanical harmonic vibrations.

for a material point that performs harmonic mechanical oscillations, the value of w can be interpreted as the number of oscillations for a certain cycle of time, equal to 2l. Therefore, the value of w was called the cyclic (or circular) frequency. If point M starts its movement not from point 1 but from point 2, then equation (4.1) will take the form: The value of f0 is called the initial phase.

29. Damped vibrations.

Let us consider free damped oscillations - oscillations whose amplitudes decrease over time due to energy losses by a real oscillatory system. Differential equation free damped oscillations linear system is given in the form

(146.1), where s- a fluctuating value that describes one or another physical process, d=const - attenuation coefficient, w 0 - cyclic frequency of free undamped oscillations of the same oscillatory system, i.e. at d = 0 (in the absence of energy losses) is called the natural frequency of the oscillatory system.

- amplitude of damped oscillations, a BUT 0 - initial amplitude. If a A(t) and BUT(t+ T) - amplitudes of two successive oscillations corresponding to times that differ by a period, then the ratio is called damping decrement, and its logarithm (146.7)- logarithmic damping decrement; N e - the number of oscillations made during the time when the amplitude decreases by e times. The logarithmic damping decrement is a constant value for a given oscillatory system. To characterize an oscillatory system, the concept is used quality factor Q, which for small values ​​of the logarithmic decrement is equal to (146.8). From formula (146.8) it follows that the quality factor is proportional to the number of oscillations N e , performed by the system during the relaxation time.

30. Forced vibrations, resonance.

Oscillations arising under the action of an external periodically changing force or an external periodically changing emf are called forced mechanical and forced electromagnetic oscillations, respectively. Consider the dependence amplitude A forced vibrations from frequency w. Mechanical and electromagnetic oscillations will be considered simultaneously, calling the oscillating value or displacement (X) an oscillating body from an equilibrium position, or by a charge (Q) capacitor.

From formula (147.8) it follows that the amplitude BUT displacement (charge) has a maximum. To determine the resonant frequency w cut, - the frequency at which the amplitude BUT displacement (charge) reaches its maximum - you need to find the maximum of the function (147.8), or, what is the same, the minimum of the radical expression. Differentiating the radical expression with respect to w and equating it to zero, we obtain the condition that determines w cut: This equality holds for w=0, ± , for which only a positive value has a physical meaning. Consequently, the resonant frequency (148.1) The phenomenon of a sharp increase in the amplitude of forced oscillations when the frequency of the driving force (the frequency of the driving alternating voltage) approaches a frequency equal to or close to the natural frequency of the oscillatory system is called resonance (mechanical or electrical, respectively). When value w cut almost coincides with the natural frequency w 0 oscillating system. Substituting (148.1) into formula (147.8), we obtain (148.2)

On fig. 210 shows the dependences of the amplitude of forced oscillations on frequency for various values d. From (148.1) and (148.2) it follows that the less d, the higher and to the right lies the maximum of this curve. If a w® 0, then all curves (see also (147.8)) reach the same non-zero limit value , which is called the static deviation. In the case of mechanical vibrations , in the case of electromagnetic U m / (L). If a w®¥, then the curves asymptotically tend to zero. The reduced set of curves is called resonance curves.

The law of conservation of energy states that the energy of the body never disappears and does not reappear, it can only turn from one form to another. This law is universal. It has its own formulation in various branches of physics. Classical mechanics considers the law of conservation of mechanical energy.

Total mechanical energy of a closed system physical bodies, between which conservative forces act, is a constant value. This is how the law of conservation of energy in Newtonian mechanics is formulated.

Closed, or isolated, is considered to be physical system, which is not affected by external forces. It does not exchange energy with the surrounding space, and its own energy, which it possesses, remains unchanged, that is, it is preserved. In such a system, only internal forces, and bodies interact with each other. It can only convert potential energy into kinetic energy and vice versa.

The simplest example of a closed system is a sniper rifle and a bullet.

Types of mechanical forces

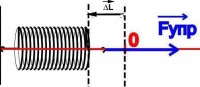
The forces that act inside a mechanical system are usually divided into conservative and non-conservative.

conservative forces are considered whose work does not depend on the trajectory of the body to which they are applied, but is determined only by the initial and final position of this body. The conservative forces are also called potential. The work of such forces in a closed loop is zero. Examples of conservative forces − gravity force, elastic force.

All other forces are called non-conservative. These include friction force and drag force. They are also called dissipative forces. These forces perform negative work during any motions in a closed mechanical system, and under their action the total mechanical energy of the system decreases (dissipates). It passes into other, non-mechanical types of energy, for example, into heat. Therefore, the law of conservation of energy in a closed mechanical system can be fulfilled only if there are no non-conservative forces in it.

The total energy of a mechanical system consists of kinetic and potential energy and is their sum. These types of energies can transform into each other.

Potential energy

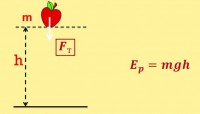
Potential energy is called the energy of interaction of physical bodies or their parts with each other. It is determined by their mutual arrangement, that is, the distance between them, and is equal to the work that needs to be done to move the body from the reference point to another point in the field of conservative forces.

Potential energy has any motionless physical body, raised to some height, since it is affected by gravity, which is a conservative force. Such energy is possessed by water at the edge of a waterfall, a sled at the top of a mountain.

Where did this energy come from? While the physical body was being raised to a height, work was done and energy was expended. It is this energy that was stored in the raised body. And now this energy is ready to do work.

The value of the potential energy of the body is determined by the height at which the body is located relative to some initial level. We can take any point we choose as a starting point.

If we consider the position of the body relative to the Earth, then potential energy body on the Earth's surface is zero. And on top h it is calculated by the formula:

E p = mɡ h ,

where m - body mass

ɡ - acceleration of gravity

h – height of the center of mass of the body relative to the Earth

ɡ \u003d 9.8 m / s 2

When a body falls from a height h1 up to height h2 gravity does work. This work is equal to the change in potential energy and has a negative value, since the magnitude of potential energy decreases as the body falls.

A = - ( E p2 - E p1) = - ∆ E p ,

where E p1 is the potential energy of the body at height h1 ,

E p2 - potential energy of a body at a height h2 .

If the body is raised to a certain height, then work is done against the forces of gravity. In this case, it has a positive value. And the value of the potential energy of the body increases.

An elastically deformed body (compressed or stretched spring). Its value depends on the stiffness of the spring and on how long it was compressed or stretched, and is determined by the formula:

E p \u003d k (∆x) 2 / 2 ,

where k - stiffness coefficient,

∆x - lengthening or contraction of the body.

The potential energy of the spring can do work.

Kinetic energy

Translated from the Greek "kinema" means "movement". The energy that a physical body receives as a result of its movement is called kinetic. Its value depends on the speed of movement.

A soccer ball rolling across the field, a sledge rolling down a mountain and continuing to move, an arrow fired from a bow - they all have kinetic energy.

If a body is at rest, its kinetic energy is zero. As soon as a force or several forces act on the body, it will begin to move. And since the body is moving, the force acting on it does work. The work of the force, under the influence of which the body from rest will go into motion and change its speed from zero to ν , is called kinetic energy body mass m .

If, at the initial moment of time, the body was already in motion, and its speed had the value v 1 , and at the end it was equal to v 2 , then the work done by the force or forces acting on the body will be equal to the increment in the kinetic energy of the body.

∆ E k = E k 2 - E k 1

If the direction of the force coincides with the direction of motion, then positive work is done, and the kinetic energy of the body increases. And if the force is directed in the direction opposite to the direction of motion, then negative work is done, and the body gives off kinetic energy.

Law of conservation of mechanical energy

Ek 1 + E p1= E k 2 + E p2

Any physical body located at some height has potential energy. But when falling, it begins to lose this energy. Where does she go? It turns out that it does not disappear anywhere, but turns into the kinetic energy of the same body.

Suppose , at some height, a load is motionlessly fixed. Its potential energy at this point is equal to the maximum value. If we let it go, it will start falling at a certain speed. Therefore, it will begin to acquire kinetic energy. But at the same time, its potential energy will begin to decrease. At the point of impact, the kinetic energy of the body will reach a maximum, and the potential energy will decrease to zero.

The potential energy of a ball thrown from a height decreases, while the kinetic energy increases. Sledges at rest on top of a mountain have potential energy. Their kinetic energy at this moment is zero. But when they start to roll down, the kinetic energy will increase, and the potential energy will decrease by the same amount. And the sum of their values ​​will remain unchanged. The potential energy of an apple hanging on a tree is converted into its kinetic energy when it falls.

These examples clearly confirm the law of conservation of energy, which says that the total energy of a mechanical system is a constant value . The value of the total energy of the system does not change, and the potential energy is converted into kinetic energy and vice versa.

By what amount the potential energy decreases, the kinetic energy will increase by the same amount. Their amount will not change.

For a closed system of physical bodies, the equality
E k1 + E p1 = E k2 + E p2,
where E k1 , E p1 - kinetic and potential energies of the system before any interaction, E k2 , E p2 - corresponding energies after it.

The process of converting kinetic energy into potential energy and vice versa can be seen by watching a swinging pendulum.

Click on the picture

Being in the extreme right position, the pendulum seems to freeze. At this moment, its height above the reference point is maximum. Therefore, the potential energy is also maximum. And the kinetic is zero, since it does not move. But the next moment the pendulum starts moving down. Its speed increases, and, therefore, its kinetic energy increases. But as the height decreases, so does the potential energy. At the bottom point, it will become equal to zero, and the kinetic energy will reach its maximum value. The pendulum will pass this point and begin to rise up to the left. Its potential energy will begin to increase, and its kinetic energy will decrease. Etc.

To demonstrate the transformation of energy, Isaac Newton invented mechanical system, which is called Newton's cradle or Newton's balls .

Click on the picture

If the first ball is deflected and then released, its energy and momentum will be transferred to the last one through three intermediate balls, which will remain motionless. And the last ball will deflect with the same speed and rise to the same height as the first one. Then the last ball will transfer its energy and momentum through the intermediate balls to the first one, and so on.

A ball laid aside has the maximum potential energy. Its kinetic energy at this moment is zero. Having started moving, it loses potential energy and acquires kinetic energy, which reaches its maximum at the moment of collision with the second ball, and potential energy becomes equal to zero. Further, the kinetic energy is transferred to the second, then the third, fourth and fifth balls. The latter, having received kinetic energy, begins to move and rises to the same height at which the first ball was at the beginning of the movement. Its kinetic energy at this moment is equal to zero, and the potential energy is equal to the maximum value. Then it starts to fall and in the same way transfers energy to the balls in reverse order.

This continues for quite a long time and could continue indefinitely if there were no non-conservative forces. But in reality, dissipative forces act in the system, under the influence of which the balls lose their energy. Their speed and amplitude gradually decrease. And eventually they stop. This confirms that the law of conservation of energy is satisfied only in the absence of non-conservative forces.

The total mechanical energy characterizes the movement and interaction of bodies, therefore, it depends on the speeds and relative position of the bodies.

The total mechanical energy of a closed mechanical system is equal to the sum of the kinetic and potential energies of the bodies of this system:

Law of energy conservation

The law of conservation of energy is a fundamental law of nature.

In Newtonian mechanics, the law of conservation of energy is formulated as follows:

The total mechanical energy of an isolated (closed) system of bodies remains constant.

In other words:

Energy does not arise from nothing and does not disappear anywhere, it can only pass from one form to another.

Classical examples of this statement are: a spring pendulum and a pendulum on a thread (with negligible damping). In the case of a spring pendulum, in the process of oscillation, the potential energy of a deformed spring (having a maximum in the extreme positions of the load) is converted into the kinetic energy of the load (reaching a maximum at the moment the load passes the equilibrium position) and vice versa. In the case of a pendulum on a thread, the potential energy of the load is converted into kinetic energy and vice versa.

2 Equipment

2.1 Dynamometer.

2.2 Laboratory stand.

2.3 Load weighing 100 g - 2 pcs.

2.4 Measuring ruler.

2.5 Piece soft tissue or felt.

3 Theoretical background

The scheme of the experimental setup is shown in Figure 1.

The dynamometer is fixed vertically in the foot of the tripod. A piece of soft cloth or felt is placed on a tripod. When hanging loads from the dynamometer, the tension of the dynamometer spring is determined by the position of the pointer. In this case, the maximum elongation (or static displacement) of the spring X 0 occurs when the elastic force of a spring with stiffness k balances the force of gravity of the load with the mass t:

kx 0 =mg, (1)

where g = 9.81 - free fall acceleration.

Consequently,

The static displacement characterizes the new equilibrium position O" of the lower end of the spring (Fig. 2).

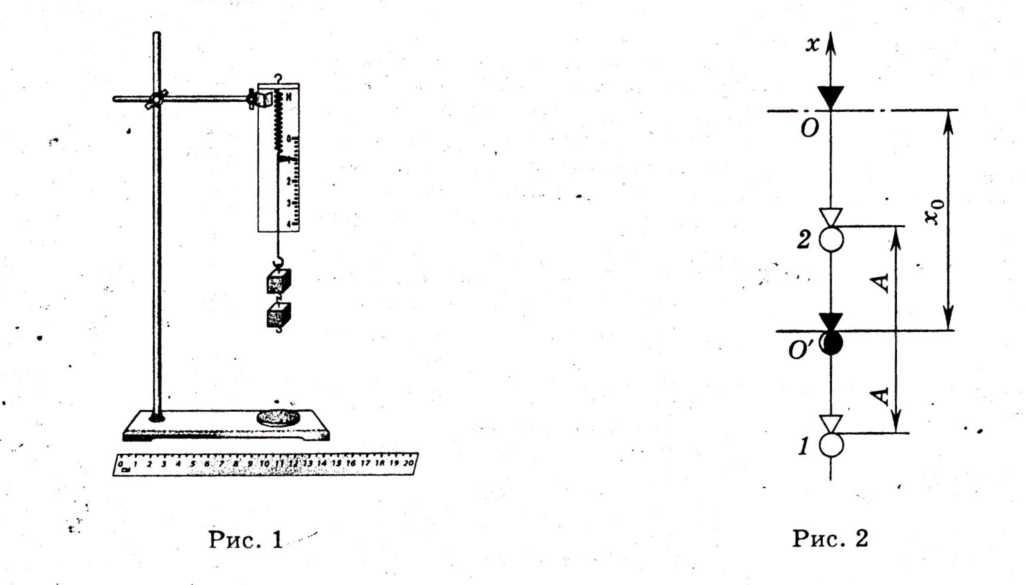
If the load is pulled down a distance BUT from point O" and release at point 1, then periodic oscillations of the load occur. At points 1 and 2, called turning points, the load stops, reversing the direction of movement. Therefore, at these points, the speed of the load v = 0.

Max speed v m ax the load will have at the midpoint O". Two forces act on the oscillating load: the constant force of gravity mg and variable elastic force kx. Potential energy of a body in a gravitational field at an arbitrary point with coordinate X is equal to mgx. The potential energy of the deformed body, respectively, is equal to .

In this case, the point X = 0, corresponding to the position of the pointer for an unstretched spring.

The total mechanical energy of the load at an arbitrary point is the sum of its potential and kinetic energy. Neglecting the forces of friction, we use the law of conservation of total mechanical energy.

Let us equate the total mechanical energy of the load at point 2 with the coordinate -(X 0 -BUT) and at point O" with coordinate -X 0 :

Expanding the brackets and performing simple transformations, we bring formula (3) to the form

Then the module of the maximum speed of loads

The stiffness of a spring can be found by measuring the static displacement X 0 . As follows from formula (1),

3.5. Laws of conservation and change of energy

3.5.1. Law of Change total mechanical energy

A change in the total mechanical energy of a system of bodies occurs when work is done by forces acting both between the bodies of the system and from external bodies.

The change in mechanical energy ∆E of a system of bodies is determined by by the law of change of total mechanical energy:

∆E \u003d E 2 - E 1 \u003d A ext + A tr (resist),

where E 1 is the total mechanical energy of the initial state of the system; E 2 - total mechanical energy of the final state of the system; A external - the work done on the bodies of the system by external forces; A tr (resist) - the work done by the forces of friction (resistance) acting inside the system.

Example 30. At a certain height, a body at rest has a potential energy equal to 56 J. By the time it falls to the Earth, the body has a kinetic energy equal to 44 J. Determine the work of the air resistance forces.

Solution. The figure shows two positions of the body: at a certain height (first) and at the moment of falling to the Earth (second). The zero level of potential energy is chosen on the surface of the Earth.

The total mechanical energy of a body relative to the Earth's surface is determined by the sum of potential and kinetic energy:

• at some height

E 1 \u003d W p 1 + W k 1;

• by the time it hits the ground

E 2 \u003d W p 2 + W k 2,

where W p 1 = 56 J is the potential energy of the body at a certain height; W k 1 = 0 - kinetic energy of a body resting at a certain height; W p 2 = 0 J - potential energy of the body at the time of falling to the Earth; W k 2 \u003d 44 J - the kinetic energy of the body by the time it falls to the Earth.

We find the work of air resistance forces from the law of change in the total mechanical energy of the body:

where E 1 = W p 1 is the total mechanical energy of the body at a certain height; E 2 \u003d W k ​​2 - the total mechanical energy of the body by the time it falls to the Earth; A ext \u003d 0 - work of external forces (external forces are absent); A resist - the work of air resistance forces.

The desired work of the air resistance forces is thus determined by the expression

A resist = W k 2 − W p 1 .

Let's do the calculation:

A resist \u003d 44 - 56 \u003d -12 J.

The work of air resistance forces is a negative value.

Example 31. Two springs with stiffness factors of 1.0 kN/m and 2.0 kN/m are connected in parallel. What work must be done to stretch the spring system by 20 cm?

Solution. The figure shows two springs with different spring rates connected in parallel.

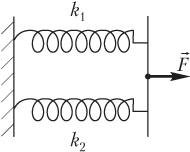
The external force F → , stretching the springs, depends on the magnitude of the deformation of the composite spring, therefore, the calculation of the work of the specified force using the formula for calculating the work of a constant force is illegal.

To calculate the work, we use the law of change in the total mechanical energy of the system:

E 2 − E 1 = A ext + A resist,

where E 1 is the total mechanical energy of the composite spring in the undeformed state; E 2 - total mechanical energy of the deformed spring; A external - work of external force (desired value); A resist = 0 - the work of the resistance forces.

The total mechanical energy of a composite spring is the potential energy of its deformation:

• for undeformed spring

E 1 \u003d W p 1 \u003d 0,

• for extended spring

E 2 \u003d W p 2 \u003d k total (Δ l) 2 2,

where k total - the total stiffness of the composite spring; ∆l - the magnitude of the stretching of the spring.

The total stiffness of two springs connected in parallel is the sum

k total \u003d k 1 + k 2,

where k 1 - coefficient of rigidity of the first spring; k 2 - coefficient of rigidity of the second spring.

We find the work of the external force from the law of change in the total mechanical energy of the body:

A ext \u003d E 2 - E 1,

substituting in this expression the formulas that determine E 1 and E 2, as well as the expression for the total stiffness coefficient of the composite spring:

A ext \u003d k total (Δ l) 2 2 − 0 \u003d (k 1 + k 2) (Δ l) 2 2.

Let's do the calculation:

A ext \u003d (1.0 + 2.0) ⋅ 10 3 ⋅ (20 ⋅ 10 − 2) 2 2 \u003d 60 J.

Example 32. A bullet with a mass of 10.0 g flying at a speed of 800 m/s hits a wall. The modulus of the force of resistance to the movement of a bullet in the wall is constant and amounts to 8.00 kN. Determine how far the bullet will penetrate the wall.

Solution. The figure shows two positions of the bullet: when it approaches the wall (first) and at the moment the bullet stops (gets stuck) in the wall (second).

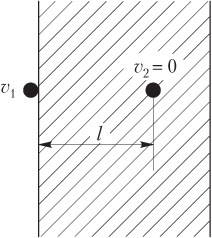
The total mechanical energy of a bullet is the kinetic energy of its movement:

• when a bullet hits a wall

E 1 \u003d W k ​​1 \u003d m v 1 2 2;

• by the time the bullet stops (gets stuck) in the wall

E 2 \u003d W k ​​2 \u003d m v 2 2 2,

where W k 1 - the kinetic energy of the bullet when approaching the wall; W k 2 - the kinetic energy of the bullet by the time it stops (gets stuck) in the wall; m is the mass of the bullet; v 1 - bullet speed module when approaching the wall; v 2 \u003d 0 - the value of the bullet speed at the moment of stopping (getting stuck) in the wall.

The distance at which the bullet will go deep into the wall, we find from the law of change in the total mechanical energy of the bullet:

E 2 − E 1 = A ext + A resist,

where E 1 \u003d m v 1 2 2 - the total mechanical energy of the bullet when approaching the wall; E 2 \u003d 0 - the total mechanical energy of the bullet by the time it stops (gets stuck) in the wall; A ext \u003d 0 - work of external forces (external forces are absent); A resist - the work of the forces of resistance.

The work of the resistance forces is determined by the product:

A resist = F resist l cos α ,

where F resist - the module of the force of resistance to the movement of the bullet; l - the distance that the bullet will go deep into the wall; α = 180° - the angle between the directions of the drag force and the direction of the bullet.

Thus, the law of change in the total mechanical energy of a bullet in an explicit form is as follows:

− m v 1 2 2 = F resist l cos 180 ° .

The desired distance is determined by the ratio

l = − m v 1 2 2 F resist cos 180 ° = m v 1 2 2 F resist

l = 10.0 ⋅ 10 − 3 ⋅ 800 2 2 ⋅ 8.00 ⋅ 10 3 = 0.40 m = 400 mm.

Page 1

The total mechanical energy of the body does not change. Energy only changes from one form to another.

The total mechanical energy of a body, which is not affected by the forces of friction and resistance, remains unchanged during its motion.

The total mechanical energy of a body is the sum of its kinetic and potential energies. Consider full energy freely falling body at different times.

Does the total mechanical energy of the body change when it falls.

What is called the total mechanical energy of the body.

Thus, the total mechanical energy of a body performing harmonic oscillations is proportional to the square of the oscillation amplitude. Therefore, the amplitude A of oscillations also does not depend on time.

As can be seen from (44.13), the total mechanical energy of the body during damped oscillations decreases with time according to an exponential law.

The sum of kinetic and potential energies forms the total mechanical energy of the body.

An absolutely elastic impact is such an impact at which the total mechanical energy of the bodies is conserved. First, the kinetic energy is partially or completely converted into the potential energy of elastic deformation. Then the bodies return to their original shape, repelling each other. As a result, the potential energy of elastic deformation again turns into kinetic energy and the bodies fly apart with velocities determined by two conditions - conservation of total energy and total impulse tel.

An absolutely elastic impact is such an impact at which the total mechanical energy of the bodies is conserved. First, the kinetic energy is partially or completely converted into the potential energy of elastic deformation. Then the bodies return to their original shape, repelling each other. As a result, the potential energy of elastic deformation again turns into kinetic energy and the bodies fly apart with velocities determined by two conditions - the conservation of the total energy and the total momentum of the bodies.

An absolutely elastic impact is such an impact at which the total mechanical energy of the bodies is conserved. First, the kinetic energy is partially or completely converted into the potential energy of elastic deformation. Then the bodies return to their original shape, repelling each other. As a result, the potential energy of elastic deformation again turns into kinetic energy and the bodies fly apart with velocities determined by two conditions - the conservation of the total energy and the total momentum of the bodies.

This work is spent on dissipating energy or changing the total mechanical energy of the body.

According to the law of energy change (see § 28), the work of the resistance force (external force) is equal to the increment of the total mechanical energy of the body.

This result is predictable, since the elastic force under which the body moves is conservative, therefore, the energy conservation law is fulfilled - the total mechanical energy of the body is conserved.

Mechanical energy characterizes the ability of a body to perform mechanical work. The total mechanical energy of a body is the sum of kinetic and potential energy.