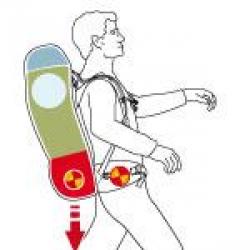
Bilimde ve hayatın diğer bazı alanlarında düzenli çokgenler. "Doğada düzenli çokgenler. Düzgün çokgenlerden parkeler" - sunum Günlük yaşamda düzenli çokgenler sunumu
İyi gün dostları!
Uzun zamandır bu projemizi size anlatacaktım ama bir türlü eller uzanmadı. Ve işte bir mucize! Eller geldi! Bu nedenle projeye "Etrafımızdaki çokgenler" adı verilir. Tahmin edebileceğiniz gibi bu 4. sınıfta kızım Alexandra ile yaptığımız matematik çalışması.
Çalışmaya yaratıcı bir şekilde yaklaştık ve matematiksel yaratıcılığımızın özetlerinizi, projelerinizi veya araştırma makalelerinizi hazırlamanız için yararlı olabileceğinden eminiz.
Eserin adını şöyle koyduk: “Matematiksel Gerilim. Çokgen Avcısı »
Ve şimdi size tüm fotoğraflarla birlikte tam metni getiriyorum. Hikaye, bu bilimsel çalışmanın yazarı olan birinci kişi ağzından anlatılıyor.

Çalışmanın amacı: çevremizdeki dünyadaki çokgenlerin pratik uygulaması.
Sorunlu soru: çokgenler hayatımızda nasıl bir yer kaplar?
Çocukluğumuzdan beri çeşitli çokgen türlerine aşinayız, ancak bunlarla çevremizdeki dünyada ne sıklıkla karşılaştığımızı bir şekilde düşünmüyoruz.
Günlük hayatta aşina olduğumuz şeylere daha yakından bakmaya ve etrafımızdaki nesnelerde matematik derslerinde çalışılan çokgenleri bulmaya karar verdim.
Bir gün, tepeden tırnağa uzun ve ağır bir cetvelle silahlanmış olarak çokgen avına çıktım.

Uzağa gitmek zorunda değildim. Onları evde aradım.
Mutfağın kapısına gittim ve irademi yumruk haline getirerek ışığı yaktım! Ve… Ah korku!!! Yüzlerce poligonal, keskin ve künt ve kesinlikle doğrudan görüş hissettim. Her yerdeydiler! Hiç tereddüt etmeden bana bakıyorlardı! Hükümdarımdan korkmadılar! Saklanmaya bile çalışmadılar! Bu bir mutfak değil! Bu gerçek bir poligonal krallık! Yüzlerce çokgen duvarlara oturdu (duvar kağıdı desenindeki dikdörtgenler). Onları saymaya bile cesaret edemedim.

En kurnaz olanı tavana yapıştırılmış (tavan karoları dikdörtgen şeklindedir). Yukarıdan şüpheyle bana baktılar.
Ve en kibirli olanlar bulaşıklara girdi ... ve hatta onlara dönüştü (tabakların üzerindeki süslemeler ve tabakların şekli farklı çokgen türleri ile temsil edilir).

Artık çokgenlerin köfte kalıplamayı sevdiğini biliyorum (hamur kalıbında altıgenler görünür).

Ne yediğime bakıyorlar. Ve hatta kedimin yedikleri için (mama kutularının kenarları dikdörtgen şeklindedir).

Korkarak mutfaktan atladım ve salona yöneldim. Ve aniden ... çokgenlerden birinin papağanlarımı yakaladığını gördüm (kafes dikdörtgen, üçgen ve dörtgen şekil öğelerinden oluşur).

Bu küstah figürinler bir çocuğu bile (yapıcı unsurlar) esirgemedi. Küçük erkek kardeşim, tehlikenin farkında olmadan onlarla coşkuyla oynadı.

Sevgili büyükannem durmadan başka bir çokgene baktı ve ona dünyada neler olduğunu gösterdi (TV ekranı bir dikdörtgendir).

Ve aniden keskin bir gıcırtı sesi geldi! "Bu ne?" diye düşündüm şok içinde. Ve raftan bir ses veren, bu çokgen krallığın başka bir temsilcisiydi (bir cep telefonu dikdörtgen paralelyüz şeklindedir).

En azından orada saklanmayı umarak çocuk odasına koştum ... Ama başaramadım.
Parlak, neşeli çokgenler, mutlu bir şekilde gülerek perdelerimizde sallandı (geometrik kumaş deseni). “Düşersin!” diye düşündüm ve masama baktım…

Yapmamalıydım ... Masamda iki karmaşık çokgen bir şeyden bahsediyordu. Biri mavi, biri kırmızı… (lambaların tavanları üçgen ve dörtgenlerin birleşimi olarak düşünülebilir).

Ve yanlarında küçük çokgen yavrular hafifçe kıkırdadılar (kalemlerin kenarları dikdörtgen ve tabanı bir altıgendir).

Bu bir daire değil! Burası çokgenlerden oluşan bir sığınak!!! Burada bir yuvaları var!
Yeni Yılı bile bizimle kutladılar (birçok Noel süsünün şekli, farklı çokgenlerin birleşimidir)! Ve biz bile bilmiyorduk...

Onlardan hiçbir yerde saklanamayacağınızı anladım. Mısır'da bile (piramitlerin yüzleri üçgen, tabanları dikdörtgendir)!

Çözüm. Bu dünya çokgenlere ait! Ve onunla uzlaşmalıyız. Ve bu çokgen yaratıklarla uyum içinde yaşamayı öğrenin.
İşte böyle alışılmadık bir projemiz var. Bu sayede günlükte Sasha beş tane daha aldı.
Power Point programında slayt şeklinde yapıldı ve sadece matematik dersinde değil, aynı zamanda diploma aldığı okul yarışması "Bilim ve Yaratıcılık" da sunuldu.
Blogumuzda başka matematiksel projeler bulacaksınız:
Hepsi bugün için!
Size ilginç yaratıcı görevler dileriz!
Dünyada sadece bir tür şekil olsaydı, örneğin dikdörtgen gibi bir şekil olsaydı ne olurdu? Bazı şeyler hiç değişmezdi: kapılar, yük römorkları, futbol sahaları - hepsi aynı görünür. Peki ya kapı kolları? Biraz tuhaf olacaklar. Peki ya araba tekerlekleri? Bu verimsiz olurdu. Peki ya futbol? Hayal etmesi bile zor. Neyse ki, dünya birçok farklı formla doludur. Doğada varlar mı? Evet ve birçoğu var.
çokgen nedir?
Bir şeklin çokgen olabilmesi için bazı şartlar gereklidir. İlk olarak, birçok kenar ve köşe olmalıdır. Ayrıca kapalı bir form olmalıdır. tüm kenarları ve açıları eşit olan bir şekildir. Buna göre yanlış olan için biraz deforme olabilirler.

Düzenli çokgen türleri
Bir düzgün çokgenin sahip olabileceği en az kenar sayısı kaçtır? Bir çizginin birçok kenarı olamaz. İki taraf da buluşamaz ve kapalı bir şekil oluşturamaz. Ve üç taraf da yapabilir - böylece bir üçgen elde edersiniz. Ve tüm kenarların ve açıların eşit olduğu düzgün çokgenlerden bahsettiğimiz için, şunu kastediyoruz:
Bir kenar daha eklerseniz, bir kare elde edersiniz. Kenarları eşit olmayan bir dikdörtgen düzgün çokgen olabilir mi? Hayır, bu şekle dikdörtgen denecek. Beşinci kenarı eklerseniz, bir beşgen elde edersiniz. Buna göre, sonsuza kadar altıgenler, yedigenler, sekizgenler ve benzeri vardır.

temel geometri
Çokgenler farklı türlerde gelir: açık, kapalı ve kendi kendine kesişen. Temel geometride, bir çokgen, kapalı bir çoklu çizgi veya kontur şeklinde sonlu bir düz çizgi parçaları zinciri ile sınırlanan düz bir şekildir. Bu parçalar kenarları veya kenarlarıdır ve iki kenarın birleştiği noktalar köşeleri ve köşeleridir. Bir çokgenin içi bazen gövdesi olarak adlandırılır.

Doğada ve insan yaşamında çokyüzlüler
Pek çok canlı türü beşgen desenlerde bol miktarda bulunurken, mineral dünyası ikili, üçlü, dörtlü ve altılı simetriyi destekler. Altıgen, maksimum yapısal verimlilik sağlayan yoğun bir şekildir. Beşgen şekillerin neredeyse hiç bulunmadığı moleküller ve kristaller alanında çok yaygındır. Steroidler, kolesterol, benzen, C ve D vitaminleri, aspirin, şeker, grafit altılı simetrinin tezahürleridir. Doğada düzenli çokyüzlüler nerede bulunur? En ünlü altıgen mimari, arılar, yaban arıları ve eşek arıları tarafından yaratılmıştır.

Altı su molekülü, her kar kristalinin çekirdeğini oluşturur. Kar tanesi böyle yapılır. Sineğin gözünün kenarları yoğun bir şekilde paketlenmiş altıgen bir düzenleme oluşturur. Doğada başka hangi düzenli çokyüzlüler var? Bunlar su ve elmas kristalleri, bazalt kolonları, gözdeki epitel hücreleri, bazı bitki hücreleri ve çok daha fazlasıdır. Böylece, doğanın yarattığı canlı ve cansız çokyüzlüler, insan yaşamında çok sayıda ve çeşitlilikte mevcuttur.

Altıgenlerin popülaritesinin sebebi nedir?
Kar taneleri, organik moleküller, kuvars kristalleri ve sütunlu bazaltlar altıgenlerdir. Bunun nedeni, içsel simetrileridir. En çarpıcı örnek, tüm yüzey çok rasyonel kullanıldığından altıgen yapısı alan eksikliğini en aza indiren peteklerdir. Neden aynı hücrelere bölünelim? Arılar, bal depolama ve yumurtlama gibi ihtiyaçları için kullanmak üzere doğada düzenli çokyüzlüler oluştururlar. Doğa neden altıgenleri tercih ediyor? Bu sorunun cevabı temel matematik ile verilebilir.
- Üçgenler. Bir kenarı yaklaşık 7,35 mm olan 428 eşkenar üçgen alın. Toplam uzunlukları 3 * 7,35 mm * 428/2 = 47,2 cm'dir.
- dikdörtgenler Kenarları yaklaşık 4,84 mm olan 428 kare alın, toplam uzunlukları 4 * 4,84 m * 428/2 = 41,4 cm'dir.
- altıgenler. Ve son olarak, kenarları 3 mm olan 428 altıgen alın, toplam uzunlukları 6 * 3 mm * 428/2 = 38,5 cm'dir.
Açık olan, altıgenlerin zaferidir. Alanı maksimuma indirmeye yardımcı olan ve daha küçük bir alana mümkün olduğunca çok şekil yerleştirmenize izin veren bu formdur. Arıların kehribar nektarını içinde sakladıkları petek, kusursuz bir altıgen kesite sahip prizma biçimli bir dizi hücreden oluşan bir hassas mühendislik harikasıdır. Balmumu duvarları çok hassas bir kalınlıkta yapılmıştır, yapışkan balın düşmesini önlemek için hücreler dikkatlice eğilir ve tüm yapı dünyanın manyetik alanıyla hizalanır. Şaşırtıcı bir şekilde, arılar çabalarını koordine ederek aynı anda çalışırlar.

Neden altıgenler? Bu basit geometri
Aynı şekil ve boyuttaki hücreleri tüm düzlemi dolduracak şekilde bir araya getirmek istiyorsanız, o zaman yalnızca üç normal şekil (tüm kenarları ve aynı açıları olan) çalışacaktır: eşkenar üçgenler, kareler ve altıgenler. Bunlardan altıgen hücreler, aynı alandaki üçgenlere veya karelere kıyasla en küçük toplam duvar uzunluğunu gerektirir.
Yani arıların altıgen seçimi mantıklı. 18. yüzyılda, bilim adamı Charles Darwin, altıgen peteklerin "iş gücünden ve balmumundan tasarruf etmek için kesinlikle ideal" olduğunu ilan etti. Doğal seçilimin arılara, diğer türlere göre daha az enerji ve zaman gerektirme avantajına sahip olan bu mum odalarını yaratma içgüdüsü verdiğine inanıyordu.

Doğadaki çokyüzlü örnekleri
Bazı böceklerin bileşik gözleri, her bir yüzün uzun ince bir retinal hücreye bağlı bir mercek olduğu bir altıgen içine yerleştirilmiştir. Biyolojik hücre kümelerinin oluşturduğu yapılar, genellikle sabunlu sudaki baloncuklarla aynı kurallara tabi şekillere sahiptir. Göz fasetinin mikroskobik yapısı bunun en güzel örneklerinden biridir. Her faset, dört normal vezikül kümesiyle aynı şekle sahip dört ışığa duyarlı hücreden oluşan bir küme içerir.
Bu sabun filmi kurallarını ve kabarcık şekillerini belirleyen nedir? Doğa, ekonomiyle arılardan daha fazla ilgilenir. Kabarcıklar ve sabun filmleri (sabun eklenmiş) sudan yapılır ve yüzey gerilimi sıvının yüzeyini mümkün olduğunca az alan verecek şekilde çeker. Bu nedenle damlalar düştüklerinde küreseldir (az ya da çok): Bir kürenin yüzey alanı, aynı hacme sahip diğer herhangi bir şekilden daha azdır. Bir mum levha üzerinde, su damlacıkları aynı nedenle küçük boncuklar halinde çekilir.
Bu yüzey gerilimi baloncuklu sal ve köpük modellerini açıklar. Köpük, en küçük duvar alanını sağlayacak en düşük toplam yüzey gerilimine sahip yapıyı arayacaktır. Sabun filmlerinin geometrisi mekanik kuvvetlerin etkileşimi tarafından belirlense de köpüğün şeklinin ne olacağını bize söylemez. Tipik bir köpük, çeşitli şekil ve boyutlarda çokyüzlü hücreler içerir. Yakından bakarsanız, doğadaki normal çokyüzlüler o kadar doğru değildir. Kenarları nadiren tamamen düzdür.

Doğru baloncuklar
Tüm baloncukların aynı boyutta olduğu "mükemmel" bir köpük yapabileceğinizi varsayalım. Kabarcık duvarının toplam alanını olabildiğince küçük yapan mükemmel hücre şekli nedir? Bu uzun yıllardır tartışıldı ve uzun bir süre ideal hücre şeklinin kenarları kare ve altıgen olan 14 kenarlı bir çokyüzlü olduğuna inanılıyordu.
1993 yılında, sekiz farklı hücre şeklinden oluşan tekrar eden bir gruptan oluşan daha ekonomik, ancak daha az düzenli bir yapı keşfedildi. Bu daha karmaşık model, 2008 Pekin Olimpiyatları sırasında yüzme stadyumunun köpük tasarımı için ilham kaynağı olarak kullanıldı.
Köpükte hücre oluşumunun kuralları, canlı hücrelerde gözlenen bazı kalıpları da kontrol eder. Yassı balonla aynı altıgen faset yığınını gösteren sadece sineğin bileşik gözü değildir. Bireysel lenslerin her birinin içindeki ışığa duyarlı hücreler de tıpkı sabun köpüğü gibi görünen kümeler halinde kümelenir.

Doğada çokyüzlülerin dünyası
Bitkilerden farelere kadar pek çok farklı organizma türünün hücreleri, bu mikroskobik yapılara sahip zarlar içerir. Ne işe yaradıklarını kimse bilmiyor ama o kadar yaygınlar ki, yararlı bir rolleri olduğunu varsaymak doğru olur. Belki de çapraz müdahalelerden kaçınarak bir biyokimyasal süreci diğerinden ayırıyorlar.
Veya belki de büyük bir çalışma düzlemi yaratmanın etkili bir yoludur, çünkü birçok biyokimyasal süreç, enzimlerin ve diğer aktif moleküllerin gömülebildiği zarların yüzeyinde gerçekleşir. Polihedranın doğadaki işlevi ne olursa olsun, karmaşık genetik yönergeler oluşturmaya zahmet etmeyin, çünkü fizik yasaları bunu sizin yerinize yapacaktır.
Bazı kelebekler, kitin adı verilen sert bir malzemeden düzenli bir labirent içeren kanatlı pullara sahiptir. Bir kanadın yüzeyindeki normal sırtlardan ve diğer yapılardan seken ışık dalgalarına maruz kalmak, bazı dalga boylarının (yani bazı renklerin) solmasına neden olurken diğerleri birbirini güçlendirir. Böylece çokgen yapı, hayvan rengi üretmek için mükemmel bir araç sunar.

Sert bir mineralden düzenli ağlar yapmak için, bazı organizmalar yumuşak, esnek zarlardan bir kalıp oluşturuyor ve ardından sert malzemeyi iç içe geçen ağlardan birinde kristalleştiriyor gibi görünüyor. Deniz faresi olarak bilinen olağandışının kitinsi dikenleri içindeki içi boş mikroskobik kanalların petek yapısı, bu tüy benzeri yapıları, ışığın yönüne bağlı olarak kırmızıdan mavimsi yeşile çevirerek ışığı yönlendirebilen doğal optik liflere dönüştürür. Bu renk değişikliği avcıları caydırmaya hizmet edebilir.

Doğa daha iyi bilir
Flora ve fauna, vahşi yaşamdaki polihedron örneklerinin yanı sıra taş ve minerallerin cansız dünyası ile doludur. Tamamen evrimsel bir bakış açısından, altıgen yapı enerji optimizasyonunda liderdir. Bariz avantajlara (yerden tasarruf) ek olarak, çokyüzlü ağlar çok sayıda yüz sağlar, bu nedenle komşuların sayısı artar ve bu da tüm yapı üzerinde faydalı bir etkiye sahiptir. Bunun nihai sonucu, bilginin çok daha hızlı yayılmasıdır. Düzenli altıgen ve düzensiz yıldız çokyüzlüler doğada neden bu kadar yaygın? Muhtemelen çok gerekli. Doğa daha iyi bilir, o daha iyi bilir.
Bir kişi, tahta küplerle oynayan iki yaşındaki bir çocuktan olgun bir matematikçiye kadar bilinçli faaliyeti boyunca çokyüzlülere ilgi gösterir. Düzenli ve yarı-düzenli cisimlerin bir kısmı doğada kristaller halinde bulunurken, bir kısmı da ancak elektron mikroskobu ile görülebilen virüsler şeklinde bulunur. polihedron nedir? Bu soruyu cevaplamak için, geometrinin kendisinin bazen uzay bilimi ve uzamsal figürler - iki boyutlu ve üç boyutlu olarak tanımlandığını hatırlayalım. İki boyutlu bir şekil, bir düzlemin bir bölümünü sınırlayan bir dizi çizgi parçası olarak tanımlanabilir. Böyle düz bir şekle çokgen denir. Bir polihedron, üç boyutlu uzayın bir bölümünü sınırlayan bir dizi çokgen olarak tanımlanabilir. Bir polihedron oluşturan çokgenlere yüzleri denir.
Antik çağlardan beri bilim adamları "ideal" veya düzenli çokgenlerle, yani eşit kenarlara ve eşit açılara sahip çokgenlerle ilgilenmişlerdir. Bir eşkenar üçgen, bir düzlemin bir bölümünü sınırlayabilecek en az sayıda kenara sahip olduğundan, en basit düzgün çokgen olarak kabul edilebilir. Bizi ilgilendiren düzgün çokgenlerin genel resmi, bir eşkenar üçgenle birlikte şunlardan oluşur: bir kare (dört kenar), bir beşgen (beş kenar), bir altıgen (altı kenar), bir sekizgen (sekiz kenar), bir ongen (on kenar), vb. Açıkçası, teorik olarak normal bir çokgenin kenar sayısında herhangi bir kısıtlama yoktur, yani düzenli çokgenlerin sayısı sonsuzdur.
Düzenli çokyüzlü nedir? Böyle bir polihedron, tüm yüzleri birbirine eşitse (veya matematikte alışılageldiği gibi uyumluysa) ve aynı zamanda normal çokgenlerse, düzenli olarak adlandırılır. Kaç tane düzgün çokyüzlü vardır? İlk bakışta, bu sorunun cevabı çok basit - ne kadar çok düzenli çokgen varsa, yani ilk bakışta, kenarları herhangi bir normal çokgen olabilen normal bir çokyüzlü oluşturabileceğiniz görülüyor. Ancak öyle değil. Zaten Öklid'in Öğelerinde, düzenli çokyüzlülerin sayısının çok sınırlı olduğu ve yüzleri yalnızca üç tür düzgün çokgen olabilen yalnızca beş düzgün çokyüzlü olduğu kesin bir şekilde kanıtlanmıştır: üçgenler, kareler ve beşgenler. Bu düzenli çokyüzlülere Platonik katılar denir. İlki tetrahedron. Yüzleri dört eşkenar üçgendir. Tetrahedron, Platonik cisimler arasında en az sayıda yüze sahiptir ve düzgün çokgenler arasında en az kenar sayısına sahip olan düz bir düzgün üçgenin üç boyutlu analoğudur. "Dörtyüzlü" kelimesi Yunanca "tetra" - dört ve "edra" - tabandan gelir. Üçgen bir piramittir. Bir sonraki gövde, küp olarak da adlandırılan bir altı yüzlüdür. Altı yüzlünün kare olan altı yüzü vardır. Oktahedronun yüzleri düzgün üçgenlerdir ve oktahedrondaki sayıları sekizdir. Bir sonraki en büyük yüz sayısı dodecahedron'dur. Yüzeyleri beşgendir ve dodekahedrondaki sayıları on ikidir. İkosahedron, beş Platonik cismi kapatır. Yüzleri düzgün üçgendir ve sayıları yirmidir.
Çalışmamda dışbükey çokyüzlülerin ana tanımları ve özellikleri ele alınmıştır. Yalnızca beş düzenli çokyüzlünün varlığı kanıtlanmıştır. Stereometri problemlerinde en yaygın olan düzgün n-gonal piramit ve düzgün dörtyüzlü için ilişkiler ayrıntılı olarak ele alınmıştır. Makale, stereometrinin bazı bölümlerinin incelenmesinde kullanılabilecek çok miktarda analitik ve açıklayıcı materyal sunmaktadır.
Platon'un çalışmaları
Platon çok ilginç bir teori yarattı. Her şeyin inşa edildiği dört "temel elementin" (toprak, su, hava ve ateş) atomlarının düzenli çokyüzlüler biçimine sahip olduğunu öne sürdü: bir tetrahedron - ateş, bir altı yüzlü (küp) - toprak, bir oktahedron - hava, bir ikosahedron - su. Beşinci polihedron - dodecahedron - "Büyük Zihin" veya "Evrenin Uyumu" nu sembolize ediyordu. Ateş, hava ve su gibi kolayca birbirine dönüşen üç elementin parçacıklarının aynı figürlerden - normal üçgenlerden - oluştuğu ortaya çıktı. Ve onlardan önemli ölçüde farklı olan dünya, farklı türde parçacıklardan oluşur - küpler veya daha doğrusu kareler. Platon, tüm dönüşümleri üçgenler yardımıyla çok net bir şekilde açıkladı. Huzursuz kaosta, iki hava parçacığı bir ateş parçacığıyla, yani iki oktahedron bir tetrahedronla karşılaşır. İki oktahedronun toplam on altı üçgen yüzü vardır, bir tetrahedronun dört yüzü vardır. Toplam yirmi. Yirmiden bir ikosahedron kolayca oluşur ve bu bir su parçacığıdır.
Platon'un kozmolojisi, o zamandan beri tüm insan biliminde kırmızı bir iplik gibi işleyen sözde ikosahedral-dodecahedral doktrininin temeli oldu. Bu doktrinin özü, dodecahedron ve icosahedron'un, kozmostan mikro dünyaya kadar tüm tezahürlerinde doğanın tipik biçimleri olduğudur.
Düzenli çokyüzlüler
Düzenli çokyüzlüler, antik çağlardan beri bilim adamlarının, inşaatçıların, mimarların ve diğerlerinin ilgisini çekmiştir. Bu çok yüzlülerin güzelliği, mükemmelliği ve uyumu karşısında şaşkına döndüler. Pisagorcular bu çokyüzlüleri ilahi olarak kabul ettiler ve onları dünyanın özü hakkındaki felsefi yazılarında kullandılar. Öklid'in ünlü "Başlangıçları" nın son 13. kitabı, düzenli çokyüzlülere ayrılmıştır.
Yüzleri eşit düzgün çokgenlerse ve her tepe noktasında aynı sayıda yüz birleşiyorsa, dışbükey bir çokyüzlünün düzenli olarak adlandırıldığını tekrarlıyoruz.
Bu tür en basit çokyüzlü "yüzleri normal üçgenler olan bir üçgen piramittir. Köşelerinin her birinde üç yüz birleşir. Dört yüzün tümüne sahip olan bu çokyüzlüye Yunanca'da "dörtyüzlü" anlamına gelen dörtyüzlü de denir. .
Bazen bir tetrahedron, keyfi bir piramit olarak da adlandırılır. Bu nedenle, normal bir çokyüzlüden bahsettiğimiz durumda, normal bir dörtyüzlü diyeceğiz.
Yüzleri düzgün üçgen olan ve her köşede dört yüzü birleşen, yüzeyi sekiz düzgün üçgenden oluşan çokyüzlüye oktahedron denir.
Her bir köşesinde beş düzgün üçgenin birleştiği ve yüzeyi yirmi düzgün üçgenden oluşan bir çokyüzlüye ikosahedron denir.
Bir dışbükey çokyüzlünün köşelerinde beşten fazla düzgün üçgen yakınsamayacağından, yüzleri düzgün üçgen olan başka hiçbir düzgün çokyüzlü yoktur.
Benzer şekilde, bir dışbükey çokyüzlünün köşelerinde yalnızca üç kare birleşebileceğinden, küpün yanı sıra yüzleri kareler olan başka düzenli çokyüzlü yoktur. Bir küpün altı kenarı vardır ve bu nedenle altı yüzlü olarak adlandırılır.
Yüzleri düzgün beşgen olan ve her tepe noktasında birleşen üç yüzü olan bir çokyüzlü. Yüzeyi on iki normal beşgenden oluşur, buna dodecahedron denir.
Beşten fazla kenarı olan düzgün çokgenler bir dışbükey Çokyüzlünün köşelerinde birleşemeyeceğinden, başka düzenli çokyüzlü yoktur ve bu nedenle yalnızca beş düzgün çokyüzlü vardır: dörtyüzlü, altıyüzlü (küp), oktahedron, dodekahedron, ikosahedron.
Düzenli çokyüzlülerin isimleri Yunanistan'dan gelmektedir. Yunanca "tetrahedron", "octahedron", "hexahedron", "dodecahedron", "icosahedron" kelimelerinden gerçek çeviride şu anlama gelir: "tetrahedron", "octahedron", "hexahedron". dodecahedron, dodecahedron. Euclid's Elements'in 13. kitabı bu güzel bedenlere adanmıştır. Ayrıca Platon'un bedenleri olarak da adlandırılırlar, çünkü Platon'un evrenin yapısına ilişkin felsefi kavramında önemli bir yer işgal ederler.
Ve şimdi bu rakamlarla ilişkili kaç tane özellik, önerme ve teoreme bakalım.
Tüm düz açıların ve tüm dihedral açıların eşit olduğu, tepe noktası S olan bir çokyüzlü açıyı ele alalım. Kenarlarında A1, A2, An noktalarını SA1 = SA2 = SAn olacak şekilde seçiyoruz. O halde A1, A2, An noktaları aynı düzlemdedir ve düzgün bir n-genin köşeleridir.
Kanıt.
Ardışık herhangi bir noktanın aynı düzlemde olduğunu kanıtlayalım. Ardışık dört nokta A1, A2, A3 ve A4'ü ele alalım. SA1 A2 A3 ve SA2 A3 A4 piramitleri eşittir, çünkü SA2 ve SA3 kenarları (tabii ki farklı piramitlerin kenarları alınır) ve bu kenarlardaki dihedral açılar birleştirilerek birleştirilebileceklerdir. Benzer şekilde SA1 A3A4 ve SA1 A2 A4 piramitlerinin de tüm kenarları eşit olduğu için eşit olduğu gösterilebilir. Bu eşitlik anlamına gelir
Son eşitlikten, A1A2A3A4 piramidinin hacminin sıfıra eşit olduğu, yani bu dört noktanın aynı düzlemde olduğu sonucu çıkar. Dolayısıyla, tüm n noktaları aynı düzlemde yer alır ve n-gon A1 A2 An'da tüm kenarlar ve açılar eşittir. Dolayısıyla, doğrudur ve lemma kanıtlanmıştır.
En fazla beş farklı düzgün çokyüzlü türü olduğunu kanıtlayalım.
Kanıt.
Düzenli bir çokyüzlünün tanımından, yalnızca üçgenlerin, dörtgenlerin ve beşgenlerin yüzleri olabileceği sonucu çıkar. Gerçekten de örneğin yüzlerin düzgün altıgen olamayacağını kanıtlayalım. Düzenli bir çokyüzlünün tanımına göre, köşelerinin her birinde en az üç yüz birleşmelidir. Ancak düzgün altıgende açılar 120° dir. Bir dışbükey çokyüzlü açının üç düzlem açısının toplamının 360° olduğu ortaya çıktı ki bu imkansızdır, çünkü bu toplam her zaman 360°'den küçüktür. Ayrıca, düzgün bir çokyüzlünün yüzleri, çok sayıda kenarı olan çokgenler olamaz.
Düzgün bir çokyüzlünün bir tepe noktasında kaç yüzün birleşebileceğini bulalım. Tüm yüzleri düzgün üçgenler ise, o zaman her köşeye beşten fazla üçgen bitişik olamaz, çünkü aksi halde bu tepe noktasındaki düzlem açılarının toplamı en az 360° olacaktır ki bu, gördüğümüz gibi, imkansızdır. Yani, düzgün bir çokyüzlünün tüm yüzleri düzgün üçgenler ise, o zaman her köşeye üç, dört veya beş üçgen bitişiktir. Benzer bir akıl yürütmeyle, yüzleri düzgün dörtgenler ve beşgenler olan düzgün bir çokyüzlünün her köşesinde tam olarak üç kenarın birleştiğinden emin oluruz.
Şimdi belirli bir tipte sabit bir kenar uzunluğuna sahip yalnızca bir çokyüzlü olduğunu kanıtlayalım. Örneğin, tüm yüzlerin düzgün beşgen olduğu durumu ele alalım. Tersini varsayalım: tüm yüzleri a kenarı olan düzgün beşgenler olan ve her bir çokyüzlünün tüm dihedral açıları birbirine eşit olan iki çokyüzlü olsun. Bir çokyüzlünün tüm dihedral açılarının mutlaka başka bir çokyüzlünün ikiyüzlü açılarına eşit olmadığına dikkat edin: şimdi bunu kanıtlayacağız.
Gösterdiğimiz gibi, her çokyüzlünün her bir köşesinden üç kenar çıkar. AB, AC ve AD kenarları bir çokyüzlünün A köşesinden ve A1B1, A1C1 ve A1D1 kenarları diğerinin A1 köşesinden çıksın. ABCD ve A1B1C1D1, A ve A1 köşelerinden çıkan eşit kenarlara ve bu köşelerde düz açılara sahip olduklarından düzgün üçgen piramitler.
Buradan, bir çokyüzlünün ikiyüzlü açılarının diğerinin ikiyüzlü açılarına eşit olduğu sonucu çıkar. Bu nedenle, ABCD ve A1B1C1D1 piramitlerini birleştirirsek, çokyüzlülerin kendileri de uyumlu olacaktır. Dolayısıyla, tüm yüzleri bir kenarı a olan düzgün beşgenler olan düzgün bir çokyüzlü varsa, o zaman böyle bir çokyüzlü benzersizdir.
Diğer çokyüzlüler benzer şekilde kabul edilir. Tüm yüzlerin üçgen olması ve dört veya beş üçgenin her köşeye bitişik olması durumunda, Lemma 2. ve bir beşgen kullanılmalıdır. Teorem kanıtlanmıştır.
Bu teoremin, tam olarak beş tür düzenli çokyüzlü olduğu anlamına gelmediğine dikkat edin. Teorem yalnızca bu tür en fazla beş tür olduğunu belirtir ve şimdi geriye beş çokyüzlü türünün tümünü sunarak bu türlerden gerçekten beş tane olduğunu kanıtlamamız kalıyor.
Düzenli n-gonal piramit
Düzenli bir n-gonal piramit düşünün. Bu polihedron, stereometrik problemlerde sıklıkla karşılaşılır ve bu nedenle, özelliklerinin daha ayrıntılı ve kapsamlı bir şekilde incelenmesi büyük ilgi görmektedir. Dahası, normal çokyüzlülerimizden biri - tetrahedron - bu.
SA1A2 An düzgün bir n-gonal piramit olsun. Aşağıdaki notasyonu tanıtalım:
a, yan nervürün taban düzlemine eğim açısıdır;
β, tabandaki dihedral açıdır;
γ, üstteki düz açıdır;
δ yan kenardaki dihedral açıdır.
O, piramidin tabanının merkezi, B A1A2 kenarının ortası, D A1A3 ve OA2 segmentlerinin kesişme noktası, C SA2 yan kenarındaki nokta, öyle ki A1CSA2, E segmentlerin kesişme noktası olsun SB ve A1C, K, A1A3 ve OV segmentlerinin kesişme noktasıdır. A1OA2= olsun. Göstermesi kolay
Ayrıca piramidin yüksekliğini H ile, apothem - m ile, yan kenar - l ile, tabanın tarafı - a ile ve r ve R ile - tabana yazılan ve açıklanan dairelerin yarıçaplarını belirtiriz. etrafında.
Aşağıda, düzenli bir n-gonal piramidin α, β, γ, δ açıları arasındaki ilişkiler teoremler şeklinde formüle edilmiştir.
düzgün dörtyüzlü
Özellikleri
Önceki bölümde elde edilen bağıntıları düzgün bir dörtyüzlüye uygulamak, sonraki için bir dizi ilginç bağıntı elde etmemizi sağlar. Bu bölümde, bu özel durum için elde edilen formülleri sunacağız ve ek olarak, örneğin hacim, toplam yüzey alanı ve benzeri gibi düzgün bir dörtyüzlünün bazı özellikleri için ifadeler bulacağız.
Önceki bölümün gösterimini takiben, kenar uzunluğu a olan normal dörtyüzlü SA1A2A3'ü ele alalım. Açıları için gösterimi aynı bırakıp hesaplıyoruz.
Düzgün bir üçgende, yüksekliğin uzunluğu eşittir. Bu üçgen düzgün olduğundan, yüksekliği hem açıortay hem de medyandır. Medyanlar, bildiğiniz gibi, kesişme noktalarına göre yukarıdan sayılarak 2: 1 oranında bölünür. Medyanların kesişme noktasını bulmak kolaydır. Dörtyüzlü düzenli olduğundan, bu nokta O noktası olacaktır - A1A2A3 normal üçgeninin merkezi. S noktasından bırakılan düzgün bir dörtyüzlünün yüksekliğinin tabanı da O noktasına çıkıntı yapar. Dolayısıyla,. SA1A2 düzgün üçgeninde, dörtyüzlünün apothem uzunluğu eşittir. Pisagor teoremini Δ SBO için uygulayalım:. Buradan.
Böylece, düzgün bir dörtyüzlünün yüksekliği eşittir.
Bir tetrahedronun tabanının alanı - normal bir üçgen:
Yani düzgün bir tetrahedronun hacmi:
Bir tetrahedronun toplam yüzey alanı, taban alanının dört katıdır.
Düzenli bir dörtyüzlü için yan yüzdeki dihedral açı, açıkça yan yüzün taban düzlemine eğim açısına eşittir:
Düzgün bir dörtyüzlünün tepe noktasındaki düzlem açısı eşittir.
Yan nervürün taban düzlemine eğim açısı şu şekilde bulunabilir:
Düzenli bir tetrahedron için yazılı bir kürenin yarıçapı, onu tetrahedronun hacmi ve toplam yüzey alanı ile ilişkilendiren iyi bilinen bir formülle bulunabilir (ikinci formülün, içinde bir kürenin olabileceği herhangi bir çokyüzlü için geçerli olduğuna dikkat edin. yazılı). Bizim durumumuzda, elimizde
Sınırlandırılmış kürenin yarıçapını bulun. Düzgün bir dörtyüzlünün çevrelediği kürenin merkezi, taban düzlemine dik olan ve kürenin merkezinden geçen SO doğrusu olduğundan ve bu doğru tabanın tüm köşelerinden eşit uzaklıkta bir nokta içermesi gerektiğinden, yüksekliğindedir. tetrahedronun. Bu O1 noktası olsun, sonra O1S=O1A2=R. Sahibiz. Pisagor teoremini BA2O1 ve BO1O üçgenlerine uygulayalım:
R = 3r, r + R = H olduğuna dikkat edin.
Hesaplamak, yani, tanımlanan kürenin merkezinden düzenli bir dörtyüzlünün kenarının göründüğü açıyı hesaplamak ilginçtir. Hadi bulalım:
Bu, kimyanın seyrinden aşina olduğumuz bir değerdir: Bu, metan molekülündeki C-H bağları arasındaki açıdır ve deneyde çok doğru bir şekilde ölçülebilir ve CH4 molekülündeki tek bir hidrojen atomu olmadığı için. Açıkça herhangi bir şey tarafından izole edildiğinden, bu molekülün düzenli bir tetrahedron şekline sahip olduğunu varsaymak mantıklıdır. Bu gerçek, bir elektron mikroskobu kullanılarak elde edilen bir metan molekülünün fotoğrafları ile doğrulanır.
Düzenli altı yüzlü (Küp)
Yüz tipi Kare
Yüz sayısı 6
Kaburga sayısı 12
Pik sayısı 8
Düz açı 90 o
Düz açıların toplamı 270 o
Simetri merkezi var mı Evet (köşegenlerin kesişme noktası)
Simetri eksenlerinin sayısı 9
Simetri düzlemlerinin sayısı 9
düzenli oktahedron
Yüz sayısı 8
Kaburga sayısı 12
Pik sayısı 6
Düz açı 60o
Tepe noktasındaki düz köşe sayısı 4
Düz açıların toplamı 240o
Simetri ekseni var mı Evet
Düzenli bir oktahedronun varlığı
ABCD karesini düşünün ve tabanda olduğu gibi, düzleminin her iki yanında yan kenarları karenin kenarlarına eşit olan dörtgen piramitler oluşturun. Ortaya çıkan çokyüzlü bir oktahedron olacaktır.
Bunu kanıtlamak için geriye tüm dihedral açıların eşit olduğunu kontrol etmemiz kalıyor. Gerçekten de ABCD karesinin merkezi O olsun. O noktasını polihedronumuzun tüm köşeleriyle birleştirerek, ortak bir O köşesine sahip sekiz üçgen piramit elde ederiz. Bunlardan birini, örneğin ABEO'yu düşünün. AO = BO = EO ve dahası, bu kenarlar ikili olarak diktir. ABEO piramidi düzgündür, çünkü tabanı düzgün bir ABE üçgenidir. Bu nedenle, tabandaki tüm dihedral açılar eşittir. Benzer şekilde, tepesi O noktasında olan sekiz piramidin tümü ve tabanları - ABCDEG oktahedronunun yüzleri - düzenlidir ve üstelik birbirine eşittir. Bu, bu oktahedronun tüm dihedral açılarının eşit olduğu anlamına gelir, çünkü bunların her biri, piramitlerin her birinin tabanındaki dihedral açının iki katıdır.
*Altı yüzlü (küp) ve sekiz yüzlü ile ilgili ilginç bir gerçeğe dikkat edin. Bir küpün 6 yüzü, 12 kenarı ve 8 köşesi varken, bir oktahedronun 8 yüzü, 12 kenarı ve 6 köşesi vardır. Yani, bir çokyüzlünün yüz sayısı diğerinin köşe sayısına eşittir ve bunun tersi de geçerlidir. Küp ve altı yüzlünün birbirine ikili olduğu söylenir. Bu aynı zamanda, bir küp alıp yüzlerinin merkezlerinde köşeleri olan bir çokyüzlü inşa ederseniz, kolayca görebileceğiniz gibi, bir oktahedron elde etmeniz gerçeğinde de kendini gösterir. Tersi de doğrudur - oktahedronun yüzlerinin merkezleri küpün köşeleri olarak işlev görür. Bu oktahedron ve küpün ikiliğidir.
Düzgün bir dörtyüzlünün yüzlerinin merkezlerini alırsak, yine düzgün bir dörtyüzlü elde ettiğimizi anlamak kolaydır. Böylece tetrahedron kendisine dualdir. *
düzenli ikosahedron
Yüz görünümü Dik üçgen
Yüz sayısı 20
Kaburga sayısı 30
Pik sayısı 12
Düz açı 60 o
Tepe noktasındaki düz köşe sayısı 5
Düz açıların toplamı 300 o
Simetri merkezi var mı Evet
Simetri eksenlerinin sayısı Birkaç
Simetri düzlemlerinin sayısı Birkaç
Düzenli bir ikosahedronun varlığı
Tüm yüzlerin düzgün üçgen olduğu ve her tepe noktasından 5 kenarın çıktığı düzgün bir çokyüzlü vardır. Bu çokyüzlünün 20 yüzü, 30 kenarı, 12 köşesi vardır ve buna icosahedron (icosi - yirmi) denir.
Kanıt
Kenarı 1 olan ABCDEG oktahedronunu ele alalım. AM = EK = CN = EQ = olacak şekilde AE, BE, CE, DE, AB ve BC kenarlarında sırasıyla M, K, N, Q, L ve P noktalarını seçin. BL = BP = x. Bu noktaları birleştiren tüm doğru parçaları birbirine eşit olacak şekilde x'i seçiyoruz.
Bunun için KM = KQ eşitliğinin sağlanmasının yeterli olduğu açıktır. Bununla birlikte, KEQ, KE ve EQ bacakları olan bir ikizkenar dik üçgen olduğundan, o zaman. MEK üçgeni için kosinüs teoremini yazıyoruz, burada:
Buradan. 1'den büyük olan ikinci kök uymuyor. x'i bu şekilde seçerek gerekli çokyüzlüyü oluşturuyoruz. Tetrahedronun merkezine göre K, L, P, N, Q ve M noktalarına simetrik olan altı nokta daha seçiyoruz ve bunları sırasıyla K1, L1, P1, N1, Q1 ve M1 olarak gösteriyoruz. K, L, P, N, Q, M, K1, L1, P1, N1, Q1 ve M1 köşelerine sahip elde edilen çokyüzlü istenendir. Tüm yüzleri düzenli üçgenlerdir, her tepe noktasından beş kenar çıkar. Şimdi tüm dihedral açılarının birbirine eşit olduğunu kanıtlayalım.
Bunu yapmak için, inşa edilen yirmi yüzün tüm köşelerinin oktahedronun merkezi olan O noktasından eşit uzaklıkta olduğunu, yani O merkezli kürenin yüzeyinde bulunduğunu not ediyoruz. düzgün bir sekiz yüzlünün varlığının ispatında olduğu gibi. Yirmi-hedronun tüm köşelerini O noktasına bağlayalım. Aynı şekilde, tabanları inşa edilen çokyüzlünün yüzleri olan üçgen piramitlerin eşitliğini ispatlıyoruz ve tüm dihedral açıların aynı olduğundan emin oluyoruz. yirmi yüzün her biri, bu eşit üçgen piramitlerin tabanındaki açıların iki katı kadardır. Bu nedenle, tüm dihedral açılar eşittir, bu da ortaya çıkan çokyüzlünün düzenli olduğu anlamına gelir. Buna ikosahedron denir.
Düzenli dodecahedron
Pentagon yüzünün görünümü (normal beşgen)
Yüz sayısı 12
Kaburga sayısı 30
Pik sayısı 20
Düz açı 108 o
Tepe noktasındaki düz köşe sayısı 3
Düz açıların toplamı 324 o
Simetri merkezi var mı evet
Simetri eksenlerinin sayısı Birkaç
Simetri düzlemlerinin sayısı Birkaç
Düzenli bir dodecahedronun varlığı
Tüm yüzleri düzgün beşgen olan ve her tepe noktasından 3 kenar çıkan düzgün bir çokyüzlü vardır. Bu polihedronun 12 yüzü, 30 kenarı ve 20 köşesi vardır ve dodecahedron (dodeka - on iki) olarak adlandırılır.
Kanıt.
Görüldüğü gibi şimdi varlığını kanıtlamaya çalıştığımız çokyüzlünün yüz ve köşe sayısı, ikosahedronun köşe ve yüz sayısına eşittir. Dolayısıyla, bu teoremde bahsedilen çokyüzlünün varlığını kanıtlarsak, o zaman kesinlikle ikosahedronun ikili olduğu ortaya çıkacaktır. Bir küp ve bir oktahedron örneğinde, ikili şekillerin birinin köşesinin diğerinin yüzlerinin merkezinde olma özelliğine sahip olduğunu gördük. Bu, bu teoremi kanıtlama fikrine yol açar.
Bir ikosahedron alın ve köşeleri yüzlerinin merkezinde olan bir çokyüzlü düşünün. İkosahedronun ortak bir köşeye sahip beş yüzünün merkezlerinin aynı düzlemde yer aldığı ve düzgün bir beşgenin köşeleri olarak hizmet ettiği açıktır (bu, lemmanın ispatında kullanılana benzer bir şekilde doğrulanabilir. ). Böylece, ikosahedronun her köşesi, yüzleri düzgün beşgen olan ve tüm dihedral açıları eşit olan yeni bir çokyüzlünün yüzüne karşılık gelir. Bu, yeni çokyüzlünün aynı tepesinden çıkan herhangi üç kenarın, normal bir üçgen piramidin yan kenarları olarak kabul edilebileceği ve ortaya çıkan tüm piramitlerin eşit olduğu (eşit yan kenarlara ve aralarında düz açılara sahip oldukları) gerçeğinden çıkar. düzenli bir üçgen piramidin açılarıdır). beşgen). Yukarıdakilerden, ortaya çıkan çokyüzlünün düzenli olduğu ve 12 yüzü, 30 kenarı ve 20 köşesi olduğu sonucu çıkar. Böyle bir polihedron, dodecahedron olarak adlandırılır.
Yani, üç boyutlu uzayda, sadece beş tür düzenli çokyüzlü vardır. Formlarını belirledik ve tüm çokyüzlülerin ikilileri olduğunu belirledik. Küp oktahedrona göre çifttir ve bunun tersi de geçerlidir. Icosahedron'dan dodecahedron'a ve tam tersi. Tetrahedron kendisine dualdir.
Düzenli çokyüzlüler için Euler formülü
Böylece, tam olarak beş düzgün çokyüzlü olduğu ortaya çıktı. Ve içlerindeki kenarların, yüzlerin, köşelerin sayısı nasıl belirlenir? Az sayıda kenarı olan çokyüzlüler için bunu yapmak zor değil, ama örneğin bir ikosahedron için bu tür bilgileri nasıl elde edebilirim? Ünlü matematikçi L. Euler, herhangi bir çokyüzlünün köşelerinin /В/, yüzlerinin /Г/ ve kenarlarının /Р/ sayısını ilişkilendiren В+Г-Р=2 formülünü elde etti. Bu formülün basitliği, mesafe veya açılarla hiçbir ilgisi olmamasıdır. Normal bir çokyüzlünün kenar, köşe ve yüz sayısını belirlemek için önce k \u003d 2y - xy + 2x sayısını buluruz, burada x bir yüze ait kenarların sayısı, y yakınsayan yüzlerin sayısıdır bir tepe noktasında. Düzgün bir çokyüzlünün yüz, köşe ve kenar sayısını bulmak için formüller kullanırız. Bundan sonra, düzenli çokyüzlülerin öğeleri hakkında bilgi sağlayan bir tabloyu doldurmak kolaydır:
Adı Köşeler (V) Kenarlar (P) Yüzler (D) Formül
Dörtyüzlü 4 6 4 4-6+4=2
Altı Yüzlü (Küp) 8 12 6 8-12+6=2
Sekizyüzlü 6 12 8 6-12+8=2
İkosahedron 12 30 20 12-30+20=2
Dodekahedron 20 30 12 20-30+12=2
Bölüm II: Hayatta düzenli çokyüzlüler
Uzay ve Dünya
Gezegenimiz de dahil olmak üzere Evrenin yapısı hakkında çokyüzlülerle ilgili birçok hipotez ve teori var. Aşağıda bunlardan bazıları var.
I. Kepler tarafından dünyanın uyumlu yapısı sisteminde düzenli çokyüzlüler önemli bir yer işgal etti. Uyum, güzellik ve evrenin matematiksel olarak düzenli yapısına olan aynı inanç, I. Kepler'i beş düzenli çokyüzlü olduğu için bunlara yalnızca altı gezegenin karşılık geldiği fikrine götürdü. Ona göre gezegenlerin küreleri, içlerinde yazılı olan Platonik katı cisimlerle birbirine bağlıdır. Her bir düzgün çokyüzlü için, yazılı ve çevrelenmiş kürelerin merkezleri çakıştığı için, tüm model, Güneş'in yer alacağı tek bir merkeze sahip olacaktır.
Büyük bir hesaplama çalışması yapan I. Kepler, keşfinin sonuçlarını 1596'da "Evrenin Sırrı" kitabında yayınladı. Satürn'ün yörüngesine bir küp, bir kübe - Jüpiter'in küresine, Jüpiter'in küresine - bir tetrahedron ve benzeri sırayla Mars küresini - bir dodecahedron, Dünya küresini birbirine sığdırır. - bir icosahedron, Venüs'ün küresi - bir oktahedron, Merkür'ün küresi. Evrenin sırrı açık görünüyor.
Bugün gezegenler arasındaki mesafelerin herhangi bir polihedra ile ilgili olmadığını söylemek güvenlidir. Bununla birlikte, I. Kepler'in "Evrenin Sırları", "Dünyanın Uyumu", düzenli çokyüzlüler olmasaydı, I. Kepler'in hareketi tanımlamada önemli bir rol oynayan üç ünlü yasası olmazdı. gezegenlerin.
Bu harika bedenleri başka nerede görebilirsin? Yüzyılımızın başındaki Alman biyolog E. Haeckel'in "Doğadaki Formların Güzelliği" adlı çok güzel kitabında şu satırlar okunabilir: "Doğa, bağrında şimdiye kadar tükenmez sayıda harika yaratık besler. güzellik ve çeşitlilikte insan sanatının yarattığı tüm formları aşar." Bu kitaptaki doğanın yaratımları güzel ve simetriktir. Bu, doğal uyumun ayrılmaz bir özelliğidir. Ancak burada tek hücreli organizmaları da görebilirsiniz - şekli ikosahedronu doğru bir şekilde taşıyan feodarii. Böylesine doğal bir geometriye ne sebep oldu? Belki de aynı sayıda yüze sahip tüm çokyüzlüler nedeniyle, en büyük hacme ve en küçük yüzey alanına sahip olan ikosahedrondur. Bu geometrik özellik, deniz mikroorganizmasının su sütununun basıncını yenmesine yardımcı olur.
Biyologların virüslerin şekliyle ilgili tartışmalarında ilgi odağı haline gelen şeyin ikosahedron olması da ilginçtir. Virüs, daha önce düşünüldüğü gibi mükemmel bir şekilde yuvarlak olamaz. Şeklini oluşturmak için çeşitli çokyüzlüler aldılar, atomların virüse akışıyla aynı açılarda onlara ışık yönlendirdiler. Sadece bir çokyüzlünün tam olarak aynı gölgeyi verdiği ortaya çıktı - ikosahedron. Yukarıda belirtilen geometrik özellikleri, genetik bilgilerin kaydedilmesine izin verir. Düzenli çokyüzlüler en avantajlı figürlerdir. Ve doğa bundan yararlanır. Bildiğimiz bazı maddelerin kristalleri düzenli çokyüzlüler biçimindedir. Böylece, küp sodyum klorür kristallerinin şeklini taşır NaCl, alüminyum-potasyum alum (KAlSO4) 2 12H2O'nun tek kristali bir oktahedron şekline sahiptir, kükürt pirit FeS kristali bir dodecahedron şekline sahiptir, antimon sodyum sülfat bir tetrahedron, bor bir ikosahedrondur. Düzenli çokyüzlüler, bazı kimyasalların kristal kafeslerinin şeklini belirler. Bu fikri aşağıdaki problemle açıklıyoruz.
Görev. CH4 metan molekülünün modeli, dört köşede hidrojen atomları ve merkezde bir karbon atomu bulunan düzenli bir tetrahedron şekline sahiptir. İki CH bağı arasındaki bağ açısını belirleyin.
Çözüm. Düzgün bir dört yüzlünün altı eşit kenarı olduğundan, yüzlerinin köşegenleri düzgün bir dört yüzlünün kenarları olacak şekilde bir küp seçmek mümkündür. Küpün merkezi aynı zamanda tetrahedronun da merkezidir, çünkü tetrahedronun dört köşesi aynı zamanda küpün köşeleridir ve etraflarında açıklanan küre, aynı düzlemde uzanmayan dört nokta tarafından benzersiz bir şekilde belirlenir. İki CH bağı arasındaki istenen j açısı, AOS açısına eşittir. AOC üçgeni ikizkenardır. Dolayısıyla, a küpün kenarı olduğunda, d tetrahedronun yan yüzünün veya kenarının köşegeninin uzunluğudur. Yani, buradan = 54.73561O ve j = 109.47O
Dünyanın şekli sorunu, eski zamanların bilim adamlarının zihinlerini sürekli meşgul ediyordu. Ve Dünya'nın küresel şekli hakkındaki hipotez doğrulandığında, Dünya'nın şeklinin bir dodecahedron olduğu fikri ortaya çıktı. Platon zaten şöyle yazmıştı: "Yukarıdan bakarsanız, 12 deri parçasından dikilmiş bir topa benziyor." Platon'un bu hipotezi, fizikçilerin, matematikçilerin ve jeologların çalışmalarında daha fazla bilimsel gelişme buldu. Böylece, Fransız jeolog de Beamont ve ünlü matematikçi Poincaré, Dünya'nın şeklinin deforme olmuş bir dodecahedron olduğuna inanıyorlardı.
Başka bir hipotez var. Bunun anlamı, Dünya'nın bir ikosahedron şekline sahip olmasıdır. Küre üzerinde iki paralel alınır - 30o kuzey ve güney enlemi. Her birinin kendi yarımküresinin kutbuna olan uzaklığı 60o, aralarındaki mesafe de 60o'dir. Bu paralellerin kuzeyinde, noktalar tam bir dairenin 1/5'i veya 72o ile işaretlenir: 32o, 104o ve 176o in meridyenleri ile kesişme noktasında. d. ve 40o ve 112o z. e.Güney paralelinde, noktalar meridyenlerle kesişme noktalarında işaretlenir ve 68o ile 140o arasında tam ortasından geçer. ve 4o, 76o ve 148o z. e.30o s paralelinde beş nokta. Şş. , beş - 30o G paralelinde. Şş. ve Dünya'nın iki kutbu ve çokyüzlünün 12 köşesini oluşturacak.
Rus jeolog S. Kislitsin de Dünya'nın on iki yüzlü şekli hakkındaki görüşünü paylaştı. 400-500 milyon yıl önce on iki yüzlü jeosferin bir jeo-ikosahedron'a dönüştüğünü varsaydı. Bununla birlikte, böyle bir geçişin eksik ve eksik olduğu ortaya çıktı, bunun sonucunda jeo-dodekahedron ikosahedron yapısında yazılı olduğu ortaya çıktı. Son yıllarda, Dünya'nın ikosahedral-dodekahedral şekli hipotezi test edildi. Bunu yapmak için bilim adamları, dodecahedronun eksenini dünyanın ekseni ile hizaladılar ve bu çokyüzlüyü onun etrafında döndürerek, kenarlarının yer kabuğundaki dev rahatsızlıklarla (örneğin, Orta Atlantik ile) çakıştığına dikkat çekti. denizaltı sırtı). Daha sonra ikosahedronu bir polihedron olarak alarak, kenarlarının yer kabuğunun daha küçük bölümleriyle (sırtlar, faylar, vb.) Çakıştığını buldular. Bu gözlemler, yer kabuğunun tektonik yapısının dodecahedron ve icosahedron şekillerine benzer olduğu hipotezini doğrulamaktadır.
Varsayımsal bir jeo-kristalin düğümleri, gezegendeki bazı anormalliklerin merkezleri gibidir: dünyanın tüm aşırı atmosferik basınç merkezlerini, kasırgaların çıktığı alanları içerirler; ikosahedronun düğüm noktalarından birinde (Gabon'da), 1,7 milyar yıl önce hala çalışan bir "doğal atomik reaktör" keşfedildi. Dev maden yatakları (örneğin, Tyumen petrol sahası), hayvanlar dünyasının anormallikleri (Baykal Gölü), insan kültürlerinin gelişme merkezleri (Eski Mısır, proto-Hint uygarlığı Mohenjo-Daro, Kuzey Moğol, vb.) birçok polihedron düğümü ile sınırlıdır.
Bir varsayım daha var. Pisagor, Platon, I. Kepler'in düzenli çokyüzlülerin dünyanın uyumlu yapısıyla bağlantısı hakkındaki fikirleri, yazarları (80'lerin başında) Moskova mühendisleri olan ilginç bir bilimsel hipotezde zamanımızda sürekliliklerini bulmuşlardır. V. Makarov ve V. Morozov. Dünyanın çekirdeğinin, gezegende meydana gelen tüm doğal süreçlerin gelişimini etkileyen, büyüyen bir kristalin şekline ve özelliklerine sahip olduğuna inanıyorlar. Bu kristalin ışınları veya daha doğrusu güç alanı, Dünya'nın ikosahedral-dodekahedral yapısını belirler; icosahedron ve dodecahedron. Yazarlar tarafından düğüm olarak adlandırılan 62 köşeleri ve kenarların orta noktaları, bazı anlaşılmaz fenomenleri açıklamayı mümkün kılan bir dizi spesifik özelliğe sahiptir.
Belki de Dünya hakkında daha fazla araştırma, görünüşe göre düzenli çokyüzlülerin önemli bir yer tuttuğu bu güzel bilimsel hipoteze karşı tutumu belirleyecektir.
Ve normal çokyüzlülerle bağlantılı olarak bir soru daha ortaya çıkıyor: aralarında boşluk kalmayacak şekilde boşluğu onlarla doldurmak mümkün mü? Bazıları düzlemi doldurabilen düzgün çokgenlere benzetilerek ortaya çıkar. Boşluğu yalnızca bir normal çokyüzlü küp yardımıyla doldurabileceğiniz ortaya çıktı. Uzay ayrıca eşkenar dörtgen dodecahedronlarla doldurulabilir. Bunu anlamak için sorunu çözmeniz gerekir.
Görev. Uzamsal bir "haç" oluşturan yedi küpün yardımıyla eşkenar dörtgen bir dodecahedron oluşturun ve alanı doldurabileceklerini gösterin.
Çözüm. Küpler alanı doldurabilir. Kübik bir kafesin bir parçasını düşünün. Orta küpü olduğu gibi bırakıyoruz ve "sınırlayıcı" küplerin her birinde, altı çift zıt kenarın tamamı boyunca düzlemler çiziyoruz. Bu durumda, "çevreleyen" küpler, kare tabanlı ve yan kenarları küpün köşegeninin yarısına eşit olan altı eşit piramide bölünecektir. El değmemiş kübe bitişik piramitler, ikincisi ile birlikte eşkenar dörtgen bir dodecahedron oluşturur. Bundan, tüm alanın eşkenar dörtgen dodecahedronlarla doldurulabileceği açıktır. Sonuç olarak, eşkenar dörtgen bir dodecahedron'un hacminin, kenarı dodecahedron yüzünün daha küçük köşegeniyle çakışan bir küpün hacminin iki katına eşit olduğunu elde ederiz.
Bu sorunu çözerek eşkenar dörtgen dodecahedronlara geldik. İlginç bir şekilde, boşlukları da boşluksuz dolduran arı hücreleri de ideal geometrik şekillerdir. Arı hücresinin üst kısmı eşkenar dörtgen dodecahedron'un bir parçasıdır.
1525'te Dürer, yüzeyleri iyi perspektif modeller olarak hizmet eden beş düzgün çokyüzlüyü sunduğu bir inceleme yazdı.
Böylece, düzenli çokyüzlüler bize bilim adamlarının dünya uyumunun sırrına yaklaşma girişimlerini ortaya çıkardı ve geometrinin karşı konulamaz çekiciliğini gösterdi.
Düzenli çokyüzlüler ve altın oran
Rönesans döneminde heykeltıraşlar, mimarlar ve sanatçılar düzenli çokyüzlülerin biçimlerine büyük ilgi gösterdiler. Örneğin Leonardo da Vinci, çokyüzlüler teorisine düşkündü ve onları sık sık tuvallerinde tasvir etti. Arkadaşı keşiş Luca Pacioli'nin (1445 - 1514) "İlahi Oran Üzerine" kitabını düzenli ve yarı düzenli çokyüzlülerin resimleriyle resmetti.
1509'da Venedik'te Luca Pacioli, İlahi Oran Üzerine'yi yayınladı. Pacioli beş Platonik katıda bulundu - düzenli çokgenler (tetrahedron, küp, oktahedron, icosahedron ve dodecahedron) "ilahi oranın" on üç tezahürü. "On ikinci, neredeyse doğaüstü mülkiyet" bölümünde, normal icosahedron'u ele alıyor. İkosahedronun her bir köşesinde, beş üçgen düzgün bir beşgen oluşturmak için birleşir. Bir ikosahedronun herhangi iki zıt kenarını birbirine bağlarsanız, kenarların toplamı büyük olana eşit olduğundan, büyük kenarı küçük olanla ilişkili olan bir dikdörtgen elde edersiniz.
Böylece, altın oran, eski bilim adamlarına göre evrenin altında yatan beş düzenli çokyüzlü geometrisinde kendini gösterir.
Büyük sanatçıların resimlerinde Platon'un katı cisimlerinin geometrisi
Geometriye de düşkün olan ünlü bir Rönesans sanatçısı A. Dürer'di. Ünlü gravürü "Melancholia"da ön planda bir dodecahedron tasvir edilmiştir.
Ressam Salvador Dali'nin "Son Akşam Yemeği" tablosunun görüntüsünü düşünün. Resmin ön planında, büyük şeffaf bir dodecahedronun arka planına karşı müritleriyle birlikte Mesih tasvir edilmiştir.
Kristaller doğal çokyüzlülerdir
Pek çok polihedron biçimi insanın kendisi tarafından değil, doğa tarafından kristaller biçiminde icat edildi.
Çoğu zaman, kristallerin harika, yanardöner polihedronlarına bakan insanlar, bunların insan tarafından değil doğa tarafından yaratıldığına inanamazlar. Bu yüzden kristallerle ilgili pek çok şaşırtıcı halk hikayesi doğdu.
İlginç yazılı materyaller günümüze ulaşmıştır, örneğin, değerli taşlara gizemli güçlerin atfedildiği, özel ritüeller ve büyülerle taş işleme yöntemlerinin tanımını içeren sözde "Ebers Papirüsü".
Nar kristalinin mutluluk getirdiğine inanılıyordu. Eşkenar dörtgen bir dodecahedron (bazen eşkenar dörtgen veya eşkenar dörtgen olarak adlandırılır) - yüzleri on iki eşit eşkenar dörtgen olan bir dodecahedron biçimine sahiptir.
Granat için, dodecahedral kristaller o kadar tipiktir ki, böyle bir çokyüzlünün şekline bir garnetohedron bile denirdi.
Granat, kayaç oluşturan ana minerallerden biridir. Skarn adı verilen granat kayalarından oluşan devasa kayalar var. Ancak değerli, güzel renkli ve şeffaf taşlar yaygın olmaktan uzaktır. Buna rağmen, şu anda çok popüler olduğu modern Çek Cumhuriyeti ve Slovakya topraklarında antik Neolitik dönemde Avrupa'da keşfedildiğinden, arkeologların en eski dekorasyon olarak gördükleri tam olarak garnet - kan kırmızısı piroptur.
Granatın, yani rhombododecahedron polyhedron'un antik çağlardan beri bilinmesi, eski Yunanca'da "kırmızı boya" anlamına gelen adının kökeni tarihi ile değerlendirilebilir. Aynı zamanda, isim, garnetlerin en yaygın rengi olan kırmızı ile ilişkilendirildi.
Garnet, değerli taş uzmanları tarafından çok değerlidir. Birinci sınıf mücevher yapımında kullanılan lal taşı, onu takan kadınlara öngörü armağanını iletme ve ağır düşünceleri onlardan uzaklaştırma yeteneğine sahipken, erkekleri şiddetli ölümden korur.
El bombaları, durumun olağandışılığını, insanların eylemlerinin tuhaflığını vurgular, duygularının saflığını ve yüceliğini vurgular.
Bu, OCAK'ta doğan insanlar için bir tılsım taşıdır.
Şekli iyi çalışılmış ve düzenli, yarı düzenli ve yıldız biçimli çokyüzlüleri temsil eden taşları düşünün.
Pirit, adını Yunanca ateş anlamına gelen pyros kelimesinden alır. Bir darbe kıvılcım çıkarır, eski zamanlarda pirit parçaları çakmaktaşı görevi görürdü. Yüzlerdeki aynasal parlaklık, piriti diğer sülfitlerden ayırır. Cilalı pirit daha da parlar. İnkaların mezarlarında arkeologlar tarafından parlatılmış piritten yapılmış aynalar bulundu. Bu nedenle piritin de çok nadir bir adı vardır - İnkaların taşı. Altına hücum salgınları sırasında, bir kuvars damarındaki pirit pulları, bir yıkama tavasındaki ıslak kumda birden fazla sıcak kafa çevirdi. Acemi taş severler şimdi bile piriti altın sanıyorlar.
Ama ona daha yakından bakalım, atasözünü dinleyelim: "Parıldayan her şey altın değildir!" piritin rengi pirinç sarısıdır. Pirit kristallerinin kenarları, güçlü bir metalik parlaklıkla dökülür. ? burada molada parlaklık daha sönük.
Piritin sertliği 6-6.5'dir, camı kolayca çizer. Sülfür sınıfındaki en sert mineraldir.
Yine de piritin görünümündeki en karakteristik özellik kristallerin şeklidir. Çoğu zaman bir küptür. Çatlaklar boyunca yuva yapan en küçük "küplerden, nervür yüksekliği 5 cm, 15 cm ve hatta 30 cm olan küplere! Ancak pirit kristalleri sadece küpler halinde kesilmez, bu mineralin cephaneliğinde zaten bildiğimiz oktahedronlar vardır. manyetit Pirit için oldukça nadirdirler.Fakat pirit, aynı adı taşıyan forma kişisel olarak hayran olmanızı sağlar - pentagondodecahedron. "Penta" beştir, bu formun tüm yüzleri beş kenarlıdır ve "dodeca" - bir düzine - toplamda on iki tane var. Pirit için bu form o kadar tipiktir ki, eski günlerde "piritohedron" adını bile almıştır. Farklı şekillerdeki yüzleri birleştiren örnekler de olabilir: bir küp ve bir pentagondodekahedron.
kaset
Kasiterit, kalayın ana cevheri olan parlak, kırılgan kahverengi bir mineraldir. Şekil çok akılda kalıcı - yüksek dört yüzlü, üstte ve altta keskin piramitler ve ortada - yine yönlü kısa bir sütun. Görünüş olarak oldukça farklı olan kasiterit kristalleri, kuvars damarlarında büyür. Chukchi Yarımadası'nda, mükemmel casiterite kristallerine sahip damarların uzun zamandır ünlü olduğu Iultin yatağı var.
Galena bir metale benziyor ve onu cevherde fark etmemek imkansız. Anında güçlü bir metalik parlaklık ve ağırlık verir. Galena neredeyse her zaman gümüşi küplerdir (veya paralelyüzlülerdir). Ve bunlar mutlaka bütün kristaller değildir. Galena, bir küpte mükemmel bir bölünmeye sahiptir. Bu, şekilsiz parçalara değil, düzgün gümüşi parlak küplere bölündüğü anlamına gelir. Doğal kristalleri bir oktahedron veya kübiktahedron şeklindedir. Galena ayrıca böyle bir özellik ile ayırt edilir: bu mineral yumuşaktır ve kimyasal olarak çok dayanıklı değildir.
ZİRKONYUM
"Zirkon" - Farsça "kral" ve "silah" kelimelerinden - altın rengi.
Zirkonyum değerli Seylan zirkonunda 1789/0'da keşfedildi. Bu elementin kaşifi M. Claport'tur. Muhteşem şeffaf ve parlak ışıltılı zirkonlar antik çağda ünlüydü. Bu taş Asya'da oldukça değerliydi.
Nükleer reaktörlerde zirkonyum çubuk kabukları ve diğer yapısal detaylar ortaya çıkmadan önce kimyagerler ve metalürjistler çok çalışmak zorunda kaldılar.
Yani zirkon etkili bir taştır - turuncu, saman sarısı, mavi - mavi, yeşil - parlar ve elmas gibi oynar.
Zirkonlar genellikle karakteristik zarif bir şekle sahip küçük düzenli kristallerle temsil edilir. Kristal kafeslerinin motifi ve buna bağlı olarak kristallerin şekli, dördüncü simetri eksenine tabidir. Zirkon kristalleri, tetragonal sengoniye aittir. Enine kesitte karedirler. Ve kristalin kendisi bir dörtgen prizmadan (bazen kenarları boyunca ikinci bir benzer prizma ile köreltilir) ve prizmayı her iki uçta tamamlayan bir dörtgen bipiramitten oluşur.
Uçlarında iki dipiramit bulunan kristaller daha da göz alıcıdır: biri üstte, diğeri ise yalnızca prizma ile üst piramit arasındaki kenarları matlaştırır.
Tuz kristalleri küp şeklindedir, buz kristalleri ve kaya kristali (kuvars) her iki tarafı bilenmiş bir kaleme benzer, yani tabanına altıgen piramitlerin yerleştirildiği altıgen prizma şeklindedir.
Elmas çoğunlukla bir oktahedron, bazen bir küp ve hatta bir kübiktahedron şeklinde bulunur.
Görüntüyü ikiye bölen İzlanda direği, eğik bir paralelyüz şeklindedir.
İlginç
Diğer tüm normal çokyüzlüler küpten dönüşümlerle elde edilebilir.
Yumurtanın bölünmesi sürecinde önce dört hücreden oluşan bir tetrahedron, ardından bir oktahedron, bir küp ve son olarak gastrulanın on iki yüzlü-ikosahedral yapısı oluşur.
Ve son olarak, belki de en önemlisi, yaşamın genetik kodunun DNA yapısı, dönen bir dodecahedron'un (zaman ekseni boyunca) dört boyutlu bir taramasıdır!
Düzenli çokyüzlülerin iyi şans getirdiğine inanılıyordu. Bu nedenle, sadece küp şeklinde değil, diğer tüm formlarda kemikler vardı. Örneğin, dodecahedron şeklindeki bir kemiğe d12 adı verildi.
Alman matematikçi August Ferdinand Möbius, “Polyhedra'nın Hacmi Üzerine” adlı çalışmasında, inanılmaz bir özelliği olan geometrik bir yüzey tanımladı: sadece bir tarafı var! Bir kağıt şeridinin uçlarını yapıştırırsanız, önce birini 180 derece döndürürseniz, bir Mobius şeridi veya şeridi elde ederiz. Bükülmüş şeridi 2 renge boyamayı deneyin - biri dışarıda, diğeri içeride. Başaramayacaksın! Ancak öte yandan, Möbius şeridinde sürünen bir karıncanın karşı tarafa geçmek için kenarını aşmasına gerek yoktur.
Lewis Carroll bir keresinde "Düzenli dışbükey çokyüzlüler meydan okurcasına azdır," dedi, "ancak sayıca çok mütevazı olan bu müfreze, muhteşem beşli, bilimin derinliklerine derinlemesine nüfuz etmeyi başardı. »
Tüm bu örnekler, Platon'un sezgisinin şaşırtıcı içgörüsünü doğrular.
Çözüm
Sunulan çalışma şunları dikkate alır:
Dışbükey çokyüzlünün tanımı;
Belirli bir çokyüzlünün köşelerinin, kenarlarının ve yüzlerinin sayısıyla ilgili Euler teoremi dahil olmak üzere dışbükey çokyüzlülerin temel özellikleri;
Düzenli bir çokyüzlünün tanımı, yalnızca beş düzgün çokyüzlünün varlığı kanıtlanmıştır;
Düzgün bir çokyüzlünün ayrılmaz bir parçası olan düzgün bir n-gonal piramidin karakteristik açıları arasındaki ilişkiler ayrıntılı olarak ele alınır;
Düzenli bir dört yüzlünün hacim, yüzey alanı ve benzeri gibi bazı özellikleri ayrıntılı olarak ele alınmıştır.
Ekler, dışbükey çokyüzlülerin ana özelliklerinin kanıtlarını ve bu yazıda yer alan diğer teoremleri içerir. Yukarıdaki teoremler ve ilişkiler, stereometrideki birçok problemin çözümünde faydalı olabilir. Çalışma, belirli stereometri konularının incelenmesinde referans ve açıklayıcı materyal olarak kullanılabilir.
Polihedronlar her yerde bizi çevreliyor: çocuk küpleri, mobilyalar, mimari yapılar vb. Günlük yaşamda onları fark etmeyi neredeyse bıraktık, ancak herkesin aşina olduğu nesnelerin tarihini bilmek çok ilginç, özellikle de çok heyecan vericiyse.
Russkikh Egor, Tarasov Dmitry
Çevremizdeki dünya bir formlar dünyasıdır, çok çeşitli ve şaşırtıcıdır. Çeşit çeşit ev eşyalarıyla çevriliyiz. Bu konuyu inceledikten sonra gerçekten çokgenlerin bizi her yerde çevrelediğini ve hayatın çeşitli alanlarında bulunduğunu gördük.
İndirmek:
Ön izleme:
https://accounts.google.com
Slayt altyazıları:
normal çokgenler
İnanılmaz çokgen
yıldız çokgenler
Doğadaki çokgenler
Doğadaki çokgenler
İlginiz için teşekkür ederiz!
Ön izleme:
Sunuların önizlemesini kullanmak için bir Google hesabı (hesabı) oluşturun ve oturum açın: https://accounts.google.com
Slayt altyazıları:
Bilimde ve diğer bazı yaşam alanlarında düzenli çokgenler Projenin yazarları: Rusların 8. sınıf öğrencileri Egor Tarasov Dmitry. Bilimsel danışman: matematik öğretmeni Rakhmankulova E.R.
Sorunlu soru Çokgenlerin hayatımızdaki rolü nedir? Çalışmanın amacı: çokgenler. Araştırma konusu: çevremizdeki dünyadaki çokgenlerin pratik uygulaması.
Amaç: bu konudaki bilginin sistemleştirilmesi ve çokgenler ve bunların pratik uygulamaları hakkında yeni bilgiler elde edilmesi. Görevler: 1. Konuyla ilgili literatürü incelemek. 2. Çevremizdeki dünyada düzgün çokgenlerin pratik uygulamasını gösterin.
Araştırma yöntemleri: 1. Bilimsel (literatür çalışması); 2. Araştırma. Hipotez: Çokgenler insan çevresinde güzellik yaratır.
normal çokgenler
Sihirli kare 4 9 2 3 5 7 8 1 6
İnanılmaz çokgen
yıldız çokgenler
Doğadaki çokgenler P3: P4: P6 = 1: 0,877: 0,816
Doğadaki çokgenler
Doğadaki çokgenler
Çevremizdeki çokgenler Parke
Sonuç Geometri olmadan hiçbir şey olmazdı, bizi çevreleyen her şey geometrik şekillerdir. Ama dikkat etmeyi unutuyoruz.
Sonuç Çevremizdeki dünya bir formlar dünyasıdır, çok çeşitli ve şaşırtıcıdır. Çeşit çeşit ev eşyalarıyla çevriliyiz. Bu konuyu inceledikten sonra gerçekten çokgenlerin bizi her yerde çevrelediğini ve hayatın çeşitli alanlarında bulunduğunu gördük.
İlginiz için teşekkür ederiz!
Ön izleme:
Sunuların önizlemesini kullanmak için bir Google hesabı (hesabı) oluşturun ve oturum açın:
"Poligonlar" - Oyun için "Poligonlar" Görevleri konusunda kendi kendine çalışma materyali. Üçgen (eşkenar). bozuk hat. dışbükey olmayan Derleyici. Soloninkina T.V. Bir çokgenin sınırladığı bir düzlemin uç kısmı. Dışbükey bir beşgen çizin. Pentagon. Düzenli çokgenler. Uzman 2.
"Bir çokgenin alanını ölçmek" - Yeni şeyler öğrenmek. 1. Bir şeklin alanı nasıl ölçülür? - Alan kavramı herkes tarafından yaşam deneyimlerinden bilinir. Abu-r-Raykhan al-Buruni. 3. Ders hedefleri: Bugünden itibaren çeşitli geometrik şekillerin alanlarını hesaplamayı öğreneceğiz. Sık sık şunu duyarız: "dairemizin alanı 63m2'dir." Cherevina Oksana Nikolaevna
"Şekillerin geometri alanları" - Alanları eşit olan şekillere eşit denir. H.S=(a?b):2. Dikdörtgen, üçgen, paralelkenar. C.S=a?b. D. Öğretmen: Ivniaminova L.A. Şekil alanları. A. B. b. Yazarlar: Zyryanova N. Jafarova A 8b notu.
"Düzenli çokgen" - Sonuç1. Düzenli çokgenler. Temel formüller. R. Dik üçgen. Sonuç 2. Düzgün bir çokgenin çevrelediği daire. R. Sonuçlar. Düzgün bir çokgenin içine çizilmiş bir daire. Düzenli altıgen. A. Formüllerin uygulanması. Herhangi bir normal çokgene bir daire ve dahası yalnızca bir daire çizebilirsiniz.
"Paralelkenar" - Paralelkenar. Bir dörtgenin karşılıklı kenarları çiftler halinde eşitse, o zaman dörtgen bir paralelkenardır. Bir dörtgenin iki kenarı eşit ve paralel ise. paralelkenar nedir? Bir paralelkenarın özellikleri. Paralelkenarda karşılıklı kenarlar ve karşılıklı açılar birbirine eşittir. Bir paralelkenarın köşegenleri kesişme noktası tarafından ikiye bölünür.
"Rhombus Kare Dikdörtgen" - "Dikdörtgen" konulu problemlerin çözülmesi. A. Doğrulama testinin yanıtları. Bul: MD + DN. Eşkenar dörtgen. Dersin amacı: “Dikdörtgen” konulu teorik materyali pekiştirmek. Teorik bağımsız çalışma + (evet), - (hayır) işaretlerini işaretleyerek tabloyu doldurun. Teorik bağımsız çalışmaya doğru cevaplar.
Konuyla ilgili toplam 19 sunum var.