O zi buna, prieteni!

De mult aveam să vă povestesc despre acest proiect al nostru, dar cumva mâinile nu au ajuns. Și iată o minune! Au sosit mainile! Deci, proiectul se numește „Poligoane din jurul nostru”. După cum probabil ați ghicit, aceasta este lucrarea de matematică pe care am făcut-o în clasa a IV-a cu fiica mea Alexandra.

Am abordat lucrarea creativ și suntem siguri că creativitatea noastră matematică vă poate fi utilă pentru a vă pregăti rezumatele, proiectele sau lucrările de cercetare.

Am intitulat lucrarea astfel: „Thriller matematic. Polygon Hunter »

Și acum vă aduc textul integral, împreună cu toate fotografiile. Povestea este spusă la persoana întâi, autorul acestei lucrări științifice.

Scopul lucrării: aplicarea practică a poligoanelor în lumea din jurul nostru.

Întrebare problematică: ce loc ocupă poligoanele în viața noastră?

Din copilărie suntem familiarizați cu diverse tipuri de poligoane, dar cât de des le întâlnim în lumea din jurul nostru, cumva nu ne gândim.

Am decis să arunc o privire mai atentă asupra lucrurilor familiare în viața de zi cu zi și să găsesc poligoane studiate la lecțiile de matematică în obiectele din jurul nostru.

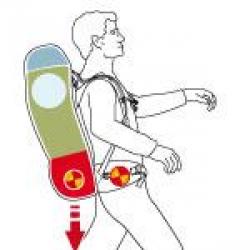
Într-o zi, înarmat până în dinți cu o riglă lungă și grea, am plecat la vânătoare de poligoane.

Nu trebuia să meargă departe. Le-am căutat acasă.

M-am dus la ușa bucătăriei și, adunându-mi voința într-un pumn, am aprins lumina! Și... O groază!!! Am simțit sute de vederi poligonale, ascuțite și tocite, precum și vederi absolut directe. Erau peste tot! Se uitau la mine fără ezitare! Nu le era frică de domnitorul meu! Nici nu au încercat să se ascundă! Aceasta nu este o bucătărie! Acesta este un adevărat regat poligonal! Sute de poligoane s-au așezat pe pereți (dreptunghiuri în modelul tapetului). Nici nu am îndrăznit să le număr.

Cei mai vicleni s-au lipit de tavan (placile de tavan sunt în formă de dreptunghiuri). M-au privit suspiciosi de sus.

Și cei mai aroganți au intrat în vase... și chiar s-au transformat în ele (ornamentul de pe vase și forma vaselor sunt reprezentate de diferite tipuri de poligoane).

Acum știu că poligoanelor le place să modeleze găluște (hexagoanele sunt vizibile în forma de găluște).

Ei urmăresc ce mănânc. Și chiar și pentru ceea ce mănâncă pisica mea (marginile cutiilor de mâncare sunt sub formă de dreptunghiuri).

Îngrozită, am sărit din bucătărie și m-am îndreptat spre hol. Și deodată am văzut... că unul dintre poligoane mi-a capturat papagalii (cușca este formată din elemente de formă dreptunghiulară, triunghiulară și pătraunghiulară).

Aceste figurine obscure nu au cruțat nici măcar un copil (elementele constructoare). Fratele meu mai mic s-a jucat cu entuziasm cu ei, neștiind pericolul.

Iubita mea bunica, fără să se oprească, s-a uitat într-un alt poligon, care i-a arătat ce se întâmplă în lume (ecranul televizorului este dreptunghi).

Și deodată se auzi un scârțâit ascuțit! „Ce este asta?” m-am gândit șocată. Și a fost un alt reprezentant al acestui regat poligonal (un telefon mobil are forma unui paralelipiped dreptunghiular) care a dat o voce de pe raft.

Am fugit la creșă, sperând să mă ascund măcar acolo... Dar nu am reușit.

Poligoane strălucitoare, vesele, care râdeau bucuroși, se legănau pe perdelele noastre (model geometric de țesătură). „Fie ca tu să cazi!”, m-am gândit și m-am uitat la masa mea...

N-ar fi trebuit să o fac... Pe masa mea, două poligoane complexe vorbeau despre ceva. Unul este albastru, celălalt este roșu... (plafondurile lămpilor pot fi considerate ca o combinație de triunghiuri și patrulatere).

Și lângă ei, puii poligonali chicoteau încet (marginile creioanelor sunt dreptunghiuri, iar baza este un hexagon).

Acesta nu este un apartament! Acesta este un bârlog de poligoane!!! Au un cuib aici!

Au sărbătorit chiar și Anul Nou alături de noi (forma multor decorațiuni de Crăciun este o combinație de diferite poligoane)! Și nici nu știam...

Mi-am dat seama că nu te poți ascunde de ei nicăieri. Chiar și în Egipt (fețele piramidelor sunt triunghiuri, bazele sunt dreptunghiuri)!

Concluzie. Această lume aparține poligoanelor! Și trebuie să ne împăcăm cu asta. Și învață să trăiești în armonie cu aceste creaturi poligonale.

Avem aici un proiect atât de neobișnuit. Datorită cărora, în jurnal, Sasha a mai obținut cinci.

A fost realizat în programul Power Point sub formă de diapozitive și prezentat nu doar la o lecție de matematică, ci și la concursul școlar „Știință și creativitate”, unde i s-a acordat și o diplomă.

Pe blogul nostru veți găsi și alte proiecte matematice:

Asta e tot pentru azi!

Vă dorim sarcini creative interesante!

Ce s-ar întâmpla dacă ar exista un singur tip de formă în lume, de exemplu, o formă cum ar fi un dreptunghi? Unele lucruri nu s-ar schimba deloc: uși, remorci de marfă, terenuri de fotbal - toate arată la fel. Dar cum rămâne cu mânerele ușilor? Ar fi puțin ciudați. Dar roțile mașinii? Acest lucru ar fi ineficient. Dar fotbalul? E greu de imaginat. Din fericire, lumea este plină de multe forme diferite. Există ele în natură? Da, și sunt o mulțime.

Ce este un poligon?

Pentru ca o figură să fie un poligon, sunt necesare anumite condiții. În primul rând, trebuie să fie multe laturi și colțuri. De asemenea, trebuie să fie o formă închisă. este o figură cu toate laturile și unghiurile egale. În consecință, pentru cel greșit, acestea pot fi ușor deformate.

Tipuri de poligoane regulate

Care este numărul minim de laturi pe care un poligon obișnuit poate avea? O singură linie nu poate avea mai multe laturi. De asemenea, cele două părți nu se pot întâlni și formează o formă închisă. Și trei laturi pot - deci obțineți un triunghi. Și din moment ce vorbim despre poligoane regulate, unde toate laturile și unghiurile sunt egale, ne referim

Dacă mai adaugi o latură, obții un pătrat. Un dreptunghi unde laturile nu sunt egale poate fi un poligon regulat? Nu, această cifră va fi numită dreptunghi. Dacă adăugați a cincea latură, obțineți un pentagon. În consecință, există hexagoane, heptagoane, octagoane și așa mai departe la infinit.

Geometrie elementară

Poligoane sunt de diferite tipuri: deschise, închise și auto-intersectante. În geometria elementară, un poligon este o figură plată, care este delimitată de un lanț finit de segmente de linie dreaptă sub forma unei polilinii sau contur închise. Aceste segmente sunt marginile sau laturile sale, iar punctele în care două margini se întâlnesc sunt vârfurile și colțurile sale. Interiorul unui poligon este uneori numit corpul său.

Poliedre în natură și viața umană

În timp ce multe forme vii abundă în modele pentagonale, lumea minerală favorizează simetria dublă, triplă, cvadruplă și șase ori. Hexagonul este o formă densă care oferă eficiență structurală maximă. Este foarte frecventă în domeniul moleculelor și al cristalelor, în care forme pentagonale nu se găsesc aproape niciodată. Steroizii, colesterolul, benzenul, vitaminele C și D, aspirina, zahărul, grafitul sunt toate manifestări ale simetriei șase. Unde se găsesc poliedre regulate în natură? Cea mai cunoscută arhitectură hexagonală este creată de albine, viespi și viespi.

Șase molecule de apă formează miezul fiecărui cristal de zăpadă. Așa se face un fulg de nea. Fațetele ochiului muștei formează un aranjament hexagonal dens. Ce alte poliedre regulate există în natură? Acestea sunt cristale de apă și diamant, coloane de bazalt, celule epiteliale din ochi, unele celule vegetale și multe altele. Astfel, poliedrele create de natură, atât animate cât și neînsuflețite, sunt prezente în viața umană într-un număr și varietate imensă.

Care este motivul popularității hexagoanelor?

Fulgii de zăpadă, moleculele organice, cristalele de cuarț și bazalții columnari sunt hexagoane. Motivul pentru aceasta este simetria lor inerentă. Cel mai frapant exemplu este fagurele, a cărui structură hexagonală minimizează lipsa de spațiu, deoarece întreaga suprafață este folosită foarte rațional. De ce să se împartă în celule identice? Albinele creează poliedre regulate în natură pentru a le folosi pentru nevoile lor, inclusiv pentru depozitarea mierii și depunerea ouălor. De ce natura preferă hexagoanele? Răspunsul la această întrebare poate fi dat de matematica elementară.

• Triunghiuri. Luați 428 de triunghiuri echilaterale cu o latură de aproximativ 7,35 mm. Lungimea lor totală este de 3 * 7,35 mm * 428/2 = 47,2 cm.
• dreptunghiuri. Luați 428 de pătrate cu latura de aproximativ 4,84 mm, lungimea lor totală este de 4 * 4,84 m * 428/2 = 41,4 cm.
• Hexagoane. Și, în cele din urmă, luați 428 de hexagoane cu o latură de 3 mm, lungimea lor totală este de 6 * 3 mm * 428/2 = 38,5 cm.

Evident este victoria hexagoanelor. Această formă este cea care ajută la minimizarea spațiului la maximum și vă permite să plasați cât mai multe figuri posibil într-o zonă mai mică. Fagurele în care albinele își depozitează nectarul de chihlimbar este o minune a ingineriei de precizie, o serie de celule în formă de prismă cu o secțiune transversală perfect hexagonală. Pereții de ceară sunt realizați la o grosime foarte precisă, celulele sunt înclinate cu grijă pentru a preveni căderea mierii lipicioase, iar întreaga structură este aliniată cu câmpul magnetic al pământului. În mod surprinzător, albinele lucrează simultan, coordonându-și eforturile.

De ce hexagoane? Este o geometrie simplă

Dacă doriți să puneți împreună celule de aceeași formă și dimensiune, astfel încât să umple întregul plan, atunci doar trei forme regulate (cu toate laturile și cu aceleași unghiuri) vor funcționa: triunghiuri echilaterale, pătrate și hexagoane. Dintre acestea, celulele hexagonale necesită cea mai mică lungime totală a peretelui în comparație cu triunghiurile sau pătratele din aceeași zonă.

Deci alegerea hexagoanelor de către albine are sens. În secolul al XVIII-lea, omul de știință Charles Darwin a declarat că fagurii hexagonali erau „absolut ideali pentru a economisi forța de muncă și ceară”. El credea că selecția naturală a dat albinelor instinctul de a crea aceste camere de ceară, care aveau avantajul de a necesita mai puțină energie și timp decât alte forme.

Exemple de poliedre în natură

Ochii compuși ai unor insecte sunt împachetati într-un hexagon, unde fiecare față este o lentilă conectată la o celulă retiniană lungă și subțire. Structurile care sunt formate din grupuri de celule biologice au adesea forme guvernate de aceleași reguli ca bulele din apă cu săpun. Structura microscopică a fațetei ochiului este unul dintre cele mai bune exemple. Fiecare fațetă conține un grup de patru celule fotosensibile, care au aceeași formă ca grupul de patru vezicule obișnuite.

Ce determină aceste reguli ale foliei de săpun și formele bulelor? Natura este chiar mai preocupată de economie decât de albine. Bulele și peliculele de săpun sunt făcute din apă (cu săpun adăugat), iar tensiunea superficială trage suprafața lichidului în așa fel încât să îi confere o suprafață cât mai mică. Acesta este motivul pentru care picăturile sunt sferice (mai mult sau mai puțin) atunci când cad: o sferă are o suprafață mai mică decât orice altă formă cu același volum. Pe o foaie de ceară, picăturile de apă sunt trase în margele mici din același motiv.

Această tensiune superficială explică modelele de plută cu bule și spumă. Spuma va căuta structura care are cea mai mică tensiune superficială totală, care va oferi cea mai mică suprafață a peretelui. Deși geometria foliilor de săpun este dictată de interacțiunea forțelor mecanice, aceasta nu ne spune care va fi forma spumei. O spumă tipică conține celule poliedrice de diferite forme și dimensiuni. Dacă te uiți cu atenție, atunci poliedrele obișnuite din natură nu sunt atât de corecte. Marginile lor sunt rareori perfect drepte.

Corectează bulele

Să presupunem că poți face o spumă „perfectă” în care toate bulele au aceeași dimensiune. Care este forma perfectă a celulei care face ca suprafața totală a peretelui bulei să fie cât mai mică posibil. Acest lucru a fost discutat de mulți ani și pentru o lungă perioadă de timp s-a crezut că forma ideală a celulei este un poliedru cu 14 laturi cu laturile pătrate și hexagonale.

În 1993, a fost descoperită o structură mai economică, deși mai puțin ordonată, constând dintr-un grup repetat de opt forme de celule diferite. Acest model mai complex a fost folosit ca inspirație pentru proiectarea cu spumă a stadionului de înot în timpul Jocurilor Olimpice de la Beijing din 2008.

Regulile de formare a celulelor în spumă controlează, de asemenea, unele dintre modelele observate în celulele vii. Nu numai ochiul compus al muștei arată aceeași împachetare hexagonală de fațete ca și bula plată. Celulele sensibile la lumină din interiorul fiecărei lentile individuale se grupează, de asemenea, în grupuri care arată exact ca bulele de săpun.

Lumea poliedrelor în natură

Celulele multor tipuri diferite de organisme, de la plante la șobolani, conțin membrane cu aceste structuri microscopice. Nimeni nu știe pentru ce sunt, dar sunt atât de răspândite încât este corect să presupunem că au un rol util. Poate că izolează un proces biochimic de altul, evitând intervențiile încrucișate.

Sau poate este doar o modalitate eficientă de a crea un plan mare de lucru, deoarece multe procese biochimice au loc pe suprafața membranelor, unde pot fi încorporate enzime și alte molecule active. Oricare ar fi funcția poliedrelor în natură, nu vă obosiți să creați instrucțiuni genetice complexe, deoarece legile fizicii o vor face pentru dvs.

Unii fluturi au solzi înaripați care conțin un labirint ordonat dintr-un material dur numit chitină. Expunerea la undele luminoase care sară pe crestele normale și alte structuri de pe suprafața unei aripi determină ca unele lungimi de undă (adică unele culori) să se estompeze, în timp ce altele se întăresc reciproc. Astfel, structura poligonală oferă un vehicul excelent pentru producerea culorii animalelor.

Pentru a face rețele ordonate dintr-un mineral rigid, unele organisme par să formeze un mucegai din membrane moi și flexibile și apoi cristalizează materialul dur într-una dintre rețelele care se întrepătrund. Structura de tip fagure a canalelor microscopice goale din țepii chitinoși ai neobișnuitului cunoscut sub numele de șoarecele de mare transformă aceste structuri asemănătoare părului în fibre optice naturale care pot ghida lumina, schimbând-o de la roșu la verde-albăstrui, în funcție de direcția luminii. Această schimbare de culoare poate servi la descurajarea prădătorilor.

Natura știe mai bine

Flora și fauna sunt pline de exemple de poliedre în viața sălbatică, precum și lumea neînsuflețită a pietrelor și mineralelor. Din punct de vedere pur evolutiv, structura hexagonală este lider în optimizarea energetică. Pe lângă avantajele evidente (economisirea spațiului), plasele poliedrice oferă un număr mare de fețe, prin urmare, numărul de vecini crește, ceea ce are un efect benefic asupra întregii structuri. Rezultatul final este că informațiile se răspândesc mult mai rapid. De ce sunt poliedre stelare regulate hexagonale și neregulate atât de comune în natură? Probabil atât de necesar. Natura știe mai bine, ea știe mai bine.

O persoană manifestă interes pentru poliedre pe parcursul activității sale conștiente - de la un copil de doi ani care se joacă cu cuburi de lemn până la un matematician matur. Unele dintre corpurile obișnuite și semi-regulate apar în natură sub formă de cristale, altele sub formă de viruși care pot fi observați doar cu un microscop electronic. Ce este un poliedru? Pentru a răspunde la această întrebare, să ne amintim că geometria însăși este uneori definită ca știința spațiului și a figurilor spațiale - bidimensionale și tridimensionale. O figură bidimensională poate fi definită ca un set de segmente de linie care mărginesc o parte a unui plan. O astfel de figură plată se numește poligon. Rezultă că un poliedru poate fi definit ca un set de poligoane care mărginesc o porțiune de spațiu tridimensional. Poligoanele care formează un poliedru se numesc fețele acestuia.

Din cele mai vechi timpuri, oamenii de știință au fost interesați de poligoane „ideale” sau regulate, adică poligoane care au laturi și unghiuri egale. Un triunghi echilateral poate fi considerat cel mai simplu poligon regulat, deoarece are cel mai mic număr de laturi care pot limita o parte a unui plan. Tabloul general al poligoanelor regulate care ne interesează, împreună cu un triunghi echilateral, este alcătuit din: un pătrat (patru laturi), un pentagon (cinci laturi), un hexagon (șase laturi), un octogon (opt laturi), un decagon (zece laturi), etc. Evident, teoretic nu există restricții privind numărul de laturi ale unui poligon regulat, adică numărul de poligoane regulate este infinit.

Ce este un poliedru regulat? Un astfel de poliedru se numește regulat dacă toate fețele sale sunt egale (sau congruente, după cum se obișnuiește în matematică) între ele și, în același timp, sunt poligoane regulate. Câte poliedre regulate există? La prima vedere, răspunsul la această întrebare este foarte simplu - câte poligoane regulate există, adică la prima vedere se pare că puteți crea un poliedru regulat, ale cărui laturi pot fi orice poligon regulat. Cu toate acestea, nu este. Deja în Elementele lui Euclid s-a dovedit riguros că numărul poliedrelor regulate este foarte limitat și că există doar cinci poliedre regulate ale căror fețe pot fi doar trei tipuri de poligoane regulate: triunghiuri, pătrate și pentagoane. Aceste poliedre regulate sunt numite solide platonice. Primul este tetraedrul. Fețele sale sunt patru triunghiuri echilaterale. Tetraedrul are cel mai puțin număr de fețe dintre solidele platonice și este analogul tridimensional al unui triunghi regulat plat, care are cel mai puțin număr de laturi dintre poligoane regulate. Cuvântul „tetraedru” provine din grecescul „tetra” – patru și „edra” – bază. Este o piramidă triunghiulară. Următorul corp este un hexaedru, numit și cub. Hexaedrul are șase fețe, care sunt pătrate. Fețele octaedrului sunt triunghiuri regulate, iar numărul lor în octaedru este opt. Următorul cel mai mare număr de fețe este dodecaedrul. Fețele sale sunt pentagoane, iar numărul lor în dodecaedru este doisprezece. Icosaedrul închide cele cinci solide platonice. Fețele sale sunt triunghiuri regulate, iar numărul lor este douăzeci.

În lucrarea mea, sunt luate în considerare principalele definiții și proprietăți ale poliedrelor convexe. Existența a doar cinci poliedre regulate a fost dovedită. Relațiile dintre piramida n-gonală regulată și tetraedrul regulat, care sunt cele mai frecvente în problemele de stereometrie, sunt luate în considerare în detaliu. Lucrarea prezintă o cantitate mare de material analitic și ilustrativ care poate fi folosit în studiul unor secțiuni de stereometrie.

studiile lui Platon

Platon a creat o teorie foarte interesantă. El a sugerat că atomii celor patru „elemente de bază” (pământ, apă, aer și foc), din care sunt construite toate lucrurile, au forma unor poliedre regulate: un tetraedru - foc, un hexaedru (cub) - pământ, un octaedru - aer, un icosaedru - apă. Al cincilea poliedru - dodecaedrul - a simbolizat „Marea Minte” sau „Armonia Universului”. Particulele din trei elemente care se transformă ușor unul în celălalt, și anume foc, aer și apă, s-au dovedit a fi formate din figuri identice - triunghiuri regulate. Și pământul, care este semnificativ diferit de ele, este format din particule de alt tip - cuburi, sau mai degrabă pătrate. Platon a explicat foarte clar toate transformările cu ajutorul triunghiurilor. În haosul agitat, două particule de aer se întâlnesc cu o particulă de foc, adică doi octaedri se întâlnesc cu un tetraedru. Două octaedre au un total de șaisprezece fețe triunghiulare, un tetraedru are patru. În total douăzeci. Din douăzeci, un icosaedru se formează cu ușurință, iar aceasta este o particulă de apă.

Cosmologia lui Platon a devenit baza așa-numitei doctrine icosaedrico-dodecaedrice, care de atunci a trecut ca un fir roșu prin toată știința umană. Esența acestei doctrine este că dodecaedrul și icosaedrul sunt forme tipice ale naturii în toate manifestările sale, de la cosmos la microlume.

Poliedre regulate

Poliedrele obișnuite au atras atenția oamenilor de știință, constructorilor, arhitecților și multor altora încă din cele mai vechi timpuri. Au fost frapați de frumusețea, perfecțiunea, armonia acestor poliedre. Pitagoreii considerau aceste poliedre ca fiind divine și le foloseau în scrierile lor filozofice despre esența lumii. Ultima, a 13-a carte a celebrului „Începuturi” lui Euclid este dedicată poliedrelor regulate.

Repetăm ​​că un poliedru convex se numește regulat dacă fețele sale sunt poligoane regulate egale și același număr de fețe converg la fiecare vârf.

Cel mai simplu astfel de poliedru regulat "este o piramidă triunghiulară, ale cărei fețe sunt triunghiuri regulate. Trei fețe converg la fiecare dintre vârfurile sale. Având toate cele patru fețe, acest poliedru este numit și tetraedru, ceea ce înseamnă "patru edre" în greacă. .

Uneori, un tetraedru este numit și o piramidă arbitrară. Prin urmare, în cazul în care vorbim despre un poliedru obișnuit, vom spune - un tetraedru obișnuit.

Un poliedru ale cărui fețe sunt triunghiuri regulate și la fiecare vârf converg patru fețe, a cărui suprafață este formată din opt triunghiuri regulate, se numește octaedru.

Un poliedru, la fiecare vârf din care converg cinci triunghiuri regulate, a cărui suprafață este formată din douăzeci de triunghiuri regulate, se numește icosaedru.

Rețineți că, deoarece mai mult de cinci triunghiuri regulate nu pot converge la vârfurile unui poliedru convex, nu există alte poliedre regulate ale căror fețe sunt triunghiuri regulate.

În mod similar, deoarece numai trei pătrate pot converge la vârfurile unui poliedru convex, nu există alte poliedre regulate cu pătrate ca fețe în afară de cub. Un cub are șase laturi și de aceea se numește hexaedru.

Un poliedru ale cărui fețe sunt pentagoane regulate și trei fețe converg la fiecare vârf. Suprafața sa este formată din douăsprezece pentagoane regulate, se numește dodecaedru.

Deoarece poligoane regulate cu mai mult de cinci laturi nu pot converge la vârfurile unui poliedru convex, nu există alte poliedre regulate și, prin urmare, există doar cinci poliedre regulate: tetraedru, hexaedru (cub), octaedru, dodecaedru, icosaedru.

Numele poliedrelor regulate provin din Grecia. În traducere literală din greacă „tetraedru”, „octaedru”, „hexaedru”, „dodecaedru”, „icosaedru” înseamnă: „tetraedru”, „octaedru”, „hexaedru”. dodecaedru, dodecaedru. A 13-a carte din Elementele lui Euclid este dedicată acestor corpuri frumoase. Ele sunt numite și corpurile lui Platon, deoarece au ocupat un loc important în conceptul filozofic al lui Platon despre structura universului.

Și acum să ne uităm la câte proprietăți, leme și teoreme asociate cu aceste cifre.

Să considerăm un unghi poliedric cu vârful S, unde toate unghiurile plate și toate unghiurile diedrice sunt egale. Alegem punctele A1, A2, An de pe marginile sale astfel încât SA1 = SA2 = SAn. Atunci punctele A1, A2, An se află în același plan și sunt vârfuri ale unui n-gon regulat.

Dovada.

Să demonstrăm că orice puncte consecutive se află în același plan. Luați în considerare patru puncte consecutive A1, A2, A3 și A4. Piramidele SA1 A2 A3 și SA2 A3 A4 sunt egale, deoarece pot fi combinate prin combinarea muchiilor SA2 și SA3 (desigur, se iau muchiile diferitelor piramide) și unghiurile diedrice de la aceste muchii. În mod similar, se poate demonstra că piramidele SA1 A3A4 și SA1 A2 A4 sunt egale, deoarece toate marginile lor sunt egale. Aceasta presupune egalitatea

Din ultima egalitate rezultă că volumul piramidei A1A2A3A4 este egal cu zero, adică aceste patru puncte se află în același plan. Prin urmare, toate n puncte se află în același plan, iar în n-gonul A1 A2 An toate laturile și unghiurile sunt egale. Prin urmare, este corect și lema este dovedită.

Să demonstrăm că există cel mult cinci tipuri diferite de poliedre regulate.

Dovada.

Din definiția unui poliedru regulat rezultă că numai triunghiurile, patruunghiurile și pentagoanele pot fi fețele acestuia. Într-adevăr, să demonstrăm, de exemplu, că fețele nu pot fi hexagoane obișnuite. Conform definiției unui poliedru regulat, cel puțin trei fețe trebuie să convergă la fiecare dintre vârfurile sale. Cu toate acestea, într-un hexagon obișnuit, unghiurile sunt de 120°. Se pare că suma a trei unghiuri plane ale unui unghi poliedric convex este de 360°, ceea ce este imposibil, deoarece această sumă este întotdeauna mai mică de 360°. Mai mult, fețele unui poliedru regulat nu pot fi poligoane cu un număr mare de laturi.

Să aflăm câte fețe pot converge la un vârf al unui poliedru regulat. Dacă toate fețele sale sunt triunghiuri regulate, atunci nu mai mult de cinci triunghiuri se pot alătura fiecărui vârf, deoarece, altfel, suma unghiurilor plane la acest vârf va fi de cel puțin 360°, ceea ce, după cum am văzut, este imposibil. Deci, dacă toate fețele unui poliedru regulat sunt triunghiuri regulate, atunci trei, patru sau cinci triunghiuri se învecinează cu fiecare vârf. Prin raționament analog, ne asigurăm că la fiecare vârf al unui poliedru regulat, ale cărui fețe sunt patrulatere și pentagoane regulate, converg exact trei muchii.

Să demonstrăm acum că există un singur poliedru de un tip dat cu o lungime fixă ​​a muchiei. Luați în considerare, de exemplu, cazul în care toate fețele sunt pentagoane regulate. Să presupunem contrariul: să fie două poliedre, ale căror fețe sunt pentagoane regulate cu latura a și toate unghiurile diedrice din fiecare poliedru sunt egale între ele. Rețineți că nu toate unghiurile diedrice ale unui poliedru sunt neapărat egale cu unghiurile diedrice ale altui poliedru: aceasta este ceea ce vom demonstra acum.

După cum am arătat, trei muchii ies din fiecare vârf al fiecărui poliedru. Lasă muchiile AB, AC și AD să iasă din vârful A al unui poliedru, iar muchiile A1B1, A1C1 și A1D1 să iasă din vârful A1 al celuilalt. ABCD și A1B1C1D1 sunt piramide triunghiulare regulate, deoarece au muchii egale care ies din vârfurile A și A1 și unghiuri plate la aceste vârfuri.

Rezultă că unghiurile diedrice ale unui poliedru sunt egale cu unghiurile diedrice ale celuilalt. Prin urmare, dacă combinăm piramidele ABCD și A1B1C1D1, atunci poliedrele înseși vor fi și ele compatibile. Prin urmare, dacă există un poliedru regulat ale cărui fețe sunt pentagoane regulate cu latura a, atunci un astfel de poliedru este unic.

Alte poliedre sunt considerate similar. În cazul în care toate fețele sunt triunghiuri și patru sau cinci triunghiuri învecinate cu fiecare vârf, ar trebui să folosiți Lema 2. și un pentagon. Teorema a fost demonstrată.

Rețineți că această teoremă nu implică faptul că există exact cinci tipuri de poliedre regulate. Teorema afirmă doar că există cel mult cinci astfel de tipuri, iar acum rămâne să demonstrăm că există într-adevăr cinci dintre aceste tipuri prezentând toate cele cinci tipuri de poliedre.

Piramida n-gonală regulată

Luați în considerare o piramidă n-gonală regulată. Acest poliedru este adesea întâlnit în probleme stereometrice și, prin urmare, un studiu mai detaliat și mai amănunțit al proprietăților sale este de mare interes. Mai mult, unul dintre poliedrele noastre obișnuite - tetraedrul - este acesta.

Fie SA1A2 An o piramidă n-gonală regulată. Să introducem următoarea notație:

α este unghiul de înclinare a nervurii laterale față de planul bazei;

β este unghiul diedru de la bază;

γ este unghiul plat din partea de sus;

δ este unghiul diedric la marginea laterală.

Fie O centrul bazei piramidei, B mijlocul muchiei A1A2, D punctul de intersecție al segmentelor A1A3 și OA2, C punctul de pe marginea laterală SA2 astfel încât A1CSA2, E punctul de intersecție al segmentelor SB și A1C, K punctul de intersecție al segmentelor A1A3 și OV. Fie A1OA2=. Este ușor de arătat

De asemenea, notăm înălțimea piramidei prin H, apotema - prin m, marginea laterală - prin l, latura bazei - prin a și prin r și R - razele cercurilor înscrise în bază și descrise. în jurul lui.

Mai jos sunt relațiile dintre unghiurile α, β, γ, δ ale unei piramide n-gonale regulate, formulate sub formă de teoreme.

tetraedru regulat

Proprietățile sale

Aplicarea relațiilor obținute în secțiunea anterioară la un tetraedru obișnuit ne permite să obținem un număr de relații interesante pentru acesta din urmă. În această secțiune, vom prezenta formulele obținute pentru acest caz specific și, în plus, vom găsi expresii pentru unele caracteristici ale unui tetraedru regulat, cum ar fi, de exemplu, volumul, suprafața totală și altele asemenea.

Urmând notarea secțiunii precedente, luați în considerare tetraedrul regulat SA1A2A3 cu lungimea muchiei a. Lăsăm notația pentru unghiurile sale la fel și le calculăm.

Într-un triunghi regulat, lungimea înălțimii este egală. Deoarece acest triunghi este regulat, înălțimea lui este atât o bisectoare, cât și o mediană. Medianele, după cum știți, sunt împărțite la punctul lor de intersecție într-un raport de 2: 1, numărând de sus. Este ușor de găsit punctul de intersecție al medianelor. Deoarece tetraedrul este regulat, acest punct va fi punctul O - centrul triunghiului regulat A1A2A3. Baza înălțimii unui tetraedru regulat, coborâtă din punctul S, se proiectează și ea spre punctul O. Prin urmare,. Într-un triunghi regulat SA1A2, lungimea apotemului tetraedrului este egală. Să aplicăm teorema lui Pitagora pentru Δ SBO:. De aici.

Astfel, înălțimea unui tetraedru obișnuit este egală cu.

Aria bazei unui tetraedru - un triunghi regulat:

Deci volumul unui tetraedru obișnuit este:

Suprafața totală a unui tetraedru este de patru ori mai mare decât aria bazei acestuia.

Unghiul diedric al feței laterale pentru un tetraedru obișnuit este în mod evident egal cu unghiul de înclinare al feței laterale față de planul de bază:

Unghiul plan la vârful unui tetraedru regulat este egal cu.

Unghiul de înclinare a nervurii laterale față de planul bazei poate fi găsit din:

Raza unei sfere înscrise pentru un tetraedru obișnuit poate fi găsită printr-o formulă binecunoscută care o raportează la volumul și aria suprafeței totale a tetraedrului (rețineți că ultima formulă este valabilă pentru orice poliedru în care o sferă poate fi înscris). În cazul nostru, avem

Aflați raza sferei circumscrise. Centrul sferei circumscris unui tetraedru regulat se află la înălțimea sa, deoarece este linia SO care este perpendiculară pe planul bazei și trece prin centrul său, iar această dreaptă trebuie să conțină un punct echidistant de toate vârfurile bazei. a tetraedrului. Fie acesta punctul O1, apoi O1S=O1A2=R. Avem. Să aplicăm teorema lui Pitagora triunghiurilor BA2O1 și BO1O:

Rețineți că R = 3r, r + R = H.

Este interesant de calculat, adică unghiul la care marginea unui tetraedru regulat este vizibilă din centrul sferei descrise. Să-l găsim:

Aceasta este o valoare familiară nouă din cursul chimiei: acesta este unghiul dintre legăturile C–H din molecula de metan, care poate fi măsurat foarte precis în experiment și din moment ce nu există niciun atom de hidrogen din molecula CH4. izolat evident de orice, este rezonabil să presupunem că această moleculă are forma unui tetraedru obișnuit. Acest fapt este confirmat de fotografiile unei molecule de metan obținute cu ajutorul unui microscop electronic.

Hexaedru regulat (cub)

Tipul feței Pătrat

Numărul de fețe 6

Numărul de coaste 12

Număr de vârfuri 8

Unghi plat 90 o

Suma unghiurilor plate 270 o

Există un centru de simetrie Da (punctul de intersecție al diagonalelor)

Numărul de axe de simetrie 9

Numărul de planuri de simetrie 9

Octaedru regulat

Numărul de fețe 8

Numărul de coaste 12

Numărul de vârfuri 6

Unghi plat 60o

Numărul de colțuri plate la vârf 4

Suma unghiurilor plate 240o

Există o axă de simetrie Da

Existența unui octaedru regulat

Luați în considerare pătratul ABCD și construiți pe el, la fel ca pe bază, pe ambele părți ale piramidelor sale plane pătrangulare, ale căror margini laterale sunt egale cu laturile pătratului. Poliedrul rezultat va fi un octaedru.

Pentru a demonstra acest lucru, rămâne să verificăm dacă toate unghiurile diedrice sunt egale. Într-adevăr, fie O centrul pătratului ABCD. Conectând punctul O cu toate vârfurile poliedrului nostru, obținem opt piramide triunghiulare cu un vârf comun O. Luați în considerare una dintre ele, de exemplu, ABEO. AO = BO = EO și, în plus, aceste muchii sunt perpendiculare perechi. Piramida ABEO este regulată, deoarece baza sa este un triunghi regulat ABE. Prin urmare, toate unghiurile diedrice de la bază sunt egale. În mod similar, toate cele opt piramide cu vârf în punctul O și baze - fețele octaedrului ABCDEG - sunt regulate și, în plus, sunt egale între ele. Aceasta înseamnă că toate unghiurile diedrice ale acestui octaedru sunt egale, deoarece fiecare dintre ele este de două ori mai mare decât unghiul diedric de la baza fiecăreia dintre piramide.

*Rețineți un fapt interesant legat de hexaedru (cub) și octaedru. Un cub are 6 fețe, 12 muchii și 8 vârfuri, în timp ce un octaedru are 8 fețe, 12 muchii și 6 vârfuri. Adică numărul de fețe ale unui poliedru este egal cu numărul de vârfuri ale celuilalt și invers. Se spune că cubul și hexaedrul sunt duali unul față de celălalt. Acest lucru se manifestă și prin faptul că, dacă luați un cub și construiți un poliedru cu vârfuri în centrele fețelor sale, atunci, după cum puteți vedea cu ușurință, obțineți un octaedru. Reversul este de asemenea adevărat - centrele fețelor octaedrului servesc drept vârfuri ale cubului. Aceasta este dualitatea octaedrului și a cubului.

Este ușor să ne dăm seama că dacă luăm centrele fețelor unui tetraedru obișnuit, atunci obținem din nou un tetraedru obișnuit. Astfel, tetraedrul este dual cu sine. *

Icosaedru regulat

Vedere față Triunghi dreptunghic

Număr de fețe 20

Număr de coaste 30

Număr de vârfuri 12

Unghi plat 60 o

Numărul de colțuri plate la vârf 5

Suma unghiurilor plate 300 o

Există un centru de simetrie Da

Numărul de axe de simetrie Mai multe

Numărul de planuri de simetrie Mai multe

Existența unui icosaedru regulat

Există un poliedru regulat în care toate fețele sunt triunghiuri regulate și din fiecare vârf ies 5 muchii. Acest poliedru are 20 de fețe, 30 de muchii, 12 vârfuri și se numește icosaedru (icosi - douăzeci).

Dovada

Luați în considerare octaedrul ABCDEG cu muchia 1. Alegeți punctele M, K, N, Q, L și P pe muchiile sale AE, BE, CE, DE, AB și respectiv BC, astfel încât AM = EK = CN = EQ = BL = BP = x. Alegem x astfel încât toate segmentele care leagă aceste puncte să fie egale între ele.

Este evident că pentru aceasta este suficient să se îndeplinească egalitatea KM = KQ. Totuși, deoarece KEQ este un triunghi dreptunghic isoscel cu catetele KE și EQ, atunci. Scriem teorema cosinusului pentru triunghiul MEK, în care:

De aici. A doua rădăcină, care este mai mare decât 1, nu se potrivește. Alegând x în acest fel, construim poliedrul necesar. Alegem încă șase puncte care sunt simetrice cu punctele K, L, P, N, Q și M față de centrul tetraedrului și le notăm ca K1, L1, P1, N1, Q1 și, respectiv, M1. Poliedrul rezultat cu vârfurile K, L, P, N, Q, M, K1, L1, P1, N1, Q1 și M1 este cel dorit. Toate fețele sale sunt triunghiuri regulate, cinci muchii ies din fiecare vârf. Să demonstrăm acum că toate unghiurile sale diedrice sunt egale între ele.

Pentru a face acest lucru, observăm că toate vârfurile celui de douăzeci de edruri construit sunt echidistante de punctul O, centrul octaedrului, adică sunt situate pe suprafața sferei cu centrul O. În continuare, procedăm în la fel ca în demonstrarea existenţei unui octaedru regulat. Să conectăm toate vârfurile celui de douăzeci de edruri cu punctul O. Exact în același mod, demonstrăm egalitatea piramidelor triunghiulare, ale căror baze sunt fețele poliedrului construit și ne asigurăm că toate unghiurile diedrice dintre cele douăzeci de edri sunt de două ori mai mari decât unghiurile de la baza acestor piramide triunghiulare egale. Prin urmare, toate unghiurile diedrice sunt egale, ceea ce înseamnă că poliedrul rezultat este regulat. Se numește icosaedru.

Dodecaedru regulat

Vedere a feței Pentagonului (pentagon obișnuit)

Numărul de fețe 12

Număr de coaste 30

Număr de vârfuri 20

Unghi plat 108 o

Numărul de colțuri plate la vârf 3

Suma unghiurilor plate 324 o

Există un centru de simetrie da

Numărul de axe de simetrie Mai multe

Numărul de planuri de simetrie Mai multe

Existența unui dodecaedru regulat

Există un poliedru regulat în care toate fețele sunt pentagoane regulate și din fiecare vârf ies 3 muchii. Acest poliedru are 12 fețe, 30 de muchii și 20 de vârfuri și se numește dodecaedru (dodeka - doisprezece).

Dovada.

După cum puteți vedea, numărul de fețe și vârfuri ale poliedrului, a cărui existență încercăm acum să o dovedim, este egal cu numărul de vârfuri și fețe ale icosaedrului. Astfel, dacă demonstrăm existența poliedrului la care se face referire în această teoremă, atunci cu siguranță se va dovedi a fi dual cu icosaedrul. Pe exemplul unui cub și al unui octaedru, am văzut că figurile duale au proprietatea că vârfurile uneia dintre ele se află în centrele fețelor celeilalte. Acest lucru duce la ideea de a demonstra această teoremă.

Luați un icosaedru și luați în considerare un poliedru cu vârfuri în centrul fețelor sale. Este evident că centrele celor cinci fețe ale icosaedrului care au un vârf comun se află în același plan și servesc ca vârfuri ale unui pentagon regulat (acest lucru poate fi verificat într-o manieră similară cu cea utilizată în demonstrarea lemei). ). Deci, fiecare vârf al icosaedrului corespunde unei fețe a unui nou poliedru, ale cărui fețe sunt pentagoane regulate și toate unghiurile diedrice sunt egale. Acest lucru rezultă din faptul că oricare trei muchii care ies din același vârf al noului poliedru pot fi considerate ca margini laterale ale unei piramide triunghiulare obișnuite și toate piramidele rezultate sunt egale (au muchii laterale egale și unghiuri plate între ele, care sunt unghiurile unei piramide triunghiulare regulate).pentagon). Din cele de mai sus, rezultă că poliedrul rezultat este regulat și are 12 fețe, 30 de muchii și 20 de vârfuri. Un astfel de poliedru se numește dodecaedru.

Deci, în spațiul tridimensional, există doar cinci tipuri de poliedre regulate. Le-am determinat forma și am stabilit că toate poliedrele au duale față de ele. Cubul este dual cu octaedrul și invers. Icosaedru la dodecaedru și invers. Tetraedrul este dual cu sine.

Formula lui Euler pentru poliedre regulate

Deci, s-a aflat că există exact cinci poliedre regulate. Și cum se determină numărul de muchii, fețe, vârfuri din ele? Acest lucru nu este dificil de făcut pentru poliedre cu un număr mic de muchii, dar cum, de exemplu, să obțineți astfel de informații pentru un icosaedru? Celebrul matematician L. Euler a obținut formula В+Г-Р=2, care raportează numărul de vârfuri /В/, fețele /Г/ și muchiile /Р/ ale oricărui poliedru. Simplitatea acestei formule este că nu are nimic de-a face cu distanța sau unghiurile. Pentru a determina numărul de muchii, vârfuri și fețe ale unui poliedru regulat, găsim mai întâi numărul k \u003d 2y - xy + 2x, unde x este numărul de muchii aparținând unei fețe, y este numărul de fețe convergente. la un vârf. Pentru a afla numărul de fețe, vârfuri și muchii ale unui poliedru obișnuit, folosim formule. După aceea, este ușor să completați un tabel care oferă informații despre elementele poliedrelor obișnuite:

Nume Noduri (V) Muchii (P) Fețe (D) Formula

Tetraedru 4 6 4 4-6+4=2

Hexaedru (Cub) 8 12 6 8-12+6=2

Octaedru 6 12 8 6-12+8=2

Icosaedru 12 30 20 12-30+20=2

Dodecaedru 20 30 12 20-30+12=2

Capitolul II: Poliedre regulate în viață

Spațiul și Pământul

Există multe ipoteze și teorii legate de poliedre despre structura Universului, inclusiv planeta noastră. Mai jos sunt câteva dintre ele.

Un loc important l-au ocupat poliedrele regulate în sistemul structurii armonioase a lumii de I. Kepler. Aceeași credință în armonie, frumusețe și structura matematică regulată a universului l-au determinat pe I. Kepler la ideea că, deoarece există cinci poliedre regulate, le corespund doar șase planete. În opinia sa, sferele planetelor sunt interconectate de solidele platonice înscrise în ele. Întrucât pentru fiecare poliedru regulat centrele sferelor înscrise și circumscrise coincid, întregul model va avea un singur centru, în care va fi situat Soarele.

După ce a făcut o muncă de calcul uriașă, în 1596 I. Kepler a publicat rezultatele descoperirii sale în cartea „Secretul Universului”. El înscrie un cub în sfera orbitei lui Saturn, într-un cub - sfera lui Jupiter, în sfera lui Jupiter - un tetraedru și așa mai departe se potrivesc succesiv unul în celălalt sfera lui Marte - un dodecaedru, sfera Pământului. - un icosaedru, sfera lui Venus - un octaedru, sfera lui Mercur. Secretul universului pare deschis.

Astăzi este sigur să spunem că distanțele dintre planete nu sunt legate de nicio poliedră. Totuși, este posibil ca fără „Secretele Universului”, „Armonia lumii” de I. Kepler, poliedre regulate, să nu fi existat trei legi celebre ale lui I. Kepler, care joacă un rol important în descrierea mișcării. a planetelor.

Unde mai poți vedea aceste corpuri uimitoare? Într-o carte foarte frumoasă a biologului german de la începutul secolului nostru, E. Haeckel, „Frumusețea formelor în natură”, se pot citi următoarele rânduri: „Natura hrănește în sânul ei un număr inepuizabil de creaturi uimitoare atât de departe. depășesc toate formele create de arta umană în frumusețe și diversitate.” Creațiile naturii din această carte sunt frumoase și simetrice. Aceasta este o proprietate inseparabilă a armoniei naturale. Dar aici puteți vedea și organisme unicelulare - feodarii, a căror formă transmite cu precizie icosaedrul. Ce a cauzat o astfel de geometrizare naturală? Poate din cauza tuturor poliedrelor cu același număr de fețe, icosaedrul este cel care are cel mai mare volum și cea mai mică suprafață. Această proprietate geometrică ajută microorganismul marin să depășească presiunea coloanei de apă.

De asemenea, este interesant că icosaedrul a fost cel care s-a dovedit a fi în centrul atenției biologilor în disputele lor cu privire la forma virușilor. Virusul nu poate fi perfect rotund, așa cum se credea anterior. Pentru a-i stabili forma, au luat diferite poliedre, au îndreptat lumina spre ei în aceleași unghiuri ca fluxul de atomi către virus. S-a dovedit că un singur poliedru dă exact aceeași umbră - icosaedrul. Proprietățile sale geometrice, menționate mai sus, permit salvarea informațiilor genetice. Poliedrele regulate sunt figurile cele mai avantajoase. Și natura profită de asta. Cristalele unor substanțe cunoscute nouă sunt sub formă de poliedre regulate. Deci, cubul prezintă forma cristalelor de clorură de sodiu NaCl, monocristalul de alaun de aluminiu-potasiu (KAlSO4) 2 12H2O are forma unui octaedru, cristalul de pirită de sulf FeS are forma unui dodecaedru, sulfatul de antimoniu de sodiu este un tetraedru, borul este un icosaedru. Poliedrele regulate determină forma rețelelor cristaline ale unor substanțe chimice. Ilustram aceasta idee cu urmatoarea problema.

Sarcină. Modelul moleculei de metan CH4 are forma unui tetraedru regulat, cu atomi de hidrogen la patru vârfuri și un atom de carbon în centru. Determinați unghiul de legătură dintre două legături CH.

Soluţie. Deoarece un tetraedru obișnuit are șase muchii egale, este posibil să alegeți un cub astfel încât diagonalele fețelor sale să fie muchiile unui tetraedru obișnuit. Centrul cubului este și centrul tetraedrului, deoarece cele patru vârfuri ale tetraedrului sunt și vârfurile cubului, iar sfera descrisă în jurul lor este determinată în mod unic de patru puncte care nu se află în același plan. Unghiul dorit j dintre două legături CH este egal cu unghiul AOS. Triunghiul AOC este isoscel. Prin urmare, unde a este latura cubului, d este lungimea diagonalei feței laterale sau a muchiei tetraedrului. Deci, de unde = 54,73561O și j = 109,47O

Întrebarea formei Pământului a ocupat în mod constant mințile oamenilor de știință din antichitate. Și când s-a confirmat ipoteza despre forma sferică a Pământului, a apărut ideea că forma Pământului este un dodecaedru. Așadar, deja Platon a scris: „Pământul, dacă îl privești de sus, arată ca o minge cusută din 12 bucăți de piele”. Această ipoteză a lui Platon a găsit o dezvoltare științifică ulterioară în lucrările fizicienilor, matematicienilor și geologilor. Așadar, geologul francez de Beamont și faimosul matematician Poincaré credeau că forma Pământului este un dodecaedru deformat.

Există o altă ipoteză. Sensul său este că Pământul are forma unui icosaedru. Pe glob sunt luate două paralele - 30o latitudine nordică și sudică. Distanța de la fiecare dintre ele până la polul emisferei sale este de 60o, între ele fiind tot de 60o. Pe nordul acestor paralele, punctele sunt marcate prin 1/5 dintr-un cerc complet, sau 72o: la intersecția cu meridianele 32o, 104o și 176o in. d. și 40o și 112o z. e. Pe paralela sudică punctele sunt marcate la intersecţiile cu meridianele, trecând exact la mijloc între numitele: 68o şi 140o in. și 4o, 76o și 148o z. e. Cinci puncte pe paralela 30o s. SH. , cinci - pe paralela de 30o S. SH. și doi poli ai Pământului și vor alcătui 12 vârfuri ale poliedrului.

De asemenea, geologul rus S. Kislitsin a împărtășit părerea despre forma dodecaedrică a Pământului. El a emis ipoteza că acum 400-500 de milioane de ani geosfera dodecaedrică s-a transformat într-un geo-icosaedru. Cu toate acestea, o astfel de tranziție s-a dovedit a fi incompletă și incompletă, drept urmare geo-dodecaedrul s-a dovedit a fi înscris în structura icosaedrului. În ultimii ani, s-a testat ipoteza formei icosaedrice-dodecaedrice a Pământului. Pentru a face acest lucru, oamenii de știință au aliniat axa dodecaedrului cu axa globului și, rotind acest poliedru în jurul lui, au atras atenția asupra faptului că marginile sale coincid cu perturbări uriașe din scoarța terestră (de exemplu, cu Atlanticul de mijloc. creasta submarină). Apoi, luând icosaedrul ca poliedru, au descoperit că marginile acestuia coincid cu diviziuni mai mici ale scoarței terestre (cresturi, falii etc.). Aceste observații confirmă ipoteza că structura tectonică a scoarței terestre este similară cu formele dodecaedrului și icosaedrului.

Nodurile unui geo-cristal ipotetic sunt, parcă, centrele anumitor anomalii de pe planetă: ele conțin toate centrele lumii de presiune atmosferică extremă, zone de unde își au originea uraganele; într-unul dintre nodurile icosaedrului (în Gabon) a fost descoperit un „reactor atomic natural” care încă mai funcționa acum 1,7 miliarde de ani. Zăcăminte minerale uriașe (de exemplu, câmpul petrolier Tyumen), anomalii ale lumii animale (Lacul Baikal), centre de dezvoltare a culturilor umane (Egiptul Antic, civilizația proto-indiană Mohenjo-Daro, Mongolia de Nord etc.) sunt limitat la multe noduri de poliedre.

Mai există o presupunere. Ideile lui Pitagora, Platon, I. Kepler despre legătura poliedrelor regulate cu structura armonioasă a lumii și-au găsit deja continuarea în timpul nostru într-o ipoteză științifică interesantă, ai cărei autori (la începutul anilor '80) au fost ingineri moscoviți. V. Makarov şi V. Morozov. Ei cred că miezul Pământului are forma și proprietățile unui cristal în creștere care afectează dezvoltarea tuturor proceselor naturale care au loc pe planetă. Razele acestui cristal, sau mai degrabă, câmpul său de forță, determină structura icosaedric-dodecaedrică a Pământului, care se manifestă prin faptul că în scoarța terestră apar, parcă, proiecții de poliedre regulate înscrise pe glob: icosaedrul și dodecaedrul. Cele 62 de vârfuri și punctele mijlocii ale muchiilor, numite noduri de către autori, au o serie de proprietăți specifice care fac posibilă explicarea unor fenomene de neînțeles.

Studiile ulterioare ale Pământului, probabil, vor determina atitudinea față de această frumoasă ipoteză științifică, în care, aparent, poliedrele regulate ocupă un loc important.

Și încă o întrebare apare în legătură cu poliedrele obișnuite: este posibil să umpleți spațiul cu ele, astfel încât să nu existe goluri între ele? Apare prin analogie cu poligoane regulate, dintre care unele pot umple planul. Se pare că puteți umple spațiul numai cu ajutorul unui cub poliedru obișnuit. Spațiul poate fi umplut și cu dodecaedre rombice. Pentru a înțelege acest lucru, trebuie să rezolvați problema.

Sarcină. Cu ajutorul a șapte cuburi care formează o „cruce” spațială, construiește un dodecaedru rombic și arată că pot umple spațiul.

Soluţie. Cuburile pot umple spațiul. Luați în considerare o parte dintr-o rețea cubică. Lăsăm neatins cubul din mijloc și în fiecare dintre cuburile „delimitate” desenăm avioane prin toate cele șase perechi de muchii opuse. În acest caz, cuburile „înconjurătoare” vor fi împărțite în șase piramide egale cu baze pătrate și margini laterale egale cu jumătate din diagonala cubului. Piramidele adiacente cubului neatins formează împreună cu acesta din urmă un dodecaedru rombic. Din aceasta este clar că întreg spațiul poate fi umplut cu dodecaedre rombice. În consecință, obținem că volumul unui dodecaedru rombic este egal cu dublul volumului unui cub a cărui muchie coincide cu diagonala mai mică a feței dodecaedrului.

Rezolvând această problemă, am ajuns la dodecaedre rombice. Interesant este că celulele de albine, care umplu, de asemenea, spațiul fără goluri, sunt, de asemenea, în mod ideal forme geometrice. Partea superioară a celulei de albine este o parte a dodecaedrului rombic.

În 1525, Dürer a scris un tratat în care a prezentat cinci poliedre regulate ale căror suprafețe servesc drept modele bune de perspectivă.

Deci, poliedrele obișnuite ne-au dezvăluit încercările oamenilor de știință de a aborda secretul armoniei mondiale și au arătat atractivitatea irezistibilă a geometriei.

Poliedre regulate și raportul de aur

În timpul Renașterii, sculptorii, arhitecții și artiștii au arătat un mare interes pentru formele poliedrelor regulate. Leonardo da Vinci, de exemplu, era pasionat de teoria poliedrelor și le-a descris adesea pe pânzele sale. A ilustrat cartea prietenului său călugărul Luca Pacioli (1445 - 1514) „Despre proporția divină” cu imagini de poliedre regulate și semiregulate.

În 1509, la Veneția, Luca Pacioli a publicat Despre proporția divină. Pacioli a găsit în cele cinci solide platonice - poligoane regulate (tetraedru, cub, octaedru, icosaedru și dodecaedru) treisprezece manifestări ale „proporției divine”. În capitolul „Despre a doisprezecea, aproape supranaturală proprietate”, el consideră icosaedrul regulat. La fiecare vârf al icosaedrului, cinci triunghiuri converg pentru a forma un pentagon regulat. Dacă conectați oricare două margini opuse ale unui icosaedru una de alta, obțineți un dreptunghi în care latura mai mare este legată de cea mai mică, deoarece suma laturilor este cu cea mai mare.

Astfel, raportul de aur se manifestă în geometria a cinci poliedre regulate, care, conform oamenilor de știință antici, stau la baza universului.

Geometria solidelor lui Platon în picturile marilor artiști

Un artist celebru al Renașterii, pasionat și de geometrie, a fost A. Dürer. În binecunoscuta sa gravură „Melancholia”, un dodecaedru a fost înfățișat în prim-plan.

Luați în considerare imaginea picturii artistului Salvador Dali „Cina cea de Taină”. În prim-planul picturii este înfățișat Hristos cu discipolii săi pe fundalul unui uriaș dodecaedru transparent.

Cristalele sunt poliedre naturale

Multe forme de poliedre nu au fost inventate de omul însuși, ci de natură sub formă de cristale.

Adesea oamenii, privind minunatele poliedre irizate ale cristalelor, nu pot să creadă că au fost create de natură, și nu de om. De aceea s-au născut atât de multe povești populare uimitoare despre cristale.

Au supraviețuit materiale scrise interesante, de exemplu, așa-numitul „Ebers Papyrus”, care conține o descriere a metodelor de tratare a pietrelor cu ritualuri și vrăji speciale, în care puterile misterioase sunt atribuite pietrelor prețioase.

Se credea că cristalul de rodie aduce fericire. Are forma unui dodecaedru rombic (uneori numit dodecaedru romboidal sau rombic) - un dodecaedru, ale cărui fețe sunt douăsprezece romburi egale.

Pentru granat, cristalele dodecaedrice sunt atât de tipice încât forma unui astfel de poliedru a fost numită chiar și garnetoedru.

Granatul este unul dintre principalele minerale care formează roca. Există roci uriașe care sunt compuse din roci granat numite skarns. Cu toate acestea, pietrele prețioase, frumos colorate și transparente sunt departe de a fi comune. În ciuda acestui fapt, tocmai granatul - piropul roșu de sânge - este cel pe care arheologii îl consideră cel mai vechi decor, deoarece a fost descoperit în Europa în neoliticul antic pe teritoriul Republicii Cehe și Slovaciei moderne, unde este în prezent foarte popular.

Faptul că granatul, adică poliedrul rombododecaedrului, este cunoscut încă din cele mai vechi timpuri poate fi judecat după istoria originii numelui său, care în greaca veche însemna „vopsea roșie”. În același timp, numele a fost asociat cu roșu - cea mai comună culoare a granatelor.

Granatul este foarte apreciat de cunoscătorii de pietre prețioase. Este folosit pentru realizarea de bijuterii de primă clasă, granatul are capacitatea de a comunica darul previziunii femeilor care îl poartă și alungă gândurile grele de la ele, în timp ce îi protejează pe bărbați de moartea violentă.

Grenadele subliniază neobișnuirea situației, excentricitatea acțiunilor oamenilor, subliniază puritatea și sublimitatea sentimentelor lor.

Aceasta este o piatră talisman pentru persoanele născute în IANUARIE.

Luați în considerare pietrele a căror formă este bine studiată și reprezintă poliedre regulate, semiregulate și în formă de stea.

Pirita își ia numele de la cuvântul grecesc pyros, care înseamnă foc. O lovitură adusă ei dă naștere unei scântei; în vremuri străvechi, bucăți de pirit serveau ca silex. Strălucirea speculară de pe fețe distinge pirita de alte sulfuri. Pirita lustruită strălucește și mai tare. Oglinzi din pirită lustruită au fost găsite de arheologi în mormintele incașilor. Prin urmare, pirita are și un nume atât de rar - piatra incașilor. În timpul epidemiei de goana aurului, paietele de pirit într-un filon de cuarț, în nisip umed pe o tigaie de spălat, au întors mai mult de un cap fierbinte. Chiar și acum, iubitorii de piatră începători confundă pirita cu aur.

Dar să aruncăm o privire mai atentă, să ascultăm proverbul: „Nu tot ce strălucește este aur!” culoarea piritei este galben-alama. Marginile cristalelor de pirita sunt turnate cu un luciu metalic puternic. ? aici, în pauză, strălucirea este mai slabă.

Duritatea piritei este de 6-6,5, zgârie ușor sticla. Este cel mai dur mineral din clasa sulfurilor.

Și totuși, cea mai caracteristică în aspectul piritei este forma cristalelor. Cel mai adesea este un cub. De la cele mai mici „cuburi care cuibăresc de-a lungul crăpăturilor, până la cuburi cu o înălțime a nervurii de 5 cm, 15 cm și chiar 30 cm! Dar cristalele de pirit nu sunt doar tăiate în cuburi, în arsenalul acestui mineral există octaedre deja cunoscute nouă din magnetit. Pentru pirit, ele sunt destul de rare.Dar pirita vă permite să admirați personal forma cu același nume - pentagondodecaedru. „Penta” este cinci, toate fețele acestei forme sunt cu cinci fețe, iar „dodeca” - o duzină - sunt în total douăsprezece.Această formă pentru pirita este atât de tipică încât în ​​vremurile vechi chiar a primit numele de „piritoedru.” Pot exista și exemplare care combină fețe de diferite forme: un cub și un pentagondodecaedru.

casetita

Cassiteritul este un mineral maro strălucitor, fragil, care este principalul minereu de staniu. Forma este foarte memorabilă - tetraedric înalt, piramide ascuțite deasupra și dedesubt, iar în mijloc - o coloană scurtă, de asemenea fațetată. Destul de diferit ca aspect, cristalele de casiterit cresc in nervuri de cuart. Pe Peninsula Chukchi se află zăcământul Iultin, unde filoanele cu cristale excelente de casiterită sunt de multă vreme faimoase.

Galena arată ca un metal și pur și simplu este imposibil să nu o observi în minereu. Oferă imediat un luciu metalic puternic și greutate. Galena este aproape întotdeauna cuburi argintii (sau paralelipipede). Și acestea nu sunt neapărat cristale întregi. Galena are un decolteu perfect într-un cub. Aceasta înseamnă că nu se sparge în fragmente fără formă, ci în cuburi strălucitoare argintii îngrijite. Cristalele sale naturale au forma unui octaedru sau cuboctaedru. Galena se distinge și printr-o astfel de proprietate: acest mineral este moale și nu foarte rezistent din punct de vedere chimic.

ZIRCONIU

„Zircon” - din cuvintele persane „rege” și „pistol” - culoare aurie.

Zirconiul a fost descoperit în 1789/0 în prețiosul zircon din Ceylon. Descoperitorul acestui element este M. Claport. Zirconii magnifici, transparente și strălucitori, erau faimoși în antichitate. Această piatră era foarte apreciată în Asia.

Chimiștii și metalurgiștii au trebuit să muncească din greu înainte ca în reactoarele nucleare să apară carcasele de tije de zirconiu și alte detalii structurale.

Deci, zirconul este o bijuterie eficientă - portocaliu, galben pai, albastru - albastru, verde - strălucește și joacă ca un diamant.

Zirconii sunt adesea reprezentați de mici cristale regulate cu o formă elegantă caracteristică. Motivul rețelei lor cristaline și, în consecință, forma cristalelor este supus celei de-a patra axe de simetrie. Cristalele de zircon aparțin singoniei tetragonale. Ele sunt pătrate în secțiune transversală. Și cristalul în sine constă dintr-o prismă tetragonală (uneori este tocită de-a lungul marginilor de o a doua prismă similară) și o bipiramidă tetragonală care completează prisma la ambele capete.

Cristalele cu două dipiramide la capete sunt și mai spectaculoase: unul la vârfuri, iar celălalt doar tocește marginile dintre prismă și piramida superioară.

Cristalele de sare au forma unui cub, cristalele de gheață și cristal de stâncă (cuarț) seamănă cu un creion șlefuit pe ambele părți, adică au forma unei prisme hexagonale, pe baza căreia sunt așezate piramide hexagonale.

Diamantul se găsește cel mai adesea sub formă de octaedru, uneori de cub și chiar de cuboctaedru.

Spatarul islandez, care bifurcă imaginea, are forma unui paralelipiped oblic.

Interesant

Toate celelalte poliedre regulate pot fi obținute din cub prin transformări.

În procesul de diviziune a oului se formează mai întâi un tetraedru de patru celule, apoi un octaedru, un cub și în final o structură dodecaedrică-icosaedrică a gastrulei.

Și, în sfârșit, poate cel mai important, structura ADN-ului codului genetic al vieții este o măturare în patru dimensiuni (de-a lungul axei timpului) a unui dodecaedru rotativ!

Se credea că poliedrele obișnuite aduc noroc. Prin urmare, au existat oase nu numai sub formă de cub, ci și în toate celelalte forme. De exemplu, un os în formă de dodecaedru se numea d12.

Matematicianul german August Ferdinand Möbius, în lucrarea sa „Despre volumul poliedrelor”, a descris o suprafață geometrică care are o proprietate incredibilă: are o singură latură! Dacă lipiți capetele unei benzi de hârtie, întorcând mai întâi una dintre ele la 180 de grade, obținem o bandă sau o bandă Mobius. Încercați să pictați panglica răsucită în 2 culori - una pe exterior și una pe interior. Nu vei reuși! Dar, pe de altă parte, o furnică care se târăște pe o bandă Möbius nu trebuie să se târască peste marginea ei pentru a ajunge pe partea opusă.

„Poliedrele convexe obișnuite sunt în mod sfidător puține”, a remarcat odată Lewis Carroll, „dar acest detașament, foarte modest ca număr, cei cinci magnifici, a reușit să pătrundă adânc în profunzimile științei. »

Toate aceste exemple confirmă percepția uimitoare a intuiției lui Platon.

Concluzie

Lucrarea prezentată are în vedere:

Definiția poliedrelor convexe;

Proprietățile de bază ale poliedrelor convexe, inclusiv teorema lui Euler care raportează numărul de vârfuri, muchii și fețe ale unui poliedru dat;

Definiția unui poliedru regulat, s-a dovedit existența a doar cinci poliedre regulate;

Relațiile dintre unghiurile caracteristice ale unei piramide n-gonale regulate, care este parte integrantă a unui poliedru regulat, sunt considerate în detaliu;

Unele caracteristici ale unui tetraedru obișnuit, cum ar fi volumul, suprafața și altele asemenea, sunt luate în considerare în detaliu.

Anexele conțin dovezi ale principalelor proprietăți ale poliedrelor convexe și alte teoreme cuprinse în această lucrare. Teoremele și relațiile de mai sus pot fi utile în rezolvarea multor probleme din stereometrie. Lucrarea poate fi folosită în studiul anumitor subiecte de stereometrie ca material de referință și ilustrativ.

Poliedrele ne înconjoară peste tot: cuburi pentru copii, mobilier, structuri arhitecturale etc. În viața de zi cu zi, aproape că am încetat să le observăm, dar este foarte interesant să cunoaștem istoria obiectelor familiare tuturor, mai ales dacă este atât de incitant.

Russkikh Egor, Tarasov Dmitri

Lumea din jurul nostru este o lume a formelor, este foarte diversă și uimitoare. Suntem înconjurați de obiecte de uz casnic de diferite feluri. După ce am studiat acest subiect, am văzut cu adevărat că poligoane ne înconjoară peste tot și se găsesc în diverse domenii ale vieții.

Descarca:

Previzualizare:

https://accounts.google.com

Subtitrări slide-uri:

Poligoane regulate

Poligon uimitor

Poligoane stelare

Poligoane în natură

Poligoane în natură

Vă mulțumim pentru atenție!

Previzualizare:

Pentru a utiliza previzualizarea prezentărilor, creați un cont Google (cont) și conectați-vă: https://accounts.google.com

Subtitrări slide-uri:

Poligoane regulate în știință și în alte sfere ale vieții Autorii proiectului: elevii din clasa a VIII-a a rușilor Egor Tarasov Dmitry. Consilier științific: profesor de matematică Rakhmankulova E.R.

Intrebare problematica. Care este rolul poligoanelor în viața noastră? Obiectul de studiu: poligoane. Subiect de cercetare: aplicarea practică a poligoanelor în lumea din jurul nostru.

Scop: sistematizarea cunoștințelor pe această temă și obținerea de noi informații despre poligoane și aplicarea lor practică. Sarcini: 1. Să studieze literatura de specialitate pe această temă. 2. Arătați aplicarea practică a poligoanelor regulate în lumea din jurul nostru.

Metode de cercetare: 1. Științifică (studiu literaturii); 2. Cercetare. Ipoteza: poligoanele creează frumusețe în mediul uman.

Poligoane regulate

Pătrat magic 4 9 2 3 5 7 8 1 6

Poligon uimitor

Poligoane stelare

Poligoane în natură P3: P4: P6 = 1: 0,877: 0,816

Poligoane în natură

Poligoane în natură

Poligoane din jurul nostru Parchet

Concluzie Fără geometrie nu ar exista nimic, tot ceea ce ne înconjoară sunt forme geometrice. Dar uităm să fim atenți.

Concluzie Lumea din jurul nostru este o lume a formelor, este foarte diversă și uimitoare. Suntem înconjurați de obiecte de uz casnic de diferite feluri. După ce am studiat acest subiect, am văzut cu adevărat că poligoane ne înconjoară peste tot și se găsesc în diverse domenii ale vieții.

Vă mulțumim pentru atenție!

Previzualizare:

Pentru a utiliza previzualizarea prezentărilor, creați un cont Google (cont) și conectați-vă:

„Poligoane” - Material pentru auto-studiu pe tema „Poligoane” Sarcini pentru joc. Triunghi (echilateral). linie frântă. Neconvex. Compilator. Soloninkina T.V. Partea de capăt a unui plan mărginită de un poligon. Desenați un pentagon convex. Pentagon. Poligoane regulate. Expertul 2.

„Măsurarea ariei unui poligon” - Învățare lucruri noi. 1. Cum se măsoară aria unei figuri? - Conceptul de zonă este cunoscut de toată lumea din experiența de viață. Abu-r-Raykhan al-Buruni. 3. Obiectivele lecției: De astăzi vom învăța să calculăm ariile diferitelor forme geometrice. Auzim adesea: „suprafața apartamentului nostru este de 63 m2”. Cherevina Oksana Nikolaevna

„Geometria zonelor figurilor” - Figurile cu arii egale se numesc egale. H.S=(a?b):2. Dreptunghi, triunghi, paralelogram. C.S=a?b. D. Profesor: Ivniaminova L.A. Zone de figuri. A. B. b. Autori: Zyryanova N. Jafarova A nota 8b.

„Poligon regulat” - Corolar1. Poligoane regulate. Formule de bază. R. Triunghi dreptunghic. Consecința 2. Un cerc circumscris unui poligon regulat. r. Consecințe. Un cerc înscris într-un poligon regulat. Hexagon obișnuit. A. Aplicarea formulelor. În orice poligon obișnuit, puteți înscrie un cerc și, în plus, doar unul.

„Paralelogram” - Paralelogram. Dacă un patrulater are laturile opuse egale în perechi, atunci patrulaterul este un paralelogram. Dacă două laturi ale unui patrulater sunt egale și paralele. Ce este un paralelogram? Caracteristicile unui paralelogram. Într-un paralelogram, laturile opuse și unghiurile opuse sunt egale. Diagonalele unui paralelogram sunt tăiate în două de punctul de intersecție.

„Rhombus Square Rectangle” - Rezolvarea problemelor pe tema „Dreptunghi. A. Răspunsuri la testul de verificare. Găsiți: MD + DN. Romb. Scopul lecției: Consolidarea materialului teoretic pe tema „Dreptunghi. Lucrare teoretică independentă Completați tabelul, notând semnele + (da), - (nu). Răspunsuri corecte la munca independentă teoretică.

În total sunt 19 prezentări la subiect