Potential energy charge in an electric field. The work done by the forces electric field when moving a positive point charge q from position 1 to position 2, represent as a change in the potential energy of this charge:

where W n1 and W n2 - potential energies of the charge q in positions 1 and 2. For small charge movement q in the field created by a positive point charge Q, the change in potential energy is

.

With the final movement of the charge q from position 1 to position 2, located at distances r 1 and r 2 off charge Q,

If the field was created by the system point charges Q 1 ,Q 2 ,¼ , Q n , then the change in the potential energy of the charge q in this field:

.

The above formulas allow you to find only change potential energy of a point charge q rather than the potential energy itself. To determine the potential energy, it is necessary to agree at what point of the field to consider it equal to zero. For the potential energy of a point charge q, located in an electric field created by another point charge Q, we get

,

where C is an arbitrary constant. Let the potential energy be zero for infinity long distance from charge Q(at r® ¥ ), then the constant C= 0 and the previous expression becomes

In this case, the potential energy is defined as work done to move a charge from a given point to a point at infinity. In the case of an electric field created by a system of point charges, the potential energy of the charge q:

.

Potential energy of a system of point charges. When electrostatic field potential energy serves as a measure of the interaction of charges. Let there be a system of point charges in space Q i(i = 1, 2, ... , n). Energy interaction of all n charges is determined by the ratio

,

where rij- the distance between the corresponding charges, and the summation is carried out in such a way that the interaction between each pair of charges is taken into account once.

The potential of the electrostatic field. The conservative force field can be described not only vector function, but an equivalent description of this field can be obtained by defining a suitable scalar value at each of its points. For an electrostatic field, this quantity is electrostatic field potential, defined as the ratio of the potential energy of the test charge q to the magnitude of this charge, j = W P / q, whence it follows that the potential is numerically equal to the potential energy that a unit positive charge has at a given point in the field. The unit of potential is Volt (1 V).

Potential of the field of a point charge Q in a homogeneous isotropic medium with permittivity e :

The principle of superposition. The potential is a scalar function, the principle of superposition is valid for it. So for the field potential of a system of point charges Q 1, Q 2 ¼ ,Qn we have

,

where ri- distance from the point of the field, which has the potential j, before charge Q i. If the charge is randomly distributed in space, then

,

where r- distance from elementary volume d x, d y, d z to the point ( x, y, z), where the potential is determined; V is the volume of space in which the charge is distributed.

Potential and work of electric field forces. Based on the definition of the potential, it can be shown that the work of the electric field forces when moving a point charge q from one point of the field to another is equal to the product of the magnitude of this charge and the potential difference at the initial and final points of the path, A=q (j 1 - j 2 ) .
If, by analogy with potential energy, we assume that at points infinitely distant from electric charges - field sources, the potential is zero, then the work of the electric field forces when moving the charge q from point 1 to infinity can be represented as A ¥ = qj 1 .
Thus, the potential â at a given point of the electrostatic field is physical quantity, numerically equal to work, performed by the forces of the electric field when moving a unit positive point charge from a given point of the field to an infinitely distant: j = A ¥ / q.
In some cases, the potential of the electric field is more clearly defined as physical quantity numerically equal to the work of external forces against the forces of the electric field when moving a single positive point charge from infinity to given point . The last definition can be conveniently written as follows:

AT modern science and technology, especially when describing phenomena occurring in the microcosm, a unit of work and energy is often used, called electron volt(eV). This is the work done in moving the charge. equal to the charge electron, between two points with a potential difference of 1 V: 1 eV = 1.60 × 10 - 1 9 Cl × 1 V = 1.60 × 10 - 1 9 J.

Questions

1) Give the definition of the potential of a given point of the field and the potential difference of two points of the field.

2) Give graphs of the field strength and potential versus distance for a uniformly charged spherical surface. Give their explanation and justification.

We begin by discussing the potential energy that a charge has in an electrostatic field. First of all, it is necessary to recall the conditions under which it is generally possible to introduce the concept of potential energy.

4.1 Conservative forces

A force is called conservative (or potential) if the work of this force does not depend on the shape of the trajectory and is determined only by the initial and final positions of the body.

Let, for example, the body under the action of a conservative force ~ moved from the initial

point 1 to end point 2 (Fig. 16). Then the work done by the force depends only on the position

points 1 and 2 themselves, but not from the trajectory of the body. For example, for trajectories 1 ! a! 2 and 1! b! 2 the value of A will be the same.

Rice. 16. On the concept of conservative force

Note that the work done by a conservative force along any closed path is zero. Indeed, let's leave point 1 along trajectory 1 ! a! 2 and go back along the trajectory 2 ! b! 1. On the first trajectory, the force will do work A, and on the second trajectory, the work will be equal to A. As a result, the total work will be zero.

So, the concept of potential energy can be introduced only in the case of a conservative force. Potential energy W is a mathematical expression that depends on the coordinates of the body, such that the work of the force is equal to the change in this expression with a minus sign:

Or, which is the same:

A = (W2 W1 ) = W1 W2 :

As you can see, the work of a conservative force is the difference between the potential energy values ​​calculated for the initial and final positions of the body, respectively.

Examples of conservative forces are well known to you. For example, gravity is conservative. The spring force is also conservative. That is why we can talk about the potential energy of a body raised above the ground, or about the potential energy of a deformed spring.

But the friction force is not conservative: the work of the friction force depends on the shape of the trajectory and is not equal to zero on a closed path. Therefore, there is no ¾potential energy of the body in the field of friction force¿.

4.2 Potentiality of the electrostatic field

It turns out that the force with which the electrostatic field acts on a charged body is also conservative. The work of this force, performed when moving the charge, is called the work of the electrostatic field. Thus, we have the most important fact:

The work of the electrostatic field does not depend on the shape of the trajectory along which the charge moves, and is determined only by the initial and final positions of the charge. The work of the field along a closed path is zero.

This fact is also called the potentiality of the electrostatic field. Like the gravity field, the electrostatic field is potential. The work of an electrostatic field is the same for all paths along which a charge can move from one fixed point in space to another.

A rigorous mathematical proof of the potentiality of an electrostatic field is out of scope school curriculum. However, ¾at the physical level of rigor¿ we can verify the validity of this fact with the help of the following simple reasoning.

It is easy to see that if the electrostatic field were not potential, then it would be possible to build a perpetual motion machine! Indeed, then there would be a closed trajectory, when the charge moves along which the field would do positive work (and no changes would occur in the surrounding bodies). We turn our charge along this trajectory, we draw an unlimited amount of energy from nowhere and all the energy problems of mankind are solved :-) But this, alas, is not observed, it blatantly contradicts the law of conservation of energy.

Since the electrostatic field is potential, we can talk about the potential energy of the charge in this field. Let's start with a simple and important case.

4.3 Potential charge energy in a uniform field

The potential energy of a body raised above the ground is equal to mgh. The case of a charge in a uniform field turns out to be very similar to this mechanical situation.

Consider a uniform electrostatic field E, the lines of intensity of which are directed along the X axis (Fig. 17). Let the positive charge q move along the line of force from point 1 (with coordinate x1) to point 2 (with coordinate x2).

0x1

Rice. 17. Movement of a charge in a uniform field

The field acts on the charge with a force ~ , which is directed along the lines of tension. Work

this force, as it is easy to see, will be equal to:

A = F (x2 x1 ) = qE(x2 x1 ):

What will change if points 1 and 2 do not lie on the same line of tension? It turns out nothing! The formula for field work will remain the same. We will verify this with the help of Fig. eighteen .

0x1

Rice. 18. Movement of a charge in a uniform field

Moving from point 1 to point 2, let's choose path 1! 3! 2, where point 3 lies on the same field line with point 1. Then the work A32 in section 32 is zero because we are moving perpendicular to the force. As a result, we get:

A = A13 + A32 = A13 = qE(x2 x1 ):

We see that the work of the field depends only on the abscissa of the initial and final positions of the charge. We write the resulting formula as follows:

A = qEx2 qEx1 = ((qEx2 ) (qEx1 )) = (W2 W1 ) = W:

Here W1 = qEx1 , W2 = qEx2 . The work of the field, in accordance with the formula (8), turns out to be equal to the change with a minus sign of the value

This value is the potential energy of the charge in a uniform electrostatic field. The x denotes the abscissa of the point at which the potential energy is sought. The zero level of potential energy in this case corresponds to the origin x = 0 and is depicted in the figures by a dotted line perpendicular to the lines of tension4.

Recall that, for the time being, q > 0 is considered. It follows from formula (9) that when a charge moves along a field line, the potential energy decreases with increasing x. This is natural: after all, the field does positive work, accelerating the charge, and kinetic energy charge increases due to the decrease in its potential energy.

It is easy to show that formula (9) remains valid for q< 0. В этом случае потенциальная энергия возрастает с ростом x. Это тоже понятно: ведь сила, с которой поле действует на заряд, теперь будет направлена влево, так что движение заряда вправо будет осуществляться против действия поля. Заряд тормозится полем, кинетическая энергия заряда уменьшается, а потенциальная энергия увеличивается.

So, an important conclusion: in the formula for potential energy, q denotes the algebraic value of the charge (taking into account the sign), and not its modulus.

4 In fact, the zero level of potential energy can be chosen anywhere. In other words, the potential energy is defined only up to an arbitrary additive constant C, i.e. W = qEx+C. There is nothing wrong with such uncertainty: the potential energy itself has physical meaning, and the difference in potential energies is equal to the work of the field. In this difference, the constant C cancels out.

4.4 Potential energy of interaction of point charges

Let two point charges q1 and q2 be in vacuum at a distance r from each other. It can be shown that the potential energy of their interaction is given by the formula:

		kq1 q2

We accept formula (10) without proof. Two features of this formula should be discussed.

First, where is the zero level of potential energy? After all, the potential energy, as can be seen from formula (10), cannot turn to zero. But in fact, the zero level exists, and it is at infinity. In other words, when the charges are located infinitely far from each other, the potential energy of their interaction is assumed to be zero (which is logical in this case, the charges already ¾do not interact¿).

Secondly, q1 and q2 are again algebraic quantities of charges, i.e., charges, taking into account their sign.

For example, the potential energy of the interaction of two similar charges will be positive. Why? If we let them go, they will start to accelerate and move away from each other. Their kinetic energy increases, so their potential energy decreases. But at infinity, the potential energy vanishes, and since it decreases to zero, then it is positive.

But the potential energy of interaction of opposite charges turns out to be negative. Indeed, let's remove them at a very large distance from each other so that the potential energy is zero and let go. The charges will begin to accelerate, approaching, and the potential energy decreases again. But if it was zero, then where should it decrease? Only towards negative values.

Formula (10) also helps to calculate the potential energy of a system of charges if the number of charges is more than two. To do this, you need to sum the energies of each pair of charges. We will not issue general formula; Let's better illustrate what has been said with a simple example, shown in Fig. 19.

Rice. 19. Interaction of three charges

If the charges q1, q2, q3 are at the vertices of a triangle with sides a, b, c, then the potential energy of their interaction is equal to:

		kq1 q2		kq2 q3		kq1 q3

4.5 Potential

From the formula W = qEx we see that the potential energy of a charge q in a uniform field is directly proportional to this charge.

We see the same thing from the formula W = kq1 q2 =r: the potential energy of a charge q1 located in the field of a point charge q2 is directly proportional to the charge q1 .

If a electric body acts on electrically charged bodies, then it is able to do the work of moving the charged bodies. The electrostatic field created by a point charge is central, that is, the force acting on a point charge in such a field is directed along the straight line connecting the source charge and the test charge. Earlier we showed that any central force is potential, that is, the work of this force does not depend on the shape of the trajectory, but is determined only by the initial and final position of the body.

Let us briefly recall the proof of this most important assertion. Let a point test charge q move in the central field created by a fixed charge Q (Fig. 174). The force acting on the test charge is determined by Coulomb's law

Where is the vector drawn from the source charge Q to point A, where the test charge is located. When a charge moves along arcs of circles centered on the charge Q (for example, along arcs AB, CD), work electrical force is equal to zero, so the vectors of force and displacement are mutually perpendicular. When moving in the radial direction (for example, along the segments BC, DE), the work depends only on the initial and final distance to the source charge. So the work of the electrostatic field when moving along the segments DE and D1E1 are obviously equal. The most beautiful proof of this statement is related to the symmetry of the field - let's rotate our system around the axis passing through the source, so that the segment D1E1 coincides with the segment DE - the distribution of the field will not change, why should the work of the field change?

Since the principle of superposition is valid for the strength of an electrostatic field, any electrostatic field is potential. Indeed, let a point charge q be in an electric field created by a system of fixed point charges Q1, Q2, … ,QN . When moving the charge to a small displacement vector, by definition, the electric field will do the work, where

The resulting force acting on the moving charge q, equal to the sum of the forces acting from each of the fixed point charges Qk. The work of this force can be calculated by the formula

In order to calculate the work on the final section of the trajectory, it is necessary to divide the trajectory into small sections (Fig. 175), then use formula (1) to calculate the work on each small section, and then sum them up

. (2) In fact, this sum is double, since each resultant force is the sum of forces, according to formula (1). Note that in formula (2) the resulting force changes, since it is calculated in different points trajectories.

As we showed earlier, the work of the electric field of a point charge does not depend on the shape of the trajectory, that is, each term from formula (1) does not depend on the shape of the trajectory, therefore, the entire sum does not depend on the shape of the trajectory. Thus, any electrostatic field is potential.

Therefore, for a point charge in an electrostatic field, one can introduce the potential energy of interaction U(x, y, z). This function has the following physical meaning: the work of the electric field when moving a point charge from one point with coordinates (x1,y1,z1) to another, with coordinates (x2,y2,z2) is equal to the change in potential energy, taken with the opposite sign:

. (3) Sign change in this definition quite logically: if the electric field has done positive work (A > 0), then its energy decreases (ΔU< 0). Для вычисления работы силы взаимодействия между двумя точечными заряженными телами достаточно подсчитать эту работу при движении вдоль радиального отрезка при изменении расстояния от r1 до r2 (Рис. 176). Если построить зависимость силы взаимодействия между зарядами от расстояния r между телами, тогда площадь под графиком этой зависимости в указанных пределах и будет равна искомой работе (Рис. 177). Зависимость силы электростатического взаимодействия от расстояния аналогична силе гравитационного взаимодействия, с одним существенным отличием: гравитационная сила всегда есть сила притяжения, а электрическая может быть как силой притяжения, так и силой отталкивания. В частности два positive charge repel. Therefore, the expression for the work of the electric field will be similar to the formula for the work of the gravitational force, but have the opposite sign

This work is equal to the decrease in the potential energy of interaction, that is, From this expression, you can determine the expression for the potential energy of the electrostatic interaction of two point charges. (4) With this definition, the potential energy of interaction of two charges of the same sign is positive and tends to zero at an infinite distance between the bodies. The force of interaction of charges of opposite signs is directed in the opposite direction, so the work of this force with an increase in the distance between the charges will be negative. However, we do not need to make any additional reservations, since formula (4) automatically takes into account the signs of the charges - if the charges are opposite, then their product (respectively, the energy) is negative. The sign of the potential energy of the interaction of charges has a very clear meaning. Charges of the same sign repel, therefore, when they “run away” to an infinitely large distance, the electric field will do positive work - therefore, initially the system of these charges has the ability to do work, therefore its energy is positive, when the charges move away from each other, their energy decreases to zero. Charges of opposite signs attract, in order to remove them to an infinite distance, external forces must do positive work. In this case, the energy of a pair of charges should increase, therefore, initially it is negative, and when the charges are removed from each other, it increases to zero. In general, the usual situation is that attraction corresponds to negative energy, and repulsion - positive. We only note that such evidence is valid only when choosing the zero level of potential energy at infinity. Formula (4) determines the potential energy of the interaction of two point charged bodies. The values ​​of the charges of the bodies Q and q enter, as expected, symmetrically into this formula. The division of charges into a source charge and a test charge is conditional, they can be completely interchanged. Therefore, it is preferable to write this formula in a symmetrical form: the interaction energy of two point charges q1 and q2 is , or both charges move, finally, regardless of the trajectories of movement of both charges. Further, it is impossible to say to which particular charge this energy “belongs”, in the future we will show that the energy of the interaction of charges is part of the energy of the electrostatic field itself, that is, it is “smeared” over the entire space where the field created by these charges exists. If the system consists of more than two charges, then to calculate the interaction energy of these charges, it is necessary to sum the interaction energies of all pairs of charges

here Uik is the interaction energy of charges qi and qk located at a distance rik from each other (Fig. 178).

40 Question:

Electrostatic field - el. stationary charge field.

Fel, acting on the charge, moves it, doing work. In a uniform electric field Fel = qE - constant

The work of the field (electronic force) does not depend on the shape of the trajectory and on a closed trajectory = zero.

POTENTIAL ENERGY OF A CHARGED BODY IN A HOMOGENEOUS ELECTROSTATIC FIELD

Electrostatic energy is the potential energy of a system of charged bodies (because they interact and are able to do work).

Since the work of the field does not depend on the shape of the trajectory, then at the same time

comparing the work formulas, we obtain the potential energy of the charge in a uniform electrostatic field

If the field does positive work (along lines of force), then the potential energy

of a charged body decreases (but according to the law of conservation of energy, the kinetic energy increases) and vice versa.

POTENTIAL OF ELECTROstatic FIELD

Energy characteristic el. fields.

It is equal to the ratio of the potential energy of the charge in the field to this charge.

A scalar value that determines the potential energy of the charge at any point in the email. fields.

The potential value is considered relative to the selected zero level.

POTENTIAL DIFFERENCE (or otherwise VOLTAGE)

This is the potential difference at the start and end points of the charge trajectory.

The voltage between two points (U) is equal to the potential difference of these points and is equal to the work of the field in moving a unit charge.

RELATIONSHIP BETWEEN FIELD STRENGTH AND POTENTIAL DIFFERENCE

§ 12.3 The work of the forces of the electrostatic field. Potential. Equipotential surfaces

A charge q pr placed at an arbitrary point of an electrostatic field with a strength E is subject to a force F = q pr E. If the charge is not fixed, then the force will make it move and, therefore, work will be done. The elementary work done by the force F when moving a point electric charge q pr from point a of the electric field to point b on a segment of the path dℓ, by definition, is equal to

(α is the angle between F and the direction of movement) (Fig. 12.13).

If work is done external forces, then dA< 0 , если силами поля, то dA >0. Integrating the last expression, we get that the work against the field forces when moving q pr from the point a to point b

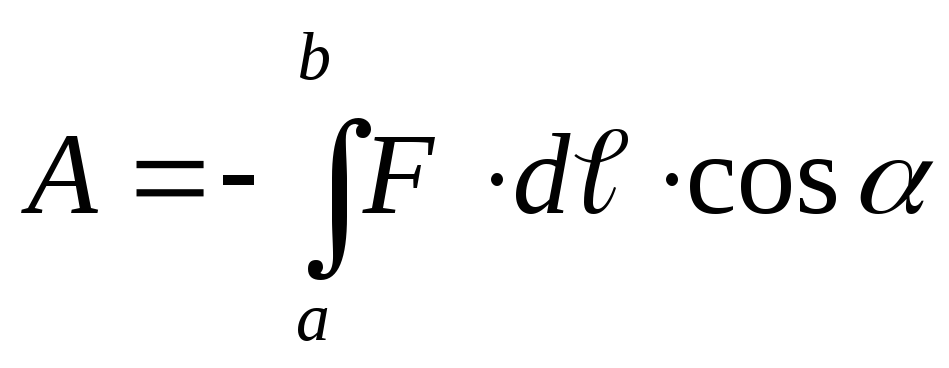(12.20)

Figure -12.13

(

- Coulomb force acting on the test charge q pr at each point of the field with strength E).

Then work

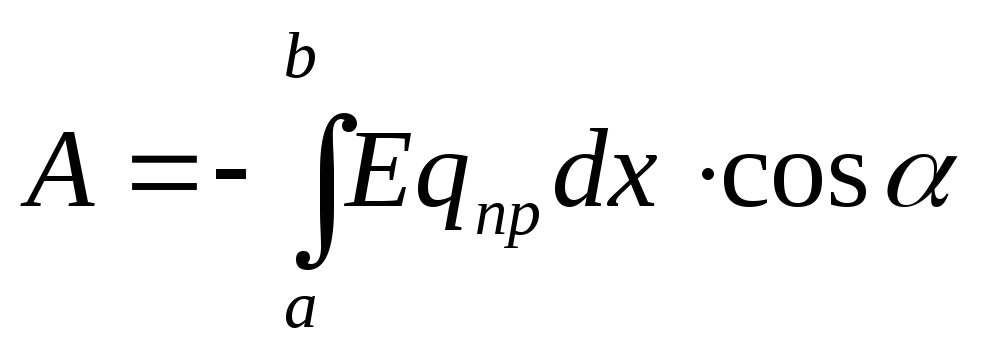(12.21)

The movement is perpendicular to the vector , hence cosα =1, work of test charge transfer q pr from a to b is equal to

(12.22)

The work of the forces of the electric field when moving the charge does not depend on the shape of the path, but depends only on relative position start and end points of the trajectory.

Therefore, the electrostatic field of a point charge ispotential , and the electrostatic forces areconservative .

This is a property of potential fields. It follows from it that the work done in an electric field along a closed circuit is equal to zero:

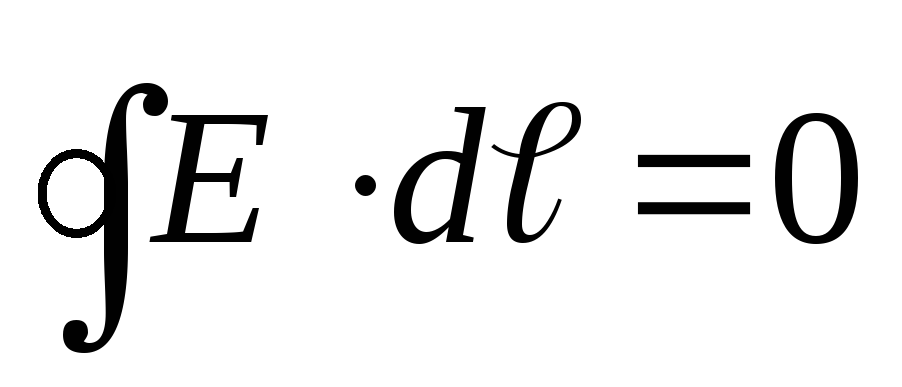(12.23)

Integral

called tension vector circulation . From the vanishing of the circulation of the vector E, it follows that the lines of the electrostatic field strength cannot be closed, they start on positive and end on negative charges.

As you know, the work of conservative forces is performed due to the loss of potential energy. Therefore, the work of the forces of the electrostatic field can be represented as the difference in potential energies that a point charge q pr has at the initial and final points of the charge field q:

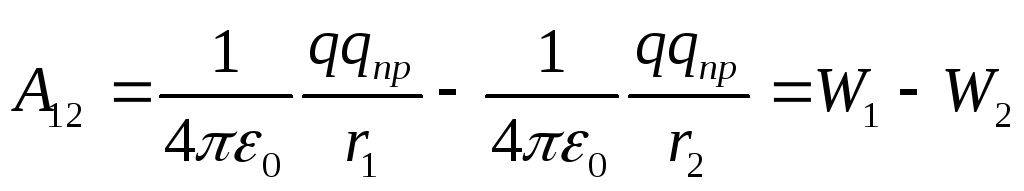(12.24)

whence it follows that the potential energy of charge q pr in the field of charge q is equal to

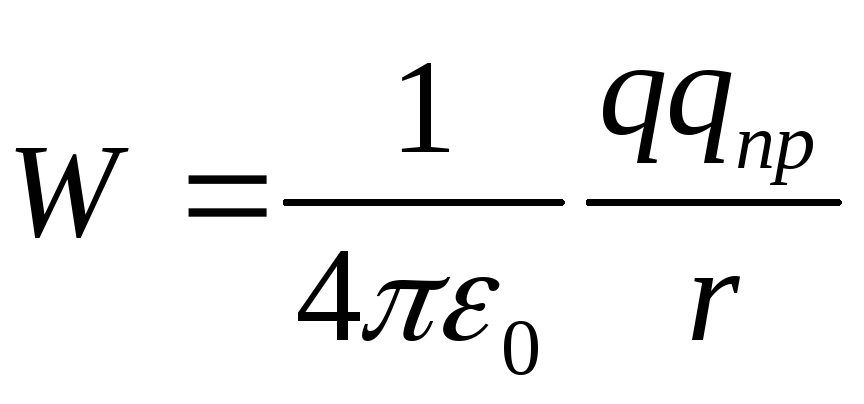(12.25)

For like charges q pr q >0 and the potential energy of their interaction (repulsion) is positive, for unlike charges q pr q< 0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

If the field is created by a system of n point charges q 1, q 2, .... q n , then the potential energy U of the charge q pr located in this field is equal to the sum of its potential energies U i created by each of the charges separately:

(12.26)

Attitude 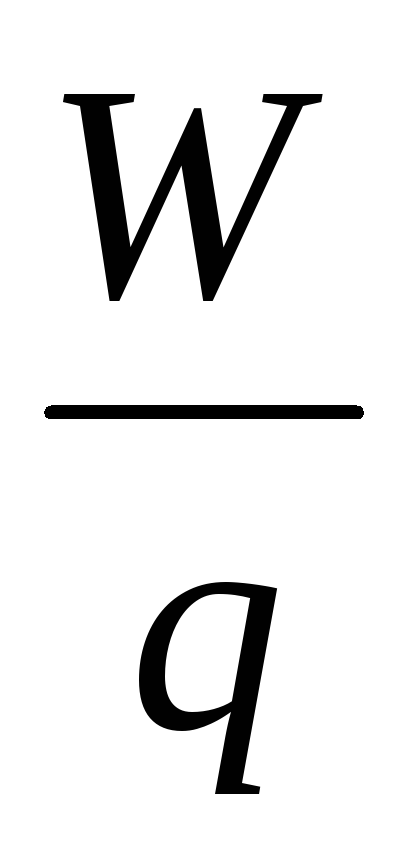do not depend on the charge q and is the energy characteristic of the electrostatic field.

A scalar physical quantity, measured by the ratio of the potential energy of a test charge in an electrostatic field to the value of this charge, is calledpotential of the electrostatic field.

(12.27)

The field potential created by a point charge q is equal to

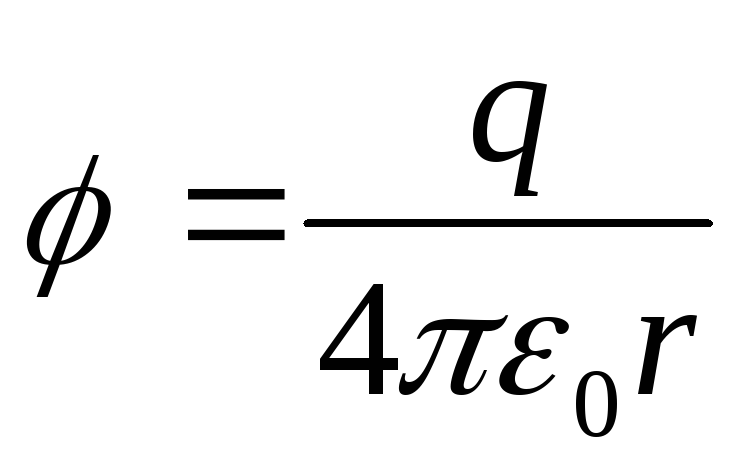(12.28)

Potential unit - volt.

The work done by the forces of the electrostatic field when moving the charge q pr from point 1 to point 2 can be represented as

those. is equal to the product of the transferred charge and the potential difference at the starting and ending points.

The potential difference of two points of the electrostatic field φ 1 -φ 2 is equal to the voltage. Then

The ratio of the work done by an electrostatic field when moving a test charge from one point of the field to another, to the value of this charge is calledvoltage between these points.

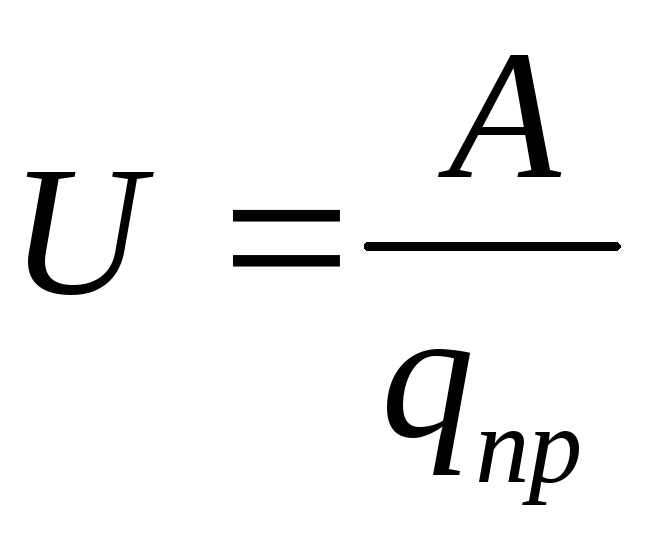(12.30)

Graphically, the electric field can be depicted not only with the help of lines of tension, but also with the help of equipotential surfaces.

Equipotential surfaces is a set of points having the same potential. The figure shows that the lines of tension (radial rays) are perpendicular to the equipotential lines.

E there are an infinite number of potential surfaces around each charge and each system of charges (Fig. 12.14). However, they are carried out so that the potential differences between any two adjacent equipotential surfaces are the same. Then the density of equipotential surfaces clearly characterizes the field strength at different points. Where these surfaces are denser, the field strength is greater. Knowing the location of equipotential lines (surfaces), it is possible to construct lines of tension, or from a known location of lines of tension, equipotential surfaces can be constructed.

§ 12.4Relationship between tension and potential

An electrostatic field has two characteristics: power (strength) and energy (potential). Tension and potential are different characteristics of the same field point, therefore, there must be a connection between them.

The work of moving a single point positive charge from one point to another along the x axis, provided that the points are infinitely close to each other and x 1 - x 2 \u003d dx, is equal to qE x dx. The same work is equal to q(φ 1 - φ 2)= -dφq. Equating both expressions, we can write

Repeating similar reasoning for the y and z axes, we can find the vector :

where

- unit vectors of coordinate axes x, y, z.

From the definition of a gradient it follows that

or

(12.31)

those. the field strength E is equal to the potential gradient with a minus sign. The minus sign is determined by the fact that tension vector E field is directed in the direction of decreasing potential.

The established relationship between the strength and potential allows, by the known field strength, to find the potential difference between two arbitrary points of this field.

Field of a uniformly charged sphere radiusR

The field strength outside the sphere is determined by the formula

(r>R)

The potential difference between the points r 1 and r 2 (r 1 >R; r 2 >R) is determined using the relation

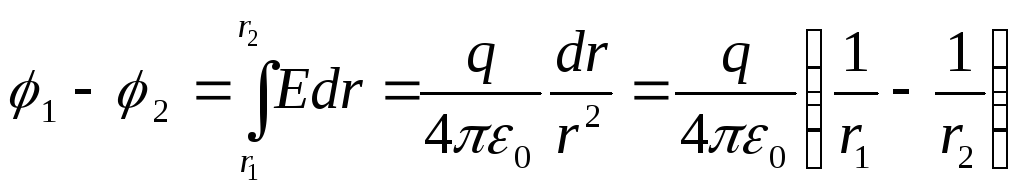
We get the potential of the sphere if r 1 = R, r 2 → ∞:

The field of a uniformly charged infinitely long cylinder

The field strength outside the cylinder (r > R) is determined by the formula

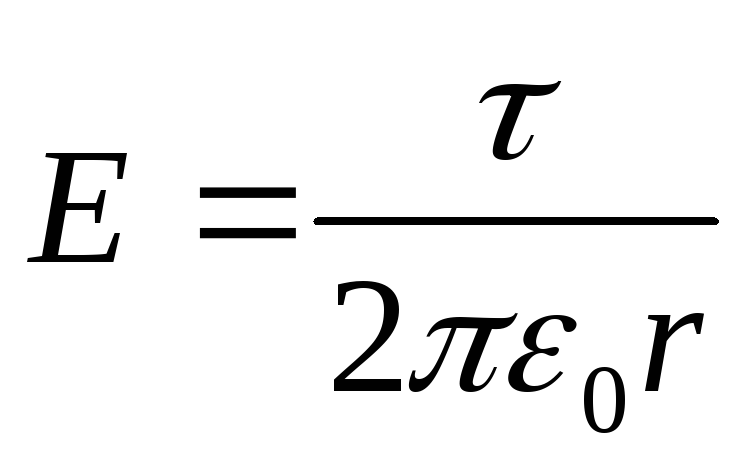
(τ is the linear density).

The potential difference between two points lying at a distance r 1 and r 2 (r 1 >R; r 2 >R) from the axis of the cylinder is equal to

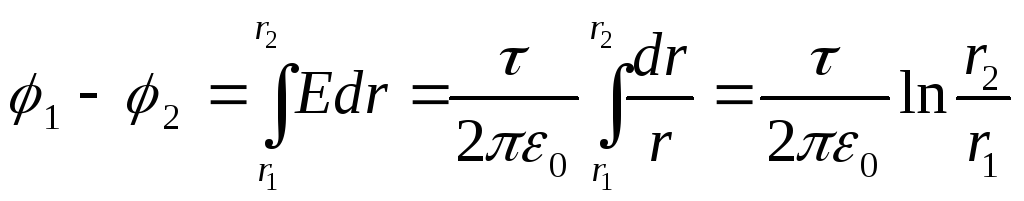(12.32)

Field of a uniformly charged infinite plane

The field strength of this plane is determined by the formula

(σ - surface density).

The potential difference between points lying at a distance x 1 and x 2 from the plane is equal to

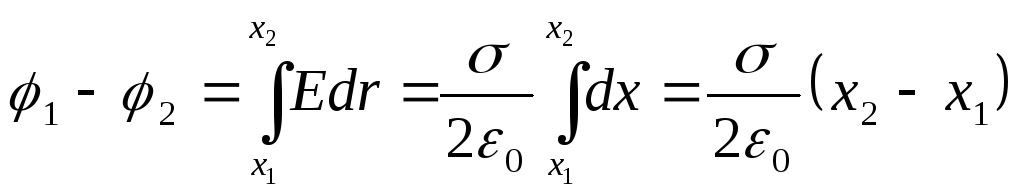(12.33)

Field of two oppositely charged infinite parallel planes

The field strength of these planes is determined by the formula

The potential difference between the planes is

(12.34)

(d is the distance between the planes).

Examples of problem solving

Example 12.1 . Three point charges Q 1 \u003d 2nC, Q 2 \u003d 3nC and Q 3 \u003d -4nC are located at the vertices of an equilateral triangle with side length a=10cm. Determine the potential energy of this system.

Given : Q 1 \u003d 2nCl \u003d 2∙10 -9 C; Q 2 \u003d 3nCl \u003d 3 ∙ 10 -9 C; and Q 3 \u003d -4nCl \u003d 4∙10 -9 C; a=10cm=0.1m.

Find : U.

R Solution: The potential energy of a system of charges is equal to the algebraic sum of the interaction energies of each of the interacting pairs of charges, i.e.

U=U 12 +U 13 +U 23

where, respectively, the potential energies of one of the charges located in the field of another charge at a distance a from him, equal

;

;

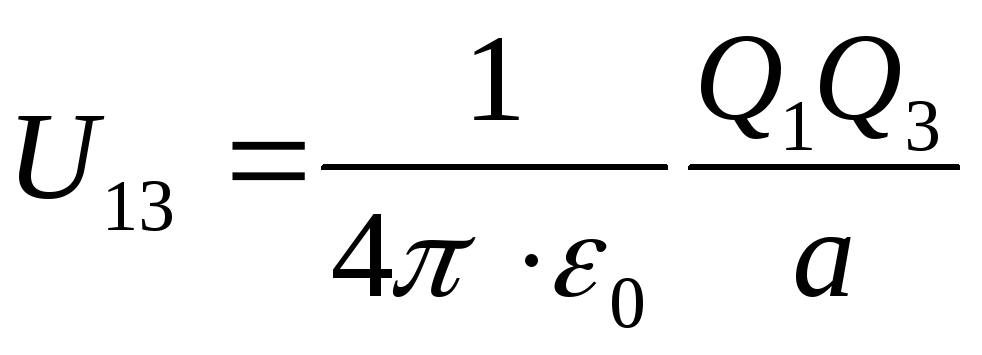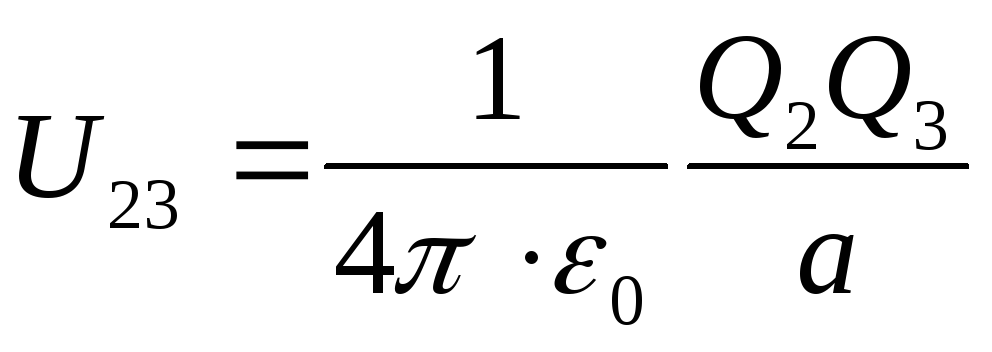(2)

We substitute formulas (2) into expression (1), find the desired potential energy of the system of charges

Answer: U \u003d -0.126 μJ.

Example 12.2 . Determine the potential in the center of the ring with an inner radius R 1 =30cm and an outer R 2 =60cm, if the charge q=5nC is evenly distributed on it.

Given: R 1 \u003d 30 cm \u003d 0.3 m; R 2 \u003d 60 cm \u003d 0.6 m; q=5nCl=5∙10 -9 C

Find : φ .

Solution: We divide the ring into concentric infinitely thin rings with an inner radius r and an outer radius (r+dr).

The area of ​​the considered thin ring (see figure) dS=2πrdr.

P 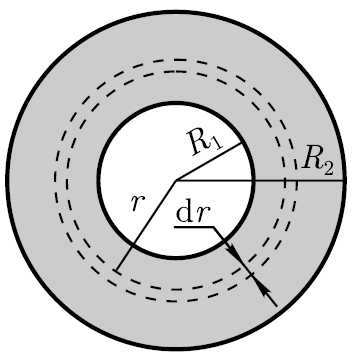potential at the center of the ring, created by an infinitely thin ring,

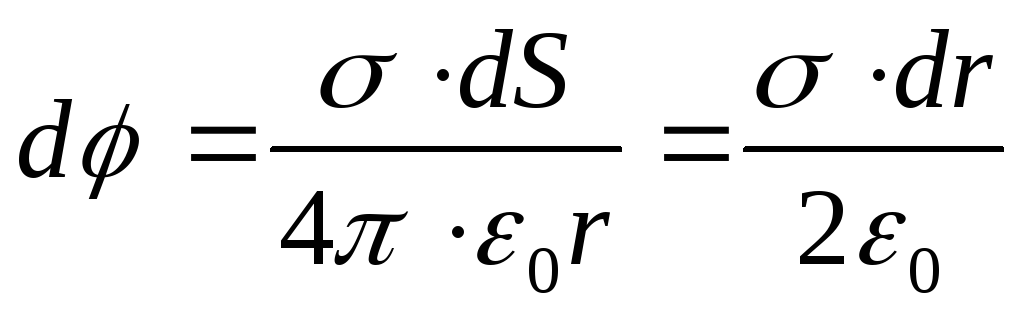
where is the surface charge density.

To determine the potential at the center of the ring, one should arithmetically add dφ from all infinitely thin rings. Then

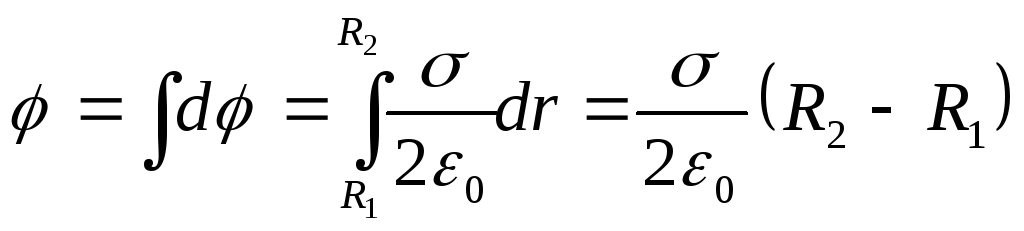
Considering that the charge of the ring Q=σS, where S= π(R 2 2 -R 1 2) is the area of ​​the ring, we obtain the desired potential at the center of the ring

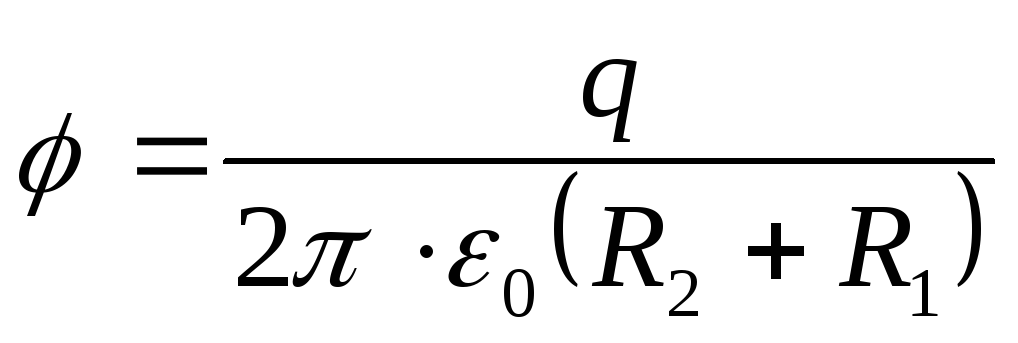
Answer : φ=25V

Example 12.3. Two point charges of the same name (q 1 =2nC andq 2 \u003d 5nC) are in vacuum at a distancer 1 = 20cm. Determine the work A that must be done to bring them closer to the distancer 2 =5cm.

Given: q 1 =2nCl=2∙10 -9 C; q 2 =5nCl=5∙10 -9 C ; r 1 = 20cm=0.2m;r 2 =5cm=0.05m.

Find : BUT.

Solution: The work done by the forces of the electrostatic field when moving the charge Q from a point in the field with a potential φ 1 to a point with a potential φ 2.

A 12 \u003d q (φ 1 - φ 2)

When similar charges approach each other, the work is done by external forces, so the work of these forces is equal in absolute value, but opposite in sign to the work of the Coulomb forces:

A \u003d -q (φ 1 - φ 2) \u003d q (φ 2 - φ 1). (one)

Potentials of points 1 and 2 of the electrostatic field

;

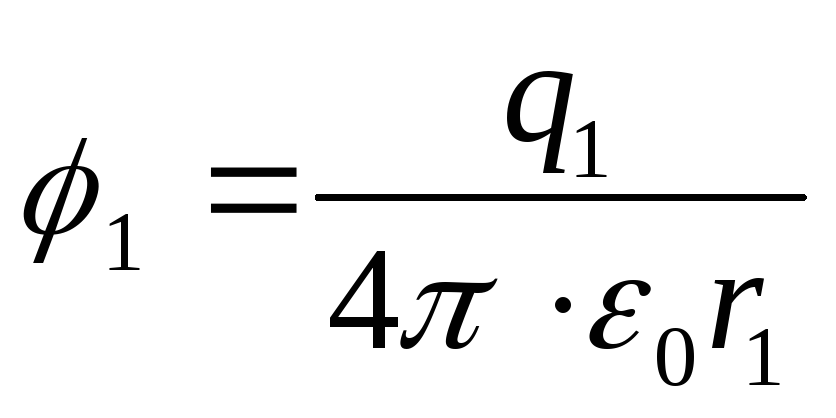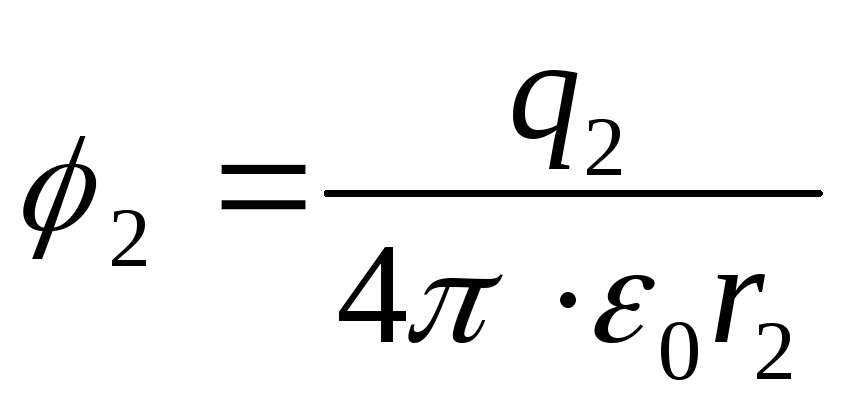(2)

Substituting formulas (2) into expression (1), we find the desired work that must be done in order to bring the charges closer,

Answer: A=1.35 μJ.

Example 12.4. An electrostatic field is created by a positively charged endless filament. A proton moving under the action of an electrostatic field along the line of tension from the filament from a distancer 1 =2cm tor 2 =10cm, changed its speed fromυ 1 =1Mm/s up toυ 2 =5Mm/s. Determine the linear density τ of the charge of the thread.

Given: q=1.6∙10 -19 C; m=1.67∙10 -27 kg; r 1 \u003d 2 cm \u003d 2 ∙ 10 -2 m; r 2 \u003d 10cm \u003d 0.1m; r 2 \u003d 5 cm \u003d 0.05 m; υ 1 \u003d 1 Mm / s \u003d 1 ∙ 10 6 m / s; up to υ 2 \u003d 5 Mm / s \u003d 5 ∙ 10 6 m / s.

Find : τ .

Solution: The work done by the forces of the electrostatic field when moving a proton from a point of the field with a potential φ 1 to a point with a potential φ 2 goes to increase the kinetic energy of the proton

q(φ 1 - φ 2) \u003d ΔT (1)

In the case of a filament, the electrostatic field is axially symmetric, so

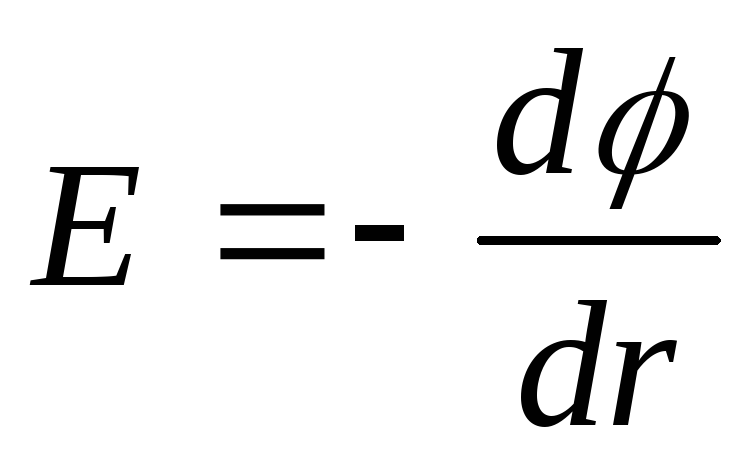or dφ=-Edr,

then the potential difference between two points located at a distance r 1 and r 2 from the thread,

(we took into account that the strength of the field created by a uniformly charged infinite thread,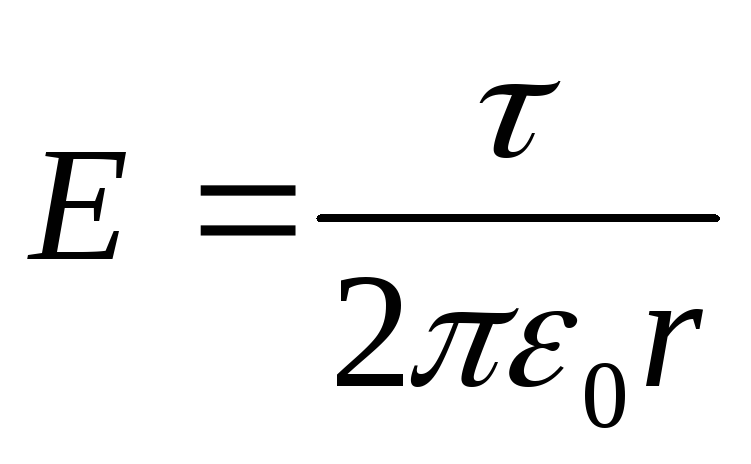

).

Substituting expression (2) into formula (1) and taking into account that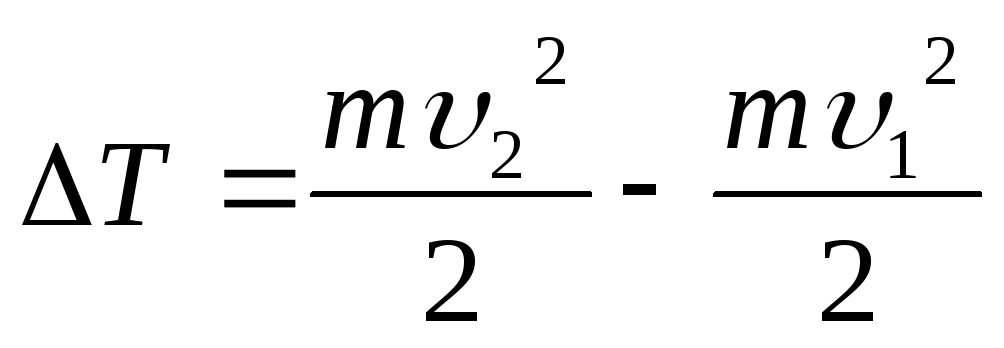

, we get

Where is the desired linear charge density of the thread

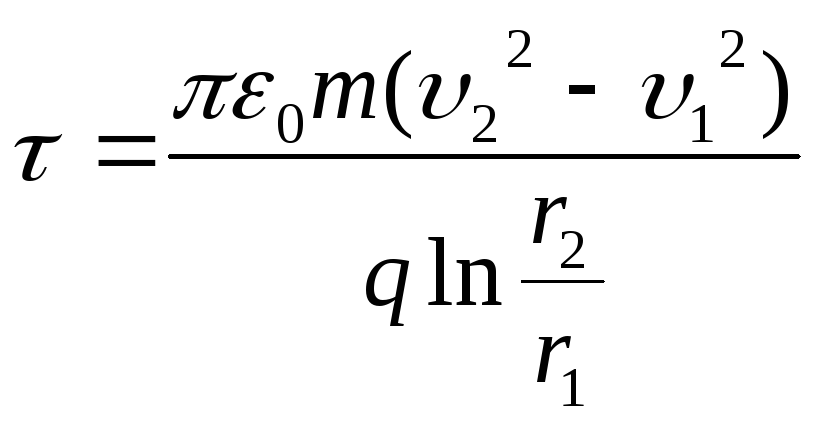
Answer : τ = 4.33 µC/m.

Example 12.5. An electrostatic field is created in a vacuum by a ball with a radiusR=8cm, uniformly charged with bulk density ρ=10nC/m 3 . Determine the potential difference between two points of this field lying at distances from the center of the ball: 1)r 1 =10cm andr 2 =15cm; 2)r 3 = 2cm andr 4 =5cm..

Given: R=8cm=8∙10 -2 m; ρ=10nC/m 3 =10∙10 -9 nC/m 3; r 1 \u003d 10 cm \u003d 10 ∙ 10 -2 m;

r 2 \u003d 15 cm \u003d 15 ∙ 10 -2 m; r 3 \u003d 2cm \u003d 2 ∙ 10 -2 m; r 4 \u003d 5 cm \u003d 5 ∙ 10 -2 m.

Find : 1) φ 1 - φ 2 ; 2) φ 3 - φ 4 .

Solution: 1) The potential difference between two points lying at a distance r 1 and r 2 from the center of the ball.

(1)

where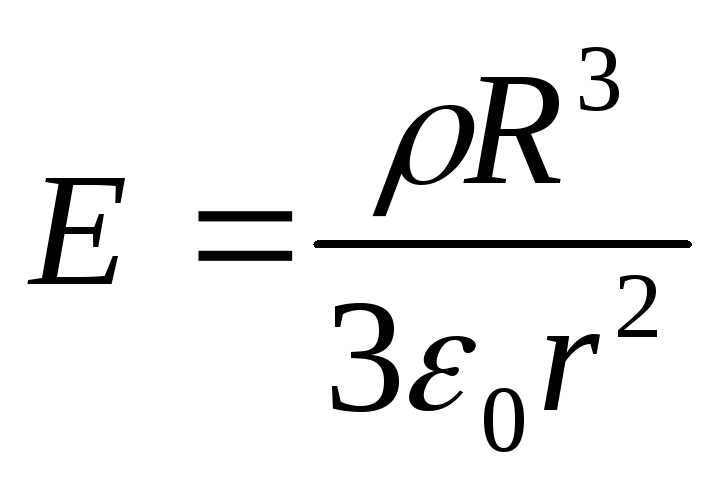

is the field strength generated by a uniformly charged ball with a bulk density ρ at any point outside the ball at a distance r from its center.

Substituting this expression into formula (1) and integrating, we obtain the desired potential difference

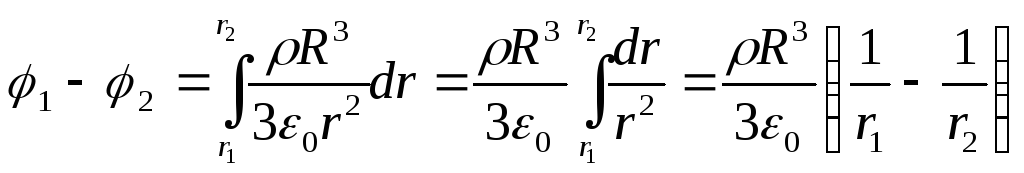
2) The potential difference between two points lying at a distance r 3 and r 4 from the center of the ball,

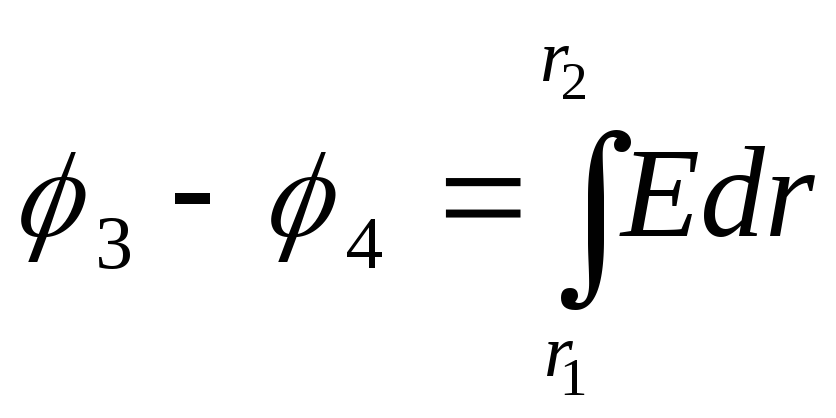(2)

where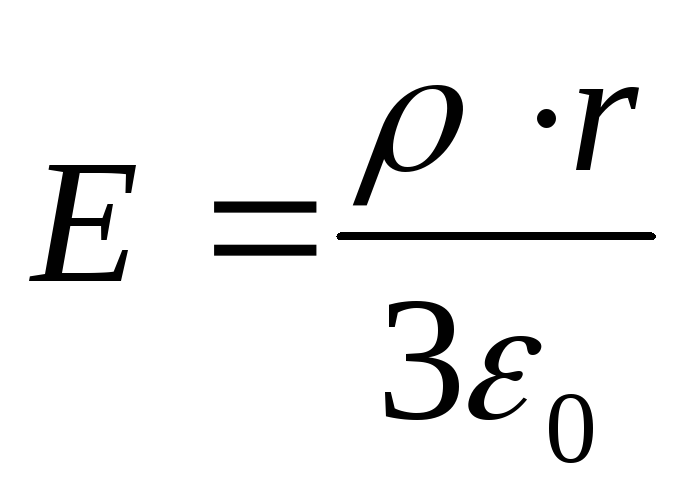

is the field strength generated by a uniformly charged ball with a volume density ρ at any point lying inside the ball at a distance r from its center.

Substituting this expression into formula (2) and integrating, we obtain the desired potential difference

Answer : 1) φ 1 - φ 2 \u003d 0.643 V; 2) φ 3 - φ 4 \u003d 0.395 V

Let us calculate the potential energy of electric charges for the simplest but very important special cases.
Potential Energy of a Charge in a Homogeneous Field Let the charge q move in a uniform electric field with a strength E from point 1 to point 2. The position of point 1 is determined by the radius vector and of point 2 by the radius vector r2. The force acting on the charge F = qE is constant. The work of the force F does not depend on the shape of the trajectory connecting points 1 and 2. This follows from the general proof of the potentiality of the electrostatic field. It is also possible to carry out a proof using a direct calculation of the work done when a charge moves along different paths in the same way as was done in Mechanics for gravitational forces. Now we will not do it.
The easiest way to calculate the work is if the charge moves along the straight line connecting point 1 and point 2 (Fig. 1.78). Displacement vector Dg = r2 - rv The work is equal to the scalar product of force and displacement:
A = F Ar^qE (r2-r1) = qE r2-qE gg (1.18.1)
On the other hand, according to (1.17.1), A \u003d ~ (W 2 ~ Comparing expressions (1.18.1) and (1.17.1), we obtain an expression for the potential energy of a charge in a uniform field:
Wp ~ -qE g. (1.18.2)
A uniform field is created, in particular, in the space between parallel plates, carrying charges opposite signs (Fig. 1.79). It is natural to choose the coordinate system so that the X axis is directed perpendicular to the plates. Then the projections En and E, are equal to zero and are expressed
at z
lower (1.18.2) takes the form:
Wp = -q(Exx + Eyy + Ezz) = ~qExx. (1.18.3)

Formula (1.18.3) is similar to the formula Wp = mgh for the potential energy of a body above the Earth's surface. The role of mass is played by charge, acceleration free fall is the field strength, and instead of the height h is the x coordinate. But the sign of the energy is different: minus instead of plus. The point here is this. The mass is always positive, and the force of gravity is necessarily directed vertically downwards. Taking into account these circumstances, the formula Wp = mgh was written. It contains the free fall acceleration module, and the height h is measured from the Earth's surface. Formula (1.18.3) is more general. The charge q can be either positive or negative; the field strength can be directed anywhere, and its projection can be either positive or negative, depending on the choice of coordinate system.
In particular, if the field strength E is directed vertically downwards, and the X axis is upwards, then
Wp = qE\x\ (1.18.4)
in exact accordance with the expression Wp = mgh.
If the electric field does positive work, then the energy of a charged body in the field decreases: AW 0. Such a movement of a charged particle is similar to the movement of a stone thrown upwards. In this case, the potential energy of the particle increases, while the kinetic energy decreases: the particle is decelerated.
Zero potential energy
Potential energy in electrodynamics is determined, as in mechanics, up to an arbitrary constant. Instead of expression (1.18.2) we could write:
W=-qE-r + C, (1.18.5)
where C is an arbitrary constant. In this case, the change in potential energy remains the same, and the work determines precisely the change in potential energy, and not the energy itself. Writing down the formula (1.18.2), we actually equated the constant C to zero. This corresponds to a certain choice of the zero level of potential energy. For example, for the case shown in Figure 1.79, the potential energy is assumed to be zero on the surface of the plate B. But, as with the action of gravitational forces, the zero level of potential energy is chosen arbitrarily. We can assume that W - O at a distance from the plate B. Then
wp=-qExx-qExx y
It is not the potential energy itself that has physical meaning, but the difference in its values, determined by the work of the field when the charge moves from the initial position to the final one.
Interaction energy of point charges
In the course of mechanics, an expression was obtained for the interaction energy of point bodies:
tі u "W \u003d -G---.
R g
If instead of point masses we take two charges q1 and q2 of opposite signs (the charges are attracted), then we can obtain a similar expression for the potential energy of their interaction:
w (1.18.6)
R y "
For charges of the same sign (charges repel), the sign of potential energy will be opposite:
w (1.18.7)
R y "
Formulas (1.18.6) and (1.18.7) can be combined into one if instead of charge modules we take their algebraic values:
W. (1.18.8)
R r v "
The potential energy sign will automatically turn out to be correct.
If the charges ql and q2 have the same signs, then the potential energy of their interaction is positive (Fig. 1.80, a). It is the greater, the smaller the distance between the charges, since the work that the Coulomb forces can do when the charges are repelled from each other will be greater. If the charges have opposite signs, then the energy is negative and its maximum value, equal to zero, is achieved at r -> oo (Fig. 1.80, b). The larger r, the more work will be done by the forces of attraction when the charges approach each other.

Rice. 1.80
When writing potential energy in the form (1.18.8), a certain choice of the zero level of potential energy has already been made. It is believed that the potential energy of infinitely distant charges is equal to zero: Wp -» 0 when r -» oo. This choice of zero level is convenient, but not required. Instead of expression (1.18.8), one could just as well write that
(1.18.9)
rg y"
where C is an arbitrary constant. This shows that the positive or negative value of the potential energy of a special physical sense does not have. The sign of the potential energy will be determined by fixing an arbitrary constant C. By changing the value of C, we can change the sign of Wp for a given distance r between charges.
Potential energy of a system of point charges
The potential energy of a system of point charges qv q2, ..., qN is equal to the sum of the potential energies of all pairs of interacting charges. For three charges
w kbSi+hbS*+hwz l
R G1.2 G1.3 G2.3
Prove it yourself using the following trick. Initially, the charges q2 and qz are at an infinite distance from the charge qv Then the charge q2 moves to a point located at a distance gl 2 from the first charge. After that, the charge qz moves to a point at a distance r1 3 from the first charge and r2 3 from the second. It is necessary to calculate the work of the Coulomb forces performed during these displacements and equate it to the change in potential energy, taken with the opposite sign.
In general, N charges
N N
wp=llk7rh> (1.18.11)
i=lfc=l (i*k)
where r; k - distance between charges of numbers ink. Coefficient - 1
2 is obtained due to the fact that when summing, the potential energy is taken into account twice in the form of identical
ri, k rk, i
Formulas for potential energy electric charge in a homogeneous field (1.18.2) and for two point charges (1.18.8) it is advisable to remember. They will meet quite often.
? 1. Is it possible to create an electrostatic
le, the lines of tension of which are parallel- ^^^^^^^
lelny, and the module of intensity of age is
em in the direction perpendicular to the
niyam (Fig. 1.81)? Rice. 1.81
Draw a graph of the dependence of the potential energy of oppositely charged particles on the distance, provided that the arbitrary constant C in the formula (1.18.9) is positive.
What will formula (1.18.8) look like if the charges are in a medium with a dielectric constant є?