Potential energy in an electrostatic field. The potential of the electrostatic field. Potential of a system of electric charges
§ 15. POTENTIAL. ENERGY OF THE SYSTEM OF ELECTRIC CHARGES. WORK ON MOVING THE CHARGE IN THE FIELD
Basic formulas
Potential electric field is a quantity equal to the ratio of the potential energy of a point positive charge placed in given point fields, to this charge;
=P/ Q,
or the potential of the electric field is a quantity equal to the ratio of the work of the field forces to move a point positive charge from a given point of the field to infinity to this charge:
=A/ Q.
The potential of the electric field at infinity is conditionally taken equal to zero.
Note that when a charge moves in an electric field, the work A v.s external forces is equal in absolute value to the work A s.p. field strength and is opposite to it in sign:
A v.s = – A s.p. .
Electric field potential created by a point charge Q on distance r from the charge
The potential of the electric field created by the metal, carrying a charge Q sphere with radius R, at a distance from the center of the sphere:
inside the sphere ( r<R)
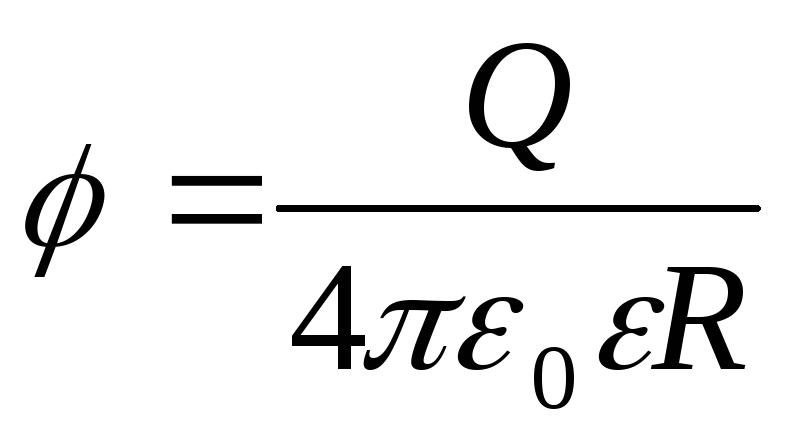 ;
;
on the surface of a sphere ( r=R)
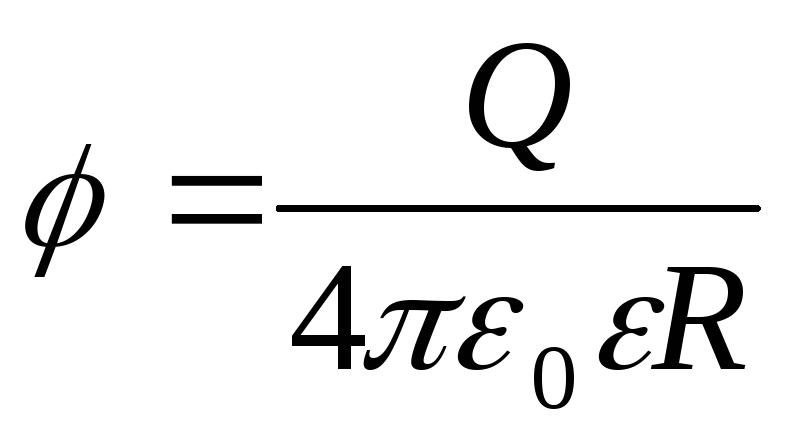 ;
;
out of scope (r>
R)
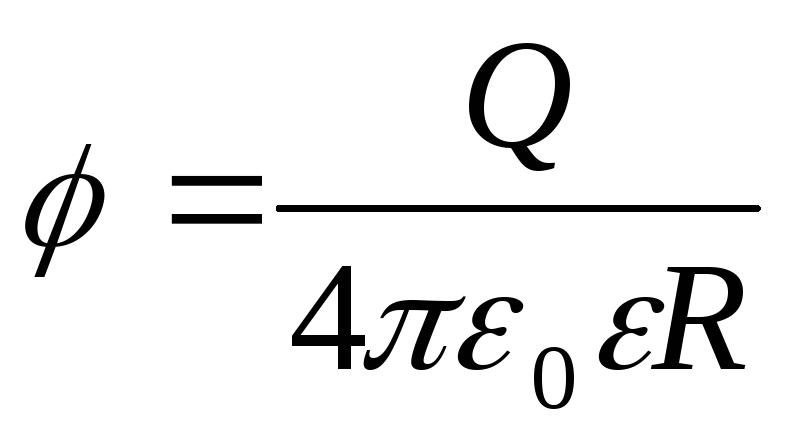 .
.
In all the formulas given for the potential of a charged sphere, is the permittivity of a homogeneous infinite dielectric surrounding the sphere.
The potential of the electric field created by the system P point charges, at a given point, in accordance with the principle of superposition of electric fields, is equal to the algebraic sum of potentials 1 , 2 , ... , n, created by individual point charges Q 1 ,Q 2 , ...,Q n :
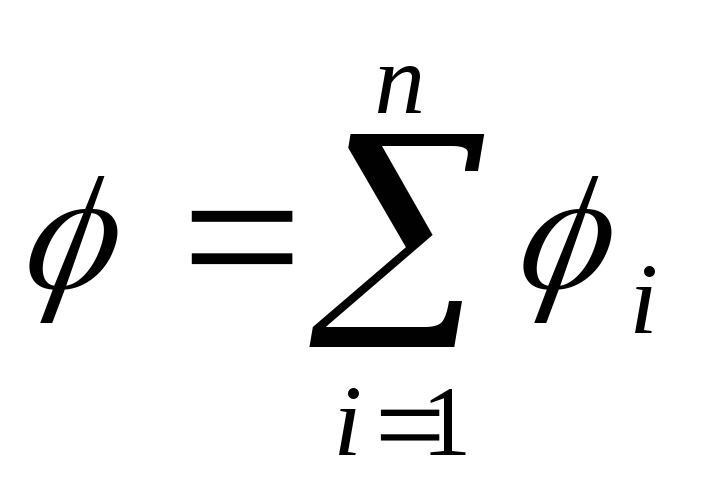
Energy W interactions of a system of point charges Q 1 ,Q 2 , ...,Q n is determined by the work that this system of charges can do when they are removed relative to each other to infinity, and is expressed by the formula
 ,
,
where i- the potential of the field created by all P- 1 charges (excluding the 1st) at the point where the charge is located Q i .
The potential is related to the strength of the electric field by the relation
E= -grad.
In the case of an electric field with spherical symmetry, this relationship is expressed by the formula
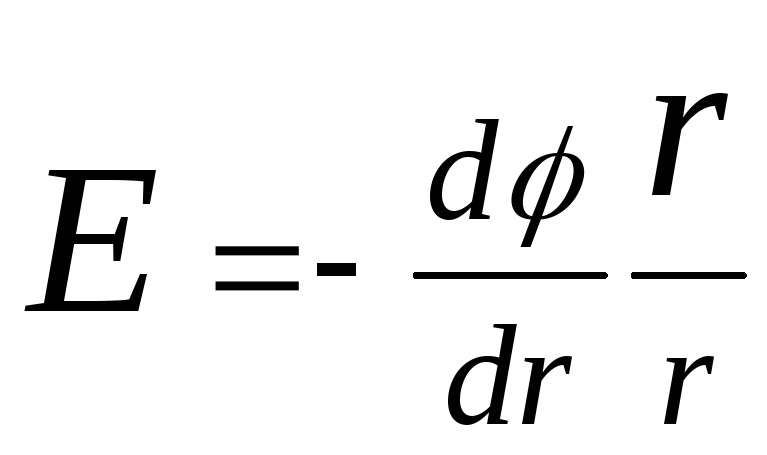 ,
,
or in scalar form
 ,
,
and in case homogeneous field, i.e., a field whose strength at each point is the same both in absolute value and in direction,
E=( 1 – 2 ,)/d,
where 1 and 2 - potentials of points of two equipotential surfaces; d - the distance between these surfaces along the electrical field line.
Work done by an electric field when moving a point charge Q from one point of the field with a potential 1 , into another with a potential 2 ,
A=Q( 1
- 2
), or  ,
,
where E l - tension vector projection E to the direction of movement; dl - movement.
In the case of a homogeneous field, the last formula takes the form
A= QElcos ,
where l- displacement; - angle between vector directions E and displacement l.
Examples of problem solving
Example 1 positive charges Q 1 \u003d 3 μC and Q 2 \u003d 20 nC are in vacuum at a distance r 1 =l.5 m apart. Define a job A, which must be done in order to bring the charges closer to a distance r 2 =1 m.
Solution. Let us assume that the first charge Q 1 remains stationary and the other Q 2 under the action of external forces moves in the field created by the charge Q 1 approaching him from a distance r 1 =t,5 m up to r 2 =1 m .
Work BUT" external force to move the charge Q from one point of the field with potential 1 into another, whose potential 2 , equal in absolute value and opposite in sign to work BUT field forces for the movement of the charge between the same points:
A "= -A.
Work BUT field forces on charge displacement A=Q( 1 - 2 ). Then work BUT" external forces can be written as
A" = –Q( 1 - 2 )=Q( 2 - 1 ). (1)
The potentials of the start and end points of the path are expressed by the formulas
 ;
;
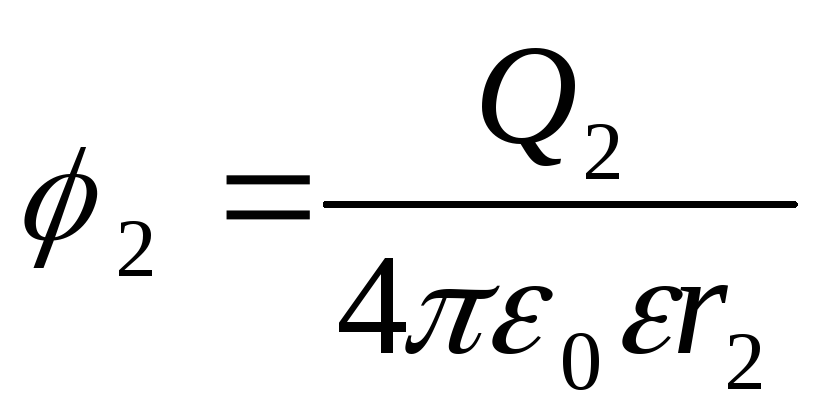 .
.
Substituting expressions 1 and 2 into formula (1) and taking into account that for this case the transferred charge Q=Q 2 , we get
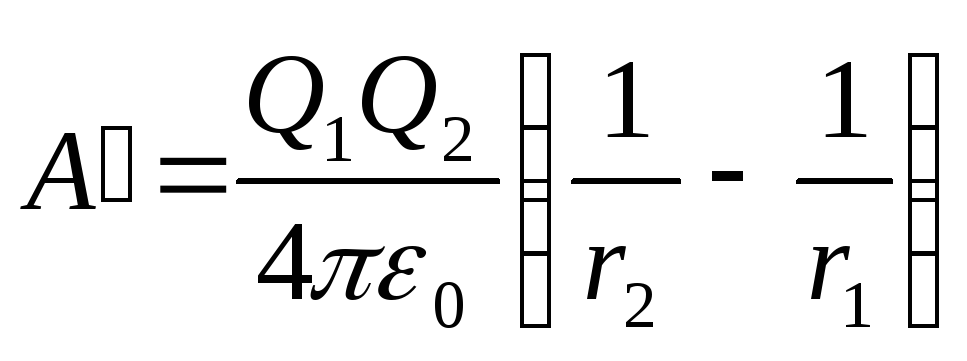 . (2)
. (2)
Considering that 1/(4 0 )=910 9 m/F, then after substituting the values of the quantities into formula (2) and calculating, we find
A"=180 µJ.
Example 2 Find a job BUT charge transfer fields Q=10 nC from point 1 exactly 2 (Fig. 15.1), located between two oppositely charged ones with a surface density \u003d 0.4 μC / m 2 infinite parallel planes, distance l between them is 3 cm.
R 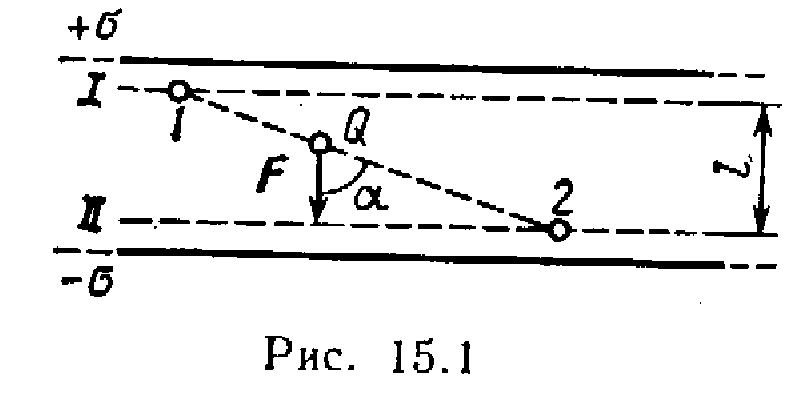 solution. There are two ways to solve the problem.
solution. There are two ways to solve the problem.
1st way. The work of the field forces to move the charge Q from the point 1 fields with potential 1 exactly 2 fields with potential 2 find by formula
A=Q( 1 - 2 ). (1)
To determine potentials at points 1 and 2 Let us draw equipotential surfaces I and II through these points. These surfaces will be planes, since the field between two uniformly charged infinite parallel planes is uniform. For such a field, the relation
1 - 2 =El, (2)
where E - field strength; l - distance between equipotential surfaces.
Field strength between parallel infinite oppositely charged planes E=/ 0 . Substituting this expression E into formula (2) and then the expression 1 - 2 into formula (1), we obtain
A= Q( / 0 ) l.
2nd way. Since the field is uniform, the force acting on the charge Q, is constant as it moves. Therefore, the work of moving the charge from the point 1 exactly 2 can be calculated using the formula
A=F r cos, (3)
where F - force acting on a charge r- charge transfer module Q from a point 1 exactly 2; is the angle between the directions of displacement and force . But F= QE= Q( / 0 ). Substituting this expression F into equality (3), as well as noticing that r cos= l, we get
A=Q(/ 0 )l. (4)
Thus, both solutions lead to the same result.
Substituting into expression (4) the value of quantities Q, , 0 and l, find
A\u003d 13.6 μJ.
Example 3 On a thin thread bent along an arc of a circle with a radius R,
uniformly distributed charge with linear density=10 nC/m. Define tension E and potential of the electric field created by such a p  distributed charge at a point O, coinciding with the center of curvature of the arc. Length l the thread is 1/3 of the circumference and is equal to 15 cm.
distributed charge at a point O, coinciding with the center of curvature of the arc. Length l the thread is 1/3 of the circumference and is equal to 15 cm.
Solution. We choose the coordinate axes so that the origin of coordinates coincides with the center of curvature of the arc, and the axis at was symmetrically located relative to the ends of the arc (Fig. 15.2). Select an element of length d on the thread l. Charged Q=d l, located in the selected area, can be considered as a point.
Let us determine the strength of the electric field at the point O. To do this, we first find the tension d E field created by the charge d Q:
 ,
,
where r-radius-vector directed away from element d l to the point at which the tension is calculated. We express the vector d E through projection dE x c and dE y on the coordinate axis:
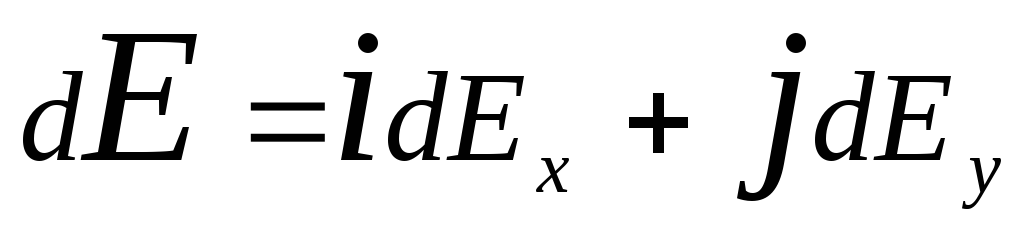 ,
,
where i and j- unit direction vectors (orths).
tension E find by integration:
 .
.
Integration is carried out along the arc of length l. Due to symmetry, the integral  equals zero. Then
equals zero. Then
 , (1)
, (1)
where 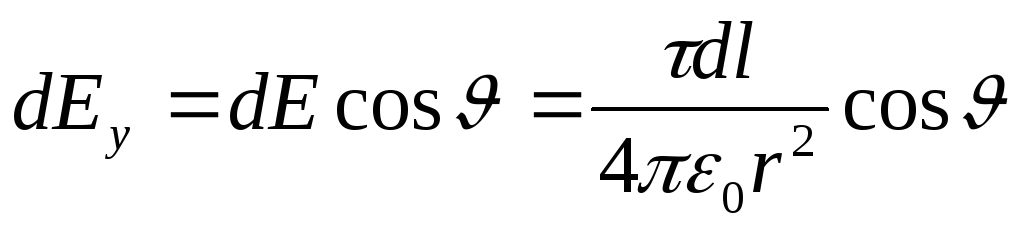 . Because r=R= const and d l=R d. then
. Because r=R= const and d l=R d. then
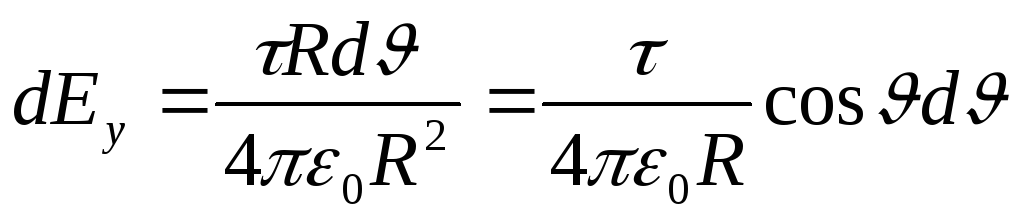
Substitute the found expression dE y in (1) and, taking into account the symmetrical location of the arc relative to the axis OU, we take the limits of integration from 0 to /3, and double the result;
 .
.
Substituting these limits and expressing R through the length of the arc (3 l= 2 r), we get
 .
.
This formula shows that the vector E coincides with the positive direction of the axis OU Substituting the value and l into the last formula and doing the calculations, we find
E\u003d 2.18 kV / m.
Let us determine the potential of the electric field at the point O. Let us first find the potential d created by the point charge d Q at the point O:

Let's replace r on the R and perform the integration:
 .Because l=2
R/3,
then
.Because l=2
R/3,
then
=/(6 0 ).
Having made calculations according to this formula, we obtain
Example4 . The electric field is created by a long cylinder with a radius R= 1cm , uniformly charged with linear density=20 nC/m. Determine the potential difference of two points of this field located at distances a 1 =0.5 cm and a 2 \u003d 2 cm from the surface of the cylinder, in its middle part.
Solution. To determine the potential difference, we use the relationship between the field strength and the change in potential E= -grad. For a field with axial symmetry, which is the field of a cylinder, this relation can be written as
E= -( d/d r) , or d= - E d r.
Integrating the last expression, we find the potential difference of two points separated by r 1 and r 2 from the axis of the cylinder;
![]() . (1)
. (1)
Since the cylinder is long and the points are taken near its middle part, the field strength can be expressed using the formula  . Substituting this expression E into equality (1), we obtain
. Substituting this expression E into equality (1), we obtain
 (2)
(2)
Since the quantities r 2 and r 1 enter the formula as a ratio, then they can be expressed in any, but only the same units:
r 1 =R+a 1 = 1.5 cm; r 2 =R+a 2 =3cm .
Substituting the magnitude values , 0 ,r 1 and r 2 into formula (2) and calculating, we find
1 - 2 =250 V.
Example 5 The electric field is created by a thin rod carrying a charge =0.1 μC/m uniformly distributed along its length. Determine the potential of the field at a point remote from the ends of the rod at a distance, equal to the length rod.
Solution. The charge on the rod cannot be considered as a point charge, therefore, directly apply the formula to calculate the potential
 , (1)
, (1)
valid only for point charges, it is impossible. But if we split the rod into elementary segments d l, then the charged l located on each of them can be considered as a point and then formula (1) will be valid. Applying this formula, we get
 , (2)
, (2)
where r - the distance of the point at which the potential is determined to the rod element.
From fig. 15.3 that d l=(r d/cos). Substituting this expression d l into formula (2), we find  .
.
Integrating the resulting expression within the limits of 1
yes 2
, we obtain the potential created by the entire charge distributed on the rod: 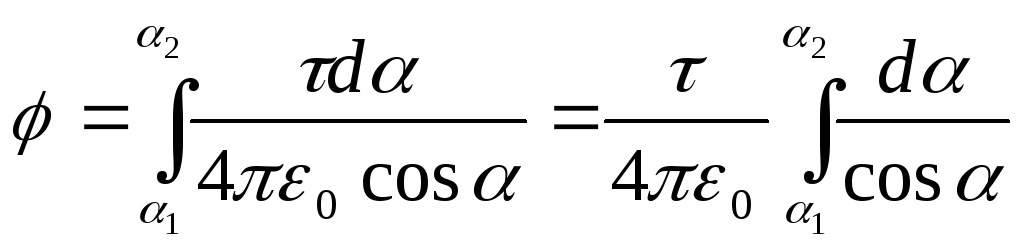 .
.
AT 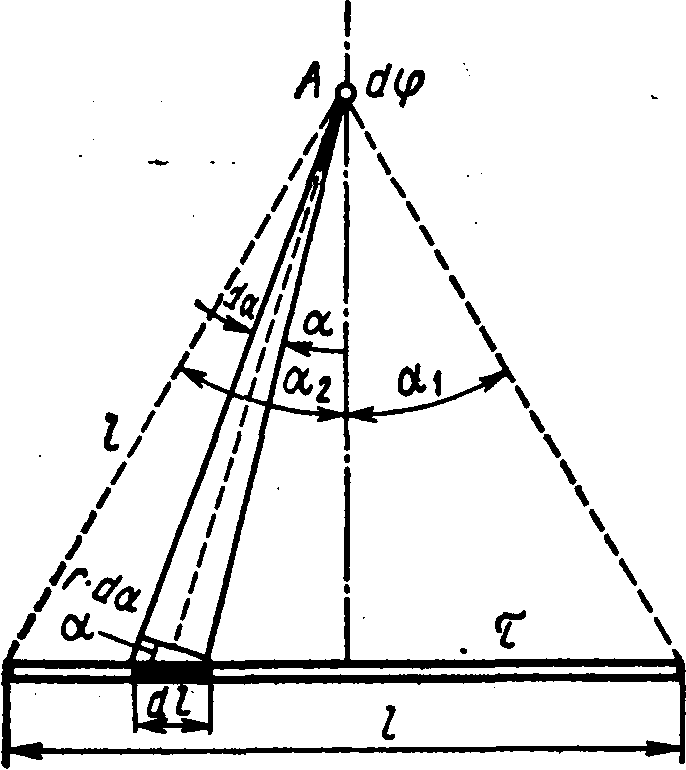 point symmetry force BUT relative to the ends of the rod we have 2
= 1
and therefore
point symmetry force BUT relative to the ends of the rod we have 2
= 1
and therefore  .
.
Consequently,
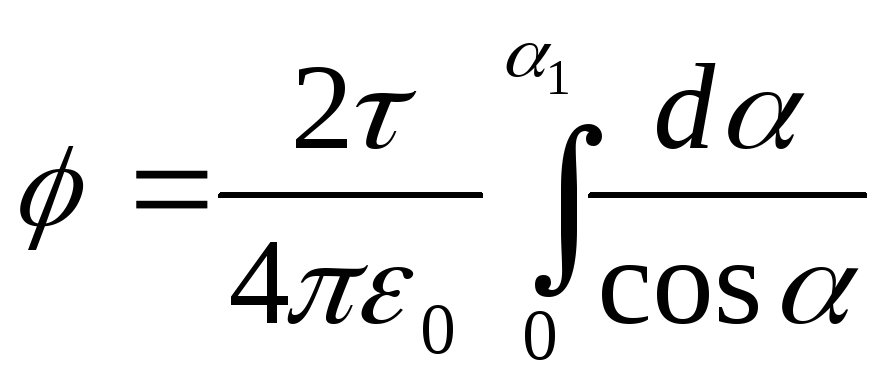 .Because
.Because 
(see Table 2), then  .
.
Substituting the limits of integration, we obtain
Having made calculations according to this formula, we find
Example 6 An electron with a speed v=1.8310 6 m/s flew into a uniform electric field in the direction opposite to the field strength vector. What potential difference U an electron must pass in order to have energy E i\u003d 13.6 eV *? (Having such an energy, an electron can ionize it when it collides with a hydrogen atom. The energy of 13.6 eV is called the ionization energy of hydrogen.)
Solution. The electron must pass such a potential difference u, so that the energy acquired W combined with kinetic energy T, which the electron had before entering the field, amounted to an energy equal to the ionization energy E i ,
i.e. W+
T=
E i .
Expressing in this formula W=
EU and T=(m v 2
/2), we get EU+(m v 2
/2)=E i. From here  .
.
___________________
* Electron-volt (eV) - the energy acquired by a particle having a charge equal to the charge of an electron that has passed through a potential difference of 1 V. This non-systemic unit of energy is currently approved for use in physics.
Let's make calculations in SI units:
U=4.15 AT.
Example 7 Determine initial speed υ 0 approach of protons located at a sufficiently long distance from each other if the minimum distance r min , by which they can get close, is 10 -11 cm.
Solution: There are repulsive forces between the two protons, as a result of which the movement of the protons will be slow. Therefore, the problem can be solved as inertial system coordinates (associated with the center of mass of two protons), and in non-inertial (associated with one of the rapidly moving protons). In the second case, Newton's laws do not hold. The application of the d'Alembert principle is difficult due to the fact that the acceleration of the system will be variable. Therefore, it is convenient to consider the problem in an inertial frame of reference.
Let us place the origin of coordinates at the center of mass of two protons. Since we are dealing with identical particles, the center of mass will be at the point that bisects the segment connecting the particles. Relative to the center of mass, the particles will have at any time the same velocities modulo. When the particles are at a sufficiently large distance from each other, the speed υ 1 each particle is equal to half υ 0 , i.e. υ 1 =υ 0 /2.
To solve the problem, we apply the law of conservation of energy, according to which the total mechanical energy E isolated system is constant, i.e.
E=T+ P ,
where T- the sum of the kinetic energies of both protons relative to the center of mass; P is the potential energy of the system of charges.
We express the potential energy in the initial P 1 and final P 2 moments of motion.
At the initial moment, according to the condition of the problem, the protons were at a great distance, so the potential energy can be neglected (P 1 =0). Therefore, for the initial moment total energy will be equal to the kinetic energy T 1 protons, i.e.
E=T l . (1)
At the final moment, when the protons approach as close as possible, the speed and kinetic energy are equal to zero, and the total energy will be equal to the potential energy P 2, i.e.
E= P 2 . (2)
Equating the right parts of equalities (1) and (2), we obtain
T 1 \u003d P 2. (3)
The kinetic energy is equal to the sum of the kinetic energies of the protons:
 (4)
(4)
Potential energy of a system of two charges Q 1 and Q 2 in vacuum is determined by the formula  , where r- distance between charges. Using this formula, we get
, where r- distance between charges. Using this formula, we get
 (5)
(5)
Taking into account equalities (4) and (5), formula (3) takes the form
 where
where 
After performing calculations according to the obtained formula, we find υ 0 =2,35 mm/s
 Example 8 An electron without an initial velocity has passed the potential difference U 0 =10
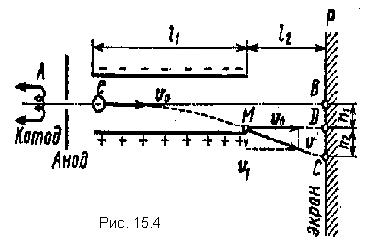
kV and flew into the space between the plates of a flat capacitor charged to a potential difference U l \u003d 100 V, along the line AB, parallel to the plates (Fig. 15.4). Distance d between the plates is 2 cm. Length l 1 capacitor plates in the direction of electron flight is equal to 20cm. Determine distance sun on the screen R, away from the condenser l 2 \u003d 1 m.
Example 8 An electron without an initial velocity has passed the potential difference U 0 =10
kV and flew into the space between the plates of a flat capacitor charged to a potential difference U l \u003d 100 V, along the line AB, parallel to the plates (Fig. 15.4). Distance d between the plates is 2 cm. Length l 1 capacitor plates in the direction of electron flight is equal to 20cm. Determine distance sun on the screen R, away from the condenser l 2 \u003d 1 m.
Solution. The motion of an electron inside the capacitor consists of two motions: 1) by inertia along the line AB at a constant speed υ 0 , acquired under the action of a potential difference U 0 , which the electron passed to the capacitor; 2) uniformly accelerated movement in the vertical direction to a positively charged plate under the action of a constant field force of the capacitor. After leaving the capacitor, the electron will move uniformly with a speed υ, which he had at the point M at the time of exit from the condenser.
From fig. 15.4 shows that the desired distance | | BC|=h 1 +h 2 , where from h 1 - the distance that the electron will move in the vertical direction while moving in the capacitor; h 2 - the distance between the point D on the screen, in which the electron would fall, moving at the exit from the capacitor in the direction of the initial velocity υ 0 , and the point C, where the electron actually hits.
Express separately h 1 and h 2 . Using the formula for the path length of uniformly accelerated motion, we find
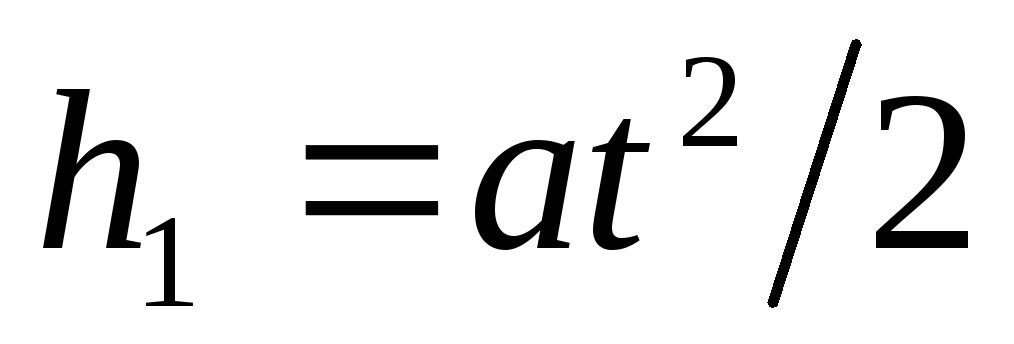 .
(1)
.
(1)
where a- acceleration received by the electron under the action of the capacitor field; t- the flight time of an electron inside a capacitor.
According to Newton's second law a=F/m, where F- the force with which the field acts on the electron; t- its mass. In its turn, F=eE=eU 1 /d, where e- electron charge; U 1 - potential difference between the capacitor plates; d- the distance between them. We find the flight time of an electron inside the capacitor from the formula for the path of uniform motion  ,
where
,
where

where l 1
is the length of the capacitor in the direction of electron flight. We find the expression for the speed from the condition of equality of the work done by the field when moving the electron and the kinetic energy acquired by it:  .
From here
.
From here
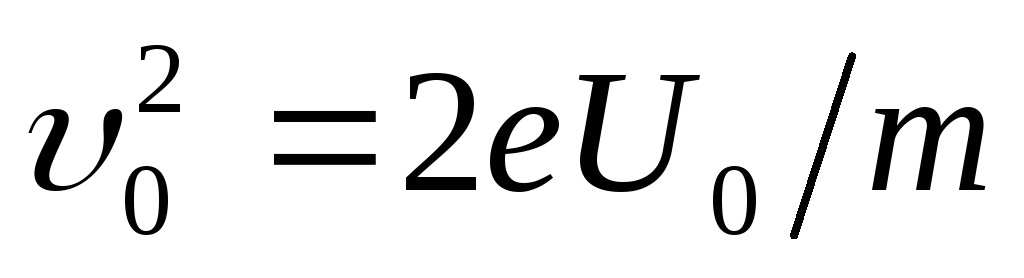 (2)
(2)
Substituting into formula (1) successively the values a,F, t and υ
0 2
from the corresponding expressions, we obtain 
Cut length h 2 find from the similarity of triangles MDC and vector:
 (3)
(3)
where υ 1 - electron speed in the vertical direction at a point M;l 2 - distance from the capacitor to the screen.
Speed υ 1 we find by the formula υ 1 =at, which, taking into account the expressions for a, F and t will take the form

Substituting the expression υ
1 into formula (3), we get  ,
or by replacing υ
0 2 by formula (3), we find
,
or by replacing υ
0 2 by formula (3), we find

Finally for the required distance | BC| will have
|BC|=
Substituting the values of quantities U 1 ,U 0 ,d,l 1 and l 2 into the last expression and performing calculations, we get | BC|=5.5 cm.
Tasks
Potential energy and field potential of point charges
15.1. point charge Q\u003d 10 nC, being at a certain point in the field, has a potential energy P \u003d 10 μJ. Find the potential φ of this field point.
5.2. When moving charge Q=20 nC between two points of the field, work was done by external forces A=4µJ. Define a job A 1 field forces and the difference Δφ of the potentials of these points of the field.
15.3. The electric field is created by a point positive charge Q 1 \u003d 6 nC. positive charge Q 2 is transferred from the point BUT this field to a point AT(Fig. 15.5). What is the change in potential energy ΔP per unit of transferred charge, if r 1 =20 cm and r 2 \u003d 50 cm?
15.4.
Electric field created by a point charge Q l \u003d 50 nC. Without using the concept of potential, calculate the work BUT in 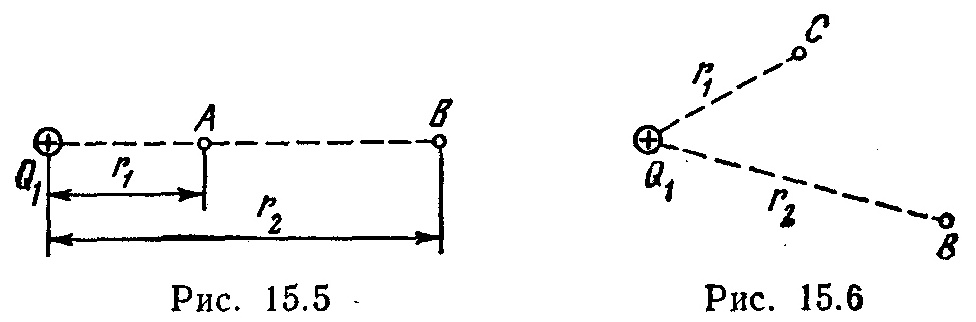 external forces to move a point charge Q 2 = -2 nC from point FROM exactly AT
external forces to move a point charge Q 2 = -2 nC from point FROM exactly AT
(Fig. 15.6), if r 1 =10 cm, r 2 \u003d 20 cm. Also determine the change ΔP of the potential energy of the system of charges.
15.5. The field is created by a point charge Q=1 nC. Determine the potential φ of the field at a point remote from the charge at a distance r=20 cm.
15.6. Determine the potential φ of the electric field at a point remote from the charges Q 1 = -0.2 µC and Q 2 =0,5 μC, respectively, on r 1 =15 mass media r 2 \u003d 25 cm. Also determine the minimum and maximum distances between charges for which a solution is possible.
15.7. Charges Q 1 \u003d 1 μC and Q 2 = -1 μC are at a distance d\u003d 10 cm. Determine the tension E and potential φ of the field at a point remote at a distance r= 10 cm from the first charge and lying on a line passing through the first charge perpendicular to the direction from Q 1 to Q 2 .
15.8. Calculate the potential energy P of a system of two point charges Q 1 =100 nC and Q 2 =10 nC at a distance d=10 cm apart.
15.9. Find the potential energy P of a system of three point charges Q 1 \u003d 10 nC, Q 2 =20 nCl and Q 3 \u003d -30 nC, located at the vertices of an equilateral triangle with side length a=10 cm.
15.10. What is potential energyП systems of four identical point charges Q\u003d 10 nC, located at the vertices of a square with a side length a\u003d 10 cm? .
15.11. Determine the potential energy P of a system of four point charges located at the vertices of a square with side length a\u003d 10 cm. The charges are the same in modulus Q=10 nC, but two of them are negative. Consider two possible cases of the arrangement of charges.
 15.12
. The field is created by two point charges +
2Q and -Q, at a distance d=12 cm apart. Determine the locus of points on the plane for which the potential is zero (write the equation for the line of zero potential).
15.12
. The field is created by two point charges +
2Q and -Q, at a distance d=12 cm apart. Determine the locus of points on the plane for which the potential is zero (write the equation for the line of zero potential).
5.13. The system consists of three charges - two of the same size Q 1 = |Q 2 |=1 μC and opposite in sign and charge Q=20 nC, located at point 1 in the middle between the other two charges of the system (Fig. 15.7). Determine the change in the potential energy ΔP of the system during charge transfer Q from point 1 to point 2. These points are removed from the negative charge Q 1 per distance a= 0,2 m.
Potential of the field of linearly distributed charges
15.14. Along a thin ring with a radius R= 10 cm uniformly distributed charge with a linear density τ= 10 nC/m. Determine the potential φ at a point lying on the axis of the ring, at a distance a= 5 cm from the center.
15.15. On a segment of a thin straight conductor, a charge is uniformly distributed with a linear density τ=10 nC/m. Calculate the potential φ created by this charge at a point located on the axis of the conductor and remote from the nearest end of the segment by a distance equal to the length of this segment.
The electrostatic field is potential, the Coulomb forces are conservative forces, and the work of conservative forces can be represented as a decrease in potential energy, i.e.
where C is the constant of integration, which is usually chosen so that when the charge q is removed to infinity - W р = 0, i.e. C=0.
We will investigate the ESP using test charges q pr 1 , q pr 2 , q pr 3 –
The potential of an electrostatic field is the energy characteristic of the field, numerically equal to the ratio of the potential energy of the test electric charge, placed at a given point of the field, to the magnitude of the charge.
Then, using relations (7.1) and (7.7), we obtain:
Knowing the distribution of charges, we can find the field potential of any system.
Field potentials are added algebraically, therefore, the calculation of potentials is usually simpler than the calculation of EF strengths.
In SI, the unit of potential is [ j ] \u003d 1J / C \u003d 1V
A unit of work of 1 eV (electron volt) is equal to the work done by the field forces on the charge equal to the charge electron, when it passes a potential difference of 1 V.
1 eV = 1.6´10 -19 C ´ 1V=1.6´10 -19 J
Video model: 1) Movement of charges in an electric field; 2) Mass spectrometer.
A body located in a potential field of forces (an electrostatic field) has potential energy due to which work is done by the forces of the field. The work of conservative forces is performed due to the loss of potential energy. Therefore, the work of the forces of the electrostatic field can be represented as the difference in potential energies possessed by point charge Q 0 at the start and end points of the charge field Q: , whence it follows that the potential energy of the charge q0 in the charge field Q is equal to ![]() . It is defined ambiguously, and up to an arbitrary constant FROM. If we assume that when the charge is removed to infinity ( r®¥) the potential energy vanishes ( U=0),
then FROM=0 and the potential energy of the charge Q 0 ,
located in the field of charge Q at a distance r from it, is equal to
. It is defined ambiguously, and up to an arbitrary constant FROM. If we assume that when the charge is removed to infinity ( r®¥) the potential energy vanishes ( U=0),
then FROM=0 and the potential energy of the charge Q 0 ,
located in the field of charge Q at a distance r from it, is equal to ![]() . For similar charges Q 0 Q> 0 and the potential energy of their interaction (repulsion) is positive, for opposite charges Q 0 Q<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.
. For similar charges Q 0 Q> 0 and the potential energy of their interaction (repulsion) is positive, for opposite charges Q 0 Q<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.
Potential j at any point of the electrostatic field there is a physical quantity determined by the potential energy of a unit positive charge placed at this point. From which it follows that the potential of the field created by a point charge Q, is equal to . The work done by the forces of the electrostatic field when moving the charge Q 0 from point 1
exactly 2
, can be represented as , i.e. equal to the product of the transferred charge and the potential difference at the initial and final points. Potential difference two points 1
and 2
in an electrostatic field is determined by the work done by the field forces when moving a unit positive charge from a point 1
exactly 2
. The work of the field forces when moving the charge Q 0 from point 1
exactly 2
can also be written in the form ![]() . The expression for the potential difference: , where integration can be performed along any line connecting the start and end points, since the work of the electrostatic field forces does not depend on the trajectory of movement.
. The expression for the potential difference: , where integration can be performed along any line connecting the start and end points, since the work of the electrostatic field forces does not depend on the trajectory of movement.
If you move the charge Q 0 from an arbitrary point outside the field, i.e. to infinity, where, by condition, the potential is zero, then the work of the forces of the electrostatic field A ¥ =Q 0 j where
Potential- a physical quantity determined by the work of moving a unit positive charge when it is removed from a given point of the field to infinity. This work is numerically equal to the work done external forces(against the forces of the electrostatic field) by moving a unit positive charge from infinity to a given point in the field. Potential unit - volt(B): 1 V is the potential of such a point in the field at which a charge of 1 C has a potential energy of 1 J (1 V = 1 J/C).
In the case of an electrostatic field, potential energy serves as a measure of the interaction of charges. Let there be a system of point charges in space Q i(i = 1, 2, ... ,n). Interaction energy of all n charges is determined by the ratio
![]()
where rij- the distance between the corresponding charges, and the summation is carried out in such a way that the interaction between each pair of charges is taken into account once.
From this it follows that the potential of the field of the system of charges is equal to algebraic the sum of the field potentials of all these charges:
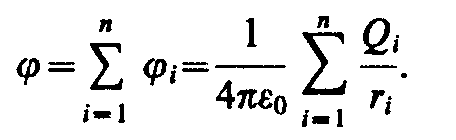
Considering the electric field created by a system of charges, one should use the principle of superposition to determine the field potential:
The potential of the electric field of a system of charges at a given point in space is equal to the algebraic sum of the potentials of the electric fields created at a given point in space by each charge of the system separately:
![]()
6. Equipotential surfaces and their properties. Relationship between potential difference and electrostatic field strength.
An imaginary surface, all points of which have the same potential, is called an equipotential surface. The equation of this surface
If the field is created by a point charge, then its potential  Thus, the equipotential surfaces in this case are concentric spheres. On the other hand, the lines of tension in the case of a point charge are radial straight lines. Therefore, the lines of tension in the case of a point charge perpendicular equipotential surfaces.
Thus, the equipotential surfaces in this case are concentric spheres. On the other hand, the lines of tension in the case of a point charge are radial straight lines. Therefore, the lines of tension in the case of a point charge perpendicular equipotential surfaces.


All points of the equipotential surface have the same potential, so the work of moving the charge along this surface is zero, i.e., the electrostatic forces acting on the charge, always directed along the normals to the equipotential surfaces. Therefore, the vector E is always normal to equipotential surfaces, and therefore the lines of the vector E orthogonal to these surfaces.
There are an infinite number of equipotential surfaces around each charge and each system of charges. However, they are usually carried out so that the potential differences between any two adjacent equipotential surfaces are the same. Then the density of equipotential surfaces clearly characterizes the field strength at different points. Where these surfaces are denser, the field strength is greater.
So, knowing the location of the electrostatic field strength lines, it is possible to construct equipotential surfaces and, conversely, from the known location of the equipotential surfaces, it is possible to determine the modulus and direction of the field strength at each point of the field.
Let's find the relationship between the strength of the electrostatic field, which is its power feature, and potential - energy characteristic of the field.
Relocation work single point positive charge from one point of the field to another along the axis X provided that the points are infinitely close to each other and x 2 -x 1 = d x, is equal to E x d x. The same work is j 1 -j 2 =dj. Equating both expressions, we can write
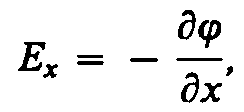
where the partial derivative symbol emphasizes that differentiation is made only with respect to X. Repeating similar reasoning for the axes at and z, we can find the vector E:

where i, j, k- unit vectors of coordinate axes x, y, z.
From the definition of a gradient it follows that
i.e. tension E field is equal to the potential gradient with a minus sign. The minus sign is determined by the fact that the intensity vector E fields directed to downward direction potential.
For a graphical representation of the potential distribution of the electrostatic field, as in the case of the gravitational field, use equipotential surfaces- surfaces, at all points of which the potential j has the same meaning.






