The components of the particle velocity v in the system K are determined by the expressions

In the system K" the velocity components v of the same particle are equal to

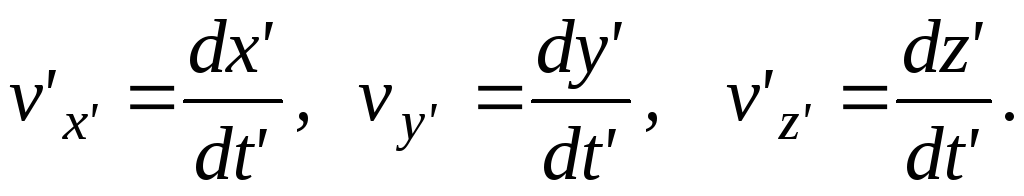
Let us find formulas relating the unprimed velocity components to the primed ones.

.

=

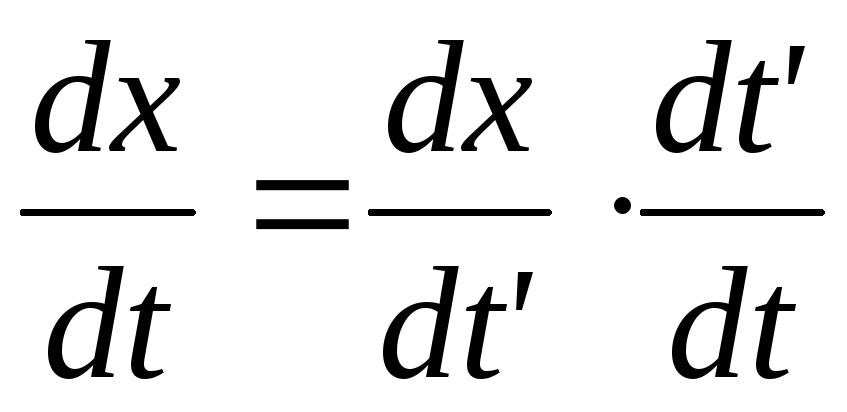Finally we get

Similarly

6.5 Relativistic momentum

An expression that ensures the invariance of the momentum conservation law can be obtained by replacing the time t with the proper time τ.

Then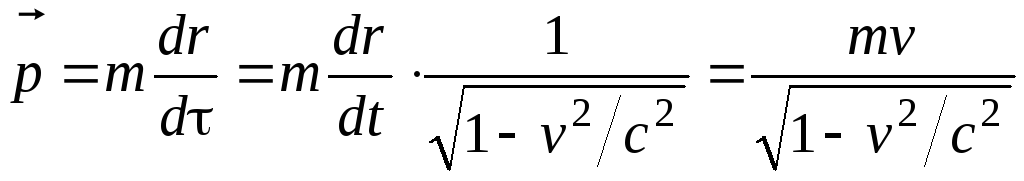

.

6.6 Relativistic expression for kinetic energy

In relativistic mechanics, the expression remains valid

.

It means that

. Whence it is clear that the force is not an invariant quantity. In addition, strength F and acceleration a not collegiate.

It is easy to get an expression for kinetic energy.

Let a body (particle) be accelerated in a rectilinear motion along constant force F, the work of which will be transformed into an increase in kinetic energy

moreover, we cannot, as before, take m out of the differentiation sign as a constant, because with v~c mconst. Because the

, change the order of differentiation with respect to the coordinate

Let us now consider in more detail the relativistic expression for the mass

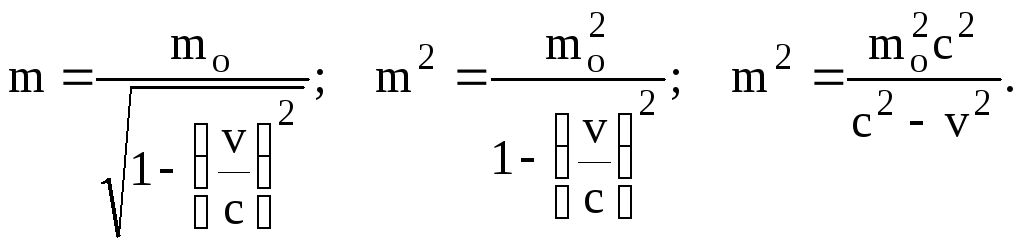
Let's simplify the last expression:

m 2 c 2 – m 2 v 2 = m o 2 c 2  m 2 c 2 = m o 2 c 2 + m 2 v 2

and differentiate taking into account the condition m o = const and c=const:

2C2mdm = 2mv2dm + 2m2vdv: 2m.

We get

With 2 dm = v 2 dm + mv dv.

Compare the right parts of the equations and equate the left parts of these equations

dW K = c 2 dm.

Let us integrate this equality taking into account that for v = 0 W K= 0, m = m o

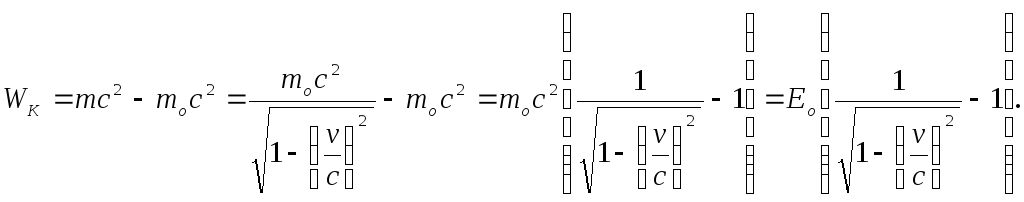
It is clear that E about = m o c 2 is the rest energy of the body, and mc 2 is the total energy of the body, and their difference W K and there is kinetic energy, the energy due to the movement of the body.

Consequences:

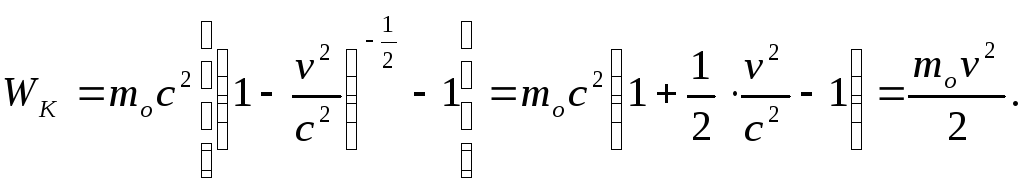
In relativistic motion, it also looks different the equation for the relationship between the momentum of a particle and its kinetic energy

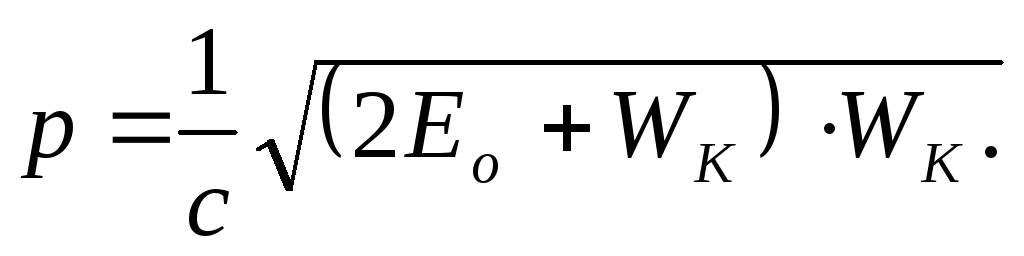
Energy and momentum in relativistic mechanics are not saved. The invariant is the expression:

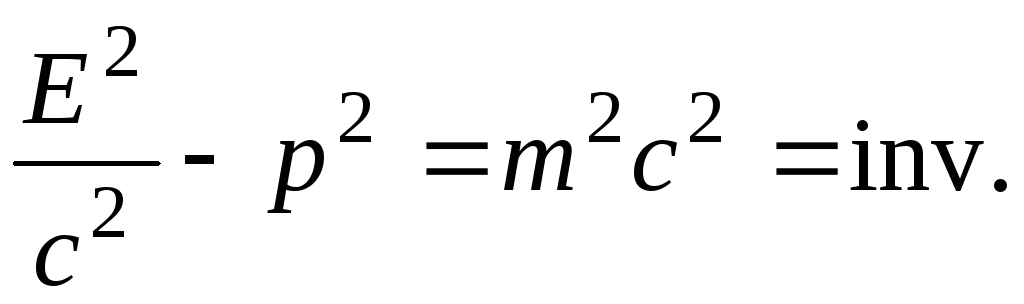
6.7 Relationship between mass and rest energy

The mass of a body and its rest energy are related by the relation E 0 = t 0 With 2 . M An important conclusion can be drawn that any change in mass Δ t accompanied by a change in the rest energy Δ E 0 , where these changes are proportional to each other.

Δ E 0 = with 2 Δ t.

This statement is calledthe law of the relationship between mass and rest energy (sometimes they simply say mass and energy).

Relationship t and E 0 leads to the fact that the total mass of interacting particles is not conserved.

Consider an example of an inelastic central impact of two identical particles moving with velocities equal in absolute value and opposite in direction. As a result of the collision, a new immobile particle is formed. In Newtonian mechanics we would have

M= m+ m=2 m; V= Vl- V 2 =0 (|V 1 |= |V 2 |)

In relativistic mechanics, the situation is somewhat different:

1) before the collision, the total energy of each particle is equal to

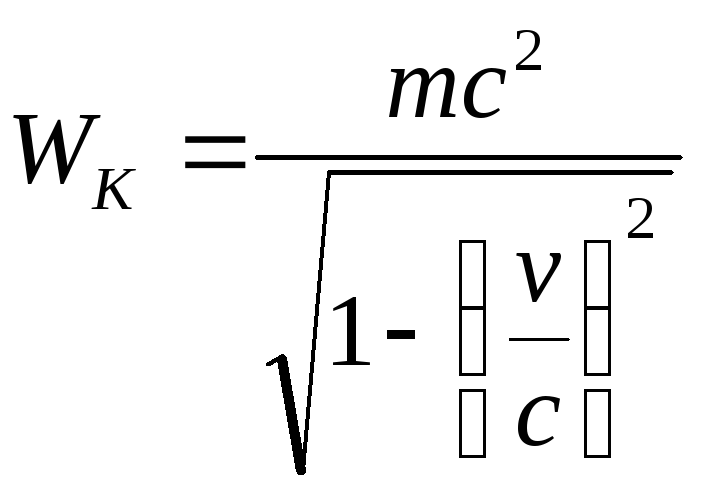
2) the total energy of the formed stationary particle

E=Ms 2

3) Apply the law of conservation of energy to this case

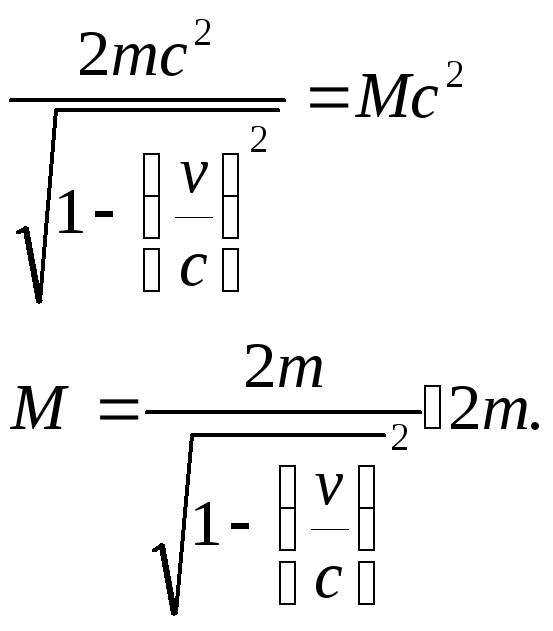
Thus, the mass of the formed particle is greater than the masses of the initial particles. This is due to the fact that the kinetic energy of the particles turned into an equivalent amount of rest energy, and this led, in turn, to an increase in mass by

Δ t = Δ E 0 /s 2 .

If we generalize the above to an arbitrary case of the motion of particles with near-light speeds, then we can write

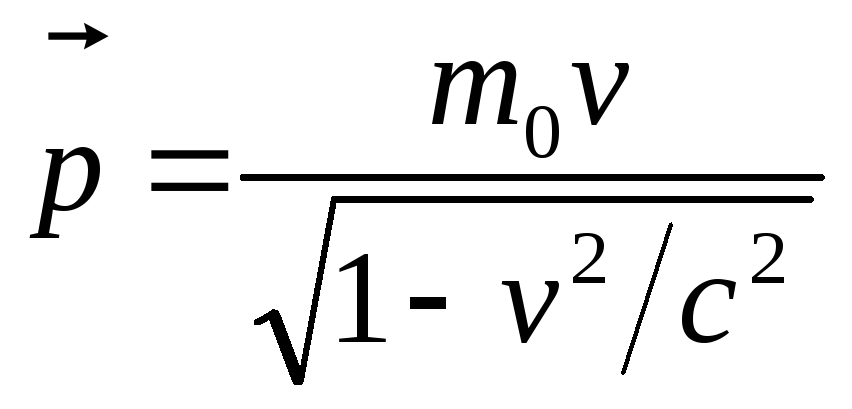
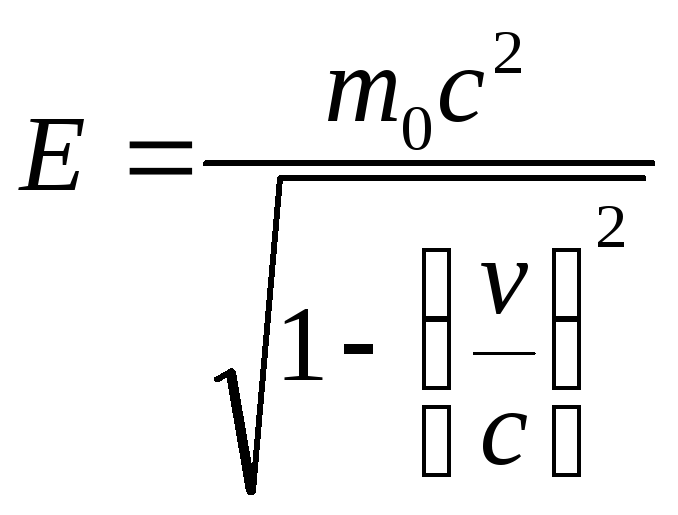
E 0 = t 0 With 2 ,

where t 0 - the mass of a particle at rest or the rest mass of a particle, V is the speed of a moving particle.

Then the mass of the moving particle m will be equal to

When an immobile particle decays into several particles flying in different directions, the opposite phenomenon is observed - the sum of the masses of the formed particles turns out to be less than the initial particle by a value equal to the total kinetic energy of these particles divided by c 2.

If we generalize our conclusions to a body consisting of N particles with masses t 1 t 2 ...tN, then the body will not disintegrate into the particles that form it, provided that the latter are connected with each other. This bond can be characterized by the binding energy ESt.. Bond energy - is the energy that

it is necessary to spend to break the connection between the particles and spread them to such distances at which the interaction of particles can be neglected.

The binding energy of the particle system will be equal to

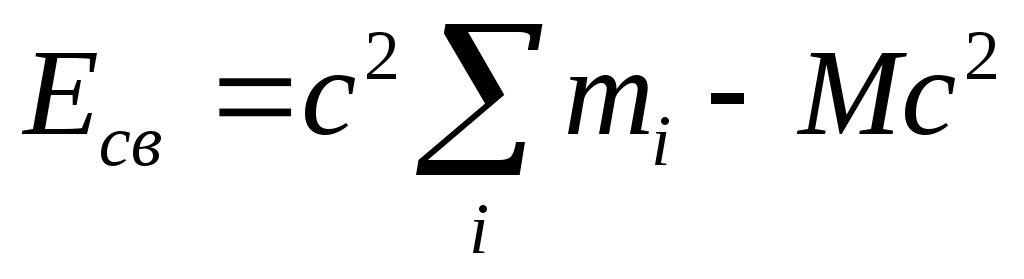
where M is the mass of the system (mass of the body).

The theory of relativity requires a revision and refinement of the laws of mechanics. As we have seen, the equations of classical dynamics (Newton's second law) satisfy the principle of relativity with respect to Galilean transformations. But the transformations of Galileo must be replaced by the transformations of Lorentz! Therefore, the equations of dynamics should be changed so that they remain unchanged when passing from one inertial system reference to another according to the Lorentz transformations. At low velocities, the equations of relativistic dynamics must pass into classical ones, because in this region their validity is confirmed by experience.

Momentum and energy. In the theory of relativity, as in classical mechanics, for a closed physical system the momentum and energy E are conserved, but the relativistic expressions for them differ from the corresponding classical ones:

where is the mass of the particle. This is the mass in the reference frame where the particle is at rest. It is often called the rest mass of the particle. It coincides with the particle mass in nonrelativistic mechanics.

It can be shown that the dependence of the momentum and energy of a particle on its velocity in the theory of relativity expressed by formulas (1) inevitably follows from the relativistic effect of time dilation in a moving frame of reference. This will be done below.

Relativistic energy and momentum (1) satisfy equations similar to the corresponding equations of classical mechanics:

relativistic mass. Sometimes the coefficient of proportionality in (1) between the speed of a particle and its momentum

is called the relativistic mass of the particle. With its help, expressions (1) for the momentum and energy of the particle can be written in a compact form

If a relativistic particle, i.e., a particle moving at a speed close to the speed of light, is given additional energy in order to increase its momentum, then its speed will increase very slightly. We can say that the energy of the particle and its momentum now increase due to the growth of its relativistic mass. This effect is observed in the work of high-energy charged particle accelerators and serves as the most convincing experimental confirmation of the theory of relativity.

Peace energy. The most remarkable thing about the formula is that a body at rest has energy: putting in we get

Energy is called rest energy.

Kinetic energy. The kinetic energy of a particle in some frame of reference is defined as the difference between its total energy and the rest energy Using (1), we have

If the speed of the particle is small compared to the speed of light, formula (6) turns into the usual expression for the kinetic energy of the particle in nonrelativistic physics.

The difference between the classical and relativistic expressions for kinetic energy becomes especially significant when the speed of the particle approaches the speed of light. At , the relativistic kinetic energy (6) increases indefinitely: a particle with a nonzero rest mass and

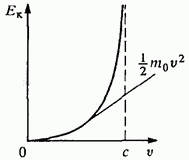
Rice. 10. Dependence of the kinetic energy of the body on the speed

moving at the speed of light would have to have infinite kinetic energy. The dependence of the kinetic energy on the particle velocity is shown in fig. ten.

Proportionality of mass and energy. It follows from formula (6) that when a body accelerates, the increment in kinetic energy is accompanied by a proportional increment in its relativistic mass. Recall that the most important property of energy is its ability to transform from one form to another in equivalent quantities during various physical processes - this is precisely the content of the law of conservation of energy. Therefore, it is natural to expect that an increase in the relativistic mass of a body will occur not only when kinetic energy is imparted to it, but also with any other increase in the body's energy, regardless of the specific type of energy. From here we can make a fundamental conclusion that the total energy of a body is proportional to its relativistic mass, regardless of what specific types of energy it consists of.

Let us clarify what has been said with the following simple example. Consider an inelastic collision of two identical bodies, moving towards each other with the same speeds, so that as a result of the collision one body is formed, which is at rest (Fig. 11a).

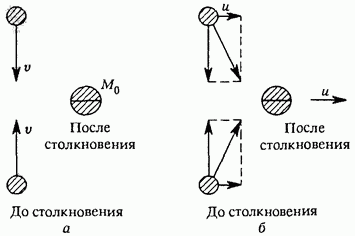
Rice. 11. Inelastic collision observed in different systems reference

Let the speed of each of the bodies before the collision be equal to and the rest mass Let us denote the rest mass of the resulting body as Now let's consider the same collision from the point of view of an observer in another reference frame K, moving relative to the original frame K to the left (Fig. 11b) with a small (nonrelativistic) speed - and.

Since then to convert the speed in the transition from K to K, you can use the classical law of addition of speeds. The law of conservation of momentum requires that the total momentum of the bodies before the collision be equal to momentum formed body. Before the collision, the total momentum of the system is where is the relativistic mass of the colliding bodies; after a collision, it is equal because, as a result, the mass of the formed body and in K can be considered equal to the rest mass. Thus, it follows from the law of conservation of momentum that the rest mass of the body formed as a result of inelastic collision is equal to the sum of the relativistic masses of the colliding particles, i.e., it is greater than the sum of the rest masses of the original particles:

The considered example of an inelastic collision of two bodies, in which the kinetic energy is converted into internal energy, shows that an increase in internal energy body is also accompanied by a proportional increase in mass. This conclusion should be extended to all types of energy: a heated body has a greater mass than a cold one, a compressed spring has a greater mass than an uncompressed one, etc.

Equivalence of energy and mass. The law of proportionality of mass and energy is one of the most remarkable conclusions of the theory of relativity. The relationship between mass and energy deserves a detailed discussion.

In classical mechanics, the mass of a body is physical quantity, which is quantitative characteristic its inert properties, i.e., a measure of inertia. This is an inert mass. On the other hand, mass characterizes the body's ability to create a gravitational field and experience force in the gravitational field. It is a gravitating, or gravitational, mass. Inertia and the ability to gravitational interactions are completely different manifestations of the properties of matter. However, the fact that the measures of these different manifestations are denoted by the same word is not accidental, but is due to the fact that both properties always exist together and are always proportional to each other, so that the measures of these properties can be expressed by the same number with an appropriate choice of units. measurements.

The equality of inertial and gravitational masses is an experimental fact, confirmed with a great degree of accuracy in the experiments of Eötvös, Dicke, and others. How should one answer the question: are inertial and gravitational mass the same or not? Their manifestations are different, but their numerical characteristics proportional to each other. This state of affairs is characterized by the word "equivalence".

A similar question arises in connection with the concepts of rest mass and rest energy in the theory of relativity. Manifestations of the properties of matter corresponding to mass and energy are indisputably different. But the theory of relativity states that these properties are inextricably linked, proportional to each other. Therefore, in this sense, one can speak of the equivalence of rest mass and rest energy. The relation (5) expressing this equivalence is called the Einstein formula. It means that any change in the energy of the system is accompanied by an equivalent change in its mass. It refers to changes various kinds internal energy at which the rest mass changes.

On the law of conservation of mass. Experience shows us that the vast majority physical processes, in which the internal energy changes, the rest mass remains unchanged. How can this be reconciled with the law of proportionality of mass and energy? The fact is that usually the overwhelming majority of internal energy (and the rest mass corresponding to it) does not participate in transformations, and as a result, it turns out that the mass determined from weighing is practically conserved, despite the fact that the body releases or absorbs energy. This is simply due to insufficient weighing accuracy. To illustrate, consider a few numerical examples.

1. Energy released during the combustion of oil, during the explosion of dynamite and during other chemical transformations, seems to us on the scale of everyday experience enormous. However, if we translate its value into the language of equivalent mass, then it turns out that this mass does not even constitute the full value of the rest mass. For example, when hydrogen combines with oxygen, about an energy is released. The rest mass of the resulting water is less than the mass of the starting materials. This change in mass is too small to be detected with modern instruments.

2. In an inelastic collision of two particles accelerated towards each other to a speed, the additional rest mass of the stuck together pair is

(At this speed, one can use the non-relativistic expression for the kinetic energy.) This value is much less than the error with which the mass can be measured

Rest mass and quantum regularities. It is natural to ask the question: why, under normal conditions, is the overwhelming majority of energy in a completely passive state and does not participate in transformations? The theory of relativity cannot answer this question. The answer must be sought in the field of quantum laws,

one of characteristic features which is the existence of stable states with discrete energy levels.

For elementary particles the energy corresponding to the rest mass is either completely converted into an active form (radiation) or not converted at all. An example is the transformation of an electron-positron pair into gamma radiation.

In atoms, the overwhelming majority of the mass is in the form of the rest mass of elementary particles, which in chemical reactions does not change. Even in nuclear reactions the energy corresponding to the rest mass of heavy particles (nucleons) that make up nuclei remains passive. But here the active part of the energy, i.e., the interaction energy of nucleons, already constitutes a noticeable fraction of the rest energy.

Thus, experimental confirmation of the relativistic law of proportionality of rest energy and rest mass should be sought in the world of elementary particle physics and nuclear physics. For example, in nuclear reactions that proceed with the release of energy, the rest mass of the final products is less than the rest mass of the nuclei entering into the reaction. The energy corresponding to this change in mass coincides with good accuracy with the experimentally measured kinetic energy of the formed particles.

How do the momentum and energy of a particle depend on its speed in relativistic mechanics?

What physical quantity is called the mass of a particle? What is rest mass? What is relativistic mass?

Show that the relativistic expression (6) for the kinetic energy transforms into the usual classical one at .

What is rest energy? What is the fundamental difference between the relativistic expression for the energy of a body and the corresponding classical one?

In which physical phenomena does the energy of rest reveal itself?

How to understand the statement about the equivalence of mass and energy? Give examples of manifestation of this equivalence.

Is the mass of a substance conserved during chemical transformations?

Derivation of the expression for momentum. Let us justify formulas (1) given above without proof by analyzing a simple mental experience. To elucidate the dependence of the particle momentum on the velocity, let us consider the picture of an absolutely elastic "sliding" collision of two identical particles. In the center of mass system, this collision has the form shown in Fig. 12a: before the collision, particles Y and 2 move towards each other with the same velocities in absolute value; after the collision, the particles fly apart in opposite directions with the same velocities in absolute value as before the collision. In other words,

in a collision, only the rotation of the velocity vectors of each of the particles occurs by the same small angle

What will the same collision look like in other frames of reference? Let us direct the x-axis along the bisector of the angle and introduce a reference frame K moving along the x-axis relative to the center-of-mass frame with a velocity equal to the x-component of the velocity of particle 1. In this reference frame, the collision pattern will look as shown in Fig. 12b: particle 1 moves parallel to the y axis, changing the direction of velocity and momentum to the opposite during the collision.

The conservation of the x-component of the total momentum of a system of particles in a collision is expressed by the relation

where are the momenta of the particles after the collision. Since (Fig. 126), the requirement of conservation of momentum means the equality of the x-components of the momentum of particles 1 and 2 in the reference frame K:

Comparing the last two equalities, we find, i.e., the y-component of the momentum of particle 1 is the same in the frames of reference K and K. In the same way, we find In other words, the y-component of the momentum of any particle, perpendicular to the direction of the relative velocity of the frames of reference, is the same in these frames. This is the main conclusion from the considered thought experiment.

But the y-component of the particle velocity has a different value in the frames of reference K and K. According to the velocity transformation formulas

where is the velocity of the system K with respect to K. Thus, in K the y-component of the velocity of particle 1 is less than in K.

This decrease in the y-component of the velocity of particle 1 during the transition from K to K is directly related to the relativistic time transformation: the same distance in K and K between the dashed lines A and B (Fig. 12b, c) particle 1 in the system K takes a longer time, than in K. If in K this time is equal to (proper time, since both events - the intersection of strokes A and B - occur in K at the same coordinate value, then in the system K this time is greater and equal to

Recalling now that the y-component of the momentum of particle 1 is the same in the systems K and K, we see that in the system K, where the y-component of the particle velocity is smaller, this particle must be assigned, as it were, a larger mass, if mass is understood, as in non-relativistic physics, the coefficient of proportionality between velocity and momentum. As already noted, this coefficient is sometimes called the relativistic mass. The relativistic mass of a particle depends on the frame of reference, i.e., it is a relative quantity. In that frame of reference, where the speed of the particle is much less than the speed of light, for the relationship between the speed and momentum of the particle, the usual classical expression is true where is the mass of the particle in the sense that it is understood in non-relativistic physics (rest mass).

Returning to fig. 12, we recall that the case of a glancing collision was considered, when the component of the particle's velocity along the y axis was much less than the component of its velocity along the x axis. In this limiting case, the relative velocity of the systems K and k included in the obtained formula practically coincides with the velocity of particle 1 in the system K. Therefore, the found value of the proportionality coefficient between the y-components of the velocity and momentum vectors is also valid for the vectors themselves. Thus, relation (3) is proved.

Derivation of the expression for energy. Let us now find out to what changes in the expression for the energy of the particle the formula for the relativistic momentum leads.

In relativistic mechanics, the force is introduced in such a way that the ratio between the particle momentum increment Dp and the force momentum is the same as in classical physics:

How can a thought experiment show that the momentum component of a particle, perpendicular to the direction of the relative velocity of two frames of reference, is the same in both of these frames? What role do symmetry considerations play in this?

Explain the relationship between the dependence of the relativistic mass of a particle on its velocity and the relativistic kinematic effect of time dilation.

How can one arrive at a relativistic formula for kinetic energy based on the proportionality between increments of kinetic energy and relativistic mass?

12.4. Energy relativistic particle

12.4.1. Energy of a relativistic particle

The total energy of a relativistic particle is the sum of the rest energy of the relativistic particle and its kinetic energy:

E \u003d E 0 + T,

Equivalence of mass and energy(Einstein's formula) allows us to determine the rest energy of a relativistic particle and its total energy as follows:

• rest energy -

E 0 \u003d m 0 c 2,

where m 0 is the rest mass of a relativistic particle (the mass of the particle in its own frame of reference); c is the speed of light in vacuum, c ≈ 3.0 ⋅ 10 8 m/s;

• total energy -

E \u003d mc 2,

where m is the mass of the moving particle (the mass of the particle moving relative to the observer with relativistic speed v); c is the speed of light in vacuum, c ≈ 3.0 ⋅ 10 8 m/s.

Relationship between masses m 0 (mass of a particle at rest) and m (mass of a moving particle) is given by

Kinetic energy relativistic particle is determined by the difference:

T = E - E 0 ,

where E is the total energy of the moving particle, E = mc 2 ; E 0 - rest energy of the indicated particle, E 0 = m 0 c 2 ; the masses m 0 and m are related by the formula

m = m 0 1 − v 2 c 2 ,

where m 0 is the mass of the particle in the frame of reference relative to which the particle is at rest; m is the mass of the particle in the frame of reference relative to which the particle moves at a speed v; c is the speed of light in vacuum, c ≈ 3.0 ⋅ 10 8 m/s.

explicitly kinetic energy relativistic particle is defined by the formula

T = m c 2 − m 0 c 2 = m 0 c 2 (1 1 − v 2 c 2 − 1) .

Example 6. The speed of a relativistic particle is 80% of the speed of light. Determine how many times the total energy of the particle is greater than its kinetic energy.

Solution . The total energy of a relativistic particle is the sum of the rest energy of the relativistic particle and its kinetic energy:

E \u003d E 0 + T,

where E is the total energy of the moving particle; E 0 - rest energy of the specified particle; T is its kinetic energy.

It follows that the kinetic energy is the difference

T = E − E 0 .

The desired value is the ratio

E T = E E − E 0 .

To simplify the calculations, we find the reciprocal of the desired:

T E = E − E 0 E = 1 − E 0 E ,

where E 0 \u003d m 0 c 2; E = mc 2 ; m 0 - rest mass; m is the mass of the moving particle; c is the speed of light in vacuum.

Substituting the expressions for E 0 and E into the relation (T /E ) gives

T E = 1 − m 0 c 2 m c 2 = 1 − m 0 m .

The relationship between the masses m 0 and m is determined by the formula

m = m 0 1 − v 2 c 2 ,

where v is the speed of the relativistic particle, v = 0.80c.

Let's express the mass ratio from here:

m 0 m = 1 − v 2 c 2

and substitute it into (T /E ):

T E = 1 − 1 − v 2 c 2 .

Let's calculate:

T E \u003d 1 - 1 - (0.80 s) 2 c 2 \u003d 1 - 0.6 \u003d 0.4.

The desired value is the inverse ratio

E T \u003d 1 0.4 \u003d 2.5.

The total energy of a relativistic particle at the indicated speed exceeds its kinetic energy by a factor of 2.5.

Total energy of a relativistic particle defined as

where is the particle mass and is its velocity. The total energy in different reference systems is different.

Energy of a body at rest (at )

Classical mechanics does not take into account the rest energy, assuming that at , the energy of a body at rest is equal to zero.

Law of energy conservation in relativistic mechanics says that total energy closed system is preserved, i.e. does not change over time.

Kinetic energy of the body is determined by the formula

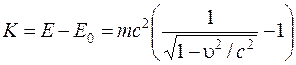, (5.26)

since total energy in relativistic dynamics is the sum of kinetic energy and rest energy.

From formulas (5.22) and (5.24) it is easy to obtain an expression relating energy and momentum:

From here we get

. (5.28)

Given that , from here we get

. (5.29)

test questions

1. What principles underlie the special theory of relativity?

2. How are Galilean transformations and Lorentz transformations related to each other?

3. What invariant quantities do you know?

4. Write a formula expressing the momentum of a particle in terms of its energy and speed.

5. Write a formula expressing the energy of a particle in terms of its momentum.

6. What is characteristic of particles with zero mass?

7. Is the law of conservation of momentum observed in the special theory of relativity?

1. How many times does the passage of time slow down at the speed of the clock u = 240,000 km/s?

2. Find the relative speed of two particles moving towards each other with speed u = c/2.

3. Write an expression for full energy particle, its kinetic energy, rest energy, particle momentum. What is the relationship between the energy and momentum of a relativistic particle?

4. During the experiment, the momentum and energy of the particle were determined. Find its speed and mass.

5. The electron begins to accelerate in a uniform electric field, the intensity of which is directed along the axis x. Draw high-quality graphs depending on x: a) complete E and kinetic To electron energies; b) electron momentum; c) electron speed.

6. Why for u =c Lorentz transformations lose their meaning?

7. Can the annihilation of an electron ( q=-e) and positron ( q=+e) produce one photon? Justify your answer using the laws of conservation of energy and momentum.