A deformed elastic body (for example, a stretched or compressed spring) is capable, returning to an undeformed state, to perform work on the bodies in contact with it. Therefore, an elastically deformed body has potential energy. It depends on the relative position of body parts, such as coils of a spring. The work that a stretched spring can do depends on the initial and final stretches of the spring. Let's find the work that can be done by the stretched spring, returning to the unstretched state, i.e., find the potential energy of the stretched spring.

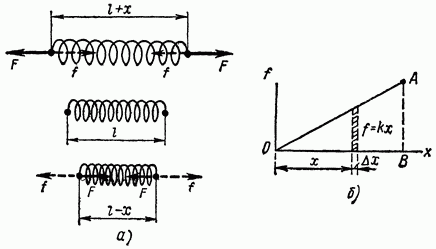
Let the stretched spring be fixed at one end, and the other end, moving, does work. It should be borne in mind that the force with which the spring acts does not remain constant, but changes in proportion to the stretch. If the initial stretch of the spring, counting from the unstretched state, was />, then the initial value of the elastic force was , where is the proportionality factor, which is called the spring stiffness. As the spring contracts, this force decreases linearly from a value to zero. So the average value of the force is . It can be shown that the work is equal to this average multiplied by the displacement of the point of application of the force:

Thus, the potential energy of a stretched spring

The same expression is obtained for a compressed spring.

In formula (98.1), the potential energy is expressed in terms of the stiffness of the spring and in terms of its extension. Replacing with , where is the elastic force corresponding to the tension (or compression) of the spring, we obtain the expression

which determines the potential energy of the spring, stretched (or compressed) force. It can be seen from this formula that, by stretching different springs with the same force, we will give them a different supply of potential energy: the stiffer the spring, i.e. the greater its elasticity, the less potential energy; and vice versa: the softer the spring, the more energy it will store for a given tensile force. This can be clearly understood, if we take into account that for the same active forces the stretching of a soft spring is greater than that of a rigid one, and therefore the product of force and the displacement of the point of application of force, i.e. work, is also greater.

This pattern has great importance, for example, when installing various springs and shock absorbers: when landing on the ground, the chassis shock absorber, compressing, must do a lot of work, damping the vertical speed of the aircraft. In a shock absorber with low rigidity, the compression will be greater, but the resulting elastic forces will be less and the aircraft will be better protected from damage. For the same reason, road shocks are felt more sharply when the bicycle tires are heavily inflated than when they are lightly inflated.

According to expression (3.12), the potential energy of the system is the maximum positive work that can be done by those acting in the system internal forces.

Calculate the potential energy of a compressed or stretched elastic spring; internal forces acting at the ends of the spring are directed against external deforming forces and are proportional in magnitude to the deformation (Fig. 1.27, a):

where is the coefficient of elasticity of the spring. Let us calculate the work that can be performed by internal forces during the transition of the spring from the deformed state to the normal (undeformed) state; this work is always positive. When the length of the spring changes by a very small amount, the forces can be considered almost constant, and their work will be equal. Graphically, this work is depicted by the area shaded in Fig. 1.27b. Full work internal forces during the transition to the normal state is obviously represented by the area of ​​the triangle. This work is the potential energy of the deformed spring

For a twisted helical spring, a similar calculation gives where is the coefficient of elasticity for torsion, and is the angle of twist. Note that in a state with zero potential energy, the internal forces are equal to zero.

For an elastically deformed solid body (or medium), one can calculate the potential energy contained in a unit volume. Let's apply the formula to a rod of length I and cross section. Then it will be the relative elongation of the body under the action of a force by normal mechanical stress. We use Hooke's law (see the formula and express the potential energy of the entire rod (see (3.14)) depending on or on the relative

elongation or tension

where is the volume of the body; modulus of longitudinal elasticity.

Thus, the value

is the energy of elastic deformation (tension or compression) contained in a unit volume of a body or an elastic medium. For a given medium with a certain modulus of longitudinal elasticity, the energy per unit volume is directly proportional to the square of the relative strain or the square of the stress a. For a given relative strain, this energy is proportional to the modulus of longitudinal elasticity. Similar expressions are obtained for other types of elastic deformations.

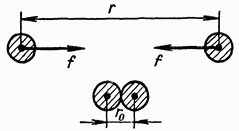
We calculate the potential energy of two bodies with masses attracted to each other according to the law of gravity. The forces of mutual attraction will do positive work if the bodies are approaching, and negative work if the bodies are moving away. Let us assume that in the initial state these bodies are at a distance and when approaching, the smallest possible distance between them (at contact) is equal to (Fig. 1.28). Then the positive work that is done by the forces of gravity during this approach can be calculated as the sum of elementary works, i.e.

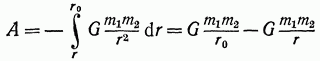
(the minus sign in front of the integral appeared due to the fact that when the distance between the bodies decreases, the value as the difference between the new and initial values ​​\u200b\u200bis negative, while the work is positive, since the bodies move in the direction of the forces). In the particular case when the distances are large and their difference is small, as is the case when a body falls on the Earth's surface from a small height, the product can be replaced by and then

The work that a body with a weight located at a height can do when it falls is called the potential energy of this body in the Earth's gravitational field.

body to the Earth, gravity does positive work and the potential energy of the body decreases.

However, if the potential energy of a system of two attracting bodies is equated to the work calculated by formula (3.15), then the potential energy of the system will be zero at But the smallest distance between bodies is not always a certain value. This circumstance prompted us to choose another, more definite state of the system, in which its potential energy is equal to zero; namely, we agreed to consider that the potential energy of any system is equal to zero if its constituent parts are removed from each other by infinitely large distances; in this case, the forces of interaction between the bodies are equal to zero.

It follows from this condition that the potential energy of a system of attracting bodies must be a negative value (and a system of repulsive bodies must be a positive value). Indeed, if from the initial state, when the distance between the bodies is infinitely large and the bodies begin to approach, for example, to a distance, then the forces of attraction do positive work and therefore the potential energy must decrease and, therefore, become less than zero. In this way,

Consequently,

For a system consisting of two interacting electric charges and potential energy is expressed by the same formula:

where constant. If the charges have different signs, then the potential energy is negative; for a system of charges of the same sign, the potential energy is a positive value. On fig. 1.29 shows graphs of the function showing the change in the potential energy of a system of attracting (1) and repelling (2) bodies with a change in the distance between them.

For a more complex system containing, for example, interacting bodies, the potential energy will be a function of the coordinates of all these bodies: is equal to For two bodies, therefore,

For a complex system consisting of many interacting bodies, the force acting on the body in the direction

for example, the axis is equal to the partial derivative:

Let's assume that at graphic image functions for some physical system the origin O is placed inside the system, and the axis is oriented in some direction of interest to us (Fig. 1.30). has a negative sign, i.e., it is directed towards the point O and will prevent the removal of the particle from the system; at point B the force is in the opposite direction.

When moving away from the point O, the potential energy will increase, therefore, the kinetic energy of the particle must decrease. If at point O the kinetic energy of the particle was equal, then it

becomes equal to zero at point A. Here the particle will stop, after which the forces acting on it will tell it to reverse motion; the particle will not be able to overcome the potential barrier and leave the system. This will be possible only if the kinetic energy is sufficiently large, for example, equal to

AT complex systems interacting bodies can also form potential wells (Fig. 1.31). If the particle is on the site, then when moving in any direction, the potential energy increases, therefore, the kinetic energy decreases (the force acting on the particle is directed towards point C). Therefore, if the kinetic energy of a particle inside the “pit” is small, then it will not be able to leave it and will perform oscillating motion around point C.

Denote by X spring extension, i.e. the difference between the lengths of the spring in the deformed and undeformed states.

When the spring returns from the deformed state to the undeformed state, the force does work.

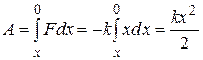. (12)

Thus, the potential energy of an elastically deformed spring

4.5.2. Potential energy gravitational attraction two material points

On fig. 5 shows two material points of mass m 1 and m 2. Their position is characterized by radius vectors and respectively. The elementary work done by the forces of gravitational attraction of these points , where is the force acting on the first material point from the second, and is the force acting on the second material point from the first; according to Newton's 3rd law =-; and are elementary displacements of material points. With this in mind, where . Considering that and are oppositely directed and that the quantity , we find . Full work

where R 1 and R2– initial and final distance between material points.

This work is equal to the change in potential energy A=W n 1 -W n 2. Taking into account (14), we find that the potential energy of the gravitational attraction of two material points

or (15)

where R or r– distance between material points.

End of work -

This topic belongs to:

Physics will be studied over 4 semesters: in the first: - physical foundations of classical and relativistic mechanics

INTRODUCTION ... PHYSICS in Greek NATURE is a science that studies the simplest and at the same time the most general laws of phenomena ...

If you need additional material on this topic, or you did not find what you were looking for, we recommend using the search in our database of works:

What will we do with the received material:

If this material turned out to be useful for you, you can save it to your page on social networks:

All topics in this section:

L E C T I A ​​N 1. K I N E M A T I C A
Kinematics is a branch of mechanics that studies the movement of bodies without considering the causes that cause movement. The movement of a body is the change in its position relative to another body in

Kinematics of a material point. Path, displacement, speed and acceleration
Rice. 1 Learn

The law of motion is given by the vector equation
. (1) With the coordinate method, the position of point A is determined by the coordinates x, y, z, and the law

Speed
The instantaneous velocity of a material point is determined by the relation

Acceleration
To characterize the rate of change of speed, a vector is introduced physical quantity called the acceleration

Angular Velocity and Angular Acceleration
Consider the motion of a material point along a circle of radius R (Fig. 5). Let for time

L E C T I O N 2 . D I N A M I ​​C A M A T E R I A L
Dynamics is a branch of mechanics devoted to the study of the motion of material bodies under the action of forces applied to them. Dynamics is based on Newton's 3 laws, formulated in 1687. They

Newton's second law
In order to formulate it, we introduce the concept of force. A force is a vector quantity that characterizes the impact on a given body from other bodies. Strength

Newton's third law
The impact of bodies on each other is always in the nature of interaction. If body 2 acts on body 1 with a force

Friction forces
They appear when adjoining bodies or their parts move relative to each other. Friction, woz

L E C T I O N 3
The set of bodies allocated for consideration is called a mechanical system. The bodies of the system can interact both with each other and with bodies that are not included in the system. In coo

Law of conservation of momentum
Consider a system consisting of n material points. Denote by the force with which material point

The center of mass and the law of its motion
In dynamics, the concept of the center of mass of a system of material points is widely used, which is usually denoted by the letter C. The position of the center of mass is determined by the radius vector

Jet propulsion. Movement of bodies with variable mass
There are many phenomena based on the law of conservation of momentum. For example, rocket flight (and work jet engines) are based on the fact that as a result of ejection of gases from the nozzle, the rocket

Conservative and non-conservative forces
All forces occurring in mechanics are usually divided into conservative and non-conservative. Strength, action

Potential energy of a system of material points
Consider a system consisting of many material points. If the position of each material point is given, then the position of the entire system or its configuration is determined by this. If the forces acting

Potential energy of a body in the uniform gravity field of the Earth
Formula (15) is also valid for homogeneous spherical bodies; in this case r is the distance between the centers of mass of such bodies. In particular, the potential energy of a body of mass m, located

Kinetic energy
Let us write the equation of motion of a material point (particle) of mass m, moving under the action of forces, the resultant of which is equal to

Law of conservation of energy in mechanics
Consider a system of n material points, which are affected by both conservative and non-conservative forces. Let us find the work that these forces do when moving the system from one

Elastic and Inelastic Collisions
When bodies collide, they deform to a greater or lesser extent. In this case, the kinetic energy of the bodies is partially or completely converted into the potential energy of elastic deformation and into internal energy.

Absolutely inelastic impact
An interesting example where there is a loss of mechanical energy under the action of dissipative forces is a completely inelastic impact, in which the potential energy of elastic deformation does not arise.

Absolutely elastic impact
This is such a blow, in which the full mechanical energy body is saved. First, the kinetic energy is partially or completely converted into the potential energy of elastic deformation. Then the bodies are returned

General physical law of conservation of energy
Classical mechanics takes into account only the kinetic energy of the macroscopic motion of bodies and their macroscopic parts, as well as their potential energy. But she is completely distracted from the inner

Moment of force and moment of impulse relative to a fixed beginning
Let O be any fixed point in the inertial frame of reference. It is called the beginning or pole. Denote by

Moment equation
Let's assume that the point O is fixed. In the case of one material point, differentiating (3), we obtain.

Law of conservation of angular momentum
If the system is closed (i.e. external forces no), then and, therefore, according to equation (6) the vector

Movement in the field of central forces
If a force of the form acts on a material point, (8) then they say that the material point finds

Degrees of freedom. Generalized coordinates
The position of a point in space can be specified by a certain number of independent coordinates, for example, three coordinates x, y, z of the Cartesian system. But this can also be done in another way. For example, instead of

Number of degrees of freedom of a rigid body
An absolutely rigid body in mechanics is an idealized system of material points, all the distances between which do not change with time during the movement of the system. To unambiguously

Equation of motion and equilibrium of a rigid body
Because solid is a mechanical system with six degrees of freedom, then six independent numerical equations or two independent vector equations are required to describe its motion.

Steiner's theorem
In mechanics, a rigid body is usually considered as mechanical system, the mass m of which is continuously distributed over the volume V of the body, so that when calculating the moment of inertia of the body, the summation

Kinetic energy in plane motion
Plane (plane-parallel) is a movement in which all points of the body move in parallel planes. We represent the plane motion of the body as forward movement with speed

Summing over all material points, we get
or, (12)

Thus, if we break the plane motion of the body into translational
the center of mass Vc and rotational with the angular velocity w around the axis passing through the center of mass of the body, then the kinetic energy decomposes into two independent terms

Power
. (16) Let's compare the basic quantities and equations of translational and rotational motions

Galilean transformations. Galileo's principle of relativity
If frames of reference move uniformly and rectilinearly relative to each other and Newton's 1st law is valid in one of them, then these frames are inertial. Galileo stated:

Postulates of the private theory of relativity
Historically, it was the law of addition of velocities (5) that showed the limitations of Galilean ideas about the properties of space and time. Indeed, according to this law, with respect to the system

Lorentz transformations
Einstein's postulates demanded a fundamental revision of ideas about the properties of space, time and motion. Let's show this with a simple example. Let us imagine that a moving reference frame

The law of addition of velocities in relativistic mechanics
Differentiating (11) with respect to and (12) with respect to

Mass in Newtonian and relativistic mechanics
When studying the motion of bodies whose velocities v are negligible compared to the speed of light c (v/c → 0), the nonrelativistic approximation takes place. In this case

Energy, momentum in relativistic mechanics
If a body is moving at a speed v relative to inertial system reference (ISO) K, then in addition to the rest energy

Basic equation of relativistic dynamics
According to (20), the relativistic momentum, while both formulas are valid for "heavy", i.e. having no

Kinetic energy of a relativistic particle
According to (19), total energy bodies (particles) in relativistic mechanics, it consists of energy

Harmonic vibrations
Rice. 1 Learn

Potential and kinetic energy
Let us establish the change in the potential and kinetic energy oscillating system. It is known that the potential energy of an elastically deformed body is equal to

Vector diagram of harmonic oscillation
Harmonic oscillation can be represented as a projection of the vector

Complex form of representation of vibrations
According to the Euler formula for complex numbers

Addition of identically directed oscillations
Consider the addition of two harmonic oscillations of the same frequency, the displacements of which and

Mathematical pendulum
This is a material point suspended on a weightless, inextensible thread. A good approximation to the mat

Spring pendulum
This is a load of mass m, suspended on an absolutely elastic spring and oscillating around the equilibrium position, Fig. 1. He was considered in paragraph 1. For him

Free damped vibrations
In addition to the elastic force F = - kx, a resistance force also acts on the body, which is proportional to the speed during slow movements, i.e.

Logarithmic damping decrement
natural logarithm ratio of the deviation of the system at times t and is called the logarithmic decrement

Forced vibrations
They arise when an external periodically changing force (force) acts on the system, (22)